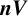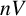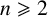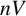1 Introduction
A well-known result of Brouwer [Reference Brouwer6] states that a nonempty totally disconnected compact metrizable space without isolated points is homeomorphic to the Cantor space
![]() $\mathfrak {C}$
. Consequently, this space arises throughout mathematics and it is unsurprising that many groups occur among its homeomorphisms. Interesting and important examples of such groups include Grigorchuk’s group of intermediate growth [Reference Grigorchuk12, Reference Grigorchuk and Satake13], which may be naturally described as consisting of certain automorphisms of a binary rooted tree, and various generalizations, such as the Gupta–Sidki groups [Reference Gupta and Sidki15] and the multi-GGS groups (see, for example, [Reference Fernández-Alcober and Zugadi-Reizabal10]); the asynchronous rational group of Grigorchuk et al. [Reference Grigorchuk, Nekrashevich and Sushchanskiĭ14]; and, particularly relevant to this paper, the groups F, T and V introduced by Richard J. Thompson [Reference Cannon, Floyd and Parry7, Reference Thompson21].
$\mathfrak {C}$
. Consequently, this space arises throughout mathematics and it is unsurprising that many groups occur among its homeomorphisms. Interesting and important examples of such groups include Grigorchuk’s group of intermediate growth [Reference Grigorchuk12, Reference Grigorchuk and Satake13], which may be naturally described as consisting of certain automorphisms of a binary rooted tree, and various generalizations, such as the Gupta–Sidki groups [Reference Gupta and Sidki15] and the multi-GGS groups (see, for example, [Reference Fernández-Alcober and Zugadi-Reizabal10]); the asynchronous rational group of Grigorchuk et al. [Reference Grigorchuk, Nekrashevich and Sushchanskiĭ14]; and, particularly relevant to this paper, the groups F, T and V introduced by Richard J. Thompson [Reference Cannon, Floyd and Parry7, Reference Thompson21].
Thompson’s group F is a
![]() $2$
-generator group with abelianization isomorphic to a free abelian group of rank
$2$
-generator group with abelianization isomorphic to a free abelian group of rank
![]() $2$
and such that its derived subgroup
$2$
and such that its derived subgroup
![]() $F'$
is simple. The other two groups T and V introduced by Thompson are both infinite simple groups. All three groups are finitely presented, with F having a small presentation with two generators and two relations. The presentations for T and V, as described in [Reference Cannon, Floyd and Parry7], both involve additional generators and relations to supplement those used for F. In particular, Thompson’s original presentation for his group V involved four generators and fourteen relations. In work by Bleak and the author [Reference Bleak and Quick2], we returned to possible presentations for V. We give there various presentations for this group: one involving infinitely many generators and an infinite family of relations. The generators in [Reference Bleak and Quick2, Theorem 1.1] correspond to transpositions of certain disjoint basic open sets of Cantor space and the relations are analogous to the Coxeter presentation for a finite symmetric group, but also include what we termed ‘split relations’ reflecting the self-similar structure of Cantor space. The second presentation, given in [Reference Bleak and Quick2, Theorem 1.2], is a finite presentation, essentially obtained by reducing the infinite presentation, with three generators and eight relations (which compares favourably in size to Thompson’s original presentation). We then produced a two-generator presentation for V by use of Tietze transformations and our smallest presentation, obtained via computational methods, is on two generators and seven relations [Reference Bleak and Quick2, Theorem 1.3]. One should also note a link between our infinite presentation for V and the geometric presentations given by Dehornoy [Reference Dehornoy8].
$F'$
is simple. The other two groups T and V introduced by Thompson are both infinite simple groups. All three groups are finitely presented, with F having a small presentation with two generators and two relations. The presentations for T and V, as described in [Reference Cannon, Floyd and Parry7], both involve additional generators and relations to supplement those used for F. In particular, Thompson’s original presentation for his group V involved four generators and fourteen relations. In work by Bleak and the author [Reference Bleak and Quick2], we returned to possible presentations for V. We give there various presentations for this group: one involving infinitely many generators and an infinite family of relations. The generators in [Reference Bleak and Quick2, Theorem 1.1] correspond to transpositions of certain disjoint basic open sets of Cantor space and the relations are analogous to the Coxeter presentation for a finite symmetric group, but also include what we termed ‘split relations’ reflecting the self-similar structure of Cantor space. The second presentation, given in [Reference Bleak and Quick2, Theorem 1.2], is a finite presentation, essentially obtained by reducing the infinite presentation, with three generators and eight relations (which compares favourably in size to Thompson’s original presentation). We then produced a two-generator presentation for V by use of Tietze transformations and our smallest presentation, obtained via computational methods, is on two generators and seven relations [Reference Bleak and Quick2, Theorem 1.3]. One should also note a link between our infinite presentation for V and the geometric presentations given by Dehornoy [Reference Dehornoy8].
In 2004, Brin [Reference Brin3] introduced, for each positive integer
![]() $n \geqslant 2$
, an analogue of Thompson’s group V that acts upon an n-dimensional version of Cantor space. He denotes this group by
$n \geqslant 2$
, an analogue of Thompson’s group V that acts upon an n-dimensional version of Cantor space. He denotes this group by
![]() $nV$
and, via the homeomorphism
$nV$
and, via the homeomorphism
![]() $\mathfrak {C}^{n} \cong \mathfrak {C}$
, this family provides us with further groups of homeomorphisms of Cantor space. Bleak and Lanoue [Reference Bleak and Lanoue1] noted that two of these groups
$\mathfrak {C}^{n} \cong \mathfrak {C}$
, this family provides us with further groups of homeomorphisms of Cantor space. Bleak and Lanoue [Reference Bleak and Lanoue1] noted that two of these groups
![]() $mV$
and
$mV$
and
![]() $nV$
are isomorphic if and only if
$nV$
are isomorphic if and only if
![]() $m = n$
. Brin observes in his first paper that the group
$m = n$
. Brin observes in his first paper that the group
![]() $2V$
is an infinite simple group, while in [Reference Brin5], he shows that all the groups
$2V$
is an infinite simple group, while in [Reference Brin5], he shows that all the groups
![]() $nV$
are simple. In the latter argument, he makes considerable reference to the baker’s maps of
$nV$
are simple. In the latter argument, he makes considerable reference to the baker’s maps of
![]() $\mathfrak {C}^{n}$
and notes that these maps can be expressed as a product of transpositions. This observation will be particularly relevant to our proof of Theorem 1.1 in Section 2 below. Furthermore, all these groups are finitely presented: in [Reference Brin4, Theorem 5], Brin observes that
$\mathfrak {C}^{n}$
and notes that these maps can be expressed as a product of transpositions. This observation will be particularly relevant to our proof of Theorem 1.1 in Section 2 below. Furthermore, all these groups are finitely presented: in [Reference Brin4, Theorem 5], Brin observes that
![]() $2V$
has a finite presentation with
$2V$
has a finite presentation with
![]() $8$
generators and
$8$
generators and
![]() $70$
relations. This method was extended by Hennig and Matucci [Reference Hennig and Matucci17] to establish a finite presentation for the groups
$70$
relations. This method was extended by Hennig and Matucci [Reference Hennig and Matucci17] to establish a finite presentation for the groups
![]() $nV$
involving
$nV$
involving
![]() $2n+4$
generators and
$2n+4$
generators and
![]() $10n^{2} + 10n + 10$
relations (see [Reference Hennig and Matucci17, Theorem 25]). Indeed, each group
$10n^{2} + 10n + 10$
relations (see [Reference Hennig and Matucci17, Theorem 25]). Indeed, each group
![]() $nV$
is of type
$nV$
is of type
![]() $\mathrm {F}_{\infty }$
, as established in [Reference Fluch, Marschler, Witzel and Zaremsky11, Reference Kochloukova, Martínez-Pérez and Nucinkas19]. In this article, it is demonstrated that these groups possess infinite presentations involving elements corresponding to transpositions of disjoint basic open sets and involving relations that have a Coxeter-like shape and reflect the self-similar nature of
$\mathrm {F}_{\infty }$
, as established in [Reference Fluch, Marschler, Witzel and Zaremsky11, Reference Kochloukova, Martínez-Pérez and Nucinkas19]. In this article, it is demonstrated that these groups possess infinite presentations involving elements corresponding to transpositions of disjoint basic open sets and involving relations that have a Coxeter-like shape and reflect the self-similar nature of
![]() $\mathfrak {C}^{n}$
(see Theorem 1.1 below). Again, these infinite presentations bear comparison with Dehornoy’s geometric presentations [Reference Dehornoy8] for F and V. In the final section of the paper, we demonstrate that the group
$\mathfrak {C}^{n}$
(see Theorem 1.1 below). Again, these infinite presentations bear comparison with Dehornoy’s geometric presentations [Reference Dehornoy8] for F and V. In the final section of the paper, we demonstrate that the group
![]() $nV$
is isomorphic to a group G with a finite presentation involving
$nV$
is isomorphic to a group G with a finite presentation involving
![]() $3$
generators and
$3$
generators and
![]() $2n^{2} + 3n + 11$
relations. It is noteworthy that the number of generators is bounded independent of the parameter n and that the number of relations significantly improves upon the presentations in [Reference Brin4, Reference Hennig and Matucci17]. In particular, the resulting finite presentation for
$2n^{2} + 3n + 11$
relations. It is noteworthy that the number of generators is bounded independent of the parameter n and that the number of relations significantly improves upon the presentations in [Reference Brin4, Reference Hennig and Matucci17]. In particular, the resulting finite presentation for
![]() $2V$
involves
$2V$
involves
![]() $3$
generators and
$3$
generators and
![]() $25$
relations.
$25$
relations.
1.1 Notation
We write
![]() $\mathfrak {C}$
for the Cantor set; that is, the collection of all infinite words from the alphabet
$\mathfrak {C}$
for the Cantor set; that is, the collection of all infinite words from the alphabet
![]() $\{0,1\}$
. We also use the set
$\{0,1\}$
. We also use the set
![]() $\{0,1\}^{\ast }$
of finite words in this alphabet and write
$\{0,1\}^{\ast }$
of finite words in this alphabet and write
![]() $\varepsilon $
to denote the empty word. If
$\varepsilon $
to denote the empty word. If
![]() $\alpha ,\beta \in \{0,1\}^{\ast }$
, then
$\alpha ,\beta \in \{0,1\}^{\ast }$
, then
![]() $\alpha \preceq \beta $
indicates that
$\alpha \preceq \beta $
indicates that
![]() $\alpha $
is a prefix of
$\alpha $
is a prefix of
![]() $\beta $
. The notation
$\beta $
. The notation
![]() $\alpha \perp \beta $
denotes that
$\alpha \perp \beta $
denotes that
![]() $\alpha \npreceq \beta $
and
$\alpha \npreceq \beta $
and
![]() $\alpha \nsucceq \beta $
, and we then say these words are incomparable. The length of a finite word
$\alpha \nsucceq \beta $
, and we then say these words are incomparable. The length of a finite word
![]() $\alpha $
, denoted by
$\alpha $
, denoted by
![]() $\mathopen {|}\alpha \mathclose {|}$
, is the number of symbols from
$\mathopen {|}\alpha \mathclose {|}$
, is the number of symbols from
![]() $\{0,1\}$
occurring in
$\{0,1\}$
occurring in
![]() $\alpha $
.
$\alpha $
.
If n is a positive integer with
![]() $n \geqslant 2$
, the higher-dimensional Thompson group
$n \geqslant 2$
, the higher-dimensional Thompson group
![]() $nV$
is defined (see below) as consisting of certain transformations defined on n-dimensional Cantor space
$nV$
is defined (see below) as consisting of certain transformations defined on n-dimensional Cantor space
![]() $\Gamma = \mathfrak {C}^{n}$
. Accordingly, we also need the set
$\Gamma = \mathfrak {C}^{n}$
. Accordingly, we also need the set
![]() $\Omega $
of sequences
$\Omega $
of sequences
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
where each
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
where each
![]() $\alpha _{i} \in \{0,1\}^{\ast }$
and we use the term address to refer to elements of
$\alpha _{i} \in \{0,1\}^{\ast }$
and we use the term address to refer to elements of
![]() $\Omega $
. These addresses are used to index the basic open subsets of
$\Omega $
. These addresses are used to index the basic open subsets of
![]() $\Gamma $
which in turn appear in the definition of the elements of
$\Gamma $
which in turn appear in the definition of the elements of
![]() $nV$
. We extend the concept of incomparability to addresses by writing
$nV$
. We extend the concept of incomparability to addresses by writing
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, for a pair of addresses
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, for a pair of addresses
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
and
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
and
![]() $\boldsymbol {\beta } = (\,\beta _{1},\beta _{2},\ldots ,\beta _{n})$
, when
$\boldsymbol {\beta } = (\,\beta _{1},\beta _{2},\ldots ,\beta _{n})$
, when
![]() $\alpha _{d} \perp \beta _{d}$
for some index d with
$\alpha _{d} \perp \beta _{d}$
for some index d with
![]() $1 \leqslant d \leqslant n$
. Similarly, for such addresses, we write
$1 \leqslant d \leqslant n$
. Similarly, for such addresses, we write
![]() $\boldsymbol {\alpha } \preceq \boldsymbol {\beta }$
when
$\boldsymbol {\alpha } \preceq \boldsymbol {\beta }$
when
![]() $\alpha _{d} \preceq \beta _{d}$
for all
$\alpha _{d} \preceq \beta _{d}$
for all
![]() $d = 1$
,
$d = 1$
,
![]() $2$
, …, n.
$2$
, …, n.
The higher-dimensional Thompson group
![]() $nV$
consists of certain homeomorphisms of
$nV$
consists of certain homeomorphisms of
![]() $\Gamma $
. We use right action notation throughout and so write
$\Gamma $
. We use right action notation throughout and so write
![]() $\boldsymbol {w}g$
for the image of
$\boldsymbol {w}g$
for the image of
![]() $\boldsymbol {w} \in \Gamma $
under
$\boldsymbol {w} \in \Gamma $
under
![]() $g \in nV$
. Let
$g \in nV$
. Let
![]() $\Gamma (\boldsymbol {\alpha }) = \{\,\boldsymbol {\alpha w}\mid \boldsymbol {w} \in \Gamma \,\}$
be the collection of all sequences in
$\Gamma (\boldsymbol {\alpha }) = \{\,\boldsymbol {\alpha w}\mid \boldsymbol {w} \in \Gamma \,\}$
be the collection of all sequences in
![]() $\Gamma $
with the address
$\Gamma $
with the address
![]() $\boldsymbol {\alpha }$
as prefix, and this is the basic open set indexed by
$\boldsymbol {\alpha }$
as prefix, and this is the basic open set indexed by
![]() $\boldsymbol {\alpha }$
. Note
$\boldsymbol {\alpha }$
. Note
![]() $\Gamma (\boldsymbol {\alpha }) \cap \Gamma (\boldsymbol {\,\beta }) = \varnothing $
if and only if
$\Gamma (\boldsymbol {\alpha }) \cap \Gamma (\boldsymbol {\,\beta }) = \varnothing $
if and only if
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and that
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and that
![]() $\Gamma (\boldsymbol {\alpha }) \supseteq \Gamma (\boldsymbol {\,\beta })$
if and only if
$\Gamma (\boldsymbol {\alpha }) \supseteq \Gamma (\boldsymbol {\,\beta })$
if and only if
![]() $\boldsymbol {\alpha } \preceq \boldsymbol {\beta }$
. An element g of
$\boldsymbol {\alpha } \preceq \boldsymbol {\beta }$
. An element g of
![]() $nV$
is then described as follows: given two partitions
$nV$
is then described as follows: given two partitions
![]() $\Gamma = \bigcup _{i=1}^{k} \Gamma (\boldsymbol {\alpha }^{(i)}) = \bigcup _{i=1}^{k} \Gamma (\boldsymbol {\,\beta }^{(i)})$
into the same number of disjoint basic open sets, we define the homeomorphism g of
$\Gamma = \bigcup _{i=1}^{k} \Gamma (\boldsymbol {\alpha }^{(i)}) = \bigcup _{i=1}^{k} \Gamma (\boldsymbol {\,\beta }^{(i)})$
into the same number of disjoint basic open sets, we define the homeomorphism g of
![]() $\Gamma $
by
$\Gamma $
by
![]() $\boldsymbol {\alpha }^{(i)}\boldsymbol {w} \mapsto \boldsymbol {\beta }^{(i)}\boldsymbol {w}$
for
$\boldsymbol {\alpha }^{(i)}\boldsymbol {w} \mapsto \boldsymbol {\beta }^{(i)}\boldsymbol {w}$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
, …, k and any
$2$
, …, k and any
![]() $\boldsymbol {w} \in \Gamma $
. Thus, each homeomorphism in
$\boldsymbol {w} \in \Gamma $
. Thus, each homeomorphism in
![]() $nV$
is given by piecewise affine maps on
$nV$
is given by piecewise affine maps on
![]() $\Gamma $
determined by two partitions of the space into the same number of basic open sets and some bijection between the parts. Figure 1 illustrates an example partition of
$\Gamma $
determined by two partitions of the space into the same number of basic open sets and some bijection between the parts. Figure 1 illustrates an example partition of
![]() $\mathfrak {C}^{3}$
; that is, a potential choice for domain or codomain partially determining an element of
$\mathfrak {C}^{3}$
; that is, a potential choice for domain or codomain partially determining an element of
![]() $3V$
. If
$3V$
. If
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
are incomparable addresses, we call the element of
$\boldsymbol {\beta }$
are incomparable addresses, we call the element of
![]() $nV$
that maps
$nV$
that maps
![]() $\boldsymbol {\alpha w} \mapsto \boldsymbol {\beta w}$
,
$\boldsymbol {\alpha w} \mapsto \boldsymbol {\beta w}$
,
![]() $\boldsymbol {\beta w} \mapsto \boldsymbol {\alpha w}$
for all
$\boldsymbol {\beta w} \mapsto \boldsymbol {\alpha w}$
for all
![]() $\boldsymbol {w} \in \Gamma $
and fixes all other points in
$\boldsymbol {w} \in \Gamma $
and fixes all other points in
![]() $\Gamma $
a transposition. This element has the effect of interchanging the basic open sets
$\Gamma $
a transposition. This element has the effect of interchanging the basic open sets
![]() $\Gamma (\boldsymbol {\alpha })$
and
$\Gamma (\boldsymbol {\alpha })$
and
![]() $\Gamma (\boldsymbol {\,\beta })$
. In what follows, we write
$\Gamma (\boldsymbol {\,\beta })$
. In what follows, we write
![]() $G_{\infty }$
for the group with the presentation given in Theorem 1.1 below. The element denoted by
$G_{\infty }$
for the group with the presentation given in Theorem 1.1 below. The element denoted by
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
that appears in that presentation corresponds, under the natural homomorphism
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
that appears in that presentation corresponds, under the natural homomorphism
![]() $G_{\infty } \to nV$
, to this transposition that interchanges
$G_{\infty } \to nV$
, to this transposition that interchanges
![]() $\Gamma (\boldsymbol {\alpha })$
and
$\Gamma (\boldsymbol {\alpha })$
and
![]() $\Gamma (\boldsymbol {\,\beta })$
.
$\Gamma (\boldsymbol {\,\beta })$
.

Figure 1 A domain or codomain partition of
![]() $\Gamma = \mathfrak {C}^{3}$
.
$\Gamma = \mathfrak {C}^{3}$
.
To describe an address in
![]() $\Omega $
, in theory, requires one to write a sequence of n finite words in
$\Omega $
, in theory, requires one to write a sequence of n finite words in
![]() $\{0,1\}$
. Such a sequence would appear quite cumbersome in our calculations particularly when appearing as entries in the transpositions with which we work. Accordingly, we present a more compact and useful notation. If
$\{0,1\}$
. Such a sequence would appear quite cumbersome in our calculations particularly when appearing as entries in the transpositions with which we work. Accordingly, we present a more compact and useful notation. If
![]() $\alpha $
is some (usually explicit) finite word in
$\alpha $
is some (usually explicit) finite word in
![]() $\{0,1\}$
, we write
$\{0,1\}$
, we write
![]() $\boldsymbol {\alpha }_{d}$
for the address all of whose entries are the empty word with the exception of the d th coordinate which equals
$\boldsymbol {\alpha }_{d}$
for the address all of whose entries are the empty word with the exception of the d th coordinate which equals
![]() $\alpha $
. Thus, for example,
$\alpha $
. Thus, for example,
![]() $\boldsymbol {010}_{d} = (\varepsilon ,\ldots ,\varepsilon ,010,\varepsilon ,\ldots ,\varepsilon )$
where
$\boldsymbol {010}_{d} = (\varepsilon ,\ldots ,\varepsilon ,010,\varepsilon ,\ldots ,\varepsilon )$
where
![]() $010$
occurs in the d th coordinate in this n-tuple. We particularly make use of this notation when we wish to append one (or more) letters from
$010$
occurs in the d th coordinate in this n-tuple. We particularly make use of this notation when we wish to append one (or more) letters from
![]() $\{0,1\}$
to particular entries in an address
$\{0,1\}$
to particular entries in an address
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
. For example, we write
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
. For example, we write
![]() $\boldsymbol {\alpha }.\boldsymbol {0}_{d}$
to indicate that we concatenate the addresses
$\boldsymbol {\alpha }.\boldsymbol {0}_{d}$
to indicate that we concatenate the addresses
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {0}_{d}$
; that is, we append the symbol
$\boldsymbol {0}_{d}$
; that is, we append the symbol
![]() $0$
to the d th coordinate
$0$
to the d th coordinate
![]() $\alpha _{d}$
of
$\alpha _{d}$
of
![]() $\boldsymbol {\alpha }$
:
$\boldsymbol {\alpha }$
:
(The use of the dot appearing in this notation is to demarcate the end of the first address
![]() $\boldsymbol {\alpha }$
and the beginning of the second and is intended to achieve clarity. Indeed, according to our notation,
$\boldsymbol {\alpha }$
and the beginning of the second and is intended to achieve clarity. Indeed, according to our notation,
![]() $\boldsymbol {\alpha 0}_{d}$
(without the dot) would indicate the address with a single nonempty entry
$\boldsymbol {\alpha 0}_{d}$
(without the dot) would indicate the address with a single nonempty entry
![]() $\alpha 0$
in the d th coordinate. The dot notation is unnecessary when concatenating two finite words in
$\alpha 0$
in the d th coordinate. The dot notation is unnecessary when concatenating two finite words in
![]() $\{0,1\}$
but helps when dealing with n-tuples.) The use of this notation can be observed within what we term the ‘split relations’ appearing in the statement of Theorem 1.1 below (see Equation (1-4)) and in the addresses labelling the parts in Figure 1. An additional piece of notation that we use is that if
$\{0,1\}$
but helps when dealing with n-tuples.) The use of this notation can be observed within what we term the ‘split relations’ appearing in the statement of Theorem 1.1 below (see Equation (1-4)) and in the addresses labelling the parts in Figure 1. An additional piece of notation that we use is that if
![]() $x \in \{0,1\}$
, then
$x \in \{0,1\}$
, then
![]() $\bar {x}$
denotes the other element in this set and then, following our above convention,
$\bar {x}$
denotes the other element in this set and then, following our above convention,
![]() $\bar {\boldsymbol {x}}_{d}$
is the sequence
$\bar {\boldsymbol {x}}_{d}$
is the sequence
![]() $(\varepsilon ,\ldots ,\varepsilon ,\bar {x},\varepsilon ,\ldots ,\varepsilon )$
, where
$(\varepsilon ,\ldots ,\varepsilon ,\bar {x},\varepsilon ,\ldots ,\varepsilon )$
, where
![]() $\bar {x}$
occurs in the d th coordinate. Finally,
$\bar {x}$
occurs in the d th coordinate. Finally,
![]() $\boldsymbol {\varepsilon }$
denotes the address
$\boldsymbol {\varepsilon }$
denotes the address
![]() $(\varepsilon ,\varepsilon ,\ldots ,\varepsilon )$
all of whose entries are the empty word.
$(\varepsilon ,\varepsilon ,\ldots ,\varepsilon )$
all of whose entries are the empty word.
To specify the relations that define our group, we define an additional notation that encodes the partial action of transpositions in
![]() $nV$
upon the basic open sets indexed by the addresses in
$nV$
upon the basic open sets indexed by the addresses in
![]() $\Omega $
. To be specific, if
$\Omega $
. To be specific, if
![]() $\boldsymbol {\alpha },\boldsymbol {\beta },\boldsymbol {\gamma } \in \Omega $
with
$\boldsymbol {\alpha },\boldsymbol {\beta },\boldsymbol {\gamma } \in \Omega $
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, we define a partial map by
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, we define a partial map by
 $$ \begin{align} \boldsymbol{\gamma} \bullet {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} = \begin{cases} \boldsymbol{\beta}\boldsymbol{\delta} &\text{if }\boldsymbol{\gamma} = \boldsymbol{\alpha}\boldsymbol{\delta} \text{ for some } \boldsymbol{\delta} \in \Omega; \\ \boldsymbol{\alpha}\boldsymbol{\delta} &\text{if } \boldsymbol{\gamma} = \boldsymbol{\beta}\boldsymbol{\delta} \text{ for some } \boldsymbol{\delta} \in \Omega; \\ \boldsymbol{\gamma} &\text{if both } \boldsymbol{\gamma} \perp \boldsymbol{\alpha} \text{ and } \boldsymbol{\gamma} \perp \boldsymbol{\beta}; \\ \text{undefined} &\text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \boldsymbol{\gamma} \bullet {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} = \begin{cases} \boldsymbol{\beta}\boldsymbol{\delta} &\text{if }\boldsymbol{\gamma} = \boldsymbol{\alpha}\boldsymbol{\delta} \text{ for some } \boldsymbol{\delta} \in \Omega; \\ \boldsymbol{\alpha}\boldsymbol{\delta} &\text{if } \boldsymbol{\gamma} = \boldsymbol{\beta}\boldsymbol{\delta} \text{ for some } \boldsymbol{\delta} \in \Omega; \\ \boldsymbol{\gamma} &\text{if both } \boldsymbol{\gamma} \perp \boldsymbol{\alpha} \text{ and } \boldsymbol{\gamma} \perp \boldsymbol{\beta}; \\ \text{undefined} &\text{otherwise}. \end{cases} \end{align} $$
Thus, we associate to the symbol
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
the partial map on the set
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
the partial map on the set
![]() $\Omega $
of addresses that performs a prefix substitution that interchanges the prefix
$\Omega $
of addresses that performs a prefix substitution that interchanges the prefix
![]() $\boldsymbol {\alpha }$
with the prefix
$\boldsymbol {\alpha }$
with the prefix
![]() $\boldsymbol {\beta }$
.
$\boldsymbol {\beta }$
.
1.2 Statement of results
In Section 2, we establish the following infinite presentation for
![]() $nV$
.
$nV$
.
Theorem 1.1. Let
![]() $n \geqslant 2$
. Let
$n \geqslant 2$
. Let
![]() $\mathcal {A}$
be the set of all symbols
$\mathcal {A}$
be the set of all symbols
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
where
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
are addresses in
$\boldsymbol {\beta }$
are addresses in
![]() $\Omega $
with
$\Omega $
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
. Then Brin’s higher-dimensional Thompson group
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
. Then Brin’s higher-dimensional Thompson group
![]() $nV$
has infinite presentation with generating set
$nV$
has infinite presentation with generating set
![]() $\mathcal {A}$
and all relations
$\mathcal {A}$
and all relations
where
![]() $\boldsymbol {\alpha }$
,
$\boldsymbol {\alpha }$
,
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
range over all addresses in
$\boldsymbol {\delta }$
range over all addresses in
![]() $\Omega $
such that
$\Omega $
such that
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
,
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
and such that both
$\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
and such that both
![]() $\boldsymbol {\alpha } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and
$\boldsymbol {\alpha } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and
![]() $\boldsymbol {\beta } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
are defined, and d ranges over all indices with
$\boldsymbol {\beta } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
are defined, and d ranges over all indices with
![]() $1 \leqslant d \leqslant n$
.
$1 \leqslant d \leqslant n$
.
We refer to relations of the form in Equation (1-3) as ‘conjugacy relations’ and those of the form in Equation (1-4) as ‘split relations’ in what follows. The latter arise due to the self-similar nature of Cantor space: to exchange prefixes
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
is equivalent to exchanging both the pairs of prefixes obtained by ‘splitting’ the d th coordinate. Note that we use exponential notation for conjugation, writing
$\boldsymbol {\beta }$
is equivalent to exchanging both the pairs of prefixes obtained by ‘splitting’ the d th coordinate. Note that we use exponential notation for conjugation, writing
![]() $g^{h}$
for
$g^{h}$
for
![]() $h^{-1}gh$
, where g and h belong to some group, and this is consistent with our use of right actions.
$h^{-1}gh$
, where g and h belong to some group, and this is consistent with our use of right actions.
We also need an additional relation that can be deduced immediately from Equation (1-3). On the face of it, if
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
are incomparable addresses in
$\boldsymbol {\beta }$
are incomparable addresses in
![]() $\Omega $
, the symbols
$\Omega $
, the symbols
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
and
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
and
![]() ${(\kern1.5pt\boldsymbol {\beta }\;\;\boldsymbol {\alpha })}$
are not necessarily the same element of the group with the given presentation. However, we expect them to correspond to the same transposition in
${(\kern1.5pt\boldsymbol {\beta }\;\;\boldsymbol {\alpha })}$
are not necessarily the same element of the group with the given presentation. However, we expect them to correspond to the same transposition in
![]() $nV$
. The ‘symmetry relation’
$nV$
. The ‘symmetry relation’
follows from Equation (1-3) by taking
![]() $\boldsymbol {\gamma } = \boldsymbol {\alpha }$
and
$\boldsymbol {\gamma } = \boldsymbol {\alpha }$
and
![]() $\boldsymbol {\delta } = \boldsymbol {\beta }$
:
$\boldsymbol {\delta } = \boldsymbol {\beta }$
:
We make use of this additional relation in Equation (1-5) throughout our arguments.
The method of proof of the above theorem is essentially to verify a family of relations for
![]() $nV$
originally found in [Reference Hennig and Matucci17]. Let
$nV$
originally found in [Reference Hennig and Matucci17]. Let
![]() $G_{\infty }$
denote the group with presentation given in Theorem 1.1. The key steps in the proof in Section 3 are to define and investigate elements in
$G_{\infty }$
denote the group with presentation given in Theorem 1.1. The key steps in the proof in Section 3 are to define and investigate elements in
![]() $G_{\infty }$
that correspond to baker’s maps. The two-dimensional baker’s map is a basic object within the study of dynamical systems (see, for example, [Reference Devaney9]) and is illustrated in Figure 2(i). In the context of n dimensions, we refer to baker’s maps that arise in the domain from a cut in the first coordinate and in the codomain from a cut in the d th coordinate. Thus, we define, in
$G_{\infty }$
that correspond to baker’s maps. The two-dimensional baker’s map is a basic object within the study of dynamical systems (see, for example, [Reference Devaney9]) and is illustrated in Figure 2(i). In the context of n dimensions, we refer to baker’s maps that arise in the domain from a cut in the first coordinate and in the codomain from a cut in the d th coordinate. Thus, we define, in
![]() $G_{\infty }$
, an element
$G_{\infty }$
, an element
![]() $B_{d}(\boldsymbol {\alpha })$
that corresponds to the element of
$B_{d}(\boldsymbol {\alpha })$
that corresponds to the element of
![]() $nV$
with support equal to
$nV$
with support equal to
![]() $\Gamma (\boldsymbol {\alpha })$
mapping
$\Gamma (\boldsymbol {\alpha })$
mapping
![]() $\mathfrak {C}^{n} \to \mathfrak {C}^{n}$
via the formula
$\mathfrak {C}^{n} \to \mathfrak {C}^{n}$
via the formula
 $$ \begin{align*} \boldsymbol{w} \mapsto \begin{cases} \boldsymbol{\alpha}.\boldsymbol{0}_{d}.\boldsymbol{u} &\text{if } \boldsymbol{w} = \boldsymbol{\alpha}.\boldsymbol{0}_{1}.\boldsymbol{u} \text{ for some } \boldsymbol{u} \in \mathfrak{C}^{n}, \\ \boldsymbol{\alpha}.\boldsymbol{1}_{d}.\boldsymbol{u} &\text{if } \boldsymbol{w} = \boldsymbol{\alpha}.\boldsymbol{1}_{1}.\boldsymbol{u} \text{ for some } \boldsymbol{u} \in \mathfrak{C}^{n}, \\ \boldsymbol{w} &\text{otherwise (that is, if } \boldsymbol{\alpha} \npreceq \boldsymbol{w}). \end{cases} \end{align*} $$
$$ \begin{align*} \boldsymbol{w} \mapsto \begin{cases} \boldsymbol{\alpha}.\boldsymbol{0}_{d}.\boldsymbol{u} &\text{if } \boldsymbol{w} = \boldsymbol{\alpha}.\boldsymbol{0}_{1}.\boldsymbol{u} \text{ for some } \boldsymbol{u} \in \mathfrak{C}^{n}, \\ \boldsymbol{\alpha}.\boldsymbol{1}_{d}.\boldsymbol{u} &\text{if } \boldsymbol{w} = \boldsymbol{\alpha}.\boldsymbol{1}_{1}.\boldsymbol{u} \text{ for some } \boldsymbol{u} \in \mathfrak{C}^{n}, \\ \boldsymbol{w} &\text{otherwise (that is, if } \boldsymbol{\alpha} \npreceq \boldsymbol{w}). \end{cases} \end{align*} $$
When we refer below to the element
![]() $B_{d}(\boldsymbol {\alpha })$
evaluating to an ‘index d’ baker’s map, we mean that it evaluates to the homeomorphism of
$B_{d}(\boldsymbol {\alpha })$
evaluating to an ‘index d’ baker’s map, we mean that it evaluates to the homeomorphism of
![]() $\mathfrak {C}^{n}$
given by this formula. All baker’s maps arising within our work will have such a form (for some address
$\mathfrak {C}^{n}$
given by this formula. All baker’s maps arising within our work will have such a form (for some address
![]() $\boldsymbol {\alpha } \in \Omega $
and some
$\boldsymbol {\alpha } \in \Omega $
and some
![]() $d \geqslant 2$
).
$d \geqslant 2$
).

Figure 2 Baker’s maps when
![]() $d = 2$
(left) and
$d = 2$
(left) and
![]() $d = 3$
(right).
$d = 3$
(right).
The elements
![]() $B_{d}(\boldsymbol {\alpha })$
in
$B_{d}(\boldsymbol {\alpha })$
in
![]() $G_{\infty }$
are defined via the formulae expressing baker’s maps in terms of transpositions found in [Reference Brin5]. In Section 2, we observe that the behaviour of baker’s maps can be deduced from the relations assumed about transpositions. Lemmas 2.2–2.4 give the properties upon which we depend. In summary, while Brin [Reference Brin5] establishes simplicity of
$G_{\infty }$
are defined via the formulae expressing baker’s maps in terms of transpositions found in [Reference Brin5]. In Section 2, we observe that the behaviour of baker’s maps can be deduced from the relations assumed about transpositions. Lemmas 2.2–2.4 give the properties upon which we depend. In summary, while Brin [Reference Brin5] establishes simplicity of
![]() $nV$
by expressing baker’s maps as products of transpositions, we use relational properties between transpositions to produce information about baker’s maps to establish our presentation in Theorem 1.1.
$nV$
by expressing baker’s maps as products of transpositions, we use relational properties between transpositions to produce information about baker’s maps to establish our presentation in Theorem 1.1.
In Section 3, we reduce our infinite presentation to a finite presentation (the relations are those listed in Relations R1–R7 in that section).
Theorem 1.2. Let
![]() $n \geqslant 2$
. Brin’s higher-dimensional Thompson group
$n \geqslant 2$
. Brin’s higher-dimensional Thompson group
![]() $nV$
has a finite presentation with three generators and
$nV$
has a finite presentation with three generators and
![]() $2n^{2} + 3n + 11$
relations.
$2n^{2} + 3n + 11$
relations.
To prove this theorem, we begin with transpositions with entries from the set
![]() $\Delta $
of addresses
$\Delta $
of addresses
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with
![]() $\mathopen {|}\alpha _{d}\mathclose {|} = 2$
for
$\mathopen {|}\alpha _{d}\mathclose {|} = 2$
for
![]() $1 \leqslant d \leqslant n$
. Thus, as a base point in an induction argument, we assume that we have a subgroup isomorphic to (a quotient of) the symmetric group of degree
$1 \leqslant d \leqslant n$
. Thus, as a base point in an induction argument, we assume that we have a subgroup isomorphic to (a quotient of) the symmetric group of degree
![]() $4^{n}$
. In an induction argument, we build further transpositions by successively conjugating the transpositions constructed at a previous stage and then finally exploit the split relations in Equation (1-4) to complete the definitions. In this way, we demonstrate that the group G with the presentations provided in Theorem 1.2 is a quotient of the group
$4^{n}$
. In an induction argument, we build further transpositions by successively conjugating the transpositions constructed at a previous stage and then finally exploit the split relations in Equation (1-4) to complete the definitions. In this way, we demonstrate that the group G with the presentations provided in Theorem 1.2 is a quotient of the group
![]() $G_{\infty }$
described in Theorem 1.1.
$G_{\infty }$
described in Theorem 1.1.
Finally, by applying Tietze transformations, we deduce the following corollary.
Corollary 1.3. Let
![]() $n \geqslant 2$
. Brin’s higher-dimensional Thompson group
$n \geqslant 2$
. Brin’s higher-dimensional Thompson group
![]() $nV$
has a finite presentation with two generators and
$nV$
has a finite presentation with two generators and
![]() $2n^{2} + 3n + 13$
relations.
$2n^{2} + 3n + 13$
relations.
Remarks 1.4. In common with the finite presentation given by Hennig–Matucci [Reference Hennig and Matucci17], the number of relations we use is quadratic in the dimension n. One could ask whether there are presentations for
![]() $nV$
on two generators but where the number of relations grows at most linearly in n. In our case, the quadratic function arises from the family of Relations R5, which is used to ensure the well definedness of transpositions
$nV$
on two generators but where the number of relations grows at most linearly in n. In our case, the quadratic function arises from the family of Relations R5, which is used to ensure the well definedness of transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
where two coordinates of
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
where two coordinates of
![]() $\boldsymbol {\alpha }$
have length
$\boldsymbol {\alpha }$
have length
![]() $3$
and all remaining coordinates of
$3$
and all remaining coordinates of
![]() $\boldsymbol {\alpha }$
and all those of
$\boldsymbol {\alpha }$
and all those of
![]() $\boldsymbol {\beta }$
have length
$\boldsymbol {\beta }$
have length
![]() $2$
. Although the growth in the number of relations relative to the dimension of the space acted upon seems reasonable, surprising results such as that of Guralnick et al. [Reference Guralnick, Kantor, Kassabov and Lubotzky16] stand in contrast to expectations. The arguments used in [Reference Guralnick, Kantor, Kassabov and Lubotzky16] employ a process that has been termed the Burnside procedure and presented in detail in the appendix of [Reference Martinez-Pérez, Matucci and Nucinkis20]. This process can be used to reduce some large presentation of a group to a much smaller one. Potentially, it could be applied to the infinite presentation found in Theorem 1.1 and one might wonder how the result would compare with Theorem 1.2. It seemed to the author that the most direct application of the Burnside procedure (if successful) would likely result in more relations. Nevertheless, it remains an interesting question whether smaller presentations exist for Brin’s groups
$2$
. Although the growth in the number of relations relative to the dimension of the space acted upon seems reasonable, surprising results such as that of Guralnick et al. [Reference Guralnick, Kantor, Kassabov and Lubotzky16] stand in contrast to expectations. The arguments used in [Reference Guralnick, Kantor, Kassabov and Lubotzky16] employ a process that has been termed the Burnside procedure and presented in detail in the appendix of [Reference Martinez-Pérez, Matucci and Nucinkis20]. This process can be used to reduce some large presentation of a group to a much smaller one. Potentially, it could be applied to the infinite presentation found in Theorem 1.1 and one might wonder how the result would compare with Theorem 1.2. It seemed to the author that the most direct application of the Burnside procedure (if successful) would likely result in more relations. Nevertheless, it remains an interesting question whether smaller presentations exist for Brin’s groups
![]() $nV$
.
$nV$
.
2 The infinite presentation for
 $nV$
$nV$
We devote this section to establishing Theorem 1.1. Accordingly, we define
![]() $G_{\infty }$
to be the group presented by the generators
$G_{\infty }$
to be the group presented by the generators
![]() $\mathcal {A} = \{\, {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}\mid \boldsymbol {\alpha },\boldsymbol {\beta } \in \Omega , \; \boldsymbol {\alpha } \perp \boldsymbol {\beta }\,\}$
subject to the family of Relations (1-2)–(1-4). In this context, we shall use the term transposition for any element
$\mathcal {A} = \{\, {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}\mid \boldsymbol {\alpha },\boldsymbol {\beta } \in \Omega , \; \boldsymbol {\alpha } \perp \boldsymbol {\beta }\,\}$
subject to the family of Relations (1-2)–(1-4). In this context, we shall use the term transposition for any element
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
appearing in the generating set
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
appearing in the generating set
![]() $\mathcal {A}$
. It was observed by Brin [Reference Brin5] that the group
$\mathcal {A}$
. It was observed by Brin [Reference Brin5] that the group
![]() $nV$
is generated by the corresponding transpositions of basic open sets of
$nV$
is generated by the corresponding transpositions of basic open sets of
![]() $\Gamma $
. It is readily verified that these homeomorphisms satisfy the relations listed in Theorem 1.1. Hence, there exists a surjective homomorphism
$\Gamma $
. It is readily verified that these homeomorphisms satisfy the relations listed in Theorem 1.1. Hence, there exists a surjective homomorphism
![]() $\phi \colon G_{\infty } \to nV$
that maps
$\phi \colon G_{\infty } \to nV$
that maps
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
to the corresponding transposition in
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
to the corresponding transposition in
![]() $nV$
. In what follows, we speak of evaluating a product g in
$nV$
. In what follows, we speak of evaluating a product g in
![]() $nV$
to mean the effect of applying the homomorphism
$nV$
to mean the effect of applying the homomorphism
![]() $\phi $
to the element
$\phi $
to the element
![]() $g \in G_{\infty }$
.
$g \in G_{\infty }$
.
We can extend the definition appearing in Equation (1-1) to a product g of transpositions, say
![]() $g = g_{1}g_{2}\ldots g_{k}$
, where each
$g = g_{1}g_{2}\ldots g_{k}$
, where each
![]() $g_{i} \in \mathcal {A}$
, by defining
$g_{i} \in \mathcal {A}$
, by defining
![]() $\boldsymbol {\alpha }\bullet g$
to equal the value obtained by successively applying Equation (1-1) with each transposition
$\boldsymbol {\alpha }\bullet g$
to equal the value obtained by successively applying Equation (1-1) with each transposition
![]() $g_{i}$
. Note that this is, strictly speaking, a function of the word in
$g_{i}$
. Note that this is, strictly speaking, a function of the word in
![]() $\mathcal {A}$
representing g rather than depending upon g as an element of
$\mathcal {A}$
representing g rather than depending upon g as an element of
![]() $G_{\infty }$
. With this extended definition, if
$G_{\infty }$
. With this extended definition, if
![]() $\boldsymbol {\alpha },\boldsymbol {\beta } \in \Omega $
with
$\boldsymbol {\alpha },\boldsymbol {\beta } \in \Omega $
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
![]() $g \in G_{\infty }$
is expressed as a product of transpositions such that both
$g \in G_{\infty }$
is expressed as a product of transpositions such that both
![]() $\boldsymbol {\alpha } \bullet g$
and
$\boldsymbol {\alpha } \bullet g$
and
![]() $\boldsymbol {\beta } \bullet g$
are defined, then it follows by repeated use of the conjugacy relations in Equation (1-3) that
$\boldsymbol {\beta } \bullet g$
are defined, then it follows by repeated use of the conjugacy relations in Equation (1-3) that
Note that
![]() $\boldsymbol {\alpha } \bullet g$
, when it is defined, coincides with the value obtained if the product g is evaluated as an element of the Brin’s higher-dimensional Thompson group
$\boldsymbol {\alpha } \bullet g$
, when it is defined, coincides with the value obtained if the product g is evaluated as an element of the Brin’s higher-dimensional Thompson group
![]() $nV$
and then
$nV$
and then
![]() $\boldsymbol {\alpha } \bullet g$
is calculated via the natural partial action of
$\boldsymbol {\alpha } \bullet g$
is calculated via the natural partial action of
![]() $nV$
upon the addresses
$nV$
upon the addresses
![]() $\Omega $
. The only difference is that there may exist some addresses
$\Omega $
. The only difference is that there may exist some addresses
![]() $\boldsymbol {\alpha }$
for which
$\boldsymbol {\alpha }$
for which
![]() $\boldsymbol {\alpha } \bullet g$
is not defined for our given word representing g but for which the corresponding transformation in
$\boldsymbol {\alpha } \bullet g$
is not defined for our given word representing g but for which the corresponding transformation in
![]() $nV$
does have an action defined upon
$nV$
does have an action defined upon
![]() $\boldsymbol {\alpha }$
. However, if
$\boldsymbol {\alpha }$
. However, if
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
and provided the words
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
and provided the words
![]() $\alpha _{i}$
are sufficiently long, then
$\alpha _{i}$
are sufficiently long, then
![]() $\boldsymbol {\alpha } \bullet g$
is defined and hence coincides with the value obtained via the partial action of
$\boldsymbol {\alpha } \bullet g$
is defined and hence coincides with the value obtained via the partial action of
![]() $nV$
upon
$nV$
upon
![]() $\Omega $
.
$\Omega $
.
We establish that
![]() $G_{\infty }$
is isomorphic to the group
$G_{\infty }$
is isomorphic to the group
![]() $nV$
by demonstrating that a family of relations found within Hennig–Matucci’s work [Reference Hennig and Matucci17] can be deduced from our defining relations. We define elements of our group
$nV$
by demonstrating that a family of relations found within Hennig–Matucci’s work [Reference Hennig and Matucci17] can be deduced from our defining relations. We define elements of our group
![]() $G_{\infty }$
that correspond to the family of generators that are used in [Reference Hennig and Matucci17]. Some are readily constructed using transpositions
$G_{\infty }$
that correspond to the family of generators that are used in [Reference Hennig and Matucci17]. Some are readily constructed using transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
but others depend upon building analogues of the baker’s maps. Brin’s paper [Reference Brin5] describes how to construct a baker’s map from transpositions in his Lemma 3. By following this recipe we are able to define the required elements of
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
but others depend upon building analogues of the baker’s maps. Brin’s paper [Reference Brin5] describes how to construct a baker’s map from transpositions in his Lemma 3. By following this recipe we are able to define the required elements of
![]() $G_{\infty }$
. Moreover, it then follows that the products of transformations we define evaluate to the required baker’s maps in
$G_{\infty }$
. Moreover, it then follows that the products of transformations we define evaluate to the required baker’s maps in
![]() $nV$
and hence we can determine the value of
$nV$
and hence we can determine the value of
![]() $\boldsymbol {\alpha } \bullet g$
for such products g provided the coordinates of
$\boldsymbol {\alpha } \bullet g$
for such products g provided the coordinates of
![]() $\boldsymbol {\alpha }$
are sufficiently long.
$\boldsymbol {\alpha }$
are sufficiently long.
If
![]() $\boldsymbol {\alpha },\boldsymbol {\beta } \in \Omega $
with
$\boldsymbol {\alpha },\boldsymbol {\beta } \in \Omega $
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and d is an index with
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and d is an index with
![]() $2 \leqslant d \leqslant n$
, we define
$2 \leqslant d \leqslant n$
, we define
We define further elements of
![]() $G_{\infty }$
in terms of this product as follows:
$G_{\infty }$
in terms of this product as follows:
 $$ \begin{align} \begin{aligned} \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) &= A_{d}(\boldsymbol{0}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) \\ \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) &= A_{d}(\boldsymbol{0}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) \\ \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{0}_{d}) &= A_{d}(\boldsymbol{1}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{1}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{1}_{1}.\boldsymbol{1}_{d}) \\ \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{1}_{d}) &= A_{d}(\boldsymbol{1}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{1}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{1}_{1}.\boldsymbol{0}_{d}), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) &= A_{d}(\boldsymbol{0}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) \\ \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) &= A_{d}(\boldsymbol{0}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) \\ \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{0}_{d}) &= A_{d}(\boldsymbol{1}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{1}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{1}_{1}.\boldsymbol{1}_{d}) \\ \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{1}_{d}) &= A_{d}(\boldsymbol{1}_{1},\boldsymbol{\gamma}) \;\, {(\boldsymbol{1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{1}_{1}.\boldsymbol{10}_{d})} \;\, A_{d}(\boldsymbol{\gamma},\boldsymbol{1}_{1}.\boldsymbol{0}_{d}), \end{aligned} \end{align} $$
where
![]() $\boldsymbol {\gamma } = (\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})$
is an address in
$\boldsymbol {\gamma } = (\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})$
is an address in
![]() $\Omega $
satisfying
$\Omega $
satisfying
![]() $\mathopen {|}\gamma _{1}\mathclose {|},\mathopen {|}\gamma _{d}\mathclose {|} \geqslant 1$
and the additional condition that
$\mathopen {|}\gamma _{1}\mathclose {|},\mathopen {|}\gamma _{d}\mathclose {|} \geqslant 1$
and the additional condition that
![]() $\boldsymbol {\gamma } \perp \boldsymbol {0}_{1}$
in the first two definitions and that
$\boldsymbol {\gamma } \perp \boldsymbol {0}_{1}$
in the first two definitions and that
![]() $\boldsymbol {\gamma } \perp \boldsymbol {1}_{1}$
in the last two definitions in Equation (2-2). Further, we then define:
$\boldsymbol {\gamma } \perp \boldsymbol {1}_{1}$
in the last two definitions in Equation (2-2). Further, we then define:
 $$ \begin{align} \begin{aligned} B_{d}(\boldsymbol{0}_{1}) &= \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) \;\, \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) \;\, {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ B_{d}(\boldsymbol{1}_{1}) &= \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{0}_{d}) \;\, \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{1}_{d}) \;\, {(\boldsymbol{1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{1}_{1}.\boldsymbol{10}_{d})} \end{aligned}. \end{align} $$
$$ \begin{align} \begin{aligned} B_{d}(\boldsymbol{0}_{1}) &= \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) \;\, \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) \;\, {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ B_{d}(\boldsymbol{1}_{1}) &= \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{0}_{d}) \;\, \hat{B}_{d}(\boldsymbol{1}_{1}.\boldsymbol{1}_{d}) \;\, {(\boldsymbol{1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{1}_{1}.\boldsymbol{10}_{d})} \end{aligned}. \end{align} $$
These three types of element are the analogues of the maps arising within the proof of [Reference Brin5, Lemma 3] and their definition precisely follows that proof. Consequently, the product
![]() $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
evaluates in the group
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
evaluates in the group
![]() $nV$
to the composite of an ‘index d’ baker’s map with support
$nV$
to the composite of an ‘index d’ baker’s map with support
![]() $\Gamma (\boldsymbol {\alpha })$
and the inverse of an ‘index d’ baker’s map with support
$\Gamma (\boldsymbol {\alpha })$
and the inverse of an ‘index d’ baker’s map with support
![]() $\Gamma (\boldsymbol {\,\beta })$
. The subsequent elements
$\Gamma (\boldsymbol {\,\beta })$
. The subsequent elements
![]() $\hat {B}_{d}(\boldsymbol {\alpha })$
and
$\hat {B}_{d}(\boldsymbol {\alpha })$
and
![]() $B_{d}(\boldsymbol {\alpha })$
both evaluate to the ‘index d’ baker’s map with support
$B_{d}(\boldsymbol {\alpha })$
both evaluate to the ‘index d’ baker’s map with support
![]() $\Gamma (\boldsymbol {\alpha })$
. The difference is that the address
$\Gamma (\boldsymbol {\alpha })$
. The difference is that the address
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
that we have first defined them upon satisfies
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
that we have first defined them upon satisfies
![]() $\mathopen {|}\alpha _{1}\mathclose {|} = 1$
for both products, but the
$\mathopen {|}\alpha _{1}\mathclose {|} = 1$
for both products, but the
![]() $\hat {B}_{d}$
version requires
$\hat {B}_{d}$
version requires
![]() $\mathopen {|}\alpha _{d}\mathclose {|} = 1$
while
$\mathopen {|}\alpha _{d}\mathclose {|} = 1$
while
![]() $B_{d}$
permits
$B_{d}$
permits
![]() $\alpha _{d}$
to be empty. One notes that to define a baker’s map on the whole space
$\alpha _{d}$
to be empty. One notes that to define a baker’s map on the whole space
![]() $\Gamma = \mathfrak {C}^{n}$
(that is, with address
$\Gamma = \mathfrak {C}^{n}$
(that is, with address
![]() $\boldsymbol {\varepsilon }$
) requires a further such definition. As this is (up to choice of index d) a single element in
$\boldsymbol {\varepsilon }$
) requires a further such definition. As this is (up to choice of index d) a single element in
![]() $G_{\infty }$
, we delay the definition of this element, which appears as
$G_{\infty }$
, we delay the definition of this element, which appears as
![]() $C_{0,d}$
below (see Equation (2-5)).
$C_{0,d}$
below (see Equation (2-5)).
To extend the baker’s maps to arbitrary addresses, we use another convenient notation. If g is an element of
![]() $G_{\infty }$
and
$G_{\infty }$
and
![]() $\boldsymbol {\delta } \in \Omega $
, we write
$\boldsymbol {\delta } \in \Omega $
, we write
![]() $\boldsymbol {\delta }.g$
for the element of
$\boldsymbol {\delta }.g$
for the element of
![]() $G_{\infty }$
obtained by inserting
$G_{\infty }$
obtained by inserting
![]() $\boldsymbol {\delta }$
as a prefix in both entries of every transposition appearing in the product g. Since Relations (1-2)–(1-4) are closed under performing such insertions, it follows that (i)
$\boldsymbol {\delta }$
as a prefix in both entries of every transposition appearing in the product g. Since Relations (1-2)–(1-4) are closed under performing such insertions, it follows that (i)
![]() $\boldsymbol {\delta }.g$
is a well-defined element of
$\boldsymbol {\delta }.g$
is a well-defined element of
![]() $G_{\infty }$
and (ii) if
$G_{\infty }$
and (ii) if
![]() $u = v$
is a relation that holds in
$u = v$
is a relation that holds in
![]() $G_{\infty }$
, then
$G_{\infty }$
, then
![]() $\boldsymbol {\delta }.u = \boldsymbol {\delta }.v$
also holds in
$\boldsymbol {\delta }.u = \boldsymbol {\delta }.v$
also holds in
![]() $G_{\infty }$
. We use the latter observation to reduce the number of calculations required.
$G_{\infty }$
. We use the latter observation to reduce the number of calculations required.
In terms of this prefix notation, observe that
for any addresses
![]() $\boldsymbol {\alpha }$
,
$\boldsymbol {\alpha }$
,
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\delta }$
with
$\boldsymbol {\delta }$
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
. For our baker’s maps, we define
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
. For our baker’s maps, we define
![]() $\hat {B}_{d}(\boldsymbol {\alpha })$
, where
$\hat {B}_{d}(\boldsymbol {\alpha })$
, where
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfies
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfies
![]() $\mathopen {|}\alpha _{1}\mathclose {|},\mathopen {|}\alpha _{d}\mathclose {|} \geqslant 1$
, by writing
$\mathopen {|}\alpha _{1}\mathclose {|},\mathopen {|}\alpha _{d}\mathclose {|} \geqslant 1$
, by writing
![]() $\boldsymbol {\alpha } = \boldsymbol {\delta }\boldsymbol {\beta }$
where
$\boldsymbol {\alpha } = \boldsymbol {\delta }\boldsymbol {\beta }$
where
![]() $\boldsymbol {\beta } \in \{ \boldsymbol {0}_{1}.\boldsymbol {0}_{d}, \boldsymbol {0}_{1}.\boldsymbol {1}_{d}, \boldsymbol {1}_{1}.\boldsymbol {0}_{d}, \boldsymbol {1}_{1}.\boldsymbol {1}_{d} \}$
and then setting
$\boldsymbol {\beta } \in \{ \boldsymbol {0}_{1}.\boldsymbol {0}_{d}, \boldsymbol {0}_{1}.\boldsymbol {1}_{d}, \boldsymbol {1}_{1}.\boldsymbol {0}_{d}, \boldsymbol {1}_{1}.\boldsymbol {1}_{d} \}$
and then setting
where
![]() $\hat {B}_{d}(\boldsymbol {\,\beta })$
is as defined in Equation (2-2). Similarly, if
$\hat {B}_{d}(\boldsymbol {\,\beta })$
is as defined in Equation (2-2). Similarly, if
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfies
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfies
![]() $\mathopen {|}\alpha _{1}\mathclose {|} \geqslant 1$
, by writing
$\mathopen {|}\alpha _{1}\mathclose {|} \geqslant 1$
, by writing
![]() $\boldsymbol {\alpha } = \boldsymbol {\delta }\boldsymbol {\beta }$
where
$\boldsymbol {\alpha } = \boldsymbol {\delta }\boldsymbol {\beta }$
where
![]() $\boldsymbol {\beta } \in \{ \boldsymbol {0}_{1}, \boldsymbol {1}_{1} \}$
, we define
$\boldsymbol {\beta } \in \{ \boldsymbol {0}_{1}, \boldsymbol {1}_{1} \}$
, we define
Note that inserting this prefix
![]() $\boldsymbol {\delta }$
into the definition in Equation (2-3) yields
$\boldsymbol {\delta }$
into the definition in Equation (2-3) yields
for any
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with
![]() $\mathopen {|}\alpha _{1}\mathclose {|} \geqslant 1$
. Now, if
$\mathopen {|}\alpha _{1}\mathclose {|} \geqslant 1$
. Now, if
![]() $\boldsymbol {\alpha }$
is an address such that both
$\boldsymbol {\alpha }$
is an address such that both
![]() $\hat {B}_{d}(\boldsymbol {\alpha })$
and
$\hat {B}_{d}(\boldsymbol {\alpha })$
and
![]() $B_{d}(\boldsymbol {\alpha })$
are defined, then they evaluate to the same baker’s map in the group
$B_{d}(\boldsymbol {\alpha })$
are defined, then they evaluate to the same baker’s map in the group
![]() $nV$
. However, the former is not defined for addresses
$nV$
. However, the former is not defined for addresses
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with
![]() $\alpha _{d}$
empty.
$\alpha _{d}$
empty.
Lemma 2.1. Let
![]() $\boldsymbol {\alpha },\boldsymbol {\beta },\boldsymbol {\gamma },\boldsymbol {\delta } \in \Omega $
be addresses with
$\boldsymbol {\alpha },\boldsymbol {\beta },\boldsymbol {\gamma },\boldsymbol {\delta } \in \Omega $
be addresses with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
![]() $\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
. Let
$\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
. Let
![]() $d,d'$
be indices in the range
$d,d'$
be indices in the range
![]() $2 \leqslant d,d' \leqslant n$
. Then:
$2 \leqslant d,d' \leqslant n$
. Then:
-
(i)
 $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })^{{(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = A_{d}(\boldsymbol {\alpha }\!\bullet \!{(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}, \boldsymbol {\beta }\!\bullet \!{(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} )$
, whenever both
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })^{{(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = A_{d}(\boldsymbol {\alpha }\!\bullet \!{(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}, \boldsymbol {\beta }\!\bullet \!{(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} )$
, whenever both
 $\boldsymbol {\alpha } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and
$\boldsymbol {\alpha } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and
 $\boldsymbol {\beta } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
are defined;
$\boldsymbol {\beta } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
are defined; -
(ii) if every pair from
 $\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
are incomparable, then
$\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
are incomparable, then
 $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
and
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
and
 $A_{d}(\boldsymbol {\gamma },\boldsymbol {\delta })$
commute;
$A_{d}(\boldsymbol {\gamma },\boldsymbol {\delta })$
commute; -
(iii)
 $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta }) = {(\boldsymbol {\alpha }.\boldsymbol {01}_{1}\;\;\boldsymbol {\alpha }.\boldsymbol {10}_{1})} \; A_{d}(\boldsymbol {\alpha }.\boldsymbol {0}_{1}, \boldsymbol {\beta }.\boldsymbol {0}_{1}) \; A_{d}(\boldsymbol {\alpha }.\boldsymbol {1}_{1}, \boldsymbol {\beta }.\boldsymbol {1}_{1}) \; {(\boldsymbol {\,\beta }.\boldsymbol {01}_{1}\;\;\boldsymbol {\beta }.\boldsymbol {10}_{1})}$
;
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta }) = {(\boldsymbol {\alpha }.\boldsymbol {01}_{1}\;\;\boldsymbol {\alpha }.\boldsymbol {10}_{1})} \; A_{d}(\boldsymbol {\alpha }.\boldsymbol {0}_{1}, \boldsymbol {\beta }.\boldsymbol {0}_{1}) \; A_{d}(\boldsymbol {\alpha }.\boldsymbol {1}_{1}, \boldsymbol {\beta }.\boldsymbol {1}_{1}) \; {(\boldsymbol {\,\beta }.\boldsymbol {01}_{1}\;\;\boldsymbol {\beta }.\boldsymbol {10}_{1})}$
; -
(iv) if
 $d' \neq d$
, then
$d' \neq d$
, then
 $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta }) = A_{d}(\boldsymbol {\alpha }.\boldsymbol {0}_{d'},\boldsymbol {\beta }.\boldsymbol {0}_{d'}) \; A_{d}(\boldsymbol {\alpha }.\boldsymbol {1}_{d'},\boldsymbol {\beta }.\boldsymbol {1}_{d'})$
.
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta }) = A_{d}(\boldsymbol {\alpha }.\boldsymbol {0}_{d'},\boldsymbol {\beta }.\boldsymbol {0}_{d'}) \; A_{d}(\boldsymbol {\alpha }.\boldsymbol {1}_{d'},\boldsymbol {\beta }.\boldsymbol {1}_{d'})$
.
Proof. Part (i) follows immediately by Equation (1-3). We deduce part (ii) by noting that Equation (2-1) expresses
![]() $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
as a product of transpositions each of which, by part (i), commutes with
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
as a product of transpositions each of which, by part (i), commutes with
![]() $A_{d}(\boldsymbol {\gamma },\boldsymbol {\delta })$
.
$A_{d}(\boldsymbol {\gamma },\boldsymbol {\delta })$
.
(iii) We expand the right-hand side using the definition of the terms
![]() $A_{d}$
and collect the transpositions using the conjugacy relations in Equation (1-3):
$A_{d}$
and collect the transpositions using the conjugacy relations in Equation (1-3):
 $$ \begin{align*} &{(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \; A_{d}(\boldsymbol{\alpha}.\boldsymbol{0}_{1},\boldsymbol{\beta}.\boldsymbol{0}_{1}) \; A_{d}(\boldsymbol{\alpha}.\boldsymbol{1}_{1},\boldsymbol{\beta}.\boldsymbol{1}_{1}) \; {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \qquad\qquad\qquad \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \; {(\boldsymbol{\alpha}.\boldsymbol{00}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{0}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{1}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1})} \\ &\quad\qquad \cdot {(\boldsymbol{\alpha}.\boldsymbol{10}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{0}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{11}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{1}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1})} \; {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{00}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{10}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{1}_{d})} \\ &\quad\qquad \cdot {(\boldsymbol{\alpha}.\boldsymbol{11}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{00}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{10}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{11}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{1}_{d})} \\ &\quad\qquad \cdot {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \;\, {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \qquad \text{(by Equation}\ ({1\hbox{-}4})) \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})}^{2} = A_{d}(\boldsymbol{\alpha},\boldsymbol{\beta}). \end{align*} $$
$$ \begin{align*} &{(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \; A_{d}(\boldsymbol{\alpha}.\boldsymbol{0}_{1},\boldsymbol{\beta}.\boldsymbol{0}_{1}) \; A_{d}(\boldsymbol{\alpha}.\boldsymbol{1}_{1},\boldsymbol{\beta}.\boldsymbol{1}_{1}) \; {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \qquad\qquad\qquad \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \; {(\boldsymbol{\alpha}.\boldsymbol{00}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{0}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{1}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1})} \\ &\quad\qquad \cdot {(\boldsymbol{\alpha}.\boldsymbol{10}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{0}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{11}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{1}_{d})} \; {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1})} \; {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{00}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{10}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{1}_{d})} \\ &\quad\qquad \cdot {(\boldsymbol{\alpha}.\boldsymbol{11}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{00}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{10}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{11}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1}.\boldsymbol{1}_{d})} \\ &\quad\qquad \cdot {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{1})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{1})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{01}_{1}\;\;\boldsymbol{\alpha}.\boldsymbol{10}_{1})} \;\, {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})} \qquad \text{(by Equation}\ ({1\hbox{-}4})) \\ &\quad= {(\boldsymbol{\alpha}.\boldsymbol{0}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \;\, {(\boldsymbol{\alpha}.\boldsymbol{1}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} \;\, {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} \;\, {(\boldsymbol{\,\beta}.\boldsymbol{01}_{1}\;\;\boldsymbol{\beta}.\boldsymbol{10}_{1})}^{2} = A_{d}(\boldsymbol{\alpha},\boldsymbol{\beta}). \end{align*} $$
(iv) Apply the split relation in Equation (1-4) in the
![]() $d'$
th coordinate to each transposition appearing in
$d'$
th coordinate to each transposition appearing in
![]() $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
. For example,
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
. For example,
![]() ${(\boldsymbol {\alpha }.\boldsymbol {0}_{1}\;\;\boldsymbol {\beta }.\boldsymbol {0}_{d})} = {(\boldsymbol {\alpha }.\boldsymbol {0}_{d'}.\boldsymbol {0}_{1}\;\;\boldsymbol {\beta }.\boldsymbol {0}_{d'}.\boldsymbol {0}_{d})} (\boldsymbol {\alpha }.\boldsymbol {1}_{d'}.\boldsymbol {0}_{1} \boldsymbol {\beta }.\boldsymbol {1}_{d'}.\boldsymbol {0}_{d})$
and similarly for the other transpositions. Every pair of addresses from
${(\boldsymbol {\alpha }.\boldsymbol {0}_{1}\;\;\boldsymbol {\beta }.\boldsymbol {0}_{d})} = {(\boldsymbol {\alpha }.\boldsymbol {0}_{d'}.\boldsymbol {0}_{1}\;\;\boldsymbol {\beta }.\boldsymbol {0}_{d'}.\boldsymbol {0}_{d})} (\boldsymbol {\alpha }.\boldsymbol {1}_{d'}.\boldsymbol {0}_{1} \boldsymbol {\beta }.\boldsymbol {1}_{d'}.\boldsymbol {0}_{d})$
and similarly for the other transpositions. Every pair of addresses from
![]() $\boldsymbol {\alpha }.\boldsymbol {0}_{d'}$
,
$\boldsymbol {\alpha }.\boldsymbol {0}_{d'}$
,
![]() $\boldsymbol {\alpha }.\boldsymbol {1}_{d'}$
,
$\boldsymbol {\alpha }.\boldsymbol {1}_{d'}$
,
![]() $\boldsymbol {\beta }.\boldsymbol {0}_{d'}$
and
$\boldsymbol {\beta }.\boldsymbol {0}_{d'}$
and
![]() $\boldsymbol {\beta }.\boldsymbol {1}_{d'}$
are incomparable so rearranging the resulting formula for
$\boldsymbol {\beta }.\boldsymbol {1}_{d'}$
are incomparable so rearranging the resulting formula for
![]() $A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
yields the claimed result.
$A_{d}(\boldsymbol {\alpha },\boldsymbol {\beta })$
yields the claimed result.
Lemma 2.2. Let
![]() $d,d'$
be indices in the range
$d,d'$
be indices in the range
![]() $2 \leqslant d,d' \leqslant n$
.
$2 \leqslant d,d' \leqslant n$
.
-
(i) If
 $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}) \in \Omega $
satisfies
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}) \in \Omega $
satisfies
 $\mathopen {|}\alpha _{1}\mathclose {|}, \mathopen {|}\alpha _{d}\mathclose {|} \geqslant 1$
and if
$\mathopen {|}\alpha _{1}\mathclose {|}, \mathopen {|}\alpha _{d}\mathclose {|} \geqslant 1$
and if
 $\boldsymbol {\zeta },\boldsymbol {\eta } \in \Omega $
are such that every pair from
$\boldsymbol {\zeta },\boldsymbol {\eta } \in \Omega $
are such that every pair from
 $\{ \boldsymbol {\alpha }, \boldsymbol {\zeta }, \boldsymbol {\eta } \}$
are incomparable, then
$\{ \boldsymbol {\alpha }, \boldsymbol {\zeta }, \boldsymbol {\eta } \}$
are incomparable, then
 $\hat {B}_{d}(\boldsymbol {\alpha })$
commutes with
$\hat {B}_{d}(\boldsymbol {\alpha })$
commutes with
 ${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
.
${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
. -
(ii) If
 $\boldsymbol {\alpha } = \boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}.\boldsymbol {y}_{d}$
for some
$\boldsymbol {\alpha } = \boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}.\boldsymbol {y}_{d}$
for some
 $\boldsymbol {\delta } \in \Omega $
and some
$\boldsymbol {\delta } \in \Omega $
and some
 $x,y \in \{0,1\}$
, then (2-4)for any address
$x,y \in \{0,1\}$
, then (2-4)for any address $$ \begin{align} \hat{B}_{d}(\boldsymbol{\alpha}) = A_{d}(\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1},\boldsymbol{\gamma}) \; {(\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma},\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1}.\bar{\boldsymbol{y}}_{d}) \end{align} $$
$$ \begin{align} \hat{B}_{d}(\boldsymbol{\alpha}) = A_{d}(\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1},\boldsymbol{\gamma}) \; {(\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma},\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{1}.\bar{\boldsymbol{y}}_{d}) \end{align} $$
 $\boldsymbol {\gamma } = (\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})$
such that
$\boldsymbol {\gamma } = (\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})$
such that
 $\boldsymbol {\gamma } \perp \boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}$
and
$\boldsymbol {\gamma } \perp \boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}$
and
 $\mathopen {|}\gamma _{1}\mathclose {|}, \mathopen {|}\gamma _{d}\mathclose {|} \geqslant 1$
.
$\mathopen {|}\gamma _{1}\mathclose {|}, \mathopen {|}\gamma _{d}\mathclose {|} \geqslant 1$
.
-
(iii) If
 $y \in \{0,1\}$
, then
$y \in \{0,1\}$
, then
 $\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {y}_{d})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {1}_{1})}} = \hat {B}_{d}(\boldsymbol {1}_{1}.\boldsymbol {y}_{d})$
.
$\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {y}_{d})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {1}_{1})}} = \hat {B}_{d}(\boldsymbol {1}_{1}.\boldsymbol {y}_{d})$
. -
(iv) If
 $y \kern1.2pt{\in}\kern1.2pt \{0,1\}$
, then
$y \kern1.2pt{\in}\kern1.2pt \{0,1\}$
, then
 $\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {y}_{d})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {10}_{1})}} \kern1.2pt{=}\kern1.2pt \hat {B}_{d}(\boldsymbol {10}_{1}.\boldsymbol {y}_{d})$
and
$\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {y}_{d})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {10}_{1})}} \kern1.2pt{=}\kern1.2pt \hat {B}_{d}(\boldsymbol {10}_{1}.\boldsymbol {y}_{d})$
and
 $\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {y}_{d})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {11}_{1})}} \kern1.2pt{=}\kern1.2pt \hat {B}_{d}(\boldsymbol {11}_{1}.\boldsymbol {y}_{d})$
.
$\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {y}_{d})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {11}_{1})}} \kern1.2pt{=}\kern1.2pt \hat {B}_{d}(\boldsymbol {11}_{1}.\boldsymbol {y}_{d})$
. -
(v) If
 $x \in \{0,1\}$
, then
$x \in \{0,1\}$
, then
 $\hat {B}_{d}(\boldsymbol {x0}_{1}.\boldsymbol {1}_{d})$
and
$\hat {B}_{d}(\boldsymbol {x0}_{1}.\boldsymbol {1}_{d})$
and
 $\hat {B}_{d}(\boldsymbol {x1}_{1}.\boldsymbol {0}_{d})$
commute.
$\hat {B}_{d}(\boldsymbol {x1}_{1}.\boldsymbol {0}_{d})$
commute. -
(vi) If
 $x,y \in \{0,1\}$
, then
$x,y \in \{0,1\}$
, then
 $\hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}) = {(\boldsymbol {x01}_{1}.\boldsymbol {y}_{d}\;\;\boldsymbol {x10}_{1}.\boldsymbol {y}_{d})} \; \hat {B}_{d}(\boldsymbol {x0}_{1}.\boldsymbol {y}_{d}) \; \hat {B}_{d}(\boldsymbol {x1}_{1}.\boldsymbol {y}_{d})$
.
$\hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}) = {(\boldsymbol {x01}_{1}.\boldsymbol {y}_{d}\;\;\boldsymbol {x10}_{1}.\boldsymbol {y}_{d})} \; \hat {B}_{d}(\boldsymbol {x0}_{1}.\boldsymbol {y}_{d}) \; \hat {B}_{d}(\boldsymbol {x1}_{1}.\boldsymbol {y}_{d})$
. -
(vii) If
 $d' \neq d$
, then
$d' \neq d$
, then
 $\hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}) = \hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}.\boldsymbol {0}_{d'}) \; \hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}.\boldsymbol {1}_{d'})$
.
$\hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}) = \hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}.\boldsymbol {0}_{d'}) \; \hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d}.\boldsymbol {1}_{d'})$
.
If we take
![]() $\boldsymbol {\delta } = \boldsymbol {\varepsilon }$
in part (ii), then it tells us that the definitions in Equation (2-2) are independent of the choice of address
$\boldsymbol {\delta } = \boldsymbol {\varepsilon }$
in part (ii), then it tells us that the definitions in Equation (2-2) are independent of the choice of address
![]() $\boldsymbol {\gamma }$
used. Consequently,
$\boldsymbol {\gamma }$
used. Consequently,
![]() $\hat {B}_{d}(\boldsymbol {\alpha })$
does depend only on the address
$\hat {B}_{d}(\boldsymbol {\alpha })$
does depend only on the address
![]() $\boldsymbol {\alpha }$
.
$\boldsymbol {\alpha }$
.
Proof. (i) Repeatedly apply the split relation in Equation (1-4) to express
![]() ${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
as a product of transpositions
${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
as a product of transpositions
![]() ${(\boldsymbol {\zeta }'\;\;\boldsymbol {\eta }')}$
having entries with sufficiently long coordinates that the values
${(\boldsymbol {\zeta }'\;\;\boldsymbol {\eta }')}$
having entries with sufficiently long coordinates that the values
![]() $\boldsymbol {\zeta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha })$
and
$\boldsymbol {\zeta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha })$
and
![]() $\boldsymbol {\eta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha })$
are defined. These values therefore coincide with those obtained when the corresponding baker’s map in
$\boldsymbol {\eta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha })$
are defined. These values therefore coincide with those obtained when the corresponding baker’s map in
![]() $nV$
is applied to
$nV$
is applied to
![]() $\boldsymbol {\zeta }'$
and
$\boldsymbol {\zeta }'$
and
![]() $\boldsymbol {\eta }'$
. Since
$\boldsymbol {\eta }'$
. Since
![]() $\boldsymbol {\zeta }$
and
$\boldsymbol {\zeta }$
and
![]() $\boldsymbol {\eta }$
are both incomparable with
$\boldsymbol {\eta }$
are both incomparable with
![]() $\boldsymbol {\alpha }$
, we conclude
$\boldsymbol {\alpha }$
, we conclude
![]() $\boldsymbol {\zeta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha }) = \boldsymbol {\zeta }'$
and
$\boldsymbol {\zeta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha }) = \boldsymbol {\zeta }'$
and
![]() $\boldsymbol {\eta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha }) = \boldsymbol {\eta }'$
. It then follows, by the conjugacy relation in Equation (1-3), that
$\boldsymbol {\eta }'\bullet \hat {B}_{d}(\boldsymbol {\alpha }) = \boldsymbol {\eta }'$
. It then follows, by the conjugacy relation in Equation (1-3), that
![]() $\hat {B}_{d}(\boldsymbol {\alpha })$
commutes with all such
$\hat {B}_{d}(\boldsymbol {\alpha })$
commutes with all such
![]() ${(\boldsymbol {\zeta }'\;\;\boldsymbol {\eta }')}$
and hence also with their product
${(\boldsymbol {\zeta }'\;\;\boldsymbol {\eta }')}$
and hence also with their product
![]() ${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
.
${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
.
(ii) One formula of the form given in Equation (2-4) for
![]() $\hat {B}_{d}(\boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}.\boldsymbol {y}_{d})$
is obtained by inserting
$\hat {B}_{d}(\boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}.\boldsymbol {y}_{d})$
is obtained by inserting
![]() $\boldsymbol {\delta }$
as prefix into the entries of the transpositions in the definition of
$\boldsymbol {\delta }$
as prefix into the entries of the transpositions in the definition of
![]() $\hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d})$
in Equation (2-2). Start with one such valid Equation (2-4) involving a particular address
$\hat {B}_{d}(\boldsymbol {x}_{1}.\boldsymbol {y}_{d})$
in Equation (2-2). Start with one such valid Equation (2-4) involving a particular address
![]() $\boldsymbol {\gamma }$
and consider another potential address
$\boldsymbol {\gamma }$
and consider another potential address
![]() $\boldsymbol {\gamma }' = (\gamma _{1}',\gamma _{2}',\ldots ,\gamma _{n}')$
satisfying
$\boldsymbol {\gamma }' = (\gamma _{1}',\gamma _{2}',\ldots ,\gamma _{n}')$
satisfying
![]() $\boldsymbol {\gamma }' \perp \boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}$
and
$\boldsymbol {\gamma }' \perp \boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{1}$
and
![]() $\mathopen {|}\gamma _{d}'\mathclose {|} \geqslant 1$
. If
$\mathopen {|}\gamma _{d}'\mathclose {|} \geqslant 1$
. If
![]() $\boldsymbol {\gamma }' \perp \boldsymbol {\gamma }$
, conjugate by
$\boldsymbol {\gamma }' \perp \boldsymbol {\gamma }$
, conjugate by
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\gamma }')}$
and use part (i) to produce the required formula for
${(\boldsymbol {\gamma }\;\;\boldsymbol {\gamma }')}$
and use part (i) to produce the required formula for
![]() $\hat {B}_{d}(\boldsymbol {\delta }.\kern1pt\boldsymbol {x}_{1}.\boldsymbol {y}_{d})$
. If
$\hat {B}_{d}(\boldsymbol {\delta }.\kern1pt\boldsymbol {x}_{1}.\boldsymbol {y}_{d})$
. If
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\gamma }'$
are not incomparable, then as
$\boldsymbol {\gamma }'$
are not incomparable, then as
![]() $\mathopen {|}\gamma _{d}\mathclose {|}, \mathopen {|}\gamma ^{\prime }_{d}\mathclose {|} \geqslant 1$
there is another address
$\mathopen {|}\gamma _{d}\mathclose {|}, \mathopen {|}\gamma ^{\prime }_{d}\mathclose {|} \geqslant 1$
there is another address
![]() $\boldsymbol {\zeta }$
, with nonempty d th coordinate, that is incomparable with all three of
$\boldsymbol {\zeta }$
, with nonempty d th coordinate, that is incomparable with all three of
![]() $\boldsymbol {\gamma }$
,
$\boldsymbol {\gamma }$
,
![]() $\boldsymbol {\gamma }'$
and
$\boldsymbol {\gamma }'$
and
![]() $\boldsymbol {\delta }.\kern1pt\boldsymbol {x}_{1}$
. Now conjugate by the product
$\boldsymbol {\delta }.\kern1pt\boldsymbol {x}_{1}$
. Now conjugate by the product
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\zeta })} \; {(\boldsymbol {\gamma }'\;\;\boldsymbol {\zeta })}$
, again using part (i), to produce the required Equation (2-4) involving the address
${(\boldsymbol {\gamma }\;\;\boldsymbol {\zeta })} \; {(\boldsymbol {\gamma }'\;\;\boldsymbol {\zeta })}$
, again using part (i), to produce the required Equation (2-4) involving the address
![]() $\boldsymbol {\gamma }'$
.
$\boldsymbol {\gamma }'$
.
Part (iii) follows immediately from the definition of the
![]() $\hat {B}_{d}$
elements.
$\hat {B}_{d}$
elements.
(iv) We establish here the first equation in the case when
![]() $y = 0$
. The other formulae are similar. First, use part (ii) to assume that in the expression of Equation (2-2) for
$y = 0$
. The other formulae are similar. First, use part (ii) to assume that in the expression of Equation (2-2) for
![]() $\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {0}_{d})$
, the address
$\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {0}_{d})$
, the address
![]() $\boldsymbol {\gamma } = (\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})$
satisfies
$\boldsymbol {\gamma } = (\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})$
satisfies
![]() $11 \preceq \gamma _{1}$
. Consequently,
$11 \preceq \gamma _{1}$
. Consequently,
![]() $\boldsymbol {\gamma } \bullet {(\boldsymbol {0}_{1}\;\;\boldsymbol {10}_{1})} = \boldsymbol {\gamma }$
and
$\boldsymbol {\gamma } \bullet {(\boldsymbol {0}_{1}\;\;\boldsymbol {10}_{1})} = \boldsymbol {\gamma }$
and
![]() $\boldsymbol {\gamma } = \boldsymbol {1}_{1}.\boldsymbol {\delta }$
, where
$\boldsymbol {\gamma } = \boldsymbol {1}_{1}.\boldsymbol {\delta }$
, where
![]() $\boldsymbol {\delta } \perp \boldsymbol {0}_{1}$
. Hence, using Lemma 2.1(i),
$\boldsymbol {\delta } \perp \boldsymbol {0}_{1}$
. Hence, using Lemma 2.1(i),
 $$ \begin{align*} &\hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d})^{{(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})}} = A_{d}(\boldsymbol{10}_{1},\boldsymbol{\gamma}) \; {(\boldsymbol{10}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{10}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma},\boldsymbol{10}_{1}.\boldsymbol{1}_{d}) \\ &\qquad = \boldsymbol{1}_{1}.( A_{d}(\boldsymbol{0}_{1},\boldsymbol{\delta}) \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\delta},\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) ) = \boldsymbol{1}_{1}.\hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) = \hat{B}_{d}(\boldsymbol{10}_{1}.\boldsymbol{0}_{d}). \end{align*} $$
$$ \begin{align*} &\hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d})^{{(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})}} = A_{d}(\boldsymbol{10}_{1},\boldsymbol{\gamma}) \; {(\boldsymbol{10}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{10}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma},\boldsymbol{10}_{1}.\boldsymbol{1}_{d}) \\ &\qquad = \boldsymbol{1}_{1}.( A_{d}(\boldsymbol{0}_{1},\boldsymbol{\delta}) \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\delta},\boldsymbol{0}_{1}.\boldsymbol{1}_{d}) ) = \boldsymbol{1}_{1}.\hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) = \hat{B}_{d}(\boldsymbol{10}_{1}.\boldsymbol{0}_{d}). \end{align*} $$
(v) Using part (ii), we can assume that
 $$ \begin{align*} \hat{B}_{d}(\boldsymbol{x0}_{1}.\boldsymbol{1}_{d}) &= A_{d}(\boldsymbol{x0}_{1},\boldsymbol{\gamma}) \; {(\boldsymbol{x0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{x0}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma},\boldsymbol{x0}_{1}.\boldsymbol{0}_{d}) \\ \hat{B}_{d}(\boldsymbol{x1}_{1}.\boldsymbol{0}_{d}) &= A_{d}(\boldsymbol{x1}_{1},\boldsymbol{\gamma}') \; {(\boldsymbol{x1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{x1}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}',\boldsymbol{x1}_{1}.\boldsymbol{1}_{d}), \end{align*} $$
$$ \begin{align*} \hat{B}_{d}(\boldsymbol{x0}_{1}.\boldsymbol{1}_{d}) &= A_{d}(\boldsymbol{x0}_{1},\boldsymbol{\gamma}) \; {(\boldsymbol{x0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{x0}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma},\boldsymbol{x0}_{1}.\boldsymbol{0}_{d}) \\ \hat{B}_{d}(\boldsymbol{x1}_{1}.\boldsymbol{0}_{d}) &= A_{d}(\boldsymbol{x1}_{1},\boldsymbol{\gamma}') \; {(\boldsymbol{x1}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{x1}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}',\boldsymbol{x1}_{1}.\boldsymbol{1}_{d}), \end{align*} $$
where
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\gamma }'$
are addresses with
$\boldsymbol {\gamma }'$
are addresses with
![]() $\boldsymbol {\gamma } \perp \boldsymbol {\gamma }'$
and
$\boldsymbol {\gamma } \perp \boldsymbol {\gamma }'$
and
![]() $\boldsymbol {x}_{1} \perp \boldsymbol {\gamma },\boldsymbol {\gamma }'$
. These commute by Lemma 2.1(i) and (ii).
$\boldsymbol {x}_{1} \perp \boldsymbol {\gamma },\boldsymbol {\gamma }'$
. These commute by Lemma 2.1(i) and (ii).
(vi) We present the case
![]() $x = y = 0$
, with the other cases established by similar calculations. Recall that
$x = y = 0$
, with the other cases established by similar calculations. Recall that
![]() $\boldsymbol {\gamma } \perp \boldsymbol {0}_{1}$
in our definition by Equation (2-2) of
$\boldsymbol {\gamma } \perp \boldsymbol {0}_{1}$
in our definition by Equation (2-2) of
![]() $\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {0}_{d})$
. In the following calculation, we begin by applying Lemma 2.1(iii) to the terms appearing in the definition of
$\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {0}_{d})$
. In the following calculation, we begin by applying Lemma 2.1(iii) to the terms appearing in the definition of
![]() $\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {0}_{d})$
:
$\hat {B}_{d}(\boldsymbol {0}_{1}.\boldsymbol {0}_{d})$
:
 $$ \begin{align*} \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; A_{d}(\boldsymbol{00}_{1},\boldsymbol{\gamma}.\boldsymbol{0}_{1}) \; A_{d}(\boldsymbol{01}_{1},\boldsymbol{\gamma}.\boldsymbol{1}_{1}) \; {(\boldsymbol{\gamma}.\boldsymbol{01}_{1}\;\;\boldsymbol{\gamma}.\boldsymbol{10}_{1})} \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ &\qquad \cdot {(\boldsymbol{\gamma}.\boldsymbol{01}_{1}\;\;\boldsymbol{\gamma}.\boldsymbol{10}_{1})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{0}_{1},\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{1}_{1},\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; A_{d}(\boldsymbol{00}_{1},\boldsymbol{\gamma}.\boldsymbol{0}_{1}) \; A_{d}(\boldsymbol{01}_{1},\boldsymbol{\gamma}.\boldsymbol{1}_{1}) \; {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \\ &\qquad \cdot {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{0}_{1},\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{1}_{1},\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; A_{d}(\boldsymbol{00}_{1},\boldsymbol{\gamma}.\boldsymbol{0}_{1}) \; {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{0}_{1},\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \\ &\qquad \cdot A_{d}(\boldsymbol{01}_{1},\boldsymbol{\gamma}.\boldsymbol{1}_{1}) \; {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{1}_{1},\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \quad \text{(using part (ii))} \\ &= {(\boldsymbol{001}_{1}.\boldsymbol{0}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{0}_{d})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}). \end{align*} $$
$$ \begin{align*} \hat{B}_{d}(\boldsymbol{0}_{1}.\boldsymbol{0}_{d}) &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; A_{d}(\boldsymbol{00}_{1},\boldsymbol{\gamma}.\boldsymbol{0}_{1}) \; A_{d}(\boldsymbol{01}_{1},\boldsymbol{\gamma}.\boldsymbol{1}_{1}) \; {(\boldsymbol{\gamma}.\boldsymbol{01}_{1}\;\;\boldsymbol{\gamma}.\boldsymbol{10}_{1})} \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ &\qquad \cdot {(\boldsymbol{\gamma}.\boldsymbol{01}_{1}\;\;\boldsymbol{\gamma}.\boldsymbol{10}_{1})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{0}_{1},\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{1}_{1},\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; A_{d}(\boldsymbol{00}_{1},\boldsymbol{\gamma}.\boldsymbol{0}_{1}) \; A_{d}(\boldsymbol{01}_{1},\boldsymbol{\gamma}.\boldsymbol{1}_{1}) \; {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \\ &\qquad \cdot {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{0}_{1},\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{1}_{1},\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; A_{d}(\boldsymbol{00}_{1},\boldsymbol{\gamma}.\boldsymbol{0}_{1}) \; {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{0}_{1},\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \\ &\qquad \cdot A_{d}(\boldsymbol{01}_{1},\boldsymbol{\gamma}.\boldsymbol{1}_{1}) \; {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \; A_{d}(\boldsymbol{\gamma}.\boldsymbol{1}_{1},\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \quad \text{(using part (ii))} \\ &= {(\boldsymbol{001}_{1}.\boldsymbol{0}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{0}_{d})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}). \end{align*} $$
(vii) This follows by applying Lemma 2.1(iv) and the split relation in Equation (1-4) to terms appearing in Equation (2-2), and then rearranging in a similar way to the proof of Lemma 2.1(iv).
Lemma 2.3. Let
![]() $d,d'$
be indices in the range
$d,d'$
be indices in the range
![]() $2 \leqslant d,d' \leqslant n$
.
$2 \leqslant d,d' \leqslant n$
.
-
(i) If
 $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}) \in \Omega $
satisfies
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}) \in \Omega $
satisfies
 $\mathopen {|}\alpha _{1}\mathclose {|} \geqslant 1$
and if
$\mathopen {|}\alpha _{1}\mathclose {|} \geqslant 1$
and if
 $\boldsymbol {\zeta }, \boldsymbol {\eta } \in \Omega $
are such that every pair from
$\boldsymbol {\zeta }, \boldsymbol {\eta } \in \Omega $
are such that every pair from
 $\{ \boldsymbol {\alpha }, \boldsymbol {\zeta }, \boldsymbol {\eta } \}$
is incomparable, then
$\{ \boldsymbol {\alpha }, \boldsymbol {\zeta }, \boldsymbol {\eta } \}$
is incomparable, then
 $B_{d}(\boldsymbol {\alpha })$
commutes with
$B_{d}(\boldsymbol {\alpha })$
commutes with
 ${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
. In particular, for any
${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
. In particular, for any
 $x \in \{0,1\}$
, the element
$x \in \{0,1\}$
, the element
 $B_{d}(\boldsymbol {x}_{1})$
commutes with any element of the form
$B_{d}(\boldsymbol {x}_{1})$
commutes with any element of the form
 $\bar {\boldsymbol {x}}_{1}.g$
.
$\bar {\boldsymbol {x}}_{1}.g$
. -
(ii)
 $B_{d}(\boldsymbol {0}_{1})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {1}_{1})}} = B_{d}(\boldsymbol {1}_{1})$
.
$B_{d}(\boldsymbol {0}_{1})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {1}_{1})}} = B_{d}(\boldsymbol {1}_{1})$
. -
(iii)
 $B_{d}(\boldsymbol {0}_{1})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {10}_{1})}} = B_{d}(\boldsymbol {10}_{1})$
and
$B_{d}(\boldsymbol {0}_{1})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {10}_{1})}} = B_{d}(\boldsymbol {10}_{1})$
and
 $B_{d}(\boldsymbol {0}_{1})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {11}_{1})}} = B_{d}(\boldsymbol {11}_{1})$
.
$B_{d}(\boldsymbol {0}_{1})^{{(\boldsymbol {0}_{1}\;\;\boldsymbol {11}_{1})}} = B_{d}(\boldsymbol {11}_{1})$
. -
(iv) If
 $x \in \{0,1\}$
, then
$x \in \{0,1\}$
, then
 $B_{d}(\boldsymbol {x}_{1}) = {(\boldsymbol {x01}_{1}\;\;\boldsymbol {x10}_{1})} \; B_{d}(\boldsymbol {x0}_{1}) \; B_{d}(\boldsymbol {x1}_{1})$
.
$B_{d}(\boldsymbol {x}_{1}) = {(\boldsymbol {x01}_{1}\;\;\boldsymbol {x10}_{1})} \; B_{d}(\boldsymbol {x0}_{1}) \; B_{d}(\boldsymbol {x1}_{1})$
. -
(v)
 $B_{d}(\boldsymbol {0}_{1})$
and
$B_{d}(\boldsymbol {0}_{1})$
and
 $B_{d'}(\boldsymbol {1}_{1})$
commute.
$B_{d'}(\boldsymbol {1}_{1})$
commute. -
(vi) If
 $d' \neq d$
, then
$d' \neq d$
, then
 $B_{d}(\boldsymbol {x}_{1}) = B_{d}(\boldsymbol {x}_{1}.\boldsymbol {0}_{d'}) \; B_{d}(\boldsymbol {x}_{1}.\boldsymbol {1}_{d'})$
.
$B_{d}(\boldsymbol {x}_{1}) = B_{d}(\boldsymbol {x}_{1}.\boldsymbol {0}_{d'}) \; B_{d}(\boldsymbol {x}_{1}.\boldsymbol {1}_{d'})$
.
Proof. The first section of part (i) is established by the same argument as used in Lemma 2.2(i) and the remainder follows immediately. Parts (ii) and (iii) follow using parts (iii) and (iv), respectively, of Lemma 2.2, while part (vi) is an extension of Lemma 2.2(vii) that is established similarly.
We establish part (iv) in the case that
![]() $x = 0$
. First, apply Lemma 2.2(vi) to the two
$x = 0$
. First, apply Lemma 2.2(vi) to the two
![]() $\hat {B}_{d}$
terms in the definition of Equation (2-3) and then use parts (i) and (v) of Lemma 2.2 to rearrange terms:
$\hat {B}_{d}$
terms in the definition of Equation (2-3) and then use parts (i) and (v) of Lemma 2.2 to rearrange terms:
 $$ \begin{align*} B_{d}(\boldsymbol{0}_{1}) &= {(\boldsymbol{001}_{1}.\boldsymbol{0}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{0}_{d})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &\qquad \cdot \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}.\boldsymbol{0}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{0}_{d})} \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \\ &\qquad \cdot \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \\ &\qquad \cdot {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \; {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \\ &\qquad \cdot \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; B_{d}(\boldsymbol{00}_{1}) \; B_{d}(\boldsymbol{01}_{1}). \end{align*} $$
$$ \begin{align*} B_{d}(\boldsymbol{0}_{1}) &= {(\boldsymbol{001}_{1}.\boldsymbol{0}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{0}_{d})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \\ &\qquad \cdot \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}.\boldsymbol{0}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{0}_{d})} \; {(\boldsymbol{001}_{1}.\boldsymbol{1}_{d}\;\;\boldsymbol{010}_{1}.\boldsymbol{1}_{d})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \\ &\qquad \cdot \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{0}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{0}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \\ &\qquad \cdot {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \; {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{00}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{00}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{00}_{1}.\boldsymbol{10}_{d})} \\ &\qquad \cdot \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{0}_{d}) \; \hat{B}_{d}(\boldsymbol{01}_{1}.\boldsymbol{1}_{d}) \; {(\boldsymbol{01}_{1}.\boldsymbol{01}_{d}\;\;\boldsymbol{01}_{1}.\boldsymbol{10}_{d})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{010}_{1})} \; B_{d}(\boldsymbol{00}_{1}) \; B_{d}(\boldsymbol{01}_{1}). \end{align*} $$
Finally, it then follows that
![]() $B_{d}(\boldsymbol {0}_{1}) = \boldsymbol {0}_{1}.( {(\boldsymbol {01}_{1}\;\;\boldsymbol {10}_{1})} \; B_{d}(\boldsymbol {0}_{1}) \; B_{d}(\boldsymbol {1}) )$
commutes with
$B_{d}(\boldsymbol {0}_{1}) = \boldsymbol {0}_{1}.( {(\boldsymbol {01}_{1}\;\;\boldsymbol {10}_{1})} \; B_{d}(\boldsymbol {0}_{1}) \; B_{d}(\boldsymbol {1}) )$
commutes with
![]() $B_{d'}(\boldsymbol {1}_{1})$
using part (i). Hence, we have established the remaining part (v).
$B_{d'}(\boldsymbol {1}_{1})$
using part (i). Hence, we have established the remaining part (v).
We now consider one of the presentations for Brin’s higher-dimensional Thompson group
![]() $nV$
given by Hennig–Matucci [Reference Hennig and Matucci17]. They define generators
$nV$
given by Hennig–Matucci [Reference Hennig and Matucci17]. They define generators
![]() $X_{m,d}$
(for
$X_{m,d}$
(for
![]() $m \geqslant 0$
and
$m \geqslant 0$
and
![]() $1 \leqslant d \leqslant n$
),
$1 \leqslant d \leqslant n$
),
![]() $C_{m,d}$
(for
$C_{m,d}$
(for
![]() $m \geqslant 0$
and
$m \geqslant 0$
and
![]() $2 \leqslant d \leqslant n$
),
$2 \leqslant d \leqslant n$
),
![]() $\pi _{m}$
(for
$\pi _{m}$
(for
![]() $m \geqslant 0$
) and
$m \geqslant 0$
) and
![]() $\bar {\pi }_{m}$
(for
$\bar {\pi }_{m}$
(for
![]() $m \geqslant 0$
) and describe eighteen families of relations (numbered (1)–(18) on pages 59 and 60 of [Reference Hennig and Matucci17]). They observe in [Reference Hennig and Matucci17, Theorem 23] that these do indeed give a presentation for
$m \geqslant 0$
) and describe eighteen families of relations (numbered (1)–(18) on pages 59 and 60 of [Reference Hennig and Matucci17]). They observe in [Reference Hennig and Matucci17, Theorem 23] that these do indeed give a presentation for
![]() $nV$
. Since we write our maps on the right, we convert the relations to our setting by reversing each one and record these now for reference. We have also changed some of the labels on Hennig–Matucci’s generators appearing in the lists so that our arguments can be unified when establishing Proposition 2.5 below. In the families of Relations (HM1)–(HM7), one should assume that
$nV$
. Since we write our maps on the right, we convert the relations to our setting by reversing each one and record these now for reference. We have also changed some of the labels on Hennig–Matucci’s generators appearing in the lists so that our arguments can be unified when establishing Proposition 2.5 below. In the families of Relations (HM1)–(HM7), one should assume that
![]() $1 \leqslant d,d' \leqslant n$
:
$1 \leqslant d,d' \leqslant n$
:
The second collection of relations is as below. Note that we have adjusted the range of the parameters in Equation (HM8) to bring it into line with the relations given by Brin (see [Reference Brin4, Equation (22)]).
Finally, in the families of Equations (HM14)–(HM18),
![]() $2 \leqslant d \leqslant n$
and
$2 \leqslant d \leqslant n$
and
![]() $1 \leqslant d' \leqslant n$
, unless otherwise indicated:
$1 \leqslant d' \leqslant n$
, unless otherwise indicated:
We now define the elements of our group
![]() $G_{\infty }$
that correspond to the above generators. In the following, d is an index with
$G_{\infty }$
that correspond to the above generators. In the following, d is an index with
![]() $2 \leqslant d \leqslant n$
. First, we set
$2 \leqslant d \leqslant n$
. First, we set
 $$ \begin{align} \begin{aligned} X_{0,1} &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \;\, {(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})} \;\, {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})}, \qquad\qquad &X_{0,d} &= X_{0,1} \: B_{d}(\boldsymbol{1}_{1}), \\ \pi_{0} &= {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})}, &\bar{\pi}_{0} &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})}, \\ C_{0,d} &= {(\boldsymbol{01}_{1}\;\;\boldsymbol{10}_{1})} \;\, B_{d}(\boldsymbol{0}_{1}) \;\, B_{d}(\boldsymbol{1}_{1}), &C_{1,d} &= B_{d}(\boldsymbol{0}_{1}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} X_{0,1} &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \;\, {(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})} \;\, {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})}, \qquad\qquad &X_{0,d} &= X_{0,1} \: B_{d}(\boldsymbol{1}_{1}), \\ \pi_{0} &= {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})}, &\bar{\pi}_{0} &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})}, \\ C_{0,d} &= {(\boldsymbol{01}_{1}\;\;\boldsymbol{10}_{1})} \;\, B_{d}(\boldsymbol{0}_{1}) \;\, B_{d}(\boldsymbol{1}_{1}), &C_{1,d} &= B_{d}(\boldsymbol{0}_{1}). \end{aligned} \end{align} $$
These are extended, for positive integers
![]() $m \geqslant 1$
, to
$m \geqslant 1$
, to
 $$ \begin{align} \begin{aligned} X_{m,d} &= \boldsymbol{0}_{1}^{m}.X_{0,d} &&\text{for }1 \leqslant d \leqslant n, \\ \pi_{m} &= \boldsymbol{0}_{1}^{m}.\pi_{0}, \\ \bar{\pi}_{m} &= \boldsymbol{0}_{1}^{m}.\bar{\pi}_{0}, \\ C_{m,d} &= \boldsymbol{0}_{1}^{m-1}.C_{1,d} &&\text{for } m \geqslant 2 \text{ and } 2 \leqslant d \leqslant n, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} X_{m,d} &= \boldsymbol{0}_{1}^{m}.X_{0,d} &&\text{for }1 \leqslant d \leqslant n, \\ \pi_{m} &= \boldsymbol{0}_{1}^{m}.\pi_{0}, \\ \bar{\pi}_{m} &= \boldsymbol{0}_{1}^{m}.\bar{\pi}_{0}, \\ C_{m,d} &= \boldsymbol{0}_{1}^{m-1}.C_{1,d} &&\text{for } m \geqslant 2 \text{ and } 2 \leqslant d \leqslant n, \end{aligned} \end{align} $$
where
![]() $\boldsymbol {0}_{1}^{m}$
denotes
$\boldsymbol {0}_{1}^{m}$
denotes
![]() $\boldsymbol {00}\ldots {}\boldsymbol {0}_{1} = (00\ldots 0,\varepsilon ,\ldots ,\varepsilon )$
with the word
$\boldsymbol {00}\ldots {}\boldsymbol {0}_{1} = (00\ldots 0,\varepsilon ,\ldots ,\varepsilon )$
with the word
![]() $00\ldots 0$
having length m.
$00\ldots 0$
having length m.
Note that, by Lemma 2.3(iv),
![]() $C_{1,d} = \boldsymbol {0}_{1}.C_{0,d}$
. Consequently, the definition of
$C_{1,d} = \boldsymbol {0}_{1}.C_{0,d}$
. Consequently, the definition of
![]() $C_{m,d}$
can be extended to include the case
$C_{m,d}$
can be extended to include the case
![]() $ m =1$
; that is,
$ m =1$
; that is,
![]() $C_{m,d} = \boldsymbol {0}_{1}^{m}.C_{0,d}$
for all
$C_{m,d} = \boldsymbol {0}_{1}^{m}.C_{0,d}$
for all
![]() $m \geqslant 1$
and all indices d in the range
$m \geqslant 1$
and all indices d in the range
![]() $2 \leqslant d \leqslant n$
. This will enable us to treat these baker’s maps in a uniform manner.
$2 \leqslant d \leqslant n$
. This will enable us to treat these baker’s maps in a uniform manner.
Lemma 2.4. Let d and
![]() $d'$
be indices in the range
$d'$
be indices in the range
![]() $2 \leqslant d,d' \leqslant n$
.
$2 \leqslant d,d' \leqslant n$
.
-
(i)
 $B_{d}(\boldsymbol {0}_{1})^{C_{0,d'}} = \boldsymbol {0}_{d'}.C_{0,d}$
and
$B_{d}(\boldsymbol {0}_{1})^{C_{0,d'}} = \boldsymbol {0}_{d'}.C_{0,d}$
and
 $B_{d}(\boldsymbol {1}_{1})^{C_{0,d'}} = \boldsymbol {1}_{d'}.C_{0,d}$
.
$B_{d}(\boldsymbol {1}_{1})^{C_{0,d'}} = \boldsymbol {1}_{d'}.C_{0,d}$
. -
(ii) If
 $d \neq d'$
, then
$d \neq d'$
, then
 $C_{0,d} = (\boldsymbol {0}_{d'}.C_{0,d}) \: (\boldsymbol {1}_{d'}.C_{0,d})$
.
$C_{0,d} = (\boldsymbol {0}_{d'}.C_{0,d}) \: (\boldsymbol {1}_{d'}.C_{0,d})$
.
By inserting the prefix
![]() $\boldsymbol {1}_{1}$
into the entries of transpositions in part (i) of this lemma, it follows with use of Lemma 2.3(iv) that:
$\boldsymbol {1}_{1}$
into the entries of transpositions in part (i) of this lemma, it follows with use of Lemma 2.3(iv) that:
Proof. (i) First note that, by suitable choice of
![]() $\boldsymbol {\gamma }$
appearing in the definition of Equation (2-2), we can express
$\boldsymbol {\gamma }$
appearing in the definition of Equation (2-2), we can express
![]() $C_{0,d'}$
as a product of transpositions whose entries have nonempty coordinates only for index
$C_{0,d'}$
as a product of transpositions whose entries have nonempty coordinates only for index
![]() $1$
and index
$1$
and index
![]() $d'$
. Consequently, provided the index
$d'$
. Consequently, provided the index
![]() $1$
and index
$1$
and index
![]() $d'$
coordinates of an address
$d'$
coordinates of an address
![]() $\boldsymbol {\zeta }$
are sufficiently long,
$\boldsymbol {\zeta }$
are sufficiently long,
![]() $\boldsymbol {\zeta } \bullet C_{0,d'}$
is defined. Furthermore,
$\boldsymbol {\zeta } \bullet C_{0,d'}$
is defined. Furthermore,
![]() $C_{0,d'}$
evaluates in
$C_{0,d'}$
evaluates in
![]() $nV$
to the (primary) baker’s map with full support on
$nV$
to the (primary) baker’s map with full support on
![]() $\Gamma $
, so this value
$\Gamma $
, so this value
![]() $\boldsymbol {\zeta } \bullet C_{0,d'}$
coincides with that obtained when we act with the baker’s map. Now if
$\boldsymbol {\zeta } \bullet C_{0,d'}$
coincides with that obtained when we act with the baker’s map. Now if
![]() $x \in \{0,1\}$
, then
$x \in \{0,1\}$
, then
![]() $(\boldsymbol {x}_{1}.\boldsymbol {\zeta }) \bullet C_{0,d'}$
is also defined (as the required coordinates are sufficiently long) and equals
$(\boldsymbol {x}_{1}.\boldsymbol {\zeta }) \bullet C_{0,d'}$
is also defined (as the required coordinates are sufficiently long) and equals
![]() $\boldsymbol {x}_{d'}.\boldsymbol {\zeta }$
in view of how the baker’s map acts.
$\boldsymbol {x}_{d'}.\boldsymbol {\zeta }$
in view of how the baker’s map acts.
If
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is any transposition, apply Equation (1-4) repeatedly to express it as a product of transpositions
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is any transposition, apply Equation (1-4) repeatedly to express it as a product of transpositions
![]() ${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
with the index
${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })}$
with the index
![]() $1$
and index d coordinates of
$1$
and index d coordinates of
![]() $\boldsymbol {\zeta }$
and
$\boldsymbol {\zeta }$
and
![]() $\boldsymbol {\eta }$
sufficiently long that the partial action of
$\boldsymbol {\eta }$
sufficiently long that the partial action of
![]() $C_{0,d'}$
upon them is defined. By inserting
$C_{0,d'}$
upon them is defined. By inserting
![]() $\boldsymbol {x}_{1}$
as a prefix into all the transpositions involved, we express
$\boldsymbol {x}_{1}$
as a prefix into all the transpositions involved, we express
![]() ${(\boldsymbol {x}_{1}.\boldsymbol {\alpha }\;\;\boldsymbol {x}_{1}.\boldsymbol {\beta })}$
as a product of transpositions
${(\boldsymbol {x}_{1}.\boldsymbol {\alpha }\;\;\boldsymbol {x}_{1}.\boldsymbol {\beta })}$
as a product of transpositions
![]() ${(\boldsymbol {x}_{1}.\boldsymbol {\zeta }\;\;\boldsymbol {x_{1}}.\boldsymbol {\eta })}$
. Since
${(\boldsymbol {x}_{1}.\boldsymbol {\zeta }\;\;\boldsymbol {x_{1}}.\boldsymbol {\eta })}$
. Since
![]() $\boldsymbol {x}_{1}.\boldsymbol {\zeta } \bullet C_{0,d'} = \boldsymbol {x}_{d'}.\boldsymbol {\zeta }$
by our above observation and similarly for
$\boldsymbol {x}_{1}.\boldsymbol {\zeta } \bullet C_{0,d'} = \boldsymbol {x}_{d'}.\boldsymbol {\zeta }$
by our above observation and similarly for
![]() $\boldsymbol {x}_{1}.\boldsymbol {\eta }$
, we deduce
$\boldsymbol {x}_{1}.\boldsymbol {\eta }$
, we deduce
We now recombine the resulting transpositions using Equation (1-4) to conclude
Now if g is any element of
![]() $G_{\infty }$
, then it is a product of transpositions and it follows from the above calculation that
$G_{\infty }$
, then it is a product of transpositions and it follows from the above calculation that
for any
![]() $x \in \{0,1\}$
. The claimed equations now follow by taking
$x \in \{0,1\}$
. The claimed equations now follow by taking
![]() $g = C_{0,d}$
and noting, by Lemma 2.3(iv), that
$g = C_{0,d}$
and noting, by Lemma 2.3(iv), that
![]() $B_{d}(\boldsymbol {x}_{1}) = \boldsymbol {x}_{1}.C_{0,d}$
.
$B_{d}(\boldsymbol {x}_{1}) = \boldsymbol {x}_{1}.C_{0,d}$
.
Part (ii) is an extension of Lemma 2.3(vi) established by a similar argument.
Proposition 2.5. The elements
![]() $X_{m,d}$
,
$X_{m,d}$
,
![]() $C_{m,d}$
,
$C_{m,d}$
,
![]() $\pi _{m}$
and
$\pi _{m}$
and
![]() $\bar {\pi }_{m}$
of
$\bar {\pi }_{m}$
of
![]() $G_{\infty }$
defined in Equations (2-5) and (2-6) satisfy Relations (HM1)–(HM18).
$G_{\infty }$
defined in Equations (2-5) and (2-6) satisfy Relations (HM1)–(HM18).
Establishing this proposition completes the proof of Theorem 1.1 since it establishes that the surjective homomorphism
![]() $\phi \colon G_{\infty } \to nV$
has trivial kernel.
$\phi \colon G_{\infty } \to nV$
has trivial kernel.
Proof. First, as observed earlier, if
![]() $u = v$
is a relation in
$u = v$
is a relation in
![]() $G_{\infty }$
, then so is
$G_{\infty }$
, then so is
![]() $\boldsymbol {0}_{1}.u = \boldsymbol {0}_{1}.v$
. Consequently, it suffices to establish each of Relations (HM1)–(HM18) only when
$\boldsymbol {0}_{1}.u = \boldsymbol {0}_{1}.v$
. Consequently, it suffices to establish each of Relations (HM1)–(HM18) only when
![]() $m = 0$
. Relations (HM8)–(HM13) are the most straightforward to verify and follow directly from the assumed relations involving transpositions (that is Equations (1-2) and (1-3)). Relation (HM6) is established in a similar manner. When
$m = 0$
. Relations (HM8)–(HM13) are the most straightforward to verify and follow directly from the assumed relations involving transpositions (that is Equations (1-2) and (1-3)). Relation (HM6) is established in a similar manner. When
![]() $q> 1$
, observe that both
$q> 1$
, observe that both
![]() $X_{q,d}$
and
$X_{q,d}$
and
![]() $C_{q,d}$
is a product of transpositions all of whose entries have
$C_{q,d}$
is a product of transpositions all of whose entries have
![]() $\boldsymbol {00}_{1}$
as a prefix. These transpositions are therefore disjoint from
$\boldsymbol {00}_{1}$
as a prefix. These transpositions are therefore disjoint from
![]() $\pi _{0}$
and Relations (HM4) and (HM17) follow. We now describe the details involved in the other relations.
$\pi _{0}$
and Relations (HM4) and (HM17) follow. We now describe the details involved in the other relations.
Note that
![]() $\boldsymbol {00}_{1} \bullet X_{0,1} = \boldsymbol {0}_{1}$
. Hence, for any
$\boldsymbol {00}_{1} \bullet X_{0,1} = \boldsymbol {0}_{1}$
. Hence, for any
![]() $g \in G_{\infty }$
,
$g \in G_{\infty }$
,
This establishes Relations (HM1), (HM2) and (HM5) in the case when
![]() $m = 0$
and
$m = 0$
and
![]() $d = 1$
, and it also establishes Relation (HM15) in the case when
$d = 1$
, and it also establishes Relation (HM15) in the case when
![]() $m = 0$
and
$m = 0$
and
![]() $d' = 1$
. We extend the first three to
$d' = 1$
. We extend the first three to
![]() $d \geqslant 2$
by use of Lemma 2.3(i) to tell us that
$d \geqslant 2$
by use of Lemma 2.3(i) to tell us that
![]() $B_{d}(\boldsymbol {1}_{1})$
commutes with each of
$B_{d}(\boldsymbol {1}_{1})$
commutes with each of
![]() $X_{q,d'}$
,
$X_{q,d'}$
,
![]() $\pi _{q}$
and
$\pi _{q}$
and
![]() $\bar {\pi }_{q}$
for
$\bar {\pi }_{q}$
for
![]() $q> 0$
. Similarly, we extend Relation (HM15) to the case when
$q> 0$
. Similarly, we extend Relation (HM15) to the case when
![]() $d' \geqslant 2$
by using the same fact to show
$d' \geqslant 2$
by using the same fact to show
![]() $B_{d'}(\boldsymbol {1}_{1})$
commutes with
$B_{d'}(\boldsymbol {1}_{1})$
commutes with
![]() $C_{q,d}$
for
$C_{q,d}$
for
![]() $q \geqslant 2$
and, by Lemma 2.3(v), also with
$q \geqslant 2$
and, by Lemma 2.3(v), also with
![]() $C_{1,d}$
.
$C_{1,d}$
.
Relation (HM3) when
![]() $m = 0$
and
$m = 0$
and
![]() $d = 1$
is established by collecting transpositions using Equation (1-3) and one application of Equation (1-4):
$d = 1$
is established by collecting transpositions using Equation (1-3) and one application of Equation (1-4):
 $$ \begin{align*} \pi_{1} \, \pi_{0} \, X_{1,1} &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{010}_{1})} \; {(\boldsymbol{010}_{1}\;\;\boldsymbol{011}_{1})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} = X_{0,1} \, \pi_{0}. \end{align*} $$
$$ \begin{align*} \pi_{1} \, \pi_{0} \, X_{1,1} &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{010}_{1})} \; {(\boldsymbol{010}_{1}\;\;\boldsymbol{011}_{1})} \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} = X_{0,1} \, \pi_{0}. \end{align*} $$
The case when
![]() $d \geqslant 2$
now follows using Lemma 2.3(i)–(iii).
$d \geqslant 2$
now follows using Lemma 2.3(i)–(iii).
We establish Relation (HM7) first in the case when
![]() $d' = 1$
and
$d' = 1$
and
![]() $m = 0$
. If
$m = 0$
. If
![]() $d \geqslant 2$
, then:
$d \geqslant 2$
, then:
 $$ \begin{align*} X_{0,1} \, X_{1,1} \, X_{0,d} &= X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \\ &= X_{0,1} \; X_{1,1} \; X_{0,1} \; {(\boldsymbol{101}_{1}\;\;\boldsymbol{110}_{1})} \; B_{d}(\boldsymbol{10}_{1}) \; B_{d}(\boldsymbol{11}_{1}) \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d}(\boldsymbol{10}_{1}) \; B_{d}(\boldsymbol{11}_{1}) &&\text{by repeated use of Equation}\ ({1\hbox{-}3}) \\ &= \pi_{1} \; X_{0,1} \; X_{1,1} \; B_{d}(\boldsymbol{01}_{1}) \; B_{d}(\boldsymbol{1}_{1}) \; X_{0,1} &&\hspace{-40pt} \text{by Lemma}\ \text{(i)--(iii) and Equation}\ ({1\hbox{-}3}) \\ &= \pi_{1} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \; X_{1,1} \; B_{d}(\boldsymbol{01}_{1}) \; X_{0,1} &&\hspace{-40pt}\text{by Lemma}\ {2.3}\text{(i) to move } B_{d}(\boldsymbol{1}_{1}) \\ &= \pi_{1} \, X_{0,d} \, X_{1,d} \, X_{0,1}. \end{align*} $$
$$ \begin{align*} X_{0,1} \, X_{1,1} \, X_{0,d} &= X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \\ &= X_{0,1} \; X_{1,1} \; X_{0,1} \; {(\boldsymbol{101}_{1}\;\;\boldsymbol{110}_{1})} \; B_{d}(\boldsymbol{10}_{1}) \; B_{d}(\boldsymbol{11}_{1}) \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d}(\boldsymbol{10}_{1}) \; B_{d}(\boldsymbol{11}_{1}) &&\text{by repeated use of Equation}\ ({1\hbox{-}3}) \\ &= \pi_{1} \; X_{0,1} \; X_{1,1} \; B_{d}(\boldsymbol{01}_{1}) \; B_{d}(\boldsymbol{1}_{1}) \; X_{0,1} &&\hspace{-40pt} \text{by Lemma}\ \text{(i)--(iii) and Equation}\ ({1\hbox{-}3}) \\ &= \pi_{1} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \; X_{1,1} \; B_{d}(\boldsymbol{01}_{1}) \; X_{0,1} &&\hspace{-40pt}\text{by Lemma}\ {2.3}\text{(i) to move } B_{d}(\boldsymbol{1}_{1}) \\ &= \pi_{1} \, X_{0,d} \, X_{1,d} \, X_{0,1}. \end{align*} $$
We can interchange the roles of d and
![]() $d'$
in Relation (HM7) by multiplying on the left by
$d'$
in Relation (HM7) by multiplying on the left by
![]() $\pi _{m+1}$
. Hence, it remains to establish the relation in the cases when both
$\pi _{m+1}$
. Hence, it remains to establish the relation in the cases when both
![]() $d,d' \geqslant 2$
. This is achieved as follows:
$d,d' \geqslant 2$
. This is achieved as follows:
 $$ \begin{align*} &X_{0,d'} \, X_{1,d'} \, X_{0,d}\\ &\quad= X_{0,d'} \; X_{1,d'} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \\ &\quad= \pi_{1} \; X_{0,1} \; X_{1,1} \; X_{0,d'} \; B_{d}(\boldsymbol{1}_{1}) &&\kern-5pt\text{by the case } d = 1 \\ &\quad= \pi_{1} \; X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d'}(\boldsymbol{1}_{1}) \; B_{d}(\boldsymbol{1}_{1}.\boldsymbol{0}_{d'}) \; B_{d}(\boldsymbol{1}_{1}.\boldsymbol{1}_{d'}) &&\kern-5pt\text{by Lemma}\ {2.3}\text{(vi)} \\ &\quad= \pi_{1} \; X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d}(\boldsymbol{10}_{1}) \; B_{d}(\boldsymbol{11}_{1}) \; B_{d'}(\boldsymbol{1}_{1}) &&\kern-5pt\text{by Equation}\ ({2\hbox{-}7}) \\ &\quad= \pi_{1} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \; X_{1,1} \; B_{d}(\boldsymbol{01}_{1}) \; X_{0,d'} &&\kern-5pt\text{by Lemma}\ {2.3}\ \text{and Equation} ({1\hbox{-}3}) \\ &\quad= \pi_{1} \, X_{0,d} \, X_{1,d} \, X_{0,d'}. \end{align*} $$
$$ \begin{align*} &X_{0,d'} \, X_{1,d'} \, X_{0,d}\\ &\quad= X_{0,d'} \; X_{1,d'} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \\ &\quad= \pi_{1} \; X_{0,1} \; X_{1,1} \; X_{0,d'} \; B_{d}(\boldsymbol{1}_{1}) &&\kern-5pt\text{by the case } d = 1 \\ &\quad= \pi_{1} \; X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d'}(\boldsymbol{1}_{1}) \; B_{d}(\boldsymbol{1}_{1}.\boldsymbol{0}_{d'}) \; B_{d}(\boldsymbol{1}_{1}.\boldsymbol{1}_{d'}) &&\kern-5pt\text{by Lemma}\ {2.3}\text{(vi)} \\ &\quad= \pi_{1} \; X_{0,1} \; X_{1,1} \; X_{0,1} \; B_{d}(\boldsymbol{10}_{1}) \; B_{d}(\boldsymbol{11}_{1}) \; B_{d'}(\boldsymbol{1}_{1}) &&\kern-5pt\text{by Equation}\ ({2\hbox{-}7}) \\ &\quad= \pi_{1} \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \; X_{1,1} \; B_{d}(\boldsymbol{01}_{1}) \; X_{0,d'} &&\kern-5pt\text{by Lemma}\ {2.3}\ \text{and Equation} ({1\hbox{-}3}) \\ &\quad= \pi_{1} \, X_{0,d} \, X_{1,d} \, X_{0,d'}. \end{align*} $$
Relation (HM14) is established by using formulae about conjugation by
![]() ${(\boldsymbol {0}_{1}\;\;\boldsymbol {1}_{1})}$
:
${(\boldsymbol {0}_{1}\;\;\boldsymbol {1}_{1})}$
:
 $$ \begin{align*} X_{0,d} \, \bar{\pi}_{0} &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; B_{d}(\boldsymbol{1}_{1}) \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{01}_{1})} \; B_{d}(\boldsymbol{0}_{1}) = {(\boldsymbol{00}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \; B_{d}(\boldsymbol{0}_{1}) = \bar{\pi}_{1} \, \pi_{0} \, C_{1,d}. \end{align*} $$
$$ \begin{align*} X_{0,d} \, \bar{\pi}_{0} &= {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{10}_{1})} \; {(\boldsymbol{10}_{1}\;\;\boldsymbol{11}_{1})} \; B_{d}(\boldsymbol{1}_{1}) \; {(\boldsymbol{0}_{1}\;\;\boldsymbol{1}_{1})} \\ &= {(\boldsymbol{00}_{1}\;\;\boldsymbol{1}_{1})} \; {(\boldsymbol{00}_{1}\;\;\boldsymbol{01}_{1})} \; B_{d}(\boldsymbol{0}_{1}) = {(\boldsymbol{00}_{1}\;\;\boldsymbol{01}_{1})} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{1}_{1})} \; B_{d}(\boldsymbol{0}_{1}) = \bar{\pi}_{1} \, \pi_{0} \, C_{1,d}. \end{align*} $$
For Relation (HM16), we collect the transpositions comprising
![]() $X_{0,1}$
to the right:
$X_{0,1}$
to the right:
 $$ \begin{align*} X_{0,1} \, C_{0,d} &= X_{0,1} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{10}_{1})} \; B_{d}(\boldsymbol{0}_{1}) \; B_{d}(\boldsymbol{1}_{1}) \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; B_{d}(\boldsymbol{00}_{1}) \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) = \pi_{1} \, C_{2,d} \, X_{0,d}. \end{align*} $$
$$ \begin{align*} X_{0,1} \, C_{0,d} &= X_{0,1} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{10}_{1})} \; B_{d}(\boldsymbol{0}_{1}) \; B_{d}(\boldsymbol{1}_{1}) \\ &= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; B_{d}(\boldsymbol{00}_{1}) \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) = \pi_{1} \, C_{2,d} \, X_{0,d}. \end{align*} $$
Finally, consider Relation (HM18) in the case when
![]() $m = 0$
. We calculate
$m = 0$
. We calculate
 $$ \begin{align*} &C_{2,d'} \, X_{0,d'} \, C_{0,d}\\ &\quad= B_{d'}(\boldsymbol{00}_{1}) \; X_{0,1} \; B_{d'}(\boldsymbol{1}_{1}) \; C_{0,d} \\ &\quad= X_{0,1} \; B_{d'}(\boldsymbol{0}_{1}) \; B_{d'}(\boldsymbol{1}_{1}) \; C_{0,d} &&\text{by Equation}\ ({1\hbox{-}3})\ \text{and Lemma}\ {2.3}\text{(i), (iii)} \\ &\quad= X_{0,1} \; C_{0,d} \; C_{0,d'} &&\text{by Lemma}\ \text{(i), (ii)} \\ &\quad= X_{0,1} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{10}_{1})} \; B_{d}(\boldsymbol{0}_{1}) \; B_{d}(\boldsymbol{1}_{1}) \; C_{0,d'} \\ &\quad= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; B_{d}(\boldsymbol{00}_{1}) \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \; C_{0,d'} &&\text{by Equation}\ ({1\hbox{-}3})\ \text{and Lemma}\ {2.3}\text{(i), (iii)} \\ &\quad= \pi_{1} \, C_{2,d} \, X_{0,d} \, C_{0,d'}, \end{align*} $$
$$ \begin{align*} &C_{2,d'} \, X_{0,d'} \, C_{0,d}\\ &\quad= B_{d'}(\boldsymbol{00}_{1}) \; X_{0,1} \; B_{d'}(\boldsymbol{1}_{1}) \; C_{0,d} \\ &\quad= X_{0,1} \; B_{d'}(\boldsymbol{0}_{1}) \; B_{d'}(\boldsymbol{1}_{1}) \; C_{0,d} &&\text{by Equation}\ ({1\hbox{-}3})\ \text{and Lemma}\ {2.3}\text{(i), (iii)} \\ &\quad= X_{0,1} \; C_{0,d} \; C_{0,d'} &&\text{by Lemma}\ \text{(i), (ii)} \\ &\quad= X_{0,1} \; {(\boldsymbol{01}_{1}\;\;\boldsymbol{10}_{1})} \; B_{d}(\boldsymbol{0}_{1}) \; B_{d}(\boldsymbol{1}_{1}) \; C_{0,d'} \\ &\quad= {(\boldsymbol{001}_{1}\;\;\boldsymbol{01}_{1})} \; B_{d}(\boldsymbol{00}_{1}) \; X_{0,1} \; B_{d}(\boldsymbol{1}_{1}) \; C_{0,d'} &&\text{by Equation}\ ({1\hbox{-}3})\ \text{and Lemma}\ {2.3}\text{(i), (iii)} \\ &\quad= \pi_{1} \, C_{2,d} \, X_{0,d} \, C_{0,d'}, \end{align*} $$
as required. This completes the proof of the proposition and the work of this section.
3 Finite presentations for
 $nV$
$nV$
In this section, we prove Theorem 1.2. In the course of our argument, we refer to two particular subsets of the collection
![]() $\Omega $
of addresses. Write
$\Omega $
of addresses. Write
![]() $\Delta = (X^{2})^{n}$
for the set of addresses
$\Delta = (X^{2})^{n}$
for the set of addresses
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfying
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfying
![]() $\mathopen {|}\alpha _{i}\mathclose {|} = 2$
for
$\mathopen {|}\alpha _{i}\mathclose {|} = 2$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
, …, n. Also define
$2$
, …, n. Also define
![]() $\Omega ^{\ast }$
to be the set of addresses
$\Omega ^{\ast }$
to be the set of addresses
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfying
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
satisfying
![]() $\mathopen {|}\alpha _{i}\mathclose {|} \geqslant 2$
for
$\mathopen {|}\alpha _{i}\mathclose {|} \geqslant 2$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
, …, n.
$2$
, …, n.
We define a presentation for a group G on three generators a, b and c, and
![]() $2n^{2} + 3n + 11$
relations. The starting point is a presentation for the symmetric group of degree
$2n^{2} + 3n + 11$
relations. The starting point is a presentation for the symmetric group of degree
![]() $4^{n}$
on two generators. According to [Reference Guralnick, Kantor, Kassabov and Lubotzky16, Theorem A], this can be achieved using merely eight relations (independent of the value of n). A recent article by Huxford [Reference Huxford18] presents corrections to the arguments and the relations given in [Reference Guralnick, Kantor, Kassabov and Lubotzky16]. Note, however, that the number of relations is unaffected and the statement of [Reference Guralnick, Kantor, Kassabov and Lubotzky16, Theorem A] remains valid.
$4^{n}$
on two generators. According to [Reference Guralnick, Kantor, Kassabov and Lubotzky16, Theorem A], this can be achieved using merely eight relations (independent of the value of n). A recent article by Huxford [Reference Huxford18] presents corrections to the arguments and the relations given in [Reference Guralnick, Kantor, Kassabov and Lubotzky16]. Note, however, that the number of relations is unaffected and the statement of [Reference Guralnick, Kantor, Kassabov and Lubotzky16, Theorem A] remains valid.
Our first family (Relation R1 below) of relations is sufficient to ensure that the generators a and b satisfy all relations that hold in the symmetric group of degree
![]() $4^{n}$
. Moreover, all the relations that we assume are satisfied if one maps a, b and c to the corresponding elements of
$4^{n}$
. Moreover, all the relations that we assume are satisfied if one maps a, b and c to the corresponding elements of
![]() $nV$
(where for c, we interpret Relation R7 in
$nV$
(where for c, we interpret Relation R7 in
![]() $nV$
). In particular, the resulting homomorphism
$nV$
). In particular, the resulting homomorphism
![]() $G \to nV$
induces a homomorphism from
$G \to nV$
induces a homomorphism from
![]() $H = \langle a,b \rangle $
onto the above symmetric group. Consequently,
$H = \langle a,b \rangle $
onto the above symmetric group. Consequently,
![]() $H \cong \operatorname {\mathrm {Sym}}(\Delta )$
and we may interpret the elements in H as defining permutations of
$H \cong \operatorname {\mathrm {Sym}}(\Delta )$
and we may interpret the elements in H as defining permutations of
![]() $\Delta $
. We therefore use the symbol
$\Delta $
. We therefore use the symbol
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Delta $
with
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Delta $
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, to denote certain elements of the subgroup H and more generally refer to permutations of
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, to denote certain elements of the subgroup H and more generally refer to permutations of
![]() $\Delta $
by which we mean the corresponding elements of this subgroup. This also means that we can speak of the support of an element
$\Delta $
by which we mean the corresponding elements of this subgroup. This also means that we can speak of the support of an element
![]() $g \in H$
and use the notation
$g \in H$
and use the notation
![]() $\boldsymbol {\gamma } \bullet g$
to denote the effect of applying g to some address
$\boldsymbol {\gamma } \bullet g$
to denote the effect of applying g to some address
![]() $\boldsymbol {\gamma } \in \Delta $
. (In some sense, this extends the notation given in Section 1.)
$\boldsymbol {\gamma } \in \Delta $
. (In some sense, this extends the notation given in Section 1.)
The third generator c will be used to construct further transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
for other addresses
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
for other addresses
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
with
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
. The details of this construction will be described later in this section, together with appropriate verifications that the resulting elements of G are well defined and satisfy the relations in Equations (1-2)–(1-4) listed in Theorem 1.1. For the remaining discussion, prior to explaining the construction, we assume the existence of the various transpositions
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
. The details of this construction will be described later in this section, together with appropriate verifications that the resulting elements of G are well defined and satisfy the relations in Equations (1-2)–(1-4) listed in Theorem 1.1. For the remaining discussion, prior to explaining the construction, we assume the existence of the various transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, each of which will be expressed as some product in G involving the generators a, b and c.
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, each of which will be expressed as some product in G involving the generators a, b and c.
To specify the relations that we assume, we fix certain elements of H. Let
![]() $\boldsymbol {\delta }^{(0)}$
,
$\boldsymbol {\delta }^{(0)}$
,
![]() $\boldsymbol {\delta }^{(1)}$
, …,
$\boldsymbol {\delta }^{(1)}$
, …,
![]() $\boldsymbol {\delta }^{(4^{n}-1)}$
be an enumeration of the addresses in
$\boldsymbol {\delta }^{(4^{n}-1)}$
be an enumeration of the addresses in
![]() $\Delta $
and define the following elements of H:
$\Delta $
and define the following elements of H:
 $$ \begin{align} \begin{aligned} p &= ( \boldsymbol{\delta}^{(n+1)} \; \boldsymbol{\delta}^{(n+2)} \, \ldots \, \boldsymbol{\delta}^{(4^{n}-1)} ) \\ q_{d} &= ( \boldsymbol{\delta}^{(0)} \; \boldsymbol{\delta}^{(1)} \, \ldots \, \boldsymbol{\delta}^{(d-1)} \; \boldsymbol{\delta}^{(d+1)} \, \ldots \, \boldsymbol{\delta}^{(n)} \; \boldsymbol{\delta}^{(n+2)} \, \ldots \, \boldsymbol{\delta}^{(4^{n}-1)} ). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} p &= ( \boldsymbol{\delta}^{(n+1)} \; \boldsymbol{\delta}^{(n+2)} \, \ldots \, \boldsymbol{\delta}^{(4^{n}-1)} ) \\ q_{d} &= ( \boldsymbol{\delta}^{(0)} \; \boldsymbol{\delta}^{(1)} \, \ldots \, \boldsymbol{\delta}^{(d-1)} \; \boldsymbol{\delta}^{(d+1)} \, \ldots \, \boldsymbol{\delta}^{(n)} \; \boldsymbol{\delta}^{(n+2)} \, \ldots \, \boldsymbol{\delta}^{(4^{n}-1)} ). \end{aligned} \end{align} $$
The relations that we assume are the following:
-
R1. eight relations involving a and b that define the symmetric group of degree
 $4^{n}$
(from [Reference Guralnick, Kantor, Kassabov and Lubotzky16, Theorem A]);
$4^{n}$
(from [Reference Guralnick, Kantor, Kassabov and Lubotzky16, Theorem A]); -
R2.
 $[c,p] = [\, c, \, {(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})} \, ] = 1$
;
$[c,p] = [\, c, \, {(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})} \, ] = 1$
; -
R3.
 $[ \, q_{d}, \, {(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})} \, ] = 1$
for
$[ \, q_{d}, \, {(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})} \, ] = 1$
for
 $d = 1$
,
$d = 1$
,
 $2$
, …, n and
$2$
, …, n and
 $x \in \{0,1\}$
;
$x \in \{0,1\}$
; -
R4.
 $[ \, c, \, {(\boldsymbol {\delta }^{(n+2)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+3)})} \, ] = 1$
for
$[ \, c, \, {(\boldsymbol {\delta }^{(n+2)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+3)})} \, ] = 1$
for
 $d = 1$
,
$d = 1$
,
 $2$
, …, n and
$2$
, …, n and
 $x \in \{0,1\}$
;
$x \in \{0,1\}$
; -
R5.
 $ {(\boldsymbol {\delta }^{(0)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(1)})}^{ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\boldsymbol {y}_{d'})}} = {(\boldsymbol {\delta }^{(0)}.\boldsymbol {y}_{d'}\;\;\boldsymbol {\delta }^{(1)})}^{ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\kern1pt\boldsymbol{x}_{d})}} $
for all choices of distinct indices
$ {(\boldsymbol {\delta }^{(0)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(1)})}^{ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\boldsymbol {y}_{d'})}} = {(\boldsymbol {\delta }^{(0)}.\boldsymbol {y}_{d'}\;\;\boldsymbol {\delta }^{(1)})}^{ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\kern1pt\boldsymbol{x}_{d})}} $
for all choices of distinct indices
 $d,d' \in \{1,2,\ldots ,n\}$
and all pairs
$d,d' \in \{1,2,\ldots ,n\}$
and all pairs
 $x,y \in \{0,1\}$
;
$x,y \in \{0,1\}$
; -
R6.
 $ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(1)})} = {(\boldsymbol {\delta }^{(0)}.\boldsymbol {0}_{d}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {0}_{d})} \; {(\boldsymbol {\delta }^{(0)}.\boldsymbol {1}_{d}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {1}_{d})} $
for
$ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(1)})} = {(\boldsymbol {\delta }^{(0)}.\boldsymbol {0}_{d}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {0}_{d})} \; {(\boldsymbol {\delta }^{(0)}.\boldsymbol {1}_{d}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {1}_{d})} $
for
 $d = 1$
,
$d = 1$
,
 $2$
, …, n; and
$2$
, …, n; and -
R7.
 $c = {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {0}_{1})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {1}_{1})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\boldsymbol {0}_{2})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\boldsymbol {1}_{2})}$
$c = {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {0}_{1})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(1)}.\boldsymbol {1}_{1})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\boldsymbol {0}_{2})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(2)}.\boldsymbol {1}_{2})}$
 $\phantom{\hspace{15pt}} \cdots \, {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n)}.\boldsymbol {0}_{n})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n)}.\boldsymbol {1}_{n})}$
.
$\phantom{\hspace{15pt}} \cdots \, {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n)}.\boldsymbol {0}_{n})} \; {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n)}.\boldsymbol {1}_{n})}$
.
We establish Theorem 1.2 by showing that the group G, generated by a, b and c subject to the
![]() $2n^{2} + 3n + 11$
relations listed in Relations R1–R7, is isomorphic to the group
$2n^{2} + 3n + 11$
relations listed in Relations R1–R7, is isomorphic to the group
![]() $nV$
.
$nV$
.
The first part of the proof of Theorem 1.2 involves the definition of all transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, for
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, for
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
with
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, as elements of the group G, verifying that these transpositions are well defined, and that they satisfy all those relations in Equations (1-2)–(1-4) listed in Theorem 1.1 involving only addresses in
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, as elements of the group G, verifying that these transpositions are well defined, and that they satisfy all those relations in Equations (1-2)–(1-4) listed in Theorem 1.1 involving only addresses in
![]() $\Omega ^{\ast }$
. (In this part of the proof, we do not consider any address
$\Omega ^{\ast }$
. (In this part of the proof, we do not consider any address
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with one or more coordinates satisfying
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
with one or more coordinates satisfying
![]() $\mathopen {|}\alpha _{i}\mathclose {|} \leqslant 1$
.) We also verify explicitly the relation listed in Equation (1-5) since we depend upon this to reduce the number of cases when verifying Equation (1-3) (see Lemma 3.1 below). The overall process is an induction argument based on the number of coordinates of an address
$\mathopen {|}\alpha _{i}\mathclose {|} \leqslant 1$
.) We also verify explicitly the relation listed in Equation (1-5) since we depend upon this to reduce the number of cases when verifying Equation (1-3) (see Lemma 3.1 below). The overall process is an induction argument based on the number of coordinates of an address
![]() $\boldsymbol {\alpha }$
having some specified length. To make this precise, we set
$\boldsymbol {\alpha }$
having some specified length. To make this precise, we set
![]() $m(\boldsymbol {\alpha }) = \max \{ \mathopen {|}\alpha _{1}\mathclose {|}, \mathopen {|}\alpha _{2}\mathclose {|}, \ldots , \mathopen {|}\alpha _{n}\mathclose {|} \}$
and define
$m(\boldsymbol {\alpha }) = \max \{ \mathopen {|}\alpha _{1}\mathclose {|}, \mathopen {|}\alpha _{2}\mathclose {|}, \ldots , \mathopen {|}\alpha _{n}\mathclose {|} \}$
and define
![]() $k(\boldsymbol {\alpha })$
to be the number of coordinates
$k(\boldsymbol {\alpha })$
to be the number of coordinates
![]() $\alpha _{i}$
satisfying
$\alpha _{i}$
satisfying
![]() $\mathopen {|}\alpha _{i}\mathclose {|} = m(\boldsymbol {\alpha })$
. The weight of
$\mathopen {|}\alpha _{i}\mathclose {|} = m(\boldsymbol {\alpha })$
. The weight of
![]() $\boldsymbol {\alpha }$
is then the ordered pair
$\boldsymbol {\alpha }$
is then the ordered pair
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m(\boldsymbol {\alpha }), k(\boldsymbol {\alpha }))$
. This pair then measures the longest coordinate of
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m(\boldsymbol {\alpha }), k(\boldsymbol {\alpha }))$
. This pair then measures the longest coordinate of
![]() $\boldsymbol {\alpha }$
and counts the number of longest coordinates in the address. Thus, for example,
$\boldsymbol {\alpha }$
and counts the number of longest coordinates in the address. Thus, for example,
![]() $\Delta $
consists of all addresses of weight
$\Delta $
consists of all addresses of weight
![]() $(2,n)$
.
$(2,n)$
.
We order weights lexicographically, so
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) < \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta })$
means either
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) < \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta })$
means either
![]() $m(\boldsymbol {\alpha }) < m(\boldsymbol {\,\beta })$
, or
$m(\boldsymbol {\alpha }) < m(\boldsymbol {\,\beta })$
, or
![]() $m(\boldsymbol {\alpha }) = m(\boldsymbol {\,\beta })$
and
$m(\boldsymbol {\alpha }) = m(\boldsymbol {\,\beta })$
and
![]() $k(\boldsymbol {\alpha }) < k(\boldsymbol {\,\beta })$
; that is, either the coordinates of
$k(\boldsymbol {\alpha }) < k(\boldsymbol {\,\beta })$
; that is, either the coordinates of
![]() $\boldsymbol {\alpha }$
are all shorter than the longest of
$\boldsymbol {\alpha }$
are all shorter than the longest of
![]() $\boldsymbol {\beta }$
or that the greatest length is the same but
$\boldsymbol {\beta }$
or that the greatest length is the same but
![]() $\boldsymbol {\alpha }$
has fewer of these longest coordinates than
$\boldsymbol {\alpha }$
has fewer of these longest coordinates than
![]() $\boldsymbol {\beta }$
.
$\boldsymbol {\beta }$
.
In each step of the induction, we assume that we already have defined transpositions whose entries have weight less than
![]() $(m,k)$
and verified all Equations (1-2)–(1-4), and also Equation (1-5), involving such transpositions. Our first stage is then to define transpositions
$(m,k)$
and verified all Equations (1-2)–(1-4), and also Equation (1-5), involving such transpositions. Our first stage is then to define transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
![]() $\boldsymbol {\beta } \in \Delta $
, or vice versa. We then verify that our definitions make sense and that all the required relations involving the newly defined transpositions are satisfied. At the second stage, we perform the same definitions and verifications for the remaining transpositions
$\boldsymbol {\beta } \in \Delta $
, or vice versa. We then verify that our definitions make sense and that all the required relations involving the newly defined transpositions are satisfied. At the second stage, we perform the same definitions and verifications for the remaining transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
with
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
with
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) \leqslant (m,k)$
. The new transpositions will always be conjugates of transpositions from
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) \leqslant (m,k)$
. The new transpositions will always be conjugates of transpositions from
![]() $\operatorname {\mathrm {Sym}}(\Delta )$
and consequently Equation (1-2) will always hold and we do not verify it explicitly.
$\operatorname {\mathrm {Sym}}(\Delta )$
and consequently Equation (1-2) will always hold and we do not verify it explicitly.
A significant part of our argument is verifying the conjugacy relations in Equation (1-3). The following lemma describes which instances of this relation are needed at each step of the induction.
Lemma 3.1. Assume that all transpositions defined at some stage of the induction satisfy
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })}$
and
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })}$
and
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}^{2} = 1$
. To verify all required conjugacy relations in Equation (1-3), it is sufficient to establish them in the following cases.
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}^{2} = 1$
. To verify all required conjugacy relations in Equation (1-3), it is sufficient to establish them in the following cases.
-
(A) Every pair from
 $\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
is incomparable. The required relation then has the form
$\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
is incomparable. The required relation then has the form  $$ \begin{align*} [ \, {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} \, , \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, ] = 1. \end{align*} $$
$$ \begin{align*} [ \, {(\boldsymbol{\alpha}\;\;\boldsymbol{\beta})} \, , \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, ] = 1. \end{align*} $$
-
(B)
 $\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
and every pair from
$\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
and every pair from
 $\{\kern1.5pt \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
is incomparable. Then,
$\{\kern1.5pt \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
is incomparable. Then,
 $\boldsymbol {\alpha } = \boldsymbol {\gamma }\boldsymbol {\eta }$
for some
$\boldsymbol {\alpha } = \boldsymbol {\gamma }\boldsymbol {\eta }$
for some
 $\boldsymbol {\eta } \in ~\Omega $
and the required relation is
$\boldsymbol {\eta } \in ~\Omega $
and the required relation is  $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{{(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{{(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
-
(C)
 $\boldsymbol {\gamma } \prec \boldsymbol {\alpha }$
,
$\boldsymbol {\gamma } \prec \boldsymbol {\alpha }$
,
 $\boldsymbol {\delta } \preceq \boldsymbol {\beta }$
and
$\boldsymbol {\delta } \preceq \boldsymbol {\beta }$
and
 $\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
. Then,
$\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
. Then,
 $\boldsymbol {\alpha } = \boldsymbol {\gamma \eta }$
and
$\boldsymbol {\alpha } = \boldsymbol {\gamma \eta }$
and
 $\boldsymbol {\beta } = \boldsymbol {\delta \theta }$
for some
$\boldsymbol {\beta } = \boldsymbol {\delta \theta }$
for some
 $\boldsymbol {\eta },\boldsymbol {\theta } \in \Omega $
and the required relation is
$\boldsymbol {\eta },\boldsymbol {\theta } \in \Omega $
and the required relation is  $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\delta\theta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\gamma\theta}\;\;\boldsymbol{\delta\eta})}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\delta\theta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\gamma\theta}\;\;\boldsymbol{\delta\eta})}. \end{align*} $$
-
(D)
 $\boldsymbol {\gamma } \prec \boldsymbol {\alpha }, \boldsymbol {\beta }$
and
$\boldsymbol {\gamma } \prec \boldsymbol {\alpha }, \boldsymbol {\beta }$
and
 $\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
. Then,
$\boldsymbol {\gamma } \perp \boldsymbol {\delta }$
. Then,
 $\boldsymbol {\alpha } = \boldsymbol {\gamma \eta }$
and
$\boldsymbol {\alpha } = \boldsymbol {\gamma \eta }$
and
 $\boldsymbol {\beta } = \boldsymbol {\gamma \theta }$
for (necessarily nonempty)
$\boldsymbol {\beta } = \boldsymbol {\gamma \theta }$
for (necessarily nonempty)
 $\boldsymbol {\eta }, \boldsymbol {\theta } \in \Omega $
and the required relation is
$\boldsymbol {\eta }, \boldsymbol {\theta } \in \Omega $
and the required relation is  $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\gamma\theta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\delta\theta})}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\gamma\theta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\delta\theta})}. \end{align*} $$
Proof. In order that
![]() $\boldsymbol {\alpha } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
be defined, we require (i)
$\boldsymbol {\alpha } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
be defined, we require (i)
![]() $\boldsymbol {\gamma } \perp \boldsymbol {\alpha }$
or
$\boldsymbol {\gamma } \perp \boldsymbol {\alpha }$
or
![]() $\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
, and (ii)
$\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
, and (ii)
![]() $\boldsymbol {\delta } \perp \boldsymbol {\alpha }$
or
$\boldsymbol {\delta } \perp \boldsymbol {\alpha }$
or
![]() $\boldsymbol {\delta } \preceq \boldsymbol {\alpha }$
. A similar pair of conditions apply when
$\boldsymbol {\delta } \preceq \boldsymbol {\alpha }$
. A similar pair of conditions apply when
![]() $\boldsymbol {\beta } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
is defined. We analyse the four resulting conditions. Furthermore, we note, for example, that if
$\boldsymbol {\beta } \bullet {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
is defined. We analyse the four resulting conditions. Furthermore, we note, for example, that if
![]() $\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
or
$\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
or
![]() $\boldsymbol {\delta } \preceq \boldsymbol {\alpha }$
, then by exploiting the symmetry
$\boldsymbol {\delta } \preceq \boldsymbol {\alpha }$
, then by exploiting the symmetry
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} = {(\boldsymbol {\delta }\;\;\boldsymbol {\gamma })}$
we may assume that in fact
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} = {(\boldsymbol {\delta }\;\;\boldsymbol {\gamma })}$
we may assume that in fact
![]() $\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
. This reduces the four conditions to the configurations described in the statement of the lemma.
$\boldsymbol {\gamma } \preceq \boldsymbol {\alpha }$
. This reduces the four conditions to the configurations described in the statement of the lemma.
3.1 Base step
As the base step of the induction, we rely upon the assumed Relation R1 to ensure that the transpositions in
![]() $H = \langle a,b \rangle $
exist and satisfy all the relations in the symmetric group of degree
$H = \langle a,b \rangle $
exist and satisfy all the relations in the symmetric group of degree
![]() $4^{n}$
; that is, we may use all transpositions
$4^{n}$
; that is, we may use all transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) = (2,n)$
, and all relations in Equations (1-2), (1-3) and (1-5) between them. (There are no relations of the form of Equation (1-4) involving only transpositions from H.)
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) = (2,n)$
, and all relations in Equations (1-2), (1-3) and (1-5) between them. (There are no relations of the form of Equation (1-4) involving only transpositions from H.)
3.2 Induction, stage 1
Let us assume that for some fixed weight
![]() $(m,k) \geqslant (3,1)$
, we have already defined all transpositions
$(m,k) \geqslant (3,1)$
, we have already defined all transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) < (m,k)$
and verified all relations in Equations (1-2)–(1-5) involving such transpositions. We now define those transpositions with one entry of weight
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) < (m,k)$
and verified all relations in Equations (1-2)–(1-5) involving such transpositions. We now define those transpositions with one entry of weight
![]() $(m,k)$
and one entry from
$(m,k)$
and one entry from
![]() $\Delta $
. The definitions and argument actually depend upon whether
$\Delta $
. The definitions and argument actually depend upon whether
![]() $(m,k) = (3,1)$
or
$(m,k) = (3,1)$
or
![]() $(m,k)> (3,1)$
. Consequently, we split into these cases.
$(m,k)> (3,1)$
. Consequently, we split into these cases.
Suppose then that
![]() $(m,k) = (3,1)$
. First, set
$(m,k) = (3,1)$
. First, set
where
![]() $d = 1$
,
$d = 1$
,
![]() $2$
, …, n and
$2$
, …, n and
![]() $x \in \{0,1\}$
. (Since d and x are nonnegative integers, the sum
$x \in \{0,1\}$
. (Since d and x are nonnegative integers, the sum
![]() $2d+x-1$
is defined.) We now define transpositions
$2d+x-1$
is defined.) We now define transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
,
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
,
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (3,1)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (3,1)$
and
![]() $\boldsymbol {\beta } \in \Delta $
. Then,
$\boldsymbol {\beta } \in \Delta $
. Then,
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
, where
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
, where
![]() $\mathopen {|}\alpha _{d}\mathclose {|} = 3$
for some index d and
$\mathopen {|}\alpha _{d}\mathclose {|} = 3$
for some index d and
![]() $\mathopen {|}\alpha _{i}\mathclose {|} = 2$
for all other indices i. Write
$\mathopen {|}\alpha _{i}\mathclose {|} = 2$
for all other indices i. Write
![]() $\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
, where
$\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
, where
![]() $\hat {\boldsymbol {\alpha }} \in \Delta $
, and choose a permutation
$\hat {\boldsymbol {\alpha }} \in \Delta $
, and choose a permutation
![]() $\sigma \in H$
that moves
$\sigma \in H$
that moves
![]() $\boldsymbol {\delta }^{(d)}$
to
$\boldsymbol {\delta }^{(d)}$
to
![]() $\hat {\boldsymbol {\alpha }}$
and
$\hat {\boldsymbol {\alpha }}$
and
![]() $\boldsymbol {\delta }^{(n+1)}$
to
$\boldsymbol {\delta }^{(n+1)}$
to
![]() $\boldsymbol {\beta }$
. We then define
$\boldsymbol {\beta }$
. We then define
in terms of the transposition defined in Equation (3-2). To achieve the symmetry required by Equation (1-5), we also define
![]() ${(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })} \mathrel {:=} {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
for such
${(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })} \mathrel {:=} {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
for such
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
. To verify that these definitions are independent of the choice of permutation
$\boldsymbol {\beta }$
. To verify that these definitions are independent of the choice of permutation
![]() $\sigma \in H$
, we use the following lemma.
$\sigma \in H$
, we use the following lemma.
Lemma 3.2
-
(i) If
 $\sigma \in H$
is a permutation of
$\sigma \in H$
is a permutation of
 $\Delta $
with support disjoint from
$\Delta $
with support disjoint from
 $\boldsymbol {\delta }^{(0)}$
,
$\boldsymbol {\delta }^{(0)}$
,
 $\boldsymbol {\delta }^{(1)}$
, …,
$\boldsymbol {\delta }^{(1)}$
, …,
 $\boldsymbol {\delta }^{(n)}$
, then
$\boldsymbol {\delta }^{(n)}$
, then
 $[c,\sigma ] = 1$
.
$[c,\sigma ] = 1$
. -
(ii) Let
 $d = 1$
,
$d = 1$
,
 $2$
, …, n and
$2$
, …, n and
 $x \in \{0,1\}$
. Then,
$x \in \{0,1\}$
. Then,
 ${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}$
commutes with every permutation in H that has support disjoint from
${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}$
commutes with every permutation in H that has support disjoint from
 $\boldsymbol {\delta }^{(d)}$
and
$\boldsymbol {\delta }^{(d)}$
and
 $\boldsymbol {\delta }^{(n+1)}$
.
$\boldsymbol {\delta }^{(n+1)}$
.
Proof. (i) Note that our permutation p, defined in Equation (3-1), and the transposition
![]() ${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
generate all the permutations of
${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
generate all the permutations of
![]() $\Delta \setminus \{ \boldsymbol {\delta }^{(0)}, \boldsymbol {\delta }^{(1)}, \ldots , \boldsymbol {\delta }^{(n)} \}$
. Hence, all permutations of the latter set commute with c by our assumed Relation R2.
$\Delta \setminus \{ \boldsymbol {\delta }^{(0)}, \boldsymbol {\delta }^{(1)}, \ldots , \boldsymbol {\delta }^{(n)} \}$
. Hence, all permutations of the latter set commute with c by our assumed Relation R2.
(ii) The disjoint transpositions
![]() ${(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}$
and
${(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}$
and
![]() ${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
commute. Consequently,
${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
commute. Consequently,
![]() ${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})} = {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}^{c^{2d+x-1}}$
commutes with
${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})} = {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}^{c^{2d+x-1}}$
commutes with
![]() ${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
by Relation R2. The definition in Equation (3-1) of the cycle
${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
by Relation R2. The definition in Equation (3-1) of the cycle
![]() $q_{d}$
ensures that it and the transposition
$q_{d}$
ensures that it and the transposition
![]() ${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
generate all permutations in H with support disjoint from
${(\boldsymbol {\delta }^{(n+2)}\;\;\boldsymbol {\delta }^{(n+3)})}$
generate all permutations in H with support disjoint from
![]() $\boldsymbol {\delta }^{(d)}$
and
$\boldsymbol {\delta }^{(d)}$
and
![]() $\boldsymbol {\delta }^{(n+1)}$
. Hence,
$\boldsymbol {\delta }^{(n+1)}$
. Hence,
![]() ${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}$
commutes with all such permutations with use of Relation R3.
${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}$
commutes with all such permutations with use of Relation R3.
We now show that the definition of
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
in Equation (3-3) does not depend on the choice of
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
in Equation (3-3) does not depend on the choice of
![]() $\sigma $
. For if
$\sigma $
. For if
![]() $\sigma _{1}$
and
$\sigma _{1}$
and
![]() $\sigma _{2}$
are two permutations of
$\sigma _{2}$
are two permutations of
![]() $\Delta $
that both move
$\Delta $
that both move
![]() $\boldsymbol {\delta }^{(d)}$
to
$\boldsymbol {\delta }^{(d)}$
to
![]() $\hat {\boldsymbol {\alpha }}$
and
$\hat {\boldsymbol {\alpha }}$
and
![]() $\boldsymbol {\delta }^{(n+1)}$
to
$\boldsymbol {\delta }^{(n+1)}$
to
![]() $\boldsymbol {\beta }$
, then
$\boldsymbol {\beta }$
, then
![]() $\sigma _{1}\sigma _{2}^{-1}$
fixes both
$\sigma _{1}\sigma _{2}^{-1}$
fixes both
![]() $\boldsymbol {\delta }^{(d)}$
and
$\boldsymbol {\delta }^{(d)}$
and
![]() $\boldsymbol {\delta }^{(n+1)}$
, so commutes with
$\boldsymbol {\delta }^{(n+1)}$
, so commutes with
![]() ${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}$
by part (ii) of the lemma. Therefore,
${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}$
by part (ii) of the lemma. Therefore,
![]() ${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}^{\sigma _{1}} = {(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}^{\sigma _{2}}$
, establishing that
${(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}^{\sigma _{1}} = {(\boldsymbol {\delta }^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+1)})}^{\sigma _{2}}$
, establishing that
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is well defined.
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is well defined.
There are no split relations in Equation (1-4) to verify at this stage, since we have not yet introduced any transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where both
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where both
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
have coordinates of length
$\boldsymbol {\beta }$
have coordinates of length
![]() $3$
. Hence, we only need to check conjugacy relations in Equation (1-3) involving the transpositions that we have introduced.
$3$
. Hence, we only need to check conjugacy relations in Equation (1-3) involving the transpositions that we have introduced.
Lemma 3.3
-
(i) Let
 $\boldsymbol {\beta },\boldsymbol {\gamma } \in \Delta $
,
$\boldsymbol {\beta },\boldsymbol {\gamma } \in \Delta $
,
 $x \in \{0,1\}$
and d be an index with
$x \in \{0,1\}$
and d be an index with
 $1 \leqslant d \leqslant n$
. If
$1 \leqslant d \leqslant n$
. If
 $\sigma \in \operatorname {\mathrm {Sym}}(\Delta )$
, then where, as above,
$\sigma \in \operatorname {\mathrm {Sym}}(\Delta )$
, then where, as above, $$ \begin{align*} {(\boldsymbol{\,\beta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\gamma})}^{\sigma} = {((\boldsymbol{\,\beta}\!\bullet\!\sigma).\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\gamma}\!\bullet\!\sigma)}, \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\,\beta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\gamma})}^{\sigma} = {((\boldsymbol{\,\beta}\!\bullet\!\sigma).\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\gamma}\!\bullet\!\sigma)}, \end{align*} $$
 $\boldsymbol {\beta }\bullet \sigma $
and
$\boldsymbol {\beta }\bullet \sigma $
and
 $\boldsymbol {\gamma }\bullet \sigma $
denote the images of
$\boldsymbol {\gamma }\bullet \sigma $
denote the images of
 $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
 $\boldsymbol {\gamma }$
under the action of
$\boldsymbol {\gamma }$
under the action of
 $\sigma \in H$
.
$\sigma \in H$
.
-
(ii) If
 $\boldsymbol {\beta } \in \Delta \setminus \{ \boldsymbol {\delta }^{(0)}, \boldsymbol {\delta }^{(1)}, \ldots , \boldsymbol {\delta }^{(n)} \}$
,
$\boldsymbol {\beta } \in \Delta \setminus \{ \boldsymbol {\delta }^{(0)}, \boldsymbol {\delta }^{(1)}, \ldots , \boldsymbol {\delta }^{(n)} \}$
,
 $1 \leqslant d \leqslant n$
and
$1 \leqslant d \leqslant n$
and
 $x \in \{0,1\}$
, then
$x \in \{0,1\}$
, then  $$ \begin{align*} {(\boldsymbol{\delta}^{(0)}\;\;\boldsymbol{\beta})}^{c^{2d+x-1}} = {(\boldsymbol{\delta}^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\delta}^{(0)}\;\;\boldsymbol{\beta})}^{c^{2d+x-1}} = {(\boldsymbol{\delta}^{(d)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}. \end{align*} $$
Proof. (i) This follows immediately from the definition of transpositions of the form
![]() ${(\boldsymbol {\,\beta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\gamma })}$
and their well definedness.
${(\boldsymbol {\,\beta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\gamma })}$
and their well definedness.
(ii) We must establish the result when
![]() $\boldsymbol {\beta } \neq \boldsymbol {\delta }^{(n+1)}$
. Take
$\boldsymbol {\beta } \neq \boldsymbol {\delta }^{(n+1)}$
. Take
![]() $\sigma = {(\boldsymbol {\delta }^{(n+1)}\;\;\boldsymbol {\beta })}$
. This commutes with c by Lemma 3.2(i). Hence,
$\sigma = {(\boldsymbol {\delta }^{(n+1)}\;\;\boldsymbol {\beta })}$
. This commutes with c by Lemma 3.2(i). Hence,
which produces the required result using part (i).
Part (i) of Lemma 3.3 establishes any instance of the conjugacy relation in Equation (1-3) when
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} \in H$
. We consider now the remaining instances of Equation (1-3) involving transpositions defined at this stage of the induction (via Equation (3-3) above) and we split into the cases listed in Lemma 3.1.
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} \in H$
. We consider now the remaining instances of Equation (1-3) involving transpositions defined at this stage of the induction (via Equation (3-3) above) and we split into the cases listed in Lemma 3.1.
(A): Consider four incomparable addresses
![]() $\boldsymbol {\alpha }$
,
$\boldsymbol {\alpha }$
,
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma }$
,
$\boldsymbol {\gamma }$
,
![]() $\boldsymbol {\delta }$
, where we may assume
$\boldsymbol {\delta }$
, where we may assume
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = (3,1)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = (3,1)$
and
![]() $\boldsymbol {\beta }, \boldsymbol {\delta } \in \Delta $
. Write
$\boldsymbol {\beta }, \boldsymbol {\delta } \in \Delta $
. Write
![]() $\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
and
$\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
and
![]() $\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\boldsymbol {y}_{d'}$
for
$\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\boldsymbol {y}_{d'}$
for
![]() $x,y \in \{0,1\}$
, indices d and
$x,y \in \{0,1\}$
, indices d and
![]() $d'$
, and some
$d'$
, and some
![]() $\hat {\boldsymbol {\alpha }}, \hat {\boldsymbol {\gamma }} \in \Delta $
. Suppose
$\hat {\boldsymbol {\alpha }}, \hat {\boldsymbol {\gamma }} \in \Delta $
. Suppose
![]() $\hat {\boldsymbol {\alpha }} \neq \hat {\boldsymbol {\gamma }}$
, so that
$\hat {\boldsymbol {\alpha }} \neq \hat {\boldsymbol {\gamma }}$
, so that
![]() $\hat {\boldsymbol {\alpha }}$
,
$\hat {\boldsymbol {\alpha }}$
,
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\hat {\boldsymbol {\gamma }}$
and
$\hat {\boldsymbol {\gamma }}$
and
![]() $\boldsymbol {\delta }$
are distinct addresses in
$\boldsymbol {\delta }$
are distinct addresses in
![]() $\Delta $
. From Lemma 3.3(i), we know
$\Delta $
. From Lemma 3.3(i), we know
![]() ${(\boldsymbol {\delta }^{(n+2)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+3)})}$
commutes with
${(\boldsymbol {\delta }^{(n+2)}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta }^{(n+3)})}$
commutes with
![]() ${(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}$
and it commutes with c by Relation R4. Hence, conjugating by
${(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}$
and it commutes with c by Relation R4. Hence, conjugating by
![]() $c^{2d'+y-1}$
, we conclude that
$c^{2d'+y-1}$
, we conclude that
Finally, conjugate by a permutation
![]() $\sigma $
in H that maps
$\sigma $
in H that maps
![]() $\boldsymbol {\delta }^{(n+2)}$
to
$\boldsymbol {\delta }^{(n+2)}$
to
![]() $\hat {\boldsymbol {\alpha }}$
,
$\hat {\boldsymbol {\alpha }}$
,
![]() $\boldsymbol {\delta }^{(n+3)}$
to
$\boldsymbol {\delta }^{(n+3)}$
to
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\delta }^{(d')}$
to
$\boldsymbol {\delta }^{(d')}$
to
![]() $\hat {\boldsymbol {\gamma }}$
and
$\hat {\boldsymbol {\gamma }}$
and
![]() $\boldsymbol {\delta }^{(n+1)}$
to
$\boldsymbol {\delta }^{(n+1)}$
to
![]() $\boldsymbol {\delta }$
to establish
$\boldsymbol {\delta }$
to establish
![]() $[ {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} , {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} ] = 1$
, as required.
$[ {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} , {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} ] = 1$
, as required.
However, if
![]() $\hat {\boldsymbol {\alpha }} = \hat {\boldsymbol {\gamma }}$
, then in order that
$\hat {\boldsymbol {\alpha }} = \hat {\boldsymbol {\gamma }}$
, then in order that
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\gamma }$
, we know that
$\boldsymbol {\alpha } \perp \boldsymbol {\gamma }$
, we know that
![]() $d = d'$
and, after suitable relabelling, we can assume
$d = d'$
and, after suitable relabelling, we can assume
![]() $x = 0$
and
$x = 0$
and
![]() $y = 1$
. We make use of Lemma 3.3(ii) to observe:
$y = 1$
. We make use of Lemma 3.3(ii) to observe:
 $$ \begin{align*} {(\boldsymbol{\delta}^{(d)}.\boldsymbol{0}_{d}\;\;\boldsymbol{\delta}^{(n+1)})} &= {(\boldsymbol{\delta}^{(0)}\;\;\boldsymbol{\delta}^{(n+1)})}^{c^{2d-1}} \\ {(\boldsymbol{\delta}^{(d)}.\boldsymbol{1}_{d}\;\;\boldsymbol{\delta}^{(n+2)})} &= {(\boldsymbol{\delta}^{(0)}\;\;\boldsymbol{\delta}^{(n+2)})}^{c^{2d}} = {(\boldsymbol{\delta}^{(1)}.\boldsymbol{0}_{1}\;\;\boldsymbol{\delta}^{(n+2)})}^{c^{2d-1}}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\delta}^{(d)}.\boldsymbol{0}_{d}\;\;\boldsymbol{\delta}^{(n+1)})} &= {(\boldsymbol{\delta}^{(0)}\;\;\boldsymbol{\delta}^{(n+1)})}^{c^{2d-1}} \\ {(\boldsymbol{\delta}^{(d)}.\boldsymbol{1}_{d}\;\;\boldsymbol{\delta}^{(n+2)})} &= {(\boldsymbol{\delta}^{(0)}\;\;\boldsymbol{\delta}^{(n+2)})}^{c^{2d}} = {(\boldsymbol{\delta}^{(1)}.\boldsymbol{0}_{1}\;\;\boldsymbol{\delta}^{(n+2)})}^{c^{2d-1}}. \end{align*} $$
By Lemma 3.3(i),
![]() ${(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}$
commutes with
${(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}$
commutes with
![]() ${(\boldsymbol {\delta }^{(1)}.\boldsymbol {0}_{1}\;\;\boldsymbol {\delta }^{(n+2)})}$
. Hence, upon conjugating by
${(\boldsymbol {\delta }^{(1)}.\boldsymbol {0}_{1}\;\;\boldsymbol {\delta }^{(n+2)})}$
. Hence, upon conjugating by
![]() $c^{2d-1}$
, we deduce
$c^{2d-1}$
, we deduce
We establish the required relation
![]() $[ {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} , {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} ] = 1$
by finally conjugating by a permutation
$[ {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} , {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} ] = 1$
by finally conjugating by a permutation
![]() $\sigma $
in H that moves
$\sigma $
in H that moves
![]() $\boldsymbol {\delta }^{(d)}$
to
$\boldsymbol {\delta }^{(d)}$
to
![]() $\hat {\boldsymbol {\alpha }}$
,
$\hat {\boldsymbol {\alpha }}$
,
![]() $\boldsymbol {\delta }^{(n+1)}$
to
$\boldsymbol {\delta }^{(n+1)}$
to
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\delta }^{(n+2)}$
to
$\boldsymbol {\delta }^{(n+2)}$
to
![]() $\boldsymbol {\delta }$
.
$\boldsymbol {\delta }$
.
(B): In view of Lemma 3.3(i) and the symmetry between
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
in the conjugacy relation, we may assume, in this case, that
$\boldsymbol {\delta }$
in the conjugacy relation, we may assume, in this case, that
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = (3,1)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = (3,1)$
and
![]() $\boldsymbol {\alpha } = \boldsymbol {\gamma }$
. The remaining addresses
$\boldsymbol {\alpha } = \boldsymbol {\gamma }$
. The remaining addresses
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\delta }$
must be from
$\boldsymbol {\delta }$
must be from
![]() $\Delta $
. Write
$\Delta $
. Write
![]() $\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\kern1pt\boldsymbol{x}_{d}$
for some
$\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\kern1pt\boldsymbol{x}_{d}$
for some
![]() $x \in \{0,1\}$
and some index d. Conjugate the equation
$x \in \{0,1\}$
and some index d. Conjugate the equation
![]() $ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}^{ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+2)})}} = {(\boldsymbol {\delta }^{(n+1)}\;\;\boldsymbol {\delta }^{(n+2)})}$
by
$ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+1)})}^{ {(\boldsymbol {\delta }^{(0)}\;\;\boldsymbol {\delta }^{(n+2)})}} = {(\boldsymbol {\delta }^{(n+1)}\;\;\boldsymbol {\delta }^{(n+2)})}$
by
![]() $c^{2d+x-1}$
to produce
$c^{2d+x-1}$
to produce
by use of Lemmas 3.2(i) and 3.3(ii). Finally, conjugate by a permutation
![]() $\sigma $
of
$\sigma $
of
![]() $\Delta $
moving
$\Delta $
moving
![]() $\boldsymbol {\delta }^{(d)}$
to
$\boldsymbol {\delta }^{(d)}$
to
![]() $\hat {\boldsymbol {\gamma }}$
,
$\hat {\boldsymbol {\gamma }}$
,
![]() $\boldsymbol {\delta }^{(n+1)}$
to
$\boldsymbol {\delta }^{(n+1)}$
to
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\delta }^{(n+2)}$
to
$\boldsymbol {\delta }^{(n+2)}$
to
![]() $\boldsymbol {\delta }$
, using Lemma 3.3(i), to establish the required relation.
$\boldsymbol {\delta }$
, using Lemma 3.3(i), to establish the required relation.
(C)/(D): Conjugacy relations of the form (C) occur only at this stage when
![]() $\boldsymbol {\gamma }, \boldsymbol {\delta } \in \Delta $
, which all then hold by Lemma 3.3. There are no type (D) relations to verify. This completes the verifications required for stage 1 of the induction when
$\boldsymbol {\gamma }, \boldsymbol {\delta } \in \Delta $
, which all then hold by Lemma 3.3. There are no type (D) relations to verify. This completes the verifications required for stage 1 of the induction when
![]() $(m,k) = (3,1)$
.
$(m,k) = (3,1)$
.
Now assume
![]() $(m,k)> (3,1)$
. Consider a pair of incomparable addresses
$(m,k)> (3,1)$
. Consider a pair of incomparable addresses
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
with
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
with
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
![]() $\boldsymbol {\beta } \in \Delta $
. To define the transposition
$\boldsymbol {\beta } \in \Delta $
. To define the transposition
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, first choose d to be the index of one of the coordinates of
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, first choose d to be the index of one of the coordinates of
![]() $\boldsymbol {\alpha }$
that has length m and write
$\boldsymbol {\alpha }$
that has length m and write
![]() $\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
, where
$\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
, where
![]() $x \in \{0,1\}$
. Then,
$x \in \{0,1\}$
. Then,
![]() $\hat {\boldsymbol {\alpha }}$
is an address with
$\hat {\boldsymbol {\alpha }}$
is an address with
![]() $\operatorname {\mathrm {wt}}(\hat {\boldsymbol {\alpha }}) < (m,k)$
and, since every coordinate of
$\operatorname {\mathrm {wt}}(\hat {\boldsymbol {\alpha }}) < (m,k)$
and, since every coordinate of
![]() $\boldsymbol {\beta }$
has length
$\boldsymbol {\beta }$
has length
![]() $2$
, it follows
$2$
, it follows
![]() $\hat {\boldsymbol {\alpha }} \perp \boldsymbol {\beta }$
also. Choose
$\hat {\boldsymbol {\alpha }} \perp \boldsymbol {\beta }$
also. Choose
![]() $\boldsymbol {\zeta } \in \Delta $
incomparable with both
$\boldsymbol {\zeta } \in \Delta $
incomparable with both
![]() $\hat {\boldsymbol {\alpha }}$
and
$\hat {\boldsymbol {\alpha }}$
and
![]() $\boldsymbol {\beta }$
. Then,
$\boldsymbol {\beta }$
. Then,
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}) = (3,1) < (m,k)$
and, by induction, both transpositions
$\operatorname {\mathrm {wt}}(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}) = (3,1) < (m,k)$
and, by induction, both transpositions
![]() ${(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}$
and
${(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}$
and
![]() ${(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\alpha }})}$
have been constructed. We then define
${(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\alpha }})}$
have been constructed. We then define
To achieve Equation (1-5), we also set
![]() ${(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })} \mathrel {:=} {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
. We must verify that the above definition is independent of the choice of the address
${(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })} \mathrel {:=} {(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
. We must verify that the above definition is independent of the choice of the address
![]() $\boldsymbol {\zeta }$
and of the index d.
$\boldsymbol {\zeta }$
and of the index d.
With the above assumptions, we make the following observations.
Lemma 3.4
-
(i) Suppose that
 $\boldsymbol {\zeta }$
and
$\boldsymbol {\zeta }$
and
 $\boldsymbol {\eta }$
are distinct addresses in
$\boldsymbol {\eta }$
are distinct addresses in
 $\Delta $
that are incomparable with both
$\Delta $
that are incomparable with both
 $\hat {\boldsymbol {\alpha }}$
and
$\hat {\boldsymbol {\alpha }}$
and
 $\boldsymbol {\beta }$
. Then,
$\boldsymbol {\beta }$
. Then,  $$ \begin{align*} {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\hat{\boldsymbol{\alpha}})}} = {(\boldsymbol{\eta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\eta}\;\;\hat{\boldsymbol{\alpha}})}}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\hat{\boldsymbol{\alpha}})}} = {(\boldsymbol{\eta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\eta}\;\;\hat{\boldsymbol{\alpha}})}}. \end{align*} $$
-
(ii) Suppose that d and
 $d'$
are both indices of coordinates of
$d'$
are both indices of coordinates of
 $\boldsymbol {\alpha }$
of length m. Write
$\boldsymbol {\alpha }$
of length m. Write
 $\boldsymbol {\alpha } = \boldsymbol {\gamma }.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}$
for some
$\boldsymbol {\alpha } = \boldsymbol {\gamma }.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}$
for some
 $x,y \in \{0,1\}$
. If
$x,y \in \{0,1\}$
. If
 $\boldsymbol {\zeta }$
is an address in
$\boldsymbol {\zeta }$
is an address in
 $\Delta $
incomparable with both
$\Delta $
incomparable with both
 $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
 $\boldsymbol {\gamma }$
, then
$\boldsymbol {\gamma }$
, then  $$ \begin{align*} {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\gamma}.\boldsymbol{y}_{d'})}} = {(\boldsymbol{\zeta}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\gamma}.\kern1pt\boldsymbol{x}_{d})}}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\gamma}.\boldsymbol{y}_{d'})}} = {(\boldsymbol{\zeta}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\gamma}.\kern1pt\boldsymbol{x}_{d})}}. \end{align*} $$
Proof. (i) As distinct addresses in
![]() $\Delta $
, certainly
$\Delta $
, certainly
![]() $\boldsymbol {\zeta }$
and
$\boldsymbol {\zeta }$
and
![]() $\boldsymbol {\eta }$
are incomparable. All addresses appearing in the following calculation have weight
$\boldsymbol {\eta }$
are incomparable. All addresses appearing in the following calculation have weight
![]() $< (m,k)$
and so, by induction,
$< (m,k)$
and so, by induction,
and the required equation then follows.
(ii) Note that our assumption that
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and
![]() $\boldsymbol {\beta } \in \Delta $
implies that
$\boldsymbol {\beta } \in \Delta $
implies that
![]() $\boldsymbol {\beta } \perp \boldsymbol {\gamma }$
. Now consider first the case when
$\boldsymbol {\beta } \perp \boldsymbol {\gamma }$
. Now consider first the case when
![]() $(m,k) = (3,2)$
, so that
$(m,k) = (3,2)$
, so that
![]() $\boldsymbol {\gamma } \in \Delta $
. We simply conjugate Relation R5 by a permutation
$\boldsymbol {\gamma } \in \Delta $
. We simply conjugate Relation R5 by a permutation
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\Delta )$
that moves
$\sigma \in \operatorname {\mathrm {Sym}}(\Delta )$
that moves
![]() $\boldsymbol {\delta }^{(0)}$
to
$\boldsymbol {\delta }^{(0)}$
to
![]() $\boldsymbol {\zeta }$
,
$\boldsymbol {\zeta }$
,
![]() $\boldsymbol {\delta }^{(1)}$
to
$\boldsymbol {\delta }^{(1)}$
to
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\delta }^{(2)}$
to
$\boldsymbol {\delta }^{(2)}$
to
![]() $\boldsymbol {\gamma }$
(using relations established in the weight
$\boldsymbol {\gamma }$
(using relations established in the weight
![]() $(3,1)$
stage) to yield the required formula.
$(3,1)$
stage) to yield the required formula.
Now consider the case when
![]() $(m,k)> (3,2)$
. Choose
$(m,k)> (3,2)$
. Choose
![]() $\boldsymbol {\delta } \in \Delta $
that is incomparable with each of
$\boldsymbol {\delta } \in \Delta $
that is incomparable with each of
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\zeta }$
. Note that
$\boldsymbol {\zeta }$
. Note that
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}) = (3,2)$
and so the transpositions with this address as an entry in the following calculation were constructed at an earlier stage. Then,
$\operatorname {\mathrm {wt}}(\boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}) = (3,2)$
and so the transpositions with this address as an entry in the following calculation were constructed at an earlier stage. Then,
and similarly
![]() ${(\boldsymbol {\zeta }.\boldsymbol {y}_{d'}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\boldsymbol {\gamma }.\kern1pt\boldsymbol{x}_{d})} \, {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = {(\boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}\;\;\boldsymbol {\beta })}$
. It therefore follows that the left-hand sides of these equations are equal, from which we deduce our required formula.
${(\boldsymbol {\zeta }.\boldsymbol {y}_{d'}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\boldsymbol {\gamma }.\kern1pt\boldsymbol{x}_{d})} \, {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = {(\boldsymbol {\delta }.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}\;\;\boldsymbol {\beta })}$
. It therefore follows that the left-hand sides of these equations are equal, from which we deduce our required formula.
It follows from part (i) of this lemma that our definition in Equation (3-4) of
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is independent of the choice of
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is independent of the choice of
![]() $\boldsymbol {\zeta }$
. Then, part (ii) shows the definition is also independent of the choice of index d. In conclusion, the transpositions
$\boldsymbol {\zeta }$
. Then, part (ii) shows the definition is also independent of the choice of index d. In conclusion, the transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
![]() $\boldsymbol {\beta } \in \Delta $
or vice versa, are well defined. The remaining work in this part of the induction is to establish the four types of conjugacy relations in Equation (1-3) and then the split relation in Equation (1-4) when they involve such transpositions.
$\boldsymbol {\beta } \in \Delta $
or vice versa, are well defined. The remaining work in this part of the induction is to establish the four types of conjugacy relations in Equation (1-3) and then the split relation in Equation (1-4) when they involve such transpositions.
(A): Consider two transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
and
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
and
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
, at least one of which was defined as in Equation (3-4) and the other possibly arriving at an early stage in the induction, such that every pair of addresses from
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
, at least one of which was defined as in Equation (3-4) and the other possibly arriving at an early stage in the induction, such that every pair of addresses from
![]() $\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
is incomparable. Exploiting the symmetry relation in Equation (1-5), we can suppose without loss of generality that one of the following sets of conditions holds:
$\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \}$
is incomparable. Exploiting the symmetry relation in Equation (1-5), we can suppose without loss of generality that one of the following sets of conditions holds:
-
(A.i)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
,
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
,
 $\boldsymbol {\beta } \in \Delta $
and
$\boldsymbol {\beta } \in \Delta $
and
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta }) < (m,k)$
; or
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta }) < (m,k)$
; or -
(A.ii)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = (m,k)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = (m,k)$
and
 $\boldsymbol {\beta }, \boldsymbol {\delta } \in \Delta $
.
$\boldsymbol {\beta }, \boldsymbol {\delta } \in \Delta $
.
In Case (A.i), write
![]() $\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
as above. Choose
$\boldsymbol {\alpha } = \hat {\boldsymbol {\alpha }}.\kern1pt\boldsymbol{x}_{d}$
as above. Choose
![]() $\boldsymbol {\zeta } \in \Delta $
that is incomparable with each of
$\boldsymbol {\zeta } \in \Delta $
that is incomparable with each of
![]() $\hat {\boldsymbol {\alpha }}$
,
$\hat {\boldsymbol {\alpha }}$
,
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
and use this, together with Lemma 3.4, in the definition in Equation (3-4) of
$\boldsymbol {\delta }$
and use this, together with Lemma 3.4, in the definition in Equation (3-4) of
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
. By induction,
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
. By induction,
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
commutes with both
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
commutes with both
![]() ${(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}$
and
${(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}$
and
![]() ${(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\alpha }})}$
and hence with
${(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\alpha }})}$
and hence with
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\alpha }})}}$
, as required. Case (A.ii) is similar, but we now write
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\alpha }})}}$
, as required. Case (A.ii) is similar, but we now write
![]() $\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\boldsymbol {y}_{d'}$
for some suitable index
$\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\boldsymbol {y}_{d'}$
for some suitable index
![]() $d'$
and choose
$d'$
and choose
![]() $\boldsymbol {\eta } \in \Delta $
incomparable with each address in
$\boldsymbol {\eta } \in \Delta $
incomparable with each address in
![]() $\{ \hat {\boldsymbol {\alpha }}, \boldsymbol {\beta }, \hat {\boldsymbol {\gamma }}, \boldsymbol {\delta }, \boldsymbol {\zeta } \}$
. We then observe that, by induction, each transposition used in the definition
$\{ \hat {\boldsymbol {\alpha }}, \boldsymbol {\beta }, \hat {\boldsymbol {\gamma }}, \boldsymbol {\delta }, \boldsymbol {\zeta } \}$
. We then observe that, by induction, each transposition used in the definition
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} = {(\boldsymbol {\eta }.\boldsymbol {y}_{d'}\;\;\boldsymbol {\delta })}^{ {(\boldsymbol {\eta }\;\;\hat {\boldsymbol {\gamma }})}}$
commutes with each one used to construct
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} = {(\boldsymbol {\eta }.\boldsymbol {y}_{d'}\;\;\boldsymbol {\delta })}^{ {(\boldsymbol {\eta }\;\;\hat {\boldsymbol {\gamma }})}}$
commutes with each one used to construct
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
. This establishes all type (A) conjugacy relations at this stage.
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
. This establishes all type (A) conjugacy relations at this stage.
(B): Consider a conjugacy relation of Equation (1-3), where
![]() $\boldsymbol {\alpha } = \boldsymbol {\gamma \eta }$
as in Lemma 3.1(B). At least one address in the relation has weight
$\boldsymbol {\alpha } = \boldsymbol {\gamma \eta }$
as in Lemma 3.1(B). At least one address in the relation has weight
![]() $(m,k)$
and the other entry in a transposition involving such an address must be in
$(m,k)$
and the other entry in a transposition involving such an address must be in
![]() $\Delta $
. Exploiting the symmetry present, there are four possibilities:
$\Delta $
. Exploiting the symmetry present, there are four possibilities:
-
(B.i)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) = (m,k)$
,
$\operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) = (m,k)$
,
 $\boldsymbol {\gamma }, \boldsymbol {\delta } \in \Delta $
and
$\boldsymbol {\gamma }, \boldsymbol {\delta } \in \Delta $
and
 $\boldsymbol {\eta } = \boldsymbol {\varepsilon }$
;
$\boldsymbol {\eta } = \boldsymbol {\varepsilon }$
; -
(B.ii)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = (m,k)$
,
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = (m,k)$
,
 $\boldsymbol {\beta } \in \Delta $
and
$\boldsymbol {\beta } \in \Delta $
and
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) < (m,k)$
;
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) < (m,k)$
; -
(B.iii)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) = (m,k)$
,
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) = (m,k)$
,
 $\boldsymbol {\beta } \in \Delta $
and
$\boldsymbol {\beta } \in \Delta $
and
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta }) < (m,k)$
; or
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }), \operatorname {\mathrm {wt}}(\boldsymbol {\delta }) < (m,k)$
; or -
(B.iv)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = (m,k)$
,
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = (m,k)$
,
 $\boldsymbol {\beta }, \boldsymbol {\delta } \in \Delta $
and
$\boldsymbol {\beta }, \boldsymbol {\delta } \in \Delta $
and
 $\operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) < (m,k)$
.
$\operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) < (m,k)$
.
(It is impossible that
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) = (m,k)$
: if this situation were to happen, then there would be some index d, where the d th coordinate of
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) = (m,k)$
: if this situation were to happen, then there would be some index d, where the d th coordinate of
![]() $\boldsymbol {\delta \eta }$
has length m. Then the d th coordinate of
$\boldsymbol {\delta \eta }$
has length m. Then the d th coordinate of
![]() $\boldsymbol {\gamma \eta }$
has length m, but that of
$\boldsymbol {\gamma \eta }$
has length m, but that of
![]() $\boldsymbol {\gamma }$
is shorter, contradicting
$\boldsymbol {\gamma }$
is shorter, contradicting
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta })$
.)
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta })$
.)
In case (B.i), write
![]() $\boldsymbol {\beta } = \hat {\boldsymbol {\beta }}.\kern1pt\boldsymbol{x}_{d}$
and choose
$\boldsymbol {\beta } = \hat {\boldsymbol {\beta }}.\kern1pt\boldsymbol{x}_{d}$
and choose
![]() $\boldsymbol {\zeta } \in \Delta $
incomparable with each of
$\boldsymbol {\zeta } \in \Delta $
incomparable with each of
![]() $\hat {\boldsymbol {\beta }}$
,
$\hat {\boldsymbol {\beta }}$
,
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
to define
$\boldsymbol {\delta }$
to define
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\gamma }\;\;\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d})}^{ {(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\beta }})}}$
and similarly for
${(\boldsymbol {\gamma }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\gamma }\;\;\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d})}^{ {(\boldsymbol {\zeta }\;\;\hat {\boldsymbol {\beta }})}}$
and similarly for
![]() ${(\boldsymbol {\delta }\;\;\boldsymbol {\beta })}$
. Then, by induction,
${(\boldsymbol {\delta }\;\;\boldsymbol {\beta })}$
. Then, by induction,
In case (B.ii), note that there is an index d such that the d th coordinate of
![]() $\boldsymbol {\gamma \eta }$
has length m and that of
$\boldsymbol {\gamma \eta }$
has length m and that of
![]() $\boldsymbol {\gamma }$
is shorter. Therefore, we can write
$\boldsymbol {\gamma }$
is shorter. Therefore, we can write
![]() $\boldsymbol {\eta } = \hat {\boldsymbol {\eta }}.\kern1pt\boldsymbol{x}_{d}$
and choose
$\boldsymbol {\eta } = \hat {\boldsymbol {\eta }}.\kern1pt\boldsymbol{x}_{d}$
and choose
![]() $\boldsymbol {\zeta } \in \Delta $
incomparable with each of
$\boldsymbol {\zeta } \in \Delta $
incomparable with each of
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
to define
$\boldsymbol {\delta }$
to define
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\boldsymbol {\gamma }\hat {\boldsymbol {\eta }})}}$
. Then,
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\boldsymbol {\gamma }\hat {\boldsymbol {\eta }})}}$
. Then,
For case (B.iii), there are two possibilities. If there is some d such that the d th coordinate of
![]() $\boldsymbol {\gamma \eta }$
and
$\boldsymbol {\gamma \eta }$
and
![]() $\boldsymbol {\delta \eta }$
both have length m, but those of
$\boldsymbol {\delta \eta }$
both have length m, but those of
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
are shorter, then we use the same argument as for case (B.ii), but now the last step in the calculation is actually the definition of
$\boldsymbol {\delta }$
are shorter, then we use the same argument as for case (B.ii), but now the last step in the calculation is actually the definition of
![]() ${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
. Otherwise, there are d and
${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
. Otherwise, there are d and
![]() $d'$
such that the d th coordinate of
$d'$
such that the d th coordinate of
![]() $\boldsymbol {\gamma \eta }$
has length m and that of
$\boldsymbol {\gamma \eta }$
has length m and that of
![]() $\boldsymbol {\gamma }$
is shorter and the
$\boldsymbol {\gamma }$
is shorter and the
![]() $d'$
th coordinate of
$d'$
th coordinate of
![]() $\boldsymbol {\delta \eta }$
has length m and that of
$\boldsymbol {\delta \eta }$
has length m and that of
![]() $\boldsymbol {\delta }$
is shorter. Moreover, by hypothesis, the d th coordinate of
$\boldsymbol {\delta }$
is shorter. Moreover, by hypothesis, the d th coordinate of
![]() $\boldsymbol {\gamma }$
must be longer than that of
$\boldsymbol {\gamma }$
must be longer than that of
![]() $\boldsymbol {\delta }$
, so has length at least
$\boldsymbol {\delta }$
, so has length at least
![]() $3$
. Choose distinct addresses
$3$
. Choose distinct addresses
![]() $\boldsymbol {\zeta }, \boldsymbol {\theta } \in \Delta $
incomparable with each of
$\boldsymbol {\zeta }, \boldsymbol {\theta } \in \Delta $
incomparable with each of
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
. We use
$\boldsymbol {\delta }$
. We use
![]() $\boldsymbol {\zeta }$
when employing Equation (3-4) to define
$\boldsymbol {\zeta }$
when employing Equation (3-4) to define
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}$
and
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}$
and
![]() ${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
, exploiting the coordinates of indices d and
${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
, exploiting the coordinates of indices d and
![]() $d'$
, respectively, having written
$d'$
, respectively, having written
![]() $\boldsymbol {\eta } = \hat {\boldsymbol {\eta }}.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}$
. Thus,
$\boldsymbol {\eta } = \hat {\boldsymbol {\eta }}.\kern1pt\boldsymbol{x}_{d}.\boldsymbol {y}_{d'}$
. Thus,
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\boldsymbol {\gamma }\hat {\boldsymbol {\eta }}.\boldsymbol {y}_{d'})}}$
and similarly for
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\zeta }\;\;\boldsymbol {\gamma }\hat {\boldsymbol {\eta }}.\boldsymbol {y}_{d'})}}$
and similarly for
![]() ${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
(as in the second set of calculations below). Furthermore,
${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
(as in the second set of calculations below). Furthermore,
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\theta \eta }) < (m,k)$
since the d th coordinate of
$\operatorname {\mathrm {wt}}(\boldsymbol {\theta \eta }) < (m,k)$
since the d th coordinate of
![]() $\boldsymbol {\theta \eta }$
is shorter than that of
$\boldsymbol {\theta \eta }$
is shorter than that of
![]() $\boldsymbol {\gamma \eta }$
. We therefore compute:
$\boldsymbol {\gamma \eta }$
. We therefore compute:
 $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})}} &= {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\gamma}\hat{\boldsymbol{\eta}}.\boldsymbol{y}_{d'})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})}} \\ &= {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\theta}\hat{\boldsymbol{\eta}}.\boldsymbol{y}_{d'})} \, {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} \\ &= {(\boldsymbol{\theta}\hat{\boldsymbol{\eta}}.\kern1pt\boldsymbol{x}_{d}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\theta\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} \\[7pt] {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} &= {(\boldsymbol{\zeta}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\delta}\hat{\boldsymbol{\eta}}.\kern1pt\boldsymbol{x}_{d})} \, {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} \\ &= {(\boldsymbol{\zeta}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\theta}\hat{\boldsymbol{\eta}}.\kern1pt\boldsymbol{x}_{d})}} \\ &= {(\boldsymbol{\theta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})}} &= {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\gamma}\hat{\boldsymbol{\eta}}.\boldsymbol{y}_{d'})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})}} \\ &= {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\theta}\hat{\boldsymbol{\eta}}.\boldsymbol{y}_{d'})} \, {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} \\ &= {(\boldsymbol{\theta}\hat{\boldsymbol{\eta}}.\kern1pt\boldsymbol{x}_{d}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\theta\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} \\[7pt] {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} &= {(\boldsymbol{\zeta}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\delta}\hat{\boldsymbol{\eta}}.\kern1pt\boldsymbol{x}_{d})} \, {(\boldsymbol{\theta}\;\;\boldsymbol{\delta})}} \\ &= {(\boldsymbol{\zeta}.\boldsymbol{y}_{d'}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\theta}\hat{\boldsymbol{\eta}}.\kern1pt\boldsymbol{x}_{d})}} \\ &= {(\boldsymbol{\theta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
Hence,
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} \, {(\boldsymbol {\gamma }\;\;\boldsymbol {\theta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
and, with use of our already verified type (A) conjugacy relation, we conclude
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} \, {(\boldsymbol {\gamma }\;\;\boldsymbol {\theta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
and, with use of our already verified type (A) conjugacy relation, we conclude
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\theta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
.
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\theta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
.
Finally, in case (B.iv), let d be the index of a coordinate of
![]() $\boldsymbol {\gamma }$
of length m. Write
$\boldsymbol {\gamma }$
of length m. Write
![]() $\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\kern1pt\boldsymbol{x}_{d}$
. Note that the d th coordinate of
$\boldsymbol {\gamma } = \hat {\boldsymbol {\gamma }}.\kern1pt\boldsymbol{x}_{d}$
. Note that the d th coordinate of
![]() $\boldsymbol {\eta }$
is empty. Choose distinct addresses
$\boldsymbol {\eta }$
is empty. Choose distinct addresses
![]() $\boldsymbol {\zeta }, \boldsymbol {\theta } \in \Delta $
that are incomparable with each of
$\boldsymbol {\zeta }, \boldsymbol {\theta } \in \Delta $
that are incomparable with each of
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\hat {\boldsymbol {\gamma }}$
and
$\hat {\boldsymbol {\gamma }}$
and
![]() $\boldsymbol {\delta }$
. The first is used in the construction of
$\boldsymbol {\delta }$
. The first is used in the construction of
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}$
. One observes that
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}$
. One observes that
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\theta \eta }.\kern1pt\boldsymbol{x}_{d}) < (m,k)$
. We calculate
$\operatorname {\mathrm {wt}}(\boldsymbol {\theta \eta }.\kern1pt\boldsymbol{x}_{d}) < (m,k)$
. We calculate
(since
![]() ${(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta })}$
and
${(\boldsymbol {\zeta }.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol {\delta })}$
and
![]() ${(\hat {\boldsymbol {\gamma }}\;\;\boldsymbol {\theta })}$
commute) so that
${(\hat {\boldsymbol {\gamma }}\;\;\boldsymbol {\theta })}$
commute) so that
 $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\hat{\boldsymbol{\gamma}}\;\;\boldsymbol{\theta})}} = {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\hat{\boldsymbol{\gamma}}\boldsymbol{\eta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\hat{\boldsymbol{\gamma}}\;\;\boldsymbol{\theta})}} &= {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\theta\eta})} \, {(\boldsymbol{\theta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\delta})}} \\ &= {(\boldsymbol{\theta\eta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\hat{\boldsymbol{\gamma}}\;\;\boldsymbol{\theta})}} = {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\hat{\boldsymbol{\gamma}}\boldsymbol{\eta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})} \, {(\hat{\boldsymbol{\gamma}}\;\;\boldsymbol{\theta})}} &= {(\boldsymbol{\zeta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\zeta}\;\;\boldsymbol{\theta\eta})} \, {(\boldsymbol{\theta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\delta})}} \\ &= {(\boldsymbol{\theta\eta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\theta}.\kern1pt\boldsymbol{x}_{d}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
Hence, by a type (A) conjugacy relation,
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}^{ {(\hat {\boldsymbol {\gamma }}\;\;\boldsymbol {\theta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
. This establishes all the type (B) conjugacy relations.
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}^{ {(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}^{ {(\hat {\boldsymbol {\gamma }}\;\;\boldsymbol {\theta })}} = {(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
. This establishes all the type (B) conjugacy relations.
(C): In the notation of Lemma 3.1(C), if it were the case that
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \theta }) = (m,k)$
, then at this stage
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\gamma \theta }) = (m,k)$
, then at this stage
![]() $\boldsymbol {\delta }, \boldsymbol {\delta \eta }, \boldsymbol {\delta \theta } \in \Delta $
, which would force
$\boldsymbol {\delta }, \boldsymbol {\delta \eta }, \boldsymbol {\delta \theta } \in \Delta $
, which would force
![]() $\boldsymbol {\eta } = \boldsymbol {\theta } = \boldsymbol {\varepsilon }$
. The conjugacy relation would reduce to one form
$\boldsymbol {\eta } = \boldsymbol {\theta } = \boldsymbol {\varepsilon }$
. The conjugacy relation would reduce to one form
![]() $g^{g} = g$
that holds in any group. Consequently, upon exploiting the symmetry in the relation, we must verify Equation (1-3) in the following two cases:
$g^{g} = g$
that holds in any group. Consequently, upon exploiting the symmetry in the relation, we must verify Equation (1-3) in the following two cases:
-
(C.i)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = (m,k)$
,
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = (m,k)$
,
 $\boldsymbol {\delta } \in \Delta $
,
$\boldsymbol {\delta } \in \Delta $
,
 $\boldsymbol {\theta } = \boldsymbol {\varepsilon }$
and
$\boldsymbol {\theta } = \boldsymbol {\varepsilon }$
and
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) < (m,k)$
; or
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma }) < (m,k)$
; or -
(C.ii)
 $\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) = (m,k)$
,
$\operatorname {\mathrm {wt}}(\boldsymbol {\gamma \eta }) = \operatorname {\mathrm {wt}}(\boldsymbol {\delta \eta }) = (m,k)$
,
 $\boldsymbol {\gamma }, \boldsymbol {\delta } \in \Delta $
and
$\boldsymbol {\gamma }, \boldsymbol {\delta } \in \Delta $
and
 $\boldsymbol {\theta } = \boldsymbol {\varepsilon }$
.
$\boldsymbol {\theta } = \boldsymbol {\varepsilon }$
.
Both are dealt with in the same manner, namely by an argument similar to case (B.ii) above.
(D)/Split: Note that, in the notation of Lemma 3.1(D), the addresses
![]() $\boldsymbol {\eta }$
and
$\boldsymbol {\eta }$
and
![]() $\boldsymbol {\theta }$
must be nonempty. However, since all the transpositions introduced via Equation (3-4) have one entry from
$\boldsymbol {\theta }$
must be nonempty. However, since all the transpositions introduced via Equation (3-4) have one entry from
![]() $\Delta $
, we conclude that no new conjugacy relations of type (D) must be verified at this stage. Similarly, there are no split relations in Equation (1-4) to verify at this stage. In conclusion, we have verified all the required relations involving the transpositions that have been introduced.
$\Delta $
, we conclude that no new conjugacy relations of type (D) must be verified at this stage. Similarly, there are no split relations in Equation (1-4) to verify at this stage. In conclusion, we have verified all the required relations involving the transpositions that have been introduced.
3.3 Induction, stage 2
At the second stage of the induction, we assume that, for the fixed weight
![]() $(m,k) \geqslant (3,1)$
, we have already defined all transpositions
$(m,k) \geqslant (3,1)$
, we have already defined all transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
satisfy
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and either
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
and either
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) < (m,k)$
, or
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) < (m,k)$
, or
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }) = (m,k)$
and
![]() $\boldsymbol {\beta } \in \Delta $
(or vice versa). The former case holds by the inductive assumption and the latter by the completion of stage 1. We also assume that we have verified all relations in Equations (1-2)–(1-5) involving these transpositions. We now define the remaining transpositions with entries of weight at most
$\boldsymbol {\beta } \in \Delta $
(or vice versa). The former case holds by the inductive assumption and the latter by the completion of stage 1. We also assume that we have verified all relations in Equations (1-2)–(1-5) involving these transpositions. We now define the remaining transpositions with entries of weight at most
![]() $(m,k)$
.
$(m,k)$
.
Assume then that
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
are incomparable addresses in
$\boldsymbol {\beta }$
are incomparable addresses in
![]() $\Omega ^{\ast }$
of which one has weight
$\Omega ^{\ast }$
of which one has weight
![]() $(m,k)$
and the other has weight at most
$(m,k)$
and the other has weight at most
![]() $(m,k)$
and is not from
$(m,k)$
and is not from
![]() $\Delta $
. Choose
$\Delta $
. Choose
![]() $\boldsymbol {\zeta } \in \Delta $
incomparable with both
$\boldsymbol {\zeta } \in \Delta $
incomparable with both
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
and define
$\boldsymbol {\beta }$
and define
At least one of the transpositions on the right-hand side is defined via stage 1, while the other (in the case that the relevant entry has weight
![]() $< (m,k)$
) may have been constructed earlier in the inductive process. We first verify that this definition is independent of the choice of
$< (m,k)$
) may have been constructed earlier in the inductive process. We first verify that this definition is independent of the choice of
![]() $\boldsymbol {\zeta }$
.
$\boldsymbol {\zeta }$
.
Lemma 3.5. Let
![]() $\boldsymbol {\alpha }$
,
$\boldsymbol {\alpha }$
,
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\zeta }$
and
$\boldsymbol {\zeta }$
and
![]() $\boldsymbol {\eta }$
be incomparable addresses in
$\boldsymbol {\eta }$
be incomparable addresses in
![]() $\Omega ^{\ast }$
with
$\Omega ^{\ast }$
with
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) \leqslant (m,k)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) \leqslant (m,k)$
and
![]() $\boldsymbol {\zeta }, \boldsymbol {\eta } \in \Delta $
. Then:
$\boldsymbol {\zeta }, \boldsymbol {\eta } \in \Delta $
. Then:
-
(i)
 ${(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}} = {(\boldsymbol {\alpha }\;\;\boldsymbol {\eta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\eta })}}$
;
${(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}} = {(\boldsymbol {\alpha }\;\;\boldsymbol {\eta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\eta })}}$
; -
(ii)
 ${(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}}$
.
${(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}}$
.
Proof. (i) In the following calculation, and indeed for many used during this stage, all the transpositions we manipulate involve one entry from
![]() $\Delta $
. Hence, the relations we rely upon hold by induction or were established in Stage 1. Observe
$\Delta $
. Hence, the relations we rely upon hold by induction or were established in Stage 1. Observe
from which the claimed equation follows.
(ii) Choose
![]() $\boldsymbol {\eta } \in \Delta $
that is incomparable with each of
$\boldsymbol {\eta } \in \Delta $
that is incomparable with each of
![]() $\boldsymbol {\alpha }$
,
$\boldsymbol {\alpha }$
,
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\zeta }$
. We then calculate
$\boldsymbol {\zeta }$
. We then calculate
so that
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })} \, {(\boldsymbol {\,\beta }\;\;\boldsymbol {\eta })}} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })} \, {(\boldsymbol {\,\beta }\;\;\boldsymbol {\eta })}}$
, from which the claimed equation follows.
${(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })} \, {(\boldsymbol {\,\beta }\;\;\boldsymbol {\eta })}} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}^{ {(\boldsymbol {\alpha }\;\;\boldsymbol {\zeta })} \, {(\boldsymbol {\,\beta }\;\;\boldsymbol {\eta })}}$
, from which the claimed equation follows.
Part (i) of this lemma tells us that the definition in Equation (3-5) of
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is independent of the choice of
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
is independent of the choice of
![]() $\boldsymbol {\zeta } \in \Delta $
. Part (ii) tells us that
$\boldsymbol {\zeta } \in \Delta $
. Part (ii) tells us that
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })}$
; that is, Equation (1-5) holds for the transpositions defined via Equation (3-5).
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })}$
; that is, Equation (1-5) holds for the transpositions defined via Equation (3-5).
Before verifying the remaining relations, we observe that
holds for every triple
![]() $\boldsymbol {\alpha }$
,
$\boldsymbol {\alpha }$
,
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\zeta }$
of pairwise incomparable addresses in
$\boldsymbol {\zeta }$
of pairwise incomparable addresses in
![]() $\Omega ^{\ast }$
with
$\Omega ^{\ast }$
with
![]() $\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) \leqslant (m,k)$
and
$\operatorname {\mathrm {wt}}(\boldsymbol {\alpha }), \operatorname {\mathrm {wt}}(\boldsymbol {\,\beta }) \leqslant (m,k)$
and
![]() $\boldsymbol {\zeta } \in \Delta $
. When one or both of
$\boldsymbol {\zeta } \in \Delta $
. When one or both of
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
have weight
$\boldsymbol {\beta }$
have weight
![]() $(m,k)$
, this is the definition in Equation (3-5) combined with Lemma 3.5(i). When they both have weight
$(m,k)$
, this is the definition in Equation (3-5) combined with Lemma 3.5(i). When they both have weight
![]() $< (m,k)$
, it follows by induction.
$< (m,k)$
, it follows by induction.
The four cases (A)–(D) of conjugacy relations in Equation (1-3) described in Lemma 3.1 are all established by the same method. We illustrate this for case (B), namely we establish
for incomparable addresses
![]() $\boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \in \Omega ^{\ast }$
and some (possibly empty)
$\boldsymbol {\beta }, \boldsymbol {\gamma }, \boldsymbol {\delta } \in \Omega ^{\ast }$
and some (possibly empty)
![]() $\boldsymbol {\eta } \in \Omega $
such that the addresses appearing in the formula all have weight
$\boldsymbol {\eta } \in \Omega $
such that the addresses appearing in the formula all have weight
![]() $\leqslant (m,k)$
. Choose distinct
$\leqslant (m,k)$
. Choose distinct
![]() $\boldsymbol {\zeta }, \boldsymbol {\theta } \in \Delta $
incomparable with each of
$\boldsymbol {\zeta }, \boldsymbol {\theta } \in \Delta $
incomparable with each of
![]() $\boldsymbol {\beta }$
,
$\boldsymbol {\beta }$
,
![]() $\boldsymbol {\gamma }$
and
$\boldsymbol {\gamma }$
and
![]() $\boldsymbol {\delta }$
, so that
$\boldsymbol {\delta }$
, so that
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\zeta })}^{{(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}}$
and
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\zeta })}^{{(\boldsymbol {\,\beta }\;\;\boldsymbol {\zeta })}}$
and
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} = {(\boldsymbol {\gamma }\;\;\boldsymbol {\theta })}^{{(\boldsymbol {\delta }\;\;\boldsymbol {\theta })}}$
. In the following calculation, all the transpositions manipulated have second entry either
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })} = {(\boldsymbol {\gamma }\;\;\boldsymbol {\theta })}^{{(\boldsymbol {\delta }\;\;\boldsymbol {\theta })}}$
. In the following calculation, all the transpositions manipulated have second entry either
![]() $\boldsymbol {\zeta }$
or
$\boldsymbol {\zeta }$
or
![]() $\boldsymbol {\theta }$
(selected from
$\boldsymbol {\theta }$
(selected from
![]() $\Delta $
):
$\Delta $
):
 $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})}} &= {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})}} \\ &= {(\boldsymbol{\theta\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})}} \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} = {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})}} &= {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})} \, {(\boldsymbol{\gamma}\;\;\boldsymbol{\theta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})}} \\ &= {(\boldsymbol{\theta\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})} \, {(\boldsymbol{\delta}\;\;\boldsymbol{\theta})}} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\zeta})}^{ {(\boldsymbol{\,\beta}\;\;\boldsymbol{\zeta})}} \end{align*} $$
and the latter is equal to
![]() ${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
. Cases (A), (C) and (D) of the conjugacy relations are established similarly.
${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
. Cases (A), (C) and (D) of the conjugacy relations are established similarly.
Finally, we establish all split relations in Equation (1-4) for this stage. If
![]() $(m,k) = (3,1)$
, then an arbitrary split relation has the form
$(m,k) = (3,1)$
, then an arbitrary split relation has the form
for incomparable
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Delta $
. This is deduced from Relation R6 by conjugating by a permutation
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Delta $
. This is deduced from Relation R6 by conjugating by a permutation
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\Delta )$
that moves
$\sigma \in \operatorname {\mathrm {Sym}}(\Delta )$
that moves
![]() $\boldsymbol {\delta }^{(0)}$
to
$\boldsymbol {\delta }^{(0)}$
to
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\delta }^{(1)}$
to
$\boldsymbol {\delta }^{(1)}$
to
![]() $\boldsymbol {\beta }$
. For the case when
$\boldsymbol {\beta }$
. For the case when
![]() $(m,k)> (3,1)$
, choose
$(m,k)> (3,1)$
, choose
![]() $\boldsymbol {\zeta }, \boldsymbol {\eta } \in \Delta $
such that every pair from
$\boldsymbol {\zeta }, \boldsymbol {\eta } \in \Delta $
such that every pair from
![]() $\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\zeta }, \boldsymbol {\eta } \}$
is incomparable. We have just established that
$\{ \boldsymbol {\alpha }, \boldsymbol {\beta }, \boldsymbol {\zeta }, \boldsymbol {\eta } \}$
is incomparable. We have just established that
![]() ${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })} = {(\boldsymbol {\zeta }.\boldsymbol {0}_{d}\;\;\boldsymbol {\eta }.\boldsymbol {0}_{d})} \, {(\boldsymbol {\zeta }.\boldsymbol {1}_{d}\;\;\boldsymbol {\eta }.\boldsymbol {1}_{d})}$
and we deduce the general case of Equation (1-4) by conjugating by
${(\boldsymbol {\zeta }\;\;\boldsymbol {\eta })} = {(\boldsymbol {\zeta }.\boldsymbol {0}_{d}\;\;\boldsymbol {\eta }.\boldsymbol {0}_{d})} \, {(\boldsymbol {\zeta }.\boldsymbol {1}_{d}\;\;\boldsymbol {\eta }.\boldsymbol {1}_{d})}$
and we deduce the general case of Equation (1-4) by conjugating by
![]() ${(\boldsymbol {\zeta }\;\;\boldsymbol {\alpha })} \, {(\boldsymbol {\eta }\;\;\boldsymbol {\beta })}$
and using the conjugacy relations in Equation (1-3) that we have already established.
${(\boldsymbol {\zeta }\;\;\boldsymbol {\alpha })} \, {(\boldsymbol {\eta }\;\;\boldsymbol {\beta })}$
and using the conjugacy relations in Equation (1-3) that we have already established.
3.4 Transpositions with short coordinates
We have now constructed all transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
with
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
with
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
and
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega ^{\ast }$
and
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, and demonstrated that all the required relations in Equations (1-2)–(1-4) (and also in Equation (1-5)) involving such transpositions hold in G. We complete the definitions by constructing the remaining transpositions
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, and demonstrated that all the required relations in Equations (1-2)–(1-4) (and also in Equation (1-5)) involving such transpositions hold in G. We complete the definitions by constructing the remaining transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
with
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
with
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega $
. Fix a sequence
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega $
. Fix a sequence
![]() $(k_{1},k_{2},\ldots ,k_{n})$
with each
$(k_{1},k_{2},\ldots ,k_{n})$
with each
![]() $k_{i} \in \{0,1,2\}$
. As an induction hypothesis, assume that we have constructed all transpositions
$k_{i} \in \{0,1,2\}$
. As an induction hypothesis, assume that we have constructed all transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, where
![]() $\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
and
$\boldsymbol {\alpha } = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})$
and
![]() $\boldsymbol {\beta } = (\,\beta _{1},\beta _{2},\ldots ,\beta _{n})$
are incomparable addresses satisfying
$\boldsymbol {\beta } = (\,\beta _{1},\beta _{2},\ldots ,\beta _{n})$
are incomparable addresses satisfying
![]() $\mathopen {|}\alpha _{i}\mathclose {|}, \mathopen {|}\,\beta _{i}\mathclose {|} \geqslant k_{i}$
for
$\mathopen {|}\alpha _{i}\mathclose {|}, \mathopen {|}\,\beta _{i}\mathclose {|} \geqslant k_{i}$
for
![]() $1 \leqslant i \leqslant d$
. (The ‘base case’ is
$1 \leqslant i \leqslant d$
. (The ‘base case’ is
![]() $(k_{1},k_{2},\ldots ,k_{n}) = (2,2,\ldots ,2)$
, for which our assumption follows from the steps just completed.) Select an index d with
$(k_{1},k_{2},\ldots ,k_{n}) = (2,2,\ldots ,2)$
, for which our assumption follows from the steps just completed.) Select an index d with
![]() $k_{d}> 0$
and for any pair of incomparable addresses
$k_{d}> 0$
and for any pair of incomparable addresses
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\beta }$
such that
$\boldsymbol {\beta }$
such that
![]() $\mathopen {|}\alpha _{i}\mathclose {|}, \mathopen {|}\,\beta _{i}\mathclose {|} \geqslant k_{i}$
for
$\mathopen {|}\alpha _{i}\mathclose {|}, \mathopen {|}\,\beta _{i}\mathclose {|} \geqslant k_{i}$
for
![]() $i \neq d$
and such that one, or possibly both, of
$i \neq d$
and such that one, or possibly both, of
![]() $\alpha _{d}$
or
$\alpha _{d}$
or
![]() $\beta _{d}$
has length
$\beta _{d}$
has length
![]() $k_{d}-1$
, define
$k_{d}-1$
, define
Both transpositions on the right-hand side exist by our assumption. Furthermore, the transpositions on the right-hand satisfy the relations in Equations (1-2) and (1-5) and commute. It follows that
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })}$
and
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })} = {(\boldsymbol {\,\beta }\;\;\boldsymbol {\alpha })}$
and
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}^{2} = 1$
. Conjugacy relations are established similarly to earlier steps, namely by considering cases (A)–(D) of Lemma 3.1. The method is the same for each case. For example, consider a case (B) conjugacy relation; that is, one of the form
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}^{2} = 1$
. Conjugacy relations are established similarly to earlier steps, namely by considering cases (A)–(D) of Lemma 3.1. The method is the same for each case. For example, consider a case (B) conjugacy relation; that is, one of the form
where some entry here has its d th coordinate of length
![]() $k_{d}-1$
. We may assume the entry with this shorter coordinate is either
$k_{d}-1$
. We may assume the entry with this shorter coordinate is either
![]() $\boldsymbol {\gamma }$
(and possibly also
$\boldsymbol {\gamma }$
(and possibly also
![]() $\boldsymbol {\gamma \eta }$
) or
$\boldsymbol {\gamma \eta }$
) or
![]() $\boldsymbol {\beta }$
. If the d th coordinate of
$\boldsymbol {\beta }$
. If the d th coordinate of
![]() $\boldsymbol {\gamma }$
has length
$\boldsymbol {\gamma }$
has length
![]() $k_{d}-1$
and that of
$k_{d}-1$
and that of
![]() $\boldsymbol {\eta }$
is empty, then we use Equation (3-6) for both
$\boldsymbol {\eta }$
is empty, then we use Equation (3-6) for both
![]() ${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}$
and
${(\boldsymbol {\gamma \eta }\;\;\boldsymbol {\beta })}$
and
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
. Note then
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
. Note then
![]() $\boldsymbol {\eta }.\kern1pt\boldsymbol{x}_{d} = \boldsymbol {x}_{d}.\boldsymbol {\eta }$
for
$\boldsymbol {\eta }.\kern1pt\boldsymbol{x}_{d} = \boldsymbol {x}_{d}.\boldsymbol {\eta }$
for
![]() $x \in \{0,1\}$
, which permits us to calculate the following conjugate:
$x \in \{0,1\}$
, which permits us to calculate the following conjugate:
 $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} &= ( {(\boldsymbol{\gamma\eta}.\boldsymbol{0}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\gamma\eta}.\boldsymbol{1}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} )^{ {(\boldsymbol{\gamma}.\boldsymbol{0}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\gamma}.\boldsymbol{1}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{1}_{d})}} \\ &= {(\boldsymbol{\delta\eta}.\boldsymbol{0}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\delta\eta}.\boldsymbol{1}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}, \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} &= ( {(\boldsymbol{\gamma\eta}.\boldsymbol{0}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\gamma\eta}.\boldsymbol{1}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} )^{ {(\boldsymbol{\gamma}.\boldsymbol{0}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\gamma}.\boldsymbol{1}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{1}_{d})}} \\ &= {(\boldsymbol{\delta\eta}.\boldsymbol{0}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\delta\eta}.\boldsymbol{1}_{d}\;\;\boldsymbol{\beta}.\boldsymbol{1}_{d})} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}, \end{align*} $$
relying upon relations that hold by the inductive assumption. The last step is either one of these assumed relations or is the definition of
![]() ${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
if it is the case that the d th coordinate of
${(\boldsymbol {\delta \eta }\;\;\boldsymbol {\beta })}$
if it is the case that the d th coordinate of
![]() $\boldsymbol {\beta }$
or
$\boldsymbol {\beta }$
or
![]() $\boldsymbol {\delta }$
has length
$\boldsymbol {\delta }$
has length
![]() $k_{d}-1$
. Alternatively, if the d th coordinate of
$k_{d}-1$
. Alternatively, if the d th coordinate of
![]() $\boldsymbol {\gamma }$
has length
$\boldsymbol {\gamma }$
has length
![]() $k_{d}-1$
and that of
$k_{d}-1$
and that of
![]() $\boldsymbol {\eta }$
is nonempty, write
$\boldsymbol {\eta }$
is nonempty, write
![]() $\boldsymbol {\eta } = \boldsymbol {x}_{d}.\hat {\boldsymbol {\eta }}$
for some
$\boldsymbol {\eta } = \boldsymbol {x}_{d}.\hat {\boldsymbol {\eta }}$
for some
![]() $x \in \{0,1\}$
and some (possibly empty)
$x \in \{0,1\}$
and some (possibly empty)
![]() $\hat {\boldsymbol {\eta }} \in \Omega $
. In this case, we use Equation (3-6) for the definition of
$\hat {\boldsymbol {\eta }} \in \Omega $
. In this case, we use Equation (3-6) for the definition of
![]() ${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and calculate
${(\boldsymbol {\gamma }\;\;\boldsymbol {\delta })}$
and calculate
 $$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} &= {(\boldsymbol{\gamma}.\kern1pt\boldsymbol{x}_{d}.\hat{\boldsymbol{\eta}}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}.\boldsymbol{0}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\gamma}.\boldsymbol{1}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{1}_{d})}} \\ &= {(\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{d}.\hat{\boldsymbol{\eta}}\;\;\boldsymbol{\beta})} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
$$ \begin{align*} {(\boldsymbol{\gamma\eta}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}\;\;\boldsymbol{\delta})}} &= {(\boldsymbol{\gamma}.\kern1pt\boldsymbol{x}_{d}.\hat{\boldsymbol{\eta}}\;\;\boldsymbol{\beta})}^{ {(\boldsymbol{\gamma}.\boldsymbol{0}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{0}_{d})} \, {(\boldsymbol{\gamma}.\boldsymbol{1}_{d}\;\;\boldsymbol{\delta}.\boldsymbol{1}_{d})}} \\ &= {(\boldsymbol{\delta}.\kern1pt\boldsymbol{x}_{d}.\hat{\boldsymbol{\eta}}\;\;\boldsymbol{\beta})} = {(\boldsymbol{\delta\eta}\;\;\boldsymbol{\beta})}. \end{align*} $$
Conjugacy relations in case (B), where the d th coordinate of
![]() $\boldsymbol {\beta }$
has length
$\boldsymbol {\beta }$
has length
![]() $k_{d}-1$
, and those in cases (A), (C) and (D) are established similarly. Finally, the split relations in Equation (1-4) involving the transpositions defined in Equation (3-6) are either simply that definition or are inherited from split relations for the terms on the right-hand side of that formula.
$k_{d}-1$
, and those in cases (A), (C) and (D) are established similarly. Finally, the split relations in Equation (1-4) involving the transpositions defined in Equation (3-6) are either simply that definition or are inherited from split relations for the terms on the right-hand side of that formula.
It now follows, using this step repeatedly, that we have constructed transpositions
![]() ${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, for
${(\boldsymbol {\alpha }\;\;\boldsymbol {\beta })}$
, for
![]() $\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega $
with
$\boldsymbol {\alpha }, \boldsymbol {\beta } \in \Omega $
with
![]() $\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, in the group G and verified all relations in Equations (1-2)–(1-4) involving these transpositions. Consequently, by Theorem 1.1, there is a homomorphism
$\boldsymbol {\alpha } \perp \boldsymbol {\beta }$
, in the group G and verified all relations in Equations (1-2)–(1-4) involving these transpositions. Consequently, by Theorem 1.1, there is a homomorphism
![]() $\phi \colon nV \to G$
mapping each transposition in
$\phi \colon nV \to G$
mapping each transposition in
![]() $nV$
to the corresponding element that we have defined in G. Moreover, Relation R7 tells us that the generator c is in the image of
$nV$
to the corresponding element that we have defined in G. Moreover, Relation R7 tells us that the generator c is in the image of
![]() $\phi $
and hence G is isomorphic to a quotient of
$\phi $
and hence G is isomorphic to a quotient of
![]() $nV$
. However, all Relations R1–R7 listed are satisfied by the corresponding elements of
$nV$
. However, all Relations R1–R7 listed are satisfied by the corresponding elements of
![]() $nV$
and so there is a homomorphism from G into
$nV$
and so there is a homomorphism from G into
![]() $nV$
with nontrivial image. The fact that
$nV$
with nontrivial image. The fact that
![]() $nV$
is simple therefore yields
$nV$
is simple therefore yields
![]() $G \cong nV$
, completing the proof of Theorem 1.2.
$G \cong nV$
, completing the proof of Theorem 1.2.
Proof of Corollary 1.3.
The subgroup
![]() $H = \langle a,b \rangle \cong \operatorname {\mathrm {Sym}}(\Delta )$
of G can be generated by a cycle x of length
$H = \langle a,b \rangle \cong \operatorname {\mathrm {Sym}}(\Delta )$
of G can be generated by a cycle x of length
![]() $4^{n}$
and a transposition t that can be assumed disjoint from c (as described via Relation R7). Note that c has odd order. Therefore, c and t are powers of
$4^{n}$
and a transposition t that can be assumed disjoint from c (as described via Relation R7). Note that c has odd order. Therefore, c and t are powers of
![]() $y = ct$
and
$y = ct$
and
![]() $\{ x, y \}$
is a generating set for G. Applying Tietze transformations to produce a presentation on generators x and y introduces two additional relations. This establishes the corollary.
$\{ x, y \}$
is a generating set for G. Applying Tietze transformations to produce a presentation on generators x and y introduces two additional relations. This establishes the corollary.
Acknowledgements
The author thanks Collin Bleak for introducing him to Brin’s family of groups
![]() $nV$
, suggesting this project for investigation and for various helpful comments. It should also be recorded that the fact that
$nV$
, suggesting this project for investigation and for various helpful comments. It should also be recorded that the fact that
![]() $nV$
can be generated by two elements, as appears in the proof of Corollary 1.3, was originally observed in collaboration with Bleak. The author also thanks Prof. Brin for his comments on a draft of this article and a referee of an earlier version for their helpful suggestions.
$nV$
can be generated by two elements, as appears in the proof of Corollary 1.3, was originally observed in collaboration with Bleak. The author also thanks Prof. Brin for his comments on a draft of this article and a referee of an earlier version for their helpful suggestions.