Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-16T16:34:51.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing time bounds for edge flipping on regular graphs

Part of: Limit theorems Combinatorial probability Stochastic processes

Published online by Cambridge University Press:  26 April 2023

Yunus Emre Demirci ,
Ümit Işlak  and
Alperen Özdemir Open the ORCID record for Alperen Özdemir [Opens in a new window]
Yunus Emre Demirci*
Affiliation:
Queen’s University
Ümit Işlak*
Affiliation:
Boğaziçi University
Alperen Özdemir*
Affiliation:
Georgia Institute of Technology
*
*Postal address: Queen’s University, Department of Mathematics and Statistics, Kingston, Ontario, Canada. Email: [email protected]
**Postal address: Boğaziçi University, Department of Mathematics, Istanbul, Turkey. Email: [email protected]
***Postal address: Georgia Institute of Technology, School of Mathematics, Atlanta, GA, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An edge flipping is a non-reversible Markov chain on a given connected graph, as defined in Chung and Graham (2012). In the same paper, edge flipping eigenvalues and stationary distributions for some classes of graphs were identified. We further study edge flipping spectral properties to show a lower bound for the rate of convergence in the case of regular graphs. Moreover, we show by a coupling argument that a cutoff occurs at 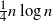$\frac{1}{4} n \log n$ for the edge flipping on the complete graph.

Keywords

Couplingedge flippinghyperplane arrangementsMarkov chainsregular graphs

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 60F05: Central limit and other weak theorems 60G42: Martingales with discrete parameter
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 4 , December 2023 , pp. 1317 - 1332
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athanasiadis, C. A. and Diaconis, P. (2010). Functions of random walks on hyperplane arrangements. Adv. Appl. Math. 45, 410–437.Google Scholar
Basu, R., Hermon, J. and Peres, Y. (2017). Characterization of cutoff for reversible Markov chains. Ann. Prob. 45, 1448–1487.CrossRefGoogle Scholar
Bidigare, P., Hanlon, P. and Rockmore, D. (1999). A combinatorial description of the spectrum for the Tsetlin library and its generalization to hyperplane arrangements. Duke Math. J. 99, 135–174.CrossRefGoogle Scholar
Brown, K. (2000). Semigroups, rings, and Markov chains. J. Theoret. Prob. 13, 871–928.Google Scholar
Brown, K. and Diaconis, P. (1998). Random walks and hyperplane arrangements. Ann. Prob. 26, 1813–1854.Google Scholar
Butler, S., Chung, F., Cummings, J. and Graham, R. (2015). Edge flipping in the complete graph. Adv. Appl. Math. 69, 46–64.CrossRefGoogle Scholar
Chung, F. and Graham, R. (2012). Edge flipping in graphs. Adv. Appl. Math. 48, 37–63.Google Scholar
Chung, F. and Hughes, J. (2014). A note on an alternating upper bound for random walks on semigroups. Discrete Appl. Math. 176, 24–29.CrossRefGoogle Scholar
Feller, W. (1968). Introduction to Probability and its Applications, Vol. 17. Wiley, Chichester.Google Scholar
Grimmett, G. and Stirzaker, D. (2020). Probability and Random Processes. Oxford University Press.Google Scholar
Levin, D. A., Peres, Y. and Wilmer, E. L. (2009). Markov Chains and Mixing Time. AMS, Providence, RI.Google Scholar
Nestoridi, E. (2017). A non-local random walk on the hypercube. Adv. Appl. Prob. 49, 1288–1299.CrossRefGoogle Scholar
Nestoridi, E. (2019). Optimal strong stationary times for random walks on the chambers of a hyperplane arrangement. Prob. Theory Relat. Fields 174, 929–943.Google Scholar
Pike, J. (2013). Eigenfunctions for random walks on hyperplane arrangements. PhD thesis, University of Southern California.Google Scholar
Salez, J. (2021). Cutoff for non-negatively curved Markov chains. Preprint, arXiv:2102.05597.Google Scholar
Saliola, F. (2012). Eigenvectors for a random walk on a left-regular band. Adv. Appl. Math. 48, 306–311.Google Scholar
Stanley, R. P. (2007). An introduction to hyperplane arrangements. Geom. Combinatorics 13, 389–496.Google Scholar
Wilson, D. B. (2004). Mixing times of lozenge tiling and card shuffling Markov chains. Ann. Appl. Prob. 14, 274–325.Google Scholar