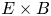1 Introduction
Non-neutral plasmas (Malmberg & deGrassie Reference Malmberg and deGrassie1975; Davidson Reference Davidson2001) have a wide range of applications in basic science and technology (Davidson Reference Davidson2001; Danielson et al. Reference Danielson, Dubin, Greaves and Surko2015). A recent review (Fajans & Surko Reference Fajans and Surko2020) describes the numerous techniques, developed over decades, for the manipulation of antimatter plasmas, with applications to positron emission tomography, material studies, positronium atoms and molecules, and antihydrogen formation.
Confinement of non-neutral plasmas is often realized in Penning–Malmberg (PM) traps (Malmberg & deGrassie Reference Malmberg and deGrassie1975). In a PM trap, transverse confinement is provided by an axial magnetic field, while longitudinal confinement and transport are controlled by manipulating the voltages on a series of cylindrical electrodes.
It was shown by O'Neil (Reference O'Neil1980) that if the canonical angular momentum of the plasma is dominated by the magnetic field contribution, azimuthally symmetric PM traps are subject to a confinement theorem that constrains radial particle transport. In this case, the total canonical angular momentum of the plasma is approximately given by
where $q$![]() is the elementary charge of the plasma species, $B$
is the elementary charge of the plasma species, $B$![]() is the axial magnetic field and $r_i$
is the axial magnetic field and $r_i$![]() is the distance of particle $i$
is the distance of particle $i$![]() from the trap axis. Azimuthal symmetry requires that the angular momentum is conserved and thus, absent of any external torques, the mean-squared radius of a magnetized non-neutral plasma must be conserved. This confinement theorem predicts very long plasma lifetimes, although in experiments, slow expansion is observed due to non-ideal trap effects. Collisions with residual background gas particles drive radial transport and limit confinement time (deGrassie & Malmberg Reference deGrassie and Malmberg1980), in agreement with theory (O'Neil Reference O'Neil1980) at high background pressure. However, radial expansion did not follow the expected behaviour as the background pressure was reduced (Driscoll, Fine & Malmberg Reference Driscoll, Fine and Malmberg1986); this was attributed (Driscoll et al. Reference Driscoll, Fine and Malmberg1986) to azimuthal asymmetries in the magnetic or electric confinement system.
from the trap axis. Azimuthal symmetry requires that the angular momentum is conserved and thus, absent of any external torques, the mean-squared radius of a magnetized non-neutral plasma must be conserved. This confinement theorem predicts very long plasma lifetimes, although in experiments, slow expansion is observed due to non-ideal trap effects. Collisions with residual background gas particles drive radial transport and limit confinement time (deGrassie & Malmberg Reference deGrassie and Malmberg1980), in agreement with theory (O'Neil Reference O'Neil1980) at high background pressure. However, radial expansion did not follow the expected behaviour as the background pressure was reduced (Driscoll, Fine & Malmberg Reference Driscoll, Fine and Malmberg1986); this was attributed (Driscoll et al. Reference Driscoll, Fine and Malmberg1986) to azimuthal asymmetries in the magnetic or electric confinement system.
A major advance in reaching long confinement times was achieved with the development (Huang et al. Reference Huang, Anderegg, Hollmann, Driscoll and O'Neil1997) of rotating wall (RW) compression. In the RW scheme, phased voltages are applied to an azimuthally sectored electrode to create a rotating electric field at the plasma. This field exerts a torque which changes the plasma angular momentum and does work on the plasma. We consider here the case where the RW frequency exceeds the plasma rotation frequency, corresponding to a final plasma state which is compressed. The plasma heats and cools during the compression, with the heating provided by the RW doing work on the plasma and the cooling provided by electron cyclotron emission. Rotating wall compression has been developed and exploited to control ion (with buffer gas cooling), electron and positron plasmas (Huang et al. Reference Huang, Bollinger, Mitchell, Itano and Dubin1998; Greaves & Surko Reference Greaves and Surko2000; Hollmann, Anderegg & Driscoll Reference Hollmann, Anderegg and Driscoll2000; Danielson & Surko Reference Danielson and Surko2005, Reference Danielson and Surko2006; Greaves & Moxom Reference Greaves and Moxom2008; Isaac et al. Reference Isaac, Baker, Mortensen, van der Werf and Charlton2011). It is now routinely used to both improve confinement and increase plasma densities (Fajans & Surko Reference Fajans and Surko2020).
In initial experiments, the coupling of the RW to the plasma was through Trivelpiece– Gould modes (Soga et al. Reference Soga, Kiwamoto, Sanpei and Aoki2003). These modes, in turn, couple to the bulk plasma via collisions and Landau damping. An alternative to the Trivelpiece–Gould coupling is known as the strong-drive regime, which is the focus of this paper. In this regime, the plasma rotation frequency almost catches up to the rotating wall frequency. Earlier papers have investigated strong-drive compression (Kiwamoto, Soga & Aoki Reference Kiwamoto, Soga and Aoki2005; Danielson, Surko & O'Neil Reference Danielson, Surko and O'Neil2007; van der Werf et al. Reference van der Werf, Isaac, Baker, Mortensen and Charlton2012). The single-particle limit was explored by van der Werf et al. (Reference van der Werf, Isaac, Baker, Mortensen and Charlton2012), a simplified torque-balance model was used to study the relation between the initial and final plasma states by Danielson et al. (Reference Danielson, Surko and O'Neil2007), and Kiwamoto et al. (Reference Kiwamoto, Soga and Aoki2005) developed a drift kinetic model, similar to what is used here, to evaluate the coupling of the RW to the plasma. In this paper, we use the ansatz that the system can be described at any time by a slowly evolving thermal equilibrium and derive a full set of coupled equations by combining equilibrium thermodynamics with the drift kinetic equation.
The key assumptions of our model are that: (i) the RW torque is generated by coupling to particles that are resonant with the RW wave (i.e. the combined $E\times B$![]() and axial motion of the particles allows them to remain in phase with the RW wave); (ii) the resonant particle coupling causes a weak perturbation to the Vlasov distribution function; (iii) the plasma evolves slowly, remaining in thermal equilibrium as the density increases and the temperature evolves; (iv) the total potential used to find the torque is calculated self-consistently; and (v) the particles lose energy via cyclotron emission. The assumptions (i) and (ii) allow us to calculate the evolution equations for the plasma temperature and rotation frequency, and use linear kinetic theory to evaluate the torque generated by resonant coupling. Under these assumptions, we avoid having to explicitly calculate any collisional integrals.
and axial motion of the particles allows them to remain in phase with the RW wave); (ii) the resonant particle coupling causes a weak perturbation to the Vlasov distribution function; (iii) the plasma evolves slowly, remaining in thermal equilibrium as the density increases and the temperature evolves; (iv) the total potential used to find the torque is calculated self-consistently; and (v) the particles lose energy via cyclotron emission. The assumptions (i) and (ii) allow us to calculate the evolution equations for the plasma temperature and rotation frequency, and use linear kinetic theory to evaluate the torque generated by resonant coupling. Under these assumptions, we avoid having to explicitly calculate any collisional integrals.
2 Thermal equilibrium model for rotating wall compression
In this section, a complete derivation of our RW model is given. In § 2.1, we derive the equations of motion (EOM) starting from thermodynamic considerations and incorporating Vlasov dynamics. In § 2.2, we find explicit expressions for the energy and angular momentum in terms of thermodynamic state variables (temperature and plasma rotation frequency). In § 2.3, we use drift kinetic theory to derive the torque that the RW imparts to the plasma. We use cgs units throughout and set $k_B = 1$![]() .
.
2.1 Thermodynamic equations for compression
In this model, we consider a cylindrical pure electron plasma in thermal equilibrium, confined to a PM trap with an axial magnetic field $\boldsymbol {B} = B\hat {z}$![]() . The state variables of the plasma are its temperature $T$
. The state variables of the plasma are its temperature $T$![]() and rotational (angular) velocity $\omega _r$
and rotational (angular) velocity $\omega _r$![]() . We neglect finite-length effects by modelling a plasma of physical length $L_p$
. We neglect finite-length effects by modelling a plasma of physical length $L_p$![]() as infinite and periodic, with periodicity length $\mathcal {L}_p = 2L_p$
as infinite and periodic, with periodicity length $\mathcal {L}_p = 2L_p$![]() (Eggleston & O'Neil Reference Eggleston and O'Neil1999). All integrals along the $z$
(Eggleston & O'Neil Reference Eggleston and O'Neil1999). All integrals along the $z$![]() -axis in this paper are understood to be over one periodic cell, $-L_p \leq z \leq L_p$
-axis in this paper are understood to be over one periodic cell, $-L_p \leq z \leq L_p$![]() .
.
Electron dynamics follows from the single-particle (sp) Hamiltonian
with
where $m_e$![]() is the electron mass, $q=-e$
is the electron mass, $q=-e$![]() is the electron charge, $\varOmega _c = {qB}/{m_e c}$
is the electron charge, $\varOmega _c = {qB}/{m_e c}$![]() is the (signed) cyclotron frequency, $c$
is the (signed) cyclotron frequency, $c$![]() is the speed of light and $\phi _0(r; T, \omega _r)$
is the speed of light and $\phi _0(r; T, \omega _r)$![]() is the mean-field electrostatic potential of the plasma. The electrostatic potential depends on the radial density profile, which, given a fixed number of electrons in the trap, is uniquely determined, and in equilibrium, on the plasma temperature and rotation frequency. The explicit dependence on the thermodynamic state variables following the semicolon (e.g. $\phi _0(r;T,\omega _r)$
is the mean-field electrostatic potential of the plasma. The electrostatic potential depends on the radial density profile, which, given a fixed number of electrons in the trap, is uniquely determined, and in equilibrium, on the plasma temperature and rotation frequency. The explicit dependence on the thermodynamic state variables following the semicolon (e.g. $\phi _0(r;T,\omega _r)$![]() ) is a reminder that we are considering equilibrium quantities that evolve by virtue of the plasma transitioning between thermal equilibrium states during compression.
) is a reminder that we are considering equilibrium quantities that evolve by virtue of the plasma transitioning between thermal equilibrium states during compression.
Though we consider only pure electron plasmas in this paper, our analysis naturally extends to positron plasmas. To facilitate this extension, we use a sign convention that readily encompasses both signs of charge. For a magnetic field pointing along $+\hat {z}$![]() , a positively charged plasma column will rotate in the $-\hat {\theta }$
, a positively charged plasma column will rotate in the $-\hat {\theta }$![]() direction under its $E\times B$
direction under its $E\times B$![]() drift. This makes the rotational angular velocity negative, $\omega _r<0$
drift. This makes the rotational angular velocity negative, $\omega _r<0$![]() , for charges with $q>0$
, for charges with $q>0$![]() . Other angular rotation frequencies follow the same convention. To summarize our sign conventions, for $q>0$
. Other angular rotation frequencies follow the same convention. To summarize our sign conventions, for $q>0$![]() , we have $\varOmega _c>0$
, we have $\varOmega _c>0$![]() , $\omega _r<0$
, $\omega _r<0$![]() and $p_\theta >0$
and $p_\theta >0$![]() (when strongly magnetized), while for $q<0$
(when strongly magnetized), while for $q<0$![]() , we have $\varOmega _c<0$
, we have $\varOmega _c<0$![]() , $\omega _r>0$
, $\omega _r>0$![]() and $p_\theta <0$
and $p_\theta <0$![]() (when strongly magnetized).
(when strongly magnetized).
The distribution function of the plasma is (using the above sign conventions)
The constant $\mathcal {Z}$![]() is determined by normalizing the distribution function to the total number of electrons in a periodic cell,
is determined by normalizing the distribution function to the total number of electrons in a periodic cell,
where $\mathcal {N}_e$![]() is the line density of electrons along the axis.
is the line density of electrons along the axis.
The equilibrium density $n_0(r; T, \omega _r)$![]() is given by
is given by
where $n_0(0; T, \omega _r)$![]() is the on-axis density. The function $\psi (r;T)$
is the on-axis density. The function $\psi (r;T)$![]() (see Dubin & O'Neil Reference Dubin and O'Neil1999) combines the electrostatic and centrifugal potentials:
(see Dubin & O'Neil Reference Dubin and O'Neil1999) combines the electrostatic and centrifugal potentials:
The Poisson equation can then be written as
with
The rotating wall perturbs the plasma out of equilibrium:
Our model avoids explicit calculations involving collisional operators even though the time scale for cooling is much longer than the collision time. This is accomplished by assuming that thermalization via collisions occurs sufficiently rapidly so that the plasma evolves through thermal equilibrium states defined by the average energy $\langle E\rangle$![]() and average angular momentum $\langle \,p_\theta \rangle$
and average angular momentum $\langle \,p_\theta \rangle$![]() . The temporal evolution of these states is found by matching the same quantities computed for the perturbed plasma after the RW perturbation has been active for a small time $\Delta t$
. The temporal evolution of these states is found by matching the same quantities computed for the perturbed plasma after the RW perturbation has been active for a small time $\Delta t$![]() .
.
Explicitly, consider the energy and angular momentum functionals
where, since $\phi$![]() is the self-field, the factor of 1/2 in the energy is necessary to avoid double-counting. In thermal equilibrium, these functionals become ordinary functions of the state variables:
is the self-field, the factor of 1/2 in the energy is necessary to avoid double-counting. In thermal equilibrium, these functionals become ordinary functions of the state variables:
Our equilibration assumption is
where $f(t_0+\Delta t)$![]() is the equilibrium distribution at $t_0$
is the equilibrium distribution at $t_0$![]() , $f(t_0)\equiv f_0$
, $f(t_0)\equiv f_0$![]() , evolved with the Vlasov equation to time $t=t_0+\Delta t$
, evolved with the Vlasov equation to time $t=t_0+\Delta t$![]() and $\phi (t_0+\Delta t)$
and $\phi (t_0+\Delta t)$![]() is the corresponding total self-consistent potential. Expanding to linear order and dividing through by $\Delta t$
is the corresponding total self-consistent potential. Expanding to linear order and dividing through by $\Delta t$![]() gives
gives
where, on the left-hand side, ${{\rm d}}/{{\rm d} t} = \dot {T}({\partial }/{\partial T}) + \dot {\omega }_r({\partial }/{\partial \omega _r})$![]() .
.
Integrals of the form
can be simplified with the Vlasov equation,
where
is the full Hamiltonian. Inserting (2.15) into (2.14) and integrating by parts to pull derivatives off of $f$![]() yields:
yields:
The second derivatives of $H$![]() cancel and we proceed to evaluate the remaining expressions with $g=p_\theta$
cancel and we proceed to evaluate the remaining expressions with $g=p_\theta$![]() and $g=K + \frac {1}{2}q\phi _0$
and $g=K + \frac {1}{2}q\phi _0$![]() .
.
For $g=p_\theta$![]() , we have
, we have

For $g=K + \frac {1}{2}q\phi _0$![]() , the terms ${\partial K}/{\partial \boldsymbol {r}}\boldsymbol {\cdot } {\partial K}/{\partial \boldsymbol {p}}$
, the terms ${\partial K}/{\partial \boldsymbol {r}}\boldsymbol {\cdot } {\partial K}/{\partial \boldsymbol {p}}$![]() cancel. Furthermore, none of the potential terms depend on $\boldsymbol {p}$
cancel. Furthermore, none of the potential terms depend on $\boldsymbol {p}$![]() , so that only remaining terms are
, so that only remaining terms are
Since $\phi _0$![]() only has radial dependence, we find
only has radial dependence, we find
To find a closed set of equations, we use linear theory to approximate the evolution of $f$![]() and $\delta \phi$
and $\delta \phi$![]() . With $f=f_0+\delta f$
. With $f=f_0+\delta f$![]() in (2.20), terms with only a single perturbed quantity vanish upon azimuthal integration because the equilibrium is azimuthally symmetric and the perturbations are linear combinations of non-zero azimuthal modes. The same argument applies to the $({\partial \phi }/{\partial t})f_0=({\partial (\delta \phi )}/{\partial t})f_0$
in (2.20), terms with only a single perturbed quantity vanish upon azimuthal integration because the equilibrium is azimuthally symmetric and the perturbations are linear combinations of non-zero azimuthal modes. The same argument applies to the $({\partial \phi }/{\partial t})f_0=({\partial (\delta \phi )}/{\partial t})f_0$![]() term in (2.13a), which thus also vanishes. Terms that are the product of two perturbations (i.e. both $\delta \phi$
term in (2.13a), which thus also vanishes. Terms that are the product of two perturbations (i.e. both $\delta \phi$![]() and $\delta f$
and $\delta f$![]() ) can be non-zero after azimuthal integration. There is also one term without any perturbations: $\int f_0(({p_r}/{2m_e})({\partial (q\phi _0)}/{\partial r}))\,{\rm d}^3\boldsymbol {r}\,{\rm d}^3\boldsymbol {p}$
) can be non-zero after azimuthal integration. There is also one term without any perturbations: $\int f_0(({p_r}/{2m_e})({\partial (q\phi _0)}/{\partial r}))\,{\rm d}^3\boldsymbol {r}\,{\rm d}^3\boldsymbol {p}$![]() ; this terms vanishes because $f_0$
; this terms vanishes because $f_0$![]() is Gaussian in $p_r$
is Gaussian in $p_r$![]() , making the full integrand odd in $p_r$
, making the full integrand odd in $p_r$![]() .
.
Putting everything together, we have
Note that ${\partial K}/{\partial \boldsymbol {p}} = {\partial \mathcal {H}_{{\rm sp}}}/{\partial \boldsymbol {p}}=\dot {\boldsymbol {r}}$![]() since the potential term has no momentum dependence. Thus, ${\partial K}/{\partial \boldsymbol {p}}\boldsymbol {\cdot } {\partial (q\delta \phi )}/{\partial \boldsymbol {r}} = \dot {r}({\partial (q\delta \phi )}/{\partial r}) + \dot {z}({\partial (q\delta \phi )}/{\partial z}) + \dot {\theta }({\partial (q\delta \phi )}/{\partial \theta })$
since the potential term has no momentum dependence. Thus, ${\partial K}/{\partial \boldsymbol {p}}\boldsymbol {\cdot } {\partial (q\delta \phi )}/{\partial \boldsymbol {r}} = \dot {r}({\partial (q\delta \phi )}/{\partial r}) + \dot {z}({\partial (q\delta \phi )}/{\partial z}) + \dot {\theta }({\partial (q\delta \phi )}/{\partial \theta })$![]() . We neglect the first term because it is proportional to the inverse of the compression time scale ($\dot {r}\partial \delta \phi /\partial r\sim \delta \phi /\tau _{{\rm comp}}\ll \dot {\theta }\partial \delta \phi /\partial \theta \sim \omega _r\delta \phi$
. We neglect the first term because it is proportional to the inverse of the compression time scale ($\dot {r}\partial \delta \phi /\partial r\sim \delta \phi /\tau _{{\rm comp}}\ll \dot {\theta }\partial \delta \phi /\partial \theta \sim \omega _r\delta \phi$![]() ). We neglect the second term because it describes the heating of particles resonant with the RW wave as their distribution flattens in a process akin to nonlinear Landau damping, which will not occur assuming that thermalization is rapid enough to maintain thermal equilibrium during compression. Since the plasma rotates coherently in equilibrium, we have $\dot {\theta }=\omega _r={\rm const.}$
). We neglect the second term because it describes the heating of particles resonant with the RW wave as their distribution flattens in a process akin to nonlinear Landau damping, which will not occur assuming that thermalization is rapid enough to maintain thermal equilibrium during compression. Since the plasma rotates coherently in equilibrium, we have $\dot {\theta }=\omega _r={\rm const.}$![]() and we can move $\omega _r$
and we can move $\omega _r$![]() outside the integral.
outside the integral.
Electrons cool via cyclotron emission and are heated by a thermal reservoir at temperature $T_{{\rm res}.}$![]() . We account for this by subtracting the term $({1}/{\tau _R})(T - T_{{\rm res}.})$
. We account for this by subtracting the term $({1}/{\tau _R})(T - T_{{\rm res}.})$![]() in the EOM for $\langle E\rangle$
in the EOM for $\langle E\rangle$![]() , where $\tau _R = {9 m_e c^3}/{8q^2\varOmega _c^2}$
, where $\tau _R = {9 m_e c^3}/{8q^2\varOmega _c^2}$![]() is the time scale for cyclotron radiation (Beck, Fajans & Malmberg Reference Beck, Fajans and Malmberg1996).
is the time scale for cyclotron radiation (Beck, Fajans & Malmberg Reference Beck, Fajans and Malmberg1996).
Lastly, we add a phenomenological drag torque $\tau _{{\rm dr}}$![]() and its corresponding heating or cooling term $P_{{\rm dr}}$
and its corresponding heating or cooling term $P_{{\rm dr}}$![]() . If the drag torque can be modelled with a potential perturbation in a manner similar to the RW torque, then $P_{{\rm dr}}=\tau _{{\rm dr}}\omega _r$
. If the drag torque can be modelled with a potential perturbation in a manner similar to the RW torque, then $P_{{\rm dr}}=\tau _{{\rm dr}}\omega _r$![]() , but in more general cases (such as collisions with background gas particles deGrassie & Malmberg Reference deGrassie and Malmberg1980), the two quantities are independent.
, but in more general cases (such as collisions with background gas particles deGrassie & Malmberg Reference deGrassie and Malmberg1980), the two quantities are independent.
Our full system of equations is then
where the last line introduces the average torque acting on the plasma.
We pause here to remark about the signs of various terms. Recall from our sign conventions in § 2.1 that electrons ($q<0$![]() ) have $\omega _r>0$
) have $\omega _r>0$![]() and $\langle \,p_\theta \rangle \sim qB\sum _i r_i^2<0$
and $\langle \,p_\theta \rangle \sim qB\sum _i r_i^2<0$![]() . For the plasma to compress, we need $\langle \,p _{\theta }\rangle$
. For the plasma to compress, we need $\langle \,p _{\theta }\rangle$![]() to become less negative (smaller $\sum _i r_i^2$
to become less negative (smaller $\sum _i r_i^2$![]() ), which requires a positive torque according to (2.22b). A positive torque and rotation frequency in turn means the first term of (2.22a) is positive, leading to energy gain and heating. This is the expected behaviour since the RW torque does work on the plasma to compress it. For $q>0$
), which requires a positive torque according to (2.22b). A positive torque and rotation frequency in turn means the first term of (2.22a) is positive, leading to energy gain and heating. This is the expected behaviour since the RW torque does work on the plasma to compress it. For $q>0$![]() (e.g. positrons), the signs are reversed: $\omega _r<0$
(e.g. positrons), the signs are reversed: $\omega _r<0$![]() , $\langle \,p_\theta \rangle >0$
, $\langle \,p_\theta \rangle >0$![]() , $\langle \tau \rangle <0$
, $\langle \tau \rangle <0$![]() , but as expected, the first term of (2.22a) remains positive since the RW still does work to compress the plasma.
, but as expected, the first term of (2.22a) remains positive since the RW still does work to compress the plasma.
Next, we rewrite (2.22a) and (2.22b) using the dimensionless variables
where $\omega _{{\rm RW}}$![]() is the angular rotation frequency of the rotating wall (the sign of $\omega _{{\rm RW}}$
is the angular rotation frequency of the rotating wall (the sign of $\omega _{{\rm RW}}$![]() will depend on the direction of rotation, but to compress electrons, we need $\omega _{{\rm RW}}>0$
will depend on the direction of rotation, but to compress electrons, we need $\omega _{{\rm RW}}>0$![]() ), $v_{\phi, 0} = {|\omega _{{\rm RW}}|}/{k_0}$
), $v_{\phi, 0} = {|\omega _{{\rm RW}}|}/{k_0}$![]() is the phase velocity of the fundamental axial RW mode and
is the phase velocity of the fundamental axial RW mode and
is the wavenumber of the fundamental mode. The variable $D$![]() is a normalized detuning between the plasma rotation and RW frequencies. Variable $D$
is a normalized detuning between the plasma rotation and RW frequencies. Variable $D$![]() is bounded above by unity so long as angular velocity of the plasma is parallel to that of the RW. Variable $D$
is bounded above by unity so long as angular velocity of the plasma is parallel to that of the RW. Variable $D$![]() is bounded below by $0$
is bounded below by $0$![]() so long as $|\omega _r| < |\omega _{{\rm RW}}|$
so long as $|\omega _r| < |\omega _{{\rm RW}}|$![]() , which is the case analysed here. When $D\approx 0$
, which is the case analysed here. When $D\approx 0$![]() , the plasma has (practically) fully compressed because $\omega _r\approx \omega _{{\rm RW}}$
, the plasma has (practically) fully compressed because $\omega _r\approx \omega _{{\rm RW}}$![]() . The variable $\varTheta = {T}/{m_e v_{\phi, 0}^2}$
. The variable $\varTheta = {T}/{m_e v_{\phi, 0}^2}$![]() is the ratio between the thermal energy of an electron and the kinetic energy of an electron that is in-phase with the fundamental RW mode. The variables $D$
is the ratio between the thermal energy of an electron and the kinetic energy of an electron that is in-phase with the fundamental RW mode. The variables $D$![]() and $\varTheta$
and $\varTheta$![]() are in bijective correspondence with $\langle \mathcal {H}\rangle$
are in bijective correspondence with $\langle \mathcal {H}\rangle$![]() and $\langle \,p _{\theta }\rangle$
and $\langle \,p _{\theta }\rangle$![]() as we show in the next section. Hereafter, we take $D$
as we show in the next section. Hereafter, we take $D$![]() and $\varTheta$
and $\varTheta$![]() to be the state variables.
to be the state variables.
In terms of these dimensionless variables, our EOM governing the energy and angular momentum dynamics of the plasma are
where

with the last line defining the dimensionless torque (and a similar relation holds between $\hat {\tau }_{{\rm dr}}$![]() and $\tau _{{\rm dr}}$
and $\tau _{{\rm dr}}$![]() ). The partial derivative matrix needed to change variables is
). The partial derivative matrix needed to change variables is

where
To arrive at a closed set of equations, we (i) express $\hat {E}$![]() , $\hat {p}_\theta$
, $\hat {p}_\theta$![]() and their partial derivatives in terms of $\varTheta$
and their partial derivatives in terms of $\varTheta$![]() and $D$
and $D$![]() , and (ii) explicitly evaluate the perturbations $\delta \phi$
, and (ii) explicitly evaluate the perturbations $\delta \phi$![]() and $\delta f$
and $\delta f$![]() and substitute them into the torque (2.22c).
and substitute them into the torque (2.22c).
2.2 Expressions for the energy and angular momentum
We begin with the expression for energy in equilibrium:
Completing the square on $p_{\theta }$![]() in the exponent of $f_0$
in the exponent of $f_0$![]() , (2.3) allows us to perform the momentum integrals as simple Gaussian expectations. We take advantage of the usual Gaussian expectation results ${\langle \,p_r^2\rangle _G}/{2m_e}={\langle \,p_z^2\rangle _G}/{2m_e}={\langle (\,p_{\theta }-\langle \,p _{\theta }\rangle )^2\rangle _G}/{2m_e r^2}={T}/{2}$
, (2.3) allows us to perform the momentum integrals as simple Gaussian expectations. We take advantage of the usual Gaussian expectation results ${\langle \,p_r^2\rangle _G}/{2m_e}={\langle \,p_z^2\rangle _G}/{2m_e}={\langle (\,p_{\theta }-\langle \,p _{\theta }\rangle )^2\rangle _G}/{2m_e r^2}={T}/{2}$![]() and $\langle \,p _{\theta }\rangle _G = \frac {1}{2}m_e (\varOmega _c+2\omega _r)r^2$
and $\langle \,p _{\theta }\rangle _G = \frac {1}{2}m_e (\varOmega _c+2\omega _r)r^2$![]() , where the $G$
, where the $G$![]() subscript reminds us that we average over a Gaussian distribution here. Simplifying the resulting expression leaves
subscript reminds us that we average over a Gaussian distribution here. Simplifying the resulting expression leaves

where $\psi$![]() was introduced in (2.6), and we performed the trivial $\theta$
was introduced in (2.6), and we performed the trivial $\theta$![]() and $z$
and $z$![]() integrals.
integrals.
We now introduce the Debye length, normalized radial coordinate, ratio of plasma rotation to cyclotron frequency and a convenient variable $\varDelta$![]() :
:
The normalization $\int n_0\,{\rm d}^3\boldsymbol {r} = N_e\implies 2{\rm \pi} n_0(r=0)\int {\rm e}^\psi r\,{\rm d} r = \mathcal {N}_e$![]() can be rewritten with the help of the Debye length and normalized radial coordinate
can be rewritten with the help of the Debye length and normalized radial coordinate
Substituting all of these in (2.33) and exchanging the remaining $\phi _0$![]() in favour of $\psi$
in favour of $\psi$![]() gives
gives
To calculate the potential at the centre of the plasma column, note that the electric field can be written as
Setting $\phi _0(R_W)=0$![]() (conducting wall at the boundary), we have
(conducting wall at the boundary), we have
This can be rewritten in terms of $\psi$![]() and $\rho$
and $\rho$![]() as
as
where $\rho _w=R_w/\lambda _D$![]() . This completes our expression for the energy in terms of $T$
. This completes our expression for the energy in terms of $T$![]() and $\omega _r$
and $\omega _r$![]() (and hence in terms of $\varTheta$
(and hence in terms of $\varTheta$![]() and $D$
and $D$![]() ). The remaining implicit dependence of $\psi$
). The remaining implicit dependence of $\psi$![]() on $T$
on $T$![]() can be uncovered by searching for $\delta$
can be uncovered by searching for $\delta$![]() such that the solution of the Poisson equation (2.7) satisfies the normalization $\int {\rm e}^\psi \rho \,{\rm d}\rho = 2q^2\mathcal {N}_e/T$
such that the solution of the Poisson equation (2.7) satisfies the normalization $\int {\rm e}^\psi \rho \,{\rm d}\rho = 2q^2\mathcal {N}_e/T$![]() .
.
The calculation of the angular momentum proceeds in a similar manner. We can take advantage of our previous result for the expectation of $p_{\theta }$![]() under Gaussian integration:
under Gaussian integration:

Substituting our dimensionless variables gives
Our final expressions for the dimensionless energy and angular momentum are thus

where $\alpha \equiv {mv_{\phi,0}^2}/{q^2\mathcal {N}_e}$![]() . As noted above, $\varDelta$
. As noted above, $\varDelta$![]() and $\varTheta$
and $\varTheta$![]() are implicitly linked by the Poisson equation. Equation (2.42) can be simplified further using the assumption $|\chi |\ll 1$
are implicitly linked by the Poisson equation. Equation (2.42) can be simplified further using the assumption $|\chi |\ll 1$![]() , as is typically the case in experiments.
, as is typically the case in experiments.
Despite the seeming complexity of the expressions (2.42) in dimensionless variables, the underlying physical quantities are straightforward averages over the plasma. So the average energy $\langle E\rangle$![]() (see (2.33)) is a sum of the average thermal energy $3T/2$
(see (2.33)) is a sum of the average thermal energy $3T/2$![]() , the average rotational kinetic energy $\langle \frac {1}{2}m_e \omega _r r^2\rangle$
, the average rotational kinetic energy $\langle \frac {1}{2}m_e \omega _r r^2\rangle$![]() and the self-energy $\langle \frac {1}{2}q\phi _0\rangle$
and the self-energy $\langle \frac {1}{2}q\phi _0\rangle$![]() . The average angular momentum $\langle \,p_\theta \rangle$
. The average angular momentum $\langle \,p_\theta \rangle$![]() (see (2.40)) is a sum of the kinetic angular momentum $\langle m_e\omega _r r^2\rangle$
(see (2.40)) is a sum of the kinetic angular momentum $\langle m_e\omega _r r^2\rangle$![]() and the magnetic field correction $({qB}/{2c})\langle r^2\rangle$
and the magnetic field correction $({qB}/{2c})\langle r^2\rangle$![]() . The evolution is driven by the average torque $\langle \tau \rangle$
. The evolution is driven by the average torque $\langle \tau \rangle$![]() , which is just the average of $\boldsymbol {r}\times \boldsymbol {F}=-q\boldsymbol {r}\times \boldsymbol {\nabla }\phi =-q({\partial \phi }/{\partial \theta })\hat {z}$
, which is just the average of $\boldsymbol {r}\times \boldsymbol {F}=-q\boldsymbol {r}\times \boldsymbol {\nabla }\phi =-q({\partial \phi }/{\partial \theta })\hat {z}$![]() .
.
We now turn to the final piece of our model: the derivation of the torque.
2.3 Derivation of the rotating wall torque
The RW torque is found by first solving for $\delta f$![]() and $\delta \phi$
and $\delta \phi$![]() , and then inserting them into (2.22c). In the previous section, the Vlasov distribution on the full six-dimensional phase space was for the thermodynamic equations. In this section, we take advantage of the small Larmor radius and use the guiding centre approximation. Our distribution will thus be over a four-dimensional phase space $(r,\theta,z,v_z)$
, and then inserting them into (2.22c). In the previous section, the Vlasov distribution on the full six-dimensional phase space was for the thermodynamic equations. In this section, we take advantage of the small Larmor radius and use the guiding centre approximation. Our distribution will thus be over a four-dimensional phase space $(r,\theta,z,v_z)$![]() , with the first three variables denoting the position of the guiding centre and the last being the guiding centre velocity along the magnetic field. See Lifshitz & Pitaevski (Reference Lifshitz and Pitaevski1981) for details on transitioning from the particle to the guiding centre phase space. From now on, all variables are assumed to refer to the guiding centre. The full distribution is
, with the first three variables denoting the position of the guiding centre and the last being the guiding centre velocity along the magnetic field. See Lifshitz & Pitaevski (Reference Lifshitz and Pitaevski1981) for details on transitioning from the particle to the guiding centre phase space. From now on, all variables are assumed to refer to the guiding centre. The full distribution is
The equilibrium distribution function, $f_0(r, v_z)$![]() , can be written as the equilibrium density, $n_0(r; \varTheta, D)$
, can be written as the equilibrium density, $n_0(r; \varTheta, D)$![]() , multiplied by a Maxwellian velocity distribution,
, multiplied by a Maxwellian velocity distribution,

with thermal velocity $v_{th} = v_{\phi,0}\sqrt {\varTheta } = \sqrt {T/m_e}$![]() .
.
The distribution function, $f(t, r, \theta, z, v_z)$![]() , evolves according to the drift kinetic equation (DKE) (Dubin & O'Neil Reference Dubin and O'Neil1999; Lifshitz & Pitaevski Reference Lifshitz and Pitaevski1981),
, evolves according to the drift kinetic equation (DKE) (Dubin & O'Neil Reference Dubin and O'Neil1999; Lifshitz & Pitaevski Reference Lifshitz and Pitaevski1981),
where $\epsilon$![]() is an effective collision frequency, $\delta f$
is an effective collision frequency, $\delta f$![]() is the perturbation of the distribution function, and $\boldsymbol {E}$
is the perturbation of the distribution function, and $\boldsymbol {E}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() are the total electric and magnetic fields. Note that $\boldsymbol {E} = -\boldsymbol {\nabla } \phi (t, r, \theta, z)$
are the total electric and magnetic fields. Note that $\boldsymbol {E} = -\boldsymbol {\nabla } \phi (t, r, \theta, z)$![]() includes the RW potential.
includes the RW potential.
We solve the linearized DKE together with the linearized Poisson equation
where
by expanding in Fourier modes:
The mode functions $\delta \phi _{m, l, s}(r)$![]() satisfy the boundary condition $\delta \phi _{m, l, s}(R_w)=1$
satisfy the boundary condition $\delta \phi _{m, l, s}(R_w)=1$![]() . For convenience, we chose the same expansion coefficients $a_{m, l, s}$
. For convenience, we chose the same expansion coefficients $a_{m, l, s}$![]() for all three of $\delta \phi$
for all three of $\delta \phi$![]() , $\delta f$
, $\delta f$![]() and $\delta n$
and $\delta n$![]() . The mode functions $\delta f_{m, l, s}$
. The mode functions $\delta f_{m, l, s}$![]() and $\delta n_{m, l, s}$
and $\delta n_{m, l, s}$![]() are then uniquely determined by $\delta \phi _{m, l, s}$
are then uniquely determined by $\delta \phi _{m, l, s}$![]() as we show below. The coefficients $a_{m, l, s}$
as we show below. The coefficients $a_{m, l, s}$![]() are determined by requiring that the RW potential at the trap radius satisfies
are determined by requiring that the RW potential at the trap radius satisfies
where $V(z) = \varPhi _0$![]() on the RW electrodes and $V(z) = 0$
on the RW electrodes and $V(z) = 0$![]() elsewhere. We picked this form to simplify our calculations, although one could modify our model to include the sectored nature of RW apparatuses. As such, only the $l = s = \pm 1$
elsewhere. We picked this form to simplify our calculations, although one could modify our model to include the sectored nature of RW apparatuses. As such, only the $l = s = \pm 1$![]() modes are non-zero in our model. The coefficients, $a_{m, l, s}$
modes are non-zero in our model. The coefficients, $a_{m, l, s}$![]() , are thus given by the usual relation $a_{m, \pm 1, \pm 1} = ({1}/{2\mathcal {L}_p})\int \cos (m k_0 z)V(z)\,{\rm d} z$
, are thus given by the usual relation $a_{m, \pm 1, \pm 1} = ({1}/{2\mathcal {L}_p})\int \cos (m k_0 z)V(z)\,{\rm d} z$![]() . Because $V(z)$
. Because $V(z)$![]() is a step function, the coefficients are
is a step function, the coefficients are
where $\mathcal {L}_e=2L_e$![]() is twice the physical electrode length.
is twice the physical electrode length.
Returning to the DKE, we insert the Fourier decompositions and linearize to find
In (2.51), we dropped the diamagnetic drift, $({m_e v_{{\rm th}}^2}/{q})({lc}/{rB})({\partial \ln n_0(r; \varTheta, D)}/{\partial r})$![]() , which is one of the terms arising from $\boldsymbol {\nabla }_{\perp }f(t, r, \theta, z, v_z)$
, which is one of the terms arising from $\boldsymbol {\nabla }_{\perp }f(t, r, \theta, z, v_z)$![]() in (2.45). This term is small for the regime of interest here (see, for example, Section IIB of Dubin & O'Neil Reference Dubin and O'Neil1999). In the absence of any diamagnetic drift,
in (2.45). This term is small for the regime of interest here (see, for example, Section IIB of Dubin & O'Neil Reference Dubin and O'Neil1999). In the absence of any diamagnetic drift,
and we use these interchangeably in the rest of the paper.
The density perturbation, $\delta n_{m, l, s}(r)$![]() , is obtained by integrating $\delta f_{m, l, s}(r, v_z)$
, is obtained by integrating $\delta f_{m, l, s}(r, v_z)$![]() over the axial velocity $v_z$
over the axial velocity $v_z$![]() . Using the plasma dispersion function $Z$
. Using the plasma dispersion function $Z$![]() (Fried & Conte Reference Fried and Conte2015), we have
(Fried & Conte Reference Fried and Conte2015), we have
where the resonance between the rotating wall and the combined electron rotational and axial motion is given by
Inserting this density perturbation into the linearized Poisson equation (2.46) yields an equation for $\delta \phi _{m, l, s}$![]() :
:

This is a homogeneous Bessel-like equation with a source term proportional to density manifesting a Debye screening effect.
The solution to this equation together with the relationship between $\delta n_{m, l, s}$![]() and $\delta \phi _{m, l, s}$
and $\delta \phi _{m, l, s}$![]() is sufficient to evaluate the torque, but further simplifications can be made. Writing
is sufficient to evaluate the torque, but further simplifications can be made. Writing
where $b_{m, l, s}$![]() is defined by (2.53), the torque (2.22c) becomes
is defined by (2.53), the torque (2.22c) becomes

In going from the second to the third line of (2.57), we summed over $s = l = \pm 1$![]() , restricted the wavenumber sum to positive $m$
, restricted the wavenumber sum to positive $m$![]() and used the fact that $\Im [b_{m,1,1}]=-\Im [b_{m,-1,-1}]$
and used the fact that $\Im [b_{m,1,1}]=-\Im [b_{m,-1,-1}]$![]() (see below).
(see below).
To explicitly evaluate $\Im [b_{m,1,1}]$![]() , express the plasma dispersion function using the Sokhotski–Plemelj formula
, express the plasma dispersion function using the Sokhotski–Plemelj formula

where $P$![]() denotes the Cauchy principal value and
denotes the Cauchy principal value and
We can now read off $b_{m, l, s}(r)$![]() from (2.58):
from (2.58):

from which we see
Since $g(r,v_z)$![]() is an odd function of $v_z$
is an odd function of $v_z$![]() , we have $\Im [b_{m,1,1}]=-\Im [b_{m,-1,-1}]$
, we have $\Im [b_{m,1,1}]=-\Im [b_{m,-1,-1}]$![]() as stated above.
as stated above.
Recalling that $f_0(\boldsymbol {r}, \boldsymbol {v}; \varTheta, D)$![]() has the Maxwellian velocity distribution given by (2.44), we obtain the desired expression for the dimensionless torque
has the Maxwellian velocity distribution given by (2.44), we obtain the desired expression for the dimensionless torque

where we have defined the dimensionless torque strength

and introduced the notation

Now it is straightforward to substitute the solution of the Poisson equation (2.55) into the torque. This completes our model.
3 Discussion and conclusion
We have developed a model for RW compression of a pure electron plasma under the assumption the plasma slowly evolves through states of thermal equilibrium. This allowed us to avoid explicitly tracking non-equilibrium dynamics and collisions, yielding tractable equations suitable for numerical study. We made several additional approximations along the way. By utilizing linearized Vlasov theory in our derivations, we have assumed that any nonlinear Vlasov effects will be muted by re-equilibration due to collisions. We have neglected finite-length effects under the assumption that the axial motion will not be significantly impacted, which limits our analysis to long plasma columns. The validity of our approximations can be tested through detailed numerical studies and experimental comparisons, which we leave for future work.
One aspect of our model that can already be validated against experiments without numerical simulations is the lack of compression beyond $\omega _r=\omega _{{\rm RW}}$![]() . That is, as the plasma rotation starts catching up to the rotating wall ($\omega _r\to \omega _{{\rm RW}}$
. That is, as the plasma rotation starts catching up to the rotating wall ($\omega _r\to \omega _{{\rm RW}}$![]() ), our torque (2.63a) vanishes since $D\to 0$
), our torque (2.63a) vanishes since $D\to 0$![]() . This sets a fundamental limit on our compression at a fixed RW frequency, even in the absence of drag torques, and has been verified experimentally (Danielson & Surko Reference Danielson and Surko2006). While this suggests our model is capable of matching the final state of plasma experiments, it remains to validate the details of the time evolution and parameter dependencies predicted by the model.
. This sets a fundamental limit on our compression at a fixed RW frequency, even in the absence of drag torques, and has been verified experimentally (Danielson & Surko Reference Danielson and Surko2006). While this suggests our model is capable of matching the final state of plasma experiments, it remains to validate the details of the time evolution and parameter dependencies predicted by the model.
Assuming our model proves sufficiently accurate for experimental purposes, its relative simplicity lends itself to further analytical approximations and numerical solutions. This, in turn, could allow for compression optimization and real-time guidance to experimentalists. We leave such considerations to future work.
Acknowledgements
The authors would like to thank T.M. O'Neil for helpful discussions and guidance in the initial formulation of this model. This work was supported by the DOE Office of Fusion Energy Science and the NSF-DOE Program in Basic Plasma Science. This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344.
Editor Francesco Califano thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.