1. Introduction
The phenomenon of inertial migration in microfluidic systems has gained significant attention since its initial observation in circular pipes by Segre & Silberberg (Reference Segre and Silberberg1962). Understanding the fundamental hydrodynamic forces acting on moving particles has been a central topic in fluid mechanics. These forces can be broadly classified into drag forces, which act parallel to the relative motion of the body, and lift forces, which act perpendicular to it. In the context of confined microchannels, the primary lift forces driving particle migration across streamlines are the shear-gradient lift force and the wall-induced lift force (Zhou & Papautsky Reference Zhou and Papautsky2013; Amini, Lee & Di Carlo Reference Amini, Lee and Di Carlo2014; Martel & Toner Reference Martel and Toner2014; Zhang et al. Reference Zhang, Yan, Yuan, Alici, Nguyen, Warkiani and Li2016). Additionally, the velocity difference between the particle and the surrounding fluid results in the Saffman lift (Saffman Reference Saffman1965), while the difference in angular velocity leads to the Magnus effect (Rubinow & Keller Reference Rubinow and Keller1961). These forces act simultaneously on a moving particle within a channel, with the shear-gradient and wall-induced lift forces typically dominating the migration process, particularly for particles that are small relative to the channel size (Asmolov Reference Asmolov1999).
To gain a better understanding of the fundamental mechanism of inertial lift, previous research has focused on analytically investigating the near-wall hydrodynamic forces (Cherukat & McLaughlin Reference Cherukat and McLaughlin1994; Asmolov Reference Asmolov1999; Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020). Asymptotic theories are particularly applicable when the particle Reynolds number (![]() $Re_p$) is less than one (
$Re_p$) is less than one (![]() $Re_p = (Ga^2)/\nu$, where
$Re_p = (Ga^2)/\nu$, where ![]() $G = (2 V_{{wall}})/H$ represents the velocity gradient of the shear, with
$G = (2 V_{{wall}})/H$ represents the velocity gradient of the shear, with ![]() $V_{{wall}}$ being the velocity of the walls at distance
$V_{{wall}}$ being the velocity of the walls at distance ![]() $H$,
$H$, ![]() $a$ the particle radius and
$a$ the particle radius and ![]() $\nu$ the kinematic viscosity of the fluid). In this regime, particles experience the competing effect of the shear-gradient force and the wall-repulsive force, as described by Ho & Leal (Reference Ho and Leal1974) and Vasseur & Cox (Reference Vasseur and Cox1977). Additional investigations of lift force profiles have also been conducted for torque-free spheres (Cox & Brenner Reference Cox and Brenner1968; Ho & Leal Reference Ho and Leal1974; Vasseur & Cox Reference Vasseur and Cox1976; Schonberg & Hinch Reference Schonberg and Hinch1989), and more recently also in pulsatile flows (Fox Reference Fox2021; Vishwanathan & Juarez Reference Vishwanathan and Juarez2021). Furthermore, Cherukat et al. experimentally investigated the shear-induced inertial migration of rigid negatively buoyant spheres using a homogeneous shear flow (Cherukat, McLaughlin & Graham Reference Cherukat, McLaughlin and Graham1994).
$\nu$ the kinematic viscosity of the fluid). In this regime, particles experience the competing effect of the shear-gradient force and the wall-repulsive force, as described by Ho & Leal (Reference Ho and Leal1974) and Vasseur & Cox (Reference Vasseur and Cox1977). Additional investigations of lift force profiles have also been conducted for torque-free spheres (Cox & Brenner Reference Cox and Brenner1968; Ho & Leal Reference Ho and Leal1974; Vasseur & Cox Reference Vasseur and Cox1976; Schonberg & Hinch Reference Schonberg and Hinch1989), and more recently also in pulsatile flows (Fox Reference Fox2021; Vishwanathan & Juarez Reference Vishwanathan and Juarez2021). Furthermore, Cherukat et al. experimentally investigated the shear-induced inertial migration of rigid negatively buoyant spheres using a homogeneous shear flow (Cherukat, McLaughlin & Graham Reference Cherukat, McLaughlin and Graham1994).
In general, when ![]() $Re_p > 1$, numerical methods are often preferred over asymptotic theories, which are only valid under specific flow conditions. For higher values of
$Re_p > 1$, numerical methods are often preferred over asymptotic theories, which are only valid under specific flow conditions. For higher values of ![]() $Re_p$ in unbounded flows, various phenomena have been observed, including streamwise vorticity mechanisms. One such phenomenon is the Lighthill–Auton lift (Lighthill Reference Lighthill1956, Reference Lighthill1957), a shear-induced lift force caused by a pair of streamwise counter-rotating vortices formed in the wake of the sphere due to inviscid vorticity tilting by ambient shear. Notably, the direction of Lighthill–Auton lift is identical to that of the Saffman lift (Auton Reference Auton1987). However, at higher Reynolds number, viscous effects induce in the vicinity of the sphere a second streamwise vorticity field, the direction of which is antiparallel to the one due to the inviscid vortex tilting mechanism and thus weakens the Lighthill–Auton lift, leading to an inversion of the lift coefficients (Shi & Rzehak Reference Shi and Rzehak2020; Shi et al. Reference Shi, Rzehak, Lucas and Magnaudet2021). Kurose & Komori reported this inversion for a rigid non-rotating sphere (Kurose & Komori Reference Kurose and Komori1999), where positive coefficients indicate a lift force directed towards the low velocity side, while negative coefficients indicate a force directed towards the high velocity side. Others conducted numerical simulations in unbounded linear shear flows and reported similar changes in the lift force coefficient sign (Lee & Wilczak Reference Lee and Wilczak2000; Bagchi & Balachandar Reference Bagchi and Balachandar2002a; Kim Reference Kim2006; Hölzer & Sommerfeld Reference Hölzer and Sommerfeld2009; Homann, Bec & Grauer Reference Homann, Bec and Grauer2013). Additional numerical studies in an unbounded flow configuration can be found in the literature for both rigid spheres and spherical bubbles (see Kim, Choi & Choi Reference Kim, Choi and Choi2005; Bluemink et al. Reference Bluemink, Lohse, Prosperetti and Van Wijngaarden2008; Sugioka & Komori Reference Sugioka and Komori2009; Santarelli & Fröhlich Reference Santarelli and Fröhlich2015, Reference Santarelli and Fröhlich2016), but they do not explore higher
$Re_p$ in unbounded flows, various phenomena have been observed, including streamwise vorticity mechanisms. One such phenomenon is the Lighthill–Auton lift (Lighthill Reference Lighthill1956, Reference Lighthill1957), a shear-induced lift force caused by a pair of streamwise counter-rotating vortices formed in the wake of the sphere due to inviscid vorticity tilting by ambient shear. Notably, the direction of Lighthill–Auton lift is identical to that of the Saffman lift (Auton Reference Auton1987). However, at higher Reynolds number, viscous effects induce in the vicinity of the sphere a second streamwise vorticity field, the direction of which is antiparallel to the one due to the inviscid vortex tilting mechanism and thus weakens the Lighthill–Auton lift, leading to an inversion of the lift coefficients (Shi & Rzehak Reference Shi and Rzehak2020; Shi et al. Reference Shi, Rzehak, Lucas and Magnaudet2021). Kurose & Komori reported this inversion for a rigid non-rotating sphere (Kurose & Komori Reference Kurose and Komori1999), where positive coefficients indicate a lift force directed towards the low velocity side, while negative coefficients indicate a force directed towards the high velocity side. Others conducted numerical simulations in unbounded linear shear flows and reported similar changes in the lift force coefficient sign (Lee & Wilczak Reference Lee and Wilczak2000; Bagchi & Balachandar Reference Bagchi and Balachandar2002a; Kim Reference Kim2006; Hölzer & Sommerfeld Reference Hölzer and Sommerfeld2009; Homann, Bec & Grauer Reference Homann, Bec and Grauer2013). Additional numerical studies in an unbounded flow configuration can be found in the literature for both rigid spheres and spherical bubbles (see Kim, Choi & Choi Reference Kim, Choi and Choi2005; Bluemink et al. Reference Bluemink, Lohse, Prosperetti and Van Wijngaarden2008; Sugioka & Komori Reference Sugioka and Komori2009; Santarelli & Fröhlich Reference Santarelli and Fröhlich2015, Reference Santarelli and Fröhlich2016), but they do not explore higher ![]() $Re$. Furthermore, numerical studies focusing on near-wall configurations are quite limited in inertia-dominated regimes, particularly for arbitrarily translating and freely rotating spheres, and practically absent for non-spherical particles. To the best of our knowledge, only a few studies have investigated near-wall dynamics in a shear flow, including works by Ekanayake et al. (Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020), Ekanayake, Berry & Harvie (Reference Ekanayake, Berry and Harvie2021), Lee & Balachandar (Reference Lee and Balachandar2010) and Shi et al. (Reference Shi, Rzehak, Lucas and Magnaudet2021).
$Re$. Furthermore, numerical studies focusing on near-wall configurations are quite limited in inertia-dominated regimes, particularly for arbitrarily translating and freely rotating spheres, and practically absent for non-spherical particles. To the best of our knowledge, only a few studies have investigated near-wall dynamics in a shear flow, including works by Ekanayake et al. (Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020), Ekanayake, Berry & Harvie (Reference Ekanayake, Berry and Harvie2021), Lee & Balachandar (Reference Lee and Balachandar2010) and Shi et al. (Reference Shi, Rzehak, Lucas and Magnaudet2021).
Recently, a study on spherical particles by Fox, Schneider & Khair (Reference Fox, Schneider and Khair2021) explored the inertia-dominated regime at higher ![]() $Re_p$ values than the previous literature did, specifically in the range
$Re_p$ values than the previous literature did, specifically in the range ![]() $1 \leq Re_p \leq 50$, using the lattice Boltzmann method (LBM). In their study, a three-dimensional shear flow was employed to examine spherical particles between two parallel walls, assuming an incompressible Newtonian fluid. The results revealed the establishment of stable off-centre equilibria through a pitchfork bifurcation due to the higher modelled
$1 \leq Re_p \leq 50$, using the lattice Boltzmann method (LBM). In their study, a three-dimensional shear flow was employed to examine spherical particles between two parallel walls, assuming an incompressible Newtonian fluid. The results revealed the establishment of stable off-centre equilibria through a pitchfork bifurcation due to the higher modelled ![]() $Re_p$. They demonstrated that above a critical
$Re_p$. They demonstrated that above a critical ![]() $Re_p$, a supercritical pitchfork bifurcation occurs, resulting in two off-centre equilibrium positions equidistant from the centre. This finding was unexpected as the symmetry of the system suggested only one stable equilibrium position halfway between the two walls. The inertial bifurcation of equilibrium positions depends on the particle's confinement ratio and is observed under steady flow conditions (Fox et al. Reference Fox, Schneider and Khair2021). The study on spherical particles also investigated neutrally and non-neutrally buoyant particles, the influence of gravity on the migration process, and explored how flow cessation and reversal affect the focusing positions.
$Re_p$, a supercritical pitchfork bifurcation occurs, resulting in two off-centre equilibrium positions equidistant from the centre. This finding was unexpected as the symmetry of the system suggested only one stable equilibrium position halfway between the two walls. The inertial bifurcation of equilibrium positions depends on the particle's confinement ratio and is observed under steady flow conditions (Fox et al. Reference Fox, Schneider and Khair2021). The study on spherical particles also investigated neutrally and non-neutrally buoyant particles, the influence of gravity on the migration process, and explored how flow cessation and reversal affect the focusing positions.
Confirming this phenomenon could be the first step towards developing a new particle separation system based on the bifurcation of the equilibrium positions due to inertial effects. Simple shear flows, which can be easily obtained experimentally using a sliding plate rheometer or a parallel band apparatus, play a crucial role in this development (Taylor Reference Taylor1934; Rust & Manga Reference Rust and Manga2002). Anand & Subramanian (Reference Anand and Subramanian2023) investigated this problem analytically, building upon the work of Fox et al. (Reference Fox, Schneider and Khair2021), using a point–particle approximation. They demonstrated that the bifurcation threshold in planar Couette flow, for both a circular cylinder and a sphere, corresponds to a critical channel Reynolds number (![]() $Re_c$) rather than
$Re_c$) rather than ![]() $Re_p$. They showed that a pair of stable off-centre positions appears when
$Re_p$. They showed that a pair of stable off-centre positions appears when ![]() $Re_c > 148$ (110) for a sphere (a circular cylinder) under the assumption of a small
$Re_c > 148$ (110) for a sphere (a circular cylinder) under the assumption of a small ![]() $Re_p$.
$Re_p$.
Previous research on inertial migration in microfluidic systems has mainly focused on spherical particles, and investigations regarding shaped particles are limited (Tohme, Magaud & Baldas Reference Tohme, Magaud and Baldas2021). Only in recent years a few devices have emerged for shape-based particle separation (Li et al. Reference Li, Muñoz, Goda and Di Carlo2017; Behdani et al. Reference Behdani, Monjezi, Carey, Weldon, Zhang, Wang and Park2018; Feng et al. Reference Feng, Hockin, Capecchi, Gale and Sant2020; Yuan et al. Reference Yuan, Yan, Zhang, Guijt, Zhao and Li2021; Zhang et al. Reference Zhang, Liu, Okano, Tang, Inoue, Yamazaki, Kamikubo, Cain, Tanaka and Inglis2022). The lack of knowledge in this area is a significant hindrance to the development of shape-based separation tools, which rely solely on the distinct morphologies of biological particles such as cancer cells and bacteria. Additionally, the study of inertial lift forces has primarily focused on confined Poiseuille channel flows, while the analysis of inertial lift forces in Couette-type flows remains surprisingly limited (Fox et al. Reference Fox, Schneider and Khair2021).
In this work, we conducted numerical simulations to explore the inertial dynamics of finite-size particles with various shapes. We investigated a wider range of ![]() $Re_p$ and, in addition to the pitchfork bifurcation of equilibrium positions observed for spheres in the study by Fox et al. (Reference Fox, Schneider and Khair2021) for
$Re_p$ and, in addition to the pitchfork bifurcation of equilibrium positions observed for spheres in the study by Fox et al. (Reference Fox, Schneider and Khair2021) for ![]() $15 < Re_p < 50$, we observed that ellipsoidal particles migrate back towards the central equilibrium position for
$15 < Re_p < 50$, we observed that ellipsoidal particles migrate back towards the central equilibrium position for ![]() $Re_p > 50$. Furthermore, in our recent study (Lauricella et al. Reference Lauricella, Zhou, Luan, Papautsky and Peng2022), we examined the inertial migration dynamics of prolate particles in a straight rectangular channel using smoothed particle hydrodynamics (SPH) at moderate
$Re_p > 50$. Furthermore, in our recent study (Lauricella et al. Reference Lauricella, Zhou, Luan, Papautsky and Peng2022), we examined the inertial migration dynamics of prolate particles in a straight rectangular channel using smoothed particle hydrodynamics (SPH) at moderate ![]() $Re$. In a fully confined channel, only the top and bottom face-centre focusing positions are possible, and a prolate particle can exhibit tumbling or logrolling behaviour, depending on its initial position, alignment and confinement ratio. Building upon the same numerical framework, we now investigate how the inertial dynamics change when the flow is confined by two parallel walls instead. Initially, we employed SPH to validate the LBM calculations conducted on spherical particles with the unexpected off-centre positions. Expanding upon the previous work by Fox et al. (Reference Fox, Schneider and Khair2021) on spheres, we aimed to examine how the distinctive off-centre positions vary concerning particle size, shape, orientation and flow conditions. Furthermore, we sought to explore higher
$Re$. In a fully confined channel, only the top and bottom face-centre focusing positions are possible, and a prolate particle can exhibit tumbling or logrolling behaviour, depending on its initial position, alignment and confinement ratio. Building upon the same numerical framework, we now investigate how the inertial dynamics change when the flow is confined by two parallel walls instead. Initially, we employed SPH to validate the LBM calculations conducted on spherical particles with the unexpected off-centre positions. Expanding upon the previous work by Fox et al. (Reference Fox, Schneider and Khair2021) on spheres, we aimed to examine how the distinctive off-centre positions vary concerning particle size, shape, orientation and flow conditions. Furthermore, we sought to explore higher ![]() $Re$ than those considered in previous studies of simplified inertial flows (see Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020; Feng et al. Reference Feng, Hockin, Capecchi, Gale and Sant2020; Fox, Schneider & Khair Reference Fox, Schneider and Khair2020; Fox et al. Reference Fox, Schneider and Khair2021). Remarkably, we discovered, for the first time, that elliptical particles can exhibit a reversal in behaviour at even larger
$Re$ than those considered in previous studies of simplified inertial flows (see Ekanayake et al. Reference Ekanayake, Berry, Stickland, Dunstan, Muir, Dower and Harvie2020; Feng et al. Reference Feng, Hockin, Capecchi, Gale and Sant2020; Fox, Schneider & Khair Reference Fox, Schneider and Khair2020; Fox et al. Reference Fox, Schneider and Khair2021). Remarkably, we discovered, for the first time, that elliptical particles can exhibit a reversal in behaviour at even larger ![]() $Re_p$ (up to
$Re_p$ (up to ![]() $Re_p = 100$, corresponding to
$Re_p = 100$, corresponding to ![]() $Re_c = 1250$), returning to a stable position at the centre. This is in contrast to the instability typically observed for perfectly spherical particles. We demonstrated that the initial location of the particle plays a crucial role in determining the final equilibrium position at higher values of
$Re_c = 1250$), returning to a stable position at the centre. This is in contrast to the instability typically observed for perfectly spherical particles. We demonstrated that the initial location of the particle plays a crucial role in determining the final equilibrium position at higher values of ![]() $Re_p$, and this behaviour differs between prolate and oblate particles. Asymmetric particles exhibited more complex and less predictable dynamics. It is important to note that all these cases involved steady flows, as unsteadiness arises for
$Re_p$, and this behaviour differs between prolate and oblate particles. Asymmetric particles exhibited more complex and less predictable dynamics. It is important to note that all these cases involved steady flows, as unsteadiness arises for ![]() $Re_p > 270$, as previously reported (see Johnson & Patel Reference Johnson and Patel1999). To further confirm this unprecedented result, finite element method (FEM) simulations were conducted, providing additional insights into the underlying physics based on the surrounding flow fields.
$Re_p > 270$, as previously reported (see Johnson & Patel Reference Johnson and Patel1999). To further confirm this unprecedented result, finite element method (FEM) simulations were conducted, providing additional insights into the underlying physics based on the surrounding flow fields.
The paper is structured as follows. Section 2 provides a detailed description of our SPH set-up and FEM model. In the initial part of § 3 (the results section), we present the validation of these numerical methods. We then proceed to discuss the dynamics of prolate particles, exploring their behaviour at high ![]() $Re$ and examining the influence of various parameters, including particle orientation, shape asymmetry,
$Re$ and examining the influence of various parameters, including particle orientation, shape asymmetry, ![]() $Re$ and initial position. The latter part of the results section focuses on a similar analysis conducted for oblate particles. Finally, in § 4, we summarize the key findings of our study and provide an outlook on future research directions.
$Re$ and initial position. The latter part of the results section focuses on a similar analysis conducted for oblate particles. Finally, in § 4, we summarize the key findings of our study and provide an outlook on future research directions.
2. Methods
2.1. The SPH model
In our study, we utilized the weakly compressible SPH formulation (Gingold & Monaghan Reference Gingold and Monaghan1977) to solve the same boundary value problem as the previous computational work conducted in Fox et al. (Reference Fox, Schneider and Khair2021). The SPH simulations involve discretizing the Navier–Stokes equations for Lagrangian particles, which represent the computational particles and are used to track variables such as position, density, velocity and energy. These variables are interpolated using a kernel function that operates over a smoothing length ![]() $h$. Only the particles within the
$h$. Only the particles within the ![]() $h$-neighbourhood contribute to the calculation of resulting quantities. In this work, we employed the Lucy kernel, as we did in our previous study (Lauricella et al. Reference Lauricella, Zhou, Luan, Papautsky and Peng2022).
$h$-neighbourhood contribute to the calculation of resulting quantities. In this work, we employed the Lucy kernel, as we did in our previous study (Lauricella et al. Reference Lauricella, Zhou, Luan, Papautsky and Peng2022).
To enforce non-penetration and non-slip boundary conditions on the wall and rigid sphere surfaces, we employed a method that extrapolates the velocity to the wall particles based on their distances to the boundary, guaranteeing proper interactions. Conservation of momentum is ensured through pairwise interactions between SPH particles, and viscous forces are incorporated using Morris’ formula (Morris, Fox & Zhu Reference Morris, Fox and Zhu1997). Particle positions and velocities are computed using a velocity Verlet algorithm. The SPH method was implemented using the molecular dynamics code LAMMPS (large-scale atomic/molecular massively parallel simulator) (Thompson et al. Reference Thompson, Aktulga, Berger, Bolintineanu, Brown, Crozier, in't Veld, Kohlmeyer, Moore and Nguyen2022), with an adapted version of the SPH-USER package (Ganzenmüller et al. Reference Ganzenmüller, Steinhauser, Van Liedekerke and Leuven2011).
Regarding the SPH simulation set-up, we aimed to replicate the same three-dimensional inertial shear flow that was previously modelled using LBM by Fox et al. (Reference Fox, Schneider and Khair2021). The SPH particles were arranged in a regular lattice within an orthogonal box, with specific regions designated to model the walls and spheroidal particles to be simulated. Periodic boundary conditions were applied in the ![]() $x$ and
$x$ and ![]() $y$ directions. The size of the simulation box can influence the results, and based on the previous work (Fox et al. Reference Fox, Schneider and Khair2021), it was determined that a box with an aspect ratio (AR) of 2 (i.e. the ratio of the box length in the
$y$ directions. The size of the simulation box can influence the results, and based on the previous work (Fox et al. Reference Fox, Schneider and Khair2021), it was determined that a box with an aspect ratio (AR) of 2 (i.e. the ratio of the box length in the ![]() $x$ direction to that in the
$x$ direction to that in the ![]() $y/z$ directions, while the
$y/z$ directions, while the ![]() $y$ and
$y$ and ![]() $z$ dimensions are the same) yielded the best accuracy for LBM. Consequently, we chose to use a box with an AR of 2, resulting in dimensions of
$z$ dimensions are the same) yielded the best accuracy for LBM. Consequently, we chose to use a box with an AR of 2, resulting in dimensions of ![]() $200~\mathrm {\mu }{\rm m} \times 100~\mathrm {\mu }{\rm m} \times 100~\mathrm {\mu }{\rm m}$. Notably, in our system, the two parallel walls are considered infinite in the
$200~\mathrm {\mu }{\rm m} \times 100~\mathrm {\mu }{\rm m} \times 100~\mathrm {\mu }{\rm m}$. Notably, in our system, the two parallel walls are considered infinite in the ![]() $x$ and
$x$ and ![]() $y$ directions, and they are separated by a distance of
$y$ directions, and they are separated by a distance of ![]() $H = 100\,\mathrm {\mu }{\rm m}$ in the
$H = 100\,\mathrm {\mu }{\rm m}$ in the ![]() $z$ direction. Hence, we identified the transverse position of the particles along the
$z$ direction. Hence, we identified the transverse position of the particles along the ![]() $z$ direction, which is where the stable and unstable equilibrium positions are located. In other words, the
$z$ direction, which is where the stable and unstable equilibrium positions are located. In other words, the ![]() $y$ and
$y$ and ![]() $z$ directions are inverted compared with the LBM model by Fox et al. (Reference Fox, Schneider and Khair2021). Figure 1(a) illustrates a schematic of the system modelled using SPH. The reference system is set such that the top wall is located at
$z$ directions are inverted compared with the LBM model by Fox et al. (Reference Fox, Schneider and Khair2021). Figure 1(a) illustrates a schematic of the system modelled using SPH. The reference system is set such that the top wall is located at ![]() $z = +50\, \mathrm {\mu }{\rm m}$, the bottom wall at
$z = +50\, \mathrm {\mu }{\rm m}$, the bottom wall at ![]() $z = -50\, \mathrm {\mu }{\rm m}$ and
$z = -50\, \mathrm {\mu }{\rm m}$ and ![]() $z = 0\, \mathrm {\mu }{\rm m}$ represents the central position.
$z = 0\, \mathrm {\mu }{\rm m}$ represents the central position.

Figure 1. Schematic of a particle between two parallel walls in the SPH model. (a) The top and bottom walls move in opposite directions with velocities ![]() $V_{{wall}} (t)$ and
$V_{{wall}} (t)$ and ![]() $-V_{{wall}} (t)$, and a three-dimensional linear shear gradient is obtained. The walls are infinite in the
$-V_{{wall}} (t)$, and a three-dimensional linear shear gradient is obtained. The walls are infinite in the ![]() $x$ and
$x$ and ![]() $y$ direction. The origin of the system is halfway between the walls, whose distance spans from
$y$ direction. The origin of the system is halfway between the walls, whose distance spans from ![]() $z = -50 \,\mathrm {\mu }{\rm m}$ to
$z = -50 \,\mathrm {\mu }{\rm m}$ to ![]() $z = +50 \,\mathrm {\mu }{\rm m}$. (b) Different initial alignments were investigated in the present study. We tested how the initial orientation affects the final rotational behaviour of the particles. For simplicity, only a prolate particle is reported in the schematic, but the same initial orientations have been used also for oblate spheroids and asymmetric particles.
$z = +50 \,\mathrm {\mu }{\rm m}$. (b) Different initial alignments were investigated in the present study. We tested how the initial orientation affects the final rotational behaviour of the particles. For simplicity, only a prolate particle is reported in the schematic, but the same initial orientations have been used also for oblate spheroids and asymmetric particles.
Throughout our investigation, we tested different initial alignments of the particles, which are depicted in figure 1(b). In our simulations, the particle is released at ![]() $y = 0$, and the confinement ratio of the particle, denoted as
$y = 0$, and the confinement ratio of the particle, denoted as ![]() $K$, is defined as
$K$, is defined as ![]() $K = a/H$, where
$K = a/H$, where ![]() $a$ represents the particle's largest radius, and
$a$ represents the particle's largest radius, and ![]() $H$ is the distance between the parallel walls. To accurately match
$H$ is the distance between the parallel walls. To accurately match ![]() $Re_p$, we adjusted the velocity gradient of the fluid, denoted as
$Re_p$, we adjusted the velocity gradient of the fluid, denoted as ![]() $G$. The velocity gradient is related to the velocity of the wall,
$G$. The velocity gradient is related to the velocity of the wall, ![]() $V_{{wall}}(t)$, and is given by the expression
$V_{{wall}}(t)$, and is given by the expression ![]() $G = (2 V_{{wall}}(t))/H$. By tuning the velocity of the moving walls, we can achieve the desired
$G = (2 V_{{wall}}(t))/H$. By tuning the velocity of the moving walls, we can achieve the desired ![]() $G$ value, which is then used to compute
$G$ value, which is then used to compute ![]() $Re_p$, using the formula
$Re_p$, using the formula ![]() $Re_p = (Ga^2)/\nu$. In this context,
$Re_p = (Ga^2)/\nu$. In this context, ![]() $\nu$ denotes the kinematic viscosity of the fluid, which we have chosen to be
$\nu$ denotes the kinematic viscosity of the fluid, which we have chosen to be ![]() $1\,{\rm mm}^{2}\,{\rm s}^{-1}$. This value aligns with the viscosity commonly encountered in inertial particle focusing experiments, such as those conducted with water.
$1\,{\rm mm}^{2}\,{\rm s}^{-1}$. This value aligns with the viscosity commonly encountered in inertial particle focusing experiments, such as those conducted with water.
In the LBM formulation employed by Fox et al. (Reference Fox, Schneider and Khair2021), the fluid is assumed to be Newtonian and incompressible. In our SPH formulation, the compressibility of the fluid is controlled by the speed of sound. Ideally, for an incompressible fluid, the speed of sound should be infinite. However, in our weakly compressible SPH formulation, we set the speed of sound to ensure flow compressibility within 3 %. This value strikes a balance between computational efficiency and obtaining accurate results, as demonstrated in the validation section of our study. Furthermore, the fluid density is set to the density of water at ambient temperature. During the simulations, the position of the particle's centre of mass is recorded in a text file, along with its angular and linear velocity. To visualize and analyse the results, we employ VMD (visual molecular dynamics) (Humphrey, Dalke & Schulten Reference Humphrey, Dalke and Schulten1996), which is a software tool commonly used for visualizing molecular systems.
2.2. The FEM model
For the FEM simulations, we used the COMSOL Multiphysics software package (COMSOL, Inc., Burlington, MA). Unlike SPH, where transient particle trajectories are obtained, in the FEM method, only the final stable equilibrium position of the particles was calculated. To obtain force curves along the ![]() $z$ direction in FEM simulations, we employed the flow at specific particle position (FSPP) approach (Bazaz et al. Reference Bazaz, Mashhadian, Ehsani, Saha, Krüger and Warkiani2020). In this approach, the particle is treated as a ‘void’ in the three-dimensional fluid domain, and it is positioned at various vertical positions between the bottom wall and the centreline (since the system exhibits symmetry, only half the distance between the parallel walls needs to be studied). The full Navier–Stokes equations are then solved, and the force on the particle is calculated by integrating the traction over the particle surface. The validity of this approach has been demonstrated by us (Naderi et al. Reference Naderi, Barilla, Zhou, Papautsky and Peng2022) and others (Di Carlo et al. Reference Di Carlo, Edd, Humphry, Stone and Toner2009; Raoufi et al. Reference Raoufi, Mashhadian, Niazmand, Asadnia, Razmjou and Warkiani2019). The independence of results on the selected box length and width was confirmed for the highest
$z$ direction in FEM simulations, we employed the flow at specific particle position (FSPP) approach (Bazaz et al. Reference Bazaz, Mashhadian, Ehsani, Saha, Krüger and Warkiani2020). In this approach, the particle is treated as a ‘void’ in the three-dimensional fluid domain, and it is positioned at various vertical positions between the bottom wall and the centreline (since the system exhibits symmetry, only half the distance between the parallel walls needs to be studied). The full Navier–Stokes equations are then solved, and the force on the particle is calculated by integrating the traction over the particle surface. The validity of this approach has been demonstrated by us (Naderi et al. Reference Naderi, Barilla, Zhou, Papautsky and Peng2022) and others (Di Carlo et al. Reference Di Carlo, Edd, Humphry, Stone and Toner2009; Raoufi et al. Reference Raoufi, Mashhadian, Niazmand, Asadnia, Razmjou and Warkiani2019). The independence of results on the selected box length and width was confirmed for the highest ![]() $Re_p$ used in the simulations.
$Re_p$ used in the simulations.
Due to the steady-state nature of the FSPP approach, it is only applicable when the particle (whether symmetric prolate or oblate) is rotating about its symmetric axis, known as ‘logrolling motion’. To generate flow in the simulations, the moving wall boundary condition is applied to the parallel walls with the values (![]() $U_W-U_P$) and (
$U_W-U_P$) and (![]() $-U_W-U_P$), where
$-U_W-U_P$), where ![]() $U_W$ and
$U_W$ and ![]() $U_P$ represent the velocities of the walls and the particle, respectively, matching the velocity
$U_P$ represent the velocities of the walls and the particle, respectively, matching the velocity ![]() $V_{{wall}}$ in our SPH set-up. This boundary condition captures both the sliding movement of the wall and the translational velocity of the particles. The rotation of the particle is modelled by directly applying a rotational velocity about the
$V_{{wall}}$ in our SPH set-up. This boundary condition captures both the sliding movement of the wall and the translational velocity of the particles. The rotation of the particle is modelled by directly applying a rotational velocity about the ![]() $y$ axis on the particle surface. As we only consider cases where the particle undergoes logrolling motion, rotation about the
$y$ axis on the particle surface. As we only consider cases where the particle undergoes logrolling motion, rotation about the ![]() $x$ axis and
$x$ axis and ![]() $z$ axis are manually set to zero. To account for the infinite length and width of the parallel walls, periodic flow conditions with
$z$ axis are manually set to zero. To account for the infinite length and width of the parallel walls, periodic flow conditions with ![]() $\Delta P = 0$ are applied in the
$\Delta P = 0$ are applied in the ![]() $x$ and
$x$ and ![]() $y$ directions. The domain is discretized using
$y$ directions. The domain is discretized using ![]() $1.5 \times 10^{6}$ tetrahedral mesh elements to accurately represent the geometry and flow behaviour.
$1.5 \times 10^{6}$ tetrahedral mesh elements to accurately represent the geometry and flow behaviour.
3. Results and discussion
3.1. Validation
To validate the accuracy of our SPH model in capturing the inertial bifurcation phenomenon, we conducted various validation tests. Previously, we successfully employed SPH to model spherical particles in inertial flows (Zhou, Peng & Papautsky Reference Zhou, Peng and Papautsky2020) as well as ellipsoidal particles (Lauricella et al. Reference Lauricella, Zhou, Luan, Papautsky and Peng2022). In our latest work on shaped particles (Lauricella et al. Reference Lauricella, Zhou, Luan, Papautsky and Peng2022), we validated the SPH model against Jeffery's theory (Jeffery Reference Jeffery1922). By comparing the period of rotation of prolate particles with the analytical solution from Jeffery's theory, we confirmed that the SPH model accurately captures the dynamics of ellipsoidal particles in a channel flow. Furthermore, we validated the SPH modelling by comparing it with microfluidic experiments on prolate particles and computational studies on oblate particles.
In the present study, we applied and validated the same methodology to systematically investigate prolate and oblate ellipsoidal particles, including asymmetric ellipsoids, in a simple shear flow between two parallel walls. The occurrence of the inertial bifurcation strongly depends on the effect of inertia. To validate our model, we compared it with the computational results obtained by Fox et al. (Reference Fox, Schneider and Khair2021) for spherical particles. They had previously validated their LBM code against perturbation theory. We replicated the migration trajectories of a freely suspended neutrally buoyant sphere with a confinement ratio ![]() $K = 0.2$, corresponding to a sphere with a radius of
$K = 0.2$, corresponding to a sphere with a radius of ![]() $20\,\mathrm {\mu }{\rm m}$ in our SPH model. The sphere was released at different transverse positions, and we tested various
$20\,\mathrm {\mu }{\rm m}$ in our SPH model. The sphere was released at different transverse positions, and we tested various ![]() $Re_p$. For consistency with prior research, we normalized the transverse position
$Re_p$. For consistency with prior research, we normalized the transverse position ![]() $z$ of the particles by dividing it by the wall distance
$z$ of the particles by dividing it by the wall distance ![]() $H$. The dimensionless quantity to which we will henceforth refer is denoted as
$H$. The dimensionless quantity to which we will henceforth refer is denoted as ![]() ${z}_0$. Specifically, the sphere was released at the transverse positions
${z}_0$. Specifically, the sphere was released at the transverse positions ![]() $z_0 = -0.1$ and
$z_0 = -0.1$ and ![]() $z_0 = -0.25$, which are the same chosen in Fox et al. (Reference Fox, Schneider and Khair2021). We assumed that a sphere starting in positions with
$z_0 = -0.25$, which are the same chosen in Fox et al. (Reference Fox, Schneider and Khair2021). We assumed that a sphere starting in positions with ![]() $z_0 > 0$, mirrored with respect to the centreline, would follow the same trajectory due to the system's symmetry (Fox et al. Reference Fox, Schneider and Khair2021). Overall, the SPH results showed good agreement with the trajectories reported by Fox et al. using LBM (figure 2).
$z_0 > 0$, mirrored with respect to the centreline, would follow the same trajectory due to the system's symmetry (Fox et al. Reference Fox, Schneider and Khair2021). Overall, the SPH results showed good agreement with the trajectories reported by Fox et al. using LBM (figure 2).

Figure 2. The SPH validation of the migration trajectory of spherical particles with ![]() $K = 0.2$ released at
$K = 0.2$ released at ![]() $z_0 = -0.1$ and
$z_0 = -0.1$ and ![]() $z_0 = -0.25$. The transverse position was normalized as
$z_0 = -0.25$. The transverse position was normalized as ![]() $z_0 = z/H$ and the time as
$z_0 = z/H$ and the time as ![]() $t_0 = tG$, with
$t_0 = tG$, with ![]() $G$ being the velocity gradient. The spheres at lower
$G$ being the velocity gradient. The spheres at lower ![]() $Re_p$ migrated to the centre while stable off-centre positions were present at higher values of
$Re_p$ migrated to the centre while stable off-centre positions were present at higher values of ![]() $Re_p$. The results agreed with the one obtained with LBM presented in Fox et al. (Reference Fox, Schneider and Khair2021), reported in the figure with dotted lines.
$Re_p$. The results agreed with the one obtained with LBM presented in Fox et al. (Reference Fox, Schneider and Khair2021), reported in the figure with dotted lines.
At ![]() $Re_p = 3$, we observed that there is only one stable equilibrium position at the centreline
$Re_p = 3$, we observed that there is only one stable equilibrium position at the centreline ![]() $H = 0$. Regardless of the initial transverse location, the spheres eventually reached this central position. However, at
$H = 0$. Regardless of the initial transverse location, the spheres eventually reached this central position. However, at ![]() $Re_p = 10$, we did not observe any off-centre positions, unlike the LBM simulation. Instead, the particles migrated towards the central position. To investigate further, we tested
$Re_p = 10$, we did not observe any off-centre positions, unlike the LBM simulation. Instead, the particles migrated towards the central position. To investigate further, we tested ![]() $Re_p = 15$ and found an off-centre stable position at
$Re_p = 15$ and found an off-centre stable position at ![]() $z_0 = -0.13$, which is very close the results reported by Fox et al. (Reference Fox, Schneider and Khair2021) for
$z_0 = -0.13$, which is very close the results reported by Fox et al. (Reference Fox, Schneider and Khair2021) for ![]() $Re_p = 10$. Similarly, good agreement was observed at
$Re_p = 10$. Similarly, good agreement was observed at ![]() $Re_p = 30$, where the sphere focused at approximately
$Re_p = 30$, where the sphere focused at approximately ![]() $z_0 = -0.24$, matching the off-centre position obtained from LBM. Some differences were observed at the beginning of the migration path, which we attribute to the incompressible fluid modelled with LBM, while our SPH formulation allows for a small degree of compressibility. The inherent difference in compressibility limited the possibility of achieving a perfect match for the entire particle trajectory.
$z_0 = -0.24$, matching the off-centre position obtained from LBM. Some differences were observed at the beginning of the migration path, which we attribute to the incompressible fluid modelled with LBM, while our SPH formulation allows for a small degree of compressibility. The inherent difference in compressibility limited the possibility of achieving a perfect match for the entire particle trajectory.
We also conducted tests under flow cessation to observe the behaviour of particles as the flow is gradually reduced and eventually stopped within a given time interval ![]() $\Delta t$. As the flow decreased, the particle experienced lower values of
$\Delta t$. As the flow decreased, the particle experienced lower values of ![]() $Re_p$, causing the equilibrium position to gradually approach the centre of the channel. In our analysis, we focused on the case of
$Re_p$, causing the equilibrium position to gradually approach the centre of the channel. In our analysis, we focused on the case of ![]() $\Delta t = 0$, where we abruptly stopped the motion of the parallel walls when the particle had already reached a stable off-centre position. In this scenario, the particle did not have enough time to reach the centreline but was instead driven inward to a new stable off-centre position until the flow had completely ceased. For instance, Fox et al. (Reference Fox, Schneider and Khair2021) observed that for
$\Delta t = 0$, where we abruptly stopped the motion of the parallel walls when the particle had already reached a stable off-centre position. In this scenario, the particle did not have enough time to reach the centreline but was instead driven inward to a new stable off-centre position until the flow had completely ceased. For instance, Fox et al. (Reference Fox, Schneider and Khair2021) observed that for ![]() $Re_p = 10$, the transverse off-centre position shifted
$Re_p = 10$, the transverse off-centre position shifted ![]() $3\,\mathrm {\mu }{\rm m}$ towards the centre of the channel within a
$3\,\mathrm {\mu }{\rm m}$ towards the centre of the channel within a ![]() $\Delta t = 0$ interval. We observed a similar behaviour for
$\Delta t = 0$ interval. We observed a similar behaviour for ![]() $Re_p = 30$, where a sphere that was initially focused on the off-centre position
$Re_p = 30$, where a sphere that was initially focused on the off-centre position ![]() $z_0 = -0.24$ shifted to a new stable equilibrium position of
$z_0 = -0.24$ shifted to a new stable equilibrium position of ![]() $z_0 = -0.18$ after the flow had ceased (figure 3). Overall, our method successfully captured the predicted supercritical pitchfork bifurcation for a neutrally buoyant sphere in a time-dependent inertial shear flow. This finding confirmed the presence of an inertial bifurcation of equilibrium positions for spherical particles, as previously observed by Fox et al. using LBM.
$z_0 = -0.18$ after the flow had ceased (figure 3). Overall, our method successfully captured the predicted supercritical pitchfork bifurcation for a neutrally buoyant sphere in a time-dependent inertial shear flow. This finding confirmed the presence of an inertial bifurcation of equilibrium positions for spherical particles, as previously observed by Fox et al. using LBM.
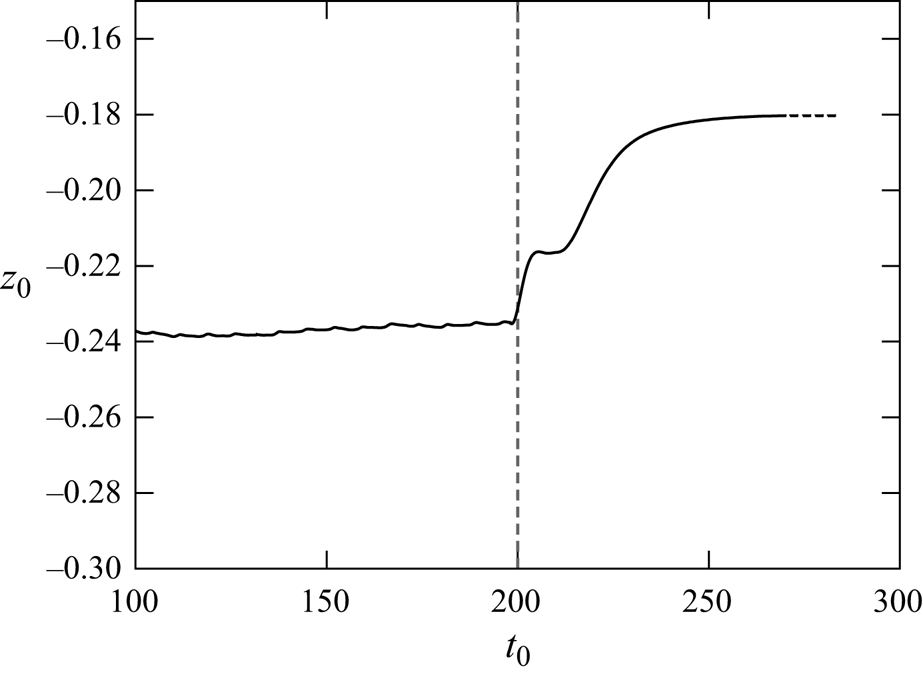
Figure 3. A spherical particle with ![]() $K = 0.2$ at
$K = 0.2$ at ![]() $Re_p = 30$ under flow cessation. The vertical dashed line represents the moment the velocity of the moving walls is set to zero. After a transient phase, the particle reached a new off-centre equilibrium position after the flow had totally ceased.
$Re_p = 30$ under flow cessation. The vertical dashed line represents the moment the velocity of the moving walls is set to zero. After a transient phase, the particle reached a new off-centre equilibrium position after the flow had totally ceased.
3.2. Prolate particles
We demonstrated the presence of the supercritical pitchfork bifurcation for prolate particles and investigated its dependence on ![]() $Re$, particle dimensions and particle orientation. The particle trajectory was shown as its transverse position plotted against computational time. To maintain consistency with the validation section, we used non-dimensional quantities by dividing the transverse position
$Re$, particle dimensions and particle orientation. The particle trajectory was shown as its transverse position plotted against computational time. To maintain consistency with the validation section, we used non-dimensional quantities by dividing the transverse position ![]() $z$ by
$z$ by ![]() $H$ and multiplying the time by the velocity gradient
$H$ and multiplying the time by the velocity gradient ![]() $G$, resulting in
$G$, resulting in ![]() $z_0 = z/H$ and
$z_0 = z/H$ and ![]() $t_0 = tG$.
$t_0 = tG$.
3.2.1. Effect of  $Re$ and initial position
$Re$ and initial position
In the first place, we used a prolate particle of AR ![]() $2:1:1$ (AR 2). We set its dimensions to
$2:1:1$ (AR 2). We set its dimensions to ![]() $40\,\mathrm {\mu } {\rm m} \times 20\,\mathrm {\mu }{\rm m} \times 20\,\mathrm {\mu }{\rm m}$, corresponding to the same confinement ratio
$40\,\mathrm {\mu } {\rm m} \times 20\,\mathrm {\mu }{\rm m} \times 20\,\mathrm {\mu }{\rm m}$, corresponding to the same confinement ratio ![]() $K = 0.2$ (defined as the largest radius
$K = 0.2$ (defined as the largest radius ![]() $a = 20\, \mathrm {\mu } {\rm m}$ divided by the distance of the parallel walls,
$a = 20\, \mathrm {\mu } {\rm m}$ divided by the distance of the parallel walls, ![]() $H = 100\,\mathrm {\mu }{\rm m}$) as the spherical particle used in the validation section. Initially, we examined the presence of off-centre positions for moderate values of the
$H = 100\,\mathrm {\mu }{\rm m}$) as the spherical particle used in the validation section. Initially, we examined the presence of off-centre positions for moderate values of the ![]() $Re_p$. For
$Re_p$. For ![]() $Re_p = 3$, a prolate particle migrated towards the single stable equilibrium position at
$Re_p = 3$, a prolate particle migrated towards the single stable equilibrium position at ![]() $H = 0$, which corresponds to the centre position. At
$H = 0$, which corresponds to the centre position. At ![]() $Re_p = 10$, a prolate particle released at
$Re_p = 10$, a prolate particle released at ![]() $z_0 = -0.1$ remained in the same position, representing a stable equilibrium point.
$z_0 = -0.1$ remained in the same position, representing a stable equilibrium point.
Next, we increased to ![]() $Re_p = 30$ and investigated the influence of the initial alignment and location of the particle on the focusing position. Figure 4 demonstrates that the initial transverse position of the particle did not affect the final equilibrium. Whether the prolate particle was released at
$Re_p = 30$ and investigated the influence of the initial alignment and location of the particle on the focusing position. Figure 4 demonstrates that the initial transverse position of the particle did not affect the final equilibrium. Whether the prolate particle was released at ![]() $z_0 = -0.1$ or
$z_0 = -0.1$ or ![]() $z_0 = -0.25$, it occupied the same stable off-centre position. However, the initial alignment of the particle (horizontal, vertical or inclined) did impact the focusing position at
$z_0 = -0.25$, it occupied the same stable off-centre position. However, the initial alignment of the particle (horizontal, vertical or inclined) did impact the focusing position at ![]() $Re_p = 30$. In figure 4, simulations were concluded at different times for computational convenience. Specifically, the simulation for the horizontally aligned particle ended earlier than the vertically aligned one. This decision was based on the assumption that the horizontally aligned particle had already reached a stable equilibrium, leading to the termination of the simulation at that point.
$Re_p = 30$. In figure 4, simulations were concluded at different times for computational convenience. Specifically, the simulation for the horizontally aligned particle ended earlier than the vertically aligned one. This decision was based on the assumption that the horizontally aligned particle had already reached a stable equilibrium, leading to the termination of the simulation at that point.

Figure 4. Symmetric prolate particles with ![]() $K = 0.2$ released at
$K = 0.2$ released at ![]() $z_0 = -0.1$ and
$z_0 = -0.1$ and ![]() $z_0 = -0.25$ in the transverse position. At
$z_0 = -0.25$ in the transverse position. At ![]() $Re_p = 30$, the stable off-centre position was dependent on the initial particle orientation (indicated in parentheses in the plot legend), but not on the initial location. Logrolling particles focused closer to the bottom wall with respect to tumbling particles.
$Re_p = 30$, the stable off-centre position was dependent on the initial particle orientation (indicated in parentheses in the plot legend), but not on the initial location. Logrolling particles focused closer to the bottom wall with respect to tumbling particles.
Then, we conducted tests on the same prolate particle at higher values of ![]() $Re_p$. The particles were initially released at a transverse position of
$Re_p$. The particles were initially released at a transverse position of ![]() $z_0 = -0.25$ with a horizontal alignment. Upon initiating the flow, the particles maintained their alignment and orientation, undergoing logrolling motion. The equilibrium positions were found to be stable and increasingly distant from the centre as
$z_0 = -0.25$ with a horizontal alignment. Upon initiating the flow, the particles maintained their alignment and orientation, undergoing logrolling motion. The equilibrium positions were found to be stable and increasingly distant from the centre as ![]() $Re_p$ increased. Specifically, we observed a focusing position of
$Re_p$ increased. Specifically, we observed a focusing position of ![]() $z_0 = -0.264$ for
$z_0 = -0.264$ for ![]() $Re_p = 30$,
$Re_p = 30$, ![]() $z_0 = -0.31$ for
$z_0 = -0.31$ for ![]() $Re_p = 50$ and
$Re_p = 50$ and ![]() $z_0 = -0.33$ for
$z_0 = -0.33$ for ![]() $Re_p = 70$ (figure 5a). Notably, for
$Re_p = 70$ (figure 5a). Notably, for ![]() $Re_p = 30$, the off-centre position was similar (slightly farther away from the centre) compared with a sphere with the same confinement ratio, which stabilized at
$Re_p = 30$, the off-centre position was similar (slightly farther away from the centre) compared with a sphere with the same confinement ratio, which stabilized at ![]() $z_0 = -0.24$. Interestingly, we identified a transitional range between
$z_0 = -0.24$. Interestingly, we identified a transitional range between ![]() $Re_p = 70$ and
$Re_p = 70$ and ![]() $90$, where the particle experiences multiple stable off-centre positions that are closer to the centre. Then, for
$90$, where the particle experiences multiple stable off-centre positions that are closer to the centre. Then, for ![]() $Re_p = 90$, the trend was completely reversed and the prolate particle migrated to the centre. After a small overshoot past the
$Re_p = 90$, the trend was completely reversed and the prolate particle migrated to the centre. After a small overshoot past the ![]() $z$ midline, the particle eventually stabilized at the centre position with a logrolling motion. This behaviour had not been observed in the previous work, as the range of
$z$ midline, the particle eventually stabilized at the centre position with a logrolling motion. This behaviour had not been observed in the previous work, as the range of ![]() $Re_p$ was below 50. Since a final steady logrolling motion was predicted using SPH, we were able to apply FEM to confirm this reversal in the bifurcation of the equilibrium location at high
$Re_p$ was below 50. Since a final steady logrolling motion was predicted using SPH, we were able to apply FEM to confirm this reversal in the bifurcation of the equilibrium location at high ![]() $Re$. The FEM simulations also confirmed the presence of stable off-centre positions, with slight variations of a few microns compared with the SPH results. The FEM results are presented in the form of force curves along the
$Re$. The FEM simulations also confirmed the presence of stable off-centre positions, with slight variations of a few microns compared with the SPH results. The FEM results are presented in the form of force curves along the ![]() $z$ direction (figure 5b). The curves represent the non-dimensional force
$z$ direction (figure 5b). The curves represent the non-dimensional force ![]() $f_0 = F/(U_w^2*(d/2)^4/H^2)$ exerted on a neutrally buoyant logrolling prolate moving freely at a specified
$f_0 = F/(U_w^2*(d/2)^4/H^2)$ exerted on a neutrally buoyant logrolling prolate moving freely at a specified ![]() $z_0$ position, with positive (negative) values indicating a centre-directed (wall-directed) force. Hence, stable (unstable) focusing positions are the locations where the force curve intersects with the
$z_0$ position, with positive (negative) values indicating a centre-directed (wall-directed) force. Hence, stable (unstable) focusing positions are the locations where the force curve intersects with the ![]() $f_0 = 0$ dashed line with a negative (positive) slope. The results are shown only for the lower half of the distance between the walls due to symmetry. Starting from
$f_0 = 0$ dashed line with a negative (positive) slope. The results are shown only for the lower half of the distance between the walls due to symmetry. Starting from ![]() $Re_p = 30$, the force exhibited negative values in the central regions and positive values near the walls (figure 5b), with a single crossing of the force curve and the dashed line at
$Re_p = 30$, the force exhibited negative values in the central regions and positive values near the walls (figure 5b), with a single crossing of the force curve and the dashed line at ![]() $z_0 = -0.22$, representing the stable off-centre focusing position. Thus, due to symmetry, we observe two symmetric stable off-centre focusing positions and an unstable saddle point at the centre for
$z_0 = -0.22$, representing the stable off-centre focusing position. Thus, due to symmetry, we observe two symmetric stable off-centre focusing positions and an unstable saddle point at the centre for ![]() $Re_p = 30$, as reported by (Fox et al. Reference Fox, Schneider and Khair2021). This trend holds with increasing
$Re_p = 30$, as reported by (Fox et al. Reference Fox, Schneider and Khair2021). This trend holds with increasing ![]() $Re_p$ up to 70, with the off-centre stable equilibrium positions moving closer to the walls, which is in agreement with the SPH results. At
$Re_p$ up to 70, with the off-centre stable equilibrium positions moving closer to the walls, which is in agreement with the SPH results. At ![]() $Re_p = 80$, the force curve crosses the dashed line with a negative slope at two off-centre points. One closer to the wall at
$Re_p = 80$, the force curve crosses the dashed line with a negative slope at two off-centre points. One closer to the wall at ![]() $z_0 = -0.3$ and the other closer to the centre at
$z_0 = -0.3$ and the other closer to the centre at ![]() $z_0 = -0.14$. Further increase of the
$z_0 = -0.14$. Further increase of the ![]() $Re_p$ up to 90 and 100 shifts the entire force curve upwards, leading to a only a single crossing with the
$Re_p$ up to 90 and 100 shifts the entire force curve upwards, leading to a only a single crossing with the ![]() $f_0 = 0$ dashed line at the centre (
$f_0 = 0$ dashed line at the centre (![]() $z_0 = 0$), confirming the findings from our SPH simulations. The phase diagram in figure 6 illustrates the equilibrium positions reached at the conclusion of the simulation, dependent on the particle Reynolds number. In this diagram, we have integrated results from both SPH simulations and FEM. The shaded grey region signifies the transition zone where multiple stable off-centre positions coexist, as mentioned earlier.
$z_0 = 0$), confirming the findings from our SPH simulations. The phase diagram in figure 6 illustrates the equilibrium positions reached at the conclusion of the simulation, dependent on the particle Reynolds number. In this diagram, we have integrated results from both SPH simulations and FEM. The shaded grey region signifies the transition zone where multiple stable off-centre positions coexist, as mentioned earlier.

Figure 5. (a) The behaviour of symmetric prolate particles with ![]() $K = 0.2$ undergoing logrolling motion at moderate and high
$K = 0.2$ undergoing logrolling motion at moderate and high ![]() $Re$ is depicted in this figure. As the
$Re$ is depicted in this figure. As the ![]() $Re_p$ increased, the off-centre positions moved progressively farther from the centre. However, for
$Re_p$ increased, the off-centre positions moved progressively farther from the centre. However, for ![]() $Re_p = 90$ this trend was reversed, and the particle migrated towards the centre position, irrespective of the initial location. The
$Re_p = 90$ this trend was reversed, and the particle migrated towards the centre position, irrespective of the initial location. The ![]() $70 < Re_p < 90$ range was found to be a transition region where there exist multistable off-centre positions closer to the centre. All the particles exhibited logrolling motion and had been released with a horizontal alignment, as indicated in the box on the right-hand side of the figure. (b) Force curves obtained from FEM simulations. Positive (negative) values indicate a centre-directed (wall-directed) force. Stable (unstable) focusing positions are the locations where the force curve intersects with the
$70 < Re_p < 90$ range was found to be a transition region where there exist multistable off-centre positions closer to the centre. All the particles exhibited logrolling motion and had been released with a horizontal alignment, as indicated in the box on the right-hand side of the figure. (b) Force curves obtained from FEM simulations. Positive (negative) values indicate a centre-directed (wall-directed) force. Stable (unstable) focusing positions are the locations where the force curve intersects with the ![]() $f_0 = 0$ dashed line with a negative (positive) slope. Results are shown only for the lower half of the distance between the walls due to symmetry.
$f_0 = 0$ dashed line with a negative (positive) slope. Results are shown only for the lower half of the distance between the walls due to symmetry.

Figure 6. The SPH and FEM data points representing the final equilibrium positions ![]() $z_0$ of a prolate particle with
$z_0$ of a prolate particle with ![]() $K = 0.2$ are depicted on a phase diagram that incorporates particle Reynolds numbers (
$K = 0.2$ are depicted on a phase diagram that incorporates particle Reynolds numbers (![]() $Re_p$) of 1, 5, 10, 20, 30, 50, 70, 80, 90 and 100. Only FEM simulations were performed for
$Re_p$) of 1, 5, 10, 20, 30, 50, 70, 80, 90 and 100. Only FEM simulations were performed for ![]() $Re_p < 30$ due to computational cost. A ‘transition region’ is observed where multiple equilibria coexist, and this phenomenon persists until
$Re_p < 30$ due to computational cost. A ‘transition region’ is observed where multiple equilibria coexist, and this phenomenon persists until ![]() $Re_p = 90$, beyond which only a singular equilibrium at the centre prevails.
$Re_p = 90$, beyond which only a singular equilibrium at the centre prevails.
3.2.2. Mechanisms of bifurcation reversal at high  $Re$
$Re$
Next, we explored the underlying mechanisms of the reversal in the bifurcation of the equilibrium position.
To the best of our knowledge, the phenomenon of migration back to the centre at higher ![]() $Re_p$ has not been previously reported in inertial shear flow. Prior studies on non-bounded flow conducted under similar flow conditions did not report this particular behaviour. Kurose & Komori (Reference Kurose and Komori1999) performed a numerical study on a non-rotating sphere in a linear shear flow, spanning a wide range of particle Reynolds numbers (
$Re_p$ has not been previously reported in inertial shear flow. Prior studies on non-bounded flow conducted under similar flow conditions did not report this particular behaviour. Kurose & Komori (Reference Kurose and Komori1999) performed a numerical study on a non-rotating sphere in a linear shear flow, spanning a wide range of particle Reynolds numbers (![]() $1 \leq Re_p \leq 500$). They observed only one instance of the lift force coefficient changing its sign for
$1 \leq Re_p \leq 500$). They observed only one instance of the lift force coefficient changing its sign for ![]() $Re_p > 60$. Other studies have investigated the behaviour of spheres in unbounded flow (Bagchi & Balachandar Reference Bagchi and Balachandar2002a,Reference Bagchi and Balachandarb), but none of them reported a second reversal in the direction of the lift force.
$Re_p > 60$. Other studies have investigated the behaviour of spheres in unbounded flow (Bagchi & Balachandar Reference Bagchi and Balachandar2002a,Reference Bagchi and Balachandarb), but none of them reported a second reversal in the direction of the lift force.
Similar observations can be made for studies conducted in bounded flows, which also do not report the behaviour observed in this study. This can be attributed mainly to the fact that the investigated ![]() $Re_p$ were close to unity (Cherukat & McLaughlin Reference Cherukat and McLaughlin1994). Recently, Shi et al. explored the flow around a rigid sphere translating in the near-wall region of a single wall-bounded flow (Shi et al. Reference Shi, Rzehak, Lucas and Magnaudet2021). In contrast to previous work, they considered the effect of rotation and explored values of
$Re_p$ were close to unity (Cherukat & McLaughlin Reference Cherukat and McLaughlin1994). Recently, Shi et al. explored the flow around a rigid sphere translating in the near-wall region of a single wall-bounded flow (Shi et al. Reference Shi, Rzehak, Lucas and Magnaudet2021). In contrast to previous work, they considered the effect of rotation and explored values of ![]() $Re_p$ greater than unity. They introduced the slip Reynolds number, defined as
$Re_p$ greater than unity. They introduced the slip Reynolds number, defined as ![]() $Re_s = |U_{{rel}}| d / \nu$, where
$Re_s = |U_{{rel}}| d / \nu$, where ![]() $|U_{{rel}}|$ represents the prescribed relative velocity of the particle to the wall (slip velocity),
$|U_{{rel}}|$ represents the prescribed relative velocity of the particle to the wall (slip velocity), ![]() $d$ is the particle diameter and
$d$ is the particle diameter and ![]() $\nu$ is the kinematic viscosity. However, their investigation only tested a maximum value of
$\nu$ is the kinematic viscosity. However, their investigation only tested a maximum value of ![]() $Re_s = 250$, corresponding to
$Re_s = 250$, corresponding to ![]() $Re_p \sim 20$ and the reversal of the lift force sign was not observed in their study.
$Re_p \sim 20$ and the reversal of the lift force sign was not observed in their study.
However, comparable phenomena to what we observed have been reported in pipe flow studies within moderately high Reynolds number regimes (Matas, Morris & Guazzelli Reference Matas, Morris and Guazzelli2004; Shao, Yu & Sun Reference Shao, Yu and Sun2008; Matas, Morris & Guazzelli Reference Matas, Morris and Guazzelli2009; Nakayama et al. Reference Nakayama, Yamashita, Yabu, Itano and Sugihara-Seki2019; Pan, Li & Glowinski Reference Pan, Li and Glowinski2021). These studies have shown experimentally, numerically and analytically the existence of three regimes of equilibria for a pipe flow. The Segré–Silberberg annulus (Segre & Silberberg Reference Segre and Silberberg1962) was observed to move closer to the tube walls for ![]() $Re_c$ up to 700. At
$Re_c$ up to 700. At ![]() $700 > Re_c > 900$ particles were detected on an inner annulus as well as the Segré–Silberberg ring. At even higher
$700 > Re_c > 900$ particles were detected on an inner annulus as well as the Segré–Silberberg ring. At even higher ![]() $Re_c$, particles were focused only on the inner annulus, indicating that the radial position of the Segré–Silberberg ring is no longer a stable equilibrium position (Nakayama et al. Reference Nakayama, Yamashita, Yabu, Itano and Sugihara-Seki2019). Although the inner annulus equilibrium position never reaches the pipe centreline in those studies, the overall behaviour resembles that of the shear flow we described earlier. Shao et al. (Reference Shao, Yu and Sun2008) attributed this complex particle migration behaviour to the interaction between the flow and the channel in terms of travelling wave structures (Hof et al. Reference Hof, Van Doorne, Westerweel, Nieuwstadt, Faisst, Eckhardt, Wedin, Kerswell and Waleffe2004; Kerswell Reference Kerswell2005; Eckhardt et al. Reference Eckhardt, Schneider, Hof and Westerweel2007; Pringle & Kerswell Reference Pringle and Kerswell2007; Shao et al. Reference Shao, Yu and Sun2008), i.e. secondary flows developed perpendicular to the main flow direction within the particle's plane, as well as both upstream and downstream of the particle.
$Re_c$, particles were focused only on the inner annulus, indicating that the radial position of the Segré–Silberberg ring is no longer a stable equilibrium position (Nakayama et al. Reference Nakayama, Yamashita, Yabu, Itano and Sugihara-Seki2019). Although the inner annulus equilibrium position never reaches the pipe centreline in those studies, the overall behaviour resembles that of the shear flow we described earlier. Shao et al. (Reference Shao, Yu and Sun2008) attributed this complex particle migration behaviour to the interaction between the flow and the channel in terms of travelling wave structures (Hof et al. Reference Hof, Van Doorne, Westerweel, Nieuwstadt, Faisst, Eckhardt, Wedin, Kerswell and Waleffe2004; Kerswell Reference Kerswell2005; Eckhardt et al. Reference Eckhardt, Schneider, Hof and Westerweel2007; Pringle & Kerswell Reference Pringle and Kerswell2007; Shao et al. Reference Shao, Yu and Sun2008), i.e. secondary flows developed perpendicular to the main flow direction within the particle's plane, as well as both upstream and downstream of the particle.
Since both the Lighthill–Auton inviscid lift, and the viscous-effect induced opposite lift, are related to streamwise vorticity fields (Lighthill Reference Lighthill1956, Reference Lighthill1957; Auton Reference Auton1987; Shi & Rzehak Reference Shi and Rzehak2020; Shi et al. Reference Shi, Rzehak, Lucas and Magnaudet2021), we also examine the streamwise vorticity fields at different particle ![]() $Re$ numbers. Figure 7 illustrates the non-dimensional streamwise vorticity,
$Re$ numbers. Figure 7 illustrates the non-dimensional streamwise vorticity, ![]() $\omega _0$, at the
$\omega _0$, at the ![]() $y$–
$y$–![]() $z$ particle plane (
$z$ particle plane (![]() $x = 0$) and both the upstream (
$x = 0$) and both the upstream (![]() $x = +0.75 d_x$) and downstream (
$x = +0.75 d_x$) and downstream (![]() $x = -0.75 d_x$) for the case of a prolate located at
$x = -0.75 d_x$) for the case of a prolate located at ![]() $z_0 = -0.2$ at
$z_0 = -0.2$ at ![]() $Re_p = 30$ and
$Re_p = 30$ and ![]() $Re_p = 100$. Here,
$Re_p = 100$. Here, ![]() $d_x$ denotes the
$d_x$ denotes the ![]() $x$ component of the prolate diameter undergoing logrolling motion. We chose this location since the prolate experiences the force in opposite directions at
$x$ component of the prolate diameter undergoing logrolling motion. We chose this location since the prolate experiences the force in opposite directions at ![]() $Re_p = 30$ and
$Re_p = 30$ and ![]() $Re_p = 100$ at
$Re_p = 100$ at ![]() $z_0 = -0.2$. Therefore, it can showcase the flow structure evolution responsible for the reversal in the bifurcation. At
$z_0 = -0.2$. Therefore, it can showcase the flow structure evolution responsible for the reversal in the bifurcation. At ![]() $Re_p = 30$, which is below the ‘transition region’, the vorticity field exhibited nearly symmetric behaviour in the vicinity of the particle. That is, the fluid flows away from the particle (figure 7b), followed by a pair of counter-rotating vortices that change rotational direction going from the upstream to the downstream (figure 7a,c). This is in agreement with the observation of Shao et al. (Reference Shao, Yu and Sun2008) in pipe flow. However, above the ‘transition region’ and at
$Re_p = 30$, which is below the ‘transition region’, the vorticity field exhibited nearly symmetric behaviour in the vicinity of the particle. That is, the fluid flows away from the particle (figure 7b), followed by a pair of counter-rotating vortices that change rotational direction going from the upstream to the downstream (figure 7a,c). This is in agreement with the observation of Shao et al. (Reference Shao, Yu and Sun2008) in pipe flow. However, above the ‘transition region’ and at ![]() $Re_p = 100$, an additional pair of counter-rotating streamwise vortices is formed at the particle plane, between the particle and the bottom wall (figure 7e), disrupting the symmetry of the pressure field in the vicinity of the particle (figure 8). This asymmetry caused higher pressure magnitudes on the wall side of the particle, ultimately pushing it upwards towards the centre. While, as reported by Fox et al., at
$Re_p = 100$, an additional pair of counter-rotating streamwise vortices is formed at the particle plane, between the particle and the bottom wall (figure 7e), disrupting the symmetry of the pressure field in the vicinity of the particle (figure 8). This asymmetry caused higher pressure magnitudes on the wall side of the particle, ultimately pushing it upwards towards the centre. While, as reported by Fox et al., at ![]() $Re_p = 10$, which is well below the ‘transition region’, the asymmetry of the flow streamlines around the particle at the off-centre focusing position produces no net hydrodynamic lift (Fox Reference Fox2021). In short, we found that the altered streamwise vorticity field and its associated secondary flow velocity at higher
$Re_p = 10$, which is well below the ‘transition region’, the asymmetry of the flow streamlines around the particle at the off-centre focusing position produces no net hydrodynamic lift (Fox Reference Fox2021). In short, we found that the altered streamwise vorticity field and its associated secondary flow velocity at higher ![]() $Re$ leads to unsymmetrical pressure distribution, which pushes the particle back to the centre.
$Re$ leads to unsymmetrical pressure distribution, which pushes the particle back to the centre.

Figure 7. Non-dimensional streamwise vorticity field, (![]() $\omega _0$ =
$\omega _0$ = ![]() $\omega H / U_W$) in the
$\omega H / U_W$) in the ![]() $y$–
$y$–![]() $z$ plane at the upstream (
$z$ plane at the upstream (![]() $x= +0.75 d_x$), particle plane (
$x= +0.75 d_x$), particle plane (![]() $x = 0$) and downstream (
$x = 0$) and downstream (![]() $x = -0.75 d_x$) at
$x = -0.75 d_x$) at ![]() $Re_p =30$ (a–c) and
$Re_p =30$ (a–c) and ![]() $Re_p = 100$ (d–f), respectively. Here,
$Re_p = 100$ (d–f), respectively. Here, ![]() $d_x$ is the
$d_x$ is the ![]() $x$ component of the prolate diameter undergoing logrolling motion. The colour map represents streamwise vorticity; arrows show in-plane velocity field.
$x$ component of the prolate diameter undergoing logrolling motion. The colour map represents streamwise vorticity; arrows show in-plane velocity field.

Figure 8. Normalized pressure distribution, ![]() $p_0 = p/p_{max}$, in the particle
$p_0 = p/p_{max}$, in the particle ![]() $y$–
$y$–![]() $z$ plane for (a)
$z$ plane for (a)![]() $~Re_p = 30$, and (b)
$~Re_p = 30$, and (b)![]() $~Re_p = 100$ where
$~Re_p = 100$ where ![]() $p_{max}$ is the maximum pressure in the
$p_{max}$ is the maximum pressure in the ![]() $y$–
$y$–![]() $z$ plane. (c) Normalized pressure along the vertical cut-line through the particle symmetric plane; here, pressure is normalized using the maximum pressure along the cut line for ease of comparison.
$z$ plane. (c) Normalized pressure along the vertical cut-line through the particle symmetric plane; here, pressure is normalized using the maximum pressure along the cut line for ease of comparison.
Finally, in an effort to further explore the phenomenon in one-wall bounded flows, we attempted to utilize FEM simulations to gain a better understanding of the influence of the wall. However, our FEM model failed to converge for cases where ![]() $H \gg 100\,\mathrm {\mu } {\rm m}$ at
$H \gg 100\,\mathrm {\mu } {\rm m}$ at ![]() $Re_p = 100$, preventing us from confirming whether this behaviour is influenced by a single wall or the presence of two parallel walls. In other words, although we showed the reversal of the pitchfork bifurcation with the particles going back can occur for two walls, it is unclear whether this can also occur for a single-wall bounded flow with further increased
$Re_p = 100$, preventing us from confirming whether this behaviour is influenced by a single wall or the presence of two parallel walls. In other words, although we showed the reversal of the pitchfork bifurcation with the particles going back can occur for two walls, it is unclear whether this can also occur for a single-wall bounded flow with further increased ![]() $Re_p$, and future investigations are needed.
$Re_p$, and future investigations are needed.
3.2.3. Effect of particle orientation
In our previous study, we observed that prolate spheroids can undergo different rotational motions in a straight microchannel (Lauricella et al. Reference Lauricella, Zhou, Luan, Papautsky and Peng2022), depending on the initial conditions. The presence of the four walls leads to more complicated dynamics, that allow a prolate particle to stabilize into a logrolling motion. However, in the existing literature, only the tumbling motion had been reported for prolate ellipsoids in inertial flows (Tohme et al. Reference Tohme, Magaud and Baldas2021).
We observed that, even in a two parallel walls configuration, a prolate particle that was initially horizontally aligned (largest radius aligned with the ![]() $y$ direction) experienced a logrolling rotational motion. If the particle was released with a vertical alignment (largest radius parallel with the
$y$ direction) experienced a logrolling rotational motion. If the particle was released with a vertical alignment (largest radius parallel with the ![]() $z$ direction), it maintained a tumbling motion. In both cases, the particles did not change their rotational motion throughout the simulation. We observed that the tumbling prolate reached the stable off-centre position
$z$ direction), it maintained a tumbling motion. In both cases, the particles did not change their rotational motion throughout the simulation. We observed that the tumbling prolate reached the stable off-centre position ![]() $z_0 = -0.22$, closer to the centre with respect to the same particle that is logrolling, which focused at
$z_0 = -0.22$, closer to the centre with respect to the same particle that is logrolling, which focused at ![]() $z_0 = -0.264$. This happened for two different starting positions at
$z_0 = -0.264$. This happened for two different starting positions at ![]() $z_0 = -0.1$ and
$z_0 = -0.1$ and ![]() $z_0 = -0.25$. The trajectory of the tumbling prolate presented small oscillations in the transverse direction, due to the rotational mode which is less stable than the logrolling behaviour. As can be noticed in figure 4, the time required to reach the stable off-centre position for a tumbling particle was approximately 30 % longer than for the particle undergoing a logrolling motion. Furthermore, we tested other alignments, including an initial ‘inclined’ orientation, by rotating the prolate particle by
$z_0 = -0.25$. The trajectory of the tumbling prolate presented small oscillations in the transverse direction, due to the rotational mode which is less stable than the logrolling behaviour. As can be noticed in figure 4, the time required to reach the stable off-centre position for a tumbling particle was approximately 30 % longer than for the particle undergoing a logrolling motion. Furthermore, we tested other alignments, including an initial ‘inclined’ orientation, by rotating the prolate particle by ![]() $15^{\circ }$ and
$15^{\circ }$ and ![]() $45^{\circ }$, as shown in figure 9(a). Shortly after this initial condition, the particle vertically aligned in the flow and underwent a tumbling motion, thereby achieving the same stable off-centre position as a particle that was vertically aligned from the beginning of the simulation. Therefore, unless the particle was released with a horizontal orientation, any substantial shift (i.e. greater than a few degrees) from this position led to a tumbling motion under the flow conditions described above. A qualitative illustration of this behaviour is shown by plotting the angular velocities of these particles in figure 9(b–d). Note that although we previously used
$45^{\circ }$, as shown in figure 9(a). Shortly after this initial condition, the particle vertically aligned in the flow and underwent a tumbling motion, thereby achieving the same stable off-centre position as a particle that was vertically aligned from the beginning of the simulation. Therefore, unless the particle was released with a horizontal orientation, any substantial shift (i.e. greater than a few degrees) from this position led to a tumbling motion under the flow conditions described above. A qualitative illustration of this behaviour is shown by plotting the angular velocities of these particles in figure 9(b–d). Note that although we previously used ![]() $\omega$ to indicate the fluid streamwise vorticity, here
$\omega$ to indicate the fluid streamwise vorticity, here ![]() $\omega$ it refers to the angular velocities of the particle. The components around the
$\omega$ it refers to the angular velocities of the particle. The components around the ![]() $x$ and
$x$ and ![]() $z$ axes of the angular velocity of a tumbling particle that had a perfect vertical alignment were zero. In this case, only the
$z$ axes of the angular velocity of a tumbling particle that had a perfect vertical alignment were zero. In this case, only the ![]() $y$-angular velocity
$y$-angular velocity ![]() $\omega _y$ was non-zero. A particle with an initial angle exhibited non-zero components of
$\omega _y$ was non-zero. A particle with an initial angle exhibited non-zero components of ![]() $\omega _x$ and
$\omega _x$ and ![]() $\omega _z$ until it stabilized on a vertical rotation, as shown in figure 9(b,d). Concurrently, the value of
$\omega _z$ until it stabilized on a vertical rotation, as shown in figure 9(b,d). Concurrently, the value of ![]() $\omega _y$ progressively increased, as shown in figure 9(c). In general, the angular velocity of tumbling particles was characterized by periodic oscillations, while it was almost constant for logrolling particles.
$\omega _y$ progressively increased, as shown in figure 9(c). In general, the angular velocity of tumbling particles was characterized by periodic oscillations, while it was almost constant for logrolling particles.

Figure 9. Symmetric prolate particles with ![]() $K = 0.2$ released with different initial orientations at
$K = 0.2$ released with different initial orientations at ![]() $z_0 = -0.1$, with
$z_0 = -0.1$, with ![]() $Re_p = 30$. (a) The trajectory of the prolate particles shows that if the particle has an initial horizontal alignment, it will keep the same orientation undergoing a logrolling motion, focusing at
$Re_p = 30$. (a) The trajectory of the prolate particles shows that if the particle has an initial horizontal alignment, it will keep the same orientation undergoing a logrolling motion, focusing at ![]() $z_0 = -0.264$. In all the other cases, i.e. initial angle or vertical alignment, the final rotational motion and off-centre position will be the same at
$z_0 = -0.264$. In all the other cases, i.e. initial angle or vertical alignment, the final rotational motion and off-centre position will be the same at ![]() $z_0 = -0.22$. (b–d) Angular velocities of the particles around the three axes. Angular velocities are in units of radians per second.
$z_0 = -0.22$. (b–d) Angular velocities of the particles around the three axes. Angular velocities are in units of radians per second.
Finally, it is important to clarify that in experimental settings, maintaining a perfectly horizontal orientation is not necessary for preserving logrolling motion. Our observations suggest that at moderate Reynolds numbers, the logrolling motion remains robust even with small fluctuations in inclination, typically of the order of a few degrees. However, an inclination of ![]() $15^{\circ }$ can shift the motion towards tumbling, as illustrated in figure 9 for
$15^{\circ }$ can shift the motion towards tumbling, as illustrated in figure 9 for ![]() $Re_p = 30$. Conversely, at higher Reynolds numbers, the augmented influence of inertia plays a stabilizing role, allowing the system to endure more substantial oscillations. In figure 10, the asymmetric prolate particle at
$Re_p = 30$. Conversely, at higher Reynolds numbers, the augmented influence of inertia plays a stabilizing role, allowing the system to endure more substantial oscillations. In figure 10, the asymmetric prolate particle at ![]() $Re_p = 70$ initially exhibited an oscillatory motion resembling kayaking. Nevertheless, as the trajectory progressed, the particle smoothly transitioned into a stable logrolling motion, evident in the form of a flat trajectory line. We also tested a prolate particle inclined by
$Re_p = 70$ initially exhibited an oscillatory motion resembling kayaking. Nevertheless, as the trajectory progressed, the particle smoothly transitioned into a stable logrolling motion, evident in the form of a flat trajectory line. We also tested a prolate particle inclined by ![]() $5^{\circ }$ at
$5^{\circ }$ at ![]() $Re_p = 100$ and it preserved the logrolling motion.
$Re_p = 100$ and it preserved the logrolling motion.

Figure 10. Asymmetric prolate particles with ![]() $K = 0.17$. The particles were released with a horizontal alignment at
$K = 0.17$. The particles were released with a horizontal alignment at ![]() $z_0 = -0.1$. For
$z_0 = -0.1$. For ![]() $Re_p = 30$ and
$Re_p = 30$ and ![]() $Re_p = 50$ the particles underwent a logrolling motion, and the trajectories exhibited some bumps due to the irregular oscillatory motion given by the asymmetry. At
$Re_p = 50$ the particles underwent a logrolling motion, and the trajectories exhibited some bumps due to the irregular oscillatory motion given by the asymmetry. At ![]() $Re_p = 100$ the particle was much more stable and underwent a logrolling motion. The particle shape is shown in the inset.
$Re_p = 100$ the particle was much more stable and underwent a logrolling motion. The particle shape is shown in the inset.
3.2.4. Effect of shape asymmetry
Finally, we studied the behaviour of an asymmetric prolate particle with a confinement ratio ![]() $K = 0.17$, similar to the symmetric cases. The creation of asymmetric particles was initiated at the outset of the simulation by employing LAMMPS-specific commands within the region category. In particular, the ‘union’ and ‘intersect’ keywords were utilized to designate and merge specified particle regions from the initial lattice of SPH particles, resulting in the generation of customized mesoscopic particles. As illustrated in figure 10, the particle in question was formed by combining a spherical component of radius
$K = 0.17$, similar to the symmetric cases. The creation of asymmetric particles was initiated at the outset of the simulation by employing LAMMPS-specific commands within the region category. In particular, the ‘union’ and ‘intersect’ keywords were utilized to designate and merge specified particle regions from the initial lattice of SPH particles, resulting in the generation of customized mesoscopic particles. As illustrated in figure 10, the particle in question was formed by combining a spherical component of radius ![]() $9\, \mathrm {\mu }{\rm m}$ with a prolate particle with an AR of 4. We released the particle with a horizontal alignment at position
$9\, \mathrm {\mu }{\rm m}$ with a prolate particle with an AR of 4. We released the particle with a horizontal alignment at position ![]() $z_0 = -0.1$ and tested
$z_0 = -0.1$ and tested ![]() $Re_p = 30, 50$ and
$Re_p = 30, 50$ and ![]() $100$. The off-centre positions were present also for the asymmetric prolate and were similar to the positions achieved by the symmetric prolate particles. However, the asymmetric shape of these particles created pronounced oscillations in the trajectory that persisted also after the particle reached the equilibrium position (figure 10). In addition, the time required to reach the stable off-centre positions was more than twice the time required for the symmetric particles, presumably a consequence of the oscillating behaviour that slows down the overall migration process. One major difference occurred at
$100$. The off-centre positions were present also for the asymmetric prolate and were similar to the positions achieved by the symmetric prolate particles. However, the asymmetric shape of these particles created pronounced oscillations in the trajectory that persisted also after the particle reached the equilibrium position (figure 10). In addition, the time required to reach the stable off-centre positions was more than twice the time required for the symmetric particles, presumably a consequence of the oscillating behaviour that slows down the overall migration process. One major difference occurred at ![]() $Re_p = 100$, where unlike the symmetric case, the particle did not reach the
$Re_p = 100$, where unlike the symmetric case, the particle did not reach the ![]() $z$ midline (
$z$ midline (![]() $H = 0$) and instead remained in the vicinity of
$H = 0$) and instead remained in the vicinity of ![]() $z_0 = -0.06$. Besides the initial horizontal orientation, we also tested the vertical and inclined orientation. The corresponding results are shown in figure 11. The tumbling asymmetric prolate took more time to reach a stable off-centre position, which oscillated around
$z_0 = -0.06$. Besides the initial horizontal orientation, we also tested the vertical and inclined orientation. The corresponding results are shown in figure 11. The tumbling asymmetric prolate took more time to reach a stable off-centre position, which oscillated around ![]() $z_0 = -0.28$. A different trajectory, but the same focusing position was achieved by the same particle which was released with an initial angle of
$z_0 = -0.28$. A different trajectory, but the same focusing position was achieved by the same particle which was released with an initial angle of ![]() $45^{\circ }$, as shown in figure 11. The inclination gradually disappeared as the particle travelled in the
$45^{\circ }$, as shown in figure 11. The inclination gradually disappeared as the particle travelled in the ![]() $x$ direction. It eventually experienced a tumbling motion and stabilized at
$x$ direction. It eventually experienced a tumbling motion and stabilized at ![]() $z_0 = -0.28$. This was also true for a smaller initial angle of
$z_0 = -0.28$. This was also true for a smaller initial angle of ![]() $20^{\circ }$. Overall, we confirmed that even in the case of asymmetric prolate ellipsoids, logrolling particles reached their stable off-centre position sooner than the tumbling particles. The time required for the logrolling particles was approximately 50 % less than that for the tumbling particles of the same size and shape. We organized the cases we tested for prolate particles and the different parameters we investigated in table 1.
$20^{\circ }$. Overall, we confirmed that even in the case of asymmetric prolate ellipsoids, logrolling particles reached their stable off-centre position sooner than the tumbling particles. The time required for the logrolling particles was approximately 50 % less than that for the tumbling particles of the same size and shape. We organized the cases we tested for prolate particles and the different parameters we investigated in table 1.

Figure 11. Asymmetric prolate particles with ![]() $K = 0.17$. The particles were released with different initial orientations. In the case of initial vertical alignment or with an angle, it always ended up tumbling, reaching the same stable off-centre position of
$K = 0.17$. The particles were released with different initial orientations. In the case of initial vertical alignment or with an angle, it always ended up tumbling, reaching the same stable off-centre position of ![]() $z_0 = -0.28$.
$z_0 = -0.28$.
Table 1. List of the cases investigated for prolate ellipsoidal particles. The confinement ratio ![]() $K$, particle AR,
$K$, particle AR, ![]() $Re_p$,
$Re_p$, ![]() $Re_c$, initial position (IP) initial orientation (refer to figure 1b), final rotational mode (logrolling (L), tumbling (T)) and final stable equilibrium position are reported. Asymmetric prolate particles are identified with ‘asy’ in the column of the AR. For these particles, their final motion is oscillating, therefore the stable focusing position is indicated as ‘average’.
$Re_c$, initial position (IP) initial orientation (refer to figure 1b), final rotational mode (logrolling (L), tumbling (T)) and final stable equilibrium position are reported. Asymmetric prolate particles are identified with ‘asy’ in the column of the AR. For these particles, their final motion is oscillating, therefore the stable focusing position is indicated as ‘average’.

3.3. Oblate particles
The unique off-centre focusing positions were exhibited also by oblate spheroids. Regardless of the initial orientation of the oblate particles we tested, they eventually reached a stable logrolling motion, with the major axis aligned with the vorticity axis. Unlike Jeffery's theory, developed for an inertialess fluid, when the effect of inertia is not negligible, the orbit followed by the particle is reduced to one. In an unbounded simple shear flow, it was already observed that an oblate particle drifts towards a logrolling motion (Huang et al. Reference Huang, Yang, Krafczyk and Lu2012; Mao & Alexeev Reference Mao and Alexeev2014). The same behaviour applied in the parallel-wall system we employed in the present investigation.
3.3.1. Effect of  $Re$ number and initial position
$Re$ number and initial position
We modelled an oblate particle with major axes ![]() $40\,\mathrm {\mu }{\rm m}\times 40\,\mathrm {\mu }{\rm m}\times 20\, \mathrm {\mu }{\rm m}$ in length, corresponding to a confinement ratio
$40\,\mathrm {\mu }{\rm m}\times 40\,\mathrm {\mu }{\rm m}\times 20\, \mathrm {\mu }{\rm m}$ in length, corresponding to a confinement ratio ![]() $K = 0.2$. We identified differences and similarities in the migration dynamics in comparison with a prolate particle with the same confinement ratio. The stable off-centre position was
$K = 0.2$. We identified differences and similarities in the migration dynamics in comparison with a prolate particle with the same confinement ratio. The stable off-centre position was ![]() $z_0 = -0.21$ for
$z_0 = -0.21$ for ![]() $Re_p = 30$, which is almost the same as a prolate particle undergoing a tumbling motion at the same
$Re_p = 30$, which is almost the same as a prolate particle undergoing a tumbling motion at the same ![]() $Re_p$. This confirmed that one key factor in determining the exclusive off-centre positions is the extension of the particle in the
$Re_p$. This confirmed that one key factor in determining the exclusive off-centre positions is the extension of the particle in the ![]() $z$ direction. Then, we increased
$z$ direction. Then, we increased ![]() $Re_p$ and noted that for
$Re_p$ and noted that for ![]() $Re_p = 50$ the off-centre position did not change (figure 12), unlike prolate particles for which we observed two different equilibria at
$Re_p = 50$ the off-centre position did not change (figure 12), unlike prolate particles for which we observed two different equilibria at ![]() $Re_p = 30$,
$Re_p = 30$, ![]() $Re_p = 50$ and
$Re_p = 50$ and ![]() $Re_p = 100$. However, if the same particle was released closer to the centre at
$Re_p = 100$. However, if the same particle was released closer to the centre at ![]() $Re_p = 50$, it reached the centre focusing position, showing that at higher values of
$Re_p = 50$, it reached the centre focusing position, showing that at higher values of ![]() $Re_p$ the initial location of the particle is crucial in determining the final equilibrium position. In addition, at
$Re_p$ the initial location of the particle is crucial in determining the final equilibrium position. In addition, at ![]() $Re_p = 60$ and
$Re_p = 60$ and ![]() $70$, the oblate particle migrated to the centre and stabilized at
$70$, the oblate particle migrated to the centre and stabilized at ![]() $z_0 = 0$ regardless of the initial starting location. For a prolate particle, the same behaviour was observed at
$z_0 = 0$ regardless of the initial starting location. For a prolate particle, the same behaviour was observed at ![]() $Re_p = 100$, and off-centre positions still existed at
$Re_p = 100$, and off-centre positions still existed at ![]() $Re_p = 70$ (figure 5a).
$Re_p = 70$ (figure 5a).

Figure 12. Symmetric oblate particles with ![]() $K = 0.2$ The particle top view is reported in the inset. For all the
$K = 0.2$ The particle top view is reported in the inset. For all the ![]() $Re_p$ values, the oblate spheroid underwent a logrolling motion. Different values of
$Re_p$ values, the oblate spheroid underwent a logrolling motion. Different values of ![]() $Re_p$ yield different off-centre positions, but with a different trend than prolate ellipsoids. The initial positions were chosen arbitrarily.
$Re_p$ yield different off-centre positions, but with a different trend than prolate ellipsoids. The initial positions were chosen arbitrarily.
3.3.2. Effect of shape asymmetry
Ultimately, analogous to the approach used for creating the asymmetric prolate particle, we applied a similar procedure by merging an oblate particle measuring ![]() $20 \,\mathrm {\mu }{\rm m}\times 10\,\mathrm {\mu }{\rm m}\times 10\,\mathrm {\mu }{\rm m}$ with a prolate particle with an AR of 2 to get the asymmetric oblate spheroid with
$20 \,\mathrm {\mu }{\rm m}\times 10\,\mathrm {\mu }{\rm m}\times 10\,\mathrm {\mu }{\rm m}$ with a prolate particle with an AR of 2 to get the asymmetric oblate spheroid with ![]() $K = 0.2$ reported in figure 13. We observed that, unlike symmetric oblate particles, the particles studied in these cases underwent a tumbling motion for a long period of time, before transitioning to a logrolling motion. We tested three values of
$K = 0.2$ reported in figure 13. We observed that, unlike symmetric oblate particles, the particles studied in these cases underwent a tumbling motion for a long period of time, before transitioning to a logrolling motion. We tested three values of ![]() $Re_p$, finding various stable off-centre positions. The particle equilibrated at
$Re_p$, finding various stable off-centre positions. The particle equilibrated at ![]() $z_0 = -0.25$ for
$z_0 = -0.25$ for ![]() $Re_p = 30$,
$Re_p = 30$, ![]() $z_0 = -0.3$ for
$z_0 = -0.3$ for ![]() $Re_p = 50$ and
$Re_p = 50$ and ![]() $z_0 = -0.32$ for
$z_0 = -0.32$ for ![]() $Re_p = 70$. However, for
$Re_p = 70$. However, for ![]() $Re_p = 30$, the stable off-centre position changed when the particle shifted to a logrolling behaviour. We observed the shift in the rotational mode only for
$Re_p = 30$, the stable off-centre position changed when the particle shifted to a logrolling behaviour. We observed the shift in the rotational mode only for ![]() $Re_p = 30$. We believe that the same transition can happen also for lower values of
$Re_p = 30$. We believe that the same transition can happen also for lower values of ![]() $Re_p$, whereas for higher
$Re_p$, whereas for higher ![]() $Re_p$ the force exerted by the fluid on the particle prevents this transition. In fact, asymmetric oblates at
$Re_p$ the force exerted by the fluid on the particle prevents this transition. In fact, asymmetric oblates at ![]() $Re_p = 50$ and
$Re_p = 50$ and ![]() $Re_p = 70$ underwent a tumbling motion, without experiencing a transition in the rotational mode. In addition, as discussed for the asymmetric prolate, the trajectory was not smooth even for asymmetric oblate spheroids, where slight bumps were present even when the particle reached a stable position. For this specific case, the oscillations increased when the particle transitioned from the tumbling to the logrolling motion, at the lowest
$Re_p = 70$ underwent a tumbling motion, without experiencing a transition in the rotational mode. In addition, as discussed for the asymmetric prolate, the trajectory was not smooth even for asymmetric oblate spheroids, where slight bumps were present even when the particle reached a stable position. For this specific case, the oscillations increased when the particle transitioned from the tumbling to the logrolling motion, at the lowest ![]() $Re_p$ tested. A summary of the simulations of oblate particles is provided in table 2.
$Re_p$ tested. A summary of the simulations of oblate particles is provided in table 2.

Figure 13. Asymmetric oblate particles with ![]() $K = 0.2$. The vertical dashed line indicates the moment when the particle at
$K = 0.2$. The vertical dashed line indicates the moment when the particle at ![]() $Re_p = 30$ transitions from a tumbling motion to logrolling. This did not happen for
$Re_p = 30$ transitions from a tumbling motion to logrolling. This did not happen for ![]() $Re_p = 50$ and
$Re_p = 50$ and ![]() $Re_p = 70$. The trajectories showed some oscillations due to the asymmetric shape, shown in the inset.
$Re_p = 70$. The trajectories showed some oscillations due to the asymmetric shape, shown in the inset.
Table 2. List of the cases investigated for oblate ellipsoidal particles. The asymmetric oblate at ![]() $Re_p = 30$ exhibited a tumbling motion with one focusing position and then transitioned into a logrolling motion with a different off-centre position. All cases showed oscillations for asymmetric particles. The initial position (IP) of the particle may play a role in determining the final equilibrium position.
$Re_p = 30$ exhibited a tumbling motion with one focusing position and then transitioned into a logrolling motion with a different off-centre position. All cases showed oscillations for asymmetric particles. The initial position (IP) of the particle may play a role in determining the final equilibrium position.

3.4. Effect of particle AR and confinement ratio on the inertial bifurcation
In this section, we present a comparison of prolate and oblate particles with different dimensions, with the main purpose of elucidating the role of each parameter (confinement ratio, volume, AR) in determining the final focusing position of the particle. While in the previous sections, we mainly investigated ellipsoids an AR of 2, here we explored different ARs and confinement ratios, and also compared ellipsoidal particles with spheres. The results were organized in order to emphasize the common features presented by particles with the same behaviour, i.e. the same focusing position and dynamics.
First, we compared spherical, prolate and oblate particles with fixed volumes at two different ![]() $Re$. For these cases we used
$Re$. For these cases we used ![]() $Re_c$, since imposing the same volume on particles with different shapes leads inevitably to different radii,
$Re_c$, since imposing the same volume on particles with different shapes leads inevitably to different radii, ![]() $a$, and, as a consequence, to different
$a$, and, as a consequence, to different ![]() $Re_p$ (since
$Re_p$ (since ![]() $Re_p = (Ga^2)/\nu$). In figure 14, we tested particles with a volume
$Re_p = (Ga^2)/\nu$). In figure 14, we tested particles with a volume ![]() $V_{1} = 4189\, \mathrm {\mu }{\rm m}^3$,
$V_{1} = 4189\, \mathrm {\mu }{\rm m}^3$, ![]() $V_{2} = 8377\,\mathrm {\mu }{\rm m}^3$ and
$V_{2} = 8377\,\mathrm {\mu }{\rm m}^3$ and ![]() $V_{3} = 16\,775\,\mathrm {\mu }{\rm m}^3$. It can be noticed that
$V_{3} = 16\,775\,\mathrm {\mu }{\rm m}^3$. It can be noticed that ![]() $V_{2}$ is twice
$V_{2}$ is twice ![]() $V_{1}$ and
$V_{1}$ and ![]() $V_{3}$ is twice
$V_{3}$ is twice ![]() $V_{2}$. The results are shown in figure 14 for
$V_{2}$. The results are shown in figure 14 for ![]() $Re_c = 375$ and
$Re_c = 375$ and ![]() $Re_c = 880$. The figure also includes the dimension of the semiaxes of each particle, reported in the legend as (p, q, r), with p being the largest semiaxis. At
$Re_c = 880$. The figure also includes the dimension of the semiaxes of each particle, reported in the legend as (p, q, r), with p being the largest semiaxis. At ![]() $Re_c = 375$, the particles exhibited similar behaviour and there were no noticeable differences for particles with different volumes. Prolate particles underwent a logrolling motion, therefore the space they occupied in the transverse position was close to the spherical particles. Oblate particles reached focusing positions that were closer to the channel centre with respect to prolate and spheres, which exhibited a similar equilibrium position instead. These differences were more pronounced as the
$Re_c = 375$, the particles exhibited similar behaviour and there were no noticeable differences for particles with different volumes. Prolate particles underwent a logrolling motion, therefore the space they occupied in the transverse position was close to the spherical particles. Oblate particles reached focusing positions that were closer to the channel centre with respect to prolate and spheres, which exhibited a similar equilibrium position instead. These differences were more pronounced as the ![]() $Re_c$ and/or the volume were increased. These results suggested that the volume of the particle did not play a significant role in determining the final off-centre position, since for a fixed volume and fixed
$Re_c$ and/or the volume were increased. These results suggested that the volume of the particle did not play a significant role in determining the final off-centre position, since for a fixed volume and fixed ![]() $Re$ the shift in the equilibrium position was solely given by the difference in the vertical extension of the particle, namely its dimension in the transverse position
$Re$ the shift in the equilibrium position was solely given by the difference in the vertical extension of the particle, namely its dimension in the transverse position ![]() $z$. However, this trend was disrupted when the particle was too large, or
$z$. However, this trend was disrupted when the particle was too large, or ![]() $Re$ was too high. For particles with volume
$Re$ was too high. For particles with volume ![]() $V_3$ at
$V_3$ at ![]() $Re_c = 880$, it can be noticed that the oblate particle went back to the centre, the prolate particle underwent a tumbling motion and hit the bottom wall, while the sphere oscillated up and down without reaching a stable equilibrium.
$Re_c = 880$, it can be noticed that the oblate particle went back to the centre, the prolate particle underwent a tumbling motion and hit the bottom wall, while the sphere oscillated up and down without reaching a stable equilibrium.

Figure 14. Spheres (S), prolate (P) and oblate (O) particles with fixed volumes. Panels (a i–iii) and (b i–iii) show the cases at ![]() $Re_c = 375$ and
$Re_c = 375$ and ![]() $Re_c = 880$, respectively; while (a i,b i), (a ii,b ii) and (a iii,b iii) correspond to a different volume,
$Re_c = 880$, respectively; while (a i,b i), (a ii,b ii) and (a iii,b iii) correspond to a different volume, ![]() $V_{1} = 4189\,\mathrm {\mu }{\rm m}^3$,
$V_{1} = 4189\,\mathrm {\mu }{\rm m}^3$, ![]() $V_{2} = 8377 \,\mathrm {\mu }{\rm m}^3$ and
$V_{2} = 8377 \,\mathrm {\mu }{\rm m}^3$ and ![]() $V_{3} = 16\,775\,\mathrm {\mu }{\rm m}^3$, respectively. Also for these cases, the normalized transverse position
$V_{3} = 16\,775\,\mathrm {\mu }{\rm m}^3$, respectively. Also for these cases, the normalized transverse position ![]() $z_0 = z / H$ was plotted against the normalized time
$z_0 = z / H$ was plotted against the normalized time ![]() $t_0 = tG$.
$t_0 = tG$.
As shown in figure 15, more cases of prolate particles in various conditions were compared, to confirm and verify some insights provided by the previous data. Solid lines correspond to ![]() $Re_p = 50$ and dashed lines correspond to
$Re_p = 50$ and dashed lines correspond to ![]() $Re_p = 30$. Prolate particles with an AR of 5 (
$Re_p = 30$. Prolate particles with an AR of 5 (![]() $20\,\mathrm {\mu }{\rm m}$,
$20\,\mathrm {\mu }{\rm m}$, ![]() $4\,\mathrm {\mu }{\rm m}$,
$4\,\mathrm {\mu }{\rm m}$, ![]() $4\,\mathrm {\mu }{\rm m}$) and AR 2 (
$4\,\mathrm {\mu }{\rm m}$) and AR 2 (![]() $10\,\mathrm {\mu }{\rm m}$,
$10\,\mathrm {\mu }{\rm m}$, ![]() $5\,\mathrm {\mu }{\rm m}$,
$5\,\mathrm {\mu }{\rm m}$, ![]() $5\,\mathrm {\mu }{\rm m}$) were shown in blue and red, respectively. Although the AR and volume of the two particles were different, the focusing position was similar and close to the centreline. This confirmed that the main factor determining the off-centre position is the dimension of the particle in the transverse position. In this case, the particles vertical dimension was 4 and
$5\,\mathrm {\mu }{\rm m}$) were shown in blue and red, respectively. Although the AR and volume of the two particles were different, the focusing position was similar and close to the centreline. This confirmed that the main factor determining the off-centre position is the dimension of the particle in the transverse position. In this case, the particles vertical dimension was 4 and ![]() $5\,\mathrm {\mu }{\rm m}$, respectively. As mentioned before, this trend held until it was reverted when the particle became too large, and the wall-repulsive force pushed it away from the wall. This can be noticed for the prolate particle with dimensions (
$5\,\mathrm {\mu }{\rm m}$, respectively. As mentioned before, this trend held until it was reverted when the particle became too large, and the wall-repulsive force pushed it away from the wall. This can be noticed for the prolate particle with dimensions (![]() $20\,\mathrm {\mu }{\rm m}$,
$20\,\mathrm {\mu }{\rm m}$, ![]() $10\,\mathrm {\mu }{\rm m}$,
$10\,\mathrm {\mu }{\rm m}$, ![]() $10\,\mathrm {\mu }{\rm m}$) and (
$10\,\mathrm {\mu }{\rm m}$) and (![]() $30\,\mathrm {\mu }{\rm m}$,
$30\,\mathrm {\mu }{\rm m}$, ![]() $15\,\mathrm {\mu }{\rm m}$,
$15\,\mathrm {\mu }{\rm m}$, ![]() $15\,\mathrm {\mu }{\rm m}$) at
$15\,\mathrm {\mu }{\rm m}$) at ![]() $Re_p = 30$, shown with the yellow and magenta dashed lines, respectively. The former was slightly closer to the bottom wall than the bigger prolate particle. When
$Re_p = 30$, shown with the yellow and magenta dashed lines, respectively. The former was slightly closer to the bottom wall than the bigger prolate particle. When ![]() $Re_p$ was increased to 50, the smaller particle moved even closer to the confining wall, whereas the bigger particle exhibited an unstable behaviour.
$Re_p$ was increased to 50, the smaller particle moved even closer to the confining wall, whereas the bigger particle exhibited an unstable behaviour.

Figure 15. Prolate particles of different dimensions at ![]() $Re_p = 30$ (dashed lines) and 50 (solid lines). The semiaxes are reported in the legend as (p, q, r), with p being the major semiaxis. It can be noted how the two main factors in determining the final transverse position
$Re_p = 30$ (dashed lines) and 50 (solid lines). The semiaxes are reported in the legend as (p, q, r), with p being the major semiaxis. It can be noted how the two main factors in determining the final transverse position ![]() $z$ (normalized as
$z$ (normalized as ![]() $z_0 = z/H$) are
$z_0 = z/H$) are ![]() $Re$ and the dimension that the particles occupy in the transverse position.
$Re$ and the dimension that the particles occupy in the transverse position.
Overall, we never observed a spherical particle stably going back to the centre at high ![]() $Re$ in this investigation. To gain a better understanding of the difference between spheres and prolate particles at high
$Re$ in this investigation. To gain a better understanding of the difference between spheres and prolate particles at high ![]() $Re$, we tested prolate particles with different ARs at
$Re$, we tested prolate particles with different ARs at ![]() $Re_p = 100$. We explored decreasing values of AR approaching 1, corresponding to a spherical particle. As shown in figure 16(a), for an AR equal or greater than 2 the particle migrated towards the centre position. As the AR was reduced further, approaching the one of a sphere, oscillations appeared in the particle trajectories. In these unsteady cases, the particles reached a stable position and remained there for a given amount of time, but then they suddenly jumped towards the top wall and moved back and forth without finding an equilibrium location in the transverse position. This instability occurred approximately after a time of
$Re_p = 100$. We explored decreasing values of AR approaching 1, corresponding to a spherical particle. As shown in figure 16(a), for an AR equal or greater than 2 the particle migrated towards the centre position. As the AR was reduced further, approaching the one of a sphere, oscillations appeared in the particle trajectories. In these unsteady cases, the particles reached a stable position and remained there for a given amount of time, but then they suddenly jumped towards the top wall and moved back and forth without finding an equilibrium location in the transverse position. This instability occurred approximately after a time of ![]() $t_0 = 300$ (figure 16), and it was not reported in Fox et al. (Reference Fox, Schneider and Khair2021) probably because the simulation time was not long enough and because they explored values of
$t_0 = 300$ (figure 16), and it was not reported in Fox et al. (Reference Fox, Schneider and Khair2021) probably because the simulation time was not long enough and because they explored values of ![]() $Re_p < 50$. In the attempt to provide an explanation for this behaviour, we hypothesized that at higher Reynolds numbers perfect spheres or prolates with low AR oscillate because of the instabilities in the
$Re_p < 50$. In the attempt to provide an explanation for this behaviour, we hypothesized that at higher Reynolds numbers perfect spheres or prolates with low AR oscillate because of the instabilities in the ![]() $x$ and
$x$ and ![]() $z$ rotations, while the elongated shape of prolates with high AR stabilize the
$z$ rotations, while the elongated shape of prolates with high AR stabilize the ![]() $x$ and
$x$ and ![]() $z$ rotations and oscillations. To test our hypothesis, we repeated the simulations for the prolate particles with ARs of 1.3 and 1.7, but manually disabled the rotations of the particle around the
$z$ rotations and oscillations. To test our hypothesis, we repeated the simulations for the prolate particles with ARs of 1.3 and 1.7, but manually disabled the rotations of the particle around the ![]() $x$ and
$x$ and ![]() $z$ axes to test whether the rotational instability is the main cause. As shown in figure 16(b), although it reduced the instability for prolates with aspect ratio 1.3 and 1.7, the oscillation still occurs for the spherical particle (AR 1). This showed that additional mechanisms exist for the oscillation of the sphere, besides the rotational instability. These results suggested that the AR of the particle might be the key parameter determining whether the particle returns to the centre, but further investigation needs to be conducted to clarify the differences between spherical and ellipsoidal particles at higher values of
$z$ axes to test whether the rotational instability is the main cause. As shown in figure 16(b), although it reduced the instability for prolates with aspect ratio 1.3 and 1.7, the oscillation still occurs for the spherical particle (AR 1). This showed that additional mechanisms exist for the oscillation of the sphere, besides the rotational instability. These results suggested that the AR of the particle might be the key parameter determining whether the particle returns to the centre, but further investigation needs to be conducted to clarify the differences between spherical and ellipsoidal particles at higher values of ![]() $Re_p$. In the pipe study by Shao et al. (Reference Shao, Yu and Sun2008), they showed how particles near the tube wall undergo oscillatory motion at high Reynolds numbers. As Reynolds number was increased further more, despite initial stability, particles experience eventual instability, transitioning to oscillatory motion primarily within
$Re_p$. In the pipe study by Shao et al. (Reference Shao, Yu and Sun2008), they showed how particles near the tube wall undergo oscillatory motion at high Reynolds numbers. As Reynolds number was increased further more, despite initial stability, particles experience eventual instability, transitioning to oscillatory motion primarily within ![]() $r= 0.4\unicode{x2013}0.7$. Notably, Shao et al. highlight the absence of a stable inner equilibrium position at higher Reynolds numbers, underscoring the challenging and sometimes elusive nature of characterizing oscillations in these systems.
$r= 0.4\unicode{x2013}0.7$. Notably, Shao et al. highlight the absence of a stable inner equilibrium position at higher Reynolds numbers, underscoring the challenging and sometimes elusive nature of characterizing oscillations in these systems.

Figure 16. (a) Prolate particles with the same dimension in the transverse position but different ARs. When the AR approached one of the spheres, the particle experienced an unstable dynamic instead of going to the centre position at ![]() $Re_p = 100$. (b) Particles with the
$Re_p = 100$. (b) Particles with the ![]() $x$ and
$x$ and ![]() $z$ rotation artificially disabled in the SPH simulations.
$z$ rotation artificially disabled in the SPH simulations.
4. Conclusions
Overall, we observed the existence of lower and upper thresholds in ![]() $Re$ values that determine the behaviour of ellipsoidal particles. Below the first threshold, these particles exhibit a stable focusing position at the centre (
$Re$ values that determine the behaviour of ellipsoidal particles. Below the first threshold, these particles exhibit a stable focusing position at the centre (![]() $H = 0$). As
$H = 0$). As ![]() $Re$ exceeds the first threshold, the particles transition to a pair of stable off-centre positions symmetrically located with respect to the centreline. Beyond the upper threshold, the particles return to a single central equilibrium position and experience multistability in certain cases. We explained the underlining mechanism of this reverse of bifurcation by altered streamwise vorticity and symmetry breaking of pressure. A summary of the key findings is reported herein.
$Re$ exceeds the first threshold, the particles transition to a pair of stable off-centre positions symmetrically located with respect to the centreline. Beyond the upper threshold, the particles return to a single central equilibrium position and experience multistability in certain cases. We explained the underlining mechanism of this reverse of bifurcation by altered streamwise vorticity and symmetry breaking of pressure. A summary of the key findings is reported herein.
The off-centre positions were consistently observed for particles of various shapes and symmetries for ![]() $Re_c < 375$. In the case of asymmetric particles, we defined an average focusing position due to the presence of regular oscillations in the particle trajectory. As
$Re_c < 375$. In the case of asymmetric particles, we defined an average focusing position due to the presence of regular oscillations in the particle trajectory. As ![]() $Re$ increases, the off-centre positions progressively shift closer to the confining walls. The dominant factor determining particle behaviour is the size of the particle in the transverse dimension (
$Re$ increases, the off-centre positions progressively shift closer to the confining walls. The dominant factor determining particle behaviour is the size of the particle in the transverse dimension (![]() $z$ axis). For particles with small vertical dimensions, such as the AR 5 prolate or
$z$ axis). For particles with small vertical dimensions, such as the AR 5 prolate or ![]() $K = 0.1$ prolate (see figure 15), the equilibrium locations are situated near the centre. As the extension of the particle along the
$K = 0.1$ prolate (see figure 15), the equilibrium locations are situated near the centre. As the extension of the particle along the ![]() $z$ axis increases, the off-centre position gradually shifts towards the wall. However, when the particle becomes too large, the trend is reversed, and the position shifts back towards the centre due to the limited space between the walls. The particle volume does not significantly impact the off-centre position at a given
$z$ axis increases, the off-centre position gradually shifts towards the wall. However, when the particle becomes too large, the trend is reversed, and the position shifts back towards the centre due to the limited space between the walls. The particle volume does not significantly impact the off-centre position at a given ![]() $Re_p$.
$Re_p$.
For ![]() $Re_c > 880$, the particle dynamics can be influenced by the particle size and AR, resulting in differences observed among different particle shapes. Spherical particles do not return stably to the centre but exhibit unstable behaviour instead. The AR may be the determining factor, as prolate particles with an AR close to unity exhibit the same unstable behaviour as spheres (see figure 16a). Prolate particles achieve a stable centre position only when a logrolling rotational mode is maintained. However, our results indicate that this is not always the case, as certain conditions can cause the particle to transition into a tumbling motion and collide with the confining walls. Oblate particles, on the other hand, tend to return to the centre at a lower
$Re_c > 880$, the particle dynamics can be influenced by the particle size and AR, resulting in differences observed among different particle shapes. Spherical particles do not return stably to the centre but exhibit unstable behaviour instead. The AR may be the determining factor, as prolate particles with an AR close to unity exhibit the same unstable behaviour as spheres (see figure 16a). Prolate particles achieve a stable centre position only when a logrolling rotational mode is maintained. However, our results indicate that this is not always the case, as certain conditions can cause the particle to transition into a tumbling motion and collide with the confining walls. Oblate particles, on the other hand, tend to return to the centre at a lower ![]() $Re_p$ than prolate particles, and the initial position of the particle may influence the final stable focusing position. For both prolate and oblate particles, we identified a transitional region of the Reynolds number where multistability exists, namely the particle can reach off-centre equilibrium positions closer to the
$Re_p$ than prolate particles, and the initial position of the particle may influence the final stable focusing position. For both prolate and oblate particles, we identified a transitional region of the Reynolds number where multistability exists, namely the particle can reach off-centre equilibrium positions closer to the ![]() $z$ midline, different from the off-centre positions reached at moderate
$z$ midline, different from the off-centre positions reached at moderate ![]() $Re_p$. For asymmetric particles, the phenomenon becomes more complex and less predictable, but the general trends observed for symmetric ellipsoidal particles are maintained.
$Re_p$. For asymmetric particles, the phenomenon becomes more complex and less predictable, but the general trends observed for symmetric ellipsoidal particles are maintained.
In conclusion, our study revealed that the pitchfork bifurcation of equilibrium positions for rigid particles in a shear flow between two parallel walls is influenced by multiple parameters, including particle size, shape, initial configuration and ![]() $Re$, and it can be reversed. Future investigations should clarify whether this behaviour is caused by the presence of one or two walls, at high
$Re$, and it can be reversed. Future investigations should clarify whether this behaviour is caused by the presence of one or two walls, at high ![]() $Re$. More work is required to elucidate the behaviour of spherical particles at high Reynolds number. Moreover, it is advisable to explore a broader range of initial configurations for ellipsoidal particles, including initial position and alignment, to gain a more accurate understanding of the existence of multiple stable equilibria within the transitional zones of
$Re$. More work is required to elucidate the behaviour of spherical particles at high Reynolds number. Moreover, it is advisable to explore a broader range of initial configurations for ellipsoidal particles, including initial position and alignment, to gain a more accurate understanding of the existence of multiple stable equilibria within the transitional zones of ![]() $Re_p$. Additionally, the examination of non-axisymmetric particles would be interesting to determine whether they exhibit dynamics similar to those we observed in fore–aft asymmetric particles. These findings open up opportunities for future research to explore the potential development of novel separation techniques and devices.
$Re_p$. Additionally, the examination of non-axisymmetric particles would be interesting to determine whether they exhibit dynamics similar to those we observed in fore–aft asymmetric particles. These findings open up opportunities for future research to explore the potential development of novel separation techniques and devices.
Funding
This work was supported by the National Science Foundation and the industrial members of the Center for Advanced Design and Manufacturing of Integrated Microfluidics (NSF I/UCRC award IIP- 1841473). G.L. and Z.P. were partially supported by NSF/DMS 1951526 and NSF/PHY 2210366. Z.P. was also partially supported by a Scholar Award from the American Society of Hematology. Simulations were conducted on the supercomputer Theta in Argonne Leadership Computing Facility (ALCF) in the Argonne National Lab under Director's Discretionary (DD) allocation Modeling Corona Virus. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under contract DE-AC02- 06CH11357.
Declaration of interests
The authors report no conflict of interest.