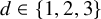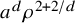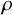1. Introduction
The study of dilute quantum gases [Reference Giorgini, Pitaevskii and StringariGPS08] has received much interest from the mathematical physics community in the recent decades. In particular, much work has been done pertaining to the ground state energies of both Fermi and Bose gases in the thermodynamic limit.
For Bose gases in
![]() $3$
dimensions, the leading term of the ground state energy was first shown by Dyson [Reference DysonDys57] as an upper bound and by Lieb–Yngvason [Reference Lieb and YngvasonLY98] as a lower bound. The leading term depends only on the density and the s-wave scattering length of the interaction. More recently, the second order correction, known as the Lee–Huang–Yang correction, was shown [Reference Fournais and SolovejFS20; Reference Fournais and SolovejFS23; Reference Yau and YinYY09]. Also, the
$3$
dimensions, the leading term of the ground state energy was first shown by Dyson [Reference DysonDys57] as an upper bound and by Lieb–Yngvason [Reference Lieb and YngvasonLY98] as a lower bound. The leading term depends only on the density and the s-wave scattering length of the interaction. More recently, the second order correction, known as the Lee–Huang–Yang correction, was shown [Reference Fournais and SolovejFS20; Reference Fournais and SolovejFS23; Reference Yau and YinYY09]. Also, the
![]() $2$
-dimensional [Reference Fournais, Girardot, Junge, Morin and OlivieriFGJMO24; Reference Lieb and YngvasonLY01] and
$2$
-dimensional [Reference Fournais, Girardot, Junge, Morin and OlivieriFGJMO24; Reference Lieb and YngvasonLY01] and
![]() $1$
-dimensional [Reference AgerskovAge23; Reference Agerskov, Reuvers and SolovejARS22] settings have been studied.
$1$
-dimensional [Reference AgerskovAge23; Reference Agerskov, Reuvers and SolovejARS22] settings have been studied.
The fermionic setting has been similarly studied in the
![]() $3$
-dimensional [Reference Falconi, Giacomelli, Hainzl and PortaFGHP21; Reference GiacomelliGia23; Reference LauritsenLau23; Reference Lauritsen and SeiringerLS24a; Reference Lauritsen and SeiringerLS24b; Reference Lieb, Seiringer and SolovejLSS05],
$3$
-dimensional [Reference Falconi, Giacomelli, Hainzl and PortaFGHP21; Reference GiacomelliGia23; Reference LauritsenLau23; Reference Lauritsen and SeiringerLS24a; Reference Lauritsen and SeiringerLS24b; Reference Lieb, Seiringer and SolovejLSS05],
![]() $2$
-dimensional [Reference Lauritsen and SeiringerLS24a; Reference Lauritsen and SeiringerLS24b; Reference Lieb, Seiringer and SolovejLSS05] and
$2$
-dimensional [Reference Lauritsen and SeiringerLS24a; Reference Lauritsen and SeiringerLS24b; Reference Lieb, Seiringer and SolovejLSS05] and
![]() $1$
-dimensional [Reference AgerskovAge23; Reference Agerskov, Reuvers and SolovejARS22; Reference Lauritsen and SeiringerLS24b] case. For fermions, the spin is important. For nonzero spin, the leading correction to the energy of the free gas is similar to the leading term for bosons and depends only on the density and the s-wave scattering length of the interaction. For fully spin-polarized (i.e., effectively spin-
$1$
-dimensional [Reference AgerskovAge23; Reference Agerskov, Reuvers and SolovejARS22; Reference Lauritsen and SeiringerLS24b] case. For fermions, the spin is important. For nonzero spin, the leading correction to the energy of the free gas is similar to the leading term for bosons and depends only on the density and the s-wave scattering length of the interaction. For fully spin-polarized (i.e., effectively spin-
![]() $0$
) fermions, the behavior is different. By the Pauli exclusion principle, the probability of two fermions of the same spin being close enough to interact is suppressed. As such, the leading correction to the energy of the free gas depends on the p-wave scattering length of the interaction instead and is much smaller for dilute gases, which makes its analysis significantly harder.
$0$
) fermions, the behavior is different. By the Pauli exclusion principle, the probability of two fermions of the same spin being close enough to interact is suppressed. As such, the leading correction to the energy of the free gas depends on the p-wave scattering length of the interaction instead and is much smaller for dilute gases, which makes its analysis significantly harder.
A natural question to consider is the extension of these results on the ground state energy to positive temperature. This has been done both for bosons [Reference Deuchert, Mayer and SeiringerDMS20; Reference Haberberger, Hainzl, Nam, Seiringer and TriayHHNST23; Reference Mayer and SeiringerMS20; Reference SeiringerSei08; Reference YinYin10] and nonzero spin fermions [Reference SeiringerSei06]. In this paper, we consider the extension for fully spin-polarized fermions. More precisely, we consider the problem of finding the pressure
![]() $\psi (\beta ,\mu )$
at positive temperature
$\psi (\beta ,\mu )$
at positive temperature
![]() $T = 1/\beta $
and chemical potential
$T = 1/\beta $
and chemical potential
![]() $\mu $
in the setting of a spin-polarized Fermi gas. We are interested in the dilute limit
$\mu $
in the setting of a spin-polarized Fermi gas. We are interested in the dilute limit
![]() $a^d\overline {\rho } \ll 1$
, where a denotes the p-wave scattering length of the interaction and
$a^d\overline {\rho } \ll 1$
, where a denotes the p-wave scattering length of the interaction and
![]() $\overline {\rho }$
denotes the particle density. In this dilute limit, we show the lower bound in dimensions
$\overline {\rho }$
denotes the particle density. In this dilute limit, we show the lower bound in dimensions
![]() $d\in \{1,2,3\}$
$d\in \{1,2,3\}$
for an explicit (temperature dependent) coefficient
![]() $c_d(\beta \mu )$
. Here,
$c_d(\beta \mu )$
. Here,
![]() $\psi $
, respectively
$\psi $
, respectively
![]() $\psi _0$
, denotes the pressure of the interacting respectively noninteracting system at inverse temperature
$\psi _0$
, denotes the pressure of the interacting respectively noninteracting system at inverse temperature
![]() $\beta $
and chemical potential
$\beta $
and chemical potential
![]() $\mu $
.
$\mu $
.
As discussed in more details in Remark 1.6 below, the term
![]() $c_d(\beta \mu ) a^d \overline {\rho }^{2+2/d}$
arises naturally from the two-body interaction and the fact that the two-body density vanishes quadratically for incident particles. In the low-temperature limit
$c_d(\beta \mu ) a^d \overline {\rho }^{2+2/d}$
arises naturally from the two-body interaction and the fact that the two-body density vanishes quadratically for incident particles. In the low-temperature limit
![]() $\beta \mu \to \infty $
, the coefficients
$\beta \mu \to \infty $
, the coefficients
![]() $c_d(\beta \mu )$
converge to the corresponding zero-temperature constants [Reference Agerskov, Reuvers and SolovejARS22; Reference Lauritsen and SeiringerLS24a; Reference Lauritsen and SeiringerLS24b]. The temperature dependence of this term can then be understood via the temperature dependence of the two-particle density of the free state.
$c_d(\beta \mu )$
converge to the corresponding zero-temperature constants [Reference Agerskov, Reuvers and SolovejARS22; Reference Lauritsen and SeiringerLS24a; Reference Lauritsen and SeiringerLS24b]. The temperature dependence of this term can then be understood via the temperature dependence of the two-particle density of the free state.
The result is valid for temperatures T at most of the order of the Fermi temperature
![]() $T_F \sim \overline {\rho }^{2/d}$
of the free gas. For larger temperatures, one should expect thermal effects to become larger than quantum effects, and thus the gas should behave more like a (high temperature) classical gas. The natural parameter capturing the temperature is the fugacity
$T_F \sim \overline {\rho }^{2/d}$
of the free gas. For larger temperatures, one should expect thermal effects to become larger than quantum effects, and thus the gas should behave more like a (high temperature) classical gas. The natural parameter capturing the temperature is the fugacity
![]() $z=e^{\beta \mu }$
. In terms of the fugacity, the constraint that the temperature satisfies
$z=e^{\beta \mu }$
. In terms of the fugacity, the constraint that the temperature satisfies
![]() $T\lesssim T_F$
reads
$T\lesssim T_F$
reads
![]() $z \gtrsim 1$
.
$z \gtrsim 1$
.
In contrast, for nonzero spin fermions, the pressure in the dilute limit is in
![]() $3$
dimensions [Reference SeiringerSei06]
$3$
dimensions [Reference SeiringerSei06]
with
![]() $\psi $
and
$\psi $
and
![]() $\psi _{0}$
the pressures of the interacting, respectively noninteracting, system,
$\psi _{0}$
the pressures of the interacting, respectively noninteracting, system,
![]() $q\geq 2$
the number of spin sectors and
$q\geq 2$
the number of spin sectors and
![]() $a_s$
the s-wave scattering length of the interaction. Notably, here the coefficient
$a_s$
the s-wave scattering length of the interaction. Notably, here the coefficient
![]() $4\pi (1-q^{-1})$
does not depend on the temperature.
$4\pi (1-q^{-1})$
does not depend on the temperature.
Our method of proof is split in two cases depending on the temperature. For sufficiently small temperatures, the result follows by a simple comparison to the zero-temperature setting and using the result of [Reference Lauritsen and SeiringerLS24b]. In the more interesting case of higher temperatures, our method of proof consists of computing the pressure of a Jastrow-type trial state using a rigorous implementation [Reference LauritsenLau23; Reference Lauritsen and SeiringerLS24b] (given in Lemma 4.4) of the fermionic cluster expansion of Gaudin–Gillespie–Ripka [Reference Gaudin, Gillespie and RipkaGGR71]. (More precisely in [Reference LauritsenLau23; Reference Lauritsen and SeiringerLS24b], we found conditions under which the formulas of [Reference Gaudin, Gillespie and RipkaGGR71] are convergent.) A similar method was employed in the zero-temperature setting [Reference Lauritsen and SeiringerLS24b], with the important difference that, because of the smoothness of the momentum distribution, the condition for convergence we obtain at positive (not too small) temperature is uniform in the volume (see Theorem 4.3). Thus, we can compute the thermodynamic limit directly, without appealing to a box method of localizing a trial state into large but finite boxes as done in [Reference Lauritsen and SeiringerLS24b].
1.1. Precise statement
To state our main theorem precisely, define the (spin-polarized) fermionic Fock space
![]() $\mathcal {F} = \bigoplus _{n=0}^\infty L_a^2\left ([0,L]^{dn}; \mathbb {C} \right ) = \bigoplus _{n=0}^\infty \bigwedge ^{n} L^2\left ([0,L]^{d}; \mathbb {C} \right )$
. On this space, we define the free Hamiltonian
$\mathcal {F} = \bigoplus _{n=0}^\infty L_a^2\left ([0,L]^{dn}; \mathbb {C} \right ) = \bigoplus _{n=0}^\infty \bigwedge ^{n} L^2\left ([0,L]^{d}; \mathbb {C} \right )$
. On this space, we define the free Hamiltonian
![]() $\mathcal {H}$
, the number operator
$\mathcal {H}$
, the number operator
![]() $\mathcal {N}$
and interaction operator
$\mathcal {N}$
and interaction operator
![]() $\mathcal {V}$
as follows (in natural units where
$\mathcal {V}$
as follows (in natural units where
![]() $\frac {\hbar }{2m}=1$
):
$\frac {\hbar }{2m}=1$
):
 $$ \begin{align*} \begin{aligned} \mathcal{H} & = (0, H_{1}, \ldots, H_{n}, \ldots), \qquad & H_n & = \sum_{j=1}^n -\Delta_{x_j}, \\ \mathcal{N} & = (0, 1, \ldots, n, \ldots), \\ \mathcal{V} & = (0,0,V_2,\ldots,V_n,\ldots), & V_n & = \sum_{1\leq i < j \leq n} v(x_i-x_j). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{H} & = (0, H_{1}, \ldots, H_{n}, \ldots), \qquad & H_n & = \sum_{j=1}^n -\Delta_{x_j}, \\ \mathcal{N} & = (0, 1, \ldots, n, \ldots), \\ \mathcal{V} & = (0,0,V_2,\ldots,V_n,\ldots), & V_n & = \sum_{1\leq i < j \leq n} v(x_i-x_j). \end{aligned} \end{align*} $$
The interacting Hamiltonian is then
![]() $\mathcal {H} + \mathcal {V}$
. In the calculations below, we will use periodic boundary conditions for convenience. The pressure does not depend on the choice of boundary conditions [Reference RobinsonRob71], and hence, we are free to choose the most convenient ones. We are interested in determining the pressure of the system described by this Hamiltonian at inverse temperature
$\mathcal {H} + \mathcal {V}$
. In the calculations below, we will use periodic boundary conditions for convenience. The pressure does not depend on the choice of boundary conditions [Reference RobinsonRob71], and hence, we are free to choose the most convenient ones. We are interested in determining the pressure of the system described by this Hamiltonian at inverse temperature
![]() $\beta $
and chemical potential
$\beta $
and chemical potential
![]() $\mu $
. We denote this by
$\mu $
. We denote this by
where
![]() $S(\varGamma ) = - \operatorname {\mathrm {Tr}} \varGamma \log \varGamma $
is the entropy of the state
$S(\varGamma ) = - \operatorname {\mathrm {Tr}} \varGamma \log \varGamma $
is the entropy of the state
![]() $\varGamma $
and
$\varGamma $
and
![]() $P[\varGamma ]$
is the pressure functional. By state we mean a density matrix (i.e., a positive trace-class operator on
$P[\varGamma ]$
is the pressure functional. By state we mean a density matrix (i.e., a positive trace-class operator on
![]() $\mathcal {F}$
of unit trace). (We suppress from the notation the dependence on the dimension d and the length L.) We denote moreover by
$\mathcal {F}$
of unit trace). (We suppress from the notation the dependence on the dimension d and the length L.) We denote moreover by
the pressure and pressure functional of the free gas. The supremum is a maximum and is achieved for the Gibbs state
Then [Reference HuangHua87, Equation (8.63)]
 $$ \begin{align} \begin{aligned} \psi_0(\beta,\mu) & = \lim_{L\to \infty} \frac{1}{L^d} \left[-\operatorname{\mathrm{Tr}}_{\mathcal{F}}\left[(\mathcal{H} - \mu \mathcal{N})\varGamma\right] + \frac{1}{\beta} S(\varGamma)\right] = \lim_{L\to\infty} \frac{1}{L^d\beta} \log Z \\[6pt] & = \frac{1}{\beta (2\pi)^d} \int_{\mathbb{R}^d} \log\left(1 + e^{\beta\mu - \beta|k|^2}\right) \,\text{d} k. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \psi_0(\beta,\mu) & = \lim_{L\to \infty} \frac{1}{L^d} \left[-\operatorname{\mathrm{Tr}}_{\mathcal{F}}\left[(\mathcal{H} - \mu \mathcal{N})\varGamma\right] + \frac{1}{\beta} S(\varGamma)\right] = \lim_{L\to\infty} \frac{1}{L^d\beta} \log Z \\[6pt] & = \frac{1}{\beta (2\pi)^d} \int_{\mathbb{R}^d} \log\left(1 + e^{\beta\mu - \beta|k|^2}\right) \,\text{d} k. \end{aligned} \end{align} $$
To state our main theorem, we moreover define the p-wave scattering length a. (See also [Reference Lieb and YngvasonLY01, Appendix A] and [Reference Seiringer and YngvasonSY20, Equations (2.9), (4.3)].)
Definition 1.1 [Reference Lauritsen and SeiringerLS24b, Definitions 1.1, 1.9 and 1.11]
The p-wave scattering length a of the interaction v in dimension d is defined by
 $$ \begin{align*} c_d a^d = \inf \left\{\int_{\mathbb{R}^d} \left(\left\vert \nabla f_0(x) \right\vert{}^2 + \frac{1}{2} v(x) f_0(x)^2\right)|x|^2 \,\text{d} x : f_0(x) \to 1 \text{ for } |x|\to \infty \right\}, \end{align*} $$
$$ \begin{align*} c_d a^d = \inf \left\{\int_{\mathbb{R}^d} \left(\left\vert \nabla f_0(x) \right\vert{}^2 + \frac{1}{2} v(x) f_0(x)^2\right)|x|^2 \,\text{d} x : f_0(x) \to 1 \text{ for } |x|\to \infty \right\}, \end{align*} $$
where
 $$ \begin{align} c_d = \begin{cases} 12\pi & d=3, \\ 4\pi & d=2, \\ 2 & d=1. \end{cases} \end{align} $$
$$ \begin{align} c_d = \begin{cases} 12\pi & d=3, \\ 4\pi & d=2, \\ 2 & d=1. \end{cases} \end{align} $$
The minimizer
![]() $f_0$
is the p-wave scattering function. (If
$f_0$
is the p-wave scattering function. (If
![]() $v(x) = +\infty $
for some x [for instance if v has a hard core,
$v(x) = +\infty $
for some x [for instance if v has a hard core,
![]() $v(x) = +\infty $
for
$v(x) = +\infty $
for
![]() $|x| < R_0$
], we interpret
$|x| < R_0$
], we interpret
![]() $v(x)\,\text {d} x$
as a measure. We suppress from the notation the dependence of a and
$v(x)\,\text {d} x$
as a measure. We suppress from the notation the dependence of a and
![]() $f_0$
on the dimension d.)
$f_0$
on the dimension d.)
The dimensionless parameter measuring the diluteness is then
![]() $a^d \overline {\rho }$
, with
$a^d \overline {\rho }$
, with
![]() $\overline {\rho }$
the particle densityFootnote 1 (in infinite volume) given by
$\overline {\rho }$
the particle densityFootnote 1 (in infinite volume) given by
![]() $\overline {\rho } = \partial _\mu \psi (\beta ,\mu )$
. We are interested in a dilute limit, meaning that
$\overline {\rho } = \partial _\mu \psi (\beta ,\mu )$
. We are interested in a dilute limit, meaning that
![]() $a^d\overline {\rho } \ll 1$
. Moreover, we are considering temperatures
$a^d\overline {\rho } \ll 1$
. Moreover, we are considering temperatures
![]() $T\lesssim T_F \sim \overline {\rho }^{2/d}$
, meaning that
$T\lesssim T_F \sim \overline {\rho }^{2/d}$
, meaning that
![]() $z \gtrsim 1$
. As mentioned in the introduction, small z corresponds to a (high-temperature) classical gas.
$z \gtrsim 1$
. As mentioned in the introduction, small z corresponds to a (high-temperature) classical gas.
We shall prove the following theorem.
Theorem 1.2. Let
![]() $v\geq 0$
be radial and of compact support. If
$v\geq 0$
be radial and of compact support. If
![]() $d=1$
, assume moreover that
$d=1$
, assume moreover that
![]() $\int \left (\left \vert \partial f_0 \right \vert {}^2 + \frac {1}{2} v f_0^2\right ) \,\text {d} x < \infty $
. For any
$\int \left (\left \vert \partial f_0 \right \vert {}^2 + \frac {1}{2} v f_0^2\right ) \,\text {d} x < \infty $
. For any
![]() $z_0> 0$
, there exists
$z_0> 0$
, there exists
![]() $c> 0$
such that if
$c> 0$
such that if
![]() $a^d\overline {\rho }_0 < c$
, then, uniformly in
$a^d\overline {\rho }_0 < c$
, then, uniformly in
![]() $z = e^{\beta \mu } \geq z_0$
, we have the lower bound
$z = e^{\beta \mu } \geq z_0$
, we have the lower bound
 $$ \begin{align*} \psi(\beta,\mu) \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} a^d \overline{\rho}_0^{2+2/d} \left[ 1 + \delta_d \right], \end{align*} $$
$$ \begin{align*} \psi(\beta,\mu) \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} a^d \overline{\rho}_0^{2+2/d} \left[ 1 + \delta_d \right], \end{align*} $$
where
![]() $\overline {\rho }_0=\partial _\mu \psi _0(\beta ,\mu )$
is the particle density of the free gas (in infinite volume), the constants
$\overline {\rho }_0=\partial _\mu \psi _0(\beta ,\mu )$
is the particle density of the free gas (in infinite volume), the constants
![]() $c_d$
are defined in Equation (1.3) and
$c_d$
are defined in Equation (1.3) and
 $$ \begin{align} \left\vert \delta_d \right\vert \leq \begin{cases} C(a^3\overline{\rho}_0)^{1/39} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^{12/13} & d=3, \\ C(a^2\overline{\rho}_0)^{1/5} \left\vert \log a^2\overline{\rho}_0 \right\vert{}^{6/5} & d=2, \\ C(a\overline{\rho}_0)^{1/7} \left\vert \log a\overline{\rho}_0 \right\vert{}^{12/7} & d=1. \end{cases} \end{align} $$
$$ \begin{align} \left\vert \delta_d \right\vert \leq \begin{cases} C(a^3\overline{\rho}_0)^{1/39} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^{12/13} & d=3, \\ C(a^2\overline{\rho}_0)^{1/5} \left\vert \log a^2\overline{\rho}_0 \right\vert{}^{6/5} & d=2, \\ C(a\overline{\rho}_0)^{1/7} \left\vert \log a\overline{\rho}_0 \right\vert{}^{12/7} & d=1. \end{cases} \end{align} $$
Here,
![]() $\operatorname {\mathrm {Li}}_s$
denotes the polylogarithm. It satisfies [NIS, Equation 25.12.16]
$\operatorname {\mathrm {Li}}_s$
denotes the polylogarithm. It satisfies [NIS, Equation 25.12.16]
 $$ \begin{align} -\operatorname{\mathrm{Li}}_{s}(-e^x) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{t^{s-1}}{e^{t-x}+1} \,\text{d} t \end{align} $$
$$ \begin{align} -\operatorname{\mathrm{Li}}_{s}(-e^x) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{t^{s-1}}{e^{t-x}+1} \,\text{d} t \end{align} $$
with
![]() $\Gamma $
the Gamma function.
$\Gamma $
the Gamma function.
We expect that the lower bound of Theorem 1.2 is, in fact, an equality (with a potentially different bound on the error term). It remains an open problem to prove this.
Remark 1.3. For better comparison with the zero-temperature result in [Reference Lauritsen and SeiringerLS24b], we find it convenient to write the correction to the pressure of the free gas in terms of the particle density (of the free gas)
![]() $\overline {\rho }_0$
. The latter is given explicitly as
$\overline {\rho }_0$
. The latter is given explicitly as
This follows from an elementary computation, which we give in Lemma 3.6 below.
To leading order
![]() $\overline {\rho } \simeq \overline {\rho }_0$
, more precisely,
$\overline {\rho } \simeq \overline {\rho }_0$
, more precisely,
Corollary 1.4. Under the same assumptions as in Theorem 1.2, we have for the particle densityFootnote 2
![]() $\overline {\rho } = \partial _\mu \psi (\beta ,\mu )$
$\overline {\rho } = \partial _\mu \psi (\beta ,\mu )$
We shall give the proof at the end of this section. In particular, the conditions of small
![]() $a^d\overline {\rho }$
and of small
$a^d\overline {\rho }$
and of small
![]() $a^d\overline {\rho }_0$
are equivalent. Moreover, the error terms of Theorem 1.2 can equally well be written with
$a^d\overline {\rho }_0$
are equivalent. Moreover, the error terms of Theorem 1.2 can equally well be written with
![]() $\overline {\rho }_0$
replaced by
$\overline {\rho }_0$
replaced by
![]() $\overline {\rho }$
.
$\overline {\rho }$
.
Remark 1.5. The additional assumption on v in dimension
![]() $d=1$
is discussed in [Reference Lauritsen and SeiringerLS24b, Remark 1.13]. If v is either smooth or has a hard core (meaning that
$d=1$
is discussed in [Reference Lauritsen and SeiringerLS24b, Remark 1.13]. If v is either smooth or has a hard core (meaning that
![]() $v(x)=+\infty $
for
$v(x)=+\infty $
for
![]() $|x|\leq a_0$
for some
$|x|\leq a_0$
for some
![]() $a_0> 0$
), this assumption is satisfied.
$a_0> 0$
), this assumption is satisfied.
Remark 1.6. The term of order
![]() $a^d \overline {\rho }_0^{2+2/d}$
depends on the temperature. This is different from the setting of spin-
$a^d \overline {\rho }_0^{2+2/d}$
depends on the temperature. This is different from the setting of spin-
![]() $\frac {1}{2}$
fermions, where the analogous term (in
$\frac {1}{2}$
fermions, where the analogous term (in
![]() $3$
dimensions) is
$3$
dimensions) is
![]() $2\pi a \overline {\rho }_0^2$
[Reference SeiringerSei06] uniformly in the temperature. That the term of order
$2\pi a \overline {\rho }_0^2$
[Reference SeiringerSei06] uniformly in the temperature. That the term of order
![]() $a^d \overline {\rho }_0^{2+2/d}$
should depend on the temperature may be heuristically understood as follows: This term arises from the fact that the two-body density vanishes quadratically for incident particles. The rate at which it vanishes depends on the exact state, and thus the temperature. Concretely, the two-particle density of the free gas (in infinite volume) satisfies
$a^d \overline {\rho }_0^{2+2/d}$
should depend on the temperature may be heuristically understood as follows: This term arises from the fact that the two-body density vanishes quadratically for incident particles. The rate at which it vanishes depends on the exact state, and thus the temperature. Concretely, the two-particle density of the free gas (in infinite volume) satisfies
 $$ \begin{align} \begin{aligned} \overline{\rho}^{(2)}(x_1,x_2) & = 2\pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \overline{\rho}_0^{2+2/d} |x_1-x_2|^2 \left[1 + O\left(\overline{\rho}_0^{2/d}|x_1-x_2|^2\right)\right], \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \overline{\rho}^{(2)}(x_1,x_2) & = 2\pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \overline{\rho}_0^{2+2/d} |x_1-x_2|^2 \left[1 + O\left(\overline{\rho}_0^{2/d}|x_1-x_2|^2\right)\right], \end{aligned} \end{align} $$
where
![]() $O\left (\overline {\rho }_0^{2/d}|x_1-x_2|^2\right )$
is understood as being bounded by
$O\left (\overline {\rho }_0^{2/d}|x_1-x_2|^2\right )$
is understood as being bounded by
![]() $C \overline {\rho }_0^{2/d}|x_1-x_2|^2$
uniformly. This follows from an elementary computation, which we give in Lemma 3.6 below.
$C \overline {\rho }_0^{2/d}|x_1-x_2|^2$
uniformly. This follows from an elementary computation, which we give in Lemma 3.6 below.
In the low-temperature limit
![]() $z \to \infty $
, we recover the zero-temperature constants in the terms of order
$z \to \infty $
, we recover the zero-temperature constants in the terms of order
![]() $a^d \overline {\rho }_0^{2+2/d}$
. The zero-temperature results read [Reference Lauritsen and SeiringerLS24b, Theorems 1.3, 1.10, 1.12]
$a^d \overline {\rho }_0^{2+2/d}$
. The zero-temperature results read [Reference Lauritsen and SeiringerLS24b, Theorems 1.3, 1.10, 1.12]
with
![]() $e(\overline {\rho }_0), e_0(\overline {\rho }_0)$
denoting the ground state energy density of the interacting, respectively the free, gas and
$e(\overline {\rho }_0), e_0(\overline {\rho }_0)$
denoting the ground state energy density of the interacting, respectively the free, gas and
 $$ \begin{align} \begin{aligned} c_{0,d} & = \begin{cases} \frac{12\pi}{5}(6\pi^2)^{2/3} & d=3, \\ 4\pi^2 & d=2, \\ \frac{2\pi^2}{3} & d=1, \end{cases} \qquad & \left\vert \delta_d \right\vert & \lesssim \begin{cases} a^2\overline{\rho}^{2/3} & d=3, \\ a^2\overline{\rho}_0\left\vert \log a^2\overline{\rho}_0 \right\vert{}^2 & d=2, \\ (a\overline{\rho}_0)^{13/17} & d=1. \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} c_{0,d} & = \begin{cases} \frac{12\pi}{5}(6\pi^2)^{2/3} & d=3, \\ 4\pi^2 & d=2, \\ \frac{2\pi^2}{3} & d=1, \end{cases} \qquad & \left\vert \delta_d \right\vert & \lesssim \begin{cases} a^2\overline{\rho}^{2/3} & d=3, \\ a^2\overline{\rho}_0\left\vert \log a^2\overline{\rho}_0 \right\vert{}^2 & d=2, \\ (a\overline{\rho}_0)^{13/17} & d=1. \end{cases} \end{aligned} \end{align} $$
Indeed, we claim that
 $$ \begin{align} 2\pi c_d \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} = c_{0,d} + O( (\log z)^{-2}) \quad \text{as } z\to \infty. \end{align} $$
$$ \begin{align} 2\pi c_d \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} = c_{0,d} + O( (\log z)^{-2}) \quad \text{as } z\to \infty. \end{align} $$
To see this, write (following [Reference WoodWoo92])
 $$ \begin{align*} -\operatorname{\mathrm{Li}}_{s}(-e^x) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{t^{s-1}}{e^{t-x}+1} \,\text{d} t = \frac{1}{\Gamma(s)} \left[\int_0^x t^{s-1} \,\text{d} t - \int_0^x \frac{t^{s-1}}{e^{x-t}+1} \,\text{d} t + \int_x^\infty \frac{t^{s-1}}{e^{t-x}+1} \,\text{d} t\right] \\ = \frac{x^{s}}{\Gamma(s+1)} - \frac{1}{\Gamma(s)} \int_0^x \frac{(x-u)^{s-1} - (x+u)^{s-1}}{e^u + 1} \,\text{d} u - \frac{1}{\Gamma(s)} \int_x^\infty \frac{(x+u)^{s-1}}{e^u+1} \,\text{d} u, \end{align*} $$
$$ \begin{align*} -\operatorname{\mathrm{Li}}_{s}(-e^x) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{t^{s-1}}{e^{t-x}+1} \,\text{d} t = \frac{1}{\Gamma(s)} \left[\int_0^x t^{s-1} \,\text{d} t - \int_0^x \frac{t^{s-1}}{e^{x-t}+1} \,\text{d} t + \int_x^\infty \frac{t^{s-1}}{e^{t-x}+1} \,\text{d} t\right] \\ = \frac{x^{s}}{\Gamma(s+1)} - \frac{1}{\Gamma(s)} \int_0^x \frac{(x-u)^{s-1} - (x+u)^{s-1}}{e^u + 1} \,\text{d} u - \frac{1}{\Gamma(s)} \int_x^\infty \frac{(x+u)^{s-1}}{e^u+1} \,\text{d} u, \end{align*} $$
where we changed variables
![]() $t= x\pm u$
. The middle and last integrals can easily be bounded as
$t= x\pm u$
. The middle and last integrals can easily be bounded as
![]() $O(x^{s-2})$
and
$O(x^{s-2})$
and
![]() $O(x^s e^{-x})$
, respectively. Thus,
$O(x^s e^{-x})$
, respectively. Thus,
and Equation (1.9) follows.
Remark 1.7. The error bounds in Theorem 1.2 are uniform in z. They arise as the worst cases of two types of bounds, one good for
![]() $z\sim 1$
and one good for
$z\sim 1$
and one good for
![]() $z \gg 1$
. In particular, for concrete values of z, the error bounds can be improved. See Propositions 1.8 and 1.9 below.
$z \gg 1$
. In particular, for concrete values of z, the error bounds can be improved. See Propositions 1.8 and 1.9 below.
Finally, we give the following:
Proof of Corollary 1.4
Note that
![]() $\psi (\beta ,\mu )$
is a convex function of
$\psi (\beta ,\mu )$
is a convex function of
![]() $\mu $
. Thus, we may bound its derivative by any difference quotient. More precisely, for any
$\mu $
. Thus, we may bound its derivative by any difference quotient. More precisely, for any ![]() , we have
, we have
Using the trivial upper bound ![]() (which is a consequence of the assumed non-negativity of the interaction potential v) and the lower bound of Theorem 1.2, we conclude that
(which is a consequence of the assumed non-negativity of the interaction potential v) and the lower bound of Theorem 1.2, we conclude that
Using the explicit formula for
![]() $\overline {\rho }_0=\partial _\mu \psi _0$
and optimizing in
$\overline {\rho }_0=\partial _\mu \psi _0$
and optimizing in ![]() , we get that
, we get that
![]() $\overline {\rho } \leq \overline {\rho }_0(1 + O( (a^d\overline {\rho }_0)^{1/2}))$
. For
$\overline {\rho } \leq \overline {\rho }_0(1 + O( (a^d\overline {\rho }_0)^{1/2}))$
. For ![]() , the argument is analogous only the direction of the inequalities is reversed.
, the argument is analogous only the direction of the inequalities is reversed.
1.2. Strategy of the proof
To prove Theorem 1.2, we distinguish two cases: that of a ‘low-temperature’ setting and that of a ‘high-temperature’ setting. For sufficiently small temperatures, we compare to the ground state energy studied in [Reference Lauritsen and SeiringerLS24b]. For larger temperatures, we consider a specific trial state
![]() $\varGamma _J$
of Jastrow-type (defined in Equation (3.1) below) and compute the pressure functional evaluated on this trial state. For these computations, we use a rigorous implementation [Reference LauritsenLau23; Reference Lauritsen and SeiringerLS24b] of the formal cluster expansion of Gaudin–Gillespie–Ripka [Reference Gaudin, Gillespie and RipkaGGR71].
$\varGamma _J$
of Jastrow-type (defined in Equation (3.1) below) and compute the pressure functional evaluated on this trial state. For these computations, we use a rigorous implementation [Reference LauritsenLau23; Reference Lauritsen and SeiringerLS24b] of the formal cluster expansion of Gaudin–Gillespie–Ripka [Reference Gaudin, Gillespie and RipkaGGR71].
Temperature-dependent errors naturally arise as powers of
![]() $\zeta := 1 + \left \vert \log z \right \vert .$
We shall prove the following propositions.
$\zeta := 1 + \left \vert \log z \right \vert .$
We shall prove the following propositions.
Proposition 1.8. Let
![]() $v\geq 0$
be radial and of compact support. If
$v\geq 0$
be radial and of compact support. If
![]() $d=1$
, assume moreover that
$d=1$
, assume moreover that
![]() $\int \left (\left \vert \partial f_0 \right \vert {}^2 + \frac {1}{2} v f_0^2\right ) \,\text {d} x < \infty $
. Then for sufficiently small
$\int \left (\left \vert \partial f_0 \right \vert {}^2 + \frac {1}{2} v f_0^2\right ) \,\text {d} x < \infty $
. Then for sufficiently small
![]() $a^d\overline {\rho }_0$
and large
$a^d\overline {\rho }_0$
and large
![]() $z = e^{\beta \mu }$
, we have
$z = e^{\beta \mu }$
, we have
 $$ \begin{align} \psi(\beta,\mu) \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} a^d \overline{\rho}_0^{2+2/d} \left[1 + \delta_d\right], \end{align} $$
$$ \begin{align} \psi(\beta,\mu) \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} a^d \overline{\rho}_0^{2+2/d} \left[1 + \delta_d\right], \end{align} $$
where
![]() $\overline {\rho }_0$
is the particle density of the free gas,
$\overline {\rho }_0$
is the particle density of the free gas,
![]() $c_d$
is defined in Equation (1.3) and
$c_d$
is defined in Equation (1.3) and
 $$ \begin{align} \left\vert \delta_d \right\vert \lesssim \begin{cases} \begin{aligned} &a^2\overline{\rho}_0^{2/3} && + (a^3\overline{\rho}_0)^{-1} \zeta^{-2} & d=3, \\ &a^2\overline{\rho}_0 \left\vert \log a^2\overline{\rho}_0 \right\vert{}^2 && + (a^2\overline{\rho}_0)^{-1} \zeta^{-2} & d=2, \\ &(a\overline{\rho}_0)^{13/17} && + (a\overline{\rho}_0)^{-1} \zeta^{-2} & d=1. \end{aligned} \end{cases} \end{align} $$
$$ \begin{align} \left\vert \delta_d \right\vert \lesssim \begin{cases} \begin{aligned} &a^2\overline{\rho}_0^{2/3} && + (a^3\overline{\rho}_0)^{-1} \zeta^{-2} & d=3, \\ &a^2\overline{\rho}_0 \left\vert \log a^2\overline{\rho}_0 \right\vert{}^2 && + (a^2\overline{\rho}_0)^{-1} \zeta^{-2} & d=2, \\ &(a\overline{\rho}_0)^{13/17} && + (a\overline{\rho}_0)^{-1} \zeta^{-2} & d=1. \end{aligned} \end{cases} \end{align} $$
Proposition 1.9. Let
![]() $v\geq 0$
be radial and of compact support. If
$v\geq 0$
be radial and of compact support. If
![]() $d=1$
, assume moreover that
$d=1$
, assume moreover that
![]() $\int \left (\left \vert \partial f_0 \right \vert {}^2 + \frac {1}{2} v f_0^2\right ) \,\text {d} x < \infty $
. Then for
$\int \left (\left \vert \partial f_0 \right \vert {}^2 + \frac {1}{2} v f_0^2\right ) \,\text {d} x < \infty $
. Then for
![]() $z = e^{\beta \mu }$
satisfying
$z = e^{\beta \mu }$
satisfying
![]() $z \gtrsim 1$
, there exists a constant
$z \gtrsim 1$
, there exists a constant
![]() $c>0$
such that if
$c>0$
such that if
![]() $a^d\overline {\rho }_0 < c$
and
$a^d\overline {\rho }_0 < c$
and
![]() $a^d \overline {\rho }_0 \zeta ^{d/2} \left \vert \log a^d\overline {\rho }_0 \right \vert < c$
, then
$a^d \overline {\rho }_0 \zeta ^{d/2} \left \vert \log a^d\overline {\rho }_0 \right \vert < c$
, then
 $$ \begin{align*} \psi(\beta,\mu) \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} a^d \overline{\rho}_0^{2+2/d} \left[ 1 + \delta_d \right], \end{align*} $$
$$ \begin{align*} \psi(\beta,\mu) \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} a^d \overline{\rho}_0^{2+2/d} \left[ 1 + \delta_d \right], \end{align*} $$
where
![]() $\overline {\rho }_0$
is the particle density of the free gas,
$\overline {\rho }_0$
is the particle density of the free gas,
![]() $c_d$
is defined in Equation (1.3) and
$c_d$
is defined in Equation (1.3) and
 $$ \begin{align} \begin{aligned} \left\vert \delta_d \right\vert & \lesssim \begin{cases} (a^3\overline{\rho}_0)^{6/15} \zeta^{-3/5} + (a^3\overline{\rho}_0) \zeta^{1/2} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^2 + (a^3\overline{\rho}_0)^{7/3} \zeta^{9/2} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^3 & d=3, \\ (a^2\overline{\rho}_0)^{1/2} \zeta^{-1/2} + (a^2\overline{\rho}_0) \zeta \left\vert \log a^2\overline{\rho}_0 \right\vert + (a^2\overline{\rho}_0)^2 \zeta^{3} \left\vert \log a^2\overline{\rho}_0 \right\vert{}^{3}, & d=2, \\ (a\overline{\rho}_0)^{1/2} \left\vert \log a\overline{\rho}_0 \right\vert{}^{1/2} + a\overline{\rho}_0 \zeta^{3/2} \left\vert \log a\overline{\rho}_0 \right\vert{}^3 & d=1. \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\vert \delta_d \right\vert & \lesssim \begin{cases} (a^3\overline{\rho}_0)^{6/15} \zeta^{-3/5} + (a^3\overline{\rho}_0) \zeta^{1/2} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^2 + (a^3\overline{\rho}_0)^{7/3} \zeta^{9/2} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^3 & d=3, \\ (a^2\overline{\rho}_0)^{1/2} \zeta^{-1/2} + (a^2\overline{\rho}_0) \zeta \left\vert \log a^2\overline{\rho}_0 \right\vert + (a^2\overline{\rho}_0)^2 \zeta^{3} \left\vert \log a^2\overline{\rho}_0 \right\vert{}^{3}, & d=2, \\ (a\overline{\rho}_0)^{1/2} \left\vert \log a\overline{\rho}_0 \right\vert{}^{1/2} + a\overline{\rho}_0 \zeta^{3/2} \left\vert \log a\overline{\rho}_0 \right\vert{}^3 & d=1. \end{cases} \end{aligned} \end{align} $$
Proposition 1.8 is a simple corollary of [Reference Lauritsen and SeiringerLS24b, Theorems 1.3, 1.10, 1.13], extending the result to small positive temperatures. Proposition 1.9 is the main new result of this paper. Most of the rest of the paper is concerned with the proof of Proposition 1.9. Theorem 1.2 is an immediate consequence:
Proof of Theorem 1.2
We use the lower bound in Proposition 1.8 for
 $$ \begin{align*} \zeta \geq \zeta_0 := \begin{cases} (a^3\overline{\rho}_0)^{-20/39} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^{-6/13} & d=3, \\ (a^2\overline{\rho}_0)^{-3/5} \left\vert \log a^2\overline{\rho}_0 \right\vert{}^{-3/5} & d=2, \\ (a\overline{\rho}_0)^{-4/7} \left\vert \log a\overline{\rho}_0 \right\vert{}^{-6/7} & d=1 \end{cases} \end{align*} $$
$$ \begin{align*} \zeta \geq \zeta_0 := \begin{cases} (a^3\overline{\rho}_0)^{-20/39} \left\vert \log a^3\overline{\rho}_0 \right\vert{}^{-6/13} & d=3, \\ (a^2\overline{\rho}_0)^{-3/5} \left\vert \log a^2\overline{\rho}_0 \right\vert{}^{-3/5} & d=2, \\ (a\overline{\rho}_0)^{-4/7} \left\vert \log a\overline{\rho}_0 \right\vert{}^{-6/7} & d=1 \end{cases} \end{align*} $$
and the lower bound in Proposition 1.9 otherwise. Theorem 1.2 follows.
We note that for
![]() $\zeta \sim \zeta _0$
, the last of the summands in Equation (1.13) (in all dimensions) dominate the error term in Proposition 1.9.
$\zeta \sim \zeta _0$
, the last of the summands in Equation (1.13) (in all dimensions) dominate the error term in Proposition 1.9.
Remark 1.10. The proof of Proposition 1.9 uses the Gaudin–Gillespie–Ripka expansion. This expansion consists of formulas for the normalization constant
![]() $Z_J$
(defined in Equation (3.1) below) and the reduced densities of the state
$Z_J$
(defined in Equation (3.1) below) and the reduced densities of the state
![]() $\varGamma _J$
; see Theorem 4.3. Both
$\varGamma _J$
; see Theorem 4.3. Both
![]() $Z_J$
and the reduced densities are given as infinite series of diagrams (defined in Definition 4.1). Using these formulas, the ‘smallest’ diagrams give the corrections of Proposition 1.9 and the remaining diagrams are error terms. To bound the error terms, we calculate the values of (finitely many) ‘small’ diagrams and give crude bounds for all (infinitely many) ‘larger’ diagrams.
$Z_J$
and the reduced densities are given as infinite series of diagrams (defined in Definition 4.1). Using these formulas, the ‘smallest’ diagrams give the corrections of Proposition 1.9 and the remaining diagrams are error terms. To bound the error terms, we calculate the values of (finitely many) ‘small’ diagrams and give crude bounds for all (infinitely many) ‘larger’ diagrams.
Remark 1.11. We expect that with the method presented here, one could improve the error bounds in Proposition 1.9 (and consequently Theorem 1.2) slightly by treating more diagrams in the Gaudin–Gillespie–Ripka expansion as small (i.e., calculating their values more precisely). See also [Reference Lauritsen and SeiringerLS24b, Remark 1.8]. This is similar to what is done in [Reference Basti, Cenatiempo, Giuliani, Olgiati, Pasqualetti and SchleinBCGOPS23; Reference LauritsenLau23]. (In [Reference Basti, Cenatiempo, Giuliani, Olgiati, Pasqualetti and SchleinBCGOPS23], the hard core Bose gas is treated with a method similar to a cluster expansion. Using such an expansion to sufficiently high order proves the bounds of [Reference Basti, Cenatiempo, Giuliani, Olgiati, Pasqualetti and SchleinBCGOPS23].)
More precisely, we expect that by treating more diagrams as small, one could improve the bounds in Proposition 1.9 to
 $$ \begin{align} \left\vert \delta_d \right\vert \lesssim O \left( \begin{cases} (a^3\overline{\rho}_0)^{6/15} \zeta^{-3/5} & d=3 \\ (a^2\overline{\rho}_0)^{1/2} \zeta^{-1/2} & d=2 \\ (a\overline{\rho}_0)^{1/2} \left\vert \log a\overline{\rho}_0 \right\vert{}^{1/2} & d=1 \end{cases} \right) + O \left((a^d\overline{\rho}_0)^{-2/d} \left(a^d\overline{\rho}_0 \zeta^{d/2} \left\vert \log a^d\overline{\rho}_0 \right\vert\right)^{n}\right) \end{align} $$
$$ \begin{align} \left\vert \delta_d \right\vert \lesssim O \left( \begin{cases} (a^3\overline{\rho}_0)^{6/15} \zeta^{-3/5} & d=3 \\ (a^2\overline{\rho}_0)^{1/2} \zeta^{-1/2} & d=2 \\ (a\overline{\rho}_0)^{1/2} \left\vert \log a\overline{\rho}_0 \right\vert{}^{1/2} & d=1 \end{cases} \right) + O \left((a^d\overline{\rho}_0)^{-2/d} \left(a^d\overline{\rho}_0 \zeta^{d/2} \left\vert \log a^d\overline{\rho}_0 \right\vert\right)^{n}\right) \end{align} $$
for any n. This would then propagate to better error terms in Theorem 1.2. More precisely, by using the bound in Proposition 1.8 for
![]() $\zeta \geq \zeta _0$
and the bound in Proposition 1.9 with error improved as in Equation (1.14) otherwise and optimising in
$\zeta \geq \zeta _0$
and the bound in Proposition 1.9 with error improved as in Equation (1.14) otherwise and optimising in
![]() $\zeta _0$
, one would improve the error bound in Theorem 1.2 to
$\zeta _0$
, one would improve the error bound in Theorem 1.2 to

for any ![]() , where
, where ![]() depends on
depends on ![]() , by taking n sufficiently large in Equation (1.14).
, by taking n sufficiently large in Equation (1.14).
The first terms in Equation (1.14) come from the precise evaluation of certain small diagrams. In dimension
![]() $d=2,3$
, one should not expect to get better bounds than this using the method presented here. In dimension
$d=2,3$
, one should not expect to get better bounds than this using the method presented here. In dimension
![]() $d=1$
, one might be able to do a more precise analysis (see Remark 5.6) and thus improve the bound.
$d=1$
, one might be able to do a more precise analysis (see Remark 5.6) and thus improve the bound.
The proof of Proposition 1.8 will be given in Section 2. It is mostly independent of the rest of the paper (Sections 3, 4 and 5), which is devoted to the proof of Proposition 1.9.
Structure of the paper
First, in Section 2, we give the proof of Proposition 1.8. Then, in Section 3, we define the trial state
![]() $\varGamma _J$
and give some preliminary computations. Next, in Section 4, we compute reduced densities of the trial state
$\varGamma _J$
and give some preliminary computations. Next, in Section 4, we compute reduced densities of the trial state
![]() $\varGamma _J$
using the (rigorous implementation of the) Gaudin–Gillespie–Ripka expansion. Finally, in Section 5, we calculate the individual terms in the pressure functional and prove Proposition 1.9. In Appendix A, we show that
$\varGamma _J$
using the (rigorous implementation of the) Gaudin–Gillespie–Ripka expansion. Finally, in Section 5, we calculate the individual terms in the pressure functional and prove Proposition 1.9. In Appendix A, we show that
![]() $\varGamma _J$
has particle density
$\varGamma _J$
has particle density
![]() $\approx \overline {\rho }_0$
.
$\approx \overline {\rho }_0$
.
2. Low temperature
In this section, we prove Proposition 1.8 by comparing to the zero-temperature problem.
Proof of Proposition 1.8
The pressures
![]() $\psi , \psi _0$
(of the interacting and noninteracting gas, respectively) are the Legendre transforms of the corresponding free energy densities
$\psi , \psi _0$
(of the interacting and noninteracting gas, respectively) are the Legendre transforms of the corresponding free energy densities
![]() $\phi , \phi _0$
. That is,
$\phi , \phi _0$
. That is,
 $$ \begin{align} \begin{aligned} \psi(\beta,\mu) & = \sup_{\tilde\rho} \left[\tilde \rho \mu - \phi(\beta,\tilde\rho)\right] \geq \overline{\rho}_0\mu - \phi(\beta,\overline{\rho}_0) \\ \psi_0(\beta,\mu) & = \sup_{\tilde\rho} \left[\tilde \rho \mu - \phi_0(\beta,\tilde\rho)\right] = \overline{\rho}_0\mu - \phi_0(\beta,\overline{\rho}_0) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \psi(\beta,\mu) & = \sup_{\tilde\rho} \left[\tilde \rho \mu - \phi(\beta,\tilde\rho)\right] \geq \overline{\rho}_0\mu - \phi(\beta,\overline{\rho}_0) \\ \psi_0(\beta,\mu) & = \sup_{\tilde\rho} \left[\tilde \rho \mu - \phi_0(\beta,\tilde\rho)\right] = \overline{\rho}_0\mu - \phi_0(\beta,\overline{\rho}_0) \end{aligned} \end{align} $$
with
![]() $\overline {\rho }_0$
the density of the free gas at chemical potential
$\overline {\rho }_0$
the density of the free gas at chemical potential
![]() $\mu $
and inverse temperature
$\mu $
and inverse temperature
![]() $\beta $
, given in Equation (1.6). We may trivially bound the free energy density by the ground state energy density e. The latter is bounded from above in [Reference Lauritsen and SeiringerLS24b, Theorems 1.3, 1.10 and 1.13]. That is,
$\beta $
, given in Equation (1.6). We may trivially bound the free energy density by the ground state energy density e. The latter is bounded from above in [Reference Lauritsen and SeiringerLS24b, Theorems 1.3, 1.10 and 1.13]. That is,
with
![]() $e_0(\overline {\rho }_0)$
denoting the ground state energy density of the free gas and
$e_0(\overline {\rho }_0)$
denoting the ground state energy density of the free gas and
![]() $c_{0,d}$
and
$c_{0,d}$
and
![]() $\delta _d$
as in Equation (1.8). By a straightforward calculation, the ground state energy density of the free gas is
$\delta _d$
as in Equation (1.8). By a straightforward calculation, the ground state energy density of the free gas is
 $$ \begin{align*} \begin{aligned} e_0(\overline{\rho}_0) & = 4\pi \frac{d^{2/d}}{d+2} \left(\frac{d}{2}\right)^{2/d} \Gamma(d/2)^{2/d} \overline{\rho}_0^{1+2/d}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} e_0(\overline{\rho}_0) & = 4\pi \frac{d^{2/d}}{d+2} \left(\frac{d}{2}\right)^{2/d} \Gamma(d/2)^{2/d} \overline{\rho}_0^{1+2/d}. \end{aligned} \end{align*} $$
By Equations (1.2), (1.6) and (1.10), we have for large
![]() $z = e^{\beta \mu }$
(see also [Reference HuangHua87, Equation (11.31)]),
$z = e^{\beta \mu }$
(see also [Reference HuangHua87, Equation (11.31)]),
 $$ \begin{align*} \begin{aligned} \psi_0(\beta,\mu) & = \beta^{-1-d/2} \frac{\left\vert {\mathbb{S}}^{d-1} \right\vert\Gamma(d/2)}{2(2\pi)^d} ( - \operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})) \\ & = 4\pi \overline{\rho}_0^{1+2/d} \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} = \frac{2}{d} e_0(\overline{\rho}_0) + O\left( \overline{\rho}_0^{1+2/d} (\beta\mu)^{-2}\right), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \psi_0(\beta,\mu) & = \beta^{-1-d/2} \frac{\left\vert {\mathbb{S}}^{d-1} \right\vert\Gamma(d/2)}{2(2\pi)^d} ( - \operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})) \\ & = 4\pi \overline{\rho}_0^{1+2/d} \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} = \frac{2}{d} e_0(\overline{\rho}_0) + O\left( \overline{\rho}_0^{1+2/d} (\beta\mu)^{-2}\right), \end{aligned} \end{align*} $$
where
![]() $\left \vert {\mathbb {S}}^{d-1} \right \vert = \frac {2\pi ^{d/2}}{\Gamma (d/2)}$
is the area of the
$\left \vert {\mathbb {S}}^{d-1} \right \vert = \frac {2\pi ^{d/2}}{\Gamma (d/2)}$
is the area of the
![]() $(d-1)$
-sphere. Thus,
$(d-1)$
-sphere. Thus,
Combining this with Equations (2.1) and (2.2), we conclude the proof of Proposition 1.8.
The rest of the paper concerns the proof of Proposition 1.9. We start with some preliminary computations.
3. Preliminaries
To prove Proposition 1.9, we will consider a finite system on a cubic box of side length L with periodic boundary conditions and bound
![]() $\psi (\beta ,\mu )$
from below by the pressure functional evaluated on the trial state
$\psi (\beta ,\mu )$
from below by the pressure functional evaluated on the trial state
 $$ \begin{align} \varGamma_J = \frac{Z}{Z_J} F \varGamma F, \qquad F = \bigoplus_{n=0}^\infty F_n, \qquad F_n = \prod_{1 \leq i < j \leq n} f(x_i - x_j), \end{align} $$
$$ \begin{align} \varGamma_J = \frac{Z}{Z_J} F \varGamma F, \qquad F = \bigoplus_{n=0}^\infty F_n, \qquad F_n = \prod_{1 \leq i < j \leq n} f(x_i - x_j), \end{align} $$
where f is some cut-off and rescaled scattering function defined in Equation (3.2) below, where
![]() $\varGamma $
is defined in Equation (1.1), and where
$\varGamma $
is defined in Equation (1.1), and where
![]() $Z_J$
is such that this is normalized with
$Z_J$
is such that this is normalized with
![]() $\operatorname {\mathrm {Tr}} \varGamma _J = 1$
. Concretely, on the n-particle space,
$\operatorname {\mathrm {Tr}} \varGamma _J = 1$
. Concretely, on the n-particle space,
![]() $\varGamma _J$
acts via the kernel
$\varGamma _J$
acts via the kernel
(Recall that
![]() $\varGamma $
acts via the kernel
$\varGamma $
acts via the kernel
![]() $Z^{-1}\varGamma _n(X_n,Y_n)$
.) The function f is more precisely
$Z^{-1}\varGamma _n(X_n,Y_n)$
.) The function f is more precisely
 $$ \begin{align} f(x) = \begin{cases} \frac{1}{1 - a^d/b^d} f_0(x) & |x|\leq b \\ 1 & |x|\geq b, \end{cases} \end{align} $$
$$ \begin{align} f(x) = \begin{cases} \frac{1}{1 - a^d/b^d} f_0(x) & |x|\leq b \\ 1 & |x|\geq b, \end{cases} \end{align} $$
where
![]() $f_0(x)$
is the p-wave scattering function defined in Definition 1.1 and b is a length to be chosen later. We will choose
$f_0(x)$
is the p-wave scattering function defined in Definition 1.1 and b is a length to be chosen later. We will choose
![]() $a \ll b \leq C \rho _0^{-1/d}$
. Here and in the following,
$a \ll b \leq C \rho _0^{-1/d}$
. Here and in the following,
![]() $\rho _0$
denotes the particle density of the free gas in finite volume. In particular, for
$\rho _0$
denotes the particle density of the free gas in finite volume. In particular, for
![]() $a^d\rho _0$
small enough, b is larger than the range of v and so f is continuous (since
$a^d\rho _0$
small enough, b is larger than the range of v and so f is continuous (since
![]() $f_0(x) = 1 - \frac {a^3}{|x|^3}$
for x outside the support of v).
$f_0(x) = 1 - \frac {a^3}{|x|^3}$
for x outside the support of v).
Notation 3.1.
-
○ We will denote expectation values of operators in the free state
 $\varGamma $
by
$\varGamma $
by
 $\left \langle \cdot \right \rangle _0$
and in the trial state
$\left \langle \cdot \right \rangle _0$
and in the trial state
 $\varGamma _J$
by
$\varGamma _J$
by
 $\left \langle \cdot \right \rangle _J$
. That is,
$\left \langle \cdot \right \rangle _J$
. That is,
 $\left \langle \mathcal {A} \right \rangle _0 = \operatorname {\mathrm {Tr}}_{\mathcal {F}}[\mathcal {A}\varGamma ]$
and
$\left \langle \mathcal {A} \right \rangle _0 = \operatorname {\mathrm {Tr}}_{\mathcal {F}}[\mathcal {A}\varGamma ]$
and
 $\left \langle \mathcal {A} \right \rangle _J = \operatorname {\mathrm {Tr}}_{\mathcal {F}}[\mathcal {A}\varGamma _J]$
for any operator
$\left \langle \mathcal {A} \right \rangle _J = \operatorname {\mathrm {Tr}}_{\mathcal {F}}[\mathcal {A}\varGamma _J]$
for any operator
 $\mathcal {A}$
on
$\mathcal {A}$
on
 $\mathcal {F}$
.
$\mathcal {F}$
. -
• We denote
 $g(x) = f(x)^2 - 1$
.
$g(x) = f(x)^2 - 1$
. -
• For any function h, we write
 $h_e = h_{ij} = h(x_i-x_j)$
for an edge
$h_e = h_{ij} = h(x_i-x_j)$
for an edge
 $e = (i,j)$
.
$e = (i,j)$
. -
• Moreover, we write
 $\gamma ^{(1)}_e = \gamma ^{(1)}_{ij} = \gamma ^{(1)}(x_i; x_j)$
for an edge
$\gamma ^{(1)}_e = \gamma ^{(1)}_{ij} = \gamma ^{(1)}(x_i; x_j)$
for an edge
 $e = (i,j)$
, where
$e = (i,j)$
, where
 $\gamma ^{(1)}$
is the
$\gamma ^{(1)}$
is the
 $1$
-particle density matrix of
$1$
-particle density matrix of
 $\varGamma $
defined in Equation (3.4) below (see also Notation 3.3).
$\varGamma $
defined in Equation (3.4) below (see also Notation 3.3). -
• We write
 $X_n = (x_1,\ldots ,x_n)$
and
$X_n = (x_1,\ldots ,x_n)$
and
 $X_{[n,m]} = (x_n,\ldots ,x_m)$
if
$X_{[n,m]} = (x_n,\ldots ,x_m)$
if
 $n\leq m$
. If
$n\leq m$
. If
 $n> m$
, then
$n> m$
, then
 $X_{[n,m]} = \varnothing $
.
$X_{[n,m]} = \varnothing $
.
Remark 3.2. The trial state
![]() $\varGamma _J$
does not have (average) particle density
$\varGamma _J$
does not have (average) particle density
![]() $\rho _0$
. However, we have that
$\rho _0$
. However, we have that
This is not needed for the proof of Proposition 1.9, however. We give the proof of (3.3) in Appendix A.
We normalize q-particle density matrices of a general state
![]() $\tilde \varGamma = (\tilde \varGamma _0, \tilde \varGamma _1,\ldots )$
as
$\tilde \varGamma = (\tilde \varGamma _0, \tilde \varGamma _1,\ldots )$
as
 $$ \begin{align} \begin{aligned} \gamma^{(q)}_{\tilde\varGamma}(X_q; Y_q) & = \sum_{n=q}^{\infty} \frac{n!}{(n-q)!} \idotsint \tilde \varGamma_n(X_{q}, X_{[q+1,n]}; Y_q, X_{[q+1,n]}) \,\text{d} X_{[q+1,n]}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \gamma^{(q)}_{\tilde\varGamma}(X_q; Y_q) & = \sum_{n=q}^{\infty} \frac{n!}{(n-q)!} \idotsint \tilde \varGamma_n(X_{q}, X_{[q+1,n]}; Y_q, X_{[q+1,n]}) \,\text{d} X_{[q+1,n]}. \end{aligned} \end{align} $$
Notation 3.3. For the Gibbs state
![]() $\varGamma = (Z^{-1}\varGamma _0,Z^{-1}\varGamma _1,\ldots )$
and the trial state
$\varGamma = (Z^{-1}\varGamma _0,Z^{-1}\varGamma _1,\ldots )$
and the trial state
![]() $\varGamma _J$
, we denote their q-particle density matrices by
$\varGamma _J$
, we denote their q-particle density matrices by
![]() $\gamma ^{(q)}(X_q;Y_q) = \gamma ^{(q)}_{\varGamma }(X_q;Y_q)$
and
$\gamma ^{(q)}(X_q;Y_q) = \gamma ^{(q)}_{\varGamma }(X_q;Y_q)$
and
![]() $\gamma ^{(q)}_J(X_q;Y_q) = \gamma ^{(q)}_{\varGamma _J}(X_q;Y_q)$
, respectively. The same applies to the q-particle densities, being then denoted
$\gamma ^{(q)}_J(X_q;Y_q) = \gamma ^{(q)}_{\varGamma _J}(X_q;Y_q)$
, respectively. The same applies to the q-particle densities, being then denoted
![]() $\rho ^{(q)}$
and
$\rho ^{(q)}$
and
![]() $\rho ^{(q)}_J$
.
$\rho ^{(q)}_J$
.
The Gibbs state
![]() $\varGamma $
is quasi-free and particle preserving. Thus, by Wick’s rule (see [Reference Bratteli and RobinsonBR97, Section 5.2.4], [Reference SolovejSol14, Theorem 10.2]), we have for the q-particle density
$\varGamma $
is quasi-free and particle preserving. Thus, by Wick’s rule (see [Reference Bratteli and RobinsonBR97, Section 5.2.4], [Reference SolovejSol14, Theorem 10.2]), we have for the q-particle density
Moreover, by translation invariance, we have that
![]() $\gamma ^{(1)}(x;y)$
is a function of
$\gamma ^{(1)}(x;y)$
is a function of
![]() $x-y$
only. With a slight abuse of notation, we then write
$x-y$
only. With a slight abuse of notation, we then write
 $$ \begin{align*} \gamma^{(1)}(x;y) = \gamma^{(1)}(x-y) = \frac{1}{L^d}\sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \hat\gamma^{(1)}(k) e^{-ik(x-y)}. \end{align*} $$
$$ \begin{align*} \gamma^{(1)}(x;y) = \gamma^{(1)}(x-y) = \frac{1}{L^d}\sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \hat\gamma^{(1)}(k) e^{-ik(x-y)}. \end{align*} $$
A simple calculation shows that (see [Reference HuangHua87, Equation (8.65)])
 $$ \begin{align*} \hat \gamma^{(1)}(k) = \frac{ze^{ - \beta|k|^2}}{1 + ze^{- \beta|k|^2}} = \frac{e^{\beta\mu - \beta|k|^2}}{1 + e^{\beta\mu - \beta|k|^2}}. \end{align*} $$
$$ \begin{align*} \hat \gamma^{(1)}(k) = \frac{ze^{ - \beta|k|^2}}{1 + ze^{- \beta|k|^2}} = \frac{e^{\beta\mu - \beta|k|^2}}{1 + e^{\beta\mu - \beta|k|^2}}. \end{align*} $$
For the proof of Proposition 1.9, we compute the pressure of the trial state
![]() $\varGamma _J$
. We have
$\varGamma _J$
. We have
 $$ \begin{align} \begin{aligned} \psi(\beta,\mu) & \geq \limsup_{L\to \infty} \frac{1}{L^d} \left[-\left\langle \mathcal{H} - \mu \mathcal{N} + \mathcal{V} \right\rangle_J + \frac{1}{\beta} S(\varGamma_J)\right] \\ & = \limsup_{L\to \infty} \frac{1}{L^d} \left[-\left\langle \mathcal{H} \right\rangle_J - \mu \left\langle \mathcal{N} \right\rangle_J - \frac{1}{2}\iint v_{12} \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 + \frac{1}{\beta} S(\varGamma_J)\right], \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \psi(\beta,\mu) & \geq \limsup_{L\to \infty} \frac{1}{L^d} \left[-\left\langle \mathcal{H} - \mu \mathcal{N} + \mathcal{V} \right\rangle_J + \frac{1}{\beta} S(\varGamma_J)\right] \\ & = \limsup_{L\to \infty} \frac{1}{L^d} \left[-\left\langle \mathcal{H} \right\rangle_J - \mu \left\langle \mathcal{N} \right\rangle_J - \frac{1}{2}\iint v_{12} \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 + \frac{1}{\beta} S(\varGamma_J)\right], \end{aligned} \end{align} $$
where
![]() $\rho ^{(2)}_J$
is the two-body reduced density of the trial state
$\rho ^{(2)}_J$
is the two-body reduced density of the trial state
![]() $\varGamma _J$
. We calculate
$\varGamma _J$
. We calculate
![]() $\rho ^{(2)}_J$
in Section 4 using the Gaudin–Gillespie–Ripka expansion, and we compute the individual terms of Equation (3.5) in Section 5 below. First, however, we need some preliminary bounds.
$\rho ^{(2)}_J$
in Section 4 using the Gaudin–Gillespie–Ripka expansion, and we compute the individual terms of Equation (3.5) in Section 5 below. First, however, we need some preliminary bounds.
3.1. Useful bounds
We recall some useful bounds on the scattering function (defined in Equation (3.2)) from [Reference Lauritsen and SeiringerLS24b].
Lemma 3.4. The scattering function f satisfies
 $$ \begin{align} \kern-1.3pt\qquad\int \left\vert 1 - f(x)^2 \right\vert |x|^n \,\text{d} x & \leq \begin{cases} C a^d \log b/a & n=0 \\ C a^d b^n & n> 0 \end{cases} \end{align} $$
$$ \begin{align} \kern-1.3pt\qquad\int \left\vert 1 - f(x)^2 \right\vert |x|^n \,\text{d} x & \leq \begin{cases} C a^d \log b/a & n=0 \\ C a^d b^n & n> 0 \end{cases} \end{align} $$
 $$ \begin{align} \int \left(\left\vert \nabla f(x) \right\vert{}^2 + \frac{1}{2} v(x) f(x)^2\right)|x|^2 \,\text{d} x & = c_d a^d \left(1 + O(a^d/b^d))\right)\qquad\qquad \end{align} $$
$$ \begin{align} \int \left(\left\vert \nabla f(x) \right\vert{}^2 + \frac{1}{2} v(x) f(x)^2\right)|x|^2 \,\text{d} x & = c_d a^d \left(1 + O(a^d/b^d))\right)\qquad\qquad \end{align} $$
 $$ \begin{align} \quad\ \kern-1pt\int \left(\left\vert \nabla f(x) \right\vert{}^2 + \frac{1}{2} v(x) f(x)^2\right)|x|^n \,\text{d} x & \leq \begin{cases} C a^{n+d-2} & n+d \leq 2d+1 \\ C a^{n+d-2}\log b/a & n+d = 2d+2 \\ C a^{2d} b^{n-d-2} & n+d \geq 2d+3 \end{cases} \end{align} $$
$$ \begin{align} \quad\ \kern-1pt\int \left(\left\vert \nabla f(x) \right\vert{}^2 + \frac{1}{2} v(x) f(x)^2\right)|x|^n \,\text{d} x & \leq \begin{cases} C a^{n+d-2} & n+d \leq 2d+1 \\ C a^{n+d-2}\log b/a & n+d = 2d+2 \\ C a^{2d} b^{n-d-2} & n+d \geq 2d+3 \end{cases} \end{align} $$
 $$ \begin{align} \kern-1.5pt\quad\left\vert \int f(x) \left\vert \nabla f(x) \right\vert |x|^n \,\text{d} x \right\vert & \leq \begin{cases} Ca^{d-1} & n=0 \\ C a^d \log b/a & n=1 \\ C a^{d} b^{n-1} & n\geq 2, \end{cases} \end{align} $$
$$ \begin{align} \kern-1.5pt\quad\left\vert \int f(x) \left\vert \nabla f(x) \right\vert |x|^n \,\text{d} x \right\vert & \leq \begin{cases} Ca^{d-1} & n=0 \\ C a^d \log b/a & n=1 \\ C a^{d} b^{n-1} & n\geq 2, \end{cases} \end{align} $$
where
![]() $c_d$
is defined in Equation (1.3).
$c_d$
is defined in Equation (1.3).
Proof. Equations (3.6), (3.7), (3.8) and (3.9) all follow from the definition of the scattering length, Definition 1.1, and the bounds [Reference Lieb and YngvasonLY01, Lemma A.1; Reference Lauritsen and SeiringerLS24b, Lemma 2.2]
 $$ \begin{align*} \left[1 - \frac{a^d}{|x|^d}\right]_+ \leq f_0(x) \leq 1, \qquad \left\vert \nabla f_0(x) \right\vert \leq \frac{da^d}{|x|^{d+1}} \quad \text{for } |x|> a, \end{align*} $$
$$ \begin{align*} \left[1 - \frac{a^d}{|x|^d}\right]_+ \leq f_0(x) \leq 1, \qquad \left\vert \nabla f_0(x) \right\vert \leq \frac{da^d}{|x|^{d+1}} \quad \text{for } |x|> a, \end{align*} $$
where the left inequality in the first inequality is an equality for x outside the support of v. We refer to [Reference Lauritsen and SeiringerLS24b, Equations (4.1) to (4.6)] for a detailed proof.
We will need the following technical lemma.
Lemma 3.5. Let
![]() $\hat \gamma (k) = z e^{-\beta |k|^2}$
. Let
$\hat \gamma (k) = z e^{-\beta |k|^2}$
. Let
![]() $p,n,m$
be non-negative integers with
$p,n,m$
be non-negative integers with
![]() $1\leq n\leq m$
. Then
$1\leq n\leq m$
. Then
 $$ \begin{align*} \begin{aligned} \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \frac{|k|^p \hat \gamma(k)^n}{(1 + \hat \gamma(k))^m} & = \frac{1}{(2\pi)^d} \int_{\mathbb{R}^d} \frac{|k|^p \hat \gamma(k)^n}{(1 + \hat\gamma(k))^m} \,\text{d} k + O\left(L^{-1} \beta \max \left\{\beta^{-1}, \mu \right\}^{\frac{p+d+1}{2}}\right) \\ & \leq C\max \left\{\beta^{-1}, \mu \right\}^{\frac{p+d}{2}} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \frac{|k|^p \hat \gamma(k)^n}{(1 + \hat \gamma(k))^m} & = \frac{1}{(2\pi)^d} \int_{\mathbb{R}^d} \frac{|k|^p \hat \gamma(k)^n}{(1 + \hat\gamma(k))^m} \,\text{d} k + O\left(L^{-1} \beta \max \left\{\beta^{-1}, \mu \right\}^{\frac{p+d+1}{2}}\right) \\ & \leq C\max \left\{\beta^{-1}, \mu \right\}^{\frac{p+d}{2}} \end{aligned} \end{align*} $$
for
![]() $z =e^{\beta \mu } \gtrsim 1$
and L sufficiently large.
$z =e^{\beta \mu } \gtrsim 1$
and L sufficiently large.
Note that
![]() $\hat {\gamma }(k) \ne \hat {\gamma }^{(1)}(k)$
. In fact,
$\hat {\gamma }(k) \ne \hat {\gamma }^{(1)}(k)$
. In fact,
![]() $\hat {\gamma }^{(1)}(k) = \frac {\hat {\gamma }(k)}{1 + \hat {\gamma }(k)}$
.
$\hat {\gamma }^{(1)}(k) = \frac {\hat {\gamma }(k)}{1 + \hat {\gamma }(k)}$
.
Proof. We interpret the sum as a Riemann sum and compare it with its corresponding integral
Writing
![]() $F_{p,n,m}(k) = \frac {|k|^p \hat {\gamma }(k)^n}{(1 + \hat {\gamma }(k))^m} $
, then
$F_{p,n,m}(k) = \frac {|k|^p \hat {\gamma }(k)^n}{(1 + \hat {\gamma }(k))^m} $
, then
 $$ \begin{align*} \begin{aligned} {\frac{1}{L^d}} \sum_{k\in \frac{2\pi}{L}{\mathbb{Z}}^d} \frac{|k|^p \hat{\gamma}(k)^n}{(1 + \hat{\gamma}(k))^m} & = {\frac{1}{(2\pi)^d}} \sum_{k\in \frac{2\pi}{L}{\mathbb{Z}}^d} \int_{\left[-\frac{\pi}{L}, {\frac{\pi}{L}}\right]^d} \left(F_{p,n,m}(k+\xi) - \int_0^1 \partial_t F_{p,n,m}(k+t\xi) \,\text{d} t\right) \,\text{d} \xi. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\frac{1}{L^d}} \sum_{k\in \frac{2\pi}{L}{\mathbb{Z}}^d} \frac{|k|^p \hat{\gamma}(k)^n}{(1 + \hat{\gamma}(k))^m} & = {\frac{1}{(2\pi)^d}} \sum_{k\in \frac{2\pi}{L}{\mathbb{Z}}^d} \int_{\left[-\frac{\pi}{L}, {\frac{\pi}{L}}\right]^d} \left(F_{p,n,m}(k+\xi) - \int_0^1 \partial_t F_{p,n,m}(k+t\xi) \,\text{d} t\right) \,\text{d} \xi. \end{aligned} \end{align*} $$
The first term is the integral
![]() $I_{p,n,m}$
. For the second term, we may bound by direct computation (defining
$I_{p,n,m}$
. For the second term, we may bound by direct computation (defining
![]() $F_{p,n,m} = 0$
for
$F_{p,n,m} = 0$
for
![]() $p < 0$
)
$p < 0$
)
 $$ \begin{align*} \begin{aligned} \left\vert \partial_t F_{p,n,m}(k+t\xi) \right\vert & \leq C |\xi| \left[F_{p-1,n,m}(k+t\xi) + \beta F_{p+1,n,m}(k+t\xi)\right] \\ & \leq C |\xi| e^{C\beta|\xi||k+\xi| + C \beta|\xi|^2} \left[F_{p-1,n,m}(k+\xi) + \beta F_{p+1,n,m}(k+\xi)\right]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\vert \partial_t F_{p,n,m}(k+t\xi) \right\vert & \leq C |\xi| \left[F_{p-1,n,m}(k+t\xi) + \beta F_{p+1,n,m}(k+t\xi)\right] \\ & \leq C |\xi| e^{C\beta|\xi||k+\xi| + C \beta|\xi|^2} \left[F_{p-1,n,m}(k+\xi) + \beta F_{p+1,n,m}(k+\xi)\right]. \end{aligned} \end{align*} $$
That is, the second term is bounded by the integral
Next, to bound the integral, we note that
![]() $F_{p,n,m}\leq F_{p,1,1}$
. First, consider
$F_{p,n,m}\leq F_{p,1,1}$
. First, consider
![]() $z \geq e$
(i.e.,
$z \geq e$
(i.e.,
![]() $\beta \mu \geq 1$
). Then we bound
$\beta \mu \geq 1$
). Then we bound
 $$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^d} e^{CL^{-1} \beta |k| } F_{p,1,1}(k) \,\text{d} k & \leq C \int_0^{\sqrt{2\mu}} e^{CL^{-1} \beta k } k^{p+d-1}\,\text{d} k + C \int_{\sqrt{2\mu}}^\infty e^{CL^{-1} \beta k } k^{p+d-1} e^{-\beta(k^2-\mu)} \,\text{d} k \\ & \leq C \mu^{\frac{p+d}{2}} e^{CL^{-1} \beta \mu^{1/2} } + C \beta^{-\frac{p+d}{2}}\int_{\sqrt{\beta\mu}}^\infty t^{p+d-1} e^{-t^2 + C L^{-1}\beta^{1/2} t} \,\text{d} t \leq C \mu^{\frac{p+d}{2}} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^d} e^{CL^{-1} \beta |k| } F_{p,1,1}(k) \,\text{d} k & \leq C \int_0^{\sqrt{2\mu}} e^{CL^{-1} \beta k } k^{p+d-1}\,\text{d} k + C \int_{\sqrt{2\mu}}^\infty e^{CL^{-1} \beta k } k^{p+d-1} e^{-\beta(k^2-\mu)} \,\text{d} k \\ & \leq C \mu^{\frac{p+d}{2}} e^{CL^{-1} \beta \mu^{1/2} } + C \beta^{-\frac{p+d}{2}}\int_{\sqrt{\beta\mu}}^\infty t^{p+d-1} e^{-t^2 + C L^{-1}\beta^{1/2} t} \,\text{d} t \leq C \mu^{\frac{p+d}{2}} \end{aligned} \end{align*} $$
for L sufficiently large.
Next, for
![]() $z < e$
, we bound
$z < e$
, we bound
 $$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^d} e^{CL^{-1} \beta |k| } F_{p,1,1}(k) \,\text{d} k & \leq C \int_{0}^\infty e^{CL^{-1} \beta k } k^{p+d-1} z e^{-\beta k^2} \,\text{d} k \\ & \leq C \beta^{-\frac{p+d}{2}}\int_{0}^\infty t^{p+d-1} e^{-t^2 + C L^{-1}\beta^{1/2} t} \,\text{d} t \leq C \beta^{-\frac{p+d}{2}} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{\mathbb{R}^d} e^{CL^{-1} \beta |k| } F_{p,1,1}(k) \,\text{d} k & \leq C \int_{0}^\infty e^{CL^{-1} \beta k } k^{p+d-1} z e^{-\beta k^2} \,\text{d} k \\ & \leq C \beta^{-\frac{p+d}{2}}\int_{0}^\infty t^{p+d-1} e^{-t^2 + C L^{-1}\beta^{1/2} t} \,\text{d} t \leq C \beta^{-\frac{p+d}{2}} \end{aligned} \end{align*} $$
for L sufficiently large. The equality in the lemma follows. We may bound
![]() $I_{p,n,m}$
in a similar manner and conclude the proof of the lemma.
$I_{p,n,m}$
in a similar manner and conclude the proof of the lemma.
Finally, we have the following lemma for the reduced densities of the free state.
Lemma 3.6. The reduced densities of the free Fermi gas satisfy
 $$ \begin{align} \rho^{(2)}(x_1,x_2) & = 2\pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \rho_0^{2+2/d} |x_1-x_2|^2 \left[1 + O(\rho_0^{2/d}|x_1-x_2|^2) +O (L^{-1} \zeta \rho_0^{-1/d} ) \right]. \end{align} $$
$$ \begin{align} \rho^{(2)}(x_1,x_2) & = 2\pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \rho_0^{2+2/d} |x_1-x_2|^2 \left[1 + O(\rho_0^{2/d}|x_1-x_2|^2) +O (L^{-1} \zeta \rho_0^{-1/d} ) \right]. \end{align} $$
Equations (3.10) and (3.11) are the finite volume analogues of Equations (1.6) and (1.7).
Remark 3.7. Note that
![]() $\beta \sim \zeta \rho _0^{-2/d}$
. (Recall that
$\beta \sim \zeta \rho _0^{-2/d}$
. (Recall that
![]() $\zeta = 1 + \left \vert \log z \right \vert $
.) Indeed, for
$\zeta = 1 + \left \vert \log z \right \vert $
.) Indeed, for
![]() $z\leq C$
, this is clear from Equation (3.10). For
$z\leq C$
, this is clear from Equation (3.10). For
![]() $z \gg 1$
, this follows from the asymptotics of the polylogarithm, Equation (1.10). Moreover, if
$z \gg 1$
, this follows from the asymptotics of the polylogarithm, Equation (1.10). Moreover, if
![]() $\beta \mu \geq 1$
, then
$\beta \mu \geq 1$
, then
![]() $\mu \sim \rho _0^{2/d}$
. In particular then, Lemma 3.5 may be reformulated as
$\mu \sim \rho _0^{2/d}$
. In particular then, Lemma 3.5 may be reformulated as
 $$ \begin{align} \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \frac{|k|^p \hat \gamma(k)^n}{(1 + \hat \gamma(k))^m} = \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d } \frac{|k|^p z^n e^{- n \beta |k|^2}}{\left(1 + z e^{-\beta|k|^2}\right)^m} \leq C\rho_0^{1+p/d} \end{align} $$
$$ \begin{align} \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \frac{|k|^p \hat \gamma(k)^n}{(1 + \hat \gamma(k))^m} = \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d } \frac{|k|^p z^n e^{- n \beta |k|^2}}{\left(1 + z e^{-\beta|k|^2}\right)^m} \leq C\rho_0^{1+p/d} \end{align} $$
for
![]() $z\gtrsim 1$
and L sufficiently large. This is the form we will later use.
$z\gtrsim 1$
and L sufficiently large. This is the form we will later use.
Proof. By translation invariance,
Moreover, by Lemma 3.5,
 $$ \begin{align*} \begin{aligned} \rho^{(1)}(0) & = \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \frac{e^{\beta\mu - \beta|k|^2}}{1 + e^{\beta\mu - \beta|k|^2}} \\[5pt] & = \frac{1}{(2\pi)^d} \int_{\mathbb{R}^d} \frac{ze^{ - \beta|k|^2}}{1 + ze^{ - \beta|k|^2}} \,\text{d} k + O\left(L^{-1}\beta \max \left\{\beta^{-1}, \mu\right\}^{\frac{d+1}{2}}\right) \\[5pt] & = \frac{\Gamma(d/2) \left\vert {\mathbb{S}}^{d-1} \right\vert}{2(2\pi)^d} \beta^{-d/2} (-\operatorname{\mathrm{Li}}_{d/2}(-z)) \left(1 + O\left(L^{-1}\beta \max \left\{\beta^{-1}, \mu\right\}^{1/2}\right)\right), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \rho^{(1)}(0) & = \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \frac{e^{\beta\mu - \beta|k|^2}}{1 + e^{\beta\mu - \beta|k|^2}} \\[5pt] & = \frac{1}{(2\pi)^d} \int_{\mathbb{R}^d} \frac{ze^{ - \beta|k|^2}}{1 + ze^{ - \beta|k|^2}} \,\text{d} k + O\left(L^{-1}\beta \max \left\{\beta^{-1}, \mu\right\}^{\frac{d+1}{2}}\right) \\[5pt] & = \frac{\Gamma(d/2) \left\vert {\mathbb{S}}^{d-1} \right\vert}{2(2\pi)^d} \beta^{-d/2} (-\operatorname{\mathrm{Li}}_{d/2}(-z)) \left(1 + O\left(L^{-1}\beta \max \left\{\beta^{-1}, \mu\right\}^{1/2}\right)\right), \end{aligned} \end{align*} $$
where
![]() $\left \vert {\mathbb {S}}^{d-1} \right \vert = \frac {2\pi ^{d/2}}{\Gamma (d/2)}$
is the surface area of the
$\left \vert {\mathbb {S}}^{d-1} \right \vert = \frac {2\pi ^{d/2}}{\Gamma (d/2)}$
is the surface area of the
![]() $(d-1)$
-sphere. Using that
$(d-1)$
-sphere. Using that
![]() $\max \left \{\beta ^{-1},\mu \right \} \sim \rho _0^{2/d}$
(which follow from this equation for L sufficiently large; see Remark 3.7), we conclude the proof of Equation (3.10).
$\max \left \{\beta ^{-1},\mu \right \} \sim \rho _0^{2/d}$
(which follow from this equation for L sufficiently large; see Remark 3.7), we conclude the proof of Equation (3.10).
Next, we consider the
![]() $2$
-particle density. By Wick’s rule, we have
$2$
-particle density. By Wick’s rule, we have
By translation invariance,
![]() $\gamma ^{(1)}(x_1;x_2)$
is a function of
$\gamma ^{(1)}(x_1;x_2)$
is a function of
![]() $x_1-x_2$
only. We expand it as a Taylor series in
$x_1-x_2$
only. We expand it as a Taylor series in
![]() $x_1-x_2$
. By symmetry of reflection in any of the axes, all odd orders and all off-diagonal second order terms vanish. Additionally, all second order terms are equal by the symmetry of permutation of the axes. That is,
$x_1-x_2$
. By symmetry of reflection in any of the axes, all odd orders and all off-diagonal second order terms vanish. Additionally, all second order terms are equal by the symmetry of permutation of the axes. That is,
 $$ \begin{align*} \begin{aligned} \gamma^{(1)}(x_1;x_2) & = \frac{1}{L^d}\sum_{k} \hat \gamma^{(1)}(k) e^{ik(x_1-x_2)} \\ & = \frac{1}{L^d}\sum_{k} \hat \gamma^{(1)}(k) \left[1 - \frac{1}{2d}|k|^2 |x_1-x_2|^2 + O(|k|^4 |x_1-x_2|^4)\right] \\ & = \rho_0- \frac{1}{2d} \left[\frac{1}{L^d} \sum_{k} |k|^2 \hat \gamma^{(1)}(k)\right] |x_1-x_2|^2 + O\left(\left[\frac{1}{L^d} \sum_{k} |k|^4 \hat \gamma^{(1)}(k)\right] |x_1-x_2|^4\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \gamma^{(1)}(x_1;x_2) & = \frac{1}{L^d}\sum_{k} \hat \gamma^{(1)}(k) e^{ik(x_1-x_2)} \\ & = \frac{1}{L^d}\sum_{k} \hat \gamma^{(1)}(k) \left[1 - \frac{1}{2d}|k|^2 |x_1-x_2|^2 + O(|k|^4 |x_1-x_2|^4)\right] \\ & = \rho_0- \frac{1}{2d} \left[\frac{1}{L^d} \sum_{k} |k|^2 \hat \gamma^{(1)}(k)\right] |x_1-x_2|^2 + O\left(\left[\frac{1}{L^d} \sum_{k} |k|^4 \hat \gamma^{(1)}(k)\right] |x_1-x_2|^4\right). \end{aligned} \end{align*} $$
(Here,
![]() $O(|k|^4 |x_1-x_2|^4)$
means a term that is bounded by
$O(|k|^4 |x_1-x_2|^4)$
means a term that is bounded by
![]() $|k|^4 |x_1-x_2|^4$
uniformly in
$|k|^4 |x_1-x_2|^4$
uniformly in
![]() $|k|^4 |x_1-x_2|^4$
, even if it is large.) For the first sum, we have by and Equation (3.10) (and writing the error term in terms of
$|k|^4 |x_1-x_2|^4$
, even if it is large.) For the first sum, we have by and Equation (3.10) (and writing the error term in terms of
![]() $\rho _0$
as above)
$\rho _0$
as above)
 $$ \begin{align*} \begin{aligned} \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} |k|^2 \hat\gamma^{(1)}(k) & = \frac{1}{(2\pi)^d} \int \frac{ze^{- \beta|k|^2}}{1 + ze^{- \beta|k|^2}} |k|^2 \,\text{d} k + O\left(L^{-1} \zeta \rho_0^{4/d}\right) \\ & = \frac{\Gamma(d/2+1) \left\vert {\mathbb{S}}^{d-1} \right\vert}{2(2\pi)^d} \beta^{-d/2-1} (-\operatorname{\mathrm{Li}}_{d/2+1}(-z)) \left(1 + O(L^{-1}\zeta \rho_0^{-1/d})\right) \\ & = 2d\pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \rho_0^{1+2/d} \left(1 + O(L^{-1}\zeta \rho_0^{-1/d})\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} |k|^2 \hat\gamma^{(1)}(k) & = \frac{1}{(2\pi)^d} \int \frac{ze^{- \beta|k|^2}}{1 + ze^{- \beta|k|^2}} |k|^2 \,\text{d} k + O\left(L^{-1} \zeta \rho_0^{4/d}\right) \\ & = \frac{\Gamma(d/2+1) \left\vert {\mathbb{S}}^{d-1} \right\vert}{2(2\pi)^d} \beta^{-d/2-1} (-\operatorname{\mathrm{Li}}_{d/2+1}(-z)) \left(1 + O(L^{-1}\zeta \rho_0^{-1/d})\right) \\ & = 2d\pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \rho_0^{1+2/d} \left(1 + O(L^{-1}\zeta \rho_0^{-1/d})\right). \end{aligned} \end{align*} $$
Using again Lemma 3.5 to bound the second sum, we conclude that
 $$ \begin{align*} \begin{aligned} \gamma^{(1)}(x_1;x_2) & = \rho_0- \pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \rho_0^{1+2/d} |x_1-x_2|^2 \\ & \qquad + O\left(L^{-1} \zeta \rho_0^{1+1/d}|x_1-x_2|^2\right) + O\left(\rho_0^{1+4/d}|x_1-x_2|^4\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \gamma^{(1)}(x_1;x_2) & = \rho_0- \pi \frac{- \operatorname{\mathrm{Li}}_{d/2+1}(-z)}{(-\operatorname{\mathrm{Li}}_{d/2}(-z))^{1+2/d}} \rho_0^{1+2/d} |x_1-x_2|^2 \\ & \qquad + O\left(L^{-1} \zeta \rho_0^{1+1/d}|x_1-x_2|^2\right) + O\left(\rho_0^{1+4/d}|x_1-x_2|^4\right). \end{aligned} \end{align*} $$
We conclude the proof of Equation (3.11).
4. Gaudin–Gillespie–Ripka expansion
We use the Gaudin–Gillespie–Ripka (GGR) expansion [Reference Gaudin, Gillespie and RipkaGGR71] to compute
![]() $Z_J$
and
$Z_J$
and
![]() $\rho ^{(q)}_J$
, the q-particle reduced densities of the trial state
$\rho ^{(q)}_J$
, the q-particle reduced densities of the trial state
![]() $\varGamma _J$
. For this, we recall some notation from [Reference Lauritsen and SeiringerLS24b].
$\varGamma _J$
. For this, we recall some notation from [Reference Lauritsen and SeiringerLS24b].
Definition 4.1 [Reference Lauritsen and SeiringerLS24b, Definition 3.1]
We define
![]() $\mathcal {G}_p^{q}$
as the set of graphs on q external vertices
$\mathcal {G}_p^{q}$
as the set of graphs on q external vertices
![]() $\{1,...,q\}$
and p internal vertices
$\{1,...,q\}$
and p internal vertices
![]() $\{q+1,...,q+p\}$
such that there are no edges between external vertices and such that all internal vertices have degree at least
$\{q+1,...,q+p\}$
such that there are no edges between external vertices and such that all internal vertices have degree at least
![]() $1$
(i.e., there is at least one edge incident to each internal vertex). We replace q and/or p with sets
$1$
(i.e., there is at least one edge incident to each internal vertex). We replace q and/or p with sets
![]() $V^*$
and V, respectively, and write
$V^*$
and V, respectively, and write
![]() $\mathcal {G}_V^{V^*}$
if we need the external and/or internal vertices to have definite indices
$\mathcal {G}_V^{V^*}$
if we need the external and/or internal vertices to have definite indices
![]() $V^*$
, respectively V. Concretely, this means that for a set of edges
$V^*$
, respectively V. Concretely, this means that for a set of edges
![]() $E\subset \{\{i,j\} : 1\leq i < j \leq q+p\} $
, the corresponding graph is in
$E\subset \{\{i,j\} : 1\leq i < j \leq q+p\} $
, the corresponding graph is in
![]() $\mathcal {G}_p^q$
if and only if
$\mathcal {G}_p^q$
if and only if
Define
![]() $\mathcal {T}_p^q\subset \mathcal {C}_p^q\subset \mathcal {G}_p^q$
as the subset of trees and connected graphs, respectively. (Define similarly
$\mathcal {T}_p^q\subset \mathcal {C}_p^q\subset \mathcal {G}_p^q$
as the subset of trees and connected graphs, respectively. (Define similarly
![]() $\mathcal {T}_V^{V^*}\subset \mathcal {C}_V^{V^*} \subset \mathcal {G}_V^{V^*}$
.) Define the functions
$\mathcal {T}_V^{V^*}\subset \mathcal {C}_V^{V^*} \subset \mathcal {G}_V^{V^*}$
.) Define the functions
 $$ \begin{align*} W_p^q = W_p^q(x_1,\ldots,x_{p+q}) = \sum_{G\in\mathcal{G}_p^q} \prod_{e\in G} g_e. \end{align*} $$
$$ \begin{align*} W_p^q = W_p^q(x_1,\ldots,x_{p+q}) = \sum_{G\in\mathcal{G}_p^q} \prod_{e\in G} g_e. \end{align*} $$
A diagram
![]() $(\pi ,G)$
(on q external and p internal vertices) is a pair of a permutation
$(\pi ,G)$
(on q external and p internal vertices) is a pair of a permutation
![]() $\pi \in \mathcal {S}_{p+q}$
and a graph
$\pi \in \mathcal {S}_{p+q}$
and a graph
![]() $G\in \mathcal {G}_p^q$
. We view the permutation
$G\in \mathcal {G}_p^q$
. We view the permutation
![]() $\pi $
as a directed graph on the
$\pi $
as a directed graph on the
![]() $p+q$
vertices. The set of all diagrams on q external and p internal vertices is denoted
$p+q$
vertices. The set of all diagrams on q external and p internal vertices is denoted
![]() $\mathcal {D}_p^q$
.
$\mathcal {D}_p^q$
.
For a diagram
![]() $(\pi ,G)$
, we will refer to G as the g-graph and
$(\pi ,G)$
, we will refer to G as the g-graph and
![]() $\pi $
as the
$\pi $
as the
![]() $\gamma $
-graph. The value of a diagram
$\gamma $
-graph. The value of a diagram
![]() $(\pi ,G) \in \mathcal {D}_p^q$
is the function
$(\pi ,G) \in \mathcal {D}_p^q$
is the function
 $$ \begin{align*} \Gamma_{\pi,G}^q(x_1,\ldots,x_q) = (-1)^{\pi} \idotsint \prod_{j=1}^{p+q} \gamma^{(1)}(x_j;x_{\pi(j)}) \prod_{e\in G} g_e \,\text{d} X_{[q+1,q+p]}. \end{align*} $$
$$ \begin{align*} \Gamma_{\pi,G}^q(x_1,\ldots,x_q) = (-1)^{\pi} \idotsint \prod_{j=1}^{p+q} \gamma^{(1)}(x_j;x_{\pi(j)}) \prod_{e\in G} g_e \,\text{d} X_{[q+1,q+p]}. \end{align*} $$
A diagram
![]() $(\pi ,G)\in \mathcal {D}_p^q$
is linked if the union of
$(\pi ,G)\in \mathcal {D}_p^q$
is linked if the union of
![]() $\pi $
and G is a connected graph. The subset of all linked diagrams is denoted
$\pi $
and G is a connected graph. The subset of all linked diagrams is denoted
![]() ${\mathcal {L}}_p^q \subset \mathcal {D}_p^q$
.
${\mathcal {L}}_p^q \subset \mathcal {D}_p^q$
.
For
![]() $q\geq 1$
, define the set
$q\geq 1$
, define the set
![]() $\tilde {{\mathcal {L}}}_p^q \subset \mathcal {D}_p^q$
as the set of all diagrams such that each linked component contains at least one external vertex. For
$\tilde {{\mathcal {L}}}_p^q \subset \mathcal {D}_p^q$
as the set of all diagrams such that each linked component contains at least one external vertex. For
![]() $q=0$
, we set
$q=0$
, we set
![]() $\tilde {\mathcal {L}}_p^0 = \mathcal {L}_p^0$
.
$\tilde {\mathcal {L}}_p^0 = \mathcal {L}_p^0$
.
If
![]() $q=0$
, we write
$q=0$
, we write
![]() $\mathcal {G}_p^q = \mathcal {G}_p$
etc. without a superscript q.
$\mathcal {G}_p^q = \mathcal {G}_p$
etc. without a superscript q.
A cluster is a connected component of the graph G.
Notation 4.2. By a picture of a diagram, such as Figure 4.1, we will also denote the value of the pictured diagram.

Figure 4.1 Example of a diagram
![]() $(\pi ,G)\in \mathcal {D}_{6}^3$
with three linked components with each linked component containing two (left linked component), one (center top linked component) and two (right linked component) clusters, respectively. Vertices labeled with
$(\pi ,G)\in \mathcal {D}_{6}^3$
with three linked components with each linked component containing two (left linked component), one (center top linked component) and two (right linked component) clusters, respectively. Vertices labeled with
![]() $*$
denote external vertices, dashed lines denote g-edges and arrows denote
$*$
denote external vertices, dashed lines denote g-edges and arrows denote
![]() $\gamma $
-edges (i.e., an arrow from i to j denotes that
$\gamma $
-edges (i.e., an arrow from i to j denotes that
![]() $\pi (i) = j$
). Note that all internal vertices have at least one incident g-edge, that external vertices may have none, and that there are no g-edges between external vertices.
$\pi (i) = j$
). Note that all internal vertices have at least one incident g-edge, that external vertices may have none, and that there are no g-edges between external vertices.
We shall in the remainder of this section prove the following theorem.
Theorem 4.3. For any
![]() $q_0$
, there exists a constant
$q_0$
, there exists a constant
![]() $c_{q_0}> 0$
independently of L such that if
$c_{q_0}> 0$
independently of L such that if
![]() $a^d\rho _0\zeta ^{d/2} \log b/a < c_{q_0}$
, then
$a^d\rho _0\zeta ^{d/2} \log b/a < c_{q_0}$
, then
 $$ \begin{align} \!\!\!Z_J & = Z \exp\left[\sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p} \Gamma_{\pi,G}\right], \end{align} $$
$$ \begin{align} \!\!\!Z_J & = Z \exp\left[\sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p} \Gamma_{\pi,G}\right], \end{align} $$
 $$ \begin{align} \rho_J^{(q)} & = \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^q} \Gamma_{\pi,G}^q \end{align} $$
$$ \begin{align} \rho_J^{(q)} & = \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^q} \Gamma_{\pi,G}^q \end{align} $$
for any
![]() $q \leq q_0$
.
$q \leq q_0$
.
Note that the p-sum in Equation (4.2) starts at
![]() $p=0$
as opposed to that in Equation (4.1). This arises from the fact that diagrams with at least one external vertex may have zero internal vertices, whereas diagrams with no external vertices have at least two internal vertices.
$p=0$
as opposed to that in Equation (4.1). This arises from the fact that diagrams with at least one external vertex may have zero internal vertices, whereas diagrams with no external vertices have at least two internal vertices.
In the proof, we will use the GGR expansion as formulated in [Reference LauritsenLau23, Lemma 3.6] and [Reference Lauritsen and SeiringerLS24b, Theorem 3.4]. For convenience, we recall it here. Note that
![]() $\frac {1}{L^d}\sum _{k\in \frac {2\pi }{L}\mathbb {Z}^d} \left \vert \hat \gamma ^{(1)}(k) \right \vert = \rho _0$
. We continue to abuse notation slightly and treat
$\frac {1}{L^d}\sum _{k\in \frac {2\pi }{L}\mathbb {Z}^d} \left \vert \hat \gamma ^{(1)}(k) \right \vert = \rho _0$
. We continue to abuse notation slightly and treat
![]() $\gamma ^{(1)}$
as a function and write
$\gamma ^{(1)}$
as a function and write
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} = \int _{[0,L]^d} \left \vert \gamma ^{(1)}(x) \right \vert \,\text {d} x$
.
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} = \int _{[0,L]^d} \left \vert \gamma ^{(1)}(x) \right \vert \,\text {d} x$
.
Lemma 4.4 [Reference LauritsenLau23, Lemma 3.6], [Reference Lauritsen and SeiringerLS24b, Theorem 3.4]
For any integer
![]() $q_0$
, there exists a constant
$q_0$
, there exists a constant
![]() $c_{q_0}> 0$
such that if
$c_{q_0}> 0$
such that if
![]() $\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} \rho _0 < c_{q_0}$
, thenFootnote 3
$\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} \rho _0 < c_{q_0}$
, thenFootnote 3
 $$ \begin{align*} \begin{aligned} \mathcal{Z} : = 1 + \sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p} \Gamma_{\pi,G} & = \exp \left[\sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p} \Gamma_{\pi,G} \right], \\[8pt] \frac{1}{\mathcal{Z}} \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p^q} \Gamma_{\pi,G}^q & = \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde {\mathcal{L}}_p^q} \Gamma_{\pi,G}^q \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{Z} : = 1 + \sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p} \Gamma_{\pi,G} & = \exp \left[\sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p} \Gamma_{\pi,G} \right], \\[8pt] \frac{1}{\mathcal{Z}} \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p^q} \Gamma_{\pi,G}^q & = \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde {\mathcal{L}}_p^q} \Gamma_{\pi,G}^q \end{aligned} \end{align*} $$
for any
![]() $q \leq q_0$
, the p-sums being absolutely convergent.
$q \leq q_0$
, the p-sums being absolutely convergent.
We shall bound
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
![]() $\left \Vert g \right \Vert {}_{L^1}$
in Lemma 4.6 below.
$\left \Vert g \right \Vert {}_{L^1}$
in Lemma 4.6 below.
4.1. Calculation of
 $Z_J$
$Z_J$
We calculate
![]() $Z_{J}$
. This is analogous to the computation in [Reference Lauritsen and SeiringerLS24b, Section 3.0.1] and [Reference LauritsenLau23, Section 3.1]. For simplicity, denote the diagonal of
$Z_{J}$
. This is analogous to the computation in [Reference Lauritsen and SeiringerLS24b, Section 3.0.1] and [Reference LauritsenLau23, Section 3.1]. For simplicity, denote the diagonal of
![]() $\varGamma _n$
by
$\varGamma _n$
by
![]() $\varGamma _n = \varGamma _n(X_n) = \varGamma _n(X_n; X_n)$
. Then
$\varGamma _n = \varGamma _n(X_n) = \varGamma _n(X_n; X_n)$
. Then
 $$ \begin{align*} Z_J & = \sum_{n=0}^{\infty} \idotsint \prod_{i<j} f_{ij}^2 \varGamma_n(X_n) \,\text{d} X_n = \sum_{n=0}^{\infty} \idotsint \prod_{i<j} (1+g_{ij}) \varGamma_n(X_n) \,\text{d} X_n. \end{align*} $$
$$ \begin{align*} Z_J & = \sum_{n=0}^{\infty} \idotsint \prod_{i<j} f_{ij}^2 \varGamma_n(X_n) \,\text{d} X_n = \sum_{n=0}^{\infty} \idotsint \prod_{i<j} (1+g_{ij}) \varGamma_n(X_n) \,\text{d} X_n. \end{align*} $$
Expanding the product and grouping all terms where p variables
![]() $x_i$
appear in the factors
$x_i$
appear in the factors
![]() $g_{ij}$
, we find the function
$g_{ij}$
, we find the function
![]() $W_p$
(evaluated on the respective p coordinates
$W_p$
(evaluated on the respective p coordinates
![]() $x_i$
). Noting further the permutation symmetry of the coordinates, we have
$x_i$
). Noting further the permutation symmetry of the coordinates, we have
 $$ \begin{align*} & = \sum_{n=0}^\infty \idotsint \left[1 + \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} W_p(X_p)\right] \varGamma_n(X_n) \,\text{d} X_n \end{align*} $$
$$ \begin{align*} & = \sum_{n=0}^\infty \idotsint \left[1 + \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} W_p(X_p)\right] \varGamma_n(X_n) \,\text{d} X_n \end{align*} $$
since there are
![]() $\frac {n!}{(n-p)!p!}$
many ways to choose p coordinates out of n coordinates. Now, if
$\frac {n!}{(n-p)!p!}$
many ways to choose p coordinates out of n coordinates. Now, if
 $$ \begin{align*} \sum_{n=0}^\infty \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} \idotsint |W_p| \varGamma_n \,\text{d} X_n < \infty, \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} \idotsint |W_p| \varGamma_n \,\text{d} X_n < \infty, \end{align*} $$
then we may interchange the two sums. A criterion for this is given in Lemma 4.5 below. Thus, if the condition of Lemma 4.5 is satisfied – namely, that
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1}$
is sufficiently small – we have
$\rho _0\left \Vert g \right \Vert {}_{L^1}$
is sufficiently small – we have
 $$ \begin{align*} \begin{aligned} Z_J & = Z \left[1 + \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p W_p \left[\frac{1}{Z}\sum_{n=p}^{\infty} \frac{n!}{(n-p)!} \idotsint \,\text{d} X_{[p+1,n]} \varGamma_n \right]\right] \\[8pt] & = Z \left[1+\sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p W_p \rho^{(p)}\right]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} Z_J & = Z \left[1 + \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p W_p \left[\frac{1}{Z}\sum_{n=p}^{\infty} \frac{n!}{(n-p)!} \idotsint \,\text{d} X_{[p+1,n]} \varGamma_n \right]\right] \\[8pt] & = Z \left[1+\sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p W_p \rho^{(p)}\right]. \end{aligned} \end{align*} $$
The free Fermi gas is a quasi-free state, and thus by Wick’s rule, we have
 $$ \begin{align*} Z_J = Z \left[1 + \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p W_p \det\left[\gamma^{(1)}_{ij}\right]_{1\leq i,j\leq p}\right]. \end{align*} $$
$$ \begin{align*} Z_J = Z \left[1 + \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p W_p \det\left[\gamma^{(1)}_{ij}\right]_{1\leq i,j\leq p}\right]. \end{align*} $$
Expanding
![]() $W_p$
and the determinant, we get
$W_p$
and the determinant, we get
 $$ \begin{align*} Z_J = Z \left[1+\sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p} \Gamma_{\pi,G}\right]. \end{align*} $$
$$ \begin{align*} Z_J = Z \left[1+\sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p} \Gamma_{\pi,G}\right]. \end{align*} $$
Applying then Lemma 4.4, we conclude that if
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
$\rho _0\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1}$
are sufficiently small, then Equation (4.1) holds.
$\rho _0\left \Vert g \right \Vert {}_{L^1}$
are sufficiently small, then Equation (4.1) holds.
4.2. Calculation of
 $\rho ^{(q)}_J$
$\rho ^{(q)}_J$
Next, we calculate the reduced densities
![]() $\rho _J^{(q)}$
of the trial state
$\rho _J^{(q)}$
of the trial state
![]() $\varGamma _J$
. This is analogous to the computations in [Reference Lauritsen and SeiringerLS24b, Sections 3.0.2–3.0.4] and [Reference LauritsenLau23, Section 3.2]. We have
$\varGamma _J$
. This is analogous to the computations in [Reference Lauritsen and SeiringerLS24b, Sections 3.0.2–3.0.4] and [Reference LauritsenLau23, Section 3.2]. We have
 $$ \begin{align*} \rho_J^{(q)}(X_q) & = \frac{1}{Z_J} \sum_{n=q}^{\infty} \frac{n!}{(n-q)!}\idotsint \prod_{1\leq i < j \leq n} f_{ij}^2 \varGamma_n(X_n) \,\text{d} X_{[q+1,n].}\qquad\qquad\qquad\qquad\qquad\quad\qquad \end{align*} $$
$$ \begin{align*} \rho_J^{(q)}(X_q) & = \frac{1}{Z_J} \sum_{n=q}^{\infty} \frac{n!}{(n-q)!}\idotsint \prod_{1\leq i < j \leq n} f_{ij}^2 \varGamma_n(X_n) \,\text{d} X_{[q+1,n].}\qquad\qquad\qquad\qquad\qquad\quad\qquad \end{align*} $$
We write
![]() $f_{ij}^2 = 1+g_{ij}$
if at least one of
$f_{ij}^2 = 1+g_{ij}$
if at least one of
![]() $i,j$
is an internal vertex and expand the product of the
$i,j$
is an internal vertex and expand the product of the
![]() $(1+g_{ij})$
’s. Grouping together those terms where p internal vertices are present, we find the function
$(1+g_{ij})$
’s. Grouping together those terms where p internal vertices are present, we find the function
![]() $W_p^q$
. Using additionally the symmetry of permutation of the coordinates, we find
$W_p^q$
. Using additionally the symmetry of permutation of the coordinates, we find
 $$ \begin{align*} &\qquad\qquad\!\!\!\!\! = \frac{1}{Z_J} \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{n=q}^{\infty} \frac{n!}{(n-q)!} \sum_{p=0}^{n-q} \frac{(n-q)!}{p! (n-q-p)!}\idotsint W_p^q(X_{p+q}) \varGamma_n(X_n) \,\text{d} X_{[q+1,n]}. \end{align*} $$
$$ \begin{align*} &\qquad\qquad\!\!\!\!\! = \frac{1}{Z_J} \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{n=q}^{\infty} \frac{n!}{(n-q)!} \sum_{p=0}^{n-q} \frac{(n-q)!}{p! (n-q-p)!}\idotsint W_p^q(X_{p+q}) \varGamma_n(X_n) \,\text{d} X_{[q+1,n]}. \end{align*} $$
By Lemma 4.5 below, we may interchange the sums if
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1}$
is sufficiently small. Then
$\rho _0\left \Vert g \right \Vert {}_{L^1}$
is sufficiently small. Then
 $$ \begin{align*} \begin{aligned} \rho_J^{(q)} & = \frac{Z}{Z_J} \prod_{1\leq i < j \leq q}\! f_{ij}^2 \sum_{p=0}^{\infty} \frac{1}{p!} \!\idotsint \!W_p^q \left[\frac{1}{Z} \sum_{n=p+q}^\infty \frac{n!}{(n-p-q)!} \!\idotsint \!\varGamma_n \,\text{d} X_{[q+p+1,n]}\kern-1pt\right] \,\text{d} X_{[q+1,q+p]} \\[7pt] & = \frac{Z}{Z_J} \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{p=0}^\infty \frac{1}{p!} \idotsint W_p^q \rho^{(p+q)} \,\text{d} X_{[q+1,q+p].} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \rho_J^{(q)} & = \frac{Z}{Z_J} \prod_{1\leq i < j \leq q}\! f_{ij}^2 \sum_{p=0}^{\infty} \frac{1}{p!} \!\idotsint \!W_p^q \left[\frac{1}{Z} \sum_{n=p+q}^\infty \frac{n!}{(n-p-q)!} \!\idotsint \!\varGamma_n \,\text{d} X_{[q+p+1,n]}\kern-1pt\right] \,\text{d} X_{[q+1,q+p]} \\[7pt] & = \frac{Z}{Z_J} \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{p=0}^\infty \frac{1}{p!} \idotsint W_p^q \rho^{(p+q)} \,\text{d} X_{[q+1,q+p].} \end{aligned} \end{align*} $$
Expanding the
![]() $W_p^q$
and using the Wick rule for the reduced densities of the free gas as above, we get
$W_p^q$
and using the Wick rule for the reduced densities of the free gas as above, we get
 $$ \begin{align*} \begin{aligned} \rho_J^{(q)} & = \frac{Z}{Z_J} \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p^q} \Gamma_{\pi,G}^q. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \rho_J^{(q)} & = \frac{Z}{Z_J} \prod_{1\leq i < j \leq q} f_{ij}^2 \sum_{p=0}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{D}_p^q} \Gamma_{\pi,G}^q. \end{aligned} \end{align*} $$
As above, by Lemma 4.4, we get that Equation (4.2) holds for
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
$\rho _0\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1}$
small enough (dependent on q).
$\rho _0\left \Vert g \right \Vert {}_{L^1}$
small enough (dependent on q).
4.3. A convergence criterion
In this section, we show the following:
Lemma 4.5. There exists a constant
![]() $c> 0$
such that if
$c> 0$
such that if
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1} < c$
, then
$\rho _0\left \Vert g \right \Vert {}_{L^1} < c$
, then
 $$ \begin{align} \frac{1}{Z} \sum_{n=0}^\infty \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} \idotsint |W_p| |\varGamma_n| \,\mathrm{d} X_n & \leq \exp( CL^d \rho_0 \left\Vert g \right\Vert{}_{L^1} ) < \infty, \end{align} $$
$$ \begin{align} \frac{1}{Z} \sum_{n=0}^\infty \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} \idotsint |W_p| |\varGamma_n| \,\mathrm{d} X_n & \leq \exp( CL^d \rho_0 \left\Vert g \right\Vert{}_{L^1} ) < \infty, \end{align} $$
and for any
![]() $q \geq 1,$
$q \geq 1,$
 $$ \begin{align} \frac{1}{Z} \sum_{n=q}^\infty \sum_{p=0}^{n-q} \frac{n!}{(n-q-p)!p!} \idotsint |W_p^q| |\varGamma_n| \,\mathrm{d} X_{[q+1,n]} & \leq C_q \rho_0^q \exp(C L^d \rho_0 \left\Vert g \right\Vert{}_{L^1}) < \infty \end{align} $$
$$ \begin{align} \frac{1}{Z} \sum_{n=q}^\infty \sum_{p=0}^{n-q} \frac{n!}{(n-q-p)!p!} \idotsint |W_p^q| |\varGamma_n| \,\mathrm{d} X_{[q+1,n]} & \leq C_q \rho_0^q \exp(C L^d \rho_0 \left\Vert g \right\Vert{}_{L^1}) < \infty \end{align} $$
uniformly in
![]() $x_1,\ldots ,x_q$
.
$x_1,\ldots ,x_q$
.
Proof. Write
 $$ \begin{align*} \begin{aligned} \frac{1}{Z} \sum_{n=0}^\infty \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} \idotsint |W_p| |\varGamma_n| \,\text{d} X_n & = \frac{1}{Z} \sum_{p=2}^\infty\sum_{n=p}^{\infty} \frac{n!}{(n-p)!p!}\idotsint \,\text{d} X_n |W_p| \varGamma_n \\[7pt] & = \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p |W_p| \rho^{(p)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{Z} \sum_{n=0}^\infty \sum_{p=2}^{n} \frac{n!}{(n-p)!p!} \idotsint |W_p| |\varGamma_n| \,\text{d} X_n & = \frac{1}{Z} \sum_{p=2}^\infty\sum_{n=p}^{\infty} \frac{n!}{(n-p)!p!}\idotsint \,\text{d} X_n |W_p| \varGamma_n \\[7pt] & = \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p |W_p| \rho^{(p)}. \end{aligned} \end{align*} $$
By splitting all graphs into their connected components, we have
 $$ \begin{align*} \idotsint \!\,\text{d} X_p \, |W_p| \rho^{(p)} = \idotsint \!\,\text{d} X_p \, \left\vert \sum_{k=1}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \binom{p}{n_1,\ldots, n_k} \chi_{(\sum n_\ell = p)} \prod_{\ell=1}^k \left[\sum_{G_\ell \in \mathcal{C}_{n_\ell}} \prod_{e_\in G_\ell} g_e\right] \right\vert \rho^{(p)}. \end{align*} $$
$$ \begin{align*} \idotsint \!\,\text{d} X_p \, |W_p| \rho^{(p)} = \idotsint \!\,\text{d} X_p \, \left\vert \sum_{k=1}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \binom{p}{n_1,\ldots, n_k} \chi_{(\sum n_\ell = p)} \prod_{\ell=1}^k \left[\sum_{G_\ell \in \mathcal{C}_{n_\ell}} \prod_{e_\in G_\ell} g_e\right] \right\vert \rho^{(p)}. \end{align*} $$
We abused notation slightly and denote by
![]() $\mathcal {C}_{n_\ell }$
the set of connected graphs on
$\mathcal {C}_{n_\ell }$
the set of connected graphs on
![]() $n_{\ell }$
specified vertices, say
$n_{\ell }$
specified vertices, say
![]() $\{\sum _{\ell ' < \ell } n_{\ell '} + 1, \ldots , \sum _{\ell ' \leq \ell } n_{\ell '}\}$
, such that no two
$\{\sum _{\ell ' < \ell } n_{\ell '} + 1, \ldots , \sum _{\ell ' \leq \ell } n_{\ell '}\}$
, such that no two
![]() $G_\ell $
’s share any vertices. Here, k is the number of connected components having sizes
$G_\ell $
’s share any vertices. Here, k is the number of connected components having sizes
![]() $n_1,\ldots ,n_k$
. Note that
$n_1,\ldots ,n_k$
. Note that
![]() $n_\ell \geq 2$
since each connected component needs at least two vertices since any vertex in a graph
$n_\ell \geq 2$
since each connected component needs at least two vertices since any vertex in a graph
![]() $G\in \mathcal {G}_p$
is internal and hence connected to at least one other vertex. The factor
$G\in \mathcal {G}_p$
is internal and hence connected to at least one other vertex. The factor
![]() $\frac {1}{k!}$
comes from counting the possible labelings of the connected component, and the factor
$\frac {1}{k!}$
comes from counting the possible labelings of the connected component, and the factor
![]() $\binom {p}{n_1 \cdots n_k}$
comes from counting the possible labelings of the vertices in the different connected components.
$\binom {p}{n_1 \cdots n_k}$
comes from counting the possible labelings of the vertices in the different connected components.
Next, we employ the tree-graph inequality [Reference UeltschiUel18]. This reads (since
![]() $0\leq g \leq 1$
)
$0\leq g \leq 1$
)
 $$ \begin{align*} \left\vert \sum_{G\in \mathcal{C}_n} \prod_{e\in G} g_e \right\vert \leq \sum_{T \in \mathcal{T}_n} \prod_{e\in T} \left\vert g_e \right\vert. \end{align*} $$
$$ \begin{align*} \left\vert \sum_{G\in \mathcal{C}_n} \prod_{e\in G} g_e \right\vert \leq \sum_{T \in \mathcal{T}_n} \prod_{e\in T} \left\vert g_e \right\vert. \end{align*} $$
Thus,
 $$ \begin{align*} \idotsint \!\,\text{d} X_p \, \frac{1}{p!} \left\vert W_p \right\vert \rho^{(p)} & \leq \sum_{k=1}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq2} \frac{1}{n_1! \cdots n_k!} \chi_{(\sum n_\ell = p)} \idotsint \!\,\text{d} X_p \prod_{\ell=1}^k \left[\sum_{T_\ell \in \mathcal{T}_{n_\ell}} \prod_{e\in T_\ell} |g_e|\right] \rho^{(p)}. \end{align*} $$
$$ \begin{align*} \idotsint \!\,\text{d} X_p \, \frac{1}{p!} \left\vert W_p \right\vert \rho^{(p)} & \leq \sum_{k=1}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq2} \frac{1}{n_1! \cdots n_k!} \chi_{(\sum n_\ell = p)} \idotsint \!\,\text{d} X_p \prod_{\ell=1}^k \left[\sum_{T_\ell \in \mathcal{T}_{n_\ell}} \prod_{e\in T_\ell} |g_e|\right] \rho^{(p)}. \end{align*} $$
Next, we bound
![]() $\rho ^{(p)}$
analogously to [Reference Lauritsen and SeiringerLS24b, Lemma 3.10]. First,
$\rho ^{(p)}$
analogously to [Reference Lauritsen and SeiringerLS24b, Lemma 3.10]. First,
![]() $\rho ^{(p)} = \det [\gamma ^{(1)}_{ij}]_{1\leq i,j\leq p}$
by the Wick rule. Next, define
$\rho ^{(p)} = \det [\gamma ^{(1)}_{ij}]_{1\leq i,j\leq p}$
by the Wick rule. Next, define
![]() $\alpha _i(k) = L^{-d/2} e^{ikx_i} \hat \gamma ^{(1)}(k) \in \ell ^2(\frac {2\pi }{L}\mathbb {Z}^d)$
. Then
$\alpha _i(k) = L^{-d/2} e^{ikx_i} \hat \gamma ^{(1)}(k) \in \ell ^2(\frac {2\pi }{L}\mathbb {Z}^d)$
. Then
![]() $\gamma ^{(1)}_{ij} = \left \langle \alpha _i \middle \vert \alpha _j \right \rangle _{\ell ^2(\frac {2\pi }{L}\mathbb {Z}^d)}$
and so by the Gram–Hadamard inequality [Reference Giuliani, Mastropietro and RychkovGMR21, Lemma D.1],
$\gamma ^{(1)}_{ij} = \left \langle \alpha _i \middle \vert \alpha _j \right \rangle _{\ell ^2(\frac {2\pi }{L}\mathbb {Z}^d)}$
and so by the Gram–Hadamard inequality [Reference Giuliani, Mastropietro and RychkovGMR21, Lemma D.1],
 $$ \begin{align*} \rho^{(p)} = \det \left[\gamma^{(1)}_{ij}\right]_{1\leq i,j\leq p} \leq \prod_{i=1}^p \Vert \alpha_i \Vert_{\ell^2(\frac{2\pi}{L} \mathbb{Z}^d)}^2 = \rho_0^p . \end{align*} $$
$$ \begin{align*} \rho^{(p)} = \det \left[\gamma^{(1)}_{ij}\right]_{1\leq i,j\leq p} \leq \prod_{i=1}^p \Vert \alpha_i \Vert_{\ell^2(\frac{2\pi}{L} \mathbb{Z}^d)}^2 = \rho_0^p . \end{align*} $$
Thus,
 $$ \begin{align*} \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p |W_p| \rho^{(p)} & \leq \sum_{k=1}^\infty \frac{1}{k! } \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{n_1!\cdots n_k!} \rho_0^{\sum n_\ell} \prod_{\ell=1}^k\left[\sum_{T_\ell \in \mathcal{T}_{n_\ell}} \idotsint \prod_{e\in T_\ell} |g_e|\right].\quad\ \end{align*} $$
$$ \begin{align*} \sum_{p=2}^\infty \frac{1}{p!} \idotsint \,\text{d} X_p |W_p| \rho^{(p)} & \leq \sum_{k=1}^\infty \frac{1}{k! } \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{n_1!\cdots n_k!} \rho_0^{\sum n_\ell} \prod_{\ell=1}^k\left[\sum_{T_\ell \in \mathcal{T}_{n_\ell}} \idotsint \prod_{e\in T_\ell} |g_e|\right].\quad\ \end{align*} $$
For each tree, the integration is over all variables; thus, by the translation invariance, the integration over the variables in the tree
![]() $T_\ell $
gives
$T_\ell $
gives
![]() $L^d (\int |g|)^{n_\ell - 1}$
. Using moreover Cayley’s formula
$L^d (\int |g|)^{n_\ell - 1}$
. Using moreover Cayley’s formula
![]() $\# \mathcal {T}_n = n^{n-2}\leq C^n n!$
, we get
$\# \mathcal {T}_n = n^{n-2}\leq C^n n!$
, we get
 $$ \begin{align*} &\qquad\qquad\qquad\qquad\qquad\ \ \qquad \leq \sum_{k=1}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{n_1!\cdots n_k!} \rho_0^{\sum n_\ell} C^{\sum n_\ell} n_1! \cdots n_k! \left(\int |g|\right)^{\sum n_\ell - k} L^{dk} \\ &\qquad\qquad\qquad\qquad\qquad\ \ \qquad = \sum_{k=1}^\infty \frac{1}{k!} \left[C\rho_0L^d \sum_{n=2}^\infty (C\rho_0\left\Vert g \right\Vert{}_{L^1})^{n-1} \right]^k \\ &\qquad\qquad\qquad\qquad\qquad\ \ \qquad \leq \exp\left(CL^d \rho_0\left\Vert g \right\Vert{}_{L^1}\right) < \infty \end{align*} $$
$$ \begin{align*} &\qquad\qquad\qquad\qquad\qquad\ \ \qquad \leq \sum_{k=1}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{n_1!\cdots n_k!} \rho_0^{\sum n_\ell} C^{\sum n_\ell} n_1! \cdots n_k! \left(\int |g|\right)^{\sum n_\ell - k} L^{dk} \\ &\qquad\qquad\qquad\qquad\qquad\ \ \qquad = \sum_{k=1}^\infty \frac{1}{k!} \left[C\rho_0L^d \sum_{n=2}^\infty (C\rho_0\left\Vert g \right\Vert{}_{L^1})^{n-1} \right]^k \\ &\qquad\qquad\qquad\qquad\qquad\ \ \qquad \leq \exp\left(CL^d \rho_0\left\Vert g \right\Vert{}_{L^1}\right) < \infty \end{align*} $$
if
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1}$
is sufficiently small.
$\rho _0\left \Vert g \right \Vert {}_{L^1}$
is sufficiently small.
The proof of Equation (4.4) is in spirit the same. Write
 $$ \begin{align*} \begin{aligned} \frac{1}{Z} \sum_{n=q}^\infty \sum_{p=0}^{n-q} \frac{n!}{(n-q-p)!p!} \idotsint |W_p^q| |\varGamma_n| \,\text{d} X_{[q+1,n]} & = \sum_{p=0}^\infty \frac{1}{p!} \idotsint \,\text{d} X_{[q+1,q+p]} |W_p^q| \rho^{(q+p)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{Z} \sum_{n=q}^\infty \sum_{p=0}^{n-q} \frac{n!}{(n-q-p)!p!} \idotsint |W_p^q| |\varGamma_n| \,\text{d} X_{[q+1,n]} & = \sum_{p=0}^\infty \frac{1}{p!} \idotsint \,\text{d} X_{[q+1,q+p]} |W_p^q| \rho^{(q+p)}. \end{aligned} \end{align*} $$
By decomposing the graphs into their connected components, we have

Here,
![]() $\kappa $
is the number of connected components having external vertices, and k is the number of connected components only with internal vertices. The partition
$\kappa $
is the number of connected components having external vertices, and k is the number of connected components only with internal vertices. The partition
![]() $(V_1^*,\ldots ,V_\kappa ^*)$
partitions the external vertices into the
$(V_1^*,\ldots ,V_\kappa ^*)$
partitions the external vertices into the
![]() $\kappa $
different connected components with external vertices, and the numbers
$\kappa $
different connected components with external vertices, and the numbers
![]() $n_1^*,\ldots ,n_\kappa ^*$
are the number of internal vertices in the connected components with external vertices. The numbers
$n_1^*,\ldots ,n_\kappa ^*$
are the number of internal vertices in the connected components with external vertices. The numbers
![]() $n_1,\ldots ,n_k$
and the combinatorial factors are as above.
$n_1,\ldots ,n_k$
and the combinatorial factors are as above.
Using the tree-graph inequality as above, we will obtain a sum of trees. (Technically, we need to use a trivial modification of the tree-graph bound adapted to the setting with external vertices as in [Reference Lauritsen and SeiringerLS24b, Section 3.1.3; Reference LauritsenLau23, Section 4.2]. One simply defines
![]() $g_e=0$
for a disallowed edge e between external vertices.) Namely, we will have factors like
$g_e=0$
for a disallowed edge e between external vertices.) Namely, we will have factors like
 $$ \begin{align*} \sum_{T_\lambda^* \in \mathcal{T}_{n_\lambda^*}^{V^*_\lambda}} \prod_{e \in T_\lambda^*} |g_e|. \end{align*} $$
$$ \begin{align*} \sum_{T_\lambda^* \in \mathcal{T}_{n_\lambda^*}^{V^*_\lambda}} \prod_{e \in T_\lambda^*} |g_e|. \end{align*} $$
We bound these as follows. If
![]() $\# V_\lambda ^* = 1$
, we do nothing and define
$\# V_\lambda ^* = 1$
, we do nothing and define
![]() $T_{\lambda ,1}^* = T_\lambda ^*$
. Otherwise, iteratively pick any edge on the path between any two external vertices and bound the factor
$T_{\lambda ,1}^* = T_\lambda ^*$
. Otherwise, iteratively pick any edge on the path between any two external vertices and bound the factor
![]() $|g_e|\leq 1$
. Remove this edge from
$|g_e|\leq 1$
. Remove this edge from
![]() $T_\lambda ^*$
. Repeating this procedure
$T_\lambda ^*$
. Repeating this procedure
![]() $\# V^*_\lambda - 1$
many times results in
$\# V^*_\lambda - 1$
many times results in
![]() $\# V^*_\lambda $
many trees all with exactly one external vertex. Label these as
$\# V^*_\lambda $
many trees all with exactly one external vertex. Label these as
![]() $T_{\lambda ,1}^*,\ldots ,T_{\lambda ,\#V_\lambda ^*}^*$
. We then have the bound
$T_{\lambda ,1}^*,\ldots ,T_{\lambda ,\#V_\lambda ^*}^*$
. We then have the bound
 $$ \begin{align*} \prod_{e \in T_\lambda^*} |g_e| \leq \prod_{\nu = 1}^{\#V_\lambda^*} \prod_{e\in T_{\lambda,\nu}^*} |g_e|. \end{align*} $$
$$ \begin{align*} \prod_{e \in T_\lambda^*} |g_e| \leq \prod_{\nu = 1}^{\#V_\lambda^*} \prod_{e\in T_{\lambda,\nu}^*} |g_e|. \end{align*} $$
Using this bound together with the Gram–Hadamard inequality as above, we get
 $$ \begin{align*} & \sum_{p=0}^\infty \frac{1}{p!} \idotsint \,\text{d} X_{[q+1,q+p]} |W_p^q| \rho^{(q+p)} \\[5pt] & \quad \leq \sum_{\kappa=1}^q \frac{1}{\kappa!} \sum_{\substack{(V_1^*,\ldots,V_\kappa^*) \\[5pt] \text{part. of } \{1,\ldots,q\} \\ V_\lambda^* \ne \varnothing}} \sum_{n_1^*,\ldots,n_\kappa^* \geq 0} \sum_{k=0}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{\prod_{\lambda=1}^\kappa n_\lambda^* ! \prod_{\ell=1}^k n_\ell !} \rho_0^{q + \sum_\lambda n_\lambda^* + \sum_\ell n_\ell} \\ & \qquad \times \sum_{T_\lambda^* \in \mathcal{T}_{n_\lambda^*}^{V_\lambda^*}} \sum_{T_\ell \in \mathcal{T}_{n_\ell}} \left[ \prod_{\lambda=1}^\kappa \prod_{\nu = 1}^{\#V_\lambda^*} \idotsint \prod_{e\in T_{\lambda,\nu}^*} |g_e| \right] \left[ \prod_{\ell=1}^k \idotsint \prod_{e\in T_{\ell}} |g_e| \right]. \end{align*} $$
$$ \begin{align*} & \sum_{p=0}^\infty \frac{1}{p!} \idotsint \,\text{d} X_{[q+1,q+p]} |W_p^q| \rho^{(q+p)} \\[5pt] & \quad \leq \sum_{\kappa=1}^q \frac{1}{\kappa!} \sum_{\substack{(V_1^*,\ldots,V_\kappa^*) \\[5pt] \text{part. of } \{1,\ldots,q\} \\ V_\lambda^* \ne \varnothing}} \sum_{n_1^*,\ldots,n_\kappa^* \geq 0} \sum_{k=0}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{\prod_{\lambda=1}^\kappa n_\lambda^* ! \prod_{\ell=1}^k n_\ell !} \rho_0^{q + \sum_\lambda n_\lambda^* + \sum_\ell n_\ell} \\ & \qquad \times \sum_{T_\lambda^* \in \mathcal{T}_{n_\lambda^*}^{V_\lambda^*}} \sum_{T_\ell \in \mathcal{T}_{n_\ell}} \left[ \prod_{\lambda=1}^\kappa \prod_{\nu = 1}^{\#V_\lambda^*} \idotsint \prod_{e\in T_{\lambda,\nu}^*} |g_e| \right] \left[ \prod_{\ell=1}^k \idotsint \prod_{e\in T_{\ell}} |g_e| \right]. \end{align*} $$
In the integrations, each tree
![]() $T_{\lambda ,\nu }^*$
is integrated over all but the one external vertex and so gives a value
$T_{\lambda ,\nu }^*$
is integrated over all but the one external vertex and so gives a value
![]() $(\int |g|)^{\# T_{\lambda ,\nu }^* - 1}$
, and each tree
$(\int |g|)^{\# T_{\lambda ,\nu }^* - 1}$
, and each tree
![]() $T_\ell $
is integrated over all coordinates giving the value
$T_\ell $
is integrated over all coordinates giving the value
![]() $(\int |g|)^{n_\ell - 1} L^d$
. Moreover,
$(\int |g|)^{n_\ell - 1} L^d$
. Moreover,
![]() $\sum _\nu (\# T_{\lambda ,\nu }^* - 1) = n_\lambda ^*$
. Thus, using additionally Cayley’s formula (trivially extended to the setting with external vertices:
$\sum _\nu (\# T_{\lambda ,\nu }^* - 1) = n_\lambda ^*$
. Thus, using additionally Cayley’s formula (trivially extended to the setting with external vertices:
![]() $\# \mathcal {T}_{n_\lambda ^*}^{V_\lambda ^*} \leq C^{n_\lambda ^* + \# V_\lambda ^*} (n_\lambda ^*+ \# V_\lambda ^*)!$
),
$\# \mathcal {T}_{n_\lambda ^*}^{V_\lambda ^*} \leq C^{n_\lambda ^* + \# V_\lambda ^*} (n_\lambda ^*+ \# V_\lambda ^*)!$
),
 $$ \begin{align*} & \quad \leq \sum_{\kappa=1}^q \frac{1}{\kappa!} \sum_{\substack{(V_1^*,\ldots,V_\kappa^*) \\ \text{part. of } \{1,\ldots,q\} \\ V_\lambda^* \ne \varnothing}} \sum_{n_1^*,\ldots,n_\kappa^* \geq 0} \sum_{k=0}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{\prod_{\lambda=1}^\kappa n_\lambda^* ! \prod_{\ell=1}^k n_\ell !} \rho_0^{q + \sum_\lambda n_\lambda^* + \sum_\ell n_\ell} \\ & \qquad \times C^{q+\sum_\lambda n_\lambda^* + \sum_\ell n_\ell} \prod_{\lambda=1}^\kappa (n_\lambda^* + \# V_\lambda^*)! \prod_{\ell=1}^k n_\ell! \left(\int |g|\right)^{\sum_\lambda n_\lambda^* + \sum_\ell n_\ell - k} L^{dk}. \end{align*} $$
$$ \begin{align*} & \quad \leq \sum_{\kappa=1}^q \frac{1}{\kappa!} \sum_{\substack{(V_1^*,\ldots,V_\kappa^*) \\ \text{part. of } \{1,\ldots,q\} \\ V_\lambda^* \ne \varnothing}} \sum_{n_1^*,\ldots,n_\kappa^* \geq 0} \sum_{k=0}^\infty \frac{1}{k!} \sum_{n_1,\ldots,n_k\geq 2} \frac{1}{\prod_{\lambda=1}^\kappa n_\lambda^* ! \prod_{\ell=1}^k n_\ell !} \rho_0^{q + \sum_\lambda n_\lambda^* + \sum_\ell n_\ell} \\ & \qquad \times C^{q+\sum_\lambda n_\lambda^* + \sum_\ell n_\ell} \prod_{\lambda=1}^\kappa (n_\lambda^* + \# V_\lambda^*)! \prod_{\ell=1}^k n_\ell! \left(\int |g|\right)^{\sum_\lambda n_\lambda^* + \sum_\ell n_\ell - k} L^{dk}. \end{align*} $$
Next, we may bound the binomial coefficients as
![]() $(n+m)! \leq 2^{n+m}n!m!$
so
$(n+m)! \leq 2^{n+m}n!m!$
so
![]() $\prod _{\lambda =1}^\kappa (n_\lambda ^* + \# V_\lambda ^*)! \leq 2^{\sum _\lambda n_\lambda ^* + q} \prod _\lambda n_\lambda ^* ! (\# V_\lambda ^*)!$
. Thus,
$\prod _{\lambda =1}^\kappa (n_\lambda ^* + \# V_\lambda ^*)! \leq 2^{\sum _\lambda n_\lambda ^* + q} \prod _\lambda n_\lambda ^* ! (\# V_\lambda ^*)!$
. Thus,
 $$ \begin{align*} & \quad \kern2pt\leq C^q \sum_{\kappa=1}^q \frac{1}{\kappa!} \sum_{\substack{(V_1^*,\ldots,V_\kappa^*) \\ \text{part. of } \{1,\ldots,q\} \\ V_\lambda^* \ne \varnothing}} \prod_{\lambda=1}^\kappa (\# V_\lambda^*)! \left[ \sum_{n^* = 0}^\infty (C \rho_0\left\Vert g \right\Vert{}_{L^1})^{n_*} \right]^{\kappa}\qquad\qquad\qquad\qquad\qquad \\ & \qquad\kern2pt \times \rho_0^q \sum_{k=0}^{\infty} \frac{1}{k!} \left[ CL^d \rho_0\sum_{n=2}^\infty \left(C\rho_0\left\Vert g \right\Vert{}_{L^1}\right)^{n-1} \right]^k \qquad\qquad\qquad\qquad\qquad\\ & \quad\kern2pt \leq C_q \rho_0^q \exp\left(CL^d \rho_0\left\Vert g \right\Vert{}_{L^1}\right) < \infty\qquad\qquad\qquad\qquad\qquad \end{align*} $$
$$ \begin{align*} & \quad \kern2pt\leq C^q \sum_{\kappa=1}^q \frac{1}{\kappa!} \sum_{\substack{(V_1^*,\ldots,V_\kappa^*) \\ \text{part. of } \{1,\ldots,q\} \\ V_\lambda^* \ne \varnothing}} \prod_{\lambda=1}^\kappa (\# V_\lambda^*)! \left[ \sum_{n^* = 0}^\infty (C \rho_0\left\Vert g \right\Vert{}_{L^1})^{n_*} \right]^{\kappa}\qquad\qquad\qquad\qquad\qquad \\ & \qquad\kern2pt \times \rho_0^q \sum_{k=0}^{\infty} \frac{1}{k!} \left[ CL^d \rho_0\sum_{n=2}^\infty \left(C\rho_0\left\Vert g \right\Vert{}_{L^1}\right)^{n-1} \right]^k \qquad\qquad\qquad\qquad\qquad\\ & \quad\kern2pt \leq C_q \rho_0^q \exp\left(CL^d \rho_0\left\Vert g \right\Vert{}_{L^1}\right) < \infty\qquad\qquad\qquad\qquad\qquad \end{align*} $$
if
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1}$
is small enough.
$\rho _0 \left \Vert g \right \Vert {}_{L^1}$
is small enough.
4.4. Calculation of
 $\left \Vert g \right \Vert {}_{L^1}, \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
$\left \Vert g \right \Vert {}_{L^1}, \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
In this section, we bound the quantities
![]() $\left \Vert g \right \Vert {}_{L^1}$
and
$\left \Vert g \right \Vert {}_{L^1}$
and
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} = \int \left \vert \gamma ^{(1)}(x) \right \vert \,\text {d} x$
. We show (recall
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} = \int \left \vert \gamma ^{(1)}(x) \right \vert \,\text {d} x$
. We show (recall
![]() $\zeta = 1 + \left \vert \log z \right \vert $
)
$\zeta = 1 + \left \vert \log z \right \vert $
)
Lemma 4.6. The quantities
![]() $\left \Vert g \right \Vert {}_{L^1}$
and
$\left \Vert g \right \Vert {}_{L^1}$
and
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
satisfy
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
satisfy
Note that these bounds are uniform in the volume
![]() $L^d$
.
$L^d$
.
Proof. The bound
![]() $\left \Vert g \right \Vert {}_{L^1} \leq C a^d \log b/a$
follows from Equation (3.6). For
$\left \Vert g \right \Vert {}_{L^1} \leq C a^d \log b/a$
follows from Equation (3.6). For
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
, we have for any (length)
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
, we have for any (length)
![]() $\lambda> 0$
,
$\lambda> 0$
,
 $$ \begin{align*} \begin{aligned} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1} & = \int_{[0,L]^d} \left\vert \gamma^{(1)}(x) \right\vert \\ & \leq \left(\int_{\mathbb{R}^d} \left\vert \gamma^{(1)}(x) \right\vert{}^2 (\lambda^2 + |x|^2)^{2} \,\text{d} x\right)^{1/2} \left(\int_{\mathbb{R}^d} \frac{1}{(\lambda^2+|x|^2)^2} \,\text{d} x \right)^{1/2} \\ & = C \lambda^{d/2-2} \left[\frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \left\vert \widehat{(\lambda^2+|x|^2)\gamma^{(1)}}(k) \right\vert{}^2\right]^{1/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1} & = \int_{[0,L]^d} \left\vert \gamma^{(1)}(x) \right\vert \\ & \leq \left(\int_{\mathbb{R}^d} \left\vert \gamma^{(1)}(x) \right\vert{}^2 (\lambda^2 + |x|^2)^{2} \,\text{d} x\right)^{1/2} \left(\int_{\mathbb{R}^d} \frac{1}{(\lambda^2+|x|^2)^2} \,\text{d} x \right)^{1/2} \\ & = C \lambda^{d/2-2} \left[\frac{1}{L^d} \sum_{k\in \frac{2\pi}{L}\mathbb{Z}^d} \left\vert \widehat{(\lambda^2+|x|^2)\gamma^{(1)}}(k) \right\vert{}^2\right]^{1/2}. \end{aligned} \end{align*} $$
Moreover, (with
![]() $\hat \gamma (k) = ze^{- \beta |k|^2}$
is as in Equation (3.12)),
$\hat \gamma (k) = ze^{- \beta |k|^2}$
is as in Equation (3.12)),
 $$ \begin{align*} \begin{aligned} \widehat{(\lambda^2+|x|^2)\gamma^{(1)}}(k) & = \left[\lambda^2 - \Delta_k\right] \hat \gamma^{(1)}(k) \\ & = \frac{\lambda^2 \hat\gamma(k)^3 + (2\lambda^2 - 4\beta^2|k|^2 - 2d\beta) \hat \gamma(k)^2 + (\lambda^2 + 4\beta^2|k|^2 - 2d\beta) \hat\gamma(k) }{(1 + \hat\gamma(k))^3}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \widehat{(\lambda^2+|x|^2)\gamma^{(1)}}(k) & = \left[\lambda^2 - \Delta_k\right] \hat \gamma^{(1)}(k) \\ & = \frac{\lambda^2 \hat\gamma(k)^3 + (2\lambda^2 - 4\beta^2|k|^2 - 2d\beta) \hat \gamma(k)^2 + (\lambda^2 + 4\beta^2|k|^2 - 2d\beta) \hat\gamma(k) }{(1 + \hat\gamma(k))^3}. \end{aligned} \end{align*} $$
Using Equation (3.12), we conclude that
 $$ \begin{align*} \frac{1}{L^d} \sum_{k\in\frac{2\pi}{L}\mathbb{Z}^d} \left\vert \widehat{(\lambda^2+|x|^2)\gamma^{(1)}}(k) \right\vert{}^2 \leq C \rho_0\left(\lambda^4 + \beta^{4}\rho_0^{4/d} + \beta^2\right) \leq C \rho_0\left(\lambda^4 + \zeta^2\beta^2\right). \end{align*} $$
$$ \begin{align*} \frac{1}{L^d} \sum_{k\in\frac{2\pi}{L}\mathbb{Z}^d} \left\vert \widehat{(\lambda^2+|x|^2)\gamma^{(1)}}(k) \right\vert{}^2 \leq C \rho_0\left(\lambda^4 + \beta^{4}\rho_0^{4/d} + \beta^2\right) \leq C \rho_0\left(\lambda^4 + \zeta^2\beta^2\right). \end{align*} $$
Thus, for
![]() $\lambda = \beta ^{1/2}\zeta ^{1/2}$
, we have
$\lambda = \beta ^{1/2}\zeta ^{1/2}$
, we have
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}\leq C \zeta ^{d/2}$
. (Recall that
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}\leq C \zeta ^{d/2}$
. (Recall that
![]() $\beta \sim \zeta \rho _0^{-2/d}$
by Remark 3.7.)
$\beta \sim \zeta \rho _0^{-2/d}$
by Remark 3.7.)
We conclude that
![]() $\rho _0\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} \leq C a^d \rho _0\zeta ^{d/2} \log b/a$
. This concludes the proof of Theorem 4.3.
$\rho _0\left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} \leq C a^d \rho _0\zeta ^{d/2} \log b/a$
. This concludes the proof of Theorem 4.3.
5. Calculation of terms in Equation (3.5)
In this section, we compute and bound the different terms in Equation (3.5) and thereby prove Proposition 1.9.
5.1. Energy
The kinetic energy of the trial state
![]() $\varGamma _J$
is
$\varGamma _J$
is
 $$ \begin{align*} \begin{aligned} \left\langle \mathcal{H} \right\rangle_J & = \frac{1}{Z_J} \sum_{n=1}^\infty \idotsint \left[(-\Delta_{X_n}) \left[F_n(X_n) \varGamma_n(X_n, Y_n) F_n(Y_n)\right] \right]_{Y_n = X_n} \,\text{d} X_n \\ & = \frac{1}{Z_J} \sum_{n=1}^\infty \idotsint \left(|\nabla_{X_n} F|^2 \varGamma_n(X_n;X_n) - F_n^2 (\Delta_{X_n} \varGamma_n)(X_n;X_n)\right) \,\text{d} X_n. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\langle \mathcal{H} \right\rangle_J & = \frac{1}{Z_J} \sum_{n=1}^\infty \idotsint \left[(-\Delta_{X_n}) \left[F_n(X_n) \varGamma_n(X_n, Y_n) F_n(Y_n)\right] \right]_{Y_n = X_n} \,\text{d} X_n \\ & = \frac{1}{Z_J} \sum_{n=1}^\infty \idotsint \left(|\nabla_{X_n} F|^2 \varGamma_n(X_n;X_n) - F_n^2 (\Delta_{X_n} \varGamma_n)(X_n;X_n)\right) \,\text{d} X_n. \end{aligned} \end{align*} $$
The second term may be calculated as (recall that
![]() $\left \langle \cdot \right \rangle _J$
means expectation in the state
$\left \langle \cdot \right \rangle _J$
means expectation in the state
![]() $\varGamma _J$
)
$\varGamma _J$
)
 $$ \begin{align*} \begin{aligned} \frac{1}{Z_J} \sum_{n=1}^\infty \idotsint F_n^2 (-\Delta_{X_n} \varGamma_n)(X_n;X_n) \,\text{d} X_n & = \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}[F^2 \mathcal{H} \varGamma] \\ & = \frac{1}{Z_J} \operatorname{\mathrm{Tr}}[ F^2 (-\partial_\beta (Z\varGamma) + \mu\mathcal{N} Z \varGamma)] \\ & = - \partial_\beta \log Z_J + \mu \left\langle \mathcal{N} \right\rangle_J. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{Z_J} \sum_{n=1}^\infty \idotsint F_n^2 (-\Delta_{X_n} \varGamma_n)(X_n;X_n) \,\text{d} X_n & = \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}[F^2 \mathcal{H} \varGamma] \\ & = \frac{1}{Z_J} \operatorname{\mathrm{Tr}}[ F^2 (-\partial_\beta (Z\varGamma) + \mu\mathcal{N} Z \varGamma)] \\ & = - \partial_\beta \log Z_J + \mu \left\langle \mathcal{N} \right\rangle_J. \end{aligned} \end{align*} $$
Here, we used that
![]() $\varGamma $
is differentiable in
$\varGamma $
is differentiable in
![]() $\beta $
in the topology of trace-class operators. This may be easily verified. For the first term, we have that
$\beta $
in the topology of trace-class operators. This may be easily verified. For the first term, we have that
 $$ \begin{align*} |\nabla_{X_n} F_n|^2 = \left[2\sum_{j<k} \left\vert \frac{\nabla f_{jk}}{f_{jk}} \right\vert{}^2 + \sum_{\substack{i,j,k \\ \text{all distinct}}} \frac{\nabla f_{ij}\nabla f_{jk}}{f_{ij} f_{jk}}\right] F_n^2. \end{align*} $$
$$ \begin{align*} |\nabla_{X_n} F_n|^2 = \left[2\sum_{j<k} \left\vert \frac{\nabla f_{jk}}{f_{jk}} \right\vert{}^2 + \sum_{\substack{i,j,k \\ \text{all distinct}}} \frac{\nabla f_{ij}\nabla f_{jk}}{f_{ij} f_{jk}}\right] F_n^2. \end{align*} $$
Thus, the full energy is
 $$ \begin{align} \begin{aligned} \left\langle \mathcal{H} - \mu\mathcal{N} + \mathcal{V} \right\rangle_J & = - \partial_\beta \log Z_J + \iint \left[\left\vert \frac{\nabla f_{12}}{f_{12}} \right\vert{}^2 + \frac{1}{2} v_{12}\right] \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 \\ & \quad + \iiint \frac{\nabla f_{12} \nabla f_{13}}{f_{12} f_{13}}\rho^{(3)}_J \,\text{d} x_1 \,\text{d} x_2 \,\text{d} x_3. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\langle \mathcal{H} - \mu\mathcal{N} + \mathcal{V} \right\rangle_J & = - \partial_\beta \log Z_J + \iint \left[\left\vert \frac{\nabla f_{12}}{f_{12}} \right\vert{}^2 + \frac{1}{2} v_{12}\right] \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 \\ & \quad + \iiint \frac{\nabla f_{12} \nabla f_{13}}{f_{12} f_{13}}\rho^{(3)}_J \,\text{d} x_1 \,\text{d} x_2 \,\text{d} x_3. \end{aligned} \end{align} $$
5.2. Entropy
We note that
![]() $\varGamma _J = \frac {Z}{Z_J} F \varGamma F$
is isospectral to
$\varGamma _J = \frac {Z}{Z_J} F \varGamma F$
is isospectral to
![]() $\frac {Z}{Z_J} \varGamma ^{1/2} F^2 \varGamma ^{1/2}$
. Moreover, since
$\frac {Z}{Z_J} \varGamma ^{1/2} F^2 \varGamma ^{1/2}$
. Moreover, since
![]() $F\leq 1$
, we have
$F\leq 1$
, we have
![]() $\varGamma ^{1/2} F^2 \varGamma ^{1/2}\leq \varGamma $
as operators. Thus, by operator monotonicity of the logarithm,
$\varGamma ^{1/2} F^2 \varGamma ^{1/2}\leq \varGamma $
as operators. Thus, by operator monotonicity of the logarithm,
 $$ \begin{align*} \begin{aligned} \operatorname{\mathrm{Tr}}\left[\varGamma_J \log \varGamma_J\right] & = \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}\left[\varGamma^{1/2} F^2 \varGamma^{1/2} \left(\log \frac{Z}{Z_J} + \log \varGamma^{1/2} F^2 \varGamma^{1/2}\right)\right] \\ & \leq \log \frac{Z}{Z_J} + \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}\left[\varGamma^{1/2} F^2 \varGamma^{1/2}\log \varGamma\right] \\ & = - \log Z_J - \beta \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}\left[F^2 \varGamma (\mathcal{H} - \mu \mathcal{N})\right] \\ & = - \log Z_J + \frac{1}{Z_J} \beta \partial_\beta \operatorname{\mathrm{Tr}}\left[F^2 Z \varGamma\right] \\ & = - \log Z_J + \beta \partial_\beta \log Z_J. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \operatorname{\mathrm{Tr}}\left[\varGamma_J \log \varGamma_J\right] & = \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}\left[\varGamma^{1/2} F^2 \varGamma^{1/2} \left(\log \frac{Z}{Z_J} + \log \varGamma^{1/2} F^2 \varGamma^{1/2}\right)\right] \\ & \leq \log \frac{Z}{Z_J} + \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}\left[\varGamma^{1/2} F^2 \varGamma^{1/2}\log \varGamma\right] \\ & = - \log Z_J - \beta \frac{Z}{Z_J} \operatorname{\mathrm{Tr}}\left[F^2 \varGamma (\mathcal{H} - \mu \mathcal{N})\right] \\ & = - \log Z_J + \frac{1}{Z_J} \beta \partial_\beta \operatorname{\mathrm{Tr}}\left[F^2 Z \varGamma\right] \\ & = - \log Z_J + \beta \partial_\beta \log Z_J. \end{aligned} \end{align*} $$
We conclude the bound on the entropy
5.3. Pressure
Combining Equations (5.1) and (5.2), the terms
![]() $\pm \partial _\beta \log Z_j$
cancel, and we conclude the bound for the pressure
$\pm \partial _\beta \log Z_j$
cancel, and we conclude the bound for the pressure
 $$ \begin{align*} \begin{aligned} L^d P[\varGamma_J] & = - \left\langle \mathcal{H} - \mu\mathcal{N} + \mathcal{V} \right\rangle_J + \frac{1}{\beta} S(\varGamma_J) \\ & \geq \frac{1}{\beta} \log Z_J - \iint \left[\left\vert \frac{\nabla f_{12}}{f_{12}} \right\vert{}^2 + \frac{1}{2} v_{12}\right] \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 - \iiint \frac{\nabla f_{12} \nabla f_{13}}{f_{12} f_{13}}\rho^{(3)}_J \,\text{d} x_1 \,\text{d} x_2 \,\text{d} x_3. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} L^d P[\varGamma_J] & = - \left\langle \mathcal{H} - \mu\mathcal{N} + \mathcal{V} \right\rangle_J + \frac{1}{\beta} S(\varGamma_J) \\ & \geq \frac{1}{\beta} \log Z_J - \iint \left[\left\vert \frac{\nabla f_{12}}{f_{12}} \right\vert{}^2 + \frac{1}{2} v_{12}\right] \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 - \iiint \frac{\nabla f_{12} \nabla f_{13}}{f_{12} f_{13}}\rho^{(3)}_J \,\text{d} x_1 \,\text{d} x_2 \,\text{d} x_3. \end{aligned} \end{align*} $$
Remark 5.1. The cancellation of the terms
![]() $\pm \partial _\beta \log Z_j$
is not essential. Namely, the energy of the trial state
$\pm \partial _\beta \log Z_j$
is not essential. Namely, the energy of the trial state
![]() $\varGamma _J$
is the energy of the free gas plus the relevant interaction term up to small errors. And the entropy of the trial state
$\varGamma _J$
is the energy of the free gas plus the relevant interaction term up to small errors. And the entropy of the trial state
![]() $\varGamma _J$
is bounded from above by the entropy of the free gas up to small errors. To see this, write
$\varGamma _J$
is bounded from above by the entropy of the free gas up to small errors. To see this, write
One can show that
![]() $\partial _\beta \log \frac {Z_J}{Z}$
is small compared to the interaction of order
$\partial _\beta \log \frac {Z_J}{Z}$
is small compared to the interaction of order
![]() $L^d a^d \rho _0^{2+2/d}$
. Thus, the energy of the trial state
$L^d a^d \rho _0^{2+2/d}$
. Thus, the energy of the trial state
![]() $\varGamma _J$
is
$\varGamma _J$
is
 $$\begin{align*}\left\langle \mathcal{H} - \mu\mathcal{N} + \mathcal{V} \right\rangle_J = \left\langle \mathcal{H} - \mu\mathcal{N} \right\rangle_0 + \iint \left[\left\vert \frac{\nabla f_{12}}{f_{12}} \right\vert{}^2 + \frac{1}{2} v_{12}\right] \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 + \text{small error}. \end{align*}$$
$$\begin{align*}\left\langle \mathcal{H} - \mu\mathcal{N} + \mathcal{V} \right\rangle_J = \left\langle \mathcal{H} - \mu\mathcal{N} \right\rangle_0 + \iint \left[\left\vert \frac{\nabla f_{12}}{f_{12}} \right\vert{}^2 + \frac{1}{2} v_{12}\right] \rho^{(2)}_J \,\text{d} x_1 \,\text{d} x_2 + \text{small error}. \end{align*}$$
Similarly, for the entropy,
 $$ \begin{align*} \begin{aligned} -\frac{1}{\beta} \log Z_J + \partial_\beta \log Z_J & = -\frac{1}{\beta}\log Z + \partial_\beta \log Z - \frac{1}{\beta} \log \frac{Z_J}{Z} + \partial_\beta \log \frac{Z_J}{Z} \\ & = -\frac{1}{\beta}S(\varGamma) - \frac{1}{\beta} \log \frac{Z_J}{Z} + \partial_\beta \log \frac{Z_J}{Z}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} -\frac{1}{\beta} \log Z_J + \partial_\beta \log Z_J & = -\frac{1}{\beta}\log Z + \partial_\beta \log Z - \frac{1}{\beta} \log \frac{Z_J}{Z} + \partial_\beta \log \frac{Z_J}{Z} \\ & = -\frac{1}{\beta}S(\varGamma) - \frac{1}{\beta} \log \frac{Z_J}{Z} + \partial_\beta \log \frac{Z_J}{Z}. \end{aligned} \end{align*} $$
We show below that
![]() $\frac {1}{\beta } \log \frac {Z_J}{Z}$
is small compared to the interaction term of size
$\frac {1}{\beta } \log \frac {Z_J}{Z}$
is small compared to the interaction term of size
![]() $L^d a^d \rho _0^{2+2/d}$
. Thus, the entropy of the trial state
$L^d a^d \rho _0^{2+2/d}$
. Thus, the entropy of the trial state
![]() $\varGamma _J$
may be bounded as
$\varGamma _J$
may be bounded as
The proof that
![]() $\partial _\beta \log \frac {Z_J}{Z}$
is small is somewhat analogous to the proof of Lemma 5.2 in Section 5.4. As we will not need it, we omit the details.
$\partial _\beta \log \frac {Z_J}{Z}$
is small is somewhat analogous to the proof of Lemma 5.2 in Section 5.4. As we will not need it, we omit the details.
By Equation (4.2), we have for
![]() $a^d\rho _0\zeta ^{d/2} \log b/a$
sufficiently small that
$a^d\rho _0\zeta ^{d/2} \log b/a$
sufficiently small that
 $$ \begin{align*} \rho_J^{(2)} = f_{12}^2 \left[\rho^{(2)} + \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^2} \Gamma_{\pi,G}^2\right]. \end{align*} $$
$$ \begin{align*} \rho_J^{(2)} = f_{12}^2 \left[\rho^{(2)} + \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^2} \Gamma_{\pi,G}^2\right]. \end{align*} $$
We may then write

The first term is the pressure of the free gas (times the volume), the second term leads to the leading order correction, and the remaining terms are error terms. We shall show in Section 5.4 below the following bounds. (Recall that
![]() $\zeta = 1 + \left \vert \log z \right \vert $
.)
$\zeta = 1 + \left \vert \log z \right \vert $
.)
Lemma 5.2. For
![]() $z\gtrsim 1$
, there exists a constant
$z\gtrsim 1$
, there exists a constant
![]() $c> 0$
such that if
$c> 0$
such that if
![]() $a^d\rho _0 \zeta ^{d/2} \left \vert \log a^d \rho _0 \right \vert < c$
, then, for sufficently large L, the error terms are bounded as
$a^d\rho _0 \zeta ^{d/2} \left \vert \log a^d \rho _0 \right \vert < c$
, then, for sufficently large L, the error terms are bounded as

In particular, we have the bounds (recalling that
![]() $a \ll b\lesssim \rho _0^{-1/d}$
)
$a \ll b\lesssim \rho _0^{-1/d}$
)

Note that this is increasing in b. For the second term in Equation (5.3) above, we use Equations (3.7), (3.8) and (3.11); thus,
 $$ \begin{align} \begin{aligned} & \iint \left[\left\vert \nabla f_{12} \right\vert{}^2 + \frac{1}{2} v_{12} f_{12}^2\right] \rho^{(2)} \,\text{d} x_1 \,\text{d} x_2 \\ & \quad = 2\pi \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} \rho_0^{2+2/d} L^d \int \left(\left\vert \nabla f \right\vert{}^2 + \frac{1}{2}v f^2\right) |x|^2 \,\text{d} x \left(1 + O(L^{-1}\zeta \rho_0^{-1/d})\right) \\ & \qquad + O\left(L^d \rho_0^{2+4/d} \int \left(\left\vert \nabla f \right\vert{}^2 + \frac{1}{2}v f^2\right) |x|^4 \,\text{d} x\right) \\ & \quad = 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} L^d a^d \rho_0^{2+2/d} \left(1 + O(a^d/b^d) + O\left(L^{-1} \zeta \rho_0^{-1/d}\right)\right) \\ & \qquad + \begin{cases} O\left(L^d a^{d+2} \rho_0^{2 + 4/d} \log b/a\right) & d \geq 2 \\ O\left(L a^2 b \rho_0^{6}\right) & d = 1, \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \iint \left[\left\vert \nabla f_{12} \right\vert{}^2 + \frac{1}{2} v_{12} f_{12}^2\right] \rho^{(2)} \,\text{d} x_1 \,\text{d} x_2 \\ & \quad = 2\pi \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} \rho_0^{2+2/d} L^d \int \left(\left\vert \nabla f \right\vert{}^2 + \frac{1}{2}v f^2\right) |x|^2 \,\text{d} x \left(1 + O(L^{-1}\zeta \rho_0^{-1/d})\right) \\ & \qquad + O\left(L^d \rho_0^{2+4/d} \int \left(\left\vert \nabla f \right\vert{}^2 + \frac{1}{2}v f^2\right) |x|^4 \,\text{d} x\right) \\ & \quad = 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} L^d a^d \rho_0^{2+2/d} \left(1 + O(a^d/b^d) + O\left(L^{-1} \zeta \rho_0^{-1/d}\right)\right) \\ & \qquad + \begin{cases} O\left(L^d a^{d+2} \rho_0^{2 + 4/d} \log b/a\right) & d \geq 2 \\ O\left(L a^2 b \rho_0^{6}\right) & d = 1, \end{cases} \end{aligned} \end{align} $$
where
![]() $c_d$
is defined in Equation (1.3). Note that the first error term is decreasing in b. This competes with the other error terms and leads to the choice of b below. Combining Equations (5.3), (5.4) and (5.5), we thus conclude the bound
$c_d$
is defined in Equation (1.3). Note that the first error term is decreasing in b. This competes with the other error terms and leads to the choice of b below. Combining Equations (5.3), (5.4) and (5.5), we thus conclude the bound
 $$ \begin{align*} \begin{aligned} & \psi(\beta,\mu) \\ & \quad \geq \limsup_{L\to \infty} P[\varGamma_J] \\ & \quad \geq \lim_{L\to \infty} \left[\frac{1}{L^d\beta} \log Z\right] - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} a^d \rho_0^{2+2/d} \\ & \qquad + \begin{cases} O \begin{pmatrix} a^{6}b^{-3} \rho_0^{8/3} + a^3 b^2 \rho_0^{10/3}\zeta^{-1} + a^6 \rho_0^{11/3}\zeta^{1/2} (\log b/a)^2 + a^{10} \rho_0^5\zeta^{9/2} (\log b/a)^3 \end{pmatrix} & d= 3, \\\\[-9pt]O \begin{pmatrix} a^{4}b^{-2} \rho_0^{3} + a^2b^2 \rho_0^{4}\zeta^{-1} + a^4 \rho_0^4\zeta \log b/a + a^{6} \rho_0^5\zeta^{3} (\log b/a)^3 \end{pmatrix} & d= 2, \\\\[-9pt] O \begin{pmatrix} a^{2}b^{-1} \rho_0^{4} + ab \rho_0^5 \log b/a + a^2 \rho_0^5 \zeta^{3/2}(\log b/a)^3 \end{pmatrix} & d=1. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \psi(\beta,\mu) \\ & \quad \geq \limsup_{L\to \infty} P[\varGamma_J] \\ & \quad \geq \lim_{L\to \infty} \left[\frac{1}{L^d\beta} \log Z\right] - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} a^d \rho_0^{2+2/d} \\ & \qquad + \begin{cases} O \begin{pmatrix} a^{6}b^{-3} \rho_0^{8/3} + a^3 b^2 \rho_0^{10/3}\zeta^{-1} + a^6 \rho_0^{11/3}\zeta^{1/2} (\log b/a)^2 + a^{10} \rho_0^5\zeta^{9/2} (\log b/a)^3 \end{pmatrix} & d= 3, \\\\[-9pt]O \begin{pmatrix} a^{4}b^{-2} \rho_0^{3} + a^2b^2 \rho_0^{4}\zeta^{-1} + a^4 \rho_0^4\zeta \log b/a + a^{6} \rho_0^5\zeta^{3} (\log b/a)^3 \end{pmatrix} & d= 2, \\\\[-9pt] O \begin{pmatrix} a^{2}b^{-1} \rho_0^{4} + ab \rho_0^5 \log b/a + a^2 \rho_0^5 \zeta^{3/2}(\log b/a)^3 \end{pmatrix} & d=1. \end{cases} \end{aligned} \end{align*} $$
Using that
![]() $\lim _{L\to \infty } \left [\frac {1}{L^d\beta } \log Z\right ] = \psi _0(\beta ,\mu )$
and optimizing in b, we find for the choices (recall that we require
$\lim _{L\to \infty } \left [\frac {1}{L^d\beta } \log Z\right ] = \psi _0(\beta ,\mu )$
and optimizing in b, we find for the choices (recall that we require
![]() $b\lesssim \rho _0^{-1/d}$
)
$b\lesssim \rho _0^{-1/d}$
)
 $$ \begin{align*} b = \begin{cases} \min \left\{ a(a^3\rho_0)^{-2/15} \zeta^{1/5}, \rho_0^{-1/3} \right\} & d=3 , \\ \min \left\{ a (a^2\rho_0)^{-1/4} \zeta^{1/4}, \rho_0^{-1/2} \right\} & d=2, \\ a (a\rho_0)^{-1/2} \left\vert \log a\rho_0 \right\vert{}^{-1/2} & d=1, \end{cases} \end{align*} $$
$$ \begin{align*} b = \begin{cases} \min \left\{ a(a^3\rho_0)^{-2/15} \zeta^{1/5}, \rho_0^{-1/3} \right\} & d=3 , \\ \min \left\{ a (a^2\rho_0)^{-1/4} \zeta^{1/4}, \rho_0^{-1/2} \right\} & d=2, \\ a (a\rho_0)^{-1/2} \left\vert \log a\rho_0 \right\vert{}^{-1/2} & d=1, \end{cases} \end{align*} $$
that
 $$ \begin{align*} \begin{aligned} \psi(\beta,\mu) & \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} a^d \rho_0^{2+2/d} \left[1 + \delta_d\right], \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \psi(\beta,\mu) & \geq \psi_0(\beta,\mu) - 2\pi c_d \frac{-\operatorname{\mathrm{Li}}_{d/2+1}(-e^{\beta\mu})}{(-\operatorname{\mathrm{Li}}_{d/2}(-e^{\beta\mu}))^{1+2/d}} a^d \rho_0^{2+2/d} \left[1 + \delta_d\right], \end{aligned} \end{align*} $$
where
![]() $\delta _d$
is as in Equation (1.13). The calculations above are valid as long as the conditions of Theorem 4.3 are satisfied – that is, if
$\delta _d$
is as in Equation (1.13). The calculations above are valid as long as the conditions of Theorem 4.3 are satisfied – that is, if
![]() $a^d \rho _0 \zeta ^{d/2} \left \vert \log a^d\rho _0 \right \vert $
is sufficiently small. This concludes the proof of Proposition 1.9. It remains to give the proof of Lemma 5.2.
$a^d \rho _0 \zeta ^{d/2} \left \vert \log a^d\rho _0 \right \vert $
is sufficiently small. This concludes the proof of Proposition 1.9. It remains to give the proof of Lemma 5.2.
5.4. Error terms (proof of Lemma 5.2)
In this section we give the following:
Proof of Lemma 5.2
To better illustrate where the different error terms come from, we will write them in terms of the quantities
![]() $\left \Vert g \right \Vert {}_{L^1}, \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
$\left \Vert g \right \Vert {}_{L^1}, \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
and
![]() $\left \Vert |\cdot |^ng \right \Vert {}_{L^1} = \int _{\mathbb {R}^d} |x|^n |g(x)| \,\text {d} x$
,
$\left \Vert |\cdot |^ng \right \Vert {}_{L^1} = \int _{\mathbb {R}^d} |x|^n |g(x)| \,\text {d} x$
,
![]() $n\geq 1$
. By Lemma 4.6 and Equation (3.6), we have the bounds
$n\geq 1$
. By Lemma 4.6 and Equation (3.6), we have the bounds
For the analysis of the error terms, we use the bounds [Reference LauritsenLau23, Equation (4.13)] and [Reference Lauritsen and SeiringerLS24b, Equations (4.10) and (4.22)]. To state these, we define for any diagram
![]() $(\pi ,G) \in \tilde {\mathcal {L}}_p^m$
the numbers
$(\pi ,G) \in \tilde {\mathcal {L}}_p^m$
the numbers
![]() $k = k(G) = k(\pi ,G)$
as the number of clusters (connected components of G; recall Definition 4.1) entirely with internal vertices (of sizes
$k = k(G) = k(\pi ,G)$
as the number of clusters (connected components of G; recall Definition 4.1) entirely with internal vertices (of sizes
![]() $n_1,\ldots ,n_k$
) and
$n_1,\ldots ,n_k$
) and
![]() $\kappa = \kappa (G) = \kappa (\pi ,G)$
as the number of clusters with each at least one external vertex (of sizes [meaning number of internal vertices]
$\kappa = \kappa (G) = \kappa (\pi ,G)$
as the number of clusters with each at least one external vertex (of sizes [meaning number of internal vertices]
![]() $n_1^*,\ldots ,n_\kappa ^*$
). Define
$n_1^*,\ldots ,n_\kappa ^*$
). Define
 $$\begin{align*}\nu^* := \sum_{\lambda=1}^\kappa n_\lambda^*, \qquad \nu := \sum_{\ell=1}^k n_\ell - 2k. \end{align*}$$
$$\begin{align*}\nu^* := \sum_{\lambda=1}^\kappa n_\lambda^*, \qquad \nu := \sum_{\ell=1}^k n_\ell - 2k. \end{align*}$$
As discussed around [Reference LauritsenLau23, Equation (4.13)] and [Reference Lauritsen and SeiringerLS24b, Equations (4.10) and (4.22)], the numbers
![]() $\nu ^*$
and
$\nu ^*$
and
![]() $\nu $
count the ‘number of added vertices’. Concretely, a diagram with k clusters of only internal vertices has at least
$\nu $
count the ‘number of added vertices’. Concretely, a diagram with k clusters of only internal vertices has at least
![]() $2k$
internal vertices. Then
$2k$
internal vertices. Then
![]() $\nu ^*$
is the number of additional internal vertices in clusters with external vertices, and
$\nu ^*$
is the number of additional internal vertices in clusters with external vertices, and
![]() $\nu $
is the number of additional internal vertices in clusters with only internal vertices.
$\nu $
is the number of additional internal vertices in clusters with only internal vertices.
The bounds [Reference LauritsenLau23, Equation (4.13)], [Reference Lauritsen and SeiringerLS24b, Equations (4.10) and (4.22)] (note that there bounds on
![]() $\left \Vert g \right \Vert {}_{L^1},\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
analogous to those of Lemma 4.6 are already used) then read for any
$\left \Vert g \right \Vert {}_{L^1},\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
analogous to those of Lemma 4.6 are already used) then read for any
![]() $k_0, \nu _0$
$k_0, \nu _0$
 $$ \begin{align} \frac{1}{p!} \left\vert \sum_{\substack{(\pi,G)\in\tilde {\mathcal{L}}_p^m \\ k(\pi,G) = k_0 \\ \nu(\pi,G) + \nu^*(\pi,G) = \nu_0}} \Gamma_{\pi,G}^m \right\vert \leq \begin{cases} C L^d \rho_0\left(C \rho_0\left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1} & m=0, \\ C_m \rho_0^m \left(C\rho_0\left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0} & m> 0, \end{cases} \qquad p=2k_0 + \nu_0, \end{align} $$
$$ \begin{align} \frac{1}{p!} \left\vert \sum_{\substack{(\pi,G)\in\tilde {\mathcal{L}}_p^m \\ k(\pi,G) = k_0 \\ \nu(\pi,G) + \nu^*(\pi,G) = \nu_0}} \Gamma_{\pi,G}^m \right\vert \leq \begin{cases} C L^d \rho_0\left(C \rho_0\left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1} & m=0, \\ C_m \rho_0^m \left(C\rho_0\left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0} & m> 0, \end{cases} \qquad p=2k_0 + \nu_0, \end{align} $$
where the constants
![]() $C,C_m$
depend only on m but not on
$C,C_m$
depend only on m but not on
![]() $\nu _0$
or
$\nu _0$
or
![]() $k_0$
(in particular, not on p).
$k_0$
(in particular, not on p).
Remark 5.3. The case
![]() $m=0$
is not included in the statement in [Reference LauritsenLau23, Equation (4.13)] and [Reference Lauritsen and SeiringerLS24b, Equations (4.10) and (4.22)]. It follows from the analysis in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1] (see also [Reference LauritsenLau23, Section 4.1]), however.
$m=0$
is not included in the statement in [Reference LauritsenLau23, Equation (4.13)] and [Reference Lauritsen and SeiringerLS24b, Equations (4.10) and (4.22)]. It follows from the analysis in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1] (see also [Reference LauritsenLau23, Section 4.1]), however.
More precisely, the analysis in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1] consists of the following steps: (1), decompose the linked diagrams in
![]() $\mathcal {L}_p$
according to the connected components of the graphs, (2) use the tree-graph inequality [Reference UeltschiUel18] to bound each sum over graphs by a sum over trees in each connected component of the graph, (3) use the Brydges–Battle–Federbush formula (see [Reference Giuliani, Mastropietro and RychkovGMR21, Appendix D]) to bound the truncated correlations, (4) compute the integrals, each being now an integral of either
$\mathcal {L}_p$
according to the connected components of the graphs, (2) use the tree-graph inequality [Reference UeltschiUel18] to bound each sum over graphs by a sum over trees in each connected component of the graph, (3) use the Brydges–Battle–Federbush formula (see [Reference Giuliani, Mastropietro and RychkovGMR21, Appendix D]) to bound the truncated correlations, (4) compute the integrals, each being now an integral of either
![]() $|g|$
or
$|g|$
or
![]() $|\gamma ^{(1)}|$
.
$|\gamma ^{(1)}|$
.
In any of the equations in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1], the only effect of the p-summation is to eliminate the factor
![]() $\chi _{(\sum _\ell n_\ell = p)}$
present in the very first equation (where there is no p-summation). That is, not performing the p-summation, all equations in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1] remain valid, only with no p-summation on their left-hand sides and with an additional factor
$\chi _{(\sum _\ell n_\ell = p)}$
present in the very first equation (where there is no p-summation). That is, not performing the p-summation, all equations in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1] remain valid, only with no p-summation on their left-hand sides and with an additional factor
![]() $\chi _{(\sum _\ell n_\ell = p)}$
on their right-hand sides. Thus, from the analysis in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1], modified by not performing the p-summation, we find the following modification of the final formula in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1]:
$\chi _{(\sum _\ell n_\ell = p)}$
on their right-hand sides. Thus, from the analysis in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1], modified by not performing the p-summation, we find the following modification of the final formula in [Reference Lauritsen and SeiringerLS24b, Section 3.1.1]:
 $$ \begin{align*} \frac{1}{p!}\left\vert \sum_{\substack{(\pi,G)\in \mathcal{L}_p \\ k(\pi,G) = k_0 \\ \nu(\pi,G) = \nu_0}} \Gamma_{\pi,G} \right\vert \leq C N \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1} \sum_{\substack{n_1,\ldots,n_{k_0}\geq 2 \\ \sum_\ell n_\ell = 2k_0 + \nu_0}} \left(\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\sum_\ell (n_\ell - 1)}, \qquad p=2k_0 + \nu_0, \end{align*} $$
$$ \begin{align*} \frac{1}{p!}\left\vert \sum_{\substack{(\pi,G)\in \mathcal{L}_p \\ k(\pi,G) = k_0 \\ \nu(\pi,G) = \nu_0}} \Gamma_{\pi,G} \right\vert \leq C N \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1} \sum_{\substack{n_1,\ldots,n_{k_0}\geq 2 \\ \sum_\ell n_\ell = 2k_0 + \nu_0}} \left(\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\sum_\ell (n_\ell - 1)}, \qquad p=2k_0 + \nu_0, \end{align*} $$
from which Equation (5.6) in the case
![]() $m=0$
follows.
$m=0$
follows.
From this bound, the natural ‘size’ of a diagram
![]() $(\pi ,G)\in \tilde {\mathcal {L}}_p^m$
is not p but rather
$(\pi ,G)\in \tilde {\mathcal {L}}_p^m$
is not p but rather
![]() $\nu + \nu ^* + k$
, since its value is (neglecting
$\nu + \nu ^* + k$
, since its value is (neglecting
![]() $\log $
’s and dependence on z)
$\log $
’s and dependence on z)
![]() $\lesssim \rho _0^m(a^d\rho _0)^{\nu + \nu ^* + k}$
. For the bounds of the terms
$\lesssim \rho _0^m(a^d\rho _0)^{\nu + \nu ^* + k}$
. For the bounds of the terms ![]() , we will bound sufficiently large diagrams by the bound in Equation (5.6) and do a more precise computation for small diagrams.
, we will bound sufficiently large diagrams by the bound in Equation (5.6) and do a more precise computation for small diagrams.
Additionally, we have the following:
Lemma 5.4. The reduced densities
![]() $\rho ^{(3)}$
and
$\rho ^{(3)}$
and
![]() $\rho ^{(4)}$
satisfy
$\rho ^{(4)}$
satisfy
 $$ \begin{align*} \begin{aligned} \rho^{(3)}(x_1,x_2,x_3) & \leq C \rho_0^{3+4/d} |x_1-x_2|^2 |x_1-x_3|^2, \\ \rho^{(4)}(x_1,x_2,x_3,x_4) & \leq C \rho_0^{4+6/d} |x_1-x_2|^2 |x_1-x_3|^2 |x_1-x_4|^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \rho^{(3)}(x_1,x_2,x_3) & \leq C \rho_0^{3+4/d} |x_1-x_2|^2 |x_1-x_3|^2, \\ \rho^{(4)}(x_1,x_2,x_3,x_4) & \leq C \rho_0^{4+6/d} |x_1-x_2|^2 |x_1-x_3|^2 |x_1-x_4|^2. \end{aligned} \end{align*} $$
Proof. Note that both
![]() $\rho ^{(3)}$
and
$\rho ^{(3)}$
and
![]() $\rho ^{(4)}$
vanish whenever two particles are incident and are invariant under permutation of the particle positions. Thus, for fixed
$\rho ^{(4)}$
vanish whenever two particles are incident and are invariant under permutation of the particle positions. Thus, for fixed
![]() $x_1$
as functions of
$x_1$
as functions of
![]() $x_j$
,
$x_j$
,
![]() $j\ne 1$
, they vanish quadratically around
$j\ne 1$
, they vanish quadratically around
![]() $x_j=x_1$
. Writing
$x_j=x_1$
. Writing
![]() $\rho ^{(q)} = \det [\gamma ^{(1)}_{ij}]_{1\leq i,j\leq q}$
using the Wick rule, Taylor expanding in
$\rho ^{(q)} = \det [\gamma ^{(1)}_{ij}]_{1\leq i,j\leq q}$
using the Wick rule, Taylor expanding in
![]() $x_j$
,
$x_j$
,
![]() $j\ne 1$
around
$j\ne 1$
around
![]() $x_j=x_1$
and using Equation (3.12) to bound the derivatives, we conclude the proof of the lemma.
$x_j=x_1$
and using Equation (3.12) to bound the derivatives, we conclude the proof of the lemma.
We first bound ![]() .
.
5.4.1. Bound of 
We have by Theorem 4.3

We use the bound in Equation (5.6) above for
![]() $m=0$
and for diagrams with
$m=0$
and for diagrams with
![]() $\nu + k \geq 2$
. These are precisely the diagrams with
$\nu + k \geq 2$
. These are precisely the diagrams with
![]() $p\geq 3$
(note that
$p\geq 3$
(note that
![]() $k\geq 1$
for any diagram
$k\geq 1$
for any diagram
![]() $(\pi ,G)\in \mathcal {L}_p$
). Thus,
$(\pi ,G)\in \mathcal {L}_p$
). Thus,
 $$ \begin{align*} \begin{aligned} \sum_{p=3}^\infty \frac{1}{p!} \left\vert \sum_{\substack{(\pi,G)\in \mathcal{L}_p}} \Gamma_{\pi,G} \right\vert & \leq C L^d \rho_0 \sum_{\substack{k_0 \geq 1 \\[5pt] \nu_0+k_0\geq 2}} \left(C\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1} \\[5pt] & = C L^d \rho_0 \left[\sum_{\nu_0=1}^\infty \left(C\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+1} + \sum_{k_0=2}^\infty \sum_{\nu_0=0}^\infty \left(C\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1}\right] \\ & \leq C L^d \rho_0^3 \left\Vert g \right\Vert{}_{L^1}^2 \left(1 + \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}\right) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{p=3}^\infty \frac{1}{p!} \left\vert \sum_{\substack{(\pi,G)\in \mathcal{L}_p}} \Gamma_{\pi,G} \right\vert & \leq C L^d \rho_0 \sum_{\substack{k_0 \geq 1 \\[5pt] \nu_0+k_0\geq 2}} \left(C\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1} \\[5pt] & = C L^d \rho_0 \left[\sum_{\nu_0=1}^\infty \left(C\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+1} + \sum_{k_0=2}^\infty \sum_{\nu_0=0}^\infty \left(C\rho_0 \left\Vert g \right\Vert{}_{L^1}\right)^{\nu_0+k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0-1}\right] \\ & \leq C L^d \rho_0^3 \left\Vert g \right\Vert{}_{L^1}^2 \left(1 + \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}\right) \end{aligned} \end{align*} $$
for sufficiently small
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
$\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
. For the diagrams with
$\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
. For the diagrams with
![]() $\nu + k=1$
, we do a more precise calculation. These are precisely the diagrams with
$\nu + k=1$
, we do a more precise calculation. These are precisely the diagrams with
![]() $p=2$
. In particular, these diagrams have
$p=2$
. In particular, these diagrams have
![]() $\nu = 0$
and
$\nu = 0$
and
![]() $k=1$
. We have then (recall that pictures of diagrams refer to their values)
$k=1$
. We have then (recall that pictures of diagrams refer to their values)

using Equation (3.11). Thus, using Lemma 4.6 and recalling that
![]() $\beta \sim \zeta \rho _0^{-2/d}$
from Remark 3.7, we conclude that
$\beta \sim \zeta \rho _0^{-2/d}$
from Remark 3.7, we conclude that

5.4.2. Bound of 
We have by Theorem 4.3
 $$\begin{align*}\rho_J^{(3)} = f_{12}^2 f_{13}^2 f_{23}^2 \left[ \rho^{(3)} + \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^3} \Gamma_{\pi,G}^3 \right]. \end{align*}$$
$$\begin{align*}\rho_J^{(3)} = f_{12}^2 f_{13}^2 f_{23}^2 \left[ \rho^{(3)} + \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^3} \Gamma_{\pi,G}^3 \right]. \end{align*}$$
We use the bound in Lemma 5.4 to bound
![]() $\rho ^{(3)}$
and the bound in Equation (5.6) on the remaining terms. (That is, a precise calculation for diagrams with
$\rho ^{(3)}$
and the bound in Equation (5.6) on the remaining terms. (That is, a precise calculation for diagrams with
![]() $\nu + \nu ^* + k =0$
and the bound in Equation (5.6) for diagrams with
$\nu + \nu ^* + k =0$
and the bound in Equation (5.6) for diagrams with
![]() $\nu + \nu ^* + k \geq 1$
.) Thus, by a similar computation as for
$\nu + \nu ^* + k \geq 1$
.) Thus, by a similar computation as for ![]() ,
,
 $$ \begin{align*} \begin{aligned} \left\vert \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^3} \Gamma_{\pi,G}^3 \right\vert & \leq C \rho_0^3 \left[ \sum_{\nu_0=1}^\infty (C\rho_0 \left\Vert g \right\Vert{}_{L^1})^{\nu_0} + \sum_{k_0=1}^\infty \sum_{\nu_0=0}^\infty (C\rho_0 \left\Vert g \right\Vert{}_{L^1})^{\nu_0 + k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0} \right] \\ & \leq C \rho_0^4 \left\Vert g \right\Vert{}_{L^1} \left(1+\left\Vert \gamma^{(1)} \right\Vert{}_{L^1}\right) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\vert \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^3} \Gamma_{\pi,G}^3 \right\vert & \leq C \rho_0^3 \left[ \sum_{\nu_0=1}^\infty (C\rho_0 \left\Vert g \right\Vert{}_{L^1})^{\nu_0} + \sum_{k_0=1}^\infty \sum_{\nu_0=0}^\infty (C\rho_0 \left\Vert g \right\Vert{}_{L^1})^{\nu_0 + k_0} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^{k_0} \right] \\ & \leq C \rho_0^4 \left\Vert g \right\Vert{}_{L^1} \left(1+\left\Vert \gamma^{(1)} \right\Vert{}_{L^1}\right) \end{aligned} \end{align*} $$
for sufficiently small
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
$\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
. Moreover,
$\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
. Moreover,
![]() $f\leq 1$
, and the support of
$f\leq 1$
, and the support of
![]() $\nabla f$
is contained a ball of radius
$\nabla f$
is contained a ball of radius
![]() $\sim b$
. Thus, by Equation (3.9) and Lemma 4.6,
$\sim b$
. Thus, by Equation (3.9) and Lemma 4.6,

Refined analysis in dimension
 $d=1$
$d=1$
In dimension
![]() $d=1$
, we need also to analyze diagrams with
$d=1$
, we need also to analyze diagrams with
![]() $k +\nu + \nu ^* = 1$
in more detail. Intuitively, this follows by ‘counting powers of
$k +\nu + \nu ^* = 1$
in more detail. Intuitively, this follows by ‘counting powers of
![]() $\rho _0$
’: the claimed leading term in Theorem 1.2 is of order
$\rho _0$
’: the claimed leading term in Theorem 1.2 is of order
![]() $a\rho _0^4$
. Thus, we need to compute precisely all diagrams for which the naive bound Equation (5.6) only gives a power
$a\rho _0^4$
. Thus, we need to compute precisely all diagrams for which the naive bound Equation (5.6) only gives a power
![]() $\leq 4$
of
$\leq 4$
of
![]() $\rho _0$
.
$\rho _0$
.
The diagrams with
![]() $k +\nu + \nu ^* = 1$
have either
$k +\nu + \nu ^* = 1$
have either
![]() $p=1$
, in which case
$p=1$
, in which case
![]() $\nu ^*=1$
, or
$\nu ^*=1$
, or
![]() $p=2$
, in which case
$p=2$
, in which case
![]() $k=1$
. For the diagrams with
$k=1$
. For the diagrams with
![]() $p=1$
for any graph, any permutation makes each linked component have at least one external vertex, and thus, we get
$p=1$
for any graph, any permutation makes each linked component have at least one external vertex, and thus, we get
 $$ \begin{align*} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_1^3} \Gamma_{\pi,G}^3 & = \sum_{G\in \mathcal{G}_1^3} \int \rho^{(4)}(x_1,x_2,x_3,x_4) \prod_{e\in G} g_e \,\text{d} x_4. \end{align*} $$
$$ \begin{align*} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_1^3} \Gamma_{\pi,G}^3 & = \sum_{G\in \mathcal{G}_1^3} \int \rho^{(4)}(x_1,x_2,x_3,x_4) \prod_{e\in G} g_e \,\text{d} x_4. \end{align*} $$
Bound all but one g-factor, by symmetry say
![]() $g_{14}$
, by
$g_{14}$
, by
![]() $|g_{ij}|\leq 1$
, and bound
$|g_{ij}|\leq 1$
, and bound
![]() $\rho ^{(4)}$
using Lemma 5.4. We conclude
$\rho ^{(4)}$
using Lemma 5.4. We conclude
 $$ \begin{align*} |\cdot| & \leq C \rho_0^{10} |x_1-x_2|^2 |x_1-x_3|^2 \int |g(z)| |z|^2 \,\text{d} z \\ & \leq C ab^2\rho_0^{10} |x_1-x_2|^2 |x_1-x_3|^2. \end{align*} $$
$$ \begin{align*} |\cdot| & \leq C \rho_0^{10} |x_1-x_2|^2 |x_1-x_3|^2 \int |g(z)| |z|^2 \,\text{d} z \\ & \leq C ab^2\rho_0^{10} |x_1-x_2|^2 |x_1-x_3|^2. \end{align*} $$
By Equation (3.9), this gives the contribution
![]() $L a^3b^{4}\rho _0^{10}$
to
$L a^3b^{4}\rho _0^{10}$
to ![]() . For
. For
![]() $p=2$
, we have the graph (recall that
$p=2$
, we have the graph (recall that
![]() $*$
’s label external vertices)
$*$
’s label external vertices)

The only
![]() $\pi $
’s for which
$\pi $
’s for which
![]() $(\pi ,G)\notin \tilde {\mathcal {L}}_2^3$
are those not connecting
$(\pi ,G)\notin \tilde {\mathcal {L}}_2^3$
are those not connecting
![]() $\{4,5\}$
to
$\{4,5\}$
to
![]() $\{1,2,3\}$
. Thus,
$\{1,2,3\}$
. Thus,
 $$ \begin{align*} \begin{aligned} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_2^3} \Gamma_{\pi,G}^3 & = \int \left[\rho^{(5)}(x_1,\ldots,x_5) - \rho^{(3)}(x_1,x_2,x_3)\rho^{(2)}(x_4,x_5)\right] g_{45} \,\text{d} x_4 \,\text{d} x_5. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_2^3} \Gamma_{\pi,G}^3 & = \int \left[\rho^{(5)}(x_1,\ldots,x_5) - \rho^{(3)}(x_1,x_2,x_3)\rho^{(2)}(x_4,x_5)\right] g_{45} \,\text{d} x_4 \,\text{d} x_5. \end{aligned} \end{align*} $$
This vanishes (quadratically) whenever any
![]() $x_i$
and
$x_i$
and
![]() $x_j$
,
$x_j$
,
![]() $i,j=1,2,3$
are incident. Thus, as with
$i,j=1,2,3$
are incident. Thus, as with
![]() $\rho ^{(3)}$
and
$\rho ^{(3)}$
and
![]() $\rho ^{(4)}$
, we bound the derivatives and use Taylor’s theorem. Denote the derivative w.r.t.
$\rho ^{(4)}$
, we bound the derivatives and use Taylor’s theorem. Denote the derivative w.r.t.
![]() $x_j$
by
$x_j$
by
![]() $\partial _{x_j}$
. We are thus interested in bounding
$\partial _{x_j}$
. We are thus interested in bounding
![]() $\partial _{x_2}^2\partial _{x_3}^2\Gamma _{\pi ,G}^3$
. By explicit computation (with the permutation denoted
$\partial _{x_2}^2\partial _{x_3}^2\Gamma _{\pi ,G}^3$
. By explicit computation (with the permutation denoted
![]() $\pi ^{-1}$
for convenience of notation), we have
$\pi ^{-1}$
for convenience of notation), we have
 $$ \begin{align*} & \partial_{x_2}^2\partial_{x_3}^2 \Gamma_{\pi^{-1},G}^3 \\ &\quad = \partial_{x_2}^2\partial_{x_3}^2 \left[ (-1)^{\pi} \frac{1}{L^5} \sum_{k_1,\ldots,k_5} \hat \gamma^{(1)}(k_1)\cdots \hat \gamma^{(1)}(k_5) \iint e^{i(k_1-k_{\pi(1)})x_1} \cdots e^{i(k_5-k_{\pi(5)})x_5} g_{45} \,\text{d} x_4 \,\text{d} x_5 \right] \\ & \quad = - (-1)^{\pi} \frac{1}{L^{4}} \sum_{k_1,\ldots,k_5} (k_2 - k_{\pi(2)})^2 (k_3 - k_{\pi(3)})^2 \hat \gamma^{(1)}(k_1)\cdots \hat \gamma^{(1)}(k_5) \\ & \qquad \times e^{i(k_1-k_{\pi(1)})x_1} \cdots e^{i(k_3-k_{\pi(3)})x_3} \hat g(k_4 -k_{\pi(4)}) \chi_{(k_5-k_{\pi(5)} + k_4 - k_{\pi(4)}=0)}, \end{align*} $$
$$ \begin{align*} & \partial_{x_2}^2\partial_{x_3}^2 \Gamma_{\pi^{-1},G}^3 \\ &\quad = \partial_{x_2}^2\partial_{x_3}^2 \left[ (-1)^{\pi} \frac{1}{L^5} \sum_{k_1,\ldots,k_5} \hat \gamma^{(1)}(k_1)\cdots \hat \gamma^{(1)}(k_5) \iint e^{i(k_1-k_{\pi(1)})x_1} \cdots e^{i(k_5-k_{\pi(5)})x_5} g_{45} \,\text{d} x_4 \,\text{d} x_5 \right] \\ & \quad = - (-1)^{\pi} \frac{1}{L^{4}} \sum_{k_1,\ldots,k_5} (k_2 - k_{\pi(2)})^2 (k_3 - k_{\pi(3)})^2 \hat \gamma^{(1)}(k_1)\cdots \hat \gamma^{(1)}(k_5) \\ & \qquad \times e^{i(k_1-k_{\pi(1)})x_1} \cdots e^{i(k_3-k_{\pi(3)})x_3} \hat g(k_4 -k_{\pi(4)}) \chi_{(k_5-k_{\pi(5)} + k_4 - k_{\pi(4)}=0)}, \end{align*} $$
where
![]() $\chi $
denotes a characteristic function. Any permutation such that
$\chi $
denotes a characteristic function. Any permutation such that
![]() $(\pi ,G) \in \tilde {\mathcal {L}}_3^2$
has
$(\pi ,G) \in \tilde {\mathcal {L}}_3^2$
has
![]() $\pi (\{4,5\}) \ne \{4,5\}$
. In particular, for the relevant permutations, the characteristic function is not identically one, and thus effectively it reduces the number of k-sums by
$\pi (\{4,5\}) \ne \{4,5\}$
. In particular, for the relevant permutations, the characteristic function is not identically one, and thus effectively it reduces the number of k-sums by
![]() $1$
. More precisely, we get for the permutations with
$1$
. More precisely, we get for the permutations with
![]() $\pi (5),\pi (4) \ne 5$
(the others are similar)
$\pi (5),\pi (4) \ne 5$
(the others are similar)
 $$ \begin{align*} & \quad = - (-1)^{\pi} \frac{1}{L^{4}} \sum_{k_1,\ldots,k_4} (k_2 - k_{\pi(2)})^2 (k_3 - k_{\pi(3)})^2 \hat \gamma^{(1)}(k_1)\cdots \hat \gamma^{(1)}(k_4) \hat \gamma^{(1)}(-k_4 + k_{\pi(4)} + k_{\pi(5)}) \\ & \qquad \times e^{i(k_1-k_{\pi(1)})x_1} \cdots e^{i(k_3-k_{\pi(3)})x_3} \hat g(k_4 -k_{\pi(4)}). \end{align*} $$
$$ \begin{align*} & \quad = - (-1)^{\pi} \frac{1}{L^{4}} \sum_{k_1,\ldots,k_4} (k_2 - k_{\pi(2)})^2 (k_3 - k_{\pi(3)})^2 \hat \gamma^{(1)}(k_1)\cdots \hat \gamma^{(1)}(k_4) \hat \gamma^{(1)}(-k_4 + k_{\pi(4)} + k_{\pi(5)}) \\ & \qquad \times e^{i(k_1-k_{\pi(1)})x_1} \cdots e^{i(k_3-k_{\pi(3)})x_3} \hat g(k_4 -k_{\pi(4)}). \end{align*} $$
Bounding
![]() $\left \vert \hat \gamma ^{(1)}(-k_4 + k_{\pi (4)} + k_{\pi (5)}) \right \vert \leq 1$
and
$\left \vert \hat \gamma ^{(1)}(-k_4 + k_{\pi (4)} + k_{\pi (5)}) \right \vert \leq 1$
and
![]() $\left \vert \hat g \right \vert \leq \left \Vert g \right \Vert {}_{L^1} \leq C a \log b/a$
, the k-sums are readily bounded by Equation (3.12). Thus, for any valid permutation
$\left \vert \hat g \right \vert \leq \left \Vert g \right \Vert {}_{L^1} \leq C a \log b/a$
, the k-sums are readily bounded by Equation (3.12). Thus, for any valid permutation
![]() $\pi $
, we have
$\pi $
, we have
By Taylor’s theorem, we conclude that
We thus get the contribution to ![]() of
of
![]() $L a^3 b^2 \rho _0^{8} \log b/a$
by Equation (3.9). Finally, using the bound in Equation (5.6) for diagrams with
$L a^3 b^2 \rho _0^{8} \log b/a$
by Equation (3.9). Finally, using the bound in Equation (5.6) for diagrams with
![]() $k+\nu +\nu ^* \geq 2$
, we get (again for suffiently small
$k+\nu +\nu ^* \geq 2$
, we get (again for suffiently small
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
$\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
)
$\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
)
 $$ \begin{align*} \sum_{p=2}^\infty \frac{1}{p!}\left\vert \sum_{\substack{(\pi,G)\in \tilde{\mathcal{L}}_p^2 \\ (k + \nu + \nu^*)(\pi,G) \geq 2}} \Gamma_{\pi,G}^2 \right\vert \leq C a^3 \rho_0^5 \zeta (\log b/a)^2. \end{align*} $$
$$ \begin{align*} \sum_{p=2}^\infty \frac{1}{p!}\left\vert \sum_{\substack{(\pi,G)\in \tilde{\mathcal{L}}_p^2 \\ (k + \nu + \nu^*)(\pi,G) \geq 2}} \Gamma_{\pi,G}^2 \right\vert \leq C a^3 \rho_0^5 \zeta (\log b/a)^2. \end{align*} $$
By Equation (3.9), this gives a contribution to ![]() of
of
![]() $L a^2 \rho _0^5 (\log b/a)^2$
. We conclude the bound
$L a^2 \rho _0^5 (\log b/a)^2$
. We conclude the bound

in dimension
![]() $d=1$
.
$d=1$
.
5.4.3. Bound of 
We use the bound in Equation (5.6) for diagrams with
![]() $\nu + \nu ^* + k \geq 3$
and a more precise analysis for the small diagrams. Write
$\nu + \nu ^* + k \geq 3$
and a more precise analysis for the small diagrams. Write
 $$ \begin{align} \sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G) \in \tilde{\mathcal{L}}_p^2} \Gamma_{\pi,G}^2 = \xi_{=1} + \xi_{=2} + \xi_{\geq 3}, \end{align} $$
$$ \begin{align} \sum_{p=2}^\infty \frac{1}{p!} \sum_{(\pi,G) \in \tilde{\mathcal{L}}_p^2} \Gamma_{\pi,G}^2 = \xi_{=1} + \xi_{=2} + \xi_{\geq 3}, \end{align} $$
where
![]() $\xi _{=j}$
is the sum of the values of all diagrams with
$\xi _{=j}$
is the sum of the values of all diagrams with
![]() $\nu + \nu ^* + k = j$
and
$\nu + \nu ^* + k = j$
and
![]() $\xi _{\geq 3}$
is the sum of the values of all diagrams with
$\xi _{\geq 3}$
is the sum of the values of all diagrams with
![]() $\nu + \nu ^* + k \geq 3$
.
$\nu + \nu ^* + k \geq 3$
.
For the large diagrams with
![]() $\nu + \nu ^* + k \geq 3$
, we have similarly as above for
$\nu + \nu ^* + k \geq 3$
, we have similarly as above for
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
$\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
sufficiently small
$\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
sufficiently small
 $$ \begin{align} \left\vert \xi_{\geq 3} \right\vert = \left\vert \sum_{p=2}^\infty \frac{1}{p!} \sum_{\substack{(\pi,G)\in \tilde{\mathcal{L}}_p^2 \\ (k+\nu+\nu^*)(\pi,G) \geq 2}} \Gamma_{\pi,G}^2 \right\vert \leq C \rho_0^5 \left\Vert g \right\Vert{}_{L^1}^3 \left(1 + \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^3\right). \end{align} $$
$$ \begin{align} \left\vert \xi_{\geq 3} \right\vert = \left\vert \sum_{p=2}^\infty \frac{1}{p!} \sum_{\substack{(\pi,G)\in \tilde{\mathcal{L}}_p^2 \\ (k+\nu+\nu^*)(\pi,G) \geq 2}} \Gamma_{\pi,G}^2 \right\vert \leq C \rho_0^5 \left\Vert g \right\Vert{}_{L^1}^3 \left(1 + \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^3\right). \end{align} $$
Diagrams with
 $k+\nu +\nu ^* = 1$
$k+\nu +\nu ^* = 1$
For the diagrams with
![]() $p=1$
and
$p=1$
and
![]() $p=2$
with
$p=2$
with
![]() $k=1$
, we do a more precise calculation. For
$k=1$
, we do a more precise calculation. For
![]() $p=1$
, there are three possible g-graphs: (Recall that
$p=1$
, there are three possible g-graphs: (Recall that
![]() $*$
’s label the external vertices)
$*$
’s label the external vertices)

Any permutation makes any of these diagrams have at least one external vertex in each linked component, and thus,
 $$\begin{align*} \sum_{(\pi,G)\in \tilde {\mathcal{L}}_1^2} \Gamma_{\pi,G}^2 & = \int \rho^{(3)}(x_1,x_2,x_3) \left[g_{13} + g_{23} + g_{13}g_{23}\right] \,\text{d} x_3. \end{align*}$$
$$\begin{align*} \sum_{(\pi,G)\in \tilde {\mathcal{L}}_1^2} \Gamma_{\pi,G}^2 & = \int \rho^{(3)}(x_1,x_2,x_3) \left[g_{13} + g_{23} + g_{13}g_{23}\right] \,\text{d} x_3. \end{align*}$$
Bounding
![]() $|g_{13} g_{23}| \leq |g_{13}|$
and recalling the bound
$|g_{13} g_{23}| \leq |g_{13}|$
and recalling the bound
![]() $\rho ^{(3)}(x_1,x_2,x_3) \leq C \rho _0^{3+4/d} |x_1-x_2|^2 |x_1-x_3|^2$
from Lemma 5.4, we get by symmetry
$\rho ^{(3)}(x_1,x_2,x_3) \leq C \rho _0^{3+4/d} |x_1-x_2|^2 |x_1-x_3|^2$
from Lemma 5.4, we get by symmetry
 $$ \begin{align} \left\vert \sum_{(\pi,G)\in \tilde {\mathcal{L}}_1^2} \Gamma_{\pi,G}^2 \right\vert & \leq C \rho_0^{3+4/d} |x_1-x_2|^2 \int |g(z)| |z|^2\,\text{d} z = C \left\Vert |\cdot|^2g \right\Vert{}_{L^1} \rho_0^{3+4/d} |x_1-x_2|^2. \end{align} $$
$$ \begin{align} \left\vert \sum_{(\pi,G)\in \tilde {\mathcal{L}}_1^2} \Gamma_{\pi,G}^2 \right\vert & \leq C \rho_0^{3+4/d} |x_1-x_2|^2 \int |g(z)| |z|^2\,\text{d} z = C \left\Vert |\cdot|^2g \right\Vert{}_{L^1} \rho_0^{3+4/d} |x_1-x_2|^2. \end{align} $$
The diagrams with
![]() $p=2$
and
$p=2$
and
![]() $k=1$
have g-graph
$k=1$
have g-graph

The only permutations
![]() $\pi $
such that
$\pi $
such that
![]() $(\pi ,G)\notin \tilde {\mathcal {L}}_2^2$
are those connecting only external to external and internal to internal (i.e., those with either
$(\pi ,G)\notin \tilde {\mathcal {L}}_2^2$
are those connecting only external to external and internal to internal (i.e., those with either
![]() $\pi (3)=3, \pi (4)=4$
or
$\pi (3)=3, \pi (4)=4$
or
![]() $\pi (3)=4, \pi (4)=3$
). Thus,
$\pi (3)=4, \pi (4)=3$
). Thus,
 $$ \begin{align} \begin{aligned} \sum_{\substack{(\pi,G)\in \tilde {\mathcal{L}}_2^2 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^2 & = \iint \left[\rho^{(4)}(x_1,\ldots,x_4) - \rho^{(2)}(x_1,x_2) \rho^{(2)}(x_3,x_4)\right] g_{34} \,\text{d} x_3 \,\text{d} x_4. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{\substack{(\pi,G)\in \tilde {\mathcal{L}}_2^2 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^2 & = \iint \left[\rho^{(4)}(x_1,\ldots,x_4) - \rho^{(2)}(x_1,x_2) \rho^{(2)}(x_3,x_4)\right] g_{34} \,\text{d} x_3 \,\text{d} x_4. \end{aligned} \end{align} $$
Clearly, this vanishes quadratically in
![]() $x_1-x_2$
since both determinants do; thus, we bound it using Taylor’s theorem, expanding in
$x_1-x_2$
since both determinants do; thus, we bound it using Taylor’s theorem, expanding in
![]() $x_1$
around
$x_1$
around
![]() $x_1=x_2$
analogously to what we did for (some of the diagrams for)
$x_1=x_2$
analogously to what we did for (some of the diagrams for) ![]() above. We treat each diagram separately. (For convenience, we denote the permutation
above. We treat each diagram separately. (For convenience, we denote the permutation
![]() $\pi ^{-1}$
.) Denoting the derivative with respect to
$\pi ^{-1}$
.) Denoting the derivative with respect to
![]() $x_1^\mu $
by
$x_1^\mu $
by
![]() $\partial ^\mu _{x_1}$
, we have
$\partial ^\mu _{x_1}$
, we have
 $$ \begin{align*} \begin{aligned} \partial_{x_1}^\mu \partial_{x_1}^{\nu} \Gamma_{\pi^{-1},G}^2 & = - \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_4} \left(k_1^\mu - k_{\pi(1)}^\mu\right) \left(k_1^\nu - k_{\pi(1)}^\nu\right) \hat \gamma^{(1)}(k_1) \hat \gamma^{(1)}(k_2) \hat \gamma^{(1)}(k_3) \hat \gamma^{(1)}(k_4) \\[5pt] & \qquad \times e^{i(k_1-k_{\pi(1)})x_1} e^{i(k_2-k_{\pi(2)})x_2} \iint e^{i(k_3-k_{\pi(3)})x_3} e^{i(k_4-k_{\pi(4)})x_4} g(x_3-x_4) \,\text{d} x_3 \,\text{d} x_4 \\[5pt] & = - \frac{1}{L^{3d}} \sum_{k_1,\ldots,k_4} \left(k_1^\mu - k_{\pi(1)}^\mu\right) \left(k_1^\nu - k_{\pi(1)}^\nu\right) \hat \gamma^{(1)}(k_1) \hat \gamma^{(1)}(k_2) \hat \gamma^{(1)}(k_3) \hat \gamma^{(1)}(k_4) \\[5pt] & \qquad \times \hat g(k_{\pi(3)}-k_3) \chi_{(k_4-k_{\pi(4)} = k_{\pi(3)} - k_3)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \partial_{x_1}^\mu \partial_{x_1}^{\nu} \Gamma_{\pi^{-1},G}^2 & = - \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_4} \left(k_1^\mu - k_{\pi(1)}^\mu\right) \left(k_1^\nu - k_{\pi(1)}^\nu\right) \hat \gamma^{(1)}(k_1) \hat \gamma^{(1)}(k_2) \hat \gamma^{(1)}(k_3) \hat \gamma^{(1)}(k_4) \\[5pt] & \qquad \times e^{i(k_1-k_{\pi(1)})x_1} e^{i(k_2-k_{\pi(2)})x_2} \iint e^{i(k_3-k_{\pi(3)})x_3} e^{i(k_4-k_{\pi(4)})x_4} g(x_3-x_4) \,\text{d} x_3 \,\text{d} x_4 \\[5pt] & = - \frac{1}{L^{3d}} \sum_{k_1,\ldots,k_4} \left(k_1^\mu - k_{\pi(1)}^\mu\right) \left(k_1^\nu - k_{\pi(1)}^\nu\right) \hat \gamma^{(1)}(k_1) \hat \gamma^{(1)}(k_2) \hat \gamma^{(1)}(k_3) \hat \gamma^{(1)}(k_4) \\[5pt] & \qquad \times \hat g(k_{\pi(3)}-k_3) \chi_{(k_4-k_{\pi(4)} = k_{\pi(3)} - k_3)}. \end{aligned} \end{align*} $$
The only permutations for which the characteristic function is identically
![]() $1$
are those with either
$1$
are those with either
![]() $\pi (3)=3, \pi (4)=4$
or
$\pi (3)=3, \pi (4)=4$
or
![]() $\pi (3)=4, \pi (4)=3$
. These are exactly the permutations that do not appear in Equation (5.11) above. Thus, similarly as for (some of the diagrams for)
$\pi (3)=4, \pi (4)=3$
. These are exactly the permutations that do not appear in Equation (5.11) above. Thus, similarly as for (some of the diagrams for) ![]() above, the characteristic function effectively reduces the number of k-sums by
above, the characteristic function effectively reduces the number of k-sums by
![]() $1$
. Bounding
$1$
. Bounding
![]() $\left \vert \hat g \right \vert \leq \left \Vert g \right \Vert {}_{L^1}$
,
$\left \vert \hat g \right \vert \leq \left \Vert g \right \Vert {}_{L^1}$
,
![]() $\hat \gamma ^{(1)} \leq 1$
for one of the
$\hat \gamma ^{(1)} \leq 1$
for one of the
![]() $\gamma ^{(1)}$
-factors, and using Equation (3.12) to bound the k-sums, we have for any diagram
$\gamma ^{(1)}$
-factors, and using Equation (3.12) to bound the k-sums, we have for any diagram
![]() $(\pi ,G)\in \tilde {\mathcal {L}}_2^2$
with G as in Equation (5.10)
$(\pi ,G)\in \tilde {\mathcal {L}}_2^2$
with G as in Equation (5.10)
We conclude the bound
 $$ \begin{align} \begin{aligned} \left\vert \sum_{\substack{(\pi,G)\in \tilde {\mathcal{L}}_2^2 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^2 \right\vert & \leq C \left\Vert g \right\Vert{}_{L^1} \rho_0^{3+2/d} |x_1-x_2|^2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\vert \sum_{\substack{(\pi,G)\in \tilde {\mathcal{L}}_2^2 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^2 \right\vert & \leq C \left\Vert g \right\Vert{}_{L^1} \rho_0^{3+2/d} |x_1-x_2|^2. \end{aligned} \end{align} $$
In particular, by combining Equations (5.9) and (5.12), we have
Diagrams with
 $k+\nu +\nu ^* = 2$
$k+\nu +\nu ^* = 2$
Finally, consider all diagrams with
![]() $k + \nu + \nu ^* = 2$
more precisely. We split these into three groups.
$k + \nu + \nu ^* = 2$
more precisely. We split these into three groups.
-
(i)
 $\nu ^* = 2$
$\nu ^* = 2$
-
(ii)
 $\nu ^*=1$
and vertices
$\nu ^*=1$
and vertices
 $\{1\}$
and
$\{1\}$
and
 $\{2\}$
are connected
$\{2\}$
are connected -
(iii) Remaining diagrams
We will use a Taylor expansion to bound the values of the diagrams in group (iii). Write
Then as
![]() $\rho _J^{(2)}(x_2;x_2)=0$
, we get from Equation (5.7)
$\rho _J^{(2)}(x_2;x_2)=0$
, we get from Equation (5.7)
Moreover,
![]() $\xi _{\text {(iii)}}$
is symmetric in exchange of
$\xi _{\text {(iii)}}$
is symmetric in exchange of
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, so the first order vanishes. We conclude by Taylor’s theorem that
$x_2$
, so the first order vanishes. We conclude by Taylor’s theorem that
 $$ \begin{align} \begin{aligned} \left\vert \xi_{\text{(iii)}}(x_1,x_2) \right\vert & \leq \left\vert \xi_{\text{(i)}}(x_2,x_2) \right\vert + \left\vert \xi_{\text{(ii)}}(x_2,x_2) \right\vert + \left\vert \xi_{=1}(x_2,x_2) \right\vert + \left\vert \xi_{\geq3}(x_2,x_2) \right\vert \\ & \quad + C \sup_{\mu,\nu} \sup_{z_1,z_2} \left\vert \partial_{x_1}^\mu \partial_{x_1}^\nu \xi_{\text{(iii)}}(z_1,z_2) \right\vert |x_1-x_2|^2, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\vert \xi_{\text{(iii)}}(x_1,x_2) \right\vert & \leq \left\vert \xi_{\text{(i)}}(x_2,x_2) \right\vert + \left\vert \xi_{\text{(ii)}}(x_2,x_2) \right\vert + \left\vert \xi_{=1}(x_2,x_2) \right\vert + \left\vert \xi_{\geq3}(x_2,x_2) \right\vert \\ & \quad + C \sup_{\mu,\nu} \sup_{z_1,z_2} \left\vert \partial_{x_1}^\mu \partial_{x_1}^\nu \xi_{\text{(iii)}}(z_1,z_2) \right\vert |x_1-x_2|^2, \end{aligned} \end{align} $$
where again
![]() $\partial _{x_1}^\mu $
denotes the derivative w.r.t.
$\partial _{x_1}^\mu $
denotes the derivative w.r.t.
![]() $x_1^\mu $
. Bounding
$x_1^\mu $
. Bounding
![]() $\partial _{x_1}^\mu \partial _{x_1}^\nu \xi _{\text {(iii)}}$
is analogous to the argument in [Reference Lauritsen and SeiringerLS24b, Proof of Lemmas 4.1 and 4.8]: For diagrams with an internal vertex connected to
$\partial _{x_1}^\mu \partial _{x_1}^\nu \xi _{\text {(iii)}}$
is analogous to the argument in [Reference Lauritsen and SeiringerLS24b, Proof of Lemmas 4.1 and 4.8]: For diagrams with an internal vertex connected to
![]() $\{1\}$
with a g-edge, we do a precise calculation as in [Reference Lauritsen and SeiringerLS24b, Proof of Lemma 4.8]. For the remaining diagrams where
$\{1\}$
with a g-edge, we do a precise calculation as in [Reference Lauritsen and SeiringerLS24b, Proof of Lemma 4.8]. For the remaining diagrams where
![]() $\{1\}$
has no incident g-edges, we modify the proof of the absolute convergence of the GGR expansion as in [Reference Lauritsen and SeiringerLS24b, Proof of Lemma 4.1].
$\{1\}$
has no incident g-edges, we modify the proof of the absolute convergence of the GGR expansion as in [Reference Lauritsen and SeiringerLS24b, Proof of Lemma 4.1].
First, the diagrams in group (iii) with an internal vertex connected to
![]() $\{1\}$
with a g-edge all have g-graph
$\{1\}$
with a g-edge all have g-graph

since
![]() $\nu ^* = 1$
and
$\nu ^* = 1$
and
![]() $k+\nu +\nu ^* = 2$
. Then
$k+\nu +\nu ^* = 2$
. Then
 $$ \begin{align*} \begin{aligned} \Gamma_{\pi^{-1},G}^2 & = (-1)^{\pi} \frac{1}{L^{5d}} \sum_{k_1,\ldots,k_5} \hat \gamma^{(1)}(k_1) \cdots \hat \gamma^{(1)}(k_5) \iiint e^{i(k_1-k_{\pi(1)}) x_1} \cdots e^{i(k_5-k_{\pi(5)}) x_5} g_{13} g_{45} \,\text{d} x_3 \,\text{d} x_4 \,\text{d} x_5 \\ & = (-1)^{\pi} \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat \gamma^{(1)}(k_1) \cdots \hat \gamma^{(1)}(k_5) e^{i(k_1 - k_{\pi(1)} + k_3 - k_{\pi(3)})x_1} e^{i(k_2-k_{\pi(2)})x_2} \\ & \quad \times \hat g(k_3-k_{\pi(3)}) \hat g(k_5 - k_{\pi(5)}) \chi_{(k_4 - k_{\pi(4)} + k_5 - k_{\pi(5)}=0)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Gamma_{\pi^{-1},G}^2 & = (-1)^{\pi} \frac{1}{L^{5d}} \sum_{k_1,\ldots,k_5} \hat \gamma^{(1)}(k_1) \cdots \hat \gamma^{(1)}(k_5) \iiint e^{i(k_1-k_{\pi(1)}) x_1} \cdots e^{i(k_5-k_{\pi(5)}) x_5} g_{13} g_{45} \,\text{d} x_3 \,\text{d} x_4 \,\text{d} x_5 \\ & = (-1)^{\pi} \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat \gamma^{(1)}(k_1) \cdots \hat \gamma^{(1)}(k_5) e^{i(k_1 - k_{\pi(1)} + k_3 - k_{\pi(3)})x_1} e^{i(k_2-k_{\pi(2)})x_2} \\ & \quad \times \hat g(k_3-k_{\pi(3)}) \hat g(k_5 - k_{\pi(5)}) \chi_{(k_4 - k_{\pi(4)} + k_5 - k_{\pi(5)}=0)}. \end{aligned} \end{align*} $$
The characteristic function
![]() $\chi $
is identically
$\chi $
is identically
![]() $1$
only if
$1$
only if
![]() $\pi (\{4,5\}) = \{4,5\}$
, but then
$\pi (\{4,5\}) = \{4,5\}$
, but then
![]() $(\pi ,G)\notin \tilde {\mathcal {L}}_3^2$
so these permutations do not appear in
$(\pi ,G)\notin \tilde {\mathcal {L}}_3^2$
so these permutations do not appear in
![]() $\xi _{\text {(iii)}}$
. Taking the derivative, bounding
$\xi _{\text {(iii)}}$
. Taking the derivative, bounding
![]() $|\hat g| \leq \left \Vert g \right \Vert {}_{L^1}$
and using Equation (3.12) to bound the k-sums, we conclude as above that
$|\hat g| \leq \left \Vert g \right \Vert {}_{L^1}$
and using Equation (3.12) to bound the k-sums, we conclude as above that
for all diagrams
![]() $(\pi ,G)\in \tilde {\mathcal {L}}_3^2$
with G as in Equation (5.15).
$(\pi ,G)\in \tilde {\mathcal {L}}_3^2$
with G as in Equation (5.15).
Next, for the diagrams with no g-edges connected to
![]() $\{1\}$
, the argument is as for the bound of
$\{1\}$
, the argument is as for the bound of
![]() $\partial _{x_1}^{\mu }\partial _{x_1}^\nu \xi _0$
in [Reference Lauritsen and SeiringerLS24b, Proof of Lemma 4.1]. Analogously to [Reference Lauritsen and SeiringerLS24b, Equations (4.19) and (4.20)], we conclude the bound (the term
$\partial _{x_1}^{\mu }\partial _{x_1}^\nu \xi _0$
in [Reference Lauritsen and SeiringerLS24b, Proof of Lemma 4.1]. Analogously to [Reference Lauritsen and SeiringerLS24b, Equations (4.19) and (4.20)], we conclude the bound (the term
![]() $1$
in the factor
$1$
in the factor
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} + 1$
arises similarly as in the bounds above from the value of diagrams with
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} + 1$
arises similarly as in the bounds above from the value of diagrams with
![]() $k=1$
)
$k=1$
)
 $$ \begin{align*} \begin{aligned} & \left\vert \partial_{x_1}^2 \sum_{\substack{(\pi,G)\in \tilde{\mathcal{L}}_3^2 \\\text{no} g\text{-edges incident to } \{1\}}} \Gamma_{\pi^{-1},G}^2 \right\vert \\[7pt] & \quad \leq C \rho_0^4 \left\Vert g \right\Vert{}_{L^1}^2 \left(\left\Vert \gamma^{(1)} \right\Vert{}_{L^1} + 1\right) \left[\rho_0^{2/d} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1} + \rho_0^{1/d} \left\Vert \partial \gamma^{(1)} \right\Vert{}_{L^1} + \left\Vert \partial^2 \gamma^{(1)} \right\Vert{}_{L^1}\right], \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \left\vert \partial_{x_1}^2 \sum_{\substack{(\pi,G)\in \tilde{\mathcal{L}}_3^2 \\\text{no} g\text{-edges incident to } \{1\}}} \Gamma_{\pi^{-1},G}^2 \right\vert \\[7pt] & \quad \leq C \rho_0^4 \left\Vert g \right\Vert{}_{L^1}^2 \left(\left\Vert \gamma^{(1)} \right\Vert{}_{L^1} + 1\right) \left[\rho_0^{2/d} \left\Vert \gamma^{(1)} \right\Vert{}_{L^1} + \rho_0^{1/d} \left\Vert \partial \gamma^{(1)} \right\Vert{}_{L^1} + \left\Vert \partial^2 \gamma^{(1)} \right\Vert{}_{L^1}\right], \end{aligned} \end{align*} $$
where with a similar abuse of notation,
Recall that
![]() $\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} \leq C \zeta ^{d/2}$
by Lemma 4.6. By a simple modification of the proof of Lemma 4.6, we may bound
$\left \Vert \gamma ^{(1)} \right \Vert {}_{L^1} \leq C \zeta ^{d/2}$
by Lemma 4.6. By a simple modification of the proof of Lemma 4.6, we may bound
![]() $\left \Vert \partial \gamma ^{(1)} \right \Vert {}_{L^1} \leq C \zeta ^{d/2} \rho _0^{1/d}$
and
$\left \Vert \partial \gamma ^{(1)} \right \Vert {}_{L^1} \leq C \zeta ^{d/2} \rho _0^{1/d}$
and
![]() $\left \Vert \partial ^2 \gamma ^{(1)} \right \Vert {}_{L^1} \leq C \zeta ^{d/2} \rho _0^{2/d}$
. Thus,
$\left \Vert \partial ^2 \gamma ^{(1)} \right \Vert {}_{L^1} \leq C \zeta ^{d/2} \rho _0^{2/d}$
. Thus,
Next, we bound
![]() $\xi _{\text {(i)}}$
. For the diagrams with
$\xi _{\text {(i)}}$
. For the diagrams with
![]() $\nu ^*=2$
, if G is any graph with
$\nu ^*=2$
, if G is any graph with
![]() $\nu ^*(G) = 2$
, then for any permutation
$\nu ^*(G) = 2$
, then for any permutation
![]() $\pi \in \mathcal {S}_4$
, we have
$\pi \in \mathcal {S}_4$
, we have
![]() $(\pi ,G)\in \tilde {\mathcal {L}}_2^2$
. Thus, using Lemma 5.4 to bound
$(\pi ,G)\in \tilde {\mathcal {L}}_2^2$
. Thus, using Lemma 5.4 to bound
![]() $\rho ^{(4)}$
and bounding some g-factors by
$\rho ^{(4)}$
and bounding some g-factors by
![]() $1$
, we get similarly to Equation (5.9)
$1$
, we get similarly to Equation (5.9)
 $$ \begin{align} \begin{aligned} \xi_{\text{(i)}} & = \sum_{\substack{G\in \mathcal{G}_2^2 \\ \nu^*(G) = 2}} \iint \rho^{(4)} \prod_{e\in G} g_e \,\text{d} x_3 \,\text{d} x_4 \\[7pt] \left\vert \xi_{\text{(i)}} \right\vert & \leq C\rho_0^{4+6/d} |x_1-x_2|^2 \iint |g(z_1)|^2 |g(z_2)|^2 (|z_1|^2 + |z_2|^2 + |x_1-x_2|^2)^2 \,\text{d} z_1 \,\text{d} z_2 \\[7pt] & \leq C \left\Vert g \right\Vert{}_{L^1}^2 \rho_0^{4+6/d} |x_1-x_2|^2 (b^2 + |x_1-x_2|^2)^{2}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \xi_{\text{(i)}} & = \sum_{\substack{G\in \mathcal{G}_2^2 \\ \nu^*(G) = 2}} \iint \rho^{(4)} \prod_{e\in G} g_e \,\text{d} x_3 \,\text{d} x_4 \\[7pt] \left\vert \xi_{\text{(i)}} \right\vert & \leq C\rho_0^{4+6/d} |x_1-x_2|^2 \iint |g(z_1)|^2 |g(z_2)|^2 (|z_1|^2 + |z_2|^2 + |x_1-x_2|^2)^2 \,\text{d} z_1 \,\text{d} z_2 \\[7pt] & \leq C \left\Vert g \right\Vert{}_{L^1}^2 \rho_0^{4+6/d} |x_1-x_2|^2 (b^2 + |x_1-x_2|^2)^{2}. \end{aligned} \end{align} $$
Finally, we bound
![]() $\xi _{\text {(ii)}}$
. All diagrams with
$\xi _{\text {(ii)}}$
. All diagrams with
![]() $\nu ^* = 1$
and
$\nu ^* = 1$
and
![]() $\{1\}$
and
$\{1\}$
and
![]() $\{2\}$
connected have g-graph
$\{2\}$
connected have g-graph

For convenience of notation, we denote the permutation in the diagram
![]() $\pi ^{-1}$
. Then
$\pi ^{-1}$
. Then
 $$ \begin{align*} \begin{aligned} & \Gamma_{\pi^{-1},G_0}^2 \\ & \quad = (-1)^{\pi} \frac{1}{L^{5d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) \\ & \qquad \times \iiint e^{i(k_1 - k_{\pi(1)})x_1} \cdots e^{i(k_5 - k_{\pi(5)})x_5} g(x_1-x_3)g(x_2-x_3) g(x_4-x_5) \,\text{d} x_3 \,\text{d} x_4 \,\text{d} x_5 \\ & \quad = (-1)^{\pi} \frac{1}{L^{5d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) e^{i\left(k_1 - k_{\pi(1)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_1} e^{i\left(k_2 - k_{\pi(2)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_2} \\ & \qquad \times \int e^{i(k_3-k_{\pi(3)}) (x_3 - \frac{x_1+x_2}{2})} g\left(\frac{x_1-x_2}{2} + \frac{x_1+x_2}{2} - x_3\right) g\left(-\frac{x_1-x_2}{2} + \frac{x_1+x_2}{2} - x_3\right) \,\text{d} x_3 \\ & \qquad \times \iint g(x_4-x_5) e^{i(k_4-k_{\pi(4)})(x_4-x_5)} e^{i(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)}) x_5} \,\text{d} x_4 \,\text{d} x_5 \\ & \quad = (-1)^{\pi} \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) \\ & \qquad \times e^{i\left(k_1 - k_{\pi(1)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_1} e^{i\left(k_2 - k_{\pi(2)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_2} \hat G_1(k_3 - k_{\pi(3)}) \hat g(k_{\pi(4)}-k_4) \chi_{(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)} = 0)}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \Gamma_{\pi^{-1},G_0}^2 \\ & \quad = (-1)^{\pi} \frac{1}{L^{5d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) \\ & \qquad \times \iiint e^{i(k_1 - k_{\pi(1)})x_1} \cdots e^{i(k_5 - k_{\pi(5)})x_5} g(x_1-x_3)g(x_2-x_3) g(x_4-x_5) \,\text{d} x_3 \,\text{d} x_4 \,\text{d} x_5 \\ & \quad = (-1)^{\pi} \frac{1}{L^{5d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) e^{i\left(k_1 - k_{\pi(1)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_1} e^{i\left(k_2 - k_{\pi(2)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_2} \\ & \qquad \times \int e^{i(k_3-k_{\pi(3)}) (x_3 - \frac{x_1+x_2}{2})} g\left(\frac{x_1-x_2}{2} + \frac{x_1+x_2}{2} - x_3\right) g\left(-\frac{x_1-x_2}{2} + \frac{x_1+x_2}{2} - x_3\right) \,\text{d} x_3 \\ & \qquad \times \iint g(x_4-x_5) e^{i(k_4-k_{\pi(4)})(x_4-x_5)} e^{i(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)}) x_5} \,\text{d} x_4 \,\text{d} x_5 \\ & \quad = (-1)^{\pi} \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) \\ & \qquad \times e^{i\left(k_1 - k_{\pi(1)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_1} e^{i\left(k_2 - k_{\pi(2)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_2} \hat G_1(k_3 - k_{\pi(3)}) \hat g(k_{\pi(4)}-k_4) \chi_{(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)} = 0)}, \end{aligned} \end{align*} $$
where
We group together pairs of diagrams
![]() $\pi $
and (using cycle notation)
$\pi $
and (using cycle notation)
![]() $\pi \cdot (4\,5) = (\pi (4)\,\pi (5)) \cdot \pi $
, meaning where
$\pi \cdot (4\,5) = (\pi (4)\,\pi (5)) \cdot \pi $
, meaning where
![]() $\pi (4)$
and
$\pi (4)$
and
![]() $\pi (5)$
are swapped. These have opposite signs. Thus,
$\pi (5)$
are swapped. These have opposite signs. Thus,
 $$ \begin{align*} \begin{aligned} & \Gamma_{\pi^{-1},G_0}^2 + \Gamma_{(\pi (4\,5))^{-1}, G_0}^2 \\ & \quad = (-1)^{\pi} \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) e^{i\left(k_1 - k_{\pi(1)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_1} e^{i\left(k_2 - k_{\pi(2)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_2} \\ & \qquad \times \hat G_1(k_3 - k_{\pi(3)}) \chi_{(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)} = 0)} \left[ \hat g(k_{\pi(4)}-k_4) - \hat g(k_{\pi(5)} - k_4) \right]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \Gamma_{\pi^{-1},G_0}^2 + \Gamma_{(\pi (4\,5))^{-1}, G_0}^2 \\ & \quad = (-1)^{\pi} \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) e^{i\left(k_1 - k_{\pi(1)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_1} e^{i\left(k_2 - k_{\pi(2)} - \frac{k_3 - k_{\pi(3)}}{2}\right)x_2} \\ & \qquad \times \hat G_1(k_3 - k_{\pi(3)}) \chi_{(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)} = 0)} \left[ \hat g(k_{\pi(4)}-k_4) - \hat g(k_{\pi(5)} - k_4) \right]. \end{aligned} \end{align*} $$
We Taylor expand
![]() $\hat g(k_{\pi (5)} - k_4)$
in
$\hat g(k_{\pi (5)} - k_4)$
in
![]() $k_{\pi (5)}$
around
$k_{\pi (5)}$
around
![]() $k_{\pi (5)} = k_{\pi (4)}$
. That is,
$k_{\pi (5)} = k_{\pi (4)}$
. That is,
where
![]() $O\left (\nabla \hat g\right )$
should be interpreted as being bounded by
$O\left (\nabla \hat g\right )$
should be interpreted as being bounded by
![]() $\left \vert \nabla \hat g(k) \right \vert \leq \int |x| |g(x)| = \left \Vert |\cdot |g \right \Vert {}_{L^1}$
uniformly in
$\left \vert \nabla \hat g(k) \right \vert \leq \int |x| |g(x)| = \left \Vert |\cdot |g \right \Vert {}_{L^1}$
uniformly in
![]() $k_{\pi (4)} - k_{\pi (5)}$
. Moreover,
$k_{\pi (4)} - k_{\pi (5)}$
. Moreover,
![]() $\left \vert \hat G_1 \right \vert \leq \left \Vert g \right \Vert {}_{L^1}$
. Thus,
$\left \vert \hat G_1 \right \vert \leq \left \Vert g \right \Vert {}_{L^1}$
. Thus,
 $$ \begin{align*} \begin{aligned} & \left\vert \Gamma_{\pi^{-1},G_0}^2 + \Gamma_{(\pi (4\,5))^{-1}, G_0}^2 \right\vert \\ & \quad \leq C \left\Vert g \right\Vert{}_{L^1} \left\Vert |\cdot|g \right\Vert{}_{L^1} \times \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) \left\vert k_{\pi(4)} - k_{\pi(5)} \right\vert \chi_{(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)} = 0)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \left\vert \Gamma_{\pi^{-1},G_0}^2 + \Gamma_{(\pi (4\,5))^{-1}, G_0}^2 \right\vert \\ & \quad \leq C \left\Vert g \right\Vert{}_{L^1} \left\Vert |\cdot|g \right\Vert{}_{L^1} \times \frac{1}{L^{4d}} \sum_{k_1,\ldots,k_5} \hat\gamma^{(1)}(k_1)\cdots \hat\gamma^{(1)}(k_5) \left\vert k_{\pi(4)} - k_{\pi(5)} \right\vert \chi_{(k_5 - k_{\pi(5)} + k_{4}-k_{\pi(4)} = 0)}. \end{aligned} \end{align*} $$
The characteristic function is not identically
![]() $1$
for linked diagrams. Indeed, if
$1$
for linked diagrams. Indeed, if
![]() $\pi (\{4,5\}) = \{4,5\}$
, then the diagram would not be linked. Thus, the characteristic function effectively reduces the number of k-sums by
$\pi (\{4,5\}) = \{4,5\}$
, then the diagram would not be linked. Thus, the characteristic function effectively reduces the number of k-sums by
![]() $1$
. Bounding similarly as above
$1$
. Bounding similarly as above
![]() $\hat \gamma ^{(1)} \leq 1$
and using finally Equation (3.12) to bound the k-sums, we conclude for any permutation
$\hat \gamma ^{(1)} \leq 1$
and using finally Equation (3.12) to bound the k-sums, we conclude for any permutation
![]() $\pi $
such that
$\pi $
such that
![]() $(\pi ,G_0)\in \tilde {\mathcal {L}}_3^2$
that
$(\pi ,G_0)\in \tilde {\mathcal {L}}_3^2$
that
Since
![]() $\pi $
and
$\pi $
and
![]() $\pi (4\, 5)$
either both give rise to linked diagrams or neither do, we conclude that
$\pi (4\, 5)$
either both give rise to linked diagrams or neither do, we conclude that
 $$ \begin{align} \left\vert \xi_{\text{(ii)}} \right\vert = \frac{1}{3!}\left\vert \sum_{(\pi,G_0) \in \tilde{\mathcal{L}}_3^2} \Gamma_{\pi,G_0} \right\vert \leq C \rho_0^{4+1/d} \left\Vert |\cdot|g \right\Vert{}_{L^1} \left\Vert g \right\Vert{}_{L^1}. \end{align} $$
$$ \begin{align} \left\vert \xi_{\text{(ii)}} \right\vert = \frac{1}{3!}\left\vert \sum_{(\pi,G_0) \in \tilde{\mathcal{L}}_3^2} \Gamma_{\pi,G_0} \right\vert \leq C \rho_0^{4+1/d} \left\Vert |\cdot|g \right\Vert{}_{L^1} \left\Vert g \right\Vert{}_{L^1}. \end{align} $$
Combining then Equations (5.8), (5.13), (5.14), (5.16), (5.17) and (5.19) and using Lemma 4.6, we conclude the bound
We conclude the bound
 $$ \begin{align*} \begin{aligned} \left\vert \sum_{p=1}^\infty {\frac{1}{p!}} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^2} \Gamma_{\pi,G}^2 \right\vert & \leq C a^{d} \rho_0^{3+2/d} \log b/a |x_1-x_2|^2 + a^{d} b^2 \rho_0^{3+4/d} |x_1-x_2|^2 \\ & \quad + C a^d \rho_0^{4+6/d} |x_1-x_2|^2 (b^2 + |x_1-x_2|^2)^2 (\log b/a)^2 + C a^{2d} b \rho_0^{4+1/d} \log b/a \\ & \quad + C a^{2d} \rho_0^{4+2/d} \zeta^{d} (\log b/a)^2 |x_1-x_2|^2 + C a^{3d} \rho_0^5 \zeta^{3d/2} (\log b/a)^3. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\vert \sum_{p=1}^\infty {\frac{1}{p!}} \sum_{(\pi,G)\in \tilde{\mathcal{L}}_p^2} \Gamma_{\pi,G}^2 \right\vert & \leq C a^{d} \rho_0^{3+2/d} \log b/a |x_1-x_2|^2 + a^{d} b^2 \rho_0^{3+4/d} |x_1-x_2|^2 \\ & \quad + C a^d \rho_0^{4+6/d} |x_1-x_2|^2 (b^2 + |x_1-x_2|^2)^2 (\log b/a)^2 + C a^{2d} b \rho_0^{4+1/d} \log b/a \\ & \quad + C a^{2d} \rho_0^{4+2/d} \zeta^{d} (\log b/a)^2 |x_1-x_2|^2 + C a^{3d} \rho_0^5 \zeta^{3d/2} (\log b/a)^3. \end{aligned} \end{align*} $$
Thus, using Lemma 3.4, we get

This concludes the proof of Lemma 5.2.
Remark 5.5 (Necessity of precise analysis of diagrams with
 $k+\nu +\nu ^*=2$
)
$k+\nu +\nu ^*=2$
)
For the bound of ![]() , we give here a precise analysis of the diagrams with
, we give here a precise analysis of the diagrams with
![]() $k+\nu +\nu ^*=2$
. In general, one should not expect this to be needed in dimensions
$k+\nu +\nu ^*=2$
. In general, one should not expect this to be needed in dimensions
![]() $d=2,3$
. More precisely, by just considering powers of
$d=2,3$
. More precisely, by just considering powers of
![]() $\rho _0$
, one would expect that diagrams with
$\rho _0$
, one would expect that diagrams with
![]() $k+\nu +\nu ^* \geq 1$
are all subleading as they carry a higher power of
$k+\nu +\nu ^* \geq 1$
are all subleading as they carry a higher power of
![]() $\rho _0$
(using Equation (5.6)) than the claimed leading term, with exponent
$\rho _0$
(using Equation (5.6)) than the claimed leading term, with exponent
![]() $2+2/d$
.
$2+2/d$
.
The reason we need a precise analysis here is the temperature dependence of our bounds: for some regime of temperatures, the bound one would get by using Equation (5.6) is not good enough.
Remark 5.6 (Optimality of the error bounds)
One should not expect the bound given in Equation (5.19) to be optimal. More precisely, in Equation (5.19), we only took into account the cancellations of pairs of diagrams. However, one should expect much more cancellations. We have
Naively, just using that
![]() $\rho ^{(5)}(x_1,\ldots ,x_5) - \rho ^{(3)}(x_1,x_2,x_3)\rho ^{(2)}(x_4,x_5)$
vanishes whenever any two of the particles
$\rho ^{(5)}(x_1,\ldots ,x_5) - \rho ^{(3)}(x_1,x_2,x_3)\rho ^{(2)}(x_4,x_5)$
vanishes whenever any two of the particles
![]() $1,2,3$
or the particles
$1,2,3$
or the particles
![]() $4,5$
are incident, we get by Taylor expansion
$4,5$
are incident, we get by Taylor expansion
Using this bound and bounding
![]() $|g_{23}|\leq 1$
, we get
$|g_{23}|\leq 1$
, we get
This bound is too large by a volume factor. (This arises since we ‘forget’ that the relevant diagrams are linked when we do the Taylor expansion.) It, however, illustrates how many more cancellations between the different permutations are present than what we used in the bound Equation (5.19) — it carries a higher power of
![]() $\rho _0$
. Using these cancellations but losing the information that diagrams are linked is what we did in [Reference Lauritsen and SeiringerLS24b].
$\rho _0$
. Using these cancellations but losing the information that diagrams are linked is what we did in [Reference Lauritsen and SeiringerLS24b].
If one could somehow see these cancellations, while still keeping the information that the diagrams have to be linked, one might be able to improve upon the bound Equation (5.19). In one dimension, this error term is actually (for some regime of temperatures) the dominant error term. Thus, by improving the analysis of these diagrams, one might improve the error term in Proposition 1.9 in
![]() $d=1$
.
$d=1$
.
A Particle density of the trial state
In this section, we give the following:
Proof of Equation (3.3)
We calculate
![]() $\left \langle \mathcal {N} \right \rangle _J$
and compare it to
$\left \langle \mathcal {N} \right \rangle _J$
and compare it to
![]() $\left \langle \mathcal {N} \right \rangle _0 = \rho _0L^d$
. We have by Equation (4.2)
$\left \langle \mathcal {N} \right \rangle _0 = \rho _0L^d$
. We have by Equation (4.2)
 $$ \begin{align*} \begin{aligned} \left\langle \mathcal{N} \right\rangle_J & = \int \rho_J^{(1)}(x) \,\text{d} x = L^d \left[\rho^{(1)} + \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p^1} \Gamma_{\pi,G}^1\right] = \left\langle \mathcal{N} \right\rangle_0 + L^d \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p^1} \Gamma_{\pi,G}^1. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\langle \mathcal{N} \right\rangle_J & = \int \rho_J^{(1)}(x) \,\text{d} x = L^d \left[\rho^{(1)} + \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p^1} \Gamma_{\pi,G}^1\right] = \left\langle \mathcal{N} \right\rangle_0 + L^d \sum_{p=1}^\infty \frac{1}{p!} \sum_{(\pi,G)\in \mathcal{L}_p^1} \Gamma_{\pi,G}^1. \end{aligned} \end{align*} $$
Next, we bound
![]() $\sum _{p=1}^\infty \frac {1}{p!} \sum _{(\pi ,G)\in \mathcal {L}_p^1} \Gamma _{\pi ,G}^1$
. We use the bound in Equation (5.6) for diagrams with
$\sum _{p=1}^\infty \frac {1}{p!} \sum _{(\pi ,G)\in \mathcal {L}_p^1} \Gamma _{\pi ,G}^1$
. We use the bound in Equation (5.6) for diagrams with
![]() $k+\nu +\nu ^* \geq 2$
, i.e., for
$k+\nu +\nu ^* \geq 2$
, i.e., for
![]() $p=2$
with
$p=2$
with
![]() $k = 0, \nu ^* = 2$
and for
$k = 0, \nu ^* = 2$
and for
![]() $p\geq 3$
. That is,
$p\geq 3$
. That is,
 $$ \begin{align*} \frac{1}{2!} \left\vert \sum_{\substack{(\pi,G)\in\mathcal{L}_2^1 \\ k(\pi,G) = 0}} \Gamma_{\pi,G}^1 \right\vert \leq C \left\Vert g \right\Vert{}_{L^1}^2 \rho_0^3, \qquad \sum_{p=3}^\infty \frac{1}{p!} \left\vert \sum_{\substack{(\pi,G)\in\mathcal{L}_p^1}} \Gamma_{\pi,G}^1 \right\vert \leq C \left\Vert g \right\Vert{}_{L^1}^2 \left(1 + \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^2\right) \rho_0^3 \end{align*} $$
$$ \begin{align*} \frac{1}{2!} \left\vert \sum_{\substack{(\pi,G)\in\mathcal{L}_2^1 \\ k(\pi,G) = 0}} \Gamma_{\pi,G}^1 \right\vert \leq C \left\Vert g \right\Vert{}_{L^1}^2 \rho_0^3, \qquad \sum_{p=3}^\infty \frac{1}{p!} \left\vert \sum_{\substack{(\pi,G)\in\mathcal{L}_p^1}} \Gamma_{\pi,G}^1 \right\vert \leq C \left\Vert g \right\Vert{}_{L^1}^2 \left(1 + \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^2\right) \rho_0^3 \end{align*} $$
for sufficiently small
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
$\rho _0 \left \Vert g \right \Vert {}_{L^1}$
and
![]() $\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
. Thus, we get
$\rho _0 \left \Vert g \right \Vert {}_{L^1} \left \Vert \gamma ^{(1)} \right \Vert {}_{L^1}$
. Thus, we get
 $$ \begin{align*} \sum_{p=1}^\infty \frac{1}{p!} \sum_{\substack{(\pi,G)\in\mathcal{L}_p^1}}\Gamma_{\pi,G}^1 = \sum_{\substack{(\pi,G)\in\mathcal{L}_1^1}}\Gamma_{\pi,G}^1 + \frac{1}{2} \sum_{\substack{(\pi,G)\in \mathcal{L}_2^1 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^1 + O\left(\left\Vert g \right\Vert{}_{L^1}^2\left(\left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^2+1\right) \rho_0^3\right). \end{align*} $$
$$ \begin{align*} \sum_{p=1}^\infty \frac{1}{p!} \sum_{\substack{(\pi,G)\in\mathcal{L}_p^1}}\Gamma_{\pi,G}^1 = \sum_{\substack{(\pi,G)\in\mathcal{L}_1^1}}\Gamma_{\pi,G}^1 + \frac{1}{2} \sum_{\substack{(\pi,G)\in \mathcal{L}_2^1 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^1 + O\left(\left\Vert g \right\Vert{}_{L^1}^2\left(\left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^2+1\right) \rho_0^3\right). \end{align*} $$
For the
![]() $p=1$
-term, there are two diagrams. Thus (where
$p=1$
-term, there are two diagrams. Thus (where
![]() $*$
labels the external vertex),
$*$
labels the external vertex),

For the
![]() $p=2$
-term with
$p=2$
-term with
![]() $k=1$
, there are
$k=1$
, there are
![]() $4$
diagrams. Thus,
$4$
diagrams. Thus,

Taylor expanding
![]() $\hat g$
and using that
$\hat g$
and using that
![]() $\int x g(x) = 0$
so
$\int x g(x) = 0$
so
![]() $\nabla \hat g(0) = 0$
, we get
$\nabla \hat g(0) = 0$
, we get
 $$ \begin{align*} \left\vert \frac{1}{2}\sum_{\substack{(\pi,G)\in \mathcal{L}_2^1 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^1 \right\vert \leq C \left\Vert |\cdot|^2g \right\Vert{}_{L^1} \rho_0^{2+2/d}. \end{align*} $$
$$ \begin{align*} \left\vert \frac{1}{2}\sum_{\substack{(\pi,G)\in \mathcal{L}_2^1 \\ k(\pi,G) = 1}} \Gamma_{\pi,G}^1 \right\vert \leq C \left\Vert |\cdot|^2g \right\Vert{}_{L^1} \rho_0^{2+2/d}. \end{align*} $$
Thus, by Lemma 4.6,
 $$ \begin{align*} \begin{aligned} \left\vert \sum_{p=1}^\infty \frac{1}{p!} \sum_{\substack{(\pi,G)\in\mathcal{L}_p^1}}\Gamma_{\pi,G}^1 \right\vert & \leq C \left\Vert |\cdot|^2g \right\Vert{}_{L^1} \rho_0^{2+2/d} + C \left\Vert g \right\Vert{}_{L^1}^2 \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^2 \rho_0^3 + C \left\Vert g \right\Vert{}_{L^1}^2 \rho_0^3 \\ & \leq C a^d b^2 \rho_0^{2+2/d} + C a^{2d} \rho_0^3 \zeta^d (\log b/a)^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\vert \sum_{p=1}^\infty \frac{1}{p!} \sum_{\substack{(\pi,G)\in\mathcal{L}_p^1}}\Gamma_{\pi,G}^1 \right\vert & \leq C \left\Vert |\cdot|^2g \right\Vert{}_{L^1} \rho_0^{2+2/d} + C \left\Vert g \right\Vert{}_{L^1}^2 \left\Vert \gamma^{(1)} \right\Vert{}_{L^1}^2 \rho_0^3 + C \left\Vert g \right\Vert{}_{L^1}^2 \rho_0^3 \\ & \leq C a^d b^2 \rho_0^{2+2/d} + C a^{2d} \rho_0^3 \zeta^d (\log b/a)^2. \end{aligned} \end{align*} $$
That is, Equation (3.3) is satisfied.
Competing interest
The authors have no competing interest to declare.
Funding statement
Financial support by the Austrian Science Fund (FWF) through grant DOI: 10.55776/I6427 (as part of the SFB/TRR 352) is gratefully acknowledged.