Introduction
The worldwide energy use for cooling by refrigerators and air conditioners is substantial. For example, in the United States, households used about 20% of all the generated electricity in 2016.1 This usage is projected to rise at least through 2050, despite steady improvements in the efficiencies of conventional cooling systems.Reference Shah, Khanna, Karali, Karali, Park, Qu and Zhou2 Today’s mainstream cooling technology, in development since the early 20th century, is based on vapor-compression cycles, and has reached about 30% of Carnot efficiency (representing the thermodynamic limit). Some alternatives, such as Peltier-based cooling using thermoelectric materials, which are a modern staple for solid-state refrigeration, realize an efficiency of only about 10% of the Carnot efficiency, and therefore have little but niche use. Ferroic cooling already exceeds the efficiency of thermoelectric systems, and has the potential to overtake that of vapor compression.Reference Kitanowski, Tušek, Tomc, Plaznik, Ožbolt and Poredoš3 However, this new technology is in the early stages, and will need some time to become cost competitive with conventional systems because of the large investment over the long research and development time older technologies have enjoyed.
This issue of MRS Bulletin introduces the state-of-the-art and ongoing developments in ferroic-caloric materials and their applications to cooling devices. In this article, we first explain a ferroic cooling cycle and describe similarities and differences between magnetocaloric, electrocaloric, and elastocaloric cooling. We then summarize the current status of materials and device development, as well as the challenges that lie ahead. We end with an outlook on possible novel applications beyond refrigeration enabled by ferroic-caloric materials.
How can ferroic materials be used in a cooling cycle?
Ferroic materials used as refrigerants in the core of ferroic cooling cycles earn the name ferroics due to peculiar transitions that alter symmetry at certain transition temperatures, T C.Reference Schmidt4 (For ferromagnetic and ferroelectric materials, TC is the Curie temperature; for ferroelastic materials it is the martensitic transition temperature.) As a result, a particular kind of ferroic order, described in a later section, is established when cooling, which can be either ferromagnetic, ferroelectric, or ferroelastic (as a starting point, one may just think ferromagnetic instead of ferroic in the rest of this section). In addition to temperature, these phase transitions can be driven by applying and removing external fields, namely magnetic, electric, or elastic fields.
To understand what makes a ferroic material suitable for a caloric application, a typical ferroic cooling cycle is sketched in Figure 1.Reference Fähler, Rößler, Kastner, Eckert, Eggeler, Emmerich, Entel, Müller, Quandt and Albe5–Reference Tishin and Spichkin8 Consider a case where the ferroic material undergoes a first-order phase transition, which is generally accompanied by latent heat, ΔL. Around T C, this phase transition can also be induced by external fields. Initially, both the material and its surroundings are at the same temperature, T. In the first step of the cooling cycle, a field strong enough to trigger a ferroic phase transition is applied adiabatically (the ferroic material does not exchange heat with the surroundings). This happens when the field change is completed much faster than it takes for the heat to flow out. Accordingly, the latent heat increases the temperature of the ferroic material by ∆T ≅ ΔL/C. Here, the material’s heat capacity, C, is assumed to be nearly constant before, during, and after application of the field. This is a simplification, as both ΔL and C may depend on the field strength, but it gives a good idea as to why a large ΔL helps induce sizable caloric effects.
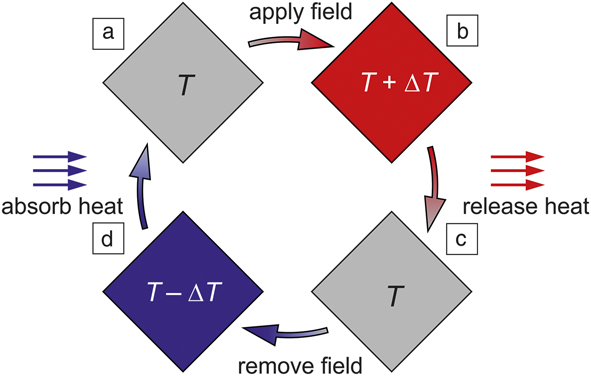
Figure 1. Schematic illustration of the ferroic cooling cycle. (a) The field is applied on a ferroic material to induce a phase transition. For a magnetocaloric material this is a magnetic field, for ferroelectric materials an electric field, for ferroelastic shape-memory alloys a mechanical stress field, and for barocaloric materials hydrostatic pressure. In the vicinity of the transition temperature, these fields increase the temperature of the ferroic material. (b) Heat is released to the external reservoir, which reduces the material’s temperature to ambient. (c) The field is switched off, which reduces the temperature of the ferroic material. (d) The sample is connected to a cold reservoir, extracting heat and closing the ferroic cooling cycle.
In the second step, the material is brought into contact with the ambient medium. This is still at T, which is now lower than T + ΔT of the material, and thus the material releases heat into the ambient surroundings, going back to its original T. In the third step, the field is removed adiabatically. Now latent heat is required to complete the transition and is taken from the material, which accordingly reduces its temperature by the same or nearly the same ∆T. In the fourth step, the ferroic-caloric material is brought into contact with the cold reservoir and absorbs heat. This is the decisive step during which ferroic cooling occurs. This also closes the cycle, which is repeated as long as cooling is required. This example assumes ΔL > 0 when the field is applied and the opposite when it is removed. Quite a few materials exhibit a so-called “inverse caloric effect” with ΔL < 0 upon field application and ΔL > 0 upon its removal.Reference Krenke, Duman, Acet, Wassermann, Moya, Mañosa and Planes9–Reference Marathe, Renggli, Sanlialp, Kararabasov, Shvatsman, Lupascu, Grunebohm and Ederer11 They are also suitable for cooling, but within the cycle illustrated in Figure 1 the words “apply” and “remove” must be switched for the inverse caloric effect.
When the ferroic material undergoes a second-order phase transition, there is no latent heat, but the external field tends to align the entities of the phase with lower symmetry. A magnetic (electric) field, for example, tends to align the magnetic spins (electric dipoles) parallel with the field direction. Compared to a disordered state, where the active entities point in any direction, this alignment reduces disorder, which is expressed by a reduction in entropy ∆S, and correspondingly heat (∆Q), because ∆Q = ∆S × T. In a simplified picture, this results in increased lattice vibrations, which increases temperature. Thus, the entropy change when applying (first step) or removing (third step) an external field is also a critical property of a ferroic-caloric material.
Both first- and second-order phase transitions are interesting and important for ferroic cooling. While first-order phase transitions can exhibit a large entropy change, ∆S, they are only usable over narrow temperature ranges around T C. Furthermore, many first-order phase transitions occur with hysteresis. The associated hysteresis lossesReference Entel and Fähler12 reduce the cooling efficiency and can even inhibit reversibility in the low fields that are feasible, for example, for consumer use. In contrast, ferroic materials with second-order phase transitions have no hysteresis, but typically demonstrate a lower entropy change, which can be used in a broader temperature range. Achieving an optimum balance offered by both types of materials remains a major challenge for ferroic cooling. Presumably, such an optimum condition can be found in materials or compositions located within the boundary separating first- and second-order transitions.
Why are ferroic materials susceptible to external fields?
The categories of ferroic transitions and conjugate fieldsReference Schmidt4 are illustrated in Figure 2. In general, ferroic materials exhibit phase transitions from a disordered state at higher temperatures to an ordered state at lower temperatures, forming domains, which are regions of “ordered entities.” In the low-temperature state, an external field can align and switch these domains. This general description becomes clearer when one considers specific types of ferroic order. In ferromagnetic materials, for example, a transition occurs from a disordered paramagnetic state above T C to an ordered ferromagnetic state below T C. The ordered entities, magnetic spins, form magnetic domains that can be aligned and switched by a magnetic field. In ferroelectric materials, the ordered entities are electric dipoles, which also form ferroelectric domains switchable by an electric field below T C. Ferroelastic materials (i.e., shape-memory alloys) exhibit diffusionless, reversible martensitic transitions from a unit cell with high symmetry (e.g., cubic) above T C toward a unit cell with lower symmetry (e.g., tetragonal) below T C. The ordered entities are low-symmetry unit cells. Domains, called martensitic variants, are formed by groups of identically aligned unit cells. These variants can be aligned by mechanical stress, or, generally speaking, by a stress field. In addition, in a number of materials, more than one ferroic order occurs in the same phase. These multiferroic materials can exhibit multicaloric effects.
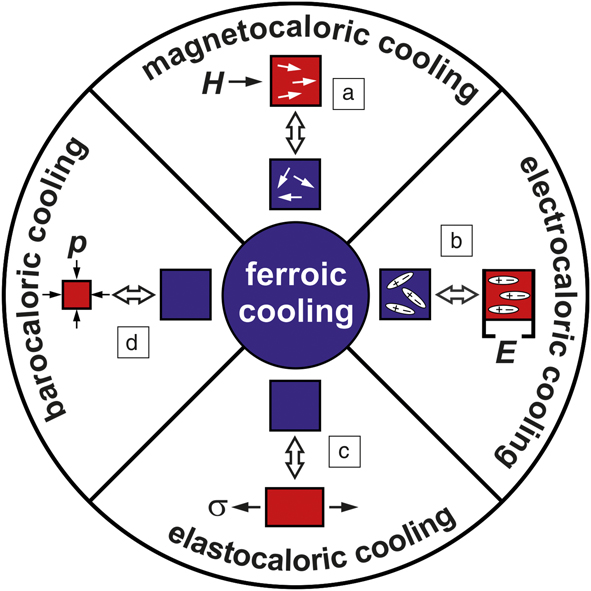
Figure 2. Different types of ferroic cooling and the susceptibilities of ferroic materials to external fields. (a) A magnetocaloric material above its Curie temperature is shown. When a magnetic field H is applied, the magnetic spins align toward the field direction. When the magnetic field is turned off, the spins point in random directions and thus have a higher entropy, which decreases the temperature of the magnetocaloric sample. (b) For ferroelectric materials, an electric field E is used to align the electric dipoles, symbolized by + and –. As with the magnetocaloric material, removing the E field increases entropy and reduces temperature. (c) Shape-memory alloys are elastocaloric materials, which exhibit a solid–solid structural transition, symbolized by the cubic unit cell (blue) and the tetragonal unit cell (red). When applying uniaxial tensile stress, σ, the long axes of the tetragonal unit cells align along the direction of the stress. Releasing this stress just above the transition temperature results in the reverse transition toward the cubic structure, which reduces temperature. (d) A barocaloric material and process is illustrated, where hydrostatic pressure, p, is used to control the transition between two phases exhibiting a difference in volume. In all cases, the blue boxes represent high-entropy, low-temperature states, and the red boxes represent low-entropy, high-temperature states.
To understand the caloric properties of ferroic materials, one must consider the following fundamental thermodynamic relationship:Reference Planes, Castan and Saxena13,Reference Stern-Taulats, Castán, Mañosa, Planes, Mathur and Moya14
Equation 1 describes the difference in Gibbs free energy, ∆G, of two phases connected by a ferroic transition. The first two terms on the right side are common for all materials and describe the differences between internal energies, ∆U, and entropies, ∆S, of both phases at a given temperature T, while the remaining contributions are specific to ferroic compounds. Hence, the third factor applies to ferromagnetic materials, where there is a difference, ∆M, between magnetizations of both phases. The product –µ0H∆M, where µ0 is the vacuum permeability, shows that a magnetic field H stabilizes the phase with higher magnetization. Around T C, where |ΔM| can be substantial, this contribution can be large enough to lower ΔG, thus inducing phase transition and supporting a magnetocaloric cooling cycle.Reference Waske, Gruner, Gottschall and Gutfleisch15–Reference Brown17
The term E∆P applies to ferroelectric materials, where both phases may have a large difference in electric polarization, ∆P, and accordingly, an electric field E can drive an electrocaloric cooling cycle.Reference Moya, Defay, Mathur and Hirose18,Reference Kobeko and Kurtschatov19 In ferroelastic materials, both phases have different crystal structures and thus a difference in spontaneous strain ∆u comes into play. Accordingly, a mechanical stress field σ can drive an elastocaloric cooling cycle.Reference Frenzel, Eggeler, Quandt, Seelecke and Kohl20–Reference Gough22 The last contribution is important for materials whose volume changes by ∆V at the transition. Then, a hydrostatic pressure p favors the lower volume phase. The resulting barocaloric cooling cycle is equivalent to a vapor-compression cycle, except that barocaloric materials remain in the solid state in both phases.Reference Mañosa, González-Alonso, Planes, Bonnot, Barrio, Tamarit, Aksoy and Acet23 Strictly speaking, a symmetry-conserving transition with volume change is not ferroic as there are no switchable entities, but due to the thermodynamic similarities, barocaloric materials may be considered as a subclass of ferroic materials. This issue does not cover barocaloric effects in detail as it is technologically difficult to realize hydrostatic pressure and efficient heat exchange to/from a solid in the same device; this has hindered the demonstration of a barocaloric cooling prototype. For the sake of completeness, we note that the elastocaloric and barocaloric effects are jointly identified as mechanocaloric effects.Reference Moya, Kar-Narayan and Mathur24
Which material properties are required to make ferroic materials suitable for caloric applications?
To achieve good caloric properties, ferroic materials must exhibit a large change in at least one order parameter (∆M, ∆P, ∆u) in a narrow temperature range. This occurs in the vicinity of T C, which defines the temperature range where ferroic cooling can be efficient. The key functional property of all ferroic-caloric materials is the field-induced adiabatic temperature change ∆T. A large |∆T| is beneficial to realize a large temperature span for cooling, but in most cases a single material cannot support the span of about 30 K needed for a useful refrigerator. Thus, commonly, a series of materials with closely spaced T C values is used. This requires that T C be tuned easily (e.g., by varying the composition).
The second key property is the change in entropy ∆S occurring simultaneously with ∆T. Broadly, ∆S defines how much heat the ferroic-caloric material can transport during one cooling cycle, so ∆S should be maximized. The maximum values for ∆T and ∆S should be triggered by low field strengths, since creating huge fields is both technologically difficult (for magnetocalorics) and destructive (dielectric breakdown in electrocalorics or loss of mechanical integrity in elastocalorics). Another important material property is good thermal conductivity to allow fast heat exchange with the surroundings. This increases the cycle frequency and the cooling power.
The ideal ferroic-caloric compound must be easily machinable or adaptable to processing, as it is necessary to shape the material to a high surface-to-volume ratio for fast heat exchange. A high-quality caloric material must also have a large heat capacity in order to serve as an effective regenerator. Additionally, low functional fatigue is important for practical devices, which need to operate for 10+ years. Aiming at cycle frequencies of ∼10 Hz, ferroic-caloric materials should survive some 109 cooling cycles. Finally, they should consist of abundant and environmentally friendly components.
In this issue
Among the four ferroic cooling approaches, magnetocaloric cooling is the most mature in terms of development. In their article in this issue, Waske et al.Reference Waske, Gruner, Gottschall and Gutfleisch15 describe in more detail the functional properties required for magnetocaloric cooling, state-of-the-art materials, and how they can be processed into effective regenerators. Zimm et al.Reference Zimm, Boeder, Mueller, Rule and Russek25 cover the application of magnetocaloric materials in refrigeration devices.
Two articles in the issue focus on elastocaloric materials, which reach the highest combination of ∆T and ∆S values among all ferroic materials, and some challenges in their implementation in cooling devices. Frenzel et al.Reference Frenzel, Eggeler, Quandt, Seelecke and Kohl20 focus on the tensile mode, which enables fast heat exchange and avoidance of functional fatigue by lattice compatibility. Hou et al.Reference Hou, Cui, Qian, Catalini, Hwang, Radermacher and Takeuchi21 discuss the use of the compression mode to reduce fatigue and demonstrate work recovery to boost efficiency.
In their article, Moya et al.Reference Moya, Defay, Mathur and Hirose18 focus on electrocaloric materials and describe how multilayer capacitors can be used for cooling applications. Though electrocaloric cooling has probably the lowest technology readiness level among the three, it promises the most direct conversion of electrical to thermal energy. The last article by Stern-Taulats et al.Reference Stern-Taulats, Castán, Mañosa, Planes, Mathur and Moya14 addresses new cooling concepts, such as coupling ferroic-caloric effects to trigger multicaloric effects.
Beyond refrigeration
The development of ferroic materials for cooling has also enabled new functionalities beyond refrigeration. This is most evident for magnetocaloric materials. The cycle sketched in Figure 1 represents a heat pump and accordingly the hot side can be used when heating is required instead of cooling.Reference Kitanowski, Tušek, Tomc, Plaznik, Ožbolt and Poredoš3 In place of using electrical energy to obtain a temperature difference by changing the magnetic field, the reverse process is also possible. Cycling the temperature of a magnetocaloric material around T C results in a change of magnetization, enabling one to switch the magnetic flux on and off. An induction coil placed around the magnetocaloric material is a simple demonstration of the so-called thermomagnetic generator that converts thermal energy into electrical. Though conceived by TeslaReference Tesla26 and EdisonReference Edison27 more than 100 years ago, working demonstrators became feasible only with advanced magnetocaloric materials.Reference Srivastava, Song, Bhatti and James28,Reference Christiaanse and Brück29 These exhibit a sharp change in magnetization with temperature, potentially allowing for harvesting low-grade waste heat commonly available below 100°C. First demonstrations of such devices work also on a miniaturized scaleReference Gueltig, Wendler, Ossmer, Ohtsuka, Miki, Takagi and Kohl30 and, with a similar approach called a thermomagnetic motor, also within the kilowatt range.31
Beyond energy, magnetocaloric materials are being explored for hyperthermia therapy, where cancer is treated by subjecting magnetic (nano-) particles within the tumor to an alternating magnetic field to generate heat. First-order magnetocaloric materials exhibit a sharp decrease in magnetization at the transition temperature, which automatically prevents overheating, preserving healthy tissue from destruction.Reference Barati, Selomulya, Sandeman and Suzuki32 These examples demonstrate that novel functional materials can also be used to address issues in areas other than refrigeration. It will be interesting to see which unexpected applications become feasible by the ongoing development of ferroic-caloric materials over time.
Acknowledgments
S.F. acknowledges funding by the German Research Foundation (DFG) through the Priority Program on Ferroic Cooling (SPP 1599). V.K.P. acknowledges funding by the Advanced Manufacturing Office of the Office of Energy Efficiency & Renewable Energy of the US Department of Energy (DOE) through the caloric materials consortium, CaloriCool, and Ames Laboratory, which is operated for the DOE by Iowa State University of Science and Technology under Contract No. DE-AC02–07CH11358. We acknowledge A. Diestel for the illustrations.

Sebastian Fähler is head of the research group on Functional Magnetic Films at the IFW Dresden, Germany. He received his PhD degree in physics at Georg August University, Germany, in 1998. He completed his Habilitation degree at TU Dresden, Germany, in 2014. His research includes ferroic cooling, (magnetic) shape-memory alloys, E-field control of magnetism, hard magnetic films, and magnetic nanowires. He has coordinated the DFG-funded German Priority Programs on magnetic shape-memory alloys (SPP 1239) and is coordinating one on ferroic cooling (SPP 1599). Fähler can be reached by email at [email protected].

Vitalij K. Pecharsky is an Anson Marston Distinguished Professor of Materials Science and Engineering, and faculty scientist at the US Department of Energy Ames Laboratory. He received his PhD degree in inorganic chemistry from Lviv State University, Ukraine, in 1979. His current research involves rare-earth, hydrogen-containing, and magnetocaloric materials. He co-edits the Journal of Alloys and Compounds and the Handbook on the Physics and Chemistry of Rare Earths. He leads two research programs funded by the Office of Science of the US Department of Energy (DOE), and also directs CaloriCool (the Caloric Materials Consortium), funded by the Office of Energy Efficiency & Renewable Energy of the DOE. Pecharsky can be reached by email at [email protected].





