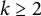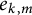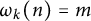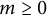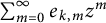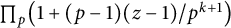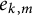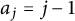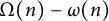1 Introduction
Let
$\omega (n)$
be the number of distinct prime factors of a positive integer n, and let
$\Omega (n)$
be the number of prime factors of n counted with multiplicity. Average behaviours of such arithmetic functions are understood via their summatory functions. It is known [Reference Hardy and Ramanujan7] (see also [Reference Hardy, Wright, Heath-Brown and Silverman8, Theorems 427–430]) that
$$ \begin{align} \begin{aligned} \sum_{n\leqslant x} \omega(n)&=x\log\log x+bx+O\biggl(\frac{x}{\log x} \biggr) \\ \sum_{n\leqslant x} \Omega(n)&=x\log\log x+\biggl(b+\sum_{p } \frac{1}{p(p-1)} \biggr)x+O\biggl(\frac{x}{\log x} \biggr); \end{aligned} \end{align} $$
here the constant b is defined by
$$ \begin{align} b&=\gamma_0+\sum_{p} \sum_{j=2}^{\infty} \frac{1}{jp^j} \end{align} $$
where
$\gamma _0$
denotes the Euler–Mascheroni constant. (In this paper,
$\sum _p$
and
$\prod _p$
always denote sums and products running over all prime numbers.) The celebrated Erdős–Kac theorem tells us that both
$\omega (n)$
and
$\Omega (n)$
can be normalized to have Gaussian limiting distribution functions.
By the asymptotic formulas (1.1), the difference
$\Omega (n)-\omega (n)$
has an average value, namely the constant
$$ \begin{align*} \lim_{x\to\infty} \frac1x \sum_{n\leqslant x} \bigl( \Omega(n)-\omega(n) \bigr) = \sum_{p} \frac{1}{p(p-1)}, \end{align*} $$
which provides motivation to study the frequency of each possible value of
${\Omega (n)-\omega (n)}$
. For any integer
$m\geqslant 0$
, define
$$ \begin{align*} \mathcal{N}_m(x)=\lbrace n\leqslant x\colon \Omega(n)-\omega(n)=m\rbrace. \end{align*} $$
Rényi [Reference Rényi10] (see also [Reference Montgomery and Vaughan9, Section 2.4]) proved that the (natural) densities
$$ \begin{align} d_m=\lim_{x\to \infty} \frac{\#\mathcal{N}_m(x)}{x} = \frac{6}{\pi^2} \sum_{\substack{f\in\mathcal{F} \\ \Omega(f)-\omega(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} \end{align} $$
exist for every
$m\geqslant 0$
, where
$\mathcal {F}$
is the set of powerful numbers (the set of positive integers all of whose prime factors have multiplicity
$\geqslant 2$
). Furthermore, he showed that these densities have the generating function
$$ \begin{align} \sum_{m=0}^{\infty}d_mz^m=\prod_{p} \biggl(1-\frac{1}{p} \biggr)\biggl(1+ \frac{1}{p-z} \biggr) \qquad (|z|<2). \end{align} $$
(Note the special case
$d_0 = \prod _p (1-\frac 1p)(1+\frac 1p) = \frac 1{\zeta (2)} = \frac 6{\pi ^2}$
for the density of squarefree numbers, which can also be confirmed by realizing that the sum in equation (1.3) contains only the single term
$f=1$
when
$m=0$
.) In particular, the smaller function
$\Omega (n)-\omega (n)$
already has a (discrete) limiting distribution function, without needing normalization in the way that the larger functions
$\omega (n)$
and
$\Omega (n)$
individually do.
As a refinement of the function
$\omega (n)$
, Liu and the first author introduced the functions
$$ \begin{align*} \omega_k(n)=\sum_{p^k \| n}1 \end{align*} $$
for each integer
$k\geqslant 1$
, so that
$\omega _k(n)$
counts the number of prime factors of n with multiplicity k and thus
$\omega (n) = \sum _{k=1}^\infty \omega _k(n)$
. They showed [Reference Elma2] that
$$ \begin{align*} \sum_{n\leqslant x} \omega_1(n)=x\log\log x+\biggl(b-\sum_{p} \frac{1}{p^2} \biggr)x+O\biggl(\frac{x}{\log x} \biggr) \end{align*} $$
where b is the constant from equation (1.2), while
$$ \begin{align} \sum_{n\leqslant x} \omega_k(n)=x\sum_{p} \frac{p-1}{p^{k+1}}+O\bigl(x^{(k+1)/(3k-1)} \log^2x\bigr) \qquad (k\geqslant 2). \end{align} $$
They also showed that the larger function
$\omega _1(n)$
has a Gaussian limiting distribution function after being normalized in the same way as the classical
$\omega (n)$
and
$\Omega (n)$
. However, since equation (1.5) shows that
$\omega _k(n)$
has an average value for each
$k\geqslant 2$
, we might expect these smaller functions to have limiting distributions without needing to be normalized.
In this paper, we obtain the limiting distribution for the functions
$\omega _k(n)$
for
$k\geqslant 2$
, analogous to the results of Rényi described above. For integers
$m\geqslant 0$
, define
$$ \begin{align} \mathcal{N}_{k,m}(x)=\lbrace n\leqslant x\colon \omega_k(n)=m\rbrace \end{align} $$
to be the set of positive integers
$n\leqslant x$
with exactly m prime factors of multiplicity k. Our main result establishes the existence of the densities
$$ \begin{align*} e_{k,m} = \lim_{x\to \infty} \frac{\#\mathcal{N}_{k,m}(x)}{x} \end{align*} $$
and gives an exact formula for the
$e_{k,m}$
involving an infinite sum.
Theorem 1.1 Uniformly for all integers
$k\geqslant 2$
and
$m\geqslant 0$
,
$$ \begin{align*} \#\mathcal{N}_{k,m}(x) = e_{k,m}x+O(x^{1/2} \log x) \end{align*} $$
with
$$ \begin{align*} e_{k,m}= \frac{6}{\pi^2} \sum_{\substack{f\in\mathcal{F} \\ \omega_k(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1}. \end{align*} $$
Remark 1.2 Note that the
$e_{k,m}$
are all nonnegative, and we can check that they do sum to
$1$
:
$$ \begin{align*} \sum_{m=0}^\infty e_{k,m} &= \sum_{m=0}^\infty \frac{6}{\pi^2} \sum_{\substack{f\in\mathcal{F} \\\omega_k(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} = \frac{6}{\pi^2} \sum_{f\in\mathcal{F}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1}. \end{align*} $$
Since the summand is a multiplicative function of f, as is the indicator function of
$\mathcal {F}$
, the right-hand side equals its Euler product
$$\begin{align*}\frac{6}{\pi^2} \prod_p \biggl( 1 + 0 + \biggl(1+\frac{1}{p} \biggr)^{-1} \biggl( \frac1{p^2} + \frac1{p^3} + \cdots \biggr) \biggr) = \frac{6}{\pi^2} \prod_p \biggl( 1-\frac1{p^2} \biggr)^{-1} = 1. \end{align*}$$
The same remark applies to the densities in equation (1.10) below.
Moreover, we obtain an identity analogous to equation (1.4) for the generating function of the densities
$e_{k,m}$
for fixed
$k\geqslant 2$
, from which we can derive an upper bound for the densities
$e_{k,m}$
when
$k\geqslant 2$
is fixed and
$m\to \infty $
.
Theorem 1.3 Let
$k\geqslant 2$
be an integer. For all
$z\in \mathbb {C}$
with
$|z|\leqslant 1$
,
$$ \begin{align} \sum_{m=0}^{\infty}e_{k,m}z^{m}=\prod_{p} \biggl(1+\frac{(p-1)(z-1)}{p^{k+1}} \biggr). \end{align} $$
Corollary 1.4 For each fixed
$k\geqslant 2$
, we have
$e_{k,m} \leqslant m^{-(k-o(1))m}$
as
$m\to \infty $
.
Remark 1.5 The proof of the upper bound in Corollary 1.4 (see Section 3) shows that for each
$k\geqslant 2$
, the bound is attained for infinitely many m; it would be interesting to try to show that
$e_{k,m} = m^{-(k-o(1))m}$
for all k and m. Moreover, the corollary and its proof show that both sides of equation (1.7) converge to entire functions, and thus Theorem 1.3 actually holds for all
$z\in \mathbb {C}$
by uniqueness of analytic continuation. The same remarks apply to the generating functions in Corollary 1.14 and the upper bounds in Corollary 1.15 below.
Some numerical values of
$e_{k,m}$
are given in Table 1. The numbers in the first column corresponding to
$m=0$
are increasing as k increases, whereas the numbers in other columns are decreasing. This behaviour stems from the fact that the case
$m=0$
indicates the nonexistence of prime factors with multiplicity k, which becomes more probable as k increases. (Note also that each number in the first column exceeds
$\frac 6{\pi ^2} \approx 0.608$
, since every squarefree number n certainly has
$\omega _k(n)=0$
for all
$k\geqslant 2$
.) On the other hand, for
$m\geqslant 1$
, the criterion
$\omega _{k}(n)=m$
indicates the existence of prime factors with multiplicity k, which becomes less probable as k increases. Details of the calculations of these values are given in Section 4, although we do note here that the calculations use the generating function in Theorem 1.3 rather than the formula for
$e_{k,m}$
in Theorem 1.1.
Table 1 Some values of
$e_{k,m}$
.
A consequence of Theorem 1.1 and Remark 1.2 is that
$\omega _k(n)$
has a limiting distribution, which is the same as the distribution of the nonnegative integer-valued random variable
$X_k$
that takes the value m with probability
$e_{k,m}$
. While it is straightforward to calculate the expectation and variance of this limiting distribution via the expressions
$$\begin{align*}\lim_{x\to\infty} \frac1x \sum_{n\leqslant x} \omega_k(n) \qquad\text{and}\qquad \lim_{x\to\infty} \frac1x \sum_{n\leqslant x} \omega_k(n)^2 - \biggl( \lim_{x\to\infty} \frac1x \sum_{n\leqslant x} \omega_k(n) \biggr)^2, \end{align*}$$
we can observe that the generating function from Theorem 1.3 provides a quick way to obtain the answers with no further input from number theory.
Corollary 1.6 The limiting distribution of
$\omega _k(n)$
has expectation
$\displaystyle \sum _{p} \frac {p-1}{p^{k+1}}$
and variance
$\displaystyle \sum _p \frac {p-1}{p^{k+1}} \biggl ( 1 - \frac {p-1}{p^{k+1}} \biggr )$
.
Remark 1.7 Not surprisingly, these quantities are the expectation and variance of the sum of infinitely many Bernoulli random variables
$B_p$
, indexed by primes p, where
$B_p$
takes the value
$1$
with probability
$(p-1)/p^{k+1}$
(the density of those integers exactly divisible by
$p^k$
).
These quantities are easy to calculate to reasonably high precision (see Section 4 for details); we record some numerical values in Table 2. The reader can confirm that the listed expectations are in good agreement with the quantities
$0e_{k,0}+1e_{k,1}+2e_{k,2}+3e_{k,3}$
as calculated from Table 1.
Table 2 Statistics of the limiting distribution of
$\omega _k(n)$
.
1.1 Generalizations
It turns out that our proof of Theorem 1.1 goes through for a far larger class of additive functions than just the
$\omega _k(n)$
. Given any sequence
$A=(a_1,a_2, a_3 ,\dots )$
of complex numbers, define the additive function
$$ \begin{align} \omega_{A}(n)=\sum_{j=1}^{\infty}a_j\omega_{j}(n), \end{align} $$
which is of course a finite sum for each integer n.
Remark 1.8 This definition generalizes all the examples we have seen so far:
-
• if
$a_j=1$
always then
$\omega _{A}(n) = \omega (n)$
; -
• if
$a_j=j$
always then
$\omega _{A}(n) = \Omega (n)$
; -
• if
$a_j=j-1$
always then
$\omega _{A}(n)=\Omega (n)-\omega (n)$
; -
• for a fixed positive integer k, if
$a_k=1$
while
$a_j=0$
for
$j\neq k$
, then
$\omega _{A}(n)=\omega _k(n)$
.
When
$a_1\ne 0$
, classical techniques show that the large function
$\frac 1{a_1} \omega _A(n)$
has the same Gaussian limiting distribution as
$\omega (n)$
and
$\Omega (n)$
when properly normalized (at least if the
$a_j$
do not grow too quickly). Therefore we restrict our attention to the smaller functions
$\omega _A(n)$
where
$a_1=0$
, which we expect to have limiting distributions without needing normalization.
For
$m\in \mathbb {C}$
, define
$$ \begin{align*} \mathcal{N}_{A,m}(x)=\lbrace n\leqslant x \colon \omega_{A}(n)=m\rbrace. \end{align*} $$
Our next result, which generalizes both equation (1.3) and Theorem 1.1, establishes the existence of the densities
$$ \begin{align} e_{A,m} = \lim_{x\to \infty} \frac{\#\mathcal{N}_{A,m}(x)}{x} \end{align} $$
and provides an exact formula for them.
Theorem 1.9 Uniformly for all sequences
$A=(0,a_2,a_3,\dots )$
of complex numbers with
$a_1=0$
and for all
$m\in \mathbb {C}$
,
$$ \begin{align*} \#\mathcal{N}_{A,m}(x) = e_{A,m}x+O(x^{1/2} \log x) \end{align*} $$
with
$$ \begin{align} e_{A,m}= \frac{6}{\pi^2} \sum_{\substack{f\in\mathcal{F} \\ \omega_A(f) = m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1}. \end{align} $$
If we now restrict to the case where the
$a_j$
(and thus all values of
$\omega _A(n)$
) are nonnegative integers, it once again makes sense to consider generating functions. Our next result generalizes both equation (1.4) and Theorem 1.3 in light of Remark 1.8.
Theorem 1.10 Let
$A=(0,a_2,a_3,\dots )$
be a sequence of nonnegative integers. For all
$z\in \mathbb {C}$
with
$|z|\leqslant 1$
,
$$ \begin{align} \sum_{m=0}^{\infty}e_{A,m}z^{m}=\prod_{p} \biggl(1-\frac{1}{p^2}+\sum_{j=2}^{\infty}z^{a_j} \biggl(\frac{1}{p^{j}}-\frac{1}{p^{j+1}} \biggr)\biggr). \end{align} $$
Remark 1.11 The Erdős–Wintner theorem [Reference Erdős3, Reference Erdős and Wintner4] (see also [Reference Tenenbaum11, Chapter III.4]) implies the existence of a limiting distribution for
$\omega _A(n)$
, as well as a formula for its characteristic function that is related to equation (1.11); indeed that approach works for any additive function f with
$f(p)=0$
for all primes p. On the other hand, our elementary approach shares the advantages of Rényi’s [Reference Rényi10] of giving formulas for the densities
$e_{A,m}$
and the means to compute their numerical values and asymptotic size.
Again Theorem 1.10 shows that
$\omega _A(n)$
has a limiting distribution when the
$a_j$
are nonnegative integers, and we can therefore generalize Corollary 1.6; we record only the expectation for simplicity.
Corollary 1.12 Let
$A=(0,a_2,a_3,\dots )$
be a sequence of nonnegative integers. The limiting distribution of
$\omega _A(n)$
has expectation
$\displaystyle \sum _{p} \sum _{j=2}^{\infty }a_j\biggl (\frac {1}{p^{j}}-\frac {1}{p^{j+1}} \biggr )$
.
Remark 1.13 It is certainly possible for this expectation to be infinite, as the example
$A=(0,2,4,8,16,\dots )$
shows. In such cases
$\frac 1x \sum _{n\leqslant x} \omega _A(n)$
grows too quickly for the mean value of
$\omega _A(n)$
to exist. Note, however, that Theorems 1.9 and 1.10 hold no matter how quickly the sequence A might grow.
We examine three specific examples of such sequences for the purposes of illustration: set
$S=(0,1,1,\dots )$
and
$E = (0,1,0,1,\dots )$
and
$O = (0,0,1,0,1,0,1,\dots )$
. Then the corresponding omega functions are
$$ \begin{align*} \omega_{{S}}(n) =\sum_{j\geqslant 2} \omega_j(n) \quad\text{and} \quad \omega_{{E}}(n) =\sum_{\substack{j\geqslant 2\\ j \text{ even}}} \omega_{j}(n) \quad\text{and} \quad \omega_{{O}}(n) =\sum_{\substack{j\geqslant 3\\ j \text{ odd}}} \omega_{j}(n) \end{align*} $$
which count, respectively, the number of primes dividing the powerful part of n (that is, the number of primes dividing n at least twice), the number of primes dividing n with even multiplicity, and the number of primes dividing n with odd multiplicity exceeding
$1$
. For integers
$m\geqslant 0$
, let
$e_{{S},m}$
and
$e_{{E},m}$
and
$e_{{O},m}$
be the corresponding densities defined in equation (1.9). An easy calculation of the right-hand side of equation (1.11) in these cases (for which each factor becomes a geometric series) yields the following generating functions:
Corollary 1.14 For all
$z\in \mathbb {C}$
with
$|z|\leqslant 1$
,
$$ \begin{align*} \sum_{m=0}^{\infty}e_{{S},m}z^{m}&=\prod_{p} \biggl(1+\frac{z-1}{p^{2}} \biggr) \\\sum_{m=0}^{\infty}e_{{E},m}z^{m}&=\prod_{p} \biggl(1+\frac{z-1}{p(p+1)} \biggr) \\\sum_{m=0}^{\infty}e_{{O},m}z^{m}&=\prod_{p} \biggl(1+\frac{z-1}{p^{2}(p+1)} \biggr). \end{align*} $$
Corollary 1.15 We have
$e_{{S},m} \leqslant m^{-(2-o(1))m}$
and
$e_{{E},m} \leqslant m^{-(2-o(1))m}$
and
$e_{{O},m} \leqslant m^{-(3-o(1))m}$
as
$m\to \infty $
.
Remark 1.16 One interesting class of functions for which our methods accomplish less than desired are functions of the form
$\omega _A(n)$
where A contains integers but not necessarily only nonnegative integers. For example, if
$A = (0,1,-1,0,0,\dots )$
then
$\omega _A(n) = \omega _2(n)-\omega _3(n)$
, while if
$A=(0,1,-1,1,-1,\dots )$
then
$\omega _A(n) = \omega _E(n) - \omega _O(n)$
. The target
$m=0$
is natural to investigate, as
$\omega _A(n) = 0$
in these two examples translates into
$\omega _2(n) = \omega _3(n)$
and
$\omega _E(n) = \omega _O(n)$
, respectively. While Theorem 1.9 gives a formula for the density of those integers n satisfying each of these equalities, our numerical techniques in Section 4 (which ultimately rely on being able to find the values of the derivatives of the appropriate generating function at
$z=0$
) are not able to approach the question of good numerical approximations to these densities.
In Section 2 we establish Theorems 1.9 and 1.10, the formula and generating function for
$e_{A,m}$
, from which Theorems 1.1 and 1.3 follow as special cases. In Section 3 we deduce Corollaries 1.4 and 1.15 (the decay rates of
$e_{k,m}$
and certain variants) from Theorem 1.3 and Corollary 1.14. Finally, in Section 4 we describe the computations leading to the numerical values in Tables 1 and 2, as well as establishing Corollaries 1.6 and 1.12 concerning the expectation and variance of the additive functions under examination.
2 Exact formula and generating function for the densities
We first prove Theorem 1.9, which will also establish the special case that is Theorem 1.1, by following the exposition of Rényi’s result (1.3) in [Reference Montgomery and Vaughan9, Section 2.4]. Recall the notation of equation (1.8), and recall that
$\mathcal {F}$
denotes the set of powerful numbers.
Lemma 2.1 Uniformly for all sequences
$A=(a_1,a_2,\dots )$
of complex numbers and all
$m\in \mathbb {C}$
,
$$\begin{align*}\sum_{\substack{f\leqslant x\\f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f^{1/2}} \prod_{p\mid f} (1-p^{-1/2} )^{-1} \ll \log x. \end{align*}$$
Proof By dropping the condition
$\omega _{A}(f)=m$
and noting that
$f\leqslant x$
implies that all prime factors of f are at most x, we have by positivity
$$ \begin{align*} \sum_{\substack{f\leqslant x \\ f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f^{1/2}} \prod_{p\mid f} (1-p^{-1/2} )^{-1}&\leqslant \sum_{\substack{f\leqslant x \\ f\in\mathcal{F}}} \frac{1}{f^{1/2}} \prod_{p\mid f} (1-p^{-1/2} )^{-1} \\&\leqslant \sum_{\substack{f\in\mathcal{F} \\ p\mid f \implies p\leqslant x}} \frac{1}{f^{1/2}} \prod_{p\mid f} (1-p^{-1/2} )^{-1}. \end{align*} $$
The right-hand side has an Euler product whose factors involve geometric series with common ratio
$p^{-1/2}$
:
$$ \begin{align*} \sum_{\substack{f\in\mathcal{F} \\ p\mid f \implies p\leqslant x}} \frac{1}{f^{1/2}} \prod_{p\mid f} (1-p^{-1/2} )^{-1} &= \prod_{p\leqslant x} \biggl(1 + \frac{(1-p^{-1/2} )^{-1}}{(p^2)^{1/2}} + \frac{(1-p^{-1/2} )^{-1}}{(p^3)^{1/2}} + \cdots \biggr) \\&= \prod_{p\leqslant x} \biggl( 1 + \frac1{(p^{1/2}-1)^2} \biggr) \\&= \prod_{p\leqslant x} \biggl( 1 - \frac1p \biggr)^{-1} \prod_{p\leqslant x} \biggl( 1 + \frac2{p(p^{1/2}-1)} \biggr); \end{align*} $$
this establishes the lemma, since the first product is asymptotic to a multiple of
$\log x$
as shown by Mertens, while the second is a convergent product of the form
$\prod _p (1+O(p^{-3/2}))$
.
Lemma 2.2 Uniformly for all sequences
$A=(a_1,a_2,\dots )$
of complex numbers and all
$m\in \mathbb {C}$
,
$$\begin{align*}\sum_{\substack{f>x \\ f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} \ll x^{-1/2}. \end{align*}$$
Proof Golomb [Reference Golomb6] proved that the number of powerful numbers up to y is asymptotic to a constant times
$y^{1/2}$
. Thus for each integer
$r\geqslant 0$
,
$$\begin{align*}\sum_{\substack{ 2^rx < f \leqslant 2^{r+1}x \\f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} < \frac1{2^rx} \sum_{\substack{ 2^rx < f \leqslant 2^{r+1}x \\f\in\mathcal{F}}} 1 \ll \frac1{2^rx} (2^{r+1}x)^{1/2} \ll 2^{-r/2}x^{-1/2}, \end{align*}$$
and consequently
$$\begin{align*}\sum_{\substack{f>x\\f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} = \sum_{r=0}^\infty \sum_{\substack{ 2^rx < f \leqslant 2^{r+1}x \\f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} \ll \sum_{r=0}^\infty 2^{-r/2}x^{-1/2} \ll x^{-1/2}. \end{align*}$$
Proof of Theorem 1.9
Fix a sequence
$A=(0,a_2,a_3,\ldots )$
of complex numbers and a target
$m\in \mathbb {C}$
. Every positive integer n can be written uniquely as
$n=qf$
where q is squarefree, f is powerful, and
$(q,f)=1$
(indeed, q is the product of the primes dividing n exactly once). In this notation, the condition
$\omega _{A}(n)=m$
is equivalent to
$\omega _{A}(f)=m$
(since
$a_1=0$
), and thus
$$ \begin{align} \#\mathcal{N}_{A,m}(x)=\sum_{\substack{f\leqslant x\\ f\in\mathcal{F} \\ \omega_A(f)=m}} \sum_{\substack{q\leqslant x/f \\ (q,f)=1}} \mu^2(q). \end{align} $$
To estimate the inner sum above, we use [Reference Montgomery and Vaughan9, Lemma 2.17] which says that for any
$y\geqslant 1$
and any positive integer f,
$$\begin{align*}\sum_{\substack{n\leqslant y\\ (n,f)=1}} \mu^2(n)=\frac{6}{\pi^2}y \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} + O\biggl(y^{1/2} \prod_{p\mid f} (1-p^{-1/2})^{-1} \biggr). \end{align*}$$
Inserting this asymptotic formula into equation (2.1) yields
$$ \begin{align*} \#\mathcal{N}_{A,m}(x) &= \frac{6}{\pi^2}x\sum_{\substack{f\leqslant x\\f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} + O\biggl(x^{1/2} \sum_{\substack{f\leqslant x\\f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f^{1/2}} \prod_{p\mid f}(1-p^{-1/2})^{-1} \biggr) \\ &= \frac{6}{\pi^2}x \biggl( \sum_{\substack{f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} - \sum_{\substack{f>x\\f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} \biggr) + O(x^{1/2}\log x) \\ &= \frac{6}{\pi^2}x \biggl( \sum_{\substack{f\in\mathcal{F} \\\omega_A(f)=m}} \frac{1}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} + O(x^{-1/2}) \biggr) + O(x^{1/2}\log x) \end{align*} $$
by Lemmas 2.1 and 2.2, which completes the proof of the theorem.
With Theorem 1.9 now established, it is a simple matter to prove Theorem 1.10, which will also establish the special case that is Theorem 1.3.
Proof of Theorem 1.10
Fix a sequence
$A=(0,a_2,a_3,\ldots )$
of nonnegative integers. Note that
$\sum _{m=0}^{\infty }e_{A,m} = 1$
(by the argument in Remark 1.2), and therefore
$\sum _{m=0}^{\infty }e_{A,m}z^{m}$
converges absolutely for any complex number z with
$|z|\leqslant 1$
. By Theorem 1.9,
$$ \begin{align*} \sum_{m=0}^{\infty}e_{A,m}z^{m}&=\frac{6}{\pi^2} \sum_{m=0}^{\infty} z^m \sum_{\substack{f\in\mathcal{F} \\\omega_A(f)=m}} \frac1{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} = \frac{6}{\pi^2} \sum_{f\in\mathcal{F}} \frac{z^{\omega_A(f)}}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1}. \end{align*} $$
Since
${z^{\omega _A(f)}}/{f} = \prod _{p^j\| f} {z^{\omega _A(p^j)}}/{p^j} = \prod _{p^j\| f} {z^{a_j}}/{p^j}$
, the right-hand side equals its Euler product
$$ \begin{align*} \frac{6}{\pi^2} \sum_{f\in\mathcal{F}} \frac{z^{\omega_A(f)}}{f} \prod_{p\mid f} \biggl(1+\frac{1}{p} \biggr)^{-1} &= \frac{6}{\pi^2} \prod_p \biggl(1+\biggl(1+\frac{1}{p} \biggr)^{-1} \sum_{j= 2}^{\infty} \frac{z^{a_j}}{p^{j}} \biggr) \\ &= \prod_p \biggl(1-\frac{1}{p^2} \biggr) \biggl(1+\biggl(1+\frac{1}{p} \biggr)^{-1} \sum_{j= 2}^{\infty} \frac{z^{a_j}}{p^{j}} \biggr) \\ &=\prod_{p} \biggl(1-\frac{1}{p^2} + \biggl(1-\frac{1}{p} \biggr) \sum_{j= 2}^{\infty} \frac{z^{a_j}}{p^{j}} \biggr), \end{align*} $$
which is equal to the right-hand side of equation (1.11), thus establishing the theorem.
3 Decay rates of the densities
In this section, we deduce Corollary 1.4 from Theorem 1.3 and Corollary 1.15 from Theorem 1.10. The key step is to give a proposition establishing the rate of growth of infinite products such as those appearing in Theorems 1.3 and 1.10, which we do after the following simple lemma for the prime-counting function
$\pi (y)$
and its logarithmically weighted version
$\theta (y)$
.
Lemma 3.1
$\pi (y)\log y - \theta (y) \sim y/\log y$
as
$y\to \infty $
.
Proof By the prime number theorem,
$$ \begin{align*} &\pi(y)\log y - \theta(y) = \bigl( {\mathop{\mathrm{li}}}(y) + O(ye^{-c\sqrt{\log y}}) \bigr) \log y - \bigl( y + O(ye^{-c\sqrt{\log y}}) \bigr) \\ &\quad= \biggl( \Big( \frac y{\log y} + \frac y{\log^2 y} + O\Big( \frac y{\log^3 y} \Big) \Big) + O\Big( \frac y{\log^3 y} \Big) \biggr) \log y - \biggl( y + O\Big( \frac y{\log^2 y} \Big) \biggr) \\ &\quad= \frac y{\log y} + O\Big( \frac y{\log^2 y} \Big).\\[-44pt] \end{align*} $$
Proposition 3.2 Fix a real number
$\kappa>1$
, and let
$R(p)$
be a positive function defined on primes p such that
$R(p) \sim p^{-\kappa }$
as
$p\to \infty $
. Define the function
$$ \begin{align*}P(x) = \prod\nolimits _p \bigl (1 + R(p)x \bigr ).\end{align*} $$
Then
$\log P(x) \asymp x^{1/\kappa }/\log x$
as
$x\to \infty $
.
Proof All implicit constants in this proof may depend on
$R(p)$
and
$\kappa $
. Choose
$p_0$
so that
$\frac 12p^{-\kappa } < R(p) < 2p^{-\kappa }$
for all
$p>p_0$
. We write
$$ \begin{align} \log P(x) &= \sum_{p\leqslant p_0} \log \bigl(1 + R(p)x \bigr) + \sum_{p_0<p\leqslant x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) + \sum_{p>x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) \notag \\ &= O(\log x) + \sum_{p_0<p\leqslant x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) + \sum_{p>x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr), \end{align} $$
since the number of terms in the first sum, and the largest value of
$R(p)$
appearing in that sum, are both bounded in terms of the function R.
In the first sum in equation (3.1),
$$\begin{align*}\tfrac12p^{-\kappa}x < R(p)x < 1 + R(p)x < (x^{1/\kappa}/p)^\kappa + 2p^{-\kappa}x = 3p^{-\kappa}x. \end{align*}$$
Therefore
$$\begin{align*}\sum_{p_0<p\leqslant x^{1/\kappa}} \log (\tfrac12 p^{-\kappa}x) \leqslant \sum_{p_0<p\leqslant x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) \leqslant \sum_{p_0<p\leqslant x^{1/\kappa}} \log (3p^{-\kappa}x). \end{align*}$$
The right-hand inequality is the same as
$$ \begin{align*} \sum_{p_0<p\leqslant x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) &\leqslant ( \log x + \log 3 ) \bigl( \pi(x^{1/k}) - \pi(p_0) \bigr) - \kappa \bigl( \theta(x^{1/k}) - \theta(p_0) \bigr) \\ &= \kappa \bigl( \pi(x^{1/\kappa})\log(x^{1/\kappa}) \kern1.3pt{-}\kern1.3pt \theta(x^{1/\kappa}) \bigr) \kern1.3pt{+}\kern1.3pt \pi(x^{1/\kappa}) \log 3 \kern1.3pt{+}\kern1.3pt O(\log x) \\ &\sim (\kappa+\log3) \frac{x^{1/\kappa}}{\log(x^{1/\kappa})} = \kappa(\kappa+\log3) \frac{{x^{1/\kappa}}}{\log x} \end{align*} $$
by Lemma 3.1. By the same calculation with
$\log \frac 12$
in place of
$\log 3$
,
$$ \begin{align*} \sum_{p_0<p\leqslant x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) &\geqslant\kappa(\kappa-\log2) \frac{{x^{1/\kappa}}}{\log x} \end{align*} $$
(note that
$\kappa -\log 2>1-\log 2$
is bounded away from
$0$
). We conclude that
$$ \begin{align} \sum_{p_0<p\leqslant x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) \asymp \frac{{x^{1/\kappa}}}{\log x}. \end{align} $$
In the second sum in equation (3.1),
$$\begin{align*}0 \leqslant \log(1+R(p)x) \leqslant R(p)x < 2p^{-\kappa} x, \end{align*}$$
and thus by partial summation,
$$ \begin{align*} 0 \leqslant \sum_{p>x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) &\leqslant \sum_{p>x^{1/\kappa}} 2p^{-\kappa} x \\ &= 2x \int_{x^{1/\kappa}}^\infty t^{-\kappa} \, d\pi(t) \\ &= 2x \biggl( \pi(t)t^{-\kappa}\bigg|_{x^{1/\kappa}}^\infty + \int_{x^{1/\kappa}}^\infty \kappa t^{-\kappa-1}\pi(t)\,dt \biggr). \end{align*} $$
The boundary term is well defined (since
$\kappa>1$
) and negative, and thus by the prime number theorem,
$$ \begin{align*} 0 \leqslant \sum_{p>x^{1/\kappa}} \log \bigl(1 + R(p)x \bigr) &\ll x \biggl( 0 + \int_{x^{1/\kappa}}^\infty t^{-\kappa-1} \frac{t}{\log t} \,dt \biggr) \\ &\ll \frac{x}{\log x} \int_{x^{1/\kappa}}^\infty t^{-\kappa} \,dt = \frac{x}{\log x} \frac{(x^{1/\kappa})^{1-\kappa}}{\kappa-1} \ll \frac{x^{1/\kappa}}{\log x}. \end{align*} $$
The proposition now follows by combining these inequalities with equations (3.1) and (3.2).
All that is left is to connect the rates of growth of the generating functions in Theorems 1.3 and 1.10 to the decay rate of their Maclaurin coefficients. We use the following classical information about entire functions [Reference Boas1, Definition 2.1.1 and Theorem 2.2.2]:
Definition 3.3 An entire function
$f(z)$
is said to be of order
$\rho $
if
$$ \begin{align*} \limsup_{r\to \infty} \frac{\log\log M_f(r)}{\log r}=\rho \end{align*} $$
where
$M_f(r)=\max _{|z|=r} |f(z)|$
. It is of finite order if it is of order
$\rho $
for some
$\rho \in \mathbb {R}$
.
Lemma 3.4 Let
$f(z) = \sum _{m=0}^{\infty } b_mz^m$
be an entire function. The function
$f(z)$
is of finite order if and only if
$$ \begin{align*} \mu=\limsup_{\substack{m\to \infty \\ b_m\ne0}} \frac{m\log m}{\log(1/|b_m|)} \end{align*} $$
is finite, and in this case
$f(z)$
is of order
$\mu $
.
Proof of Corollary 1.4
Set
$$ \begin{align*} P(x)=\prod_{p} \biggl(1+\frac{p-1}{p^{k+1}} x \biggr) \quad\text{and}\quad Q(z) = \sum_{m=0}^{\infty}e_{k,m}z^{m} = \prod_{p} \biggl(1+\frac{p-1}{p^{k+1}} (z-1) \biggr). \end{align*} $$
When
$|z|=r$
, note that
$$\begin{align*}|Q(z)| \leqslant \prod_{p} \biggl(1+\frac{p-1}{p^{k+1}} (|z|+1) \biggr) = P\big( r+1 \big); \end{align*}$$
thus by Proposition 3.2 with
$\kappa =k$
and
$R(p) = (p-1)/p^{k+1}$
,
$$\begin{align*}\log |Q(z)| \ll \frac{(r+1)^{1/k}}{\log(r+1)} \ll \frac{r^{1/k}}{\log r}. \end{align*}$$
On the other hand, when
$z=r>3$
is real, then
$$\begin{align*}\log |Q(r)| = \log P(r-1) \gg \frac{(r-1)^{1/k}}{\log(r-1)} \gg \frac{r^{1/k}}{\log r} \end{align*}$$
again by Proposition 3.2. Together these last estimates show that
$\log M_Q(r) \asymp {r^{1/k}}/{\log r}$
, which implies that
$$\begin{align*}\limsup_{r\to \infty} \frac{\log\log M_Q(r)}{\log r} = \limsup_{r\to \infty} \frac{\log(r^{1/k}) - \log\log r + O(1)}{\log r} = \frac1k. \end{align*}$$
In particular,
$Q(z)$
has order
$\frac 1k$
by Definition 3.3; consequently, by Lemma 3.4,
$$ \begin{align*} \limsup_{\substack{m\to \infty \\ e_{k,m}\ne0}} \frac{m\log m}{\log(1/|e_{k,m}|)}=\frac{1}{k}. \end{align*} $$
We know that
$e_{k,m}>0$
by Theorem 1.1, and so
$$ \begin{align*} \frac{m\log m}{\log(1/e_{k,m})} \leqslant \frac{1}{k}+o(1) \end{align*} $$
with asymptotic equality for infinitely many m; we conclude that
$$ \begin{align*} e_{k,m} \leqslant m^{-(k-o(1))m} \end{align*} $$
which completes the proof of the corollary.
Proof of Corollary 1.14
The proof is the same as the proof of Corollary 1.4, except that
$Q(z)$
is changed to each of the three products
$$ \begin{align*} \sum_{m=0}^{\infty}e_{{S},m}z^{m}&=\prod_{p} \biggl(1+\frac{z-1}{p^{2}} \biggr) \\\sum_{m=0}^{\infty}e_{{E},m}z^{m}&=\prod_{p} \biggl(1+\frac{z-1}{p(p+1)} \biggr) \\\sum_{m=0}^{\infty}e_{{O},m}z^{m}&=\prod_{p} \biggl(1+\frac{z-1}{p^{2}(p+1)} \biggr) \end{align*} $$
in turn, with corresponding modifications to
$P(x)$
and
$R(p)$
; instead of with
$\kappa =k$
, the appeal to Proposition 3.2 is made with
$\kappa =2$
in the first two cases and
$\kappa =3$
in the last case, and the rest of the proof goes through in exactly the same way.
4 Numerical calculations of densities, expectations, and variances
We now describe how we used the generating functions in Theorem 1.3 to facilitate the calculation of the densities
$e_{k,m}$
in Table 1 to the indicated high level of precision. Our approach is based on observations of Marcus Lai (private communication).
Proposition 4.1 Let
$P(z)$
be any function with Maclaurin series
$$\begin{align*}P(z) = \sum_{n=0}^\infty C(n) z^n, \end{align*}$$
so that
$C(n) = \frac 1{n!} P^{(n)}(0)$
for every
$n\ge 0$
. Define
$$\begin{align*}S(0,z) = \log P(z) \quad\text{and}\quad S(n,z) = \frac{d^n}{dz^n} S(0,z) \end{align*}$$
for all
$n\ge 1$
; and define
$S(n) = S(n,0)$
and
$\tilde S(n) = \frac 1{(n-1)!} S(n)$
. Then for any
$n\ge 1$
,
$$ \begin{align*} P^{(n)}(z) &= \sum_{k=0}^{n-1} \binom{n-1}k P^{(k)}(z) S(n-k,z). \end{align*} $$
In particular, for
$n\ge 1$
,
$$ \begin{align} C(n) = \frac1n \sum_{k=0}^{n-1} C(k) \tilde S(n-k), \end{align} $$
so that for example
$$ \begin{align*} C(1) &=C(0)\tilde{S}(1)= P(0) \tilde S(1), \\ C(2) &=\frac{1}{2} \bigl(C(0)\tilde{S}(2)+C(1)\tilde{S}(1)\bigr) =\frac{P(0)}{2} \bigl( \tilde S(1)^2 + \tilde S(2) \bigr), \\ C(3) &=\frac{1}{3} \bigl(C(0)\tilde{S}(3)+C(1)\tilde{S}(2)+C(2)\tilde{S}(1)\bigr) = \frac{P(0)}{6} \bigl( {\tilde S(1)^3} + 3 \tilde S(1) \tilde S(2) + 2 \tilde S(3) \bigr). \end{align*} $$
Proof We first verify that
$$\begin{align*}P'(z) = P(z)\frac{P'(z)}{P(z)} = P(z) \frac d{dz} \log P(z) = P(z) \frac d{dz} S(0,z) = P(z) S(1,z), \end{align*}$$
which is the case
$n=1$
of the first identity. The general case of the first identity now follows from using the product rule
$n-1$
times in a row on this initial identity
$P'(z) = P(z) S(1,z)$
. The second identity follows by plugging in
$z=0$
into the first identity and recalling that
$C(n) = \frac 1{n!} P^{(n)}(0)$
.
We apply this recursive formula (with subscripts inserted throughout the notation for clarity) with
$C(m) = e_{k,m}$
, so that
$$ \begin{align} P_k(z) = \sum_{m=0}^\infty e_{k,m} z^m = \prod_p \biggl( 1 + \frac{(p-1)(z-1)}{p^{k+1}} \biggr) \end{align} $$
by Theorem 1.3. We compute
$$ \begin{align} S_k(0,z) &= \sum_p \log \biggl( 1 + \frac{(p-1)(z-1)}{p^{k+1}} \biggr) \notag \\ S_k(1,z) &= \frac d{dz} \sum_p \log \biggl( 1 + \frac{(p-1)(z-1)}{p^{k+1}} \biggr) = \sum_p \biggl( z+\frac{p^{k+1}}{p-1}-1 \biggr)^{-1} \\ S_k(n,z) &= \frac{d^{n-1}}{dz^{n-1}} \sum_p \biggl( z+\frac{p^{k+1}}{p-1}-1 \biggr)^{-1} = \sum_p (-1)^{n-1} (n-1)! \biggl( z+\frac{p^{k+1}}{p-1}-1 \biggr)^{-n}, \notag \end{align} $$
so that
$$ \begin{align} \tilde S_k(n) =(-1)^{n-1} \sum_p \biggl( \frac{p^{k+1}}{p-1}-1 \biggr)^{-n}. \end{align} $$
Therefore equation (4.1) becomes
$$\begin{align*}e_{k,m} = \frac1m \sum_{j=0}^{m-1} e_{k,j} \tilde S_k(m-j), \end{align*}$$
and in particular we have
$$ \begin{align*} e_{k,0} &=\prod_{p} \biggl(1-\frac{p-1}{p^{k+1}} \biggr), \\ e_{k,1} &= e_{k,0} \tilde S_k(1), \\ e_{k,2} &= \frac{e_{k,0}}{2} \bigl( \tilde S_k(1)^2 + \tilde S_k(2) \bigr), \\[5pt] e_{k,3} &= \frac{e_{k,0}}{6} \bigl( {\tilde S_k(1)^3} + 3 \tilde S_k(1) \tilde S_k2) + 2 \tilde S_k(3) \bigr). \end{align*} $$
Remark 4.2 We coded these formulas, and the one in equation (4.4), into SageMath and calculated approximations to them where we truncated the infinite product and sums to run over primes
$p\leqslant 10^7$
, resulting in the densities appearing in Table 1 (the cases
$k=2,3,4,5$
and
$m=0,1,2,3$
). While we do not include a formal analysis of the error arising from these truncations, we have listed the densities to nine decimal places to display our confidence in that level of precision.
Finally, we extract the expectations and variances of various limiting distributions from their generating functions by relating those quantities to derivatives of their generating functions.
Proof of Corollary 1.6
Let
$X_k$
be the discrete random variable whose distribution is the same as the limiting distribution of
$\omega _k(n)$
; then the generating function of this distribution is the function
$P_k(z)$
in equation (4.2). Proposition 4.1 and equations (4.2)–(4.3) tell us that
$$ \begin{align*} P_k'(1) &= P_k(1) S_k(1,1) =1\cdot \sum_p \frac{p-1}{p^{k+1}} = \sum_p \frac{p-1}{p^{k+1}} \\[5pt] P_k"(1) &= P_k'(1) S_k(1,1) + P_k(1) S_k(2,1) \\[5pt] &= \sum_p \frac{p-1}{p^{k+1}} \cdot \sum_p \frac{p-1}{p^{k+1}} + 1\biggl( - \sum_p \biggl( \frac{p-1}{p^{k+1}} \biggr)^2 \biggr) = \biggl( \sum_p \frac{p-1}{p^{k+1}} \biggr)^2 - \sum_p \biggl( \frac{p-1}{p^{k+1}} \biggr)^2 \end{align*} $$
But now by standard results from probability [Reference Feller5, Chapter XI, Theorems 2–3],
$$ \begin{align*} \mathbb{E}[X_k] &= P_k'(1) = \sum_p \frac{p-1}{p^{k+1}} \\ \sigma^2[X_k] &= P_k"(1)+P_k'(1)-P_k'(1)^2 = \sum_p \frac{p-1}{p^{k+1}} - \sum_p \biggl( \frac{p-1}{p^{k+1}} \biggr)^2 \end{align*} $$
which is equivalent to the statement of the corollary.
Remark 4.3 As before, we used SageMath to calculate truncations of these infinite sums, running over primes
$p\leqslant 10^7$
, to generate the approximate expectations and variances listed in Table 2 for
$k=2,3,4,5$
.
Proof of Corollary 1.12
Let
$X_A$
be the random variable whose distribution is the same as the limiting distribution of
$\omega _A(n)$
. Using the same approach starting from the generating function (1.10), we see that
$$ \begin{align*} \mathbb{E} & [X_A] = P_A'(1) = \frac d{dz} \prod_{p} \biggl(1-\frac{1}{p^2}+\sum_{j=2}^{\infty}z^{a_j} \biggl(\frac{1}{p^{j}}-\frac{1}{p^{j+1}} \biggr)\biggr) \bigg|_{z=1} \\ &= \biggl\{ \prod_{p} \biggl(1-\frac{1}{p^2}+\sum_{j=2}^{\infty}z^{a_j} \biggl(\frac{1}{p^{j}}-\frac{1}{p^{j+1}} \biggr)\biggr) \sum_p \frac d{dz} \log \biggl(1-\frac{1}{p^2}+\sum_{j=2}^{\infty}z^{a_j} \biggl(\frac{1}{p^{j}}-\frac{1}{p^{j+1}} \biggr)\biggr) \biggr\} \bigg|_{z=1} \\ &= 1 \sum_p \biggl(0+\sum_{j=2}^{\infty} a_jz^{a_j-1} \biggl(\frac{1}{p^{j}}-\frac{1}{p^{j+1}} \biggr) \biggr) \bigg/ \biggl(1-\frac{1}{p^2}+\sum_{j=2}^{\infty}z^{a_j} \biggl(\frac{1}{p^{j}}-\frac{1}{p^{j+1}} \biggr) \biggr) \bigg|_{z=1} \\ &= \sum_p \sum_{j=2}^{\infty} a_j \biggl(\frac{1}{p^{j}}-\frac{1}{p^{j+1}} \biggr) \bigg/ 1 \end{align*} $$
as claimed.
Acknowledgments
We thank Marcus Lai and Paul Péringuey for helpful discussions related to the calculations in Section 4, and we are grateful to the Pacific Institute for the Mathematical Sciences (PIMS) whose welcoming environment contributed to this project. The first author was supported by a University of Lethbridge postdoctoral fellowship. The second author was supported in part by a Natural Sciences and Engineering Council of Canada Discovery Grant.
