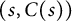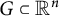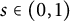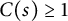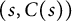1 Introduction
Harnack’s inequality is a fundamental result in the study of partial differential equations (PDEs), with applications across various branches of mathematics, particularly in the theory of elliptic and parabolic equations. The Harnack inequality typically concerns positive solutions to elliptic or parabolic equations in divergence form. In the case of elliptic equations, which describe steady-state problems such as heat conduction or electrostatics, the inequality establishes bounds on the solutions by comparing the maximum and minimum values within a domain. Moreover, the German mathematician Axel Harnack developed the original formulation of this inequality for harmonic functions in the plane (see [Reference Kassmann18] for more details). It should be noted that this inequality was first published in 1887 in the book [Reference Harnack11].
In the context of the theory of PDEs, the current formulation of the Harnack inequality for harmonic functions is expressed as follows:
Harnack inequality. Let
![]() $B^n(x,r)$
be a Euclidean ball centered at x with the radius
$B^n(x,r)$
be a Euclidean ball centered at x with the radius
![]() $r\in (0,1)$
such that the concentric ball
$r\in (0,1)$
such that the concentric ball
![]() $B^n(x,2r)$
is contained in a domain
$B^n(x,2r)$
is contained in a domain
![]() $G \subset \mathbb {R}^n$
,
$G \subset \mathbb {R}^n$
,
![]() $n\geq 2$
. Then there exists a positive constant C depending on n such that
$n\geq 2$
. Then there exists a positive constant C depending on n such that
holds for all nonnegative harmonic functions
![]() $u:G\rightarrow \mathbb {R}$
.
$u:G\rightarrow \mathbb {R}$
.
We recall that a real-valued function
![]() $u: G\subset \mathbb {R}^n \rightarrow \mathbb {R}$
is called harmonic in a domain
$u: G\subset \mathbb {R}^n \rightarrow \mathbb {R}$
is called harmonic in a domain
![]() $G \subset \mathbb {R}^n$
if it is twice continuously differentiable and satisfies the Laplace equation
$G \subset \mathbb {R}^n$
if it is twice continuously differentiable and satisfies the Laplace equation
![]() $\sum _{i=1}^{n}\partial ^2 u/\partial x_i^2=0$
. The progress of potential analysis linked to the Laplace equation hinges on the key role of Harnack’s inequality (1.1) (see [Reference Helms13]).
$\sum _{i=1}^{n}\partial ^2 u/\partial x_i^2=0$
. The progress of potential analysis linked to the Laplace equation hinges on the key role of Harnack’s inequality (1.1) (see [Reference Helms13]).
Subsequently, we revisit a definition presented in [Reference Vuorinen24]. Define
![]() $\mathbb {R}^+$
as the set
$\mathbb {R}^+$
as the set
![]() $\{x\in \mathbb {R}:x>0\}$
.
$\{x\in \mathbb {R}:x>0\}$
.
Definition 1.1 Consider a proper subdomain G of
![]() $\mathbb {R}^n$
, and let
$\mathbb {R}^n$
, and let
![]() $u:G\rightarrow \mathbb {R}^+\cup \{0\}$
be a continuous function. We say that u satisfies the Harnack inequality in G if there exist numbers
$u:G\rightarrow \mathbb {R}^+\cup \{0\}$
be a continuous function. We say that u satisfies the Harnack inequality in G if there exist numbers
![]() $s\in (0,1)$
and
$s\in (0,1)$
and
![]() $C(s)\geq 1$
such that
$C(s)\geq 1$
such that
holds, whenever
![]() $B^n(x,r)\subset G$
and
$B^n(x,r)\subset G$
and
![]() $B_x=\overline {B}^n(x,sr)$
. A function that meets this condition is referred to as a Harnack function.
$B_x=\overline {B}^n(x,sr)$
. A function that meets this condition is referred to as a Harnack function.
Here are some examples:
Example 1.1 (i) Let
![]() $u:G\rightarrow \mathbb {R}^+$
be a continuous function on a domain G with
$u:G\rightarrow \mathbb {R}^+$
be a continuous function on a domain G with
![]() $0<m\leq u(x)\leq M<\infty $
. Then u satisfies (1.2) with
$0<m\leq u(x)\leq M<\infty $
. Then u satisfies (1.2) with
![]() $C(s)=M/m$
for all
$C(s)=M/m$
for all
![]() $x\in G$
.
$x\in G$
.
(ii) Let G be a domain, and let
![]() $d(x, \partial G)$
be the minimum distance from x to the boundary of G. If
$d(x, \partial G)$
be the minimum distance from x to the boundary of G. If
![]() $u:G\rightarrow \mathbb {R}^+$
is defined as
$u:G\rightarrow \mathbb {R}^+$
is defined as
![]() $u(x)=\alpha \,d(x, \partial G)^\beta $
, where
$u(x)=\alpha \,d(x, \partial G)^\beta $
, where
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $\beta \neq 0$
, then u satisfies (1.2) with
$\beta \neq 0$
, then u satisfies (1.2) with
![]() $C(s)=((1+s)/(1-s))^{|\beta |}$
.
$C(s)=((1+s)/(1-s))^{|\beta |}$
.
(iii) All nonnegative harmonic functions satisfy (1.2) with a constant
![]() $C(s)$
such that
$C(s)$
such that
![]() $C(s)\rightarrow 1$
as
$C(s)\rightarrow 1$
as
![]() $s\rightarrow 0^+$
(see [Reference Gilbarg and Trudinger8, p. 16]).
$s\rightarrow 0^+$
(see [Reference Gilbarg and Trudinger8, p. 16]).
(iv) Let
![]() $u(z)=\arg z$
and
$u(z)=\arg z$
and
![]() $G=\mathbb {R}^2\,{\backslash}\, \{x\in \mathbb {R}: x\geq 0\}$
. Then u satisfies (1.2) in G with
$G=\mathbb {R}^2\,{\backslash}\, \{x\in \mathbb {R}: x\geq 0\}$
. Then u satisfies (1.2) in G with
![]() $C(s)=(4+\pi )/(4-\pi )$
, where
$C(s)=(4+\pi )/(4-\pi )$
, where
![]() $s=1/2$
(see [Reference Hariri, Klén and Vuorinen10, Exercise 6.33(1)]).
$s=1/2$
(see [Reference Hariri, Klén and Vuorinen10, Exercise 6.33(1)]).
In this paper, we study the
![]() $(s, C(s))$
-Harnack inequality, which is defined as follows, where
$(s, C(s))$
-Harnack inequality, which is defined as follows, where
![]() $s\in (0,1)$
and
$s\in (0,1)$
and
![]() $C(s)\geq 1$
.
$C(s)\geq 1$
.
Definition 1.2 Under the assumptions of Definition 1.1, for
![]() $s\in (0,1)$
and
$s\in (0,1)$
and
![]() $C_s\geq 1$
we say that u satisfies the
$C_s\geq 1$
we say that u satisfies the
![]() $(s, C(s))$
-Harnack inequality in a domain
$(s, C(s))$
-Harnack inequality in a domain
![]() $G\subset \mathbb {R}^n$
, if the inequality (1.2) holds. A function satisfying (1.2) for all
$G\subset \mathbb {R}^n$
, if the inequality (1.2) holds. A function satisfying (1.2) for all
![]() $s\in (0,1)$
is called the
$s\in (0,1)$
is called the
![]() $(s,C(s))$
-Harnack function.
$(s,C(s))$
-Harnack function.
This paper is organized as follows: Section 2 provides the essential notations and definitions required for the discussions in this paper. In Section 3, we investigate the behavior of the
![]() $(s, C(s))$
-Harnack functions and the Harnack metric. Lastly, Section 4 presents a version of the harmonic Schwarz lemma and improves the Schwarz–Pick estimate for a real-valued harmonic function.
$(s, C(s))$
-Harnack functions and the Harnack metric. Lastly, Section 4 presents a version of the harmonic Schwarz lemma and improves the Schwarz–Pick estimate for a real-valued harmonic function.
2 Preliminaries
This section establishes a foundation for our subsequent discussions by introducing essential notations and definitions.
Let sh, ch, th, and arth denote the hyperbolic functions
![]() $\sinh $
,
$\sinh $
,
![]() $\cosh $
,
$\cosh $
,
![]() $\tanh $
, and
$\tanh $
, and
![]() $\mathrm {arctanh}$
, respectively. Consider the Euclidean space
$\mathrm {arctanh}$
, respectively. Consider the Euclidean space
![]() $\mathbb {R}^n$
with
$\mathbb {R}^n$
with
![]() $n \geq 2$
and define
$n \geq 2$
and define
![]() $\mathbb {H}^n = \{x=(x_1, \ldots , x_n) \in \mathbb {R}^n : x_n> 0\}$
as the Poincaré half-space or the upper half-plane. The ball with center x in
$\mathbb {H}^n = \{x=(x_1, \ldots , x_n) \in \mathbb {R}^n : x_n> 0\}$
as the Poincaré half-space or the upper half-plane. The ball with center x in
![]() $\mathbb {R}^n$
and radius
$\mathbb {R}^n$
and radius
![]() $r>0$
is denoted as
$r>0$
is denoted as
![]() $B^n(x,r)$
, defined as the set
$B^n(x,r)$
, defined as the set
![]() $\{y\in \mathbb {R}^n:|y-x|<r\}$
. Correspondingly, the sphere sharing the same center and radius is
$\{y\in \mathbb {R}^n:|y-x|<r\}$
. Correspondingly, the sphere sharing the same center and radius is
![]() $S^{n-1}(x,r)=\{y\in \mathbb {R}^n:|y-x|=r\}$
. The unit ball will be denoted by
$S^{n-1}(x,r)=\{y\in \mathbb {R}^n:|y-x|=r\}$
. The unit ball will be denoted by
![]() $\mathbb {B}^n=B^n(0,1)$
. Also,
$\mathbb {B}^n=B^n(0,1)$
. Also,
![]() $\overline {B}^n(x,r)=\{y\in \mathbb {R}^n:|y-x|\leq r\}$
. For any x within a domain G in
$\overline {B}^n(x,r)=\{y\in \mathbb {R}^n:|y-x|\leq r\}$
. For any x within a domain G in
![]() $\mathbb {R}^n$
, the Euclidean distance
$\mathbb {R}^n$
, the Euclidean distance
![]() $d_G(x)$
is defined as the minimum distance from x to the boundary of G, denoted by
$d_G(x)$
is defined as the minimum distance from x to the boundary of G, denoted by
![]() $d_G(x)=d(x,\partial G)=\inf \{|x-w|: w\in \partial G\}$
. In the hyperbolic space
$d_G(x)=d(x,\partial G)=\inf \{|x-w|: w\in \partial G\}$
. In the hyperbolic space
![]() $\mathbb {H}^n$
, the hyperbolic distance
$\mathbb {H}^n$
, the hyperbolic distance
![]() $\rho $
is characterized by the differential equation
$\rho $
is characterized by the differential equation
![]() $\mathrm {d}\rho =|\mathrm {d}x|/x_n$
. Explicit formulas for the distances between points in both the upper half-space
$\mathrm {d}\rho =|\mathrm {d}x|/x_n$
. Explicit formulas for the distances between points in both the upper half-space
![]() $\mathbb {H}^n$
and the unit ball
$\mathbb {H}^n$
and the unit ball
![]() $\mathbb {B}^n$
, respectively, are as follows (see [Reference Hariri, Klén and Vuorinen10, (4.8), p. 52; (4.16), p. 55]):
$\mathbb {B}^n$
, respectively, are as follows (see [Reference Hariri, Klén and Vuorinen10, (4.8), p. 52; (4.16), p. 55]):
 $$ \begin{align*} \mathrm{ch} \rho_{\mathbb{H}^n}(x,y)= 1+\frac{|x-y|^2}{2d_{\mathbb{H}^n}(x)d_{\mathbb{H}^n}(y)},\quad x,y\in \mathbb{H}^n \end{align*} $$
$$ \begin{align*} \mathrm{ch} \rho_{\mathbb{H}^n}(x,y)= 1+\frac{|x-y|^2}{2d_{\mathbb{H}^n}(x)d_{\mathbb{H}^n}(y)},\quad x,y\in \mathbb{H}^n \end{align*} $$
and
 $$ \begin{align*} \mathrm{sh}^2 \frac{\rho_{\mathbb{B}^n}(x,y)}{2}=\frac{|x-y|^2}{(1-|x|^2)(1-|y|^2)},\quad x,y\in \mathbb{B}^n. \end{align*} $$
$$ \begin{align*} \mathrm{sh}^2 \frac{\rho_{\mathbb{B}^n}(x,y)}{2}=\frac{|x-y|^2}{(1-|x|^2)(1-|y|^2)},\quad x,y\in \mathbb{B}^n. \end{align*} $$
The quasihyperbolic distance, denoted as
![]() $k_G(x, y)$
, between points x and y in the domain G, is formally defined as the infimum of the integral along rectifiable curves
$k_G(x, y)$
, between points x and y in the domain G, is formally defined as the infimum of the integral along rectifiable curves
![]() $\gamma \subset G$
containing both x and y. This integral is calculated as the quotient of the absolute value of the differential element
$\gamma \subset G$
containing both x and y. This integral is calculated as the quotient of the absolute value of the differential element
![]() $\mathrm {d}x$
by the distance function
$\mathrm {d}x$
by the distance function
![]() $d_G(x)$
, as given by the expression:
$d_G(x)$
, as given by the expression:
Gehring and Palka introduced the metric
![]() $k_G(x,y)$
in [Reference Gehring and Palka7, p. 173] and provided a proof for the sharp inequalities (see [Reference Gehring and Palka7, Lemma 2.1]). These inequalities are expressed as follows:
$k_G(x,y)$
in [Reference Gehring and Palka7, p. 173] and provided a proof for the sharp inequalities (see [Reference Gehring and Palka7, Lemma 2.1]). These inequalities are expressed as follows:
 $$ \begin{align} k_G(x,y)\geq \left|\log \frac{d_G(x)}{d_G(y)}\right| \end{align} $$
$$ \begin{align} k_G(x,y)\geq \left|\log \frac{d_G(x)}{d_G(y)}\right| \end{align} $$
and
 $$ \begin{align} k_G(x,y)\geq \log \left(1+\frac{|x-y|}{d_G(x)}\right). \end{align} $$
$$ \begin{align} k_G(x,y)\geq \log \left(1+\frac{|x-y|}{d_G(x)}\right). \end{align} $$
For a detailed discussion, we refer to [Reference Hariri, Klén and Vuorinen10], p. 68. It is well-known that (see [Reference Gehring and Palka7], p. 174)
For any open set
![]() $\Omega $
in
$\Omega $
in
![]() $\mathbb {R}^n$
, where
$\mathbb {R}^n$
, where
![]() $\Omega $
is not equal to the entire space
$\Omega $
is not equal to the entire space
![]() $\mathbb {R}^n$
, the distance ratio metric is defined by
$\mathbb {R}^n$
, the distance ratio metric is defined by
 $$ \begin{align*} j_\Omega(x, y)=\log\left(1+\frac{|x-y|}{\min\{d_\Omega(x),d_\Omega(y)\}} \right),\quad x, y\in \Omega. \end{align*} $$
$$ \begin{align*} j_\Omega(x, y)=\log\left(1+\frac{|x-y|}{\min\{d_\Omega(x),d_\Omega(y)\}} \right),\quad x, y\in \Omega. \end{align*} $$
When
![]() $\Omega \in \{\mathbb {B}^n, \mathbb {H}^n\}$
as per [Reference Hariri, Klén and Vuorinen10, Lemma 4.9], the following double-inequality holds:
$\Omega \in \{\mathbb {B}^n, \mathbb {H}^n\}$
as per [Reference Hariri, Klén and Vuorinen10, Lemma 4.9], the following double-inequality holds:
Modulus of a curve family. Let
![]() $\Gamma $
be a family of curves in
$\Gamma $
be a family of curves in
![]() $\mathbb {R}^n$
. Also, let
$\mathbb {R}^n$
. Also, let
![]() $\mathcal {F}(\Gamma )$
denote the family of all nonnegative Borel-measurable functions
$\mathcal {F}(\Gamma )$
denote the family of all nonnegative Borel-measurable functions
![]() $\sigma :\mathbb {R}^n\to \mathbb {R} \cup \{\infty \}$
such that
$\sigma :\mathbb {R}^n\to \mathbb {R} \cup \{\infty \}$
such that
![]() $\int _\gamma \sigma \mathrm {d}\tau \geq 1$
for each locally rectifiable curve
$\int _\gamma \sigma \mathrm {d}\tau \geq 1$
for each locally rectifiable curve
![]() $\gamma \in \Gamma $
. The modulus of a curve family
$\gamma \in \Gamma $
. The modulus of a curve family
![]() $\Gamma \subset \mathbb {R}^n$
is defined by (see [Reference Hariri, Klén and Vuorinen10], p. 104)
$\Gamma \subset \mathbb {R}^n$
is defined by (see [Reference Hariri, Klén and Vuorinen10], p. 104)
where m stands for the n-dimensional Lebesgue measure.
We denote by
![]() $\Delta (E,F;G)$
the family of all closed nonconstant curves joining two non-empty sets E and F in a domain G, where E, F, and G are subsets of
$\Delta (E,F;G)$
the family of all closed nonconstant curves joining two non-empty sets E and F in a domain G, where E, F, and G are subsets of
![]() $\overline {\mathbb {R}}^n$
.
$\overline {\mathbb {R}}^n$
.
Modulus metric. Let G be a proper subdomain of
![]() $\overline {\mathbb {R}}^n$
. The modulus metric is defined by
$\overline {\mathbb {R}}^n$
. The modulus metric is defined by
where the infimum is taken over all continuous paths
![]() $C_{xy}$
in G joining x and y, represented by a continuous function
$C_{xy}$
in G joining x and y, represented by a continuous function
![]() $\gamma :[0,1]\rightarrow G$
satisfying
$\gamma :[0,1]\rightarrow G$
satisfying
![]() $\gamma (0)=x$
and
$\gamma (0)=x$
and
![]() $\gamma (1)=y$
. The definition of modulus metric is illustrated in Figure 1.
$\gamma (1)=y$
. The definition of modulus metric is illustrated in Figure 1.

Figure 1 Conformal invariant
![]() $\mu _G(x,y)$
.
$\mu _G(x,y)$
.
Uniformity. (See [Reference Hariri, Klén and Vuorinen10, Definition 6.1]) A domain G of
![]() $\mathbb {R}^n$
, where
$\mathbb {R}^n$
, where
![]() $G\neq \mathbb {R}^n$
, is termed uniform if there exists a constant
$G\neq \mathbb {R}^n$
, is termed uniform if there exists a constant
![]() $A=A(G)\geq 1$
such that
$A=A(G)\geq 1$
such that
![]() $k_G(x,y)\leq A j_G(x,y)$
for all
$k_G(x,y)\leq A j_G(x,y)$
for all
![]() $x,y\in G$
. The unit ball
$x,y\in G$
. The unit ball
![]() $\mathbb {B}^n$
and the upper half-space
$\mathbb {B}^n$
and the upper half-space
![]() $\mathbb {H}^n$
are examples of uniform domains with the constant
$\mathbb {H}^n$
are examples of uniform domains with the constant
![]() $2$
, as implied by (2.3) and (2.4), respectively.
$2$
, as implied by (2.3) and (2.4), respectively.
Absolutely continuous on lines (ACL). Consider
![]() $\mathbb {R}^{n-1}_j$
as the set
$\mathbb {R}^{n-1}_j$
as the set
![]() $\mathbb {R}^{n-1}_j=\{x\in \mathbb {R}^n: x_j=0\}$
, where
$\mathbb {R}^{n-1}_j=\{x\in \mathbb {R}^n: x_j=0\}$
, where
![]() $j=1,2,\ldots ,n$
. Suppose that
$j=1,2,\ldots ,n$
. Suppose that
![]() $T_j:\mathbb {R}^n\rightarrow \mathbb {R}^{n-1}_j$
is an onto orthogonal projection
$T_j:\mathbb {R}^n\rightarrow \mathbb {R}^{n-1}_j$
is an onto orthogonal projection
![]() $T_j x=x-x_je_j$
and
$T_j x=x-x_je_j$
and
![]() $Q=\{x\in \mathbb {R}^n: a_j\leq x_j\leq b_j\}$
is a closed n-interval. A mapping
$Q=\{x\in \mathbb {R}^n: a_j\leq x_j\leq b_j\}$
is a closed n-interval. A mapping
![]() $\phi : Q \rightarrow \mathbb {R}$
is called absolutely continuous on lines, abbreviated as ACL, if it is absolutely continuous on almost every line segment in Q, parallel to the coordinate axes
$\phi : Q \rightarrow \mathbb {R}$
is called absolutely continuous on lines, abbreviated as ACL, if it is absolutely continuous on almost every line segment in Q, parallel to the coordinate axes
![]() $e_1,\ldots ,e_n$
. More precisely, if
$e_1,\ldots ,e_n$
. More precisely, if
![]() $E_j$
is the set of all
$E_j$
is the set of all
![]() $x\in T_j Q$
such that the mapping
$x\in T_j Q$
such that the mapping
![]() $t\mapsto \phi (x+te_j)$
is not absolutely continuous on
$t\mapsto \phi (x+te_j)$
is not absolutely continuous on
![]() $[a_j,b_j]$
, then
$[a_j,b_j]$
, then
![]() $m_{n-1}(E_j)=0$
for all
$m_{n-1}(E_j)=0$
for all
![]() $j=1,\ldots ,n$
.
$j=1,\ldots ,n$
.
For an open set
![]() $\Omega $
in
$\Omega $
in
![]() $\mathbb {R}^n$
, an ACL mapping
$\mathbb {R}^n$
, an ACL mapping
![]() $\phi :\Omega \rightarrow \mathbb {R}$
is said to be ACL
$\phi :\Omega \rightarrow \mathbb {R}$
is said to be ACL
![]() $^n$
,
$^n$
,
![]() $n\geq 1$
, if
$n\geq 1$
, if
![]() $\phi $
is locally
$\phi $
is locally
![]() $L^n$
-integrable in
$L^n$
-integrable in
![]() $\Omega $
and if the partial derivatives
$\Omega $
and if the partial derivatives
![]() $\partial _j \phi $
(which exist a.e. and are measurable) of
$\partial _j \phi $
(which exist a.e. and are measurable) of
![]() $\phi $
are locally
$\phi $
are locally
![]() $L^n$
-integrable as well (see [Reference Martio, Ryazanov, Srebro and Yakubov20, p. 22]).
$L^n$
-integrable as well (see [Reference Martio, Ryazanov, Srebro and Yakubov20, p. 22]).
Quasiregular mappings. Consider a domain
![]() $G\subset \mathbb {R}^n$
. A mapping
$G\subset \mathbb {R}^n$
. A mapping
![]() $f: G \rightarrow \mathbb {R}^n$
is said to be K-quasiregular if f belongs to ACL
$f: G \rightarrow \mathbb {R}^n$
is said to be K-quasiregular if f belongs to ACL
![]() $^n$
and if there exists a constant
$^n$
and if there exists a constant
![]() $K\geq 1$
satisfying the inequality
$K\geq 1$
satisfying the inequality
almost everywhere in G. Here,
![]() $f'(x)$
and
$f'(x)$
and
![]() $J_f(x)$
represent the formal derivative and the Jacobian determinant of f at the point x, respectively.
$J_f(x)$
represent the formal derivative and the Jacobian determinant of f at the point x, respectively.
Quasiconformal mappings. Let G,
![]() $G'$
be domains in
$G'$
be domains in
![]() $\overline {\mathbb {R}}^n=\mathbb {R}^n\cup \{\infty \}$
,
$\overline {\mathbb {R}}^n=\mathbb {R}^n\cup \{\infty \}$
,
![]() $K\geq 1$
and let
$K\geq 1$
and let
![]() $f:G\rightarrow G'$
be a homeomorphism. Then, f is K-quasiconformal if and only if the following conditions are satisfied:
$f:G\rightarrow G'$
be a homeomorphism. Then, f is K-quasiconformal if and only if the following conditions are satisfied:
-
• f is ACL
 $^n$
;
$^n$
; -
• f is differentiable;
-
• for almost all
 $x\in G$
where
$x\in G$
where $$ \begin{align*} |f'(x)|^n/K\leq |J_f(x)|\leq K L (f'(x))^n, \end{align*} $$
$$ \begin{align*} |f'(x)|^n/K\leq |J_f(x)|\leq K L (f'(x))^n, \end{align*} $$
 $L(\lambda )=\min _{|\phi |=1}|\lambda \phi |$
.
$L(\lambda )=\min _{|\phi |=1}|\lambda \phi |$
.
The Harnack inequality provides a basis for defining a Harnack (pseudo) metric. Consider
![]() $\mathcal {H}^+(G)$
as the class of all positive harmonic functions u in G.
$\mathcal {H}^+(G)$
as the class of all positive harmonic functions u in G.
Harnack metric. For arbitrary
![]() $x, y \in G$
, the Harnack metric is defined by
$x, y \in G$
, the Harnack metric is defined by
 $$ \begin{align*} h_G(x,y)=\sup\left|\log \frac{u(x)}{u(y)}\right|, \end{align*} $$
$$ \begin{align*} h_G(x,y)=\sup\left|\log \frac{u(x)}{u(y)}\right|, \end{align*} $$
where the supremum is taken over all
![]() $u\in \mathcal {H}^+(G)$
. This metric has been investigated in various contexts, including studies in [Reference Bear and Smith3, Reference Chirka5, Reference Herron and Minda15, Reference Herron14, Reference Köhn19, Reference Shiga22].
$u\in \mathcal {H}^+(G)$
. This metric has been investigated in various contexts, including studies in [Reference Bear and Smith3, Reference Chirka5, Reference Herron and Minda15, Reference Herron14, Reference Köhn19, Reference Shiga22].
3
 $(s, C(s))$
-Harnack functions and Harnack metric
$(s, C(s))$
-Harnack functions and Harnack metric
In this section, we present our results on
![]() $(s, C(s))$
-Harnack functions and the Harnack metric under K-quasiconformal and K-quasiregular mappings. We start with the following:
$(s, C(s))$
-Harnack functions and the Harnack metric under K-quasiconformal and K-quasiregular mappings. We start with the following:
Lemma 3.1
All positive harmonic functions on
![]() $B^n(x,r)\subset \mathbb {R}^n$
are
$B^n(x,r)\subset \mathbb {R}^n$
are
![]() $(s, C(s))$
-Harnack with
$(s, C(s))$
-Harnack with
for all
![]() $s\in (0,1)$
.
$s\in (0,1)$
.
Proof Let u be any positive harmonic function on
![]() $B^n(x,r)$
and
$B^n(x,r)$
and
![]() $0<\delta <r$
. Then, by [Reference Helms13, Theorem 3.2.1], we have
$0<\delta <r$
. Then, by [Reference Helms13, Theorem 3.2.1], we have
 $$ \begin{align} \frac{u(x_1)}{u(x_2)}\leq \frac{r^2}{r^2-\delta^2}\left(\frac{r+\delta}{r-\delta}\right)^n \end{align} $$
$$ \begin{align} \frac{u(x_1)}{u(x_2)}\leq \frac{r^2}{r^2-\delta^2}\left(\frac{r+\delta}{r-\delta}\right)^n \end{align} $$
for all
![]() $x_1,x_2\in B^n(x,\delta )$
. Now, it is enough to put
$x_1,x_2\in B^n(x,\delta )$
. Now, it is enough to put
![]() $\delta =r s$
in (3.1) since
$\delta =r s$
in (3.1) since
![]() $rs<r$
for all
$rs<r$
for all
![]() $s\in (0,1)$
.
$s\in (0,1)$
.
Theorem 3.2
(i) Let
![]() $s\in (0,1)$
and
$s\in (0,1)$
and
![]() $u:\mathbb {B}^{n} \rightarrow (0,\infty )$
be a Harnack function. Then for all
$u:\mathbb {B}^{n} \rightarrow (0,\infty )$
be a Harnack function. Then for all
![]() $x,y\in \mathbb {B}^n$
$x,y\in \mathbb {B}^n$
 $$ \begin{align*} u(x)\leq C(s)^{1+t} u(y), \qquad t=\frac{\log((1+r)/(1-r))}{\log((1+s)/(1-s))}, \end{align*} $$
$$ \begin{align*} u(x)\leq C(s)^{1+t} u(y), \qquad t=\frac{\log((1+r)/(1-r))}{\log((1+s)/(1-s))}, \end{align*} $$
where
![]() $r=\mathrm {th}(\rho _{\mathbb {B}^n}(x,y)/2)$
and
$r=\mathrm {th}(\rho _{\mathbb {B}^n}(x,y)/2)$
and
![]() $C(s)\geq 1$
. (ii) If u is a positive harmonic function,
$C(s)\geq 1$
. (ii) If u is a positive harmonic function,
![]() $x\in \mathbb {B}^n$
,
$x\in \mathbb {B}^n$
,
![]() $s\in (0,1)$
and
$s\in (0,1)$
and
![]() $y\in S^{n-1}(x, s(1-|x|))$
, then
$y\in S^{n-1}(x, s(1-|x|))$
, then
Proof (i) The proof follows from Definition 1.2 and [Reference Hariri, Klén and Vuorinen10, Lemma 6.23]. (ii) It follows from [Reference Hariri, Klén and Vuorinen10, Lemma 4.9(1)] that
 $$ \begin{align*} \rho_{\mathbb{B}^n}(x,y)\geq j_{\mathbb{B}^n}(x,y)\geq \log\left(1+\frac{s(1-|x|)}{1-|x|}\right)=\log(1+s). \end{align*} $$
$$ \begin{align*} \rho_{\mathbb{B}^n}(x,y)\geq j_{\mathbb{B}^n}(x,y)\geq \log\left(1+\frac{s(1-|x|)}{1-|x|}\right)=\log(1+s). \end{align*} $$
This completes the proof.
We continue with the following result on quasiregular mappings; in fact, we show that if
![]() $f: G\rightarrow \mathbb {R}^n$
is a quasiregular mapping, and if
$f: G\rightarrow \mathbb {R}^n$
is a quasiregular mapping, and if
![]() $\partial fG$
satisfies some additional conditions, then the function
$\partial fG$
satisfies some additional conditions, then the function
![]() $u(x)=d_{fG}(f(x))$
,
$u(x)=d_{fG}(f(x))$
,
![]() $(x\in G)$
, satisfies the
$(x\in G)$
, satisfies the
![]() $(s, C(s))$
-Harnack inequality.
$(s, C(s))$
-Harnack inequality.
Remark 3.3 It is important to clarify that the theorem presented herein diverges from Theorem 5.2 in [Reference Sugawa, Vuorinen and Zhang23]. Specifically, our theorem assumes that
![]() $fG$
is a A-uniform domain with a connected boundary, while Sugawa et al. [Reference Sugawa, Vuorinen and Zhang23] regarded
$fG$
is a A-uniform domain with a connected boundary, while Sugawa et al. [Reference Sugawa, Vuorinen and Zhang23] regarded
![]() $\partial fG$
as uniformly perfect. The connectedness of
$\partial fG$
as uniformly perfect. The connectedness of
![]() $\partial fG$
is decisive in the following theorem, as demonstrated in Remark 3.5. Conversely, in the proof of Theorem 5.2, Sugawa et al. [Reference Sugawa, Vuorinen and Zhang23] employ the definition of the modulus metric
$\partial fG$
is decisive in the following theorem, as demonstrated in Remark 3.5. Conversely, in the proof of Theorem 5.2, Sugawa et al. [Reference Sugawa, Vuorinen and Zhang23] employ the definition of the modulus metric
![]() $\mu _G$
to establish an upper bound, whereas we utilize a general upper bound derived from Lemma 10.6(2) of [Reference Hariri, Klén and Vuorinen10] for
$\mu _G$
to establish an upper bound, whereas we utilize a general upper bound derived from Lemma 10.6(2) of [Reference Hariri, Klén and Vuorinen10] for
![]() $y\in {B}^n(x,s d_G(x))$
. Moreover, the constant
$y\in {B}^n(x,s d_G(x))$
. Moreover, the constant
![]() $C(s)$
obtained here is more generality than the constant obtained by Sugawa et al. in [Reference Sugawa, Vuorinen and Zhang23].
$C(s)$
obtained here is more generality than the constant obtained by Sugawa et al. in [Reference Sugawa, Vuorinen and Zhang23].
Theorem 3.4 Let G be a proper subdomain of
![]() $\mathbb {R}^n$
, and let
$\mathbb {R}^n$
, and let
![]() $f: G\rightarrow \mathbb {R}^n$
be a K-quasiregular mapping such that
$f: G\rightarrow \mathbb {R}^n$
be a K-quasiregular mapping such that
![]() $fG\subset \mathbb {R}^n$
is a A-uniform domain. Also, let
$fG\subset \mathbb {R}^n$
is a A-uniform domain. Also, let
![]() $\partial fG$
be connected such that it consists of at least two points. Then, the function
$\partial fG$
be connected such that it consists of at least two points. Then, the function
![]() $u(x)=d_{fG}(f(x))$
,
$u(x)=d_{fG}(f(x))$
,
![]() $(x\in G)$
, satisfies the
$(x\in G)$
, satisfies the
![]() $(s, C(s))$
-Harnack inequality with the constant
$(s, C(s))$
-Harnack inequality with the constant
 $$ \begin{align} C(s)=\exp\left(\frac{A K_I(f)}{c_n}\omega_{n-1}\left(\log \frac{s d_G(x)}{|x-y|}\right)^{1-n}\right),\quad s\in(0,1), \end{align} $$
$$ \begin{align} C(s)=\exp\left(\frac{A K_I(f)}{c_n}\omega_{n-1}\left(\log \frac{s d_G(x)}{|x-y|}\right)^{1-n}\right),\quad s\in(0,1), \end{align} $$
for
![]() $y\in B_{x,s}={B}^n(x,s d_G(x))$
, where
$y\in B_{x,s}={B}^n(x,s d_G(x))$
, where
![]() $\omega _{n-1}$
is the
$\omega _{n-1}$
is the
![]() $(n-1)$
-dimensional surface area of
$(n-1)$
-dimensional surface area of
![]() $S^{n-1}$
,
$S^{n-1}$
,
![]() $K_I(f)$
is the inner dilatation of f, and
$K_I(f)$
is the inner dilatation of f, and
![]() $c_n$
is a constant number depending only on n.
$c_n$
is a constant number depending only on n.
Proof Since
![]() $\partial fG$
is a connected domain and
$\partial fG$
is a connected domain and
![]() $fG$
is a A-uniform domain, by [Reference Hariri, Klén and Vuorinen10, Lemma 10.8(1)] and by definition, we have
$fG$
is a A-uniform domain, by [Reference Hariri, Klén and Vuorinen10, Lemma 10.8(1)] and by definition, we have
where
![]() $A\geq 1$
, and
$A\geq 1$
, and
![]() $c_n$
is a constant number depending on n. Also, by [Reference Hariri, Klén and Vuorinen10, Theorem 15.36(1)], the following inequality
$c_n$
is a constant number depending on n. Also, by [Reference Hariri, Klén and Vuorinen10, Theorem 15.36(1)], the following inequality
holds for a nonconstant quasiregular mapping
![]() $f: G\rightarrow \mathbb {R}^n$
, where
$f: G\rightarrow \mathbb {R}^n$
, where
![]() $K_I(f)\geq 1$
is the inner dilatation of f. It follows from [Reference Hariri, Klén and Vuorinen10, Lemma 10.6(2)] that if
$K_I(f)\geq 1$
is the inner dilatation of f. It follows from [Reference Hariri, Klén and Vuorinen10, Lemma 10.6(2)] that if
![]() $x\in G$
and
$x\in G$
and
![]() $y\in B_{x,s}={B}^n(x,s d_G(x))$
with
$y\in B_{x,s}={B}^n(x,s d_G(x))$
with
![]() $x\neq y$
, then
$x\neq y$
, then
 $$ \begin{align} \mu_G(x,y)\leq \mu_{B_{x,s}}(x,y)\leq \omega_{n-1}\left(\log \frac{1}{r} \right)^{1-n}, \end{align} $$
$$ \begin{align} \mu_G(x,y)\leq \mu_{B_{x,s}}(x,y)\leq \omega_{n-1}\left(\log \frac{1}{r} \right)^{1-n}, \end{align} $$
where
![]() $r=|x-y|/(sd_G(x))$
. Now, by (2.1) and (3.3)–(3.5), we obtain
$r=|x-y|/(sd_G(x))$
. Now, by (2.1) and (3.3)–(3.5), we obtain
 $$ \begin{align*} \left|\log \frac{d_{fG}(f(x))}{d_{fG}(f(y))}\right| &\leq k_{fG}(f(x),f(y))\leq \frac{A}{c_n}\mu_{fG}(f(x),f(y))\leq \frac{A K_I(f)}{c_n}\mu_{G}(x,y) \\ &\leq \frac{AK_I(f)}{c_n}\mu_{B_{x,s}}(x,y)\leq \frac{AK_I(f)}{c_n}\omega_{n-1}\left(\log \frac{s d_G(x)}{|x-y|}\right)^{1-n}. \end{align*} $$
$$ \begin{align*} \left|\log \frac{d_{fG}(f(x))}{d_{fG}(f(y))}\right| &\leq k_{fG}(f(x),f(y))\leq \frac{A}{c_n}\mu_{fG}(f(x),f(y))\leq \frac{A K_I(f)}{c_n}\mu_{G}(x,y) \\ &\leq \frac{AK_I(f)}{c_n}\mu_{B_{x,s}}(x,y)\leq \frac{AK_I(f)}{c_n}\omega_{n-1}\left(\log \frac{s d_G(x)}{|x-y|}\right)^{1-n}. \end{align*} $$
This establishes the desired inequality (3.2), and thus concludes the proof.
Remark 3.5 In Theorem 3.4, the connectedness of
![]() $\partial fG$
is crucial. However, it is noteworthy that the statement of Theorem 3.4 can be invalidated by the existence of an analytic function
$\partial fG$
is crucial. However, it is noteworthy that the statement of Theorem 3.4 can be invalidated by the existence of an analytic function
![]() $f:\mathbb {B}^2\rightarrow \mathbb {B}^2\,{\backslash}\, \{0\}=f\mathbb {B}^2$
. An explicit example of such a function is defined by
$f:\mathbb {B}^2\rightarrow \mathbb {B}^2\,{\backslash}\, \{0\}=f\mathbb {B}^2$
. An explicit example of such a function is defined by
![]() $f:\mathbb {B}^2\rightarrow \mathbb {B}^2\,{\backslash}\, \{0\}$
as
$f:\mathbb {B}^2\rightarrow \mathbb {B}^2\,{\backslash}\, \{0\}$
as
Let
![]() $x_p = (e^p - 1)/(e^p + 1)$
for
$x_p = (e^p - 1)/(e^p + 1)$
for
![]() $p = 1, 2, \ldots $
. Considering
$p = 1, 2, \ldots $
. Considering
![]() $f(x_p) = \exp (-e^p)$
and
$f(x_p) = \exp (-e^p)$
and
![]() $f(x_{p+1}) = \exp (-e^{p+1})$
, we can deduce
$f(x_{p+1}) = \exp (-e^{p+1})$
, we can deduce
 $$ \begin{align*} \left|\frac{f(x_p)}{f(x_{p+1})}\right| = \frac{\exp(e^{p+1})}{\exp(e^p)}. \end{align*} $$
$$ \begin{align*} \left|\frac{f(x_p)}{f(x_{p+1})}\right| = \frac{\exp(e^{p+1})}{\exp(e^p)}. \end{align*} $$
Additionally, employing a straightforward calculation, we can infer from (2.2) that
 $$ \begin{align*} \left(\log \frac{sd(x_p)}{|x_p - x_{p+1}|}\right)^{1-n} \leq \left(\log \frac{s}{\exp(k_{\mathbb{B}^2}(x_p,x_{p+1}))-1}\right)^{1-n}. \end{align*} $$
$$ \begin{align*} \left(\log \frac{sd(x_p)}{|x_p - x_{p+1}|}\right)^{1-n} \leq \left(\log \frac{s}{\exp(k_{\mathbb{B}^2}(x_p,x_{p+1}))-1}\right)^{1-n}. \end{align*} $$
Moreover, due to
![]() $k_{\mathbb {B}^2}(x,y)\leq 2 j_{\mathbb {B}^2}(x,y)$
, the preceding inequality leads to
$k_{\mathbb {B}^2}(x,y)\leq 2 j_{\mathbb {B}^2}(x,y)$
, the preceding inequality leads to
 $$ \begin{align*} \left(\log \frac{sd(x_p)}{|x_p-x_{p+1}|}\right)^{1-n}\leq \left(\log \frac{s}{\exp(2j_{\mathbb{B}^2}(x_p,x_{p+1}))-1}\right)^{1-n}. \end{align*} $$
$$ \begin{align*} \left(\log \frac{sd(x_p)}{|x_p-x_{p+1}|}\right)^{1-n}\leq \left(\log \frac{s}{\exp(2j_{\mathbb{B}^2}(x_p,x_{p+1}))-1}\right)^{1-n}. \end{align*} $$
Finally, by applying Theorem 3.4 and utilizing (2.4), we derive
 $$ \begin{align*} \frac{\exp(e^{p+1})}{\exp(e^p)}\leq \exp\left(\frac{A K_I(f)}{c_n}\omega_{n-1}\left(\log \frac{s}{\exp(2\rho_{\mathbb{B}^2}(x_p,x_{p+1}))-1}\right)^{1-n}\right). \end{align*} $$
$$ \begin{align*} \frac{\exp(e^{p+1})}{\exp(e^p)}\leq \exp\left(\frac{A K_I(f)}{c_n}\omega_{n-1}\left(\log \frac{s}{\exp(2\rho_{\mathbb{B}^2}(x_p,x_{p+1}))-1}\right)^{1-n}\right). \end{align*} $$
As
![]() $\rho _{\mathbb {B}^2}(x_p,x_{p+1})=1$
, the right-hand side of the last inequality remains bounded. However, the left-hand side of the same inequality diverges to infinity as p approaches infinity. Consequently, we can infer that the assertion in Theorem 3.4 loses validity when
$\rho _{\mathbb {B}^2}(x_p,x_{p+1})=1$
, the right-hand side of the last inequality remains bounded. However, the left-hand side of the same inequality diverges to infinity as p approaches infinity. Consequently, we can infer that the assertion in Theorem 3.4 loses validity when
![]() $\partial fG$
includes isolated points.
$\partial fG$
includes isolated points.
In the following, we shall study the Harnack metric
![]() $h_G(x,y)$
, where G is a proper subdomain of
$h_G(x,y)$
, where G is a proper subdomain of
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
Theorem 3.6 Let
![]() $s\in (0,1)$
and
$s\in (0,1)$
and
![]() $C(s)\geq 1$
. (i) If G is a proper subdomain of
$C(s)\geq 1$
. (i) If G is a proper subdomain of
![]() $\mathbb {R}^n$
, then
$\mathbb {R}^n$
, then
 $$ \begin{align*} h_G(x,y)\leq \left(1+\frac{k_G(x,y)}{2\log(1+s)}\right)\log C(s). \end{align*} $$
$$ \begin{align*} h_G(x,y)\leq \left(1+\frac{k_G(x,y)}{2\log(1+s)}\right)\log C(s). \end{align*} $$
(ii) If
![]() $G=\mathbb {B}^n$
or
$G=\mathbb {B}^n$
or
![]() $G=\mathbb {H}^n$
, then we have
$G=\mathbb {H}^n$
, then we have
 $$ \begin{align*} h_G(x,y)\leq \left(1+\frac{\rho_G(x,y)}{\log[(1+s)/(1-s)]}\right)\log C(s). \end{align*} $$
$$ \begin{align*} h_G(x,y)\leq \left(1+\frac{\rho_G(x,y)}{\log[(1+s)/(1-s)]}\right)\log C(s). \end{align*} $$
Proof (i) Let
![]() $u:G\rightarrow (0,\infty )$
be a Harnack function. By [Reference Hariri, Klén and Vuorinen10, Lemma 6.23], we have
$u:G\rightarrow (0,\infty )$
be a Harnack function. By [Reference Hariri, Klén and Vuorinen10, Lemma 6.23], we have
 $$ \begin{align*} \frac{u(x)}{u(y)}\leq C(s)^{1+t}\Leftrightarrow \log \frac{u(x)}{u(y)}\leq (1+t)\log C(s), \end{align*} $$
$$ \begin{align*} \frac{u(x)}{u(y)}\leq C(s)^{1+t}\Leftrightarrow \log \frac{u(x)}{u(y)}\leq (1+t)\log C(s), \end{align*} $$
where
![]() $t=k_G(x,y)/(2\log (1+s))$
. The claim is now a direct consequence of the Harnack metric definition. (ii) According to [Reference Hariri, Klén and Vuorinen10, Lemma 6.23], the proof closely resembles that of part (i), so we skip the details.
$t=k_G(x,y)/(2\log (1+s))$
. The claim is now a direct consequence of the Harnack metric definition. (ii) According to [Reference Hariri, Klén and Vuorinen10, Lemma 6.23], the proof closely resembles that of part (i), so we skip the details.
To prove the next results, the following two lemmas will be helpful.
Lemma 3.7 [Reference Bear2, Corollary 1] For all
![]() $x,y\in \mathbb {B}^n$
,
$x,y\in \mathbb {B}^n$
,
Lemma 3.8 [Reference Bear and Smith3, Lemma 2.5] If
![]() $x,y\in \mathbb {H}^n$
, then
$x,y\in \mathbb {H}^n$
, then
Theorem 3.9
(i) If
![]() $f: \mathbb {B}^n \rightarrow f \mathbb {B}^n$
is a nonconstant K-quasiregular mapping with
$f: \mathbb {B}^n \rightarrow f \mathbb {B}^n$
is a nonconstant K-quasiregular mapping with
![]() $f\mathbb {B}^n \subset \mathbb {B}^n$
, then the inequality
$f\mathbb {B}^n \subset \mathbb {B}^n$
, then the inequality
holds for all
![]() $x, y \in \mathbb {B}^n$
.
$x, y \in \mathbb {B}^n$
.
(ii) If
![]() $f: \mathbb {B}^n \rightarrow f \mathbb {B}^n=\mathbb {B}^n$
is a K-quasiconformal mapping, then the inequality
$f: \mathbb {B}^n \rightarrow f \mathbb {B}^n=\mathbb {B}^n$
is a K-quasiconformal mapping, then the inequality
holds, where
![]() $\alpha =K^{1/(1-n)}$
and b is a constant depending on K and n. Here, b tends to
$\alpha =K^{1/(1-n)}$
and b is a constant depending on K and n. Here, b tends to
![]() $1$
as K tends to
$1$
as K tends to
![]() $1$
.
$1$
.
Proof (i) By [Reference Hariri, Klén and Vuorinen10, Theorem 16.2(2)], we have
for all
![]() $x,y\in \mathbb {B}^n$
, where
$x,y\in \mathbb {B}^n$
, where
![]() $f:\mathbb {B}^n\rightarrow f\mathbb {B}^n\subset \mathbb {B}^n$
is a K-quasiregular mapping. It follows also from Lemma 3.7 that, for
$f:\mathbb {B}^n\rightarrow f\mathbb {B}^n\subset \mathbb {B}^n$
is a K-quasiregular mapping. It follows also from Lemma 3.7 that, for
![]() $x,y\in \mathbb {B}^n$
$x,y\in \mathbb {B}^n$
Now, combining (3.7) and (3.6) with Lemma 3.7 gives the desired result. (ii) Let
![]() $f: \mathbb {B}^n \rightarrow f \mathbb {B}^n=\mathbb {B}^n$
be a K-quasiconformal mapping and
$f: \mathbb {B}^n \rightarrow f \mathbb {B}^n=\mathbb {B}^n$
be a K-quasiconformal mapping and
![]() $x,y\in \mathbb {B}^n$
. Then, by Corollary 18.5 in [Reference Hariri, Klén and Vuorinen10], we have
$x,y\in \mathbb {B}^n$
. Then, by Corollary 18.5 in [Reference Hariri, Klén and Vuorinen10], we have
where
![]() $\alpha =K^{1/(1-n)}$
and b is a constant depending on K and n. Now, by (3.8), and using Lemma 3.7, the conclusion is obtained.
$\alpha =K^{1/(1-n)}$
and b is a constant depending on K and n. Now, by (3.8), and using Lemma 3.7, the conclusion is obtained.
Theorem 3.10 Let
![]() $f:\mathbb {H}^n\rightarrow \mathbb {H}^n$
be a nonconstant K-quasiregular mapping such that
$f:\mathbb {H}^n\rightarrow \mathbb {H}^n$
be a nonconstant K-quasiregular mapping such that
![]() $f\mathbb {H}^n\subset \mathbb {H}^n$
. Then
$f\mathbb {H}^n\subset \mathbb {H}^n$
. Then
where
![]() $K\geq 1$
.
$K\geq 1$
.
Proof If
![]() $f:\mathbb {H}^n\rightarrow \mathbb {H}^n$
is a nonconstant K-quasiregular mapping such that
$f:\mathbb {H}^n\rightarrow \mathbb {H}^n$
is a nonconstant K-quasiregular mapping such that
![]() $f\mathbb {H}^n\subset \mathbb {H}^n$
, then by [Reference Hariri, Klén and Vuorinen10, Theorem 16.2(2)], we have
$f\mathbb {H}^n\subset \mathbb {H}^n$
, then by [Reference Hariri, Klén and Vuorinen10, Theorem 16.2(2)], we have
where
![]() $K\geq 1$
. Also, by Lemma 3.8, for all
$K\geq 1$
. Also, by Lemma 3.8, for all
![]() $x,y\in f\mathbb {H}^n\subset \mathbb {H}^n$
, we have
$x,y\in f\mathbb {H}^n\subset \mathbb {H}^n$
, we have
The result now follows from (3.9), (3.10), and Lemma 3.8. The proof is now complete.
For
![]() $r\in (0,1)$
and
$r\in (0,1)$
and
![]() $K\in [1,\infty )$
, the function
$K\in [1,\infty )$
, the function
![]() $\varphi _K:[0,1]\rightarrow [0,1]$
is defined as follows:
$\varphi _K:[0,1]\rightarrow [0,1]$
is defined as follows:
 $$ \begin{align*} \varphi_K(r)=\mu^{-1}\left(\frac{\mu(r)}{K}\right), \quad \varphi_K(0)=0; \varphi_K(1)=1, \end{align*} $$
$$ \begin{align*} \varphi_K(r)=\mu^{-1}\left(\frac{\mu(r)}{K}\right), \quad \varphi_K(0)=0; \varphi_K(1)=1, \end{align*} $$
where
![]() $\mu :(0,1)\rightarrow (0,\infty )$
is a decreasing homeomorphism given by
$\mu :(0,1)\rightarrow (0,\infty )$
is a decreasing homeomorphism given by

and F represents the Gaussian hypergeometric function. For additional information about the function
![]() $\varphi _K(r)$
and its approximation, readers are encouraged to consult [Reference Kargar, Rainio and Vuorinen17].
$\varphi _K(r)$
and its approximation, readers are encouraged to consult [Reference Kargar, Rainio and Vuorinen17].
Theorem 3.11 If
![]() $f:\mathbb {B}^2\rightarrow \mathbb {B}^2$
is a nonconstant K-quasiregular mapping, then
$f:\mathbb {B}^2\rightarrow \mathbb {B}^2$
is a nonconstant K-quasiregular mapping, then
for all
![]() $x,y\in \mathbb {B}^2$
, where
$x,y\in \mathbb {B}^2$
, where
![]() $c(K)=2\mathrm {arth}(\varphi _K(\mathrm {th}(1/2)))$
. In particular,
$c(K)=2\mathrm {arth}(\varphi _K(\mathrm {th}(1/2)))$
. In particular,
![]() $c(1)=1$
.
$c(1)=1$
.
Proof Let
![]() $f:\mathbb {B}^2\rightarrow \mathbb {B}^2$
be a nonconstant K-quasiregular mapping. Then, by Theorem [Reference Hariri, Klén and Vuorinen10, Theorem 16.39], we have
$f:\mathbb {B}^2\rightarrow \mathbb {B}^2$
be a nonconstant K-quasiregular mapping. Then, by Theorem [Reference Hariri, Klén and Vuorinen10, Theorem 16.39], we have
for all
![]() $x,y\in \mathbb {B}^2$
, where
$x,y\in \mathbb {B}^2$
, where
![]() $c(K)=2\mathrm {arth}(\varphi _K(\mathrm {th}(1/2)))$
. The desired assertion can be obtained by utilizing Lemma 3.7 and inequality (3.11).
$c(K)=2\mathrm {arth}(\varphi _K(\mathrm {th}(1/2)))$
. The desired assertion can be obtained by utilizing Lemma 3.7 and inequality (3.11).
4 Harmonic Schwarz lemma
This section first generalizes the Schwarz lemma for harmonic functions in the complex plane utilizing the Poisson integral formula. Then, it improves the Schwarz–Pick estimate for a real-valued harmonic function. First, we recall that the classical Schwarz lemma states that if
![]() $u:\mathbb {B}^2\rightarrow \mathbb {B}^2$
is a holomorphic function with
$u:\mathbb {B}^2\rightarrow \mathbb {B}^2$
is a holomorphic function with
![]() $u(0)=0$
, then:
$u(0)=0$
, then:
-
•
 $|u(z)|\leq |z|$
for all
$|u(z)|\leq |z|$
for all
 $z\in \mathbb {B}^2$
;
$z\in \mathbb {B}^2$
; -
•
 $|u'(0)|\leq 1$
.
$|u'(0)|\leq 1$
.
Heinz (see [Reference Heinz12]) has obtained an improvement of the classical Schwarz lemma for a complex-valued harmonic function (see Lemma 4.1). A complex-valued function
![]() $f:G \to \mathbb {C}$
, where
$f:G \to \mathbb {C}$
, where
![]() $f= u + i v$
is said to be harmonic if both
$f= u + i v$
is said to be harmonic if both
![]() $u:G \to \mathbb {R}$
and
$u:G \to \mathbb {R}$
and
![]() $v:G \to \mathbb {R}$
are harmonic in the sense defined above.
$v:G \to \mathbb {R}$
are harmonic in the sense defined above.
Lemma 4.1 Let
![]() $u:\mathbb {B}^2\rightarrow \mathbb {B}^2$
be a complex-valued harmonic function with
$u:\mathbb {B}^2\rightarrow \mathbb {B}^2$
be a complex-valued harmonic function with
![]() $u(0)=0$
. Then
$u(0)=0$
. Then
The inequality is sharp for each point
![]() $z\in \mathbb {B}^2$
.
$z\in \mathbb {B}^2$
.
The following Theorem 4.2 is known as the Poisson integral formula (see, for example, [Reference Gwynne9]).
Theorem 4.2 Let u be a complex-valued function continuous on
![]() $\overline {B}^2(a,R)$
,
$\overline {B}^2(a,R)$
,
![]() $(R>0)$
, and harmonic on
$(R>0)$
, and harmonic on
![]() ${B}^2(a,R)$
. Then for
${B}^2(a,R)$
. Then for
![]() $r\in [0,R)$
and
$r\in [0,R)$
and
![]() $t\in \mathbb {R}$
the following formulas hold:
$t\in \mathbb {R}$
the following formulas hold:
 $$ \begin{align} u\left(a+r e^{i t}\right)=\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{R^2-r^2}{R^2+r^2-2rR \cos(t-\theta)}u\left(a+R e^{i \theta}\right)\mathrm{d}\theta \end{align} $$
$$ \begin{align} u\left(a+r e^{i t}\right)=\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{R^2-r^2}{R^2+r^2-2rR \cos(t-\theta)}u\left(a+R e^{i \theta}\right)\mathrm{d}\theta \end{align} $$
and
Motivated by Lemma 4.1 and applying Theorem 4.2, we derive the following Theorem 4.3 which is an extension of the above Schwarz lemma:
Theorem 4.3 Let
![]() $0< r<R$
and
$0< r<R$
and
![]() $M>0$
. If u is a complex-valued harmonic mapping in the disk
$M>0$
. If u is a complex-valued harmonic mapping in the disk
![]() $B^2(a,R)$
such that
$B^2(a,R)$
such that
![]() $|u(w)|\leq M$
for all
$|u(w)|\leq M$
for all
![]() $w\in B^2(a,R)$
, then
$w\in B^2(a,R)$
, then
 $$ \begin{align*} \left|u(a+z)-\frac{R^2-|z|^2}{R^2+|z|^2}u(a)\right|\leq\frac{2M}{\pi}\arctan\left(\frac{2R|z|}{R^2-|z|^2}\right),\quad z=re^{i t}. \end{align*} $$
$$ \begin{align*} \left|u(a+z)-\frac{R^2-|z|^2}{R^2+|z|^2}u(a)\right|\leq\frac{2M}{\pi}\arctan\left(\frac{2R|z|}{R^2-|z|^2}\right),\quad z=re^{i t}. \end{align*} $$
The result is sharp.
Proof Suppose that
![]() $0<r<R$
. Applying formula (4.1) for
$0<r<R$
. Applying formula (4.1) for
![]() $z=r$
, we obtain
$z=r$
, we obtain
 $$ \begin{align*} &u\left(a+r\right)-\frac{R^2-r^2}{R^2+r^2}u(a)\\ &\quad=\frac{1}{2\pi}\int_{-\pi}^{\pi} \left(\frac{R^2-r^2}{R^2+r^2-2rR \cos(\theta)}-\frac{R^2-r^2}{R^2+r^2} \right)u\left(a+Re^{i\theta}\right)\mathrm{d}\theta\\ &\quad= \frac{rR(R^2-r^2)}{\pi(R^2+r^2)}\int_{-\pi}^{\pi}\frac{\cos(\theta)}{R^2+r^2-2rR \cos(\theta)} u\left(a+Re^{i\theta}\right)\mathrm{d}\theta. \end{align*} $$
$$ \begin{align*} &u\left(a+r\right)-\frac{R^2-r^2}{R^2+r^2}u(a)\\ &\quad=\frac{1}{2\pi}\int_{-\pi}^{\pi} \left(\frac{R^2-r^2}{R^2+r^2-2rR \cos(\theta)}-\frac{R^2-r^2}{R^2+r^2} \right)u\left(a+Re^{i\theta}\right)\mathrm{d}\theta\\ &\quad= \frac{rR(R^2-r^2)}{\pi(R^2+r^2)}\int_{-\pi}^{\pi}\frac{\cos(\theta)}{R^2+r^2-2rR \cos(\theta)} u\left(a+Re^{i\theta}\right)\mathrm{d}\theta. \end{align*} $$
By the last equality and the assumption
![]() $|u|\leq M$
, we obtain
$|u|\leq M$
, we obtain
 $$ \begin{align} \left|u\left(a+r\right)-\frac{R^2-r^2}{R^2+r^2}u(a)\right|\leq M\frac{rR(R^2-r^2)}{\pi(R^2+r^2)}\int_{-\pi}^{\pi}\frac{|\cos(\theta)|}{R^2+r^2-2rR \cos(\theta)} \mathrm{d}\theta. \end{align} $$
$$ \begin{align} \left|u\left(a+r\right)-\frac{R^2-r^2}{R^2+r^2}u(a)\right|\leq M\frac{rR(R^2-r^2)}{\pi(R^2+r^2)}\int_{-\pi}^{\pi}\frac{|\cos(\theta)|}{R^2+r^2-2rR \cos(\theta)} \mathrm{d}\theta. \end{align} $$
Now, we calculate the integral
It is easy to check that
 $$ \begin{align*} I&=\int_{-\pi/2}^{\pi/2}\left(\frac{\cos(\theta)}{R^2+r^2-2rR \cos(\theta)}+\frac{\cos(\theta)}{R^2+r^2+2rR \cos(\theta)}\right) \mathrm{d}\theta\\ &=2(R^2+r^2)\int_{-\pi/2}^{\pi/2}\frac{\cos(\theta)}{(R^2+r^2)^2-4r^2 R^2 \cos^2(\theta)}\mathrm{d}\theta\\ &=4(R^2+r^2)\int_{0}^{\pi/2}\frac{\cos(\theta)}{(R^2-r^2)^2+4r^2 R^2 \sin^2(\theta)}\mathrm{d}\theta\\ &=\frac{2(R^2+r^2)}{rR(R^2-r^2)}\arctan\left(\frac{2rR}{R^2-r^2}\right). \end{align*} $$
$$ \begin{align*} I&=\int_{-\pi/2}^{\pi/2}\left(\frac{\cos(\theta)}{R^2+r^2-2rR \cos(\theta)}+\frac{\cos(\theta)}{R^2+r^2+2rR \cos(\theta)}\right) \mathrm{d}\theta\\ &=2(R^2+r^2)\int_{-\pi/2}^{\pi/2}\frac{\cos(\theta)}{(R^2+r^2)^2-4r^2 R^2 \cos^2(\theta)}\mathrm{d}\theta\\ &=4(R^2+r^2)\int_{0}^{\pi/2}\frac{\cos(\theta)}{(R^2-r^2)^2+4r^2 R^2 \sin^2(\theta)}\mathrm{d}\theta\\ &=\frac{2(R^2+r^2)}{rR(R^2-r^2)}\arctan\left(\frac{2rR}{R^2-r^2}\right). \end{align*} $$
Thus, from (4.3) follows that
 $$ \begin{align*} \left|u\left(a+r\right)-\frac{R^2-r^2}{R^2+r^2}u(a)\right|\leq \frac{2M}{\pi}\arctan\left(\frac{2rR}{R^2-r^2}\right), \end{align*} $$
$$ \begin{align*} \left|u\left(a+r\right)-\frac{R^2-r^2}{R^2+r^2}u(a)\right|\leq \frac{2M}{\pi}\arctan\left(\frac{2rR}{R^2-r^2}\right), \end{align*} $$
which implies the desired result. It is easy to see that the result is sharp for the function
or one of its rotations, where
![]() $0<r<R$
and
$0<r<R$
and
![]() $M>0$
, completing the proof.
$M>0$
, completing the proof.
Remark 4.4 It should be noted that Theorem 4.3 is also an extension of [Reference Pavlović21, Theorem 3.6.1]. Indeed, Pavlović proved that if
![]() $f:\mathbb {B}^2\rightarrow \overline {\mathbb {B}}^2$
is a complex-valued harmonic function, then the following sharp inequality holds:
$f:\mathbb {B}^2\rightarrow \overline {\mathbb {B}}^2$
is a complex-valued harmonic function, then the following sharp inequality holds:
 $$ \begin{align*} \left|u(z)-\frac{1-|z|^2}{1+|z|^2}u(0)\right|\leq\frac{4}{\pi}\arctan |z|,\quad z=re^{i t}. \end{align*} $$
$$ \begin{align*} \left|u(z)-\frac{1-|z|^2}{1+|z|^2}u(0)\right|\leq\frac{4}{\pi}\arctan |z|,\quad z=re^{i t}. \end{align*} $$
Let
![]() $\nabla u$
be the gradient of u at x defined by
$\nabla u$
be the gradient of u at x defined by
In 1989 (see [Reference Colonna6]), Colonna proved the following Schwarz–Pick estimate for complex-valued harmonic functions u from the unit disk
![]() $\mathbb {B}^2$
to itself:
$\mathbb {B}^2$
to itself:
 $$ \begin{align*} \left|\frac{\partial u(z)}{\partial z}\right|+\left|\frac{\partial u(z)}{\partial \overline{z}}\right|\leq \frac{4}{\pi}\frac{1}{1-|z|^2}, \quad z\in \mathbb{B}^2. \end{align*} $$
$$ \begin{align*} \left|\frac{\partial u(z)}{\partial z}\right|+\left|\frac{\partial u(z)}{\partial \overline{z}}\right|\leq \frac{4}{\pi}\frac{1}{1-|z|^2}, \quad z\in \mathbb{B}^2. \end{align*} $$
If u is a real-valued function, Kalaj and Vuorinen established the above Schwarz–Pick estimate as the following theorem; refer to [Reference Kalaj and Vuorinen16, Theorem 1.8] for details.
Theorem 4.5 Let u be a real harmonic function of the unit disk into
![]() $(-1, 1)$
. Then the following sharp inequality holds:
$(-1, 1)$
. Then the following sharp inequality holds:
 $$ \begin{align*} |\nabla u(z)|\leq \frac{4}{\pi}\frac{1-|u(z)|^2}{1-|z|^2}, \quad z\in \mathbb{B}^2. \end{align*} $$
$$ \begin{align*} |\nabla u(z)|\leq \frac{4}{\pi}\frac{1-|u(z)|^2}{1-|z|^2}, \quad z\in \mathbb{B}^2. \end{align*} $$
In accordance with the findings of Chen [Reference Chen4, Theorem 1.2], the subsequent result has been derived:
Theorem 4.6 Let u be a real harmonic mapping of
![]() $\mathbb {B}^2$
into the open interval
$\mathbb {B}^2$
into the open interval
![]() $(-1,1)$
. Then
$(-1,1)$
. Then
 $$ \begin{align*} |\nabla u(z)|\leq \frac{4}{\pi}\frac{\cos \left(\frac{\pi}{2}u(z)\right)}{1-|z|^2} \end{align*} $$
$$ \begin{align*} |\nabla u(z)|\leq \frac{4}{\pi}\frac{\cos \left(\frac{\pi}{2}u(z)\right)}{1-|z|^2} \end{align*} $$
holds for
![]() $z\in \mathbb {B}^2$
. The inequality is sharp for any
$z\in \mathbb {B}^2$
. The inequality is sharp for any
![]() $z\in \mathbb {B}^2$
and any value of
$z\in \mathbb {B}^2$
and any value of
![]() $u(z)$
, and the equality occurs for some point in
$u(z)$
, and the equality occurs for some point in
![]() $\mathbb {B}^2$
if and only if
$\mathbb {B}^2$
if and only if
![]() $u(z)=(4 \mathrm {Re}\{\arctan \, f(z)\})/\pi $
,
$u(z)=(4 \mathrm {Re}\{\arctan \, f(z)\})/\pi $
,
![]() $z\in \mathbb {B}^2$
with a Möbius transformation f of
$z\in \mathbb {B}^2$
with a Möbius transformation f of
![]() $\mathbb {B}^2$
onto itself.
$\mathbb {B}^2$
onto itself.
In the subsequent discussion, we aim to expand upon Theorem 4.5 in the following manner: Furthermore, it is worth noting that our extension encompasses the findings presented in Theorem 6.26 of [Reference Axler, Bourdon and Ramey1].
Theorem 4.7 Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two real numbers such that
$\beta $
be two real numbers such that
![]() $\alpha <\beta $
. If
$\alpha <\beta $
. If
![]() $u:\mathbb {B}^2\rightarrow (\alpha ,\beta )$
is a real-valued harmonic function, then we have
$u:\mathbb {B}^2\rightarrow (\alpha ,\beta )$
is a real-valued harmonic function, then we have
 $$ \begin{align*} |\nabla u(z)|\leq \frac{2(\beta-\alpha)}{\pi}\frac{1-\frac{4}{(\beta-\alpha)^2} \left|u(z)-\frac{\alpha+\beta}{2}\right|{}^2}{1-|z|^2},\quad z\in \mathbb{B}^2. \end{align*} $$
$$ \begin{align*} |\nabla u(z)|\leq \frac{2(\beta-\alpha)}{\pi}\frac{1-\frac{4}{(\beta-\alpha)^2} \left|u(z)-\frac{\alpha+\beta}{2}\right|{}^2}{1-|z|^2},\quad z\in \mathbb{B}^2. \end{align*} $$
The result is sharp.
Proof Define
![]() $v(z)$
as
$v(z)$
as
 $$ \begin{align*} v(z)=\frac{2}{\beta-\alpha}\left(u(z)-\frac{\alpha+\beta}{2}\right),\quad z\in \mathbb{B}^2, \end{align*} $$
$$ \begin{align*} v(z)=\frac{2}{\beta-\alpha}\left(u(z)-\frac{\alpha+\beta}{2}\right),\quad z\in \mathbb{B}^2, \end{align*} $$
where
![]() $u:\mathbb {B}^2\rightarrow (\alpha ,\beta )$
is a real-valued harmonic function,
$u:\mathbb {B}^2\rightarrow (\alpha ,\beta )$
is a real-valued harmonic function,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are real numbers such that
$\beta $
are real numbers such that
![]() $\alpha <\beta $
. Then it is clear that v is a harmonic function of the unit disk
$\alpha <\beta $
. Then it is clear that v is a harmonic function of the unit disk
![]() $\mathbb {B}^2$
into
$\mathbb {B}^2$
into
![]() $(-1,1)$
. Therefore, v satisfies the assumption of Theorem 4.5. Moreover, we have
$(-1,1)$
. Therefore, v satisfies the assumption of Theorem 4.5. Moreover, we have
 $$ \begin{align*} \frac{2}{\beta-\alpha}|\nabla u|=|\nabla v|\leq \frac{4}{\pi}\frac{1-\frac{4}{(\beta-\alpha)^2} \left|u(z)-\frac{\alpha+\beta}{2}\right|{}^2}{1-|z|^2},\quad z\in \mathbb{B}^2, \end{align*} $$
$$ \begin{align*} \frac{2}{\beta-\alpha}|\nabla u|=|\nabla v|\leq \frac{4}{\pi}\frac{1-\frac{4}{(\beta-\alpha)^2} \left|u(z)-\frac{\alpha+\beta}{2}\right|{}^2}{1-|z|^2},\quad z\in \mathbb{B}^2, \end{align*} $$
which implies the desired result. To show that the result is sharp, we take the harmonic function
 $$ \begin{align*} \ell(z)=\frac{\alpha+\beta}{2}+\frac{\beta-\alpha}{\pi}\arctan \frac{2y}{1-x^2-y^2},\quad z\in \mathbb{B}^2. \end{align*} $$
$$ \begin{align*} \ell(z)=\frac{\alpha+\beta}{2}+\frac{\beta-\alpha}{\pi}\arctan \frac{2y}{1-x^2-y^2},\quad z\in \mathbb{B}^2. \end{align*} $$
It is easy to see
![]() $\alpha <\ell (z)<\beta $
. A simple calculation yields
$\alpha <\ell (z)<\beta $
. A simple calculation yields
 $$ \begin{align*} |\nabla \ell(0)|=\frac{2(\beta-\alpha)}{2}=\frac{2(\beta-\alpha)}{2}\cdot \frac{1-\frac{4}{(\beta-\alpha)^2}\left|\frac{\alpha+\beta}{2}-\frac{\alpha+\beta}{2} \right|{}^2}{1-0^2}, \end{align*} $$
$$ \begin{align*} |\nabla \ell(0)|=\frac{2(\beta-\alpha)}{2}=\frac{2(\beta-\alpha)}{2}\cdot \frac{1-\frac{4}{(\beta-\alpha)^2}\left|\frac{\alpha+\beta}{2}-\frac{\alpha+\beta}{2} \right|{}^2}{1-0^2}, \end{align*} $$
which is the desired conclusion.
Applying Theorem 4.6, we get the following result:
Theorem 4.8 If
![]() $u:\mathbb {B}^2\rightarrow (\alpha ,\beta )$
is an into harmonic mapping, then
$u:\mathbb {B}^2\rightarrow (\alpha ,\beta )$
is an into harmonic mapping, then
 $$ \begin{align*} |\nabla u(z)|\leq \frac{2(\beta-\alpha)}{\pi}\frac{\cos \left(\frac{\pi}{\beta-\alpha}\left(u(z)-\frac{\alpha+\beta}{2}\right)\right)}{1-|z|^2}, \end{align*} $$
$$ \begin{align*} |\nabla u(z)|\leq \frac{2(\beta-\alpha)}{\pi}\frac{\cos \left(\frac{\pi}{\beta-\alpha}\left(u(z)-\frac{\alpha+\beta}{2}\right)\right)}{1-|z|^2}, \end{align*} $$
where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are real numbers such that
$\beta $
are real numbers such that
![]() $\alpha <\beta $
. The result is sharp.
$\alpha <\beta $
. The result is sharp.
Proof The proof is the same as the proof of Theorem 4.7, therefore, we omit the details.
We conclude this paper by presenting the following open question:
Open question. What is the connection between the Harnack metric h and the hyperbolic metric
![]() $\rho $
in a simply connected Jordan domain in the complex plane
$\rho $
in a simply connected Jordan domain in the complex plane
![]() $\mathbb {C}$
?
$\mathbb {C}$
?
Acknowledgments
The author thanks Professor Matti Vuorinen for his encouragement and many useful discussions throughout the writing process. He also thanks the editor and the anonymous reviewer for their insightful comments and valuable suggestions on this paper, which have greatly enhanced its quality and depth.