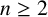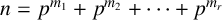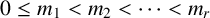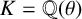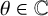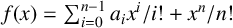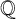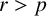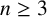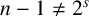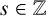1 Introduction
Let
$K = \mathbb Q(\theta )$
be an algebraic number field with
$\theta $
in the ring
${\mathbb Z}_K$
of algebraic integers of K. Let
$f(x)$
be the minimal polynomial of
$\theta $
having degree n over the field
$\mathbb Q$
of rational numbers. It is well known that
${\mathbb Z}_K$
is a free abelian group of rank n. A number field K is said to be monogenic if there exists some
$\beta \in {\mathbb Z}_K$
such that
${\mathbb Z}_K = {\mathbb Z}[\beta ].$
In this case,
$\{1, \beta ,\ldots ,\beta ^{n-1}\}$
is an integral basis of K; such an integral basis of K is called a power integral basis or briefly a power basis of K. If K does not possess any power basis, we say that K is nonmonogenic. Quadratic and cyclotomic fields are monogenic. In algebraic number theory, it is important to know whether a number field is monogenic or not. The first example of a nonmonogenic number field was given by Dedekind in 1878; he proved that the cubic field
$\mathbb Q(\eta )$
is not monogenic when
$\eta $
is a root of the polynomial
$x^3-x^2-2x-8$
(see [Reference Narkiewicz15, page 64]). The problems of testing the monogenity of number fields and constructing power integral bases have been intensively studied (see [Reference Gaál7] for an overview of the latest developments).
Throughout this paper,
$\mathop {\mathrm {ind}} \theta $
denotes the index of the subgroup
${\mathbb Z}[\theta ]$
in
${\mathbb Z}_K $
and
$i(K)$
stands for the index of the field K defined by
$ i(K) = \gcd \{\mathop {\mathrm {ind}} \alpha \mid {\text {} K=\mathbb Q(\alpha ) {\text { and }} \alpha \in {\mathbb Z}_K} \}.$
A prime number p dividing
$i(K)$
is called a prime common index divisor of K. Note that if K is monogenic, then
$i(K)=1$
. Therefore, a number field having a prime common index divisor is nonmonogenic. However, there exist nonmonogenic number fields having
$i(K)=1$
, for example,
$K=\mathbb Q(\sqrt [3]{175})$
is not monogenic and has
$i(K)=1$
. Nakahara [Reference Nakahara14] studied the index of noncyclic but abelian biquadratic number fields. Gaál et al. [Reference Gaál, Pethö and Pohst8] characterised the field indices of biquadratic number fields having Galois group
$V_4$
. Ahmad et al. [Reference Ahmad, Nakahara and Hameed1, Reference Ahmad, Nakahara and Husnine2] proved that for a square free integer m not congruent to
$\pm 1\bmod 9$
, a pure field
$\mathbb Q(m^{1/6})$
having degree
$6$
over
$\mathbb Q$
is monogenic when
$m\equiv 2$
or
$3\bmod 4$
and it is nonmonogenic when
$m\equiv 1\bmod 4$
. Gaál and Remete [Reference Gaál and Remete9] studied monogenity of number fields of the type
$\mathbb Q(m^{1/n})$
where
$3\leq n\leq 9$
and m is square free. Gaál [Reference Gaál6] and Jakhar and Kaur [Reference Jakhar and Kaur10] studied monogenity of number fields defined by some sextic irreducible trinomials.
Let
$a_0, \ldots , a_{n-1}$
be integers. It is known that the polynomial
$$ \begin{align} f(x) = a_0 + a_1x+ a_2\frac{x^2}{2!} + \cdots +a_{n-1}\frac{x^{n-1}}{(n-1)!} + \frac{x^n}{n!} \end{align} $$
of degree n is irreducible over
$\mathbb Q$
if one of the following conditions is satisfied:
-
(1)
$\gcd (a_0, n!) = 1$
(see [Reference Coleman5, Reference Schur16]); -
(2)
$\gcd (a_0a_1\cdots a_{n-1}, n) = 1$
(see [Reference Jindal and Khanduja11, Theorem 1.2]).
Let p be a prime number. Let
$n\geq 2$
be an integer given by
$n = p^{m_1} + p^{m_2} + \cdots + p^{m_r}$
, where
$0\leq m_1 < m_2 < \cdots < m_r$
are integers. Let
$K = \mathbb Q(\theta )$
with
$\theta $
a root of an irreducible polynomial
$f(x)$
over
$\mathbb Q$
, where
$f(x)$
is given by (1.1) and
$a_0, \ldots , a_{n-1}$
are integers not divisible by p. We provide necessary and sufficient conditions so that
$p \mid i(K)$
for
$n\geq 2.$
As an application, we give a family of number fields which are nonmonogenic. Precisely stated, we prove the following result.
Theorem 1.1. Let p be a prime number. Let
$n\geq 2$
be an integer given by
${n = p^{m_1} + p^{m_2} + \cdots + p^{m_r}}$
, where
$0\leq m_1 < m_2 < \cdots < m_r$
are integers. Let
$a_0, a_1, \ldots , a_{n-1}$
be integers not divisible by p. Let
$K = \mathbb Q(\theta )$
be an algebraic number field with
$\theta $
a root of an irreducible polynomial
$f(x) = x^n+ n! \sum _{i=0}^{n-1}a_i x^i/i!$
over
$\mathbb Q$
. Then:
-
(1)
$p{\mathbb Z}_K = \wp _1^{e_1}\cdots \wp _r^{e_r},$
where the
$\wp _i$
are distinct prime ideals lying above the prime p with index of ramification
$e_i = p^{m_i}$
and residual degree one for each i; -
(2) p divides
$i(K)$
if and only if
$r>p$
.
In particular, if
$r>p$
, then K is always nonmonogenic.
The following corollary is an immediate consequence of the theorem.
Corollary 1.2. Let
$n\geq 2$
be an integer with
$2$
-adic expansion
$n = 2^{m_1} + 2^{m_2} + \cdots + 2^{m_r}$
, where
$0\leq m_1 < m_2 < \cdots < m_r$
. Let
$a_0, a_1, \ldots , a_{n-1}$
be odd integers. Let
$K = \mathbb Q(\theta )$
be an algebraic number field with
$\theta $
a root of an irreducible polynomial
$f(x) = x^n+ n! \sum _{i=0}^{n-1}a_i x^i/i!$
over
$\mathbb Q$
. If
$r> 2$
, then K is nonmonogenic.
As an application of this corollary, we obtain the following result.
Corollary 1.3. Let
$n\geq 2$
be an integer with
$2$
-adic expansion
$n = 2^{m_1} + 2^{m_2} + \cdots + 2^{m_r}$
, where
$0\leq m_1 < m_2 < \cdots < m_r$
. Let
$K = \mathbb Q(\theta )$
be an algebraic number field with
$\theta $
a root of a truncated exponential Taylor polynomial
$f(x) = 1 + x + x^2/2! + \cdots + x^n/n!$
. Assume that
$r\geq 3$
. Then K is always nonmonogenic.
Example 1.4. This example provides a family of nonmonogenic algebraic number fields. Let
$n\geq 3$
be an odd integer such that
$n-1 \neq 2^s$
for any
$s\in {\boldsymbol N}$
. If
$K = \mathbb Q(\theta )$
is an algebraic number field with
$\theta \in {\mathbb C}$
a root of
$f(x) = \sum _{i=0}^{n}{x^i}/{i!}$
, then K is nonmonogenic by Corollary 1.3.
Remark 1.5. If we take
$r < 3$
, then K can be monogenic. For example, consider
$n = 3$
,
$r = 2$
and
$f(x) = x^3 + 3x^2+ 6x + 6$
in Corollary 1.3. It can be easily checked that the discriminant of
$f(x)$
is
$-2^3\cdot 3^3.$
Let
$K = \mathbb Q(\theta )$
with
$\theta $
a root of
$f(x)$
. Since
$f(x)$
is an Eisenstein polynomial with respect to
$3$
, in view of a basic result [Reference Khanduja12, Theorem 2.18], we see that
$3\nmid [{\mathbb Z}_K : {\mathbb Z}[\theta ]].$
Further note that
$f(x) \equiv x^2(x+1) \pmod 2$
. Hence, using Dedekind’s criterion [Reference Khanduja12, page 78], it is easy to see that
$2\nmid [{\mathbb Z}_K : {\mathbb Z}[\theta ]]$
. Therefore, in view of the formula
$D_f = [{\mathbb Z}_K : {\mathbb Z}[\theta ]]^2d_K$
, where
$D_f$
denotes the discriminant of the polynomial
$f(x)$
and
$d_K$
denotes the discriminant of K, it follows that
${\mathbb Z}_K = {\mathbb Z}[\theta ].$
Hence, K is monogenic.
2 Preliminary results
Let
$K=\mathbb Q(\theta )$
be an algebraic number field with
$\theta $
a root of a monic irreducible polynomial
$f(x)$
belonging to
${\mathbb Z}[x]$
. In what follows,
${\mathbb Z}_K$
stands for the ring of algebraic integers of K. For a rational prime p, let
${\mathbb F}_p$
be the finite field with p elements and
${\mathbb Z}_p$
denote the ring of p-adic integers. Throughout the paper,
$f(x)\rightarrow \overline {f(x)}$
stands for the canonical homomorphism from
${\mathbb Z}_p[x]$
onto
${\mathbb F}_p[x]$
. For a prime p and a nonzero m belonging to the ring
${\mathbb Z}_p$
of p-adic integers,
$v_p(m)$
denotes the highest power of p dividing m. The following lemma will play an important role in the proof of the theorem.
Lemma 2.1 [Reference Narkiewicz15, Theorem 4.34].
Let K be an algebraic number field and p be a rational prime. Then p is a prime common index divisor of K if and only if for some positive integer h, the number of distinct prime ideals of
${\mathbb Z}_K$
lying above p having residual degree h is greater than the number of monic irreducible polynomials of degree h in
${\mathbb F}_p[x]$
.
The following simple result will also be used. Its proof is omitted.
Lemma 2.2. Let p be a prime number. If
$n = c_0 + c_1p + \cdots + c_rp^r$
is the representation of the positive integer n in base p with
$0\leq c_i < p$
for each i, then
$$ \begin{align*}v_p(n!) = \frac{n-(c_0+c_1+\cdots + c_r)}{p-1}.\end{align*} $$
3 A short introduction to prime ideal factorisation based on Newton polygons
In 1894, Hensel developed a powerful approach for finding prime ideals of
${\mathbb Z}_K$
over a rational prime p. He showed that for every prime p, the prime ideals of
${\mathbb Z}_K$
lying above p are in one-to-one correspondence with monic irreducible factors of
$f(x)$
in
$\mathbb Q_p[x]$
. Newton polygons are very helpful for finding the factors of
$f(x)$
in
$\mathbb Q_p[x]$
. This is a standard method which is rather technical but efficient to apply. Therefore, we first introduce the notion of Gauss valuation and
$\phi $
-Newton polygon, where
$\phi (x)$
belonging to
${\mathbb Z}_p[x]$
is a monic polynomial with
$\overline {\phi }(x)$
irreducible over
${\mathbb F}_p$
.
Definition 3.1. The Gauss valuation of the field
$\mathbb Q_p(x)$
of rational functions in an indeterminate x extends the valuation
$v_p$
of
$\mathbb Q_p$
and is defined on
$\mathbb Q_p[x]$
by
$$ \begin{align*} v_{p,x}(a_0+a_1x+a_2x^2+\cdots+a_sx^s)= \displaystyle\min_{1\leq i\leq s}\{v_p(a_i)\}, \quad a_i\in \mathbb Q_p. \end{align*} $$
Definition 3.2. Let p be a rational prime. Let
$\phi (x)\in {\mathbb Z}_p[x]$
be a monic polynomial which is irreducible modulo p and
$f(x)\in {\mathbb Z}_p[x]$
be a monic polynomial not divisible by
$\phi (x)$
. Let
$\sum _{i=0}^{n}a_i(x)\phi (x)^i$
, with
$\deg a_i(x)<\deg \phi (x)$
,
$a_n(x)\neq 0$
, be the
$\phi (x)$
-expansion of
$f(x)$
obtained by dividing
$f(x)$
by the successive powers of
$\phi (x)$
. Let
$P_i$
stand for the point in the plane having coordinates
$(i,v_{p,x}(a_{n-i}(x)))$
when
$a_{n-i}(x)\neq 0$
,
$0\leq i\leq n$
. Let
$\mu _{ij}$
denote the slope of the line joining the point
$P_i$
to
$P_j$
if
$a_{n-i}(x)a_{n-j}(x)\neq 0$
. Let
$i_1$
be the largest positive index not exceeding n such that
$$ \begin{align*}\mu_{0i_1}=\min\{\mu_{0j}~|~0<j\leq n,~a_{n-j}(x)\neq0\}.\end{align*} $$
If
$i_1<n,$
let
$i_2$
be the largest index such that
$i_1<i_2\leq n$
with
$$ \begin{align*}\mu_{i_1i_2}=\min\{\mu_{i_1j}~|~i_1<j\leq n,~a_{n-j}(x)\neq0\},\end{align*} $$
and so on. The
$\phi $
-Newton polygon of
$f(x)$
with respect to p is the polygonal path having segments
$P_{0}P_{i_1},P_{i_1}P_{i_2},\ldots ,P_{i_{k-1}}P_{i_k}$
with
$i_k=n$
. These segments are called the edges of the
$\phi $
-Newton polygon and their slopes form a strictly increasing sequence; these slopes are nonnegative as
$f(x)$
is a monic polynomial with coefficients in
${\mathbb Z}_p$
.
Definition 3.3. Let
$\phi (x) \in {\mathbb Z}_p[x]$
be a monic polynomial which is irreducible modulo a rational prime p having a root
$\alpha $
in the algebraic closure
$\widetilde {\mathbb Q}_{p}$
of
$\mathbb Q_p$
. Let
$f(x) \in {\mathbb Z}_p[x]$
be a monic polynomial not divisible by
$\phi (x)$
whose
$\phi (x)$
-expansion is given by
$\phi (x)^n + a_{n-1}(x)\phi (x)^{n-1} + \cdots + a_0(x)$
and such that
$\overline {f}(x)$
is a power of
$\overline {\phi }(x)$
. Suppose that the
$\phi $
-Newton polygon of
$f(x)$
with respect to p consists of a single edge, say S, having positive slope
${l}/{e}$
with
$l, e$
coprime, that is,
$$ \begin{align*}\min\bigg\{\frac{v_{p,x}(a_{n-i}(x))}{i} \ \bigg|\ 1\leq i\leq n\bigg\} = \frac{v_{p,x}(a_0(x))}{n} = \frac{l}{e},\end{align*} $$
so that n is divisible by e, say
$n=et$
, and
$v_{p,x}(a_{n-ej}(x)) \geq lj$
with
$1\leq j\leq t$
. Thus, the polynomial
$b_j(x):={a_{n-ej}(x)}/{p^{lj}}$
has coefficients in
${\mathbb Z}_p$
and
$b_j(\alpha )\in {\mathbb Z}_p[\alpha ]$
for
$1\leq j \leq t$
. The polynomial
$T(Y)$
in the indeterminate Y defined by
$T(Y) = Y^t + \sum _{j=1}^{t} \overline {b_j}(\overline {\alpha })Y^{t-j}$
with coefficients in
${\mathbb F}_p[\overline {\alpha }]\cong {{\mathbb F}_p[x]}/{\langle \phi (x)\rangle }$
is called the residual polynomial of
$f (x)$
with respect to
$(\phi ,S)$
.
The following weaker version of the theorem of the product, originally due to Ore, will be used in the proof of main result (see [Reference Cohen, Movahhedi and Salinier4, Theorem 1.5], [Reference Khanduja and Kumar13, Theorem 1.1]).
Theorem 3.4. Let
$\phi (x) \in {\mathbb Z}_p[x]$
be a monic polynomial which is irreducible modulo a rational prime p having a root
$\alpha $
in the algebraic closure
$\widetilde {\mathbb Q}_{p}$
of
$\mathbb Q_p$
. Let
$g(x) \in {\mathbb Z}_p[x]$
be a monic polynomial not divisible by
$\phi (x)$
whose
$\phi (x)$
-expansion is given by
$\phi (x)^n + a_{n-1}(x)\phi (x)^{n-1} + \cdots + a_0(x)$
and such that
$\overline {f}(x)$
is a power of
$\overline {\phi }(x)$
. Suppose that the
$\phi $
-Newton polygon of
$g(x)$
with respect to the prime p has k edges
$S_1, \ldots , S_k$
having slopes
$\lambda _1 < \cdots < \lambda _k$
. Then:
-
(1)
$g(x) = g_1(x)\cdots g_k(x)$
, where each
$g_i(x) \in {\mathbb Z}_{{p}}[x]$
is a monic polynomial of degree
$\ell _i\deg (\phi (x))$
and whose
$\phi $
-Newton polygon has a single edge, say
$S_i'$
, which is a translate of
$S_i$
such that
$\ell _i$
is the length of the horizontal projection of
$S_i$
; -
(2) the residual polynomial
$T_i(Y) \in {{\mathbb F}}_{p}[\overline {\alpha }][Y]$
of
$g_i(x)$
with respect to (
$\phi ,~S_i'$
) has degree
$\ell _i/e_i$
, where
$e_i$
is the smallest positive integer such that
$e_i\lambda _i \in {\mathbb Z}.$
The next definition extends the notion of residual polynomial to more general polynomials
$f(x)$
.
Definition 3.5. Let
$p, \phi (x), \alpha $
be as in Definition 3.3. Let
$g(x)\in {\mathbb Z}_p[x]$
be a monic polynomial not divisible by
$\phi (x)$
such that
$\overline {g}(x)$
is a power of
$\overline {\phi }(x)$
. Let
$\lambda _1 < \cdots < \lambda _k$
be the slopes of the edges of the
$\phi $
-Newton polygon of
$g(x)$
and
$S_i$
denote the edge with slope
$\lambda _i$
. In view of Theorem 3.4, we can write
$g(x) = g_1(x)\cdots g_k(x)$
, where the
$\phi $
-Newton polygon of
$g_i(x) \in {\mathbb Z}_{{p}}[x]$
has a single edge, say
$S_i'$
, which is a translate of
$S_i$
. Let
$T_i(Y)$
belonging to
${{\mathbb F}}_{p}[\overline {\alpha }][Y]$
denote the residual polynomial of
$g_i(x)$
with respect to (
$\phi ,~S_i'$
) as in Definition 3.3. For convenience, the polynomial
$T_i(Y)$
will be referred to as the residual polynomial of
$g(x)$
with respect to
$(\phi ,S_i)$
. The polynomial
$g(x)$
is said to be p-regular with respect to
$\phi $
if none of the polynomials
$T_i(Y)$
has a repeated root in the algebraic closure of
${\mathbb F}_p$
,
$1\leq i\leq k$
. In general, if
$f(x)$
belonging to
${\mathbb Z}_p[x]$
is a monic polynomial and
$\overline {f}(x) = \overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$
is its factorisation modulo p into irreducible polynomials with each
$\phi _i(x)$
belonging to
${\mathbb Z}_p[x]$
monic and
$e_i> 0$
, then by Hensel’s lemma [Reference Borevich and Shafarevich3, Ch. 4, Section 3], there exist monic polynomials
$f_1(x), \ldots , f_r(x)$
belonging to
${\mathbb Z}_{{p}}[x]$
such that
$f(x) = f_1(x)\cdots f_r(x)$
and
$\overline {f}_i(x) = \overline {\phi }_i(x)^{e_i}$
for each i. The polynomial
$f(x)$
is said to be p-regular (with respect to
$\phi _1, \ldots , \phi _r$
) if each
$f_i(x)$
is
${p}$
-regular with respect to
$\phi _i$
.
We provide a simple example of a p-regular polynomial with respect to any monic polynomial
$\phi (x) \in {\mathbb Z}[x]$
which is irreducible modulo a prime p.
Example 3.6. If
$p, \phi (x)$
are as above and
$g(x) \neq \phi (x)$
belonging to
${\mathbb Z}_p[x]$
is a monic polynomial with
$\overline {g}(x) = \overline {\phi }(x)$
, then the
$\phi $
-Newton polygon of
$g(x)$
with respect to p is a line segment S joining the point
$(0,0)$
with
$(1,b)$
for some
$b>0$
. Consequently, the polynomial associated to
$g(x)$
with respect to
$(\phi , S)$
is linear and
$g(x)$
is p-regular with respect to
$\phi $
.
To determine the number of distinct prime ideals of
${\mathbb Z}_K$
lying above a rational prime p, we will use the following theorem which is a weaker version of [Reference Khanduja and Kumar13, Theorem 1.2].
Theorem 3.7. Let
$L=\mathbb Q(\xi )$
be an algebraic number field with
$\xi $
satisfying an irreducible polynomial
$g(x)\in {\mathbb Z}[x]$
and p be a rational prime. Let
$ \overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$
be the factorisation of
$g(x)$
modulo p into powers of distinct irreducible polynomials over
${\mathbb F}_p$
with each
$\phi _i(x)\neq g(x)$
belonging to
${\mathbb Z}[x]$
monic. Suppose that the
$\phi _i$
-Newton polygon of
$g(x)$
has
$k_i$
edges, say
$S_{ij}$
, having slopes
$\lambda _{ij}={l_{ij}}/{e_{ij}} $
with
$\gcd (l_{ij},~e_{ij})=1$
for
$1\leq j\leq k_i$
. If
$T_{ij}(Y) = \prod _{s=1}^{s_{ij}}U_{ijs}(Y)$
is the factorisation of the residual polynomial
$T_{ij}(Y)$
into distinct irreducible factors over
${\mathbb F}_p$
with respect to
$(\phi _i,~S_{ij})$
for
$1\leq j\leq k_i$
, then
$$ \begin{align*}p{\mathbb Z}_L=\displaystyle\prod_{i=1}^{r}\displaystyle\prod_{j=1}^{k_i}\displaystyle\prod_{s=1}^{s_{ij}}\mathfrak p_{ijs}^{e_{ij}},\end{align*} $$
where
$\mathfrak p_{ijs}$
are distinct prime ideals of
${\mathbb Z}_L$
having residual degree
$\deg \phi _i(x)\cdot \deg U_{ijs}(Y).$
4 Proof of Theorem 1.1
Proof. Observe that
$p\leq n.$
We first show that x is the only repeated factor of
$f(x)$
modulo p. If
$p \mid n$
, then clearly
$f(x) \equiv x^n \pmod p$
. If
$p\nmid n$
, then assume that
$j, 0\leq j\leq n-2$
, is the smallest index such that p divides
$n-j$
. Keeping in mind that
$p\nmid a_i$
, we see that
$f(x)$
is congruent to
$$ \begin{align*} & x^n + na_{n-1}x^{n-1} + \cdots + a_{n-j}\frac{n!}{(n-j)!}x^{n-j} \\ &\quad \equiv x^{n-j}\bigg(x^j +na_{n-1}x^{j-1} + \cdots + a_{n-j}\frac{n!}{(n-j)!}\bigg) \bmod p. \end{align*} $$
Note that
$p\nmid j$
. Otherwise, if
$p \mid j$
, then since
$p \mid (n-j)$
, we have
$p \mid n$
, which is a contradiction. Hence, the polynomial
$x^j +\overline {n}\overline {a}_{n-1}x^{j-1} + \cdots + \overline {a}_{n-j}\overline {{n!}/{(n-j)!}}$
belonging to
${\mathbb Z}/p{\mathbb Z}[x]$
is a separable polynomial. It follows that x is the only repeated factor of
$f(x)$
modulo p.
Now we show that
$f(x)$
is p-regular with respect to
$\phi (x) = x$
. Recall that
$p\nmid a_i$
. By the definition of the p-Newton polygon, we see that it will be the polygonal path formed by the lower edges along the convex hull of the points of the set S defined by
$$ \begin{align*}S = \bigg\{\bigg(i, v_p\bigg(\frac{n!}{(n-i)!}\bigg)\bigg) \ \bigg|\ 0\leq i\leq n\bigg\}.\end{align*} $$
By hypothesis,
$n = p^{m_1} + p^{m_2} + \cdots + p^{m_r}$
, where
$0\leq m_1 < m_2 < \cdots <m_r$
. Let
$\ell _i$
denote the integer
$$ \begin{align*} \ell_i = p^{m_1} + \cdots + p^{m_i}, ~~~1\leq i\leq r. \end{align*} $$
Set
$\ell _0 = 0.$
As in [Reference Coleman5], using Lemma 2.2 and keeping in mind that
$v_p(a_i) = 0$
for each i, it can be easily checked that the p-Newton polygon of
$f(x)$
consists of r edges, and the ith edge is the line segment having vertices
$(\ell _{i-1}, v_p(n!/(n-\ell _{i-1})!))$
and
${(\ell _{i}, v_p(n!/(n-\ell _{i})!))}$
. So by Lemma 2.2, the slope
$\lambda _i$
of the ith edge of the p-Newton polygon of
$f(x)$
is
$$ \begin{align*} \lambda_i = \frac{-v_p((n-\ell_i)!) + v_p((n-\ell_{i-1})!)}{\ell_i - \ell_{i-1}} = \frac{\ell_i - \ell_{i-1} -1}{(\ell_i - \ell_{i-1})(p-1)} = \frac{p^{m_i} - 1}{p^{m_i}(p-1)}. \end{align*} $$
Observe that
$f(x)$
can have an edge with slope zero if and only if
$m_1 = 0$
. Also,
$m_1$
can be zero only when
$p\nmid n$
. Therefore, in view of Hensel’s lemma and Theorem 3.4, we can write
$f(x) = g_1(x)\cdots g_r(x)$
, where
$g_i(x) \in {\mathbb Z}_p[x]$
has degree
$\ell _i - \ell _{i-1} = p^{m_i}$
and the p-Newton polygon of
$g_i(x)$
has a single edge, say
$S_i$
, with slope
$\lambda _i$
. When
$\lambda _i> 0$
, the polynomial, say
$T_i(y) \in {\mathbb F}_p[y]$
, associated to
$g_i(x)$
with respect to
$(x, S_i)$
is linear. Hence,
$f(x)$
is p-regular with respect to
$\phi (x) = x.$
So, by Theorem 3.7,
$$ \begin{align*}p{\mathbb Z}_K = \wp_1^{e_1}\cdots \wp_r^{e_r},\end{align*} $$
where the
$\wp _i$
are distinct prime ideals lying above prime p with index of ramification
$e_i = p^{m_i}$
and residual degree one for each i. Hence, by Lemma 2.1,
$p \mid i(K)$
if and only if
$r> p.$
This completes the proof of the theorem.
Acknowledgement
The author appreciates the anonymous referee’s suggestions, which have enhanced the quality of this paper.
