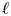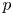1. Introduction
This paper is a sequel of sorts to the first author's paper [Reference KedlayaKed23a], although there is no logical dependence between the two. Both papers concern themselves with analogues of ‘Drinfeld's lemma’ in étale cohomology and, in particular, with corresponding statements in ![]() $p$-adic cohomology; however, there are some differences in scope and methodology which we highlight below.
$p$-adic cohomology; however, there are some differences in scope and methodology which we highlight below.
1.0.1 Drinfeld's lemma was first introduced in his proof of the Langlands correspondence for ![]() $\operatorname {GL}_2$ over global function fields of characteristic
$\operatorname {GL}_2$ over global function fields of characteristic ![]() $p>0$ (see [Reference DrinfeldDri80]). Let us briefly review the result. Let
$p>0$ (see [Reference DrinfeldDri80]). Let us briefly review the result. Let ![]() $X_1,X_2$ be two connected schemes over
$X_1,X_2$ be two connected schemes over ![]() $k=\mathbb {F}_p$. The scheme
$k=\mathbb {F}_p$. The scheme ![]() $X:=X_1\times _k X_2$ is equipped with two endomorphisms
$X:=X_1\times _k X_2$ is equipped with two endomorphisms ![]() $F_{1}, F_{2}$, obtained by base changes of the absolute Frobenius on
$F_{1}, F_{2}$, obtained by base changes of the absolute Frobenius on ![]() $X_1,X_2$, respectively. We consider the category
$X_1,X_2$, respectively. We consider the category ![]() $\mathcal {C}(X,\Phi )$ of objects
$\mathcal {C}(X,\Phi )$ of objects ![]() $(T,F_{ \{1\}},F_{ \{2\}})$ consisting of a finite étale morphism
$(T,F_{ \{1\}},F_{ \{2\}})$ consisting of a finite étale morphism ![]() $T\to X$ and isomorphisms
$T\to X$ and isomorphisms ![]() $F_{ \{i\}}\colon T\times _{X,F_i}X \xrightarrow {\sim } T$ commuting with each other, whose composition is the relative Frobenius morphism
$F_{ \{i\}}\colon T\times _{X,F_i}X \xrightarrow {\sim } T$ commuting with each other, whose composition is the relative Frobenius morphism ![]() $F_{T/X}$ of
$F_{T/X}$ of ![]() $T$ over
$T$ over ![]() $X$. This category is a Galois category and we denote by
$X$. This category is a Galois category and we denote by ![]() $\pi _1(X,\Phi,\overline {x})$ the Galois group defined by a geometric point
$\pi _1(X,\Phi,\overline {x})$ the Galois group defined by a geometric point ![]() $\overline {x}$ of
$\overline {x}$ of ![]() $X$. Then Drinfeld's lemma says that the projection maps
$X$. Then Drinfeld's lemma says that the projection maps ![]() $X\to X_i$ induce an isomorphism of profinite groups:
$X\to X_i$ induce an isomorphism of profinite groups:
(See [Reference LauLau04, Theorem 8.1.4] or [Reference KedlayaKed19, Theorem 4.2.12]. For the key case where ![]() $X_2$ is a geometric point, see also [Reference LafforgueLaf18, Lemme 8.11].)
$X_2$ is a geometric point, see also [Reference LafforgueLaf18, Lemme 8.11].)
A closely related result is that any quasicompact open immersion which is stable under the ![]() $F_i$ is covered by products of open immersions into the
$F_i$ is covered by products of open immersions into the ![]() $X_i$. (See [Reference LauLau04, Lemma 9.2.1] or [Reference KedlayaKed19, Theorem 4.3.6]. For the key case where
$X_i$. (See [Reference LauLau04, Lemma 9.2.1] or [Reference KedlayaKed19, Theorem 4.3.6]. For the key case where ![]() $X_2$ is a geometric point, see also [Reference LafforgueLaf18, Lemme 8.12].) These two results together allow us to view lisse
$X_2$ is a geometric point, see also [Reference LafforgueLaf18, Lemme 8.12].) These two results together allow us to view lisse ![]() $\ell$-adic sheaves with ‘partial Frobenius’ on
$\ell$-adic sheaves with ‘partial Frobenius’ on ![]() $X$ as
$X$ as ![]() $\ell$-adic representations of
$\ell$-adic representations of ![]() $\pi _1(X_1,\overline {x})\times \pi _1(X_2,\overline {x})$, and to work with constructible sheaves with partial Frobenius on
$\pi _1(X_1,\overline {x})\times \pi _1(X_2,\overline {x})$, and to work with constructible sheaves with partial Frobenius on ![]() $X$ via stratifications coming from
$X$ via stratifications coming from ![]() $X_1$ and
$X_1$ and ![]() $X_2$. We refer to [Reference LauLau04] and [Reference KedlayaKed19, Lecture 4] for more detailed expositions.
$X_2$. We refer to [Reference LauLau04] and [Reference KedlayaKed19, Lecture 4] for more detailed expositions.
1.0.2 Drinfeld's lemma also plays an essential role in V. Lafforgue's work [Reference LafforgueLaf18] on the automorphic-to-Galois direction of the Langlands correspondence for reductive groups over a global function field ![]() $F$. Roughly speaking, V. Lafforgue showed that the space of cuspidal automorphic functions (with values in
$F$. Roughly speaking, V. Lafforgue showed that the space of cuspidal automorphic functions (with values in ![]() $\overline {\mathbb {Q}}_{\ell }$) of a reductive group
$\overline {\mathbb {Q}}_{\ell }$) of a reductive group ![]() $G$ over
$G$ over ![]() $F$ admits a decomposition indexed by certain
$F$ admits a decomposition indexed by certain ![]() $\ell$-adic Langlands parameters. This decomposition is obtained by investigating the
$\ell$-adic Langlands parameters. This decomposition is obtained by investigating the ![]() $\ell$-adic cohomology of certain moduli stacks of shtukas for
$\ell$-adic cohomology of certain moduli stacks of shtukas for ![]() $G$. Moreover, he conjectured that this decomposition should be
$G$. Moreover, he conjectured that this decomposition should be ![]() $\ell$-independent and indexed by certain motivic Langlands parameters.
$\ell$-independent and indexed by certain motivic Langlands parameters.
In particular, we expect that there is a variant of V. Lafforgue's result in terms of ![]() $p$-adic Langlands parameters, corresponding to Abe's adaptation of the work of L. Lafforgue from
$p$-adic Langlands parameters, corresponding to Abe's adaptation of the work of L. Lafforgue from ![]() $\ell$-adic to
$\ell$-adic to ![]() $p$-adic coefficients [Reference AbeAbe18b]. In this adaptation, the
$p$-adic coefficients [Reference AbeAbe18b]. In this adaptation, the ![]() $p$-adic analogues of lisse
$p$-adic analogues of lisse ![]() $\ell$-adic sheaves are overconvergent
$\ell$-adic sheaves are overconvergent ![]() $F$-isocrystals. In addition to those objects, we may also consider the larger category of convergent
$F$-isocrystals. In addition to those objects, we may also consider the larger category of convergent ![]() $F$-isocrystals, which admit no
$F$-isocrystals, which admit no ![]() $\ell$-adic analogue but play an important role in the
$\ell$-adic analogue but play an important role in the ![]() $p$-adic setup.
$p$-adic setup.
Recently, Drinfeld proposed an unconditional definition of motivic Langlands parameters [Reference DrinfeldDri18]. Inspired by this work, we consider ![]() $p$-adic Langlands parameters as homomorphisms of the Tannakian group of the category of overconvergent
$p$-adic Langlands parameters as homomorphisms of the Tannakian group of the category of overconvergent ![]() $F$-isocrystals over a curve to the Langlands dual group of
$F$-isocrystals over a curve to the Langlands dual group of ![]() $G$.
$G$.
1.0.3 From this perspective, we prove a Tannakian form of Drinfeld's lemma for overconvergent/convergent ![]() $F$-isocrystals, which aims to establish the aforementioned result for
$F$-isocrystals, which aims to establish the aforementioned result for ![]() $p$-adic Langlands parameters. Note that another ingredient of V. Lafforgue's approach, the geometric Satake equivalence, was established for
$p$-adic Langlands parameters. Note that another ingredient of V. Lafforgue's approach, the geometric Satake equivalence, was established for ![]() $F$-isocrystals by the second author and Zhu [Reference Xu and ZhuXZ22].
$F$-isocrystals by the second author and Zhu [Reference Xu and ZhuXZ22].
Keep the notation of § 1.0.1. Given an overconvergent (respectively, convergent) isocrystal ![]() $\mathscr {E}$ on
$\mathscr {E}$ on ![]() $X$, a partial Frobenius structure on
$X$, a partial Frobenius structure on ![]() $\mathscr {E}$ consists of two isomorphisms
$\mathscr {E}$ consists of two isomorphisms ![]() $\varphi _i\colon F_i^*(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$ such that
$\varphi _i\colon F_i^*(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$ such that ![]() $\varphi _1\circ F_1^*(\varphi _2)= \varphi _2\circ F_2^*(\varphi _1)$; this composition, in particular, provides
$\varphi _1\circ F_1^*(\varphi _2)= \varphi _2\circ F_2^*(\varphi _1)$; this composition, in particular, provides ![]() $\mathscr {E}$ with the structure of an
$\mathscr {E}$ with the structure of an ![]() $F$-isocrystal. The category
$F$-isocrystal. The category ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ (respectively,
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ (respectively, ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$) of overconvergent (respectively, convergent) isocrystals with a partial Frobenius structure is a Tannakian category and we denote by
$\operatorname {\mathbf {\Phi -Isoc}}(X)$) of overconvergent (respectively, convergent) isocrystals with a partial Frobenius structure is a Tannakian category and we denote by ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$ (respectively,
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$ (respectively, ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)$) the associated Tannakian group (with respect to a fiber functor).
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)$) the associated Tannakian group (with respect to a fiber functor).
Theorem 1.0.4 (Theorems 2.2.4, 3.3.2, and 3.5.1)
(i) Suppose each ![]() $X_i$ is geometrically connected (respectively, smooth and geometrically connected) over
$X_i$ is geometrically connected (respectively, smooth and geometrically connected) over ![]() $k$. The pullback functors of projections
$k$. The pullback functors of projections ![]() $p_i\colon X\to X_i$ induce a canonical isomorphism of Tannakian groups:
$p_i\colon X\to X_i$ induce a canonical isomorphism of Tannakian groups:
 \begin{align}
\begin{aligned} p_1^{\circ}\times
p_2^{\circ}\colon
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}}(X)&\xrightarrow{\sim}
\pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_1)\times
\pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_2) \nonumber\\
\text{(respectively, }
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}}}(X)&\xrightarrow{\sim}
\pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_1)\times
\pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_2)), \end{aligned}\end{align}
\begin{align}
\begin{aligned} p_1^{\circ}\times
p_2^{\circ}\colon
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}}(X)&\xrightarrow{\sim}
\pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_1)\times
\pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_2) \nonumber\\
\text{(respectively, }
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}}}(X)&\xrightarrow{\sim}
\pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_1)\times
\pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_2)), \end{aligned}\end{align}
where ![]() $\pi _1^{\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}}$ (respectively,
$\pi _1^{\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}}$ (respectively, ![]() $\pi _1^{\operatorname {\mathbf {F-Isoc}}}$) denotes the Tannakian group of the category of overconvergent (respectively, convergent)
$\pi _1^{\operatorname {\mathbf {F-Isoc}}}$) denotes the Tannakian group of the category of overconvergent (respectively, convergent) ![]() $F$-isocrystals over
$F$-isocrystals over ![]() $\overline {\mathbb {Q}}_p$, and similarly with
$\overline {\mathbb {Q}}_p$, and similarly with ![]() $F$ replaced by
$F$ replaced by ![]() $\Phi$.
$\Phi$.
(ii) Suppose each ![]() $X_i$ is smooth and geometrically connected over
$X_i$ is smooth and geometrically connected over ![]() $k$. By taking connected components in the above isomorphism, we recover the isomorphism (1.0.1.1).
$k$. By taking connected components in the above isomorphism, we recover the isomorphism (1.0.1.1).
In the overconvergent case, we also establish a similar isomorphism for overconvergent isocrystals which can be equipped with a Frobenius structure but do not carry a specified one. This roughly corresponds to passing from arithmetic to geometric fundamental groups in the ![]() $\ell$-adic setting.
$\ell$-adic setting.
1.0.5 In very recent work [Reference KedlayaKed22c], the first author has established a relative version of the ![]() $p$-adic local monodromy theorem for differential modules with a Frobenius structure over an annulus [Reference AndréAnd02, Reference MebkhoutMeb02, Reference KedlayaKed04a]. An application is the local monodromy theorem for modules with an integrable connection and a partial Frobenius structure over polyannuli [Reference KedlayaKed22c, Theorem 3.3.6]. We formulate these results in terms of a Tannakian form of local Drinfeld's lemma (Theorem 5.0.1) and discuss some related constructions.
$p$-adic local monodromy theorem for differential modules with a Frobenius structure over an annulus [Reference AndréAnd02, Reference MebkhoutMeb02, Reference KedlayaKed04a]. An application is the local monodromy theorem for modules with an integrable connection and a partial Frobenius structure over polyannuli [Reference KedlayaKed22c, Theorem 3.3.6]. We formulate these results in terms of a Tannakian form of local Drinfeld's lemma (Theorem 5.0.1) and discuss some related constructions.
We remark that variants of local Drinfeld's lemma for ![]() $\ell$-adic sheaves are key ingredients of the local Langlands correspondence of Genestier and V. Lafforgue [Reference Genestier and LafforgueGL17] and of Fargues and Scholze [Reference Fargues and ScholzeFS21].
$\ell$-adic sheaves are key ingredients of the local Langlands correspondence of Genestier and V. Lafforgue [Reference Genestier and LafforgueGL17] and of Fargues and Scholze [Reference Fargues and ScholzeFS21].
Inspired by Berger's thesis [Reference BergerBer02], we expect to deduce a ‘de Rham implies potentially semistable’ result for ![]() $p$-adic representations of powers of Galois groups from local Drinfeld's lemma. There are some related results in this direction: (i) the overconvergence of multivariate
$p$-adic representations of powers of Galois groups from local Drinfeld's lemma. There are some related results in this direction: (i) the overconvergence of multivariate ![]() $(\varphi,\Gamma )$-modules has been proved by the first author, Carter, and Zábrádi [Reference Carter, Kedlaya and ZábrádiCKZ21]; (ii) multivariable de Rham representations and the associated
$(\varphi,\Gamma )$-modules has been proved by the first author, Carter, and Zábrádi [Reference Carter, Kedlaya and ZábrádiCKZ21]; (ii) multivariable de Rham representations and the associated ![]() $p$-adic differential equations are studied by Brinon, Chiarellotto, and Mazzari [Reference Brinon, Chiarellotto and MazzariBCM21].
$p$-adic differential equations are studied by Brinon, Chiarellotto, and Mazzari [Reference Brinon, Chiarellotto and MazzariBCM21].
1.0.6 We now describe the structure of the paper.
The proof of Theorem 1.0.4 in the overconvergent case is given in § 2. A key ingredient is Proposition 2.2.8, which says that the pushforward functor (for arithmetic ![]() $\mathscr {D}$-modules) of the projection
$\mathscr {D}$-modules) of the projection ![]() $p_i\colon X\to X_i$ (
$p_i\colon X\to X_i$ (![]() $i=1,2$) sends overconvergent isocrystals on
$i=1,2$) sends overconvergent isocrystals on ![]() $X$, which can be equipped with a partial Frobenius structure, to overconvergent isocrystals on
$X$, which can be equipped with a partial Frobenius structure, to overconvergent isocrystals on ![]() $X_i$. Combined with a criterion of Esnault, Hai, and Sun [Reference Esnault, Hai and SunEHS07] on exact sequences of Tannakian groups, we conclude Theorem 1.0.4(i) in the overconvergent case.
$X_i$. Combined with a criterion of Esnault, Hai, and Sun [Reference Esnault, Hai and SunEHS07] on exact sequences of Tannakian groups, we conclude Theorem 1.0.4(i) in the overconvergent case.
The proof in the convergent case is contained in § 3 and follows a similar line as in [Reference KedlayaKed23a]. We study unit-root and diagonally unit-root convergent isocrystals with a partial Frobenius structure (Propositions 3.1.8 and 3.2.2), and the diagonal (respectively, partial) Frobenius slope filtrations (Theorems 3.1.10 and 3.4.1). These tools allow us to define a pushforward functor along the projection ![]() $p_i\colon X\to X_i$ from
$p_i\colon X\to X_i$ from ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$ to
$\operatorname {\mathbf {\Phi -Isoc}}(X)$ to ![]() $\operatorname {\mathbf {F-Isoc}}(X_i)$. Then we deduce Theorem 1.0.4(i) in the convergent case by a similar argument as in the overconvergent case.
$\operatorname {\mathbf {F-Isoc}}(X_i)$. Then we deduce Theorem 1.0.4(i) in the convergent case by a similar argument as in the overconvergent case.
We upgrade the isomorphism (1.0.4.1) in an ![]() $\ell$-independent form à la Drinfeld [Reference DrinfeldDri18] in § 4 (see Proposition 4.2.4 and (4.2.6.1)).
$\ell$-independent form à la Drinfeld [Reference DrinfeldDri18] in § 4 (see Proposition 4.2.4 and (4.2.6.1)).
The last section is devoted to the local Drinfeld's lemma.
1.0.7 We now compare more carefully the results of this paper with those of [Reference KedlayaKed23a]. In [Reference KedlayaKed23a], each ![]() $X_i$ is required to be smooth over some perfect field
$X_i$ is required to be smooth over some perfect field ![]() $k_i$, but it is not required that
$k_i$, but it is not required that ![]() $k_i$ be either finite or independent of
$k_i$ be either finite or independent of ![]() $i$. The more restricted situation considered here (in which
$i$. The more restricted situation considered here (in which ![]() $k_i = \mathbb {F}_p$ for all
$k_i = \mathbb {F}_p$ for all ![]() $i$) is sufficient for the application to geometric Langlands; moreover, it is not immediately apparent how to reproduce the Tannakian formulation in the setting of [Reference KedlayaKed23a].
$i$) is sufficient for the application to geometric Langlands; moreover, it is not immediately apparent how to reproduce the Tannakian formulation in the setting of [Reference KedlayaKed23a].
Another important difference with [Reference KedlayaKed23a] is in the overall structure of the arguments. Therein, the convergent case is treated first, using the isomorphism (1.0.1.1) as input, and then the overconvergent case is deduced as a corollary; herein, we obtain the overconvergent case directly using cohomological methods, deduce (1.0.1.1) as a corollary, and finally recover the convergent case.
Notation. Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p>0$,
$p>0$, ![]() $K$ a complete discrete valuation field of characteristic zero with residue field
$K$ a complete discrete valuation field of characteristic zero with residue field ![]() $k$, and
$k$, and ![]() $\mathscr {O}_K$ its ring of integers. Let
$\mathscr {O}_K$ its ring of integers. Let ![]() $s$ be a positive integer and
$s$ be a positive integer and ![]() $q=p^s$. We assume, moreover, that the
$q=p^s$. We assume, moreover, that the ![]() $s$th Frobenius automorphism
$s$th Frobenius automorphism ![]() $k\xrightarrow {\sim } k$,
$k\xrightarrow {\sim } k$, ![]() $x\mapsto x^q$ lifts to an automorphism
$x\mapsto x^q$ lifts to an automorphism ![]() $\sigma \colon \mathscr {O}_K\xrightarrow {\sim } \mathscr {O}_K$.
$\sigma \colon \mathscr {O}_K\xrightarrow {\sim } \mathscr {O}_K$.
In this article, we mainly work with the case where ![]() $(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$ (and
$(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$ (and ![]() $K$ is, therefore, a finite extension of
$K$ is, therefore, a finite extension of ![]() $\mathbb {Q}_p$). In this case, we fix an algebraic closure
$\mathbb {Q}_p$). In this case, we fix an algebraic closure ![]() $\overline {\mathbb {Q}}_p$ of
$\overline {\mathbb {Q}}_p$ of ![]() $K$.
$K$.
In the following, a ![]() $k$-variety
$k$-variety ![]() $X$ means a separated scheme of finite type over
$X$ means a separated scheme of finite type over ![]() $k$. We denote the
$k$. We denote the ![]() $s$th Frobenius morphism on
$s$th Frobenius morphism on ![]() $X$ by
$X$ by ![]() $F_X$.
$F_X$.
When using the notation ![]() $\prod$ for a product of schemes, the product is taken over
$\prod$ for a product of schemes, the product is taken over ![]() $k$.
$k$.
2. Drinfeld's lemma for overconvergent  $F$-isocrystals
$F$-isocrystals
2.1 Generalities on Tannakian categories
In the following, we study some general constructions in the Tannakian formalism. Let ![]() $E$ be a field of characteristic zero. Let
$E$ be a field of characteristic zero. Let ![]() $\operatorname {Vec}_E$ denote the category of finite-dimensional
$\operatorname {Vec}_E$ denote the category of finite-dimensional ![]() $E$-vector spaces. For any neutral Tannakian category
$E$-vector spaces. For any neutral Tannakian category ![]() $\mathscr {C}$ over
$\mathscr {C}$ over ![]() $E$ with respect to a fiber functor
$E$ with respect to a fiber functor ![]() $\omega$, we use
$\omega$, we use ![]() $\pi _1(\mathscr {C},\omega )$ to denote its Tannakian group (i.e. the group of natural automorphisms of
$\pi _1(\mathscr {C},\omega )$ to denote its Tannakian group (i.e. the group of natural automorphisms of ![]() $\omega$). We omit
$\omega$). We omit ![]() $\omega$ from the notation if there is no risk of confusion.
$\omega$ from the notation if there is no risk of confusion.
2.1.1 Let ![]() $\widetilde {\mathscr {C}}$ be a Tannakian category over
$\widetilde {\mathscr {C}}$ be a Tannakian category over ![]() $E$, neutralized by a fiber functor
$E$, neutralized by a fiber functor ![]() $\omega \colon \widetilde {\mathscr {C}}\to \operatorname {Vec}_F$, where
$\omega \colon \widetilde {\mathscr {C}}\to \operatorname {Vec}_F$, where ![]() $F$ is a finite extension of
$F$ is a finite extension of ![]() $E$. Suppose there exist
$E$. Suppose there exist ![]() $E$-linear tensor equivalences
$E$-linear tensor equivalences ![]() $\tau _i\colon \widetilde {\mathscr {C}}\to \widetilde {\mathscr {C}}$ and isomorphisms of tensor functors
$\tau _i\colon \widetilde {\mathscr {C}}\to \widetilde {\mathscr {C}}$ and isomorphisms of tensor functors ![]() $\eta _i\colon \omega \circ \tau _i\xrightarrow {\sim } \omega$ for
$\eta _i\colon \omega \circ \tau _i\xrightarrow {\sim } \omega$ for ![]() $i=1,2,\dots,n$. Moreover, we assume that there exist natural isomorphisms
$i=1,2,\dots,n$. Moreover, we assume that there exist natural isomorphisms ![]() $\sigma _{ij}\colon \tau _i\circ \tau _j \simeq \tau _{j}\circ \tau _i$ for
$\sigma _{ij}\colon \tau _i\circ \tau _j \simeq \tau _{j}\circ \tau _i$ for ![]() $i,j$ such that the following diagram commutes.
$i,j$ such that the following diagram commutes.

Since ![]() $\omega$ is faithful, such an isomorphism
$\omega$ is faithful, such an isomorphism ![]() $\sigma _{ij}$ is unique. In the following, for every
$\sigma _{ij}$ is unique. In the following, for every ![]() $i=1,\dots,n$, we fix a quasi-inverse
$i=1,\dots,n$, we fix a quasi-inverse ![]() $\tau _i^{-1}$ of
$\tau _i^{-1}$ of ![]() $\tau _i$. For
$\tau _i$. For ![]() $m\in \mathbb {Z}$, we set
$m\in \mathbb {Z}$, we set ![]() $\tau _i^m$ to be the
$\tau _i^m$ to be the ![]() $|m|$th composition of
$|m|$th composition of ![]() $\tau _i$ (or
$\tau _i$ (or ![]() $\tau _i^{-1}$ if
$\tau _i^{-1}$ if ![]() $m<0$) and define
$m<0$) and define ![]() $\eta _i^m\colon \omega \circ \tau _i^m \xrightarrow {\sim } \omega$ by the composition of
$\eta _i^m\colon \omega \circ \tau _i^m \xrightarrow {\sim } \omega$ by the composition of ![]() $\eta _i$ (or the inverse of
$\eta _i$ (or the inverse of ![]() $\eta _i$ if
$\eta _i$ if ![]() $m<0$).
$m<0$).
We define a category ![]() $\mathscr {C}_0$ as follows: an object
$\mathscr {C}_0$ as follows: an object ![]() $(\mathscr {E},\varphi _1,\dots,\varphi _{n})$ consists of an object
$(\mathscr {E},\varphi _1,\dots,\varphi _{n})$ consists of an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\widetilde {\mathscr {C}}$ and isomorphisms
$\widetilde {\mathscr {C}}$ and isomorphisms ![]() $\varphi _i\colon \tau _i(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$ such that
$\varphi _i\colon \tau _i(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$ such that ![]() $\varphi _j\circ \tau _j(\varphi _i)=\varphi _i\circ \tau _i(\varphi _j)$ via
$\varphi _j\circ \tau _j(\varphi _i)=\varphi _i\circ \tau _i(\varphi _j)$ via ![]() $\sigma _{ij}$. Morphisms of
$\sigma _{ij}$. Morphisms of ![]() $\mathscr {C}_0$ are morphisms of
$\mathscr {C}_0$ are morphisms of ![]() $\widetilde {\mathscr {C}}$ compatible with the
$\widetilde {\mathscr {C}}$ compatible with the ![]() $\varphi _i$. We have a canonical functor
$\varphi _i$. We have a canonical functor
By [Reference DeligneDel07, § 2.5] and a similar argument to [Reference Xu and ZhuXZ22, Proposition 3.4.5], we can show that ![]() $\mathscr {C}_0$ is a Tannakian category over
$\mathscr {C}_0$ is a Tannakian category over ![]() $E$ neutralized by
$E$ neutralized by ![]() $\omega$ over
$\omega$ over ![]() $\operatorname {Vec}_F$.
$\operatorname {Vec}_F$.
We say an object of ![]() $\mathscr {C}_0$ is constant if its image in
$\mathscr {C}_0$ is constant if its image in ![]() $\widetilde {\mathscr {C}}$ is isomorphic to a finite direct sum of the unit object.
$\widetilde {\mathscr {C}}$ is isomorphic to a finite direct sum of the unit object.
Recall [Reference BertolinBer08, § 2] that a Tannakian subcategory of ![]() $\widetilde {\mathscr {C}}$ is a strictly full abelian subcategory closed under
$\widetilde {\mathscr {C}}$ is a strictly full abelian subcategory closed under ![]() $\otimes$, duals, and subobjects (and, thus, quotients). The constant objects of
$\otimes$, duals, and subobjects (and, thus, quotients). The constant objects of ![]() $\mathscr {C}_0$ form a Tannakian subcategory
$\mathscr {C}_0$ form a Tannakian subcategory ![]() $\mathscr {C}_{0,\operatorname {cst}}$ of
$\mathscr {C}_{0,\operatorname {cst}}$ of ![]() $\mathscr {C}_0$ (see [Reference BertolinBer08, § 2]).
$\mathscr {C}_0$ (see [Reference BertolinBer08, § 2]).
Let ![]() $\mathscr {C}$ be the smallest Tannakian subcategory of
$\mathscr {C}$ be the smallest Tannakian subcategory of ![]() $\widetilde {\mathscr {C}}$ containing the essential image of
$\widetilde {\mathscr {C}}$ containing the essential image of ![]() $\mathscr {C}_0$ (i.e. generated by the subquotients of the essential image of
$\mathscr {C}_0$ (i.e. generated by the subquotients of the essential image of ![]() $\mathscr {C}_0$).
$\mathscr {C}_0$).
2.1.2 In the following, we assume that ![]() $\widetilde {\mathscr {C}}$ is neutral over
$\widetilde {\mathscr {C}}$ is neutral over ![]() $E$ by
$E$ by ![]() $\omega \colon \widetilde {\mathscr {C}}\to \operatorname {Vec}_E$. Then so are
$\omega \colon \widetilde {\mathscr {C}}\to \operatorname {Vec}_E$. Then so are ![]() $\mathscr {C},\mathscr {C}_0$ and
$\mathscr {C},\mathscr {C}_0$ and ![]() $\mathscr {C}_{0,\operatorname {cst}}$. We prove the following results by a similar approach of [Reference D'AddezioD'Ad20, Appendix], where D'Addezio treated the case
$\mathscr {C}_{0,\operatorname {cst}}$. We prove the following results by a similar approach of [Reference D'AddezioD'Ad20, Appendix], where D'Addezio treated the case ![]() $n=1$. A similar discussion appeared in [Reference Heinloth, Ngô and YunHNY13, Appendix 2] and [Reference Xu and ZhuXZ22, § 3.4].
$n=1$. A similar discussion appeared in [Reference Heinloth, Ngô and YunHNY13, Appendix 2] and [Reference Xu and ZhuXZ22, § 3.4].
Proposition 2.1.3 (i) The canonical functors ![]() $\mathscr {C}_{0,\operatorname {cst}}\to \mathscr {C}_0\to \mathscr {C}$ induce a short exact sequence
$\mathscr {C}_{0,\operatorname {cst}}\to \mathscr {C}_0\to \mathscr {C}$ induce a short exact sequence
(ii) The category ![]() $\mathscr {C}_{0,\operatorname {cst}}$ is equivalent to the category of representations of
$\mathscr {C}_{0,\operatorname {cst}}$ is equivalent to the category of representations of ![]() $\mathbb {Z}^n$ over
$\mathbb {Z}^n$ over ![]() $E$ and the Tannakian group
$E$ and the Tannakian group ![]() $\pi _1(\mathscr {C}_{0,\operatorname {cst}})$ is isomorphic to the pro-algebraic completion of
$\pi _1(\mathscr {C}_{0,\operatorname {cst}})$ is isomorphic to the pro-algebraic completion of ![]() $\mathbb {Z}^n$.
$\mathbb {Z}^n$.
In view of [Reference Deligne and MilneDM82, Proposition 2.21] and the definition of ![]() $\mathscr {C}$, the morphism
$\mathscr {C}$, the morphism ![]() $\pi _1(\mathscr {C}) \to \pi _1(\mathscr {C}_0)$ (respectively,
$\pi _1(\mathscr {C}) \to \pi _1(\mathscr {C}_0)$ (respectively, ![]() $\pi _1(\mathscr {C}_0)\to \pi _1(\mathscr {C}_{0,\operatorname {cst}})$) is a closed immersion (respectively, faithfully flat). We use the following criterion to prove the exactness.
$\pi _1(\mathscr {C}_0)\to \pi _1(\mathscr {C}_{0,\operatorname {cst}})$) is a closed immersion (respectively, faithfully flat). We use the following criterion to prove the exactness.
Theorem 2.1.4 ([Reference Deligne and MilneDM82, Proposition 2.21], [Reference Esnault, Hai and SunEHS07, Theorem A.1])
We consider a sequence of affine group schemes over ![]() $E$:
$E$:
and the associated functors:
(i) The map ![]() $p\colon G\to A$ is faithfully flat if and only if
$p\colon G\to A$ is faithfully flat if and only if ![]() $p^*(\mathbf {Rep}_E(A))$ is a full subcategory of
$p^*(\mathbf {Rep}_E(A))$ is a full subcategory of ![]() $\mathbf {Rep}_E(G)$, closed under taking subquotients.
$\mathbf {Rep}_E(G)$, closed under taking subquotients.
(ii) The map ![]() $q\colon L\to G$ is a closed immersion if and only if any object of
$q\colon L\to G$ is a closed immersion if and only if any object of ![]() $\mathbf {Rep}_E(L)$ is a subquotient of an object
$\mathbf {Rep}_E(L)$ is a subquotient of an object ![]() $q^*(V)$ for some
$q^*(V)$ for some ![]() $V\in \mathbf {Rep}_E(G)$.
$V\in \mathbf {Rep}_E(G)$.
(iii) Assume that ![]() $q$ is a closed immersion and
$q$ is a closed immersion and ![]() $p$ is faithfully flat. Then the sequence (2.1.4.1) is exact if and only if the following conditions are satisfied.
$p$ is faithfully flat. Then the sequence (2.1.4.1) is exact if and only if the following conditions are satisfied.
(a) For an object
 $V\in \mathbf {Rep}_E(G)$,
$V\in \mathbf {Rep}_E(G)$,  $q^*(V)$ in
$q^*(V)$ in  $\mathbf {Rep}_E(L)$ is trivial if and only if
$\mathbf {Rep}_E(L)$ is trivial if and only if  $V\simeq p^*U$ for some object
$V\simeq p^*U$ for some object  $U$ in
$U$ in  $\mathbf {Rep}_E(A)$.
$\mathbf {Rep}_E(A)$.(b) Let
 $W_0$ be the maximal trivial subobject of
$W_0$ be the maximal trivial subobject of  $q^*(V)$ in
$q^*(V)$ in  $\mathbf {Rep}_E(L)$. Then there exists a subobject
$\mathbf {Rep}_E(L)$. Then there exists a subobject  $V_0$ of
$V_0$ of  $V$ in
$V$ in  $\mathbf {Rep}_E(G)$ such that
$\mathbf {Rep}_E(G)$ such that  $q^*(V_0)\simeq W_0$.
$q^*(V_0)\simeq W_0$.(c) Any object of
 $\mathbf {Rep}_E(L)$ is a subobject of an object in the essential image of
$\mathbf {Rep}_E(L)$ is a subobject of an object in the essential image of  $q^*$.
$q^*$.
For any ![]() $E$-algebra
$E$-algebra ![]() $R$ and
$R$ and ![]() $1\le i \le n$, the above structure defines a homomorphism:
$1\le i \le n$, the above structure defines a homomorphism:
In view of (2.1.1.1), the images of ![]() $u_i,u_j$ commute with each other. We thus obtain an action of
$u_i,u_j$ commute with each other. We thus obtain an action of ![]() $\mathbb {Z}^n$ on
$\mathbb {Z}^n$ on ![]() $\pi _1(\mathscr {C})$ and this allows us to define a group scheme
$\pi _1(\mathscr {C})$ and this allows us to define a group scheme ![]() $\pi _1(\mathscr {C})\rtimes \mathbb {Z}^n$ over
$\pi _1(\mathscr {C})\rtimes \mathbb {Z}^n$ over ![]() $E$, which we denote by
$E$, which we denote by ![]() $W(\mathscr {C}_0)$.
$W(\mathscr {C}_0)$.
Lemma 2.1.5 (i) There exist a canonical equivalence of categories ![]() $\mathscr {C}_0\xrightarrow {\sim } \mathbf {Rep}_{E}(W(\mathscr {C}_0))$ and a canonical morphism of group schemes
$\mathscr {C}_0\xrightarrow {\sim } \mathbf {Rep}_{E}(W(\mathscr {C}_0))$ and a canonical morphism of group schemes ![]() $\iota \colon W(\mathscr {C}_0)\to \pi _1(\mathscr {C}_0)$ such that the following diagram is
$\iota \colon W(\mathscr {C}_0)\to \pi _1(\mathscr {C}_0)$ such that the following diagram is ![]() $2$-commutative.
$2$-commutative.

Moreover, the image of ![]() $\iota$ is Zariski-dense in
$\iota$ is Zariski-dense in ![]() $\pi _1(\mathscr {C}_0)$.
$\pi _1(\mathscr {C}_0)$.
(ii) The subgroup ![]() $\pi _1(\mathscr {C})$ of
$\pi _1(\mathscr {C})$ of ![]() $\pi _1(\mathscr {C}_0)$ is normal. In particular, every object of
$\pi _1(\mathscr {C}_0)$ is normal. In particular, every object of ![]() $\mathscr {C}$ is a subobject of an object in the essential image of
$\mathscr {C}$ is a subobject of an object in the essential image of ![]() $\mathscr {C}_0$.
$\mathscr {C}_0$.
Proof. (i) We construct a functor
Given an object ![]() $(\mathscr {E},\varphi _i)$ of
$(\mathscr {E},\varphi _i)$ of ![]() $\mathscr {C}_0$, we construct a representation
$\mathscr {C}_0$, we construct a representation ![]() $\rho$ of
$\rho$ of ![]() $W(\mathscr {C}_0)(E)$ on
$W(\mathscr {C}_0)(E)$ on ![]() $\omega (\mathscr {E})$. For any element
$\omega (\mathscr {E})$. For any element ![]() $(g,m_1,\dots,m_n)\in \pi _1(\mathscr {C})(E)\rtimes \mathbb {Z}^n$, we define
$(g,m_1,\dots,m_n)\in \pi _1(\mathscr {C})(E)\rtimes \mathbb {Z}^n$, we define ![]() $\rho (g,m_i)$ as the composition:
$\rho (g,m_i)$ as the composition:
In view of the definition of ![]() $u_i$ (2.1.4.3), one checks that the above formula defines a representation. Then we obtain the above functor and we can check that it is an equivalence.
$u_i$ (2.1.4.3), one checks that the above formula defines a representation. Then we obtain the above functor and we can check that it is an equivalence.
By the Tannakian reconstruction theorem [Reference Deligne and MilneDM82, Theorem 2.11], ![]() $\pi _1(\mathscr {C}_0)$ is the pro-algebraic completion of
$\pi _1(\mathscr {C}_0)$ is the pro-algebraic completion of ![]() $W(\mathscr {C}_0)$ and the image of
$W(\mathscr {C}_0)$ and the image of ![]() $\iota$ is therefore Zariski-dense.
$\iota$ is therefore Zariski-dense.
(ii) The second assertion follows from the first one by Theorem 2.1.4(iii)(c). Let ![]() $H$ denote the normalizer of
$H$ denote the normalizer of ![]() $\pi _1(\mathscr {C})$ in
$\pi _1(\mathscr {C})$ in ![]() $\pi _1(\mathscr {C}_0)$. As
$\pi _1(\mathscr {C}_0)$. As ![]() $\pi _1(\mathscr {C})$ is normal in
$\pi _1(\mathscr {C})$ is normal in ![]() $W(\mathscr {C}_0)$, the image of
$W(\mathscr {C}_0)$, the image of ![]() $\iota \colon W(\mathscr {C}_0)\to \pi _1(\mathscr {C}_0)$ is contained in
$\iota \colon W(\mathscr {C}_0)\to \pi _1(\mathscr {C}_0)$ is contained in ![]() $H$. As
$H$. As ![]() $\iota$ has Zariski-dense image by assertion (i), this implies that
$\iota$ has Zariski-dense image by assertion (i), this implies that ![]() $H=\pi _1(\mathscr {C}_0)$ and the assertion follows.
$H=\pi _1(\mathscr {C}_0)$ and the assertion follows.
Proof of Proposition 2.1.3 (i) We know the exactness at the left and the exactness on the right follows from [Reference Deligne and MilneDM82, Proposition 2.21]. We use Theorem 2.1.4 to verify the exactness. Condition (a) follows from the definition. Given an object ![]() $(V,\varphi _1,\dots,\varphi _n)$ of
$(V,\varphi _1,\dots,\varphi _n)$ of ![]() $\mathscr {C}_0$, the maximal trivial subobject
$\mathscr {C}_0$, the maximal trivial subobject ![]() $W_0$ of
$W_0$ of ![]() $V$ in
$V$ in ![]() $\mathscr {C}$ is preserved by the
$\mathscr {C}$ is preserved by the ![]() $\varphi _i$. Therefore condition (b) is verified. Condition (c) is proved in Lemma 2.1.5(ii).
$\varphi _i$. Therefore condition (b) is verified. Condition (c) is proved in Lemma 2.1.5(ii).
(ii) The assertion follows from Lemma 2.1.5 applied to the category ![]() $\operatorname {Vec}_E$.
$\operatorname {Vec}_E$.
2.2 Tannakian form of Drinfeld's lemma for overconvergent  $F$-isocrystals
$F$-isocrystals
2.2.1 Let ![]() $X$ be a
$X$ be a ![]() $k$-variety. We denote by
$k$-variety. We denote by ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively,
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively, ![]() $\operatorname {\mathbf {Isoc}}(X/K)$) the category of overconvergent (respectively, convergent) isocrystals over
$\operatorname {\mathbf {Isoc}}(X/K)$) the category of overconvergent (respectively, convergent) isocrystals over ![]() $X$ relative to
$X$ relative to ![]() $K$. If we apply the construction of § 2.1.1 to the Tannakian category
$K$. If we apply the construction of § 2.1.1 to the Tannakian category ![]() $\widetilde {\mathscr {C}}=\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively,
$\widetilde {\mathscr {C}}=\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively, ![]() $\operatorname {\mathbf {Isoc}}(X/K)$) over
$\operatorname {\mathbf {Isoc}}(X/K)$) over ![]() $k$ and the (
$k$ and the (![]() $s$th) Frobenius pull-back functor
$s$th) Frobenius pull-back functor ![]() $\tau =F_X^*$, then
$\tau =F_X^*$, then ![]() $\mathscr {C}_0$ corresponds to the category
$\mathscr {C}_0$ corresponds to the category ![]() $\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X/K)$ (respectively,
$\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X/K)$ (respectively, ![]() $\operatorname {\mathbf {F-Isoc}}(X/K)$) of overconvergent (respectively, convergent)
$\operatorname {\mathbf {F-Isoc}}(X/K)$) of overconvergent (respectively, convergent) ![]() $F$-isocrystals over
$F$-isocrystals over ![]() $X/(K,\sigma )$. We set
$X/(K,\sigma )$. We set ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X/K):=\mathscr {C}$, the Tannakian full subcategory of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X/K):=\mathscr {C}$, the Tannakian full subcategory of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ generated by subquotients of overconvergent isocrystals which admit a (
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ generated by subquotients of overconvergent isocrystals which admit a (![]() $s$th) Frobenius structure, considered in [Reference AbeAbe18b].
$s$th) Frobenius structure, considered in [Reference AbeAbe18b].
2.2.2 In the following, we assume ![]() $(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$.
$(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$.
The above construction can be generalized as follows. For ![]() $i=1,\ldots,n$, let
$i=1,\ldots,n$, let ![]() $X_i$ be a
$X_i$ be a ![]() $k$-variety and set
$k$-variety and set ![]() $X:=X_1\times _k \cdots \times _k X_n$. We define a morphism
$X:=X_1\times _k \cdots \times _k X_n$. We define a morphism ![]() $F_i\colon X\to X$ by the (
$F_i\colon X\to X$ by the (![]() $s$th) Frobenius morphism
$s$th) Frobenius morphism ![]() $F_{X_i}$ of
$F_{X_i}$ of ![]() $X_i$ on the component
$X_i$ on the component ![]() $X_i$ and the identity map on other components. The morphisms
$X_i$ and the identity map on other components. The morphisms ![]() $F_i$ commute with each other and their composition is equal to
$F_i$ commute with each other and their composition is equal to ![]() $F_X$. The morphisms
$F_X$. The morphisms ![]() $F_i$ induce tensor equivalences
$F_i$ induce tensor equivalences
commuting with each other and their composition is equal to ![]() $F^*_X$.
$F^*_X$.
Given an overconvergent (respectively, convergent) isocrystal ![]() $\mathscr {E}$ over
$\mathscr {E}$ over ![]() $X/K$, a partial (
$X/K$, a partial ( ![]() $s$th) Frobenius structure on
$s$th) Frobenius structure on ![]() $\mathscr {E}$ consists of isomorphisms
$\mathscr {E}$ consists of isomorphisms ![]() $\varphi _i\colon F_i^{*}(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$ for
$\varphi _i\colon F_i^{*}(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$ for ![]() $i=1,\dots, n$ such that
$i=1,\dots, n$ such that ![]() $\varphi _i\circ F_i^{*}(\varphi _j)=\varphi _j\circ F_j^{*}(\varphi _i)$. For
$\varphi _i\circ F_i^{*}(\varphi _j)=\varphi _j\circ F_j^{*}(\varphi _i)$. For ![]() $i=1,\dots,n$,
$i=1,\dots,n$, ![]() $\varphi _i$ is called the
$\varphi _i$ is called the ![]() $i$th partial Frobenius structure (on
$i$th partial Frobenius structure (on ![]() $\mathscr {E}$). Note that the composition of the
$\mathscr {E}$). Note that the composition of the ![]() $\varphi _i$ (in any order) forms a Frobenius structure on
$\varphi _i$ (in any order) forms a Frobenius structure on ![]() $\mathscr {E}$.
$\mathscr {E}$.
If we apply the construction of 2.1.1 to ![]() $(\widetilde {\mathscr {C}}=\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively,
$(\widetilde {\mathscr {C}}=\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively, ![]() $\operatorname {\mathbf {Isoc}}(X/K)$);
$\operatorname {\mathbf {Isoc}}(X/K)$); ![]() $F_1^{*},\ldots,F_n^{*})$, then
$F_1^{*},\ldots,F_n^{*})$, then ![]() $\mathscr {C}_0$ corresponds to the category of overconvergent (convergent) isocrystals over
$\mathscr {C}_0$ corresponds to the category of overconvergent (convergent) isocrystals over ![]() $X$ with a partial Frobenius structure, which we denote by
$X$ with a partial Frobenius structure, which we denote by ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X/K)$ (respectively,
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X/K)$ (respectively, ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$). We set
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$). We set ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K):=\mathscr {C}$, the full subcategory of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K):=\mathscr {C}$, the full subcategory of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$, generated by subquotients of overconvergent isocrystals which admits a
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$, generated by subquotients of overconvergent isocrystals which admits a ![]() $s$th partial Frobenius structure.
$s$th partial Frobenius structure.
We denote by ![]() $F_i\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively,
$F_i\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X/K)$ (respectively, ![]() $F_i\text {-}\operatorname {\mathbf {Isoc}}(X/K)$) the category of pairs
$F_i\text {-}\operatorname {\mathbf {Isoc}}(X/K)$) the category of pairs ![]() $(\mathscr {E},\varphi _i)$ consisting of an overconvergent (respectively, convergent) isocrystal with an
$(\mathscr {E},\varphi _i)$ consisting of an overconvergent (respectively, convergent) isocrystal with an ![]() $i$th partial Frobenius structure.
$i$th partial Frobenius structure.
Let ![]() $k'/k$ be a finite extension of degree
$k'/k$ be a finite extension of degree ![]() $a$ and set
$a$ and set ![]() $K':=\operatorname {W}(k')\otimes _{\operatorname {W}(k)}K$. (We denote the Witt vector functor by
$K':=\operatorname {W}(k')\otimes _{\operatorname {W}(k)}K$. (We denote the Witt vector functor by ![]() $\operatorname {W}$ to reduce confusion with the notation
$\operatorname {W}$ to reduce confusion with the notation ![]() $W(\mathscr {C}_0)$ from Lemma 2.1.5.) Set
$W(\mathscr {C}_0)$ from Lemma 2.1.5.) Set ![]() $X_{k'}:=X\otimes _k k'$. Then we have a canonical functor of extension of scalars:
$X_{k'}:=X\otimes _k k'$. Then we have a canonical functor of extension of scalars:
2.2.3 The category ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)$ defined above is a Tannakian category over
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)$ defined above is a Tannakian category over ![]() $K$ and may not be neutral. For any algebraic extension
$K$ and may not be neutral. For any algebraic extension ![]() $L$ of
$L$ of ![]() $K$ in
$K$ in ![]() $\overline {\mathbb {Q}}_p$, we set
$\overline {\mathbb {Q}}_p$, we set ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /L):=\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)\otimes _K L$. When
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /L):=\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)\otimes _K L$. When ![]() $L=\overline {\mathbb {Q}}_p$, this category is a neutral Tannakian category over
$L=\overline {\mathbb {Q}}_p$, this category is a neutral Tannakian category over ![]() $\overline {\mathbb {Q}}_p$ (with respect to a fiber functor) and we omit
$\overline {\mathbb {Q}}_p$ (with respect to a fiber functor) and we omit ![]() $/\overline {\mathbb {Q}}_p$ from the notation. We denote by
$/\overline {\mathbb {Q}}_p$ from the notation. We denote by ![]() $\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )$ (respectively,
$\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )$ (respectively, ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$, respectively
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$, respectively ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)$) the Tannakian group of
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)$) the Tannakian group of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ (respectively,
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ (respectively, ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$,
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$, ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$) over
$\operatorname {\mathbf {\Phi -Isoc}}(X)$) over ![]() $\overline {\mathbb {Q}}_p$. When
$\overline {\mathbb {Q}}_p$. When ![]() $n=1$ (i.e. partial Frobenius structures reduce to a Frobenius structure), we omit
$n=1$ (i.e. partial Frobenius structures reduce to a Frobenius structure), we omit ![]() $\Phi$ from the notation or replace it with
$\Phi$ from the notation or replace it with ![]() $F$.
$F$.
The pullback functor ![]() $p_{i}^*$ induces a canonical tensor functor
$p_{i}^*$ induces a canonical tensor functor
 \begin{equation} \begin{gathered}
p_i^{*}\colon \operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}(X_i) \to \operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}(X)\\
\text{(respectively, } \mathbf{Isoc}^{{{\dagger}}{{\dagger}}}(X_i)\to
\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}(X,\Phi),\ \text{respectively, }
\operatorname{\mathbf{F-Isoc}}(X_i)\to \operatorname{\mathbf{\Phi-Isoc}}(X))\\
(\mathscr{E}_i,\varphi_i) \mapsto (p_i^{*}\mathscr{E}_i, \operatorname{id},\ldots,p_i^{*}(\varphi_i),\ldots,\operatorname{id}).
\end{gathered} \end{equation}
\begin{equation} \begin{gathered}
p_i^{*}\colon \operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}(X_i) \to \operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}(X)\\
\text{(respectively, } \mathbf{Isoc}^{{{\dagger}}{{\dagger}}}(X_i)\to
\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}(X,\Phi),\ \text{respectively, }
\operatorname{\mathbf{F-Isoc}}(X_i)\to \operatorname{\mathbf{\Phi-Isoc}}(X))\\
(\mathscr{E}_i,\varphi_i) \mapsto (p_i^{*}\mathscr{E}_i, \operatorname{id},\ldots,p_i^{*}(\varphi_i),\ldots,\operatorname{id}).
\end{gathered} \end{equation}
By the Künneth formula, the functor ![]() $p_i^*\colon \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)\to \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ is fully faithful. It induces a canonical
$p_i^*\colon \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)\to \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ is fully faithful. It induces a canonical ![]() $\overline {\mathbb {Q}}_p$-homomorphism
$\overline {\mathbb {Q}}_p$-homomorphism
 \begin{gather*} p_i^{\circ}\colon
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}}(X) \to
\pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_i)\\
\text{(respectively, }
\pi_1^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X,\Phi)\to
\pi_{1}^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X_i),\ \text{respectively, }
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}}}(X) \to
\pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_i)).
\end{gather*}
\begin{gather*} p_i^{\circ}\colon
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}}(X) \to
\pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_i)\\
\text{(respectively, }
\pi_1^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X,\Phi)\to
\pi_{1}^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X_i),\ \text{respectively, }
\pi_1^{\operatorname{\mathbf{\Phi-Isoc}}}(X) \to
\pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_i)).
\end{gather*}
The Tannakian form of Drinfeld's lemma can be summarized as follows. Its proof will occupy most of the remainder of § 2.2.
Theorem 2.2.4 Assume each ![]() $X_i$ is a geometrically connected
$X_i$ is a geometrically connected ![]() $k$-variety. The following canonical homomorphisms are isomorphisms:
$k$-variety. The following canonical homomorphisms are isomorphisms:
 \begin{equation} \prod_{i=1}^n p_i^{\circ}\colon \pi_1^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \pi_{1}^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X_i), \quad \prod_{i=1}^n p_i^{\circ}\colon \pi_1^{\operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}}(X) \xrightarrow{\sim} \prod_{i=1}^n \pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_i) . \end{equation}
\begin{equation} \prod_{i=1}^n p_i^{\circ}\colon \pi_1^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \pi_{1}^{\mathbf{Isoc}^{{{\dagger}}{{\dagger}}}}(X_i), \quad \prod_{i=1}^n p_i^{\circ}\colon \pi_1^{\operatorname{\mathbf{\Phi-Isoc}^{{{\dagger}}}}}(X) \xrightarrow{\sim} \prod_{i=1}^n \pi_1^{\operatorname{\mathbf{F-Isoc}^{{{\dagger}}}}}(X_i) . \end{equation} We first establish some basic properties of the category ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$.
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$.
Proposition 2.2.5 (i) An irreducible object of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ belongs to
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ belongs to ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ if and only if it can be equipped with an
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ if and only if it can be equipped with an ![]() $s'$th partial Frobenius structure for some
$s'$th partial Frobenius structure for some ![]() $s|s'$.
$s|s'$.
(ii) (D’Addezio and Esnault [Reference D'Addezio and EsnaultDE22]) The category ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ is closed under extension. Every object of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ is closed under extension. Every object of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ can be embedded into an object of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ can be embedded into an object of ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$.
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$.
(iii) The category ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ is equivalent to the thick full subcategory of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ is equivalent to the thick full subcategory of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ generated by those objects which can be equipped with an
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ generated by those objects which can be equipped with an ![]() $s'$th partial Frobenius structure for some
$s'$th partial Frobenius structure for some ![]() $s|s'$.
$s|s'$.
Proof. (i) Given an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$, the partial Frobenius pullbacks permute the isomorphism classes of the irreducible constituents of
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$, the partial Frobenius pullbacks permute the isomorphism classes of the irreducible constituents of ![]() $\mathscr {E}$ in
$\mathscr {E}$ in ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X)$. We thus conclude that an irreducible object
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X)$. We thus conclude that an irreducible object ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ admits
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ admits ![]() $s'$th partial Frobenius structure for some
$s'$th partial Frobenius structure for some ![]() $s|s'$.
$s|s'$.
On the other hand, if an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ is irreducible equipped with an
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ is irreducible equipped with an ![]() $s'(=st)$th partial Frobenius structure for some
$s'(=st)$th partial Frobenius structure for some ![]() $t\in \mathbb {N}$, then
$t\in \mathbb {N}$, then ![]() $\mathscr {E}$ is a subobject of
$\mathscr {E}$ is a subobject of
 \[ \mathscr{F}:=\bigoplus_{j_1=0}^{t-1} \cdots \bigoplus_{j_n=0}^{t-1} F_1^{j_1*}\circ\cdots\circ F_{n}^{j_n*}(\mathscr{E}), \]
\[ \mathscr{F}:=\bigoplus_{j_1=0}^{t-1} \cdots \bigoplus_{j_n=0}^{t-1} F_1^{j_1*}\circ\cdots\circ F_{n}^{j_n*}(\mathscr{E}), \]
which admits an ![]() $s$th Frobenius structure. Therefore,
$s$th Frobenius structure. Therefore, ![]() $\mathscr {E}$ belongs to
$\mathscr {E}$ belongs to ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$.
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$.
(ii) When ![]() $n=1$, assertion (ii) is proved in [Reference D'Addezio and EsnaultDE22, Theorem 5.4]. The general case can be showed in a similar way as in [Reference D'Addezio and EsnaultDE22, Theorem 5.4].
$n=1$, assertion (ii) is proved in [Reference D'Addezio and EsnaultDE22, Theorem 5.4]. The general case can be showed in a similar way as in [Reference D'Addezio and EsnaultDE22, Theorem 5.4].
(iii) Assertion (iii) follows from assertions (i) and (ii).
2.2.6 We will use the theory of holonomic (arithmetic) ![]() $\mathscr {D}$-modules and their six functors formalism developed in [Reference Abe and CaroAC18, Reference AbeAbe18b]. Let
$\mathscr {D}$-modules and their six functors formalism developed in [Reference Abe and CaroAC18, Reference AbeAbe18b]. Let ![]() $L$ be an extension of
$L$ be an extension of ![]() $K$ in
$K$ in ![]() $\overline {\mathbb {Q}}_p$,
$\overline {\mathbb {Q}}_p$, ![]() $\mathfrak {T}:=\{k,\mathscr {O}_K,K,L\}$ the associated geometric base tuple and
$\mathfrak {T}:=\{k,\mathscr {O}_K,K,L\}$ the associated geometric base tuple and ![]() $\mathfrak {T}_F:=\{k,\mathscr {O}_K,K,L,s,\operatorname {id}_L\}$ the associated arithmetic base tuple [Reference AbeAbe18b, 1.4.10, 2.4.14].
$\mathfrak {T}_F:=\{k,\mathscr {O}_K,K,L,s,\operatorname {id}_L\}$ the associated arithmetic base tuple [Reference AbeAbe18b, 1.4.10, 2.4.14].
Let ![]() $X$ be a
$X$ be a ![]() $k$-variety. There exists an
$k$-variety. There exists an ![]() $L$-linear triangulated category
$L$-linear triangulated category ![]() $\operatorname {D}(X/L)$ (respectively,
$\operatorname {D}(X/L)$ (respectively, ![]() $\operatorname {D}(X/L_F)$) relative to the geometric base tuple
$\operatorname {D}(X/L_F)$) relative to the geometric base tuple ![]() $\mathfrak {T}$ (respectively, arithmetic base tuple
$\mathfrak {T}$ (respectively, arithmetic base tuple ![]() $\mathfrak {T}_F$). This category is denoted by
$\mathfrak {T}_F$). This category is denoted by ![]() $\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/\mathfrak {T})$ or
$\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/\mathfrak {T})$ or ![]() $\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/L)$ (respectively,
$\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/L)$ (respectively, ![]() $\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/\mathfrak {T}_F)$ or
$\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/\mathfrak {T}_F)$ or ![]() $\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/L_F)$) in [Reference AbeAbe18b, 1.1.1, 2.1.16]. For
$\operatorname {D}^{\operatorname {b}}_{\operatorname {hol}}(X/L_F)$) in [Reference AbeAbe18b, 1.1.1, 2.1.16]. For ![]() $\blacktriangle \in \{\emptyset,F\}$, there exists a holonomic t-structure on
$\blacktriangle \in \{\emptyset,F\}$, there exists a holonomic t-structure on ![]() $\operatorname {D}(X/L_{\blacktriangle })$, whose heart is denoted by
$\operatorname {D}(X/L_{\blacktriangle })$, whose heart is denoted by ![]() $\operatorname {Hol}(X/L_{\blacktriangle })$, called the category of holonomic modules. We denote by
$\operatorname {Hol}(X/L_{\blacktriangle })$, called the category of holonomic modules. We denote by ![]() $\mathcal {H}^*$ the cohomological functor for holonomic t-structure.
$\mathcal {H}^*$ the cohomological functor for holonomic t-structure.
The six functors formalism for ![]() $\operatorname {D}(X/L)$ (respectively,
$\operatorname {D}(X/L)$ (respectively, ![]() $\operatorname {D}(X/L_F)$) has been established recently. We refer to [Reference AbeAbe18b, § 2.3] for details and to [Reference AbeAbe18b, 1.1.3] for a summary.
$\operatorname {D}(X/L_F)$) has been established recently. We refer to [Reference AbeAbe18b, § 2.3] for details and to [Reference AbeAbe18b, 1.1.3] for a summary.
2.2.7 Let ![]() $X$ be a smooth and quasiprojective geometrically connected
$X$ be a smooth and quasiprojective geometrically connected ![]() $k$-variety of dimension
$k$-variety of dimension ![]() $d_X$. The category
$d_X$. The category ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X)$ (respectively,
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X)$ (respectively, ![]() $\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X)$) is equivalent to the full subcategory
$\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X)$) is equivalent to the full subcategory ![]() $\operatorname {Sm}(X/\overline {\mathbb {Q}}_p)$ (respectively,
$\operatorname {Sm}(X/\overline {\mathbb {Q}}_p)$ (respectively, ![]() $\operatorname {Sm}(X/\overline {\mathbb {Q}}_{p,F})$) consisting of smooth objects of the category
$\operatorname {Sm}(X/\overline {\mathbb {Q}}_{p,F})$) consisting of smooth objects of the category ![]() $\operatorname {Hol}(X/\overline {\mathbb {Q}}_p)[-d_X]$ (respectively,
$\operatorname {Hol}(X/\overline {\mathbb {Q}}_p)[-d_X]$ (respectively, ![]() $\operatorname {Hol}(X/\overline {\mathbb {Q}}_{p,F})[-d_X]$) of holonomic arithmetic
$\operatorname {Hol}(X/\overline {\mathbb {Q}}_{p,F})[-d_X]$) of holonomic arithmetic ![]() $\mathscr {D}$-modules shifted by the dimension
$\mathscr {D}$-modules shifted by the dimension ![]() $-d_X$ (see [Reference AbeAbe18b, 1.1.3 (12)]).
$-d_X$ (see [Reference AbeAbe18b, 1.1.3 (12)]).
We briefly review the pushforward and pullback functors for a smooth morphism ![]() $f\colon X\to Y$ of relative dimension
$f\colon X\to Y$ of relative dimension ![]() $d$ between quasiprojective geometrically connected
$d$ between quasiprojective geometrically connected ![]() $k$-varieties following [Reference AbeAbe18b, 1.2.8]. We have an adjoint pair
$k$-varieties following [Reference AbeAbe18b, 1.2.8]. We have an adjoint pair ![]() $(f_+,f^+[2d])$
$(f_+,f^+[2d])$
The functor ![]() $f^+[d]$ is exact and induces a fully faithful functor [Reference Xu and ZhuXZ22, Proposition 2.1.6]:
$f^+[d]$ is exact and induces a fully faithful functor [Reference Xu and ZhuXZ22, Proposition 2.1.6]:
If ![]() $d_X$ (respectively,
$d_X$ (respectively, ![]() $d_Y$) denotes the dimension of
$d_Y$) denotes the dimension of ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$), the functor
$Y$), the functor
is a right adjoint of ![]() $f^*:=f^+$ and is left exact. Its right derived functor
$f^*:=f^+$ and is left exact. Its right derived functor ![]() $\operatorname {R} f_*$ is compatible with
$\operatorname {R} f_*$ is compatible with ![]() $f_+$.
$f_+$.
Moreover, there exists a canonical isomorphism (Poincaré duality [Reference AbeAbe18b, 1.5.13]):
Proposition 2.2.8 Assume each ![]() $X_i$ is smooth and quasiprojective over
$X_i$ is smooth and quasiprojective over ![]() $k$.
$k$.
(i) The functor
 $p_{i,*}$ sends objects of
$p_{i,*}$ sends objects of  $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ to
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ to  $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)$ (respectively,
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)$ (respectively,  $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ to
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ to  $\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X_i)$).
$\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X_i)$).(ii) The functor
 $p_{i,*}\colon \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )\to \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)$ is a right adjoint of
$p_{i,*}\colon \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )\to \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)$ is a right adjoint of  $p_i^*$ (2.2.3.1). The adjoint morphism
$p_i^*$ (2.2.3.1). The adjoint morphism  $\operatorname {id}\to p_{i,*}p_i^*$ is an isomorphism and
$\operatorname {id}\to p_{i,*}p_i^*$ is an isomorphism and  $p_i^*p_{i,*}\to \operatorname {id}$ is injective.
$p_i^*p_{i,*}\to \operatorname {id}$ is injective.
2.2.9 Let ![]() $Y:=Y_1\times _k Y_2$ be a product of two geometrically connected
$Y:=Y_1\times _k Y_2$ be a product of two geometrically connected ![]() $k$-varieties,
$k$-varieties, ![]() $k'$ a perfect field over
$k'$ a perfect field over ![]() $k$,
$k$, ![]() $\mathscr {O}_{K'}:=\operatorname {W}(k')\otimes _{\operatorname {W}(k)}\mathscr {O}_K$, equipped with a lift
$\mathscr {O}_{K'}:=\operatorname {W}(k')\otimes _{\operatorname {W}(k)}\mathscr {O}_K$, equipped with a lift ![]() $\sigma '$ of the
$\sigma '$ of the ![]() $s$th Frobenius automorphism of
$s$th Frobenius automorphism of ![]() $k'$ defined by that of
$k'$ defined by that of ![]() $\operatorname {W}(k')$ and
$\operatorname {W}(k')$ and ![]() $\operatorname {id}_{\mathscr {O}_K}$. We set
$\operatorname {id}_{\mathscr {O}_K}$. We set ![]() $K':=\mathscr {O}_{K'}[{1}/{p}]$.
$K':=\mathscr {O}_{K'}[{1}/{p}]$.
We denote by ![]() $F_1\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(Y_{1,k'}/K')$ (respectively,
$F_1\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(Y_{1,k'}/K')$ (respectively, ![]() $F_1\text {-}\operatorname {\mathbf {Isoc}}(Y_{1,k'}/K')$) the category of pairs
$F_1\text {-}\operatorname {\mathbf {Isoc}}(Y_{1,k'}/K')$) the category of pairs ![]() $(\mathscr {E},\phi )$ consisting of an object
$(\mathscr {E},\phi )$ consisting of an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(Y_{1,k'}/K')$ (respectively,
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(Y_{1,k'}/K')$ (respectively, ![]() $\operatorname {\mathbf {Isoc}}(Y_{1,k'}/K')$) and an isomorphism
$\operatorname {\mathbf {Isoc}}(Y_{1,k'}/K')$) and an isomorphism ![]() $\phi \colon (F_{Y_1}\otimes \operatorname {id}_{k'})^*(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$.
$\phi \colon (F_{Y_1}\otimes \operatorname {id}_{k'})^*(\mathscr {E})\xrightarrow {\sim } \mathscr {E}$.
A point ![]() $i\colon \operatorname {Spec}(k')\to Y_2$ induces a natural functor:
$i\colon \operatorname {Spec}(k')\to Y_2$ induces a natural functor:
 \begin{align} \begin{aligned} \iota\colon F_1\text{-}\operatorname{\mathbf{Isoc}^{{{\dagger}}}}(Y/K) & \to F_1\text{-}\operatorname{\mathbf{Isoc}^{{{\dagger}}}}(Y_{1,k'}/K'), \enspace \text{(respectively, } F_1\text{-}\operatorname{\mathbf{Isoc}}(Y/K)\to F_1\text{-}\operatorname{\mathbf{Isoc}}(Y_{1,k'}/K') ),\\ (\mathscr{E},\varphi) & \mapsto ((\operatorname{id}_{Y_1}\times i)^*(\mathscr{E}),(\operatorname{id}_{Y_1}\times i)^*\varphi). \end{aligned} \end{align}
\begin{align} \begin{aligned} \iota\colon F_1\text{-}\operatorname{\mathbf{Isoc}^{{{\dagger}}}}(Y/K) & \to F_1\text{-}\operatorname{\mathbf{Isoc}^{{{\dagger}}}}(Y_{1,k'}/K'), \enspace \text{(respectively, } F_1\text{-}\operatorname{\mathbf{Isoc}}(Y/K)\to F_1\text{-}\operatorname{\mathbf{Isoc}}(Y_{1,k'}/K') ),\\ (\mathscr{E},\varphi) & \mapsto ((\operatorname{id}_{Y_1}\times i)^*(\mathscr{E}),(\operatorname{id}_{Y_1}\times i)^*\varphi). \end{aligned} \end{align}
When ![]() $k'$ is a finite extension of
$k'$ is a finite extension of ![]() $k$ of degree
$k$ of degree ![]() $a$, we associate an
$a$, we associate an ![]() $F$-isocrystal over
$F$-isocrystal over ![]() $Y_{1,k'}/K'$ to an object of
$Y_{1,k'}/K'$ to an object of ![]() $F_1\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(Y_{1,k'}/K')$ by composing its Frobenius structure
$F_1\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(Y_{1,k'}/K')$ by composing its Frobenius structure ![]() $a$ times.
$a$ times.
When ![]() $Y_2=\operatorname {Spec}(k)$, we regard the above functor as the functor of extension of scalars:
$Y_2=\operatorname {Spec}(k)$, we regard the above functor as the functor of extension of scalars:
2.2.10. Proof of Proposition 2.2.8
(i) It suffices to prove the assertion for objects of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)$. We may assume
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)$. We may assume ![]() $i=1$. We set
$i=1$. We set ![]() $X':=\prod _{i=2}^n X_i$.
$X':=\prod _{i=2}^n X_i$.
(a) We first prove the assertion for an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)$ equipped with a partial Frobenius structure
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi /K)$ equipped with a partial Frobenius structure ![]() $(\varphi _1,\ldots,\varphi _n)$. There exists an open subscheme
$(\varphi _1,\ldots,\varphi _n)$. There exists an open subscheme ![]() $U_1$ of
$U_1$ of ![]() $X_1$ such that
$X_1$ such that ![]() $p_{1,*}(\mathscr {E})|_{U_1}$ is smooth. In view of their fibers, the adjoint morphism of overconvergent isocrystals:
$p_{1,*}(\mathscr {E})|_{U_1}$ is smooth. In view of their fibers, the adjoint morphism of overconvergent isocrystals:
is injective. The first partial Frobenius ![]() $\varphi _1$ on
$\varphi _1$ on ![]() $\mathscr {E}$ induces a Frobenius structure
$\mathscr {E}$ induces a Frobenius structure ![]() $\phi _1$ on
$\phi _1$ on ![]() $p_{1,*}(\mathscr {E})|_{U_1}$ and the above morphism is compatible with the first partial Frobenius structures
$p_{1,*}(\mathscr {E})|_{U_1}$ and the above morphism is compatible with the first partial Frobenius structures ![]() $p_1^*(\phi _1)$ and
$p_1^*(\phi _1)$ and ![]() $\varphi _1$. Let
$\varphi _1$. Let ![]() $k'$ be a perfect closure of
$k'$ be a perfect closure of ![]() $k(X')$ and
$k(X')$ and ![]() $K':=\operatorname {W}(k')[{1}/{p}]$. By the exactness of the functor
$K':=\operatorname {W}(k')[{1}/{p}]$. By the exactness of the functor ![]() $\iota$, defined in (2.2.9.1), we obtain an injection in
$\iota$, defined in (2.2.9.1), we obtain an injection in ![]() $F_1\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(U_{1,k'}/K')$:
$F_1\text {-}\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(U_{1,k'}/K')$:
By [Reference KedlayaKed07, Proposition 5.3.1], the left-hand side extends to a subobject ![]() $\mathscr {F}'$ of
$\mathscr {F}'$ of ![]() $\iota (\mathscr {E})$ of
$\iota (\mathscr {E})$ of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X_{1,k'}/K')$.
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X_{1,k'}/K')$.
We claim that there exists an overconvergent isocrystal ![]() $\mathscr {F}$ of
$\mathscr {F}$ of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X_1/K)$ extending
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X_1/K)$ extending ![]() $p_{1,*}(\mathscr {E})|_{U_1}$ such that
$p_{1,*}(\mathscr {E})|_{U_1}$ such that ![]() $\iota _{k'/k}(\mathscr {F})\simeq \mathscr {F}'$. By Kedlaya and Shiho's purity theorem [Reference KedlayaKed22a, Theorem 5.1], we may assume that the boundary
$\iota _{k'/k}(\mathscr {F})\simeq \mathscr {F}'$. By Kedlaya and Shiho's purity theorem [Reference KedlayaKed22a, Theorem 5.1], we may assume that the boundary ![]() $D:=X_1-U_1$ is a smooth divisor. Since the local monodromy of
$D:=X_1-U_1$ is a smooth divisor. Since the local monodromy of ![]() $\mathscr {F}'$ around
$\mathscr {F}'$ around ![]() $D_{k'}$ is constant [Reference KedlayaKed07, Theorem 5.2.1], then so is the local monodromy of
$D_{k'}$ is constant [Reference KedlayaKed07, Theorem 5.2.1], then so is the local monodromy of ![]() $p_{1,*}(\mathscr {E})|_{U_1}$ around
$p_{1,*}(\mathscr {E})|_{U_1}$ around ![]() $D$. Then the claim follows.
$D$. Then the claim follows.
Moreover, the Frobenius structure on ![]() $p_{1,*}(\mathscr {E})|_{U_1}$ extends to
$p_{1,*}(\mathscr {E})|_{U_1}$ extends to ![]() $\mathscr {F}$. Finally, by full faithfullness of pullback for holonomic
$\mathscr {F}$. Finally, by full faithfullness of pullback for holonomic ![]() $\mathscr {D}$-modules along
$\mathscr {D}$-modules along ![]() $U_1\to X_1$ (see [Reference Xu and ZhuXZ22, Proposition 2.1.6]), we deduce that
$U_1\to X_1$ (see [Reference Xu and ZhuXZ22, Proposition 2.1.6]), we deduce that ![]() $\mathscr {F}$ is isomorphic to
$\mathscr {F}$ is isomorphic to ![]() $p_{1,*}(\mathscr {E})$. Then the assertion in this case follows.
$p_{1,*}(\mathscr {E})$. Then the assertion in this case follows.
(b) An object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ can be embedded into an object
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ can be embedded into an object ![]() $\mathscr {F}$, which can be equipped with a partial Frobenius structure (Proposition 2.2.5(ii)). As
$\mathscr {F}$, which can be equipped with a partial Frobenius structure (Proposition 2.2.5(ii)). As ![]() $p_{1,*}$ is left exact, we have an injection to a smooth object
$p_{1,*}$ is left exact, we have an injection to a smooth object ![]() $\mathscr {N}$ of
$\mathscr {N}$ of ![]() $\operatorname {Hol}(X_1/\overline {\mathbb {Q}}_{p,F})[-d_{X_1}]$:
$\operatorname {Hol}(X_1/\overline {\mathbb {Q}}_{p,F})[-d_{X_1}]$:
It remains to show that ![]() $\mathscr {M}$ is also smooth. We first consider the case where
$\mathscr {M}$ is also smooth. We first consider the case where ![]() $X_1$ is a curve. Let
$X_1$ is a curve. Let ![]() $U_1$ be an open subset of
$U_1$ be an open subset of ![]() $X_1$ on which
$X_1$ on which ![]() $\mathscr {M}$ is smooth. By applying [Reference Xu and ZhuXZ22, Corollary 2.3.4] to
$\mathscr {M}$ is smooth. By applying [Reference Xu and ZhuXZ22, Corollary 2.3.4] to ![]() $\mathscr {M}|_{U_1}$, the exactness of pullback on smooth modules and of the nearby cycle functor, we deduce the smoothness of
$\mathscr {M}|_{U_1}$, the exactness of pullback on smooth modules and of the nearby cycle functor, we deduce the smoothness of ![]() $\mathscr {M}$ from that of
$\mathscr {M}$ from that of ![]() $\mathscr {N}$.
$\mathscr {N}$.
In general, there is a dense open subscheme ![]() $j\colon U_1\to X_1$ and a smooth object
$j\colon U_1\to X_1$ and a smooth object ![]() $\mathscr {L}$ on
$\mathscr {L}$ on ![]() $U_1$ such that
$U_1$ such that ![]() $\mathscr {M}|_{U_1}\simeq \mathscr {L}$. Let
$\mathscr {M}|_{U_1}\simeq \mathscr {L}$. Let ![]() $c\colon C\to X_1$ be a morphism from a smooth curve to
$c\colon C\to X_1$ be a morphism from a smooth curve to ![]() $X$ such that
$X$ such that ![]() $c(C)\cap U_1$ is non-empty and
$c(C)\cap U_1$ is non-empty and ![]() $p_c\colon C\times _k X'\to C$ the projection. By the above argument,
$p_c\colon C\times _k X'\to C$ the projection. By the above argument, ![]() $p_{c,*}( (c\times \operatorname {id})^*\mathscr {E})$ is smooth and the pullback
$p_{c,*}( (c\times \operatorname {id})^*\mathscr {E})$ is smooth and the pullback ![]() $c^*\mathscr {L}$ extends to an overconvergent isocrystal on
$c^*\mathscr {L}$ extends to an overconvergent isocrystal on ![]() $C$. By Shiho's cut-by-curves theorem [Reference ShihoShi11a] and Kedlaya and Shiho's purity theorem,
$C$. By Shiho's cut-by-curves theorem [Reference ShihoShi11a] and Kedlaya and Shiho's purity theorem, ![]() $\mathscr {L}$ can be extended to an overconvergent isocrystal over
$\mathscr {L}$ can be extended to an overconvergent isocrystal over ![]() $X$. By full faithfulness of pullback along
$X$. By full faithfulness of pullback along ![]() $U_1\to X_1$, we deduce that
$U_1\to X_1$, we deduce that ![]() $\mathscr {M}$ is isomorphic to the extension of
$\mathscr {M}$ is isomorphic to the extension of ![]() $\mathscr {L}$ to
$\mathscr {L}$ to ![]() $X_1$. This finishes the proof.
$X_1$. This finishes the proof.
(ii) The isomorphism ![]() $\operatorname {id}\to p_{i,*}p_i^*$ follows from the Künneth formula [Reference AbeAbe18b, Proposition 1.1.7]. In view of fibers at closed points, the injectivity of
$\operatorname {id}\to p_{i,*}p_i^*$ follows from the Künneth formula [Reference AbeAbe18b, Proposition 1.1.7]. In view of fibers at closed points, the injectivity of ![]() $p_i^*p_{i,*}\to \operatorname {id}$ follows.
$p_i^*p_{i,*}\to \operatorname {id}$ follows.
2.2.11 We now turn to the proof of Theorem 2.2.4. We first prove Theorem 2.2.4 for ![]() $\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}$ under the additional hypothesis that each
$\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}$ under the additional hypothesis that each ![]() $X_i$ is smooth and quasiprojective over
$X_i$ is smooth and quasiprojective over ![]() $k$.
$k$.
Proof. As we work with arithmetic ![]() $\mathscr {D}$-modules with coefficients in
$\mathscr {D}$-modules with coefficients in ![]() $\overline {\mathbb {Q}}_p$, we may enlarge the base field
$\overline {\mathbb {Q}}_p$, we may enlarge the base field ![]() $k$ as in [Reference AbeAbe18b, 1.4.11]. Therefore, we may assume there exists a
$k$ as in [Reference AbeAbe18b, 1.4.11]. Therefore, we may assume there exists a ![]() $k$-point
$k$-point ![]() $x$ of
$x$ of ![]() $X_1$. We consider the following diagram.
$X_1$. We consider the following diagram.

We denote by ![]() $\operatorname {\mathbf {\Phi }^{\prime }-\mathbf {Isoc}^{{{\dagger}} }}(X')$ the category of overconvergent isocrystals over
$\operatorname {\mathbf {\Phi }^{\prime }-\mathbf {Isoc}^{{{\dagger}} }}(X')$ the category of overconvergent isocrystals over ![]() $X'$ with a partial Frobenius structure and
$X'$ with a partial Frobenius structure and ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X',\Phi ')$ the Tannakian subcategory of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X',\Phi ')$ the Tannakian subcategory of ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X')$ generated by those object which can be equipped with some partial Frobenius structure. The morphism
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X')$ generated by those object which can be equipped with some partial Frobenius structure. The morphism ![]() $u$ induces a tensor functor
$u$ induces a tensor functor
and a homomorphism ![]() $u^{\circ }\colon \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X',\Phi ')\to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )$. Consider the following commutative diagram.
$u^{\circ }\colon \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X',\Phi ')\to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )$. Consider the following commutative diagram.

Here the upper sequence is defined as before and the lower sequence is exact. By induction, it suffices to show the exactness of the upper sequence. In the following, we will do it by checking the conditions of Theorem 2.1.4 for the functors:
where ![]() $p_1^{*}$ is defined as in (2.2.3.1). We use the functor
$p_1^{*}$ is defined as in (2.2.3.1). We use the functor ![]() $p_{i,*}$ defined in Proposition 2.2.8(i).
$p_{i,*}$ defined in Proposition 2.2.8(i).
(i) Let ![]() $\mathscr {E}$ be an object of
$\mathscr {E}$ be an object of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_1)$ and
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_1)$ and ![]() $\mathscr {F}$ a subobject of
$\mathscr {F}$ a subobject of ![]() $p_1^*(\mathscr {E})$. We need to show that
$p_1^*(\mathscr {E})$. We need to show that ![]() $\mathscr {F}$ is the image under
$\mathscr {F}$ is the image under ![]() $p_1^*$ of a subobject of
$p_1^*$ of a subobject of ![]() $\mathscr {E}$. If
$\mathscr {E}$. If ![]() $\mathscr {G}$ denotes the quotient
$\mathscr {G}$ denotes the quotient ![]() $p_1^*(\mathscr {E})/\mathscr {F}$, by applying
$p_1^*(\mathscr {E})/\mathscr {F}$, by applying ![]() $p_1^*p_{1,*}$ we obtain a commutative diagram.
$p_1^*p_{1,*}$ we obtain a commutative diagram.

Here ![]() $\beta$ is the identity, whereas
$\beta$ is the identity, whereas ![]() $\alpha,\gamma$ are injective by Proposition 2.2.8(ii). Then
$\alpha,\gamma$ are injective by Proposition 2.2.8(ii). Then ![]() $\delta$ is surjective. We deduce that
$\delta$ is surjective. We deduce that ![]() $\alpha$ is an isomorphism. Then we conclude that
$\alpha$ is an isomorphism. Then we conclude that ![]() $\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi ) \to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X_1)$ is faithfully flat by [Reference Deligne and MilneDM82, Proposition 2.21].
$\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi ) \to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X_1)$ is faithfully flat by [Reference Deligne and MilneDM82, Proposition 2.21].
(ii) and (iii)(c) Since ![]() $u$ is a section of
$u$ is a section of ![]() $p'\colon X=X_1\times _k X'\to X'$, we deduce condition (iii)(c) of Theorem 2.1.4 for
$p'\colon X=X_1\times _k X'\to X'$, we deduce condition (iii)(c) of Theorem 2.1.4 for ![]() $u^{\circ }\colon \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X',\Phi ')\to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )$. Then
$u^{\circ }\colon \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X',\Phi ')\to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )$. Then ![]() $u^{\circ }$ is a closed immersion by [Reference Deligne and MilneDM82, Proposition 2.21].
$u^{\circ }$ is a closed immersion by [Reference Deligne and MilneDM82, Proposition 2.21].
(iii)(b) Given an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$, the maximal trivial subobject of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$, the maximal trivial subobject of ![]() $u^{*}\mathscr {E}$ in the category
$u^{*}\mathscr {E}$ in the category ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X',\Phi ')$ is
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X',\Phi ')$ is ![]() $g^{*}g_{*}u^{*}\mathscr {E}$. Since
$g^{*}g_{*}u^{*}\mathscr {E}$. Since ![]() $u^+(\mathscr {E})[2d]\simeq u^!(\mathscr {E})$, we have
$u^+(\mathscr {E})[2d]\simeq u^!(\mathscr {E})$, we have ![]() $g^{*}g_{*}u^{*}\mathscr {E}\simeq u^* p_1^*p_{1,*}\mathscr {E}$ by smooth base change. Then condition (b) follows from the fact that
$g^{*}g_{*}u^{*}\mathscr {E}\simeq u^* p_1^*p_{1,*}\mathscr {E}$ by smooth base change. Then condition (b) follows from the fact that ![]() $p_1^*p_{1,*}\to \operatorname {id}$ is injective by Proposition 2.2.8(ii).
$p_1^*p_{1,*}\to \operatorname {id}$ is injective by Proposition 2.2.8(ii).
(iii)(a) If an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ comes from the essential image of
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ comes from the essential image of ![]() $p_1^{*}$, then
$p_1^{*}$, then ![]() $u^*(\mathscr {E})$ is trivial. Conversely, in view of condition (iii)(b), if
$u^*(\mathscr {E})$ is trivial. Conversely, in view of condition (iii)(b), if ![]() $u^*(\mathscr {E})$ is trivial, then
$u^*(\mathscr {E})$ is trivial, then ![]() $\mathscr {E}\simeq p_1^*p_{1,*}(\mathscr {E})$. This verifies condition (a).
$\mathscr {E}\simeq p_1^*p_{1,*}(\mathscr {E})$. This verifies condition (a).
We now upgrade the previous argument to eliminate the smooth quasiprojective hypothesis.
Lemma 2.2.12 The categories ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X), \operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X), \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X, \Phi )$ admit descent with respect to any proper hypercoverings of the
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X), \operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X), \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X, \Phi )$ admit descent with respect to any proper hypercoverings of the ![]() $X_i$.
$X_i$.
Proof. Descent for ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ is established in [Reference LazdaLaz22, Theorem 5.1]. This then implies descent for
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$ is established in [Reference LazdaLaz22, Theorem 5.1]. This then implies descent for ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$; we deduce descent for
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$; we deduce descent for ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X, \Phi )$ using Proposition 2.2.5.
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X, \Phi )$ using Proposition 2.2.5.
2.2.13. Proof of Theorem 2.2.4 for  $\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}$ with general
$\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}$ with general  $X_i$
$X_i$
By de Jong's alterations theorem [Reference de JongdeJ96], there exist smooth, connected, and quasiprojective ![]() $k$-varieties
$k$-varieties ![]() $Y_i$ and proper surjective, generic étale maps
$Y_i$ and proper surjective, generic étale maps ![]() $\pi _i\colon Y_i\to X_i$ for
$\pi _i\colon Y_i\to X_i$ for ![]() $i=1,2,\ldots,n$. We use the hypercovering produced by the
$i=1,2,\ldots,n$. We use the hypercovering produced by the ![]() $\pi _i$ to show that the upper sequence in (2.2.11.2) is exact, by again checking the conditions of Theorem 2.1.4.
$\pi _i$ to show that the upper sequence in (2.2.11.2) is exact, by again checking the conditions of Theorem 2.1.4.
We set ![]() $Y:=\prod _{i=1}^n Y_i$ and
$Y:=\prod _{i=1}^n Y_i$ and ![]() $\pi \colon Y\to X$ to be the product
$\pi \colon Y\to X$ to be the product ![]() $\prod _{i=1}^n \pi _i$. By induction, it suffices to treat the case where
$\prod _{i=1}^n \pi _i$. By induction, it suffices to treat the case where ![]() $Y_i=X_i$ for
$Y_i=X_i$ for ![]() $i=2,\dots,n$. Consider the following diagram.
$i=2,\dots,n$. Consider the following diagram.

By induction hypotheses, we may assume the exactness of the second line. We will deduce the exactness of the first line from the second one. The above diagram corresponds to the top two lines in the following diagram.

Here ![]() $Y_1^{(2)}:=Y_1\times _{X_1}Y_1$ and
$Y_1^{(2)}:=Y_1\times _{X_1}Y_1$ and ![]() $Y^{(2)}:=Y\times _X Y$. We check the conditions of 2.1.4 for the first line.
$Y^{(2)}:=Y\times _X Y$. We check the conditions of 2.1.4 for the first line.
(i) Let ![]() $U$ be an object of
$U$ be an object of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_1)$ and
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_1)$ and ![]() $V_0$ a subobject of
$V_0$ a subobject of ![]() $p_1^*(U)$. By exactness of the second line, we deduce that there exists a subobject
$p_1^*(U)$. By exactness of the second line, we deduce that there exists a subobject ![]() $U_{0,Y}$ of
$U_{0,Y}$ of ![]() $\pi _1^*(U)$ over
$\pi _1^*(U)$ over ![]() $Y_1$ such that
$Y_1$ such that ![]() $p_1^*(U_{0,Y})\simeq \pi ^*(V_0)$ as subobjects of
$p_1^*(U_{0,Y})\simeq \pi ^*(V_0)$ as subobjects of ![]() $\pi ^*(p_1^*(U))$. As the functor
$\pi ^*(p_1^*(U))$. As the functor ![]() $p_1^*\colon \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(Y_1^{(2)})\to \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(Y^{(2)},\Phi )$ is fully faithful, the descent data on
$p_1^*\colon \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(Y_1^{(2)})\to \mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(Y^{(2)},\Phi )$ is fully faithful, the descent data on ![]() $\pi ^*(V_0)$ gives rise to a descent data on
$\pi ^*(V_0)$ gives rise to a descent data on ![]() $U_0$. In this way, we obtain a subobject
$U_0$. In this way, we obtain a subobject ![]() $U_{0}$ of
$U_{0}$ of ![]() $U$ over
$U$ over ![]() $X_1$, sent to
$X_1$, sent to ![]() $V_0\to p_1^*(U)$ via
$V_0\to p_1^*(U)$ via ![]() $p_1^*$. Hence, the map
$p_1^*$. Hence, the map ![]() $p_1^\circ \colon \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )\to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X_1)$ is faithfully flat.
$p_1^\circ \colon \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi )\to \pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X_1)$ is faithfully flat.
Conditions (ii) and (iii)(c) follow from the same argument as in the smooth and quasiprojective case.
(iii)(a) Let ![]() $V$ be an object of
$V$ be an object of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ such that
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ such that ![]() $u^*(V)$ is trivial. Then there exists an object
$u^*(V)$ is trivial. Then there exists an object ![]() $U_Y$ over
$U_Y$ over ![]() $Y_1$ such that
$Y_1$ such that ![]() $p_1^*(U_Y)\simeq \pi ^*(V)$. The descent data on
$p_1^*(U_Y)\simeq \pi ^*(V)$. The descent data on ![]() $\pi ^*(V)$ induces a descent data on
$\pi ^*(V)$ induces a descent data on ![]() $U_Y$, which gives rise to an object
$U_Y$, which gives rise to an object ![]() $U$ on
$U$ on ![]() $X_1$, sent to
$X_1$, sent to ![]() $V$ via
$V$ via ![]() $p_1^*$.
$p_1^*$.
(iii)(b) Let ![]() $V$ be an object of
$V$ be an object of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$,
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$, ![]() $W_0$ be the maximal trivial subobject of
$W_0$ be the maximal trivial subobject of ![]() $u^*(V)$. By exactness of the second line, there exists a subobject
$u^*(V)$. By exactness of the second line, there exists a subobject ![]() $V_0$ of
$V_0$ of ![]() $\pi ^*(V)$ on
$\pi ^*(V)$ on ![]() $Y$, sent to
$Y$, sent to ![]() $W_0$ via
$W_0$ via ![]() $u^*$. Since
$u^*$. Since ![]() $u^*$ is faithful, we deduce that the descent data on
$u^*$ is faithful, we deduce that the descent data on ![]() $\pi ^*(V)$ preserves
$\pi ^*(V)$ preserves ![]() $V_0$. This gives rise to a subobject of
$V_0$. This gives rise to a subobject of ![]() $V$, sent to the trivial object
$V$, sent to the trivial object ![]() $W_0$.
$W_0$.
2.2.14. Proof of Theorem 2.2.4 for  $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}$
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}$
By Proposition 2.1.3(i), we have a commutative diagram:

where the first and second lines are exact. By Proposition 2.1.3(ii), the right vertical arrow identifies with the projection of the pro-algebraic completion of ![]() $\mathbb {Z}^n$ to the pro-algebraic completion of
$\mathbb {Z}^n$ to the pro-algebraic completion of ![]() $\mathbb {Z}$ and is therefore an isomorphism. The assertion follows from that the left vertical arrow is an isomorphism.
$\mathbb {Z}$ and is therefore an isomorphism. The assertion follows from that the left vertical arrow is an isomorphism.
3. Drinfeld's lemma for convergent  $\Phi$-isocrystals
$\Phi$-isocrystals
In this section, we assume ![]() $(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$, and
$(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$, and ![]() $X_i$ denotes a
$X_i$ denotes a ![]() $k$-variety for
$k$-variety for ![]() $i=1,\ldots,n$ and
$i=1,\ldots,n$ and ![]() $X:=\prod _{i=1}^n X_i$. Except in §§ 3.1.1–3.1.3, we assume each
$X:=\prod _{i=1}^n X_i$. Except in §§ 3.1.1–3.1.3, we assume each ![]() $X_i$ is smooth and geometrically connected over
$X_i$ is smooth and geometrically connected over ![]() $k$.
$k$.
3.1 Unit-root and diagonally unit-root convergent  $\Phi$-isocrystals
$\Phi$-isocrystals
3.1.1 We first define the partial Frobenius slopes at a closed point of ![]() $X$.
$X$.
Let ![]() $(\mathscr {E},\varphi _i)$ be an object of
$(\mathscr {E},\varphi _i)$ be an object of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$,
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$, ![]() $x\in |X|$ a closed point,
$x\in |X|$ a closed point, ![]() $K_x:=\operatorname {W}(k_x)\otimes _{\operatorname {W}(k)}K$, and
$K_x:=\operatorname {W}(k_x)\otimes _{\operatorname {W}(k)}K$, and ![]() $a:=[k_x:k]$. We take the extension of scalars to
$a:=[k_x:k]$. We take the extension of scalars to ![]() $k_x$ (2.2.2.1) and then take its fiber
$k_x$ (2.2.2.1) and then take its fiber ![]() $(\mathscr {E}_x,\varphi _1^a|_x,\ldots,\varphi _n^a|_x)$ at
$(\mathscr {E}_x,\varphi _1^a|_x,\ldots,\varphi _n^a|_x)$ at ![]() $x$, which is an object of
$x$, which is an object of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(\operatorname {Spec}(k_x)/K_x)$ with respect to the
$\operatorname {\mathbf {\Phi -Isoc}}(\operatorname {Spec}(k_x)/K_x)$ with respect to the ![]() $sa$th power of Frobenius, that is a
$sa$th power of Frobenius, that is a ![]() $K_x$-vector space together with commuting linear automorphisms
$K_x$-vector space together with commuting linear automorphisms ![]() $\varphi _i^a|_x$. This allows us to define the
$\varphi _i^a|_x$. This allows us to define the ![]() $i$th partial Frobenius slopes of
$i$th partial Frobenius slopes of ![]() $(\mathscr {E},\varphi _i)$ at
$(\mathscr {E},\varphi _i)$ at ![]() $x$ for
$x$ for ![]() $i=1,\ldots,n$ by Dieudonné–Manin theory.
$i=1,\ldots,n$ by Dieudonné–Manin theory.
We have a surjection from points of ![]() $X$ to products of points of the
$X$ to products of points of the ![]() $X_i$:
$X_i$:
 \[ \pi\colon |X|\twoheadrightarrow \prod_{i=1}^n |X_i|. \]
\[ \pi\colon |X|\twoheadrightarrow \prod_{i=1}^n |X_i|. \]
Let ![]() $(x_i)_{i=1}^n\in \prod |X_i|$ be a tuple of closed points. To simplify notation, assume that there exists a finite extension
$(x_i)_{i=1}^n\in \prod |X_i|$ be a tuple of closed points. To simplify notation, assume that there exists a finite extension ![]() $k'$ of
$k'$ of ![]() $k$ such that
$k$ such that ![]() $k_{x_i}\simeq k'$ (this can always be enforced by enlarging
$k_{x_i}\simeq k'$ (this can always be enforced by enlarging ![]() $k$). We have a decomposition
$k$). We have a decomposition
indexed by ![]() $G:=\big ( \prod \operatorname {Gal}(k'/k) \big )/\operatorname {Gal}(k'/k)$, for the diagonal action. For an object
$G:=\big ( \prod \operatorname {Gal}(k'/k) \big )/\operatorname {Gal}(k'/k)$, for the diagonal action. For an object ![]() $(\mathscr {E},\varphi _i)$ of
$(\mathscr {E},\varphi _i)$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(\prod _k x_i/K)$,
$\operatorname {\mathbf {\Phi -Isoc}}(\prod _k x_i/K)$, ![]() $\mathscr {E}$ corresponds to a direct sum of vector spaces over
$\mathscr {E}$ corresponds to a direct sum of vector spaces over ![]() $K'$, indexed by
$K'$, indexed by ![]() $G$. If
$G$. If ![]() $a=[k':k]$, then the
$a=[k':k]$, then the ![]() $a$th power of each partial Frobenius
$a$th power of each partial Frobenius ![]() $\varphi _{i}^a$ preserves each component.
$\varphi _{i}^a$ preserves each component.
Lemma 3.1.2 The partial Frobenius slopes at a point ![]() $x\in |X|$ depend only on its image
$x\in |X|$ depend only on its image ![]() $\pi (x)=(x_1,\ldots,x_n)\in \prod |X_i|$.
$\pi (x)=(x_1,\ldots,x_n)\in \prod |X_i|$.
Proof. We keep the above notation. Since ![]() $G$ acts transitively on each component of (3.1.1.1), the action induces isomorphisms between the pullback of
$G$ acts transitively on each component of (3.1.1.1), the action induces isomorphisms between the pullback of ![]() $(\mathscr {E}_x,\varphi _{i,x}^a)$ to each component and the claim follows.
$(\mathscr {E}_x,\varphi _{i,x}^a)$ to each component and the claim follows.
Definition 3.1.3 Let ![]() $(\mathscr {E},\varphi _1,\ldots,\varphi _n)$ be an object of
$(\mathscr {E},\varphi _1,\ldots,\varphi _n)$ be an object of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$.
$\operatorname {\mathbf {\Phi -Isoc}}(X)$.
(i) We say the
 $i$th partial Frobenius structure
$i$th partial Frobenius structure  $\varphi _i\colon F_i^*(\mathscr {E})\to \mathscr {E}$ is unit-root, if its slope at each closed point is zero.
$\varphi _i\colon F_i^*(\mathscr {E})\to \mathscr {E}$ is unit-root, if its slope at each closed point is zero.(ii) We say
 $\mathscr {E}$ is unit-root, if every partial Frobenius structure
$\mathscr {E}$ is unit-root, if every partial Frobenius structure  $\varphi _i$ is unit-root.
$\varphi _i$ is unit-root.(iii) We say
 $\mathscr {E}$ is diagonally unit-root if the associated convergent
$\mathscr {E}$ is diagonally unit-root if the associated convergent  $F$-isocrystal is unit-root.
$F$-isocrystal is unit-root.
3.1.4 In the following, we assume each ![]() $X_i$ is a smooth geometrically connected
$X_i$ is a smooth geometrically connected ![]() $k$-variety. Then so is
$k$-variety. Then so is ![]() $X$.
$X$.
Let ![]() $x$ be a closed point of
$x$ be a closed point of ![]() $X$ and
$X$ and ![]() $\overline {x}$ the associated geometric point. Recall [Reference CrewCre87] that there exists a canonical equivalence between the category of continuous
$\overline {x}$ the associated geometric point. Recall [Reference CrewCre87] that there exists a canonical equivalence between the category of continuous ![]() $K$-representations of
$K$-representations of ![]() $\pi _1^{{\unicode{x00E9}}{\text t}}(X,\overline {x})$ and the category of unit-root convergent
$\pi _1^{{\unicode{x00E9}}{\text t}}(X,\overline {x})$ and the category of unit-root convergent ![]() $F$-isocrystals over
$F$-isocrystals over ![]() $X/K$:
$X/K$:
Via the equivalence between the left-hand side and the category ![]() $\operatorname {\mathbf {LocSys}}(X,K)$ of lisse
$\operatorname {\mathbf {LocSys}}(X,K)$ of lisse ![]() $K$-sheaves over
$K$-sheaves over ![]() $X$, we have
$X$, we have
The above equivalence is compatible with the following operations.
(i) The pullback functoriality along a morphism between smooth connected
 $k$-varieties.
$k$-varieties.(ii) Extensions of scalars.
Recall that a lisse ![]() $K$-sheaf
$K$-sheaf ![]() $\mathbb {L}$ over
$\mathbb {L}$ over ![]() $X$ is equipped with the Frobenius correspondence [Reference GrothendieckSGA5, XIV=XV]:
$X$ is equipped with the Frobenius correspondence [Reference GrothendieckSGA5, XIV=XV]:
Lemma 3.1.5 Let ![]() $(\mathscr {E},\varphi )$ be a unit-root convergent
$(\mathscr {E},\varphi )$ be a unit-root convergent ![]() $F$-isocrystal over
$F$-isocrystal over ![]() $X$ and
$X$ and ![]() $\mathbb {L}$ the associated sheaf. Then the Frobenius structure
$\mathbb {L}$ the associated sheaf. Then the Frobenius structure ![]() $\varphi \colon (F_X^*\mathscr {E},F_X^*\varphi )\xrightarrow {\sim } (\mathscr {E},\varphi )$ gives rise to the above isomorphism
$\varphi \colon (F_X^*\mathscr {E},F_X^*\varphi )\xrightarrow {\sim } (\mathscr {E},\varphi )$ gives rise to the above isomorphism ![]() $\phi _{\mathbb {L}}$.
$\phi _{\mathbb {L}}$.
Proof. In view of the construction of (3.1.4.1), we may reduce to the case where ![]() $\mathbb {L}$ is a lisse
$\mathbb {L}$ is a lisse ![]() $\mathscr {O}_K/p^n \mathscr {O}_K$-sheaf for some
$\mathscr {O}_K/p^n \mathscr {O}_K$-sheaf for some ![]() $n$, and we may assume
$n$, and we may assume ![]() $X$ is affine and admits a smooth lifting
$X$ is affine and admits a smooth lifting ![]() $\mathfrak {X}_n$ to
$\mathfrak {X}_n$ to ![]() $\mathscr {O}_K/p^n\mathscr {O}_K$, equipped with a Frobenius lift. After taking pullback along a finite étale morphism trivializing
$\mathscr {O}_K/p^n\mathscr {O}_K$, equipped with a Frobenius lift. After taking pullback along a finite étale morphism trivializing ![]() $\mathbb {L}$, we may moreover assume that
$\mathbb {L}$, we may moreover assume that ![]() $\mathbb {L}$ is a trivial
$\mathbb {L}$ is a trivial ![]() $\mathscr {O}_K/p^n\mathscr {O}_K$-module. In this case, the assertion is clear.
$\mathscr {O}_K/p^n\mathscr {O}_K$-module. In this case, the assertion is clear.
Remark 3.1.6 When ![]() $X=x=\operatorname {Spec}(k)$, we will view
$X=x=\operatorname {Spec}(k)$, we will view ![]() $\phi _{\mathbb {L}}$ as an endomorphism on
$\phi _{\mathbb {L}}$ as an endomorphism on ![]() $\mathbb {L}$ in such a way that the action on the geometric fiber
$\mathbb {L}$ in such a way that the action on the geometric fiber ![]() $\mathbb {L}_{\overline {x}}$ coincides with the action of the geometric Frobenius
$\mathbb {L}_{\overline {x}}$ coincides with the action of the geometric Frobenius ![]() $F_k\in \operatorname {Gal}(\overline {k}/k)$.
$F_k\in \operatorname {Gal}(\overline {k}/k)$.
3.1.7 Let ![]() $i$ be an integer
$i$ be an integer ![]() $\in [1,n]$. The
$\in [1,n]$. The ![]() $i$th partial Frobenius
$i$th partial Frobenius ![]() $F_i$ of
$F_i$ of ![]() $X$ is a homeomorphism and induces an equivalence of étale topoi of
$X$ is a homeomorphism and induces an equivalence of étale topoi of ![]() $X$. Let
$X$. Let ![]() $(\mathscr {E},\varphi _1,\ldots,\varphi _n)$ be a diagonally unit-root convergent
$(\mathscr {E},\varphi _1,\ldots,\varphi _n)$ be a diagonally unit-root convergent ![]() $\Phi$-isocrystal over
$\Phi$-isocrystal over ![]() $X$ and
$X$ and ![]() $\mathbb {L}$ the lisse
$\mathbb {L}$ the lisse ![]() $K$-sheaf over
$K$-sheaf over ![]() $X$ associated to
$X$ associated to ![]() $(\mathscr {E},\varphi )$. The
$(\mathscr {E},\varphi )$. The ![]() $i$th partial Frobenius structure
$i$th partial Frobenius structure ![]() $\varphi _i$ induces an isomorphism of sheaves:
$\varphi _i$ induces an isomorphism of sheaves:
The isomorphisms ![]() $\phi _i$ commute with each other in the following sense: for any
$\phi _i$ commute with each other in the following sense: for any ![]() $1\le i,j \le n$, the identifications
$1\le i,j \le n$, the identifications
induce an equality ![]() $\phi _j\circ F_j^*(\phi _i)=\phi _i\circ F_i^*(\phi _j)$. The composition of
$\phi _j\circ F_j^*(\phi _i)=\phi _i\circ F_i^*(\phi _j)$. The composition of ![]() $\phi _i$ coincides with the isomorphism
$\phi _i$ coincides with the isomorphism ![]() $\phi _{\mathbb {L}}$ (3.1.4.3). The above construction is clearly functorial.
$\phi _{\mathbb {L}}$ (3.1.4.3). The above construction is clearly functorial.
Proposition 3.1.8 The category of diagonally unit-root ![]() $\Phi$-isocrystals over
$\Phi$-isocrystals over ![]() $X$ is equivalent to the category of pairs
$X$ is equivalent to the category of pairs ![]() $(\mathbb {L},\{\phi _i\}_{i=1}^n)$ consisting of a lisse
$(\mathbb {L},\{\phi _i\}_{i=1}^n)$ consisting of a lisse ![]() $K$-sheaf
$K$-sheaf ![]() $\mathbb {L}$ over
$\mathbb {L}$ over ![]() $X$ together with isomorphisms
$X$ together with isomorphisms ![]() $\phi _i\colon F_i^*(\mathbb {L})\xrightarrow {\sim } \mathbb {L}$ commuting to each other and whose composition is
$\phi _i\colon F_i^*(\mathbb {L})\xrightarrow {\sim } \mathbb {L}$ commuting to each other and whose composition is ![]() $\phi _{\mathbb {L}}$ (3.1.4.3). The morphisms in the latter category are morphisms of
$\phi _{\mathbb {L}}$ (3.1.4.3). The morphisms in the latter category are morphisms of ![]() $\operatorname {\mathbf {LocSys}}(X,K)$ compatible with the
$\operatorname {\mathbf {LocSys}}(X,K)$ compatible with the ![]() $\phi _i$.
$\phi _i$.
Proof. We construct a quasi-inverse of the functor in § 3.1.7. Let ![]() $(\mathbb {L},\{\phi _i\}_{i=1}^n)$ be a collection of data as above and
$(\mathbb {L},\{\phi _i\}_{i=1}^n)$ be a collection of data as above and ![]() $(\mathscr {E},\varphi )$ the unit-root
$(\mathscr {E},\varphi )$ the unit-root ![]() $F$-isocrystal over
$F$-isocrystal over ![]() $X$ associated to
$X$ associated to ![]() $\mathbb {L}$. By functoriality of (3.1.4.2),
$\mathbb {L}$. By functoriality of (3.1.4.2), ![]() $\phi _i$ induces an
$\phi _i$ induces an ![]() $i$th partial Frobenius structure
$i$th partial Frobenius structure ![]() $\varphi _i$ on
$\varphi _i$ on ![]() $\mathscr {E}$. The commutativity of the
$\mathscr {E}$. The commutativity of the ![]() $\varphi _i$, and the fact that the composition of the
$\varphi _i$, and the fact that the composition of the ![]() $\varphi _i$ equals
$\varphi _i$ equals ![]() $\varphi$, follow from the corresponding properties of the
$\varphi$, follow from the corresponding properties of the ![]() $\phi _i$. This construction is clearly functorial and provide a quasi-inverse of § 3.1.7.
$\phi _i$. This construction is clearly functorial and provide a quasi-inverse of § 3.1.7.
Corollary 3.1.9 Let ![]() $(\mathscr {E},\varphi _i)$ be a diagonally unit-root
$(\mathscr {E},\varphi _i)$ be a diagonally unit-root ![]() $\Phi$-isocrystal over
$\Phi$-isocrystal over ![]() $X$. Then for
$X$. Then for ![]() $i=1,2,\ldots,n$, the
$i=1,2,\ldots,n$, the ![]() $i$th partial Frobenius slopes of
$i$th partial Frobenius slopes of ![]() $\mathscr {E}$ are constant on
$\mathscr {E}$ are constant on ![]() $|X|$.
$|X|$.
Proof. Let ![]() $(\mathbb {L},\{\phi _i\}_{i=1}^n)$ be the associated data in Proposition 3.1.8. Then the
$(\mathbb {L},\{\phi _i\}_{i=1}^n)$ be the associated data in Proposition 3.1.8. Then the ![]() $i$th partial Frobenius slope of
$i$th partial Frobenius slope of ![]() $\mathscr {E}$ at
$\mathscr {E}$ at ![]() $x\in X(k)$ can be calculated by that of
$x\in X(k)$ can be calculated by that of ![]() $\phi _{i,\overline {x}}$ on
$\phi _{i,\overline {x}}$ on ![]() $\mathbb {L}_{\overline {x}}$ (with the convention of Remark 3.1.6). Since
$\mathbb {L}_{\overline {x}}$ (with the convention of Remark 3.1.6). Since ![]() $\mathbb {L}$ admits a lisse
$\mathbb {L}$ admits a lisse ![]() $\mathscr {O}_K$-sheaf as an integral model, the slopes of
$\mathscr {O}_K$-sheaf as an integral model, the slopes of ![]() $\phi _i$ at each fibers
$\phi _i$ at each fibers ![]() $\mathbb {L}_{\overline {x}}$ are constant as function on
$\mathbb {L}_{\overline {x}}$ are constant as function on ![]() $x\in X(k)$.
$x\in X(k)$.
The corollary follows from applying the previous argument to extensions of scalars of ![]() $(\mathscr {E},\varphi _i)$ (§ 3.4.1).
$(\mathscr {E},\varphi _i)$ (§ 3.4.1).
Theorem 3.1.10 Let ![]() $(\mathscr {E},\varphi _i)$ be a convergent
$(\mathscr {E},\varphi _i)$ be a convergent ![]() $\Phi$-isocrystal over
$\Phi$-isocrystal over ![]() $X$. Suppose that the diagonal Newton polygon of
$X$. Suppose that the diagonal Newton polygon of ![]() $(\mathscr {E},\varphi _i)$ is constant as a function on
$(\mathscr {E},\varphi _i)$ is constant as a function on ![]() $|X|$.
$|X|$.
(i) There exists a filtration
of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$ and an increasing sequence
$\operatorname {\mathbf {\Phi -Isoc}}(X)$ and an increasing sequence ![]() $\mu _1<\mu _2<\cdots <\mu _{\ell }$ of rational numbers such that for
$\mu _1<\mu _2<\cdots <\mu _{\ell }$ of rational numbers such that for ![]() $j=1,\dots,\ell$, the diagonal Newton polygon of
$j=1,\dots,\ell$, the diagonal Newton polygon of ![]() $\mathscr {E}_j/\mathscr {E}_{j-1}$ is constant with slope
$\mathscr {E}_j/\mathscr {E}_{j-1}$ is constant with slope ![]() $\mu _j$. Moreover, the filtration and sequence are both uniquely determined by this condition. (We call it the diagonal slope filtration of
$\mu _j$. Moreover, the filtration and sequence are both uniquely determined by this condition. (We call it the diagonal slope filtration of ![]() $\mathscr {E}$.)
$\mathscr {E}$.)
(ii) For each partial Frobenius structure ![]() $\varphi _i$ of
$\varphi _i$ of ![]() $\mathscr {E}$, its Newton polygon is also constant on
$\mathscr {E}$, its Newton polygon is also constant on ![]() $|X|$.
$|X|$.
Proof. (i) There exists a slope filtration (3.1.10.1) as convergent ![]() $F$-isocrystals [Reference KedlayaKed22a, Corollary 4.2]. It suffices to show that each partial Frobenius
$F$-isocrystals [Reference KedlayaKed22a, Corollary 4.2]. It suffices to show that each partial Frobenius ![]() $\varphi _i$ preserves this filtration, that is the composition
$\varphi _i$ preserves this filtration, that is the composition ![]() $F_i^*(\mathscr {E}_j)\xrightarrow {\varphi _i} \mathscr {E} \to \mathscr {E}/\mathscr {E}_j$ vanishes. Then uniqueness follows from that of the slope filtration for
$F_i^*(\mathscr {E}_j)\xrightarrow {\varphi _i} \mathscr {E} \to \mathscr {E}/\mathscr {E}_j$ vanishes. Then uniqueness follows from that of the slope filtration for ![]() $F$-isocrystals.
$F$-isocrystals.
We reduce to checking the above claim at the fiber of each closed point ![]() $x\in |X|$. We may assume there exists a finite extension
$x\in |X|$. We may assume there exists a finite extension ![]() $k'/k$ of degree
$k'/k$ of degree ![]() $a$ such that
$a$ such that ![]() $x\simeq \operatorname {Spec}(k')$ as in § 3.1.1. Then the fiber of the Frobenius structure
$x\simeq \operatorname {Spec}(k')$ as in § 3.1.1. Then the fiber of the Frobenius structure ![]() $\varphi _x^a$ is a linear automorphism of
$\varphi _x^a$ is a linear automorphism of ![]() $\mathscr {E}_x$, and its generalized eigenspace decomposition is a refinement of the filtration
$\mathscr {E}_x$, and its generalized eigenspace decomposition is a refinement of the filtration ![]() $\mathscr {E}_{0,x}\subset \cdots \subset \mathscr {E}_{\ell,x}$. Since each partial Frobenius structure
$\mathscr {E}_{0,x}\subset \cdots \subset \mathscr {E}_{\ell,x}$. Since each partial Frobenius structure ![]() $\varphi _{i,x}$ commutes with
$\varphi _{i,x}$ commutes with ![]() $\varphi _{x}^a$,
$\varphi _{x}^a$, ![]() $\varphi _{i,x}$ preserves each generalized eigenspace of
$\varphi _{i,x}$ preserves each generalized eigenspace of ![]() $\varphi _x^a$. Then the assertion follows.
$\varphi _x^a$. Then the assertion follows.
(ii) By assertion (i), we may reduce to the case where ![]() $\mathscr {E}$ is diagonally unit-root after twisting. In this case, assertion (ii) follows from Corollary 3.1.9.
$\mathscr {E}$ is diagonally unit-root after twisting. In this case, assertion (ii) follows from Corollary 3.1.9.
3.2 A variant of Crew's theorem for unit-root convergent  $\Phi$-isocrystals
$\Phi$-isocrystals
3.2.1 We denote by ![]() $\mathcal {C}(X,\Phi )$ the category of objects
$\mathcal {C}(X,\Phi )$ the category of objects ![]() $(T,\{F_{ \{i\}}\}_{i=1}^n)$ consisting of a finite étale morphism
$(T,\{F_{ \{i\}}\}_{i=1}^n)$ consisting of a finite étale morphism ![]() $T\to X=X_1\times _k\cdots \times _k X_n$ and isomorphisms
$T\to X=X_1\times _k\cdots \times _k X_n$ and isomorphisms ![]() $F_{ \{i\}}\colon T\times _{X,F_i}X \xrightarrow {\sim } T$ commuting with each other, i.e.
$F_{ \{i\}}\colon T\times _{X,F_i}X \xrightarrow {\sim } T$ commuting with each other, i.e. ![]() $F_{ \{i\}}\circ F_{ \{j\}}\times _{X,F_j}X= F_{ \{j\}}\circ F_{ \{i\}}\times _{X,F_i}X$, whose composition is the relative Frobenius morphism
$F_{ \{i\}}\circ F_{ \{j\}}\times _{X,F_j}X= F_{ \{j\}}\circ F_{ \{i\}}\times _{X,F_i}X$, whose composition is the relative Frobenius morphism ![]() $F_{T/X}$ of
$F_{T/X}$ of ![]() $T$ over
$T$ over ![]() $X$. A morphism in this category is a morphism above
$X$. A morphism in this category is a morphism above ![]() $X$ compatible with the
$X$ compatible with the ![]() $F_{ \{i\}}$. Note that an object of
$F_{ \{i\}}$. Note that an object of ![]() $\mathcal {C}(X,\Phi )$ is equivalent to the data of a pair
$\mathcal {C}(X,\Phi )$ is equivalent to the data of a pair ![]() $(T, \{\varphi _{T,i}\}_{i=1}^n)$ consisting of a finite étale morphism
$(T, \{\varphi _{T,i}\}_{i=1}^n)$ consisting of a finite étale morphism ![]() $T\to X$ together with morphisms
$T\to X$ together with morphisms ![]() $\varphi _{T,i}\colon T\to T$ above
$\varphi _{T,i}\colon T\to T$ above ![]() $F_i$, commuting with each other, whose composition is the Frobenius morphism
$F_i$, commuting with each other, whose composition is the Frobenius morphism ![]() $F_T$.
$F_T$.
This category is a Galois category and we denote by ![]() $\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ the Galois group defined by the fiber functor associated to
$\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ the Galois group defined by the fiber functor associated to ![]() $\overline {x}$. We have the following equivalence:
$\overline {x}$. We have the following equivalence:
• the category of continuous actions of
 $\pi _1(X,\Phi,\overline {x})$ on finite sets;
$\pi _1(X,\Phi,\overline {x})$ on finite sets;• the category of locally constant constructible sheaves
 $\mathbb {L}$ of
$\mathbb {L}$ of  $X_{{\unicode{x00E9}}{\text t}}$, equipped with a partial Frobenius structure
$X_{{\unicode{x00E9}}{\text t}}$, equipped with a partial Frobenius structure  $\phi _i\colon F_i^*(\mathbb {L})\xrightarrow {\sim } \mathbb {L}$, commuting with each other, whose composition is the Frobenius correspondence
$\phi _i\colon F_i^*(\mathbb {L})\xrightarrow {\sim } \mathbb {L}$, commuting with each other, whose composition is the Frobenius correspondence  $\phi _{\mathbb {L}}$.
$\phi _{\mathbb {L}}$.
Proposition 3.2.2 There is a canonical equivalence between the category of continuous representations of ![]() $\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ on finite-dimensional
$\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ on finite-dimensional ![]() $K$-vector spaces and the full subcategory
$K$-vector spaces and the full subcategory ![]() $\operatorname {\mathbf {\Phi -Isoc}}^{\operatorname {ur}}(X/K)$ of
$\operatorname {\mathbf {\Phi -Isoc}}^{\operatorname {ur}}(X/K)$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ consisting of unit-root convergent
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ consisting of unit-root convergent ![]() $\Phi$-isocrystals.
$\Phi$-isocrystals.
3.2.3 Let ![]() $\pi$ be a uniformizer of
$\pi$ be a uniformizer of ![]() $\mathscr {O}_K$. We set
$\mathscr {O}_K$. We set ![]() $R:=\mathscr {O}_K$ and
$R:=\mathscr {O}_K$ and ![]() $R_n:=\mathscr {O}_K/\pi ^n \mathscr {O}_K$ for
$R_n:=\mathscr {O}_K/\pi ^n \mathscr {O}_K$ for ![]() $n\ge 1$. We may reduce to the case where each
$n\ge 1$. We may reduce to the case where each ![]() $X_i$ is affine and admits a smooth formal lifting
$X_i$ is affine and admits a smooth formal lifting ![]() $\mathfrak {X}_i$ to
$\mathfrak {X}_i$ to ![]() $R$ and a lifting
$R$ and a lifting ![]() $F_{\mathfrak {X}_i}\colon \mathfrak {X}_i\to \mathfrak {X}_i$ of the Frobenius
$F_{\mathfrak {X}_i}\colon \mathfrak {X}_i\to \mathfrak {X}_i$ of the Frobenius ![]() $F_{X_i}$. We set
$F_{X_i}$. We set ![]() $\mathfrak {X}:=\prod _{\operatorname {W}(k)} \mathfrak {X}_i$ and denote by
$\mathfrak {X}:=\prod _{\operatorname {W}(k)} \mathfrak {X}_i$ and denote by ![]() $F_{i,\mathfrak {X}}\colon \mathfrak {X}\to \mathfrak {X}$ the product of
$F_{i,\mathfrak {X}}\colon \mathfrak {X}\to \mathfrak {X}$ the product of ![]() $F_{\mathfrak {X}_i}$ and the identity maps on other components.
$F_{\mathfrak {X}_i}$ and the identity maps on other components.
A unit-root ![]() $\Phi$-lattice on
$\Phi$-lattice on ![]() $\mathfrak {X}/R$ is a locally free
$\mathfrak {X}/R$ is a locally free ![]() $\mathscr {O}_{\mathfrak {X}}$-module of finite rank together with isomorphisms
$\mathscr {O}_{\mathfrak {X}}$-module of finite rank together with isomorphisms ![]() $\varphi _i\colon F_{i,\mathfrak {X}}^*(M)\xrightarrow {\sim } M$ commuting with each other. We first establish an equivalence following [Reference CrewCre87]:
$\varphi _i\colon F_{i,\mathfrak {X}}^*(M)\xrightarrow {\sim } M$ commuting with each other. We first establish an equivalence following [Reference CrewCre87]:
Let ![]() $V$ be a continuous
$V$ be a continuous ![]() $R$-linear representation of
$R$-linear representation of ![]() $\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$. For
$\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$. For ![]() $n\ge 1$, let
$n\ge 1$, let ![]() $G_n$ be the image of
$G_n$ be the image of ![]() $\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ in
$\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ in ![]() $\operatorname {GL}(V/\pi ^nV)$, which corresponds to a Galois cover
$\operatorname {GL}(V/\pi ^nV)$, which corresponds to a Galois cover ![]() $Y^{(n)}\to X$ and
$Y^{(n)}\to X$ and ![]() $\pi _n\colon \mathfrak {Y}_n^{(n)}\to \mathfrak {X}_n$ its lifting to
$\pi _n\colon \mathfrak {Y}_n^{(n)}\to \mathfrak {X}_n$ its lifting to ![]() $R_n$. Moreover, each isomorphism
$R_n$. Moreover, each isomorphism ![]() $F_{ \{i\}}$ uniquely lifts to an isomorphism
$F_{ \{i\}}$ uniquely lifts to an isomorphism ![]() $F_{ \{i\}}\colon F_{i,\mathfrak {X}}^*(\mathfrak {Y}_n^{(n)})\xrightarrow {\sim } \mathfrak {Y}_n^{(n)}$, which commute with each other. As in [Reference CrewCre87], we consider a locally free
$F_{ \{i\}}\colon F_{i,\mathfrak {X}}^*(\mathfrak {Y}_n^{(n)})\xrightarrow {\sim } \mathfrak {Y}_n^{(n)}$, which commute with each other. As in [Reference CrewCre87], we consider a locally free ![]() $\mathscr {O}_{\mathfrak {X}_n}$-module (respectively,
$\mathscr {O}_{\mathfrak {X}_n}$-module (respectively, ![]() $\mathscr {O}_{\mathfrak {X}}$-module)
$\mathscr {O}_{\mathfrak {X}}$-module)
Then the isomorphism ![]() $F_{ \{i\}}$ induces an isomorphism
$F_{ \{i\}}$ induces an isomorphism ![]() $F_{i,\mathfrak {X}}^*(M_n)\xrightarrow {\sim } M_n$ and gives rise to a unit-root partial Frobenius structure
$F_{i,\mathfrak {X}}^*(M_n)\xrightarrow {\sim } M_n$ and gives rise to a unit-root partial Frobenius structure
In this way, we obtain the functor ![]() $\iota$ as in (3.2.3.1).
$\iota$ as in (3.2.3.1).
Conversely, given a unit-root ![]() $\Phi$-lattice
$\Phi$-lattice ![]() $(\mathscr {E},\varphi _i)$ on
$(\mathscr {E},\varphi _i)$ on ![]() $\mathfrak {X}/R$, the associated unit-root
$\mathfrak {X}/R$, the associated unit-root ![]() $F$-lattice
$F$-lattice ![]() $(\mathscr {E},\varphi )$ defines a lisse
$(\mathscr {E},\varphi )$ defines a lisse ![]() $R$-sheaf
$R$-sheaf ![]() $\mathbb {L}$ on
$\mathbb {L}$ on ![]() $X$ by [Reference CrewCre87, Theorem 2.2]. The partial Frobenius structures
$X$ by [Reference CrewCre87, Theorem 2.2]. The partial Frobenius structures ![]() $\varphi _i$ define isomorphisms
$\varphi _i$ define isomorphisms ![]() $\phi _i\colon F_i^*(\mathbb {L})\xrightarrow {\sim } \mathbb {L}$ commuting with each other. Then we obtain a continuous
$\phi _i\colon F_i^*(\mathbb {L})\xrightarrow {\sim } \mathbb {L}$ commuting with each other. Then we obtain a continuous ![]() $R$-representation of
$R$-representation of ![]() $\pi _1(X,\Phi,\overline {x})$ on
$\pi _1(X,\Phi,\overline {x})$ on ![]() $\mathbb {L}_{\overline {x}}$. The above construction is functorial and defines a quasi-inverse of
$\mathbb {L}_{\overline {x}}$. The above construction is functorial and defines a quasi-inverse of ![]() $\iota$.
$\iota$.
Lemma 3.2.4 The isomorphism ![]() $\varphi _i$ is horizontal with respect to the canonical convergent connection
$\varphi _i$ is horizontal with respect to the canonical convergent connection ![]() $\nabla$ on
$\nabla$ on ![]() $M^{\operatorname {rig}}$ (see [Reference CrewCre87, Proposition 2.3]).
$M^{\operatorname {rig}}$ (see [Reference CrewCre87, Proposition 2.3]).
Proof. Let ![]() $\Delta$ be the formal completion of the diagonal map
$\Delta$ be the formal completion of the diagonal map ![]() $\mathfrak {X}\to \mathfrak {X}\times _{R}\mathfrak {X}$ and
$\mathfrak {X}\to \mathfrak {X}\times _{R}\mathfrak {X}$ and ![]() $p_1,p_2\colon \Delta \to \mathfrak {X}$ the natural projections. For
$p_1,p_2\colon \Delta \to \mathfrak {X}$ the natural projections. For ![]() $n\ge 1$, we set
$n\ge 1$, we set ![]() $\Delta _n:=\Delta \otimes _{R}R_n$. Let
$\Delta _n:=\Delta \otimes _{R}R_n$. Let ![]() $p_i^*\mathfrak {Y}_{n}^{(n)}$ be the fiber product
$p_i^*\mathfrak {Y}_{n}^{(n)}$ be the fiber product ![]() $\mathfrak {Y}_{n}^{(n)}\times _{\mathfrak {X}_n,p_i}\Delta _n$. The map
$\mathfrak {Y}_{n}^{(n)}\times _{\mathfrak {X}_n,p_i}\Delta _n$. The map ![]() $\mathfrak {Y}_n^{(n)}\to \mathfrak {X}_n \xrightarrow {diag} \Delta _n$ gives rise to formal thickenings
$\mathfrak {Y}_n^{(n)}\to \mathfrak {X}_n \xrightarrow {diag} \Delta _n$ gives rise to formal thickenings ![]() $\mathfrak {Y}_n^{(n)}\to p_i^*\mathfrak {Y}_{n}^{(n)}$. Recall (see [Reference CrewCre87, Proposition 2.3]) that, since
$\mathfrak {Y}_n^{(n)}\to p_i^*\mathfrak {Y}_{n}^{(n)}$. Recall (see [Reference CrewCre87, Proposition 2.3]) that, since ![]() $\mathfrak {Y}_n^{(n)}\to \mathfrak {X}_n$ is étale, there exists a unique isomorphism
$\mathfrak {Y}_n^{(n)}\to \mathfrak {X}_n$ is étale, there exists a unique isomorphism ![]() $p_1^*\mathfrak {Y}_n^{(n)}\xrightarrow {\sim } p_2^*\mathfrak {Y}_n^{(n)}$ which fits into the following diagram.
$p_1^*\mathfrak {Y}_n^{(n)}\xrightarrow {\sim } p_2^*\mathfrak {Y}_n^{(n)}$ which fits into the following diagram.

By uniqueness, this isomorphism is compatible with the ![]() $G_n$-action, the partial Frobenius maps on
$G_n$-action, the partial Frobenius maps on ![]() $\mathfrak {Y}_n^{(n)}$, and the canonical connection on
$\mathfrak {Y}_n^{(n)}$, and the canonical connection on ![]() $M$. Then the lemma follows.
$M$. Then the lemma follows.
3.2.5. Proof of Proposition 3.2.2
By the above lemma, we have a fully faithful functor
It suffices to show that the functor in Proposition 3.2.2 is essentially surjective.
Let ![]() $(\mathscr {M},\varphi _i)$ be a unit-root
$(\mathscr {M},\varphi _i)$ be a unit-root ![]() $\Phi$-isocrystal on
$\Phi$-isocrystal on ![]() $X/K$ and
$X/K$ and ![]() $(\mathbb {L},\phi _i)$ the associated data in Proposition 3.1.8. There exists a
$(\mathbb {L},\phi _i)$ the associated data in Proposition 3.1.8. There exists a ![]() $R$-lattice
$R$-lattice ![]() $\mathbb {L}^{\circ }$ of
$\mathbb {L}^{\circ }$ of ![]() $\mathbb {L}$ such that
$\mathbb {L}$ such that ![]() $\phi _{\mathbb {L}}$ induces an isomorphism
$\phi _{\mathbb {L}}$ induces an isomorphism ![]() $F_X^*(\mathbb {L}^{\circ })\xrightarrow {\sim } \mathbb {L}^{\circ }$. As
$F_X^*(\mathbb {L}^{\circ })\xrightarrow {\sim } \mathbb {L}^{\circ }$. As ![]() $\varphi _i$ is unit-root, we claim there exist integers
$\varphi _i$ is unit-root, we claim there exist integers ![]() $r,s$ such that for every integer
$r,s$ such that for every integer ![]() $m\ge 0$, we have
$m\ge 0$, we have
Indeed, let ![]() $x\in |X|$ be a closed point with degree
$x\in |X|$ be a closed point with degree ![]() $[k_x:k]=a$. The linear action of
$[k_x:k]=a$. The linear action of ![]() $\phi _{i,x}^a$ on the fiber
$\phi _{i,x}^a$ on the fiber ![]() $\mathbb {L}^{\circ }_{\overline {x}}$ is unit-root and satisfies the above properties [Reference CrewCre87, Proposition 1.11]. Then the claim follows.
$\mathbb {L}^{\circ }_{\overline {x}}$ is unit-root and satisfies the above properties [Reference CrewCre87, Proposition 1.11]. Then the claim follows.
Following [Reference CrewCre87], we consider
Then ![]() $\phi _i$ induces an isomorphism
$\phi _i$ induces an isomorphism ![]() $F_i^*\mathbb {L}_i\xrightarrow {\sim } \mathbb {L}_i$.
$F_i^*\mathbb {L}_i\xrightarrow {\sim } \mathbb {L}_i$.
By repeating the above argument to each ![]() $\phi _i$, we obtain a
$\phi _i$, we obtain a ![]() $R$-lattice
$R$-lattice ![]() $\widetilde {\mathbb {L}}$ of
$\widetilde {\mathbb {L}}$ of ![]() $\mathbb {L}$ such that
$\mathbb {L}$ such that ![]() $\phi _i$ induces an isomorphism
$\phi _i$ induces an isomorphism ![]() $F_i^*(\widetilde {\mathbb {L}})\xrightarrow {\sim } \widetilde {\mathbb {L}}$ for every
$F_i^*(\widetilde {\mathbb {L}})\xrightarrow {\sim } \widetilde {\mathbb {L}}$ for every ![]() $i$. Then the data
$i$. Then the data ![]() $(\widetilde {\mathbb {L}},\phi _i)$ descend to a representation of
$(\widetilde {\mathbb {L}},\phi _i)$ descend to a representation of ![]() $\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$. In view of Proposition 3.1.8, this defines a quasi-inverse of the previous construction. The proposition follows.
$\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$. In view of Proposition 3.1.8, this defines a quasi-inverse of the previous construction. The proposition follows.
3.3 Original Drinfeld's lemma
Following an argument of Drinfeld and Kedlaya [Reference Drinfeld and KedlayaDK17, Appendix B], we recover the original Drinfeld's lemma from Theorem 2.2.4 and Proposition 3.2.2.
3.3.1 We say a representation of ![]() $\mathbf {Rep}^{\operatorname {cont}}_K(\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x}))$ is smooth if the action of
$\mathbf {Rep}^{\operatorname {cont}}_K(\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x}))$ is smooth if the action of ![]() $\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ factors through a finite quotient. In view of étale descent for overconvergent
$\pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})$ factors through a finite quotient. In view of étale descent for overconvergent ![]() $F$-isocrystals, the canonical functor
$F$-isocrystals, the canonical functor
factors through ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$. It induces canonical homomorphisms:
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$. It induces canonical homomorphisms:
Since the functor (3.3.1.1) is fully faithful, the composition is an epimorphism.
Writing ![]() $\mathbf {Fet}(X_i)$ for the category of finite étale schemes over
$\mathbf {Fet}(X_i)$ for the category of finite étale schemes over ![]() $X_i$, the canonical functor
$X_i$, the canonical functor
induces a canonical homomorphism ![]() $\widetilde {p}_i\colon \pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})\to \pi _1^{{\unicode{x00E9}}{\text t}}(X_i,\overline {x}_i)$, where
$\widetilde {p}_i\colon \pi _1^{{\unicode{x00E9}}{\text t}}(X,\Phi,\overline {x})\to \pi _1^{{\unicode{x00E9}}{\text t}}(X_i,\overline {x}_i)$, where ![]() $\overline {x}_i:=p_i(\overline {x})$. In view of the construction, the above morphism is compatible with the projection, that is, the following diagram commutes.
$\overline {x}_i:=p_i(\overline {x})$. In view of the construction, the above morphism is compatible with the projection, that is, the following diagram commutes.

Theorem 3.3.2 (i) The homomorphisms (3.3.1.2) induce isomorphisms
(ii) If we apply ![]() $\pi _0$ to the isomorphism (2.2.4.1), we obtain the original Drinfeld's lemma:
$\pi _0$ to the isomorphism (2.2.4.1), we obtain the original Drinfeld's lemma:
 \[ \pi_1(X,\Phi,\overline{x})\xrightarrow{\sim} \prod_{i=1}^n \pi_1^{{\unicode{x00E9}}{\text t}}(X_i,\overline{x}_i). \]
\[ \pi_1(X,\Phi,\overline{x})\xrightarrow{\sim} \prod_{i=1}^n \pi_1^{{\unicode{x00E9}}{\text t}}(X_i,\overline{x}_i). \]
Proof. (i) We first show that for any finite group ![]() $\Gamma$, any tensor functor
$\Gamma$, any tensor functor
factors through ![]() $\mathbf {Rep}_{\overline {\mathbb {Q}}_p}^{\operatorname {cont}}(\pi _1(X,\Phi,\overline {x}))$. By Proposition 3.2.2, it suffices to show that objects in the essential image of the above functor are unit-root at each point of
$\mathbf {Rep}_{\overline {\mathbb {Q}}_p}^{\operatorname {cont}}(\pi _1(X,\Phi,\overline {x}))$. By Proposition 3.2.2, it suffices to show that objects in the essential image of the above functor are unit-root at each point of ![]() $|X|$. This can be shown by a similar argument to [Reference Drinfeld and KedlayaDK17, Proposition B.4.1].
$|X|$. This can be shown by a similar argument to [Reference Drinfeld and KedlayaDK17, Proposition B.4.1].
Moreover, we deduce that the above functor factors through ![]() $\mathbf {Rep}_{\overline {\mathbb {Q}}_p}^{\operatorname {smooth}}(\pi _1(X,\Phi,\overline {x}))$ as in [Reference Drinfeld and KedlayaDK17, Proposition B.4.1].
$\mathbf {Rep}_{\overline {\mathbb {Q}}_p}^{\operatorname {smooth}}(\pi _1(X,\Phi,\overline {x}))$ as in [Reference Drinfeld and KedlayaDK17, Proposition B.4.1].
Hence, the kernel of the canonical epimorphism ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)\twoheadrightarrow \pi _1(X,\Phi,\overline {x})$ is the neutral component of
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)\twoheadrightarrow \pi _1(X,\Phi,\overline {x})$ is the neutral component of ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)$. We obtain the isomorphism
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)$. We obtain the isomorphism ![]() $\pi _0(\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X))\xrightarrow {\sim } \pi _1(X,\Phi,\overline {x})$.
$\pi _0(\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X))\xrightarrow {\sim } \pi _1(X,\Phi,\overline {x})$.
By a full faithfulness result à la Kedlaya (Proposition 3.3.3), ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)\to \pi _1(X,\Phi,\overline {x})$ is an epimorphism. Then by [Reference Drinfeld and KedlayaDK17, Lemma B.7.4], we deduce the isomorphism
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)\to \pi _1(X,\Phi,\overline {x})$ is an epimorphism. Then by [Reference Drinfeld and KedlayaDK17, Lemma B.7.4], we deduce the isomorphism ![]() $\pi _0(\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X))\xrightarrow {\sim } \pi _1(X,\Phi,\overline {x})$.
$\pi _0(\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X))\xrightarrow {\sim } \pi _1(X,\Phi,\overline {x})$.
(ii) Assertion (ii) follows from assertion (i), Theorem 2.2.4, and the commutative diagram (3.3.1.3).
Proposition 3.3.3 (i) The canonical functor ![]() $\iota _{\Phi }\colon \operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X/K)\to \operatorname {\mathbf {\Phi -Isoc}}(X/K)$ is fully faithful.
$\iota _{\Phi }\colon \operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X/K)\to \operatorname {\mathbf {\Phi -Isoc}}(X/K)$ is fully faithful.
(ii) For ![]() $i=1,\dots,n$, let
$i=1,\dots,n$, let ![]() $U_i\subset X_i$ be an open immersion with dense image and set
$U_i\subset X_i$ be an open immersion with dense image and set ![]() $U:= \prod _{i=1}^n U_i$. Then the following restriction functors are fully faithful:
$U:= \prod _{i=1}^n U_i$. Then the following restriction functors are fully faithful:
Proof. (i) Consider the following diagram.

The vertical arrows are faithful and ![]() $\iota _F$ is fully faithful [Reference KedlayaKed04b]. Hence, it remains to show the fullness of
$\iota _F$ is fully faithful [Reference KedlayaKed04b]. Hence, it remains to show the fullness of ![]() $\iota _{\Phi }$.
$\iota _{\Phi }$.
Given two objects ![]() $(\mathscr {E},\varphi _i),(\mathscr {E}',\varphi '_i)$ of
$(\mathscr {E},\varphi _i),(\mathscr {E}',\varphi '_i)$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ and a morphism
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ and a morphism ![]() $f\colon \mathscr {E}\to \mathscr {E}'$ of
$f\colon \mathscr {E}\to \mathscr {E}'$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$,
$\operatorname {\mathbf {\Phi -Isoc}}(X)$, ![]() $f$ extends to a morphism
$f$ extends to a morphism ![]() $f^{{{\dagger}} }\colon \mathscr {E}\to \mathscr {E}'$ of overconvergent
$f^{{{\dagger}} }\colon \mathscr {E}\to \mathscr {E}'$ of overconvergent ![]() $F$-isocrystals by the full faithfulness of
$F$-isocrystals by the full faithfulness of ![]() $\iota _F$. Since the canonical functor
$\iota _F$. Since the canonical functor ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)\to \operatorname {\mathbf {Isoc}}(X)$ is faithful, we deduce that
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)\to \operatorname {\mathbf {Isoc}}(X)$ is faithful, we deduce that ![]() $f^{{{\dagger}} }$ is compatible with partial Frobenius structures.
$f^{{{\dagger}} }$ is compatible with partial Frobenius structures.
(ii) By assertion (i), it suffices to prove the assertion for convergent ![]() $\Phi$-isocrystals. By [Reference KedlayaKed22a, Theorem 5.3] and a similar argument as in assertion (i), it suffices to show its fullness.
$\Phi$-isocrystals. By [Reference KedlayaKed22a, Theorem 5.3] and a similar argument as in assertion (i), it suffices to show its fullness.
Given two objects ![]() $(\mathscr {E},\varphi _i),(\mathscr {E}',\varphi '_i)$ of
$(\mathscr {E},\varphi _i),(\mathscr {E}',\varphi '_i)$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ and a morphism
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ and a morphism ![]() $f\colon \mathscr {E}\to \mathscr {E}'$ of
$f\colon \mathscr {E}\to \mathscr {E}'$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(U/K)$. Then
$\operatorname {\mathbf {\Phi -Isoc}}(U/K)$. Then ![]() $f$ extends to a morphism
$f$ extends to a morphism ![]() $g\colon \mathscr {E}\to \mathscr {E}'$ of convergent
$g\colon \mathscr {E}\to \mathscr {E}'$ of convergent ![]() $F$-isocrystals on
$F$-isocrystals on ![]() $X$. The compatibility between
$X$. The compatibility between ![]() $f$ and partial Frobenius structures follows from [Reference KedlayaKed22a, Theorem 5.3].
$f$ and partial Frobenius structures follows from [Reference KedlayaKed22a, Theorem 5.3].
3.4 Partial Frobenius slope filtrations
Theorem 3.4.1 Suppose that an object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ has a constant diagonal Newton polygon on
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ has a constant diagonal Newton polygon on ![]() $|X|$. Then for
$|X|$. Then for ![]() $i=1,\dots,n$,
$i=1,\dots,n$, ![]() $\mathscr {E}$ admits a filtration
$\mathscr {E}$ admits a filtration
in ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ and an ascending sequence
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ and an ascending sequence ![]() $\mu _1 < \cdots < \mu _l$ of rational numbers such that for
$\mu _1 < \cdots < \mu _l$ of rational numbers such that for ![]() $j=1,\dots,l$, the
$j=1,\dots,l$, the ![]() $i$th partial Frobenius slope of
$i$th partial Frobenius slope of ![]() $\mathscr {E}^{(i)}_j/\mathscr {E}^{(i)}_{j-1}$ equals to
$\mathscr {E}^{(i)}_j/\mathscr {E}^{(i)}_{j-1}$ equals to ![]() $\mu _j$. Moreover, the filtration and sequence are both uniquely determined by this condition. (We call it the
$\mu _j$. Moreover, the filtration and sequence are both uniquely determined by this condition. (We call it the ![]() $i$th partial slope filtration of
$i$th partial slope filtration of ![]() $\mathscr {E}$.)
$\mathscr {E}$.)
Lemma 3.4.2 Suppose that ![]() $\mathscr {E} \in \operatorname {\mathbf {\Phi -Isoc}}(X/K)$ is diagonally unit-root.
$\mathscr {E} \in \operatorname {\mathbf {\Phi -Isoc}}(X/K)$ is diagonally unit-root.
(i) Then there exists a decomposition in ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$
indexed by tuples ![]() $(d_1,\dots,d_n) \in \mathbb {Q}^n$ with
$(d_1,\dots,d_n) \in \mathbb {Q}^n$ with ![]() $d_1 + \cdots + d_n = 0$, in which
$d_1 + \cdots + d_n = 0$, in which ![]() $\mathscr {E}_{d_1,\dots,d_n}$ has the constant partial Frobenius slopes
$\mathscr {E}_{d_1,\dots,d_n}$ has the constant partial Frobenius slopes ![]() $(d_1,\ldots,d_n)$ on
$(d_1,\ldots,d_n)$ on ![]() $|X|$.
$|X|$.
(ii) After taking extension of scalars, each ![]() $\Phi$-isocrystal
$\Phi$-isocrystal ![]() $\mathscr {E}_{d_1,\ldots,d_n}$ is isomorphic to successive extensions of
$\mathscr {E}_{d_1,\ldots,d_n}$ is isomorphic to successive extensions of ![]() $\Phi$-isocrystals
$\Phi$-isocrystals ![]() $\mathscr {E}_1\boxtimes \mathscr {E}_2\boxtimes \cdots \boxtimes \mathscr {E}_n$, where
$\mathscr {E}_1\boxtimes \mathscr {E}_2\boxtimes \cdots \boxtimes \mathscr {E}_n$, where ![]() $\mathscr {E}_i\in \operatorname {\mathbf {F-Isoc}}(X_i/K)$ is isoclinic of slope
$\mathscr {E}_i\in \operatorname {\mathbf {F-Isoc}}(X_i/K)$ is isoclinic of slope ![]() $d_i$.
$d_i$.
Proof. (i) Let ![]() $(\mathbb {L},\phi _i)$ be the data associated to
$(\mathbb {L},\phi _i)$ be the data associated to ![]() $\mathscr {E}$ in Proposition 3.1.8. Let
$\mathscr {E}$ in Proposition 3.1.8. Let ![]() $x\in |X|$ be a closed point of degree
$x\in |X|$ be a closed point of degree ![]() $a$ and
$a$ and ![]() $(V=\mathbb {L}_{\overline {x}},\rho )$ the associated
$(V=\mathbb {L}_{\overline {x}},\rho )$ the associated ![]() $\pi _1(X,\overline {x})$-representation. Since
$\pi _1(X,\overline {x})$-representation. Since ![]() $\phi _{i,\overline {x}}$ commute with each other,
$\phi _{i,\overline {x}}$ commute with each other, ![]() $V$ admits a decomposition
$V$ admits a decomposition
according to partial Frobenius slopes of ![]() $(\phi _{1,\overline {x}},\ldots,\phi _{n,\overline {x}})$. It remains to show that each component is invariant under the
$(\phi _{1,\overline {x}},\ldots,\phi _{n,\overline {x}})$. It remains to show that each component is invariant under the ![]() $\pi _1(X,\overline {x})$-action. Note that each
$\pi _1(X,\overline {x})$-action. Note that each ![]() $\phi _{i,\overline {x}}$ preserves
$\phi _{i,\overline {x}}$ preserves ![]() $V_{d_1,\ldots,d_n}$, as then does their composition
$V_{d_1,\ldots,d_n}$, as then does their composition ![]() $\phi _{\mathbb {L},\overline {x}}$.
$\phi _{\mathbb {L},\overline {x}}$.
Since ![]() $F_X^a$ induces an identity on étale fundamental groups
$F_X^a$ induces an identity on étale fundamental groups ![]() $F_X^a\colon \pi _1(X,\overline {x})=\pi _1(X,\overline {x})$,
$F_X^a\colon \pi _1(X,\overline {x})=\pi _1(X,\overline {x})$, ![]() $\phi _{\mathbb {L},\overline {x}}^a$ is an automorphism of the representation
$\phi _{\mathbb {L},\overline {x}}^a$ is an automorphism of the representation ![]() $(V,\rho )$. Since
$(V,\rho )$. Since ![]() $\phi _{\mathbb {L},\overline {x}}^a$ commutes with the action of
$\phi _{\mathbb {L},\overline {x}}^a$ commutes with the action of ![]() $\pi _1(X,\overline {x})$ on
$\pi _1(X,\overline {x})$ on ![]() $V$, we deduce that the
$V$, we deduce that the ![]() $\pi _1(X,\overline {x})$-action also preserves each component
$\pi _1(X,\overline {x})$-action also preserves each component ![]() $V_{d_1,\ldots,d_n}$. Then assertion (i) follows.
$V_{d_1,\ldots,d_n}$. Then assertion (i) follows.
(ii) After taking extension of scalars and twisting, we may assume ![]() $\mathscr {F}=\mathscr {E}_{d_1,\ldots,d_n}$ is unit-root. We prove the assertion by induction on
$\mathscr {F}=\mathscr {E}_{d_1,\ldots,d_n}$ is unit-root. We prove the assertion by induction on ![]() $n$. Let
$n$. Let ![]() $\overline {x}$ be a geometric point of
$\overline {x}$ be a geometric point of ![]() $X$. By Proposition 3.2.2 and Theorem 3.3.2,
$X$. By Proposition 3.2.2 and Theorem 3.3.2, ![]() $\mathscr {E}$ corresponds to a continuous
$\mathscr {E}$ corresponds to a continuous ![]() $K$-linear representation
$K$-linear representation ![]() $V$ of
$V$ of ![]() $\pi _1(X_1,\overline {x})\times \cdots \times \pi _1(X_n,\overline {x})$. Let
$\pi _1(X_1,\overline {x})\times \cdots \times \pi _1(X_n,\overline {x})$. Let ![]() $W$ be an irreducible sub-
$W$ be an irreducible sub-![]() $\pi _1(X_n,\overline {x})$-representation of
$\pi _1(X_n,\overline {x})$-representation of ![]() $V$. Then
$V$. Then ![]() $W$ corresponds to a unit-root
$W$ corresponds to a unit-root ![]() $F$-isocrystal
$F$-isocrystal ![]() $\mathscr {F}_n$ on
$\mathscr {F}_n$ on ![]() $X_n$, and
$X_n$, and ![]() $\operatorname {Hom}_{\pi _1(X_n,\overline {x})}(W,V)$, viewed as a
$\operatorname {Hom}_{\pi _1(X_n,\overline {x})}(W,V)$, viewed as a ![]() $\pi _1(X_1,\overline {x})\times \cdots \times \pi _1(X_{n-1},\overline {x})$-representation, corresponds to a unit-root
$\pi _1(X_1,\overline {x})\times \cdots \times \pi _1(X_{n-1},\overline {x})$-representation, corresponds to a unit-root ![]() $\Phi$-isocrystal
$\Phi$-isocrystal ![]() $\mathscr {E}'$ on
$\mathscr {E}'$ on ![]() $X_1\times _k\cdots \times _k X_{n-1}$. We obtain a monomorphism
$X_1\times _k\cdots \times _k X_{n-1}$. We obtain a monomorphism ![]() $\mathscr {E}'\boxtimes \mathscr {F}_n\to \mathscr {F}$. Applying the induction hypothesis to
$\mathscr {E}'\boxtimes \mathscr {F}_n\to \mathscr {F}$. Applying the induction hypothesis to ![]() $\mathscr {E}'$, then assertion (ii) follows.
$\mathscr {E}'$, then assertion (ii) follows.
Lemma 3.4.3 Let ![]() $\mathscr {E},\mathscr {E}'$ be two objects of
$\mathscr {E},\mathscr {E}'$ be two objects of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ with constant partial Frobenius slopes
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)$ with constant partial Frobenius slopes ![]() $(\mu _i)_{i=1}^n,(\mu _i')_{i=1}^n$ respectively.
$(\mu _i)_{i=1}^n,(\mu _i')_{i=1}^n$ respectively.
(i) If
 $\operatorname {Hom}_{\operatorname {\mathbf {\Phi -Isoc}}(X/K)}(\mathscr {E}',\mathscr {E})\neq 0$, then
$\operatorname {Hom}_{\operatorname {\mathbf {\Phi -Isoc}}(X/K)}(\mathscr {E}',\mathscr {E})\neq 0$, then  $\mu _i=\mu _i'$ for every
$\mu _i=\mu _i'$ for every  $i=1,\dots,n$.
$i=1,\dots,n$.(ii) If
 $\operatorname {Ext}_{\operatorname {\mathbf {\Phi -Isoc}}(X/K)}(\mathscr {E}',\mathscr {E})\neq 0$, then
$\operatorname {Ext}_{\operatorname {\mathbf {\Phi -Isoc}}(X/K)}(\mathscr {E}',\mathscr {E})\neq 0$, then  $\mu _i\ge \mu _i'$ for every
$\mu _i\ge \mu _i'$ for every  $i=1,\dots,n$.
$i=1,\dots,n$.
Proof. (i) Let ![]() $i$ be an integer,
$i$ be an integer, ![]() $X':=\prod _{j\neq i} X_j$ and
$X':=\prod _{j\neq i} X_j$ and ![]() $k'$ a closed point of
$k'$ a closed point of ![]() $X'$. We apply the exact and faithful functor (2.2.9.1) to the pullback along
$X'$. We apply the exact and faithful functor (2.2.9.1) to the pullback along ![]() $\operatorname {Spec}(k')\to X'$ to obtain convergent
$\operatorname {Spec}(k')\to X'$ to obtain convergent ![]() $F$-isocrystals on
$F$-isocrystals on ![]() $X_{i,k'}/K'$. Then the assertion follows from the corresponding assertion for convergent
$X_{i,k'}/K'$. Then the assertion follows from the corresponding assertion for convergent ![]() $F$-isocrystals.
$F$-isocrystals.
(ii) We will deduce this vanishing result of ![]() $\operatorname {Ext}$ from the case of
$\operatorname {Ext}$ from the case of ![]() $F$-isocrystals, which is known (it follows from the existence of the usual slope filtration). We set
$F$-isocrystals, which is known (it follows from the existence of the usual slope filtration). We set ![]() $\mathscr {F}:=\mathscr {H}om(\mathscr {E}',\mathscr {E})$. By Lemma 3.4.2(ii), we may reduce to the case where
$\mathscr {F}:=\mathscr {H}om(\mathscr {E}',\mathscr {E})$. By Lemma 3.4.2(ii), we may reduce to the case where ![]() $\mathscr {F}\simeq \mathscr {F}_1\boxtimes \cdots \boxtimes \mathscr {F}_n$, with
$\mathscr {F}\simeq \mathscr {F}_1\boxtimes \cdots \boxtimes \mathscr {F}_n$, with ![]() $\mathscr {F}_i\in \operatorname {\mathbf {F-Isoc}}(X_i/K)$ after taking extension of scalars. Suppose
$\mathscr {F}_i\in \operatorname {\mathbf {F-Isoc}}(X_i/K)$ after taking extension of scalars. Suppose ![]() $\mu _i'>\mu _i$ for some integer
$\mu _i'>\mu _i$ for some integer ![]() $i\in [1,n]$. We consider the extension group
$i\in [1,n]$. We consider the extension group ![]() $\operatorname {Ext}^1_{F_i\text {-}\operatorname {\mathbf {Isoc}}(X/K)}(\mathscr {E}',\mathscr {E})$, which fits into the following diagram.
$\operatorname {Ext}^1_{F_i\text {-}\operatorname {\mathbf {Isoc}}(X/K)}(\mathscr {E}',\mathscr {E})$, which fits into the following diagram.
Since the slope of ![]() $\mathscr {F}_i$ is
$\mathscr {F}_i$ is ![]() $>0$, we obtain the vanishing of
$>0$, we obtain the vanishing of ![]() $\operatorname {H}^0(X_i,\mathscr {F}_i)^{\varphi _i=\operatorname {id}},\operatorname {H}^0(X_i,\mathscr {F}_i)/(\varphi _i-\operatorname {id})$, and
$\operatorname {H}^0(X_i,\mathscr {F}_i)^{\varphi _i=\operatorname {id}},\operatorname {H}^0(X_i,\mathscr {F}_i)/(\varphi _i-\operatorname {id})$, and ![]() $\operatorname {H}^1(X_i,\mathscr {F}_i)^{\varphi _i=\operatorname {id}}$; note that the last case follows from the assertion (ii) for convergent
$\operatorname {H}^1(X_i,\mathscr {F}_i)^{\varphi _i=\operatorname {id}}$; note that the last case follows from the assertion (ii) for convergent ![]() $F$-isocrystals. We conclude that the middle term of (3.4.3.1) vanishes by the Künneth formula [Reference AbeAbe14, Lemma 4.5]. Then the assertion follows.
$F$-isocrystals. We conclude that the middle term of (3.4.3.1) vanishes by the Künneth formula [Reference AbeAbe14, Lemma 4.5]. Then the assertion follows.
3.4.4. Proof of Theorem 3.4.1
By Theorem 3.1.10, each partial Newton polygon of ![]() $\mathscr {E}$ is also constant. Then we apply Lemma 3.4.2 to the successive quotients of the diagonal slope filtration; this yields a filtration in which each successive quotient has the property that every
$\mathscr {E}$ is also constant. Then we apply Lemma 3.4.2 to the successive quotients of the diagonal slope filtration; this yields a filtration in which each successive quotient has the property that every ![]() $i$th partial Frobenius slope has a fixed value, but these values may not occur in ascending order. However, using Lemma 3.4.3 we can reorder the successive quotients to enforce this condition.
$i$th partial Frobenius slope has a fixed value, but these values may not occur in ascending order. However, using Lemma 3.4.3 we can reorder the successive quotients to enforce this condition.
3.5 Drinfeld's lemma for convergent  $\Phi$-isocrystals
$\Phi$-isocrystals
Recall that the category ![]() $\operatorname {\mathbf {F-Isoc}}(X/K)\otimes _K \overline {\mathbb {Q}}_p$ (respectively,
$\operatorname {\mathbf {F-Isoc}}(X/K)\otimes _K \overline {\mathbb {Q}}_p$ (respectively, ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X/K)\otimes _K\overline {\mathbb {Q}}_p$) is denoted by
$\operatorname {\mathbf {\Phi -Isoc}}(X/K)\otimes _K\overline {\mathbb {Q}}_p$) is denoted by ![]() $\operatorname {\mathbf {F-Isoc}}(X)$ (respectively,
$\operatorname {\mathbf {F-Isoc}}(X)$ (respectively, ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$) and is neutral Tannakian over
$\operatorname {\mathbf {\Phi -Isoc}}(X)$) and is neutral Tannakian over ![]() $\overline {\mathbb {Q}}_p$. With the notation of § 2.2.3, we show a version of Drinfeld's lemma for convergent
$\overline {\mathbb {Q}}_p$. With the notation of § 2.2.3, we show a version of Drinfeld's lemma for convergent ![]() $F$-isocrystals as in Theorem 2.2.4.
$F$-isocrystals as in Theorem 2.2.4.
Theorem 3.5.1 Assume ![]() $X_i$ is a smooth geometrically connected
$X_i$ is a smooth geometrically connected ![]() $k$-variety. The following canonical homomorphism is an isomorphism:
$k$-variety. The following canonical homomorphism is an isomorphism:
 \begin{equation} \prod_{i=1}^n p_i^{\circ}\colon \pi_1^{\operatorname{\mathbf{\Phi-Isoc}}}(X) \xrightarrow{\sim} \prod_{i=1}^n \pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_i) . \end{equation}
\begin{equation} \prod_{i=1}^n p_i^{\circ}\colon \pi_1^{\operatorname{\mathbf{\Phi-Isoc}}}(X) \xrightarrow{\sim} \prod_{i=1}^n \pi_1^{\operatorname{\mathbf{F-Isoc}}}(X_i) . \end{equation}Proposition 3.5.2 The pullback functor:
is fully faithful and its essential image is closed under subquotients.
Proof. We may assume ![]() $i=n$ and set
$i=n$ and set ![]() $X':=\prod _{i=1}^{n-1}X_i$.
$X':=\prod _{i=1}^{n-1}X_i$.
(i) We first prove the full faithfulness. By Proposition 3.3.3, we may assume each ![]() $X_i$ is affine and admits a smooth formal lifting
$X_i$ is affine and admits a smooth formal lifting ![]() $\mathfrak {X}_i$ over
$\mathfrak {X}_i$ over ![]() $\mathscr {O}_K$. Let
$\mathscr {O}_K$. Let ![]() $(\mathscr {E},\varphi )$ be an object of
$(\mathscr {E},\varphi )$ be an object of ![]() $\operatorname {\mathbf {F-Isoc}}(X_n)$. Since each
$\operatorname {\mathbf {F-Isoc}}(X_n)$. Since each ![]() $X_i$ is smooth and geometrically connected, the canonical morphism
$X_i$ is smooth and geometrically connected, the canonical morphism
is an isomorphism by the Künneth formula for the sheaf of differential operators [Reference AbeAbe14, Lemma 4.5] and for quasicoherent modules. Then we deduce a canonical isomorphism:
The full faithfulness follows from the above isomorphism applied to internal homomorphisms.
(ii) Next we treat the second assertion. Let ![]() $\mathscr {E}$ be an object of
$\mathscr {E}$ be an object of ![]() $\operatorname {\mathbf {F-Isoc}}(X_n)$ and
$\operatorname {\mathbf {F-Isoc}}(X_n)$ and ![]() $p_n^*(\mathscr {E})\to \mathscr {F}$ a surjection in
$p_n^*(\mathscr {E})\to \mathscr {F}$ a surjection in ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$. By enlarging
$\operatorname {\mathbf {\Phi -Isoc}}(X)$. By enlarging ![]() $k$ (2.2.2.1), we may assume there exists a
$k$ (2.2.2.1), we may assume there exists a ![]() $k$-point
$k$-point ![]() $x$ of
$x$ of ![]() $X'$. We will show that the surjection
$X'$. We will show that the surjection ![]() $\mathscr {E}\to \mathscr {G}:=(x\times _k \operatorname {id}_{X_n})^*(\mathscr {F})$ over
$\mathscr {E}\to \mathscr {G}:=(x\times _k \operatorname {id}_{X_n})^*(\mathscr {F})$ over ![]() $X_n$ is isomorphic to
$X_n$ is isomorphic to ![]() $p_n^*(\mathscr {E})\to \mathscr {F}$ after pullback via
$p_n^*(\mathscr {E})\to \mathscr {F}$ after pullback via ![]() $p_n^*$.
$p_n^*$.
Let ![]() $U$ be a dense open subset of
$U$ be a dense open subset of ![]() $X$ such that the diagonal Newton polygon of
$X$ such that the diagonal Newton polygon of ![]() $\mathscr {F}$ is constant, which is preserved by partial Frobenius morphisms. By Drinfeld's lemma for open immersions [Reference LauLau04, Lemma 9.2.1], [Reference KedlayaKed19, Theorem 4.3.6], and Proposition 3.3.3, we may assume that the diagonal Newton polygons of
$\mathscr {F}$ is constant, which is preserved by partial Frobenius morphisms. By Drinfeld's lemma for open immersions [Reference LauLau04, Lemma 9.2.1], [Reference KedlayaKed19, Theorem 4.3.6], and Proposition 3.3.3, we may assume that the diagonal Newton polygons of ![]() $p_n^*(\mathscr {E})$ and
$p_n^*(\mathscr {E})$ and ![]() $\mathscr {F}$ are constant on
$\mathscr {F}$ are constant on ![]() $|X|$ after shrinking
$|X|$ after shrinking ![]() $X_i$. Then the set of each partial Newton polygon of
$X_i$. Then the set of each partial Newton polygon of ![]() $\mathscr {F}$ is also constant on
$\mathscr {F}$ is also constant on ![]() $|X|$. To show the claim, we may reduce to the case where the Frobenius slopes of
$|X|$. To show the claim, we may reduce to the case where the Frobenius slopes of ![]() $\mathscr {E}$ are constant on
$\mathscr {E}$ are constant on ![]() $X_n$ by applying Theorem 3.1.10 to
$X_n$ by applying Theorem 3.1.10 to ![]() $p_n^*(\mathscr {E})\to \mathscr {F}$. Moreover, we may assume
$p_n^*(\mathscr {E})\to \mathscr {F}$. Moreover, we may assume ![]() $\mathscr {E}$ is unit-root by twisting. Then
$\mathscr {E}$ is unit-root by twisting. Then ![]() $\mathscr {F}$ is also a unit-root
$\mathscr {F}$ is also a unit-root ![]() $\Phi$-isocrystal. By Proposition 3.2.2 and Theorem 3.3.2, for a geometric point
$\Phi$-isocrystal. By Proposition 3.2.2 and Theorem 3.3.2, for a geometric point ![]() $\overline {y}$ of
$\overline {y}$ of ![]() $X$, the action of
$X$, the action of ![]() $\prod _{i=1}^{n-1}\pi _1(X_i,\overline {y})$ on
$\prod _{i=1}^{n-1}\pi _1(X_i,\overline {y})$ on ![]() $p_n^*(\mathscr {E})_{\overline {y}}$ is trivial. Then the same holds for
$p_n^*(\mathscr {E})_{\overline {y}}$ is trivial. Then the same holds for ![]() $\mathscr {F}$ and the assertion follows.
$\mathscr {F}$ and the assertion follows.
Proposition 3.5.3 (i) The functor ![]() $p_i^*:\operatorname {\mathbf {F-Isoc}}(X_i)\to \operatorname {\mathbf {\Phi -Isoc}}(X)$ admits a right adjoint
$p_i^*:\operatorname {\mathbf {F-Isoc}}(X_i)\to \operatorname {\mathbf {\Phi -Isoc}}(X)$ admits a right adjoint ![]() $p_{i,*}$. Moreover, the canonical morphism
$p_{i,*}$. Moreover, the canonical morphism ![]() $\operatorname {id}\to p_{i,*}p_i^*$ is an isomorphism and
$\operatorname {id}\to p_{i,*}p_i^*$ is an isomorphism and ![]() $p_i^*p_{i,*}\to \operatorname {id}$ is injective.
$p_i^*p_{i,*}\to \operatorname {id}$ is injective.
(ii) The functor ![]() $p_{i,*}$ commutes with the base change of
$p_{i,*}$ commutes with the base change of ![]() $g\colon Y\to X_i$.
$g\colon Y\to X_i$.
Proof. (i) Let ![]() $\mathscr {E}$ be an object of
$\mathscr {E}$ be an object of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$. By Proposition 3.5.2, the collection of subobjects of
$\operatorname {\mathbf {\Phi -Isoc}}(X)$. By Proposition 3.5.2, the collection of subobjects of ![]() $\mathscr {E}$ which belong to the essential image of
$\mathscr {E}$ which belong to the essential image of ![]() $p^*_i$ has a maximal element
$p^*_i$ has a maximal element ![]() $\mathscr {F}$. Then we define
$\mathscr {F}$. Then we define ![]() $p_{i,*}(\mathscr {E})$ to be the object of
$p_{i,*}(\mathscr {E})$ to be the object of ![]() $\operatorname {\mathbf {F-Isoc}}(X_i)$ of which
$\operatorname {\mathbf {F-Isoc}}(X_i)$ of which ![]() $\mathscr {F}$ is a pullback.
$\mathscr {F}$ is a pullback.
Let ![]() $f:\mathscr {E}_1\to \mathscr {E}_2$ be a morphism of
$f:\mathscr {E}_1\to \mathscr {E}_2$ be a morphism of ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$. Let
$\operatorname {\mathbf {\Phi -Isoc}}(X)$. Let ![]() $\mathscr {G}$ be the image of
$\mathscr {G}$ be the image of ![]() $p_i^*(p_{i,*}(\mathscr {E}_1))$ in
$p_i^*(p_{i,*}(\mathscr {E}_1))$ in ![]() $\mathscr {E}_2$. By Proposition 3.5.2,
$\mathscr {E}_2$. By Proposition 3.5.2, ![]() $\mathscr {G}$ belongs to the essential image of
$\mathscr {G}$ belongs to the essential image of ![]() $p_i^*$ and the functoriality of
$p_i^*$ and the functoriality of ![]() $p_{i,*}$ follows. The second assertion is clear.
$p_{i,*}$ follows. The second assertion is clear.
(ii) By Lemma 3.3.3, we may assume that the diagonal Newton polygon of ![]() $\mathscr {E}$ is constant on
$\mathscr {E}$ is constant on ![]() $|X|$. By Theorem 3.1.10, we may moreover assume that
$|X|$. By Theorem 3.1.10, we may moreover assume that ![]() $\mathscr {E}$ is diagonally unit-root after twisting the
$\mathscr {E}$ is diagonally unit-root after twisting the ![]() $i$th partial Frobenius structure. Then
$i$th partial Frobenius structure. Then ![]() $p_{i,*}(\mathscr {E})$ is unit-root and
$p_{i,*}(\mathscr {E})$ is unit-root and ![]() $p_i^*(p_{i,*}(\mathscr {E}))$ lies in the unit-root component
$p_i^*(p_{i,*}(\mathscr {E}))$ lies in the unit-root component ![]() $\mathscr {E}_{(0,\ldots,0)}$ of
$\mathscr {E}_{(0,\ldots,0)}$ of ![]() $\mathscr {E}$ (cf. Lemma 3.4.2). Moreover, the unit-root
$\mathscr {E}$ (cf. Lemma 3.4.2). Moreover, the unit-root ![]() $F$-isocrystal
$F$-isocrystal ![]() $p_{i,*}(\mathscr {E})$ over
$p_{i,*}(\mathscr {E})$ over ![]() $X_i$ can be identified with the
$X_i$ can be identified with the ![]() $\prod _{j\neq i}\pi _1(X_j,\overline {x})$-invariant part of the
$\prod _{j\neq i}\pi _1(X_j,\overline {x})$-invariant part of the ![]() $\pi _1(X,\Phi,\overline {x})$-representation associated to
$\pi _1(X,\Phi,\overline {x})$-representation associated to ![]() $\mathscr {E}_{(0,\ldots,0)}$ via Proposition 3.2.2. The base change property follows from this identification in view of Theorem 3.3.2.
$\mathscr {E}_{(0,\ldots,0)}$ via Proposition 3.2.2. The base change property follows from this identification in view of Theorem 3.3.2.
3.5.4. Proof of Theorem 3.5.1
The proof is similar to that of § 2.2.11(a). We keep the notation of § 2.2.11. It suffices to show the exactness of the following sequence:
We verify the exactness using Theorem 2.1.4.
Condition (i) follows from Proposition 3.5.2. Conditions (ii) and (iii)(c) can be verified in the same way as in § 2.2.11(a). Finally, as in § 2.2.11, we verify conditions (iii)(a) and (b) using functor ![]() $p_{i,*}$ and its base change property Proposition 3.5.3. This finishes the proof.
$p_{i,*}$ and its base change property Proposition 3.5.3. This finishes the proof.
Remark 3.5.5 The functor ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)\to \operatorname {\mathbf {\Phi -Isoc}}(X)$ induces a canonical morphism
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)\to \operatorname {\mathbf {\Phi -Isoc}}(X)$ induces a canonical morphism ![]() $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)\to \pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$, which fits into the following diagram.
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}}}(X)\to \pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$, which fits into the following diagram.

In view of the above diagram, the pushforward functor for convergent ![]() $\Phi$-isocrystals is compatible with that for overconvergent
$\Phi$-isocrystals is compatible with that for overconvergent ![]() $\Phi$-isocrystals.
$\Phi$-isocrystals.
Corollary 3.5.6 Any object ![]() $\mathscr {E}$ of
$\mathscr {E}$ of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ (respectively,
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X,\Phi )$ (respectively, ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$, respectively,
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$, respectively, ![]() $\operatorname {\mathbf {\Phi -Isoc}}(X)$) is a subobject (or quotient) of an object of the form
$\operatorname {\mathbf {\Phi -Isoc}}(X)$) is a subobject (or quotient) of an object of the form ![]() $\boxtimes _{i=1}^n \mathscr {E}_i$, where each
$\boxtimes _{i=1}^n \mathscr {E}_i$, where each ![]() $\mathscr {E}_i$ is an object of
$\mathscr {E}_i$ is an object of ![]() $\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)$ (respectively,
$\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }(X_i)$ (respectively, ![]() $\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X_i)$, respectively,
$\operatorname {\mathbf {F-Isoc}^{{{\dagger}} }}(X_i)$, respectively, ![]() $\operatorname {\mathbf {F-Isoc}}(X)$).
$\operatorname {\mathbf {F-Isoc}}(X)$).
Proof. It suffices to show the assertion about the quotient. By induction, we can reduce to the case where ![]() $n=2$. We set
$n=2$. We set ![]() $G:=\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi ), G_i:=\pi _1^{\operatorname {\mathbf {Isoc}^{{{\dagger}} }}}(X_i)$. Let
$G:=\pi _1^{\mathbf {Isoc}^{{{\dagger}} {{\dagger}} }}(X,\Phi ), G_i:=\pi _1^{\operatorname {\mathbf {Isoc}^{{{\dagger}} }}}(X_i)$. Let ![]() $V$ be a representation of
$V$ be a representation of ![]() $G\simeq G_1\times G_2$ corresponding to
$G\simeq G_1\times G_2$ corresponding to ![]() $\mathscr {E}$. We have morphisms of
$\mathscr {E}$. We have morphisms of ![]() $G_1\times G_2$-representations:
$G_1\times G_2$-representations:
where ![]() $G_1$ only acts at the first component of
$G_1$ only acts at the first component of ![]() $V\otimes V^{\vee }\otimes V$ and
$V\otimes V^{\vee }\otimes V$ and ![]() $G_2$ acts diagonally. By composing with
$G_2$ acts diagonally. By composing with ![]() $V\xrightarrow {\operatorname {coev}\otimes \operatorname {id}} V\otimes V^{\vee }\otimes V$, we see that the above composition is surjective. This finishes the proof.
$V\xrightarrow {\operatorname {coev}\otimes \operatorname {id}} V\otimes V^{\vee }\otimes V$, we see that the above composition is surjective. This finishes the proof.
4. A variant for  $\widehat {\Pi }^{\operatorname {mot}}$
$\widehat {\Pi }^{\operatorname {mot}}$
In [Reference DrinfeldDri18], Drinfeld considered the ![]() $\ell$-adic pro-semisimple completion of the étale fundamental group and showed this object is independent of
$\ell$-adic pro-semisimple completion of the étale fundamental group and showed this object is independent of ![]() $\ell$ up to conjugation by elements of the neutral component. In this section, we incorporate Drinfeld's lemma in that setting.
$\ell$ up to conjugation by elements of the neutral component. In this section, we incorporate Drinfeld's lemma in that setting.
Throughout § 4, we assume ![]() $(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$, let
$(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$, let ![]() $X_i$ be smooth geometrically connected
$X_i$ be smooth geometrically connected ![]() $k$-varieties for
$k$-varieties for ![]() $i=1,\ldots,n$ and set
$i=1,\ldots,n$ and set ![]() $X:=\prod _{i=1}^n X_i$.
$X:=\prod _{i=1}^n X_i$.
4.1 On semisimplicity of the monodromy group
In this subsection, we discuss the semisimplicity of the monodromy group for an overconvergent ![]() $\Phi$-isocrystal following [Reference DeligneDel80, Reference CrewCre92].
$\Phi$-isocrystal following [Reference DeligneDel80, Reference CrewCre92].
An ![]() $n$-twist is a
$n$-twist is a ![]() $\Phi$-isocrystal on
$\Phi$-isocrystal on ![]() $\operatorname {Spec}(k)/K$ of rank 1. Let
$\operatorname {Spec}(k)/K$ of rank 1. Let ![]() $\chi :=(\chi _i)_{i=1}^n$ be an
$\chi :=(\chi _i)_{i=1}^n$ be an ![]() $n$-twist and
$n$-twist and ![]() $\mathscr {E}$ an overconvergent
$\mathscr {E}$ an overconvergent ![]() $\Phi$-isocrystal. We denote by
$\Phi$-isocrystal. We denote by ![]() $\mathscr {E}(\chi )$ the tensor product
$\mathscr {E}(\chi )$ the tensor product ![]() $\mathscr {E}\otimes f^*(\chi )$, where
$\mathscr {E}\otimes f^*(\chi )$, where ![]() $f:X\to \operatorname {Spec}(k)$ is the structure morphism. We first prove a result in the rank one case, generalizing a result of Abe [Reference AbeAbe18a, Lemma 6.1].
$f:X\to \operatorname {Spec}(k)$ is the structure morphism. We first prove a result in the rank one case, generalizing a result of Abe [Reference AbeAbe18a, Lemma 6.1].
Lemma 4.1.1 Let ![]() $\mathscr {E}$ be an overconvergent
$\mathscr {E}$ be an overconvergent ![]() $\Phi$-isocrystal of rank one over
$\Phi$-isocrystal of rank one over ![]() $X$. Then there exists an
$X$. Then there exists an ![]() $n$-twist
$n$-twist ![]() $\chi$ such that
$\chi$ such that ![]() $\mathscr {E}(\chi )$ has finite order.
$\mathscr {E}(\chi )$ has finite order.
Proof. After twisting, we may assume ![]() $\mathscr {E}$ is unit-root. Let
$\mathscr {E}$ is unit-root. Let ![]() $\rho$ be the character of
$\rho$ be the character of ![]() $\pi _1(X,\Phi,\overline {x})$ associated to
$\pi _1(X,\Phi,\overline {x})$ associated to ![]() $\mathscr {E}$ (Proposition 3.2.2) and
$\mathscr {E}$ (Proposition 3.2.2) and ![]() $\rho _i$ the restriction of
$\rho _i$ the restriction of ![]() $\rho$ to
$\rho$ to ![]() $\pi _1(X_i,\overline {x})$ (Theorem 3.3.2). We may shrink each
$\pi _1(X_i,\overline {x})$ (Theorem 3.3.2). We may shrink each ![]() $X_i$ and, in particular, we may assume that
$X_i$ and, in particular, we may assume that ![]() $X_i$ admits a smooth compactification
$X_i$ admits a smooth compactification ![]() $X_i\to \overline {X}_i$ such that the complement is a simple normal crossing divisor. Using [Reference ShihoShi11b, Theorem 4.3], [Reference Katz and LangKL81, Theorem 2], and the same argument of [Reference CrewCre87, Corollary 4.13], one can show that some power
$X_i\to \overline {X}_i$ such that the complement is a simple normal crossing divisor. Using [Reference ShihoShi11b, Theorem 4.3], [Reference Katz and LangKL81, Theorem 2], and the same argument of [Reference CrewCre87, Corollary 4.13], one can show that some power ![]() $\mathscr {E}^{\otimes N}$ is geometrically trivial, i.e. its underlying overconvergent isocrystal is trivial. Then
$\mathscr {E}^{\otimes N}$ is geometrically trivial, i.e. its underlying overconvergent isocrystal is trivial. Then ![]() $\rho ^{\otimes N}$ factors through the quotient
$\rho ^{\otimes N}$ factors through the quotient ![]() $\pi _1(X,\Phi,\overline {x})\to \widehat {\mathbb {Z}}^n$ and each
$\pi _1(X,\Phi,\overline {x})\to \widehat {\mathbb {Z}}^n$ and each ![]() $\rho _i^{\otimes N}$ is also geometrically trivial. Hence, the unit-root convergent
$\rho _i^{\otimes N}$ is also geometrically trivial. Hence, the unit-root convergent ![]() $F$-isocrystal
$F$-isocrystal ![]() $\mathscr {E}_i$ over
$\mathscr {E}_i$ over ![]() $X_i$ associated to
$X_i$ associated to ![]() $\rho _i$ is overconvergent. We may take suitable twists
$\rho _i$ is overconvergent. We may take suitable twists ![]() $\chi _i$ such that each
$\chi _i$ such that each ![]() $\mathscr {E}_i(\chi _i)$ has finite order [Reference AbeAbe18a, Lemma 6.1]. Then the assertion follows.
$\mathscr {E}_i(\chi _i)$ has finite order [Reference AbeAbe18a, Lemma 6.1]. Then the assertion follows.
This allows us to conclude the following corollary.
Corollary 4.1.2 Let ![]() $\mathscr {E}$ be an overconvergent
$\mathscr {E}$ be an overconvergent ![]() $\Phi$-isocrystal over
$\Phi$-isocrystal over ![]() $X$. After taking a finite extension of
$X$. After taking a finite extension of ![]() $K$, there exist an integer
$K$, there exist an integer ![]() $m\ge 1$,
$m\ge 1$, ![]() $n$-twists
$n$-twists ![]() $\chi _i$ for
$\chi _i$ for ![]() $1\le i\le m$, and a decomposition of the semisimplification of
$1\le i\le m$, and a decomposition of the semisimplification of ![]() $\mathscr {E}$:
$\mathscr {E}$:
 \[ \mathscr{E}^{\operatorname{ss}}\simeq \bigoplus_{i=1}^m \mathscr{F}_i(\chi_i), \]
\[ \mathscr{E}^{\operatorname{ss}}\simeq \bigoplus_{i=1}^m \mathscr{F}_i(\chi_i), \]
where ![]() $\mathscr {F}_i$ is an irreducible overconvergent
$\mathscr {F}_i$ is an irreducible overconvergent ![]() $\Phi$-isocrystal of finite order determinant for each
$\Phi$-isocrystal of finite order determinant for each ![]() $i$.
$i$.
Definition 4.1.3 We say ![]() $\mathscr {E}$ is untwisted if we can choose each
$\mathscr {E}$ is untwisted if we can choose each ![]() $\chi _i$ to be the trivial
$\chi _i$ to be the trivial ![]() $\Phi$-isocrystal on
$\Phi$-isocrystal on ![]() $\operatorname {Spec}(k)$ in the above corollary.
$\operatorname {Spec}(k)$ in the above corollary.
4.1.4 Let ![]() $\mathscr {E}$ be an object of
$\mathscr {E}$ be an object of ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$. We denote by
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$. We denote by ![]() $G_{\operatorname {geo}}(\mathscr {E})$ (respectively,
$G_{\operatorname {geo}}(\mathscr {E})$ (respectively, ![]() $G_{\operatorname {arith}}(\mathscr {E})$) its geometric (respectively, arithmetic) monodromy group over
$G_{\operatorname {arith}}(\mathscr {E})$) its geometric (respectively, arithmetic) monodromy group over ![]() $\overline {\mathbb {Q}}_p$, which is defined by the Tannakian full subcategory of
$\overline {\mathbb {Q}}_p$, which is defined by the Tannakian full subcategory of ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ (respectively,
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ (respectively, ![]() $\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$) whose objects are subquotients of
$\operatorname {\mathbf {Isoc}^{{{\dagger}} }}(X)$) whose objects are subquotients of ![]() $\mathscr {E}^{\otimes m}\otimes \mathscr {E}^{\vee, \otimes n}$ for some
$\mathscr {E}^{\otimes m}\otimes \mathscr {E}^{\vee, \otimes n}$ for some ![]() $m,n$. Recall that the radical of
$m,n$. Recall that the radical of ![]() $G_{\operatorname {geo}}(\mathscr {E})$ is unipotent [Reference CrewCre92, Theorem 4.9].
$G_{\operatorname {geo}}(\mathscr {E})$ is unipotent [Reference CrewCre92, Theorem 4.9].
Given a field ![]() $E$, by a semisimple group (respectively, reductive group) over
$E$, by a semisimple group (respectively, reductive group) over ![]() $E$, we mean an algebraic group of finite type over
$E$, we mean an algebraic group of finite type over ![]() $E$ whose neutral component is semisimple (respectively, reductive).
$E$ whose neutral component is semisimple (respectively, reductive).
By a similar argument to [Reference D'AddezioD'Ad20, Theorem 3.4.7], we conclude the following result for ![]() $\Phi$-isocrystals.
$\Phi$-isocrystals.
Proposition 4.1.5 The following properties are equivalent.
(i) The neutral component of
 $G_{\operatorname {arith}}(\mathscr {E})/G_{\operatorname {geo}}(\mathscr {E})$ is unipotent.
$G_{\operatorname {arith}}(\mathscr {E})/G_{\operatorname {geo}}(\mathscr {E})$ is unipotent.(ii) The radical of
 $G_{\operatorname {arith}}(\mathscr {E})$ is unipotent.
$G_{\operatorname {arith}}(\mathscr {E})$ is unipotent.(iii) The object
 $\mathscr {E}$ is untwisted.
$\mathscr {E}$ is untwisted.
Corollary 4.1.6 Let ![]() $\mathscr {E}$ be a semisimple object of
$\mathscr {E}$ be a semisimple object of ![]() $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$.
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$.
(i) The geometric monodromy group
 $G_{\operatorname {geo}}(\mathscr {E})$ is semisimple.
$G_{\operatorname {geo}}(\mathscr {E})$ is semisimple.(ii) If the determinant of each irreducible component of
 $\mathscr {E}$ has finite order, then
$\mathscr {E}$ has finite order, then  $G_{\operatorname {arith}}(\mathscr {E})$ is semisimple.
$G_{\operatorname {arith}}(\mathscr {E})$ is semisimple.
Proof. Assertion (i) follows from the fact that the radical of ![]() $G_{\operatorname {geo}}(\mathscr {E})$ is unipotent and the argument of [Reference DeligneDel80, Corollaire 1.3.9]. Assertion (ii) can be shown in a similar way using Proposition 4.1.5.
$G_{\operatorname {geo}}(\mathscr {E})$ is unipotent and the argument of [Reference DeligneDel80, Corollaire 1.3.9]. Assertion (ii) can be shown in a similar way using Proposition 4.1.5.
4.2 Pro-semisimple completion of the fundamental group of a smooth variety with partial Frobenius
4.2.1 Let ![]() $E$ be an algebraically closed field. We refer to [Reference DrinfeldDri18, § 2.1.1] for the notion of pro-semisimple groups and pro-reductive groups. Following [Reference DrinfeldDri18, § 1.2.3],
$E$ be an algebraically closed field. We refer to [Reference DrinfeldDri18, § 2.1.1] for the notion of pro-semisimple groups and pro-reductive groups. Following [Reference DrinfeldDri18, § 1.2.3], ![]() $\operatorname {Pro-red}(E)$ denotes the groupoid whose objects are pro-reductive groups over
$\operatorname {Pro-red}(E)$ denotes the groupoid whose objects are pro-reductive groups over ![]() $E$ and whose morphisms are as follows: a morphism
$E$ and whose morphisms are as follows: a morphism ![]() $G_1\to G_2$ is an isomorphism of group schemes
$G_1\to G_2$ is an isomorphism of group schemes ![]() $G_1\xrightarrow {\sim } G_2$ defined up to composing with automorphisms of
$G_1\xrightarrow {\sim } G_2$ defined up to composing with automorphisms of ![]() $G_2$ of the form
$G_2$ of the form ![]() $x\mapsto gxg^{-1}$,
$x\mapsto gxg^{-1}$, ![]() $g\in G_2^{\circ }$. Let
$g\in G_2^{\circ }$. Let ![]() $\operatorname {Pro-ss}(E)\subset \operatorname {Pro-red}(E)$ be the full subcategory formed by pro-semisimple groups.
$\operatorname {Pro-ss}(E)\subset \operatorname {Pro-red}(E)$ be the full subcategory formed by pro-semisimple groups.
For any pro-algebraic group ![]() $G$ over
$G$ over ![]() $E$, we denote by
$E$, we denote by ![]() $G^{\operatorname {red}}$ (respectively,
$G^{\operatorname {red}}$ (respectively, ![]() $G^{\operatorname {ss}}$) its pro-reductive (respectively, pro-semi-simple) quotient.
$G^{\operatorname {ss}}$) its pro-reductive (respectively, pro-semi-simple) quotient.
4.2.2 Fix an algebraic closure ![]() $\overline {\mathbb {Q}}$ of
$\overline {\mathbb {Q}}$ of ![]() $\mathbb {Q}$. Let
$\mathbb {Q}$. Let ![]() $\lambda$ be a non-Archimedean place of
$\lambda$ be a non-Archimedean place of ![]() $\overline {\mathbb {Q}}$,
$\overline {\mathbb {Q}}$, ![]() $\ell$ the prime that
$\ell$ the prime that ![]() $\lambda$ divides
$\lambda$ divides ![]() $\ell$,
$\ell$, ![]() $\overline {\mathbb {Q}}_{\lambda }$ the direct limit of
$\overline {\mathbb {Q}}_{\lambda }$ the direct limit of ![]() $E_{\lambda }$ for subfields
$E_{\lambda }$ for subfields ![]() $E\subset \overline {\mathbb {Q}}$ finite over
$E\subset \overline {\mathbb {Q}}$ finite over ![]() $\mathbb {Q}$. Let
$\mathbb {Q}$. Let ![]() $(\widetilde {X},\Phi )$ (respectively,
$(\widetilde {X},\Phi )$ (respectively, ![]() $\widetilde {X}_i$) be the universal cover of the category
$\widetilde {X}_i$) be the universal cover of the category ![]() $\mathcal {C}(X,\Phi )$ (3.2.1) (respectively, the universal étale cover of
$\mathcal {C}(X,\Phi )$ (3.2.1) (respectively, the universal étale cover of ![]() $X_i$) and
$X_i$) and ![]() $\Pi (X,\Phi )$ the automorphism group of
$\Pi (X,\Phi )$ the automorphism group of ![]() $(\widetilde {X},\Phi )/X$, which is isomorphic to
$(\widetilde {X},\Phi )/X$, which is isomorphic to ![]() $\pi _1(X,\Phi,\overline {x})$ after choosing a base point. When
$\pi _1(X,\Phi,\overline {x})$ after choosing a base point. When ![]() $n=1$, we write
$n=1$, we write ![]() $\Pi (X)$ for
$\Pi (X)$ for ![]() $\Pi (X,\Phi )$.
$\Pi (X,\Phi )$.
Following Drinfeld, we define a pro-semisimple group ![]() $\widehat {\Pi }_{\lambda }(X,\Phi )$ over
$\widehat {\Pi }_{\lambda }(X,\Phi )$ over ![]() $\overline {\mathbb {Q}}_{\lambda }$ as follows.
$\overline {\mathbb {Q}}_{\lambda }$ as follows.
(i) When
 $\ell =p$, we denote by
$\ell =p$, we denote by  $\mathcal {T}_{\lambda }(X,\Phi )$ the full subcategory of
$\mathcal {T}_{\lambda }(X,\Phi )$ the full subcategory of  $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ of semisimple objects
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ of semisimple objects  $M$ such that the determinant of each irreducible component of
$M$ such that the determinant of each irreducible component of  $M$ has finite order. This category is a Tannakian full subcategory of
$M$ has finite order. This category is a Tannakian full subcategory of  $\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ and we denote by
$\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}(X)$ and we denote by  $\widehat {\Pi }_{\lambda }(X,\Phi )$ its Tannakian group. By Corollary 4.1.6, the quotient
$\widehat {\Pi }_{\lambda }(X,\Phi )$ its Tannakian group. By Corollary 4.1.6, the quotient  $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)\to \widehat {\Pi }_{\lambda }(X,\Phi )$, induced by the inclusion functor, identifies with the pro-semisimple quotient of
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)\to \widehat {\Pi }_{\lambda }(X,\Phi )$, induced by the inclusion functor, identifies with the pro-semisimple quotient of  $\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$.
$\pi _1^{\operatorname {\mathbf {\Phi -Isoc}^{{{\dagger}} }}}(X)$.(ii) When
 $\ell \neq p$, we define
$\ell \neq p$, we define  $\widehat {\Pi }_{\ell }(X,\Phi )$ to be the
$\widehat {\Pi }_{\ell }(X,\Phi )$ to be the  $\ell$-adic pro-semisimple completion of
$\ell$-adic pro-semisimple completion of  $\Pi (X,\Phi )$ and set
$\Pi (X,\Phi )$ and set  $\widehat {\Pi }_{\lambda }(X,\Phi )=\widehat {\Pi }_{\ell }(X,\Phi )\otimes _{\mathbb {Q}_{\ell }}\overline {\mathbb {Q}}_{\lambda }$ (see [Reference DrinfeldDri18, § 1.2.1]).
$\widehat {\Pi }_{\lambda }(X,\Phi )=\widehat {\Pi }_{\ell }(X,\Phi )\otimes _{\mathbb {Q}_{\ell }}\overline {\mathbb {Q}}_{\lambda }$ (see [Reference DrinfeldDri18, § 1.2.1]).There is an equivalent definition: we define a full subcategory
 $\mathcal {T}_{\lambda }(X,\Phi )$ of the category of lisse
$\mathcal {T}_{\lambda }(X,\Phi )$ of the category of lisse  $\overline {\mathbb {Q}}_{\lambda }$-sheaves on
$\overline {\mathbb {Q}}_{\lambda }$-sheaves on  $X$ with a partial Frobenius structure, formed by semisimple objects
$X$ with a partial Frobenius structure, formed by semisimple objects  $M$ such that the determinant of each irreducible component of
$M$ such that the determinant of each irreducible component of  $M$ has finite order as in part (i). It is a Tannakian category over
$M$ has finite order as in part (i). It is a Tannakian category over  $\overline {\mathbb {Q}}_{\lambda }$ and the associated Tannakian group is isomorphic to
$\overline {\mathbb {Q}}_{\lambda }$ and the associated Tannakian group is isomorphic to  $\widehat {\Pi }_{\lambda }(X,\Phi )$ (cf. [Reference DrinfeldDri18, § 3.6] in the case
$\widehat {\Pi }_{\lambda }(X,\Phi )$ (cf. [Reference DrinfeldDri18, § 3.6] in the case  $n=1$).
$n=1$).
The embedding ![]() $\overline {\mathbb {Q}}\to \overline {\mathbb {Q}}_{\lambda }$ induces an equivalence [Reference DrinfeldDri18, Proposition 2.2.5]:
$\overline {\mathbb {Q}}\to \overline {\mathbb {Q}}_{\lambda }$ induces an equivalence [Reference DrinfeldDri18, Proposition 2.2.5]:
We denote by ![]() $\widehat {\Pi }_{(\lambda )}(X,\Phi )$ the object of
$\widehat {\Pi }_{(\lambda )}(X,\Phi )$ the object of ![]() $\operatorname {Pro-ss}(\overline {\mathbb {Q}})$ associated to
$\operatorname {Pro-ss}(\overline {\mathbb {Q}})$ associated to ![]() $\widehat {\Pi }_{\lambda }(X,\Phi )$ by above equivalence. When
$\widehat {\Pi }_{\lambda }(X,\Phi )$ by above equivalence. When ![]() $n=1$, we omit
$n=1$, we omit ![]() $\Phi$ from the above notation.
$\Phi$ from the above notation.
By Drinfeld's lemma, there exists a canonical isomorphism over ![]() $\overline {\mathbb {Q}}_{\lambda }$:
$\overline {\mathbb {Q}}_{\lambda }$:
 \[ \widehat{\Pi}_{\lambda}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \widehat{\Pi}_{\lambda}(X_i). \]
\[ \widehat{\Pi}_{\lambda}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \widehat{\Pi}_{\lambda}(X_i). \]
When ![]() $\lambda$ divides
$\lambda$ divides ![]() $p$, it follows from taking the pro-semisimple quotient of (2.2.4.1); when
$p$, it follows from taking the pro-semisimple quotient of (2.2.4.1); when ![]() $\lambda$ does not divide
$\lambda$ does not divide ![]() $p$, it follows from (3.3.2.1) and taking the
$p$, it follows from (3.3.2.1) and taking the ![]() $\ell$-adic pro-semisimple completion. Via the equivalence (4.2.2.1), we obtain an isomorphism over
$\ell$-adic pro-semisimple completion. Via the equivalence (4.2.2.1), we obtain an isomorphism over ![]() $\overline {\mathbb {Q}}$:
$\overline {\mathbb {Q}}$:
 \begin{equation} \widehat{\Pi}_{(\lambda)}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \widehat{\Pi}_{(\lambda)}(X_i). \end{equation}
\begin{equation} \widehat{\Pi}_{(\lambda)}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \widehat{\Pi}_{(\lambda)}(X_i). \end{equation}4.2.3 We review some constructions in [Reference DrinfeldDri18]. For each ![]() $i$, let
$i$, let ![]() $|\widetilde {X}_i|^\circ$ be the set of closed points of
$|\widetilde {X}_i|^\circ$ be the set of closed points of ![]() $\widetilde {X}_i$. We have a canonical
$\widetilde {X}_i$. We have a canonical ![]() $\Pi (X_i)$-equivariant map [Reference DrinfeldDri18, (1.1)]:
$\Pi (X_i)$-equivariant map [Reference DrinfeldDri18, (1.1)]:
where ![]() $F_{\tilde {x}}$ denotes the geometric Frobenius automorphism at
$F_{\tilde {x}}$ denotes the geometric Frobenius automorphism at ![]() $\widetilde {x}$.
$\widetilde {x}$.
The set ![]() $\Pi (X_i)$ contains a dense subset
$\Pi (X_i)$ contains a dense subset ![]() $\Pi _{\operatorname {Fr}}(X_i)$ formed by the elements
$\Pi _{\operatorname {Fr}}(X_i)$ formed by the elements ![]() $F_{\tilde {x}}^n$ for
$F_{\tilde {x}}^n$ for ![]() $\tilde {x}\in |\widetilde {X}_i|^\circ$ and
$\tilde {x}\in |\widetilde {X}_i|^\circ$ and ![]() $n\in \mathbb {Z}_{\ge 0}$. The group
$n\in \mathbb {Z}_{\ge 0}$. The group ![]() $\Pi (X_i)$ acts on
$\Pi (X_i)$ acts on ![]() $\Pi _{\operatorname {Fr}}(X_i)$ by conjugation. We denote by
$\Pi _{\operatorname {Fr}}(X_i)$ by conjugation. We denote by ![]() $\widetilde {\Pi }_{\operatorname {Fr}}(X_i):=\mathbb {Z}_{\ge 0}\times |\widetilde {X}|^\circ$. One has the canonical
$\widetilde {\Pi }_{\operatorname {Fr}}(X_i):=\mathbb {Z}_{\ge 0}\times |\widetilde {X}|^\circ$. One has the canonical ![]() $\Pi (X_i)$-equivariant surjection:
$\Pi (X_i)$-equivariant surjection:
For any pro-reductive group ![]() $G$, let
$G$, let ![]() $[G]$ denote the geometric invariant theory (GIT) quotient of
$[G]$ denote the geometric invariant theory (GIT) quotient of ![]() $G$ by the conjugation action of the neutral component
$G$ by the conjugation action of the neutral component ![]() $G^{\circ }$. By Theorem 3.3.2, we have an adjoint action of
$G^{\circ }$. By Theorem 3.3.2, we have an adjoint action of ![]() $\Pi (X,\Phi )$ on
$\Pi (X,\Phi )$ on ![]() $[\widehat {\Pi }_{(\lambda )}(X,\Phi )]$ and a canonical
$[\widehat {\Pi }_{(\lambda )}(X,\Phi )]$ and a canonical ![]() $\Pi (X,\Phi )$-equivariant map
$\Pi (X,\Phi )$-equivariant map ![]() $[\widehat {\Pi }_{(\lambda )}(X,\Phi )]\twoheadrightarrow \Pi (X,\Phi )$.
$[\widehat {\Pi }_{(\lambda )}(X,\Phi )]\twoheadrightarrow \Pi (X,\Phi )$.
The map (4.2.3.1) has a canonical lift to a ![]() $\Pi (X_i)$-equivariant map (cf. [Reference DrinfeldDri18, §§ 7.2.4, 7.3.5])
$\Pi (X_i)$-equivariant map (cf. [Reference DrinfeldDri18, §§ 7.2.4, 7.3.5])
By the companion theorem [Reference AbeAbe18b, Reference Abe and EsnaultAE19, Reference KedlayaKed22b, Reference KedlayaKed23b], the above map factors as [Reference DrinfeldDri18, Corollary 7.4.2]
For any non-Archimedean place ![]() $\lambda$ of
$\lambda$ of ![]() $\overline {\mathbb {Q}}$, we have the following diagram of sets.
$\overline {\mathbb {Q}}$, we have the following diagram of sets.
Via the isomorphism (4.2.2.2), we obtain the following diagram of sets.
 \begin{equation} \prod_{i=1}^n \Pi_{\operatorname{Fr}}(X_i) \to [\widehat{\Pi}_{(\lambda)}(X,\Phi)](\overline{\mathbb{Q}})\twoheadrightarrow \Pi(X,\Phi)\end{equation}
\begin{equation} \prod_{i=1}^n \Pi_{\operatorname{Fr}}(X_i) \to [\widehat{\Pi}_{(\lambda)}(X,\Phi)](\overline{\mathbb{Q}})\twoheadrightarrow \Pi(X,\Phi)\end{equation}The result of [Reference DrinfeldDri18, Theorem 1.4.1] can be generalized as follow.
Proposition 4.2.4 Let ![]() $\lambda, \lambda '$ be non-Archimedean places of
$\lambda, \lambda '$ be non-Archimedean places of ![]() $\overline {\mathbb {Q}}$. There exists a unique isomorphism
$\overline {\mathbb {Q}}$. There exists a unique isomorphism
in the category ![]() $\operatorname {Pro-ss}(\overline {\mathbb {Q}})$ which sends the diagram (4.2.3.3) to the corresponding diagram for
$\operatorname {Pro-ss}(\overline {\mathbb {Q}})$ which sends the diagram (4.2.3.3) to the corresponding diagram for ![]() $\widehat {\Pi }_{(\lambda ')}$.
$\widehat {\Pi }_{(\lambda ')}$.
Proof. When ![]() $n=1$ (i.e. we do not consider partial Frobenius structures), Drinfeld proved the above result for higher-dimensional smooth geometrically connected
$n=1$ (i.e. we do not consider partial Frobenius structures), Drinfeld proved the above result for higher-dimensional smooth geometrically connected ![]() $k$-varieties if
$k$-varieties if ![]() $\lambda,\lambda '$ do not divide
$\lambda,\lambda '$ do not divide ![]() $p$ and the result in the curve case when
$p$ and the result in the curve case when ![]() $\lambda$ or
$\lambda$ or ![]() $\lambda '$ divides
$\lambda '$ divides ![]() $p$ (see [Reference DrinfeldDri18, Theorem 1.4.1, 5.2.1]). Now we can obtain the full generality of the theorem in the case
$p$ (see [Reference DrinfeldDri18, Theorem 1.4.1, 5.2.1]). Now we can obtain the full generality of the theorem in the case ![]() $n=1$ using the recent breakthrough in the companion theorem for
$n=1$ using the recent breakthrough in the companion theorem for ![]() $p$-adic coefficients [Reference Abe and EsnaultAE19, Reference KedlayaKed22b, Reference KedlayaKed23b] over smooth
$p$-adic coefficients [Reference Abe and EsnaultAE19, Reference KedlayaKed22b, Reference KedlayaKed23b] over smooth ![]() $k$-varieties and the same argument of [Reference DrinfeldDri18].
$k$-varieties and the same argument of [Reference DrinfeldDri18].
In general, the isomorphism ![]() $\prod _{i=1}^n \widehat {\Pi }_{(\lambda )}(X_i)\xrightarrow {\sim } \prod _{i=1}^n \widehat {\Pi }_{(\lambda ')}(X_i)$, obtained in the case
$\prod _{i=1}^n \widehat {\Pi }_{(\lambda )}(X_i)\xrightarrow {\sim } \prod _{i=1}^n \widehat {\Pi }_{(\lambda ')}(X_i)$, obtained in the case ![]() $n=1$, induces an isomorphism
$n=1$, induces an isomorphism ![]() $\widehat {\Pi }_{(\lambda )}(X,\Phi )\xrightarrow {\sim } \widehat {\Pi }_{(\lambda ')}(X,\Phi )$, which fits into the following diagram.
$\widehat {\Pi }_{(\lambda )}(X,\Phi )\xrightarrow {\sim } \widehat {\Pi }_{(\lambda ')}(X,\Phi )$, which fits into the following diagram.

In view of the definition of (4.2.3.3), the required properties and the uniqueness follows from the case ![]() $n=1$.
$n=1$.
Corollary 4.2.5 The neutral component ![]() $\widehat {\Pi }^{\circ }_{(\lambda )}(X,\Phi )$ is simply connected.
$\widehat {\Pi }^{\circ }_{(\lambda )}(X,\Phi )$ is simply connected.
Proof. We may assume that ![]() $\lambda$ is coprime to
$\lambda$ is coprime to ![]() $p$. Then the statement follows from isomorphism (4.2.2.2) and [Reference DrinfeldDri18, Proposition 3.3.4].
$p$. Then the statement follows from isomorphism (4.2.2.2) and [Reference DrinfeldDri18, Proposition 3.3.4].
4.2.6 Let ![]() $\lambda$ be a non-Archimedean place of
$\lambda$ be a non-Archimedean place of ![]() $\overline {\mathbb {Q}}$. In [Reference DrinfeldDri18, § 6], Drinfeld defined a pro-reductive group
$\overline {\mathbb {Q}}$. In [Reference DrinfeldDri18, § 6], Drinfeld defined a pro-reductive group ![]() $\widehat {\Pi }^{\operatorname {mot}}_{(\lambda )}$ over
$\widehat {\Pi }^{\operatorname {mot}}_{(\lambda )}$ over ![]() $\overline {\mathbb {Q}}$ (independent of
$\overline {\mathbb {Q}}$ (independent of ![]() $\lambda$ up to unique isomorphisms) and introduced an unconditional definition of motivic Langlands parameters proposed by V. Lafforgue [Reference LafforgueLaf18].
$\lambda$ up to unique isomorphisms) and introduced an unconditional definition of motivic Langlands parameters proposed by V. Lafforgue [Reference LafforgueLaf18].
Now we introduce its variant ![]() $\widehat {\Pi }^{\operatorname {mot}}_{(\lambda )}(X,\Phi )$ with partial Frobenius. Let
$\widehat {\Pi }^{\operatorname {mot}}_{(\lambda )}(X,\Phi )$ with partial Frobenius. Let ![]() $\mathcal {W}_p\subset \overline {\mathbb {Q}}^{\times }$ denote the subgroup of
$\mathcal {W}_p\subset \overline {\mathbb {Q}}^{\times }$ denote the subgroup of ![]() $p$-Weil numbers. For every
$p$-Weil numbers. For every ![]() $n\ge 1$, we set
$n\ge 1$, we set ![]() $D_n:=\operatorname {Hom}(\mathcal {W}_p,\mathbb {G}_m^n)$ and
$D_n:=\operatorname {Hom}(\mathcal {W}_p,\mathbb {G}_m^n)$ and ![]() $D_{n,\lambda }:=D_n\otimes _{\overline {\mathbb {Q}}}\overline {\mathbb {Q}}_{\lambda }$ (see [Reference DrinfeldDri18, § 6.1]). Note that the group
$D_{n,\lambda }:=D_n\otimes _{\overline {\mathbb {Q}}}\overline {\mathbb {Q}}_{\lambda }$ (see [Reference DrinfeldDri18, § 6.1]). Note that the group ![]() $\pi _0(D_n)$ identifies with the group
$\pi _0(D_n)$ identifies with the group ![]() $\operatorname {Hom}(\mu _{\infty }(\overline {\mathbb {Q}}),\mathbb {G}_m^n)\simeq \widehat {\mathbb {Z}}^n$.
$\operatorname {Hom}(\mu _{\infty }(\overline {\mathbb {Q}}),\mathbb {G}_m^n)\simeq \widehat {\mathbb {Z}}^n$.
On the other hand, we have a canonical surjection:
Following [Reference DrinfeldDri18, § 6.1], we define ![]() $\widehat {\Pi }_{(\lambda )}^{\operatorname {mot}}(X,\Phi )$ as the fiber product of
$\widehat {\Pi }_{(\lambda )}^{\operatorname {mot}}(X,\Phi )$ as the fiber product of ![]() $\widehat {\Pi }_{(\lambda )}(X,\Phi )$ and
$\widehat {\Pi }_{(\lambda )}(X,\Phi )$ and ![]() $D_{n}$ over
$D_{n}$ over ![]() $\widehat {\mathbb {Z}}^{n}$. Then we can upgrade the isomorphism (4.2.2.2) to be an isomorphism in
$\widehat {\mathbb {Z}}^{n}$. Then we can upgrade the isomorphism (4.2.2.2) to be an isomorphism in ![]() $\operatorname {Pro-red}(\overline {\mathbb {Q}})$:
$\operatorname {Pro-red}(\overline {\mathbb {Q}})$:
 \begin{equation} \widehat{\Pi}_{(\lambda)}^{\operatorname{mot}}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \widehat{\Pi}_{(\lambda)}^{\operatorname{mot}}(X_i). \end{equation}
\begin{equation} \widehat{\Pi}_{(\lambda)}^{\operatorname{mot}}(X,\Phi)\xrightarrow{\sim} \prod_{i=1}^n \widehat{\Pi}_{(\lambda)}^{\operatorname{mot}}(X_i). \end{equation}
Note that the above isomorphism is independent of ![]() $\lambda$ by Proposition 4.2.4.
$\lambda$ by Proposition 4.2.4.
5. Local Drinfeld's lemma over polyannuli
We assume ![]() $(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$. For a connected subinterval
$(k,\sigma )=(\mathbb {F}_q,\operatorname {id}_{\mathscr {O}_K})$. For a connected subinterval ![]() $I$ of
$I$ of ![]() $(0,\infty )$, we denote by
$(0,\infty )$, we denote by ![]() $A_K[I]$ the rigid annulus
$A_K[I]$ the rigid annulus ![]() $|t|\in I$ over
$|t|\in I$ over ![]() $K$. Recall that the Robba ring
$K$. Recall that the Robba ring ![]() $\mathcal {R}$ over
$\mathcal {R}$ over ![]() $K$ is defined as
$K$ is defined as
Let ![]() $n$ be a positive integer. We consider the
$n$ be a positive integer. We consider the ![]() $n$-fold Robba ring
$n$-fold Robba ring ![]() $\mathcal {R}^n$ over
$\mathcal {R}^n$ over ![]() $K$:
$K$:
 \begin{align*} \mathcal{R}^n &:= \lim_{\varepsilon_1,\ldots,\varepsilon_n\to 1} \mathscr{O}\bigg(\prod_{i=1}^n A_K[\varepsilon_i,1[\bigg)\\ &= \bigg\{\sum_{I=(i_1,\ldots,i_n)} a_I \underline{t}^I ;~ |a_I|\underline{\rho}^I \to 0 ~(|i_1|+\cdots+|i_n|\to \infty), \forall \rho_i\in [\varepsilon_i,1[ \text{ for some } \varepsilon_i\in\, ]0,1[ \bigg\}, \end{align*}
\begin{align*} \mathcal{R}^n &:= \lim_{\varepsilon_1,\ldots,\varepsilon_n\to 1} \mathscr{O}\bigg(\prod_{i=1}^n A_K[\varepsilon_i,1[\bigg)\\ &= \bigg\{\sum_{I=(i_1,\ldots,i_n)} a_I \underline{t}^I ;~ |a_I|\underline{\rho}^I \to 0 ~(|i_1|+\cdots+|i_n|\to \infty), \forall \rho_i\in [\varepsilon_i,1[ \text{ for some } \varepsilon_i\in\, ]0,1[ \bigg\}, \end{align*}
where ![]() $\underline {t}^I:=t_1^{i_1}\cdots t_n^{i_n}$ and
$\underline {t}^I:=t_1^{i_1}\cdots t_n^{i_n}$ and ![]() $\rho ^I:=\rho _1^{i_1}\cdots \rho _n^{i_n}$. For any algebraic extension
$\rho ^I:=\rho _1^{i_1}\cdots \rho _n^{i_n}$. For any algebraic extension ![]() $L/K$, we set
$L/K$, we set
Let ![]() $h$ be an integer
$h$ be an integer ![]() $\ge 1$, and
$\ge 1$, and ![]() $\sigma$ a continuous automorphism of
$\sigma$ a continuous automorphism of ![]() $\overline {\mathbb {Q}}_p$ lifting the
$\overline {\mathbb {Q}}_p$ lifting the ![]() $h$th Frobenius on
$h$th Frobenius on ![]() $\overline {k}$ and preserving each finite extension
$\overline {k}$ and preserving each finite extension ![]() $L$ of
$L$ of ![]() $K$. We denote by
$K$. We denote by ![]() $\phi _i\colon \mathcal {R}^n\to \mathcal {R}^n$ the
$\phi _i\colon \mathcal {R}^n\to \mathcal {R}^n$ the ![]() $K$-linear endomorphism defined by
$K$-linear endomorphism defined by ![]() $t_i\mapsto t_i^{p^h}$ and
$t_i\mapsto t_i^{p^h}$ and ![]() $t_j\mapsto t_j$ if
$t_j\mapsto t_j$ if ![]() $j\neq i$.
$j\neq i$.
We consider the category ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ of free
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ of free ![]() $\mathcal {R}^n$-modules of finite rank equipped with an integrable
$\mathcal {R}^n$-modules of finite rank equipped with an integrable ![]() $K$-linear connection and we denote by
$K$-linear connection and we denote by ![]() $\operatorname {\mathbf {MIC}}^{\operatorname {uni}}(\mathcal {R}^n/K)$ its full subcategory consisting of unipotent objects, which is isomorphic to a successive extension of the trivial connection over
$\operatorname {\mathbf {MIC}}^{\operatorname {uni}}(\mathcal {R}^n/K)$ its full subcategory consisting of unipotent objects, which is isomorphic to a successive extension of the trivial connection over ![]() $\mathcal {R}^n$.
$\mathcal {R}^n$.
A partial Frobenius structure of order ![]() $h$ (respectively, a partial Frobenius structure) on an object
$h$ (respectively, a partial Frobenius structure) on an object ![]() $(M,\nabla )$ of
$(M,\nabla )$ of ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ consists of isomorphisms
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ consists of isomorphisms ![]() $\varphi _i\colon (\sigma \circ \phi _i)^*(M,\nabla )\simeq (M,\nabla )$ of
$\varphi _i\colon (\sigma \circ \phi _i)^*(M,\nabla )\simeq (M,\nabla )$ of ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ commuting with each other (respectively, without specifying order
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ commuting with each other (respectively, without specifying order ![]() $h$). We denote by
$h$). We denote by ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K,\Phi )$ the full subcategory of
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K,\Phi )$ the full subcategory of ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ consisting of objects whose irreducible subquotients can be equipped with a partial Frobenius structure (of order
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K)$ consisting of objects whose irreducible subquotients can be equipped with a partial Frobenius structure (of order ![]() $h'$ with
$h'$ with ![]() $h|h'$). Note that a unipotent object lies in
$h|h'$). Note that a unipotent object lies in ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K,\Phi )$.
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K,\Phi )$.
Let ![]() $K^{\operatorname {ur}}$ be the maximal unramified extension of
$K^{\operatorname {ur}}$ be the maximal unramified extension of ![]() $K$ in
$K$ in ![]() $\overline {\mathbb {Q}}_p$. We can extend above definition to free
$\overline {\mathbb {Q}}_p$. We can extend above definition to free ![]() $\mathcal {R}^n_{K^{\operatorname {ur}}}$-modules of finite rank with an integrable
$\mathcal {R}^n_{K^{\operatorname {ur}}}$-modules of finite rank with an integrable ![]() $K^{\operatorname {ur}}$-linear connection. Note that an object of
$K^{\operatorname {ur}}$-linear connection. Note that an object of ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}})$ comes from the extension of scalars of an object of
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}})$ comes from the extension of scalars of an object of ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{L}/L)$ for an unramified finite extension
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{L}/L)$ for an unramified finite extension ![]() $L/K$.
$L/K$.
Let ![]() $\mathcal {K}:=k( (t))$,
$\mathcal {K}:=k( (t))$, ![]() $G_{\mathcal {K}}:=\operatorname {Gal}(\mathcal {K}^{}/\mathcal {K})$, and
$G_{\mathcal {K}}:=\operatorname {Gal}(\mathcal {K}^{}/\mathcal {K})$, and ![]() $I_{\mathcal {K}}$ the inertia subgroup of the Galois group
$I_{\mathcal {K}}$ the inertia subgroup of the Galois group ![]() $G_{\mathcal {K}}$. We reformulate the local monodromy theorem for
$G_{\mathcal {K}}$. We reformulate the local monodromy theorem for ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K,\Phi )$ (see [Reference KedlayaKed22c, Theorem 3.3.6]) as follows; this generalizes André's result [Reference AndréAnd02, Théorème 7.1.1] to polyannuli.
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n/K,\Phi )$ (see [Reference KedlayaKed22c, Theorem 3.3.6]) as follows; this generalizes André's result [Reference AndréAnd02, Théorème 7.1.1] to polyannuli.
Theorem 5.0.1 The category ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}},\Phi )$ is a neutral Tannakian category over
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}},\Phi )$ is a neutral Tannakian category over ![]() $K^{\operatorname {ur}}$ and its Tannakian group is isomorphic to
$K^{\operatorname {ur}}$ and its Tannakian group is isomorphic to ![]() $(I_{\mathcal {K}}\times \mathbb {G}_{a})^n$.
$(I_{\mathcal {K}}\times \mathbb {G}_{a})^n$.
5.1 Unipotent connections on polyannuli
Proposition 5.1.1 The functor ![]() $(V,N_1,\ldots,N_n) \mapsto (V\otimes _K \mathcal {R},\nabla _{\mathcal {N}})$, where the connection
$(V,N_1,\ldots,N_n) \mapsto (V\otimes _K \mathcal {R},\nabla _{\mathcal {N}})$, where the connection ![]() $\nabla _{\mathcal {N}}$ is defined by
$\nabla _{\mathcal {N}}$ is defined by
 \[ \nabla_{\mathcal{N}}(v \otimes 1):= \sum_{i=1}^n N_iv\otimes \frac{dt_i}{t_i}, \]
\[ \nabla_{\mathcal{N}}(v \otimes 1):= \sum_{i=1}^n N_iv\otimes \frac{dt_i}{t_i}, \]
induces an equivalence of tensor categories between the category of finite dimensional ![]() $K$-vector spaces with
$K$-vector spaces with ![]() $n$ commuting nilpotent operators
$n$ commuting nilpotent operators ![]() $\mathcal {N}=(N_1,\ldots,N_n)$ and the category
$\mathcal {N}=(N_1,\ldots,N_n)$ and the category ![]() $\operatorname {\mathbf {MIC}}^{\operatorname {uni}}(\mathcal {R}^n/K)$.
$\operatorname {\mathbf {MIC}}^{\operatorname {uni}}(\mathcal {R}^n/K)$.
Proof. We construct a quasi-inverse of the above functor. Let ![]() $(M,\nabla )$ be a unipotent connection on a polyannulus
$(M,\nabla )$ be a unipotent connection on a polyannulus ![]() $\prod _{i=1}^n A_K[\varepsilon _i,1[$. The operators
$\prod _{i=1}^n A_K[\varepsilon _i,1[$. The operators ![]() $\partial _i:=\nabla (t_i ({d}/{d t_i}))$ on
$\partial _i:=\nabla (t_i ({d}/{d t_i}))$ on ![]() $M$ commute with each other; set
$M$ commute with each other; set ![]() $\partial :=\partial _1\circ \cdots \circ \partial _n$. Since
$\partial :=\partial _1\circ \cdots \circ \partial _n$. Since ![]() $(M,\nabla )$ is unipotent, the
$(M,\nabla )$ is unipotent, the ![]() $K$-vector space
$K$-vector space ![]() $V:=\cup _{n\ge 1} (\operatorname {Ker} \partial )^n$ has the same rank as
$V:=\cup _{n\ge 1} (\operatorname {Ker} \partial )^n$ has the same rank as ![]() $M$. We claim that the operator
$M$. We claim that the operator ![]() $\partial _i$ is nilpotent on
$\partial _i$ is nilpotent on ![]() $V$. Indeed, if
$V$. Indeed, if ![]() $x$ is a point of the polyannulus
$x$ is a point of the polyannulus ![]() $\prod _{j\neq i} A_K[\varepsilon _j,1[$, then its fiber
$\prod _{j\neq i} A_K[\varepsilon _j,1[$, then its fiber ![]() $(M_x,\nabla _x)$ is a unipotent connection over the annulus
$(M_x,\nabla _x)$ is a unipotent connection over the annulus ![]() $A_{K(x)}[\varepsilon _i,1[$. We deduce that
$A_{K(x)}[\varepsilon _i,1[$. We deduce that ![]() $\partial _i$ is nilpotent on
$\partial _i$ is nilpotent on ![]() $V\otimes _K K(x)$ and the claim follows. Then
$V\otimes _K K(x)$ and the claim follows. Then
defines a quasi-inverse functor. The proposition follows.
Remark 5.1.2 Unlike the case of an annulus [Reference MatsudaMat02, Lemma 4.3], a unipotent object on a polyannulus may not admit a Frobenius structure.
5.1.3. Proof of Theorem 5.0.1
Let ![]() $(M,\nabla )$ be an object of
$(M,\nabla )$ be an object of ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}},\Phi )$ defined on a polyannulus
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}},\Phi )$ defined on a polyannulus ![]() $\prod _{i=1}^n A_{K^{\operatorname {ur}}}[\varepsilon _i,1[$. By [Reference KedlayaKed22c, Theorem 3.3.6], there exist eligible étale covers
$\prod _{i=1}^n A_{K^{\operatorname {ur}}}[\varepsilon _i,1[$. By [Reference KedlayaKed22c, Theorem 3.3.6], there exist eligible étale covers ![]() $\{Y_i\to A_{K^{\operatorname {ur}}}[\varepsilon _i,1[\}_{i=1}^n$ such that the pullback of
$\{Y_i\to A_{K^{\operatorname {ur}}}[\varepsilon _i,1[\}_{i=1}^n$ such that the pullback of ![]() $(M,\nabla )$ to
$(M,\nabla )$ to ![]() $\prod _{i=1}^n Y_i$ is unipotent. Then by Proposition 5.1.1, we obtain a fiber functor:
$\prod _{i=1}^n Y_i$ is unipotent. Then by Proposition 5.1.1, we obtain a fiber functor:
by forgetting nilpotent operators. This makes ![]() $\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}},\Phi )$ into a neutral Tannakian category over
$\operatorname {\mathbf {MIC}}(\mathcal {R}^n_{K^{\operatorname {ur}}}/K^{\operatorname {ur}},\Phi )$ into a neutral Tannakian category over ![]() $K^{\operatorname {ur}}$. In this way, we obtain a continuous action of
$K^{\operatorname {ur}}$. In this way, we obtain a continuous action of ![]() $I_{\mathcal {K}}^n$ on
$I_{\mathcal {K}}^n$ on ![]() $\omega (M,\nabla )$ via
$\omega (M,\nabla )$ via ![]() $I_{\mathcal {K}}^n\to \prod \operatorname {Aut}(Y_i/A_{K^{\operatorname {ur}}}[I])$, which commutes with the action of nilpotent operators. Then the theorem follows.
$I_{\mathcal {K}}^n\to \prod \operatorname {Aut}(Y_i/A_{K^{\operatorname {ur}}}[I])$, which commutes with the action of nilpotent operators. Then the theorem follows.
5.2 Construction of Weil–Deligne representations
In this subsection, we briefly review representations of a self-product of the Weil group of ![]() $\mathcal {K}$ associated to differential modules with a partial Frobenius structure on polyannuli, following [Reference MarmoraMar08].
$\mathcal {K}$ associated to differential modules with a partial Frobenius structure on polyannuli, following [Reference MarmoraMar08].
5.2.1 Recall that ![]() $q=p^s$ is the cardinality of
$q=p^s$ is the cardinality of ![]() $k$. We denote by
$k$. We denote by ![]() $\Phi \text {-}\mathbf {MIC}(\mathcal {R}^n/K)$ the category of free modules over
$\Phi \text {-}\mathbf {MIC}(\mathcal {R}^n/K)$ the category of free modules over ![]() $\mathcal {R}^n$ equipped with an integrable
$\mathcal {R}^n$ equipped with an integrable ![]() $K$-linear connection and a partial Frobenius structure of order
$K$-linear connection and a partial Frobenius structure of order ![]() $s$.
$s$.
We denote by ![]() $\operatorname {\mathbf {Del}}_{K^{\operatorname {ur}}}(G_{\mathcal {K}}^n)$ the category of triples
$\operatorname {\mathbf {Del}}_{K^{\operatorname {ur}}}(G_{\mathcal {K}}^n)$ the category of triples ![]() $(V,\varphi _1,\ldots,\varphi _n,N_1,\ldots,N_n)$ consisting of a continuous semilinear representation of
$(V,\varphi _1,\ldots,\varphi _n,N_1,\ldots,N_n)$ consisting of a continuous semilinear representation of ![]() $G_{\mathcal {K}}^n$ on a finite-dimensional
$G_{\mathcal {K}}^n$ on a finite-dimensional ![]() $K^{\operatorname {ur}}$-vector space
$K^{\operatorname {ur}}$-vector space ![]() $V$ (with discrete topology),
$V$ (with discrete topology), ![]() $\sigma$-semilinear equivariant Frobenius isomorphisms
$\sigma$-semilinear equivariant Frobenius isomorphisms ![]() $\{\varphi _i\}_{i=1}^n$ on
$\{\varphi _i\}_{i=1}^n$ on ![]() $V$ commuting with each other, and equivariant monodromy operators
$V$ commuting with each other, and equivariant monodromy operators ![]() $\{N_i\colon V\to V\}_{i=1}^n$ commuting with each other satisfying
$\{N_i\colon V\to V\}_{i=1}^n$ commuting with each other satisfying ![]() $N_i\varphi _j=q^{\delta _{ij}}\varphi _jN_i$ for
$N_i\varphi _j=q^{\delta _{ij}}\varphi _jN_i$ for ![]() $i,j=1,\ldots,n$.
$i,j=1,\ldots,n$.
The proof of Theorem 5.0.1 shows that there exists a canonical tensor functor:
5.2.2 Let ![]() $W_{\mathcal {K}}$ be the Weil group of
$W_{\mathcal {K}}$ be the Weil group of ![]() $\mathcal {K}$ and
$\mathcal {K}$ and ![]() $v_i\colon W_{\mathcal {K}}^n\to \mathbb {Z}$ the projection on the
$v_i\colon W_{\mathcal {K}}^n\to \mathbb {Z}$ the projection on the ![]() $i$th component. We consider the category
$i$th component. We consider the category ![]() $\mathbf {Rep}_{K^{\operatorname {ur}}}(\operatorname {WD}^n_{\mathcal {K}})$ of pairs
$\mathbf {Rep}_{K^{\operatorname {ur}}}(\operatorname {WD}^n_{\mathcal {K}})$ of pairs ![]() $(V,N_1,\ldots,N_n)$ consisting of a continuous linear representation
$(V,N_1,\ldots,N_n)$ consisting of a continuous linear representation ![]() $\rho$ of
$\rho$ of ![]() $W_{\mathcal {K}}^n$ on a finite-dimensional
$W_{\mathcal {K}}^n$ on a finite-dimensional ![]() $K^{\operatorname {ur}}$-vector space
$K^{\operatorname {ur}}$-vector space ![]() $V$ (with discrete topology), monodromy operators
$V$ (with discrete topology), monodromy operators ![]() $\{N_i\}_{i=1}^n$ commuting with each other satisfying
$\{N_i\}_{i=1}^n$ commuting with each other satisfying ![]() $N_i\rho (g)=q^{v_i(g)}\rho (g)N_i$ for
$N_i\rho (g)=q^{v_i(g)}\rho (g)N_i$ for ![]() $i=1,\ldots,n$, and
$i=1,\ldots,n$, and ![]() $g\in W_{\mathcal {K}}^n$. When
$g\in W_{\mathcal {K}}^n$. When ![]() $n=1$, this is the category of Weil–Deligne representations of
$n=1$, this is the category of Weil–Deligne representations of ![]() $W_{\mathcal {K}}$.
$W_{\mathcal {K}}$.
We have a Frobenius linearization functor
sending ![]() $(V,\varphi _i,N_i)$ to a continuous linear representation
$(V,\varphi _i,N_i)$ to a continuous linear representation ![]() $\rho$ of
$\rho$ of ![]() $W_{\mathcal {K}}^n$ on
$W_{\mathcal {K}}^n$ on ![]() $V$ defined by
$V$ defined by
 \[ \rho(g)(m):=g\bigg(\prod_{i=1}^n \varphi^{v_i(g)}_i(m)\bigg), \]
\[ \rho(g)(m):=g\bigg(\prod_{i=1}^n \varphi^{v_i(g)}_i(m)\bigg), \]
together with monodromy operators ![]() $\{N_i\}_{i=1}^n$. In summary, we obtain a tensor functor:
$\{N_i\}_{i=1}^n$. In summary, we obtain a tensor functor:
Conflicts of Interest
None.