1. Introduction
Farmland prices play a critical role in the agricultural economy. Farmland is the primary store of farmers’ wealth and is the leading source of collateral in agricultural loans (Nickerson et al., Reference Nickerson, Morehart, Kuethe, Beckman, Ifft and Williams2012). As a result, changes in aggregate farmland prices influence lenders’ ability and willingness to provide liquidity to the agricultural sector (Briggeman, Gunderson, and Gloy, Reference Briggeman, Gunderson and Gloy2009). The recent experiences of the farmland markets have brought increased interest in the future of farm real estate prices. Between 2003 and 2013, farmland values in many parts of the United States exhibited unprecedented appreciation rates. The sudden increase in appreciation rates was troubling to many market participants given prior evidence that farmland prices have a tendency to overreact to short-run changes in market fundamentals (Falk and Lee, Reference Falk and Lee1998). Many researchers questioned the degree to which farmland prices were in a “bubble” (Olsen and Stokes, Reference Olsen and Stokes2015; Stokes and Cox, Reference Stokes and Cox2014).
Farmland prices, however, are difficult to forecast empirically. At a parcel level, farmland prices are determined by a complex set of factors, including agricultural productivity, locational amenities, and farm policy (Ifft, Kuethe, and Morehart, Reference Ifft, Kuethe and Morehart2015). In addition, a number of economic factors, including broader real estate market trends and overall macroeconomic conditions, influence the dynamics of aggregate farmland prices (Kuethe, Hubbs, and Morehart, Reference Kuethe, Hubbs and Morehart2014; Stokes and Cox, Reference Stokes and Cox2014). However, a growing body of literature suggests that subjective forecasts of economic variables derived from aggregate opinions of market participants and experts may outperform traditional empirical forecasts (see Faust and Wright, Reference Faust, Wright, Elliot and Timmermann2013). In the case of farmland price forecasts, previous studies demonstrate that qualitative opinion surveys of agricultural bankers conducted by Federal Reserve banks provide useful information on the future direction of farm real estate values (Covey, Reference Covey1999; Zakrzewicz, Brorsen, and Briggeman, Reference Zakrzewicz, Brorsen and Briggeman2013).
Although Covey (Reference Covey1999) and Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013) examine the accuracy of probability forecasts provided by the Federal Reserve surveys using qualitative forecast evaluation methods, this study examines the degree to which these surveys satisfy the properties of forecast optimality as defined by Diebold and Lopez (Reference Diebold, Lopez, Maddala and Rao1996). According to Diebold and Lopez (Reference Diebold, Lopez, Maddala and Rao1996), a forecast is optimal if it is both unbiased and efficient. A forecast is unbiased if it does not consistently differ from observed outcomes, and a forecast is efficient if it contains all information available at the time of the forecast. The empirical tests of forecast optimality are difficult to estimate for qualitative forecasts.
The Federal Reserve surveys are qualitative because they ask respondents whether they believe farmland values in the next quarter (3 months) are likely to be higher, lower, or stable (no change). This form of elicitation is not unique to the Federal Reserve surveys but is common across an array of economic surveys, such as the Livingston Survey and the University of Michigan Surveys of Consumers. The use of categorical (qualitative) responses to measure expectations was originally developed because it was believed that respondents would be unlikely to complete a survey that requires exact cardinal responses (Theil, Reference Theil1955). In addition, it is believed that categorical responses are less likely to be subject to measurement error than direct attempts at cardinal measurement (Pesaran, Reference Pesaran, Malgrange and Muett1984, p. 34). Because qualitative forecasts are common in economic and business surveys, econometricians have developed a number of empirical techniques to convert categorical expectations into quantitative estimates of the underlying distribution of respondents’ cardinal expectations (Nardo, Reference Nardo2003; Smith and McAleer, Reference Smith and McAleer1995). Quantified qualitative survey data have been used extensively in other areas of applied economics to test higher-order forecast properties, like bias and efficiencies (Pesaran and Weale, Reference Pesaran, Weale, Elliot, Granger and Timmerman2006), yet the methods have received limited application in the agricultural economics literature.
This study uses qualitative forecast evaluation methods to examine the accuracy of quarterly farm real estate price forecast of the Federal Reserve Bank of Chicago's Land Values and Credit Conditions Survey in a manner similar to Covey (Reference Covey1999) and Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013). Similar to Covey (Reference Covey1999), we find that bankers’ predictions are less accurate than those of a naïve relative frequency forecast, and they predict more positive and negative price movements than observed. We then convert the qualitative responses to quantitative expectations and subject the quantified forecasts to additional tests of forecast optimality. The tests suggest that the bankers’ forecasts are unbiased but inefficient. In other words, the inaccuracy of the bankers’ predictions is likely the result of the inability to fully reflect all information available at the time of the forecast.
2. Data
Each quarter, the Federal Reserve Bank of Chicago's Land Values and Credit Conditions Survey collects current and expected credit market information from agricultural bankers throughout the Federal Reserve's Seventh District. The Federal Reserve publishes regular updates of the survey results through the Federal Reserve Bank of Chicago's AgLetter (Oppedahl, Reference Oppedahl2016). In addition, the “Agricultural Finance Databook,” assembled by the Federal Reserve Bank of Kansas City (2016), provides archived summary statistics from the survey from 1991: quarter 1 (Q1) through 2016: Q1 (101 quarterly observations).
The Land Values and Credit Conditions Survey population includes all member banks that have a volume of agricultural loans that exceeds a threshold that was specified when the survey was initiated in 1972 (Federal Reserve Bank of Kansas City, 2016). The Seventh District spans the northern portions of Illinois and Indiana, southern Wisconsin, the lower peninsula of Michigan, and the entire state of Iowa. For most states in the district, the threshold of 25% was applied, but in Michigan, a 10% threshold was used. The sample has undergone periodic review, but the latest survey results are based on the responses of about 450 banks (Federal Reserve Bank of Kansas City, 2016). According to the “Agricultural Finance Databook,” the Seventh District is home to approximately 25% of the nation's agricultural banks.
In addition to farmland price expectations, the survey asks respondents to provide a point estimate of the average value for “good quality” farmland in their area. Because the Federal Reserve is a regulatory agency, it does not publish the survey's point estimates to prevent the information from being used as a benchmark for farmland sales (Zakrzewicz, Brorsen, and Briggeman, Reference Zakrzewicz, Brorsen and Briggeman2012). Instead, the Federal Reserve provides average percentage changes from the previous quarter derived from the aggregate point estimates. Prior studies demonstrate that these percentage changes and point estimates are consistent with market transaction prices (Zakrzewicz, Brorsen, and Briggeman, Reference Zakrzewicz, Brorsen and Briggeman2012), as well as aggregate farmland values reported by similar, annual surveys of farmers and other farmland market experts (Kuethe and Ifft, Reference Kuethe and Ifft2013).
3. Qualitative Evaluation of Bankers’ Forecasts of Farmland Values
Qualitative forecast evaluation methods compare the proportion of respondents who provide each categorical response (up, stable, and down) to observed outcomes, where the observed outcomes are similarly classified into complimentary categories (up, stable, and down). Formally, the three categorical responses up, stable, and down are indexed by k (K = 3), and the proportion of respondents who provide each categorical response, also called the probability forecast, are denoted fk
. As such, the probability forecasts represent the exhaustive set of possible outcomes such that
![]() $\mathop \sum \nolimits^ {f_k} = 1$
. The observed outcome is similarly expressed by a set of indicator variables:
$\mathop \sum \nolimits^ {f_k} = 1$
. The observed outcome is similarly expressed by a set of indicator variables:
Thus, classifying the quantitative outcomes into categories (i.e., defining dk ) is one of the critical assumptions of qualitative forecast evaluation. Covey (Reference Covey1999) found that between 1981 and 1986 at least a 4% change in value had occurred in quarters in which a majority of respondents indicated a belief in a future up or down trend. As a result, a period of “stable” price trend is defined as an outcome in which the reported price changes was within a boundary of ±4%. This definition was retained by Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013) and also employed in our analysis.Footnote 1
The relationship between probability forecasts and observed outcomes can be measured using Brier's (Reference Brier1950) probability score (PS). PS measures the accuracy of qualitative forecasts using the sum of squared errors between the probabilistic forecasts and the realized outcome indicator variables:
 $$\begin{equation}
P{S_t} = \frac{1}{T}\mathop \sum \limits_{t = 1}^T {\left( {{d_{k,t}} - {f_{k,t}}} \right)^2},
\end{equation}$$
$$\begin{equation}
P{S_t} = \frac{1}{T}\mathop \sum \limits_{t = 1}^T {\left( {{d_{k,t}} - {f_{k,t}}} \right)^2},
\end{equation}$$
where fk
is the forecasted probability of kth directional movement at time t, and d
k, t
is the outcome indicator variable for the kth directional movement at time t. A PS of 0 occurs when a forecast of absolute certainty is realized in the following period. Thus, a lower PS is associated with better forecast accuracy. The mean probability score (
![]() $\overline {PS} $
) measures the accuracy of forecast across all categories over an entire observation period:
$\overline {PS} $
) measures the accuracy of forecast across all categories over an entire observation period:
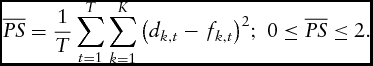 $$\begin{equation}
\overline {PS} = \frac{1}{T}\mathop \sum \limits_{t = 1}^T \mathop \sum \limits_{k = 1}^K {\left( {{d_{k,t}} - {f_{k,t}}} \right)^2};\ 0 \le \overline {PS} \le 2.
\end{equation}$$
$$\begin{equation}
\overline {PS} = \frac{1}{T}\mathop \sum \limits_{t = 1}^T \mathop \sum \limits_{k = 1}^K {\left( {{d_{k,t}} - {f_{k,t}}} \right)^2};\ 0 \le \overline {PS} \le 2.
\end{equation}$$
![]() $\overline {PS} $
is interpreted similarly, and a lower
$\overline {PS} $
is interpreted similarly, and a lower
![]() $\overline {PS} $
is associated with better forecast accuracy.
$\overline {PS} $
is associated with better forecast accuracy.
Both PS and
![]() $\overline {PS} $
provide measures of the forecast accuracy based on the squared deviation between the forecast and observed outcome. However, the measures do not lend themselves to statistical tests of the compatibility of the forecast and to observed outcomes. As a result, we use Speigelhalter's (Reference Spiegelhalter1986) z-statistic to test whether the forecasts are compatible with the observed outcomes. The z-statistic is defined as follows:
$\overline {PS} $
provide measures of the forecast accuracy based on the squared deviation between the forecast and observed outcome. However, the measures do not lend themselves to statistical tests of the compatibility of the forecast and to observed outcomes. As a result, we use Speigelhalter's (Reference Spiegelhalter1986) z-statistic to test whether the forecasts are compatible with the observed outcomes. The z-statistic is defined as follows:
 $$\begin{equation}
z = \frac{{\mathop \sum \nolimits_{t = 1}^T \left( {{d_{k,t}} - {f_{k,t}}} \right)\left( {1 - 2{f_{k,t}}} \right)}}{{\sqrt {\mathop \sum \nolimits_{t = 1}^T {{\left( {1 - 2{f_{k,t}}} \right)}^2}{f_{k,t}}\left( {1 - {f_{k,t}}} \right)} }}.
\end{equation}$$
$$\begin{equation}
z = \frac{{\mathop \sum \nolimits_{t = 1}^T \left( {{d_{k,t}} - {f_{k,t}}} \right)\left( {1 - 2{f_{k,t}}} \right)}}{{\sqrt {\mathop \sum \nolimits_{t = 1}^T {{\left( {1 - 2{f_{k,t}}} \right)}^2}{f_{k,t}}\left( {1 - {f_{k,t}}} \right)} }}.
\end{equation}$$
The significance of the z-statistic can be assessed using a standard normal table, with absolute z-statistic values in excess of 1.96 representing forecasts that are incompatible with the realized farmland price changes at a significance level of approximately 0.05.
The qualitative forecasts are compared against three naïve models: (1) a uniform distribution model in which the probability of each directional movement is equal across all outcomes (fk
= 1/K for all k = 1, . . ., K); (2) a relative frequency model that assigns probabilities based on the relative in-sample frequency of all actual outcomes (
![]() ${f_k} = {\bar{d}_k}$
for all k = 1, . . ., K, where
${f_k} = {\bar{d}_k}$
for all k = 1, . . ., K, where
![]() ${\bar{d}_k}$
is the relative outcome frequency across all T periods); and (3) a no-change forecast in which the full probability weight is assigned to the “stable” category.Footnote
2
${\bar{d}_k}$
is the relative outcome frequency across all T periods); and (3) a no-change forecast in which the full probability weight is assigned to the “stable” category.Footnote
2
The Brier's
![]() $\overline {PS} $
and Speigelhalter's z-statistic for the bankers’ probability forecasts, as well as those of the three naïve forecasts, are reported in Table 1. In order to be consistent with prior studies, “stable” price changes are defined as quarters in which the price change was in the range of ±4%. The results suggest that only the bankers’ probability forecasts and the naïve relative forecast are compatible with the observed data. For upward price movements, the Brier's
$\overline {PS} $
and Speigelhalter's z-statistic for the bankers’ probability forecasts, as well as those of the three naïve forecasts, are reported in Table 1. In order to be consistent with prior studies, “stable” price changes are defined as quarters in which the price change was in the range of ±4%. The results suggest that only the bankers’ probability forecasts and the naïve relative forecast are compatible with the observed data. For upward price movements, the Brier's
![]() $\overline {PS} $
of the bankers’ probability forecast is less than that of the naïve relative forecast. However, because the absolute Speigelhalter's z-statistic for the bankers’ forecast exceeds that of the naïve relative price forecast, the naïve relative forecast is more statistically consistent, or calibrated, with the observed farmland price changes. Thus, our results are consistent with Covey (Reference Covey1999) who found that “bankers failed to assign realistic probabilities as well as the relative frequency model” (p. 447). The results are contrasted by Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013) who found that the Federal Reserve Bank of Kansas City survey respondents outperformed both the uniform and relative probability naïve forecast models. It is important to note, however, that the period examined by Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013) contained only increasing or stable prices, and the period examined in our study, as well as that of Covey (Reference Covey1999), contains increasing, stable, and downward price movements.
$\overline {PS} $
of the bankers’ probability forecast is less than that of the naïve relative forecast. However, because the absolute Speigelhalter's z-statistic for the bankers’ forecast exceeds that of the naïve relative price forecast, the naïve relative forecast is more statistically consistent, or calibrated, with the observed farmland price changes. Thus, our results are consistent with Covey (Reference Covey1999) who found that “bankers failed to assign realistic probabilities as well as the relative frequency model” (p. 447). The results are contrasted by Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013) who found that the Federal Reserve Bank of Kansas City survey respondents outperformed both the uniform and relative probability naïve forecast models. It is important to note, however, that the period examined by Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013) contained only increasing or stable prices, and the period examined in our study, as well as that of Covey (Reference Covey1999), contains increasing, stable, and downward price movements.
Table 1. Brier's Mean Probability Score (
![]() $\overline {PS} $
)
$\overline {PS} $
)
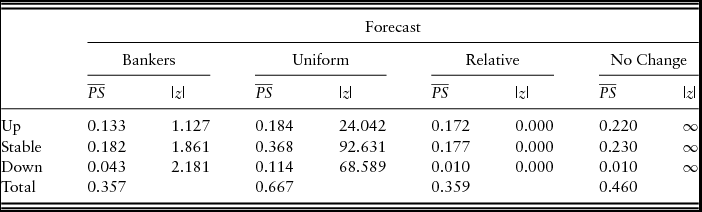
Note: 1991: quarter 1 (Q1) to 2016: Q1 (101 observations).
In order to understand why the bankers’ probability forecast does not outperform the naïve relative probability forecast model, we rely on the PS decomposition developed by Yates (Reference Yates1982). The decomposition is an expression of equation (2), such that
where
![]() $\bar{d}$
is the relative outcome frequency over all T periods observed (mean outcome frequency) and
$\bar{d}$
is the relative outcome frequency over all T periods observed (mean outcome frequency) and
![]() $\bar{d}( {1 - \bar{d}} ) = {\rm{Var}}( d )$
;
$\bar{d}( {1 - \bar{d}} ) = {\rm{Var}}( d )$
;
![]() $\bar{f}$
is the mean probability forecast over all T periods and
$\bar{f}$
is the mean probability forecast over all T periods and
![]() $\bar{f}( {1 - \bar{f}} ) = {\rm{Var}}( f )$
; and Cov(f, d) is the covariance between the forecast probability and the outcome indicator variable. The covariance between the forecast probability and the outcome indicator variable can also be expressed as follows:
$\bar{f}( {1 - \bar{f}} ) = {\rm{Var}}( f )$
; and Cov(f, d) is the covariance between the forecast probability and the outcome indicator variable. The covariance between the forecast probability and the outcome indicator variable can also be expressed as follows:
where λ is the slope of the regression line when forecast values are regressed on outcomes. When the outcome is expressed as a binary variable (taking the value of 0 or 1), the slope is defined as follows:
where
![]() ${\bar{f}_c}$
is the mean probability forecast for the Tc
periods in which the predicted outcome is observed at the end of the forecast horizon:
${\bar{f}_c}$
is the mean probability forecast for the Tc
periods in which the predicted outcome is observed at the end of the forecast horizon:
 $$\begin{equation}
{\bar{f}_c} = \frac{1}{{{T_c}}}\mathop \sum \limits_m {f_{c,m}};\ m = 1, \ldots ,{T_c}.\
\end{equation}$$
$$\begin{equation}
{\bar{f}_c} = \frac{1}{{{T_c}}}\mathop \sum \limits_m {f_{c,m}};\ m = 1, \ldots ,{T_c}.\
\end{equation}$$
The mean probability forecast when the predicted outcome is not observed,
![]() ${\bar{f}_0}$
, is similarly defined for the remaining To
observations, such that Tc
+ To
= T. Thus, the slope measures the change in forecast probability given that the predicted outcome is observed at the end of the forecast horizon. Alternately, it is the increase in the number of bankers providing accurate predictions when the predicted outcome is observed in the next quarter. The optimal slope is 1, and it occurs when the respondents have perfect foresight. In addition, Yates (Reference Yates1982) demonstrates that bias of the forecast can be evaluated using the formula
${\bar{f}_0}$
, is similarly defined for the remaining To
observations, such that Tc
+ To
= T. Thus, the slope measures the change in forecast probability given that the predicted outcome is observed at the end of the forecast horizon. Alternately, it is the increase in the number of bankers providing accurate predictions when the predicted outcome is observed in the next quarter. The optimal slope is 1, and it occurs when the respondents have perfect foresight. In addition, Yates (Reference Yates1982) demonstrates that bias of the forecast can be evaluated using the formula
![]() $\bar{f} - \bar{d}$
.
$\bar{f} - \bar{d}$
.
The bias and slope for the bankers’ forecasts are reported in Table 2. The positive bias scores for up and down price movements suggest that bankers predicted more positive and negative movements than observed. Thus, bankers overpredict positive and negative price movements, or alternatively, stable price environments occur more frequently than bankers predict. This is also suggested by the negative bias score for stable price movements, which implies that bankers underpredicted the frequency of stable price movements over the observation period. However, it is important to note that bias is directly related to the definition of “stable” price movements, and we retain the definition of ±4% (Covey, Reference Covey1999; Zakrzewicz, Brorsen, and Briggeman, Reference Zakrzewicz, Brorsen and Briggeman2013).
Table 2. Bias and Slope Scores
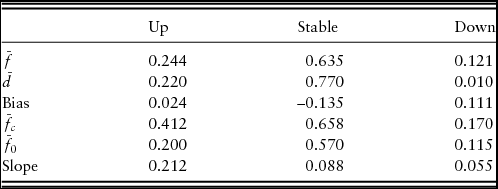
Note: 1991: quarter 1 (Q1) to 2016: Q1 (101 observations).
The slope score of each potential price movement, however, is positive, which suggests that bankers possess some ability to discriminate information regarding the future movement of farmland values. The proportion of bankers who predicted upward price movements is 21.2% higher in quarters in which farmland values subsequently increased. Similarly, the proportion of bankers who accurately predicted stable and downward price movements increased by 8.8% and 5.5% in quarters in which farmland values subsequently remained stable or decreased, respectively. Thus, bankers are most skilled at predicting upward price movements.
In sum, qualitative forecast evaluation suggests that agricultural bankers possess some skill at predicting directional movements of future farmland values, yet the bankers overpredict downward and upward price movements and underpredict stable prices. This finding introduces a number of important questions related to how the bankers formulate their short-run forecasts. Specifically, do bankers fully incorporate new information in forming their expectations? Although qualitative forecast evaluation methods provide some indication on the accuracy of bankers’ probability forecasts, the methods cannot fully address this issue or examine why bankers’ probability forecasts may fail to outperform the naïve benchmark forecasts. As a result, we examine the optimality of bankers’ probability forecasts through survey quantification methods.
4. Quantifying Qualitative Forecasts
The most widely employed survey quantification method is the probability method originally proposed by Theil (Reference Theil1952) and later formalized by Carlson and Parkin (Reference Carlson and Parkin1975), Pesaran (Reference Pesaran1987), and Cunningham, Smith, and Weale (Reference Cunningham, Smith, Weale, Begg and Henry1998). The probability method assumes that the categorical responses are derived from a continuous distribution of expectations. When respondents believe that the expected change is small or close to zero, they provide a categorical response of “stable” or “no change.” In order for respondents to provide a directional change, their expectations must exceed some threshold value. For example, in our case, agricultural bankers answer “down” (D i, t ) if they expect mean farmland prices in the next quarter t + 1 to be smaller than some nonzero threshold value a i, t (i.e., E t [Δ P i, t + 1] < a i, t , where the expected value of the change in farm real estate E t [Δ P i, t + 1] is defined as E t [P i, t + 1] − P i, t and is measured in percentage points). Similarly, respondents answer “up” (U i, t ) if E t [Δ P i, t + 1] is greater than some threshold value b i, t (E t [Δ P i, t + 1] > b i, t ). Finally, if their expected percentage change in farmland values in the next quarter E t [Δ P i, t + 1] is within the lower and upper boundary of the indifference interval a i, t and b i, t (a i, t ⩽ E t [Δ P i, t + 1] ⩽ b i, t ), agricultural bankers answer “stable” (S i, t ). That is, the probability method assumes that there is some “indifference interval” around zero within which respondents report the expected change in farmland values is zero (stable), and outside of this region, they report expected negative or positive price changes (down or up, respectively).
To estimate the underlying distribution of cardinal expectations, it is typically assumed that the distributions of expectations are independent across respondents and that they have a common form with finite mean and variance. Further, it assumed that the upper and lower boundaries are identical for all respondents in the population (a i, t = at ; b i, t = bt ). Then, the survey results can be interpreted as a sampling from some aggregate distribution. Thus, the share of agricultural bankers who expect an increase or decrease in farmland prices converges to the population values:
 $$\begin{equation}
{r_t} = {{\rm{\Phi }}^{ - 1}}\left( {1 - {U_t}} \right) = \frac{{{b_t} - {{\rm{E}}_t}\left[ {\Delta\ {P_{i,t + 1}}} \right]}}{{{\sigma _{t + 1}}}},\\
\end{equation}$$
$$\begin{equation}
{r_t} = {{\rm{\Phi }}^{ - 1}}\left( {1 - {U_t}} \right) = \frac{{{b_t} - {{\rm{E}}_t}\left[ {\Delta\ {P_{i,t + 1}}} \right]}}{{{\sigma _{t + 1}}}},\\
\end{equation}$$
 $$\begin{equation}
{f_t} = {{\rm{\Phi }}^{ - 1}}\left( {{D_t}} \right) = \frac{{{a_t} - {{\rm{E}}_t}{{\rm{E}}_t}\left[ {\Delta\ {P_{i,t + 1}}} \right]}}{{{\sigma _{t + 1}}}}.
\end{equation}$$
$$\begin{equation}
{f_t} = {{\rm{\Phi }}^{ - 1}}\left( {{D_t}} \right) = \frac{{{a_t} - {{\rm{E}}_t}{{\rm{E}}_t}\left[ {\Delta\ {P_{i,t + 1}}} \right]}}{{{\sigma _{t + 1}}}}.
\end{equation}$$
Most studies assume that the underlying distribution is a standard normal, such that σ t + 1 = 1, so the mean of the aggregate distribution of farm real estate expectations can be expressed as follows:
To make the estimation of E t [Δ P i, t + 1] tractable, Carlson and Parkin (Reference Carlson and Parkin1975) assume symmetric and time-invariant boundaries: c = −at = bt . In addition, it is assumed that on average the expectations are correct:
 $$\begin{equation}
\frac{1}{T}\mathop \sum \limits_{t = 1}^T {{\rm{E}}_t}\left[ {\Delta\ {P_{i,t + 1}}} \right] = \frac{1}{T}\mathop \sum \limits_{t = 1}^T \left( {{P_t} - {P_{t - 1}}} \right).
\end{equation}$$
$$\begin{equation}
\frac{1}{T}\mathop \sum \limits_{t = 1}^T {{\rm{E}}_t}\left[ {\Delta\ {P_{i,t + 1}}} \right] = \frac{1}{T}\mathop \sum \limits_{t = 1}^T \left( {{P_t} - {P_{t - 1}}} \right).
\end{equation}$$
In our case, this assumption is supported by the qualitative forecast evaluation. Substituting c = −at = bt in equation (10), equation (11) becomes
 $$\begin{equation}
\mathop \sum \limits_{t = 1}^T \frac{{c\left( {{f_t} + {r_t}} \right)}}{{{f_t} - {r_t}}} = \mathop \sum \limits_{t = 1}^T \left( {{P_t} - {P_{t - 1}}} \right),
\end{equation}$$
$$\begin{equation}
\mathop \sum \limits_{t = 1}^T \frac{{c\left( {{f_t} + {r_t}} \right)}}{{{f_t} - {r_t}}} = \mathop \sum \limits_{t = 1}^T \left( {{P_t} - {P_{t - 1}}} \right),
\end{equation}$$
which yields the following estimate of c:
 $$\begin{equation}
\hat{c} = \left[ {\mathop \sum \limits_{t = 1}^T \left( {{P_t} - {P_{t - 1}}} \right)} \right]\Bigg/\left( {\mathop \sum \limits_{t = 1}^T \frac{{{f_t} + {r_t}}}{{{f_t} - {r_t}}}} \right).
\end{equation}$$
$$\begin{equation}
\hat{c} = \left[ {\mathop \sum \limits_{t = 1}^T \left( {{P_t} - {P_{t - 1}}} \right)} \right]\Bigg/\left( {\mathop \sum \limits_{t = 1}^T \frac{{{f_t} + {r_t}}}{{{f_t} - {r_t}}}} \right).
\end{equation}$$
It is important to note that no empirical method is a panacea, and the probability method has a number of limitations that have been widely debated in the literature (see, e.g., Lahiri and Zhao, Reference Lahiri and Zhao2015; Nardo, Reference Nardo2003). Several studies have argued against the assumption of distribution for individual preferences (see Nardo, Reference Nardo2003). When the assumptions of the distribution of underlying assumptions are violated, the probability method may mischaracterize the aggregate distribution of cardinal expectations, and as a result, many studies consider alternative distributions for the underlying preferences. The standard practice is to select the distribution that minimizes some measure of fit between the quantified expectations and the observed outcomes, but as pointed out by Seitz (Reference Seitz1988), it is not possible to examine the accuracy of alternative distribution assumptions fully without access to the individual survey responses. In our case, unfortunately, the individual survey responses are not released by the Federal Reserve. Other researchers have developed alternative methods for quantifying qualitative survey responses that do not require individual survey responses (see Nardo, Reference Nardo2003; Smith and McAleer, Reference Smith and McAleer1995). However, these often require additional sources of information that are not available in the present analysis. For example, the regression method of Pesaran (Reference Pesaran, Malgrange and Muett1984) uses judgments, or projections of current values relative to the past, as a proxy for the distribution of (future) expectations.
The probability method derives a series of expectations that has the same dimensionality as the underlying observation series (Carlson and Parkin, Reference Carlson and Parkin1975), but in our case, the underlying observation series requires additional assumptions. As mentioned previously, the Federal Reserve does not publicly report the point estimates of farmland prices provided by the respondents. Instead, the Federal Reserve reports the estimated percentage change from the previous survey quarter (Zakrzewicz, Brorsen, and Briggeman, Reference Zakrzewicz, Brorsen and Briggeman2012). More specifically, if the actual value of farmland in quarter t is At , the Federal Reserve reports the estimated percentage change from the previous quarter APt = ln (At /A t − 1). Thus, to quantify the qualitative expectations, we create an index for the “market value of good farmland,” beginning with a base value of 100 for the quarter prior to the observation period (following Kuethe and Ifft, Reference Kuethe and Ifft2013).
The quarterly index value derived from the Federal Reserve Bank of Chicago is plotted from 1991: Q1 to 2016: Q1 in Figure 1. For comparison, the figure also includes similar indexes created for the five states included in the Seventh Federal Reserve District. The state-level indexes were derived from the annual state-level average per acre value of farm real estate reported by the U.S. Department of Agriculture (USDA), National Agricultural Statistics Service (2016). The figure suggests that the Federal Reserve Bank of Chicago price index roughly follows the same general pattern as the state-level indexes, yet the index also differs for three important reasons. One, the Federal Reserve Bank of Chicago survey specifically asks for the average “market value of good farmland,” whereas the USDA considers the average value of all land qualities. Two, the USDA values are for “farm real estate,” which includes all buildings, structures, and improvements. These features are not explicitly addressed in the Federal Reserve survey. Three, with the exception of Iowa, the Seventh Federal Reserve District only encompasses a portion of each state. For example, the Seventh District covers the northern portions of Illinois and Indiana, which contain the most productive, and therefore most valuable, farmland in each state. This shortcoming is not likely to affect the results if price changes are constant over time. However, if the value of lower-quality farmland is either slower or faster to change than high-quality farmland, the aggregates may differ substantially from the corresponding state values.
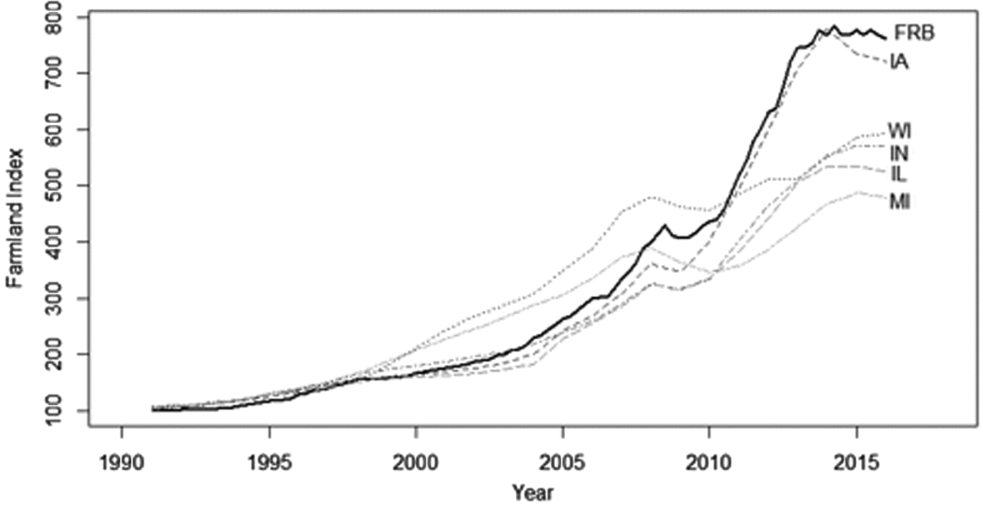
Figure 1. Federal Reserve Farmland Price Index and U.S. Department of Agriculture State-Level Indexes (FRB, Federal Reserve Board)
We apply the probability method to the aggregate farmland price index and the probability forecasts of each of the three price change categories using three alternative specifications of the assumed distribution of respondent expectations: standard normal, logistic, and t. Among the three candidate distributions, the logistic distribution yielded the lowest mean absolute error and root mean square error.Footnote
3
The logistic distribution estimation yields an indifference interval of
![]() $\hat{c} = 0.074$
. Thus, agricultural bankers will only provide an answer of “up” (“down”) when they expect farmland prices in the next quarter to increase (decrease) by 7.4%. It is important to note that this empirical finding differs substantially from the assumed definition of “stable” price movements of ±4% used in the qualitative forecast evaluation and in prior studies (Covey, Reference Covey1999; Zakrzewicz, Brorsen, and Briggeman, Reference Zakrzewicz, Brorsen and Briggeman2013). It implies that lenders require a stronger signal of an expected price change to deviate from the stable price prediction than previously assumed in the literature.
$\hat{c} = 0.074$
. Thus, agricultural bankers will only provide an answer of “up” (“down”) when they expect farmland prices in the next quarter to increase (decrease) by 7.4%. It is important to note that this empirical finding differs substantially from the assumed definition of “stable” price movements of ±4% used in the qualitative forecast evaluation and in prior studies (Covey, Reference Covey1999; Zakrzewicz, Brorsen, and Briggeman, Reference Zakrzewicz, Brorsen and Briggeman2013). It implies that lenders require a stronger signal of an expected price change to deviate from the stable price prediction than previously assumed in the literature.
The quantified expectations, their estimated 95% confidence interval, and their forecast error are plotted in Figure 2. The forecast error is defined as et = ln (At ) − ln (Ft ), where At is the aggregate quarterly farmland price index derived from the Federal Reserve reported data and Ft is the imputed one quarter ahead cardinal forecast for the same period.
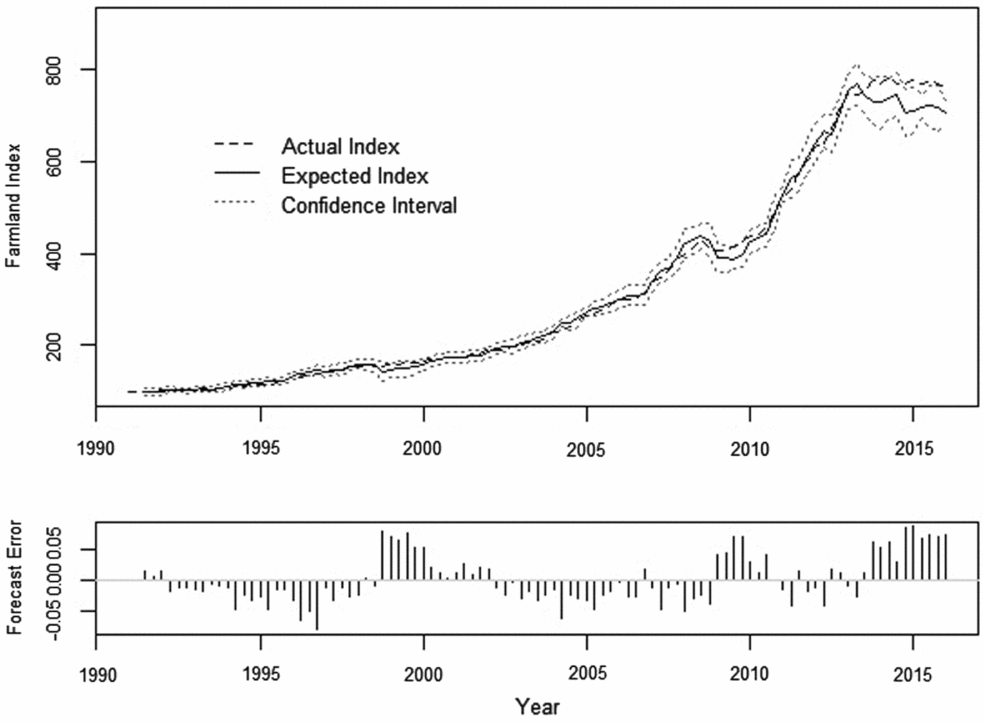
Figure 2. Quantified Farmland Forecast and Forecast Error, 1991: quarter 1 (Q1) to 2016: Q1 (101 observations)
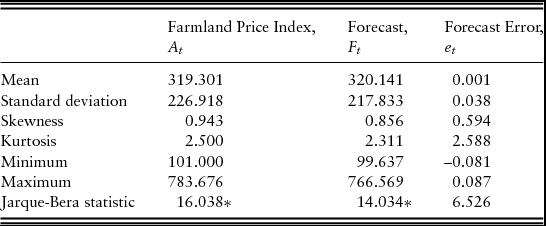
The summary statistics of the farmland price index, the forecast, and forecast error are reported in Table 3. The statistics suggest that the distribution of quantified farmland expectations closely mirrors that of the farmland price index. A t-test statistic value of –0.027 fails to reject the null hypothesis of equal means, and an F-test statistic value of 1.085 fails to reject the null hypothesis of equal variances. Finally, a Jarque-Bera test statistic of 6.526 suggests that forecast error is distributed normally.
Table 3. Summary Statistics
Note: Asterisk (*) indicates α ⩽ 0.01; 1991: quarter 1 (Q1) to 2016: Q1 (101 observations).
5. Quantitative Forecast Evaluation
The quantified expectations series allows us to test the degree to which the bankers’ forecasts of farmland prices are optimal. A forecast is optimal if it is both unbiased and efficient (Diebold and Lopez, Reference Diebold, Lopez, Maddala and Rao1996). A forecast is unbiased if it does not consistently differ from observed outcomes, and a forecast is efficient if it contains all information available at the time of the forecast. The existing literature provides a number of weak (necessary but not sufficient) empirical testing procedures for both unbiasedness and efficiency of cardinal forecasts.
The primary test of forecast bias was developed by Mincer and Zarnowitz (Reference Mincer, Zarnowitz and Mincer1969). The test examines the relationship between forecast values and observed outcomes using the regression:
The null hypothesis of unbiasedness is evaluated by the joint test (θ1, θ2) = (0, 1). In other words, the forecasts are perfectly, positively correlated with observed outcomes.
The results of the Mincer-Zarnowitz test of forecast bias are reported in Table 4. Using t-tests on the two coefficients of equation (14) individually, we find that θ1 is indistinguishable from 0, yet we fail to reject the null hypothesis that θ2 is equal to 1. In addition, we fail to reject the joint test of the null hypothesis (θ1, θ2) = (0, 1). Thus, the Mincer-Zarnowitz test suggests that the bankers’ yield an unbiased forecast of future farm real estate values.
Table 4. Mincer-Zarnowitz Bias Test Results
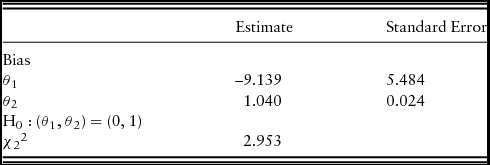
Note: Regression coefficients from equation (14), At = θ1 + θ2 Ft + ε t , calculated using the Newey-West heteroskedasticity and autocorrelation consistent estimator and χ2 2 test of the joint bias test, H0: (θ1, θ2) = (0, 1), 1991: quarter 1 (Q1) to 2016: Q1 (101 observations).
The correlation between observed and forecasted values, however, may be spurious if either series contains a unit root. As a result, Diebold and Lopez (Reference Diebold, Lopez, Maddala and Rao1996) develop a test of unbiasedness based on the notion that the optimal forecast errors should have a mean of zero, or alternatively, the forecast errors do not have a predictable nonzero value. The test regresses the forecast errors on a constant:
The null hypothesis of unbiasedness is evaluated by testing γ = 0.
The results of the Diebold-Lopez (Reference Diebold, Lopez, Maddala and Rao1996) test of forecast bias are reported in Table 5. The estimated coefficient γ is indistinguishable from zero, and we therefore fail to reject the null hypothesis that the bankers’ forecasts are unbiased predictors of future farm real estate values.
Table 5. Diebold-Lopez Bias Test Results

Notes: Regression coefficient from equation (15), et = γ + ε t , calculated using the Newey-West heteroskedasticity and autocorrelation consistent estimator. The null hypothesis that the forecast is unbiased suggests that γ is indistinguishable from zero; 1991: quarter 1 (Q1) to 2016: Q1 (101 observations).
Forecasts are (weakly) efficient if the forecast error is orthogonal to both the level of the forecasted price change and the prior forecast error (Nordhaus, Reference Nordhaus1987). In other words, there is no systematic relationship between the forecast error and the level of forecasts or previous errors (memoryless property). Forecast efficiency can be tested through the two regression equations:
Table 6. Nordhaus Efficiency Test Results

Notes: Efficiency tests based on equations (16a) and (16b) calculated using the Newey-West heteroskedasticity and autocorrelation consistent estimator. Efficiency implies β = 0 and ρ = 0; asterisk (*) indicates α ⩽ 0.01; 1991: quarter 1 (Q1) to 2016: Q1 (101 observations).
In both cases, we reject the null hypothesis that the slope coefficient is indistinguishable from zero and can conclude that the bankers’ forecasts of farmland prices are inefficient. Specifically, forecast errors are negatively correlated with the level of forecast price changes. Thus, in periods of appreciating prices, bankers overpredict subsequent price increases, or bankers provide overly optimistic (pessimistic) predictions of price changes during price increases (decreases). This is consistent with the findings of the qualitative forecast evaluation that suggested that bankers overpredict upward and downward price movements and underpredict stable price environments. In addition, aggregate forecasts errors in one period are positively correlated with aggregate forecast errors in the next period. In other words, respondents’ errors, in aggregate, are persistent from one period to the next, or the respondents, in aggregate, do not adjust from their prior mistakes.
6. Conclusions
Farmland plays an important role in the financial health of the agricultural sector. It accounts for a substantial portion of the value of the sector's asset base. It serves as both a store of wealth and a source of collateral. As a result, changes in farm real estate values affect lenders’ capacity to provide liquidity to the agricultural sector (Briggeman, Gunderson, and Gloy, Reference Briggeman, Gunderson and Gloy2009). Two prior studies examine the accuracy of quarterly farmland price forecasts collected by Federal Reserve banks through qualitative forecast evaluation methods, and the studies offer somewhat conflicting results. Covey's (Reference Covey1999) analysis of the survey conducted by the Federal Reserve Bank of Chicago suggest that bankers’ probability forecasts are not as accurate as the naïve relative frequency forecast rule. However, using a similar, unpublished survey conducted by the Federal Reserve Bank of Kansas City, Zakrzewicz, Brorsen, and Briggeman (Reference Zakrzewicz, Brorsen and Briggeman2013) suggest that bankers outperform both the relative frequency and uniform naïve forecast models. Using more recent data from the Federal Reserve Bank of Chicago survey, our qualitative forecast evaluation finds results similar to those of Covey (Reference Covey1999).
Our qualitative forecast evaluation, therefore, necessitates the question of “why do lenders fail to outperform the naïve relative frequency rule?” Although this question is difficult to address using qualitative survey data, we rely on survey quantification methods to test whether the bankers’ forecasts are biased or inefficient. The results suggest that lenders’ short-run forecasts are unbiased, yet the forecasts are inefficient. That is, aggregate forecast errors are inversely related to forecasted price levels and positively associated with prior forecast errors.
It is import to note that our study was conducted using published aggregate survey responses (probability forecasts). The finding that aggregate forecast errors are correlated with previous aggregate forecast errors suggests that, on average, respondents do not learn from their prior mistakes. This result, in turn, suggests that further study is warranted. Similar models could be constructed using the individual survey response, and one could test whether individual respondents are biased or inefficient. In addition, these models could examine issues of heterogeneity, particularly as they relate to local market conditions. This effort is left for future research.










