Dronamraju (Reference Dronamraju2017, p. 82) asserts that ‘population genetics’ began as an attempt to ‘marry Darwin's theory of evolution with the science of genetics that was founded by . . . Mendel’. He states that the ‘next important step’ (in population genetics theory) was the introduction of the Hardy–Weinberg law in 1908 (Hardy, Reference Hardy1908; Weinberg, Reference Weinberg1908). He says that the law is strictly valid only if the following conditions are valid:

1. (1) the population must be large enough so that sampling errors can be ignored;

2. (2) there must be no mutation;

3. (3) there must be no selective mating;

4. (4) there must be no selection.

Conditions similar to the above four can be found in many introductory texts on population genetics, generally in relation to autosomal loci, as were the original formulations. It appears that Dronamraju is excluding assortative mating in the third of his conditions and may intend that the selection of mates should be random. As can be seen from references cited below, random mating is not a necessary requirement for the maintenance of Hardy–Weinberg proportions. The purpose of this paper is to show that the same is true of an X-linked locus.

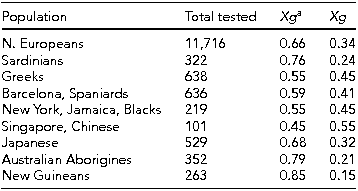
We take locus Xg as envisaged by Mann et al. (Reference Mann, Cahan, Gelb, Fisher, Hamper, Tippett and Race1962) as archetypical. These authors give the set of estimated genotype frequencies reproduced in Table 1. They used the gene frequencies among males to represent the population frequencies and applied Hardy–Weinberg proportions to calculate the female genotype frequencies. In Table 1, the frequency of Xg ^a in males is 0.6169 and the combined frequency of Xg ^a Xg ^a and Xg Xg ^a in females is 0.8532. This is in approximate agreement with the frequencies of Xg(a₊) (60% in males and 90% in females) given by Mueller and Young (Reference Mueller and Young1995). In our notation, introduced below, Xg is given the label U, and Xg ^a label T. Johnson (Reference Johnson2011) and Tippett and Ellis (Reference Tippett and Ellis1998) review the XG system.

TABLE 1 Estimated Genotype Frequencies at the Xg Locus

Mann et al. (Reference Mann, Cahan, Gelb, Fisher, Hamper, Tippett and Race1962) give ‘certain rules which may be laid down for an X-borne dominant antigen’ (p. 9); for example, that from the mating positive × positive, there can be no negative daughters. In this article, the alleles are treated as co-dominant. In their analysis, these authors calculate the proportions of expected matings by assuming, for example, that the frequency of Xg(a-) father by Xg(a-) mother is the product of the respective genotype frequencies, that is, equivalent to random mating frequencies. They compute the expected proportions of Xg(a+) and Xg(a-) male and female children from the observed numbers of female genotype frequencies and use them to calculate the expected numbers of male and female children of each type. These are then compared with the observed numbers from 50 sibships, finding satisfactory agreement with the hypothesis of X-linked inheritance. In their analysis, because of dominance, there are four mating types. In our analysis, there are six mating pair combinations.

Johnson (Reference Johnson2011) states ‘the function of the Xg^a protein is unknown’ (p. 68). Tippett and Ellis (Reference Tippett and Ellis1998) state ‘. . . anti-Xg^a does not appear to be clinically significant’ (p. 234). They give a table of gene frequencies that are reproduced in Table 2. In the light of this, it seems not unreasonable to treat the Xg locus as an example of a stable polymorphism with equally viable genotypes.

TABLE 2 Xg ^a Gene Frequencies in Different Populations

The monograph of Thomas Nagylaki (Reference Nagylaki1977) gives a sound account of basic population genetics as it existed at the time of publication. In most respects, the theory as expounded by Nagylaki is still current. In the chapter entitled ‘Panmictic Populations’, Nagylaki starts with ‘the genetic structure of a randomly mating population in the absence of selection, mutation, and random drift’ (p. 33). He says of this theory: ‘This part of population genetics was the first to be understood, and a thorough grasp of its principles is required for the formulation and interpretation of most evolutionary models’ (p. 33).

Nagylaki (Reference Nagylaki1977) gives theory for several alleles at an autosomal locus whereas we take only two. Also, he uses ordered genotype frequencies, so that in his notation, when P_ij (= P_ji) designates the frequency of ordered A_iA_j genotypes, 2P_ij, i ≠ j, is the frequency of unordered A_iA_j heterozygotes. For convenience, we use unordered genotypes so that a single subscript serves to distinguish genotypes. Using his notation, Nagylaki calculates allele frequencies as

$$\begin{equation*} {p_i} = \sum\nolimits_j {{P_{ij}}.} \end{equation*}$$

It is relevant to quote from Nagylaki's (Reference Nagylaki1977, p. 34) monograph:

By Mendel's Law of Segregation, p_i is the frequency of A_i in the gametic output of the population.

If mating occurs without regard to the genotype at the A-locus, random union of gametes yields the genotypic proportions

$$\begin{equation*} {P'_{ij}} = {p_i}{p_j} \end{equation*}$$

in the next generation. Therefore, the gene frequencies do not change,

$$\begin{equation*} {p'_i} = \sum\limits_j {{{P'}_{ij}} = {p_i},} \end{equation*}$$

and Hardy–Weinberg proportions,

$$\begin{equation*} {P'_{ij}} = {p'_i}{p'_j}, \end{equation*}$$

are attained in a single generation.

Nagylaki (Reference Nagylaki1977, p. 34) states further that ‘The most important aspect of the Hardy-Weinberg law is the constancy of the allelic frequencies’.

Nagylaki also considers matings explicitly but soon resorts to random mating. He introduces different frequencies for the two sexes and reaches the identity

$$\begin{equation*} {P'_{ij}} = {Q'_{ij}} = {\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}({p_i}{q_j} + {p_j}{q_i}), \end{equation*}$$

where P and p apply to male and Q and q apply to female entities. He uses the same approach for autosomal and X-linked loci to reach what he calls ‘generalized Hardy–Weinberg proportions’ (Nagylaki, Reference Nagylaki1977, p. 36).

The point which we emphasize is that, in respect of Hardy–Weinberg equilibrium, using frequencies of mating pairs, it is not necessary to invoke random mating. It is implicit in a formula of Stark (Reference Stark1980) that, for an autosomal locus, Hardy–Weinberg frequencies are consistent with non-random mating. Stark (Reference Stark2006) showed that Hardy–Weinberg frequencies can be attained in a single round of non-random mating. Stark and Seneta (Reference Stark and Seneta2013, Reference Stark and Seneta2014) show how general genotypic proportions can be maintained.

Nagylaki (Reference Nagylaki1977) shows that for an X-linked locus with random mating, not only are gene frequencies equalized in the two sexes, but Hardy–Weinberg proportions are approached rapidly. In this paper, we assume that gene frequencies in males are the same as those in females.

The object of this paper is to show how a general equilibrium at an X-linked locus can be sustained in females. Just as in autosomal loci, Hardy–Weinberg frequencies can be maintained with non-random mating at an X-linked locus. The condition required to maintain equilibrium is given in the next section. The boundaries of the region of admissible points of equilibrium are given in the following section.

The Mating System

This is a model for a single X-linked locus with two alleles U and T with frequencies in the population q and p (q + p = 1). We have in mind the human population in which females have two X chromosomes and males one. We assume that the population is in equilibrium, the genotypes equally viable and the gene frequencies the same in both sexes. The frequencies of genotypes UU, UT, TT in the females are denoted, respectively, f ₀, f ₁, f ₂ (f ₀ + f ₁ + f ₂ = 1) and the frequencies of male hemizygotes U and T are denoted, respectively, m ₀and m ₁ (m ₀ + m ₁ = 1). The frequency of U in females is ${f_0} + {\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}\ {f_1} = q$ and in males is m ₀ = q. Without loss of generality, q is taken to be less than or equal to ½.

The mating scheme is represented by

$$\begin{equation*} \left[ {\begin{array}{@{}*{3}{l}@{}} {U \times UU}&\quad {U \times UT}&\quad {U \times TT}\\ {T \times UU}&\quad {T \times UT}&\quad {T \times TT} \end{array}} \right] \end{equation*}$$

with commensurate mating frequencies given by the matrix

$$\begin{equation*} C = \left[ {\begin{array}{@{}*{3}{l}@{}} {{f_{00}}}&\quad {{f_{01}}}&\quad {{f_{02}}}\\ {{f_{10}}}&\quad {{f_{11}}}&\quad {{f_{12}}} \end{array}} \right]. \end{equation*}$$

The row sums of C are q and p and the column sums are f ₀, f ₁, f ₂, so these are the parental frequency distributions. We use C in the extended row vector form

$$\begin{equation*} u' = \{ {f_{00}},{f_{01}},{f_{02}},{f_{10}},{f_{11}},{f_{12}}\} . \end{equation*}$$

To follow the progression of generations, which are assumed to be discrete and non-overlapping, we need Mendel's coefficients of heredity, given in matrix form, for female offspring, by

$$\begin{equation*} M = \left[ {\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1&{{\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}}&0&0&0&0\\[4pt] 0&{{\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}}&1&1&{{\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}}&0\\[4pt] 0&0&0&0&{{\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}}&1 \end{array}} \right]. \end{equation*}$$

Then, the frequency distribution of juvenile females is calculated from

$$\begin{equation*} j' = (Mu)' \end{equation*}$$

which in detail is

$$\begin{equation*} j = \{ {f_{00}} + {\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}{f_{01}},{\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}{f_{01}} + {f_{02}} + {f_{10}} + {\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}{f_{11}},{\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}{f_{11}} + {f_{12}}\} '. \end{equation*}$$

The distribution of male juveniles is q of type U and p of type T.

The main point of interest is to specify the properties of C which satisfy

(1) $$\begin{equation} j = \{ {f_0},{f_1},{f_2}\} ', \end{equation}$$

that is, that the distribution of juvenile females is the same as the distribution of adult females. The special distribution

(2) $$\begin{equation} a^\ast = \{ {q^2},5pq,{p^2}\} ' \end{equation}$$

will be referred to as the Hardy–Weinberg distribution even though both Hardy and Weinberg considered only the case of an autosomal locus. Other distributions can be put in the form

(3) $$\begin{equation} a = \{ {q^2} + Fpq,2pq - 2Fpq,{p^2} + Fpq\} '. \end{equation}$$

Parameter F, as well as q, serves to specify details of the system.

Equation (1) is satisfied if

(4) $$\begin{equation} {f_{01}} = 2{f_{10}}. \end{equation}$$

If q = 1/3, F = 1/12, a = {7/54, 22/54, 25/54}',

(5) $$\begin{equation} C = \frac{1}{{54}}\left[ {\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 3&8&7\\ 4&{14}&{18} \end{array}} \right] \end{equation}$$

has property (4), thereby satisfying condition (1). Matrix (5) is only one of an infinite number which could be found to satisfy (1). The force of (4) can be seen by exploiting the fact that the elements of the first row of C sum to q, as do the sum of the elements of the first column and half of each element of the second column, leading to the identity:

(6) $$\begin{equation} {f_{00}} + {f_{01}} + {f_{02}} = {f_{00}} + {f_{10}} + {\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}({f_{01}} + {f_{11}}). \end{equation}$$

Substituting from (4) into (6) leads to the implied property

(7) $$\begin{equation} {f_{11}} = 2{f_{02}}. \end{equation}$$

Identity (4) ensures that juvenile females of type UU have frequency f ₀, (7) that those of type TT have frequency f ₂, and the heterozygotes have frequency f ₁since the frequencies sum to unity. Thus, given the marginal sums of C, nominating elements f ₀₁and f ₁₀, which conform to (4) and are compatible with marginal quantities, enable the construction of C satisfying (1).

Taking F = 0 produces the Hardy–Weinberg distribution among adult females. Random mating, defined by

(8) $$\begin{equation} {f_{sd}} = {m_s} \times {f_d},\;s = 0,1;d = 0,1,2, \end{equation}$$

satisfies (1), but is only one of an infinite number of mating schemes with this property.

Admissible Points of Equilibria

The mating matrix C must be consistent with various mathematical, as well as biological constraints. These are conveniently depicted by points within and on the sides of a figure defined by the pair of coordinates F and f ₀₁, using a unique planar figure for each value of q. Figure 1 displays the admissible region, whose vertices are QVDE, for q = 2/5. Given a value of q, for a given F, admissible definitions of C are represented by points (values off ₀₁)along the vertical line above F within or on the boundary of the appropriate polygon QVDE. The base of the defining triangle extends from ${\raise0.7ex\hbox{${ - q}$} \! / \!\lower0.7ex\hbox{$p$}}$ to 1, the admissible range of F. The maximum height of the triangle is f ₀₁ = q, when F = (2p − 1)/(2p), the mid-point of the base. The equation of the side of the triangle from ${\raise0.7ex\hbox{${ - q}$} \! / \!\lower0.7ex\hbox{$p$}}$ to the vertex is f ₀₁ = 2(q ² + Fpq) and of the side from 1 to the vertex is f ₀₁ = 2pq − 2Fpq. When ${\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$3$}} < q \le {\raise0.7ex\hbox{$1$} \! / \!\lower0.7ex\hbox{$2$}}$, the line with equation f ₀₁ = 2p(q − p − 2Fq)is another boundary. These three equations, together with f ₀₁ = 0, define the admissible region of the system for a specified value of q. Point Z in Figure 1 has {F, f ₀₁} coordinates {0, 0}, Q has coordinates {(2q – 1)/(2q), 0} and point E coordinates {(3pq – 1)/(3pq), 2q – ⅔}. Figure 1 shows the point of random mating (R) when F = 0 and ${f_{01}} = {\raise0.7ex\hbox{${24}$} \! / \!\lower0.7ex\hbox{${125}$}}$ highlighting the fact that random mating is only one point of an infinite number, on the vertical line through R, which are consistent with Hardy–Weinberg frequencies. When q ≤ ⅓, points O and Q coalesce, so that the boundary of the admissible region is OVD.

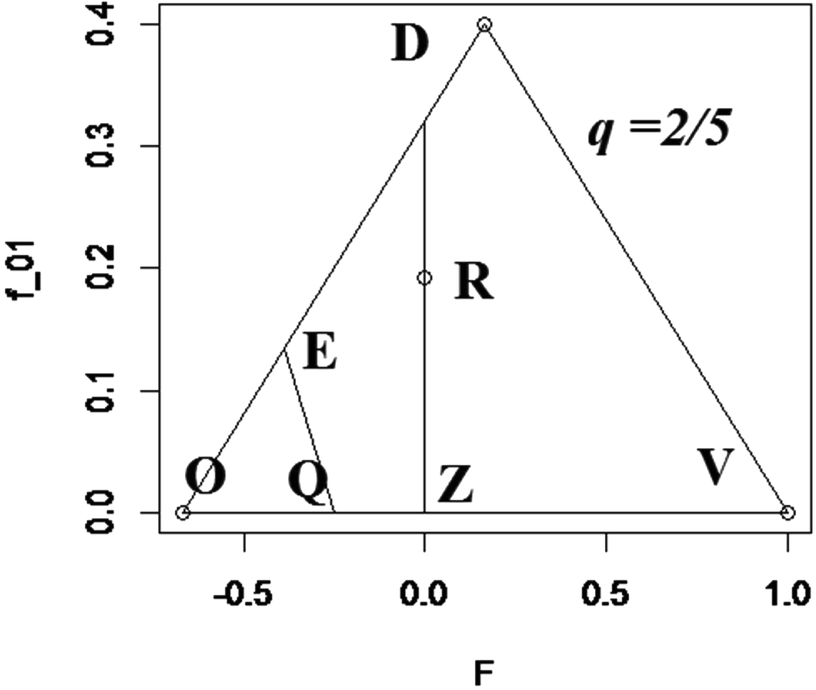
FIGURE 1 Admissible region, defined by QVDE, when q = 2/5; R indicates point of random mating.