INTRODUCTION
Durum wheat (Triticum turgidum L. var. durum) is the only species able to provide the raw material for traditional pasta making. It is a key crop for Italian agriculture in terms of both national consumption and exportation. Grain protein concentration (GPC) has a positive effect on the rheological and cooking properties of pasta (Dexter & Matsuo Reference Dexter and Matsuo1977; Cubadda et al. Reference Cubadda, Carcea, Marconi and Trivisonno2007). More specifically, gluten plays a key role in determining the quality of the derived products. By increasing the GPC, the fraction of gluten also increases and its quality improves (Dexter & Matsuo Reference Dexter and Matsuo1977). For these reasons, in global wheat trade the higher the GPC, the higher the price paid to farmers.
However, the high variability of climatic conditions in Mediterranean countries makes it difficult to guarantee a stable GPC and the quality standards requested by grain dealers (Borghi et al. Reference Borghi, Corbellini, Minoia, Palumbo, Di Fonzo and Perenzin1997; Troccoli et al. Reference Troccoli, Borrelli, De Vita, Fares and Di Fonzo2000). Further, farmers of southern European regions suffer from competition with imported wheat and quality has become an even more important issue. In this respect, correct management of nitrogen (N) fertilization through N applications late in the season (between booting [growth stage BBCH4; Lancashire et al. Reference Lancashire, Bleiholder, Langeluddecke, Stauss, van den Boom, Weber and Witzen-Berger1991] and flowering stages [BBCH6]), is effective in promoting GPC (Strong Reference Strong1982; Bly & Woodard Reference Bly and Woodard2003) and in improving grain quality. Modelling can support decision-making concerning late fertilization by providing an early assessment of the harvest quality in terms of GPC.
In most wheat models, such as CERES-wheat (Ritchie & Otter Reference Ritchie, Otter and Willis1985), SWHEAT (van Keulen & Seligman Reference van Keulen and Seligman1987), AFRCWHEAT2 (Porter Reference Porter1993) and APSIM-N-wheat (Asseng et al. Reference Asseng, Bar-Tal, Bowden, Keating, Van Herwaarden, Palta, Huth and Probert2002), GPC is determined by soil N availability and plant N demand. The latter is positively related to leaf area expansion, and thus the ability of leaf biomass to store N.
Therefore, models assume a ‘source-limited’ nature of grain protein deposition and leaf area index (LAI) (green leaf area per unit ground surface area) is the main descriptor of the source of N available for translocation. However, while wheat crop models perform well in assessing yield, inconsistent results have been observed for GPC (Weiss & Moreno-Sotomayer Reference Weiss and Moreno-Sotomayer2006). Consequently, the current algorithms need to be reviewed and GPC modelling remains a challenge.
CERES-wheat, as reported extensively in Basso et al. (Reference Basso, Liu and Ritchie2016), is among the most used crop simulation models, successfully applied to simulate worldwide crop growth and yield forecasting in response to climate and climate change, soil and management. Based on that, the model CERES-wheat (DSSAT-CSM v4) was recently applied in a long-term analysis of durum wheat production in Central Italy, with the aim of identifying the main system components with a predictive power for yield, and then to formulate a simplified yield forecasting index suitable for operational applications (Dalla Marta et al. Reference Dalla Marta, Orlando, Mancini, Guasconi, Motha, Qu and Orlandini2015).
Starting from that point, and based on the good performance of the model in predicting yield, the main goal of the present study is to expand that research by using CERES-wheat, a widely used crop simulation model, as the basis for the development of a simple forecasting index for grain protein content assessment (SFIpro) in durum wheat. This overarching objective was achieved by: (i) development of a new equation for GPC simulation in durum wheat; (ii) identification of the main variables affecting modelled GPC using a long-term simulation study; (iii) development of the SFIpro forecasting index, based on the results of these long-term simulations; and (iv) assessment of SFIpro performance, through comparison between forecasted and observed GPC.
MATERIALS AND METHODS
Study area and crop model performance in simulating grain protein concentration
The long-term modelling developed in the present study was focused on Val d'Orcia (Central Italy, 43°02′N, 11°68′E, 320 m a.s.l.), where durum wheat is the most traditionally grown crop. The area has an average annual temperature of 13·6 °C and a cumulative precipitation of 715 mm. Wheat is grown in ‘Typic Ustorthents fine, mixed, calcareous, mesic’ soils (Soil Survey Staff 2014), moderately deep, weakly alkaline, with a silty–clay–loam texture.
The CERES-wheat simulation model (DSSAT-CSM version 4.0) used in the present study is a predictive and deterministic model, designed to simulate the effects of cultivar, crop management, weather and soil on crop growth, development and production (Ritchie & Otter Reference Ritchie, Otter and Willis1985). The model operates on a daily timestep and the minimum meteorological inputs include precipitation (mm), solar radiation (MJ/m2), and maximum and minimum air temperatures (°C) (Jones & Kiniry Reference Jones and Kiniry1986). The daily weather data for the period 1955–2011 were collected from six weather stations located in Val d'Orcia; Table 1 shows the main physical and chemical characteristics of the soil profile used to initialize the model.
Table 1. Main chemical and physical characteristics of soil from the study area, and input soil profile used to initialize the simulation model CERES-wheat
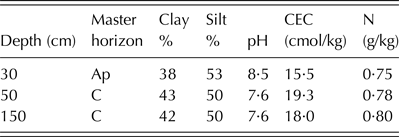
CEC, cation-exchange capacity; N, nitrogen.
In most wheat simulation models, including CERES-wheat, GPC is obtained as the result of independent functions for dry matter and N accumulation into the grain, with the latter predicted through estimating N uptake by plant and N distribution into grains. The model assumes that under optimal growing conditions, the rate and duration of starch deposition during grain filling are mainly determined by factors operating within or close to the grain itself, and are therefore sink-limited (Fischer et al. Reference Fischer, Aguilar and Laing1977). On the other hand, the rate and duration of protein deposition are determined by factors external to the grain and therefore are mainly source-limited (Jenner et al. Reference Jenner, Ugalde and Aspinall1991). The calculation of N uptake assumes limitation either by crop demand or by N availability. Therefore, N assimilation depends on N supply from the soil and on leaf area expansion, and thus on the leaf biomass able to store N and translocate it into the grain during grain filling. The source-limited assumption implies that grain protein accumulation depends on the N content of above-ground biomass at the beginning of the grain filling. In optimal conditions, N available in the biomass is translocated into the grain, and during grain filling the model simulates grain N based on sink size, which is a function of the daily rate of dry matter accumulation and the number of grains per plant.
The CERES-wheat model was previously calibrated and validated for winter durum wheat cvar Claudio, widespread in the study area, in a previous study (Dalla Marta et al. (Reference Dalla Marta, Orlando, Mancini, Guasconi, Motha, Qu and Orlandini2015). The crop productive potential and the timing of the phenological stages (Zadoks et al. Reference Zadoks, Chang and Konzak1974) were calibrated by the genetic coefficients of the ‘Winter-Europe’ genotype adjusted on the basis of the best fit between the simulated and measured yields and onset dates of the main crop stages (Dalla Marta et al. Reference Dalla Marta, Orlando, Mancini, Guasconi, Motha, Qu and Orlandini2015).
However, significant differences between ordinary and durum wheat have been observed in field studies in relation to the qualitative response of the crop in the Mediterranean environment. Cossani et al. (Reference Cossani, Slafer and Savin2011) observed on average 5 g/kg more grain maximum N concentration for cvar Claudio compared with ordinary wheat. Therefore, as a first step in the present study, the model routine for GPC was revised to make it more appropriate for modelling durum wheat and cvar. Claudio in particular, using the CERES-wheat outputs for biomass dry matter and N concentration. Building on the assumptions of the GPC sub-model, a new equation for GPC simulation was developed (Eqn (1)). This equation assumes that the total available N (TN) from the biomass is translocated into the grain and that its ratio with the grain N sink (NS) determines the N concentration. Hence,
where 0·5 is the additional factor due to the genetic difference between durum and ordinary wheat (Cossani et al. Reference Cossani, Slafer and Savin2011) and 5·7 is the conversion factor from grain N to protein content (Spratt Reference Spratt1979).
Total available nitrogen is the total N available for translocation from above-ground biomass into the grain at the beginning of grain filling. In this respect, leaves and stems are the most important N reserves in wheat; therefore in the current work plant straw was considered as the N source, disregarding any contribution from spikes and roots. Therefore, in Eqn (1), TN was computed as the total leaf and stem biomass (g DM/plant) multiplied by the appropriate N concentration simulated by the model. The biomass weight per hectare at the beginning of grain filling was converted into biomass per plant on the basis of an average plant density of 500 stems/m2.
The size of the grain NS was computed as equal to the grain weight increase per plant simulated during the grain-filling stage, depending on the difference between the grain dry matter at the watery ripe stage and at the fully ripe stage (Weiss & Moreno-Sotomayer Reference Weiss and Moreno-Sotomayer2006).
The performance of the CERES-wheat model variants, i.e. with and without the new GPC equation, in terms of GPC prediction was evaluated by a correlation analysis between simulated and observed data (Table 2). The variety trials of the Regional Agency for Development and Innovation in the Agro-forestry Sector (ARSIA) supplied the crop data for model calibration. Data were available for 10 years (1998–2009) on one field per year. Once calibrated, CERES-wheat was validated using a dataset from field monitoring carried out by the Siena Provincial Agrarian Consortium (CAPSI) in collaboration with the Department of Agrifood Production and Environmental Sciences – University of Florence (DISPAA). The data were available over three growing seasons (2009–2011), for a total number of 20 fields (nine in 2009, seven in 2010 and four in 2011). The ARSIA and CAPSI datasets supplied information concerning crop management (e.g. sowing, plant density and fertilization plans), plant phenology and harvest (e.g. yield, grain humidity and GPC). The following fitting coefficients were calculated: root-mean-square error (RMSE; Fox Reference Fox1981; from 0 to +∞, optimum 0), relative root-mean-square error (RRMSE; Jørgensen et al. Reference Jørgensen, Kamp-Nielsen, Christensen, Windolf-Nielsen and Westergaard1986; from 0 to +∞, optimum 0), model efficiency (EF; Nash & Sutcliffe Reference Nash and Sutcliffe1970; from –∞ to 1, optimum 1; Eqn (2)) and the coefficient of residual mass (CRM; Loague & Green Reference Loague and Green1991; from –∞ to +∞, optimum 0; Eqn (3)):
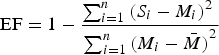 $${\rm \; EF} = 1 - \displaystyle{{\sum\nolimits_{i = 1}^n {{(S_i - M_i)}^2} {\rm \; }} \over {\sum\nolimits_{i = 1}^n {{(M_i - \bar M)}^2}}}$$
$${\rm \; EF} = 1 - \displaystyle{{\sum\nolimits_{i = 1}^n {{(S_i - M_i)}^2} {\rm \; }} \over {\sum\nolimits_{i = 1}^n {{(M_i - \bar M)}^2}}}$$
where S and M are the simulated and measured data, respectively.
Table 2. Performance of CERES-wheat crop model, with and without the new equation for simulation of grain protein concentration

RMSE, root-mean-square error; RRMSE, relative root-mean-square error; EF, model efficiency; CRM, coefficient of residual mass.
Development and validation of a simplified forecasting index for grain protein concentration
After assessment of the model performance in simulating GPC with the new equation, it was used for a long-term simulation aiming to identify the main variables affecting GPC in the CERES-wheat model. Following previous work carried out on yield simulation, the procedure described in Dalla Marta et al. (Reference Dalla Marta, Orlando, Mancini, Guasconi, Motha, Qu and Orlandini2015) was adopted for evaluating the impact of status (LAI) and forcing (weather indices) variables on GPC. Accordingly, using the model initialization described by Dalla Marta et al. (Reference Dalla Marta, Orlando, Mancini, Guasconi, Motha, Qu and Orlandini2015), CERES-wheat was run over the 56-year period from 1955 to 2011, with the new GPC equation. A correlation analysis was carried out, using the output of the long-term simulation (GPC and LAI) and the observed monthly weather indices (Table 3), in order to describe the relationship between GPC and both LAI and the weather indices. The values of the proposed prediction factors are calculated at the key crop growth stages of tillering, heading and grain filling, corresponding to stages 2, 5 and 7, respectively, of the Biologische Bundesanstalt, Bundessortenamt und Chemische Industrie (BBCH) phenological scale for cereals (Lancashire et al. Reference Lancashire, Bleiholder, Langeluddecke, Stauss, van den Boom, Weber and Witzen-Berger1991).
Table 3. Correlations between grain protein concentration, weather indices and plant LAI during the crop cycle
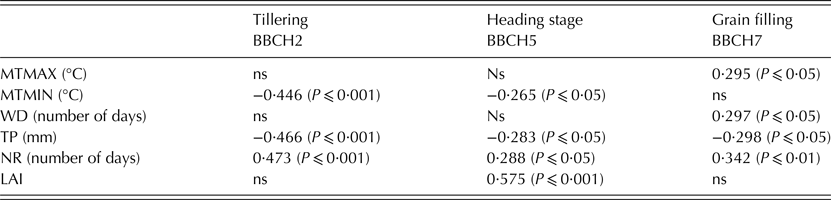
ns, not significant; MTMAX, monthly mean maximum temperature; MTMIN, monthly mean minimum temperature; WD, warm days (maximum temperature above monthly 56-years average); TP, monthly total precipitation; NR, days without rainfall; LAI, leaf area index.
A backward stepwise multiple regression (SPSS.18) was performed, with GPC as the dependent variable, and LAI and weather indices (Table 3) as prediction factors in order to develop a simplified forecasting index (SFIpro) for GPC, of the form described in Eqn (4):
where Y is the GPC at harvest taken from each year of the long-term simulation output; β 0 the intercept value; β 1, β 2, …, β n the regression coefficients of the predictor variables X 1, X 2, …, X n , respectively.
The SFIpro was validated against field data collected on ten fields per year during two growing seasons (2010 and 2011 harvests) in order to assess its potential as an operational tool and therefore to study the ability of CERES-wheat to determine the main variables affecting GPC. In monitored fields, different crop management were considered according to the agronomic practices commonly adopted by each farmer (Table 4). At harvest, ten samples were collected following an X scheme with two repetitions (i.e. five sampling points per field, one point in the centre and four points around the centre, forming a cross). Each sample consisted of plants collected from an area of 1 m2. Grain moisture content was measured after oven-drying (105 °C for 24 h), the GPC and grain gluten concentration were determined with an Infratec System 1241 Grain Analyser (FOSS, Denmark), and the yield was recorded by a precision mini thresher. To better understand the model performances, a second validation of SFIpro was carried out separately on two groups of fields classified in terms of the LAI values during the heading stage (BBCH stage 5) (LAI5) recorded in field. Fields where crop LAI was in the II and III quartiles were grouped as intermediate LAI (LAIint) (1 ⩽ LAI5 ⩽ 2) (ten fields), and fields where crop LAI was in I and IV quartiles were grouped as extreme LAI (LAIext) (LAI5 < 1 and LAI5 > 2) (four and six fields, respectively). Fields belonging to the same growing season showed a heterogeneous distribution between LAIint and LAIext, indicating that LAI5 is affected both by the seasonal weather and by the different crop management adopted by each farmer.
Table 4. Sowing date and fertilizers applied during the growing seasons 2009–2010 and 2010–2011
DAS, days after sowing; P, phosphorus; N, nitrogen.
In order to investigate how SFIpro performance was related to different LAI and thus the relationship between GPC and LAI, correlation analyses between forecasted and observed GPC and between observed yield and observed GPC were performed separately for the LAIint and LAIext groups.
RESULTS
Results concerning the performance of CERES-wheat in terms of GPC simulation, with both the standard and new equation, are shown in Table 2. The correlation between observed and simulated GPC was significant (P ⩽ 0·01), but for operational use it cannot be considered satisfactory for either the standard model routine or the new equation. However, the new equation is an improvement, enhancing the values of all the measures of fit considered (Table 2).
Analysis of the long-term simulations shows that CERES-wheat predictions of GPC are affected significantly by weather conditions during tillering, heading and grain-filling growth stages (Table 3). The model identified drought conditions as a promoter of GPC with significant negative correlations at all growth stages with monthly total precipitation (TP) (P ⩽ 0·001 at BBCH2 and 7; P ⩽ 0·05 at BBCH5) and corresponding positive correlations with days without rainfall (NR) (P ⩽ 0·001 at BBCH2 and 7; P ⩽ 0·05 at BBCH5). The model produced different impacts due to temperature depending on crop growth stage. Higher GPC values were simulated with cold conditions, described by low monthly mean minimum temperature (MTMIN) at tillering and heading stages and, conversely, with warm temperatures at the grain-filling stage, with positive correlations between GPC and monthly mean maximum temperature (MTMAX) and warm days (WD – maximum temperature above monthly 56-year average). Concerning status variables, LAI significantly affected GPC with a positive correlation, but only at the heading stage (LAI5) (P ⩽ 0·001) (Table 3).
The analysis showed that the main status and forcing variables affecting GPC were LAI at heading stage and rainfall distribution at tillering, respectively. Then, accounting for only these variables the SFIpro was described by the multiple regression as follows (Eqn (5)):
where Y is the GPC, LAI5 is the LAI at BBCH stage 5 and NR2 is the number of dry days during BBCH stage 2.
Unfortunately, the developed SFIpro failed at validation. In fact, the correlation between GPC assessed through SFIpro and that observed in the field monitoring was significantly negative (R 2 = 0·406; P ⩽ 0·01) (Fig. 1), showing complete disagreement between modelled and observed GPC.

Fig. 1. Scatter plot between grain protein concentration (GPC) values assessed by SFIpro and those observed. Data given on dry matter basis.
One reason for this failure is that LAIint and LAIext clearly showed different trends in the correlation between modelled and observed GPC. In LAIext, a highly significant and negative correlation was found (R 2 = 0·810; P ⩽ 0·001) (Fig. 2), confirming the failure of SFIpro, whereas for LAIint the SFIpro was able to describe the GPC variability, showing a significant positive correlation between observed and forecasted data (R 2 = 0·604; P ⩽ 0·01) (Fig. 2). Different behaviour was also shown by LAIint and LAIext as regards the correlation between yield and GPC observed during field monitoring. In LAIint, no significant relationship was found between the two harvest components (results not shown), while in LAIext the GPC was negatively correlated to yield (R 2 = 0·595; P ⩽ 0·01) (Fig. 3).
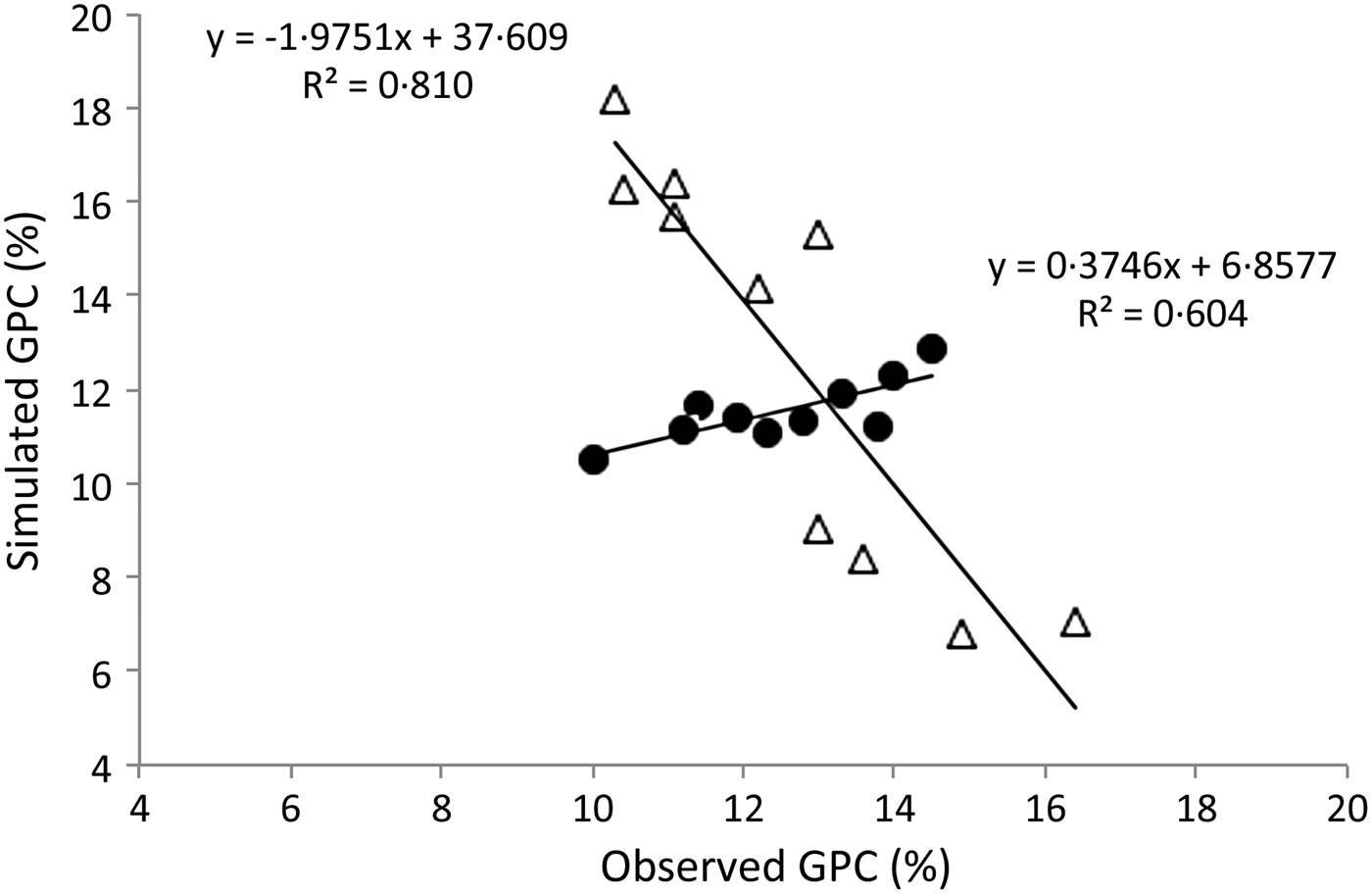
Fig. 2. Scatter plot between grain protein concentration (GPC) values assessed by SFIpro and those observed in LAIint (fields group with 1 ⩽ LAI ⩽ 2) fields (solid circles) and LAIext (LAI < 1 and LAI > 2) fields (empty circles). Data given on dry matter basis.
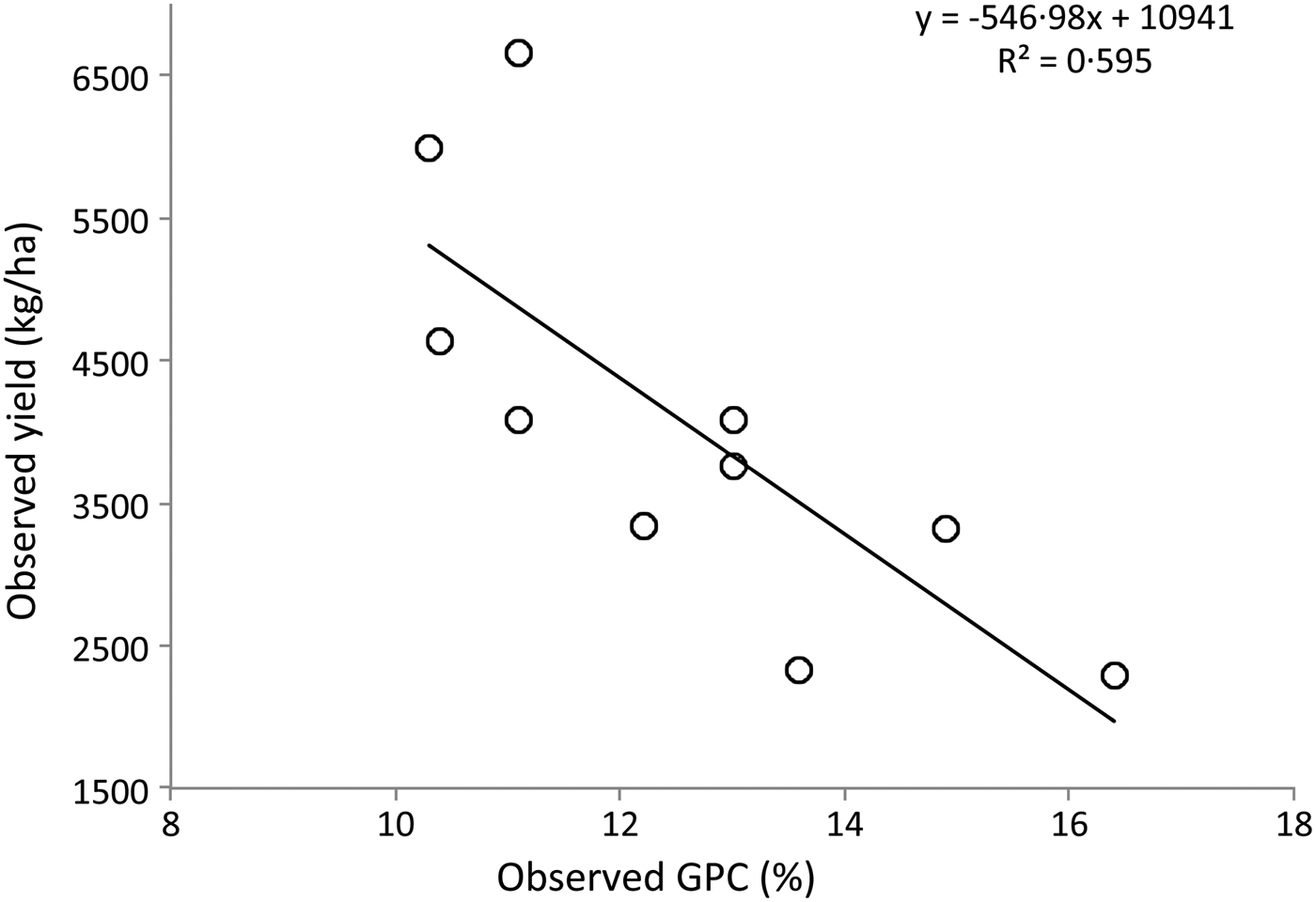
Fig. 3. Scatter plot between observed grain protein concentration (GPC) and yield of LAIext (LAI < 1 and LAI > 2) fields. Data given on dry matter basis.
In the field data, grain gluten concentration closely tracked the GPC trend with a R 2 = 0·973 (P ⩽ 0·001) between the two variables (data not shown), confirming the ability of GPC to describe this key determinant of harvest quality, and the relevance of the modelling of the dynamics underlying protein deposition and accumulation in optimizing crop management.
DISCUSSION
Although the CERES-wheat model has previously been parameterized for winter durum wheat cvar Claudio regarding phenology and yield, the model uses a GPC algorithm, which was originally developed for common wheat (the Triticum aestivum genotype) (Nuttal et al. Reference Nuttal, O'Leary, Panozzo, Walker, Barlow and Fitzgerald2015). However, durum wheat is richer in protein, specifically gluten, as this is crucial for pasta making. Compared to common wheat (T. aestivum), the literature shows that, in Mediterranean areas, durum wheat has a significantly higher average grain N concentration under the same climatic conditions (Cossani et al. Reference Cossani, Slafer and Savin2011). Therefore, the current work developed a new equation (Eqn (1)) to account for such issues, resulting in improved simulation of GPC compared to the standard GPC model routine. In fact, application of the new equation reduced the mean squared error, mainly thanks to a reduction of underestimation. Nevertheless, performance was still poor (R 2 = 0·423), confirming that simulation of GPC for durum wheat remains problematic, in accordance with the findings of other authors (Asseng et al. Reference Asseng, Bar-Tal, Bowden, Keating, Van Herwaarden, Palta, Huth and Probert2002; Weiss & Moreno-Sotomayer Reference Weiss and Moreno-Sotomayer2006).
The results of a long-term simulation study showed that in the model water-limited conditions in early crop development and during heading, enhanced GPC, as well as heat and water stress during the grain-filling stage. However, the scientific literature provides inconclusive results concerning the impact of temperature on GPC during vegetative growth, especially when long-term analyses are considered. For example, Orlandini et al. (Reference Orlandini, Mancini, Grifoni, Orlando, Dalla Marta and Capecchi2011) found no significant correlation between GPC and average monthly temperature. Smith and Gooding (Reference Smith and Gooding1996) and Garrido-Lestache et al. (Reference Garrido-Lestache, López-Bellido and López-Bellido2005) found that the temperature trend in the pre-anthesis period was not able to explain the variability in GPC. Ludwig and Asseng (Reference Ludwig and Asseng2006) suggested that higher temperatures could cause either an increase or a decrease in GPC.
CERES-wheat, in common with other wheat crop growth models, assumes that protein deposition is based on N uptake by the plant, which in turn is estimated on the basis of soil N availability and crop demand (Nuttal et al. Reference Nuttal, O'Leary, Panozzo, Walker, Barlow and Fitzgerald2015). The latter is determined by the model in relation to leaf biomass or leaf area. Therefore, the higher the value of plant LAI, the greater the GPC simulated by the model. However, a positive relationship between LAI and GPC is only partially confirmed in the scientific literature. On one hand, studies have identified wheat leaves as the main source of amino acids for grain protein synthesis (Dalling Reference Dalling, Harper, Schrader and Howell1985), reporting that total leaf N at anthesis is positively related to GPC (Wang et al. Reference Wang, Huang, Zhao, Yang and Wang2003; Li et al. Reference Li, Zhu, Tian, You, Zhou and Cao2005). On the other hand, Orlandini et al. (Reference Orlandini, Mancini, Grifoni, Orlando, Dalla Marta and Capecchi2011) and Wang et al. (Reference Wang, Wang, Liu, Huang, Zhao and Wang2004) found a negative correlation between LAI retrieved by remote-sensing indices and GPC, while others again found no significant interaction between these two variables (Freeman et al. Reference Freeman, Raun, Johnson, Mullen, Stone and Solie2003; Liu et al. Reference Liu, Wang, Bao, Huang, Ma and Zhao2006; Xue et al. Reference Xue, Cao and Yang2007). Bonfil et al. (Reference Bonfil, Karnieli, Raz, Mufradi, Asido, Egozi, Hoffman and Schmilovitch2004) and Smith and Gooding (Reference Smith and Gooding1999) suggested that a higher biomass production and vegetative proliferation promoted by meteorological conditions would dilute the N within the plant, and a grain with a low protein level would be harvested. In this situation, LAI and total N content in the leaf biomass at heading stage would not be consistently successful in predicting GPC. Neither the standard nor the new model assumptions for the simulation of GPC take this issue into account.
For these reasons, SFIpro, built using data from CERES wheat model simulations, completely failed the GPC assessment when applied to the complete observed dataset. However, by separately analysing the performance of SFIpro on a portion of the observed dataset, differentiating according to the LAI measured at the field level, the results achieved were very different. The SFIpro was able to assess GPC trend when the observed LAI values were within an intermediate range. Thus, in the case of LAIint (1 ⩽ LAI ⩽ 2), CERES-wheat assumptions for GPC simulation were confirmed, and increasing values of LAI were associated with an increase in GPC.
On the other hand, SFIpro completely failed the GPC assessment for LAIext (LAI < 1 and LAI > 2). In this case, a high LAI was accompanied by low measured GPC, contrary to model assumption. Similarly, with a low LAI, high GPC was observed. These results are reflected in the observed inverse relationship between GPC and yield that was observed for extreme (LAIext), but not intermediate (LAIint) LAI. As already discussed, weather conditions that discourage vegetative proliferation, and therefore leaf development, can lead to a reduction in grain size and weight, with a lower yield but a relative increase in the GPC, with the converse applying under conditions of strong vegetative proliferation. In this regard, Meinke et al. (Reference Meinke, Rabbinge, Hammer, Van Keulen and Jamieson1998) pointed out the inability of the models to predict the N percentage of the kernel due to its sensitivity to slight dry matter changes. In particular, Cossani et al. (Reference Cossani, Slafer and Savin2011) highlighted how in durum wheat the impact of a yield increase on GPC is more evident, observing that in the Mediterranean environment an increase in grain weight is accompanied by a more pronounced decrease in grain N compared with common wheat.
Finally, these results suggest that SFIpro being based on the model simulations has shown the same difficulties in capturing the inverse relationship between yield and GPC. An increase in LAI beyond a threshold promoted the yield, so that the benefits for grain protein accumulation, related to the greater total N content in leaves, were minimized. Similarly, very low LAI values, leading to a reduction in grain weight and yield, were able to promote the GPC despite lower N available for the grain protein deposition. It is possible that this nonlinear relationship between LAI and GPC could be the basis of the disagreement in literature discussed above, concerning the correlation between the remotely sensed LAI and GPC.
CONCLUSIONS
The aim of the current research was the development of a simplified forecasting index for the assessment of GPC in durum wheat, based on the identification of the main status and forcing variables affecting GPC implemented in the CERES-wheat model. The model showed significant correlations between GPC and the number of dry days during tillering and LAI at heading stage, and so these two variables were included in the developed forecasting index. However, during validation, the index performed well in forecasting GPC when crop LAI5 (i.e. LAI at the heading stage) ranged between 1 and 2, while poor performances were obtained where LAI5 was lower (LAI5 < 1) or higher (LAI5 > 2).
These results suggest that the relationship between LAI and GPC is nonlinear and that the CERES-wheat assumption of ‘source-limited’ protein deposition in grain is only partially confirmed, being valid for an intermediate range of LAI. For this reason, further research is required in order to better understand and formalize the relation between LAI and grain protein accumulation so improving the model's potential to assess in advance this parameter, which is one of the main factors determining the quality of durum wheat.










