Impact Statement

One method that climate scientists use to find structures in environmental data is unsupervised classification, where a machine learning model sorts data, such as temperatures from different parts of the ocean, into groups or classes. This paper proposes a new way of determining if an unsupervised classification model has “over-fit” the data available, which means it is using too many classes. This method will be useful for climate scientists using unsupervised classification for studying climate model data, as current criteria commonly used often don’t provide an upper limit on the number of classes.

2. Data and Methods

This section is arranged as follows: first, we describe the dataset of temperature profiles from the UK-ESM CMIP6 simulations (Section 2.1), then we describe the form of the GMMs we fit to those data (Section 2.2). Finally, in Section 2.3, we describe the different methods we will compare to select the number of classes: the BIC, the silhouette score, and the newly defined EDC.

2.2. Classification scheme

Figure 1 gives an overview of the classification process, which is carried out independently for each ensemble member described in Section 2.1. As an initial step, the raw dataset is normalized so that each depth level has mean zero and standard deviation one. We choose to normalize because the variance in the raw profiles is dominated by the near-surface (Figure 1a), and we wish the classification to be dependent on the structures of the profiles over the full depth considered rather than dominated by surface temperatures.

Figure 1. An overview of the classification process using 1200 random Southern Ocean profiles from the year 2000. Raw profiles (a), are normalized (b) so each depth level has a mean of zero and a standard deviation of one. (c) The profiles are transformed into PCA space. Two PCs are shown here; each point corresponds to one temperature profile. (d) The data are classified according to a GMM. Three classes are chosen to generate this example, with an equi-probability surface shown for each, separately.

Each profile is $ L=30 $ -dimensional (determined by the number of depth levels between 100m and 2km in the model). The large number of dimensions makes computation expensive and hinders the usefulness of distance metrics on the normalized dataset. Principal component analysis (PCA) (Abdi and Williams, Reference Abdi and Williams2010) is employed as a dimensionality-reduction step. The dataset in PC space is given by

(1) $$ {\mathbf{x}}_i=\mathrm{P}{\mathbf{T}}_i, $$

where $ {\mathbf{T}}_i $ is the $ i $ th temperature profile in depth space, $ {\mathbf{x}}_i $ is the same profile in PC space, and P is the projection matrix. In the following analysis, $ M=3 $ principal components are used––the first three PCs are sufficient to explain $ 99.8\% $ of the variance in the training dataset.

The training dataset is fitted to a GMM (Anderson and Moore, Reference Anderson and Moore2012) as in Jones et al. (Reference Jones, Holt, Meijers and Shuckburgh2019). This assumes that the data points $ {\mathbf{x}}_i $ are sampled from a joint distribution over profiles $ \mathbf{x} $ and class $ k $ (a Gaussian mixture), with probability

(2) $$ {\rho}_k\left(\mathbf{x}\right)={\lambda}_k\mathbf{\mathcal{N}}\left(\mathbf{x};{\boldsymbol{\mu}}_k,{\Sigma}_k\right), $$

where

(3) $$ \mathbf{\mathcal{N}}\left(\mathbf{x};{\boldsymbol{\mu}}_k,{\Sigma}_k\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^M\mid {\Sigma}_k\mid }}\exp \left[-\frac{1}{2}{\left(\mathbf{x}-{\boldsymbol{\mu}}_k\right)}^T{\Sigma}_k^{-1}\left(\mathbf{x}-{\boldsymbol{\mu}}_k\right)\right] $$

is a multivariate Gaussian distribution with mean $ {\boldsymbol{\mu}}_k $ and covariance matrix $ {\Sigma}_k $ , and

(4) $$ {\lambda}_k\in \left[0,1\right],\sum \limits_{k=1}^K{\lambda}_k=1 $$

is any distribution over the set $ \left\{{k}_i\right\}=\left[1,K\right] $ where $ K $ is the total number of classes. The marginal distribution of the profiles $ \mathbf{x} $ is

(5) $$ \rho \left(\mathbf{x}\right)=\sum \limits_{k=1}^K{\rho}_k\left(\mathbf{x}\right). $$

This work uses the GMM classification model from the scikit-learn Python package (Pedregosa et al., Reference Pedregosa, Varoquaux, Gramfort, Michel, Thirion, Grisel, Blondel, Prettenhofer, Weiss, Dubourg, Vanderplas, Passos, Cournapeau, Brucher, Perrot and Duchesnay2011). This implements an expectation-maximization algorithm to learn the set of parameters $ \left\{{\lambda}_k,{\boldsymbol{\mu}}_k,{\Sigma}_k\right\} $ from the training dataset. Each data point is then assigned to a single class according to the Gaussian distribution it most likely belongs to, that is, the class with the greatest probability $ {\rho}_k\left({\mathbf{x}}_i\right) $ :

(6) $$ {k}_i=\underset{k}{\arg \hskip0.35em \max}\hskip0.35em {\rho}_k\left({\mathbf{x}}_i\right). $$

The final result of the classification is a function that maps from a temperature profile to a class index, which is used to classify the full dataset, including the training data, for that ensemble member:

(7) $$ f:{\mathbf{T}}_i\hskip0.35em \mapsto \hskip0.35em {k}_i, $$

as well as providing the probability distributions $ {\rho}_k $ . This allows one to define the overall certainty of the model as the sum of the log-likelihoods $ \mathrm{\mathcal{L}}(K) $ over all $ N $ profiles:

(8) $$ \mathrm{\mathcal{L}}(K)=\sum \limits_i^N\log \left(\rho \left({\mathbf{x}}_i\right)\right), $$

which is a measure of how well a given GMM represents the data.

2.3. Definition of metrics to determine the optimal number of classes

We here define three criteria for determining the optimal number of classes that we will use to analyze our results: the BIC, the silhouette coefficient, and a novel method, the EDC.

2.3.1. BIC

The BIC is a cost metric that rewards a high total likelihood of the data $ \mathrm{\mathcal{L}}(K) $ , while regularizing based on the estimated number of free parameters in the GMM $ {N}_f(K) $ .

(9) $$ \mathrm{BIC}(K)=-2\mathrm{\mathcal{L}}(K)+{N}_f(K)\ln (N), $$

(10) $$ {N}_f(K)=K-1+ KM+\frac{1}{2} KM\left(M-1\right). $$

A low BIC implies that the model fits the data well, while also avoiding overfitting. An optimal value of $ K $ can be determined by, for example, a minimum in the BIC curve, or for a value of $ K $ above which there are diminishing returns, determined by looking at the $ \Delta $ BIC curve, that is the change in score for adding an extra class. The AIC is similarly defined but weights the number of free parameters differently.

2.3.2. Silhouette coefficient

The silhouette coefficient is a measure of how well the clusters in a model are separated from each other. For each classified sample, the sample silhouette coefficient $ {S}_i $ is based on comparing the mean distance between point $ i $ and all other points in the same cluster ( $ {a}_i $ ), and the mean distance between point $ i $ and all points in the “nearest” cluster ( $ {b}_i $ ):

(11) $$ {S}_i=\frac{b_i-{a}_i}{\mathit{\max}\left({a}_i,{b}_i\right)}. $$

Note that in our example, the distance between samples is calculated in PCA space, the space on which the samples are classified (see Figure 1d), and not in geographical space.

$ {S}_i $ can vary from −1 (a “poor” score, indicating the sample is closer to samples in the neighboring class than its own) to 1 (a “good” score, indicating the sample is far from samples in the neighboring class), whereas a score of 0 indicates overlapping classes. The overall silhouette coefficient for a given model is the mean of the sample silhouettes, that is, SIL $ \equiv 1/N\hskip0.35em {\sum}_i^N{S}_i $ . Maximizing the silhouette coefficient therefore desirable for applications where well-separated classes is a priority.

2.3.3. Ensemble difference criterion

If multiple realizations of the dataset are available, for example different ensemble members of UK-ESM, the simulated data can be leveraged to determine a physically-motivated and unambiguous value of the maximum number of classes.

First, we define a map between class indices in different ensembles

(12) $$ {f}^{E_1\to {E}_2}(k)=\underset{l}{\arg \min }{\left\Vert {\mathbf{T}}_k^{E_1}-{\mathbf{T}}_l^{E_2}\right\Vert}^2, $$

where $ {\mathbf{T}}_i^{E_j} $ is the mean temperature profile of the $ i $ th class in ensemble $ {E}_j $ , such that $ {f}^{E_1\to {E}_2}(k) $ is the index of the class in ensemble $ {E}_2 $ that is most similar to the class with index $ k $ in ensemble $ {E}_1 $ .

Here “most similar” is defined as the profile that minimizes the Euclidean distance in temperature/depth space, but the method is not dependent on this exact choice as long as it is allows one to identify correspondences between classes from different GMMs. Other maps could include, for example, the Euclidean distance between class centers in PCA space, the variance of each depth level, or the mean temperature of each class. We tested calculating the Euclidean distances in PCA space for the results reported here (in Sections 3 and 4.3), and most mappings were identical to those using temperature/depth space, with occasional differences for one class in a given ensemble member (not shown).

The EDC requires that, having defined $ {f}^{E_1\to {E}_2}(k) $ :

(13) $$ {\forall}_{x,y}\hskip0.1em {f}^{E_x\leftrightarrow {E}_y},x,y\in E $$

where $ x $ and $ y $ are pairs of ensemble members, and $ \leftrightarrow $ indicates the map is bijective, that is each element in ensemble $ x $ maps to one and only one member in ensemble $ y $ , and vice versa. If this is satisfied, the model passes the EDC, if it is not, the EDC is violated. In practice, to find the maximum number of classes allowed by the EDC, one successively increases K until the EDC is violated.

3. Comparison with Observations

We first compare an eight-class GMM fit on the model data, as described in Section 2, with the results of Jones et al. (Reference Jones, Holt, Meijers and Shuckburgh2019), who fit an eight class GMM on Argo data from the same time period. We present this in order to provide the context for discussing the choice of class number in Section 4, and leave detailed discussion of the physical interpretation of these results to another study.

Whilst an ideal model would exactly reproduce the “true” Southern Ocean, and would therefore have the same number of appropriate classes, we do not expect the number of classes most appropriate for the UK-ESM data is necessarily the same as the number of classes appropriate for the Argo data. This is partly because the Argo data are under-sampled in many regions (see Jones et al., Reference Jones, Holt, Meijers and Shuckburgh2019), whereas the UK-ESM data is not, inevitably leading to datasets with different properties. Even if the observations had better coverage, the Southern Ocean is imperfectly replicated by any climate model and therefore does not necessarily support the same number of classes. Nonetheless, it is informative to assess how well the results of observations and modeling studies match, in order to understand in which ways results from the modelled data might apply to the real world.

In order to compare the classification across ensembles, it is first necessary to align the classes between the ensembles, as the GMM labels the classes 1–8 at random each time it is fit. Thus, for each ensemble member, the classes are first sorted from coldest to warmest by the class mean profile temperature value at the shallowest level (5 m). Figure 2b shows the ensemble mode (i.e., most common) class for each point in the domain, across the dataset time period (2001–2017) and all seven ensemble members after sorting by surface temperature (which are shown individually in the Supplementary Material, Figures S1 and S2).

Figure 2. Comparison of the class assignments from Argo (a, Jones et al., Reference Jones, Holt, Meijers and Shuckburgh2019) and the ensemble mode class from UK-ESM (b), for 2001–2017. See text for further details. The ocean fronts from Kim and Orsi (Reference Kim and Orsi2014) are marked by the colored lines as labeled.

Note that, for eight classes, sorting by surface temperature does not always result in alignment between the classes that are closest to one another when considering the overall Euclidean distance between mean profiles at all depths, see Figure 7 and the discussion in Section 4.

Despite this, there is relatively little inter-ensemble variation in the mean temperature profiles for the classes sorted in this manner: Figure 3b shows the ensemble and time mean profiles (solid lines), with the standard deviations of the time mean profiles from each ensemble (dotted lines) smaller than the ensemble mean of the temporal standard deviations (dashed lines). For comparison, Figure 3a shows the mean and standard deviations of the temperature profiles from Jones et al. (Reference Jones, Holt, Meijers and Shuckburgh2019), sorted by the shallowest temperature.

Figure 3. The mean temperature profiles for an eight-class GMM from Jones et al. (Reference Jones, Holt, Meijers and Shuckburgh2019) (a) compared with the ensemble mean profiles from this study (b). Dashed lines indicate the standard deviation across samples for the Argo data, and the ensemble average of the temporal standard deviations for the UK-ESM data. The dotted line indicates the ensemble standard deviation in the temporal mean profiles for the UK-ESM data. Red arrows indicate the mapping from a UK-ESM class to the closest class in the Argo data, and the blue arrows indicate the same for the Argo classes and the closest classes in the UK-ESM data.

Comparing the mean profiles between the two observationally-derived GMM and the model-derived GMM using the mean Euclidean distance in temperature/depth space (see Section 4.3 for more details), we can map from each class in one model to the class it is most similar to in the other model (blue and red arrows in Figure 3).

The two GMMs show some structural similarities with the coldest four classes (1-4) largely being circumpolar, with boundaries somewhat aligned with the climatological ACC fronts from Kim and Orsi (Reference Kim and Orsi2014), marked in Figure 2. The warmer classes (5–8) show a more basin dominated structure in both models. There are, however, differences in the detailed structures: within the Southern Boundary (yellow line) the UK-ESM model has two distinct classes, 1 and 2, whereas the Argo model has only one (class 1). This could be due to the extreme sparsity of Argo data close to the continent, as well as the fact it is likely to be from Austral summer only (when the region is ice-free), whereas the UK-ESM data is year-round.

Both models then have two circumpolar classes that lie roughly between the Southern Boundary and the SAF––classes 3 and 4 in UK-ESM and 2 and 3 in Argo, with mean profiles that match well (see arrows in Figure 3). Both class 5 in UK-ESM and class 4 in Argo extend in a roughly zonal band from the South West coast of South America westward to the south Indian ocean, and show similar mean profiles. This suggests the structure of the ACC is a strong bound on the water properties, producing similar class boundaries in physical space and similar mean profiles in both models.

The geographic distributions of the warmest classes is most different between the two models, with classes 5 to 8 in the Argo model mostly confined to a single basin or sub-region. The three sub-tropical class in the UK-ESM model show a more cross-basin structure. This could be because there are fewer sub-tropical classes in the UK-ESM model than the Argo model, (three vs four). This can be tested by increasing the number of classes in the UK-ESM model to nine. This does lead to an extra sub-tropical class in the model, but the structure is no more similar to the Argo data than for the eight class model (see Figures S3 and S4 in the Supplementary Material).

The difference in structures of the sub-tropical classes between the two models could also be because the temperature profiles in this region are too similar to cluster well. This is indicated by the very similar structure of the warmest mean profiles in Figure 3, and may indicate that the datasets do not robustly support eight unique classes. A comparison of various methods to find a robust choice of classes is carried out in the next section.

4. Choosing the Number of Classes

The key free parameter in the fitting of a GMM is the total number of classes $ K $ . Choosing a value of $ K $ presents a trade-off: low values will exhibit fewer structures and may fail to capture some of the underlying covariance structure whereas high values risk overfitting, losing physical interpretability and predictability. We here compare the results of three criteria, defined in Section 2.3: the BIC, the silhouette coefficient, and the EDC.

4.1. Bayesian information criterion

The BIC and $ \Delta $ BIC curves for three ensemble members, clustered into a range of class numbers, as described in Section 2.2, is shown in Figure 4. We only calculated the curve for the first three members due to the computational expense of fitting multiple models. There is no clear minimum in the BIC curve (Figure 4a) for up to 20 classes, so no clearly optimal value of $ K $ . The $ \Delta $ BIC curve (Figure 4b) shows that adding an extra class leads to the largest improvements for 3 and 4 classes, then the gains begin to diminish for $ >5 $ classes. However, there is large variability between and within ensemble members, and some class values lead to an increase in the BIC for a given ensemble member.

Figure 4. (a) BIC curves and (b) $ \Delta $ BIC curves for three of the ensembles.

For this study, the BIC and AIC were almost identical for all clustering models studied (not shown), indicating the dominance of the log-likelihood term over the free-parameter term in equation 9, likely because of the low-dimensionality of the problem ( $ M=3 $ ).

4.2. Silhouette coefficient

The SIL and $ \Delta $ SIL curves for three ensemble members, clustered into a range of class numbers, as described in Section 2.2, are shown in Figure 5. For each ensemble member, we calculate the SIL for a random subset of 10,000 samples (approx. 1.6%) from the training set, due to the computational intensity of the calculation. Conversely to the BIC (Section 4.1), it is desirable to maximize the SIL score.

Figure 5. (a) SIL curves and (b) $ \Delta $ SIL curves for three of the ensembles.

The overall maximum SIL is for two classes, and there appears to be a local maximum at five classes for the three ensembles shown. As with the BIC, there is large variability both between and within ensemble members, especially at higher numbers of classes.

4.3. Ensemble difference criterion

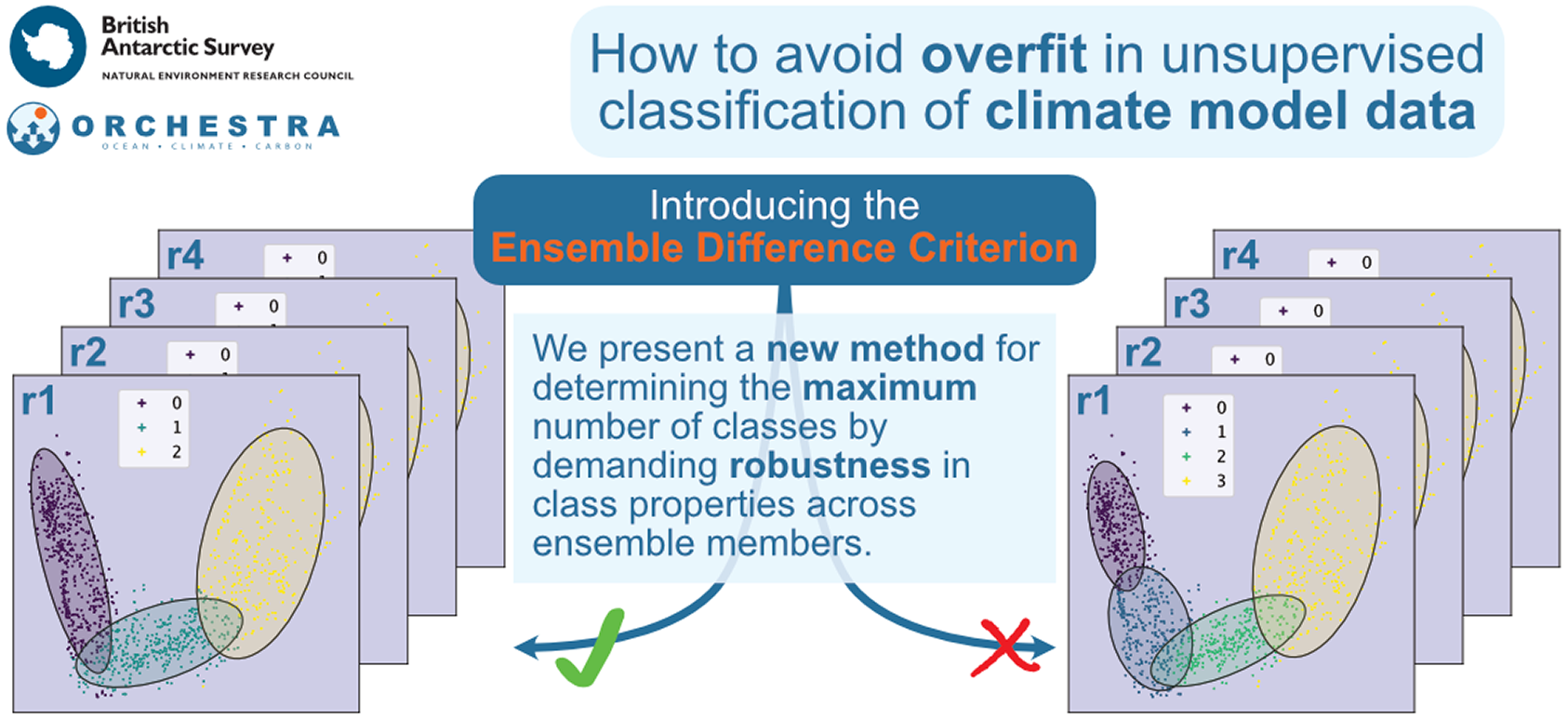
An example of using the EDC for the UK-ESM data is shown in Figures 6 and 7. Figure 6 shows an example of matching between 7-class GMMs fit to two ensemble members. The matching is successful because the map is bijective for all ensemble pairs (only one is shown here): each class in one model is matched by only one class in any other model.

Figure 6. An example of using the ensemble difference criterion (EDC) to match classes resulting from a 7-class GMM of two different ensemble members (r1i1p1f2 and r2i1p1f2).

Figure 7. An example of using the ensemble difference criterion (EDC) to match classes resulting from a 8-class GMM of two different ensemble members (r1i1p1f2 and r2i1p1f2). Note that the map between classes of each ensemble is not bijective––3 and 4 in the first ensemble are both matched to class 6 in the second (highlighted in red).

Figure 7 shows an example of matching between 8-class GMMs fit to the same two ensemble members. The matching is not bijective in this case. For example, classes 3 and 4 in the r1i1p1f2 model are both closer to class 6 in the r2i1p1f2 model than to any other. The mapping fails for all pairs between the seven ensembles (only one is shown here), with some mappings finding three classes match to the same referent. The EDC thus determines 7 classes as the maximum supported by this dataset.

6. Summary

Unsupervised classification studies are becoming increasingly common in the study of observed and simulated climate data. In many cases, techniques such as GMMs and K-means clustering have been remarkably successful at identifying structures that are coherent in time and space, despite not being provided with temporal or spatial information. The property driven-approach of these methods is attractive when the aim is to objectively identify structures. That is not to say that domain knowledge is un-necessary, and in fact experience of the climate system is required to interpret the results and place them in context.

Unsupervised classification methods generally require no external input beyond the data, and the number of classes into which the data should be divided. However, there is not necessarily an obvious choice for this number, which is a relatively unconstrained free parameter. In practice, most studies use statistical criteria such as the BIC or Silhouette score to compare the results of training the model multiple times for a range of number of classes.

In this paper, we have demonstrated a novel new method for determining over-fit, the EDC, which can be used, for example, on climate data from ensemble simulations. In demanding robustness of the class definitions between different ensemble members, the EDC provides a definitive upper limit on the number of classes supported by the data.

In the example presented here, the GMM classification of Southern Ocean temperature profiles from historical climate simulations of the UK-ESM model, we find that the BIC does not give a strong constraint on over-fitting, and so the EDC is an extremely useful extra tool. Taking into account the information provided by the BIC, the EDC, and Silhouette scores, we find our data can support between four and seven classes.

For reference, we also compare an eight class GMM based on the UK-ESM data with a previous eight class GMM based on Argo observations. We find that there is good agreement between GMMs within the ACC region; however, there are too few Argo observations South of the Southern Boundary to provide a good match with the UK-ESM data in this region. Additionally, the sub-tropical classes don’t match well between GMMs, either because the simulations don’t reproduce the temperature structure of the observed sub-tropical Southern Ocean, or because the temperature profiles are not distinct enough in these regions to support robust classes for an eight class model.