No CrossRef data available.
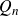 $Q_n$
$Q_n$Published online by Cambridge University Press: 08 May 2023
Let BG be the classifying space of an algebraic group G over the field 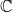 ${\mathbb C}$ of complex numbers. There are smooth projective approximations X of
${\mathbb C}$ of complex numbers. There are smooth projective approximations X of 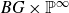 $BG\times {\mathbb P}^{\infty}$, by Ekedahl. We compute a new stable birational invariant of X defined by the difference of two coniveau filtrations of X, by Benoist and Ottem. Hence we give many examples such that two coniveau filtrations are different.
$BG\times {\mathbb P}^{\infty}$, by Ekedahl. We compute a new stable birational invariant of X defined by the difference of two coniveau filtrations of X, by Benoist and Ottem. Hence we give many examples such that two coniveau filtrations are different.