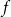1. Introduction
To every matroid
![]() $\mathsf {M}$
one may associate its base polytope
$\mathsf {M}$
one may associate its base polytope
![]() $\mathscr {P}(\mathsf {M})$
, carrying all the information of the matroid. Not only this polytope plays a prominent role in combinatorial optimisation [Reference Schrijver46] but also is of fundamental importance in tropical geometry [Reference Maclagan and Sturmfels39, Reference Joswig32], the theory of valuations [Reference Derksen and Fink18, Reference Ardila and Sanchez8], combinatorial Hodge theory, and the study of matroid invariants [Reference Berget, Eur, Spink and Tseng10, Reference Eur, Huh and Larson19, Reference Ferroni and Schröter23].
$\mathscr {P}(\mathsf {M})$
, carrying all the information of the matroid. Not only this polytope plays a prominent role in combinatorial optimisation [Reference Schrijver46] but also is of fundamental importance in tropical geometry [Reference Maclagan and Sturmfels39, Reference Joswig32], the theory of valuations [Reference Derksen and Fink18, Reference Ardila and Sanchez8], combinatorial Hodge theory, and the study of matroid invariants [Reference Berget, Eur, Spink and Tseng10, Reference Eur, Huh and Larson19, Reference Ferroni and Schröter23].
A question that arises naturally in the study of a convex polytope
![]() $\mathscr {P}\subseteq \mathbb {R}^n$
is how many faces of each dimension
$\mathscr {P}\subseteq \mathbb {R}^n$
is how many faces of each dimension
![]() $\mathscr {P}$
has. The
f-vector of
$\mathscr {P}$
has. The
f-vector of
![]() $\mathscr {P}$
is defined by
$\mathscr {P}$
is defined by
where
![]() $f_i \,:\!= \#\{\text {$i$-dimensional faces of $\mathscr {P}$}\}$
for each
$f_i \,:\!= \#\{\text {$i$-dimensional faces of $\mathscr {P}$}\}$
for each
![]() $i\in \{0,\ldots, d\}$
and
$i\in \{0,\ldots, d\}$
and
![]() $d\,:\!=\dim \mathscr {P}$
. In particular, the number of vertices of
$d\,:\!=\dim \mathscr {P}$
. In particular, the number of vertices of
![]() $\mathscr {P}$
is just
$\mathscr {P}$
is just
![]() $f_0$
, the number of facets of
$f_0$
, the number of facets of
![]() $\mathscr {P}$
is
$\mathscr {P}$
is
![]() $f_{d-1}$
, and
$f_{d-1}$
, and
![]() $f_d=1$
.
$f_d=1$
.
The difficulty of calculating the
![]() $f$
-vector may vary drastically depending on the polytope
$f$
-vector may vary drastically depending on the polytope
![]() $\mathscr {P}$
, on the properties it possesses, or on how it is described; for some concrete examples of the computation of
$\mathscr {P}$
, on the properties it possesses, or on how it is described; for some concrete examples of the computation of
![]() $f$
-vectors and certain related problems, see [Reference Ziegler48]. The family of possible vectors arising as the
$f$
-vectors and certain related problems, see [Reference Ziegler48]. The family of possible vectors arising as the
![]() $f$
-vector of a polytope is notoriously hard, and their classification is open in dimensions as low as four, see [Reference Ziegler50]. Even in the case of
$f$
-vector of a polytope is notoriously hard, and their classification is open in dimensions as low as four, see [Reference Ziegler50]. Even in the case of
![]() $0/1$
-polytopes of fixed dimension, although the set of possible
$0/1$
-polytopes of fixed dimension, although the set of possible
![]() $f$
-vectors is finite, much remains to be discovered, see [Reference Ziegler49].
$f$
-vectors is finite, much remains to be discovered, see [Reference Ziegler49].
In this article, we will initiate the study of the explicit face enumeration of matroid polytopes, by focusing on the well-structured subclass of split matroids. The face structure of some special classes as positroids and lattice path matroids appeared in previous work, however without an explicit enumeration. The class of split matroids was introduced by Joswig and Schröter in [Reference Joswig and Schröter33] to study tropical linear spaces. They have received considerable attention in the past few years, including a forbidden minor characterisation [Reference Cameron and Mayhew17], hypergraphs descriptions [Reference Bérczi, Király, Schwarcz, Yamaguchi and Yokoi13], Tutte polynomial inequalities [Reference Ferroni and Schröter22], subdivisions and computation of valuations [Reference Ferroni and Schröter23], and conjectures about exchange properties on the bases [Reference Bérczi and Schwarcz15] which are related to White’s conjecture.
Even though the
![]() $f$
-vector of the matroid base polytope constitutes an invariant of the matroid
$f$
-vector of the matroid base polytope constitutes an invariant of the matroid
![]() $\mathsf {M}$
under isomorphisms, it is not valuative; see Example 2.2 below. This makes its computation considerably subtler and difficult. In particular, for the case of split matroids we require a non-trivial modification of the machinery presented in [Reference Ferroni and Schröter23].
$\mathsf {M}$
under isomorphisms, it is not valuative; see Example 2.2 below. This makes its computation considerably subtler and difficult. In particular, for the case of split matroids we require a non-trivial modification of the machinery presented in [Reference Ferroni and Schröter23].
One important reason why split matroids deserve to be studied is that they encompass the classes of paving and copaving matroids. A long-standing conjecture often attributed to Crapo and Rota, appearing in print in [Reference Mayhew, Newman, Welsh and Whittle38], predicts that asymptotically almost all matroids are sparse paving. There is some evidence supporting this assertion [Reference Pendavingh and van der Pol43], but another intriguing conjecture affirms that even restricting to the enumeration of non sparse paving matroids, the class of split matroids will continue to be predominant [Reference Ferroni and Schröter23, Conjecture 4.11].
As of today, the problem of face enumeration of matroid polytopes has not been approached systematically in the literature, and to the best of our knowledge there are no prior articles addressing their computation. Nonetheless, there are some results that could be of interest in the study of
![]() $f$
-vectors of certain classes of matroids. The computation of the cd-index of matroid polytopes of rank two appears in work by Kim [Reference Kim34]. In [Reference An, Jung and Kim5] An, Jung, and Kim investigated the lattice of faces of the base polytopes of lattice path matroids. In [Reference Ardila, Rincón and Williams7] Ardila, Rincón and Williams approached the lattice of faces of positroids, whereas in [Reference Oh and Xiang41] Oh and Xiang studied the facets of positroid polytopes. In [Reference Grande and Sanyal27] Grande and Sanyal used the faces of matroid polytopes to characterise their
$f$
-vectors of certain classes of matroids. The computation of the cd-index of matroid polytopes of rank two appears in work by Kim [Reference Kim34]. In [Reference An, Jung and Kim5] An, Jung, and Kim investigated the lattice of faces of the base polytopes of lattice path matroids. In [Reference Ardila, Rincón and Williams7] Ardila, Rincón and Williams approached the lattice of faces of positroids, whereas in [Reference Oh and Xiang41] Oh and Xiang studied the facets of positroid polytopes. In [Reference Grande and Sanyal27] Grande and Sanyal used the faces of matroid polytopes to characterise their
![]() $k$
-levelness. In all of the aforementioned cases, although combinatorial descriptions and properties of the faces of the polytope are provided, an explicit enumeration of them does not seem direct or easy. In [Reference Postnikov, Reiner and Williams42] Postnikov, Reiner, and Williams described the
$k$
-levelness. In all of the aforementioned cases, although combinatorial descriptions and properties of the faces of the polytope are provided, an explicit enumeration of them does not seem direct or easy. In [Reference Postnikov, Reiner and Williams42] Postnikov, Reiner, and Williams described the
![]() $h$
-vector of simple generalised permutohedra; however, although the class of generalised permutohedra encompasses the family of matroid base polytopes, these fail to be simple when the rank or the corank are greater than one.
$h$
-vector of simple generalised permutohedra; however, although the class of generalised permutohedra encompasses the family of matroid base polytopes, these fail to be simple when the rank or the corank are greater than one.
In particular, perhaps as a reminiscence of the situation for polytopes in general (and even for
![]() $0/1$
-polytopes), questions about properties of
$0/1$
-polytopes), questions about properties of
![]() $f$
-vectors of matroid polytopes are widely open.
$f$
-vectors of matroid polytopes are widely open.
1.1 Main results
As mentioned before, the fact that the face numbers are not valuations makes the computation of the
![]() $f$
-vector of matroid polytopes a delicate task. In the case of split matroids, we need more data than just the number of cyclic flats of each rank and size. Some information on their pairwise intersection is necessary.
$f$
-vector of matroid polytopes a delicate task. In the case of split matroids, we need more data than just the number of cyclic flats of each rank and size. Some information on their pairwise intersection is necessary.
In order to express the
![]() $f$
-vector of a polytope
$f$
-vector of a polytope
![]() $\mathscr {P}$
in a more compact fashion, we will often refer to the
f-polynomial, which is defined via:
$\mathscr {P}$
in a more compact fashion, we will often refer to the
f-polynomial, which is defined via:
 \begin{equation*} f_{\mathscr {P}}(t)\, :\!= \sum _{i=0}^d f_i\cdot t^i.\end{equation*}
\begin{equation*} f_{\mathscr {P}}(t)\, :\!= \sum _{i=0}^d f_i\cdot t^i.\end{equation*}
Following the notation and terminology of [Reference Ferroni and Schröter23], whenever we have a matroid
![]() $\mathsf {M}$
of rank
$\mathsf {M}$
of rank
![]() $k$
and cardinality
$k$
and cardinality
![]() $n$
, we denote by
$n$
, we denote by
![]() $\unicode {x03BB}_{r,h}$
the number of stressed subsets of rank
$\unicode {x03BB}_{r,h}$
the number of stressed subsets of rank
![]() $r$
and size
$r$
and size
![]() $h$
with non-empty cover that
$h$
with non-empty cover that
![]() $\mathsf {M}$
has. For a connected split matroid, the number
$\mathsf {M}$
has. For a connected split matroid, the number
![]() $\unicode {x03BB}_{r,h}$
counts also the number of proper non-empty cyclic flats of rank
$\unicode {x03BB}_{r,h}$
counts also the number of proper non-empty cyclic flats of rank
![]() $r$
and size
$r$
and size
![]() $h$
. Although one of the main results of that article establishes that the numbers
$h$
. Although one of the main results of that article establishes that the numbers
![]() $\unicode {x03BB}_{r,h}$
are enough to compute any valuative invariant on
$\unicode {x03BB}_{r,h}$
are enough to compute any valuative invariant on
![]() $\mathsf {M}$
, we need further data to compute the
$\mathsf {M}$
, we need further data to compute the
![]() $f$
-vector.
$f$
-vector.
For a matroid
![]() $\mathsf {M}$
as before, we will denote by
$\mathsf {M}$
as before, we will denote by
![]() $\unicode {x03BC}_{\alpha, \beta, a,b}$
the number of modular pairs of cyclic flats
$\unicode {x03BC}_{\alpha, \beta, a,b}$
the number of modular pairs of cyclic flats
![]() $\{F_1,F_2\}$
such that
$\{F_1,F_2\}$
such that
![]() $a = |F_1\smallsetminus F_2|$
,
$a = |F_1\smallsetminus F_2|$
,
![]() $b = |F_2\smallsetminus F_1|$
,
$b = |F_2\smallsetminus F_1|$
,
![]() $\alpha = \textrm {rk}(F_1)-\textrm {rk}(F_1\cap F_2)$
, and
$\alpha = \textrm {rk}(F_1)-\textrm {rk}(F_1\cap F_2)$
, and
![]() $\beta = \textrm {rk}(F_2)-\textrm {rk}(F_1\cap F_2)$
; see also equation (⋆) below.
$\beta = \textrm {rk}(F_2)-\textrm {rk}(F_1\cap F_2)$
; see also equation (⋆) below.
The following constitutes the main result of this article and is stated as Theorem2.5 further below. It tells us that the numbers
![]() $\unicode {x03BC}_{\alpha, \beta, a,b}$
are the precise additional datum needed to perform the computation of the
$\unicode {x03BC}_{\alpha, \beta, a,b}$
are the precise additional datum needed to perform the computation of the
![]() $f$
-vector of a split matroid polytope. Moreover, the statement tells us concretely how to calculate the number of faces of given dimension.
$f$
-vector of a split matroid polytope. Moreover, the statement tells us concretely how to calculate the number of faces of given dimension.
Theorem.
Let
![]() $\mathsf {M}$
be a connected split matroid of rank
$\mathsf {M}$
be a connected split matroid of rank
![]() $k$
on
$k$
on
![]() $n$
elements. The number of faces of its base polytope
$n$
elements. The number of faces of its base polytope
![]() $\mathscr {P}(\mathsf {M})$
is given by the polynomial
$\mathscr {P}(\mathsf {M})$
is given by the polynomial
where the first sum ranges over all values with
![]() $0\lt r\lt h\lt n$
and the second sum ranges over the values
$0\lt r\lt h\lt n$
and the second sum ranges over the values
![]() $0\lt \alpha \lt a$
,
$0\lt \alpha \lt a$
,
![]() $0\lt \beta \lt b$
for which either
$0\lt \beta \lt b$
for which either
![]() $a\lt b$
or
$a\lt b$
or
![]() $a=b$
and
$a=b$
and
![]() $\alpha \leq \beta$
.
$\alpha \leq \beta$
.
In the above theorem, the expressions
![]() $u_{r,k,h,n}(t)$
and
$u_{r,k,h,n}(t)$
and
![]() $w_{\alpha, \beta, a,b}(t)$
are polynomials that depend only on their subindices. We present in Propositions 2.7 and 2.8 explicit (but complicated) formulas for them which allow us or a computer to calculate the face numbers effortlessly. A formula for the
$w_{\alpha, \beta, a,b}(t)$
are polynomials that depend only on their subindices. We present in Propositions 2.7 and 2.8 explicit (but complicated) formulas for them which allow us or a computer to calculate the face numbers effortlessly. A formula for the
![]() $f$
-vector of the hypersimplex
$f$
-vector of the hypersimplex
![]() $\Delta _{k,n}$
is also given explicitly in Example 2.1. In particular, the entire calculation can be done without the necessity of building costly face lattices or computing convex hulls.
$\Delta _{k,n}$
is also given explicitly in Example 2.1. In particular, the entire calculation can be done without the necessity of building costly face lattices or computing convex hulls.
As direct but interesting application of our result, we provide closed expressions for the
![]() $f$
-vector of sparse paving matroids, a class that made a prominent appearance in the theory of the extension complexity of independence polytopes [Reference Rothvoß45]. We also prove a fairly explicit formula for the
$f$
-vector of sparse paving matroids, a class that made a prominent appearance in the theory of the extension complexity of independence polytopes [Reference Rothvoß45]. We also prove a fairly explicit formula for the
![]() $f$
-vector of arbitrary rank two matroids, which is of independent interest due to the connection of these polytopes with edge polytopes of complete multipartite graphs [Reference Ohsugi and Hibi40].
$f$
-vector of arbitrary rank two matroids, which is of independent interest due to the connection of these polytopes with edge polytopes of complete multipartite graphs [Reference Ohsugi and Hibi40].
2. The number of faces of split matroids
2.1 The set up
Throughout this paper, we will assume that the reader is familiar with the usual terminology and notation in matroid theory. For the notions and machinery introduced very recently, in particular about stressed subsets, relaxations, and Schubert elementary split matroids, we refer the reader to our previous article [Reference Ferroni and Schröter23, Sections 3–4]. Regarding split matroids and elementary split matroids, the reader can consult the same article as well as [Reference Joswig and Schröter33, Reference Bérczi, Király, Schwarcz, Yamaguchi and Yokoi13]. However, basic knowledge on polytopes should be enough to follow the arguments and methods in this manuscript.
For a
![]() $d$
-dimensional polytope
$d$
-dimensional polytope
![]() $\mathscr {P}$
, we denote by
$\mathscr {P}$
, we denote by
![]() $f(\mathscr {P})\,:\!=(f_0,\ldots, f_d)$
its
$f(\mathscr {P})\,:\!=(f_0,\ldots, f_d)$
its
![]() $f$
-vector, and by
$f$
-vector, and by
 \begin{equation*} f_{\mathscr {P}}(t)\, :\!= \sum _{i=0}^{d} f_i\ t^i \end{equation*}
\begin{equation*} f_{\mathscr {P}}(t)\, :\!= \sum _{i=0}^{d} f_i\ t^i \end{equation*}
its
![]() $f$
-polynomial. In both cases,
$f$
-polynomial. In both cases,
![]() $f_i$
denotes the number of
$f_i$
denotes the number of
![]() $i$
-dimensional faces of
$i$
-dimensional faces of
![]() $\mathscr {P}$
. Notice that we omit the inclusion of
$\mathscr {P}$
. Notice that we omit the inclusion of
![]() $f_{-1}\,:\!=1$
for the empty set in both the
$f_{-1}\,:\!=1$
for the empty set in both the
![]() $f$
-vector and the
$f$
-vector and the
![]() $f$
-polynomial, but we do include
$f$
-polynomial, but we do include
![]() $f_d=1$
for the polytope itself. A basic property of
$f_d=1$
for the polytope itself. A basic property of
![]() $f$
-polynomials that we will use without explicitly mentioning is the fact that it behaves multiplicatively under cartesian products of polytopes, i.e.,
$f$
-polynomials that we will use without explicitly mentioning is the fact that it behaves multiplicatively under cartesian products of polytopes, i.e.,
![]() $f_{\mathscr {P}_1\times \mathscr {P}_2}(t) = f_{\mathscr {P}_1}(t) \cdot f_{\mathscr {P}_2}(t)$
. Another basic property that we use implicitly is that a matroid on a ground set of size
$f_{\mathscr {P}_1\times \mathscr {P}_2}(t) = f_{\mathscr {P}_1}(t) \cdot f_{\mathscr {P}_2}(t)$
. Another basic property that we use implicitly is that a matroid on a ground set of size
![]() $n$
with exactly
$n$
with exactly
![]() $c$
connected components has a base polytope of dimension
$c$
connected components has a base polytope of dimension
![]() $\dim \mathscr {P}(\mathsf {M}) = n - c$
, which is the product of the base polytopes of its
$\dim \mathscr {P}(\mathsf {M}) = n - c$
, which is the product of the base polytopes of its
![]() $c$
direct summands.
$c$
direct summands.
2.1.1 Essential notation
Following [Reference Ferroni and Schröter23], whenever we have a matroid
![]() $\mathsf {M}$
, unless specified otherwise, the rank of the matroid is denoted by
$\mathsf {M}$
, unless specified otherwise, the rank of the matroid is denoted by
![]() $k$
and the size of its ground set is denoted by
$k$
and the size of its ground set is denoted by
![]() $n$
. We reserve the letters
$n$
. We reserve the letters
![]() $r$
and
$r$
and
![]() $h$
for the rank and the size of stressed subsets that
$h$
for the rank and the size of stressed subsets that
![]() $\mathsf {M}$
may possess.
$\mathsf {M}$
may possess.
Our aim is to find formulas for the number of faces of a matroid base polytope
![]() $\mathscr {P}(\mathsf {M})$
whenever the matroid
$\mathscr {P}(\mathsf {M})$
whenever the matroid
![]() $\mathsf {M}$
is connected, i.e.,
$\mathsf {M}$
is connected, i.e.,
![]() $\mathscr {P}(\mathsf {M})\subseteq \mathbb {R}^n$
is of dimension
$\mathscr {P}(\mathsf {M})\subseteq \mathbb {R}^n$
is of dimension
![]() $n-1$
, and split. Note that under the assumption of connectedness, the classes of split matroids and elementary split matroids coincide [Reference Bérczi, Király, Schwarcz, Yamaguchi and Yokoi13, Theorem 11]. Since the base polytope of a direct sum of matroids
$n-1$
, and split. Note that under the assumption of connectedness, the classes of split matroids and elementary split matroids coincide [Reference Bérczi, Király, Schwarcz, Yamaguchi and Yokoi13, Theorem 11]. Since the base polytope of a direct sum of matroids
![]() $\mathsf {M}_1\oplus \mathsf {M}_2$
is the cartesian product of
$\mathsf {M}_1\oplus \mathsf {M}_2$
is the cartesian product of
![]() $\mathscr {P}(\mathsf {M}_1)$
and
$\mathscr {P}(\mathsf {M}_1)$
and
![]() $\mathscr {P}(\mathsf {M}_2)$
, the
$\mathscr {P}(\mathsf {M}_2)$
, the
![]() $f$
-vector of any disconnected split matroid can be recovered from the
$f$
-vector of any disconnected split matroid can be recovered from the
![]() $f$
-vector of the connected components, all of which are split as well.
$f$
-vector of the connected components, all of which are split as well.
The most basic example of a matroid polytope is the hypersimplex
![]() $\Delta _{k,n}$
, the matroid base polytope of the uniform matroid
$\Delta _{k,n}$
, the matroid base polytope of the uniform matroid
![]() $\mathsf {U}_{k,n}$
of rank
$\mathsf {U}_{k,n}$
of rank
![]() $k$
on
$k$
on
![]() $n$
elements.
$n$
elements.
Example 2.1.
The face enumeration of hypersimplices is encoded in the following
![]() $f$
-polynomial:
$f$
-polynomial:
 \begin{align*} f_{\mathscr {P}(\mathsf {U}_{k,n})}(t) = f_{\Delta _{k,n}}(t) &= \binom {n}{k} + \sum ^{n-1}_{i=1} \binom {n}{i+1}\sum _{j = 1}^{i} \binom {n-i-1}{k-j}\cdot t^i \enspace . \end{align*}
\begin{align*} f_{\mathscr {P}(\mathsf {U}_{k,n})}(t) = f_{\Delta _{k,n}}(t) &= \binom {n}{k} + \sum ^{n-1}_{i=1} \binom {n}{i+1}\sum _{j = 1}^{i} \binom {n-i-1}{k-j}\cdot t^i \enspace . \end{align*}
This formula can be obtained by contracting and deleting the elements of
![]() $\mathsf {U}_{k,n}$
. That is, by intersecting with hyperplanes of the form
$\mathsf {U}_{k,n}$
. That is, by intersecting with hyperplanes of the form
![]() $x_i=0$
or
$x_i=0$
or
![]() $x_i=1$
(and forgetting the coordinate
$x_i=1$
(and forgetting the coordinate
![]() $i$
), which leads to lower dimensional hypersimplices. For a detailed proof see for example [Reference Hibi, Li and Ohsugi30
, Corollary 4].
$i$
), which leads to lower dimensional hypersimplices. For a detailed proof see for example [Reference Hibi, Li and Ohsugi30
, Corollary 4].
The next example is similar to the one in [Reference Ferroni20 Remark 5.9] and gives a glimpse of the subtlety of the
![]() $f$
-vector as a matroid invariant. In general, we see that the assignment
$f$
-vector as a matroid invariant. In general, we see that the assignment
![]() $\mathsf {M} \mapsto f_{\mathscr {P}(\mathsf {M})}(t)$
is an invariant of the matroid
$\mathsf {M} \mapsto f_{\mathscr {P}(\mathsf {M})}(t)$
is an invariant of the matroid
![]() $\mathsf {M}$
that fails to be valuative. Hence, its computation is a more delicate task, even for the case of paving or split matroids. In these cases, we cannot rely on the strength of [Reference Ferroni and Schröter23, Theorem 5.3] – that result asserts that the evaluation of a valuative invariant on a split matroid
$\mathsf {M}$
that fails to be valuative. Hence, its computation is a more delicate task, even for the case of paving or split matroids. In these cases, we cannot rely on the strength of [Reference Ferroni and Schröter23, Theorem 5.3] – that result asserts that the evaluation of a valuative invariant on a split matroid
![]() $\mathsf {M}$
can be achieved by knowing relatively little about the matroid
$\mathsf {M}$
can be achieved by knowing relatively little about the matroid
![]() $\mathsf {M}$
, consisting in its rank
$\mathsf {M}$
, consisting in its rank
![]() $k$
, its size
$k$
, its size
![]() $n$
, and parameters
$n$
, and parameters
![]() $\unicode {x03BB}_{r,h}$
which denote the number of stressed subsets with non-empty cover of rank
$\unicode {x03BB}_{r,h}$
which denote the number of stressed subsets with non-empty cover of rank
![]() $r$
and size
$r$
and size
![]() $h$
that
$h$
that
![]() $\mathsf {M}$
has. If one is interested in knowing the
$\mathsf {M}$
has. If one is interested in knowing the
![]() $f$
-vector of
$f$
-vector of
![]() $\mathscr {P}(\mathsf {M})$
, the matroidal information we just mentioned is far from being enough. One of the main difficulties in order to carry out the enumeration of the faces of
$\mathscr {P}(\mathsf {M})$
, the matroidal information we just mentioned is far from being enough. One of the main difficulties in order to carry out the enumeration of the faces of
![]() $\mathscr {P}(\mathsf {M})$
consists of first identifying what matroid data we need in addition to the parameters mentioned before.
$\mathscr {P}(\mathsf {M})$
consists of first identifying what matroid data we need in addition to the parameters mentioned before.
Example 2.2.
Consider the four matroids
![]() $\mathsf {U}_{3,6}$
,
$\mathsf {U}_{3,6}$
,
![]() $\mathsf {M}$
,
$\mathsf {M}$
,
![]() $\mathsf {N}_1$
, and
$\mathsf {N}_1$
, and
![]() $\mathsf {N}_2$
with ground set rank three, whose families of bases are given as follows:
$\mathsf {N}_2$
with ground set rank three, whose families of bases are given as follows:
 \begin{align*} \mathscr {B}(\mathsf {U}_{3,6})\, &:\!= \binom {[6]}{3}, &\mathscr {B}(\mathsf {N}_1)\, &:\!= \binom {[6]}{3} \smallsetminus \{\{1,2,3\}, \{4,5,6\}\}\\ \mathscr {B}(\mathsf {M}) \,&:\!= \binom {[6]}{3} \smallsetminus \{\{1,2,3\}\}, &\mathscr {B}(\mathsf {N}_2)\, &:\!= \binom {[6]}{3} \smallsetminus \{\{1,2,3\}, \{3,4,5\}\}. \end{align*}
\begin{align*} \mathscr {B}(\mathsf {U}_{3,6})\, &:\!= \binom {[6]}{3}, &\mathscr {B}(\mathsf {N}_1)\, &:\!= \binom {[6]}{3} \smallsetminus \{\{1,2,3\}, \{4,5,6\}\}\\ \mathscr {B}(\mathsf {M}) \,&:\!= \binom {[6]}{3} \smallsetminus \{\{1,2,3\}\}, &\mathscr {B}(\mathsf {N}_2)\, &:\!= \binom {[6]}{3} \smallsetminus \{\{1,2,3\}, \{3,4,5\}\}. \end{align*}
The
![]() $f$
-vectors of their base polytopes are, respectively:
$f$
-vectors of their base polytopes are, respectively:
All of these matroids are sparse paving. In particular, the two matroids
![]() $\mathsf {N}_1$
and
$\mathsf {N}_1$
and
![]() $\mathsf {N}_2$
have, e.g., the same Tutte polynomial and the same Ehrhart polynomial – in fact, via [Reference Ferroni and Schröter23
, Corollary 5.4] any valuative invariant on these two matroids yields the same result. Yet, observe that their
$\mathsf {N}_2$
have, e.g., the same Tutte polynomial and the same Ehrhart polynomial – in fact, via [Reference Ferroni and Schröter23
, Corollary 5.4] any valuative invariant on these two matroids yields the same result. Yet, observe that their
![]() $f$
-vectors differ in the third and the fourth entries.
$f$
-vectors differ in the third and the fourth entries.
2.2 Schubert elementary split matroids and a technical lemma
By using [Reference Ferroni and Schröter23, Corollary 3.29], we see that the intersection of the hypersimplex
![]() $\Delta _{k,n}$
with the half-space of a single split hyperplane leads to the polytope:
$\Delta _{k,n}$
with the half-space of a single split hyperplane leads to the polytope:
 \begin{equation} \mathscr {P}\left(\mathsf {\Lambda }_{k-r,k,n-h,n}\right) = \left \{x\in \Delta _{k,n}\vphantom {\sum _{i=1}^h x_i\leq r}\ :\ \sum _{i=1}^h x_i\leq r\vphantom {x\in \Delta _{k,n}}\right \} \enspace, \end{equation}
\begin{equation} \mathscr {P}\left(\mathsf {\Lambda }_{k-r,k,n-h,n}\right) = \left \{x\in \Delta _{k,n}\vphantom {\sum _{i=1}^h x_i\leq r}\ :\ \sum _{i=1}^h x_i\leq r\vphantom {x\in \Delta _{k,n}}\right \} \enspace, \end{equation}
for appropriate values
![]() $r$
and
$r$
and
![]() $h$
. This is the base polytope of the Schubert elementary split matroid
$h$
. This is the base polytope of the Schubert elementary split matroid
![]() $\mathsf {\Lambda }_{k-r,k,n-h,n}$
, a matroid having exactly three cyclic flats: the empty set, the entire ground set, and one proper cyclic flat of size
$\mathsf {\Lambda }_{k-r,k,n-h,n}$
, a matroid having exactly three cyclic flats: the empty set, the entire ground set, and one proper cyclic flat of size
![]() $h$
and rank
$h$
and rank
![]() $r$
. For the purposes of this paper, the reader may regard equation (1) as the definition of Schubert elementary split matroids.
$r$
. For the purposes of this paper, the reader may regard equation (1) as the definition of Schubert elementary split matroids.
Let us introduce some notation that will help us formulate later our main results in a more compact fashion:
The
![]() $i$
-th coefficient of this polynomial is the difference between the number of
$i$
-th coefficient of this polynomial is the difference between the number of
![]() $i$
-dimensional faces of the hypersimplex
$i$
-dimensional faces of the hypersimplex
![]() $\Delta _{k,n}$
and the number of
$\Delta _{k,n}$
and the number of
![]() $i$
-dimensional faces of the Schubert elementary split matroid
$i$
-dimensional faces of the Schubert elementary split matroid
![]() $\mathsf {\Lambda }_{k-r,k,n-h,n}$
. A non-obvious property is that some of these coefficients may be negative while other are positive – moreover, the actual sign of each individual coefficient a priori depends on the four parameters
$\mathsf {\Lambda }_{k-r,k,n-h,n}$
. A non-obvious property is that some of these coefficients may be negative while other are positive – moreover, the actual sign of each individual coefficient a priori depends on the four parameters
![]() $r,k,h,n$
.
$r,k,h,n$
.
Before we go on, let us introduce a second polynomial, which will play an important role in the sequel. For fixed numbers
![]() $0\lt \alpha \lt a$
and
$0\lt \alpha \lt a$
and
![]() $0\lt \beta \lt b$
let us define,
$0\lt \beta \lt b$
let us define,
Later, in Proposition 2.7, we provide a compact formula for the polynomial
![]() $w_{\alpha, \beta, a,b}(t)$
and a formula for the polynomial
$w_{\alpha, \beta, a,b}(t)$
and a formula for the polynomial
![]() $u_{r,k,h,n}(t)$
in Proposition 2.8 both of which can be used to compute these polynomials, bypassing the computation of
$u_{r,k,h,n}(t)$
in Proposition 2.8 both of which can be used to compute these polynomials, bypassing the computation of
![]() $f$
-vectors of Schubert elementary split matroids using the polytopes themselves.
$f$
-vectors of Schubert elementary split matroids using the polytopes themselves.
Remark 2.3. The intuition of why it is reasonable to consider and define the complicated expression above stems from [Reference Ferroni and Schröter23, Example 5.2]. As follows from the explanation there, if the assignment
![]() $\mathsf {M}\mapsto f_{\mathscr {P}(\mathsf {M})}(t)$
were valuative, then the defining formula for
$\mathsf {M}\mapsto f_{\mathscr {P}(\mathsf {M})}(t)$
were valuative, then the defining formula for
![]() $w_{\alpha, \beta, a,b}(t)$
would actually be identically zero. The polynomial
$w_{\alpha, \beta, a,b}(t)$
would actually be identically zero. The polynomial
![]() $w_{\alpha, \beta, a,b}(t)$
quantifies (in a certain way) how far the map
$w_{\alpha, \beta, a,b}(t)$
quantifies (in a certain way) how far the map
![]() $\mathsf {M}\mapsto f_{\mathscr {P}(\mathsf {M})}(t)$
is from being valuative.
$\mathsf {M}\mapsto f_{\mathscr {P}(\mathsf {M})}(t)$
is from being valuative.
The following lemma is the key in the proof of our main result. Its proof constitutes arguably the most technical part of the paper. In the Lemma and the text below we denote the Schubert elementary split matroid of rank
![]() $k$
on
$k$
on
![]() $n$
elements with proper cyclic flat
$n$
elements with proper cyclic flat
![]() $F$
by
$F$
by
![]() $\mathsf {\Lambda }_{k,n}^{F}$
. This matroid is isomorphic to the matroid
$\mathsf {\Lambda }_{k,n}^{F}$
. This matroid is isomorphic to the matroid
![]() $\mathsf {\Lambda }_{k-\operatorname {rk} F,k,n-|F|,n}$
. Similarly, for a set
$\mathsf {\Lambda }_{k-\operatorname {rk} F,k,n-|F|,n}$
. Similarly, for a set
![]() $N$
of coordinates we use the notation
$N$
of coordinates we use the notation
![]() $\Delta _{k,N}\cong \Delta _{k,|N|}$
to indicate the coordinates of the hypersimplex.
$\Delta _{k,N}\cong \Delta _{k,|N|}$
to indicate the coordinates of the hypersimplex.
Lemma 2.4.
Let
![]() $\mathsf {N}$
be a rank
$\mathsf {N}$
be a rank
![]() $k$
split matroid on
$k$
split matroid on
![]() $[n]$
whose cyclic flats are the four sets
$[n]$
whose cyclic flats are the four sets
![]() $\varnothing$
,
$\varnothing$
,
![]() $F$
,
$F$
,
![]() $G$
, and
$G$
, and
![]() $F\cup G=[n]$
of rank
$F\cup G=[n]$
of rank
![]() $0$
,
$0$
,
![]() $r_F$
,
$r_F$
,
![]() $r_G$
, and
$r_G$
, and
![]() $k$
, respectively. Then
$k$
, respectively. Then
if
![]() $|F\cap G| + k \lt r_F+r_G$
, and
$|F\cap G| + k \lt r_F+r_G$
, and
where
![]() $c = |F\cap G|$
if
$c = |F\cap G|$
if
![]() $|F\cap G| + k = r_F+r_G$
otherwise.
$|F\cap G| + k = r_F+r_G$
otherwise.
Proof.
Note that either the matroid
![]() $\mathsf {N}$
is connected or it is the direct sum
$\mathsf {N}$
is connected or it is the direct sum
![]() $\mathsf {U}_{r_F,|F|}\oplus \mathsf {U}_{r_G,|G|}$
. The matroid polytope of the latter is
$\mathsf {U}_{r_F,|F|}\oplus \mathsf {U}_{r_G,|G|}$
. The matroid polytope of the latter is
![]() $\mathscr {P}(\mathsf {U}_{r_F,|F|}\oplus \mathsf {U}_{r_G,|G|}) = \Delta _{r_F,|F|}\times \Delta _{r_G,|G|}$
with
$\mathscr {P}(\mathsf {U}_{r_F,|F|}\oplus \mathsf {U}_{r_G,|G|}) = \Delta _{r_F,|F|}\times \Delta _{r_G,|G|}$
with
![]() $f$
-polynomial
$f$
-polynomial
![]() $f_{\Delta _{r_F,|F|}}(t)\cdot f_{\Delta _{r_G,|G|}}(t)$
. Moreover, in this case
$f_{\Delta _{r_F,|F|}}(t)\cdot f_{\Delta _{r_G,|G|}}(t)$
. Moreover, in this case
![]() $|F\cap G| = 0$
and
$|F\cap G| = 0$
and
![]() $k=r_F+r_G$
. Thus formula (4) applies by definition of
$k=r_F+r_G$
. Thus formula (4) applies by definition of
![]() $w_{r_F,r_G,|F|,|G|}$
. From now on, we assume that
$w_{r_F,r_G,|F|,|G|}$
. From now on, we assume that
![]() $\mathsf {N}$
is connected.
$\mathsf {N}$
is connected.
We compare the faces of the polytope
![]() $\mathscr {P}(\mathsf {N})$
with those of
$\mathscr {P}(\mathsf {N})$
with those of
![]() $\Delta _{k,n}$
. By [Reference Joswig and Schröter33, Proposition 7] every
$\Delta _{k,n}$
. By [Reference Joswig and Schröter33, Proposition 7] every
![]() $d$
-face of
$d$
-face of
![]() $\mathscr {P}(\mathsf {N})=\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F}\right)\cap \mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{G}\right)$
, and also
$\mathscr {P}(\mathsf {N})=\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F}\right)\cap \mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{G}\right)$
, and also
![]() $\mathscr {P}_F\,:\!=\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F}\right)$
or
$\mathscr {P}_F\,:\!=\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F}\right)$
or
![]() $\mathscr {P}_G\,:\!=\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{G}\right)$
lies in a
$\mathscr {P}_G\,:\!=\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{G}\right)$
lies in a
![]() $d$
-face of the hypersimplex
$d$
-face of the hypersimplex
![]() $\Delta _{k,n}$
or in at least one of the hyperplanes
$\Delta _{k,n}$
or in at least one of the hyperplanes
![]() $H_F=\{x\in \mathbb {R}^n\,|\,\sum _{i\in F} x_i = r_F\}$
and
$H_F=\{x\in \mathbb {R}^n\,|\,\sum _{i\in F} x_i = r_F\}$
and
![]() $H_G=\{x\in \mathbb {R}^n\,|\,\sum _{i\in G} x_i = r_G\}$
. Notice further that by [Reference Joswig and Schröter33, Proposition 14] we have that
$H_G=\{x\in \mathbb {R}^n\,|\,\sum _{i\in G} x_i = r_G\}$
. Notice further that by [Reference Joswig and Schröter33, Proposition 14] we have that
![]() $|F\cap G| + k \leq r_F+r_G$
. Thus, the statement of the lemma indeed covers all possible cases. Furthermore, this shows that there is no point in the hypersimplex
$|F\cap G| + k \leq r_F+r_G$
. Thus, the statement of the lemma indeed covers all possible cases. Furthermore, this shows that there is no point in the hypersimplex
![]() $\Delta _{k,n}$
violating both of the inequalities
$\Delta _{k,n}$
violating both of the inequalities
![]() $\sum _{i\in F} x_i \leq r_F$
and
$\sum _{i\in F} x_i \leq r_F$
and
![]() $\sum _{i\in G} x_i \leq r_G$
simultaneously. We will use this crucial fact several times further below without recalling it explicitly. A first consequence is that the two hyperplanes
$\sum _{i\in G} x_i \leq r_G$
simultaneously. We will use this crucial fact several times further below without recalling it explicitly. A first consequence is that the two hyperplanes
![]() $H_F$
and
$H_F$
and
![]() $H_G$
split a face of
$H_G$
split a face of
![]() $\Delta _{k,n}$
into at most three maximal dimensional polytopes.
$\Delta _{k,n}$
into at most three maximal dimensional polytopes.
Now, let us analyse the various cases. If
![]() $Q'$
is a
$Q'$
is a
![]() $d$
-dimensional face of
$d$
-dimensional face of
![]() $\mathscr {P}(\mathsf {N})$
and not contained in a
$\mathscr {P}(\mathsf {N})$
and not contained in a
![]() $d$
-face of the hypersimplex
$d$
-face of the hypersimplex
![]() $\Delta _{k,n}$
, then either
$\Delta _{k,n}$
, then either
![]() $Q'$
lies in exactly one of the hyperplanes
$Q'$
lies in exactly one of the hyperplanes
![]() $H_F$
and
$H_F$
and
![]() $H_G$
or in both. If it is in exactly one of them, say
$H_G$
or in both. If it is in exactly one of them, say
![]() $H_F$
, then
$H_F$
, then
![]() $Q'$
is a
$Q'$
is a
![]() $d$
-dimensional face of
$d$
-dimensional face of
![]() $\mathscr {P}_F$
and not a
$\mathscr {P}_F$
and not a
![]() $d$
-dimensional face of
$d$
-dimensional face of
![]() $\mathscr {P}_G$
. If the
$\mathscr {P}_G$
. If the
![]() $d$
-dimensional face
$d$
-dimensional face
![]() $Q'$
lies in both hyperplanes, then
$Q'$
lies in both hyperplanes, then
![]() $Q'$
lies in a
$Q'$
lies in a
![]() $(d+1)$
-dimensional face
$(d+1)$
-dimensional face
![]() $Q$
of
$Q$
of
![]() $\Delta _{k,n}$
, which is subdivided into two parts. We discuss this situation in detail further below in this proof.
$\Delta _{k,n}$
, which is subdivided into two parts. We discuss this situation in detail further below in this proof.
Let us now assume
![]() $Q$
is a
$Q$
is a
![]() $d$
-dimensional face of
$d$
-dimensional face of
![]() $\Delta _{k,n}$
. We will go through the three possibilities of how many cells
$\Delta _{k,n}$
. We will go through the three possibilities of how many cells
![]() $Q$
is subdivided into by
$Q$
is subdivided into by
![]() $H_F$
and
$H_F$
and
![]() $H_G$
. If
$H_G$
. If
![]() $Q$
remains undivided then either it is a face of
$Q$
remains undivided then either it is a face of
![]() $\mathscr {P}(\mathsf {N})$
and also of both
$\mathscr {P}(\mathsf {N})$
and also of both
![]() $\mathscr {P}_F$
and
$\mathscr {P}_F$
and
![]() $\mathscr {P}_G$
, or it is not a face of
$\mathscr {P}_G$
, or it is not a face of
![]() $\mathscr {P}(\mathsf {N})$
and thus a face of exactly one of the two polyhedra
$\mathscr {P}(\mathsf {N})$
and thus a face of exactly one of the two polyhedra
![]() $\mathscr {P}_F$
and
$\mathscr {P}_F$
and
![]() $\mathscr {P}_G$
. In the case that the face
$\mathscr {P}_G$
. In the case that the face
![]() $Q$
is subdivided into three parts of dimension
$Q$
is subdivided into three parts of dimension
![]() $d$
, it contributes a
$d$
, it contributes a
![]() $d$
-face to each of the four polytopes as well. It remains to analyse the situation in which
$d$
-face to each of the four polytopes as well. It remains to analyse the situation in which
![]() $Q$
is subdivided into two polytopes
$Q$
is subdivided into two polytopes
![]() $Q'$
and
$Q'$
and
![]() $Q''$
. It cannot happen that both of these polytopes are faces of
$Q''$
. It cannot happen that both of these polytopes are faces of
![]() $\mathscr {P}(\mathsf {N})$
. If one of them, say
$\mathscr {P}(\mathsf {N})$
. If one of them, say
![]() $Q'$
, is a face of
$Q'$
, is a face of
![]() $\mathscr {P}(\mathsf {N})$
then
$\mathscr {P}(\mathsf {N})$
then
![]() $Q'$
is a face of one of the polytopes
$Q'$
is a face of one of the polytopes
![]() $\mathscr {P}_F$
and
$\mathscr {P}_F$
and
![]() $\mathscr {P}_G$
, while
$\mathscr {P}_G$
, while
![]() $Q$
is a face of the other. In total,
$Q$
is a face of the other. In total,
![]() $Q$
and
$Q$
and
![]() $Q'$
contribute a
$Q'$
contribute a
![]() $d$
-dimensional face to each of the four polytopes. If neither
$d$
-dimensional face to each of the four polytopes. If neither
![]() $Q'$
nor
$Q'$
nor
![]() $Q''$
is a face of
$Q''$
is a face of
![]() $\mathscr {P}(\mathsf {N})$
then
$\mathscr {P}(\mathsf {N})$
then
![]() $Q'$
and
$Q'$
and
![]() $Q''$
meet in a
$Q''$
meet in a
![]() $(d-1)$
-face
$(d-1)$
-face
![]() $\widetilde {Q}\subsetneq Q$
, which is a face of the three polytopes
$\widetilde {Q}\subsetneq Q$
, which is a face of the three polytopes
![]() $\mathscr {P}(\mathsf {N})$
,
$\mathscr {P}(\mathsf {N})$
,
![]() $\mathscr {P}_F$
and
$\mathscr {P}_F$
and
![]() $\mathscr {P}_G$
. Moreover, the
$\mathscr {P}_G$
. Moreover, the
![]() $d$
-dimensional face
$d$
-dimensional face
![]() $Q'$
is a face of one of the two polytopes
$Q'$
is a face of one of the two polytopes
![]() $\mathscr {P}_F$
and
$\mathscr {P}_F$
and
![]() $\mathscr {P}_G$
, while
$\mathscr {P}_G$
, while
![]() $Q''$
is a
$Q''$
is a
![]() $d$
-dimensional face of the other one. The
$d$
-dimensional face of the other one. The
![]() $(d-1)$
-dimensional face
$(d-1)$
-dimensional face
![]() $\widetilde {Q}$
is not a face of the hypersimplex
$\widetilde {Q}$
is not a face of the hypersimplex
![]() $\Delta _{k,n}$
and sits in both hyperplanes
$\Delta _{k,n}$
and sits in both hyperplanes
![]() $H_F$
and
$H_F$
and
![]() $H_G$
. Every
$H_G$
. Every
![]() $(d-1)$
-dimensional face of
$(d-1)$
-dimensional face of
![]() $\mathscr {P}(\mathsf {N})$
that is not a face of
$\mathscr {P}(\mathsf {N})$
that is not a face of
![]() $\Delta _{k,n}$
but lies in both
$\Delta _{k,n}$
but lies in both
![]() $H_F$
and
$H_F$
and
![]() $H_G$
must be contained in a
$H_G$
must be contained in a
![]() $d$
-face of
$d$
-face of
![]() $\Delta _{k,n}$
as we mentioned at the beginning of this proof. Let us investigate the situation further. There must exist four pairwise disjoint sets
$\Delta _{k,n}$
as we mentioned at the beginning of this proof. Let us investigate the situation further. There must exist four pairwise disjoint sets
![]() $A,B,C,D$
that partition the ground set
$A,B,C,D$
that partition the ground set
![]() $[n]$
such that
$[n]$
such that
where
![]() $C$
consists of all coordinates which are one and
$C$
consists of all coordinates which are one and
![]() $D$
of those which are
$D$
of those which are
![]() $0$
, and
$0$
, and
where
![]() $\alpha = r_F-|C\cap F|$
,
$\alpha = r_F-|C\cap F|$
,
![]() $\beta = r_G-|C\cap G|$
,
$\beta = r_G-|C\cap G|$
,
![]() $A\subseteq F\smallsetminus G$
, and
$A\subseteq F\smallsetminus G$
, and
![]() $B\subseteq G\smallsetminus F$
. The inclusions follow (up to interchanging the roles of
$B\subseteq G\smallsetminus F$
. The inclusions follow (up to interchanging the roles of
![]() $A$
and
$A$
and
![]() $B$
) from the fact that both hyperplanes
$B$
) from the fact that both hyperplanes
![]() $H_F$
and
$H_F$
and
![]() $H_G$
induce the same split of
$H_G$
induce the same split of
![]() $\Delta _{\alpha +\beta, A\cup B}$
. From this we get
$\Delta _{\alpha +\beta, A\cup B}$
. From this we get
![]() $k-|C| = \alpha + \beta =r_F-|F\cap C|+r_G-|G\cap C|$
and hence
$k-|C| = \alpha + \beta =r_F-|F\cap C|+r_G-|G\cap C|$
and hence
We obtain
![]() $F\cap G \subseteq C \subseteq F\cup G$
, and also the equality
$F\cap G \subseteq C \subseteq F\cup G$
, and also the equality
![]() $|F\cap G|+k = r_F+r_G$
. Furthermore, every choice of such
$|F\cap G|+k = r_F+r_G$
. Furthermore, every choice of such
![]() $C$
,
$C$
,
![]() $A\subseteq F\smallsetminus G$
and
$A\subseteq F\smallsetminus G$
and
![]() $B\subseteq G\smallsetminus F$
leads to a face that sits in both hyperplanes and in a higher dimensional face of
$B\subseteq G\smallsetminus F$
leads to a face that sits in both hyperplanes and in a higher dimensional face of
![]() $\Delta _{k,n}$
. Hence, for the inclusion-wise maximal such face we have to pick
$\Delta _{k,n}$
. Hence, for the inclusion-wise maximal such face we have to pick
![]() $C=F\cap G$
and
$C=F\cap G$
and
![]() $D=[n]\smallsetminus (F\cup G)$
. We see that the expression
$D=[n]\smallsetminus (F\cup G)$
. We see that the expression
counts exactly the two types of faces. In summary, our comparison verifies the formulas of equations (3) and (4) and thus the proof is complete.
2.3 Face counting of split matroids
For a connected split matroid
![]() $\mathsf {M}$
, let us define the following numbers that we have already mentioned in the introduction. The number of stressed subsets with non-empty cover having rank
$\mathsf {M}$
, let us define the following numbers that we have already mentioned in the introduction. The number of stressed subsets with non-empty cover having rank
![]() $r$
and size
$r$
and size
![]() $h$
, denoted by
$h$
, denoted by
![]() $\unicode {x03BB}_{r,h}$
– recall that by [Reference Ferroni and Schröter23, Proposition 3.9], in a connected split matroid this is the same as the number of proper non-empty cyclic flats of rank
$\unicode {x03BB}_{r,h}$
– recall that by [Reference Ferroni and Schröter23, Proposition 3.9], in a connected split matroid this is the same as the number of proper non-empty cyclic flats of rank
![]() $r$
and size
$r$
and size
![]() $h$
. We also need the numbers
$h$
. We also need the numbers
![]() $\unicode {x03BC}_{\alpha, \beta, a,b}$
of (unordered) modular pairs
$\unicode {x03BC}_{\alpha, \beta, a,b}$
of (unordered) modular pairs
![]() $\{F_1,F_2\}$
of proper non-empty cyclic flats, i.e.,
$\{F_1,F_2\}$
of proper non-empty cyclic flats, i.e.,
![]() $F_1$
and
$F_1$
and
![]() $F_2$
fulfilling the modularity property,
$F_2$
fulfilling the modularity property,
where the indices denote the following quantities:
Note that the set
![]() $F_1\cap F_2 \subsetneq F_1 \subsetneq [n]$
can not contain a circuit if
$F_1\cap F_2 \subsetneq F_1 \subsetneq [n]$
can not contain a circuit if
![]() $\mathsf {M}$
is a connected split matroid, thus it is an independent set, i.e.,
$\mathsf {M}$
is a connected split matroid, thus it is an independent set, i.e.,
![]() $\operatorname {rk}(F_1\cap F_2)=|F_1\cap F_2|$
.
$\operatorname {rk}(F_1\cap F_2)=|F_1\cap F_2|$
.
In terms of these numbers and variables, our main result is the following theorem.
Theorem 2.5.
Let
![]() $\mathsf {M}$
be a connected split matroid of rank
$\mathsf {M}$
be a connected split matroid of rank
![]() $k$
on
$k$
on
![]() $n$
elements. The number of faces of its base polytope
$n$
elements. The number of faces of its base polytope
![]() $\mathscr {P}(\mathsf {M})$
is given by the polynomial
$\mathscr {P}(\mathsf {M})$
is given by the polynomial
where the first sum ranges over all values with
![]() $0\lt r\lt h\lt n$
and the second sum ranges over the values
$0\lt r\lt h\lt n$
and the second sum ranges over the values
![]() $0\lt \alpha \lt a$
,
$0\lt \alpha \lt a$
,
![]() $0\lt \beta \lt b$
for which either
$0\lt \beta \lt b$
for which either
![]() $a\lt b$
or
$a\lt b$
or
![]() $a=b$
and
$a=b$
and
![]() $\alpha \leq \beta$
.
$\alpha \leq \beta$
.
Before moving towards the proof of this result, let us digress about the meaning of its statement. On one hand, note that the polynomials
![]() $f_{\Delta _{k,n}}(t)$
,
$f_{\Delta _{k,n}}(t)$
,
![]() $u_{r,k,h,n}(t)$
and
$u_{r,k,h,n}(t)$
and
![]() $w_{\alpha, \beta, a,b}(t)$
can be precomputed for all the occurring instances of the variables which appear as subindices. The first non-trivial fact that is deduced by our statement is that in addition to the parameters
$w_{\alpha, \beta, a,b}(t)$
can be precomputed for all the occurring instances of the variables which appear as subindices. The first non-trivial fact that is deduced by our statement is that in addition to the parameters
![]() $\unicode {x03BB}_{r,h}$
, which always appear in the computation of a valuative invariant, the precise additional matroidal datum needed to compute the
$\unicode {x03BB}_{r,h}$
, which always appear in the computation of a valuative invariant, the precise additional matroidal datum needed to compute the
![]() $f$
-vector consists of the numbers
$f$
-vector consists of the numbers
![]() $\unicode {x03BC}_{\alpha, \beta, a,b}$
. Surprisingly, the last sum in equation (5) does not take into consideration the rank nor the size of the matroid
$\unicode {x03BC}_{\alpha, \beta, a,b}$
. Surprisingly, the last sum in equation (5) does not take into consideration the rank nor the size of the matroid
![]() $\mathsf {M}$
itself, only the intersection data for the modular pairs of flats. The second non-trivial fact is that it explains how to put together this information in order to effectively computing the
$\mathsf {M}$
itself, only the intersection data for the modular pairs of flats. The second non-trivial fact is that it explains how to put together this information in order to effectively computing the
![]() $f$
-vector of
$f$
-vector of
![]() $\mathscr {P}(\mathsf {M})$
for a split matroid, circumventing the necessity of constructing the polytope.
$\mathscr {P}(\mathsf {M})$
for a split matroid, circumventing the necessity of constructing the polytope.
Proof of Theorem 2.5.
We follow the guidance of the proof of Lemma 2.4 and compare the faces of
![]() $\mathscr {P}(\mathsf {M})$
with those of
$\mathscr {P}(\mathsf {M})$
with those of
![]() $\Delta _{k,n}$
taking into account the polytopes
$\Delta _{k,n}$
taking into account the polytopes
![]() $\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F_j}\right)$
for the various cyclic flats
$\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F_j}\right)$
for the various cyclic flats
![]() $F_j$
. We recall that there is no point in
$F_j$
. We recall that there is no point in
![]() $\Delta _{k,n}$
that violates more than one of the inequalities
$\Delta _{k,n}$
that violates more than one of the inequalities
![]() $\sum _{i\in F_j} x_i \leq \operatorname {rk} F_j$
.
$\sum _{i\in F_j} x_i \leq \operatorname {rk} F_j$
.
Now, if
![]() $Q$
is a
$Q$
is a
![]() $d$
-face of
$d$
-face of
![]() $\Delta _{k,n}$
that contains a
$\Delta _{k,n}$
that contains a
![]() $d$
-face of
$d$
-face of
![]() $\mathscr {P}(\mathsf {M})$
then every polytope
$\mathscr {P}(\mathsf {M})$
then every polytope
![]() $\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F_i}\right)$
has a
$\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F_i}\right)$
has a
![]() $d$
-face that is contained in
$d$
-face that is contained in
![]() $Q$
. Hence, these faces do not contribute to any
$Q$
. Hence, these faces do not contribute to any
![]() $u_{r,k,h,n}$
or
$u_{r,k,h,n}$
or
![]() $w_{\alpha, \beta, a,b}$
. If
$w_{\alpha, \beta, a,b}$
. If
![]() $Q$
is a
$Q$
is a
![]() $d$
-face of
$d$
-face of
![]() $\Delta _{k,n}$
whose interior has no point in common with
$\Delta _{k,n}$
whose interior has no point in common with
![]() $\mathscr {P}(\mathsf {M})$
, then all these points lie beyond exactly one of the split hyperplanes
$\mathscr {P}(\mathsf {M})$
, then all these points lie beyond exactly one of the split hyperplanes
![]() $\sum _{i\in F_j} x_i = \operatorname {rk} F_j$
. Therefore,
$\sum _{i\in F_j} x_i = \operatorname {rk} F_j$
. Therefore,
![]() $Q$
contributes
$Q$
contributes
![]() $1$
to
$1$
to
![]() $f_{\Delta _{k,n}}(t)$
and to
$f_{\Delta _{k,n}}(t)$
and to
![]() $u_{\operatorname {rk}_{F_j},k,|F_j|,n}(t)$
, but not to the other polynomials. It remains again to look at the
$u_{\operatorname {rk}_{F_j},k,|F_j|,n}(t)$
, but not to the other polynomials. It remains again to look at the
![]() $(d-1)$
-faces
$(d-1)$
-faces
![]() $\widetilde {Q}$
of
$\widetilde {Q}$
of
![]() $\mathscr {P}(\mathsf {M})$
that are contained in the interior of the
$\mathscr {P}(\mathsf {M})$
that are contained in the interior of the
![]() $d$
-face
$d$
-face
![]() $Q$
of
$Q$
of
![]() $\Delta _{k,n}$
. Note that
$\Delta _{k,n}$
. Note that
![]() $\widetilde {Q}$
is a hyperplane in
$\widetilde {Q}$
is a hyperplane in
![]() $Q$
that separates two of the vertices of
$Q$
that separates two of the vertices of
![]() $Q$
. Each of the two vertices can only violate one of the inequalities, thus
$Q$
. Each of the two vertices can only violate one of the inequalities, thus
![]() $\widetilde {Q}$
is a face of exactly two of the polytopes
$\widetilde {Q}$
is a face of exactly two of the polytopes
![]() $\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F_j}\right)$
.
$\mathscr {P}\left(\mathsf {\Lambda }_{k,n}^{F_j}\right)$
.
Let us assume that
![]() $\overline {Q}$
is inclusion-wise maximal among all these
$\overline {Q}$
is inclusion-wise maximal among all these
![]() $(d-1)$
-faces of
$(d-1)$
-faces of
![]() $\mathscr {P}(\mathsf {M})$
in the relative interior of
$\mathscr {P}(\mathsf {M})$
in the relative interior of
![]() $d$
-faces of
$d$
-faces of
![]() $\Delta _{k,n}$
. Then there must be pairwise disjoint sets
$\Delta _{k,n}$
. Then there must be pairwise disjoint sets
![]() $C$
and
$C$
and
![]() $D$
in the complement of
$D$
in the complement of
![]() $F\cup G$
such that
$F\cup G$
such that
![]() $\overline {Q}$
is a face of
$\overline {Q}$
is a face of
where
![]() $F$
and
$F$
and
![]() $G$
are the two cyclic flats for which
$G$
are the two cyclic flats for which
![]() $\overline {Q}$
is a face of
$\overline {Q}$
is a face of
![]() $\mathsf {\Lambda }_{k,n}^{F}$
and
$\mathsf {\Lambda }_{k,n}^{F}$
and
![]() $\mathsf {\Lambda }_{k,n}^{G}$
. It follows that
$\mathsf {\Lambda }_{k,n}^{G}$
. It follows that
![]() $k-|C|\leq \operatorname {rk}_{\mathsf {M}}(F\cup G)$
as
$k-|C|\leq \operatorname {rk}_{\mathsf {M}}(F\cup G)$
as
![]() $\overline {Q}$
is a face of
$\overline {Q}$
is a face of
![]() $\mathscr {P}(\mathsf {M})$
. Furthermore, applying Lemma 2.4 to the matroid
$\mathscr {P}(\mathsf {M})$
. Furthermore, applying Lemma 2.4 to the matroid
![]() $(\mathsf {M}\smallsetminus D) / C$
, i.e., the contraction and the deletion of
$(\mathsf {M}\smallsetminus D) / C$
, i.e., the contraction and the deletion of
![]() $D$
in
$D$
in
![]() $\mathsf {M}$
, which is a split matroid of rank
$\mathsf {M}$
, which is a split matroid of rank
![]() $k-|C|$
on
$k-|C|$
on
![]() $F\cup G$
, yields that the hyperplanes of
$F\cup G$
, yields that the hyperplanes of
![]() $F$
and
$F$
and
![]() $G$
coincide only if
$G$
coincide only if
![]() $k-|C|=\operatorname {rk} F + \operatorname {rk} G - |F\cap G|$
. Moreover, because
$k-|C|=\operatorname {rk} F + \operatorname {rk} G - |F\cap G|$
. Moreover, because
![]() $\mathsf {M}$
is a connected split matroid we get
$\mathsf {M}$
is a connected split matroid we get
Thus
![]() $k-|C| = \operatorname {rk} F\cup G$
and
$k-|C| = \operatorname {rk} F\cup G$
and
![]() $|F\cap G| = \operatorname {rk} F + \operatorname {rk} G - \operatorname {rk}(F\cup G)$
. Furthermore, Lemma 2.4 shows also that the faces
$|F\cap G| = \operatorname {rk} F + \operatorname {rk} G - \operatorname {rk}(F\cup G)$
. Furthermore, Lemma 2.4 shows also that the faces
![]() $\widetilde {Q}$
and
$\widetilde {Q}$
and
![]() $Q$
contribute a summand
$Q$
contribute a summand
![]() $t^{d-1}$
and
$t^{d-1}$
and
![]() $t^{d}$
to the corresponding
$t^{d}$
to the corresponding
![]() $w_{\alpha, \beta, a,b}(t)$
. This completes our proof.
$w_{\alpha, \beta, a,b}(t)$
. This completes our proof.
Example 2.6.
Let us take a look again at Example 2.2
. The matroids
![]() $\mathsf {N}_1$
and
$\mathsf {N}_1$
and
![]() $\mathsf {N}_2$
are sparse paving, have rank
$\mathsf {N}_2$
are sparse paving, have rank
![]() $k=3$
and size
$k=3$
and size
![]() $n=6$
. In each case the proper non-empty cyclic flats are exactly the non-bases, yielding for both matroids
$n=6$
. In each case the proper non-empty cyclic flats are exactly the non-bases, yielding for both matroids
![]() $\unicode {x03BB}_{2,3}=2$
. One can compute the corresponding polynomial,
$\unicode {x03BB}_{2,3}=2$
. One can compute the corresponding polynomial,
![]() $u_{2,3,3,6}(t) = 1+9t+9t^2-t^4$
. In
$u_{2,3,3,6}(t) = 1+9t+9t^2-t^4$
. In
![]() $\mathsf {N}_1$
, the intersection of the only pair of proper non-empty cyclic flats,
$\mathsf {N}_1$
, the intersection of the only pair of proper non-empty cyclic flats,
![]() $F_1=\{1,2,3\}$
and
$F_1=\{1,2,3\}$
and
![]() $F_2=\{4,5,6\}$
, does not satisfy the property (
⋆
), because
$F_2=\{4,5,6\}$
, does not satisfy the property (
⋆
), because
![]() $\textrm {rk}(F_1\cap F_2)+\textrm {rk}(F_1\cup F_2)=0+3$
, whereas
$\textrm {rk}(F_1\cap F_2)+\textrm {rk}(F_1\cup F_2)=0+3$
, whereas
![]() $\textrm {rk}(F_1)+\textrm {rk}(F_2) = 2 + 2 = 4$
.
$\textrm {rk}(F_1)+\textrm {rk}(F_2) = 2 + 2 = 4$
.
For
![]() $\mathsf {N}_2$
, the situation is different, as
$\mathsf {N}_2$
, the situation is different, as
![]() $F_1 = \{1,2,3\}$
and
$F_1 = \{1,2,3\}$
and
![]() $F_2=\{3,4,5\}$
indeed satisfy (
⋆
), and we have
$F_2=\{3,4,5\}$
indeed satisfy (
⋆
), and we have
![]() $a = |F_1\smallsetminus F_2|=2$
,
$a = |F_1\smallsetminus F_2|=2$
,
![]() $b = |F_2\smallsetminus F_1|=2$
,
$b = |F_2\smallsetminus F_1|=2$
,
![]() $\alpha = \textrm {rk}(F_1)-|F_1\cap F_2| = 2 - 1 = 1$
, and
$\alpha = \textrm {rk}(F_1)-|F_1\cap F_2| = 2 - 1 = 1$
, and
![]() $\beta =\textrm {rk}(F_2)-|F_1\cap F_2| = 2 - 1=1$
, so that
$\beta =\textrm {rk}(F_2)-|F_1\cap F_2| = 2 - 1=1$
, so that
![]() $\unicode {x03BC}_{1,1,2,2}=1$
and we have to subratct
$\unicode {x03BC}_{1,1,2,2}=1$
and we have to subratct
![]() $w_{1,1,2,2}(t) = t^2+t^3$
to obtain the correct
$w_{1,1,2,2}(t) = t^2+t^3$
to obtain the correct
![]() $f$
-polynomial, as we expected.
$f$
-polynomial, as we expected.
2.4 Explicit formulas
The polynomials
![]() $u_{r,k,h,n}(t)$
and
$u_{r,k,h,n}(t)$
and
![]() $w_{\alpha, \beta, a,b}(t)$
in Theorem2.5 are defined in terms of
$w_{\alpha, \beta, a,b}(t)$
in Theorem2.5 are defined in terms of
![]() $f$
-vectors of specific matroid polytopes. In this subsection we will present explicit descriptions for these polynomials, enabling us to do the face enumeration of a split matroid polytope, without any convex hull or face lattice computation. To express the formulas in a compact form, we will make use of multinomial coefficients. Let
$f$
-vectors of specific matroid polytopes. In this subsection we will present explicit descriptions for these polynomials, enabling us to do the face enumeration of a split matroid polytope, without any convex hull or face lattice computation. To express the formulas in a compact form, we will make use of multinomial coefficients. Let
![]() $i,j,\ell$
be non negative integers, then
$i,j,\ell$
be non negative integers, then
We begin with an explicit formula for the polynomials
![]() $w_{\alpha, \beta, a,b}(t)$
.
$w_{\alpha, \beta, a,b}(t)$
.
Proposition 2.7.
For any
![]() $0 \lt \alpha \lt a$
and
$0 \lt \alpha \lt a$
and
![]() $0 \lt \beta \lt b$
, the following formula holds:
$0 \lt \beta \lt b$
, the following formula holds:
 \begin{equation*} w_{\alpha, \beta, a,b}(t) = \sum _{i=0}^{a-\alpha -1} \sum _{j=0}^{\alpha -1} \sum _{i'=0}^{b-\beta -1} \sum _{j'=0}^{\beta -1} \binom {a}{i,j}\binom {b}{i',j'} \cdot (1+t) \cdot t^{a+b-i-j-i'-j'-2} \enspace . \end{equation*}
\begin{equation*} w_{\alpha, \beta, a,b}(t) = \sum _{i=0}^{a-\alpha -1} \sum _{j=0}^{\alpha -1} \sum _{i'=0}^{b-\beta -1} \sum _{j'=0}^{\beta -1} \binom {a}{i,j}\binom {b}{i',j'} \cdot (1+t) \cdot t^{a+b-i-j-i'-j'-2} \enspace . \end{equation*}
Proof.
We are revisiting the proof of Lemma 2.4. We observe the following: the faces counted by
![]() $w_{\alpha, \beta, a,b}(t)$
come in pairs, namely the faces of
$w_{\alpha, \beta, a,b}(t)$
come in pairs, namely the faces of
![]() $\Delta _{\alpha, a}\times \Delta _{\beta, b}$
that do not lie in the boundary of
$\Delta _{\alpha, a}\times \Delta _{\beta, b}$
that do not lie in the boundary of
![]() $\Delta _{\alpha +\beta, a+b}$
and the faces of
$\Delta _{\alpha +\beta, a+b}$
and the faces of
![]() $\Delta _{k,n}$
one dimension higher. Furthermore, these faces are obtained by deleting and contracting elements such that the hyperplane
$\Delta _{k,n}$
one dimension higher. Furthermore, these faces are obtained by deleting and contracting elements such that the hyperplane
![]() $\sum _{\ell =1}^a x_\ell = \alpha$
still induces a split. Deleting
$\sum _{\ell =1}^a x_\ell = \alpha$
still induces a split. Deleting
![]() $i$
and contracting
$i$
and contracting
![]() $j$
of the first
$j$
of the first
![]() $a$
elements as well as deleting
$a$
elements as well as deleting
![]() $i'$
and contracting
$i'$
and contracting
![]() $j'$
of the other
$j'$
of the other
![]() $b$
elements then leads to such a pair of faces of dimension
$b$
elements then leads to such a pair of faces of dimension
![]() $a+b-i-j-i'-j'-2$
and
$a+b-i-j-i'-j'-2$
and
![]() $a+b-i-j-i'-j'-1$
. Expressing the ways of choosing the elements with multinomial coefficients leads to the desired formula.
$a+b-i-j-i'-j'-1$
. Expressing the ways of choosing the elements with multinomial coefficients leads to the desired formula.
For the polynomials
![]() $u_{r,k,h,n}(t)$
we provide the following formula.
$u_{r,k,h,n}(t)$
we provide the following formula.
Proposition 2.8.
For any
![]() $0\lt r\lt k\lt n$
and
$0\lt r\lt k\lt n$
and
![]() $r\lt h\lt n$
the following formula holds
$r\lt h\lt n$
the following formula holds
 \begin{equation*} u_{r,k,h,n}(t) = p_{r,k,h,n}(t) - p'_{r,h}(t)\cdot p'_{k-r,n-h}(t)\cdot (1+t) + \sum _{i = r+1}^k \binom {h}{i}\binom {n-h}{k-i} \end{equation*}
\begin{equation*} u_{r,k,h,n}(t) = p_{r,k,h,n}(t) - p'_{r,h}(t)\cdot p'_{k-r,n-h}(t)\cdot (1+t) + \sum _{i = r+1}^k \binom {h}{i}\binom {n-h}{k-i} \end{equation*}
where
![]() $p^{\prime}_{r,h}(t) =f_{\Delta _{r,h}}(t)-\binom {h}{r}$
and
$p^{\prime}_{r,h}(t) =f_{\Delta _{r,h}}(t)-\binom {h}{r}$
and
 \begin{equation*} p_{r,k,h,n}(t) = \sum _{j=0}^{h-r-1} \sum _{i=0}^{\min \{h-j,k-1\}} \sum _{\ell = 0}^{\min \{k-i-1,k-r-1\}} \sum _{m=0}^{\min \{n-h-\ell, n-k-j-1\}} \binom {h}{i,j}\binom {n-h}{\ell, m} \cdot t^{n-1-i-j-\ell -m}. \end{equation*}
\begin{equation*} p_{r,k,h,n}(t) = \sum _{j=0}^{h-r-1} \sum _{i=0}^{\min \{h-j,k-1\}} \sum _{\ell = 0}^{\min \{k-i-1,k-r-1\}} \sum _{m=0}^{\min \{n-h-\ell, n-k-j-1\}} \binom {h}{i,j}\binom {n-h}{\ell, m} \cdot t^{n-1-i-j-\ell -m}. \end{equation*}
Proof.
We begin by counting the faces of
![]() $\Delta _{k,n}$
that are not faces of
$\Delta _{k,n}$
that are not faces of
![]() $\mathscr {P}(\mathsf {\Lambda }_{k-r,k,n-h,n})$
. There are two types of such faces. Those that are entirely beyond the splitting hyperplane, and the ones that are separated by the hyperplane. Clearly there are
$\mathscr {P}(\mathsf {\Lambda }_{k-r,k,n-h,n})$
. There are two types of such faces. Those that are entirely beyond the splitting hyperplane, and the ones that are separated by the hyperplane. Clearly there are
![]() $\sum _{i=r+1}^k\binom {h}{i}\binom {n-h}{k-i}$
vertices of
$\sum _{i=r+1}^k\binom {h}{i}\binom {n-h}{k-i}$
vertices of
![]() $\Delta _{k,n}$
that are cut off by the hyperplane
$\Delta _{k,n}$
that are cut off by the hyperplane
![]() $\sum _{i=1}^h x_i = r$
. The other faces are precisely those containing such a vertex. Hence we count faces for which more than
$\sum _{i=1}^h x_i = r$
. The other faces are precisely those containing such a vertex. Hence we count faces for which more than
![]() $r$
of the first
$r$
of the first
![]() $h$
coordinates can be chosen to be one, where in total we have
$h$
coordinates can be chosen to be one, where in total we have
![]() $k$
coordinates equal to one. We do so by picking coordinates whose value we fix, the remaining coordinates can either be zero or one, and the total number of ones is precisely
$k$
coordinates equal to one. We do so by picking coordinates whose value we fix, the remaining coordinates can either be zero or one, and the total number of ones is precisely
![]() $k$
. Moreover, we do not want to fix all coordinates, i.e., we can fix at most
$k$
. Moreover, we do not want to fix all coordinates, i.e., we can fix at most
![]() $k-1$
coordinates to be equal to one and at most
$k-1$
coordinates to be equal to one and at most
![]() $n-k-1$
of them to be zero.
$n-k-1$
of them to be zero.
Say we fix
![]() $i$
coordinates in
$i$
coordinates in
![]() $\{1,\ldots, h\}$
to be one and
$\{1,\ldots, h\}$
to be one and
![]() $j$
to be zero. Then
$j$
to be zero. Then
![]() $0 \leq j\lt h-r$
and
$0 \leq j\lt h-r$
and
![]() $0\leq i \lt k$
as well as
$0\leq i \lt k$
as well as
![]() $i+j\leq h$
, since there are only
$i+j\leq h$
, since there are only
![]() $h$
coordinates to select from. Similarly, we fix
$h$
coordinates to select from. Similarly, we fix
![]() $\ell$
ones in the last
$\ell$
ones in the last
![]() $n-h$
coordinates and
$n-h$
coordinates and
![]() $m\geq 0$
zeros. Then
$m\geq 0$
zeros. Then
![]() $0\leq \ell \lt k-i$
and
$0\leq \ell \lt k-i$
and
![]() $\ell \lt k-r$
as it must be allowed to move another
$\ell \lt k-r$
as it must be allowed to move another
![]() $1$
to the first coordinates to get there more than
$1$
to the first coordinates to get there more than
![]() $r$
out of the
$r$
out of the
![]() $k$
ones. Furthermore,
$k$
ones. Furthermore,
![]() $\ell +m\leq n-h$
as we select
$\ell +m\leq n-h$
as we select
![]() $\ell +m$
out of
$\ell +m$
out of
![]() $\{h+1,\ldots, n\}$
and
$\{h+1,\ldots, n\}$
and
![]() $m+j \lt n-k$
because otherwise we would have fixed all zeros and hence also the ones. Clearly, there are
$m+j \lt n-k$
because otherwise we would have fixed all zeros and hence also the ones. Clearly, there are
![]() $\binom {h}{i,j}$
ways to select the
$\binom {h}{i,j}$
ways to select the
![]() $i$
and
$i$
and
![]() $j$
first coordinates and
$j$
first coordinates and
![]() $\binom {h}{\ell, m}$
ways to fix the
$\binom {h}{\ell, m}$
ways to fix the
![]() $\ell$
ones and
$\ell$
ones and
![]() $m$
zeros in the last coordinates. Every fixed coordinate reduces the dimension and hence counts
$m$
zeros in the last coordinates. Every fixed coordinate reduces the dimension and hence counts
![]() $p_{r,k,h,n}(t)$
these type of faces that are not vertices.
$p_{r,k,h,n}(t)$
these type of faces that are not vertices.
Now we count the
![]() $(d-1)$
-faces of
$(d-1)$
-faces of
![]() $\mathsf {\Lambda }_{r,k,h,n}$
that split a
$\mathsf {\Lambda }_{r,k,h,n}$
that split a
![]() $d$
-face of
$d$
-face of
![]() $\Delta _{k,n}$
. These are exactly the faces of
$\Delta _{k,n}$
. These are exactly the faces of
![]() $\Delta _{r,h}\times \Delta _{k-r,n-h}$
that contain a product of edges, i.e., are not of the from
$\Delta _{r,h}\times \Delta _{k-r,n-h}$
that contain a product of edges, i.e., are not of the from
![]() $\Delta _{r,h}\times \{v\}$
or
$\Delta _{r,h}\times \{v\}$
or
![]() $\{w\}\times \Delta _{k-r,n-h}$
for vertices
$\{w\}\times \Delta _{k-r,n-h}$
for vertices
![]() $v$
of
$v$
of
![]() $\Delta _{k-r,n-h}$
and
$\Delta _{k-r,n-h}$
and
![]() $w$
of
$w$
of
![]() $\Delta _{k,h}$
. Thus these faces are enumerated by the polynomial
$\Delta _{k,h}$
. Thus these faces are enumerated by the polynomial
![]() $p'_{r,h}(t)\times p'_{k-r,n-h}(t)$
. Each of these faces contributes
$p'_{r,h}(t)\times p'_{k-r,n-h}(t)$
. Each of these faces contributes
![]() $-t^{d-1}$
to
$-t^{d-1}$
to
![]() $u_{r,k,h,n}(t)$
. Furthermore, the
$u_{r,k,h,n}(t)$
. Furthermore, the
![]() $d$
-faces of
$d$
-faces of
![]() $\Delta _{k,n}$
that are separated by such a split do not contribute to
$\Delta _{k,n}$
that are separated by such a split do not contribute to
![]() $u_{r,k,h,n}(t)$
. Therefore we subtract
$u_{r,k,h,n}(t)$
. Therefore we subtract
![]() $p'_{r,h}(t)\cdot p'_{k-r,n-h}(t)\cdot (1+t)$
from
$p'_{r,h}(t)\cdot p'_{k-r,n-h}(t)\cdot (1+t)$
from
![]() $p_{r,k,h,n}(t)$
to obtain the polynomial
$p_{r,k,h,n}(t)$
to obtain the polynomial
![]() $u_{r,k,h,n}(t)$
.
$u_{r,k,h,n}(t)$
.
In the following we will specialise Theorem2.5 to some common and interesting classes of matroids. We begin with an example.
Example 2.9.
Let
![]() $\mathsf {M}$
be the projective geometry
$\mathsf {M}$
be the projective geometry
![]() $\mathrm {PG}(2,3)$
. This is a matroid on
$\mathrm {PG}(2,3)$
. This is a matroid on
![]() $n=13$
elements of rank
$n=13$
elements of rank
![]() $k=3$
. It is split as it is in fact paving. This matroid has
$k=3$
. It is split as it is in fact paving. This matroid has
![]() $13$
stressed hyperplanes, i.e., rank
$13$
stressed hyperplanes, i.e., rank
![]() $k-1=2$
flats, all of which have cardinality
$k-1=2$
flats, all of which have cardinality
![]() $h=4$
. In other words, we have
$h=4$
. In other words, we have
![]() $\unicode {x03BB}_{2,4} = 13$
. In particular, to use the formula of Theorem
2.5
, the polynomial
$\unicode {x03BB}_{2,4} = 13$
. In particular, to use the formula of Theorem
2.5
, the polynomial
is required. Since projective geometries are modular matroids, any pair of distinct proper non-empty cyclic flats fulfills the property (
⋆
). Also, every pair of them intersect in a single element. Moreover, for every pair of these cyclic flats we have
![]() $a = |F_1\smallsetminus F_2| = 3$
, and by symmetry
$a = |F_1\smallsetminus F_2| = 3$
, and by symmetry
![]() $b = |F_1\smallsetminus F_2| = 3$
. Additionally,
$b = |F_1\smallsetminus F_2| = 3$
. Additionally,
![]() $\alpha =\textrm {rk}(F_1) - |F_1\cap F_2| = 2 - 1 = 1$
and again by symmetry
$\alpha =\textrm {rk}(F_1) - |F_1\cap F_2| = 2 - 1 = 1$
and again by symmetry
![]() $\beta =\textrm {rk}(F_2) - |F_1\cap F_2| = 1$
. Therefore there is a single non-vanishing coefficient
$\beta =\textrm {rk}(F_2) - |F_1\cap F_2| = 1$
. Therefore there is a single non-vanishing coefficient
![]() $\unicode {x03BC}_{\alpha, \beta, a,b}$
which is
$\unicode {x03BC}_{\alpha, \beta, a,b}$
which is
It remains to compute:
Now applying Theorem 2.5 , we obtain:
 \begin{align*} f_{\mathscr {P}(\mathrm {PG}(2,3))}(t) &= f_{\Delta _{3,13}}(t) - 13 \, u_{2,3,4,13}(t) - 78 \, w_{1,1,3,3}(t)\\ &= t^{12} + 39 \, t^{11} + 455\, t^{10} + 2704\, t^{9} + 9893\, t^{8} + 24414\, t^{7} + 42666\, t^{6} + \\ &\qquad 54054\, t^{5} + 49608\, t^{4} + 31707\, t^{3} + 12870\, t^{2} + 2808\, t + 234 \enspace . \end{align*}
\begin{align*} f_{\mathscr {P}(\mathrm {PG}(2,3))}(t) &= f_{\Delta _{3,13}}(t) - 13 \, u_{2,3,4,13}(t) - 78 \, w_{1,1,3,3}(t)\\ &= t^{12} + 39 \, t^{11} + 455\, t^{10} + 2704\, t^{9} + 9893\, t^{8} + 24414\, t^{7} + 42666\, t^{6} + \\ &\qquad 54054\, t^{5} + 49608\, t^{4} + 31707\, t^{3} + 12870\, t^{2} + 2808\, t + 234 \enspace . \end{align*}
2.5 Face numbers of sparse paving matroids
As mentioned in the introduction, it is conjectured that almost all matroids are sparse paving; see [Reference Mayhew, Newman, Welsh and Whittle38] for the details. Furthermore, many famous examples of matroids fall into this class; notable examples are the Fano matroid, the Vámos matroid, the complete graph on four vertices, and the duals of each of them. Sparse paving and paving matroids are split, so we can make use of our main result. For sparse paving matroids all the proper cyclic flats are circuit hyperplanes, i.e., of rank
![]() $r=k-1$
and size
$r=k-1$
and size
![]() $h=k$
. Using these parameters, Theorem2.5 simplifies to the following statement.
$h=k$
. Using these parameters, Theorem2.5 simplifies to the following statement.
Corollary 2.10.
Let
![]() $\mathsf {M}$
be a connected sparse paving matroid of rank
$\mathsf {M}$
be a connected sparse paving matroid of rank
![]() $k$
on
$k$
on
![]() $n$
elements having exactly
$n$
elements having exactly
![]() $\unicode {x03BB}$
circuit-hyperplanes, and let
$\unicode {x03BB}$
circuit-hyperplanes, and let
![]() $\unicode {x03BC}$
count the pair of circuit-hyperplanes which have
$\unicode {x03BC}$
count the pair of circuit-hyperplanes which have
![]() $k-2$
elements in common. Then
$k-2$
elements in common. Then
where
![]() $u(t)$
is given by
$u(t)$
is given by
 \begin{align*} 1-k\cdot (n-k)\cdot (t+1)+\left ((n-k)\cdot (t+1)^{k+1} + k\cdot (t+1)^{n-k+1}-n\cdot (t+1)\right )\cdot t^{-1}\\ +\left ((t+1)^k+(t+1)^{n-k}-(t+1)^n-1\right )\cdot t^{-2}\enspace . \end{align*}
\begin{align*} 1-k\cdot (n-k)\cdot (t+1)+\left ((n-k)\cdot (t+1)^{k+1} + k\cdot (t+1)^{n-k+1}-n\cdot (t+1)\right )\cdot t^{-1}\\ +\left ((t+1)^k+(t+1)^{n-k}-(t+1)^n-1\right )\cdot t^{-2}\enspace . \end{align*}
Proof.
By substituting
![]() $r$
by
$r$
by
![]() $k-1$
and
$k-1$
and
![]() $h$
with
$h$
with
![]() $k$
in Proposition 2.8 we obtain
$k$
in Proposition 2.8 we obtain
where
![]() $p_{k-1,k,k,n}(t)$
is equal to
$p_{k-1,k,k,n}(t)$
is equal to
 \begin{align*} \sum _{i=0}^{k-1}\binom {k}{i}\sum _{m=0}^{n-k-1} \binom {n-k}{m}\cdot t^{n-k-m}\cdot t^{k-i}\cdot t^{-1} &= \left ((t+1)^k-1\right )\cdot \left ((t+1)^{n-k}-1\right )\cdot t^{-1} \enspace . \end{align*}
\begin{align*} \sum _{i=0}^{k-1}\binom {k}{i}\sum _{m=0}^{n-k-1} \binom {n-k}{m}\cdot t^{n-k-m}\cdot t^{k-i}\cdot t^{-1} &= \left ((t+1)^k-1\right )\cdot \left ((t+1)^{n-k}-1\right )\cdot t^{-1} \enspace . \end{align*}
Furthermore, the polytope
![]() $\Delta _{k-1,k}$
is an affine transformation of
$\Delta _{k-1,k}$
is an affine transformation of
![]() $\Delta _{1,k}$
hence
$\Delta _{1,k}$
hence
 \begin{equation*} p'_{k-1,k}(t) = p'_{1,k}(t) = \sum _{i=2}^k \binom {k}{i}\cdot t^{i-1} = \left ((t+1)^k-1-k\cdot t\right )\cdot t^{-1}\enspace . \end{equation*}
\begin{equation*} p'_{k-1,k}(t) = p'_{1,k}(t) = \sum _{i=2}^k \binom {k}{i}\cdot t^{i-1} = \left ((t+1)^k-1-k\cdot t\right )\cdot t^{-1}\enspace . \end{equation*}
Using the same formula for
![]() $p'_{1,n-k}(t)$
leads to the desired formula.
$p'_{1,n-k}(t)$
leads to the desired formula.
As was mentioned earlier, there are many famous matroids that are sparse paving. We saw four sparse paving matroids in the running Example 2.2. In the next example we take a look at a family of sparse paving matroids with maximum number of circuit-hyperplanes. This example demonstrates that one can derive a bit more from our calculations.
Example 2.11.
Let
![]() $m\geq 3$
. Consider the rank
$m\geq 3$
. Consider the rank
![]() $k=4$
matroid
$k=4$
matroid
![]() $\mathsf {M}$
whose bases are the quadruples of affinely independent binary vectors of length
$\mathsf {M}$
whose bases are the quadruples of affinely independent binary vectors of length
![]() $m$
. This is a sparse paving matroid on
$m$
. This is a sparse paving matroid on
![]() $n=2^m$
elements with the maximum number
$n=2^m$
elements with the maximum number
![]() $\unicode {x03BB} = \frac {1}{4}\binom {n}{3}$
of circuit-hyperplanes, as every three points define a circuit. A simple double counting argument reveals that the number of pairs of these circuit-hyperplanes that share two elements is
$\unicode {x03BB} = \frac {1}{4}\binom {n}{3}$
of circuit-hyperplanes, as every three points define a circuit. A simple double counting argument reveals that the number of pairs of these circuit-hyperplanes that share two elements is
![]() $\unicode {x03BC}=\frac {3n-12}{8}\binom {n}{3}$
. The polytope
$\unicode {x03BC}=\frac {3n-12}{8}\binom {n}{3}$
. The polytope
![]() $\mathscr {P}(\mathsf {M})$
has
$\mathscr {P}(\mathsf {M})$
has
![]() $\frac {6n^2-57n+132}{8}\binom {n}{3}$
many square faces all of which are induced by split hyperplanes, and hence can be read off from the quadratic term of the product
$\frac {6n^2-57n+132}{8}\binom {n}{3}$
many square faces all of which are induced by split hyperplanes, and hence can be read off from the quadratic term of the product
![]() $p'_{3,4}(t)\cdot p'_{1,n-4}(t)$
, and
$p'_{3,4}(t)\cdot p'_{1,n-4}(t)$
, and
![]() $ \left (4\,\binom {n-3}{2}-\binom {n-4}{4}+\binom {n}{4}-3\,n^2+17\,n-20\right )\frac {1}{4}\,\binom {n}{3}$
many triangular faces that are also faces of the hypersimplex
$ \left (4\,\binom {n-3}{2}-\binom {n-4}{4}+\binom {n}{4}-3\,n^2+17\,n-20\right )\frac {1}{4}\,\binom {n}{3}$
many triangular faces that are also faces of the hypersimplex
![]() $\Delta _{4,n}$
, e.g., for
$\Delta _{4,n}$
, e.g., for
![]() $m=3$
the matroid is the binary affine cube and its polytope has
$m=3$
the matroid is the binary affine cube and its polytope has
![]() $420$
square and
$420$
square and
![]() $448$
triangular faces.
$448$
triangular faces.
2.6 Face numbers of rank two matroids
A loopless matroid of rank two is trivially paving, and hence a split matroid. This allows us to use the strength of Theorem2.5 to compute their
![]() $f$
-vectors.
$f$
-vectors.
The key is the following elementary observation. The hyperplanes, i.e., the flats of rank one, of a loopless matroid of rank two form a partition of the ground set, and conversely, any partition of the ground set defines precisely a single rank two matroid having each part as a flat. The bases of the matroid are obtained by taking two elements of the ground set, not belonging to the same part.
Base polytopes of matroids of rank two have made prominent appearances throughout algebraic combinatorics, under various guises. Notably, as is pointed out in [Reference Ferroni and Higashitani21, Section 6.1], they coincide with edge polytopes of complete multipartite graphs – we refer to that paper for the precise definition of edge polytopes and a short overview of them. In this vein, the work of Ohsugi and Hibi [Reference Ohsugi and Hibi40] addresses the edge polytopes of complete multipartite graphs, motivated both from toric geometry and graph theory. In particular, the content of [Reference Ohsugi and Hibi40, Theorem 2.5] provides a formula for the
![]() $f$
-vector of the edge polytope of an arbitrary complete multipartite graph, and thus for general rank two matroid polytopes. Let us point out that there appears to be an error in the formula as they stated it – in particular within the quantity they denote by
$f$
-vector of the edge polytope of an arbitrary complete multipartite graph, and thus for general rank two matroid polytopes. Let us point out that there appears to be an error in the formula as they stated it – in particular within the quantity they denote by
![]() $\alpha _i$
. As an application of Theorem2.5 we can give another formula for the
$\alpha _i$
. As an application of Theorem2.5 we can give another formula for the
![]() $f$
-vector of these polytopes.
$f$
-vector of these polytopes.
Corollary 2.12.
Let
![]() $\mathsf {M}$
be a loopless matroid of rank two having
$\mathsf {M}$
be a loopless matroid of rank two having
![]() $s$
hyperplanes with cardinalities
$s$
hyperplanes with cardinalities
![]() $h_1,\ldots, h_s$
. number of
$h_1,\ldots, h_s$
. number of
![]() $i$
-dimensional faces of
$i$
-dimensional faces of
![]() $\mathscr {P}(\mathsf {M})$
or, equivalently, the edge polytope of a complete multipartite graph with parts of sizes
$\mathscr {P}(\mathsf {M})$
or, equivalently, the edge polytope of a complete multipartite graph with parts of sizes
![]() $h_1,\ldots, h_s$
is given by:
$h_1,\ldots, h_s$
is given by:
 \begin{equation*}f_i(\mathscr {P}(\mathsf {M})) = \binom {n+1}{i+2}\!+(s-1)\binom {n}{i+2} - \!\sum _{j\lt \ell } \!\binom {h_j+h_\ell +1}{i+2} \!+ (s-2)\!\sum _{j=1}^s\! \binom {h_j+1}{i+2} - \!\sum _{j=1}^s \!\binom {n-h_j}{i+2}.\end{equation*}
\begin{equation*}f_i(\mathscr {P}(\mathsf {M})) = \binom {n+1}{i+2}\!+(s-1)\binom {n}{i+2} - \!\sum _{j\lt \ell } \!\binom {h_j+h_\ell +1}{i+2} \!+ (s-2)\!\sum _{j=1}^s\! \binom {h_j+1}{i+2} - \!\sum _{j=1}^s \!\binom {n-h_j}{i+2}.\end{equation*}
Proof.
It is straightforward to check the formula for the case
![]() $s=2$
, that is
$s=2$
, that is
![]() $\mathscr {P}(\mathsf {M}) = \Delta _{1,h_1}\times \Delta _{1,h_2}$
. If
$\mathscr {P}(\mathsf {M}) = \Delta _{1,h_1}\times \Delta _{1,h_2}$
. If
![]() $s\gt 2$
then
$s\gt 2$
then
![]() $\mathsf {M}$
is connected and we may apply Theorem2.5. Observe that all pairs of flats are trivially modular, and they are pairwise disjoint. Thus, the non-vanishing coefficients are
$\mathsf {M}$
is connected and we may apply Theorem2.5. Observe that all pairs of flats are trivially modular, and they are pairwise disjoint. Thus, the non-vanishing coefficients are
![]() $\unicode {x03BC}_{1,1,h_j,h_\ell }$
. In the following we omit parts of the long and tedious calculations but indicate the main steps. For
$\unicode {x03BC}_{1,1,h_j,h_\ell }$
. In the following we omit parts of the long and tedious calculations but indicate the main steps. For
![]() $k=2$
and
$k=2$
and
![]() $r=1$
using some change of summation and the Vandermonde identity we obtain
$r=1$
using some change of summation and the Vandermonde identity we obtain
 \begin{align*} \sum _{j\lt l} w_{1,1,h_j,h_\ell }(t) =\sum _{i=2}^{n-1} \left ( \sum _{j\lt \ell } \binom {h_j+h_\ell }{i+2} -\sum _{j=1}^s \left ((s-1)\binom {h_j}{i+2}+(n-h_j)\binom {h_j}{i+1}\right )\right )\cdot t^i\, (1+t). \end{align*}
\begin{align*} \sum _{j\lt l} w_{1,1,h_j,h_\ell }(t) =\sum _{i=2}^{n-1} \left ( \sum _{j\lt \ell } \binom {h_j+h_\ell }{i+2} -\sum _{j=1}^s \left ((s-1)\binom {h_j}{i+2}+(n-h_j)\binom {h_j}{i+1}\right )\right )\cdot t^i\, (1+t). \end{align*}
Similarly, we get this formula for
![]() $p'_{1,h_j}(t)\cdot p'_{1,n-h_j}(t)\cdot (1+t)$
$p'_{1,h_j}(t)\cdot p'_{1,n-h_j}(t)\cdot (1+t)$
 \begin{align*} \sum _{i=2}^{n-1} \left (\binom {n}{i+2}-\binom {n-h_j}{i+2}-h\binom {n-h_j}{i+1}-(n-h_j)\binom {h_j}{i+1}-\binom {h_j}{i+2}\right )\cdot t^i\,(1+t) \end{align*}
\begin{align*} \sum _{i=2}^{n-1} \left (\binom {n}{i+2}-\binom {n-h_j}{i+2}-h\binom {n-h_j}{i+1}-(n-h_j)\binom {h_j}{i+1}-\binom {h_j}{i+2}\right )\cdot t^i\,(1+t) \end{align*}
and for
![]() $p_{1,2,h_j,n}(t)$
the expression
$p_{1,2,h_j,n}(t)$
the expression
 \begin{align*} \sum _{i=1}^{n-1}\left (\binom {n}{i+2}-\binom {n-h_j}{i+2}-h\binom {n-h_j}{i+1}\right )t^{i+1} +\sum _{i=1}^{n-1}\left (h_j\binom {n-1}{i+1}-h_j\binom {n-h_j}{i+1}\right )\cdot t^i \end{align*}
\begin{align*} \sum _{i=1}^{n-1}\left (\binom {n}{i+2}-\binom {n-h_j}{i+2}-h\binom {n-h_j}{i+1}\right )t^{i+1} +\sum _{i=1}^{n-1}\left (h_j\binom {n-1}{i+1}-h_j\binom {n-h_j}{i+1}\right )\cdot t^i \end{align*}
where the two sums correspond to the indices
![]() $i=0$
and
$i=0$
and
![]() $i=1$
in the definition of
$i=1$
in the definition of
![]() $p_{r,k,h,n}(t)$
. This gives us
$p_{r,k,h,n}(t)$
. This gives us
![]() $u_{1,2,h_j,n}(t) = p_{1,2,h_j,n}(t)-p'_{1,h_j}(t)p'_{1,n-h_j}(t)(t+1)+\binom {h_j}{2}$
and hence
$u_{1,2,h_j,n}(t) = p_{1,2,h_j,n}(t)-p'_{1,h_j}(t)p'_{1,n-h_j}(t)(t+1)+\binom {h_j}{2}$
and hence
![]() $\sum _{j=1}^s u_{1,2,h_j,n}$
. We also need
$\sum _{j=1}^s u_{1,2,h_j,n}$
. We also need
 \begin{align*} f_{\Delta _{2,n}}(t) &= \binom {n}{2} + \sum _{i=1}^{n-1} \binom {n}{i+1}\sum _{j=1}^i \binom {n-i-1}{2-j}\cdot t^i = \binom {n}{2} + 3\binom {n}{3} \, t +\sum _{i=2}^{n-1}\binom {n}{i+1}(n-i) \cdot t^i \enspace . \end{align*}
\begin{align*} f_{\Delta _{2,n}}(t) &= \binom {n}{2} + \sum _{i=1}^{n-1} \binom {n}{i+1}\sum _{j=1}^i \binom {n-i-1}{2-j}\cdot t^i = \binom {n}{2} + 3\binom {n}{3} \, t +\sum _{i=2}^{n-1}\binom {n}{i+1}(n-i) \cdot t^i \enspace . \end{align*}
Now putting the pieces together, applying Pascal’s identity, and cancelling many terms, one may obtain the desired formula of the statement (where additional effort is required for the constant, linear and quadratic term).
Remark 2.13.
Kim described in [Reference Kim34] how the cd-indices of polytopes change when performing hyperplane splits. From this, he derived a formula for the cd-index of rank two matroid base polytopes. This formula depends on the cd-index of polytopes of rank two matroids with
![]() $1$
,
$1$
,
![]() $2$
, and
$2$
, and
![]() $3$
hyperplanes. While there are explicit expressions for the cd-index when the matroid has
$3$
hyperplanes. While there are explicit expressions for the cd-index when the matroid has
![]() $1$
or
$1$
or
![]() $2$
hyperplanes, the case with
$2$
hyperplanes, the case with
![]() $3$
hyperplanes remains unsolved. We point out that the cd-index contains more information than the
$3$
hyperplanes remains unsolved. We point out that the cd-index contains more information than the
![]() $f$
-vector – however, recovering the
$f$
-vector – however, recovering the
![]() $f$
-vector from the cd-index is often a very laborious task.
$f$
-vector from the cd-index is often a very laborious task.
3. Final remarks and open problems
Steinitz characterised
![]() $f$
-vectors of
$f$
-vectors of
![]() $3$
-polytopes. Since then, the
$3$
-polytopes. Since then, the
![]() $f$
-vectors of
$f$
-vectors of
![]() $4$
-polytopes have been intensively studied. In spite of the great interest from mathematicians, only little is known about the face numbers of higher dimensional polytopes [Reference Ziegler50] or
$4$
-polytopes have been intensively studied. In spite of the great interest from mathematicians, only little is known about the face numbers of higher dimensional polytopes [Reference Ziegler50] or
![]() $0/1$
-polytopes [Reference Ziegler49]. The contribution of this paper is an explicit formula for
$0/1$
-polytopes [Reference Ziegler49]. The contribution of this paper is an explicit formula for
![]() $f$
-vectors of split matroids. However, many questions and problems regarding
$f$
-vectors of split matroids. However, many questions and problems regarding
![]() $f$
-vectors of
$f$
-vectors of
![]() $0/1$
-polytopes, or even the class of matroid polytopes itself, remain broadly open. This last section aims to propose a few problems and questions in this underexplored area of discrete geometry.
$0/1$
-polytopes, or even the class of matroid polytopes itself, remain broadly open. This last section aims to propose a few problems and questions in this underexplored area of discrete geometry.
3.1 Explicit formulas for other polytopes
Besides the base polytope studied in this paper, another famous polytope that one may associate to a matroid is the so-called independence polytope. This polytope is defined as the convex hull of the indicator vectors of all the independent sets, i.e., subsets of bases, of the matroid, and it contains the base polytope as a facet.
A natural challenge that we raise is to provide a good way of computing the
![]() $f$
-vectors of these polytopes.
$f$
-vectors of these polytopes.
Problem 3.1.
Find a formula for the
![]() $f$
-vector of the independent set polytope for (connected) split matroids.
$f$
-vector of the independent set polytope for (connected) split matroids.
We speculate that one can approach this problem by using modifications of the ideas and the techniques that we presented in this article.
On the other hand, it is also natural to ask about the problem of finding a formula for
![]() $f$
-vectors of matroid base polytopes or independence polytopes for arbitrary matroids. These two problems appear to be considerably more difficult. Nonetheless, we pose the following broad question.
$f$
-vectors of matroid base polytopes or independence polytopes for arbitrary matroids. These two problems appear to be considerably more difficult. Nonetheless, we pose the following broad question.
Question 3.2.
Can the approach of splitting polytopes, or treating the
![]() $f$
-vector as a valuation with an error term, be used to obtain an explicit formula for the
$f$
-vector as a valuation with an error term, be used to obtain an explicit formula for the
![]() $f$
-vector of an arbitrary matroid polytope? Independently of the details of the computation, what is the precise matroidal data that one needs in order to recover the
$f$
-vector of an arbitrary matroid polytope? Independently of the details of the computation, what is the precise matroidal data that one needs in order to recover the
![]() $f$
-vector?
$f$
-vector?
Note that all matroid polytopes are cut out of the hypersimplex by intersecting it with split hyperplanes – or, more precisely, with half-spaces whose boundary is a split hyperplane – which are weakly compatible, i.e., that may intersect in the interior of the hypersimplex.
Also, every matroid base polytopes can be obtained by slicing pieces off of a unit cube. Unit cubes themselves possess many split hyperplanes; see [Reference Herrmann and Joswig28] for more details. Therefore, it seems reasonable to attempt to generalise the techniques and ideas of the present paper beyond the class of matroid polytopes, in order to include other classes of
![]() $0/1$
-polytopes.
$0/1$
-polytopes.
Problem 3.3.
Describe the
![]() $f$
-vectors of
$f$
-vectors of
![]() $0/1$
-polytopes in terms of their supporting split hyperplanes.
$0/1$
-polytopes in terms of their supporting split hyperplanes.
3.2 The shape of f-vectors of matroid polytopes
A recent trend in matroid theory is that of proving unimodal and log-concave inequalities for various vectors of numbers associated to matroids. A finite sequence of numbers
![]() $(a_0,\ldots, a_n)$
is said to be unimodal if there exists some index
$(a_0,\ldots, a_n)$
is said to be unimodal if there exists some index
![]() $0\leq j\leq n$
with the property that
$0\leq j\leq n$
with the property that
If all the
![]() $a_i$
’s are positive, a stronger condition is that of log-concavity, which asserts that for each index
$a_i$
’s are positive, a stronger condition is that of log-concavity, which asserts that for each index
![]() $1\leq j\leq n-1$
the inequalities
$1\leq j\leq n-1$
the inequalities
![]() $a_j^2\geq a_{j-1}a_{j+1}$
hold.
$a_j^2\geq a_{j-1}a_{j+1}$
hold.
There are two objects that, in other contexts, can be referred to as “the
![]() $f$
-vector of a matroid,” though they hold no direct relation with the
$f$
-vector of a matroid,” though they hold no direct relation with the
![]() $f$
-vector we studied in this paper. The first of them comes from considering a matroid as a pure simplicial complex with the property that each vertex-induced subcomplex is shellable [Reference Björner12]. In this case, one can define the
$f$
-vector we studied in this paper. The first of them comes from considering a matroid as a pure simplicial complex with the property that each vertex-induced subcomplex is shellable [Reference Björner12]. In this case, one can define the
![]() $f$
-vector of a matroid to be the
$f$
-vector of a matroid to be the
![]() $f$
-vector of this simplicial complex. This has been object of intensive research and several open problems and conjectures exist in the literature regarding this
$f$
-vector of this simplicial complex. This has been object of intensive research and several open problems and conjectures exist in the literature regarding this
![]() $f$
-vector, for instance Stanley’s conjecture asserting that the corresponding
$f$
-vector, for instance Stanley’s conjecture asserting that the corresponding
![]() $h$
-vector is a pure
$h$
-vector is a pure
![]() $O$
-sequence (see [Reference Stanley and Birkhäuser47]). In [Reference Adiprasito, Huh and Katz4] these
$O$
-sequence (see [Reference Stanley and Birkhäuser47]). In [Reference Adiprasito, Huh and Katz4] these
![]() $f$
-vectors are proved to be log-concave. The second object that sometimes is referred to as “the
$f$
-vectors are proved to be log-concave. The second object that sometimes is referred to as “the
![]() $f$
-vector of a matroid” is the vector having as coordinates the number of flats of the matroid of each rank, i.e., the Whitney numbers of the second kind of
$f$
-vector of a matroid” is the vector having as coordinates the number of flats of the matroid of each rank, i.e., the Whitney numbers of the second kind of
![]() $\mathsf {M}$
. This object has also received some attention in the recent years; one of the main open problems regarding this
$\mathsf {M}$
. This object has also received some attention in the recent years; one of the main open problems regarding this
![]() $f$
-vector was the so-called “Top-Heavy Conjecture,” which was settled in [Reference Braden, Huh, Matherne, Proudfoot and Wang11]. It remains as an open problem to prove or disprove the unimodality of the Whitney numbers of the second kind.
$f$
-vector was the so-called “Top-Heavy Conjecture,” which was settled in [Reference Braden, Huh, Matherne, Proudfoot and Wang11]. It remains as an open problem to prove or disprove the unimodality of the Whitney numbers of the second kind.
In a similar vein, it is quite inviting to ask the following question.
Question 3.4.
Are the
![]() $f$
-vectors of matroid base polytopes unimodal, or even log-concave?
$f$
-vectors of matroid base polytopes unimodal, or even log-concave?
It is known that there are simplicial polytopes having a non-unimodal
![]() $f$
-vector; see [Reference Ziegler48, Chapter 8.6]. However, let us point out that, within the existing literature, we were not able to find any examples of non-unimodal
$f$
-vector; see [Reference Ziegler48, Chapter 8.6]. However, let us point out that, within the existing literature, we were not able to find any examples of non-unimodal
![]() $f$
-vectors for the general class of all
$f$
-vectors for the general class of all
![]() $0/1$
-polytopes. We have been able to verify the log-concavity of the
$0/1$
-polytopes. We have been able to verify the log-concavity of the
![]() $f$
-vectors of the following classes of matroids, in some cases relying critically on the results of this paper:
$f$
-vectors of the following classes of matroids, in some cases relying critically on the results of this paper:
-
• All matroids on a ground set of size at most
 $9$
.
$9$
. -
• Split matroids on a ground set of size at most
 $12$
.
$12$
. -
• Sparse paving matroids on a ground set of size at most
 $40$
.
$40$
. -
• Split matroids with four cyclic flats as in Lemma 2.4 of size at most
 $50$
.
$50$
. -
• Schubert elementary split matroids on a ground set of size at most
 $100$
.
$100$
. -
• Lattice path matroids on a ground set of size at most
 $13$
.
$13$
. -
• Rank two matroids on a ground set of size at most
 $60$
.
$60$
.
Matroid base polytopes have many remarkable properties. One that is particularly relevant is that their vertex-edge graph, i.e., the
![]() $1$
-skeleton of the polytope, determines the entire polytope up to a rigid transformation; see [Reference Holzmann, Norton and Tobey31, Reference Pineda-Villavicencio and Schröter44] for more precise statements. Similarly, the data of the
$1$
-skeleton of the polytope, determines the entire polytope up to a rigid transformation; see [Reference Holzmann, Norton and Tobey31, Reference Pineda-Villavicencio and Schröter44] for more precise statements. Similarly, the data of the
![]() $2$
-skeleton of a matroidal subdivision describes the subdivision completely; this technique has been used in several articles, see for example [Reference Herrmann, Joswig and Speyer29]. It is tempting to ask whether the enumerative information encoded in the first few entries of the
$2$
-skeleton of a matroidal subdivision describes the subdivision completely; this technique has been used in several articles, see for example [Reference Herrmann, Joswig and Speyer29]. It is tempting to ask whether the enumerative information encoded in the first few entries of the
![]() $f$
-vector of a matroid base polytope is already sufficient to derive the remaining entries. More precisely, we ask for the following constant.
$f$
-vector of a matroid base polytope is already sufficient to derive the remaining entries. More precisely, we ask for the following constant.
Problem 3.5.
Is it true that there exists a number
![]() $c$
such that the first
$c$
such that the first
![]() $c$
entries of the
$c$
entries of the
![]() $f$
-vector of some matroid i.e.,
$f$
-vector of some matroid i.e.,
![]() $f_0, \ldots, f_{c-1}$
, are enough to determine the complete
$f_0, \ldots, f_{c-1}$
, are enough to determine the complete
![]() $f$
-vector of
$f$
-vector of
![]() $\mathsf {M}$
If it is true, what is the smallest such
$\mathsf {M}$
If it is true, what is the smallest such
![]() $c$
?
$c$
?
One may consider various versions of the above problem, where the size or the rank of the matroid are part of the input or not. Further slight modifications consist of restricting to only connected matroids, or to matroids belonging to a specific class. Our computer experiments indicate that
![]() $c=5$
suffices for all connected matroids on up to nine elements. This number cannot be smaller as we found two matroids of rank four on nine elements that agree on the sequence
$c=5$
suffices for all connected matroids on up to nine elements. This number cannot be smaller as we found two matroids of rank four on nine elements that agree on the sequence
![]() $f_0$
,
$f_0$
,
![]() $f_1$
,
$f_1$
,
![]() $f_2$
,
$f_2$
,
![]() $f_3$
but not on the number of
$f_3$
but not on the number of
![]() $4$
-faces
$4$
-faces
![]() $f_4$
. Their
$f_4$
. Their
![]() $f$
-vectors are:
$f$
-vectors are:
On the other hand, as a consequence of Corollary 2.10, if one restricts to all sparse paving matroids of rank
![]() $k$
on
$k$
on
![]() $n$
elements, knowing the number of vertices
$n$
elements, knowing the number of vertices
![]() $f_0$
and
$f_0$
and
![]() $2$
-dimensional faces
$2$
-dimensional faces
![]() $f_2$
suffices to recover
$f_2$
suffices to recover
![]() $\unicode {x03BB}$
and
$\unicode {x03BB}$
and
![]() $\unicode {x03BC}$
, and hence the entire
$\unicode {x03BC}$
, and hence the entire
![]() $f$
-vector. Thus, in this version of the problem the answer is
$f$
-vector. Thus, in this version of the problem the answer is
![]() $c=3$
.
$c=3$
.
3.3 A digression on the extension complexity of split matroids
A motivation to study the face enumeration of matroid polytopes stems from the work of Rothvoss [Reference Rothvoß45], Conforti, Kaibel, Walter, and Weltge [Reference Conforti, Kaibel, Walter and Weltge16], and Kaibel, Lee, Walter, and Weltge [Reference Kaibel, Lee, Walter and Weltge35] on the extension complexity of matroid polytopes (see also the corrigendum [Reference Kaibel, Lee, Walter and Weltge36], and the article by Aprile and Fiorini [Reference Aprile and Fiorini3]). The special case of hypersimplices is discussed in work by Grande, Padrol, and Sanyal [Reference Grande, Padrol and Sanyal25], and the case of
![]() $2$
-level matroids is the main focus of [Reference Aprile, Cevallos and Faenza1, Reference Aprile, Conforti, Fiorini, Faenza, Huynh and Macchia2].
$2$
-level matroids is the main focus of [Reference Aprile, Cevallos and Faenza1, Reference Aprile, Conforti, Fiorini, Faenza, Huynh and Macchia2].
Given a lattice polytope
![]() $\mathscr {P}\subseteq \mathbb {R}^n$
, an extended formulation of
$\mathscr {P}\subseteq \mathbb {R}^n$
, an extended formulation of
![]() $\mathscr {P}$
is another lattice polytope
$\mathscr {P}$
is another lattice polytope
![]() $\mathscr {Q}\subseteq \mathbb {R}^m$
together with a projection map
$\mathscr {Q}\subseteq \mathbb {R}^m$
together with a projection map
![]() $\pi :\mathbb {R}^m \to \mathbb {R}^n$
which projects
$\pi :\mathbb {R}^m \to \mathbb {R}^n$
which projects
![]() $\mathscr {Q}$
onto
$\mathscr {Q}$
onto
![]() $\mathscr {P}$
. The complexity of an extended formulation is the number of facets of the polytope
$\mathscr {P}$
. The complexity of an extended formulation is the number of facets of the polytope
![]() $\mathscr {Q}$
. The extension complexity of
$\mathscr {Q}$
. The extension complexity of
![]() $\mathscr {P}$
, denoted
$\mathscr {P}$
, denoted
![]() $\operatorname {xc}(\mathscr {P})$
, is the minimum complexity of an extended formulation of
$\operatorname {xc}(\mathscr {P})$
, is the minimum complexity of an extended formulation of
![]() $\mathscr {P}$
.
$\mathscr {P}$
.
One of the main tools for finding lower bounds on the extension complexity are the rectangular covering numbers, but these numbers grow at most quadratically in the size of the ground set [Reference Kaibel, Lee, Walter and Weltge35, Proposition 2]. Furthermore, the extension complexity of regular matroids is polynomial [Reference Aprile and Fiorini3]. The extension complexity of matroid polytopes is also related to the “hitting number” of the base polytope, see [Reference Aprile6].
Rothvoss [Reference Rothvoß45, Corollary 6] provedFootnote
1
that for all
![]() $n$
there exists a matroid
$n$
there exists a matroid
![]() $\mathsf {M}$
on
$\mathsf {M}$
on
![]() $n$
elements whose base polytope has extension complexity
$n$
elements whose base polytope has extension complexity
![]() $\operatorname {xc}(\mathscr {P}(\mathsf {M})) \in \Omega \left (\frac {2^{n/2}}{n^{5/4} \sqrt {\log (2n)}}\right )$
. Moreover, Rothvoss’ proof is non-constructive and relies only on an enumerative result of matroids, that therefore guarantees that whatever these examples are, they must belong to the class of sparse paving matroids, and are therefore split matroids. Thus it remains a notorious open problem to find an explicit family of matroids having exponential extension complexity. In fact, having one would yield an explicit infinite family of Boolean functions requiring superlogarithmic depth circuits, according to an observation attributed to Göös in [Reference Aprile and Fiorini3, Section 8] and [37]; see also the relevant [Reference Göös, Jain and Watson24].
$\operatorname {xc}(\mathscr {P}(\mathsf {M})) \in \Omega \left (\frac {2^{n/2}}{n^{5/4} \sqrt {\log (2n)}}\right )$
. Moreover, Rothvoss’ proof is non-constructive and relies only on an enumerative result of matroids, that therefore guarantees that whatever these examples are, they must belong to the class of sparse paving matroids, and are therefore split matroids. Thus it remains a notorious open problem to find an explicit family of matroids having exponential extension complexity. In fact, having one would yield an explicit infinite family of Boolean functions requiring superlogarithmic depth circuits, according to an observation attributed to Göös in [Reference Aprile and Fiorini3, Section 8] and [37]; see also the relevant [Reference Göös, Jain and Watson24].
Although we cannot compute explicitly the extension complexity of split matroid polytopes, we conjecture that the following natural family of sparse paving matroids might have the desired exponential extension complexity.
Conjecture 3.6.
For each positive integer
![]() $n$
, let us denote by
$n$
, let us denote by
![]() $\mathsf {S}_n$
the sparse paving matroid on
$\mathsf {S}_n$
the sparse paving matroid on
![]() $[n]$
of rank
$[n]$
of rank
![]() $\lfloor \frac {n}{2}\rfloor$
, having the maximal possible number of circuit-hyperplanes, and whose set of bases is lexicographically minimal
Footnote
2
. Then
$\lfloor \frac {n}{2}\rfloor$
, having the maximal possible number of circuit-hyperplanes, and whose set of bases is lexicographically minimal
Footnote
2
. Then
 \begin{equation*}\operatorname {xc}(\mathscr {P}(\mathsf {S}_n)) \in \Omega \left (\frac {2^{n/2}}{n^{5/4} \sqrt {\log (2n)}}\right ).\end{equation*}
\begin{equation*}\operatorname {xc}(\mathscr {P}(\mathsf {S}_n)) \in \Omega \left (\frac {2^{n/2}}{n^{5/4} \sqrt {\log (2n)}}\right ).\end{equation*}
Observe that the explicit determination of the matroid
![]() $\mathsf {S}_n$
is yet another open problem, related to the construction of binary codes with constant weight and Hamming distance
$\mathsf {S}_n$
is yet another open problem, related to the construction of binary codes with constant weight and Hamming distance
![]() $4$
, as well as stable subsets of Johnson graphs. In particular, we point out that it remains an open problem to determine the matroid
$4$
, as well as stable subsets of Johnson graphs. In particular, we point out that it remains an open problem to determine the matroid
![]() $\mathsf {S}_{20}$
– in fact, its number of circuit-hyperplanes seems to be unknown, though it is between
$\mathsf {S}_{20}$
– in fact, its number of circuit-hyperplanes seems to be unknown, though it is between
![]() $13452$
and
$13452$
and
![]() $16652$
(see [Reference Agrell, Vardy and Zeger9, Table I]).
$16652$
(see [Reference Agrell, Vardy and Zeger9, Table I]).
Although we cannot prove this conjecture, at least we can prove that the number of facets of
![]() $\mathscr {P}(\mathsf {S}_n)$
is indeed exponential.
$\mathscr {P}(\mathsf {S}_n)$
is indeed exponential.
Proposition 3.7.
Let
![]() $\mathsf {S}_n$
be the matroid described in the prior statement. The number of facets of
$\mathsf {S}_n$
be the matroid described in the prior statement. The number of facets of
![]() $\mathscr {P}(\mathsf {S}_n)$
satisfies:
$\mathscr {P}(\mathsf {S}_n)$
satisfies:
Proof.
By Corollary 2.10 the number of facets of
![]() $\mathsf {S}_n$
is
$\mathsf {S}_n$
is
![]() $2n+\unicode {x03BB}$
(whenever
$2n+\unicode {x03BB}$
(whenever
![]() $n\gt 4$
) where
$n\gt 4$
) where
![]() $\unicode {x03BB}$
is the number of circuit-hyperplanes of
$\unicode {x03BB}$
is the number of circuit-hyperplanes of
![]() $\mathsf {S}_n$
. As follows from a result of Graham and Sloane in [Reference Graham and Sloane26], the maximal possible value of
$\mathsf {S}_n$
. As follows from a result of Graham and Sloane in [Reference Graham and Sloane26], the maximal possible value of
![]() $\unicode {x03BB}$
is at least
$\unicode {x03BB}$
is at least
![]() $\frac {1}{n}\binom {2n}{n}$
; see for example [Reference Ferroni and Schröter23, Lemma 4.14].
$\frac {1}{n}\binom {2n}{n}$
; see for example [Reference Ferroni and Schröter23, Lemma 4.14].
Remark 3.8.
Even though the number of facets of a matroid polytope can be exponential, for arbitrary
![]() $0/1$
-polytopes in
$0/1$
-polytopes in
![]() $\mathbb {R}^n$
it is known that the number of facets can be larger than
$\mathbb {R}^n$
it is known that the number of facets can be larger than
![]() $\left (\frac {cn}{\log n}\right )^{n/4}$
, via a random construction [Reference Bárány and Pór14].
$\left (\frac {cn}{\log n}\right )^{n/4}$
, via a random construction [Reference Bárány and Pór14].
Funding statement
LF is a member at the Institute for Advanced Study, funded by the Minerva Research Foundation, he was also partially supported by the Swedish Research Council grant 2018-03968. BS is supported by the Swedish Research Council grant 2022-04224.