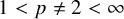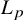1 Introduction
Schur multipliers are linear maps on matrix algebras with a great impact on geometric group theory, operator algebras and functional analysis. Their definition is rather simple on discrete spaces
![]() $S_M(A) = (M(j,k) A_{jk})_{jk}$
. It easily extends to nonatomic
$S_M(A) = (M(j,k) A_{jk})_{jk}$
. It easily extends to nonatomic
![]() $\sigma $
-finite measure spaces
$\sigma $
-finite measure spaces
![]() $(\Omega ,\mu )$
by restricting to operators A in
$(\Omega ,\mu )$
by restricting to operators A in
![]() $L_2(\Omega ,\mu )$
admitting a kernel representation over
$L_2(\Omega ,\mu )$
admitting a kernel representation over
![]() $\Omega \times \Omega $
. Their role in geometric group theory and operator algebras was first analyzed by Haagerup. His pioneering work on free groups [Reference Haagerup20] and the research thereafter on semisimple lattices [Reference de Cannière and Haagerup4, Reference Cowling and Haagerup13] encoded deep geometric properties via approximation properties with Schur multipliers. Other interesting links can be found in [Reference Bennett1, Reference Harcharras22, Reference Pisier37, Reference Pisier39, Reference Pisier41, Reference Pisier and Shlyakhtenko42, Reference Potapov and Sukochev44].
$\Omega \times \Omega $
. Their role in geometric group theory and operator algebras was first analyzed by Haagerup. His pioneering work on free groups [Reference Haagerup20] and the research thereafter on semisimple lattices [Reference de Cannière and Haagerup4, Reference Cowling and Haagerup13] encoded deep geometric properties via approximation properties with Schur multipliers. Other interesting links can be found in [Reference Bennett1, Reference Harcharras22, Reference Pisier37, Reference Pisier39, Reference Pisier41, Reference Pisier and Shlyakhtenko42, Reference Potapov and Sukochev44].
In 2011, stronger rigidity properties of high rank lattices were discovered by studying
![]() $L_p$
-approximations [Reference de Laat and de la Salle27, Reference Lafforgue and de la Salle28]. First, there are no
$L_p$
-approximations [Reference de Laat and de la Salle27, Reference Lafforgue and de la Salle28]. First, there are no
![]() $L_p$
-approximations by means of Fourier or Schur multipliers over
$L_p$
-approximations by means of Fourier or Schur multipliers over
![]() $\mathrm {SL}_n(\mathbf {R})$
for
$\mathrm {SL}_n(\mathbf {R})$
for
![]() $p> 2+ \alpha _n$
, with
$p> 2+ \alpha _n$
, with
![]() $\alpha _n \to 0$
as
$\alpha _n \to 0$
as
![]() $n \to \infty $
. Second, it turns out that this unprecedented pathology leads to a strong form of nonamenability which is potentially useful to distinguish the group von Neumann algebras of
$n \to \infty $
. Second, it turns out that this unprecedented pathology leads to a strong form of nonamenability which is potentially useful to distinguish the group von Neumann algebras of
![]() $\mathrm {PSL}_n(\mathbf {Z})$
for different values of
$\mathrm {PSL}_n(\mathbf {Z})$
for different values of
![]() $n \ge 3$
, the most iconic form of Connes’ rigidity conjecture. This has strongly motivated our recent work [Reference Conde-Alonso, González-Pérez, Parcet and Tablate10, Reference Parcet, Ricard and de la Salle35] with several forms of the Hörmander-Mikhlin theorem. Nevertheless, there is still much to learn about less regular multipliers. A key point in [Reference Lafforgue and de la Salle28] was a careful analysis of Schur multipliers over the n-sphere for symbols of the form
$n \ge 3$
, the most iconic form of Connes’ rigidity conjecture. This has strongly motivated our recent work [Reference Conde-Alonso, González-Pérez, Parcet and Tablate10, Reference Parcet, Ricard and de la Salle35] with several forms of the Hörmander-Mikhlin theorem. Nevertheless, there is still much to learn about less regular multipliers. A key point in [Reference Lafforgue and de la Salle28] was a careful analysis of Schur multipliers over the n-sphere for symbols of the form
![]() $M_\varphi (x,y) = \varphi (\langle x,y \rangle )$
. More precisely, the boundedness of
$M_\varphi (x,y) = \varphi (\langle x,y \rangle )$
. More precisely, the boundedness of
![]() $S_{M_\varphi }$
on the Schatten class
$S_{M_\varphi }$
on the Schatten class
![]() $S_p$
for
$S_p$
for
![]() $p> 2 + \frac {2}{n-1}$
imposes Hölder regularity conditions on
$p> 2 + \frac {2}{n-1}$
imposes Hölder regularity conditions on
![]() $\varphi $
. This article grew from the analysis of the spherical Hilbert transform
$\varphi $
. This article grew from the analysis of the spherical Hilbert transform
Is it
![]() $S_p$
-bounded for some
$S_p$
-bounded for some
![]() $\frac {2n}{n+1} < p \neq 2 < \frac {2n}{n-1}$
? Its
$\frac {2n}{n+1} < p \neq 2 < \frac {2n}{n-1}$
? Its
![]() $S_p$
-boundedness is equivalent to that of
$S_p$
-boundedness is equivalent to that of
![]() $\frac 12 (1+iH_{\mathbf {S}})$
– whose symbol is
$\frac 12 (1+iH_{\mathbf {S}})$
– whose symbol is
![]() $\chi _\Sigma $
with
$\chi _\Sigma $
with
![]() $\Sigma = \{(x,y): \langle x,y\rangle>0\}$
– and it is worth noting the analogy with the ball multiplier problem, which was only known to be unbounded for p outside this range before Fefferman’s celebrated contribution [Reference Fefferman15]. Our main result completely solves this problem:
$\Sigma = \{(x,y): \langle x,y\rangle>0\}$
– and it is worth noting the analogy with the ball multiplier problem, which was only known to be unbounded for p outside this range before Fefferman’s celebrated contribution [Reference Fefferman15]. Our main result completely solves this problem:
![]() $H_{\mathbf {S}}$
is
$H_{\mathbf {S}}$
is
![]() $S_p$
-unbounded unless
$S_p$
-unbounded unless
![]() $n=1$
or
$n=1$
or
![]() $p=2$
. We characterize
$p=2$
. We characterize
![]() $S_p$
-boundedness for a lot more idempotents.
$S_p$
-boundedness for a lot more idempotents.
Let
![]() $M,N$
be two differentiable manifolds with the Lebesgue measure coming from any Riemmanian structure on them. Consider a
$M,N$
be two differentiable manifolds with the Lebesgue measure coming from any Riemmanian structure on them. Consider a
![]() $\mathcal {C}^1$
-domain
$\mathcal {C}^1$
-domain
![]() $\Sigma \subset M \times N$
so that its boundary
$\Sigma \subset M \times N$
so that its boundary
![]() $\partial \Sigma $
is a smooth hypersurface, which is locally represented by level sets of some real-valued
$\partial \Sigma $
is a smooth hypersurface, which is locally represented by level sets of some real-valued
![]() $\mathcal {C}^1$
-functions with nonvanishing gradients. We say that
$\mathcal {C}^1$
-functions with nonvanishing gradients. We say that
![]() $\partial \Sigma $
is transverse at a point
$\partial \Sigma $
is transverse at a point
![]() $(x,y)$
when the tangent space of
$(x,y)$
when the tangent space of
![]() $\partial \Sigma $
at
$\partial \Sigma $
at
![]() $(x,y)$
maps surjectively on each factor
$(x,y)$
maps surjectively on each factor
![]() $T_x M$
and
$T_x M$
and
![]() $T_y N$
. In that case, both sections
$T_y N$
. In that case, both sections
become codimension
![]() $1$
manifolds on some neighbourhood of y and x, respectively.
$1$
manifolds on some neighbourhood of y and x, respectively.
Theorem A. Let
![]() $p \in (1,\infty ) \setminus \{2\}$
and consider a
$p \in (1,\infty ) \setminus \{2\}$
and consider a
![]() $\mathcal {C}^1$
-domain
$\mathcal {C}^1$
-domain
![]() $\Sigma \subset M \times N$
. Then the following statements are equivalent for any transverse point
$\Sigma \subset M \times N$
. Then the following statements are equivalent for any transverse point
![]() $(x_0,y_0) \in \partial \Sigma \hskip -2pt :$
$(x_0,y_0) \in \partial \Sigma \hskip -2pt :$
-
(1)
 $S_p$
-boundedness. The idempotent Schur multiplier
$S_p$
-boundedness. The idempotent Schur multiplier
 $S_\Sigma $
whose symbol equals
$S_\Sigma $
whose symbol equals
 $1$
on
$1$
on
 $\Sigma $
and
$\Sigma $
and
 $0$
elsewhere is bounded on
$0$
elsewhere is bounded on
 $S_p(L_2(U), L_2(V))$
for some pair of neighbourhoods
$S_p(L_2(U), L_2(V))$
for some pair of neighbourhoods
 $U,V$
of
$U,V$
of
 $x_0, y_0$
in
$x_0, y_0$
in
 $M,N$
.
$M,N$
. -
(2) Zero-curvature condition. There are neighbourhoods
 $U,V$
of
$U,V$
of
 $x_0, y_0$
in
$x_0, y_0$
in
 $M,N$
such that the tangent spaces
$M,N$
such that the tangent spaces
 $T_y (\partial \Sigma _{x_1})$
and
$T_y (\partial \Sigma _{x_1})$
and
 $T_y (\partial \Sigma _{x_2})$
coincide for any pair of points
$T_y (\partial \Sigma _{x_2})$
coincide for any pair of points
 $(x_1,y), (x_2,y) \in \partial \Sigma \cap (U \times V)$
.
$(x_1,y), (x_2,y) \in \partial \Sigma \cap (U \times V)$
. -
(3) Triangular truncation representation. There are neighbourhoods
 $U,V$
of the points
$U,V$
of the points
 $x_0, y_0$
in
$x_0, y_0$
in
 $M,N$
and
$M,N$
and
 $\mathcal {C}^1$
-functions
$\mathcal {C}^1$
-functions
 $f_1: U \to \mathbf {R}$
and
$f_1: U \to \mathbf {R}$
and
 $f_2: V \to \mathbf {R}$
, such that
$f_2: V \to \mathbf {R}$
, such that
 $\Sigma \cap (U \times V) = \big \{(x,y) \in U \times V: f_1(x)>f_2(y) \big \}$
.
$\Sigma \cap (U \times V) = \big \{(x,y) \in U \times V: f_1(x)>f_2(y) \big \}$
.
Theorem A characterizes the local geometry of
![]() $S_p$
-bounded idempotent Schur multipliers and vastly amplifies the ball multiplier theorem [Reference Fefferman15]. A first interesting consequence is that this property does not depend on the value of p. It is important to insist here that the characterization is local. If the global aspects are taken into account, the
$S_p$
-bounded idempotent Schur multipliers and vastly amplifies the ball multiplier theorem [Reference Fefferman15]. A first interesting consequence is that this property does not depend on the value of p. It is important to insist here that the characterization is local. If the global aspects are taken into account, the
![]() $S_p$
-boundedness of idempotent Schur multipliers does depend on p: in the discrete setting, whenever
$S_p$
-boundedness of idempotent Schur multipliers does depend on p: in the discrete setting, whenever
![]() $p<q$
with p is an even integer, there is an idempotent Schur multiplier that is
$p<q$
with p is an even integer, there is an idempotent Schur multiplier that is
![]() $S_p$
-bounded but not
$S_p$
-bounded but not
![]() $S_q$
-bounded [Reference Harcharras22]. Remark 2.7 provides other examples where the local theorem fails to be global.
$S_q$
-bounded [Reference Harcharras22]. Remark 2.7 provides other examples where the local theorem fails to be global.
Theorem A is only interesting when M and N have dimension at least
![]() $2$
. When M or N is a discrete space – in other words,
$2$
. When M or N is a discrete space – in other words,
![]() $\dim M = 0$
or
$\dim M = 0$
or
![]() $\dim N = 0$
– it is obvious just by taking
$\dim N = 0$
– it is obvious just by taking
![]() $U=\{x_0\}$
or
$U=\{x_0\}$
or
![]() $V = \{y_0\}$
. Similarly, when
$V = \{y_0\}$
. Similarly, when
![]() $\dim M = 1$
or
$\dim M = 1$
or
![]() $\dim N = 1$
, condition (3) always holds by the implicit function theorem, and the other conditions are also easily seen to always hold. However, in dimension at least
$\dim N = 1$
, condition (3) always holds by the implicit function theorem, and the other conditions are also easily seen to always hold. However, in dimension at least
![]() $2$
, the conditions become restrictive. A simple example of a transverse domain that fails to satisfy (2) or (3) at any boundary point is shown in Figure 1 above.
$2$
, the conditions become restrictive. A simple example of a transverse domain that fails to satisfy (2) or (3) at any boundary point is shown in Figure 1 above.

Figure 1 Failure of (2) for spherical Hilbert transforms
![]() $H_{{\mathbf {S},\delta }}$
. Here
$H_{{\mathbf {S},\delta }}$
. Here
![]() $H_{{\mathbf {S},\delta }} = -i (2S_{\Sigma _\delta } - \mathrm {id})$
with
$H_{{\mathbf {S},\delta }} = -i (2S_{\Sigma _\delta } - \mathrm {id})$
with
![]() $\Sigma _\delta = \big \{(x,y) \in \mathbf {S}^n \times \mathbf {S}^n : \langle x,y \rangle> \delta \big \}$
for
$\Sigma _\delta = \big \{(x,y) \in \mathbf {S}^n \times \mathbf {S}^n : \langle x,y \rangle> \delta \big \}$
for
![]() $n = 2$
.
$n = 2$
.
The implication (3)
![]() $\Rightarrow $
(1) is the easy one. By known techniques, it follows from the classical
$\Rightarrow $
(1) is the easy one. By known techniques, it follows from the classical
![]() $S_p$
-boundedness of the triangular projection
$S_p$
-boundedness of the triangular projection
![]() $(A_{jk}) \mapsto (\chi _{j \geq k} A_{jk})$
with
$(A_{jk}) \mapsto (\chi _{j \geq k} A_{jk})$
with
![]() $j,k \in \mathbf {N}$
, closely related to the
$j,k \in \mathbf {N}$
, closely related to the
![]() $L_p$
-boundedness of the Hilbert transform. On the contrary, the converse implication (1)
$L_p$
-boundedness of the Hilbert transform. On the contrary, the converse implication (1)
![]() $\Rightarrow $
(3) is certainly unexpected. It says that the triangular projection is the only local model for
$\Rightarrow $
(3) is certainly unexpected. It says that the triangular projection is the only local model for
![]() $S_p$
-bounded idempotents. Our proof decomposes in two independent parts. The implication (1)
$S_p$
-bounded idempotents. Our proof decomposes in two independent parts. The implication (1)
![]() $\Rightarrow $
(2) is very much analytical. By well-known Fourier-Schur transference results, Fefferman’s theorem corresponds to the case
$\Rightarrow $
(2) is very much analytical. By well-known Fourier-Schur transference results, Fefferman’s theorem corresponds to the case
![]() $M=N=\mathbf {R}^n$
and domains
$M=N=\mathbf {R}^n$
and domains
![]() $\Sigma = \big \{ (x,y): x-y \in \Omega \big \}$
for a Euclidean
$\Sigma = \big \{ (x,y): x-y \in \Omega \big \}$
for a Euclidean
![]() $\mathcal {C}^1$
-domain
$\mathcal {C}^1$
-domain
![]() $\Omega $
. Transversality trivially holds at every boundary point in this case. In the general case, the main idea (Lemma 2.3) is a new connection between Schur and Fourier multipliers: it gives an
$\Omega $
. Transversality trivially holds at every boundary point in this case. In the general case, the main idea (Lemma 2.3) is a new connection between Schur and Fourier multipliers: it gives an
![]() $L_p$
square-function inequality for half-space multipliers out of the
$L_p$
square-function inequality for half-space multipliers out of the
![]() $S_p$
-boundedness of
$S_p$
-boundedness of
![]() $S_\Sigma $
. This is a noncommutative form of Meyer’s lemma, which derived such a square inequality from
$S_\Sigma $
. This is a noncommutative form of Meyer’s lemma, which derived such a square inequality from
![]() $L_p$
-bounded Fourier multipliers, and which was a key part in the proof of the ball multiplier theorem. However, the implication (2)
$L_p$
-bounded Fourier multipliers, and which was a key part in the proof of the ball multiplier theorem. However, the implication (2)
![]() $\Rightarrow $
(3) is a purely geometric statement about hypersurfaces in product manifolds (Theorem 2.5) to which we failed to find a straightforward proof.
$\Rightarrow $
(3) is a purely geometric statement about hypersurfaces in product manifolds (Theorem 2.5) to which we failed to find a straightforward proof.
It is rather surprising to us that Theorem A holds for Schur multipliers on general manifolds which – contrary to Euclidean spaces, where Fefferman’s result held so far – lack to admit a Fourier transform connection. Also observe that when we take
![]() $M=N=\mathbf {R}^n$
and write
$M=N=\mathbf {R}^n$
and write
for a normal vector to
![]() $\partial \Sigma $
at
$\partial \Sigma $
at
![]() $(x,y)$
, transversality means that both n-dimensional components
$(x,y)$
, transversality means that both n-dimensional components
![]() $\mathbf {n}_1, \mathbf {n}_2$
are nonzero. The zero-curvature condition means that
$\mathbf {n}_1, \mathbf {n}_2$
are nonzero. The zero-curvature condition means that
![]() $\mathbf {n}_2(x_1,y)$
and
$\mathbf {n}_2(x_1,y)$
and
![]() $\mathbf {n}_2(x_2,y)$
are parallel—equivalent forms in terms of
$\mathbf {n}_2(x_2,y)$
are parallel—equivalent forms in terms of
![]() $\mathbf {n}_1(x,y_1)$
and
$\mathbf {n}_1(x,y_1)$
and
![]() $\mathbf {n}_1(x,y_2)$
instead, or simpler formulations for
$\mathbf {n}_1(x,y_2)$
instead, or simpler formulations for
![]() $\mathcal {C}^2$
-domains will be also discussed. In a different direction, a global (nonlocal) characterization of
$\mathcal {C}^2$
-domains will be also discussed. In a different direction, a global (nonlocal) characterization of
![]() $S_p$
-bounded idempotent Schur multipliers also follows for relatively compact fully transverse domains
$S_p$
-bounded idempotent Schur multipliers also follows for relatively compact fully transverse domains
![]() $\Sigma $
.
$\Sigma $
.
Theorem A has profound consequences for Fourier multipliers on Lie group von Neumann algebras. Smooth Fourier multipliers on group algebras were intensively investigated over the last decade [Reference Caspers5, Reference Conde-Alonso, González-Pérez, Parcet and Tablate11, Reference González-Pérez, Junge and Parcet18, Reference Junge, Mei and Parcet24, Reference Junge, Mei and Parcet25, Reference Mei, Ricard and Xu32, Reference Parcet, Ricard and de la Salle35]. The nonsmooth theory concerns a longstanding search to classify idempotent Fourier
![]() $L_p$
-multipliers, but their geometric behavior is very sensitive to the underlying group. Harcharras investigated noncommutative
$L_p$
-multipliers, but their geometric behavior is very sensitive to the underlying group. Harcharras investigated noncommutative
![]() $\Lambda (p)$
-sets in [Reference Harcharras22]. Bożejko and Fendler [Reference Bożejko and Fendler3] studied an analog of Fefferman’s ball multiplier theorem in the free group for
$\Lambda (p)$
-sets in [Reference Harcharras22]. Bożejko and Fendler [Reference Bożejko and Fendler3] studied an analog of Fefferman’s ball multiplier theorem in the free group for
![]() $|1/p-1/2|> 1/6$
. More recently, Mei and Ricard found a large class of free Hilbert transforms in their remarkable work [Reference Mei and Ricard31]. The search for Hilbert transforms on general groups also includes crossed products and groups acting on tree-like structures [Reference González-Pérez, Parcet and Xia19, Reference Parcet and Rogers36].
$|1/p-1/2|> 1/6$
. More recently, Mei and Ricard found a large class of free Hilbert transforms in their remarkable work [Reference Mei and Ricard31]. The search for Hilbert transforms on general groups also includes crossed products and groups acting on tree-like structures [Reference González-Pérez, Parcet and Xia19, Reference Parcet and Rogers36].
In this paper, we shall give a complete characterization of the local boundary behavior for completely bounded idempotent Fourier multipliers on arbitrary Lie groups. We say that a function
![]() ${m: \mathrm {G} \to \mathbf {C}}$
defines locally at
${m: \mathrm {G} \to \mathbf {C}}$
defines locally at
![]() $g_0 \in \mathrm {G}$
a completely bounded Fourier
$g_0 \in \mathrm {G}$
a completely bounded Fourier
![]() $L_p$
-multiplier if there is a function
$L_p$
-multiplier if there is a function
![]() ${\varphi : \mathrm {G} \to \mathbf {C}}$
equal to
${\varphi : \mathrm {G} \to \mathbf {C}}$
equal to
![]() $1$
on a neighbourhood of
$1$
on a neighbourhood of
![]() $g_0$
such that
$g_0$
such that
![]() $\varphi m$
defines (globally) a completely bounded Fourier
$\varphi m$
defines (globally) a completely bounded Fourier
![]() $L_p$
-multiplier. Our result is more easily stated for simply connected groups. We refer to Section 3 for various characterizations of local Fourier multipliers and for the statement of our result below on general Lie groups (Theorem 3.3).
$L_p$
-multiplier. Our result is more easily stated for simply connected groups. We refer to Section 3 for various characterizations of local Fourier multipliers and for the statement of our result below on general Lie groups (Theorem 3.3).
Theorem B. Let
![]() $p \in (1,\infty )\setminus \{2\}$
. Let
$p \in (1,\infty )\setminus \{2\}$
. Let
![]() $\mathrm {G}$
be a simply connected Lie group,
$\mathrm {G}$
be a simply connected Lie group,
![]() $\Omega \subset \mathrm {G}$
a
$\Omega \subset \mathrm {G}$
a
![]() $\mathcal {C}^1$
-domain and
$\mathcal {C}^1$
-domain and
![]() $g_0 \in \partial \Omega $
a point in the boundary of
$g_0 \in \partial \Omega $
a point in the boundary of
![]() $\Omega $
. The following are equivalent:
$\Omega $
. The following are equivalent:
-
(1)
 $\chi _\Omega $
defines locally at
$\chi _\Omega $
defines locally at
 $g_0$
a completely bounded Fourier
$g_0$
a completely bounded Fourier
 $L_p$
-multiplier.
$L_p$
-multiplier. -
(2) There is a smooth action
 $\mathrm {G} \to \mathrm {Diff}(\mathbf {R})$
by diffeomorphisms on the real line, such that
$\mathrm {G} \to \mathrm {Diff}(\mathbf {R})$
by diffeomorphisms on the real line, such that
 $\Omega $
coincides on a neighbourhood of
$\Omega $
coincides on a neighbourhood of
 $g_0$
with
$g_0$
with
 $\{g \in \mathrm {G} \mid g \cdot 0> g_0 \cdot 0\}$
.
$\{g \in \mathrm {G} \mid g \cdot 0> g_0 \cdot 0\}$
.
Alternatively, this means that
![]() $\partial \Omega $
is locally a coset of a codimension
$\partial \Omega $
is locally a coset of a codimension
![]() $1$
subgroup. There are two ingredients in the proof of Theorem B. The first is Theorem A. The second is a general result relating local complete
$1$
subgroup. There are two ingredients in the proof of Theorem B. The first is Theorem A. The second is a general result relating local complete
![]() $L_p$
-boundedness of Fourier and Schur multipliers for arbitrary locally compact groups. Such a result is known to be true globally at the endpoints
$L_p$
-boundedness of Fourier and Schur multipliers for arbitrary locally compact groups. Such a result is known to be true globally at the endpoints
![]() $p=1,\infty $
[Reference Bożejko and Fendler3] or when the group
$p=1,\infty $
[Reference Bożejko and Fendler3] or when the group
![]() $\mathrm {G}$
is amenable [Reference Caspers and de la Salle7, Reference Neuwirth and Ricard34]. The eventuality that it could be true locally is a recent observation [Reference Parcet, Ricard and de la Salle35] for even integers
$\mathrm {G}$
is amenable [Reference Caspers and de la Salle7, Reference Neuwirth and Ricard34]. The eventuality that it could be true locally is a recent observation [Reference Parcet, Ricard and de la Salle35] for even integers
![]() $p \in 2 \mathbf {Z}_+$
and unimodular groups
$p \in 2 \mathbf {Z}_+$
and unimodular groups
![]() $\mathrm {G}$
. In Theorem 3.1 below, we manage to prove it in full generality as a crucial step towards Theorem B.
$\mathrm {G}$
. In Theorem 3.1 below, we manage to prove it in full generality as a crucial step towards Theorem B.
Lie himself classified Lie groups admitting (local) actions by diffeomorphisms on the real line [Reference Lie30]. This classification into three types (translation, affine and projective) gives rise to the following three fundamental examples of a group
![]() $\mathrm {G}$
with a smooth domain
$\mathrm {G}$
with a smooth domain
![]() $\Omega $
:
$\Omega $
:
-
i) The real line
 $\mathrm {G}_1 = \mathbf {R}$
with
$\mathrm {G}_1 = \mathbf {R}$
with
 $\Omega _1 = (0,\infty )$
.
$\Omega _1 = (0,\infty )$
. -
ii) The affine group
 $\mathrm {G}_2 = \operatorname {\mathrm {Aff}}_+(\mathbf {R})$
Footnote 1 and
$\mathrm {G}_2 = \operatorname {\mathrm {Aff}}_+(\mathbf {R})$
Footnote 1 and
 $\Omega _2 = \{ax+b: b> 0\}$
.
$\Omega _2 = \{ax+b: b> 0\}$
. -
iii) The universal covering group
 $\mathrm {G}_3 = \widetilde {\mathrm {PSL}}_2(\mathbf {R})$
Footnote 2 with
$\mathrm {G}_3 = \widetilde {\mathrm {PSL}}_2(\mathbf {R})$
Footnote 2 with
 $\Omega _3 = \{g: \alpha _g(0)> 0\}$
.
$\Omega _3 = \{g: \alpha _g(0)> 0\}$
.
The domains
![]() $\Omega _j$
define global (not just local) completely bounded idempotent Fourier
$\Omega _j$
define global (not just local) completely bounded idempotent Fourier
![]() $L_p$
-multipliers for
$L_p$
-multipliers for
![]() $1<p<\infty $
.
$1<p<\infty $
.
![]() $\Omega _1$
gives the classical Hilbert transform
$\Omega _1$
gives the classical Hilbert transform
![]() $H = -i(2 T_{\chi _{\Omega _1}} - \mathrm {id})$
.
$H = -i(2 T_{\chi _{\Omega _1}} - \mathrm {id})$
.
![]() $L_p$
-boundedness for the domain
$L_p$
-boundedness for the domain
![]() $\Omega _3$
follows from recent Cotlar identities for unimodular groups [Reference González-Pérez, Parcet and Xia19].
$\Omega _3$
follows from recent Cotlar identities for unimodular groups [Reference González-Pérez, Parcet and Xia19].
![]() $\mathrm {G}_2$
is nonunimodular, and
$\mathrm {G}_2$
is nonunimodular, and
![]() $L_p$
-boundedness for
$L_p$
-boundedness for
![]() $\Omega _2$
is properly justified in Example 3.8. The basic models
$\Omega _2$
is properly justified in Example 3.8. The basic models
![]() $H_j = -i(2T_{\chi _{\Omega _j}} - \mathrm {id})$
will be referred to as classical, affine and projective Hilbert transforms. We find very surprising that every other idempotent Fourier multiplier locally comes from a surjective homomorphism on one of these three groups.
$H_j = -i(2T_{\chi _{\Omega _j}} - \mathrm {id})$
will be referred to as classical, affine and projective Hilbert transforms. We find very surprising that every other idempotent Fourier multiplier locally comes from a surjective homomorphism on one of these three groups.
Corollary B1. Conditions (1) and (2) in Theorem B are equivalent to the following
![]() $:$
$:$
-
(3) There is
 $j\in \{1,2,3\}$
and a smooth surjective homomorphism
$j\in \{1,2,3\}$
and a smooth surjective homomorphism
 $f\colon \mathrm {G} \to \mathrm {G}_j$
such that the domain
$f\colon \mathrm {G} \to \mathrm {G}_j$
such that the domain
 $\Omega $
coincides on a neighbourhood of
$\Omega $
coincides on a neighbourhood of
 $g_0$
with
$g_0$
with
 $g_0 f^{-1}(\Omega _j)$
.
$g_0 f^{-1}(\Omega _j)$
.
When
![]() $\mathrm {G}=\mathbf {R}^n$
, a homomorphism as in Corollary B1 above is of the form
$\mathrm {G}=\mathbf {R}^n$
, a homomorphism as in Corollary B1 above is of the form
![]() $\mathbf {R}^n \ni \xi \mapsto c\langle \xi , u \rangle \in \mathbf {R}$
for
$\mathbf {R}^n \ni \xi \mapsto c\langle \xi , u \rangle \in \mathbf {R}$
for
![]() $c \in \mathbf {R}^*$
and
$c \in \mathbf {R}^*$
and
![]() $u \in \mathbf {S}^{n-1}$
. Thus, Corollary B1 recovers that
$u \in \mathbf {S}^{n-1}$
. Thus, Corollary B1 recovers that
![]() $L_p$
-bounded idempotent Fourier multipliers in the Euclidean setting locally correspond (up to translations) to half-space multipliers with symbol
$L_p$
-bounded idempotent Fourier multipliers in the Euclidean setting locally correspond (up to translations) to half-space multipliers with symbol
![]() $m_u(\xi ) = \chi _{\langle \xi ,u \rangle> 0}$
for some
$m_u(\xi ) = \chi _{\langle \xi ,u \rangle> 0}$
for some
![]() $u \in \mathbf {S}^{n-1}$
. This is well understood since Fefferman’s solution to the Ball multiplier problem. Note in passing that these half-space multipliers are directional extensions of the Riesz projection
$u \in \mathbf {S}^{n-1}$
. This is well understood since Fefferman’s solution to the Ball multiplier problem. Note in passing that these half-space multipliers are directional extensions of the Riesz projection
![]() $R = \frac 12 (i H + \mathrm {id})$
. By analogy, we could rephrase Corollary B1 by saying that every Fourier
$R = \frac 12 (i H + \mathrm {id})$
. By analogy, we could rephrase Corollary B1 by saying that every Fourier
![]() $L_p$
-idempotent on an arbitrary Lie group arises as a directional amplification of one of the three fundamental models of Riesz projections above.
$L_p$
-idempotent on an arbitrary Lie group arises as a directional amplification of one of the three fundamental models of Riesz projections above.
Theorem B and Corollary B1 give very satisfactory descriptions of completely bounded Fourier idempotents in arbitrary Lie groups. It is certainly surprising that these multipliers are modeled out of exactly three fundamental examples, the classical Hilbert transform and its affine and projective variants. It also shows that every
![]() $\mathcal {C}^1$
-idempotent is automatically
$\mathcal {C}^1$
-idempotent is automatically
![]() $\mathcal {C}^\infty $
. This rigidity property collides head-on with the much more flexible scenario of Theorem A.
$\mathcal {C}^\infty $
. This rigidity property collides head-on with the much more flexible scenario of Theorem A.
Corollary B2. Let
![]() $p \in (1, \infty ) \setminus \{2\}$
and let
$p \in (1, \infty ) \setminus \{2\}$
and let
![]() $\mathrm {G}$
be a Lie group
$\mathrm {G}$
be a Lie group
![]() $:$
$:$
-
i) If
 $\mathrm {G}$
is simply connected and nilpotent, every cb-
$\mathrm {G}$
is simply connected and nilpotent, every cb-
 $L_p$
-bounded smooth Fourier idempotent is locally of the form
$L_p$
-bounded smooth Fourier idempotent is locally of the form
 $R \circ \varphi $
, for the classical Riesz projection R and some continuous homomorphism
$R \circ \varphi $
, for the classical Riesz projection R and some continuous homomorphism
 $\varphi : \mathrm {G} \to \mathbf {R}$
.
$\varphi : \mathrm {G} \to \mathbf {R}$
. -
ii) If
 $\mathrm {G}$
is a simple Lie group which is not locally isomorphic to
$\mathrm {G}$
is a simple Lie group which is not locally isomorphic to
 $\mathrm {SL}_2(\mathbf {R})$
, then
$\mathrm {SL}_2(\mathbf {R})$
, then
 $\mathrm {G}$
does not carry any smooth Fourier idempotent which is locally completely
$\mathrm {G}$
does not carry any smooth Fourier idempotent which is locally completely
 $L_p$
-bounded on its group von Neumann algebra.
$L_p$
-bounded on its group von Neumann algebra. -
iii) If
 $\mathrm {G}$
is locally isomorphic to
$\mathrm {G}$
is locally isomorphic to
 $\mathrm {SL}_2(\mathbf {R})$
, then
$\mathrm {SL}_2(\mathbf {R})$
, then
 $\mathrm {G}$
carries a unique local Fourier idempotent which is completely
$\mathrm {G}$
carries a unique local Fourier idempotent which is completely
 $L_p$
-bounded on its group algebra
$L_p$
-bounded on its group algebra
 $($
up to left/right translations
$($
up to left/right translations
 $)$
given by
$)$
given by
 $g \mapsto \frac 12 \big ( 1 + \mathrm {sgn} \, \mathrm {Tr} (g e_{12}) \big )$
.
$g \mapsto \frac 12 \big ( 1 + \mathrm {sgn} \, \mathrm {Tr} (g e_{12}) \big )$
.
As an illustration for stratified Lie groups,
![]() $\varphi $
corresponds on the Lie algebra level with the projection onto any 1-dimensional subspace of the first stratum. The second statement spotlights the singular nature of harmonic analysis over simple Lie groups. It also yields an alternative way to justify that the spherical Hilbert transform
$\varphi $
corresponds on the Lie algebra level with the projection onto any 1-dimensional subspace of the first stratum. The second statement spotlights the singular nature of harmonic analysis over simple Lie groups. It also yields an alternative way to justify that the spherical Hilbert transform
![]() $H_{\mathbf {S}}$
is not
$H_{\mathbf {S}}$
is not
![]() $L_p$
-bounded for any
$L_p$
-bounded for any
![]() $p \neq 2$
. Finally, as we shall justify, the third statement gives a straightforward solution (in the negative) to Problem A in [Reference González-Pérez, Parcet and Xia19]. We refer to [Reference Pisier38, Reference Pisier40] for the operator space background necessary for this paper.
$p \neq 2$
. Finally, as we shall justify, the third statement gives a straightforward solution (in the negative) to Problem A in [Reference González-Pérez, Parcet and Xia19]. We refer to [Reference Pisier38, Reference Pisier40] for the operator space background necessary for this paper.
The plan of the paper is as follows. Section 2 is devoted to idempotent Schur multipliers. It contains the proof of Theorem A and several discussions, including our analysis of the spherical Hilbert transform. Section 3 is devoted to Fourier multipliers. It contains the proof of Theorem B and its corollaries. The proof relies on a result of independent interest on the local transference between Fourier and Schur multipliers for arbitrary locally compact groups, Theorem 3.1.
2 Idempotent Schur multipliers
In this section, we give a complete proof of Theorem A. We begin by recalling some particularly flexible changes of variables for Schur symbols, which preserve the
![]() $S_p$
-norm of the corresponding Schur multipliers on nonatomic spaces. Then, we prove the implications (1)
$S_p$
-norm of the corresponding Schur multipliers on nonatomic spaces. Then, we prove the implications (1)
![]() $\Rightarrow $
(2)
$\Rightarrow $
(2)
![]() $\Rightarrow $
(3)
$\Rightarrow $
(3)
![]() $\Rightarrow $
(1) in Theorem A separately. We shall finish with some comments and applications to spherical Hilbert transforms.
$\Rightarrow $
(1) in Theorem A separately. We shall finish with some comments and applications to spherical Hilbert transforms.
2.1 Schur multipliers
Let
![]() $(X,\mu )$
and
$(X,\mu )$
and
![]() $(Y,\nu )$
be
$(Y,\nu )$
be
![]() $\sigma $
-finite measure spaces. Given
$\sigma $
-finite measure spaces. Given
![]() $1\leq p<\infty $
, let
$1\leq p<\infty $
, let
![]() $S_p(L_2(Y),L_2(X))$
be the space all of bounded linear operators
$S_p(L_2(Y),L_2(X))$
be the space all of bounded linear operators
![]() $T: L_2(Y) \to L_2(X)$
with
$T: L_2(Y) \to L_2(X)$
with
![]() $\operatorname {\mathrm {Tr}}|T|^p <\infty $
, which is a Banach space for the norm below
$\operatorname {\mathrm {Tr}}|T|^p <\infty $
, which is a Banach space for the norm below
When
![]() $p=2$
, the Schatten class
$p=2$
, the Schatten class
![]() $S_2(L_2(Y),L_2(X))$
is the space of Hilbert-Schmidt operators
$S_2(L_2(Y),L_2(X))$
is the space of Hilbert-Schmidt operators
![]() $L_2(Y) \to L_2(X)$
. It coincides with
$L_2(Y) \to L_2(X)$
. It coincides with
![]() $L_2(X\times Y)$
, regarding any
$L_2(X\times Y)$
, regarding any
![]() $L_2$
-function
$L_2$
-function
![]() $(x,y) \mapsto K(x,y)$
as the kernel of the corresponding Hilbert-Schmidt operator
$(x,y) \mapsto K(x,y)$
as the kernel of the corresponding Hilbert-Schmidt operator
Given a bounded measurable function
![]() $m \colon X\times Y\to \mathbf {C}$
, the Schur
$m \colon X\times Y\to \mathbf {C}$
, the Schur
![]() $S_p$
-multiplier with symbol m is defined (when it exists) as the unique bounded linear map
$S_p$
-multiplier with symbol m is defined (when it exists) as the unique bounded linear map
![]() $S_m$
on
$S_m$
on
![]() $S_p(L_2(Y),L_2(X))$
which assigns
$S_p(L_2(Y),L_2(X))$
which assigns
![]() $T_K = ( K(x,y) )_{x\in X, y \in Y} \in S_2 \cap S_p$
to
$T_K = ( K(x,y) )_{x\in X, y \in Y} \in S_2 \cap S_p$
to
![]() $( m(x,y) K(x,y) )_{x \in X, y \in XY} = S_m (T_K)$
. We shall write
$( m(x,y) K(x,y) )_{x \in X, y \in XY} = S_m (T_K)$
. We shall write
![]() $\left \|m\right \|_{MS_p}$
for its norm, with the convention
$\left \|m\right \|_{MS_p}$
for its norm, with the convention
![]() $\left \|m\right \|_{MS_p}=\infty $
if
$\left \|m\right \|_{MS_p}=\infty $
if
![]() $S_m$
does not exist. By definition, if it exists,
$S_m$
does not exist. By definition, if it exists,
![]() $S_m$
is unchanged when m is modified on a measure
$S_m$
is unchanged when m is modified on a measure
![]() $0$
subset, so we can and will often consider
$0$
subset, so we can and will often consider
![]() $S_m$
for
$S_m$
for
![]() $m \in L_\infty (X\times Y)$
.
$m \in L_\infty (X\times Y)$
.
The following general fact will be crucial in our proof of Theorem A. It evidences a much greater flexibility of Schur multipliers compared to Fourier multipliers. The proof follows from [Reference Lafforgue and de la Salle28], we include the argument below.
Lemma 2.1. Let
![]() $(X,\mu ),(X',\mu '),(Y,\nu ),(Y',\nu ')$
be atomless
$(X,\mu ),(X',\mu '),(Y,\nu ),(Y',\nu ')$
be atomless
![]() $\sigma $
-finite measure spaces and
$\sigma $
-finite measure spaces and
![]() $f\colon X \to X'$
and
$f\colon X \to X'$
and
![]() $g\colon Y \to Y'$
be measurable maps. Assume the pushforward measures
$g\colon Y \to Y'$
be measurable maps. Assume the pushforward measures
![]() $f_* \mu $
and
$f_* \mu $
and
![]() $g_* \nu $
are absolutely continuous with respect to the measures
$g_* \nu $
are absolutely continuous with respect to the measures
![]() $\mu '$
and
$\mu '$
and
![]() $\nu '$
, respectively. Then, for every
$\nu '$
, respectively. Then, for every
![]() $m \in L_\infty (X' \times Y')$
,
$m \in L_\infty (X' \times Y')$
,
The absolute continuity of
![]() $f_*\mu $
and
$f_*\mu $
and
![]() $g_* \nu $
is necessary. Indeed, otherwise there would exist a bounded measurable function
$g_* \nu $
is necessary. Indeed, otherwise there would exist a bounded measurable function
![]() $m\colon X'\times Y'\to \mathbf {C}$
with
$m\colon X'\times Y'\to \mathbf {C}$
with
![]() $m=0 \mu '\otimes \nu '$
-almost everywhere but
$m=0 \mu '\otimes \nu '$
-almost everywhere but
![]() $\widetilde {m}:(x,y)\mapsto m(f(x),g(y))$
does not vanish almost
$\widetilde {m}:(x,y)\mapsto m(f(x),g(y))$
does not vanish almost
![]() $\mu \otimes \nu $
-almost everywhere. And in particular,
$\mu \otimes \nu $
-almost everywhere. And in particular,
Proof. The inequality
follows directly from [Reference Lafforgue and de la Salle28, Lemma 1.9] and the absolute continuity assumption. So our goal will be to prove the following equality:
To lighten the notation, let us assume that
![]() $(X,\mu )=(Y,\nu )$
,
$(X,\mu )=(Y,\nu )$
,
![]() $(X',\mu ')=(Y',\nu ')$
and
$(X',\mu ')=(Y',\nu ')$
and
![]() $f=g$
. Let
$f=g$
. Let
![]() $\mathcal B, \mathcal B'$
be the underlying
$\mathcal B, \mathcal B'$
be the underlying
![]() $\sigma $
-algebras, and consider
$\sigma $
-algebras, and consider
![]() $\mathcal A:=f^{-1}(\mathcal B')$
. Then f allows to identify
$\mathcal A:=f^{-1}(\mathcal B')$
. Then f allows to identify
![]() $L_2(X',\mathcal B',f_*\mu )$
with
$L_2(X',\mathcal B',f_*\mu )$
with
![]() $L_2(X,\mathcal A,\mu )$
. In particular,
$L_2(X,\mathcal A,\mu )$
. In particular,
and similarly for the cb-norm. However, [Reference Lafforgue and de la Salle28, Lemma 1.13] implies that the cb norms of
![]() $m \circ (f\times f)$
on
$m \circ (f\times f)$
on
![]() $S_p(L_2(\mathcal A,\mu ))$
and
$S_p(L_2(\mathcal A,\mu ))$
and
![]() $S_p(L_2(\mathcal B,\mu ))$
coincide, so we deduce
$S_p(L_2(\mathcal B,\mu ))$
coincide, so we deduce
Then [Reference Lafforgue and de la Salle28, Theorem 1.18] allows us to conclude. Indeed, our assumptions that
![]() $\mu $
and
$\mu $
and
![]() $\mu '$
have no atoms imply that both cb-norms are equal to their norms.
$\mu '$
have no atoms imply that both cb-norms are equal to their norms.
2.2 Proof of Theorem A: Boundedness implies zero-curvature
In this paragraph, we prove (1)
![]() $\Rightarrow $
(2) from the statement of Theorem A. The proof of this implication follows the same path as in Fefferman’s solution of the ball multiplier theorem [Reference Fefferman15]. The first step in his argument is a reduction due to Yves Meyer [Reference Fefferman15, Lemma 1] from the ball multiplier to square function estimates for half-space multipliers. Given a nonzero vector
$\Rightarrow $
(2) from the statement of Theorem A. The proof of this implication follows the same path as in Fefferman’s solution of the ball multiplier theorem [Reference Fefferman15]. The first step in his argument is a reduction due to Yves Meyer [Reference Fefferman15, Lemma 1] from the ball multiplier to square function estimates for half-space multipliers. Given a nonzero vector
![]() $u \in \mathbf {R}^n$
, let
$u \in \mathbf {R}^n$
, let
![]() $H_u$
denote the corresponding u-directional half-space multiplier
$H_u$
denote the corresponding u-directional half-space multiplier
Lemma 2.2 (Meyer).
Assume that the ball multiplier in
![]() $\mathbf {R}^2$
is
$\mathbf {R}^2$
is
![]() $L_p$
-bounded with norm
$L_p$
-bounded with norm
![]() $\leq C$
. For every integer N, every sequence of unit vectors
$\leq C$
. For every integer N, every sequence of unit vectors
![]() $u_1, u_e, \ldots , u_N \in \mathbf {R}^2$
and functions
$u_1, u_e, \ldots , u_N \in \mathbf {R}^2$
and functions
![]() $f_1, f_2, \ldots , f_N \in L_p(\mathbf {R}^2)$
, the following inequality holds
$f_1, f_2, \ldots , f_N \in L_p(\mathbf {R}^2)$
, the following inequality holds
![]() $\hskip 1pt :$
$\hskip 1pt :$
 $$ \begin{align} \Big\| \Big( \sum_{j=1}^N \big| H_{u_j}(f_j) \big|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^2)} \leq C \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^2)}. \end{align} $$
$$ \begin{align} \Big\| \Big( \sum_{j=1}^N \big| H_{u_j}(f_j) \big|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^2)} \leq C \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^2)}. \end{align} $$
The second step in the argument in [Reference Fefferman15] is the proof that (2.1) does not hold if
![]() $p\geq 2$
. The argument relies on Besicovitch’s construction for the Kakeya needle problem. The key new idea we introduce is a form of Meyer’s Lemma 2.2 that is valid for Schur multipliers. It shows that, under the assumption that the indicator function of a domain
$p\geq 2$
. The argument relies on Besicovitch’s construction for the Kakeya needle problem. The key new idea we introduce is a form of Meyer’s Lemma 2.2 that is valid for Schur multipliers. It shows that, under the assumption that the indicator function of a domain
![]() $\Sigma $
defines an
$\Sigma $
defines an
![]() $S_p$
-bounded Schur multiplier with norm
$S_p$
-bounded Schur multiplier with norm
![]() $\leq C$
, the square function estimate (2.1) will hold whenever
$\leq C$
, the square function estimate (2.1) will hold whenever
![]() $u_1,\dots ,u_N$
are normal vectors to
$u_1,\dots ,u_N$
are normal vectors to
![]() $\partial \Sigma _{x_j}$
at a given point y. To make this precise, we introduce some notation: if
$\partial \Sigma _{x_j}$
at a given point y. To make this precise, we introduce some notation: if
![]() $\Sigma \subset \mathbf {R}^n$
is a
$\Sigma \subset \mathbf {R}^n$
is a
![]() $\mathcal {C}^1$
-domain and
$\mathcal {C}^1$
-domain and
![]() $z \in \partial \Sigma $
, let
$z \in \partial \Sigma $
, let
![]() $\mathbf {n}(z) = (\mathbf {n}_1(z),\mathbf {n}_2(z)) \in \mathbf {R}^n \oplus \mathbf {R}^n$
be a normal to
$\mathbf {n}(z) = (\mathbf {n}_1(z),\mathbf {n}_2(z)) \in \mathbf {R}^n \oplus \mathbf {R}^n$
be a normal to
![]() $\partial \Sigma $
at z pointing away from
$\partial \Sigma $
at z pointing away from
![]() $\Sigma $
.
$\Sigma $
.
Lemma 2.3. Let
![]() $U,V \subset \mathbf {R}^n$
be open subsets and
$U,V \subset \mathbf {R}^n$
be open subsets and
![]() $\Sigma \subset U \times V$
a
$\Sigma \subset U \times V$
a
![]() $\mathcal {C}^1$
-domain. Assume that the Schur multiplier
$\mathcal {C}^1$
-domain. Assume that the Schur multiplier
![]() $S_\Sigma $
whose symbol is the characteristic function of
$S_\Sigma $
whose symbol is the characteristic function of
![]() $\Sigma $
is bounded on
$\Sigma $
is bounded on
![]() $S_p(L_2(U),L_2(V))$
with norm C. Let
$S_p(L_2(U),L_2(V))$
with norm C. Let
![]() $x_1, x_2, \ldots , x_N \in U$
and
$x_1, x_2, \ldots , x_N \in U$
and
![]() $y \in V$
such that
$y \in V$
such that
![]() $z_j = (x_j,y)$
is a transverse point in the boundary
$z_j = (x_j,y)$
is a transverse point in the boundary
![]() $\partial \Sigma $
for every
$\partial \Sigma $
for every
![]() $j=1,2,\ldots ,N$
. Define
$j=1,2,\ldots ,N$
. Define
![]() $u_j = \mathbf {n}_2(z_j)$
and consider functions
$u_j = \mathbf {n}_2(z_j)$
and consider functions
![]() $f_1, f_2, \ldots , f_N \in L_p(\mathbf {R}^n)$
. Then, we have
$f_1, f_2, \ldots , f_N \in L_p(\mathbf {R}^n)$
. Then, we have
 $$\begin{align*}\Big\| \Big( \sum_{j=1}^N \big| H_{u_j}(f_j) \big|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} \leq C \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)}. \end{align*}$$
$$\begin{align*}\Big\| \Big( \sum_{j=1}^N \big| H_{u_j}(f_j) \big|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} \leq C \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)}. \end{align*}$$
Proof. Given
![]() $u \in \mathbf {R}^n \setminus \{0\}$
, define
$u \in \mathbf {R}^n \setminus \{0\}$
, define
 $$\begin{align*}m_u(\xi,\eta) = \chi_{\langle \xi-\eta,u\rangle>0} = \begin{cases} 1 & \textrm{if }\langle \xi-\eta,u\rangle >0\\ 0 & \textrm{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}m_u(\xi,\eta) = \chi_{\langle \xi-\eta,u\rangle>0} = \begin{cases} 1 & \textrm{if }\langle \xi-\eta,u\rangle >0\\ 0 & \textrm{otherwise.} \end{cases} \end{align*}$$
Then, the proof relies on the following two claims:
-
(A) Let
 $(x,y)$
be a transverse point in the boundary of
$(x,y)$
be a transverse point in the boundary of
 $\partial \Sigma $
and let
$\partial \Sigma $
and let
 $T \in \mathrm {GL}_n(\mathbf {R})$
be such that
$T \in \mathrm {GL}_n(\mathbf {R})$
be such that
 $T^* \mathbf {n}_1(x,y) = - \mathbf {n}_2(x,y)$
. Then, the following identity holds for almost every
$T^* \mathbf {n}_1(x,y) = - \mathbf {n}_2(x,y)$
. Then, the following identity holds for almost every
 $\xi ,\eta \in \mathbf {R}^n$
:
$\xi ,\eta \in \mathbf {R}^n$
:  $$\begin{align*}\lim_{\varepsilon\to 0^+} \chi_\Sigma \big( x+\varepsilon T\xi, y+\varepsilon \eta \big) = m_{\mathbf{n}_2(x,y)}(\xi,\eta).\end{align*}$$
$$\begin{align*}\lim_{\varepsilon\to 0^+} \chi_\Sigma \big( x+\varepsilon T\xi, y+\varepsilon \eta \big) = m_{\mathbf{n}_2(x,y)}(\xi,\eta).\end{align*}$$
-
(B) Let
 $u_j$
be as in the statement. Then the Schur multiplier is bounded on
$u_j$
be as in the statement. Then the Schur multiplier is bounded on $$\begin{align*}M:\big( (\xi,j),\eta \big) \in \big( \mathbf{R}^n \times\{1,\dots,N\} \big) \times \mathbf{R}^n \mapsto m_{u_j}(\xi,\eta)\end{align*}$$
$$\begin{align*}M:\big( (\xi,j),\eta \big) \in \big( \mathbf{R}^n \times\{1,\dots,N\} \big) \times \mathbf{R}^n \mapsto m_{u_j}(\xi,\eta)\end{align*}$$
 $S_p(L_2(\mathbf {R}^n),L_2(\mathbf {R}^n \times \{1,2,\ldots ,N\}))$
with norm
$S_p(L_2(\mathbf {R}^n),L_2(\mathbf {R}^n \times \{1,2,\ldots ,N\}))$
with norm
 $\le C$
.
$\le C$
.
Assuming the validity of the above claims, we may now conclude the proof using standard transference ideas that go back at least to the work of Bożejko and Fendler [Reference Bożejko and Fendler2]. Consider
![]() $f_1,f_2,\dots ,f_N \in L_p(\mathbf {R}^n)$
. If
$f_1,f_2,\dots ,f_N \in L_p(\mathbf {R}^n)$
. If
![]() $e_{j,1}$
denotes the standard elementary matrices, if
$e_{j,1}$
denotes the standard elementary matrices, if
![]() $C=\sum _{j=1}^N c_j e_{j,1}$
, we have
$C=\sum _{j=1}^N c_j e_{j,1}$
, we have
![]() $|C|^p=(C^*C)^{\frac p 2} = (\sum _j |c_j|^2)^{\frac p 2} e_{1,1}$
. Taking
$|C|^p=(C^*C)^{\frac p 2} = (\sum _j |c_j|^2)^{\frac p 2} e_{1,1}$
. Taking
![]() $c_j=f_j(x)$
and integrating with respect to x, we get
$c_j=f_j(x)$
and integrating with respect to x, we get
 $$\begin{align*}\Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} = \Big\| \sum_{j=1}^N f_j \otimes e_{j,1} \Big\|_{L_p(\mathbf{R}^n;S_p)}.\end{align*}$$
$$\begin{align*}\Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} = \Big\| \sum_{j=1}^N f_j \otimes e_{j,1} \Big\|_{L_p(\mathbf{R}^n;S_p)}.\end{align*}$$
We know from [Reference Caspers and de la Salle7, Theorem 5.2] that there is an ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\mathbf {N}$
and a completely isometric map
$\mathbf {N}$
and a completely isometric map
that intertwines Fourier and Schur multipliers. The notation
![]() $\prod _{\mathcal {U}} S_p(L_2(\mathbf {R}^n))$
stands for the Banach space ultraproduct, that is the quotient of
$\prod _{\mathcal {U}} S_p(L_2(\mathbf {R}^n))$
stands for the Banach space ultraproduct, that is the quotient of
 $$\begin{align*}\prod_{\alpha \in \mathbf{N}} S_p(L_2(\mathbf{R}^n)):=\Big\{(A_\alpha)_{\alpha \in \mathbf{N}}\mid A_\alpha \in S_p(L_2(\mathbf{R}^n)), \sup_\alpha \|A_\alpha\|_p<\infty\Big\}\end{align*}$$
$$\begin{align*}\prod_{\alpha \in \mathbf{N}} S_p(L_2(\mathbf{R}^n)):=\Big\{(A_\alpha)_{\alpha \in \mathbf{N}}\mid A_\alpha \in S_p(L_2(\mathbf{R}^n)), \sup_\alpha \|A_\alpha\|_p<\infty\Big\}\end{align*}$$
by its closed subspace
![]() $\{(A_\alpha )_\alpha \mid \lim _{\alpha \to \mathcal {U}} \|A_\alpha \|_p=0\}$
. Pick a representative
$\{(A_\alpha )_\alpha \mid \lim _{\alpha \to \mathcal {U}} \|A_\alpha \|_p=0\}$
. Pick a representative
![]() $(A_{j,\alpha })_{\alpha \in \mathbf {N}}$
of
$(A_{j,\alpha })_{\alpha \in \mathbf {N}}$
of
![]() $j_p(f_j)$
. This gives that
$j_p(f_j)$
. This gives that
![]() $(S_{m_u}(A_{j,\alpha }))_{\alpha \in \mathbf {N}}$
is a representative of
$(S_{m_u}(A_{j,\alpha }))_{\alpha \in \mathbf {N}}$
is a representative of
![]() $j_p(H_u(f_j))$
for every
$j_p(H_u(f_j))$
for every
![]() $u \in \mathbf {R}^n$
. That
$u \in \mathbf {R}^n$
. That
![]() $j_p$
is a complete isometry gives
$j_p$
is a complete isometry gives
 $$ \begin{align} \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} = \lim_{\alpha \to \mathcal{U}} \Big\| \sum_{j=1}^N A_{j,\alpha} \otimes e_{j,1} \Big\|_{S_p}, \end{align} $$
$$ \begin{align} \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} = \lim_{\alpha \to \mathcal{U}} \Big\| \sum_{j=1}^N A_{j,\alpha} \otimes e_{j,1} \Big\|_{S_p}, \end{align} $$
and applying it to
![]() $H_{u_j}(f_j)$
instead of
$H_{u_j}(f_j)$
instead of
![]() $f_j$
, we obtain
$f_j$
, we obtain
 $$\begin{align*}\Big\| \Big( \sum_{j=1}^N |H_{u_j}(f_j)|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} = \lim_{\alpha \to \mathcal{U}} \Big\| \sum_{j=1}^N S_{m_{u_j}} (A_{j,\alpha}) \otimes e_{j,1} \Big\|_{S_p}.\end{align*}$$
$$\begin{align*}\Big\| \Big( \sum_{j=1}^N |H_{u_j}(f_j)|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} = \lim_{\alpha \to \mathcal{U}} \Big\| \sum_{j=1}^N S_{m_{u_j}} (A_{j,\alpha}) \otimes e_{j,1} \Big\|_{S_p}.\end{align*}$$
In the preceding equality and in what follows, if
![]() $A_1,\dots ,A_N \in S_p(L_2(\mathbf {R}^n))$
, we see the sum
$A_1,\dots ,A_N \in S_p(L_2(\mathbf {R}^n))$
, we see the sum
![]() $\sum _{j=1}^N A_j \otimes e_{j,1}$
as the element of
$\sum _{j=1}^N A_j \otimes e_{j,1}$
as the element of
![]() $S_p(L_2(\mathbf {R}^n),L_2(\mathbf {R}^n \times \{1,2,\ldots ,N\}))$
mapping
$S_p(L_2(\mathbf {R}^n),L_2(\mathbf {R}^n \times \{1,2,\ldots ,N\}))$
mapping
![]() $g \in L_2(\mathbf {R}^n)$
to the function
$g \in L_2(\mathbf {R}^n)$
to the function
![]() $(\xi ,j) \in \mathbf {R}^n \times \{1,2,\ldots ,N\} \mapsto (A_jg)(\xi )$
. In the particular case when
$(\xi ,j) \in \mathbf {R}^n \times \{1,2,\ldots ,N\} \mapsto (A_jg)(\xi )$
. In the particular case when
![]() $A_j \in S_p \cap S_2$
has kernel
$A_j \in S_p \cap S_2$
has kernel
![]() $K_j \in L_2(\mathbf {R}^n \times \mathbf {R}^n)$
,
$K_j \in L_2(\mathbf {R}^n \times \mathbf {R}^n)$
,
![]() $\sum _{j=1}^N A_j \otimes e_{j,1}$
maps g to the function
$\sum _{j=1}^N A_j \otimes e_{j,1}$
maps g to the function
![]() $(\xi ,j)\mapsto \int K_j(\xi ,\eta ) g(\eta ) d\eta $
, so it is the Hilbert-Schmidt operator with kernel
$(\xi ,j)\mapsto \int K_j(\xi ,\eta ) g(\eta ) d\eta $
, so it is the Hilbert-Schmidt operator with kernel
![]() $((\xi ,j),\eta )\mapsto K_j(\xi ,\eta )$
. Similarly,
$((\xi ,j),\eta )\mapsto K_j(\xi ,\eta )$
. Similarly,
![]() $\sum _{j=1}^N S_{m_j}(A_j)\otimes e_{j,1}$
is the Hilbert-Schmidt operators with kernel
$\sum _{j=1}^N S_{m_j}(A_j)\otimes e_{j,1}$
is the Hilbert-Schmidt operators with kernel
![]() $((\xi ,j),\eta )\mapsto m_j(\xi ,\eta ) K_j(\xi ,\eta )$
. Therefore, we have
$((\xi ,j),\eta )\mapsto m_j(\xi ,\eta ) K_j(\xi ,\eta )$
. Therefore, we have
 $$ \begin{align} S_M\Big(\sum_{j=1}^N A_j \otimes e_{j,1}\Big) = \sum_{j=1}^N S_{m_j}(A_j)\otimes e_{j,1}, \end{align} $$
$$ \begin{align} S_M\Big(\sum_{j=1}^N A_j \otimes e_{j,1}\Big) = \sum_{j=1}^N S_{m_j}(A_j)\otimes e_{j,1}, \end{align} $$
where
![]() $S_M$
is the Schur multiplier appearing in claim (B). Claim (B) therefore implies that (2.3) holds for every
$S_M$
is the Schur multiplier appearing in claim (B). Claim (B) therefore implies that (2.3) holds for every
![]() $A_1,\dots ,A_N \in S_p(L_2(\mathbf {R}^n))$
and that the
$A_1,\dots ,A_N \in S_p(L_2(\mathbf {R}^n))$
and that the
![]() $S_p$
-norm of (2.3) is
$S_p$
-norm of (2.3) is
![]() $\leq C\|\sum _{j=1}^N A_j \otimes e_{j,1}\|_p$
.
$\leq C\|\sum _{j=1}^N A_j \otimes e_{j,1}\|_p$
.
Let us apply this with
![]() $A_j=A_{j,\alpha }$
. According to claim (2.2), we get
$A_j=A_{j,\alpha }$
. According to claim (2.2), we get
 $$ \begin{align*}\Big\| \Big( \sum_{j=1}^N |H_{u_j}(f_j)|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} & \leq C \lim_{\alpha \to \mathcal{U}} \Big\| \sum_{j=1}^N A_{j,\alpha} \otimes e_{j,1} \Big\|_{S_p}\\ &= C \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)}. \end{align*} $$
$$ \begin{align*}\Big\| \Big( \sum_{j=1}^N |H_{u_j}(f_j)|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)} & \leq C \lim_{\alpha \to \mathcal{U}} \Big\| \sum_{j=1}^N A_{j,\alpha} \otimes e_{j,1} \Big\|_{S_p}\\ &= C \Big\| \Big( \sum_{j=1}^N |f_j|^2 \Big)^{\frac{1}{2}} \Big\|_{L_p(\mathbf{R}^n)}. \end{align*} $$
Thus, the assertion is a consequence of claim (B), for which we need to justify claim (A) first. To do so, we can assume that
![]() $\Sigma = f^{-1}(-\infty ,0)$
for a
$\Sigma = f^{-1}(-\infty ,0)$
for a
![]() $\mathcal {C}^1$
-submersion
$\mathcal {C}^1$
-submersion
![]() $f \colon U \times V \to \mathbf {R}$
. Then
$f \colon U \times V \to \mathbf {R}$
. Then
![]() $\nabla f(x,y)= (\nabla _x f(x,y),\nabla _y f(x,y))$
is a normal vector to the boundary
$\nabla f(x,y)= (\nabla _x f(x,y),\nabla _y f(x,y))$
is a normal vector to the boundary
![]() $\partial \Sigma = f^{-1}(0)$
at every
$\partial \Sigma = f^{-1}(0)$
at every
![]() $(x,y) \in \partial \Sigma $
, pointing away from
$(x,y) \in \partial \Sigma $
, pointing away from
![]() $\Sigma $
. Thus, replacing f by a positive multiple, we can assume that its gradient is
$\Sigma $
. Thus, replacing f by a positive multiple, we can assume that its gradient is
![]() $(\mathbf {n}_1(x,y),\mathbf {n}_2(x,y))$
. Then, the Taylor expansion of f gives
$(\mathbf {n}_1(x,y),\mathbf {n}_2(x,y))$
. Then, the Taylor expansion of f gives
 $$ \begin{align*} f \big( x+\varepsilon T \xi, y+\varepsilon \eta \big) & = \varepsilon \big\langle \mathbf{n}_1(x,y), T\xi \big\rangle + \varepsilon \big\langle \mathbf{n}_2(x,y), \eta \big\rangle + o(\varepsilon) \\ & = \varepsilon \big\langle \mathbf{n}_2(x,y), \eta - \xi \big\rangle + o(\varepsilon). \end{align*} $$
$$ \begin{align*} f \big( x+\varepsilon T \xi, y+\varepsilon \eta \big) & = \varepsilon \big\langle \mathbf{n}_1(x,y), T\xi \big\rangle + \varepsilon \big\langle \mathbf{n}_2(x,y), \eta \big\rangle + o(\varepsilon) \\ & = \varepsilon \big\langle \mathbf{n}_2(x,y), \eta - \xi \big\rangle + o(\varepsilon). \end{align*} $$
Therefore, if
![]() $\eta - \xi $
is not orthogonal to
$\eta - \xi $
is not orthogonal to
![]() $\mathbf {n}_2(x,y)$
(a condition that holds for almost every
$\mathbf {n}_2(x,y)$
(a condition that holds for almost every
![]() $\xi $
and
$\xi $
and
![]() $\eta $
), we have
$\eta $
), we have
![]() $\chi _\Sigma (x+\varepsilon T\xi , y+\varepsilon \eta ) =m_{\mathbf {n}_2(x,y)}(\xi ,\eta )$
for every
$\chi _\Sigma (x+\varepsilon T\xi , y+\varepsilon \eta ) =m_{\mathbf {n}_2(x,y)}(\xi ,\eta )$
for every
![]() $\varepsilon>0$
small enough. This proves claim (A).
$\varepsilon>0$
small enough. This proves claim (A).
To prove claim (B) we apply (A). More precisely, let
![]() $T_j \in \mathrm {GL}_n(\mathbf {R})$
be such that
$T_j \in \mathrm {GL}_n(\mathbf {R})$
be such that
![]() $T_j^* \mathbf {n}_1(x_j,y) = - \mathbf {n}_2(x_j,y) = - u_j$
for every
$T_j^* \mathbf {n}_1(x_j,y) = - \mathbf {n}_2(x_j,y) = - u_j$
for every
![]() $j = 1,2,\ldots ,N$
. The existence of these maps is clear, because by the transversality assumption, both
$j = 1,2,\ldots ,N$
. The existence of these maps is clear, because by the transversality assumption, both
![]() $\mathbf {n}_1(x_j,y)$
and
$\mathbf {n}_1(x_j,y)$
and
![]() $\mathbf {n}_2(x_j,y)$
are nonzero vectors in
$\mathbf {n}_2(x_j,y)$
are nonzero vectors in
![]() $\mathbf {R}^n$
and
$\mathbf {R}^n$
and
![]() $\mathrm {GL}_n(\mathbf {R})$
acts transitively on them. By Lemma 2.1, the Schur multiplier with symbol
$\mathrm {GL}_n(\mathbf {R})$
acts transitively on them. By Lemma 2.1, the Schur multiplier with symbol
is bounded with norm
![]() $\leq C$
for every
$\leq C$
for every
![]() $\varepsilon>0$
. Taking
$\varepsilon>0$
. Taking
![]() $\varepsilon \to 0^+$
, we obtain that the almost everywhere limit of
$\varepsilon \to 0^+$
, we obtain that the almost everywhere limit of
![]() $m_\varepsilon $
is
$m_\varepsilon $
is
![]() $S_p$
-bounded with norm
$S_p$
-bounded with norm
![]() $\leq C$
. However, this limit is
$\leq C$
. However, this limit is
![]() $m_{u_j}(\xi ,\eta )$
from claim (A). This proves claim (B).
$m_{u_j}(\xi ,\eta )$
from claim (A). This proves claim (B).
Remark 2.4. Taking
for a smooth domain
![]() $\Omega $
, Lemma 2.3 reduces to the classical Meyer’s lemma.
$\Omega $
, Lemma 2.3 reduces to the classical Meyer’s lemma.
Proof of (1)
 $\Rightarrow $
(2) in Theorem A.
$\Rightarrow $
(2) in Theorem A.
Let us assume that (1) in Theorem A holds. By taking charts, we can and will assume that M and N are open subsets of
![]() $\mathbf {R}^{m}$
and
$\mathbf {R}^{m}$
and
![]() $\mathbf {R}^n$
, respectively. We shall further assume that
$\mathbf {R}^n$
, respectively. We shall further assume that
![]() $m=n$
. For instance, if
$m=n$
. For instance, if
![]() $m<n$
, we can replace M by
$m<n$
, we can replace M by
![]() $M \times \mathbf {R}^{n-m}$
and
$M \times \mathbf {R}^{n-m}$
and
![]() $\Sigma $
by
$\Sigma $
by
By the transversality assumption, the map
![]() $z \mapsto \mathbf {n}_2(z)/\|\mathbf {n}_2(z)\|$
is continuous on a neighbourhood of the transverse point
$z \mapsto \mathbf {n}_2(z)/\|\mathbf {n}_2(z)\|$
is continuous on a neighbourhood of the transverse point
![]() $(x_0,y_0)$
in Theorem A. Moreover, for y close to
$(x_0,y_0)$
in Theorem A. Moreover, for y close to
![]() $y_0$
, we have that
$y_0$
, we have that
![]() $\partial \Sigma ^y$
is locally a manifold, so is connected. Thus, if (2) was not true, there would exist y close to
$\partial \Sigma ^y$
is locally a manifold, so is connected. Thus, if (2) was not true, there would exist y close to
![]() $y_0$
such that the subset of the sphere
$y_0$
such that the subset of the sphere
![]() $X = \{\mathbf {n}_2(x',y)/\|\mathbf {n}_2(x',y)\|: x' \in \partial \Sigma ^y \cap U\}$
contains a connected subset not reduced to a point. According to (1) and Lemma 2.3, this would imply that the square function inequality holds uniformly in
$X = \{\mathbf {n}_2(x',y)/\|\mathbf {n}_2(x',y)\|: x' \in \partial \Sigma ^y \cap U\}$
contains a connected subset not reduced to a point. According to (1) and Lemma 2.3, this would imply that the square function inequality holds uniformly in
![]() $L_p(\mathbf {R}^n)$
for any finite set in X. However, Fefferman’s main result in his proof of the ball multiplier theorem [Reference Fefferman15] claims that such a uniform inequality cannot hold. In fact, Fefferman stated it for
$L_p(\mathbf {R}^n)$
for any finite set in X. However, Fefferman’s main result in his proof of the ball multiplier theorem [Reference Fefferman15] claims that such a uniform inequality cannot hold. In fact, Fefferman stated it for
![]() $n=2$
, but the result in arbitrary dimension follows from the
$n=2$
, but the result in arbitrary dimension follows from the
![]() $2$
-dimensional case by K. de Leeuw’s restriction theorem [Reference de Leeuw29]. Hence, the zero-curvature condition (2) must hold.
$2$
-dimensional case by K. de Leeuw’s restriction theorem [Reference de Leeuw29]. Hence, the zero-curvature condition (2) must hold.
2.3 Proof of Theorem A: Zero-curvature implies triangular truncations
The implication (2)
![]() $\Rightarrow $
(3) is a general geometric statement concerning transverse hypersurfaces in manifolds of product type. Let
$\Rightarrow $
(3) is a general geometric statement concerning transverse hypersurfaces in manifolds of product type. Let
![]() $M,N$
be manifolds of dimension
$M,N$
be manifolds of dimension
![]() $m,n$
. Following the terminology in the Introduction, we say that a
$m,n$
. Following the terminology in the Introduction, we say that a
![]() $\mathcal {C}^1$
-submanifold
$\mathcal {C}^1$
-submanifold
![]() $\Pi \subset M \times N$
of codimension
$\Pi \subset M \times N$
of codimension
![]() $1$
is said to be transverse at
$1$
is said to be transverse at
![]() $z=(x,y) \in \Pi $
if the tangent space of
$z=(x,y) \in \Pi $
if the tangent space of
![]() $\Pi $
at z maps surjectively on each factor
$\Pi $
at z maps surjectively on each factor
![]() $T_x M$
and
$T_x M$
and
![]() $T_y N$
. In that case,
$T_y N$
. In that case,
![]() $\Pi _x = \{y' \in N \mid (x,y') \in \Pi \}$
and
$\Pi _x = \{y' \in N \mid (x,y') \in \Pi \}$
and
![]() $\Pi ^y = \{x' \in M \mid (x',y) \in \Pi \}$
are manifolds on a neighbourhood y and x, respectively.
$\Pi ^y = \{x' \in M \mid (x',y) \in \Pi \}$
are manifolds on a neighbourhood y and x, respectively.
Theorem 2.5. Let
![]() $\Pi \subset M \times N$
be a
$\Pi \subset M \times N$
be a
![]() $\mathcal {C}^1$
-submanifold of codimension
$\mathcal {C}^1$
-submanifold of codimension
![]() $1$
that is transverse at
$1$
that is transverse at
![]() ${z_0=(x_0,y_0)\in \Pi }$
. Then, the following are equivalent
${z_0=(x_0,y_0)\in \Pi }$
. Then, the following are equivalent
![]() $\hskip 1pt :$
$\hskip 1pt :$
-
(a) There are neighbourhoods
 $U,V$
of
$U,V$
of
 $x_0$
and
$x_0$
and
 $y_0$
in
$y_0$
in
 $M,N$
such that for every
$M,N$
such that for every
 $x,x' \in U$
and
$x,x' \in U$
and
 $y \in V$
with
$y \in V$
with
 $(x,y),(x',y) \in \Pi $
,
$(x,y),(x',y) \in \Pi $
,
 $T_y \Pi _x = T_y \Pi _{x'}$
.
$T_y \Pi _x = T_y \Pi _{x'}$
. -
(b) There are neighbourhoods
 $U,V$
of
$U,V$
of
 $x_0$
and
$x_0$
and
 $y_0$
in
$y_0$
in
 $M,N$
such that for every
$M,N$
such that for every
 $x \in U$
and
$x \in U$
and
 $y,y' \in V$
with
$y,y' \in V$
with
 $(x,y),(x,y') \in \Pi $
,
$(x,y),(x,y') \in \Pi $
,
 $T_x \Pi ^y = T_x \Pi ^{y'}$
.
$T_x \Pi ^y = T_x \Pi ^{y'}$
. -
(c) There are neighbourhoods
 $U,V$
of
$U,V$
of
 $x_0$
and
$x_0$
and
 $y_0$
in
$y_0$
in
 $M,N$
and
$M,N$
and
 $C^1$
submersions
$C^1$
submersions
 $f \colon U \to \mathbf {R}$
and
$f \colon U \to \mathbf {R}$
and
 $g \colon V \to \mathbf {R}$
with
$g \colon V \to \mathbf {R}$
with
 $\Pi \cap (U \times V) = \{(x,y) \in U \times V \mid f(x)=g(y)\}$
.
$\Pi \cap (U \times V) = \{(x,y) \in U \times V \mid f(x)=g(y)\}$
.
The difficult direction in Theorem 2.5 is (a)
![]() $\Rightarrow $
(c). Both conditions are invariant by diffeomorphisms of product type, that is of the form
$\Rightarrow $
(c). Both conditions are invariant by diffeomorphisms of product type, that is of the form
![]() $(x,y)\mapsto (\phi (x),\psi (y))$
. It will be useful to have a description of a local normal form (that is of an element in every orbit) of transverse manifolds.
$(x,y)\mapsto (\phi (x),\psi (y))$
. It will be useful to have a description of a local normal form (that is of an element in every orbit) of transverse manifolds.
Lemma 2.6. Consider a
![]() $\mathcal {C}^1$
-submanifold
$\mathcal {C}^1$
-submanifold
![]() $\Pi \subset M \times N$
of codimension
$\Pi \subset M \times N$
of codimension
![]() $1$
that is transverse at
$1$
that is transverse at
![]() ${z_0=(x_0,y_0)\in \Pi} $
. Then, there are diffeomorphisms
${z_0=(x_0,y_0)\in \Pi} $
. Then, there are diffeomorphisms
![]() $\phi $
and
$\phi $
and
![]() $\psi $
from neighbourhoods U and V of
$\psi $
from neighbourhoods U and V of
![]() $x_0$
and
$x_0$
and
![]() $y_0$
, respectively, into
$y_0$
, respectively, into
![]() $\mathbf {R}^m$
and
$\mathbf {R}^m$
and
![]() $\mathbf {R}^n$
satisfying that
$\mathbf {R}^n$
satisfying that
![]() $\phi (x_0) = 0 = \psi (y_0)$
and such that
$\phi (x_0) = 0 = \psi (y_0)$
and such that
for some
![]() $\mathcal {C}^1$
function
$\mathcal {C}^1$
function
![]() $g \colon \mathbf {R}^{m-1} \times \mathbf {R}^n \to \mathbf {R}$
satisfying
$g \colon \mathbf {R}^{m-1} \times \mathbf {R}^n \to \mathbf {R}$
satisfying
![]() $g(0,y)=y_1$
for every y.
$g(0,y)=y_1$
for every y.
Proof. By the transversality assumption that
![]() $T_{z_0}\Pi $
surjects onto
$T_{z_0}\Pi $
surjects onto
![]() $T_{y_0} M$
, we see that
$T_{y_0} M$
, we see that
![]() $T_{z_0} \Pi \cap (T_{x_0}M \oplus 0) \neq T_{x_0} M \oplus 0$
. Thus, by applying a local diffeomorphism
$T_{z_0} \Pi \cap (T_{x_0}M \oplus 0) \neq T_{x_0} M \oplus 0$
. Thus, by applying a local diffeomorphism
![]() $\phi :M \to \mathbf {R}^m$
, we can assume that
$\phi :M \to \mathbf {R}^m$
, we can assume that
![]() $M=\mathbf {R}^m$
,
$M=\mathbf {R}^m$
,
![]() $x_0=0$
and
$x_0=0$
and
![]() $(1,0, \ldots ,0)\notin T_{z_0} \Pi $
. Then by the implicit function theorem, there is a
$(1,0, \ldots ,0)\notin T_{z_0} \Pi $
. Then by the implicit function theorem, there is a
![]() $\mathcal {C}^1$
function
$\mathcal {C}^1$
function
![]() $h \colon \mathbf {R}^{m-1} \times N \to \mathbf {R}$
such that, on a neighbourhood of
$h \colon \mathbf {R}^{m-1} \times N \to \mathbf {R}$
such that, on a neighbourhood of
![]() $(0,y_0)$
,
$(0,y_0)$
,
The function
![]() $h(0,\cdot )$
vanishes at
$h(0,\cdot )$
vanishes at
![]() $y_0$
and, by the second half of the transversality assumption, has nonzero differential at
$y_0$
and, by the second half of the transversality assumption, has nonzero differential at
![]() $y_0$
. By the implicit function theorem (or the surjection theorem) again, there is a diffeomorphism
$y_0$
. By the implicit function theorem (or the surjection theorem) again, there is a diffeomorphism
![]() $\psi $
from a neighbourhood of
$\psi $
from a neighbourhood of
![]() $y_0$
into
$y_0$
into
![]() $\mathbf {R}^n$
vanishing at
$\mathbf {R}^n$
vanishing at
![]() $y_0$
and such that
$y_0$
and such that
![]() $h(0,y) = \psi (y)_1$
for every y close enough to
$h(0,y) = \psi (y)_1$
for every y close enough to
![]() $y_0$
. This proves the lemma with
$y_0$
. This proves the lemma with
![]() $g(0,y)=h(0,\psi ^{-1}(y))$
.
$g(0,y)=h(0,\psi ^{-1}(y))$
.
Proof of Theorem 2.5.
By symmetry of the two variables, it is enough to prove (a)
![]() $\Leftrightarrow $
(c). The implication (c)
$\Leftrightarrow $
(c). The implication (c)
![]() $\Rightarrow $
(a) is clear with the same U and V because in that case,
$\Rightarrow $
(a) is clear with the same U and V because in that case,
![]() $T_y \Pi _x$
is the kernel of
$T_y \Pi _x$
is the kernel of
![]() $d_y g$
, which is independent of x. It remains to prove the implication (a)
$d_y g$
, which is independent of x. It remains to prove the implication (a)
![]() $\Rightarrow $
(c). Observe that both conditions are unchanged if we replace
$\Rightarrow $
(c). Observe that both conditions are unchanged if we replace
![]() $(x_0,y_0,\Pi )$
by
$(x_0,y_0,\Pi )$
by
![]() $(\phi (x_0),\psi (y_0),\phi \times \psi (\Pi ))$
for local diffeomorphisms. Therefore, by the normal form Lemma 2.6, we may assume that
$(\phi (x_0),\psi (y_0),\phi \times \psi (\Pi ))$
for local diffeomorphisms. Therefore, by the normal form Lemma 2.6, we may assume that
![]() $M \times N=\mathbf {R}^m \times \mathbf {R}^n$
,
$M \times N=\mathbf {R}^m \times \mathbf {R}^n$
,
![]() $(x_0,y_0)=(0,0)$
and
$(x_0,y_0)=(0,0)$
and
for some
![]() $\mathcal {C}^1$
function
$\mathcal {C}^1$
function
![]() $g\colon \mathbf {R}^{m-1}\times \mathbf {R}^n \to \mathbf {R}$
satisfying
$g\colon \mathbf {R}^{m-1}\times \mathbf {R}^n \to \mathbf {R}$
satisfying
![]() $g(0,y)=y_1$
. Then, for every
$g(0,y)=y_1$
. Then, for every
![]() $(x,y) \in \Pi $
with
$(x,y) \in \Pi $
with
![]() $x=(x_1,\tilde {x})$
, we have
$x=(x_1,\tilde {x})$
, we have
![]() $T_y \Pi _x = \ker ( d_y g(\tilde x,y))$
. Let
$T_y \Pi _x = \ker ( d_y g(\tilde x,y))$
. Let
![]() $\tilde U \subset \mathbf {R}^{m-1},\tilde V \subset V$
be square neighbourhoods of
$\tilde U \subset \mathbf {R}^{m-1},\tilde V \subset V$
be square neighbourhoods of
![]() $0$
such that
$0$
such that
![]() $(g(\tilde x,y),\tilde x) \in U$
for
$(g(\tilde x,y),\tilde x) \in U$
for
![]() $(\tilde x,y) \in \tilde U \times \tilde V$
. Then for every such
$(\tilde x,y) \in \tilde U \times \tilde V$
. Then for every such
![]() $\tilde x,y$
, condition (a) applied to
$\tilde x,y$
, condition (a) applied to
![]() $x=(g(\tilde x,y),\tilde x)$
and
$x=(g(\tilde x,y),\tilde x)$
and
![]() $x' = (g(0,y),0)$
yields
$x' = (g(0,y),0)$
yields
![]() $\ker d_y g( \tilde x,y) = \ker d_y g(0,y) = \operatorname {span}(e_2,\dots ,e_n)$
. In particular,
$\ker d_y g( \tilde x,y) = \ker d_y g(0,y) = \operatorname {span}(e_2,\dots ,e_n)$
. In particular,
![]() $\partial _{y_j} g(\tilde x,y)=0$
for every
$\partial _{y_j} g(\tilde x,y)=0$
for every
![]() $j \geq 2$
, so (since
$j \geq 2$
, so (since
![]() $\tilde V$
is a square)
$\tilde V$
is a square)
![]() $g(\tilde x,y) = w(\tilde x,y_1)$
for certain
$g(\tilde x,y) = w(\tilde x,y_1)$
for certain
![]() $\mathcal {C}^1$
function
$\mathcal {C}^1$
function
![]() $w:\mathbf {R}^{m-1}\times \mathbf {R} \to \mathbf {R}$
satisfying
$w:\mathbf {R}^{m-1}\times \mathbf {R} \to \mathbf {R}$
satisfying
![]() $w(0,s)=s$
for all s. By the implicit function theorem, we get
$w(0,s)=s$
for all s. By the implicit function theorem, we get
locally for a
![]() $\mathcal {C}^1$
function
$\mathcal {C}^1$
function
![]() $u \colon \mathbf {R}^m \to \mathbf {R}$
. This completes the proof of Theorem 2.5.
$u \colon \mathbf {R}^m \to \mathbf {R}$
. This completes the proof of Theorem 2.5.
2.4 Proof of Theorem A: Transference on triangular truncations
We record finally the easy last implication, which completes the proof of Theorem A.
Proof of (3)
 $\Rightarrow $
(1) in Theorem A.
$\Rightarrow $
(1) in Theorem A.
This is immediate from the classical boundedness of the triangular projection on Schatten p-classes for
![]() $1 < p < \infty $
(due to Macaev [Reference Macaev48]; see also [Reference Gohberg and Krein17, Chap III, §6]) and the transference Lemma 2.1 above.
$1 < p < \infty $
(due to Macaev [Reference Macaev48]; see also [Reference Gohberg and Krein17, Chap III, §6]) and the transference Lemma 2.1 above.
2.5 Relatively compact domains
Using a partition of unity argument, it is not difficult to prove that Theorem A holds globally for relatively compact fully transverse domains
![]() $\Sigma $
. More precisely, let
$\Sigma $
. More precisely, let
![]() $p \in (1,\infty )\setminus \{2\}$
and consider a relatively compact domain
$p \in (1,\infty )\setminus \{2\}$
and consider a relatively compact domain
![]() $\Sigma $
in
$\Sigma $
in
![]() $M \times N$
which is transverse at every point of
$M \times N$
which is transverse at every point of
![]() $\partial \Sigma $
. Then
$\partial \Sigma $
. Then
![]() $S_\Sigma $
is an
$S_\Sigma $
is an
![]() $S_p$
-bounded multiplier if and only if any of the equivalent conditions (2) and (3) in the statement of Theorem A holds at every point of the boundary.
$S_p$
-bounded multiplier if and only if any of the equivalent conditions (2) and (3) in the statement of Theorem A holds at every point of the boundary.
Remark 2.7. The fact that
![]() $\Sigma $
is relatively compact is crucial in the preceding argument. For instance, (2) holds trivially at every boundary point for every fully transverse
$\Sigma $
is relatively compact is crucial in the preceding argument. For instance, (2) holds trivially at every boundary point for every fully transverse
![]() $\mathcal {C}^1$
-domain of
$\mathcal {C}^1$
-domain of
![]() $\mathbf {R}\times \mathbf {R}$
. But there are examples of such domains – which are Toeplitz, arising from Fourier symbols – that do not define an
$\mathbf {R}\times \mathbf {R}$
. But there are examples of such domains – which are Toeplitz, arising from Fourier symbols – that do not define an
![]() $S_p$
multiplier for any
$S_p$
multiplier for any
![]() $p \neq 2$
. An explicit construction is given in [Reference Caspers, Parcet, Perrin and Ricard6, Appendix A].
$p \neq 2$
. An explicit construction is given in [Reference Caspers, Parcet, Perrin and Ricard6, Appendix A].
At this point, it is interesting to observe the difference here between Fourier and Schur idempotents. We know from Fefferman’s theorem [Reference Fefferman15] that there are no Fourier
![]() $L_p$
-idempotents associated to smooth compact domains. However, there are plenty such Schur idempotents: necessarily nonToeplitz, since Toeplitz symbols give rise to Fourier idempotents. A funny instance is precisely given by other forms of ball multipliers
$L_p$
-idempotents associated to smooth compact domains. However, there are plenty such Schur idempotents: necessarily nonToeplitz, since Toeplitz symbols give rise to Fourier idempotents. A funny instance is precisely given by other forms of ball multipliers
![]() $\Sigma _R = \{ (x,y) \hskip -1pt \in \hskip -1pt \mathbf {R}^n \times \mathbf {R}^n\hskip -2pt : |x|^2 + |y|^2 < R^2 \}$
, which are clearly
$\Sigma _R = \{ (x,y) \hskip -1pt \in \hskip -1pt \mathbf {R}^n \times \mathbf {R}^n\hskip -2pt : |x|^2 + |y|^2 < R^2 \}$
, which are clearly
![]() $S_p$
-bounded and have been recently used by Chuah-Liu-Mei in their recent paper [Reference Chuah, Liu and Mei9, Example 4.4]. Theorem A proves in addition that the spheres
$S_p$
-bounded and have been recently used by Chuah-Liu-Mei in their recent paper [Reference Chuah, Liu and Mei9, Example 4.4]. Theorem A proves in addition that the spheres
![]() $\partial \Sigma _R$
satisfy the zero-curvature condition (2). More intriguing examples are the spherical Hilbert transforms defined in the Introduction as
$\partial \Sigma _R$
satisfy the zero-curvature condition (2). More intriguing examples are the spherical Hilbert transforms defined in the Introduction as
More generally, we also define
![]() $H_{\mathbf {S},\delta } = -i (2S_{\Sigma _\delta } - \mathrm {id})$
with
$H_{\mathbf {S},\delta } = -i (2S_{\Sigma _\delta } - \mathrm {id})$
with
![]() $S_{\Sigma _\delta }(A) = (\chi _{\langle x,y \rangle> \delta } A_{xy})$
for
$S_{\Sigma _\delta }(A) = (\chi _{\langle x,y \rangle> \delta } A_{xy})$
for
![]() $\delta \in (-1,1)$
. The case
$\delta \in (-1,1)$
. The case
![]() $\delta = 0$
corresponds to the spherical transform
$\delta = 0$
corresponds to the spherical transform
![]() $H_{\mathbf {S}}$
above.
$H_{\mathbf {S}}$
above.
Corollary 2.8. Let us fix
![]() $1 < p \neq 2 < \infty $
. Then, the n-dimensional spherical Hilbert transforms
$1 < p \neq 2 < \infty $
. Then, the n-dimensional spherical Hilbert transforms
![]() $H_{\mathbf {S},\delta }$
are all
$H_{\mathbf {S},\delta }$
are all
![]() $S_p$
-bounded for
$S_p$
-bounded for
![]() $n = 1$
and
$n = 1$
and
![]() $S_p$
-unbounded for
$S_p$
-unbounded for
![]() $n \ge 2$
.
$n \ge 2$
.
Proof. Spherical Hilbert transforms
![]() $H_{\mathbf {S},\delta }$
arise from relatively compact domains
$H_{\mathbf {S},\delta }$
arise from relatively compact domains
![]() $\Sigma _\delta $
whose boundary is fully transverse. In particular, we may apply Theorem A. In dimension
$\Sigma _\delta $
whose boundary is fully transverse. In particular, we may apply Theorem A. In dimension
![]() $1$
, the assertion follows immediately since the zero-curvature condition (2) is trivially satisfied. Alternatively, the symbol can be expressed as a triangular truncation in terms of the polar coordinates of x and y. When
$1$
, the assertion follows immediately since the zero-curvature condition (2) is trivially satisfied. Alternatively, the symbol can be expressed as a triangular truncation in terms of the polar coordinates of x and y. When
![]() $n \ge 2$
, it is easily checked that the tangent spaces at
$n \ge 2$
, it is easily checked that the tangent spaces at
![]() $\partial \Sigma _{x_1}$
and
$\partial \Sigma _{x_1}$
and
![]() $\partial \Sigma _{x_2}$
differ at their intersection points. This was illustrated for
$\partial \Sigma _{x_2}$
differ at their intersection points. This was illustrated for
![]() $n=2$
in Figure 1. Theorem A implies the assertion.
$n=2$
in Figure 1. Theorem A implies the assertion.
Remark 2.9. Alternatively, Corollary 2.8 also follows as a special case of Corollary B2. Indeed, Lemma 2.1 implies that
![]() $H_{\mathbf {S},\delta }$
has the same norm as the Schur multiplier on
$H_{\mathbf {S},\delta }$
has the same norm as the Schur multiplier on
![]() $\mathrm {SO}(n+1) \times \mathrm {SO}(n+1)$
with symbol
$\mathrm {SO}(n+1) \times \mathrm {SO}(n+1)$
with symbol
![]() $(g,h)\mapsto \mathrm {sgn}( (g^{-1}h)_{1,1})$
, which by [Reference Caspers and de la Salle7] coincides with the cb-norm of the Fourier multipler with symbol
$(g,h)\mapsto \mathrm {sgn}( (g^{-1}h)_{1,1})$
, which by [Reference Caspers and de la Salle7] coincides with the cb-norm of the Fourier multipler with symbol
![]() $g\mapsto \mathrm {sgn}(g_{1,1})$
. But for
$g\mapsto \mathrm {sgn}(g_{1,1})$
. But for
![]() $n\geq 2$
,
$n\geq 2$
,
![]() $\mathrm {SO}(n+1)$
is a simple Lie group not locally isomorphic to
$\mathrm {SO}(n+1)$
is a simple Lie group not locally isomorphic to
![]() $\mathrm {SL}_2(\mathbf {R})$
, so it does not carry any idempotent multiplier.
$\mathrm {SL}_2(\mathbf {R})$
, so it does not carry any idempotent multiplier.
Remark 2.10. We may also consider symbols
![]() $\Sigma _\delta = \{(x,y) \in \mathbf {R}^n: \langle x,y \rangle> \delta \}$
in the full Euclidean space for
$\Sigma _\delta = \{(x,y) \in \mathbf {R}^n: \langle x,y \rangle> \delta \}$
in the full Euclidean space for
![]() $n \ge 2$
. In this case, Theorem A gives
$n \ge 2$
. In this case, Theorem A gives
![]() $S_p$
-unboundedness for
$S_p$
-unboundedness for
![]() $(n,\delta ) \neq (2,0)$
. By [Reference Lafforgue and de la Salle28, Theorem 1.18] and since
$(n,\delta ) \neq (2,0)$
. By [Reference Lafforgue and de la Salle28, Theorem 1.18] and since
![]() $S_{\Sigma _0} = H_{\mathbf {S},0} \otimes \mathrm {id}_{\mathbf {R}_+}$
, it turns out that
$S_{\Sigma _0} = H_{\mathbf {S},0} \otimes \mathrm {id}_{\mathbf {R}_+}$
, it turns out that
![]() $S_p$
-boundedness for
$S_p$
-boundedness for
![]() $(n,\delta ) = (2,0)$
follows from Corollary 2.8.
$(n,\delta ) = (2,0)$
follows from Corollary 2.8.
2.6 Curvature on smoother domains
Our curvature condition (2) admits an alternative formulation under additional regularity. Let
![]() $\Sigma $
be a
$\Sigma $
be a
![]() $\mathcal {C}^2$
-domain. Then
$\mathcal {C}^2$
-domain. Then
![]() $\Sigma \cap (U \times V) = \big \{ (x, y) : F(x, y)> 0 \big \}$
for some
$\Sigma \cap (U \times V) = \big \{ (x, y) : F(x, y)> 0 \big \}$
for some
![]() $\mathcal {C}^2$
-function
$\mathcal {C}^2$
-function
![]() $F: M \times N \to \mathbf {R}$
and small enough neighbourhoods
$F: M \times N \to \mathbf {R}$
and small enough neighbourhoods
![]() $U,V$
. Our curvature condition holds if and only if we have
$U,V$
. Our curvature condition holds if and only if we have
for
![]() $(u,v) \in \ker d_xF(x, y) \times \ker d_yF(x, y)$
at every
$(u,v) \in \ker d_xF(x, y) \times \ker d_yF(x, y)$
at every
![]() $(x, y) \in \partial \Sigma \cap (U \times V)$
. The argument is quite simple. By fixing boundary points
$(x, y) \in \partial \Sigma \cap (U \times V)$
. The argument is quite simple. By fixing boundary points
![]() $(x,y)$
and vectors
$(x,y)$
and vectors
![]() $(u,v)$
as specified above, let
$(u,v)$
as specified above, let
![]() $\gamma : [0,1] \to \partial \Sigma ^y \cap U$
be a curve with
$\gamma : [0,1] \to \partial \Sigma ^y \cap U$
be a curve with
![]() $\gamma (0) = x$
and
$\gamma (0) = x$
and
![]() $\gamma '(0)=u$
, and set
$\gamma '(0)=u$
, and set
![]() $h(s) = d_yF(\gamma (s),y)$
. The curvature condition (2) means that
$h(s) = d_yF(\gamma (s),y)$
. The curvature condition (2) means that
![]() $h(s) = \alpha (s) h(0)$
for some nonvanishing function
$h(s) = \alpha (s) h(0)$
for some nonvanishing function
![]() $\alpha : [0,1] \to \mathbf {R}$
. In particular, we get
$\alpha : [0,1] \to \mathbf {R}$
. In particular, we get
Reciprocally, assume that the
![]() $\mathcal {C}^2$
-curvature condition above holds. Consider a curve
$\mathcal {C}^2$
-curvature condition above holds. Consider a curve
![]() $\gamma \colon [0,1] \to \partial \Sigma ^y \cap U$
and define h as above. Since we have
$\gamma \colon [0,1] \to \partial \Sigma ^y \cap U$
and define h as above. Since we have
![]() $\gamma '(s) \in \ker d_xF(\gamma (s),y)$
and
$\gamma '(s) \in \ker d_xF(\gamma (s),y)$
and
![]() $h'(s) = \gamma '(s)^{\mathrm {t}} \cdot d_xd_yF(\gamma (s),y)$
by construction, it turns out that
$h'(s) = \gamma '(s)^{\mathrm {t}} \cdot d_xd_yF(\gamma (s),y)$
by construction, it turns out that
![]() $\langle h'(s),v \rangle $
equals
$\langle h'(s),v \rangle $
equals
![]() $\langle d_xd_yF(\gamma (s),y), \gamma '(s) \otimes v \rangle $
for any
$\langle d_xd_yF(\gamma (s),y), \gamma '(s) \otimes v \rangle $
for any
![]() $v \in \ker d_yF(\gamma (s),y)$
. Applying the
$v \in \ker d_yF(\gamma (s),y)$
. Applying the
![]() $\mathcal {C}^2$
-curvature condition, this implies that
$\mathcal {C}^2$
-curvature condition, this implies that
![]() $h'(s)$
is parallel to
$h'(s)$
is parallel to
![]() $h(s)$
for every s, which leads to the ODE
$h(s)$
for every s, which leads to the ODE
 $$\begin{align*}\left. \begin{array}{rcl} h'(s) & = \lambda(s) h(s) \\ h(0) & = d_yF(x,y) \end{array} \right\} \Rightarrow h(s) = \exp \Big( \int_0^s \lambda(t)dt \Big) h(0) = \alpha(s) h(0)\end{align*}$$
$$\begin{align*}\left. \begin{array}{rcl} h'(s) & = \lambda(s) h(s) \\ h(0) & = d_yF(x,y) \end{array} \right\} \Rightarrow h(s) = \exp \Big( \int_0^s \lambda(t)dt \Big) h(0) = \alpha(s) h(0)\end{align*}$$
for a nonvanishing
![]() $\alpha : [0,1] \to \mathbf {R}$
. This implies condition (2) in Theorem A.
$\alpha : [0,1] \to \mathbf {R}$
. This implies condition (2) in Theorem A.
Remark 2.11. In this form, (2) is invariant under exchanging x and y, which is clear a posteriori without the
![]() $\mathcal {C}^2$
assumption, since both (1) and (3) are. However, condition (2) in Theorem A seems new, while its
$\mathcal {C}^2$
assumption, since both (1) and (3) are. However, condition (2) in Theorem A seems new, while its
![]() $\mathcal {C}^2$
-form above is quite similar to the rotational curvature
$\mathcal {C}^2$
-form above is quite similar to the rotational curvature
![]() $\det [d_xd_y F(x,y)] $
defined by Stein in [Reference Stein45, XI.3.1].
$\det [d_xd_y F(x,y)] $
defined by Stein in [Reference Stein45, XI.3.1].
2.7 On the transversality condition
The transversality assumption has been essential in our proofs of (1)
![]() $\Rightarrow $
(2)
$\Rightarrow $
(2)
![]() $\Rightarrow $
(3) in Theorem A, but it is not clear that it is really needed for the statement. Indeed, conditions (1) and (3) make sense without it, and (2) is already meaningful if one only assumes that
$\Rightarrow $
(3) in Theorem A, but it is not clear that it is really needed for the statement. Indeed, conditions (1) and (3) make sense without it, and (2) is already meaningful if one only assumes that
![]() $\mathbf {n}_2(x_0,y_0) \neq 0$
, and we do not have an example where the equivalence fails. It is likely that such examples can be found, but probably not for domains with analytic boundary. We leave these questions as open problems. In the degenerate case where
$\mathbf {n}_2(x_0,y_0) \neq 0$
, and we do not have an example where the equivalence fails. It is likely that such examples can be found, but probably not for domains with analytic boundary. We leave these questions as open problems. In the degenerate case where
![]() $\mathbf {n}_1$
is identically
$\mathbf {n}_1$
is identically
![]() $0$
, or equivalently when
$0$
, or equivalently when
![]() $\Sigma $
is locally of the form
$\Sigma $
is locally of the form
![]() $\Sigma = \{(x,y): y \in \Omega \}$
, all conditions in Theorem A hold. The
$\Sigma = \{(x,y): y \in \Omega \}$
, all conditions in Theorem A hold. The
![]() $S_p$
-boundedness is in that case even true for
$S_p$
-boundedness is in that case even true for
![]() $1 \leq p \leq \infty $
because the Schur multiplier whose symbol is the indicator function of
$1 \leq p \leq \infty $
because the Schur multiplier whose symbol is the indicator function of
![]() $\Sigma $
is just the right-multiplication by the orthogonal projection on
$\Sigma $
is just the right-multiplication by the orthogonal projection on
![]() $L_2(\Omega )$
.
$L_2(\Omega )$
.
3 Idempotent Fourier multipliers on Lie groups
Let
![]() $\mathrm {G}$
be a Lie group, that we equip with a left Haar measure. As to every locally compact group, we can associate to it the following:
$\mathrm {G}$
be a Lie group, that we equip with a left Haar measure. As to every locally compact group, we can associate to it the following:
-
• Its von Neumann algebra
 $\mathcal {L} \mathrm {G}$
.
$\mathcal {L} \mathrm {G}$
. -
• The noncommutative
 $L_p$
spaces
$L_p$
spaces
 $L_p(\mathcal {L} \mathrm {G})$
for
$L_p(\mathcal {L} \mathrm {G})$
for
 $1 \leq p < \infty $
.
$1 \leq p < \infty $
. -
• The Fourier
 $L_p$
-multipliers
$L_p$
-multipliers
 $T_m$
with symbol
$T_m$
with symbol
 $m\colon \mathrm {G} \to \mathbf {C}$
.
$m\colon \mathrm {G} \to \mathbf {C}$
.
The group von Neumann algebra
![]() $\mathcal {L} \mathrm {G}$
is the weak-
$\mathcal {L} \mathrm {G}$
is the weak-
![]() $*$
closure in
$*$
closure in
![]() $B(L_2(\mathrm {G}))$
of the algebra of convolution operators
$B(L_2(\mathrm {G}))$
of the algebra of convolution operators
![]() $\lambda (f):\xi \in L_2(\mathrm {G}) \mapsto f \ast \xi $
for
$\lambda (f):\xi \in L_2(\mathrm {G}) \mapsto f \ast \xi $
for
![]() $f \in \mathcal {C}_c(\mathrm {G})$
. When
$f \in \mathcal {C}_c(\mathrm {G})$
. When
![]() $\mathrm {G}$
is unimodular, its
$\mathrm {G}$
is unimodular, its
![]() $L_p$
-theory is quite elementary:
$L_p$
-theory is quite elementary:
![]() $\mathcal {L} \mathrm {G}$
carries a natural semifinite trace
$\mathcal {L} \mathrm {G}$
carries a natural semifinite trace
![]() $\tau $
given by
$\tau $
given by
![]() $\tau ( \lambda (f)^* \lambda (f)) = \int |f(g)|^2 dg$
for every
$\tau ( \lambda (f)^* \lambda (f)) = \int |f(g)|^2 dg$
for every
![]() $f \in L_2(\mathrm {G})$
with
$f \in L_2(\mathrm {G})$
with
![]() $\lambda (f) \in \mathcal {L} \mathrm {G}$
;
$\lambda (f) \in \mathcal {L} \mathrm {G}$
;
![]() $L_p(\mathcal {L} \mathrm {G})$
is then defined as the completion of
$L_p(\mathcal {L} \mathrm {G})$
is then defined as the completion of
![]() $\{x \in \mathcal {L} \mathrm {G} : \|x\|_p<\infty \}$
for the norm
$\{x \in \mathcal {L} \mathrm {G} : \|x\|_p<\infty \}$
for the norm
![]() $\|x\|_p = \tau ( |x|^p)^{1/p}$
. It turns out that
$\|x\|_p = \tau ( |x|^p)^{1/p}$
. It turns out that
![]() $L_p(\mathcal {L} \mathrm {G})$
contains
$L_p(\mathcal {L} \mathrm {G})$
contains
![]() $\{\lambda (f) : f \in \mathcal {C}_c(\mathrm {G})\ast \mathcal {C}_c(\mathrm {G})\}$
as a dense subspace. A bounded measurable
$\{\lambda (f) : f \in \mathcal {C}_c(\mathrm {G})\ast \mathcal {C}_c(\mathrm {G})\}$
as a dense subspace. A bounded measurable
![]() $m \colon \mathrm {G} \to \mathbf {C}$
defines a Fourier
$m \colon \mathrm {G} \to \mathbf {C}$
defines a Fourier
![]() $L_p$
-multiplier if
$L_p$
-multiplier if
![]() $\lambda (f) \mapsto \lambda (mf)$
extends to a bounded map
$\lambda (f) \mapsto \lambda (mf)$
extends to a bounded map
![]() $T_m$
on
$T_m$
on
![]() $L_p(\mathcal {L} \mathrm {G})$
. These definitions are more involved for nonunimodular groups and will be recalled in Section 3.3 below.
$L_p(\mathcal {L} \mathrm {G})$
. These definitions are more involved for nonunimodular groups and will be recalled in Section 3.3 below.
When
![]() $p=1,\infty $
, a bounded measurable function
$p=1,\infty $
, a bounded measurable function
![]() $m \colon \mathrm {G}\to \mathbf {C}$
defines a completely bounded Fourier
$m \colon \mathrm {G}\to \mathbf {C}$
defines a completely bounded Fourier
![]() $L_p$
-multiplier if and only if the Schur multiplier associated to the symbol
$L_p$
-multiplier if and only if the Schur multiplier associated to the symbol
![]() $(g,h)\mapsto m(g h^{-1})$
– called the Herz-Schur multiplier with symbol m and denoted
$(g,h)\mapsto m(g h^{-1})$
– called the Herz-Schur multiplier with symbol m and denoted
![]() $S_m$
– is completely
$S_m$
– is completely
![]() $S_p$
-bounded, with same norms [Reference Bożejko and Fendler3]. For amenable groups, the same holds for
$S_p$
-bounded, with same norms [Reference Bożejko and Fendler3]. For amenable groups, the same holds for
![]() $1 < p < \infty $
[Reference Caspers and de la Salle7, Reference Neuwirth and Ricard34], and it is an intriguing open problem whether this holds beyond amenable groups. We shall use that this always holds locally. This phenomenon was discovered recently [Reference Parcet, Ricard and de la Salle35, Theorem 1.4] when p is an even integer and
$1 < p < \infty $
[Reference Caspers and de la Salle7, Reference Neuwirth and Ricard34], and it is an intriguing open problem whether this holds beyond amenable groups. We shall use that this always holds locally. This phenomenon was discovered recently [Reference Parcet, Ricard and de la Salle35, Theorem 1.4] when p is an even integer and
![]() $\mathrm {G}$
unimodular, and the following generalizes this to the general case; see [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi8] for other local results of similar nature. In what follows, the Fourier support of an element
$\mathrm {G}$
unimodular, and the following generalizes this to the general case; see [Reference Caspers, Janssens, Krishnaswamy-Usha and Miaskiwskyi8] for other local results of similar nature. In what follows, the Fourier support of an element
![]() $x \in L_p(\mathcal {L} \mathrm {G})$
will refer to the smallest closed subset
$x \in L_p(\mathcal {L} \mathrm {G})$
will refer to the smallest closed subset
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $T_m(x)=0$
for every Fourier
$T_m(x)=0$
for every Fourier
![]() $L_p$
-multiplier with symbol m whose support is a compact subset of
$L_p$
-multiplier with symbol m whose support is a compact subset of
![]() $\mathrm {G}\setminus \Lambda $
. When
$\mathrm {G}\setminus \Lambda $
. When
![]() $\mathrm {G}$
is unimodular and
$\mathrm {G}$
is unimodular and
![]() $x=\lambda (f)$
for
$x=\lambda (f)$
for
![]() $f \in \mathcal {C}_c(\mathrm {G}) \ast \mathcal {C}_c(\mathrm {G})$
, it is easy to see that this coincides with the support of the function f.
$f \in \mathcal {C}_c(\mathrm {G}) \ast \mathcal {C}_c(\mathrm {G})$
, it is easy to see that this coincides with the support of the function f.
Theorem 3.1. Let
![]() $\mathrm {G}$
be a locally compact group and consider a bounded measurable function
$\mathrm {G}$
be a locally compact group and consider a bounded measurable function
![]() ${m \colon \mathrm {G} \to \mathbf {C}}$
. Then, the following are equivalent for
${m \colon \mathrm {G} \to \mathbf {C}}$
. Then, the following are equivalent for
![]() $p \in (1,\infty )$
and
$p \in (1,\infty )$
and
![]() $g_0 \in \mathrm {G} \hskip -3pt :$
$g_0 \in \mathrm {G} \hskip -3pt :$
-
(a) There is a neighbourhood U of
 $g_0$
such that the restriction
$g_0$
such that the restriction
 $T_{m,U}$
of
$T_{m,U}$
of
 $T_m$
to the space of elements of
$T_m$
to the space of elements of
 $L_p(\mathcal {L} \mathrm {G})$
Fourier supported in U is completely bounded.
$L_p(\mathcal {L} \mathrm {G})$
Fourier supported in U is completely bounded. -
(b) There exists a function
 $\varphi \colon \mathrm {G} \to \mathbf {C}$
which equals
$\varphi \colon \mathrm {G} \to \mathbf {C}$
which equals
 $1$
on a neighbourhood of
$1$
on a neighbourhood of
 $g_0$
such that
$g_0$
such that
 $\varphi m$
defines a completely bounded Fourier multiplier on
$\varphi m$
defines a completely bounded Fourier multiplier on
 $L_p(\mathcal {L} \mathrm {G})$
.
$L_p(\mathcal {L} \mathrm {G})$
. -
(c) There are open sets
 $V,W \subset \mathrm {G}$
with
$V,W \subset \mathrm {G}$
with
 $g_0 \in V W^{-1}$
such that the function
$g_0 \in V W^{-1}$
such that the function
 $(g,h) \in V \times W \mapsto m(g h^{-1})$
defines a completely bounded Schur multiplier on the Schatten class
$(g,h) \in V \times W \mapsto m(g h^{-1})$
defines a completely bounded Schur multiplier on the Schatten class
 $S_p(L_2(V),L_2(W))$
.
$S_p(L_2(V),L_2(W))$
.
When these conditions hold, we say that m defines locally at
![]() $g_0$
a completely bounded Fourier
$g_0$
a completely bounded Fourier
![]() $L_p$
-multiplier. The proof is given in Section 3.2. We can record the following consequence, which is immediate by looking at condition (c).
$L_p$
-multiplier. The proof is given in Section 3.2. We can record the following consequence, which is immediate by looking at condition (c).
Corollary 3.2. Let
![]() $\mathrm {G}$
be a connected Lie group and denote by
$\mathrm {G}$
be a connected Lie group and denote by
![]() $\widetilde {\mathrm {G}}$
its universal cover. Let
$\widetilde {\mathrm {G}}$
its universal cover. Let
![]() $\tilde {g}_0 \in \widetilde {\mathrm {G}}$
be any lift of
$\tilde {g}_0 \in \widetilde {\mathrm {G}}$
be any lift of
![]() $g_0 \in \mathrm {G}$
. Then
$g_0 \in \mathrm {G}$
. Then
![]() $m \colon \mathrm {G} \to \mathbf {C}$
defines locally at
$m \colon \mathrm {G} \to \mathbf {C}$
defines locally at
![]() $g_0$
a completely bounded Fourier
$g_0$
a completely bounded Fourier
![]() $L_p$
-multiplier over
$L_p$
-multiplier over
![]() $\mathcal {L} \mathrm {G}$
if and only its lift
$\mathcal {L} \mathrm {G}$
if and only its lift
![]() $\widetilde {m}$
defines locally at
$\widetilde {m}$
defines locally at
![]() $\tilde {g}_0$
a completely bounded Fourier
$\tilde {g}_0$
a completely bounded Fourier
![]() $L_p$
-multiplier as well.
$L_p$
-multiplier as well.
3.1 Idempotent multipliers
Now we are ready to prove Theorem B and also Corollaries B1 and B2 from the Introduction. In fact, we shall prove a slightly expanded version of Theorem B which includes non-simply connected groups and Corollary B1 at once. The groups
![]() $\mathrm {G}_1,\mathrm {G}_2,\mathrm {G}_3$
in the statement below refer to the real line
$\mathrm {G}_1,\mathrm {G}_2,\mathrm {G}_3$
in the statement below refer to the real line
![]() $\mathbf {R}$
,
$\mathbf {R}$
,
![]() $\operatorname {\mathrm {Aff}}_+(\mathbf {R})$
and
$\operatorname {\mathrm {Aff}}_+(\mathbf {R})$
and
![]() $\widetilde {\mathrm {PSL}}_2(\mathbf {R})$
as in the Introduction.
$\widetilde {\mathrm {PSL}}_2(\mathbf {R})$
as in the Introduction.
Theorem 3.3. Let
![]() $p \in (1,\infty )\setminus \{2\}$
. Let
$p \in (1,\infty )\setminus \{2\}$
. Let
![]() $\mathrm {G}$
be a connected Lie group,
$\mathrm {G}$
be a connected Lie group,
![]() $\Omega \subset \mathrm {G}$
a
$\Omega \subset \mathrm {G}$
a
![]() $\mathcal {C}^1$
-domain and
$\mathcal {C}^1$
-domain and
![]() $g_0 \in \partial \Omega $
a point in the boundary of
$g_0 \in \partial \Omega $
a point in the boundary of
![]() $\Omega $
. Consider the following conditions
$\Omega $
. Consider the following conditions
![]() $:$
$:$
-
(1)
 $\chi _\Omega $
defines locally at
$\chi _\Omega $
defines locally at
 $g_0$
a completely bounded Fourier
$g_0$
a completely bounded Fourier
 $L_p$
-multiplier.
$L_p$
-multiplier. -
(2) There is a smooth action
 $\mathrm {G} \to \mathrm {Diff}(\mathbf {R})$
by diffeomorphisms on the real line, such that
$\mathrm {G} \to \mathrm {Diff}(\mathbf {R})$
by diffeomorphisms on the real line, such that
 $\Omega $
coincides on a neighbourhood of
$\Omega $
coincides on a neighbourhood of
 $g_0$
with
$g_0$
with
 $\{g \in \mathrm {G} \mid g \cdot 0> g_0 \cdot 0\}$
.
$\{g \in \mathrm {G} \mid g \cdot 0> g_0 \cdot 0\}$
. -
(3) There is
 $j\in \{1,2,3\}$
and a smooth surjective homomorphism
$j\in \{1,2,3\}$
and a smooth surjective homomorphism
 $f\colon \mathrm {G} \to \mathrm {G}_j$
such that the domain
$f\colon \mathrm {G} \to \mathrm {G}_j$
such that the domain
 $\Omega $
coincides on a neighbourhood of
$\Omega $
coincides on a neighbourhood of
 $g_0$
with
$g_0$
with
 $g_0 f^{-1}(\Omega _j)$
.
$g_0 f^{-1}(\Omega _j)$
. -
(4)
 $\partial \Omega = g_0 \exp (\mathfrak {h})$
locally near
$\partial \Omega = g_0 \exp (\mathfrak {h})$
locally near
 $g_0$
for some codimension
$g_0$
for some codimension
 $1$
Lie subalgebra
$1$
Lie subalgebra
 $\mathfrak {h} \subset \mathfrak {g}$
.
$\mathfrak {h} \subset \mathfrak {g}$
.
Then
![]() $(1) \Leftrightarrow (4) \Leftarrow (2) \Leftrightarrow (3)$
. If
$(1) \Leftrightarrow (4) \Leftarrow (2) \Leftrightarrow (3)$
. If
![]() $\mathrm {G}$
is simply connected, then we also have
$\mathrm {G}$
is simply connected, then we also have
![]() $(4) \Rightarrow (2)$
.
$(4) \Rightarrow (2)$
.
Proof. The main difficulty is to prove the equivalence (1)
![]() $\Leftrightarrow $
(4), which we leave to the end of the proof. The implication (2)
$\Leftrightarrow $
(4), which we leave to the end of the proof. The implication (2)
![]() $\Rightarrow $
(4) is clear, with
$\Rightarrow $
(4) is clear, with
![]() $\mathrm {H} = \exp (\mathfrak {h})$
the stabilizer of
$\mathrm {H} = \exp (\mathfrak {h})$
the stabilizer of
![]() $0$
. Under the assumption that
$0$
. Under the assumption that
![]() $\mathrm {G}$
is simply connected, the converse (4)
$\mathrm {G}$
is simply connected, the converse (4)
![]() $\Rightarrow $
(2) holds by a Theorem of Mostow [Reference Mostow33], which implies that
$\Rightarrow $
(2) holds by a Theorem of Mostow [Reference Mostow33], which implies that
![]() $\mathrm {H}$
is a closed subgroup. Therefore,
$\mathrm {H}$
is a closed subgroup. Therefore,
![]() $\mathrm {G}/\mathrm {H}$
is a
$\mathrm {G}/\mathrm {H}$
is a
![]() $1$
-dimensional manifold that is simply connected, and so is diffeomorphic to
$1$
-dimensional manifold that is simply connected, and so is diffeomorphic to
![]() $\mathbf {R}$
. The implication (3)
$\mathbf {R}$
. The implication (3)
![]() $\Rightarrow $
(2) is also clear because
$\Rightarrow $
(2) is also clear because
![]() $\mathrm {G}_j$
is given as a group of diffeomorphisms of
$\mathrm {G}_j$
is given as a group of diffeomorphisms of
![]() $\mathbf {R}$
with
$\mathbf {R}$
with
![]() $\Omega _j=\{g \in \mathrm {G}_j\mid g \cdot 0>0\}$
. The converse (2)
$\Omega _j=\{g \in \mathrm {G}_j\mid g \cdot 0>0\}$
. The converse (2)
![]() $\Rightarrow $
(3) follows from Lie’s classification of (local) actions by diffeomorphism on the real line [Reference Lie30]; see also [Reference Tits47] for modern presentations and [Reference Ghys16] for the global aspect. More precisely, the fact that
$\Rightarrow $
(3) follows from Lie’s classification of (local) actions by diffeomorphism on the real line [Reference Lie30]; see also [Reference Tits47] for modern presentations and [Reference Ghys16] for the global aspect. More precisely, the fact that
![]() $g_0$
belongs to the boundary of
$g_0$
belongs to the boundary of
![]() $\Omega $
implies that
$\Omega $
implies that
![]() $0$
is not fixed by
$0$
is not fixed by
![]() $\mathrm {G}$
and – here we use that
$\mathrm {G}$
and – here we use that
![]() $\mathrm {G}$
is connected – the
$\mathrm {G}$
is connected – the
![]() $\mathrm {G}$
-orbit of
$\mathrm {G}$
-orbit of
![]() $0$
is an open interval, so by identifying it with
$0$
is an open interval, so by identifying it with
![]() $\mathbf {R}$
, we can assume that the
$\mathbf {R}$
, we can assume that the
![]() $\mathrm {G}$
-action is transitive. In that case, the image of
$\mathrm {G}$
-action is transitive. In that case, the image of
![]() $\mathrm {G}$
in
$\mathrm {G}$
in
![]() $\mathrm {Diff}(\mathbf {R})$
is one of the three groups in condition (3) of Corollary B1, see [Reference Ghys16, Section 4.1] for the details.
$\mathrm {Diff}(\mathbf {R})$
is one of the three groups in condition (3) of Corollary B1, see [Reference Ghys16, Section 4.1] for the details.
Next, let us focus on the equivalence (1)
![]() $\Leftrightarrow $
(4) for general Lie groups. If we translate
$\Leftrightarrow $
(4) for general Lie groups. If we translate
![]() $\Omega $
by
$\Omega $
by
![]() $g_0^{-1}$
, we may assume that
$g_0^{-1}$
, we may assume that
![]() $g_0=e$
and the tangent space of
$g_0=e$
and the tangent space of
![]() $\mathrm {G}$
at
$\mathrm {G}$
at
![]() $g_0$
identifies with its Lie algebra
$g_0$
identifies with its Lie algebra
![]() $\mathfrak {g}$
. Also, the tangent space of
$\mathfrak {g}$
. Also, the tangent space of
![]() $\partial \Omega $
at
$\partial \Omega $
at
![]() $g_0$
identifies with a codimension
$g_0$
identifies with a codimension
![]() $1$
subspace
$1$
subspace
![]() $\mathfrak h$
of
$\mathfrak h$
of
![]() $\mathfrak g$
. Define the
$\mathfrak g$
. Define the
![]() $\mathcal {C}^1$
-manifold
$\mathcal {C}^1$
-manifold
Its sections
![]() $\widetilde {\Omega }_g$
and
$\widetilde {\Omega }_g$
and
![]() $\widetilde {\Omega }^h$
are left and right translates of the
$\widetilde {\Omega }^h$
are left and right translates of the
![]() $\mathcal {C}^1$
-domain
$\mathcal {C}^1$
-domain
![]() $\Omega $
$\Omega $
In particular,
![]() $\widetilde {\Omega }$
is transverse at every point of its boundary. By Lemma 2.1 and Theorem 3.1, we know that (1) is equivalent to the existence of a neighbourhood of the identity
$\widetilde {\Omega }$
is transverse at every point of its boundary. By Lemma 2.1 and Theorem 3.1, we know that (1) is equivalent to the existence of a neighbourhood of the identity
![]() $U \subset \mathrm {G}$
such that
$U \subset \mathrm {G}$
such that
![]() $\chi _{\widetilde {\Omega }}$
defines a Schur multiplier on
$\chi _{\widetilde {\Omega }}$
defines a Schur multiplier on
![]() $S_p(L_2(U))$
. By Theorem A, this is equivalent to the existence of a neighbourhood of the identity
$S_p(L_2(U))$
. By Theorem A, this is equivalent to the existence of a neighbourhood of the identity
![]() $V \subset \mathrm {G}$
such that both conditions below hold:
$V \subset \mathrm {G}$
such that both conditions below hold:
By the above idenfications (3.1), if we denote by
![]() $L_x,R_x\colon \mathrm {G}\to \mathrm {G}$
the left and right multiplication by x, these conditions are equivalent to the existence of a neighbourhood of the identity W such that
$L_x,R_x\colon \mathrm {G}\to \mathrm {G}$
the left and right multiplication by x, these conditions are equivalent to the existence of a neighbourhood of the identity W such that
Indeed, taking
![]() $x_j = g_j h$
for
$x_j = g_j h$
for
![]() $j=1,2$
we have
$j=1,2$
we have
Composing by
![]() $(d_{x_2} L_{g_2^{-1}})^{-1} = d_h L_{g_2}$
, and using
$(d_{x_2} L_{g_2^{-1}})^{-1} = d_h L_{g_2}$
, and using
![]() $(d_h L_{g_2}) \circ (d_{x_1} L_{g_1^{-1}})= d_{x_1} L_{x_2x_1^{-1}}$
by the chain rule, we see that (3.2) is equivalent to (3.4). The equivalence for right multiplication maps is entirely similar. Next, recalling that
$(d_h L_{g_2}) \circ (d_{x_1} L_{g_1^{-1}})= d_{x_1} L_{x_2x_1^{-1}}$
by the chain rule, we see that (3.2) is equivalent to (3.4). The equivalence for right multiplication maps is entirely similar. Next, recalling that
![]() $T_e \partial \Omega = \mathfrak {h}$
, the above conditions can be written in the equivalent forms:
$T_e \partial \Omega = \mathfrak {h}$
, the above conditions can be written in the equivalent forms:
If we remember that
![]() $\operatorname {\mathrm {Ad}}_x =d_e (R_{x^{-1}} L_x)$
, we obtain that this system is equivalent to
$\operatorname {\mathrm {Ad}}_x =d_e (R_{x^{-1}} L_x)$
, we obtain that this system is equivalent to
![]() $d_{e} L_x(\mathfrak {h}) =T_x \partial \Omega $
and
$d_{e} L_x(\mathfrak {h}) =T_x \partial \Omega $
and
![]() $\operatorname {\mathrm {Ad}}_x \mathfrak {h} = \mathfrak {h}$
for every
$\operatorname {\mathrm {Ad}}_x \mathfrak {h} = \mathfrak {h}$
for every
![]() $x \in \partial \Omega \cap W$
. Therefore, we have proved that (1) at
$x \in \partial \Omega \cap W$
. Therefore, we have proved that (1) at
![]() $g_0=e$
is equivalent to the existence of a neighbourhood of the identity W such that
$g_0=e$
is equivalent to the existence of a neighbourhood of the identity W such that
![]() $T_x \partial \Omega = d_e L_x( \mathfrak {h})$
and
$T_x \partial \Omega = d_e L_x( \mathfrak {h})$
and
![]() $\operatorname {\mathrm {Ad}}_x \mathfrak {h} = \mathfrak {h}$
for every
$\operatorname {\mathrm {Ad}}_x \mathfrak {h} = \mathfrak {h}$
for every
![]() $x \in \partial \Omega \cap W$
. These conditions clearly hold if
$x \in \partial \Omega \cap W$
. These conditions clearly hold if
![]() $\mathfrak {h}$
is a Lie algebra and
$\mathfrak {h}$
is a Lie algebra and
![]() $\partial \Omega $
locally coincides with the exponential of a neighbourhood of
$\partial \Omega $
locally coincides with the exponential of a neighbourhood of
![]() $0$
in
$0$
in
![]() $\mathfrak {h}$
. Conversely, assume
$\mathfrak {h}$
. Conversely, assume
![]() $T_x \partial \Omega = d_e L_x(\mathfrak {h})$
and
$T_x \partial \Omega = d_e L_x(\mathfrak {h})$
and
![]() $\operatorname {\mathrm {Ad}}_x(\mathfrak {h}) = \mathfrak {h}$
for every
$\operatorname {\mathrm {Ad}}_x(\mathfrak {h}) = \mathfrak {h}$
for every
![]() $x \in \partial \Omega \cap W$
. Making x go to the identity element e in the second condition, we deduce that
$x \in \partial \Omega \cap W$
. Making x go to the identity element e in the second condition, we deduce that
![]() $\operatorname {\mathrm {ad}}_{\mathrm {X}}(\mathfrak h) \subset \mathfrak {h}$
for every
$\operatorname {\mathrm {ad}}_{\mathrm {X}}(\mathfrak h) \subset \mathfrak {h}$
for every
![]() $\mathrm {X} \in \mathfrak {h}$
. That is,
$\mathrm {X} \in \mathfrak {h}$
. That is,
![]() $\mathfrak {h}$
is a Lie subalgebra. By the local uniqueness of a manifold in
$\mathfrak {h}$
is a Lie subalgebra. By the local uniqueness of a manifold in
![]() $\mathrm {G}$
containing e and whose tangent space at x is
$\mathrm {G}$
containing e and whose tangent space at x is
![]() $d_e L_x(\mathfrak {h})$
(Frobenius’ theorem), we deduce that
$d_e L_x(\mathfrak {h})$
(Frobenius’ theorem), we deduce that
![]() $\partial \Omega $
is locally the exponential of a neighbourhood of
$\partial \Omega $
is locally the exponential of a neighbourhood of
![]() $0$
in
$0$
in
![]() $\mathfrak {h}$
. This completes the proof.
$\mathfrak {h}$
. This completes the proof.
Remark 3.4. By a partition of the unity argument, the following global form of Theorem 3.3 holds: if
![]() $p \in (1,\infty )\setminus \{2\}$
,
$p \in (1,\infty )\setminus \{2\}$
,
![]() $\mathrm {G}$
is a connected Lie group and
$\mathrm {G}$
is a connected Lie group and
![]() $\Omega \subset \mathrm {G}$
a relatively compact
$\Omega \subset \mathrm {G}$
a relatively compact
![]() $\mathcal {C}^1$
-domain, then
$\mathcal {C}^1$
-domain, then
![]() $\chi _\Omega $
defines a Fourier cb-
$\chi _\Omega $
defines a Fourier cb-
![]() $L_p$
-multiplier if and only if the condition (4) holds for every point
$L_p$
-multiplier if and only if the condition (4) holds for every point
![]() $g_0$
in the boundary of
$g_0$
in the boundary of
![]() $\Omega $
.
$\Omega $
.
Proof of Corollary B2.
Assertion i) follows since the quotient of a nilpotent Lie algebra remains nilpotent, so the nonnilpotent examples in Theorem 3.3 (3) cannot happen when
![]() $\mathrm {G}$
is nilpotent. Assertions ii) and iii) follow immediately from Lie’s classification [Reference Lie30]: up to isomorphism, there is a unique pair
$\mathrm {G}$
is nilpotent. Assertions ii) and iii) follow immediately from Lie’s classification [Reference Lie30]: up to isomorphism, there is a unique pair
![]() $(\mathfrak {h},\mathfrak {g})$
where
$(\mathfrak {h},\mathfrak {g})$
where
![]() $\mathfrak {g}$
is a simple Lie algebra and
$\mathfrak {g}$
is a simple Lie algebra and
![]() $\mathfrak {h}$
is a codimension
$\mathfrak {h}$
is a codimension
![]() $1$
subalgebra. It is given by
$1$
subalgebra. It is given by
![]() $\mathfrak {g}=\mathfrak {sl}_2$
and
$\mathfrak {g}=\mathfrak {sl}_2$
and
![]() $\mathfrak {h}$
the subalgebra of upper-triangular matrices. This completes the proof.
$\mathfrak {h}$
the subalgebra of upper-triangular matrices. This completes the proof.
3.2 Local Fourier-Schur transference
The rest of this paper will be devoted to justify Theorem 3.1. We will sometimes consider the Fourier algebra
![]() $A(\mathrm {G})$
of
$A(\mathrm {G})$
of
![]() $\mathrm {G}$
[Reference Eymard14] – that is,
$\mathrm {G}$
[Reference Eymard14] – that is,
A form of the following lemma was proved in [Reference Parcet, Ricard and de la Salle35, Lemma 1.3] for p an even integer and
![]() $\mathrm {G}$
unimodular, which was enough for the applications there. Here, we need a form valid for every p and every locally compact group.
$\mathrm {G}$
unimodular, which was enough for the applications there. Here, we need a form valid for every p and every locally compact group.
Lemma 3.5. Let
![]() $V,W\subset \mathrm {G}$
be open sets and
$V,W\subset \mathrm {G}$
be open sets and
![]() $g_0 \in V W^{-1}$
. Then, there are a neighbourhood U of
$g_0 \in V W^{-1}$
. Then, there are a neighbourhood U of
![]() $g_0$
, a constant C, and maps
$g_0$
, a constant C, and maps
![]() $J_p\colon L_p(\mathcal {L} \mathrm {G}) \to S_p(L_2(V),L_2(W))$
for
$J_p\colon L_p(\mathcal {L} \mathrm {G}) \to S_p(L_2(V),L_2(W))$
for
![]() $1\leq p\leq \infty $
intertwining Fourier and Herz-Schur multipliers and such that
$1\leq p\leq \infty $
intertwining Fourier and Herz-Schur multipliers and such that
for every
![]() $n\geq 1$
and every
$n\geq 1$
and every
![]() $x \in M_n \otimes L_p(\mathcal {L} \mathrm {G})$
which is Fourier supported in U.
$x \in M_n \otimes L_p(\mathcal {L} \mathrm {G})$
which is Fourier supported in U.
Remark 3.6. The proof of Lemma 3.5 that we present was kindly communicated to us by Éric Ricard. Our original proof was more complicated but worked whenever U is a relatively compact subset of
![]() $V W^{-1}$
. The simpler version above is, however, enough to prove the main implication (c)
$V W^{-1}$
. The simpler version above is, however, enough to prove the main implication (c)
![]() $\Rightarrow $
(a) in Theorem 3.1, and by using a partition of the unity argument in the Fourier algebra of
$\Rightarrow $
(a) in Theorem 3.1, and by using a partition of the unity argument in the Fourier algebra of
![]() $\mathrm {G}$
[Reference Eymard14], it is not hard to deduce that this implication holds actually whenever U is a relatively compact subset of
$\mathrm {G}$
[Reference Eymard14], it is not hard to deduce that this implication holds actually whenever U is a relatively compact subset of
![]() $VW^{-1}$
.
$VW^{-1}$
.
For the reader’s convenience, we first prove Lemma 3.5 and Theorem 3.1 for unimodular groups and explain in the next paragraph how to modify the definition of Fourier multiplier and the argument for nonunimodular groups.
Proof of Lemma 3.5 for
 $\mathrm {G}$
unimodular.
$\mathrm {G}$
unimodular.
Translating V and W, we can assume that the identity belongs to V and W and
![]() $g_0=e$
. Let U be a neighbourhood of e such that
$g_0=e$
. Let U be a neighbourhood of e such that
![]() $U \subset V$
and
$U \subset V$
and
![]() $U^{-1} U \subset W$
. Let
$U^{-1} U \subset W$
. Let
![]() $\phi = \frac {1}{|U|} \chi _U$
and
$\phi = \frac {1}{|U|} \chi _U$
and
![]() $\psi = \chi _{U^{-1} U}$
, so that
$\psi = \chi _{U^{-1} U}$
, so that
Consider the map
where we identify
![]() $\phi ,\psi $
with the operators of multiplication by
$\phi ,\psi $
with the operators of multiplication by
![]() $\phi ,\psi $
. The convention is that
$\phi ,\psi $
. The convention is that
![]() $0^{\frac 1 \infty } = 0$
. We claim that the maps
$0^{\frac 1 \infty } = 0$
. We claim that the maps
![]() $J_p$
are completely bounded with cb-norm
$J_p$
are completely bounded with cb-norm
whenever
![]() $1 \le p \le \infty $
. By interpolation, it is enough to justify the extreme cases
$1 \le p \le \infty $
. By interpolation, it is enough to justify the extreme cases
![]() $p=1$
and
$p=1$
and
![]() $p=\infty $
. The case
$p=\infty $
. The case
![]() $p = \infty $
is clear. For the case
$p = \infty $
is clear. For the case
![]() $p=1$
, we factorize
$p=1$
, we factorize
![]() $x = x_1 x_2$
so that
$x = x_1 x_2$
so that
![]() $J_1(x) = \phi x_1 \cdot x_2 \psi $
. Take them so that
$J_1(x) = \phi x_1 \cdot x_2 \psi $
. Take them so that
![]() $\|x\|_1 = \|x_1\|_2 \|x_2\|_2$
, and it suffices to show that both factors are bounded in
$\|x\|_1 = \|x_1\|_2 \|x_2\|_2$
, and it suffices to show that both factors are bounded in
![]() $S_2(L_2(\mathrm {G})) \simeq L_2(\mathrm {G} \times \mathrm {G})$
by
$S_2(L_2(\mathrm {G})) \simeq L_2(\mathrm {G} \times \mathrm {G})$
by
![]() $\|\phi \|_{L_2(\mathrm {G})} \|x_1\|_{L_2(\mathcal {L} \mathrm {G})}$
and
$\|\phi \|_{L_2(\mathrm {G})} \|x_1\|_{L_2(\mathcal {L} \mathrm {G})}$
and
![]() $\|\psi \|_{L_2(\mathrm {G})} \|x_2\|_{L_2(\mathcal {L} \mathrm {G})}$
, respectively. Using that
$\|\psi \|_{L_2(\mathrm {G})} \|x_2\|_{L_2(\mathcal {L} \mathrm {G})}$
, respectively. Using that
the expected bounds follow from Plancherel theorem
![]() $L_2 (\mathcal {L} \mathrm {G}) \simeq L_2(\mathrm {G})$
. Moreover when
$L_2 (\mathcal {L} \mathrm {G}) \simeq L_2(\mathrm {G})$
. Moreover when
![]() $x= \lambda (f)$
, the operator
$x= \lambda (f)$
, the operator
![]() $J_p(x)$
has kernel
$J_p(x)$
has kernel
![]() $(\phi (g)^{1/p} f(gh^{-1}) \psi (h)^{1/p})$
. Thus, it is clear that the map
$(\phi (g)^{1/p} f(gh^{-1}) \psi (h)^{1/p})$
. Thus, it is clear that the map
![]() $J_p$
intertwines the Fourier multiplier with symbol
$J_p$
intertwines the Fourier multiplier with symbol
![]() $g \mapsto m(g)$
and the Schur multiplier with symbol
$g \mapsto m(g)$
and the Schur multiplier with symbol
![]() $(g,h) \mapsto m(gh^{-1})$
.
$(g,h) \mapsto m(gh^{-1})$
.
The inequality
![]() $C^{-1}\|x\|_p \leq \|J_p(x)\|_p$
is a bit more involved. Let
$C^{-1}\|x\|_p \leq \|J_p(x)\|_p$
is a bit more involved. Let
![]() $f \in M_n \otimes \mathcal {C}_c(U)$
with
$f \in M_n \otimes \mathcal {C}_c(U)$
with
![]() $\lambda (f) \in L_p(M_n \otimes \mathcal {L} \mathrm {G})$
and assume that
$\lambda (f) \in L_p(M_n \otimes \mathcal {L} \mathrm {G})$
and assume that
![]() $x = \lambda (f)$
by density. Let q be the conjugate exponent of p and
$x = \lambda (f)$
by density. Let q be the conjugate exponent of p and
![]() $\gamma \in M_n \otimes \mathcal {C}_c(\mathrm {G})$
with
$\gamma \in M_n \otimes \mathcal {C}_c(\mathrm {G})$
with
![]() $\lambda (\gamma ) \in L_q(M_n \otimes \mathcal {L} \mathrm {G})$
. Then we have
$\lambda (\gamma ) \in L_q(M_n \otimes \mathcal {L} \mathrm {G})$
. Then we have
 $$ \begin{align*} \operatorname{\mathrm{Tr}} \otimes \operatorname{\mathrm{Tr}}_n \big( J_p(\lambda(f)) J_{q} (\lambda(\gamma))^* \big) & = \operatorname{\mathrm{Tr}}_n \int_{\mathrm{G} \times \mathrm{G}} \phi(g) f \gamma^*(gh^{-1}) \psi(h) ds dt\\ & = \int_{\mathrm{G}} \operatorname{\mathrm{Tr}}_n \big( f(g) \gamma(g)^* \big) \Big[ \int_{\mathrm{G}} \phi(gh) \psi(h) \, dh \Big] \, dg\\ & = \int_{\mathrm{G}} \operatorname{\mathrm{Tr}}_n \big( f(g) \gamma(g)^* \big) \, dg = \tau\otimes \operatorname{\mathrm{Tr}}_n \big( \lambda(f) \lambda(\gamma)^* \big). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Tr}} \otimes \operatorname{\mathrm{Tr}}_n \big( J_p(\lambda(f)) J_{q} (\lambda(\gamma))^* \big) & = \operatorname{\mathrm{Tr}}_n \int_{\mathrm{G} \times \mathrm{G}} \phi(g) f \gamma^*(gh^{-1}) \psi(h) ds dt\\ & = \int_{\mathrm{G}} \operatorname{\mathrm{Tr}}_n \big( f(g) \gamma(g)^* \big) \Big[ \int_{\mathrm{G}} \phi(gh) \psi(h) \, dh \Big] \, dg\\ & = \int_{\mathrm{G}} \operatorname{\mathrm{Tr}}_n \big( f(g) \gamma(g)^* \big) \, dg = \tau\otimes \operatorname{\mathrm{Tr}}_n \big( \lambda(f) \lambda(\gamma)^* \big). \end{align*} $$
In the last line, we used that
![]() $\int _{\mathrm {G}} \phi (gh) \psi (h) \, dh=1$
on
$\int _{\mathrm {G}} \phi (gh) \psi (h) \, dh=1$
on
![]() $\mathrm {supp} f \subset U$
. By Hölder’s inequality, we get
$\mathrm {supp} f \subset U$
. By Hölder’s inequality, we get
 $$ \begin{align*} \big| \tau\otimes \operatorname{\mathrm{Tr}}_n( \lambda(f) \lambda(\gamma)^*) \big| & \leq \|J_p(\lambda(f))\|_p \|J_q(\lambda(\gamma)\|_q\\ & \leq \|J_q\|_{\mathrm{cb}} \|J_p(\lambda(f))\|_p \|\lambda(\gamma)\|_q\\ & \leq \|J_q\|_{\mathrm{cb}} \|\lambda(\gamma)\|_q \|J_p(\lambda(f))\|_p. \end{align*} $$
$$ \begin{align*} \big| \tau\otimes \operatorname{\mathrm{Tr}}_n( \lambda(f) \lambda(\gamma)^*) \big| & \leq \|J_p(\lambda(f))\|_p \|J_q(\lambda(\gamma)\|_q\\ & \leq \|J_q\|_{\mathrm{cb}} \|J_p(\lambda(f))\|_p \|\lambda(\gamma)\|_q\\ & \leq \|J_q\|_{\mathrm{cb}} \|\lambda(\gamma)\|_q \|J_p(\lambda(f))\|_p. \end{align*} $$
Taking the sup over
![]() $\gamma $
, we get
$\gamma $
, we get
![]() $C^{-1}\|x\|_p \leq \|J_p(x)\|_p$
for
$C^{-1}\|x\|_p \leq \|J_p(x)\|_p$
for
![]() $C = \|J_q\|_{\mathrm {cb}}< \infty $
.
$C = \|J_q\|_{\mathrm {cb}}< \infty $
.
With the same argument as in [Reference Parcet, Ricard and de la Salle35], we deduce the following:
Proof of Theorem 3.1.
The implication (a)
![]() $\Rightarrow $
(b) is easy. Indeed, if (a) holds and
$\Rightarrow $
(b) is easy. Indeed, if (a) holds and
![]() $\varphi \in A(\mathrm {G})$
is supported in U and equal to
$\varphi \in A(\mathrm {G})$
is supported in U and equal to
![]() $1$
on a neighbourhood of
$1$
on a neighbourhood of
![]() $g_0$
(for the construction of
$g_0$
(for the construction of
![]() $\varphi $
, see the proof of Lemma 3.5), then
$\varphi $
, see the proof of Lemma 3.5), then
![]() $T_\varphi $
is completely bounded on
$T_\varphi $
is completely bounded on
![]() $L_p(\mathcal {L} \mathrm {G})$
for every
$L_p(\mathcal {L} \mathrm {G})$
for every
![]() $1 \leq p \leq \infty $
, and takes values in the space of elements Fourier supported in U. In particular,
$1 \leq p \leq \infty $
, and takes values in the space of elements Fourier supported in U. In particular,
![]() $T_{m\varphi } = T_{m,U}\circ T_\varphi $
is also completely bounded. The implication (b)
$T_{m\varphi } = T_{m,U}\circ T_\varphi $
is also completely bounded. The implication (b)
![]() $\Rightarrow $
(c) follows from [Reference Caspers and de la Salle7, Theorem 4.2], which implies that
$\Rightarrow $
(c) follows from [Reference Caspers and de la Salle7, Theorem 4.2], which implies that
defines a completely bounded Fourier
![]() $L_p$
-multiplier. Thus, we get (c) if
$L_p$
-multiplier. Thus, we get (c) if
![]() $V,W$
are chosen so that
$V,W$
are chosen so that
![]() $\varphi =1$
on
$\varphi =1$
on
![]() $V W^{-1}$
. Finally, (c)
$V W^{-1}$
. Finally, (c)
![]() $\Rightarrow $
(a) follows from Lemma 3.5.
$\Rightarrow $
(a) follows from Lemma 3.5.
3.3 Nonunimodular groups
Let
![]() $\mathrm {G}$
be an arbitrary locally compact group with modular function
$\mathrm {G}$
be an arbitrary locally compact group with modular function
![]() $\Delta \colon \mathrm {G} \to \mathbf {R}_+$
. Our choice of
$\Delta \colon \mathrm {G} \to \mathbf {R}_+$
. Our choice of
![]() $\Delta $
is characterized by the following identity for all
$\Delta $
is characterized by the following identity for all
![]() $f \in \mathcal {C}_c(\mathrm {G})$
$f \in \mathcal {C}_c(\mathrm {G})$
When
![]() $\mathrm {G}$
is not unimodular – that is,
$\mathrm {G}$
is not unimodular – that is,
![]() $\Delta $
is not the constant
$\Delta $
is not the constant
![]() $1$
function – the natural weight
$1$
function – the natural weight
![]() $\lambda (f)^* \lambda (f) \mapsto \int |f|^2$
on
$\lambda (f)^* \lambda (f) \mapsto \int |f|^2$
on
![]() $\mathcal {L} \mathrm {G}$
is not tracial. Even when
$\mathcal {L} \mathrm {G}$
is not tracial. Even when
![]() $\mathcal {L} \mathrm {G}$
is semifinite, it is better to work with the general definition of
$\mathcal {L} \mathrm {G}$
is semifinite, it is better to work with the general definition of
![]() $L_p$
spaces associated to a von Neumann algebra. Several concrete descriptions are possible: Haagerup’s original one [Reference Haagerup21], Kosaki’s complex interpolation [Reference Kosaki26], Connes-Hilsum’s [Reference Connes12, Reference Hilsum23]…; see [Reference Pisier, Xu, Johnson and Lindenstrauss43]. Here, we will use the Connes-Hilsum spatial description because we want to rely on some results from [Reference Caspers and de la Salle7, Reference Terp46], to which we refer for precise definitions. In that case,
$L_p$
spaces associated to a von Neumann algebra. Several concrete descriptions are possible: Haagerup’s original one [Reference Haagerup21], Kosaki’s complex interpolation [Reference Kosaki26], Connes-Hilsum’s [Reference Connes12, Reference Hilsum23]…; see [Reference Pisier, Xu, Johnson and Lindenstrauss43]. Here, we will use the Connes-Hilsum spatial description because we want to rely on some results from [Reference Caspers and de la Salle7, Reference Terp46], to which we refer for precise definitions. In that case,
![]() $L_p(\mathcal {L} \mathrm {G})$
is realized as a space of unbounded operators on
$L_p(\mathcal {L} \mathrm {G})$
is realized as a space of unbounded operators on
![]() $L_2(\mathrm {G})$
.
$L_2(\mathrm {G})$
.
In [Reference Caspers and de la Salle7], Caspers and the second-named author defined Fourier
![]() $L_p$
-multipliers for symbols that ensure that the Fourier multiplier is completely bounded for every
$L_p$
-multipliers for symbols that ensure that the Fourier multiplier is completely bounded for every
![]() $1 \leq p \leq \infty $
. Here, we extend the definition, allowing to talk about Fourier multipliers for a single p, and possibly only bounded. The shortest way to do so properly in this context is by using Terp’s Hausdorff-Young inequality [Reference Terp46].
$1 \leq p \leq \infty $
. Here, we extend the definition, allowing to talk about Fourier multipliers for a single p, and possibly only bounded. The shortest way to do so properly in this context is by using Terp’s Hausdorff-Young inequality [Reference Terp46].
Informally, a typical element of
![]() $L_p(\mathcal {L} \mathrm {G})$
is of the form
$L_p(\mathcal {L} \mathrm {G})$
is of the form
![]() $\lambda (f) \Delta ^{\frac 1 p}$
– where we are identifying the function
$\lambda (f) \Delta ^{\frac 1 p}$
– where we are identifying the function
![]() $\Delta $
with the densely defined operator of multiplication by
$\Delta $
with the densely defined operator of multiplication by
![]() $\Delta $
on
$\Delta $
on
![]() $L_2(\mathrm {G})$
– for some suitable function f. Keeping at the informal level, the Fourier multiplier with symbol
$L_2(\mathrm {G})$
– for some suitable function f. Keeping at the informal level, the Fourier multiplier with symbol
![]() $m \colon \mathrm {G}\to \mathbf {C}$
should be, whenever it exists, the operator acting as follows:
$m \colon \mathrm {G}\to \mathbf {C}$
should be, whenever it exists, the operator acting as follows:
Making this definition precise requires some lengthy and unpleasant discussions about domains/cores of unbounded operators, but fortunately, we can rely on the results from [Reference Terp46], where these discussions have been performed. We shall need to distinguish the cases
![]() $p\geq 2$
and
$p\geq 2$
and
![]() $p \leq 2$
. Let
$p \leq 2$
. Let
![]() $q=\frac {p}{p-1}$
be the conjugate exponent of p. When
$q=\frac {p}{p-1}$
be the conjugate exponent of p. When
![]() $p\geq 2$
, the Fourier transform
$p\geq 2$
, the Fourier transform
is an injective norm
![]() $1$
linear map with dense image, where
$1$
linear map with dense image, where
![]() $\mathcal {F}_q(f)$
is defined as a suitable extension of
$\mathcal {F}_q(f)$
is defined as a suitable extension of
![]() $\lambda (f) \Delta ^{1/p}$
; see [Reference Terp46, Theorem 4.5]. When
$\lambda (f) \Delta ^{1/p}$
; see [Reference Terp46, Theorem 4.5]. When
![]() $p\leq 2$
, the adjoint of
$p\leq 2$
, the adjoint of
![]() $\mathcal {F}_p$
gives a norm
$\mathcal {F}_p$
gives a norm
![]() $1$
injective map with dense image
$1$
injective map with dense image
![]() $\overline {\mathcal F}_p\colon L_p(\mathcal {L} \mathrm {G}) \to L_q(\mathrm {G})$
. If
$\overline {\mathcal F}_p\colon L_p(\mathcal {L} \mathrm {G}) \to L_q(\mathrm {G})$
. If
![]() $I_q$
denotes the isometry of
$I_q$
denotes the isometry of
![]() $L_q(\mathrm {G})$
defined by
$L_q(\mathrm {G})$
defined by
![]() $I_q(f)(g) = f(g^{-1}) \Delta (g)^{-1/q}$
, we know from [Reference Terp46, Proposition 1.15] that every element x of
$I_q(f)(g) = f(g^{-1}) \Delta (g)^{-1/q}$
, we know from [Reference Terp46, Proposition 1.15] that every element x of
![]() $L_p(\mathcal {L} \mathrm {G})$
is a suitable extension of
$L_p(\mathcal {L} \mathrm {G})$
is a suitable extension of
![]() $\lambda (f) \Delta ^{1/p}$
for
$\lambda (f) \Delta ^{1/p}$
for
![]() $f = I_q \circ \overline {\mathcal F}_p(x) \in L_q(\mathrm {G})$
. In the particular case
$f = I_q \circ \overline {\mathcal F}_p(x) \in L_q(\mathrm {G})$
. In the particular case
![]() $p=2$
, these two statements together yield Plancherel’s formula:
$p=2$
, these two statements together yield Plancherel’s formula:
![]() $\mathcal F_2$
is a unitary. If
$\mathcal F_2$
is a unitary. If
![]() $p=1$
, the image of
$p=1$
, the image of
![]() $\overline {\mathcal {F}}_1$
is the Fourier algebra
$\overline {\mathcal {F}}_1$
is the Fourier algebra
![]() $A(\mathrm {G})$
, and following standard notation, we write
$A(\mathrm {G})$
, and following standard notation, we write
Definition 3.7. Let
![]() $1 < p < \infty $
and
$1 < p < \infty $
and
![]() $m \in L_\infty (\mathrm {G})$
. We say that m defines a bounded Fourier
$m \in L_\infty (\mathrm {G})$
. We say that m defines a bounded Fourier
![]() $L_p$
-multiplier when the condition below holds according to the value of
$L_p$
-multiplier when the condition below holds according to the value of
![]() $p \hskip -2pt:$
$p \hskip -2pt:$
-
• Case
 $p \geq 2$
. The map (densely defined on
$p \geq 2$
. The map (densely defined on $$\begin{align*}\mathcal{F}_{q}(f) \mapsto \mathcal{F}_{q}(mf)\end{align*}$$
$$\begin{align*}\mathcal{F}_{q}(f) \mapsto \mathcal{F}_{q}(mf)\end{align*}$$
 $\mathcal {F}_q( L_q(\mathrm {G}))$
) extends to a bounded map
$\mathcal {F}_q( L_q(\mathrm {G}))$
) extends to a bounded map
 $T_m$
on
$T_m$
on
 $L_p(\mathcal {L} \mathrm {G})$
.
$L_p(\mathcal {L} \mathrm {G})$
.
-
• Case
 $p \leq 2$
. The multiplication by m preserves the image of
$p \leq 2$
. The multiplication by m preserves the image of
 $I_q \circ \overline {\mathcal F}_p$
when the map
$I_q \circ \overline {\mathcal F}_p$
when the map
 $T_m:x\mapsto (I_q \circ \overline {\mathcal F}_p)^{-1}( m (I_q \circ \overline {\mathcal F}_p(x)))$
is a bounded map on
$T_m:x\mapsto (I_q \circ \overline {\mathcal F}_p)^{-1}( m (I_q \circ \overline {\mathcal F}_p(x)))$
is a bounded map on
 $L_p(\mathcal {L} \mathrm {G})$
.
$L_p(\mathcal {L} \mathrm {G})$
.
We say that m defines a completely bounded Fourier
![]() $L_p$
-multiplier when m defines a bounded Fourier
$L_p$
-multiplier when m defines a bounded Fourier
![]() $L_p$
-multiplier and the Fourier multiplier
$L_p$
-multiplier and the Fourier multiplier
![]() $T_m$
is completely bounded.
$T_m$
is completely bounded.
It follows from the above definition that m defines a (completely) bounded
![]() $L_p$
multiplier if and only it defines a (completely) bounded
$L_p$
multiplier if and only it defines a (completely) bounded
![]() $L_q$
multiplier, and in that case,
$L_q$
multiplier, and in that case,
Once we have polished the definition of Fourier
![]() $L_p$
-multipliers in nonunimodular group von Neumann algebras, we can extend a Cotlar identity from [Reference González-Pérez, Parcet and Xia19] to arbitrary locally compact groups.
$L_p$
-multipliers in nonunimodular group von Neumann algebras, we can extend a Cotlar identity from [Reference González-Pérez, Parcet and Xia19] to arbitrary locally compact groups.
Example 3.8. Let
![]() $\mathrm {G} \to \mathrm {Homeo}_+(\mathbf {R})$
be a continuous action of a connected Lie group. Then, the indicator function m of
$\mathrm {G} \to \mathrm {Homeo}_+(\mathbf {R})$
be a continuous action of a connected Lie group. Then, the indicator function m of
![]() $\{g \in \mathrm {G} \mid g \cdot 0>0\}$
defines a completely bounded
$\{g \in \mathrm {G} \mid g \cdot 0>0\}$
defines a completely bounded
![]() $L_p$
Fourier multiplier on G with completely bounded norm
$L_p$
Fourier multiplier on G with completely bounded norm
![]() $\leq 2 \max \{p,\frac {p}{p-1}\}$
.
$\leq 2 \max \{p,\frac {p}{p-1}\}$
.
Proof. Let m be the indicator function of
![]() $\{g \in \mathrm {G} \mid g \cdot 0>0\}$
. It suffices to prove the following implication for every
$\{g \in \mathrm {G} \mid g \cdot 0>0\}$
. It suffices to prove the following implication for every
![]() $2 \leq p<\infty $
: if m defines a completely bounded Fourier
$2 \leq p<\infty $
: if m defines a completely bounded Fourier
![]() $L_p$
-multiplier with norm
$L_p$
-multiplier with norm
![]() $\leq C_p$
, then it defines a completely bounded Fourier
$\leq C_p$
, then it defines a completely bounded Fourier
![]() $L_{2p}$
-multiplier with norm
$L_{2p}$
-multiplier with norm
![]() $\leq 2 C_p$
. Indeed, using that
$\leq 2 C_p$
. Indeed, using that
![]() $C_2=\|m\|_\infty =1$
, we deduce
$C_2=\|m\|_\infty =1$
, we deduce
![]() $C_{2^N} \leq 2^N$
for every integer N, so by interpolation,
$C_{2^N} \leq 2^N$
for every integer N, so by interpolation,
![]() $C_p \leq 2p$
for all
$C_p \leq 2p$
for all
![]() $p\geq 2$
. By duality, the conclusion also holds for
$p\geq 2$
. By duality, the conclusion also holds for
![]() $p\leq 2$
.
$p\leq 2$
.
Let r be the dual exponent of
![]() $2p$
. Let
$2p$
. Let
![]() $f \in \mathcal {C}_c(\mathrm {G})$
and consider
$f \in \mathcal {C}_c(\mathrm {G})$
and consider
![]() $X =\mathcal {F}_r(f)$
and
$X =\mathcal {F}_r(f)$
and
![]() $Y=\mathcal F_r(mf)$
; these are well-defined elements of
$Y=\mathcal F_r(mf)$
; these are well-defined elements of
![]() $L_{2p}(\mathcal {L} G)$
by [Reference Terp46]. Then, we claim that the equality below holds:
$L_{2p}(\mathcal {L} G)$
by [Reference Terp46]. Then, we claim that the equality below holds:
Indeed, this inequality is equivalent to the almost everywhere equality
which follows for the fact that
![]() $m(g^{-1}) m(g^{-1}h) = m(h) m(g^{-1}) + m(h^{-1})m(g^{-1}h)$
for almost every
$m(g^{-1}) m(g^{-1}h) = m(h) m(g^{-1}) + m(h^{-1})m(g^{-1}h)$
for almost every
![]() $g,h \in \mathrm {G}$
. If the whole group
$g,h \in \mathrm {G}$
. If the whole group
![]() $\mathrm {G}$
fixes
$\mathrm {G}$
fixes
![]() $0$
, this is obvious because m is identically
$0$
, this is obvious because m is identically
![]() $0$
. Otherwise, the stabilizer of
$0$
. Otherwise, the stabilizer of
![]() $0$
is a closed subgroup, so it has measure
$0$
is a closed subgroup, so it has measure
![]() $0$
and it is enough to justify the equality for
$0$
and it is enough to justify the equality for
![]() $h \cdot 0 \neq 0$
. Set
$h \cdot 0 \neq 0$
. Set
![]() $(\alpha ,\beta ) = (g \cdot 0 ,h \cdot 0)$
and observe that
$(\alpha ,\beta ) = (g \cdot 0 ,h \cdot 0)$
and observe that
![]() $m(g^{-1}) m(g^{-1}h)=1$
if and only if
$m(g^{-1}) m(g^{-1}h)=1$
if and only if
![]() $\alpha < \min \{0, \beta \}$
. Similarly, we have
$\alpha < \min \{0, \beta \}$
. Similarly, we have
![]() $m(h) m(g^{-1}) = 1$
iff
$m(h) m(g^{-1}) = 1$
iff
![]() $\alpha < 0 < \beta $
and
$\alpha < 0 < \beta $
and
![]() $m(h^{-1})m(g^{-1}h)=1$
iff
$m(h^{-1})m(g^{-1}h)=1$
iff
![]() $\alpha < \beta < 0$
. Therefore, the expected identity reduces to the trivial one
$\alpha < \beta < 0$
. Therefore, the expected identity reduces to the trivial one
![]() $\chi _{\alpha < 0 \wedge \beta } = \chi _{\alpha < 0 < \beta } + \chi _{\alpha < \beta < 0}$
. This justifies (3.9), both sides of which are in
$\chi _{\alpha < 0 \wedge \beta } = \chi _{\alpha < 0 < \beta } + \chi _{\alpha < \beta < 0}$
. This justifies (3.9), both sides of which are in
![]() $L_{p}(\mathcal {L} \mathrm {G})$
. Thus, taking the norm and applying the triangle inequality, the hypothesis and Hölder’s inequality leads to
$L_{p}(\mathcal {L} \mathrm {G})$
. Thus, taking the norm and applying the triangle inequality, the hypothesis and Hölder’s inequality leads to
We deduce
![]() $\|Y\|_{2p} \leq 2 C_{p} \|X\|_{2p}$
. Since
$\|Y\|_{2p} \leq 2 C_{p} \|X\|_{2p}$
. Since
![]() $\mathcal {C}_c(\mathrm {G})$
is dense in
$\mathcal {C}_c(\mathrm {G})$
is dense in
![]() $L_r(\mathrm {G})$
, we obtain that m defines a Fourier
$L_r(\mathrm {G})$
, we obtain that m defines a Fourier
![]() $L_{2p}$
-multiplier with norm
$L_{2p}$
-multiplier with norm
![]() $\leq 2C_p$
. A similar argument gives the same bound for the completely bounded norm, which concludes the proof.
$\leq 2C_p$
. A similar argument gives the same bound for the completely bounded norm, which concludes the proof.
Remark 3.9. The Cotlar-type identity from [Reference González-Pérez, Parcet and Xia19] is refined in some cases by (3.9).
The following summarizes the properties that we need.
Lemma 3.10. Let
![]() $1 \leq p \leq \infty $
and consider functions
$1 \leq p \leq \infty $
and consider functions
![]() $\phi ,\psi \in L_{2p}(\mathrm {G})$
, which we identify with
$\phi ,\psi \in L_{2p}(\mathrm {G})$
, which we identify with
![]() $($
possibly unbounded
$($
possibly unbounded
![]() $)$
multiplication operators on
$)$
multiplication operators on
![]() $L_2(\mathrm {G})$
. Then
$L_2(\mathrm {G})$
. Then
![]() $\hskip 1pt $
$\hskip 1pt $
-
• Given
 $x\in L_{2p}(\mathcal {L} \mathrm {G})$
,
$x\in L_{2p}(\mathcal {L} \mathrm {G})$
,
 $x \phi $
is densely defined and closable. In fact, its closure
$x \phi $
is densely defined and closable. In fact, its closure
 $[x\phi ]$
belongs to
$[x\phi ]$
belongs to
 $S_{2p}(L_2(\mathrm {G}))$
and has
$S_{2p}(L_2(\mathrm {G}))$
and has
 $S_{2p}$
-norm
$S_{2p}$
-norm
 $\leq \|\phi \|_{L_{2p}(\mathrm {G})} \|x\|_{L_{2p}(\mathcal {L} \mathrm {G})}$
.
$\leq \|\phi \|_{L_{2p}(\mathrm {G})} \|x\|_{L_{2p}(\mathcal {L} \mathrm {G})}$
. -
• There exists a bounded linear map
 $L_p(\mathcal {L} \mathrm {G}) \to S_p(L_2(\mathrm {G}))$
Footnote 3 sending
$L_p(\mathcal {L} \mathrm {G}) \to S_p(L_2(\mathrm {G}))$
Footnote 3 sending
 $y^* x$
to
$y^* x$
to
 $[y \psi ^*]^* [x \phi ]$
for every
$[y \psi ^*]^* [x \phi ]$
for every
 $x,y \in L_{2p}(\mathcal {L} \mathrm {G})$
. It has norm
$x,y \in L_{2p}(\mathcal {L} \mathrm {G})$
. It has norm
 $\leq \|\phi \|_{L_{2p}(\mathrm {G})} \|\psi \|_{L_{2p}(\mathrm {G})}$
.
$\leq \|\phi \|_{L_{2p}(\mathrm {G})} \|\psi \|_{L_{2p}(\mathrm {G})}$
. -
• If q denotes the conjugate exponent of p, consider
 $\phi ',\psi ' \in L_{2q}(\mathrm {G})$
and
$\phi ',\psi ' \in L_{2q}(\mathrm {G})$
and
 $y \in L_{q}(\mathcal {L} \mathrm {G})$
. Then, we have (3.10)where
$y \in L_{q}(\mathcal {L} \mathrm {G})$
. Then, we have (3.10)where $$ \begin{align} \operatorname{\mathrm{Tr}} \big( \phi x \psi (\phi' y \psi')^* \big) = \operatorname{\mathrm{tr}}( T_m(x) y^*), \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Tr}} \big( \phi x \psi (\phi' y \psi')^* \big) = \operatorname{\mathrm{tr}}( T_m(x) y^*), \end{align} $$
 $m \in A(\mathrm {G})$
is the function
$m \in A(\mathrm {G})$
is the function
 $\displaystyle m(g) = \int _{\mathrm {G}} (\phi \overline {\phi '})(h) (\psi \overline {\psi '})(g^{-1} h) \, dh$
.
$\displaystyle m(g) = \int _{\mathrm {G}} (\phi \overline {\phi '})(h) (\psi \overline {\psi '})(g^{-1} h) \, dh$
.
Proof. When
![]() $\phi =\psi $
are indicator functions, the first two points were proved in [Reference Caspers and de la Salle7, Proposition 3.3, Theorem 5.2]. The same argument applies in our case. Let us justify identity (3.10). First, observe that
$\phi =\psi $
are indicator functions, the first two points were proved in [Reference Caspers and de la Salle7, Proposition 3.3, Theorem 5.2]. The same argument applies in our case. Let us justify identity (3.10). First, observe that
![]() $\phi \overline {\phi '}$
and
$\phi \overline {\phi '}$
and
![]() $\psi \overline {\phi '}$
belong to
$\psi \overline {\phi '}$
belong to
![]() $L_2(\mathrm {G})$
by Hölder’s inequality, so that m indeed belongs to
$L_2(\mathrm {G})$
by Hölder’s inequality, so that m indeed belongs to
![]() $A(\mathrm {G})$
. In particular, m defines a completely bounded
$A(\mathrm {G})$
. In particular, m defines a completely bounded
![]() $L_1$
and
$L_1$
and
![]() $L_\infty $
Fourier multiplier. Thus, it also defines a Fourier
$L_\infty $
Fourier multiplier. Thus, it also defines a Fourier
![]() $L_p$
-multiplier [Reference Caspers and de la Salle7, Definition-Proposition 3.5]. Therefore, by interpolation [Reference Caspers and de la Salle7, Section 6], it suffices to prove (3.10) for
$L_p$
-multiplier [Reference Caspers and de la Salle7, Definition-Proposition 3.5]. Therefore, by interpolation [Reference Caspers and de la Salle7, Section 6], it suffices to prove (3.10) for
![]() $p=1$
and
$p=1$
and
![]() $p=\infty $
. These two cases are formally equivalent, and we just consider
$p=\infty $
. These two cases are formally equivalent, and we just consider
![]() $p=\infty $
. In that case,
$p=\infty $
. In that case,
![]() $y\in L_1(\mathcal {L} \mathrm {G})$
corresponds to an element
$y\in L_1(\mathcal {L} \mathrm {G})$
corresponds to an element
![]() $f \in A(\mathrm {G})$
and
$f \in A(\mathrm {G})$
and
![]() $\phi ' y \psi '$
is the trace class operator with kernel
$\phi ' y \psi '$
is the trace class operator with kernel
see [Reference Caspers and de la Salle7, Lemma 3.4]. By a weak-
![]() $*$
density argument, it is enough to prove (3.10) for
$*$
density argument, it is enough to prove (3.10) for
![]() $x=\lambda (g_0)$
for some
$x=\lambda (g_0)$
for some
![]() $g_0 \in \mathrm {G}$
. In that case,
$g_0 \in \mathrm {G}$
. In that case,
![]() $T_m(x) = m(g_0) \lambda (g_0)$
and we obtain
$T_m(x) = m(g_0) \lambda (g_0)$
and we obtain
![]() $\operatorname {\mathrm {tr}}( T_m(x) y^*) = m(g_0) \overline {f(g_0^{-1})}$
. We can compute
$\operatorname {\mathrm {tr}}( T_m(x) y^*) = m(g_0) \overline {f(g_0^{-1})}$
. We can compute
 $$ \begin{align*} \operatorname{\mathrm{Tr}} \big( \phi x \psi (\phi' y \psi')^* \big) & = \operatorname{\mathrm{Tr}} \big( \lambda(g_0) \psi \overline{\psi'} y^* \phi \overline{\phi'} \big) \\ [5pt] & = \operatorname{\mathrm{Tr}} \Big[ \Big( \psi \overline{\psi'})(g_0^{-1}g) \overline{f(g_0^{-1} g h^{-1} )} (\phi \overline{\phi'})(h) \Big)_{g,h \in \mathrm{G}} \Big]\\ & = \int_{\mathrm{G}} (\psi \overline{\psi'})(g_0^{-1}g) \overline{f(g_0^{-1})} (\phi \overline{\phi'})(g) \, dg = m(g_0) \overline{f(g_0^{-1})}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Tr}} \big( \phi x \psi (\phi' y \psi')^* \big) & = \operatorname{\mathrm{Tr}} \big( \lambda(g_0) \psi \overline{\psi'} y^* \phi \overline{\phi'} \big) \\ [5pt] & = \operatorname{\mathrm{Tr}} \Big[ \Big( \psi \overline{\psi'})(g_0^{-1}g) \overline{f(g_0^{-1} g h^{-1} )} (\phi \overline{\phi'})(h) \Big)_{g,h \in \mathrm{G}} \Big]\\ & = \int_{\mathrm{G}} (\psi \overline{\psi'})(g_0^{-1}g) \overline{f(g_0^{-1})} (\phi \overline{\phi'})(g) \, dg = m(g_0) \overline{f(g_0^{-1})}. \end{align*} $$
This justifies the identity (3.10) and completes the proof of the lemma.
Lemma 3.10 allows us to adapt the proof of Lemma 3.5 from the unimodular case.
Proof of Lemma 3.5, general case.
We take
![]() $\phi ,\psi \in \mathcal {C}_c(\mathrm {G})$
as in the proof in the unimodular case, and set
$\phi ,\psi \in \mathcal {C}_c(\mathrm {G})$
as in the proof in the unimodular case, and set
![]() $m(g) = \int \phi (gh) \psi (h) dh$
. By Lemma 3.10, we can define completely bounded maps
$m(g) = \int \phi (gh) \psi (h) dh$
. By Lemma 3.10, we can define completely bounded maps
which intertwine Fourier and Schur multipliers. Now, if
![]() $x \in L_p(M_n \otimes \mathcal {L} \mathrm {G})$
is Fourier supported in U and
$x \in L_p(M_n \otimes \mathcal {L} \mathrm {G})$
is Fourier supported in U and
![]() $y \in L_q(M_n \otimes \mathcal {L} \mathrm {G})$
– for q being the dual exponent of p – we get
$y \in L_q(M_n \otimes \mathcal {L} \mathrm {G})$
– for q being the dual exponent of p – we get
 $$ \begin{align*} \operatorname{\mathrm{tr}}(x y^*) & = \operatorname{\mathrm{tr}}\big( T_{m}(x) y^*\big) = \operatorname{\mathrm{Tr}} \big( J_p(x) J_q (y)^* \big)\\ & \leq \|J_p(x)\|_{S_p} \|J_q(y)\|_{S_q} \leq \|J_q\|_{\mathrm{cb}} \|y\|_{L_q(\mathcal{L} \mathrm{G})} \|J_p(x)\|_{S_p}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{tr}}(x y^*) & = \operatorname{\mathrm{tr}}\big( T_{m}(x) y^*\big) = \operatorname{\mathrm{Tr}} \big( J_p(x) J_q (y)^* \big)\\ & \leq \|J_p(x)\|_{S_p} \|J_q(y)\|_{S_q} \leq \|J_q\|_{\mathrm{cb}} \|y\|_{L_q(\mathcal{L} \mathrm{G})} \|J_p(x)\|_{S_p}. \end{align*} $$
The first line is because
![]() $m=1$
on U and x is Fourier supported in U, and by (3.10). The last line is Hölder’s inequality. Taking suprema over y in the unit ball of
$m=1$
on U and x is Fourier supported in U, and by (3.10). The last line is Hölder’s inequality. Taking suprema over y in the unit ball of
![]() $L_q(\mathcal {L} \mathrm {G})$
gives
$L_q(\mathcal {L} \mathrm {G})$
gives
![]() $\|x\|_{L_p(\mathcal {L} \mathrm {G})} \leq \|J_q\|_{\mathrm {cb}} \|J_p(x)\|_{S_p}$
.
$\|x\|_{L_p(\mathcal {L} \mathrm {G})} \leq \|J_q\|_{\mathrm {cb}} \|J_p(x)\|_{S_p}$
.
3.4 The group
 $\mathrm {SL}_2(\mathbf {R})$
$\mathrm {SL}_2(\mathbf {R})$
Consider the symbol
 $$\begin{align*}m_0 \Big[ \begin{pmatrix} a & b\\c&d \end{pmatrix} \Big] = \frac12 \Big( 1 + \mathrm{sgn} (ac+bd) \Big).\end{align*}$$
$$\begin{align*}m_0 \Big[ \begin{pmatrix} a & b\\c&d \end{pmatrix} \Big] = \frac12 \Big( 1 + \mathrm{sgn} (ac+bd) \Big).\end{align*}$$
This was identified in [Reference González-Pérez, Parcet and Xia19] as the canonical Hilbert transform (Riesz projection would be more accurate though) in
![]() $\mathrm {SL}_2(\mathbf {Z})$
. Its complete
$\mathrm {SL}_2(\mathbf {Z})$
. Its complete
![]() $L_p$
-boundedness follows for
$L_p$
-boundedness follows for
![]() $1 < p < \infty $
from a Cotlar-type identity. The same problem in
$1 < p < \infty $
from a Cotlar-type identity. The same problem in
![]() $\mathrm {SL}_2(\mathbf {R})$
was left open in [Reference González-Pérez, Parcet and Xia19, Problem A]. Now this is solved by condition (4) in Theorem 3.3, which disproves cb-
$\mathrm {SL}_2(\mathbf {R})$
was left open in [Reference González-Pérez, Parcet and Xia19, Problem A]. Now this is solved by condition (4) in Theorem 3.3, which disproves cb-
![]() $L_p$
-boundedness for any
$L_p$
-boundedness for any
![]() $p \neq 2$
. However, according to Corollary B2, the map
$p \neq 2$
. However, according to Corollary B2, the map
 $$\begin{align*}m (g) = m \Big[ \begin{pmatrix} a & b\\c&d \end{pmatrix} \Big] := \frac12 \big( 1 + \mathrm{sgn}(c) \big) = m_0 (gg^{\mathrm{t}}) \end{align*}$$
$$\begin{align*}m (g) = m \Big[ \begin{pmatrix} a & b\\c&d \end{pmatrix} \Big] := \frac12 \big( 1 + \mathrm{sgn}(c) \big) = m_0 (gg^{\mathrm{t}}) \end{align*}$$
does define, locally at every point of its boundary, a completely bounded Fourier
![]() $L_p$
-multiplier for every
$L_p$
-multiplier for every
![]() $1<p<\infty $
. But, is it globally
$1<p<\infty $
. But, is it globally
![]() $L_p$
-bounded? Is it completely
$L_p$
-bounded? Is it completely
![]() $L_p$
-bounded as well? We leave these problems open for future attempts.
$L_p$
-bounded as well? We leave these problems open for future attempts.
3.5 Stratified Lie groups
A Lie algebra
![]() $\mathfrak {g}$
is called graded when there exists a finite family of subspaces
$\mathfrak {g}$
is called graded when there exists a finite family of subspaces
![]() $\mathrm {W}_1, \mathrm {W}_2, \ldots , \mathrm {W}_N$
of the Lie algebra satisfying conditions below:
$\mathrm {W}_1, \mathrm {W}_2, \ldots , \mathrm {W}_N$
of the Lie algebra satisfying conditions below:
 $$\begin{align*}\mathfrak{g} = \bigoplus_{j = 1}^N \mathrm{W}_j \qquad \text{and} \qquad [\mathrm{W}_j, \mathrm{W}_k] \subset \mathrm{W}_{j+k}.\end{align*}$$
$$\begin{align*}\mathfrak{g} = \bigoplus_{j = 1}^N \mathrm{W}_j \qquad \text{and} \qquad [\mathrm{W}_j, \mathrm{W}_k] \subset \mathrm{W}_{j+k}.\end{align*}$$
A simply connected Lie group
![]() $\mathrm {G}$
is called stratified when its Lie algebra
$\mathrm {G}$
is called stratified when its Lie algebra
![]() $\mathfrak {g}$
is graded and the first stratum
$\mathfrak {g}$
is graded and the first stratum
![]() $\mathrm {W}_1$
generates
$\mathrm {W}_1$
generates
![]() $\mathfrak {g}$
as an algebra. Stratified Lie groups are nilpotent and include, among many other examples, Heisenberg groups. According to Corollary B2, idempotent multipliers are of the form
$\mathfrak {g}$
as an algebra. Stratified Lie groups are nilpotent and include, among many other examples, Heisenberg groups. According to Corollary B2, idempotent multipliers are of the form
![]() $R \circ \varphi $
, for the classical Riesz projection
$R \circ \varphi $
, for the classical Riesz projection
![]() $R = \frac 12 (iH + \mathrm {id})$
and some continuous homomorphism
$R = \frac 12 (iH + \mathrm {id})$
and some continuous homomorphism
![]() $\varphi : \mathrm {G} \to \mathbf {R}$
. A quick look at Theorem 3.3 shows that
$\varphi : \mathrm {G} \to \mathbf {R}$
. A quick look at Theorem 3.3 shows that
![]() $\varphi $
corresponds on the Lie algebra with the projection onto any 1-dimensional subspace of the first stratum, since codimension 1 Lie subalgebras are exactly those codimension 1 subspaces leaving out a vector in the first stratum.
$\varphi $
corresponds on the Lie algebra with the projection onto any 1-dimensional subspace of the first stratum, since codimension 1 Lie subalgebras are exactly those codimension 1 subspaces leaving out a vector in the first stratum.
Competing interest
The authors have no competing interests to declare.
Financial support
The research of JP and ET was partially supported by the Spanish Research Grant PID2022-141354NB-I00 ‘Fronteras del Análisis Armónico’ (MCIN) as well as Severo Ochoa Grant CEX2019-000904-S (ICMAT), funded by MCIN/AEI 10.13039/501100011033. The research of MdlS was partially supported by the Charles Simonyi Endowment at the Institute for Advanced Study, and the ANR projects ANCG ANR-19-CE40-0002 and PLAGE ANR-24-CE40-3137. ET was supported as well by Spanish Ministry of Universities with a FPU Grant with reference FPU19/00837.