No CrossRef data available.
Article contents
Efficiency of reversible MCMC methods: elementary derivations and applications to composite methods
Published online by Cambridge University Press: 18 September 2024
Abstract
We review criteria for comparing the efficiency of Markov chain Monte Carlo (MCMC) methods with respect to the asymptotic variance of estimates of expectations of functions of state, and show how such criteria can justify ways of combining improvements to MCMC methods. We say that a chain on a finite state space with transition matrix P efficiency-dominates one with transition matrix Q if for every function of state it has lower (or equal) asymptotic variance. We give elementary proofs of some previous results regarding efficiency dominance, leading to a self-contained demonstration that a reversible chain with transition matrix P efficiency-dominates a reversible chain with transition matrix Q if and only if none of the eigenvalues of 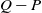 $Q-P$ are negative. This allows us to conclude that modifying a reversible MCMC method to improve its efficiency will also improve the efficiency of a method that randomly chooses either this or some other reversible method, and to conclude that improving the efficiency of a reversible update for one component of state (as in Gibbs sampling) will improve the overall efficiency of a reversible method that combines this and other updates. It also explains how antithetic MCMC can be more efficient than independent and identically distributed sampling. We also establish conditions that can guarantee that a method is not efficiency-dominated by any other method.
$Q-P$ are negative. This allows us to conclude that modifying a reversible MCMC method to improve its efficiency will also improve the efficiency of a method that randomly chooses either this or some other reversible method, and to conclude that improving the efficiency of a reversible update for one component of state (as in Gibbs sampling) will improve the overall efficiency of a reversible method that combines this and other updates. It also explains how antithetic MCMC can be more efficient than independent and identically distributed sampling. We also establish conditions that can guarantee that a method is not efficiency-dominated by any other method.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust



