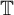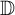1 Introduction
Let E be a closed subset of the unit circle
![]() $\mathbb {T} = \{ z \in \mathbb {C} : |z| = 1 \}$
of the complex plane
$\mathbb {T} = \{ z \in \mathbb {C} : |z| = 1 \}$
of the complex plane
![]() $\mathbb {C}$
, and let the notation
$\mathbb {C}$
, and let the notation
![]() $dm$
stand for the Lebesgue measure, normalized by the condition
$dm$
stand for the Lebesgue measure, normalized by the condition
![]() $m(\mathbb {T}) = 1$
. The following question has been studied by Khrushchev in [Reference Khrushchev12]. What conditions on the set E guarantee the existence of a nonzero measurable function h supported on E for which the Cauchy transform, or Cauchy integral,
$m(\mathbb {T}) = 1$
. The following question has been studied by Khrushchev in [Reference Khrushchev12]. What conditions on the set E guarantee the existence of a nonzero measurable function h supported on E for which the Cauchy transform, or Cauchy integral,
 $$ \begin{align} C_{h1_E}(z) := \int_{\mathbb{T}} \frac{h(\zeta)1_E(\zeta)}{1-z\overline{\zeta}} dm(\zeta) = \int_E \frac{h(\zeta)}{1-z\overline{\zeta}} dm(\zeta), \quad z \in \mathbb{D}, \end{align} $$
$$ \begin{align} C_{h1_E}(z) := \int_{\mathbb{T}} \frac{h(\zeta)1_E(\zeta)}{1-z\overline{\zeta}} dm(\zeta) = \int_E \frac{h(\zeta)}{1-z\overline{\zeta}} dm(\zeta), \quad z \in \mathbb{D}, \end{align} $$
which is an analytic function in the unit disk
![]() $\mathbb {D} = \{ z \in \mathbb {C} : |z| < 1 \}$
, can be smoothly extended to the closed disk
$\mathbb {D} = \{ z \in \mathbb {C} : |z| < 1 \}$
, can be smoothly extended to the closed disk
![]() $\overline {\mathbb {D}}$
? In the above formula, and throughout the article,
$\overline {\mathbb {D}}$
? In the above formula, and throughout the article,
![]() $1_E$
denotes the indicator function of the set E.
$1_E$
denotes the indicator function of the set E.
For the question to be interesting, the set E should contain no arc A of
![]() $\mathbb {T}$
. Indeed, if E contains an arc A, then certainly any function
$\mathbb {T}$
. Indeed, if E contains an arc A, then certainly any function
![]() $s :\mathbb {T} \to \mathbb {C}$
in
$s :\mathbb {T} \to \mathbb {C}$
in
![]() $C^{\infty }$
with support on A will be transformed into a function
$C^{\infty }$
with support on A will be transformed into a function
![]() $C_s$
which is a member of
$C_s$
which is a member of
![]() $\mathcal {A}^{\infty }$
. Here,
$\mathcal {A}^{\infty }$
. Here,
![]() $\mathcal {A}^{\infty }$
denotes the algebra of analytic functions in
$\mathcal {A}^{\infty }$
denotes the algebra of analytic functions in
![]() $\mathbb {D}$
for which the derivatives of any order extend continuously to
$\mathbb {D}$
for which the derivatives of any order extend continuously to
![]() $\overline {\mathbb {D}}$
. The containment
$\overline {\mathbb {D}}$
. The containment
![]() $C_s \in \mathcal {A}^{\infty }$
follows in this case readily from the rapid rate of decay of Fourier coefficients
$C_s \in \mathcal {A}^{\infty }$
follows in this case readily from the rapid rate of decay of Fourier coefficients
![]() $\{s_n\}_n$
of the smooth function s, and the fact that
$\{s_n\}_n$
of the smooth function s, and the fact that
![]() $C_s(z) = \sum _{n=0}^{\infty } s_nz^n$
.
$C_s(z) = \sum _{n=0}^{\infty } s_nz^n$
.
By
![]() $\mathcal {A}$
, we will denote the class of analytic functions in
$\mathcal {A}$
, we will denote the class of analytic functions in
![]() $\mathbb {D}$
which admit a continuous extension to
$\mathbb {D}$
which admit a continuous extension to
![]() $\overline {\mathbb {D}}$
, and by
$\overline {\mathbb {D}}$
, and by
![]() $\mathcal {A}^n$
we denote those functions for which the nth derivative admits such an extension, that is,
$\mathcal {A}^n$
we denote those functions for which the nth derivative admits such an extension, that is,
![]() $f^{(n)} \in \mathcal {A}$
. Thus,
$f^{(n)} \in \mathcal {A}$
. Thus,
![]() $\mathcal {A}^{\infty } = \cap _{n \geq 1} \mathcal {A}^n$
. Khrushchev in [Reference Khrushchev12] has solved the existence part of the above stated problem in full. For a general closed set E, he establishes the existence of a nonzero measurable function h, with support only on E, such that
$\mathcal {A}^{\infty } = \cap _{n \geq 1} \mathcal {A}^n$
. Khrushchev in [Reference Khrushchev12] has solved the existence part of the above stated problem in full. For a general closed set E, he establishes the existence of a nonzero measurable function h, with support only on E, such that
![]() $C_h$
given by (1.1) is in the class
$C_h$
given by (1.1) is in the class
![]() $\mathcal {A}$
. Moreover, he proves that there exists a nonzero measurable function h supported on E for which the transform (1.1) is a function in
$\mathcal {A}$
. Moreover, he proves that there exists a nonzero measurable function h supported on E for which the transform (1.1) is a function in
![]() $\mathcal {A}^{\infty }$
essentially if and only if E contains a Beurling–Carleson set of positive Lebesgue measure. A set E is a Beurling–Carleson set if it is closed and if the condition
$\mathcal {A}^{\infty }$
essentially if and only if E contains a Beurling–Carleson set of positive Lebesgue measure. A set E is a Beurling–Carleson set if it is closed and if the condition
is satisfied, where
![]() $\{A_n\}_n$
is the system of disjoint open subarcs of
$\{A_n\}_n$
is the system of disjoint open subarcs of
![]() $\mathbb {T}$
union of which equals the complement
$\mathbb {T}$
union of which equals the complement
![]() $\mathbb {T} \setminus E$
, and
$\mathbb {T} \setminus E$
, and
![]() $|A|$
denotes the length of the arc A. The class of Beurling–Carleson sets has a rich history, and appears notably in the solution of boundary zero set problems for smooth analytic functions, and zero set problems for Bergman spaces (see, for instance, Carleson’s paper [Reference Carleson5] and Korenblum’s paper [Reference Korenblum14]). In [Reference Limani and Malman18], the present authors found that Beurling–Carleson sets play an important role in smooth approximation theory in de Branges–Rovnyak spaces, another classical and well-studied family of Hilbert spaces of analytic functions.
$|A|$
denotes the length of the arc A. The class of Beurling–Carleson sets has a rich history, and appears notably in the solution of boundary zero set problems for smooth analytic functions, and zero set problems for Bergman spaces (see, for instance, Carleson’s paper [Reference Carleson5] and Korenblum’s paper [Reference Korenblum14]). In [Reference Limani and Malman18], the present authors found that Beurling–Carleson sets play an important role in smooth approximation theory in de Branges–Rovnyak spaces, another classical and well-studied family of Hilbert spaces of analytic functions.
A notable feature of the proofs of the abovementioned results of Khrushchev in [Reference Khrushchev12] is that they are non-constructive. One of the aims of this article is to show that, in the case in which Beurling–Carleson sets and the class
![]() $\mathcal {A}^{\infty }$
are involved, the theorem of Khrushchev can be obtained in a rather elementary and explicit way by using modifications of other known constructions.
$\mathcal {A}^{\infty }$
are involved, the theorem of Khrushchev can be obtained in a rather elementary and explicit way by using modifications of other known constructions.
Theorem A Let E be a Beurling–Carleson set of positive Lebesgue measure.Then there exists an explicit formula for a measurable function
![]() $h = h1_E$
for which the Cauchy transform given by (
1.1
) belongs to
$h = h1_E$
for which the Cauchy transform given by (
1.1
) belongs to
![]() $\mathcal {A}^{\infty }$
.
$\mathcal {A}^{\infty }$
.
The above result is established in Section 3 as a special case of Proposition 3.1, which deals with a slightly more general situation, and which will be useful for our further applications. We remark that the very interesting problem of giving an explicit formula for h supported on any given closed set E such that
![]() $C_{h1_E}$
is in
$C_{h1_E}$
is in
![]() $\mathcal {A}$
remains open, and the approach presented here is not applicable.
$\mathcal {A}$
remains open, and the approach presented here is not applicable.
Our ultimate application of the construction of smooth Cauchy transforms is to the approximation theory in de Branges–Rovnyak spaces
![]() $\mathcal {H}(b)$
. For background on the theory of
$\mathcal {H}(b)$
. For background on the theory of
![]() $\mathcal {H}(b)$
-spaces, see [Reference Fricain and Mashreghi6, Reference Fricain and Mashreghi7, Reference Sarason21]. A basic problem in the theory is to identify what functions are contained in the space
$\mathcal {H}(b)$
-spaces, see [Reference Fricain and Mashreghi6, Reference Fricain and Mashreghi7, Reference Sarason21]. A basic problem in the theory is to identify what functions are contained in the space
![]() $\mathcal {H}(b)$
and how this depends on the structure of the symbol b, which is any analytic function mapping the disk
$\mathcal {H}(b)$
and how this depends on the structure of the symbol b, which is any analytic function mapping the disk
![]() $\mathbb {D}$
into itself. It has been established by Sarason (see [Reference Sarason21]) that the analytic polynomials are contained and norm-dense in the space
$\mathbb {D}$
into itself. It has been established by Sarason (see [Reference Sarason21]) that the analytic polynomials are contained and norm-dense in the space
![]() $\mathcal {H}(b)$
if and only if the weight
$\mathcal {H}(b)$
if and only if the weight
has an integrable logarithm on
![]() $\mathbb {T}$
:
$\mathbb {T}$
:
Moreover, it is also known that any
![]() $\mathcal {H}(b)$
-space contains a dense subset of functions in
$\mathcal {H}(b)$
-space contains a dense subset of functions in
![]() $\mathcal {A}$
(see [Reference Aleman and Malman2]). In particular, considering the usual inner–outer factorization of
$\mathcal {A}$
(see [Reference Aleman and Malman2]). In particular, considering the usual inner–outer factorization of
![]() $b = \theta b_0$
into an inner function
$b = \theta b_0$
into an inner function
![]() $\theta $
and an outer function
$\theta $
and an outer function
![]() $b_0$
, the inner factor
$b_0$
, the inner factor
![]() $\theta $
plays no role in the context of approximations by analytic polynomials or functions continuous up to the boundary. The situation is different in the context of approximations by functions in the class
$\theta $
plays no role in the context of approximations by analytic polynomials or functions continuous up to the boundary. The situation is different in the context of approximations by functions in the class
![]() $\mathcal {A}^{\infty }$
or
$\mathcal {A}^{\infty }$
or
![]() $\mathcal {A}^n$
, or even the Hölder classes. A combination of results in [Reference Limani and Malman16, Reference Limani and Malman18] shows that the functions in the class
$\mathcal {A}^n$
, or even the Hölder classes. A combination of results in [Reference Limani and Malman16, Reference Limani and Malman18] shows that the functions in the class
![]() $\mathcal {A}^n$
will be dense in the space
$\mathcal {A}^n$
will be dense in the space
![]() $\mathcal {H}(b)$
if the outer factor of b is “good” and the “bad” part of the singularities of the inner factor of b is appropriately located on
$\mathcal {H}(b)$
if the outer factor of b is “good” and the “bad” part of the singularities of the inner factor of b is appropriately located on
![]() $\mathbb {T}$
, with respect to the outer factor. More precisely, it was found in [Reference Aleman and Malman2] that if weight
$\mathbb {T}$
, with respect to the outer factor. More precisely, it was found in [Reference Aleman and Malman2] that if weight
![]() $\Delta $
appearing above is of the form
$\Delta $
appearing above is of the form
where each set
![]() $E_n$
is a Beurling–Carleson set of positive Lebesgue measure, and each
$E_n$
is a Beurling–Carleson set of positive Lebesgue measure, and each
![]() $w_n$
is a nonnegative weight satisfying
$w_n$
is a nonnegative weight satisfying
then the functions in
![]() $\mathcal {A}^n$
are dense in
$\mathcal {A}^n$
are dense in
![]() $\mathcal {H}(b)$
if b is outer. Note that the two conditions above say something about the “good” structure of the support set of the weight
$\mathcal {H}(b)$
if b is outer. Note that the two conditions above say something about the “good” structure of the support set of the weight
![]() $\Delta $
(being a union of “good” sets satisfying the Beurling–Carleson condition), and something about
$\Delta $
(being a union of “good” sets satisfying the Beurling–Carleson condition), and something about
![]() $\Delta $
not being too small on the support. In [Reference Limani and Malman18], examples are highlighted in which bad support and small size of
$\Delta $
not being too small on the support. In [Reference Limani and Malman18], examples are highlighted in which bad support and small size of
![]() $\Delta $
both independently prohibit such approximations in
$\Delta $
both independently prohibit such approximations in
![]() $\mathcal {H}(b)$
, not only by functions in
$\mathcal {H}(b)$
, not only by functions in
![]() $\mathcal {A}^{\infty }$
, but even by functions in the Hölder classes. In the presence of a nontrivial inner factor
$\mathcal {A}^{\infty }$
, but even by functions in the Hölder classes. In the presence of a nontrivial inner factor
![]() $\theta = BS_{\nu }$
of b, where B is a Blaschke product and
$\theta = BS_{\nu }$
of b, where B is a Blaschke product and
![]() $S_{\nu }$
is a singular inner function, results of [Reference Limani and Malman16, Reference Limani and Malman18] show that what matters is the location on
$S_{\nu }$
is a singular inner function, results of [Reference Limani and Malman16, Reference Limani and Malman18] show that what matters is the location on
![]() $\mathbb {T}$
of the support of a certain part of the singular measure
$\mathbb {T}$
of the support of a certain part of the singular measure
![]() $\nu $
. To describe this mechanism, we will need to introduce a simple decomposition of the measure
$\nu $
. To describe this mechanism, we will need to introduce a simple decomposition of the measure
![]() $\nu $
, which has appeared already in a similar context in [Reference Limani and Malman17] and also in work of Roberts in [Reference Roberts20]. Namely, the measure
$\nu $
, which has appeared already in a similar context in [Reference Limani and Malman17] and also in work of Roberts in [Reference Roberts20]. Namely, the measure
![]() $\nu $
can be expressed as a sum
$\nu $
can be expressed as a sum
where the two measures are mutually singular, there exists an increasing sequence of Beurling–Carleson sets of Lebesgue measure zero
![]() $\{F_n\}_{n \geq 1}$
such that
$\{F_n\}_{n \geq 1}$
such that
and
for any Beurling–Carleson set F of Lebesgue measure zero. The part
![]() $\nu _{\mathcal {C}}$
plays no role in our approximation problem. However, the support of
$\nu _{\mathcal {C}}$
plays no role in our approximation problem. However, the support of
![]() $\nu _{\mathcal {K}}$
must necessarily be located on the support of
$\nu _{\mathcal {K}}$
must necessarily be located on the support of
![]() $\Delta $
for approximations by smooth functions to be possible. Moreover, if the conditions (1.5) and (1.6) are satisfied and the mass of
$\Delta $
for approximations by smooth functions to be possible. Moreover, if the conditions (1.5) and (1.6) are satisfied and the mass of
![]() $\nu _{\mathcal {K}}$
is located appropriately in the sense that
$\nu _{\mathcal {K}}$
is located appropriately in the sense that
then indeed functions in the class
![]() $\mathcal {A}^n$
are dense in
$\mathcal {A}^n$
are dense in
![]() $\mathcal {H}(b)$
. This was established by a duality argument in [Reference Limani and Malman18], using also the results of [Reference Limani and Malman16]. We will sharpen this result by proving density of functions in
$\mathcal {H}(b)$
. This was established by a duality argument in [Reference Limani and Malman18], using also the results of [Reference Limani and Malman16]. We will sharpen this result by proving density of functions in
![]() $\mathcal {A}^{\infty }$
. Thus, we will prove (using duality) the following approximation result, which is the strongest that we are aware of.
$\mathcal {A}^{\infty }$
. Thus, we will prove (using duality) the following approximation result, which is the strongest that we are aware of.
Theorem B Let
![]() $b: \mathbb {D} \to \mathbb {D}$
be an analytic function with singular inner factor
$b: \mathbb {D} \to \mathbb {D}$
be an analytic function with singular inner factor
![]() $S_{\nu }$
such that the weight
$S_{\nu }$
such that the weight
![]() $\Delta $
given by (
1.3
) has the form (
1.5
) for some sequence
$\Delta $
given by (
1.3
) has the form (
1.5
) for some sequence
![]() $\{E_n\}_n$
of Beurling–Carleson sets of positive measure and satisfies (
1.6
) and such that the part
$\{E_n\}_n$
of Beurling–Carleson sets of positive measure and satisfies (
1.6
) and such that the part
![]() $\nu _{\mathcal {K}}$
in the decomposition (
1.7
) of
$\nu _{\mathcal {K}}$
in the decomposition (
1.7
) of
![]() $\nu $
satisfies (
1.8
). Then
$\nu $
satisfies (
1.8
). Then
![]() $\mathcal {A}^{\infty } \cap \mathcal {H}(b)$
is norm-dense in
$\mathcal {A}^{\infty } \cap \mathcal {H}(b)$
is norm-dense in
![]() $\mathcal {H}(b)$
.
$\mathcal {H}(b)$
.
A more detailed exposition of why this approximation result is close to the best possible also appears in [Reference Limani and Malman18].
The proof of Theorem B presented here is long, but it is self-contained and the constructive proof of the theorem of Khrushchev mentioned above plays a crucial role in our development. In [Reference Limani and Malman18], a duality approach to the smooth approximation problem in
![]() $\mathcal {H}(b)$
is presented, and it is based on a connection with two problems in analysis which are of independent interest: an operator irreducibility problem and an inner factor permanence problem. We will need to study both of these problems in detail to prove Theorem B.
$\mathcal {H}(b)$
is presented, and it is based on a connection with two problems in analysis which are of independent interest: an operator irreducibility problem and an inner factor permanence problem. We will need to study both of these problems in detail to prove Theorem B.
In Section 5, we deal with the irreducibility problem. Let X be some space of functions defined on a domain in the complex plane which contains the analytic polynomials and is invariant under the forward shift operator
![]() $M_z : f(z) \mapsto zf(z)$
, where z is the coordinate function (or identity function) of the complex plane. We denote by D the closure of the analytic polynomials in X. In many important cases, the functions in X live on the closed unit disk
$M_z : f(z) \mapsto zf(z)$
, where z is the coordinate function (or identity function) of the complex plane. We denote by D the closure of the analytic polynomials in X. In many important cases, the functions in X live on the closed unit disk
![]() $\overline {\mathbb {D}}$
, the operator
$\overline {\mathbb {D}}$
, the operator
![]() $M_z$
is a contraction (in the sense that
$M_z$
is a contraction (in the sense that
![]() $\|M_zf\|_X \leq \|f\|_X$
holds for all
$\|M_zf\|_X \leq \|f\|_X$
holds for all
![]() $f \in X$
), and a question or assumption which appears in several contexts (see, for instance, [Reference Aleman and Malman2, Reference Aleman, Richter and Sundberg3, Reference Kriete and MacCluer15]) is related to the existence of invariant subspaces of the operator
$f \in X$
), and a question or assumption which appears in several contexts (see, for instance, [Reference Aleman and Malman2, Reference Aleman, Richter and Sundberg3, Reference Kriete and MacCluer15]) is related to the existence of invariant subspaces of the operator
![]() $M_z: D \to D$
on which it acts as an isometry. In the particular case
$M_z: D \to D$
on which it acts as an isometry. In the particular case
![]() $X = L^2(\mu )$
, where
$X = L^2(\mu )$
, where
![]() $\mu $
is a positive Borel measure compactly supported in the complex plane, the closure of analytic polynomials is usually denoted by
$\mu $
is a positive Borel measure compactly supported in the complex plane, the closure of analytic polynomials is usually denoted by
![]() $\mathcal {P}^2(\mu )$
. If
$\mathcal {P}^2(\mu )$
. If
![]() $\mu $
is a positive measure of the form
$\mu $
is a positive measure of the form
(
![]() $dA$
and
$dA$
and
![]() $d\textit {m}$
being the area measure of
$d\textit {m}$
being the area measure of
![]() $\mathbb {D}$
and Lebesgue measure of
$\mathbb {D}$
and Lebesgue measure of
![]() $\mathbb {T}$
, respectively), then the condition that
$\mathbb {T}$
, respectively), then the condition that
![]() $M_z$
is completely nonisometric on the closure of polynomials
$M_z$
is completely nonisometric on the closure of polynomials
![]() $D := \mathcal {P}^2(\mu )$
is precisely the condition which ensures that
$D := \mathcal {P}^2(\mu )$
is precisely the condition which ensures that
![]() $\mathcal {P}^2(\mu )$
can be identified with a genuine space of analytic functions in
$\mathcal {P}^2(\mu )$
can be identified with a genuine space of analytic functions in
![]() $\mathbb {D}$
. If not, then
$\mathbb {D}$
. If not, then
![]() $\mathcal {P}^2(\mu )$
will contain as a subset a space of the form
$\mathcal {P}^2(\mu )$
will contain as a subset a space of the form
![]() $L^2(1_Fd\textit {m})$
, for some measurable subset F of E, on which
$L^2(1_Fd\textit {m})$
, for some measurable subset F of E, on which
![]() $M_z$
obviously acts as an isometry. In the context of
$M_z$
obviously acts as an isometry. In the context of
![]() $\mathcal {P}^2(\mu )$
-spaces, the nonexistence of a subspaces of the type
$\mathcal {P}^2(\mu )$
-spaces, the nonexistence of a subspaces of the type
![]() $L^2(1_Fd\textit {m})$
goes under the name of irreducibility (see [Reference Aleman, Richter and Sundberg3, Reference Thomson24]). It is known that if E is a Beurling–Carleson set, then the corresponding shift operator will be completely nonisometric on
$L^2(1_Fd\textit {m})$
goes under the name of irreducibility (see [Reference Aleman, Richter and Sundberg3, Reference Thomson24]). It is known that if E is a Beurling–Carleson set, then the corresponding shift operator will be completely nonisometric on
![]() $\mathcal {P}^2(\mu )$
. This follows essentially from Khrushchev’s work in [Reference Khrushchev12]. However, if we replace
$\mathcal {P}^2(\mu )$
. This follows essentially from Khrushchev’s work in [Reference Khrushchev12]. However, if we replace
![]() $dA$
by a weighted version
$dA$
by a weighted version
![]() $\rho \,dA$
in (1.9), where
$\rho \,dA$
in (1.9), where
![]() $\rho $
is some function which decays rapidly to zero near the boundary of
$\rho $
is some function which decays rapidly to zero near the boundary of
![]() $\mathbb {D}$
, or if we replace E by a set more complicated than a Beurling–Carleson set, then it might very well happen that
$\mathbb {D}$
, or if we replace E by a set more complicated than a Beurling–Carleson set, then it might very well happen that
![]() $M_z$
admits an invariant subspace on which it acts as an isometry (see [Reference Kriete and MacCluer15] and in particular [Reference Khrushchev12] for details). In Section 5, we construct a special family of smooth Cauchy transforms and employ it in a functional analytic argument to establish that
$M_z$
admits an invariant subspace on which it acts as an isometry (see [Reference Kriete and MacCluer15] and in particular [Reference Khrushchev12] for details). In Section 5, we construct a special family of smooth Cauchy transforms and employ it in a functional analytic argument to establish that
![]() $M_z$
is completely nonisometric on a wide range of Hilbert spaces of analytic functions which are structurally similar to the
$M_z$
is completely nonisometric on a wide range of Hilbert spaces of analytic functions which are structurally similar to the
![]() $\mathcal {P}^2(\mu )$
-spaces discussed here, but much bigger. More precisely, we will work with spaces which we denote below by
$\mathcal {P}^2(\mu )$
-spaces discussed here, but much bigger. More precisely, we will work with spaces which we denote below by
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
and which we will equip with a norm defined on an analytic polynomial
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
and which we will equip with a norm defined on an analytic polynomial
![]() $p(z) = \sum _k p_kz^k$
by
$p(z) = \sum _k p_kz^k$
by
 $$ \begin{align} \|p\|^2_{\mathcal{D}(\boldsymbol{\alpha}^{-1}, w)} := \sum_k \frac{|p_k|^2}{\alpha_k} + \int_E |p|^2 w\,d\textit{m}, \end{align} $$
$$ \begin{align} \|p\|^2_{\mathcal{D}(\boldsymbol{\alpha}^{-1}, w)} := \sum_k \frac{|p_k|^2}{\alpha_k} + \int_E |p|^2 w\,d\textit{m}, \end{align} $$
for some rapidly increasing positive sequence
![]() $\boldsymbol {\alpha } = \{\alpha _k\}_k$
and a Beurling–Carleson set E with weight w. Our development in particular implies the abovementioned results for
$\boldsymbol {\alpha } = \{\alpha _k\}_k$
and a Beurling–Carleson set E with weight w. Our development in particular implies the abovementioned results for
![]() $\mathcal {P}^2(\mu )$
-spaces, and even their extensions from [Reference Limani and Malman16], but the method of proof is completely different, arguably much more straightforward, and the result actually reaches further. We remark that a wealth of information on the behavior of
$\mathcal {P}^2(\mu )$
-spaces, and even their extensions from [Reference Limani and Malman16], but the method of proof is completely different, arguably much more straightforward, and the result actually reaches further. We remark that a wealth of information on the behavior of
![]() $\mathcal {P}^2(\mu )$
-spaces which are spaces of analytic functions can be found in [Reference Aleman, Richter and Sundberg3].
$\mathcal {P}^2(\mu )$
-spaces which are spaces of analytic functions can be found in [Reference Aleman, Richter and Sundberg3].
In Section 6, we will study the inner factor permanence problem. In the problem setting, we let
![]() $\mathcal {H}$
be a space of analytic
$\mathcal {H}$
be a space of analytic
![]() $\mathbb {D}$
which includes at least
$\mathbb {D}$
which includes at least
![]() $H^{\infty }$
, the algebra of bounded analytic functions. Assume that
$H^{\infty }$
, the algebra of bounded analytic functions. Assume that
![]() $\mathcal {H}$
carries a norm (or at least some other type of topological structure) and we have a convergent sequence of the form
$\mathcal {H}$
carries a norm (or at least some other type of topological structure) and we have a convergent sequence of the form
where
![]() $\theta $
is an inner function, and all other appearing functions are bounded and analytic in
$\theta $
is an inner function, and all other appearing functions are bounded and analytic in
![]() $\mathbb {D}$
. Then, in particular, f admits an inner–outer factorization
$\mathbb {D}$
. Then, in particular, f admits an inner–outer factorization
![]() $f = IU$
into an inner function I and an outer function U. We ask: is I divisible by
$f = IU$
into an inner function I and an outer function U. We ask: is I divisible by
![]() $\theta $
? In other words, does the inner factor
$\theta $
? In other words, does the inner factor
![]() $\theta $
get passed onto the limit
$\theta $
get passed onto the limit
![]() $f \in H^{\infty }$
in the metric induced by the norm
$f \in H^{\infty }$
in the metric induced by the norm
![]() $\| \cdot \|_{\mathcal {H}}$
? We will call this property permanence of an inner function
$\| \cdot \|_{\mathcal {H}}$
? We will call this property permanence of an inner function
![]() $\theta $
in the corresponding metric. The problem is only interesting for singular inner functions, since a Blaschke product B will be passed onto the limit in any reasonable norm defined on analytic functions. In the context of the usual
$\theta $
in the corresponding metric. The problem is only interesting for singular inner functions, since a Blaschke product B will be passed onto the limit in any reasonable norm defined on analytic functions. In the context of the usual
![]() $L^2$
-norm computed on the circle, it is of course well known that any inner function
$L^2$
-norm computed on the circle, it is of course well known that any inner function
![]() $\theta $
satisfies the permanence property, but for many other metrics, a more interesting situation occurs. Here, a principal set of examples consists of the weighted
$\theta $
satisfies the permanence property, but for many other metrics, a more interesting situation occurs. Here, a principal set of examples consists of the weighted
![]() $L^2$
-metrics on the unit disk
$L^2$
-metrics on the unit disk
![]() $\mathbb {D}$
. A singular inner function has the form
$\mathbb {D}$
. A singular inner function has the form
where
![]() $\nu $
is a finite positive singular Borel measure on
$\nu $
is a finite positive singular Borel measure on
![]() $\mathbb {T}$
. Recall the decomposition (1.7) above, which induces according to (1.11) a factorization
$\mathbb {T}$
. Recall the decomposition (1.7) above, which induces according to (1.11) a factorization
![]() $S_{\nu } = S_{\nu _{\mathcal {C}}}S_{\nu _{\mathcal {K}}}$
. The part
$S_{\nu } = S_{\nu _{\mathcal {C}}}S_{\nu _{\mathcal {K}}}$
. The part
![]() $S_{\nu _{\mathcal {C}}}$
is passed onto the limit under convergence of bounded functions in the weighted Bergman spaces norms with polynomially decreasing weights. That is, if
$S_{\nu _{\mathcal {C}}}$
is passed onto the limit under convergence of bounded functions in the weighted Bergman spaces norms with polynomially decreasing weights. That is, if
![]() $\nu = \nu _{\mathcal {C}}$
in (1.7), then for
$\nu = \nu _{\mathcal {C}}$
in (1.7), then for
![]() $\theta = S_{\nu }$
, we have that
$\theta = S_{\nu }$
, we have that
 $$ \begin{gather*} \lim_{n \to \infty} \int_{\mathbb{D}} |\theta f_n - f|^2 (1-|z|^2)^C dA(z) = 0 \\ \Rightarrow f/\theta \in H^{\infty} \end{gather*} $$
$$ \begin{gather*} \lim_{n \to \infty} \int_{\mathbb{D}} |\theta f_n - f|^2 (1-|z|^2)^C dA(z) = 0 \\ \Rightarrow f/\theta \in H^{\infty} \end{gather*} $$
whenever
![]() $f_n, f$
are all bounded analytic functions, and
$f_n, f$
are all bounded analytic functions, and
![]() $C>-1$
. In contrast,
$C>-1$
. In contrast,
![]() $S_{\nu _{\mathcal {K}}}$
can vanish under the same circumstances. A proof for the first claim appears in [Reference Limani and Malman17], whereas the second is a consequence of a deep cyclicity theorem for inner functions which was independently established by Roberts in [Reference Roberts20] and Korenblum in [Reference Korenblum14]. In Section 6, a carefully constructed family of smooth Cauchy transforms will help us to implement a functional analytic argument and establish this inner factor permanence for a very large class of singular inner functions and a range of spaces
$S_{\nu _{\mathcal {K}}}$
can vanish under the same circumstances. A proof for the first claim appears in [Reference Limani and Malman17], whereas the second is a consequence of a deep cyclicity theorem for inner functions which was independently established by Roberts in [Reference Roberts20] and Korenblum in [Reference Korenblum14]. In Section 6, a carefully constructed family of smooth Cauchy transforms will help us to implement a functional analytic argument and establish this inner factor permanence for a very large class of singular inner functions and a range of spaces
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
mentioned above. The result is a technical extension of the one appearing in the article [Reference Limani and Malman16], in which the present authors investigated this principle for the topologies induced by the abovementioned
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
mentioned above. The result is a technical extension of the one appearing in the article [Reference Limani and Malman16], in which the present authors investigated this principle for the topologies induced by the abovementioned
![]() $\mathcal {P}^2(\mu )$
-spaces.
$\mathcal {P}^2(\mu )$
-spaces.
Our results on the spaces
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
are used in Section 7 in which we implement the duality approach from [Reference Limani and Malman18] to prove Theorem B.
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
are used in Section 7 in which we implement the duality approach from [Reference Limani and Malman18] to prove Theorem B.
2 Construction of an analytic “cutoff” function
We start off by presenting the constructing of a certain analytic function with strong decay properties near a given Beurling–Carleson set. The reason for calling it a cutoff function, as in the name of the section, will become clear from the proof of the coming application in Proposition 3.1. Our construction is a straightforward adaptation of a technique from [Reference Hedenmalm, Korenblum and Zhu10], more precisely from Lemma 7.11 of that work. We could have also followed the ideas of [Reference Novinger19] or [Reference Taylor and Williams23]. The proof is included for the reader’s convenience and because the construction is crucial for our development.
Lemma 2.1 Let E be a Beurling–Carleson set, of either zero or positive Lebesgue measure. There exists an analytic function
![]() $g: \mathbb {D} \to \mathbb {D}$
that extends analytically across
$g: \mathbb {D} \to \mathbb {D}$
that extends analytically across
![]() $\mathbb {T} \setminus E$
, and if
$\mathbb {T} \setminus E$
, and if
![]() $G: \mathbb {T} \to \mathbb {C}$
is defined by
$G: \mathbb {T} \to \mathbb {C}$
is defined by
where
![]() $1_{\mathbb {T}\setminus E}$
denotes the indicator function of the set
$1_{\mathbb {T}\setminus E}$
denotes the indicator function of the set
![]() $\mathbb {T} \setminus E$
, then G is a smooth function on
$\mathbb {T} \setminus E$
, then G is a smooth function on
![]() $\mathbb {T}$
, and we have the estimate
$\mathbb {T}$
, and we have the estimate
for each pair of nonnegative integer N and m. Here,
![]() $G^{(m)}$
denotes the mth derivative of G with respect to the variable t, and
$G^{(m)}$
denotes the mth derivative of G with respect to the variable t, and
![]() $\text {dist}( \cdot , \cdot ) $
denotes the distance between two closed sets.
$\text {dist}( \cdot , \cdot ) $
denotes the distance between two closed sets.
Proof Let
![]() $\cup _{n \in \mathbb {N}} A_n = \mathbb {T} \setminus E$
be the complement of E with respect to
$\cup _{n \in \mathbb {N}} A_n = \mathbb {T} \setminus E$
be the complement of E with respect to
![]() $\mathbb {T}$
. For each subarc
$\mathbb {T}$
. For each subarc
![]() $A_n$
, we perform the classical Whitney decomposition
$A_n$
, we perform the classical Whitney decomposition
![]() $A_n = \cup _{k \in \mathbb {Z}} A_{n,k}$
. More precisely, let
$A_n = \cup _{k \in \mathbb {Z}} A_{n,k}$
. More precisely, let
![]() $A_{n,0}$
be the arc with the same midpoint as
$A_{n,0}$
be the arc with the same midpoint as
![]() $A_n$
but having one-third of the length of
$A_n$
but having one-third of the length of
![]() $A_n$
. For this choice of the length, we have
$A_n$
. For this choice of the length, we have
![]() $|A_{n,0}| = \text {dist}( A_{n,0}, E ) $
. The arcs
$|A_{n,0}| = \text {dist}( A_{n,0}, E ) $
. The arcs
![]() $A_{n,-1}$
and
$A_{n,-1}$
and
![]() $A_{n,1}$
should be chosen adjacent to
$A_{n,1}$
should be chosen adjacent to
![]() $A_{n,0}$
from the left and the right, respectively, and their lengths should be chosen, again, such that
$A_{n,0}$
from the left and the right, respectively, and their lengths should be chosen, again, such that
![]() $|A_{n,-1}| = \text {dist}( A_{n,-1}, E ) $
and
$|A_{n,-1}| = \text {dist}( A_{n,-1}, E ) $
and
![]() $|A_{n,1}| = \text {dist}( A_{n,1}, E ) $
. It is easy to see that the correct choice is
$|A_{n,1}| = \text {dist}( A_{n,1}, E ) $
. It is easy to see that the correct choice is
![]() $|A_{n,1}| = |A_{n,-1}| = \frac {|A_n|}{6}.$
Proceeding in this manner, we will obtain a decomposition
$|A_{n,1}| = |A_{n,-1}| = \frac {|A_n|}{6}.$
Proceeding in this manner, we will obtain a decomposition
where, for each arc
![]() $A_{n,k}$
, we have
$A_{n,k}$
, we have
A straightforward computation based on (2.3) will show that
Let
![]() $\{B_j\}_j$
be a relabeling of the arcs
$\{B_j\}_j$
be a relabeling of the arcs
![]() $\{A_{n,k}\}_{n,k}$
and {
$\{A_{n,k}\}_{n,k}$
and {
![]() $\lambda _j\}_j$
a positive sequence tending to infinity such that
$\lambda _j\}_j$
a positive sequence tending to infinity such that
Now, let
![]() $r_j = 1 + |B_j|$
,
$r_j = 1 + |B_j|$
,
![]() $b_j \in \mathbb {T}$
be the midpoint of the arc
$b_j \in \mathbb {T}$
be the midpoint of the arc
![]() $B_j$
, and consider the function
$B_j$
, and consider the function
 $$ \begin{align} h(z) = \sum_{j} h_j(z) = \sum_j \frac{\lambda_j b_j|B_j| \log(1/|B_j|)}{r_jb_j - z}, \quad z \in \mathbb{D}. \end{align} $$
$$ \begin{align} h(z) = \sum_{j} h_j(z) = \sum_j \frac{\lambda_j b_j|B_j| \log(1/|B_j|)}{r_jb_j - z}, \quad z \in \mathbb{D}. \end{align} $$
It is not hard to see that the real part of
![]() $h(z)$
is positive in
$h(z)$
is positive in
![]() $\mathbb {D}$
. In fact, the real part of the jth term in the sum is
$\mathbb {D}$
. In fact, the real part of the jth term in the sum is
 $$ \begin{gather*} \operatorname{Re} h_j(z) = \lambda_j |B_j| \log(1/|B_j|)\frac{\operatorname{Re} (r_j - \overline{z}b_j)}{|r_jb_j - z|^2}> 0, \end{gather*} $$
$$ \begin{gather*} \operatorname{Re} h_j(z) = \lambda_j |B_j| \log(1/|B_j|)\frac{\operatorname{Re} (r_j - \overline{z}b_j)}{|r_jb_j - z|^2}> 0, \end{gather*} $$
where the last inequality follows from
![]() $\operatorname {Re} (r_j - \overline {z}b_j)> 0$
, which is a consequence of the inequalities
$\operatorname {Re} (r_j - \overline {z}b_j)> 0$
, which is a consequence of the inequalities
![]() $r_j> 1$
and
$r_j> 1$
and
![]() $|\overline {z}b_j| < 1$
. It follows that
$|\overline {z}b_j| < 1$
. It follows that
is bounded by 1 in modulus for
![]() $z \in \mathbb {D}$
. Moreover, the series defining
$z \in \mathbb {D}$
. Moreover, the series defining
![]() $h(z)$
converges also for
$h(z)$
converges also for
![]() $z \in B_j$
, and h extends analytically across each
$z \in B_j$
, and h extends analytically across each
![]() $B_j$
, because the poles
$B_j$
, because the poles
![]() $\{r_jb_j\}_j$
of h cluster only at the set E. For
$\{r_jb_j\}_j$
of h cluster only at the set E. For
![]() $z \in B_j$
, we have that the quantities
$z \in B_j$
, we have that the quantities
![]() $|r_jb_j - z|$
and
$|r_jb_j - z|$
and
![]() $\operatorname {Re}(r_j - \overline {z}b_j)$
are both approximately equal to
$\operatorname {Re}(r_j - \overline {z}b_j)$
are both approximately equal to
![]() $|B_j|$
, and so
$|B_j|$
, and so
for some positive constant c. Since
![]() $|B_j|$
equals the distance from
$|B_j|$
equals the distance from
![]() $B_j$
to E, for
$B_j$
to E, for
![]() $z \in B_j$
, we obtain that
$z \in B_j$
, we obtain that
for some positive constant
![]() $C> 0$
independent of j. Note that as z tends to E along the complement
$C> 0$
independent of j. Note that as z tends to E along the complement
![]() $\mathbb {T} \setminus E$
, it needs to pass through infinitely many intervals
$\mathbb {T} \setminus E$
, it needs to pass through infinitely many intervals
![]() $B_j$
. Since
$B_j$
. Since
![]() $\lambda _j$
tends to infinity, we obtain that
$\lambda _j$
tends to infinity, we obtain that
as
![]() $z \to E$
along the complement of E on
$z \to E$
along the complement of E on
![]() $\mathbb {T}$
, for any choice of positive integer N. Now, for
$\mathbb {T}$
, for any choice of positive integer N. Now, for
![]() $e^{it} \in \mathbb {T} \setminus E$
, the derivatives
$e^{it} \in \mathbb {T} \setminus E$
, the derivatives
![]() $G^{(m)}(e^{it})$
have the form
$G^{(m)}(e^{it})$
have the form
![]() $H(e^{it})G(e^{it})$
, where H is a linear combination of products of derivatives of
$H(e^{it})G(e^{it})$
, where H is a linear combination of products of derivatives of
![]() $h(e^{it})$
with respect to t. But a glance at (2.4) shows that such a product cannot grow faster than a constant multiple of
$h(e^{it})$
with respect to t. But a glance at (2.4) shows that such a product cannot grow faster than a constant multiple of
![]() $\text {dist}( e^{it}, E ) ^{-n}$
for
$\text {dist}( e^{it}, E ) ^{-n}$
for
![]() $e^{it} \in \mathbb {T} \setminus E$
, for some positive integer
$e^{it} \in \mathbb {T} \setminus E$
, for some positive integer
![]() $n=n_m$
depending only on the number of derivatives m taken. Now, according to the definition of G in (2.1), it follows that the estimate (2.2) holds whenever
$n=n_m$
depending only on the number of derivatives m taken. Now, according to the definition of G in (2.1), it follows that the estimate (2.2) holds whenever
![]() $e^{it} \in \mathbb {T} \setminus E$
. Using this, it is now also evident from the definition in (2.1) that G is continuous on
$e^{it} \in \mathbb {T} \setminus E$
. Using this, it is now also evident from the definition in (2.1) that G is continuous on
![]() $\mathbb {T}$
. In fact, it is straightforward to verify that whenever
$\mathbb {T}$
. In fact, it is straightforward to verify that whenever
![]() $e^{it} \in E$
, the function G is differentiable as many times as we wish, with
$e^{it} \in E$
, the function G is differentiable as many times as we wish, with
![]() $G^{(m)}(e^{it})=0$
for any positive integer m. This shows that G is smooth on all of
$G^{(m)}(e^{it})=0$
for any positive integer m. This shows that G is smooth on all of
![]() $\mathbb {T}$
and thus completes the proof of this lemma.
$\mathbb {T}$
and thus completes the proof of this lemma.
Note the fact that the proof above gives an explicit computable formula for the cutoff function g. It is given in terms of the Beurling–Carleson set E and is presented in equations (2.4) and (2.5).
3 A constructive proof of Khrushchev’s theorem
3.1 Smooth Cauchy transforms
As before, let E be a Beurling–Carleson set of positive measure. Lemma 2.1 will allow us to construct, and give explicit formulas for, measurable functions supported on E which have a smooth Cauchy transform. Thus, we will now give the constructive proof of the theorem of Khrushchev from his seminal work [Reference Khrushchev12].
Proposition 3.1 (Construction of smooth Cauchy transforms)
Let E be a Beurling–Carleson set of positive measure such that
![]() $E \neq \mathbb {T}$
, and let w be a bounded positive measurable function with support on E which satisfies
$E \neq \mathbb {T}$
, and let w be a bounded positive measurable function with support on E which satisfies
![]() $\int _E \log (w) d\textit {m}> -\infty $
. Let W be the outer function
$\int _E \log (w) d\textit {m}> -\infty $
. Let W be the outer function
and let g be the function associated with E, which is given by Lemma 2.1. Consider the set
consisting of functions on
![]() $\mathbb {T}$
, where
$\mathbb {T}$
, where
![]() $\zeta $
is the coordinate function on
$\zeta $
is the coordinate function on
![]() $\mathbb {T}$
. Then the Cauchy transform
$\mathbb {T}$
. Then the Cauchy transform
 $$ \begin{align} C_{s1_E}(z) := \int_E \frac{s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta) \end{align} $$
$$ \begin{align} C_{s1_E}(z) := \int_E \frac{s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta) \end{align} $$
is a nonzero function in
![]() $\mathcal {A}^{\infty }$
for each nonzero
$\mathcal {A}^{\infty }$
for each nonzero
![]() $s \in K$
, the restrictions to E of elements of the set K form a dense subset of
$s \in K$
, the restrictions to E of elements of the set K form a dense subset of
![]() $L^2(1_E d\textit {m})$
, and the set
$L^2(1_E d\textit {m})$
, and the set
is dense in
![]() $H^2$
.
$H^2$
.
Certainly, our more general form of the theorem, together with the density statements, is obtainable by Khrushchev’s methods from [Reference Khrushchev12]. We therefore emphasize that our main contribution in this context are the explicit formulas for the measurable functions supported on E for which the Cauchy transform is an analytic function in
![]() $\mathcal {A}^{\infty }$
. More precisely, the formulas for the functions in K are given by the equations (2.4), (2.5), and (3.1).
$\mathcal {A}^{\infty }$
. More precisely, the formulas for the functions in K are given by the equations (2.4), (2.5), and (3.1).
The density statements in Proposition 3.1 will be useful for our further applications. It is not our point to prove these density statements constructively. In this part of the proof, we will use the following well-known theorem.
Lemma 3.2 (Beurling–Wiener theorem)
Let
![]() $M_{\overline {\zeta }}:L^2(\mathbb {T}) \to L^2(\mathbb {T})$
be the operator of multiplication by
$M_{\overline {\zeta }}:L^2(\mathbb {T}) \to L^2(\mathbb {T})$
be the operator of multiplication by
![]() $\overline {\zeta }$
. The closed
$\overline {\zeta }$
. The closed
![]() $M_{\overline {\zeta }}$
-invariant subspaces of
$M_{\overline {\zeta }}$
-invariant subspaces of
![]() $L^2(\mathbb {T})$
are of the form
$L^2(\mathbb {T})$
are of the form
where F is a measurable subset of
![]() $\mathbb {T}$
, or of the form
$\mathbb {T}$
, or of the form
where U is a unimodular function.
For a proof of the Beurling–Wiener theorem, see, for instance, [Reference Helson11].
Proof of Proposition 3.1 Since s is a conjugate analytic and satisfies
![]() $\int _{\mathbb {T}} s d\textit {m} = 0$
, we have
$\int _{\mathbb {T}} s d\textit {m} = 0$
, we have
 $$\begin{align*}\int_{\mathbb{T}} \frac{s(\zeta)}{1-z \overline{\zeta}}dm(\zeta) = 0\end{align*}$$
$$\begin{align*}\int_{\mathbb{T}} \frac{s(\zeta)}{1-z \overline{\zeta}}dm(\zeta) = 0\end{align*}$$
for each
![]() $z \in \mathbb {D}$
. This implies that
$z \in \mathbb {D}$
. This implies that
 $$ \begin{align} C_{s1_E}(z) = \int_E \frac{s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta) = -\int_{\mathbb{T} \setminus E} \frac{s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta). \end{align} $$
$$ \begin{align} C_{s1_E}(z) = \int_E \frac{s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta) = -\int_{\mathbb{T} \setminus E} \frac{s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta). \end{align} $$
Consider now the function
![]() $S(e^{it}) : = s(e^{it})1_{\mathbb {T} \setminus E}(e^{it}) = \overline {e^{it}p(e^{it})G(e^{it})W(e^{it})}$
. From the formula (3.1) for W, it is clear that this function extends analytically across
$S(e^{it}) : = s(e^{it})1_{\mathbb {T} \setminus E}(e^{it}) = \overline {e^{it}p(e^{it})G(e^{it})W(e^{it})}$
. From the formula (3.1) for W, it is clear that this function extends analytically across
![]() $\mathbb {T} \setminus E$
, and a simple differentiation argument shows that the derivatives in the variable t of the function
$\mathbb {T} \setminus E$
, and a simple differentiation argument shows that the derivatives in the variable t of the function
![]() $W(e^{it})$
admit a bound
$W(e^{it})$
admit a bound
for
![]() $e^{it} \in \mathbb {T} \setminus E$
. Thus, by (2.2) of Lemma 2.1 and the definition in (3.2), the derivatives of any order of S tends to zero as
$e^{it} \in \mathbb {T} \setminus E$
. Thus, by (2.2) of Lemma 2.1 and the definition in (3.2), the derivatives of any order of S tends to zero as
![]() $e^{it}$
tends to E along
$e^{it}$
tends to E along
![]() $\mathbb {T} \setminus E$
, and it is not hard to see that the derivatives of S vanish on E. Thus,
$\mathbb {T} \setminus E$
, and it is not hard to see that the derivatives of S vanish on E. Thus,
![]() $S \in C^{\infty }$
. It follows that the Fourier coefficients
$S \in C^{\infty }$
. It follows that the Fourier coefficients
![]() $S_n$
of S satisfy
$S_n$
of S satisfy
![]() $|S_n| \leq C|n|^{-M}$
for each positive integer M and some constant
$|S_n| \leq C|n|^{-M}$
for each positive integer M and some constant
![]() $C = C(M)> 0$
. Obviously, then, (3.5) implies that the function
$C = C(M)> 0$
. Obviously, then, (3.5) implies that the function
![]() $C_{s1_E}(z) = -\sum _{n = 0}^{\infty } S_nz^n$
is in
$C_{s1_E}(z) = -\sum _{n = 0}^{\infty } S_nz^n$
is in
![]() $\mathcal {A}^{\infty }$
. It is nonzero if s is nonzero because the positive Fourier coefficients cannot vanish for the function
$\mathcal {A}^{\infty }$
. It is nonzero if s is nonzero because the positive Fourier coefficients cannot vanish for the function
![]() $s1_E$
which is identically zero on the set
$s1_E$
which is identically zero on the set
![]() $\mathbb {T} \setminus E$
of positive Lebesgue measure.
$\mathbb {T} \setminus E$
of positive Lebesgue measure.
The density in
![]() $L^2(1_E d\textit {m})$
of the restrictions to E of elements of the set K is an easy consequence of the invariance of K under multiplication by
$L^2(1_E d\textit {m})$
of the restrictions to E of elements of the set K is an easy consequence of the invariance of K under multiplication by
![]() $\overline {\zeta }$
and the Beurling–Wiener theorem (Lemma 3.2). Indeed, the restriction to E of an element of K is nonzero almost everywhere on E, but obviously zero on
$\overline {\zeta }$
and the Beurling–Wiener theorem (Lemma 3.2). Indeed, the restriction to E of an element of K is nonzero almost everywhere on E, but obviously zero on
![]() $\mathbb {T} \setminus E$
. It follows from Lemma 3.2 that the closure of K in
$\mathbb {T} \setminus E$
. It follows from Lemma 3.2 that the closure of K in
![]() $L^2(1_E d\textit {m})$
could not be anything else than the full space.
$L^2(1_E d\textit {m})$
could not be anything else than the full space.
The set
![]() $C_EK$
is certainly contained in
$C_EK$
is certainly contained in
![]() $H^2$
, and the density in
$H^2$
, and the density in
![]() $H^2$
follows from the classical Beurling theorem for the Hardy spaces. More precisely, the set
$H^2$
follows from the classical Beurling theorem for the Hardy spaces. More precisely, the set
![]() $C_EK$
is invariant under the backward shift operator
$C_EK$
is invariant under the backward shift operator
Indeed, we have that
 $$ \begin{align} \frac{C_{s1_E}(z) - C_{s1_E}(0)}{z} = \int_E \frac{\overline{\zeta}s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta) = C_{\overline{\zeta} {s1_E}}(z). \end{align} $$
$$ \begin{align} \frac{C_{s1_E}(z) - C_{s1_E}(0)}{z} = \int_E \frac{\overline{\zeta}s(\zeta)}{1-z\overline{\zeta}}d\textit{m}(\zeta) = C_{\overline{\zeta} {s1_E}}(z). \end{align} $$
By Beurling’s theorem, the closure of
![]() $C_EK$
is either all of
$C_EK$
is either all of
![]() $H^2$
, or it coincides with a model space
$H^2$
, or it coincides with a model space
![]() $K_{\theta }$
of functions which have boundary values on
$K_{\theta }$
of functions which have boundary values on
![]() $\mathbb {T}$
of the form
$\mathbb {T}$
of the form
![]() $\theta \overline {h}, h \in zH^2$
, for some nonzero inner function
$\theta \overline {h}, h \in zH^2$
, for some nonzero inner function
![]() $\theta $
. If we would be in the second case, then there would exist a function
$\theta $
. If we would be in the second case, then there would exist a function
![]() $k \in zH^2$
such that on the circle
$k \in zH^2$
such that on the circle
![]() $\mathbb {T}$
we would have the equality
$\mathbb {T}$
we would have the equality
![]() $s1_E = C_{s1_E} + \overline {k} = \theta \overline {h} + \overline {k}$
, and consequently
$s1_E = C_{s1_E} + \overline {k} = \theta \overline {h} + \overline {k}$
, and consequently
![]() $\overline {\theta }s1_E \in \overline {H^2}$
. This is a contradiction, since
$\overline {\theta }s1_E \in \overline {H^2}$
. This is a contradiction, since
![]() $\overline {\theta }s1_E$
vanishes on a set of positive measure.
$\overline {\theta }s1_E$
vanishes on a set of positive measure.
3.2 A technical improvement
Sets of the form K as in (3.2) have another useful property, one of which will be employed in the coming applications. The property is that the set
![]() $C_E K$
defined in (3.4) is contained in a single Hilbert space consisting purely of functions which are in
$C_E K$
defined in (3.4) is contained in a single Hilbert space consisting purely of functions which are in
![]() $\mathcal {A}^{\infty }$
. This applies to many sets similar to K, as we shall see next.
$\mathcal {A}^{\infty }$
. This applies to many sets similar to K, as we shall see next.
More precisely, take the function
![]() $s_0 := \overline {\zeta g W} \in K$
, i.e., the one where
$s_0 := \overline {\zeta g W} \in K$
, i.e., the one where
![]() $p = 1$
in (3.2). The only property of K that we will use in the proof is that it is of the form
$p = 1$
in (3.2). The only property of K that we will use in the proof is that it is of the form
For an analytic polynomial
![]() $p(z) = \sum _{n=0}^{d} p_nz^n$
, we let
$p(z) = \sum _{n=0}^{d} p_nz^n$
, we let
 $$ \begin{align} \tilde{p}(z) := \sum_{n=0}^{d} \overline{p_n}z^n \end{align} $$
$$ \begin{align} \tilde{p}(z) := \sum_{n=0}^{d} \overline{p_n}z^n \end{align} $$
and define the operator
 $$ \begin{align} p(L) := \sum_{n=0}^{d} p_nL^n, \end{align} $$
$$ \begin{align} p(L) := \sum_{n=0}^{d} p_nL^n, \end{align} $$
where L is the backward shift operator defined in (3.7). Every other element of
![]() $C_EK$
can be expressed as
$C_EK$
can be expressed as
![]() $p(L)C_{s_01_E}$
for some analytic polynomial. This claim is a consequence of the formula
$p(L)C_{s_01_E}$
for some analytic polynomial. This claim is a consequence of the formula
 $$ \begin{align} p(L)C_{s_01_E}(z) = \int_{E} \frac{\overline{\zeta \tilde{p} g W}}{1 - z\overline{\zeta}} d\textit{m}(\zeta), \end{align} $$
$$ \begin{align} p(L)C_{s_01_E}(z) = \int_{E} \frac{\overline{\zeta \tilde{p} g W}}{1 - z\overline{\zeta}} d\textit{m}(\zeta), \end{align} $$
which, in turn, is a consequence of (3.8). Thus, the Taylor coefficients in the family
![]() $C_EK$
have similar asymptotic behavior, and we exploit this fact in the following way. Being a function in
$C_EK$
have similar asymptotic behavior, and we exploit this fact in the following way. Being a function in
![]() $\mathcal {A}^{\infty }$
, the Taylor coefficients
$\mathcal {A}^{\infty }$
, the Taylor coefficients
![]() $\{ S_k \}_{k=0}^{\infty }$
of
$\{ S_k \}_{k=0}^{\infty }$
of
![]() $C_{s_01_E}$
satisfy
$C_{s_01_E}$
satisfy
 $$ \begin{align} \sum_{k=0}^{\infty} k^N |S_k|^2 < \infty \end{align} $$
$$ \begin{align} \sum_{k=0}^{\infty} k^N |S_k|^2 < \infty \end{align} $$
for all positive integers N. It follows that for each
![]() $N \geq 1$
, there exists a positive integer
$N \geq 1$
, there exists a positive integer
![]() $K(N)$
such that
$K(N)$
such that
 $$ \begin{align} \sum_{k=K(N)}^{\infty} k^N |S_k|^2 < \frac{1}{2^N}. \end{align} $$
$$ \begin{align} \sum_{k=K(N)}^{\infty} k^N |S_k|^2 < \frac{1}{2^N}. \end{align} $$
We may assume that
![]() $\{K(N)\}_{N \geq 1}$
is increasing. Set
$\{K(N)\}_{N \geq 1}$
is increasing. Set
![]() $K(0) = 0$
and define a sequence
$K(0) = 0$
and define a sequence
![]() $\{\alpha _k\}_{k=0}^{\infty }$
by
$\{\alpha _k\}_{k=0}^{\infty }$
by
This sequence is increasing, and satisfies
 $$ \begin{align} \sum_{k=0}^{\infty} \alpha_k|S_k|^2 = \sum_{N=0}^{\infty} \sum_{k=K(N)}^{K(N+1)-1} k^N |S_k|^2 \leq \sum_{N=0}^{\infty} \frac{1}{2^N} < \infty. \end{align} $$
$$ \begin{align} \sum_{k=0}^{\infty} \alpha_k|S_k|^2 = \sum_{N=0}^{\infty} \sum_{k=K(N)}^{K(N+1)-1} k^N |S_k|^2 \leq \sum_{N=0}^{\infty} \frac{1}{2^N} < \infty. \end{align} $$
Moreover, since
![]() $\alpha _k \geq k^{N+1}$
if
$\alpha _k \geq k^{N+1}$
if
![]() $k \geq K(N+1)$
, we have that
$k \geq K(N+1)$
, we have that
for any positive integer N.
Definition 3.3 A sequence of positive numbers
![]() $\boldsymbol {\alpha } = \{ \alpha _k\}_{k=0}^{\infty }$
is rapidly increasing if
$\boldsymbol {\alpha } = \{ \alpha _k\}_{k=0}^{\infty }$
is rapidly increasing if
holds for each positive integer N.
Thus, we have constructed above a rapidly increasing sequence. In the coming application, we will also need the very mild condition
which we can safely assume. Indeed, by replacing
![]() $\alpha _k$
by
$\alpha _k$
by
![]() $\min (\alpha _k, k^{\sqrt {k}})$
, we still have a sequence which is rapidly increasing, and moreover
$\min (\alpha _k, k^{\sqrt {k}})$
, we still have a sequence which is rapidly increasing, and moreover
We now make a somewhat trivial observation, which will, however, be important in the sequel. Because the sequence
![]() $\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
is increasing, it also follows that whenever an analytic function f has a Taylor series which satisfies (3.14), then so does the backward shift
$\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
is increasing, it also follows that whenever an analytic function f has a Taylor series which satisfies (3.14), then so does the backward shift
![]() $Lf$
of this function. Thus, also
$Lf$
of this function. Thus, also
![]() $p(L)f$
satisfies this property, for all analytic polynomials p (and, in fact, so does appropriately defined
$p(L)f$
satisfies this property, for all analytic polynomials p (and, in fact, so does appropriately defined
![]() $h(L)f$
for any bounded analytic function h; see Proposition 4.1). Using also the formula (3.11), we have proved the following technical result.
$h(L)f$
for any bounded analytic function h; see Proposition 4.1). Using also the formula (3.11), we have proved the following technical result.
Proposition 3.4 Let
![]() $s_0$
be a measurable function on
$s_0$
be a measurable function on
![]() $\mathbb {T}$
for which the Cauchy transform
$\mathbb {T}$
for which the Cauchy transform
![]() $C_{s_0}$
is a function in
$C_{s_0}$
is a function in
![]() $\mathcal {A}^{\infty }$
. Then there exists a rapidly increasing sequence
$\mathcal {A}^{\infty }$
. Then there exists a rapidly increasing sequence
![]() $\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
satisfying
$\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
satisfying
and such that
 $$\begin{align*}\sum_{k=0}^{\infty} \alpha_k|f_k|^2 < \infty \end{align*}$$
$$\begin{align*}\sum_{k=0}^{\infty} \alpha_k|f_k|^2 < \infty \end{align*}$$
for all functions f which are Cauchy transforms
![]() $f = C_s$
of a function s from the set
$f = C_s$
of a function s from the set
4 Weighted sequence spaces
We will explore the Hilbert spaces implicitly appearing in Proposition 3.4 a little more, and prove a few basic facts about their duality and operators acting on them. The main results of the following Sections 5 and 6 will be stated in the context of these Hilbert spaces. All results in this section are certainly well known, so we include the proofs for completeness.
4.1 Definition and duality
For a sequence of positive numbers
![]() $\boldsymbol {\alpha } = \{ \alpha _k\}_{k=0}^{\infty }$
, we define the Hilbert space
$\boldsymbol {\alpha } = \{ \alpha _k\}_{k=0}^{\infty }$
, we define the Hilbert space
![]() $X(\boldsymbol {\alpha })$
to consist of formal power series
$X(\boldsymbol {\alpha })$
to consist of formal power series
![]() $f(z) = \sum _{k=0}^{\infty } f_nz^n$
which satisfy
$f(z) = \sum _{k=0}^{\infty } f_nz^n$
which satisfy
 $$ \begin{align} \|f\|^2_{X(\boldsymbol{\alpha})} := \sum_{k=0}^{\infty} \alpha_k|f_k|^2 < \infty. \end{align} $$
$$ \begin{align} \|f\|^2_{X(\boldsymbol{\alpha})} := \sum_{k=0}^{\infty} \alpha_k|f_k|^2 < \infty. \end{align} $$
It is obvious that if
![]() $\boldsymbol {\alpha }$
is rapidly increasing, then
$\boldsymbol {\alpha }$
is rapidly increasing, then
![]() $X(\boldsymbol {\alpha }) \subset \mathcal {A}^{\infty }$
. We define the dual sequence
$X(\boldsymbol {\alpha }) \subset \mathcal {A}^{\infty }$
. We define the dual sequence
![]() $\boldsymbol {\alpha ^{-1}}$
by the equation
$\boldsymbol {\alpha ^{-1}}$
by the equation
The space
![]() $X(\boldsymbol {\alpha ^{-1}})$
is isometrically isomorphic to the dual space of
$X(\boldsymbol {\alpha ^{-1}})$
is isometrically isomorphic to the dual space of
![]() $X(\boldsymbol {\alpha })$
under the pairing which maps
$X(\boldsymbol {\alpha })$
under the pairing which maps
![]() $f \in X(\boldsymbol {\alpha })$
,
$f \in X(\boldsymbol {\alpha })$
,
![]() $g \in X(\boldsymbol {\alpha ^{-1}})$
to the complex number
$g \in X(\boldsymbol {\alpha ^{-1}})$
to the complex number
where the sequences
![]() $\{f_k\}_{k=0}^{\infty }$
and
$\{f_k\}_{k=0}^{\infty }$
and
![]() $\{g_k\}_{k=0}^{\infty }$
are the coefficients in the formal power series expansions of f and g, respectively.
$\{g_k\}_{k=0}^{\infty }$
are the coefficients in the formal power series expansions of f and g, respectively.
In fact, for us, the spaces
![]() $X(\boldsymbol {\alpha })$
and
$X(\boldsymbol {\alpha })$
and
![]() $X(\boldsymbol {\alpha }^{-1})$
will always be genuine spaces of analytic functions on
$X(\boldsymbol {\alpha }^{-1})$
will always be genuine spaces of analytic functions on
![]() $\mathbb {D}$
. Indeed, a property which ensures this is
$\mathbb {D}$
. Indeed, a property which ensures this is
![]() $\lim _{k \to \infty } \alpha _k^{1/k} = 1$
. The sequences appearing in our context will be the ones constructed in Proposition 3.4 and their dual sequences, so we can safely assume below that this assumption is always satisfied. To see indeed that the assumption
$\lim _{k \to \infty } \alpha _k^{1/k} = 1$
. The sequences appearing in our context will be the ones constructed in Proposition 3.4 and their dual sequences, so we can safely assume below that this assumption is always satisfied. To see indeed that the assumption
![]() $\lim _{k \to \infty } \beta _k^{1/k} = 1$
implies that the radius of convergence of a formal power series
$\lim _{k \to \infty } \beta _k^{1/k} = 1$
implies that the radius of convergence of a formal power series
![]() $f \in X(\boldsymbol {\beta })$
is equal to at least 1, we compute
$f \in X(\boldsymbol {\beta })$
is equal to at least 1, we compute
 $$\begin{align*}\limsup_{k\to \infty} |f_k|^{1/k} = \limsup_{k \to \infty} \frac{ (\beta_k |f_k|^2)^{1/2k}}{\beta_k^{1/2k}} \leq \limsup_{k \to \infty} \frac{1}{\beta_k^{1/2k}} = 1,\end{align*}$$
$$\begin{align*}\limsup_{k\to \infty} |f_k|^{1/k} = \limsup_{k \to \infty} \frac{ (\beta_k |f_k|^2)^{1/2k}}{\beta_k^{1/2k}} \leq \limsup_{k \to \infty} \frac{1}{\beta_k^{1/2k}} = 1,\end{align*}$$
where, in the next-to-last step, we used that
so that
This shows that the radius of convergence of
![]() $f \in X(\boldsymbol {\beta })$
is indeed equal to at least 1.
$f \in X(\boldsymbol {\beta })$
is indeed equal to at least 1.
Finally, an obvious but important property of the presented duality pairing is that if f and g happen to be functions in
![]() $H^2$
, then we have that (4.2) equals
$H^2$
, then we have that (4.2) equals
In other words, the duality pairing coincides with the usual
![]() $L^2(\mathbb {T})$
-duality pairing in the case f and g are functions in
$L^2(\mathbb {T})$
-duality pairing in the case f and g are functions in
![]() $H^2$
. We shall often implicitly use this property.
$H^2$
. We shall often implicitly use this property.
4.2 Toeplitz operators
The usual Toeplitz operator with symbol
![]() $h \in L^{\infty }(\mathbb {T})$
acts on an
$h \in L^{\infty }(\mathbb {T})$
acts on an
![]() $H^2$
-function f by the formula
$H^2$
-function f by the formula
 $$\begin{align*}T_{h} f(z) := \int_{\mathbb{T}} \frac{f(\zeta)h(\zeta)}{1-\overline{\zeta}z}\,d\textit{m}(\zeta). \end{align*}$$
$$\begin{align*}T_{h} f(z) := \int_{\mathbb{T}} \frac{f(\zeta)h(\zeta)}{1-\overline{\zeta}z}\,d\textit{m}(\zeta). \end{align*}$$
If p is a polynomial, then
where
![]() $\tilde {p}(L)$
is defined according to (3.10) and where
$\tilde {p}(L)$
is defined according to (3.10) and where
![]() $\tilde {p}(z)$
is given by (3.9). If h is in
$\tilde {p}(z)$
is given by (3.9). If h is in
![]() $H^{\infty }$
, then we can equivalently define the operator
$H^{\infty }$
, then we can equivalently define the operator
![]() $T_h$
as the mapping taking the function
$T_h$
as the mapping taking the function
![]() $f(z), z \in \mathbb {D}$
, to the function
$f(z), z \in \mathbb {D}$
, to the function
![]() $h(z)f(z), z \in \mathbb {D}$
. We denote by
$h(z)f(z), z \in \mathbb {D}$
. We denote by
![]() $M_h$
the multiplication operator
$M_h$
the multiplication operator
which acts on the space of all holomorphic functions on
![]() $\mathbb {D}$
. If h is analytic and
$\mathbb {D}$
. If h is analytic and
![]() $f \in H^2$
, then it is well known that
$f \in H^2$
, then it is well known that
![]() $T_hf = M_hf$
. We say that the Toeplitz operator is co-analytic, or has a co-analytic symbol, if it is of the form
$T_hf = M_hf$
. We say that the Toeplitz operator is co-analytic, or has a co-analytic symbol, if it is of the form
![]() $T_{\overline {h}}$
for
$T_{\overline {h}}$
for
![]() $h \in H^{\infty }$
.
$h \in H^{\infty }$
.
Proposition 4.1 Let
![]() $\boldsymbol {\alpha }$
be a sequence of positive numbers such that the corresponding
$\boldsymbol {\alpha }$
be a sequence of positive numbers such that the corresponding
![]() $X(\boldsymbol {\alpha })$
space consists of analytic functions in
$X(\boldsymbol {\alpha })$
space consists of analytic functions in
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
-
(i) If
 $\boldsymbol {\alpha }$
is increasing, then
$\boldsymbol {\alpha }$
is increasing, then
 $X(\boldsymbol {\alpha })$
is continuously contained in
$X(\boldsymbol {\alpha })$
is continuously contained in
 $H^2$
, and the Toeplitz operators with bounded co-analytic symbols are bounded on
$H^2$
, and the Toeplitz operators with bounded co-analytic symbols are bounded on
 $X(\boldsymbol {\alpha })$
.
$X(\boldsymbol {\alpha })$
. -
(ii) If
 $\boldsymbol {\alpha }$
is decreasing, then the operators
$\boldsymbol {\alpha }$
is decreasing, then the operators
 $M_h$
with bounded analytic symbols are bounded on
$M_h$
with bounded analytic symbols are bounded on
 $X(\boldsymbol {\alpha })$
.
$X(\boldsymbol {\alpha })$
.
In both cases, the corresponding operators have a norm which is less than or equal to the supremum norm of the corresponding symbol.
Proof We prove
![]() $(i)$
. It is clear that
$(i)$
. It is clear that
![]() $X(\boldsymbol {\alpha })$
is continuously contained in
$X(\boldsymbol {\alpha })$
is continuously contained in
![]() $H^2$
. A direct computation shows that
$H^2$
. A direct computation shows that
![]() $\boldsymbol {\alpha }$
being increasing implies that the backward shift operator L in (3.7) is a contraction on
$\boldsymbol {\alpha }$
being increasing implies that the backward shift operator L in (3.7) is a contraction on
![]() $X(\boldsymbol {\alpha })$
. There certainly exists no subspace of
$X(\boldsymbol {\alpha })$
. There certainly exists no subspace of
![]() $X(\boldsymbol {\alpha })$
on which L acts as a unitary (or even an isometry), so the Nagy–Foias functional calculus (see [Reference Sz-Nagy, Foias, Bercovici and Kérchy22] for details) allows us to define the operator
$X(\boldsymbol {\alpha })$
on which L acts as a unitary (or even an isometry), so the Nagy–Foias functional calculus (see [Reference Sz-Nagy, Foias, Bercovici and Kérchy22] for details) allows us to define the operator
for any bounded analytic function h, in such a way that the definition is consistent with (3.10) for polynomials h, the operator norm of
![]() $h(L)$
is at most
$h(L)$
is at most
![]() $\|h\|_{\infty }$
, and if
$\|h\|_{\infty }$
, and if
almost everywhere on
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
then
![]() $h_n(L)$
converges in the strong operator topology to
$h_n(L)$
converges in the strong operator topology to
![]() $h(L)$
. In fact, the operators
$h(L)$
. In fact, the operators
![]() $h(L)$
are co-analytic Toeplitz operators with symbol
$h(L)$
are co-analytic Toeplitz operators with symbol
![]() $\overline {\tilde {h}}$
, where
$\overline {\tilde {h}}$
, where
![]() $\tilde {h}(z) = \overline {h(\overline {z})}$
. To see this, fix
$\tilde {h}(z) = \overline {h(\overline {z})}$
. To see this, fix
![]() $h \in H^{\infty }$
and let
$h \in H^{\infty }$
and let
![]() $\{h_n\}_n$
be the Fejér polynomials for h, so that the above properties of the Nagy–Foias functional calculus imply that
$\{h_n\}_n$
be the Fejér polynomials for h, so that the above properties of the Nagy–Foias functional calculus imply that
![]() $h_n(L)f \to h(L)f$
in the norm of
$h_n(L)f \to h(L)f$
in the norm of
![]() $X(\boldsymbol {\alpha })$
, for any
$X(\boldsymbol {\alpha })$
, for any
![]() $f \in X(\boldsymbol {\alpha })$
. The same is true in the norm of
$f \in X(\boldsymbol {\alpha })$
. The same is true in the norm of
![]() $H^2$
. Recalling (4.3), for
$H^2$
. Recalling (4.3), for
![]() $z \in \mathbb {D}$
, we get
$z \in \mathbb {D}$
, we get
Thus,
![]() $h(L) = T_{\overline {\tilde {h}}}$
, and by reversing roles of h and
$h(L) = T_{\overline {\tilde {h}}}$
, and by reversing roles of h and
![]() $\tilde {h}$
, we see that the Nagy–Foias functional calculus for L on
$\tilde {h}$
, we see that the Nagy–Foias functional calculus for L on
![]() $X(\boldsymbol {\alpha })$
is a bijection onto the co-analytic Toeplitz operators.
$X(\boldsymbol {\alpha })$
is a bijection onto the co-analytic Toeplitz operators.
Next, we prove
![]() $(ii)$
. If
$(ii)$
. If
![]() $\boldsymbol {\alpha }$
is decreasing, then the dual sequence
$\boldsymbol {\alpha }$
is decreasing, then the dual sequence
![]() $\boldsymbol {\alpha ^{-1}}$
is increasing, so by
$\boldsymbol {\alpha ^{-1}}$
is increasing, so by
![]() $(i)$
we can define
$(i)$
we can define
![]() $T_{\overline {h}}^*: X(\boldsymbol {\alpha }) \to X(\boldsymbol {\alpha })$
as the adjoint of
$T_{\overline {h}}^*: X(\boldsymbol {\alpha }) \to X(\boldsymbol {\alpha })$
as the adjoint of
![]() $T_{\overline {h}}: X(\boldsymbol {\alpha ^{-1}}) \to X(\boldsymbol {\alpha ^{-1}})$
with respect to our duality pairing (4.2) between the spaces. Let
$T_{\overline {h}}: X(\boldsymbol {\alpha ^{-1}}) \to X(\boldsymbol {\alpha ^{-1}})$
with respect to our duality pairing (4.2) between the spaces. Let
![]() $f \in X(\boldsymbol {\alpha })$
,
$f \in X(\boldsymbol {\alpha })$
,
![]() $\lambda \in \mathbb {D}$
, and
$\lambda \in \mathbb {D}$
, and
![]() $s_{\lambda }(z) = \frac {1}{1-\overline {\lambda }z}$
. Recall that
$s_{\lambda }(z) = \frac {1}{1-\overline {\lambda }z}$
. Recall that
![]() $s_{\lambda }$
is an eigenvector of
$s_{\lambda }$
is an eigenvector of
![]() $T_{\overline {h}}$
, with eigenvalue
$T_{\overline {h}}$
, with eigenvalue
![]() $\overline {h(\lambda )}$
. We compute
$\overline {h(\lambda )}$
. We compute
Thus, the adjoints of the co-analytic Toeplitz operators on
![]() $X(\boldsymbol {\alpha ^{-1})}$
are multiplication operators on
$X(\boldsymbol {\alpha ^{-1})}$
are multiplication operators on
![]() $X(\boldsymbol {\alpha )}$
. The operator norm of
$X(\boldsymbol {\alpha )}$
. The operator norm of
![]() $T_{\overline {h}}^*$
equals to operator norm of
$T_{\overline {h}}^*$
equals to operator norm of
![]() $T_{\overline {h}}$
, which is at most
$T_{\overline {h}}$
, which is at most
![]() $\|h\|_{\infty }$
, as was noted in the proof of part
$\|h\|_{\infty }$
, as was noted in the proof of part
![]() $(i)$
. The proof is complete.
$(i)$
. The proof is complete.
5 Completely nonisometric shifts
5.1 A big Hilbert space with a completely nonisometric shift
In the next proposition, we construct a Hilbert space of analytic functions on
![]() $\mathbb {D}$
which has desirable properties and which is strictly larger than any space
$\mathbb {D}$
which has desirable properties and which is strictly larger than any space
![]() $\mathcal {P}^2(\mu )$
with measure
$\mathcal {P}^2(\mu )$
with measure
![]() $\mu $
being of the form
$\mu $
being of the form
and C being any positive number. This Hilbert space will play an important role in the proof of the main result of Section 7. Another application is presented in Corollary 5.3. We note that a similar result certainly can be reached by methods of Khrushchev developed in [Reference Khrushchev12], but our proof below is different, and relies fully on construction of smooth Cauchy transforms.
Proposition 5.1 Let E be a Beurling–Carleson set of positive Lebesgue measure, and let w be a bounded positive measurable function which is supported on E and satisfies
![]() $\int _E \log (w) d\textit {m}> -\infty $
. For a sequence
$\int _E \log (w) d\textit {m}> -\infty $
. For a sequence
![]() $\boldsymbol {\alpha }$
, consider the product space
$\boldsymbol {\alpha }$
, consider the product space
and the norm closure
of the linear manifold
There exists a rapidly increasing sequence
![]() $\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
such that the space
$\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
such that the space
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
has the following property:
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
has the following property:
![]() $f_1 \equiv 0$
implies that
$f_1 \equiv 0$
implies that
![]() $f_2 \equiv 0$
, for any tuple
$f_2 \equiv 0$
, for any tuple
![]() $(f_1, f_2) \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
.
$(f_1, f_2) \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
.
Proof The proof is very simple in principle. We will use the set K in (3.2) in combination with the sequence constructed in Proposition 3.4, and this will provide us with enough functionals on
![]() $X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
to conclude that
$X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
to conclude that
![]() $f_1 \equiv 0$
implies
$f_1 \equiv 0$
implies
![]() $f_2 \equiv 0$
, by a straightforward duality argument involving the Beurling–Wiener theorem.
$f_2 \equiv 0$
, by a straightforward duality argument involving the Beurling–Wiener theorem.
For each
![]() $s \in K$
, consider the functional
$s \in K$
, consider the functional
which we define on the set
![]() $\{ (p,p) \in X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m}) : p \text { analytic polynomial}\}$
. By construction, these functionals are the zero functionals, since the functions
$\{ (p,p) \in X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m}) : p \text { analytic polynomial}\}$
. By construction, these functionals are the zero functionals, since the functions
![]() $C_{s1_E}$
and
$C_{s1_E}$
and
![]() $s1_E$
have coinciding Fourier coefficients indexed by nonnegative numbers. Apply Proposition 3.4 to produce a rapidly increasing sequence
$s1_E$
have coinciding Fourier coefficients indexed by nonnegative numbers. Apply Proposition 3.4 to produce a rapidly increasing sequence
![]() $\boldsymbol {\alpha }$
such that
$\boldsymbol {\alpha }$
such that
![]() $C_{s1_E} \in X(\boldsymbol {\alpha })$
for all
$C_{s1_E} \in X(\boldsymbol {\alpha })$
for all
![]() $s \in K$
. The constructed functionals are then continuous with respect to the metric
$s \in K$
. The constructed functionals are then continuous with respect to the metric
![]() $X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
. Indeed, we see from (3.2) that
$X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
. Indeed, we see from (3.2) that
![]() $s = wq$
on E, where q is a bounded function, and so
$s = wq$
on E, where q is a bounded function, and so
by Cauchy–Schwarz inequality.
Now, let
![]() $(f_1, f_2)$
lie
$(f_1, f_2)$
lie
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
and assume that
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
and assume that
![]() $f_1 \equiv 0$
. Fix a sequence of polynomials
$f_1 \equiv 0$
. Fix a sequence of polynomials
![]() $\{p_n\}_{n=1}^{\infty }$
such that
$\{p_n\}_{n=1}^{\infty }$
such that
![]() $(p_n, p_n) \to (f_1, f_2) = (0, f_2)$
in the norm of
$(p_n, p_n) \to (f_1, f_2) = (0, f_2)$
in the norm of
![]() $X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
. Then
$X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
. Then
![]() $(0, f_2)$
is annihilated by any functional in (5.1), and so
$(0, f_2)$
is annihilated by any functional in (5.1), and so
By the density statements in Proposition 3.1, we conclude that
![]() $f_2 \equiv 0$
.
$f_2 \equiv 0$
.
Let us take another look at the space
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
appearing above, assuming that it is satisfying the conclusion of Propoition 5.1. If
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
appearing above, assuming that it is satisfying the conclusion of Propoition 5.1. If
![]() $(f, f_1)$
and
$(f, f_1)$
and
![]() $(f, f_2)$
are two tuples in
$(f, f_2)$
are two tuples in
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
with coinciding first coordinate, then
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
with coinciding first coordinate, then
![]() $(0, f_1 - f_2) \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
, and the above result implies that
$(0, f_1 - f_2) \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
, and the above result implies that
![]() $f_1 \equiv f_2$
. In particular, the projection
$f_1 \equiv f_2$
. In particular, the projection
![]() $(f,f_1) \mapsto f$
onto the first coordinate is an injective mapping from such tuples to analytic functions on
$(f,f_1) \mapsto f$
onto the first coordinate is an injective mapping from such tuples to analytic functions on
![]() $\mathbb {D}$
. But this means that
$\mathbb {D}$
. But this means that
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
is in essence a space of analytic functions in which the analytic polynomials are dense.
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
is in essence a space of analytic functions in which the analytic polynomials are dense.
We make three more very simple but important observations.
Proposition 5.2 Let
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
be as in Propoition 5.1, and identify it with a space of analytic functions on
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
be as in Propoition 5.1, and identify it with a space of analytic functions on
![]() $\mathbb {D}$
as described above.
$\mathbb {D}$
as described above.
-
(i)
 $M_z: \mathcal {D}(\boldsymbol {\alpha }^{-1},w) \to \mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
is completely nonisometric.
$M_z: \mathcal {D}(\boldsymbol {\alpha }^{-1},w) \to \mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
is completely nonisometric. -
(ii) If
 $f \in H^2$
, then
$f \in H^2$
, then
 $f \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
and the corresponding tuple equals
$f \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
and the corresponding tuple equals
 $(f,f)$
, where in the second coordinate f is interpreted in the sense of boundary values of f on
$(f,f)$
, where in the second coordinate f is interpreted in the sense of boundary values of f on
 $\mathbb {T}$
.
$\mathbb {T}$
. -
(iii) Every bounded analytic function h defines a multiplication operator
 $M_h$
on
$M_h$
on
 $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
, with norm at most
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
, with norm at most
 $\|h\|_{\infty }$
.
$\|h\|_{\infty }$
.
Proof Part
![]() $(i)$
follows from the paragraph above. The only way a function
$(i)$
follows from the paragraph above. The only way a function
![]() $f \in \mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
satisfies
$f \in \mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
satisfies
![]() $\|M_z f\|_{\mathcal {D}(\boldsymbol {\alpha }^{-1},w)} = \|f\|_{\mathcal {D}(\boldsymbol {\alpha }^{-1},w)}$
is if f vanishes on
$\|M_z f\|_{\mathcal {D}(\boldsymbol {\alpha }^{-1},w)} = \|f\|_{\mathcal {D}(\boldsymbol {\alpha }^{-1},w)}$
is if f vanishes on
![]() $\mathbb {D}$
, which does not happen by Propoition 5.1.
$\mathbb {D}$
, which does not happen by Propoition 5.1.
Part
![]() $(ii)$
follows in a similar way. We need to note only that since
$(ii)$
follows in a similar way. We need to note only that since
![]() $\boldsymbol {\alpha ^{-1}}$
is decreasing and w is bounded, then for a suitable sequence
$\boldsymbol {\alpha ^{-1}}$
is decreasing and w is bounded, then for a suitable sequence
![]() $\{p_n\}_n$
of Taylor polynomials of
$\{p_n\}_n$
of Taylor polynomials of
![]() $f \in H^2$
, the tuples
$f \in H^2$
, the tuples
![]() $(p_n, p_n)$
will converge in the norm of
$(p_n, p_n)$
will converge in the norm of
![]() $X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w \, d\textit {m})$
to
$X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w \, d\textit {m})$
to
![]() $(f,f)$
. By part
$(f,f)$
. By part
![]() $(i)$
, or the discussion in the paragraph above, there is only one tuple in
$(i)$
, or the discussion in the paragraph above, there is only one tuple in
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
which has f as the first coordinate. So the tuple representing
$\mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
which has f as the first coordinate. So the tuple representing
![]() $f \in H^2 \cap \mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
is precisely
$f \in H^2 \cap \mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
is precisely
![]() $(f,f)$
.
$(f,f)$
.
To prove part
![]() $(iii)$
, let h be a bounded analytic function and
$(iii)$
, let h be a bounded analytic function and
![]() $\{h_n\}_n$
its Fejér means. Let
$\{h_n\}_n$
its Fejér means. Let
![]() $\{p_n\}_n$
be a sequence of polynomials converging to
$\{p_n\}_n$
be a sequence of polynomials converging to
![]() $f \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
. Then Proposition 4.1 implies that
$f \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
. Then Proposition 4.1 implies that
![]() $\{h_np_n\}_n$
is a norm-bounded sequence in
$\{h_np_n\}_n$
is a norm-bounded sequence in
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
. The weak limit of this sequence equals
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
. The weak limit of this sequence equals
![]() $hf \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
, and
$hf \in \mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
, and
The last inequality is again a consequence of Proposition 4.1.
5.2 An uncertainty-type principle
The significance of Propoition 5.1 might not be easy to appreciate. In this section, which is independent of the rest of the article, we want to highlight how such a result can be applied in the theory of
![]() $\mathcal {P}^2(\mu )$
-spaces and how it relates to a classical result in the theory of Hardy spaces.
$\mathcal {P}^2(\mu )$
-spaces and how it relates to a classical result in the theory of Hardy spaces.
Recall that a square integrable function f on
![]() $\mathbb {T}$
which lies in the
$\mathbb {T}$
which lies in the
![]() $L^2$
-closure of the analytic polynomials (that is, in the Hardy space
$L^2$
-closure of the analytic polynomials (that is, in the Hardy space
![]() $H^2$
) cannot vanish on a set of positive measure. Thus, the spectral smallness of f (vanishing of negative Fourier coefficients of f) implies that the function cannot be too small. A beautiful exposition of this result, and other manifestations of the uncertainty principle in harmonic analysis, can be found in [Reference Havin and Jöricke9]. A combination of the deep work of Aleman, Richter, and Sundberg in [Reference Aleman, Richter and Sundberg3] and our Propoition 5.1 will establish the following result of similar nature.
$H^2$
) cannot vanish on a set of positive measure. Thus, the spectral smallness of f (vanishing of negative Fourier coefficients of f) implies that the function cannot be too small. A beautiful exposition of this result, and other manifestations of the uncertainty principle in harmonic analysis, can be found in [Reference Havin and Jöricke9]. A combination of the deep work of Aleman, Richter, and Sundberg in [Reference Aleman, Richter and Sundberg3] and our Propoition 5.1 will establish the following result of similar nature.
Corollary 5.3 (An uncertainty-type principle for a class of
 $\,\mathcal {P}^2(\mu )$
-spaces)
$\,\mathcal {P}^2(\mu )$
-spaces)
Let
![]() $C> -1$
and E be a Beurling–Carleson set of positive measure. Let w be a bounded positive measurable function which is supported on E and satisfies
$C> -1$
and E be a Beurling–Carleson set of positive measure. Let w be a bounded positive measurable function which is supported on E and satisfies
![]() $\int _E \log (w) d\textit {m}> -\infty $
. Consider the measure
$\int _E \log (w) d\textit {m}> -\infty $
. Consider the measure
and the classical Lebesgue space
![]() $L^2(\mu )$
. Let
$L^2(\mu )$
. Let
![]() $\mathcal {P}^2(\mu )$
be the closure of analytic polynomials in
$\mathcal {P}^2(\mu )$
be the closure of analytic polynomials in
![]() $L^2(\mu )$
. Then we have that
$L^2(\mu )$
. Then we have that
![]() $f \neq 0$
almost everywhere with respect to
$f \neq 0$
almost everywhere with respect to
![]() $\mu $
, for any nonzero
$\mu $
, for any nonzero
![]() $f \in \mathcal {P}^2(\mu )$
.
$f \in \mathcal {P}^2(\mu )$
.
Proof A computation shows that for
![]() $f(z) = \sum _{k=0}^{\infty } f_kz^k$
, we have
$f(z) = \sum _{k=0}^{\infty } f_kz^k$
, we have
where the weights
![]() $\beta _k(C)$
satisfy the asymptotics
$\beta _k(C)$
satisfy the asymptotics
This means that convergence of polynomials
![]() $\{p_n\}_n$
in
$\{p_n\}_n$
in
![]() $\mathcal {P}^2(\mu )$
implies convergence of
$\mathcal {P}^2(\mu )$
implies convergence of
![]() $(p_n, p_n)$
in the space
$(p_n, p_n)$
in the space
![]() $X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
appearing in Propoition 5.1, and a direct consequence is that
$X(\boldsymbol {\alpha }^{-1}) \oplus L^2(w d\textit {m})$
appearing in Propoition 5.1, and a direct consequence is that
![]() $\mathcal {P}^2(\mu )$
contains no nonzero function which vanishes on
$\mathcal {P}^2(\mu )$
contains no nonzero function which vanishes on
![]() $\mathbb {D}$
. In particular,
$\mathbb {D}$
. In particular,
![]() $\mathcal {P}^2(\mu )$
does not contain the characteristic function of any subset of
$\mathcal {P}^2(\mu )$
does not contain the characteristic function of any subset of
![]() $\mathbb {T}$
of positive measure, and every element
$\mathbb {T}$
of positive measure, and every element
![]() $f \in \mathcal {P}^2(\mu )$
has a unique restriction
$f \in \mathcal {P}^2(\mu )$
has a unique restriction
![]() $f|\mathbb {D}$
to
$f|\mathbb {D}$
to
![]() $\mathbb {D}$
, which of course is an analytic function. In particular, the space satisfies the assumptions of [Reference Aleman, Richter and Sundberg3, Theorem A], and the conclusion of that theorem is that for any
$\mathbb {D}$
, which of course is an analytic function. In particular, the space satisfies the assumptions of [Reference Aleman, Richter and Sundberg3, Theorem A], and the conclusion of that theorem is that for any
![]() $f \in \mathcal {P}^2(\mu )$
, its restriction
$f \in \mathcal {P}^2(\mu )$
, its restriction
![]() $f|\mathbb {D}$
has a nontangential limit almost everywhere with respect to
$f|\mathbb {D}$
has a nontangential limit almost everywhere with respect to
![]() $\mu |\mathbb {T}$
, and this limit agrees almost everywhere with
$\mu |\mathbb {T}$
, and this limit agrees almost everywhere with
![]() $f|\mathbb {T}$
. If f would vanish on a set of positive
$f|\mathbb {T}$
. If f would vanish on a set of positive
![]() $\mu |\mathbb {T}$
-measure, then a classical theorem of Privalov (see, for instance, [Reference Koosis13]) can be used to deduce that
$\mu |\mathbb {T}$
-measure, then a classical theorem of Privalov (see, for instance, [Reference Koosis13]) can be used to deduce that
![]() $f \equiv 0$
throughout
$f \equiv 0$
throughout
![]() $\overline {\mathbb {D}}$
.
$\overline {\mathbb {D}}$
.
In the above result, we can obviously replace the part
![]() $d\mu |\mathbb {T} = w d\textit {m}$
with a more general weight w which is carried by a countable union
$d\mu |\mathbb {T} = w d\textit {m}$
with a more general weight w which is carried by a countable union
![]() $\{E_n\}_n$
of Beurling–Carleson sets of positive measure, and where the weight w is
$\{E_n\}_n$
of Beurling–Carleson sets of positive measure, and where the weight w is
![]() $\log $
-integrable on each set
$\log $
-integrable on each set
![]() $E_n$
separately.
$E_n$
separately.
We want to remark also that the use of the very deep and general Aleman–Richter–Sundberg theorem from [Reference Aleman, Richter and Sundberg3] in the above proof can likely be avoided, and the existence of nontangential limits on E for functions f in
![]() $\mathcal {P}^2(\mu )$
of the described form, or even in the space
$\mathcal {P}^2(\mu )$
of the described form, or even in the space
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
, is likely accessible in a more straightforward way (see the introductory section of the article [Reference Aleman, Richter and Sundberg3] for an exposition of previously attained special cases of the Aleman–Richter–Sundberg theorem).
$\mathcal {D}(\boldsymbol {\alpha }^{-1},w)$
, is likely accessible in a more straightforward way (see the introductory section of the article [Reference Aleman, Richter and Sundberg3] for an exposition of previously attained special cases of the Aleman–Richter–Sundberg theorem).
6 A permanence principle for inner factors
In this section, we study the inner factor permanence problem for the spaces appearing in the previous sections. We start by formally stating the property which we are investigating.
Definition 6.1 Let
![]() $\mathcal {H}$
be a topological space of analytic functions which contains
$\mathcal {H}$
be a topological space of analytic functions which contains
![]() $H^{\infty }$
, and let
$H^{\infty }$
, and let
![]() $\theta $
be a given inner function. We say that the pair
$\theta $
be a given inner function. We say that the pair
![]() $(\mathcal {H}, \theta )$
satisfies the permanence property if
$(\mathcal {H}, \theta )$
satisfies the permanence property if
in the sense of the topology of
![]() $\mathcal {H}$
, implies that
$\mathcal {H}$
, implies that
![]() $f/\theta $
is bounded, whenever
$f/\theta $
is bounded, whenever
![]() $f_n,f$
are bounded analytic functions.
$f_n,f$
are bounded analytic functions.
Let us go back to the setting of Propositions 5.1 and 5.2 where the Hilbert space
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
appears. We noted that if
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
appears. We noted that if
![]() $\boldsymbol {\alpha }$
is suitably chosen, then
$\boldsymbol {\alpha }$
is suitably chosen, then
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
is in fact a space of analytic functions, and it contains
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
is in fact a space of analytic functions, and it contains
![]() $H^2$
. Thus, the above question of inner factor permanence makes sense in the context of the norm on
$H^2$
. Thus, the above question of inner factor permanence makes sense in the context of the norm on
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
.
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
.
Weaker versions of the following results appear in [Reference Limani and Malman16], where circumstances allow for statements in much less technical form. This is a consequence of the fact that the sequences
![]() $\boldsymbol {\alpha }$
which appear in [Reference Limani and Malman16] increase only polynomially. Below, we show that by fixing some singular inner function
$\boldsymbol {\alpha }$
which appear in [Reference Limani and Malman16] increase only polynomially. Below, we show that by fixing some singular inner function
![]() $\theta $
of some particular structure, we can alter the methods in [Reference Limani and Malman16] and construct a space
$\theta $
of some particular structure, we can alter the methods in [Reference Limani and Malman16] and construct a space
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
where the sequence
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
where the sequence
![]() $\boldsymbol {\alpha }$
is rapidly increasing and in which the permanence principle in Definition 6.1 holds for that given
$\boldsymbol {\alpha }$
is rapidly increasing and in which the permanence principle in Definition 6.1 holds for that given
![]() $\theta $
. The corresponding results for
$\theta $
. The corresponding results for
![]() $\mathcal {P}^2(\mu )$
-spaces from [Reference Limani and Malman16] are corollaries (we state them in Corollary 6.5), but we will need the full strength of the results established below in the principal application to come.
$\mathcal {P}^2(\mu )$
-spaces from [Reference Limani and Malman16] are corollaries (we state them in Corollary 6.5), but we will need the full strength of the results established below in the principal application to come.
Lemma 6.2 Let
![]() $\theta = S_{\nu }$
be a fixed singular inner function for which in the decomposition (
1.7
) of
$\theta = S_{\nu }$
be a fixed singular inner function for which in the decomposition (
1.7
) of
![]() $\nu $
, the part
$\nu $
, the part
![]() $\nu _{\mathcal {C}}$
is supported on a single Beurling–Carleson set F of Lebesgue measure zero, and
$\nu _{\mathcal {C}}$
is supported on a single Beurling–Carleson set F of Lebesgue measure zero, and
![]() $\nu _{\mathcal {K}} \equiv 0$
. Then there exists a rapidly increasing sequence
$\nu _{\mathcal {K}} \equiv 0$
. Then there exists a rapidly increasing sequence
![]() $\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
(which depends on
$\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
(which depends on
![]() $\theta $
) such that the pair
$\theta $
) such that the pair
![]() $(X(\boldsymbol {\alpha }^{-1}), \theta )$
satisfies the permanence property in Definition 6.1.
$(X(\boldsymbol {\alpha }^{-1}), \theta )$
satisfies the permanence property in Definition 6.1.
Proof The idea of the proof is as follows: Let u be a function in
![]() $K_{\theta }$
, the orthogonal complement of
$K_{\theta }$
, the orthogonal complement of
![]() $\theta H^2$
in
$\theta H^2$
in
![]() $H^2$
, and let
$H^2$
, and let
![]() $\Lambda _u$
be the (in general, unbounded with respect to the norm on
$\Lambda _u$
be the (in general, unbounded with respect to the norm on
![]() $X(\boldsymbol {\alpha ^{-1}})$
) linear functional
$X(\boldsymbol {\alpha ^{-1}})$
) linear functional
which is defined for
![]() $f \in H^2 \subset X(\boldsymbol {\alpha ^{-1}})$
. If
$f \in H^2 \subset X(\boldsymbol {\alpha ^{-1}})$
. If
![]() $\Lambda _u$
can be extended to a bounded linear functional on
$\Lambda _u$
can be extended to a bounded linear functional on
![]() $X(\boldsymbol {\alpha ^{-1}})$
for u in a dense subset of
$X(\boldsymbol {\alpha ^{-1}})$
for u in a dense subset of
![]() $K_{\theta }$
, then
$K_{\theta }$
, then
![]() $\|\theta f_n - f\|_{X(\boldsymbol {\alpha }^{-1})} \to 0$
, with
$\|\theta f_n - f\|_{X(\boldsymbol {\alpha }^{-1})} \to 0$
, with
![]() $f_n, f \in H^2$
, will imply that f is orthogonal to
$f_n, f \in H^2$
, will imply that f is orthogonal to
![]() $K_{\theta }$
in
$K_{\theta }$
in
![]() $H^2$
. Indeed, in such a case, we will have
$H^2$
. Indeed, in such a case, we will have
for all u in a dense subset of
![]() $K_{\theta }$
, and so
$K_{\theta }$
, and so
![]() $f \in (K_{\theta })^{\perp } = \theta H^2$
. This of course means that
$f \in (K_{\theta })^{\perp } = \theta H^2$
. This of course means that
![]() $f/\theta \in H^2$
. We will show that such a dense set can be constructed under the stated assumption, for some rapidly increasing sequence
$f/\theta \in H^2$
. We will show that such a dense set can be constructed under the stated assumption, for some rapidly increasing sequence
![]() $\boldsymbol {\alpha }$
. The proof will involve construction of a new set of smooth Cauchy transforms similar to those in (3.4), and an application of Proposition 3.4.
$\boldsymbol {\alpha }$
. The proof will involve construction of a new set of smooth Cauchy transforms similar to those in (3.4), and an application of Proposition 3.4.
Note that
![]() $\theta $
extends analytically across the set
$\theta $
extends analytically across the set
![]() $\mathbb {T} \setminus F$
, and a simple differentiation argument and the formula (1.11) shows that we have the following estimate:
$\mathbb {T} \setminus F$
, and a simple differentiation argument and the formula (1.11) shows that we have the following estimate:
Let
![]() $g = g_F$
be the function decaying rapidly near F, which is given by Lemma 2.1. We conclude, similarly to as in the proof of Proposition 3.1, that the set of functions on
$g = g_F$
be the function decaying rapidly near F, which is given by Lemma 2.1. We conclude, similarly to as in the proof of Proposition 3.1, that the set of functions on
![]() $\mathbb {T}$
defined by
$\mathbb {T}$
defined by
consists of functions in
![]() $C^{\infty }(\mathbb {T})$
, and thus the Cauchy transform of any function in this set is in
$C^{\infty }(\mathbb {T})$
, and thus the Cauchy transform of any function in this set is in
![]() $\mathcal {A}^{\infty }$
. Let
$\mathcal {A}^{\infty }$
. Let
![]() $P_+$
denote the projection operator from
$P_+$
denote the projection operator from
![]() $L^2(\mathbb {T})$
to the Hardy space
$L^2(\mathbb {T})$
to the Hardy space
![]() $H^2$
. Then
$H^2$
. Then
![]() $P_+f = C_f$
, interpreted as functions on the circle. We now verify that the Cauchy transforms of elements of
$P_+f = C_f$
, interpreted as functions on the circle. We now verify that the Cauchy transforms of elements of
![]() $K_1$
are members of
$K_1$
are members of
![]() $K_{\theta }$
. Let
$K_{\theta }$
. Let
![]() $\big \langle \cdot , \cdot \big \rangle _{L^2}$
denote the usual inner product for
$\big \langle \cdot , \cdot \big \rangle _{L^2}$
denote the usual inner product for
![]() $L^2(\mathbb {T})$
. For
$L^2(\mathbb {T})$
. For
![]() $s = \theta \overline {\zeta p g_F}$
and any
$s = \theta \overline {\zeta p g_F}$
and any
![]() $h \in H^2$
, we have
$h \in H^2$
, we have
where the last integral vanishes because the integrand represents the boundary function of an analytic function with a zero at the origin. Thus,
![]() $C_{s} \in K_{\theta }$
for any
$C_{s} \in K_{\theta }$
for any
![]() $s \in K_{\theta }$
. We now verify that this set of Cauchy transforms is dense in
$s \in K_{\theta }$
. We now verify that this set of Cauchy transforms is dense in
![]() $K_{\theta }$
. If
$K_{\theta }$
. If
![]() $f \in K_{\theta }$
, then
$f \in K_{\theta }$
, then
![]() $f\overline {\theta } = \overline {\zeta f_0}$
as boundary functions, where
$f\overline {\theta } = \overline {\zeta f_0}$
as boundary functions, where
![]() $f_0 \in H^2$
. Orthogonality of
$f_0 \in H^2$
. Orthogonality of
![]() $f \in K_{\theta }$
to all functions
$f \in K_{\theta }$
to all functions
![]() $C_s, s\in K_1$
, means that
$C_s, s\in K_1$
, means that
Since
![]() $g_F$
is outer, the set
$g_F$
is outer, the set
is dense in
![]() $H^2$
, and so the above implies
$H^2$
, and so the above implies
![]() $f_0 \equiv 0$
, which means that
$f_0 \equiv 0$
, which means that
![]() $f \equiv 0$
. We have thus constructed a dense set of functions in
$f \equiv 0$
. We have thus constructed a dense set of functions in
![]() $K_{\theta }$
to which Proposition 3.4 applies, and the conclusion is that the Cauchy transforms we constructed are all contained in some space
$K_{\theta }$
to which Proposition 3.4 applies, and the conclusion is that the Cauchy transforms we constructed are all contained in some space
![]() $X(\boldsymbol {\alpha })$
defined by a rapidly increasing sequence
$X(\boldsymbol {\alpha })$
defined by a rapidly increasing sequence
![]() $\boldsymbol {\alpha }$
. Then the space
$\boldsymbol {\alpha }$
. Then the space
![]() $X(\boldsymbol {\alpha ^{-1}})$
satisfies the permanence principle for
$X(\boldsymbol {\alpha ^{-1}})$
satisfies the permanence principle for
![]() $\theta $
, by the observation in the first paragraph of this proof.
$\theta $
, by the observation in the first paragraph of this proof.
Lemma 6.3 Let E be a Beurling–Carleson set of positive Lebesgue measure, and let w be a weight supported on E and satisfying
![]() $\int _E \log (w) \, d\textit {m}> -\infty $
. Let
$\int _E \log (w) \, d\textit {m}> -\infty $
. Let
![]() $\theta = S_{\nu }$
be a fixed singular inner function for which
$\theta = S_{\nu }$
be a fixed singular inner function for which
![]() $\nu $
is supported on the set E. There exists a rapidly increasing sequence
$\nu $
is supported on the set E. There exists a rapidly increasing sequence
![]() $\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
(which depends on
$\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
(which depends on
![]() $E, w$
, and
$E, w$
, and
![]() $\theta $
) for which the conclusion of Propoition 5.1 holds, and moreover the pair
$\theta $
) for which the conclusion of Propoition 5.1 holds, and moreover the pair
![]() $(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w) , \theta )$
satisfies the permanence property in Definition 6.1.
$(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w) , \theta )$
satisfies the permanence property in Definition 6.1.
The difference from Lemma 6.2 is that Lemma 6.3 also applies to the case when
![]() $\nu _{\mathcal {K}}$
in (1.7) is nonzero.
$\nu _{\mathcal {K}}$
in (1.7) is nonzero.
Proof We follow the same idea as in the proof of Lemma 6.2. From the weight w, we construct the outer function W given by the formula (3.1). For the set E, we construct the corresponding function
![]() $g = g_E$
as in Lemma 2.1, and we define
$g = g_E$
as in Lemma 2.1, and we define
This time, the Cauchy transforms of the functions in
![]() $K_2$
are not necessarily smooth. However, they are again contained and dense in
$K_2$
are not necessarily smooth. However, they are again contained and dense in
![]() $K_{\theta }$
, as in Lemma 6.2. The only difference in the proof, which we skip, is that the set in (6.3) is replaced by
$K_{\theta }$
, as in Lemma 6.2. The only difference in the proof, which we skip, is that the set in (6.3) is replaced by
which is dense in
![]() $H^2$
by the fact that W and
$H^2$
by the fact that W and
![]() $g_E$
are outer.
$g_E$
are outer.
For
we define the Cauchy transform
![]() $u_0 := C_{s_0}$
. We can decompose
$u_0 := C_{s_0}$
. We can decompose
![]() $u_0$
according to
$u_0$
according to
 $$ \begin{align} u_0(z) = \int_{\mathbb{T}} \frac{s_0(\zeta)}{1-\overline{\zeta}z} \, dm(\zeta) &= \int_{\mathbb{T} \setminus E} \frac{s_0(\zeta)}{1-\overline{\zeta}z} \, dm(\zeta) + \int_{E} \frac{s_0(\zeta)}{1-\overline{\zeta}z} \, dm(\zeta) \nonumber \\ &:= u_1(z) + u_2(z). \end{align} $$
$$ \begin{align} u_0(z) = \int_{\mathbb{T}} \frac{s_0(\zeta)}{1-\overline{\zeta}z} \, dm(\zeta) &= \int_{\mathbb{T} \setminus E} \frac{s_0(\zeta)}{1-\overline{\zeta}z} \, dm(\zeta) + \int_{E} \frac{s_0(\zeta)}{1-\overline{\zeta}z} \, dm(\zeta) \nonumber \\ &:= u_1(z) + u_2(z). \end{align} $$
The estimates in (3.6) and (6.2) show that in
![]() $s_01_{\mathbb {T} \setminus E}$
is a function in
$s_01_{\mathbb {T} \setminus E}$
is a function in
![]() $C^{\infty }$
, and thus
$C^{\infty }$
, and thus
![]() $u_1 \in \mathcal {A}^{\infty }$
. Consequently, by Proposition 3.4, there exists a rapidly increasing sequence
$u_1 \in \mathcal {A}^{\infty }$
. Consequently, by Proposition 3.4, there exists a rapidly increasing sequence
![]() $\boldsymbol {\beta }$
such that
$\boldsymbol {\beta }$
such that
![]() $C_{s1_{\mathbb {T} \setminus E}}$
is in
$C_{s1_{\mathbb {T} \setminus E}}$
is in
![]() $X(\boldsymbol {\beta ^{-1}})$
, for all
$X(\boldsymbol {\beta ^{-1}})$
, for all
![]() $s \in K_2$
. Apply now Propoition 5.1 to E and w to obtain another rapidly increasing sequence
$s \in K_2$
. Apply now Propoition 5.1 to E and w to obtain another rapidly increasing sequence
![]() $\boldsymbol {\gamma }$
such that the conclusion of that proposition holds, and let
$\boldsymbol {\gamma }$
such that the conclusion of that proposition holds, and let
![]() $\boldsymbol {\alpha }$
be the termwise minimum of
$\boldsymbol {\alpha }$
be the termwise minimum of
![]() $\boldsymbol {\beta }$
and
$\boldsymbol {\beta }$
and
![]() $\boldsymbol {\gamma }$
:
$\boldsymbol {\gamma }$
:
Then
![]() $\boldsymbol {\alpha }$
is again a rapidly increasing sequence, the conclusion of Propoition 5.1 holds, and
$\boldsymbol {\alpha }$
is again a rapidly increasing sequence, the conclusion of Propoition 5.1 holds, and
![]() $C_{s1_{\mathbb {T} \setminus E}}$
is in
$C_{s1_{\mathbb {T} \setminus E}}$
is in
![]() $X(\boldsymbol {\alpha })$
, for all
$X(\boldsymbol {\alpha })$
, for all
![]() $s \in K_2$
.
$s \in K_2$
.
Moreover, the linear functional
defined on analytic polynomials f, is bounded in the metric of
![]() $L^2(w \,d\textit {m})$
. Indeed, recall that
$L^2(w \,d\textit {m})$
. Indeed, recall that
![]() $|W| = w$
on the set E, and so we have
$|W| = w$
on the set E, and so we have
for some constant
![]() $c> 0$
, since
$c> 0$
, since
![]() $\overline {\theta } \zeta g_E$
is bounded. The same argument shows also that
$\overline {\theta } \zeta g_E$
is bounded. The same argument shows also that
![]() $C_{s1_E}$
defines a bounded linear functional on the analytic polynomials in the metric of
$C_{s1_E}$
defines a bounded linear functional on the analytic polynomials in the metric of
![]() $L^2(w \, d\textit {m})$
, for all
$L^2(w \, d\textit {m})$
, for all
![]() $s \in K_2$
.
$s \in K_2$
.
We let
![]() $v = C_s$
for
$v = C_s$
for
![]() $s \in K_2$
,
$s \in K_2$
,
![]() $v_1 = C_{s1_{\mathbb {T} \setminus E}}$
, and
$v_1 = C_{s1_{\mathbb {T} \setminus E}}$
, and
![]() $v_2 = C_{s1_{E}}$
, so that
$v_2 = C_{s1_{E}}$
, so that
![]() $v = v_1 + v_2$
, and go back to the definition of the functional
$v = v_1 + v_2$
, and go back to the definition of the functional
![]() $\Lambda _u$
in (6.1). We have just verified that we can decompose it according to (6.4)
$\Lambda _u$
in (6.1). We have just verified that we can decompose it according to (6.4)
in such a way that the first piece defines a continuous linear functional on the analytic polynomials in the metric of
![]() $X(\boldsymbol {\alpha ^{-1}})$
, and the second piece defines a continuous linear functional on the analytic polynomials in the metric of
$X(\boldsymbol {\alpha ^{-1}})$
, and the second piece defines a continuous linear functional on the analytic polynomials in the metric of
![]() $L^2(w \, d\textit {m})$
. But then, these functionals extend continuously to
$L^2(w \, d\textit {m})$
. But then, these functionals extend continuously to
![]() $\mathcal {D}(\boldsymbol {\alpha ^{-1}}, w)$
, and by the density of
$\mathcal {D}(\boldsymbol {\alpha ^{-1}}, w)$
, and by the density of
![]() $\{ C_s : s \in K_2 \}$
in
$\{ C_s : s \in K_2 \}$
in
![]() $K_{\theta }$
and the argument in the first paragraph of the proof of Lemma 6.2, we conclude that the pair
$K_{\theta }$
and the argument in the first paragraph of the proof of Lemma 6.2, we conclude that the pair
![]() $(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w) , \theta )$
satisfies the permanence property.
$(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w) , \theta )$
satisfies the permanence property.
Corollary 6.4 (An inner factor permanence principle)
Let E be a Beurling–Carleson set of positive Lebesgue measure, and let w be a weight supported on E and satisfies
![]() $\int _E \log (w) \, d\textit {m}> -\infty $
. Let
$\int _E \log (w) \, d\textit {m}> -\infty $
. Let
![]() $\theta = S_{\nu }$
be a fixed singular inner function such that in the decomposition (
1.7
), the part
$\theta = S_{\nu }$
be a fixed singular inner function such that in the decomposition (
1.7
), the part
![]() $\nu _{\mathcal {C}}$
satisfies
$\nu _{\mathcal {C}}$
satisfies
![]() $\nu _{\mathcal {C}}(F) = \nu _{\mathcal {C}}(\mathbb {T})$
for a single fixed Beurling–Carleson set F of Lebesgue measure zero, and
$\nu _{\mathcal {C}}(F) = \nu _{\mathcal {C}}(\mathbb {T})$
for a single fixed Beurling–Carleson set F of Lebesgue measure zero, and
![]() $\nu _{\mathcal {K}}$
is supported on E. There exists a rapidly increasing sequence
$\nu _{\mathcal {K}}$
is supported on E. There exists a rapidly increasing sequence
![]() $\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
(which depends on
$\boldsymbol {\alpha } = \{\alpha _k\}_{k=0}^{\infty }$
(which depends on
![]() $E, w$
, and
$E, w$
, and
![]() $\theta $
) for which the conclusion of Propoition 5.1 holds, and moreover the pair
$\theta $
) for which the conclusion of Propoition 5.1 holds, and moreover the pair
![]() $(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w) , \theta )$
satisfies the permanence property in Definition 6.1.
$(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w) , \theta )$
satisfies the permanence property in Definition 6.1.
Proof The required rapidly increasing sequence
![]() $\boldsymbol {\alpha }$
is the one obtained by constructing the termwise minimum of the sequences given by Lemmas 6.2 and 6.3.
$\boldsymbol {\alpha }$
is the one obtained by constructing the termwise minimum of the sequences given by Lemmas 6.2 and 6.3.
The above result is essentially optimal. Indeed, if
![]() $\nu = \nu _{\mathcal {K}}$
in (1.7) and
$\nu = \nu _{\mathcal {K}}$
in (1.7) and
![]() $\nu (\mathbb {T} \setminus E)> 0$
, then
$\nu (\mathbb {T} \setminus E)> 0$
, then
![]() $S_{\nu }$
will be divisible by an inner function which is cyclic in
$S_{\nu }$
will be divisible by an inner function which is cyclic in
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
(and so certainly cannot satisfy the permanence property). This can be seen from the corresponding cyclicity result in [Reference Limani and Malman16] for the class of
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
(and so certainly cannot satisfy the permanence property). This can be seen from the corresponding cyclicity result in [Reference Limani and Malman16] for the class of
![]() $\mathcal {P}^2(\mu )$
-spaces appearing in Corollary 5.3. In the other direction, we note that the main inner factor permanence result in [Reference Limani and Malman16] is an immediate consequence of Corollary 6.4. Here is the statement.
$\mathcal {P}^2(\mu )$
-spaces appearing in Corollary 5.3. In the other direction, we note that the main inner factor permanence result in [Reference Limani and Malman16] is an immediate consequence of Corollary 6.4. Here is the statement.
Corollary 6.5 (The permanence principle for a class of
 $\mathcal {P}^2(\mu )$
-spaces)
$\mathcal {P}^2(\mu )$
-spaces)
Let
![]() $C> -1$
and E be a Beurling–Carleson set of positive measure. Let w be a bounded positive measurable function which is supported on E and satisfies
$C> -1$
and E be a Beurling–Carleson set of positive measure. Let w be a bounded positive measurable function which is supported on E and satisfies
![]() $\int _E \log (w) d\textit {m}> -\infty $
. Consider the measure
$\int _E \log (w) d\textit {m}> -\infty $
. Consider the measure
and the classical Lebesgue space
![]() $L^2(\mu )$
. Let
$L^2(\mu )$
. Let
![]() $\mathcal {P}^2(\mu )$
be the closure of analytic polynomials in
$\mathcal {P}^2(\mu )$
be the closure of analytic polynomials in
![]() $L^2(\mu )$
. If
$L^2(\mu )$
. If
![]() $\theta = S_{\nu }$
be a singular inner function such that in the decomposition (
1.7
) the part
$\theta = S_{\nu }$
be a singular inner function such that in the decomposition (
1.7
) the part
![]() $\nu _{\mathcal {K}}$
is supported on E, then the pair
$\nu _{\mathcal {K}}$
is supported on E, then the pair
![]() $(\mathcal {P}^2(\mu ), \theta )$
satisfies the permanence property in Definition 6.1.
$(\mathcal {P}^2(\mu ), \theta )$
satisfies the permanence property in Definition 6.1.
We skip the proof, which is similar to the proof of Corollary 5.3.
7 Density of smooth functions in extreme
 $\mathcal {H}(b)$
-spaces
$\mathcal {H}(b)$
-spaces
This final section is devoted to the proof of density of smooth functions in the class of de Branges–Rovnyak spaces described in Section 1.
7.1 A little background on
 $\mathcal {H}(b)$
$\mathcal {H}(b)$
The following construction of the
![]() $\mathcal {H}(b)$
-space appears in [Reference Aleman and Malman2].
$\mathcal {H}(b)$
-space appears in [Reference Aleman and Malman2].
Proposition 7.1 Let b be an extreme point of the unit ball of
![]() $H^{\infty }$
,
$H^{\infty }$
,
and let
![]() $\Delta = \sqrt {1-|b|^2}$
be a function on the circle
$\Delta = \sqrt {1-|b|^2}$
be a function on the circle
![]() $\mathbb {T}$
, defined in terms of boundary values of b on
$\mathbb {T}$
, defined in terms of boundary values of b on
![]() $\mathbb {T}$
. For
$\mathbb {T}$
. For
![]() $f\in \mathcal {H}(b)$
, the equation
$f\in \mathcal {H}(b)$
, the equation
has a unique solution
![]() $g\in L^2(E)$
, and the map
$g\in L^2(E)$
, and the map
![]() $J:\mathcal {H}(b)\to H^2\oplus L^2(E)$
defined by
$J:\mathcal {H}(b)\to H^2\oplus L^2(E)$
defined by
is an isometry. Moreover,
The benefit of the above described way of constructing the
![]() $\mathcal {H}(b)$
-space (that is, using the embedding J above, and an orthogonal complement) is that it will be particularly easy to implement our duality argument.
$\mathcal {H}(b)$
-space (that is, using the embedding J above, and an orthogonal complement) is that it will be particularly easy to implement our duality argument.
We need only one more lemma before going into the final proof.
Lemma 7.2 Let
![]() $b = \theta u$
be an extreme point of the unit ball of
$b = \theta u$
be an extreme point of the unit ball of
![]() $H^{\infty }$
, where
$H^{\infty }$
, where
![]() $\theta $
and u are the inner and outer factors of b, respectively. Furthermore, let
$\theta $
and u are the inner and outer factors of b, respectively. Furthermore, let
![]() $\{\theta _n\}_n$
be a sequence of inner divisors of
$\{\theta _n\}_n$
be a sequence of inner divisors of
![]() $\theta $
such that
$\theta $
such that
for all
![]() $z \in \mathbb {D}$
, and let
$z \in \mathbb {D}$
, and let
![]() $\{E_n\}_n$
be an increasing sequence of subsets of
$\{E_n\}_n$
be an increasing sequence of subsets of
![]() $\mathbb {T}$
such that
$\mathbb {T}$
such that
up to a set of Lebesgue measure zero. For
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $u_n$
be the outer function with modulus
$u_n$
be the outer function with modulus
on
![]() $\mathbb {T}$
. Set
$\mathbb {T}$
. Set
![]() $b_n = \theta _n u_n$
. Then
$b_n = \theta _n u_n$
. Then
![]() $\mathcal {H}(b_n)$
is contractively contained in
$\mathcal {H}(b_n)$
is contractively contained in
![]() $\mathcal {H}(b)$
, and
$\mathcal {H}(b)$
, and
![]() $\cup _n \mathcal {H}(b_n)$
is norm-dense in
$\cup _n \mathcal {H}(b_n)$
is norm-dense in
![]() $\mathcal {H}(b)$
.
$\mathcal {H}(b)$
.
Proof Let
![]() $k_b$
and
$k_b$
and
![]() $k_{b_n}$
be the reproducing kernels of
$k_{b_n}$
be the reproducing kernels of
![]() $\mathcal {H}(b)$
and
$\mathcal {H}(b)$
and
![]() $\mathcal {H}(b_n)$
, respectively. Note that the assumptions imply that
$\mathcal {H}(b_n)$
, respectively. Note that the assumptions imply that
![]() $b_n$
divides b, in the sense that
$b_n$
divides b, in the sense that
Then
 $$\begin{align*}k_b(\lambda,z) - k_{b_n}(\lambda, z) = \frac{\overline{b_n(\lambda)} b_n(z) - \overline{b(\lambda)}b(z)}{1-\overline{\lambda}z} = \overline{b_n(\lambda)}b_n(z)\frac{1 - \overline{b/b_n(\lambda)}b/b_n(z)}{1-\overline{\lambda}z} \end{align*}$$
$$\begin{align*}k_b(\lambda,z) - k_{b_n}(\lambda, z) = \frac{\overline{b_n(\lambda)} b_n(z) - \overline{b(\lambda)}b(z)}{1-\overline{\lambda}z} = \overline{b_n(\lambda)}b_n(z)\frac{1 - \overline{b/b_n(\lambda)}b/b_n(z)}{1-\overline{\lambda}z} \end{align*}$$
is clearly a positive definite kernel, so by standard theory of reproducing kernel Hilbert spaces (see, for instance, [Reference Aronszajn4] or [Reference Agler and McCarthy1]), it follows that
![]() $\mathcal {H}(b_n)$
is contractively contained in
$\mathcal {H}(b_n)$
is contractively contained in
![]() $\mathcal {H}(b)$
. Moreover, contractivity of the containment means that
$\mathcal {H}(b)$
. Moreover, contractivity of the containment means that
 $$\begin{align*}\|k_{b_n}(\lambda, \cdot)\|^2_{\mathcal{H}(b)} \leq \|k_{b_n}(\lambda, \cdot)\|^2_{\mathcal{H}(b_n)} = \frac{1-|b_n(\lambda)|^2}{1-|\lambda|^2} \leq \frac{1-|b(\lambda)|^2}{1-|\lambda|^2}, \end{align*}$$
$$\begin{align*}\|k_{b_n}(\lambda, \cdot)\|^2_{\mathcal{H}(b)} \leq \|k_{b_n}(\lambda, \cdot)\|^2_{\mathcal{H}(b_n)} = \frac{1-|b_n(\lambda)|^2}{1-|\lambda|^2} \leq \frac{1-|b(\lambda)|^2}{1-|\lambda|^2}, \end{align*}$$
where in the last step we used (7.3). So, for fixed
![]() $\lambda $
, the functions
$\lambda $
, the functions
![]() $k_{b_n}(\lambda , \cdot )$
are norm-bounded in
$k_{b_n}(\lambda , \cdot )$
are norm-bounded in
![]() $\mathcal {H}(b)$
. It is not hard to see from the usual construction of the outer functions that
$\mathcal {H}(b)$
. It is not hard to see from the usual construction of the outer functions that
![]() $u_n(z) \to u(z)$
as
$u_n(z) \to u(z)$
as
![]() $n \to \infty $
, for every
$n \to \infty $
, for every
![]() $z \in \mathbb {D}$
. Consequently,
$z \in \mathbb {D}$
. Consequently,
![]() $b_n(z) \to b(z)$
for each
$b_n(z) \to b(z)$
for each
![]() $z \in \mathbb {D}$
, and even
$z \in \mathbb {D}$
, and even
Together with the norm estimate above, this means that for any fixed
![]() $\lambda \in \mathbb {D}$
, a suitable subsequence of the kernels
$\lambda \in \mathbb {D}$
, a suitable subsequence of the kernels
![]() $k_{b_n}(\lambda , \cdot )$
will converge weakly in
$k_{b_n}(\lambda , \cdot )$
will converge weakly in
![]() $\mathcal {H}(b)$
to
$\mathcal {H}(b)$
to
![]() $k_b(\lambda , \cdot )$
. Elementary functional analysis now ensures that
$k_b(\lambda , \cdot )$
. Elementary functional analysis now ensures that
![]() $\cup _n \mathcal {H}(b_n)$
is dense in
$\cup _n \mathcal {H}(b_n)$
is dense in
![]() $\mathcal {H}(b)$
.
$\mathcal {H}(b)$
.
We remark that a simple consequence of the contractive containment of
![]() $\mathcal {H}(b_n)$
in
$\mathcal {H}(b_n)$
in
![]() $\mathcal {H}(b)$
is the following: density of
$\mathcal {H}(b)$
is the following: density of
![]() $\mathcal {A}^{\infty } \cap \mathcal {H}(b_n)$
in
$\mathcal {A}^{\infty } \cap \mathcal {H}(b_n)$
in
![]() $\mathcal {H}(b_n)$
for each n implies density of
$\mathcal {H}(b_n)$
for each n implies density of
![]() $\mathcal {A}^{\infty } \cap \mathcal {H}(b)$
in
$\mathcal {A}^{\infty } \cap \mathcal {H}(b)$
in
![]() $\mathcal {H}(b)$
.
$\mathcal {H}(b)$
.
7.2 The density theorem
In the proof below, we use the duality pairing
![]() $\big \langle \cdot , \cdot \big \rangle $
appearing in Section 4.1. For a set S in either
$\big \langle \cdot , \cdot \big \rangle $
appearing in Section 4.1. For a set S in either
![]() $X(\boldsymbol {\alpha })$
or
$X(\boldsymbol {\alpha })$
or
![]() $X(\boldsymbol {\alpha ^{-1}})$
, we denote by
$X(\boldsymbol {\alpha ^{-1}})$
, we denote by
![]() $S^{\perp }$
the linear space of elements in the other space which is annihilated by S under the duality. Basic Hilbert space theory says that
$S^{\perp }$
the linear space of elements in the other space which is annihilated by S under the duality. Basic Hilbert space theory says that
![]() $(S^{\perp })^{\perp }$
is the norm-closure of S.
$(S^{\perp })^{\perp }$
is the norm-closure of S.
For convenience, we restate the Theorem B of Section 1.
Theorem 7.3 (
 $\mathcal {A}^{\infty }$
-density theorem in
$\mathcal {A}^{\infty }$
-density theorem in
 $\,\mathcal {H}(b)$
-spaces)
$\,\mathcal {H}(b)$
-spaces)
Let
![]() $b = \theta u$
be an extreme point of the unit ball of
$b = \theta u$
be an extreme point of the unit ball of
![]() $H^{\infty }$
satisfying the following assumptions.
$H^{\infty }$
satisfying the following assumptions.
-
(i) There exists an increasing sequence
 $\{E_n\}_n$
of Beurling–Carleson sets of positive measure such that, up to a set of Lebesgue measure zero, we have the equality
$\{E_n\}_n$
of Beurling–Carleson sets of positive measure such that, up to a set of Lebesgue measure zero, we have the equality  $$\begin{align*}E := \{ \zeta \in \mathbb{T} : |b(\zeta)| < 1 \} = \cup_n E_n \end{align*}$$
$$\begin{align*}E := \{ \zeta \in \mathbb{T} : |b(\zeta)| < 1 \} = \cup_n E_n \end{align*}$$
and
 $$\begin{align*}\int_{E_n} \log (1-|b|^2) \, d\textit{m}> -\infty, \quad \text{ for all } n. \end{align*}$$
$$\begin{align*}\int_{E_n} \log (1-|b|^2) \, d\textit{m}> -\infty, \quad \text{ for all } n. \end{align*}$$
-
(ii) If
 $\theta = BS_{\nu }$
, where B is a Blaschke product and
$\theta = BS_{\nu }$
, where B is a Blaschke product and
 $\nu $
is the measure defining the singular inner factor as in (
1.11
), then in the decomposition (
1.7
), the part
$\nu $
is the measure defining the singular inner factor as in (
1.11
), then in the decomposition (
1.7
), the part
 $\nu _{\mathcal {K}}$
which vanishes on Beurling–Carleson sets of Lebesgue measure zero satisfies
$\nu _{\mathcal {K}}$
which vanishes on Beurling–Carleson sets of Lebesgue measure zero satisfies
 $\nu _{\mathcal {K}}(\cup _n E_n) = \nu _{\mathcal {K}} (\mathbb {T})$
, where
$\nu _{\mathcal {K}}(\cup _n E_n) = \nu _{\mathcal {K}} (\mathbb {T})$
, where
 $\{E_n\}_n$
are the sets in
$\{E_n\}_n$
are the sets in
 $(i)$
.
$(i)$
.
Then
![]() $\mathcal {A}^{\infty } \cap \mathcal {H}(b)$
is norm-dense in
$\mathcal {A}^{\infty } \cap \mathcal {H}(b)$
is norm-dense in
![]() $\mathcal {H}(b)$
.
$\mathcal {H}(b)$
.
Before going into the proof, we remind the reader of what was remarked in Section 1, that the condition
![]() $\nu _{\mathcal {K}}(\cup _n E_n) = \nu _{\mathcal {K}} (\mathbb {T})$
appearing in
$\nu _{\mathcal {K}}(\cup _n E_n) = \nu _{\mathcal {K}} (\mathbb {T})$
appearing in
![]() $(ii)$
above is essentially necessary, and that some type of structure condition on the set E, and a size condition on the weight
$(ii)$
above is essentially necessary, and that some type of structure condition on the set E, and a size condition on the weight
![]() $(1-|b|^2)$
, also are necessary (examples are mentioned in [Reference Limani and Malman18]).
$(1-|b|^2)$
, also are necessary (examples are mentioned in [Reference Limani and Malman18]).
The proof below is essentially the same as the one given in the context of
![]() $\mathcal {P}^2(\mu )$
-spaces in [Reference Limani and Malman18].
$\mathcal {P}^2(\mu )$
-spaces in [Reference Limani and Malman18].
Proof By Lemma 7.2 and the remark following it, we can assume that E is a Beurling–Carleson set of positive measure, and the inner factor has a factorization
where
![]() $\nu _{\mathcal {C}}$
is supported on a single Beurling–Carleson set F of Lebesgue measure zero.
$\nu _{\mathcal {C}}$
is supported on a single Beurling–Carleson set F of Lebesgue measure zero.
We set
![]() $w := \Delta ^2 = (1-|b|^2)1_E,$
and apply Corollary 6.4 to the data
$w := \Delta ^2 = (1-|b|^2)1_E,$
and apply Corollary 6.4 to the data
![]() $E, F, S_{\nu _{\mathcal {C}}}, S_{\nu _{\mathcal {K}}}$
to obtain a rapidly increasing sequence
$E, F, S_{\nu _{\mathcal {C}}}, S_{\nu _{\mathcal {K}}}$
to obtain a rapidly increasing sequence
![]() $\boldsymbol {\alpha }$
and a space
$\boldsymbol {\alpha }$
and a space
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
which satisfies the conclusion of Corollary 6.4. Since
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
which satisfies the conclusion of Corollary 6.4. Since
![]() $\boldsymbol {\alpha }$
is rapidly increasing, the space
$\boldsymbol {\alpha }$
is rapidly increasing, the space
![]() $X(\boldsymbol {\alpha })$
consists of functions in
$X(\boldsymbol {\alpha })$
consists of functions in
![]() $\mathcal {A}^{\infty }$
. We will show that
$\mathcal {A}^{\infty }$
. We will show that
![]() $X(\boldsymbol {\alpha }) \cap \mathcal {H}(b)$
is dense in
$X(\boldsymbol {\alpha }) \cap \mathcal {H}(b)$
is dense in
![]() $\mathcal {H}(b)$
.
$\mathcal {H}(b)$
.
Assume that
![]() $f \in \mathcal {H}(b)$
is orthogonal to all functions in
$f \in \mathcal {H}(b)$
is orthogonal to all functions in
![]() $X(\boldsymbol {\alpha }) \cap \mathcal {H}(b)$
. In terms of the embedding J appearing in Proposition 7.1, this means that the tuple
$X(\boldsymbol {\alpha }) \cap \mathcal {H}(b)$
. In terms of the embedding J appearing in Proposition 7.1, this means that the tuple
![]() $Jf := (f,g)$
is orthogonal in
$Jf := (f,g)$
is orthogonal in
![]() $H^2 \oplus L^2(E)$
to all tuples in
$H^2 \oplus L^2(E)$
to all tuples in
![]() $J(X(\boldsymbol {\alpha }) \cap \mathcal {H}(b))$
. By the definition of the duality pairing appearing in Section 4.1, this means that
$J(X(\boldsymbol {\alpha }) \cap \mathcal {H}(b))$
. By the definition of the duality pairing appearing in Section 4.1, this means that
annihilates
Now, from (7.2), we see that the set
![]() $J(X(\boldsymbol {\alpha }) \cap \mathcal {H}(b)) \subset X(\boldsymbol {\alpha }) \oplus L^2(E)$
can be expressed as the pre-annihilator. Then
$J(X(\boldsymbol {\alpha }) \cap \mathcal {H}(b)) \subset X(\boldsymbol {\alpha }) \oplus L^2(E)$
can be expressed as the pre-annihilator. Then
We are in a Hilbert space setting, so it follows from the duality remarks above that there exists a sequence
![]() $\{h_n\}_n$
of functions in
$\{h_n\}_n$
of functions in
![]() $H^2$
, such that
$H^2$
, such that
![]() $(bh_n, \Delta h_n)$
converges to
$(bh_n, \Delta h_n)$
converges to
![]() $(f,g)$
in the norm of
$(f,g)$
in the norm of
![]() $X(\boldsymbol {\alpha ^{-1}}) \oplus L^2(E)$
. By passing to a subsequence, we may assume that the convergence of
$X(\boldsymbol {\alpha ^{-1}}) \oplus L^2(E)$
. By passing to a subsequence, we may assume that the convergence of
![]() $\Delta h_n$
to g happens also pointwise almost everywhere on E. Multiplying the second coordinate by the bounded function b, we read that the elements
$\Delta h_n$
to g happens also pointwise almost everywhere on E. Multiplying the second coordinate by the bounded function b, we read that the elements
![]() $(bh_n, \Delta b h_n)$
converge to
$(bh_n, \Delta b h_n)$
converge to
![]() $(f,bg)$
in the norm
$(f,bg)$
in the norm
![]() $X(\boldsymbol {\alpha ^{-1}}) \oplus L^2(E)$
, and in particular the tuples
$X(\boldsymbol {\alpha ^{-1}}) \oplus L^2(E)$
, and in particular the tuples
![]() $(bh_n, \Delta b h_n)$
form a Cauchy sequence. In fact, since
$(bh_n, \Delta b h_n)$
form a Cauchy sequence. In fact, since
![]() $w = \Delta ^2$
, this is equivalent to
$w = \Delta ^2$
, this is equivalent to
so the sequence
![]() $(bh_n, bh_n)$
converges in the space
$(bh_n, bh_n)$
converges in the space
![]() $\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
which is a space of analytic functions. The limit function must be
$\mathcal {D}(\boldsymbol {\alpha }^{-1}, w)$
which is a space of analytic functions. The limit function must be
![]() $f \in H^2$
, by the above. Now, we apply part
$f \in H^2$
, by the above. Now, we apply part
![]() $(ii)$
of Proposition 5.2, which tells us that
$(ii)$
of Proposition 5.2, which tells us that
![]() $bh_n \to f$
pointwise on the set E (it is precisely at this point where
$bh_n \to f$
pointwise on the set E (it is precisely at this point where
![]() $M_z$
being completely nonisometric on
$M_z$
being completely nonisometric on
![]() $D(\boldsymbol {\alpha ^{-1}}, w)$
is crucial, else the sequence
$D(\boldsymbol {\alpha ^{-1}}, w)$
is crucial, else the sequence
![]() $\{bh_n\}_n$
could potentially converge to something else than f). Thus, we have
$\{bh_n\}_n$
could potentially converge to something else than f). Thus, we have
for almost every
![]() $\zeta \in E$
. Thus,
$\zeta \in E$
. Thus,
![]() $g = \Delta f/b$
on E. All in all, we have identified the tuple
$g = \Delta f/b$
on E. All in all, we have identified the tuple
![]() $Jf$
as
$Jf$
as
Moreover, by the permanence property of
![]() $(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w),\theta ) $
, f is divisible by the inner factor
$(\mathcal {D}(\boldsymbol {\alpha }^{-1}, w),\theta ) $
, f is divisible by the inner factor
![]() $\theta $
of b.
$\theta $
of b.
Note that on
![]() $\mathbb {T}$
, we have
$\mathbb {T}$
, we have
Since the right-hand side is square-integrable, so is the left. Since the inner factor of f is divisible by the inner factor of b, we conclude that
![]() $f/b$
is a function in the Smirnov class of the unit disk which has square-integrable boundary values, and so
$f/b$
is a function in the Smirnov class of the unit disk which has square-integrable boundary values, and so
![]() $f/b \in H^2$
(see [Reference Garnett8, Chapter 2]). But by (7.1), we get
$f/b \in H^2$
(see [Reference Garnett8, Chapter 2]). But by (7.1), we get
So
![]() $f/b \equiv 0$
, and hence
$f/b \equiv 0$
, and hence
![]() $f \equiv 0$
. The proof is complete.
$f \equiv 0$
. The proof is complete.
Acknowledgement
The authors gratefully thank the referee for the valuable comments and suggestions that we have received, in particular regarding the statement of Lemma 2.1.