We have recently discovered that the implicit assumption that
![]() $N_{2}=0$
for a monolayer suspension in the paper by Wilson & Davis (Reference Wilson and Davis2002) was an error: the repercussions of this error are corrected below. For dilute systems, we neglected to calculate the second normal stress difference, which is negative. In concentrated systems, the viscosity is rather larger than reported (although the trends remain the same), and the second normal stress difference is negative; but the first normal stress difference
$N_{2}=0$
for a monolayer suspension in the paper by Wilson & Davis (Reference Wilson and Davis2002) was an error: the repercussions of this error are corrected below. For dilute systems, we neglected to calculate the second normal stress difference, which is negative. In concentrated systems, the viscosity is rather larger than reported (although the trends remain the same), and the second normal stress difference is negative; but the first normal stress difference
![]() $N_{1}$
is now observed to change sign and become positive for concentrated systems.
$N_{1}$
is now observed to change sign and become positive for concentrated systems.
The behaviour of the viscosity and of
![]() $N_{1}$
are of particular interest in the light of developments in the field since the publication of the original paper. There has been a growth of interest in the influence of roughness on suspension rheology via solid contact and friction, and its role in strong shear thickening. Since our original paper, experiments by Lootens et al. (Reference Lootens, van Damme, Hémar and Hébraud2005) were able to make the first quantitative measurements of normal stress differences in a jamming suspension by using artificially roughened particles. They found negative
$N_{1}$
are of particular interest in the light of developments in the field since the publication of the original paper. There has been a growth of interest in the influence of roughness on suspension rheology via solid contact and friction, and its role in strong shear thickening. Since our original paper, experiments by Lootens et al. (Reference Lootens, van Damme, Hémar and Hébraud2005) were able to make the first quantitative measurements of normal stress differences in a jamming suspension by using artificially roughened particles. They found negative
![]() $N_{1}$
at low shear rates far from the jamming transition, but large positive fluctuations of
$N_{1}$
at low shear rates far from the jamming transition, but large positive fluctuations of
![]() $N_{1}$
during jamming. Much more recently, Royer, Blair & Hudson (Reference Royer, Blair and Hudson2016) carried out experiments on continuously shear-thickening suspensions; they also found a transition in
$N_{1}$
during jamming. Much more recently, Royer, Blair & Hudson (Reference Royer, Blair and Hudson2016) carried out experiments on continuously shear-thickening suspensions; they also found a transition in
![]() $N_{1}$
from negative to positive with increasing volume fraction and shear rate, but in this case without any associated sharp change in the viscosity. This behaviour has also been replicated in simulations by Mari et al. (Reference Mari, Seto, Morris and Denn2015), using a model which needs to incorporate both frictional contact and hydrodynamic forces, but also Brownian motion and a short-range colloidal repulsive force.
$N_{1}$
from negative to positive with increasing volume fraction and shear rate, but in this case without any associated sharp change in the viscosity. This behaviour has also been replicated in simulations by Mari et al. (Reference Mari, Seto, Morris and Denn2015), using a model which needs to incorporate both frictional contact and hydrodynamic forces, but also Brownian motion and a short-range colloidal repulsive force.
Equation and figure numbers preceded by the letter C denote corrected versions of the original items; additional equations are numbered with a following letter. In addition to the material changes already mentioned, there was a small typographical error in equation (2.8):
Dilute systems
For dilute systems, equations (2.26)–(2.27) and (2.30)–(2.33), while correct, do not capture all the interesting components of the stresslet for non-contacting particles; the omitted contributions are
and the contact stresslets for rolling:
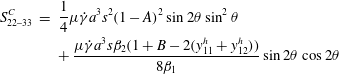 $$\begin{eqnarray}\displaystyle S_{22{-}33}^{C} & = & \displaystyle \frac{1}{4}\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}s^{2}(1-A)^{2}\sin 2\unicode[STIX]{x1D703}\sin ^{2}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}s\unicode[STIX]{x1D6FD}_{2}(1+B-2(y_{11}^{h}+y_{12}^{h}))}{8\unicode[STIX]{x1D6FD}_{1}}\sin 2\unicode[STIX]{x1D703}\cos 2\unicode[STIX]{x1D703}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{22{-}33}^{C} & = & \displaystyle \frac{1}{4}\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}s^{2}(1-A)^{2}\sin 2\unicode[STIX]{x1D703}\sin ^{2}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}s\unicode[STIX]{x1D6FD}_{2}(1+B-2(y_{11}^{h}+y_{12}^{h}))}{8\unicode[STIX]{x1D6FD}_{1}}\sin 2\unicode[STIX]{x1D703}\cos 2\unicode[STIX]{x1D703}\end{eqnarray}$$
and slipping:
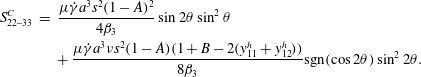 $$\begin{eqnarray}\displaystyle S_{22{-}33}^{C} & = & \displaystyle \frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}s^{2}(1-A)^{2}}{4\unicode[STIX]{x1D6FD}_{3}}\sin 2\unicode[STIX]{x1D703}\sin ^{2}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}\unicode[STIX]{x1D708}s^{2}(1-A)(1+B-2(y_{11}^{h}+y_{12}^{h}))}{8\unicode[STIX]{x1D6FD}_{3}}\text{sgn}(\cos 2\unicode[STIX]{x1D703})\sin ^{2}2\unicode[STIX]{x1D703}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{22{-}33}^{C} & = & \displaystyle \frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}s^{2}(1-A)^{2}}{4\unicode[STIX]{x1D6FD}_{3}}\sin 2\unicode[STIX]{x1D703}\sin ^{2}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D6FE}}a^{3}\unicode[STIX]{x1D708}s^{2}(1-A)(1+B-2(y_{11}^{h}+y_{12}^{h}))}{8\unicode[STIX]{x1D6FD}_{3}}\text{sgn}(\cos 2\unicode[STIX]{x1D703})\sin ^{2}2\unicode[STIX]{x1D703}.\qquad\end{eqnarray}$$

Figure 3a. Plot of the normalised second normal stress difference
![]() ${\tilde{N}}_{2}$
against the roughness height
${\tilde{N}}_{2}$
against the roughness height
![]() $\unicode[STIX]{x1D701}$
. The lower (solid) curve represents the case of no friction,
$\unicode[STIX]{x1D701}$
. The lower (solid) curve represents the case of no friction,
![]() $\unicode[STIX]{x1D708}=0$
, and the upper (dotted) curve the opposite extreme,
$\unicode[STIX]{x1D708}=0$
, and the upper (dotted) curve the opposite extreme,
![]() $\unicode[STIX]{x1D708}\rightarrow \infty$
.
$\unicode[STIX]{x1D708}\rightarrow \infty$
.

Figure C5. Dependence of first normal stress difference
![]() $N_{1}$
on area fraction
$N_{1}$
on area fraction
![]() $c$
. Roughness heights (a)
$c$
. Roughness heights (a)
![]() $\unicode[STIX]{x1D701}=10^{-3}$
, (b)
$\unicode[STIX]{x1D701}=10^{-3}$
, (b)
![]() $\unicode[STIX]{x1D701}=10^{-2}$
. For the smaller roughness height we could not obtain results for
$\unicode[STIX]{x1D701}=10^{-2}$
. For the smaller roughness height we could not obtain results for
![]() $c>0.4$
. In each graph, the curves represent the relevant dilute theory (at both
$c>0.4$
. In each graph, the curves represent the relevant dilute theory (at both
![]() $\unicode[STIX]{x1D708}=0$
and
$\unicode[STIX]{x1D708}=0$
and
![]() $\unicode[STIX]{x1D708}\rightarrow \infty$
); the two curves on each graph are indistinguishable from one another. The symbols are our simulation results at
$\unicode[STIX]{x1D708}\rightarrow \infty$
); the two curves on each graph are indistinguishable from one another. The symbols are our simulation results at
![]() $\unicode[STIX]{x1D708}=0$
(
$\unicode[STIX]{x1D708}=0$
(
![]() $+$
) and
$+$
) and
![]() $\unicode[STIX]{x1D708}\rightarrow \infty$
(
$\unicode[STIX]{x1D708}\rightarrow \infty$
(
![]() $\times$
). For
$\times$
). For
![]() $c\geqslant 0.4$
we found we could not simulate in the true limit
$c\geqslant 0.4$
we found we could not simulate in the true limit
![]() $\unicode[STIX]{x1D708}\rightarrow \infty$
so these results are for
$\unicode[STIX]{x1D708}\rightarrow \infty$
so these results are for
![]() $\unicode[STIX]{x1D708}=10$
.
$\unicode[STIX]{x1D708}=10$
.

Figure C5a. Dependence of second normal stress difference
![]() $N_{2}$
on area fraction
$N_{2}$
on area fraction
![]() $c$
. Roughness heights (a)
$c$
. Roughness heights (a)
![]() $\unicode[STIX]{x1D701}=10^{-3}$
, (b)
$\unicode[STIX]{x1D701}=10^{-3}$
, (b)
![]() $\unicode[STIX]{x1D701}=10^{-2}$
. For the smaller roughness height we could not obtain results for
$\unicode[STIX]{x1D701}=10^{-2}$
. For the smaller roughness height we could not obtain results for
![]() $c>0.4$
. Points are our Stokesian dynamics simulation results at
$c>0.4$
. Points are our Stokesian dynamics simulation results at
![]() $\unicode[STIX]{x1D708}=0$
(
$\unicode[STIX]{x1D708}=0$
(
![]() $+$
) and
$+$
) and
![]() $\unicode[STIX]{x1D708}\rightarrow \infty$
(
$\unicode[STIX]{x1D708}\rightarrow \infty$
(
![]() $\times$
). For
$\times$
). For
![]() $c\geqslant 0.4$
we could not simulate in the true limit
$c\geqslant 0.4$
we could not simulate in the true limit
![]() $\unicode[STIX]{x1D708}\rightarrow \infty$
so these results are for
$\unicode[STIX]{x1D708}\rightarrow \infty$
so these results are for
![]() $\unicode[STIX]{x1D708}=10$
. In both cases the results from dilute theory are indistinguishable from zero on this scale.
$\unicode[STIX]{x1D708}=10$
. In both cases the results from dilute theory are indistinguishable from zero on this scale.
The resultant contributions to the macroscopic stress are
in which we have defined the new coefficient
The normal stress difference that results from these new equations is plotted in figure 3a .
Concentrated systems
For concentrated suspensions, there was a coding error corresponding to the assumption of zero second normal stress difference. When corrected, this makes only minor quantitative changes to the viscosity; however, the first normal stress difference
![]() $N_{1}$
, which was reported as negative, is now found to be positive for denser suspensions (shown in figure C5). In addition, we report that the second normal stress difference
$N_{1}$
, which was reported as negative, is now found to be positive for denser suspensions (shown in figure C5). In addition, we report that the second normal stress difference
![]() $N_{2}$
is negative, shown in new figure C5a
.
$N_{2}$
is negative, shown in new figure C5a
.






