1. Introduction
Extensive networks of hydrological drainage channels, located deep beneath the thick ice of the Antarctic ice sheet’s interior, are responsible for transporting mass, in the form of subglacial meltwater produced at the base of the ice cover, to other regions of the ice sheet (Reference Dowdeswell and SiegertDowdeswell and Siegert, 1999). Such subglacial networks may have important consequences for ice flow, mass-balance studies and subglacial lake formation. Therefore knowledge of their location is required to properly model ice-sheet dynamics. Direct mapping of these features is not straightforward since it requires information on basal ice parameters. Radio-echo sounding (RES) measures ice-sheet thickness, from which bedrock topography and basal boundary conditions can be inferred, but the existing data coverage for Antarctica is sparse (Reference Lythe and VaughanLythe and others, 2000). Surface elevation data from the European Remote-sensing Satellite-1 (ERS-1) radar altimeter (RA) can provide indirect information on the location of some subglacial lakes, but there are several limitations, including low spatial resolution (∼2.5 km at 70˚ S). Moreover, subglacial lakes are identified by the flat ice surface above, which is produced because basal shear stress tends to zero as the ice reaches hydrostatic equilibrium over subglacial lake waters. Lakes smaller than about 4 or 5 km across, however, are unlikely to form this characteristic flat surface, as the thick ice above them may not be in hydrostatic equilibrium (Reference Dowdeswell and SiegertDowdeswell and Siegert, 1999), so that the classical technique is ill suited. A further limitation is that a large number of features related to ice flow are superimposed and are therefore difficult to unambiguously distinguish (e.g. lakes, inland slope breaks, glacier flowlines, en echelon features due to lateral shear stress, 100 km scale undulations and 20km scale undulations due to ice flow over rough bedrock (Reference Rémy, Shaeffer and LegrésyRémy and others, 1999)). Despite these limitations, the existence of subglacial drainage channels has been proposed through analysis of ERS RA data by Reference Siegert and RidleySiegert and Ridley (1998a) from Adventure Trench, East Antarctica, and confirmed recently by Reference Rémy, Testut, Legrésy, Forieri, Bianchi and TabaccoRémy and others (2003) at Dome C, using ERS RA data coupled with field measurements.
In previous work, we have shown that subtle surface features observed in RA digital elevation models (DEMs) can be enhanced by generating maps of a parameter that describes the curvature of the surface topography (Reference Rémy and TabaccoRémy and Tabacco, 2000), which permits subglacial channels to be mapped more faithfully than by the raw DEM. We applied this approach at Dome C (Reference Rémy, Testut, Legrésy, Forieri, Bianchi and TabaccoRémy and others 2003), in the region selected for the deep-drilling project EPICA (European Project for Ice Coring in Antarctica), to search for subglacial hydrological networks. Extensive in situ, airborne and satellite datasets compiled for the EPICA site selection allowed us to confirm the results of our approach. A product that was particularly useful for validating our results was a high-resolution bedrock map derived from extensive airborne RES measurements (Reference Tabacco, Passerini, Corbelli and GormanTabacco and others, 1998). In this paper, we describe the approach in detail, and then demonstrate its success by applying it to the Wilkes Land sector of East Antarctica. We make an enlargement around the Mertz Glacier region and compare the results there with other data. Finally we apply the method to the entire Antarctic ice sheet.
2. Method
Surface elevation data are provided for the Antarctic ice sheet by a 2.5 km DEM generated using altimetry from the geodetic (168 day) phase of the ERS-1 RA collected during 1994/95 (Reference Rémy, Shaeffer and LegrésyRémy and others, 1999). The dense spatial sampling of this phase provides surface topography at the 2.5km scale at an accuracy of < 1m for much of the ice sheet, as far south as 81.2˚ S (the orbit extent of ERS).
To enhance the topographic features of the ERS DEM we define a surface curvature (Cy) parameter, which is the derivative of the surface slope in the cross-slope direction over a 5 km scale, normalized by the surface slope. Normalizing by the surface slope both emphasizes weak topographic features usually found over flat areas, and directly relates Cy to the ice direction. If x is the slope direction, y the cross-slope direction and h(x, y) the surface topography, we define Cy as:
To calculate Cy from the ERS RA DEM, we fit the surface topography with a bi-quadratic function with a search radius of 5 km around each grid node. The curvature radius is deduced from the first and second derivatives using classical procedures. The surface slope, used for normalization, is estimated on a 20 km scale to enhance smaller-scale features. The same length scale (20 km) is used in the estimation of the slope direction.
Our technique is also well suited to detecting change in ice flow due to sliding, even over a small area, because the sliding areas are surrounded by two symmetrical topographic anomalies (Reference Rémy, Shaeffer and LegrésyRémy and others, 1999). Such bumps and troughs in the topography, of a few metres in amplitude and a few kilometres in wavelength, are associated with an abrupt transition in basal condition. From weak to strong sliding friction and from strong to weak friction, they induce a strong negative curvature and a strong positive curvature respectively. In the case of Vostok lake, these topographic anomalies are 12m in amplitude and around 10 km in wavelength, so that our curvature parameter is greater, by an order of magnitude, than the curvature induced by surface undulations, This is examined further in the next section.
Note at the kilometre scale, the choice of the curvature does not play an important role. For example, the map of d2 h/dx2 at the kilometre scale shows the same kind of features as at larger scales. This choice only leads to change in the intensity, depending on the direction of the basal anomaly with respect to the flow direction. We choose this curvature because it is directly linked with the flow and thus is more adapted to detect flow anomalies.
The Cy parameter is plotted in Figure 1 for an area in the vicinity of Dome C. We focus on one of the features previously observed by Reference Rémy, Testut, Legrésy, Forieri, Bianchi and TabaccoRémy and others (2003) and we superimpose on the figure the lakes detected by Reference Siegert and RidleySiegert and Ridley (1998b) and by Reference Tabacco, Passerini, Corbelli and GormanTabacco and others (1998). The topographic signature is characterized by two adjacent features of opposite sign and they are clearly visible. The pattern of Cy clearly exhibits an elongated feature that links several lakes. Reference Rémy, Testut, Legrésy, Forieri, Bianchi and TabaccoRémy and others (2003) also showed that these features run along the bedrock valleys in a downslope direction. Moreover, they presented evidence which suggested that some portions of these features exhibited basal sliding, suggesting that some lakes are connected.
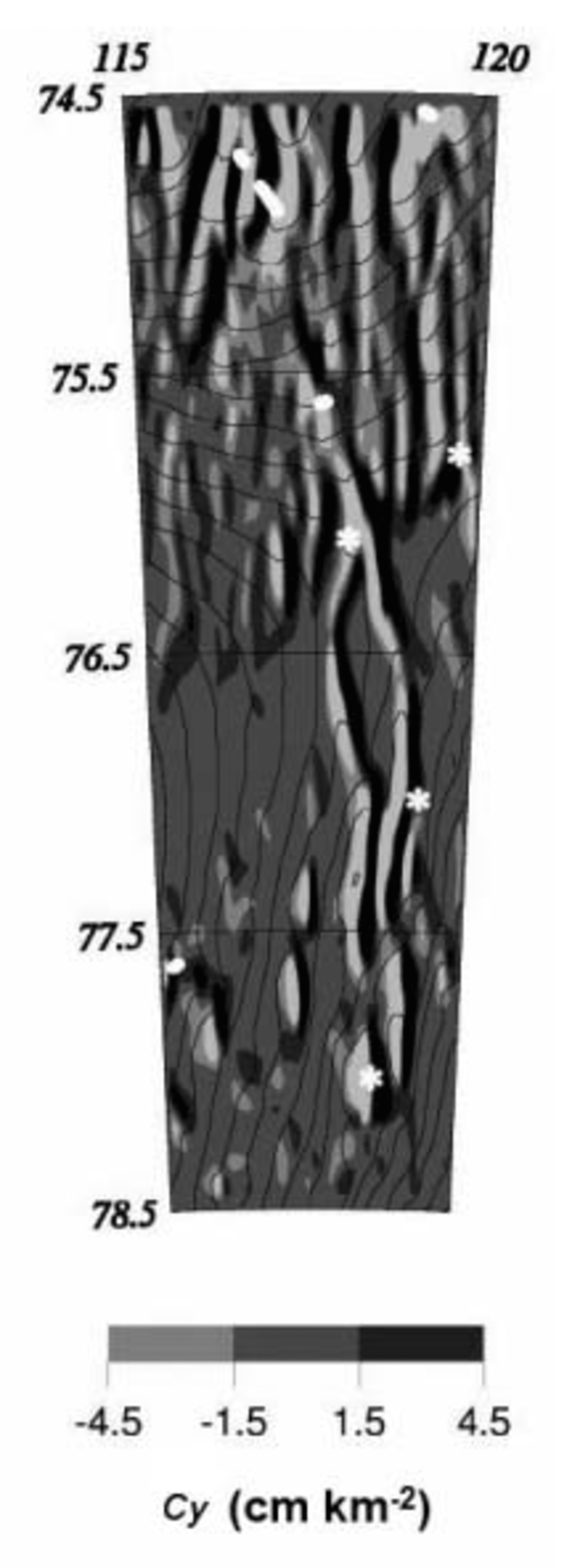
Fig. 1. Map of the surface curvature parameter (Cy ; see Equation 1) in the vicinity of the Dome C area. Siegert’s lakes (Reference Siegert and RidleySiegert and Ridley, 1998a) are marked with a star, while Tabacco’s lakes (Reference Tabacco, Passerini, Corbelli and GormanTabacco and others, 1998) are shown with a thick line. This parameter exhibits elongated features that link the lakes and run along the bedrock valleys. Surface elevation contours, every 10 m, are superimposed. The extreme negative Cy values are in white, while the extreme positive values are in black.
3. Results and Discussion
3.1. Wilkes Land
The histogram of the Cy parameter for the Wilkes Land region is plotted in Figure 2, and its distribution is mapped in Figure 3. The histogram is not Gaussian, with >60% of the values between –1.5 and 1.5 cm km–2, corresponding to typical features induced by surface undulations. Indeed, if one assumes, for simplicity, that the average undulations within this sector can be modelled as dome-shaped features of amplitude 5m and of length 20 km with an average surface slope of 2mkm–1, the maximum induced curvature normalized by the slope is 0.2 cm km–2. About 20% of the Cy distribution has extreme values corresponding to strong perturbations; for example, Cy induced by change in ice flow surrounding Vostok (12m of amplitude and < 10 km of wavelength) is about ten times greater than for typical undulations. High values of Cy can be correlated to a change in ice flow, except near the coast where the ice thickness is low and surface undulations change rapidly.
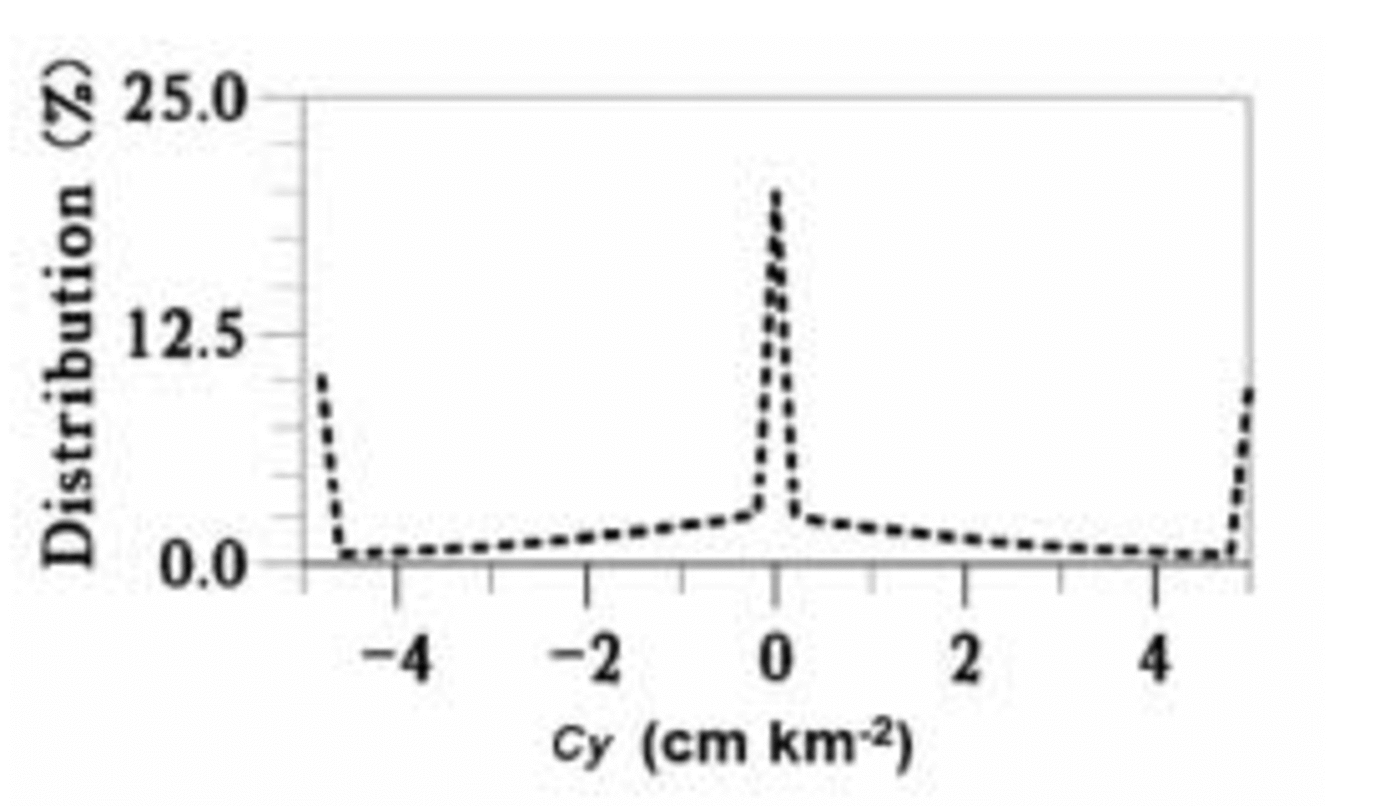
Fig. 2. Histogram of the normalized surface curvature parameter (Cy ) over the Wilkes Land region.
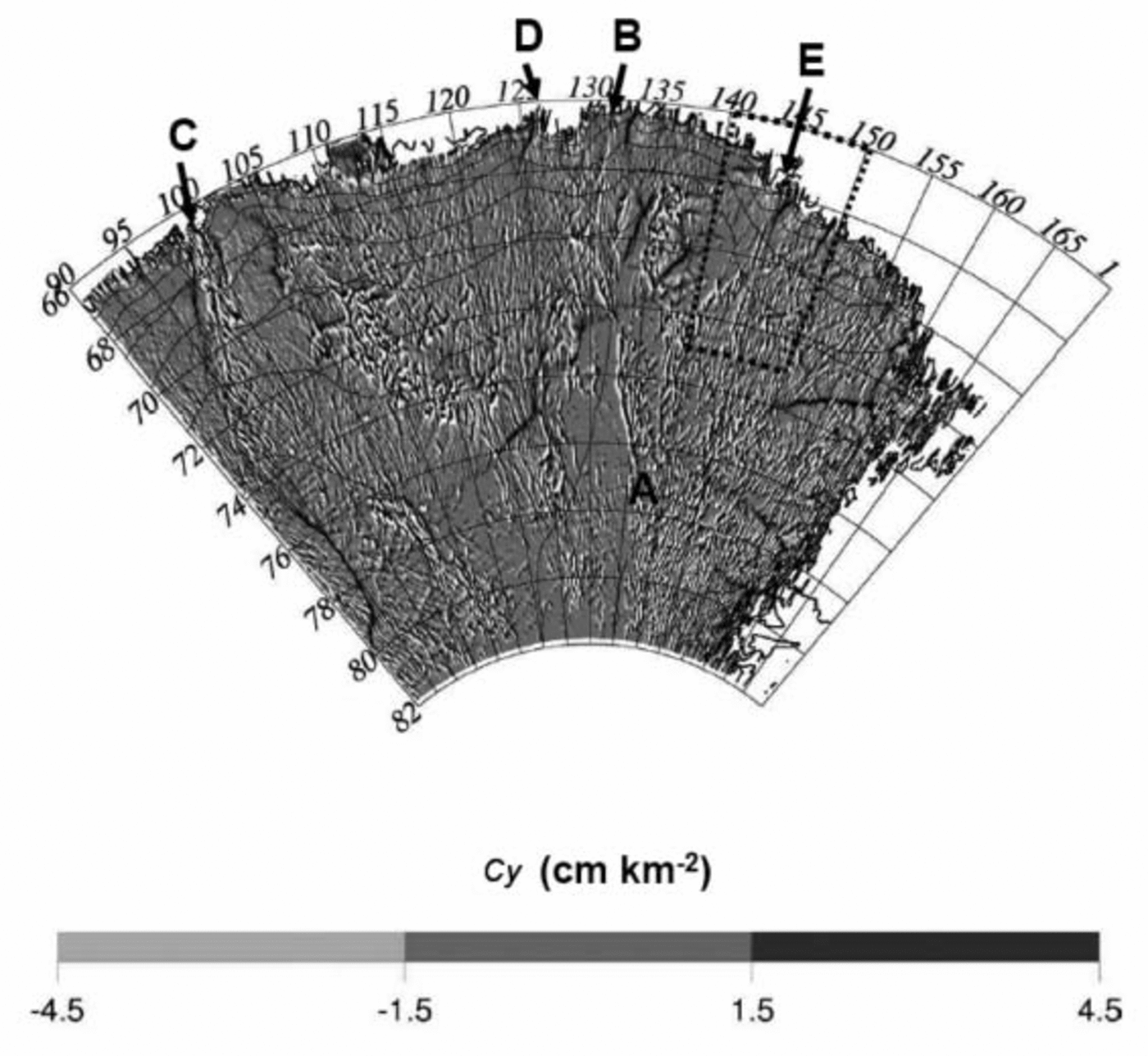
Fig. 3. Map of the normalized surface curvature parameter (Cy ) over the Wilkes Land region. The extreme negative Cy values are in white, while the extreme positive values are in black. The principal features referred to in the text are marked A–E. The box delineates the boundary of Figure 4.
The suspected hydrological systems, characterized by two adjacent curvatures of opposite sign, are clearly visible even at the global scale. The Cy map reveals well-delineated, large inland zones of alternate high and low amplitudes, as well as a series of longitudinal features. For instance, just above the Aurora Subglacial Basin (70–74˚ S, 107–115˚ E) we observe a confused pattern. At this location, both the ice
thickness (4000 m; Reference Lythe and VaughanLythe and others, 2000) and the ice velocity (10–20ma–1; Reference Testut, Hurd, Coleman, Rémy and LegrésyTestut and others, 2003) are large, so that the basal temperature is at the melting point. The same is true near the Astrolabe Subglacial Basin (69–71˚ S, 135–137˚ E) and near the Vostok area. These high values are not generated by the bedrock topography since both theoretical and empirical studies suggest the ratio between bedrock and surface roughness (the damping factor) decreases when ice thickness increases (Reference Budd and CarterBudd and Carter, 1971; Reference Rémy, Shaeffer and LegrésyRémy and others, 1999). Also the surface curvature induced by bedrock features is lower than we observe here. The difference probably results from small-scale variations in basal conditions, concentrated in some areas.
Many of the longitudinal features in Figure 3 are coherent and can be followed over large regions. The longest feature that we can distinguish begins at point A (76.5˚ S, 135˚ E), heads towards the point 72˚ S, 132˚ E, and continues up to the coast at point B, east of Porpoise Bay (62.2˚ S, 132˚ E). This feature is coherent over about 400 km. The up-slope part of this feature, just above the Adventure Subglacial Trench, has been previously identified by Reference Siegert and RidleySiegert and Ridley (1998a) as a possible hydrological system. Reference Testut, Tabacco, Bianchi and RémyTestut and others (2000) also observed a major anomaly in the ice flow, between Dome C and Terra Nova Bay just above this trench, and estimated the basal temperature at the melting point. This trench was associated with a high surface curvature 10 km wide and several hundred km long crossing the area.
Other elongated features directly link the ice sheet with the coast. One of the more interesting examples of elongated features directly joining the coast runs several hundred kilometres to reach the Queen Mary Coast near longitude 100˚ E, just to the east of the Shackleton Ice Shelf (C in Fig. 3). In the easterly direction, a 150 km-scale feature runs in a north-northeasterly direction, joining the coast at longitude 127˚ E (D in Fig. 3), west of Porpoise Bay.
Mertz Glacier region
A closer look at the Mertz Glacier region is interesting, and Figure 4a shows an enlargement of the features running parallel along 144˚E (E in Fig. 3) between 73˚ S and 68˚ S which flow towards the Mertz Glacier drainage basin. We compare that map with an ERS synthetic aperture radar (SAR) interferogram, corresponding to the Mertz Glacier drainage basin and to its grounding zone (Fig. 4b). The interferogram was constructed with an ERS SAR image pair from the tandem mission, so the images had only 24 hours separation (Reference Legrésy, Wendt, Tabacco, Rémy and DietrichLegrésy and others, 2004). The arrow indicates the direction of the SAR line-of-sight, and one fringe in the interferogram corresponds to 28 mm displacement projected in the line-of-sight. The orbit baseline is short, so the interferogram is free of topographic fringes. Although the SAR look direction is not optimum, we see clearly from the flow velocity direction that, in addition to the main flow coming from the west and turning north, a secondary tributary comes from the south on the eastern side of the glacier. This second tributary corresponds to the downslope end of the observed elongated feature visible in Figure 4a.
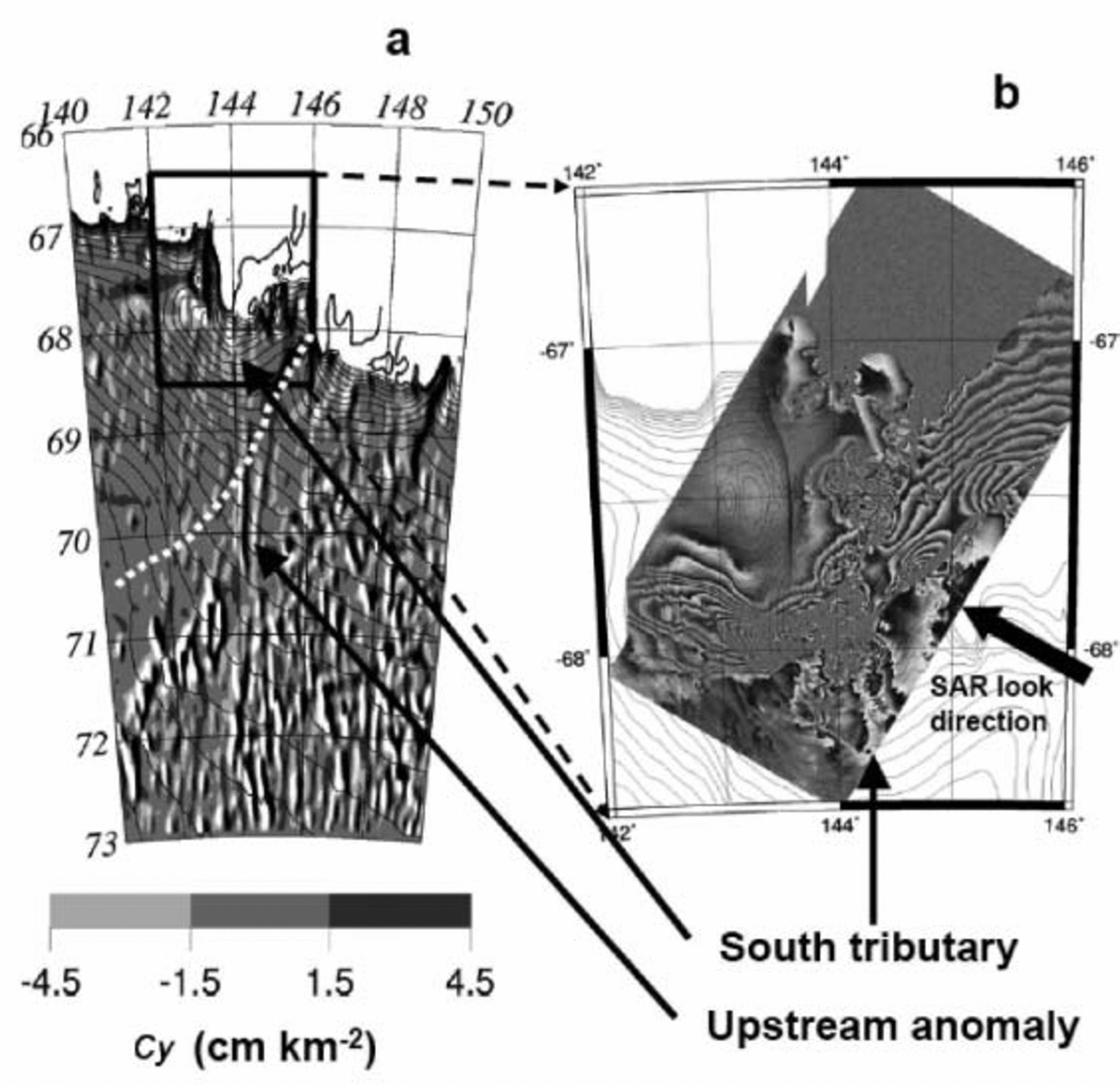
Fig. 4. Enlargement of the Mertz Glacier sector. The surface curvature is on the left, with elevation contours from 0 to 2600 m each 100 m, and the interferogram is on the right. The dotted white line corresponds to the eastern limit of the Mertz Glacier drainage basin.
To confirm that these networks correspond to effective perturbations of the ice flow, we plotted the drainage limits of the glaciers assuming that flowlines follow the largest slope. In the case of the Mertz Glacier drainage, the surface anomaly crosses the Ninnis Glacier drainage basin.
These observations could be explained by three possible scenarios:
(i) these features correspond to bedrock valleys which are not seen in available radar measurements, and the bedrock topographic anomaly affects the ice surface topography.
(ii) the features correspond to changing basal conditions induced by either melting or the presence of basal streams. In this case, they may correspond to some under-ice ‘rivers’ exporting water out of the ice cap, and the large-scale flow remains unperturbed.
(iii) these features correspond to important hydrological production areas, leading to outflow valleys in the bedrock corresponding to large glaciers as mentioned above. They may also disturb the larger scale as the flow no longer follows the dominant slope direction. Therefore, when tracing the limits of the drainage basins, one should take account of these features and perhaps adjust the direction of the flowline. At drainage limits, a small error in the position of the flowline may increase or decrease significantly the drainage area attributed to a given glacier.
Reference Dowdeswell and SiegertDowdeswell and Siegert (2003) argued that warm-based, fast-flowing ice streams provide a possible route by which subglacial water is connected to the ice-sheet margin. The examples shown here suggest that part of the inland subglacial water must be connected to the coast by ‘subglacial rivers’. The subglacial rivers detected here are not systematically linked to fast-flowing ice streams. One reason is probably that most of the fast ice streams are identified with the help of the surface topography by assuming that the flow follows the greatest slope direction, while the elongated features reaching the coast do not always follow the surface slope. However, the feature labelled C in Figure 3 seems to correspond well to one branch of the fast streams reaching the Shackleton Ice Shelf. Due to the lack of bedrock topography measurements in this sector, it is difficult to conclude whether this suspected subglacial river is linked with the bedrock topography or not. Above all, it is not possible to estimate the pressure gradient driving the water.
3.2. Antarctic continent
At the large scale, we choose the root mean square (rms) of Cy to map the hydrological signal. The rms is estimated over a 5×5 km grid with a search radius of 15km as shown in Figure 5. Even at this scale, connections to the coast can be distinguished: for instance, we recognize the elongated large feature of Figure 3 (labelled C) and another one running along latitude 75˚ S at longitudes 140–160˚ E.
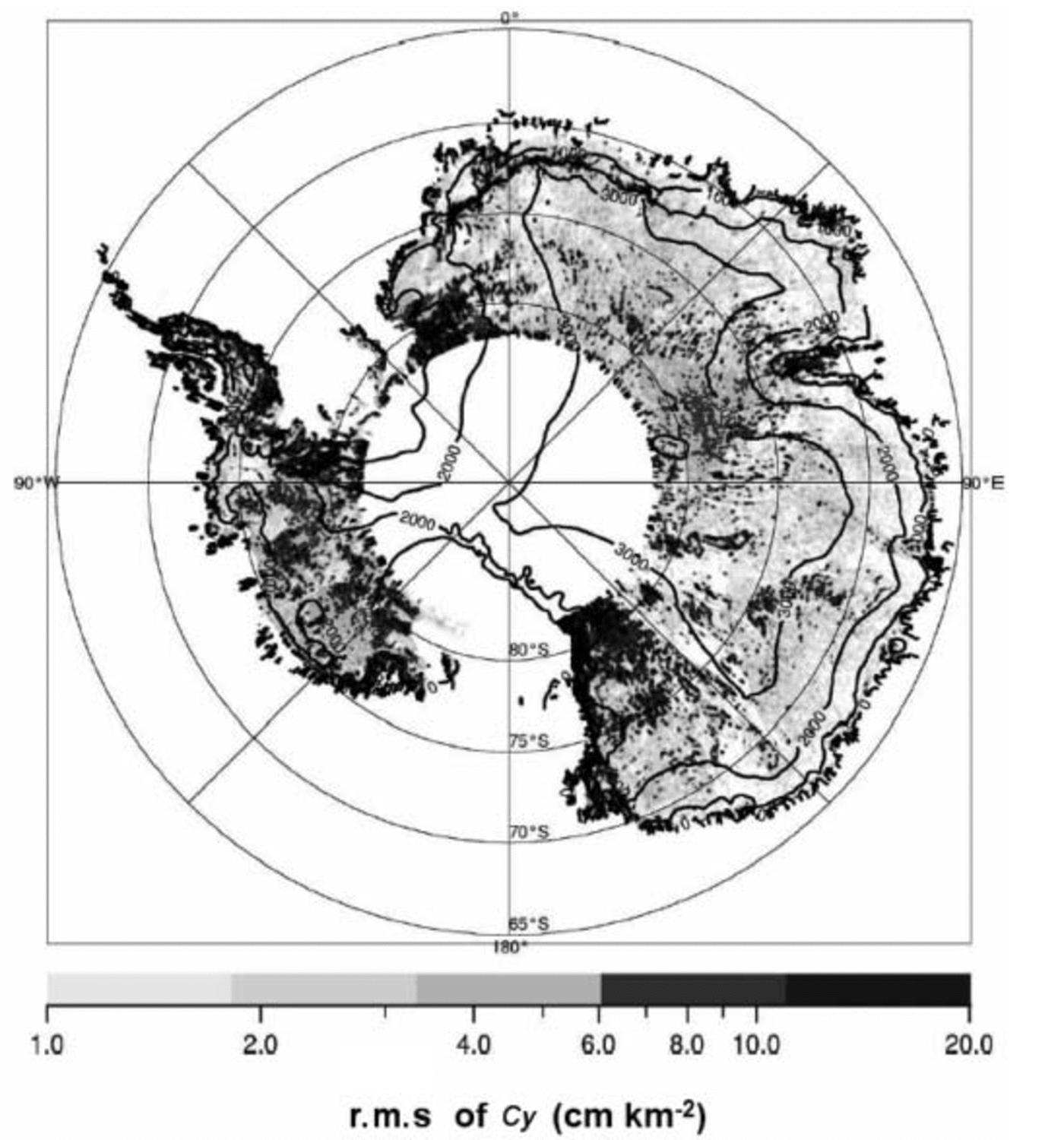
Fig. 5. Map of Cy rms over the portion of the Antarctic ice sheet lying within ERS coverage (north of 81.2˚ S). Surface elevation contours from the ERS DEM are overlaid.
We can distinguish some areas with high Cy amplitudes in the Victoria Land sector (77–82˚ S, 135–150˚ E), above Vincennes Subglacial Basin (72.5˚ S, 115˚ E), around Dome C and Vostok, in the up-slope direction of the Amery Ice Shelf (74–80˚ S, 60–80˚ E), in the Filchner Ice Shelf and Recovery Glacier drainage sector (78–82˚ S, 15–40˚ W) and in West Antarctica around MacAyeal Ice Stream (former Ice Stream E) and the Thwaites Glacier catchment. Most of these sectors show a highly convergent ice flow. This can be explained by the fact that these areas are characterized by fast-flow regions and an enhanced basal temperature. Conversely, we can question whether the presence of a hydrological system may strongly enhance the flow. Note that near the coast, because of the thin ice covering the mountainous topography, some of the strong signal may be induced by bedrock features.
Unfortunately, the area of overlap between the coverage of the RES data used by Reference Dowdeswell and SiegertDowdeswell and Siegert (1999) to identify subglacial lakes, and the ERS RA data used in this paper is small. Only a sector to the south of 80˚S for the West Antarctic and a part of Wilkes Land is common to both datasets. Even if the correspondence between high Cy values and lake areas is relatively good for both these sectors (especially near Hercules Dome and Dome C), the overlap region is not large enough for conclusions to be drawn.
We observe that the distribution of high surface curvature values is not homogeneous but rather skewed toward the western part of Antarctica. This can be explained by the distribution of the geothermal flux, even if poorly known. First, Reference Siegert and DowdeswellSiegert and Dowdeswell (1996) used the presence of lakes to estimate the geothermal flux, which is the greatest unknown in the basal temperature estimation. They found an east–west gradient where the geothermal flux in the Hercules Dome region, West Antarctic ice sheet, is 10–15mW m–2 greater than in the Dome C region and 20–25mW m–2 greater than in the Ridge B region. This gradient is in good agreement with theory. Indeed, if one agrees with Reference Pollack, Hurter and JohnsonPollack and others (1993) that we can link the age of the geological provinces with the geothermal flow, the geothermal flux should decrease from west to east with the age of the Antarctic crust.
Some well-defined areas of different ranges of Cy rms can be observed. For instance, the meridian 135˚ E between 82˚ S and 75˚ S clearly divides a zone of high Cy (in the east) from a zone of low Cy (in the west) with an abrupt transition. It seems difficult to explain this by an abrupt change in basal temperature due to ice flow. Also, the two demarcated sectors have no link with large-scale bedrock morphology and cannot be explained by deflections or convergence of subglacial water. The transition may correspond to that between the broad sedimentary Wilkes Subglacial Basin on one side and the more varied relief of the Belgica Highlands and various subglacial troughs on the other. Another hypothesis is that an abrupt change in geothermal flux yields a clear difference in basal melting conditions. One can observe that the middle part of this elongated feature (near 75˚ S) corresponds exactly with the Adventure Trench (at this place parallel to the meridian 135˚ E), just to the west of the Wilkes Subglacial Basin (Reference FerraccioliFerraccioli and others, 2001). These authors collected gravimetric, magnetic and bedrock morphology data along the International Trans-Antarctic Scientific Expedition (ITASE) traverse, following the latitude 75˚ S from Terra Nova Bay (160˚ E) to Dome C (126˚ E). They observed a strong magnetic anomaly gradient between 135˚ and 145˚ E that they interpreted as the eastern edge of the Precambrian East Antarctic Craton just on the western flank of the Wilkes Subglacial Basin. The position of the observed elongated feature here, just in the western part of the magnetic anomaly gradient, could then be explained by a change in the rock properties.
4. Conclusion
We have confirmed the existence of several hydrological networks beneath the Antarctic ice sheet that have been proposed by Reference Siegert and RidleySiegert and Ridley (1998a) and Reference Rémy, Testut, Legrésy, Forieri, Bianchi and TabaccoRémy and others (2003). Our approach uses a surface curvature technique to enhance subtle surface features observed in the ice-sheet surface topography derived from ERS radar altimetry. We have identified several elongated features corresponding to hydrological systems, which cross the continent over distances greater than a few hundred kilometres. Some of these features are connected to the ice-sheet margin, although the low number of such features means that transportation of subglacial meltwater within these channels does not significantly contribute to mass loss for the ice sheet on the continental scale.
For the Mertz Glacier drainage basin, we detect a flow anomaly related to a suspected hydrological system. This confirms that the existence of basal hydrological networks may affect the ice-flow dynamics and, on the local scale, mass loss to the ocean.
On the continental scale, the areas where the higher concentrations of elongated features are found correspond to areas of convergent flow. It is difficult to conclude whether the flow is due to basal melting, especially affecting the convergent-flow area, or whether the presence of hydrological systems strongly enhances the flow over a large region. Also, the suspected hydrological systems become more and more numerous as one moves from the eastern to the western part of Antarctica and could thus be related to geothermal flux. If this is confirmed, one has a means to better constrain this poorly known parameter. The distinctive delineation revealed between a poorly and a highly dense hydrological area along 1358 E may correspond to the limit between old East Antarctica and young West Antarctica.
Confirmation of the link between these observed topographic features and the presence of hydrological networks requires more extensive RES measurements. Such datasets may also help us to understand better the impact of ice flow and ice modelling.
Acknowledgements
We thank two anonymous reviewers, the Scientific Editor H. Fricker, and R. Coleman for help with improving this paper.







