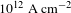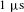1 Introduction
The advent of laser pulses of ps or shorter duration and of very high power opened a basically new physics topic which includes relativistic effects[Reference Mourou, Tajima and Bulanov1, Reference Tajima and Mourou2]. One of these phenomena is the interaction of these laser pulses at very high intensities with solid-state density, targets resulting in a basically different nature compared with ns pulses[Reference Hora, Badziak, Read, Li, Liang, Liu, Shang, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied3, Reference Hora4]. The ps laser–target interaction case shows a direct conversion of laser energy into directed macroscopic motion of plasma blocks with nearly no losses of thermal or instability processes. In contrast to this high efficiency energy conversion, the ns interaction is based on the conversion of laser energy into quiver motions of electrons and the electron temperatures increases by collisions. Through thermal equipartition between ions and electrons, the ion temperature increases and its pressure then determines the plasma dynamics with compression or expansion of the irradiated plasma. This difference was drastically measured for the first time as an ultrahigh acceleration by Sauerbrey[Reference Sauerbrey5] from the Doppler effect of the motion of the generated plasma moving against the laser beam. The acceleration of
![]() $2\times 10^{20}~\text{cm}~\text{s}^{-2}$
was 100 000 times higher than any acceleration detected before in a laboratory and had values known from neutron stars or similar astrophysical objects. These accelerations were known from numerical evaluations of the plasma theory when the laser intensities were high enough that the dynamics was no longer determined by thermal pressures but by forces due to the laser fields as a kind of ponderomotive force. The more detailed analysis needed the inclusion of the optical properties of plasma into the Maxwellian stress tensor[Reference Hora6] where an acceleration of plasma blocks resulted in values of above
$2\times 10^{20}~\text{cm}~\text{s}^{-2}$
was 100 000 times higher than any acceleration detected before in a laboratory and had values known from neutron stars or similar astrophysical objects. These accelerations were known from numerical evaluations of the plasma theory when the laser intensities were high enough that the dynamics was no longer determined by thermal pressures but by forces due to the laser fields as a kind of ponderomotive force. The more detailed analysis needed the inclusion of the optical properties of plasma into the Maxwellian stress tensor[Reference Hora6] where an acceleration of plasma blocks resulted in values of above
![]() $10^{20}~\text{cm}~\text{s}^{-2}$
under similar conditions as the experiments[Reference Sauerbrey5]. The application of the nonthermal, efficient ultrahigh acceleration for a new approach for nuclear fusion[Reference Hora7] led to an alternative kind of shock ignition[Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou8, Reference Moustaizis, Lalousis and Hora9]. Parallel to these ultrahigh accelerations, ultrahigh ion current densities were detected[Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikowa, Kraska, Laska, Parys, Perina, Pfeifer, Rohlena, Skala, Ullschmied, Wolowski and Woryna10] in the space charge neutral directed motion of the plasma blocks with homogeneous high ion energies exceeding ion current densities of
$10^{20}~\text{cm}~\text{s}^{-2}$
under similar conditions as the experiments[Reference Sauerbrey5]. The application of the nonthermal, efficient ultrahigh acceleration for a new approach for nuclear fusion[Reference Hora7] led to an alternative kind of shock ignition[Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou8, Reference Moustaizis, Lalousis and Hora9]. Parallel to these ultrahigh accelerations, ultrahigh ion current densities were detected[Reference Hora, Badziak, Boody, Höpfl, Jungwirth, Kralikowa, Kraska, Laska, Parys, Perina, Pfeifer, Rohlena, Skala, Ullschmied, Wolowski and Woryna10] in the space charge neutral directed motion of the plasma blocks with homogeneous high ion energies exceeding ion current densities of
![]() $10^{12}~\text{A}~\text{cm}^{-2}$
. These values are more than million times higher than those of the best ion accelerators. The following evaluations consider the application of a basically new approach to fusion energy due to the completely new conditions for muon catalyzed fusion (
$10^{12}~\text{A}~\text{cm}^{-2}$
. These values are more than million times higher than those of the best ion accelerators. The following evaluations consider the application of a basically new approach to fusion energy due to the completely new conditions for muon catalyzed fusion (
![]() $\unicode[STIX]{x03BC}$
CF)[Reference Eliezer, Tajima and Rosenbluth11–Reference Cohen13]. As an example, it should be mentioned how the very high density interaction by lasers compared with accelerators, that led to a change of the efficiency of antiproton interaction from about
$\unicode[STIX]{x03BC}$
CF)[Reference Eliezer, Tajima and Rosenbluth11–Reference Cohen13]. As an example, it should be mentioned how the very high density interaction by lasers compared with accelerators, that led to a change of the efficiency of antiproton interaction from about
![]() $10^{-9}{-}10^{-2}$
[Reference Christopoulos, Hora, Stening, Loeb and Scheid14] such that the design of an interstellar space mission may be considered possible by using antihydrogen as fuel[Reference Hora and Loeb15].
$10^{-9}{-}10^{-2}$
[Reference Christopoulos, Hora, Stening, Loeb and Scheid14] such that the design of an interstellar space mission may be considered possible by using antihydrogen as fuel[Reference Hora and Loeb15].
In the near future, Petawatt or Exawatt–Zetawatt[Reference Mourou, Tajima and Bulanov1, Reference Tajima and Mourou2] laser systems like ELI[16] and especially the IZEST[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima17, Reference Mourou, Brocklesby, Tajima and Limpert18] and the fiber based laser system will be investigated for the ICAN project; thus, it will be able to attain intensities up to
![]() $10^{25}$
and
$10^{25}$
and
![]() $10^{29}~\text{W}~\text{cm}^{-2}$
, respectively. For the case of ELI it is expected to reach maximum power of 200 PW for pulse duration of the order of fs, while IZEST is predicted to be in the TW regime in terms of power, with pulse duration of the order of attoseconds or zettaseconds. In the case of the ICAN–IZEST project a laser beam with 100 Hz rap rate and output efficiency up to 30% will enable unique applications such as the proton acceleration, the neutron production and the gamma–gamma collider, etc. The recent development of the ELI-NP Laser Infrastructure in Romania[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19] allows to study muon production and
$10^{29}~\text{W}~\text{cm}^{-2}$
, respectively. For the case of ELI it is expected to reach maximum power of 200 PW for pulse duration of the order of fs, while IZEST is predicted to be in the TW regime in terms of power, with pulse duration of the order of attoseconds or zettaseconds. In the case of the ICAN–IZEST project a laser beam with 100 Hz rap rate and output efficiency up to 30% will enable unique applications such as the proton acceleration, the neutron production and the gamma–gamma collider, etc. The recent development of the ELI-NP Laser Infrastructure in Romania[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19] allows to study muon production and
![]() $\unicode[STIX]{x03BC}$
CF induced by PW laser beams. The surface muon production[Reference Bungau, Cywinski, Bungau, King and Lord20] from proton beam interaction with a solid target presents a local maximum in the range of 300–350 MeV[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19, Reference Bungau, Cywinski, Lord, King and Bungau21–Reference Turcu, Balascuta, Negoita, Jaroszynski and Mckenna24]. Experiments on laser-driven proton acceleration by high power, ps laser pulse interaction with ultrathin solid targets or with specific solid target configuration could be planned and performed in existing kJ
$\unicode[STIX]{x03BC}$
CF induced by PW laser beams. The surface muon production[Reference Bungau, Cywinski, Bungau, King and Lord20] from proton beam interaction with a solid target presents a local maximum in the range of 300–350 MeV[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19, Reference Bungau, Cywinski, Lord, King and Bungau21–Reference Turcu, Balascuta, Negoita, Jaroszynski and Mckenna24]. Experiments on laser-driven proton acceleration by high power, ps laser pulse interaction with ultrathin solid targets or with specific solid target configuration could be planned and performed in existing kJ
![]() $/$
PW laser facilities as the GEKKO-LFEX[Reference Azechi25, Reference Fujioka, Zhang, Yamamoto, Ohira, Fujii, Ishihara, Johzaki, Sunahara, Arikawa, Shigemori, Hironaka, Sakawa, Nakata, Kawanaka, Nagatomo, Shiraga, Miyanaga, Norimatsu, Nishimura and Azechi26], the ORION[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett27] and the PETAL[Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28, Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel29]. Recent development of kJ
$/$
PW laser facilities as the GEKKO-LFEX[Reference Azechi25, Reference Fujioka, Zhang, Yamamoto, Ohira, Fujii, Ishihara, Johzaki, Sunahara, Arikawa, Shigemori, Hironaka, Sakawa, Nakata, Kawanaka, Nagatomo, Shiraga, Miyanaga, Norimatsu, Nishimura and Azechi26], the ORION[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett27] and the PETAL[Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28, Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel29]. Recent development of kJ
![]() $/$
PW laser systems[Reference Danson, Hillier, Hopps and Neely30] in worldwide laser facilities enable to perform preliminary experiments on muon production by proton beam interaction with solid targets and investigate fusion process in magnetized plasmas with applications to astrophysics[Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28–Reference Danson, Hillier, Hopps and Neely30] or energy production[Reference Azechi25, Reference Fujioka, Zhang, Yamamoto, Ohira, Fujii, Ishihara, Johzaki, Sunahara, Arikawa, Shigemori, Hironaka, Sakawa, Nakata, Kawanaka, Nagatomo, Shiraga, Miyanaga, Norimatsu, Nishimura and Azechi26, Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28–Reference Danson, Hillier, Hopps and Neely30].
$/$
PW laser systems[Reference Danson, Hillier, Hopps and Neely30] in worldwide laser facilities enable to perform preliminary experiments on muon production by proton beam interaction with solid targets and investigate fusion process in magnetized plasmas with applications to astrophysics[Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28–Reference Danson, Hillier, Hopps and Neely30] or energy production[Reference Azechi25, Reference Fujioka, Zhang, Yamamoto, Ohira, Fujii, Ishihara, Johzaki, Sunahara, Arikawa, Shigemori, Hironaka, Sakawa, Nakata, Kawanaka, Nagatomo, Shiraga, Miyanaga, Norimatsu, Nishimura and Azechi26, Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28–Reference Danson, Hillier, Hopps and Neely30].
2 Description of the operation of the proposed new scheme for fusion
During the last few years there has been an increase interest to develop laboratory prototypes of compact magnetic fusion devices[Reference Mcguire31–Reference Hora33]. These devices will be operating with intermediate plasma densities (
![]() $10^{16}{-}10^{18}~\text{cm}^{-3}$
), compared to Tokamak machines which operate at lower plasma density and to ICF machines which operate at much higher plasma density.
$10^{16}{-}10^{18}~\text{cm}^{-3}$
), compared to Tokamak machines which operate at lower plasma density and to ICF machines which operate at much higher plasma density.
The proposed new fusion scheme is based on a compact magnetic fusion device which is divided in two parts with different plasma densities, plasma temperatures and different external applied magnetic field. Both magnetic configurations are in cylindrical symmetry and in mirror-like topology. The first part of the device has a relatively small volume (about
![]() $1~\text{cm}^{3}$
) magnetic device with mirror-like topology capable to support 90–100 T magnetic field[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19, Reference Moustaizis, Auvray, Hora, Lalousis, Larour and Mourou34], initial plasma density up to
$1~\text{cm}^{3}$
) magnetic device with mirror-like topology capable to support 90–100 T magnetic field[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19, Reference Moustaizis, Auvray, Hora, Lalousis, Larour and Mourou34], initial plasma density up to
![]() $10^{20}{-}10^{21}~\text{cm}^{-3}$
and plasma temperature no higher than 100 eV. This first part is used to ignite spark fusion by
$10^{20}{-}10^{21}~\text{cm}^{-3}$
and plasma temperature no higher than 100 eV. This first part is used to ignite spark fusion by
![]() $\unicode[STIX]{x03BC}$
CF in its volume. More details for the small magnetic configuration (see Figures 17 and 58(a) in Ref. [Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19]) and its operation can be found in the technical report of the ELI-NP laser infrastructure[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19]. The plasma trapping in the small magnetic configuration is
$\unicode[STIX]{x03BC}$
CF in its volume. More details for the small magnetic configuration (see Figures 17 and 58(a) in Ref. [Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19]) and its operation can be found in the technical report of the ELI-NP laser infrastructure[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19]. The plasma trapping in the small magnetic configuration is
![]() $1~\unicode[STIX]{x03BC}\text{s}$
, in order to enable
$1~\unicode[STIX]{x03BC}\text{s}$
, in order to enable
![]() $\unicode[STIX]{x03BC}$
CF reactions (see Figures 1 and 2) during the period of the lifetime of the muons (
$\unicode[STIX]{x03BC}$
CF reactions (see Figures 1 and 2) during the period of the lifetime of the muons (
![]() $2.2~\unicode[STIX]{x03BC}\text{s}$
). After
$2.2~\unicode[STIX]{x03BC}\text{s}$
). After
![]() $1~\unicode[STIX]{x03BC}\text{s}$
the alpha particles produced from the spark fusion part of the device generate sufficient alpha heating (see Figures 3 and 4) in order to trigger (initiate) the fusion[Reference Lalousis, Throumoulopoulos and Poulipoulis35] process in the plasma (
$1~\unicode[STIX]{x03BC}\text{s}$
the alpha particles produced from the spark fusion part of the device generate sufficient alpha heating (see Figures 3 and 4) in order to trigger (initiate) the fusion[Reference Lalousis, Throumoulopoulos and Poulipoulis35] process in the plasma (
![]() $10^{17}~\text{cm}^{-3}$
) of the second part of the device and achieve the optimum fusion temperature and reaction rate after 0.05 s (see Figure 3). For a lower plasma density of the order of
$10^{17}~\text{cm}^{-3}$
) of the second part of the device and achieve the optimum fusion temperature and reaction rate after 0.05 s (see Figure 3). For a lower plasma density of the order of
![]() $10^{16}~\text{cm}^{-3}$
the optimum plasma temperature and maximum reaction rate are achieved after 0.02 s (see Figure 4).
$10^{16}~\text{cm}^{-3}$
the optimum plasma temperature and maximum reaction rate are achieved after 0.02 s (see Figure 4).

Figure 1. Full description of muon catalysis fusion cycle.

Figure 2. Reduced
![]() $\unicode[STIX]{x03BC}$
CF catalyzed cycle.
$\unicode[STIX]{x03BC}$
CF catalyzed cycle.

Figure 3. Temporal evolution of the reaction rate, plasma ion density and plasma ion temperature. The blue arrow indicates the end of operation of the
![]() $\unicode[STIX]{x03BC}$
CF in the spark fusion part of the device which correspond to
$\unicode[STIX]{x03BC}$
CF in the spark fusion part of the device which correspond to
![]() $1~\unicode[STIX]{x03BC}\text{s}$
.
$1~\unicode[STIX]{x03BC}\text{s}$
.
The second part of the proposed device is composed by a volume in cylindrical symmetry with a diameter of 45 cm and 45 cm in the axial direction, with mirror-like magnetic topology, capable of trapping a plasma with density of
![]() $10^{16}{-}10^{17}~\text{cm}^{-3}$
and initial plasma temperature up to 300 or 800 eV for duration much shorter than 1 s (see Figure 3). The external applied magnetic field for the second part of the device is fixed to 8–9 T. For both parts of the proposed compact magnetic fusion device the selected initial values of the plasmas and the magnetic fields allow a beta plasma value in the range of 1–1.5. In the spark fusion part of the proposed device the fusion reactions in the low temperature plasma will be initiated by
$10^{16}{-}10^{17}~\text{cm}^{-3}$
and initial plasma temperature up to 300 or 800 eV for duration much shorter than 1 s (see Figure 3). The external applied magnetic field for the second part of the device is fixed to 8–9 T. For both parts of the proposed compact magnetic fusion device the selected initial values of the plasmas and the magnetic fields allow a beta plasma value in the range of 1–1.5. In the spark fusion part of the proposed device the fusion reactions in the low temperature plasma will be initiated by
![]() $\unicode[STIX]{x03BC}$
CF in D–T plasma. After
$\unicode[STIX]{x03BC}$
CF in D–T plasma. After
![]() $1~\unicode[STIX]{x03BC}\text{s}$
of operation the spark fusion part of the device produces sufficient alphas in order to trigger the fusion process, via alpha heating, in the second part of the device. The proposed new scheme works in two steps having different characteristic times of operation, enabling in the first step to produce alpha particles by
$1~\unicode[STIX]{x03BC}\text{s}$
of operation the spark fusion part of the device produces sufficient alphas in order to trigger the fusion process, via alpha heating, in the second part of the device. The proposed new scheme works in two steps having different characteristic times of operation, enabling in the first step to produce alpha particles by
![]() $\unicode[STIX]{x03BC}$
CF fusion reactions in the spark part of the device and use the alpha heating effect in the second step to increase the initial plasma temperature of 300 or 800 eV to the optimum fusion temperature of 25 keV (see Figure 3) in the second part of the device. The selection of these plasma temperatures (300 or 800 eV) is to emphasize on the alpha heating effect and study the triggering fusion process of the low temperature plasma. We use a multi-fluid global particle and energy balance code[Reference Lalousis, Throumoulopoulos and Poulipoulis35] to calculate the temporal evolution of the plasma parameters, the effect of alpha heating in the second part of the device and the necessary time interval for the reaction rate to reach the max value which gives the neutron production of the device. The numerical simulation for the two-step operation of the device will be presented and discussed in the next paragraphs.
$\unicode[STIX]{x03BC}$
CF fusion reactions in the spark part of the device and use the alpha heating effect in the second step to increase the initial plasma temperature of 300 or 800 eV to the optimum fusion temperature of 25 keV (see Figure 3) in the second part of the device. The selection of these plasma temperatures (300 or 800 eV) is to emphasize on the alpha heating effect and study the triggering fusion process of the low temperature plasma. We use a multi-fluid global particle and energy balance code[Reference Lalousis, Throumoulopoulos and Poulipoulis35] to calculate the temporal evolution of the plasma parameters, the effect of alpha heating in the second part of the device and the necessary time interval for the reaction rate to reach the max value which gives the neutron production of the device. The numerical simulation for the two-step operation of the device will be presented and discussed in the next paragraphs.

Figure 4. Temporal evolution of the reaction rate, and plasma ion temperature. The blue arrow indicates the end of operation of the
![]() $\unicode[STIX]{x03BC}$
CF in the spark fusion part of the device which correspond to
$\unicode[STIX]{x03BC}$
CF in the spark fusion part of the device which correspond to
![]() $1~\unicode[STIX]{x03BC}\text{s}$
.
$1~\unicode[STIX]{x03BC}\text{s}$
.
3 Development of
 $\unicode[STIX]{x03BC}$
CF for conditions opened by laser induced ultrahigh ion densities
$\unicode[STIX]{x03BC}$
CF for conditions opened by laser induced ultrahigh ion densities
Up until now muon production is based on accelerators where a proton beam accelerates and collides with a solid target to produce pions that decay to positive and negative muons[Reference Frank36–Reference Sakharov39]. Our aim is to study
![]() $\unicode[STIX]{x03BC}$
CF in D–T mixture where muons are created from the interaction of a proton beam, which is created and accelerated by a high-intensity laser beam, with a solid target. Only negative muons are useful and contribute to the muon catalyzed fusion. The following paragraphs and sections of the text will refer to the term
$\unicode[STIX]{x03BC}$
CF in D–T mixture where muons are created from the interaction of a proton beam, which is created and accelerated by a high-intensity laser beam, with a solid target. Only negative muons are useful and contribute to the muon catalyzed fusion. The following paragraphs and sections of the text will refer to the term
![]() $\unicode[STIX]{x03BC}$
CF instead of the term negative
$\unicode[STIX]{x03BC}$
CF instead of the term negative
![]() $\unicode[STIX]{x03BC}$
CF. The reason for this choice is that the use of a laser based accelerator will be advantageous as will lead to relatively smaller scale facilities more tunable in operating parameters. Also the expected number of accelerated particles will be higher by few orders of magnitude compared to the conventional accelerator case.
$\unicode[STIX]{x03BC}$
CF. The reason for this choice is that the use of a laser based accelerator will be advantageous as will lead to relatively smaller scale facilities more tunable in operating parameters. Also the expected number of accelerated particles will be higher by few orders of magnitude compared to the conventional accelerator case.
Use of muons as a catalyst in p–D fusion was first examined by Frank in 1947[Reference Frank36] and the first experimental proof was demonstrated by Alvarez in 1956[Reference Alvarez, Bradner, Crawford, Crawford, Falk-Vairant, Good, Gow, Rosenfeld, Solmitz, Stevenson, Ticho and Tripp37]. Muon catalyzed D–T fusion was described in the work of Sakharov in 1948[Reference Sakharov38, Reference Sakharov39] and was further discussed by Jackson in 1957[Reference Jackson40]. In 1987, Eliezer et al.
[Reference Eliezer, Tajima and Rosenbluth11] proposed a muon catalyzed fusion–fission device. Studies on
![]() $\unicode[STIX]{x03BC}$
CF in relatively large magnetic devices[Reference Petitjean41] and detailed investigation on
$\unicode[STIX]{x03BC}$
CF in relatively large magnetic devices[Reference Petitjean41] and detailed investigation on
![]() $\unicode[STIX]{x03BC}$
CF process[Reference Eliezer and Henis42] including fusion devices with magnetic trapping conditions[Reference Eliezer and Henis42, Reference Tajima, Eliezer, Kulsrud, Jones, Rafelski and Monkhorst43] enable to propose schemes for energy production plants[Reference Eliezer and Henis42–Reference Petrov44]. An analytical description can be seen in many works[Reference Eliezer and Henis42, Reference Nagamine45–Reference Gershtein, Petrov, Ponomarev, Somov and Faifman47]. The full cycle describing the process is shown in Figure 1
[Reference Nagamine45]. There the injected muons in the D
$\unicode[STIX]{x03BC}$
CF process[Reference Eliezer and Henis42] including fusion devices with magnetic trapping conditions[Reference Eliezer and Henis42, Reference Tajima, Eliezer, Kulsrud, Jones, Rafelski and Monkhorst43] enable to propose schemes for energy production plants[Reference Eliezer and Henis42–Reference Petrov44]. An analytical description can be seen in many works[Reference Eliezer and Henis42, Reference Nagamine45–Reference Gershtein, Petrov, Ponomarev, Somov and Faifman47]. The full cycle describing the process is shown in Figure 1
[Reference Nagamine45]. There the injected muons in the D
![]() $_{2}$
, T
$_{2}$
, T
![]() $_{2}$
mixture form muonic atoms (d
$_{2}$
mixture form muonic atoms (d
![]() $\unicode[STIX]{x03BC}$
or t
$\unicode[STIX]{x03BC}$
or t
![]() $\unicode[STIX]{x03BC}$
) and afterwards they react again with either D, T and as a result molecules such as dd
$\unicode[STIX]{x03BC}$
) and afterwards they react again with either D, T and as a result molecules such as dd
![]() $\unicode[STIX]{x03BC}$
, dt
$\unicode[STIX]{x03BC}$
, dt
![]() $\unicode[STIX]{x03BC}$
or tt
$\unicode[STIX]{x03BC}$
or tt
![]() $\unicode[STIX]{x03BC}$
are formed, leading to fusion reactions, with the above seen products. After the reaction most of the muons are available for a second
$\unicode[STIX]{x03BC}$
are formed, leading to fusion reactions, with the above seen products. After the reaction most of the muons are available for a second
![]() $\unicode[STIX]{x03BC}$
CF cycle. However as the cross-section for the formation of tt
$\unicode[STIX]{x03BC}$
CF cycle. However as the cross-section for the formation of tt
![]() $\unicode[STIX]{x03BC}$
and dd
$\unicode[STIX]{x03BC}$
and dd
![]() $\unicode[STIX]{x03BC}$
is lower (about
$\unicode[STIX]{x03BC}$
is lower (about
![]() $10^{2}$
times) than the cross-section for dt
$10^{2}$
times) than the cross-section for dt
![]() $\unicode[STIX]{x03BC}$
, the following reduced cycle can describe the catalysis in good agreement with Figure 2
[Reference Harms, Schoepf, Miley and Kingdon48].
$\unicode[STIX]{x03BC}$
, the following reduced cycle can describe the catalysis in good agreement with Figure 2
[Reference Harms, Schoepf, Miley and Kingdon48].
The numerical solution of a set of differential equations[Reference Nagamine45, Reference Harms, Schoepf, Miley and Kingdon48] that describe the
![]() $\unicode[STIX]{x03BC}$
CF cycle allows us to follow the temporal evolution of neutron and alpha production due to
$\unicode[STIX]{x03BC}$
CF cycle allows us to follow the temporal evolution of neutron and alpha production due to
![]() $\unicode[STIX]{x03BC}$
CF. We use the same set of differential equations as presented and discussed in details in Ref. [Reference Harms, Schoepf, Miley and Kingdon48] and without including estimation on muon losses due to annihilation or other physical processes occurred during the propagation and the separation of positive and negative muons before their interaction with the fusion fuel. The main critical parameter for
$\unicode[STIX]{x03BC}$
CF. We use the same set of differential equations as presented and discussed in details in Ref. [Reference Harms, Schoepf, Miley and Kingdon48] and without including estimation on muon losses due to annihilation or other physical processes occurred during the propagation and the separation of positive and negative muons before their interaction with the fusion fuel. The main critical parameter for
![]() $\unicode[STIX]{x03BC}$
CF (
$\unicode[STIX]{x03BC}$
CF (
![]() $\unicode[STIX]{x03BC}$
dt) is the muon sticking probability,
$\unicode[STIX]{x03BC}$
dt) is the muon sticking probability,
![]() $\unicode[STIX]{x1D714}$
, expressing the capture of a muon by an alpha particle (
$\unicode[STIX]{x1D714}$
, expressing the capture of a muon by an alpha particle (
![]() $\unicode[STIX]{x1D6FC}$
or He) that is generated from fusion reaction. This phenomenon leads to muon loss and the mechanism to reactivate the stuck muons from
$\unicode[STIX]{x1D6FC}$
or He) that is generated from fusion reaction. This phenomenon leads to muon loss and the mechanism to reactivate the stuck muons from
![]() $\unicode[STIX]{x03BC}\unicode[STIX]{x1D6FC}$
atoms is called muon regeneration or muon stripping and its fraction is symbolized as
$\unicode[STIX]{x03BC}\unicode[STIX]{x1D6FC}$
atoms is called muon regeneration or muon stripping and its fraction is symbolized as
![]() $R$
[Reference Nagamine45, Reference Harms, Schoepf, Miley and Kingdon48]. Thus the effective sticking probability is
$R$
[Reference Nagamine45, Reference Harms, Schoepf, Miley and Kingdon48]. Thus the effective sticking probability is
![]() $\unicode[STIX]{x1D714}_{s}^{\text{eff}}=(1-R)\unicode[STIX]{x1D714}_{s}^{0}$
.
$\unicode[STIX]{x1D714}_{s}^{\text{eff}}=(1-R)\unicode[STIX]{x1D714}_{s}^{0}$
.
![]() $\unicode[STIX]{x1D714}_{s}^{0}$
is the initial sticking probability. Optimization mechanisms of
$\unicode[STIX]{x1D714}_{s}^{0}$
is the initial sticking probability. Optimization mechanisms of
![]() $R$
, as well as numerical estimates can be seen in Refs. [Reference Eliezer and Henis42, Reference Kimura and Bonasera49–Reference Hu51]. The optimal value for
$R$
, as well as numerical estimates can be seen in Refs. [Reference Eliezer and Henis42, Reference Kimura and Bonasera49–Reference Hu51]. The optimal value for
![]() $\unicode[STIX]{x1D714}_{s}^{0}$
is in the range of 0.007–0.0008 and for
$\unicode[STIX]{x1D714}_{s}^{0}$
is in the range of 0.007–0.0008 and for
![]() $\unicode[STIX]{x1D714}_{s}^{\text{eff}}$
after muon regeneration is 0.0007 or lower. The main factor in order to create a sustainable
$\unicode[STIX]{x1D714}_{s}^{\text{eff}}$
after muon regeneration is 0.0007 or lower. The main factor in order to create a sustainable
![]() $\unicode[STIX]{x03BC}$
CF process is the available number of
$\unicode[STIX]{x03BC}$
CF process is the available number of
![]() $\unicode[STIX]{x03BC}$
that will participate in the fusion reactions. In recent simulations of the collision of a proton beam with various solid targets for the parameters of the ISIS-UK muon facility, the results showed that about
$\unicode[STIX]{x03BC}$
that will participate in the fusion reactions. In recent simulations of the collision of a proton beam with various solid targets for the parameters of the ISIS-UK muon facility, the results showed that about
![]() $10^{4}\unicode[STIX]{x03BC}$
will be created[Reference Bungau, Cywinski, Bungau, King and Lord20, Reference Bungau, Cywinski, Bungau, King and Lord52, Reference Bungau, Cywinski, Bungau, King and Lord53]. These experimental results confirm the necessity for high muon production by laser proton acceleration and interaction with solid targets in order to have efficient
$10^{4}\unicode[STIX]{x03BC}$
will be created[Reference Bungau, Cywinski, Bungau, King and Lord20, Reference Bungau, Cywinski, Bungau, King and Lord52, Reference Bungau, Cywinski, Bungau, King and Lord53]. These experimental results confirm the necessity for high muon production by laser proton acceleration and interaction with solid targets in order to have efficient
![]() $\unicode[STIX]{x03BC}$
CF in an experimental device. In addition muon creation from laser vacuum interaction was studied[Reference Sakharov38, Reference Sakharov39], but with relatively low production efficiency. The
$\unicode[STIX]{x03BC}$
CF in an experimental device. In addition muon creation from laser vacuum interaction was studied[Reference Sakharov38, Reference Sakharov39], but with relatively low production efficiency. The
![]() $\unicode[STIX]{x03BC}$
CF depends also on the temperature of the D–T plasma. The international literature[Reference Eliezer, Tajima and Rosenbluth11–Reference Cohen13, Reference Eliezer and Henis42, Reference Kimura and Bonasera49–Reference Hu51, Reference Breunlich54–Reference Pahlavani and Motevalli56] enables parametric studies of
$\unicode[STIX]{x03BC}$
CF depends also on the temperature of the D–T plasma. The international literature[Reference Eliezer, Tajima and Rosenbluth11–Reference Cohen13, Reference Eliezer and Henis42, Reference Kimura and Bonasera49–Reference Hu51, Reference Breunlich54–Reference Pahlavani and Motevalli56] enables parametric studies of
![]() $\unicode[STIX]{x03BC}$
CF as a function of the plasma temperature and estimate sticking coefficient and the number of fusions per muon (
$\unicode[STIX]{x03BC}$
CF as a function of the plasma temperature and estimate sticking coefficient and the number of fusions per muon (
![]() $f/\unicode[STIX]{x03BC}$
) which for low temperature plasma could be up to
$f/\unicode[STIX]{x03BC}$
) which for low temperature plasma could be up to
![]() $1000f/\unicode[STIX]{x03BC}$
[Reference Eliezer and Henis42, Reference Breunlich54, Reference Pahlavani and Motevalli56]. But the experimental results are limited and there is not yet experimental setup using the proposed scheme of operation of the compact magnetic fusion device. For our purpose we initiate the calculations by using moderate parameters for the
$1000f/\unicode[STIX]{x03BC}$
[Reference Eliezer and Henis42, Reference Breunlich54, Reference Pahlavani and Motevalli56]. But the experimental results are limited and there is not yet experimental setup using the proposed scheme of operation of the compact magnetic fusion device. For our purpose we initiate the calculations by using moderate parameters for the
![]() $\unicode[STIX]{x03BC}$
CF in order to have
$\unicode[STIX]{x03BC}$
CF in order to have
![]() $250f/\unicode[STIX]{x03BC}{-}300f/\unicode[STIX]{x03BC}$
. Multi-kJ and PW laser beams can accelerate protons to energies up to 300 MeV. The high energy proton production by ps ultrahigh-intensity laser beam interaction with solid target present the main advantage compared to conventional accelerators because the number of produced protons could be up to
$250f/\unicode[STIX]{x03BC}{-}300f/\unicode[STIX]{x03BC}$
. Multi-kJ and PW laser beams can accelerate protons to energies up to 300 MeV. The high energy proton production by ps ultrahigh-intensity laser beam interaction with solid target present the main advantage compared to conventional accelerators because the number of produced protons could be up to
![]() $10^{15}{-}10^{16}$
per laser pulse. For a production of
$10^{15}{-}10^{16}$
per laser pulse. For a production of
![]() $10^{-5}\unicode[STIX]{x03BC}/\text{p}$
(results from the ISIS-UK facility and Ref. [Reference Ferrari, Sala, Fasso and Ranft23]), the number of the generated muons is up to
$10^{-5}\unicode[STIX]{x03BC}/\text{p}$
(results from the ISIS-UK facility and Ref. [Reference Ferrari, Sala, Fasso and Ranft23]), the number of the generated muons is up to
![]() $10^{10}{-}10^{11}$
per laser pulse. Under these conditions the estimated value for the laser beam energy is hundreds of kJ which is relatively high for the actual laser facilities. In the future laser installations such as the IZEST could deliver this energy. But for near future laser installation energy of few kJ (PETAL class laser) or 30 kJ like the ELI project will be available. These laser installations emphasize the benefits of laser based accelerator compared to the conventional accelerators for muon production.
$10^{10}{-}10^{11}$
per laser pulse. Under these conditions the estimated value for the laser beam energy is hundreds of kJ which is relatively high for the actual laser facilities. In the future laser installations such as the IZEST could deliver this energy. But for near future laser installation energy of few kJ (PETAL class laser) or 30 kJ like the ELI project will be available. These laser installations emphasize the benefits of laser based accelerator compared to the conventional accelerators for muon production.
In the international bibliography there are proposals for high current, high efficient and high energy proton beams production by high-intensity laser pulse interaction with solid targets[Reference Hora7, Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima17, Reference Mourou, Brocklesby, Tajima and Limpert18]. The accelerated proton beam in the energy range of 300–350 MeV will interact with a solid target of graphite or other suitable material to generate a pion beam. The pions decay and produce surface muons[Reference Bungau, Cywinski, Bungau, King and Lord20–Reference Turcu, Balascuta, Negoita, Jaroszynski and Mckenna24]. In the following section we explore numerically the operation of the proposed device using laser beam energy for the muon production from hundreds of kJ (exotic case) to tens of kJ. These calculations allow to appreciate the laser development and to evaluate the potential use of the proposed device for energy production.
4 Numerical simulation describing the fusion process in the proposed device
We consider in the spark fusion part (first part) of the device a plasma mixture of D–T with density of
![]() $N_{\text{d}}=N_{\text{t}}=10^{21}~\text{cm}^{-3}$
and plasma temperature lower than 100 eV. The application of an external magnetic field of 100 T with mirror-like topology allows plasma trapping for
$N_{\text{d}}=N_{\text{t}}=10^{21}~\text{cm}^{-3}$
and plasma temperature lower than 100 eV. The application of an external magnetic field of 100 T with mirror-like topology allows plasma trapping for
![]() $1~\unicode[STIX]{x03BC}\text{s}$
[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19, Reference Moustaizis, Auvray, Hora, Lalousis, Larour and Mourou34]. A solid disc (first solid target) placed near the magnetic mirror of the configuration and the interaction with high contrast PW (or higher) laser beam produce high energy and high density proton beam up to 350 MeV due to plasma block acceleration. The high energy proton beam interacts with a second solid surface placed perpendicular to proton beam and just after the first disc in order to produce pions which decay to muons[Reference Bungau, Cywinski, Bungau, King and Lord20]. In the extreme case the interaction of hundreds of kJ of laser beam with a thin solid target produces
$1~\unicode[STIX]{x03BC}\text{s}$
[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19, Reference Moustaizis, Auvray, Hora, Lalousis, Larour and Mourou34]. A solid disc (first solid target) placed near the magnetic mirror of the configuration and the interaction with high contrast PW (or higher) laser beam produce high energy and high density proton beam up to 350 MeV due to plasma block acceleration. The high energy proton beam interacts with a second solid surface placed perpendicular to proton beam and just after the first disc in order to produce pions which decay to muons[Reference Bungau, Cywinski, Bungau, King and Lord20]. In the extreme case the interaction of hundreds of kJ of laser beam with a thin solid target produces
![]() $2\times 10^{16}$
protons (p). The interaction of this beam with a solid surface (e.g., of graphite) generates
$2\times 10^{16}$
protons (p). The interaction of this beam with a solid surface (e.g., of graphite) generates
![]() $2\times 10^{11}$
surface muons (
$2\times 10^{11}$
surface muons (
![]() $\unicode[STIX]{x03BC}$
) in a volume of
$\unicode[STIX]{x03BC}$
) in a volume of
![]() $1~\text{cm}^{3}$
of the spark fusion part of the device. This number of muons is introduced as initial conditions for numerical solutions of the coupled differential equations describing the
$1~\text{cm}^{3}$
of the spark fusion part of the device. This number of muons is introduced as initial conditions for numerical solutions of the coupled differential equations describing the
![]() $\unicode[STIX]{x03BC}$
CF with the appropriate parameters as described in textbooks[Reference Nagamine45, Reference Harms, Schoepf, Miley and Kingdon48]. The plasma temperature is less than 100 eV. The main result correspond to the production of
$\unicode[STIX]{x03BC}$
CF with the appropriate parameters as described in textbooks[Reference Nagamine45, Reference Harms, Schoepf, Miley and Kingdon48]. The plasma temperature is less than 100 eV. The main result correspond to the production of
![]() $10^{14}$
alphas in the
$10^{14}$
alphas in the
![]() $1~\text{cm}^{3}$
volume of the spark fusion part of the device after
$1~\text{cm}^{3}$
volume of the spark fusion part of the device after
![]() $1~\unicode[STIX]{x03BC}\text{s}$
of operation. This value of alpha corresponds approximately to
$1~\unicode[STIX]{x03BC}\text{s}$
of operation. This value of alpha corresponds approximately to
![]() $300f/\unicode[STIX]{x03BC}$
. Subsequently the simulation introduces the alphas in order to trigger the fusion process in the second part of the device. We simulate the temporal evolution of the plasma parameters and the reaction rate using a global particle and energy balance code[Reference Lalousis, Throumoulopoulos and Poulipoulis35]. In the second part of the device the initial values of the plasma density is
$300f/\unicode[STIX]{x03BC}$
. Subsequently the simulation introduces the alphas in order to trigger the fusion process in the second part of the device. We simulate the temporal evolution of the plasma parameters and the reaction rate using a global particle and energy balance code[Reference Lalousis, Throumoulopoulos and Poulipoulis35]. In the second part of the device the initial values of the plasma density is
![]() $10^{17}~\text{cm}^{-3}$
, the plasma temperature is 300 eV and the applied external magnetic field is 9 T. Figure 3 show the temporal evolution of the plasma ion density, plasma temperature and reaction rate due to the initial alpha production in the spark fusion part of the device and consequently the alpha heating effect of the plasma in the second part of the device. The important result of the simulation is that the alpha heating effect begins to be important after 0.04 s and the reaction rate reaches the maximum value at 0.05 s after the end of the
$10^{17}~\text{cm}^{-3}$
, the plasma temperature is 300 eV and the applied external magnetic field is 9 T. Figure 3 show the temporal evolution of the plasma ion density, plasma temperature and reaction rate due to the initial alpha production in the spark fusion part of the device and consequently the alpha heating effect of the plasma in the second part of the device. The important result of the simulation is that the alpha heating effect begins to be important after 0.04 s and the reaction rate reaches the maximum value at 0.05 s after the end of the
![]() $\unicode[STIX]{x03BC}$
CF operation in the spark fusion part of the device. The blue arrow indicates the end of the operation of the spark fusion part. The maximum reaction rate corresponds to a value of
$\unicode[STIX]{x03BC}$
CF operation in the spark fusion part of the device. The blue arrow indicates the end of the operation of the spark fusion part. The maximum reaction rate corresponds to a value of
![]() $1.5\times 10^{24}~\text{m}^{-3}~\text{s}^{-1}$
. The volume integration and the time integration allow estimating
$1.5\times 10^{24}~\text{m}^{-3}~\text{s}^{-1}$
. The volume integration and the time integration allow estimating
![]() $10^{19}$
neutrons produced after 0.06 s of the operation of the proposed device. The plasma ion density drops dramatically after 0.06 s due to high reaction rate, and the ion temperature increases is due to alpha heating. The plasma temperature for the maximum value of the reaction rate corresponds to 25 keV. This value of the temperature is achieved in the plasma of the second part of the device which initially was at a temperature of 300 eV. The reaction rate decrease after 0.06 s following the plasma density and if we like to maintain the fusion process with high reaction rate a pellet injection could be used for refueling the device. Under these conditions a continuous operation of the device is possible similar to the Tokamak machines but with a more compact magnetic fusion configuration.
$10^{19}$
neutrons produced after 0.06 s of the operation of the proposed device. The plasma ion density drops dramatically after 0.06 s due to high reaction rate, and the ion temperature increases is due to alpha heating. The plasma temperature for the maximum value of the reaction rate corresponds to 25 keV. This value of the temperature is achieved in the plasma of the second part of the device which initially was at a temperature of 300 eV. The reaction rate decrease after 0.06 s following the plasma density and if we like to maintain the fusion process with high reaction rate a pellet injection could be used for refueling the device. Under these conditions a continuous operation of the device is possible similar to the Tokamak machines but with a more compact magnetic fusion configuration.
Similar numerical results are obtained with a plasma density of
![]() $5\times 10^{16}~\text{cm}^{-3}$
in the second part of the device. The other plasma parameters and magnetic field values for both part of the device remain the same. Figure 4 shows the temporal evolution of the reaction rate and the plasma temperature. The main change for this case is the characteristic time of the alpha heating effect which arrives 0.01 s after the end of the
$5\times 10^{16}~\text{cm}^{-3}$
in the second part of the device. The other plasma parameters and magnetic field values for both part of the device remain the same. Figure 4 shows the temporal evolution of the reaction rate and the plasma temperature. The main change for this case is the characteristic time of the alpha heating effect which arrives 0.01 s after the end of the
![]() $\unicode[STIX]{x03BC}$
CF operation in the spark fusion part of the device. The reaction rate reaches the maximum value after 0.02 s which is a factor of two compared to the previous case. The maximum value for the reaction rate in this case is about
$\unicode[STIX]{x03BC}$
CF operation in the spark fusion part of the device. The reaction rate reaches the maximum value after 0.02 s which is a factor of two compared to the previous case. The maximum value for the reaction rate in this case is about
![]() $4.5\times 10^{23}~\text{m}^{-3}~\text{s}^{-1}$
, which correspond to a factor of three less, compare to the previous case. Also in this case the maximum value of the reaction corresponds to the fusion temperature of 25 keV. The same comments are applicable concerning the temperature effect and the refueling process as in the previous case.
$4.5\times 10^{23}~\text{m}^{-3}~\text{s}^{-1}$
, which correspond to a factor of three less, compare to the previous case. Also in this case the maximum value of the reaction corresponds to the fusion temperature of 25 keV. The same comments are applicable concerning the temperature effect and the refueling process as in the previous case.
As we explain in the previous paragraph the production of
![]() $10^{16}$
protons with energy up to 350 MeV per laser pulse is an extreme case for laser infrastructures because the necessary energy of the laser pulse must be hundreds of kJ. The results presented in Figures 3 and 4 could stimulate efforts for both laser system development and experimental studies on compact magnetic fusion devices. If the laser energy decreases to a few kJ (PETAL class laser system) or to tens of kJ (35 kJ), as will be the case for the IZEST project, the production of protons will be decreased by a factor of 100 or 10, respectively, and future experiments for high density proton generation by laser interaction with thin solid targets will be feasible. For this reason, we simulate the operation of the proposed device with laser energies close to actual laser facilities or to the near future laser facilities. Figure 5 shows the temporal evolution of the reaction rate due to alpha heating effect in the second part of the device for different alpha productions in the spark fusion part of the device. The different curves in Figure 5 correspond to different proton, muon and consequently alpha production in the spark fusion part of the device. The alpha density correspond to
$10^{16}$
protons with energy up to 350 MeV per laser pulse is an extreme case for laser infrastructures because the necessary energy of the laser pulse must be hundreds of kJ. The results presented in Figures 3 and 4 could stimulate efforts for both laser system development and experimental studies on compact magnetic fusion devices. If the laser energy decreases to a few kJ (PETAL class laser system) or to tens of kJ (35 kJ), as will be the case for the IZEST project, the production of protons will be decreased by a factor of 100 or 10, respectively, and future experiments for high density proton generation by laser interaction with thin solid targets will be feasible. For this reason, we simulate the operation of the proposed device with laser energies close to actual laser facilities or to the near future laser facilities. Figure 5 shows the temporal evolution of the reaction rate due to alpha heating effect in the second part of the device for different alpha productions in the spark fusion part of the device. The different curves in Figure 5 correspond to different proton, muon and consequently alpha production in the spark fusion part of the device. The alpha density correspond to
![]() $2\times 10^{11}~\text{cm}^{-3}$
(deep green
$2\times 10^{11}~\text{cm}^{-3}$
(deep green
![]() $2\times 10^{17}~\text{m}^{-3}$
), to
$2\times 10^{17}~\text{m}^{-3}$
), to
![]() $10^{12}~\text{cm}^{-3}$
(blue
$10^{12}~\text{cm}^{-3}$
(blue
![]() $10^{18}~\text{m}^{-3}$
),
$10^{18}~\text{m}^{-3}$
),
![]() $5\times 10^{12}~\text{cm}^{-3}$
(green
$5\times 10^{12}~\text{cm}^{-3}$
(green
![]() $5\times 10^{18}~\text{m}^{-3}$
) and to
$5\times 10^{18}~\text{m}^{-3}$
) and to
![]() $10^{13}~\text{cm}^{-3}$
(red
$10^{13}~\text{cm}^{-3}$
(red
![]() $10^{19}~\text{m}^{-3}$
). We simulate the operation of the device for initial plasma densities up to
$10^{19}~\text{m}^{-3}$
). We simulate the operation of the device for initial plasma densities up to
![]() $10^{16}~\text{cm}^{-3}$
and plasma temperature up to 800 eV, in the second part of the device. All the other parameters and the values of the magnetic fields in both parts of the device remain the same as was for the simulations of Figures 3 and 4. The main results is that for all values of alpha particles there exists triggering of fusion process in the second part of the device but for later time intervals as the alpha particle density decreases. The reaction rate for the lower value of alphas change (increases) very slow and reach the max value for a time interval longer than 10 s. For all cases there is manifestation of the alpha heating effect with main interest for the case of
$10^{16}~\text{cm}^{-3}$
and plasma temperature up to 800 eV, in the second part of the device. All the other parameters and the values of the magnetic fields in both parts of the device remain the same as was for the simulations of Figures 3 and 4. The main results is that for all values of alpha particles there exists triggering of fusion process in the second part of the device but for later time intervals as the alpha particle density decreases. The reaction rate for the lower value of alphas change (increases) very slow and reach the max value for a time interval longer than 10 s. For all cases there is manifestation of the alpha heating effect with main interest for the case of
![]() $10^{13}~\text{cm}^{-3}$
(red curve of Figure 5) and
$10^{13}~\text{cm}^{-3}$
(red curve of Figure 5) and
![]() $5\times 10^{12}~\text{cm}^{-3}$
(green curve in Figure 5) for which the max of reaction rate correspond to a time interval less than 1 s after the end of operation of
$5\times 10^{12}~\text{cm}^{-3}$
(green curve in Figure 5) for which the max of reaction rate correspond to a time interval less than 1 s after the end of operation of
![]() $\unicode[STIX]{x03BC}$
CF in the spark fusion part of the device.
$\unicode[STIX]{x03BC}$
CF in the spark fusion part of the device.

Figure 5. Temporal evolution of the reaction rate. The curves correspond to different initial values of the alpha particles produced by the
![]() $\unicode[STIX]{x03BC}$
CF in the spark part of the device: (a) red
$\unicode[STIX]{x03BC}$
CF in the spark part of the device: (a) red
![]() $10^{19}~\text{m}^{-3}$
, green
$10^{19}~\text{m}^{-3}$
, green
![]() $5\times 10^{18}~\text{m}^{-3}$
, blue
$5\times 10^{18}~\text{m}^{-3}$
, blue
![]() $10^{18}~\text{m}^{-3}$
and deep green
$10^{18}~\text{m}^{-3}$
and deep green
![]() $2\times 10^{17}~\text{m}^{-3}$
.
$2\times 10^{17}~\text{m}^{-3}$
.
5 Conclusions
In view of the basically new aspects of generation of ultrahigh space charge neutral relativistic ion densities[Reference Hora4, Reference Hora7, Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou8] based on the ultrahigh acceleration of plasma blocks[Reference Hora, Badziak, Read, Li, Liang, Liu, Shang, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied3, Reference Sauerbrey5, Reference Hora6], the mechanism of generation of ultrahigh density beams of protons with energies above of hundreds of MeV[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima17, Reference Mourou, Brocklesby, Tajima and Limpert18] opens a new access to
![]() $\unicode[STIX]{x03BC}$
CF[Reference Eliezer, Tajima and Rosenbluth11]. This was experienced by extending the results derived for relativistic ion beams[Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou8] following the application of petawatt to exawatt laser pulses for a new scheme of compact laser-driven compact magnetic fusion device. Laser-driven proton beam acceleration by high power laser beam interaction with ultrathin solid target is under investigation in the existing kJ
$\unicode[STIX]{x03BC}$
CF[Reference Eliezer, Tajima and Rosenbluth11]. This was experienced by extending the results derived for relativistic ion beams[Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou8] following the application of petawatt to exawatt laser pulses for a new scheme of compact laser-driven compact magnetic fusion device. Laser-driven proton beam acceleration by high power laser beam interaction with ultrathin solid target is under investigation in the existing kJ
![]() $/$
PW laser facilities as the GEKKO-LFEX[Reference Azechi25, Reference Fujioka, Zhang, Yamamoto, Ohira, Fujii, Ishihara, Johzaki, Sunahara, Arikawa, Shigemori, Hironaka, Sakawa, Nakata, Kawanaka, Nagatomo, Shiraga, Miyanaga, Norimatsu, Nishimura and Azechi26], ORION[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett27] and PETAL[Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28, Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel29]. Preliminary experiments in existing kJ
$/$
PW laser facilities as the GEKKO-LFEX[Reference Azechi25, Reference Fujioka, Zhang, Yamamoto, Ohira, Fujii, Ishihara, Johzaki, Sunahara, Arikawa, Shigemori, Hironaka, Sakawa, Nakata, Kawanaka, Nagatomo, Shiraga, Miyanaga, Norimatsu, Nishimura and Azechi26], ORION[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett27] and PETAL[Reference Blanchot, Behar, Berthier, Busserole, Chappuis, Damiens-Dupont, Garcia, Granet, Grosset-Grange, Goossens, Hilsz, Laborde, Lacombe, Laniesse, Lavastre, Luce, Macias, Mazataud, Miquel, Néauport, Noailles, Patelli, Perrot-Minot, Present, Raffestin, Remy, Rouyer and Valla28, Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel29]. Preliminary experiments in existing kJ
![]() $/$
PW laser facilities[Reference Danson, Hillier, Hopps and Neely30] allow the development of experimental setups and diagnostics for muon production by proton beam interaction with solid targets. High muon production by proton beam interaction with solid targets is scheduled for the new ELI-NP laser infrastructure enabling the systematic study[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19] of
$/$
PW laser facilities[Reference Danson, Hillier, Hopps and Neely30] allow the development of experimental setups and diagnostics for muon production by proton beam interaction with solid targets. High muon production by proton beam interaction with solid targets is scheduled for the new ELI-NP laser infrastructure enabling the systematic study[Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir19] of
![]() $\unicode[STIX]{x03BC}$
CF process and their potential application in compact magnetic fusion devices. Our numerical simulations confirm the importance of
$\unicode[STIX]{x03BC}$
CF process and their potential application in compact magnetic fusion devices. Our numerical simulations confirm the importance of
![]() $\unicode[STIX]{x03BC}$
CF and alpha heating effect for the potential operation of compact magnetic fusion devices in the intermediate plasma density range with low initial plasma temperature. The main advantage of the proposed device is that the fusion process initiated in very low plasma temperature by
$\unicode[STIX]{x03BC}$
CF and alpha heating effect for the potential operation of compact magnetic fusion devices in the intermediate plasma density range with low initial plasma temperature. The main advantage of the proposed device is that the fusion process initiated in very low plasma temperature by
![]() $\unicode[STIX]{x03BC}$
CF and the triggering of the fusion process of the device is due to the alpha heating effect. The initial plasma density of
$\unicode[STIX]{x03BC}$
CF and the triggering of the fusion process of the device is due to the alpha heating effect. The initial plasma density of
![]() $10^{16}~\text{cm}^{-3}$
of the second part of the proposed device is favorable for operation because the reaction rate reaches the max value in shorter time than this corresponding to initial plasma density of
$10^{16}~\text{cm}^{-3}$
of the second part of the proposed device is favorable for operation because the reaction rate reaches the max value in shorter time than this corresponding to initial plasma density of
![]() $10^{17}~\text{cm}^{-3}$
. From these results it is obvious that alpha heating effect is not important in the spark fusion part of the device due to high plasma density, low initial plasma temperature and short operation time of
$10^{17}~\text{cm}^{-3}$
. From these results it is obvious that alpha heating effect is not important in the spark fusion part of the device due to high plasma density, low initial plasma temperature and short operation time of
![]() $1~\unicode[STIX]{x03BC}\text{s}$
. The neutron production reach the value of the
$1~\unicode[STIX]{x03BC}\text{s}$
. The neutron production reach the value of the
![]() $5\times 10^{19}$
neutrons for an operation much less than 1 s. Pellet injection could be used for continuous operation of the proposed device. Simplified evaluations without taking into account the plasma losses in the proposed device allows estimating a power of about 100 MW by applying Tokamak blanket techniques for energy conversion. The alpha avalanche process[Reference Eliezer, Hora, Korn, Nissin and Martinez Val57] enhances the alpha heating effect in the case of p
$5\times 10^{19}$
neutrons for an operation much less than 1 s. Pellet injection could be used for continuous operation of the proposed device. Simplified evaluations without taking into account the plasma losses in the proposed device allows estimating a power of about 100 MW by applying Tokamak blanket techniques for energy conversion. The alpha avalanche process[Reference Eliezer, Hora, Korn, Nissin and Martinez Val57] enhances the alpha heating effect in the case of p
![]() $^{11}$
B fusion reaction with interest for future investigations on compact magnetic fusion devices working with the attractive aneutronic fusion fuel. These results promote the development of new high power laser systems and their coupling with compact magnetic fusion devices for clean energy production.
$^{11}$
B fusion reaction with interest for future investigations on compact magnetic fusion devices working with the attractive aneutronic fusion fuel. These results promote the development of new high power laser systems and their coupling with compact magnetic fusion devices for clean energy production.