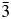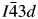I. INTRODUCTION
Synthetic anhydrous analogues of the silicate framework minerals leucite (KAlSi2O6) and pollucite (CsAlSi2O6) can be prepared with the general formulae A 2BSi5O12 and ACSi2O6; where A is a monovalent alkali metal cation, B is a divalent cation, and C is a trivalent cation. These structures all have the same topology with B and C cations partially substituting onto tetrahedrally coordinated sites (T-sites) in the silicate framework and charge balancing A cations sitting in extra-framework channels. The A cations can be replaced by ion exchange, Cs containing silicate framework minerals are of potential technological interest as storage media for radioactive Cs from nuclear waste (Gatta et al., Reference Gatta, Rotiroti, Fisch, Kadiyski and Armbruster2008).
We have used X-ray and neutron powder diffraction to determine and Rietveld refine the ambient temperature crystal structures of leucite analogues with the general formulae A 2BSi5O12 and ACSi2O6. Crystal structures have been refined in the Ia 
$\bar{3}$d cubic and I41/a tetragonal space groups (A = K, Rb, Cs; B = Mg, Mn, Co, Cu, Zn; C = Fe3+, Ga; Bell and Henderson, Reference Bell and Henderson1994a, Reference Bell and Henderson1994b, Reference Bell and Henderson2018, Reference Bell and Henderson2020; Bell et al., Reference Bell, Henderson, Redfern, Cernik, Champness, Fitch and Kohn1994a, Reference Bell, Knight, Henderson and Fitch2010). These structures all have disordered T-site cations and also have A cation sites fully occupied with either K, Rb, or Cs. Crystal structures have also been refined at ambient temperature for P21/c monoclinic crystal structures of leucite analogues with the general formulae A 2BSi5O12 (A = K, B = Mg, Fe2+, Co, Zn; Bell et al., Reference Bell, Henderson, Redfern, Cernik, Champness, Fitch and Kohn1994a; Bell and Henderson, Reference Bell and Henderson2018) and also for Pbca orthorhombic (A = Rb; B = Mg, Mn, Ni, Cd; Bell and Henderson, Reference Bell and Henderson1996, Reference Bell and Henderson2009, Reference Bell and Henderson2016) and (A = Cs; B = Mg, Mn, Co, Ni, Cu, Zn, Cd; Bell et al., Reference Bell, Redfern, Henderson and Kohn1994b, Reference Bell, Knight, Henderson and Fitch2010; Bell and Henderson, Reference Bell and Henderson1996, Reference Bell and Henderson2009). These structures all have ordered T-site cations and also have A cation sites fully occupied with either K, Rb, or Cs. Cs2ZnSi5O12 undergoes a reversible phase transition from Pbca to 
$Pa\bar{3}$ on heating to 566 K (Bell and Henderson, Reference Bell and Henderson2012). K2MgSi5O12 and K2ZnSi5O12 both undergo phase transitions from P21/c to Pbca on heating to 622 K (K2MgSi5O12; Redfern and Henderson, Reference Redfern and Henderson1996) and over the temperature range 843–868 K (K2ZnSi5O12; Bell et al., Reference Bell, Clegg and Henderson2021). KGaSi2O6 undergoes a phase transition from I41/a to Ia 
$\bar{3}$d over the temperature range 673–970 K (Bell and Henderson, Reference Bell and Henderson2020). Cs2X 2+Si5O12 (X = Cd, Cu, Zn) all retain the cation ordered Pbca orthorhombic structure below 10 K (Bell, Reference Bell2021).
RbCsX 2+Si5O12 (X = Mg, Ni, Cd) leucite analogues, with two different extra-framework alkali metal cations, all have the Pbca structure with ordered T-site cations (Bell and Henderson, Reference Bell and Henderson2019). For X = Ni and Cd, these structures have disordered extra-framework cations, but, for X = Mg, there is partial extra-framework cation ordering.
In this paper, we report the Rietveld refinements (Rietveld, Reference Rietveld1969) of three more T-site cation-disordered synthetic leucite analogues with stoichiometries of Cs2NiSi5O12, RbGaSi2O6, and CsGaSi2O6.
II. EXPERIMENTAL
A. Sample synthesis
All three samples were prepared from appropriate stoichiometric mixtures of Rb2CO3, Cs2CO3, SiO2, NiO, and Ga2O3. The starting mixture for Cs2NiSi5O12 was loaded into a platinum crucible and heated for 24 h at 873 K to decompose the carbonate. The mixture was then heated at 1673 K for 90 min before quenching by dipping the base of the crucible in water. The resultant glass was then reground and heated at 1393 K for 5 days; this produced a dark blue powdered sample. The starting mixtures for RbGaSi2O6 and CsGaSi2O6 were also loaded into platinum crucibles. Both mixtures were heated at 10 K min−1 from room temperature to 873 K; the temperature was then maintained at 873 K for 12 h, in order to decompose carbonates. The mixtures were then heated to 1473 K at 10 K min−1 and the temperature was then maintained at 1473 K for 10 h. Each crucible was removed from the furnace and quenched by dipping the base of the crucible in water. The resultant glasses were then reground and heated up at 1473 K for 7 days before cooling at 2 K min−1 to room temperature. This produced white powdered samples.
B. X-ray powder diffraction data collection
After heating the samples were removed from the metal capsules, ground with a mortar and pestle and then mounted on low-background silicon wafers with a drop of acetone prior to ambient temperature X-ray powder diffraction (XRD).
For Cs2NiSi5O12, data were collected on a PANalytical Empyrean diffractometer using CoKα X-rays with an iron β-filter and a 3.3473° 2θ wide 255 channel PIXCEL-3D area detector. Data were collected in a single scan over 66 h using Data Collector 5.1a (PANalytical, 2014). These data were collected over the range 12–140° 2θ with a step width of 0.0131° 2θ and an effective counting time of 5998 s per point, the beam size was defined with a 20 mm mask, fixed divergence antiscatter (¼°) slit and automatic divergence slit with a 15-mm long beam footprint. These diffracted intensities were converted from the automatic divergence slit mode to the fixed divergence slit mode in HighScore Plus (PANalytical, 2009) prior to data analysis.
For the RbGaSi2O6 and CsGaSi2O6 samples, data were collected on a PANalytical X'Pert Pro MPD using CuKα X-rays, with a nickel β-filter and a 3.3473° 2θ wide 255 channel PIXCEL-1D area detector. These data were collected over the range 8–100° 2θ with a step width of 0.0131° 2θ using Data Collector 5.5a (PANalytical, 2017). The beam size was defined with a 20 mm mask, fixed antiscatter (¼°) and divergence (⅛°) slits. For RbGaSi2O6, a single-scan was collected lasting 33 h and an effective counting time of 4175 s per point. For CsGaSi2O6, a single-scan was collected lasting 24 h and an effective counting time of 3035 s per point.
No smoothing or α 2 stripping was done on any of these data. Both diffractometers were calibrated with an external NIST 640e silicon standard.
C. XRD data analysis
All powder diffraction data were using HighScore Plus and the ICDD Powder Diffraction File. Analysis of the powder diffraction data for Cs2NiSi5O12 showed that this sample was single-phase cubic and the position of the Bragg reflections in the powder diffraction data matched the cubic pattern PDF# 00-037-0335 for Cs2NiSi5O12. However, analysis of the powder diffraction data for RbGaSi2O6 showed that this sample consisted of two phases. The main phase was I41/a tetragonal RbGaSi2O6 PDF# 00-037-0350 with C2/m monoclinic Ga2O3 PDF# 00-043-1012 as a minor phase. A similar analysis of CsGaSi2O6 also showed 
$I\bar{4}3d$ cubic pattern PDF# 00-050-0175 for CsGaSi2O6 as the main phase and C2/m monoclinic Ga2O3 PDF# 00-043-1012 as a minor phase.
Rietveld refinements were done using FULLPROF (Rodríguez-Carvajal, Reference Rodríguez-Carvajal1993). Backgrounds were fitted by linear interpolation between a set of background points with refinable heights. The Thompson-Cox-Hastings Pseudo-Voigt function (van Laar and Yelon, Reference van Laar and Yelon1984), convoluted with asymmetry due to axial divergence (Finger et al., Reference Finger, Cox and Jephcoat1994), was used to model the profile shape.
The crystal structure of Cs2NiSi5O12 was refined using the Ia 
$\bar{3}$d cubic structure of Cs2CuSi5O12 (Bell et al., Reference Bell, Knight, Henderson and Fitch2010) as the starting model. In this starting model, Ni replaced Cu on the disordered T-site. In this crystal structure, there is one Ia 
$\bar{3}$d 16b Wyckoff special position site which is 100% occupied by Cs, there is one 48 g special position site which is 1/6th occupied by Ni and 5/6th by Si (T-site occupancies were not refined) and there is a 96 h general position 100% occupied by O. A stoichiometry of Cs2NiSi5O12 was assumed. The isotropic temperature factors of the T-site atoms Si and Ni were constrained to be the same. It should be noted that one of the authors (AMTB) published a Pbca orthorhombic structure for Cs2NiSi5O12, with ordered T-site cations and a, b, and c being very close but slightly different (Bell and Henderson, Reference Bell and Henderson1996). However, the XRD data for this sample did not show the slight orthorhombic distortion that was seen in the synchrotron XRD data used for the earlier structure refinement.
The crystal structure of RbGaSi2O6 was refined using the I41/a structure of KGaSi2O6 (Bell and Henderson, Reference Bell and Henderson2020) as the starting model with Rb replacing K on the extra-framework cation site. In this crystal structure, all atoms were located on the I41/a 16f Wyckoff general position. There is one 16f position for Rb, three 16f positions for T-sites (disordered 1/3rd Ga and 2/3rd Si, T-site occupancies were not refined), and six 16f positions for O. The isotropic temperature factors of the T-site atoms Si and Ga were constrained to be the same on each T-site but were allowed to vary between different T-sites. All isotropic temperature factors for the six O sites were constrained to have the same value. As was done for KGaSi2O6 the T–O interatomic distances were soft constrained to be 1.68 ± 0.02 Å (the average bond distance for tetrahedral Si–O and Ga–O) assuming complete T-site disorder (1/3Ga:2/3Si on each T-site) as it was not possible to refine chemically sensible T-site occupancies. Rietveld refinements in noncubic leucite structures without soft interatomic distance constraints tend to give unrealistic interatomic T–O distances.
The crystal structure of CsGaSi2O6 was refined using the 
$I\bar{4}3d$ cubic structure of RbBSi2O6 (Filatov et al., Reference Filatov, Paufler, Georgievskaya, Levin, Meyer and Bubnova2011) as the starting model. This matched the space group assignment of the CsGaSi2O6 PDF# 00-050-0175. In this starting model, Ga replaced B on the disordered T-site, which is occupied by 1/3rd Ga and 2/3rd Si (T-site occupancies were not refined), and Cs replaced Rb on the extra-framework cation site. In this crystal structure, there is one 
$I\bar{4}3d$ 16c Wyckoff special position site which is 100% occupied by Cs. There are also three 
$I\bar{4}3d$ 48e Wyckoff general position sites, one of these is occupied by the disordered Ga/Si T-site and two are 100% occupied by O. The Rietveld refinements for RbGaSi2O6 and CsGaSi2O6 both used the crystal structure of Ga2O3 (da Silva et al., Reference da Silva, Sosman, Yokaichiya, Mazzocchi, Parente, Mestnik-Filho, Henry and Bordallo2012) to fit the minor phase. The RbGaSi2O6 sample contained 11.8(1) wt.% Ga2O3 and the CsGaSi2O6 sample contained 9.2(1) wt.% Ga2O3.
VESTA (Momma and Izumi, Reference Momma and Izumi2011) was used to plot crystal structures.
III. RESULTS AND DISCUSSION
Crystal structures have been refined for Cs2NiSi5O12, RbGaSi2O6, and CsGaSi2O6 leucite analogues from XRD data. All refined structures have disordered T-site cations. Cs2NiSi5O12 is isostructural with Ia 
$\bar{3}$d cubic Cs2CuSi5O12; RbGaSi2O6 is isostructural with I41/a tetragonal KGaSi2O6; and CsGaSi2O6 is isostructural with 
$I\bar{4}3d$ cubic RbBSi2O6. Table I shows the comparison of the refined lattice parameters for Cs2NiSi5O12, RbGaSi2O6, and CsGaSi2O6 with the Cs2CuSi5O12 (Bell et al., Reference Bell, Knight, Henderson and Fitch2010), KGaSi2O6 (Bell and Henderson, Reference Bell and Henderson2020), and RbBSi2O6 (Filatov et al., Reference Filatov, Paufler, Georgievskaya, Levin, Meyer and Bubnova2011) starting structures used for Rietveld refinement. Tables II–VII similarly show refined interatomic distances and angles; the mean T–O distances are close to the constraint distances, the mean O–T–O angles are close to the ideal tetrahedral angle of 109.47°. Table VIII similarly shows the tetrahedral angle variances for the T-sites (Robinson et al., Reference Robinson, Gibbs and Ribbe1971) in the silicate framework structures.
TABLE I. Refined lattice parameters compared with those for starting structures
TABLE II. Refined interatomic distances, Ia 
$\bar{3}$d cubic structures
TABLE III. Refined interatomic angles, Ia 
$\bar{3}$d cubic structures
TABLE IV. Refined interatomic distances (Å)
I41/a tetragonal structures. AGaSi2O6 (A = K, Rb). T = disordered Si/Ga.
TABLE V. Refined interatomic angles (°)
I41/a tetragonal structures. AGaSi2O6 (A = K, Rb). T = disordered Si/Ga.
TABLE VI. Refined interatomic distances (Å)
$I\bar{4}3d$ cubic structures. A = Cs/Rb, T = disordered Si/Ga and Si/B.
TABLE VII. Refined interatomic angles (°)
$I\bar{4}3d$ cubic structures. A = Cs/Rb, T = disordered Si/Ga and Si/B
A. Cs2NiSi5O12 structure
Figures 1 and 2 respectively show the Rietveld difference and the VESTA crystal structure plots for the refined crystal structure of Cs2NiSi5O12. Table I shows that this crystal structure has a unit cell volume that is slightly larger than the isostructural Cs2CuSi5O12 which was used as a starting model for Rietveld refinement. However, the ionic radius (Shannon, Reference Shannon1976) for Ni2+ (0.69 Å) is smaller than that for Cu2+ (0.71 Å), it would be expected that the smaller ionic radius for Ni2+ would result in a smaller unit cell compared with that for Cs2CuSi5O12. This discrepancy may be due to Cs2NiSi5O12 not having the assumed stoichiometry. Table II shows that one set of Cs–O distances is slightly larger for Cs2NiSi5O12 compared with Cs2CuSi5O12. However, the other set of Cs–O distances are equivalent between error limits. Table II also shows that both sets of T–O distances are equivalent between error limits for Cs2NiSi5O12 and Cs2CuSi5O12. Table III shows that two of the six O–T–O angles are different between error limits for Cs2NiSi5O12 and Cs2CuSi5O12, but the T–O–T angles are equivalent between error limits for Cs2NiSi5O12 and Cs2CuSi5O12. Table VIII shows that tetrahedral distortions for Cs2NiSi5O12 and Cs2CuSi5O12 are very close.
Figure 1. Rietveld difference plot for Cs2NiSi5O12. Red circles represent observed data points, the blue line represents calculated data points, the green line represents difference curve, and black crosses represent positions of Bragg reflections. R-factors for this refinement were: R p = 21.5314%, R wp = 11.5115%, R exp = 4.7035%, χ 2 = 6.2111.
Figure 2. VESTA Ia 
$\bar{3}$d cubic structure plot for Cs2Ni2+Si5O12, viewed down [111] showing a channel for extra-framework light blue Cs+ cations. Disordered (Si/Ni)O4 tetrahedra are shown in gray with O2− anions are shown in red.
B. RbGaSi2O6 structure
Figures 3 and 4 respectively show the Rietveld difference and the VESTA crystal structure plots for the refined crystal structure of RbGaSi2O6. Note that Figure 4 shows that this tetragonal crystal structure has a slightly collapsed silicate framework structure compared with the cubic structure in Figure 2. Table I shows that the crystal structure of RbGaSi2O6 has a larger unit cell volume than that of KGaSi2O6 which was used as a starting model for Rietveld refinement, this reflects the difference in the ionic radii for Rb+ (1.72 Å) and K+ (1.64 Å) cations (Shannon, Reference Shannon1976). However, the ambient temperature c/a ratio for RbGaSi2O6 is 1.032, which is smaller than the ambient temperature c/a ratio for KGaSi2O6, which is 1.053. When KGaSi2O6 is heated the c/a ratio decreases before a phase transition from I41/a to Ia 
$\bar{3}$d over the temperature range 673–970 K (Bell and Henderson, Reference Bell and Henderson2020). It would be interesting to do a high-temperature XRD experiment on RbGaSi2O6 as this smaller c/a ratio would suggest that this leucite analogue would undergo a phase transition from I41/a to Ia 
$\bar{3}$d at a lower temperature than KGaSi2O6. Table IV shows larger A–O distances for A = Rb compared with A = K, also reflecting the ionic radii difference. The mean T–O distances for RbGaSi2O6 and KGaSi2O6 are the same within error limits. Table IV shows that the mean O–T–O and T–O–T angles for RbGaSi2O6 and KGaSi2O6 are the same within error limits. Table VIII shows that mean tetrahedral distortion for KGaSi2O6 is larger than that for RbGaSi2O6, this reflects the greater collapse (Taylor and Henderson, Reference Taylor and Henderson1968) of the silicate framework structure with the smaller K+ cation compared with the larger Rb+ cation.
Figure 3. Rietveld difference plot for RbGaSi2O6. Red circles represent observed data points, the blue line represents calculated data points, and the green line represents difference curve. The upper line of black crosses represent positions of Bragg reflections for RbGaSi2O6 and the lower line of black crosses represent positions of Bragg reflections for Ga2O3 impurity. R-factors for this refinement were: R p = 10.1855%, R wp = 8.2308%, R exp = 2.7240%, χ 2 = 9.2667.
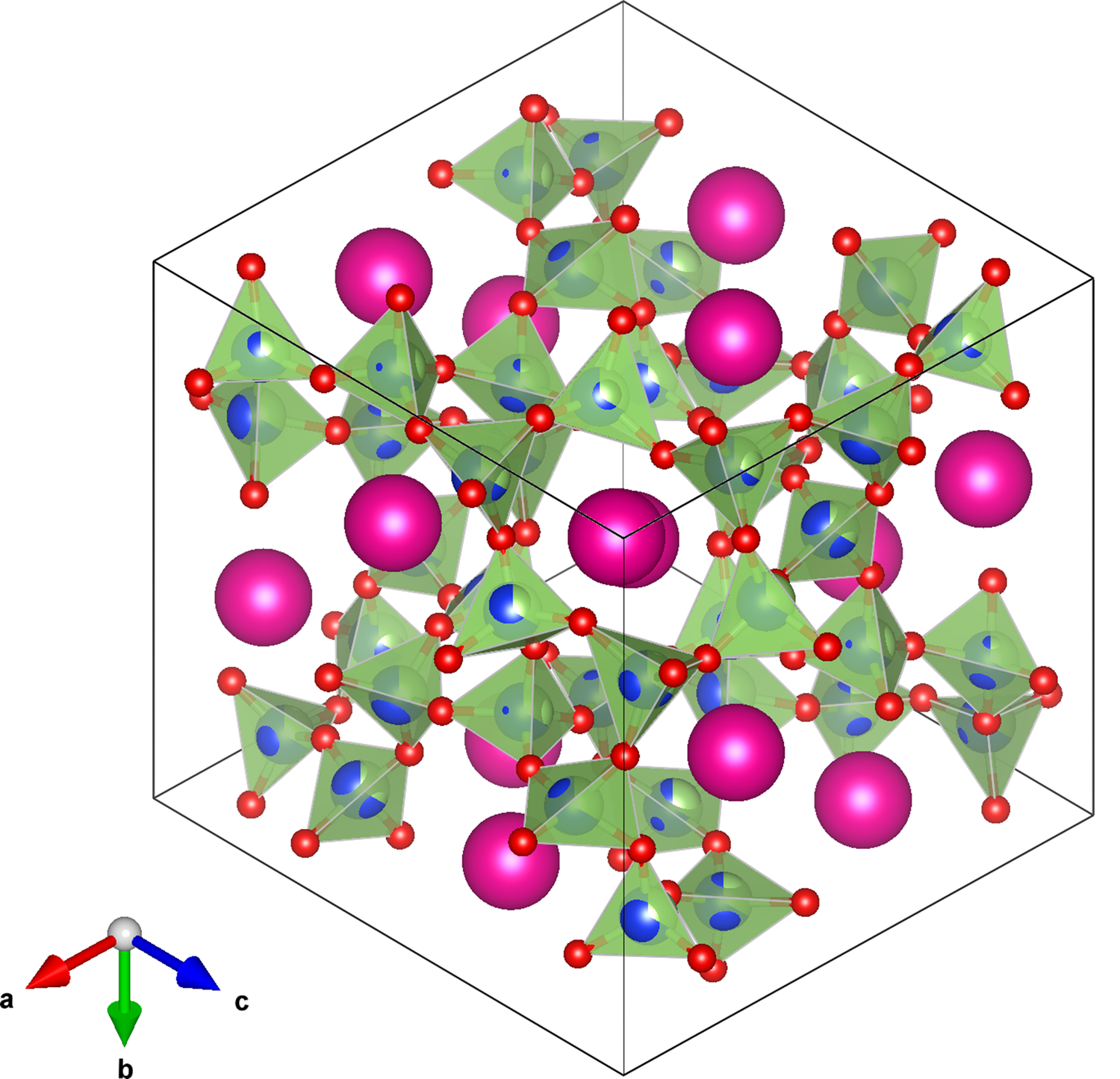
Figure 4. VESTA I41/a tetragonal structure plot for RbGaSi2O6, viewed down [1–11] showing a channel for extra-framework pink Rb+ cations. Disordered (Si/Ga)O4 tetrahedra are shown in light green with O2− anions are shown in red.
TABLE VIII. Tetrahedral angle variance [σ 2, deg2]: σ 2= Σ(θ–109.47)2/5 (Robinson et al., Reference Robinson, Gibbs and Ribbe1971), where θ is the O–T–O tetrahedral angle.
Mean variance and standard deviation is given for the three tetrahedral sites in each I41/a structure. Variance is given for the single tetrahedral site in each Ia 
$\bar{3}$d and 
$I\bar{4}3d$ structure.
C. CsGaSi2O6 structure
Figures 5 and 6 respectively show the Rietveld difference and the VESTA crystal structure plots for the refined crystal structure of CsGaSi2O6. Table I shows that the crystal structure of CsGaSi2O6 has a larger a unit-cell volume than that of RbBSi2O6 which was used as a starting model for Rietveld refinement, this reflects the differences in the ionic radii for Cs+ (2.02 Å), Ga3+ (0.61 Å), Rb+ (1.86 Å), and B3+ (0.25 Å) cations (Shannon, Reference Shannon1976). CsGaSi2O6 has the 
$I\bar{4}3d$ cubic crystal structure, unlike RbGaSi2O6, which has the I41/a tetragonal structure. These differences in cation size mean that the silicate framework for the RbGaSi2O6 is more collapsed (Taylor and Henderson, Reference Taylor and Henderson1968) than for CsGaSi2O6, and consequently, there is a lowering of symmetry for the crystal structure. Table VI shows that for CsGaSi2O6 the A–O and T–O distances are larger than those for the RbBSi2O6 due to the differences in ionic radii for the cations present in these crystal structures. Table VII shows that three of the six O–T–O angles are different between error limits for CsGaSi2O6 and RbBSi2O6. The mean T–O–T angles for CsGaSi2O6 are smaller than those for RbBSi2O6, reflecting the greater framework collapse of RbBSi2O6 compared with CsGaSi2O6. Table VIII shows that tetrahedral distortion for CsGaSi2O6 is larger than that for RbBSi2O6. This reflects the greater distortion of the silicate framework structure by incorporation of the larger Ga3+ cation into the framework compared with the smaller B3+ cation.
Figure 5. Rietveld difference plot for CsGaSi2O6. Red circles represent observed data points, the blue line represents calculated data points, and the green line represents difference curve. The upper line of black crosses represent positions of Bragg reflections for CsGaSi2O6 and the lower line of black crosses represent positions of Bragg reflections for Ga2O3 impurity. R-factors for this refinement were: R p = 9.9377%, R wp = 8.0887%, R exp = 2.5680%, χ 2 = 10.4871.
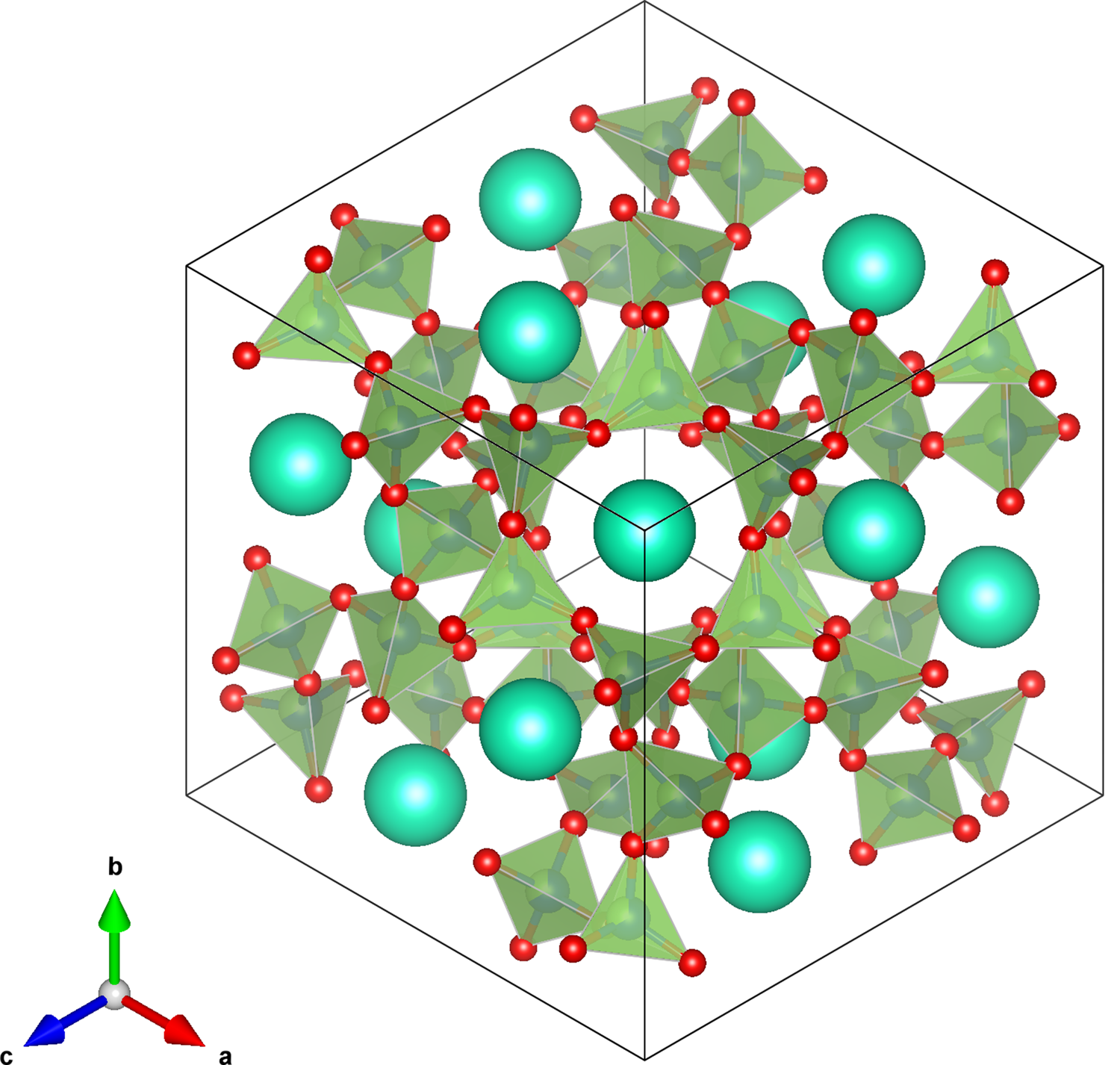
Figure 6. VESTA 
$I\bar{4}3d$ cubic structure plot for CsGaSi2O6, viewed down [111] showing a channel for extra-framework light blue Cs+ cations. Disordered (Si/Ga)O4 tetrahedra are shown in light green with O2− anions are shown in red.
The R-factors for this refinement of the CsGaSi2O6 crystal structure in 
$I\bar{4}3d$ were: R p = 9.9377%, R wp = 8.0887%, R exp = 2.5680%, χ 2 = 10.4871. However, it should be noted that a refinement of the CsGaSi2O6 crystal structure in Ia 
$\bar{3}$d, using the cubic structure of CsAlSi2O6 (Yanase et al., Reference Yanase, Kobayashi, Shibasaki and Mitamura1997) as a starting structure, gave the following R-factors: R p = 10.3604%, R wp = 8.4084%, R exp = 2.5708%, χ 2 = 11.5234. These R-factors are only slightly worse than those for 
$I\bar{4}3d$, suggesting that the crystal structures in these two different space groups show some similarities. Ia 
$\bar{3}$d is a supergroup of 
$I\bar{4}3d$, it would also be interesting to try a high-temperature XRD experiment on CsGaSi2O6 to see if there might be a phase transition from 
$I\bar{4}3d$ to Ia 
$\bar{3}$d.
IV. CONCLUSIONS
Crystal structures have been refined for Cs2NiSi5O12, RbGaSi2O6, and CsGaSi2O6 synthetic leucite analogues. All refined structures have disordered T-site cations. Cs2NiSi5O12 is isostructural with Ia 
$\bar{3}$d cubic Cs2CuSi5O12; RbGaSi2O6 is isostructural with I41/a tetragonal KGaSi2O6, and CsGaSi2O6 is isostructural with 
$I\bar{4}3d$ cubic RbBSi2O6.
V. DEPOSITED DATA
CIF files with information related to crystal structure, interatomic distances, and angles, and powder diffraction data for Cs2NiSi5O12, RbGaSi2O6, and CsGaSi2O6 synthetic leucite analogues were deposited with the ICDD. You may request these data from ICDD at [email protected].
ACKNOWLEDGEMENTS
We wish to acknowledge the use of the EPSRC funded National Chemical Database Service hosted by the Royal Society of Chemistry. We also wish to thank Ms Mirjam Skof of Sheffield Hallam University for her assistance with the use of a glove box.
Open access
