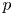1. Introduction
Let ![]() $F$ be a local non-Archimedean field. In 1980, Zelevinsky [Reference ZelevinskyZel80] defined an involution
$F$ be a local non-Archimedean field. In 1980, Zelevinsky [Reference ZelevinskyZel80] defined an involution ![]() $\tau \mapsto \hat \tau$ on the Grothendieck group of finite-length smooth representations of
$\tau \mapsto \hat \tau$ on the Grothendieck group of finite-length smooth representations of ![]() $\mathrm {GL}_n(F)$ and conjectured that this involution should preserve irreducibility. Assuming this conjecture, in 1986, Mœglin and Waldspurger [Reference Mœglin and WaldspurgerMW86] studied the involution and gave an algorithm for computing the Langlands (or Zelevinsky) data of
$\mathrm {GL}_n(F)$ and conjectured that this involution should preserve irreducibility. Assuming this conjecture, in 1986, Mœglin and Waldspurger [Reference Mœglin and WaldspurgerMW86] studied the involution and gave an algorithm for computing the Langlands (or Zelevinsky) data of ![]() $\hat \tau$ for every irreducible representation
$\hat \tau$ for every irreducible representation ![]() $\tau$ of
$\tau$ of ![]() $\mathrm {GL}_n(F)$. Later, another explicit formula was given by Knight and Zelevinsky [Reference Knight and ZelevinskyKZ96].
$\mathrm {GL}_n(F)$. Later, another explicit formula was given by Knight and Zelevinsky [Reference Knight and ZelevinskyKZ96].
Motivated by the Alvis–Curtis duality for finite groups [Reference AlvisAlv79, Reference AlvisAlv82, Reference CurtisCur80], Kato [Reference KatoKat93] defined an involution on the Grothendieck group of smooth finite-length Iwahori-fixed representations of a split reductive group over ![]() $F$. In 1996, Aubert showed that Kato's involution could be extended to the category of finite-length smooth representations of any reductive group
$F$. In 1996, Aubert showed that Kato's involution could be extended to the category of finite-length smooth representations of any reductive group ![]() $G$ and proved that it indeed preserves irreducibility. Furthermore, using different approaches, Schneider and Stuhler [Reference Schneider and StuhlerSS97], as well as Bernstein, Bezrukavnikov and Kazhdan [Reference BernsteinBer92, Reference Bernstein, Bezrukavnikov and KazhdanBBK18, Reference BezrukavnikovBez04], defined involutions on the category of smooth representations of
$G$ and proved that it indeed preserves irreducibility. Furthermore, using different approaches, Schneider and Stuhler [Reference Schneider and StuhlerSS97], as well as Bernstein, Bezrukavnikov and Kazhdan [Reference BernsteinBer92, Reference Bernstein, Bezrukavnikov and KazhdanBBK18, Reference BezrukavnikovBez04], defined involutions on the category of smooth representations of ![]() $G$. For irreducible representations of
$G$. For irreducible representations of ![]() $\mathrm {GL}_n(F)$, all these involutions coincide (up to the contragredient and up to a sign) with the involution defined by Zelevinsky.
$\mathrm {GL}_n(F)$, all these involutions coincide (up to the contragredient and up to a sign) with the involution defined by Zelevinsky.
For simplicity, when restricted to the set of irreducible smooth representations of a reductive group ![]() $G$, this involution is commonly known as the Zelevinsky–Aubert duality, and it is the main topic of this article. This duality has many interesting applications to Koszul duality (see [Reference Mirković and RicheMR15]) and to the Langlands program (see for example [Reference TadićTad18] or [Reference WaldspurgerWal18]). One important property of the Zelevinsky–Aubert duality is that it does not preserve the fact of being tempered. For this reason, in the proof of Arthur's local classification, the first step beyond tempered representations is to consider the Zelevinsky–Aubert dual of tempered representations [Reference ArthurArt13, § 7]. However, one expects that the duality will preserve unitarity, so it should be an important tool for determining the unitary dual of classical groups [Reference TadićTad22].
$G$, this involution is commonly known as the Zelevinsky–Aubert duality, and it is the main topic of this article. This duality has many interesting applications to Koszul duality (see [Reference Mirković and RicheMR15]) and to the Langlands program (see for example [Reference TadićTad18] or [Reference WaldspurgerWal18]). One important property of the Zelevinsky–Aubert duality is that it does not preserve the fact of being tempered. For this reason, in the proof of Arthur's local classification, the first step beyond tempered representations is to consider the Zelevinsky–Aubert dual of tempered representations [Reference ArthurArt13, § 7]. However, one expects that the duality will preserve unitarity, so it should be an important tool for determining the unitary dual of classical groups [Reference TadićTad22].
Our goal is to extend the result of Mœglin and Waldspurger to the Zelevinsky–Aubert duality, that is, we give an algorithm for computing the Langlands data of ![]() $\hat \pi$ in terms of those of
$\hat \pi$ in terms of those of ![]() $\pi$, for every irreducible representation
$\pi$, for every irreducible representation ![]() $\pi$ of
$\pi$ of ![]() $G$. As we will use the endoscopic classification of Arthur [Reference ArthurArt13] and Mœglin's construction of the local packets [Reference MœglinMœg11], we focus on the case where
$G$. As we will use the endoscopic classification of Arthur [Reference ArthurArt13] and Mœglin's construction of the local packets [Reference MœglinMœg11], we focus on the case where ![]() $F$ is a local non-Archimedean field of characteristic
$F$ is a local non-Archimedean field of characteristic ![]() $0$ and
$0$ and ![]() $G$ is either a symplectic or an odd special orthogonal group.
$G$ is either a symplectic or an odd special orthogonal group.
There have been several attempts to explicitly describe the Zelevinsky–Aubert duality. There are some partial results due to Mœglin [Reference MœglinMœg06], Matić [Reference MatićMat17, Reference MatićMat19], Jantzen [Reference JantzenJan18a] and the first author of the present paper [Reference AtobeAto22b]. In order to explain the novelties of the present article, let us introduce some notation.
Let ![]() $G$ be a connected algebraic reductive group defined over
$G$ be a connected algebraic reductive group defined over ![]() $F$. Fix a minimal parabolic subgroup
$F$. Fix a minimal parabolic subgroup ![]() $P_0$ of
$P_0$ of ![]() $G$. We denote by
$G$. We denote by ![]() $\mathrm {Ind}_P^G$ the normalized parabolic induction and by
$\mathrm {Ind}_P^G$ the normalized parabolic induction and by ![]() $\mathrm {Jac}_P^G$ its left adjoint functor, the Jacquet functor.
$\mathrm {Jac}_P^G$ its left adjoint functor, the Jacquet functor.
Let ![]() $\Pi$ be a smooth finite-length representation of
$\Pi$ be a smooth finite-length representation of ![]() $G$. We consider the virtual semisimple representation
$G$. We consider the virtual semisimple representation
where ![]() $P = MN$ runs over all standard parabolic subgroups of
$P = MN$ runs over all standard parabolic subgroups of ![]() $G$ and
$G$ and ![]() $A_M$ is the maximal split torus of the center of
$A_M$ is the maximal split torus of the center of ![]() $M$. Then Aubert [Reference AubertAub95] showed that if
$M$. Then Aubert [Reference AubertAub95] showed that if ![]() $\pi$ is irreducible, there exists a sign
$\pi$ is irreducible, there exists a sign ![]() $\epsilon \in \{\pm 1\}$ such that
$\epsilon \in \{\pm 1\}$ such that ![]() $\hat {\pi } = \epsilon \cdot D_{G}(\pi )$ is also an irreducible representation. We call the map
$\hat {\pi } = \epsilon \cdot D_{G}(\pi )$ is also an irreducible representation. We call the map ![]() $\pi \mapsto \hat \pi$ the Zelevinsky–Aubert duality.
$\pi \mapsto \hat \pi$ the Zelevinsky–Aubert duality.
This map has the following important properties.
(1) The dual of
 $\hat \pi$ is equal to
$\hat \pi$ is equal to  $\pi$, i.e. the map
$\pi$, i.e. the map  $\pi \mapsto \hat \pi$ is an involution.
$\pi \mapsto \hat \pi$ is an involution.(2) If
 $\pi$ is supercuspidal, then
$\pi$ is supercuspidal, then  $\hat \pi = \pi$.
$\hat \pi = \pi$.(3) The duality commutes with Jacquet functors (see (2.1)).
Let us now restrict ourselves to the case where ![]() $G=G_n$ is either the split special orthogonal group
$G=G_n$ is either the split special orthogonal group ![]() $\mathrm {SO}_{2n+1}(F)$ or the symplectic group
$\mathrm {SO}_{2n+1}(F)$ or the symplectic group ![]() $\mathrm {Sp}_{2n}(F)$ of rank
$\mathrm {Sp}_{2n}(F)$ of rank ![]() $n$. In this case, when
$n$. In this case, when ![]() $\pi$ (respectively
$\pi$ (respectively ![]() $\tau _i$) is a smooth representation of
$\tau _i$) is a smooth representation of ![]() $G_{n_0}$ (respectively
$G_{n_0}$ (respectively ![]() $\mathrm {GL}_{d_i}(F)$), with
$\mathrm {GL}_{d_i}(F)$), with ![]() $d_1+\cdots +d_r+n_0=n$, we denote by
$d_1+\cdots +d_r+n_0=n$, we denote by
the normalized parabolically induced representation of ![]() $\tau _1 \boxtimes \cdots \boxtimes \tau _r \boxtimes \pi$ from the standard parabolic subgroup
$\tau _1 \boxtimes \cdots \boxtimes \tau _r \boxtimes \pi$ from the standard parabolic subgroup ![]() $P$ of
$P$ of ![]() $G_n$ with Levi subgroup isomorphic to
$G_n$ with Levi subgroup isomorphic to ![]() $\mathrm {GL}_{d_1}(F) \times \cdots \times \mathrm {GL}_{d_r}(F) \times G_{n_0}$.
$\mathrm {GL}_{d_1}(F) \times \cdots \times \mathrm {GL}_{d_r}(F) \times G_{n_0}$.
Given an irreducible representation ![]() $\pi$ of
$\pi$ of ![]() $G_n$ and a supercuspidal non-self-dual representation
$G_n$ and a supercuspidal non-self-dual representation ![]() $\rho$ of
$\rho$ of ![]() $\mathrm {GL}_d(F)$, there exists a unique
$\mathrm {GL}_d(F)$, there exists a unique ![]() $k\geq 0$ and a unique irreducible representation
$k\geq 0$ and a unique irreducible representation ![]() $\pi _0$ of
$\pi _0$ of ![]() $G_{n_0}$, with
$G_{n_0}$, with ![]() $n=dk+n_0$, such that
$n=dk+n_0$, such that
•
 $\pi$ is a unique irreducible subrepresentation of
(1.1)
$\pi$ is a unique irreducible subrepresentation of
(1.1) \begin{equation} \underbrace{\rho \times\cdots\times \rho}_{k \text{ times}}\rtimes \pi_0; \end{equation}
\begin{equation} \underbrace{\rho \times\cdots\times \rho}_{k \text{ times}}\rtimes \pi_0; \end{equation}•
 $k$ is maximal, in the sense that for every irreducible representation
$k$ is maximal, in the sense that for every irreducible representation  $\pi '_0$ of
$\pi '_0$ of  $G_{n_0-d}$,
$G_{n_0-d}$,  $\pi _0$ is not a subrepresentation of
$\pi _0$ is not a subrepresentation of  $\rho \rtimes \pi '_0$.
$\rho \rtimes \pi '_0$.
We call ![]() $\pi _0$ the highest
$\pi _0$ the highest ![]() $\rho$-derivative of
$\rho$-derivative of ![]() $\pi$ and denote it by
$\pi$ and denote it by ![]() $D_\rho ^{\max }(\pi )$. An important consequence of the commutativity of the Zelevinsky–Aubert duality with Jacquet functors is that
$D_\rho ^{\max }(\pi )$. An important consequence of the commutativity of the Zelevinsky–Aubert duality with Jacquet functors is that
where ![]() $\rho ^\vee$ denotes the contragredient of
$\rho ^\vee$ denotes the contragredient of ![]() $\rho$.
$\rho$.
We can now describe the main idea of the algorithm for explicating the Zelevinsky–Aubert dual of an irreducible representation ![]() $\pi$ of
$\pi$ of ![]() $G_n$. It is a two-step procedure as follows.
$G_n$. It is a two-step procedure as follows.
Step 1. If there exists a supercuspidal non-self-dual representation ![]() $\rho$ of
$\rho$ of ![]() $\mathrm {GL}_d(F)$ such that
$\mathrm {GL}_d(F)$ such that ![]() $D_\rho ^{\max }(\pi ) \neq \pi$, then we give an explicit formula for the Langlands data of
$D_\rho ^{\max }(\pi ) \neq \pi$, then we give an explicit formula for the Langlands data of ![]() $D_\rho ^{\max }(\pi )$ in terms of those of
$D_\rho ^{\max }(\pi )$ in terms of those of ![]() $\pi$. By induction we can compute the Langlands data of
$\pi$. By induction we can compute the Langlands data of ![]() $D_{\rho }^{\max }(\pi ){\widehat {\;}}$. We finally give an explicit formula for the Langlands data of
$D_{\rho }^{\max }(\pi ){\widehat {\;}}$. We finally give an explicit formula for the Langlands data of ![]() $\hat \pi$ in terms of those of
$\hat \pi$ in terms of those of ![]() $D_{\rho }^{\max }(\pi ){\widehat {\;}} = D_{\rho ^\vee }^{\max }(\hat \pi )$.
$D_{\rho }^{\max }(\pi ){\widehat {\;}} = D_{\rho ^\vee }^{\max }(\hat \pi )$.
Step 2. Assume finally that for all supercuspidal representations ![]() $\rho$ of
$\rho$ of ![]() $\mathrm {GL}_d(F)$ such that
$\mathrm {GL}_d(F)$ such that ![]() $\pi$ is a subrepresentation of
$\pi$ is a subrepresentation of ![]() $\rho \times \pi _0$ for some irreducible representation
$\rho \times \pi _0$ for some irreducible representation ![]() $\pi _0$ of
$\pi _0$ of ![]() $G_{n-d}$, we have that
$G_{n-d}$, we have that ![]() $\rho$ is self-dual. Then the following hold.
$\rho$ is self-dual. Then the following hold.
• If
 $\pi$ is tempered, then
$\pi$ is tempered, then  $\pi$ is ‘almost supercuspidal’, and we can compute its Zelevinsky–Aubert dual explicitly (see § 5.3, in particular Proposition 5.4).
$\pi$ is ‘almost supercuspidal’, and we can compute its Zelevinsky–Aubert dual explicitly (see § 5.3, in particular Proposition 5.4).• If
 $\pi$ is not tempered, then we show that there exists a supercuspidal self-dual representation
$\pi$ is not tempered, then we show that there exists a supercuspidal self-dual representation  $\rho$ of
$\rho$ of  $\mathrm {GL}_d(F)$ such that
$\mathrm {GL}_d(F)$ such that  $\pi$ is a unique irreducible subrepresentation of
for some irreducible representation
$\pi$ is a unique irreducible subrepresentation of
for some irreducible representation \[ \underbrace{\Delta_\rho[0,-1] \times\cdots\times \Delta_\rho[0,-1]}_{k \text{ times}}\rtimes \pi_0 \]
\[ \underbrace{\Delta_\rho[0,-1] \times\cdots\times \Delta_\rho[0,-1]}_{k \text{ times}}\rtimes \pi_0 \]
 $\pi _0$ of
$\pi _0$ of  $G_{n_0}$, with
$G_{n_0}$, with  $n=2dk+n_0$, and some positive integer
$n=2dk+n_0$, and some positive integer  $k$ maximal as above, where
$k$ maximal as above, where  $\Delta _\rho [0,-1]$ is a Steinberg representation (see § 2.3 for a precise definition). We call
$\Delta _\rho [0,-1]$ is a Steinberg representation (see § 2.3 for a precise definition). We call  $\pi _0$ the highest
$\pi _0$ the highest  $\Delta _\rho [0,-1]$-derivative and denote it by
$\Delta _\rho [0,-1]$-derivative and denote it by  $D_{\Delta _\rho [0,-1]}^{\max }(\pi )$. Similar to (1.2), this derivative satisfies a formula
where
$D_{\Delta _\rho [0,-1]}^{\max }(\pi )$. Similar to (1.2), this derivative satisfies a formula
where \[ D_{\Delta_\rho[0,-1]}^{\max}(\pi){\widehat{\;}} = D_{Z_\rho[0,1]}^{\max}(\hat\pi), \]
\[ D_{\Delta_\rho[0,-1]}^{\max}(\pi){\widehat{\;}} = D_{Z_\rho[0,1]}^{\max}(\hat\pi), \]
 $D_{Z_\rho [0,1]}^{\max }(\hat \pi )$ is the highest
$D_{Z_\rho [0,1]}^{\max }(\hat \pi )$ is the highest  $Z_\rho [0,1]$-derivative of
$Z_\rho [0,1]$-derivative of  $\hat \pi$ (see § 3.4). As in Step 1, this allows us to compute by induction the Zelevinsky–Aubert dual of
$\hat \pi$ (see § 3.4). As in Step 1, this allows us to compute by induction the Zelevinsky–Aubert dual of  $\pi$. The precise algorithm is explained in § 4.
$\pi$. The precise algorithm is explained in § 4.
Let us first remark on the self-duality condition on ![]() $\rho$. When
$\rho$. When ![]() $\rho$ is self-dual, a representation of the form (1.1) may have several irreducible subrepresentations and there is no simple way of distinguishing them. The same problem was already observed by Jantzen [Reference JantzenJan18a]. For these reasons he just considered what is called the half-integral case.
$\rho$ is self-dual, a representation of the form (1.1) may have several irreducible subrepresentations and there is no simple way of distinguishing them. The same problem was already observed by Jantzen [Reference JantzenJan18a]. For these reasons he just considered what is called the half-integral case.
This also explains one of the differences between the case of ![]() $\mathrm {GL}_n(F)$ and the case of classical groups that we treat in this article. In the former case, induced representations of the form
$\mathrm {GL}_n(F)$ and the case of classical groups that we treat in this article. In the former case, induced representations of the form ![]() $\rho \times \pi _0$, with
$\rho \times \pi _0$, with ![]() $\rho$ supercuspidal, always have a unique irreducible subrepresentation. The second difference is that for
$\rho$ supercuspidal, always have a unique irreducible subrepresentation. The second difference is that for ![]() $\mathrm {GL}_n(F)$ it is much easier to explicate the Langlands data of this subrepresentation in terms of those of
$\mathrm {GL}_n(F)$ it is much easier to explicate the Langlands data of this subrepresentation in terms of those of ![]() $\pi$. However, the most intricate part of this article is to explicitly describe, in terms of Langlands data, the correspondence
$\pi$. However, the most intricate part of this article is to explicitly describe, in terms of Langlands data, the correspondence ![]() $\pi \leftrightarrow D_{\tau }^{\max }(\pi )$ for
$\pi \leftrightarrow D_{\tau }^{\max }(\pi )$ for ![]() $\tau$ either supercuspidal non-self-dual or of the form
$\tau$ either supercuspidal non-self-dual or of the form ![]() $Z_\rho [0,1]$; see Theorems 7.1, 7.4 and 8.1. To explicate these formulas, we use matching functions as in [Reference Lapid and MínguezLM16] and
$Z_\rho [0,1]$; see Theorems 7.1, 7.4 and 8.1. To explicate these formulas, we use matching functions as in [Reference Lapid and MínguezLM16] and ![]() $A$-parameters. These results are interesting in their own right. In particular, we get a combinatorial criterion for the irreducibility of parabolically induced representations of the form
$A$-parameters. These results are interesting in their own right. In particular, we get a combinatorial criterion for the irreducibility of parabolically induced representations of the form ![]() $\rho \rtimes \pi _0$ with
$\rho \rtimes \pi _0$ with ![]() $\rho$ non-self-dual supercuspidal and
$\rho$ non-self-dual supercuspidal and ![]() $\pi _0$ irreducible; see Corollary 7.2. Moreover, the explicit formulas established in this paper are used in [Reference AtobeAto22a] to make Mœglin's construction of local
$\pi _0$ irreducible; see Corollary 7.2. Moreover, the explicit formulas established in this paper are used in [Reference AtobeAto22a] to make Mœglin's construction of local ![]() $A$-packets more computable.
$A$-packets more computable.
The paper is organized as follows. In § 2, we recall some general results on representation theory of ![]() $p$-adic classical groups. In § 3, we define
$p$-adic classical groups. In § 3, we define ![]() $\rho$-derivatives and other derivatives, and we prove some general results about them, in particular their compatibility with the Zelevinsky–Aubert duality. In § 4 we give our algorithm for computing the Zelevinsky–Aubert dual using derivatives and socles. We will prove explicit formulas for these derivatives and socles in several situations in §§ 6–8. To do this, we review Arthur's theory of endoscopic classification in § 5 and the theory of matching functions at the beginning of § 6.
$\rho$-derivatives and other derivatives, and we prove some general results about them, in particular their compatibility with the Zelevinsky–Aubert duality. In § 4 we give our algorithm for computing the Zelevinsky–Aubert dual using derivatives and socles. We will prove explicit formulas for these derivatives and socles in several situations in §§ 6–8. To do this, we review Arthur's theory of endoscopic classification in § 5 and the theory of matching functions at the beginning of § 6.
2. Notation and preliminaries
In this section we introduce some notation, in particular the functors of induction and restriction, Tadić's formula and Jantzen's decomposition.
2.1 Notation
Throughout this article, we fix a non-Archimedean locally compact field ![]() $F$ of characteristic zero with normalized absolute value
$F$ of characteristic zero with normalized absolute value ![]() $|\cdot |$. Let
$|\cdot |$. Let ![]() $G$ be the group of
$G$ be the group of ![]() $F$-points of a connected reductive group defined over
$F$-points of a connected reductive group defined over ![]() $F$, with the usual topology. We will only consider smooth representations of
$F$, with the usual topology. We will only consider smooth representations of ![]() $G$, that is, representations such that the stabilizer of every vector is an open subgroup of
$G$, that is, representations such that the stabilizer of every vector is an open subgroup of ![]() $G$, and we write
$G$, and we write ![]() $\mathrm {Rep}(G)$ for the category of smooth complex representations of
$\mathrm {Rep}(G)$ for the category of smooth complex representations of ![]() $G$ of finite length. Denote by
$G$ of finite length. Denote by ![]() $\mathrm {Irr}(G)$ the set of equivalence classes of irreducible objects of
$\mathrm {Irr}(G)$ the set of equivalence classes of irreducible objects of ![]() $\mathrm {Rep}(G)$. Let
$\mathrm {Rep}(G)$. Let ![]() $\mathscr {R}(G)$ be the Grothendieck group of
$\mathscr {R}(G)$ be the Grothendieck group of ![]() $\mathrm {Rep}(G)$. The canonical map from the objects of
$\mathrm {Rep}(G)$. The canonical map from the objects of ![]() $\mathrm {Rep}(G)$ to
$\mathrm {Rep}(G)$ to ![]() $\mathscr {R} (G)$ will be denoted by
$\mathscr {R} (G)$ will be denoted by ![]() $\pi \mapsto [\pi ]$.
$\pi \mapsto [\pi ]$.
For ![]() $\pi, \pi ' \in \mathrm {Rep}(G)$ we write
$\pi, \pi ' \in \mathrm {Rep}(G)$ we write ![]() $\pi \hookrightarrow \pi '$ (respectively
$\pi \hookrightarrow \pi '$ (respectively ![]() $\pi \twoheadrightarrow \pi '$) if there exists an injective (respectively surjective) morphism from
$\pi \twoheadrightarrow \pi '$) if there exists an injective (respectively surjective) morphism from ![]() $\pi$ to
$\pi$ to ![]() $\pi '$.
$\pi '$.
Fix a minimal ![]() $F$-parabolic subgroup
$F$-parabolic subgroup ![]() $P_0$ of
$P_0$ of ![]() $G$. A parabolic subgroup
$G$. A parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ is said to be standard if it contains
$G$ is said to be standard if it contains ![]() $P_0$. Henceforth, the letter
$P_0$. Henceforth, the letter ![]() $P$ will always denote a standard parabolic subgroup of
$P$ will always denote a standard parabolic subgroup of ![]() $G$ with an implicit standard Levi decomposition
$G$ with an implicit standard Levi decomposition ![]() $P=MU$. Let
$P=MU$. Let ![]() $\Sigma$ denote the set of roots of
$\Sigma$ denote the set of roots of ![]() $G$ with respect to
$G$ with respect to ![]() $P_0$, and let
$P_0$, and let ![]() $\Delta$ be a basis of
$\Delta$ be a basis of ![]() $\Sigma$. For
$\Sigma$. For ![]() $\Theta \subset \Delta$ let
$\Theta \subset \Delta$ let ![]() $P_\Theta$ denote the standard parabolic subgroup of
$P_\Theta$ denote the standard parabolic subgroup of ![]() $G$ corresponding to
$G$ corresponding to ![]() $\Theta$ and let
$\Theta$ and let ![]() $M_\Theta$ be a corresponding standard Levi subgroup. Let
$M_\Theta$ be a corresponding standard Levi subgroup. Let ![]() $W$ be the Weyl group of
$W$ be the Weyl group of ![]() $G$.
$G$.
Let ![]() $\tau$ be a representation of
$\tau$ be a representation of ![]() $M$, regarded as a representation of
$M$, regarded as a representation of ![]() $P$ on which
$P$ on which ![]() $U$ acts trivially. We denote by
$U$ acts trivially. We denote by ![]() $\mathrm {Ind}_P^G\tau$ the representation of
$\mathrm {Ind}_P^G\tau$ the representation of ![]() $G$ parabolically induced from
$G$ parabolically induced from ![]() $\tau$. (We will always mean the normalized induction.) We view
$\tau$. (We will always mean the normalized induction.) We view ![]() $\mathrm {Ind}_P^G$ as a functor. Its left adjoint, the Jacquet functor with respect to
$\mathrm {Ind}_P^G$ as a functor. Its left adjoint, the Jacquet functor with respect to ![]() $P$, will be denoted by
$P$, will be denoted by ![]() $\mathrm {Jac}_P^G$.
$\mathrm {Jac}_P^G$.
An irreducible representation ![]() $\pi$ of
$\pi$ of ![]() $G$ is said to be supercuspidal if it is not a composition factor of any representation of the form
$G$ is said to be supercuspidal if it is not a composition factor of any representation of the form ![]() $\mathrm {Ind}^{G}_P(\tau )$ with
$\mathrm {Ind}^{G}_P(\tau )$ with ![]() $P$ a proper parabolic subgroup of
$P$ a proper parabolic subgroup of ![]() $G$ and
$G$ and ![]() $\tau$ a representation of
$\tau$ a representation of ![]() $M$. We write
$M$. We write ![]() $\mathscr {C}(G)$ for the subset of
$\mathscr {C}(G)$ for the subset of ![]() $\mathrm {Irr}(G)$ consisting of supercuspidal representations. For any
$\mathrm {Irr}(G)$ consisting of supercuspidal representations. For any ![]() $\pi \in \mathrm {Rep}(G)$, we denote by
$\pi \in \mathrm {Rep}(G)$, we denote by ![]() $\pi ^\vee$ the contragredient of
$\pi ^\vee$ the contragredient of ![]() $\pi$. (The sets
$\pi$. (The sets ![]() $\mathrm {Irr}(G)$ and
$\mathrm {Irr}(G)$ and ![]() $\mathscr {C}(G)$ are invariant under
$\mathscr {C}(G)$ are invariant under ![]() $^\vee$.)
$^\vee$.)
Let ![]() $\Pi$ be a smooth representation of
$\Pi$ be a smooth representation of ![]() $G$ of finite length. The socle of
$G$ of finite length. The socle of ![]() $\Pi$ is the largest semisimple subrepresentation of
$\Pi$ is the largest semisimple subrepresentation of ![]() $\Pi$. It is denoted by
$\Pi$. It is denoted by ![]() $\mathrm {soc}(\Pi )$. We say that
$\mathrm {soc}(\Pi )$. We say that ![]() $\Pi$ is socle irreducible (SI) if
$\Pi$ is socle irreducible (SI) if ![]() $\mathrm {soc}(\Pi )$ is irreducible and occurs with multiplicity one in
$\mathrm {soc}(\Pi )$ is irreducible and occurs with multiplicity one in ![]() $[\Pi ]$.
$[\Pi ]$.
2.2 The Zelevinsky–Aubert duality
We consider the map
 \begin{align*} D_{G} \colon \mathscr{R}(G) & \longrightarrow \mathscr{R}(G)\\ \pi &\longmapsto \sum_{P}(-1)^{\dim A_M} \big[\mathrm{Ind}_P^{G}(\mathrm{Jac}_{P}^G(\pi))\big], \end{align*}
\begin{align*} D_{G} \colon \mathscr{R}(G) & \longrightarrow \mathscr{R}(G)\\ \pi &\longmapsto \sum_{P}(-1)^{\dim A_M} \big[\mathrm{Ind}_P^{G}(\mathrm{Jac}_{P}^G(\pi))\big], \end{align*}
where ![]() $P = MN$ runs over all standard parabolic subgroups of
$P = MN$ runs over all standard parabolic subgroups of ![]() $G$. Aubert [Reference AubertAub95] showed that if
$G$. Aubert [Reference AubertAub95] showed that if ![]() $\pi$ is irreducible, then there exists a sign
$\pi$ is irreducible, then there exists a sign ![]() $\epsilon \in \{\pm 1\}$ such that
$\epsilon \in \{\pm 1\}$ such that ![]() $\hat {\pi } = \epsilon \cdot D_{G}(\pi )$ is also an irreducible representation. We call the map
$\hat {\pi } = \epsilon \cdot D_{G}(\pi )$ is also an irreducible representation. We call the map
the Zelevinsky–Aubert duality.
It has the following important properties.
(1) For any
 $\pi \in \mathrm {Irr}(G)$, the dual of
$\pi \in \mathrm {Irr}(G)$, the dual of  $\hat \pi$ is equal to
$\hat \pi$ is equal to  $\pi$, that is, the map
$\pi$, that is, the map  $\pi \mapsto \hat \pi$ is an involution [Reference AubertAub95, Théorème 1.7(3)].
$\pi \mapsto \hat \pi$ is an involution [Reference AubertAub95, Théorème 1.7(3)].(2) If
 $\pi \in \mathscr {C}(G)$, then
$\pi \in \mathscr {C}(G)$, then  $\hat \pi = \pi$ [Reference AubertAub95, Théorème 1.7(4)].
$\hat \pi = \pi$ [Reference AubertAub95, Théorème 1.7(4)].(3) Let
 $\Theta \subset \Delta$ and consider the standard parabolic subgroup
$\Theta \subset \Delta$ and consider the standard parabolic subgroup  $P=P_\Theta$ with Levi decomposition
$P=P_\Theta$ with Levi decomposition  $P=MN$. Let
$P=MN$. Let  $w_0$ be the longest element in the set
$w_0$ be the longest element in the set  $\{w\in W\mid w^{-1}(\Theta )>0\}$ and let
$\{w\in W\mid w^{-1}(\Theta )>0\}$ and let  $P'$ be the standard parabolic subgroup with Levi subgroup
$P'$ be the standard parabolic subgroup with Levi subgroup  $M'=w^{-1}(M)$. Then we have (cf. [Reference AubertAub95, Théorème 1.7(2)])
(2.1)
$M'=w^{-1}(M)$. Then we have (cf. [Reference AubertAub95, Théorème 1.7(2)])
(2.1) \begin{equation} \mathrm{Jac}_P^G \circ D_G= {\rm Ad}(w_0)\circ D_{M'} \circ \mathrm{Jac}_{P'}^G. \end{equation}
\begin{equation} \mathrm{Jac}_P^G \circ D_G= {\rm Ad}(w_0)\circ D_{M'} \circ \mathrm{Jac}_{P'}^G. \end{equation}
2.3 Representations of general linear groups
Set ![]() $\mathrm {Irr}^\mathrm {GL} := \bigcup _{n\ge 0}\mathrm {Irr} (\mathrm {GL}_n(F))$, and let
$\mathrm {Irr}^\mathrm {GL} := \bigcup _{n\ge 0}\mathrm {Irr} (\mathrm {GL}_n(F))$, and let ![]() $\mathscr {C}^\mathrm {GL} \subset \mathrm {Irr}^\mathrm {GL}$ be the subset of supercuspidal representations of
$\mathscr {C}^\mathrm {GL} \subset \mathrm {Irr}^\mathrm {GL}$ be the subset of supercuspidal representations of ![]() $\mathrm {GL}_n(F)$ for every
$\mathrm {GL}_n(F)$ for every ![]() $n>0$. We write
$n>0$. We write ![]() $\mathscr {R}^\mathrm {GL} := \bigoplus _{n \geq 0} \mathscr {R}(\mathrm {GL}_n(F))$.
$\mathscr {R}^\mathrm {GL} := \bigoplus _{n \geq 0} \mathscr {R}(\mathrm {GL}_n(F))$.
Let ![]() $d_1, \ldots, d_r$ be some positive integers. Let
$d_1, \ldots, d_r$ be some positive integers. Let ![]() $\tau _i \in \mathrm {Rep}(\mathrm {GL}_{d_i}(F))$ for
$\tau _i \in \mathrm {Rep}(\mathrm {GL}_{d_i}(F))$ for ![]() $1 \leq i \leq r$. It is customary to denote the normalized parabolically induced representation by
$1 \leq i \leq r$. It is customary to denote the normalized parabolically induced representation by
This product induces a ![]() $\mathbb {Z}$-graded ring structure on
$\mathbb {Z}$-graded ring structure on ![]() $\mathscr {R}^\mathrm {GL}$. We denote the multiplication by
$\mathscr {R}^\mathrm {GL}$. We denote the multiplication by ![]() $m$. If
$m$. If ![]() $\tau _1 = \cdots = \tau _r = \tau$, we will write
$\tau _1 = \cdots = \tau _r = \tau$, we will write ![]() $\tau ^r = \tau \times \cdots \times \tau$ (
$\tau ^r = \tau \times \cdots \times \tau$ (![]() $r$ times).
$r$ times).
The Jacquet functor for ![]() $\mathrm {GL}_{m}(F)$ along the maximal parabolic subgroup
$\mathrm {GL}_{m}(F)$ along the maximal parabolic subgroup ![]() $P_{(d,m-d)}$ with Levi subgroup isomorphic to
$P_{(d,m-d)}$ with Levi subgroup isomorphic to ![]() $\mathrm {GL}_{d}(F) \times \mathrm {GL}_{m-d}(F)$ is denoted by
$\mathrm {GL}_{d}(F) \times \mathrm {GL}_{m-d}(F)$ is denoted by ![]() $\mathrm {Jac}_{(d,m-d)} = \mathrm {Jac}_{P_{(d,m-d)}}^{\mathrm {GL}_m(F)}$. It induces a co-multiplication, that is, a ring homomorphism
$\mathrm {Jac}_{(d,m-d)} = \mathrm {Jac}_{P_{(d,m-d)}}^{\mathrm {GL}_m(F)}$. It induces a co-multiplication, that is, a ring homomorphism
 \begin{align*} m^\ast \colon \mathscr{R}^\mathrm{GL} &\longrightarrow \mathscr{R}^\mathrm{GL}\otimes \mathscr{R}^\mathrm{GL} \nonumber\\ \tau & \longmapsto \sum_{n \geq 0} \biggl(\sum_{n_1+n_2=n}\bigl[\mathrm{Jac}_{(n_1,n_2)}(\tau)\bigr]\biggr). \end{align*}
\begin{align*} m^\ast \colon \mathscr{R}^\mathrm{GL} &\longrightarrow \mathscr{R}^\mathrm{GL}\otimes \mathscr{R}^\mathrm{GL} \nonumber\\ \tau & \longmapsto \sum_{n \geq 0} \biggl(\sum_{n_1+n_2=n}\bigl[\mathrm{Jac}_{(n_1,n_2)}(\tau)\bigr]\biggr). \end{align*}
We finally take
to be the composition ![]() $M^\ast = (m\otimes 1) \circ (\cdot ^\vee \otimes m^\ast ) \circ s \circ m^\ast$, where
$M^\ast = (m\otimes 1) \circ (\cdot ^\vee \otimes m^\ast ) \circ s \circ m^\ast$, where ![]() $s \colon \mathscr {R}^\mathrm {GL}\otimes \mathscr {R}^\mathrm {GL} \to \mathscr {R}^\mathrm {GL}\otimes \mathscr {R}^\mathrm {GL}$ denotes the transposition
$s \colon \mathscr {R}^\mathrm {GL}\otimes \mathscr {R}^\mathrm {GL} \to \mathscr {R}^\mathrm {GL}\otimes \mathscr {R}^\mathrm {GL}$ denotes the transposition ![]() $s(\sum _i \tau _i\otimes \tau '_i)=\sum _i \tau '_i\otimes \tau _i$.
$s(\sum _i \tau _i\otimes \tau '_i)=\sum _i \tau '_i\otimes \tau _i$.
If ![]() $\tau \in \mathrm {Irr}^\mathrm {GL}$, there exist
$\tau \in \mathrm {Irr}^\mathrm {GL}$, there exist ![]() $\rho _1, \ldots, \rho _r \in \mathscr {C}^\mathrm {GL}$ such that
$\rho _1, \ldots, \rho _r \in \mathscr {C}^\mathrm {GL}$ such that ![]() $\tau$ is a subrepresentation of
$\tau$ is a subrepresentation of ![]() $\rho _1 \times \cdots \times \rho _r$. The set
$\rho _1 \times \cdots \times \rho _r$. The set ![]() $\mathrm {scusp}(\pi ) := \{\rho _1, \ldots, \rho _r \}$ is uniquely determined by
$\mathrm {scusp}(\pi ) := \{\rho _1, \ldots, \rho _r \}$ is uniquely determined by ![]() $\pi$ and is called the supercuspidal support of
$\pi$ and is called the supercuspidal support of ![]() $\tau$.
$\tau$.
For ![]() $\pi \in \mathrm {Rep}(\mathrm {GL}_n(F))$ and a character
$\pi \in \mathrm {Rep}(\mathrm {GL}_n(F))$ and a character ![]() $\chi$ of
$\chi$ of ![]() $F^\times$, we denote by
$F^\times$, we denote by ![]() $\pi \cdot \chi$ the representation obtained from
$\pi \cdot \chi$ the representation obtained from ![]() $\pi$ by twisting by the character
$\pi$ by twisting by the character ![]() $\chi \circ \det$. If
$\chi \circ \det$. If ![]() $\rho \in \mathscr {C}^\mathrm {GL}$, we denote by
$\rho \in \mathscr {C}^\mathrm {GL}$, we denote by ![]() $\mathbb {Z}_\rho = \{\rho |\cdot |^a \mid a\in \mathbb {Z}\}$ the line of
$\mathbb {Z}_\rho = \{\rho |\cdot |^a \mid a\in \mathbb {Z}\}$ the line of ![]() $\rho$.
$\rho$.
A segment ![]() $[x,y]_\rho$ is a sequence of supercuspidal representations of the form
$[x,y]_\rho$ is a sequence of supercuspidal representations of the form
where ![]() $\rho \in \mathscr {C}^\mathrm {GL}$ and
$\rho \in \mathscr {C}^\mathrm {GL}$ and ![]() $x,y \in \mathbb {R}$ with
$x,y \in \mathbb {R}$ with ![]() $x-y \in \mathbb {Z}$ and
$x-y \in \mathbb {Z}$ and ![]() $x \geq y$.
$x \geq y$.
One can associate with a segment ![]() $[x,y]_\rho$ two irreducible representations of
$[x,y]_\rho$ two irreducible representations of ![]() $\mathrm {GL}_{d(x-y+1)}(F)$. We denote by
$\mathrm {GL}_{d(x-y+1)}(F)$. We denote by ![]() $\Delta _{\rho }[x,y]$ the Steinberg representation of
$\Delta _{\rho }[x,y]$ the Steinberg representation of ![]() $\mathrm {GL}_{d(x-y+1)}(F)$, i.e. the unique irreducible subrepresentation of
$\mathrm {GL}_{d(x-y+1)}(F)$, i.e. the unique irreducible subrepresentation of
and we also write ![]() $Z_\rho [y,x]$ for its unique irreducible quotient. For example, when
$Z_\rho [y,x]$ for its unique irreducible quotient. For example, when ![]() $\rho = \mathbf {1}_{\mathrm {GL}_1(F)}$, we have
$\rho = \mathbf {1}_{\mathrm {GL}_1(F)}$, we have ![]() $Z_\rho [-(n-1)/2,(n-1)/2] = \mathbf {1}_{\mathrm {GL}_n(F)}$.
$Z_\rho [-(n-1)/2,(n-1)/2] = \mathbf {1}_{\mathrm {GL}_n(F)}$.
The Steinberg representation ![]() $\Delta _{\rho }[x,y]$ is an essentially discrete series, and all essentially discrete series are of this form [Reference ZelevinskyZel80, Theorem 9.3]. By convention, we take
$\Delta _{\rho }[x,y]$ is an essentially discrete series, and all essentially discrete series are of this form [Reference ZelevinskyZel80, Theorem 9.3]. By convention, we take ![]() $\Delta _\rho [x,x+1]= Z_\rho [x+1,x]$ to be the trivial representation of the trivial group
$\Delta _\rho [x,x+1]= Z_\rho [x+1,x]$ to be the trivial representation of the trivial group ![]() $\mathrm {GL}_0(F)$.
$\mathrm {GL}_0(F)$.
If the segments ![]() $[x_1,y_1]_{\rho _1}, \ldots, [x_r,y_r]_{\rho _r}$ are such that
$[x_1,y_1]_{\rho _1}, \ldots, [x_r,y_r]_{\rho _r}$ are such that ![]() $x_i \geq y_i$ and
$x_i \geq y_i$ and ![]() $x_1+y_1 \leq \cdots \leq x_r+y_r$, then the socle (Langlands subrepresentation)
$x_1+y_1 \leq \cdots \leq x_r+y_r$, then the socle (Langlands subrepresentation)
is irreducible. When ![]() $\rho _1 = \cdots = \rho _r$,
$\rho _1 = \cdots = \rho _r$, ![]() $x_1 < \cdots < x_r$,
$x_1 < \cdots < x_r$, ![]() $y_1 < \cdots < y_r$ and
$y_1 < \cdots < y_r$ and ![]() $x_1 \equiv \cdots \equiv x_r \bmod \mathbb {Z}$, we call it a ladder representation. As a special case, when
$x_1 \equiv \cdots \equiv x_r \bmod \mathbb {Z}$, we call it a ladder representation. As a special case, when ![]() $x_i = x_1+i-1$ and
$x_i = x_1+i-1$ and ![]() $y_i = y_1+i-1$ for
$y_i = y_1+i-1$ for ![]() $1 \leq i \leq r$, the ladder representation
$1 \leq i \leq r$, the ladder representation ![]() $L(\Delta _\rho [x_1,y_1], \ldots, \Delta _\rho [x_r,y_r])$ is also called a Speh representation.
$L(\Delta _\rho [x_1,y_1], \ldots, \Delta _\rho [x_r,y_r])$ is also called a Speh representation.
The Jacquet modules of ![]() $\Delta _\rho [x,y]$ and
$\Delta _\rho [x,y]$ and ![]() $Z_\rho [y,x]$ are given by
$Z_\rho [y,x]$ are given by
respectively (see [Reference ZelevinskyZel80, Propositions 3.4 and 9.5]). For Jacquet modules of ladder representations, see [Reference Kret and LapidKL12, Theorem 2.1].
2.4 Representations of classical groups
In this paper, we let ![]() $G_n$ be either the split special orthogonal group
$G_n$ be either the split special orthogonal group ![]() $\mathrm {SO}_{2n+1}(F)$ or the symplectic group
$\mathrm {SO}_{2n+1}(F)$ or the symplectic group ![]() $\mathrm {Sp}_{2n}(F)$ of rank
$\mathrm {Sp}_{2n}(F)$ of rank ![]() $n$. Set
$n$. Set ![]() $\mathrm {Irr}^{G} := \bigcup _{n \geq 0} \mathrm {Irr} (G_n)$ and
$\mathrm {Irr}^{G} := \bigcup _{n \geq 0} \mathrm {Irr} (G_n)$ and ![]() $\mathscr {R}^G := \bigoplus _{n \geq 0} \mathscr {R}(G_{n})$, where the union and the direct sum are taken over groups of the same type. Let
$\mathscr {R}^G := \bigoplus _{n \geq 0} \mathscr {R}(G_{n})$, where the union and the direct sum are taken over groups of the same type. Let ![]() $\mathscr {C}^G \subset \mathrm {Irr}^G$ be the subset of supercuspidal representations of
$\mathscr {C}^G \subset \mathrm {Irr}^G$ be the subset of supercuspidal representations of ![]() $G_n$ for every
$G_n$ for every ![]() $n \geq 0$ of the same type.
$n \geq 0$ of the same type.
Fix a rational Borel subgroup of ![]() $G_n$. Let
$G_n$. Let ![]() $P$ be the standard parabolic subgroup of
$P$ be the standard parabolic subgroup of ![]() $G_n$ with Levi subgroup isomorphic to
$G_n$ with Levi subgroup isomorphic to ![]() $\mathrm {GL}_{d_1}(F) \times \cdots \times \mathrm {GL}_{d_r}(F) \times G_{n_0}$. Let
$\mathrm {GL}_{d_1}(F) \times \cdots \times \mathrm {GL}_{d_r}(F) \times G_{n_0}$. Let ![]() $\pi \in \mathrm {Rep}(G_{n_0})$ and let
$\pi \in \mathrm {Rep}(G_{n_0})$ and let ![]() $\tau _i \in \mathrm {Rep}(\mathrm {GL}_{d_i}(F))$ for
$\tau _i \in \mathrm {Rep}(\mathrm {GL}_{d_i}(F))$ for ![]() $1 \leq i \leq r$. We denote the normalized parabolically induced representation by
$1 \leq i \leq r$. We denote the normalized parabolically induced representation by
As in the case of general linear groups, the Jacquet functors give rise, at the level of Grothendieck groups, to a map
 \begin{align*} \mu^\ast \colon \mathscr{R}^G &\longrightarrow \mathscr{R}^\mathrm{GL}\otimes \mathscr{R}^G \\ \mathscr{R}(G_n) \ni \pi &\longmapsto \sum_{k=0}^{n} \bigl[\mathrm{Jac}_{P_k}^{G_n}(\pi)\bigr], \end{align*}
\begin{align*} \mu^\ast \colon \mathscr{R}^G &\longrightarrow \mathscr{R}^\mathrm{GL}\otimes \mathscr{R}^G \\ \mathscr{R}(G_n) \ni \pi &\longmapsto \sum_{k=0}^{n} \bigl[\mathrm{Jac}_{P_k}^{G_n}(\pi)\bigr], \end{align*}
where ![]() $P_k$ is the standard parabolic subgroup of
$P_k$ is the standard parabolic subgroup of ![]() $G_n$ with Levi subgroup isomorphic to
$G_n$ with Levi subgroup isomorphic to ![]() $\mathrm {GL}_{k}(F) \times G_{n-k}$. The geometric lemma at the level of Grothendieck groups is commonly known in this case as Tadić's formula.
$\mathrm {GL}_{k}(F) \times G_{n-k}$. The geometric lemma at the level of Grothendieck groups is commonly known in this case as Tadić's formula.
Proposition 2.1 (Tadić's formula [Reference TadićTad95])
For ![]() $\tau \in \mathscr {R}^{\mathrm {GL}}$ and
$\tau \in \mathscr {R}^{\mathrm {GL}}$ and ![]() $\pi \in \mathscr {R}^G$, we have
$\pi \in \mathscr {R}^G$, we have
We will also use the MVW-functor [Reference Mœglin, Vignéras and WaldspurgerMVW87]. It is a covariant functor
satisfying the following properties:
• if
 $\pi \in \mathrm {Irr} (G_n)$, then
$\pi \in \mathrm {Irr} (G_n)$, then  $\pi ^\mathrm {MVW}$ is isomorphic to
$\pi ^\mathrm {MVW}$ is isomorphic to  $\pi ^\vee$;
$\pi ^\vee$;•
 $(\tau \rtimes \pi )^\mathrm {MVW} \cong \tau \rtimes \pi ^\mathrm {MVW}$ for any
$(\tau \rtimes \pi )^\mathrm {MVW} \cong \tau \rtimes \pi ^\mathrm {MVW}$ for any  $\pi \in \mathrm {Rep}(G_{n_0})$ and any
$\pi \in \mathrm {Rep}(G_{n_0})$ and any  $\tau \in \mathrm {Rep}(\mathrm {GL}_{d}(F))$ with
$\tau \in \mathrm {Rep}(\mathrm {GL}_{d}(F))$ with  $n=n_0+d$.
$n=n_0+d$.
The Zelevinsky–Aubert duality extends by linearity to a map ![]() $D^G: \mathscr {R}^G \rightarrow \mathscr {R}^G$. With this notation, the compatibility of the duality with Jacquet functors in (2.1) stands:
$D^G: \mathscr {R}^G \rightarrow \mathscr {R}^G$. With this notation, the compatibility of the duality with Jacquet functors in (2.1) stands:
where
 \begin{align*} d^G \colon \mathscr{R}^\mathrm{GL} \otimes \mathscr{R}^G &\longrightarrow \mathscr{R}^\mathrm{GL}\otimes \mathscr{R}^G \\ \sum_i \tau_i \otimes \pi_i &\longmapsto \sum_i \hat{\tau}_i^\vee \otimes \hat{\pi}_i. \end{align*}
\begin{align*} d^G \colon \mathscr{R}^\mathrm{GL} \otimes \mathscr{R}^G &\longrightarrow \mathscr{R}^\mathrm{GL}\otimes \mathscr{R}^G \\ \sum_i \tau_i \otimes \pi_i &\longmapsto \sum_i \hat{\tau}_i^\vee \otimes \hat{\pi}_i. \end{align*}
Let ![]() $[x_1,y_1]_{\rho _1}, \ldots, [x_r,y_r]_{\rho _r}$ be some segments with
$[x_1,y_1]_{\rho _1}, \ldots, [x_r,y_r]_{\rho _r}$ be some segments with ![]() $\rho _i \in \mathscr {C}(\mathrm {GL}_{d_i}(F))$ being unitary for
$\rho _i \in \mathscr {C}(\mathrm {GL}_{d_i}(F))$ being unitary for ![]() $1 \leq i \leq r$, and let
$1 \leq i \leq r$, and let ![]() $\pi _\mathrm {temp}$ be an irreducible tempered representation of
$\pi _\mathrm {temp}$ be an irreducible tempered representation of ![]() $G_{n_0}$. A parabolically induced representation of the form
$G_{n_0}$. A parabolically induced representation of the form
is called a standard module if ![]() $x_1+y_1 \leq \cdots \leq x_r+y_r < 0$.
$x_1+y_1 \leq \cdots \leq x_r+y_r < 0$.
The Langlands classification says that any standard module is SI, and that any irreducible representation ![]() $\pi$ of
$\pi$ of ![]() $G_n$ is the unique irreducible subrepresentation (Langlands subrepresentation) of a standard module
$G_n$ is the unique irreducible subrepresentation (Langlands subrepresentation) of a standard module ![]() $\Delta _{\rho _1}[x_1,y_1] \times \cdots \times \Delta _{\rho _r}[x_r,y_r] \rtimes \pi _\mathrm {temp}$ with
$\Delta _{\rho _1}[x_1,y_1] \times \cdots \times \Delta _{\rho _r}[x_r,y_r] \rtimes \pi _\mathrm {temp}$ with ![]() $n=n_0 + \sum _{i=1}^r d_i(x_i-y_i+1)$, which is unique up to isomorphism. For more details, see [Reference KonnoKon03]. In this case, we write
$n=n_0 + \sum _{i=1}^r d_i(x_i-y_i+1)$, which is unique up to isomorphism. For more details, see [Reference KonnoKon03]. In this case, we write ![]() $\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ and refer to
$\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ and refer to ![]() $(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ as the Langlands data of
$(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ as the Langlands data of ![]() $\pi$.
$\pi$.
2.5 The Jantzen decomposition
If ![]() $\pi \in \mathrm {Irr}(G_n)$, there exist
$\pi \in \mathrm {Irr}(G_n)$, there exist ![]() $\rho _1, \ldots, \rho _r \in \mathscr {C}^\mathrm {GL}$ and
$\rho _1, \ldots, \rho _r \in \mathscr {C}^\mathrm {GL}$ and ![]() $\sigma \in \mathscr {C}^G$ such that
$\sigma \in \mathscr {C}^G$ such that ![]() $\pi$ is a subrepresentation of
$\pi$ is a subrepresentation of ![]() $\rho _1 \times \cdots \times \rho _r \rtimes \sigma$. The set
$\rho _1 \times \cdots \times \rho _r \rtimes \sigma$. The set
is uniquely determined by ![]() $\pi$ and is called the supercuspidal support of
$\pi$ and is called the supercuspidal support of ![]() $\pi$. For
$\pi$. For ![]() $\sigma \in \mathscr {C}^G$, we put
$\sigma \in \mathscr {C}^G$, we put ![]() $\mathrm {Irr}_\sigma := \{\pi \in \mathrm {Irr}^G \mid \sigma \in \mathrm {scusp}(\pi )\}$.
$\mathrm {Irr}_\sigma := \{\pi \in \mathrm {Irr}^G \mid \sigma \in \mathrm {scusp}(\pi )\}$.
In this paragraph, we fix a supercuspidal representation ![]() $\sigma \in \mathscr {C}^G$.
$\sigma \in \mathscr {C}^G$.
Definition 2.2 Recall that ![]() $\mathbb {Z}_\rho = \{\rho |\cdot |^a \mid a\in \mathbb {Z}\}$ is the line of
$\mathbb {Z}_\rho = \{\rho |\cdot |^a \mid a\in \mathbb {Z}\}$ is the line of ![]() $\rho$ for
$\rho$ for ![]() $\rho \in \mathscr {C}^\mathrm {GL}$.
$\rho \in \mathscr {C}^\mathrm {GL}$.
• We say that
 $\rho$ is good if
$\rho$ is good if  $\mathbb {Z}_\rho = \mathbb {Z}_{\rho ^\vee }$ and
$\mathbb {Z}_\rho = \mathbb {Z}_{\rho ^\vee }$ and  $\rho ' \rtimes \sigma$ is reducible for some
$\rho ' \rtimes \sigma$ is reducible for some  $\rho ' \in \mathbb {Z}_\rho$.
$\rho ' \in \mathbb {Z}_\rho$.• We say that
 $\rho$ is bad if
$\rho$ is bad if  $\mathbb {Z}_\rho = \mathbb {Z}_{\rho ^\vee }$ and
$\mathbb {Z}_\rho = \mathbb {Z}_{\rho ^\vee }$ and  $\rho ' \rtimes \sigma$ is irreducible for all
$\rho ' \rtimes \sigma$ is irreducible for all  $\rho ' \in \mathbb {Z}_\rho$.
$\rho ' \in \mathbb {Z}_\rho$.• We say that
 $\rho$ is ugly if
$\rho$ is ugly if  $\mathbb {Z}_\rho \neq \mathbb {Z}_{\rho ^\vee }$.
$\mathbb {Z}_\rho \neq \mathbb {Z}_{\rho ^\vee }$.
Every supercuspidal representation is either good, bad or ugly.
Remark 2.3 It is known that
• the notions of good and bad are independent of
 $\sigma$;
$\sigma$;• if
 $\rho '|\cdot |^z$ is good or bad with
$\rho '|\cdot |^z$ is good or bad with  $\rho '$ unitary and
$\rho '$ unitary and  $z\in \mathbb {R}$, then
$z\in \mathbb {R}$, then  $\rho '$ is self-dual and
$\rho '$ is self-dual and  $z \in (1/2)\mathbb {Z}$;
$z \in (1/2)\mathbb {Z}$;• if
 $\rho '|\cdot |^{z_1}, \rho '|\cdot |^{z_2}$ are both good or both bad, then
$\rho '|\cdot |^{z_1}, \rho '|\cdot |^{z_2}$ are both good or both bad, then  $z_1-z_2 \in \mathbb {Z}$.
$z_1-z_2 \in \mathbb {Z}$.
See Remark 5.1 below.
Definition 2.4
(1) We say that two good (respectively bad) supercuspidal representations
 $\rho$ and
$\rho$ and  $\rho '$ are line equivalent if
$\rho '$ are line equivalent if  $\mathbb {Z}_\rho =\mathbb {Z}_{\rho '}$. We denote by
$\mathbb {Z}_\rho =\mathbb {Z}_{\rho '}$. We denote by  $\mathscr {C}^{{\rm good}}$ (respectively
$\mathscr {C}^{{\rm good}}$ (respectively  $\mathscr {C}^{\rm bad}$) a set of representatives of good (respectively bad) representations under this equivalence relation.
$\mathscr {C}^{\rm bad}$) a set of representatives of good (respectively bad) representations under this equivalence relation.(2) Similarly, we say that two ugly representations
 $\rho$ and
$\rho$ and  $\rho '$ are line equivalent if
$\rho '$ are line equivalent if  $\mathbb {Z}_\rho \cup \mathbb {Z}_{\rho ^\vee } = \mathbb {Z}_{\rho '}\cup \mathbb {Z}_{\rho ^{'\vee }}$. We denote by
$\mathbb {Z}_\rho \cup \mathbb {Z}_{\rho ^\vee } = \mathbb {Z}_{\rho '}\cup \mathbb {Z}_{\rho ^{'\vee }}$. We denote by  $\mathscr {C}^{\rm ugly}$ a set of representatives of ugly representations under this equivalence relation.
$\mathscr {C}^{\rm ugly}$ a set of representatives of ugly representations under this equivalence relation.
Definition 2.5 Let ![]() $\pi \in \mathrm {Irr}_\sigma$.
$\pi \in \mathrm {Irr}_\sigma$.
(1) If
we say that \[ \mathrm{scusp}(\pi) \subset \biggl(\bigcup_{\rho \in \mathscr{C}^{{\rm good}}} \mathbb{Z}_\rho \biggr) \cup \{\sigma\}, \]
\[ \mathrm{scusp}(\pi) \subset \biggl(\bigcup_{\rho \in \mathscr{C}^{{\rm good}}} \mathbb{Z}_\rho \biggr) \cup \{\sigma\}, \]
 $\pi$ is of good parity. We write
$\pi$ is of good parity. We write  $\mathrm {Irr}_\sigma ^{\rm good}$ for the set of such representations.
$\mathrm {Irr}_\sigma ^{\rm good}$ for the set of such representations.(2) If
 $\mathrm {scusp}(\pi ) \subset \mathbb {Z}_\rho \cup \{\sigma \}$ for some bad representation
$\mathrm {scusp}(\pi ) \subset \mathbb {Z}_\rho \cup \{\sigma \}$ for some bad representation  $\rho$, we say that
$\rho$, we say that  $\pi$ is of bad parity (or of
$\pi$ is of bad parity (or of  $\rho$-bad parity if we want to specify
$\rho$-bad parity if we want to specify  $\rho$). We write
$\rho$). We write  $\mathrm {Irr}_\sigma ^{\rho {\rm -bad}}$ for the set of such representations.
$\mathrm {Irr}_\sigma ^{\rho {\rm -bad}}$ for the set of such representations.(3) If
 $\mathrm {scusp}(\pi ) \subset (\mathbb {Z}_\rho \cup \mathbb {Z}_{\rho ^\vee }) \cup \{\sigma \}$ for some ugly representation
$\mathrm {scusp}(\pi ) \subset (\mathbb {Z}_\rho \cup \mathbb {Z}_{\rho ^\vee }) \cup \{\sigma \}$ for some ugly representation  $\rho$, we say that
$\rho$, we say that  $\pi$ is ugly (or
$\pi$ is ugly (or  $\rho$-ugly if we want to specify
$\rho$-ugly if we want to specify  $\rho$). We write
$\rho$). We write  $\mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$ for the set of such representations.
$\mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$ for the set of such representations.
Ugly representations are easy to deal with owing to the following proposition, which reduces every problem to a similar problem for general linear groups.
Proposition 2.6 Let ![]() $\pi \in \mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$. Then there exists an irreducible representation
$\pi \in \mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$. Then there exists an irreducible representation ![]() $\tau$ of
$\tau$ of ![]() $\mathrm {GL}_m(F)$ with
$\mathrm {GL}_m(F)$ with ![]() $\mathrm {scusp}(\tau ) \subset \mathbb {Z}_\rho$ such that
$\mathrm {scusp}(\tau ) \subset \mathbb {Z}_\rho$ such that ![]() $\pi = \tau \rtimes \sigma$ (irreducible induction).
$\pi = \tau \rtimes \sigma$ (irreducible induction).
Proof. We can write
for some ![]() $x_i, y_j \in \mathbb {Z}$. There exist irreducible subquotients
$x_i, y_j \in \mathbb {Z}$. There exist irreducible subquotients ![]() $\tau _1$ of
$\tau _1$ of ![]() $\rho |\cdot |^{x_1} \times \cdots \times \rho |\cdot |^{x_r}$ and
$\rho |\cdot |^{x_1} \times \cdots \times \rho |\cdot |^{x_r}$ and ![]() $\tau _2$ of
$\tau _2$ of ![]() $\rho ^\vee |\cdot |^{-y_1} \times \cdots \times \rho ^\vee |\cdot |^{-y_s}$ such that this inclusion factors through
$\rho ^\vee |\cdot |^{-y_1} \times \cdots \times \rho ^\vee |\cdot |^{-y_s}$ such that this inclusion factors through ![]() $\pi \hookrightarrow \tau _1 \times \tau _2 \rtimes \sigma$. As
$\pi \hookrightarrow \tau _1 \times \tau _2 \rtimes \sigma$. As ![]() $\rho$ is ugly, we can apply [Reference Lapid and TadićLT20, Lemma 6.2] to
$\rho$ is ugly, we can apply [Reference Lapid and TadićLT20, Lemma 6.2] to ![]() $\tau _2 \rtimes \sigma$ and see that
$\tau _2 \rtimes \sigma$ and see that ![]() $\tau _2 \rtimes \sigma$ is irreducible. Hence
$\tau _2 \rtimes \sigma$ is irreducible. Hence ![]() $\pi \hookrightarrow \tau _1 \times \tau _2^\vee \rtimes \sigma$. Take an irreducible subquotient
$\pi \hookrightarrow \tau _1 \times \tau _2^\vee \rtimes \sigma$. Take an irreducible subquotient ![]() $\tau$ of
$\tau$ of ![]() $\tau _1 \times \tau _2^\vee$ such that
$\tau _1 \times \tau _2^\vee$ such that ![]() $\pi \hookrightarrow \tau \rtimes \sigma$. Then by [Reference Lapid and TadićLT20, Lemma 6.2] again, we conclude that
$\pi \hookrightarrow \tau \rtimes \sigma$. Then by [Reference Lapid and TadićLT20, Lemma 6.2] again, we conclude that ![]() $\tau \rtimes \sigma$ is irreducible.
$\tau \rtimes \sigma$ is irreducible.
Remark 2.7 More precisely, by the Langlands classification, one can take ![]() $\tau _1$ and
$\tau _1$ and ![]() $\tau _2$ in the proof of this proposition so that
$\tau _2$ in the proof of this proposition so that
with ![]() $x'_1+y'_1 \leq \cdots \leq x'_{r'}+y'_{r'} \leq 0$ and
$x'_1+y'_1 \leq \cdots \leq x'_{r'}+y'_{r'} \leq 0$ and ![]() $x''_1+y''_1 \leq \cdots \leq x''_{r''}+y''_{r''} \leq 0$. Then since
$x''_1+y''_1 \leq \cdots \leq x''_{r''}+y''_{r''} \leq 0$. Then since ![]() $\tau _2^\vee = L(\Delta _{\rho }[-y''_{r''},-x''_{r''}], \ldots, \Delta _{\rho }[-y''_{1},-x''_{1}])$ and
$\tau _2^\vee = L(\Delta _{\rho }[-y''_{r''},-x''_{r''}], \ldots, \Delta _{\rho }[-y''_{1},-x''_{1}])$ and ![]() $\pi = \mathrm {soc}(\tau _1 \times \tau _2^\vee \rtimes \sigma ) \hookrightarrow \mathrm {soc}(\tau _1 \times \tau _2^\vee ) \rtimes \sigma$, one can take
$\pi = \mathrm {soc}(\tau _1 \times \tau _2^\vee \rtimes \sigma ) \hookrightarrow \mathrm {soc}(\tau _1 \times \tau _2^\vee ) \rtimes \sigma$, one can take ![]() $\tau$ to be
$\tau$ to be
Let ![]() $\pi \in \mathrm {Irr}_\sigma$. Then Jantzen [Reference JantzenJan97] defined representations
$\pi \in \mathrm {Irr}_\sigma$. Then Jantzen [Reference JantzenJan97] defined representations ![]() $\pi ^{\rm good} \in \mathrm {Irr}_\sigma ^{\rm good}$,
$\pi ^{\rm good} \in \mathrm {Irr}_\sigma ^{\rm good}$, ![]() $\pi ^{\rho {\rm -bad}} \in \mathrm {Irr}_\sigma ^{\rho {\rm -bad}}$ and
$\pi ^{\rho {\rm -bad}} \in \mathrm {Irr}_\sigma ^{\rho {\rm -bad}}$ and ![]() $\pi ^{\rho {\rm -ugly}} \in \mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$ as follows:
$\pi ^{\rho {\rm -ugly}} \in \mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$ as follows:
•
 $\pi ^{\rm good}$ is the unique representation in
$\pi ^{\rm good}$ is the unique representation in  $\mathrm {Irr}_\sigma ^{\rm good}$ such that
$\mathrm {Irr}_\sigma ^{\rm good}$ such that  $\pi \hookrightarrow \tau \times \pi ^{\rm good}$ with no good representations in
$\pi \hookrightarrow \tau \times \pi ^{\rm good}$ with no good representations in  $\mathrm {scusp}(\tau )$;
$\mathrm {scusp}(\tau )$;• if
 $\rho$ is a bad supercuspidal representation, then
$\rho$ is a bad supercuspidal representation, then  $\pi ^{\rho {\rm -bad}}$ is the unique representation in
$\pi ^{\rho {\rm -bad}}$ is the unique representation in  $\mathrm {Irr}_\sigma ^{\rho {\rm -bad}}$ such that
$\mathrm {Irr}_\sigma ^{\rho {\rm -bad}}$ such that  $\pi \hookrightarrow \tau \times \pi ^{\rho {\rm -bad} }$ with
$\pi \hookrightarrow \tau \times \pi ^{\rho {\rm -bad} }$ with  $\mathrm {scusp}(\tau ) \cap \mathbb {Z}_\rho =\emptyset$;
$\mathrm {scusp}(\tau ) \cap \mathbb {Z}_\rho =\emptyset$;• if
 $\rho$ is an ugly supercuspidal representation, then
$\rho$ is an ugly supercuspidal representation, then  $\pi ^{\rho {\rm -ugly}}$ is the unique representation in
$\pi ^{\rho {\rm -ugly}}$ is the unique representation in  $\mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$ such that
$\mathrm {Irr}_\sigma ^{\rho {\rm -ugly}}$ such that  $\pi \hookrightarrow \tau \times \pi ^{\rho {\rm -ugly}}$ with
$\pi \hookrightarrow \tau \times \pi ^{\rho {\rm -ugly}}$ with  $\mathrm {scusp}(\tau ) \cap (\mathbb {Z}_\rho \cup \mathbb {Z}_{\rho ^\vee }) = \emptyset$.
$\mathrm {scusp}(\tau ) \cap (\mathbb {Z}_\rho \cup \mathbb {Z}_{\rho ^\vee }) = \emptyset$.
The following theorem is a special case of Jantzen's decomposition.
Theorem 2.8 [Reference JantzenJan97, Theorem 9.3]
The map
 \begin{align*}
\Psi \colon
\mathrm{Irr}_\sigma &\longrightarrow
\mathrm{Irr}_\sigma^{\rm good} \sqcup \biggl
(\,\bigsqcup_{\rho\in
\mathscr{C}^{\rm bad}}
\mathrm{Irr}_\sigma^{\rho{\rm -bad}} \biggr)
\sqcup \biggl(\,\bigsqcup_{\rho\in
\mathscr{C}^{\rm ugly}}
\mathrm{Irr}_\sigma^{\rho{\rm -ugly}}
\biggr) \\ \pi &\longmapsto \bigl(
\pi^{\rm good},
\{\pi^{\rho{\rm -bad}}\}_\rho,
\{\pi^{\rho{\rm -ugly}}\}_\rho \bigr)
\end{align*}
\begin{align*}
\Psi \colon
\mathrm{Irr}_\sigma &\longrightarrow
\mathrm{Irr}_\sigma^{\rm good} \sqcup \biggl
(\,\bigsqcup_{\rho\in
\mathscr{C}^{\rm bad}}
\mathrm{Irr}_\sigma^{\rho{\rm -bad}} \biggr)
\sqcup \biggl(\,\bigsqcup_{\rho\in
\mathscr{C}^{\rm ugly}}
\mathrm{Irr}_\sigma^{\rho{\rm -ugly}}
\biggr) \\ \pi &\longmapsto \bigl(
\pi^{\rm good},
\{\pi^{\rho{\rm -bad}}\}_\rho,
\{\pi^{\rho{\rm -ugly}}\}_\rho \bigr)
\end{align*}
is bijective. Moreover, it commutes with the Zelevinsky–Aubert duality in the sense that
In practice, this theorem enables us to reduce the problem of making the Zelevinsky–Aubert duality explicit to the case where the representation is either ugly or of good or bad parity.
3. The theory of  $\rho$-derivatives
$\rho$-derivatives
Let ![]() $d>0$ be an integer. In this section, we fix
$d>0$ be an integer. In this section, we fix ![]() $\rho \in \mathscr {C}(\mathrm {GL}_d(F))$. We recall the definition of
$\rho \in \mathscr {C}(\mathrm {GL}_d(F))$. We recall the definition of ![]() $\rho$-derivatives in [Reference Lapid and TadićLT20] and introduce the notions of
$\rho$-derivatives in [Reference Lapid and TadićLT20] and introduce the notions of ![]() $\Delta _\rho [0,-1]$-derivative and
$\Delta _\rho [0,-1]$-derivative and ![]() $Z_\rho [0,1]$-derivative. One should not confuse these notions with the Bernstein–Zelevinsky notion of derivatives.
$Z_\rho [0,1]$-derivative. One should not confuse these notions with the Bernstein–Zelevinsky notion of derivatives.
3.1 Definitions
We treat first the case of general linear groups. For ![]() $\tau \in \mathrm {Rep}(\mathrm {GL}_n(F))$, define semisimple representations
$\tau \in \mathrm {Rep}(\mathrm {GL}_n(F))$, define semisimple representations ![]() $L_\rho ^{(k)}(\tau )$ and
$L_\rho ^{(k)}(\tau )$ and ![]() $R_\rho ^{(k)}(\tau )$ of
$R_\rho ^{(k)}(\tau )$ of ![]() $\mathrm {GL}_{n-dk}(F)$ so that
$\mathrm {GL}_{n-dk}(F)$ so that
 \begin{align*} \big[\mathrm{Jac}_{(dk,n-dk)}(\tau)\big] &= \rho^k \boxtimes L_{\rho}^{(k)}(\tau) + \sum_i \tau_i \boxtimes \sigma_i,\\ \big[\mathrm{Jac}_{(n-dk,dk)}(\tau)\big] &= R_{\rho}^{(k)}(\tau) \boxtimes \rho^k + \sum_i \sigma'_i \boxtimes \tau'_i, \end{align*}
\begin{align*} \big[\mathrm{Jac}_{(dk,n-dk)}(\tau)\big] &= \rho^k \boxtimes L_{\rho}^{(k)}(\tau) + \sum_i \tau_i \boxtimes \sigma_i,\\ \big[\mathrm{Jac}_{(n-dk,dk)}(\tau)\big] &= R_{\rho}^{(k)}(\tau) \boxtimes \rho^k + \sum_i \sigma'_i \boxtimes \tau'_i, \end{align*}
where ![]() $\tau _i$ and
$\tau _i$ and ![]() $\tau '_i$ are irreducible representations of
$\tau '_i$ are irreducible representations of ![]() $\mathrm {GL}_{dk}(F)$ which are not isomorphic to
$\mathrm {GL}_{dk}(F)$ which are not isomorphic to ![]() $\rho ^k$. We call
$\rho ^k$. We call ![]() $L_\rho ^{(k)}(\tau )$ (respectively
$L_\rho ^{(k)}(\tau )$ (respectively ![]() $R_\rho ^{(k)}(\tau )$) the
$R_\rho ^{(k)}(\tau )$) the ![]() $k$th left
$k$th left ![]() $\rho$-derivative (respectively the
$\rho$-derivative (respectively the ![]() $k$th right
$k$th right ![]() $\rho$-derivative) of
$\rho$-derivative) of ![]() $\tau$.
$\tau$.
Definition 3.1
(1) If
 $L_{\rho }^{(k)}(\tau ) \not = 0$ but
$L_{\rho }^{(k)}(\tau ) \not = 0$ but  $L_{\rho }^{(k+1)}(\tau ) =0$, we say that
$L_{\rho }^{(k+1)}(\tau ) =0$, we say that  $L_{\rho }^{(k)}(\tau )$ is the highest left
$L_{\rho }^{(k)}(\tau )$ is the highest left  $\rho$-derivative. We define the highest right
$\rho$-derivative. We define the highest right  $\rho$-derivative similarly.
$\rho$-derivative similarly.(2) When
 $L_{\rho }^{(1)}(\tau ) =0$ (respectively
$L_{\rho }^{(1)}(\tau ) =0$ (respectively  $R_{\rho }^{(1)}(\tau ) =0$), we say that
$R_{\rho }^{(1)}(\tau ) =0$), we say that  $\tau$ is left
$\tau$ is left  $\rho$-reduced (respectively right
$\rho$-reduced (respectively right  $\rho$-reduced).
$\rho$-reduced).
Similarly we now treat the case of ![]() $G_n$. Again let
$G_n$. Again let ![]() $k \geq 0$, and now let
$k \geq 0$, and now let ![]() $P_{dk}$ be the standard parabolic subgroup of
$P_{dk}$ be the standard parabolic subgroup of ![]() $G_n$ with Levi subgroup of the form
$G_n$ with Levi subgroup of the form ![]() $\mathrm {GL}_{dk}(F) \times G_{n-dk}$. For
$\mathrm {GL}_{dk}(F) \times G_{n-dk}$. For ![]() $\Pi \in \mathrm {Rep}(G_n)$, define a semisimple representation
$\Pi \in \mathrm {Rep}(G_n)$, define a semisimple representation ![]() $D_\rho ^{(k)}(\Pi )$ of
$D_\rho ^{(k)}(\Pi )$ of ![]() $G_{n-dk}$ so that
$G_{n-dk}$ so that
where ![]() $\tau _i$ is an irreducible representation of
$\tau _i$ is an irreducible representation of ![]() $\mathrm {GL}_{dk}(F)$ which is not isomorphic to
$\mathrm {GL}_{dk}(F)$ which is not isomorphic to ![]() $\rho ^k$. We call
$\rho ^k$. We call ![]() $D_\rho ^{(k)}(\Pi )$ the
$D_\rho ^{(k)}(\Pi )$ the ![]() $k$th
$k$th ![]() $\rho$-derivative of
$\rho$-derivative of ![]() $\Pi$.
$\Pi$.
Definition 3.2
(1) If
 $D_{\rho }^{(k)}(\Pi ) \not = 0$ but
$D_{\rho }^{(k)}(\Pi ) \not = 0$ but  $D_{\rho }^{(k+1)}(\Pi ) =0$, we say that
$D_{\rho }^{(k+1)}(\Pi ) =0$, we say that  $D_{\rho }^{(k)}(\Pi )$ is the highest
$D_{\rho }^{(k)}(\Pi )$ is the highest  $\rho$-derivative.
$\rho$-derivative.(2) When
 $D_{\rho }^{(1)}(\Pi ) =0$, we say that
$D_{\rho }^{(1)}(\Pi ) =0$, we say that  $\Pi$ is
$\Pi$ is  $\rho$-reduced.
$\rho$-reduced.
3.2 The non-self-dual case
If ![]() $\pi$ is irreducible and
$\pi$ is irreducible and ![]() $\rho$ is not self-dual, then the highest
$\rho$ is not self-dual, then the highest ![]() $\rho$-derivative
$\rho$-derivative ![]() $D_\rho ^{(k)}(\pi )$ is irreducible and
$D_\rho ^{(k)}(\pi )$ is irreducible and ![]() $\pi$ is isomorphic to the unique irreducible subrepresentation of
$\pi$ is isomorphic to the unique irreducible subrepresentation of ![]() $\rho ^k \rtimes D_{\rho }^{(k)}(\pi )$ (see [Reference JantzenJan14, Lemma 3.1.3] and [Reference AtobeAto22b, Proposition 2.7]). Using these properties, we can show the following.
$\rho ^k \rtimes D_{\rho }^{(k)}(\pi )$ (see [Reference JantzenJan14, Lemma 3.1.3] and [Reference AtobeAto22b, Proposition 2.7]). Using these properties, we can show the following.
Proposition 3.3 Let ![]() $\pi$ be an irreducible representation of
$\pi$ be an irreducible representation of ![]() $G_n$ and
$G_n$ and ![]() $r$ a non-negative integer. If
$r$ a non-negative integer. If ![]() $\rho$ is not self-dual, then
$\rho$ is not self-dual, then ![]() $\rho ^r \rtimes \pi$ is SI.
$\rho ^r \rtimes \pi$ is SI.
Proof. Consider the highest ![]() $\rho$-derivative
$\rho$-derivative ![]() $D_{\rho }^{(k)}(\pi )$. If
$D_{\rho }^{(k)}(\pi )$. If ![]() $\pi ' \hookrightarrow \rho ^r \rtimes \pi$, then
$\pi ' \hookrightarrow \rho ^r \rtimes \pi$, then ![]() $\pi ' \hookrightarrow \rho ^{k+r} \rtimes D_{\rho }^{(k)}(\pi )$. In particular,
$\pi ' \hookrightarrow \rho ^{k+r} \rtimes D_{\rho }^{(k)}(\pi )$. In particular, ![]() $D_{\rho }^{(k+r)}(\pi ') = D_{\rho }^{(k)}(\pi )$. However, since
$D_{\rho }^{(k+r)}(\pi ') = D_{\rho }^{(k)}(\pi )$. However, since
by Tadić's formula (Proposition 2.1), we see that ![]() $\pi '$ is determined uniquely. Hence
$\pi '$ is determined uniquely. Hence ![]() $\mathrm {soc}(\rho ^r \rtimes \pi )$ is irreducible and satisfies
$\mathrm {soc}(\rho ^r \rtimes \pi )$ is irreducible and satisfies
These equations imply that ![]() $\mathrm {soc}(\rho ^r \rtimes \pi )$ appears with multiplicity one in
$\mathrm {soc}(\rho ^r \rtimes \pi )$ appears with multiplicity one in ![]() $[\rho ^r \rtimes \pi ]$.
$[\rho ^r \rtimes \pi ]$.
We set
 \[ S_\rho^{(r)}(\pi) = \underbrace{S_\rho^{(1)} \circ \cdots \circ S_\rho^{(1)}}_{r\text{ times}}(\pi) = \mathrm{soc}(\rho^r \rtimes \pi) \]
\[ S_\rho^{(r)}(\pi) = \underbrace{S_\rho^{(1)} \circ \cdots \circ S_\rho^{(1)}}_{r\text{ times}}(\pi) = \mathrm{soc}(\rho^r \rtimes \pi) \]
for any ![]() $\pi \in \mathrm {Irr}(G_n)$.
$\pi \in \mathrm {Irr}(G_n)$.
3.3 The self-dual case
Recall from [Reference AtobeAto22b, Proposition 2.7] that the highest ![]() $\rho$-derivative
$\rho$-derivative ![]() $D_\rho ^{(k)}(\pi )$ of an irreducible representation is isotypic, i.e.
$D_\rho ^{(k)}(\pi )$ of an irreducible representation is isotypic, i.e. ![]() $D_\rho ^{(k)}(\pi ) = m \cdot \pi _0$ with some irreducible representation
$D_\rho ^{(k)}(\pi ) = m \cdot \pi _0$ with some irreducible representation ![]() $\pi _0$ and a certain multiplicity
$\pi _0$ and a certain multiplicity ![]() $m > 0$. In this case, we have
$m > 0$. In this case, we have ![]() $\pi \hookrightarrow \rho ^k \rtimes \pi _0$, but
$\pi \hookrightarrow \rho ^k \rtimes \pi _0$, but ![]() $\mathrm {soc}(\rho ^k \rtimes \pi _0)$ can be reducible.
$\mathrm {soc}(\rho ^k \rtimes \pi _0)$ can be reducible.
We give a criterion for ![]() $\rho ^r \rtimes \pi$ being SI.
$\rho ^r \rtimes \pi$ being SI.
Proposition 3.4 Suppose that ![]() $\rho$ is self-dual. Let
$\rho$ is self-dual. Let ![]() $\pi \in \mathrm {Irr}(G_n)$, and let
$\pi \in \mathrm {Irr}(G_n)$, and let ![]() $r$ be a positive integer. The following are equivalent:
$r$ be a positive integer. The following are equivalent:
(a)
 $\rho ^r \rtimes \pi$ is SI;
$\rho ^r \rtimes \pi$ is SI;(b)
 $\rho ^r \rtimes \pi$ is irreducible;
$\rho ^r \rtimes \pi$ is irreducible;(c)
 $\rho ^r \rtimes \pi$ has an irreducible subquotient
$\rho ^r \rtimes \pi$ has an irreducible subquotient  $\pi '$ such that
$\pi '$ such that  $D_{\rho }^{(k+r)}(\pi ') = 2^r \cdot D_{\rho }^{(k)}(\pi )$, where
$D_{\rho }^{(k+r)}(\pi ') = 2^r \cdot D_{\rho }^{(k)}(\pi )$, where  $D_{\rho }^{(k)}(\pi )$ is the highest
$D_{\rho }^{(k)}(\pi )$ is the highest  $\rho$-derivative of
$\rho$-derivative of  $\pi$.
$\pi$.
Proof. We use here the MVW-functor; see § 2.4. As we assume that ![]() $\rho$ is self-dual, if an irreducible representation
$\rho$ is self-dual, if an irreducible representation ![]() $\pi '$ satisfies
$\pi '$ satisfies ![]() $\pi ' \hookrightarrow \rho ^r \rtimes \pi$, by taking the MVW-functor and the contragredient functor we have
$\pi ' \hookrightarrow \rho ^r \rtimes \pi$, by taking the MVW-functor and the contragredient functor we have ![]() $\rho ^r \rtimes \pi \twoheadrightarrow \pi '$.
$\rho ^r \rtimes \pi \twoheadrightarrow \pi '$.
Now we assume that ![]() $\mathrm {soc}(\rho ^r \rtimes \pi )$ is irreducible but
$\mathrm {soc}(\rho ^r \rtimes \pi )$ is irreducible but ![]() $\rho ^r \rtimes \pi$ is reducible. The above remark implies that the quotient
$\rho ^r \rtimes \pi$ is reducible. The above remark implies that the quotient ![]() $(\rho ^r \rtimes \pi ) / \mathrm {soc}(\rho ^r \rtimes \pi )$ has an irreducible quotient isomorphic to
$(\rho ^r \rtimes \pi ) / \mathrm {soc}(\rho ^r \rtimes \pi )$ has an irreducible quotient isomorphic to ![]() ${\mathrm {soc}(\rho ^r \rtimes \pi)}$. This means that
${\mathrm {soc}(\rho ^r \rtimes \pi)}$. This means that ![]() $\mathrm {soc}(\rho ^r \rtimes \pi )$ appears with multiplicity greater than one in
$\mathrm {soc}(\rho ^r \rtimes \pi )$ appears with multiplicity greater than one in ![]() $[\rho ^r \rtimes \pi ]$. Hence (a) implies (b). As the opposite implication is obvious, (a) and (b) are equivalent.
$[\rho ^r \rtimes \pi ]$. Hence (a) implies (b). As the opposite implication is obvious, (a) and (b) are equivalent.
Note that ![]() $D_{\rho }^{(k+r)}(\rho ^r \rtimes \pi ) = 2^r \cdot D_{\rho }^{(k)}(\pi )$. In particular, (b) implies (c). On the other hand, let
$D_{\rho }^{(k+r)}(\rho ^r \rtimes \pi ) = 2^r \cdot D_{\rho }^{(k)}(\pi )$. In particular, (b) implies (c). On the other hand, let ![]() $\pi '$ be an irreducible subquotient of
$\pi '$ be an irreducible subquotient of ![]() $\rho ^r \rtimes \pi$ such that
$\rho ^r \rtimes \pi$ such that ![]() $D_{\rho }^{(k+r)}(\pi ') = 2^r \cdot D_{\rho }^{(k)}(\pi )$. Then
$D_{\rho }^{(k+r)}(\pi ') = 2^r \cdot D_{\rho }^{(k)}(\pi )$. Then ![]() $\pi '$ must be a subrepresentation of
$\pi '$ must be a subrepresentation of ![]() $\rho ^r \rtimes \pi$, and
$\rho ^r \rtimes \pi$, and ![]() $(\rho ^r \rtimes \pi )/\pi '$ has no irreducible quotient. Hence
$(\rho ^r \rtimes \pi )/\pi '$ has no irreducible quotient. Hence ![]() $\pi ' = \rho ^r \rtimes \pi$ so that
$\pi ' = \rho ^r \rtimes \pi$ so that ![]() $\rho ^r \rtimes \pi$ is irreducible.
$\rho ^r \rtimes \pi$ is irreducible.
3.4  $\Delta _\rho [0,-1]$-derivatives and
$\Delta _\rho [0,-1]$-derivatives and  $Z_\rho [0,1]$-derivatives
$Z_\rho [0,1]$-derivatives
In the case where ![]() $\rho$ is self-dual,
$\rho$ is self-dual, ![]() $\rho$-derivatives are difficult. Therefore, we define some other derivatives in this paragraph. These will be key ingredients in making the Zelevinsky–Aubert duality explicit. In this subsection we assume that
$\rho$-derivatives are difficult. Therefore, we define some other derivatives in this paragraph. These will be key ingredients in making the Zelevinsky–Aubert duality explicit. In this subsection we assume that ![]() $\rho \in \mathscr {C}(\mathrm {GL}_d(F))$ is self-dual.
$\rho \in \mathscr {C}(\mathrm {GL}_d(F))$ is self-dual.
Let ![]() $\Pi \in \mathrm {Rep}(G_n)$. Define the
$\Pi \in \mathrm {Rep}(G_n)$. Define the ![]() $\Delta _\rho [0,-1]$-derivative
$\Delta _\rho [0,-1]$-derivative ![]() $D_{\Delta _\rho [0,-1]}^{(k)}(\Pi )$ and the
$D_{\Delta _\rho [0,-1]}^{(k)}(\Pi )$ and the ![]() $Z_\rho [0,1]$-derivative
$Z_\rho [0,1]$-derivative ![]() $D_{Z_\rho [0,1]}^{(k)}(\Pi )$ by the semisimple representations of
$D_{Z_\rho [0,1]}^{(k)}(\Pi )$ by the semisimple representations of ![]() $G_{n-2dk}$ satisfying
$G_{n-2dk}$ satisfying
where ![]() $\tau _i \in \mathrm {Irr}(\mathrm {GL}_{2dk}(F))$ such that
$\tau _i \in \mathrm {Irr}(\mathrm {GL}_{2dk}(F))$ such that ![]() $\tau _i \not \cong \Delta _\rho [0,-1]^k, Z_\rho [0,1]^k$.
$\tau _i \not \cong \Delta _\rho [0,-1]^k, Z_\rho [0,1]^k$.
Typically, when the supercuspidal representation ![]() $\rho$ is clear from the context, we will write
$\rho$ is clear from the context, we will write ![]() $[0,-1]$-derivative for short instead of
$[0,-1]$-derivative for short instead of ![]() $\Delta _\rho [0,-1]$-derivative, and
$\Delta _\rho [0,-1]$-derivative, and ![]() $[0,1]$-derivative instead of
$[0,1]$-derivative instead of ![]() $Z_\rho [0,1]$-derivative. We also write
$Z_\rho [0,1]$-derivative. We also write ![]() $D_{[0,-1]}^{(k)}(\Pi ) := D_{\Delta _\rho [0,-1]}^{(k)}(\Pi )$ and
$D_{[0,-1]}^{(k)}(\Pi ) := D_{\Delta _\rho [0,-1]}^{(k)}(\Pi )$ and ![]() $D_{[0,1]}^{(k)}(\Pi ) := D_{Z_\rho [0,1]}^{(k)}(\Pi )$. Similar to Definition 3.2, we define the notion of highest
$D_{[0,1]}^{(k)}(\Pi ) := D_{Z_\rho [0,1]}^{(k)}(\Pi )$. Similar to Definition 3.2, we define the notion of highest ![]() $[0,-1]$-derivative (respectively highest
$[0,-1]$-derivative (respectively highest ![]() $[0,1]$-derivative) and the property of being
$[0,1]$-derivative) and the property of being ![]() $\Delta _\rho [0,-1]$-reduced (respectively
$\Delta _\rho [0,-1]$-reduced (respectively ![]() $Z_\rho [0,1]$-reduced).
$Z_\rho [0,1]$-reduced).
Lemma 3.5 Fix ![]() $\rho \in \mathscr {C}(\mathrm {GL}_d(F))$ and
$\rho \in \mathscr {C}(\mathrm {GL}_d(F))$ and ![]() $\epsilon \in \{\pm 1\}$. Let
$\epsilon \in \{\pm 1\}$. Let ![]() $\pi \in \mathrm {Irr}(G_n)$. Suppose that
$\pi \in \mathrm {Irr}(G_n)$. Suppose that ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^{\epsilon }$-reduced. Let
$\rho |\cdot |^{\epsilon }$-reduced. Let ![]() $D_{\rho }^{(k_0)}(\pi ) = m \cdot \pi _0$ be the highest
$D_{\rho }^{(k_0)}(\pi ) = m \cdot \pi _0$ be the highest ![]() $\rho$-derivative of
$\rho$-derivative of ![]() $\pi$ (with multiplicity
$\pi$ (with multiplicity ![]() $m > 0$) and let
$m > 0$) and let ![]() $\pi _1 = D_{\rho |\cdot |^{\epsilon }}^{(k_1)}(\pi _0)$ be the highest
$\pi _1 = D_{\rho |\cdot |^{\epsilon }}^{(k_1)}(\pi _0)$ be the highest ![]() $\rho |\cdot |^{\epsilon }$-derivative of
$\rho |\cdot |^{\epsilon }$-derivative of ![]() $\pi _0$. Then the following hold:
$\pi _0$. Then the following hold:
(1)
 $k_0 \geq k_1$;
$k_0 \geq k_1$;(2)
 $D_{[0,\epsilon ]}^{(k_1)}(\pi )$ is the highest
$D_{[0,\epsilon ]}^{(k_1)}(\pi )$ is the highest  $[0,\epsilon ]$-derivative;
$[0,\epsilon ]$-derivative;(3)
 $D_{[0,\epsilon ]}^{(k_1)}(\pi )$ is
$D_{[0,\epsilon ]}^{(k_1)}(\pi )$ is  $\rho |\cdot |^{\epsilon }$-reduced.
$\rho |\cdot |^{\epsilon }$-reduced.
Proof. Note that ![]() $\pi \hookrightarrow \rho ^{k_0} \times (\rho |\cdot |^{\epsilon })^{k_1} \rtimes \pi _1$. If
$\pi \hookrightarrow \rho ^{k_0} \times (\rho |\cdot |^{\epsilon })^{k_1} \rtimes \pi _1$. If ![]() $k_1 > k_0$, then no irreducible subquotient of
$k_1 > k_0$, then no irreducible subquotient of ![]() $\rho ^{k_0} \times (\rho |\cdot |^{\epsilon })^{k_1}$ is left
$\rho ^{k_0} \times (\rho |\cdot |^{\epsilon })^{k_1}$ is left ![]() $\rho |\cdot |^{\epsilon }$-reduced. Since
$\rho |\cdot |^{\epsilon }$-reduced. Since ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^{\epsilon }$-reduced, we must have
$\rho |\cdot |^{\epsilon }$-reduced, we must have ![]() $k_0 \geq k_1$ and
$k_0 \geq k_1$ and
 \[ \pi \hookrightarrow \begin{cases} Z_\rho[0,1]^{k_1} \times \rho^{k_0-k_1} \rtimes \pi_1 & \text{if } \epsilon = 1, \\ \Delta_\rho[0,-1]^{k_1} \times \rho^{k_0-k_1} \rtimes \pi_1 & \text{if } \epsilon = -1. \end{cases} \]
\[ \pi \hookrightarrow \begin{cases} Z_\rho[0,1]^{k_1} \times \rho^{k_0-k_1} \rtimes \pi_1 & \text{if } \epsilon = 1, \\ \Delta_\rho[0,-1]^{k_1} \times \rho^{k_0-k_1} \rtimes \pi_1 & \text{if } \epsilon = -1. \end{cases} \]
Now we claim that ![]() $\pi _1$ is
$\pi _1$ is ![]() $\rho$-reduced. This is trivial when
$\rho$-reduced. This is trivial when ![]() $k_1 = 0$. If
$k_1 = 0$. If ![]() $k_1 > 0$ and
$k_1 > 0$ and ![]() $\pi _1$ is not
$\pi _1$ is not ![]() $\rho$-reduced, since
$\rho$-reduced, since ![]() $\pi _0$ is
$\pi _0$ is ![]() $\rho$-reduced, we can find a representation
$\rho$-reduced, we can find a representation ![]() $\pi _1' \not = 0$ such that
$\pi _1' \not = 0$ such that
 \[ \pi_0 \hookrightarrow \begin{cases} \Delta_\rho[1,0] \rtimes \pi_1' & \text{if } \epsilon = 1, \\ Z_\rho[-1,0] \rtimes \pi_1' & \text{if } \epsilon = -1. \end{cases} \]
\[ \pi_0 \hookrightarrow \begin{cases} \Delta_\rho[1,0] \rtimes \pi_1' & \text{if } \epsilon = 1, \\ Z_\rho[-1,0] \rtimes \pi_1' & \text{if } \epsilon = -1. \end{cases} \]
Since ![]() $\pi \hookrightarrow \rho ^{k_0} \rtimes \pi _0$, this implies that
$\pi \hookrightarrow \rho ^{k_0} \rtimes \pi _0$, this implies that ![]() $D_{\rho |\cdot |^{\epsilon }}^{(1)}(\pi ) \not = 0$, which is a contradiction, so we obtain the claim.
$D_{\rho |\cdot |^{\epsilon }}^{(1)}(\pi ) \not = 0$, which is a contradiction, so we obtain the claim.
Since ![]() $\pi _1$ is
$\pi _1$ is ![]() $\rho$-reduced and
$\rho$-reduced and ![]() $\rho |\cdot |^{\epsilon }$-reduced, we see that
$\rho |\cdot |^{\epsilon }$-reduced, we see that ![]() $D_{[0,\epsilon ]}^{(1)}(\rho ^{k_0-k_1} \rtimes \pi _1) = 0$ by Tadić's formula (Proposition 2.1). Hence
$D_{[0,\epsilon ]}^{(1)}(\rho ^{k_0-k_1} \rtimes \pi _1) = 0$ by Tadić's formula (Proposition 2.1). Hence ![]() $D_{[0,\epsilon ]}^{(k_1)}(\pi )$ is the highest
$D_{[0,\epsilon ]}^{(k_1)}(\pi )$ is the highest ![]() $[0,\epsilon ]$-derivative. Since it is a subrepresentation of
$[0,\epsilon ]$-derivative. Since it is a subrepresentation of ![]() $[\rho ^{k_0-k_1} \rtimes \pi _1]$, we see that
$[\rho ^{k_0-k_1} \rtimes \pi _1]$, we see that ![]() $D_{[0, \epsilon ]}^{(k_1)}(\pi )$ is
$D_{[0, \epsilon ]}^{(k_1)}(\pi )$ is ![]() $\rho |\cdot |^{\epsilon }$-reduced.
$\rho |\cdot |^{\epsilon }$-reduced.
In the next proposition, we will use the following simple lemma on representations of general linear groups.
Lemma 3.6 Let ![]() $k>0$ and let
$k>0$ and let ![]() $\tau \in \mathrm {Rep}(\mathrm {GL}_{2dk}(F))$. Suppose that
$\tau \in \mathrm {Rep}(\mathrm {GL}_{2dk}(F))$. Suppose that
•
 $\tau$ is left
$\tau$ is left  $\rho |\cdot |^{-1}$-reduced (respectively left
$\rho |\cdot |^{-1}$-reduced (respectively left  $\rho |\cdot |^1$-reduced);
$\rho |\cdot |^1$-reduced);•
 $[\tau ]$ contains
$[\tau ]$ contains  $\Delta _\rho [0,-1]^k$ (respectively
$\Delta _\rho [0,-1]^k$ (respectively  $Z_\rho [0,1]^k$).
$Z_\rho [0,1]^k$).
Then there is a surjection ![]() $\tau \twoheadrightarrow \Delta _\rho [0,-1]^k$ (respectively
$\tau \twoheadrightarrow \Delta _\rho [0,-1]^k$ (respectively ![]() $\tau \twoheadrightarrow Z_\rho [0,1]^k$).
$\tau \twoheadrightarrow Z_\rho [0,1]^k$).
Proof. We may assume that all irreducible constituents of ![]() $\tau$ have the same supercuspidal support. They are all left
$\tau$ have the same supercuspidal support. They are all left ![]() $\rho |\cdot |^{-1}$-reduced (respectively left
$\rho |\cdot |^{-1}$-reduced (respectively left ![]() $\rho |\cdot |^1$-reduced), as is
$\rho |\cdot |^1$-reduced), as is ![]() $\tau$. By [Reference ZelevinskyZel80, Example 11.3], the irreducible representations of
$\tau$. By [Reference ZelevinskyZel80, Example 11.3], the irreducible representations of ![]() $\mathrm {GL}_{2dk}(F)$ which have the same supercuspidal support as
$\mathrm {GL}_{2dk}(F)$ which have the same supercuspidal support as ![]() $\Delta _\rho [0,-1]^k$ (respectively
$\Delta _\rho [0,-1]^k$ (respectively ![]() $Z_\rho [0,1]^k$) are of the form
$Z_\rho [0,1]^k$) are of the form ![]() $\Delta _\rho [0,-1]^a \times Z_\rho [-1,0]^b$ (respectively
$\Delta _\rho [0,-1]^a \times Z_\rho [-1,0]^b$ (respectively ![]() $\Delta _\rho [1,0]^a \times Z_\rho [0,1]^b$) for some
$\Delta _\rho [1,0]^a \times Z_\rho [0,1]^b$) for some ![]() $a,b \geq 0$ with
$a,b \geq 0$ with ![]() $a+b = k$. Among them,
$a+b = k$. Among them, ![]() $\Delta _\rho [0,-1]^k$ (respectively
$\Delta _\rho [0,-1]^k$ (respectively ![]() $Z_\rho [0,1]^k$) is characterized as the only left
$Z_\rho [0,1]^k$) is characterized as the only left ![]() $\rho |\cdot |^{-1}$-reduced (respectively left
$\rho |\cdot |^{-1}$-reduced (respectively left ![]() $\rho |\cdot |^1$-reduced) representation. Therefore, we have
$\rho |\cdot |^1$-reduced) representation. Therefore, we have ![]() $\tau \twoheadrightarrow \Delta _\rho [0,-1]^k$ (respectively
$\tau \twoheadrightarrow \Delta _\rho [0,-1]^k$ (respectively ![]() $\tau \twoheadrightarrow Z_\rho [0,1]^k$).
$\tau \twoheadrightarrow Z_\rho [0,1]^k$).
Now we can prove the irreducibility of the highest ![]() $[0,\pm 1]$-derivatives of
$[0,\pm 1]$-derivatives of ![]() $\rho |\cdot |^{\pm 1}$-reduced irreducible representations.
$\rho |\cdot |^{\pm 1}$-reduced irreducible representations.
Proposition 3.7 Let ![]() $\pi \in \mathrm {Irr}(G_n)$. Suppose that
$\pi \in \mathrm {Irr}(G_n)$. Suppose that ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^{-1}$-reduced (respectively
$\rho |\cdot |^{-1}$-reduced (respectively ![]() $\rho |\cdot |^1$-reduced). Then the highest
$\rho |\cdot |^1$-reduced). Then the highest ![]() $[0,-1]$-derivative
$[0,-1]$-derivative ![]() $D_{[0,-1]}^{(k)}(\pi )$ (respectively the highest
$D_{[0,-1]}^{(k)}(\pi )$ (respectively the highest ![]() $[0,1]$-derivative
$[0,1]$-derivative ![]() $D_{[0,1]}^{(k)}(\pi )$) is irreducible. Moreover,
$D_{[0,1]}^{(k)}(\pi )$) is irreducible. Moreover, ![]() $\Delta _\rho [0,-1]^r \rtimes \pi$ (respectively
$\Delta _\rho [0,-1]^r \rtimes \pi$ (respectively ![]() $Z_\rho [0,1]^r \rtimes \pi$) is SI.
$Z_\rho [0,1]^r \rtimes \pi$) is SI.
Proof. We prove the assertions only for ![]() $[0,1]$. By the previous lemma, there exists an irreducible subrepresentation of
$[0,1]$. By the previous lemma, there exists an irreducible subrepresentation of ![]() $\pi _{[0,1]}$ of the highest
$\pi _{[0,1]}$ of the highest ![]() $[0,1]$-derivative
$[0,1]$-derivative ![]() $D_{[0,1]}^{(k)}(\pi )$ such that
$D_{[0,1]}^{(k)}(\pi )$ such that
or, equivalently,
Since ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^1$-reduced, so is
$\rho |\cdot |^1$-reduced, so is ![]() $\pi _0$. Hence, by Tadić's formula (Proposition 2.1) for
$\pi _0$. Hence, by Tadić's formula (Proposition 2.1) for
we see that
Therefore, ![]() $0 \not = D_{[0,1]}^{(k)}(\pi ) \subset \pi _0$ so that
$0 \not = D_{[0,1]}^{(k)}(\pi ) \subset \pi _0$ so that ![]() $D_{[0,1]}^{(k)}(\pi ) = \pi _0$. Moreover, this implies that
$D_{[0,1]}^{(k)}(\pi ) = \pi _0$. Moreover, this implies that ![]() $Z_\rho [0,1]^k \rtimes \pi _0$ is SI.
$Z_\rho [0,1]^k \rtimes \pi _0$ is SI.
When ![]() $\pi '$ is an irreducible subrepresentation of
$\pi '$ is an irreducible subrepresentation of ![]() $Z_\rho [0,1]^r \rtimes \pi$, we have
$Z_\rho [0,1]^r \rtimes \pi$, we have ![]() $\pi ' \subset \mathrm {soc}(Z_\rho [0,1]^{k+r} \rtimes \pi _0)$. In particular,
$\pi ' \subset \mathrm {soc}(Z_\rho [0,1]^{k+r} \rtimes \pi _0)$. In particular, ![]() $\pi '$ is unique and appears with multiplicity one in
$\pi '$ is unique and appears with multiplicity one in ![]() $[Z_\rho [0,1]^{k+r} \rtimes \pi _0]$ and hence in
$[Z_\rho [0,1]^{k+r} \rtimes \pi _0]$ and hence in ![]() $[Z_\rho [0,1]^r \rtimes \pi ]$. Therefore,
$[Z_\rho [0,1]^r \rtimes \pi ]$. Therefore, ![]() $Z_\rho [0,1]^r \rtimes \pi$ is SI.
$Z_\rho [0,1]^r \rtimes \pi$ is SI.
For simplicity, we set
for an irreducible representation ![]() $\pi$ of
$\pi$ of ![]() $G_n$ which is
$G_n$ which is ![]() $\rho |\cdot |^1$-reduced.
$\rho |\cdot |^1$-reduced.
The highest ![]() $[0,-1]$-derivatives are easy in a special case.
$[0,-1]$-derivatives are easy in a special case.
Proposition 3.8 Let ![]() $\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ be an irreducible representation of
$\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ be an irreducible representation of ![]() $G_n$. Suppose that
$G_n$. Suppose that ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^z$-reduced for all
$\rho |\cdot |^z$-reduced for all ![]() $z \not = 0$ and that there exists
$z \not = 0$ and that there exists ![]() $i \in \{1, \ldots, r\}$ such that
$i \in \{1, \ldots, r\}$ such that ![]() $\rho _i \cong \rho$. Then
$\rho _i \cong \rho$. Then ![]() $\min \{x_i \mid \rho _i \cong \rho \} = 0$, and the highest
$\min \{x_i \mid \rho _i \cong \rho \} = 0$, and the highest ![]() $[0,-1]$-derivative
$[0,-1]$-derivative ![]() $D_{[0,-1]}^{(k)}(\pi )$ of
$D_{[0,-1]}^{(k)}(\pi )$ of ![]() $\pi$ is given by
$\pi$ is given by
with
 \[ z_i = \begin{cases} -2 & \text{if } \rho_i \cong \rho, \, x_i = 0, \\ x_i & \text{otherwise}. \end{cases} \]
\[ z_i = \begin{cases} -2 & \text{if } \rho_i \cong \rho, \, x_i = 0, \\ x_i & \text{otherwise}. \end{cases} \]
In particular,
Proof. With ![]() $x := \min \{x_i \mid \rho _i \cong \rho \}$, we see that
$x := \min \{x_i \mid \rho _i \cong \rho \}$, we see that ![]() $\pi$ is not
$\pi$ is not ![]() $\rho |\cdot |^x$-reduced. Hence we must have
$\rho |\cdot |^x$-reduced. Hence we must have ![]() $x = 0$. Moreover, we note that if
$x = 0$. Moreover, we note that if ![]() $\rho _i \cong \rho$ and
$\rho _i \cong \rho$ and ![]() $x_i = 0$, then
$x_i = 0$, then ![]() $y_i \leq -1$ since
$y_i \leq -1$ since ![]() $x_i+y_i < 0$.
$x_i+y_i < 0$.
We remark that ![]() $D_\rho ^{(l)}(\pi _\mathrm {temp})$ is tempered since
$D_\rho ^{(l)}(\pi _\mathrm {temp})$ is tempered since ![]() $\rho$ is self-dual (see [Reference AtobeAto20, Theorem 4.2(1) and (4)]), so
$\rho$ is self-dual (see [Reference AtobeAto20, Theorem 4.2(1) and (4)]), so ![]() $D_\rho ^{(l)}(\pi _\mathrm {temp})$ is
$D_\rho ^{(l)}(\pi _\mathrm {temp})$ is ![]() $\rho |\cdot |^{-1}$-reduced by Casselman's criterion (see e.g. [Reference KonnoKon03, Lemma 2.4]). Hence by Lemma 3.5, with
$\rho |\cdot |^{-1}$-reduced by Casselman's criterion (see e.g. [Reference KonnoKon03, Lemma 2.4]). Hence by Lemma 3.5, with ![]() $k$ as in the statement,
$k$ as in the statement, ![]() $D_{[0,-1]}^{(k)}(\pi )$ is the highest
$D_{[0,-1]}^{(k)}(\pi )$ is the highest ![]() $[0,-1]$-derivative.
$[0,-1]$-derivative.
Set ![]() $\tau := L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r])$. Then
$\tau := L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r])$. Then ![]() $\pi \hookrightarrow \tau \rtimes \pi _\mathrm {temp}$. Since
$\pi \hookrightarrow \tau \rtimes \pi _\mathrm {temp}$. Since ![]() $\min \{x_i \mid \rho _i \cong \rho \} = 0$ and
$\min \{x_i \mid \rho _i \cong \rho \} = 0$ and ![]() $y_i < 0$, we see that
$y_i < 0$, we see that ![]() $\tau \hookrightarrow \Delta _{\rho }[0,-1]^k \times \tau '$ with
$\tau \hookrightarrow \Delta _{\rho }[0,-1]^k \times \tau '$ with ![]() $\tau ' := L(\Delta _{\rho _1}[z_1,y_1], \ldots, \Delta _{\rho _r}[z_r,y_r])$. Hence
$\tau ' := L(\Delta _{\rho _1}[z_1,y_1], \ldots, \Delta _{\rho _r}[z_r,y_r])$. Hence
By the Frobenius reciprocity, we have a non-zero map
which must factor through a non-zero map
Since ![]() $D_{[0,-1]}^{(k)}(\pi )$ is irreducible by Proposition 3.7 and since
$D_{[0,-1]}^{(k)}(\pi )$ is irreducible by Proposition 3.7 and since ![]() $\tau ' \rtimes \pi _\mathrm {temp}$ is SI, we deduce that
$\tau ' \rtimes \pi _\mathrm {temp}$ is SI, we deduce that
This completes the proof.
3.5 The Zelevinsky–Aubert duality and derivatives
We deduce the following compatibility between derivatives and duality.
Proposition 3.9 Let ![]() $\pi \in \mathrm {Irr}(G_n)$ and
$\pi \in \mathrm {Irr}(G_n)$ and ![]() $\rho \in \mathscr {C}(\mathrm {GL}_d(F))$.
$\rho \in \mathscr {C}(\mathrm {GL}_d(F))$.
(1) If
 $D_{\rho }^{(k)}(\pi )$ is the highest
$D_{\rho }^{(k)}(\pi )$ is the highest  $\rho$-derivative, then
$\rho$-derivative, then
 \[ D_{\rho}^{(k)}(\pi){\widehat{\;}} = D_{\rho^\vee}^{(k)}(\hat\pi). \]
\[ D_{\rho}^{(k)}(\pi){\widehat{\;}} = D_{\rho^\vee}^{(k)}(\hat\pi). \]
(2) If
 $\rho$ is self-dual,
$\rho$ is self-dual,  $\pi$ is
$\pi$ is  $\rho |\cdot |^{-1}$-reduced and
$\rho |\cdot |^{-1}$-reduced and  $D_{\Delta _\rho [0,-1]}^{(k)}(\pi )$ is the highest
$D_{\Delta _\rho [0,-1]}^{(k)}(\pi )$ is the highest  $\Delta _\rho [0,-1]$-derivative, then
$\Delta _\rho [0,-1]$-derivative, then
 \[ D_{\Delta_\rho[0,-1]}^{(k)}(\pi){\widehat{\;}} = D_{Z_\rho[0,1]}^{(k)}(\hat\pi). \]
\[ D_{\Delta_\rho[0,-1]}^{(k)}(\pi){\widehat{\;}} = D_{Z_\rho[0,1]}^{(k)}(\hat\pi). \]
Proof. This is a consequence of the commutativity of the Jacquet functor with the duality; see (2.2).
4. The algorithm
In this section we give an algorithm for computing the Zelevinsky–Aubert dual of an irreducible representation ![]() $\pi$. Thanks to Jantzen's decomposition (see § 2.5), we can reduce
$\pi$. Thanks to Jantzen's decomposition (see § 2.5), we can reduce ![]() $\pi$ to the case where
$\pi$ to the case where ![]() $\pi$ is either ugly or of good or bad parity. Then we proceed as follows.
$\pi$ is either ugly or of good or bad parity. Then we proceed as follows.
Remark 4.1 Assume that we can compute ![]() $\hat \pi _0$ for all irreducible representations of
$\hat \pi _0$ for all irreducible representations of ![]() $G_{n_0}$ for
$G_{n_0}$ for ![]() $n_0 < n$. Let
$n_0 < n$. Let ![]() $\pi$ be an irreducible representation of
$\pi$ be an irreducible representation of ![]() $G_n$.
$G_n$.
(1) If there exists
 $\rho \in \mathscr {C}^\mathrm {GL}$ such that
$\rho \in \mathscr {C}^\mathrm {GL}$ such that  $\rho$ is not self-dual and such that
$\rho$ is not self-dual and such that  $D_{\rho }^{(k)}(\pi )$ is the highest
$D_{\rho }^{(k)}(\pi )$ is the highest  $\rho$-derivative with
$\rho$-derivative with  $k \geq 1$, then
$k \geq 1$, then
 \[ \hat\pi = S_{\rho^\vee}^{(k)}\bigl( D_{\rho}^{(k)}(\pi){\widehat{\;}} \bigr). \]
\[ \hat\pi = S_{\rho^\vee}^{(k)}\bigl( D_{\rho}^{(k)}(\pi){\widehat{\;}} \bigr). \]
(2) Otherwise, and if
 $\pi$ is not tempered, one can find
$\pi$ is not tempered, one can find  $\rho \in \mathscr {C}^\mathrm {GL}$ such that
$\rho \in \mathscr {C}^\mathrm {GL}$ such that  $\rho$ is self-dual and
$\rho$ is self-dual and  $D_{\Delta _\rho [0,-1]}^{(k)}(\pi )$ is the highest
$D_{\Delta _\rho [0,-1]}^{(k)}(\pi )$ is the highest  $\Delta _\rho [0,-1]$-derivative with
$\Delta _\rho [0,-1]$-derivative with  $k \geq 1$. Then
$k \geq 1$. Then
 \[ \hat\pi = S_{Z_\rho[0,1]}^{(k)}\bigl( D_{\Delta_\rho[0,-1]}^{(k)}(\pi){\widehat{\;}} \bigr). \]
\[ \hat\pi = S_{Z_\rho[0,1]}^{(k)}\bigl( D_{\Delta_\rho[0,-1]}^{(k)}(\pi){\widehat{\;}} \bigr). \]
(3) Otherwise, and if
 $\pi$ is tempered, one can use an explicit formula for
$\pi$ is tempered, one can use an explicit formula for  $\hat \pi$ (Proposition 5.4 below).
$\hat \pi$ (Proposition 5.4 below).
In order to run the algorithm, we need the following formulas.
• Explicit formulas for the highest
 $\rho$-derivative
$\rho$-derivative  $D_{\rho }^{(k)}(\pi )$ and for the socle
$D_{\rho }^{(k)}(\pi )$ and for the socle  $S_{\rho }^{(k)}(\pi )$ for any
$S_{\rho }^{(k)}(\pi )$ for any  $\rho \in \mathscr {C}^\mathrm {GL}$ which is not self-dual: these are given in Proposition 6.1 if
$\rho \in \mathscr {C}^\mathrm {GL}$ which is not self-dual: these are given in Proposition 6.1 if  $\rho$ is ugly or if the exponent of
$\rho$ is ugly or if the exponent of  $\rho$ is negative, and in Theorem 7.1 (respectively Theorem 7.4) if the exponent of
$\rho$ is negative, and in Theorem 7.1 (respectively Theorem 7.4) if the exponent of  $\rho$ is positive and
$\rho$ is positive and  $\rho$ is in the good (respectively bad) case.
$\rho$ is in the good (respectively bad) case.• Explicit formulas for the
 $\Delta _\rho [0,-1]$-derivative
$\Delta _\rho [0,-1]$-derivative  $D_{\Delta _\rho [0,-1]}^{(k)}(\pi )$ and the socle
$D_{\Delta _\rho [0,-1]}^{(k)}(\pi )$ and the socle  $S_{Z_\rho [0,1]}^{(k)}(\pi )$ when
$S_{Z_\rho [0,1]}^{(k)}(\pi )$ when  $\rho$ is self-dual and
$\rho$ is self-dual and  $\pi$ is non-tempered and
$\pi$ is non-tempered and  $\rho |\cdot |^z$-reduced for all
$\rho |\cdot |^z$-reduced for all  $z \not = 0$: these are established in Proposition 3.8 for the
$z \not = 0$: these are established in Proposition 3.8 for the  $\Delta _\rho [0,-1]$-derivative and in Theorem 8.1 for the socle, respectively.
$\Delta _\rho [0,-1]$-derivative and in Theorem 8.1 for the socle, respectively.• An explicit formula for
 $\hat \pi$ when
$\hat \pi$ when  $\pi$ is tempered such that
$\pi$ is tempered such that  $\pi$ is
$\pi$ is  $\rho |\cdot |^z$-reduced for all
$\rho |\cdot |^z$-reduced for all  $z \not = 0$: this is given in Proposition 5.4.
$z \not = 0$: this is given in Proposition 5.4.
In the rest of the paper, we will prove all these formulas.
5. The endoscopic classification
In §§ 7.1 and 8.3 below, we will give explicit formulas for several derivatives and socles in the good-parity case. In these formulas, certain special irreducible representations ![]() $\pi _A$ play an important and mysterious role. These special representations
$\pi _A$ play an important and mysterious role. These special representations ![]() $\pi _A$ are of Arthur type, and the mystery comes from Arthur's theory of the endoscopic classification [Reference ArthurArt13]. In this section, we review his theory.
$\pi _A$ are of Arthur type, and the mystery comes from Arthur's theory of the endoscopic classification [Reference ArthurArt13]. In this section, we review his theory.
5.1  $A$-parameters
$A$-parameters
We denote by ![]() $W_F$ the Weil group of
$W_F$ the Weil group of ![]() $F$. A homomorphism
$F$. A homomorphism
is called an ![]() $A$-parameter for
$A$-parameter for ![]() $\mathrm {GL}_n(F)$ if
$\mathrm {GL}_n(F)$ if
•
 $\psi (\mathrm {Frob}) \in \mathrm {GL}_n(\mathbb {C})$ is semisimple and all its eigenvalues have absolute value
$\psi (\mathrm {Frob}) \in \mathrm {GL}_n(\mathbb {C})$ is semisimple and all its eigenvalues have absolute value  $1$, where
$1$, where  $\mathrm {Frob}$ is a fixed (geometric) Frobenius element;
$\mathrm {Frob}$ is a fixed (geometric) Frobenius element;•
 $\psi |W_F$ is smooth, i.e. has an open kernel;
$\psi |W_F$ is smooth, i.e. has an open kernel;•
 $\psi |\mathrm {SL}_2(\mathbb {C}) \times \mathrm {SL}_2(\mathbb {C})$ is algebraic.
$\psi |\mathrm {SL}_2(\mathbb {C}) \times \mathrm {SL}_2(\mathbb {C})$ is algebraic.
The local Langlands correspondence for ![]() $\mathrm {GL}_d(F)$ asserts that there is a canonical bijection between the set of irreducible unitary supercuspidal representations of
$\mathrm {GL}_d(F)$ asserts that there is a canonical bijection between the set of irreducible unitary supercuspidal representations of ![]() $\mathrm {GL}_d(F)$ and the set of irreducible
$\mathrm {GL}_d(F)$ and the set of irreducible ![]() $d$-dimensional representations of
$d$-dimensional representations of ![]() $W_F$ of bounded image. We identify these two sets and use the symbol
$W_F$ of bounded image. We identify these two sets and use the symbol ![]() $\rho$ for their elements.
$\rho$ for their elements.
Any such irreducible representation of ![]() $W_F \times \mathrm {SL}_2(\mathbb {C}) \times \mathrm {SL}_2(\mathbb {C})$ is of the form
$W_F \times \mathrm {SL}_2(\mathbb {C}) \times \mathrm {SL}_2(\mathbb {C})$ is of the form ![]() $\rho \boxtimes S_a \boxtimes S_b$, where
$\rho \boxtimes S_a \boxtimes S_b$, where ![]() $S_a$ is the unique irreducible algebraic representation of
$S_a$ is the unique irreducible algebraic representation of ![]() $\mathrm {SL}_2(\mathbb {C})$ of dimension
$\mathrm {SL}_2(\mathbb {C})$ of dimension ![]() $a$. We write
$a$. We write ![]() $\rho \boxtimes S_a = \rho \boxtimes S_a \boxtimes S_1$ and
$\rho \boxtimes S_a = \rho \boxtimes S_a \boxtimes S_1$ and ![]() $\rho = \rho \boxtimes S_1 \boxtimes S_1$ for short. For an
$\rho = \rho \boxtimes S_1 \boxtimes S_1$ for short. For an ![]() $A$-parameter
$A$-parameter ![]() $\psi$, the multiplicity of
$\psi$, the multiplicity of ![]() $\rho \boxtimes S_a \boxtimes S_b$ in
$\rho \boxtimes S_a \boxtimes S_b$ in ![]() $\psi$ is denoted by
$\psi$ is denoted by ![]() $m_\psi (\rho \boxtimes S_a \boxtimes S_b)$. When
$m_\psi (\rho \boxtimes S_a \boxtimes S_b)$. When ![]() $\psi = \bigoplus _{i \in I} \rho _i \boxtimes S_{a_i} \boxtimes S_{b_i}$ is an
$\psi = \bigoplus _{i \in I} \rho _i \boxtimes S_{a_i} \boxtimes S_{b_i}$ is an ![]() $A$-parameter of
$A$-parameter of ![]() $\mathrm {GL}_n(F)$, we define
$\mathrm {GL}_n(F)$, we define ![]() $\tau _\psi$ by the product of Speh representations (see § 2.3)
$\tau _\psi$ by the product of Speh representations (see § 2.3)
Now we consider a split odd special orthogonal group ![]() $\mathrm {SO}_{2n+1}(F)$ or a symplectic group
$\mathrm {SO}_{2n+1}(F)$ or a symplectic group ![]() $\mathrm {Sp}_{2n}(F)$. We call
$\mathrm {Sp}_{2n}(F)$. We call ![]() $\psi$ an
$\psi$ an ![]() $A$-parameter for
$A$-parameter for ![]() $\mathrm {SO}_{2n+1}(F)$ if it is an
$\mathrm {SO}_{2n+1}(F)$ if it is an ![]() $A$-parameter for
$A$-parameter for ![]() $\mathrm {GL}_{2n}(F)$ of symplectic type, i.e.
$\mathrm {GL}_{2n}(F)$ of symplectic type, i.e.
Similarly, ![]() $\psi$ is called an
$\psi$ is called an ![]() $A$-parameter for
$A$-parameter for ![]() $\mathrm {Sp}_{2n}(F)$ if it is an
$\mathrm {Sp}_{2n}(F)$ if it is an ![]() $A$-parameter for
$A$-parameter for ![]() $\mathrm {GL}_{2n+1}(F)$ of orthogonal type with the trivial determinant, i.e.
$\mathrm {GL}_{2n+1}(F)$ of orthogonal type with the trivial determinant, i.e.
For ![]() $G_n = \mathrm {SO}_{2n+1}(F)$ (respectively
$G_n = \mathrm {SO}_{2n+1}(F)$ (respectively ![]() $G_n = \mathrm {Sp}_{2n}(F)$), we let
$G_n = \mathrm {Sp}_{2n}(F)$), we let ![]() $\Psi (G_n)$ be the set of
$\Psi (G_n)$ be the set of ![]() $\widehat {G_n}$-conjugacy classes of
$\widehat {G_n}$-conjugacy classes of ![]() $A$-parameters for
$A$-parameters for ![]() $G_n$, where
$G_n$, where ![]() $\widehat {G_n} = \mathrm {Sp}_{2n}(\mathbb {C})$ (respectively
$\widehat {G_n} = \mathrm {Sp}_{2n}(\mathbb {C})$ (respectively ![]() $\widehat {G_n} = \mathrm {SO}_{2n+1}(\mathbb {C})$). We say that
$\widehat {G_n} = \mathrm {SO}_{2n+1}(\mathbb {C})$). We say that
•
 $\psi \in \Psi (G_n)$ is tempered if the restriction of
$\psi \in \Psi (G_n)$ is tempered if the restriction of  $\psi$ to the second
$\psi$ to the second  $\mathrm {SL}_2(\mathbb {C})$ is trivial;
$\mathrm {SL}_2(\mathbb {C})$ is trivial;•
 $\psi \in \Psi (G_n)$ is of good parity if
$\psi \in \Psi (G_n)$ is of good parity if  $\psi$ is a sum of irreducible self-dual representations of the same type as
$\psi$ is a sum of irreducible self-dual representations of the same type as  $\psi$.
$\psi$.
We denote by ![]() $\Psi _\mathrm {temp}(G_n) := \Phi _\mathrm {temp}(G_n)$ (respectively
$\Psi _\mathrm {temp}(G_n) := \Phi _\mathrm {temp}(G_n)$ (respectively ![]() $\Psi _\mathrm {gp}(G_n)$) the subset of
$\Psi _\mathrm {gp}(G_n)$) the subset of ![]() $\Psi (G_n)$ consisting of tempered
$\Psi (G_n)$ consisting of tempered ![]() $A$-parameters (respectively
$A$-parameters (respectively ![]() $A$-parameters of good parity). Also, we put
$A$-parameters of good parity). Also, we put ![]() $\Phi _\mathrm {gp}(G_n) := \Phi _\mathrm {temp}(G_n) \cap \Psi _\mathrm {gp}(G_n)$. Set
$\Phi _\mathrm {gp}(G_n) := \Phi _\mathrm {temp}(G_n) \cap \Psi _\mathrm {gp}(G_n)$. Set ![]() $\Psi _*(G) := \bigcup _{n \geq 0}\Psi _*(G_n)$ and
$\Psi _*(G) := \bigcup _{n \geq 0}\Psi _*(G_n)$ and ![]() $\Phi _*(G) := \bigcup _{n \geq 0}\Phi _*(G_n)$ for
$\Phi _*(G) := \bigcup _{n \geq 0}\Phi _*(G_n)$ for ![]() $* \in \{\emptyset, \mathrm {temp}, \mathrm {gp}\}$.
$* \in \{\emptyset, \mathrm {temp}, \mathrm {gp}\}$.
For ![]() $\psi \in \Psi (G)$, a component group
$\psi \in \Psi (G)$, a component group ![]() $\mathcal {S}_\psi$ is defined. We recall the definition only in the case where
$\mathcal {S}_\psi$ is defined. We recall the definition only in the case where ![]() $\psi \in \Psi _\mathrm {gp}(G)$. Hence we can write
$\psi \in \Psi _\mathrm {gp}(G)$. Hence we can write ![]() $\psi = \bigoplus _{i=1}^{r} \psi _i$, where
$\psi = \bigoplus _{i=1}^{r} \psi _i$, where ![]() $\psi _i$ is an irreducible self-dual representation of the same type as
$\psi _i$ is an irreducible self-dual representation of the same type as ![]() $\psi$. We define an enhanced component group
$\psi$. We define an enhanced component group ![]() $\mathcal {A}_\psi$ as
$\mathcal {A}_\psi$ as
 \[ \mathcal{A}_\psi := \bigoplus_{i=1}^r \, (\mathbb{Z}/2\mathbb{Z})\alpha_{\psi_i}. \]
\[ \mathcal{A}_\psi := \bigoplus_{i=1}^r \, (\mathbb{Z}/2\mathbb{Z})\alpha_{\psi_i}. \]
Specifically, ![]() $\mathcal {A}_\psi$ is a free
$\mathcal {A}_\psi$ is a free ![]() $\mathbb {Z}/2\mathbb {Z}$-module of rank
$\mathbb {Z}/2\mathbb {Z}$-module of rank ![]() $r$ with a basis
$r$ with a basis ![]() $\{\alpha _{\psi _i}\}$ associated with the irreducible components
$\{\alpha _{\psi _i}\}$ associated with the irreducible components ![]() $\{\psi _i\}$. Define the component group
$\{\psi _i\}$. Define the component group ![]() $\mathcal {S}_\psi$ as the quotient of
$\mathcal {S}_\psi$ as the quotient of ![]() $\mathcal {A}_\psi$ by the subgroup generated by the elements
$\mathcal {A}_\psi$ by the subgroup generated by the elements
•
 $z_\psi := \sum _{i=1}^r \alpha _{\psi _i}$; and
$z_\psi := \sum _{i=1}^r \alpha _{\psi _i}$; and•
 $\alpha _{\psi _i} + \alpha _{\psi _{i'}}$ such that
$\alpha _{\psi _i} + \alpha _{\psi _{i'}}$ such that  $\psi _i \cong \psi _{i'}$.
$\psi _i \cong \psi _{i'}$.
Let ![]() $\widehat {\mathcal {S}_\psi }$ and
$\widehat {\mathcal {S}_\psi }$ and ![]() $\widehat {\mathcal {A}_\psi }$ be the Pontryagin duals of
$\widehat {\mathcal {A}_\psi }$ be the Pontryagin duals of ![]() $\mathcal {S}_\psi$ and
$\mathcal {S}_\psi$ and ![]() $\mathcal {A}_\psi$, respectively. Via the canonical surjection
$\mathcal {A}_\psi$, respectively. Via the canonical surjection ![]() $\mathcal {A}_\psi \twoheadrightarrow \mathcal {S}_\psi$, we may regard
$\mathcal {A}_\psi \twoheadrightarrow \mathcal {S}_\psi$, we may regard ![]() $\widehat {\mathcal {S}_\psi }$ as a subgroup of
$\widehat {\mathcal {S}_\psi }$ as a subgroup of ![]() $\widehat {\mathcal {A}_\psi }$. For
$\widehat {\mathcal {A}_\psi }$. For ![]() $\eta \in \widehat {\mathcal {A}_\psi }$, we write
$\eta \in \widehat {\mathcal {A}_\psi }$, we write ![]() $\eta (\alpha _{\psi _i}) = \eta (\psi _i)$.
$\eta (\alpha _{\psi _i}) = \eta (\psi _i)$.
Let ![]() $\mathrm {Irr}_\mathrm {unit}(G_n)$ (respectively
$\mathrm {Irr}_\mathrm {unit}(G_n)$ (respectively ![]() $\mathrm {Irr}_\mathrm {temp}(G_n)$) be the set of equivalence classes of irreducible unitary (respectively tempered) representations of
$\mathrm {Irr}_\mathrm {temp}(G_n)$) be the set of equivalence classes of irreducible unitary (respectively tempered) representations of ![]() $G_n$. For
$G_n$. For ![]() $\psi \in \Psi (G_n)$, Arthur [Reference ArthurArt13, Theorem 2.2.1] defined a multiset
$\psi \in \Psi (G_n)$, Arthur [Reference ArthurArt13, Theorem 2.2.1] defined a multiset ![]() $\Pi _\psi$ over
$\Pi _\psi$ over ![]() $\mathrm {Irr}_\mathrm {unit}(G_n)$, which is called the
$\mathrm {Irr}_\mathrm {unit}(G_n)$, which is called the ![]() $A$-packet for
$A$-packet for ![]() $G_n$ associated with
$G_n$ associated with ![]() $\psi$. It has the following properties.
$\psi$. It has the following properties.
• The multiset
 $\Pi _\psi$ is actually a (multiplicity-free) subset of
$\Pi _\psi$ is actually a (multiplicity-free) subset of  $\mathrm {Irr}_\mathrm {unit}(G_n)$ (Mœglin [Reference MœglinMœg11]).
$\mathrm {Irr}_\mathrm {unit}(G_n)$ (Mœglin [Reference MœglinMœg11]).• There exists a map
 $\Pi _\psi \rightarrow \widehat {\mathcal {S}_\psi }$,
$\Pi _\psi \rightarrow \widehat {\mathcal {S}_\psi }$,  $\pi \mapsto \left \langle \cdot \, ,\pi \right \rangle _\psi$. If
$\pi \mapsto \left \langle \cdot \, ,\pi \right \rangle _\psi$. If  $\phi \in \Phi _\mathrm {temp}(G)$, it is a bijection. When
$\phi \in \Phi _\mathrm {temp}(G)$, it is a bijection. When  $\pi \in \Pi _\phi$ corresponds to
$\pi \in \Pi _\phi$ corresponds to  $\eta \in \widehat {\mathcal {S}_\phi }$, we write
$\eta \in \widehat {\mathcal {S}_\phi }$, we write  $\pi = \pi (\phi, \eta )$.
$\pi = \pi (\phi, \eta )$.• There is a canonical decomposition into a disjoint union
 \[ \mathrm{Irr}_\mathrm{temp}(G_n) = \bigsqcup_{\phi \in \Phi_\mathrm{temp}(G_n)}\Pi_\phi. \]
\[ \mathrm{Irr}_\mathrm{temp}(G_n) = \bigsqcup_{\phi \in \Phi_\mathrm{temp}(G_n)}\Pi_\phi. \]
• If
 $\psi = \psi _1 \oplus \psi _0 \oplus \psi _1^\vee$ for some irreducible representation
$\psi = \psi _1 \oplus \psi _0 \oplus \psi _1^\vee$ for some irreducible representation  $\psi _1$, then there exists a canonical injection
$\psi _1$, then there exists a canonical injection  $\mathcal {S}_{\psi _0} \hookrightarrow \mathcal {S}_{\psi }$, and
for every
$\mathcal {S}_{\psi _0} \hookrightarrow \mathcal {S}_{\psi }$, and
for every \[ \tau_{\psi_1}
\rtimes \pi_0 \cong \bigoplus_{\substack{\pi \in \Pi_\psi \\
\left\langle \cdot\,, \pi
\right\rangle_\psi|\mathcal{S}_{\psi_0} = \left\langle
\cdot\,, \pi_0 \right\rangle_{\psi_0}}} \pi \]
\[ \tau_{\psi_1}
\rtimes \pi_0 \cong \bigoplus_{\substack{\pi \in \Pi_\psi \\
\left\langle \cdot\,, \pi
\right\rangle_\psi|\mathcal{S}_{\psi_0} = \left\langle
\cdot\,, \pi_0 \right\rangle_{\psi_0}}} \pi \]
 $\pi _0 \in \Pi _{\psi _0}$ (see [Reference ArthurArt13, Proposition 2.4.3]).
$\pi _0 \in \Pi _{\psi _0}$ (see [Reference ArthurArt13, Proposition 2.4.3]).
Remark 5.1 Let ![]() $\rho \in \mathscr {C}^\mathrm {GL}$ be unitary and
$\rho \in \mathscr {C}^\mathrm {GL}$ be unitary and ![]() $x \geq 0$ a real number. Then the following statements are equivalent.
$x \geq 0$ a real number. Then the following statements are equivalent.
(1) For any
 $\pi (\phi, \eta )$ with
$\pi (\phi, \eta )$ with  $\phi \in \Phi _\mathrm {gp}(G)$ and
$\phi \in \Phi _\mathrm {gp}(G)$ and  $\eta \in \widehat {\mathcal {S}_\phi }$, there exists
$\eta \in \widehat {\mathcal {S}_\phi }$, there exists  $m \in \mathbb {Z}$ such that
$m \in \mathbb {Z}$ such that  $\rho |\cdot |^{x+m} \rtimes \pi (\phi, \eta )$ is reducible.
$\rho |\cdot |^{x+m} \rtimes \pi (\phi, \eta )$ is reducible.(2) For some
 $\pi (\phi, \eta )$ with
$\pi (\phi, \eta )$ with  $\phi \in \Phi _\mathrm {gp}(G)$ and
$\phi \in \Phi _\mathrm {gp}(G)$ and  $\eta \in \widehat {\mathcal {S}_\phi }$, there exists
$\eta \in \widehat {\mathcal {S}_\phi }$, there exists  $m \in \mathbb {Z}$ such that
$m \in \mathbb {Z}$ such that  $\rho |\cdot |^{x+m} \rtimes \pi (\phi, \eta )$ is reducible.
$\rho |\cdot |^{x+m} \rtimes \pi (\phi, \eta )$ is reducible.(3) We have that
 $x \in (1/2)\mathbb {Z}$ and
$x \in (1/2)\mathbb {Z}$ and  $\rho \boxtimes S_{2x+1}$ is self-dual of the same type as elements of
$\rho \boxtimes S_{2x+1}$ is self-dual of the same type as elements of  $\Phi _\mathrm {gp}(G)$, i.e.
$\Phi _\mathrm {gp}(G)$, i.e.
•
 $x \in \mathbb {Z}$ and
$x \in \mathbb {Z}$ and  $\rho$ is self-dual of the same type as elements of
$\rho$ is self-dual of the same type as elements of  $\Phi _\mathrm {gp}(G)$; or
$\Phi _\mathrm {gp}(G)$; or•
 $x \in (1/2)\mathbb {Z} \!\setminus \! \mathbb {Z}$ and
$x \in (1/2)\mathbb {Z} \!\setminus \! \mathbb {Z}$ and  $\rho$ is self-dual of the opposite type to elements of
$\rho$ is self-dual of the opposite type to elements of  $\Phi _\mathrm {gp}(G)$.
$\Phi _\mathrm {gp}(G)$.
This follows, for example, from [Reference Mœglin and WaldspurgerMW12, Théorème (i)] and [Reference JantzenJan18b, Theorem 4.7]. In particular, ![]() $\rho |\cdot |^x$ is good in the sense of Definition 2.2 if and only if
$\rho |\cdot |^x$ is good in the sense of Definition 2.2 if and only if ![]() $\rho \boxtimes S_{2x+1}$ is self-dual of the same type as elements of
$\rho \boxtimes S_{2x+1}$ is self-dual of the same type as elements of ![]() $\Phi _\mathrm {gp}(G)$. Also, an irreducible representation
$\Phi _\mathrm {gp}(G)$. Also, an irreducible representation ![]() $\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ is of good parity if and only if
$\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ is of good parity if and only if ![]() $\pi _\mathrm {temp} = \pi (\phi, \eta )$ with
$\pi _\mathrm {temp} = \pi (\phi, \eta )$ with ![]() $\phi \in \Phi _\mathrm {gp}(G)$ and
$\phi \in \Phi _\mathrm {gp}(G)$ and ![]() $\rho _i \boxtimes S_{2|x_i|+1}$ is self-dual of the same type as
$\rho _i \boxtimes S_{2|x_i|+1}$ is self-dual of the same type as ![]() $\phi$ for all
$\phi$ for all ![]() $i = 1, \ldots, r$.
$i = 1, \ldots, r$.
5.2 A special example
Now we consider a special ![]() $A$-parameter of the form
$A$-parameter of the form
for ![]() $t \geq 1$,
$t \geq 1$, ![]() $\phi \in \Phi _\mathrm {gp}(G)$ and
$\phi \in \Phi _\mathrm {gp}(G)$ and ![]() $x \in (1/2)\mathbb {Z}$ with
$x \in (1/2)\mathbb {Z}$ with ![]() $x > 0$ such that
$x > 0$ such that ![]() $\rho \boxtimes S_{2x+1}$ is self-dual of the same type as
$\rho \boxtimes S_{2x+1}$ is self-dual of the same type as ![]() $\phi$.
$\phi$.
For ![]() $l \in \mathbb {Z}/2\mathbb {Z}$ and for
$l \in \mathbb {Z}/2\mathbb {Z}$ and for ![]() $\eta$ in a certain subset
$\eta$ in a certain subset ![]() $\widehat {\mathcal {S}_{\psi,l}}$ of
$\widehat {\mathcal {S}_{\psi,l}}$ of ![]() $\widehat {\mathcal {S}_\psi }$ (depending on
$\widehat {\mathcal {S}_\psi }$ (depending on ![]() $l$), we define
$l$), we define ![]() $\pi (\psi, l, \eta )$ as follows. When
$\pi (\psi, l, \eta )$ as follows. When ![]() $l = 1$, we set
$l = 1$, we set ![]() $\widehat {\mathcal {S}_{\psi,1}} := \widehat {\mathcal {S}_\phi } = \{ \eta \in \widehat {\mathcal {S}_\psi } \mid \eta (\rho \boxtimes S_{2x} \boxtimes S_2) = 1\}$ and
$\widehat {\mathcal {S}_{\psi,1}} := \widehat {\mathcal {S}_\phi } = \{ \eta \in \widehat {\mathcal {S}_\psi } \mid \eta (\rho \boxtimes S_{2x} \boxtimes S_2) = 1\}$ and
When ![]() $l = 0$ and
$l = 0$ and ![]() $x \geq 1$, we let
$x \geq 1$, we let ![]() $\widehat {\mathcal {S}_{\psi,0}}$ be the subset of
$\widehat {\mathcal {S}_{\psi,0}}$ be the subset of ![]() $\widehat {\mathcal {S}_\psi }$ consisting of
$\widehat {\mathcal {S}_\psi }$ consisting of ![]() $\eta$ that satisfy
$\eta$ that satisfy
•
 $\eta (\rho \boxtimes S_{2x} \boxtimes S_2) = \eta (\rho \boxtimes S_{2x-1})$ if
$\eta (\rho \boxtimes S_{2x} \boxtimes S_2) = \eta (\rho \boxtimes S_{2x-1})$ if  $\rho \boxtimes S_{2x-1} \subset \phi$;
$\rho \boxtimes S_{2x-1} \subset \phi$;•
 $\eta (\rho \boxtimes S_{2x} \boxtimes S_2) = (-1)^{t}\eta (\rho \boxtimes S_{2x+1})$ if
$\eta (\rho \boxtimes S_{2x} \boxtimes S_2) = (-1)^{t}\eta (\rho \boxtimes S_{2x+1})$ if  $\rho \boxtimes S_{2x+1} \subset \phi$;
$\rho \boxtimes S_{2x+1} \subset \phi$;•
 $\eta (z_\phi ) = (-1)^t$.
$\eta (z_\phi ) = (-1)^t$.
When ![]() $l = 0$ and
$l = 0$ and ![]() $x = 1/2$, we let
$x = 1/2$, we let ![]() $\widehat {\mathcal {S}_{\psi,0}}$ be the subset of
$\widehat {\mathcal {S}_{\psi,0}}$ be the subset of ![]() $\widehat {\mathcal {S}_\psi }$ consisting of
$\widehat {\mathcal {S}_\psi }$ consisting of ![]() $\eta$ that satisfy
$\eta$ that satisfy
•
 $\eta (\rho \boxtimes S_{1} \boxtimes S_2) = -1$;
$\eta (\rho \boxtimes S_{1} \boxtimes S_2) = -1$;•
 $\eta (\rho \boxtimes S_{2}) = (-1)^{t}$ if
$\eta (\rho \boxtimes S_{2}) = (-1)^{t}$ if  $\rho \boxtimes S_{2} \subset \phi$;
$\rho \boxtimes S_{2} \subset \phi$;•
 $\eta (z_\phi ) = (-1)^t$.
$\eta (z_\phi ) = (-1)^t$.
For ![]() $\eta \in \widehat {\mathcal {S}_{\psi,0}}$, we define
$\eta \in \widehat {\mathcal {S}_{\psi,0}}$, we define
Here, we regard ![]() $\eta$ as a character of the component group of
$\eta$ as a character of the component group of ![]() $\phi + \rho \boxtimes (S_{2x-1}+S_{2x+1})$ by setting
$\phi + \rho \boxtimes (S_{2x-1}+S_{2x+1})$ by setting
 \[ \begin{cases} \eta(\rho \boxtimes S_{2x-1}) = (-1)^t\eta(\rho \boxtimes S_{2x+1}) = \eta(\rho \boxtimes S_{2x} \boxtimes S_2) & \text{if } x \geq 1,\\ \eta(\rho \boxtimes S_{2}) = (-1)^{t} & \text{if } x = 1/2. \end{cases} \]
\[ \begin{cases} \eta(\rho \boxtimes S_{2x-1}) = (-1)^t\eta(\rho \boxtimes S_{2x+1}) = \eta(\rho \boxtimes S_{2x} \boxtimes S_2) & \text{if } x \geq 1,\\ \eta(\rho \boxtimes S_{2}) = (-1)^{t} & \text{if } x = 1/2. \end{cases} \]
By specifying Mœglin's construction of ![]() $\Pi _\psi$, we have the following.
$\Pi _\psi$, we have the following.
Proposition 5.2 Let ![]() $\psi = \phi \oplus (\rho \boxtimes S_{2x} \boxtimes S_2)^{t} \in \Psi _\mathrm {gp}(G)$ with
$\psi = \phi \oplus (\rho \boxtimes S_{2x} \boxtimes S_2)^{t} \in \Psi _\mathrm {gp}(G)$ with ![]() $t \geq 1$. Then
$t \geq 1$. Then
Moreover, the map ![]() $\Pi _\psi \rightarrow \widehat {\mathcal {S}_\psi }$ is given by
$\Pi _\psi \rightarrow \widehat {\mathcal {S}_\psi }$ is given by ![]() $\left \langle \cdot \,,\pi (\psi, l ,\eta ) \right \rangle _\psi = \varepsilon _{l,\eta }$, where
$\left \langle \cdot \,,\pi (\psi, l ,\eta ) \right \rangle _\psi = \varepsilon _{l,\eta }$, where
 \begin{align*} \varepsilon_{l,\eta}(\rho \boxtimes S_d) &= \eta(\rho \boxtimes S_d), \\ \varepsilon_{l,\eta}(\rho \boxtimes S_{2x} \boxtimes S_2) &= \begin{cases} (-1)^{l-1} & \text{if } x \geq 1, \\ \eta(\rho \boxtimes S_{1} \boxtimes S_2) & \text{if } x = 1/2. \end{cases} \end{align*}
\begin{align*} \varepsilon_{l,\eta}(\rho \boxtimes S_d) &= \eta(\rho \boxtimes S_d), \\ \varepsilon_{l,\eta}(\rho \boxtimes S_{2x} \boxtimes S_2) &= \begin{cases} (-1)^{l-1} & \text{if } x \geq 1, \\ \eta(\rho \boxtimes S_{1} \boxtimes S_2) & \text{if } x = 1/2. \end{cases} \end{align*}
Proof. The ![]() $A$-packet
$A$-packet ![]() $\Pi _\psi$ was constructed by Mœglin explicitly; see [Reference XuXu17a, § 8] for details. For
$\Pi _\psi$ was constructed by Mœglin explicitly; see [Reference XuXu17a, § 8] for details. For ![]() $x \geq 1$, its construction was computed in [Reference AtobeAto22b, Proposition 3.13]. The same calculation can be applied to
$x \geq 1$, its construction was computed in [Reference AtobeAto22b, Proposition 3.13]. The same calculation can be applied to ![]() $x = 1/2$. By [Reference XuXu17a, Corollary 8.10], the map
$x = 1/2$. By [Reference XuXu17a, Corollary 8.10], the map ![]() $\Pi _\psi \rightarrow \widehat {\mathcal {S}_\psi }$ is given by
$\Pi _\psi \rightarrow \widehat {\mathcal {S}_\psi }$ is given by ![]() $\left \langle \cdot \,,\pi (\psi, l ,\eta ) \right \rangle _\psi = \varepsilon _{l,\eta } \cdot \epsilon _\psi ^{M/W}$ for some character
$\left \langle \cdot \,,\pi (\psi, l ,\eta ) \right \rangle _\psi = \varepsilon _{l,\eta } \cdot \epsilon _\psi ^{M/W}$ for some character ![]() $\epsilon _\psi ^{M/W} \in \widehat {\mathcal {S}_{\psi }}$. By definition (see [Reference XuXu17a, Definitions 5.2, 5.5 and 8.1]), one can easily see that
$\epsilon _\psi ^{M/W} \in \widehat {\mathcal {S}_{\psi }}$. By definition (see [Reference XuXu17a, Definitions 5.2, 5.5 and 8.1]), one can easily see that ![]() $\epsilon _\psi ^{M/W} = \mathbf {1}$ in our case.
$\epsilon _\psi ^{M/W} = \mathbf {1}$ in our case.
Using this description, we obtain the formula for the highest ![]() $\rho |\cdot |^x$-derivatives and socles.
$\rho |\cdot |^x$-derivatives and socles.
Theorem 5.3 Fix ![]() $\phi \in \Phi _\mathrm {gp}(G)$ and write
$\phi \in \Phi _\mathrm {gp}(G)$ and write ![]() $m = m_{\phi }(\rho \boxtimes S_{2x+1})$ and
$m = m_{\phi }(\rho \boxtimes S_{2x+1})$ and ![]() $m' = m_{\phi }(\rho \boxtimes S_{2x-1})$. Consider
$m' = m_{\phi }(\rho \boxtimes S_{2x-1})$. Consider ![]() $\psi = \phi \oplus (\rho \boxtimes S_{2x} \boxtimes S_2)^t \in \Psi _\mathrm {gp}(G)$ with
$\psi = \phi \oplus (\rho \boxtimes S_{2x} \boxtimes S_2)^t \in \Psi _\mathrm {gp}(G)$ with ![]() $t \geq 0$. Let
$t \geq 0$. Let ![]() $\pi (\psi, l, \eta ) \in \Pi _{\psi }$ be such that
$\pi (\psi, l, \eta ) \in \Pi _{\psi }$ be such that ![]() $\eta (\rho \boxtimes S_{2x-1})\eta (\rho \boxtimes S_{2x+1}) = (-1)^t$ if
$\eta (\rho \boxtimes S_{2x-1})\eta (\rho \boxtimes S_{2x+1}) = (-1)^t$ if ![]() $mm' \not = 0$. Here, if
$mm' \not = 0$. Here, if ![]() $x=1/2$, we formally understand that
$x=1/2$, we formally understand that ![]() $m'=1$ and
$m'=1$ and ![]() $\eta (\rho \boxtimes S_0) = 1$. Let
$\eta (\rho \boxtimes S_0) = 1$. Let ![]() $s$ be a non-negative integer such that
$s$ be a non-negative integer such that ![]() $s=0$ if
$s=0$ if ![]() $x=1/2$. Then the highest
$x=1/2$. Then the highest ![]() $\rho |\cdot |^x$-derivative of
$\rho |\cdot |^x$-derivative of ![]() $\mathrm {soc}((\rho |\cdot |^{-x})^{s} \rtimes \pi (\psi, l ,\eta ))$ is given by
$\mathrm {soc}((\rho |\cdot |^{-x})^{s} \rtimes \pi (\psi, l ,\eta ))$ is given by
 \begin{align*} & D_{\rho|\cdot|^x}^{(m+\max\{s-m',0\})}\bigl(\mathrm{soc}\bigl((\rho|\cdot|^{-x})^{s}
\rtimes \pi(\psi, l ,\eta)\bigr)\bigr)\\ & \quad = \mathrm{soc}\bigl(
(\rho|\cdot|^{-x})^{\min\{s,m'\}} \rtimes \pi\bigl(\psi -
(\rho \boxtimes S_{2x+1})^m + (\rho \boxtimes S_{2x-1})^m,
l+m, \eta\bigr)\bigr),
\end{align*}
\begin{align*} & D_{\rho|\cdot|^x}^{(m+\max\{s-m',0\})}\bigl(\mathrm{soc}\bigl((\rho|\cdot|^{-x})^{s}
\rtimes \pi(\psi, l ,\eta)\bigr)\bigr)\\ & \quad = \mathrm{soc}\bigl(
(\rho|\cdot|^{-x})^{\min\{s,m'\}} \rtimes \pi\bigl(\psi -
(\rho \boxtimes S_{2x+1})^m + (\rho \boxtimes S_{2x-1})^m,
l+m, \eta\bigr)\bigr),
\end{align*}
where we set ![]() $\eta (\rho \boxtimes S_{2x-1}) = (-1)^t \eta (\rho \boxtimes S_{2x+1})$ if needed. In particular,
$\eta (\rho \boxtimes S_{2x-1}) = (-1)^t \eta (\rho \boxtimes S_{2x+1})$ if needed. In particular,
 \begin{align*} &S_{\rho|\cdot|^x}^{(1)}\bigl(\mathrm{soc}\big((\rho|\cdot|^{-x})^{s} \rtimes \pi(\psi, l ,\eta)\big)\bigr)\\ &\quad = \begin{cases} \mathrm{soc}\bigl((\rho|\cdot|^{-x})^{s} \rtimes \pi(\psi - \rho \boxtimes S_{2x-1} + \rho \boxtimes S_{2x+1}, l-1, \eta) \bigr) & \text{if } s < m',\\ \mathrm{soc}\bigl((\rho|\cdot|^{-x})^{s+1} \rtimes \pi(\psi, l ,\eta)\bigr) & \text{if } s \geq m', \end{cases} \end{align*}
\begin{align*} &S_{\rho|\cdot|^x}^{(1)}\bigl(\mathrm{soc}\big((\rho|\cdot|^{-x})^{s} \rtimes \pi(\psi, l ,\eta)\big)\bigr)\\ &\quad = \begin{cases} \mathrm{soc}\bigl((\rho|\cdot|^{-x})^{s} \rtimes \pi(\psi - \rho \boxtimes S_{2x-1} + \rho \boxtimes S_{2x+1}, l-1, \eta) \bigr) & \text{if } s < m',\\ \mathrm{soc}\bigl((\rho|\cdot|^{-x})^{s+1} \rtimes \pi(\psi, l ,\eta)\bigr) & \text{if } s \geq m', \end{cases} \end{align*}
where we set ![]() $\eta (\rho \boxtimes S_{2x+1}) = (-1)^t \eta (\rho \boxtimes S_{2x-1})$.
$\eta (\rho \boxtimes S_{2x+1}) = (-1)^t \eta (\rho \boxtimes S_{2x-1})$.
Proof. When ![]() $x \geq 1$ (respectively
$x \geq 1$ (respectively ![]() $x=1/2$), the formula for the highest
$x=1/2$), the formula for the highest ![]() $\rho |\cdot |^x$-derivatives was obtained in [Reference AtobeAto22b, Theorem 4.1] (respectively in [Reference JantzenJan18a, Theorem 3.3]). It implies the formula for socles.
$\rho |\cdot |^x$-derivatives was obtained in [Reference AtobeAto22b, Theorem 4.1] (respectively in [Reference JantzenJan18a, Theorem 3.3]). It implies the formula for socles.
5.3 Zelevinsky–Aubert duals of certain tempered representations
The initial step of our algorithm for computing the Zelevinsky–Aubert duals (Algorithm 4.1(3)) is to compute ![]() $\hat \pi$ for tempered
$\hat \pi$ for tempered ![]() $\pi$ such that
$\pi$ such that ![]() $\pi$ is
$\pi$ is ![]() $\rho '$-reduced for every non-self-dual
$\rho '$-reduced for every non-self-dual ![]() $\rho '\in \mathscr {C}^\mathrm {GL}$. If
$\rho '\in \mathscr {C}^\mathrm {GL}$. If ![]() $\pi = \pi (\phi, \eta )$ for
$\pi = \pi (\phi, \eta )$ for ![]() $\phi \in \Phi _\mathrm {gp}(G)$, then
$\phi \in \Phi _\mathrm {gp}(G)$, then ![]() $\pi$ satisfies this condition if and only if
$\pi$ satisfies this condition if and only if
 $~(\ast )$ if
$~(\ast )$ if  $\rho \boxtimes S_{d} \subset \phi$ with
$\rho \boxtimes S_{d} \subset \phi$ with  $d \geq 2$, then
$d \geq 2$, then  $m_\phi (\rho \boxtimes S_{d}) =1$,
$m_\phi (\rho \boxtimes S_{d}) =1$,  $\rho \boxtimes S_{d-2} \subset \phi$ and
$\rho \boxtimes S_{d-2} \subset \phi$ and  $\eta (\rho \boxtimes S_{d}) \not = \eta (\rho \boxtimes S_{d-2})$.
$\eta (\rho \boxtimes S_{d}) \not = \eta (\rho \boxtimes S_{d-2})$.
See [Reference AtobeAto20, Theorem 4.2]. Here, we formally understand that ![]() $\rho \boxtimes S_0 \subset \phi$ and
$\rho \boxtimes S_0 \subset \phi$ and ![]() $\eta (\rho \boxtimes S_0) = +1$ if
$\eta (\rho \boxtimes S_0) = +1$ if ![]() $\rho$ is self-dual of the opposite type to
$\rho$ is self-dual of the opposite type to ![]() $\phi$.
$\phi$.
Proposition 5.4 Let ![]() $\pi = \pi (\phi, \eta )$ with
$\pi = \pi (\phi, \eta )$ with ![]() $\phi \in \Phi _\mathrm {gp}(G)$. Assume that
$\phi \in \Phi _\mathrm {gp}(G)$. Assume that ![]() $\pi$ satisfies the above condition
$\pi$ satisfies the above condition ![]() $(\ast )$. Write
$(\ast )$. Write
and set
Suppose that ![]() $y_1 \geq \cdots \geq y_t > 0 = y_{t+1} = \cdots = y_r$. Then
$y_1 \geq \cdots \geq y_t > 0 = y_{t+1} = \cdots = y_r$. Then
where
 \[ \phi' = \phi - \bigoplus_{i=1}^t \rho_i \boxtimes (S_1+S_{2y_i+1}) \]
\[ \phi' = \phi - \bigoplus_{i=1}^t \rho_i \boxtimes (S_1+S_{2y_i+1}) \]
and
 \[ \eta'(\rho \boxtimes S_{d}) = \begin{cases} -\eta(\rho \boxtimes S_d) & \text{if } \rho \in \{\rho_1, \ldots, \rho_r\}, \\ \eta(\rho \boxtimes S_d) & \text{otherwise}. \end{cases} \]
\[ \eta'(\rho \boxtimes S_{d}) = \begin{cases} -\eta(\rho \boxtimes S_d) & \text{if } \rho \in \{\rho_1, \ldots, \rho_r\}, \\ \eta(\rho \boxtimes S_d) & \text{otherwise}. \end{cases} \]
Proof. Set
Write ![]() $m_\phi (\rho _i) = 2k_i > 0$ and
$m_\phi (\rho _i) = 2k_i > 0$ and ![]() $m_{\phi }(\rho '_j) = 2k'_j+1$. Then, by [Reference AtobeAto20, Theorem 4.2], we have
$m_{\phi }(\rho '_j) = 2k'_j+1$. Then, by [Reference AtobeAto20, Theorem 4.2], we have
This is ![]() $\pi (\phi '', \eta '')$ up to multiplicity, where
$\pi (\phi '', \eta '')$ up to multiplicity, where
 \[ \phi'' = \phi - \biggl(\bigoplus_{j=1}^{r'}{\rho'_j}^{2k_j'}\biggr) - \biggl(\bigoplus_{i=1}^r\rho_i \boxtimes (S_1^{2k_i-1}+S_{2y_i+1})\biggr) \]
\[ \phi'' = \phi - \biggl(\bigoplus_{j=1}^{r'}{\rho'_j}^{2k_j'}\biggr) - \biggl(\bigoplus_{i=1}^r\rho_i \boxtimes (S_1^{2k_i-1}+S_{2y_i+1})\biggr) \]
and
 \[ \eta''(\rho \boxtimes S_{d}) = \begin{cases} -\eta(\rho \boxtimes S_d) & \text{if } \rho \in \{\rho_1, \ldots, \rho_t\}, \\ \eta(\rho \boxtimes S_d) & \text{if } \rho \not\in \{\rho_1, \ldots, \rho_r\}. \end{cases} \]
\[ \eta''(\rho \boxtimes S_{d}) = \begin{cases} -\eta(\rho \boxtimes S_d) & \text{if } \rho \in \{\rho_1, \ldots, \rho_t\}, \\ \eta(\rho \boxtimes S_d) & \text{if } \rho \not\in \{\rho_1, \ldots, \rho_r\}. \end{cases} \]
For ![]() $t < i \leq r$, we note that
$t < i \leq r$, we note that ![]() $\rho _i \not \subset \phi ''$ so that
$\rho _i \not \subset \phi ''$ so that ![]() $\eta ''(\rho _i \boxtimes S_d)$ does not appear. In particular,
$\eta ''(\rho _i \boxtimes S_d)$ does not appear. In particular, ![]() $\pi (\phi '', \eta '')$ is supercuspidal. By [Reference AtobeAto22b, Theorem 2.13], with
$\pi (\phi '', \eta '')$ is supercuspidal. By [Reference AtobeAto22b, Theorem 2.13], with ![]() $\phi '$ as in the statement, we have
$\phi '$ as in the statement, we have
for some ![]() $\eta ' \in \mathcal {A}_{\phi '}$ such that
$\eta ' \in \mathcal {A}_{\phi '}$ such that ![]() $\eta '' = \eta '|\mathcal {A}_{\phi ''}$ via the canonical inclusion
$\eta '' = \eta '|\mathcal {A}_{\phi ''}$ via the canonical inclusion ![]() $\mathcal {A}_{\phi ''} \hookrightarrow \mathcal {A}_{\phi '}$. Since
$\mathcal {A}_{\phi ''} \hookrightarrow \mathcal {A}_{\phi '}$. Since ![]() $\mathcal {S}_{\phi '}$ is generated by
$\mathcal {S}_{\phi '}$ is generated by ![]() $\mathcal {S}_{\phi ''}$ and the image of
$\mathcal {S}_{\phi ''}$ and the image of ![]() $\{\alpha _{\rho _i} \mid i > t\}$, the remaining task is to determine
$\{\alpha _{\rho _i} \mid i > t\}$, the remaining task is to determine ![]() $\eta '(\rho _{i_0})$ for
$\eta '(\rho _{i_0})$ for ![]() $i_0 > t$. To do this, by replacing
$i_0 > t$. To do this, by replacing ![]() $\pi$ with
$\pi$ with
we may assume that ![]() $\pi \subset \rho ^k \rtimes \sigma$ with
$\pi \subset \rho ^k \rtimes \sigma$ with ![]() $\sigma$ supercuspidal such that
$\sigma$ supercuspidal such that ![]() $\rho \rtimes \sigma$ is semisimple of length two. If we write
$\rho \rtimes \sigma$ is semisimple of length two. If we write ![]() $\rho \rtimes \sigma = \pi _+ \oplus \pi _-$, then
$\rho \rtimes \sigma = \pi _+ \oplus \pi _-$, then ![]() $\rho ^{k-1} \rtimes \pi _{\pm }$ is irreducible and its Zelevinsky–Aubert dual is given by
$\rho ^{k-1} \rtimes \pi _{\pm }$ is irreducible and its Zelevinsky–Aubert dual is given by ![]() $\rho ^{k-1} \rtimes \hat \pi _{\pm }$. By [Reference AubertAub95, Corollaire 1.10], we know that
$\rho ^{k-1} \rtimes \hat \pi _{\pm }$. By [Reference AubertAub95, Corollaire 1.10], we know that ![]() $\hat \pi _{\pm } = \pi _{\mp }$. Hence we see that
$\hat \pi _{\pm } = \pi _{\mp }$. Hence we see that ![]() $\eta '(\rho _{i_0}) = -\eta (\rho _{i_0})$, as desired.
$\eta '(\rho _{i_0}) = -\eta (\rho _{i_0})$, as desired.
If ![]() $\pi$ is tempered, of
$\pi$ is tempered, of ![]() $\rho$-bad parity and
$\rho$-bad parity and ![]() $\rho |\cdot |^z$-reduced for all
$\rho |\cdot |^z$-reduced for all ![]() $z \not = 0$, then
$z \not = 0$, then ![]() $\pi$ must be of the form
$\pi$ must be of the form ![]() $\pi = \rho ^m \rtimes \sigma$ for some
$\pi = \rho ^m \rtimes \sigma$ for some ![]() $m \geq 0$ and
$m \geq 0$ and ![]() $\sigma$ supercuspidal. In particular, we have
$\sigma$ supercuspidal. In particular, we have ![]() $\hat \pi = \pi$. Similarly, if
$\hat \pi = \pi$. Similarly, if ![]() $\pi$ is tempered, ugly and
$\pi$ is tempered, ugly and ![]() $\rho '$-reduced for all non-self-dual
$\rho '$-reduced for all non-self-dual ![]() $\rho '\in \mathscr {C}^\mathrm {GL}$, then
$\rho '\in \mathscr {C}^\mathrm {GL}$, then ![]() $\pi$ must be supercuspidal so that
$\pi$ must be supercuspidal so that ![]() $\hat \pi = \pi$.
$\hat \pi = \pi$.
6. Best matching functions: the ugly and negative cases
To give formulas for derivatives and socles, following [Reference Lapid and MínguezLM16, § 5.3] we introduce the notion of best matching functions. We then use these functions to explicate the ugly and the negative case.
6.1 Best matching functions
Let ![]() $A$ and
$A$ and ![]() $B$ be totally ordered finite sets with respect to
$B$ be totally ordered finite sets with respect to ![]() $\geq _A$ and
$\geq _A$ and ![]() $\geq _B$, respectively. For
$\geq _B$, respectively. For ![]() $a \in A$, write
$a \in A$, write ![]() $A_{>a} := \{a' \in A \mid a' >_A a\}$. We consider a relation
$A_{>a} := \{a' \in A \mid a' >_A a\}$. We consider a relation ![]() $\rightsquigarrow$ between
$\rightsquigarrow$ between ![]() $B$ and
$B$ and ![]() $A$ such that
$A$ such that
We say that such a relation is traversable. In this case, we define a subset ![]() $A^0$ of
$A^0$ of ![]() $A$ and an injective map
$A$ and an injective map ![]() $f \colon A^0 \rightarrow B$ recursively by
$f \colon A^0 \rightarrow B$ recursively by
 \begin{align*} & a \in A^0 \iff \exists\, b \in B\setminus f(A^0 \cap A_{>a})\text{ such that }b \rightsquigarrow a, \\ &\text{in which case }f(a) := \min\{b \in B \setminus f(A^0 \cap A_{>a}) \mid b \rightsquigarrow a\}. \end{align*}
\begin{align*} & a \in A^0 \iff \exists\, b \in B\setminus f(A^0 \cap A_{>a})\text{ such that }b \rightsquigarrow a, \\ &\text{in which case }f(a) := \min\{b \in B \setminus f(A^0 \cap A_{>a}) \mid b \rightsquigarrow a\}. \end{align*}
Let ![]() $B^0 := f(A^0)$ be the image of
$B^0 := f(A^0)$ be the image of ![]() $f$. We call the bijection
$f$. We call the bijection ![]() $f \colon A^0 \rightarrow B^0$ the best matching function between
$f \colon A^0 \rightarrow B^0$ the best matching function between ![]() $A$ and
$A$ and ![]() $B$. By [Reference Lapid and MínguezLM16, Lemma 5.7], the domain
$B$. By [Reference Lapid and MínguezLM16, Lemma 5.7], the domain ![]() $A^0$ is equal to
$A^0$ is equal to ![]() $A$ if and only if Hall's criterion is satisfied, i.e. for any subset
$A$ if and only if Hall's criterion is satisfied, i.e. for any subset ![]() $A' \subset A$,
$A' \subset A$,
When one of ![]() $A$ or
$A$ or ![]() $B$ is the empty set, note that we have
$B$ is the empty set, note that we have ![]() $A^0 = B^0 = \emptyset$. We set
$A^0 = B^0 = \emptyset$. We set ![]() $A^{\rm c}=A\setminus A^0$ and
$A^{\rm c}=A\setminus A^0$ and ![]() $B^{\rm c} = B \setminus B^0$.
$B^{\rm c} = B \setminus B^0$.
6.2 Derivatives and socles in the ugly and negative cases
Fix ![]() $\rho \in \mathscr {C}^\mathrm {GL}$ and
$\rho \in \mathscr {C}^\mathrm {GL}$ and ![]() $x \in \mathbb {R}$. In this subsection, we give explicit formulas using the best matching functions for the highest
$x \in \mathbb {R}$. In this subsection, we give explicit formulas using the best matching functions for the highest ![]() $\rho |\cdot |^x$-derivatives
$\rho |\cdot |^x$-derivatives ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$ and the socles
$D_{\rho |\cdot |^x}^{(k)}(\pi )$ and the socles ![]() $S_{\rho |\cdot |^x}^{(1)}(\pi ) = \mathrm {soc}(\rho |\cdot |^x \rtimes \pi )$ in the case where
$S_{\rho |\cdot |^x}^{(1)}(\pi ) = \mathrm {soc}(\rho |\cdot |^x \rtimes \pi )$ in the case where ![]() $\rho |\cdot |^x$ is ugly or where
$\rho |\cdot |^x$ is ugly or where ![]() $\rho$ is self-dual and
$\rho$ is self-dual and ![]() $x$ is negative.
$x$ is negative.
Let ![]() $\pi \in \mathrm {Irr}(G_n)$. By Remark 2.7 and the Langlands classification, we can write
$\pi \in \mathrm {Irr}(G_n)$. By Remark 2.7 and the Langlands classification, we can write ![]() $\pi = \mathrm {soc}(L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]) \rtimes \pi _\mathrm {temp})$, where
$\pi = \mathrm {soc}(L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]) \rtimes \pi _\mathrm {temp})$, where
• if
 $\rho |\cdot |^x$ is ugly, then
$\rho |\cdot |^x$ is ugly, then  $\rho _i = \rho$ for all
$\rho _i = \rho$ for all  $i = 1, \ldots, r$,
$i = 1, \ldots, r$,  $x_1+y_1 \leq \cdots \leq x_r+y_r$ and
$x_1+y_1 \leq \cdots \leq x_r+y_r$ and  $\pi _\mathrm {temp} = \sigma$ is supercuspidal;
$\pi _\mathrm {temp} = \sigma$ is supercuspidal;• if
 $\rho$ is self-dual and
$\rho$ is self-dual and  $x$ is negative, then
$x$ is negative, then  $x_1+y_1 \leq \cdots \leq x_r+y_r < 0$ and
$x_1+y_1 \leq \cdots \leq x_r+y_r < 0$ and  $\pi _\mathrm {temp}$ is tempered.
$\pi _\mathrm {temp}$ is tempered.
To unify the notation, let us call ![]() $(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ the inducing data.
$(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r]; \pi _\mathrm {temp})$ the inducing data.
Define an ordered set ![]() $A_{\rho |\cdot |^x}$ by
$A_{\rho |\cdot |^x}$ by
with
We define a relation ![]() $\rightsquigarrow$ between
$\rightsquigarrow$ between ![]() $A_{\rho |\cdot |^x}$ and
$A_{\rho |\cdot |^x}$ and ![]() $A_{\rho |\cdot |^{x-1}}$ by
$A_{\rho |\cdot |^{x-1}}$ by
Namely, ![]() $a' \rightsquigarrow a$ if and only if
$a' \rightsquigarrow a$ if and only if ![]() $L(\Delta _\rho [x_a,y_a], \Delta _\rho [x_{a'},y_{a'}])$ is a ladder representation. Note that this relation is traversable. Let
$L(\Delta _\rho [x_a,y_a], \Delta _\rho [x_{a'},y_{a'}])$ is a ladder representation. Note that this relation is traversable. Let ![]() $f \colon A_{\rho |\cdot |^{x-1}}^0 \rightarrow A_{\rho |\cdot |^{x}}^0$ be the best matching function. In the next proposition, we obtain explicit formulas for the highest
$f \colon A_{\rho |\cdot |^{x-1}}^0 \rightarrow A_{\rho |\cdot |^{x}}^0$ be the best matching function. In the next proposition, we obtain explicit formulas for the highest ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$ and the socle
$D_{\rho |\cdot |^x}^{(k)}(\pi )$ and the socle ![]() $S_{\rho |\cdot |^x}^{(1)}(\pi )$.
$S_{\rho |\cdot |^x}^{(1)}(\pi )$.
Proposition 6.1 Suppose that ![]() $\rho |\cdot |^x$ is ugly or that
$\rho |\cdot |^x$ is ugly or that ![]() $\rho$ is self-dual and
$\rho$ is self-dual and ![]() $x$ is negative. With notation as above, the highest
$x$ is negative. With notation as above, the highest ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the unique irreducible subrepresentation of
$D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the unique irreducible subrepresentation of ![]() $L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r]) \rtimes \pi _\mathrm {temp}$, where
$L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r]) \rtimes \pi _\mathrm {temp}$, where
 \[ x_i' = \begin{cases} x-1 & \text{if } i \in A_{\rho|\cdot|^{x}}^{\rm c},\\ x_i & \text{otherwise}. \end{cases} \]
\[ x_i' = \begin{cases} x-1 & \text{if } i \in A_{\rho|\cdot|^{x}}^{\rm c},\\ x_i & \text{otherwise}. \end{cases} \]
In particular, ![]() $k = |A_{\rho |\cdot |^{x}}^{\rm c}|$. Moreover, the following hold.
$k = |A_{\rho |\cdot |^{x}}^{\rm c}|$. Moreover, the following hold.
(a) If
 $A_{\rho |\cdot |^{x-1}}^{\rm c}\neq \emptyset$, then the inducing data of
$A_{\rho |\cdot |^{x-1}}^{\rm c}\neq \emptyset$, then the inducing data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by replacing
$\pi$ by replacing  $x_a = x-1$ with
$x_a = x-1$ with  $x$, where
$x$, where  $a$ is the minimum element of
$a$ is the minimum element of  $A_{\rho |\cdot |^{x-1}}^{\rm c}$.
$A_{\rho |\cdot |^{x-1}}^{\rm c}$.(b) If
 $A_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$, then the inducing data of
$A_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$, then the inducing data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by inserting
$\pi$ by inserting  $\rho |\cdot |^x = \Delta _\rho [x,x]$.
$\rho |\cdot |^x = \Delta _\rho [x,x]$.
Proof. Since ![]() $\rho |\cdot |^x$ is ugly or
$\rho |\cdot |^x$ is ugly or ![]() $\rho$ is self-dual and
$\rho$ is self-dual and ![]() $x$ negative, we have
$x$ negative, we have
 \begin{align*} D_{\rho|\cdot|^x}^{(k)}(\pi) &= \mathrm{soc}\bigl( L_{\rho|\cdot|^x}^{(k)}(L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r])) \rtimes \pi_\mathrm{temp} \bigr),\\ S_{\rho|\cdot|^x}^{(1)}(\pi) &= \mathrm{soc}\bigl( \mathrm{soc}(\rho|\cdot|^x \times L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r])) \rtimes \pi_\mathrm{temp} \bigr). \end{align*}
\begin{align*} D_{\rho|\cdot|^x}^{(k)}(\pi) &= \mathrm{soc}\bigl( L_{\rho|\cdot|^x}^{(k)}(L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r])) \rtimes \pi_\mathrm{temp} \bigr),\\ S_{\rho|\cdot|^x}^{(1)}(\pi) &= \mathrm{soc}\bigl( \mathrm{soc}(\rho|\cdot|^x \times L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r])) \rtimes \pi_\mathrm{temp} \bigr). \end{align*}
Therefore, the proposition is essentially a problem for general linear groups, which was treated in [Reference Lapid and MínguezLM16, Theorem 5.11].
7. Explicit formulas for derivatives and socles: the positive case
In this section, we give explicit formulas for the highest derivatives and the socles of several parabolically induced representations in the positive case. The main results are Theorem 7.1, where we describe derivatives and socles in the good-parity case, and Theorem 7.4, in which the bad-parity case is treated. In Corollary 7.2 we deduce a result on irreducibility of certain parabolic inductions.
Throughout this section we fix ![]() $\rho \in \mathscr {C}^\mathrm {GL}$ self-dual and
$\rho \in \mathscr {C}^\mathrm {GL}$ self-dual and ![]() $x \in (1/2)\mathbb {Z}$ with
$x \in (1/2)\mathbb {Z}$ with ![]() $x > 0$.
$x > 0$.
7.1 The good-parity case
In this subsection, we assume that ![]() $\pi \in \mathrm {Irr}(G_n)$ is of good parity and that
$\pi \in \mathrm {Irr}(G_n)$ is of good parity and that ![]() $\rho \boxtimes S_{2x+1}$ is self-dual of the same type as elements in
$\rho \boxtimes S_{2x+1}$ is self-dual of the same type as elements in ![]() $\Phi _\mathrm {gp}(G)$. Write
$\Phi _\mathrm {gp}(G)$. Write ![]() $\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _{r'}}[x_{r'},y_{r'}]; \pi (\phi, \eta ))$ as a Langlands subrepresentation so that
$\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _{r'}}[x_{r'},y_{r'}]; \pi (\phi, \eta ))$ as a Langlands subrepresentation so that ![]() $x_1+y_1 \leq \cdots \leq x_{r'}+y_{r'} <0$ and
$x_1+y_1 \leq \cdots \leq x_{r'}+y_{r'} <0$ and ![]() $\phi \in \Phi _\mathrm {gp}(G)$. Set
$\phi \in \Phi _\mathrm {gp}(G)$. Set
and ![]() $r = r'-t$. Then we can rewrite
$r = r'-t$. Then we can rewrite
where we set ![]() $\pi _A := L(\Delta _\rho [x-1,-x]^t; \pi (\phi, \eta ))$.
$\pi _A := L(\Delta _\rho [x-1,-x]^t; \pi (\phi, \eta ))$.
If ![]() $m_\phi (\rho \boxtimes S_{2x+1}) \not = 0$,
$m_\phi (\rho \boxtimes S_{2x+1}) \not = 0$, ![]() $m_\phi (\rho \boxtimes S_{2x-1}) \not = 0$ and
$m_\phi (\rho \boxtimes S_{2x-1}) \not = 0$ and ![]() $\eta (\rho \boxtimes S_{2x+1})\eta (\rho \boxtimes S_{2x-1}) = (-1)^{t+1}$, set
$\eta (\rho \boxtimes S_{2x+1})\eta (\rho \boxtimes S_{2x-1}) = (-1)^{t+1}$, set
and ![]() $l := 0$. Otherwise, set
$l := 0$. Otherwise, set ![]() $\psi := \phi + (\rho \boxtimes S_{2x} \boxtimes S_2)^t$ and
$\psi := \phi + (\rho \boxtimes S_{2x} \boxtimes S_2)^t$ and ![]() $l := 1$. Then
$l := 1$. Then ![]() $\pi _A = \pi (\psi, l, \eta ) \in \Pi _\psi$ by Proposition 5.2. Set
$\pi _A = \pi (\psi, l, \eta ) \in \Pi _\psi$ by Proposition 5.2. Set ![]() $m := m_\psi (\rho \boxtimes S_{2x+1})$ and
$m := m_\psi (\rho \boxtimes S_{2x+1})$ and ![]() $m' := m_\psi (\rho \boxtimes S_{2x-1})$. Then the highest
$m' := m_\psi (\rho \boxtimes S_{2x-1})$. Then the highest ![]() $\rho |\cdot |^x$-derivative of
$\rho |\cdot |^x$-derivative of ![]() $\mathrm {soc}((\rho |\cdot |^{-x})^s \rtimes \pi _A)$ is described in Theorem 5.3.
$\mathrm {soc}((\rho |\cdot |^{-x})^s \rtimes \pi _A)$ is described in Theorem 5.3.
Note that ![]() $x_i \geq y_i$ for all
$x_i \geq y_i$ for all ![]() $i = 1, \ldots, r$. Define ordered sets
$i = 1, \ldots, r$. Define ordered sets
with
 \begin{alignat*}{4}
a \geq a' & \iff y_a \geq y_{a'} & \quad & \text{for }a,a' \in A_{\rho|\cdot|^{x}},\\
b \geq b' & \iff x_b \leq x_{b'} & \quad & \text{for }b,b' \in B_{\rho|\cdot|^x}.
\end{alignat*}
\begin{alignat*}{4}
a \geq a' & \iff y_a \geq y_{a'} & \quad & \text{for }a,a' \in A_{\rho|\cdot|^{x}},\\
b \geq b' & \iff x_b \leq x_{b'} & \quad & \text{for }b,b' \in B_{\rho|\cdot|^x}.
\end{alignat*}
Notice that any two of ![]() $A_{\rho |\cdot |^{x-1}}, A_{\rho |\cdot |^{x}}, B_{\rho |\cdot |^{x-1}}$ and
$A_{\rho |\cdot |^{x-1}}, A_{\rho |\cdot |^{x}}, B_{\rho |\cdot |^{x-1}}$ and ![]() $B_{\rho |\cdot |^{x}}$ have no intersection. Define relations
$B_{\rho |\cdot |^{x}}$ have no intersection. Define relations ![]() $\rightsquigarrow$ between
$\rightsquigarrow$ between ![]() $A_{\rho |\cdot |^{x}}$ and
$A_{\rho |\cdot |^{x}}$ and ![]() $A_{\rho |\cdot |^{x-1}}$ and between
$A_{\rho |\cdot |^{x-1}}$ and between ![]() $B_{\rho |\cdot |^{x}}$ and
$B_{\rho |\cdot |^{x}}$ and ![]() $B_{\rho |\cdot |^{x-1}}$ by
$B_{\rho |\cdot |^{x-1}}$ by
 \begin{alignat*}{4}
A_{\rho|\cdot|^{x}} & \ni a' \rightsquigarrow a \in
A_{\rho|\cdot|^{x-1}} & \iff & y_{a'} > y_a, \\
B_{\rho|\cdot|^{x}} & \ni b' \rightsquigarrow b \in B_{\rho|\cdot|^{x-1}} & \iff & x_{b'} < x_b, \end{alignat*}
\begin{alignat*}{4}
A_{\rho|\cdot|^{x}} & \ni a' \rightsquigarrow a \in
A_{\rho|\cdot|^{x-1}} & \iff & y_{a'} > y_a, \\
B_{\rho|\cdot|^{x}} & \ni b' \rightsquigarrow b \in B_{\rho|\cdot|^{x-1}} & \iff & x_{b'} < x_b, \end{alignat*}
respectively. Note that these relations are traversable. Let ![]() $f \colon A_{\rho |\cdot |^{x-1}}^0 \rightarrow A_{\rho |\cdot |^{x}}^0$ and
$f \colon A_{\rho |\cdot |^{x-1}}^0 \rightarrow A_{\rho |\cdot |^{x}}^0$ and ![]() $g \colon B_{\rho |\cdot |^{x-1}}^0 \rightarrow B_{\rho |\cdot |^{x}}^0$ be the best matching functions. Write
$g \colon B_{\rho |\cdot |^{x-1}}^0 \rightarrow B_{\rho |\cdot |^{x}}^0$ be the best matching functions. Write ![]() $B_{\rho |\cdot |^{x}}^{\rm c}= \{i_1, \ldots, i_{s}\}$ with
$B_{\rho |\cdot |^{x}}^{\rm c}= \{i_1, \ldots, i_{s}\}$ with ![]() $i_1 < \cdots < i_{s}$. Notice that
$i_1 < \cdots < i_{s}$. Notice that ![]() $s > 0$ only if
$s > 0$ only if ![]() $x > 1$.
$x > 1$.
Theorem 7.1 With notation as above, suppose that ![]() $x > 0$,
$x > 0$, ![]() $x \in (1/2)\mathbb {Z}$ and
$x \in (1/2)\mathbb {Z}$ and ![]() $\rho \boxtimes S_{2x+1}$ is self-dual of the same type as
$\rho \boxtimes S_{2x+1}$ is self-dual of the same type as ![]() $\phi$. Then the highest
$\phi$. Then the highest ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the unique irreducible subrepresentation of
$D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the unique irreducible subrepresentation of ![]() $L(\Delta _{\rho _1}[x'_1,y'_1], \ldots, \Delta _{\rho _r}[x'_r,y'_r]) \rtimes \pi _A'$, where
$L(\Delta _{\rho _1}[x'_1,y'_1], \ldots, \Delta _{\rho _r}[x'_r,y'_r]) \rtimes \pi _A'$, where
 \begin{align*} x_i' &= \begin{cases} -1 & \text{if } i \in A_{\rho|\cdot|^{x}}^{\rm c},\\ x_i & \text{otherwise}, \end{cases} \\ y_i' &= \begin{cases} -(x-1) & \text{if } i=i_j, \: j > m'+\max\{|A_{\rho|\cdot|^{x-1}}^{\rm c}|-m,0\}, \\ y_i & \text{otherwise}, \end{cases} \end{align*}
\begin{align*} x_i' &= \begin{cases} -1 & \text{if } i \in A_{\rho|\cdot|^{x}}^{\rm c},\\ x_i & \text{otherwise}, \end{cases} \\ y_i' &= \begin{cases} -(x-1) & \text{if } i=i_j, \: j > m'+\max\{|A_{\rho|\cdot|^{x-1}}^{\rm c}|-m,0\}, \\ y_i & \text{otherwise}, \end{cases} \end{align*}
and ![]() $\pi _A' = \pi (\psi ', l', \eta )$ with
$\pi _A' = \pi (\psi ', l', \eta )$ with
and
In particular,
Moreover, the following hold.
(a) If
 $m+\max \{|B_{\rho |\cdot |^{x}}^{\rm c}|-m',0\} < |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then the Langlands data of
$m+\max \{|B_{\rho |\cdot |^{x}}^{\rm c}|-m',0\} < |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by replacing
$\pi$ by replacing  $x_a = x-1$ with
$x_a = x-1$ with  $x$, where
$x$, where  $a$ is the minimum element of
$a$ is the minimum element of  $A_{\rho |\cdot |^{x-1}}^{\rm c}$.
$A_{\rho |\cdot |^{x-1}}^{\rm c}$.(b) If
 $|B_{\rho |\cdot |^{x}}^{\rm c}| < m'$ and
$|B_{\rho |\cdot |^{x}}^{\rm c}| < m'$ and  $m \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, the Langlands data of
$m \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by replacing
$\pi$ by replacing  $\pi _A = \pi (\psi, l, \eta )$ with
$\pi _A = \pi (\psi, l, \eta )$ with
 \[ S_{\rho|\cdot|^x}^{(1)}(\pi_A) = \pi\bigl(\psi - (\rho \boxtimes S_{2x-1}) + (\rho \boxtimes S_{2x+1}), l-1, \eta\bigr). \]
\[ S_{\rho|\cdot|^x}^{(1)}(\pi_A) = \pi\bigl(\psi - (\rho \boxtimes S_{2x-1}) + (\rho \boxtimes S_{2x+1}), l-1, \eta\bigr). \]
(c) If
 $|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'$,
$|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'$,  $m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and
$m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and  $B_{\rho |\cdot |^{x-1}}^{\rm c} \not = \emptyset$, the Langlands data of
$B_{\rho |\cdot |^{x-1}}^{\rm c} \not = \emptyset$, the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by replacing
$\pi$ by replacing  $y_b = -(x-1)$ with
$y_b = -(x-1)$ with  $-x$, where
$-x$, where  $b$ is the minimum element of
$b$ is the minimum element of  $B_{\rho |\cdot |^{x-1}}^{\rm c}$.
$B_{\rho |\cdot |^{x-1}}^{\rm c}$.(d) If
 $|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'$,
$|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'$,  $m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and
$m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and  $B_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$, then the Langlands data of
$B_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$, then the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by inserting
$\pi$ by inserting  $\rho |\cdot |^{-x} = \Delta _{\rho }[-x,-x]$.
$\rho |\cdot |^{-x} = \Delta _{\rho }[-x,-x]$.
Proof. To obtain the formula for the highest derivative, we use Jantzen's algorithm [Reference JantzenJan18a, § 3.3] together with [Reference Lapid and MínguezLM16, Theorem 5.11] and Theorem 5.3.
(1) Recall that
with ![]() $\pi _A = L(\Delta _\rho [x-1,-x]^t; \pi (\phi, \eta ))$ and
$\pi _A = L(\Delta _\rho [x-1,-x]^t; \pi (\phi, \eta ))$ and ![]() $\Delta _{\rho _i}[x_i,y_i] \not \cong \Delta _\rho [x-1,-x]$ for all
$\Delta _{\rho _i}[x_i,y_i] \not \cong \Delta _\rho [x-1,-x]$ for all ![]() $i = 1, \ldots,r$.
$i = 1, \ldots,r$.
(2) By [Reference Lapid and MínguezLM16, Theorem 5.11], we can compute the highest right ![]() $\rho |\cdot |^{-x}$-derivative
$\rho |\cdot |^{-x}$-derivative
where
 \[ y_i'' = \begin{cases} -(x-1) & \text{if } i \in B_{\rho|\cdot|^{x}}^{\rm c}, \\ y_i & \text{otherwise}. \end{cases} \]
\[ y_i'' = \begin{cases} -(x-1) & \text{if } i \in B_{\rho|\cdot|^{x}}^{\rm c}, \\ y_i & \text{otherwise}. \end{cases} \]
In particular, ![]() $s = |B_{\rho |\cdot |^{x}}^{\rm c}|$. Claim 1 in [Reference JantzenJan18a, § 3.3] says that
$s = |B_{\rho |\cdot |^{x}}^{\rm c}|$. Claim 1 in [Reference JantzenJan18a, § 3.3] says that
with ![]() $\pi _1 := \mathrm {soc}((\rho |\cdot |^{-x})^s \rtimes \pi _A)$.
$\pi _1 := \mathrm {soc}((\rho |\cdot |^{-x})^s \rtimes \pi _A)$.
(3) By Theorem 5.3, the highest ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $\pi _2 := D_{\rho |\cdot |^x}^{(k_1)}(\pi _1)$ of
$\pi _2 := D_{\rho |\cdot |^x}^{(k_1)}(\pi _1)$ of ![]() $\pi _1$ is
$\pi _1$ is
with ![]() $k_1 = m + \max \{s-m', 0\}$. Claim 2 in [Reference JantzenJan18a, § 3.3] says that
$k_1 = m + \max \{s-m', 0\}$. Claim 2 in [Reference JantzenJan18a, § 3.3] says that
(4) We will apply [Reference Lapid and MínguezLM16, Theorem 5.11] to compute the highest left ![]() $\rho |\cdot |^x$-derivative of
$\rho |\cdot |^x$-derivative of ![]() $L(\Delta _{\rho _1}[x_1,y_1''], \ldots, \Delta _{\rho _r}[x_r,y_r''], (\rho |\cdot |^x)^{k_1})$. To do this, we have to replace
$L(\Delta _{\rho _1}[x_1,y_1''], \ldots, \Delta _{\rho _r}[x_r,y_r''], (\rho |\cdot |^x)^{k_1})$. To do this, we have to replace ![]() $A_{\rho |\cdot |^x}$ with
$A_{\rho |\cdot |^x}$ with ![]() $A_{\rho |\cdot |^x} \cup \{r+1, \ldots, r+k_1\}$, where we set
$A_{\rho |\cdot |^x} \cup \{r+1, \ldots, r+k_1\}$, where we set ![]() $\Delta _{\rho _i}[x_i,y_i] = \rho |\cdot |^x$ for
$\Delta _{\rho _i}[x_i,y_i] = \rho |\cdot |^x$ for ![]() $i = r+1, \ldots, r+k_1$. Note that any
$i = r+1, \ldots, r+k_1$. Note that any ![]() $a' \in \{r+1, \ldots, r+k_1\}$ is bigger than any element of
$a' \in \{r+1, \ldots, r+k_1\}$ is bigger than any element of ![]() $A_{\rho |\cdot |^x}$ with respect to the order of
$A_{\rho |\cdot |^x}$ with respect to the order of ![]() $A_{\rho |\cdot |^x} \cup \{r+1, \ldots, r+k_1\}$, and
$A_{\rho |\cdot |^x} \cup \{r+1, \ldots, r+k_1\}$, and ![]() $a' \rightsquigarrow a$ for every
$a' \rightsquigarrow a$ for every ![]() $a \in A_{\rho |\cdot |^{x-1}}$. Hence the image of the resulting best matching function is
$a \in A_{\rho |\cdot |^{x-1}}$. Hence the image of the resulting best matching function is
Therefore, with ![]() $k_2 = \min \{k_1, |A_{\rho |\cdot |^{x-1}}^{\rm c}|\}$ and
$k_2 = \min \{k_1, |A_{\rho |\cdot |^{x-1}}^{\rm c}|\}$ and ![]() $k = |A_{\rho |\cdot |^{x}}^{\rm c}| + k_1-k_2$, the highest left
$k = |A_{\rho |\cdot |^{x}}^{\rm c}| + k_1-k_2$, the highest left ![]() $\rho |\cdot |^x$-derivative is
$\rho |\cdot |^x$-derivative is
 \begin{align*} &L_{\rho|\cdot|^x}^{(k)} \bigl(L(\Delta_{\rho_1}[x_1,y_1''], \ldots, \Delta_{\rho_r}[x_r,y_r''], (\rho|\cdot|^x)^{k_1})\bigr)\\ &\quad = L(\Delta_{\rho_1}[x_1',y_1''], \ldots, \Delta_{\rho_r}[x_r',y_r''], (\rho|\cdot|^x)^{k_2}), \end{align*}
\begin{align*} &L_{\rho|\cdot|^x}^{(k)} \bigl(L(\Delta_{\rho_1}[x_1,y_1''], \ldots, \Delta_{\rho_r}[x_r,y_r''], (\rho|\cdot|^x)^{k_1})\bigr)\\ &\quad = L(\Delta_{\rho_1}[x_1',y_1''], \ldots, \Delta_{\rho_r}[x_r',y_r''], (\rho|\cdot|^x)^{k_2}), \end{align*}
where ![]() $x_i'$ is as in the statement of this theorem. Then the highest
$x_i'$ is as in the statement of this theorem. Then the highest ![]() $\rho |\cdot |^x$-derivative of
$\rho |\cdot |^x$-derivative of ![]() $\pi$ is
$\pi$ is
(5) Claim 3 in [Reference JantzenJan18a, § 3.3] says that
By Theorem 5.3, we have
where ![]() $\pi _A'$ is as in the statement of this theorem and
$\pi _A'$ is as in the statement of this theorem and ![]() $s' = \min \{s,m'\} + \max \{k_2-m,0\}$. Note that
$s' = \min \{s,m'\} + \max \{k_2-m,0\}$. Note that ![]() $s' \leq s$.
$s' \leq s$.
(6) Finally, note that
• if
 $s'=s$, then
$s'=s$, then  $m'+\max \{|A_{\rho |\cdot |^{x-1}}^{\rm c}|-m,0\} \geq s$, so that
$m'+\max \{|A_{\rho |\cdot |^{x-1}}^{\rm c}|-m,0\} \geq s$, so that  $y_i' = y_i$ for all
$y_i' = y_i$ for all  $i=1, \ldots, r$;
$i=1, \ldots, r$;• if
 $s' < s$, then
$s' < s$, then  $s > m'$ and
$s > m'$ and  $k_1 = m+s-m' > k_2 = |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, so that
$k_1 = m+s-m' > k_2 = |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, so that  $s' = m'+\max \{|A_{\rho |\cdot |^{x-1}}^{\rm c}|-m,0\}$.
$s' = m'+\max \{|A_{\rho |\cdot |^{x-1}}^{\rm c}|-m,0\}$.
By [Reference Lapid and MínguezLM16, Theorem 5.11], we have
 \begin{align*} &\mathrm{soc}\big( L(\Delta_{\rho_1}[x_1',y_1''], \ldots, \Delta_{\rho_r}[x_r',y_r'']) \times (\rho|\cdot|^{-x})^{s'} \big)\\ &\quad = L(\Delta_{\rho_1}[x_1',y_1'], \ldots, \Delta_{\rho_r}[x_r',y_r']), \end{align*}
\begin{align*} &\mathrm{soc}\big( L(\Delta_{\rho_1}[x_1',y_1''], \ldots, \Delta_{\rho_r}[x_r',y_r'']) \times (\rho|\cdot|^{-x})^{s'} \big)\\ &\quad = L(\Delta_{\rho_1}[x_1',y_1'], \ldots, \Delta_{\rho_r}[x_r',y_r']), \end{align*}
where ![]() $y_i'$ is as in the statement of this theorem. Claim 4 in [Reference JantzenJan18a, § 3.3] says that
$y_i'$ is as in the statement of this theorem. Claim 4 in [Reference JantzenJan18a, § 3.3] says that
This gives the Langlands data of ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$.
$D_{\rho |\cdot |^x}^{(k)}(\pi )$.
Recall that ![]() $S_{\rho |\cdot |^x}^{(1)}(\pi )$ is an irreducible representation determined by the relation
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ is an irreducible representation determined by the relation
One can easily check this equation for the representations given in (a), (b), (c) and (d).
As an application of Proposition 6.1 and Theorem 7.1, we have a combinatorial irreducibility criterion for ![]() $\rho |\cdot |^x \rtimes \pi$ as follows.
$\rho |\cdot |^x \rtimes \pi$ as follows.
Corollary 7.2 With notation as above, suppose that ![]() $x >0$,
$x >0$, ![]() $x \in (1/2)\mathbb {Z}$ and
$x \in (1/2)\mathbb {Z}$ and ![]() $\rho \boxtimes S_{2x+1}$ is self-dual of the same type as
$\rho \boxtimes S_{2x+1}$ is self-dual of the same type as ![]() $\phi$. Then the parabolically induced representation
$\phi$. Then the parabolically induced representation ![]() $\rho |\cdot |^x \rtimes \pi$ is irreducible if and only if all of the following conditions hold:
$\rho |\cdot |^x \rtimes \pi$ is irreducible if and only if all of the following conditions hold:
•
 $A_{\rho |\cdot |^{-x-1}}^{\rm c} = \emptyset$;
$A_{\rho |\cdot |^{-x-1}}^{\rm c} = \emptyset$;•
 $|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m_\psi (\rho \boxtimes S_{2x-1})$;
$|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m_\psi (\rho \boxtimes S_{2x-1})$;•
 $m_\psi (\rho \boxtimes S_{2x+1}) +|B_{\rho |\cdot |^{x}}^{\rm c}| -m_\psi (\rho \boxtimes S_{2x-1}) \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$;
$m_\psi (\rho \boxtimes S_{2x+1}) +|B_{\rho |\cdot |^{x}}^{\rm c}| -m_\psi (\rho \boxtimes S_{2x-1}) \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$;•
 $B_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$.
$B_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$.
Proof. Since ![]() $\rho |\cdot |^x$ is not self-dual, by Proposition 3.3,
$\rho |\cdot |^x$ is not self-dual, by Proposition 3.3, ![]() $\rho |\cdot |^x \rtimes \pi$ is SI so that both
$\rho |\cdot |^x \rtimes \pi$ is SI so that both ![]() $S_{\rho |\cdot |^x}^{(1)}(\pi )$ and
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ and ![]() $S_{\rho |\cdot |^{-x}}^{(1)}(\pi )$ occur with multiplicity one in
$S_{\rho |\cdot |^{-x}}^{(1)}(\pi )$ occur with multiplicity one in ![]() $[\rho |\cdot |^x \rtimes \pi ]$. Hence
$[\rho |\cdot |^x \rtimes \pi ]$. Hence ![]() $\rho |\cdot |^x \rtimes \pi$ is irreducible if and only if
$\rho |\cdot |^x \rtimes \pi$ is irreducible if and only if ![]() $S_{\rho |\cdot |^x}^{(1)}(\pi ) \cong S_{\rho |\cdot |^{-x}}^{(1)}(\pi )$. By Proposition 6.1 and Theorem 7.1, this is equivalent to the case where the Langlands data of
$S_{\rho |\cdot |^x}^{(1)}(\pi ) \cong S_{\rho |\cdot |^{-x}}^{(1)}(\pi )$. By Proposition 6.1 and Theorem 7.1, this is equivalent to the case where the Langlands data of ![]() $S_{\rho |\cdot |^{-x}}^{(1)}(\pi )$ and
$S_{\rho |\cdot |^{-x}}^{(1)}(\pi )$ and ![]() $S_{\rho |\cdot |^x}^{(1)}(\pi )$ are obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ are obtained from those of ![]() $\pi$ by inserting
$\pi$ by inserting ![]() $\rho |\cdot |^{-x}$.
$\rho |\cdot |^{-x}$.
As a special case, when ![]() $\pi = \pi (\phi, \eta )$ is tempered, since
$\pi = \pi (\phi, \eta )$ is tempered, since ![]() $A_{\rho ^\vee |\cdot |^{-x-1}}, A_{\rho |\cdot |^{x-1}}, A_{\rho |\cdot |^x}, B_{\rho |\cdot |^{x-1}}$ and
$A_{\rho ^\vee |\cdot |^{-x-1}}, A_{\rho |\cdot |^{x-1}}, A_{\rho |\cdot |^x}, B_{\rho |\cdot |^{x-1}}$ and ![]() $B_{\rho |\cdot |^x}$ are all the empty set, we see that
$B_{\rho |\cdot |^x}$ are all the empty set, we see that ![]() $\rho |\cdot |^x \rtimes \pi$ if and only if
$\rho |\cdot |^x \rtimes \pi$ if and only if ![]() $m_\psi (\rho \boxtimes S_{2x-1}) = 0$, which is equivalent to
$m_\psi (\rho \boxtimes S_{2x-1}) = 0$, which is equivalent to
•
 $\phi \not \supset \rho \boxtimes S_{2x-1}$; or
$\phi \not \supset \rho \boxtimes S_{2x-1}$; or•
 $m_\phi (\rho \boxtimes S_{2x-1}) = 1$,
$m_\phi (\rho \boxtimes S_{2x-1}) = 1$,  $m_\phi (\rho \boxtimes S_{2x+1}) > 0$ and
$m_\phi (\rho \boxtimes S_{2x+1}) > 0$ and  $\eta (\rho \boxtimes S_{2x-1}) \not = \eta (\rho \boxtimes S_{2x+1})$.
$\eta (\rho \boxtimes S_{2x-1}) \not = \eta (\rho \boxtimes S_{2x+1})$.
This special case was already known to Jantzen [Reference JantzenJan18b, Theorem 4.7].
7.2 The bad-parity case
We now treat the bad-parity case. Specifically, we assume that ![]() $\rho \boxtimes S_{2x+1}$ is self-dual of the opposite type to elements in
$\rho \boxtimes S_{2x+1}$ is self-dual of the opposite type to elements in ![]() $\Phi _\mathrm {gp}(G)$, and we take
$\Phi _\mathrm {gp}(G)$, and we take ![]() $\pi \in \mathrm {Irr}(G_n)$ such that
$\pi \in \mathrm {Irr}(G_n)$ such that ![]() $\mathrm {scusp}(\pi ) \subset \mathbb {Z}_{\rho |\cdot |^x} \cup \{\sigma \}$ for some
$\mathrm {scusp}(\pi ) \subset \mathbb {Z}_{\rho |\cdot |^x} \cup \{\sigma \}$ for some ![]() $\sigma \in \mathscr {C}^G$.
$\sigma \in \mathscr {C}^G$.
We remark that Jantzen's algorithm [Reference JantzenJan18a, § 3.3] for computing the highest ![]() $\rho |\cdot |^x$-derivatives can be applied to the bad-parity case. According to this algorithm (see (2) in the proof of Theorem 7.1), we have to deal with a
$\rho |\cdot |^x$-derivatives can be applied to the bad-parity case. According to this algorithm (see (2) in the proof of Theorem 7.1), we have to deal with a ![]() $\rho |\cdot |^x$-bad representation of the form
$\rho |\cdot |^x$-bad representation of the form
with ![]() $\phi \in \Phi _\mathrm {temp}(G_n)$ and
$\phi \in \Phi _\mathrm {temp}(G_n)$ and ![]() $s,t \geq 0$. Here, we may assume that
$s,t \geq 0$. Here, we may assume that ![]() $s = 0$ if
$s = 0$ if ![]() $x=1/2$ since
$x=1/2$ since ![]() $\rho |\cdot |^{-1/2} = \Delta _\rho [-1/2,-1/2]$. By the assumption of bad parity, if we write
$\rho |\cdot |^{-1/2} = \Delta _\rho [-1/2,-1/2]$. By the assumption of bad parity, if we write ![]() $\sigma = \pi (\phi _\sigma, \eta _\sigma )$, then
$\sigma = \pi (\phi _\sigma, \eta _\sigma )$, then ![]() $\phi = \phi _\sigma \oplus (\bigoplus _{i=1}^r (\rho \boxtimes S_{2x_i+1})^{m_i})$ with
$\phi = \phi _\sigma \oplus (\bigoplus _{i=1}^r (\rho \boxtimes S_{2x_i+1})^{m_i})$ with ![]() $x_i \in x + \mathbb {Z}$ so that
$x_i \in x + \mathbb {Z}$ so that ![]() $\mathcal {S}_\phi \cong \mathcal {S}_{\phi _\sigma }$, and
$\mathcal {S}_\phi \cong \mathcal {S}_{\phi _\sigma }$, and ![]() $\eta = \eta _\sigma$. Moreover, the multiplicity
$\eta = \eta _\sigma$. Moreover, the multiplicity ![]() $m_i$ is even for all
$m_i$ is even for all ![]() $i$. The following result is an extension of [Reference JantzenJan18a, Propositions 8.5 and 8.6].
$i$. The following result is an extension of [Reference JantzenJan18a, Propositions 8.5 and 8.6].
Proposition 7.3 With notation as above, when ![]() $x=1/2$, we assume here that
$x=1/2$, we assume here that ![]() $s=0$. Set
$s=0$. Set ![]() $m := m_\phi (\rho \boxtimes S_{2x+1})$ and
$m := m_\phi (\rho \boxtimes S_{2x+1})$ and ![]() $m' := m_\phi (\rho \boxtimes S_{2x-1})$, both of which are even. Take
$m' := m_\phi (\rho \boxtimes S_{2x-1})$, both of which are even. Take ![]() $\kappa \in \{0,1\}$ such that
$\kappa \in \{0,1\}$ such that ![]() $t \equiv \kappa \bmod 2$. Then the highest
$t \equiv \kappa \bmod 2$. Then the highest ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi _1)$ is equal to
$D_{\rho |\cdot |^x}^{(k)}(\pi _1)$ is equal to
with ![]() $k = m+\kappa +\max \{s-m'-\kappa,0\}$.
$k = m+\kappa +\max \{s-m'-\kappa,0\}$.
Proof. If we write ![]() $\pi _0 := \pi (\phi - (\rho \boxtimes S_{2x+1})^m - (\rho \boxtimes S_{2x-1})^{m'}, \eta )$, then
$\pi _0 := \pi (\phi - (\rho \boxtimes S_{2x+1})^m - (\rho \boxtimes S_{2x-1})^{m'}, \eta )$, then
is an irreducible induction. Moreover,
is always irreducible by [Reference Mœglin and WaldspurgerMW12, Théorème (i)]. Also, any subquotient of ![]() $\Delta _\rho [x-1,-x] \times \Delta _\rho [x,-(x-1)]$ is
$\Delta _\rho [x-1,-x] \times \Delta _\rho [x,-(x-1)]$ is ![]() $\Delta _\rho [x-1,-(x-1)] \times \Delta _\rho [x,-x]$ or
$\Delta _\rho [x-1,-(x-1)] \times \Delta _\rho [x,-x]$ or ![]() $L_0 := L(\Delta _\rho [x-1,-x], \Delta _\rho [x,-(x-1)])$, both of which commute with all of
$L_0 := L(\Delta _\rho [x-1,-x], \Delta _\rho [x,-(x-1)])$, both of which commute with all of ![]() $\Delta _\rho [x-1,-(x-1)]$,
$\Delta _\rho [x-1,-(x-1)]$, ![]() $\Delta _\rho [x,-x]$ and
$\Delta _\rho [x,-x]$ and ![]() $\Delta _\rho [x-1,-x]$ (see for example [Reference TadićTad14, Theorem 1.1]).
$\Delta _\rho [x-1,-x]$ (see for example [Reference TadićTad14, Theorem 1.1]).
First we assume that ![]() $t$ is even. By considering the Langlands data, we have
$t$ is even. By considering the Langlands data, we have
 \begin{align*} &\mathrm{soc}\bigl( \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0 \bigr)\\ &\quad \hookrightarrow L_0^{{t}/2} \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0\\ &\quad \hookrightarrow \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0. \end{align*}
\begin{align*} &\mathrm{soc}\bigl( \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0 \bigr)\\ &\quad \hookrightarrow L_0^{{t}/2} \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0\\ &\quad \hookrightarrow \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0. \end{align*}
Since the middle induced representation is unitary and the last induced representation is a standard module and so is SI, we see that the first inclusion map is an isomorphism. In particular, ![]() $\pi _1$ is equal to the socle of
$\pi _1$ is equal to the socle of
 \begin{align*} &(\rho|\cdot|^{-x})^s \times L_0^{{t}/2} \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0\\ &\quad \cong L_0^{{t}/2} \times (\rho|\cdot|^{-x})^s \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0. \end{align*}
\begin{align*} &(\rho|\cdot|^{-x})^s \times L_0^{{t}/2} \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0\\ &\quad \cong L_0^{{t}/2} \times (\rho|\cdot|^{-x})^s \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0. \end{align*}
Therefore, we may replace ![]() $(\rho |\cdot |^{-x})^s \times \Delta _\rho [x-1,-(x-1)]^{{m'}/2}$ with
$(\rho |\cdot |^{-x})^s \times \Delta _\rho [x-1,-(x-1)]^{{m'}/2}$ with
where ![]() $L_1 := L(\rho |\cdot |^{-x}, \Delta _\rho [x-1,-(x-1)])$. Moreover, since
$L_1 := L(\rho |\cdot |^{-x}, \Delta _\rho [x-1,-(x-1)])$. Moreover, since ![]() $\rho |\cdot |^{-x} \times \Delta _\rho [x,-x]^{{m}/2} \rtimes \pi _0$ is irreducible by [Reference Mœglin and WaldspurgerMW12, Théorème (i)], if
$\rho |\cdot |^{-x} \times \Delta _\rho [x,-x]^{{m}/2} \rtimes \pi _0$ is irreducible by [Reference Mœglin and WaldspurgerMW12, Théorème (i)], if ![]() $s \geq {m'}/2$, then we may replace
$s \geq {m'}/2$, then we may replace ![]() $(\ast )$ with
$(\ast )$ with
where ![]() $L_2 := L(\rho |\cdot |^{-x}, \Delta _\rho [x-1,-(x-1)], \rho |\cdot |^x)$. Note that if
$L_2 := L(\rho |\cdot |^{-x}, \Delta _\rho [x-1,-(x-1)], \rho |\cdot |^x)$. Note that if ![]() $x \geq 1$, then by [Reference Lapid and MínguezLM16, Proposition 5.15(3)] the ladder representations
$x \geq 1$, then by [Reference Lapid and MínguezLM16, Proposition 5.15(3)] the ladder representations ![]() $L_0$,
$L_0$, ![]() $L_1$ and
$L_1$ and ![]() $L_2$ commute with all of
$L_2$ commute with all of
Therefore, with
the ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the highest and is a subrepresentation of
$D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the highest and is a subrepresentation of
 \[ \begin{cases}
L_0^{{t}/2} \times L_1^{s} \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2-s+{m}/2} \rtimes \pi_0 &
\text{if } s \leq {m'}/{2},\\ L_0^{{t}/2} \times
L_2^{s-{m'}/2} \times L_1^{m'-s} \times
\Delta_\rho[x-1,-(x-1)]^{{m}/2} \rtimes \pi_0 & \text{if }
{m'}/{2} < s \leq m', \\ L_0^{{t}/2} \times
L_2^{{m'}/2} \times \Delta_\rho[x-1,-(x-1)]^{{m}/2} \rtimes
\pi_0 & \text{if } s > m'. \end{cases}
\]
\[ \begin{cases}
L_0^{{t}/2} \times L_1^{s} \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2-s+{m}/2} \rtimes \pi_0 &
\text{if } s \leq {m'}/{2},\\ L_0^{{t}/2} \times
L_2^{s-{m'}/2} \times L_1^{m'-s} \times
\Delta_\rho[x-1,-(x-1)]^{{m}/2} \rtimes \pi_0 & \text{if }
{m'}/{2} < s \leq m', \\ L_0^{{t}/2} \times
L_2^{{m'}/2} \times \Delta_\rho[x-1,-(x-1)]^{{m}/2} \rtimes
\pi_0 & \text{if } s > m'. \end{cases}
\]
Since ![]() $L_2 \times L_1 \cong L_1 \times L_2$ by [Reference Lapid and MínguezLM16, Corollary 6.2] and since
$L_2 \times L_1 \cong L_1 \times L_2$ by [Reference Lapid and MínguezLM16, Corollary 6.2] and since ![]() $L_1 \rtimes \sigma$ is irreducible by [Reference Lapid and TadićLT20, Theorem 1.2], this representation is a subrepresentation of
$L_1 \rtimes \sigma$ is irreducible by [Reference Lapid and TadićLT20, Theorem 1.2], this representation is a subrepresentation of
 \[ \begin{cases} (\rho|\cdot|^{-x})^s \times \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2} \rtimes \pi_0 & \text{if } s \leq m',\\ (\rho|\cdot|^{-x})^{m'} \times \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2} \rtimes \pi_0 & \text{if } s > m'. \end{cases} \]
\[ \begin{cases} (\rho|\cdot|^{-x})^s \times \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2} \rtimes \pi_0 & \text{if } s \leq m',\\ (\rho|\cdot|^{-x})^{m'} \times \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2} \rtimes \pi_0 & \text{if } s > m'. \end{cases} \]
Since ![]() $\Delta _\rho [x-1,-(x-1)]^{({m'+m})/2} \rtimes \pi _0 = \pi (\phi - (\rho \boxtimes S_{2x+1})^m + (\rho \boxtimes S_{2x-1})^{m}, \eta )$, we obtain the case where
$\Delta _\rho [x-1,-(x-1)]^{({m'+m})/2} \rtimes \pi _0 = \pi (\phi - (\rho \boxtimes S_{2x+1})^m + (\rho \boxtimes S_{2x-1})^{m}, \eta )$, we obtain the case where ![]() $t$ is even.
$t$ is even.
Next, assume that ![]() $t$ is odd. By considering the Langlands data, we have
$t$ is odd. By considering the Langlands data, we have
 \begin{align*} &\mathrm{soc}\bigl( \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0 \bigr)\\ &\quad \hookrightarrow L_0^{({t-1})/2} \times \Delta_\rho[x-1,-x] \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0\\ &\quad \cong L_0^{({t-1})/2} \times \Delta_\rho[x,-(x-1)] \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0. \end{align*}
\begin{align*} &\mathrm{soc}\bigl( \Delta_\rho[x-1,-x]^t \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0 \bigr)\\ &\quad \hookrightarrow L_0^{({t-1})/2} \times \Delta_\rho[x-1,-x] \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0\\ &\quad \cong L_0^{({t-1})/2} \times \Delta_\rho[x,-(x-1)] \times \Delta_\rho[x-1,-(x-1)]^{{m'}/2} \times \Delta_\rho[x,-x]^{{m}/2} \rtimes \pi_0. \end{align*}
Note that the middle induced representation is SI since it is a subrepresentation of a standard module. On the other hand, by taking the MVW-functor and the contragredient functor, we see that the unique irreducible subrepresentation of the middle induced representation is also an irreducible quotient of the last induced representation. By the last isomorphism, this means that ![]() $L_0^{({t-1})/2} \times \Delta _\rho [x,-(x-1)] \times \Delta _\rho [x-1,-(x-1)]^{{m'}/2} \times \Delta _\rho [x,-x]^{{m}/2} \rtimes \pi _0$ is irreducible. Therefore, by the same argument as in the case where
$L_0^{({t-1})/2} \times \Delta _\rho [x,-(x-1)] \times \Delta _\rho [x-1,-(x-1)]^{{m'}/2} \times \Delta _\rho [x,-x]^{{m}/2} \rtimes \pi _0$ is irreducible. Therefore, by the same argument as in the case where ![]() $t$ is even, with
$t$ is even, with ![]() $k = m + 1 + \max \{s-m'-1,0\}$, the
$k = m + 1 + \max \{s-m'-1,0\}$, the ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$ is highest and is a subrepresentation of
$D_{\rho |\cdot |^x}^{(k)}(\pi )$ is highest and is a subrepresentation of
 \[ \begin{cases} (\rho|\cdot|^{-x})^s \times \Delta_\rho[x-1,-x]^{t-1} \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2+1} \rtimes \pi_0 & \text{if } s \leq m'+1,\\ (\rho|\cdot|^{-x})^{m'+1} \times \Delta_\rho[x-1,-x]^{t-1} \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2+1} \rtimes \pi_0 & \text{if } s > m'+1. \end{cases} \]
\[ \begin{cases} (\rho|\cdot|^{-x})^s \times \Delta_\rho[x-1,-x]^{t-1} \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2+1} \rtimes \pi_0 & \text{if } s \leq m'+1,\\ (\rho|\cdot|^{-x})^{m'+1} \times \Delta_\rho[x-1,-x]^{t-1} \times \Delta_\rho[x-1,-(x-1)]^{({m'+m})/2+1} \rtimes \pi_0 & \text{if } s > m'+1. \end{cases} \]
Since ![]() $\Delta _\rho [x-1,-(x-1)]^{({m'+m})/2+1} \rtimes \pi _0 = \pi (\phi - (\rho \boxtimes S_{2x+1})^m + (\rho \boxtimes S_{2x-1})^{m+2}, \eta )$, we obtain the case where
$\Delta _\rho [x-1,-(x-1)]^{({m'+m})/2+1} \rtimes \pi _0 = \pi (\phi - (\rho \boxtimes S_{2x+1})^m + (\rho \boxtimes S_{2x-1})^{m+2}, \eta )$, we obtain the case where ![]() $t$ is odd.
$t$ is odd.
Now we consider the general case. Let ![]() $\pi = L(\Delta _\rho [x_1,y_1], \ldots, \Delta _\rho [x_{r'},y_{r'}]; \pi (\phi, \eta ))$ with
$\pi = L(\Delta _\rho [x_1,y_1], \ldots, \Delta _\rho [x_{r'},y_{r'}]; \pi (\phi, \eta ))$ with ![]() $x_1+y_1 \leq \cdots \leq x_{r'}+y_{r'} < 0$ and
$x_1+y_1 \leq \cdots \leq x_{r'}+y_{r'} < 0$ and ![]() $\phi \in \Phi _\mathrm {temp}(G)$. If we define
$\phi \in \Phi _\mathrm {temp}(G)$. If we define ![]() $t, r \geq 0$ with
$t, r \geq 0$ with ![]() $t+r = r'$ as in § 7.1, we can rewrite
$t+r = r'$ as in § 7.1, we can rewrite
where
•
 $x_1+y_1 \leq \cdots \leq x_r+y_r < 0$;
$x_1+y_1 \leq \cdots \leq x_r+y_r < 0$;•
 $\pi _A := L(\Delta _\rho [x-1,-x]^t; \pi (\phi, \eta ))$;
$\pi _A := L(\Delta _\rho [x-1,-x]^t; \pi (\phi, \eta ))$;•
 $[x_i,y_i] \not = [x-1,-x]$ for all
$[x_i,y_i] \not = [x-1,-x]$ for all  $i = 1, \ldots,r$.
$i = 1, \ldots,r$.
Set ![]() $m := m_\phi (\rho \boxtimes S_{2x+1})$ and
$m := m_\phi (\rho \boxtimes S_{2x+1})$ and ![]() $m' := m_\phi (\rho \boxtimes S_{2x-1})$, both of which are even. Take
$m' := m_\phi (\rho \boxtimes S_{2x-1})$, both of which are even. Take ![]() $\kappa \in \{0,1\}$ such that
$\kappa \in \{0,1\}$ such that ![]() $t \equiv \kappa \bmod 2$.
$t \equiv \kappa \bmod 2$.
Define
As in the previous paragraph, we regard ![]() $A_{\rho |\cdot |^{x}}$ and
$A_{\rho |\cdot |^{x}}$ and ![]() $A_{\rho |\cdot |^{x-1}}$ (respectively
$A_{\rho |\cdot |^{x-1}}$ (respectively ![]() $B_{\rho |\cdot |^{x}}$ and
$B_{\rho |\cdot |^{x}}$ and ![]() $B_{\rho |\cdot |^{x-1}}$) as ordered sets and take the traversal relation
$B_{\rho |\cdot |^{x-1}}$) as ordered sets and take the traversal relation ![]() $\rightsquigarrow$. Let
$\rightsquigarrow$. Let ![]() $f \colon A_{\rho |\cdot |^{x-1}}^0 \rightarrow A_{\rho |\cdot |^{x}}^0$ (respectively
$f \colon A_{\rho |\cdot |^{x-1}}^0 \rightarrow A_{\rho |\cdot |^{x}}^0$ (respectively ![]() $g \colon B_{\rho |\cdot |^{x-1}}^0 \rightarrow B_{\rho |\cdot |^{x}}^0$) be the best matching function. Write
$g \colon B_{\rho |\cdot |^{x-1}}^0 \rightarrow B_{\rho |\cdot |^{x}}^0$) be the best matching function. Write ![]() $B_{\rho |\cdot |^{x}}^{\rm c} = \{i_1, \ldots, i_{s}\}$ with
$B_{\rho |\cdot |^{x}}^{\rm c} = \{i_1, \ldots, i_{s}\}$ with ![]() $i_1 < \cdots < i_{s}$. Note that
$i_1 < \cdots < i_{s}$. Note that ![]() $s > 0$ only if
$s > 0$ only if ![]() $x > 1$.
$x > 1$.
Theorem 7.4 With notation as above, suppose that ![]() $x > 0$,
$x > 0$, ![]() $x \in (1/2)\mathbb {Z}$ and
$x \in (1/2)\mathbb {Z}$ and ![]() $\rho \boxtimes S_{2x+1}$ is self-dual of the opposite type to elements in
$\rho \boxtimes S_{2x+1}$ is self-dual of the opposite type to elements in ![]() $\Phi _\mathrm {gp}(G)$. Then the highest
$\Phi _\mathrm {gp}(G)$. Then the highest ![]() $\rho |\cdot |^x$-derivative
$\rho |\cdot |^x$-derivative ![]() $D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the unique irreducible subrepresentation of
$D_{\rho |\cdot |^x}^{(k)}(\pi )$ is the unique irreducible subrepresentation of ![]() $L(\Delta _{\rho _1}[x'_1,y'_1], \ldots, \Delta _{\rho _r}[x'_r,y'_r]) \rtimes \pi _A'$, where
$L(\Delta _{\rho _1}[x'_1,y'_1], \ldots, \Delta _{\rho _r}[x'_r,y'_r]) \rtimes \pi _A'$, where
 \begin{align*} x_i' &= \begin{cases} x-1 & \text{if } i \in A_{\rho|\cdot|^{x}}^{\rm c},\\ x_i & \text{otherwise}, \end{cases} \\ y_i' &= \begin{cases} -(x-1) & \text{if } \text{$i=i_j$, $j > m'+\kappa+\max\{|A_{\rho|\cdot|^{x-1}}^{\rm c}|-m-\kappa,0\}$}, \\ y_i & \text{otherwise} \end{cases} \end{align*}
\begin{align*} x_i' &= \begin{cases} x-1 & \text{if } i \in A_{\rho|\cdot|^{x}}^{\rm c},\\ x_i & \text{otherwise}, \end{cases} \\ y_i' &= \begin{cases} -(x-1) & \text{if } \text{$i=i_j$, $j > m'+\kappa+\max\{|A_{\rho|\cdot|^{x-1}}^{\rm c}|-m-\kappa,0\}$}, \\ y_i & \text{otherwise} \end{cases} \end{align*}
and
• if
 $m+\kappa \leq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then
$m+\kappa \leq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then  $\pi _A' = \pi _A$;
$\pi _A' = \pi _A$;• if
 $m+\kappa > |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then
according to whether
$m+\kappa > |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then
according to whether \[ \pi_A' = \begin{cases} L \bigl(\Delta_\rho[x-1,-x]^{t-\kappa}; \pi(\phi - (\rho \boxtimes S_{2x+1})^{m-v} + (\rho \boxtimes S_{2x-1})^{m-v+2\kappa}, \eta) \bigr),\\ L\bigl( \Delta_\rho[x-1,-x]^{t-\kappa+1}; \pi(\phi - (\rho \boxtimes S_{2x+1})^{m-v+1} + (\rho \boxtimes S_{2x-1})^{m-v-1+2\kappa}, \eta) \bigr) \end{cases} \]
\[ \pi_A' = \begin{cases} L \bigl(\Delta_\rho[x-1,-x]^{t-\kappa}; \pi(\phi - (\rho \boxtimes S_{2x+1})^{m-v} + (\rho \boxtimes S_{2x-1})^{m-v+2\kappa}, \eta) \bigr),\\ L\bigl( \Delta_\rho[x-1,-x]^{t-\kappa+1}; \pi(\phi - (\rho \boxtimes S_{2x+1})^{m-v+1} + (\rho \boxtimes S_{2x-1})^{m-v-1+2\kappa}, \eta) \bigr) \end{cases} \]
 $v = |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ is even or odd.
$v = |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ is even or odd.
In particular,
Moreover, the following hold.
(a) If
 $m+\kappa +\max \{|B_{\rho |\cdot |^{x}}^{\rm c}|-m'-\kappa,0\} < |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then the Langlands data of
$m+\kappa +\max \{|B_{\rho |\cdot |^{x}}^{\rm c}|-m'-\kappa,0\} < |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, then the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by replacing
$\pi$ by replacing  $x_a = x-1$ with
$x_a = x-1$ with  $x$, where
$x$, where  $a$ is the minimum element of
$a$ is the minimum element of  $A_{\rho |\cdot |^{x-1}}^{\rm c}$.
$A_{\rho |\cdot |^{x-1}}^{\rm c}$.(b) If
 $|B_{\rho |\cdot |^{x}}^{\rm c}| < m'+\kappa$ and
$|B_{\rho |\cdot |^{x}}^{\rm c}| < m'+\kappa$ and  $m+\kappa \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, the Langlands data of
$m+\kappa \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$, the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by replacing
$\pi$ by replacing  $\pi _A$ with
$\pi _A$ with
 \[ S_{\rho|\cdot|^x}^{(1)}(\pi_A) = \begin{cases} L\big( \Delta_\rho[x-1,-x]^{t+1}; \pi(\phi - (\rho \boxtimes S_{2x-1})^2, \eta) \big) & \text{if } \kappa = 0, \\ L\big( \Delta_\rho[x-1,-x]^{t-1}; \pi(\phi + (\rho \boxtimes S_{2x+1})^2, \eta) \big) & \text{if } \kappa = 1. \end{cases} \]
\[ S_{\rho|\cdot|^x}^{(1)}(\pi_A) = \begin{cases} L\big( \Delta_\rho[x-1,-x]^{t+1}; \pi(\phi - (\rho \boxtimes S_{2x-1})^2, \eta) \big) & \text{if } \kappa = 0, \\ L\big( \Delta_\rho[x-1,-x]^{t-1}; \pi(\phi + (\rho \boxtimes S_{2x+1})^2, \eta) \big) & \text{if } \kappa = 1. \end{cases} \]
(c) If
 $|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'+\kappa$,
$|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'+\kappa$,  $m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and
$m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and  $B_{\rho |\cdot |^{x-1}}^{\rm c} \not = \emptyset$, the Langlands data of
$B_{\rho |\cdot |^{x-1}}^{\rm c} \not = \emptyset$, the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by replacing
$\pi$ by replacing  $y_b = -(x-1)$ with
$y_b = -(x-1)$ with  $-x$, where
$-x$, where  $b$ is the minimum element of
$b$ is the minimum element of  $B_{\rho |\cdot |^{x-1}}^{\rm c}$.
$B_{\rho |\cdot |^{x-1}}^{\rm c}$.(d) If
 $|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'+\kappa$,
$|B_{\rho |\cdot |^{x}}^{\rm c}| \geq m'+\kappa$,  $m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and
$m+|B_{\rho |\cdot |^{x}}^{\rm c}|-m' \geq |A_{\rho |\cdot |^{x-1}}^{\rm c}|$ and  $B_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$, then the Langlands data of
$B_{\rho |\cdot |^{x-1}}^{\rm c} = \emptyset$, then the Langlands data of  $S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of
$S_{\rho |\cdot |^x}^{(1)}(\pi )$ can be obtained from those of  $\pi$ by inserting
$\pi$ by inserting  $\rho |\cdot |^{-x} = \Delta _{\rho }[-x,-x]$.
$\rho |\cdot |^{-x} = \Delta _{\rho }[-x,-x]$.
Proof. By a similar argument to that for Theorem 7.1, we obtain the assertions by applying Jantzen's algorithm [Reference JantzenJan18a, § 3.3] together with [Reference Lapid and MínguezLM16, Theorem 5.11] and Proposition 7.3.
As a consequence, one can obtain an analogous criterion to Corollary 7.2 for the irreducibility of ![]() $\rho |\cdot |^x \rtimes \pi$. We leave the details to the reader.
$\rho |\cdot |^x \rtimes \pi$. We leave the details to the reader.
8. Explicit formulas for derivatives and socles: a non-cuspidal case
Fix ![]() $\rho \in \mathscr {C}^\mathrm {GL}$ self-dual. In this section, we consider
$\rho \in \mathscr {C}^\mathrm {GL}$ self-dual. In this section, we consider ![]() $\pi \in \mathrm {Irr}(G_n)$ of good or
$\pi \in \mathrm {Irr}(G_n)$ of good or ![]() $\rho$-bad parity such that
$\rho$-bad parity such that
(a)
 $\pi$ is
$\pi$ is  $\rho |\cdot |^1$-reduced; and
$\rho |\cdot |^1$-reduced; and(b)
 $\pi$ is
$\pi$ is  $\rho |\cdot |^z$-reduced for all
$\rho |\cdot |^z$-reduced for all  $z < 0$.
$z < 0$.
Recall that if an irreducible representation ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^1$-reduced, Proposition 3.7 says that
$\rho |\cdot |^1$-reduced, Proposition 3.7 says that ![]() $Z_\rho [0,1]^k \rtimes \pi$ is SI. In this subsection, we determine the highest
$Z_\rho [0,1]^k \rtimes \pi$ is SI. In this subsection, we determine the highest ![]() $[0,1]$-derivative
$[0,1]$-derivative ![]() $\pi ' = D_{[0,1]}^{(k)}(\pi )$ of
$\pi ' = D_{[0,1]}^{(k)}(\pi )$ of ![]() $\pi$, and we show how to recover the Langlands data of
$\pi$, and we show how to recover the Langlands data of ![]() $\pi$ in terms of those of
$\pi$ in terms of those of ![]() $\pi '$.
$\pi '$.
8.1 A reduction step
In this subsection, we reduce the computation to a particular case that will be treated at the end of the section.
We write ![]() $\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r], \Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ as a Langlands subrepresentation, where
$\pi = L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r], \Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ as a Langlands subrepresentation, where
•
 $\phi \in \Phi _\mathrm {temp}(G)$;
$\phi \in \Phi _\mathrm {temp}(G)$;•
 $t \geq 0$;
$t \geq 0$;•
 $x_1+y_1 \leq \cdots \leq x_r+y_r < 0$;
$x_1+y_1 \leq \cdots \leq x_r+y_r < 0$;•
 $\Delta _{\rho _i}[x_i,y_i] \not \cong \Delta _\rho [0,-1]$ for
$\Delta _{\rho _i}[x_i,y_i] \not \cong \Delta _\rho [0,-1]$ for  $i=1, \ldots,r$.
$i=1, \ldots,r$.
We know by the assumption (b) that ![]() $x_i \geq 0$ if
$x_i \geq 0$ if ![]() $\rho _i \cong \rho$. Also, by the last condition above, we have
$\rho _i \cong \rho$. Also, by the last condition above, we have ![]() $y_i \not = -1$ if
$y_i \not = -1$ if ![]() $\rho _i \cong \rho$. Set
$\rho _i \cong \rho$. Set ![]() $\pi _A := L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$.
$\pi _A := L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$.
To rephrase the assumption (a), we recall Jantzen's algorithm [Reference JantzenJan18a, § 3.3]. Let ![]() $\pi _A' := D_{\rho |\cdot |^1}^{(l)}(\pi _A)$ be the highest
$\pi _A' := D_{\rho |\cdot |^1}^{(l)}(\pi _A)$ be the highest ![]() $\rho |\cdot |^1$-derivative of
$\rho |\cdot |^1$-derivative of ![]() $\pi _A$. It can be computed thanks to Theorem 5.3 and Proposition 7.3. Then Claim 2 in [Reference JantzenJan18a, § 3.3] says that
$\pi _A$. It can be computed thanks to Theorem 5.3 and Proposition 7.3. Then Claim 2 in [Reference JantzenJan18a, § 3.3] says that
According to Jantzen's algorithm, ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^1$-reduced if and only if
$\rho |\cdot |^1$-reduced if and only if ![]() $L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r], (\rho |\cdot |^1)^{l})$ is left
$L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r], (\rho |\cdot |^1)^{l})$ is left ![]() $\rho |\cdot |^1$-reduced. For
$\rho |\cdot |^1$-reduced. For ![]() $i = r+1, \ldots, r+l$, we set
$i = r+1, \ldots, r+l$, we set ![]() $\Delta _{\rho _i}[x_i,y_i] = \rho |\cdot |^{1}$. Define
$\Delta _{\rho _i}[x_i,y_i] = \rho |\cdot |^{1}$. Define
As in § 6.2, we regard these sets as totally ordered sets, and we define a traversable relation ![]() $\rightsquigarrow$ between
$\rightsquigarrow$ between ![]() $A_{\rho |\cdot |^1}$ and
$A_{\rho |\cdot |^1}$ and ![]() $A_\rho$. Let
$A_\rho$. Let ![]() $f \colon A_{\rho }^0 \rightarrow A_{\rho |\cdot |^1}^0$ be the best matching function. Then by [Reference Lapid and MínguezLM16, Theorem 5.11],
$f \colon A_{\rho }^0 \rightarrow A_{\rho |\cdot |^1}^0$ be the best matching function. Then by [Reference Lapid and MínguezLM16, Theorem 5.11], ![]() $L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r], (\rho |\cdot |^1)^{l})$ is left
$L(\Delta _{\rho _1}[x_1,y_1], \ldots, \Delta _{\rho _r}[x_r,y_r], (\rho |\cdot |^1)^{l})$ is left ![]() $\rho |\cdot |^1$-reduced if and only if
$\rho |\cdot |^1$-reduced if and only if ![]() $A_{\rho |\cdot |^{1}}^{\rm c} = \emptyset$. Let
$A_{\rho |\cdot |^{1}}^{\rm c} = \emptyset$. Let ![]() $D_{[0,1]}^{(k_A)}(\pi _A')$ be the highest
$D_{[0,1]}^{(k_A)}(\pi _A')$ be the highest ![]() $[0,1]$-derivative of
$[0,1]$-derivative of ![]() $\pi _A'$. We will explicitly compute it in Propositions 8.3 and 8.4 below.
$\pi _A'$. We will explicitly compute it in Propositions 8.3 and 8.4 below.
Theorem 8.1 Let ![]() $\pi \in \mathrm {Irr}(G_n)$ be of good or
$\pi \in \mathrm {Irr}(G_n)$ be of good or ![]() $\rho$-bad parity and satisfy the assumptions (a) and (b). We use the above notation. Then the highest
$\rho$-bad parity and satisfy the assumptions (a) and (b). We use the above notation. Then the highest ![]() $[0,1]$-derivative
$[0,1]$-derivative ![]() $D_{[0,1]}^{(k)}(\pi )$ is the unique irreducible subrepresentation of
$D_{[0,1]}^{(k)}(\pi )$ is the unique irreducible subrepresentation of
where
 \[ x'_i = \begin{cases} -1 & \text{if } i \in A_\rho^0, \\ 0 & \text{if } i \in A_{\rho|\cdot|^1}, \\ x_i & \text{otherwise}. \end{cases} \]
\[ x'_i = \begin{cases} -1 & \text{if } i \in A_\rho^0, \\ 0 & \text{if } i \in A_{\rho|\cdot|^1}, \\ x_i & \text{otherwise}. \end{cases} \]
In particular, ![]() $k = k_A + r_1$ with
$k = k_A + r_1$ with ![]() $r_1 := |A_{\rho |\cdot |^1}| = |A_\rho ^0|$.
$r_1 := |A_{\rho |\cdot |^1}| = |A_\rho ^0|$.
Proof. Since ![]() $x_i \geq 0$ if
$x_i \geq 0$ if ![]() $\rho _i \cong \rho$, we see that
$\rho _i \cong \rho$, we see that ![]() $\Delta _{\rho _i}[x_i,y_i] \times Z_{\rho }[0,1] \cong Z_\rho [0,1] \times \Delta _{\rho _i}[x_i,y_i]$ for all
$\Delta _{\rho _i}[x_i,y_i] \times Z_{\rho }[0,1] \cong Z_\rho [0,1] \times \Delta _{\rho _i}[x_i,y_i]$ for all ![]() $i = 1, \ldots, r+l$ (see for example [Reference TadićTad14, Theorem 1.1]). Hence
$i = 1, \ldots, r+l$ (see for example [Reference TadićTad14, Theorem 1.1]). Hence
 \begin{align*} \pi &\hookrightarrow L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l}) \rtimes \pi_A'\\ &\hookrightarrow L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l}) \times Z_\rho[0,1]^{k_A} \rtimes D_{[0,1]}^{(k_A)}(\pi_A')\\ &\cong Z_\rho[0,1]^{k_A} \times L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l}) \rtimes D_{[0,1]}^{(k_A)}(\pi_A'). \end{align*}
\begin{align*} \pi &\hookrightarrow L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l}) \rtimes \pi_A'\\ &\hookrightarrow L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l}) \times Z_\rho[0,1]^{k_A} \rtimes D_{[0,1]}^{(k_A)}(\pi_A')\\ &\cong Z_\rho[0,1]^{k_A} \times L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l}) \rtimes D_{[0,1]}^{(k_A)}(\pi_A'). \end{align*}
We claim that
To see this, by [Reference Lapid and MínguezLM16, Proposition 5.6] it is enough to show that
 \begin{align*} &L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l})\\ &\quad = \mathrm{soc}\big( \rho^{r_1+k'} \times \mathrm{soc} \big( (\rho|\cdot|^1)^{r_1} \times L_\rho^{(k')} (L(\Delta_{\rho_1}[x'_1,y_1], \ldots, \Delta_{\rho_r}[x'_r,y_r]) ) \big) \big), \end{align*}
\begin{align*} &L(\Delta_{\rho_1}[x_1,y_1], \ldots, \Delta_{\rho_r}[x_r,y_r], (\rho|\cdot|^1)^{l})\\ &\quad = \mathrm{soc}\big( \rho^{r_1+k'} \times \mathrm{soc} \big( (\rho|\cdot|^1)^{r_1} \times L_\rho^{(k')} (L(\Delta_{\rho_1}[x'_1,y_1], \ldots, \Delta_{\rho_r}[x'_r,y_r]) ) \big) \big), \end{align*}
where ![]() $L_\rho ^{(k')} (L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r]) )$ is the highest left
$L_\rho ^{(k')} (L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r]) )$ is the highest left ![]() $\rho$-derivative. By our assumptions and by the definition of
$\rho$-derivative. By our assumptions and by the definition of ![]() $x_i'$, we see that
$x_i'$, we see that ![]() $k' = r_0-r_1$ with
$k' = r_0-r_1$ with ![]() $r_0 = |A_\rho |$ and that
$r_0 = |A_\rho |$ and that
with
 \begin{align*} x_i^{(1)} &= \begin{cases} -1 & \text{if } i \in A_{\rho}^{\rm c}, \\ x_i' & \text{otherwise} \end{cases} \\ &= \begin{cases} -1 & \text{if } i \in A_\rho, \\ 0 & \text{if } i \in A_{\rho|\cdot|^1}, \\ x_i & \text{otherwise}. \end{cases} \end{align*}
\begin{align*} x_i^{(1)} &= \begin{cases} -1 & \text{if } i \in A_{\rho}^{\rm c}, \\ x_i' & \text{otherwise} \end{cases} \\ &= \begin{cases} -1 & \text{if } i \in A_\rho, \\ 0 & \text{if } i \in A_{\rho|\cdot|^1}, \\ x_i & \text{otherwise}. \end{cases} \end{align*}
Since ![]() $x_i^{(1)} \not = 1$ if
$x_i^{(1)} \not = 1$ if ![]() $\rho _i \cong \rho$, we have
$\rho _i \cong \rho$, we have
 \begin{align*} &\mathrm{soc} \bigl( (\rho|\cdot|^1)^{r_1} \times L_\rho^{(r_0-r_1)} (L(\Delta_{\rho_1}[x'_1,y_1], \ldots, \Delta_{\rho_r}[x'_r,y_r]) ) \bigr)\\ &\quad = L(\Delta_{\rho_1}[x_1^{(2)},y_1], \ldots, \Delta_{\rho_{r+l}}[x_{r+l}^{(2)},y_{r+l}]) \end{align*}
\begin{align*} &\mathrm{soc} \bigl( (\rho|\cdot|^1)^{r_1} \times L_\rho^{(r_0-r_1)} (L(\Delta_{\rho_1}[x'_1,y_1], \ldots, \Delta_{\rho_r}[x'_r,y_r]) ) \bigr)\\ &\quad = L(\Delta_{\rho_1}[x_1^{(2)},y_1], \ldots, \Delta_{\rho_{r+l}}[x_{r+l}^{(2)},y_{r+l}]) \end{align*}
with
 \begin{align*} x_i^{(2)} &= \begin{cases} -1 & \text{if } i \in A_\rho, \\ 1 & \text{if } i \in A_{\rho|\cdot|^1}, \\ x_i & \text{otherwise}. \end{cases} \end{align*}
\begin{align*} x_i^{(2)} &= \begin{cases} -1 & \text{if } i \in A_\rho, \\ 1 & \text{if } i \in A_{\rho|\cdot|^1}, \\ x_i & \text{otherwise}. \end{cases} \end{align*}
In particular, we note that ![]() $\Delta _{\rho _i}[x_i^{(2)},y_i] \cong \rho |\cdot |^1$ for
$\Delta _{\rho _i}[x_i^{(2)},y_i] \cong \rho |\cdot |^1$ for ![]() $i > r$. Since
$i > r$. Since ![]() $x_i^{(2)} \not = 0$ if
$x_i^{(2)} \not = 0$ if ![]() $\rho _i \cong \rho$, we have
$\rho _i \cong \rho$, we have
Hence we obtain the claim.
By the claim, we have
Moreover, by Tadić's formula (Proposition 2.1) together with the facts that
•
 $L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r])$ is left
$L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r])$ is left  $\rho |\cdot |^1$-reduced;
$\rho |\cdot |^1$-reduced;•
 $L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r])$ is right
$L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r])$ is right  $\rho$-reduced and right
$\rho$-reduced and right  $\rho |\cdot |^{-1}$-reduced; and
$\rho |\cdot |^{-1}$-reduced; and•
 $D_{[0,1]}^{(k_A)}(\pi _A')$ is
$D_{[0,1]}^{(k_A)}(\pi _A')$ is  $Z_\rho [0,1]$-reduced and
$Z_\rho [0,1]$-reduced and  $\rho |\cdot |^1$-reduced
$\rho |\cdot |^1$-reduced
we see that ![]() $L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r]) \rtimes D_{[0,1]}^{(k_A)}(\pi _A')$ is
$L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r]) \rtimes D_{[0,1]}^{(k_A)}(\pi _A')$ is ![]() $Z_\rho [0,1]$-reduced and
$Z_\rho [0,1]$-reduced and ![]() $\rho |\cdot |^1$-reduced. Therefore,
$\rho |\cdot |^1$-reduced. Therefore, ![]() $D_{[0,1]}^{(k_A+r_1)}(\pi )$ is the highest
$D_{[0,1]}^{(k_A+r_1)}(\pi )$ is the highest ![]() $[0,1]$-derivative, and
$[0,1]$-derivative, and
Since the induced representation in the right-hand side is a subrepresentation of a standard module, it is SI. In particular, ![]() $D_{[0,1]}^{(k_A+r_1)}(\pi )$ is the unique irreducible subrepresentation of this induced representation.
$D_{[0,1]}^{(k_A+r_1)}(\pi )$ is the unique irreducible subrepresentation of this induced representation.
We give now the converse of Theorem 8.1. Namely, when ![]() $\pi$ is of good or
$\pi$ is of good or ![]() $\rho$-bad parity and satisfies the assumptions (a) and (b), we will recover the Langlands data of
$\rho$-bad parity and satisfies the assumptions (a) and (b), we will recover the Langlands data of ![]() $\pi$ from those of
$\pi$ from those of ![]() $D_{[0,1]}^{(k)}(\pi )$.
$D_{[0,1]}^{(k)}(\pi )$.
Write ![]() $D_{[0,1]}^{(k)}(\pi ) = L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r], (\rho |\cdot |^{-1})^s, \Delta _\rho [0,-1]^t; \pi (\phi ', \eta '))$ as a Langlands subrepresentation, where
$D_{[0,1]}^{(k)}(\pi ) = L(\Delta _{\rho _1}[x'_1,y_1], \ldots, \Delta _{\rho _r}[x'_r,y_r], (\rho |\cdot |^{-1})^s, \Delta _\rho [0,-1]^t; \pi (\phi ', \eta '))$ as a Langlands subrepresentation, where
•
 $\phi ' \in \Phi _\mathrm {temp}(G)$;
$\phi ' \in \Phi _\mathrm {temp}(G)$;•
 $s, t \geq 0$;
$s, t \geq 0$;•
 $x'_1+y_1 \leq \cdots \leq x'_r+y_r < 0$;
$x'_1+y_1 \leq \cdots \leq x'_r+y_r < 0$;•
 $\Delta _{\rho _i}[x'_i,y_i] \not \cong \rho |\cdot |^{-1}, \Delta _\rho [0,-1]$ for
$\Delta _{\rho _i}[x'_i,y_i] \not \cong \rho |\cdot |^{-1}, \Delta _\rho [0,-1]$ for  $i=1, \ldots,r$.
$i=1, \ldots,r$.
Set ![]() $\pi ''_A := L((\rho |\cdot |^{-1})^s, \Delta _\rho [0,-1]^t; \pi (\phi ', \eta '))$. Define
$\pi ''_A := L((\rho |\cdot |^{-1})^s, \Delta _\rho [0,-1]^t; \pi (\phi ', \eta '))$. Define
 \begin{align*} B_{\rho|\cdot|^{-1}} &:= \{i \in \{1, \ldots, r\} \mid \rho_i \cong \rho,\, x'_i = -1\},\\ B_{\rho} &:= \{i \in \{1, \ldots, r\} \mid \rho_i \cong \rho,\, x'_i = 0\} \end{align*}
\begin{align*} B_{\rho|\cdot|^{-1}} &:= \{i \in \{1, \ldots, r\} \mid \rho_i \cong \rho,\, x'_i = -1\},\\ B_{\rho} &:= \{i \in \{1, \ldots, r\} \mid \rho_i \cong \rho,\, x'_i = 0\} \end{align*}
with the best matching function ![]() $f' \colon B_{\rho |\cdot |^{-1}}^0 \rightarrow B_\rho ^0$. By Theorem 8.1, we see that
$f' \colon B_{\rho |\cdot |^{-1}}^0 \rightarrow B_\rho ^0$. By Theorem 8.1, we see that ![]() $x'_i \not = 1$ if
$x'_i \not = 1$ if ![]() $\rho _i \cong \rho$. Also, if we set
$\rho _i \cong \rho$. Also, if we set ![]() $r_1 := |B_{\rho |\cdot |^{-1}}|$,
$r_1 := |B_{\rho |\cdot |^{-1}}|$, ![]() $k_A := k-r_1$ and
$k_A := k-r_1$ and ![]() $l := r_1 - |B_\rho ^0|$, then we have
$l := r_1 - |B_\rho ^0|$, then we have ![]() $k_A \geq 0$ and
$k_A \geq 0$ and ![]() $l \geq 0$.
$l \geq 0$.
Corollary 8.2 Let ![]() $\pi \in \mathrm {Irr}(G_n)$ be of good or
$\pi \in \mathrm {Irr}(G_n)$ be of good or ![]() $\rho$-bad parity and satisfy the assumptions (a) and (b). Then
$\rho$-bad parity and satisfy the assumptions (a) and (b). Then ![]() $\pi$ is the unique irreducible subrepresentation of
$\pi$ is the unique irreducible subrepresentation of
where
 \[ x_i = \begin{cases} 0 & \text{if } i \in B_{\rho|\cdot|^{-1}}, \\ 1 & \text{if } i \in B_\rho^0, \\ x_i' & \text{otherwise} \end{cases} \]
\[ x_i = \begin{cases} 0 & \text{if } i \in B_{\rho|\cdot|^{-1}}, \\ 1 & \text{if } i \in B_\rho^0, \\ x_i' & \text{otherwise} \end{cases} \]
and
Proof. This follows from Theorem 8.1.
8.2 The representation  $\pi _A$ in the bad-parity case
$\pi _A$ in the bad-parity case
We use the same notation as in the previous subsection. It remains to give an explicit formula for the highest ![]() $[0,1]$-derivative of
$[0,1]$-derivative of ![]() $\pi '_A$ and show how to recover the Langlands data of
$\pi '_A$ and show how to recover the Langlands data of ![]() $\pi '_A$ from those of its highest
$\pi '_A$ from those of its highest ![]() $[0,1]$-derivative.
$[0,1]$-derivative.
We treat the bad-parity case first, which is much simpler. Recall that ![]() $\pi _A = L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ with
$\pi _A = L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ with ![]() $\phi \in \Phi _\mathrm {temp}(G)$. Let
$\phi \in \Phi _\mathrm {temp}(G)$. Let ![]() $\pi _A' := D_{\rho |\cdot |^1}^{(l)}(\pi _A)$ be the highest
$\pi _A' := D_{\rho |\cdot |^1}^{(l)}(\pi _A)$ be the highest ![]() $\rho |\cdot |^1$-derivative of
$\rho |\cdot |^1$-derivative of ![]() $\pi _A$. By Proposition 7.3,
$\pi _A$. By Proposition 7.3, ![]() $\pi '_A = L(\Delta _\rho [0,-1]^{t-\kappa }; \pi (\phi ', \eta '))$ with
$\pi '_A = L(\Delta _\rho [0,-1]^{t-\kappa }; \pi (\phi ', \eta '))$ with ![]() $\kappa \in \{0,1\}$,
$\kappa \in \{0,1\}$, ![]() $t \equiv \kappa \bmod 2$ and
$t \equiv \kappa \bmod 2$ and ![]() $\phi ' \in \Phi _\mathrm {temp}(G)$ which does not contain
$\phi ' \in \Phi _\mathrm {temp}(G)$ which does not contain ![]() $\rho \boxtimes S_3$. In particular,
$\rho \boxtimes S_3$. In particular, ![]() $t-\kappa$ is even. Hence what we have to prove is the following.
$t-\kappa$ is even. Hence what we have to prove is the following.
Proposition 8.3 Let ![]() $\pi = L(\Delta _\rho [0,-1]^{t}; \pi (\phi, \eta ))$ be of
$\pi = L(\Delta _\rho [0,-1]^{t}; \pi (\phi, \eta ))$ be of ![]() $\rho$-bad parity with
$\rho$-bad parity with ![]() $t$ even and
$t$ even and ![]() $\phi \in \Phi _\mathrm {temp}(G)$ such that
$\phi \in \Phi _\mathrm {temp}(G)$ such that ![]() $\phi \not \supset \rho \boxtimes S_3$. Then the highest
$\phi \not \supset \rho \boxtimes S_3$. Then the highest ![]() $[0,1]$-derivative of
$[0,1]$-derivative of ![]() $\pi$ is
$\pi$ is
Proof. Write ![]() $m := m_\phi (\rho )$, which is even. Since
$m := m_\phi (\rho )$, which is even. Since
 \begin{align*} \pi &\hookrightarrow \rho^{t+{m}/2} \rtimes L((\rho|\cdot|^{-1})^t; \pi(\phi-\rho^m,\eta))\\ & \cong \rho^{t+{m}/2} \times (\rho|\cdot|^{-1})^t \rtimes \pi(\phi-\rho^m,\eta)\\ & \cong \rho^{t+{m}/2} \times (\rho|\cdot|^{1})^t \rtimes \pi(\phi-\rho^m,\eta), \end{align*}
\begin{align*} \pi &\hookrightarrow \rho^{t+{m}/2} \rtimes L((\rho|\cdot|^{-1})^t; \pi(\phi-\rho^m,\eta))\\ & \cong \rho^{t+{m}/2} \times (\rho|\cdot|^{-1})^t \rtimes \pi(\phi-\rho^m,\eta)\\ & \cong \rho^{t+{m}/2} \times (\rho|\cdot|^{1})^t \rtimes \pi(\phi-\rho^m,\eta), \end{align*}
we see that ![]() $D_{[0,1]}^{(t)}(\pi )$ is the highest
$D_{[0,1]}^{(t)}(\pi )$ is the highest ![]() $[0,1]$-derivative and
$[0,1]$-derivative and
Since the right-hand side is irreducible, this inclusion is an isomorphism.
By this proposition, it is easy to recover ![]() $\pi$ from its highest
$\pi$ from its highest ![]() $[0,1]$-derivative.
$[0,1]$-derivative.
8.3 The representation  $\pi _A$ in the good-parity case
$\pi _A$ in the good-parity case
To finish our algorithm we need to consider the case where ![]() $\pi = L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ with
$\pi = L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ with ![]() $\phi \in \Phi _\mathrm {gp}(G)$ and
$\phi \in \Phi _\mathrm {gp}(G)$ and ![]() $\eta \in \widehat {\mathcal {S}_\phi }$, and
$\eta \in \widehat {\mathcal {S}_\phi }$, and ![]() $\rho$ is self-dual of the same type as
$\rho$ is self-dual of the same type as ![]() $\phi$. Furthermore, we assume that
$\phi$. Furthermore, we assume that ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^1$-reduced, which is equivalent to the statement that if
$\rho |\cdot |^1$-reduced, which is equivalent to the statement that if ![]() $\rho \boxtimes S_3 \subset \phi$, then
$\rho \boxtimes S_3 \subset \phi$, then ![]() $m_\phi (\rho ) > 0$,
$m_\phi (\rho ) > 0$, ![]() $m_\phi (\rho \boxtimes S_3) = 1$ and
$m_\phi (\rho \boxtimes S_3) = 1$ and ![]() $\eta (\rho )\eta (\rho \boxtimes S_3) \not = (-1)^t$. We determine the highest
$\eta (\rho )\eta (\rho \boxtimes S_3) \not = (-1)^t$. We determine the highest ![]() $[0,1]$-derivative of
$[0,1]$-derivative of ![]() $\pi$.
$\pi$.
Proposition 8.4 Let ![]() $\pi = L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ with
$\pi = L(\Delta _\rho [0,-1]^t; \pi (\phi, \eta ))$ with ![]() $\phi \in \Phi _\mathrm {gp}(G)$ and
$\phi \in \Phi _\mathrm {gp}(G)$ and ![]() $\eta \in \widehat {\mathcal {S}_\phi }$. Suppose that
$\eta \in \widehat {\mathcal {S}_\phi }$. Suppose that ![]() $\rho$ is self-dual of the same type as
$\rho$ is self-dual of the same type as ![]() $\phi$ and that
$\phi$ and that ![]() $\pi$ is
$\pi$ is ![]() $\rho |\cdot |^1$-reduced. Write
$\rho |\cdot |^1$-reduced. Write ![]() $m := m_\phi (\rho )$.
$m := m_\phi (\rho )$.
(1) If
 $\rho \boxtimes S_3 \subset \phi$ and
$\rho \boxtimes S_3 \subset \phi$ and  $m$ is odd, then the highest
$m$ is odd, then the highest  $[0,1]$-derivative of
$[0,1]$-derivative of  $\pi$ is
$\pi$ is
 \[ D_{[0,1]}^{(t)}(\pi) = \begin{cases} \pi(\phi, \eta) & \text{if } t \equiv 0 \bmod 2, \\ L(\rho|\cdot|^{-1}; \pi(\phi+\rho-\rho \boxtimes S_3, \eta)) & \text{if } t \equiv 1 \bmod 2. \end{cases} \]
\[ D_{[0,1]}^{(t)}(\pi) = \begin{cases} \pi(\phi, \eta) & \text{if } t \equiv 0 \bmod 2, \\ L(\rho|\cdot|^{-1}; \pi(\phi+\rho-\rho \boxtimes S_3, \eta)) & \text{if } t \equiv 1 \bmod 2. \end{cases} \]
(2) If
 $\rho \boxtimes S_3 \subset \phi$ and
$\rho \boxtimes S_3 \subset \phi$ and  $m$ is even, then the highest
$m$ is even, then the highest  $[0,1]$-derivative of
$[0,1]$-derivative of  $\pi$ is
$\pi$ is
 \[ D_{[0,1]}^{(t+1)}(\pi) = \pi(\phi - \rho \boxtimes (S_1+S_3), \eta_{t+1}). \]
\[ D_{[0,1]}^{(t+1)}(\pi) = \pi(\phi - \rho \boxtimes (S_1+S_3), \eta_{t+1}). \]
(3) If
 $\rho \boxtimes S_3 \not \subset \phi$ and
$\rho \boxtimes S_3 \not \subset \phi$ and  $m$ is odd, then the highest
$m$ is odd, then the highest  $[0,1]$-derivative of
$[0,1]$-derivative of  $\pi$ is
$\pi$ is
 \[ \begin{cases} D_{[0,1]}^{(0)}(\pi) = \pi(\phi, \eta) & \text{if } t = 0, \\ D_{[0,1]}^{(t-1)}(\pi) = L(\rho|\cdot|^{-1}; \pi(\phi + \rho^2, \eta)) & \text{if } t > 0,\, t \equiv 0 \bmod 2,\\ D_{[0,1]}^{(t-1)}(\pi) = L(\Delta_\rho[0,-1]; \pi(\phi, \eta)) & \text{if } t > 0,\, t \equiv 1 \bmod 2. \end{cases} \]
\[ \begin{cases} D_{[0,1]}^{(0)}(\pi) = \pi(\phi, \eta) & \text{if } t = 0, \\ D_{[0,1]}^{(t-1)}(\pi) = L(\rho|\cdot|^{-1}; \pi(\phi + \rho^2, \eta)) & \text{if } t > 0,\, t \equiv 0 \bmod 2,\\ D_{[0,1]}^{(t-1)}(\pi) = L(\Delta_\rho[0,-1]; \pi(\phi, \eta)) & \text{if } t > 0,\, t \equiv 1 \bmod 2. \end{cases} \]
(4) If
 $\rho \boxtimes S_3 \not \subset \phi$ and
$\rho \boxtimes S_3 \not \subset \phi$ and  $m$ is even, then the highest
$m$ is even, then the highest  $[0,1]$-derivative of
$[0,1]$-derivative of  $\pi$ is
$\pi$ is
 \[ D_{[0,1]}^{(t)}(\pi) = \pi(\phi, \eta_t). \]
\[ D_{[0,1]}^{(t)}(\pi) = \pi(\phi, \eta_t). \]
Here, in (2) and (4) we set
 \[ \eta_t(\rho' \boxtimes S_d) = \begin{cases} (-1)^t \eta(\rho) & \text{if } \rho' \boxtimes S_d \cong \rho, \\ \eta(\rho' \boxtimes S_d) & \text{otherwise}. \end{cases} \]
\[ \eta_t(\rho' \boxtimes S_d) = \begin{cases} (-1)^t \eta(\rho) & \text{if } \rho' \boxtimes S_d \cong \rho, \\ \eta(\rho' \boxtimes S_d) & \text{otherwise}. \end{cases} \]
Proof. We note that ![]() $\pi \hookrightarrow \rho ^{t+u} \times L((\rho |\cdot |^{-1})^{t}; \pi (\phi - \rho ^{2u}, \eta ))$ in all cases, where
$\pi \hookrightarrow \rho ^{t+u} \times L((\rho |\cdot |^{-1})^{t}; \pi (\phi - \rho ^{2u}, \eta ))$ in all cases, where ![]() $m = 2u+1$ or
$m = 2u+1$ or ![]() $m = 2u$. We will apply Theorem 7.1 to
$m = 2u$. We will apply Theorem 7.1 to ![]() $L((\rho |\cdot |^{-1})^{t}; \pi (\phi - \rho ^{2u}, \eta ))$ and
$L((\rho |\cdot |^{-1})^{t}; \pi (\phi - \rho ^{2u}, \eta ))$ and ![]() $x=1$ in each case.
$x=1$ in each case.
To show (1), write ![]() $m = 2u+1$. By Theorem 7.1, we have
$m = 2u+1$. By Theorem 7.1, we have
 \[ \pi \hookrightarrow \rho^{t+u} \times (\rho|\cdot|^{1})^{t} \rtimes \begin{cases} \pi(\phi-\rho^{2u}, \eta) & \text{if } t \equiv 0 \bmod 2, \\ L(\rho|\cdot|^{-1}; \pi(\phi - \rho^{2u-1} - \rho \boxtimes S_3, \eta)) & \text{if } t \equiv 1 \bmod 2. \end{cases} \]
\[ \pi \hookrightarrow \rho^{t+u} \times (\rho|\cdot|^{1})^{t} \rtimes \begin{cases} \pi(\phi-\rho^{2u}, \eta) & \text{if } t \equiv 0 \bmod 2, \\ L(\rho|\cdot|^{-1}; \pi(\phi - \rho^{2u-1} - \rho \boxtimes S_3, \eta)) & \text{if } t \equiv 1 \bmod 2. \end{cases} \]
Note that ![]() $\rho ^u \rtimes \pi (\phi -\rho ^{2u}, \eta ) = \pi (\phi, \eta )$ and
$\rho ^u \rtimes \pi (\phi -\rho ^{2u}, \eta ) = \pi (\phi, \eta )$ and ![]() $\rho ^u \rtimes L(\rho |\cdot |^{-1}; \pi (\phi - \rho ^{2u-1} - \rho \boxtimes S_3, \eta )) = L(\rho |\cdot |^{-1}; \pi (\phi + \rho - \rho \boxtimes S_3, \eta ))$ are both irreducible by [Reference ArthurArt13, Proposition 2.4.3] and Mœglin's construction (see [Reference XuXu17a, § 8]). Hence
$\rho ^u \rtimes L(\rho |\cdot |^{-1}; \pi (\phi - \rho ^{2u-1} - \rho \boxtimes S_3, \eta )) = L(\rho |\cdot |^{-1}; \pi (\phi + \rho - \rho \boxtimes S_3, \eta ))$ are both irreducible by [Reference ArthurArt13, Proposition 2.4.3] and Mœglin's construction (see [Reference XuXu17a, § 8]). Hence
 \begin{align*} \pi \hookrightarrow Z_\rho[0,1]^t \rtimes \begin{cases} \pi(\phi, \eta) & \text{if } t \equiv 0 \bmod 2, \\ L(\rho|\cdot|^{-1}; \pi(\phi + \rho - \rho \boxtimes S_3, \eta)) & \text{if } t \equiv 1 \bmod 2. \end{cases} \end{align*}
\begin{align*} \pi \hookrightarrow Z_\rho[0,1]^t \rtimes \begin{cases} \pi(\phi, \eta) & \text{if } t \equiv 0 \bmod 2, \\ L(\rho|\cdot|^{-1}; \pi(\phi + \rho - \rho \boxtimes S_3, \eta)) & \text{if } t \equiv 1 \bmod 2. \end{cases} \end{align*}
This shows (1).
To show (2), write ![]() $m = 2u$. Note that
$m = 2u$. Note that ![]() $u > 0$ and
$u > 0$ and ![]() $\eta (\rho \boxtimes S_3) = (-1)^{t+1}\eta (\rho )$. Hence
$\eta (\rho \boxtimes S_3) = (-1)^{t+1}\eta (\rho )$. Hence
This implies that
 \begin{align*} \pi &\hookrightarrow Z_\rho[0,1]^{t+1} \times \rho^{u-1} \rtimes \pi(\phi-\rho^{2u-1}-\rho \boxtimes S_3, \eta_{t+1})\\ &= Z_\rho[0,1]^{t+1} \rtimes \pi(\phi-\rho-\rho \boxtimes S_3, \eta_{t+1}), \end{align*}
\begin{align*} \pi &\hookrightarrow Z_\rho[0,1]^{t+1} \times \rho^{u-1} \rtimes \pi(\phi-\rho^{2u-1}-\rho \boxtimes S_3, \eta_{t+1})\\ &= Z_\rho[0,1]^{t+1} \rtimes \pi(\phi-\rho-\rho \boxtimes S_3, \eta_{t+1}), \end{align*}
which shows (2).
To show (3), note that when ![]() $t=0$, it is clear that
$t=0$, it is clear that ![]() $\pi$ is
$\pi$ is ![]() $Z_\rho [0,1]$-reduced (Lemma 3.5). Suppose that
$Z_\rho [0,1]$-reduced (Lemma 3.5). Suppose that ![]() $t > 0$. Write
$t > 0$. Write ![]() $m = 2u+1$. Since
$m = 2u+1$. Since
we have
By [Reference ArthurArt13, Proposition 2.4.3] and Mœglin's construction (see [Reference XuXu17a, § 8]), we have
In particular, ![]() $D_{[0,1]}^{(t-1)}(\pi )$ is the highest
$D_{[0,1]}^{(t-1)}(\pi )$ is the highest ![]() $[0,1]$-derivative and is isomorphic to one of the two direct summands in the right-hand side. Now we note that
$[0,1]$-derivative and is isomorphic to one of the two direct summands in the right-hand side. Now we note that ![]() $L(\Delta _\rho [0,-1], \Delta _\rho [1,0]) \cong \mathrm {soc}(Z_\rho [0,1] \times Z_\rho [-1,0])$. When
$L(\Delta _\rho [0,-1], \Delta _\rho [1,0]) \cong \mathrm {soc}(Z_\rho [0,1] \times Z_\rho [-1,0])$. When ![]() $t$ is odd, by [Reference ArthurArt13, Proposition 2.4.3] we have
$t$ is odd, by [Reference ArthurArt13, Proposition 2.4.3] we have
Since ![]() $L(\Delta _\rho [0,-1]; \pi (\phi, \eta ))$ is
$L(\Delta _\rho [0,-1]; \pi (\phi, \eta ))$ is ![]() $\rho |\cdot |^1$-reduced and
$\rho |\cdot |^1$-reduced and ![]() $Z_\rho [0,1]$-reduced, by considering Tadić's formula (Proposition 2.1) we see that
$Z_\rho [0,1]$-reduced, by considering Tadić's formula (Proposition 2.1) we see that
which implies that ![]() $D_{[0,1]}^{(t-1)}(\pi ) = L(\Delta _\rho [0,-1]; \pi (\phi, \eta ))$. When
$D_{[0,1]}^{(t-1)}(\pi ) = L(\Delta _\rho [0,-1]; \pi (\phi, \eta ))$. When ![]() $t = 2$, by [Reference ArthurArt13, Proposition 2.4.3], we have
$t = 2$, by [Reference ArthurArt13, Proposition 2.4.3], we have
 \begin{align*} \pi &\hookrightarrow L(\Delta_\rho[0,-1], \Delta_\rho[1,0]) \rtimes \pi(\phi, \eta)\\ & \cong \mathrm{soc}(Z_\rho[0,1] \times Z_\rho[-1,0]) \rtimes \pi(\phi, \eta)\\ &\hookrightarrow Z_\rho[0,1] \times \rho|\cdot|^{-1} \rtimes \pi(\phi + \rho^2, \eta), \end{align*}
\begin{align*} \pi &\hookrightarrow L(\Delta_\rho[0,-1], \Delta_\rho[1,0]) \rtimes \pi(\phi, \eta)\\ & \cong \mathrm{soc}(Z_\rho[0,1] \times Z_\rho[-1,0]) \rtimes \pi(\phi, \eta)\\ &\hookrightarrow Z_\rho[0,1] \times \rho|\cdot|^{-1} \rtimes \pi(\phi + \rho^2, \eta), \end{align*}
which implies that ![]() $D_{[0,1]}^{(1)}(\pi ) = L(\rho |\cdot |^{-1}; \pi (\phi + \rho ^{2}, \eta ))$. When
$D_{[0,1]}^{(1)}(\pi ) = L(\rho |\cdot |^{-1}; \pi (\phi + \rho ^{2}, \eta ))$. When ![]() $t > 2$ is even, we have
$t > 2$ is even, we have
 \begin{align*} \pi &\hookrightarrow L(\Delta_\rho[0,-1], \Delta_\rho[1,0])^{({t-2})/2} \rtimes L(\Delta_\rho[0,-1]^2; \pi(\phi, \eta))\\ &\hookrightarrow Z_\rho[0,1] \times L(\Delta_\rho[0,-1], \Delta_\rho[1,0])^{({t-2})/2} \rtimes L\big(\rho|\cdot|^{-1}; \pi(\phi + \rho^{2}, \eta)\big). \end{align*}
\begin{align*} \pi &\hookrightarrow L(\Delta_\rho[0,-1], \Delta_\rho[1,0])^{({t-2})/2} \rtimes L(\Delta_\rho[0,-1]^2; \pi(\phi, \eta))\\ &\hookrightarrow Z_\rho[0,1] \times L(\Delta_\rho[0,-1], \Delta_\rho[1,0])^{({t-2})/2} \rtimes L\big(\rho|\cdot|^{-1}; \pi(\phi + \rho^{2}, \eta)\big). \end{align*}
Here, we note that ![]() $Z_\rho [0,1] \times L(\Delta _\rho [0,-1], \Delta _\rho [1,0])$ is irreducible by [Reference TadićTad14, Theorem 1.1]. Since
$Z_\rho [0,1] \times L(\Delta _\rho [0,-1], \Delta _\rho [1,0])$ is irreducible by [Reference TadićTad14, Theorem 1.1]. Since ![]() $L(\rho |\cdot |^{-1}; \pi (\phi + \rho ^{2}, \eta ))$ is
$L(\rho |\cdot |^{-1}; \pi (\phi + \rho ^{2}, \eta ))$ is ![]() $\rho |\cdot |^1$-reduced and
$\rho |\cdot |^1$-reduced and ![]() $Z_\rho [0,1]$-reduced, by considering Tadić's formula (Proposition 2.1) we see that
$Z_\rho [0,1]$-reduced, by considering Tadić's formula (Proposition 2.1) we see that
 \begin{align*} & D_{[0,1]}^{(t-1)}\bigl( Z_\rho[0,1] \times L(\Delta_\rho[0,-1],
\Delta_\rho[1,0])^{({t-2})/2} \rtimes L(\rho|\cdot|^{-1};
\pi(\phi + \rho^{2}, \eta)) \bigr) \\ & \quad =
L\bigl(\rho|\cdot|^{-1}; \pi(\phi + \rho^{2},
\eta)\bigr),\end{align*}
\begin{align*} & D_{[0,1]}^{(t-1)}\bigl( Z_\rho[0,1] \times L(\Delta_\rho[0,-1],
\Delta_\rho[1,0])^{({t-2})/2} \rtimes L(\rho|\cdot|^{-1};
\pi(\phi + \rho^{2}, \eta)) \bigr) \\ & \quad =
L\bigl(\rho|\cdot|^{-1}; \pi(\phi + \rho^{2},
\eta)\bigr),\end{align*}
which implies that ![]() $D_{[0,1]}^{(t-1)}(\pi ) = L(\rho |\cdot |^{-1}; \pi (\phi + \rho ^{2}, \eta ))$. Thus we obtain (3).
$D_{[0,1]}^{(t-1)}(\pi ) = L(\rho |\cdot |^{-1}; \pi (\phi + \rho ^{2}, \eta ))$. Thus we obtain (3).
To show (4), write ![]() $m = 2u$. Since
$m = 2u$. Since
we have
In particular, this shows (4) when ![]() $u=0$. Hereafter we assume that
$u=0$. Hereafter we assume that ![]() $u > 0$. Then
$u > 0$. Then
To show ![]() $\pi \hookrightarrow Z_\rho [0,1]^{t} \rtimes \pi (\phi, \eta _t)$, we use an argument inspired by Mœglin's construction of
$\pi \hookrightarrow Z_\rho [0,1]^{t} \rtimes \pi (\phi, \eta _t)$, we use an argument inspired by Mœglin's construction of ![]() $A$-packets.
$A$-packets.
Write ![]() $\phi = \rho ^{m} \oplus (\bigoplus _{i=1}^r \rho _i \boxtimes S_{d_i})$ with
$\phi = \rho ^{m} \oplus (\bigoplus _{i=1}^r \rho _i \boxtimes S_{d_i})$ with ![]() $d_1 \leq \cdots \leq d_r$ and
$d_1 \leq \cdots \leq d_r$ and ![]() $d_i > 3$ if
$d_i > 3$ if ![]() $\rho _i \cong \rho$. Choose
$\rho _i \cong \rho$. Choose ![]() $\phi _> = (\bigoplus _{j=1}^{m} \rho \boxtimes S_{2x_j+1}) \oplus (\bigoplus _{i=1}^r \rho _i \boxtimes S_{d_i'})$ such that
$\phi _> = (\bigoplus _{j=1}^{m} \rho \boxtimes S_{2x_j+1}) \oplus (\bigoplus _{i=1}^r \rho _i \boxtimes S_{d_i'})$ such that
•
 $x_j \in \mathbb {Z}$ with
$x_j \in \mathbb {Z}$ with  $x_j > 1$;
$x_j > 1$;•
 $d_i' \equiv d_i \bmod 2$ with
$d_i' \equiv d_i \bmod 2$ with  $d_i' \geq d_i$;
$d_i' \geq d_i$;•
 $2x_1+1 < \cdots < 2x_{m}+1 < d_1' < \cdots < d_r'$.
$2x_1+1 < \cdots < 2x_{m}+1 < d_1' < \cdots < d_r'$.
Define ![]() $\eta _> \in \widehat {\mathcal {S}_{\phi _>}}$ by
$\eta _> \in \widehat {\mathcal {S}_{\phi _>}}$ by ![]() $\eta _>(\rho \boxtimes S_{2x_j+1}) = (-1)^t\eta (\rho )$ and
$\eta _>(\rho \boxtimes S_{2x_j+1}) = (-1)^t\eta (\rho )$ and ![]() $\eta _>(\rho _i \boxtimes S_{d_i'}) = \eta (\rho _i \boxtimes S_{d_i})$. Then
$\eta _>(\rho _i \boxtimes S_{d_i'}) = \eta (\rho _i \boxtimes S_{d_i})$. Then ![]() $\pi (\phi,\eta _t) = J_2 \circ J_1(\pi (\phi _>, \eta _>))$ with
$\pi (\phi,\eta _t) = J_2 \circ J_1(\pi (\phi _>, \eta _>))$ with
 \begin{align*} J_1 &= \mathrm{Jac}_{\rho|\cdot|^{x_{m}}, \ldots, \rho|\cdot|^1} \circ \cdots \circ \mathrm{Jac}_{\rho|\cdot|^{x_{1}}, \ldots, \rho|\cdot|^1},\\ J_2 &= \mathrm{Jac}_{\rho_t|\cdot|^{({d_r'-1})/2}, \ldots, \rho_t|\cdot|^{({d_r+1})/2}} \circ \cdots \circ \mathrm{Jac}_{\rho_1|\cdot|^{({d_1'-1})/2}, \ldots, \rho_1|\cdot|^{({d_1+1})/2}}, \end{align*}
\begin{align*} J_1 &= \mathrm{Jac}_{\rho|\cdot|^{x_{m}}, \ldots, \rho|\cdot|^1} \circ \cdots \circ \mathrm{Jac}_{\rho|\cdot|^{x_{1}}, \ldots, \rho|\cdot|^1},\\ J_2 &= \mathrm{Jac}_{\rho_t|\cdot|^{({d_r'-1})/2}, \ldots, \rho_t|\cdot|^{({d_r+1})/2}} \circ \cdots \circ \mathrm{Jac}_{\rho_1|\cdot|^{({d_1'-1})/2}, \ldots, \rho_1|\cdot|^{({d_1+1})/2}}, \end{align*}
where we set ![]() $\mathrm {Jac}_{\rho |\cdot |^{x}, \ldots, \rho |\cdot |^y} = D_{\rho |\cdot |^y}^{(1)} \circ \cdots \circ D_{\rho |\cdot |^x}^{(1)}$. Since
$\mathrm {Jac}_{\rho |\cdot |^{x}, \ldots, \rho |\cdot |^y} = D_{\rho |\cdot |^y}^{(1)} \circ \cdots \circ D_{\rho |\cdot |^x}^{(1)}$. Since ![]() $\phi _>$ contains neither
$\phi _>$ contains neither ![]() $\rho$ nor
$\rho$ nor ![]() $\rho \boxtimes S_3$, by the argument in the previous paragraph we have
$\rho \boxtimes S_3$, by the argument in the previous paragraph we have
By Theorem 7.1, using the assumption that ![]() $m \equiv 0 \bmod 2$, we see that
$m \equiv 0 \bmod 2$, we see that
On the other hand, since
by [Reference XuXu17b, Lemma 5.7], and since ![]() $Z_\rho [0,1] \times \Delta _\rho [x,1] \cong \Delta _\rho [x,1] \times Z_\rho [0,1]$ if
$Z_\rho [0,1] \times \Delta _\rho [x,1] \cong \Delta _\rho [x,1] \times Z_\rho [0,1]$ if ![]() $x \geq 1$, we see that
$x \geq 1$, we see that
 \begin{align*} &J_2 \circ J_1 (\mathrm{soc}(Z_\rho[0,1]^t \rtimes \pi(\phi_>, \eta_>)))\\ &\quad\hookrightarrow J_2 \circ J_1 (Z_\rho[0,1]^t \rtimes \pi(\phi_>, \eta_>))\\ &\quad\hookrightarrow J_2 \circ J_1 (\Delta_{\rho}[x_1,1] \times \cdots \times \Delta_\rho[x_{m},1] \times Z_\rho[0,1]^t \rtimes J_1(\pi(\phi_>, \eta_>)))\\ &\quad=J_2(Z_\rho[0,1]^t \rtimes J_1(\pi(\phi_>, \eta_>))). \end{align*}
\begin{align*} &J_2 \circ J_1 (\mathrm{soc}(Z_\rho[0,1]^t \rtimes \pi(\phi_>, \eta_>)))\\ &\quad\hookrightarrow J_2 \circ J_1 (Z_\rho[0,1]^t \rtimes \pi(\phi_>, \eta_>))\\ &\quad\hookrightarrow J_2 \circ J_1 (\Delta_{\rho}[x_1,1] \times \cdots \times \Delta_\rho[x_{m},1] \times Z_\rho[0,1]^t \rtimes J_1(\pi(\phi_>, \eta_>)))\\ &\quad=J_2(Z_\rho[0,1]^t \rtimes J_1(\pi(\phi_>, \eta_>))). \end{align*}
Finally, since ![]() $(d_i+1)/2 > 2$ if
$(d_i+1)/2 > 2$ if ![]() $\rho _i \cong \rho$, we have
$\rho _i \cong \rho$, we have
Therefore we conclude that ![]() $\pi \hookrightarrow Z_\rho [0,1]^t \rtimes \pi (\phi, \eta _t)$. This completes the proof of (4).
$\pi \hookrightarrow Z_\rho [0,1]^t \rtimes \pi (\phi, \eta _t)$. This completes the proof of (4).
Finally, we state the converse of Proposition 8.4 in terms of ![]() $A$-parameters.
$A$-parameters.
Corollary 8.5 Let ![]() $\pi = L(\Delta _\rho [0,1]^t; \pi (\phi, \eta ))$ be the same as in Proposition 8.4, and let
$\pi = L(\Delta _\rho [0,1]^t; \pi (\phi, \eta ))$ be the same as in Proposition 8.4, and let ![]() $D_{[0,1]}^{(k)}(\pi )$ be the highest
$D_{[0,1]}^{(k)}(\pi )$ be the highest ![]() $[0,1]$-derivative of
$[0,1]$-derivative of ![]() $\pi$. Suppose that
$\pi$. Suppose that ![]() $k > 0$. Then one can write
$k > 0$. Then one can write ![]() $D_{[0,1]}^{(k)}(\pi ) = L((\rho |\cdot |^{-1})^{s'}, \Delta _\rho [0,1]^{t'}; \pi (\phi ', \eta '))$ with
$D_{[0,1]}^{(k)}(\pi ) = L((\rho |\cdot |^{-1})^{s'}, \Delta _\rho [0,1]^{t'}; \pi (\phi ', \eta '))$ with ![]() $s'+t'+m_{\phi '}(\rho \boxtimes S_3) \leq 1$. Moreover, with
$s'+t'+m_{\phi '}(\rho \boxtimes S_3) \leq 1$. Moreover, with ![]() $m' := m_{\phi '}(\rho )$, the following hold.
$m' := m_{\phi '}(\rho )$, the following hold.
(1) If
 $s'=1$, then
$s'=1$, then  $m' \geq 2$,
$m' \geq 2$,  $k \equiv 1\bmod 2$ and
$k \equiv 1\bmod 2$ and
 \[ \pi = \pi(\phi' - \rho^2 + (\rho \boxtimes S_2 \boxtimes S_2)^{k+1},m',\eta'). \]
\[ \pi = \pi(\phi' - \rho^2 + (\rho \boxtimes S_2 \boxtimes S_2)^{k+1},m',\eta'). \]
(2) If
 $t'=1$, then
$t'=1$, then  $m' \equiv 1 \bmod 2$,
$m' \equiv 1 \bmod 2$,  $k \equiv 0 \bmod 2$ and
$k \equiv 0 \bmod 2$ and
 \[ \pi = \pi(\phi' + (\rho \boxtimes S_2 \boxtimes S_2)^{k+1},1,\eta'). \]
\[ \pi = \pi(\phi' + (\rho \boxtimes S_2 \boxtimes S_2)^{k+1},1,\eta'). \]
(3) If
 $m_{\phi '}(\rho \boxtimes S_3) = 1$, then
$m_{\phi '}(\rho \boxtimes S_3) = 1$, then  $m' \equiv 1 \bmod 2$,
$m' \equiv 1 \bmod 2$,  $k \equiv 0 \bmod 2$ and
$k \equiv 0 \bmod 2$ and
 \[ \pi = \pi(\phi' + (\rho \boxtimes S_2 \boxtimes S_2)^{k},1,\eta'). \]
\[ \pi = \pi(\phi' + (\rho \boxtimes S_2 \boxtimes S_2)^{k},1,\eta'). \]
(4) If
 $s'+t'+m_{\phi '}(\rho \boxtimes S_3) = 0$, then
where
$s'+t'+m_{\phi '}(\rho \boxtimes S_3) = 0$, then
where \[ \pi = \pi(\phi' + (\rho \boxtimes S_2 \boxtimes S_2)^{k},m'+1,\eta'_k), \]
\[ \pi = \pi(\phi' + (\rho \boxtimes S_2 \boxtimes S_2)^{k},m'+1,\eta'_k), \]
 $\eta _k'(\rho ) = (-1)^{k}\eta '(\rho )$.
$\eta _k'(\rho ) = (-1)^{k}\eta '(\rho )$.
Proof. This follows from Proposition 8.4.
9. Some examples of Zelevinsky–Aubert duality
By the results in the previous sections, we have completed Algorithm 4.1 for computing the Zelevinsky–Aubert duality. In this section, we give some examples. Here we set ![]() $\rho := \mathbf {1}_{\mathrm {GL}_1(F)}$ and drop
$\rho := \mathbf {1}_{\mathrm {GL}_1(F)}$ and drop ![]() $\rho$ from the notation. For example, we write
$\rho$ from the notation. For example, we write ![]() $\Delta [x,y] := \Delta _\rho [x,y]$ and
$\Delta [x,y] := \Delta _\rho [x,y]$ and ![]() $Z[y,x] := Z_\rho [y,x]$. When
$Z[y,x] := Z_\rho [y,x]$. When ![]() $\phi = \bigoplus _{i=1}^r S_{d_i} \in \Phi _\mathrm {gp}(G)$ and
$\phi = \bigoplus _{i=1}^r S_{d_i} \in \Phi _\mathrm {gp}(G)$ and ![]() $\eta (S_{d_i}) = \eta _i \in \{\pm 1\}$, we write
$\eta (S_{d_i}) = \eta _i \in \{\pm 1\}$, we write ![]() $\pi (\phi, \eta ) = \pi (d_1^{\eta _1}, \ldots, d_r^{\eta _r})$.
$\pi (\phi, \eta ) = \pi (d_1^{\eta _1}, \ldots, d_r^{\eta _r})$.
9.1 Example 1
Let us compute the Zelevinsky–Aubert dual of
Note that it is of good parity, and it is ![]() $|\cdot |^z$-reduced for
$|\cdot |^z$-reduced for ![]() $z \not = 0$ by Theorem 7.1. By Algorithm 4.1, we have the following commutative diagram.
$z \not = 0$ by Theorem 7.1. By Algorithm 4.1, we have the following commutative diagram.

For the computation of ![]() $S_{Z[0,1]}^{(2)}$, by Corollaries 8.2 and 8.5 and Theorem 5.3, we have
$S_{Z[0,1]}^{(2)}$, by Corollaries 8.2 and 8.5 and Theorem 5.3, we have
 \begin{align*} S_{Z[0,1]}^{(2)}\bigl(L(\Delta[-1,-2]; \pi(1^+))\bigr) &= \mathrm{soc}\bigl( \Delta[0,-2] \rtimes S_{|\cdot|^1}^{(1)} \circ S_{Z[0,1]}^{(1)}(\pi(1^+)) \bigr)\\ &= \mathrm{soc}\bigl( \Delta[0,-2] \rtimes S_{|\cdot|^1}^{(1)}(\pi(1^-,1^-,3^+)) \bigr)\\ &= L\bigl( \Delta[0,-2], \Delta[0,-1]; \pi(3^+) \bigr). \end{align*}
\begin{align*} S_{Z[0,1]}^{(2)}\bigl(L(\Delta[-1,-2]; \pi(1^+))\bigr) &= \mathrm{soc}\bigl( \Delta[0,-2] \rtimes S_{|\cdot|^1}^{(1)} \circ S_{Z[0,1]}^{(1)}(\pi(1^+)) \bigr)\\ &= \mathrm{soc}\bigl( \Delta[0,-2] \rtimes S_{|\cdot|^1}^{(1)}(\pi(1^-,1^-,3^+)) \bigr)\\ &= L\bigl( \Delta[0,-2], \Delta[0,-1]; \pi(3^+) \bigr). \end{align*}
In conclusion, we see that ![]() $L(\Delta [0,-2], \Delta [0,-1]; \pi (3^+))$ is fixed by the Zelevinsky–Aubert duality.
$L(\Delta [0,-2], \Delta [0,-1]; \pi (3^+))$ is fixed by the Zelevinsky–Aubert duality.
9.2 Example 2
Next, let us compute the Zelevinsky–Aubert dual of
for ![]() $\epsilon \in \{\pm \}$. First, we compute derivatives as follows.
$\epsilon \in \{\pm \}$. First, we compute derivatives as follows.

By Proposition 5.4, we have ![]() $\hat \pi (1^+,1^+,1^+) = \pi (1^+,1^+,1^+)$ and
$\hat \pi (1^+,1^+,1^+) = \pi (1^+,1^+,1^+)$ and ![]() $\hat \pi (1^-,1^-,3^+) = L(\Delta [0,-1]; \pi (1^+))$. Next we compute socles as follows.
$\hat \pi (1^-,1^-,3^+) = L(\Delta [0,-1]; \pi (1^+))$. Next we compute socles as follows.

Therefore, we conclude that
 \begin{align*} \hat\pi(1^+,1^+,3^+,5^-,5^-) &= L\big(|\cdot|^{-2}, \Delta[-1,-2], |\cdot|^{-1}; \pi(1^-,1^-,1^-,1^-,3^+)\big),\\ \hat\pi(1^-,1^-,3^+,5^-,5^-) &= L\big(|\cdot|^{-2}, |\cdot|^{-1}, \Delta[0,-2]; \pi(1^-,1^-,3^+)\big). \end{align*}
\begin{align*} \hat\pi(1^+,1^+,3^+,5^-,5^-) &= L\big(|\cdot|^{-2}, \Delta[-1,-2], |\cdot|^{-1}; \pi(1^-,1^-,1^-,1^-,3^+)\big),\\ \hat\pi(1^-,1^-,3^+,5^-,5^-) &= L\big(|\cdot|^{-2}, |\cdot|^{-1}, \Delta[0,-2]; \pi(1^-,1^-,3^+)\big). \end{align*}
Similarly, one can prove that ![]() $\hat \pi (3^+,5^-,5^-) = L(|\cdot |^{-2}, \Delta [-1,-2], |\cdot |^{-1} ; \pi (1^-,1^-,3^+))$. Hence we see that
$\hat \pi (3^+,5^-,5^-) = L(|\cdot |^{-2}, \Delta [-1,-2], |\cdot |^{-1} ; \pi (1^-,1^-,3^+))$. Hence we see that
 \begin{align*} \mathbf{1}_{\mathrm{GL}_1(F)} &\rtimes L\big(|\cdot|^{-2}, \Delta[-1,-2], |\cdot|^{-1} ; \pi(1^-,1^-,3^+)\big)\\ &\cong L\big(|\cdot|^{-2}, \Delta[-1,-2], |\cdot|^{-1}; \pi(1^-,1^-,1^-,1^-,3^+)\big)\\ &\oplus L\big(|\cdot|^{-2}, |\cdot|^{-1}, \Delta[0,-2]; \pi(1^-,1^-,3^+)\big). \end{align*}
\begin{align*} \mathbf{1}_{\mathrm{GL}_1(F)} &\rtimes L\big(|\cdot|^{-2}, \Delta[-1,-2], |\cdot|^{-1} ; \pi(1^-,1^-,3^+)\big)\\ &\cong L\big(|\cdot|^{-2}, \Delta[-1,-2], |\cdot|^{-1}; \pi(1^-,1^-,1^-,1^-,3^+)\big)\\ &\oplus L\big(|\cdot|^{-2}, |\cdot|^{-1}, \Delta[0,-2]; \pi(1^-,1^-,3^+)\big). \end{align*}
In these computations we also proved, for example, that ![]() $L(\Delta [0,-2]; \pi (1^-,1^-,3^+))$ is fixed by the Zelevinsky–Aubert duality. This fact does not follow from results in [Reference AtobeAto22b]. As in this example, even if
$L(\Delta [0,-2]; \pi (1^-,1^-,3^+))$ is fixed by the Zelevinsky–Aubert duality. This fact does not follow from results in [Reference AtobeAto22b]. As in this example, even if ![]() $\pi$ is tempered, we need to compute
$\pi$ is tempered, we need to compute ![]() $S_{Z[0,1]}^{(k)}$ in general.
$S_{Z[0,1]}^{(k)}$ in general.
Acknowledgements
We would like to thank E. Lapid and C. Mœglin for useful discussions. The first author was supported by JSPS KAKENHI grant no. 19K14494.