Article contents
Irreducible modules of modular Lie superalgebras and super version of the first Kac–Weisfeiler conjecture
Published online by Cambridge University Press: 11 December 2023
Abstract
Suppose 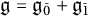 $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$ is a finite-dimensional restricted Lie superalgebra over an algebraically closed field
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$ is a finite-dimensional restricted Lie superalgebra over an algebraically closed field 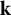 $\mathbf {k}$ of characteristic
$\mathbf {k}$ of characteristic 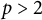 $p>2$. In this article, we propose a conjecture for maximal dimensions of irreducible modules over the universal enveloping algebra
$p>2$. In this article, we propose a conjecture for maximal dimensions of irreducible modules over the universal enveloping algebra 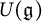 $U(\mathfrak {g})$ of
$U(\mathfrak {g})$ of 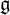 $\mathfrak {g}$, as a super generalization of the celebrated first Kac–Weisfeiler conjecture. It is demonstrated that the conjecture holds for all basic classical Lie superalgebras and all completely solvable restricted Lie superalgebras. In this process, we investigate irreducible representations of solvable Lie superalgebras.
$\mathfrak {g}$, as a super generalization of the celebrated first Kac–Weisfeiler conjecture. It is demonstrated that the conjecture holds for all basic classical Lie superalgebras and all completely solvable restricted Lie superalgebras. In this process, we investigate irreducible representations of solvable Lie superalgebras.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
This work is partially supported by the National Natural Science Foundation of China (Grant Nos. 12071136, 11771279, and 12271345), supported in part by Science and Technology Commission of Shanghai Municipality (Grant No. 22DZ2229014).
References
- 1
- Cited by



