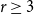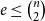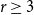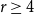1. Introduction
Given integers
![]() $n \ge r \ge 2$
, let
$n \ge r \ge 2$
, let
![]() $T_{r}(n)$
denote the balanced complete
$T_{r}(n)$
denote the balanced complete
![]() $r$
-partite graph on
$r$
-partite graph on
![]() $n$
vertices, and let
$n$
vertices, and let
![]() $t_{r}(n)$
denote the number of edges in
$t_{r}(n)$
denote the number of edges in
![]() $T_{r}(n)$
. The celebrated Turán Theorem [Reference Turán24] (with the case
$T_{r}(n)$
. The celebrated Turán Theorem [Reference Turán24] (with the case
![]() $r=3$
proved earlier by Mantel [Reference Mantel13]) states that, for
$r=3$
proved earlier by Mantel [Reference Mantel13]) states that, for
![]() $n \ge r \ge 3$
, every
$n \ge r \ge 3$
, every
![]() $n$
-vertex graph with at least
$n$
-vertex graph with at least
![]() $t_{r-1}(n)+1$
edges contains a copy of an
$t_{r-1}(n)+1$
edges contains a copy of an
![]() $r$
-clique
$r$
-clique
![]() $K_{r}$
, that is, a complete graph on
$K_{r}$
, that is, a complete graph on
![]() $r$
vertices. An unpublished result of Rademacher from 1941 (see [Reference Erdős3]) states that, in fact, every
$r$
vertices. An unpublished result of Rademacher from 1941 (see [Reference Erdős3]) states that, in fact, every
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $t_{2}(n)+1$
edges contains at least
$t_{2}(n)+1$
edges contains at least
![]() $\left \lfloor n/2\right \rfloor$
copies of
$\left \lfloor n/2\right \rfloor$
copies of
![]() $K_{3}$
. The graph obtained from
$K_{3}$
. The graph obtained from
![]() $T_{2}(n)$
by adding one edge to the larger part shows that the bound
$T_{2}(n)$
by adding one edge to the larger part shows that the bound
![]() $\left \lfloor n/2\right \lfloor$
is tight. Rademacher’s theorem motivated Erdős [Reference Erdős3] to consider the following more general question, now referred to as the Erdős–Rademacher problem: determine
$\left \lfloor n/2\right \lfloor$
is tight. Rademacher’s theorem motivated Erdős [Reference Erdős3] to consider the following more general question, now referred to as the Erdős–Rademacher problem: determine
where an
![]() $(n,e)$
-graph means a graph with
$(n,e)$
-graph means a graph with
![]() $n$
vertices and
$n$
vertices and
![]() $e$
edges and
$e$
edges and
![]() $N(K_r,G)$
denotes the number of
$N(K_r,G)$
denotes the number of
![]() $r$
-cliques in
$r$
-cliques in
![]() $G$
.
$G$
.
This problem has attracted a lot of attention and has been actively studied since it first appeared. Various results covering special ranges of
![]() $(n,e)$
were obtained (see e.g. [Reference Bollobás2, Reference Erdős4–Reference Goodman7, Reference Lovász and Simonovits11, Reference Lovász and Simonovits12, Reference Moon and Moser14, Reference Nikiforov18–Reference Nordhaus and Stewart20]) until Razborov [Reference Razborov22] determined the asymptotic value of
$(n,e)$
were obtained (see e.g. [Reference Bollobás2, Reference Erdős4–Reference Goodman7, Reference Lovász and Simonovits11, Reference Lovász and Simonovits12, Reference Moon and Moser14, Reference Nikiforov18–Reference Nordhaus and Stewart20]) until Razborov [Reference Razborov22] determined the asymptotic value of
![]() $g_{3}(n,e)$
using flag algebras. Later, using different methods, Nikiforov [Reference Nikiforov17] determined the asymptotic value of
$g_{3}(n,e)$
using flag algebras. Later, using different methods, Nikiforov [Reference Nikiforov17] determined the asymptotic value of
![]() $g_r(n,e)$
for
$g_r(n,e)$
for
![]() $r=4$
and Reiher [Reference Reiher23] did this for all
$r=4$
and Reiher [Reference Reiher23] did this for all
![]() $r \ge 5$
. For some further related results, we refer the reader to [Reference Balogh and Clemen1, Reference Kim, Liu, Pikhurko and Sharifzadeh8, Reference Liu and Mubayi10, Reference Mubayi15, Reference Mubayi16, Reference Pikhurko and Razborov21, Reference Xiao and Katona25].
$r \ge 5$
. For some further related results, we refer the reader to [Reference Balogh and Clemen1, Reference Kim, Liu, Pikhurko and Sharifzadeh8, Reference Liu and Mubayi10, Reference Mubayi15, Reference Mubayi16, Reference Pikhurko and Razborov21, Reference Xiao and Katona25].
Determining the exact value of
![]() $g_{r}(n,e)$
seems very challenging due to multiple (conjectured) extremal constructions. Given
$g_{r}(n,e)$
seems very challenging due to multiple (conjectured) extremal constructions. Given
![]() $n$
and
$n$
and
![]() $e$
in
$e$
in
![]() $\mathbb{N}\,:\!=\,\{1,2,\dots \}$
with
$\mathbb{N}\,:\!=\,\{1,2,\dots \}$
with
![]() $e \le \binom{n}{2}$
, let
$e \le \binom{n}{2}$
, let
that is,
![]() $k$
is the smallest chromatic number that an
$k$
is the smallest chromatic number that an
![]() $(n,e)$
-graph can have. Let
$(n,e)$
-graph can have. Let
![]() $\mathcal{H}_{1}(n,e)$
(resp.
$\mathcal{H}_{1}(n,e)$
(resp.
![]() $\mathcal{K}(n,e)$
) denote the family of
$\mathcal{K}(n,e)$
) denote the family of
![]() $(n,e)$
-graphs that can be obtained from a complete
$(n,e)$
-graphs that can be obtained from a complete
![]() $(k-1)$
-partite (resp. complete multipartite) graph by adding a triangle-free graph into one part. Note that the only difference between these two definitions is that we restrict the number of parts to
$(k-1)$
-partite (resp. complete multipartite) graph by adding a triangle-free graph into one part. Note that the only difference between these two definitions is that we restrict the number of parts to
![]() $k-1$
when defining
$k-1$
when defining
![]() $\mathcal{H}_{1}(n,e)$
; thus
$\mathcal{H}_{1}(n,e)$
; thus
![]() $\mathcal{H}_1(n,e) \subseteq \mathcal{K}(n,e)$
. Lovász and Simonovits [Reference Lovász and Simonovits11] conjectured that for every integer
$\mathcal{H}_1(n,e) \subseteq \mathcal{K}(n,e)$
. Lovász and Simonovits [Reference Lovász and Simonovits11] conjectured that for every integer
![]() $r\ge 3$
there exists
$r\ge 3$
there exists
![]() $n_0$
such that, for all positive integers
$n_0$
such that, for all positive integers
![]() $n \ge n_0$
and
$n \ge n_0$
and
![]() $e\le \binom{n}{2}$
, it holds that
$e\le \binom{n}{2}$
, it holds that
that is, at least one
![]() $g_r(n,e)$
-extremal graph is in
$g_r(n,e)$
-extremal graph is in
![]() $\mathcal{K}(n,e)$
. Note that (3) trivially holds for
$\mathcal{K}(n,e)$
. Note that (3) trivially holds for
![]() $e\le t_{r-1}(n)$
when
$e\le t_{r-1}(n)$
when
![]() $g_r(n,e)=0$
.
$g_r(n,e)=0$
.
Erdős in [Reference Erdős3] (resp. [Reference Erdős4]) showed that (3) is true for
![]() $r = 3$
when
$r = 3$
when
![]() $e \le t_2(n) + 3$
(resp.
$e \le t_2(n) + 3$
(resp.
![]() $e\le t_2(n)+cn$
for some constant
$e\le t_2(n)+cn$
for some constant
![]() $c\gt 0$
). Lovász and Simonovits [Reference Lovász and Simonovits11] (see also Nikiforov and Khadzhiivanov [Reference Nikiforov and Khadzhiivanov19]) extended the result of Erdős to all
$c\gt 0$
). Lovász and Simonovits [Reference Lovász and Simonovits11] (see also Nikiforov and Khadzhiivanov [Reference Nikiforov and Khadzhiivanov19]) extended the result of Erdős to all
![]() $e$
satisfying
$e$
satisfying
![]() $e \le t_2(n) + \lfloor n/2 \rfloor$
. Later, Lovász and Simonovits [Reference Lovász and Simonovits12] proved (3) for
$e \le t_2(n) + \lfloor n/2 \rfloor$
. Later, Lovász and Simonovits [Reference Lovász and Simonovits12] proved (3) for
![]() $r \ge 3$
when
$r \ge 3$
when
![]() $e/\binom{n}{2}$
lies in a small upper neighbourhood of
$e/\binom{n}{2}$
lies in a small upper neighbourhood of
![]() $1-1/m$
for some integer
$1-1/m$
for some integer
![]() $m \ge r-1$
. More recently, Liu, Pikhurko and Staden [Reference Liu, Pikhurko and Staden9] determined
$m \ge r-1$
. More recently, Liu, Pikhurko and Staden [Reference Liu, Pikhurko and Staden9] determined
![]() $g_{3}(n,e)$
for all positive integers
$g_{3}(n,e)$
for all positive integers
![]() $n$
when
$n$
when
![]() $e \le (1-o(1))\binom{n}{2}$
. Determining the exact value of
$e \le (1-o(1))\binom{n}{2}$
. Determining the exact value of
![]() $g_{r}(n,e)$
for
$g_{r}(n,e)$
for
![]() $r \ge 4$
is still wide open in general.
$r \ge 4$
is still wide open in general.
Given
![]() $n, e\in \mathbb N$
with
$n, e\in \mathbb N$
with
![]() $e \le \binom{n}{2}$
, let
$e \le \binom{n}{2}$
, let
![]() $\boldsymbol{a}^{\ast }=\boldsymbol{a}^{\ast }(n,e) \in \mathbb{N}^{k}$
be the unique vector such that
$\boldsymbol{a}^{\ast }=\boldsymbol{a}^{\ast }(n,e) \in \mathbb{N}^{k}$
be the unique vector such that
where
![]() $k = k(n,e)$
is as defined in (2). Thus
$k = k(n,e)$
is as defined in (2). Thus
![]() $a_k^{\ast }$
is the smallest possible part size that a
$a_k^{\ast }$
is the smallest possible part size that a
![]() $k$
-partite
$k$
-partite
![]() $(n,e)$
-graph can have. Also, let
$(n,e)$
-graph can have. Also, let
 \begin{align*} m^{\ast } = m^{\ast }(n,e) & \,:\!=\, \sum _{\{i,j\}\in \binom{[k]}{2}}a_{i}^{\ast }a_{j}^{\ast } -e, \quad \text{and}\quad \\ h^{\ast }_{r}(n,e) & \,:\!=\, \sum _{I\in \binom{[k]}{r}}\prod _{i\in I}a_i^{\ast } - m^{\ast }\cdot \sum _{I^{\prime}\in \binom{[k-2]}{r-2}}\prod _{j\in I^{\prime}}a_j^{\ast }, \end{align*}
\begin{align*} m^{\ast } = m^{\ast }(n,e) & \,:\!=\, \sum _{\{i,j\}\in \binom{[k]}{2}}a_{i}^{\ast }a_{j}^{\ast } -e, \quad \text{and}\quad \\ h^{\ast }_{r}(n,e) & \,:\!=\, \sum _{I\in \binom{[k]}{r}}\prod _{i\in I}a_i^{\ast } - m^{\ast }\cdot \sum _{I^{\prime}\in \binom{[k-2]}{r-2}}\prod _{j\in I^{\prime}}a_j^{\ast }, \end{align*}
where
![]() $[k]\,:\!=\,\{1,\dots, k\}$
and
$[k]\,:\!=\,\{1,\dots, k\}$
and
![]() $\binom{X}{k}\,:\!=\{Y\subseteq X\;:\;|Y|=k\}$
. Let
$\binom{X}{k}\,:\!=\{Y\subseteq X\;:\;|Y|=k\}$
. Let
![]() $T\,:\!=\, K[A_{1}^{\ast }, \ldots, A_{k}^{\ast }]$
be the complete
$T\,:\!=\, K[A_{1}^{\ast }, \ldots, A_{k}^{\ast }]$
be the complete
![]() $k$
-partite graph with parts
$k$
-partite graph with parts
![]() $A_1^{\ast },\dots, A_{k}^{\ast }$
where
$A_1^{\ast },\dots, A_{k}^{\ast }$
where
![]() $|A_{i}^{\ast }| = a_{i}^{\ast }$
for
$|A_{i}^{\ast }| = a_{i}^{\ast }$
for
![]() $i\in [k]$
. Let
$i\in [k]$
. Let
![]() $H^{\ast } = H^{\ast }(n,e)$
be the graph obtained from
$H^{\ast } = H^{\ast }(n,e)$
be the graph obtained from
![]() $T$
by removing an
$T$
by removing an
![]() $m^{\ast }$
-edge star whose centre lies in
$m^{\ast }$
-edge star whose centre lies in
![]() $A_{k}^{\ast }$
and whose leaves lie in
$A_{k}^{\ast }$
and whose leaves lie in
![]() $A_{k-1}^{\ast }$
. It is not hard to see (see e.g. the calculation in (10)) that
$A_{k-1}^{\ast }$
. It is not hard to see (see e.g. the calculation in (10)) that
![]() $0\le m^{\ast }\le a_{k-1}^{\ast }-a_{k}^{\ast }$
, so the graph
$0\le m^{\ast }\le a_{k-1}^{\ast }-a_{k}^{\ast }$
, so the graph
![]() $H^{\ast }$
is well-defined. Also, let
$H^{\ast }$
is well-defined. Also, let
![]() $\mathcal{H}_{1}^{\ast }(n,e)$
be the family defined as follows: If
$\mathcal{H}_{1}^{\ast }(n,e)$
be the family defined as follows: If
![]() $m^{\ast } = 0$
, take all graphs obtained from
$m^{\ast } = 0$
, take all graphs obtained from
![]() $T$
by replacing, for some
$T$
by replacing, for some
![]() $i\in [k-1]$
, the bipartite graph
$i\in [k-1]$
, the bipartite graph
![]() $T[A_{i}^{\ast }\cup A_{k}^{\ast }]$
with an arbitrary triangle-free graph with
$T[A_{i}^{\ast }\cup A_{k}^{\ast }]$
with an arbitrary triangle-free graph with
![]() $a_{i}^{\ast }a_{k}^{\ast }$
edges. If
$a_{i}^{\ast }a_{k}^{\ast }$
edges. If
![]() $m^{\ast }\gt 0$
, take all graphs obtained from
$m^{\ast }\gt 0$
, take all graphs obtained from
![]() $T$
by replacing
$T$
by replacing
![]() $T[A_{k-1}^{\ast }\cup A_{k}^{\ast }]$
with an arbitrary triangle-free graph with
$T[A_{k-1}^{\ast }\cup A_{k}^{\ast }]$
with an arbitrary triangle-free graph with
![]() $a_{k-1}^{\ast }a_{k}^{\ast } - m^{\ast }$
edges. Observe that
$a_{k-1}^{\ast }a_{k}^{\ast } - m^{\ast }$
edges. Observe that
![]() $\mathcal{H}_1^{\ast }(n,e) \subseteq \mathcal{H}_1(n,e)$
and every graph in
$\mathcal{H}_1^{\ast }(n,e) \subseteq \mathcal{H}_1(n,e)$
and every graph in
![]() $\mathcal{H}_{1}^{\ast }(n,e)$
has the same number of
$\mathcal{H}_{1}^{\ast }(n,e)$
has the same number of
![]() $r$
-cliques (see Fact 2.2); also, the graph
$r$
-cliques (see Fact 2.2); also, the graph
![]() $H^*=H^*(n,e)$
is contained in
$H^*=H^*(n,e)$
is contained in
![]() $\mathcal{H}_1^{\ast }(n,e)$
.
$\mathcal{H}_1^{\ast }(n,e)$
.
Sharpening the Lovász–Simonovits Conjecture, Pikhurko and Razborov [Reference Pikhurko and Razborov21, Conjecture 1.4] conjectured that, for
![]() $r\ge 4$
and sufficiently large
$r\ge 4$
and sufficiently large
![]() $n$
, every
$n$
, every
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $e\le \binom{n}{2}$
edges and that contains the minimum number of
$e\le \binom{n}{2}$
edges and that contains the minimum number of
![]() $K_r$
is in
$K_r$
is in
![]() $\mathcal{K}(n,e)$
. However, we show here that this conjecture is false (see Theorem 1.1 and Proposition 1.2) and present an amended version (see Conjecture 1.3) as follows.
$\mathcal{K}(n,e)$
. However, we show here that this conjecture is false (see Theorem 1.1 and Proposition 1.2) and present an amended version (see Conjecture 1.3) as follows.
First, we write explicitly the value of
![]() $g_{r}(n,e)$
predicted by the Lovász–Simonovits Conjecture. (We also refer the reader to [Reference Liu, Pikhurko and Staden9, Proposition 1.5] where similar results are proved for
$g_{r}(n,e)$
predicted by the Lovász–Simonovits Conjecture. (We also refer the reader to [Reference Liu, Pikhurko and Staden9, Proposition 1.5] where similar results are proved for
![]() $r=3$
.)
$r=3$
.)
Theorem 1.1.
Suppose that
![]() $r,n,e\in \mathbb N$
satisfy
$r,n,e\in \mathbb N$
satisfy
![]() $n \ge r \ge 3$
and
$n \ge r \ge 3$
and
![]() $e \le \binom{n}{2}$
. Then
$e \le \binom{n}{2}$
. Then
Moreover, if
![]() $r\ge 4$
and
$r\ge 4$
and
![]() $e\gt t_{r-1}(n)$
, then
$e\gt t_{r-1}(n)$
, then
Note that, since
![]() $\mathcal{H}_1^{\ast }(n,e)\subseteq \mathcal{H}_1(n,e)$
, Theorem 1.1 remains true if we replace
$\mathcal{H}_1^{\ast }(n,e)\subseteq \mathcal{H}_1(n,e)$
, Theorem 1.1 remains true if we replace
![]() $\mathcal{K}(n,e)$
by
$\mathcal{K}(n,e)$
by
![]() $\mathcal{H}_1(n,e)$
. In fact, the later version of the Lovász–Simonovits Conjecture from [Reference Lovász and Simonovits12] states that, for all sufficiently large
$\mathcal{H}_1(n,e)$
. In fact, the later version of the Lovász–Simonovits Conjecture from [Reference Lovász and Simonovits12] states that, for all sufficiently large
![]() $n\ge n_0(r)$
, at least one
$n\ge n_0(r)$
, at least one
![]() $g_r(n,e)$
-extremal graph is in
$g_r(n,e)$
-extremal graph is in
![]() $\mathcal{H}_1(n,e)$
. By (4), these two conjectures are equivalent. One should be able to show with some extra work that (5) also holds for
$\mathcal{H}_1(n,e)$
. By (4), these two conjectures are equivalent. One should be able to show with some extra work that (5) also holds for
![]() $r=3$
(it is also implied by the results in [Reference Liu, Pikhurko and Staden9] that (5) holds for most
$r=3$
(it is also implied by the results in [Reference Liu, Pikhurko and Staden9] that (5) holds for most
![]() $e$
, given
$e$
, given
![]() $n$
). Since our main focus is the case
$n$
). Since our main focus is the case
![]() $r\ge 4$
, we do not pursue this strengthening here.
$r\ge 4$
, we do not pursue this strengthening here.
Given integers
![]() $n,e \in \mathbb{N}$
with
$n,e \in \mathbb{N}$
with
![]() $e\le \binom{n}{2}$
, we define the family
$e\le \binom{n}{2}$
, we define the family
![]() $\mathcal{H}_{2}^{\ast }(n,e)$
as follows (with
$\mathcal{H}_{2}^{\ast }(n,e)$
as follows (with
![]() $k, \boldsymbol{a}^{\ast }, m^{\ast }$
being as before). Take those graphs in
$k, \boldsymbol{a}^{\ast }, m^{\ast }$
being as before). Take those graphs in
![]() $\mathcal{H}_{1}^{\ast }(n,e)$
that are
$\mathcal{H}_{1}^{\ast }(n,e)$
that are
![]() $k$
-partite, along with the following family. Take disjoint sets
$k$
-partite, along with the following family. Take disjoint sets
![]() $A_{1}, \ldots, A_{k}$
of sizes
$A_{1}, \ldots, A_{k}$
of sizes
![]() $a_{1}^{\ast }, \ldots, a_{k}^{\ast }$
, respectively, and let
$a_{1}^{\ast }, \ldots, a_{k}^{\ast }$
, respectively, and let
![]() $m\,:\!=\, m^{\ast }$
. If
$m\,:\!=\, m^{\ast }$
. If
![]() $m^{\ast } = 0$
and
$m^{\ast } = 0$
and
![]() $a_{1}^{\ast } \ge a_{k}^{\ast }+2$
, then we also allow
$a_{1}^{\ast } \ge a_{k}^{\ast }+2$
, then we also allow
![]() $\left (|A_{1}|, \ldots, |A_{k}|\right ) = \left (a_{2}^{\ast }, \ldots, a_{k-1}^{\ast }, a_{1}^{\ast }-1, a_{k}^{\ast }+1\right )$
and let
$\left (|A_{1}|, \ldots, |A_{k}|\right ) = \left (a_{2}^{\ast }, \ldots, a_{k-1}^{\ast }, a_{1}^{\ast }-1, a_{k}^{\ast }+1\right )$
and let
![]() $m\,:\!=\,a_1^{\ast }-a_k^{\ast }-1$
. Take all graphs obtained from
$m\,:\!=\,a_1^{\ast }-a_k^{\ast }-1$
. Take all graphs obtained from
![]() $K[A_{1}, \ldots, A_{k}]$
by removing any
$K[A_{1}, \ldots, A_{k}]$
by removing any
![]() $m$
edges, each connecting
$m$
edges, each connecting
![]() $B_i$
to
$B_i$
to
![]() $A_i$
for some
$A_i$
for some
![]() $i\in I$
, where
$i\in I$
, where
![]() $I\,:\!=\, \left \{i\in [k-1]\,\colon\, |A_{i}| = |A_{k-1}|\right \}$
and
$I\,:\!=\, \left \{i\in [k-1]\,\colon\, |A_{i}| = |A_{k-1}|\right \}$
and
![]() $\left \{B_i\colon i\in I\right \}$
are some pairwise disjoint subsets of
$\left \{B_i\colon i\in I\right \}$
are some pairwise disjoint subsets of
![]() $A_{k}$
. Clearly, every graph in
$A_{k}$
. Clearly, every graph in
![]() $\mathcal{H}_{2}^{\ast }(n,e)$
is an
$\mathcal{H}_{2}^{\ast }(n,e)$
is an
![]() $(n,e)$
-graph.
$(n,e)$
-graph.
Proposition 1.2.
Suppose that
![]() $n \ge r \ge 4$
and
$n \ge r \ge 4$
and
![]() $t_{r-1}(n)\lt e \le \binom{n}{2}$
are integers. Then
$t_{r-1}(n)\lt e \le \binom{n}{2}$
are integers. Then
Also, there are infinitely many pairs
![]() $(n,e) \in \mathbb{N}^2$
with
$(n,e) \in \mathbb{N}^2$
with
![]() $t_{r-1}(n) \lt e \le \binom{n}{2}$
such that
$t_{r-1}(n) \lt e \le \binom{n}{2}$
such that
![]() $\mathcal{H}_{2}^{\ast }(n,e) \setminus \mathcal{H}_{1}^{\ast }(n,e) \neq \emptyset$
.
$\mathcal{H}_{2}^{\ast }(n,e) \setminus \mathcal{H}_{1}^{\ast }(n,e) \neq \emptyset$
.
We propose the following amended conjecture.
Conjecture 1.3.
Let
![]() $r \ge 4$
be fixed. For every sufficiently large integer
$r \ge 4$
be fixed. For every sufficiently large integer
![]() $n$
and every integer
$n$
and every integer
![]() $e$
with
$e$
with
![]() $t_{r-1}(n)\lt e \le \binom{n}{2}$
, it holds that
$t_{r-1}(n)\lt e \le \binom{n}{2}$
, it holds that
For comparison with the case
![]() $r=3$
, the exact result of Liu, Pikhurko and Staden [Reference Liu, Pikhurko and Staden9] valid for
$r=3$
, the exact result of Liu, Pikhurko and Staden [Reference Liu, Pikhurko and Staden9] valid for
![]() $e\le (1-o(1))\binom{n}{2}$
states that the set of
$e\le (1-o(1))\binom{n}{2}$
states that the set of
![]() $g_3(n,e)$
-extremal graphs is exactly
$g_3(n,e)$
-extremal graphs is exactly
![]() $\mathcal{H}_{0}^{\ast }(n,e)\cup \mathcal{H}_{2}^{\ast }(n,e)$
for a certain explicit family
$\mathcal{H}_{0}^{\ast }(n,e)\cup \mathcal{H}_{2}^{\ast }(n,e)$
for a certain explicit family
![]() $\mathcal{H}_{0}^{\ast }(n,e)\supseteq \mathcal{H}_{1}^{\ast }(n,e)$
, where the inclusion is strict for infinitely many pairs
$\mathcal{H}_{0}^{\ast }(n,e)\supseteq \mathcal{H}_{1}^{\ast }(n,e)$
, where the inclusion is strict for infinitely many pairs
![]() $(n,e)$
. However, for
$(n,e)$
. However, for
![]() $r\ge 4$
and
$r\ge 4$
and
![]() $e\gt t_{r-1}(n)$
, every graph in
$e\gt t_{r-1}(n)$
, every graph in
![]() $\mathcal{H}_{0}^{\ast }(n,e)\setminus \mathcal{H}_{1}^{\ast }(n,e)$
can be shown to have more
$\mathcal{H}_{0}^{\ast }(n,e)\setminus \mathcal{H}_{1}^{\ast }(n,e)$
can be shown to have more
![]() $K_r$
’s than
$K_r$
’s than
![]() $H^{\ast }(n,e)$
. (Basically, each such graph is obtained from a complete
$H^{\ast }(n,e)$
. (Basically, each such graph is obtained from a complete
![]() $(k-1)$
-partite graph by adding edges into more than one part and cannot minimise the number of
$(k-1)$
-partite graph by adding edges into more than one part and cannot minimise the number of
![]() $K_r$
’s for
$K_r$
’s for
![]() $r\ge 4$
by Lemma 2.5.)
$r\ge 4$
by Lemma 2.5.)
For the purposes of this paper (namely for Proposition 1.2), only the difference
![]() $\mathcal{H}_{2}^{\ast }(n,e)\setminus \mathcal{H}_{1}^{\ast }(n,e)$
matters; we use the current definitions merely so that the families
$\mathcal{H}_{2}^{\ast }(n,e)\setminus \mathcal{H}_{1}^{\ast }(n,e)$
matters; we use the current definitions merely so that the families
![]() $\mathcal{H}_i^{\ast }(n,e)$
and
$\mathcal{H}_i^{\ast }(n,e)$
and
![]() $\mathcal{H}_i(n,e)$
are the same as in [Reference Liu, Pikhurko and Staden9].
$\mathcal{H}_i(n,e)$
are the same as in [Reference Liu, Pikhurko and Staden9].
The rest of the paper of organised as follows. In the next section, we present some definitions and preliminary results. As a step towards proving Theorem 1.1, we first find extremal graphs in a certain family
![]() $\mathcal{H}_0(n,e)$
in Section 3 (see Proposition 3.1 for the exact statement). We derive Theorem 1.1 in Section 4. The proof of Proposition 1.2 is presented in Section 5.
$\mathcal{H}_0(n,e)$
in Section 3 (see Proposition 3.1 for the exact statement). We derive Theorem 1.1 in Section 4. The proof of Proposition 1.2 is presented in Section 5.
2. Preliminaries
Given
![]() $\ell$
pairwise disjoint sets
$\ell$
pairwise disjoint sets
![]() $A_1, \ldots, A_{\ell }$
, we use
$A_1, \ldots, A_{\ell }$
, we use
![]() $K[A_1, \ldots, A_{\ell }]$
to denote the complete
$K[A_1, \ldots, A_{\ell }]$
to denote the complete
![]() $\ell$
-partite graph with parts
$\ell$
-partite graph with parts
![]() $A_1, \ldots, A_{\ell }$
; if we care only about the isomorphism type of this graph (i.e. only the sizes of the parts matter), we may instead write
$A_1, \ldots, A_{\ell }$
; if we care only about the isomorphism type of this graph (i.e. only the sizes of the parts matter), we may instead write
![]() $K_{a_1, \ldots, a_{\ell }}$
, where
$K_{a_1, \ldots, a_{\ell }}$
, where
![]() $a_i\,:\!=\,|A_i|$
for
$a_i\,:\!=\,|A_i|$
for
![]() $i\in [\ell ]$
.
$i\in [\ell ]$
.
Let
![]() $G=(V,E)$
be a graph. By
$G=(V,E)$
be a graph. By
![]() $|G|$
we denote the number of edges in
$|G|$
we denote the number of edges in
![]() $G$
. Let
$G$
. Let
![]() $\overline{G} \,:\!=\, \left (V,\binom{V}{2}\setminus E\right )$
denote the complement of
$\overline{G} \,:\!=\, \left (V,\binom{V}{2}\setminus E\right )$
denote the complement of
![]() $G$
. The subgraph of
$G$
. The subgraph of
![]() $G$
induced by a set
$G$
induced by a set
![]() $A\subseteq V$
is
$A\subseteq V$
is
![]() $G[A]\,:\!=\,\left (A,\binom{A}{2}\cap E\right )$
. For disjoint
$G[A]\,:\!=\,\left (A,\binom{A}{2}\cap E\right )$
. For disjoint
![]() $A,B\subseteq V$
, we use
$A,B\subseteq V$
, we use
![]() $G[A,B]$
to denote the induced bipartite graph with parts
$G[A,B]$
to denote the induced bipartite graph with parts
![]() $A$
and
$A$
and
![]() $B$
(which consists of edges connecting
$B$
(which consists of edges connecting
![]() $A$
to
$A$
to
![]() $B$
).
$B$
).
In the remainder of this note, we assume unless it is stated otherwise that
![]() $r,n,e\in \mathbb N$
satisfy
$r,n,e\in \mathbb N$
satisfy
![]() $r\ge 3$
and
$r\ge 3$
and
![]() $e\le \binom{n}{2}$
(and we minimise the number of
$e\le \binom{n}{2}$
(and we minimise the number of
![]() $r$
-cliques over
$r$
-cliques over
![]() $(n,e)$
-graphs). Also,
$(n,e)$
-graphs). Also,
![]() $k=k(n,e)$
is defined in (2).
$k=k(n,e)$
is defined in (2).
Given a family
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $(n,e)$
-graphs, we use
$(n,e)$
-graphs, we use
![]() $\mathcal{F}^{\min }$
to denote the collection of graphs
$\mathcal{F}^{\min }$
to denote the collection of graphs
![]() $F \in \mathcal{F}$
with the minimum number of
$F \in \mathcal{F}$
with the minimum number of
![]() $K_r$
’s (over all graphs in
$K_r$
’s (over all graphs in
![]() $\mathcal{F}$
). For convenience, we set
$\mathcal{F}$
). For convenience, we set
![]() $N(K_0, G) \,:\!=\, 1$
and
$N(K_0, G) \,:\!=\, 1$
and
![]() $N(K_{-1}, G) \,:\!=\, 0$
for all graphs
$N(K_{-1}, G) \,:\!=\, 0$
for all graphs
![]() $G$
.
$G$
.
Let the family
![]() $\mathcal{H}_{0}(n,e)$
be the collection of all
$\mathcal{H}_{0}(n,e)$
be the collection of all
![]() $(n,e)$
-graphs that can be obtained from an
$(n,e)$
-graphs that can be obtained from an
![]() $n$
-vertex complete
$n$
-vertex complete
![]() $(k-1)$
-partite graph by adding a (possibly empty) triangle-free graph into each part. It is clear from the definition that
$(k-1)$
-partite graph by adding a (possibly empty) triangle-free graph into each part. It is clear from the definition that
![]() $\mathcal{H}_1(n,e) \subseteq \mathcal{H}_{0}(n,e)$
.
$\mathcal{H}_1(n,e) \subseteq \mathcal{H}_{0}(n,e)$
.
The following fact follows from some simple calculations (with the argument for Part (i) being the same as in (10)).
Fact 2.1.
Let
![]() $k, \boldsymbol{a}^{\ast }, m^{\ast }, H^{\ast }$
, and
$k, \boldsymbol{a}^{\ast }, m^{\ast }, H^{\ast }$
, and
![]() $h_r^{\ast }(n,e)$
be as defined in Section
1
. Then it holds for all
$h_r^{\ast }(n,e)$
be as defined in Section
1
. Then it holds for all
![]() $r \ge 3$
that
$r \ge 3$
that
-
(i)
 $0 \le m^{\ast } \le a_{k-1}^{\ast } - a_{k}^{\ast }$
,
$0 \le m^{\ast } \le a_{k-1}^{\ast } - a_{k}^{\ast }$
, -
(ii)
 $|K_{a_{1}^{\ast }, \ldots, a_{k}^{\ast }}| - |K_{a_{1}^{\ast }, \ldots, a_{k-2}^{\ast }, a_{k-1}^{\ast }+1, a_{k}^{\ast }-1}| = a_{k-1}^{\ast } - a_{k}^{\ast }+1$
,
$|K_{a_{1}^{\ast }, \ldots, a_{k}^{\ast }}| - |K_{a_{1}^{\ast }, \ldots, a_{k-2}^{\ast }, a_{k-1}^{\ast }+1, a_{k}^{\ast }-1}| = a_{k-1}^{\ast } - a_{k}^{\ast }+1$
, -
(iii)
 $N(K_r, H^{\ast }) = h^{\ast }_{r}(n,e) \ge g_r(n,e)$
.
$N(K_r, H^{\ast }) = h^{\ast }_{r}(n,e) \ge g_r(n,e)$
.
We also need the following simple facts for counting
![]() $r$
-cliques in some special classes of graphs.
$r$
-cliques in some special classes of graphs.
Fact 2.2.
Let
![]() $G$
be a graph,
$G$
be a graph,
![]() $S \subseteq V(G)$
be a vertex set, and
$S \subseteq V(G)$
be a vertex set, and
![]() $\overline{S}\,:\!=\, V(G)\setminus S$
. Suppose that the induced subgraph
$\overline{S}\,:\!=\, V(G)\setminus S$
. Suppose that the induced subgraph
![]() $G[S]$
is triangle-free, and the induced bipartite graph
$G[S]$
is triangle-free, and the induced bipartite graph
![]() $G[S,\overline{S}]$
is complete. Then
$G[S,\overline{S}]$
is complete. Then
Fact 2.3.
Suppose that
![]() $G$
is a graph obtained from
$G$
is a graph obtained from
![]() $K[V_1, \ldots, V_{\ell }]$
by adding a triangle-free graph. Let
$K[V_1, \ldots, V_{\ell }]$
by adding a triangle-free graph. Let
![]() $S\,:\!=\, V_1 \cup V_2$
and
$S\,:\!=\, V_1 \cup V_2$
and
![]() $\overline{S} \,:\!=\, V(G)\setminus S$
. Then
$\overline{S} \,:\!=\, V(G)\setminus S$
. Then
 \begin{align*} N(K_{r}, G) \ =\ & |G[V_1]|\cdot |G[V_2]|\cdot N(K_{r-4}, G[\overline{S}]) \\ & + \left (|G[V_1]|\cdot |V_2| + |G[V_2]|\cdot |V_1|\right ) \cdot N(K_{r-3}, G[\overline{S}]) \\ & + |G[S]|\cdot N(K_{r-2}, G[\overline{S}]) + |S|\cdot N(K_{r-1}, G[\overline{S}]) + N(K_{r}, G[\overline{S}]). \end{align*}
\begin{align*} N(K_{r}, G) \ =\ & |G[V_1]|\cdot |G[V_2]|\cdot N(K_{r-4}, G[\overline{S}]) \\ & + \left (|G[V_1]|\cdot |V_2| + |G[V_2]|\cdot |V_1|\right ) \cdot N(K_{r-3}, G[\overline{S}]) \\ & + |G[S]|\cdot N(K_{r-2}, G[\overline{S}]) + |S|\cdot N(K_{r-1}, G[\overline{S}]) + N(K_{r}, G[\overline{S}]). \end{align*}
Fact 2.4.
Let
![]() $G$
be a graph,
$G$
be a graph,
![]() $S \subseteq V(G)$
, and
$S \subseteq V(G)$
, and
![]() $\overline{S} \,:\!=\, V(G)\setminus S$
. Suppose that the induced subgraph
$\overline{S} \,:\!=\, V(G)\setminus S$
. Suppose that the induced subgraph
![]() $G[S]$
is
$G[S]$
is
![]() $3$
-partite, and the induced bipartite subgraph
$3$
-partite, and the induced bipartite subgraph
![]() $G[S, \overline{S}]$
is complete. Then
$G[S, \overline{S}]$
is complete. Then
We will also use the following results.
Lemma 2.5.
Let
![]() $r\ge 4$
and let
$r\ge 4$
and let
![]() $n,e\in \mathbb{N}$
satisfy
$n,e\in \mathbb{N}$
satisfy
![]() $t_{r-1}(n)\lt e\le \binom{n}{2}$
. Suppose that
$t_{r-1}(n)\lt e\le \binom{n}{2}$
. Suppose that
![]() $G \in \mathcal{H}^{\min }_{0}(n,e)$
is a graph with a vertex partition
$G \in \mathcal{H}^{\min }_{0}(n,e)$
is a graph with a vertex partition
![]() $V(G) = B_1\cup \ldots \cup B_{k-1}$
such that
$V(G) = B_1\cup \ldots \cup B_{k-1}$
such that
![]() $G$
is the union of
$G$
is the union of
![]() $K[B_1, \ldots, B_{k-1}]$
with a triangle-free graph. Then
$K[B_1, \ldots, B_{k-1}]$
with a triangle-free graph. Then
![]() $G$
contains at most one part
$G$
contains at most one part
![]() $B_i$
which is partially full, meaning that
$B_i$
which is partially full, meaning that
![]() $0 \lt |G[B_i]|\lt t_{2}(|B_i|)$
.
$0 \lt |G[B_i]|\lt t_{2}(|B_i|)$
.
Proof. Suppose to the contrary that
![]() $G$
contains two partially full parts
$G$
contains two partially full parts
![]() $B_i$
and
$B_i$
and
![]() $B_j$
for some
$B_j$
for some
![]() $1 \le i \lt j \le k-1$
. Let
$1 \le i \lt j \le k-1$
. Let
![]() $x\,:\!=\, |G[B_i]|$
,
$x\,:\!=\, |G[B_i]|$
,
![]() $\sigma \,:\!=\, |G[B_i]|+|G[B_j]|$
and
$\sigma \,:\!=\, |G[B_i]|+|G[B_j]|$
and
![]() $H\,:\!=\,G[V(G)\setminus (B_i\cup B_j)]$
. Observe from Fact 2.3 that there exist constants
$H\,:\!=\,G[V(G)\setminus (B_i\cup B_j)]$
. Observe from Fact 2.3 that there exist constants
![]() $C_2, C_3, C_4$
depending on
$C_2, C_3, C_4$
depending on
![]() $|B_i|$
,
$|B_i|$
,
![]() $|B_j|$
and
$|B_j|$
and
![]() $H$
(but not on
$H$
(but not on
![]() $x$
) such that
$x$
) such that
Let
![]() $G_i$
be the graph obtained from
$G_i$
be the graph obtained from
![]() $G$
by moving one edge from
$G$
by moving one edge from
![]() $G[B_j]$
to
$G[B_j]$
to
![]() $G[B_i]$
and rearranging the latter graph to be still
$G[B_i]$
and rearranging the latter graph to be still
![]() $K_3$
-free, which is possible by Mantel’s theorem. Similarly, let
$K_3$
-free, which is possible by Mantel’s theorem. Similarly, let
![]() $G_j$
be the graph obtained from
$G_j$
be the graph obtained from
![]() $G$
by moving one edge from
$G$
by moving one edge from
![]() $G[B_i]$
to
$G[B_i]$
to
![]() $G[B_j]$
. Note that
$G[B_j]$
. Note that
![]() $N(K_r, G_i) = P(x+1)$
and
$N(K_r, G_i) = P(x+1)$
and
![]() $N(K_r, G_j) = P(x-1)$
. Since
$N(K_r, G_j) = P(x-1)$
. Since
![]() $e> t_{r-1}(n)$
, we have
$e> t_{r-1}(n)$
, we have
Thus
![]() $\min \left \{N(K_r, G_i), N(K_r, G_j)\right \} \lt N(K_r, G)$
, contradicting the minimality of
$\min \left \{N(K_r, G_i), N(K_r, G_j)\right \} \lt N(K_r, G)$
, contradicting the minimality of
![]() $G$
.
$G$
.
The following simple inequality from [Reference Liu, Pikhurko and Staden9] will be useful. For completeness, we include its short proof here.
Lemma 2.6 ([Reference Liu, Pikhurko and Staden9, Lemma 4.5]). For all integers
![]() $a\ge 1$
,
$a\ge 1$
,
![]() $k \ge 2$
, and
$k \ge 2$
, and
![]() $n \ge ak$
, we have
$n \ge ak$
, we have
Proof. Let
![]() $a_1 \ge \dots \ge a_{k-1}$
denote the part sizes of
$a_1 \ge \dots \ge a_{k-1}$
denote the part sizes of
![]() $T_{k-1}(n-a)$
. If we increase its number of vertices by one, then the part sizes of the new Turán graph, up to reordering, can be obtained by increasing
$T_{k-1}(n-a)$
. If we increase its number of vertices by one, then the part sizes of the new Turán graph, up to reordering, can be obtained by increasing
![]() $a_{k-1}$
by one. Thus the difference between the expressions in (7) is
$a_{k-1}$
by one. Thus the difference between the expressions in (7) is
which is positive since
![]() $a_{k-1} \ge \left \lfloor (n-a)/(k-1)\right \lfloor \ge \left \lfloor (ak-a)/(k-1)\right \rfloor = a$
.
$a_{k-1} \ge \left \lfloor (n-a)/(k-1)\right \lfloor \ge \left \lfloor (ak-a)/(k-1)\right \rfloor = a$
.
3. Extremal graphs in
 $\mathcal{H}_0(n,e)$
$\mathcal{H}_0(n,e)$
As an intermediate step towards Theorem 1.1, we will first prove the following result, which determines the extremal graphs in
![]() $\mathcal{H}_{0}(n,e)$
.
$\mathcal{H}_{0}(n,e)$
.
Proposition 3.1.
For all integers
![]() $n \ge r\ge 4$
and
$n \ge r\ge 4$
and
![]() $t_{r-1}(n)\lt e\le \binom{n}{2}$
, we have that
$t_{r-1}(n)\lt e\le \binom{n}{2}$
, we have that
![]() $\mathcal{H}^{\min }_{0}(n,e) = \mathcal{H}^{\ast }_{1}(n,e)$
.
$\mathcal{H}^{\min }_{0}(n,e) = \mathcal{H}^{\ast }_{1}(n,e)$
.
We will use this result later to prove Theorem 1.1 by induction on the number of parts in a graph in
![]() $\mathcal{K}(n,e)$
. Note that, in general, neither
$\mathcal{K}(n,e)$
. Note that, in general, neither
![]() $\mathcal{K}(n,e)$
nor
$\mathcal{K}(n,e)$
nor
![]() $\mathcal{H}_0(n,e)$
is a subfamily of the other. However, when we work on the structure of extremal graphs in
$\mathcal{H}_0(n,e)$
is a subfamily of the other. However, when we work on the structure of extremal graphs in
![]() $\mathcal{K}(n,e)$
in the proof of Theorem 1.1, some intermediate graphs may be in
$\mathcal{K}(n,e)$
in the proof of Theorem 1.1, some intermediate graphs may be in
![]() $\mathcal{H}_0(n,e)$
.
$\mathcal{H}_0(n,e)$
.
We need some further preliminaries before we can prove Proposition 3.1.
Given a graph
![]() $G \in \mathcal{H}^{\min }_{0}(n,e)$
with partition
$G \in \mathcal{H}^{\min }_{0}(n,e)$
with partition
![]() $B_1, \ldots, B_{k-1}$
, we apply the following modification to
$B_1, \ldots, B_{k-1}$
, we apply the following modification to
![]() $G$
to obtain a new graph
$G$
to obtain a new graph
![]() $H^{\prime}= H^{\prime}(G) \in \mathcal{H}^{\min }_{0}(n,e)$
. Note that, in fact, these steps do not depend on
$H^{\prime}= H^{\prime}(G) \in \mathcal{H}^{\min }_{0}(n,e)$
. Note that, in fact, these steps do not depend on
![]() $r$
.
$r$
.
-
Step 1: If there is a part
 $B_i$
that is partially full in
$B_i$
that is partially full in
 $G$
, then let
$G$
, then let
 $B\,:\!=\, B_i$
(by Lemma 2.5, such
$B\,:\!=\, B_i$
(by Lemma 2.5, such
 $B_i$
is unique if it exists). Otherwise, take an arbitrary
$B_i$
is unique if it exists). Otherwise, take an arbitrary
 $i\in [k-1]$
with
$i\in [k-1]$
with
 $|G[B_i]| = t_2(|B_i|)$
and let
$|G[B_i]| = t_2(|B_i|)$
and let
 $B\,:\!=\, B_i$
. Since
$B\,:\!=\, B_i$
. Since
 $|G| \gt t_{k-1}(n)$
,
$|G| \gt t_{k-1}(n)$
,
 $|G[B_i]|$
cannot be
$|G[B_i]|$
cannot be
 $0$
for all
$0$
for all
 $i \in [k-1]$
. Thus, the set
$i \in [k-1]$
. Thus, the set
 $B$
is well-defined.
$B$
is well-defined. -
Step 2: Note that
 $G-B$
is a complete multipartite graph. Let
$G-B$
is a complete multipartite graph. Let
 $A_1, \ldots, A_{t-2}$
denote its parts. Let
$A_1, \ldots, A_{t-2}$
denote its parts. Let
 $a_i \,:\!=\, |A_i|$
for
$a_i \,:\!=\, |A_i|$
for
 $i\in [t-2]$
and assume that
$i\in [t-2]$
and assume that
 $a_1 \ge \dots \ge a_{t-2}$
. Note that each original part
$a_1 \ge \dots \ge a_{t-2}$
. Note that each original part
 $B_\ell$
is either
$B_\ell$
is either
 $B$
, some
$B$
, some
 $A_i$
, or the union of two parts
$A_i$
, or the union of two parts
 $A_i$
and
$A_i$
and
 $A_j$
.
$A_j$
. -
Step 3: Choose integers
 $a_{t-1} \ge a_t \ge 1$
such thatNote that this is possible by Mantel’s theorem since
$a_{t-1} \ge a_t \ge 1$
such thatNote that this is possible by Mantel’s theorem since \begin{align*} a_{t-1}+a_{t} = |B| \quad \text{and}\quad (a_{t-1}+1)(a_t-1) \lt |G[B]| \le a_{t-1}a_{t}. \end{align*}
\begin{align*} a_{t-1}+a_{t} = |B| \quad \text{and}\quad (a_{t-1}+1)(a_t-1) \lt |G[B]| \le a_{t-1}a_{t}. \end{align*}
 $G[B]$
is triangle-free. Let
$G[B]$
is triangle-free. Let
 $A_{t-1}\sqcup A_t = B$
be a partition with
$A_{t-1}\sqcup A_t = B$
be a partition with
 $|A_{t-1}|=a_{t-1}$
and
$|A_{t-1}|=a_{t-1}$
and
 $|A_{t}| = a_t$
. If
$|A_{t}| = a_t$
. If
 $|G[B]| = t_2(|B|)$
, then
$|G[B]| = t_2(|B|)$
, then
 $a_{t-1}=\lceil |B|/2\rceil$
and
$a_{t-1}=\lceil |B|/2\rceil$
and
 $a_t=\lfloor |B|/2\rfloor$
and we assume that
$a_t=\lfloor |B|/2\rfloor$
and we assume that
 $A_{t-1}\sqcup A_t = B$
is the original partition of
$A_{t-1}\sqcup A_t = B$
is the original partition of
 $G[B]$
with the two parts labelled so that
$G[B]$
with the two parts labelled so that
 $|A_{t-1}|\ge |A_t|$
.
$|A_{t-1}|\ge |A_t|$
.
-
Step 4: Let
 $H^{\prime}$
be obtained from
$H^{\prime}$
be obtained from
 $K[A_1, \ldots, A_t]$
by removing a star whose centre lies in
$K[A_1, \ldots, A_t]$
by removing a star whose centre lies in
 $A_t$
and
$A_t$
and
 $m^{\prime}$
leaves lie in
$m^{\prime}$
leaves lie in
 $A_{t-1}$
, where(9)This is possible because, by Step 3,
$A_{t-1}$
, where(9)This is possible because, by Step 3, \begin{equation} m^{\prime}\,:\!=\, \sum _{ij\in \binom{[t]}{2}}a_ia_j - e = a_{t-1}a_t - |G[B]|. \end{equation}
(10)
\begin{equation} m^{\prime}\,:\!=\, \sum _{ij\in \binom{[t]}{2}}a_ia_j - e = a_{t-1}a_t - |G[B]|. \end{equation}
(10) \begin{align} 0 \le m^{\prime} = a_{t-1}a_t - |G[B]| \le a_{t-1}a_{t} - \left ((a_{t-1}+1)(a_t-1)+1\right ) = a_{t-1}-a_t. \end{align}
\begin{align} 0 \le m^{\prime} = a_{t-1}a_t - |G[B]| \le a_{t-1}a_{t} - \left ((a_{t-1}+1)(a_t-1)+1\right ) = a_{t-1}-a_t. \end{align}
Notice that to obtain
![]() $H^{\prime}$
we only change the structure of
$H^{\prime}$
we only change the structure of
![]() $G$
on
$G$
on
![]() $B$
while keeping
$B$
while keeping
![]() $|G[B]| = |H^{\prime}[B]|$
. Thus,
$|G[B]| = |H^{\prime}[B]|$
. Thus,
![]() $H^{\prime}\in \mathcal{H}_0(n,e)$
and, since
$H^{\prime}\in \mathcal{H}_0(n,e)$
and, since
![]() $G[B, V(G)\setminus B]$
is complete bipartite and
$G[B, V(G)\setminus B]$
is complete bipartite and
![]() $G[B]$
is triangle-free, it follows from Fact 2.2 that
$G[B]$
is triangle-free, it follows from Fact 2.2 that
![]() $N(K_r, H^{\prime}) = N(K_r, G)$
, and hence,
$N(K_r, H^{\prime}) = N(K_r, G)$
, and hence,
![]() $H^{\prime}\in \mathcal{H}_0^{\min }(n,e)$
.
$H^{\prime}\in \mathcal{H}_0^{\min }(n,e)$
.
Lemma 3.2.
For all
![]() $r\ge 3$
, integers
$r\ge 3$
, integers
![]() $n$
and
$n$
and
![]() $e$
with
$e$
with
![]() $t_{r-1}(n)\lt e\le \binom{n}{2}$
and
$t_{r-1}(n)\lt e\le \binom{n}{2}$
and
![]() $G\in \mathcal{H}_{0}^{\min }(n,e)$
, the graph
$G\in \mathcal{H}_{0}^{\min }(n,e)$
, the graph
![]() $H^{\prime}$
produced by Steps 1–4 above is isomorphic to
$H^{\prime}$
produced by Steps 1–4 above is isomorphic to
![]() $H^{\ast }(n,e)$
.
$H^{\ast }(n,e)$
.
Proof. To prove that
![]() $H^{\prime} \cong H^{\ast }(n,e)$
, it suffices to show that
$H^{\prime} \cong H^{\ast }(n,e)$
, it suffices to show that
![]() $t = k$
and
$t = k$
and
![]() $(|A_1|, \ldots, |A_{t}|) = \boldsymbol{a}^{\ast }$
, where
$(|A_1|, \ldots, |A_{t}|) = \boldsymbol{a}^{\ast }$
, where
![]() $k$
and
$k$
and
![]() $\boldsymbol{a}^{\ast }$
are as defined in Section 1.
$\boldsymbol{a}^{\ast }$
are as defined in Section 1.
Claim 3.3.
If
![]() $m^{\prime}=0$
, then
$m^{\prime}=0$
, then
![]() $|H^{\prime}[A_{h}\cup A_{i} \cup A_j]| \gt t_{2}(a_h+a_i+a_j)$
for all
$|H^{\prime}[A_{h}\cup A_{i} \cup A_j]| \gt t_{2}(a_h+a_i+a_j)$
for all
![]() $\{h,i,j\}\in \binom{[t]}{3}$
. If
$\{h,i,j\}\in \binom{[t]}{3}$
. If
![]() $m^{\prime}\gt 0$
, then
$m^{\prime}\gt 0$
, then
![]() $|H^{\prime}[A_{h}\cup A_{t-1} \cup A_t]| \gt t_{2}(a_h+a_{t-1}+a_t)$
for all
$|H^{\prime}[A_{h}\cup A_{t-1} \cup A_t]| \gt t_{2}(a_h+a_{t-1}+a_t)$
for all
![]() $h\in [t-2]$
.
$h\in [t-2]$
.
Proof. Let
![]() $S\,:\!=\, A_{h}\cup A_{i} \cup A_j$
, with
$S\,:\!=\, A_{h}\cup A_{i} \cup A_j$
, with
![]() $\{i,j\}=\{t-1,t\}$
if
$\{i,j\}=\{t-1,t\}$
if
![]() $m^{\prime}\gt 0$
. Suppose to the contrary that
$m^{\prime}\gt 0$
. Suppose to the contrary that
![]() $|H^{\prime}[S]| \le t_{2}(|S|)$
. Then let
$|H^{\prime}[S]| \le t_{2}(|S|)$
. Then let
![]() $G_1$
be a new graph obtained from
$G_1$
be a new graph obtained from
![]() $H^{\prime}$
by replacing
$H^{\prime}$
by replacing
![]() $H^{\prime}[S]$
with a bipartite graph of the same size. Note that the induced bipartite graph
$H^{\prime}[S]$
with a bipartite graph of the same size. Note that the induced bipartite graph
![]() $H^{\prime}[S, \overline{S}]$
is complete. (Indeed, this is trivially true if
$H^{\prime}[S, \overline{S}]$
is complete. (Indeed, this is trivially true if
![]() $m^{\prime}=0$
as then
$m^{\prime}=0$
as then
![]() $H^{\prime} = K[A_{1}, \ldots, A_{t}]$
; if
$H^{\prime} = K[A_{1}, \ldots, A_{t}]$
; if
![]() $m^{\prime}\gt 0$
, then the only non-complete pair is
$m^{\prime}\gt 0$
, then the only non-complete pair is
![]() $[A_{t-1}, A_{t}]$
, but both sets lie in
$[A_{t-1}, A_{t}]$
, but both sets lie in
![]() $S$
.) Since
$S$
.) Since
![]() $H^{\prime}$
is
$H^{\prime}$
is
![]() $t$
-partite, the graph
$t$
-partite, the graph
![]() $G_1$
is
$G_1$
is
![]() $(t-1)$
-partite (and with at most one non-complete pair of parts). By Steps 2–3, we have
$(t-1)$
-partite (and with at most one non-complete pair of parts). By Steps 2–3, we have
![]() $t \le 2(k-1)$
. So we can represent
$t \le 2(k-1)$
. So we can represent
![]() $G_1$
as the union of a complete
$G_1$
as the union of a complete
![]() $(k-1)$
-partite graph and a triangle-free graph, which implies that
$(k-1)$
-partite graph and a triangle-free graph, which implies that
![]() $G_1 \in \mathcal{H}_0(n,e)$
. It is easy to see from Fact 2.4 that
$G_1 \in \mathcal{H}_0(n,e)$
. It is easy to see from Fact 2.4 that
![]() $N(K_r, G_1) \le N(K_r, H^{\prime})$
, since
$N(K_r, G_1) \le N(K_r, H^{\prime})$
, since
![]() $0 = N(K_3, G_1[S]) \le N(K_3, H^{\prime}[S])$
. So it follows from the minimality of
$0 = N(K_3, G_1[S]) \le N(K_3, H^{\prime}[S])$
. So it follows from the minimality of
![]() $H^{\prime}$
that
$H^{\prime}$
that
![]() $N(K_3, H^{\prime}[S]) = 0$
. If
$N(K_3, H^{\prime}[S]) = 0$
. If
![]() $\{t-1, t\}$
is not a subset of
$\{t-1, t\}$
is not a subset of
![]() $\{h,i,j\}$
, then
$\{h,i,j\}$
, then
![]() $H^{\prime}[S]$
is a complete
$H^{\prime}[S]$
is a complete
![]() $3$
-partite graph and contains at least one traingle, contradicting
$3$
-partite graph and contains at least one traingle, contradicting
![]() $N(K_3, H^{\prime}[S]) = 0$
. Therefore,
$N(K_3, H^{\prime}[S]) = 0$
. Therefore,
![]() $\{t-1, t\} \subseteq \{h,i,j\}$
. By symmetry, we may assume that
$\{t-1, t\} \subseteq \{h,i,j\}$
. By symmetry, we may assume that
![]() $\{t-1, t\} = \{i,j\}$
(thus being consistent with our earlier assumption if
$\{t-1, t\} = \{i,j\}$
(thus being consistent with our earlier assumption if
![]() $m^{\prime}\gt 0$
). Note that
$m^{\prime}\gt 0$
). Note that
![]() $|H[A_{t-1}, A_{t}]| \ge 1$
, since otherwise, we would have
$|H[A_{t-1}, A_{t}]| \ge 1$
, since otherwise, we would have
![]() $m^{\prime} \ge a_{t-1}a_{t} \gt a_{t-1}-a_{t}$
, contradicting (10). Note that each edge in
$m^{\prime} \ge a_{t-1}a_{t} \gt a_{t-1}-a_{t}$
, contradicting (10). Note that each edge in
![]() $H[A_{t-1}, A_{t}]$
is in
$H[A_{t-1}, A_{t}]$
is in
![]() $|A_{h}|$
triangles in
$|A_{h}|$
triangles in
![]() $H[S]$
, contradicting
$H[S]$
, contradicting
![]() $N(K_3, H^{\prime}[S]) = 0$
.
$N(K_3, H^{\prime}[S]) = 0$
.
Claim 3.4.
If
![]() $m^{\prime}\gt 0$
, then
$m^{\prime}\gt 0$
, then
![]() $a_{t-2} \ge a_{t-1}$
.
$a_{t-2} \ge a_{t-1}$
.
Proof. Suppose to the contrary that
![]() $a_{t-2} \le a_{t-1}-1$
. Then let
$a_{t-2} \le a_{t-1}-1$
. Then let
![]() $G_2$
be a new graph obtained from
$G_2$
be a new graph obtained from
![]() $H^{\prime}$
by moving edges from
$H^{\prime}$
by moving edges from
![]() $[A_{t-2}, A_{t}]$
to
$[A_{t-2}, A_{t}]$
to
![]() $[A_{t-1}, A_{t}]$
until this is no longer possible. Let
$[A_{t-1}, A_{t}]$
until this is no longer possible. Let
![]() $S\,:\!=\, A_{t-2} \cup A_{t-1} \cup A_{t}$
. If
$S\,:\!=\, A_{t-2} \cup A_{t-1} \cup A_{t}$
. If
![]() $A_{t-2} \cup A_t$
is an independent set in
$A_{t-2} \cup A_t$
is an independent set in
![]() $G_2$
(i.e. if
$G_2$
(i.e. if
![]() $m^{\prime} \ge a_{t-2}a_{t}$
), then
$m^{\prime} \ge a_{t-2}a_{t}$
), then
![]() $|H^{\prime}[S]| = |G_2[S]| \le t_2(|S|)$
, contradicting Claim 3.3. Thus
$|H^{\prime}[S]| = |G_2[S]| \le t_2(|S|)$
, contradicting Claim 3.3. Thus
![]() $G_2[S]$
can be viewed as a graph obtained from
$G_2[S]$
can be viewed as a graph obtained from
![]() $K[A_{t-2}, A_{t-1}, A_{t}]$
by removing
$K[A_{t-2}, A_{t-1}, A_{t}]$
by removing
![]() $m^{\prime}$
edges from
$m^{\prime}$
edges from
![]() $K[A_{t-2}, A_{t}]$
. So
$K[A_{t-2}, A_{t}]$
. So
![]() $G_2 \in \mathcal{H}_0(n,e)$
. Note that
$G_2 \in \mathcal{H}_0(n,e)$
. Note that
which combined with Fact 2.4 implies that
![]() $N(K_r, G_2) - N(K_r, H^{\prime})\lt 0$
, contradicting the minimality of
$N(K_r, G_2) - N(K_r, H^{\prime})\lt 0$
, contradicting the minimality of
![]() $H^{\prime}$
.
$H^{\prime}$
.
If
![]() $m^{\prime}\gt 0$
, let
$m^{\prime}\gt 0$
, let
![]() $C_i\,:\!=\, A_i$
for
$C_i\,:\!=\, A_i$
for
![]() $i\in [t]$
. If
$i\in [t]$
. If
![]() $m^{\prime}=0$
, let
$m^{\prime}=0$
, let
![]() $C_1, \ldots, C_t$
be a relabelling of
$C_1, \ldots, C_t$
be a relabelling of
![]() $A_1, \ldots, A_t$
so that the sizes of the sets are non-increasing. Regardless of the value of
$A_1, \ldots, A_t$
so that the sizes of the sets are non-increasing. Regardless of the value of
![]() $m^{\prime}$
, the following statements clearly hold:
$m^{\prime}$
, the following statements clearly hold:
-
(i)
 $c_1 \ge \dots \ge c_{t}$
, where
$c_1 \ge \dots \ge c_{t}$
, where
 $c_i \,:\!=\, |C_i|$
for
$c_i \,:\!=\, |C_i|$
for
 $i\in [t]$
,
$i\in [t]$
, -
(ii)
 $0 \le m^{\prime} \le c_{t-1}-c_{t}$
,
$0 \le m^{\prime} \le c_{t-1}-c_{t}$
, -
(iii) Claim 3.3 applies to all triples
 $\{C_i, C_{t-1}, C_{t}\}$
for
$\{C_i, C_{t-1}, C_{t}\}$
for
 $i\in [t-2]$
.
$i\in [t-2]$
.
The rest of the proof is written so that it works for both
![]() $m^{\prime}=0$
and
$m^{\prime}=0$
and
![]() $m^{\prime}\gt 0$
.
$m^{\prime}\gt 0$
.
Claim 3.5.
We have
![]() $c_1 \le c_{t-1} + 1$
.
$c_1 \le c_{t-1} + 1$
.
Proof. Let
![]() $S\,:\!=\, C_1 \cup C_{t-1} \cup C_{t}$
. Note that
$S\,:\!=\, C_1 \cup C_{t-1} \cup C_{t}$
. Note that
Suppose to the contrary that
![]() $c_1 \ge c_{t-1}+2$
. Then
$c_1 \ge c_{t-1}+2$
. Then
![]() $m^{\prime\prime} \ge m^{\prime}+1$
. Take a partition
$m^{\prime\prime} \ge m^{\prime}+1$
. Take a partition
![]() $C^{\prime}_{1} \cup C^{\prime}_{t-1} \cup C^{\prime}_{t} = S$
of sizes
$C^{\prime}_{1} \cup C^{\prime}_{t-1} \cup C^{\prime}_{t} = S$
of sizes
![]() $c_1-1, c_{t-1}+1, c_{t}$
, respectively. Let
$c_1-1, c_{t-1}+1, c_{t}$
, respectively. Let
![]() $H_{S}$
be the graph obtained from
$H_{S}$
be the graph obtained from
![]() $K[C^{\prime}_{1}, C^{\prime}_{t-1}, C^{\prime}_{t}]$
by removing
$K[C^{\prime}_{1}, C^{\prime}_{t-1}, C^{\prime}_{t}]$
by removing
![]() $m^{\prime\prime}$
edges between
$m^{\prime\prime}$
edges between
![]() $C^{\prime}_{t-1}$
and
$C^{\prime}_{t-1}$
and
![]() $C^{\prime}_{t}$
. This is possible since
$C^{\prime}_{t}$
. This is possible since
![]() $m^{\prime\prime} \le (c_{t-1}+1)c_{t}$
. (Indeed, otherwise
$m^{\prime\prime} \le (c_{t-1}+1)c_{t}$
. (Indeed, otherwise
![]() $|H^{\prime}[S]| \le (c_1-1)(c_{t-1}+c_{t}+1) \le t_{2}(|S|)$
, contradicting Claim 3.3.) We have
$|H^{\prime}[S]| \le (c_1-1)(c_{t-1}+c_{t}+1) \le t_{2}(|S|)$
, contradicting Claim 3.3.) We have
![]() $|H_{S}| = |H^{\prime}[S]|$
. Let
$|H_{S}| = |H^{\prime}[S]|$
. Let
![]() $H^{\prime\prime}$
be the graph obtained from
$H^{\prime\prime}$
be the graph obtained from
![]() $H^{\prime}$
by replacing
$H^{\prime}$
by replacing
![]() $H^{\prime}[S]$
with
$H^{\prime}[S]$
with
![]() $H_{S}$
. Note that
$H_{S}$
. Note that
![]() $H^{\prime\prime} \in \mathcal{H}_{0}(n,e)$
. It follows from
$H^{\prime\prime} \in \mathcal{H}_{0}(n,e)$
. It follows from
![]() $m^{\prime} \le c_{t-1}-c_{t}$
that
$m^{\prime} \le c_{t-1}-c_{t}$
that
 \begin{eqnarray*} N(K_3, H^{\prime}[S]) - N(K_3, H^{\prime\prime}[S]) & =& \left (c_1c_{t-1}c_{t} - m^{\prime}c_1\right ) \\ & -& \left ((c_1-1)(c_{t-1}+1)c_{t} - (m^{\prime}-c_{t-1}+c_1-1)(c_1-1)\right ) \\ & \ge & (c_1 - c_{t})(c_1-c_{t-1}-2)+1 \ \ge 1, \end{eqnarray*}
\begin{eqnarray*} N(K_3, H^{\prime}[S]) - N(K_3, H^{\prime\prime}[S]) & =& \left (c_1c_{t-1}c_{t} - m^{\prime}c_1\right ) \\ & -& \left ((c_1-1)(c_{t-1}+1)c_{t} - (m^{\prime}-c_{t-1}+c_1-1)(c_1-1)\right ) \\ & \ge & (c_1 - c_{t})(c_1-c_{t-1}-2)+1 \ \ge 1, \end{eqnarray*}
which combined with Fact 2.4 implies that
![]() $N(K_r, H^{\prime}) - N(K_r, H^{\prime\prime}) \gt 0$
, contradicting the minimality of
$N(K_r, H^{\prime}) - N(K_r, H^{\prime\prime}) \gt 0$
, contradicting the minimality of
![]() $H^{\prime}$
.
$H^{\prime}$
.
Claim 3.6.
We have
![]() $t = k$
.
$t = k$
.
Proof. It suffices to show that
![]() $t_{t-1}(n)\lt e \le t_{t}(n)$
. The upper bound
$t_{t-1}(n)\lt e \le t_{t}(n)$
. The upper bound
![]() $e \le t_{t}(n)$
is trivial, since
$e \le t_{t}(n)$
is trivial, since
![]() $H^{\prime}$
is
$H^{\prime}$
is
![]() $t$
-partite. So it remains to show that
$t$
-partite. So it remains to show that
![]() $e \gt t_{t-1}(n)$
. Let
$e \gt t_{t-1}(n)$
. Let
![]() $T\,:\!=\, H^{\prime}[C_1 \cup \dots \cup C_{t-1}]$
. It follows from Claim 3.5 that
$T\,:\!=\, H^{\prime}[C_1 \cup \dots \cup C_{t-1}]$
. It follows from Claim 3.5 that
![]() $T \cong T_{t-1}(n-c_t)$
. Therefore,
$T \cong T_{t-1}(n-c_t)$
. Therefore,
On the other hand, by viewing
![]() $T_{t-1}(n)$
as a graph obtained from
$T_{t-1}(n)$
as a graph obtained from
![]() $T_{t-1}(n-c_t)$
by adding
$T_{t-1}(n-c_t)$
by adding
![]() $c_t$
new vertices into some parts, we obtain
$c_t$
new vertices into some parts, we obtain
By combining these two inequalities, we obtain
proving that
![]() $e \gt t_{t-1}(n)$
.
$e \gt t_{t-1}(n)$
.
Claim 3.7.
The sequence
![]() $\left (|C_1|, \ldots, |C_{k}|\right )$
of part sizes is equal to
$\left (|C_1|, \ldots, |C_{k}|\right )$
of part sizes is equal to
![]() $\boldsymbol{a}^{\ast } = \boldsymbol{a}^{\ast }(n,e)$
.
$\boldsymbol{a}^{\ast } = \boldsymbol{a}^{\ast }(n,e)$
.
Proof. Recall that
![]() $t=k$
and, by (11), we have that
$t=k$
and, by (11), we have that
Let us show that
![]() $c_k$
is the smallest nonnegative integer
$c_k$
is the smallest nonnegative integer
![]() $a$
satisfying
$a$
satisfying
This inequality holds for
![]() $a=c_k$
by (12). Note that
$a=c_k$
by (12). Note that
![]() $c_k \le n/k$
as it is the smallest among
$c_k \le n/k$
as it is the smallest among
![]() $c_1 + \dots + c_k = n$
. Thus, by Lemma 2.6, it is enough to check that
$c_1 + \dots + c_k = n$
. Thus, by Lemma 2.6, it is enough to check that
![]() $a=c_k-1$
violates this condition. Notice that
$a=c_k-1$
violates this condition. Notice that
Therefore, it follows from
![]() $m^{\prime} \le c_{k-1}-c_{k}$
that
$m^{\prime} \le c_{k-1}-c_{k}$
that
as desired.
Thus
![]() $c_k=a_k^{\ast }$
and (since
$c_k=a_k^{\ast }$
and (since
![]() $t=k$
by Claim 3.6) we have
$t=k$
by Claim 3.6) we have
![]() $(c_1,\dots, c_k)=\boldsymbol{a}^{\ast }$
by Claim 3.5, as desired.
$(c_1,\dots, c_k)=\boldsymbol{a}^{\ast }$
by Claim 3.5, as desired.
Also, it follows from the definitions that
![]() $m^{\prime} = m^{\ast }$
and thus
$m^{\prime} = m^{\ast }$
and thus
![]() $H^{\prime}$
is isomorphic to
$H^{\prime}$
is isomorphic to
![]() $H^{\ast }(n,e)$
. This completes the proof of Lemma 3.2.
$H^{\ast }(n,e)$
. This completes the proof of Lemma 3.2.
Now we are ready to prove Proposition 3.1.
Proof of Proposition
3.1. Let
![]() $G\in \mathcal{H}^{\min }_{0}(n,e)$
be arbitrary. Let
$G\in \mathcal{H}^{\min }_{0}(n,e)$
be arbitrary. Let
![]() $B_1, \ldots, B_{k-1}$
be a vertex partition such that
$B_1, \ldots, B_{k-1}$
be a vertex partition such that
![]() $G$
is the union of
$G$
is the union of
![]() $K[B_1, \ldots, B_{k-1}]$
with a triangle-free graph
$K[B_1, \ldots, B_{k-1}]$
with a triangle-free graph
![]() $J$
. Let
$J$
. Let
![]() $b_i\,:\!=\, |B_i|$
for
$b_i\,:\!=\, |B_i|$
for
![]() $i\in [k-1]$
. Apply Steps 1–4 to
$i\in [k-1]$
. Apply Steps 1–4 to
![]() $G$
to obtain a
$G$
to obtain a
![]() $k$
-partite graph
$k$
-partite graph
![]() $H^{\prime}$
with parts
$H^{\prime}$
with parts
![]() $A_1, \ldots, A_{k}$
. By Lemma 3.2, we have
$A_1, \ldots, A_{k}$
. By Lemma 3.2, we have
![]() $H^{\prime} \cong H^{\ast } \,:\!=\, H^{\ast }(n,e)$
. Assume that
$H^{\prime} \cong H^{\ast } \,:\!=\, H^{\ast }(n,e)$
. Assume that
![]() $|A_i| = a^{\ast }_i$
for
$|A_i| = a^{\ast }_i$
for
![]() $i\in [k]$
and that all missing edges of
$i\in [k]$
and that all missing edges of
![]() $H^{\prime}$
(if any exist) go between
$H^{\prime}$
(if any exist) go between
![]() $A_{k-1}$
and
$A_{k-1}$
and
![]() $A_{k}$
.
$A_{k}$
.
The following claim follows from the definitions of Steps 1–4.
Claim 3.8.
If
![]() $i\in [k-1]$
satisfies
$i\in [k-1]$
satisfies
![]() $|G[B_i]| \in \left \{0, t_{2}(b_i)\right \}$
, then
$|G[B_i]| \in \left \{0, t_{2}(b_i)\right \}$
, then
![]() $H^{\prime}[B_i] = G[B_i]$
.
$H^{\prime}[B_i] = G[B_i]$
.
Since
![]() $H^{\prime}$
is
$H^{\prime}$
is
![]() $k$
-partite, it follows from the definitions of Steps 1–4 that exactly one part
$k$
-partite, it follows from the definitions of Steps 1–4 that exactly one part
![]() $B_p$
of
$B_p$
of
![]() $G$
is divided into
$G$
is divided into
![]() $A_q \cup A_s$
in Steps 2–3, where, say,
$A_q \cup A_s$
in Steps 2–3, where, say,
![]() $1\le q \lt s \le k$
, while the remaining parts of
$1\le q \lt s \le k$
, while the remaining parts of
![]() $G$
correspond to the remaining parts of
$G$
correspond to the remaining parts of
![]() $H^{\prime}$
. In particular,
$H^{\prime}$
. In particular,
![]() $b_p = a_{q}^{\ast } + a_{s}^{\ast }$
.
$b_p = a_{q}^{\ast } + a_{s}^{\ast }$
.
Claim 3.9.
We have
![]() $|G[B_p]|\gt 0$
.
$|G[B_p]|\gt 0$
.
Proof. It follows from
![]() $m^{\ast } \le a_{k-1}^{\ast } - a_{k}^{\ast }$
that
$m^{\ast } \le a_{k-1}^{\ast } - a_{k}^{\ast }$
that
Combined with Claim 3.8, we see that
![]() $|G[B_p]|\gt 0$
.
$|G[B_p]|\gt 0$
.
Suppose first that
![]() $m^{\ast } = 0$
. Then
$m^{\ast } = 0$
. Then
![]() $H^{\prime} = K[A_1, \ldots, A_{k}]$
, and
$H^{\prime} = K[A_1, \ldots, A_{k}]$
, and
![]() $G$
can be obtained from
$G$
can be obtained from
![]() $H^{\prime}$
by replacing
$H^{\prime}$
by replacing
![]() $H^{\prime}[A_{q}\cup A_{s}]$
with
$H^{\prime}[A_{q}\cup A_{s}]$
with
![]() $G[B_p]$
. Moreover,
$G[B_p]$
. Moreover,
![]() $G[B_{p}]$
is a triangle-free graph with
$G[B_{p}]$
is a triangle-free graph with
![]() $a^{\ast }_{q} + a^{\ast }_{s}$
vertices and
$a^{\ast }_{q} + a^{\ast }_{s}$
vertices and
![]() $a^{\ast }_{q} a^{\ast }_{s}$
edges. If
$a^{\ast }_{q} a^{\ast }_{s}$
edges. If
![]() $a^{\ast }_{s} = a^{\ast }_{k}$
, then it follows from the definition of
$a^{\ast }_{s} = a^{\ast }_{k}$
, then it follows from the definition of
![]() $\mathcal{H}_{1}^{\ast }(n,e)$
that
$\mathcal{H}_{1}^{\ast }(n,e)$
that
![]() $G \in \mathcal{H}_{1}^{\ast }(n,e)$
. Otherwise,
$G \in \mathcal{H}_{1}^{\ast }(n,e)$
. Otherwise,
![]() $|a^{\ast }_{q} - a^{\ast }_{s}| \le 1$
(by the definition of
$|a^{\ast }_{q} - a^{\ast }_{s}| \le 1$
(by the definition of
![]() $\boldsymbol{a}^{\ast }$
), and hence,
$\boldsymbol{a}^{\ast }$
), and hence,
![]() $G[B_p]\cong T_{2}(a^{\ast }_{q} + a^{\ast }_{s})$
. This implies that
$G[B_p]\cong T_{2}(a^{\ast }_{q} + a^{\ast }_{s})$
. This implies that
![]() $G$
does not contain any partially full part, and hence,
$G$
does not contain any partially full part, and hence,
![]() $G = H^{\prime} \in \mathcal{H}_{1}^{\ast }(n,e)$
.
$G = H^{\prime} \in \mathcal{H}_{1}^{\ast }(n,e)$
.
Suppose that
![]() $m^{\ast } \gt 0$
. Since
$m^{\ast } \gt 0$
. Since
![]() $G[A_i,A_j]$
is complete for all
$G[A_i,A_j]$
is complete for all
![]() $\{i,j\} \neq \{q,s\}$
and
$\{i,j\} \neq \{q,s\}$
and
![]() $H^{\prime}[A_i,A_j]$
is complete iff
$H^{\prime}[A_i,A_j]$
is complete iff
![]() $\{i,j\} \neq \{k-1, k\}$
, we have
$\{i,j\} \neq \{k-1, k\}$
, we have
![]() $\{q,s\} = \{k-1, k\}$
. Thus
$\{q,s\} = \{k-1, k\}$
. Thus
![]() $G$
can be obtained from
$G$
can be obtained from
![]() $K[A_1, \ldots, A_{k}]$
by replacing
$K[A_1, \ldots, A_{k}]$
by replacing
![]() $K[A_{k-1} \cup A_k]$
with a triangle-free graph with
$K[A_{k-1} \cup A_k]$
with a triangle-free graph with
![]() $a^{\ast }_{k-1}a^{\ast }_k - m^{\ast }$
edges. This gives
$a^{\ast }_{k-1}a^{\ast }_k - m^{\ast }$
edges. This gives
![]() $G \in \mathcal{H}_{1}^{\ast }(n,e)$
. We conclude that
$G \in \mathcal{H}_{1}^{\ast }(n,e)$
. We conclude that
![]() $\mathcal{H}^{\min }_{0}(n,e) \subseteq \mathcal{H}^{\ast }_{1}(n,e)$
. Since
$\mathcal{H}^{\min }_{0}(n,e) \subseteq \mathcal{H}^{\ast }_{1}(n,e)$
. Since
![]() $\mathcal{H}^{\ast }_{1}(n,e) \subseteq \mathcal{H}_0(n,e)$
and every graph in
$\mathcal{H}^{\ast }_{1}(n,e) \subseteq \mathcal{H}_0(n,e)$
and every graph in
![]() $\mathcal{H}^{\ast }_{1}(n,e)$
contains the same number of
$\mathcal{H}^{\ast }_{1}(n,e)$
contains the same number of
![]() $K_r$
’s, we have
$K_r$
’s, we have
![]() $\mathcal{H}^{\min }_{0}(n,e) = \mathcal{H}^{\ast }_{1}(n,e)$
.
$\mathcal{H}^{\min }_{0}(n,e) = \mathcal{H}^{\ast }_{1}(n,e)$
.
4. Proof of Theorem 1.1
With Proposition 3.1 in hand, we are now ready to prove Theorem 1.1.
Proof of Theorem
1.1. Fix integers
![]() $n \ge r \ge 3$
and
$n \ge r \ge 3$
and
![]() $e \le \binom{n}{2}$
. Notice that (4) can be reduced to
$e \le \binom{n}{2}$
. Notice that (4) can be reduced to
![]() $\min \big \{N(K_r, G)\,\colon\, G\in \mathcal{K}(n,e)\big \} \ge h_{r}^{\ast }(n,e)$
, since the other direction is trivially true. Suppose that
$\min \big \{N(K_r, G)\,\colon\, G\in \mathcal{K}(n,e)\big \} \ge h_{r}^{\ast }(n,e)$
, since the other direction is trivially true. Suppose that
![]() $G \in \mathcal{K}^{\min }(n,e)$
is a graph obtained from a complete
$G \in \mathcal{K}^{\min }(n,e)$
is a graph obtained from a complete
![]() $\ell$
-partite graph by adding a triangle-free graph to one part. We aim to show that
$\ell$
-partite graph by adding a triangle-free graph to one part. We aim to show that
![]() $N(K_r, G) \ge h_{r}^{\ast }(n,e)$
when
$N(K_r, G) \ge h_{r}^{\ast }(n,e)$
when
![]() $r\ge 3$
and, in addition,
$r\ge 3$
and, in addition,
![]() $G \in \mathcal{H}_{1}^{\ast }(n,e)$
when
$G \in \mathcal{H}_{1}^{\ast }(n,e)$
when
![]() $r \ge 4$
and
$r \ge 4$
and
![]() $e\gt t_{r-1}(n)$
. We prove this statement by induction on
$e\gt t_{r-1}(n)$
. We prove this statement by induction on
![]() $\ell + r$
. Notice that if
$\ell + r$
. Notice that if
![]() $\ell = k-1$
(where
$\ell = k-1$
(where
![]() $k= k(n,e)$
) and
$k= k(n,e)$
) and
![]() $r \ge 4$
, then
$r \ge 4$
, then
![]() $G \in \mathcal{H}_{0}(n,e)$
, and it follows from Proposition 3.1 that
$G \in \mathcal{H}_{0}(n,e)$
, and it follows from Proposition 3.1 that
![]() $G \in \mathcal{H}_{1}^{\ast }(n,e)$
, as desired. If
$G \in \mathcal{H}_{1}^{\ast }(n,e)$
, as desired. If
![]() $\ell = k-1$
and
$\ell = k-1$
and
![]() $r=3$
, then
$r=3$
, then
![]() $G \in \mathcal{H}_{0}(n,e)$
, and it follows from [Reference Liu, Pikhurko and Staden9, Proposition 1.5] that
$G \in \mathcal{H}_{0}(n,e)$
, and it follows from [Reference Liu, Pikhurko and Staden9, Proposition 1.5] that
![]() $N(K_3, G) \ge h_{3}^{\ast }(n,e)$
. So the statement is true for all pairs
$N(K_3, G) \ge h_{3}^{\ast }(n,e)$
. So the statement is true for all pairs
![]() $(\ell, r)$
with
$(\ell, r)$
with
![]() $\ell = k-1$
and
$\ell = k-1$
and
![]() $r\ge 3$
, and this serves as our base case.
$r\ge 3$
, and this serves as our base case.
Assume that
![]() $\ell \ge k$
and
$\ell \ge k$
and
![]() $r \ge 3$
. Let
$r \ge 3$
. Let
![]() $U_1 \cup \dots \cup U_{\ell } = V(G)$
be a partition such that
$U_1 \cup \dots \cup U_{\ell } = V(G)$
be a partition such that
![]() $G$
is obtained from the complete
$G$
is obtained from the complete
![]() $\ell$
-partite graph
$\ell$
-partite graph
![]() $K[U_1, \ldots, U_{\ell }]$
by adding a triangle-free graph into
$K[U_1, \ldots, U_{\ell }]$
by adding a triangle-free graph into
![]() $U_{\ell }$
. We can assume that
$U_{\ell }$
. We can assume that
![]() $U_{\ell }$
is not an independent set (otherwise consider instead the
$U_{\ell }$
is not an independent set (otherwise consider instead the
![]() $(\ell -1)$
-partition of
$(\ell -1)$
-partition of
![]() $V(G)$
where
$V(G)$
where
![]() $U_{\ell -1}$
and
$U_{\ell -1}$
and
![]() $U_\ell$
are merged together).
$U_\ell$
are merged together).
First, we prove (4). Assume that
![]() $\ell \ge r-1$
, as otherwise
$\ell \ge r-1$
, as otherwise
![]() $h_r^{\ast }(n,e)=0$
and there is nothing to do. Note that
$h_r^{\ast }(n,e)=0$
and there is nothing to do. Note that
![]() $U_{\ell }$
is as large as any other part: if some part
$U_{\ell }$
is as large as any other part: if some part
![]() $U_i$
has strictly larger size then by moving all edges from
$U_i$
has strictly larger size then by moving all edges from
![]() $U_\ell$
to
$U_\ell$
to
![]() $U_i$
(by
$U_i$
(by
![]() $|U_i|\gt |U_\ell |$
there is enough space for this) we strictly decrease the number of
$|U_i|\gt |U_\ell |$
there is enough space for this) we strictly decrease the number of
![]() $r$
-cliques (since
$r$
-cliques (since
![]() $\ell \ge r-1$
), a contradiction. By relabelling parts
$\ell \ge r-1$
), a contradiction. By relabelling parts
![]() $U_1, \ldots, U_{\ell -1}$
, we may assume that
$U_1, \ldots, U_{\ell -1}$
, we may assume that
![]() $U_{1}$
is of smallest size among
$U_{1}$
is of smallest size among
![]() $U_1, \ldots, U_{\ell -1}$
. Let
$U_1, \ldots, U_{\ell -1}$
. Let
![]() $\hat{G}$
denote the induced subgraph of
$\hat{G}$
denote the induced subgraph of
![]() $G$
on
$G$
on
![]() $U_2 \cup \dots \cup U_{\ell }$
. Let
$U_2 \cup \dots \cup U_{\ell }$
. Let
![]() $\hat{n} \,:\!=\, n-|U_{1}|$
and
$\hat{n} \,:\!=\, n-|U_{1}|$
and
![]() $\hat{e} \,:\!=\, |\hat{G}|$
. Let
$\hat{e} \,:\!=\, |\hat{G}|$
. Let
![]() $\hat{k} \,:\!=\, k(\hat{n}, \hat{e})$
be as defined in (2) (while we reserve
$\hat{k} \,:\!=\, k(\hat{n}, \hat{e})$
be as defined in (2) (while we reserve
![]() $k$
for
$k$
for
![]() $k(n,e)$
).
$k(n,e)$
).
Claim 4.1.
We have
![]() $\hat{k} \le k$
.
$\hat{k} \le k$
.
Proof. Let
![]() $H^{\ast } = H^{\ast }(n,e)$
be the
$H^{\ast } = H^{\ast }(n,e)$
be the
![]() $k$
-partite graph as defined in Section 1. Assume that
$k$
-partite graph as defined in Section 1. Assume that
![]() $A_1^{\ast }, \ldots, A_{k}^{\ast }$
are the corresponding parts of
$A_1^{\ast }, \ldots, A_{k}^{\ast }$
are the corresponding parts of
![]() $H^{\ast }$
of sizes
$H^{\ast }$
of sizes
![]() $a_1^{\ast } \ge \dots \ge a_{k}^{\ast }$
, respectively. It is clear that
$a_1^{\ast } \ge \dots \ge a_{k}^{\ast }$
, respectively. It is clear that
![]() $|A_1^{\ast }| \ge \frac{n}{k}$
. It follows from the minimality of
$|A_1^{\ast }| \ge \frac{n}{k}$
. It follows from the minimality of
![]() $U_{1}$
that
$U_{1}$
that
![]() $|U_{1}| \le \frac{n-|U_{\ell }|}{\ell -1} \le \frac{n}{k} \le |A_1^{\ast }|$
. Let
$|U_{1}| \le \frac{n-|U_{\ell }|}{\ell -1} \le \frac{n}{k} \le |A_1^{\ast }|$
. Let
![]() $W_1 \subseteq A_1^{\ast }$
be a set of size
$W_1 \subseteq A_1^{\ast }$
be a set of size
![]() $|U_1|$
and let
$|U_1|$
and let
![]() $H^{\prime}$
be the induced subgraph of
$H^{\prime}$
be the induced subgraph of
![]() $H^{\ast }$
on
$H^{\ast }$
on
![]() $V(H)\setminus W_1$
. Observe that
$V(H)\setminus W_1$
. Observe that
![]() $H^{\prime}$
is still a
$H^{\prime}$
is still a
![]() $k$
-partite graph and
$k$
-partite graph and
![]() $|H^{\prime}| \ge |\hat{G}|$
. So it follows from the definition that
$|H^{\prime}| \ge |\hat{G}|$
. So it follows from the definition that
![]() $\hat{k} \le k$
.
$\hat{k} \le k$
.
Note that
![]() $\hat{G}$
can be viewed as a graph obtained from a complete
$\hat{G}$
can be viewed as a graph obtained from a complete
![]() $(\ell -1)$
-partite graph by adding a triangle-free graph into one part; in particular,
$(\ell -1)$
-partite graph by adding a triangle-free graph into one part; in particular,
![]() $\hat{G}\in \mathcal{K}(\hat{n},\hat{e})$
. Let
$\hat{G}\in \mathcal{K}(\hat{n},\hat{e})$
. Let
![]() $\hat{H}$
be
$\hat{H}$
be
![]() $H^{\ast }(\hat{n}, \hat{e})$
and let
$H^{\ast }(\hat{n}, \hat{e})$
and let
![]() $G^{\prime}$
be the graph obtained from
$G^{\prime}$
be the graph obtained from
![]() $G$
by replacing
$G$
by replacing
![]() $\hat{G}$
with
$\hat{G}$
with
![]() $\hat{H}$
. It follows from the inductive hypothesis that
$\hat{H}$
. It follows from the inductive hypothesis that
Hence,
finishing the inductive step for proving (4).
Now suppose that
![]() $r \ge 4$
and
$r \ge 4$
and
![]() $e\gt t_{r-1}(n)$
, and suppose for contradiction that
$e\gt t_{r-1}(n)$
, and suppose for contradiction that
![]() $G\not \in \mathcal{H}_1^{\ast }(n,e)$
. Reusing the notation introduced above, let us first derive a contradiction from assuming that
$G\not \in \mathcal{H}_1^{\ast }(n,e)$
. Reusing the notation introduced above, let us first derive a contradiction from assuming that
![]() $\hat{G} \not \in \mathcal{H}_1^{\ast }(\hat{n}, \hat{e})$
.
$\hat{G} \not \in \mathcal{H}_1^{\ast }(\hat{n}, \hat{e})$
.
If
![]() $\hat{e} \gt t_{r-1}(\hat{n})$
, then it follows from the inductive hypothesis that
$\hat{e} \gt t_{r-1}(\hat{n})$
, then it follows from the inductive hypothesis that
Therefore,
contradicting the minimality of
![]() $G$
.
$G$
.
So suppose that
![]() $\hat{e} \le t_{r-1}(\hat{n})$
. We have that
$\hat{e} \le t_{r-1}(\hat{n})$
. We have that
![]() $\ell \ge k \ge r$
. Recall that
$\ell \ge k \ge r$
. Recall that
![]() $\hat{G}$
is a graph obtained from an
$\hat{G}$
is a graph obtained from an
![]() $(\ell -1)$
-partite graph by adding a non-empty triangle-free graph. Thus, we have
$(\ell -1)$
-partite graph by adding a non-empty triangle-free graph. Thus, we have
![]() $N(K_r, \hat{H}) = 0 \lt N(K_r, \hat{G})$
. In addition, by (4), we have
$N(K_r, \hat{H}) = 0 \lt N(K_r, \hat{G})$
. In addition, by (4), we have
![]() $N(K_{r-1}, \hat{H}) = h_{r-1}^{\ast }(\hat{n}, \hat{e}) \le N(K_{r-1}, \hat{G})$
. But then the same calculation as in (13) gives a contradiction to the minimality of
$N(K_{r-1}, \hat{H}) = h_{r-1}^{\ast }(\hat{n}, \hat{e}) \le N(K_{r-1}, \hat{G})$
. But then the same calculation as in (13) gives a contradiction to the minimality of
![]() $G$
.
$G$
.
Thus we have that
![]() $\hat{G} \in \mathcal{H}_1^{\ast }(\hat{n}, \hat{e})$
. Let
$\hat{G} \in \mathcal{H}_1^{\ast }(\hat{n}, \hat{e})$
. Let
![]() $\hat{A}_1^{\ast } \cup \ldots \cup \hat{A}_{\hat{k}}^{\ast } = V(\hat{G})$
be the partition of
$\hat{A}_1^{\ast } \cup \ldots \cup \hat{A}_{\hat{k}}^{\ast } = V(\hat{G})$
be the partition of
![]() $\hat{G}$
as in the definition of
$\hat{G}$
as in the definition of
![]() $\mathcal{H}_{1}^{\ast }(\hat{n},\hat{e})$
. Let
$\mathcal{H}_{1}^{\ast }(\hat{n},\hat{e})$
. Let
![]() $B_1 \,:\!=\, U_1 \cup \hat{A}_1^{\ast }$
,
$B_1 \,:\!=\, U_1 \cup \hat{A}_1^{\ast }$
,
![]() $B_i \,:\!=\, \hat{A}_i^{\ast }$
for
$B_i \,:\!=\, \hat{A}_i^{\ast }$
for
![]() $2\le i\le \hat{k}-2$
, and
$2\le i\le \hat{k}-2$
, and
![]() $B_{\hat{k}-1}\,:\!=\,\hat{A}_{\hat{k}-1}\cup \hat{A}_{\hat{k}}$
. We can view
$B_{\hat{k}-1}\,:\!=\,\hat{A}_{\hat{k}-1}\cup \hat{A}_{\hat{k}}$
. We can view
![]() $G$
as a graph obtained from
$G$
as a graph obtained from
![]() $K[B_1, \ldots, B_{\hat{k}-1}]$
by adding triangle-free graphs into two parts, namely
$K[B_1, \ldots, B_{\hat{k}-1}]$
by adding triangle-free graphs into two parts, namely
![]() $G[B_1]$
and
$G[B_1]$
and
![]() $G[B_{\hat{k}-1}]$
. Since
$G[B_{\hat{k}-1}]$
. Since
![]() $\hat{k} \le k$
by Claim 4.1, it holds that
$\hat{k} \le k$
by Claim 4.1, it holds that
![]() $G \in \mathcal{H}_{0}(n,e)$
. Therefore, it follows from Proposition 3.1 that
$G \in \mathcal{H}_{0}(n,e)$
. Therefore, it follows from Proposition 3.1 that
![]() $G \in \mathcal{H}_{1}^{\ast }(n,e)$
, finishing the proof of Theorem 1.1.
$G \in \mathcal{H}_{1}^{\ast }(n,e)$
, finishing the proof of Theorem 1.1.
Let us remark that if we replace the family
![]() $\mathcal{K}(n,e)$
in Theorem 1.1 by the larger family
$\mathcal{K}(n,e)$
in Theorem 1.1 by the larger family
![]() $\mathcal{K}^{\prime}(n,e)$
that consists of all graphs obtained from a complete partite graph by adding a triangle-free graph (that is, we allow to add edges into more than one part) then the theorem will remain true. Indeed, for
$\mathcal{K}^{\prime}(n,e)$
that consists of all graphs obtained from a complete partite graph by adding a triangle-free graph (that is, we allow to add edges into more than one part) then the theorem will remain true. Indeed, for
![]() $r\ge 4$
, the proof of Lemma 2.5 (which in fact works for any number of parts) shows that every extremal graph
$r\ge 4$
, the proof of Lemma 2.5 (which in fact works for any number of parts) shows that every extremal graph
![]() $\mathcal{K}^{\prime}(n,e)$
has at most one partially full part and thus belongs to
$\mathcal{K}^{\prime}(n,e)$
has at most one partially full part and thus belongs to
![]() $\mathcal{K}(n,e)$
. For
$\mathcal{K}(n,e)$
. For
![]() $r=3$
, the equality in (4), will also remain true (again by the proof of Lemma 2.5 except the inequality in (6) becomes equality).
$r=3$
, the equality in (4), will also remain true (again by the proof of Lemma 2.5 except the inequality in (6) becomes equality).
5. Proof of Proposition 1.2
Proof of Proposition
1.2. First, we prove that
![]() $N(K_r, H) = h_{r}^{\ast }(n,e)$
for all
$N(K_r, H) = h_{r}^{\ast }(n,e)$
for all
![]() $H\in \mathcal{H}_{2}^{\ast }(n,e)$
. Fix
$H\in \mathcal{H}_{2}^{\ast }(n,e)$
. Fix
![]() $H \in \mathcal{H}_{2}^{\ast }(n,e)$
.
$H \in \mathcal{H}_{2}^{\ast }(n,e)$
.
First consider the case when
![]() $(|A_1|,\dots, |A_k|)=\boldsymbol{a}^{\ast }$
, where the sets
$(|A_1|,\dots, |A_k|)=\boldsymbol{a}^{\ast }$
, where the sets
![]() $A_1,\dots, A_k$
are as in the definition of
$A_1,\dots, A_k$
are as in the definition of
![]() $\mathcal{H}_{2}^{\ast }(n,e)$
. Let
$\mathcal{H}_{2}^{\ast }(n,e)$
. Let
![]() $K \,:\!=\, K[A_1, \ldots, A_k]$
, and
$K \,:\!=\, K[A_1, \ldots, A_k]$
, and
![]() $m_i^{\ast } \,:\!=\, |\overline{H}[B_i, A_i]|$
for
$m_i^{\ast } \,:\!=\, |\overline{H}[B_i, A_i]|$
for
![]() $i\in I\,:\!=\, \left \{j \in [k-1]\,\colon\, |A_j| = |A_{k-1}|\right \}$
. Note from the definition of
$i\in I\,:\!=\, \left \{j \in [k-1]\,\colon\, |A_j| = |A_{k-1}|\right \}$
. Note from the definition of
![]() $I$
that for all
$I$
that for all
![]() $i\in I$
, we have that
$i\in I$
, we have that
because we count
![]() $r$
-cliques in two isomorphic graphs. Therefore,
$r$
-cliques in two isomorphic graphs. Therefore,
 \begin{align} N(K_r, K) - N(K_r, H) & = \sum _{i\in I}m_i^{\ast } \cdot N(K_{r-2}, K[A_1, \ldots, A_{i-1}, A_{i+1}, \dots, A_{k-1}]) \notag \\ & = \sum _{i\in I}m_i^{\ast } \cdot N(K_{r-2}, K[A_1, \ldots, A_{k-2}]) \notag \\ & = m^{\ast } \cdot N(K_{r-2}, K[A_1, \ldots, A_{k-2}]) = N(K_r, K) - N(K_r, H^{\ast }). \end{align}
\begin{align} N(K_r, K) - N(K_r, H) & = \sum _{i\in I}m_i^{\ast } \cdot N(K_{r-2}, K[A_1, \ldots, A_{i-1}, A_{i+1}, \dots, A_{k-1}]) \notag \\ & = \sum _{i\in I}m_i^{\ast } \cdot N(K_{r-2}, K[A_1, \ldots, A_{k-2}]) \notag \\ & = m^{\ast } \cdot N(K_{r-2}, K[A_1, \ldots, A_{k-2}]) = N(K_r, K) - N(K_r, H^{\ast }). \end{align}
It follows that
![]() $N(K_r, H) = N(K_r, H^{\ast }) = h^{\ast }(n,e)$
, as desired.
$N(K_r, H) = N(K_r, H^{\ast }) = h^{\ast }(n,e)$
, as desired.
Now suppose that
![]() $(|A_1|,\dots, |A_k|)\not =\boldsymbol{a}^{\ast }$
. Recall that then
$(|A_1|,\dots, |A_k|)\not =\boldsymbol{a}^{\ast }$
. Recall that then
![]() $m^{\ast } = 0$
,
$m^{\ast } = 0$
,
![]() $(|A_{1}|, \ldots, |A_{k}|) = (a_{2}^{\ast }, \ldots, a_{k-1}^{\ast }, a_{1}^{\ast }-1, a_{k}^{\ast }+1)$
,
$(|A_{1}|, \ldots, |A_{k}|) = (a_{2}^{\ast }, \ldots, a_{k-1}^{\ast }, a_{1}^{\ast }-1, a_{k}^{\ast }+1)$
,
![]() $m = a_{1}^{\ast } - a_{k}^{\ast } +1$
, and
$m = a_{1}^{\ast } - a_{k}^{\ast } +1$
, and
![]() $H$
is a graph obtained from
$H$
is a graph obtained from
![]() $K[A_1, \ldots, A_{k}]$
by removing some
$K[A_1, \ldots, A_{k}]$
by removing some
![]() $m$
edges. We may assume that these
$m$
edges. We may assume that these
![]() $m$
edges were removed from parts
$m$
edges were removed from parts
![]() $[A_{k-1}, A_{k}]$
, since this does not affect the value of
$[A_{k-1}, A_{k}]$
, since this does not affect the value of
![]() $N(K_r, H)$
by the calculation in (14). Now, by viewing
$N(K_r, H)$
by the calculation in (14). Now, by viewing
![]() $H$
as a graph obtained from
$H$
as a graph obtained from
![]() $K[A_{1}, \ldots, A_{k}]$
by replacing
$K[A_{1}, \ldots, A_{k}]$
by replacing
![]() $K[A_{k-1}, A_k]$
with a triangle-free graph, we see that
$K[A_{k-1}, A_k]$
with a triangle-free graph, we see that
![]() $H \in \mathcal{H}_{1}^{\ast }(n,e)$
, and hence,
$H \in \mathcal{H}_{1}^{\ast }(n,e)$
, and hence,
![]() $N(K_r, H) = h^{\ast }(n,e)$
.
$N(K_r, H) = h^{\ast }(n,e)$
.
Next, we show that there are infinitely many pairs
![]() $(n,e) \in \mathbb{N}^2$
with
$(n,e) \in \mathbb{N}^2$
with
![]() $t_{r-1}(n) \lt e \le \binom{n}{2}$
such that
$t_{r-1}(n) \lt e \le \binom{n}{2}$
such that
![]() $\mathcal{H}_{2}^{\ast }(n,e) \setminus \mathcal{H}_{1}^{\ast }(n,e) \neq \emptyset$
. It is enough to chose
$\mathcal{H}_{2}^{\ast }(n,e) \setminus \mathcal{H}_{1}^{\ast }(n,e) \neq \emptyset$
. It is enough to chose
![]() $(n,e)$
so that
$(n,e)$
so that
![]() $a_{k-2}^{\ast }=a_{k-1}^{\ast }$
and
$a_{k-2}^{\ast }=a_{k-1}^{\ast }$
and
![]() $m^{\ast },a_k^{\ast }\ge 2$
; the choice that we use (in (15) below) is rather arbitrary.
$m^{\ast },a_k^{\ast }\ge 2$
; the choice that we use (in (15) below) is rather arbitrary.
Take any integers
![]() $p \ge r-1$
,
$p \ge r-1$
,
![]() $q \ge 100$
, and
$q \ge 100$
, and
![]() $2 \le m \le q$
. Let
$2 \le m \le q$
. Let
![]() $n \,:\!=\, 2pq+ q$
and
$n \,:\!=\, 2pq+ q$
and
![]() $e \,:\!=\, \binom{p}{2}(2q)^2 + 2pq^2 - m$
. Note that
$e \,:\!=\, \binom{p}{2}(2q)^2 + 2pq^2 - m$
. Note that
![]() $e+m$
is the number of edges in the complete
$e+m$
is the number of edges in the complete
![]() $(p+1)$
-partite graph
$(p+1)$
-partite graph
![]() $K_{2q,\dots, 2q,q}$
with
$K_{2q,\dots, 2q,q}$
with
![]() $p$
parts of size
$p$
parts of size
![]() $2q$
and one part of size
$2q$
and one part of size
![]() $q$
. The choice of
$q$
. The choice of
![]() $(p,q,m)$
ensures that
$(p,q,m)$
ensures that
By
![]() $e< e+m\le t_{p+1}(n)$
, we have that
$e< e+m\le t_{p+1}(n)$
, we have that
![]() $k(n,e) = p$
.
$k(n,e) = p$
.
Let us show that
![]() $a_{p}^{\ast } = q$
. By Lemma 2.6, it is enough to show that
$a_{p}^{\ast } = q$
. By Lemma 2.6, it is enough to show that
![]() $(q-1)(n-q-1)+t_{k-1}(n-q-1)\lt e$
. The left-hand side here is the size of the graph obtained from the complete partite graph
$(q-1)(n-q-1)+t_{k-1}(n-q-1)\lt e$
. The left-hand side here is the size of the graph obtained from the complete partite graph
![]() $K_{2q,\dots, 2q,q}$
by moving a vertex from the part of size
$K_{2q,\dots, 2q,q}$
by moving a vertex from the part of size
![]() $q$
into one of size
$q$
into one of size
![]() $2q$
. This results in losing
$2q$
. This results in losing
![]() $q+1\gt m$
edges, giving the required. Thus,
$q+1\gt m$
edges, giving the required. Thus,
Let
![]() $V_1 \cup \dots \cup V_{p+1} = [n]$
be a partition such that
$V_1 \cup \dots \cup V_{p+1} = [n]$
be a partition such that
![]() $|V_1| = \dots = |V_p| = 2q$
and
$|V_1| = \dots = |V_p| = 2q$
and
![]() $|V_{p+1}|=q$
. Fix
$|V_{p+1}|=q$
. Fix
![]() $m$
distinct vertices
$m$
distinct vertices
![]() $v_1, \ldots, v_m \in V_{p+1}$
, and choose a vertex
$v_1, \ldots, v_m \in V_{p+1}$
, and choose a vertex
![]() $u_i \in V_i$
for every
$u_i \in V_i$
for every
![]() $i\in [m]$
. Let
$i\in [m]$
. Let
![]() $G$
be the graph obtained from
$G$
be the graph obtained from
![]() $K[V_1, \ldots, V_{p-1}]$
by removing pairs in
$K[V_1, \ldots, V_{p-1}]$
by removing pairs in
![]() $\{\{v_i, u_i\}\,\colon\, i\in [m]\}$
. It is easy to see that
$\{\{v_i, u_i\}\,\colon\, i\in [m]\}$
. It is easy to see that
![]() $G \in \mathcal{H}_{2}^{\ast }(n,e) \setminus \mathcal{H}_{1}^{\ast }(n,e)$
, proving Proposition 1.2.
$G \in \mathcal{H}_{2}^{\ast }(n,e) \setminus \mathcal{H}_{1}^{\ast }(n,e)$
, proving Proposition 1.2.
Acknowledgements
The authors would like to thank the anonymous referee for helpful comments.
Funding
Research was supported by ERC Advanced Grant 101020255 and Leverhulme Research Project Grant RPG-2018-424.