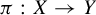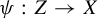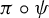1 Introduction
1.1 Background and statement of main results
In a foundational paper [Reference Shannon10] in information theory, Shannon introduced a model of a noisy communication channel, in which the input and output are modeled by stationary probability measures on a space of sequences of symbols. Shannon gave conditions under which the input can be recovered from the output, at least with an acceptable rate of error or ambiguity, in the case of a Bernoulli source, and this work has since been extended to more general sources [Reference Kieffer4].
This paper is motivated by the particular question of when one can ensure zero error, not just almost surely as in information theory but, in fact, deterministically. A deterministic channel can be modeled by a sliding block code, that is, a continuous, shift-commuting map on a subshift, on which a stationary process could be supported. In this model, we can apply techniques of symbolic dynamics to investigate the effects of deterministic noise [Reference Marcus, Petersen, Williams, Beals, Beck, Bellow and Hajian8], also called distortion [Reference Shannon10], which we can interpret as a failure of injectivity of the sliding block code representing the channel, even in the absence of random errors.
The main result of this paper, Theorem 1.1, determines the extent to which the non-injectivity of a sliding block code on a mixing shift of finite type (SFT) can be avoided by restricting to a subshift of the domain. Interpreting the sliding block code as a channel with deterministic noise, Theorem 1.1 characterizes the sources with entropy strictly lower than that of the output which can be transmitted without error or ambiguity. Note that, given the difference in entropy, there is a finite procedure to check whether the periodic point condition holds; see §2.2.
Theorem 1.1. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with topological entropy strictly less than that of Y. Then there exists a subshift
$\pi : X \to Y$
a factor code. Let Z be a subshift with topological entropy strictly less than that of Y. Then there exists a subshift
![]() $Z'$
of X conjugate to Z such that
$Z'$
of X conjugate to Z such that
![]() $\pi |_{Z'}$
is injective if and only if for every
$\pi |_{Z'}$
is injective if and only if for every
![]() $n \geq 1$
, the number of periodic points of least period n in Z is at most the number of periodic points of least period n in Y with a
$n \geq 1$
, the number of periodic points of least period n in Z is at most the number of periodic points of least period n in Y with a
![]() $\pi $
-preimage of equal least period.
$\pi $
-preimage of equal least period.
Theorem 1.1 is a generalization of the following theorem of Krieger in the case of unequal entropy; in particular, Theorem 1.1 reduces to Theorem 1.2 in the case where
![]() $Y=X$
and
$Y=X$
and
![]() $\pi $
is the identity.
$\pi $
is the identity.
Theorem 1.2. [Reference Krieger5, Theorem 2]
Let Y be a mixing shift of finite type and Z a subshift. Then there is a subshift
![]() $Z' \subseteq Y$
conjugate to Z if and only if Z and Y are conjugate or the (topological) entropy of Z is strictly less than that of Y and, for every
$Z' \subseteq Y$
conjugate to Z if and only if Z and Y are conjugate or the (topological) entropy of Z is strictly less than that of Y and, for every
![]() $n \geq 1$
, the number of periodic points of least period n in Z is at most the corresponding number in Y.
$n \geq 1$
, the number of periodic points of least period n in Z is at most the corresponding number in Y.
We note that with
![]() $X,Y,Z,\pi $
as in the statement of Theorem 1.1, clearly there exists a subshift
$X,Y,Z,\pi $
as in the statement of Theorem 1.1, clearly there exists a subshift
![]() $Z'$
of X conjugate to Z such that
$Z'$
of X conjugate to Z such that
![]() $\pi |_{Z'}$
is injective if and only if there exists a sliding block code
$\pi |_{Z'}$
is injective if and only if there exists a sliding block code
![]() $\psi : Z \to X$
such that
$\psi : Z \to X$
such that
![]() $\pi \circ \psi $
is injective, in which case
$\pi \circ \psi $
is injective, in which case
![]() $Z' = \psi (Z) \subset X$
. To verify the ‘only if’ statement in Theorem 1.1, suppose that there is a subshift
$Z' = \psi (Z) \subset X$
. To verify the ‘only if’ statement in Theorem 1.1, suppose that there is a subshift
![]() $Z'$
of X conjugate to Z such that
$Z'$
of X conjugate to Z such that
![]() $\pi |_{Z'}$
is injective. Let
$\pi |_{Z'}$
is injective. Let
![]() $y \in \pi (Z')$
be periodic. Let
$y \in \pi (Z')$
be periodic. Let
![]() $x = \pi |_{Z'}^{-1}(y)$
be the unique preimage of y in
$x = \pi |_{Z'}^{-1}(y)$
be the unique preimage of y in
![]() $Z'$
. Then the orbit of x is in bijection with the orbit of y; otherwise,
$Z'$
. Then the orbit of x is in bijection with the orbit of y; otherwise,
![]() $\pi $
would fail to be injective on the orbit of x, which is contained in
$\pi $
would fail to be injective on the orbit of x, which is contained in
![]() $Z'$
. In particular, x has finite orbit, so x is periodic, moreover with
$Z'$
. In particular, x has finite orbit, so x is periodic, moreover with
![]() $\mathrm {per}(x) = \mathrm {per}(y)$
. Thus, every periodic point in
$\mathrm {per}(x) = \mathrm {per}(y)$
. Thus, every periodic point in
![]() $\pi (Z') \subset Y$
has a periodic preimage in
$\pi (Z') \subset Y$
has a periodic preimage in
![]() $Z' \subset X$
of equal least period, which shows the necessity of the stated condition.
$Z' \subset X$
of equal least period, which shows the necessity of the stated condition.
Both Theorems 1.1 and 1.2 give conditions for the existence of an embedding in terms of entropy and a periodic point condition. The following corollary, which we prove in §5, shows that the periodic point condition can be removed in exchange for a small loss of injectivity.
Corollary 1.3. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with topological entropy strictly less than that of Y. Then there exist a subshift
$\pi : X \to Y$
a factor code. Let Z be a subshift with topological entropy strictly less than that of Y. Then there exist a subshift
![]() $Z'$
, a finite-to-one factor code
$Z'$
, a finite-to-one factor code
![]() $\chi : Z' \to Z$
, and a sliding block code
$\chi : Z' \to Z$
, and a sliding block code
![]() ${\psi : Z' \to X}$
such that
${\psi : Z' \to X}$
such that
![]() $\pi \circ \psi $
is injective. Moreover, if Z is mixing sofic with positive entropy (that is, Z does not consist of a single fixed point), then
$\pi \circ \psi $
is injective. Moreover, if Z is mixing sofic with positive entropy (that is, Z does not consist of a single fixed point), then
![]() $Z'$
can be taken to be a mixing SFT and
$Z'$
can be taken to be a mixing SFT and
![]() $\chi $
can be taken to be almost invertible.
$\chi $
can be taken to be almost invertible.
The code
![]() $\chi $
is in fact injective except on points in
$\chi $
is in fact injective except on points in
![]() $Z'$
whose images in Z are backward-asymptotic to one of finitely many periodic points in Z. See Lemma 2.3 and Remark 2.4. From Corollary 1.3, we can immediately conclude the following, with h denoting the topological entropy of a subshift.
$Z'$
whose images in Z are backward-asymptotic to one of finitely many periodic points in Z. See Lemma 2.3 and Remark 2.4. From Corollary 1.3, we can immediately conclude the following, with h denoting the topological entropy of a subshift.
Corollary 1.4. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. For any
$\pi : X \to Y$
a factor code. For any
![]() $\varepsilon> 0$
, there exists a mixing SFT
$\varepsilon> 0$
, there exists a mixing SFT
![]() $Z \subset X$
with
$Z \subset X$
with
![]() $h(Z)> h(Y) - \varepsilon $
such that
$h(Z)> h(Y) - \varepsilon $
such that
![]() $\pi |_Z$
is injective.
$\pi |_Z$
is injective.
1.2 Overview of the proof and organization of the paper
The proof of Theorem 1.1 adapts the strategy used to prove Theorem 1.2 in [Reference Krieger5, Reference Lind and Marcus6] and related results in [Reference Boyle1]. The outline of the proof is as follows. We use a marker set, as in the proof of Theorem 1.2, to break points in Z into moderate blocks and long periodic blocks, separated by marker coordinates. We code these separately using certain ‘data blocks’ in Y, some of moderate length and some long and periodic, where the long periodic data blocks come from periodic points with
![]() $\pi $
-preimages of equal least period in X. A block in Z between marker coordinates is coded to a data block in Y which is shorter by an additive constant, so that there are gaps between the data blocks that are filled with repetitions of a ‘blank’ symbol. We then lift the data blocks from Y to data blocks from X, then replace the blanks with a ‘stamp’ block from X to form a valid point in X. The stamp block is chosen to ensure that once the point in X is coded into Y by
$\pi $
-preimages of equal least period in X. A block in Z between marker coordinates is coded to a data block in Y which is shorter by an additive constant, so that there are gaps between the data blocks that are filled with repetitions of a ‘blank’ symbol. We then lift the data blocks from Y to data blocks from X, then replace the blanks with a ‘stamp’ block from X to form a valid point in X. The stamp block is chosen to ensure that once the point in X is coded into Y by
![]() $\pi $
, the locations of the stamp, and thus of the marker coordinates, can be recognized.
$\pi $
, the locations of the stamp, and thus of the marker coordinates, can be recognized.
The strategy, thus described, primarily involves a series of ‘interfaces’ between different coding constructions, which we give in §3. However, to establish the existence of subshifts with the properties required to make these interfaces work, we require a certain number of asymptotic calculations involving entropy, periodic points, and overlaps in long words or blocks. This quantitative material is deferred mainly to §4, with the results required to establish Corollary 1.3 being deferred to §5. This organizational decision has the effect of separating several results from their proofs by several pages. To mitigate difficulties in following the argument, those results are restated before their proofs, with the specific effects for each section or subsection noted where appropriate. It is highly recommended that the reader become familiar with the main constructions in §§3.1 and 3.2, the final synthesis in the proof of Theorem 1.1 being found at the end of §3.2, before spending significant time on the rest of the paper.
1.3 Remaining questions
The statement of Theorem 1.2 is false for X merely mixing sofic and, to date, there is no known characterization of the subshifts that embed into a given mixing sofic shift, though some sufficient conditions are known [Reference Boyle1, Reference Thomsen11]. Theorem 1.1 sheds some light on this problem, without resolving it. Salo and Törmä [Reference Salo9] have answered the following related question: let Y be a mixing sofic shift and
![]() $Z \subset Y$
a mixing SFT. For which such
$Z \subset Y$
a mixing SFT. For which such
![]() $Y,Z$
do there exist a mixing SFT extension
$Y,Z$
do there exist a mixing SFT extension
![]() $\pi : X \to Y$
and a (mixing SFT)
$\pi : X \to Y$
and a (mixing SFT)
![]() $Z' \subset X$
such that
$Z' \subset X$
such that
![]() $\pi |_{Z'}: Z' \to Z$
is a conjugacy? However, it is unclear how the conditions given in that answer compare to those in Theorem 1.1, or to the results given in [Reference Thomsen11]. As a final related question, when Y is an SFT and Z is conjugate to Y, the existence of an SFT
$\pi |_{Z'}: Z' \to Z$
is a conjugacy? However, it is unclear how the conditions given in that answer compare to those in Theorem 1.1, or to the results given in [Reference Thomsen11]. As a final related question, when Y is an SFT and Z is conjugate to Y, the existence of an SFT
![]() $Z' \subset X$
conjugate to Z such that
$Z' \subset X$
conjugate to Z such that
![]() $\pi |_{Z'}: Z' \to Y$
is a conjugacy, that is, is surjective as well as injective, has been studied in [Reference Han, Marcus and Wu3], continuing the work from [Reference Marcus, Petersen, Williams, Beals, Beck, Bellow and Hajian8].
$\pi |_{Z'}: Z' \to Y$
is a conjugacy, that is, is surjective as well as injective, has been studied in [Reference Han, Marcus and Wu3], continuing the work from [Reference Marcus, Petersen, Williams, Beals, Beck, Bellow and Hajian8].
2 Conventions, definitions, and background on symbolic dynamics
2.1 Subshifts and sliding block codes
Let
![]() $\mathcal {A}$
be a finite set with the discrete topology, which we will call an alphabet. The set
$\mathcal {A}$
be a finite set with the discrete topology, which we will call an alphabet. The set
![]() $\mathcal {A}^{\mathbb {Z}}$
of bi-infinite sequences over
$\mathcal {A}^{\mathbb {Z}}$
of bi-infinite sequences over
![]() $\mathcal {A}$
, equipped with the product topology, is called the full shift over
$\mathcal {A}$
, equipped with the product topology, is called the full shift over
![]() $\mathcal {A}$
, so called because the shift action
$\mathcal {A}$
, so called because the shift action
![]() $\sigma : \mathcal {A}^{\mathbb {Z}} \to \mathcal {A}^{\mathbb {Z}}$
, given by
$\sigma : \mathcal {A}^{\mathbb {Z}} \to \mathcal {A}^{\mathbb {Z}}$
, given by
![]() $(\sigma x)_i = x_{i+1}$
, is a homeomorphism. A closed, shift-invariant subset of the full shift is called a subshift. The topology on
$(\sigma x)_i = x_{i+1}$
, is a homeomorphism. A closed, shift-invariant subset of the full shift is called a subshift. The topology on
![]() $\mathcal {A}^{\mathbb {Z}}$
is generated by cylinders, which are sets of the form
$\mathcal {A}^{\mathbb {Z}}$
is generated by cylinders, which are sets of the form
where
![]() $w \in \mathcal {A}^n$
is a block or word of length
$w \in \mathcal {A}^n$
is a block or word of length
![]() $n \in \mathbb {N}$
, and
$n \in \mathbb {N}$
, and
![]() $i \in \mathbb {Z}$
. Note that by shift-invariance, for any subshift
$i \in \mathbb {Z}$
. Note that by shift-invariance, for any subshift
![]() $X \subset \mathcal {A}^{\mathbb {Z}}$
and any block
$X \subset \mathcal {A}^{\mathbb {Z}}$
and any block
![]() $w \in \mathcal {A}^*$
, we have
$w \in \mathcal {A}^*$
, we have
![]() $X \cap [w]_i \neq \emptyset $
for some
$X \cap [w]_i \neq \emptyset $
for some
![]() $i \in \mathbb {Z}$
if and only if
$i \in \mathbb {Z}$
if and only if
![]() $X \cap [w]_i \neq \emptyset $
for all
$X \cap [w]_i \neq \emptyset $
for all
![]() $i \in \mathbb {Z}$
.
$i \in \mathbb {Z}$
.
A subshift
![]() $X \subset \mathcal {A}^{\mathbb {Z}}$
is characterized by the set
$X \subset \mathcal {A}^{\mathbb {Z}}$
is characterized by the set
![]() $\mathcal {B}(X)$
of blocks
$\mathcal {B}(X)$
of blocks
![]() $w \in \mathcal {A}^*$
(where
$w \in \mathcal {A}^*$
(where
![]() $\mathcal {A}*$
is the set of all finite blocks or words over
$\mathcal {A}*$
is the set of all finite blocks or words over
![]() $\mathcal {A}$
) such that
$\mathcal {A}$
) such that
![]() $X \cap [w] \neq \emptyset $
, called the language of X. When the intended subshift X is clear, we write
$X \cap [w] \neq \emptyset $
, called the language of X. When the intended subshift X is clear, we write
![]() $[w]_i$
for
$[w]_i$
for
![]() $X \cap [w]_i$
. We write
$X \cap [w]_i$
. We write
![]() ${\mathcal {B}_n(X) = \mathcal {B}(X) \cap \mathcal {A}^n}$
. We can equivalently characterize a subshift by a set of forbidden words
${\mathcal {B}_n(X) = \mathcal {B}(X) \cap \mathcal {A}^n}$
. We can equivalently characterize a subshift by a set of forbidden words
![]() ${\mathcal {F} \subset \mathcal {A}^*}$
, writing
${\mathcal {F} \subset \mathcal {A}^*}$
, writing
![]() $\mathsf {X}_{\mathcal {F}} := \overline {\mathcal {A}^{\mathbb {Z}} \setminus \bigcup _{w \in \mathcal {F}} \bigcup _{i \in \mathbb {Z}} [w]_i }$
. Note that, in general,
$\mathsf {X}_{\mathcal {F}} := \overline {\mathcal {A}^{\mathbb {Z}} \setminus \bigcup _{w \in \mathcal {F}} \bigcup _{i \in \mathbb {Z}} [w]_i }$
. Note that, in general,
![]() $\mathcal {F} \subsetneq \mathcal {A}^* \setminus \mathcal {B}(\mathsf {X}_{\mathcal {F}})$
. For a given subshift
$\mathcal {F} \subsetneq \mathcal {A}^* \setminus \mathcal {B}(\mathsf {X}_{\mathcal {F}})$
. For a given subshift
![]() $X \subset \mathcal {A}^{\mathbb {Z}}$
, there may be several different sets of forbidden words
$X \subset \mathcal {A}^{\mathbb {Z}}$
, there may be several different sets of forbidden words
![]() $\mathcal {F} \subset \mathcal {A}^*$
such that
$\mathcal {F} \subset \mathcal {A}^*$
such that
![]() $X = \mathsf {X}_{\mathcal {F}}$
. An SFT is a subshift X such that
$X = \mathsf {X}_{\mathcal {F}}$
. An SFT is a subshift X such that
![]() $X = \mathsf {X}_{\mathcal {F}}$
for some finite set
$X = \mathsf {X}_{\mathcal {F}}$
for some finite set
![]() $\mathcal {F}$
. A k-step SFT over
$\mathcal {F}$
. A k-step SFT over
![]() $\mathcal {A}$
is an SFT of the form
$\mathcal {A}$
is an SFT of the form
![]() $X = \mathsf {X}_{\mathcal {F}}$
for some set
$X = \mathsf {X}_{\mathcal {F}}$
for some set
![]() $\mathcal {F} \subset \mathcal {A}^{k+1}$
.
$\mathcal {F} \subset \mathcal {A}^{k+1}$
.
It is a theorem (the Curtis–Hedlund–Lyndon theorem) that, for subshifts
![]() $X,Y$
, a function
$X,Y$
, a function
![]() $\phi : X \to Y$
is continuous and shift-equivariant if and only if it is a sliding block code, which means that there exist
$\phi : X \to Y$
is continuous and shift-equivariant if and only if it is a sliding block code, which means that there exist
![]() $m,n \geq 0$
and
$m,n \geq 0$
and
![]() $\Phi : \mathcal {B}_{m+n+1}(X) \to \mathcal {B}_1(Y)$
such that for every
$\Phi : \mathcal {B}_{m+n+1}(X) \to \mathcal {B}_1(Y)$
such that for every
![]() $x \in X$
and every
$x \in X$
and every
![]() $i \in \mathbb {Z}$
,
$i \in \mathbb {Z}$
,
![]() $\phi (x)_i = \Phi (x_{[i-m,i+n]})$
. By an abuse of notation, we will refer to the map on blocks,
$\phi (x)_i = \Phi (x_{[i-m,i+n]})$
. By an abuse of notation, we will refer to the map on blocks,
![]() $\Phi $
, by the same symbol as the map on points,
$\Phi $
, by the same symbol as the map on points,
![]() $\phi $
. For instance, we do this throughout with
$\phi $
. For instance, we do this throughout with
![]() $\pi $
as in Theorem 1.1. We say that
$\pi $
as in Theorem 1.1. We say that
![]() $\phi $
is a k-block code if
$\phi $
is a k-block code if
![]() $m+n+1=k$
. A factor code is a surjective sliding block code, and for a sliding block code
$m+n+1=k$
. A factor code is a surjective sliding block code, and for a sliding block code
![]() $\phi $
defined on a subshift X, we say that the image
$\phi $
defined on a subshift X, we say that the image
![]() $\phi (X)$
is a factor of X, and that X, or more properly
$\phi (X)$
is a factor of X, and that X, or more properly
![]() $\phi : X \to \phi (X)$
, is an extension of
$\phi : X \to \phi (X)$
, is an extension of
![]() $\phi (X)$
. A sofic shift (from the Hebrew swpy, ‘sofi’, meaning ‘finite’) is any factor of a shift of finite type. An injective sliding block code is called an embedding and a bijective sliding block code is called a conjugacy. The properties of being sofic and of finite type are both invariant under conjugacy.
$\phi (X)$
. A sofic shift (from the Hebrew swpy, ‘sofi’, meaning ‘finite’) is any factor of a shift of finite type. An injective sliding block code is called an embedding and a bijective sliding block code is called a conjugacy. The properties of being sofic and of finite type are both invariant under conjugacy.
A subshift X is said to be irreducible if for all
![]() $u, w \in \mathcal {B}(X)$
, there exists
$u, w \in \mathcal {B}(X)$
, there exists
![]() $v \in \mathcal {B}(X)$
such that
$v \in \mathcal {B}(X)$
such that
![]() $uvw \in \mathcal {B}(X)$
, and strongly irreducible with gap
$uvw \in \mathcal {B}(X)$
, and strongly irreducible with gap
![]() $g \geq 1$
if, for any
$g \geq 1$
if, for any
![]() $u,w$
, we can take always take
$u,w$
, we can take always take
![]() $v \in \mathcal {B}_g(X)$
. Any factor of an irreducible (respectively strongly irreducible) subshift is irreducible (respectively strongly irreducible). A periodic point in a subshift X is a point
$v \in \mathcal {B}_g(X)$
. Any factor of an irreducible (respectively strongly irreducible) subshift is irreducible (respectively strongly irreducible). A periodic point in a subshift X is a point
![]() $x \in X$
with
$x \in X$
with
![]() $x = \sigma ^n x$
for some
$x = \sigma ^n x$
for some
![]() $n \geq 1$
—we say that x has period n. The least period
$n \geq 1$
—we say that x has period n. The least period
![]() $\mathrm {per}(x)$
of a periodic point x is the least n such that
$\mathrm {per}(x)$
of a periodic point x is the least n such that
![]() $\sigma ^n x = x$
. Note that
$\sigma ^n x = x$
. Note that
![]() $| \{ \sigma ^n x \, | \, n \in \mathbb {Z} \} | = \mathrm {per}(x)$
. We write
$| \{ \sigma ^n x \, | \, n \in \mathbb {Z} \} | = \mathrm {per}(x)$
. We write
![]() $P(X)$
for the set of periodic points in a subshift X,
$P(X)$
for the set of periodic points in a subshift X,
![]() $Q_n(X)$
for the set of periodic points of least period n, and
$Q_n(X)$
for the set of periodic points of least period n, and
![]() $q_n(X) = |Q_n(X)|$
. The number of periodic points of a given least period is a conjugacy invariant.
$q_n(X) = |Q_n(X)|$
. The number of periodic points of a given least period is a conjugacy invariant.
It is a theorem that periodic points are dense in any irreducible shift of finite type. The period
![]() $\mathrm {per}(X)$
of an irreducible shift of finite type X is the gcd of the periods of the periodic points of X. An irreducible SFT with period
$\mathrm {per}(X)$
of an irreducible shift of finite type X is the gcd of the periods of the periodic points of X. An irreducible SFT with period
![]() $1$
is said to be aperiodic. An irreducible SFT is strongly irreducible if and only if it is aperiodic, if and only if it has periodic points of all sufficiently high periods. For irreducible sofic shifts, strong irreducibility is equivalent to having periodic points of all sufficiently high periods, which clearly implies that the periods have gcd
$1$
is said to be aperiodic. An irreducible SFT is strongly irreducible if and only if it is aperiodic, if and only if it has periodic points of all sufficiently high periods. For irreducible sofic shifts, strong irreducibility is equivalent to having periodic points of all sufficiently high periods, which clearly implies that the periods have gcd
![]() $1$
, but the reverse implication fails. For example, consider the odd shift over
$1$
, but the reverse implication fails. For example, consider the odd shift over
![]() $\{ 0,1 \}$
, in which the block
$\{ 0,1 \}$
, in which the block
![]() $10^n1$
is permitted only for odd n. This is an irreducible sofic shift which contains the fixed point
$10^n1$
is permitted only for odd n. This is an irreducible sofic shift which contains the fixed point
![]() $0^{\infty }$
, so the periods of periodic points trivially have gcd
$0^{\infty }$
, so the periods of periodic points trivially have gcd
![]() $1$
. However, the odd shift has no other periodic points of odd period. We follow the convention of the literature in referring to strongly irreducible sofic shifts (in particular, SFTs) as mixing sofic shifts (mixing SFTs), because they are also characterized by a topological mixing property, but we will not use that property explicitly, so we do not define it here.
$1$
. However, the odd shift has no other periodic points of odd period. We follow the convention of the literature in referring to strongly irreducible sofic shifts (in particular, SFTs) as mixing sofic shifts (mixing SFTs), because they are also characterized by a topological mixing property, but we will not use that property explicitly, so we do not define it here.
The following definition is new and we use it extensively.
Definition 2.1. Let X and Y be subshifts and let
![]() $\pi : X \to Y$
be a factor code. We write
$\pi : X \to Y$
be a factor code. We write
![]() $R_n(\pi )$
for the set of periodic points
$R_n(\pi )$
for the set of periodic points
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $y = \pi (x)$
for some periodic point
$y = \pi (x)$
for some periodic point
![]() $x \in X$
with
$x \in X$
with
![]() $\mathrm {per}(x) = \mathrm {per}(y)$
. We write
$\mathrm {per}(x) = \mathrm {per}(y)$
. We write
![]() $r_n(\pi ) = |R_n(\pi )|$
.
$r_n(\pi ) = |R_n(\pi )|$
.
For a subshift X, the (topological) entropy of X is the value
![]() $h(X) = \inf _{n \geq 1} ({1}/{n}) \log |\mathcal {B}_n(X)|$
; in fact, the limit
$h(X) = \inf _{n \geq 1} ({1}/{n}) \log |\mathcal {B}_n(X)|$
; in fact, the limit
![]() $\lim _{n \to \infty } ({1}/{n}) \log |\mathcal {B}_n(X)|$
exists and is equal to
$\lim _{n \to \infty } ({1}/{n}) \log |\mathcal {B}_n(X)|$
exists and is equal to
![]() $h(X)$
. For a mixing sofic shift (in particular, a mixing SFT) X, we also have
$h(X)$
. For a mixing sofic shift (in particular, a mixing SFT) X, we also have
![]() $h(X) = \lim _{n \to \infty } ({1}/{n}) \log q_n(X)$
. Entropy is non-increasing under factor codes and is thus a conjugacy invariant, though certainly not a complete invariant. For any irreducible sofic shift X and any proper subshift
$h(X) = \lim _{n \to \infty } ({1}/{n}) \log q_n(X)$
. Entropy is non-increasing under factor codes and is thus a conjugacy invariant, though certainly not a complete invariant. For any irreducible sofic shift X and any proper subshift
![]() $V \subset X$
, we have
$V \subset X$
, we have
![]() $h(V) < h(X)$
[Reference Lind and Marcus6, Corollary 4.4.9]. In §4, we use the following lemma of Marcus, which allows us to approximate a sofic shift from the inside by SFTs in terms of entropy.
$h(V) < h(X)$
[Reference Lind and Marcus6, Corollary 4.4.9]. In §4, we use the following lemma of Marcus, which allows us to approximate a sofic shift from the inside by SFTs in terms of entropy.
Lemma 2.2. [Reference Marcus7, Proposition 3]
Let Y be a sofic shift. For every
![]() $\varepsilon> 0$
, there exists an irreducible SFT
$\varepsilon> 0$
, there exists an irreducible SFT
![]() $U \subseteq Y$
with
$U \subseteq Y$
with
![]() $h(U)> h(Y) - \varepsilon $
.
$h(U)> h(Y) - \varepsilon $
.
For any subshift X and any
![]() $k \geq 1$
, we can form the kth higher block shift
$k \geq 1$
, we can form the kth higher block shift
![]() $X^{[k]}$
with alphabet
$X^{[k]}$
with alphabet
![]() $\mathcal {B}_k(X)$
, where
$\mathcal {B}_k(X)$
, where
if and only if for each
![]() $i,j$
, we have
$i,j$
, we have
![]() $a_{i,j} = a_{i+1,j-1}$
, so that
$a_{i,j} = a_{i+1,j-1}$
, so that
and
![]() $a_1 a_2 \ldots a_{k+\ell } \in \mathcal {B}(X)$
. Observe that X and
$a_1 a_2 \ldots a_{k+\ell } \in \mathcal {B}(X)$
. Observe that X and
![]() $X^{[k]}$
are conjugate for any subshift X and any
$X^{[k]}$
are conjugate for any subshift X and any
![]() $k \geq 1$
. Moreover, if X is an m-step SFT and
$k \geq 1$
. Moreover, if X is an m-step SFT and
![]() $k \leq m-1$
, then
$k \leq m-1$
, then
![]() $X^{[k]}$
is an
$X^{[k]}$
is an
![]() $(m-k)$
-step SFT. In particular, every SFT is conjugate to a
$(m-k)$
-step SFT. In particular, every SFT is conjugate to a
![]() $1$
-step SFT, and every sliding block code on an SFT can be written as a composition of a conjugacy and a
$1$
-step SFT, and every sliding block code on an SFT can be written as a composition of a conjugacy and a
![]() $1$
-block code. We will therefore frequently assume without loss of generality (WLOG) that a given sliding block code on an SFT is a
$1$
-block code. We will therefore frequently assume without loss of generality (WLOG) that a given sliding block code on an SFT is a
![]() $1$
-block code on a
$1$
-block code on a
![]() $1$
-step SFT.
$1$
-step SFT.
For a sliding block code on an irreducible shift of finite type, either every fiber is a finite set (indeed, of bounded cardinality), in which case the code is said to be finite-to-one and the entropy of the image is equal to that of the domain, or every fiber is uncountable, and the entropy of the image is strictly less than that of the domain. In the finite-to-one case, the minimum fiber cardinality is generic and is known as the degree. In particular, a code (on an irreducible SFT) with degree one is said to be almost invertible. It is a theorem that every irreducible (respectively mixing) sofic shift is an almost invertible factor of an irreducible (respectively mixing) SFT. We use the following construction of almost invertible codes, known as the ‘blowing-up lemma’, in the proof of Corollary 1.3 in §5.
Lemma 2.3. [Reference Lind and Marcus6, Lemma 10.3.2]
Let Z be a mixing SFT and let
![]() $z \in Z$
be a periodic point with least period p. Let
$z \in Z$
be a periodic point with least period p. Let
![]() $M \geq 1$
. Then there exist a mixing SFT
$M \geq 1$
. Then there exist a mixing SFT
![]() $Z'$
and an almost invertible factor code
$Z'$
and an almost invertible factor code
![]() $\chi : Z' \to Z$
such that the preimage of the orbit of z under
$\chi : Z' \to Z$
such that the preimage of the orbit of z under
![]() $\chi $
is a single orbit of length
$\chi $
is a single orbit of length
![]() $Mp$
.
$Mp$
.
Remark 2.4. Note that in [Reference Lind and Marcus6], the extension
![]() $\chi $
in Lemma 2.3 is only stated to be finite-to-one, but the existence of periodic points having unique preimage already implies almost invertibility. Indeed, the construction in [Reference Lind and Marcus6], based on work in [Reference Boyle1], in fact shows that
$\chi $
in Lemma 2.3 is only stated to be finite-to-one, but the existence of periodic points having unique preimage already implies almost invertibility. Indeed, the construction in [Reference Lind and Marcus6], based on work in [Reference Boyle1], in fact shows that
![]() $\chi $
is injective except on the points that are backward-asymptotic to points in the preimage of the orbit of z, where we say that two points
$\chi $
is injective except on the points that are backward-asymptotic to points in the preimage of the orbit of z, where we say that two points
![]() $z,z'$
are backward-asymptotic if
$z,z'$
are backward-asymptotic if
![]() $d(\sigma ^n z, \sigma ^n z') \to 0$
as
$d(\sigma ^n z, \sigma ^n z') \to 0$
as
![]() $n \to - \infty $
.
$n \to - \infty $
.
2.2 Markers and Markov approximations
We now recall the constructions with markers and long periodic blocks that are at the heart of the proof of Theorem 1.1. For an alphabet
![]() $\mathcal {A}$
, we say that a block
$\mathcal {A}$
, we say that a block
![]() $w = w_1 \ldots w_n \in \mathcal {A}^n$
is k-periodic, or has self-overlap of
$w = w_1 \ldots w_n \in \mathcal {A}^n$
is k-periodic, or has self-overlap of
![]() $n-k$
, if
$n-k$
, if
![]() $w_{[k+1,n]} = w_{[1,n-k]}$
, that is, for
$w_{[k+1,n]} = w_{[1,n-k]}$
, that is, for
![]() $1 \leq i \leq n-k$
, we have
$1 \leq i \leq n-k$
, we have
![]() $w_i = w_{i+k}$
. A given block may be k-periodic for several different k.
$w_i = w_{i+k}$
. A given block may be k-periodic for several different k.
Lemma 2.5. [Reference Boyle1, Lemma 2.3]
Let Z be a subshift, let
![]() $N \geq 1$
, and
$N \geq 1$
, and
![]() $a, b \in \mathbb {Z}$
with
$a, b \in \mathbb {Z}$
with
![]() ${b - a \geq 2N}$
. Let
${b - a \geq 2N}$
. Let
![]() $z \in Z$
. If for every
$z \in Z$
. If for every
![]() $i \in [a+N,b-N]$
there exists
$i \in [a+N,b-N]$
there exists
![]() $p \leq N-1$
such that
$p \leq N-1$
such that
![]() $z_{[i-N,i+N]}$
is p-periodic, then there is at most one periodic point
$z_{[i-N,i+N]}$
is p-periodic, then there is at most one periodic point
![]() $\zeta \in Z$
with
$\zeta \in Z$
with
![]() $\mathrm {per}(\zeta ) \leq N-1$
and
$\mathrm {per}(\zeta ) \leq N-1$
and
![]() $\zeta _{[a,b]} = z_{[a,b]}$
. If Z is a
$\zeta _{[a,b]} = z_{[a,b]}$
. If Z is a
![]() $1$
-step SFT, then such a
$1$
-step SFT, then such a
![]() $\zeta $
exists.
$\zeta $
exists.
Lemma 2.6. [Reference Krieger5, Lemma 2]
Let Z be a subshift. For any
![]() $N \geq 1$
, there exists a subset
$N \geq 1$
, there exists a subset
![]() $F \subset Z$
, which can be taken to be a finite union of cylinders, such that:
$F \subset Z$
, which can be taken to be a finite union of cylinders, such that:
-
(1) the sets
 $\sigma ^i F$
,
$\sigma ^i F$
,
 $0 \leq i \leq N-1$
, are all disjoint; and
$0 \leq i \leq N-1$
, are all disjoint; and -
(2) if
 $z \notin \sigma ^i F$
for all
$z \notin \sigma ^i F$
for all
 $-(N-1) \leq i \leq (N-1)$
, then
$-(N-1) \leq i \leq (N-1)$
, then
 $z_{[-N,N]}$
is p-periodic for some
$z_{[-N,N]}$
is p-periodic for some
 $p \leq N-1$
.
$p \leq N-1$
.
For any subshift X and any
![]() $n \geq 1$
, we can form the nth Markov approximation
$n \geq 1$
, we can form the nth Markov approximation
![]() $X_n$
, which is the SFT defined by allowing precisely the blocks of length n which appear in X. Clearly,
$X_n$
, which is the SFT defined by allowing precisely the blocks of length n which appear in X. Clearly,
![]() $X_{n+1} \subset X_n$
. It is an exercise to show that for any
$X_{n+1} \subset X_n$
. It is an exercise to show that for any
![]() $\varepsilon> 0$
and any
$\varepsilon> 0$
and any
![]() $N \geq 1$
, there exists
$N \geq 1$
, there exists
![]() ${N' \geq N}$
such that
${N' \geq N}$
such that
![]() $h(X_{N'}) < h(X) + \varepsilon $
and
$h(X_{N'}) < h(X) + \varepsilon $
and
![]() $q_n(X_{N'}) = q_n(X)$
for all
$q_n(X_{N'}) = q_n(X)$
for all
![]() $n \leq N$
. In Lemma 2.7, we use the Markov approximation, together with higher block shifts, to show that in the proof of Theorem 1.1, we can assume WLOG that Z is a
$n \leq N$
. In Lemma 2.7, we use the Markov approximation, together with higher block shifts, to show that in the proof of Theorem 1.1, we can assume WLOG that Z is a
![]() $1$
-step SFT, which allows us to apply Lemma 2.5.
$1$
-step SFT, which allows us to apply Lemma 2.5.
We remark that there are versions of Lemma 2.6 which obviate the need for Lemma 2.5. However, for our purposes in this paper, embedding Z into an SFT has the additional benefit that the rate of convergence of
![]() $({1}/{n}) \log q_n(Z)$
to
$({1}/{n}) \log q_n(Z)$
to
![]() $h(Z)$
can be easily estimated when Z is an SFT (see e.g. [Reference Lind and Marcus6, pp. 349–351]), which gives a procedure for deciding whether a given
$h(Z)$
can be easily estimated when Z is an SFT (see e.g. [Reference Lind and Marcus6, pp. 349–351]), which gives a procedure for deciding whether a given
![]() $X,Y,\pi ,Z$
satisfy the periodic point condition in Theorem 1.1, assuming that
$X,Y,\pi ,Z$
satisfy the periodic point condition in Theorem 1.1, assuming that
![]() $h(Z) < h(Y)$
(namely, compute
$h(Z) < h(Y)$
(namely, compute
![]() $N \geq 1$
such that for all
$N \geq 1$
such that for all
![]() $n \geq N$
,
$n \geq N$
,
![]() $q_n(Z) < r_n(\pi )$
, then check all
$q_n(Z) < r_n(\pi )$
, then check all
![]() $n \leq N$
to determine whether
$n \leq N$
to determine whether
![]() $q_n(Z) \leq r_n(\pi )$
).
$q_n(Z) \leq r_n(\pi )$
).
Lemma 2.7. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with
$\pi : X \to Y$
a factor code. Let Z be a subshift with
![]() $h(Z) < h(Y)$
and
$h(Z) < h(Y)$
and
![]() $q_n(Z) \leq r_n(\pi )$
for all
$q_n(Z) \leq r_n(\pi )$
for all
![]() $n \geq 1$
. Then there exists a
$n \geq 1$
. Then there exists a
![]() $1$
-step SFT
$1$
-step SFT
![]() $Z'$
such that Z embeds into
$Z'$
such that Z embeds into
![]() $Z'$
,
$Z'$
,
![]() $h(Z') < h(Y)$
, and
$h(Z') < h(Y)$
, and
![]() $q_n(Z') \leq r_n(\pi )$
for all
$q_n(Z') \leq r_n(\pi )$
for all
![]() $n \geq 1$
.
$n \geq 1$
.
We defer the proof of Lemma 2.7 to §5, as the proof uses a quantitative result (Proposition 4.3) that is otherwise most at home in §4.
3 Coding
In §3.1, we introduce two coding constructions, namely subshifts with blanks adjoined, Definition 3.1, and stamps, Definition 3.2, then use them to create one side of an interface between Z on the one hand and
![]() $\pi : X \to Y$
on the other. In §3.2, we use markers in Z to construct the other side of this interface. To construct subshifts with the properties required to make this interface work, we need a construction of particular SFTs using stamps, which we give in §3.3, and some quantitative estimates using the construction in §3.3, which we defer until §4.2.
$\pi : X \to Y$
on the other. In §3.2, we use markers in Z to construct the other side of this interface. To construct subshifts with the properties required to make this interface work, we need a construction of particular SFTs using stamps, which we give in §3.3, and some quantitative estimates using the construction in §3.3, which we defer until §4.2.
3.1 Blanks and stamps
As outlined in §1, the proof of Theorem 1.1 involves coding Z into X via certain intermediate subshifts which consist of long ‘data’ blocks separated by blanks. We now define this construction precisely.
Definition 3.1. (Subshift with blanks adjoined)
Let W be a subshift and let
![]() ${N, \ell \geq 1}$
with
${N, \ell \geq 1}$
with
![]() $\ell < N$
. Let
$\ell < N$
. Let
![]() $*$
be a symbol not appearing in the alphabet of W. Let
$*$
be a symbol not appearing in the alphabet of W. Let
![]() $M \subset \bigcup _{n=1}^{2N} \mathcal {B}(W)$
be a set of blocks and let
$M \subset \bigcup _{n=1}^{2N} \mathcal {B}(W)$
be a set of blocks and let
![]() $Q \subset \bigcup _{n=1}^{2N-1} Q_n(W)$
be a set of periodic points. Denote by
$Q \subset \bigcup _{n=1}^{2N-1} Q_n(W)$
be a set of periodic points. Denote by
![]() $\mathrm {Blanks}(M,Q,N,*,\ell )$
the subshift in which each point is of the form
$\mathrm {Blanks}(M,Q,N,*,\ell )$
the subshift in which each point is of the form
![]() $\ldots w_{-1} *^{\ell } w_0 *^{\ell } w_1 \ldots $
where either
$\ldots w_{-1} *^{\ell } w_0 *^{\ell } w_1 \ldots $
where either
![]() $w_i \in M$
or
$w_i \in M$
or
![]() $w_i = y_T$
where
$w_i = y_T$
where
![]() $y \in Q$
and
$y \in Q$
and
![]() $T=(-\infty ,0], [0, +\infty ), (-\infty , \infty )$
, or
$T=(-\infty ,0], [0, +\infty ), (-\infty , \infty )$
, or
![]() $[0,m]$
with
$[0,m]$
with
![]() $m \geq 2N$
.
$m \geq 2N$
.
The purpose of the
![]() $\mathrm {Blanks}$
construction is to provide an interface between the channel
$\mathrm {Blanks}$
construction is to provide an interface between the channel
![]() $\pi : X \to Y$
and the subshift Z to be embedded. One side of this interface, namely the embedding of a
$\pi : X \to Y$
and the subshift Z to be embedded. One side of this interface, namely the embedding of a
![]() $\mathrm {Blanks}$
subshift into X, is specified in Proposition 3.6. The construction involves particular blocks, which we call stamps, that can be unambiguously recognized in the following sense.
$\mathrm {Blanks}$
subshift into X, is specified in Proposition 3.6. The construction involves particular blocks, which we call stamps, that can be unambiguously recognized in the following sense.
Definition 3.2. (Stamp)
Let Y be a subshift,
![]() $W \subset Y$
a proper subshift, and
$W \subset Y$
a proper subshift, and
![]() $k \geq 1$
. We say that
$k \geq 1$
. We say that
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
is a
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
is a
![]() $(Y,W,k)$
stamp if for all
$(Y,W,k)$
stamp if for all
![]() $u_1, u_2 \in \mathcal {B}(W)$
and
$u_1, u_2 \in \mathcal {B}(W)$
and
![]() $v_1, v_2 \in \mathcal {B}_k(Y)$
,
$v_1, v_2 \in \mathcal {B}_k(Y)$
,
![]() $\mu $
appears exactly once in
$\mu $
appears exactly once in
![]() $u_1 v_1 \mu v_2 u_2$
.
$u_1 v_1 \mu v_2 u_2$
.
Remark 3.3. In Definition 3.2, continuing with the notation there, we do not explicitly require
![]() $u_1 v_1 \mu v_2 u_2$
to be legal in Y. Doing so would neither affect the results nor simplify the proofs. In all of the examples we consider, such blocks will, in fact, be legal in Y.
$u_1 v_1 \mu v_2 u_2$
to be legal in Y. Doing so would neither affect the results nor simplify the proofs. In all of the examples we consider, such blocks will, in fact, be legal in Y.
Proposition 3.4. Let Y be a strongly irreducible subshift with gap g and
![]() $W \subset Y$
a proper subshift. For every
$W \subset Y$
a proper subshift. For every
![]() $k \geq g$
and every sufficiently large n, there exists a
$k \geq g$
and every sufficiently large n, there exists a
![]() $(Y,W,k)$
stamp of length n.
$(Y,W,k)$
stamp of length n.
We defer the proof of Proposition 3.4 to §4.1, but before applying stamps in Proposition 3.6, we prove a lemma that expresses how stamps are actually used in our constructions.
Lemma 3.5. Let Y be a subshift,
![]() $W \subset Y$
a proper subshift,
$W \subset Y$
a proper subshift,
![]() $k \geq 1$
, and
$k \geq 1$
, and
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
a
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
a
![]() $(Y,W,k)$
stamp. Let
$(Y,W,k)$
stamp. Let
![]() $N \geq |\mu |$
. Then for any
$N \geq |\mu |$
. Then for any
![]() $\gamma ^{\pm } \in \mathcal {B}_k(Y)$
and any
$\gamma ^{\pm } \in \mathcal {B}_k(Y)$
and any
![]() $w \in \mathcal {B}(W)$
with
$w \in \mathcal {B}(W)$
with
![]() ${|w| \geq N}$
, the stamp
${|w| \geq N}$
, the stamp
![]() $\mu $
appears exactly twice in the block
$\mu $
appears exactly twice in the block
![]() $\mu \gamma ^- w \gamma ^+ \mu $
.
$\mu \gamma ^- w \gamma ^+ \mu $
.
Proof. By the hypotheses on
![]() $\mu $
,
$\mu $
,
![]() $\gamma ^{\pm }$
, and w, and Definition 3.2,
$\gamma ^{\pm }$
, and w, and Definition 3.2,
![]() $\mu $
appears exactly once in each subblock
$\mu $
appears exactly once in each subblock
![]() $\mu \gamma ^- w$
,
$\mu \gamma ^- w$
,
![]() $w \gamma ^+ \mu $
. An appearance of
$w \gamma ^+ \mu $
. An appearance of
![]() $\mu $
other than at the positions explicitly indicated must therefore overlap both of these subblocks. Since
$\mu $
other than at the positions explicitly indicated must therefore overlap both of these subblocks. Since
![]() $|w| \geq |\mu |$
,
$|w| \geq |\mu |$
,
![]() $\mu $
must therefore be a subblock of w, contradicting the hypothesis that
$\mu $
must therefore be a subblock of w, contradicting the hypothesis that
![]() $w \in \mathcal {B}(W)$
and
$w \in \mathcal {B}(W)$
and
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
.
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
.
We now give one of the main coding constructions (Proposition 3.6), embedding a subshift with blanks adjoined, and with blocks from a subshift
![]() $V \subset X$
, into X via a sliding block code
$V \subset X$
, into X via a sliding block code
![]() $\gamma $
, such that
$\gamma $
, such that
![]() $\pi \circ \gamma $
is injective. The large amount of data in the statement is representative of the complexity of the construction and the modular nature of the proof. As indicated in §2.1, we abuse notation and write
$\pi \circ \gamma $
is injective. The large amount of data in the statement is representative of the complexity of the construction and the modular nature of the proof. As indicated in §2.1, we abuse notation and write
![]() $\pi $
for both a
$\pi $
for both a
![]() $1$
-block factor code and the map on symbols by which it is induced.
$1$
-block factor code and the map on symbols by which it is induced.
Proposition 3.6. Let X be a mixing SFT with gap g, let Y be a mixing sofic shift, and let
![]() $\pi : X \to Y$
be a
$\pi : X \to Y$
be a
![]() $1$
-block factor code.
$1$
-block factor code.
Let
![]() $V \subset X$
,
$V \subset X$
,
![]() $W = \pi (V) \subset Y$
be proper subshifts. Let
$W = \pi (V) \subset Y$
be proper subshifts. Let
![]() $*$
be a symbol not appearing in the alphabets of
$*$
be a symbol not appearing in the alphabets of
![]() $X,Y$
. Let
$X,Y$
. Let
![]() $N \geq 1$
. Let
$N \geq 1$
. Let
![]() $M \subset \bigcup _{n=1}^{2N-1} \mathcal {B}_n(W)$
be a collection of blocks, and let
$M \subset \bigcup _{n=1}^{2N-1} \mathcal {B}_n(W)$
be a collection of blocks, and let
![]() $R \subset \bigcup _{n=1}^{N-1} R_n(\pi |_V)$
be a union of finite (that is, periodic) orbits in W with
$R \subset \bigcup _{n=1}^{N-1} R_n(\pi |_V)$
be a union of finite (that is, periodic) orbits in W with
![]() $\pi $
-preimages of equal cardinality in V. Let
$\pi $
-preimages of equal cardinality in V. Let
![]() $\kappa : M \to \mathcal {B}(V)$
be an injection such that
$\kappa : M \to \mathcal {B}(V)$
be an injection such that
![]() $\pi \circ \kappa (w) = w$
for each
$\pi \circ \kappa (w) = w$
for each
![]() $w \in M$
, and let
$w \in M$
, and let
![]() . Similarly, let
. Similarly, let
![]() $\unicode{x3bb} : R \to P(V)$
be a shift-commuting injection such that
$\unicode{x3bb} : R \to P(V)$
be a shift-commuting injection such that
![]() $\pi \circ \unicode{x3bb} (y) = y$
for each
$\pi \circ \unicode{x3bb} (y) = y$
for each
![]() $y \in R$
, and let
$y \in R$
, and let
![]() . Then for any
. Then for any
![]() $\ell \geq 1$
,
$\ell \geq 1$
,
![]() $\mathrm {Blanks}(M,R,N,*,\ell )$
and
$\mathrm {Blanks}(M,R,N,*,\ell )$
and
![]() are conjugate.
are conjugate.
Moreover, let
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
be a
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
be a
![]() $(Y,W,g)$
stamp such that
$(Y,W,g)$
stamp such that
![]() $|\mu | \leq N$
, and suppose that
$|\mu | \leq N$
, and suppose that
![]() $M \subset \bigcup _{n=N}^{2N-1} \mathcal {B}_n(W)$
, that is, M contains no blocks of length less than N. Then there exists a sliding block code
$M \subset \bigcup _{n=N}^{2N-1} \mathcal {B}_n(W)$
, that is, M contains no blocks of length less than N. Then there exists a sliding block code
![]() such that
such that
![]() $\pi \circ \gamma $
is injective.
$\pi \circ \gamma $
is injective.
Proof. First, the conjugacy. Let
![]() $W[*] = \mathrm {Blanks}(M,R,N,*,\ell )$
and
$W[*] = \mathrm {Blanks}(M,R,N,*,\ell )$
and
![]() . Consider the
. Consider the
![]() $1$
-block code
$1$
-block code
![]() $\pi [*]$
defined on
$\pi [*]$
defined on
![]() $V[*]$
by the block map
$V[*]$
by the block map
![]() $\pi [*](a) = \pi (a)$
for a in the alphabet of V and
$\pi [*](a) = \pi (a)$
for a in the alphabet of V and
![]() $\pi [*](*) = *$
. We claim that
$\pi [*](*) = *$
. We claim that
![]() $W[*] = \pi [*](V[*])$
and that
$W[*] = \pi [*](V[*])$
and that
![]() $\pi [*]: V[*] \to W[*]$
is a conjugacy. To see that
$\pi [*]: V[*] \to W[*]$
is a conjugacy. To see that
![]() $\pi [*](V[*]) \subseteq W[*]$
, note that any
$\pi [*](V[*]) \subseteq W[*]$
, note that any
![]() $\xi \in V[*]$
is of the form
$\xi \in V[*]$
is of the form
where either
![]() or
or
![]() $w_i = x_T$
for some
$w_i = x_T$
for some
![]() and T an interval with
and T an interval with
![]() $2N+1 \leq |T|$
. If
$2N+1 \leq |T|$
. If
![]() , then
, then
![]() $\pi (w_i) \in M$
; if
$\pi (w_i) \in M$
; if
![]() $w_i = x_T$
for some
$w_i = x_T$
for some
![]() , then
, then
![]() $\pi (w_i) = \pi (x)_T$
and
$\pi (w_i) = \pi (x)_T$
and
![]() ${\pi (x) \in R}$
. Therefore,
${\pi (x) \in R}$
. Therefore,
This shows that indeed
![]() $\pi [*](V[*]) \subseteq W[*]$
. Similarly, any
$\pi [*](V[*]) \subseteq W[*]$
. Similarly, any
![]() $\eta \in W[*]$
is of the form
$\eta \in W[*]$
is of the form
where either
![]() $w_i \in M$
or
$w_i \in M$
or
![]() $w_i = y_T$
for some
$w_i = y_T$
for some
![]() $y \in R$
and T an interval with
$y \in R$
and T an interval with
![]() $2N+1 \leq |T| \leq \infty $
. For
$2N+1 \leq |T| \leq \infty $
. For
![]() $\eta $
of this form, using Lemma 2.5, we can use the injections
$\eta $
of this form, using Lemma 2.5, we can use the injections
![]() $\kappa $
,
$\kappa $
,
![]() $\unicode{x3bb} $
to reconstruct a unique
$\unicode{x3bb} $
to reconstruct a unique
![]() $\xi \in V[*]$
such that
$\xi \in V[*]$
such that
![]() $\pi [*](\xi ) = \eta $
, which shows that
$\pi [*](\xi ) = \eta $
, which shows that
![]() $W[*] \subseteq \pi [*](V[*])$
.
$W[*] \subseteq \pi [*](V[*])$
.
We now suppose that each block in M has length at least N and that we have a
![]() $(Y,W,g)$
stamp
$(Y,W,g)$
stamp
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
such that
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
such that
![]() $|\mu | \leq N$
. Under these assumptions, we construct a sliding block code
$|\mu | \leq N$
. Under these assumptions, we construct a sliding block code
![]() $\gamma : V[*] \to X$
and show that
$\gamma : V[*] \to X$
and show that
![]() $\pi \circ \gamma $
is injective. Fix a
$\pi \circ \gamma $
is injective. Fix a
![]() $\pi $
-preimage
$\pi $
-preimage
![]() of
of
![]() $\mu $
, and let
$\mu $
, and let
![]() $\ell = |\mu | + 2g$
. Using the hypothesis that X is a mixing
$\ell = |\mu | + 2g$
. Using the hypothesis that X is a mixing
![]() $1$
-step SFT, define maps
$1$
-step SFT, define maps
![]() $\gamma ^{\pm }: \mathcal {B}_1(V) \to \mathcal {B}_g(X)$
such that, for
$\gamma ^{\pm }: \mathcal {B}_1(V) \to \mathcal {B}_g(X)$
such that, for
![]() $a, b \in \mathcal {B}_1(V)$
, we have
$a, b \in \mathcal {B}_1(V)$
, we have
![]() . We then have a sliding block code
. We then have a sliding block code
![]() $\gamma : V[*] \to X$
, given by replacing each block
$\gamma : V[*] \to X$
, given by replacing each block
![]() $b *^{\ell } a$
by
$b *^{\ell } a$
by
![]() , and leaving the non-blank symbols unchanged.
, and leaving the non-blank symbols unchanged.
Let
Then,
where
![]() $a_i, b_i$
are respectively the initial and terminal symbols of
$a_i, b_i$
are respectively the initial and terminal symbols of
![]() $v_i$
. In turn, we have
$v_i$
. In turn, we have
Moreover, by Lemma 3.5 and the lower bound on lengths of blocks in M, it follows that
![]() $\mu $
appears in
$\mu $
appears in
![]() $\pi \circ \gamma (\xi )$
only where
$\pi \circ \gamma (\xi )$
only where
appears at the same position in
![]() $\gamma (\xi )$
. By replacing, in
$\gamma (\xi )$
. By replacing, in
![]() $\pi \circ \gamma (\xi )$
, each appearance of
$\pi \circ \gamma (\xi )$
, each appearance of
![]() $\mu $
, and the blocks of length k to the left and right of
$\mu $
, and the blocks of length k to the left and right of
![]() $\mu $
, with
$\mu $
, with
![]() $*^{\ell }$
, we obtain the point
$*^{\ell }$
, we obtain the point
![]() $\ldots *^{\ell } \pi (v_0) *^{\ell } \ldots = \pi [*](\xi ) \in \mathrm {Blanks}(M,R,N,*,\ell )$
, from which
$\ldots *^{\ell } \pi (v_0) *^{\ell } \ldots = \pi [*](\xi ) \in \mathrm {Blanks}(M,R,N,*,\ell )$
, from which
![]() $\xi $
can be recovered since
$\xi $
can be recovered since
![]() $\pi [*]$
is a conjugacy.
$\pi [*]$
is a conjugacy.
3.2 Blanks and markers
We now prove a lemma that encapsulates the use of marker constructions in our proof of Theorem 1.1.
Lemma 3.7. Let
![]() $Z,W$
be subshifts with Z a
$Z,W$
be subshifts with Z a
![]() $1$
-step SFT. Let
$1$
-step SFT. Let
![]() $N,\ell \geq 1$
be such that
$N,\ell \geq 1$
be such that
![]() $q_n(Z) \leq q_n(W)$
for
$q_n(Z) \leq q_n(W)$
for
![]() $n \leq N-1$
and
$n \leq N-1$
and
![]() $|\mathcal {B}_n(Z)| \leq |\mathcal {B}_{n-\ell }(W)|$
for
$|\mathcal {B}_n(Z)| \leq |\mathcal {B}_{n-\ell }(W)|$
for
![]() $N+\ell \leq n \leq 2N+\ell -1$
. Let
$N+\ell \leq n \leq 2N+\ell -1$
. Let
![]() $M \subset \bigcup _{n=N}^{2N-1} \mathcal {B}_{n}(W)$
and
$M \subset \bigcup _{n=N}^{2N-1} \mathcal {B}_{n}(W)$
and
![]() $Q \subset \bigcup _{n=1}^{N-1} Q_n(W)$
be a union of finite (that is, periodic) orbits such that
$Q \subset \bigcup _{n=1}^{N-1} Q_n(W)$
be a union of finite (that is, periodic) orbits such that
![]() $|\mathcal {B}_n(Z)| \leq |M \cap \mathcal {B}_{n-\ell }(W)|$
for
$|\mathcal {B}_n(Z)| \leq |M \cap \mathcal {B}_{n-\ell }(W)|$
for
![]() $N+\ell \leq n \leq 2N+\ell -1$
, and
$N+\ell \leq n \leq 2N+\ell -1$
, and
![]() $q_n(Z) \leq |Q \cap Q_n(W)|$
for
$q_n(Z) \leq |Q \cap Q_n(W)|$
for
![]() $n \leq N-1$
. Then Z embeds into
$n \leq N-1$
. Then Z embeds into
![]() $\mathrm {Blanks}(M,Q,N,*,\ell )$
.
$\mathrm {Blanks}(M,Q,N,*,\ell )$
.
Remark 3.8. The lower bound on the length of blocks in M is not in fact needed for Lemma 3.7, but it is needed to apply Lemma 3.7 in conjunction with Proposition 3.6 in the proof of Theorem 1.1 below.
Proof. Let F be a marker set for Z with parameter N. For
![]() $z \in Z$
, let
$z \in Z$
, let
![]() $A(z) = \{ i \in \mathbb {Z} \, | \, \sigma ^i z \in F \}$
. Enumerate each
$A(z) = \{ i \in \mathbb {Z} \, | \, \sigma ^i z \in F \}$
. Enumerate each
![]() $A(z)$
as
$A(z)$
as
![]() $\{ a_j(z) \}_{j \in J(z)}$
where the index set
$\{ a_j(z) \}_{j \in J(z)}$
where the index set
![]() $J(z)$
may be the empty set, or a finite set, or the integers, or the positive or negative natural numbers, and where
$J(z)$
may be the empty set, or a finite set, or the integers, or the positive or negative natural numbers, and where
![]() $a_j(z) < a_{j+1}(z)$
for each j. We refer to the elements of
$a_j(z) < a_{j+1}(z)$
for each j. We refer to the elements of
![]() $A(z)$
as marker coordinates for z. Say that T is a marker interval for z if:
$A(z)$
as marker coordinates for z. Say that T is a marker interval for z if:
![]() $T = [a_j(z), a_{j+1}(z))$
where
$T = [a_j(z), a_{j+1}(z))$
where
![]() $a_j(z), a_{j+1}(z)$
are both defined; or
$a_j(z), a_{j+1}(z)$
are both defined; or
![]() $T=[a_0(z), \infty )$
if
$T=[a_0(z), \infty )$
if
![]() $a_0(z) = \max A(z) < \infty $
; or
$a_0(z) = \max A(z) < \infty $
; or
![]() $T=(-\infty , a_0(z)]$
if
$T=(-\infty , a_0(z)]$
if
![]() $a_0(z) = \min A(z)> -\infty $
; or
$a_0(z) = \min A(z)> -\infty $
; or
![]() $T=(-\infty , \infty )$
if
$T=(-\infty , \infty )$
if
![]() $A(z) = \emptyset $
.
$A(z) = \emptyset $
.
We construct an embedding of Z into
![]() $\mathrm {Blanks}(M,Q,N,*,\ell )$
by constructing a function
$\mathrm {Blanks}(M,Q,N,*,\ell )$
by constructing a function
![]() $\Phi $
that maps a block occurring between marker coordinates to a data block padded with
$\Phi $
that maps a block occurring between marker coordinates to a data block padded with
![]() $*^{\ell }$
. Let
$*^{\ell }$
. Let
![]() $c_n: Q_n(Z) \to Q_n(W)$
be shift-commuting injections for
$c_n: Q_n(Z) \to Q_n(W)$
be shift-commuting injections for
![]() $n \leq N-1$
. Let
$n \leq N-1$
. Let
![]() $d_n: \mathcal {B}_n(Z) \to \mathcal {B}_{n-\ell }(W)$
be injections for
$d_n: \mathcal {B}_n(Z) \to \mathcal {B}_{n-\ell }(W)$
be injections for
![]() $N+\ell \leq n \leq 2N+\ell -1$
. For a block
$N+\ell \leq n \leq 2N+\ell -1$
. For a block
![]() ${w \in \mathcal {B}_n(Z)}$
with
${w \in \mathcal {B}_n(Z)}$
with
![]() $N+\ell \leq n \leq 2N+\ell -1$
, let
$N+\ell \leq n \leq 2N+\ell -1$
, let
![]() $\Phi (w) = *^{\ell } d_n(w)$
. For
$\Phi (w) = *^{\ell } d_n(w)$
. For
![]() $z \in Z$
periodic with
$z \in Z$
periodic with
![]() $n = \mathrm {per}(z) \leq N-1$
, if
$n = \mathrm {per}(z) \leq N-1$
, if
![]() $m \geq 2N+\ell $
, let
$m \geq 2N+\ell $
, let
![]() $\Phi (z_{[0,m]}) = *^{\ell } c_n(z)_{[\ell ,m]}$
. Similarly, let
$\Phi (z_{[0,m]}) = *^{\ell } c_n(z)_{[\ell ,m]}$
. Similarly, let
![]() $\Phi (z_{[0,\infty )}) = *^{\ell } c_n(z)_{[\ell ,\infty )}$
. Finally, let
$\Phi (z_{[0,\infty )}) = *^{\ell } c_n(z)_{[\ell ,\infty )}$
. Finally, let
![]() $\Phi (z_{(-\infty ,0]}) = c_n(z)_{(-\infty ,0]}$
and let
$\Phi (z_{(-\infty ,0]}) = c_n(z)_{(-\infty ,0]}$
and let
![]() $\Phi (z) = c_n(z)$
. Observe that
$\Phi (z) = c_n(z)$
. Observe that
![]() $\Phi $
is injective, by Lemma 2.5.
$\Phi $
is injective, by Lemma 2.5.
Define
![]() $\phi : Z \to W$
by declaring that
$\phi : Z \to W$
by declaring that
![]() $\phi (z)_T = \Phi (z_T)$
whenever T is a marker interval for z. We need to show that
$\phi (z)_T = \Phi (z_T)$
whenever T is a marker interval for z. We need to show that
![]() $\phi $
is an embedding. Certainly
$\phi $
is an embedding. Certainly
![]() $\phi $
is shift-commuting, since if T is a marker interval for z, then
$\phi $
is shift-commuting, since if T is a marker interval for z, then
![]() $T-1$
is a marker interval for
$T-1$
is a marker interval for
![]() $\sigma z$
, so
$\sigma z$
, so
Thus, indeed
![]() $\phi (\sigma z) = \sigma \phi (z)$
. Moreover,
$\phi (\sigma z) = \sigma \phi (z)$
. Moreover,
![]() $\phi $
is injective because the appearances of
$\phi $
is injective because the appearances of
![]() $\beta $
in
$\beta $
in
![]() $\phi (z)$
allow us to reconstruct the marker coordinates, and then the injectivity of
$\phi (z)$
allow us to reconstruct the marker coordinates, and then the injectivity of
![]() $\Phi $
allows us to reconstruct
$\Phi $
allows us to reconstruct
![]() $z_T$
for each marker interval T for z.
$z_T$
for each marker interval T for z.
We need to show finally that
![]() $\phi $
is continuous, that is, that for
$\phi $
is continuous, that is, that for
![]() $z \in Z$
,
$z \in Z$
,
![]() $\phi (z)_0$
depends only on
$\phi (z)_0$
depends only on
![]() $z_{[-L,L]}$
for some finite L independent of z. To see this, let
$z_{[-L,L]}$
for some finite L independent of z. To see this, let
![]() $L'$
be such that F is a union of cylinders on
$L'$
be such that F is a union of cylinders on
![]() $[-L',L']$
. Let
$[-L',L']$
. Let
![]() $L = L'+2N$
. By examining
$L = L'+2N$
. By examining
![]() $z_{[-L,L]}$
, we can determine whether there are marker coordinates for z in
$z_{[-L,L]}$
, we can determine whether there are marker coordinates for z in
![]() $[-2N,0)$
and/or
$[-2N,0)$
and/or
![]() $[0,2N]$
. If each of these intervals contains a marker coordinate, then
$[0,2N]$
. If each of these intervals contains a marker coordinate, then
![]() $\phi (z)_0$
is determined by
$\phi (z)_0$
is determined by
![]() $z_T$
, where
$z_T$
, where
![]() $T \subset [-2N,2N]$
is the unique marker interval for z containing
$T \subset [-2N,2N]$
is the unique marker interval for z containing
![]() $0$
. If at least one of
$0$
. If at least one of
![]() $[-2N,0), [0,2N]$
has no marker coordinates, then
$[-2N,0), [0,2N]$
has no marker coordinates, then
![]() $0$
is in a long marker interval for z. If there is a marker coordinate in
$0$
is in a long marker interval for z. If there is a marker coordinate in
![]() $(-\ell ,0]$
, then
$(-\ell ,0]$
, then
![]() $\phi (z)_0 = *$
. Otherwise, by Lemma 2.5,
$\phi (z)_0 = *$
. Otherwise, by Lemma 2.5,
![]() $\phi (z)_0$
is determined by any subblock
$\phi (z)_0$
is determined by any subblock
![]() $z_{[a,b]}$
where
$z_{[a,b]}$
where
![]() $a < 0 \leq b$
,
$a < 0 \leq b$
,
![]() $b-a \geq 2N$
, and
$b-a \geq 2N$
, and
![]() $[a,b]$
contains no marker coordinate for z. This concludes the proof that
$[a,b]$
contains no marker coordinate for z. This concludes the proof that
![]() $\phi $
is continuous.
$\phi $
is continuous.
The remainder of the proof of Theorem 1.1 follows from the following proposition, the proof of which is taken up in §4.
Proposition 3.9. Let X be a mixing SFT with gap g, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with
$\pi : X \to Y$
a factor code. Let Z be a subshift with
![]() $h(Z) < h(Y)$
and
$h(Z) < h(Y)$
and
![]() $q_n(Z) \leq r_n(\pi )$
for every
$q_n(Z) \leq r_n(\pi )$
for every
![]() $n \geq 1$
. Then there exist:
$n \geq 1$
. Then there exist:
![]() $N \geq 1$
, subshifts
$N \geq 1$
, subshifts
![]() $V \subset X$
,
$V \subset X$
,
![]() $W = \pi (V) \subset Y$
, and a
$W = \pi (V) \subset Y$
, and a
![]() $(Y,W,g)$
stamp
$(Y,W,g)$
stamp
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
, such that
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
, such that
![]() $|\mu | \leq N$
,
$|\mu | \leq N$
,
![]() $q_n(Z) \leq r_n(\pi |_V)$
for
$q_n(Z) \leq r_n(\pi |_V)$
for
![]() $n \leq N-1$
and
$n \leq N-1$
and
![]() $|\mathcal {B}_n(Z)| \leq |\mathcal {B}_{n-\ell }(W)|$
for
$|\mathcal {B}_n(Z)| \leq |\mathcal {B}_{n-\ell }(W)|$
for
![]() $N+\ell \leq n \leq 2N+\ell -1$
, where
$N+\ell \leq n \leq 2N+\ell -1$
, where
![]() $\ell = |\mu | + 2g$
.
$\ell = |\mu | + 2g$
.
We state Theorem 1.1 in an equivalent form using the notation developed so far (as opposed to the statement in the introduction, where notation was minimized for clarity on a reader’s first encounter with the result), and give the proof.
Theorem. (Theorem 1.1)
Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with
$\pi : X \to Y$
a factor code. Let Z be a subshift with
![]() $h(Y) < h(Z)$
. Then there exists a sliding block code
$h(Y) < h(Z)$
. Then there exists a sliding block code
![]() $\psi : Z \to X$
such that
$\psi : Z \to X$
such that
![]() $\pi \circ \psi $
is injective, if and only if for every
$\pi \circ \psi $
is injective, if and only if for every
![]() $n \geq 1$
, we have
$n \geq 1$
, we have
![]() $q_n(Z) \leq r_n(\pi )$
.
$q_n(Z) \leq r_n(\pi )$
.
Proof of Theorem 1.1
By Lemma 2.7, assume WLOG that Z is a
![]() $1$
-step SFT. Let N,
$1$
-step SFT. Let N,
![]() $\ell $
,
$\ell $
,
![]() $V \subset X$
,
$V \subset X$
,
![]() $W = \pi (V) \subset Y$
, and
$W = \pi (V) \subset Y$
, and
![]() $\mu $
be as in Proposition 3.9. Let
$\mu $
be as in Proposition 3.9. Let
![]() $M \subset \bigcup _{n=N}^{2N-1} \mathcal {B}_{n}(W)$
be as in Lemma 3.7, and let
$M \subset \bigcup _{n=N}^{2N-1} \mathcal {B}_{n}(W)$
be as in Lemma 3.7, and let
![]() $R \subset \bigcup _{n=1}^{N-1} R_n(\pi |_V)$
be a union of finite orbits, such that
$R \subset \bigcup _{n=1}^{N-1} R_n(\pi |_V)$
be a union of finite orbits, such that
![]() $q_n(Z) \leq |R \cap R_n(\pi |_V)|$
for
$q_n(Z) \leq |R \cap R_n(\pi |_V)|$
for
![]() $n \leq N-1$
. Each of the orbits in R is, by the definition of
$n \leq N-1$
. Each of the orbits in R is, by the definition of
![]() $R_n$
, necessarily the image of an orbit with equal cardinality in V. Here, R takes the role that Q plays in Lemma 3.7, but in Lemma 3.7, there was no channel
$R_n$
, necessarily the image of an orbit with equal cardinality in V. Here, R takes the role that Q plays in Lemma 3.7, but in Lemma 3.7, there was no channel
![]() $\pi $
, and thus no preimage requirement, hence the change in notation. By Lemma 3.7, let
$\pi $
, and thus no preimage requirement, hence the change in notation. By Lemma 3.7, let
![]() $\phi : Z \to \mathrm {Blanks}(M,R,N,*,\ell )$
be an embedding.
$\phi : Z \to \mathrm {Blanks}(M,R,N,*,\ell )$
be an embedding.
Let
![]() ,
,
![]() be as in Proposition 3.6, let
be as in Proposition 3.6, let
![]() be a conjugacy, and let
be a conjugacy, and let
![]() be an embedding such that
be an embedding such that
![]() $\pi \circ \gamma $
is injective (by Proposition 3.6, using
$\pi \circ \gamma $
is injective (by Proposition 3.6, using
![]() $\mu $
). Then
$\mu $
). Then
![]() $\psi = \gamma \circ (\pi [*])^{-1} \circ \phi : Z \to X$
is a sliding block code such that
$\psi = \gamma \circ (\pi [*])^{-1} \circ \phi : Z \to X$
is a sliding block code such that
![]() $\pi \circ \psi $
is injective.
$\pi \circ \psi $
is injective.
3.3 Stamps and SFTs
In this subsection, we prove Lemma 3.11, which, in conjunction with Lemma 2.2, allows us, in Proposition 4.4, to construct a mixing SFT
![]() $V \subset X$
such that the image
$V \subset X$
such that the image
![]() $\pi (V) \subset Y$
is a proper subshift of Y but has entropy at least
$\pi (V) \subset Y$
is a proper subshift of Y but has entropy at least
![]() $h(Y) - \varepsilon $
for a given
$h(Y) - \varepsilon $
for a given
![]() $\varepsilon> 0$
. It may be possible to give a more efficient construction of such a V, but we have not found one. We first prove Lemma 3.10, which is related to the characterization of SFTs among S-gap shifts [Reference Dastjerdi and Jangjoo2, Theorem 3.3].
$\varepsilon> 0$
. It may be possible to give a more efficient construction of such a V, but we have not found one. We first prove Lemma 3.10, which is related to the characterization of SFTs among S-gap shifts [Reference Dastjerdi and Jangjoo2, Theorem 3.3].
Lemma 3.10. Let X be a mixing SFT with gap g and let
![]() $V_0 \subset X$
be an SFT. Let
$V_0 \subset X$
be an SFT. Let
![]() $k \geq g$
and let
$k \geq g$
and let
![]() $\mu \in \mathcal {B}(X) \setminus \mathcal {B}(V_0)$
be an
$\mu \in \mathcal {B}(X) \setminus \mathcal {B}(V_0)$
be an
![]() $(X,V_0,k)$
stamp. Let
$(X,V_0,k)$
stamp. Let
![]() $N \geq |\mu |$
and let
$N \geq |\mu |$
and let
![]() $V_1 \subset X$
be the closure of the set of points of the form
$V_1 \subset X$
be the closure of the set of points of the form
where, for each i,
![]() $\gamma ^{\pm }_i \in \mathcal {B}_k(X)$
and
$\gamma ^{\pm }_i \in \mathcal {B}_k(X)$
and
![]() $v_i \in \mathcal {B}(V_0)$
with
$v_i \in \mathcal {B}(V_0)$
with
![]() $|v_i| \geq N$
. Then
$|v_i| \geq N$
. Then
![]() $V_1$
is a mixing SFT.
$V_1$
is a mixing SFT.
Proof. Assume without loss of generality that X is a
![]() $1$
-step SFT. We first perform a small recoding for convenience, specifically to make it easier to recognize stamps, by replacing X by a conjugate shift
$1$
-step SFT. We first perform a small recoding for convenience, specifically to make it easier to recognize stamps, by replacing X by a conjugate shift
![]() . For each
. For each
![]() $x \in X$
, define
$x \in X$
, define
![]() as follows: if
as follows: if
![]() $x_{[i,i+|\mu |)} = \mu $
, then for each
$x_{[i,i+|\mu |)} = \mu $
, then for each
![]() $i \in [-k, |\mu |+k)$
, let
$i \in [-k, |\mu |+k)$
, let
![]() $a = x_i$
and let
$a = x_i$
and let
![]() , where for symbols
, where for symbols
![]() $a,b$
in the alphabet of X, we have
$a,b$
in the alphabet of X, we have
![]() if and only if
if and only if
![]() $a=b$
, and the set of symbols with hats is disjoint from the alphabet of X. If there is no
$a=b$
, and the set of symbols with hats is disjoint from the alphabet of X. If there is no
![]() $j \in (i-(|\mu |+k), i+k]$
with
$j \in (i-(|\mu |+k), i+k]$
with
![]() $x_{[j,j+|\mu |)} = \mu $
, then let
$x_{[j,j+|\mu |)} = \mu $
, then let
![]() . Clearly, the map
. Clearly, the map
![]() is a sliding block code, and it is just as clearly injective, since we recover x from
is a sliding block code, and it is just as clearly injective, since we recover x from
![]() by dropping hats. Therefore,
by dropping hats. Therefore,
![]() is a mixing SFT, conjugate to X.
is a mixing SFT, conjugate to X.
Denote by
![]() the image of
the image of
![]() $V_1$
under the map
$V_1$
under the map
![]() . Let
. Let
![]() $\ell = |\mu | + 2k$
. Since
$\ell = |\mu | + 2k$
. Since
![]() $\mu $
is an
$\mu $
is an
![]() $(X,V_0,k)$
stamp and
$(X,V_0,k)$
stamp and
![]() $N \geq |\mu |$
, blocks of the form
$N \geq |\mu |$
, blocks of the form
![]() $\gamma ^+_i \mu \gamma ^-_{i+1}$
do not overlap in any point in
$\gamma ^+_i \mu \gamma ^-_{i+1}$
do not overlap in any point in
![]() $V_1$
by Lemma 3.5, so symbols with hats occur in
$V_1$
by Lemma 3.5, so symbols with hats occur in
![]() in blocks of length exactly
in blocks of length exactly
![]() $\ell $
. The blocks of symbols with hats are separated by blocks from
$\ell $
. The blocks of symbols with hats are separated by blocks from
![]() $V_0$
. Since
$V_0$
. Since
![]() is the image of
is the image of
![]() $V_1$
under a conjugacy
$V_1$
under a conjugacy
![]() ,
,
![]() $V_1$
is an SFT if and only if
$V_1$
is an SFT if and only if
![]() is an SFT.
is an SFT.
Let
![]() $m \geq \max {N,\ell }$
be such that
$m \geq \max {N,\ell }$
be such that
![]() and
and
![]() $V_0$
are m-step SFTs. We claim that if
$V_0$
are m-step SFTs. We claim that if
![]() is such that
is such that
![]() for all
for all
![]() $i \in \mathbb {Z}$
, then
$i \in \mathbb {Z}$
, then
![]() , which means precisely that V is an m-step SFT. To prove this claim, let
, which means precisely that V is an m-step SFT. To prove this claim, let
![]() $\mathcal {F} \subset \mathcal {B}_{m+1}(X)$
be the set of blocks of length
$\mathcal {F} \subset \mathcal {B}_{m+1}(X)$
be the set of blocks of length
![]() $m+1$
which contain at least one of the following: a block of length greater than
$m+1$
which contain at least one of the following: a block of length greater than
![]() $\ell $
in which all symbols have hats; a block without hats that is not in
$\ell $
in which all symbols have hats; a block without hats that is not in
![]() $\mathcal {B}(V_0)$
; a block of symbols with hats of length less than
$\mathcal {B}(V_0)$
; a block of symbols with hats of length less than
![]() $\ell $
, bounded on both sides by symbols without hats; or a block of symbols without hats, of length less than N, bounded on both sides by symbols with hats. Note that
$\ell $
, bounded on both sides by symbols without hats; or a block of symbols without hats, of length less than N, bounded on both sides by symbols with hats. Note that
![]() $\mathcal {F}$
is disjoint from
$\mathcal {F}$
is disjoint from
![]() . Suppose that
. Suppose that
![]() for all
for all
![]() $i \in \mathbb {Z}$
. Then any block of symbols with hats in
$i \in \mathbb {Z}$
. Then any block of symbols with hats in
![]() has length exactly
has length exactly
![]() $\ell $
, and is thus of the form
$\ell $
, and is thus of the form
![]() $\gamma ^+ \mu \gamma ^-$
, where
$\gamma ^+ \mu \gamma ^-$
, where
![]() $\gamma ^{\pm } \in \mathcal {B}_g(X)$
(with hats added). Furthermore, the blocks separating the blocks with hats must have length at least N and must be in
$\gamma ^{\pm } \in \mathcal {B}_g(X)$
(with hats added). Furthermore, the blocks separating the blocks with hats must have length at least N and must be in
![]() $\mathcal {B}(V_0)$
, since every subblock of length
$\mathcal {B}(V_0)$
, since every subblock of length
![]() $m+1$
is in
$m+1$
is in
![]() $\mathcal {B}(V_0)$
and
$\mathcal {B}(V_0)$
and
![]() $V_0$
is an m-step SFT. Thus, indeed
$V_0$
is an m-step SFT. Thus, indeed
![]() , so
, so
![]() is indeed an SFT.
is indeed an SFT.
To see that
![]() $V_1$
is irreducible, let
$V_1$
is irreducible, let
![]() $u_-, u_+ \in \mathcal {B}(V_1)$
. We need to construct
$u_-, u_+ \in \mathcal {B}(V_1)$
. We need to construct
![]() $u_0 \in \mathcal {B}(V)$
such that
$u_0 \in \mathcal {B}(V)$
such that
![]() $u_- u_0 u_+ \in \mathcal {B}(V_1)$
. We do so as follows. Extend
$u_- u_0 u_+ \in \mathcal {B}(V_1)$
. We do so as follows. Extend
![]() $u_-$
on the right to form a block
$u_-$
on the right to form a block
![]() $v_- \in \mathcal {B}(V_1)$
, which begins with
$v_- \in \mathcal {B}(V_1)$
, which begins with
![]() $u_-$
and ends with
$u_-$
and ends with
![]() $\gamma ^+_{-1} \mu \gamma ^-_0$
where
$\gamma ^+_{-1} \mu \gamma ^-_0$
where
![]() $\gamma ^+_{-1}, \gamma ^-_0 \in \mathcal {B}_k(V_1)$
. (It is possible that
$\gamma ^+_{-1}, \gamma ^-_0 \in \mathcal {B}_k(V_1)$
. (It is possible that
![]() $u_-$
overlaps
$u_-$
overlaps
![]() $\gamma ^+_{-1} \mu \gamma ^-_0$
.) Let
$\gamma ^+_{-1} \mu \gamma ^-_0$
.) Let
![]() $v_0 \in \mathcal {B}_N(V_0)$
be such that
$v_0 \in \mathcal {B}_N(V_0)$
be such that
![]() $v_- v_0 \in \mathcal {B}(X)$
. Similarly, extend
$v_- v_0 \in \mathcal {B}(X)$
. Similarly, extend
![]() $u_+$
on the left to form a block
$u_+$
on the left to form a block
![]() $v_+ \in \mathcal {B}(V_1)$
which ends with
$v_+ \in \mathcal {B}(V_1)$
which ends with
![]() $u_+$
and begins with
$u_+$
and begins with
![]() $\gamma ^+_0 \mu \gamma ^-_1$
, where
$\gamma ^+_0 \mu \gamma ^-_1$
, where
![]() $\gamma ^+_0, \gamma ^-_1 \in \mathcal {B}_k(V_1)$
and
$\gamma ^+_0, \gamma ^-_1 \in \mathcal {B}_k(V_1)$
and
![]() $v_0 \gamma ^+_0 \in \mathcal {B}(X)$
. Let
$v_0 \gamma ^+_0 \in \mathcal {B}(X)$
. Let
![]() $x^{\pm } \in \mathcal {B}(V_1)$
be such that
$x^{\pm } \in \mathcal {B}(V_1)$
be such that
![]() $x^-_{[0,\infty )}$
begins with
$x^-_{[0,\infty )}$
begins with
![]() $v_-$
and
$v_-$
and
![]() $x^+_{(-\infty ,-1]}$
ends with
$x^+_{(-\infty ,-1]}$
ends with
![]() $v^+$
. Let
$v^+$
. Let
![]() $x = x^-_{(-\infty ,-1]} v_- v_0 v_+ x^+_{[0,\infty )}$
. Then
$x = x^-_{(-\infty ,-1]} v_- v_0 v_+ x^+_{[0,\infty )}$
. Then
![]() $x \in X$
, since X is a
$x \in X$
, since X is a
![]() $1$
-step SFT. Moreover,
$1$
-step SFT. Moreover,
![]() $x \in V_1$
, since the tails
$x \in V_1$
, since the tails
![]() $x^-_{(-\infty ,-1]} v_-$
and
$x^-_{(-\infty ,-1]} v_-$
and
![]() $v_+ x^+_{[0,\infty )}$
appear in
$v_+ x^+_{[0,\infty )}$
appear in
![]() $V_1$
and are joined together in a way that creates no violations of the restrictions defining
$V_1$
and are joined together in a way that creates no violations of the restrictions defining
![]() $V_1$
. Letting
$V_1$
. Letting
![]() $u_0$
be the block appearing between
$u_0$
be the block appearing between
![]() $u_-, u_+$
, such that
$u_-, u_+$
, such that
![]() $v_- v_0 v_+ = u_- u_0 u_+ \in \mathcal {B}(V)$
, the construction is complete, showing that
$v_- v_0 v_+ = u_- u_0 u_+ \in \mathcal {B}(V)$
, the construction is complete, showing that
![]() $V_1$
is indeed irreducible.
$V_1$
is indeed irreducible.
To see that
![]() $V_1$
is mixing, let
$V_1$
is mixing, let
![]() $u_1, u_2 \in \mathcal {B}(V_0)$
with
$u_1, u_2 \in \mathcal {B}(V_0)$
with
![]() $|u_1|> m$
, where m is as above, and
$|u_1|> m$
, where m is as above, and
![]() $|u_2| = |u_1| + 1$
. Let
$|u_2| = |u_1| + 1$
. Let
![]() $\gamma ^{\pm }_i \in \mathcal {B}(X)$
,
$\gamma ^{\pm }_i \in \mathcal {B}(X)$
,
![]() $i = 1,2$
, be such that
$i = 1,2$
, be such that
![]() $u_i \gamma ^+_i \mu \gamma ^-_i u_i \in \mathcal {B}(X)$
. Then
$u_i \gamma ^+_i \mu \gamma ^-_i u_i \in \mathcal {B}(X)$
. Then
![]() $x_i = (u_i \gamma ^+_i \mu \gamma ^-_i)^{\infty } \in V_1$
for both
$x_i = (u_i \gamma ^+_i \mu \gamma ^-_i)^{\infty } \in V_1$
for both
![]() $i=1,2$
. Indeed, certainly
$i=1,2$
. Indeed, certainly
![]() $x_i \in X$
, since
$x_i \in X$
, since
![]() $u_i \gamma ^+_i \mu \gamma ^-_i u_i \in \mathcal {B}(X)$
and X is a
$u_i \gamma ^+_i \mu \gamma ^-_i u_i \in \mathcal {B}(X)$
and X is a
![]() $1$
-step SFT. Moreover,
$1$
-step SFT. Moreover,
![]() $\mathrm {per}(x_i)$
divides
$\mathrm {per}(x_i)$
divides
![]() $\ell + |u_i|$
, and
$\ell + |u_i|$
, and
![]() $\gcd (\ell + |u_1|, \ell + |u_2|) = \gcd (\ell + |u_1|, \ell + |u_1| + 1) = 1$
, so
$\gcd (\ell + |u_1|, \ell + |u_2|) = \gcd (\ell + |u_1|, \ell + |u_1| + 1) = 1$
, so
![]() $\gcd ( \mathrm {per}(x_1), \mathrm {per}(x_2) ) = 1$
. Since
$\gcd ( \mathrm {per}(x_1), \mathrm {per}(x_2) ) = 1$
. Since
![]() $V_1$
is an irreducible SFT with periodic points of coprime periods,
$V_1$
is an irreducible SFT with periodic points of coprime periods,
![]() $V_1$
is mixing.
$V_1$
is mixing.
As advertised, we now use Lemma 3.10 to prove the following lemma, which is applied in the proof of Proposition 4.4, which, in turn, is the main input to the proof of Proposition 3.9.
Lemma 3.11. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a
$\pi : X \to Y$
a
![]() $1$
-block factor code. Let
$1$
-block factor code. Let
![]() $W_0 \subsetneq Y$
be an SFT. Then there exists a mixing SFT
$W_0 \subsetneq Y$
be an SFT. Then there exists a mixing SFT
![]() $V_1 \subset X$
with
$V_1 \subset X$
with
![]() $W_0 \subset \pi (V_1) \subsetneq Y$
.
$W_0 \subset \pi (V_1) \subsetneq Y$
.
Proof. Let
![]() $V_0 = \pi ^{-1}(W_0) \subset X$
. Note that
$V_0 = \pi ^{-1}(W_0) \subset X$
. Note that
![]() $V_0$
is an SFT since
$V_0$
is an SFT since
![]() $W_0$
is an SFT. Let g be the mixing gap of X. Let
$W_0$
is an SFT. Let g be the mixing gap of X. Let
![]() $y \in Y \setminus W_0$
be a periodic point with least period
$y \in Y \setminus W_0$
be a periodic point with least period
![]() $k \geq g$
. Such a y certainly exists because periodic points are dense in Y and
$k \geq g$
. Such a y certainly exists because periodic points are dense in Y and
![]() $W_0$
is a proper subshift. Let
$W_0$
is a proper subshift. Let
![]() $k'$
be such that
$k'$
be such that
![]() $y_{[0,k')} \notin \mathcal {B}_{k'}(W_0)$
. Let
$y_{[0,k')} \notin \mathcal {B}_{k'}(W_0)$
. Let
![]() $\ell = k+k'$
. Then every
$\ell = k+k'$
. Then every
![]() $\ell $
-block in y is forbidden in
$\ell $
-block in y is forbidden in
![]() $W_0$
. In particular, for any
$W_0$
. In particular, for any
![]() $x \in \pi ^{-1}(\{ y \})$
and any
$x \in \pi ^{-1}(\{ y \})$
and any
![]() $i \in \mathbb {Z}$
, we have
$i \in \mathbb {Z}$
, we have
![]() $x_{[i,i+\ell )} \notin \mathcal {B}(V_0)$
.
$x_{[i,i+\ell )} \notin \mathcal {B}(V_0)$
.
By Proposition 3.4, let
![]() $\mu $
be an
$\mu $
be an
![]() $(X,V_0,g)$
stamp. Let
$(X,V_0,g)$
stamp. Let
![]() $V_1$
consist of the closure of the set of points of the form
$V_1$
consist of the closure of the set of points of the form
![]() $\ldots v_{-1} \gamma ^+_{-1} \mu \gamma ^-_0 v_0 \gamma ^+_0 \mu \gamma ^-_1 v_1 \ldots \in X$
where each
$\ldots v_{-1} \gamma ^+_{-1} \mu \gamma ^-_0 v_0 \gamma ^+_0 \mu \gamma ^-_1 v_1 \ldots \in X$
where each
![]() $v_i \in \mathcal {B}(V_0)$
with
$v_i \in \mathcal {B}(V_0)$
with
![]() $|v_i| \geq \ell $
and each
$|v_i| \geq \ell $
and each
![]() $\gamma ^{\pm }_i \in \mathcal {B}_g(X)$
. By Lemma 3.10,
$\gamma ^{\pm }_i \in \mathcal {B}_g(X)$
. By Lemma 3.10,
![]() $V_1$
is indeed a mixing SFT. Note that every point in
$V_1$
is indeed a mixing SFT. Note that every point in
![]() $V_1$
contains
$V_1$
contains
![]() $\ell $
-blocks permitted in
$\ell $
-blocks permitted in
![]() $V_0$
, so
$V_0$
, so
![]() $V_1$
is disjoint from
$V_1$
is disjoint from
![]() $\pi ^{-1}(\{ y \})$
, and therefore
$\pi ^{-1}(\{ y \})$
, and therefore
![]() $\pi (V_1) \subsetneq Y$
. In particular, since
$\pi (V_1) \subsetneq Y$
. In particular, since
![]() $V_0 \subseteq V_1$
, we have
$V_0 \subseteq V_1$
, we have
![]() $\pi (W_0) \subseteq V_1 \subsetneq Y$
.
$\pi (W_0) \subseteq V_1 \subsetneq Y$
.
4 Counting
In this section, we prove Proposition 3.4 and Proposition 3.9, which state the existence and properties respectively of the stamps and the shifts
![]() $V \subset X, W \subset Y$
used in §3. Section 4.1 contains two results required for the proof of Proposition 3.4, one (Lemma 4.1) showing that most blocks in a subshift with positive entropy have little self-overlap, and the other (Lemma 4.2) showing that one can assume, at the cost of a small loss of entropy, that a given sufficiently long block appears syndetically in a mixing sofic shift. Section 4.2 then gives a crucial asymptotic result on the number of periodic points in Y with a preimage of equal least period in X, and applies the results from §3.3 to construct the shifts V and W.
$V \subset X, W \subset Y$
used in §3. Section 4.1 contains two results required for the proof of Proposition 3.4, one (Lemma 4.1) showing that most blocks in a subshift with positive entropy have little self-overlap, and the other (Lemma 4.2) showing that one can assume, at the cost of a small loss of entropy, that a given sufficiently long block appears syndetically in a mixing sofic shift. Section 4.2 then gives a crucial asymptotic result on the number of periodic points in Y with a preimage of equal least period in X, and applies the results from §3.3 to construct the shifts V and W.
4.1 Self-overlap and stamps
We begin by showing that most blocks have very little self-overlap, which we use both to construct stamps and to determine the asymptotic number of periodic points in Y with a
![]() $\pi $
-preimage of equal least period.
$\pi $
-preimage of equal least period.
Lemma 4.1. Let Y be a subshift with
![]() $h(Y)> 0$
. For every
$h(Y)> 0$
. For every
![]() $\alpha \in (0,1)$
, there exist
$\alpha \in (0,1)$
, there exist
![]() $N \geq 1$
and
$N \geq 1$
and
![]() $b> 0$
such that for every
$b> 0$
such that for every
![]() $n \geq N$
, there are at least
$n \geq N$
, there are at least
![]() $(1-\exp (-bn)) \exp (n h(Y))$
blocks
$(1-\exp (-bn)) \exp (n h(Y))$
blocks
![]() $w \in \mathcal {B}_n(Y)$
with no self-overlap of more than
$w \in \mathcal {B}_n(Y)$
with no self-overlap of more than
![]() $\alpha n$
.
$\alpha n$
.
Proof. Let
![]() $\varepsilon = \tfrac 12 (\alpha ^{-1} -1 )h(Y)$
, so that
$\varepsilon = \tfrac 12 (\alpha ^{-1} -1 )h(Y)$
, so that
![]() $\alpha (h(Y) + \varepsilon ) < h(Y)$
. Let
$\alpha (h(Y) + \varepsilon ) < h(Y)$
. Let
![]() $r = \exp (h(Y))$
and
$r = \exp (h(Y))$
and
![]() $s = \exp (h(Y) + \varepsilon )$
. Note that
$s = \exp (h(Y) + \varepsilon )$
. Note that
![]() $s^{\alpha } < r < s$
and that
$s^{\alpha } < r < s$
and that
![]() $r^n \leq |\mathcal {B}_n(Y)|$
for every n. Let
$r^n \leq |\mathcal {B}_n(Y)|$
for every n. Let
![]() $N_0$
be large enough that for all
$N_0$
be large enough that for all
![]() $n \geq N_0$
, we have
$n \geq N_0$
, we have
![]() $|\mathcal {B}_n(Y)| \leq s^n$
. Let
$|\mathcal {B}_n(Y)| \leq s^n$
. Let
![]() $C_1 = \sum _{k=1}^{N_0 -1} |\mathcal {B}_k(Y)|$
. Then the number of blocks in X of length n with self-overlap of more than
$C_1 = \sum _{k=1}^{N_0 -1} |\mathcal {B}_k(Y)|$
. Then the number of blocks in X of length n with self-overlap of more than
![]() $\alpha n$
is at most
$\alpha n$
is at most
 $$ \begin{align*} \sum_{k=1}^{\lceil \alpha n \rceil } |\mathcal{B}_k(Y)| &\leq \sum_{k=1}^{N_0 -1} |\mathcal{B}_k(Y)| + \sum_{k=N_0}^{\lceil \alpha n \rceil } |\mathcal{B}_k(Y)| \\ &\leq C_1 + \sum_{k=N_0}^{\lceil \alpha n \rceil } s^k \\ &\leq C_1 + \frac{ s^{\alpha n + 2} - s^{N_0} }{s-1} \\ &\leq C_2 s^{\alpha n}, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{\lceil \alpha n \rceil } |\mathcal{B}_k(Y)| &\leq \sum_{k=1}^{N_0 -1} |\mathcal{B}_k(Y)| + \sum_{k=N_0}^{\lceil \alpha n \rceil } |\mathcal{B}_k(Y)| \\ &\leq C_1 + \sum_{k=N_0}^{\lceil \alpha n \rceil } s^k \\ &\leq C_1 + \frac{ s^{\alpha n + 2} - s^{N_0} }{s-1} \\ &\leq C_2 s^{\alpha n}, \end{align*} $$
where
Let
![]() $N> ({ (1-\alpha )h(Y) - \alpha \varepsilon })/{\log C_2}$
. Then, for
$N> ({ (1-\alpha )h(Y) - \alpha \varepsilon })/{\log C_2}$
. Then, for
![]() $n \geq N$
, the number of blocks in Y of length n with no self-overlap by more than
$n \geq N$
, the number of blocks in Y of length n with no self-overlap by more than
![]() $\alpha n$
is at least
$\alpha n$
is at least
 $$ \begin{align*} |\mathcal{B}_n(Y)| - \sum_{k=1}^{\lceil \alpha n \rceil } |\mathcal{B}_k(Y)| &\geq r^n - C_2 s^{\alpha n} \\ &= r^n \bigg( 1 - C_2 \bigg( \frac{s^{\alpha}}{r} \bigg)^n \bigg) \\ &> (1- \exp(-bn)) \exp(nh(Y)), \end{align*} $$
$$ \begin{align*} |\mathcal{B}_n(Y)| - \sum_{k=1}^{\lceil \alpha n \rceil } |\mathcal{B}_k(Y)| &\geq r^n - C_2 s^{\alpha n} \\ &= r^n \bigg( 1 - C_2 \bigg( \frac{s^{\alpha}}{r} \bigg)^n \bigg) \\ &> (1- \exp(-bn)) \exp(nh(Y)), \end{align*} $$
where we can take
 $$ \begin{align*} b &= \frac{1}{2} \log \bigg( C_2 \bigg( \frac{r}{s^{\alpha}} \bigg)^N \bigg) \\ &= (1-\alpha)h(Y) - \alpha \varepsilon - \frac{1}{N} \log C_2, \end{align*} $$
$$ \begin{align*} b &= \frac{1}{2} \log \bigg( C_2 \bigg( \frac{r}{s^{\alpha}} \bigg)^N \bigg) \\ &= (1-\alpha)h(Y) - \alpha \varepsilon - \frac{1}{N} \log C_2, \end{align*} $$
which is positive by the choice of N.
We now control the entropy loss incurred by requiring a given long block to appear syndetically.
Lemma 4.2. Let Y be a strongly irreducible subshift with
![]() $h(Y)> 0$
. For every
$h(Y)> 0$
. For every
![]() $\varepsilon> 0$
, there exist
$\varepsilon> 0$
, there exist
![]() $\beta \in (0,1)$
and
$\beta \in (0,1)$
and
![]() $N \geq 1$
such that for every
$N \geq 1$
such that for every
![]() $n \geq N$
and every
$n \geq N$
and every
![]() $\theta \in \mathcal {B}_{\lfloor \beta n \rfloor }(Y)$
, the subshift
$\theta \in \mathcal {B}_{\lfloor \beta n \rfloor }(Y)$
, the subshift
![]() $S \subset Y$
consisting of points
$S \subset Y$
consisting of points
![]() $y \in Y$
in which
$y \in Y$
in which
![]() $\theta $
appears at least once in
$\theta $
appears at least once in
![]() $y_{[i,i+n)}$
for every
$y_{[i,i+n)}$
for every
![]() $i \in \mathbb {Z}$
has entropy at least
$i \in \mathbb {Z}$
has entropy at least
![]() $h(Y) - \varepsilon $
.
$h(Y) - \varepsilon $
.
Proof. Let g be the gap for Y. Let
![]() $\beta = \min \{ \varepsilon /(8 h(Y)), 1/2 \}$
and let
$\beta = \min \{ \varepsilon /(8 h(Y)), 1/2 \}$
and let
![]() $N = \lceil 4(2g+1)h(Y)/\varepsilon \rceil $
. Let
$N = \lceil 4(2g+1)h(Y)/\varepsilon \rceil $
. Let
![]() $n \geq N$
and fix
$n \geq N$
and fix
![]() $\theta \in \mathcal {B}_{\lfloor \beta n \rfloor }(Y)$
. For
$\theta \in \mathcal {B}_{\lfloor \beta n \rfloor }(Y)$
. For
![]() $m \geq n$
, and for all
$m \geq n$
, and for all
![]() $u_1, \ldots , u_k \in \mathcal {B}_{\lfloor (1-2\beta )n \rfloor -2g}(Y)$
, where
$u_1, \ldots , u_k \in \mathcal {B}_{\lfloor (1-2\beta )n \rfloor -2g}(Y)$
, where
![]() $k = \lfloor m/n \rfloor $
, there exist
$k = \lfloor m/n \rfloor $
, there exist
![]() $v^{\pm }_1, \ldots , v^{\pm }_k \in \mathcal {B}_g(Y)$
and
$v^{\pm }_1, \ldots , v^{\pm }_k \in \mathcal {B}_g(Y)$
and
![]() $v_0 \in \mathcal {B}_{m-kn}(Y)$
such that
$v_0 \in \mathcal {B}_{m-kn}(Y)$
such that
Therefore, by manipulation of logarithms and the fact that
![]() $h(Y) = \inf _{\ell \geq 1} ({1}/{\ell }) \log |\mathcal {B}_{\ell }(Y) |$
by definition,
$h(Y) = \inf _{\ell \geq 1} ({1}/{\ell }) \log |\mathcal {B}_{\ell }(Y) |$
by definition,
 $$ \begin{align*} |\mathcal{B}_m(S)| &\geq |\mathcal{B}_{\lfloor (1-2\beta)n\rfloor - 2g}(Y)|^{\lfloor m/n \rfloor} \\ \frac{1}{m} \log |\mathcal{B}_m(S)| &\geq \frac{1}{m} \log ( |\mathcal{B}_{\lfloor (1-2\beta)n\rfloor - 2g}(Y)|^{(m-1)/n} ) \\ &= \bigg( 1 - \frac{1}{m} \bigg) \frac{1}{n} \log |\mathcal{B}_{\lfloor (1-2\beta)n\rfloor - 2g}(Y)| \\ &\geq \bigg( 1 - \frac{1}{m} \bigg) \frac{1}{n} ( \lfloor(1-2\beta)n\rfloor - 2g) h(Y) \\ &> h(Y) - \varepsilon/2 \end{align*} $$
$$ \begin{align*} |\mathcal{B}_m(S)| &\geq |\mathcal{B}_{\lfloor (1-2\beta)n\rfloor - 2g}(Y)|^{\lfloor m/n \rfloor} \\ \frac{1}{m} \log |\mathcal{B}_m(S)| &\geq \frac{1}{m} \log ( |\mathcal{B}_{\lfloor (1-2\beta)n\rfloor - 2g}(Y)|^{(m-1)/n} ) \\ &= \bigg( 1 - \frac{1}{m} \bigg) \frac{1}{n} \log |\mathcal{B}_{\lfloor (1-2\beta)n\rfloor - 2g}(Y)| \\ &\geq \bigg( 1 - \frac{1}{m} \bigg) \frac{1}{n} ( \lfloor(1-2\beta)n\rfloor - 2g) h(Y) \\ &> h(Y) - \varepsilon/2 \end{align*} $$
for large enough m, where the final inequality follows from the choices of
![]() $\beta $
and N. We conclude that
$\beta $
and N. We conclude that
![]() $h(S) = \liminf _{m \to \infty } ({1}/{m}) |\mathcal {B}_n(S)|> h(Y) - \varepsilon $
.
$h(S) = \liminf _{m \to \infty } ({1}/{m}) |\mathcal {B}_n(S)|> h(Y) - \varepsilon $
.
Proposition 3.4. Let Y be a strongly irreducible subshift with gap g and
![]() $W \subset Y$
a proper subshift. For every
$W \subset Y$
a proper subshift. For every
![]() $k \geq g$
and every sufficiently large n, there exists a
$k \geq g$
and every sufficiently large n, there exists a
![]() $(Y,W,k)$
stamp of length n.
$(Y,W,k)$
stamp of length n.
Proof. It is clearly enough to prove the result for
![]() $u_1, u_2$
sufficiently long, since we can then pass to subwords of
$u_1, u_2$
sufficiently long, since we can then pass to subwords of
![]() $u_1,u_2$
. By Lemma 4.2, let
$u_1,u_2$
. By Lemma 4.2, let
![]() $\beta \in (0,1)$
, m sufficiently large, and
$\beta \in (0,1)$
, m sufficiently large, and
![]() $\theta \in \mathcal {B}_{\lfloor \beta m \rfloor }(Y) \setminus \mathcal {B}(W)$
be such that the subshift
$\theta \in \mathcal {B}_{\lfloor \beta m \rfloor }(Y) \setminus \mathcal {B}(W)$
be such that the subshift
![]() $S \subset Y$
defined by requiring at least one appearance of
$S \subset Y$
defined by requiring at least one appearance of
![]() $\theta $
in any block of length m has
$\theta $
in any block of length m has
![]() $h(S)> 0$
. Let
$h(S)> 0$
. Let
![]() $\alpha \in (0,1)$
be arbitrary, and let
$\alpha \in (0,1)$
be arbitrary, and let
![]() $n> (m+k)/(1-\alpha )$
be large enough that, by Lemma 4.1, there exists
$n> (m+k)/(1-\alpha )$
be large enough that, by Lemma 4.1, there exists
![]() $\mu \in \mathcal {B}_n(S)$
such that
$\mu \in \mathcal {B}_n(S)$
such that
![]() $\mu $
has no self-overlap by more than
$\mu $
has no self-overlap by more than
![]() $\alpha n$
, in particular, by more than
$\alpha n$
, in particular, by more than
![]() $n-(m+k)$
.
$n-(m+k)$
.
Let
![]() $u_1 \in \mathcal {B}_{k_1}(U)$
,
$u_1 \in \mathcal {B}_{k_1}(U)$
,
![]() $u_2 \in \mathcal {B}_{k_2}(U)$
with
$u_2 \in \mathcal {B}_{k_2}(U)$
with
![]() $k_1, k_2 \geq m$
and let
$k_1, k_2 \geq m$
and let
![]() $v_1, v_2 \in \mathcal {B}_{k}(Y)$
. Then
$v_1, v_2 \in \mathcal {B}_{k}(Y)$
. Then
![]() $\mu $
cannot appear in
$\mu $
cannot appear in
![]() $u_1 v_2 \mu v_2 u_2$
except at the position explicitly indicated. Indeed,
$u_1 v_2 \mu v_2 u_2$
except at the position explicitly indicated. Indeed,
![]() $\mu $
cannot appear at a position shifted by at most
$\mu $
cannot appear at a position shifted by at most
![]() $m+k$
—otherwise,
$m+k$
—otherwise,
![]() $\mu $
would overlap itself by too much—and it cannot appear at a position shifted by more than
$\mu $
would overlap itself by too much—and it cannot appear at a position shifted by more than
![]() $m+k$
, as it would then overlap with
$m+k$
, as it would then overlap with
![]() $u_1$
or
$u_1$
or
![]() $u_2$
in a block of length at least m, contradicting the fact that
$u_2$
in a block of length at least m, contradicting the fact that
![]() $\mu \in \mathcal {B}(S)$
, and thus has
$\mu \in \mathcal {B}(S)$
, and thus has
![]() $\theta $
as a subword.
$\theta $
as a subword.
4.2 Entropy and periodic points
We first show that at least a positive fraction of periodic points in Y of sufficient least period have a preimage of equal least period, and in particular that their growth is exponential with rate
![]() $h(Y)$
.
$h(Y)$
.
Proposition 4.3. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Then
$\pi : X \to Y$
a factor code. Then
![]() $\lim _{n \to \infty } ({1}/{n}) \log r_n(\pi ) = h(Y)$
.
$\lim _{n \to \infty } ({1}/{n}) \log r_n(\pi ) = h(Y)$
.
Proof. Let g be the mixing gap of X. By Lemma 4.1, let
![]() $b> 0$
and
$b> 0$
and
![]() $N> 3g$
be such that, for all
$N> 3g$
be such that, for all
![]() $n \geq N$
, the number of blocks in Y of length
$n \geq N$
, the number of blocks in Y of length
![]() $n-g$
with no self-overlap by more than
$n-g$
with no self-overlap by more than
![]() $n/3$
is at least
$n/3$
is at least
![]() $c \exp (nh(Y))$
, where we may take
$c \exp (nh(Y))$
, where we may take
![]() $c = \tfrac 12 \exp (-g h(X))$
. For each block
$c = \tfrac 12 \exp (-g h(X))$
. For each block
![]() $v \in \mathcal {B}_{n-g}(Y)$
, there exists a periodic point
$v \in \mathcal {B}_{n-g}(Y)$
, there exists a periodic point
![]() $x \in X$
with
$x \in X$
with
![]() $\pi (x)_{[0,n-g)} = v$
such that
$\pi (x)_{[0,n-g)} = v$
such that
![]() $\mathrm {per}(x)$
divides n. Thus,
$\mathrm {per}(x)$
divides n. Thus,
![]() $\pi (x)$
is also periodic with least period dividing n. Moreover, if v has no self-overlap by more than
$\pi (x)$
is also periodic with least period dividing n. Moreover, if v has no self-overlap by more than
![]() $n/3$
, then in fact
$n/3$
, then in fact
![]() $\mathrm {per}(\pi (x)) = n$
. Therefore,
$\mathrm {per}(\pi (x)) = n$
. Therefore,
![]() ${r_n(\pi ) \geq c \exp (n h(Y))}$
, so
${r_n(\pi ) \geq c \exp (n h(Y))}$
, so
![]() $\liminf _{n \to \infty } ({1}/{n}) \log r_n(\pi ) \geq h(Y)$
, matching
$\liminf _{n \to \infty } ({1}/{n}) \log r_n(\pi ) \geq h(Y)$
, matching
which concludes the proof.
We now assemble the quantitative results proven so far.
Proposition 4.4. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let
$\pi : X \to Y$
a factor code. Let
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $N_0 \geq 1$
. Then there exist
$N_0 \geq 1$
. Then there exist
![]() $N_1 \geq N_0$
and proper subshifts
$N_1 \geq N_0$
and proper subshifts
![]() $W \subsetneq Y$
,
$W \subsetneq Y$
,
![]() $V = \pi ^{-1}(W) \subset X$
, such that:
$V = \pi ^{-1}(W) \subset X$
, such that:
![]() $h(W)> h(Y) - \varepsilon $
; for
$h(W)> h(Y) - \varepsilon $
; for
![]() $n \leq N_1$
,
$n \leq N_1$
,
![]() $r_n(\pi |_V) = r_n(\pi )$
; and for
$r_n(\pi |_V) = r_n(\pi )$
; and for
![]() $n \geq N_1$
,
$n \geq N_1$
,
![]() $r_n(\pi |_V)> \exp (n (h(Y) - \varepsilon ))$
.
$r_n(\pi |_V)> \exp (n (h(Y) - \varepsilon ))$
.
Proof. By Lemmas 2.2 and 3.11, let
![]() $V_1 \subset X$
be a mixing SFT such that
$V_1 \subset X$
be a mixing SFT such that
![]() $h(Y) - \varepsilon /2 < h(\pi (V_1)) < h(Y)$
. Let
$h(Y) - \varepsilon /2 < h(\pi (V_1)) < h(Y)$
. Let
![]() $W_1 = \pi (V_1)$
. By Proposition 4.3, let
$W_1 = \pi (V_1)$
. By Proposition 4.3, let
![]() $N_1 \geq N_0$
be such that for any
$N_1 \geq N_0$
be such that for any
![]() $n \geq N_1$
, we have
$n \geq N_1$
, we have
![]() $({1}/{n}) \log r_n(\pi |_{V_1})> h(W_1) - \varepsilon /2 > h(Y) - \varepsilon $
. Let
$({1}/{n}) \log r_n(\pi |_{V_1})> h(W_1) - \varepsilon /2 > h(Y) - \varepsilon $
. Let
![]() $W = W_1 \cup \bigcup _{n=1}^{N_1} R_n(\pi )$
and
$W = W_1 \cup \bigcup _{n=1}^{N_1} R_n(\pi )$
and
![]() $V = \pi ^{-1}(W)$
. Then
$V = \pi ^{-1}(W)$
. Then
![]() $r_n(\pi |_V) = r_n(\pi )$
for all
$r_n(\pi |_V) = r_n(\pi )$
for all
![]() $n \leq N_1$
.
$n \leq N_1$
.
To see that
![]() $W \neq Y$
, observe that the only n-blocks in W that may not be in
$W \neq Y$
, observe that the only n-blocks in W that may not be in
![]() $W_1$
are those in the low-order periodic points that have been adjoined, which are bounded in number by a constant. That is,
$W_1$
are those in the low-order periodic points that have been adjoined, which are bounded in number by a constant. That is,
![]() $|\mathcal {B}_n(W)| \leq |\mathcal {B}_n(W_1)| + C$
for all
$|\mathcal {B}_n(W)| \leq |\mathcal {B}_n(W_1)| + C$
for all
![]() $n \geq N_1$
, where we can take
$n \geq N_1$
, where we can take
![]() ${C = \sum _{k=1}^{N_1} k |R_k(\pi )|}$
. Thus,
${C = \sum _{k=1}^{N_1} k |R_k(\pi )|}$
. Thus,
![]() $h(W) = h(W_1) < h(Y)$
.
$h(W) = h(W_1) < h(Y)$
.
Proposition 4.4 is the final input to the proof of Proposition 3.9, and thus of Theorem 1.1.
Proposition 3.9. Let X be a mixing SFT with gap g, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with
$\pi : X \to Y$
a factor code. Let Z be a subshift with
![]() $h(Z) < h(Y)$
and
$h(Z) < h(Y)$
and
![]() $q_n(Z) \leq r_n(\pi )$
for every
$q_n(Z) \leq r_n(\pi )$
for every
![]() $n \geq 1$
. Then there exist:
$n \geq 1$
. Then there exist:
![]() $N \geq 1$
, subshifts
$N \geq 1$
, subshifts
![]() $V \subset X$
,
$V \subset X$
,
![]() $W = \pi (V) \subset Y$
, and a
$W = \pi (V) \subset Y$
, and a
![]() $(Y,W,g)$
stamp
$(Y,W,g)$
stamp
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
, such that
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
, such that
![]() $|\mu | \leq N$
,
$|\mu | \leq N$
,
![]() $q_n(Z) \leq r_n(\pi |_V)$
for
$q_n(Z) \leq r_n(\pi |_V)$
for
![]() $n \leq N-1$
and
$n \leq N-1$
and
![]() $|\mathcal {B}_n(Z)| \leq |\mathcal {B}_{n-\ell }(W)|$
for
$|\mathcal {B}_n(Z)| \leq |\mathcal {B}_{n-\ell }(W)|$
for
![]() $N+\ell \leq n \leq 2N+\ell -1$
, where
$N+\ell \leq n \leq 2N+\ell -1$
, where
![]() $\ell = |\mu | + 2g$
.
$\ell = |\mu | + 2g$
.
Proof. Let
![]() $\varepsilon = h(Y) - h(Z)$
. Let
$\varepsilon = h(Y) - h(Z)$
. Let
![]() $N_0 \geq 1$
be large enough that for all
$N_0 \geq 1$
be large enough that for all
![]() $n \geq N_0$
,
$n \geq N_0$
,
By Proposition 4.4, let
![]() $W \subset Y$
,
$W \subset Y$
,
![]() $V = \pi ^{-1}(W) \subset X$
, and
$V = \pi ^{-1}(W) \subset X$
, and
![]() $N_1 \geq N_0$
be such that
$N_1 \geq N_0$
be such that
![]() $h(W)> h(Y) - {\varepsilon }/{4}$
,
$h(W)> h(Y) - {\varepsilon }/{4}$
,
![]() $r_n(\pi |_V) = r_n(\pi )$
for all
$r_n(\pi |_V) = r_n(\pi )$
for all
![]() $n \leq N_1$
, and
$n \leq N_1$
, and
![]() $({1}/{n}) \log r_n(\pi |_V)> h(Y) - {\varepsilon }/{4}$
for all
$({1}/{n}) \log r_n(\pi |_V)> h(Y) - {\varepsilon }/{4}$
for all
![]() $n \geq N_1$
. Note that
$n \geq N_1$
. Note that
![]() $h(W)> h(Z) + {\varepsilon }/{2}$
and that
$h(W)> h(Z) + {\varepsilon }/{2}$
and that
![]() $q_n(Z) \leq r_n(\pi |_V)$
for all
$q_n(Z) \leq r_n(\pi |_V)$
for all
![]() $n \geq 1$
.
$n \geq 1$
.
Let g be the mixing gap of X. By Proposition 3.4, let
![]() $\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
be a
$\mu \in \mathcal {B}(Y) \setminus \mathcal {B}(W)$
be a
![]() $(Y,W,g)$
stamp. Let
$(Y,W,g)$
stamp. Let
![]() $\ell = |\mu | + 2g$
. Then since
$\ell = |\mu | + 2g$
. Then since
![]() $h(Z) < h(W)$
, there exists N sufficiently large so that for all
$h(Z) < h(W)$
, there exists N sufficiently large so that for all
![]() $n \geq N$
, in particular, for
$n \geq N$
, in particular, for
![]() $N+\ell \leq n \leq 2N+\ell -1$
, we have
$N+\ell \leq n \leq 2N+\ell -1$
, we have
![]() $|\mathcal {B}_n(Z)| < |\mathcal {B}_{n-\ell }(W)|$
.
$|\mathcal {B}_n(Z)| < |\mathcal {B}_{n-\ell }(W)|$
.
5 Proofs of Lemma 2.7 and Corollary 1.3
We first use Proposition 4.3, along with facts about Markov approximations in §2.2, to prove Lemma 2.7, which reduces Theorem 1.1 to the case where Z is a
![]() $1$
-step SFT.
$1$
-step SFT.
Lemma 2.7. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with
$\pi : X \to Y$
a factor code. Let Z be a subshift with
![]() $h(Z) < h(Y)$
and
$h(Z) < h(Y)$
and
![]() $q_n(Z) \leq r_n(\pi )$
for all
$q_n(Z) \leq r_n(\pi )$
for all
![]() $n \geq 1$
. Then there exists a
$n \geq 1$
. Then there exists a
![]() $1$
-step SFT
$1$
-step SFT
![]() $Z'$
such that Z embeds into
$Z'$
such that Z embeds into
![]() $Z'$
,
$Z'$
,
![]() $h(Z') < h(Y)$
, and
$h(Z') < h(Y)$
, and
![]() $q_n(Z') \leq r_n(\pi )$
for all
$q_n(Z') \leq r_n(\pi )$
for all
![]() $n \geq 1$
.
$n \geq 1$
.
Proof. We use the properties of Markov approximations mentioned in §2. Let
![]() $\varepsilon = h(Y)-h(Z)$
. Let
$\varepsilon = h(Y)-h(Z)$
. Let
![]() $m_0$
be such that
$m_0$
be such that
![]() $h(Z_{m_0}) < h(Z) + \varepsilon /3$
, where
$h(Z_{m_0}) < h(Z) + \varepsilon /3$
, where
![]() $Z_{m_0}$
is the
$Z_{m_0}$
is the
![]() $m_0$
th Markov approximation to Z, and such that, by Proposition 4.3, for all
$m_0$
th Markov approximation to Z, and such that, by Proposition 4.3, for all
![]() $n \geq m_0$
,
$n \geq m_0$
,
![]() $({1}/{n}) \log r_n(\pi )> h(Y) - \varepsilon /3$
. Let
$({1}/{n}) \log r_n(\pi )> h(Y) - \varepsilon /3$
. Let
![]() $m_1 \geq m_0$
be such that
$m_1 \geq m_0$
be such that
![]() $({1}/{n}) \log q_n(Z_{m_0}) < h(Z_{m_0}) + \varepsilon /3$
for all
$({1}/{n}) \log q_n(Z_{m_0}) < h(Z_{m_0}) + \varepsilon /3$
for all
![]() $n \geq m_1$
. Let
$n \geq m_1$
. Let
![]() $m_2 \geq m_1$
be such that for all periodic points
$m_2 \geq m_1$
be such that for all periodic points
![]() $z \in P(Z_{m_1}) \setminus Z$
(under the natural embedding
$z \in P(Z_{m_1}) \setminus Z$
(under the natural embedding
![]() $Z \hookrightarrow Z_{m_1}$
) with
$Z \hookrightarrow Z_{m_1}$
) with
![]() $\mathrm {per}(z) \leq m_1$
, we have
$\mathrm {per}(z) \leq m_1$
, we have
![]() $z_{[0,m_2)} \notin \mathcal {B}_{m_2}(Z)$
. Then
$z_{[0,m_2)} \notin \mathcal {B}_{m_2}(Z)$
. Then
![]() $Z_{m_2}$
satisfies
$Z_{m_2}$
satisfies
![]() $q_n(Z_{m_2}) = q_n(Z) \leq r_n(\pi )$
for all
$q_n(Z_{m_2}) = q_n(Z) \leq r_n(\pi )$
for all
![]() $n \leq m_1$
. Moreover, since
$n \leq m_1$
. Moreover, since
![]() $Z_{m_2} \subset Z_{m_0}$
,
$Z_{m_2} \subset Z_{m_0}$
,
![]() $({1}/{n}) \log q_n(Z_{m_2}) \leq ({1}/{n}) \log q_n(Z_{m_0})$
for all n; in particular,
$({1}/{n}) \log q_n(Z_{m_2}) \leq ({1}/{n}) \log q_n(Z_{m_0})$
for all n; in particular,
 $$ \begin{align*} \frac{1}{n} \log q_n(Z_{m_2}) &< h(Z_{m_0}) + \varepsilon/3 \\ &< h(Z) + 2\varepsilon/3 \\ &= h(Y) - \varepsilon/3 \\ &< \frac{1}{n} \log r_n(\pi) \end{align*} $$
$$ \begin{align*} \frac{1}{n} \log q_n(Z_{m_2}) &< h(Z_{m_0}) + \varepsilon/3 \\ &< h(Z) + 2\varepsilon/3 \\ &= h(Y) - \varepsilon/3 \\ &< \frac{1}{n} \log r_n(\pi) \end{align*} $$
for all
![]() $n \geq m_1$
. Taking
$n \geq m_1$
. Taking
![]() $Z' = Z_{m_2}^{[m_2]}$
to be the
$Z' = Z_{m_2}^{[m_2]}$
to be the
![]() $m_2$
th higher block shift, the lemma is proved.
$m_2$
th higher block shift, the lemma is proved.
To prove Corollary 1.3, in the mixing sofic case, we use Lemma 2.3 to handle low-order periodic point obstructions, with periodic points of sufficiently high order controlled by Proposition 4.3. To handle the arbitrary case, we first give an improved Markov approximation (Lemma 5.2), embedding an arbitrary subshift into a mixing SFT with only slightly greater entropy. The construction uses Lemma 3.10; in Lemma 5.1, we estimate the entropy of the mixing SFT constructed in Lemma 3.10. For convenience, we recall Lemma 3.10.
Lemma 3.10. Let X be a mixing SFT with gap g and let
![]() $V_0 \subset X$
be an SFT. Let
$V_0 \subset X$
be an SFT. Let
![]() $k \geq g$
and let
$k \geq g$
and let
![]() $\mu \in \mathcal {B}(X) \setminus \mathcal {B}(V_0)$
be an
$\mu \in \mathcal {B}(X) \setminus \mathcal {B}(V_0)$
be an
![]() $(X,V_0,k)$
stamp. Let
$(X,V_0,k)$
stamp. Let
![]() $N \geq |\mu |$
and let
$N \geq |\mu |$
and let
![]() $V_1 \subset X$
be the closure of the set of points of the form
$V_1 \subset X$
be the closure of the set of points of the form
where for each i,
![]() $\gamma ^{\pm }_i \in \mathcal {B}_k(X)$
and
$\gamma ^{\pm }_i \in \mathcal {B}_k(X)$
and
![]() $v_i \in \mathcal {B}(V_0)$
with
$v_i \in \mathcal {B}(V_0)$
with
![]() $|v_i| \geq N$
. Then
$|v_i| \geq N$
. Then
![]() $V_1$
is a mixing SFT.
$V_1$
is a mixing SFT.
Lemma 5.1. Let X be a mixing SFT with gap g and let
![]() $V_0 \subset X$
be an SFT. Let
$V_0 \subset X$
be an SFT. Let
![]() $k \geq g$
and let
$k \geq g$
and let
![]() $\mu \in \mathcal {B}(X) \setminus \mathcal {B}(V_0)$
be an
$\mu \in \mathcal {B}(X) \setminus \mathcal {B}(V_0)$
be an
![]() $(X,V_0,k)$
stamp. For any
$(X,V_0,k)$
stamp. For any
![]() $\varepsilon> 0$
, there exists
$\varepsilon> 0$
, there exists
![]() $N \geq |\mu |$
such that
$N \geq |\mu |$
such that
![]() $h(V_1) < h(V_0) + \varepsilon $
, where
$h(V_1) < h(V_0) + \varepsilon $
, where
![]() $V_1$
(depending on N) is as in Lemma 3.10.
$V_1$
(depending on N) is as in Lemma 3.10.
Proof. Let
![]() $N_0 {\kern-1.2pt}\geq{\kern-1.2pt} 1$
be such that for all
$N_0 {\kern-1.2pt}\geq{\kern-1.2pt} 1$
be such that for all
![]() $n {\kern-1.2pt}\geq{\kern-1.2pt} N_0$
, we have
$n {\kern-1.2pt}\geq{\kern-1.2pt} N_0$
, we have
![]() $({1}/{n}) \log |\mathcal {B}_n(V_0)| {\kern-1.2pt}<{\kern-1.2pt} h(V_0) + \varepsilon /4$
. Let
$({1}/{n}) \log |\mathcal {B}_n(V_0)| {\kern-1.2pt}<{\kern-1.2pt} h(V_0) + \varepsilon /4$
. Let
![]() $N> 2N_0$
be such that
$N> 2N_0$
be such that
We will show that
![]() $({1}/{n}) \log |\mathcal {B}_N(V_1)| < h(V_0) + \varepsilon $
. Consider a block of length N in
$({1}/{n}) \log |\mathcal {B}_N(V_1)| < h(V_0) + \varepsilon $
. Consider a block of length N in
![]() $V_1$
. Such a block can contain at most one full or partial block of the form
$V_1$
. Such a block can contain at most one full or partial block of the form
![]() $\gamma ^+ \mu \gamma ^-$
, where
$\gamma ^+ \mu \gamma ^-$
, where
![]() $\gamma ^{\pm } \in \mathcal {B}_k(X)$
. The
$\gamma ^{\pm } \in \mathcal {B}_k(X)$
. The
![]() $\mu $
, if present, can begin at any of the N positions. The rest of the block of length N, outside the block
$\mu $
, if present, can begin at any of the N positions. The rest of the block of length N, outside the block
![]() $\gamma ^+ \mu \gamma ^-$
, consists of one or two blocks from
$\gamma ^+ \mu \gamma ^-$
, consists of one or two blocks from
![]() $V_0$
, with length totaling at most N. We thus have
$V_0$
, with length totaling at most N. We thus have
If
![]() $0 \leq \ell \leq N_0$
, then
$0 \leq \ell \leq N_0$
, then
![]() $|\mathcal {B}_{\ell }(V_0)| |\mathcal {B}_{N-\ell }(V_0)| \leq |\mathcal {B}_{N_0}(V_0)| |\mathcal {B}_{N}(V_0)|$
, so
$|\mathcal {B}_{\ell }(V_0)| |\mathcal {B}_{N-\ell }(V_0)| \leq |\mathcal {B}_{N_0}(V_0)| |\mathcal {B}_{N}(V_0)|$
, so
 $$ \begin{align*} \frac{1}{N} \log ( |\mathcal{B}_{\ell}(V_0)| |\mathcal{B}_{N-\ell}(V_0)| ) &\leq \frac{1}{N} \log |\mathcal{B}_{N_0}(V_0)| + \frac{1}{N} \log |\mathcal{B}_{N}(V_0)| \\ &< h(V_0) + \frac{\varepsilon}{2}. \end{align*} $$
$$ \begin{align*} \frac{1}{N} \log ( |\mathcal{B}_{\ell}(V_0)| |\mathcal{B}_{N-\ell}(V_0)| ) &\leq \frac{1}{N} \log |\mathcal{B}_{N_0}(V_0)| + \frac{1}{N} \log |\mathcal{B}_{N}(V_0)| \\ &< h(V_0) + \frac{\varepsilon}{2}. \end{align*} $$
If
![]() $N_0 \leq \ell \leq N/2$
, then
$N_0 \leq \ell \leq N/2$
, then
 $$ \begin{align*} \frac{1}{N} \log ( |\mathcal{B}_{\ell}(V_0)| |\mathcal{B}_{N-\ell}(V_0)| ) &< \frac{1}{N} \bigg( \ell \bigg(h(V_0) + \frac{\varepsilon}{4} \bigg) + (N-\ell) \bigg(h(V_0) + \frac{\varepsilon}{4} \bigg) \bigg) \\ &= h(V_0) + \frac{\varepsilon}{4}. \end{align*} $$
$$ \begin{align*} \frac{1}{N} \log ( |\mathcal{B}_{\ell}(V_0)| |\mathcal{B}_{N-\ell}(V_0)| ) &< \frac{1}{N} \bigg( \ell \bigg(h(V_0) + \frac{\varepsilon}{4} \bigg) + (N-\ell) \bigg(h(V_0) + \frac{\varepsilon}{4} \bigg) \bigg) \\ &= h(V_0) + \frac{\varepsilon}{4}. \end{align*} $$
Therefore,
 $$ \begin{align*} \frac{1}{N} \log |\mathcal{B}_N(V_1)| &< \frac{1}{N} \log N + \frac{1}{N} \log |\mathcal{B}_k(X)|^2 + h(V_0) + \frac{\varepsilon}{2} \\ &< h(V_0) + \varepsilon \end{align*} $$
$$ \begin{align*} \frac{1}{N} \log |\mathcal{B}_N(V_1)| &< \frac{1}{N} \log N + \frac{1}{N} \log |\mathcal{B}_k(X)|^2 + h(V_0) + \frac{\varepsilon}{2} \\ &< h(V_0) + \varepsilon \end{align*} $$
by the above choice of N.
We now give the aforementioned lemma improving the construction of the Markov approximation. For completeness, we include a proof using Lemma 3.10.
Lemma 5.2. Let Z be a subshift and let
![]() $\varepsilon> 0$
. Then there exists a mixing SFT V containing Z with
$\varepsilon> 0$
. Then there exists a mixing SFT V containing Z with
![]() $h(V) < h(Z) + \varepsilon $
.
$h(V) < h(Z) + \varepsilon $
.
Proof. Let m be large enough that
![]() $h(Z_m) < h(Z) + \varepsilon /2$
, where
$h(Z_m) < h(Z) + \varepsilon /2$
, where
![]() $Z_m$
is the mth Markov approximation to Z. Let X be the full shift on the alphabet of Z. Certainly,
$Z_m$
is the mth Markov approximation to Z. Let X be the full shift on the alphabet of Z. Certainly,
![]() $Z_m \subseteq X$
. If
$Z_m \subseteq X$
. If
![]() $Z_m = X$
, then we can take
$Z_m = X$
, then we can take
![]() $V=X$
. If
$V=X$
. If
![]() $Z_m \neq X$
, then by Proposition 3.4, let
$Z_m \neq X$
, then by Proposition 3.4, let
![]() $\mu $
be an
$\mu $
be an
![]() $(X,Z_m,k)$
stamp for some
$(X,Z_m,k)$
stamp for some
![]() $k \geq 0$
. Let
$k \geq 0$
. Let
![]() $V_0 = Z_m$
and
$V_0 = Z_m$
and
![]() $V=V_1$
as in Lemma 3.10 where N is large enough that, by Lemma 5.1, we have
$V=V_1$
as in Lemma 3.10 where N is large enough that, by Lemma 5.1, we have
![]() $h(V) < \varepsilon /2$
. Thus, V is indeed a mixing SFT containing Z with
$h(V) < \varepsilon /2$
. Thus, V is indeed a mixing SFT containing Z with
![]() $h(V) < h(Z) + \varepsilon $
.
$h(V) < h(Z) + \varepsilon $
.
We can now prove Corollary 1.3.
Corollary 1.3. Let X be a mixing SFT, Y a mixing sofic shift, and
![]() $\pi : X \to Y$
a factor code. Let Z be a subshift with topological entropy strictly less than that of Y. Then there exist a subshift
$\pi : X \to Y$
a factor code. Let Z be a subshift with topological entropy strictly less than that of Y. Then there exist a subshift
![]() $Z'$
, a finite-to-one factor code
$Z'$
, a finite-to-one factor code
![]() $\chi : Z' \to Z$
, and a sliding block code
$\chi : Z' \to Z$
, and a sliding block code
![]() $\psi : Z' \to X$
such that
$\psi : Z' \to X$
such that
![]() $\pi \circ \psi $
is injective. Moreover, if Z is mixing sofic with positive entropy (that is, Z does not consist of a single fixed point), then
$\pi \circ \psi $
is injective. Moreover, if Z is mixing sofic with positive entropy (that is, Z does not consist of a single fixed point), then
![]() $Z'$
can be taken to be a mixing SFT and
$Z'$
can be taken to be a mixing SFT and
![]() $\chi $
can be taken to be almost invertible.
$\chi $
can be taken to be almost invertible.
Proof. We first consider the case in which Z is mixing sofic. Let
![]() be a mixing SFT and
be a mixing SFT and
![]() an almost invertible factor code. If already
an almost invertible factor code. If already
![]() for all
for all
![]() $n \geq 1$
, then we can take
$n \geq 1$
, then we can take
![]() and apply Theorem 1.1 immediately to construct the claimed embedding
and apply Theorem 1.1 immediately to construct the claimed embedding
![]() $\psi : Z' \to X$
. However, if
$\psi : Z' \to X$
. However, if
![]() for some n, so that
for some n, so that
![]() violate the hypotheses of Theorem 1.1, then we need to construct a further extension of
violate the hypotheses of Theorem 1.1, then we need to construct a further extension of
![]() which satisfies the hypotheses of Theorem 1.1. The construction, consisting of a tower of extensions via Lemma 2.3, is as follows.
which satisfies the hypotheses of Theorem 1.1. The construction, consisting of a tower of extensions via Lemma 2.3, is as follows.
By Proposition 4.3, since
![]() , there are at most finitely many n such that
, there are at most finitely many n such that
![]() . Let N denote the greatest such n. Let
. Let N denote the greatest such n. Let
![]() . That is, C is the number of periodic points by which
. That is, C is the number of periodic points by which
![]() violate the hypotheses of Theorem 1.1. For
violate the hypotheses of Theorem 1.1. For
![]() $1 \leq k \leq N$
and
$1 \leq k \leq N$
and
![]() , let
, let
![]() $z_{k,\ell }$
be periodic points with pairwise disjoint orbits, such that
$z_{k,\ell }$
be periodic points with pairwise disjoint orbits, such that
![]() $\mathrm {per}(z_{k,\ell }) = k$
. For a given k, the union of the orbits of the points
$\mathrm {per}(z_{k,\ell }) = k$
. For a given k, the union of the orbits of the points
![]() $z_{k,\ell }$
has cardinality
$z_{k,\ell }$
has cardinality
![]() . Let
. Let
![]() (counting orbits, rather than points), and let
(counting orbits, rather than points), and let
![]() $\{ z^{(j)} \}_{j=1}^{C'} = \{ z_{k,\ell } \}_{k,\ell }$
be an enumeration of the points
$\{ z^{(j)} \}_{j=1}^{C'} = \{ z_{k,\ell } \}_{k,\ell }$
be an enumeration of the points
![]() $z_{k,\ell }$
.
$z_{k,\ell }$
.
Again by Proposition 4.3, let
![]() $M> N$
be large enough that for all
$M> N$
be large enough that for all
![]() $n \geq M$
, we have
$n \geq M$
, we have
. We now repeatedly apply Lemma 2.3. Let
. For
![]() $1 \leq j \leq C'$
, let
$1 \leq j \leq C'$
, let
![]() $Z^{(j)}$
be a mixing SFT and
$Z^{(j)}$
be a mixing SFT and
![]() $\chi ^{(j)}: Z^{(j)} \to Z^{(j-1)}$
an almost invertible factor code such that the preimage of the orbit of
$\chi ^{(j)}: Z^{(j)} \to Z^{(j-1)}$
an almost invertible factor code such that the preimage of the orbit of
![]() $z^{(j)}$
under
$z^{(j)}$
under
![]() $\chi ^{(j)}$
is a single orbit of length
$\chi ^{(j)}$
is a single orbit of length
![]() $M \mathrm {per}(z^{(j)})$
, and such that every periodic point in
$M \mathrm {per}(z^{(j)})$
, and such that every periodic point in
![]() $Z^{(j-1)}$
not in the orbit of
$Z^{(j-1)}$
not in the orbit of
![]() $z^{(j)}$
has a unique preimage under
$z^{(j)}$
has a unique preimage under
![]() $\chi ^{(j)}$
. Let
$\chi ^{(j)}$
. Let
![]() $\eta ^{(1)} = \chi ^{(1)}$
and
$\eta ^{(1)} = \chi ^{(1)}$
and
![]() $\eta ^{(j+1)} = \eta ^{(j)} \circ \chi ^{(j+1)}$
. Let
$\eta ^{(j+1)} = \eta ^{(j)} \circ \chi ^{(j+1)}$
. Let
![]() $Z' = Z^{(C')}$
and
$Z' = Z^{(C')}$
and
. Certainly,
![]() $\eta $
is almost invertible, so
$\eta $
is almost invertible, so
. We claim that
![]() $q_n(Z') \leq r_n(\pi )$
for all
$q_n(Z') \leq r_n(\pi )$
for all
![]() $n \geq 1$
. Indeed, for each j, if
$n \geq 1$
. Indeed, for each j, if
![]() $\mathrm {per}(z^{(j)}) = k$
, then we have
$\mathrm {per}(z^{(j)}) = k$
, then we have
![]() $q_k(Z^{(j)}) = q_k(Z^{(j-1)}) - k$
,
$q_k(Z^{(j)}) = q_k(Z^{(j-1)}) - k$
,
![]() $q_{Mk}(Z^{(j)}) = q_{Mk}(Z^{(j-1)}) + Mk$
, and
$q_{Mk}(Z^{(j)}) = q_{Mk}(Z^{(j-1)}) + Mk$
, and
![]() $q_n(Z^{(j)}) = q_n(Z^{(j-1)})$
for all
$q_n(Z^{(j)}) = q_n(Z^{(j-1)})$
for all
![]() $n \notin \{ k, Mk \}$
. Therefore,
$n \notin \{ k, Mk \}$
. Therefore,
![]() $q_k( Z' ) = r_k(\pi )$
and
$q_k( Z' ) = r_k(\pi )$
and

where the last inequality follows from the choice of M. Therefore,
![]() $X,Y,\pi ,Z'$
satisfy the hypotheses of Theorem 1.1, so there exists a sliding block code
$X,Y,\pi ,Z'$
satisfy the hypotheses of Theorem 1.1, so there exists a sliding block code
![]() $\psi : Z' \to X$
such that
$\psi : Z' \to X$
such that
![]() $\pi \circ \psi $
is injective. This concludes the proof in the case where Z is mixing sofic.
$\pi \circ \psi $
is injective. This concludes the proof in the case where Z is mixing sofic.
We now handle the general case, where Z is an arbitrary subshift with
![]() $h(Z) < h(Y)$
. By Lemma 5.2, let V be a mixing SFT containing Z with
$h(Z) < h(Y)$
. By Lemma 5.2, let V be a mixing SFT containing Z with
![]() $h(V) < h(Y)$
. By the mixing sofic case, let
$h(V) < h(Y)$
. By the mixing sofic case, let
![]() $V'$
be a mixing SFT such that
$V'$
be a mixing SFT such that
![]() $X,Y,\pi ,V'$
satisfy the hypotheses of Theorem 1.1, and let
$X,Y,\pi ,V'$
satisfy the hypotheses of Theorem 1.1, and let
![]() $\chi : V' \to V$
be an almost invertible factor code. Let
$\chi : V' \to V$
be an almost invertible factor code. Let
![]() $Z' = \chi ^{-1}(Z)$
. Then
$Z' = \chi ^{-1}(Z)$
. Then
![]() $\chi |_{Z'}$
is still finite-to-one, which concludes the proof.
$\chi |_{Z'}$
is still finite-to-one, which concludes the proof.
Acknowledgments
I thank Tom Meyerovitch for posing the question that led to this work and suggesting the argument for Proposition 4.3, and more generally for offering, with Brian Marcus, very generous advice and supervision. For helpful and interesting conversations about the relationship between this work and the embedding problem for sofic shifts, I also thank Mike Boyle and Klaus Thomsen. Finally, I thank the anonymous reviewer for their very careful reading and their detailed report.