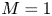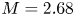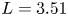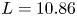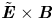1 Introduction
Historically, mirror research has prioritized the main issues with mirror confinement: stabilizing the interchange instability, stabilizing velocity-space (loss-cone-driven) instabilities and minimizing axial electron heat losses. Nevertheless, cross-field transport remains an important topic in magnetic-confinement fusion reactor development, in both linear and toroidal geometries. Insight into edge-relevant turbulence, and its coupling to interchange and other mirror-driven instabilities, performed in a basic plasma science device may be useful for a mirror-based reactor. Although not at fusion-relevant core temperatures or densities, the Large Plasma Device (LAPD) operates at conditions similar to the edge of fusion devices and can provide insight into the physical processes in that region. Mirror machines are once again rising in prominence as a candidate for commercial fusion reactors with the advent of highly funded commercial ventures and high-field high-temperature superconducting magnets (Endrizzi et al. Reference Endrizzi2023; Forest et al. Reference Forest2024), so development of a functional understanding of cross-field transport in mirrors is imperative. A characterization of edge fluctuations has been undertaken, with emphasis on interpreting these fluctuations within the context of a mirror.
Non-classical cross-field particle transport is often caused by low-frequency, large-amplitude fluctuations. These fluctuations are the result of various instabilities. One such process is the ‘universal’ drift instability, which appears in the presence of a density gradient and finite resistivity. Drift-wave turbulence and the effect on transport has been extensively studied in the past (Horton Reference Horton1999; Tynan, Fujisawa & McKee Reference Tynan, Fujisawa and McKee2009). In the presence of sufficiently high rotation or sheared flow, rotational interchange and the Kelvin–Helmholtz instabilities also contribute or couple to these fluctuations.
Various gradient-, rotation- and shear-driven instabilities (and suppression of such) have been studied previously in the LAPD experimentally (Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2012, Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2013; Schaffner Reference Schaffner2013) and in simulations using BOUT, a three-dimensional fluid turbulence code, and an eigenvalue solver (Popovich et al. Reference Popovich, Umansky, Carter and Friedman2010). The LAPD has a sufficiently high spontaneous rotation rate that rotation-driven instabilities may be excited without artificial drive. Simulations using BOUT++ (Friedman et al. Reference Friedman, Carter, Umansky, Schaffner and Joseph2013) have also suggested that a rapidly growing nonlinear instability may dominate over all other linear instabilities.
Imposing a magnetic mirror configuration introduces magnetic curvature. The alignment of the curvature vector with a pressure gradient vector component causes the flute-like interchange instability if no stabilization mechanism is present. This interchange mode could couple to finite parallel wavenumber, $k_\parallel$![]() drift waves. The coupling of drift waves to curvature-induced interchange modes has been studied in toroidal devices such as TORPEX (Fasoli et al. Reference Fasoli, Labit, McGrath, Müller, Plyushchev, Podestà and Poli2006; Poli et al. Reference Poli, Brunner, Diallo, Fasoli, Furno, Labit, Müller, Plyushchev and Podestà2006), where curvature was seen as the driving component for the unstable drift-interchange modes. Drift-like fluctuations have also been observed in the GAMMA-10 mirror (Mase et al. Reference Mase, Itakura, Inutake, Ishii, Jeong, Hattori and Miyoshi1991; Yoshikawa et al. Reference Yoshikawa2010). Flute-like modes and drift waves have been studied in other linear devices, such as Mirabelle (Brochard, Gravier & Bonhomme Reference Brochard, Gravier and Bonhomme2005), where the appearance of flute-like modes or drift waves were controlled by varying the field and limiter diameter.
drift waves. The coupling of drift waves to curvature-induced interchange modes has been studied in toroidal devices such as TORPEX (Fasoli et al. Reference Fasoli, Labit, McGrath, Müller, Plyushchev, Podestà and Poli2006; Poli et al. Reference Poli, Brunner, Diallo, Fasoli, Furno, Labit, Müller, Plyushchev and Podestà2006), where curvature was seen as the driving component for the unstable drift-interchange modes. Drift-like fluctuations have also been observed in the GAMMA-10 mirror (Mase et al. Reference Mase, Itakura, Inutake, Ishii, Jeong, Hattori and Miyoshi1991; Yoshikawa et al. Reference Yoshikawa2010). Flute-like modes and drift waves have been studied in other linear devices, such as Mirabelle (Brochard, Gravier & Bonhomme Reference Brochard, Gravier and Bonhomme2005), where the appearance of flute-like modes or drift waves were controlled by varying the field and limiter diameter.
The rotational interchange and curvature interchange can both be flute-like modes. Rotational interchange (also called the ‘centrifugal instability’) is driven by the aligned centrifugal force and pressure gradient vectors, but curvature-driven interchange is instead driven by magnetic curvature and is typically referred to as simply the ‘flute’ or ‘interchange’ instability. Rotational interchange (Jassby Reference Jassby1972) has been observed in the LAPD in the past (Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2012; Schaffner Reference Schaffner2013), and the curvature-driven interchange instability has been observed in many other mirror machines (Wickham & Vandegrift Reference Wickham and Vandegrift1982; Ferron et al. Reference Ferron, Wong, Dimonte and Leikind1983; Post Reference Post1987).
Biasing or modifying the electrical connection of the plasma with the end wall has proven to be a important actuator in many mirror machines such as TMX-U (Hooper et al. Reference Hooper, Baldwin, Fowler, Kane and Turner1984), GAMMA-10 (Mase et al. Reference Mase, Itakura, Inutake, Ishii, Jeong, Hattori and Miyoshi1991) and GDT (Bagryansky et al. Reference Bagryansky, Lizunov, Zuev, Kolesnikov and Solomachin2003; Bagryansky, Beklemishev & Soldatkina Reference Bagryansky, Beklemishev and Soldatkina2007; Beklemishev et al. Reference Beklemishev, Bagryansky, Chaschin and Soldatkina2010), and will be utilized on WHAM (Endrizzi et al. Reference Endrizzi2023). Active biasing was not attempted in this study, but the intrinsic rotation and strong electrical connection to the source region may provide a useful analogue for edge biasing in other mirror machines.
The LAPD exhibits a high degree of turbulence so it is difficult to identify the dispersion relation of the modes that are present. Nevertheless, the LAPD has good coverage of perpendicular spectra using correlation-plane techniques, and some measure of parallel spectra using the correlation between two axially separated probes. A space–time spectral characterization of the many instabilities present in this low beta (ratio of plasma pressure to magnetic pressure), moderate aspect ratio, gas-dynamic trap regime is attempted.
This goal of this study was to investigate the changes to turbulence and transport in LAPD mirror configurations. Of particular interest were the potential coupling of the interchange instability with drift waves or other modes, and the effect of the mirror geometry on cross-field particle flux. Presented is a characterization of the observed modes and the effect of introducing a mirror geometry. This paper is organized as follows. Section 2 discusses the configuration of the LAPD and the diagnostics used. Section 3 covers the changes seen when imposing a magnetic mirror configuration on profiles, particle flux, drift waves, turbulence and magnetic fluctuations. Section 4 explores the changes in two dimensions ($x\unicode{x2013}y$![]() plane) structure. Section 5 discusses the active and expected instabilities and reasons for their modification. Section 6 summarizes the study and discusses the requirements for a deeper investigation.
plane) structure. Section 5 discusses the active and expected instabilities and reasons for their modification. Section 6 summarizes the study and discusses the requirements for a deeper investigation.
2 Device configuration
2.1 The Large Plasma Device
The LAPD is a 20 m long, 1 m diameter basic plasma device at UCLA (Gekelman et al. Reference Gekelman2016). The LAPD has a variable magnetic field, from 250 G to 1.6 kG and can be varied axially. Probes inserted into the plasma can collect high-resolution, temporal information on density, temperature, potential and magnetic field fluctuations. In this study, the plasma was formed using an emissive, 72 cm diameter barium-oxide (BaO) cathode (mapped to 60 cm in a flat field) and a 72 cm diameter, 50 % transparent molybdenum anode that accelerate electrons across a configurable 40–70 V potential; voltages of $60$![]() and 63 V were used in this study. The source has since been upgraded to a lanthanum hexaboride (LaB6) cathode (Qian et al. Reference Qian2023) that enables access to higher-density, higher-temperature regimes, but all the data in this study are from plasma formed by a BaO cathode.
and 63 V were used in this study. The source has since been upgraded to a lanthanum hexaboride (LaB6) cathode (Qian et al. Reference Qian2023) that enables access to higher-density, higher-temperature regimes, but all the data in this study are from plasma formed by a BaO cathode.
The flexible magnetic geometry of the LAPD was used to construct a variety of magnetic mirror configurations. The discharge current, fill pressure and other machine parameters were held constant. The typical plasma parameters observed in this study can be seen in table 2. Data at several mirror ratios and lengths were collected (see table 1) but emphasis is placed on the short cell because the highest mirror ratio possible ($M=2.68$![]() ) with a $500$
) with a $500$![]() Gauss midplane field could be accessed and probes were able to be placed outside of the mirror cell. An overview of the axial magnetic field for the short mirror configurations and probe locations can be seen in figure 1. The 2- or 3-cell mirror configurations were also explored but are not examined in this study. All results presented below are from the short mirror-cell configuration unless otherwise specified.
Gauss midplane field could be accessed and probes were able to be placed outside of the mirror cell. An overview of the axial magnetic field for the short mirror configurations and probe locations can be seen in figure 1. The 2- or 3-cell mirror configurations were also explored but are not examined in this study. All results presented below are from the short mirror-cell configuration unless otherwise specified.
Table 1. Magnetic mirror lengths and ratios. The lengths are measured where the curvature changes sign and the ratio is the maximum divided by the minimum. Approximately $3.5$![]() m must be added to the length if the good-curvature region is included. In the case of small asymmetries, the field strengths were averaged before calculation of the mirror ratio.
m must be added to the length if the good-curvature region is included. In the case of small asymmetries, the field strengths were averaged before calculation of the mirror ratio.

Table 2. The LAPD machine information and plasma parameters in the core and peak-fluctuation region ($x=x_\text {PF}$![]() ) at the midplane in this study. Dashed quantities are assumed to be identical to core quantities.
) at the midplane in this study. Dashed quantities are assumed to be identical to core quantities.


Figure 1. Cartoon of the LAPD and the coordinate system used. Only four of the eleven mirror configurations studied are plotted for clarity (mirrors of the same length have similar shapes and simply scale with mirror ratio). Diagnostic set varied by datarun; unlabelled diagnostics were used in both dataruns.
2.2 Diagnostics
All diagnostics were recorded with an effective sampling rate of 6.25 MHz (16-sample average at 100 Msps) and a spatial resolution of 0.5 cm. When necessary, averaging over time is done in the approximate steady-state period of the plasma discharge ($4.8$![]() to $11.2$
to $11.2$![]() ms from the 1 kA trigger signal). Unless otherwise noted, all data presented will be from probes inside the mirror region ($z \approx 7$
ms from the 1 kA trigger signal). Unless otherwise noted, all data presented will be from probes inside the mirror region ($z \approx 7$![]() m). An example of a raw ion saturation current – $I_\text {sat}=0.6 S n_e e \frac{\sqrt{T_e}}{m_i}$
m). An example of a raw ion saturation current – $I_\text {sat}=0.6 S n_e e \frac{\sqrt{T_e}}{m_i}$![]() , where $S$
, where $S$![]() is effective area, $n_e$
is effective area, $n_e$![]() electron density, $e$
electron density, $e$![]() elementary charge, $T_e$
elementary charge, $T_e$![]() electron temperature, and $m_i$
electron temperature, and $m_i$![]() ion mass – signal and processing steps can be seen in figure 2. The raw signals are detrended by subtracting the mean across shots to obtain the fluctuations only. Fast Fourier transformations are then taken of these fluctuations for calculating power spectra and cross-correlated quantities. Frequencies above 200 kHz are dominated by electronics and instrumentation noise and thus are also ignored. Fluctuation power profiles can then be constructed.
ion mass – signal and processing steps can be seen in figure 2. The raw signals are detrended by subtracting the mean across shots to obtain the fluctuations only. Fast Fourier transformations are then taken of these fluctuations for calculating power spectra and cross-correlated quantities. Frequencies above 200 kHz are dominated by electronics and instrumentation noise and thus are also ignored. Fluctuation power profiles can then be constructed.

Figure 2. Raw data and basic processing steps for LAPD probe diagnostics as demonstrated by an $I_\text {sat}$![]() trace from a DR1, $M=1$
trace from a DR1, $M=1$![]() mirror at 26 cm. Data are truncated from 4.8 to 11.2 ms ($a$
mirror at 26 cm. Data are truncated from 4.8 to 11.2 ms ($a$![]() ) and detrended ($b$
) and detrended ($b$![]() ). Power spectral density is calculated ($c$
). Power spectral density is calculated ($c$![]() ), and a power profiles can be constructed ($d$
), and a power profiles can be constructed ($d$![]() ). The shaded regions are excluded from this analysis.
). The shaded regions are excluded from this analysis.
The data presented were collected in two phases. The first phase (‘datarun’), DR1, collected Langmuir probe ($I_\text {sat}$![]() and Vf – floating potential) and magnetic fluctuation (‘Bdot’) (Everson et al. Reference Everson, Pribyl, Constantin, Zylstra, Schaeffer, Kugland and Niemann2009) traces. Fifty shots were taken at each position for every configuration. The second phase, DR2, was conducted with a similar set of diagnostics focused on temperature measurements (swept and triple probe) and the two-dimensional $x$
and Vf – floating potential) and magnetic fluctuation (‘Bdot’) (Everson et al. Reference Everson, Pribyl, Constantin, Zylstra, Schaeffer, Kugland and Niemann2009) traces. Fifty shots were taken at each position for every configuration. The second phase, DR2, was conducted with a similar set of diagnostics focused on temperature measurements (swept and triple probe) and the two-dimensional $x$![]() –$y$
–$y$![]() structure. Fifteen shots were taken at each position, except for Langmuir sweeps with 64 shots. When appropriate, all data for each position were shot averaged. The parameter ‘$I_\text {sat}$
structure. Fifteen shots were taken at each position, except for Langmuir sweeps with 64 shots. When appropriate, all data for each position were shot averaged. The parameter ‘$I_\text {sat}$![]() ’ will be used interchangeably with ‘density’ and be presented with units of density (assuming a flat electron temperature $T_e = 4.5$
’ will be used interchangeably with ‘density’ and be presented with units of density (assuming a flat electron temperature $T_e = 4.5$![]() eV profile).
eV profile).
3 Mirror-induced changes
3.1 Profile modification
Because the field at the plasma source increases with $M$![]() , the midplane plasma expands by a factor of $\sqrt {M}$
, the midplane plasma expands by a factor of $\sqrt {M}$![]() . The physical locations of the peak-fluctuation region – $x_{\rm PF}$
. The physical locations of the peak-fluctuation region – $x_{\rm PF}$![]() (maximum gradient) – and the cathode radius $x_c$
(maximum gradient) – and the cathode radius $x_c$![]() can be seen in table 3. This expansion leads to broader plasma profiles and decreased core density but these profiles are similar in the core and at $x_{\rm PF}$
can be seen in table 3. This expansion leads to broader plasma profiles and decreased core density but these profiles are similar in the core and at $x_{\rm PF}$![]() when magnetically mapped to the cathode radius $x_c$
when magnetically mapped to the cathode radius $x_c$![]() , as seen in figure 3. Dips between the core ($x/x_c=0)$
, as seen in figure 3. Dips between the core ($x/x_c=0)$![]() and the peak-fluctuation region ($x=x_{\rm PF})$
and the peak-fluctuation region ($x=x_{\rm PF})$![]() are seen, but fluctuation power from this region ($x/x_c = 0.5$
are seen, but fluctuation power from this region ($x/x_c = 0.5$![]() to $0.7$
to $0.7$![]() ) is not significant (figure 7) so this region is not the focus of this study. The line-integrated density as measured by a 56 GHz heterodyne interferometer increases up to ${\sim }35\,\%$
) is not significant (figure 7) so this region is not the focus of this study. The line-integrated density as measured by a 56 GHz heterodyne interferometer increases up to ${\sim }35\,\%$![]() from the $M=1$
from the $M=1$![]() case of ${\approx }8 \times 10^{13}\ {\rm cm}^{-2}$
case of ${\approx }8 \times 10^{13}\ {\rm cm}^{-2}$![]() (figure 4) but does not increase past a mirror ratio of 2.3. Discharge power increases only slightly ($3\,\%$
(figure 4) but does not increase past a mirror ratio of 2.3. Discharge power increases only slightly ($3\,\%$![]() ) at higher mirror ratios, suggesting negligible impact on density. Langmuir sweeps and triple probe measurements of $T_e$
) at higher mirror ratios, suggesting negligible impact on density. Langmuir sweeps and triple probe measurements of $T_e$![]() (DR2) show slightly (less than 25 %) depressed core and slightly elevated edge $T_e$
(DR2) show slightly (less than 25 %) depressed core and slightly elevated edge $T_e$![]() with increasing mirror ratio (figure 5) but otherwise remains unaffected. The temperature affects $I_\text {sat}$
with increasing mirror ratio (figure 5) but otherwise remains unaffected. The temperature affects $I_\text {sat}$![]() measurements through the $\sqrt {T_e}$
measurements through the $\sqrt {T_e}$![]() term so small changes are insignificant. The low temperatures indicate that the plasma is collisional given the length scales of the system (as seen in table 2) and isotropic. Plasma potential decreases across the plasma (figure 6) when the mirror ratio exceeds 1.9. This drop in plasma potential may be caused by the grounding of the anode to the wall, which should begin at $M=1.93$
term so small changes are insignificant. The low temperatures indicate that the plasma is collisional given the length scales of the system (as seen in table 2) and isotropic. Plasma potential decreases across the plasma (figure 6) when the mirror ratio exceeds 1.9. This drop in plasma potential may be caused by the grounding of the anode to the wall, which should begin at $M=1.93$![]() given the 72 cm anode and 100 cm vessel diameters. The reason for the local minimum in the $M=2.68$
given the 72 cm anode and 100 cm vessel diameters. The reason for the local minimum in the $M=2.68$![]() is unknown. This potential profile creates a sheared $\boldsymbol {E} \boldsymbol {\times } \boldsymbol {B}$
is unknown. This potential profile creates a sheared $\boldsymbol {E} \boldsymbol {\times } \boldsymbol {B}$![]() velocity profile (figure 6) limited to $500\ {\rm m}\ {\rm s}^{-1}$
velocity profile (figure 6) limited to $500\ {\rm m}\ {\rm s}^{-1}$![]() in the core and exceeding ${\sim }3\ {\rm km}\ {\rm s}^{-1}$
in the core and exceeding ${\sim }3\ {\rm km}\ {\rm s}^{-1}$![]() at the far edge. The flow does not exceed 4 % of the sound speed (table 2) in the core or gradient ($x=x_{\rm PF}$
at the far edge. The flow does not exceed 4 % of the sound speed (table 2) in the core or gradient ($x=x_{\rm PF}$![]() ) region. The mirror ratio does not appear to significantly alter azimuthal flow. The floating potential (Vf) profile also exhibits similar behaviour to the plasma potential (figure 6), but is modified by the presence of primary electrons.
) region. The mirror ratio does not appear to significantly alter azimuthal flow. The floating potential (Vf) profile also exhibits similar behaviour to the plasma potential (figure 6), but is modified by the presence of primary electrons.
Table 3. The $x_c$![]() and $x_{\rm PF}$
and $x_{\rm PF}$![]() locations for each mirror ratio when scaled by the expected magnetic expansion.
locations for each mirror ratio when scaled by the expected magnetic expansion.


Figure 3. Midplane $I_\text {sat}$![]() profile, shot averaged and time averaged from 4.8 to 11.2 ms (we have assumed $T_e = 4.5$
profile, shot averaged and time averaged from 4.8 to 11.2 ms (we have assumed $T_e = 4.5$![]() eV based on triple probe and Langmuir sweep measurements). Effective area was calibrated using a nearby interferometer. Profile shape remains similar in the core and gradient region when mapped to the cathode radius $x_c$
eV based on triple probe and Langmuir sweep measurements). Effective area was calibrated using a nearby interferometer. Profile shape remains similar in the core and gradient region when mapped to the cathode radius $x_c$![]() . The dips in profiles at higher $M$
. The dips in profiles at higher $M$![]() below $x=x_\text {PF}$
below $x=x_\text {PF}$![]() are of unknown origin and are not the focus of this study. Shot-to-shot variation is less than 5 % for $x \leqslant 0.95 x_c$
are of unknown origin and are not the focus of this study. Shot-to-shot variation is less than 5 % for $x \leqslant 0.95 x_c$![]() and less than 9 % for $x \leqslant 1.4 x_c$
and less than 9 % for $x \leqslant 1.4 x_c$![]() for all cases.
for all cases.

Figure 4. Line-integrated density as measured by a 56 GHz heterodyne interferometer as a function of mirror ratio, taken from four discharges for each mirror configuration. Density increases up to a mirror ratio of 2.3, where it appears to level off. The interferometer is located in the mirror-cell bad-curvature region at 9.59 m, 1.3 m closer to the cathode from the midplane.

Figure 5. The value of $T_e$![]() from Langmuir sweeps (DR2) at the midplane. Triple probe results are nearly identical. The increased temperatures directly at the plasma edge, indicated by dotted portions of the curves, are likely artefacts caused by sheath expansion in lower densities. Changes in mirror ratio lead to at most a 25 % change in $T_e$
from Langmuir sweeps (DR2) at the midplane. Triple probe results are nearly identical. The increased temperatures directly at the plasma edge, indicated by dotted portions of the curves, are likely artefacts caused by sheath expansion in lower densities. Changes in mirror ratio lead to at most a 25 % change in $T_e$![]() . The plasma is collisional and isotropic.
. The plasma is collisional and isotropic.

Figure 6. Plasma potential Vp ($a$![]() ) and derived $\boldsymbol {E}\boldsymbol {\times }\boldsymbol {B}$
) and derived $\boldsymbol {E}\boldsymbol {\times }\boldsymbol {B}$![]() velocity profiles ($b$
velocity profiles ($b$![]() ) from Langmuir sweeps at the midplane. The range $x/x_c > 1.2$
) from Langmuir sweeps at the midplane. The range $x/x_c > 1.2$![]() has been excluded from the graph for greater clarity in the core and gradient region. The electric field was calculated by taking the gradient of the spline-smoothed plasma potential profile. The Mach number (in per cent) is calculated using the approximate sound speed evaluated at $x=x_{\rm PF}$
has been excluded from the graph for greater clarity in the core and gradient region. The electric field was calculated by taking the gradient of the spline-smoothed plasma potential profile. The Mach number (in per cent) is calculated using the approximate sound speed evaluated at $x=x_{\rm PF}$![]() (table 2). The overall structure of the flows does not appreciably change when mirror ratio is varied.
(table 2). The overall structure of the flows does not appreciably change when mirror ratio is varied.
3.2 Reduced particle flux
The density fluctuation power peaks at the steepest gradient region ($x_{\rm PF} = x/x_c \sim 0.88)$![]() as expected, as seen in figure 7. Here, $x_{\rm PF}$
as expected, as seen in figure 7. Here, $x_{\rm PF}$![]() occurs at nearly the same magnetically mapped coordinate for each mirror ratio. These density fluctuations are a large driver of changes in the cross-field particle flux (3.1). The Vf fluctuations also peak at the same location, but the total power across mirror ratios is similar and, relative to density fluctuations, much lower in the core. Core density fluctuations below 2 kHz are substantial in the core at lower mirror ratios, possibly caused by hollow profiles, non-uniform cathode emissivity or probe perturbations, but are outside the scope of this study.
occurs at nearly the same magnetically mapped coordinate for each mirror ratio. These density fluctuations are a large driver of changes in the cross-field particle flux (3.1). The Vf fluctuations also peak at the same location, but the total power across mirror ratios is similar and, relative to density fluctuations, much lower in the core. Core density fluctuations below 2 kHz are substantial in the core at lower mirror ratios, possibly caused by hollow profiles, non-uniform cathode emissivity or probe perturbations, but are outside the scope of this study.

Figure 7. The $I_\text {sat}$![]() ($a$
($a$![]() ) and $B_\perp$
) and $B_\perp$![]() ($b$
($b$![]() ) fluctuation power profiles for signals 2 kHz and up at $z=8.3$
) fluctuation power profiles for signals 2 kHz and up at $z=8.3$![]() m (midplane) and $z=7.7$
m (midplane) and $z=7.7$![]() m, respectively. The lower-frequency components in $I_\text {sat}$
m, respectively. The lower-frequency components in $I_\text {sat}$![]() are associated with bulk profile evolution, dominate the core region and are not the focus of this study.
are associated with bulk profile evolution, dominate the core region and are not the focus of this study.
A spectral decomposition technique is used to calculate the time-averaged particle flux (Powers Reference Powers1974) as seen in figure 8
where $k$![]() is the azimuthal wavenumber component, $\gamma$
is the azimuthal wavenumber component, $\gamma$![]() is the coherency, $\alpha$
is the coherency, $\alpha$![]() is the cross-phase, $P$
is the cross-phase, $P$![]() is the power spectrum and $\omega$
is the power spectrum and $\omega$![]() is the frequency. This method is more robust than the naive time integration of $n (t ) \tilde {E} ( t )$
is the frequency. This method is more robust than the naive time integration of $n (t ) \tilde {E} ( t )$![]() because it accounts for the coherency of the density-potential fluctuations. This representation also enables inspection of each contributing term in the event of surprising or problematic results. A plot of the $I_\text {sat}$
because it accounts for the coherency of the density-potential fluctuations. This representation also enables inspection of each contributing term in the event of surprising or problematic results. A plot of the $I_\text {sat}$![]() -Vf phase can be seen in figure 9. The flattened particle flux in the core is likely caused by primary electrons emitted by the cathode. These electrons have long mean free paths (greater than a few metres) and sample fluctuations along the length of the machine, mixing the phases of these fluctuations. Since the floating potential is set by the hotter electron population, the measured Vf fluctuations are no longer related to the local plasma potential fluctuations of a wave by bulk $T_e$
-Vf phase can be seen in figure 9. The flattened particle flux in the core is likely caused by primary electrons emitted by the cathode. These electrons have long mean free paths (greater than a few metres) and sample fluctuations along the length of the machine, mixing the phases of these fluctuations. Since the floating potential is set by the hotter electron population, the measured Vf fluctuations are no longer related to the local plasma potential fluctuations of a wave by bulk $T_e$![]() (Carter & Maggs Reference Carter and Maggs2009). These primary electrons have a significant effect in the core within the region mapped to the cathode $x \lesssim x_c$
(Carter & Maggs Reference Carter and Maggs2009). These primary electrons have a significant effect in the core within the region mapped to the cathode $x \lesssim x_c$![]() . The $I_\text {sat}$
. The $I_\text {sat}$![]() fluctuations are not affected.
fluctuations are not affected.

Figure 8. Cross-field, $\tilde {E_y} \times B$![]() fluctuation-based particle flux (calculated using (3.1)) with respect to mirror ratio. A monotonic decrease in particle flux is observed with increasing mirror ratio at the midplane. Particle flux is normalized by plasma circumference to the $M=1$
fluctuation-based particle flux (calculated using (3.1)) with respect to mirror ratio. A monotonic decrease in particle flux is observed with increasing mirror ratio at the midplane. Particle flux is normalized by plasma circumference to the $M=1$![]() case to account for the geometry-induced decrease in particle flux caused by a larger-diameter plasma.
case to account for the geometry-induced decrease in particle flux caused by a larger-diameter plasma.

Figure 9. Phase ($a$![]() ) and coherency ($b$
) and coherency ($b$![]() ) of $I_\text {sat}$
) of $I_\text {sat}$![]() current and Vf near $x_{\rm PF}$
current and Vf near $x_{\rm PF}$![]() at the midplane, smoothed. Positive phase means $I_\text {sat}$
at the midplane, smoothed. Positive phase means $I_\text {sat}$![]() leads Vf. Peaks in coherency occur between 3 and 5 kHz and at the drift-Alvén wave peaks between 12 and 25 kHz. These coherency peaks tend to have larger phase shifts than other nearby frequencies.
leads Vf. Peaks in coherency occur between 3 and 5 kHz and at the drift-Alvén wave peaks between 12 and 25 kHz. These coherency peaks tend to have larger phase shifts than other nearby frequencies.
Azimuthal wavenumber is measured by two Vf probe tips $0.5$![]() cm apart. This wavenumber estimation technique yields good agreement with correlation-plane measurements (figure 17). Note that $\tilde {E}$
cm apart. This wavenumber estimation technique yields good agreement with correlation-plane measurements (figure 17). Note that $\tilde {E}$![]() is not directly measured – it is instead calculated through the $k(\omega ) \sqrt {P_{\phi \phi } (\omega )}$
is not directly measured – it is instead calculated through the $k(\omega ) \sqrt {P_{\phi \phi } (\omega )}$![]() terms.
terms.
The $\tilde {E} \times B$![]() particle flux clearly decreases with mirror ratio; most of this decrease is attributed to the decrease in density fluctuation power. The particle flux for each mirror ratio was normalized to the $M=1$
particle flux clearly decreases with mirror ratio; most of this decrease is attributed to the decrease in density fluctuation power. The particle flux for each mirror ratio was normalized to the $M=1$![]() case via the plasma circumference to compensate for the increased plasma surface area at the same magnetically mapped coordinate $x/x_c$
case via the plasma circumference to compensate for the increased plasma surface area at the same magnetically mapped coordinate $x/x_c$![]() . This particle flux is of the order of Bohm diffusion $D_B = \frac {1}{16} {T_e}/{B} \approx 6.25 \ \text {m}^{2}\ \text {s}^{-1}$
. This particle flux is of the order of Bohm diffusion $D_B = \frac {1}{16} {T_e}/{B} \approx 6.25 \ \text {m}^{2}\ \text {s}^{-1}$![]() , as observed in other transport studies (Maggs, Carter & Taylor Reference Maggs, Carter and Taylor2007).
, as observed in other transport studies (Maggs, Carter & Taylor Reference Maggs, Carter and Taylor2007).
The $T_e$![]() profiles and fluctuations may affect particle fluxes but measurements of both were not taken in the same datarun; nevertheless, a quantification of the effect of $T_e$
profiles and fluctuations may affect particle fluxes but measurements of both were not taken in the same datarun; nevertheless, a quantification of the effect of $T_e$![]() on particle flux is attempted. The $T_e$
on particle flux is attempted. The $T_e$![]() fluctuations affect $I_\text {sat}$
fluctuations affect $I_\text {sat}$![]() -based density measurements through the $T_e^{-1/2}$
-based density measurements through the $T_e^{-1/2}$![]() term, and triple probe and Langmuir sweep $T_e$
term, and triple probe and Langmuir sweep $T_e$![]() measurements suggest that temperature gradients have a negligible impact. A naive incorporation of temperature fluctuation data from DR2 into particle fluxes from DR1 suggests that cross-field particle flux may be underestimated by up to $50\,\%$
measurements suggest that temperature gradients have a negligible impact. A naive incorporation of temperature fluctuation data from DR2 into particle fluxes from DR1 suggests that cross-field particle flux may be underestimated by up to $50\,\%$![]() via the $I_\text {sat}$
via the $I_\text {sat}$![]() temperature term, but the trend and relative fluxes across mirror ratios remain unchanged. Such a naive incorporation should be treated with suspicion because of the sensitive nature of the flux with respect to the gradient and the differences in profiles between DR1 and DR2. These difference in profiles may be caused by the cathode condition, deposits on the anode or a different gas mix and are difficult to account for.
temperature term, but the trend and relative fluxes across mirror ratios remain unchanged. Such a naive incorporation should be treated with suspicion because of the sensitive nature of the flux with respect to the gradient and the differences in profiles between DR1 and DR2. These difference in profiles may be caused by the cathode condition, deposits on the anode or a different gas mix and are difficult to account for.
3.3 Drift waves
The $I_\text {sat}$![]() fluctuation power spectra in the region of peak power $x \sim x_\text {PF}$
fluctuation power spectra in the region of peak power $x \sim x_\text {PF}$![]() , also where the density gradient is strongest, can be seen in figure 10. Notably, the fluctuation peaks shift to higher frequencies and decrease in total fluctuation power. The shift in frequency may be the Doppler shift caused by the change in $\boldsymbol {E}\boldsymbol {\times }\boldsymbol {B}$
, also where the density gradient is strongest, can be seen in figure 10. Notably, the fluctuation peaks shift to higher frequencies and decrease in total fluctuation power. The shift in frequency may be the Doppler shift caused by the change in $\boldsymbol {E}\boldsymbol {\times }\boldsymbol {B}$![]() plasma rotation seen in figure 6 at the location $x/x_c \approx x_\text {PF}$
plasma rotation seen in figure 6 at the location $x/x_c \approx x_\text {PF}$![]() . The shift in frequency is somewhat smaller than what would be expected from the field line-averaged increase in Alfvén speed at the longest possible wavelength. The phase angle of $I_\text {sat}$
. The shift in frequency is somewhat smaller than what would be expected from the field line-averaged increase in Alfvén speed at the longest possible wavelength. The phase angle of $I_\text {sat}$![]() and Vf provides insight into the nature of the driving instability. Including a non-zero resistivity $\eta$
and Vf provides insight into the nature of the driving instability. Including a non-zero resistivity $\eta$![]() in the drift wave leads to a small phase shift $\delta$
in the drift wave leads to a small phase shift $\delta$![]() between the density and potential. This phase shift $\delta$
between the density and potential. This phase shift $\delta$![]() in a collisional plasmas is of the order of $\delta \approx \omega \nu _e / k_\parallel ^2 \bar {v}_e^2$
in a collisional plasmas is of the order of $\delta \approx \omega \nu _e / k_\parallel ^2 \bar {v}_e^2$![]() (Horton Reference Horton1999). Estimating this quantity using measured and typical values ($k_\parallel = 0.18\ {\rm rad}\ {\rm m}^{-1}$
(Horton Reference Horton1999). Estimating this quantity using measured and typical values ($k_\parallel = 0.18\ {\rm rad}\ {\rm m}^{-1}$![]() , $\bar {v}_e = 1300\ {\rm km}\ {\rm s}^{-1}$
, $\bar {v}_e = 1300\ {\rm km}\ {\rm s}^{-1}$![]() , $\nu _e = 3.7$
, $\nu _e = 3.7$![]() MHz, $\omega = 12$
MHz, $\omega = 12$![]() kHz) yields a substantial phase shift of $\delta \approx 46^\circ$
kHz) yields a substantial phase shift of $\delta \approx 46^\circ$![]() , which roughly agrees with the phase shifts in figure 9, although the implied increased phase shift at higher frequencies does not agree with measurements.
, which roughly agrees with the phase shifts in figure 9, although the implied increased phase shift at higher frequencies does not agree with measurements.

Figure 10. The $I_\text {sat}$![]() (density) fluctuation power averaged over a 1 cm region around $x_\text {PF}$
(density) fluctuation power averaged over a 1 cm region around $x_\text {PF}$![]() at the midplane. The fluctuation power is largely featureless below 2 kHz and beyond 40 kHz aside from electronics noise.
at the midplane. The fluctuation power is largely featureless below 2 kHz and beyond 40 kHz aside from electronics noise.
As seen in figure 9, the phase shift between $I_\text {sat}$![]() and Vf fluctuations is larger below 10 kHz, implying the presence of additional modes beyond or significant modification of resistive drift-wave fluctuations. The phase difference between two Vf probes, $3.83$
and Vf fluctuations is larger below 10 kHz, implying the presence of additional modes beyond or significant modification of resistive drift-wave fluctuations. The phase difference between two Vf probes, $3.83$![]() m apart, was used to calculate the parallel wavelength ${2 {\rm \pi}}/{\lambda } = k_\parallel = \phi _{\text {Vf1}, \text {Vf2}} / \Delta z$
m apart, was used to calculate the parallel wavelength ${2 {\rm \pi}}/{\lambda } = k_\parallel = \phi _{\text {Vf1}, \text {Vf2}} / \Delta z$![]() assuming the wavelengths are greater than 7.66 m. The two probes mapped to the same field line only in the $M=1$
assuming the wavelengths are greater than 7.66 m. The two probes mapped to the same field line only in the $M=1$![]() configuration, so parallel wavenumbers are available only for the flat case. Parallel wavenumbers are theoretically calculable from two-dimensional correlation planes but the coherency dropped dramatically when a mirror geometry was introduced.
configuration, so parallel wavenumbers are available only for the flat case. Parallel wavenumbers are theoretically calculable from two-dimensional correlation planes but the coherency dropped dramatically when a mirror geometry was introduced.
A 34 m wavelength mode likely contributes to the measured $k_\parallel$![]() from $3$
from $3$![]() to ${\gtrsim }10$
to ${\gtrsim }10$![]() kHz (figure 11). Drift waves are long-wavelength modes so coherent density and potential fluctuations along the flux tube are expected. The coherency is a measure of similarity of the spectral content of two signals, in this case Vf probes 1 and 2. The coherency is defined as $\gamma = {|\langle P_{1,2} \rangle |}/{\langle |P_{1,1}|^2 \rangle \langle |P_{2,2}|^2 \rangle }$
kHz (figure 11). Drift waves are long-wavelength modes so coherent density and potential fluctuations along the flux tube are expected. The coherency is a measure of similarity of the spectral content of two signals, in this case Vf probes 1 and 2. The coherency is defined as $\gamma = {|\langle P_{1,2} \rangle |}/{\langle |P_{1,1}|^2 \rangle \langle |P_{2,2}|^2 \rangle }$![]() , where $P_{x,y}$
, where $P_{x,y}$![]() is the cross-spectrum between signals $x$
is the cross-spectrum between signals $x$![]() and $y$
and $y$![]() and the angle brackets $\langle \rangle$
and the angle brackets $\langle \rangle$![]() denote the mean over shots. The coherency between the two Vf probes drops off with increasing frequency, with a slight bump at around 12 kHz. There are several candidates for the driving mechanism of the 3–5 kHz mode, but the 12 kHz mode is most likely a drift-Alfvén wave.
denote the mean over shots. The coherency between the two Vf probes drops off with increasing frequency, with a slight bump at around 12 kHz. There are several candidates for the driving mechanism of the 3–5 kHz mode, but the 12 kHz mode is most likely a drift-Alfvén wave.

Figure 11. Values of $k_\parallel$![]() ($a$
($a$![]() ) and coherency $\gamma$
) and coherency $\gamma$![]() ($b$
($b$![]() ) as a function of frequency. Only results from the $M=1$
) as a function of frequency. Only results from the $M=1$![]() case are available, but it is clear that there are long (${\gtrsim }34$
case are available, but it is clear that there are long (${\gtrsim }34$![]() m) wavelength modes at 3 and 12 kHz. The probes used for calculating $k_\parallel$
m) wavelength modes at 3 and 12 kHz. The probes used for calculating $k_\parallel$![]() were located at the midplane ($z=8.31$
were located at the midplane ($z=8.31$![]() ) and $z=12.14$
) and $z=12.14$![]() m, 3.83 m apart.
m, 3.83 m apart.
3.4 Turbulence modification
The wavenumber–power relation in figure 12 shows decreased fluctuation power when a mirror configuration is introduced. However, there is no discernible trend when the mirror ratio is increased further. The exponential nature of the curve also remains unchanged. The greatest decrease in fluctuation power occurred at low and high $k_y$![]() values, around $10$
values, around $10$![]() and $70\ {\rm rad}\ {\rm m}^{-1}$
and $70\ {\rm rad}\ {\rm m}^{-1}$![]() . The shape of the power-$k_y$
. The shape of the power-$k_y$![]() curves follow an exponential distribution, and is inconsistent with a two-dimensional drift-wave turbulent cascade (Wakatani Hasegawa $k^{-3}$
curves follow an exponential distribution, and is inconsistent with a two-dimensional drift-wave turbulent cascade (Wakatani Hasegawa $k^{-3}$![]() ) (Wakatani & Hasegawa Reference Wakatani and Hasegawa1984). The steep dropoff in fluctuation power with $k_y$
) (Wakatani & Hasegawa Reference Wakatani and Hasegawa1984). The steep dropoff in fluctuation power with $k_y$![]() suggests that higher-wavenumber fluctuations do not have a significant effect on transport.
suggests that higher-wavenumber fluctuations do not have a significant effect on transport.

Figure 12. Fluctuation power summed for each $k_y$![]() for frequencies up to 100 kHz, smoothed. The contribution to fluctuation power is negligible past 100 kHz. The fluctuation power decreases substantially when a mirror configuration is introduced, but no trend is seen otherwise and the $k_y$
for frequencies up to 100 kHz, smoothed. The contribution to fluctuation power is negligible past 100 kHz. The fluctuation power decreases substantially when a mirror configuration is introduced, but no trend is seen otherwise and the $k_y$![]() spectra remain exponential. Note the logarithmic scale.
spectra remain exponential. Note the logarithmic scale.
Previous simulations in a flat field (Friedman Reference Friedman2013) predicted frequency and wavenumber spectra that can be fit with many power laws or exponentials, but the data presented here (figures 10, 13, 12) appear to follow an exponential relationship within measurement variation.

Figure 13. The $B_\perp$![]() fluctuation power averaged at the core from 0 to 3 cm ($a$
fluctuation power averaged at the core from 0 to 3 cm ($a$![]() ) and around the peak-fluctuation point $(x \sim x_{\rm PF})$
) and around the peak-fluctuation point $(x \sim x_{\rm PF})$![]() ($b$
($b$![]() ). Fluctuation power decreases across the board with mirror ratio except for core frequencies close to $\varOmega _{\rm ci}$
). Fluctuation power decreases across the board with mirror ratio except for core frequencies close to $\varOmega _{\rm ci}$![]() . Peaks around 10–30 kHz at $x_{\rm PF}$
. Peaks around 10–30 kHz at $x_{\rm PF}$![]() are consistent (region 2) with drift-Alfvén waves and the near-cyclotron frequency features in the core may be resonating Alfvén waves created by the magnetic mirror. Frequencies below 2 kHz are dominated by instrumentation noise and thus excluded.
are consistent (region 2) with drift-Alfvén waves and the near-cyclotron frequency features in the core may be resonating Alfvén waves created by the magnetic mirror. Frequencies below 2 kHz are dominated by instrumentation noise and thus excluded.
Turbulence measurements can be directly compared with theoretical predictions and other devices, as summarized by Liewer (Reference Liewer1985). For saturated drift-wave turbulence, one expects the normalized fluctuation level $\tilde {n}/n \sim 1/\langle k_\perp \rangle L_n$![]() , where $k_\perp$
, where $k_\perp$![]() is some typical wavenumber. The power-weighted $k_y$
is some typical wavenumber. The power-weighted $k_y$![]() (calculated from figure 12) was approximately $15\ {\rm rad}\ {\rm m}^{-1}$
(calculated from figure 12) was approximately $15\ {\rm rad}\ {\rm m}^{-1}$![]() , which is an order of magnitude too small to satisfy this relationship. The $\tilde {n}/n$
, which is an order of magnitude too small to satisfy this relationship. The $\tilde {n}/n$![]() scaling with $\rho _s / L_n$
scaling with $\rho _s / L_n$![]() , however, is roughly consistent with drift-wave turbulence level saturation: the latter is ${\approx }3$
, however, is roughly consistent with drift-wave turbulence level saturation: the latter is ${\approx }3$![]() times larger. These comparisons suggest that the large, low-frequency fluctuations (${\sim }3$
times larger. These comparisons suggest that the large, low-frequency fluctuations (${\sim }3$![]() kHz, which had even smaller $k_y$
kHz, which had even smaller $k_y$![]() ) may have a drift-wave turbulence component but are dominantly driven by other instabilities. No trend is seen in $\rho _s / L_n$
) may have a drift-wave turbulence component but are dominantly driven by other instabilities. No trend is seen in $\rho _s / L_n$![]() and $1/k_y L_n$
and $1/k_y L_n$![]() when the mirror ratio is varied.
when the mirror ratio is varied.
Core fluctuations appear to decrease dramatically, as seen in the $I_\text {sat}$![]() fluctuation power (figure 7). The $I_\text {sat}$
fluctuation power (figure 7). The $I_\text {sat}$![]() decorrelation time increases from ${\sim }0.7$
decorrelation time increases from ${\sim }0.7$![]() ms for $M=1$
ms for $M=1$![]() to ${\sim }2.5$
to ${\sim }2.5$![]() ms for $M=2.68$
ms for $M=2.68$![]() . At $x=x_{\rm PF}$
. At $x=x_{\rm PF}$![]() , decorrelation times for all mirror ratios remained at $0.2$
, decorrelation times for all mirror ratios remained at $0.2$![]() ms.
ms.
3.5 Magnetic fluctuations
The perpendicular magnetic fluctuation ($B_\perp$![]() ) component of the drift-Alfvén wave can be seen in figure 13. These $B_\perp$
) component of the drift-Alfvén wave can be seen in figure 13. These $B_\perp$![]() fluctuations are spatially and spectrally coincident with the electrostatic fluctuations (figure 10). Drift-Alfvén waves have been studied in the LAPD in the past (Maggs & Morales Reference Maggs and Morales1997; Vincena & Gekelman Reference Vincena and Gekelman2006); strong coupling is observed for $\beta _e > m_e / m_i$
fluctuations are spatially and spectrally coincident with the electrostatic fluctuations (figure 10). Drift-Alfvén waves have been studied in the LAPD in the past (Maggs & Morales Reference Maggs and Morales1997; Vincena & Gekelman Reference Vincena and Gekelman2006); strong coupling is observed for $\beta _e > m_e / m_i$![]() (the electron-ion mass ratio), which is satisfied in this study. The Alfvén speed $\omega / k_\parallel = v_A = B/\sqrt {4 {\rm \pi}n M}$
(the electron-ion mass ratio), which is satisfied in this study. The Alfvén speed $\omega / k_\parallel = v_A = B/\sqrt {4 {\rm \pi}n M}$![]() (given $\omega \ll \varOmega _{\rm ci}$
(given $\omega \ll \varOmega _{\rm ci}$![]() ) when averaged over the entire column ranges from ${\sim }450$
) when averaged over the entire column ranges from ${\sim }450$![]() to ${\sim }1600\ {\rm km}\ {\rm s}^{-1}$
to ${\sim }1600\ {\rm km}\ {\rm s}^{-1}$![]() . A $k_\parallel$
. A $k_\parallel$![]() corresponding to a wavelength $\lambda = 34$
corresponding to a wavelength $\lambda = 34$![]() m roughly falls within the bound established by the kinetic and inertial Alfvén wave dispersion relations at the frequency peaks observed at $x \sim x_{\rm PF}$
m roughly falls within the bound established by the kinetic and inertial Alfvén wave dispersion relations at the frequency peaks observed at $x \sim x_{\rm PF}$![]() seen in figure 13. The lengthening of field lines caused by curvature accounts for at most $10\,\%$
seen in figure 13. The lengthening of field lines caused by curvature accounts for at most $10\,\%$![]() of the change in frequency.
of the change in frequency.
The spatial extent of the $B_\perp$![]() features identified in figure 13 are plotted in figure 14. Feature 1 at ${\approx }6$
features identified in figure 13 are plotted in figure 14. Feature 1 at ${\approx }6$![]() kHz shows increased fluctuation amplitudes at $x=0$
kHz shows increased fluctuation amplitudes at $x=0$![]() for mirror ratios 1.9 and above, but for $M=1$
for mirror ratios 1.9 and above, but for $M=1$![]() and $M=1.47$
and $M=1.47$![]() there is no increase in fluctuation power. A similar feature, but at a much smaller level, is observed in the $I_\text {sat}$
there is no increase in fluctuation power. A similar feature, but at a much smaller level, is observed in the $I_\text {sat}$![]() fluctuation power in the core as well. This core feature may be caused by the hole in the core seen in the $I_\text {sat}$
fluctuation power in the core as well. This core feature may be caused by the hole in the core seen in the $I_\text {sat}$![]() profile (figure 3) driving low-amplitude waves or instabilities. Feature 2 in figure 14 is the magnetic component of the drift-Alfvén wave. The fluctuation power peaks at the gradient region and corresponds with the peak in density fluctuations (figure 7).
profile (figure 3) driving low-amplitude waves or instabilities. Feature 2 in figure 14 is the magnetic component of the drift-Alfvén wave. The fluctuation power peaks at the gradient region and corresponds with the peak in density fluctuations (figure 7).

Figure 14. The $B_\perp$![]() fluctuation power profiles for the three regions shown in figure 13: region 1 (6 kHz) ($a$
fluctuation power profiles for the three regions shown in figure 13: region 1 (6 kHz) ($a$![]() ), region 2, where frequencies are taken from the peaks of the drift-Alfvén waves for each mirror ratio, ($b$
), region 2, where frequencies are taken from the peaks of the drift-Alfvén waves for each mirror ratio, ($b$![]() ) and region 3 (114 kHz) ($c$
) and region 3 (114 kHz) ($c$![]() ).
).
Feature 3 is particularly interesting because this the only fluctuating quantity to increase with mirror ratio, seen in figure 15. This feature may be broad evanescent Alfvénic fluctuations from the plasma source. These fluctuations have been observed in the LAPD in the source region alongside an Alfvén wave maser (Maggs, Morales & Carter Reference Maggs, Morales and Carter2005). Note that the Alfvén maser cannot enter the mirror cell at mirror ratios greater than 1.75 because the Alfvén maser resonates at 0.57 $f_{\rm ci}$![]() but the midplane is always at or near 500 G.
but the midplane is always at or near 500 G.

Figure 15. Summed fluctuation power of $B_\perp$![]() in the core ($x/x_c \leqslant 0.3$
in the core ($x/x_c \leqslant 0.3$![]() ) as a function of mirror length and ratio. ($a$
) as a function of mirror length and ratio. ($a$![]() ) The fluctuation power is normalized by the sum of the full-spectrum summed power. ($b$
) The fluctuation power is normalized by the sum of the full-spectrum summed power. ($b$![]() ) The frequency of the power distribution >50 kHz weighted by the fluctuation power.
) The frequency of the power distribution >50 kHz weighted by the fluctuation power.
The sub-$2$![]() kHz modes in $B_\perp$
kHz modes in $B_\perp$![]() and the harmonics of these modes are nearly constant in power across the entire plasma; these features are likely perturbations from the magnet power supplies and thus ignored. The lack of radial, azimuthal and axial structure in these magnetic signals below 2 kHz and narrow bandwidth indicate a non-plasma origin. Significant radial and azimuthal structure in $B_\perp$
and the harmonics of these modes are nearly constant in power across the entire plasma; these features are likely perturbations from the magnet power supplies and thus ignored. The lack of radial, azimuthal and axial structure in these magnetic signals below 2 kHz and narrow bandwidth indicate a non-plasma origin. Significant radial and azimuthal structure in $B_\perp$![]() fluctuation power starts to appear in frequencies larger than 4 kHz.
fluctuation power starts to appear in frequencies larger than 4 kHz.
4 Two-dimensional structure
The perpendicular magnetic field structure is measured by collecting $x\unicode{x2013}y$![]() planar Bdot (${\rm d}B_{\{x, y, z \} } / {\rm d}t$
planar Bdot (${\rm d}B_{\{x, y, z \} } / {\rm d}t$![]() ) data alongside a stationary, axially separated $I_\text {sat}$
) data alongside a stationary, axially separated $I_\text {sat}$![]() reference probe (DR2). This probe provides a phase reference for the magnetic field fluctuations, allowing a two-dimensional map of relative phase to be constructed over many shots. Only the region around $x_{\rm PF}$
reference probe (DR2). This probe provides a phase reference for the magnetic field fluctuations, allowing a two-dimensional map of relative phase to be constructed over many shots. Only the region around $x_{\rm PF}$![]() was measured because of constraints on probe movement. The amplitude and phases for each magnetic field component are then used to reconstruct the local magnetic fluctuation vector $\boldsymbol {B}$
was measured because of constraints on probe movement. The amplitude and phases for each magnetic field component are then used to reconstruct the local magnetic fluctuation vector $\boldsymbol {B}$![]() . The axial current density structure, $j_z$
. The axial current density structure, $j_z$![]() , can be derived from this vector field. $\boldsymbol {B}$
, can be derived from this vector field. $\boldsymbol {B}$![]() and the corresponding $j_z$
and the corresponding $j_z$![]() for the flat-field ($M=1$
for the flat-field ($M=1$![]() ) case can be seen in figure 16. Two main current channels can be seen with the magnetic fields circulating around them. This structure quickly decoheres in time as expected in a turbulent plasma. At higher mirror ratios, the field magnitude and corresponding current density decrease (which was also seen in DR1: figure 13).
) case can be seen in figure 16. Two main current channels can be seen with the magnetic fields circulating around them. This structure quickly decoheres in time as expected in a turbulent plasma. At higher mirror ratios, the field magnitude and corresponding current density decrease (which was also seen in DR1: figure 13).

Figure 16. Perpendicular magnetic field and the derived current density for the flat-field ($M=1$![]() ) case using a Bdot probe with an axially separated $I_\text {sat}$
) case using a Bdot probe with an axially separated $I_\text {sat}$![]() reference (DR2). The $x\unicode{x2013}y$
reference (DR2). The $x\unicode{x2013}y$![]() plane was centred near $x_{\rm PF}$
plane was centred near $x_{\rm PF}$![]() .
.
Using two, axially separated, correlated $I_\text {sat}$![]() measurements (DR2), with one collecting $x\unicode{x2013}y$
measurements (DR2), with one collecting $x\unicode{x2013}y$![]() planar data, the azimuthal mode number $m$
planar data, the azimuthal mode number $m$![]() (radially integrated) was calculated. Higher-frequency and higher-$m$
(radially integrated) was calculated. Higher-frequency and higher-$m$![]() features are seen with increasing mirror ratio (figure 17). The increased frequencies may be caused by a change in Doppler shift by the $\boldsymbol {E} \boldsymbol {\times }\boldsymbol {B}$
features are seen with increasing mirror ratio (figure 17). The increased frequencies may be caused by a change in Doppler shift by the $\boldsymbol {E} \boldsymbol {\times }\boldsymbol {B}$![]() flow. This higher-$m$
flow. This higher-$m$![]() trend suggests that azimuthal structures do not scale with increased plasma radius but instead remain roughly the same size. The limited planar probe movement caused an increase in the lower bound on $m$
trend suggests that azimuthal structures do not scale with increased plasma radius but instead remain roughly the same size. The limited planar probe movement caused an increase in the lower bound on $m$![]() at higher mirror ratios. At mirror ratios 1.47 and higher, the lower-frequency component (<10 kHz) appears to decrease significantly in amplitude. Calculating $k_\perp$
at higher mirror ratios. At mirror ratios 1.47 and higher, the lower-frequency component (<10 kHz) appears to decrease significantly in amplitude. Calculating $k_\perp$![]() from $m$
from $m$![]() evaluated at $x \sim x_c$
evaluated at $x \sim x_c$![]() yields similar $k_y$
yields similar $k_y$![]() values as the two-tip technique (figure 18). The average $k_y$
values as the two-tip technique (figure 18). The average $k_y$![]() for a given frequency can be calculated using two Vf tips on the same probe by calculating the phase difference and dividing by the spatial separation of $5$
for a given frequency can be calculated using two Vf tips on the same probe by calculating the phase difference and dividing by the spatial separation of $5$![]() mm: $k_y = \phi _{\text {vf1},\text {vf2}} / \Delta y$
mm: $k_y = \phi _{\text {vf1},\text {vf2}} / \Delta y$![]() (Beall, Kim & Powers Reference Beall, Kim and Powers1982). The maximum $|k_y|$
(Beall, Kim & Powers Reference Beall, Kim and Powers1982). The maximum $|k_y|$![]() measurable before aliasing is ${\rm \pi} / \Delta y \approx 628\ {\rm rad}\ {\rm m}^{-1}$
measurable before aliasing is ${\rm \pi} / \Delta y \approx 628\ {\rm rad}\ {\rm m}^{-1}$![]() . As seen in figure 18, the $k_y$
. As seen in figure 18, the $k_y$![]() spectrum remains similar across mirror ratios, but the wavenumber extends further into higher frequencies with increasing mirror ratio. These azimuthal mode numbers and gradient scale lengths are consistent with linear simulations using the three-dimensional fluid code BOUT (Popovich et al. Reference Popovich, Umansky, Carter and Friedman2010) in the flat, unbiased case.
spectrum remains similar across mirror ratios, but the wavenumber extends further into higher frequencies with increasing mirror ratio. These azimuthal mode numbers and gradient scale lengths are consistent with linear simulations using the three-dimensional fluid code BOUT (Popovich et al. Reference Popovich, Umansky, Carter and Friedman2010) in the flat, unbiased case.

Figure 17. Azimuthal mode number $m$![]() amplitudes calculated from two axially separated, correlated, $I_\text {sat}$
amplitudes calculated from two axially separated, correlated, $I_\text {sat}$![]() probes. Increasing mirror ratio ($a$
probes. Increasing mirror ratio ($a$![]() –$e$
–$e$![]() ) leads to increased $m$
) leads to increased $m$![]() at higher frequencies. (DR2).
at higher frequencies. (DR2).

Figure 18. The value of $k_y$![]() averaged about $x_{\rm PF}$
averaged about $x_{\rm PF}$![]() and smoothed for each mirror ratio calculated using two vertically separated Vf tips on the same probe. Little change is seen in $k_y$
and smoothed for each mirror ratio calculated using two vertically separated Vf tips on the same probe. Little change is seen in $k_y$![]() at lower frequencies but higher frequencies tend towards larger $k_y$
at lower frequencies but higher frequencies tend towards larger $k_y$![]() at higher mirror ratios.
at higher mirror ratios.
5 Discussion
5.1 Lack of mirror-driven instabilities
No evidence is seen for mirror-driven instabilities – curvature, loss cone or otherwise. Given the LAPD parameters in this study (tables 1 and 2), the collision frequencies are sufficiently high such that the mirror is in the gas-dynamic regime: losses out of the mirror throat are governed by gas-dynamic equations rather than free streaming through the loss cone. To be in the gas-dynamic regime, the mirror length must exceed the mean free path of the ions (Ivanov & Prikhodko Reference Ivanov and Prikhodko2013)
where $L$![]() is the mirror length, $\lambda _{\rm ii}$
is the mirror length, $\lambda _{\rm ii}$![]() is the ion mean free path and $M$
is the ion mean free path and $M$![]() is the mirror ratio. These collisions populate the loss cone and maintain a (cold) Maxwellian distribution, eliminating the possibility of loss-cone-, ion-driven instabilities like the Alfvén-ion cyclotron (AIC) (Casper & Smith Reference Casper and Smith1982) or drift-cyclotron loss-cone (DCLC) (Simonen Reference Simonen1976; Kanaev Reference Kanaev1979) instabilities that have been observed in other (historic) devices.
is the mirror ratio. These collisions populate the loss cone and maintain a (cold) Maxwellian distribution, eliminating the possibility of loss-cone-, ion-driven instabilities like the Alfvén-ion cyclotron (AIC) (Casper & Smith Reference Casper and Smith1982) or drift-cyclotron loss-cone (DCLC) (Simonen Reference Simonen1976; Kanaev Reference Kanaev1979) instabilities that have been observed in other (historic) devices.
The paraxial, approximate interchange growth rate is (Post Reference Post1987; Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011)
which yields $\varGamma _0 \approx 1.2$![]() kHz using $L_M \approx 7$
kHz using $L_M \approx 7$![]() m and $L_P = 17$
m and $L_P = 17$![]() m. Here, $c_s$
m. Here, $c_s$![]() is used instead of $\overline {v_i}$
is used instead of $\overline {v_i}$![]() because $T_i \ll T_e$
because $T_i \ll T_e$![]() and the mirror length $L$
and the mirror length $L$![]() is split to distinguish between the contributions of the plasma length and mirror length to inertia and to curvature drive, respectively. Interchange is not visible, in part because the aspect ratio of these mirrors is quite large, limiting the growth rate of interchange. The length of the mirror (3.5 m), radius of curvature (6–7 m) and plasma column (17 m) are much larger than the radius of the plasma (0.5 m maximum), so the plasma inertia is large relative to the instability drivers. Line tying to the cathode may further lower the growth rate. The hot cathode used for plasma formation could function as a thermionic endplate that can supply current to short out the flute-like interchange perturbations. Line tying has been seen in flux rope experiments on the LAPD using a hotter, denser source (Van Compernolle et al. Reference Van Compernolle, Gekelman, Pribyl and Cooper2011), also in other devices (Fornaca, Kiwamoto & Rynn Reference Fornaca, Kiwamoto and Rynn1979), and is why interchange was not seen in the earliest mirror machines (Post Reference Post1987). Note that the plasma terminates on the cathode or end plates before the magnetic field flares out, so there is no contribution to stability from an expander tank as seen in other GDTs (Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011; Ivanov & Prikhodko Reference Ivanov and Prikhodko2013). Finite Larmor radius (FLR) effects may provide a stabilizing effect for larger azimuthal mode numbers. At the highest mirror ratio, assuming a plasma radius of $a_0 =\sqrt {2.68} * x_{\rm PF}=43$
is split to distinguish between the contributions of the plasma length and mirror length to inertia and to curvature drive, respectively. Interchange is not visible, in part because the aspect ratio of these mirrors is quite large, limiting the growth rate of interchange. The length of the mirror (3.5 m), radius of curvature (6–7 m) and plasma column (17 m) are much larger than the radius of the plasma (0.5 m maximum), so the plasma inertia is large relative to the instability drivers. Line tying to the cathode may further lower the growth rate. The hot cathode used for plasma formation could function as a thermionic endplate that can supply current to short out the flute-like interchange perturbations. Line tying has been seen in flux rope experiments on the LAPD using a hotter, denser source (Van Compernolle et al. Reference Van Compernolle, Gekelman, Pribyl and Cooper2011), also in other devices (Fornaca, Kiwamoto & Rynn Reference Fornaca, Kiwamoto and Rynn1979), and is why interchange was not seen in the earliest mirror machines (Post Reference Post1987). Note that the plasma terminates on the cathode or end plates before the magnetic field flares out, so there is no contribution to stability from an expander tank as seen in other GDTs (Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011; Ivanov & Prikhodko Reference Ivanov and Prikhodko2013). Finite Larmor radius (FLR) effects may provide a stabilizing effect for larger azimuthal mode numbers. At the highest mirror ratio, assuming a plasma radius of $a_0 =\sqrt {2.68} * x_{\rm PF}=43$![]() cm, the FLR stability criterion $({m}/{2})({\rho _i L}/{a_0^2}) > 1$
cm, the FLR stability criterion $({m}/{2})({\rho _i L}/{a_0^2}) > 1$![]() (Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011) suggests a stabilizing effect may be present for azimuthal mode numbers $m > 4$
(Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011) suggests a stabilizing effect may be present for azimuthal mode numbers $m > 4$![]() .
.
If the curvature-induced interchange instability were observable, then introducing a mirror configuration would lead to new features in $I_\text {sat}$![]() and Bdot fluctuations. In particular, low-frequency mode(s) – likely less than 10 kHz given the low $m$
and Bdot fluctuations. In particular, low-frequency mode(s) – likely less than 10 kHz given the low $m$![]() number and plasma rotation rates – would be observed growing from the pressure gradient region. For onset of the interchange instability, the mirror curvature or plasma pressure would need to be increased but the precise conditions required for this onset are not yet known for the LAPD.
number and plasma rotation rates – would be observed growing from the pressure gradient region. For onset of the interchange instability, the mirror curvature or plasma pressure would need to be increased but the precise conditions required for this onset are not yet known for the LAPD.
Interchange could also be at least partially stabilized by the continuous production of electrons in the core that are electrostatically trapped by the ambipolar potential (Guest & Harris Reference Guest and Harris1971). The intuition behind this stabilization mechanism is as follows: electrons are continuously produced via ionization of neutrals, and any change in the local potential will cause more or fewer electrons to be lost out the ends of the device along that field line, counteracting the potential change. This stabilization mechanism has been experimentally demonstrated to completely suppress interchange when the ambipolar potential $\varPhi \gtrsim 6T_e$![]() (Komori et al. Reference Komori, Higuchi, Suetsugu, Yonesu and Kawai1987).
(Komori et al. Reference Komori, Higuchi, Suetsugu, Yonesu and Kawai1987).
The $\boldsymbol {E} \boldsymbol {\times } \boldsymbol {B}$![]() shear flow present (figure 6) may also make a contribution to the stabilization of interchange (Bagryansky et al. Reference Bagryansky, Lizunov, Zuev, Kolesnikov and Solomachin2003, Reference Bagryansky, Beklemishev and Soldatkina2007; Beklemishev et al. Reference Beklemishev, Bagryansky, Chaschin and Soldatkina2010; Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011). The estimated shearing rate is between 3 and 10 kHz, which is greater than the estimated ${\approx }1.2$
shear flow present (figure 6) may also make a contribution to the stabilization of interchange (Bagryansky et al. Reference Bagryansky, Lizunov, Zuev, Kolesnikov and Solomachin2003, Reference Bagryansky, Beklemishev and Soldatkina2007; Beklemishev et al. Reference Beklemishev, Bagryansky, Chaschin and Soldatkina2010; Ryutov et al. Reference Ryutov, Berk, Cohen, Molvik and Simonen2011). The estimated shearing rate is between 3 and 10 kHz, which is greater than the estimated ${\approx }1.2$![]() kHz growth rate of the interchange mode.
kHz growth rate of the interchange mode.
5.2 Instabilities driving turbulence
Rotational interchange can be significant driver of the broadband turbulence spectrum in the LAPD, particularly when a biased limiter is installed. This observation has been confirmed by both linear simulations (Popovich et al. Reference Popovich, Umansky, Carter and Friedman2010) and biasing experiments (Schaffner Reference Schaffner2013).
This rotational interchange mode has the following attributes, as summarized by Jassby (Reference Jassby1972): flute-like ($k_\parallel =0)$![]() , $|e\tilde {\phi }/T_e|/|\tilde {n}/n| \gtrsim 1$
, $|e\tilde {\phi }/T_e|/|\tilde {n}/n| \gtrsim 1$![]() , radial potential phase variation $45$
, radial potential phase variation $45$![]() to $90^\circ$
to $90^\circ$![]() , maximum possible $|e\tilde {\phi }/T_e| < 1$
, maximum possible $|e\tilde {\phi }/T_e| < 1$![]() . All of these attributes are seen for the lower-frequency (3 kHz) mode. The Vf radial phase variation when $M>1$
. All of these attributes are seen for the lower-frequency (3 kHz) mode. The Vf radial phase variation when $M>1$![]() is not clearly seen because the coherency is dramatically reduced along the field line. The rotational interchange mode could couple with the drift wave at $k_\parallel = {\rm \pi}/ L \sim 0.37\ {\rm rad}\ {\rm m}^{-1}$
is not clearly seen because the coherency is dramatically reduced along the field line. The rotational interchange mode could couple with the drift wave at $k_\parallel = {\rm \pi}/ L \sim 0.37\ {\rm rad}\ {\rm m}^{-1}$![]() ($n=0.5$
($n=0.5$![]() ), which has been observed in the past (Schaffner Reference Schaffner2013) and likely present here. Estimates of shearing rate from the $\boldsymbol {E}\boldsymbol {\times }\boldsymbol {B}$
), which has been observed in the past (Schaffner Reference Schaffner2013) and likely present here. Estimates of shearing rate from the $\boldsymbol {E}\boldsymbol {\times }\boldsymbol {B}$![]() flow velocity profile (figure 6), calculated fluctuation ratios and radial phase shift variation suggest that Kelvin–Helmholtz-driven turbulence is not significant, if present at all. Historically, biasing a limiter has been required to clearly observe the Kelvin–Helmholtz instability (Horton et al. Reference Horton, Perez, Carter and Bengtson2005; Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2012; Schaffner Reference Schaffner2013).
flow velocity profile (figure 6), calculated fluctuation ratios and radial phase shift variation suggest that Kelvin–Helmholtz-driven turbulence is not significant, if present at all. Historically, biasing a limiter has been required to clearly observe the Kelvin–Helmholtz instability (Horton et al. Reference Horton, Perez, Carter and Bengtson2005; Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2012; Schaffner Reference Schaffner2013).
Low-frequency density fluctuations may also be driven by a flute-like conducting-wall temperature-gradient instability which only requires an electron temperature gradient to grow (even with straight field lines) (Berk, Ryutov & Tsidulko Reference Berk, Ryutov and Tsidulko1991). Simulations of turbulence in the LAPD suggest the possible presence of these conducting-wall modes (CWMs) which have the highest growth rate for $m \leqslant 20$![]() (Friedman et al. Reference Friedman, Carter, Umansky, Schaffner and Joseph2013). This lower-$m$
(Friedman et al. Reference Friedman, Carter, Umansky, Schaffner and Joseph2013). This lower-$m$![]() mode could be responsible for the peak around $3$
mode could be responsible for the peak around $3$![]() kHz in the $M=1$
kHz in the $M=1$![]() $I_\text {sat}$
$I_\text {sat}$![]() fluctuation (figure 10) and azimuthal mode numbers (figure 17) and for the low-frequency low-$k_\parallel$
fluctuation (figure 10) and azimuthal mode numbers (figure 17) and for the low-frequency low-$k_\parallel$![]() or flute-like behaviour (figure 11). This CWM may also be responsible for flatter electron temperature profiles seen in previous studies (Schaffner Reference Schaffner2013; Perks et al. Reference Perks, Mordijck, Carter, Van Compernolle, Vincena, Rossi and Schaffner2022) (figure 5).
or flute-like behaviour (figure 11). This CWM may also be responsible for flatter electron temperature profiles seen in previous studies (Schaffner Reference Schaffner2013; Perks et al. Reference Perks, Mordijck, Carter, Van Compernolle, Vincena, Rossi and Schaffner2022) (figure 5).
These linearly unstable modes may be outgrown by a rapidly growing nonlinear instability that couples to drift-like modes, as suggested by simulations (Friedman et al. Reference Friedman, Carter, Umansky, Schaffner and Joseph2013). This nonlinear instability is driven by the density gradient at an axial mode number of $n=0$![]() and nonlinearly transfers energy to $n \neq 0$
and nonlinearly transfers energy to $n \neq 0$![]() fluctuations.
fluctuations.
The CWM and nonlinear instability may be present in these mirror experiments but the spectra are adequately explained by linearly unstable modes. Precise identification these modes requires further study; neither of these instabilities have been directly observed in the LAPD.
5.3 Causes of particle flux reduction
The reduction in particle flux explained by a reduction in density fluctuations likely caused by a increased gradient scale length $L_n = {n}/{\boldsymbol {\nabla } n }$![]() (figure 19), decreasing the linear drift-wave growth rate and saturation level seen in § 3.4. This gradient length reduction may also reduce the growth rate of the rotational interchange instability, which may be the dominate driver for the low-frequency large-amplitude density fluctuations.
(figure 19), decreasing the linear drift-wave growth rate and saturation level seen in § 3.4. This gradient length reduction may also reduce the growth rate of the rotational interchange instability, which may be the dominate driver for the low-frequency large-amplitude density fluctuations.

Figure 19. Gradient scale length $L_n$![]() and the associated term in the drift-wave growth rate $L_n^{-2}$
and the associated term in the drift-wave growth rate $L_n^{-2}$![]() . This scale length was calculated over a 3 cm region around $x_\text {PF}$
. This scale length was calculated over a 3 cm region around $x_\text {PF}$![]() (peak-fluctuation region) at the midplane. Increasing the mirror ratio increases the gradient scale length, which suggests weakening of the underlying instability driver.
(peak-fluctuation region) at the midplane. Increasing the mirror ratio increases the gradient scale length, which suggests weakening of the underlying instability driver.
The decorrelation time of $I_\text {sat}$![]() time series data is around 0.15 ms at $x_\text {PF}$
time series data is around 0.15 ms at $x_\text {PF}$![]() . An estimate of the $\boldsymbol {E \times B}$
. An estimate of the $\boldsymbol {E \times B}$![]() flow shear from figure 6 (DR2) yields a shearing time between 0.1 and 0.3 ms at $x_\text {PF}$
flow shear from figure 6 (DR2) yields a shearing time between 0.1 and 0.3 ms at $x_\text {PF}$![]() . These times suggest that spontaneous flow shear may be important for suppressing turbulence, as seen in other studies (Cho et al. Reference Cho2005; Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2013), at all mirror ratios. However, no clear trend in shearing strength is seen with mirror ratio.
. These times suggest that spontaneous flow shear may be important for suppressing turbulence, as seen in other studies (Cho et al. Reference Cho2005; Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2013), at all mirror ratios. However, no clear trend in shearing strength is seen with mirror ratio.
It is important to note that the electron thermal diffusion time along the field line is very long compared with the frequency of the drift wave ($\omega \gtrsim k_\parallel \bar {v}_e^2 / \nu _{\rm ei}$![]() ) (Goldston Reference Goldston1995) so the electron temperature along the field line may not be constant on the drift-wave time scale. This factor is not taken into account in this analysis but may have substantial impact on interpretations of the measured phase shift.
) (Goldston Reference Goldston1995) so the electron temperature along the field line may not be constant on the drift-wave time scale. This factor is not taken into account in this analysis but may have substantial impact on interpretations of the measured phase shift.
6 Conclusions and future work
Turbulence and transport were studied in mirrors with varying lengths and ratios using the flexible magnetic geometry of the LAPD. Particle flux and fluctuation amplitudes decreased up to a factor of two when the mirror ratio was increased. The primary drivers of turbulence were identified as the rotational interchange mode, caused by spontaneous rotation, and unstable drift-Alfvén waves driven by the density gradient. The decrease in density fluctuation amplitudes can be attributed to an increase in the gradient scale length caused by the dimensionally wider plasma at the mirror midplane. Despite imposing a mirror configuration, no signs of mirror-driven instabilities were observed. The highly collisional, GDT-like plasma produced suppressed any velocity space instabilities. The interchange growth rate was likely suppressed to an undetectable level by line tying, in-cell electron production and shear flow.
Future experiments in hotter regimes with the new LaB6 cathode (Qian et al. Reference Qian2023) will need to be performed to evaluate the robustness of these results, particularly concerning the stabilization of curvature-induced interchange. Additionally, the source field should be matched to the mirror midplane field so that the plasma remains at the same radius to isolate geometric effects. Simultaneous measurements using flux and/or vorticity probes and $I_\text {sat}$![]() are needed to concretely determine if azimuthal flow shear is modified by the mirror field, and to quantify the effect of flows on rotational interchange and drift-wave instability drive in general. Multiple simultaneous axial measurements of potential would enable better understanding of the axial wavenumber and identification of possible modes.
are needed to concretely determine if azimuthal flow shear is modified by the mirror field, and to quantify the effect of flows on rotational interchange and drift-wave instability drive in general. Multiple simultaneous axial measurements of potential would enable better understanding of the axial wavenumber and identification of possible modes.
Acknowledgements
Editor Cary Forest thanks the referees for their advice in evaluating this article.
Funding
This work was performed at the Basic Plasma Science Facility, which is a DOE Office of Science, FES collaborative user facility and is funded by DOE (DE-FC02-07ER54918) and the National Science Foundation (NSF-PHY 1036140). The authors would like to thank Dr G. Rossi and Dr S. Vincena for probe set-up and assistance with data collection, and Dr M. Abler, Professor W. Gekelman and Professor G. Morales for insightful discussion.
Declaration of interests
The authors report no conflict of interest.
Data availability
The data and code supporting this study are available from the corresponding author upon reasonable request.