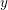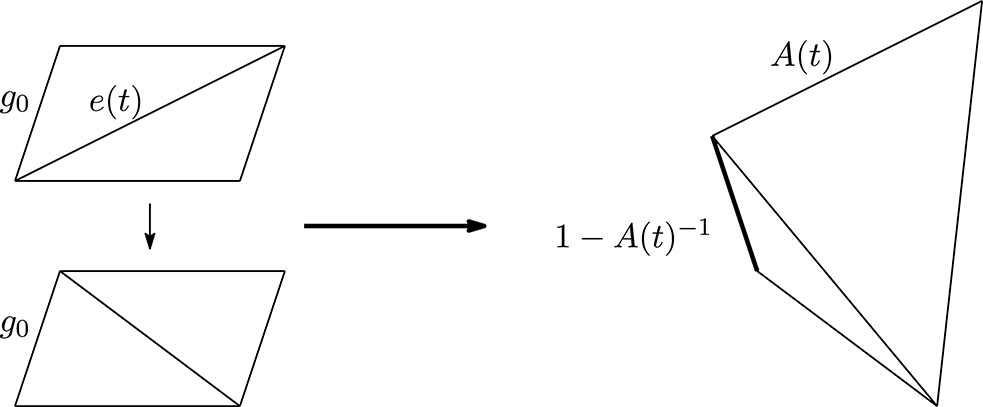0 Introduction
0.1 Cluster algebras
Cluster algebras were introduced by Fomin and Zelevinsky [Reference Fomin and ZelevinskyFZ02] around 2000. Since then, many authors have uncovered beautiful connections between the theory of cluster algebras and a wide range of mathematics such as
∙ dual canonical bases and their relations with preprojective algebras and quiver varieties [Reference Bernstein, Fomin and ZelevinskyBFZ05], [Reference LeclercLec10], [Reference NakajimaNak11a], [Reference KimuraKim12]
∙ total positivity [Reference FominFom10]
∙ (higher) Teichmüller theory and its quantization [Reference Fock and GoncharovFG06, Reference Fock and GoncharovFG07, Reference Fock and GoncharovFG09], [Reference TeschnerTes07, Reference TeschnerTes]
∙ 2-dimensional hyperbolic geometry [Reference Gekhtman, Shapiro and VainshteinGSV03], [Reference Fomin, Shapiro and ThurstonFST08]
∙ cluster categories [Reference KellerKel10], [Reference AmiotAmi09], [Reference PlamondonPla11]
∙ discrete integrable systems [Reference KedemKed08], [Reference Kuniba, Nakanishi and SuzukiKNS11]
∙ Donaldson–Thomas theory [Reference Kontsevich and SoibelmanKS], [Reference NagaoNag13]
∙ supersymmetric gauge theories [Reference Gaiotto, Moore and NeitzkeGMN], [Reference Cecotti, Neitzke and VafaCNV], [Reference Eager and FrancoEF12].
The goal of this paper is to add yet another item to this list: the theory of hyperbolic
![]() $3$
-manifolds. This paper is a companion to [Reference Terashima and YamazakiTY14], which discusses the application of cluster algebras to the physics of 3d
$3$
-manifolds. This paper is a companion to [Reference Terashima and YamazakiTY14], which discusses the application of cluster algebras to the physics of 3d
![]() ${\mathcal{N}}=2$
supersymmetric gauge theories.
${\mathcal{N}}=2$
supersymmetric gauge theories.
0.2 Hyperbolic
 $3$
-manifolds
$3$
-manifolds
A hyperbolic
![]() $3$
-manifold (with cusps) has a decomposition into ideal tetrahedra. This makes it possible for us to compute invariants of the
$3$
-manifold (with cusps) has a decomposition into ideal tetrahedra. This makes it possible for us to compute invariants of the
![]() $3$
-manifold, such as the hyperbolic volume and the Chern–Simons invariant [Reference Neumann and ZagierNZ85, Reference NeumannNeu92].
$3$
-manifold, such as the hyperbolic volume and the Chern–Simons invariant [Reference Neumann and ZagierNZ85, Reference NeumannNeu92].
An ideal tetrahedron is parametrized by a complex number called a shape parameter. Given a topological decomposition of the
![]() $3$
-manifold into ideal tetrahedra, we need to find shape parameters which satisfy edge-gluing equations (§4.2) in order to obtain a hyperbolic structure on the
$3$
-manifold into ideal tetrahedra, we need to find shape parameters which satisfy edge-gluing equations (§4.2) in order to obtain a hyperbolic structure on the
![]() $3$
-manifold. Moreover, the cusp equations (§4.4) should hold for the complete hyperbolic structure. In general, it is a rather nontrivial problem to systematically find solutions of these equations.
$3$
-manifold. Moreover, the cusp equations (§4.4) should hold for the complete hyperbolic structure. In general, it is a rather nontrivial problem to systematically find solutions of these equations.
In this paper, we study mapping tori
![]() $M_{\unicode[STIX]{x1D711}}$
of mapping classes
$M_{\unicode[STIX]{x1D711}}$
of mapping classes
![]() $\unicode[STIX]{x1D711}$
of a surface
$\unicode[STIX]{x1D711}$
of a surface
![]() $\unicode[STIX]{x1D6F4}$
with punctures. We mainly discuss the case that the mapping torus admits a hyperbolic structure.
$\unicode[STIX]{x1D6F4}$
with punctures. We mainly discuss the case that the mapping torus admits a hyperbolic structure.
The main results of this paper are summarized as follows:
∙ Solving the periodicity equation in Theorem 4.4 for cluster transformations, we get a solution of the edge-gluing equations of the mapping torus
 $M_{\unicode[STIX]{x1D711}}$
with an ideal triangulation induced by the cluster transformations.
$M_{\unicode[STIX]{x1D711}}$
with an ideal triangulation induced by the cluster transformations.∙ Shape parameters of tetrahedra are given by the cluster
 $y$
-variables, where the initial values of the
$y$
-variables, where the initial values of the
 $y$
-variables are taken to be the solution of the periodicity equation.
$y$
-variables are taken to be the solution of the periodicity equation.∙ The cusp condition is written as a simple condition on a product of the initial values of the
 $y$
-variables.
$y$
-variables.
Remark 0.1. The complete hyperbolic structure gives a nonzero solution of the periodicity equation, thanks to the result of [Reference Kitayama and TerashimaKT15, Corollary 2.6].
Remark 0.2. This paper has grown up from our attempts to formulate the results of [Reference Kashaev and NakanishiKN11] and [Reference Terashima and YamazakiTY11, Reference Terashima and YamazakiTY13] in mathematically rigorously.
In [Reference Terashima and YamazakiTY11], the authors conjectured an equivalence of the partition function of a
![]() $3d$
$3d$
![]() ${\mathcal{N}}=2$
gauge theory on a duality wall and that of the
${\mathcal{N}}=2$
gauge theory on a duality wall and that of the
![]() $\text{SL}(2,\mathbb{R})$
Chern–Simons theory on a mapping torus. This is a
$\text{SL}(2,\mathbb{R})$
Chern–Simons theory on a mapping torus. This is a
![]() $3d/3d$
counterpart of the
$3d/3d$
counterpart of the
![]() $4d/2d$
correspondence, known as the AGT relation [Reference Alday, Gaiotto and TachikawaAGT10].
$4d/2d$
correspondence, known as the AGT relation [Reference Alday, Gaiotto and TachikawaAGT10].
In [Reference Terashima and YamazakiTY13], the authors demonstrated that a limit of the 3d N = 2 partition function reproduces the hyperbolic volume of the mapping torus in the case of the once-punctured torus by using quantum cluster transformations. The key observation in [Reference Terashima and YamazakiTY13] was that the shape parameters satisfying edge-gluing equations (as previously analyzed in [Reference GuéritaudGué06]) appear at the saddle point.
In [Reference Kashaev and NakanishiKN11], it was shown that classical dilogarithm identities [Reference NakanishiNak11c] naturally emerge from quantum dilogarithm identities [Reference KellerKel11], [Reference NagaoNag11] by the saddle-point method.
It will be interesting to learn from physics about the “quantum” aspects of hyperbolic geometry of
![]() $3$
-manifolds.
$3$
-manifolds.
Remark 0.3. There is a known relation between cluster transformations and integrable systems [Reference Fomin and ZelevinskyFZ03, Reference KellerKel13, Reference NakanishiNak11b, Reference KedemKed08]. With this, our theorem, which connects cluster transformations to
![]() $3$
-manifolds, gives a natural explanation for mysterious and interesting relations between
$3$
-manifolds, gives a natural explanation for mysterious and interesting relations between
![]() $3$
-manifolds and conformal field theories/integrable systems, originally found in [Reference Gliozzi and TateoGT96, Reference Nahm, Recknagel and TerhoevenNRT93, Reference Dupont and SahDS94]. We illustrate this point by an example in the final subsection (the corresponding
$3$
-manifolds and conformal field theories/integrable systems, originally found in [Reference Gliozzi and TateoGT96, Reference Nahm, Recknagel and TerhoevenNRT93, Reference Dupont and SahDS94]. We illustrate this point by an example in the final subsection (the corresponding
![]() $3$
-manifold is not hyperbolic).
$3$
-manifold is not hyperbolic).
The differences between the two setups, (a) integrable systems and (b) hyperbolic
![]() $3$
-manifolds, can be stated in several different languages:
$3$
-manifolds, can be stated in several different languages:
∙ We have periodicity conditions on the cluster
 $y$
-variables both in (a) and in (b). However, in (a), periodicity is imposed as identities of rational functions on
$y$
-variables both in (a) and in (b). However, in (a), periodicity is imposed as identities of rational functions on
 $y_{i}$
’s, whereas in (b) we solve the periodicity equations to determine values of
$y_{i}$
’s, whereas in (b) we solve the periodicity equations to determine values of
 $y_{i}$
, which in turn determines the hyperbolic structure of the mapping tori.
$y_{i}$
, which in turn determines the hyperbolic structure of the mapping tori.∙ In (a), the product of the quantum dilogarithms associated to the sequence of mutations is equal to
 $1$
(quantum dilogarithm identity [Reference KellerKel11]). In (b), the product gives a nontrivial action of the mapping class in the quantum Teichmüller theory.
$1$
(quantum dilogarithm identity [Reference KellerKel11]). In (b), the product gives a nontrivial action of the mapping class in the quantum Teichmüller theory.∙ In terms of surface triangulations and flips, after a sequence of flips, in (a) we get the original triangulation (up to a permutation of vertices), while in (b) we get the original triangulation pulled back by the mapping class.
∙ A mutation provides a derived equivalence of
 $3$
-dimensional Calabi–Yau categories associated to quivers with potential [Reference Keller and YangKY11]. In (a), the composition of the derived equivalences is an identity functor, while in (b) it gives the action of the mapping class on the derived category (see [Reference NagaoNag]).
$3$
-dimensional Calabi–Yau categories associated to quivers with potential [Reference Keller and YangKY11]. In (a), the composition of the derived equivalences is an identity functor, while in (b) it gives the action of the mapping class on the derived category (see [Reference NagaoNag]).∙ The derived equivalence induced by mutation corresponds to a wall crossing in the space of stability conditions, and a sequence of mutations gives a new chamber. In (a), the new chamber coincides with the original one, while in (b) the chamber is obtained from the original one by the action of the mapping class on the space of stability conditions. In other words, the former is the wall crossing associated with a contractible cycle, whereas the latter corresponds to a noncontractible cycle with nontrivial monodromies (cf. [Reference Andriyash, Denef, Jafferis and MooreADJM12]).
1 Cluster algebras
1.1 Quiver mutation
In this paper, we always assume that a quiver has
∙ the vertex set
 $I=\{1,\ldots ,n\}$
, and
$I=\{1,\ldots ,n\}$
, and∙ no loops and oriented
 $2$
-cycles (see Figure 1).
$2$
-cycles (see Figure 1).
Figure 1. A loop (left) and an oriented
![]() $2$
-cycle (right) of a quiver.
$2$
-cycle (right) of a quiver.
For vertices
![]() $i$
and
$i$
and
![]() $j\in I$
, we define
$j\in I$
, we define
Note that the quiver
![]() $Q$
is uniquely determined by the skew-symmetric matrix
$Q$
is uniquely determined by the skew-symmetric matrix
![]() $\overline{Q}(i,j)$
(or equivalently
$\overline{Q}(i,j)$
(or equivalently
![]() $Q(i,j)$
) under the assumption aboveFootnote
1
.
$Q(i,j)$
) under the assumption aboveFootnote
1
.
For the vertex
![]() $k$
, we define a new quiver
$k$
, we define a new quiver
![]() $\unicode[STIX]{x1D707}_{k}Q$
(mutation of
$\unicode[STIX]{x1D707}_{k}Q$
(mutation of
![]() $Q$
at vertex
$Q$
at vertex
![]() $k$
) by an antisymmetric matrix
$k$
) by an antisymmetric matrix
1.2 Cluster variables
Given a sequence
![]() $\mathbf{k}=(k_{1},\ldots ,k_{l})$
of vertices and “time” parameters
$\mathbf{k}=(k_{1},\ldots ,k_{l})$
of vertices and “time” parameters
![]() $t=0,\ldots ,l$
, we define
$t=0,\ldots ,l$
, we define
For initial values
![]() $x_{i}(0)=x_{i}$
and
$x_{i}(0)=x_{i}$
and
![]() $y_{i}(0)=y_{i}$
, we define the cluster
$y_{i}(0)=y_{i}$
, we define the cluster
![]() $x$
-variables
$x$
-variables
![]() $x_{i}(t)$
and the cluster
$x_{i}(t)$
and the cluster
![]() $y$
-variables (coefficients)
$y$
-variables (coefficients)
![]() $y_{i}(t)$
(
$y_{i}(t)$
(
![]() $i\in I$
) by
$i\in I$
) by
and
2 Triangulated surfaces and quivers
Let
![]() $\unicode[STIX]{x1D6F4}$
be a closed connected oriented surface and
$\unicode[STIX]{x1D6F4}$
be a closed connected oriented surface and
![]() $M$
be a finite set of points on
$M$
be a finite set of points on
![]() $\unicode[STIX]{x1D6F4}$
, called punctures. We assume that
$\unicode[STIX]{x1D6F4}$
, called punctures. We assume that
![]() $M$
is nonempty and
$M$
is nonempty and
![]() $(\unicode[STIX]{x1D6F4},M)$
is not a sphere with less than four punctures.
$(\unicode[STIX]{x1D6F4},M)$
is not a sphere with less than four punctures.
We choose an ideal triangulation
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $\unicode[STIX]{x1D6F4}$
, i.e., we decompose
$\unicode[STIX]{x1D6F4}$
, i.e., we decompose
![]() $\unicode[STIX]{x1D6F4}$
into triangles whose vertices are located at the punctures. We will not allow self-folded arcs (see Figure 2) in this paper.
$\unicode[STIX]{x1D6F4}$
into triangles whose vertices are located at the punctures. We will not allow self-folded arcs (see Figure 2) in this paper.

Figure 2. We do not allow self-folded triangles as in this figure.
2.1 Quiver associated to a triangulation
For a triangulation
![]() $\unicode[STIX]{x1D70F}$
without self-folded arcs we will define a quiver
$\unicode[STIX]{x1D70F}$
without self-folded arcs we will define a quiver
![]() $Q_{\unicode[STIX]{x1D70F}}$
whose vertex set
$Q_{\unicode[STIX]{x1D70F}}$
whose vertex set
![]() $I$
is the set of arcs in
$I$
is the set of arcs in
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
For a triangle
![]() $\unicode[STIX]{x1D6E5}$
and arcs
$\unicode[STIX]{x1D6E5}$
and arcs
![]() $i$
and
$i$
and
![]() $j$
, we define a skew-symmetric integer matrix
$j$
, we define a skew-symmetric integer matrix
![]() $\overline{Q}^{\unicode[STIX]{x1D6E5}}$
by
$\overline{Q}^{\unicode[STIX]{x1D6E5}}$
by
 $$\begin{eqnarray}\overline{Q}^{\unicode[STIX]{x1D6E5}}(i,j):=\left\{\begin{array}{@{}ll@{}}1\quad & \unicode[STIX]{x1D6E5}\text{ has sides }i\text{ and }j,\text{with }i\text{ following }j\\ \quad & \text{in the clockwise order},\\ -1\quad & \text{the same holds, but in the counter-clockwise order,}\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\overline{Q}^{\unicode[STIX]{x1D6E5}}(i,j):=\left\{\begin{array}{@{}ll@{}}1\quad & \unicode[STIX]{x1D6E5}\text{ has sides }i\text{ and }j,\text{with }i\text{ following }j\\ \quad & \text{in the clockwise order},\\ -1\quad & \text{the same holds, but in the counter-clockwise order,}\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
We define
where the sum is taken over all triangles in
![]() $\unicode[STIX]{x1D70F}$
. Let
$\unicode[STIX]{x1D70F}$
. Let
![]() $Q_{\unicode[STIX]{x1D70F}}$
denote the quiver associated to the matrix
$Q_{\unicode[STIX]{x1D70F}}$
denote the quiver associated to the matrix
![]() $\overline{Q}_{\unicode[STIX]{x1D70F}}$
.
$\overline{Q}_{\unicode[STIX]{x1D70F}}$
.
For an arc
![]() $i$
in the triangulation
$i$
in the triangulation
![]() $\unicode[STIX]{x1D70F}$
, we can flip the edge
$\unicode[STIX]{x1D70F}$
, we can flip the edge
![]() $i$
to get a new triangulation
$i$
to get a new triangulation
![]() $f_{i}(\unicode[STIX]{x1D70F})$
. This operation is compatible with a mutation at vertex
$f_{i}(\unicode[STIX]{x1D70F})$
. This operation is compatible with a mutation at vertex
![]() $i$
:
$i$
:
2.2 Mapping class group action
For a triangulation
![]() $\unicode[STIX]{x1D70F}$
, we define
$\unicode[STIX]{x1D70F}$
, we define
For a puncture
![]() $m\in M$
, take a sufficiently small circle around
$m\in M$
, take a sufficiently small circle around
![]() $m$
and let
$m$
and let
![]() $e_{1},\ldots ,e_{n}$
be the sequence of arcs which intersect with the circle, where
$e_{1},\ldots ,e_{n}$
be the sequence of arcs which intersect with the circle, where
![]() $e_{1},\ldots ,e_{n}$
may have multiplicity. We define
$e_{1},\ldots ,e_{n}$
may have multiplicity. We define
and
Let us fix a mapping class
![]() $\unicode[STIX]{x1D711}$
. Then the two triangulations
$\unicode[STIX]{x1D711}$
. Then the two triangulations
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})$
are related by a sequence of flips, together with appropriate changes of labels. More formally, there exists a sequence
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})$
are related by a sequence of flips, together with appropriate changes of labels. More formally, there exists a sequence
such that the two triangulations
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})$
are related by the sequence of flips associated to
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})$
are related by the sequence of flips associated to
![]() $\mathbf{k}$
(see [Reference Fomin, Shapiro and ThurstonFST08, Proposition 3.8]). Note that a flip provides a canonical bijection of the edges of the triangulations. We can represent the composition of the bijections by a permutation
$\mathbf{k}$
(see [Reference Fomin, Shapiro and ThurstonFST08, Proposition 3.8]). Note that a flip provides a canonical bijection of the edges of the triangulations. We can represent the composition of the bijections by a permutation
![]() $\unicode[STIX]{x1D70E}\in \mathfrak{S}_{I}$
. We define the automorphisms
$\unicode[STIX]{x1D70E}\in \mathfrak{S}_{I}$
. We define the automorphisms
by
Thanks to the result [Reference Fomin, Shapiro and ThurstonFST08, Theorem 3.10] and the pentagon relation of cluster transformations,
![]() $\text{CT}_{\unicode[STIX]{x1D711}}$
and
$\text{CT}_{\unicode[STIX]{x1D711}}$
and
![]() $\text{CT}_{\unicode[STIX]{x1D711}}^{\vee }$
are independent of the choices of the sequences of flips and provides a well-defined action of the mapping class group on
$\text{CT}_{\unicode[STIX]{x1D711}}^{\vee }$
are independent of the choices of the sequences of flips and provides a well-defined action of the mapping class group on
![]() $T(\unicode[STIX]{x1D70F})$
.
$T(\unicode[STIX]{x1D70F})$
.
3 Pseudo-Anosov mapping tori
Let
![]() $\unicode[STIX]{x1D70F}$
,
$\unicode[STIX]{x1D70F}$
,
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() $\mathbf{k}$
and
$\mathbf{k}$
and
![]() $\unicode[STIX]{x1D70E}$
be as in §2.2. We assume that no triangles are self-folded.
$\unicode[STIX]{x1D70E}$
be as in §2.2. We assume that no triangles are self-folded.
Let
![]() $h=h(t)$
be the edge flipped at
$h=h(t)$
be the edge flipped at
![]() $t$
and
$t$
and
![]() $h^{\prime }$
be the edge after the flip. Let
$h^{\prime }$
be the edge after the flip. Let
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
and
$c$
and
![]() $d$
be the edges of the quadrilateral in the triangulations whose diagonals are
$d$
be the edges of the quadrilateral in the triangulations whose diagonals are
![]() $h$
and
$h$
and
![]() $h^{\prime }$
. We associate a topological tetrahedron
$h^{\prime }$
. We associate a topological tetrahedron
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(t)$
whose edges are labeled by
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}(t)$
whose edges are labeled by
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
,
$c$
,
![]() $d$
,
$d$
,
![]() $h$
and
$h$
and
![]() $h^{\prime }$
(see Figure 3).
$h^{\prime }$
(see Figure 3).

Figure 3. A flip in a 2d triangulation can be traded for a 3d tetrahedron.
For any pseudo-Anosov mapping class
![]() $\unicode[STIX]{x1D711}$
, this provides a topological tetrahedron decomposition of the mapping torus [Reference AgolAgo11]. A mapping class
$\unicode[STIX]{x1D711}$
, this provides a topological tetrahedron decomposition of the mapping torus [Reference AgolAgo11]. A mapping class
![]() $\unicode[STIX]{x1D711}$
is pseudo-Anosov if and only if the mapping torus has a hyperbolic structure.
$\unicode[STIX]{x1D711}$
is pseudo-Anosov if and only if the mapping torus has a hyperbolic structure.

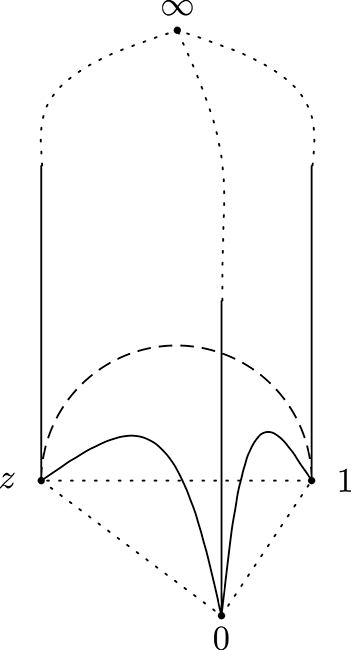
Figure 4. An ideal tetrahedron with shape parameter
![]() $z$
.
$z$
.
4 Equations for hyperbolic structure
4.1 Shape parameters
For an ideal tetrahedron in
![]() $\mathbb{H}^{3}$
with vertices
$\mathbb{H}^{3}$
with vertices
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $z$
and
$z$
and
![]() $\infty$
(Figure 4), we associate the shape parameter
$\infty$
(Figure 4), we associate the shape parameter
![]() $z$
with the edge connecting
$z$
with the edge connecting
![]() $0$
and
$0$
and
![]() $\infty$
. For an ideal tetrahedron, a pair of mutually nonintersecting edges has a common shape parameter, and the shape parameters for the three pairs of mutually nonintersecting edges are given by (Figure 5)
$\infty$
. For an ideal tetrahedron, a pair of mutually nonintersecting edges has a common shape parameter, and the shape parameters for the three pairs of mutually nonintersecting edges are given by (Figure 5)
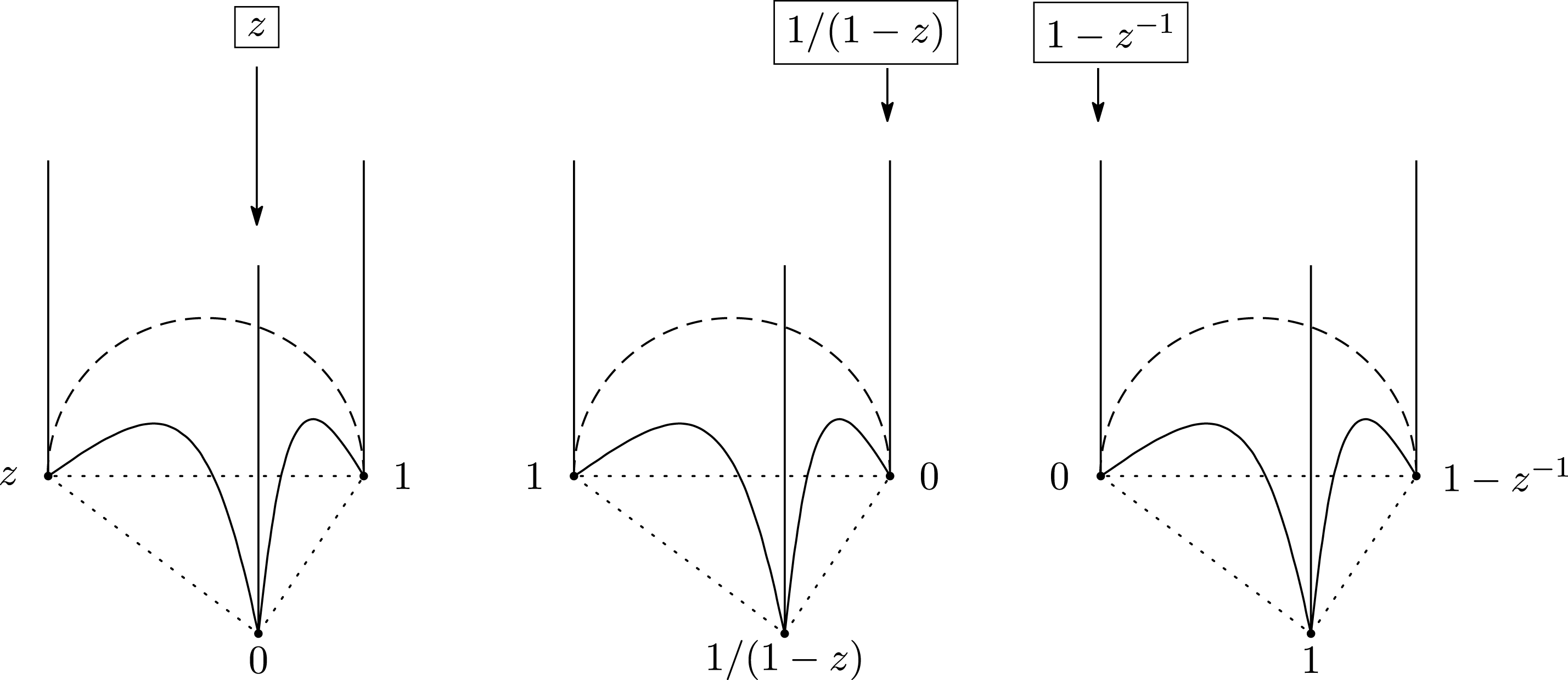
Figure 5. The three shape parameters of an ideal tetrahedron.
We take a sequence of flips and associated topological decomposition of the mapping torus as in §3. For
![]() $t\in \mathbb{Z}$
, let
$t\in \mathbb{Z}$
, let
![]() $\unicode[STIX]{x1D6E5}(t)$
denote the
$\unicode[STIX]{x1D6E5}(t)$
denote the
![]() $t$
th tetrahedron, where
$t$
th tetrahedron, where
![]() $\unicode[STIX]{x1D6E5}(t)$
and
$\unicode[STIX]{x1D6E5}(t)$
and
![]() $\unicode[STIX]{x1D6E5}(t+l)$
are identified for any
$\unicode[STIX]{x1D6E5}(t+l)$
are identified for any
![]() $t$
. Let
$t$
. Let
![]() $Z(t)$
denote the shape parameter of
$Z(t)$
denote the shape parameter of
![]() $\unicode[STIX]{x1D6E5}(t)$
at the edge
$\unicode[STIX]{x1D6E5}(t)$
at the edge
![]() $h(t)$
, the edge flipped at time
$h(t)$
, the edge flipped at time
![]() $t$
. Note that the sequence
$t$
. Note that the sequence
![]() $(Z(t))$
satisfies shape parameter periodicity
$(Z(t))$
satisfies shape parameter periodicity
For a tetrahedron
![]() $\unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6E5}$
, let
![]() $\unicode[STIX]{x1D6E5}_{1}$
be the set of edges of
$\unicode[STIX]{x1D6E5}_{1}$
be the set of edges of
![]() $\unicode[STIX]{x1D6E5}$
. We define
$\unicode[STIX]{x1D6E5}$
. We define
Let
![]() $\widetilde{E}$
denote the set of all edges in the tetrahedron decomposition of
$\widetilde{E}$
denote the set of all edges in the tetrahedron decomposition of
![]() $\unicode[STIX]{x1D6F4}\times \mathbb{R}$
and
$\unicode[STIX]{x1D6F4}\times \mathbb{R}$
and
![]() $\unicode[STIX]{x1D70B}:\overline{E}\rightarrow \widetilde{E}$
be the canonical surjection.
$\unicode[STIX]{x1D70B}:\overline{E}\rightarrow \widetilde{E}$
be the canonical surjection.
Given parameters
![]() $(Z(t))_{t\in \mathbb{Z}}$
, we can define associated parameter
$(Z(t))_{t\in \mathbb{Z}}$
, we can define associated parameter
![]() $Z_{e}=Z_{e}(t)$
for any
$Z_{e}=Z_{e}(t)$
for any
![]() $t\in \mathbb{Z}$
and
$t\in \mathbb{Z}$
and
![]() $e\in \unicode[STIX]{x1D6E5}(t)_{1}$
as the shape parameter of
$e\in \unicode[STIX]{x1D6E5}(t)_{1}$
as the shape parameter of
![]() $\unicode[STIX]{x1D6E5}(t)$
on the edge
$\unicode[STIX]{x1D6E5}(t)$
on the edge
![]() $e$
, which is determined as in (4).
$e$
, which is determined as in (4).
4.2 Edge-gluing conditions
Suppose that the shape parameters
![]() $(Z(t))_{t\in \mathbb{Z}}$
give an ideal tetrahedron decompositionFootnote
2
. This holds if and only if the following three conditions are satisfied.
$(Z(t))_{t\in \mathbb{Z}}$
give an ideal tetrahedron decompositionFootnote
2
. This holds if and only if the following three conditions are satisfied.
First, we need the shape parameter periodicity condition as already discussed in (5). Second, we need
so that the tetrahedron is positively oriented. Third, for each edge
![]() $g\in \widetilde{E}$
, the product of all the shape parameters associated to the elements in
$g\in \widetilde{E}$
, the product of all the shape parameters associated to the elements in
![]() $\unicode[STIX]{x1D70B}^{-1}(g)$
must be
$\unicode[STIX]{x1D70B}^{-1}(g)$
must be
![]() $1$
([Reference ThurstonThu79], see Figure 6):
$1$
([Reference ThurstonThu79], see Figure 6):

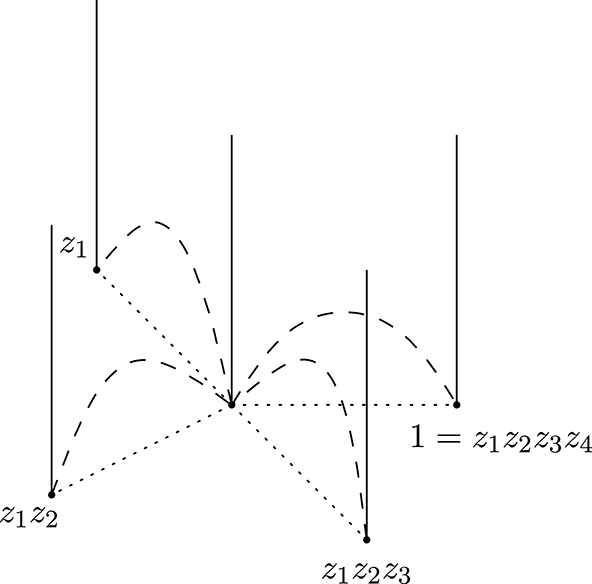
Figure 6. The edge-gluing equation around an edge.
4.3
 $y$
-variables and gluing conditions
$y$
-variables and gluing conditions
Proposition 4.1. Let
![]() $e(t)\in \unicode[STIX]{x1D70F}(t)_{1}$
be the edge which we flip at
$e(t)\in \unicode[STIX]{x1D70F}(t)_{1}$
be the edge which we flip at
![]() $t$
and
$t$
and
![]() $e^{\prime }(t+1)\in \unicode[STIX]{x1D70F}(t+1)_{1}$
be the edge which appears after the flip. The edge-gluing equation is satisfied for the shape parameters
$e^{\prime }(t+1)\in \unicode[STIX]{x1D70F}(t+1)_{1}$
be the edge which appears after the flip. The edge-gluing equation is satisfied for the shape parameters

Figure 7. An edge
![]() $g$
in a tetrahedron decomposition appears at time
$g$
in a tetrahedron decomposition appears at time
![]() $t_{1}$
and disappears at time
$t_{1}$
and disappears at time
![]() $t_{2}$
.
$t_{2}$
.
Proof. Let
![]() $g\in \widetilde{E}$
be an edge which appears at the
$g\in \widetilde{E}$
be an edge which appears at the
![]() $t_{1}$
th flip at
$t_{1}$
th flip at
![]() $\bar{g}^{\prime }$
and disappears at the
$\bar{g}^{\prime }$
and disappears at the
![]() $t_{2}$
th flip
$t_{2}$
th flip
![]() $\bar{g}^{\prime \prime }$
(Figure 7). Let
$\bar{g}^{\prime \prime }$
(Figure 7). Let
![]() $\bar{g}_{1}$
(resp.
$\bar{g}_{1}$
(resp.
![]() $\bar{g}_{2}$
) be the unique element in
$\bar{g}_{2}$
) be the unique element in
![]() $\unicode[STIX]{x1D6E5}(t_{1})_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)$
(resp. in
$\unicode[STIX]{x1D6E5}(t_{1})_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)$
(resp. in
![]() $\unicode[STIX]{x1D6E5}(t_{2})_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)$
). The gluing equation associated with
$\unicode[STIX]{x1D6E5}(t_{2})_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)$
). The gluing equation associated with
![]() $g$
is
$g$
is
 $$\begin{eqnarray}\displaystyle 1 & = & \displaystyle \mathop{\prod }_{t=t_{1}}^{t_{2}}\mathop{\prod }_{\bar{g}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)}Z_{\bar{g}}\nonumber\\ \displaystyle & = & \displaystyle Z(t_{1})\times \left(\mathop{\prod }_{t=t_{1}+1}^{t_{2}-1}\mathop{\prod }_{\bar{g}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)}Z_{\bar{g}}\right)\times Z(t_{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1 & = & \displaystyle \mathop{\prod }_{t=t_{1}}^{t_{2}}\mathop{\prod }_{\bar{g}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)}Z_{\bar{g}}\nonumber\\ \displaystyle & = & \displaystyle Z(t_{1})\times \left(\mathop{\prod }_{t=t_{1}+1}^{t_{2}-1}\mathop{\prod }_{\bar{g}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)}Z_{\bar{g}}\right)\times Z(t_{2}).\nonumber\end{eqnarray}$$
For this equation, we will show
 $$\begin{eqnarray}Z(t_{1})\times \left(\mathop{\prod }_{t=t_{1}+1}^{T}\mathop{\prod }_{\bar{g}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)}Z_{\bar{g}}\right)=-y_{g_{0}}(T+1)^{-1},\end{eqnarray}$$
$$\begin{eqnarray}Z(t_{1})\times \left(\mathop{\prod }_{t=t_{1}+1}^{T}\mathop{\prod }_{\bar{g}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(g)}Z_{\bar{g}}\right)=-y_{g_{0}}(T+1)^{-1},\end{eqnarray}$$
where
![]() $g_{0}$
is the edge corresponding to
$g_{0}$
is the edge corresponding to
![]() $g$
which
$g$
which
![]() $\unicode[STIX]{x1D70F}(t)$
(
$\unicode[STIX]{x1D70F}(t)$
(
![]() $t=t_{1}+1,\ldots ,t_{2}$
) have in common. We show the equation above by induction with respect to
$t=t_{1}+1,\ldots ,t_{2}$
) have in common. We show the equation above by induction with respect to
![]() $T$
. The claim for
$T$
. The claim for
![]() $T=t_{1}$
trivially follows from the definition (6). Let us assume the above statement for
$T=t_{1}$
trivially follows from the definition (6). Let us assume the above statement for
![]() $T\rightarrow T-1$
. To show the statement for
$T\rightarrow T-1$
. To show the statement for
![]() $T$
, we need to show
$T$
, we need to show
We will show this by classifying the positional relation of
![]() $g_{0}$
and
$g_{0}$
and
![]() $e(t)$
.
$e(t)$
.
∙
 $g_{0}$
and
$g_{0}$
and
 $e(t)$
have no triangle in common: both side of the equation above is
$e(t)$
have no triangle in common: both side of the equation above is
 $1$
.
$1$
.∙
 $g_{0}$
and
$g_{0}$
and
 $e(t)$
have a single triangle in common:
$e(t)$
have a single triangle in common: –
 $\overline{Q_{t}}(e(t),g_{0})=1$
(see Figure 8):
$\overline{Q_{t}}(e(t),g_{0})=1$
(see Figure 8):  $$\begin{eqnarray}(\text{LHS})\overset{\text{ equation (4) }}{=}1-Z(t)^{-1}\overset{\text{ equation (2) }}{=}(\text{RHS}),\end{eqnarray}$$
$$\begin{eqnarray}(\text{LHS})\overset{\text{ equation (4) }}{=}1-Z(t)^{-1}\overset{\text{ equation (2) }}{=}(\text{RHS}),\end{eqnarray}$$
–
 $\overline{Q_{t}}(e(t),g_{0})=-1$
:
$\overline{Q_{t}}(e(t),g_{0})=-1$
:  $$\begin{eqnarray}(\text{LHS})\overset{\text{ equation (4) }}{=}(1-Z(t))^{-1}\overset{\text{ equation (2) }}{=}(\text{RHS}),\end{eqnarray}$$
$$\begin{eqnarray}(\text{LHS})\overset{\text{ equation (4) }}{=}(1-Z(t))^{-1}\overset{\text{ equation (2) }}{=}(\text{RHS}),\end{eqnarray}$$
∙
 $g_{0}$
and
$g_{0}$
and
 $e(t)$
have two triangles in common:
$e(t)$
have two triangles in common:–
 $\overline{Q_{t}}(e(t),g_{0})=\pm 2$
(see Figure 9):
$\overline{Q_{t}}(e(t),g_{0})=\pm 2$
(see Figure 9):  $$\begin{eqnarray}(\text{LHS})\overset{\text{ equation (4) }}{=}(1-Z(t)^{\mp })^{\pm 2}\overset{\text{ equation (2) }}{=}(\text{RHS}),\end{eqnarray}$$
$$\begin{eqnarray}(\text{LHS})\overset{\text{ equation (4) }}{=}(1-Z(t)^{\mp })^{\pm 2}\overset{\text{ equation (2) }}{=}(\text{RHS}),\end{eqnarray}$$
–
 $\overline{Q_{t}}(e(t),g_{0})=0$
: this cannot happen because we prohibit self-folded edges in this paper (see Figure 10).
$\overline{Q_{t}}(e(t),g_{0})=0$
: this cannot happen because we prohibit self-folded edges in this paper (see Figure 10).

Figure 8. The case with
![]() $\overline{Q_{t}}(e(t),g_{0})=1$
.
$\overline{Q_{t}}(e(t),g_{0})=1$
.
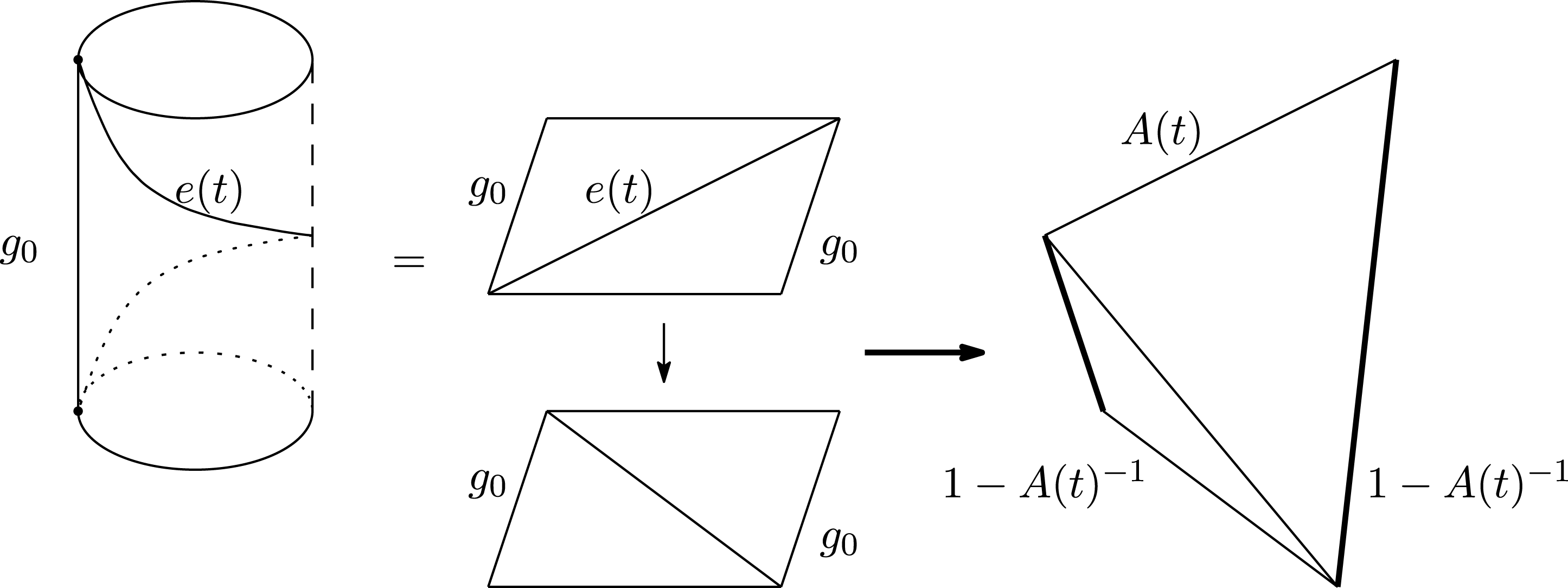
Figure 9. The case with
![]() $\overline{Q_{t}}(e(t),g_{0})=2$
.
$\overline{Q_{t}}(e(t),g_{0})=2$
.
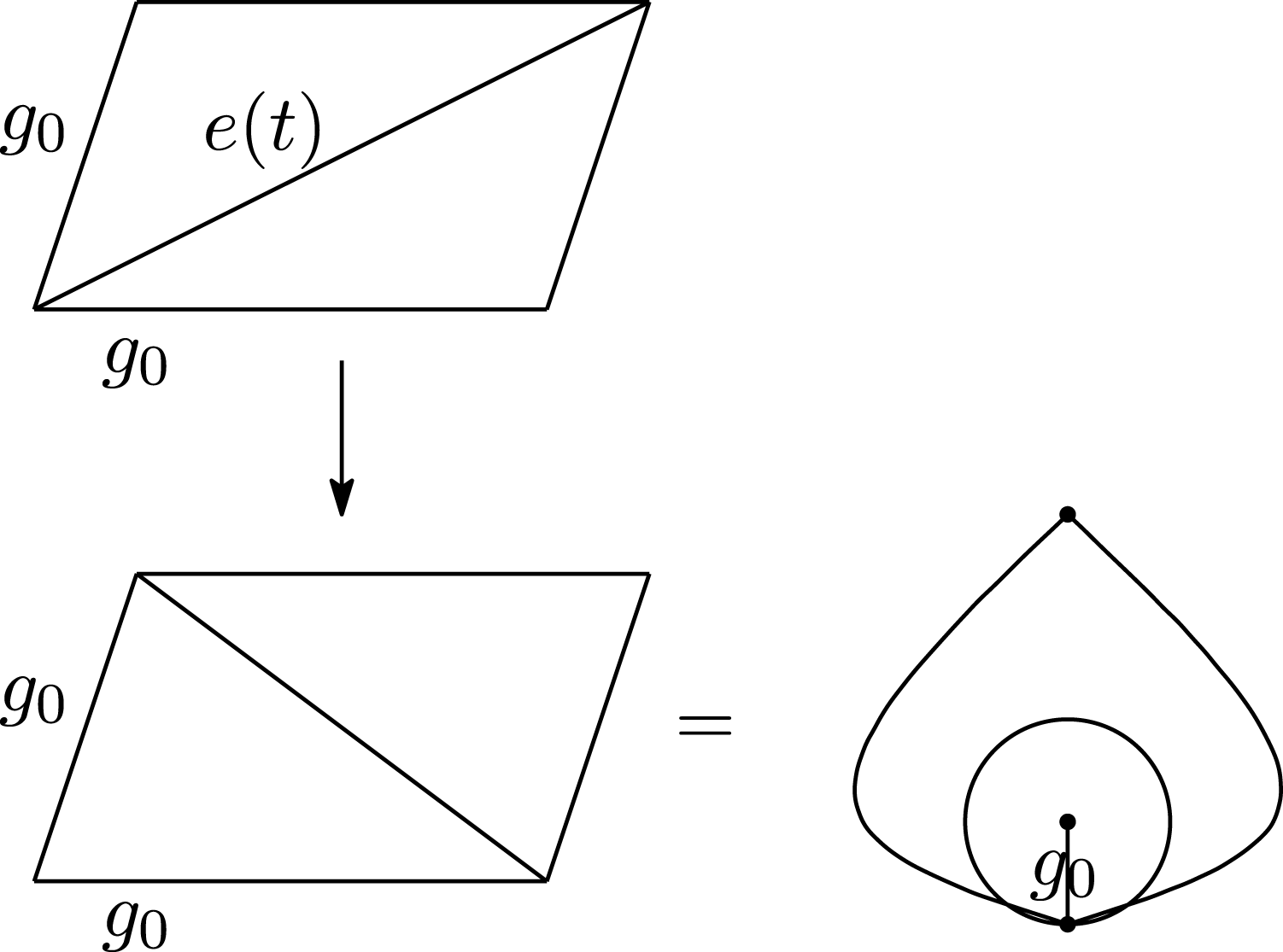
Figure 10. The case with
![]() $\overline{Q_{t}}(e(t),g_{0})=0$
.
$\overline{Q_{t}}(e(t),g_{0})=0$
.
4.4 Complete hyperbolic structures
Patching ideal tetrahedra with corners removed, we get a hyperbolic
![]() $3$
-manifold with boundaries, each of which is isomorphic to a torus. Note that such a boundary torus has two directions: the direction of “time” parameter
$3$
-manifold with boundaries, each of which is isomorphic to a torus. Note that such a boundary torus has two directions: the direction of “time” parameter
![]() $t$
(time direction) and the direction of the original surface (surface direction)Footnote
3
.
$t$
(time direction) and the direction of the original surface (surface direction)Footnote
3
.
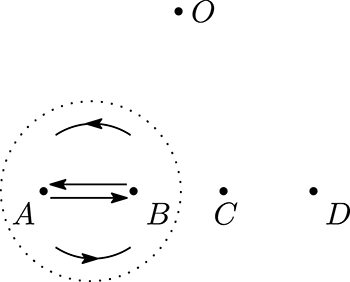
The intersection of a removed corner and a boundary torus gives a triangle on the torus with a shape parameter for each angle.
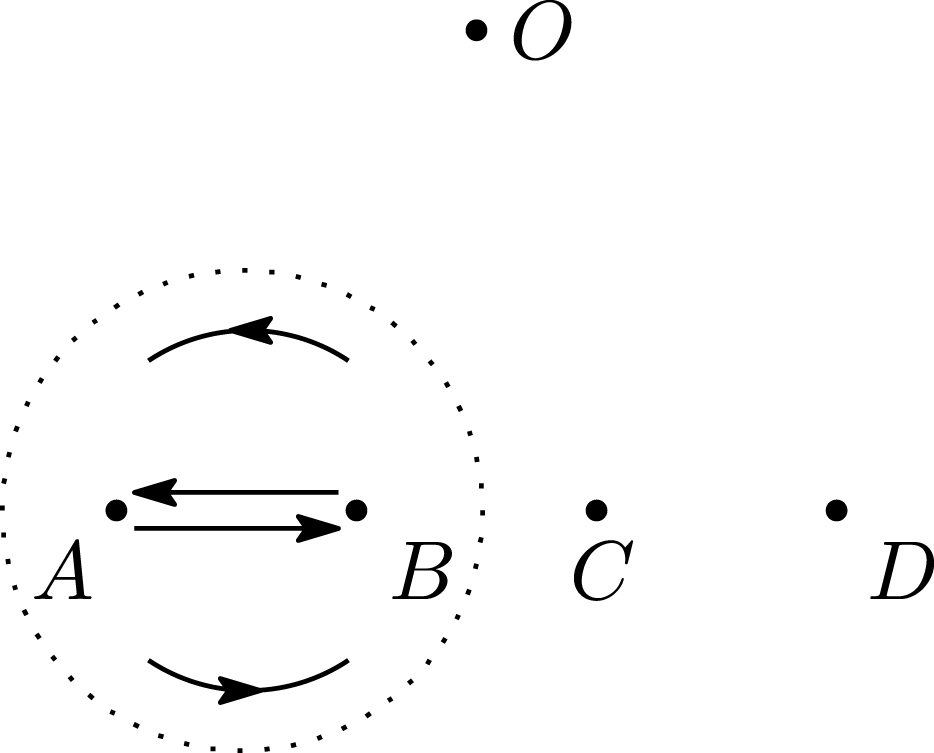
Figure 11. A Dehn half-twist
![]() $\unicode[STIX]{x1D70E}_{1}$
along a circle containing
$\unicode[STIX]{x1D70E}_{1}$
along a circle containing
![]() $A$
and
$A$
and
![]() $B$
.
$B$
.
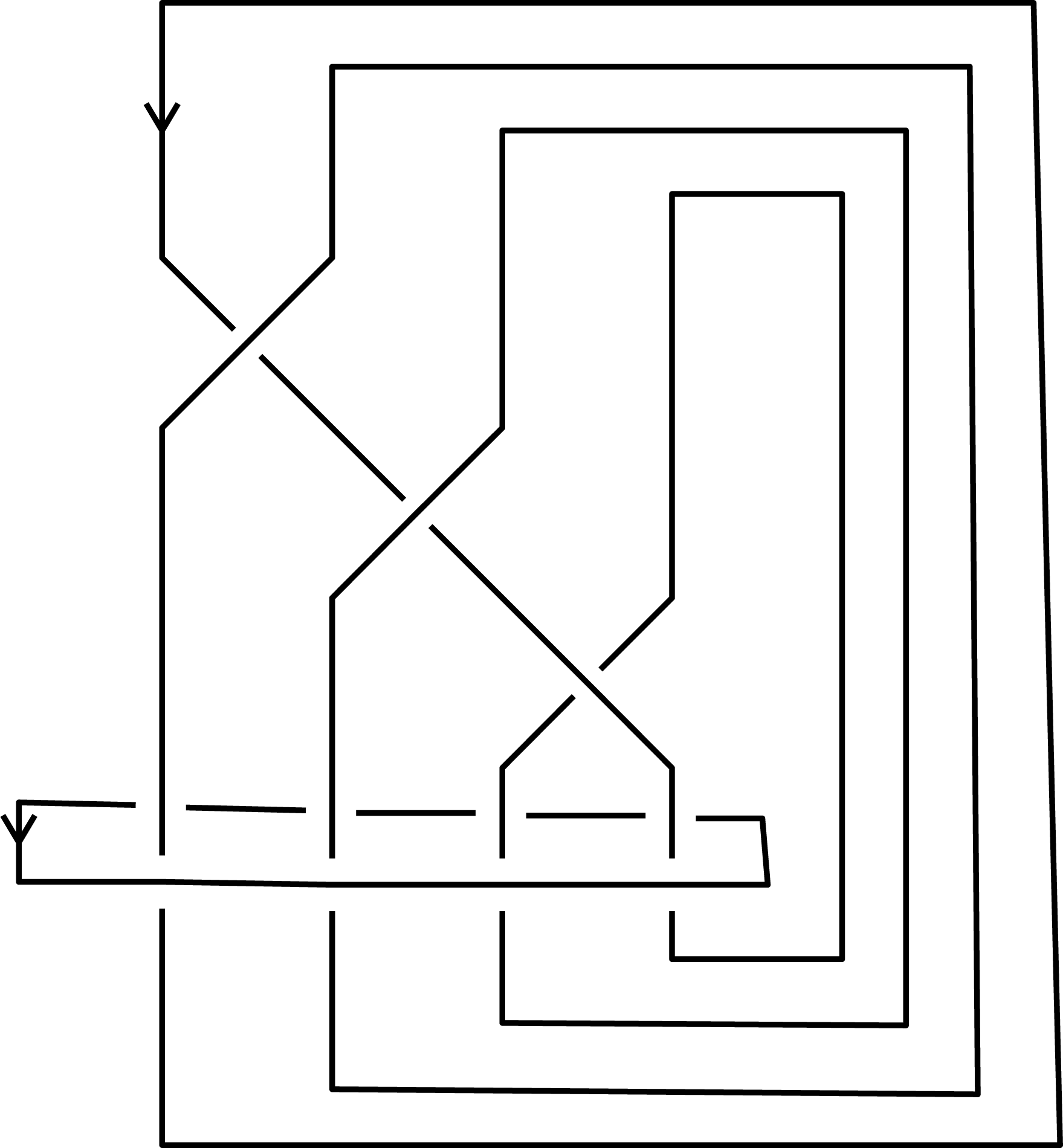
Figure 12. The link corresponding to
![]() $\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{3}^{-1}$
.
$\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{3}^{-1}$
.

Figure 13. A triangulation of the five-punctured sphere.
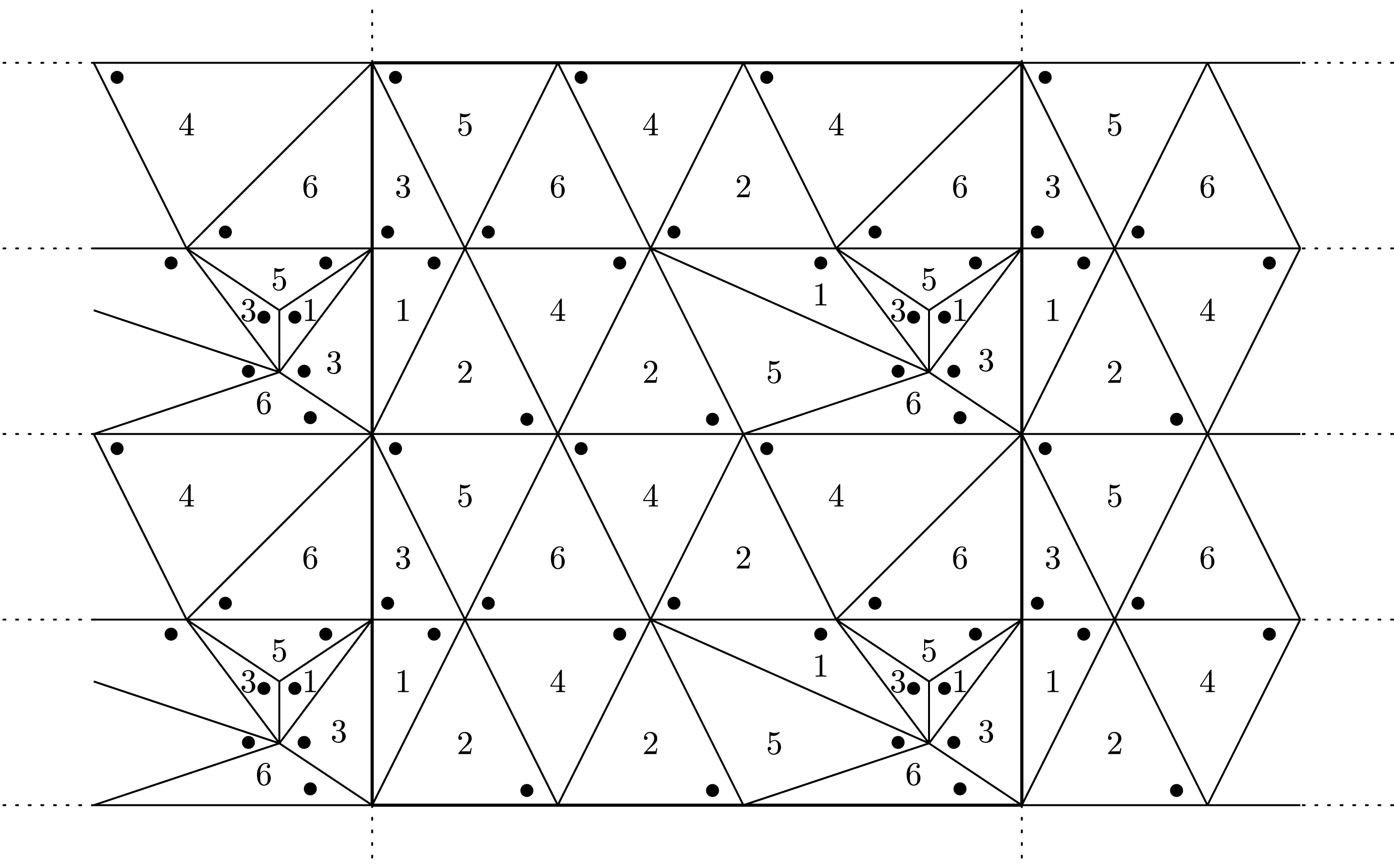
Figure 14. The triangulation of the boundary torus. A triangle with number
![]() $t$
represents the
$t$
represents the
![]() $t$
th tetrahedron
$t$
th tetrahedron
![]() $\unicode[STIX]{x1D6E5}(t)$
, whose modulus
$\unicode[STIX]{x1D6E5}(t)$
, whose modulus
![]() $Z(t)$
corresponds to a dihedral angle represented by a black dot.
$Z(t)$
corresponds to a dihedral angle represented by a black dot.
Example 4.2. We take a five-punctured sphere. Let
![]() $A$
,
$A$
,
![]() $B$
,
$B$
,
![]() $C$
,
$C$
,
![]() $D$
,
$D$
,
![]() $O$
be the punctures and
$O$
be the punctures and
![]() $\unicode[STIX]{x1D70E}_{1}$
(resp.
$\unicode[STIX]{x1D70E}_{1}$
(resp.
![]() $\unicode[STIX]{x1D70E}_{2}$
or
$\unicode[STIX]{x1D70E}_{2}$
or
![]() $\unicode[STIX]{x1D70E}_{3}$
) be the Dehn half-twist along a circle containing
$\unicode[STIX]{x1D70E}_{3}$
) be the Dehn half-twist along a circle containing
![]() $A$
and
$A$
and
![]() $B$
(resp.
$B$
(resp.
![]() $B$
and
$B$
and
![]() $C$
, or
$C$
, or
![]() $C$
and
$C$
and
![]() $D$
) in the anticlock direction (see Figure 11). Note that
$D$
) in the anticlock direction (see Figure 11). Note that
![]() $\unicode[STIX]{x1D70E}_{1}$
,
$\unicode[STIX]{x1D70E}_{1}$
,
![]() $\unicode[STIX]{x1D70E}_{2}$
and
$\unicode[STIX]{x1D70E}_{2}$
and
![]() $\unicode[STIX]{x1D70E}_{3}$
generate the braid group
$\unicode[STIX]{x1D70E}_{3}$
generate the braid group
![]() $B_{4}$
. We take
$B_{4}$
. We take
∙
 $\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{3}^{-1}$
as a mapping class;
$\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{3}^{-1}$
as a mapping class;∙ the triangulation as in Figure 13;
∙
 $8$
,
$8$
,
 $9$
,
$9$
,
 $5$
,
$5$
,
 $7$
,
$7$
,
 $1$
,
$1$
,
 $8$
as a sequence of edges which we flipFootnote
4
.
$8$
as a sequence of edges which we flipFootnote
4
.
The mapping torus is the complement of the two-component link in
![]() $S^{2}\times S^{1}$
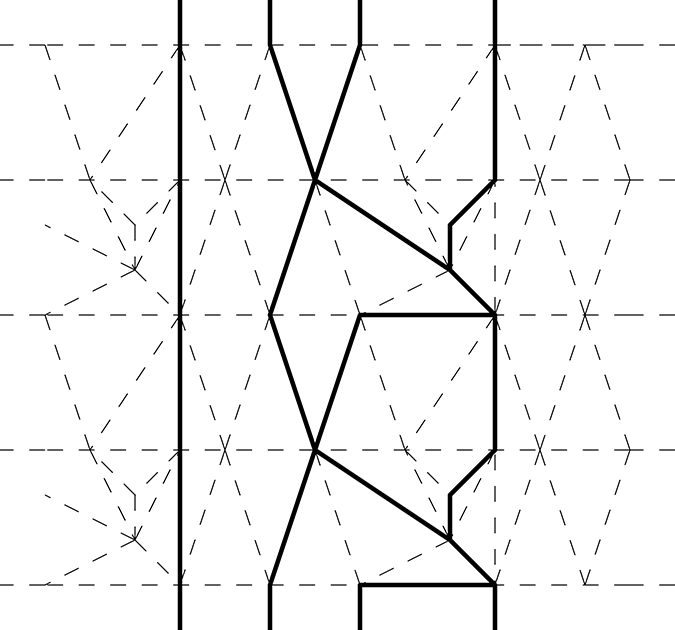
(Figure 12), and hence we have two boundary components. We show the triangulation of the universal cover of one of the components in Figure 14.
$S^{2}\times S^{1}$
(Figure 12), and hence we have two boundary components. We show the triangulation of the universal cover of one of the components in Figure 14.
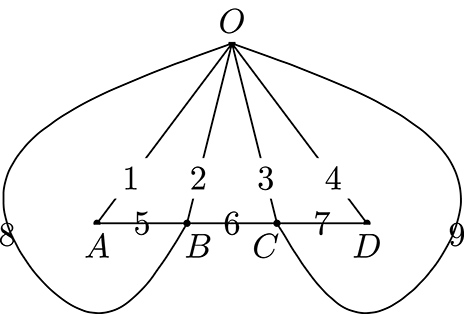
Fix a puncture
![]() $m\in M$
of the surface and a time parameter
$m\in M$
of the surface and a time parameter
![]() $t_{0}$
. Let
$t_{0}$
. Let
![]() $F_{i}$
(
$F_{i}$
(
![]() $i\in \mathbb{Z}/n\mathbb{Z}$
) be the triangle in
$i\in \mathbb{Z}/n\mathbb{Z}$
) be the triangle in
![]() $\unicode[STIX]{x1D70F}(t_{0})$
which is adjacent to
$\unicode[STIX]{x1D70F}(t_{0})$
which is adjacent to
![]() $e_{i-1}$
,
$e_{i-1}$
,
![]() $m$
and
$m$
and
![]() $e_{i}$
, where
$e_{i}$
, where
![]() $(e_{1},\ldots ,e_{n})$
is the sequence of arcs around
$(e_{1},\ldots ,e_{n})$
is the sequence of arcs around
![]() $m$
as before.
$m$
as before.
On the boundary torus,
![]() $e_{i}$
represents a vertex and
$e_{i}$
represents a vertex and
![]() $F_{i}$
represents an edge connecting
$F_{i}$
represents an edge connecting
![]() $e_{i-1}$
and
$e_{i-1}$
and
![]() $e_{i}$
. The union of
$e_{i}$
. The union of
![]() $F_{i}$
’s provides a (piecewise linear) closed curve on the boundary torusFootnote
5
. We call this a vertical line (see Figure 15).
$F_{i}$
’s provides a (piecewise linear) closed curve on the boundary torusFootnote
5
. We call this a vertical line (see Figure 15).
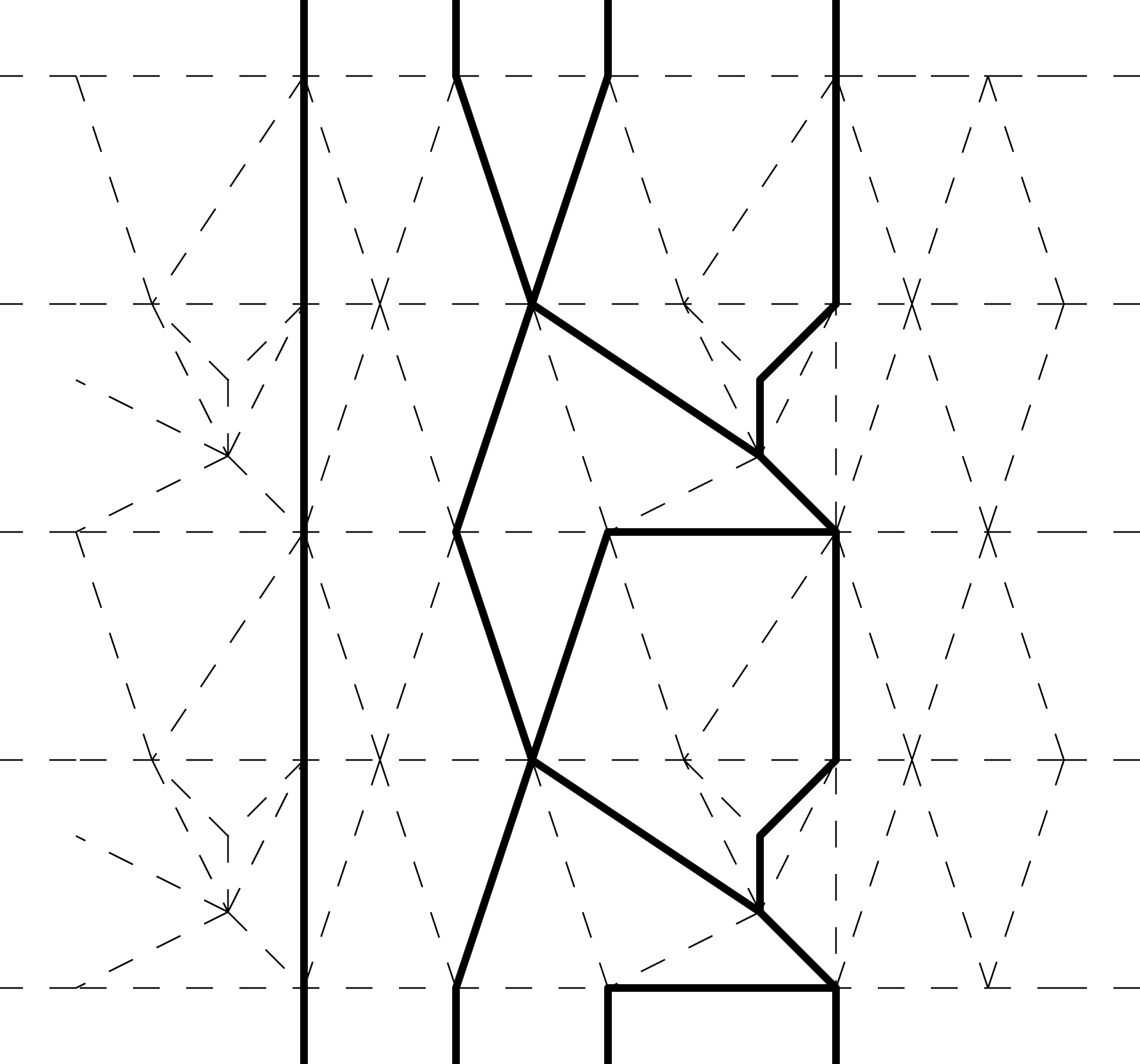
Figure 15. Vertical lines, drawn in the triangulation of Figure 14.
The holonomy of along a cycle in the surface direction is given as follows. A vertical line divides the boundary torus into two parts. We fix one of them. For a vertex
![]() $e_{i}$
on the vertical line, we take all angles in the universal cover which have
$e_{i}$
on the vertical line, we take all angles in the universal cover which have
![]() $e_{i}$
as the vertex and which are on the given side of the vertical line. We denote by
$e_{i}$
as the vertex and which are on the given side of the vertical line. We denote by
![]() $H_{i}$
the product of the shape parameters associated to these angles. Then we have
$H_{i}$
the product of the shape parameters associated to these angles. Then we have
A hyperbolic structure given by a sequence of shape parameters is complete if and only if the following condition holds:
![]()
In Figure 7, we study the set of all tetrahedra which are adjacent to an edge. In this setting, the vertical line divides the set of these tetrahedra into two groups: tetrahedra which appear before/after
![]() $t=t_{0}$
. Hence we have
$t=t_{0}$
. Hence we have
 $$\begin{eqnarray}H_{i}=Z(t_{1})\times \left(\mathop{\prod }_{t=t_{1}+1}^{t_{0}-1}\mathop{\prod }_{\bar{e}_{i}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(e_{i})}Z_{\bar{e_{i}}}\right).\end{eqnarray}$$
$$\begin{eqnarray}H_{i}=Z(t_{1})\times \left(\mathop{\prod }_{t=t_{1}+1}^{t_{0}-1}\mathop{\prod }_{\bar{e}_{i}\in \unicode[STIX]{x1D6E5}(t)_{1}\cap \unicode[STIX]{x1D70B}^{-1}(e_{i})}Z_{\bar{e_{i}}}\right).\end{eqnarray}$$
By (7), the right hand side equals
![]() $-y_{e_{i}}(t_{0})$
. Therefore the holonomy (8) is equivalent with
$-y_{e_{i}}(t_{0})$
. Therefore the holonomy (8) is equivalent with
![]() $y_{m}(t_{0})=\prod _{i=1}^{n}y_{e_{i}}(t_{0})$
(recall (3)). We can show this product is independent on the choice of
$y_{m}(t_{0})=\prod _{i=1}^{n}y_{e_{i}}(t_{0})$
(recall (3)). We can show this product is independent on the choice of
![]() $t_{0}$
, either by induction or by using the edge-gluing conditions (vertical lines at different choices of
$t_{0}$
, either by induction or by using the edge-gluing conditions (vertical lines at different choices of
![]() $t_{0}$
are homologous in the triangulation of the boundary torus).
$t_{0}$
are homologous in the triangulation of the boundary torus).
In summary, we get the following description of the holonomy:
Proposition 4.3. For a sequence of shape parameters determined by the result of Proposition 4.1, the holonomy around a puncture
![]() $m$
in the surface direction is equal to
$m$
in the surface direction is equal to
![]() $y_{m}$
.
$y_{m}$
.
4.5 Main theorem
Let us summarize our results in the form of a theorem:
Theorem 4.4. Let
![]() $(y_{e})_{e\in \unicode[STIX]{x1D70F}_{1}}$
be nonzero complex numbers such that
$(y_{e})_{e\in \unicode[STIX]{x1D70F}_{1}}$
be nonzero complex numbers such that
![]() $y_{m}=1$
for any puncture
$y_{m}=1$
for any puncture
![]() $m\in M$
. Assume that
$m\in M$
. Assume that
![]() $y_{h}(t)\Big|_{y_{e}(0)=y_{e}}$
is well defined for any
$y_{h}(t)\Big|_{y_{e}(0)=y_{e}}$
is well defined for any
![]() $h$
and
$h$
and
![]() $t$
and that the periodicity equation is satisfied
$t$
and that the periodicity equation is satisfied
Let us define the shape parameters
![]() $Z(t)$
by
$Z(t)$
by
where
![]() $e(t)$
is the edge flipped at time
$e(t)$
is the edge flipped at time
![]() $t$
, and suppose that
$t$
, and suppose that
![]() $Z(t)\neq 0,1$
for any
$Z(t)\neq 0,1$
for any
![]() $t$
. Then
$t$
. Then
![]() $(Z(t))$
satisfies the edge-gluing equations in §4.2 and the cusp condition in §4.4.
$(Z(t))$
satisfies the edge-gluing equations in §4.2 and the cusp condition in §4.4.
This theorem gives a systematic method to identify for hyperbolic structures on mapping tori, formulated in the language of cluster algebras. For a genuine hyperbolic structure we also need to verify
![]() $\text{Im}(Z(t))>0$
; see the examples in the next section.
$\text{Im}(Z(t))>0$
; see the examples in the next section.
5 Examples
In the last section, we demonstrate Theorem 4.4 in the case of a once-punctured torus and of a five-punctured sphere. The examples are chosen for the sake of simplicity, and the same methods apply to more general mapping classes of more general punctured surfaces (recall Remark 0.1). We also discuss an example of the six-punctured disc, to show that our formulation covers the nonhyperbolic cases not covered in Theorem 4.4.

Figure 16. Example: once-punctured torus and
![]() $LR$
.
$LR$
.
5.1 Once-punctured torus and
 $LR$
$LR$
Let us start with a once-punctured torus. We take a sequence of two flips as in Figure 16. This is the mapping class studied in [Reference Terashima and YamazakiTY13, §3.1]. Then the shape parameter periodicity conditions are
 $$\begin{eqnarray}\displaystyle y_{1} & = & \displaystyle y_{2}^{-1}\left(1+y_{1}^{-1}(1+y_{2}^{-1})^{2}\right)^{-2},\nonumber\\ \displaystyle y_{2} & = & \displaystyle y_{3}(1+y_{2})^{2}\left(1+y_{1}(1+y_{2}^{-1})^{-2}\right)^{2},\nonumber\\ \displaystyle y_{3} & = & \displaystyle y_{1}^{-1}(1+y_{2}^{-1})^{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{1} & = & \displaystyle y_{2}^{-1}\left(1+y_{1}^{-1}(1+y_{2}^{-1})^{2}\right)^{-2},\nonumber\\ \displaystyle y_{2} & = & \displaystyle y_{3}(1+y_{2})^{2}\left(1+y_{1}(1+y_{2}^{-1})^{-2}\right)^{2},\nonumber\\ \displaystyle y_{3} & = & \displaystyle y_{1}^{-1}(1+y_{2}^{-1})^{2},\nonumber\end{eqnarray}$$
and the cusp condition is
Solving these equations, we get a solution
By Theorem 4.4, shape parameters
 $$\begin{eqnarray}\displaystyle Z(0) & = & \displaystyle -y_{2}(0)=-y_{2}=\frac{1+\sqrt{-3}}{2},\nonumber\\ \displaystyle Z(1) & = & \displaystyle -y_{1}(1)=-y_{1}(1+y_{2}^{-1})^{-2}=\frac{1+\sqrt{-3}}{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z(0) & = & \displaystyle -y_{2}(0)=-y_{2}=\frac{1+\sqrt{-3}}{2},\nonumber\\ \displaystyle Z(1) & = & \displaystyle -y_{1}(1)=-y_{1}(1+y_{2}^{-1})^{-2}=\frac{1+\sqrt{-3}}{2},\nonumber\end{eqnarray}$$
satisfy edge-gluing conditions. Moreover, the imaginary parts of
![]() $Z(0)$
and
$Z(0)$
and
![]() $Z(1)$
are positive, and we obtain a complete hyperbolic structure on the mapping torus. The parameters coincide with the ones in [Reference Terashima and YamazakiTY13, §3.1].
$Z(1)$
are positive, and we obtain a complete hyperbolic structure on the mapping torus. The parameters coincide with the ones in [Reference Terashima and YamazakiTY13, §3.1].
5.2 Five-punctured sphere and
 $\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{3}^{-1}$
$\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{3}^{-1}$
Let us take the example of a five-punctured sphere in Example 4.2.
The cusp conditions are
and the shape parameter periodicity conditions are
 $$\begin{eqnarray}\displaystyle y_{6} & = & \displaystyle \frac{1}{y_{1}y_{5}y_{8}^{2}y_{9}}\Bigl((1+y_{5}+y_{5}y_{8})((1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})\nonumber\\ \displaystyle & & \displaystyle +\,y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9}))\Bigr),\nonumber\\ \displaystyle y_{1} & = & \displaystyle y_{2}(1+y_{5}+y_{5}y_{8}),\nonumber\\ \displaystyle y_{2} & = & \displaystyle \frac{y_{3}y_{7}y_{9}(1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9}))}{(1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})+y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9})},\nonumber\\ \displaystyle y_{9} & = & \displaystyle \frac{y_{4}(1+(1+y_{7})(1+y_{8})y_{9})(1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9}))}{(1+y_{5}+y_{5}y_{8})(1+y_{9}+y_{8}y_{9})},\nonumber\\ \displaystyle y_{8} & = & \displaystyle \frac{y_{1}y_{8}y_{9}}{1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9})},\nonumber\\ \displaystyle y_{5} & = & \displaystyle \frac{y_{5}y_{6}y_{8}}{1+y_{5}+y_{5}y_{8}},\nonumber\\ \displaystyle y_{4} & = & \displaystyle \frac{(1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})+y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9})}{y_{7}y_{8}y_{9}},\nonumber\\ \displaystyle y_{3} & = & \displaystyle \frac{y_{8}(1+y_{9}+y_{8}y_{9})}{(1+(1+y_{7})(1+y_{8})y_{9})(1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9}))},\nonumber\\ \displaystyle y_{7} & = & \displaystyle \frac{y_{1}y_{5}y_{7}y_{8}y_{9}}{(1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})+y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{6} & = & \displaystyle \frac{1}{y_{1}y_{5}y_{8}^{2}y_{9}}\Bigl((1+y_{5}+y_{5}y_{8})((1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})\nonumber\\ \displaystyle & & \displaystyle +\,y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9}))\Bigr),\nonumber\\ \displaystyle y_{1} & = & \displaystyle y_{2}(1+y_{5}+y_{5}y_{8}),\nonumber\\ \displaystyle y_{2} & = & \displaystyle \frac{y_{3}y_{7}y_{9}(1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9}))}{(1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})+y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9})},\nonumber\\ \displaystyle y_{9} & = & \displaystyle \frac{y_{4}(1+(1+y_{7})(1+y_{8})y_{9})(1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9}))}{(1+y_{5}+y_{5}y_{8})(1+y_{9}+y_{8}y_{9})},\nonumber\\ \displaystyle y_{8} & = & \displaystyle \frac{y_{1}y_{8}y_{9}}{1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9})},\nonumber\\ \displaystyle y_{5} & = & \displaystyle \frac{y_{5}y_{6}y_{8}}{1+y_{5}+y_{5}y_{8}},\nonumber\\ \displaystyle y_{4} & = & \displaystyle \frac{(1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})+y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9})}{y_{7}y_{8}y_{9}},\nonumber\\ \displaystyle y_{3} & = & \displaystyle \frac{y_{8}(1+y_{9}+y_{8}y_{9})}{(1+(1+y_{7})(1+y_{8})y_{9})(1+y_{9}+y_{8}y_{9}+y_{5}(1+y_{8})(1+(1+y_{8}+y_{1}y_{8})y_{9}))},\nonumber\\ \displaystyle y_{7} & = & \displaystyle \frac{y_{1}y_{5}y_{7}y_{8}y_{9}}{(1+y_{9}+y_{7}y_{9})(1+y_{9}+y_{8}y_{9})+y_{5}(1+(1+y_{7})(1+y_{8})y_{9})(1+(1+y_{8}+y_{1}y_{8})y_{9})}.\nonumber\end{eqnarray}$$
Solving the shape parameter periodicity conditions with cusp conditions, we get
![]() $14$
solutions. We take one of the solutions
$14$
solutions. We take one of the solutions
 $$\begin{eqnarray}\displaystyle y_{1} & = & \displaystyle 1.781241-0.294452\times \sqrt{-1},\nonumber\\ \displaystyle y_{2} & = & \displaystyle 1,\nonumber\\ \displaystyle y_{3} & = & \displaystyle -0.304877+0.754529\times \sqrt{-1},\nonumber\\ \displaystyle y_{4} & = & \displaystyle 0.460355+1.139318\times \sqrt{-1},\nonumber\\ \displaystyle y_{5} & = & \displaystyle 0.546473+0.0903361\times \sqrt{-1},\nonumber\\ \displaystyle y_{6} & = & \displaystyle 1.155478+1.893847\times \sqrt{-1},\nonumber\\ \displaystyle y_{7} & = & \displaystyle 0.304877-0.754529\times \sqrt{-1},\nonumber\\ \displaystyle y_{8} & = & \displaystyle 0.304877-0.754529\times \sqrt{-1},\nonumber\\ \displaystyle y_{9} & = & \displaystyle -0.14865-0.664193\times \sqrt{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{1} & = & \displaystyle 1.781241-0.294452\times \sqrt{-1},\nonumber\\ \displaystyle y_{2} & = & \displaystyle 1,\nonumber\\ \displaystyle y_{3} & = & \displaystyle -0.304877+0.754529\times \sqrt{-1},\nonumber\\ \displaystyle y_{4} & = & \displaystyle 0.460355+1.139318\times \sqrt{-1},\nonumber\\ \displaystyle y_{5} & = & \displaystyle 0.546473+0.0903361\times \sqrt{-1},\nonumber\\ \displaystyle y_{6} & = & \displaystyle 1.155478+1.893847\times \sqrt{-1},\nonumber\\ \displaystyle y_{7} & = & \displaystyle 0.304877-0.754529\times \sqrt{-1},\nonumber\\ \displaystyle y_{8} & = & \displaystyle 0.304877-0.754529\times \sqrt{-1},\nonumber\\ \displaystyle y_{9} & = & \displaystyle -0.14865-0.664193\times \sqrt{-1}.\nonumber\end{eqnarray}$$
Following the algorithm in Theorem 4.4, we get the following six parameters
 $$\begin{eqnarray}\displaystyle & & \displaystyle 0.754529\times \sqrt{-1}-0.304877,\nonumber\\ \displaystyle & & \displaystyle 0.754529\times \sqrt{-1}+0.695123,\nonumber\\ \displaystyle & & \displaystyle 0.294452\times \sqrt{-1}-0.781241,\nonumber\\ \displaystyle & & \displaystyle 0.754529\times \sqrt{-1}+0.695122,\nonumber\\ \displaystyle & & \displaystyle 0.475124\times \sqrt{-1}+0.311704,\nonumber\\ \displaystyle & & \displaystyle 1.139320\times \sqrt{-1}+0.460354,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0.754529\times \sqrt{-1}-0.304877,\nonumber\\ \displaystyle & & \displaystyle 0.754529\times \sqrt{-1}+0.695123,\nonumber\\ \displaystyle & & \displaystyle 0.294452\times \sqrt{-1}-0.781241,\nonumber\\ \displaystyle & & \displaystyle 0.754529\times \sqrt{-1}+0.695122,\nonumber\\ \displaystyle & & \displaystyle 0.475124\times \sqrt{-1}+0.311704,\nonumber\\ \displaystyle & & \displaystyle 1.139320\times \sqrt{-1}+0.460354,\nonumber\end{eqnarray}$$
whose imaginary parts are positive, which provide a complete hyperbolic structure. The volume of the mapping torus computed from the parameters above isFootnote 6
This coincides with the value computed by SnapPea/SnapPy [Reference Culler, Dunfield and WeeksCDW].
5.3 Nonhyperbolic example
Our formalism discussed in this paper applies to in general nonhyperbolic 3-manifolds which are themselves not covered in Theorem 4.4. To illustrate this point, let us consider a disk with six points, and we consider the
![]() $1/6$
rotation as a mapping class. The mapping class is realized as a sequence of three flips as in Figure 17.
$1/6$
rotation as a mapping class. The mapping class is realized as a sequence of three flips as in Figure 17.
Figure 17. A nonhyperbolic example, associated with the
![]() $1/6$
rotation of the six-punctured disc.
$1/6$
rotation of the six-punctured disc.
The periodicity conditions are
Note that indices of edges in the boundary are rotated. The
![]() $y$
-variables are given by
$y$
-variables are given by
 $$\begin{eqnarray}\displaystyle y_{1}(3) & = & \displaystyle y_{1}^{-1}(1+y_{2})^{-1},\nonumber\\ \displaystyle y_{2}(3) & = & \displaystyle y_{2}^{-1}(1+y_{1}(1+y_{2}))(1+y_{3}(1+y_{2})),\nonumber\\ \displaystyle y_{3}(3) & = & \displaystyle y_{3}^{-1}(1+y_{2})^{-1},\nonumber\\ \displaystyle y_{4}(3) & = & \displaystyle y_{4}(1+y_{1}^{-1}(1+y_{2})^{-1})^{-1},\nonumber\\ \displaystyle y_{5}(3) & = & \displaystyle y_{5}(1+y_{1}(1+y_{2})),\nonumber\\ \displaystyle y_{6}(3) & = & \displaystyle y_{6}(1+y_{2}^{-1})^{-1}(1+y_{1}^{-1}(1+y_{2})^{-1})^{-1},\nonumber\\ \displaystyle y_{7}(3) & = & \displaystyle y_{7}(1+y_{3}^{-1}(1+y_{2})^{-1})^{-1},\nonumber\\ \displaystyle y_{8}(3) & = & \displaystyle y_{8}(1+y_{3}(1+y_{2})),\nonumber\\ \displaystyle y_{9}(3) & = & \displaystyle y_{9}(1+y_{2}^{-1})^{-1}(1+y_{3}^{-1}(1+y_{2})^{-1})^{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{1}(3) & = & \displaystyle y_{1}^{-1}(1+y_{2})^{-1},\nonumber\\ \displaystyle y_{2}(3) & = & \displaystyle y_{2}^{-1}(1+y_{1}(1+y_{2}))(1+y_{3}(1+y_{2})),\nonumber\\ \displaystyle y_{3}(3) & = & \displaystyle y_{3}^{-1}(1+y_{2})^{-1},\nonumber\\ \displaystyle y_{4}(3) & = & \displaystyle y_{4}(1+y_{1}^{-1}(1+y_{2})^{-1})^{-1},\nonumber\\ \displaystyle y_{5}(3) & = & \displaystyle y_{5}(1+y_{1}(1+y_{2})),\nonumber\\ \displaystyle y_{6}(3) & = & \displaystyle y_{6}(1+y_{2}^{-1})^{-1}(1+y_{1}^{-1}(1+y_{2})^{-1})^{-1},\nonumber\\ \displaystyle y_{7}(3) & = & \displaystyle y_{7}(1+y_{3}^{-1}(1+y_{2})^{-1})^{-1},\nonumber\\ \displaystyle y_{8}(3) & = & \displaystyle y_{8}(1+y_{3}(1+y_{2})),\nonumber\\ \displaystyle y_{9}(3) & = & \displaystyle y_{9}(1+y_{2}^{-1})^{-1}(1+y_{3}^{-1}(1+y_{2})^{-1})^{-1}.\nonumber\end{eqnarray}$$
A solution of the periodicity conditions is
 $$\begin{eqnarray}\displaystyle y_{1} & = & \displaystyle {\textstyle \frac{1}{2}},\qquad y_{2}=3,\qquad y_{3}={\textstyle \frac{1}{2}},\qquad y_{4}=\sqrt{3},\qquad y_{5}={\textstyle \frac{1}{\sqrt{3}}},\nonumber\\ \displaystyle y_{6} & = & \displaystyle {\textstyle \frac{2}{\sqrt{3}}},\qquad y_{7}=\sqrt{3},\qquad y_{8}={\textstyle \frac{1}{\sqrt{3}}},\qquad y_{9}={\textstyle \frac{2}{\sqrt{3}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y_{1} & = & \displaystyle {\textstyle \frac{1}{2}},\qquad y_{2}=3,\qquad y_{3}={\textstyle \frac{1}{2}},\qquad y_{4}=\sqrt{3},\qquad y_{5}={\textstyle \frac{1}{\sqrt{3}}},\nonumber\\ \displaystyle y_{6} & = & \displaystyle {\textstyle \frac{2}{\sqrt{3}}},\qquad y_{7}=\sqrt{3},\qquad y_{8}={\textstyle \frac{1}{\sqrt{3}}},\qquad y_{9}={\textstyle \frac{2}{\sqrt{3}}}.\nonumber\end{eqnarray}$$
Shape parameters of three tetrahedra evaluated at the solution above are
 $$\begin{eqnarray}\displaystyle Z(0) & = & \displaystyle -y_{2}(0)=-y_{2}=-3,\nonumber\\ \displaystyle Z(1) & = & \displaystyle -y_{1}(1)=-y_{1}(1+y_{2})=-2,\nonumber\\ \displaystyle Z(2) & = & \displaystyle -y_{3}(2)=-y_{3}(1+y_{2})=-2.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z(0) & = & \displaystyle -y_{2}(0)=-y_{2}=-3,\nonumber\\ \displaystyle Z(1) & = & \displaystyle -y_{1}(1)=-y_{1}(1+y_{2})=-2,\nonumber\\ \displaystyle Z(2) & = & \displaystyle -y_{3}(2)=-y_{3}(1+y_{2})=-2.\nonumber\end{eqnarray}$$
Substituting shape parameters to the Rogers dilogarithm
![]() $L(x)$
, we have (with
$L(x)$
, we have (with
![]() $Z(i)^{\prime \prime }=(1-Z(i))^{-1}$
)
$Z(i)^{\prime \prime }=(1-Z(i))^{-1}$
)
which is the complexified volume of the
![]() $3$
-manifold. This is identified with the central charge of
$3$
-manifold. This is identified with the central charge of
![]() $\hat{\text{sl}}(2)$
WZW model at the level
$\hat{\text{sl}}(2)$
WZW model at the level
![]() $4$
(see Remark 0.3).
$4$
(see Remark 0.3).
Acknowledgments
K. N. is supported by the Grant-in-Aid for Research Activity Start-up (No. 22840023) and for Scientific Research (S) (No. 22224001). Y. T. is supported in part by the Grants-in-Aid for Scientific Research, JSPS (No. 22740036). M. Y. would like to thank PCTS and its anonymous donor for generous support. We would like to thank H. Fuji, A. Kato, S. Kojima, H. Masai, T. Nakanishi, S. Terashima, T. Yoshida and D. Xie for helpful conversation.