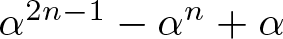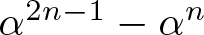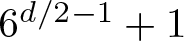1. Introduction
Recall that a Salem number is a real algebraic integer α > 1 whose conjugates over ![]() ${\mathbb Q}$ except for α itself all lie in the disc
${\mathbb Q}$ except for α itself all lie in the disc ![]() $|z| \leq 1$ with at least one conjugate lying on the boundary
$|z| \leq 1$ with at least one conjugate lying on the boundary ![]() $|z|=1$. The Salem number α is reciprocal, so it has even degree
$|z|=1$. The Salem number α is reciprocal, so it has even degree ![]() $d \geq 4$ over
$d \geq 4$ over ![]() ${\mathbb Q}$, the conjugate α −1 and d − 2 unimodular conjugates of the form
${\mathbb Q}$, the conjugate α −1 and d − 2 unimodular conjugates of the form ![]() ${\rm e}^{\pm {\rm i}\phi_j}$,
${\rm e}^{\pm {\rm i}\phi_j}$, ![]() $j=1,\dots,d/2-1$, where
$j=1,\dots,d/2-1$, where ![]() $0 \lt \phi_1 \lt \cdots \lt \phi_{d/2-1} \lt \pi$. A Pisot number is a real algebraic integer greater than 1 whose other conjugates over
$0 \lt \phi_1 \lt \cdots \lt \phi_{d/2-1} \lt \pi$. A Pisot number is a real algebraic integer greater than 1 whose other conjugates over ![]() ${\mathbb Q}$ (if any) all lie in the open disc
${\mathbb Q}$ (if any) all lie in the open disc ![]() $|z| \lt 1$.
$|z| \lt 1$.
Various properties of Salem numbers have been investigated in [Reference Flammang6–Reference McKee and Smyth8, Reference Salem12, Reference Salem13, Reference Smyth15, Reference Stankov17] (see also a survey [Reference Smyth16]), while their relations with Pisot numbers have been explored in, for example, [Reference Akiyama and Kwon1, Reference Boyd2, Reference Dubickas5, Reference McKee and Smyth9, Reference McKee and Smyth10, Reference Zaïmi18, Reference Zaïmi19]. For example, an old result of Salem [Reference Salem12] asserts that every Pisot number is a limit point of the set of Salem numbers. In [Reference Siegel14], Siegel showed that the smallest Pisot number is the root ![]() $\theta=1.3247\dots$ of
$\theta=1.3247\dots$ of ![]() $x^3-x-1=0$, while the smallest Salem number is not known, and it is not even known whether the set of Salem numbers is bounded away from 1.
$x^3-x-1=0$, while the smallest Salem number is not known, and it is not even known whether the set of Salem numbers is bounded away from 1.
In [Reference Dubickas5], the author investigated various sumsets and difference sets involving Salem and Pisot numbers. In this note, we will prove the following new result in this direction.
Theorem 1. Every Salem number is expressible as a difference of two Pisot numbers.
More explicitly, we will show the following:
Theorem 2. For each Salem number α of degree ![]() $d \geq 4$, there exist infinitely many
$d \geq 4$, there exist infinitely many ![]() $n \in {\mathbb N}$ for which
$n \in {\mathbb N}$ for which ![]() $\alpha^{2n-1}-\alpha^n+\alpha$ and
$\alpha^{2n-1}-\alpha^n+\alpha$ and ![]() $\alpha^{2n-1}-\alpha^n$ are both Pisot numbers of degree d. The smallest such n is at most
$\alpha^{2n-1}-\alpha^n$ are both Pisot numbers of degree d. The smallest such n is at most ![]() $6^{d/2-1}+1$.
$6^{d/2-1}+1$.
In [Reference Salem12, p. 69] (see also [Reference Salem13, p. 35]), Salem himself proved that every Salem number is expressible as a quotient of two Pisot numbers. On the other hand, the author showed that every positive algebraic number is a quotient of two Mahler measures [Reference Dubickas4, Theorem 1]. Recall that the Mahler measure ![]() $M(\alpha)$ of a non-zero algebraic number α is the modulus of the product of its conjugates lying outside the unit circle and the leading coefficient of its minimal polynomial in
$M(\alpha)$ of a non-zero algebraic number α is the modulus of the product of its conjugates lying outside the unit circle and the leading coefficient of its minimal polynomial in ![]() ${\mathbb Z}[x]$. Thus, for a real algebraic number α > 1, we have
${\mathbb Z}[x]$. Thus, for a real algebraic number α > 1, we have ![]() $M(\alpha) \geq \alpha$ with equality if and only if α is a Salem or a Pisot number. Therefore, the following theorem generalizes both these results.
$M(\alpha) \geq \alpha$ with equality if and only if α is a Salem or a Pisot number. Therefore, the following theorem generalizes both these results.
Theorem 3. Every real positive algebraic number α of degree d is expressible as a quotient of two Pisot numbers of degree d from the field ![]() ${\mathbb Q}(\alpha)$.
${\mathbb Q}(\alpha)$.
In the next section, we will recall a few simple results, which will be used in the proofs. Then, in § 3, we will prove Theorems 2 and 3. Evidently, Theorem 2 implies Theorem 1.
2. Auxiliary results
In the proof of Theorem 2, we will use the next version of Dirichlet’s approximation theorem [Reference Dirichlet4] (see, e.g., [Reference Pethő, Pohst and Bertók11, p. 423]).
Lemma 4. Let ![]() $\lambda_1, \lambda_2, \ldots, \lambda_N$ be real numbers. Then, for each Q > 1, there is a positive integer
$\lambda_1, \lambda_2, \ldots, \lambda_N$ be real numbers. Then, for each Q > 1, there is a positive integer ![]() $q \leq Q$ such that
$q \leq Q$ such that
 \begin{equation*}
\|\lambda_j q\| \lt Q^{-1/N}
\end{equation*}
\begin{equation*}
\|\lambda_j q\| \lt Q^{-1/N}
\end{equation*}for ![]() $j=1,2,\ldots,N$.
$j=1,2,\ldots,N$.
Throughout, ![]() $\|y\|$ stands for the distance between
$\|y\|$ stands for the distance between ![]() $y \in {\mathbb R}$ and the nearest integer.
$y \in {\mathbb R}$ and the nearest integer.
Let α be a Salem number of degree ![]() $d \geq 4$ with conjugates α −1 and
$d \geq 4$ with conjugates α −1 and ![]() ${\rm e}^{\pm {\rm i} \phi_j}$,
${\rm e}^{\pm {\rm i} \phi_j}$, ![]() $j=1,\ldots,N$, over
$j=1,\ldots,N$, over ![]() ${\mathbb Q}$, where
${\mathbb Q}$, where ![]() $0 \lt \phi_1 \lt \cdots \lt \phi_N \lt \pi$ and
$0 \lt \phi_1 \lt \cdots \lt \phi_N \lt \pi$ and ![]() $d=2N+2$. In [Reference Salem13, p. 32], Salem showed that the numbers
$d=2N+2$. In [Reference Salem13, p. 32], Salem showed that the numbers ![]() $\pi,\phi_1,\ldots,\phi_N$ are linearly independent over
$\pi,\phi_1,\ldots,\phi_N$ are linearly independent over ![]() ${\mathbb Q}$ (the argument is attributed to Pisot). In particular, Salem’s result implies that
${\mathbb Q}$ (the argument is attributed to Pisot). In particular, Salem’s result implies that
Lemma 5. The numbers ![]() $\phi_j/\pi$,
$\phi_j/\pi$, ![]() $j=1,\ldots,N$, are all irrational.
$j=1,\ldots,N$, are all irrational.
Note that in case ![]() $\phi_j/\pi \in {\mathbb Q}$, the conjugate
$\phi_j/\pi \in {\mathbb Q}$, the conjugate ![]() ${\rm e}^{{\rm i}\phi_j}$ of a Salem number must be a root of unity, which is impossible, because all the conjugates of a root of unity over
${\rm e}^{{\rm i}\phi_j}$ of a Salem number must be a root of unity, which is impossible, because all the conjugates of a root of unity over ![]() ${\mathbb Q}$ must be roots of unity themselves, but Salem number is not a root of unity. This also implies Lemma 5.
${\mathbb Q}$ must be roots of unity themselves, but Salem number is not a root of unity. This also implies Lemma 5.
Next, we record the following observation:
Lemma 6. Let α be a real algebraic number of degree ![]() $d \geq 2$ with conjugates
$d \geq 2$ with conjugates ![]() $\alpha_1=\alpha,\alpha_2,\ldots,\alpha_d$ over
$\alpha_1=\alpha,\alpha_2,\ldots,\alpha_d$ over ![]() ${\mathbb Q}$, and let f be a non-constant polynomial with rational coefficients such that
${\mathbb Q}$, and let f be a non-constant polynomial with rational coefficients such that ![]() $f(\alpha) \gt 0$ and
$f(\alpha) \gt 0$ and ![]() $|f(\alpha_j)| \lt 1$ for
$|f(\alpha_j)| \lt 1$ for ![]() $j=2,\ldots,d$. If
$j=2,\ldots,d$. If ![]() $f(\alpha) \in {\mathbb Q}(\alpha)$ is an algebraic integer, then it is a Pisot number of degree d.
$f(\alpha) \in {\mathbb Q}(\alpha)$ is an algebraic integer, then it is a Pisot number of degree d.
Proof. Note that
is the list of conjugates of an algebraic integer ![]() $f(\alpha)$ over
$f(\alpha)$ over ![]() ${\mathbb Q}$, possibly repeated several times. In particular, this implies that
${\mathbb Q}$, possibly repeated several times. In particular, this implies that ![]() $f(\alpha_j) \ne 0$ for
$f(\alpha_j) \ne 0$ for ![]() $j=2,\ldots,d$. Furthermore,
$j=2,\ldots,d$. Furthermore, ![]() $f(\alpha) \geq 1$, since otherwise
$f(\alpha) \geq 1$, since otherwise ![]() $0 \lt f(\alpha) \lt 1$, and hence there is a non-zero algebraic integer
$0 \lt f(\alpha) \lt 1$, and hence there is a non-zero algebraic integer ![]() $f(\alpha)$ with all conjugates in
$f(\alpha)$ with all conjugates in ![]() $|z| \lt 1$, including
$|z| \lt 1$, including ![]() $f(\alpha)$. But then the modulus of the product of the conjugates of
$f(\alpha)$. But then the modulus of the product of the conjugates of ![]() $f(\alpha)$ must be smaller than 1, which is impossible. Also, if
$f(\alpha)$ must be smaller than 1, which is impossible. Also, if ![]() $f(\alpha) = 1$, then its conjugates
$f(\alpha) = 1$, then its conjugates ![]() $f(\alpha_j)$,
$f(\alpha_j)$, ![]() $j=2,\dots,d$, are all equal to 1, which is not the case. Consequently,
$j=2,\dots,d$, are all equal to 1, which is not the case. Consequently, ![]() $f(\alpha) \gt 1$. Since
$f(\alpha) \gt 1$. Since ![]() $f(\alpha)$ is the only conjugate of
$f(\alpha)$ is the only conjugate of ![]() $f(\alpha)$ outside the unit circle, all
$f(\alpha)$ outside the unit circle, all ![]() $f(\alpha_j)$,
$f(\alpha_j)$, ![]() $j=2,\dots,d$, lying in
$j=2,\dots,d$, lying in ![]() $|z| \lt 1$ must be distinct, whence the result.
$|z| \lt 1$ must be distinct, whence the result.
3. Proofs of Theorems 2 and 3
Proof of Theorem 2.
Let α be a Salem number of degree ![]() $d \geq 4$ with conjugates
$d \geq 4$ with conjugates ![]() $\alpha_2=\alpha^{-1}$ and
$\alpha_2=\alpha^{-1}$ and ![]() $\{\alpha_3,\ldots,\alpha_d\}=\{{\rm e}^{\pm {\rm i} \phi_1},\ldots,{\rm e}^{\pm {\rm i} \phi_N}\}$, where
$\{\alpha_3,\ldots,\alpha_d\}=\{{\rm e}^{\pm {\rm i} \phi_1},\ldots,{\rm e}^{\pm {\rm i} \phi_N}\}$, where ![]() $N=d/2-1$. Applying Lemma Reference Dirichlet4 to the N irrational numbers
$N=d/2-1$. Applying Lemma Reference Dirichlet4 to the N irrational numbers ![]() $\lambda_1=\phi_1/(2\pi), \ldots, \lambda_N=\phi_N/(2\pi)$ (see Lemma 5), we derive that for any Q > 1, there is an integer q in the range
$\lambda_1=\phi_1/(2\pi), \ldots, \lambda_N=\phi_N/(2\pi)$ (see Lemma 5), we derive that for any Q > 1, there is an integer q in the range ![]() $1 \leq q \leq Q$ for which
$1 \leq q \leq Q$ for which
 \begin{equation}
0 \lt \|q\phi_j/(2\pi)\| \lt Q^{-1/N}=Q^{-2/(d-2)}.
\end{equation}
\begin{equation}
0 \lt \|q\phi_j/(2\pi)\| \lt Q^{-1/N}=Q^{-2/(d-2)}.
\end{equation} Put ![]() $n=q+1$ and consider the numbers
$n=q+1$ and consider the numbers
We will show that β and γ are both Pisot numbers of degree d in the field ![]() ${\mathbb Q}(\alpha)$, provided that
${\mathbb Q}(\alpha)$, provided that
 \begin{equation}
Q^{-2/(d-2)} \leq \frac{1}{6},
\end{equation}
\begin{equation}
Q^{-2/(d-2)} \leq \frac{1}{6},
\end{equation}that is, ![]() $Q \geq 6^{d/2-1}$. Of course, by letting
$Q \geq 6^{d/2-1}$. Of course, by letting ![]() $Q \to \infty$ in Equation (1), we will produce infinitely many q satisfying Equation (1), and so infinitely many
$Q \to \infty$ in Equation (1), we will produce infinitely many q satisfying Equation (1), and so infinitely many ![]() $n \in {\mathbb N}$ for which
$n \in {\mathbb N}$ for which ![]() $\beta, \gamma
\in {\mathbb Q}(\alpha)$ defined in Equation (2) are both Pisot numbers of degree d.
$\beta, \gamma
\in {\mathbb Q}(\alpha)$ defined in Equation (2) are both Pisot numbers of degree d.
We begin with the number ![]() $\gamma=f(\alpha)$, where
$\gamma=f(\alpha)$, where ![]() $f(x)=x^{2n-1}-x^n$ due to Equation (2). First,
$f(x)=x^{2n-1}-x^n$ due to Equation (2). First, ![]() $\gamma=f(\alpha) \gt 0$ is an algebraic integer lying in the field
$\gamma=f(\alpha) \gt 0$ is an algebraic integer lying in the field ![]() ${\mathbb Q}(\alpha)$. In order to apply Lemma 6, we need to show that
${\mathbb Q}(\alpha)$. In order to apply Lemma 6, we need to show that ![]() $|f(\alpha_j)| \lt 1$ for
$|f(\alpha_j)| \lt 1$ for ![]() $j=2,\dots,d$.
$j=2,\dots,d$.
Observe that, by Equation (2),
It is clear that ![]() $-1 \lt \alpha^{-2n+1}-\alpha^{-n} \lt 0$ because α > 1. So
$-1 \lt \alpha^{-2n+1}-\alpha^{-n} \lt 0$ because α > 1. So ![]() $f(\alpha_2)$ lies in
$f(\alpha_2)$ lies in ![]() $|z| \lt 1$. Next, fix a conjugate
$|z| \lt 1$. Next, fix a conjugate ![]() $\alpha^{\prime}={\rm e}^{\pm {\rm i} \phi_j}$ of α. It remains to check that for any choice of the sign ± the number
$\alpha^{\prime}={\rm e}^{\pm {\rm i} \phi_j}$ of α. It remains to check that for any choice of the sign ± the number
 \begin{equation*}f(\alpha^{\prime})=(\alpha^{\prime})^{2n-1}-(\alpha^{\prime})^{n}={\rm e}^{\pm {\rm i} \phi_j n}({\rm e}^{\pm {\rm i} \phi_j (n-1)}-1)={\rm e}^{\pm {\rm i} \phi_j (q+1)}({\rm e}^{\pm {\rm i} \phi_j q}-1)\end{equation*}
\begin{equation*}f(\alpha^{\prime})=(\alpha^{\prime})^{2n-1}-(\alpha^{\prime})^{n}={\rm e}^{\pm {\rm i} \phi_j n}({\rm e}^{\pm {\rm i} \phi_j (n-1)}-1)={\rm e}^{\pm {\rm i} \phi_j (q+1)}({\rm e}^{\pm {\rm i} \phi_j q}-1)\end{equation*} lies in ![]() $|z| \lt 1$. In view of
$|z| \lt 1$. In view of ![]() $|f(\alpha^{\prime})|=2|\,\sin(q\phi_j/2)|$, this is equivalent to
$|f(\alpha^{\prime})|=2|\,\sin(q\phi_j/2)|$, this is equivalent to ![]() $|\sin(q \phi_j/2)| \lt 1/2$. This happens if and only if
$|\sin(q \phi_j/2)| \lt 1/2$. This happens if and only if
for some ![]() $k \in {\mathbb Z}$ or, equivalently,
$k \in {\mathbb Z}$ or, equivalently, ![]() $\|q \phi_j/(2\pi)\| \lt 1/6$, which is indeed the case by Equations (1) and (3). This completes our verification. Therefore,
$\|q \phi_j/(2\pi)\| \lt 1/6$, which is indeed the case by Equations (1) and (3). This completes our verification. Therefore, ![]() $\gamma=f(\alpha) \in {\mathbb Q}(\alpha)$ is a Pisot number of degree d by Lemma 6.
$\gamma=f(\alpha) \in {\mathbb Q}(\alpha)$ is a Pisot number of degree d by Lemma 6.
Now, let us consider the number ![]() $\beta=f(\alpha)$ defined in Equation (2), where
$\beta=f(\alpha)$ defined in Equation (2), where ![]() $f(x)=x^{2n-1}-x^n+x$. It is clear that
$f(x)=x^{2n-1}-x^n+x$. It is clear that ![]() $f(\alpha) \gt \alpha \gt 1$ is an algebraic integer. This time, we find that
$f(\alpha) \gt \alpha \gt 1$ is an algebraic integer. This time, we find that
In view of α > 1 and ![]() $n \geq 2$, we obtain
$n \geq 2$, we obtain ![]() $0 \lt \alpha^{-2n+1}-\alpha^{-n}+\alpha^{-1} \lt 1$, so
$0 \lt \alpha^{-2n+1}-\alpha^{-n}+\alpha^{-1} \lt 1$, so ![]() $f(\alpha_2)$ is in
$f(\alpha_2)$ is in ![]() $|z| \lt 1$. Next, as above, fix a conjugate
$|z| \lt 1$. Next, as above, fix a conjugate ![]() $\alpha^{\prime}={\rm e}^{\pm {\rm i} \phi_j}$ of α. This time, we need to show that for any choice of the sign ± the number
$\alpha^{\prime}={\rm e}^{\pm {\rm i} \phi_j}$ of α. This time, we need to show that for any choice of the sign ± the number
 \begin{align*}f(\alpha^{\prime}) &=(\alpha^{\prime})^{2n-1}-(\alpha^{\prime})^{n}+\alpha^{\prime}={\rm e}^{\pm {\rm i} \phi_j n}\left({\rm e}^{\pm {\rm i} \phi_j (n-1)}-1+{\rm e}^{\mp {\rm i} \phi_j (n-1)}\right)\\ &= e^{\pm i \phi_j (q+1)}(2\cos(q\phi_j)-1)
\end{align*}
\begin{align*}f(\alpha^{\prime}) &=(\alpha^{\prime})^{2n-1}-(\alpha^{\prime})^{n}+\alpha^{\prime}={\rm e}^{\pm {\rm i} \phi_j n}\left({\rm e}^{\pm {\rm i} \phi_j (n-1)}-1+{\rm e}^{\mp {\rm i} \phi_j (n-1)}\right)\\ &= e^{\pm i \phi_j (q+1)}(2\cos(q\phi_j)-1)
\end{align*} lies in the open disc ![]() $|z| \lt 1$. This is true if and only if
$|z| \lt 1$. This is true if and only if ![]() $0 \lt \cos(q\phi_j) \lt 1$. The latter inequalities hold whenever
$0 \lt \cos(q\phi_j) \lt 1$. The latter inequalities hold whenever
for some ![]() $k \in {\mathbb Z}$ or, equivalently,
$k \in {\mathbb Z}$ or, equivalently, ![]() $0 \lt \|q \phi_j/(2\pi)\| \lt 1/4$. This is true by Equations (1), (3) and
$0 \lt \|q \phi_j/(2\pi)\| \lt 1/4$. This is true by Equations (1), (3) and ![]() $1/6 \lt 1/4$. As before, by Lemma 6, we conclude that
$1/6 \lt 1/4$. As before, by Lemma 6, we conclude that ![]() $\beta=f(\alpha) \gt 1$ is a Pisot number of degree d.
$\beta=f(\alpha) \gt 1$ is a Pisot number of degree d.
Finally, selecting ![]() $Q=6^{d/2-1}$, by Equations (1) and (3), we see that the smallest
$Q=6^{d/2-1}$, by Equations (1) and (3), we see that the smallest ![]() $q \in {\mathbb N}$ for which Equation (1) is true satisfies
$q \in {\mathbb N}$ for which Equation (1) is true satisfies ![]() $1 \leq q \leq 6^{d/2-1}$. This completes the proof of the last assertion of the theorem because the integer
$1 \leq q \leq 6^{d/2-1}$. This completes the proof of the last assertion of the theorem because the integer ![]() $n=q+1$ is in the range
$n=q+1$ is in the range ![]() $2 \leq n \leq 6^{d/2-1}+1$.
$2 \leq n \leq 6^{d/2-1}+1$.
Proof of Theorem 3
Let α be a positive algebraic number of degree d over ![]() ${\mathbb Q}$ with conjugates
${\mathbb Q}$ with conjugates ![]() $\alpha_1=\alpha,\alpha_2,\ldots,\alpha_d$. The claim is trivial for d = 1, since every integer
$\alpha_1=\alpha,\alpha_2,\ldots,\alpha_d$. The claim is trivial for d = 1, since every integer ![]() $k \geq 2$ is a Pisot number and every positive rational number is a quotient of two such numbers. Assume that
$k \geq 2$ is a Pisot number and every positive rational number is a quotient of two such numbers. Assume that ![]() $d \geq 2$, and let m be a positive integer for which
$d \geq 2$, and let m be a positive integer for which ![]() $m\alpha$ is an algebraic integer.
$m\alpha$ is an algebraic integer.
Fix a positive number u < 1 satisfying
and a positive number v > 1 satisfying
Select a Pisot number ![]() $\beta \in {\mathbb Q}(\alpha)$ of degree d (see Theorem 2 in [Reference Salem13, p. 3]). A natural power of β is also a Pisot number of degree d, so by replacing β by its large power if necessary, we can assume that
$\beta \in {\mathbb Q}(\alpha)$ of degree d (see Theorem 2 in [Reference Salem13, p. 3]). A natural power of β is also a Pisot number of degree d, so by replacing β by its large power if necessary, we can assume that ![]() $\beta \gt v$ and that the other d − 1 conjugates of β over
$\beta \gt v$ and that the other d − 1 conjugates of β over ![]() ${\mathbb Q}$ are all in
${\mathbb Q}$ are all in ![]() $|z| \lt u$.
$|z| \lt u$.
Write this β in the form ![]() $\beta=f(\alpha)$, where f is a non-constant polynomial of degree at most d − 1 with rational coefficients. Then, the numbers
$\beta=f(\alpha)$, where f is a non-constant polynomial of degree at most d − 1 with rational coefficients. Then, the numbers ![]() $\beta_j=f(\alpha_j)$,
$\beta_j=f(\alpha_j)$, ![]() $j=1,\ldots,d$, are the conjugates of
$j=1,\ldots,d$, are the conjugates of ![]() $\beta=\beta_1$ over
$\beta=\beta_1$ over ![]() ${\mathbb Q}$. Recall that, by the choice of β, we have
${\mathbb Q}$. Recall that, by the choice of β, we have
We claim that under assumption on the constants ![]() $u \in (0,1)$ as in Equation (4) and v > 1 as in Equation (5), the numbers
$u \in (0,1)$ as in Equation (4) and v > 1 as in Equation (5), the numbers ![]() $m \alpha\beta \in {\mathbb Q}(\alpha)$ and
$m \alpha\beta \in {\mathbb Q}(\alpha)$ and ![]() $m\beta \in {\mathbb Q}(\alpha)$ are both Pisot numbers of degree d. This will complete our proof, since their quotient is α.
$m\beta \in {\mathbb Q}(\alpha)$ are both Pisot numbers of degree d. This will complete our proof, since their quotient is α.
First, ![]() $m\beta$ is a Pisot number, since it is an algebraic integer greater than m > 1, whose other conjugates
$m\beta$ is a Pisot number, since it is an algebraic integer greater than m > 1, whose other conjugates ![]() $m\beta_j$,
$m\beta_j$, ![]() $j=2,\ldots,d$, all lie in
$j=2,\ldots,d$, all lie in ![]() $|z| \lt 1$ by
$|z| \lt 1$ by ![]() $|\beta_j| \lt u$ and Equation (4). Of course,
$|\beta_j| \lt u$ and Equation (4). Of course, ![]() $m\beta \in {\mathbb Q}(\alpha)$ is of degree d over
$m\beta \in {\mathbb Q}(\alpha)$ is of degree d over ![]() ${\mathbb Q}$, since so is β.
${\mathbb Q}$, since so is β.
Second, the number ![]() $m\alpha\beta=m\alpha f(\alpha) \in {\mathbb Q}(\alpha)$ is a positive algebraic integer, since so are
$m\alpha\beta=m\alpha f(\alpha) \in {\mathbb Q}(\alpha)$ is a positive algebraic integer, since so are ![]() $m\alpha$ and β. It is greater than 1 by
$m\alpha$ and β. It is greater than 1 by ![]() $\beta \gt v$ and Equation (5). Its other conjugates are
$\beta \gt v$ and Equation (5). Its other conjugates are ![]() $m\alpha_j f(\alpha_j)=m \alpha_j \beta_j$,
$m\alpha_j f(\alpha_j)=m \alpha_j \beta_j$, ![]() $j=2,\dots,d$. They are all in
$j=2,\dots,d$. They are all in ![]() $|z| \lt 1$ due to
$|z| \lt 1$ due to ![]() $|\beta_j| \lt u$ and Equation (4). Hence,
$|\beta_j| \lt u$ and Equation (4). Hence, ![]() $m \alpha f(\alpha) \in {\mathbb Q}(\alpha)$ is a Pisot number of degree d over
$m \alpha f(\alpha) \in {\mathbb Q}(\alpha)$ is a Pisot number of degree d over ![]() ${\mathbb Q}$ by Lemma 6 applied to the polynomial
${\mathbb Q}$ by Lemma 6 applied to the polynomial ![]() $mxf(x) \in {\mathbb Q}[x]$.
$mxf(x) \in {\mathbb Q}[x]$.
Therefore, ![]() $m \alpha\beta \in {\mathbb Q}(\alpha)$ and
$m \alpha\beta \in {\mathbb Q}(\alpha)$ and ![]() $m\beta \in {\mathbb Q}(\alpha)$ indeed are both Pisot numbers of degree d, which finishes the proof.
$m\beta \in {\mathbb Q}(\alpha)$ indeed are both Pisot numbers of degree d, which finishes the proof.
Competing Interests
The author declares none.