Article contents
Deloopings of Hurwitz spaces
Published online by Cambridge University Press: 13 September 2024
Abstract
For a partially multiplicative quandle (PMQ) 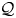 ${\mathcal {Q}}$ we consider the topological monoid
${\mathcal {Q}}$ we consider the topological monoid 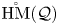 $\mathring {\mathrm {HM}}({\mathcal {Q}})$ of Hurwitz spaces of configurations in the plane with local monodromies in
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ of Hurwitz spaces of configurations in the plane with local monodromies in 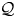 ${\mathcal {Q}}$. We compute the group completion of
${\mathcal {Q}}$. We compute the group completion of 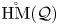 $\mathring {\mathrm {HM}}({\mathcal {Q}})$: it is the product of the (discrete) enveloping group
$\mathring {\mathrm {HM}}({\mathcal {Q}})$: it is the product of the (discrete) enveloping group 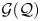 ${\mathcal {G}}({\mathcal {Q}})$ with a component of the double loop space of the relative Hurwitz space
${\mathcal {G}}({\mathcal {Q}})$ with a component of the double loop space of the relative Hurwitz space 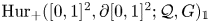 $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$; here
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$; here 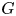 $G$ is any group giving rise, together with
$G$ is any group giving rise, together with 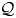 ${\mathcal {Q}}$, to a PMQ–group pair. Under the additional assumption that
${\mathcal {Q}}$, to a PMQ–group pair. Under the additional assumption that 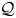 ${\mathcal {Q}}$ is finite and rationally Poincaré and that
${\mathcal {Q}}$ is finite and rationally Poincaré and that 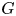 $G$ is finite, we compute the rational cohomology ring of
$G$ is finite, we compute the rational cohomology ring of 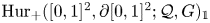 $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$.
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$.
- Type
- Research Article
- Information
- Copyright
- © 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 2
- Cited by



