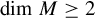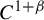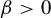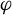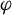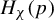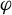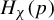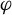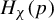1 Introduction
When studying a complex system of many possible configurations and its dynamics, one approach is to find a measure on the space of all possible configurations of the system which is invariant under its dynamics, to represent a distribution of possible events when the system is in equilibrium. The collection of all possible such invariant measures could be very big, and the field of thermodynamic formalism offers canonical ways to single out specific invariant measures of importance.
One way to single out measures of importance, is by the notion of equilibrium states: probability measures which maximize a dynamic quantity with respect to some potential (function) on the system. More explicitly, let M be the space of states of the system (a compact boundaryless Riemannian manifold), let
![]() $f\in \mathrm {Diff}^{1+}(M)$
be the dynamics of the system, and let
$f\in \mathrm {Diff}^{1+}(M)$
be the dynamics of the system, and let
![]() $\varphi :M\rightarrow \mathbb {R}$
be a bounded measurable potential on M; then an equilibrium state of
$\varphi :M\rightarrow \mathbb {R}$
be a bounded measurable potential on M; then an equilibrium state of
![]() $\varphi $
maximizes
$\varphi $
maximizes
![]() $\mu \mapsto h_{\mu }(f)+\int _M \varphi \,d\mu $
, where
$\mu \mapsto h_{\mu }(f)+\int _M \varphi \,d\mu $
, where
![]() $h_{\mu }(f)$
is the metric entropy of
$h_{\mu }(f)$
is the metric entropy of
![]() $\mu $
with respect to f.
$\mu $
with respect to f.
Two important instances of this notion are measures of maximal entropy (when
![]() $\varphi \equiv ~0$
), and Sinai–Ruelle–Bowen (SRB) measures (when
$\varphi \equiv ~0$
), and Sinai–Ruelle–Bowen (SRB) measures (when
![]() $\varphi $
is the geometric potential, that is, minus the logarithm of the Jacobian of f when restricted to the dynamics on unstable leaves). The fact that equilibrium states of the geometric potential (when
$\varphi $
is the geometric potential, that is, minus the logarithm of the Jacobian of f when restricted to the dynamics on unstable leaves). The fact that equilibrium states of the geometric potential (when
![]() $\sup \{h_{\mu }(f)+\int \varphi \,d\mu \}=0$
) are SRB measures is highly non-trivial, and it is due to Ledrappier and Young [Reference Ledrappier and YoungLY85a]. It is an instance of their more general formula to compute the entropy of general measures via local dimension of conditional measures on unstable leaves (see also [Reference Ledrappier and YoungLY85b]). When f preserves a smooth measure, the entropy formula is due to Pesin [Reference PesinPes77].
$\sup \{h_{\mu }(f)+\int \varphi \,d\mu \}=0$
) are SRB measures is highly non-trivial, and it is due to Ledrappier and Young [Reference Ledrappier and YoungLY85a]. It is an instance of their more general formula to compute the entropy of general measures via local dimension of conditional measures on unstable leaves (see also [Reference Ledrappier and YoungLY85b]). When f preserves a smooth measure, the entropy formula is due to Pesin [Reference PesinPes77].
SRB measures are measures which have conditional measures which are absolutely continuous with respect to the induced Riemannian volume on unstable leaves, when disintegrated by a measurable partition subordinated to the foliation of unstable leaves (see Rokhlin’s disintegration theorem). Hyperbolic and ergodic SRB measures are of physical importance, as the set of points which satisfy the forward-time Birkhoff’s ergodic theorem are of positive Riemannian volume (and thus, by convention, are observable in an experiment or a simulation). This property is due to Pesin’s absolute continuity theorem (see [Reference Katok, Strelcyn, Ledrappier and PrzytyckiKSLP86, Reference PesinPes77, Reference Pugh and ShubPS89]). Tsujii showed a converse, a condition via Lyapunov exponents on orbits such that a physical measure must be an ergodic hyperbolic SRB, see [Reference TsujiiTsu91].
While SRB measures are important, it is not clear what generality systems admit them. Sinai had shown their existence in Anosov systems, and Bowen and Ruelle in Axiom A systems. The dual characterization through conditional leaf measures, and as an equilibrium state, by Ledrappier and Young, offered a new way to test whether a system admits an SRB measure.
Singling out measures of importance through their conditional leaf measures is another important tool in thermodynamic formalism, in addition to the notion of equilibrium states. Some important examples of this are the Margulis construction for the measure of maximal entropy through its leaf measures [Reference MargulisMar70] and the extension of the horocyclic flow to high dimension variable negative curvature manifolds (see [Reference Bowen and MarcusBM77, Reference MarcusMar75]). Unstable leaves can be viewed as the equivalence class of an equivalence relation on orbits. The notion of defining measures by conditional measures on unstable leaves has been further generalized and studied as an equivalence class of orbits on manifolds (see [Reference SeriesSer80]) and symbolic spaces (see [Reference SeriesSer80, Reference Petersen and SchmidtPS97]).
Given a Hölder continuous potential, the idea of an equilibrium state is well defined, but it is not clear how to generally define the leaf measures corresponding to a potential. The Margulis leaf measures are conformal, that is, when pushed forward, they remain invariant up to a factor of
![]() $e^{-h_{\mathrm {top}}(f)}$
, where
$e^{-h_{\mathrm {top}}(f)}$
, where
![]() $h_{\mathrm {top}}(f)=\sup \{h_{\mu }(f):\mu \text { is an invariant probability measure}\}$
. Similarly, the conditional leaf measures of SRB measures are the induced Riemannian volume, which gains a factor of
$h_{\mathrm {top}}(f)=\sup \{h_{\mu }(f):\mu \text { is an invariant probability measure}\}$
. Similarly, the conditional leaf measures of SRB measures are the induced Riemannian volume, which gains a factor of
![]() $\exp $
(geometric potential). We therefore are looking for a family of conditional leaf measures which are conformal with respect to our potential. More explicitly, if
$\exp $
(geometric potential). We therefore are looking for a family of conditional leaf measures which are conformal with respect to our potential. More explicitly, if
![]() $\varphi $
is a bounded measurable potential and
$\varphi $
is a bounded measurable potential and
![]() $V^u$
is a local unstable leaf, we wish to find measures which satisfy
$V^u$
is a local unstable leaf, we wish to find measures which satisfy
![]() $m_{V^u}\circ f^{-1}=e^{\varphi -P(\varphi )}\cdot m_{f[V^u]}$
, where
$m_{V^u}\circ f^{-1}=e^{\varphi -P(\varphi )}\cdot m_{f[V^u]}$
, where
![]() $P(\varphi )$
is the pressure of
$P(\varphi )$
is the pressure of
![]() $\varphi $
(the quantity which an equilibrium state maximizes), which acts as a calibrating factor. In [Reference Climenhaga, Pesin and ZelerowiczCPZ19, Reference Climenhaga, Pesin and ZelerowiczCPZ20], Climenhaga, Pesin, and Zelerowicz give a construction using Carathéodory dimension. Their construction works for a general Hölder continuous potential in the partially hyperbolic setup with some restrictions on the central stable foliation and on the transitivity of the system (see the remark after Definition 2.15 for more details).
$\varphi $
(the quantity which an equilibrium state maximizes), which acts as a calibrating factor. In [Reference Climenhaga, Pesin and ZelerowiczCPZ19, Reference Climenhaga, Pesin and ZelerowiczCPZ20], Climenhaga, Pesin, and Zelerowicz give a construction using Carathéodory dimension. Their construction works for a general Hölder continuous potential in the partially hyperbolic setup with some restrictions on the central stable foliation and on the transitivity of the system (see the remark after Definition 2.15 for more details).
The result of Ledrappier and Young connects the two approaches of singling out measures of importance as equilibrium states and through conditional measures on unstable leaves. This naturally raises the question of extending their result for more potentials than just the geometric potential. Given a Grassmann–Hölder continuous potential, we give a construction of an invariant and absolutely continuous family of leaf measures which give a necessary and sufficient condition for the existence of a hyperbolic local equilibrium state via a leaf condition, and which act as the conditional leaf measures of the equilibrium state when it exists. We prove a Ledrappier–Young property, such that if the potential admits a hyperbolic local equilibrium state and a conformal system of measures, then the conditional measures of the equilibrium state are equivalent to the conformal measures on a set of full measure, and, in particular, the conformal measures give a positive measure to the hyperbolic points. For the definitions of a hyperbolic local equilibrium state, the leaf condition, and a Grassmann–Hölder continuous potential, see §2. In particular, Grassmann–Hölder continuity applies to the family of potentials
![]() $\{t\cdot \varphi \}_{t\in [0,1]}$
, where
$\{t\cdot \varphi \}_{t\in [0,1]}$
, where
![]() $\varphi $
is the geometric potential, and this family varies continuously between the
$\varphi $
is the geometric potential, and this family varies continuously between the
![]() $0$
potential and the geometric potential.
$0$
potential and the geometric potential.
2 Basic definitions and main results
Throughout this paper, M is a Riemannian, boundaryless, and compact manifold of dimension
![]() $d\geq 2$
, and
$d\geq 2$
, and
![]() $f\in \mathrm {Diff}^{1+\beta }(M), \beta>0$
. Fix
$f\in \mathrm {Diff}^{1+\beta }(M), \beta>0$
. Fix
![]() $\chi>0$
. See Appendix A for the special notation used within this paper.
$\chi>0$
. See Appendix A for the special notation used within this paper.
2.1 Basic definitions
Definition 2.1. (
 $\chi $
-summable points)
$\chi $
-summable points)
A point
![]() $x\in M$
is called
$x\in M$
is called
![]() $\chi $
-summable if there is a unique splitting
$\chi $
-summable if there is a unique splitting
![]() $T_xM=H^s(x)\oplus H^u(x)$
such that
$T_xM=H^s(x)\oplus H^u(x)$
such that
 $$ \begin{align*} \sup_{\xi_s\in H^s(x),|\xi_s|=1}\sum_{m=0}^\infty|d_xf^m\xi_s|^2e^{2\chi m}<\infty, \quad \sup_{{\xi_u\in H^u(x),|\xi_u|=1}}\sum_{m=0}^\infty|d_xf^{-m}\xi_u|^2e^{2\chi m}<\infty. \end{align*} $$
$$ \begin{align*} \sup_{\xi_s\in H^s(x),|\xi_s|=1}\sum_{m=0}^\infty|d_xf^m\xi_s|^2e^{2\chi m}<\infty, \quad \sup_{{\xi_u\in H^u(x),|\xi_u|=1}}\sum_{m=0}^\infty|d_xf^{-m}\xi_u|^2e^{2\chi m}<\infty. \end{align*} $$
Let
![]() $\chi $
-summ define the set of
$\chi $
-summ define the set of
![]() $\chi $
-summable points. An f-invariant probability measure carried by
$\chi $
-summable points. An f-invariant probability measure carried by
![]() $\chi $
-
$\chi $
-
![]() $\mathrm {summ}$
is called
$\mathrm {summ}$
is called
![]() $\chi $
-hyperbolic.
$\chi $
-hyperbolic.
For each
![]() $x \in \chi \text {-}\mathrm {summ}$
, write
$x \in \chi \text {-}\mathrm {summ}$
, write
![]() $s(x):=\mathrm {dim}(H^s(x)),u(x):=\mathrm {dim}(H^u(x))$
. Note that
$s(x):=\mathrm {dim}(H^s(x)),u(x):=\mathrm {dim}(H^u(x))$
. Note that
![]() $\chi $
-summ is f-invariant and
$\chi $
-summ is f-invariant and
![]() $H^s(\cdot ), H^u(\cdot )$
are invariant under
$H^s(\cdot ), H^u(\cdot )$
are invariant under
![]() $d_\cdot f$
.
$d_\cdot f$
.
Theorem 2.2. (Pesin–Oseledec reduction theorem)
For each point
![]() $x \in \chi \text {-}\mathrm {summ}$
, there exists an invertible linear map
$x \in \chi \text {-}\mathrm {summ}$
, there exists an invertible linear map
![]() $C_\chi (x):\mathbb {R}^d\rightarrow T_xM$
, which depends measurably on x, such that
$C_\chi (x):\mathbb {R}^d\rightarrow T_xM$
, which depends measurably on x, such that
![]() $C_\chi (x)[\mathbb {R}^{s(x)}\times \{0\}]=H^s(x),C_\chi (x)[\{0\}\times \mathbb {R}^{u(x)}]=H^u(x)$
. Here,
$C_\chi (x)[\mathbb {R}^{s(x)}\times \{0\}]=H^s(x),C_\chi (x)[\{0\}\times \mathbb {R}^{u(x)}]=H^u(x)$
. Here,
![]() $C_\chi (\cdot )$
are chosen measurably on
$C_\chi (\cdot )$
are chosen measurably on
![]() $\chi \text {-}\mathrm {summ}$
, and the choice is unique up to a composition with an orthogonal mapping of the ‘stable’ and of the ‘unstable’ subspaces of the tangent space. In addition,
$\chi \text {-}\mathrm {summ}$
, and the choice is unique up to a composition with an orthogonal mapping of the ‘stable’ and of the ‘unstable’ subspaces of the tangent space. In addition,
 $$ \begin{align*} C_\chi^{-1}(f(x))\circ d_xf\circ C_\chi(x)=\begin{pmatrix}D_s(x) & \\ & D_u(x) \end{pmatrix}\!, \end{align*} $$
$$ \begin{align*} C_\chi^{-1}(f(x))\circ d_xf\circ C_\chi(x)=\begin{pmatrix}D_s(x) & \\ & D_u(x) \end{pmatrix}\!, \end{align*} $$
where
![]() $D_s(x),D_u(x)$
are square matrices of dimensions
$D_s(x),D_u(x)$
are square matrices of dimensions
![]() $s(x),u(x)$
, respectively, and
$s(x),u(x)$
, respectively, and
![]() $\|D_s(x)\|,\|D_u^{-1}(x)\|\kern1.3pt{\leq}\kern1.3pt e^{-\chi },\|D_s^{-1}(x)\|,\|D_u(x)\|\kern1.3pt{\leq}\kern1.3pt \kappa $
for some constant
$\|D_s(x)\|,\|D_u^{-1}(x)\|\kern1.3pt{\leq}\kern1.3pt e^{-\chi },\|D_s^{-1}(x)\|,\|D_u(x)\|\kern1.3pt{\leq}\kern1.3pt \kappa $
for some constant
![]() ${\kappa \kern1.3pt{=}\kern1.3pt\kappa (f,\chi )\kern1.3pt{>}\kern1.3pt 1}$
.
${\kappa \kern1.3pt{=}\kern1.3pt\kappa (f,\chi )\kern1.3pt{>}\kern1.3pt 1}$
.
The Pesin–Oseledec reduction theorem has many different versions, which are suitable for different setups. We use the version which appears, with proof, in [Reference Ben OvadiaBO18, Theorem 2.4].
It is possible to show that
![]() $\|C_\chi ^{-1}(x)\|^2=\sup \nolimits _{\kern-1pt\overset {|\xi _s+\xi _u|=1,}{\xi _s\in H^s(x), \xi _u\in H^u(x)}}\!\{2\sum \nolimits _{m\geq 0}|d_xf^m\xi _s|^2e^{2\chi m} + 2\sum \nolimits _{m\geq 0}|d_xf^{-m}\xi _u|^2e^{2\chi m}\}$
. In addition,
$\|C_\chi ^{-1}(x)\|^2=\sup \nolimits _{\kern-1pt\overset {|\xi _s+\xi _u|=1,}{\xi _s\in H^s(x), \xi _u\in H^u(x)}}\!\{2\sum \nolimits _{m\geq 0}|d_xf^m\xi _s|^2e^{2\chi m} + 2\sum \nolimits _{m\geq 0}|d_xf^{-m}\xi _u|^2e^{2\chi m}\}$
. In addition,
![]() $\|C_\chi (\cdot )\|\leq 1$
. See [Reference Ben OvadiaBO18, Theorem 2.4, Lemma 2.9] for details. Here,
$\|C_\chi (\cdot )\|\leq 1$
. See [Reference Ben OvadiaBO18, Theorem 2.4, Lemma 2.9] for details. Here,
![]() $\|C_\chi ^{-1}(x)\|$
serves as a measurement of the hyperbolicity of x: a greater norm means a worse hyperbolicity (that is, slow contraction/expansion on stable/unstable spaces, or small angle between the stable and unstable spaces).
$\|C_\chi ^{-1}(x)\|$
serves as a measurement of the hyperbolicity of x: a greater norm means a worse hyperbolicity (that is, slow contraction/expansion on stable/unstable spaces, or small angle between the stable and unstable spaces).
Definition 2.3. Let
![]() $\epsilon>0$
and let
$\epsilon>0$
and let
![]() $x \in \chi \text {-}\mathrm {summ}$
, then
$x \in \chi \text {-}\mathrm {summ}$
, then
 $$ \begin{align*} Q_\epsilon(x):=\max\bigg\{Q\in \{e^{{-\ell\epsilon}/{3}}\}_{\ell\in\mathbb{N}}:Q\leq \frac{1}{3^{{6}/{\beta}}}\epsilon^{{90}/{\beta}}\|C^{-1}_\chi(x)\|^{{-48}/{\beta}}\bigg\}.\end{align*} $$
$$ \begin{align*} Q_\epsilon(x):=\max\bigg\{Q\in \{e^{{-\ell\epsilon}/{3}}\}_{\ell\in\mathbb{N}}:Q\leq \frac{1}{3^{{6}/{\beta}}}\epsilon^{{90}/{\beta}}\|C^{-1}_\chi(x)\|^{{-48}/{\beta}}\bigg\}.\end{align*} $$
Definition 2.4. (Recurrent
 $\epsilon $
-weak temperability)
$\epsilon $
-weak temperability)
Let
![]() $\epsilon>0$
. A point
$\epsilon>0$
. A point
![]() $x\in \chi \text {-}\mathrm {summ}$
is called
$x\in \chi \text {-}\mathrm {summ}$
is called
![]() $\epsilon $
-weakly temperable if
$\epsilon $
-weakly temperable if
![]() $\text {there exists } q:\{f^n(x)\}_{n\in \mathbb {Z}}\rightarrow \{e^{{-\ell \epsilon }/{3}}\}_{\ell \in \mathbb {N}}$
such that:
$\text {there exists } q:\{f^n(x)\}_{n\in \mathbb {Z}}\rightarrow \{e^{{-\ell \epsilon }/{3}}\}_{\ell \in \mathbb {N}}$
such that:
-
(1)
 ${q\circ f}/{q}=e^{\pm \epsilon }$
;
${q\circ f}/{q}=e^{\pm \epsilon }$
; -
(2)
 $\text {for all } n\in \mathbb {Z}$
,
$\text {for all } n\in \mathbb {Z}$
,
 $q(f^n(x))\leq Q_\epsilon (f^n(x))$
.
$q(f^n(x))\leq Q_\epsilon (f^n(x))$
.
If, in addition to items (1) and (2),
![]() $q:\{f^n(x)\}_{n\in \mathbb {Z}}\rightarrow \{e^{-{\ell \epsilon }/{3}}\}_{\ell \in \mathbb {N}}$
can be chosen to also satisfy:
$q:\{f^n(x)\}_{n\in \mathbb {Z}}\rightarrow \{e^{-{\ell \epsilon }/{3}}\}_{\ell \in \mathbb {N}}$
can be chosen to also satisfy:
-
(3)
 $\limsup \nolimits _{n\rightarrow \pm \infty }q(f^n(x))>0$
;
$\limsup \nolimits _{n\rightarrow \pm \infty }q(f^n(x))>0$
;
then we say that x is recurrently
![]() $\epsilon $
-weakly temperable. A function
$\epsilon $
-weakly temperable. A function
![]() $q:\{f^n(x)\}_{n\in \mathbb {Z}}\rightarrow \{e^{{-\ell \epsilon }/{3}}\}_{\ell \in \mathbb {N}}$
which satisfies items (1) and (2), is called an
$q:\{f^n(x)\}_{n\in \mathbb {Z}}\rightarrow \{e^{{-\ell \epsilon }/{3}}\}_{\ell \in \mathbb {N}}$
which satisfies items (1) and (2), is called an
![]() $\epsilon $
-weakly tempered kernel of x. Define
$\epsilon $
-weakly tempered kernel of x. Define
![]() $\mathrm {WT}_\chi ^\epsilon := \{x\in \chi \text {-}\mathrm {summ}:x\text { is } \epsilon \text {-weakly temperable}\}$
, and
$\mathrm {WT}_\chi ^\epsilon := \{x\in \chi \text {-}\mathrm {summ}:x\text { is } \epsilon \text {-weakly temperable}\}$
, and
![]() $\mathrm {RWT}_\chi ^\epsilon := \{x\in \chi \text {-}\mathrm {summ}:x \text { is recurrently } \epsilon \text {-weakly temperable}\}$
.
$\mathrm {RWT}_\chi ^\epsilon := \{x\in \chi \text {-}\mathrm {summ}:x \text { is recurrently } \epsilon \text {-weakly temperable}\}$
.
Remark. Every point
![]() $x\in \mathrm {WT}^\epsilon _\chi $
(for sufficiently small
$x\in \mathrm {WT}^\epsilon _\chi $
(for sufficiently small
![]() $\epsilon>0$
) admits a global unstable manifold
$\epsilon>0$
) admits a global unstable manifold
![]() $W^u(x)=\{y\in M: d(f^{-n}(x),f^{-n}(y))\xrightarrow [n\rightarrow \infty ]{}0\}$
, and a global stable manifold
$W^u(x)=\{y\in M: d(f^{-n}(x),f^{-n}(y))\xrightarrow [n\rightarrow \infty ]{}0\}$
, and a global stable manifold
![]() $W^s(x)=\{y\in M: d(f^{n}(x),f^{n}(y))\xrightarrow [n\rightarrow \infty ]{}0\}$
, which are immersed submanifolds tangent to
$W^s(x)=\{y\in M: d(f^{n}(x),f^{n}(y))\xrightarrow [n\rightarrow \infty ]{}0\}$
, which are immersed submanifolds tangent to
![]() $H^u(x)$
and
$H^u(x)$
and
![]() $H^s(x)$
, respectively. See [Reference Brin and StuckBS02, §5.6] for more details. In Definition 3.12, we give an alternative (yet equivalent) notion of global stable/unstable manifolds.
$H^s(x)$
, respectively. See [Reference Brin and StuckBS02, §5.6] for more details. In Definition 3.12, we give an alternative (yet equivalent) notion of global stable/unstable manifolds.
Claim 2.5.
![]() $\text {For all } \epsilon>0$
and
$\text {For all } \epsilon>0$
and
![]() $\epsilon '\in (0, \tfrac 23\epsilon ]$
,
$\epsilon '\in (0, \tfrac 23\epsilon ]$
,
![]() $\mathrm {RWT}_\chi ^{\epsilon '}\subseteq \mathrm {RWT}_\chi ^{\epsilon }$
, and
$\mathrm {RWT}_\chi ^{\epsilon '}\subseteq \mathrm {RWT}_\chi ^{\epsilon }$
, and
![]() $\mathrm {WT}_\chi ^{\epsilon '}\subseteq \mathrm {WT}_\chi ^{\epsilon }$
.
$\mathrm {WT}_\chi ^{\epsilon '}\subseteq \mathrm {WT}_\chi ^{\epsilon }$
.
For proof, see [Reference Ben OvadiaBO20, Claim 2.6].
Lemma 2.6.
![]() $\text {There exists } \epsilon _\chi>0$
which depends on
$\text {There exists } \epsilon _\chi>0$
which depends on
![]() $M,f,\beta $
and
$M,f,\beta $
and
![]() $\chi $
such that
$\chi $
such that
![]() $\text {for all} \epsilon \in (0,\epsilon _\chi ]$
,
$\text {for all} \epsilon \in (0,\epsilon _\chi ]$
,
![]() $\mathrm {RWT}_\chi ^\epsilon $
has a Markov partition and a finite-to-one coding with a Hölder continuous factor map, where the induced coding space is locally compact.
$\mathrm {RWT}_\chi ^\epsilon $
has a Markov partition and a finite-to-one coding with a Hölder continuous factor map, where the induced coding space is locally compact.
See [Reference Ben OvadiaBO20] for full details regarding the terms ‘Markov partition’ and ‘factor map’. See also Theorems 3.2–3.7 for more details regarding the notion of ‘a finite-to-one coding’.
Definition 2.7
Remark.
![]() $\mathrm {RWT}_\chi $
carries all
$\mathrm {RWT}_\chi $
carries all
![]() $\chi $
-hyperbolic f-invariant probability measures; and its definition depends only on the quality of hyperbolicity of the orbits of its elements. In the following parts of this paper, when
$\chi $
-hyperbolic f-invariant probability measures; and its definition depends only on the quality of hyperbolicity of the orbits of its elements. In the following parts of this paper, when
![]() $\chi>0$
is fixed, the subscript of
$\chi>0$
is fixed, the subscript of
![]() $\epsilon _\chi $
would be omitted to ease notation.
$\epsilon _\chi $
would be omitted to ease notation.
Definition 2.8. (Pesin set)
![]() $\text {For all } N\geq 1$
, the set
$\text {For all } N\geq 1$
, the set
 $$ \begin{align*}\Lambda_N:=\bigg\{x\in \mathrm{WT}_\chi^\epsilon\ {:}\ \text{there exists } \epsilon\text{-weakly tempered kernel of }x\text{ such that }q(x)\geq \frac{1}{N}\bigg\}\end{align*} $$
$$ \begin{align*}\Lambda_N:=\bigg\{x\in \mathrm{WT}_\chi^\epsilon\ {:}\ \text{there exists } \epsilon\text{-weakly tempered kernel of }x\text{ such that }q(x)\geq \frac{1}{N}\bigg\}\end{align*} $$
is called the Pesin set of level N (also sometimes called level set or Pesin level set).
Definition 2.9. (Positively recurrent points)
![]() $\text {For all } N \geq 1$
, denote by
$\text {For all } N \geq 1$
, denote by
![]() $\Lambda _N$
the Pesin set of level N. Let
$\Lambda _N$
the Pesin set of level N. Let

For the next definition, we assume without loss of generalization that
![]() $\text {there exists } s\in \{1,\ldots ,d-1\}$
such that for all points
$\text {there exists } s\in \{1,\ldots ,d-1\}$
such that for all points
![]() $x\in \mathrm {WT}_\chi ^\epsilon $
,
$x\in \mathrm {WT}_\chi ^\epsilon $
,
![]() $\mathrm {dim}H^s(x)=s$
. This is possible, since we may simply split
$\mathrm {dim}H^s(x)=s$
. This is possible, since we may simply split
![]() $\mathrm {WT}_\chi ^\epsilon $
into
$\mathrm {WT}_\chi ^\epsilon $
into
![]() $d-1$
disjoint sets, and all results apply to each subset.
$d-1$
disjoint sets, and all results apply to each subset.
Definition 2.10. (Grassmann–Hölder continuity)
Let
![]() $TM$
be the tangent bundle of M, and let
$TM$
be the tangent bundle of M, and let
![]() $x,y\in \mathrm {WT}_\chi ^\epsilon $
. Let
$x,y\in \mathrm {WT}_\chi ^\epsilon $
. Let
![]() $d_s(H^s(x),H^s(y))$
be the Grassmannian distance (of subspaces of dimension s, over
$d_s(H^s(x),H^s(y))$
be the Grassmannian distance (of subspaces of dimension s, over
![]() $TM$
) between the stable space of x and stable space of y. Similarly, let
$TM$
) between the stable space of x and stable space of y. Similarly, let
![]() $d_u(H^u(x),H^u(y))$
be the Grassmannian (of subspaces of dimension
$d_u(H^u(x),H^u(y))$
be the Grassmannian (of subspaces of dimension
![]() $d-s$
, over
$d-s$
, over
![]() $TM$
) distance between the unstable space of x and stable space of y. The Lyapunov distance on
$TM$
) distance between the unstable space of x and stable space of y. The Lyapunov distance on
![]() $\mathrm {WT}_\chi ^\epsilon $
is
$\mathrm {WT}_\chi ^\epsilon $
is
![]() $d_{GH}(x,y):=d(x,y)+ d_s(H^s(x),H^s(y))+ d_u(H^u(x),H^u(y))$
. A function
$d_{GH}(x,y):=d(x,y)+ d_s(H^s(x),H^s(y))+ d_u(H^u(x),H^u(y))$
. A function
![]() $\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
is called Grassmann–Hölder continuous if it is Hölder continuous with respect to
$\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
is called Grassmann–Hölder continuous if it is Hölder continuous with respect to
![]() $d_{GH}(\cdot ,\cdot )$
.
$d_{GH}(\cdot ,\cdot )$
.
Let
![]() $E\supseteq \mathrm {WT}_\chi ^\epsilon $
be a measurable subset of
$E\supseteq \mathrm {WT}_\chi ^\epsilon $
be a measurable subset of
![]() $\bigcup \{W^u(x):x\in \mathrm {WT}_\chi ^\epsilon \}$
. A function
$\bigcup \{W^u(x):x\in \mathrm {WT}_\chi ^\epsilon \}$
. A function
![]() $\varphi :E\rightarrow \mathbb {R}$
is called unstable-Grassmann–Hölder continuous on E if it is Hölder continuous with respect to
$\varphi :E\rightarrow \mathbb {R}$
is called unstable-Grassmann–Hölder continuous on E if it is Hölder continuous with respect to
![]() $d(\cdot ,\cdot )+d_u(\cdot ,\cdot )$
on E, where for
$d(\cdot ,\cdot )+d_u(\cdot ,\cdot )$
on E, where for
![]() $x\in \bigcup \{W^u(x):x\in \mathrm {WT}_\chi ^\epsilon \}$
,
$x\in \bigcup \{W^u(x):x\in \mathrm {WT}_\chi ^\epsilon \}$
,
![]() $H^u(x)$
is defined as
$H^u(x)$
is defined as
![]() $T_xW^u(x)$
(which is well defined).
$T_xW^u(x)$
(which is well defined).
As
![]() $f\in \mathrm {Diff}^{1+\beta }(M)$
,
$f\in \mathrm {Diff}^{1+\beta }(M)$
,
![]() $\text {for all } t>0$
, the scaled geometric potential
$\text {for all } t>0$
, the scaled geometric potential
![]() $\varphi _t(x)=-t\cdot \log \mathrm {Jac}(d_xf|_{H^u(x)})$
is unstable-
$\varphi _t(x)=-t\cdot \log \mathrm {Jac}(d_xf|_{H^u(x)})$
is unstable-
![]() $\text {Grassmann}\text{--}\text{H}\ddot{\text{o}}\text{lder continuous}$
. Every Hölder continuous potential is unstable-
$\text {Grassmann}\text{--}\text{H}\ddot{\text{o}}\text{lder continuous}$
. Every Hölder continuous potential is unstable-
![]() $\text{Grassmann}\text{--}\text{H}\ddot{\text{o}}\text{lder continuous}$
, and every unstable-
$\text{Grassmann}\text{--}\text{H}\ddot{\text{o}}\text{lder continuous}$
, and every unstable-
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential on
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential on
![]() $\mathrm {WT}_\chi ^\epsilon $
is
$\mathrm {WT}_\chi ^\epsilon $
is
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
.
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
.
Note also that a
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential must be bounded, since M has a finite diameter.
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential must be bounded, since M has a finite diameter.
Definition 2.11. (Ergodic homoclinic class)
The ergodic homoclinic class of a hyperbolic periodic point p (with respect to
![]() $\chi $
) is
$\chi $
) is
Here,
![]() $o(p)=\{f^k(p)\}$
,
$o(p)=\{f^k(p)\}$
,
![]() $\pitchfork $
denotes transverse intersections of full codimension, and
$\pitchfork $
denotes transverse intersections of full codimension, and
![]() $W^{s/u}(\cdot )$
are the global stable and unstable manifolds of the point, respectively.
$W^{s/u}(\cdot )$
are the global stable and unstable manifolds of the point, respectively.
See the remark after Definition 2.4 for the definition of global stable and unstable leaves. Definition 2.11 was introduced in [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and UresRHRHTU11], with a set of Lyapunov regular points replacing
![]() $\mathrm {RWT}_\chi $
. By a well-known argument, using the inclination lemma (see [Reference Brin and StuckBS02, Theorem 5.7.2]), every two ergodic homoclinic classes are either disjoint modulo all conservative measures, or coincide. (Conservative measures are measures which satisfy Poincaré’s recurrence theorem: for any set of positive measure, almost every point in it returns to it infinitely often.) We caution the reader that
$\mathrm {RWT}_\chi $
. By a well-known argument, using the inclination lemma (see [Reference Brin and StuckBS02, Theorem 5.7.2]), every two ergodic homoclinic classes are either disjoint modulo all conservative measures, or coincide. (Conservative measures are measures which satisfy Poincaré’s recurrence theorem: for any set of positive measure, almost every point in it returns to it infinitely often.) We caution the reader that
![]() $H_\chi (p)$
is not closed, and that this definition is different from the definition in [Reference NewhouseNew72].
$H_\chi (p)$
is not closed, and that this definition is different from the definition in [Reference NewhouseNew72].
Every ergodic
![]() $\chi $
-hyperbolic probability is carried by a unique ergodic homoclinic class (see Claim 3.15).
$\chi $
-hyperbolic probability is carried by a unique ergodic homoclinic class (see Claim 3.15).
Definition 2.12. (Local equilibrium state)
Let
![]() $\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
$\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
![]() $\text {Grassmann}\text{--}\text{H}\ddot{\text{o}}\text{lder} \text { continuous}$
potential. Let
$\text {Grassmann}\text{--}\text{H}\ddot{\text{o}}\text{lder} \text { continuous}$
potential. Let
![]() $\mu $
be a
$\mu $
be a
![]() $\chi $
-hyperbolic f-invariant ergodic probability measure. Let
$\chi $
-hyperbolic f-invariant ergodic probability measure. Let
![]() $H_\chi (p)$
be the unique ergodic homoclinic class which carries
$H_\chi (p)$
be the unique ergodic homoclinic class which carries
![]() $\mu $
. Here,
$\mu $
. Here,
![]() $\mu $
is called a hyperbolic local equilibrium state of
$\mu $
is called a hyperbolic local equilibrium state of
![]() $\varphi $
on
$\varphi $
on
![]() $H_\chi (p)$
if
$H_\chi (p)$
if
 $$ \begin{align*}h_\mu(f)&+\int \varphi \,d\mu=\sup\bigg\{h_\nu(f)\\&+\int \varphi \,d\nu:\nu\text{ is an }f\text{-invariant probability measure on }H_\chi(p)\bigg\}.\end{align*} $$
$$ \begin{align*}h_\mu(f)&+\int \varphi \,d\mu=\sup\bigg\{h_\nu(f)\\&+\int \varphi \,d\nu:\nu\text{ is an }f\text{-invariant probability measure on }H_\chi(p)\bigg\}.\end{align*} $$
Note that
![]() $\int \varphi \,d\mu <\infty $
since
$\int \varphi \,d\mu <\infty $
since
![]() $\varphi $
is bounded since it is
$\varphi $
is bounded since it is
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
.
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
.
Definition 2.13. (Local pressure)
Let p be a periodic
![]() $\chi $
-hyperbolic point, and let
$\chi $
-hyperbolic point, and let
![]() $H_\chi (p)$
be its ergodic homoclinic class. The local pressure of
$H_\chi (p)$
be its ergodic homoclinic class. The local pressure of
![]() $\varphi $
on
$\varphi $
on
![]() $H_\chi (p)$
is
$H_\chi (p)$
is
 $$ \begin{align*}P_{H_\chi(p)} (\varphi):= \sup\bigg\{h_\nu(f)+\!\int\!\! \varphi \,d\nu:\nu\text{ is an }f\text{-invariant probability measure on }H_\chi(p)\bigg\}.\end{align*} $$
$$ \begin{align*}P_{H_\chi(p)} (\varphi):= \sup\bigg\{h_\nu(f)+\!\int\!\! \varphi \,d\nu:\nu\text{ is an }f\text{-invariant probability measure on }H_\chi(p)\bigg\}.\end{align*} $$
The boundedness of
![]() $\varphi $
implies
$\varphi $
implies
![]() $P_{H_\chi (p)}(\varphi )<\infty $
. Let E be as in Definition 2.10.
$P_{H_\chi (p)}(\varphi )<\infty $
. Let E be as in Definition 2.10.
Definition 2.14. Given a sequence of
![]() $C^1$
embedded submanifolds,
$C^1$
embedded submanifolds,
![]() $V^u_n$
, we write
$V^u_n$
, we write
![]() $V^u_n\xrightarrow [n\rightarrow \infty ]{C^1} V^u$
, where
$V^u_n\xrightarrow [n\rightarrow \infty ]{C^1} V^u$
, where
![]() $V^u$
is an embedded submanifold, if
$V^u$
is an embedded submanifold, if
![]() $\sup _{x\in V^u_n}\inf _{y\in V^u}\{d(x,y)+d_{TM}(T_xV^u_n,T_yV^u)\}\xrightarrow [n\rightarrow \infty ]{}0$
.
$\sup _{x\in V^u_n}\inf _{y\in V^u}\{d(x,y)+d_{TM}(T_xV^u_n,T_yV^u)\}\xrightarrow [n\rightarrow \infty ]{}0$
.
Definition 2.15. (
 $\varphi $
-conformal system of measures)
$\varphi $
-conformal system of measures)
Let
![]() $\varphi :E\rightarrow \mathbb {R}$
be an unstable-
$\varphi :E\rightarrow \mathbb {R}$
be an unstable-
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential. Let
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential. Let
![]() $H_\chi (p)$
be the ergodic homoclinic class of a
$H_\chi (p)$
be the ergodic homoclinic class of a
![]() $\chi $
-hyperbolic and periodic point p. A
$\chi $
-hyperbolic and periodic point p. A
![]() $\varphi $
-conformal system of measures on
$\varphi $
-conformal system of measures on
![]() $H_\chi (p)$
is a collection of non-zero (finite) Radon measures
$H_\chi (p)$
is a collection of non-zero (finite) Radon measures
![]() $\{m_{V^u}\}$
indexed by the collection of local (‘local’ here means diffeomorphic to a ball, and bounded, in the induced metric) unstable leaves of points in
$\{m_{V^u}\}$
indexed by the collection of local (‘local’ here means diffeomorphic to a ball, and bounded, in the induced metric) unstable leaves of points in
![]() $H_\chi (p)$
such that
$H_\chi (p)$
such that
![]() $m_{V^u}$
is supported on
$m_{V^u}$
is supported on
![]() $V^u$
, and:
$V^u$
, and:
-
(1)
 $V^u_n\xrightarrow [n\rightarrow \infty ]{C^1}V^u$
implies
$V^u_n\xrightarrow [n\rightarrow \infty ]{C^1}V^u$
implies
 $m_{V^u_n} ^\varphi (1) \xrightarrow [n\rightarrow \infty ]{} m_{V^u} ^\varphi (1) $
;
$m_{V^u_n} ^\varphi (1) \xrightarrow [n\rightarrow \infty ]{} m_{V^u} ^\varphi (1) $
; -
(2) for every local unstable leaf of a point in
 $H_\chi (p)$
,
$H_\chi (p)$
,
 $V^u$
,
$V^u$
,  $$ \begin{align*}m^\varphi_{V^u}\circ f^{-1}=e^{\varphi-P_{H_\chi(p)}(\varphi)}\cdot m^\varphi_{f[V^u]},\end{align*} $$
$$ \begin{align*}m^\varphi_{V^u}\circ f^{-1}=e^{\varphi-P_{H_\chi(p)}(\varphi)}\cdot m^\varphi_{f[V^u]},\end{align*} $$
where
 $m^\varphi _{ V^u}, m^\varphi _{ f[V^u]} $
are the
$m^\varphi _{ V^u}, m^\varphi _{ f[V^u]} $
are the
 $\varphi $
-conformal measures on the local unstable leaves
$\varphi $
-conformal measures on the local unstable leaves
 $V^u, f[V^u]$
, respectively.
$V^u, f[V^u]$
, respectively.
An example of a conformal family of measures is the Riemannian volume on unstable leaves. It is
![]() $ \varphi $
-conformal with
$ \varphi $
-conformal with
![]() $\varphi $
being the geometric potential
$\varphi $
being the geometric potential
![]() $-\log \mathrm {Jac}(df|_{\text {unstable leaves}})$
, when the pressure is
$-\log \mathrm {Jac}(df|_{\text {unstable leaves}})$
, when the pressure is
![]() $0$
(e.g. when an SRB exists).
$0$
(e.g. when an SRB exists).
It is not clear a priori when do conformal families exist. In [Reference Climenhaga, Pesin and ZelerowiczCPZ20], Climenhaga, Pesin, and Zelerowicz give a construction of such families in the partially hyperbolic setup using the Carathéodory dimension structure (which extends their result in the uniformly hyperbolic setup [Reference Climenhaga, Pesin and ZelerowiczCPZ19]), under the assumption that
![]() $\varphi $
has the Bowen property (that is, uniformly summable variations on stable and unstable leaves, under a certain regularity assumption). Searching for an object which exists always as an alternative to conformal measures is the motivation for the next definition of invariant families.
$\varphi $
has the Bowen property (that is, uniformly summable variations on stable and unstable leaves, under a certain regularity assumption). Searching for an object which exists always as an alternative to conformal measures is the motivation for the next definition of invariant families.
Definition 2.16. (
 $\varphi $
-invariant family of leaf measures)
$\varphi $
-invariant family of leaf measures)
Let
![]() $\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
$\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential. Let
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential. Let
![]() $H_\chi (p)$
be the ergodic homoclinic class of a periodic
$H_\chi (p)$
be the ergodic homoclinic class of a periodic
![]() $\chi $
-hyperbolic point p such that
$\chi $
-hyperbolic point p such that
![]() $P_{H_\chi (p)}(\varphi )<\infty $
. A
$P_{H_\chi (p)}(\varphi )<\infty $
. A
![]() $\varphi $
-invariant family of leaf measures on
$\varphi $
-invariant family of leaf measures on
![]() $H_\chi (p)$
is a family
$H_\chi (p)$
is a family
![]() $\mathcal {F} $
of non-zero and finite measures such that:
$\mathcal {F} $
of non-zero and finite measures such that:
-
(1)
 $\text {for all } \mu \in \mathcal {F} $
,
$\text {for all } \mu \in \mathcal {F} $
,
 $\mu $
is carried by
$\mu $
is carried by
 $WT_\chi ^\epsilon $
, and its support is contained in a local unstable leaf of a point
$WT_\chi ^\epsilon $
, and its support is contained in a local unstable leaf of a point
 $x\in H_\chi (p)$
;
$x\in H_\chi (p)$
; -
(2)
 $\text {there exists }$
a map
$\text {there exists }$
a map
 $A:\cup \{\mathrm {supp}(\mu ')\}_{\mu '\in \mathcal {F} }\rightarrow \mathbb {R}$
which is measurable when restricted to measurable sets, such that
$A:\cup \{\mathrm {supp}(\mu ')\}_{\mu '\in \mathcal {F} }\rightarrow \mathbb {R}$
which is measurable when restricted to measurable sets, such that
 $\text {for all } \mu \in \mathcal {F} $
,
$\text {for all } \mu \in \mathcal {F} $
,
 $\mu \circ \!f^{-1}=e^{-P_{H_\chi (p)} (\varphi )}\!\sum _{i=1}^{N_{\mu }}e^{\phi (\mu ^{(i)})}\mu ^{(i)}$
, where
$\mu \circ \!f^{-1}=e^{-P_{H_\chi (p)} (\varphi )}\!\sum _{i=1}^{N_{\mu }}e^{\phi (\mu ^{(i)})}\mu ^{(i)}$
, where
 $\mu ^{(i)}\!\in \mathcal {F} $
for all
$\mu ^{(i)}\!\in \mathcal {F} $
for all
 $1\leq i\leq N(\mu )<\infty $
, and
$1\leq i\leq N(\mu )<\infty $
, and
 $\phi (\mu ^{(i)}) $
is a constant such that
$\phi (\mu ^{(i)}) $
is a constant such that
 $\phi (\mu ^{(i)})=\varphi (x)+A(x)-A(f^{-1}(x))$
for
$\phi (\mu ^{(i)})=\varphi (x)+A(x)-A(f^{-1}(x))$
for
 $\mu ^{(i)}$
-almost every (a.e.)
$\mu ^{(i)}$
-almost every (a.e.)
 $x\in M$
where
$x\in M$
where
 $\varphi $
is defined;
$\varphi $
is defined; -
(3)
 $\text {there exists a } \sigma $
-compact metric space X such that
$\text {there exists a } \sigma $
-compact metric space X such that
 $\mathcal {F} =\{\mu _{x}\}_{x\in X}$
and
$\mathcal {F} =\{\mu _{x}\}_{x\in X}$
and
 $x_n\rightarrow y\Rightarrow \mu _{x_n}\xrightarrow []{\text {weak-}*}~\mu _{y}$
.
$x_n\rightarrow y\Rightarrow \mu _{x_n}\xrightarrow []{\text {weak-}*}~\mu _{y}$
.
The measures in
![]() $\mathcal {F} $
are not required to be mutually singular.
$\mathcal {F} $
are not required to be mutually singular.
One cannot expect uniqueness of such a family, as the Radon–Nikodym derivative of the push-forwards can always be changed by a coboundary.
2.2 Main results
Theorem A. Let
![]() $\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
$\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
![]() $H_\chi (p)$
be the ergodic homoclinic class of a periodic
$H_\chi (p)$
be the ergodic homoclinic class of a periodic
![]() $\chi $
-hyperbolic point p. Then
$\chi $
-hyperbolic point p. Then
![]() $H_\chi (p)$
admits a
$H_\chi (p)$
admits a
![]() $\varphi $
-invariant family of leaf measures,
$\varphi $
-invariant family of leaf measures,
![]() $\mathcal {F}_{H_\chi (p)}(\varphi )$
.
$\mathcal {F}_{H_\chi (p)}(\varphi )$
.
(See Theorem 5.7.) While conformal families of measures are generally a simpler object for calculations, their general existence is a hard problem which is only solved in a few setups (we mention a few in §1). The main advantage of invariant families is that they exist with (almost) no preceding assumptions. Furthermore, when a conformal family does exist, and so does an equilibrium state for the respective potential, the invariant family of measures must coincide in measure-class with the conformal family. See Theorem E.
In the following statement,
![]() $\mathcal {F}_{H_\chi (p)}(\varphi )$
is as constructed in Theorem A. That is, in Theorem A, we construct an invariant family, and the leaf condition applies to any invariant family as constructed by that theorem. We remind the reader that the invariant family need not be unique, as the leaf measures can always be changed by a coboundary factor. In addition, we use the notation
$\mathcal {F}_{H_\chi (p)}(\varphi )$
is as constructed in Theorem A. That is, in Theorem A, we construct an invariant family, and the leaf condition applies to any invariant family as constructed by that theorem. We remind the reader that the invariant family need not be unique, as the leaf measures can always be changed by a coboundary factor. In addition, we use the notation
![]() $\varphi _n(q):=\sum _{k=0}^{n-1}\varphi (f^{-k}(q))$
in the following statement.
$\varphi _n(q):=\sum _{k=0}^{n-1}\varphi (f^{-k}(q))$
in the following statement.
Definition 2.17. (
 $\varphi $
-leaf condition)
$\varphi $
-leaf condition)
Let
![]() $\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
$\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential. Let
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential. Let
![]() $H_\chi (p)$
be an ergodic homoclinic class of a
$H_\chi (p)$
be an ergodic homoclinic class of a
![]() $\chi $
-hyperbolic periodic point p. We say that the
$\chi $
-hyperbolic periodic point p. We say that the
![]() $\varphi $
-leaf condition is satisfied for
$\varphi $
-leaf condition is satisfied for
![]() $H_\chi (p)$
, if
$H_\chi (p)$
, if
![]() $\text {there exists } \mu \in \mathcal {F}_{H_\chi (p)}(\varphi )$
such that
$\text {there exists } \mu \in \mathcal {F}_{H_\chi (p)}(\varphi )$
such that
![]() $\mu (\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
.
$\mu (\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
.
Theorem B. Let
![]() $\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
$\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
![]() $H_\chi (p)$
be an ergodic homoclinic class of a
$H_\chi (p)$
be an ergodic homoclinic class of a
![]() $\chi $
-hyperbolic periodic point p such that p belongs to a Pesin level set
$\chi $
-hyperbolic periodic point p such that p belongs to a Pesin level set
![]() $ \Lambda _{l }$
. Then,
$ \Lambda _{l }$
. Then,
![]() $\varphi $
admits a
$\varphi $
admits a
![]() $\chi $
-hyperbolic local equilibrium state on
$\chi $
-hyperbolic local equilibrium state on
![]() $H_\chi (p)$
if and only if
$H_\chi (p)$
if and only if
![]() $\sum _{n\geq 1}\sum _{f^n(q)=q,q\in H_\chi (p)\cap \Lambda _l}e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )}=\infty $
and the
$\sum _{n\geq 1}\sum _{f^n(q)=q,q\in H_\chi (p)\cap \Lambda _l}e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )}=\infty $
and the
![]() $\varphi $
-leaf condition is satisfied for
$\varphi $
-leaf condition is satisfied for
![]() $H_\chi (p)$
. If the local equilibrium state exists, then it is unique and the
$H_\chi (p)$
. If the local equilibrium state exists, then it is unique and the
![]() $\varphi $
-invariant family is its conditional measures (in the explicit sense given by equation (11)).
$\varphi $
-invariant family is its conditional measures (in the explicit sense given by equation (11)).
(See Theorem 6.1.) Note that if the assumption above holds for one l, then it holds for all
![]() $l'\geq l$
, since
$l'\geq l$
, since
![]() $\Lambda _{l'}\supseteq \Lambda _l$
. Theorems 6.1 and 5.7 yield the following corollary.
$\Lambda _{l'}\supseteq \Lambda _l$
. Theorems 6.1 and 5.7 yield the following corollary.
Corollary C. Local equilibrium states of
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potentials have local product structure.
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potentials have local product structure.
Local product structure for a non-uniformly hyperbolic measure means that every Pesin block can be covered by finitely many sets with a local product structure, on which the measure can be approximated by the product of a measure on a local stable leaf and a measure on a local unstable leaf (see Corollary 6.2). This follows from the absolute continuity property of the
![]() $\varphi $
-invariant family we construct. This extends previous results for the Axiom A setup (see [Reference HaydnHay94, Reference LeplaideurLep00]).
$\varphi $
-invariant family we construct. This extends previous results for the Axiom A setup (see [Reference HaydnHay94, Reference LeplaideurLep00]).
Corollary D.
![]() $(M,f)$
admits a
$(M,f)$
admits a
![]() $\chi $
-hyperbolic equilibrium state for
$\chi $
-hyperbolic equilibrium state for
![]() $\varphi $
if and only if there exists an ergodic homoclinic class
$\varphi $
if and only if there exists an ergodic homoclinic class
![]() $H_\chi (p)$
which satisfies the assumptions of Theorem B, and in addition,
$H_\chi (p)$
which satisfies the assumptions of Theorem B, and in addition,
![]() $P_{H_\chi (p)}(\varphi )=P_{\mathrm {top}}(\varphi )$
(
$P_{H_\chi (p)}(\varphi )=P_{\mathrm {top}}(\varphi )$
(
![]() $= \sup \{h_\nu (f)+\int \! \varphi \,d\nu :\nu \text { is an }f\text {-inv. probability on }M\}$
).
$= \sup \{h_\nu (f)+\int \! \varphi \,d\nu :\nu \text { is an }f\text {-inv. probability on }M\}$
).
Theorem E. Let
![]() $\varphi :WT_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
$\varphi :WT_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
![]() $H_\chi (p)$
be an ergodic homoclinic class of a
$H_\chi (p)$
be an ergodic homoclinic class of a
![]() $\chi $
-hyperbolic periodic point p which admits a (unique)
$\chi $
-hyperbolic periodic point p which admits a (unique)
![]() $\chi $
-hyperbolic equilibrium state for
$\chi $
-hyperbolic equilibrium state for
![]() $\varphi $
,
$\varphi $
,
![]() $\nu _\varphi $
. Assume that
$\nu _\varphi $
. Assume that
![]() $H_\chi (p)$
admits a
$H_\chi (p)$
admits a
![]() $\varphi $
-conformal system of measures. Let
$\varphi $
-conformal system of measures. Let
![]() $\mathcal {F}_{H_\chi (p)}(\varphi )$
be any
$\mathcal {F}_{H_\chi (p)}(\varphi )$
be any
![]() $\varphi $
-invariant family of conditional leaf measures as constructed in Theorem A, then there is a sub-family
$\varphi $
-invariant family of conditional leaf measures as constructed in Theorem A, then there is a sub-family
![]() $\mathcal {F}'$
which disintegrates
$\mathcal {F}'$
which disintegrates
![]() $\nu _\varphi $
(as in Theorem B), and for which the following holds. For any
$\nu _\varphi $
(as in Theorem B), and for which the following holds. For any
![]() $\mu \in \mathcal {F} '$
, given a local unstable leaf
$\mu \in \mathcal {F} '$
, given a local unstable leaf
![]() $V^u_{\mathrm {loc}}$
which carries
$V^u_{\mathrm {loc}}$
which carries
![]() $\mu $
, and a corresponding
$\mu $
, and a corresponding
![]() $\varphi $
-conformal measure on
$\varphi $
-conformal measure on
![]() $V^u_{\mathrm {loc}}$
,
$V^u_{\mathrm {loc}}$
,
![]() $m^\varphi _{ V^u_{\mathrm {loc}}}$
, there exists a measurable set of full
$m^\varphi _{ V^u_{\mathrm {loc}}}$
, there exists a measurable set of full
![]() $\mu $
-measure,
$\mu $
-measure,
![]() $E_\mu $
, such that
$E_\mu $
, such that
![]() $\mu \sim m^\varphi _{ V^u_{\mathrm {loc}}}|_{E_\mu }$
. In particular,
$\mu \sim m^\varphi _{ V^u_{\mathrm {loc}}}|_{E_\mu }$
. In particular,
![]() $m^\varphi _{ V^u_{\mathrm {loc}}} (\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
.
$m^\varphi _{ V^u_{\mathrm {loc}}} (\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
.
(See Theorem 6.3.) The last property holds in particular when
![]() $\varphi $
is unstable-
$\varphi $
is unstable-
![]() $\text {Grassmann}\text{--} \text {H}\ddot{\text{o}}\text{lder continuous}$
and is defined on unstable leaves, and thus we a priori have no reason to know that its conformal measures ‘see’ the hyperbolic points.
$\text {Grassmann}\text{--} \text {H}\ddot{\text{o}}\text{lder continuous}$
and is defined on unstable leaves, and thus we a priori have no reason to know that its conformal measures ‘see’ the hyperbolic points.
If
![]() $\varphi $
is the geometric potential, then the
$\varphi $
is the geometric potential, then the
![]() $\varphi $
-conformal measures exist and are the induced Riemannian volume of the unstable leaves, and this theorem proves that every
$\varphi $
-conformal measures exist and are the induced Riemannian volume of the unstable leaves, and this theorem proves that every
![]() $\chi $
-hyperbolic equilibrium state of the geometric potential with pressure
$\chi $
-hyperbolic equilibrium state of the geometric potential with pressure
![]() $0$
has absolutely continuous conditional measures (and thus is an SRB measure). This is a new proof to the result by Ledrappier and Young in [Reference Ledrappier and YoungLY85a], when restricting to hyperbolic measures; and extends it to additional potentials.
$0$
has absolutely continuous conditional measures (and thus is an SRB measure). This is a new proof to the result by Ledrappier and Young in [Reference Ledrappier and YoungLY85a], when restricting to hyperbolic measures; and extends it to additional potentials.
Remark. In several of the main results, we use the assumption
![]() $\sum \nolimits _{n\geq 1}\sum \nolimits _{f^n(q)=q, q\in H_\chi (p)\cap \Lambda _l} e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )} =\infty $
for some hyperbolic periodic point p which belongs to a level set
$\sum \nolimits _{n\geq 1}\sum \nolimits _{f^n(q)=q, q\in H_\chi (p)\cap \Lambda _l} e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )} =\infty $
for some hyperbolic periodic point p which belongs to a level set
![]() $\Lambda _{l}$
(where
$\Lambda _{l}$
(where
![]() $\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
is a
$\varphi :\mathrm {WT}_\chi ^\epsilon \rightarrow \mathbb {R}$
is a
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential). This assumption is used to show that
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential). This assumption is used to show that
![]() $\varphi $
is recurrent (see §4.2) when lifted to an irreducible component which codes
$\varphi $
is recurrent (see §4.2) when lifted to an irreducible component which codes
![]() $H_\chi (p)$
(see §3.3). This assumption is always used together with the leaf condition (see Definition 2.17). We do not know if the first assumption can be omitted (that is, does the leaf condition imply recurrence of the lifted potential). We were not able to prove that using the methods of this paper. The difference between this paper and [Reference Ben OvadiaBO21], where the leaf condition is sufficient, is the overlapping property of leaf measures (that is, the Lebesgue measures of two unstable leaves which intersect coincide on the intersection). Here, we use a coding to construct our
$H_\chi (p)$
(see §3.3). This assumption is always used together with the leaf condition (see Definition 2.17). We do not know if the first assumption can be omitted (that is, does the leaf condition imply recurrence of the lifted potential). We were not able to prove that using the methods of this paper. The difference between this paper and [Reference Ben OvadiaBO21], where the leaf condition is sufficient, is the overlapping property of leaf measures (that is, the Lebesgue measures of two unstable leaves which intersect coincide on the intersection). Here, we use a coding to construct our
![]() $\varphi $
-invariant family of leaf measures and, to gain a bound on the overlapping of measures, we must use the bound on the multiplicity of the coding map
$\varphi $
-invariant family of leaf measures and, to gain a bound on the overlapping of measures, we must use the bound on the multiplicity of the coding map
![]() $\widehat {\pi }$
; which in turn is only bounded on the recurrent part of the symbolic space in our construction; and hence the need for recurrence. There are other constructions of codings with better multiplicity bounds for the coding map (e.g. [Reference BuzziBuz20]), though those multiplicity improvements come at the expense of other properties which are necessary for this paper.
$\widehat {\pi }$
; which in turn is only bounded on the recurrent part of the symbolic space in our construction; and hence the need for recurrence. There are other constructions of codings with better multiplicity bounds for the coding map (e.g. [Reference BuzziBuz20]), though those multiplicity improvements come at the expense of other properties which are necessary for this paper.
3 Preliminary constructions
3.1 Symbolic dynamics
Sinai [Reference SinaĭSin68] and Adler and Weiss [Reference Adler and WeissAW70] constructed Markov partitions and for Anosov diffeomorphims and linear toral automorphisms, respectively. In [Reference SarigSar13], Sarig constructed a Markov partition for non-uniformly hyperbolic surface diffeomorphisms. We extended his results to manifolds of any dimension greater or equal to 2 in [Reference Ben OvadiaBO18]. In [Reference Ben OvadiaBO20], we modify the codings from [Reference Ben OvadiaBO18, Reference SarigSar13] and introduce the set
![]() $\mathrm {RWT}_\chi $
. Here,
$\mathrm {RWT}_\chi $
. Here,
![]() $\mathrm {RWT}_\chi $
is defined canonically, and still consists of all recurrently codable points (see Proposition 3.8) in the modified symbolic dynamics. In the following section, we review those results.
$\mathrm {RWT}_\chi $
is defined canonically, and still consists of all recurrently codable points (see Proposition 3.8) in the modified symbolic dynamics. In the following section, we review those results.
As M is compact,
![]() $\text {there exists } r=r(M)>0,\rho =\rho (M)>0$
such that the exponential map
$\text {there exists } r=r(M)>0,\rho =\rho (M)>0$
such that the exponential map
is injective.
Definition 3.1. (Pesin charts)
When
![]() $\epsilon \leq r$
, the following is well defined since
$\epsilon \leq r$
, the following is well defined since
![]() $C_\chi (\cdot )$
is a contraction (see [Reference Ben OvadiaBO18, Lemma 2.9]):
$C_\chi (\cdot )$
is a contraction (see [Reference Ben OvadiaBO18, Lemma 2.9]):
-
(1)
 $\psi _x^\eta :=\exp _x\circ C_\chi (x):\{v\in T_xM:|v|\leq \eta \}\rightarrow B_\rho (x)$
,
$\psi _x^\eta :=\exp _x\circ C_\chi (x):\{v\in T_xM:|v|\leq \eta \}\rightarrow B_\rho (x)$
,
 $\eta \in (0,Q_\epsilon (x)]$
is called a Pesin chart;
$\eta \in (0,Q_\epsilon (x)]$
is called a Pesin chart; -
(2) a double Pesin chart is an ordered couple
 $\psi _x^{p^s, p^u}:=(\psi _x^{p^s}, \psi _x^{p^u})$
, where
$\psi _x^{p^s, p^u}:=(\psi _x^{p^s}, \psi _x^{p^u})$
, where
 $\psi _x^{p^s}$
and
$\psi _x^{p^s}$
and
 $\psi _x^{p^u}$
are Pesin charts.
$\psi _x^{p^u}$
are Pesin charts.
Theorem 3.2.
![]() $\text {For all } \chi>0$
such that there exists a
$\text {For all } \chi>0$
such that there exists a
![]() $\chi $
-hyperbolic periodic point p,
$\chi $
-hyperbolic periodic point p,
![]() $\text {there exists }$
a countable and locally finite (finite out-going and in-going degree at each vertex) directed graph
$\text {there exists }$
a countable and locally finite (finite out-going and in-going degree at each vertex) directed graph
![]() $\mathcal {G}= (\mathcal {V},\mathcal {E})$
which induces a topological Markov shift
$\mathcal {G}= (\mathcal {V},\mathcal {E})$
which induces a topological Markov shift
![]() $ \Sigma :=\{\underline {u}\in \mathcal {V}^{\mathbb {Z}}: (u_i,u_{i+1})\in \mathcal {E},\text { for all } i\in \mathbb {Z}\}$
such that
$ \Sigma :=\{\underline {u}\in \mathcal {V}^{\mathbb {Z}}: (u_i,u_{i+1})\in \mathcal {E},\text { for all } i\in \mathbb {Z}\}$
such that
![]() $\Sigma $
admits a factor map
$\Sigma $
admits a factor map
![]() $\pi :\Sigma \rightarrow M$
with the following properties:
$\pi :\Sigma \rightarrow M$
with the following properties:
-
(1)
 $\sigma :\Sigma \rightarrow \Sigma $
is defined by
$\sigma :\Sigma \rightarrow \Sigma $
is defined by
 $(\sigma \underline {u})_i:=u_{i+1}$
,
$(\sigma \underline {u})_i:=u_{i+1}$
,
 $i\in \mathbb {Z}$
(the left-shift) and satisfies
$i\in \mathbb {Z}$
(the left-shift) and satisfies
 $\pi \circ \sigma =f\circ \pi $
;
$\pi \circ \sigma =f\circ \pi $
; -
(2)
 $\pi $
is a Hölder continuous map with respect to the metric
$\pi $
is a Hölder continuous map with respect to the metric
 $d(\underline {u},\underline {v}):=\exp (-\min \{i\geq 0:u_i\neq v_i\text { or } u_{-i}\neq v_{-i}\})$
;
$d(\underline {u},\underline {v}):=\exp (-\min \{i\geq 0:u_i\neq v_i\text { or } u_{-i}\neq v_{-i}\})$
; -
(3) let
 $\Sigma ^\#:=\{\underline {u}\in \Sigma :\text {there exists } n_k,m_k\uparrow \infty \text { such that }u_{n_k}=u_{n_0}, u_{-m_k}=u_{-m_0},\text{ for} \text{ all } k\geq 0\}$
, then
$\Sigma ^\#:=\{\underline {u}\in \Sigma :\text {there exists } n_k,m_k\uparrow \infty \text { such that }u_{n_k}=u_{n_0}, u_{-m_k}=u_{-m_0},\text{ for} \text{ all } k\geq 0\}$
, then
 $\pi [\Sigma ^\#]$
carries all f-invariant,
$\pi [\Sigma ^\#]$
carries all f-invariant,
 $\chi $
-hyperbolic probability measures.
$\chi $
-hyperbolic probability measures.
This theorem is the content of [Reference Ben OvadiaBO18, Theorem 3.13] (and, similarly, the content of [Reference SarigSar13, Theorem 4.16] when
![]() $d=2$
). Here,
$d=2$
). Here,
![]() $\mathcal {V}$
is a collection of double Pesin charts (see Definition 3.1), which is discrete.
$\mathcal {V}$
is a collection of double Pesin charts (see Definition 3.1), which is discrete.
Definition 3.3
-
(1)
 $\text {For all } u\in \mathcal {V}$
,
$\text {For all } u\in \mathcal {V}$
,
 $Z(u):=\pi [\{\underline {u}\in \Sigma ^\#:u_0=u\}]$
,
$Z(u):=\pi [\{\underline {u}\in \Sigma ^\#:u_0=u\}]$
,
 $\mathcal {Z}:=\{Z(u):u\in \mathcal {V}\}$
.
$\mathcal {Z}:=\{Z(u):u\in \mathcal {V}\}$
. -
(2)
 $\mathcal {R}$
is defined to be a countable partition of
$\mathcal {R}$
is defined to be a countable partition of
 $\bigcup \nolimits _{v\in \mathcal {V}}Z(v)=\pi [\Sigma ^\#]$
such that:
$\bigcup \nolimits _{v\in \mathcal {V}}Z(v)=\pi [\Sigma ^\#]$
such that:-
(a)
 $\mathcal {R}$
is a refinement of
$\mathcal {R}$
is a refinement of
 $\mathcal {Z}$
:
$\mathcal {Z}$
:
 $\text {for all } Z\in \mathcal {Z},R\in \mathcal {R}$
,
$\text {for all } Z\in \mathcal {Z},R\in \mathcal {R}$
,
 $R\cap Z\neq \varnothing \Rightarrow R\subseteq Z$
;
$R\cap Z\neq \varnothing \Rightarrow R\subseteq Z$
; -
(b)
 $\text {for all } v\in \mathcal {V}$
,
$\text {for all } v\in \mathcal {V}$
,
 $\#\{R\in \mathcal {R}:R\subseteq Z(v)\}<\infty $
[Reference SarigSar13, §11];
$\#\{R\in \mathcal {R}:R\subseteq Z(v)\}<\infty $
[Reference SarigSar13, §11]; -
(c) the rectangles property:
 $\text {for all } R\in \mathcal {R},\text { for all } x,y\in R\ \text{there exists } !\! z:=[x,y]_R\in R$
, such that
$\text {for all } R\in \mathcal {R},\text { for all } x,y\in R\ \text{there exists } !\! z:=[x,y]_R\in R$
, such that
 $\text {for all } i\geq 0, R(f^i(z))= R(f^i(y)), R(f^{-i}(z))= R(f^{-i}(x))$
, where
$\text {for all } i\geq 0, R(f^i(z))= R(f^i(y)), R(f^{-i}(z))= R(f^{-i}(x))$
, where
 $R(t):=$
the unique partition member of
$R(t):=$
the unique partition member of
 $\mathcal {R}$
which contains t, for
$\mathcal {R}$
which contains t, for
 $t\in \pi [\Sigma ^\#]$
.
$t\in \pi [\Sigma ^\#]$
.
-
-
(3)
 $\text {For all } R,S\in \mathcal {R}$
, we say
$\text {For all } R,S\in \mathcal {R}$
, we say
 $R\rightarrow S$
if
$R\rightarrow S$
if
 $R\cap f^{-1}[S]\neq \varnothing $
, and let
$R\cap f^{-1}[S]\neq \varnothing $
, and let
 $\widehat {\mathcal {E}}:=\{(R,S)\in \mathcal {R}^2\text { such that }R\to S\}$
.
$\widehat {\mathcal {E}}:=\{(R,S)\in \mathcal {R}^2\text { such that }R\to S\}$
. -
(4)
 $\widehat {\Sigma }:=\{\underline {R}\in \mathcal {R}^{\mathbb {Z}}: R_i\rightarrow R_{i+1},\text{for all } i\in \mathbb {Z}\}$
.
$\widehat {\Sigma }:=\{\underline {R}\in \mathcal {R}^{\mathbb {Z}}: R_i\rightarrow R_{i+1},\text{for all } i\in \mathbb {Z}\}$
.
Remark. Given
![]() $\mathcal {Z}$
, the definition of
$\mathcal {Z}$
, the definition of
![]() $\mathcal {R}$
is proper, since such a refining partition as
$\mathcal {R}$
is proper, since such a refining partition as
![]() $\mathcal {R}$
exists by the Bowen–Sinai refinement, see [Reference SarigSar13, §11.1]. By property (2)(b), and since
$\mathcal {R}$
exists by the Bowen–Sinai refinement, see [Reference SarigSar13, §11.1]. By property (2)(b), and since
![]() $\Sigma $
is locally compact (see Theorem 3.2, local-finiteness of
$\Sigma $
is locally compact (see Theorem 3.2, local-finiteness of
![]() $\mathcal {G}$
implies local-compactness of
$\mathcal {G}$
implies local-compactness of
![]() $\Sigma $
),
$\Sigma $
),
![]() $\widehat {\Sigma }$
is also locally compact.
$\widehat {\Sigma }$
is also locally compact.
Definition 3.4
-
(1)
 $\widehat {\Sigma }^\#:=\{\underline {R}\in \widehat {\Sigma }:\text {there exists } n_k,m_k\uparrow \infty \text { such that }R_{n_k}\ {=}\ R_{n_0}, R_{-m_k}\ {=}\ R_{-m_0},\ \text{for} \text{all}\ k\geq 0\}$
.
$\widehat {\Sigma }^\#:=\{\underline {R}\in \widehat {\Sigma }:\text {there exists } n_k,m_k\uparrow \infty \text { such that }R_{n_k}\ {=}\ R_{n_0}, R_{-m_k}\ {=}\ R_{-m_0},\ \text{for} \text{all}\ k\geq 0\}$
. -
(2) Two partition members
 $R,S\in \mathcal {R}$
are said to be affiliated if
$R,S\in \mathcal {R}$
are said to be affiliated if
 $\text {there exists } u,v\in \mathcal {V}$
such that
$\text {there exists } u,v\in \mathcal {V}$
such that
 $R\subseteq Z(u), S\subseteq Z(v)$
and
$R\subseteq Z(u), S\subseteq Z(v)$
and
 $Z(u)\cap Z(v)\neq \varnothing $
(this terminology is due to O. Sarig [Reference SarigSar13, §12.3]).
$Z(u)\cap Z(v)\neq \varnothing $
(this terminology is due to O. Sarig [Reference SarigSar13, §12.3]).
Claim 3.5. (Local finiteness of the cover
 $\mathcal {Z}$
)
$\mathcal {Z}$
)
For all
![]() $Z\in \mathcal {Z}$
,
$Z\in \mathcal {Z}$
,
![]() $\#\{Z'\kern1.2pt{\in}\kern1.2pt \mathcal {Z}:Z'\cap Z\kern1.2pt{\neq}\kern1.2pt \varnothing \} \kern1.2pt{<}\kern1.2pt\infty $
.
$\#\{Z'\kern1.2pt{\in}\kern1.2pt \mathcal {Z}:Z'\cap Z\kern1.2pt{\neq}\kern1.2pt \varnothing \} \kern1.2pt{<}\kern1.2pt\infty $
.
This claim is the content of [Reference Ben OvadiaBO18, Theorem 5.2] (and similarly [Reference SarigSar13, Theorem 10.2] when
![]() $d=2$
).
$d=2$
).
Remark. By Claim 3.5 and Definition 3.3(2)(b), it follows that every partition member of
![]() $\mathcal {R}$
has only a finite number of partition members affiliated to it.
$\mathcal {R}$
has only a finite number of partition members affiliated to it.
Definition 3.6. Let
![]() $R\in \mathcal {R}$
,
$R\in \mathcal {R}$
,
![]() $N(R):=\#\{S\in \mathcal {R}: S\text { is affiliated to }R\}$
.
$N(R):=\#\{S\in \mathcal {R}: S\text { is affiliated to }R\}$
.
Theorem 3.7. Given
![]() $\widehat {\Sigma }$
from Definition 3.3, there exists a factor map
$\widehat {\Sigma }$
from Definition 3.3, there exists a factor map
![]() $\widehat {\pi }:\widehat {\Sigma }\rightarrow M$
such that:
$\widehat {\pi }:\widehat {\Sigma }\rightarrow M$
such that:
-
(1)
 $\widehat {\pi }$
is Hölder continuous with respect to the metric
$\widehat {\pi }$
is Hölder continuous with respect to the metric
 $d(\underline {R},\underline {S})=\exp (-\min \{i\geq 0: R_i\neq S_i\text { or }R_{-i}\neq S_{-i}\})$
;
$d(\underline {R},\underline {S})=\exp (-\min \{i\geq 0: R_i\neq S_i\text { or }R_{-i}\neq S_{-i}\})$
; -
(2)
 $f\circ \widehat {\pi }=\widehat {\pi }\circ \sigma $
, where
$f\circ \widehat {\pi }=\widehat {\pi }\circ \sigma $
, where
 $\sigma $
denotes the left-shift on
$\sigma $
denotes the left-shift on
 $\widehat {\Sigma }$
;
$\widehat {\Sigma }$
; -
(3)
 $\widehat {\pi }|_{\widehat {\Sigma }^\#}$
is finite-to-one;
$\widehat {\pi }|_{\widehat {\Sigma }^\#}$
is finite-to-one; -
(4)
 $\text {for all } \underline {R}\in \widehat {\Sigma }$
,
$\text {for all } \underline {R}\in \widehat {\Sigma }$
,
 $\widehat {\pi }(\underline {R})\in \overline {R_0}$
;
$\widehat {\pi }(\underline {R})\in \overline {R_0}$
; -
(5)
 $\widehat {\pi }[\widehat {\Sigma }^\#]$
carries all
$\widehat {\pi }[\widehat {\Sigma }^\#]$
carries all
 $\chi $
-hyperbolic invariant probability measures.
$\chi $
-hyperbolic invariant probability measures.
This theorem is the content of the main theorem of [Reference Ben OvadiaBO18, Theorem 1.1] (and similarly the content of [Reference SarigSar13, Theorem 1.3] when
![]() $d = 2$
). Note that the fibers of
$d = 2$
). Note that the fibers of
![]() $\widehat {\pi }$
being finite in
$\widehat {\pi }$
being finite in
![]() $\widehat {\Sigma }^\#$
does not imply being uniformly bounded.
$\widehat {\Sigma }^\#$
does not imply being uniformly bounded.
Proposition 3.8. We have
![]() .
.
This is the content of [Reference Ben OvadiaBO20, Proposition 4.11, Corollary 4.12].
3.2 Maximal dimension unstable leaves
Definition 3.9. An unstable leaf (of f) in M,
![]() $V^u$
, is a
$V^u$
, is a
![]() $C^{1+{\beta }/{3}}$
embedded Riemannian submanifold of M, such that
$C^{1+{\beta }/{3}}$
embedded Riemannian submanifold of M, such that
![]() $\text {for all } x,y\in V^u$
,
$\text {for all } x,y\in V^u$
,
![]() $\limsup \nolimits _{n\rightarrow \infty } {1}/{n}\log d(f^{-n}(x),f^{-n}(y))<0$
. Similarly, a stable leaf is an unstable leaf of
$\limsup \nolimits _{n\rightarrow \infty } {1}/{n}\log d(f^{-n}(x),f^{-n}(y))<0$
. Similarly, a stable leaf is an unstable leaf of
![]() $f^{-1}$
.
$f^{-1}$
.
Definition 3.10. An unstable leaf is called an unstable leaf of maximal dimension if it is not contained in any unstable leaf of a greater dimension.
Note that if
![]() $x\in \mathrm {RWT}_\chi $
belongs to an unstable leaf of maximal dimension
$x\in \mathrm {RWT}_\chi $
belongs to an unstable leaf of maximal dimension
![]() $V^u$
, then
$V^u$
, then
![]() $\mathrm {dim}H^u(x)=\mathrm {dim}V^u$
. This can be seen using the following claim.
$\mathrm {dim}H^u(x)=\mathrm {dim}V^u$
. This can be seen using the following claim.
Claim 3.11. For all
![]() $\underline {u}\in \Sigma $
, there exists a maximal dimension unstable leaf
$\underline {u}\in \Sigma $
, there exists a maximal dimension unstable leaf
![]() $V^u(\underline {u})$
, which depends only on
$V^u(\underline {u})$
, which depends only on
![]() $(u_i)_{i\leq 0}$
, and a maximal dimension stable leaf
$(u_i)_{i\leq 0}$
, and a maximal dimension stable leaf
![]() $V^s(\underline {u})$
, which depends only on
$V^s(\underline {u})$
, which depends only on
![]() $(u_{i})_{i\geq 0}$
, such that
$(u_{i})_{i\geq 0}$
, such that
![]() $\{\pi (\underline {u})\}=V^u(\underline {u})\cap V^s(\underline {u})$
, and
$\{\pi (\underline {u})\}=V^u(\underline {u})\cap V^s(\underline {u})$
, and
![]() $f[V^s(\underline {u})]\subset V^s(\sigma \underline {u})$
and
$f[V^s(\underline {u})]\subset V^s(\sigma \underline {u})$
and
![]() $f^{-1}[V^u(\underline {u})]\subset V^u(\sigma ^{-1}\underline {u})$
.
$f^{-1}[V^u(\underline {u})]\subset V^u(\sigma ^{-1}\underline {u})$
.
This is the content of [Reference Ben OvadiaBO18, Propositions 3.12, 4.4, Theorem 3.13] (and similarly [Reference SarigSar13, Propositions 4.15, 6.3, Theorem 4.16] when
![]() $d=2$
). By construction,
$d=2$
). By construction,
![]() $V^s(\underline {u}),V^u(\underline {u})$
are local, in the sense that they have finite (intrinsic) diameter.
$V^s(\underline {u}),V^u(\underline {u})$
are local, in the sense that they have finite (intrinsic) diameter.
3.3 Ergodic homoclinic classes and maximal irreducible components
Definition 3.12. Let
![]() $x\in \mathrm {RWT}_\chi $
and let
$x\in \mathrm {RWT}_\chi $
and let
![]() $\underline {u}\in \Sigma ^\#$
such that
$\underline {u}\in \Sigma ^\#$
such that
![]() $ \pi (\underline {u})=x$
. The global stable (respectively unstable) manifold of x is
$ \pi (\underline {u})=x$
. The global stable (respectively unstable) manifold of x is
![]() $W^s(x):=\bigcup _{n\geq 0}f^{-n}[V^s(\sigma ^n\underline {u})]$
(respectively
$W^s(x):=\bigcup _{n\geq 0}f^{-n}[V^s(\sigma ^n\underline {u})]$
(respectively
![]() $W^u(x):=\bigcup _{n\geq 0}f^{n}[V^u(\sigma ^{-n}\underline {u})]$
).
$W^u(x):=\bigcup _{n\geq 0}f^{n}[V^u(\sigma ^{-n}\underline {u})]$
).
This definition is proper and is independent of the choice of
![]() $\underline {u}$
by the construction of
$\underline {u}$
by the construction of
![]() $V^u(\underline {u})$
. For more details, see [Reference Ben OvadiaBO18, Definitions 2.23 and 3.2]. Recall the remark after Definition 2.4.
$V^u(\underline {u})$
. For more details, see [Reference Ben OvadiaBO18, Definitions 2.23 and 3.2]. Recall the remark after Definition 2.4.
Let p be a periodic point in
![]() $\chi \text {-}\mathrm {summ}$
, that is, a hyperbolic periodic point. Since p is periodic,
$\chi \text {-}\mathrm {summ}$
, that is, a hyperbolic periodic point. Since p is periodic,
![]() $\|C^{-1}_\chi (\cdot )\|$
is bounded along the orbit of p, and therefore
$\|C^{-1}_\chi (\cdot )\|$
is bounded along the orbit of p, and therefore
![]() $p\in \mathrm {RWT}_\chi $
.
$p\in \mathrm {RWT}_\chi $
.
Definition 3.13. Let
![]() $\Sigma '$
be a topological Markov shift. A cylinder
$\Sigma '$
be a topological Markov shift. A cylinder
![]() $[R_0,\ldots ,R_n]$
,
$[R_0,\ldots ,R_n]$
,
![]() $n\geq 0$
, is the set
$n\geq 0$
, is the set
![]() $\{\underline {R}'\in \Sigma ': R_i'=R_i \text { for all } i=0,\ldots ,n\}$
. An element of a topological Markov shift is called a chain.
$\{\underline {R}'\in \Sigma ': R_i'=R_i \text { for all } i=0,\ldots ,n\}$
. An element of a topological Markov shift is called a chain.
Definition 3.14. Consider the Markov partition
![]() $\mathcal {R}$
from Definition 3.3.
$\mathcal {R}$
from Definition 3.3.
-
(1) For any
 $a,b\in \mathcal {R}$
,
$a,b\in \mathcal {R}$
,
 $n\in \mathbb {N}$
, we write
$n\in \mathbb {N}$
, we write
 $a\xrightarrow []{n}b$
if there exists a non-empty cylinder
$a\xrightarrow []{n}b$
if there exists a non-empty cylinder
 $[W_1,\ldots ,W_{n}]$
such that
$[W_1,\ldots ,W_{n}]$
such that
 $W_1=a$
and
$W_1=a$
and
 $W_n=b$
.
$W_n=b$
. -
(2) Define
 $\sim \subseteq \mathcal {R}\kern1pt{\times}\kern1pt \mathcal {R}$
by
$\sim \subseteq \mathcal {R}\kern1pt{\times}\kern1pt \mathcal {R}$
by
 $R\kern1pt{\sim}\kern1pt S\ \text { if and only if there exists } n_{RS},n_{SR}\kern1pt{\in}\kern1pt \mathbb {N}\text { such that } R\kern-1pt\xrightarrow []{n_{RS}}S,S\xrightarrow []{n_{SR}}R$
. The relation
$R\kern1pt{\sim}\kern1pt S\ \text { if and only if there exists } n_{RS},n_{SR}\kern1pt{\in}\kern1pt \mathbb {N}\text { such that } R\kern-1pt\xrightarrow []{n_{RS}}S,S\xrightarrow []{n_{SR}}R$
. The relation
 $\sim $
is transitive and symmetric. When restricted to
$\sim $
is transitive and symmetric. When restricted to
 $\{R\in \mathcal {R}:R\sim R\}$
, it is also reflexive, and thus an equivalence relation. Denote the corresponding equivalence class of some representative
$\{R\in \mathcal {R}:R\sim R\}$
, it is also reflexive, and thus an equivalence relation. Denote the corresponding equivalence class of some representative
 $R\in \mathcal {R}$
,
$R\in \mathcal {R}$
,
 $R\sim R$
, by
$R\sim R$
, by
 $\langle R\rangle $
.
$\langle R\rangle $
. -
(3) A maximal irreducible component in
 $\widehat {\Sigma }$
, corresponding to
$\widehat {\Sigma }$
, corresponding to
 $R\in \mathcal {R}$
such that
$R\in \mathcal {R}$
such that
 $R\sim R$
, is
$R\sim R$
, is
 $\{\underline {R}\in \widehat {\Sigma }: \underline {R}\in \langle R\rangle ^{\mathbb {Z}}\}$
.
$\{\underline {R}\in \widehat {\Sigma }: \underline {R}\in \langle R\rangle ^{\mathbb {Z}}\}$
. -
(4) If a topological Markov shift is a maximal irreducible component of itself, we call it irreducible.
If
![]() $\widetilde {\Sigma }$
is a maximal irreducible component of
$\widetilde {\Sigma }$
is a maximal irreducible component of
![]() $\widehat {\Sigma }$
, then
$\widehat {\Sigma }$
, then
![]() $\widehat {\pi }[\widetilde {\Sigma }^\#]$
is a subset of an ergodic homoclinic class, where
$\widehat {\pi }[\widetilde {\Sigma }^\#]$
is a subset of an ergodic homoclinic class, where
![]() $\widetilde {\Sigma }^\#:= \widehat {\Sigma }^\#\cap \widetilde {\Sigma }$
.
$\widetilde {\Sigma }^\#:= \widehat {\Sigma }^\#\cap \widetilde {\Sigma }$
.
Recall Definition 2.11.
Claim 3.15. Let
![]() $\mu $
be an f-invariant ergodic probability measure which is carried by
$\mu $
be an f-invariant ergodic probability measure which is carried by
![]() $\mathrm {RWT}_\chi $
. Then there exists a unique ergodic homoclinic class
$\mathrm {RWT}_\chi $
. Then there exists a unique ergodic homoclinic class
![]() $H_\chi (p)$
, where p is a
$H_\chi (p)$
, where p is a
![]() $\chi $
-hyperbolic periodic point, which carries
$\chi $
-hyperbolic periodic point, which carries
![]() $\mu $
.
$\mu $
.
For proof, see [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and UresRHRHTU11].
Proposition 3.16. Let p be a periodic
![]() $\chi $
-hyperbolic point. Then, there exists a maximal irreducible component,
$\chi $
-hyperbolic point. Then, there exists a maximal irreducible component,
![]() $\widetilde {\Sigma }\subseteq \widehat {\Sigma }$
, such that
$\widetilde {\Sigma }\subseteq \widehat {\Sigma }$
, such that
![]() $\widehat {\pi }[\widetilde {\Sigma }^\#]\supseteq H_\chi (p)\cap \widehat {\pi }[\widehat {\Sigma }^{\#\#}]$
, where
$\widehat {\pi }[\widetilde {\Sigma }^\#]\supseteq H_\chi (p)\cap \widehat {\pi }[\widehat {\Sigma }^{\#\#}]$
, where
In particular,
![]() $\widehat {\pi }[\widetilde {\Sigma }^\#]=H_\chi (p)$
modulo all conservative measures.
$\widehat {\pi }[\widetilde {\Sigma }^\#]=H_\chi (p)$
modulo all conservative measures.
This is the content of [Reference Ben OvadiaBO20, Theorem 5.9], and is based on the result of Buzzi, Crovisier, and Sarig in [Reference Buzzi, Crovisier and SarigBCS22] for homoclinic classes of the type of Newhouse [Reference NewhouseNew72], and the f-invariant,
![]() $\chi $
-hyperbolic, probability measures which they carry.
$\chi $
-hyperbolic, probability measures which they carry.
3.4 The canonical part of the symbolic space
Definition 3.17
 $$ \begin{align*}\widehat{\Sigma}_L&:=\{(R_i)_{i\leq0}\in \mathcal{R}^{-\mathbb{N}}\ {:}\ \text{for all } i\leq 0, R_{i-1}\rightarrow R_i\},\text{ }\sigma_R:\widehat{\Sigma}_L\rightarrow\widehat{\Sigma}_L,\sigma_R((R_i)_{i\leq0})\\&\,=(R_{i-1})_{i\leq0}. \end{align*} $$
$$ \begin{align*}\widehat{\Sigma}_L&:=\{(R_i)_{i\leq0}\in \mathcal{R}^{-\mathbb{N}}\ {:}\ \text{for all } i\leq 0, R_{i-1}\rightarrow R_i\},\text{ }\sigma_R:\widehat{\Sigma}_L\rightarrow\widehat{\Sigma}_L,\sigma_R((R_i)_{i\leq0})\\&\,=(R_{i-1})_{i\leq0}. \end{align*} $$
Note that
![]() $\sigma _R$
is the right-shift, not the left-shift. To prevent any confusion, we will always notate
$\sigma _R$
is the right-shift, not the left-shift. To prevent any confusion, we will always notate
![]() $\sigma _R$
with a subscript R (for ‘right’), when considering the right-shift.
$\sigma _R$
with a subscript R (for ‘right’), when considering the right-shift.
Definition 3.18. (The canonical coding
 $\underline {R}(\cdot )$
)
$\underline {R}(\cdot )$
)
Recall that
![]() $R(x)$
is the unique
$R(x)$
is the unique
![]() $\mathcal {R}$
-element which contains x. Given
$\mathcal {R}$
-element which contains x. Given
One should note that
![]() $\widehat {\pi }(\underline {R}(x))=x,\underline {R}(x)\in \widehat {\Sigma }^\circ $
(see Definition 3.21 for
$\widehat {\pi }(\underline {R}(x))=x,\underline {R}(x)\in \widehat {\Sigma }^\circ $
(see Definition 3.21 for
![]() $\widehat {\Sigma }^\circ $
).
$\widehat {\Sigma }^\circ $
).
Definition 3.19
 $$ \begin{align*}\text{ For all } \underline{R}\in\widehat{\Sigma}_L,\quad W^u(\underline{R}):=\bigcap_{j=0}^\infty f^j[R_{-j}].\end{align*} $$
$$ \begin{align*}\text{ For all } \underline{R}\in\widehat{\Sigma}_L,\quad W^u(\underline{R}):=\bigcap_{j=0}^\infty f^j[R_{-j}].\end{align*} $$
Here,
![]() $W^u(\underline {R})$
might be empty, and is not expected to be an immersed submanifold. It is a subset of
$W^u(\underline {R})$
might be empty, and is not expected to be an immersed submanifold. It is a subset of
![]() $\mathrm {RWT}_\chi $
. We have the following important property.
$\mathrm {RWT}_\chi $
. We have the following important property.
Corollary 3.20.
![]() $\text {For all } \underline {R}\in \widehat {\Sigma }_L$
,
$\text {For all } \underline {R}\in \widehat {\Sigma }_L$
,

See [Reference Ben OvadiaBO21, Corollary 3.19] for proof.
Definition 3.21. We have
where
![]() $\widehat {\Sigma }^\#_L:=\{(R_i)_{i\leq 0}:(R_i)_{i\in \mathbb {Z}}\in \widehat {\Sigma }^\#\}$
. We call
$\widehat {\Sigma }^\#_L:=\{(R_i)_{i\leq 0}:(R_i)_{i\in \mathbb {Z}}\in \widehat {\Sigma }^\#\}$
. We call
![]() $\widehat {\Sigma }^\circ ,\widehat {\Sigma }^\circ _L$
the canonical parts of the respective symbolic spaces.
$\widehat {\Sigma }^\circ ,\widehat {\Sigma }^\circ _L$
the canonical parts of the respective symbolic spaces.
Note that
![]() $\underline {R}(\cdot )$
is the inverse of
$\underline {R}(\cdot )$
is the inverse of
![]() $\widehat {\pi }|_{\widehat {\Sigma }^\circ }$
, and that
$\widehat {\pi }|_{\widehat {\Sigma }^\circ }$
, and that
![]() $\widehat {\Sigma }^\circ _L=(\widehat {\Sigma }^\circ )_L:=\{(R_{i})_{i\leq 0}: (R_i)_{\in \mathbb {Z}}\in \widehat {\Sigma }^\circ \}$
.
$\widehat {\Sigma }^\circ _L=(\widehat {\Sigma }^\circ )_L:=\{(R_{i})_{i\leq 0}: (R_i)_{\in \mathbb {Z}}\in \widehat {\Sigma }^\circ \}$
.
Claim 3.22. We claim that
See [Reference Ben OvadiaBO21, Corollary 3.21] for proof.
Lemma 3.23. If
![]() $R_0\rightarrow R_1$
, where
$R_0\rightarrow R_1$
, where
![]() $R_0,R_1\in \mathcal {R}$
, and
$R_0,R_1\in \mathcal {R}$
, and
![]() $R_0\subseteq Z(u_0)$
,
$R_0\subseteq Z(u_0)$
,
![]() $u_0\in \mathcal {V}$
, then
$u_0\in \mathcal {V}$
, then
![]() $\text {there exists } u_1\in \mathcal {V}$
such that
$\text {there exists } u_1\in \mathcal {V}$
such that
![]() $u_0\rightarrow u_1$
and
$u_0\rightarrow u_1$
and
![]() $R_1\subseteq Z(u_1)$
. Analogously, if
$R_1\subseteq Z(u_1)$
. Analogously, if
![]() $R_0\rightarrow R_1$
and
$R_0\rightarrow R_1$
and
![]() $R_1\subseteq Z(v_1)$
, then
$R_1\subseteq Z(v_1)$
, then
![]() $\text {there exists } v_0$
such that
$\text {there exists } v_0$
such that
![]() $v_0\rightarrow v_1$
and
$v_0\rightarrow v_1$
and
![]() $R_0\subseteq Z(v_0)$
.
$R_0\subseteq Z(v_0)$
.
See [Reference Ben OvadiaBO21, Lemma 4.1] for proof.
Definition 3.24. Given a chain
![]() $\underline {R}\in \widehat {\Sigma }_L$
, we say that a chain
$\underline {R}\in \widehat {\Sigma }_L$
, we say that a chain
![]() $\underline {u}\in \mathcal {V}^{-\mathbb {N}}$
covers the chain
$\underline {u}\in \mathcal {V}^{-\mathbb {N}}$
covers the chain
![]() $\underline {R}$
if
$\underline {R}$
if
![]() $\underline {u}$
is admissible and
$\underline {u}$
is admissible and
![]() $R_i\subseteq Z(u_i)$
for all
$R_i\subseteq Z(u_i)$
for all
![]() $i\leq 0$
. We write
$i\leq 0$
. We write
![]() $\underline {u}\curvearrowright \underline {R}$
.
$\underline {u}\curvearrowright \underline {R}$
.
By Lemma 3.23, for every chain
![]() $\underline {R}\in \widehat {\Sigma }_L$
, the collection of chains which cover
$\underline {R}\in \widehat {\Sigma }_L$
, the collection of chains which cover
![]() $\underline {R}$
is not empty.
$\underline {R}$
is not empty.
Definition 3.25. We have
![]() $\Sigma _L:=\{(u_i)_{i\leq 0}:\underline {u}\in \Sigma \}$
.
$\Sigma _L:=\{(u_i)_{i\leq 0}:\underline {u}\in \Sigma \}$
.
Proposition 3.26. For all
![]() $\underline {R}\in \widehat {\Sigma }_L$
,
$\underline {R}\in \widehat {\Sigma }_L$
,
![]() $\text {there exists }$
a local unstable leaf of maximal dimension
$\text {there exists }$
a local unstable leaf of maximal dimension
![]() $V^u(\underline {R})$
such that
$V^u(\underline {R})$
such that
![]() $f^{-1}[V^u(\underline {R})]\subseteq V^u(\sigma _R\underline {R})$
, and
$f^{-1}[V^u(\underline {R})]\subseteq V^u(\sigma _R\underline {R})$
, and
![]() $V^u(\underline {R})$
is an open submanifold of M, with finite and positive induced Riemannian volume. In addition,
$V^u(\underline {R})$
is an open submanifold of M, with finite and positive induced Riemannian volume. In addition,
![]() $V^u(\underline {R})\subseteq \psi _{x}[\{v:|v|_\infty \leq p^u\}]$
for all
$V^u(\underline {R})\subseteq \psi _{x}[\{v:|v|_\infty \leq p^u\}]$
for all
![]() $u=\psi _{x}^{p^s,p^u}\in \mathcal {V}$
such that
$u=\psi _{x}^{p^s,p^u}\in \mathcal {V}$
such that
![]() $Z(u)\supseteq R_0$
, and
$Z(u)\supseteq R_0$
, and
![]() $\underline {R}\mapsto V^u(\underline {R})$
is continuous in
$\underline {R}\mapsto V^u(\underline {R})$
is continuous in
![]() $C^1$
-norm in any local choice of coordinates. Moreover,
$C^1$
-norm in any local choice of coordinates. Moreover,
![]() $V^u(\underline {R})\subseteq V^u(\underline {u}) \text {for all } \underline {u}\in \Sigma _L$
such that
$V^u(\underline {R})\subseteq V^u(\underline {u}) \text {for all } \underline {u}\in \Sigma _L$
such that
![]() $\underline {u}\curvearrowright \underline {R}$
.
$\underline {u}\curvearrowright \underline {R}$
.
See [Reference Ben OvadiaBO21, §4.1] for proof. (Note that
![]() $W^u(\underline {R})\subseteq V^u(\underline {R})\cap \mathrm {RWT}_\chi $
.)
$W^u(\underline {R})\subseteq V^u(\underline {R})\cap \mathrm {RWT}_\chi $
.)
4 A Markovian and absolutely continuous family of measures on the symbolic space
4.1 The Ruelle operator and Sinai’s theorem
Definition 4.1. (Ruelle operator)
Let
![]() $\widetilde {\Sigma }_L$
be a one-sided irreducible locally compact topological Markov shift (of negative chains), and let
$\widetilde {\Sigma }_L$
be a one-sided irreducible locally compact topological Markov shift (of negative chains), and let
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a Hölder continuous potential. The associated Ruelle operator
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a Hölder continuous potential. The associated Ruelle operator
![]() $L_\phi :C(\widetilde {\Sigma }_L)\rightarrow C(\widetilde {\Sigma }_L)$
is defined by
$L_\phi :C(\widetilde {\Sigma }_L)\rightarrow C(\widetilde {\Sigma }_L)$
is defined by
 $$ \begin{align*}(L_\phi h)(\underline{R}):=\sum_{\widetilde{\sigma}_R\underline{S}=\underline{R}}e^{\phi(\underline{S})}h(\underline{S}),\end{align*} $$
$$ \begin{align*}(L_\phi h)(\underline{R}):=\sum_{\widetilde{\sigma}_R\underline{S}=\underline{R}}e^{\phi(\underline{S})}h(\underline{S}),\end{align*} $$
where
![]() $h\in C(\widetilde {\Sigma }_L)$
, and
$h\in C(\widetilde {\Sigma }_L)$
, and
![]() $\widetilde {\sigma }_R:\widetilde {\Sigma }_L\rightarrow \widetilde {\Sigma }_L$
is the right-shift.
$\widetilde {\sigma }_R:\widetilde {\Sigma }_L\rightarrow \widetilde {\Sigma }_L$
is the right-shift.
Definition 4.2. Let X be a topological Markov shift (either one-sided or two-sided). A function
![]() $\widehat {\varphi }:X\rightarrow \mathbb {R}$
is called weakly Hölder continuous if
$\widehat {\varphi }:X\rightarrow \mathbb {R}$
is called weakly Hölder continuous if
![]() $\text {there exists } C>0,\alpha >0$
, such that
$\text {there exists } C>0,\alpha >0$
, such that
![]() $\text {for all } \underline {x},\underline {y}\in X$
such that
$\text {for all } \underline {x},\underline {y}\in X$
such that
![]() $d(\underline {x},\underline {y})\leq e^{-1}$
, we have
$d(\underline {x},\underline {y})\leq e^{-1}$
, we have
![]() $|\widehat {\varphi }(\underline {x})-\widehat {\varphi }(\underline {y})|\leq C\cdot d(\underline {x},\underline {y})^\alpha $
.
$|\widehat {\varphi }(\underline {x})-\widehat {\varphi }(\underline {y})|\leq C\cdot d(\underline {x},\underline {y})^\alpha $
.
This notion is introduced in [Reference SarigSar09], with the weaker assumption of
![]() $d(\underline {x},\underline {y})\leq e^{-2}$
.
$d(\underline {x},\underline {y})\leq e^{-2}$
.
Recall Definition 2.10.
Claim 4.3. Let
![]() $\varphi :WT_\chi ^\epsilon \rightarrow \mathbb {R}$
be a potential which is
$\varphi :WT_\chi ^\epsilon \rightarrow \mathbb {R}$
be a potential which is
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
. Let
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
. Let
![]() $\widehat {\varphi }:\widehat {\Sigma }\rightarrow \mathbb {R}$
,
$\widehat {\varphi }:\widehat {\Sigma }\rightarrow \mathbb {R}$
,
![]() $\widehat {\varphi }:=\varphi \circ \widehat {\pi }$
, be the lift of
$\widehat {\varphi }:=\varphi \circ \widehat {\pi }$
, be the lift of
![]() $\varphi $
. Then
$\varphi $
. Then
![]() $\widehat {\varphi }$
is weakly Hölder continuous on
$\widehat {\varphi }$
is weakly Hölder continuous on
![]() $\widehat {\Sigma }$
.
$\widehat {\Sigma }$
.
This follows from [Reference Ben OvadiaBO18, Proposition 6.1].
Theorem 4.4. (Sinai)
Let
![]() $\varphi : \mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be a
$\varphi : \mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Then there exist two functions
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Then there exist two functions
![]() such that
such that
![]() $\varphi ^*(x)= \varphi ^*((R(f^{-i}(x)))_{i\geq 0})$
depends only on the past of the itinerary of x,
$\varphi ^*(x)= \varphi ^*((R(f^{-i}(x)))_{i\geq 0})$
depends only on the past of the itinerary of x,
![]() $\varphi ^*=\varphi +A-A\circ f^{-1}$
, A is bounded, and
$\varphi ^*=\varphi +A-A\circ f^{-1}$
, A is bounded, and
![]() $\widehat {A}:=A\circ \widehat {\pi }, \phi :=\varphi ^*\circ \widehat {\pi }$
are weakly Hölder continuous.
$\widehat {A}:=A\circ \widehat {\pi }, \phi :=\varphi ^*\circ \widehat {\pi }$
are weakly Hölder continuous.
This theorem appears in Sinai’s fundamental paper [Reference SinaĭSin72]. He states it in the context of a topological Markov shift with a finite alphabet (for the countable case, see [Reference DaonDao13]). We give the proof in the case when a countable Markov partition exists.
Proof. First,
![]() $\text {for all } a\in \mathcal {R}$
, fix a point
$\text {for all } a\in \mathcal {R}$
, fix a point
![]() $y_a\in a$
.
$y_a\in a$
.
![]() , define
, define
![]() $x^*:=[x,y_{R(x)}]_{R(x)} \in R(x)$
, where
$x^*:=[x,y_{R(x)}]_{R(x)} \in R(x)$
, where
![]() $R(x)$
is unique partition element of
$R(x)$
is unique partition element of
![]() $\mathcal {R}$
which contains x, and
$\mathcal {R}$
which contains x, and
![]() $[\cdot ,\cdot ]_{R(x)}$
denotes the Smale bracket of two points in
$[\cdot ,\cdot ]_{R(x)}$
denotes the Smale bracket of two points in
![]() $R(x)$
(the right-hand term yields its future, and the left-hand terms yields its past). Define
$R(x)$
(the right-hand term yields its future, and the left-hand terms yields its past). Define
![]() ,
,
By Claim 4.3,
![]() $\widehat {\varphi }:=\varphi \circ \widehat {\pi }$
is weakly Hölder continuous. In addition,
$\widehat {\varphi }:=\varphi \circ \widehat {\pi }$
is weakly Hölder continuous. In addition,
![]() $d(\underline {R}(f^{-n}(x)), \underline {R}(f^{-n} (x^*)))\leq e^{-n}$
. Let
$d(\underline {R}(f^{-n}(x)), \underline {R}(f^{-n} (x^*)))\leq e^{-n}$
. Let
![]() $C>0,\theta \in (0,1)$
be the weak Hölder constants of
$C>0,\theta \in (0,1)$
be the weak Hölder constants of
![]() $\widehat {\varphi }$
such that
$\widehat {\varphi }$
such that
![]() $d(\underline {R}^{(1)}, \underline {R}^{(2)})\leq e^{-n}\Rightarrow |\widehat {\varphi }(\underline {R}^{(1)})-\widehat {\varphi }(\underline {R}^{(2)})|\leq C\cdot \theta ^n$
. Then,
$d(\underline {R}^{(1)}, \underline {R}^{(2)})\leq e^{-n}\Rightarrow |\widehat {\varphi }(\underline {R}^{(1)})-\widehat {\varphi }(\underline {R}^{(2)})|\leq C\cdot \theta ^n$
. Then,
![]() $\widehat {A}$
is a uniformly convergent series with uniformly bounded and equicontinuous summands, and so
$\widehat {A}$
is a uniformly convergent series with uniformly bounded and equicontinuous summands, and so
![]() $\widehat {A}$
is bounded and continuous. In particular, A is also bounded.
$\widehat {A}$
is bounded and continuous. In particular, A is also bounded.
Let
![]() $\varphi ^*:=\varphi +A-A\circ f^{-1}$
and
$\varphi ^*:=\varphi +A-A\circ f^{-1}$
and
![]() $\phi :=\varphi ^*\circ \widehat {\pi }$
. The weak Hölder continuity of
$\phi :=\varphi ^*\circ \widehat {\pi }$
. The weak Hölder continuity of
![]() $\widehat {A}=A\circ \widehat {\pi }$
and of
$\widehat {A}=A\circ \widehat {\pi }$
and of
![]() $\phi $
follows from the weak Hölder continuity of
$\phi $
follows from the weak Hölder continuity of
![]() $\widehat {\varphi }$
and the proof of the finite alphabet case in [Reference SinaĭSin72], whose details are given in [Reference BowenBow75, Lemma 1.6].
$\widehat {\varphi }$
and the proof of the finite alphabet case in [Reference SinaĭSin72], whose details are given in [Reference BowenBow75, Lemma 1.6].
It remains to show that
![]() $\varphi (x)= \varphi ((R(f^{-i}(x)))_{i\geq 0})$
.
$\varphi (x)= \varphi ((R(f^{-i}(x)))_{i\geq 0})$
.
 $$ \begin{align*} \varphi^*(x)&=\varphi(x)+A(x)-A(f^{-1}(x))\\ &=\varphi(x)\kern1.2pt{+} \sum_{n\geq0}\kern-1.5pt \varphi(f^{-n}(x^*))\kern1.2pt{-}\kern1.2pt\varphi(f^{-n}(x))\kern1.2pt{-}\sum_{n\geq0} \kern-1.5pt\varphi(f^{-n}((f^{-1}(x))^*))-\varphi(f^{-n-1}(x))\\ &=\varphi(x^*)+ \sum_{n\geq0} \varphi(f^{-n}(f^{-1}(x^*)))-\varphi(f^{-n}((f^{-1}(x))^*)). \end{align*} $$
$$ \begin{align*} \varphi^*(x)&=\varphi(x)+A(x)-A(f^{-1}(x))\\ &=\varphi(x)\kern1.2pt{+} \sum_{n\geq0}\kern-1.5pt \varphi(f^{-n}(x^*))\kern1.2pt{-}\kern1.2pt\varphi(f^{-n}(x))\kern1.2pt{-}\sum_{n\geq0} \kern-1.5pt\varphi(f^{-n}((f^{-1}(x))^*))-\varphi(f^{-n-1}(x))\\ &=\varphi(x^*)+ \sum_{n\geq0} \varphi(f^{-n}(f^{-1}(x^*)))-\varphi(f^{-n}((f^{-1}(x))^*)). \end{align*} $$
The last expression depends only on
![]() $(R(f^{-i}(x)))_{i\geq 0}$
.
$(R(f^{-i}(x)))_{i\geq 0}$
.
Remark. Although
![]() $\widehat {\varphi },\widehat {A},\phi $
are defined on
$\widehat {\varphi },\widehat {A},\phi $
are defined on
![]() $\widehat {\Sigma }^\circ $
, they extend continuously to
$\widehat {\Sigma }^\circ $
, they extend continuously to
![]() $\widehat {\Sigma }$
because of their uniform moduli of continuity and the fact that
$\widehat {\Sigma }$
because of their uniform moduli of continuity and the fact that
![]() $\widehat {\Sigma }^\circ $
is dense in
$\widehat {\Sigma }^\circ $
is dense in
![]() $\widehat {\Sigma }$
. Thus,
$\widehat {\Sigma }$
. Thus,
![]() $\phi :\widehat {\Sigma }_L\rightarrow \mathbb {R}$
is well defined and weakly Hölder continuous.
$\phi :\widehat {\Sigma }_L\rightarrow \mathbb {R}$
is well defined and weakly Hölder continuous.
4.2 Recurrence, harmonic functions, and conformal measures
As before,
![]() $\widetilde {\Sigma }_L$
is a maximal irreducible component of
$\widetilde {\Sigma }_L$
is a maximal irreducible component of
![]() $\widehat {\Sigma }_L$
, and
$\widehat {\Sigma }_L$
, and
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
is a weakly Hölder continuous potential.
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
is a weakly Hölder continuous potential.
In this section, we use the Gurevich pressure, and we begin by recalling its definition. For a weakly Hölder potential
![]() $\zeta :\widehat {\Sigma }_L\rightarrow \mathbb {R}$
, the local partition functions are for
$\zeta :\widehat {\Sigma }_L\rightarrow \mathbb {R}$
, the local partition functions are for
![]() $n\geq 1$
,
$n\geq 1$
,
 $$ \begin{align*}Z_n(\zeta,R):=\sum\limits_{\underline{S}\in \widehat{\Sigma}_L\cap[R],\sigma_R^n\underline{S}=\underline{S}}e^{\sum_{k=0}^{n-1}\zeta(\sigma_R^k\underline{S})}, \end{align*} $$
$$ \begin{align*}Z_n(\zeta,R):=\sum\limits_{\underline{S}\in \widehat{\Sigma}_L\cap[R],\sigma_R^n\underline{S}=\underline{S}}e^{\sum_{k=0}^{n-1}\zeta(\sigma_R^k\underline{S})}, \end{align*} $$
where the sum has finitely many terms since
![]() $\widehat {\Sigma }_L$
is locally compact. The Gurevich pressure of the potential
$\widehat {\Sigma }_L$
is locally compact. The Gurevich pressure of the potential
![]() $\zeta $
is
$\zeta $
is
When
![]() $\widehat {\Sigma }_L$
is irreducible, the limit is independent of the choice of the symbol R (see [Reference SarigSar09, Proposition 3.2]). We say that the potential
$\widehat {\Sigma }_L$
is irreducible, the limit is independent of the choice of the symbol R (see [Reference SarigSar09, Proposition 3.2]). We say that the potential
![]() $\zeta $
is recurrent if for some symbol R,
$\zeta $
is recurrent if for some symbol R,
In this case, the sum diverges for all R, see [Reference SarigSar09, Corollary 3.1]. We say that the potential
![]() $\zeta $
is positive recurrent if it is recurrent, and for some symbol R,
$\zeta $
is positive recurrent if it is recurrent, and for some symbol R,
 $$ \begin{align*}\sum_{n\geq1}n\cdot e^{-nP_G(\zeta)} \sum\limits_{\substack{\underline{S}\in \widehat{\Sigma}_L\cap[R]\text{, such that }\sigma_R^n\underline{S}=\underline{S},\\ \text{ and}\ \text{for all } 0< l<n, S_{-l}\neq R}}e^{\sum_{k=0}^{n-1}\zeta(\sigma_R^k\underline{S})}<\infty.\end{align*} $$
$$ \begin{align*}\sum_{n\geq1}n\cdot e^{-nP_G(\zeta)} \sum\limits_{\substack{\underline{S}\in \widehat{\Sigma}_L\cap[R]\text{, such that }\sigma_R^n\underline{S}=\underline{S},\\ \text{ and}\ \text{for all } 0< l<n, S_{-l}\neq R}}e^{\sum_{k=0}^{n-1}\zeta(\sigma_R^k\underline{S})}<\infty.\end{align*} $$
Again, this property turns out to be independent of R. For more details, see [Reference SarigSar09, §3.1.3]. For a detailed review of the properties of recurrent potentials, see [Reference SarigSar09].
Definition 4.5. Let
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential such that
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential such that
![]() $P_G(\phi )<\infty $
, where
$P_G(\phi )<\infty $
, where
![]() $\widetilde {\Sigma }_L$
is a maximal irreducible component of
$\widetilde {\Sigma }_L$
is a maximal irreducible component of
![]() $\widehat {\Sigma }_L$
. A positive and continuous function
$\widehat {\Sigma }_L$
. A positive and continuous function
![]() $\psi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}^+$
is called
$\psi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}^+$
is called
![]() $\phi $
-harmonic if
$\phi $
-harmonic if
![]() $L_\phi \psi = e^{P_G(\phi )}\psi $
. A non-zero Radon measure p on
$L_\phi \psi = e^{P_G(\phi )}\psi $
. A non-zero Radon measure p on
![]() $\widetilde {\Sigma }_L$
is called
$\widetilde {\Sigma }_L$
is called
![]() $\phi $
-conformal if
$\phi $
-conformal if
![]() $L_\phi ^*p= e^{P_G(\phi )}p$
, where
$L_\phi ^*p= e^{P_G(\phi )}p$
, where
![]() $L_\phi ^*$
is the dual operator of
$L_\phi ^*$
is the dual operator of
![]() $L_\phi $
.
$L_\phi $
.
Note that
![]() $\widetilde {\Sigma }_L$
may be non-compact, and thus p may be infinite.
$\widetilde {\Sigma }_L$
may be non-compact, and thus p may be infinite.
Theorem 4.6. Let
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential, where
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential, where
![]() $\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. If
$\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. If
![]() $P_G(\phi )<\infty $
, then there exist a
$P_G(\phi )<\infty $
, then there exist a
![]() $\phi $
-harmonic function
$\phi $
-harmonic function
![]() $\psi $
and a
$\psi $
and a
![]() $\phi $
-conformal measure p.
$\phi $
-conformal measure p.
This theorem is due to work of Sarig [Reference SarigSar99, Reference SarigSar01], Cyr [Reference CyrCyr10], and Shwartz [Reference ShwartzShw19]. Sarig had proven that when
![]() $\phi $
is recurrent,
$\phi $
is recurrent,
![]() $\psi $
and p exist and are unique up to scaling. In the transient case, Cyr showed the existence of a
$\psi $
and p exist and are unique up to scaling. In the transient case, Cyr showed the existence of a
![]() $\phi $
-conformal measure, and Shwartz proved the existence of a
$\phi $
-conformal measure, and Shwartz proved the existence of a
![]() $\phi $
-harmonic function with a weakly Hölder logarithm. In the transient case, the
$\phi $
-harmonic function with a weakly Hölder logarithm. In the transient case, the
![]() $\phi $
-harmonic functions and the
$\phi $
-harmonic functions and the
![]() $\phi $
-conformal measures are not always unique up to scaling. For the structure of the set of these objects, see [Reference ShwartzShw19].
$\phi $
-conformal measures are not always unique up to scaling. For the structure of the set of these objects, see [Reference ShwartzShw19].
Lemma 4.7. Let
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential, where
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential, where
![]() $\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. Let
$\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. Let
![]() $\psi :\widetilde {\Sigma }_L \rightarrow \mathbb {R}^+$
be a
$\psi :\widetilde {\Sigma }_L \rightarrow \mathbb {R}^+$
be a
![]() $\phi $
-harmonic function. Then
$\phi $
-harmonic function. Then
![]() $\log \psi $
is weakly Hölder continuous.
$\log \psi $
is weakly Hölder continuous.
In the recurrent case, Sarig proves it in [Reference SarigSar09, Proposition 3.4]. In the transient case, it follows from the proof of Theorem 5.7 in [Reference ShwartzShw19]. Shwartz shows in the proof that
![]() $\log \psi $
is uniformly continuous. A close inspection of his argument tells that, in fact, if
$\log \psi $
is uniformly continuous. A close inspection of his argument tells that, in fact, if
![]() $\phi $
is weakly Hölder continuous, then so is
$\phi $
is weakly Hölder continuous, then so is
![]() $\log \psi $
. (It follows from the estimate on
$\log \psi $
. (It follows from the estimate on
![]() $o_n(1)$
, which depends on the regularity of the coboundary function
$o_n(1)$
, which depends on the regularity of the coboundary function
![]() $\psi $
, where one can see that if
$\psi $
, where one can see that if
![]() $\phi $
is weakly Hölder continuous, then so is
$\phi $
is weakly Hölder continuous, then so is
![]() $\psi $
([Reference ShwartzShw19, Proposition 5.4], see also Theorem 4.4 of the present paper). In particular, the error term
$\psi $
([Reference ShwartzShw19, Proposition 5.4], see also Theorem 4.4 of the present paper). In particular, the error term
![]() $o_n(1)$
is exponentially small in n.
$o_n(1)$
is exponentially small in n.
4.3 Recurrence and periodic orbits
Lemma 4.8. Let
![]() $\varphi : \mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be a
$\varphi : \mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential, and let
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential, and let
![]() $\phi :\widehat {\Sigma }_L\rightarrow \mathbb {R}$
be a corresponding weakly Hölder continuous one-sided potential given by Theorem 4.4 and the remark following it. Let
$\phi :\widehat {\Sigma }_L\rightarrow \mathbb {R}$
be a corresponding weakly Hölder continuous one-sided potential given by Theorem 4.4 and the remark following it. Let
![]() $H_\chi (p)$
be an ergodic homoclinic class of a periodic and
$H_\chi (p)$
be an ergodic homoclinic class of a periodic and
![]() $\chi $
-hyperbolic point p, and let
$\chi $
-hyperbolic point p, and let
![]() $\widetilde {\Sigma }$
be a maximal irreducible component of
$\widetilde {\Sigma }$
be a maximal irreducible component of
![]() $\widehat {\Sigma }$
such that
$\widehat {\Sigma }$
such that
![]() $\widehat {\pi }[\widetilde {\Sigma }^\#]= H_\chi (p)$
modulo conservative measures (see Proposition 3.16). Then,
$\widehat {\pi }[\widetilde {\Sigma }^\#]= H_\chi (p)$
modulo conservative measures (see Proposition 3.16). Then,
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
is recurrent if and only if
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
is recurrent if and only if
 $$ \begin{align*}\sum_{n\geq1}\sum_{\substack{f^n(q)=q,\\q\in H_\chi(p)\cap \Lambda_l}}e^{\varphi_n(q)-n\cdot P_{H_\chi(p)}(\varphi)}=\infty,\end{align*} $$
$$ \begin{align*}\sum_{n\geq1}\sum_{\substack{f^n(q)=q,\\q\in H_\chi(p)\cap \Lambda_l}}e^{\varphi_n(q)-n\cdot P_{H_\chi(p)}(\varphi)}=\infty,\end{align*} $$
where
![]() $\Lambda _l$
is a level set such that
$\Lambda _l$
is a level set such that
![]() $p\in \Lambda _{l\cdot e^{-2\sqrt [3]{\epsilon }}}$
and
$p\in \Lambda _{l\cdot e^{-2\sqrt [3]{\epsilon }}}$
and
![]() $\varphi _n(q)=\sum _{k=0}^{n-1}\varphi (f^{-k}(q))$
.
$\varphi _n(q)=\sum _{k=0}^{n-1}\varphi (f^{-k}(q))$
.
Proof. We start with the ‘if’ part. Let
![]() $q\in H_\chi (p)\cap \Lambda _l$
be a periodic
$q\in H_\chi (p)\cap \Lambda _l$
be a periodic
![]() $\chi $
-hyperbolic point of period n. By Proposition 3.16, q has a (periodic) coding in
$\chi $
-hyperbolic point of period n. By Proposition 3.16, q has a (periodic) coding in
![]() $\widetilde {\Sigma }$
. (Let
$\widetilde {\Sigma }$
. (Let
![]() $\underline {R}\in \widehat {\Sigma }^\#\cap \widehat {\pi }^{-1}[\{q\}]$
. Then for any
$\underline {R}\in \widehat {\Sigma }^\#\cap \widehat {\pi }^{-1}[\{q\}]$
. Then for any
![]() $m\geq 0$
,
$m\geq 0$
,
![]() $\widehat {\pi }(\sigma ^{m\cdot n}\underline {R})=q$
, whence by the finiteness of
$\widehat {\pi }(\sigma ^{m\cdot n}\underline {R})=q$
, whence by the finiteness of
![]() $\widehat {\Sigma }^\#\cap \widehat {\pi }^{-1}[\{q\}]$
,
$\widehat {\Sigma }^\#\cap \widehat {\pi }^{-1}[\{q\}]$
,
![]() $\text {there exists } m_1,m_2 \in \mathbb {N}$
such that
$\text {there exists } m_1,m_2 \in \mathbb {N}$
such that
![]() $\sigma ^{m_1\cdot n}\underline {R}=\sigma ^{m_2\cdot n}\underline {R}$
, and so
$\sigma ^{m_1\cdot n}\underline {R}=\sigma ^{m_2\cdot n}\underline {R}$
, and so
![]() $\sigma ^{m\cdot n}\underline {R}=\underline {R}$
with
$\sigma ^{m\cdot n}\underline {R}=\underline {R}$
with
![]() $m=\max \{m_1,m_2\}-\min \{m_1,m_2\}$
.) Let
$m=\max \{m_1,m_2\}-\min \{m_1,m_2\}$
.) Let
![]() $\underline {S}^q$
be such a periodic coding.
$\underline {S}^q$
be such a periodic coding.
By [Reference Ben OvadiaBO21, Claim 7.6], there is a finite collection of symbols
![]() $\mathcal {R}_l\subseteq \mathcal {R}$
, which depends only on l, and which contains
$\mathcal {R}_l\subseteq \mathcal {R}$
, which depends only on l, and which contains
![]() $S_0^q$
.
$S_0^q$
.
By [Reference Ben OvadiaBO18, Theorem 1.3], there exists
![]() $C_l=\max \{N(R)^2:R\in \mathcal {R}_l\}\in \mathbb {N}$
such that
$C_l=\max \{N(R)^2:R\in \mathcal {R}_l\}\in \mathbb {N}$
such that
![]() $|\widehat {\pi }^{-1}[\{q\}]\cap \widetilde {\Sigma }^\#|\leq C_l$
(see Definition 3.6 for the definition of
$|\widehat {\pi }^{-1}[\{q\}]\cap \widetilde {\Sigma }^\#|\leq C_l$
(see Definition 3.6 for the definition of
![]() $N(R)$
). In addition, by Theorem 4.4,
$N(R)$
). In addition, by Theorem 4.4,
![]() $\text {there exists } C:=2\|A\|_\infty <\infty $
such that
$\text {there exists } C:=2\|A\|_\infty <\infty $
such that
Since
![]() $\varphi $
is bounded (recall remark after Definition 2.10), so is
$\varphi $
is bounded (recall remark after Definition 2.10), so is
![]() $\phi $
. By the spectral decomposition (see [Reference SarigSar15, Theorem 2.5]), we may assume without loss of generality that
$\phi $
. By the spectral decomposition (see [Reference SarigSar15, Theorem 2.5]), we may assume without loss of generality that
![]() $(\widetilde {\Sigma },\sigma )$
is topologically mixing (otherwise apply the proof to each mixing component of a suitable period of
$(\widetilde {\Sigma },\sigma )$
is topologically mixing (otherwise apply the proof to each mixing component of a suitable period of
![]() $\sigma _R$
). By the variational principle (see [Reference SarigSar09, Theorem 4.4] and [Reference Iommi, Jordan and ToddIJT15] when the potential is not bounded), the Gurevich pressure of
$\sigma _R$
). By the variational principle (see [Reference SarigSar09, Theorem 4.4] and [Reference Iommi, Jordan and ToddIJT15] when the potential is not bounded), the Gurevich pressure of
![]() $\phi $
on
$\phi $
on
![]() $\widetilde {\Sigma }_L$
,
$\widetilde {\Sigma }_L$
,
![]() $P_G(\phi )$
, satisfies
$P_G(\phi )$
, satisfies
 $$ \begin{align*}P_G(\phi)=\sup\{h_{\nu}(\widetilde{\sigma}_R)+\int_{\widetilde{\Sigma}_L} \phi \,d\nu:\nu\text{ is an invariant probability measure on }\widetilde{\Sigma}_L\}.\end{align*} $$
$$ \begin{align*}P_G(\phi)=\sup\{h_{\nu}(\widetilde{\sigma}_R)+\int_{\widetilde{\Sigma}_L} \phi \,d\nu:\nu\text{ is an invariant probability measure on }\widetilde{\Sigma}_L\}.\end{align*} $$
Every invariant probability measure on
![]() $\widetilde {\Sigma }_L$
,
$\widetilde {\Sigma }_L$
,
![]() $\nu $
, extends uniquely to an invariant probability measure on
$\nu $
, extends uniquely to an invariant probability measure on
![]() $\widetilde {\Sigma }$
,
$\widetilde {\Sigma }$
,
![]() $\nu '$
, such that
$\nu '$
, such that
![]() $\nu '\circ \tau ^{-1}=\nu $
and
$\nu '\circ \tau ^{-1}=\nu $
and
![]() $h_{\nu }(\widetilde {\sigma }_R)= h_{\nu '}(\sigma )$
, where
$h_{\nu }(\widetilde {\sigma }_R)= h_{\nu '}(\sigma )$
, where
![]() $\tau :\widetilde {\Sigma }\rightarrow \widetilde {\Sigma }_L$
is the projection onto the non-positive coordinates. Thus,
$\tau :\widetilde {\Sigma }\rightarrow \widetilde {\Sigma }_L$
is the projection onto the non-positive coordinates. Thus,
In addition, every invariant probability measure on
![]() $H_\chi (p)$
,
$H_\chi (p)$
,
![]() $\mu $
, lifts to a an invariant probability measure on
$\mu $
, lifts to a an invariant probability measure on
![]() $\widetilde {\Sigma }$
,
$\widetilde {\Sigma }$
,
![]() $\mu '$
, such that
$\mu '$
, such that
![]() $\mu '\circ \widehat {\pi }^{-1}=\mu $
and
$\mu '\circ \widehat {\pi }^{-1}=\mu $
and
![]() $h_{\mu }(f)= h_{\mu '}(\sigma )$
. Then, we get
$h_{\mu }(f)= h_{\mu '}(\sigma )$
. Then, we get
By the Ruelle inequality, the topological entropy of f is finite, and since
![]() $\varphi $
is bounded,
$\varphi $
is bounded,
![]() $P_{H_\chi (p)}(\varphi )<\infty $
.
$P_{H_\chi (p)}(\varphi )<\infty $
.
For every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\text {there exists } a_n,b_n\in \mathcal {R}_l$
such that
$\text {there exists } a_n,b_n\in \mathcal {R}_l$
such that
 $$ \begin{align*} \sum_{\substack{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l\\ \underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\# ,S^q_0=a_n,S^q_n={b_n}}}e^{\phi_n(\underline{S}^q)}\geq \frac{1}{|\mathcal{R}_l|^2}\cdot \sum_{\substack{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l \\ \underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\#}}e^{\phi_n(\underline{S}^q)}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l\\ \underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\# ,S^q_0=a_n,S^q_n={b_n}}}e^{\phi_n(\underline{S}^q)}\geq \frac{1}{|\mathcal{R}_l|^2}\cdot \sum_{\substack{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l \\ \underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\#}}e^{\phi_n(\underline{S}^q)}. \end{align*} $$
For every
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\text {for all } q\in H_\chi (p)\cap \Lambda _l$
such that
$\text {for all } q\in H_\chi (p)\cap \Lambda _l$
such that
![]() $f^n(q)=q$
,
$f^n(q)=q$
,
![]() $|\widehat {\pi }^{-1}[\{q\}]\cap \widetilde {\Sigma }^\#| \leq C_l$
. By assumption,
$|\widehat {\pi }^{-1}[\{q\}]\cap \widetilde {\Sigma }^\#| \leq C_l$
. By assumption,
![]() $\infty =\sum \nolimits _{n\geq 1}\sum \nolimits _{f^n(q)=q,q\in H_\chi (p)\cap \Lambda _l}e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )}$
. Recall equation (1), then by the pigeonhole principle,
$\infty =\sum \nolimits _{n\geq 1}\sum \nolimits _{f^n(q)=q,q\in H_\chi (p)\cap \Lambda _l}e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )}$
. Recall equation (1), then by the pigeonhole principle,
![]() $\text {there exists } a,b\in \mathcal {R}_l$
and
$\text {there exists } a,b\in \mathcal {R}_l$
and
![]() $n_k\uparrow \infty $
such that
$n_k\uparrow \infty $
such that
![]() $a_{n_k}=a$
and
$a_{n_k}=a$
and
![]() $b_{n_k}=b$
, and so that the following sum is infinite:
$b_{n_k}=b$
, and so that the following sum is infinite:
 $$ \begin{align*} \infty=\sum_{k\geq0 }\sum_{\substack{f^{n_k}(q)=q,q\in H_\chi(p)\cap \Lambda_l \\\underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\# ,S^q_0=a,S^q_{n_k}=b }}e^{\phi_{n_k}(S^q)-n_k\cdot P_{G}(\phi)}. \end{align*} $$
$$ \begin{align*} \infty=\sum_{k\geq0 }\sum_{\substack{f^{n_k}(q)=q,q\in H_\chi(p)\cap \Lambda_l \\\underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\# ,S^q_0=a,S^q_{n_k}=b }}e^{\phi_{n_k}(S^q)-n_k\cdot P_{G}(\phi)}. \end{align*} $$
Let
![]() $C_H'>0,\gamma \in (0,1)$
be the Hölder constant and Hölder exponent of
$C_H'>0,\gamma \in (0,1)$
be the Hölder constant and Hölder exponent of
![]() $\phi $
, respectively. Let
$\phi $
, respectively. Let
![]() $C_H:=C_H'\cdot \sum _{n\geq 0}\gamma ^n<\infty $
.
$C_H:=C_H'\cdot \sum _{n\geq 0}\gamma ^n<\infty $
.
Let
![]() $\underline {W}$
be an admissible word such that
$\underline {W}$
be an admissible word such that
![]() $W_0=b$
and
$W_0=b$
and
![]() $W_{m-1}=a$
, where
$W_{m-1}=a$
, where
![]() $m:=|\underline {W}|$
. For every finite word
$m:=|\underline {W}|$
. For every finite word
![]() $\underline {W}'$
such that
$\underline {W}'$
such that
![]() $W^{\prime }_0=W^{\prime }_{|\underline {W}'|-1}$
, let
$W^{\prime }_0=W^{\prime }_{|\underline {W}'|-1}$
, let
![]() $\underline {S}^{\underline {W}'} $
denote the periodic extension of
$\underline {S}^{\underline {W}'} $
denote the periodic extension of
![]() $\underline {W}'$
to a bi-infinite chain (in
$\underline {W}'$
to a bi-infinite chain (in
![]() $\widetilde {\Sigma }^\#$
).
$\widetilde {\Sigma }^\#$
).
For every
![]() $n\geq 0$
, for every finite word
$n\geq 0$
, for every finite word
![]() $\underline {W}'$
such that
$\underline {W}'$
such that
![]() $|\underline {W}'|=n$
, every extension of
$|\underline {W}'|=n$
, every extension of
![]() $\underline {W}'$
to
$\underline {W}'$
to
![]() $\widetilde {\Sigma }^\#$
which codes a periodic point in
$\widetilde {\Sigma }^\#$
which codes a periodic point in
![]() $H_\chi (p)\cap \Lambda _l$
of period n must code the same point, by the shadowing lemma (see [Reference Ben OvadiaBO18, Proposition 3.12(4)]). Therefore,
$H_\chi (p)\cap \Lambda _l$
of period n must code the same point, by the shadowing lemma (see [Reference Ben OvadiaBO18, Proposition 3.12(4)]). Therefore,
 $$ \begin{align*} \infty&= \sum_{k\geq0}\sum_{\substack{f^{n_k}(q)=q,q\in H_\chi(p)\cap \Lambda_l \\ \underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\# ,S^q_0=a,S^q_{n_k}=b}}e^{\phi_{n_k}(\underline{S}^q)-n_k\cdot P_G(\phi)}\nonumber\\[6pt] &\leq C_l e^{C_H'\sum_{j=1}^{n_k}\gamma^j} \sum_{k\geq0} \sum_{\overset{}{ \widetilde{\underline{W}}:|\widetilde{\underline{W}}|=n_k, \widetilde{W}_0=a,\widetilde{W}_{n_k-1}=b}}e^{\phi_{n_k}(\underline{S} ^{( \widetilde{\underline{W}}\cdot\underline{W})}) -n_k\cdot P_G(\phi)}\nonumber\\[6pt] &\leq C_l e^{m\cdot(\|\varphi\|_\infty+P_G(\phi))+C_H}\cdot \sum_{k\geq0}\sum_{\underline{S}\in\widetilde{\Sigma}: \sigma^{n_k+m}\underline{S}=\underline{S},S_0=a} e^{\phi_{n_k+m}(\underline{S}) -(n_k+m)\cdot P_G(\phi)}\nonumber\\[6pt] &\leq C_l e^{m\cdot(\|\varphi\|_\infty+P_G(\phi))+C_H}\cdot\sum_{n\geq 1} \sum_{\underline{S}\in\widetilde{\Sigma}: \sigma^{n}\underline{S}=\underline{S},S_0=a} e^{\phi_{n}(\underline{S}) -n\cdot P_G(\phi)}.\nonumber \end{align*} $$
$$ \begin{align*} \infty&= \sum_{k\geq0}\sum_{\substack{f^{n_k}(q)=q,q\in H_\chi(p)\cap \Lambda_l \\ \underline{S}^q\in\widehat{\pi}^{-1}[\{q\}]\cap \widetilde{\Sigma}^\# ,S^q_0=a,S^q_{n_k}=b}}e^{\phi_{n_k}(\underline{S}^q)-n_k\cdot P_G(\phi)}\nonumber\\[6pt] &\leq C_l e^{C_H'\sum_{j=1}^{n_k}\gamma^j} \sum_{k\geq0} \sum_{\overset{}{ \widetilde{\underline{W}}:|\widetilde{\underline{W}}|=n_k, \widetilde{W}_0=a,\widetilde{W}_{n_k-1}=b}}e^{\phi_{n_k}(\underline{S} ^{( \widetilde{\underline{W}}\cdot\underline{W})}) -n_k\cdot P_G(\phi)}\nonumber\\[6pt] &\leq C_l e^{m\cdot(\|\varphi\|_\infty+P_G(\phi))+C_H}\cdot \sum_{k\geq0}\sum_{\underline{S}\in\widetilde{\Sigma}: \sigma^{n_k+m}\underline{S}=\underline{S},S_0=a} e^{\phi_{n_k+m}(\underline{S}) -(n_k+m)\cdot P_G(\phi)}\nonumber\\[6pt] &\leq C_l e^{m\cdot(\|\varphi\|_\infty+P_G(\phi))+C_H}\cdot\sum_{n\geq 1} \sum_{\underline{S}\in\widetilde{\Sigma}: \sigma^{n}\underline{S}=\underline{S},S_0=a} e^{\phi_{n}(\underline{S}) -n\cdot P_G(\phi)}.\nonumber \end{align*} $$
Therefore,
![]() $\phi $
is recurrent on
$\phi $
is recurrent on
![]() $\widetilde {\Sigma }$
.
$\widetilde {\Sigma }$
.
It remains to show the ‘only if’ part. Assume that
![]() $\phi $
is recurrent on
$\phi $
is recurrent on
![]() $\widetilde {\Sigma }$
, then
$\widetilde {\Sigma }$
, then
![]() $\text {for all } a\in \mathcal {R}_l$
,
$\text {for all } a\in \mathcal {R}_l$
,
 $$ \begin{align*}\sum\limits_{n\geq 1} \sum\limits_{\overset{\underline{S}\in\widetilde{\Sigma}:}{ \sigma^{n}\underline{S}=\underline{S},S_0=a}} e^{\phi_{n}(\underline{S}) -n\cdot P_G(\phi)}=\infty.\end{align*} $$
$$ \begin{align*}\sum\limits_{n\geq 1} \sum\limits_{\overset{\underline{S}\in\widetilde{\Sigma}:}{ \sigma^{n}\underline{S}=\underline{S},S_0=a}} e^{\phi_{n}(\underline{S}) -n\cdot P_G(\phi)}=\infty.\end{align*} $$
Choose
![]() $a\in \mathcal {R}_l$
such that
$a\in \mathcal {R}_l$
such that
![]() $[a]\cap \widehat {\pi }^{-1}[\{p\}]\cap \widetilde {\Sigma }^\#\neq \varnothing $
.
$[a]\cap \widehat {\pi }^{-1}[\{p\}]\cap \widetilde {\Sigma }^\#\neq \varnothing $
.
![]() $\text {For all } n\geq 1$
, every periodic chain
$\text {For all } n\geq 1$
, every periodic chain
![]() $\underline {S}\in \widetilde {\Sigma }\cap [a]$
of period n codes a periodic point of period n in
$\underline {S}\in \widetilde {\Sigma }\cap [a]$
of period n codes a periodic point of period n in
![]() $H_\chi (p)\cap \Lambda _l$
(see [Reference Ben OvadiaBO18, Theorem 4.13]). There can be no more than
$H_\chi (p)\cap \Lambda _l$
(see [Reference Ben OvadiaBO18, Theorem 4.13]). There can be no more than
![]() $C_l$
chains which code the same point, and thus
$C_l$
chains which code the same point, and thus
 $$ \begin{align*}\infty&=\sum_{n\geq 1} \sum_{\underline{S}\in\widetilde{\Sigma}: \sigma^{n}\underline{S}=\underline{S},S_0=a} e^{\phi_{n}(\underline{S}) -n\cdot P_G(\phi)}\\ &\leq C_l e^Ce^{C_H}\sum_{n\geq 1} \sum_{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l} e^{\varphi_{n}(q) -n\cdot P_{H_\chi(p)}(\varphi)}.\\[-4.8pc]\end{align*} $$
$$ \begin{align*}\infty&=\sum_{n\geq 1} \sum_{\underline{S}\in\widetilde{\Sigma}: \sigma^{n}\underline{S}=\underline{S},S_0=a} e^{\phi_{n}(\underline{S}) -n\cdot P_G(\phi)}\\ &\leq C_l e^Ce^{C_H}\sum_{n\geq 1} \sum_{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l} e^{\varphi_{n}(q) -n\cdot P_{H_\chi(p)}(\varphi)}.\\[-4.8pc]\end{align*} $$
5 Absolutely continuous invariant family of leaf measures
The following theorem is a version of the Ledrappier theorem ([Reference LedrappierLed74], [Reference Ledrappier, Lima and SarigLLS16, Theorem 3.3]). We give a new proof here which is good for our needs, while the previous proofs provide a formula for the measures of cylinders.
Theorem 5.1. Let
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential such that
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential such that
![]() $P_G(\phi )<\infty $
, where
$P_G(\phi )<\infty $
, where
![]() $\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. Let
$\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. Let
![]() $\psi $
be a
$\psi $
be a
![]() $\phi $
-harmonic function on
$\phi $
-harmonic function on
![]() $\widetilde {\Sigma }_L$
. Then,
$\widetilde {\Sigma }_L$
. Then,
![]() $\text {there exists }$
a family of probability measures on
$\text {there exists }$
a family of probability measures on
![]() $\widetilde {\Sigma }$
,
$\widetilde {\Sigma }$
,
![]() $\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
, such that
$\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
, such that
![]() $\text {for all } \underline {R}\in \widetilde {\Sigma }_L$
,
$\text {for all } \underline {R}\in \widetilde {\Sigma }_L$
,
![]() $\widehat {p}_{\underline {R}}$
is carried by
$\widehat {p}_{\underline {R}}$
is carried by
![]() $ \{\underline {v}\in \widetilde {\Sigma }:v_i=R_i,\text { for all } i\leq 0\}$
and
$ \{\underline {v}\in \widetilde {\Sigma }:v_i=R_i,\text { for all } i\leq 0\}$
and
![]() $\widehat {p}_{\underline {R}}\circ \sigma ^{-1}=\sum _{\widetilde {\sigma }_R\underline {S}=\underline {R}}e^{\phi (\underline {S})+\log \psi (\underline {S})-\log \psi \circ \widetilde {\sigma }_R(\underline {S})-P_G(\phi )} \widehat {p}_{\underline {S}}$
, where
$\widehat {p}_{\underline {R}}\circ \sigma ^{-1}=\sum _{\widetilde {\sigma }_R\underline {S}=\underline {R}}e^{\phi (\underline {S})+\log \psi (\underline {S})-\log \psi \circ \widetilde {\sigma }_R(\underline {S})-P_G(\phi )} \widehat {p}_{\underline {S}}$
, where
![]() $\widetilde {\sigma }_R:=\sigma _R|_{\widetilde {\Sigma }_L}$
.
$\widetilde {\sigma }_R:=\sigma _R|_{\widetilde {\Sigma }_L}$
.
Proof. Fix
![]() $[R]\subseteq \widetilde {\Sigma }_L$
, and let
$[R]\subseteq \widetilde {\Sigma }_L$
, and let
![]() $\underline {R}\in \widetilde {\Sigma }_L\cap [R]$
. Let
$\underline {R}\in \widetilde {\Sigma }_L\cap [R]$
. Let
![]() $\tau :\widehat {\Sigma }\rightarrow \widehat {\Sigma }_L$
be the projection to the non-positive coordinates. Write
$\tau :\widehat {\Sigma }\rightarrow \widehat {\Sigma }_L$
be the projection to the non-positive coordinates. Write
![]() $\widetilde {\phi }:=\phi +\log \psi -\log \psi \circ \widetilde {\sigma }_R-P_G(\phi )$
, and
$\widetilde {\phi }:=\phi +\log \psi -\log \psi \circ \widetilde {\sigma }_R-P_G(\phi )$
, and
![]() $\widetilde {\phi }_n:=\sum _{k=0}^{n-1}\widetilde {\phi }\circ \widetilde {\sigma }_R^k$
. It follows that
$\widetilde {\phi }_n:=\sum _{k=0}^{n-1}\widetilde {\phi }\circ \widetilde {\sigma }_R^k$
. It follows that
![]() $L_{\widetilde {\phi }}1=1$
. Define
$L_{\widetilde {\phi }}1=1$
. Define
 $$ \begin{align}\widehat{p}_{\underline{R}}^{(\,n)}:=\sum_{\widetilde{\sigma}_R^n\underline{S}=\underline{R}}e^{\widetilde{\phi}_n(\underline{S})}\delta_{\sigma^{-n}\underline{S}^\pm}, \end{align} $$
$$ \begin{align}\widehat{p}_{\underline{R}}^{(\,n)}:=\sum_{\widetilde{\sigma}_R^n\underline{S}=\underline{R}}e^{\widetilde{\phi}_n(\underline{S})}\delta_{\sigma^{-n}\underline{S}^\pm}, \end{align} $$
where
![]() $\delta _{\underline {S}^{\pm }}$
is a Dirac measure with mass at the chain
$\delta _{\underline {S}^{\pm }}$
is a Dirac measure with mass at the chain
![]() $\underline {S}^{\pm }$
, and
$\underline {S}^{\pm }$
, and
![]() $\underline {S}^{\pm }$
is some (any) choice of a chain in
$\underline {S}^{\pm }$
is some (any) choice of a chain in
![]() $\tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }$
. We will show that the limit
$\tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }$
. We will show that the limit
![]() $\widehat {p}_{\underline {R}}^{(\,n)}\xrightarrow [n\rightarrow \infty ]{\text {weak-}*}\widehat {p}_{\underline {R}}$
exists, and is independent of the choice of the representatives
$\widehat {p}_{\underline {R}}^{(\,n)}\xrightarrow [n\rightarrow \infty ]{\text {weak-}*}\widehat {p}_{\underline {R}}$
exists, and is independent of the choice of the representatives
![]() $\underline {S}^\pm \in \tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }$
.
$\underline {S}^\pm \in \tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }$
.
Step 1. For all
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $\widehat {p}_{\underline {R}}^{(\,n)}(1)=(L_{\widetilde {\phi }}^n1)(\underline {R})= 1$
. Here,
$\widehat {p}_{\underline {R}}^{(\,n)}(1)=(L_{\widetilde {\phi }}^n1)(\underline {R})= 1$
. Here,
![]() $\{\widetilde {\underline {R}}\in \widetilde {\Sigma }\cap [R]: \widetilde {R}_i=R_i\text { for all} i\leq 0\}$
is a compact set which carries
$\{\widetilde {\underline {R}}\in \widetilde {\Sigma }\cap [R]: \widetilde {R}_i=R_i\text { for all} i\leq 0\}$
is a compact set which carries
![]() $\widehat {p}_{\underline {R}}^{(\,n)}$
,
$\widehat {p}_{\underline {R}}^{(\,n)}$
,
![]() $\text {for all } n\geq 1$
. Thus,
$\text {for all } n\geq 1$
. Thus,
![]() $\text {there exists } n_k\uparrow \infty $
and a probability
$\text {there exists } n_k\uparrow \infty $
and a probability
![]() $\widehat {p}_{\underline {R}}$
on
$\widehat {p}_{\underline {R}}$
on
![]() $\{\widetilde {\underline {R}}\in \widetilde {\Sigma }\cap [R]: \widetilde {R}_i=R_i,\text { for all } i\leq 0\}$
such that
$\{\widetilde {\underline {R}}\in \widetilde {\Sigma }\cap [R]: \widetilde {R}_i=R_i,\text { for all } i\leq 0\}$
such that
![]() $\widehat {p}_{\underline {R}}^{(n_k)}\xrightarrow [k\rightarrow \infty ]{}\widehat {p}_{\underline {R}} $
.
$\widehat {p}_{\underline {R}}^{(n_k)}\xrightarrow [k\rightarrow \infty ]{}\widehat {p}_{\underline {R}} $
.
Step 2. Let
![]() $[\underline {w}]_a:=\sigma ^{a}[w_a,w_{a+1},\ldots ,w_{b-1},w_b]$
, where
$[\underline {w}]_a:=\sigma ^{a}[w_a,w_{a+1},\ldots ,w_{b-1},w_b]$
, where
![]() $a,b\in \mathbb {Z}$
and
$a,b\in \mathbb {Z}$
and
![]() $a\leq b$
. Let
$a\leq b$
. Let
![]() $n,m\geq 0$
. Observe the following conditions.
$n,m\geq 0$
. Observe the following conditions.
-
(1) If
 $b\leq 0$
,
$b\leq 0$
,
 if
if
 $\underline {R}\in [\underline {w}]_a$
, and
$\underline {R}\in [\underline {w}]_a$
, and
 otherwise.
otherwise. -
(2) If
 $a\leq 0\leq b$
,
$a\leq 0\leq b$
,
 (and in particular, this equals
(and in particular, this equals
 $0$
if
$0$
if
 $w_0\neq R$
).
$w_0\neq R$
). -
(3) Assume
 $\underline {w}=R,w_1,\ldots ,w_b$
, then
$\underline {w}=R,w_1,\ldots ,w_b$
, then
 $[\underline {w}]_a=[\underline {w}]$
. If
$[\underline {w}]_a=[\underline {w}]$
. If
 $n>b$
, (4)
$n>b$
, (4)
Note that equation (4) holds regardless of the choice of
 $\underline {S}^\pm ,\underline {Q}^\pm $
.
$\underline {S}^\pm ,\underline {Q}^\pm $
.
Step 3. Let
![]() $\underline {w}=(R,w_1,\ldots ,w_{b-1},w_b)$
,
$\underline {w}=(R,w_1,\ldots ,w_{b-1},w_b)$
,
![]() $b\geq 1$
,
$b\geq 1$
,
![]() $l \geq 1$
. For all
$l \geq 1$
. For all
![]() $n=b+l>b$
,
$n=b+l>b$
,

This is a constant sequence for all
![]() $n> b$
. (Having a consistent explicit formula for the limit measure of shifted cylinders allows us to use it as a definition and apply the Carathéodory extension theorem; however, we choose to present the argument which uses weak-
$n> b$
. (Having a consistent explicit formula for the limit measure of shifted cylinders allows us to use it as a definition and apply the Carathéodory extension theorem; however, we choose to present the argument which uses weak-
![]() $*$
limits for future computations.) Therefore, since the cylinders (and their shifts) generate the Borel sigma algebra, and
$*$
limits for future computations.) Therefore, since the cylinders (and their shifts) generate the Borel sigma algebra, and
![]() $\widehat {p}_{\underline {R}}^{(n_k)}\xrightarrow [k\rightarrow \infty ]{\text {weak-}*}\widehat {p}_{\underline {R}}$
, we get that
$\widehat {p}_{\underline {R}}^{(n_k)}\xrightarrow [k\rightarrow \infty ]{\text {weak-}*}\widehat {p}_{\underline {R}}$
, we get that
![]() $\widehat {p}_{\underline {R}}^{(\,n)}\xrightarrow [n\rightarrow \infty ]{\text {weak-}*}\widehat {p}_{\underline {R}}$
; and the limit is independent of the choice of
$\widehat {p}_{\underline {R}}^{(\,n)}\xrightarrow [n\rightarrow \infty ]{\text {weak-}*}\widehat {p}_{\underline {R}}$
; and the limit is independent of the choice of
![]() $\underline {S}^\pm \in \tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }$
for a chain
$\underline {S}^\pm \in \tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }$
for a chain
![]() $\underline {S}\in \widetilde {\Sigma }_L$
in equation (3). In addition, it follows that
$\underline {S}\in \widetilde {\Sigma }_L$
in equation (3). In addition, it follows that
![]() $ \text { for all } n\geq 0$
,
$ \text { for all } n\geq 0$
,
 $$ \begin{align} \widehat{p}_{\underline{R}}\circ \sigma^{-n}=\sum_{\widetilde{\sigma}_R^n\underline{S}=\underline{R}}e^{\widetilde{\phi}_n(\underline{S})}\widehat{p}_{\underline{S}}.\\[-34pt]\nonumber \end{align} $$
$$ \begin{align} \widehat{p}_{\underline{R}}\circ \sigma^{-n}=\sum_{\widetilde{\sigma}_R^n\underline{S}=\underline{R}}e^{\widetilde{\phi}_n(\underline{S})}\widehat{p}_{\underline{S}}.\\[-34pt]\nonumber \end{align} $$
This construction could a priori depend on the choice of
![]() $\psi $
; and in the case that
$\psi $
; and in the case that
![]() $\phi $
is transient,
$\phi $
is transient,
![]() $\psi $
may not be unique. We later show applications in setups which imply the recurrence of
$\psi $
may not be unique. We later show applications in setups which imply the recurrence of
![]() $\phi $
, and thus remove the need to choose
$\phi $
, and thus remove the need to choose
![]() $\psi $
.
$\psi $
.
Corollary 5.2. (Absolute continuity)
Let
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential such that
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be a weakly Hölder continuous potential such that
![]() $P_G(\phi )<\infty $
, where
$P_G(\phi )<\infty $
, where
![]() $\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. Let
$\widetilde {\Sigma }_L$
is an irreducible locally compact one-sided topological Markov shift. Let
![]() $\psi $
be a
$\psi $
be a
![]() $\phi $
-harmonic function on
$\phi $
-harmonic function on
![]() $\widetilde {\Sigma }_L$
. Let
$\widetilde {\Sigma }_L$
. Let
![]() $\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
be the measures constructed in Theorem 5.1. Let
$\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
be the measures constructed in Theorem 5.1. Let
![]() $[R]\subseteq \widetilde {\Sigma }_L$
, let
$[R]\subseteq \widetilde {\Sigma }_L$
, let
![]() $\underline {R},\widetilde {\underline {R}}\in \widetilde {\Sigma }_L\cap [R]$
, and let
$\underline {R},\widetilde {\underline {R}}\in \widetilde {\Sigma }_L\cap [R]$
, and let
be the holonomy map
![]() $\underline {v}\mapsto (\widetilde {R}_i)_{i\leq 0}\cdot (v_i)_{i\geq 0}$
, where
$\underline {v}\mapsto (\widetilde {R}_i)_{i\leq 0}\cdot (v_i)_{i\geq 0}$
, where
![]() $\cdot $
denotes an admissible concatenation. Then,
$\cdot $
denotes an admissible concatenation. Then,
![]() $\widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}$
is a continuous and invertible map such that
$\widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}$
is a continuous and invertible map such that
![]() $\widehat {p}_{\underline {R}}\circ \widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}^{-1}\sim \widehat {p}_{\widetilde {\underline {R}}}$
.
$\widehat {p}_{\underline {R}}\circ \widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}^{-1}\sim \widehat {p}_{\widetilde {\underline {R}}}$
.
Proof. Let
![]() $\psi $
be the
$\psi $
be the
![]() $\phi $
-harmonic function which is used in Theorem 5.1, and write
$\phi $
-harmonic function which is used in Theorem 5.1, and write
![]() $\widetilde {\phi }:=\phi +\log \psi -\log \psi \circ \widetilde {\sigma }_R-P_G(\phi )$
and
$\widetilde {\phi }:=\phi +\log \psi -\log \psi \circ \widetilde {\sigma }_R-P_G(\phi )$
and
![]() $\widetilde {\phi }_n:=\sum _{k=0}^{n-1}\widetilde {\phi }\circ \widetilde {\sigma }_R^k$
. By Lemma 4.7 by the local compactness of
$\widetilde {\phi }_n:=\sum _{k=0}^{n-1}\widetilde {\phi }\circ \widetilde {\sigma }_R^k$
. By Lemma 4.7 by the local compactness of
![]() $\widetilde {\Sigma }_L$
, the weak Hölder continuity of
$\widetilde {\Sigma }_L$
, the weak Hölder continuity of
![]() $\phi $
, implies that
$\phi $
, implies that
![]() $\widetilde {\phi }$
is weakly Hölder continuous.
$\widetilde {\phi }$
is weakly Hölder continuous.
Let
![]() $[\underline {w}]_a:=\sigma ^a[w_a,w_{a+1},\ldots ,w_{b-1},w_b]$
, where
$[\underline {w}]_a:=\sigma ^a[w_a,w_{a+1},\ldots ,w_{b-1},w_b]$
, where
![]() $a,b\in \mathbb {Z}$
and
$a,b\in \mathbb {Z}$
and
![]() $a\leq b$
, and write
$a\leq b$
, and write
![]() . Let
. Let
![]() $j \geq 0$
, and fix an extension
$j \geq 0$
, and fix an extension
![]() $\underline {S}^{\pm ,(j)}\in \tau ^{-1}[\{\underline {S}\}]$
for each
$\underline {S}^{\pm ,(j)}\in \tau ^{-1}[\{\underline {S}\}]$
for each
![]() $\underline {S}\in \widetilde {\sigma }_R^{-j}[\{\widetilde {\underline {R}}\}]$
, where
$\underline {S}\in \widetilde {\sigma }_R^{-j}[\{\widetilde {\underline {R}}\}]$
, where
![]() $\tau : \widetilde {\Sigma }\rightarrow \widetilde {\Sigma }_L$
is the projection to the non-positive coordinates. Let
$\tau : \widetilde {\Sigma }\rightarrow \widetilde {\Sigma }_L$
is the projection to the non-positive coordinates. Let
![]() $\{\widehat {p}_{\underline {R}}\}_{\widetilde {\Sigma }_L}$
be the measures constructed in Theorem 5.1. By steps 2 and 3 in Theorem 5.1,
$\{\widehat {p}_{\underline {R}}\}_{\widetilde {\Sigma }_L}$
be the measures constructed in Theorem 5.1. By steps 2 and 3 in Theorem 5.1,
 $$ \begin{align} \widehat{p}_{\widetilde{\underline{R}}}(g)=\lim_{j\rightarrow\infty}\sum_{\widetilde{\sigma}_R^j\underline{S}=\widetilde{\underline{R}}}e^{\widetilde{\phi}_j(\underline{S})}\delta_{\sigma^{-j}\underline{S}^{\pm,(j)}}(g). \end{align} $$
$$ \begin{align} \widehat{p}_{\widetilde{\underline{R}}}(g)=\lim_{j\rightarrow\infty}\sum_{\widetilde{\sigma}_R^j\underline{S}=\widetilde{\underline{R}}}e^{\widetilde{\phi}_j(\underline{S})}\delta_{\sigma^{-j}\underline{S}^{\pm,(j)}}(g). \end{align} $$
Moreover, by step 3 in Theorem 5.1, this limit is independent of the choice of
![]() $\{\underline {S}^{\pm ,(j)}\}_{j\geq 0}$
. Thus, similarly,
$\{\underline {S}^{\pm ,(j)}\}_{j\geq 0}$
. Thus, similarly,
 $$ \begin{align} \widehat{p}_{\underline{R}}(g\circ\widehat{\Gamma}_{\underline{R}\,\widetilde{\underline{R}}})=\lim_{j\rightarrow\infty}\sum_{\widetilde{\sigma}_R^j\widetilde{\underline{S}}=\underline{R}}e^{\widetilde{\phi}_j(\widetilde{\underline{S}})}\delta_{\widehat{\Gamma}_{\underline{R}\,\widetilde{\underline{R}}}(\sigma^{-j}\underline{S}^{\pm,(j)})}(g), \end{align} $$
$$ \begin{align} \widehat{p}_{\underline{R}}(g\circ\widehat{\Gamma}_{\underline{R}\,\widetilde{\underline{R}}})=\lim_{j\rightarrow\infty}\sum_{\widetilde{\sigma}_R^j\widetilde{\underline{S}}=\underline{R}}e^{\widetilde{\phi}_j(\widetilde{\underline{S}})}\delta_{\widehat{\Gamma}_{\underline{R}\,\widetilde{\underline{R}}}(\sigma^{-j}\underline{S}^{\pm,(j)})}(g), \end{align} $$
where
![]() $\text {for all } j\geq 0$
,
$\text {for all } j\geq 0$
,
![]() $\text {for all } \widetilde {\underline {S}}\in \widetilde {\sigma }_R^{-j}[\{\underline {R}\}]$
,
$\text {for all } \widetilde {\underline {S}}\in \widetilde {\sigma }_R^{-j}[\{\underline {R}\}]$
,
![]() $\tau (\sigma ^{j}\widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}(\sigma ^{-j}\underline {S}^{\pm ,(j)}))=\widetilde {\underline {S}}$
.
$\tau (\sigma ^{j}\widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}(\sigma ^{-j}\underline {S}^{\pm ,(j)}))=\widetilde {\underline {S}}$
.
Let
![]() $C>0,\gamma \in (0,1)$
be the Hölder constant and Hölder exponent of
$C>0,\gamma \in (0,1)$
be the Hölder constant and Hölder exponent of
![]() $\widetilde {\phi }$
, respectively.
$\widetilde {\phi }$
, respectively.
![]() $\text {For all } j\geq 0$
,
$\text {For all } j\geq 0$
,
![]() $\text {for all } \underline {S}\in \widetilde {\sigma }_R^{-j}[\{\widetilde {\underline {R}}\}]$
, write
$\text {for all } \underline {S}\in \widetilde {\sigma }_R^{-j}[\{\widetilde {\underline {R}}\}]$
, write
![]() $\widetilde {\underline {S}}:= \tau (\sigma ^{j}\widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}(\sigma ^{-j}\underline {S}^{\pm ,(j)}))\in \widetilde {\sigma }_R^{-j}[\{\underline {R}\}]$
. Write
$\widetilde {\underline {S}}:= \tau (\sigma ^{j}\widehat {\Gamma }_{\underline {R}\,\widetilde {\underline {R}}}(\sigma ^{-j}\underline {S}^{\pm ,(j)}))\in \widetilde {\sigma }_R^{-j}[\{\underline {R}\}]$
. Write
![]() $d(\underline {R},\widetilde {\underline {R}})=e^{-n}$
,
$d(\underline {R},\widetilde {\underline {R}})=e^{-n}$
,
![]() $n\geq 1$
. Then,
$n\geq 1$
. Then,
Write
![]() $\widetilde {C}_\phi :=\exp ( C\cdot \sum _{k\geq 0}\gamma ^k) \in (0,\infty )$
. Then,
$\widetilde {C}_\phi :=\exp ( C\cdot \sum _{k\geq 0}\gamma ^k) \in (0,\infty )$
. Then,
Remark. The proof of Corollary 5.1 shows something a little stronger than absolute continuity, it shows that
![]() $\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is a continuous family with a uniform modulus of continuity for the holonomies.
$\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is a continuous family with a uniform modulus of continuity for the holonomies.
Definition 5.3. Let
![]() $\widetilde {\Sigma }$
be a maximal irreducible component of
$\widetilde {\Sigma }$
be a maximal irreducible component of
![]() $\widehat {\Sigma }$
, and let
$\widehat {\Sigma }$
, and let
![]() $\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
be the family of measures given by Theorem 5.1, when
$\{\widehat {p}_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
be the family of measures given by Theorem 5.1, when
![]() $P_G(\phi |_{\widetilde {\Sigma }_L})<\infty $
. Define
$P_G(\phi |_{\widetilde {\Sigma }_L})<\infty $
. Define
![]() $\text {for all} \underline {R}\in \widetilde {\Sigma }_L$
,
$\text {for all} \underline {R}\in \widetilde {\Sigma }_L$
,
![]() $\widehat {\mu }_{\underline {R}}:=\psi (\underline {R})\cdot \widehat {p}_{\underline {R}}$
, where
$\widehat {\mu }_{\underline {R}}:=\psi (\underline {R})\cdot \widehat {p}_{\underline {R}}$
, where
![]() $\psi $
is the
$\psi $
is the
![]() $\phi $
-harmonic function on
$\phi $
-harmonic function on
![]() $\widetilde {\Sigma }_L$
which is fixed in Theorem 5.1.
$\widetilde {\Sigma }_L$
which is fixed in Theorem 5.1.
Corollary 5.4. The family of measures
![]() $\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
from Definition 5.3 satisfies:
$\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
from Definition 5.3 satisfies:
![]() $\widehat {\mu }_{\underline {R}}\circ \sigma ^{-1}=e^{-P_G(\phi )}\sum \nolimits _{\widetilde {\sigma }_R\underline {S}=\underline {R}}e^{\phi (\underline {S})} \widehat {\mu }_{\underline {S}}$
. In addition,
$\widehat {\mu }_{\underline {R}}\circ \sigma ^{-1}=e^{-P_G(\phi )}\sum \nolimits _{\widetilde {\sigma }_R\underline {S}=\underline {R}}e^{\phi (\underline {S})} \widehat {\mu }_{\underline {S}}$
. In addition,
![]() $\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is an absolutely continuous family of measures.
$\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is an absolutely continuous family of measures.
The invariance follows from Definition 5.3 and from equation (6). The absolute continuity follows from Corollary 5.2.
Corollary 5.5. When
![]() $\phi $
is recurrent, the family
$\phi $
is recurrent, the family
![]() $\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is the unique (up to scaling) continuous family of measures which satisfies
$\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is the unique (up to scaling) continuous family of measures which satisfies
![]() $\widehat {\mu }_{\underline {R}}\circ \sigma ^{-1}= e^{-P_{G}(\phi )}\sum _{\widetilde {\sigma }_R\underline {S}=\underline {R}}e^{\phi (\underline {S})}\widehat {\mu }_{\underline {S}}$
.
$\widehat {\mu }_{\underline {R}}\circ \sigma ^{-1}= e^{-P_{G}(\phi )}\sum _{\widetilde {\sigma }_R\underline {S}=\underline {R}}e^{\phi (\underline {S})}\widehat {\mu }_{\underline {S}}$
.
Proof. Let p and
![]() $\psi $
be versions of the (unique up to scaling)
$\psi $
be versions of the (unique up to scaling)
![]() $\phi $
-conformal measure and
$\phi $
-conformal measure and
![]() $\phi $
-harmonic function on
$\phi $
-harmonic function on
![]() $\widetilde {\Sigma }_L$
, respectively. Then,
$\widetilde {\Sigma }_L$
, respectively. Then,
![]() $\widehat {\mu }=\int \widehat {\mu }_{\underline {R}}\,dp(\underline {R})$
is a
$\widehat {\mu }=\int \widehat {\mu }_{\underline {R}}\,dp(\underline {R})$
is a
![]() $\sigma $
-invariant measure on
$\sigma $
-invariant measure on
![]() $\widetilde {\Sigma }$
. By [Reference SarigSar01, Theorem 1], the recurrence of
$\widetilde {\Sigma }$
. By [Reference SarigSar01, Theorem 1], the recurrence of
![]() $\phi $
implies that p is conservative and finite on cylinders. Thus,
$\phi $
implies that p is conservative and finite on cylinders. Thus,
![]() $\widehat {\mu }$
must be conservative as well. Fix
$\widehat {\mu }$
must be conservative as well. Fix
![]() $[R]\subseteq \widetilde {\Sigma }_L$
, and let
$[R]\subseteq \widetilde {\Sigma }_L$
, and let
![]() $[R,R_{-n+2},\ldots ,R_{-1},R]$
be an admissible cylinder. Then,
$[R,R_{-n+2},\ldots ,R_{-1},R]$
be an admissible cylinder. Then,
 $$ \begin{align} &\widehat{\mu}([R,R_{-n+2},\ldots,R_{-1},R])\nonumber\\&\quad=\int \widehat{\mu}_{\underline{R}}([R,R_{-n+2},\ldots,R_{-1},R])\,dp\propto(\psi\cdot p)([R,R_{-n+2},\ldots,R_{-1},R]).\end{align} $$
$$ \begin{align} &\widehat{\mu}([R,R_{-n+2},\ldots,R_{-1},R])\nonumber\\&\quad=\int \widehat{\mu}_{\underline{R}}([R,R_{-n+2},\ldots,R_{-1},R])\,dp\propto(\psi\cdot p)([R,R_{-n+2},\ldots,R_{-1},R]).\end{align} $$
This determines
![]() $\widehat {\mu }_{\underline {R}}$
for p-a.e.
$\widehat {\mu }_{\underline {R}}$
for p-a.e.
![]() $\underline {R}$
(up to a scaling constant), and since p gives a positive volume to every cylinder [Reference SarigSar99, Reference SarigSar01], the continuity of the family
$\underline {R}$
(up to a scaling constant), and since p gives a positive volume to every cylinder [Reference SarigSar99, Reference SarigSar01], the continuity of the family
![]() $\{\widehat {\mu }_{\underline {R}} \}_{\underline {R}\in \widetilde {\Sigma }_L}$
determines the family uniquely.
$\{\widehat {\mu }_{\underline {R}} \}_{\underline {R}\in \widetilde {\Sigma }_L}$
determines the family uniquely.
Definition 5.6. (Leaf measures)
Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential, let
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
potential, let
![]() $\widetilde {\Sigma }_L$
be a maximal irreducible component of
$\widetilde {\Sigma }_L$
be a maximal irreducible component of
![]() $\widehat {\Sigma }_L$
, and let
$\widehat {\Sigma }_L$
, and let
![]() $\underline {R}\in \widetilde {\Sigma }_L$
. The corresponding leaf measure is
$\underline {R}\in \widetilde {\Sigma }_L$
. The corresponding leaf measure is
![]() $\mu _{\underline {R}}:=\widehat {\mu } _{\underline {R}}\circ \widehat {\pi }^{-1}$
, where
$\mu _{\underline {R}}:=\widehat {\mu } _{\underline {R}}\circ \widehat {\pi }^{-1}$
, where
![]() $\widehat {\mu } _{\underline {R}}$
is as in Definition 5.3.
$\widehat {\mu } _{\underline {R}}$
is as in Definition 5.3.
Theorem 5.7. Let
![]() $\varphi :\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be a
$\varphi :\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let
![]() $H_\chi (p)$
be an ergodic homoclinic class of a periodic and
$H_\chi (p)$
be an ergodic homoclinic class of a periodic and
![]() $\chi $
-hyperbolic point p. Then there exists a corresponding family of leaf measures which is
$\chi $
-hyperbolic point p. Then there exists a corresponding family of leaf measures which is
![]() $\varphi $
-invariant, and is absolutely continuous.
$\varphi $
-invariant, and is absolutely continuous.
-
(1) Leaf measures:
 $\text {for all }\underline {R}\in \widetilde {\Sigma }_L$
,
$\text {for all }\underline {R}\in \widetilde {\Sigma }_L$
,
 $\mu _{\underline {R}}$
is carried by
$\mu _{\underline {R}}$
is carried by
 $\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i, \text { for all} i\leq 0\}]\subseteq V^u(\underline {R})$
.
$\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i, \text { for all} i\leq 0\}]\subseteq V^u(\underline {R})$
. -
(2)
 $\varphi $
-invariance up to a bounded coboundary:
$\varphi $
-invariance up to a bounded coboundary:
 $\text {for all }\underline {R}\in \widetilde {\Sigma }_L$
,
$\text {for all }\underline {R}\in \widetilde {\Sigma }_L$
,  $$ \begin{align*}\mu_{\underline{R}}\circ f^{-1}=e^{-P_{H_\chi(p)}(\varphi)}\cdot\sum_{\widetilde{\sigma}_R\underline{S}=\underline{R}}e^{A-A\circ f^{-1}}\cdot e^{\varphi}\cdot\mu_{\underline{S}},\end{align*} $$
$$ \begin{align*}\mu_{\underline{R}}\circ f^{-1}=e^{-P_{H_\chi(p)}(\varphi)}\cdot\sum_{\widetilde{\sigma}_R\underline{S}=\underline{R}}e^{A-A\circ f^{-1}}\cdot e^{\varphi}\cdot\mu_{\underline{S}},\end{align*} $$
where
 $A:\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
is bounded and given by Theorem 4.4.
$A:\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
is bounded and given by Theorem 4.4. -
(3) Absolute continuity: for any cylinder
 $ [R]\subseteq \widetilde {\Sigma }_L$
, and for any two chains
$ [R]\subseteq \widetilde {\Sigma }_L$
, and for any two chains
 $ \underline {R},\underline {S}\in \widetilde {\Sigma }_L\cap [R]$
, let be the holonomy map along the stable leaves of
$ \underline {R},\underline {S}\in \widetilde {\Sigma }_L\cap [R]$
, let be the holonomy map along the stable leaves of $$ \begin{align*}\Gamma_{\underline{R}\,\underline{S}}: \widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\}] \rightarrow \widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=S_i,\text{ for all } i\leq0\}] \end{align*} $$
$$ \begin{align*}\Gamma_{\underline{R}\,\underline{S}}: \widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\}] \rightarrow \widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=S_i,\text{ for all } i\leq0\}] \end{align*} $$
 $\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i,\text { for all } i\leq 0\}]$
(it is well defined on the rectangle
$\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i,\text { for all } i\leq 0\}]$
(it is well defined on the rectangle
 $\widehat {\pi }[[R]]$
). Then,
$\widehat {\pi }[[R]]$
). Then,
 $(\mu _{\underline {R}}\circ \Gamma _{\underline {R}\,\underline {S}}^{-1})(g)=C_\phi ^{\pm 1}\cdot \mu _{\underline {S}}(g)$
for every
$(\mu _{\underline {R}}\circ \Gamma _{\underline {R}\,\underline {S}}^{-1})(g)=C_\phi ^{\pm 1}\cdot \mu _{\underline {S}}(g)$
for every
 $g\in C(V^u(\underline {S}))$
, where
$g\in C(V^u(\underline {S}))$
, where
 $C_\phi>0$
is a global constant depending only on
$C_\phi>0$
is a global constant depending only on
 $\phi $
(and a fixed corresponding harmonic function).
$\phi $
(and a fixed corresponding harmonic function).
Here,
![]() $\mathcal {F}_{H_\chi (p)}(\varphi ):=\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is a
$\mathcal {F}_{H_\chi (p)}(\varphi ):=\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
is a
![]() $\varphi $
-invariant family of leaf measures (see Definition 2.16).
$\varphi $
-invariant family of leaf measures (see Definition 2.16).
Proof. Let
![]() $A,\phi :\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be given by Theorem 4.4 such that
$A,\phi :\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be given by Theorem 4.4 such that
![]() $\varphi =\varphi ^*+A- A\circ f^{-1}$
, where A is bounded and
$\varphi =\varphi ^*+A- A\circ f^{-1}$
, where A is bounded and
![]() $\phi =\varphi ^*\circ \widehat {\pi }:\widehat {\Sigma }\rightarrow \mathbb {R}$
is well defined and weakly Hölder continuous by the remark after Theorem 4.4; and
$\phi =\varphi ^*\circ \widehat {\pi }:\widehat {\Sigma }\rightarrow \mathbb {R}$
is well defined and weakly Hölder continuous by the remark after Theorem 4.4; and
![]() $\phi (\underline {R})$
depends only on the negative coordinates of
$\phi (\underline {R})$
depends only on the negative coordinates of
![]() $\underline {R}$
.
$\underline {R}$
.
Let
![]() $\widetilde {\Sigma }$
be a maximal irreducible component of
$\widetilde {\Sigma }$
be a maximal irreducible component of
![]() $\widehat {\Sigma }$
such that
$\widehat {\Sigma }$
such that
![]() $\widehat {\pi }[\widetilde {\Sigma }^\#]=H_\chi (p)$
modulo all conservative measures (see Proposition 3.16). Let
$\widehat {\pi }[\widetilde {\Sigma }^\#]=H_\chi (p)$
modulo all conservative measures (see Proposition 3.16). Let
![]() $[R]\subseteq \widetilde {\Sigma }_L$
, and let
$[R]\subseteq \widetilde {\Sigma }_L$
, and let
![]() $\underline {R},\underline {S}\in [R]\cap \widetilde {\Sigma }_L$
.
$\underline {R},\underline {S}\in [R]\cap \widetilde {\Sigma }_L$
.
Since
![]() $\varphi $
is bounded, so is
$\varphi $
is bounded, so is
![]() $\phi $
. By the spectral decomposition, we may assume without loss of generality that
$\phi $
. By the spectral decomposition, we may assume without loss of generality that
![]() $(\widetilde {\Sigma },\sigma )$
is topologically mixing (see [Reference SarigSar15, Theorem 2.5]). Thus, by the variational principle, see [Reference SarigSar09, Theorem 4.4] (and the fact that
$(\widetilde {\Sigma },\sigma )$
is topologically mixing (see [Reference SarigSar15, Theorem 2.5]). Thus, by the variational principle, see [Reference SarigSar09, Theorem 4.4] (and the fact that
![]() $\widehat {\pi }|_{\widetilde {\Sigma }^\#}$
is finite-to-one which allows to lift probabilities while preserving the entropy),
$\widehat {\pi }|_{\widetilde {\Sigma }^\#}$
is finite-to-one which allows to lift probabilities while preserving the entropy),
![]() $P_G(\phi |_{\widetilde {\Sigma }})=P_{H_\chi (p)}(\varphi )<\infty $
. (Every invariant probability measure can be decomposed into its ergodic components, and each component lifts to an invariant probability measure. Then this lift is N-to-one for some
$P_G(\phi |_{\widetilde {\Sigma }})=P_{H_\chi (p)}(\varphi )<\infty $
. (Every invariant probability measure can be decomposed into its ergodic components, and each component lifts to an invariant probability measure. Then this lift is N-to-one for some
![]() $N\in \mathbb {N}$
since the cardinality of fibers is an invariant function. Finite extensions preserve entropy, and entropy is affine.) Then we may assume without loss of generality that
$N\in \mathbb {N}$
since the cardinality of fibers is an invariant function. Finite extensions preserve entropy, and entropy is affine.) Then we may assume without loss of generality that
![]() $P_G(\phi |_{\widetilde {\Sigma }_L})=0$
, otherwise replace
$P_G(\phi |_{\widetilde {\Sigma }_L})=0$
, otherwise replace
![]() $\phi $
by
$\phi $
by
![]() $\phi -P_G(\phi |_{\widetilde {\Sigma }_L})$
.
$\phi -P_G(\phi |_{\widetilde {\Sigma }_L})$
.
-
(1) We have
Thus, $$ \begin{align*} &\mu_{\underline{R}}(\widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\}])\\[3pt]&\quad=\widehat{\mu}_{\underline{R}}\circ\widehat{\pi}^{\,-1}(\widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\}])\\[3pt]&\quad\geq \widehat{\mu}_{\underline{R}}(\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\})=\widehat{\mu}_{\underline{R}}(1)= \mu_{\underline{R}}(1). \end{align*} $$
$$ \begin{align*} &\mu_{\underline{R}}(\widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\}])\\[3pt]&\quad=\widehat{\mu}_{\underline{R}}\circ\widehat{\pi}^{\,-1}(\widehat{\pi}[\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\}])\\[3pt]&\quad\geq \widehat{\mu}_{\underline{R}}(\{\underline{v}\in\widetilde{\Sigma}:v_i=R_i,\text{ for all } i\leq0\})=\widehat{\mu}_{\underline{R}}(1)= \mu_{\underline{R}}(1). \end{align*} $$
 $\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }: v_i=R_i, \text { for all } i\leq 0\}] \subseteq V^u(\underline {R})$
has full measure.
$\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }: v_i=R_i, \text { for all } i\leq 0\}] \subseteq V^u(\underline {R})$
has full measure.
-
(2) By the relation
 $\widehat {\pi }\circ \sigma =f\circ \widehat {\pi }$
and Corollary 5.4, For a continuous test function
$\widehat {\pi }\circ \sigma =f\circ \widehat {\pi }$
and Corollary 5.4, For a continuous test function $$ \begin{align*} \mu_{\underline{R}}\circ f^{-1}&= \widehat{\mu}_{\underline{R}}\circ\widehat{\pi} ^{-1}\circ f^{-1}=(\widehat{\mu}_{\underline{R}}\circ \sigma^{-1})\circ \widehat{\pi}^{-1}\\[3pt]&= \bigg(\sum_{\widetilde{\sigma}_R\underline{Q}=\underline{R}}e^{\phi(\underline{Q})}\widehat{\mu}_{\underline{Q}}\bigg)\circ \widehat{\pi}^{-1}= \sum_{\widetilde{\sigma}_R\underline{Q}=\underline{R}}e^{\phi(\underline{Q})}\mu_{\underline{Q}}. \end{align*} $$
$$ \begin{align*} \mu_{\underline{R}}\circ f^{-1}&= \widehat{\mu}_{\underline{R}}\circ\widehat{\pi} ^{-1}\circ f^{-1}=(\widehat{\mu}_{\underline{R}}\circ \sigma^{-1})\circ \widehat{\pi}^{-1}\\[3pt]&= \bigg(\sum_{\widetilde{\sigma}_R\underline{Q}=\underline{R}}e^{\phi(\underline{Q})}\widehat{\mu}_{\underline{Q}}\bigg)\circ \widehat{\pi}^{-1}= \sum_{\widetilde{\sigma}_R\underline{Q}=\underline{R}}e^{\phi(\underline{Q})}\mu_{\underline{Q}}. \end{align*} $$
 $g\in C(V^u(\underline {Q}))$
, This completes the
$g\in C(V^u(\underline {Q}))$
, This completes the $$ \begin{align*} e^{\phi}\cdot \mu_{\underline{Q}}(g)&=\int\limits_{\substack{\underline{Q}'\in\widetilde{\Sigma}:\\ Q_i=Q_i',\text{ for all } i\leq0}} e^{\varphi^*\circ\widehat{\pi}}g\circ\widehat{\pi} \,d\widehat{\mu}_{\underline{Q}}\\&= \int\limits_{\substack{\underline{Q}'\in\widetilde{\Sigma}: \\ Q_i=Q_i',\text{ for all } i\leq0}} (e^{\varphi^*}g)\circ \widehat{\pi} \,d\widehat{\mu}_{\underline{Q}}=(e^{\varphi+A-A\circ f^{-1}}\cdot \mu_{\underline{Q}})(g). \end{align*} $$
$$ \begin{align*} e^{\phi}\cdot \mu_{\underline{Q}}(g)&=\int\limits_{\substack{\underline{Q}'\in\widetilde{\Sigma}:\\ Q_i=Q_i',\text{ for all } i\leq0}} e^{\varphi^*\circ\widehat{\pi}}g\circ\widehat{\pi} \,d\widehat{\mu}_{\underline{Q}}\\&= \int\limits_{\substack{\underline{Q}'\in\widetilde{\Sigma}: \\ Q_i=Q_i',\text{ for all } i\leq0}} (e^{\varphi^*}g)\circ \widehat{\pi} \,d\widehat{\mu}_{\underline{Q}}=(e^{\varphi+A-A\circ f^{-1}}\cdot \mu_{\underline{Q}})(g). \end{align*} $$
 $\varphi $
-invariance up to a bounded coboundary.
$\varphi $
-invariance up to a bounded coboundary.
-
(3) Let
 $\Gamma _{\underline {R}\,\underline {S}}: \widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i,\text { for all } i\leq 0\}] \rightarrow \widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=S_i,\text { for all } i\leq 0\}] $
be the holonomy map along the stable leaves of points in
$\Gamma _{\underline {R}\,\underline {S}}: \widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i,\text { for all } i\leq 0\}] \rightarrow \widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=S_i,\text { for all } i\leq 0\}] $
be the holonomy map along the stable leaves of points in
 $\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i, \text {for all } i\leq 0\}]$
. Let
$\widehat {\pi }[\{\underline {v}\in \widetilde {\Sigma }:v_i=R_i, \text {for all } i\leq 0\}]$
. Let
 $\widehat {\Gamma }_{\underline {R}\,\underline {S}}:\{\underline {v}\in \widetilde {\Sigma }: v_i=R_i,\text { for all } i\leq 0\}\rightarrow \{\underline {v}\in \widetilde {\Sigma }: v_i=S_i, \text {for all } i\leq 0\}$
be a continuous and invertible map such that
$\widehat {\Gamma }_{\underline {R}\,\underline {S}}:\{\underline {v}\in \widetilde {\Sigma }: v_i=R_i,\text { for all } i\leq 0\}\rightarrow \{\underline {v}\in \widetilde {\Sigma }: v_i=S_i, \text {for all } i\leq 0\}$
be a continuous and invertible map such that
 $\underline {v}\mapsto (S_i)_{i\leq 0}\cdot (v_i)_{i\geq 0}$
, where
$\underline {v}\mapsto (S_i)_{i\leq 0}\cdot (v_i)_{i\geq 0}$
, where
 $\cdot $
denotes an admissible concatenation. Let
$\cdot $
denotes an admissible concatenation. Let
 $g\in C(V^u(\underline {S}))$
, and write
$g\in C(V^u(\underline {S}))$
, and write
 $\widehat {g}:=g\circ \widehat {\pi }\in C(\{\underline {v}\in \widetilde {\Sigma }:v_i=S_i,\text { for all } i\leq 0\})$
. It follows that
$\widehat {g}:=g\circ \widehat {\pi }\in C(\{\underline {v}\in \widetilde {\Sigma }:v_i=S_i,\text { for all } i\leq 0\})$
. It follows that
 $\Gamma _{\underline {R}\,\underline {S}}\circ \widehat {\pi }=\widehat {\pi }\circ \widehat {\Gamma }_{\underline {R}\,\underline {S}}$
, and so
$\Gamma _{\underline {R}\,\underline {S}}\circ \widehat {\pi }=\widehat {\pi }\circ \widehat {\Gamma }_{\underline {R}\,\underline {S}}$
, and so
 $(\mu _{\underline {R}}\circ \Gamma _{\underline {R}\,\underline {S}}^{-1})(g)=(\widehat {\mu }_{\underline {R}}\circ \widehat {\Gamma }_{\underline {R}\,\underline {S}}^{-1})(\widehat {g})= \psi (\underline {R})\cdot (\widehat {p}_{\underline {R}}\circ \widehat {\Gamma }_{\underline {R}\,\underline {S}}^{-1})(\widehat {g}) $
and
$(\mu _{\underline {R}}\circ \Gamma _{\underline {R}\,\underline {S}}^{-1})(g)=(\widehat {\mu }_{\underline {R}}\circ \widehat {\Gamma }_{\underline {R}\,\underline {S}}^{-1})(\widehat {g})= \psi (\underline {R})\cdot (\widehat {p}_{\underline {R}}\circ \widehat {\Gamma }_{\underline {R}\,\underline {S}}^{-1})(\widehat {g}) $
and
 $\mu _{\underline {S}}(g)= \psi (\underline {S})\cdot \widehat {p}_{\underline {S}}(\widehat {g})$
. By Lemma 4.7,
$\mu _{\underline {S}}(g)= \psi (\underline {S})\cdot \widehat {p}_{\underline {S}}(\widehat {g})$
. By Lemma 4.7,
 $\mathrm {Var}_1(\log \psi )<\infty $
. Thus, by equation (9), we are done.
$\mathrm {Var}_1(\log \psi )<\infty $
. Thus, by equation (9), we are done.
Remark. Absolute continuity implies a local product structure. Other related important properties of hyperbolic equilibrium states of Hölder continuous potentials are true, such as being Bernoulli up to a period. This has been proven when
![]() $\dim M=2$
in [Reference SarigSar11] and for the setup of countable Markov shifts in [Reference DaonDao13]. Sarig’s proof extends, as it only uses the fact that the equilibrium state can be coded as an equilibrium state on a countable Markov shift of a weakly Hölder continuous potential. In [Reference DaonDao13], Daon relaxes the assumption on the regularity of the potential to the Walters property.
$\dim M=2$
in [Reference SarigSar11] and for the setup of countable Markov shifts in [Reference DaonDao13]. Sarig’s proof extends, as it only uses the fact that the equilibrium state can be coded as an equilibrium state on a countable Markov shift of a weakly Hölder continuous potential. In [Reference DaonDao13], Daon relaxes the assumption on the regularity of the potential to the Walters property.
6 Proofs of the main results
6.1 Local equilibrium states and the leaf condition
Theorem 6.1. Let M be a compact Riemannian manifold without boundary and of dimension
![]() $d\geq 2$
. Let
$d\geq 2$
. Let
![]() $f\in \mathrm {Diff}^{1+\beta }(M)$
,
$f\in \mathrm {Diff}^{1+\beta }(M)$
,
![]() $\beta>0$
. Fix
$\beta>0$
. Fix
![]() $\chi>0$
and
$\chi>0$
and
![]() $\epsilon =\epsilon _\chi $
as in Lemma 2.6. Let
$\epsilon =\epsilon _\chi $
as in Lemma 2.6. Let
![]() $\varphi :M\rightarrow \mathbb {R}$
be a
$\varphi :M\rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let p be a
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential. Let p be a
![]() $\chi $
-hyperbolic periodic point. Then, there exists a
$\chi $
-hyperbolic periodic point. Then, there exists a
![]() $\chi $
-hyperbolic local equilibrium state of
$\chi $
-hyperbolic local equilibrium state of
![]() $\varphi $
on
$\varphi $
on
![]() $H_\chi (p)$
if and only if the following two conditions hold:
$H_\chi (p)$
if and only if the following two conditions hold:
-
(1) we have
where $$ \begin{align*}\sum_{n\geq1}\sum_{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l}e^{\varphi_n(q)-n\cdot P_{H_\chi(p)}(\varphi)}=\infty,\end{align*} $$
$$ \begin{align*}\sum_{n\geq1}\sum_{f^n(q)=q,q\in H_\chi(p)\cap \Lambda_l}e^{\varphi_n(q)-n\cdot P_{H_\chi(p)}(\varphi)}=\infty,\end{align*} $$
 $\Lambda _l$
is a level set such that
$\Lambda _l$
is a level set such that
 $p\in \Lambda _{l\cdot e^{-2\sqrt [3]{\epsilon }}}$
; and
$p\in \Lambda _{l\cdot e^{-2\sqrt [3]{\epsilon }}}$
; and
-
(2) there exists a leaf measure
 $\mu \in \mathcal {F}_{H_\chi (p)}(\varphi )$
such that where
$\mu \in \mathcal {F}_{H_\chi (p)}(\varphi )$
such that where $$ \begin{align*}\mu(\mathrm{RWT}_\chi^{\mathrm{PR}})>0,\end{align*} $$
$$ \begin{align*}\mu(\mathrm{RWT}_\chi^{\mathrm{PR}})>0,\end{align*} $$
 $\mathcal {F}_{H_\chi (p)}(\varphi )$
is any
$\mathcal {F}_{H_\chi (p)}(\varphi )$
is any
 $\varphi $
-invariant family of measures given by Theorem 5.7.
$\varphi $
-invariant family of measures given by Theorem 5.7.
If a
![]() $\chi $
-hyperbolic local equilibrium state of
$\chi $
-hyperbolic local equilibrium state of
![]() $\varphi $
exists on
$\varphi $
exists on
![]() $H_\chi (p)$
, then its conditional measures on unstable leaves (in the explicit sense of equation (11)) are proportional to the members of the
$H_\chi (p)$
, then its conditional measures on unstable leaves (in the explicit sense of equation (11)) are proportional to the members of the
![]() $\varphi $
-invariant family of measures; and it is unique.
$\varphi $
-invariant family of measures; and it is unique.
Proof. The ‘only if’ direction is straightforward: let
![]() $\mu $
be a
$\mu $
be a
![]() $\chi $
-hyperbolic local equilibrium state of
$\chi $
-hyperbolic local equilibrium state of
![]() $\varphi $
on
$\varphi $
on
![]() $H_\chi (p)$
. Let
$H_\chi (p)$
. Let
![]() $\widetilde {\Sigma }$
be a maximal irreducible component which lifts all conservative measures on
$\widetilde {\Sigma }$
be a maximal irreducible component which lifts all conservative measures on
![]() $H_\chi (p)$
(see Proposition 3.16). Lift
$H_\chi (p)$
(see Proposition 3.16). Lift
![]() $\mu $
to an ergodic,
$\mu $
to an ergodic,
![]() $\sigma $
-invariant, probability measure on
$\sigma $
-invariant, probability measure on
![]() $\widetilde {\Sigma }$
,
$\widetilde {\Sigma }$
,
![]() $\widehat {\mu }$
, such that
$\widehat {\mu }$
, such that
![]() $\widehat {\mu }\circ \widehat {\pi }^{-1}=\mu $
, and
$\widehat {\mu }\circ \widehat {\pi }^{-1}=\mu $
, and
![]() $h_{\widehat {\mu }}(\sigma )+\int \varphi \circ \widehat {\pi } \,d\widehat {\mu }= h_\mu (f)+\int \varphi \,d\mu $
. This is possible by choosing a suitable ergodic component of
$h_{\widehat {\mu }}(\sigma )+\int \varphi \circ \widehat {\pi } \,d\widehat {\mu }= h_\mu (f)+\int \varphi \,d\mu $
. This is possible by choosing a suitable ergodic component of
![]() $\int {1}/{|N_x|}\sum _{\underline {v}\in N_x}\delta _{\underline {v}}\,d\mu (x)$
, where
$\int {1}/{|N_x|}\sum _{\underline {v}\in N_x}\delta _{\underline {v}}\,d\mu (x)$
, where
![]() $N_x:=\widehat {\pi }^{-1}[\{x\}]\cap \widehat {\Sigma }^\#$
. Let
$N_x:=\widehat {\pi }^{-1}[\{x\}]\cap \widehat {\Sigma }^\#$
. Let
![]() $\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be given by Theorem 4.4 and the remark which follows it, and let
$\phi :\widetilde {\Sigma }_L\rightarrow \mathbb {R}$
be given by Theorem 4.4 and the remark which follows it, and let
![]() $\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
be given by Definition 5.3.
$\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
be given by Definition 5.3.
By the spectral decomposition (see [Reference SarigSar15, Theorem 2.5]), we may assume without loss of generality that
![]() $(\widetilde {\Sigma }_L,\widetilde {\sigma }_R) $
is topologically mixing. It follows that
$(\widetilde {\Sigma }_L,\widetilde {\sigma }_R) $
is topologically mixing. It follows that
 $$ \begin{align*} &h_{\widehat{\mu}}(\sigma)+\int \phi \,d\widehat{\mu}=\sup\{h_{\widehat{\nu}}(\sigma)+\int \phi \,d\widehat{\nu}:\widehat{\nu}\text{ is an invariant probability measure on }\widetilde{\Sigma}\}\\ &\quad= \sup\{h_{\widehat{\nu}\circ\tau^{-1}}(\widetilde{\sigma}_R) +\int \phi \,d\widehat{\nu}\circ\tau^{-1}:\widehat{\nu}\text{ is an invariant probability measure on }\widetilde{\Sigma}\}, \end{align*} $$
$$ \begin{align*} &h_{\widehat{\mu}}(\sigma)+\int \phi \,d\widehat{\mu}=\sup\{h_{\widehat{\nu}}(\sigma)+\int \phi \,d\widehat{\nu}:\widehat{\nu}\text{ is an invariant probability measure on }\widetilde{\Sigma}\}\\ &\quad= \sup\{h_{\widehat{\nu}\circ\tau^{-1}}(\widetilde{\sigma}_R) +\int \phi \,d\widehat{\nu}\circ\tau^{-1}:\widehat{\nu}\text{ is an invariant probability measure on }\widetilde{\Sigma}\}, \end{align*} $$
where
![]() $\tau :\widetilde {\Sigma }\rightarrow \widetilde {\Sigma }_L$
is the projection onto the non-positive coordinates. Every invariant probability
$\tau :\widetilde {\Sigma }\rightarrow \widetilde {\Sigma }_L$
is the projection onto the non-positive coordinates. Every invariant probability
![]() $\nu $
on
$\nu $
on
![]() $\widetilde {\Sigma }_L$
can be lifted to an invariant probability measure on
$\widetilde {\Sigma }_L$
can be lifted to an invariant probability measure on
![]() $\widetilde {\Sigma }$
,
$\widetilde {\Sigma }$
,
![]() $\widehat {\nu }$
, such that
$\widehat {\nu }$
, such that
![]() $\widehat {\nu }\circ \tau ^{-1}=\nu $
and
$\widehat {\nu }\circ \tau ^{-1}=\nu $
and
![]() $h_{\nu }(\widetilde {\sigma }_R)=h_{\widehat {\nu }}(\sigma )$
. Thus,
$h_{\nu }(\widetilde {\sigma }_R)=h_{\widehat {\nu }}(\sigma )$
. Thus,
 $$ \begin{align*}&h_{\widehat{\mu}\circ\tau^{-1}}(\widetilde{\sigma}_R)+\int \phi \,d\widehat{\mu}\circ\tau^{-1}\\&\quad=\sup\{h_{\nu}(\sigma)+\int \phi \,d\nu:\nu\text{ is an invariant probability measure on }\widetilde{\Sigma}_L\}.\end{align*} $$
$$ \begin{align*}&h_{\widehat{\mu}\circ\tau^{-1}}(\widetilde{\sigma}_R)+\int \phi \,d\widehat{\mu}\circ\tau^{-1}\\&\quad=\sup\{h_{\nu}(\sigma)+\int \phi \,d\nu:\nu\text{ is an invariant probability measure on }\widetilde{\Sigma}_L\}.\end{align*} $$
Therefore, by [Reference Buzzi and SarigBS03],
![]() $\phi $
is recurrent on
$\phi $
is recurrent on
![]() $\widetilde {\Sigma }_L$
. Thus, by Lemma 4.8,
$\widetilde {\Sigma }_L$
. Thus, by Lemma 4.8,
![]() $\sum \nolimits _{n\geq 1}\sum \nolimits _{\substack {f^n(q)=q,\\ q\in H_\chi (p)\cap \Lambda _l}} e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )}=\infty $
.
$\sum \nolimits _{n\geq 1}\sum \nolimits _{\substack {f^n(q)=q,\\ q\in H_\chi (p)\cap \Lambda _l}} e^{\varphi _n(q)-n\cdot P_{H_\chi (p)}(\varphi )}=\infty $
.
By [Reference SarigSar09, Theorem 4.5],
![]() $\widehat {\mu }\circ \tau ^{-1}=\psi \cdot p$
, where
$\widehat {\mu }\circ \tau ^{-1}=\psi \cdot p$
, where
![]() $\psi $
is the
$\psi $
is the
![]() $\phi $
-harmonic function and p is the
$\phi $
-harmonic function and p is the
![]() $\phi $
-conformal measure, scaled such that
$\phi $
-conformal measure, scaled such that
![]() $\psi \cdot p(1)=1$
, and
$\psi \cdot p(1)=1$
, and
![]() $\psi ,p$
are unique up to a scaling. Then, by equation (10),
$\psi ,p$
are unique up to a scaling. Then, by equation (10),
![]() $\widehat {\mu }=\int _{\widetilde {\Sigma }_L} \widehat {\mu }_{\underline {R}}\,dp(\underline {R})$
. Thus,
$\widehat {\mu }=\int _{\widetilde {\Sigma }_L} \widehat {\mu }_{\underline {R}}\,dp(\underline {R})$
. Thus,
![]() $\mu =\int \mu _{\underline {R}}\,dp$
, where
$\mu =\int \mu _{\underline {R}}\,dp$
, where
![]() $\{\mu _{\underline {S}}\}_{\underline {S}\in \widetilde {\Sigma }_L}$
is the
$\{\mu _{\underline {S}}\}_{\underline {S}\in \widetilde {\Sigma }_L}$
is the
![]() $\varphi $
-invariant family of leaf measures as in Theorem 5.7. In addition,
$\varphi $
-invariant family of leaf measures as in Theorem 5.7. In addition,
![]() $\mu $
is carried by
$\mu $
is carried by
![]() $\mathrm {RWT}_\chi ^{\mathrm {PR}}$
since it is an invariant probability measure. This concludes the ‘only if’ direction.
$\mathrm {RWT}_\chi ^{\mathrm {PR}}$
since it is an invariant probability measure. This concludes the ‘only if’ direction.
We now turn to the ‘if’ direction:
![]() $\phi $
is recurrent on
$\phi $
is recurrent on
![]() $\widetilde {\Sigma }_L$
by Lemma 4.8. Let p be a
$\widetilde {\Sigma }_L$
by Lemma 4.8. Let p be a
![]() $\phi $
-conformal measure carried by
$\phi $
-conformal measure carried by
![]() $\widetilde {\Sigma }_L^\#$
, and let
$\widetilde {\Sigma }_L^\#$
, and let
![]() $\{\mu _{\underline {S}}\}_{\underline {S}\in \widetilde {\Sigma }_L}$
be the
$\{\mu _{\underline {S}}\}_{\underline {S}\in \widetilde {\Sigma }_L}$
be the
![]() $\phi $
-invariant family of leaf measures given by Theorem 5.7. By [Reference SarigSar01, Theorem 1], p is ergodic and conservative. Let
$\phi $
-invariant family of leaf measures given by Theorem 5.7. By [Reference SarigSar01, Theorem 1], p is ergodic and conservative. Let
 $$ \begin{align} \mu:=\int_{\widetilde{\Sigma}_L}\mu_{\underline{R}}\,dp(\underline{R}). \end{align} $$
$$ \begin{align} \mu:=\int_{\widetilde{\Sigma}_L}\mu_{\underline{R}}\,dp(\underline{R}). \end{align} $$
Recall that
![]() $\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
are carried by local unstable leaves, and are the projection of a family of measures given by a measurable partition of
$\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
are carried by local unstable leaves, and are the projection of a family of measures given by a measurable partition of
![]() $\widetilde {\Sigma }$
parameterized by
$\widetilde {\Sigma }$
parameterized by
![]() $\widetilde {\Sigma }_L$
. It follows that
$\widetilde {\Sigma }_L$
. It follows that
![]() $\mu $
is an ergodic, f-invariant, and conservative measure on
$\mu $
is an ergodic, f-invariant, and conservative measure on
![]() $H_\chi (p)$
, and that
$H_\chi (p)$
, and that
![]() $\mu $
is finite on Pesin level sets. This measure is finite if and only if
$\mu $
is finite on Pesin level sets. This measure is finite if and only if
![]() $\phi $
is positive recurrent. For full details of the proof of these properties, see [Reference Ben OvadiaBO21, Theorem 6.2]. (In that proof,
$\phi $
is positive recurrent. For full details of the proof of these properties, see [Reference Ben OvadiaBO21, Theorem 6.2]. (In that proof,
![]() $\phi $
denotes the geometric potential, but the proof is identical for general weakly Hölder continuous functions.)
$\phi $
denotes the geometric potential, but the proof is identical for general weakly Hölder continuous functions.)
Note that
![]() $\mu (1)=p(\psi )$
, where
$\mu (1)=p(\psi )$
, where
![]() $\psi $
is the unique (up to scaling)
$\psi $
is the unique (up to scaling)
![]() $\phi $
-harmonic function on
$\phi $
-harmonic function on
![]() $\widetilde {\Sigma }_L$
. By [Reference SarigSar99, Theorem 8], if
$\widetilde {\Sigma }_L$
. By [Reference SarigSar99, Theorem 8], if
![]() $h_{\mathrm {top}}(\sigma ),\infty $
, then
$h_{\mathrm {top}}(\sigma ),\infty $
, then
![]() $\mu (1)<\infty $
if and only if
$\mu (1)<\infty $
if and only if
![]() $\psi \cdot p$
is an equilibrium state of
$\psi \cdot p$
is an equilibrium state of
![]() $\phi $
on
$\phi $
on
![]() $\widetilde {\Sigma }_L$
(and thus
$\widetilde {\Sigma }_L$
(and thus
![]() $\mu $
is a local
$\mu $
is a local
![]() $\chi $
-hyperbolic equilibrium state of
$\chi $
-hyperbolic equilibrium state of
![]() $\varphi $
on
$\varphi $
on
![]() $H_\chi (p)$
).
$H_\chi (p)$
).
By assumption,
![]() $\text {there exists } \underline {R}\in \widetilde {\Sigma }_L$
such that
$\text {there exists } \underline {R}\in \widetilde {\Sigma }_L$
such that
![]() $\mu _{\underline {R}}(\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
. By [Reference Ben OvadiaBO21, Theorem 6.8],
$\mu _{\underline {R}}(\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
. By [Reference Ben OvadiaBO21, Theorem 6.8],
![]() $\mu $
is finite. This concludes the ‘if’ direction.
$\mu $
is finite. This concludes the ‘if’ direction.
The proof so far shows that the local equilibrium state can always be disintegrated into conditional measures on unstable leaves, where the conditional measures are
![]() $\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
.
$\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
.
We proceed to show the uniqueness of the
![]() $\chi $
-hyperbolic local equilibrium state, when it exists. We saw that
$\chi $
-hyperbolic local equilibrium state, when it exists. We saw that
![]() $\mu =\widehat {\mu }\circ \widehat {\pi }^{-1}$
where
$\mu =\widehat {\mu }\circ \widehat {\pi }^{-1}$
where
![]() $\widehat {\mu }$
is an equilibrium state for
$\widehat {\mu }$
is an equilibrium state for
![]() $\phi $
on
$\phi $
on
![]() $\widetilde {\Sigma }$
. By [Reference Buzzi and SarigBS03],
$\widetilde {\Sigma }$
. By [Reference Buzzi and SarigBS03],
![]() $\widehat {\mu }$
is unique and satisfies a variational principle on
$\widehat {\mu }$
is unique and satisfies a variational principle on
![]() $\widetilde {\Sigma }$
. It follows that a
$\widetilde {\Sigma }$
. It follows that a
![]() $\chi $
-hyperbolic local equilibrium state is unique on
$\chi $
-hyperbolic local equilibrium state is unique on
![]() $H_\chi (p)$
.
$H_\chi (p)$
.
Remark. If
![]() $\text {there exists } p\in \Lambda _\ell $
such that
$\text {there exists } p\in \Lambda _\ell $
such that
![]() $\sum _{n\geq 1}\sum _{f^n(q)=q, q\in H_\chi (p)\cap \Lambda _\ell } e^{\varphi _n(q)-n P_{H_\chi (p)}(\varphi )}=\infty $
, then
$\sum _{n\geq 1}\sum _{f^n(q)=q, q\in H_\chi (p)\cap \Lambda _\ell } e^{\varphi _n(q)-n P_{H_\chi (p)}(\varphi )}=\infty $
, then
![]() $\sum _{n\geq 1}\sum _{f^n(q)=q, q\in H_\chi (p)\cap \Lambda _{\ell e^{2\sqrt [3]\epsilon }}}e^{\varphi _n(q)-n P_{H_\chi (p)}(\varphi )}=\infty $
. Similarly, if
$\sum _{n\geq 1}\sum _{f^n(q)=q, q\in H_\chi (p)\cap \Lambda _{\ell e^{2\sqrt [3]\epsilon }}}e^{\varphi _n(q)-n P_{H_\chi (p)}(\varphi )}=\infty $
. Similarly, if
![]() $p\in \Lambda _{\ell e^{-2\sqrt [3]\epsilon }}$
, then
$p\in \Lambda _{\ell e^{-2\sqrt [3]\epsilon }}$
, then
![]() $p\in \Lambda _{\ell }$
. Then the condition in Theorem 6.1(2) can be relaxed so
$p\in \Lambda _{\ell }$
. Then the condition in Theorem 6.1(2) can be relaxed so
![]() $p\in \Lambda _l$
.
$p\in \Lambda _l$
.
Corollary 6.2. Let
![]() $\mu $
be a local equilibrium state of a
$\mu $
be a local equilibrium state of a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential, then
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential, then
![]() $\mu $
has a local product structure.
$\mu $
has a local product structure.
Proof. We show that every Pesin level set can be covered by finitely many disjoint small sets with a local product structure, on which the measure has a product structure. The proof is given in two steps. In the first step, we write
![]() $\mu $
as the projection of an equilibrium state of a specifically chosen maximal irreducible component of
$\mu $
as the projection of an equilibrium state of a specifically chosen maximal irreducible component of
![]() $\widehat {\Sigma }$
. The second step is to use the first step to show the local product structure.
$\widehat {\Sigma }$
. The second step is to use the first step to show the local product structure.
Step 1. Recall Definition 3.14, and let
![]() $\langle R\rangle $
be the equivalence class of
$\langle R\rangle $
be the equivalence class of
![]() $R\in \mathcal {R}$
with respect to
$R\in \mathcal {R}$
with respect to
![]() $\sim $
, whenever
$\sim $
, whenever
![]() $\text {there exists } n$
such that
$\text {there exists } n$
such that
![]() $f^{-n}[R]\cap R\neq \varnothing $
. Write
$f^{-n}[R]\cap R\neq \varnothing $
. Write
![]() , and note that
, and note that
![]() $\Lambda _{\langle R\rangle } $
is f-invariant. In addition, there exist at most countably many different such sets, which exhaust all invariant probability measures which are carried by
$\Lambda _{\langle R\rangle } $
is f-invariant. In addition, there exist at most countably many different such sets, which exhaust all invariant probability measures which are carried by
![]() $\mathrm {RWT}_\chi $
. Therefore,
$\mathrm {RWT}_\chi $
. Therefore,
![]() $\text {there exists } R\in \mathcal {R}$
such that
$\text {there exists } R\in \mathcal {R}$
such that
![]() $\mu (\Lambda _{\langle R\rangle })=1$
.
$\mu (\Lambda _{\langle R\rangle })=1$
.
Recall Definition 3.21. Let
![]() $\widetilde {\Sigma }:=\langle R\rangle ^{\mathbb {Z}}\cap \widehat {\Sigma }$
, and note that
$\widetilde {\Sigma }:=\langle R\rangle ^{\mathbb {Z}}\cap \widehat {\Sigma }$
, and note that
![]() $\mu \circ \underline {R}^{-1}$
is a shift-invariant probability measure on
$\mu \circ \underline {R}^{-1}$
is a shift-invariant probability measure on
![]() $\widetilde {\Sigma }$
, which is carried by
$\widetilde {\Sigma }$
, which is carried by
![]() $\widetilde {\Sigma }\cap \widehat {\Sigma }^\circ $
(recall Definition 3.18). Moreover, one can check that
$\widetilde {\Sigma }\cap \widehat {\Sigma }^\circ $
(recall Definition 3.18). Moreover, one can check that
![]() $\mu \circ \underline {R}^{-1}$
is an equilibrium state for
$\mu \circ \underline {R}^{-1}$
is an equilibrium state for
![]() $\phi $
, where
$\phi $
, where
![]() $\mu $
is a local equilibrium state for
$\mu $
is a local equilibrium state for
![]() $\varphi $
, and
$\varphi $
, and
![]() $\phi $
is given by Theorem 4.4. Therefore,
$\phi $
is given by Theorem 4.4. Therefore,
![]() $\phi $
is positive recurrent on
$\phi $
is positive recurrent on
![]() $\widetilde {\Sigma }_L$
, and as in Theorem 6.1,
$\widetilde {\Sigma }_L$
, and as in Theorem 6.1,
![]() $\mu \circ \underline {R}^{-1}=\int _{\widetilde {\Sigma }_L}\widehat {\nu }_{\underline {S}}\,dq(\underline {S})$
, where q is a
$\mu \circ \underline {R}^{-1}=\int _{\widetilde {\Sigma }_L}\widehat {\nu }_{\underline {S}}\,dq(\underline {S})$
, where q is a
![]() $\phi $
-conformal measure on
$\phi $
-conformal measure on
![]() $\widetilde {\Sigma }_L$
. Thus, in particular, q is carried by
$\widetilde {\Sigma }_L$
. Thus, in particular, q is carried by
![]() $\widetilde {\Sigma }_L^\circ :=\widetilde {\Sigma }_L\cap \widehat {\Sigma }^\circ _L$
and
$\widetilde {\Sigma }_L^\circ :=\widetilde {\Sigma }_L\cap \widehat {\Sigma }^\circ _L$
and
![]() $\widehat {\nu }_{\underline {S}}$
is carried by
$\widehat {\nu }_{\underline {S}}$
is carried by
![]() $\widetilde {\Sigma }^\circ :=\widetilde {\Sigma }\cap \widehat {\Sigma }^\circ $
for q-a.e.
$\widetilde {\Sigma }^\circ :=\widetilde {\Sigma }\cap \widehat {\Sigma }^\circ $
for q-a.e.
![]() $\underline {S}\in \widetilde {\Sigma }_L^\circ $
.
$\underline {S}\in \widetilde {\Sigma }_L^\circ $
.
Step 2. Let K be a Pesin level set such that
![]() $\mu (K)>0$
. We cover K mod
$\mu (K)>0$
. We cover K mod
![]() $\mu $
by finitely many partition elements
$\mu $
by finitely many partition elements
![]() $\{R_i\}_{i=1,\ldots ,N}$
where
$\{R_i\}_{i=1,\ldots ,N}$
where
![]() $R_i\in \langle R\rangle $
. We show that for (without loss of generality)
$R_i\in \langle R\rangle $
. We show that for (without loss of generality)
![]() $R:=R_1$
,
$R:=R_1$
,
![]() $\mu |_{R}$
has a product structure.
$\mu |_{R}$
has a product structure.
First, note that
![]() $\mu =\int _{\widetilde {\Sigma }_L^\circ } \widehat {\nu }_{\underline {S}}\circ \widehat {\pi }^{-1}\,dq(\underline {S})$
, and so for q-a.e.
$\mu =\int _{\widetilde {\Sigma }_L^\circ } \widehat {\nu }_{\underline {S}}\circ \widehat {\pi }^{-1}\,dq(\underline {S})$
, and so for q-a.e.
![]() $\underline {R}\in \widetilde {\Sigma }_L^\circ $
, if
$\underline {R}\in \widetilde {\Sigma }_L^\circ $
, if
![]() $\widehat {\nu }_{\underline {R}}\circ \widehat {\pi }^{-1} (\widehat {\pi }[\tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }^\circ ])>0$
, then
$\widehat {\nu }_{\underline {R}}\circ \widehat {\pi }^{-1} (\widehat {\pi }[\tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }^\circ ])>0$
, then
![]() $\text {there exists } \underline {S}^\pm \in \tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }^\circ $
and
$\text {there exists } \underline {S}^\pm \in \tau ^{-1}[\{\underline {S}\}]\cap \widetilde {\Sigma }^\circ $
and
![]() $\underline {R}^\pm \in \tau ^{-1}[\{\underline {R}\}]\cap \widetilde {\Sigma }^\circ $
such that
$\underline {R}^\pm \in \tau ^{-1}[\{\underline {R}\}]\cap \widetilde {\Sigma }^\circ $
such that
![]() $\widehat {\pi }(\underline {R}^\pm )= \widehat {\pi }(\underline {S}^\pm )$
; whence
$\widehat {\pi }(\underline {R}^\pm )= \widehat {\pi }(\underline {S}^\pm )$
; whence
![]() $\underline {S}^\pm =\underline {R}^\pm $
, and so
$\underline {S}^\pm =\underline {R}^\pm $
, and so
![]() $\underline {S}=\underline {R}$
.
$\underline {S}=\underline {R}$
.
Therefore,
![]() $\mu =\sum _{S\in \langle R\rangle }\int _{[S]\cap \widetilde {\Sigma }_L^\circ }\widehat {\nu }_{\underline {S}}\circ \widehat {\pi }^{-1} \,dq(\underline {S})$
, where the sum is over mutually singular measures. Then
$\mu =\sum _{S\in \langle R\rangle }\int _{[S]\cap \widetilde {\Sigma }_L^\circ }\widehat {\nu }_{\underline {S}}\circ \widehat {\pi }^{-1} \,dq(\underline {S})$
, where the sum is over mutually singular measures. Then
![]() $\mu |_R= \int _{[R]\cap \widetilde {\Sigma }_L^\circ }\widehat {\nu }_{\underline {S}}\circ \widehat {\pi }^{-1} \,dq(\underline {S})$
is given by its disintegration into mutually singular measures on local unstable leaves. By Theorem 5.7,
$\mu |_R= \int _{[R]\cap \widetilde {\Sigma }_L^\circ }\widehat {\nu }_{\underline {S}}\circ \widehat {\pi }^{-1} \,dq(\underline {S})$
is given by its disintegration into mutually singular measures on local unstable leaves. By Theorem 5.7,
![]() $\mu |_R$
has a product structure.
$\mu |_R$
has a product structure.
6.2 Ledrappier–Young property for hyperbolic equilibrium states
In the celebrated results of [Reference Ledrappier and YoungLY85a, Reference Ledrappier and YoungLY85b], Ledrappier and Young prove a general formula for the entropy of invariant probability measures of diffeomorphisms in terms of the local dimensions of their conditional measures. One very important application of their theory is the characterization of SRB measures as those which satisfy Pesin’s entropy formula, extending the previous same result of Ledrappier for hyperbolic SRB measures [Reference LedrappierLed84]. That is, an ergodic and hyperbolic invariant probability measure,
![]() $\mu $
, which satisfies the following two properties must have conditional measures on unstable local manifolds which are absolutely continuous with respect to the induced Riemannian volume measure. Let
$\mu $
, which satisfies the following two properties must have conditional measures on unstable local manifolds which are absolutely continuous with respect to the induced Riemannian volume measure. Let
![]() $\varphi (x):= -\log \mathrm {Jac}(d_xf|_{H^u(x)}):\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
(the geometric potential), then:
$\varphi (x):= -\log \mathrm {Jac}(d_xf|_{H^u(x)}):\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
(the geometric potential), then:
-
(1) we have
where the geometric potential in the integrand is well defined almost everywhere for every hyperbolic invariant probability measure; $$ \begin{align*}h_{\mu}(f)+\int \varphi \,d\mu=\sup\bigg\{h_{\nu}(f)+\int \varphi \,d\nu: \nu\text{ is an} \begin{array}{ll} \text{erg.}\\ \text{hyp.}\\ f\text{-inv.}\end{array}\text{prob.}\bigg\},\end{align*} $$
$$ \begin{align*}h_{\mu}(f)+\int \varphi \,d\mu=\sup\bigg\{h_{\nu}(f)+\int \varphi \,d\nu: \nu\text{ is an} \begin{array}{ll} \text{erg.}\\ \text{hyp.}\\ f\text{-inv.}\end{array}\text{prob.}\bigg\},\end{align*} $$
-
(2)
 $\sup \{h_{\nu }(f)+\int \varphi \,d\nu : \nu \text { is an erg. hyp. } f\text {-inv. prob.}\}=0$
.
$\sup \{h_{\nu }(f)+\int \varphi \,d\nu : \nu \text { is an erg. hyp. } f\text {-inv. prob.}\}=0$
.
Note that
![]() $P_G(\phi |_{\widetilde {\Sigma }_L})\leq 0$
is always true, because of the Ruelle–Margulis inequality [Reference RuelleRue78]. The fact that SRB measures satisfy items (1), (2) is due to Ledrappier and Strelcyn [Reference Ledrappier and StrelcynLS82]. A different way to write this characterization, is the following. Let
$P_G(\phi |_{\widetilde {\Sigma }_L})\leq 0$
is always true, because of the Ruelle–Margulis inequality [Reference RuelleRue78]. The fact that SRB measures satisfy items (1), (2) is due to Ledrappier and Strelcyn [Reference Ledrappier and StrelcynLS82]. A different way to write this characterization, is the following. Let
![]() $\mu $
be an ergodic hyperbolic invariant probability measure. Then
$\mu $
be an ergodic hyperbolic invariant probability measure. Then
![]() $\mu $
is an SRB measure if and only if:
$\mu $
is an SRB measure if and only if:
-
(1)
 $\phi $
is positive recurrent when lifted to an irreducible component
$\phi $
is positive recurrent when lifted to an irreducible component
 $\widetilde {\Sigma }_L\subseteq \widehat {\Sigma }_L$
(see §4.2), where
$\widetilde {\Sigma }_L\subseteq \widehat {\Sigma }_L$
(see §4.2), where
 $\phi $
is given by Theorem 4.4 applied to
$\phi $
is given by Theorem 4.4 applied to
 $\varphi (x) $
;
$\varphi (x) $
; -
(2)
 $P_G(\phi |_{\widetilde {\Sigma }_L})=0$
.
$P_G(\phi |_{\widetilde {\Sigma }_L})=0$
.
It follows that conditions (1) and (2) above are satisfied
![]() $\Leftrightarrow \mu _{V^u}\ll m_{V^u}$
, where
$\Leftrightarrow \mu _{V^u}\ll m_{V^u}$
, where
![]() $\mu _{V^u}$
is a conditional measure of
$\mu _{V^u}$
is a conditional measure of
![]() $\mu $
with respect to a measurable partition of local unstable leaves
$\mu $
with respect to a measurable partition of local unstable leaves
![]() $\{V^u\}$
, and
$\{V^u\}$
, and
![]() $m_{V^u}$
is the induced Riemannian volume of
$m_{V^u}$
is the induced Riemannian volume of
![]() $V^u$
(the conformal measure of the geometric potential
$V^u$
(the conformal measure of the geometric potential
![]() $\varphi $
on
$\varphi $
on
![]() $V^u$
).
$V^u$
).
In this section, we extend this result by replacing the geometric potential
![]() $\varphi $
by a general potential which is
$\varphi $
by a general potential which is
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
, and by replacing the induced Riemannian volume
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
, and by replacing the induced Riemannian volume
![]() $m_{V^u}$
by any
$m_{V^u}$
by any
![]() $\varphi $
-conformal family. We obtain a new proof different to that of Ledrappier in the hyperbolic case [Reference LedrappierLed84], and to that of Ledrappier and Young in the general case [Reference Ledrappier and YoungLY85a].
$\varphi $
-conformal family. We obtain a new proof different to that of Ledrappier in the hyperbolic case [Reference LedrappierLed84], and to that of Ledrappier and Young in the general case [Reference Ledrappier and YoungLY85a].
Theorem 6.3. Let M be a compact Riemannian manifold without boundary, and of dimension
![]() $d\geq 2$
. Let
$d\geq 2$
. Let
![]() $f\in \mathrm {Diff}^{1+\beta }(M)$
,
$f\in \mathrm {Diff}^{1+\beta }(M)$
,
![]() $\beta>0$
, let
$\beta>0$
, let
![]() $\chi>0$
and
$\chi>0$
and
![]() $\epsilon =\epsilon _\chi>0$
as in Lemma 2.6. Let
$\epsilon =\epsilon _\chi>0$
as in Lemma 2.6. Let
![]() $\varphi :WT_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
$\varphi :WT_\chi ^\epsilon \rightarrow \mathbb {R}$
be a
![]() ${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential (recall Definition 2.10). Let q be a
${Grassmann}\text{--} {H}\ddot{{o}}{lder\ continuous}$
potential (recall Definition 2.10). Let q be a
![]() $\chi $
-hyperbolic periodic point. Assume that
$\chi $
-hyperbolic periodic point. Assume that
![]() $H_\chi (q)$
admits a (unique)
$H_\chi (q)$
admits a (unique)
![]() $\chi $
-hyperbolic equilibrium state of
$\chi $
-hyperbolic equilibrium state of
![]() $\varphi $
,
$\varphi $
,
![]() $\nu $
. For any family of conditional measures as in Theorem 6.1,
$\nu $
. For any family of conditional measures as in Theorem 6.1,
![]() $\mathcal {F}_{H_\chi (q)}(\varphi )$
, there is a sub-family
$\mathcal {F}_{H_\chi (q)}(\varphi )$
, there is a sub-family
![]() $\mathcal {F}'$
which disintegrates
$\mathcal {F}'$
which disintegrates
![]() $\nu $
as in Theorem 6.1, and for which the following holds. Fix
$\nu $
as in Theorem 6.1, and for which the following holds. Fix
![]() $\mu \in \mathcal {F} '$
which is carried by a local unstable leaf
$\mu \in \mathcal {F} '$
which is carried by a local unstable leaf
![]() $V^u$
. Assume that
$V^u$
. Assume that
![]() $H_\chi (q)$
admits a
$H_\chi (q)$
admits a
![]() $\varphi $
-conformal system of measures
$\varphi $
-conformal system of measures
![]() $\mathcal {C}:=\{m^\varphi _{W^u}:W^u\text { is a local unstable leaf of }H_\chi (q)\}$
. Then,
$\mathcal {C}:=\{m^\varphi _{W^u}:W^u\text { is a local unstable leaf of }H_\chi (q)\}$
. Then,
![]() $\mu \ll m^\varphi _{V^u}$
. In particular,
$\mu \ll m^\varphi _{V^u}$
. In particular,
![]() $m_{V^u}^\varphi $
gives a positive measure to
$m_{V^u}^\varphi $
gives a positive measure to
![]() $\mathrm {RWT}_\chi ^{\mathrm {PR}}$
.
$\mathrm {RWT}_\chi ^{\mathrm {PR}}$
.
Proof. Let
![]() $\phi :\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be given by Theorem 4.4. As in the proof of Theorem 5.7, let
$\phi :\mathrm {RWT}_\chi \rightarrow \mathbb {R}$
be given by Theorem 4.4. As in the proof of Theorem 5.7, let
![]() $\widetilde {\Sigma }$
be a maximal irreducible component of
$\widetilde {\Sigma }$
be a maximal irreducible component of
![]() $\widehat {\Sigma }$
such that
$\widehat {\Sigma }$
such that
![]() $\widehat {\pi }[\widetilde {\Sigma }^\#]=H_\chi (q)$
modulo conservative measures; and write
$\widehat {\pi }[\widetilde {\Sigma }^\#]=H_\chi (q)$
modulo conservative measures; and write
![]() $\mathcal {F}_{H_\chi (q)}(\varphi )=\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
.
$\mathcal {F}_{H_\chi (q)}(\varphi )=\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L}$
.
Denote the lift of
![]() $\nu $
to
$\nu $
to
![]() $\widetilde {\Sigma }$
by
$\widetilde {\Sigma }$
by
![]() $\widehat {\nu }$
. As in the proof of Theorem 6.1,
$\widehat {\nu }$
. As in the proof of Theorem 6.1,
![]() $\phi $
is positive recurrent on
$\phi $
is positive recurrent on
![]() $\widetilde {\Sigma }$
and
$\widetilde {\Sigma }$
and
![]() $\widehat {\nu }=\int _{\widetilde {\Sigma }_L}\widehat {\mu }_{\underline {R}}\,dp(\underline {R})$
, where p is the unique (up to scaling)
$\widehat {\nu }=\int _{\widetilde {\Sigma }_L}\widehat {\mu }_{\underline {R}}\,dp(\underline {R})$
, where p is the unique (up to scaling)
![]() $\phi $
-conformal measure on
$\phi $
-conformal measure on
![]() $\widetilde {\Sigma }_L$
. In [Reference SarigSar99], Sarig showed that when
$\widetilde {\Sigma }_L$
. In [Reference SarigSar99], Sarig showed that when
![]() $\phi $
is positive recurrent, p is conservative, and is carried by
$\phi $
is positive recurrent, p is conservative, and is carried by
![]() $\widetilde {\Sigma }_L^\#$
. Set
$\widetilde {\Sigma }_L^\#$
. Set
![]() $ \mathcal {F}':=\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L^\#}$
. Write
$ \mathcal {F}':=\{\mu _{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }_L^\#}$
. Write
![]() $\mu =\mu _{\underline {R}}$
, where
$\mu =\mu _{\underline {R}}$
, where
![]() $\underline {R}\in \widetilde {\Sigma }_L^\#$
. (Note that the absolute continuity of holonomies and the existence of a measure
$\underline {R}\in \widetilde {\Sigma }_L^\#$
. (Note that the absolute continuity of holonomies and the existence of a measure
![]() $\mu '\in \mathcal {F}'$
such that
$\mu '\in \mathcal {F}'$
such that
![]() $\mu '(\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
imply that also
$\mu '(\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
imply that also
![]() $\mu (\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
.) Let
$\mu (\mathrm {RWT}_\chi ^{\mathrm {PR}})>0$
.) Let
![]() $S\in \mathcal {R}$
be a symbol which repeats infinitely often in
$S\in \mathcal {R}$
be a symbol which repeats infinitely often in
![]() $\underline {R}$
.
$\underline {R}$
.
Let
![]() $K\in \mathbb {N}$
be
$K\in \mathbb {N}$
be
![]() $N(R_0)\cdot N(S)$
(see Definition 3.6). This is a bound on the number of sequences in
$N(R_0)\cdot N(S)$
(see Definition 3.6). This is a bound on the number of sequences in
![]() $\widehat {\Sigma }^\#$
which code the same point and such that this point can be coded by a sequence which has
$\widehat {\Sigma }^\#$
which code the same point and such that this point can be coded by a sequence which has
![]() $R_0$
repeat infinitely often in the future and S repeat infinitely often in the past (see [Reference Ben OvadiaBO18, Theorem 1.3]). Choose
$R_0$
repeat infinitely often in the future and S repeat infinitely often in the past (see [Reference Ben OvadiaBO18, Theorem 1.3]). Choose
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\underline {S},\underline {Q}\in \widetilde {\Sigma }_L$
such that
$\underline {S},\underline {Q}\in \widetilde {\Sigma }_L$
such that
![]() $\sigma _R^n\underline {S}=\sigma _R^n\underline {Q}=\underline {R} $
and
$\sigma _R^n\underline {S}=\sigma _R^n\underline {Q}=\underline {R} $
and
![]() $S_0=Q_0=R_0$
. Let
$S_0=Q_0=R_0$
. Let
![]() $\underline {S}^\pm ,\underline {Q}^\pm \in \widetilde {\Sigma } $
which return to
$\underline {S}^\pm ,\underline {Q}^\pm \in \widetilde {\Sigma } $
which return to
![]() $[R_0]$
infinitely often in the future and such that
$[R_0]$
infinitely often in the future and such that
![]() $S^\pm _i=S_i,\text { for all } i\leq 0$
and
$S^\pm _i=S_i,\text { for all } i\leq 0$
and
![]() $Q^\pm _i=Q_i, \text { for all } i\leq 0$
. Define
$Q^\pm _i=Q_i, \text { for all } i\leq 0$
. Define
![]() $x:=\widehat {\pi }(\underline {S}^\pm ),y:=\widehat {\pi }(\underline {Q}^\pm ),z:=\widehat {\pi }([\underline {S}^\pm ,\underline {Q}^\pm ]_{R_0})$
, where
$x:=\widehat {\pi }(\underline {S}^\pm ),y:=\widehat {\pi }(\underline {Q}^\pm ),z:=\widehat {\pi }([\underline {S}^\pm ,\underline {Q}^\pm ]_{R_0})$
, where
![]() $[\underline {S}^\pm ,\underline {Q}^\pm ]_R$
is the Smale bracket of
$[\underline {S}^\pm ,\underline {Q}^\pm ]_R$
is the Smale bracket of
![]() $\underline {S}^\pm $
and
$\underline {S}^\pm $
and
![]() $ \underline {Q}^\pm $
in
$ \underline {Q}^\pm $
in
![]() $[R_0]$
. If
$[R_0]$
. If
![]() $V^u(\underline {S})\cap V^u(\underline {Q}) \neq \varnothing $
, then by [Reference Ben OvadiaBO18, Proposition 3.12],
$V^u(\underline {S})\cap V^u(\underline {Q}) \neq \varnothing $
, then by [Reference Ben OvadiaBO18, Proposition 3.12],
![]() $x=z=y$
.
$x=z=y$
.
Then for each
![]() $\underline {S}\in \widetilde {\sigma }_R^{-n}[\{\underline {R}\}]\cap [R_0]$
, the number of
$\underline {S}\in \widetilde {\sigma }_R^{-n}[\{\underline {R}\}]\cap [R_0]$
, the number of
![]() $\underline {Q}\in \widetilde {\sigma }_R^{-n}[\{\underline {R}\}]\cap [R_0]$
such that
$\underline {Q}\in \widetilde {\sigma }_R^{-n}[\{\underline {R}\}]\cap [R_0]$
such that
![]() $V^u(\underline {S})\cap V^u(\underline {Q})\neq \varnothing $
is bounded by K. That is,
$V^u(\underline {S})\cap V^u(\underline {Q})\neq \varnothing $
is bounded by K. That is,
Define on
![]() $V^u(\underline {R})$
the density function
$V^u(\underline {R})$
the density function
![]() , then for any
, then for any
![]() $n\geq 1$
,
$n\geq 1$
,
Let
![]() $c_{R_0}:=\min \{\sup \{m_{V^u(\underline {R}')}^\varphi (1):\underline {R}'\in [R_0]\}^{-1},\inf \{m_{V^u(\underline {R}')}^\varphi (1):\underline {R}'\in [R_0]\}\}$
. This is positive by the continuity of
$c_{R_0}:=\min \{\sup \{m_{V^u(\underline {R}')}^\varphi (1):\underline {R}'\in [R_0]\}^{-1},\inf \{m_{V^u(\underline {R}')}^\varphi (1):\underline {R}'\in [R_0]\}\}$
. This is positive by the continuity of
![]() $\mathcal {C}$
, since
$\mathcal {C}$
, since
![]() $[R_0]$
is compact and
$[R_0]$
is compact and
![]() $\underline {R}'\mapsto V^u(\underline {R}')$
is continuous in
$\underline {R}'\mapsto V^u(\underline {R}')$
is continuous in
![]() $C^1$
-norm (see Definition 2.15).
$C^1$
-norm (see Definition 2.15).
Let
![]() $g\in C(V^u(\underline {R}))$
such that g is L-Lipschitz, and
$g\in C(V^u(\underline {R}))$
such that g is L-Lipschitz, and
![]() $\|g\|_\infty \leq 1$
. Write
$\|g\|_\infty \leq 1$
. Write
![]() $\widehat {g}:=g\circ \widehat {\pi }$
, and so
$\widehat {g}:=g\circ \widehat {\pi }$
, and so
![]() $\mu _{\underline {R}}(g)=\widehat {\mu }_{\underline {R}}(\widehat {g})$
. Let
$\mu _{\underline {R}}(g)=\widehat {\mu }_{\underline {R}}(\widehat {g})$
. Let

Note that
![]() $|\widehat {\omega }_n|\leq 1$
. By Birkhoff’s ergodic theorem, and the absolute continuity of
$|\widehat {\omega }_n|\leq 1$
. By Birkhoff’s ergodic theorem, and the absolute continuity of
![]() $\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }}$
with respect to holonomies (see Corollary 5.2), for
$\{\widehat {\mu }_{\underline {R}}\}_{\underline {R}\in \widetilde {\Sigma }}$
with respect to holonomies (see Corollary 5.2), for
![]() $\widehat {\mu }_{\underline {R}}$
-a.e.
$\widehat {\mu }_{\underline {R}}$
-a.e.
![]() $\underline {R}^\pm $
,
$\underline {R}^\pm $
,
![]() $\widehat {\omega }_n(\underline {R}^\pm )\xrightarrow [n\rightarrow \infty ]{}\widehat {\nu }([R_0])$
, and so
$\widehat {\omega }_n(\underline {R}^\pm )\xrightarrow [n\rightarrow \infty ]{}\widehat {\nu }([R_0])$
, and so
![]() $\widehat {g}(\underline {R}^\pm )\cdot \widehat {\omega }_n(\underline {R}^\pm )\xrightarrow [n\rightarrow \infty ]{}\widehat {\nu }([R_0])\cdot \widehat {g}(\underline {R}^\pm )$
. Then, by Lebesgue’s dominated convergence theorem,
$\widehat {g}(\underline {R}^\pm )\cdot \widehat {\omega }_n(\underline {R}^\pm )\xrightarrow [n\rightarrow \infty ]{}\widehat {\nu }([R_0])\cdot \widehat {g}(\underline {R}^\pm )$
. Then, by Lebesgue’s dominated convergence theorem,
Since
![]() $\widehat {\pi }$
is Hölder continuous, and g is L-Lipschitz,
$\widehat {\pi }$
is Hölder continuous, and g is L-Lipschitz,
![]() $\widehat {g}$
is Hölder continuous as well. Let
$\widehat {g}$
is Hölder continuous as well. Let
![]() $H_L>0, \theta \in (0,1)$
such that
$H_L>0, \theta \in (0,1)$
such that
![]() $d(\underline {R}^\pm ,\underline {S}^\pm )\leq e^{-n}\Rightarrow |\widehat {g}(\underline {R}^\pm )-\widehat {g}(\underline {S}^\pm )|\leq H_L\cdot \theta ^n$
.
$d(\underline {R}^\pm ,\underline {S}^\pm )\leq e^{-n}\Rightarrow |\widehat {g}(\underline {R}^\pm )-\widehat {g}(\underline {S}^\pm )|\leq H_L\cdot \theta ^n$
.
For every
![]() $ n\geq 1$
and
$ n\geq 1$
and
![]() $ \underline {S}\in \widetilde {\Sigma }_L$
such that
$ \underline {S}\in \widetilde {\Sigma }_L$
such that
![]() $\sigma _R^n\underline {S}=\underline {R}$
, fix
$\sigma _R^n\underline {S}=\underline {R}$
, fix
![]() $\underline {S}^\pm \in \widetilde {\Sigma }$
such that
$\underline {S}^\pm \in \widetilde {\Sigma }$
such that
![]() $S^\pm _i=S_i \text { for all } i\leq 0$
. By [Reference Ben OvadiaBO18, Proposition 4.4],
$S^\pm _i=S_i \text { for all } i\leq 0$
. By [Reference Ben OvadiaBO18, Proposition 4.4],
where
![]() $\mathrm {diam}_{V^u(\underline {R})}$
denotes the diameter with respect to the induced Riemannian metric on
$\mathrm {diam}_{V^u(\underline {R})}$
denotes the diameter with respect to the induced Riemannian metric on
![]() $V^u(\underline {R})$
.
$V^u(\underline {R})$
.
Let
![]() $\underline {W}=(R_0,W_1,\ldots ,W_{n-2},R_0)$
be an admissible word of length
$\underline {W}=(R_0,W_1,\ldots ,W_{n-2},R_0)$
be an admissible word of length
![]() $n\geq 1$
. We estimate
$n\geq 1$
. We estimate
![]() $\widehat {\mu }_{\underline {R}}([\underline {W}])$
. First, we write
$\widehat {\mu }_{\underline {R}}([\underline {W}])$
. First, we write
![]() $[\underline {W}]= \sigma ^{-n}\sigma ^n[\underline {W}] $
. Next, by Corollary 5.5,
$[\underline {W}]= \sigma ^{-n}\sigma ^n[\underline {W}] $
. Next, by Corollary 5.5,
 $$ \begin{align*} \widehat{\mu}_{\underline{R}}([\underline{W}]) &= \widehat{\mu}_{\underline{R}}(\sigma^{-n}\sigma^n[\underline{W}])= e^{-n P_{G}(\phi)}\sum_{\widetilde{\sigma}_R^n\underline{S}=\underline{R}}e^{\phi_n(\underline{S})}\widehat{\mu}_{\underline{S}} (\sigma^n[\underline{W}])\\ &= e^{-n P_{G}(\phi)+\phi_n(\underline{R} \cdot \underline{W})}\widehat{\mu}_{\underline{R} \cdot\underline{W}} (1) , \end{align*} $$
$$ \begin{align*} \widehat{\mu}_{\underline{R}}([\underline{W}]) &= \widehat{\mu}_{\underline{R}}(\sigma^{-n}\sigma^n[\underline{W}])= e^{-n P_{G}(\phi)}\sum_{\widetilde{\sigma}_R^n\underline{S}=\underline{R}}e^{\phi_n(\underline{S})}\widehat{\mu}_{\underline{S}} (\sigma^n[\underline{W}])\\ &= e^{-n P_{G}(\phi)+\phi_n(\underline{R} \cdot \underline{W})}\widehat{\mu}_{\underline{R} \cdot\underline{W}} (1) , \end{align*} $$
where
![]() $\cdot $
denotes an admissible concatenation. Recall that
$\cdot $
denotes an admissible concatenation. Recall that
![]() $\widehat {\mu }_{\underline {R}'}(1)=\psi (\underline {R}')$
, where
$\widehat {\mu }_{\underline {R}'}(1)=\psi (\underline {R}')$
, where
![]() $\psi $
is the unique (up to scaling)
$\psi $
is the unique (up to scaling)
![]() $\phi $
-harmonic function on
$\phi $
-harmonic function on
![]() $\widetilde {\Sigma }_L$
. Then for
$\widetilde {\Sigma }_L$
. Then for
![]() $C_{R_0}:=\max _{[R_0]}\{\psi ,\psi ^{-1}\}$
,
$C_{R_0}:=\max _{[R_0]}\{\psi ,\psi ^{-1}\}$
,
Since
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $\varphi $
-conformal family, we get that for all
$\varphi $
-conformal family, we get that for all
![]() $n\geq 1$
and for every
$n\geq 1$
and for every
![]() $ \underline {S}\in \widetilde {\sigma }_R^{-n}[\{\underline {R}\}]$
,
$ \underline {S}\in \widetilde {\sigma }_R^{-n}[\{\underline {R}\}]$
,
We wish to estimate
![]() $\varphi _n(\cdot )$
on
$\varphi _n(\cdot )$
on
![]() $V^u(\underline {S})$
. For that, we need the non-trivial fact that
$V^u(\underline {S})$
. For that, we need the non-trivial fact that
![]() $d_{\mathrm {TM}}(f^{-i}(x),f^{-i}(y))$
decreases exponentially fast in
$d_{\mathrm {TM}}(f^{-i}(x),f^{-i}(y))$
decreases exponentially fast in
![]() $i\geq 0$
. This is true since
$i\geq 0$
. This is true since
![]() $V^u(\underline {S})$
is contained in the graph of a function with a Hölder continuous derivative (and
$V^u(\underline {S})$
is contained in the graph of a function with a Hölder continuous derivative (and
![]() $d(f^{-i}(x),f^{-i}(y))\leq 4e^{-({\chi }/{2})i}$
), and the Hölder constant and exponent do not depend on the choice of
$d(f^{-i}(x),f^{-i}(y))\leq 4e^{-({\chi }/{2})i}$
), and the Hölder constant and exponent do not depend on the choice of
![]() $\underline {S}\in [R_0]$
. For more details, see [Reference Ben OvadiaBO18, Definition 3.1]. Thus, since
$\underline {S}\in [R_0]$
. For more details, see [Reference Ben OvadiaBO18, Definition 3.1]. Thus, since
![]() $\varphi $
is
$\varphi $
is
![]() $\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
, we get that
$\text{Grassmann}\text{--} \text{H}\ddot{\text{o}}\text{lder continuous}$
, we get that
![]() $\text {there exists } C_\varphi>0$
such that
$\text {there exists } C_\varphi>0$
such that
![]() $\text {for all } x,y\in V^u(\underline {S})$
,
$\text {for all } x,y\in V^u(\underline {S})$
,
![]() $\sup _{n'\geq 0}|\varphi _{n'}(x)-\varphi _{n'}(y)|\leq C_\varphi $
. Using the fact that
$\sup _{n'\geq 0}|\varphi _{n'}(x)-\varphi _{n'}(y)|\leq C_\varphi $
. Using the fact that
![]() $V^u(\underline {S})$
contains a point with a coding in
$V^u(\underline {S})$
contains a point with a coding in
![]() $\widetilde {\Sigma }^\#$
, together with Theorem 4.4, where
$\widetilde {\Sigma }^\#$
, together with Theorem 4.4, where
![]() $\varphi =\phi +A-A\circ f^{-1}$
with
$\varphi =\phi +A-A\circ f^{-1}$
with
![]() $\|A\|_\infty <\infty $
, we get for all
$\|A\|_\infty <\infty $
, we get for all
![]() $n\geq 1$
,
$n\geq 1$
,
 $$ \begin{align} m^\varphi_{V^u(\underline{R})}(f^{-n}[V^u(\underline{S})])&=e^{\pm (C_\varphi+2\|A\|)}e^{\phi_n(\underline{S})-nP_{H_\chi(q)}(\varphi)}\cdot m_{V^u(\underline{S})}(1)\nonumber\\&= (c_{R_0}^{-1}e^{C_\varphi+2\|A\|})^{\pm1}e^{\phi_n(\underline{S})-nP_G(\phi)}. \end{align} $$
$$ \begin{align} m^\varphi_{V^u(\underline{R})}(f^{-n}[V^u(\underline{S})])&=e^{\pm (C_\varphi+2\|A\|)}e^{\phi_n(\underline{S})-nP_{H_\chi(q)}(\varphi)}\cdot m_{V^u(\underline{S})}(1)\nonumber\\&= (c_{R_0}^{-1}e^{C_\varphi+2\|A\|})^{\pm1}e^{\phi_n(\underline{S})-nP_G(\phi)}. \end{align} $$
In the last equality, we used the fact that
![]() $P_{G}(\phi )=P_{H_\chi (q)}(\varphi )$
(recall equation (2)).
$P_{G}(\phi )=P_{H_\chi (q)}(\varphi )$
(recall equation (2)).
The last identity we need before the main computation of the proof is the following: for any
![]() $n\geq 1$
,
$n\geq 1$
,

On the left-hand side,
![]() acts as a density for
acts as a density for
![]() $\widehat {\mu }_{\underline {R}}$
, and on the right-hand side,
$\widehat {\mu }_{\underline {R}}$
, and on the right-hand side,
![]() $\widehat {\mu }_{\underline {R}}|_{[\underline {W}]}$
is the restriction of the measure to the respective cylinder.
$\widehat {\mu }_{\underline {R}}|_{[\underline {W}]}$
is the restriction of the measure to the respective cylinder.
We are now able to use the estimates and identities from equations (12), (15), (16), (17), and (18) to get
![]() $\text {for all } n\geq 1$
,
$\text {for all } n\geq 1$
,

Write
![]() $\theta _1:=\max \{\theta ,e^{-{\chi }/{2}}\} \in (0,1)$
,
$\theta _1:=\max \{\theta ,e^{-{\chi }/{2}}\} \in (0,1)$
,
![]() $\widetilde {C}_{R_0}:=4 e^{C_\varphi +2\|A\|}c_{R_0}^{-1}C_{R_0}\cdot \sum _{k\geq 0}\theta _1^k<\infty $
. Thus,
$\widetilde {C}_{R_0}:=4 e^{C_\varphi +2\|A\|}c_{R_0}^{-1}C_{R_0}\cdot \sum _{k\geq 0}\theta _1^k<\infty $
. Thus,
![]() $\text {for all } n\geq 1$
,
$\text {for all } n\geq 1$
,
By summing and averaging equation (19) N times, and by equation (14) (recall the definition of
![]() $\widehat {\omega }_N$
in equation (13)),
$\widehat {\omega }_N$
in equation (13)),
 $$ \begin{align*} K\cdot m_{V^u(\underline{R})}^\varphi(g)&\geq\frac{1}{N}\sum_{n=1}^{N}(\rho_n\cdot m_{V^u(\underline{R})}^\varphi)(g)= \pm\frac{1}{N}2LK\cdot H_L\cdot\widetilde{C}_{R_0}\\ &\quad+\widetilde{C}_{R_0}^{\pm1}\cdot\widehat{\mu}_{\underline{R}}(\widehat{\omega}_N\widehat{g})\xrightarrow[N\rightarrow\infty]{} \widehat{\nu}([R_0])\widetilde{C}_{R_0}^{\pm1}\mu_{\underline{R}}(g). \end{align*} $$
$$ \begin{align*} K\cdot m_{V^u(\underline{R})}^\varphi(g)&\geq\frac{1}{N}\sum_{n=1}^{N}(\rho_n\cdot m_{V^u(\underline{R})}^\varphi)(g)= \pm\frac{1}{N}2LK\cdot H_L\cdot\widetilde{C}_{R_0}\\ &\quad+\widetilde{C}_{R_0}^{\pm1}\cdot\widehat{\mu}_{\underline{R}}(\widehat{\omega}_N\widehat{g})\xrightarrow[N\rightarrow\infty]{} \widehat{\nu}([R_0])\widetilde{C}_{R_0}^{\pm1}\mu_{\underline{R}}(g). \end{align*} $$
Since
![]() $\mathrm {Lip}(V^u(\underline {R}))$
is dense in
$\mathrm {Lip}(V^u(\underline {R}))$
is dense in
![]() $\|\cdot \|_\infty $
-norm in
$\|\cdot \|_\infty $
-norm in
![]() $C(V^u(\underline {R}))$
, by the Riesz–Kakutani–Markov representation theorem,
$C(V^u(\underline {R}))$
, by the Riesz–Kakutani–Markov representation theorem,
![]() $\mu _{\underline {R}}\leq \widehat {\nu }([R_0])^{-1}\cdot K\cdot \widetilde {C}_{R_0}\cdot m_{V^u(\underline {R})}^\varphi $
.
$\mu _{\underline {R}}\leq \widehat {\nu }([R_0])^{-1}\cdot K\cdot \widetilde {C}_{R_0}\cdot m_{V^u(\underline {R})}^\varphi $
.
Remarks. We make the following remarks.
-
(1) In fact, the proof shows that not only
 $\mu _{\underline {R}}\ll m_{V^u(\underline {R})}^\varphi $
, but that
$\mu _{\underline {R}}\ll m_{V^u(\underline {R})}^\varphi $
, but that
 $\mu _{\underline {R}}= (\widehat {\nu }([R_0])^{-1}\cdot K\cdot \widetilde {C}_{R_0})^{\pm 1} \!\cdot m_{V^u(\underline {R})}^\varphi |_{E_{\underline {R}}^{R_0}}$
, where
$\mu _{\underline {R}}= (\widehat {\nu }([R_0])^{-1}\cdot K\cdot \widetilde {C}_{R_0})^{\pm 1} \!\cdot m_{V^u(\underline {R})}^\varphi |_{E_{\underline {R}}^{R_0}}$
, where
 $E_{\underline {R}}^{R_0}:=\widehat {\pi }[\{\underline {R}^\pm \in \widetilde {\Sigma }\ {:}\ \text{for all } i\leq 0, R^\pm _i=R_i\text { and} \#\{j\geq 0:R^\pm _j=R_0\}=\infty \}] $
carries
$E_{\underline {R}}^{R_0}:=\widehat {\pi }[\{\underline {R}^\pm \in \widetilde {\Sigma }\ {:}\ \text{for all } i\leq 0, R^\pm _i=R_i\text { and} \#\{j\geq 0:R^\pm _j=R_0\}=\infty \}] $
carries
 $\mu _{\underline {R}}$
.
$\mu _{\underline {R}}$
. -
(2) In addition, the proof shows that the
 $\varphi $
-conformal family of measures is unique up to equivalence of the leaf measures, when restricted to sets like
$\varphi $
-conformal family of measures is unique up to equivalence of the leaf measures, when restricted to sets like
 $E_{\underline {R}}^{R_0}$
; and it works for a
$E_{\underline {R}}^{R_0}$
; and it works for a
 $\varphi $
-conformal family where the transformation law is not exactly
$\varphi $
-conformal family where the transformation law is not exactly
 $e^{\varphi _n-n\cdot P_{H_\chi (p)}(\varphi )}$
, but merely up to a multiplicative constant uniform in n.
$e^{\varphi _n-n\cdot P_{H_\chi (p)}(\varphi )}$
, but merely up to a multiplicative constant uniform in n.
Acknowledgements
I would like to thank the Eberly College of Science in the Pennsylvania State University for excellent working conditions. I am grateful to the referee who read this manuscript with care and who provided many helpful suggestions which improved this manuscript and the presentation of the results in it. I would also like to thank Prof. Omri Sarig for reading this manuscript and for his wise and useful input.
A Appendix. Special notation
 $$\begin{align*}\begin{array}{ll} \mathrm{WT} & \text{weakly temperable points (Definition}~2.4)\\\mathrm{RWT} & \text{recurrently weakly temperable points (Definition}~2.4,\\&\text{Definition~2.7)}\\\Sigma & \text{infinite-to-one Markov extension (Theorem}~3.2)\\\widehat{\Sigma} & \text{finite-to-one Markov extension (Definition}~3.3)\\\mathcal{R} & \text{Markov partition (Definition}~3.3)\\\widetilde{\Sigma} & \text{maximal irreducible component of }\widehat{\Sigma} \text{ (Definition}~3.14)\\\widehat{\Sigma}^\circ & \text{itineraries of orbits in the Markov partition (Definition}~3.18)\\X_L, X\in \{\Sigma,\widehat{\Sigma},\widetilde{\Sigma},\Sigma^\circ\} & \{(x_i)_{i\leq0}: (x_i)_{i\in\mathbb{Z}}\in X\} \end{array}\end{align*}$$
$$\begin{align*}\begin{array}{ll} \mathrm{WT} & \text{weakly temperable points (Definition}~2.4)\\\mathrm{RWT} & \text{recurrently weakly temperable points (Definition}~2.4,\\&\text{Definition~2.7)}\\\Sigma & \text{infinite-to-one Markov extension (Theorem}~3.2)\\\widehat{\Sigma} & \text{finite-to-one Markov extension (Definition}~3.3)\\\mathcal{R} & \text{Markov partition (Definition}~3.3)\\\widetilde{\Sigma} & \text{maximal irreducible component of }\widehat{\Sigma} \text{ (Definition}~3.14)\\\widehat{\Sigma}^\circ & \text{itineraries of orbits in the Markov partition (Definition}~3.18)\\X_L, X\in \{\Sigma,\widehat{\Sigma},\widetilde{\Sigma},\Sigma^\circ\} & \{(x_i)_{i\leq0}: (x_i)_{i\in\mathbb{Z}}\in X\} \end{array}\end{align*}$$
 $$\begin{align*}\begin{array}{ll}X^\#, X\in \{\Sigma,\widehat{\Sigma},\widetilde{\Sigma}\} & \{x\in X:\text{there exists } a,b: x_i=a, x_{-j}=b\text{ for infinitely}\\&\text{many positive }i\text{ and positive }j\}\\X^\#_L, X\in \{\Sigma,\widehat{\Sigma},\widetilde{\Sigma}\} & \{x\in X_L:\text{there exists } a: x_{-i}=a\text{ for infinitely many}\\&\text{positive }i\}\\\sigma_R & \text{the right-shift (Definition}~3.17)\\\widetilde{\sigma}_R & \text{the restriction of the right-shift to }\widetilde{\Sigma}_L \text{ (Definition}~4.1)\end{array}\end{align*}$$
$$\begin{align*}\begin{array}{ll}X^\#, X\in \{\Sigma,\widehat{\Sigma},\widetilde{\Sigma}\} & \{x\in X:\text{there exists } a,b: x_i=a, x_{-j}=b\text{ for infinitely}\\&\text{many positive }i\text{ and positive }j\}\\X^\#_L, X\in \{\Sigma,\widehat{\Sigma},\widetilde{\Sigma}\} & \{x\in X_L:\text{there exists } a: x_{-i}=a\text{ for infinitely many}\\&\text{positive }i\}\\\sigma_R & \text{the right-shift (Definition}~3.17)\\\widetilde{\sigma}_R & \text{the restriction of the right-shift to }\widetilde{\Sigma}_L \text{ (Definition}~4.1)\end{array}\end{align*}$$