VIEWS OF SEMANTIC REPRESENTATIONS

Our daily lives, as humans, are full of tasks that require exploiting world knowledge that we have accumulated throughout our lifetime. This world knowledge includes, for example, information about how to perform some functions in our daily lives such as driving cars, eating fruit and vegetables, and information about the behavior of some creatures such as the barking of dogs. Based on our cumulative experiences, we are able to extract and store such knowledge about the world in semantic memory. Semantic memory refers to human memory of word meaning and includes many types of information about concepts (McRae, Reference McRae and Ross2004). For example, from our past encounters with the concept cat, we know that it is an animal, it has whiskers, and it is related to other concepts such as kitten and tiger. We also know from our experiences that the meaning of the word test, for example, is related to the meaning of experiment, trial, quiz, and exam. These meanings we know about the words from our past experiences are what can be referred to as the semantic representations of the words.

There have been many different views and models explaining the nature of semantic representations and how they are stored and retrieved. Virtually, all developers of semantic memory models to a great extent agree that the humans’ semantic system exhibits a general structure and some regularity that is assumed to be shared by individual humans; they also acknowledge that individual differences to a lesser extent may influence the semantic structure (Buchanan, Westbury, & Burgess, Reference Buchanan, Westbury and Burgess2001). The models of semantic representations attempt to capture the structural regularities in either the objects found in the world or the structural regularities in the relationships between words found in language. Accordingly, these models represent two major views based on the type of information they stipulate about word meaning, object-based theories and language-based theories. The object-based view represents word meaning in terms of some observable properties or features (e.g., color, taste, smell, etc.) or categories (e.g., animal, plant, bird, etc.). The language-based view defines the meaning of a word in relation to other words in language (i.e., how a word is used in language); words can be related to each other by means of associations (i.e., words that are semantically associated with each other, e.g., hair and brush) or by means of co-occurring in similar contexts in text (e.g., movie and game both appear in the contexts of entertainment and enjoyment). What follows is a brief description of the object-based view, highlighting the issues related to the feature-based view, which is considered a representative view of the object-based theories. Then, this description will be followed by a brief comparison to the language-based theories.

The feature-based view of semantics postulates that the meaning of a word (especially concrete words) comprises multiple types of knowledge, including visual knowledge (e.g., shape, size, color, and characteristic motion), knowledge associated with sounds that the objects/entities produce (e.g., loud, etc.), how they smell (e.g., smelly, smells nice, is scented, etc.), taste (e.g., musty, sweet, sour, etc.), and feel (e.g., hard, damp, cold, etc.). In addition, the meaning of a word includes knowledge about the typical behavior of creatures (e.g., meows, barks, etc.), situational/event-based knowledge (e.g., what the objects are used for, such as cutting; where they can typically be found, such as in the kitchen; and who typically used them, such as farmers).

The above-mentioned types of conceptual representations of words are called semantic features (McRae, Cree, Seidenberg, & McNorgan, Reference McRae, Cree, Seidenberg and McNorgan2005; Rosch & Mervis, Reference Rosch and Mervis1975). The feature-based conceptual representations are empirically derived from feature production norms using feature-listing tasks. In such tasks, human participants are asked to list the semantic features of some basic-level concepts (e.g., orange or cat). Recently, McRae et al. (Reference McRae, Cree, Seidenberg and McNorgan2005) developed feature production norms for 541 basic-level concepts of living and nonliving things over 3 years. In their norms, each subject enlisted the features of 20 or 24 concepts, and each concept was presented to 30 participants. For each concept in their feature production norms, information is provided about the number of features, number of distinguishing features (e.g., barks or meows), ratings of the distinctiveness of the features, the likelihood that a feature would appear in a certain concept, and distributional statistics about feature correlations (i.e., the tendency of two features to occur in the same basic-level concepts). Under the feature-based view, words are considered semantically similar (i.e., semantic neighbors) if they have several overlapping semantic features. In this sense, robin and canary are thought of as semantic neighbors because they share some features in common such as bird, can fly, small, can sing, etc.; Cree & McRae, Reference Cree and McRae2003).

Featural representations were hypothesized to underlie our implicit statistical knowledge of feature correlations and our explicit theory-based knowledge (Holyoak & Spellman, Reference Holyoak and Spellman1993; Lin & Murphy, Reference Lin and Murphy1997). To explain, both humans and connectionist networks were found to naturally encode the extent to which certain pairs of features co-occur across concepts (Cree, McRae, & McNorgan, Reference Cree, McRae and McNorgan1999; McRae, Cree, Westmacott, & de Sa, Reference McRae, Cree, Westmacott and de Sa1999; McRae, de Sa, & Seidenberg, Reference McRae, de Sa and Seidenberg1997), suggesting that our brain's neurons (and those of the connectionist network) learn correlations (Saffran, Aslin, & Newport, Reference Saffran, Aslin and Newport1996; Jusczyk, Cutler, & Redanz, Reference Jusczyk, Cutler and Redanz1993). For example, people tend to list feature pairs such as <has wings> and <has feathers> when they are asked to list the features associated with some concepts such as robin, pigeon, and canary (McRae, Reference McRae and Ross2004). In addition, people sometimes have an explicit theory about why two features co-occur based on the relationship between features. To illustrate, people reported that <has wings> was causally related to <flies> (Ahn, Marsh, Luhmann, & Lee, Reference Ahn, Marsh, Luhmann and Lee2002; Murphy & Medin, Reference Murphy and Medin1985).

The conceptual representations derived from the feature production norms could account for some experimental phenomena such as semantic similarity priming (Cree et al., Reference Cree, McRae and McNorgan1999; McRae et al., Reference McRae, de Sa and Seidenberg1997), feature verification (McRae et al., Reference McRae, Cree, Westmacott and de Sa1999; Solmon & Barsalou, 2001), categorization (Smith, Shoben, & Rips, Reference Smith, Shoben and Rips1974), and conceptual combination (Smith, Osherson, Rips, & Keane, 1988). As such, the feature production norms have been argued to provide some insight into important aspects of word meaning (McRae, Reference McRae and Ross2004; Medin, Reference Medin1989).

Some major challenging questions, however, were raised against the feature-based view of semantic memory. One challenging question is how the various semantic features that represent the meaning of a concept bind together as a coherent unified whole, so that the features are effortlessly perceived as being aspects of a single concept (Roskies, Reference Roskies1999; von der Malsburg, Reference von der Malsburg1999). Consider, for example, how the shape feature of an object binds with the feature of the location of that object so that both shape and location features provide a unified representation of the object. To solve this binding problem, a number of hypotheses were proposed including von der Malsburg's (Reference von der Malsburg1999) temporal synchrony of neuronal firing rate (i.e., temporally synchronizing the activity of different neurons), Simmons and Barsalou's (Reference Simmons and Barsalou2003) hierarchy of convergence zones (i.e., a set of processing units that encode activity among multiple input units; Damasio, Reference Damasio1989), and Patterson, Nestor, and Rogers's (Reference Patterson, Nestor and Rogers2007) single convergence zones. It is beyond the scope of this article to review these hypotheses. To date, it is not clear which solution is most viable (McRae & Jones, Reference McRae, Jones and Reisberg2013).

Another question that was raised against the feature-based view is how words that have no observable or physical properties such as abstract words and sophisticated verbs are represented in terms of semantic features. The feature-based view is mainly based on research that has been carried out on concrete words and observable actions (verbs; McRae & Jones, Reference McRae, Jones and Reisberg2013). The feature-based representation view cannot sufficiently capture the meaning of abstract concepts (Shallice & Cooper, Reference Shallice and Cooper2013), particularly as abstract words do not have sensory referents in the world (Paivio, 1986). In an attempt to provide a resolution to this issue, some researchers suggested that the cognitive organization of abstract concepts might be partially different from the cognitive organization of concrete concepts (Plaut & Shallice, Reference Plaut and Shallice1993). Thus, Plaut and Shallice along with other researchers proposed some models that instantiated the meaning of abstract words and sophisticated verbs using a mechanism that was different from the mechanism used to instantiate the meaning of concrete words (McRae & Jones, Reference McRae, Jones and Reisberg2013). To date, however, there have not been any feature-based models that specify one common mechanism for constructing the semantic representations for all types of words.

Another limitation of the feature-based view is that the feature production norms were collected for a few hundred words that were mostly concrete nouns and observable actions. This is due to the hand-coding (and laborious) nature of the feature-listing tasks that were used to develop the norms. This seems to be an obstacle for the feature-based view that provides the semantic representations for a limited number of words and limited topics. All these issues are resolved when considering the language-based models, especially those that derive semantic representations from large-scale text corpora instead of embodied experiences collected from participants.

In contrast to the object-based view, the language-based view postulates that word meaning does not have to be represented in terms of structural regularities of the semantic features of words themselves. Instead, the language-based view captures word meaning by the patterns of word usage in language (i.e., how a word is used in relation to other words in language). As such, the history of a word's usage in language is what gives the word its meaning. The history of word usage can be derived either from tasks whereby participants are asked to write the first related word that came into mind when they saw another word (association-based semantics) or from recording the systematic patterns of the words that co-occurred around a given word (co-occurrence-based semantics). Two words are considered semantically similar (or semantic neighbors) under this view if they are semantically associated with each other (association norms; Nelson, McEvoy, & Schreiber, Reference Nelson, McEvoy and Schreiber1998) or if they appear in similar contexts in large samples of text (i.e., their distributions in text or their global co-occurrence; Lund & Burgess, Reference Lund and Burgess1996). The associational-based semantic representations, just like in the object-based view, were developed using tasks to elicit associations from human participants. In such tasks, the number of distinct responses that two or more participants enlisted is tallied (e.g., the association norms developed by Nelson et al., Reference Nelson, McEvoy and Schreiber1998). Because of the (hand-coding) nature of the tasks from which associations were developed, associates were collected for a limited number of words (5,019 words in Nelson et al.’s, Reference Nelson, McEvoy and Schreiber1998, association norms), which is one of the limitations of the associational-based semantic representations. For this reason, the global co-occurrence-based semantic (distributional-based view) can be argued to be more successful in terms of deriving semantic representations for millions of words from large corpora of text. This review will focus on co-occurrence-based semantic representations.

DISTRIBUTIONAL SEMANTIC VIEW

The distributional semantic view stipulates that the representation of the meaning of a given word can be derived from the other words that tend to co-occur within large samples of text (i.e., its distribution in text). These other words that co-occur with a given word are called the semantic neighbors of the word. Precisely, semantic neighbors under the distributional semantic view can be defined as words that are situated in close proximity to each other in texts (first-order co-occurrences) as well as different words that have in common the same words that co-occur with them, regardless of whether they appear in close proximity to each other in a text (second-order co-occurrences; Lund & Burgess, Reference Lund and Burgess1996; Shaoul & Westbury, Reference Shaoul, Westbury, McCarthy and Boonthum-Denecke2012). To illustrate, consider the phrase in the previous sentence, “situated in close proximity to . . . .” Situated and proximity appear close to each other in this phrase, and as such they are thought of as first-order co-occurring words. Now consider another phrase, “situated in a close location to . . .,” for the sake of argument. You will notice that both proximity in the former phrase and location in the latter phrase appear in similar linguistic contexts (i.e., share some co-occurring words), and therefore they are considered second-order co-occurring words. To understand the rest of this review, the remainder of this section will specify the theoretical grounding of this view and how distributional semantic models are built.

Distributional semantic view: Modeling

Some distributional semantic models are used to derive semantic representations by analyzing a text corpus. Before explaining how the models of distributional semantics were built to do this, it is important to lay down some basic terminologies used in the literature of distributional semantic models.

Distributional semantic modeling: Terminologies

Semantic space is a space that is used to spatially represent word meaning as presented in Figure 1. As can be seen from this figure, words are represented as points in this space. The distance between one point (i.e., a word) and another reflects the degree of semantic similarity between the two words. Words that are close to one another in this space are considered semantically similar. Therefore, what is actually being modeled in semantic space is the semantic similarity between words as a function of their proximity from one another in an n-dimensional space where n can reflects the number of dimensions (i.e., the number of co-occurrence words). In Figure 1, only a two-dimensional space is visualized for simplification.

Figure 1. A geometric representation of a hypothetical two-dimensional space. The words (refinery, tanker, crew, and sea) are represented as points in two dimensions (i.e., co-occurring words) of load and ship. The spatial proximity between words reflects how the words are close or similar in their meanings. For instance, in this space tanker is close to refinery while it is relatively distant from sea. Therefore, one can infer that the meaning of tanker is more similar to the meaning of refinery than to the meaning of sea.

To arrive at the geometric representations of semantic space (as illustrated in Figure 1), distributional semantic models are used to first collect distributional information (profiles) for words in a matrix of co-occurrence counts (see Tables 1 and 2), and then transform such distributional data to geometric representations. The distributional information of a word refers to the sum of all its environments (Harris, Reference Harris and Harris1970, p. 775). The environments of a given word can be the words that surround the given word in a line, sentence, or phrase (i.e., neighboring words), or they can be the documents in which the word appears. Thus, the distributional semantic models are used to populate a word-by-word matrix or word-by-document matrix. A word-by-document matrix is used to assess the relationships between words and the number of documents in which they appear (i.e., the similarity between documents) while a word-by-word matrix is used to directly measure co-occurrences between different words (i.e., the similarity between words). Since the focus of this article is on the effect of the degree of similarity between a word and the other words that co-occur with it in language, distributional semantic models that are used to produce word-by-word matrices (i.e., that define the context/environment in which a word appears as its neighboring words in text) will be central to this article and will be further discussed in the remainder of this article.

Table 1. A one-word ahead and one-word behind (raw) co-occurrence matrix

Table 2. A (hypothetical) co-occurrence matrix

Note: In this matrix, “tanker” co-occurs 83 times with “ship” and 62 times with “load.” Also, “tanker,” “oil” and “refinery” have similar co-occurrence counts in each of the three dimensions (“ship,” “load,” and “carry”).

To give a simple example of a word-by-word matrix, consider the example of, Tankers offload oil to refineries. If we consider the context of a target word as one word ahead and one word behind the target word, then the context of offload will be tankers and oil. Producing a co-occurrence matrix for the previous sentence according to a one-word ahead and one-word behind criterion should look like the co-occurrence matrix presented in Table 1.

A distributional semantic model is used to build a co-occurrence matrix based on large samples of text from a large-scale corpus of hundreds of millions or billions of words. Thus, after summing the co-occurrence counts for each word in the corpus and after applying some mathematical and statistical techniques that will be discussed later in this article, the resultant co-occurrence matrix will be somewhat similar to the simplified co-occurrence matrix presented in Table 2. This table shows that the word tanker, in this hypothetical example, co-occurs 83 times with the word ship. The rows in this matrix represent target words and the columns represent contexts (i.e., dimensions) or words that co-occur with the target word in text.

A co-occurrence matrix consists of distributional vectors containing the values found in the cells of a row. For example, the distributional vector of tanker in the co-occurrence matrix presented in Table 2 is X_tanker = (67, 62, 83, . . .). Each value in the vector is called a dimension or feature. To reiterate, the values in the matrix represent co-occurrence counts (frequencies; e.g., the number of times tanker co-occurs with ship). Thus, each value in a vector specifies one attribute or characteristic of the word in the space. The vector of a word specifies the location of the word in an n-dimensional space. However, knowing that the location of the word tanker is (67, 62, 83) in a three-dimensional space, for example, is not informative of anything, except its location in semantic space. As such, knowing the location itself is meaningless. When we consider the location of a word (e.g., tanker) in relation to its proximity to the locations of other words (e.g., refinery, oil, sea, etc.) in semantic space, then these locations become meaningful with respect to specifying which words are closer and therefore semantically similar to a given word than other words. The ultimate goal of a word-by-word distributional semantic model is to represent semantic similarity between words, by spatially modeling word meaning, in terms of the proximity between words in a high-dimensional semantic space.

To measure how similar or different the meanings of words are in a high-dimensional semantic space, similarity or distance measures are used. Similarity measures indicate how similar two vectors are and give high scores for similar vectors. Distance measures, in contrast, indicate how different two vectors are, and give low scores for similar vectors. One example of the similarity measures is cosine similarity, which is the angle between two arrows/vectors (see the angles between the vectors in Figure 2). In Figure 2, the angle between tanker and sea is larger than the angle between tanker and refinery. As such, the cosine angular distances indicate that vectors of tanker and refinery are more similar than the vectors of tanker and sea. Cosine similarity measures how similar two vectors in a scale of [0,1], where 0 indicates no similarity and 1 indicates maximal similarity. An example of the distance measures is the Euclidean distance, which measures the straight distance between two points (see the dashed lines between the vectors in Figure 2). In Figure 2, the Euclidean distance between tanker and sea is larger than the distance between tanker and refinery. As such, the vectors of tanker and sea are more different than the vectors between tanker and refinery. It is worth mentioning that the results of applying similarity and distance measures are equivalent if the vectors are normalized (as will be explained below); both distance and similarity measures give similar accounts of how close two words are in semantic space (Evert & Lenci, Reference Evert and Lenci2009).

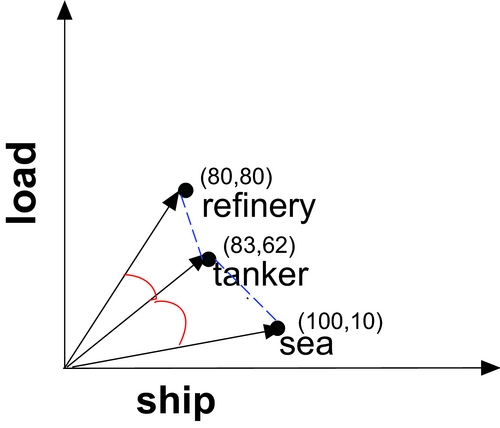
Figure 2. A (hypothetical) two-dimensional semantic space; in this space, the vectors of three words (tanker, refinery, and sea) are geometrically represented in terms of their co-occurrences with two dimensions (ship and load). In this hypothetical example, sea co-occurs 100 times with ship and 10 times with load. The illustration of this space also shows that words that have similar values in the same dimensions are located close together in the space. For example, both tanker and refinery have similar values of 80 and 85, respectively, in the dimension of ship and 62 and 80, respectively, in the dimension of load. Thus, the vectors of tanker and refinery are much closer to each other in this space compared to sea, which has very different values in these two dimensions. The Euclidean distance between sea and tanker (the dashed line) is larger than the distance between refinery and tanker. In addition, the cosine angular distance (the angle) between sea and tanker is larger than the cosine angular distance between refinery and tanker.

As can be seen from Figure 2, the angle and the distance between refinery and tanker is less than the angle and the distance between sea and either refinery or tanker. Therefore, it can be seen that the distributional profiles of refinery and tanker are similar in this semantic space and, hence, the words refinery and tanker are semantically similar while sea is less related to any of these words. Thus, the distance between two vectors indicates how similar the contexts of usage of the two words represented by the vectors are.

Distributional semantic modeling: Building steps

Building a word-by-word distributional model generally involves three main steps. The first step involves selecting the corpus from which co-occurrence information is extracted. In the second step, the corpus is linguistically processed so that it can be used by the model. This step involves detecting and eliminating unwanted text (e.g., removing non-English documents from the corpus), converting all words in the corpus to uppercase letters so that the differences in capitalization is eliminated (e.g., Door and door are converted to DOOR), adding a space to separate the possessives (’s) from the words, and replacing the hyphens in the hyphenated words with a space (e.g., first-class is converted to FIRST CLASS). In this way, the linguistic processing helps the model to detect identical words (e.g., Door: door; first-class: first class), and treat them as equivalent.

In the third step, mathematical and statistical processing for the linguistically processed corpus takes place. The mathematical and statistical processing involves building a matrix of co-occurrence frequencies, weighting the co-occurrence frequencies, smoothing the matrix by reducing its dimensionality, and measuring the similarity or distance between vectors. The basic mathematical and statistical processing is explained below.

To build a co-occurrence matrix, the number of times another word co-occurs with a target word is counted (e.g., how often does tanker occur in the context of load?). Words are considered to have co-occurred with a target word if they appear immediately adjacent to the target word as well as if they are separated from the target word by a number of intervening words in a line of a written text. The maximum number of intervening words that are considered to co-occur with a target word is called window size. The frequencies of co-occurrences are populated one window at a time in a way that the window slides forward one word at a time until all words in the corpus are processed (see Figure 3). Distributional models differ in the type of window (e.g., windows of words, sentences, paragraphs, or whole documents); the discussion in this article will be limited to only word-based distributional models as mentioned before. The models also differ in the size of the window (i.e., how many words fall in the window) and its extension (i.e., how many words to the left and to the right of the target word).

Figure 3. A visualization of a sliding window (five words ahead and five words behind the target word) with inverse linear ramp weighting. In this example, the first target word is the word interactive, and the second target word is the word teaching. The tables below show the vectors that appear ahead and behind the target words; these vectors would be contained in the co-occurrence matrix after weighting the counts from the sliding window (but before normalizing the rows; based on Shaoul & Westbury, Reference Shaoul, Westbury, McCarthy and Boonthum-Denecke2012).

By recording every window movement, the co-occurrence matrix is compiled. For every target word in this matrix, there is a row and some columns as presented in Tables 1 and 2. If the window is used to count co-occurrences symmetrically in both directions (to the left and right of the target word) within the window, then the resultant word-by-word co-occurrence matrix is symmetric in the sense that the rows and columns for a target word both contain the same co-occurrence counts. If the window is used to count co-occurrences in only one direction (to the left or right words from the target word), then the resultant matrix is directional in the sense that the rows and columns contain co-occurrence counts in different directions. To explain, a left-directional co-occurrence matrix gives co-occurrence counts with the preceding (left in English) words within the window; the values in a row are co-occurrence counts of the target word with the left words in the window while the values in a column are the co-occurrence counts with the right words in the window. A right-directional co-occurrence matrix populates counts of co-occurrences with the succeeding (right in English) words within the window; a row contains co-occurrence counts of the target word with the right words within the window while a column contains counts of co-occurrence counts with the left words within the window.

It should be noted that the above-described directional information is discarded in the final stages of applying an algorithm to concatenate the row and column vectors (Sahlgren, 2006). Thus, it does not matter whether a directional or symmetric word-by-word matrix is used, as it will be the case that words that have occurred with the same other words in a particular corpus being analyzed will have similar representations when comparing their vectors (Sahlgren, 2006).

Once the co-occurrence matrix is populated from the whole corpus, the co-occurrence counts in the cells are weighted using a weighting scheme that assigns weights to the context words based on their distances from the target word in the window. Applying a weighting function involves multiplying co-occurrence frequencies by a number reflecting the distance of the context word from the target word in the window. One of the weighting functions used in some distributional models is called linear ramp, which gives more weight to the co-occurrence neighbors that are located closely to the target word. To illustrate, consider that we have a five-word window (i.e., five words to the left and five words to the right of the target word). If a linear ramp function is applied as a weighting scheme to the co-occurrence counts, then the co-occurrence frequency of the neighboring word that appears directly adjacent to the target word in either direction will be multiplied by five in this five-word window. The co-occurrence frequency of the next neighboring word out in either direction will be multiplied by four, while the co-occurrence frequency of the word that appears at the edge of the window in either direction will be multiplied by one. Another type of weighting functions that is used in other models is the inverse linear ramp, which gives more weight to the co-occurrence neighbors that are located far away from the target words. Implementing the inverse linear ramp as a weighting scheme gives less weight to the closer words that often tend to be function words, and therefore, high-frequency words. Since function words convey little semantic information, the raw co-occurrence statistics could simply reflect frequencies that are correlated with syntactic functions along semantic relationships between words (Durda & Buchanan, Reference Durda and Buchanan2008; Rhode, Gonnerman, & Plaut, Reference Rohde, Gonnerman and Plaut2005). Through the application of this type of inverse weighting schemes, the effect of function words is minimized (for a brief review of other types of weighting functions, see Shaoul & Westbury, Reference Shaoul and Westbury2010a).

The weighted co-occurrences are then stored in a raw co-occurrence matrix that contains the weighted frequencies of co-occurrences for all possible combinations of words in all possible positions in the window (before and after the target word in the window). At this point, due to passing the sliding window over a large corpus, the consequent weighted (raw) co-occurrence matrix is very large, which can be computationally laborious and impossible, and also very sparse at the same time since most words rarely co-occur with each other in a corpus (i.e., most of the cells in the co-occurrence matrix will contain co-occurrence counts of zeros).

To solve the issues of the high-dimensionality and the sparseness of the vectors of the data, the sparse (raw) co-occurrence matrix is compressed by reducing its dimensions (columns). Dimensionality reduction is achieved by filtering out some words in the matrix based on linguistic or statistical criteria. Filtering out words based on linguistic criteria involves removing the words that belong to a closed grammatical class (e.g., function words) as these words are assumed to have little semantic information. These closed class words, constituting a small number of words in language, have orthographic frequencies (i.e., how often the words appear in a corpus) much higher than the orthographic frequencies of the rest of open class words (Zipf, Reference Zipf1949). Accordingly, the closed class words have very high co-occurrence frequencies with almost all words in the corpus. Therefore, the vectors of closed class words are very dense with large values, making them much closer to all other words than low-frequency words. The problem with the linguistic criterion as a form of dimensionality reduction is that it removes only a few words from the data because the majority of words in language belong to open grammatical classes. Statistical criteria involve removing words with some undesired statistical characteristics, for example, very high and very low frequency. Removing very high- and very low-frequency words, thus, to some extent resembles linguistic filtering since very high-frequency words tend to belong to closed grammatical classes. The statistical filtering not only removes closed class words but also succeeds in removing words belonging to open grammatical classes. The result of reducing the dimensionality of the matrix is a low-dimensional space with denser information.

Finally, similarity between words (vectors) is compared using similarity or distance measures. The similarity measures give the mean distance between a target word and all its co-occurrence neighbors. Thus, semantic similarity indexes how near or similar the target word's neighbors are to the target word in terms of similarity of their contextual usage in language. An example of a similarity metric that is implemented in many models is the cosine similarity that measures the angle between two vectors. It was suggested that semantic similarity measures (both similarity and distance metrics) should be normalized for (or take out the effect of) vector length (i.e., the number of dimensions contained in each vector) because similarity measures result in making the words with many and large co-occurrence counts too similar to most other words while distance measures result in making words with many co-occurrence counts too far from other words (Widdows, Reference Widdows2004). This problem can be avoided by directly using cosine similarity since it normalizes vectors for their respective length; thus, cosine similarity is a popular technique to compute normalized vector similarity (Sahlgren, 2006).

Readers interested in some examples of distributional semantic models can review Hyperspace Analogue to Language (HAL; Lund & Burgess, Reference Lund and Burgess1996), latent semantic analysis (a document-based model developed by Landauer & Dumais, Reference Landauer and Dumais1997), and High Dimensional Explorer (HiDEx; Shaoul & Westbury, Reference Shaoul and Westbury2006, Reference Shaoul and Westbury2010a). The reminder of this section will be devoted to discuss the how semantic neighborhood (size and density) has been calculated using HiDEx as it was empirically tested to provide empirical justifications for the optimal parameters that should be considered when building up distributional semantic models.

Shaoul and Westbury (Reference Shaoul and Westbury2006, Reference Shaoul and Westbury2010a) developed a model called HiDEx, that itself was based on a previous model, HAL (Lund & Burgess, Reference Lund and Burgess1996). HiDEx was developed to better explain the variance due to semantic similarity in response latency data for lexical decision and semantic decision tasks. In HiDEx, statistical and mathematical techniques are applied to establish first-order co-occurrences that are obtained from a large corpus, and these are then used to derive second-order co-occurrences. Shaoul and Westbury (Reference Shaoul and Westbury2010a) obtained first-order co-occurrences through the use of a sliding window, within which the co-occurrence frequencies of a particular word, referred to as the target word, with other words in the window were recorded. They found that a window size of 10 words behind, and 0 or 5 words ahead of the target word, best captured variance in lexical and semantic decision responses to that target word. Next in their procedure, the first-order co-occurrence values for the corpus were “weighted” such that more weight was apportioned to a word's co-occurrence neighbors located further away from the target word in this window. This inverse ramp-weighting scheme gives less weight to the closer words that tend to be high-frequency function words. Since function words convey little semantic information, if these words were weighted more heavily, then first-order co-occurrence statistics might reflect more the frequencies that are correlated with syntactic function among semantic relationships between words (Durda & Buchanan, Reference Durda and Buchanan2008; Rhode, Gonnerman, & Plaut, Reference Rohde, Gonnerman and Plaut2005). Through the application of inverse ramp weighting, the contribution of function words to the semantic neighborhood index is minimized. The consequent weighted co-occurrence matrix is very sparse because most words rarely co-occur with each other.

To decrease the sparseness of the matrix, Shaoul and Westbury summed the weighted co-occurrence frequencies in the window and used these to create a second-order co-occurrence matrix. Each word in this matrix is represented by a vector containing the summed co-occurrence frequencies (often referred to as elements, or features) of the target word with the other words falling in the window. This resulted in a large matrix, which they then reduced through selection of the most frequent element in each vector. Words with similar vectors, to use a hypothetical example, say, research and study, may have vectors such as X_research = (69, 35, 80. . .), X_study = (60, 29, 90. . .), specifying that these words would be located close to each other in semantic space. In contrast, words with less similar vectors, for example, research and culture, X_research = (69, 35, 80. . .), X_culture = (34, 59, 10. . .), would be more distant from each other (see Figure 4). Very high-frequency words (mostly function words) usually will have very high co-occurrence values with all the words in the corpus, and therefore, to reduce their influence, Shaoul and Westbury normalized each vector by dividing its elements by the orthographic frequency of the target word. Thus, the index of semantic neighborhood for a word that is produced in HiDEx does not covary with orthographic frequency.

Figure 4. A (hypothetical) two-dimensional space; in this space, the vectors of three words (research, study, and culture) are geometrically represented in terms of their co-occurrences with two dimensions (conduct and answer). For example, in this hypothetical example, culture co-occurred 10 times with conduct and 5 times with answer. The illustration of this space also shows that words that have similar values in the same dimensions are located close together in the space. For example, both study and research have similar values of 100 and 80, respectively, in the dimension of conduct and 100 and 85, respectively, with the dimension of answer. Thus, the vectors of study and research are much close to each other in this space compared to culture that have very different values in these two dimensions.

Finally, Shaoul and Westbury used the word vectors themselves to compute contextual similarity. To do this, they computed the mean distance between the vectors of a word and the words comprising its semantic neighborhood. To do this, Shaoul and Westbury used a multiple of the standard deviation of the distances between a word's vector and vectors for each of its semantic neighbors to compute a threshold, and then they used this threshold as a cutoff, with the number of semantic neighbors that fell within this threshold determining the word's semantic neighborhood size (NCount).

To briefly explain this final aspect of the semantic neighborhood definition procedure, Shaoul and Westbury then identified a set of word pairs that co-occurred at least once in the corpus. Then, 5%–10% of the total number of pairs (constituting billions of word pairs) were randomly selected, and the distances between each selected word pair (usually represented as the cosines of the angles between the vectors representing the words) were then calculated to obtain a representative measure of the standard deviation of all distances, and in turn, Shaol and Westbury used this to define a threshold of neighborhood membership (i.e., which words are, and which words are not, considered semantic neighbors of the target word in question). The neighborhood membership threshold was set at 1.5 SD below the mean distance (approximately 6.7% of the average distance between any two words). Since most words have a weak or no relationship, this cutoff point ensures that a neighbor is counted as part of a word's neighborhood only if it is one of the closest 6.7% of the large number of the randomly selected pairs. Due to the thresholded nature of the neighborhood specification, some proportion of a word's co- occurrence neighbors will not be categorized as semantic neighbors, and in this way, the number of semantic neighbors a particular word has will vary, with some words having more semantic neighbors than others, and some words even having none.

After obtaining a measure of a word's semantic neighborhood in HiDEx, a measure can then be obtained called the average radius of co-occurrence (ARC), which is the average cosine or distance between a target word and all its semantic neighbors within the threshold (see Figure 5). Since ARC is an average distance measure, it reflects how close (or distant) a word's semantic neighbors are, and to this extent, ARC indexes semantic neighborhood density (SND). A word that has more close semantic neighbors is more similar to its neighbors in terms of contextual usage (i.e., they appear quite frequently in similar contexts). A word that has more distant neighbors indicates that this word has a less frequent contextual usage to its neighbors. In this way, ARC captures and represents the average similarity of a word to its co-occurrence neighbors that fall inside its neighborhood threshold. The resulting ARC value ranges from 0 to 1, where 0 indicates no similarity and 1 indicates maximal similarity (with no negative values since frequencies of co-occurrence cannot be negative). Words that have neighbors that are more similar to them have higher ARC values. When a word has no neighbors (as a consequence of the thresholded neighborhood), the word is assigned an ARC value that reflects the distance between the word and its closest neighbor (the first co-occurrence neighbor outside the threshold). In sum, in line with Shaol and Westbury (Reference Shaoul and Westbury2006, Reference Shaoul and Westbury2010a), the ARC values are an index of a word's SND, and the influence of SND on word identification during normal reading is our focus in this paper.

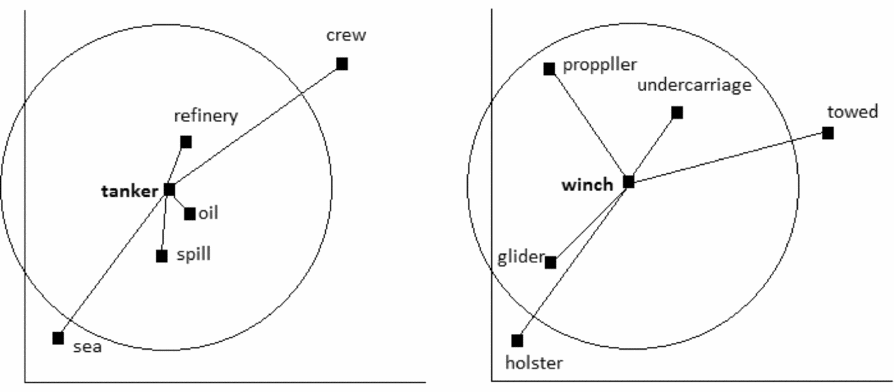
Figure 5. A two-dimensional visualization of the neighborhood membership threshold. The words tanker and winch in this example have three semantic neighbors (based on Shaoul & Westbury, Reference Shaoul and Westbury2010a). The semantic neighbors are close to tanker, whereas the semantic neighbors are distant from winch. Thus, tanker has a higher average radius of co-occurrence value than winch.

EMPIRICAL STUDIES ON THE EFFECTS OF SND

Several studies have been conducted to examine the language-based SND effects in lexical processing; these studies varied in terms of the specific SND measures used to define semantic neighborhoods and the type of behavioral tasks used in their experiments. To reiterate, the current article will use the term dense semantic neighborhood words to refer to words whose semantic neighbors are close and, thus, semantically similar to them in semantic space, and will use the term sparse semantic neighborhood words to refer to words whose semantic neighbors are distant and, thus, semantically different from them in semantic space. Generally, the findings from many studies produced convergent evidence that denser semantic neighborhood words were responded to faster than sparser semantic neighborhood words in tasks that rely on the familiarity of the presented words to make responses such as lexical decision tasksFootnote ¹ (e.g., Buchanan et al., Reference Buchanan, Westbury and Burgess2001; Shaoul & Westbury, Reference Shaoul and Westbury2010a). On the contrary, the findings about the SND effects in tasks that require excessive processing of the meaningFootnote ² of the presented words are mixed, with some findings indicating a facilitatory effect (Siakaluk, Buchanan, & Westbury, Reference Siakaluk, Buchanan and Westbury2003) while other findings showing an inhibitory effect (Shaoul & Westbury, Reference Shaoul and Westbury2010a), and still other findings demonstrating a null effect of SND (Yap, Pexman, Wellsby, Hargreaves, & Huff, Reference Yap, Pexman, Wellsby, Hargreaves and Huff2012; Yap, Tan, Pexman, & Hargreaves, Reference Yap, Tan, Pexman and Hargreaves2011). An example of such tasks is the semantic categorization task whereby participants are asked to make responses as to whether some presented visual words are concrete or nonconcrete (living or nonliving; or animal or nonanimal), as quickly and as accurately as they can.

In this section, some of these studies will be reviewed; the review will focus on the studies that used a co-occurrence-based definition of semantic neighborhoods, with limited reference to the findings of the associational-based SND effects. This section will discuss the findings of the earlier studies conducted on the co-occurrence-based SND effects, and then the review will turn to describing the findings of the most recent studies that explored the SND effects. This will be followed by a discussion of Shaoul and Westbury's (Reference Shaoul and Westbury2010a) study in which they used the SND measures derived from their model (HiDEx). In so doing, the consistencies and inconsistencies between the findings of the studies will be highlighted, mentioning the differences in the methodologies of the reviewed studies. Finally, the section will discuss how the SND effects were interpreted in the context of visual word recognition models.

One of the earliest and most influential studies that explored the SND effects was conducted by Buchanan et al. (Reference Buchanan, Westbury and Burgess2001). Buchanan et al. conducted a series of experiments in which they examined the effects of semantic neighborhood size (i.e., the number of semantic neighbors) in lexical processing using lexical decision tasks and naming tasks. One of the measures of semantic neighborhood size they used was HAL's semantic distance, which they defined as the mean distance between the target word and its 10 closest semantic neighbors in semantic space. Using hierarchal regression analyses, Buchanan et al. tested whether HAL's semantic distance could predict the speed with which words were recognized in lexical decision tasks and naming tasks. They removed the role of other lexical variables by entering them first before HAL's semantic distance in the regression analyses in the following order: log frequency, number of orthographic neighbors, word length, number of semantic associates, and semantic distance. They found that HAL's semantic distance predicted lexical decision latencies and, to some extent, naming latencies. The findings also showed that there was a positive partial correlation (and a semi-partial correlation) between lexical decision latencies and semantic distance, reflecting that as semantic distance decreased, the response latencies decreased as well. Thus, their finding in the first experiment clearly showed that words with denser semantic neighborhoods (decreased semantic distance between words and their respective closest semantic neighbors) resulted in quicker lexical decision latencies compared to words with sparser semantic neighborhoods.

To assess whether the facilitatory SND effects were not due to a confounding effect of a traditional semantic variable (imageability ratings), Buchanan et al. (Reference Buchanan, Westbury and Burgess2001) included imageability in a hierarchal regression analysis. Their findings indicated that semantic distance accounted for a unique variance in lexical decision latencies even after partialing out the contribution of imageability. Then, Buchanan et al. followed their regression analyses with some factorial experiments to further examine the effects of semantic distance. They observed that words with large semantic neighborhood size (i.e., words with low semantic distance) were responded to faster than words with small semantic neighborhood size (i.e., words with high semantic distance), even after partialing out the effect of imageability from their analyses. They also found that the effect of semantic distance was larger for low-frequency words as opposed to high-frequency words. That is, lexical decision latencies for low-frequency words appeared to be influenced by semantic distance more than those for high-frequency words. One limitation of Buchanan et al.’s (Reference Buchanan, Westbury and Burgess2001) study as they themselves noted is that they used a cutoff point in terms of a fixed number of the closest semantic neighbors (10 semantic neighbors in their case) to define the semantic neighborhoods of the words they used in their experiments. Instead, they recommended defining semantic neighborhoods by using a cutoff point in terms of distances and then counting the number of semantic neighbors falling within the specified distance, which was how Shaoul and Westbury (Reference Shaoul and Westbury2006, Reference Shaoul and Westbury2010a) defined semantic neighborhoods in their HiDEx model.

To test whether the findings of Buchanan et al. (Reference Buchanan, Westbury and Burgess2001) could be extended to other visual word recognition tasks, Siakaluk et al. (Reference Siakaluk, Buchanan and Westbury2003) used two types of semantic categorization tasks that were assumed to be more sensitive to semantic effects and that were thought to require accessing word meaning before making responses to the presented stimuli (Forster & Shen, Reference Forster and Shen1996). The two types of semantic categorization tasks were a yes/no task in which participants were asked to respond to both experimental words (nonanimals) and nonexperimental words (animals) and a go/no-go task in which participants were asked to respond to only experimental items. They also used Buchanan et al.’s (Reference Buchanan, Westbury and Burgess2001) definition of semantic distance. Using a one-way analysis of variance to analyze the data of their first experiment (a yes/no task), the results showed that the main effect of semantic distance was just significant in the subject analysis and was not significant in the item analysis. A post hoc analysis showed that the responses to low semantic distance (i.e., denser semantic neighborhood) words were 15 ms faster than responses to matched high semantic distance (i.e., sparser semantic neighborhood) words. To determine that the lack of effect of semantic distance was not due to another semantic variable (subjective frequency, or familiarity), they entered subjective frequency into a regression analysis, and found that semantic distance accounted for only a modest amount of variance (3%) above and beyond subjective frequency. Thus, the researchers concluded that this lack of semantic distance effect in their first semantic categorization task was not due to a possible confounding variable of subjective frequency.

Instead, Siakaluk et al. hypothesized that this lack of semantic distance effect in their first semantic categorization task might be due to the differences between the responses made in lexical decision tasks and responses made in their yes/no semantic categorization tasks. To explain, yes responses were expected to be made to the experimental stimuli (words) in the case of lexical decision tasks, whereas no responses were expected to be made to the experimental stimuli (animal-ness) in the case of yes/no semantic categorization tasks. Thereby, Siakaluk et al. conducted a second experiment in which they employed a go/no-go semantic categorization task, which was assumed to require participants to make yes-like responses to only the experimental stimuli similar to the responses made in lexical decision tasks and, hence, increasing the chance of observing the effect of semantic distance. The findings of their second experiment indicated that the effect of semantic distance was significant; low semantic distance words (i.e., denser semantic neighborhood words) were categorized 41 ms faster than words with high semantic distance (i.e., sparser semantic neighborhood words).

These two studies of Buchanan et al. (Reference Buchanan, Westbury and Burgess2001) and Siakaluk et al. (Reference Siakaluk, Buchanan and Westbury2003) so far suggest that the effects of SND do appear in tasks that require making responses based on the familiarity of the orthography of words (and accessing words’ meanings to some extent) rather than in tasks that require deep semantic processing that does not necessarily reflect processes taking place in lexical processing during normal reading. This observation is supported by the findings of other more recent studies that replicated Buchanan et al.’s (Reference Buchanan, Westbury and Burgess2001) facilitatory effect of SND on lexical decision latencies using different measures of SND (Pexman, Hargreaves, Siakaluk, Bonder, & Pope, Reference Pexman, Hargreaves, Siakaluk, Bodner and Pope2008; Shaoul & Westbury, Reference Shaoul and Westbury2010a; Yap et al., Reference Yap, Tan, Pexman and Hargreaves2011, Reference Yap, Pexman, Wellsby, Hargreaves and Huff2012). However, the facilitatory SND effect on semantic decision latencies found by Siakaluk et al. (Reference Siakaluk, Buchanan and Westbury2003) could not be replicated later. The findings of the SND effects on semantic tasks are inconsistent, with some researchers observing an inhibitory effect (Shaoul & Westbury, Reference Shaoul and Westbury2010a) and others demonstrating a nonsignificant effect (Pexman et al., Reference Pexman, Hargreaves, Siakaluk, Bodner and Pope2008; Yap et al., Reference Yap, Tan, Pexman and Hargreaves2011, Reference Yap, Pexman, Wellsby, Hargreaves and Huff2012).

These above-cited studies used different measures of SND. For example, Pexman et al. (Reference Pexman, Hargreaves, Siakaluk, Bodner and Pope2008) found that the number of semantic neighbors derived from co-occurrence information in a high dimensional semantic space (Durda, Buchanan, & Caron, Reference Durda, Buchanan and Caron2006) significantly predicted only the lexical decision latencies, but not the semantic categorization latencies. This finding was later replicated by Yap et al. (Reference Yap, Tan, Pexman and Hargreaves2011) and Yap et al. (Reference Yap, Pexman, Wellsby, Hargreaves and Huff2012) using different measures of co-occurrence-based semantic neighborhoods. Yap et al. (Reference Yap, Tan, Pexman and Hargreaves2011) used the mean cosine similarity between a target word and its closest 5,000 neighbors in a high dimensional space as a measure of SND, and Yap et al. (Reference Yap, Pexman, Wellsby, Hargreaves and Huff2012) used the ARC metric described in this article. All these studies found that the effects of semantic neighborhoods were only present in lexical decision tasks, with denser semantic neighborhood words (i.e., words with semantic neighbors that are more similar to them) responded to faster than words with sparser semantic neighborhoods.

Another piece of recent empirical evidence that showed the consistency of the findings of the facilitatory SND effects on lexical decision latencies and the inconsistencies of the SND effects on semantic decision latencies is the study carried out by Shaoul and Westbury (Reference Shaoul and Westbury2010a). In particular, Shaoul and Westbury tested whether HiDEx's indices of SND could explain differences in lexical and semantic decision data better than the original HAL's parameters (window size and weighting scheme). When using inverse ramp as a weighting function and a window size of 10 words behind and 0 or 5 words ahead, they reported that SND predicted response latencies better than using the original HAL's parameters of a linear ramp weighting scheme and a 10-word window. Specifically, they demonstrated that words with higher SND produced shorter lexical decision responses, consistent with the findings of the previous studies (Buchanan et al., Reference Buchanan, Westbury and Burgess2001; Pexman et al., Reference Pexman, Hargreaves, Siakaluk, Bodner and Pope2008; Yap et al., Reference Yap, Tan, Pexman and Hargreaves2011, Reference Yap, Pexman, Wellsby, Hargreaves and Huff2012). Shaoul and Westbury also investigated the SND effect in other tasks that required more extensive semantic processing. Specifically, Shaoul and Westbury used two semantic decision tasks in which they asked participants to make explicit semantic judgments about whether two words in a pair were or were not related (yes/no semantic decision task), and to make responses only to word pairs that were semantically related (a go/no-go task). They observed an inhibitory effect of increased SND (i.e., increased SND resulted in longer decision latencies in both tasks), contrary to the facilitatory SND findings observed by Siakaluk et al. (Reference Siakaluk, Buchanan and Westbury2003) in their semantic tasks. Recall that Siakaluk et al.’s semantic tasks are slightly different from those of Shaoul and Westbury.

The inconsistency between Shaoul and Westbury's findings and those of Siakaluk et al.’s results can probably be attributed to differences in the types of semantic decision tasks used in the two studies. Shaoul and Westbury's decision tasks involved judgments as to the semantic relatedness of sequentially presented word pairs while Siakaluk et al.’s decision tasks involved judgments about single words. Although Shaoul and Westbury's task was not, strictly speaking, a semantic priming lexical decision task, the format of presenting a target word to which a response was required immediately after a preceding word is certainly a close approximation to a priming paradigm. It is at least possible that the response latencies in their experiments may have reflected the influence of the preceding word on processing of the subsequent target word (see Moss & Tyler, Reference Moss and Tyler1995, for a review of semantic priming effects). In addition, as Shaoul and Westbury themselves noted, their decision latencies were much longer than those found in the other studies employing semantic categorization tasks in which participants made responses to single words (e.g., Binder, Westbury, McKiernan, Possing, & Medler, Reference Binder, Westbury, McKiernan, Possing and Medler2005; Siakaluk et al., Reference Siakaluk, Buchanan and Westbury2003). It is therefore possible that decision times in this study reflected post-lexical processes associated with decision formation. In addition, the inconsistency could be ascribed to differences in the operationalization of SND in the two studies. While Siakaluk et al. used the N closest words to define SND, Shaoul and Westbury used the distance between a target word and all its semantic neighbors within the threshold to defined SND. It seems likely that methodological and SND operationalization differences caused the differing patterns of effects.

Broadly, on the basis of the complete body of research discussed above, it appears that consistent and pronounced facilitatory SND effects are obtained in tasks that tap into simple word identification processes rather than those that require extensive processing of the meaning of words. In all of these studies, the researchers interpreted the facilitatory effects of SND within an interactive model of word recognition in which all the (orthographic, phonological, and semantic) levels are connected by bidirectional activation links (i.e., an interactive activation based framework as per McClelland & Rumelhart, Reference McClelland and Rumelhart1981). Such models assume feedforward and feedback activation between their distinct units that are dedicated to processing orthography, phonology, and semantic information. These models also assume interactivity between the units of processing in the sense that activation from one unit (or more) can affect the processing of other units. These models explain the SND effects as follows: a target word with a denser semantic neighborhood (i.e., the average similarity between the word and its neighbors is high) will receive more activation from its close co-occurrence neighbors at the semantic level, and the increased semantic activation is fed back from the semantic level to the orthographic (word) level. Consequently, the orthographic representation of the target word will be facilitated. This in turn results in speeded lexical decision responses (e.g., Buchanan et al., Reference Buchanan, Westbury and Burgess2001).

At this point, it is fair to mention Mirman and Magnuson's (Reference Mirman and Magnuson2008) study that was often cited as providing a contrast to the facilitatory effect of the increased SND in lexical decision tasks found in the above-reviewed studies. However, the findings of Mirman and Magnuson's study should be read with a caveat as the SND measures used in their study were defined in terms of a feature-based measure rather than a co-occurrence-based measure. Specifically, in their second experiment, Mirman and Magnuson (Reference Mirman and Magnuson2008) showed that a facilitatory effect could arise as a consequence of distant (i.e., less similar) semantic neighbors rather than close (i.e., more similar) semantic neighbors. In their study, near semantic neighbors slowed semantic and lexical decision times while distant semantic neighbors speeded decision times. Training an attractor dynamic network, Mirman and Magnuson studied the effect of near and distant neighbors by examining the correlation between the number of near and distant neighbors with errors in settling into a correct activity pattern of semantic units for a concept. Their findings showed a strong positive correlation with number of near neighbors (i.e., high number of near neighbors was linked to making more settling errors), indicating an inhibitory effect of near neighbors. The findings also revealed that there was no reliable correlation with the number of distant neighbors, except for a dip to the negative side (i.e., more distant neighbors was associated with fewer errors), indicating a facilitatory effect of distant neighbors. Interpreting their findings in terms of attractor dynamics, the researchers suggested that distant neighbors are far away from the target word, creating a gravitational gradient for faster settling into attractor basins, while near neighbors slowed the settling process because their basins of attraction are closer to the target word's basin of attraction.

However, it should be noted that Mirman and Magnuson, in their second experiment, defined near versus distant neighbors in terms of the cosine or distance between the target's semantic features (e.g., taste, color, function, etc.) and the semantic features of other words in the corpus they used, rather than in terms of the distance between the co-occurrence neighbors and their respective target words. As mentioned earlier, the feature-based view of semantics defines semantic similarity (and presumably semantic neighbors) as a function of shared semantic features, while the distributional-based view defines semantic similarity in terms of co-occurrence within similar contexts. For instance, movie and play are considered semantic neighbors under the distributional view because they tend to occur within similar semantic contexts, while they are not considered semantic neighbors under the feature-based view because they do not share semantic features. Thus, the feature-based semantic similarity (i.e., how much a target word shares semantic features with other words) is based on a different theoretical account than the distributional hypothesis, and is therefore not synonymous with the semantic similarity of co-occurrence neighbors. As such, feature-based SND does not speak directly to co-occurrence-based SND, and consequently, the effect of semantic similarity of neighbors, defined in terms of shared semantic features, found in Mirman and Magnuson's (Reference Mirman and Magnuson2008) study, may not apply to the effect of semantic similarity of neighbors as defined in terms of shared co-occurrence neighbors. Since the focus of this article is on co-occurrence-based SND, Mirman and Magnuson's findings of SND effects may not be comparable to those findings of the studies that used co-occurrence-based semantic representations to define semantic neighborhoods. In addition, the researchers used features norms (McRae et al., Reference McRae, Cree, Seidenberg and McNorgan2005) that were developed for only concrete words (i.e., Mirman and Magnuson's stimuli were only concrete words). However, co-occurrence-based SND has been computed for both concrete and abstract words. It has been shown that the lexical processing of concrete versus abstract words is not necessarily similar. For example, Danguecan and Buchanan (Reference Danguecan and Buchanan2016) found that the SND effect (operationalized using WINDSOR; Macdonald, Reference Macdonald2013) were consistent for abstract words in comparison to inconsistent SND effect for concrete words across different processing tasks (lexical decision, sentence relatedness, and progressive demasking). As such, the findings of Mirman and Magnuson are only limited to concrete words that have been shown to have inconsistent (or lack of) SND effect compared to abstract words (see Reilly & Desai, Reference Reilly and Desai2017).

While the focus of this article is on the co-occurrence-based SND, a brief review of the findings pertaining to the associational-based SND is necessary in order to compare both language-based definitions of SND and, hence, provide an overview of how the language-based SND in general influences lexical processing. Buchanan et al. (Reference Buchanan, Westbury and Burgess2001) investigated the effect of semantic neighborhood size as defined by number of associates (Nelson et al., Reference Nelson, McEvoy and Schreiber1998) along with HAL's semantic distance, and found that the effect of the associational-based semantic neighborhood size was facilitatory, however, and was weaker than the effect of semantic distance they derived from HAL. This finding of Buchanan et al. was replicated later by Yap et al. (Reference Yap, Tan, Pexman and Hargreaves2011), who found that the number of associates did not predict response latencies in lexical decision and naming tasks. Other researchers found a robust effect of semantic neighborhood size as defined by the number of associates on lexical decision latencies (e.g., Dunãbeitia, Avileś, & Carreiras, Reference Duñabeitia, Avilés and Carreiras2008; Locker, Simpson, & Yates, Reference Locker, Simpson and Yates2003, Yates, Locker, & Simpson, Reference Yates, Locker and Simpson2003). Particularly, these studies found that words with larger semantic neighborhoods (large number of associates) were responded to faster than words with smaller semantic neighborhoods in lexical decision tasks (Dunãbeitia et al., Reference Duñabeitia, Avilés and Carreiras2008; Locker et al., Reference Locker, Simpson and Yates2003; Yates et al., Reference Yates, Locker and Simpson2003), naming, progressive demasking, and sentence reading in Spanish (Dunãbeitia et al., Reference Duñabeitia, Avilés and Carreiras2008). The study of Dunãbeitia et al. (Reference Duñabeitia, Avilés and Carreiras2008) clearly indicated that Spanish words with a high number of associates were read for a shorter time than matched words with low number of associates as evident in gaze duration (21 ms shorter) and total reading time (23 ms shorter). Thus, their study suggests that semantic neighborhood effects may appear in early measures of lexical processing (such as gaze duration), indicating that semantic neighborhoods, as defined by at least the associational-based models, influence lexical processing during normal reading in Spanish.

In sum, the visual word recognition studies and, to some extent, eye movement studies produced convergent evidence that words with denser semantic neighborhoods (i.e., words with more similar semantic neighbors) are recognized faster than words with sparser semantic neighborhoods (i.e., words with fewer similar semantic neighbors) in tasks that depend on the familiarity of words to make responses (e.g., lexical decision tasks). The SND effects are less clear and have proved inconsistent across studies that used tasks that require participants to do excessive processing of the meaning of words before making responses (e.g., semantic categorization tasks) due to the nature of such tasks as discussed in this section. The facilitatory effect was explained within interactive models that assume strengthened feedback from the semantic level to the orthographic level.

THEORETICAL IMPLICATIONS

The review of the SND effects presented in this article indicates that word meaning, defined by the degree of semantic similarity between a given word and all its semantic neighbors, can constrain unique word identification. The present review also offers a characterization of semantic involvement in lexical identification. The findings reviewed in this article suggest that a word's semantic neighbors are more, or less, active during lexical identification. As such, these findings theoretically imply that the assumptions about semantic processing are similar to the assumptions about orthographic and phonological processing during lexical identification in reading. To explain, orthographically, phonologically, and semantically similar candidates are activated along with the perceived target word during lexical identification. In the case of this article, the findings suggest that a word's orthographic representation (e.g., MOVIE) can activate multiple semantic neighbors (e.g., game, theatre, cinema, etc.) within the semantic system during word identification in normal reading. The activation of semantic neighbors feeds back to the word level within the period that the candidate set is being reduced via processes of between-level activation and within-level inhibition. Therefore, it appears that the SND characteristics (i.e., semantic information) of a word can be accessed before the full identification of the word, and thus, can constrain the unique identification of a word's orthographic form.

The conclusions drawn from the findings of the reviewed studies in this article are inconsistent with word identification models that assume that word meaning does not influence lexical processing. For example, serial search models of word recognition (e.g., Forster, Reference Forster, Wales and Walk1976) assume that the meaning of a word can be accessed only after the processing of its orthographic (or phonological) representation has been completed, and a unique word has been identified and selected for further processing. To briefly reiterate, under these models, when a target word is perceived, the word is searched for in the orthographic file until a word in the orthographic file matches the perceptual properties of the perceived word. At this point, the search is terminated and a pointer in the orthographic file is used to check the properties of the word in the orthographic file against those in the master file. If the properties of the word in the orthographic file match the properties of the word in the master file, the word is successfully identified. Once a unique word has been identified, semantic information associated with the identified word can then be retrieved.

Thus, serial search models assume that the meaning of a word cannot influence the processing of its orthographic representation. That is, these models predict that SND will influence a stage that is independent of the stage influenced by the word-level variables (e.g., orthographic neighborhood size and word frequency) in lexical processing (as per Sternberg, 1969). However, there was no evidence in the reviewed findings that this was the case. The findings showed that SND interacted with word-level variables, suggesting that SND and word-level variables influenced a common processing stage.

The reviewed findings, nevertheless, are consistent with the interactive models of word identification (e.g., McClelland & Rumelhart, Reference McClelland and Rumelhart1981) that assume that activation feeds forward from lower levels to higher levels shortly after processing at the lower levels has begun. Activation also feeds back from the higher levels to the lower levels. According to Stolz and Besner's (Reference Stolz and Besner1996) embellished interactive-activation (IA) model (McClelland & Rumelhart, Reference McClelland and Rumelhart1981), the visual information of a perceived word partially activates the word unit corresponding to the target word and, to a lesser extent, the word units corresponding to orthographically similar words. Shortly after a word's orthographic representation is activated at the word level, activation from the word level feeds forward to the semantic level, activating its semantic representation. The activation of the word's semantic representation feeds back to the word level, contributing to resolving the competition between orthographic competitors (those of the actual word and its orthographic neighbors). Therefore, the embellished IA model predicts that SND and word-level variables can influence a common stage of lexical processing. That is, a word's semantic representation can be accessed and can influence lexical processing before processing at the word level has been completed. The facilitatory effects of increasing SND can be accounted for by the embellished IA model. According to the embellished IA model, the closely packed semantic neighbors will provide a greater amount of activation at the semantic level. Therefore, a great amount of activation will feed back from the semantic level to the word level, contributing to resolving the competition between the orthographic neighbors at the word level. As such, high SND can facilitate word identification.

As such, the findings of the reviewed studies clearly support a word identification model such as the embellished IA model that assumes that orthographic processing and word meaning processing are cascaded in time. That is, these findings ultimately imply that in order that a lexical identification model provides a comprehensive account of word identification, the model needs to integrate a mechanism by which it explains the influence of the semantic characteristics of words before the completion of unique word identification. This is exactly what the embellished IA model was developed for.

Another fundamental question that remains to be addressed here concerns the credibility of the reviewed findings in terms of informing our understanding of the influence of word meaning in lexical identification during normal reading. Recall that semantic representations in the present article were defined in terms of semantic distributional models. To remind the reader, distributional semantic models are theoretically based on the distributional hypothesis that postulates that two words that occur in similar contexts are considered semantically similar. Distributional semantic models have been used to model the meanings of words by analyzing and comparing their distributional profiles in large-scale corpora of text. The statistical distributions of words in text delineate some important aspects of their meaning. This section will give a general discussion on the capability of distributional semantic models to capture informative aspects of word meaning.

Distributional semantic models can potentially extract semantic information from linguistic contexts (i.e., text data). Humans also learn word meaning from extralinguistic contexts based on their perception and interactions with the objects in the world (de Vega, Graesser, & Glenberg, Reference de Vega, Graesser, Glenberg, Vega, Glenberg and Graesser2008). In other words, many words are learned from past perceptual experiences (or circumstances) in which the words were uttered (McRae et al., Reference McRae, Cree, Seidenberg and McNorgan2005). Therefore, both linguistic information and sensorimotor information constitute important aspects of words’ semantic representations. The results of many studies suggest that language captures and encodes much perceptual information and that linguistic contexts can be used to extract referential word meaning (Connell & Ramscar, Reference Connell, Ramscar, Moore and Stenning2001; Durda & Buchanan, Reference Durda and Buchanan2008; Kintsch, Reference Kintsch, Landauer, McNamara, Dennis and Kintsch2007, Reference Kintsch, de Vega, Glenberg and Graesser2008; Louwerse & Zwaan, Reference Louwerse and Zwaan2009; Riordan & Jones, Reference Riordan and Jones2010). For example, Riordan and Jones found that though distributional and featural models tended to emphasize different aspects of word meaning, these two types of semantic models encoded much redundant information about word meaning. Their findings also suggest that children rely on perceptual cues about the referents of the words at the early stages of learning their first language. As they gain more perceptual information, children tend to rely on statistical cues (i.e., the distribution of words in the language) to develop and refine semantic similarity relations between words. Thus, such findings clearly indicate that co-occurrence vectors obtained from distributional semantic models contain an amount of information about the words they represent, including perceptually grounded information (Shaoul & Westbury, Reference Shaoul, Westbury, McCarthy and Boonthum-Denecke2012).

The notion of semantic similarity used in distributional semantic models, though it may seem broad, has been shown to be psychologically plausible. To explain, human subjects appear to understand the concept of semantic similarity when they are instructed to make judgments about the semantic similarity of word pairs (e.g., Miller & Charles, Reference Miller and Charles1991). Moreover, many researchers have demonstrated that the participants’ agreement (intersubject agreement) about the semantic similarity of word pairs is very high (e.g., Miller & Charles, Reference Miller and Charles1991; Rubenstein & Goodenough, Reference Rubenstein and Goodenough1965). Given that researchers in the area of word identification are interested in investigating the psychological phenomena occurring in word identification, the notion of semantic similarity in its broad meaning does not need to be further specified in terms of conventional semantic relations (e.g., synonyms, antonyms, hyponyms, etc.).

It should be noted that most research investigating SND during word identification operationalizes SND using only word-based semantic models (e.g., HAL, HiDEx, and WINDSOR). If SND is to be established as a psychologically relevant construct and not an idiosyncratic measurement of a specific family of distributional semantic models, then SND derived from word-based models should be validated using other families of distributional semantic models (sentence-based and document-based models). Until now, the focus of research using sentence-based models is on the compositional meaning rather than word meaning. As such, future studies examining the effect of SND should use multiple classes of models to demonstrate the psychological relevance of this construct.

To sum up, distributional semantic models were found to successfully handle a variety of semantic tasks, which highlights the importance of considering distributional data in modeling word meaning and the capability of this research field. Of more theoretical interest to this article, distributional semantic models can potentially capture informative aspects of word meaning (both linguistic and referential meanings), and the broad notion of semantic similarity adopted in these models has been shown to be psychologically plausible.