2. Methodology

We solve the compressible Navier–Stokes equations using our flow solver STREAmS (Bernardini et al. Reference Bernardini, Modesti, Salvadore and Pirozzoli2021, Reference Bernardini, Modesti, Salvadore, Sathyanarayana, Posta and Pirozzoli2023); additional details on the numerical method are reported in Appendix A. The streamwise momentum equation is forced in such a way as to maintain a constant mass flow rate. Periodicity is exploited in the streamwise and spanwise directions, and isothermal no-slip boundary conditions are used at the channel walls. Let $h$ be the half-width of the channel, with DNS carried out in a computational domain $L_x\times L_y\times L_z=6{\rm \pi} h \times 2 h\times 2{\rm \pi} h$. A uniform bulk cooling or heating term is added to the entropy equation to guarantee that the mixed mean temperature, defined as

(2.1a–c)\begin{equation} T_m = \frac{1}{2h \rho_b u_b}\int_{0}^{2h}\bar{\rho}\, \bar{u}\,\bar{T} \,\mathrm{d}y,\quad \rho_b=\frac{1}{2h}\int_{0}^{2h}\bar{\rho}\,\mathrm{d}y,\quad u_b = \frac{1}{2h \rho_b}\int_{0}^{2h}\bar{\rho}\, \bar{u} \,\mathrm{d}y, \end{equation}

remains exactly constant in time. Here, $\rho _b$ and $u_b$ are the bulk density and velocity, respectively. In the following, an overline is used to indicate Reynolds averaging in time and in the homogeneous spatial directions, and a prime is used to denote fluctuations thereof. As is common in variable-density flows, we also use Favre averages, denoted with a tilde as $\tilde {f}=\overline {\rho f}/\bar {\rho }$, and a double prime will indicate fluctuations thereof.

A $+$ superscript is used to denote normalization by wall units, namely by friction velocity $u_{\tau } = (\tau _w/\bar {\rho }_w)^{1/2}$ (where $\tau _w= \mu _w\,{\rm d} \tilde {u}/{\rm d} y\vert _w$ is the mean wall shear stress), and the associated viscous length scale $\delta _v=\nu _w/u_\tau$, where the subscript $w$ denotes quantities evaluated at the wall. For inner normalization of the mean temperature, we use the friction temperature $\theta _{\tau } = q_w/(\rho _w c_p u_{\tau })$, where $q_w = \lambda _w \,{\rm d} \tilde {T}/{\rm d} y\vert _w$ is the mean wall heat flux, $c_p=\gamma /(\gamma -1) R$ is the specific heat capacity at constant pressure, $R$ is the air constant, and $\lambda _w$ is the thermal conductivity at the wall, evaluated as $\lambda = \mu c_p/\textit {Pr}$, with Prandtl number set to $\textit {Pr}=0.72$.

Twenty DNS have been carried out at bulk Mach number $M_b=u_b/c_m=0.2$ (where $c_m$ is the speed of sound at the mixed mean temperature) and bulk Reynolds number $\textit {Re}_b=2\rho _b u_b h/\mu _m\approx 9000\unicode{x2013}70\,000$ (see table 1), where $\mu _m = \mu (T_m)$ is the dynamic viscosity evaluated at the mixed mean temperature, as obtained from Sutherland's law (White Reference White1974). The Mach number is low enough that compressibility effects are negligible, as it turns out, in order to isolate variable-property effects. We consider various mean-to-wall temperature ratios, namely $T_m/T_w=0.4,0.5,0.7,0.8,1.5,2,2.5,3$, resulting in friction Reynolds numbers in the range $\textit {Re}_\tau =u_\tau h/\nu _w\approx 150\unicode{x2013}3200$, where $\nu _w$ is the kinematic viscosity at the wall. For the case of mean-to-wall temperature ratio $T_m/T_w=0.5$, we also study the effect of varying the dimensional wall temperature, considering cases with $T_w=800$ and $293.15$ K. This temperature range is rather wide and covers most applications of forced air convection of which we are aware. Cases with wall heating approach the condensation temperature of air ($\approx$90 K), and cases with wall cooling feature temperature variations in the range $220\ {\rm K} \lesssim T \lesssim 1000\ {\rm K}$, involving temperature values beyond those normally found in heat exchangers. For each value of the mean-to-wall temperature ratio, we have two flow cases, denoted with the letters L and H, depending on whether the Reynolds number is comparatively ‘low’ or ‘high’ (see table 1). For two flow cases with mean-to-wall temperature ratio $T_m/T_w=0.5$ and $T_m/T_w=2$ we also consider a ‘very high’ Reynolds number case, denoted with VH. In the present study, we consider pure forced convection, neglecting the effect of buoyancy because in forced air convection applications the Richardson number is typically very small. For instance, cooling channels of turbine blades have bulk velocity $u_b\approx 30\unicode{x2013}60$ m s$^{-1}$ and temperature variations of order $400$ K, leading to Richardson numbers of the order $\textit {Ri}\approx 10^{-5}$.

Table 1. Flow parameters for plane channel flow DNS. Box dimensions are $6{\rm \pi} h \times 2h \times 2{\rm \pi} h$ for all flow cases; $\textit {Re}_b = 2 \rho _b h u_b / \nu _m$ is the bulk Reynolds number, and $\textit {Re}_{\tau } = h u_{\tau } / \nu _w$ is the friction Reynolds number; $\textit {Re}_{\tau,cp} = y_{cp}(h)/\delta _v$ is the equivalent friction Reynolds number, defined in equation; $T_m$ and $T_w$ are the mixed mean temperature and the wall temperature, respectively; $C_f = 2 \tau _w /(\rho _b u_b^2)$ is the friction coefficient; $\textit {St}=q_w/[\rho _b C_p u_b (T_w-T_m)]$ is the Stanton number; $\textit {Nu}=\textit {St}\,\textit {Re}_b\,\textit {Pr}$ is the Nusselt number; $\Delta x$ and $\Delta z$ are the mesh spacings in the streamwise and spanwise directions, and $\Delta y_w$ is the mesh spacing at the wall; and the $*$ superscript indicates normalization with equivalent constant-property viscous length scale $\delta _{v,cp}$, defined in (4.16c).

3. Instantaneous temperature field

We begin our analysis by inspecting the instantaneous velocity and temperature fields of flow cases H05-A (wall heating) and H3 (wall cooling) in figure 1. Both cases exhibit the qualitative features that characterize wall turbulence, with high-speed cold (or hot) flow structures protruding towards the walls, and low-speed hot (or cold) fluid regions protruding towards the channel centre. Despite sharing the general features of wall turbulence, we also note a significant effect of the thermodynamic and fluid property variations between cases with wall heating and wall cooling. First, we observe that the friction Reynolds number values reported in table 1 are not indicative of actual separation of scales in constant-property flows. For instance, flow case with wall heating H05-A ($T_m/T_w=0.5$) has a relatively low friction Reynolds number ($\textit {Re}_\tau =360$), but it exhibits finer eddies than one would expect at this Reynolds number. This effect can be traced to strong viscosity variations within the near-wall and core flow regions. The opposite is true for wall cooling; for instance, flow case H3 ($T_m/T_w=3$) has a higher friction Reynolds number ($\textit {Re}_\tau =1420$), but small scales are absent and the flow appears to be a ‘low-pass filtered’ version of the heated case, in which only large structures survive. In fact, in flow case H3 we observe large structures extending from one wall to beyond the channel centreline, whereas those are masked by smaller eddies in flow case H05-A.

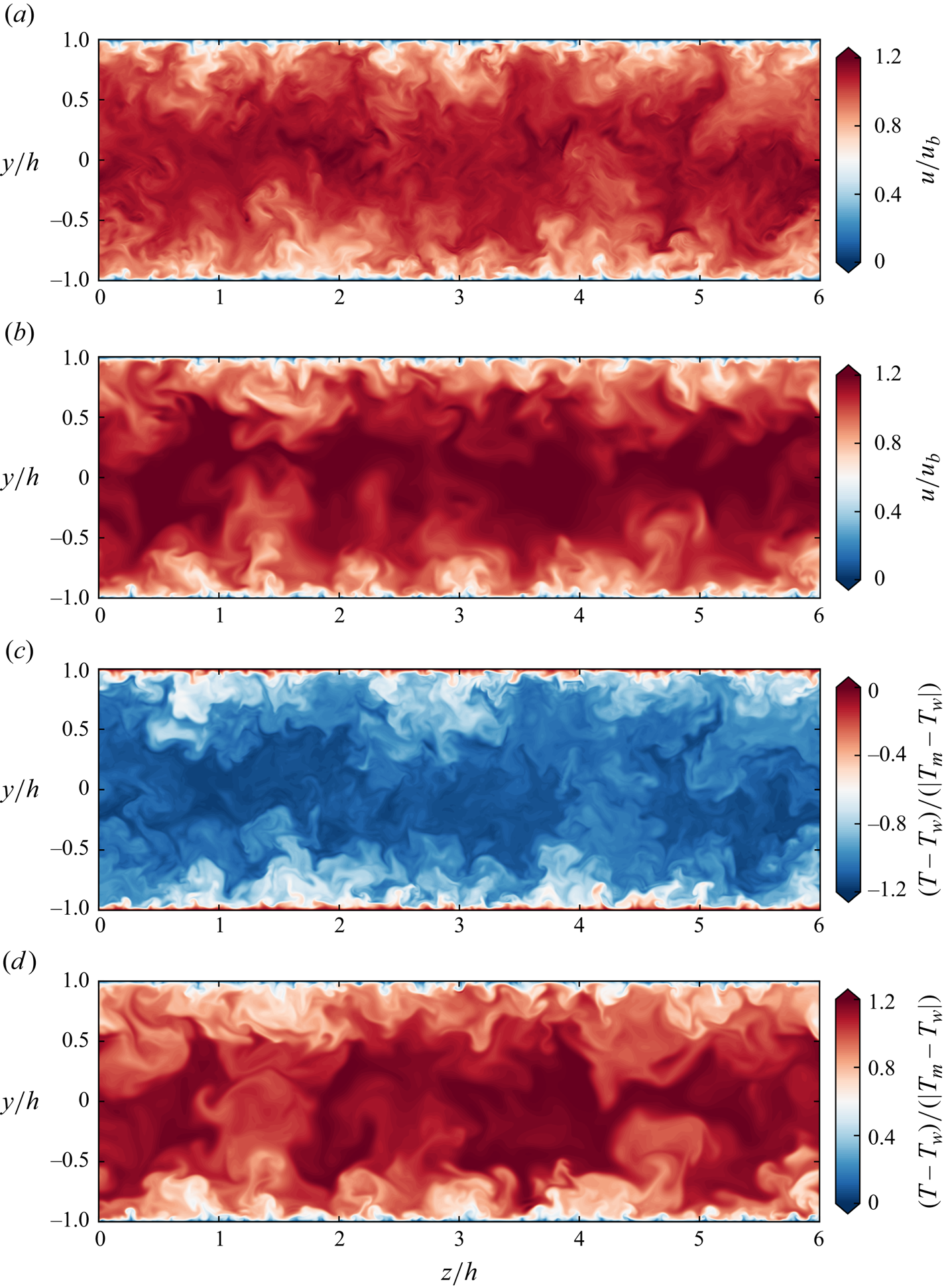
Figure 1. Instantaneous (a,b) velocity and (c,d) temperature fields in a cross-stream plane, for flow cases (a,c) H05-A (wall heating, $\textit {Re}_\tau =360$, $T_m/T_w=0.5$) and (b,d) H3 (wall cooling, $\textit {Re}_\tau =1420$, $T_m/T_w=3$).

We note that the instantaneous velocity and temperature fields are highly correlated, which is to be expected due to the similarity of the underlying equations and the near-unity value of the Prandtl number, hence the Reynolds analogy holds qualitatively also for the case of variable fluid properties. Close scrutiny of the kinematic and thermal fields reveals that temperature has finer structures as compared to velocity, which is due partly to the Prandtl number being lower than unity, and partly to the effect of the pressure gradient term in the momentum equation (A1b), which is absent in the energy equation (A1c) (Pirozzoli et al. Reference Pirozzoli, Bernardini and Orlandi2016). The occurrence of sharper eddy boundaries in passive scalars compared to the velocity field, even at unit Prandtl number, is a well-known feature that has been reported by several authors (Kim, Guezennec & Stretch Reference Kim, Guezennec and Stretch1990; Abe & Antonia Reference Abe and Antonia2017), and it has been associated with the unmixedness of the scalar, as the absence of the pressure gradient results in reduced heat transport as compared to momentum transport.

4. Mean flow field and variable-property transformations

We begin the mean flow analysis by comparing the mean velocity and temperature profiles to the equivalent statistics for the constant-property case. For that purpose, we rely both on DNS data of constant-property plane channel flow with passive scalar transport at $\textit {Pr}=0.71$ from Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016), and on synthetic composite profiles, which are obtained by matching inner-layer velocity and temperature profiles with the corresponding outer-layer distributions. The inner-layer profiles are obtained by integrating the eddy viscosity of Musker (Reference Musker1979) for the velocity, and the eddy diffusivity proposed by Pirozzoli (Reference Pirozzoli2023) for the temperature profile. In the outer layer, we use Clauser's hypothesis of uniform eddy viscosity (Clauser & Francis Reference Clauser and Francis1956) and uniform eddy diffusivity (Pirozzoli et al. Reference Pirozzoli, Bernardini and Orlandi2016). A complete derivation of the composite profiles is available in Pirozzoli & Modesti (Reference Pirozzoli and Modesti2024). Figure 2 shows that the composite profiles of mean temperature and velocity for the constant-property case are essentially indistinguishable from the DNS data, with the advantage that the synthetic profiles are available at any Reynolds number and Prandtl number.

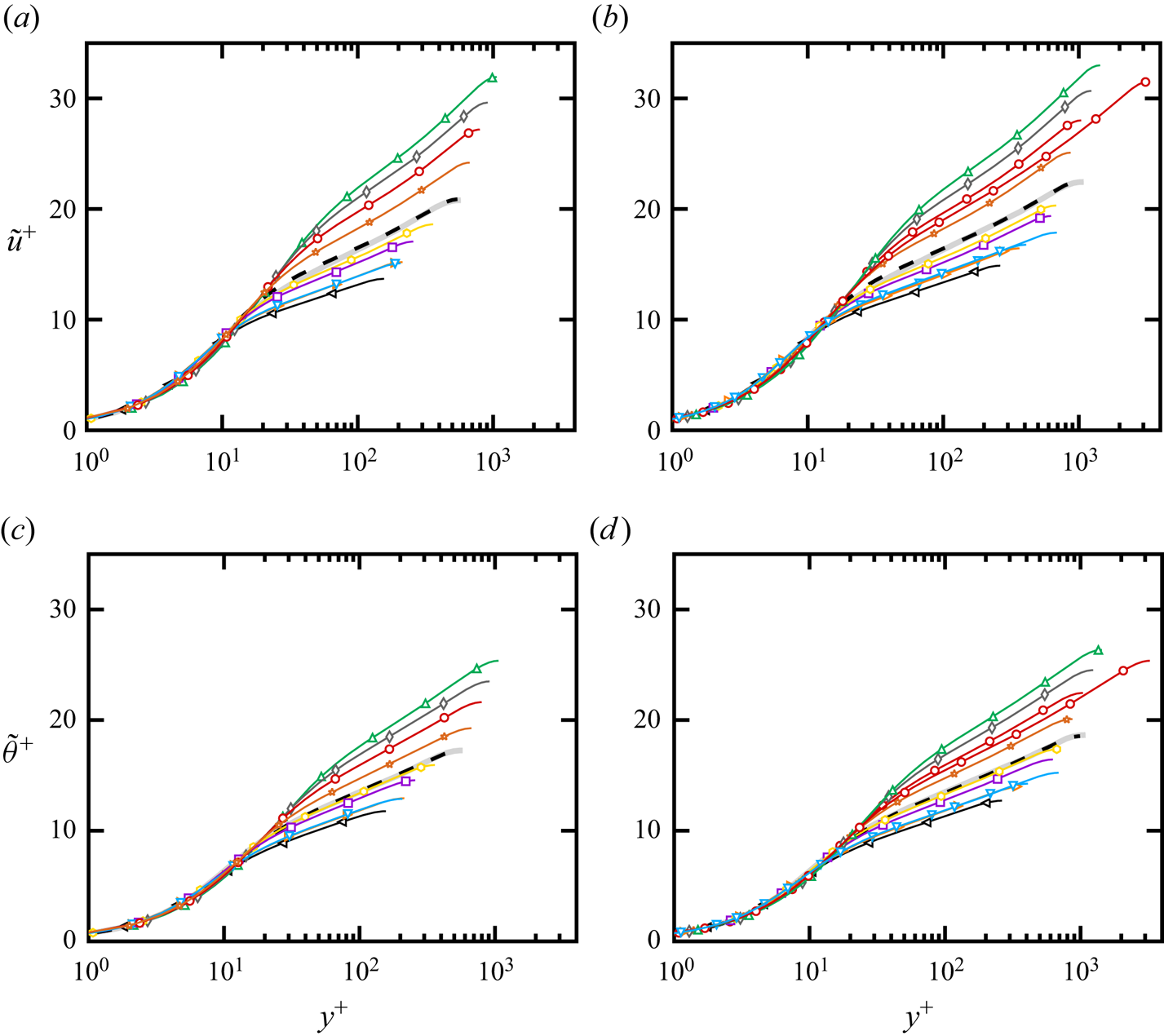
Figure 2. (a,b) Mean velocity and (c,d) mean temperature profiles for (a,c) L flow cases and (b,d) H flow cases. Symbols indicate DNS data for different mean-to-wall temperature ratios: $T_m /T_w = 0.4$ (left triangles), $T_m /T_w = 0.5$, $T_w=800$ K (downward triangles), $T_m /T_w = 0.5$, $T_w=273.25$ K (right triangles), $T_m /T_w = 0.7$ (squares), $T_m /T_w = 0.8$ (hexagons), $T_m /T_w = 1.5$ (stars), $T_m /T_w = 2$ (circles), $T_m /T_w = 2.5$ (diamonds), $T_m /T_w = 3$ (upward triangles). The grey solid lines indicate the mean velocity and temperature profiles of the constant-property case at $\textit {Pr}=0.72$, obtained using the composite profiles of Pirozzoli & Modesti (Reference Pirozzoli and Modesti2024). The dashed black lines indicate DNS of constant-property channel flow from Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016) at $\textit {Pr}=0.71$.

We note that the statistics of the variable-property DNS are substantially different from those in the constant-property case when scaled in classical wall units. All the flow cases exhibit deviations from the reference, starting from the buffer region, and becoming more evident in the logarithmic region, where both the logarithmic slope and the additive constant deviate from the constant-property references. Hence we conclude that in the variable-property case, the law-of-the-wall for both the mean velocity and temperature is not universal, but rather depends on the specific mean-to-wall temperature ratio.

In analogy with what is done for compressible flows, we assume that the effects of density and viscosity variations can be accounted for using suitable convolution integrals (Modesti & Pirozzoli Reference Modesti and Pirozzoli2016)

(4.1a–c)\begin{equation} y_{cp}=\int_0^y f_{cp} \, {\mathrm d} y, \quad u_{cp}=\int_0^{\tilde{u}} g_{cp} \, {\mathrm d}\tilde{u}, \quad \theta_{cp}=\int_0^{\tilde{\theta}} h_{cp} \, {\mathrm d}\tilde{\theta}, \end{equation}

with kernel functions $f_{cp}$, $g_{cp}$, $h_{cp}$ to be specified such that the flow properties are mapped to the universal, constant-property case, denoted with the ‘$cp$’ subscript. In order to account for the variable-property effect, we consider the streamwise mean momentum balance equation

(4.2)\begin{equation} \overline{\mu'\,\frac{\mathrm{d} u'}{\mathrm{d} y}} + \bar{\mu}\,\frac{\mathrm{d} \tilde{u}}{\mathrm{d} y} - \bar{\rho}\,\widetilde{u''v''} = \bar{\rho}_w u_{\tau}^2 (1-\eta), \end{equation}

where $\eta =y/h$. Following Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023), we then introduce an eddy viscosity for the turbulent shear stress, such that $-\bar {\rho }\,\widetilde {u''v''} = \bar {\rho }\nu _T\,\mathrm {d}\tilde {u}/\mathrm {d} y$. Substituting the transformations (4.1a–c) into the streamwise mean momentum balance equation, and assuming $\overline {\mu '\,\mathrm {d} u'/\mathrm {d} y}\approx 0$, one obtains

(4.3)\begin{equation} \frac{\bar{\mu}}{\mu_w}\,\frac{f_{cp}}{g_{cp}}\left(1 + \frac{\nu_T}{\nu}\right)\frac{\mathrm{d}u_{cp}^+}{\mathrm{d} y_{cp}^+} = 1-\eta. \end{equation}

Comparing (4.3) with the constant-property counterpart

(4.4)\begin{equation} \left(1 + \frac{\nu_{T,cp}}{\nu_{cp}}\right)\frac{\mathrm{d}u_{cp}^+}{\mathrm{d} y_{cp}^+} = 1-\eta, \end{equation}

we find the following relation between the two kernel functions $f_{cp}$ and $g_{cp}$:

(4.5)\begin{equation} \frac{\bar{\mu}}{\mu_w}\,\frac{f_{cp}}{g_{cp}}\left(1+\frac{\nu_T}{\nu}\right)=1+\frac{\nu_{T,cp}}{\nu_{cp}}. \end{equation}

A second condition is needed, which we find by enforcing that van Driest scaling (van Driest Reference van Driest1951) holds in the logarithmic region, as done by Trettel & Larsson (Reference Trettel and Larsson2016). With this condition, we find

(4.6a,b)\begin{equation} f_{cp}=\frac {\mathrm{d}}{\mathrm{d} y} \left( \frac y{R^{1/2} N} \right),\quad g_{cp}=\left(\frac{1 + \nu_T/\nu}{1+\nu_{T,cp}/\nu}\right)R N\,\frac {\mathrm{d}}{\mathrm{d} y} \left( \frac y{R^{1/2} N} \right), \end{equation}

where $N=\bar {\nu }/\nu _w$ and $R=\bar {\rho }/\bar {\rho }_w$. The kernel functions (4.6a,b) are formally equivalent to the velocity transformation derived by Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023) for a high-speed turbulent boundary layer, with eddy viscosities to be specified. Using the model eddy viscosity of Musker (Reference Musker1979) for the baseline case of constant-property flow, herein we extend the model to account for variable-property effects by including an ad hoc correction depending on the mean-to-wall temperature ratio

(4.7a,b)\begin{equation} \frac{\nu_{T,cp}}{\nu} = \frac{(\kappa y_{cp}^+)^3}{(\kappa y_{cp}^+)^2 + C_{v1}^2},\quad \displaystyle\frac{\nu_T}{\nu} = \frac{(\kappa y_{cp}^+)^3}{(\kappa y_{cp}^+)^2 + C_{v1}^2 + \varphi(T_m/T_w)}, \end{equation}

where $\kappa =0.387$ is the assumed Kármán constant, and $C_{v1}=7.3$. Fitting the present DNS data (only flow cases at ‘high Reynolds numbers’, denoted as H, have been taken into account), we have determined empirically the following expressions for the additive function $\varphi$:

(4.8)\begin{equation} \varphi(T_m/T_w) =\begin{cases} -32\log{(T_m/T_w)} - 59(1-T_m/T_w)^2, & T_m/T_w<1,\\ 5.6(1-T_m/T_w), & T_m/T_w>1. \end{cases} \end{equation}

Similarly to what is done for the mean velocity, a transformation for the mean temperature profile is obtained starting from the mean energy balance equation

(4.9)\begin{equation} \underbrace{\overline{\lambda'\,\frac{\mathrm{d} \theta'}{\mathrm{d} y}}}_{\textit{fluctuating conduction}} +\underbrace{\bar{\lambda}\,\frac{\mathrm{d} \tilde{\theta}}{\mathrm{d} y}}_{\textit{mean conduction}} \underbrace{{}- C_p\bar{\rho}\,\widetilde{\theta''v''}}_{\textit{turbulent convection}} + \underbrace{\varPsi}_{\textit{dissipation}} = \underbrace{q_w (1-\mathcal{R})}_{\textit{total heat flux}}, \end{equation}

where

(4.10a,b)$$\begin{gather} \mathcal{R}(\eta) =\frac{1}{\rho_b} \int_0^\eta \bar{\rho}(\eta)\,\mathrm{d}\eta, \quad \varPsi = \int_0^y \epsilon \, \mathrm{d} y -\int_0^y \frac{\rho}{\rho_b}\int_0^1\epsilon \, \mathrm{d}\eta\,\mathrm{d} y, \end{gather}$$

(4.10c)$$\begin{gather}\epsilon = \displaystyle\overline{\sigma_{ij}\,\frac{\partial u_i}{\partial x_j}} - \overline{u_i\,\frac{\partial p}{\partial x_i}}. \end{gather}$$

The relative importance of the different terms in (4.6) is analysed in figure 3, for representative flow cases with wall heating and wall cooling. Figure 3 shows that the mean temperature balance of variable-property flows is qualitatively similar to what is found in passive scalar convection, with mean conduction dominating the near-wall region, and turbulent convection dominating the overall balance away from the wall. However, notable differences are the nonlinearity of the total heat flux (on account of the definition of $\mathcal {R}$) and the presence of additional terms that are small but not zero. Indeed, very close to the wall, we find a small contribution from the fluctuating conduction term, which, however, remains much smaller than the mean conduction. We recall that in the mean momentum equation (4.2) the fluctuating diffusion term $\overline {\mu '\,\mathrm {d} u'/\mathrm {d} y}$ was neglected, which yields a similar contribution to momentum balance as $\overline {\lambda '\,\mathrm {d} T'/\mathrm {d} y}$ yields to the temperature balance (not shown). The dissipation remains negligible for all cases considered here, due to the small Mach number under scrutiny, confirming that all flow cases can be regarded as representative of incompressible flow. We also note that the total stress $\mathcal {R}(\eta )$ in (4.10) is indistinguishable from the sum of the components, indicating excellent statistical convergence of the results.

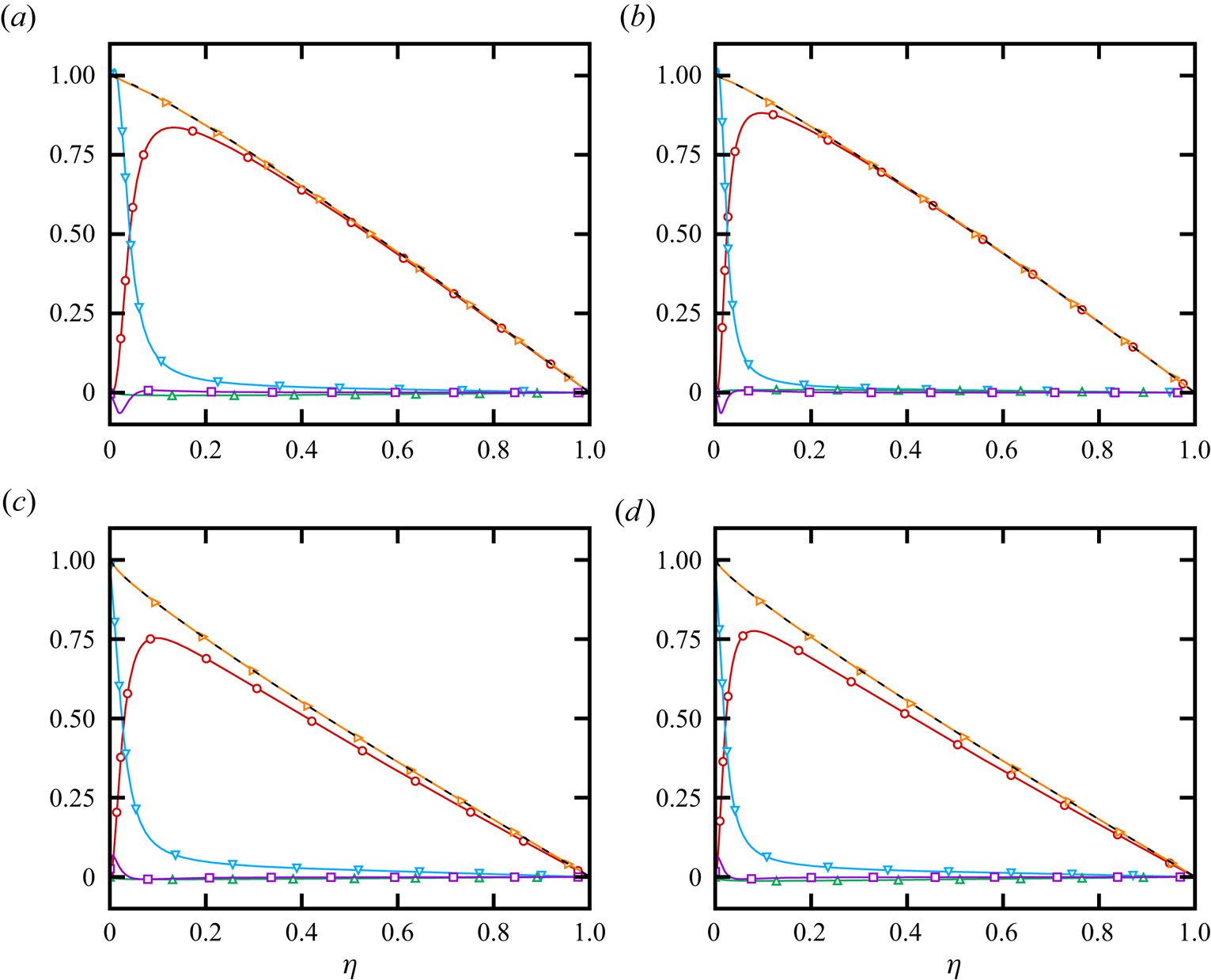
Figure 3. Mean energy balance as in (4.9) for flow cases (a) L05-A ($\textit {Re}_\tau =212$, $T_m/T_w=0.5$), (b) H05-A ($\textit {Re}_\tau =360$, $T_m/T_w=0.5$), (c) L3 ($\textit {Re}_\tau =1051$, $T_m/T_w=3$), and (d) H3 ($\textit {Re}_\tau =1420$, $T_m/T_w=3$). The symbols indicate mean conduction (downward triangles), fluctuating conduction (squares), turbulent convection (circles), dissipation (upward triangles), total heat flux $\mathcal {R({\eta })}$ in (4.9) (dashed black line), and sum of the different contributions (right triangles).

Based on the DNS data, we then assume $\varPsi \approx 0$ and $\overline {\lambda '\,\mathrm {d} \theta '/\mathrm {d} y}\approx 0$, and in analogy with what is done for the turbulent shear stress, we model the turbulent heat flux by introducing a thermal eddy diffusivity, such that

(4.11)\begin{equation} \widetilde{\theta''v''}\,\frac{1-\eta}{1-\mathcal{R}} =-\alpha_T\, \frac{\mathrm{d}\tilde{\theta}}{\mathrm{d} y}. \end{equation}

Following the same procedure as used for the mean momentum equation, we then determine the corresponding kernel function

(4.12)\begin{equation} h_{cp}=\left(\frac{1 + \alpha_T/\alpha}{1+\alpha_{T,cp}/\alpha}\right)\frac{1-\eta}{1-\mathcal{R}}\,R N\,\frac {\mathrm{d}}{\mathrm{d} y} \left( \frac y{R^{1/2} N} \right), \end{equation}

where $\alpha =\lambda /(\rho c_p)$ is the thermal diffusivity coefficient. Following Pirozzoli (Reference Pirozzoli2023), we model the turbulent diffusivity as

(4.13a,b)\begin{equation} \displaystyle\frac{\alpha_{T,cp}}{\alpha} = \frac{(\kappa_\theta y_{cp}^+)^3}{(\kappa_\theta y_{cp}^+)^2 + C_{v3}^2},\quad \displaystyle\frac{\alpha_T}{\alpha} = \frac{(\kappa_\theta y_{cp}^+)^3}{(\kappa_\theta y_{cp}^+)^2 + C_{v3}^2 + \beta(T_m/T_w)}, \end{equation}

with constants $\kappa _\theta =0.459$, $C_{v3}= 10$. As for the mean velocity, the dependency of the eddy thermal diffusivity on mean-to-wall temperature ratio is accounted for empirically by fitting the DNS data, to obtain

(4.14)\begin{align} \beta(T_m/T_w) =\begin{cases} (1-T_m/T_w)[141 - 507(T_m/T_w) + 608(T_m/T_w)^2], & T_m/T_w<1,\\ -28\log{(T_m/T_w)} + 1.6(1-T_m/T_w)^2, & T_m/T_w>1. \end{cases} \end{align}

To summarize, the kernel functions (4.6a,b) and (4.12) are rooted in the mean momentum balance and temperature balance equations, with eddy viscosity and eddy conductivity to be specified. This is, in our opinion, more robust that relying entirely on data-driven transformations (Volpiani et al. Reference Volpiani, Iyer, Pirozzoli and Larsson2020). Nonetheless, we are not aware of any exact result in turbulence theory that does not include constants to be determined from experience or simulation, and the present case is no exception. Here, the constants $\kappa$, $\kappa _{\theta }$, $C_{v1}$ and $C_{v3}$ were determined once and for all for constant-property flow (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021; Pirozzoli & Modesti Reference Pirozzoli and Modesti2023). The only added ingredients here are the functions $\varphi$ in (4.8) and $\beta$ in (4.14), which account empirically for the dependency on the bulk-to-wall temperature ratio. We note that both (4.8) and (4.14) show different functional dependency for heating and cooling, which is aligned with empirical formulas for the Nusselt number and friction coefficient reported in the literature (Petukhov Reference Petukhov1970; Yeh & Stepka Reference Yeh and Stepka1984), featuring different coefficients or functions for the two cases.

In figure 4, we plot the transformed mean velocity and temperature profiles using the kernel functions (4.6a,b) and (4.13a,b), and compare the results with the reference constant-property case. The universality of the various distributions is quite remarkable, given the wide range of variation of the flow properties that we are considering. The accuracy of the velocity and temperature transformations also supports the validity of the assumptions made to derive the kernel functions for the convolution integrals (4.1a–c). We point out that the coefficients inferred from DNS have been calibrated only for flow cases H, and they are successfully applied to lower or higher Reynolds numbers with similar accuracy, showing substantial independence from the Reynolds number. These transformations allow us to define an equivalent channel height $h_{cp}$, which we use to introduce an equivalent constant-property friction Reynolds number,

(4.15a,b)\begin{equation} \textit{Re}_{\tau,cp} = \frac{h_{cp}}{\delta_{v}}, \quad h_{cp} = \int_0^hf_{cp}\,\mathrm{d} y. \end{equation}

The equivalent channel height $h_{cp}$ is larger than $h$ for heating, and smaller for cooling, leading to higher or lower equivalent constant-property friction Reynolds numbers, respectively. The definition given in (4.15a,b) can also be used to define an equivalent constant-property friction velocity, and an equivalent viscous length scale, namely

(4.16a–c)\begin{equation} \textit{Re}_{\tau,cp} = \frac{u_{\tau,cp}h}{\bar{\nu}_w}, \quad u_{\tau,cp}=\frac{\bar{\nu}_w}{\delta_{v,cp}}, \quad \delta_{v,cp} = \frac{h}{h_{cp}}\,\delta_v. \end{equation}

Values of the equivalent constant-property Reynolds numbers are reported in table 1, which can be used as a guide to interpret the instantaneous flow field in figure 1, where flow cases with heating show finer eddies than for cooling because their effective Reynolds number is higher.

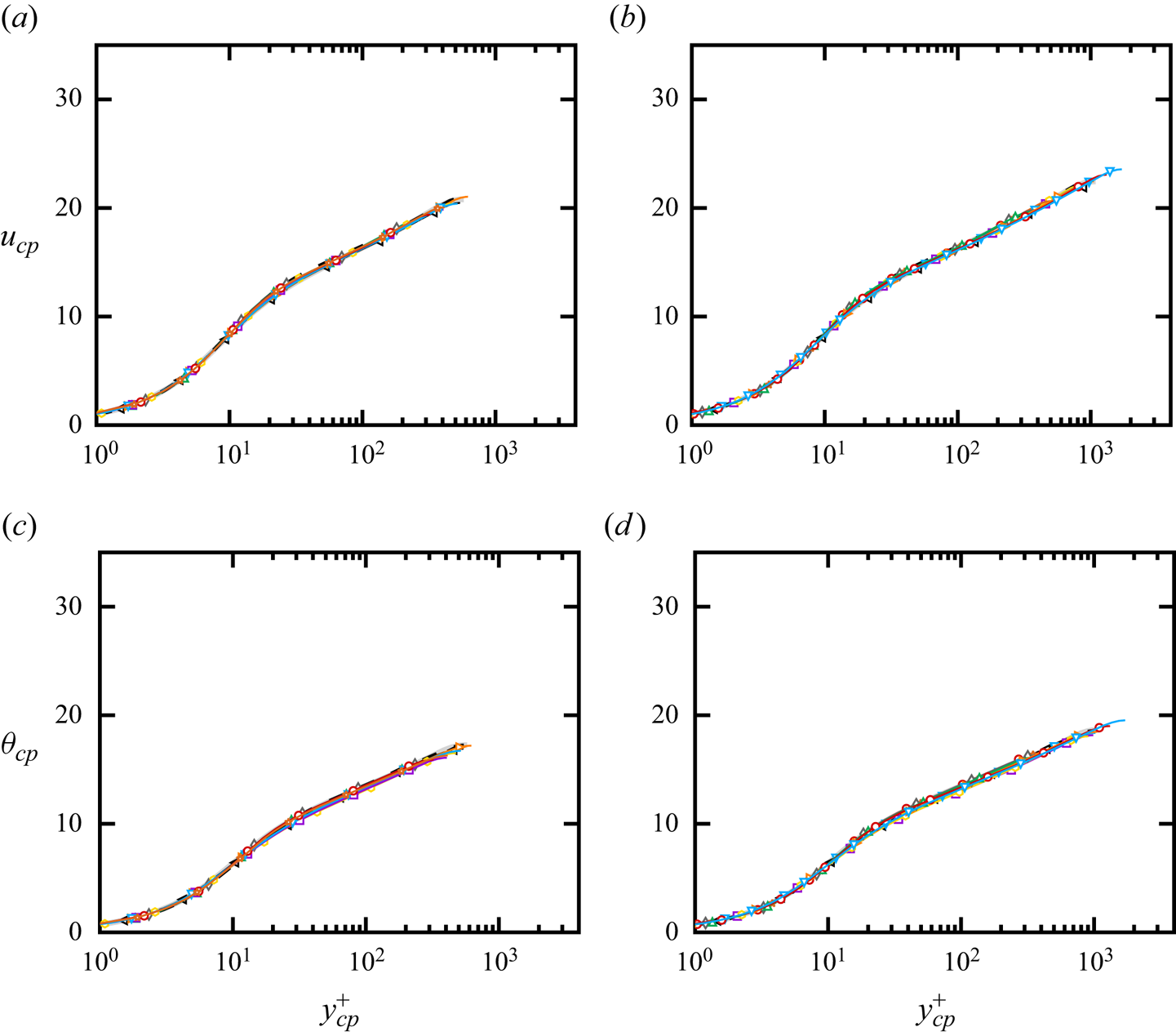
Figure 4. (a,b) Mean velocity and (c,d) mean temperature profiles transformed using (4.1a–c) with kernel functions (4.6a,b) and (4.13a,b), for (a,c) L flow cases and (b,d) H flow cases. Symbols indicate DNS data for different mean-to-wall temperature ratios: $T_m /T_w = 0.4$ (left triangles), $T_m /T_w = 0.5$, $T_w=800$ K (downward triangles), $T_m /T_w = 0.5$, $T_w=273.25$ K (right triangles), $T_m /T_w = 0.7$ (squares), $T_m /T_w = 0.8$ (hexagons), $T_m /T_w = 1.5$ (stars), $T_m /T_w = 2$ (circles), $T_m /T_w = 2.5$ (diamonds), $T_m /T_w = 3$ (upward triangles). The grey solid lines indicate the reference mean velocity and temperature profiles of the constant-property case at $\textit {Pr}=0.72$, obtained using the synthetic velocity profile of Musker (Reference Musker1979) and the synthetic temperature profile of Pirozzoli (Reference Pirozzoli2023). The dashed black lines indicate DNS of constant-property channel flow from Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016) at $\textit {Pr}=0.71$.

5. Wall friction and heat transfer

The variable-property transformations developed in the previous section are very useful, especially as they enable the prediction of the heat transfer and friction coefficients. For that purpose, the only required inputs are the reference constant-property mean velocity and mean temperature profiles. As discussed previously, in the current work we consider the composite profiles developed in the work of Pirozzoli & Modesti (Reference Pirozzoli and Modesti2024). However, different choices are possible, and one could, for instance, use the model for the mean velocity by Nagib & Chauhan (Reference Nagib and Chauhan2008), and the model for the mean temperature by Kader (Reference Kader1981), although the latter might result in less accurate temperature profiles due to inconsistencies in the near-wall region. Starting from those, application of theinverses of transformations (4.1a–c),

(5.1a––c)\begin{equation} y=\int_0^y \frac{1}{f_{cp}} \, {\mathrm d}y_{cp}, \quad \tilde{u}=\int_0^{u_{cp}} \frac{1}{g_{cp}} \, {\mathrm d}u_{cp}, \quad \tilde{\theta}=\int_0^{\theta_{cp}} \frac{1}{h_{cp}} \, {\mathrm d}\theta_{cp}, \end{equation}

allows us to determine the actual variable-property profiles, for any given mean-to-wall temperature ratio and Reynolds number. The key technical difficulty is that the kernel functions $f_{cp}$, $g_{cp}$, $h_{cp}$ depend on the actual temperature in the variable-property case, hence an iterative procedure is necessary, as for compressible flow (Kumar & Larsson Reference Kumar and Larsson2022; Hasan et al. Reference Hasan, Larsson, Pirozzoli and Pecnik2024). The iterative procedure is presented in Algorithm 1, and it can be summarized as follows.

1. (i) Generate the constant-property profiles for a target friction Reynolds number $\textit {Re}_{\tau,cp}$.

2. (ii) Initialize kernel functions $f_{cp}$, $g_{cp}$, $h_{cp}$ using the constant-property temperature profile.

3. (iii) Calculate the backward convolution integrals (5.1a–c) to find $y$, $u$, $\theta$.

4. (iv) Update the kernels $f_{cp}$, $g_{cp}$, $h_{cp}$ using the newly calculated temperature $\theta$.

5. (v) Calculate the friction coefficient, the Stanton number and $\textit {Re}_{\tau,cp}$.

6. (vi) Update the constant-property profiles based on the updated $\textit {Re}_{\tau,cp}$.

Note that two nested loops are required for this iterative algorithm. This is because the constant-property profiles are also recalculated at each step in order to converge towards the target friction Reynolds number $\textit {Re}_{\tau,cp}$.

Algorithm 1 Inverse variable-property transformation, where $\varepsilon_{\textit{Re}_{\tau}}$ and $\varepsilon$ are the tolerances for the iterative algorithm, which in our case are set to $10^{-9}$ and $10^{-10}$, respectively.

Figure 5 shows the resulting friction coefficient $C_f=2\tau _w/(\rho _bu_b^2)$ and the Stanton number $\textit {St} = q_w/[\rho _b C_p u_b(T_w-T_m)]$. Whereas the data for the constant-property case (black pentagons) fall on top of the corresponding theoretical curves (light grey), we find significant deviations thereof in cases with property variations. In particular, we note that cases with a heated wall yield reduced friction and heat flux, whereas cases with a cooled wall yield an increase of momentum and heat transfer, with a scatter around the constant-property case of $\pm$25 % for both the friction coefficient and the Stanton number. We also report the heat transfer in terms of Nusselt number $\textit {Nu} = \textit {Re}_b\,\textit {St}\,\textit {Pr}$, although this representation tends to hide differences within a few per cent, thus the Stanton number should be preferred for accurate evaluation of theories. Theoretical predictions relying on use of the variable-property transformations (4.1a–c) are shown in the figure with solid lines of matching colours, and of course those are not universal as well. Notably, figure 5 shows that the resulting predictions match the DNS data to within 1–2 % accuracy for all cases, for both the friction and heat transfer coefficients, as shown quantitatively in figure 6. We further find that the analogy between momentum and heat transfer holds also in the case of variable-property flows, as the Reynolds analogy factor stays close to the constant property case, although this information alone is obviously not sufficient to recover the heat transfer and friction coefficients from the constant-property case. Note that the Reynolds analogy factor is not unity even in the constant-property case because $\textit {Pr}=0.72$.

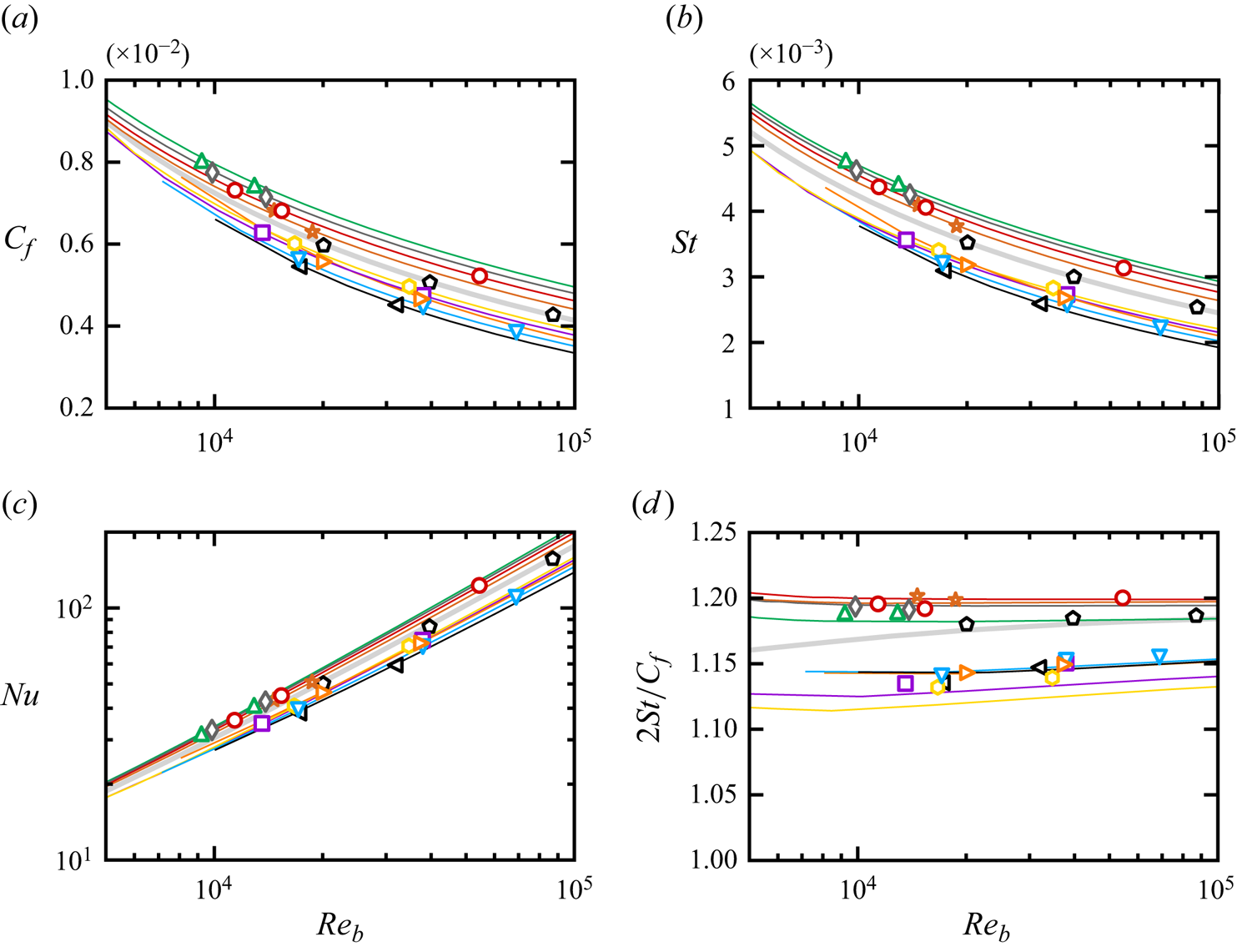
Figure 5. (a) Friction coefficient, (b) Stanton number, (c) Nusselt number and (d) Reynolds analogy factor as functions of the bulk Reynolds number $\textit {Re}_b=2h\rho _bu_b/\mu _m$. Solid lines indicate predictions obtained by inverting the variable-property transformations (4.1a–c), and symbols indicate DNS data for different mean-to-wall temperature ratios, with matching colours: $T_m /T_w = 0.4$ (black left triangles), $T_m /T_w = 0.5$, $T_w=800$ K (orange downward triangles), $T_m /T_w = 0.5$, $T_w=273.25$ K (blue right triangles), $T_m /T_w = 0.7$ (purple squares), $T_m /T_w = 0.8$ (gold hexagons), $T_m /T_w = 1.5$ (brown stars), $T_m /T_w = 2$ (red circles), $T_m /T_w = 2.5$ (grey diamonds), $T_m /T_w = 3$ (green upward triangles). Black pentagons refer to DNS data of passive scalars in plane channel flow with $\textit {Pr}=0.71$ from Pirozzoli et al. (Reference Pirozzoli, Bernardini and Orlandi2016).

Figure 6. Percentage difference between DNS data and predicted (a) friction coefficient and (b) Stanton number as functions of the bulk Reynolds number $\textit {Re}_b=2h\rho _bu_b/\mu _m$. Symbols indicate DNS data for different mean-to-wall temperature ratios: $T_m /T_w = 0.4$ (left triangles), $T_m /T_w = 0.5$, $T_w=800$ K (downward triangle), $T_m /T_w = 0.5$, $T_w=273.25$ K (right triangles), $T_m /T_w = 0.7$ (squares), $T_m /T_w = 0.8$ (hexagons), $T_m /T_w = 1.5$ (stars), $T_m /T_w = 2$ (circles), $T_m /T_w = 2.5$ (grey diamonds), $T_m /T_w = 3$ (upward triangles).