Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T10:52:56.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Noncommutative strong maximals and almost uniform convergence in several directions

Part of: Probability theory on algebraic and topological structures Groups and semigroups of linear operators, their generalizations and applications Measure-theoretic ergodic theory Harmonic analysis in several variables Individual linear operators as elements of algebraic systems

Published online by Cambridge University Press:  20 November 2020

José M. Conde-Alonso Open the ORCID record for José M. Conde-Alonso [Opens in a new window] ,
Adrián M. González-Pérez  and
Javier Parcet
José M. Conde-Alonso
Affiliation:
UAM - Departamento de Matemáticas, 7 Francisco Tomás y Valiente, 28049Madrid, Spain; E-mail: [email protected]
Adrián M. González-Pérez
Affiliation:
IMPAN (Instytut Matematyczny Polskiej Akademii Nauk), ul. Sniadekich 8, 00-656 Warsaw; E-mail: [email protected]
Javier Parcet
Affiliation:
Consejo Superior de Investigaciones Científicas - ICMAT, 23 Nicolás Cabrera, 28049Madrid, Spain; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our first result is a noncommutative form of the Jessen-Marcinkiewicz-Zygmund theorem for the maximal limit of multiparametric martingales or ergodic means. It implies bilateral almost uniform convergence (a noncommutative analogue of almost everywhere convergence) with initial data in the expected Orlicz spaces. A key ingredient is the introduction of the 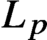$L_p$ -norm of the 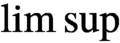$\limsup $ of a sequence of operators as a localized version of a 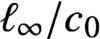$\ell _\infty /c_0$ -valued 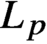$L_p$ -space. In particular, our main result gives a strong 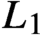$L_1$ -estimate for the 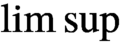$\limsup $ —as opposed to the usual weak 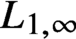$L_{1,\infty }$ -estimate for the 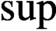$\mathop {\mathrm {sup}}\limits $ —with interesting consequences for the free group algebra.

Let 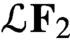$\mathcal{L} \mathbf{F} _2$ denote the free group algebra with 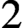$2$ generators, and consider the free Poisson semigroup generated by the usual length function. It is an open problem to determine the largest class inside 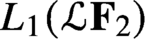$L_1(\mathcal{L} \mathbf{F} _2)$ for which the free Poisson semigroup converges to the initial data. Currently, the best known result is 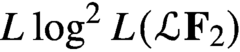$L \log ^2 L(\mathcal{L} \mathbf{F} _2)$ . We improve this result by adding to it the operators in 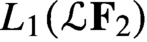$L_1(\mathcal{L} \mathbf{F} _2)$ spanned by words without signs changes. Contrary to other related results in the literature, this set grows exponentially with length. The proof relies on our estimates for the noncommutative 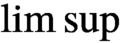$\limsup $ together with new transference techniques.

We also establish a noncommutative form of Córdoba/Feffermann/Guzmán inequality for the strong maximal: more precisely, a weak 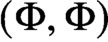$(\Phi ,\Phi )$ inequality—as opposed to weak 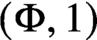$(\Phi ,1)$ —for noncommutative multiparametric martingales and $\Phi (s) = s (1 + \log _+ s)^{2 + \varepsilon }$ . This logarithmic power is an 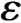$\varepsilon $ -perturbation of the expected optimal one. The proof combines a refinement of Cuculescu’s construction with a quantum probabilistic interpretation of M. de Guzmán’s original argument. The commutative form of our argument gives the simplest known proof of this classical inequality. A few interesting consequences are derived for Cuculescu’s projections.

Keywords

von Neumann algebrasnoncommutative Lp-martingalesergodic meanmaximal operators

MSC classification

Primary: 42B99: None of the above, but in this section 47C15: Operators in $C^*$- or von Neumann algebras
Secondary: 28D99: None of the above, but in this section 47D07: Markov semigroups and applications to diffusion processes 60B99: None of the above, but in this section
Type
Analysis
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e57
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Bekjan, T., Chen, Z. and Osekowski, A., ‘Noncommutative maximal inequalities associated with convex functions’, Trans. Amer. Math. Soc. 369(1) (2017), 409–427.CrossRefGoogle Scholar
Bennett, C. and Sharpley, R.C., Interpolation of Operators (Academic Press, 1988).Google Scholar
Blecher, D.P. and Merdy, C.L., Operator Algebras and Their Modules: An Operator Space Approach, London Mathematical Society Monographs (Clarendon, 2004).CrossRefGoogle Scholar
Choda, M., ‘Reduced free products of completely positive maps and entropy for free product of automorphisms’, Publ. Res. Inst. Math. Sci. 32(2) (1996), 371–382.CrossRefGoogle Scholar
Cordoba, A. and Fefferman, R., ‘A geometric proof of the strong maximal theorem’, Ann. of Math. (2) 102(1) (1975), 95–100.Google Scholar
Cuculescu, I., ‘Martingales on von Neumann algebras’, J. Multivariate Analysis 1(1), 1971, 17–27.CrossRefGoogle Scholar
Defant, A., Classical Summation in Commutative and Noncommutative L ${}_{\mathsf{p}}$ -Spaces, vol. 2021 of Lecture Notes in Mathematics (Springer Berlin Heidelberg, Berlin, Heidelberg, 2011).Google Scholar
Dirksen, S., ‘Weak-type interpolation for noncommutative maximal operators’, J. Operat. Theor. 73(2) (2015), 515–532.CrossRefGoogle Scholar
Doob, J. L., Stochastic Processes vol. 101 (New York, Wiley, 1953).Google Scholar
Dunford, N. and Schwartz, J. T., ‘Convergence almost everywhere of operator averages’, J. Ration. Mech. Anal 5(1) (1956), 129–178.Google Scholar
Effros, E.G. and Ruan, Z.-J., Operator Spaces , vol. 23 of London Mathematical Society Monographs New Series (The Clarendon Press, Oxford University Press, New York, 2000).Google Scholar
Folland, G.B., A Course in Abstract Harmonic Analysis, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1995).Google Scholar
Folland, G.B., Real analysis, Modern Techniques and Their applications, Pure and Applied Mathematics , second edn. (John Wiley & Sons, Inc., New York, 1999).Google Scholar
de Guzmán, M., ‘An inequality for the Hardy-Littlewood maximal operator with respect to the product of differentiation bases’, Studia Math 49 (1972), 265–286.Google Scholar
Haagerup, U., ‘An example of a non nuclear ${C}^{\ast }$ -algebra, which has the metric approximation property’, Invent. Math. 50(3) (1978), 279–293.CrossRefGoogle Scholar
Haagerup, U., ‘Operator-valued weights in von Neumann algebras. I’, J. Funct. Anal. 32(2) (1979), 175–206.CrossRefGoogle Scholar
Hardy, G.H. and Littlewood, J.E., ‘A maximal theorem with function-theoretic applications’, Acta Math. 54 (1930), 81–116.CrossRefGoogle Scholar
Hong, G., Junge, M. and Parcet, J., ‘Algebraic Davis decomposition and asymmetric Doob inequalities’, Commun. Math. Phys 346(3), (September 2016), 995–1019.CrossRefGoogle Scholar
Hong, G. and Sun, M., ‘Noncommutative multi-parameter Wiener-Wintner type ergodic theorem’, J. Funct. Anal. 275(5) (2018), 1100–1137.CrossRefGoogle Scholar
Hu, Y., ‘Noncommutative extrapolation theorems and applications’, Ill. J. Math. 53(2) (2009), 463–482.CrossRefGoogle Scholar
Jajte, R., Strong Limit Theorems in Non-Commutative Probability (Lecture Notes in Mathematics (Springer-Verlag, Berlin Heidelberg, 1985).CrossRefGoogle Scholar
Jajte, R., Strong Limit Theorems in Noncommutative ${L}^2$ -Spaces (Lecture Notes in Mathematics (Springer-Verlag, Berlin Heidelberg, 1991).Google Scholar
Jessen, B., Marcinkiewicz, J. and Zygmund, A., ‘Note on the differentiability of multiple integrals’, Fundam. Math. 25(1) (1935), 217–234.CrossRefGoogle Scholar
Junge, M., ‘Doob’s inequality for non-commutative martingales’, J. Reine Angew. Math. 549 (2002), 149–190.Google Scholar
Junge, M., ‘Fubini’s theorem for ultraproducts of noncommutative ${L}_p$ -spaces’, Can. J. Math. 56(5) (2004), 983–1021.CrossRefGoogle Scholar
Junge, M., Mei, T. and Parcet, J., ‘Noncommutative Riesz transforms—dimension free bounds and Fourier multipliers’, J. Eur. Math. Soc. 20(3) (2018).Google Scholar
Junge, M. and Parcet, J., ‘Mixed-norm inequalities and operator space ${L}_p$ -embedding theory’, Mem. Amer. Math. Soc. 203(953) (2010.Google Scholar
Junge, M. and Xu, Q., ‘Noncommutative maximal ergodic theorems’, J. Am. Math. Soc. 20(2) (2007), 385–439.CrossRefGoogle Scholar
Kunze, W., ‘Noncommutative Orlicz Spaces and Generalized Arens Algebras’, Math. Nachr. 147(1) (1990), 123–138.CrossRefGoogle Scholar
Lance, E.C., ‘Ergodic theorems for convex sets and operator algebras’, Invent. Math. 37(3) (1976), 201–214.CrossRefGoogle Scholar
Litvinov, S., ‘Uniform equicontinuity of sequences of measurable operators and non-commutative ergodic theorems’, Proc. Amer. Math. Soc. 140(7) (2012), 2401–2409.CrossRefGoogle Scholar
Mei, T. and Ricard, É., ‘Free Hilbert transforms’, Duke Math. J. 166(11) (2017), 2153–2182.CrossRefGoogle Scholar
Mei, T. and Xu, Q., ‘Free Fourier multipliers associated with the first segment’ (September 2019), arXiv 1909.06879.Google Scholar
Ornstein, D., ‘On the pointwise behavior of iterates of a self-adjoint operator’, J. Appl. Math. Mech. 18(5), 1968, 473–477.Google Scholar
Pedersen, G. K., ${C}^{\ast }$ -algebras and their automorphism groups, vol. 14 of London Mathematical Society Monographs (Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], London-New York, 1979).Google Scholar
Pisier, G., ‘Non-commutative vector valued ${L}_p$ -spaces and completely $p$ -summing maps’, Astérisque (247) (1998).Google Scholar
Pisier, G., Introduction to Operator Space Theory , vol. 294 of London Mathematical Society Lecture Note Series (Cambridge University Press, Cambridge, 2003).Google Scholar
Pisier, G. and Xu, Q., ‘Non-commutative ${L}^p$ -spaces’, in: Handbook of the Geometry of Banach Spaces vol. 2 (North-Holland, Amsterdam, 2003), 1459–1517.CrossRefGoogle Scholar
Pisier, G., Martingales in Banach Spaces vol. 155 (Cambridge University Press, 2016).Google Scholar
Pisier, G. and Xu, Q., ‘Non-commutative martingale inequalities’, Comm. Math. Phys. 189(3) (1997), 667–698.CrossRefGoogle Scholar
Ryan, R.A., Introduction to Tensor Products of Banach Spaces , Springer Monographs in Mathematics (Springer London, 2013).Google Scholar
Stein, E.M., ‘A note on the class $LlogL$ ’, Studia Math. 3(32) (1969), 305–310.CrossRefGoogle Scholar
Stein, E.M., Topics in Harmonic Analysis Related to the Littlewood-Paley theory , Annals of Mathematics Studies no. 63 (Princeton University Press, Princeton, NJ, 1970).Google Scholar
Takesaki, M., Theory of Operator Algebras I , vol. 124 of Encyclopaedia of Mathematical Sciences (Springer-Verlag, Berlin, 2002).Google Scholar
Takesaki, M., Theory of Operator Algebras II , vol. 125 of Encyclopaedia of Mathematical Sciences (Springer-Verlag, Berlin, 2003).Google Scholar
Tao, T., ‘A converse extrapolation theorem for translation-invariant operators’, J. Funct. Anal. 180(1) (2001), 1–10.CrossRefGoogle Scholar
Tao, T., ‘Failure of the ${L}^1$ pointwise and maximal ergodic theorems for the free group’, in: Forum Math. Sigma vol. 3 (Cambridge University Press, 2015).Google Scholar
Terp, M., ‘ ${L}^p$ spaces associated with von Neumann algebras’, Notes, Math. Institute, Copenhagen Univ 3 (1981).Google Scholar
Voiculescu, D. V., Dykema, K. J. and Nica, A., Free Random Variables (American Mathematical Society, 1992).CrossRefGoogle Scholar
Yano, S., ‘Notes on Fourier analysis (XXIX): An extrapolation theorem’, J. Math. Soc. Jpn. 3(2) (1951), 296–305.CrossRefGoogle Scholar
Yeadon, F. J., ‘Ergodic theorems for semifinite von Neumann algebras I’, J. London Math. Soc. 16(2), 1977, 326–332.CrossRefGoogle Scholar
Yeadon, F. J., ‘Ergodic theorems for semifinite von Neumann algebras: II’, Math. Proc. Camb. Philos. Soc. 88 (1980), 135–147.CrossRefGoogle Scholar
Yosida, K. and Kakutani, S., ‘Birkhoff’s Ergodic Theorem and the Maximal Ergodic Theorem’, Proc. Imp. Academy 15(6) (1939), 165–168.CrossRefGoogle Scholar
Yosida, K. and Kakutani, S., ‘Operator-Theoretical Treatment of Markoff’s Process and Mean Ergodic Theorem’, Ann. Math. 42(1)(1941), 188–228.CrossRefGoogle Scholar