The factorial model proposed by Kielanowski(Reference Kielanowski and Blaxter1) describes metabolisable energy (ME) utilisation as the sum of three factors, namely maintenance, the total cost of protein retention (PR) and the total cost of fat retention (FR). It follows that in a regression context maintenance can be estimated by the intercept (INT) in the simple regression relationship between ME intake (MEI) and energy retention (ER) or the INT in the multiple regression relationship between MEI and both PR and FR. As energy balance does not necessarily imply both protein and fat balance(2), these INT are not necessarily identical. However, estimates of the two possible INT may not differ much, as indicated by a comparison between regression estimates from Tables 1.11 and 1.12 by the Agricultural Research Council (ARC)(2).
A third possibility for the estimation of maintenance is from a measurement of fasting heat production (HP), scaled by the efficiency of the utilisation of ME below maintenance. It is the purpose of the present paper to show that INT estimates of maintenance agree with fasting HP estimates if they are supplemented with estimates of the cost of body protein resynthesis. This finding is in agreement with the hypothesis that the ordinary regression estimate of PR efficiency (k P) is deflated by the effects of body protein resynthesis. It also implies that the fasting HP estimate of maintenance should be used in conjunction with the theoretical (stoichiometric) efficiency of protein synthesis (PS).
From the foregoing approximate equalities one would expect that regression estimates of FR efficiency (k F) should be approximately equal to theoretical estimates of fat synthesis efficiency. Experimental evidence confirms this conjecture.
Theory and methods
Turnover-related protein retention efficiency
Taking turnover into account, k P can be defined(Reference Bergen, Merkel, Pearson and Dutson3) as:
where PR is in kg/d and PS corresponds to the given rate of PR, allowing for turnover. The coefficient 22·6 represents the energy equivalent of protein (MJ/kg) and 3·766 the cost of synthesis based on the assumption that 5 mol ATP will arrange 1 mol of peptide bonds. Whittemore et al. (Reference Whittemore, Green and Knap4) give an equivalent definition with coefficients of 23·6 and 3·92.
For ease in application, PR and PS will be measured in energy units (MJ/d). It follows that equation (1) becomes:
If there is no turnover, PR = PS and k P = 6/7 = 0·86, given as theoretical (stoichiometric) value in texts such as Blaxter(Reference Blaxter5).
It is customary to partition MEI into energy intake devoted to maintenance (IM), PR (IPR) and FR, all measured in terms of MJ/d, or represented in symbols by:
where IFR is intake devoted to FR.
A popular model derived from equation (3) is expressed in the regression equation, also employed by the ARC(2):
with INT representing the part of MEI devoted to maintenance.
It is axiomatic that the rate of PR is equal to the difference between the rate of PS and the rate of protein breakdown (PB):
Then, from equations (2) and (5):
where 6/7 is the theoretical (stoichiometric) efficiency of PS and PB/6 represents the cost of protein resynthesis. If equation (6) is substituted into equation (4), it follows that:
A comparison between equations (3), (4) and (7 shows that two sets of possibilities exist for consideration, i.e.:
or:
From the point of view of practical application both equations (8) and (9) may represent useful approximations. However, from a conceptual point of view there seems to be only one ultimate definition of maintenance, i.e. the intake at which both PR and FR are equal to zero. Algebraically both equations (8) and (9) represent such a conceptual point of zero retention maintenance. The only way to differentiate between equations (8) and (9) would, therefore, be on the basis of experimental evidence. However, obtaining both PR and FR equal to zero under experimental conditions may be very difficult to achieve as fat reserves may be used to fuel PR(2). A practical alternative may be to approximate maintenance by the intake at zero ER. This can be done by deriving maintenance from fasting HP. Conventionally, maintenance derived from fasting HP is symbolically expressed as:
where k M represents maintenance efficiency.
For easy reference, estimates of IM obtained by employing equation (9) will be denoted by IMI and IM estimated by employing equation (10) by IMH.
It is general experience that the application of ordinary regression analysis to the estimation of k P and k F results in estimates of k P that deviate markedly from the theoretical synthesis efficiency 6/7(Reference Blaxter5), and that are approximately equal to an average value of k P in equation (2). This average value of k P is, in turn, dependent on average values of PR and PS determined by experimental feed intake levels(Reference Roux6, Reference Roux7). HP at maintenance contains the heat loss due to PS involved in the turnover of body protein. This corresponds to PB/6 in equation (6). Hence our central hypothesis is that the maintenance portion of equation (9) would be approximately equal to equation (10). The implied inequality between maintenance in equations (8) and (10) must, therefore, necessarily follow from the fact that in equation (8) PB/6 is accommodated in k P. In the final analysis the difference between equations (8) and (9) lies in the different allocation of PB/6 between maintenance and k P. Using the allocation in equation (9) has the advantage that it is unnecessary to estimate k P, as PS efficiency can be used in its place.
In geometrical terms the inequality between the maintenance terms in equations (8) and (9) arises from a curvilinear relationship between intake and PR which can be described by a variable tangent gradient defined by 1/k P from equation (2). In ordinary linear regression this curvilinear relationship will be approximated by a straight line. This will cause no problem with extrapolation to maintenance for feed intakes near to maintenance. However, with even the lowest feeding levels in most pig efficiency experiments generally higher than half of ad libitum intake(Reference Roux6), the linear approximation to a curvilinear relationship causes the underestimation of zero retention maintenance by the INT term in equation (4).
Ignoring turnover in fat retention efficiency
It is possible to define k F in a similar fashion as k P in equation (1). The coefficients involved would have to depend on the energy content of fat, diet composition as well as the proportion of body fat resynthesised from endogenous fat moieties. This notwithstanding, it is reasoned in the present communication that measurement error in ordinary regression estimates is of such magnitude that it would at present be impossible to distinguish between correspondence to k F with or without turnover. Hence, I will proceed by showing that regression estimates are in satisfactory agreement with theoretical estimates of fat synthesis efficiency.
Experimental evidence
Estimates of the cost of the resynthesis of existing protein
Perhaps the most important requirement to test the hypothesis on the equivalence of the maintenance portion of equations (9) and (10) is estimation of the cost of resynthesis of existing body protein by PB/6. The most extensive measurements on whole-body breakdown rates for growing pigs are on three-quarter Large White one-quarter Landrace female pigs(Reference Reeds, Fuller, Cadenhead, Lobley and McDonald8, Reference Fuller, Reeds, Cadenhead and Seve9). Estimates from these sources(Reference Reeds, Fuller, Cadenhead, Lobley and McDonald8, Reference Fuller, Reeds, Cadenhead and Seve9) are combined with estimates of INT and fasting HP/k M from the literature in Table 1.
Table 1 A comparison between estimates of maintenance requirement (MJ/kg live body mass (W)0·60 per d) from intercepts (INT) corrected for protein resynthesis* and from fasting heat production (HP)†
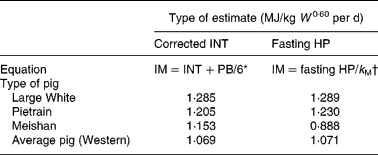
IM, intake devoted to maintenance; PB, protein breakdown; k M, maintenance efficiency.
* Equation (9).
The Meishan estimates are included in Table 1 to show that if breeds or experimental procedures are not carefully matched, widely divergent maintenance estimates can be obtained by the methods of equations (9) and (10). The agreement between the other estimates is remarkable, providing strong evidence that equations (9) and (10) should give similar answers under comparable circumstances.
The estimation of protein breakdown/6
On the assumption of a 6·25 g/g conversion of N to protein and a gross energy content of protein of 23·6 kJ/g, the values of PB/6 from equation (5) for equally weighted treatment averages are 0·199 (se 0·00 650; n 23)(Reference Reeds, Fuller, Cadenhead, Lobley and McDonald8) and 0·230 (se 0·00 878; n 32) MJ/kg W 0·60 per d(Reference Fuller, Reeds, Cadenhead and Seve9), respectively, where W indicates the live body mass of the animals. Weighted according to the number of observations in each experiment the average is:
with se 0·00 579, the value that will be accepted for present purposes.
It is noted that PB/6 can also be indirectly estimated from equation (6) as PB/6 = PR(1/k P − 7/6). The harmonic mean of k P for twenty-two pig experiments with average live mass of 49·8 kg is k P = 0·525(Reference Klein, Hoffmann, Bock, Eggum, Low and Zebrowska10). For comparable average live mass, seven sex/breed combinations(Reference Noblet, Karege, Dubois and van Milgen11) give PR = 3·4 MJ/d, on average. Accepting this as fairly representative, from equation (6):

This is in fair agreement with and not significantly different from equation (11), since the difference of 0·026 is smaller than the se = 0·032 for equation (12).
The agreement between the estimates contained in equations (11) and (12) provides strong support for the validity of the idea that the difference between k P and the theoretical efficiency of PS is due to the resynthesis of existing body protein.
The value of maintenance efficiency
The value of k M accepted for conventional growth diets by the ARC(2) is k M = 0·81. The maximum estimate from fourteen diets, widely different in chemical composition, mostly formulated for maintenance purposes(Reference Noblet, Shi and Dubios12), is in agreement with the ARC(2):
As the average of a sample of mainly maintenance diets would be too low, equation (13) represents the value accepted for growth diets in the present paper.
Maintenance from fasting heat production
An overlap of breeds(Reference Noblet, Karege, Dubois and van Milgen11, Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13), together with common experimental procedures of the Station de Recherches Porcines (Saint-Gilles, France), allow meaningful comparisons between the estimates obtained from equations (9) and (10) in Table 1.
Large Whites
No significant difference was observed(Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) for the difference between castrates and males, so that the average resting fasting metabolism for Large Whites is fasting HP = 0·990 MJ/kg W 0·60. To make the estimates between equations (9) and (10) comparable, an estimate for activity was added of 0·0485(Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) of the total fasting HP (fasting HP = resting fasting HP+activity HP). This gives IMH = (0·990+0·050)/0·807 = 1·289 MJ/kg W 0·60 per d.
No sex differences exist in the maintenance INT between different sexes of Large Whites, so that they average INT = 1·068 MJ/kg W 0·60 per d(Reference Noblet, Karege, Dubois and van Milgen11). Hence, from equations (9) and (11) IMI = 1·068+0·217 = 1·285 MJ/kg W 0·60 per d, giving excellent agreement between IMH and IMI.
Pietrain and Meishan pigs
The estimates for Pietrain males and Meishan castrates in Table 1 are obtainable from the same sources(Reference Noblet, Karege, Dubois and van Milgen11, Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) and in the same fashion as for Large Whites. Similar to Large Whites, the two Pietrain estimates in Table 1 are in excellent agreement. In the following the possible reasons for the Meishan discrepancy will be explored.
Meishan discrepancy
van Milgen et al. (Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) noted that their estimate of Meishan resting fasting HP of 0·660 MJ/kg W 0·60 per d was markedly lower than 0·749 MJ/kg W 0·60 per d, obtained on similar pigs, in an earlier study(Reference Bernier, Dubois and Noblet14). Including a correction for movement(Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13), the Bernier et al. (Reference Bernier, Dubois and Noblet14) estimate is 0·817 MJ/kg W 0·60 per d, relatively near to other estimates(Reference Yen, Nienaber, Klindt and Crouse15, Reference Yen, Hansen, Nienaber and Nelssen16) of 0·842 and 0·888, respectively. The weighted combined estimate(Reference Bernier, Dubois and Noblet14–Reference Yen, Hansen, Nienaber and Nelssen16) is 0·848 MJ/kg W 0·60 per d. This gives IMH = 0·848/0·807 = 1·051 MJ/kg W 0·60 per d.
For comparable body mass, Meishan castrates have much lower proportions of muscle mass to empty body mass than Large White castrates(Reference Noblet, Karege, Dubois and van Milgen11). Taking muscle and viscera together, the Meishan:Large White muscle+viscera ratio is 0·717. Correcting equation (11) with this ratio for the lesser protein content of Meishans, PB/6 = 0·156 MJ/kg W 0·60 per d is obtained. This can be combined with the INT value for Meishan castrates(Reference Noblet, Karege, Dubois and van Milgen11) to give IMI = 0·936+0·156 = 1·092 MJ/kg W 0·60 per d. This body composition-corrected estimate of IMI is in reasonable agreement with the estimate of IMH from the previous paragraph. Hence there is conjecture that the Meishan discrepancy in Table 1 is mainly due to a fasting sensitivity to environmental circumstances of the breed, together with an inapplicable scaling of breakdown rate in relation to body mass, derived for Western pigs.
The average pig
Evidence has been provided for the virtual identity of IMI in equation (9) and IMH in equation (10) on Large Whites and Pietrains (Table 1), together with a sizeable discrepancy for Chinese Meishan pigs. It is, therefore, of interest to enquire if equations (9) and (10) can be assumed identical for the average Western pig. Provided that HP due to residual digestive and absorptive processes can be accounted for, a short duration of fasting is probably more representative for the producing animal than long-term fasting. van Milgen et al. (Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) cite evidence for a rapid decrease in HP during day 1 of fasting, followed by a more gradual decrease afterwards. This gradual decrease in HP is probably due to changes in the mass of portal-drained viscera and the liver and represents, therefore, an abnormal physiological state for a normally growing animal(Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13). Hence, the resting fasting heat production used in the construction of Table 1 was 24 h for 25 kg pigs and 30 h for 40 and 60 kg pigs(Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13). Therefore, all references with unadjusted fasting periods of 30 h or less(Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) were used in the construction of Table 2.
Table 2 Fasting metabolism (heat production) in different experiment, type and breed combinations with fasting periods less than 30 h
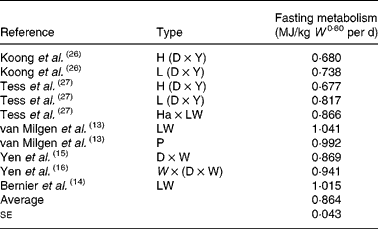
W, live body mass; H, high backfat line; D, Duroc; Y, Yorkshire; L, low backfat line; Ha, Hampshire; LW, Large White; P, Pietrain; W, White.
Since both breed and type of pig as well as experimental circumstances are important determinants of fasting HP, the observations are listed according to these criteria. This seems the best available way of obtaining as representative a sample of Western pigs as possible. The average total fasting HP in Table 2 is 0·864; this gives IMH = 0·864/0·807 = 1·071 MJ/kg W 0·60 per d.
To obtain a representative INT value for equation (9), the INT in Table 1.12(2) in MJ/kg W 0·75 is transformed to MJ/kg W 0·60 by use of live body masses at the midpoint of the indicated body mass interval. This gives a mean value of INT = 0·852 MJ/kg W 0·60 (se 0·027; n 11). Together with equation (11), IMI = 1·069 MJ/kg W 0·60 per d is obtained, almost identical to IMH for the average Western pig.
Calculating the theoretical efficiency of fat synthesis
The theoretical efficiency of fat synthesis can be calculated from regression equations for digestible energy (DE) and ME given in Table 3(Reference Noblet, Fortune, Shi and Dubois17). The energy values contained in the regression coefficients were obtained from the energy values of sixty-one diets measured in 45 kg growing Large White boars. For example, the ME potentially available from 1 kg DM of a diet with 428 g DM starch/kg would be 17·49 × 428 = 7486 kJ/kg DM. Most of the coefficients in Table 3 are exactly the same as in the original(Reference Noblet, Fortune, Shi and Dubois17), except those for retained digestible crude protein (CP) and energy metabolisable CP. Both can be obtained as follows. It is assumed that the energy contribution of retained digestible CP to ME is the same as digestible CP to DE. Since the decline in the contribution of digestible CP from DE to ME is due to urinary energy loss, z is solved in the equation:
where the meaning of 23·01 and 20·04 is given in Table 3, and 0·539 and 0·461 are the average proportions of retained digestible CP and energy metabolisable CP in the diets(Reference Noblet, Fortune, Shi and Dubois17). A regression coefficient for energy metabolisable CP is obtained: z = 16·57 (MJ/kg).
Table 3 Estimation of the theoretical efficiency of body fat synthesis from the diet averages in the study by Noblet et al. (Reference Noblet, Fortune, Shi and Dubois17)
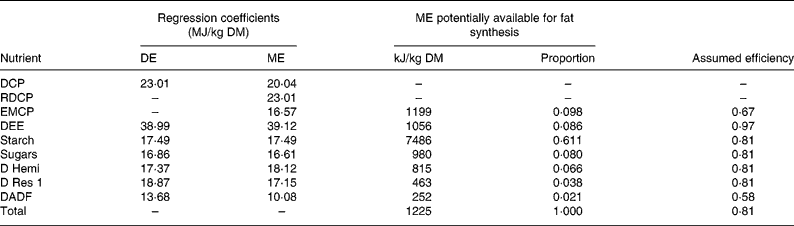
ME, metabolisable energy; DE, digestible energy; DCP, digestible crude protein; RDCP, retained digestible crude protein; EMCP, energy metabolisable crude protein; DEE, digestible ether extract; D Hemi, digestible neutral-detergent fibre minus digestible acid-detergent fibre; D Res 1, digestible organic matter minus other nutrients in Table 3; DADF, digestible acid-detergent fibre.
The difference between DE- and ME-associated regression coefficients of 23·01–16·57 = 6·44 must be due to energy loss in the urine coincident with the excretion of N-containing substances. The estimate of 6·44 is in reasonable agreement with the value of 7·2 MJ/kg protein deaminated favoured by Whittemore et al. (Reference Whittemore, Green and Knap18).
The ME potentially available for fat synthesis is then obtained by multiplying the ME regression coefficients by the diet composition (g/kg DM). The assumed efficiencies of dietary protein, fat and carbohydrate follow from Baldwin(Reference Baldwin19) and van Milgen(Reference van Milgen20) and are in close agreement with those given by Blaxter(Reference Blaxter5). (Blaxter's(Reference Blaxter5) values are generally 1 percentage point lower than the others, presumably an allowance for the cost of transport.) The efficiency for fat synthesis from fermented fibre is from Green & Whittemore(Reference Green and Whittemore21).
It is necessary to remember that k F is usually calculated from ME values. Hence, the efficiency from ME to fat in Table 3 is needed. The efficiency from digestible CP to body fat is 0·67(Reference Baldwin19). Since the urine N-associated energy loss will be accommodated by use of the ME-regression coefficient, the efficiency from digestible CP to body fat is considered applicable to the energy metabolisable CP-situation in Table 3. This argument is in agreement with the exposition in Whittemore et al. (Reference Whittemore, Green and Knap18), as the urinary excretion cost is also considered by them separately from the deamination cost, which is necessarily included in the efficiency from digestible CP to fat. The efficiency of digestible ether extract is from Baldwin(Reference Baldwin19) and van Milgen(Reference van Milgen20). The efficiency of the carbohydrates in Table 3 is taken to be 0·81, the value calculated for glucose(Reference Baldwin19, Reference van Milgen20). The efficiency for DE to fat for fibre is 0·46(Reference Green and Whittemore21). Hence, assuming a 20 % loss in the form of methane(Reference Green and Whittemore21), an efficiency of ME to body fat for digestible acid-detergent fibre is obtained of 0·46/0·80 = 0·58.
The average energy obtained from fermentation can be calculated from methane energy loss, as equal to 303 kJ/kg DM(Reference Noblet, Fortune, Shi and Dubois17). This is only slightly higher than the contribution of 252 kJ/kg DM from digestible acid-detergent fibre in Table 3. Therefore, in agreement with the relatively large difference between DE and ME, fibre-derived efficiency is only attributed to digestible acid-detergent fibre in Table 3.
On the simplifying assumption that the energy use for fat synthesis from all sources is equally likely, the total efficiency of fat synthesis of the diet can be obtained from Table 3 by calculation of the arithmetic mean with weights according to the relative amounts of component substrates of ME. This gives a total theoretical efficiency for fat synthesis of 0·81.
Quiniou et al. (Reference Quiniou, Dourmad and Noblet22) give enough information on diet composition to allow similar calculations (Table 4) as in Table 3. Digestibilities(Reference Noblet, Fortune, Shi and Dubois17, Reference Noblet and Shi23) were taken into consideration. The total theoretical efficiency calculated from Table 4, in a similar fashion to Table 3, is 0·79.
Table 4 Estimation of the theoretical efficiency of body fat synthesis from the diet averages in the study by Quiniou et al. (Reference Quiniou, Dourmad and Noblet22)
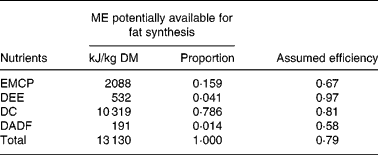
ME, metabolisable energy; EMCP, energy metabolisable crude protein; DEE, digestible ether extract; DC, digestible carbohydrates; DADF, digestible acid-detergent fibre.
Comparison with empirical estimates
The estimate of Quiniou et al. (Reference Quiniou, Dourmad and Noblet22) by ordinary multiple regression is k F = 0·81 (se 0·02), obviously not significantly different from a theoretically expected synthesis value of 0·79. Remarkably, the estimate in the model with the smallest se(Reference Noblet, Karege, Dubois and van Milgen11) is k F = 0·814 (se 0·015), also in acceptable agreement with the estimates in Tables 3 and 4.
In general the estimates of k F in the literature are very variable. For growing pigs they range from 0·69 to 1·00(Reference Klein, Hoffmann, Bock, Eggum, Low and Zebrowska10), with a harmonic mean k F = 0·80 (se 0·020; n 21), identical to the average of the theoretical values in Tables 3 and 4.
Combined maintenance, protein and fat retention
To test the theory in a combined fashion for estimates of energy required for maintenance, protein and fat synthesis an energy balance sheet was constructed (Table 5) from two experiments in the literature(Reference Noblet, Fortune, Shi and Dubois17, Reference Quiniou, Dourmad and Noblet22) with enough information on their diets for the calculation of theoretical efficiencies of fat synthesis. Line 1 simply represents the total energy devoted to PS with theoretical efficiency 6/7. The theoretical k-values employed in the calculation of line 2 are from Tables 3 and 4, respectively. The relationship between MEI and HP, both measured in MJ/d given by Noblet et al. (Reference Noblet, Fortune, Shi and Dubois17), is HP = 0·749 W 0·60+0·26 ME. Since MEI = HP+ER, it follows by substitution that MEI = 1·012 W 0·60+1·35 ER. The INT estimate in Table 5 follows by taking ER = 0.
Table 5 Energy balance sheets for two experiments (Noblet et al. (Reference Noblet, Fortune, Shi and Dubois17) and Quiniou et al. (Reference Quiniou, Dourmad and Noblet22)) in the literature
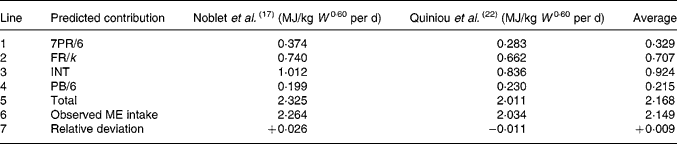
W, live body mass; PR, protein retention; FR, fat retention; k, theoretical fat synthesis efficiency; INT, intercept; PB, protein breakdown; ME, metabolisable energy.
The protein content of feed has a noticeable effect on PB. Hence the value of PB/6 in line 4 assumed for Noblet et al. (Reference Noblet, Fortune, Shi and Dubois17), with average CP content of 157 g/kg DM, is from Reeds et al. (Reference Reeds, Fuller, Cadenhead, Lobley and McDonald8) with diets of somewhat lower protein content than Fuller et al. (Reference Fuller, Reeds, Cadenhead and Seve9). The value in line 4 for INT in Quiniou et al. (Reference Quiniou, Dourmad and Noblet22) is the average of INT calculated by them from ordinary regression of MEI on PR and FR. The value of PB/6 is from Fuller et al. (Reference Fuller, Reeds, Cadenhead and Seve9) since the average CP content of the diets in Quiniou et al. (Reference Quiniou, Dourmad and Noblet22) is 246 g/kg DM.
The total predicted energy devoted to maintenance, PR and FR is in reasonable agreement with the average observed intakes of both experiments, with relative deviations, (total ME − observed ME)/observed ME, near to +0·03 and − 0·01 respectively. The average relative deviation is approximately +0·01.
The conclusion follows that the theoretical efficiencies of protein and fat synthesis can be incorporated in prediction equations for average MEI with reasonable accuracy.
Accommodating improved pigs
Chwalibog et al. (Reference Chwalibog, Jakobsen, Tausen and Thorbek24) provide evidence that, presumably due to selection for higher PR and lower body fat content, comparable fasting HP in Danish Landrace pigs increased from 0·666 to 0·986 MJ/kg W 0·60 per d over a 20-year period. As some of the evidence in the present paper is from early work it is, perhaps, important to indicate in which way the present approach might be applicable to improved pigs.
From observations on twelve improved Danish Landrace male castrates(Reference Chwalibog, Jakobsen, Tausen and Thorbek24) maintenance can be estimated by subtraction from MEI of PR and FR divided by estimates of protein and fat synthesis efficiencies respectively (Tables 3 and 4). This gives maintenance = 2·097 − 0·273/0·86 − 0·417/0·80 = 1·258 MJ/kg W 0·60 per d. On day 3 of fasting, HP was 1·062 MJ/kg W 0·60 per d. From equations (10) and (13), this gives maintenance = 1·062/0·81 = 1·311 MJ/kg W 0·60 per d. Besides confirming theory, this reasonable agreement between subtraction and fasting HP maintenance indicates that the essentials of the suggested methods remain applicable to improved pigs. For appropriate estimates of ME requirements the only necessity would be to use applicable estimates of fasting HP.
To accommodate changes in protein content it may be of value to transform (11) to:
from protein = 0·160W recommended by the ARC(2) for pigs at the time of its publication. For situations where estimates of body composition in terms of muscle, viscera and fat are available, van Milgen et al. (Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) provide a formula for the estimation of fasting HP that may be able to accommodate changes due to breeding improvement, as the likely causes of differences between types of pigs are taken into consideration.
Discussion
To understand the conclusions of the present paper one should realise that the results of regression analyses reflect correlation rather than causation. This provides the reason why protein regression coefficients include both the costs of synthesis of new protein and the resynthesis of existing body protein. Furthermore, the linear approximation of basically curvilinear relationships depends on the limits of measurement. Confining measurement to intakes reasonably far from maintenance may cause regression INT estimates of maintenance not to agree with fasting HP estimates. Nevertheless, it follows from this exposition that the main difference between causal and regression analysis approaches is in the apportioning of body protein resynthesis costs between maintenance and PR. Hence, it is concluded that, under comparable circumstances, there are two approximately equal estimates of growth energy requirements in pigs. First, total energy requirements can be estimated from maintenance estimated from fasting HP plus retention costs from theoretical efficiencies of protein and fat synthesis. This is in pigs approximately equal to the second possibility of estimation, namely the energy requirement estimated from multiple regression INT maintenance together with k P and k F associated with the regression coefficients.
The approximate equality between the two methods opens up the possibility of easier and cheaper ways of estimating growth energy requirements. The estimate of theoretical PS efficiency is 6/7 and theoretical fat synthesis efficiency can easily be calculated from feed composition by the method displayed in Table 3. Also fasts of short duration(Reference van Milgen, Bernier, Lecozler, Dubois and Noblet13) should be cheaper and easier than the full-scale measurements necessary for the application of multiple regression methods. In cases where body composition can be estimated, maintenance can also be obtained by subtraction of the total cost of new tissue synthesis from intake, quite possibly with increased accuracy of estimation. In addition, the use of the synthesis efficiency of protein in estimates of energy requirements offers relief from the problems associated with feeding level and age-variable k P indicated by (1).
As the costs of protein and fat synthesis depend on fixed biochemical reactions, there is no scope for breeding improvement in synthesis efficiencies. This leaves breeding for the efficiency of maintenance as the only option for breeding of growth efficiency. That there are possibilities in this direction is shown by the fact that maintenance depends on body composition, which is amenable to change by selection. Furthermore, Luiting(Reference Luiting, van der Heide, Huisman, Kanis and Osse25) provides evidence that efficiency in use of energy for maintenance is heritable and should respond to selection pressures.
Acknowledgements
There are, as far as I (C. Z. R.) can discern, no conflicts of interest. The motivation for the study was to investigate the possibility of breeding for improved food efficiency. I gratefully received some personal research remuneration from the University of Pretoria.







