Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-10T23:23:01.110Z Has data issue: false hasContentIssue false
  • English
  • Français

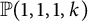A note on the smooth blowups of $\mathbb {P}(1,1,1,k)$ in torus-invariant subvarieties

Part of: Special varieties Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  29 March 2023

Daniel Cavey
Daniel Cavey*
Affiliation:
Department of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF, UK
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This papers classifies toric Fano threefolds with singular locus 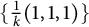$\{ \frac {1}{k}(1,1,1) \}$ for 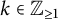$k \in \mathbb {Z}_{\geq 1}$ building on the work of Batyrev (1981, Nauk SSSR Ser. Mat. 45, 704–717) and Watanabe–Watanabe (1982, Tokyo J. Math. 5, 37–48). This is achieved by completing an equivalent problem in the language of Fano polytopes. Furthermore, we identify birational relationships between entries of the classification. For a fixed value 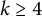$k \geq 4$, there are exactly two such toric Fano threefolds linked by a blowup in a torus-invariant line.

Keywords

Fano threefoldscascadesFano polytopescyclic quotient singularities

MSC classification

Primary: 14M25: Toric varieties, Newton polyhedra
Secondary: 14J30: $3$-folds 14J45: Fano varieties
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 4 , December 2023 , pp. 1152 - 1163
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by Evans’ EPSRC Grant EP/P02095X/2.

References

Batyrev, V., Toroidal Fano 3-folds . Izv. Akad. Nauk SSSR Ser. Mat. 45(1981), no. 4, 704–717.Google Scholar
Batyrev, V., On the classification of toric Fano $4$ -folds . J. Math. Sci. 94(1999), 1021–1050; in Algebraic geometry, 9, New York.CrossRefGoogle Scholar
Cavey, D. and Prince, T., De Pezzo surfaces with a single $1/k\left(1,1\right)$ singularity . J. Math. Soc. Japan 72(2020), no. 2, 465–505, July 2018.CrossRefGoogle Scholar
Hensley, D., Lattice vertex polytopes with interior lattice points . Pacific J. Math. 105(1983), no. 1, 183–191.CrossRefGoogle Scholar
Kasprzyk, A. M., Toric Fano three-folds with terminal singularities . Tohoku Math. J. (2) 58(2006), no. 1, 101–121.CrossRefGoogle Scholar
Kasprzyk, A. M., Canonical toric Fano threefolds . Canad. J. Math. 62(2010), no. 6, 1293–1309.CrossRefGoogle Scholar
Kreuzer, M. and Skarke, H., On the classification of reflexive polyhedra . Comm. Math. Phys. 185(1997), no. 2, 495–508.CrossRefGoogle Scholar
Kreuzer, M. and Skarke, H., Classification of reflexive polyhedra in three dimensions . Adv. Theor. Math. Phys. 2(1998), no. 4, 853–871.CrossRefGoogle Scholar
Kreuzer, M. and Skarke, H., Complete classification of reflexive polyhedra in four dimensions . Adv. Theor. Math. Phys. 4(2000), no. 6, 1209–1230.CrossRefGoogle Scholar
Lagarias, J. C. and Ziegler, G. M., Bounds for lattice polytopes containing a fixed number of interior points in a sublattice . Canad. J. Math. 43(1991), no. 5, 1022–1035.CrossRefGoogle Scholar
Mori, S. and Mukai, S., Classification of Fano $3$ -folds with ${B}_2\ge 2$ . I . Manuscripta Math. 36(1981/1982), no. 2, 147–162.CrossRefGoogle Scholar
Reid, M. and Suzuki, K., Cascades of projections from log del Pezzo surfaces . In: Number theory and algebraic geometry, London Mathematical Society Lecture Note Series, 303, Cambridge University Press, Cambridge, 2003, pp. 227–249.Google Scholar
The Graded Ring Database. http://www.grdb.co.uk (accessed 30 November 2022).Google Scholar
Watanabe, K. and Watanabe, M., The classification of Fano $3$ -folds with torus embeddings . Tokyo J. Math. 5(1982), no. 1, 37–48.CrossRefGoogle Scholar