Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-05T20:44:04.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Microlocal Euler classes and Hochschild homology

Part of: (Co)homology theory Partial differential equations

Published online by Cambridge University Press:  18 July 2013

Masaki Kashiwara  and
Pierre Schapira
Masaki Kashiwara
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Japan Department of Mathematical Sciences, Seoul National University, Republic of Korea ([email protected])
Pierre Schapira
Affiliation:
Institut de Mathématiques, Université Pierre et Marie Curie, France Mathematics Research Unit, University of Luxemburg, Luxemburg ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define the notion of a trace kernel on a manifold 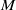$M$. Roughly speaking, it is a sheaf on 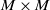$M\times M$ for which the formalism of Hochschild homology applies. We associate a microlocal Euler class with such a kernel, a cohomology class with values in the relative dualizing complex of the cotangent bundle 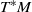${T}^{\ast } M$ over 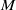$M$, and we prove that this class is functorial with respect to the composition of kernels.

This generalizes, unifies and simplifies various results from (relative) index theorems for constructible sheaves, 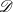$\mathscr{D}$-modules and elliptic pairs.

Keywords

sheavesD-modulesmicrolocal sheaf theoryEuler classes

MSC classification

Secondary: 14F05: Sheaves, derived categories of sheaves and related constructions 35A27: Microlocal methods; methods of sheaf theory and homological algebra in PDE
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 3 , July 2014 , pp. 487 - 516
Copyright
©Cambridge University Press 2013 

References

Bressler, P., Nest, R. and Tsygan, B., Riemann–Roch theorems via deformation quantization. I, II, Adv. Math. 167 (2002), 1–25, 26–73.CrossRefGoogle Scholar
Brylinski, J.-L. and Getzler, E., The homology of algebras of pseudodifferential symbols and the noncommutative residue, K-Theory 1 (1987), 385–403.CrossRefGoogle Scholar
Caldararu, A., The Mukai pairing II: the Hochschild–Kostant–Rosenberg isomorphism, Adv. Math. 194 (2005), 34–66.CrossRefGoogle Scholar
Caldararu, A. and Willerton, S., The Mukai pairing I: a categorical approach, New York J. Math. 16 (2010), arXiv:0707.2052.Google Scholar
Fang, B., Liu, M., Treumann, D. and Zaslow, E., The coherent–constructible correspondence and Fourier–Mukai transforms, Acta Math. Sin. (Engl. Ser.) 27 (2) (2011), 275–308, arXiv:1009.3506.CrossRefGoogle Scholar
Grivaux, J., On a conjecture of Kashiwara relating Chern and Euler classes of $\mathscr{O} $ -modules, J. Differential Geom. (2012), arXiv:0910.5384.CrossRefGoogle Scholar
Guillermou, S., Lefschetz class of elliptic pairs, Duke Math. J. 85 (2) (1996), 273–314.CrossRefGoogle Scholar
Kashiwara, M., Index theorem for maximally overdetermined systems of linear partial differential equation I, Proc. Japan Acad. 49 (1973), 803–804.Google Scholar
Kashiwara, M., Index theorem for constructible sheaves, in Systèmes différentiels et singularités, Astérisque, Volume 130, pp. 196–209 (Soc. Math. France, 1985).Google Scholar
Kashiwara, M., Letter to P. Schapira, unpublished, 18/11/1991.Google Scholar
Kashiwara, M., D-modules and microlocal calculus, Translations of Mathematical Monographs, Volume 217 (American Math. Soc., 2003).Google Scholar
Kashiwara, M. and Schapira, P., Microlocal study of sheaves, Astérisque, Volume 128 (Soc. Math. France, 1985).Google Scholar
Kashiwara, M. and Schapira, P., Sheaves on manifolds, Grundlehren der Math. Wiss., Volume 292 (Springer-Verlag, 1990).CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Moderate and formal cohomology associated with constructible sheaves, Mem. Soc. Math. Fr. (N.S.) 64 (1996).Google Scholar
Kashiwara, M. and Schapira, P., Deformation quantization modules, Astérisque, Volume 345 (Soc. Math. France, 2012), arXiv:math.arXiv:1003.3304.Google Scholar
Keller, B., On the cyclic homology of exact categories, J. Pure Appl. Algebra 136 (1999), 1–56.CrossRefGoogle Scholar
McCarthy, R., The cyclic homology of an exact category, J. Pure Appl. Algebra 93 (1994), 251–296.CrossRefGoogle Scholar
Nadler, D. and Zaslow, E., Constructible sheaves and the Fukaya category, J. Amer. Math. Soc. 22 (2009), 233–286.CrossRefGoogle Scholar
McPherson, R., Chern classes for singular varieties, Ann. of Math. (2) 100 (1974), 423–432.CrossRefGoogle Scholar
Ramadoss, A. C., The relative Riemann–Roch theorem from Hochschild homology, New York J. Math. 14 (2008), 643–717, arXiv:math/0603127.Google Scholar
Ramadoss, A. C., Tang, X. and Tseng, H.-H., Hochschild Lefschetz class for $\mathscr{D}$ -modules, arXiv:math/1203.6885.Google Scholar
Sato, M., Kawai, T. and Kashiwara, M., Microfunctions and pseudo-differential equations, in Hyperfunctions and pseudo-differential equations, Proceedings Katata 1971 (ed. Komatsu, ). Lecture Notes in Math., Volume 287, pp. 265–529 (Springer-Verlag, 1973).Google Scholar
Schapira, P. and Schneiders, J-P., Index theorem for elliptic pairs, Astérisque, Volume 224 (Soc. Math. France, 1994).Google Scholar