Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-20T04:25:06.182Z Has data issue: false hasContentIssue false
  • English
  • Français

Addendum to “Limit Sets of Typical Homeomorphisms”

Published online by Cambridge University Press:  20 November 2018

Nilson C. Bernardes Jr.
Nilson C. Bernardes Jr.*
Affiliation:
Departamento de Matemática Aplicada, Instituto de Matemática, Universidade Federal do Rio de Janeiro, Caixa POstal 68530, Rio de Janeiro, RJ, 21945-970, Brasil e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given an integer 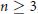$n\,\ge \,3$, a metrizable compact topological $n$-manifold 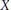$X$ with boundary, and a finite positive Borel measure 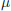$\mu$ on 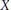$X$, we prove that for the typical homeomorphism $f:\,X\,\to \,X$, it is true that for 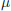$\mu$-almost every point $x$ in 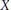$X$ the restriction of 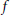$f$ (respectively of 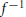${{f}^{-1}}$) to the omega limit set 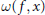$\omega \left( f,\,x \right)$ (respectively to the alpha limit set 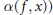$\alpha \left( f,\,x \right)$) is topologically conjugate to the universal odometer.

Keywords

37B2054H2028C1554C3554E52topological manifoldshomeomorphismsmeasuresBaire categorylimit sets
Type
Addendum
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 2 , 14 June 2014 , pp. 240 - 244
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

The author was partially supported by CAPES: Bolsista - Proc. no BEX 4012/11-9.

References

[1] Bernardes, N. C. Jr., Limit sets of typical continuous functions. J. Math. Anal. Appl. 319(2006), no. 2, 651–659. http://dx.doi.org/10.1016/j.jmaa.2005.06.056 CrossRefGoogle Scholar
[2] Bernardes, N. C. Jr., On the predictability of discrete dynamical systems. III. J. Math. Anal. Appl. 339(2008), no. 1, 58–69. http://dx.doi.org/10.1016/j.jmaa.2007.06.029 CrossRefGoogle Scholar
[3] Bernardes, N. C. Jr., Limit sets of typical homeomorphisms. Canad. Math. Bull. 55(2012), no. 2, 225–232. http://dx.doi.org/10.4153/CMB-2011-066-2 CrossRefGoogle Scholar
[4] Block, L. and Keesling, J., A characterization of adding machine maps. Topology Appl. 140(2004), no. 2–3, 151–161. http://dx.doi.org/10.1016/j.topol.2003.07.006 CrossRefGoogle Scholar
[5] Buescu, J. and I. Stewart, , Lyapunov stability and adding machines. Ergodic Theory Dynam. Systems 15(1995), no. 2, 271–290.Google Scholar
[6] D’Aniello, E., Darji, U. B., and Steele, T. H., Ubiquity of odometers in topological dynamical systems.Topology Appl. 156(2008), no. 2, 240–245. http://dx.doi.org/10.1016/j.topol.2008.07.003 CrossRefGoogle Scholar