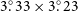1. Introduction
Supernova remnants (SNRs) are essential ingredients in the evolution of every galaxy, as they are one of the main sources of interstellar medium (ISM) enrichment. They significantly impact the structure and physical properties of the surrounding ISM (Filipović & Tothill Reference Filipović and Tothill2021). It is well understood that the census of the Galactic SNR population is incomplete (Foster et al. Reference Foster, Cooper, Reich, Kothes and West2013; Dokara et al. Reference Dokara2021; Ball et al. Reference Ball2023). Some 300+ such objects are confirmed (Green Reference Green2022; Ferrand & Safi-Harb Reference Ferrand and Safi-Harb2012) with the expectation that up to
$\sim$
2 000 additional SNRs remain undiscovered in the Milky Way (Ranasinghe & Leahy Reference Ranasinghe and Leahy2022). As recently shown in Ball et al. (Reference Ball2023), a significant number of the missing Galactic SNRs are expected to have a low-surface brightness or be located in complex regions where clear distinctions from other source types (e.g. Hii regions) are challenging. It is also well known that new, bright, small-sized (compact), and presumably young SNRs are not likely to be found in abundance (Ranasinghe, Leahy, & Stil Reference Ranasinghe, Leahy and Stil2021) and Smeaton et al. (2024, in press).
At the same time, among the 300-strong Galactic SNR population, there are a significant number of these objects whose measured position and extent are based on poorer resolution observations. This is due to the observations being conducted using the previous generation of instruments, such as the Very Large Array (VLA), Parkes/Murriyang, the Australia Telescope Compact Array (ATCA), Effelsberg, Molonglo Observatory Synthesis Telescope (MOST), and the synthesis telescope at the Dominion Radio Astrophysical Observatory (DRAO ST) as part of the Canadian Galactic Plane Survey (CGPS, Taylor et al. Reference Taylor2003). Thus, the newer generation of radio telescopes, such as Australian Square Kilometre Array Pathfinder (ASKAP) (Johnston et al. Reference Johnston2007; Norris et al. Reference Norris2011; Norris et al. Reference Norris2021; Hotan et al. Reference Hotan2021; Koribalski Reference Koribalski2022), MeerKAT (Jonas & MeerKAT Team 2016), MurchisonWidefield Array (MWA) (Beardsley et al. Reference Beardsley2019), and Low-Frequency Array (LOFAR) (van Haarlem et al. Reference van Haarlem2013) are imperative in improving these previous measurements, as well as discovering new Galactic SNRs.
As shown in several recent studies, discoveries such as the intergalactic SNR J0624–6948 (Filipović et al. Reference Filipović2022), the Galactic SNRs G288.8–6.3 (Filipović et al. Reference Filipović2023; Burger-Scheidlin et al. Reference Burger-Scheidlin2024), G181.1–9.5 (Kothes et al. Reference Kothes, Reich, Foster and Reich2017), Hoinga (Becker et al. Reference Becker2021), G118.4+37.0 (Calvera; Arias et al. Reference Arias2022), J1818.0–1607 (Ibrahim et al. Reference Ibrahim2023), G308.73+1.38 (Raspberry; Lazarević et al. Reference Lazarević2024b), G312.65+2.87 (Unicycle; Smeaton et al. 2024), and G121.1–1.9 (Khabibullin et al. Reference Khabibullin, Churazov, Bykov, Chugai and Sunyaev2023) demonstrate the ability of these newer telescopes to discover new Galactic SNRs. These SNRs are mainly located well outside the Galactic Plane, where they can preserve their original circular SNR shape for longer timeframes due to the presumably low-density environment while also displaying a lower surface-brightness as compared to typical SNRs.
G278.94+1.35, here named Diprotodon (see Appendix A), is a Galactic SNR originally established by Woermann & Jonas (Reference Woermann and Jonas1988) using the South African 26-m Hartesbeesthoek radio telescope at 1.6 GHz (restoring B.S.Footnote
a
= 30
$^\prime$
; S = 25.2
$\pm$
4 Jy) and 2.3 GHz (B.S. = 20
$^\prime$
; S = 20.7
$\pm$
3 Jy). Duncan et al. (Reference Duncan, Haynes, Stewart and Jones1995) used the Parkes 64-m radio-telescope at 1.4 GHz (B.S. = 18
$^\prime$
; S = 28.3
$\pm$
3 Jy) and 2.4 GHz (B.S. = 11
$^\prime$
; S = 20
$\pm$
2 Jy) to study the morphology and polarisation of Diprotodon. Finally, Whiteoak & Green (Reference Whiteoak and Green1996) detected some parts of Diprotodon in the MOST survey at 843 MHz (B.S.
$=43^{\prime\prime}\times53^{\prime\prime}$
). All these radio studies confirmed Diprotodon as having a faint and incomplete shell. Diprotodon has also been detected and confirmed optically with H
$\alpha$
(Stupar & Parker Reference Stupar and Parker2009; Stupar & Parker Reference Stupar and Parker2011), as well as in gamma rays in the energy range 0.5–500 GeV, which revealed a source larger than the then known radio shell (Araya Reference Araya2020). Several studies investigated if any of the pulsars that are found in the vicinity of Diprotodon could be associated with the SNR itself, but no convincing relationship between a pulsar and Diprotodon was established, including PSR J0940-5428 (Michailidis et al. Reference Michailidis, Pühlhofer, Santangelo, Becker and Sasaki2024). Most recently, Michailidis et al. (Reference Michailidis, Pühlhofer, Santangelo, Becker and Sasaki2024) presented eROSITA’s detection of Diprotodon’s X-ray counterpart showing that the X-ray emission is soft, coming from a narrow range of energies between 0.3 and 1.5 keV.
The original distance of 3 kpc was established using Parkes 64-m OH observations (Green et al. Reference Green, Frail, Goss and Otrupcek1997). Shan et al. (Reference Shan2019) refined this value to 2.7
$\pm$
0.3 kpc using optical extinction. This was determined with the red clump star method, which could be somewhat unreliable as uncertainties are typically highly underestimated. With realistic uncertainties considered, this distance estimate should have a much larger error. Michailidis et al. (Reference Michailidis, Pühlhofer, Santangelo, Becker and Sasaki2024) also considered a distance of
$\sim$
400 pc that could be associated with local/nearby pulsars. With this caution in mind, and in the absence of any more reliable distance estimate, we initially adopt 2.7
$\pm$
0.3 kpc as the assumed distance to Diprotodon. However, after in-depth analysis (Section 3), we argue that the most likely distance to this SNR is at
$\sim$
1 kpc.
2. Observations and data processing
2.1 Radio observations
2.1.1 ASKAP data
Our serendipitous detection of Diprotodon was enabled by the ASKAP-Evolutionary Map of the Universe (EMU) project (AS201), which observed this area of the radio sky in July 2023 with a complete set of 36 ASKAP antennas at the central frequency of 943.4 MHz and bandwidth of 288 MHz. All data are available through the Australian Commonwealth Scientific and Industrial Research Organisation (CSIRO) ASKAP Science Data Archive (CASDAFootnote
b
). The observations containing this object are the tiles EMU_0954–55 and 1005–51 corresponding to ASKAP scheduling blocks SB51428 and SB54774. The data were processed using the ASKAPsoft pipelines (SB51428 was made with V.2.5.18 and SB54774 was with V.2.8.3.), which included multi-frequency synthesis imaging, multi-scale cleaning, self-calibration, and convolution to a common beam size. (Guzman et al. Reference Guzman2019). The resulting 943 MHz EMU image has a root mean squared (rms) sensitivity of
$\sigma$
= 25
$\mu$
Jy beam
$^{-1}$
and a synthesised beam of
$15^{\prime\prime}\times15^{\prime\prime}$
(Fig. 1).
Figure 1. ASKAP radio-continuum intensity image of Diprotodon at 943 MHz. The green-dashed, 95
$^\prime$
–diameter circle indicates the previously measured extent, while the yellow dash ellipse indicates the new boundaries of Diprotodon’s radio emission (
$3{{{{.\!^\circ}}}}33\times3{{{{.\!^\circ}}}}23$
). In the top right corner, we show the scaled size of the Moon (
$0{{{{.\!^\circ}}}}5$
), while in the top left corner, we show the animal Diprotodon.
2.1.2 GLEAM data
We examined several radio surveys to search for Diprotodon and to derive the flux density as a function of frequency. Only surveys with sensitivity to scales at least that of its diameter (
$3{{{{.\!^\circ}}}}33$
) can be used so that it is not resolved out. At the lowest frequency, we used data taken by the MWA (Tingay et al. Reference Tingay2013; Wayth et al. Reference Wayth2018) for the GaLactic and ExtragalacticAll-sky MWA (GLEAM; Wayth et al. Reference Wayth2015) survey, at the edge of the 103–134 MHz source-finding mosaics generated by Hurley-Walker et al. (Reference Hurley-Walker2017) (Fig. 2). The resolution of this 118-MHz image is
$3{{{{.\mkern-4mu^{\prime}}}}}2$
$3{{{{.\mkern-4mu^\prime}}}}2$
, and the RMS noise is 55 mJy beam
$^{-1}$
(measured from a patch with no sources and little Galactic emission).
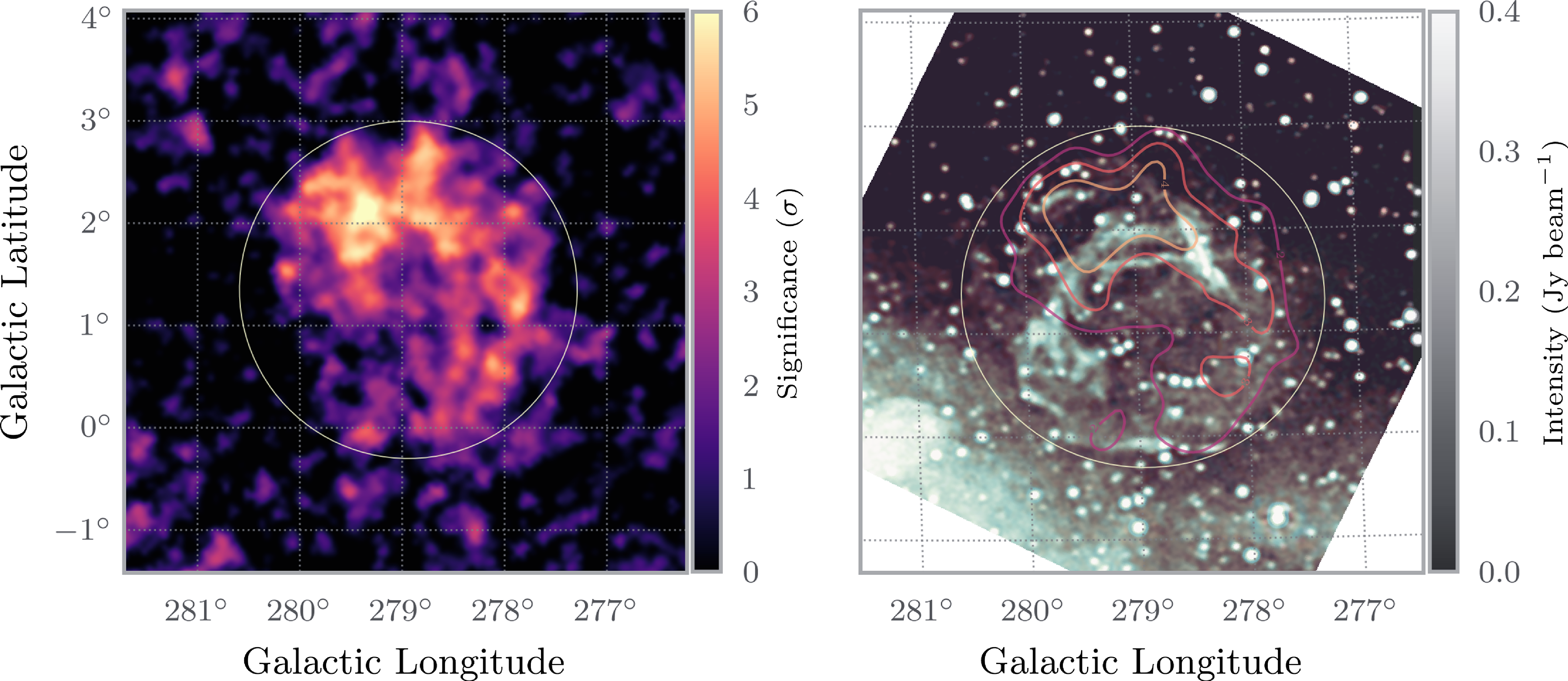
Figure 2. Left: Significance map (in units of
$\sigma$
) of the gamma-ray emission from Diprotodon obtained with Fermi-LAT events for energies above 1 GeV. Right: GaLactic and Extragalactic All-sky MWA (GLEAM) RGB intensity image of Diprotodon where R is (red) at 88 MHz, B (blue) at 118 MHz and G (green) at 154 MHz. The contours correspond to 2, 3, and 4
$\sigma$
significance levels shown in the Fermi-LAT map on the left. The circle represents the measured diameter of Diprotodon of
$3{{{{.\!^\circ}}}}33\times3{{{{.\!^\circ}}}}23$
.
To remove the contaminating point sources from the data, we followed established methods (Tian & Leahy Reference Tian and Leahy2005; Becker et al. Reference Becker2021; Araya et al. Reference Araya, Hurley-Walker and Quirós-Araya2022; Ball et al. Reference Ball2023). We performed source-finding on the MWA image, using Aegean Footnote c (Hancock et al. Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012; Hancock, Trott, & Hurley-Walker Reference Hancock, Trott and Hurley-Walker2018) and its companion tool, the Background and Noise Estimator (BANE). We subtracted the MWA point sources from the image using a further ancillary tool AeRes, and from the resulting image, we measured Diprotodon’s flux density (Section 3.2).
2.1.3 HI4PI, SGPS, and NANTEN data
We also searched for possible detection of Hi and CO clouds associated with Diprotodon using the Effelsberg and Parkes HI4PI survey (HI4PI Collaboration et al. 2016) and the NANTEN
$^{12}$
CO(J = 1–0) data (Mizuno & Fukui Reference Mizuno, Fukui, Clemens, Shah and Brainerd2004). The angular resolutions of Hi and CO data are
$\sim16{{{{.\mkern-4mu^\prime}}}}2$
and
$\sim2{{{{.\mkern-4mu^\prime}}}}6$
, respectively. The typical noise fluctuation is
$\sim$
0.04 K at the velocity resolution of 1.3 km s
$^{-1}$
for the Hi data, and
$\sim$
0.2 K at the velocity resolution of 1 km s
$^{-1}$
for the CO data. Details of these results are presented in Section 3.3.
The southern part of Diprotodon – seen in Galactic coordinates – is covered by the Southern Galactic Plane Survey (SGPS, McClure-Griffiths et al. Reference McClure-Griffiths2005). The SGPS contains a Hi spectral line survey covering Galactic longitudes from 253
$^\circ$
to 358
$^\circ$
and latitudes from –
$1{{{{.\!^\circ}}}}5$
to
$+1{{{{.\!^\circ}}}}5$
. The survey combines observations with the ATCA and the Parkes telescopes, giving a spatial resolution of
$\sim$
2
$^\prime$
.
2.2 Fermi-LAT observations
The Fermi Large Area Telescope (LAT) is a converter/tracker observatory detecting photons at high energies from
$\sim$
20 MeV to
$ \gt $
1 TeV and surveying the entire sky since 2008 (Atwood et al. Reference Atwood2009). We used Pass 8 data collected from 04 August 2008 to 30 June 2023 in the energy range of 0.2 GeV–500 GeV. We used fermitools version 2.2.0 through the fermipy package version 1.1.6 to analyse the data. We selected front and back-converted events with good quality in the SOURCE class using the options evclass = 128, evtype = 3, DATA_QUAL
$ \gt $
0, and having zenith angles lower than
$90^\circ$
to avoid contamination from gamma rays from Earth’s limb. We used the corresponding response functions P8R3_SOURCE_V3 and binned the data with a spatial scale of
$0{{{{.\!^\circ}}}}05$
per pixel and ten bins in energy for exposure calculation.
The analysis of LAT data is based on the maximum likelihood technique (Mattox et al. Reference Mattox1996) by which the morphological and spectral parameters of the sources in the region of interest (RoI) are fit to account for the number of events in each spatial and energy bin. Given the relatively large point-spread function of the LAT, we collected events from a
$20^\circ \times 20^\circ$
RoI centred at the coordinates RA(J2000) = 10
$^\textrm{h}$
00
$^\textrm{m}$
00
${{{{.\mkern-4mu^s}}}}0$
and Dec(J2000) = –53
$^\circ$
00
$^\prime$
00
${{{{.\!\!^{\prime\prime}}}}}0$
and included in the model all sources located within 25
$^\circ$
of the RoI centre found in the latest incremental version of the Fermi Large Area Telescope Fourth Source Catalog (4FGL-DR4, Abdollahi et al. Reference Abdollahi2020; Ballet et al. Reference Ballet, Bruel, Burnett and Lott2023), based on the first 14 yr of data. We also included in the model the Galactic diffuse emission using the file gll_iem_v07.fits and the isotropic and residual cosmic-ray background as described by iso_P8R3_SOURCE_V3_v1.txt.Footnote
d
Energy dispersion correction was not applied to the isotropic component as recommended by the LAT team.Footnote
e
In the 4FGL-DR4 catalogue, the emission associated with Diprotodon is described by a spatial template based on the analysis by Araya (Reference Araya2020) and labelled 4FGL J1000.0–5312e. The source is described by a ring with an outer diameter of
$2{{{{.\!^\circ}}}}88$
.
Figure 3. Diprotodon RGB image made of ASKAP smoothed 15
$^{\prime\prime}$
(red), WISE W3 (green) and WISE W4 (blue). The dash box marks the nearby Hii region that is in the line of sight (Section 2.3).
The detection significance of a source (in
$\sigma$
) having one additional free parameter in the model is obtained from the square root of the test statistic (TS), defined as
$-2\log(\mathcal{L}_0/\mathcal{L})$
, with
$\mathcal{L}$
and
$\mathcal{L}_0$
the maximum likelihood functions for a model including a source and for the model without this additional source, respectively. To maximise the likelihood in the initial step, we fit the spectral normalisation of the sources found within
$10^\circ$
of the RoI centre as well as all the spectral parameters of the sources found within
$5^\circ$
using events with energies above 0.2 GeV. In the next step, we improved the background model by adding new point sources at the locations of TS maxima exceeding a value of 16 in the residual emission obtained with the standard 4FGL-DR4 model. This was particularly important at the lowest energies of the analysis because of the presence of considerable background gamma-ray excesses in the RoI. In the next fit, we optimised the values of the spectral parameters of the new sources located up to
$12^\circ$
from the centre. For the rest of the analysis of the spectrum and morphology of Diprotodon, due to a large number of free parameters, we only kept free the spectral normalisations of the sources located within
$8^\circ$
and the spectral indices and normalisations of the sources located within
$5^\circ$
of the centre.
To visualise the gamma-ray emission from the SNR, we calculated a significance map for events having energies above 1 GeV. We removed the source 4FGL J1000.0–5312e from the model and placed a putative point source at each pixel in the map to fit its spectral normalisation (in this case, the additional parameter). The differential spectral model used for the point source is a simple power-law with a fixed index of 2. The resulting significance map is seen in Fig. 2, clearly showing the SNR.
2.3 WISE View of Diprotodon
In Fig. 3 we show a 4
$^{\circ}\times4^{\circ}$
mosaic of the area centred on Diprotodon and its local environment as traced in the mid-infrared by the Wide-Field Infrared Survey Explorer (WISE) bands of W3 (12
$\mu$
m) and W4 (23
$\mu$
m)Footnote
f
. The mosaics were created using the WISE WXSC pipeline (Jarrett et al. Reference Jarrett2012) with native resolution (
$6.5^{\prime\prime}$
in W3 and
$12.0^{\prime\prime}$
in W4) and supersampled with
$1^{\prime\prime}$
pixels. As described in Jarrett et al. (Reference Jarrett2013); Jarrett et al. (Reference Jarrett2019), the WISE bands were carefully designed to sample both stellar emission (W1 and W2), and ISM star-formation-excited gas/dust emission (W3 and W4). As expected, the stellar density is extremely high at these low Galactic latitudes, reaching the confusion limit of the WISE imaging resolution for bands W1 and W2.
Meanwhile, the star-formation-excited ISM exhibits a complex filamentary structure, with tendrils reaching down from the Galactic Plane (bottom-right in Fig. 3) penetrating through the SNR shell (at least in projection). There are also signs of shock gas compression in the sharp filamentary structures to the west and northwest of the upper shell. Similar to the SNR, the ISM emission is lower density on the eastern side, consistent with the radio-continuum (Fig. 1) where the kinematics are hinting at a cavity blowout on the South and West side. Nevertheless, across this tangled ISM emission is too complex to be directly associated with the Diprotodon or its initial blast wave.
3 Results
We have serendipitously found a large-scale object in our new ASKAP-EMU survey (Norris et al. Reference Norris2021) which we identify as a previously known Galactic SNR G278.94+1.35 (Fig. 1). Following this ASKAP Diprotodon detection, we also identified this radio source in the GLEAM and Fermi-LAT surveys. Our detection and classification of this Galactic SNR is primarily based on the object morphology, size, and multi-frequency appearance of Diprotodon with the method described in (Hurley-Walker et al. Reference Hurley-Walker2019, Section 2.4), (Filipović et al. Reference Filipović2022), and Bozzetto et al. (Reference Bozzetto2023).
3.1 Diprotodon’s extent
Previous measurements of Diprotodon’s size and central position were limited by the instruments’ poor resolution and sensitivity. It was suggested to have a diameter of
$\sim$
95
$^\prime$
(Green Reference Green2022) as shown in Fig. 1 (green dashed circle). However, Araya (Reference Araya2020) indicated that Diprotodon might extend in gamma rays beyond the above estimate. Also, Fesen et al., (in preparation) showed new large-scale H
${\alpha}$
and [O iii] images of Diprotodon. The initial comparison with our radio-continuum images didn’t show any feature alignment. This is no surprise as we have found similar tendencies in other specifically [O iii] dominate SNR as they are primarily confined to unusually low-density ISM regions. Here, we measured the extent of Diprotodon in all three: ASKAP and GLEAM radio-continuum and Fermi-LAT gamma-ray images.
We used the Minkowski tensor analysis tool BANANAFootnote
g
(Collischon et al. Reference Collischon, Sasaki, Mecke, Points and Klatt2021) to determine the centre and extent of Diprotodon. We found that Diprotodon SNR is centred at RA(J2000) = 9
$^\textrm{h}$
59
$^\textrm{m}$
50
${{{{.\mkern-4mu^s}}}}5$
and Dec(J2000) = –53
$^\circ$
19
$^\prime$
50
$^{\prime\prime}$
(
$l\,=\,278{{{{.\!^\circ}}}}94$
and
$b\,=\,+1{{{{.\!^\circ}}}}35$
). We measure Diprotodon to have an angular size of, at most, 200
$^\prime$
$\times$
194
$^\prime$
(
$3{{{{.\!^\circ}}}}33\times3{{{{.\!^\circ}}}}23$
at a position angle of 0
$^\circ$
). This makes Diprotodon one of the largest known SNRs in the sky according to the Green (Reference Green2022) catalogue and estimates by Vukotić et al. (2019), with the largest being the well-known Vela SNR (
$\sim$
8
$^\circ$
; Bock, Turtle, & Green Reference Bock, Turtle and Green1998). Diprotodon is only somewhat smaller than the SNRs G70.0–21.5 (330
$^\prime$
$\times$
240
$^\prime$
), G65.3+5.7 (310
$^\prime$
$\times$
240
$^\prime$
), G74.0–8.5 (Cygnus Loop; 230
$^\prime$
$\times$
160
$^\prime$
), and possibly G159.6+7.3 (240
$^\prime$
$\times$
180
$^\prime$
). Finally, the recently discovered Galactic SNR Hoinga (Becker et al. Reference Becker2021) also shows a large angular scale with a diameter of
$4{{{{.\!^\circ}}}}4$
at a distance of
$\sim$
500 pc.
Even more surprisingly, at a distance of 2.7 kpc (Shan et al. Reference Shan2019), Diprotodon would have a staggering physical size of 157
$\times$
154 pc, tucked in a presumably low-density region in between Carina-Sagittarius and Perseus spiral arm with its centre some 65 pc above the Galactic Plane. From Vukotić et al. (2019), only Galactic SNRs G65.1+0.6 at a distance of 9.2 kpc would have a larger diameter of 179.5 pc. However, Wang et al. (Reference Wang2020) found that G65.1+0.6 is more likely to be closer at 4.16 kpc, which makes its physical size
$\sim$
109 pc (
$\pm10\%$
). Vukotić et al. (2019) also list SNR G312.4–0.4 at the distance of 14 kpc – to be of 154.8 pc in size – but again, optical extinction suggests a distance of only 4.4 kpc, which makes its physical size significantly smaller. Therefore, if it has a distance of 2.7 kpc, Diprotodon may be the physically largest Galactic SNR known.
In the nearby Magellanic Clouds (MCs), we found a number of large-size SNRs and SNR candidates (Bozzetto et al. Reference Bozzetto2017; Maggi et al. Reference Maggi2019; Yew et al. Reference Yew2021; Bozzetto et al. Reference Bozzetto2023; Cotton et al. Reference Cotton2024), some of which span up to 155 pc. The two largest confirmed MCs SNRs are RXJ050736–6847.8 (D = 154.8 pc; Maitra et al. Reference Maitra2021) and 0450–7050 (D = 120.2 pc; Cajko, Crawford, & Filipovic Reference Cajko, Crawford and Filipovic2009) would be of comparable size to Diprotodon.
Certainly, there are several bubbles and superbubbles such as the Large Milky Cloud (LMC) 30 Doradus C that would be the same size as Diprotodon (Yamane et al. Reference Yamane2021; Sano et al. Reference Sano2017; Kavanagh et al. Reference Kavanagh2015; De Horta et al. Reference De Horta2014). However, they are all composed of multiple Supernova (SN) explosions, and therefore, one could expect a larger extent. Another possible example of a large shell-like structure is the Galactic North Polar Spur with its suggested size of up to 300 pc, which is likely a local superbubble wrapped just outside of our Local Bubble (West et al. Reference West, Landecker, Gaensler, Jaffe and Hill2021).
Such a large-size SNR is expected to be rather aged (
$\sim$
10
$^5$
yr) or in its late evolution stages. However, we note that Diprotodon’s almost circular shape across such a large field of view suggests that the SNR is still expanding in, presumably, rarefied ambient density.
3.2 Diprotodon’s radio spectral index
To estimate Diprotodon’s radio spectral index (defined by
$S \propto \nu^{\alpha}$
, where S is flux density,
$\nu$
is the frequency, and
$\alpha$
is the spectral index), we used the GLEAM detection in the 103–134 MHz range (which gave the best signal-to-noise) and fitted a 2D plane to the background. We then integrated the flux density inside the SNR defined polygon, where we avoided including bright sources in the background calculation. The total flux density of Diprotodon after background subtraction is 105
$\pm$
11 Jy. As shown in the case of Ancora (Filipović et al. Reference Filipović2023) and given Diprotodon’s considerable angular size (especially for the low surface brightness and extended emission), we did not attempt to estimate Diprotodon’s flux density at 943 MHz.
Using previous flux density measurements of Woermann & Jonas (Reference Woermann and Jonas1988) and Duncan et al. (Reference Duncan, Haynes, Stewart and Jones1995), we obtain
$\alpha=-0.55\pm0.01$
(Fig. 4). Combined with the above-measured angular size, this gives a radio surface brightness at 1 GHz of
$\Sigma=1.3\times10^{-22}$
W m
$^{-2}$
Hz
$^{-1}$
sr
$^{-1}$
(assuming the emission to be spread smoothly over the SNR boundaries defined above). However, we note that these earlier flux density measurements did not include the full extent of Diprotodon’s radio continuum emission but, at the same time, included background source contribution.
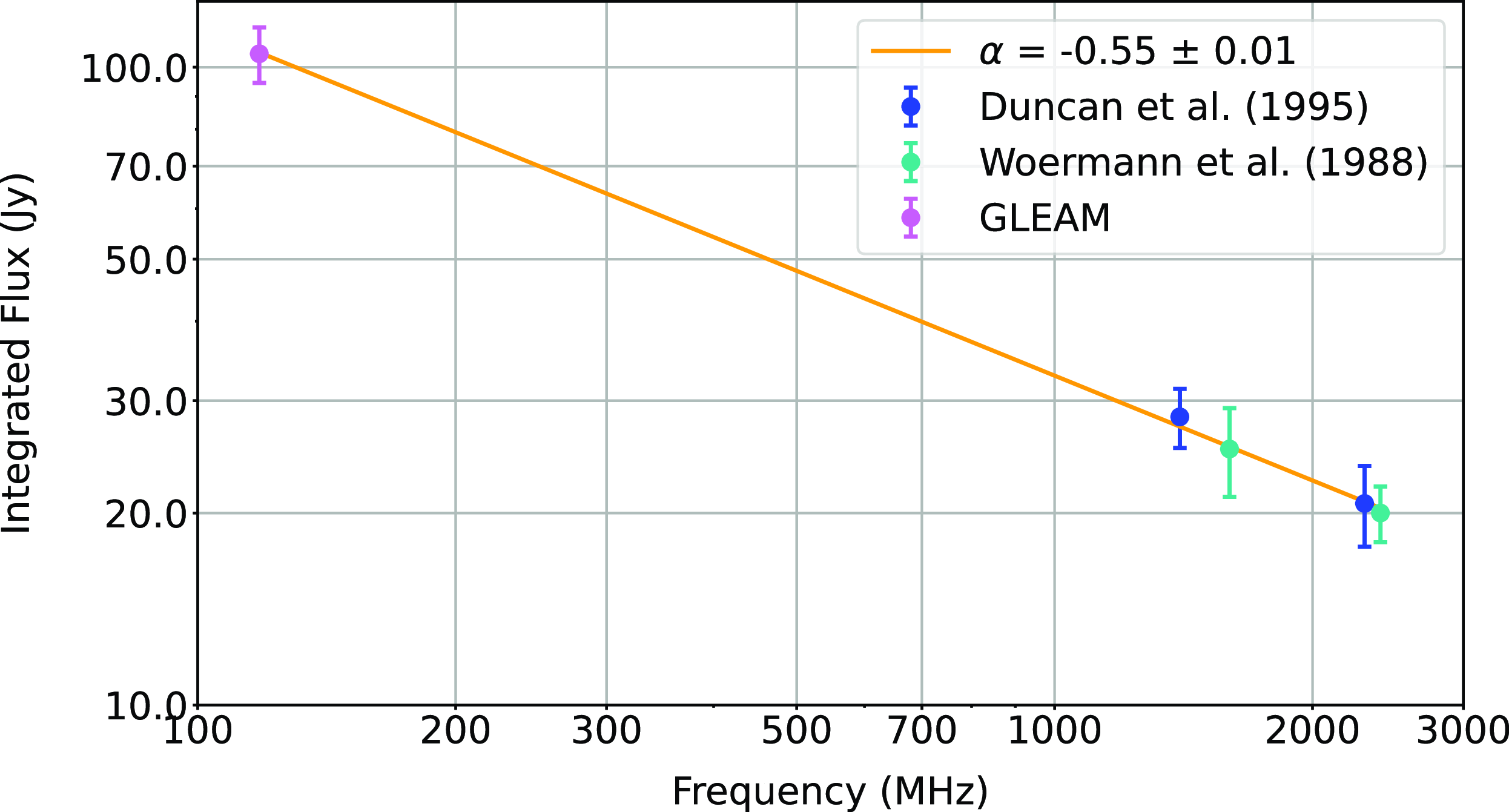
Figure 4. Diprotodon’s radio flux densities as a function of frequency. A power-law fit based on flux density from GLEAM (pink point), measurements from Woermann & Jonas (Reference Woermann and Jonas1988) (blue points) and Duncan et al. (Reference Duncan, Haynes, Stewart and Jones1995) (green points) with SNR estimated
$S_\mathrm{1\,GHz}$
= 32.8 Jy and
$\alpha = -0.55\pm0.01$
.
Nevertheless, this spectral index of
$\alpha = -0.55\pm0.01$
is representative and typical for the average shell type SNRs observed for the Galaxy and range of nearby galaxies SNRs (Reynolds, Gaensler, & Bocchino Reference Reynolds, Gaensler and Bocchino2012; Galvin & Filipovic Reference Galvin and Filipovic2014; Bozzetto et al. Reference Bozzetto2017; Maggi et al. Reference Maggi2019; Filipović & Tothill Reference Filipović and Tothill2021; Bozzetto et al. Reference Bozzetto2023; Ranasinghe & Leahy Reference Ranasinghe and Leahy2023). It certainly strongly indicates that non-thermal radio emission dominates across Diprotodon apart from the western side, as also noted by Duncan et al. (Reference Duncan, Haynes, Stewart and Jones1995). This is where Diprotodon is superimposed with the most likely unrelated Galactic bubble E116 (centred at l =
$277{{{{.\!^\circ}}}}725$
and b = +
$0{{{{.\!^\circ}}}}658$
) (Hanaoka et al. Reference Hanaoka2019) that can be seen in our WISE-IR images (Fig. 3).
The above estimate of Diprotodon’s radio surface brightness and originally suggested physical size of 157 pc places this object well outside of the SNR
$\Sigma-D$
diagram (Urošević Reference Urošević2020; Pavlović et al. Reference Pavlović2018, their fig. 3). This indicates that either of the two estimates could be potentially wrong. One would expect that such a large SNR would have a low surface brightness. Even if the estimate of Diprotodon’s SNR surface brightness is an order of magnitude lower (
$\Sigma\sim10^{-23}$
W m
$^{-2}$
Hz
$^{-1}$
sr
$^{-1}$
) it would still suggest an intrinsic diameter of
$\sim$
90-110 pc. For a selected sample of 110 Galactic SNRs, Vukotić et al. (2019) present a distance calibration for radio surface brightness at 1 GHz vs diameter relation, using a cross-validation kernel smoothing. Diprotodon’s 1 GHz surface brightness of
$\Sigma=1.3\times10^{-22}$
W m
$^{-2}$
Hz
$^{-1}$
sr
$^{-1}$
corresponds to the distance of
$\sim$
576 pc and a diameter of
$\sim$
33 pc. Given the significant amount of predicted missing flux density, this estimate should be taken as the lower limit of Diprotodon’s distance and diameter.
3.3 Diprotodon in Hi and CO surveys
To reveal the physical relation between Diprotodon and its surroundings, we analysed the archival Hi data taken from HI4PI (HI4PI Collaboration et al. 2016), SGPS (McClure-Griffiths et al. Reference McClure-Griffiths2005), and the CO data from the NANTEN telescope (Mizuno & Fukui Reference Mizuno, Fukui, Clemens, Shah and Brainerd2004).
3.3.1 Diprotodon in the HI4PI and NANTEN surveys
Figs. 5(a) and (c) show the distributions of Hi and CO superposed with the GeV gamma-ray contours and radio shell boundaries (dashed circles). We found a cavity-like distribution of Hi in the velocity range from
$-13$
to –1 km s
$^{-1}$
. The Hi clouds nicely trace the radio-shell boundary of Diprotodon, especially in the southern half of the shell. We also find filamentary molecular clouds in the northern edge of the SNR. The other CO clouds are distributed as clumpy inside or on the edge of the radio-shell boundary. We note that there is no obvious correlation between the CO clumps and GeV gamma-ray peaks. Interestingly, such a spatial anticorrelation is also seen between the Hi and GeV-gamma-ray peaks.
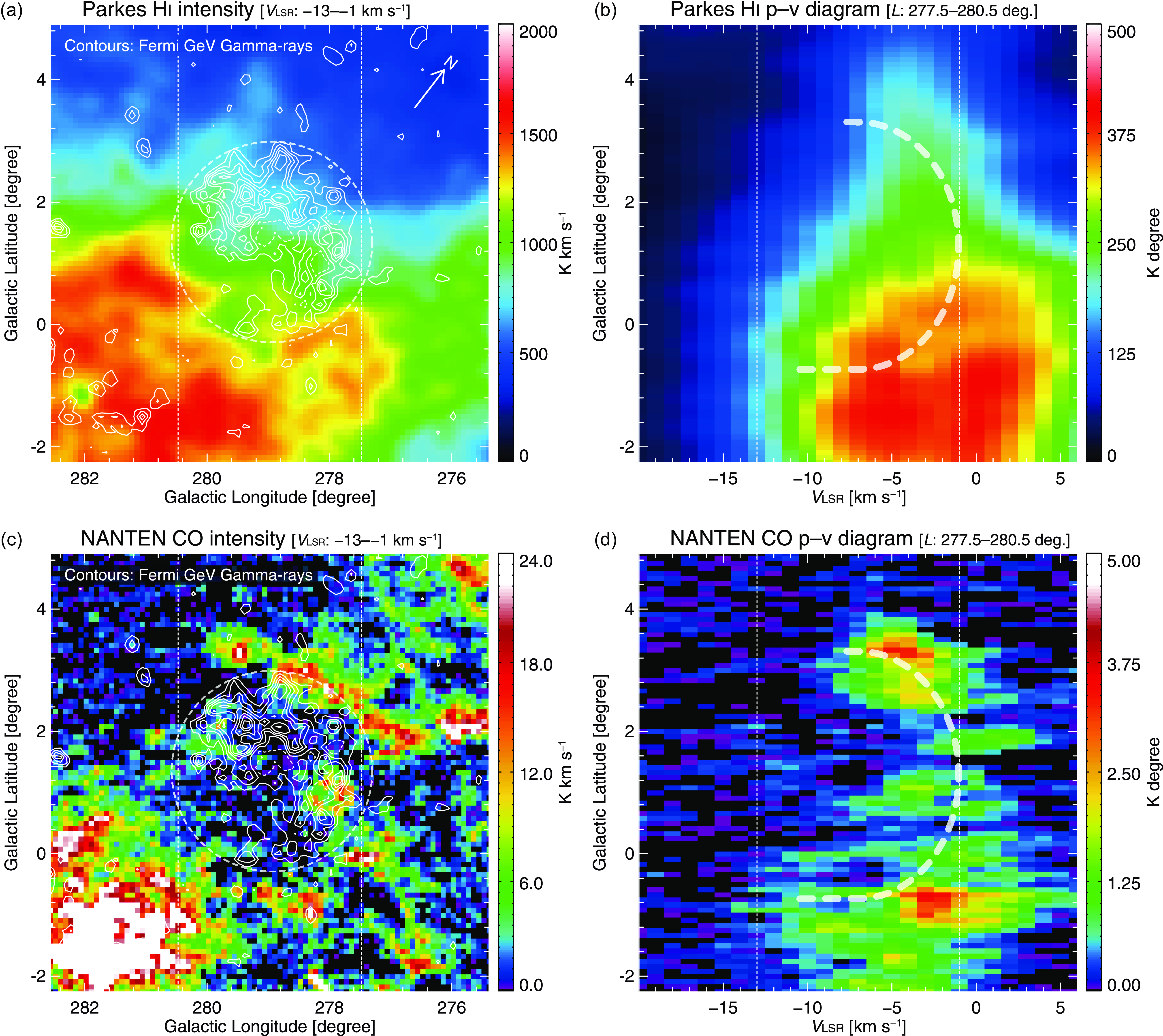
Figure 5. Velocity integrated intensity maps and position–velocity diagrams of Hi (a, b) and CO (c, d). The integration velocity range is from −13 to
$-1$
km s
$^{-1}$
for each intensity map and from
$277{{{{.\!^\circ}}}}5$
to
$280{{{{.\!^\circ}}}}5$
in Galactic latitude for each position–velocity diagram (dashed vertical lines). Superposed contours represent the GeV gamma rays whose lowest contour and intervals are
$5\sigma$
levels. The dashed white circle represents Diprotodon’s radio shell boundary. The dashed curves in the position–velocity diagrams indicate the boundaries of the CO and Hi cavities (see the text).
Figs. 5(b) and (d) show the position–velocity diagrams of Hi and CO. We find a hollowed distribution of CO and a velocity gradient of Hi whose spatial extents are roughly consistent with these of the radio-shell boundaries. Such spatial and velocity distributions of CO and Hi generally indicate an expanding motion of the molecular and atomic hydrogen gas, which could be formed by SN blastwaves and/or strong stellar winds from the progenitor system (e.g. Koo et al. Reference Koo, Reach, Heiles, Fesen and Shull1990; Koo & Heiles Reference Koo and Heiles1991). In other words, these Hi and CO clouds are possibly physically associated with Diprotodon. If this is the case, the systemic velocity of Diprotodon is in a range of Fig. 9 (top-right panel), corresponding to an almost tangent velocity in this direction. Therefore, this implies that the smaller distance of
$\sim$
1.2 kpc for Diprotodon is not in contradiction in terms of kinematic distances with other estimates shown in Sections 3.3.2 and 3.4. In any case, additional high-resolution Hi observations are needed to test this possibility.
To estimate the mass and density of molecular and atomic hydrogen gas, we used the following equations:
\begin{eqnarray}M_\mathrm{HI} = m_{\mathrm{p}} \Omega D^2 \sum_{i} N_i(\mathrm{H}{\mathrm{\tiny{I}}}),\end{eqnarray}
\begin{eqnarray}M_\mathrm{CO} = m_{\mathrm{p}}\Omega D^2 \sum_{i} N_i(\mathrm{H}_2),\end{eqnarray}
where
$m_\mathrm{p}$
is the hydrogen mass,
$\Omega$
is the solid angle for each data pixel, D is the distance to the source, N(Hi) is the atomic hydrogen column density, and N(H
$_2$
) is the molecular hydrogen column density. Here, we ignore the He abundance of molecular clouds. N(Hi) can be derived as
$1.823 \times 10^{18}\;W$
(Hi), where W(Hi) is the Hi integrated intensity. We also used a relation N(H
$_2$
) =
$2\times W$
(CO)
$\cdot$
$X_\mathrm{CO}$
, where W(CO) is the integrated intensity of CO and
$X_\mathrm{CO}$
is the CO-to-H
$_2$
conversion factor. Here we adopted
$X_\mathrm{CO} = 2\times 10^{20}$
cm
$^{-2}$
(K km s
$^{-1}$
)
$^{-1}$
(Bolatto, Wolfire, & Leroy Reference Bolatto, Wolfire and Leroy2013). We then obtained
$M_\mathrm{HI} \sim 3.8\times10^5\;{\rm M}_{\odot}$
and
$M_\mathrm{CO} \sim 3.3\times10^5\;{\rm M}_{\odot}$
within the radio shell boundary of the SNR. The number densities of Hi,
$n_\mathrm{p}$
(Hi), and H
$_2$
,
$n_\mathrm{p}$
(H
$_2$
), were also estimated to be
$\sim$
12 cm
$^{-3}$
and
$\sim$
10 cm
$^{-3}$
, respectively. We then obtain the total interstellar proton density
$n_\mathrm{p}$
(H
$_2$
+Hi) to be
$\sim$
22 cm
$^{-3}$
. We note that this density represents the upper limit as it was calculated by summing up all gas densities along the line of sight.
3.3.2 Diprotodon in the Southern Galactic Plane Survey
Using SGPS, we focus our attention on the long straight shell at the bottom of Diprotodon, which is parallel to the Galactic plane at a Galactic latitude of just below 0
$^\circ$
. To produce such a flat structure, the blast wave must be expanding in a strong density gradient in this direction. Such a density gradient is expected towards the Galactic plane. A density jump, which could be visible in the Hi line data, can also produce a flat straight shell such as the one we see in Diprotodon.
At small negative radial velocities, we find widespread dark absorption features in the Hi data from the SGPS indicative of Hi self-absorption (HISA) (see Fig. 6). HISA is generated when Galactic rotation produces two different distances with the same radial velocity. If we find dense cold Hi gas at the near distance and warm Hi gas at the far distance, the bright emission of the background gas is absorbed by the denser foreground gas, producing dark shadows as seen in Fig. 6. We find a concentration of HISA just below the bottom straight shell of the SNR. The top border of the HISA is slightly curved, with Diprotodon sitting just above it. This is a strong coincidence indicating that Diprotodon’s southern shell is running into dense Hi and possibly molecular gas, which is slowing down the expansion of the blastwave and forces the shell to follow the curved edge of the HISA area.
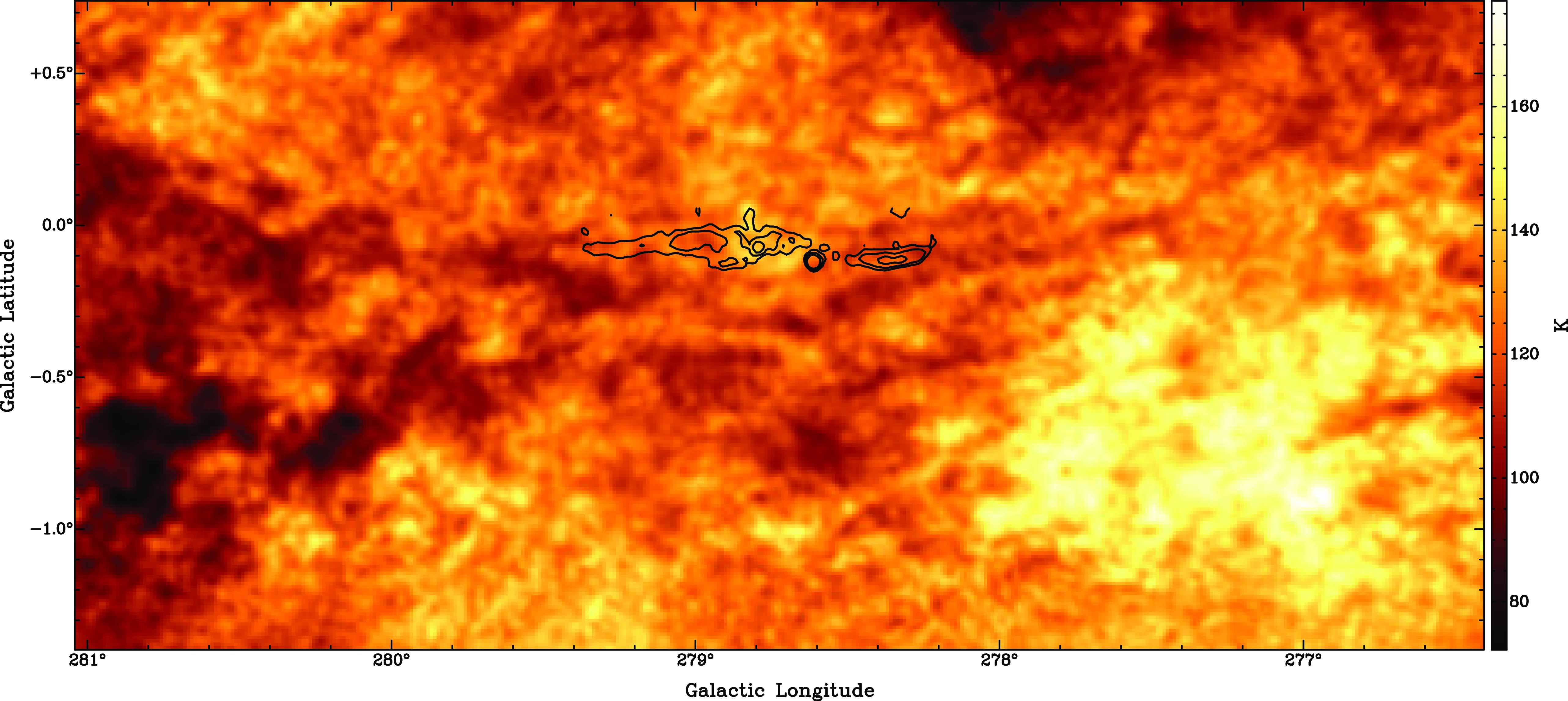
Figure 6. Hi line map taken from the SGPS (McClure-Griffiths et al. Reference McClure-Griffiths2005). For this image, we averaged the three velocity channels between
$-3.3$
and
$-1.6$
km s
$^{-1}$
. The black contours, taken from the continuum part of the SGPS (Haverkorn et al. Reference Haverkorn, Gaensler, McClure-Griffiths, Dickey and Green2006), indicate the flat southern shell of Diprotodon.
In Fig. 7, we show three sample Hi spectra taken just below the SNR’s southern shell in the left, centre, and right parts. The narrow HISA absorption lines are obvious on top of the bright Hi background emission. They show centre velocities around
$-3$
km s
$^{-1}$
.
Figure 7. Hi spectra taken at three different positions just below the straight southern shell of Diprotodon. The spectra were taken at 279.33
$^\circ$
,
$-0.18+^\circ$
(top), 278.67
$^\circ$
,
$-0.33+^\circ$
(middle) and 278.41
$^\circ$
,
$-0.23+^\circ$
(bottom). Peak absorption velocities are
$-3.3$
km s
$^{-1}$
(top),
$-2.5$
km s
$^{-1}$
(middle), and
$-2.6$
km s
$^{-1}$
(bottom).
We show the model rotation curve in the direction of Galactic longitude 279
$^\circ$
in Fig. 8. This is based on trigonometric parallax and proper motion measurements of molecular masers (Reid et al. Reference Reid2019). We find negative radial velocities up to a distance of 2.5 kpc. This is where the line of sight goes through the inner Galaxy with a tangent point velocity of about
$-3$
km s
$^{-1}$
at a distance of 1.2 kpc. As a line of sight through the inner Galaxy naturally produces a rotation curve with two different distances at a given radial velocity, we find the perfect environment for the production of HISA. The direction we are looking at is along our own Galactic spiral arm. In the approximately opposite direction, there is the Cygnus X region, which also exhibits lots of HISA (Gottschalk et al. Reference Gottschalk, Kothes, Matthews, Landecker and Dent2012).
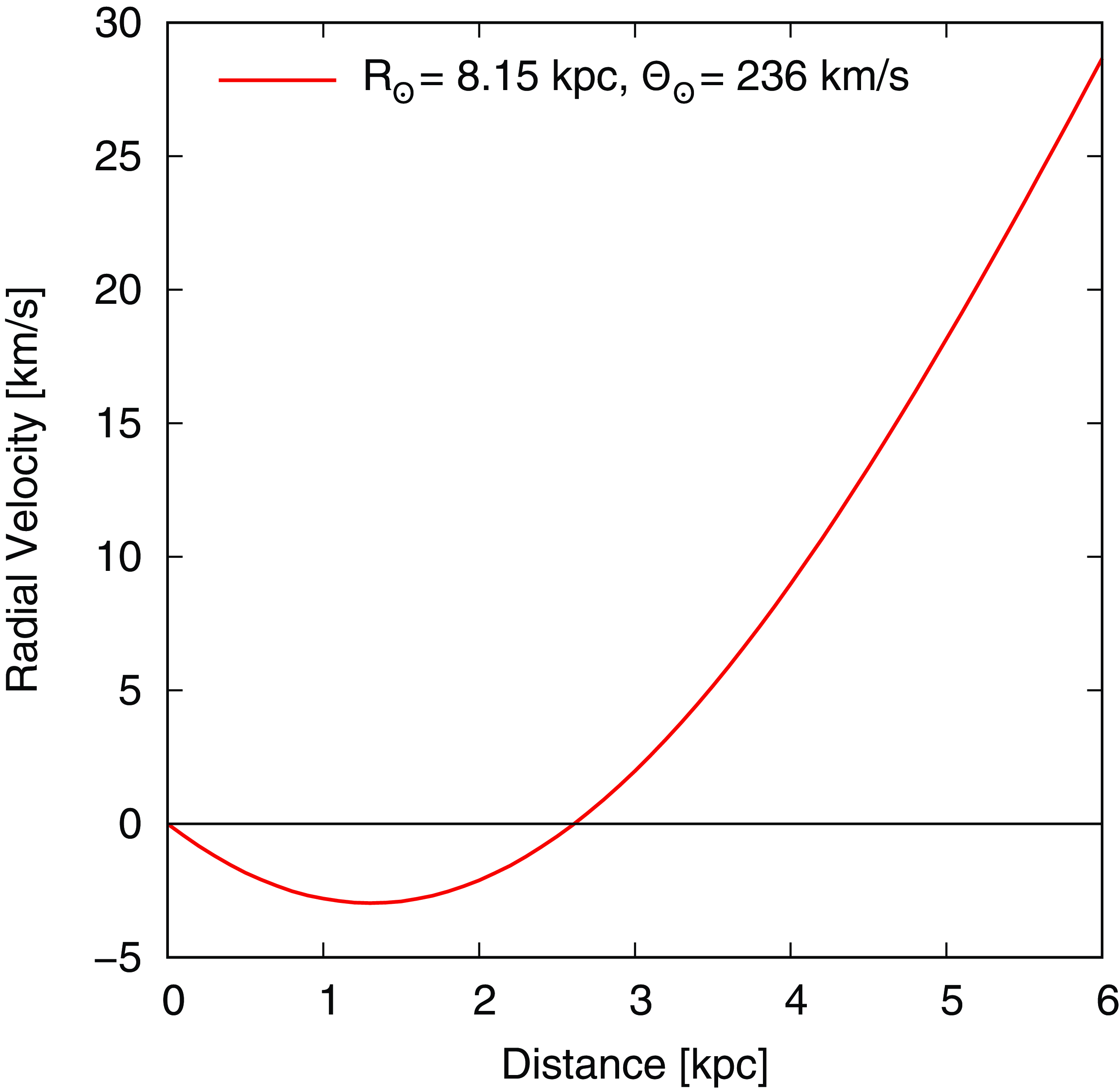
Figure 8. Galactic rotation curve in the direction of Diprotodon (Galactic Longitude = 279
$^\circ$
). We used the latest rotation curve published by Reid et al. (Reference Reid2019), based on trigonometric parallax and proper motion measurements of molecular masers.
The association of Diprotodon with this HISA gives the SNR a systemic velocity of about
$-3$
km s
$^{-1}$
. The radial velocity does not change much with distance (Fig. 8); therefore, the distance is not tightly constrained. However, as the SNR is related to HISA, it must be at the near distance because, at the far distance, it cannot produce HISA. This puts an upper limit of 1.2 kpc – the location of the tangent point – on the distance to Diprotodon which means that the SNR is in our local spiral arm – the Orion spur.
3.4 Diprotodon’s location in the Milky way
In Fig. 1, which shows Diprotodon in galactic coordinates, we can see a clear flattening of the SNR side that is touching b = 0
$^\circ$
while the opposite side (at 2
$^\circ+ \lt b \lt $
3
$^\circ$
) is more circular. It is possible that we see the double shell morphology in the radio image. The lack of emission to the west could be due to the Hii region along the line of sight as shown in Fig. 1, and not an intrinsic effect.
We examine the morphology of Diprotodon in the context of the large-scale Galactic magnetic field. Following the method of West et al. (Reference West2016), we model the synchrotron emission of an SNR that explodes into the Galactic magnetic field model of (Jansson & Farrar Reference Jansson and Farrar2012, hereafter, JF12) towards the direction of Diprotodon. In the top part of Fig. 9, we show a plot of the magnetic field vectors from JF12 with the direction to Diprotodon shown with an arrow. The bottom part of Fig. 9 shows the sequence of models shown at steps of increasing distance from 0.5, 1, 2, 3, etc. to 10 kpc (left to right).
The models at the range of
$\sim$
2–5 kpc distance look like a complete ring. This indicates that the model magnetic field for this direction and these distances is oriented nearly entirely along the line of sight. The expected synchrotron intensity would be low with the magnetic field in this orientation. In addition, the geometry is also not consistent with the morphology that we observe in Diprotodon (see Fig. 1). Comparing with Diprotodon’s observed morphology, we find that the models are consistent with a distance
$\leq+1$
kpc or
$ \gt +5$
kpc, but since
$ \gt +5$
kpc would make Diprotodon’s size unreasonably large, a distance
$\leq+1$
kpc seems the most likely scenario.
Thus, this modelling does not support the 2.7 kpc distance to Diprotodon. We suggest that it is consistent with SNR being located much closer, that is, at
$d_{{\tiny kpc}}\leq 1$
kpc where
$d_{{\tiny kpc}}$
is the distance in units of kpc. From now on, we consider that the distance to Diprotodon is at 1 kpc, which gives it a dimension of 58
$\times$
56 pc.
3.5 Diprotodon’s GeV extension and spectrum
To measure the extent and location of the gamma-ray source, we performed a scan of the parameter space to maximise the likelihood for events with energies above 1 GeV and a uniform disc hypothesis. The resulting size and location agree with those of the spatial template in the 4FGL-DR4 catalogue (4FGL J1000.0–5312e), corresponding to an angular diameter of
$2{{{{.\!^\circ}}}}88$
, and we adopt this morphology for the rest of the analysis.
We used events with energies above 0.2 GeV to study the spectrum of the source. It is described by a log-parabola in the 4FGL-DR4 catalogue. We compared fits using a simple power law and a log-parabola, and the latter is preferred at the
$6.6\sigma$
level when using the standard Galactic diffuse emission model (gll_iem_v07.fits). However, we found that the spectrum below
$\sim+1$
GeV is significantly affected by the modelling of the diffuse Galactic emission. We repeated the analysis using the eight alternative models for the Galactic diffuse emission developed by Acero et al. (Reference Acero2016).Footnote
h
They were designed to explore some of the systematic effects on source parameters caused by uncertainties in the interstellar emission, including uncertainties in the cosmic ray source distribution, the height of the cosmic ray propagation halo and the spin temperature used to derive the H i column density from the 21 cm line data. A simple power-law function was preferred for the Diprotodon spectrum in all the alternative models. A fit using a simple power law,
$\frac{dN}{dE} = N_0 E^{-\Gamma}$
, results in a spectral index
$\Gamma = 1.680 \pm 0.005_{{\tiny stat}}\pm 0.14_{{\tiny sys}}$
. We estimated the systematic error as in Acero et al. (Reference Acero2016) with the fits using the alternative diffuse emission models. More statistics at low energies will be needed to confirm or discard any spectral curvature for the SNR. On the other hand, at higher energies, no spectral curvature is significantly detected above 1 GeV using the standard Galactic diffuse emission model. The difference in the source TS in fits using a log-parabola and a simple power law is 5.1. The spectral index and luminosity above 1 GeV are
$1.79\pm 0.02_{{\tiny stat}}$
and
$\sim 5.8\times10^{33}\,d_{{\tiny kpc}}^2$
erg s
$^{-1}$
, respectively.
To get flux points, we divided the data into 15 logarithmically-spaced energy intervals and fit the spectral normalisation of 4FGL J1000.0–5312e, assuming a simple power law spectrum with index 2 in each interval. We estimated a systematic uncertainty of 13% for the spectral normalisation in the 0.2–500 GeV energy range using the alternative diffuse emission models described above and added this uncertainty to the statistical uncertainties of the flux points in quadrature.
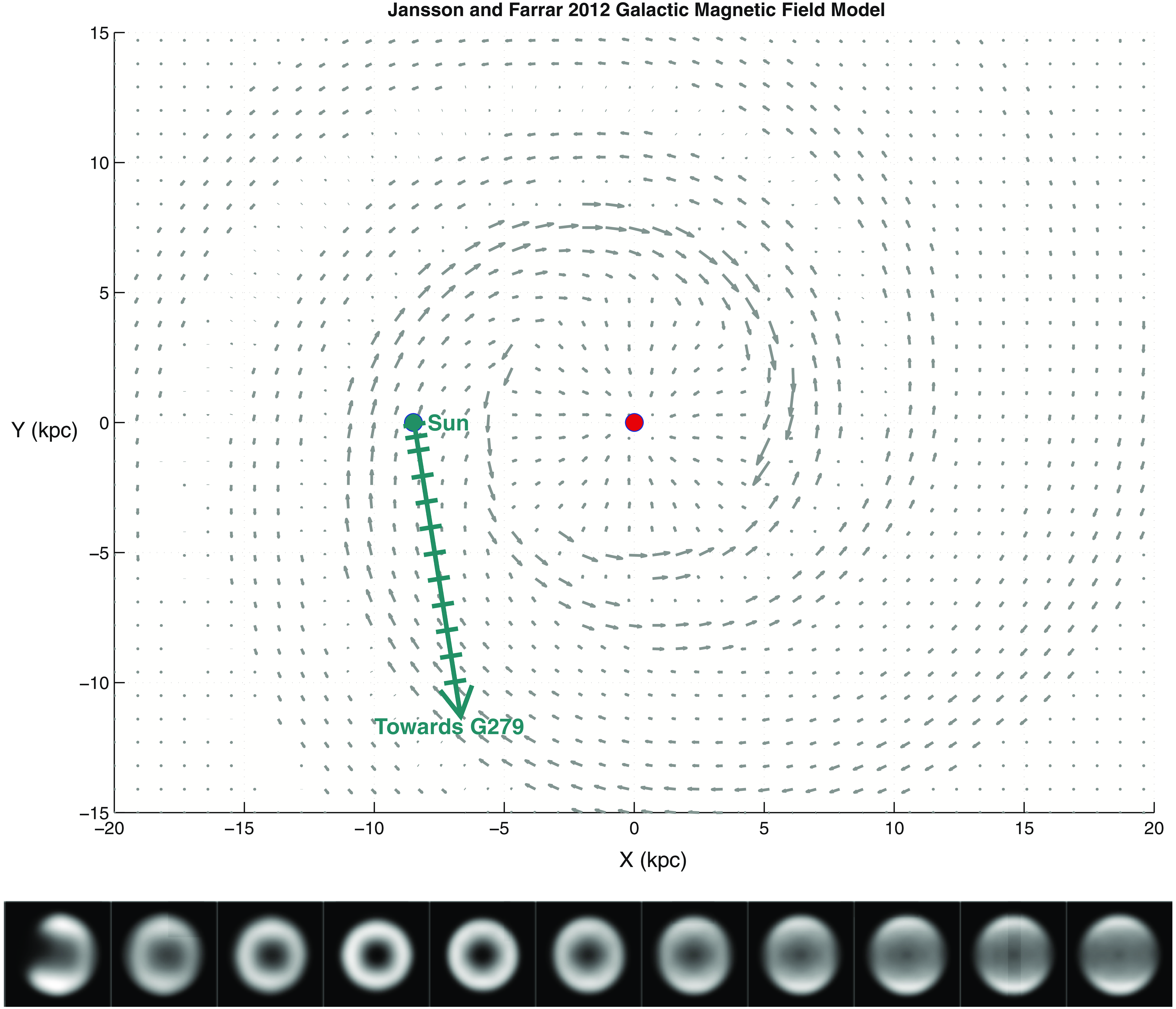
Figure 9. Top: Large-scale mean magnetic field model of JF12 shown in a top-down view. The arrow indicates the direction towards G278.94+1.35. The tick marks show 1 kpc steps along the line-of-sight, with the exception of the first tick, which is shown at 0.5 kpc. Bottom: Model images of the synchrotron emission that comes from an SNR exploding into an ambient magnetic field defined by the JF12 model. The first model image is shown for a distance of 0.5 kpc, and the subsequent model images show 1 kpc steps, from 1 kpc to 10 kpc (left to right).
4. Diprotodon’s mystery
4.1 Diprotodon’s evolutionary status
Diprotodon’s multi-frequency filamentary structure (morphology) and spectral index are strong indications of predominantly synchrotron emission from electrons. Therefore, we should expect gamma rays from the same particles. The fact is that Stupar & Parker (Reference Stupar and Parker2011) detected enhanced [S ii] emission across several Diprotodon’s filaments, suggesting that they are still in the radiative phase. It is most likely that Diprotodon grew to such an extent in a low-density environment so it can still have a well-defined forward shock.
To estimate and evaluate the true evolutionary status of Diprotodon, we use the above-mentioned
$\Sigma-D$
evolutionary tracks and a more realistic diameter estimate of
$\sim$
58 pc (Section 3.4). As Diprotodon is positioned at the bottom right corner of the
$\Sigma-D$
diagram, we can conclude that it is an evolutionary advanced and low surface brightness SNR in the radiative phase of evolution, and in this way is similar to the SNR Ancora (see: Filipović et al. Reference Filipović2023; Burger-Scheidlin et al. Reference Burger-Scheidlin2024, their fig. 4). It most likely evolved in a medium-density interstellar environment with densities
$\sim$
0.2 cm
$^{-3}$
and the energy of the SN explosion can be assumed to be the canonical 10
$^{51}$
erg.
The next important issue for the determination of Diprotodon’s evolutionary stage is from associated magnetic field values. To estimate Diprotodon’s magnetic field, we used the equipartition model from http://poincare.matf.bg.ac.rs/ arbo/eqp. This method uses modelling and simple parameters to estimate intrinsic magnetic field strength, energy contained in the magnetic field and cosmic ray particles using radio synchrotron emission (Arbutina et al. Reference Arbutina, Urošević, Andjelić, Pavlović and Vukotić2012; Arbutina et al. 2013; Urošević, Pavlović, & Arbutina Reference Urošević, Pavlović and Arbutina2018). We use
$\alpha=-0.55$
, radius
$\theta$
= 98 arcmin,
$\kappa=0$
,
$S_\textrm{1\,GHz}$
= 32.8 Jy, and
$f=0.018$
and found that the mean electron equipartition field over the whole of Diprotodon varies from
$13.7\,\mu$
G for 2.7 kpc distance to
$19.6\,\mu$
G for distance of 0.75 kpc distance, with an estimated minimum energy of
$E_\textrm{ min}=1.7\times10^{49}-7.6\times10^{47}$
erg. The original model, developed in Arbutina et al. (Reference Arbutina, Urošević, Andjelić, Pavlović and Vukotić2012), yields a mean ion equipartition (
$\kappa\neq 0$
) field of 35.7
$\mu$
G (for distance 2.7 kpc) to 51.2
$\mu$
G (for distance 0.75 kpc), with an estimated minimum energy of
$E_\textrm{min}=1.2\times10^{50}-5.2\times10^{48}$
erg.
4.1.1 Diprotodon in the radiative phase
Even at a distance of
$\sim$
1 kpc and diameter of
$\sim$
57 pc, Diprotodon is in the radiative phase and not the Sedov–Taylor or adiabatic phase. To determine the evolutionary phase of an SNR, we can compare the width of the shells and filaments with the radius of the remnant. For a Sedov–Taylor phase SNR the compression ratio is 4 (Sedov Reference Sedov1959), which translates into a shell width-to-radius ratio of about 1:10. A younger SNR would have a much wider shell, as we can detect synchrotron emission from the outer shell and the convection zone between swept up material and ejecta (e.g. Gull Reference Gull1973). For a radiative SNRs, we find large compression ratios of several 10s or even 100s.
To determine the width of an SNR’s shell we have to consider that this is a three-dimensional object and the emission we observe is projected onto the plane of the sky. We cannot simply measure the width of the projected shell, as it also contains emission from the spherically expanding shell part that is moving away from us and towards us. The emission peaks of the shells mark the longest line of sight through the synchrotron emitting region. This is the inner edge of the shell projected onto the plane of the sky. The radial distance between that peak and the outer edge of the shell emission indicates the width of the actual three-dimensional shell. In Diprotodon, which shows a wealth of thin filaments that are expected for a fragmenting radiative forward shock, this width is typically not greater than 1
$^\prime$
. The projected emission from the fragmented shell fills a large projected volume in the northeast, compared to the south, where only one isolated filament is present. This gives a ratio of the shell width to the radius of the SNR of around 0.006, which translates to a compression ratio of about 50, which is clearly well beyond the Sedov–Taylor phase. A more quantitative analysis would require the extraction of radial emission profiles, which is beyond the scope of this paper based on the available data.
Using the study of radiative SNRs by Cioffi et al. (Reference Cioffi, McKee and Bertschinger1988), we can calculate the time
$t_\textrm{PDS}$
and radius
$R_\textrm{PDS}$
at which an SNR enters the radiative phase, or as they call it the pressure driven snowplow (PDS) phase, given intrinsic parameters for the explosion energy,
$E_{51}$
given in
$10^{51}$
erg, and the ambient number density,
$n_0$
given in cm
$^{-3}$
:
\begin{equation} t_\textrm{PDS} = 1.33\times 10^4 \frac{E_{51}^{3/14}}{n_0^{4/7}}\;\textrm{yr}\end{equation}
\begin{equation} R_\textrm{PDS} = 14.0 \frac{E_{51}^{2/7}}{n_0^{3/7}}\;\textrm{pc}.\end{equation}
Assuming a distance of
$d_{{\tiny kpc}}$
= 1 kpc gives Diprotodon an average diameter of
$\sim$
60 pc. For explosion energies
$E_{51}$
of 0.1 and 1.0, which can be considered lower and upper limits, we derive ambient densities
$n_0$
of 0.17 and 0.036 cm
$^{-3}$
and ages t of 54 and 36 kyr, respectively, for the time the SNR enters the PDS phase. As Diprotodon is clearly well into the radiative phase, the values for the ambient density and the ages are lower limits.
In Table 1, we show some possible scenarios for Diprotodon for three different explosion energies between a lower limit of
$10^{50}$
erg and an upper limit of
$10^{51}$
erg for a Type-Ia explosion. The
$3.2\times 10^{50}$
erg are the logarithmic average of the lower and upper limit and correspond according to Pejcha & Prieto (Reference Pejcha and Prieto2015) to a type IIP explosion with an ejecta mass of 10
${\rm M}_\odot$
. If we now assume
$n_0 = 0.2$
cm
$^{-3}$
and
$E_0 = 10^{51}$
erg, suggested as a possible scenario based on the radio surface brightness study in Section 4.1, Diprotodon would be about 40 kyr.
Table 1. Age t in yr for Diprotodon for different intrinsic parameters
$n_0$
in cm
$^{-3}$
and
$E_0$
in
$10^{51}$
erg. The distance was assumed to be 1 kpc, which translates to a mean radius of about 30 pc. ‘S-T’ indicates that the SNR would not have reached the PDS phase yet. ‘Merged’ indicates that this SNR would merge with its environment before reaching a radius of 30 pc.
Another possible scenario is a well-structured environment in which the SNR first expands inside a low-density cavity and enters the radiative phase by crushing into higher-density clouds. This may explain the higher-than-expected radio surface brightness for such an extensive SNR and the bright gamma-ray emission, as the evolutionary development of the SNR is stalled until it reaches the clouds. However, in this scenario, we would expect to find a cloud outside of each bright, highly compressed radio shell, which is clearly not seen in our data.
Here argued the radiative phase of Diprotodon’s evolution is at odds with the eROSITA X-ray study (Michailidis et al. Reference Michailidis, Pühlhofer, Santangelo, Becker and Sasaki2024) that shows an oxygen-rich, ejecta-dominated SNR, with the plasma in a non-equilibrium state, favouring a somewhat younger age and a smaller size of only
$\sim$
20 pc. While temperatures of 0.3 or 0.6 keV point to cooler and more evolved remnants, but that could be due to interaction with denser material that agrees with the gamma-ray emission. Nevertheless, it is important to keep in mind that not all properties of this remnant necessarily indicate that it is among the largest or oldest.
4.2 Large and aged SNR that shines in gamma rays
The most unusual fact is that such an extensive SNR is detected in GeV gamma rays with a hard spectrum. This is certainly quite unexpected and challenges our understanding of the evolution of such objects. This type of gamma-ray spectrum is typical of young (and therefore smaller) TeV shell-like SNRs such as RCW 86, Vela Jr, and RX J
$1713.7-3946$
(Ajello et al. Reference Ajello2016; Tanaka et al. Reference Tanaka2011; Abdo et al. Reference Abdo2011). An example of a puzzling SNR with an angular size of
$\sim$
3
$^\circ$
that shows a dynamically young GeV spectrum while exhibiting morphological features of an evolved object is G150.3+4.5 (Gao & Han Reference Gao and Han2014; Devin et al. Reference Devin2020). There are other objects seen in gamma rays that could be (evolved) SNRs, such as the shell-like TeV source HESS J1912+101 (Aharonian et al.Aharonian, Akhperjanian, Barres de Almeida, Bazer-Bachi, Behera, Beilicke, Benbow, Bernlöhr, Boisson, Bolz, Borrel, Braun, Brion, Brown, Bühler, Bulik, Büsching, Boutelier, Carrigan, Chadwick, Chounet, Clapson, Coignet, Cornils, Costamante, Dalton, Degrange, Dickinson, Djannati-Ata, Domainko, O’C. Drury, Dubois, Dubus, Dyks, Egberts, Emmanoulopoulos, Espigat, Farnier, Feinstein, Fiasson, Förster, Fontaine, Funk, Fü 2008; Reich & Sun Reference Reich and Sun2019); and others of unknown type with hard GeV spectra having no known counterparts at lower energies such as G350.6–4.7 (3
${{{{.\!^\circ}}}}4$
wide, Araya Reference Araya2018; Ackermann et al. Reference Ackermann2018) and 2HWC J2006+341 (Albert et al. Reference Albert2020). However, none of the known evolved Galactic SNRs have a hard GeV emission while also having a similar physical size to Diprotodon.
There are a few aspects to this problem. So far, the sample of detected gamma-ray sources is somewhat biased to what we can actually see. Young (
$\sim$
1 000 yr) SNRs are predominantly leptonic as they usually evolve in low-density media, but can efficiently accelerate electrons. With time, leptonic emission (inverse-Compton) becomes suppressed due to electrons losing energy via synchrotron radiation. The TeV emission starts to decrease after
$\sim$
3 000 yr (Brose et al. Reference Brose, Pohl, Sushch, Petruk and Kuzyo2020), but GeV emission should also start to decrease at some point. So, for aged SNRs, we should not see much gamma-ray emission from electrons. On the other hand, dynamically old SNRs that we observe are predominantly hadronic with a soft spectrum (Ackermann et al. Reference Ackermann2013; Giuliani & AGILE Team 2011; Jogler & Funk Reference Jogler and Funk2016; Ambrogi et al. Reference Ambrogi2019; de Oña Wilhelmi et al. Reference de Oña Wilhelmi2020), which agrees with theoretical expectations and can be explained as a combined effect of the decrease of the maximum energy to which particles can be accelerated with time and particle escape (Celli et al. Reference Celli, Morlino, Gabici and Aharonian2019a; Brose et al. Reference Brose, Pohl, Sushch, Petruk and Kuzyo2020), or alternatively by weakening of the shock due to propagation in the hot shocked wind of the progenitor star (Das et al. Reference Das2022). Protons do not lose energy as electrons and hence can generate gamma-ray emission at late times. Dynamically old SNRs also usually show strong evidence of cloud interaction that causes deceleration of the shock and provides target material for hadronic interaction.
Supposedly, the age (
$\sim10^4$
–
$10^5$
yr) of Diprotodon naturally indicates a hadronic nature of the GeV gamma-ray emission. However, this scenario is in tension with a lack of clear correlation of the gamma-ray emission with gas distribution (see Section 3.3). The hadronic scenario also requires protons to be accelerated to a hard spectrum up to
$\sim+10$
TeV, which would be somewhat surprising (see further discussion in Section 4.3). The observed hard gamma-ray spectrum could be more naturally explained in the case of a much younger age of the remnant both in the hadronic scenario and the leptonic scenario (through the curvature of the IC spectrum imposed by the cut-off in the electron spectrum and/or the spectral break resulted from synchrotron cooling).
4.3 Diprotodon’s spectral energy distribution modeling
To help understand the particle nature of the Fermi-LAT emission from Diprotodon, we applied a model that matches the non-thermal emission from a steady-state population of particles (electrons and protons) accelerated by Diprotodon in a single zone of magnetic field B to the radio and GeV fluxes. The model assumes particles are injected according to a power law + exponential cutoff distribution
$\sim E^{-\Gamma}\exp(\!-E/E_\textrm{cut})$
with photon index
$\Gamma = 2$
. The exponential cutoff energy
$E_\textrm{cut}$
is used to represent the maximum particle energies (
$E_\textrm{ cut,e}$
and
$E_\textrm{cut,p}$
for electrons and protons, respectively) expected from acceleration limits, radiative energy losses, and potentially particle losses due to their escape from the SNR region. The total energy of protons and electrons (erg) is denoted
$W_p$
and
$W_e$
, respectively.
Photon production from synchrotron, inverse-Compton (IC), Bremsstrahlung, proton-proton (PP) collisions, and secondary synchrotron processes were considered. The PP collision cross section and secondary particle distributions are defined by Kafexhiu et al. (Reference Kafexhiu, Aharonian, Taylor and Vila2014). The IC emission is assumed to result from three low-energy photon fields – the cosmic microwave background (CMB), infrared photons, and optical photons from starlight. The PP collision rate is governed by the ISM target density n (cm
$^{-3}$
), where we used
$n=20$
cm
$^{-3}$
(
$n=5$
cm
$^{-3}$
for the leptonic dominated case) based on our ISM studies discussed earlier. We note that this value represents an upper limit calculated from the column density along the line of sight.
We assume Diprotodon to be at a 1.0 kpc distance (see Section 3.3), resulting in a physical diameter of
$D_\textrm{SNR}$
= 58 pc. We consider contributions from both the leptonic and hadronic components to the Fermi-LAT GeV emission. For the IC seed photons, we used values typical of the Galactic average for the infrared and optical photon fields (e.g. see Vernetto & Lipari Reference Vernetto and Lipari2016), as the infrared image (Fig. 3) and O-star catalogues do not suggest any significant enhancements. Thus, we assume energy densities of 0.3 eV cm
$^{-3}$
for both of these fields and thermal black-body temperatures of 30 and 2 600 K, respectively, for the infrared and optical fields.
Some constraints are also available from the X-ray and TeV gamma-ray domains. Just recently, Michailidis et al. (Reference Michailidis, Pühlhofer, Santangelo, Becker and Sasaki2024) revealed a thermal X-ray counterpart to the SNR using observations with the eROSITA telescope. They also noted some hints for this emission in their analysis of ROSAT PSPC data. The thermal X-ray spectra are consistent with a dual-temperature shock-heated gas model (with a number of spectral lines), with kT = 0.34 and 0.60 keV, respectively. In our model, we treat this as an upper limit to any non-thermal X-ray emission by including a dual-temperature thermal Bremmsstralung approximation (
$\sim+T^{-0.5}\exp(\!-E/kT)$
) normalised to the total energy flux, 1.48
$\times 10^{-9}$
erg cm
$^{-2}$
s
$^{-1}$
quoted by Michailidis et al. (Reference Michailidis, Pühlhofer, Santangelo, Becker and Sasaki2024) in the 0.2–4.0 keV energy range. For upper limits in the TeV gamma-ray range, we used the available integral
$E \gt 1$
TeV flux upper limits from the H.E.S.S. Galactic Plane Survey (HGPS) (H. E. S. S. Collaboration et al. 2018) summed over a
$0{{{{.\!^\circ}}}}2$
region. We first found the
$0{{{{.\!^\circ}}}}2$
upper limit averaged over the SNR region and then scaled this value by the ratio
$R_\textrm{SNR}$
/
$0{{{{.\!^\circ}}}}2$
. This result was then differentiated and converted to an energy flux in the 1–10 TeV energy range assuming a differential photon index
$\Gamma=2.3$
as assumed by H. E. S. S. Collaboration et al. (2018).
Results are shown in Fig. 10 along with the parameters found to adequately match the radio and Fermi-LAT fluxes. A reasonable match was found when assuming a magnetic field
$B=30\,\mu$
G,
$E_\textrm{cut,p}=100$
TeV,
$E_\textrm{cut,e}=5$
TeV, total energy
$W_{p+e}=0.3\times10^{49}(d/1\,\textrm{kpc})$
erg and electron energy assumed to be
$W_e=2.4 \times 10^{47}(d/1\,\textrm{kpc})$
erg. These particle energy budgets are similar to the canonical expectation for an SNR and to local measurements of the electron spectrum. Emission components from the non-thermal Bremsstrahlung and secondary synchrotron processes are negligible and are therefore not shown. The 5 TeV electron cutoff energy is constrained by the eROSITA thermal emission and is consistent with the expectation for mature (
$ \gt +10^4$
yr) SNRs, where maximum electron energies are limited by synchrotron losses (e.g. Reynolds Reference Reynolds2008). The 100 TeV proton cutoff energy as constrained by the TeV upper limit from H.E.S.S. represents the upper limit on the maximum proton energy. The GeV emission up to
$\sim$
400 GeV is clearly positioned inside the radio structures, implying that particles up to at least
$\sim$
4 TeV or so are confined at the current epoch. Although it is expected that an SNR could accelerate protons up to 100 TeV and higher, these high energies are normally reached only during the early stages of the SNR evolution (e.g. Bell et al. Reference Bell, Schure, Reville and Giacinti2013). The hard broad-band spectrum of the GeV gamma-ray emission suggests the presence of recently accelerated protons to at least 4 TeV. However, such proton acceleration in mature SNRs is not expected to reach significantly higher energies than this due to deceleration of the shock and less effective amplification of the magnetic field (e.g. Brose et al. Reference Brose, Pohl, Sushch, Petruk and Kuzyo2020). We do note that a lower proton cutoff energy approaching 10–20 TeV in our model would also provide a satisfactory match to the data if we were not aiming to meet the H.E.S.S. upper limit.
Figure 10. Top-left: Model spectral energy distribution from hadronic (PP) and leptonic (synchrotron and IC emission) particle populations applied to Diprotodon for the SNR at 1.0 kpc distance with radius
$R_\textrm{SNR}=29$
pc. Cutoff energies
$E_\textrm{cut, e,p}$
= 5 and 100 TeV were used for the injected electrons and protons. Additional model parameters are shown. The top-right panel uses a modified density
$n^\prime(E_p)$
in the PP component that considers energy-dependant penetration into dense ISM clumps over an age 35 kyr. A clump radius
$R_\textrm{cl}=0.1$
pc and clump magnetic field
$B_\textrm{cl} = 6B$
were assumed. The bottom-left and bottom-right panels illustrate minor variations in magnetic field,
$W_p$
and
$W_e$
to produce leptonic- and hadronic-dominant scenarios, using the same particle cutoff energies as per the top panels, and a modified density as per the top-right panel. The 95% confidence level HESS upper limit is shown on all panels (converted from an integral limit for
$E \gt 1$
TeV to a differential limit over the 1 to 10 TeV energy range assuming a spectral index of −2.3 as used by H. E. S. S. Collaboration et al. 2018). In all panels, the eROSITA thermal Bremsstrahlung component (eROSITA-TB, see text) is treated as an upper limit to the synchrotron emission.
For energies below a few GeV, we note that our PP model overestimates the observed fluxes and upper limits by factors of about 2–5 (Fig. 10 top-left panel). In the framework of our one-zone stationary model, this could be addressed by using a slightly harder proton spectrum, for example,
$\Gamma$
= 1.8–1.9. However, the radio fluxes from the SNR suggest
$\Gamma \sim 2.0$
–2.1 for electrons, and recent theoretical studies also support the likelihood of indices steeper than 2.0 in SNR shock acceleration (e.g. Bell, Matthews, & Blundell Reference Bell, Matthews and Blundell2019; Malkov & Aharonian Reference Malkov and Aharonian2019), although the potential for harder indices in shock acceleration for some circumstances has been discussed (e.g. Malkov Reference Malkov1999; Perri & Zimbardo Reference Perri and Zimbardo2012). The vast majority of dynamically old hadronic dominated GeV gamma-ray SNRs exhibit a very soft spectrum (Ackermann et al. Reference Ackermann2013; Giuliani & AGILE Team 2011; Jogler & Funk Reference Jogler and Funk2016; Ambrogi et al. Reference Ambrogi2019; de Oña Wilhelmi et al. Reference de Oña Wilhelmi2020). However, along with the Diprotodon SNR we study here, a few other SNRs (presumably mature in age) with a hard spectrum below 10 GeV have also been detected (e.g. Zeng et al. Reference Zeng, Xin, Zhang and Liu2021; Araya et al. Reference Araya, Hurley-Walker and Quirós-Araya2022; Eppens et al. Reference Eppens2024).
A potential explanation for the hard GeV spectrum, if viewed in terms of a hadronic scenario, might come from the energy-dependant diffusive penetration of protons into the ISM gas, which could be important in the case of clumpy ISM inside the SNR if it results from a core-collapse supernova event. In this case, the dense (10
$^{3-4}$
cm
$^{-3}$
) clumps that survive the SNR shock and gas turbulence induced by it may comprise a reasonable fraction of the gas mass downstream of the shock. This issue has already been discussed in application to the young (1 600 yr), gamma-ray-bright SNR RXJ 1713.7–3946, where a very hard (
$ \lt +100$
GeV) spectrum is observed (e.g. Inoue et al. Reference Inoue and Yamazaki2012; Gabici & Aharonian Reference Gabici and Aharonian2014), and in the GeV emission from nearby molecular clouds (Yang et al. Reference Yang2023). Recent measurements of the ISM towards some SNRs with ALMA have revealed the presence of sub-pc-scale ISM clumps (e.g. Sano et al. Reference Sano2020; Sano et al. Reference Sano2021). Following Inoue et al. (Reference Inoue and Yamazaki2012) the penetration depth of protons in pc units can be given by
$l_\textrm{pd}(E_p) = 0.1 \sqrt{\eta (E_p/10\textrm{TeV}) (t_\textrm{age}/10^3\textrm{yr}) / (B_\textrm{ cl}/100\,\mu\textrm{G})}$
. Here,
$E_p$
is the proton energy,
$t_\textrm{age}$
is the SNR age,
$B_\textrm{cl}$
is the clump magnetic field and
$\eta\sim (B/\delta B)^2$
is a turbulence parameter based on magnetic field fluctuation estimates.
As a potential first look at this effect as applied to our model, we follow Inoue et al. (Reference Inoue and Yamazaki2012) who suggest
$\eta=1$
and a clump radius of
$R_\textrm{cl} = 0.1$
pc. To adjust our model PP component, we apply an effective ISM density
$n^\prime(E_p) = n \zeta(E_p)$
, where
$\zeta(E_p) = 1 - [(R_\textrm{cl} - l_\textrm{pd}(E_p))/R_\textrm{cl}]^3$
represents the energy-dependent ratio of clump volume intercepted by protons to the total clump volume, under a constant clump density assumption. We note that
$\zeta(E_p)$
is upper bound to 1.0 for cases where the protons fully penetrate the clump. Detailed simulations of the SNR shock influence on dense clumps (e.g. Inoue et al. Reference Inoue and Yamazaki2012; Celli et al. Reference Celli, Morlino, Gabici and Aharonian2019b) suggest clump magnetic fields can reach values of 100
$\mu$
G or more inside and around the shock-disrupted boundary. To achieve these values, in our application, we simply assume the clump magnetic field is 6
$\times$
larger than the SNR averaged field,
$B_\textrm{cl} = 6 B$
. Results in Fig. 10 (top-right panel) assuming an age 35 kyr show that with the modified density, the PP component
$ \lt 10$
GeV can be satisfactorily reduced to match the observations.
Our simple model assumes that (1) most of the gas is in the form of clumps and (2) the gamma-ray emissivity dominantly arises from these clumps. For the gas density averaged over the SNR volume
$n= f n_\textrm{cl} + (1-f)n_\textrm{icl}$
for a clump volume filling factor f, clump density
$n_\textrm{cl}$
and inter-clump density
$n_\textrm{icl}$
, condition (1) requires
$n_\textrm{cl} \gt \gt (1-f) f^{-1} n_\textrm{icl}$
. Following this, from condition (2), it can be shown that we require
$n_\textrm{cl} \gt \gt (1/\zeta(E_p) -1) n_\textrm{icl}$
. A further condition, that the clumps do not significantly affect the SNR’s dynamical evolution (compared to effects produced by large pc-scale gas clouds), would require a small filling factor
$f \lt $
0.1 (e.g. Slavin et al. Reference Slavin2017). While we do not have as yet any observations to confirm the presence of such clumps inside this SNR, those observed by ALMA inside the young core-collapse SNR RXJ 1713.7–3946 (Sano et al. Reference Sano2020) at least so far satisfy the above-mentioned conditions.
We also show in Fig. 10 (bottom left and right panels) results after applying modest adjustments to parameters n, B,
$W_p+e$
and
$W_e$
to achieve either a dominantly leptonic or hadronic scenario. All of these parameters could be considered feasible for a mature SNR. The lower densities
$n=5$
cm
$^{-3}$
used in the leptonic-dominant scenario could be realised if one assumes some of the ISM gas in the –13 to –1 km/s velocity range lies just outside of the SNR shock. Taking into account that the peak of GeV gamma-ray emission is not spatially coincident with the peak of the gas distribution, the effective density for hadronic interactions could be even smaller. A lower gas density (
$n \sim 1$
cm
$^{-3}$
or less) might infer that much of the gas revealed by the HI and CO observations could have been contacted by the SNR in recent times, and it would be more consistent with the low densities used in the evolutionary model (Table 1, which would define our inter-clump density
$n_\textrm{ icl}$
) to estimate the SNR’s age. A consequence of this would be a factor 5–10 or so increase in
$W_p$
and a lowering of the
$W_e/W_p$
ratio, but still within a range of acceptable values.
Overall, our spectral energy distribution modelling for the SNR suggests contributions from both leptonic and hadronic processes to the GeV emission, and that either a dominantly leptonic or hadronic scenario is feasible while facing some difficulties. A modification to the hadronic component to account for energy-dependent penetration into a clumpy ISM might offer a way to match the steeply falling emission below 10 GeV. The expected cutoff at 5 TeV energies or thereabouts for electrons in a mature SNR (e.g. see Eq. 10 of Brose et al. (Reference Brose, Pohl, Sushch, Petruk and Kuzyo2020) assuming a shock speed
$\sim$
300 km/s and upstream magnetic field of 5–10
$\mu$
G) would however limit the level of
$ \gt $
1 TeV IC emission. A model with full-time-dependent energy losses and acceleration would be needed to more accurately predict the electron and proton cutoff energies.
Future TeV gamma-ray observations by H.E.S.S. and the Cherenkov Telescope Array (CTA) will therefore be crucial in testing hadronic vs. leptonic models, and the maximum energies of the associated particles. It should also be noted that the age of the remnant, which is still poorly constrained, is a crucial parameter in determining the nature of the gamma-ray emission.
4.4 Gamma-ray emission from a relic pulsar wind nebula?
We investigated the possibility that the gamma-ray emission from Diprotodon arises from a relic population of electron–positron pairs produced in a pulsar wind nebulae (PWN) during the first few millennia of the system and later mixed in with remnant material. Building upon previous work by Gelfand, Slane, & Zhang (Reference Gelfand, Slane and Zhang2009), Martin et al. (Reference Martin2024) developed a model for the dynamics and radiation from a PWN growing inside an SNR, including the possibility of particle escape from the PWN to the SNR and then from the SNR to the ISM. In this new model framework, a population of relativistic electron-positron pairs builds up and spreads across the whole PWN-SNR system. This is described qualitatively below, and the whole formalism is provided in Martin et al. (Reference Martin2024).
In the present case, we consider the possibility that particles escaped from the nebula into the remnant and still trapped downstream of its forward shock at the current age of the system are responsible for the observed gamma-ray emission. The original nebula is thought to have completely dissolved by now, and the pulsar may have escaped the system owing to its natal kick (but see the more quantitative discussion of this scenario at the end of the section), such that this population of trapped electron-positron pairs is all that remains from the PWN.
If the SN explosion gave birth to a neutron star, a PWN rapidly develops at the centre of the SNR, fed by relativistic electron-positron pairs and turbulent magnetic field resulting from the conversion of rotational energy of the neutron star. It is bounded on the inner side by the pulsar wind termination shock, where spin-down power conversion occurs (by mechanisms not specified in the model), and on the outer side by a shell of swept-up stellar ejecta, produced as the PWN expands (and assumed to be geometrically thin in the model). The dynamics of the PWN is controlled by the pressure imbalance between the nebula’s interior and the ejecta’s pressure immediately ahead of its outer frontier, taking into account the bounding shell inertia.
In the model of Martin et al. (Reference Martin2024), particles in the PWN experience a combination of advection and resonant scattering with magnetic turbulence (assumed to be Alfvenic), which is described as an isotropic diffusion process in position. Particles can escape the nebula over a typical time scale set by the time needed to cross the radius of the PWN at any given age. The process is energy-dependent and statistically favours the escape of the highest-energy pairs first. These escaping particles then enter the SNR volume, where they will be confined by the magnetic barrier that develops at the forward shock (which is a prerequisite for diffusive shock acceleration, ensuring that particles remain in the accelerator for long enough). This magnetic barrier can be characterised by the maximum momentum of the particles that can be confined in the remnant, and the latter evolves in time, first increasing linearly with time until Sedov–Taylor transition and then decreasing following a power law (Celli et al. Reference Celli, Morlino, Gabici and Aharonian2019a). As a result, at ages past the Sedov–Taylor transition, the remnant is progressively depleted of its highest-energy particles.
For aged systems, the electron-positron pairs originally energised by the pulsar are spread over three zones (the PWN, the SNR, and the ISM), and each population has a specific spectral distribution. The corresponding electromagnetic radiation is computed, with IC scattering in the ambient radiation field producing gamma-ray photons, while synchrotron radiation is responsible for emission in the radio to X-ray band. The radiation field used in IC scattering is the one defined in Section 4.3. The magnetic field involved in synchrotron radiation is defined for the nebula from the fraction of spin-down power injected as magnetic energy, while it is a free parameter for both the SNR and the ISM volumes.
In the case of Diprotodon, the model predicts gamma-ray emission matching the observations for the following main parametersFootnote
i
: (i) an assumed distance of 1.0 kpc; (ii) for the SNR, a mass of 15 M
$_\odot$
, the kinetic energy of
$5\times10^{50}$
erg, and an ambient density of 0.03 H cm
$^{-3}$
; (iii) for the pulsar, an initial spin-down power of
$7 \times 10^{37}$
erg/s, an initial spin-down time scale of 3 000 yr, and a braking index of 3; (iv) for energy injection in the nebula, a fraction of 90% of the spin-down power going into pairs, injected with a broken-power-law spectrum with index 1.8 and 2.6, respectively, above and below the break energy of 50 GeV and an exponential cutoff at 500 TeV, while the remaining 10% are evenly shared between large-scale magnetic field and Alfvenic turbulence with a largest spatial scale of 2% of the PWN radius. The parameters for the remnant and the pulsar are typical of the Galactic population. The initial properties obtained for the pulsar can be translated into an initial period of 55 ms and a magnetic field of
$4.6\times10^{12}$
G, which agrees very well with the typical values inferred for these parameters from the known pulsar population (Faucher-Giguère & Kaspi Reference Faucher-Giguère and Kaspi2006; Watters & Romani Reference Watters and Romani2011). Similarly, the properties of the remnant agree well with those inferred from a large sample of Galactic SNRs (Leahy, Ranasinghe, & Gelowitz Reference Leahy, Ranasinghe and Gelowitz2020).
With such parameters, the SNRs grows to about 30 pc at an age of 25 kyr, at which time it is still in the Sedov–Taylor stage. The reverse shock hits the nebula at about 20 kyr, and numerical hydrodynamical simulations show that significant mixing, if not full disruption of the nebula ensues (e.g. Kolb et al. Reference Kolb, Blondin, Slane and Temim2017). At this time, however, most of the particles have already escaped the PWN and are trapped within the SNR (about
$10^{48}$
erg total particle energy). As time goes by, the magnetic barrier at the forward shock weakens, such that only particles with energies below
$\sim+150$
TeV remain in the SNR at an age of 100 kyr (under the assumption that particle confinement at the forward shock reached a maximum energy of 1 PeV at Sedov–Taylor transition, with a subsequent decay in time following a power law with index 2).
The predicted gamma-ray emission from the remnant is displayed in Fig. 11. It matches the signal inferred from Fermi-LAT data regarding flux level and spectral shape, and it is consistent with the upper limit from H.E.S.S. The H.E.S.S. upper limit constrains the cutoff energy of the particle injection spectrum and the magnetic field strength in the remnant. Using 500 TeV for the former, the GHz radio intensity is saturated for an average magnetic field of 5
$\mu$
G in the remnant. The corresponding radio synchrotron emission falls short of the flux density measured at 0.1 GHz, despite using parameters for the particle spectrum that are at the end of the ranges inferred for younger PWNs (a low-energy power-law index of 1.8, below a break energy of 50 GeV; see Torres et al. Reference Torres, Cillis, Martn and de Oña Wilhelmi2014). This suggests that a second population of particles is responsible for most of the radio emission, a possibility that is supported by the fact that the radio and gamma-ray morphologies overlap only partially. Such a population could, for instance, be composed of particles accelerated at the forward shock and subsequently advected downstream of it, which would account for the steeper spectral index. In that case, and if the average magnetic field in the remnant has a strength lower than 5
$\mu$
G, the relic population of electron-positron pairs have a subdominant contribution to the synchrotron emission and are observable only through their inverse-Compton gamma-ray emission.
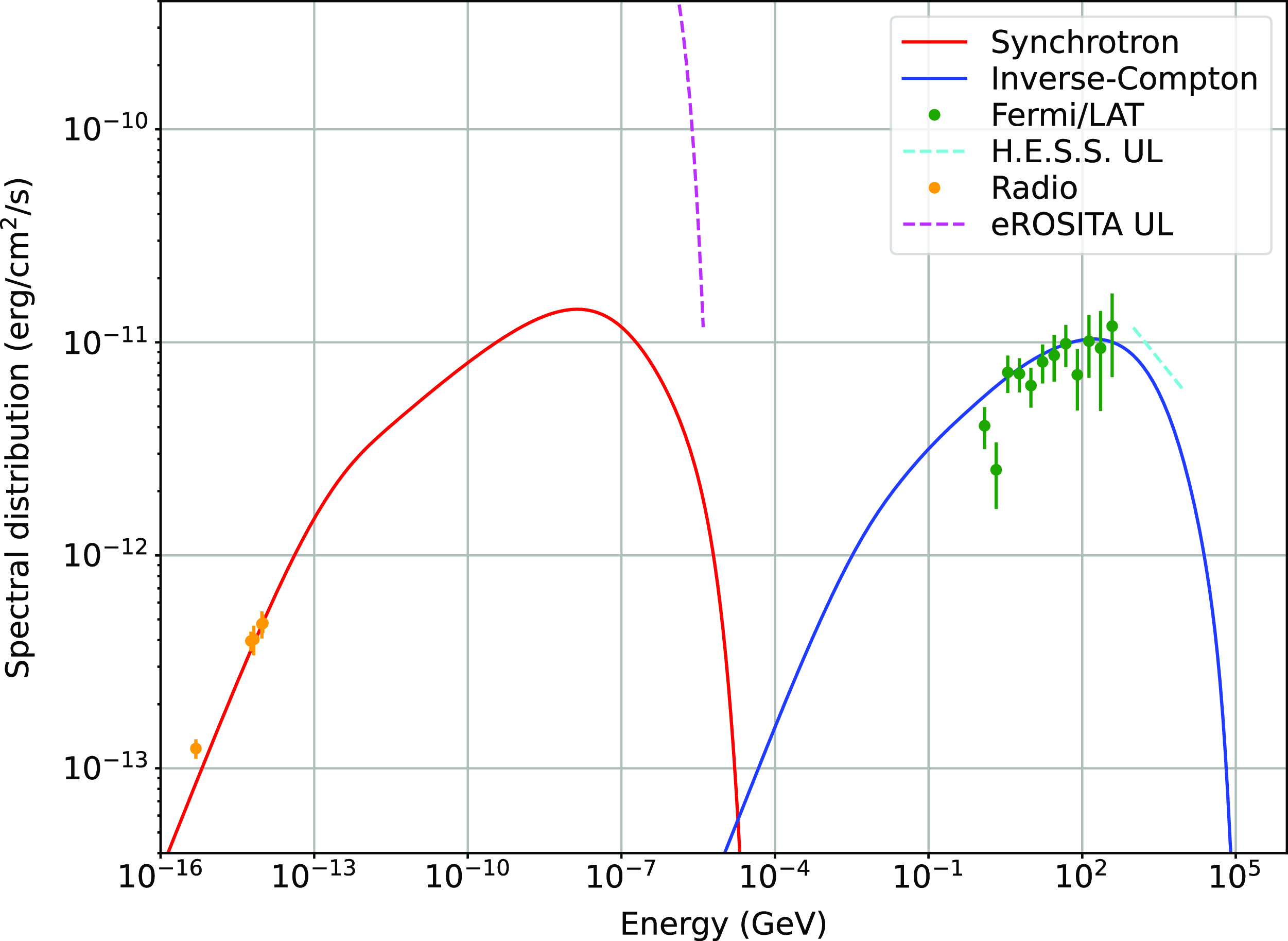
Figure 11. Predicted broadband spectral energy distribution when interpreting the gamma-ray emission as arising from a relic PWN, using the model of Martin et al. (Reference Martin2024). The dashed lines indicate upper limits on the emission.
Eventually, the relic PWN scenario can account for three observables: (i) gamma-ray emission not being positionally coincident with interstellar gas, a priori discarding a hadronic emission mechanism and favouring a leptonic origin; (ii) gamma-ray emission seemingly being pushed away from the galactic plane, which can be ascribed to the reverse shock crushing of the nebula occurring first on the low-latitude side, as the remnant ran into the gas density gradient of the Galactic plane; (iii) a flat gamma-ray spectrum over
$\sim$
1 GeV–1 TeV at a relatively advanced age, not characteristic of evolved SNRs with ages 50–100 kyr.
Validating this interpretation would ideally require identifying the pulsar of the system via its magnetospheric or nebular emission. With the assumed model parameters, this pulsar would have a spin-down luminosity of
$8\times10^{35}$
erg/s and a period of 170 ms at the assumed age of 25 kyr. Yet, the pulsar may have moved away from the system as a result of its natal kick, although that involves relatively large velocities (about 1 200 km s
$^{-1}$
to travel
$\sim$
30 pc in
$\sim$
25 kyr, which is at the high end of the natal kick velocity distribution inferred in Verbunt, Igoshev, & Cator Reference Verbunt, Igoshev and Cator2017). Also, such large pulsar velocities would create an observable radio trail as in several other known systems (Pavan et al. Reference Pavan2014; Alsaberi et al. Reference Alsaberi2019; Lazarević et al. Reference Lazarević2024a). There are five pulsars in the ATNF pulsar catalogue (version 2.0.0) within 2
$^\circ$
of the remnant’s centre, and all of them have characteristic ages above 100 kyr, and spin-down powers of the order of
$10^{34}$
erg s
$^{-1}$
at most (for PSR J0954–5430). This would tend to disfavour the relic PWN interpretation, although one cannot exclude that the required pulsar evaded detection because of unfavourable beaming, or that the emission from the (possibly bow-shock) wind nebula is out of reach of the currently available observations. A close inspection of the eROSITA observations of the remnant and its outskirts is warranted to establish if this scenario deserves further consideration.
5. Conclusion
We present new high-resolution and sensitive radio-continuum images of the Diprotodon Galactic SNR G278.94+1.35. Our ASKAP 943 MHz image at the resolution of 15
$^{\prime\prime}\times15^{\prime\prime}$
(RMS of 25
$\mu$
Jy beam
$^{-1}$
) shows an object with an unusually large angular extent of
$\sim 3{{{{.\!^\circ}}}}3$
across. We suggest that Diprotodon is at
$\sim$
1 kpc distance and in the radiative phase of evolution. Coupled with a somewhat unexpected hard Fermi-LAT gamma-ray spectrum, this extensive (
$\sim$
D = 57 pc) object challenges our theoretical predictions about the SNR evolution.
Acknowledgement
This scientific work uses data obtained from Inyarrimanha Ilgari Bundara/the Murchison Radio-astronomy Observatory. We acknowledge the Wajarri Yamaji People as the Traditional Owners and native title holders of the Observatory site. CSIRO’s ASKAP radio telescope is part of the Australia Telescope National Facility (ATNF).Footnote j
This work is based (in part) on observations made with the Spitzer Space Telescope, which was operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA.
Funding statements
Operation of ASKAP is funded by the Australian Government with support from the National Collaborative Research Infrastructure Strategy. ASKAP uses the resources of the Pawsey Supercomputing Research Centre. Establishment of ASKAP, Inyarrimanha Ilgari Bundara, the CSIRO Murchison Radio-astronomy Observatory and the Pawsey Supercomputing Research Centre are initiatives of the Australian Government, with support from the Government of Western Australia and the Science and Industry Endowment Fund.
MDF, GR, and SL acknowledge Australian Research Council (ARC) funding through grant DP200100784. N.H.-W. is the recipient of ARC Future Fellowship project number FT190100231. SD is the recipient of an ARC Discovery Early Career Award (DE210101738) funded by the Australian Government. HS acknowledges funding from JSPS KAKENHI Grant Number 21H01136. DU and BA acknowledge the financial support provided by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia through the contract 451-03-66/2024-03/200104 and for support through the joint project of the Serbian Academy of Sciences and Arts and Bulgarian Academy of Sciences ‘Optical search for Galactic and extragalactic supernova remnants’. BA additionally acknowledges the funding provided by the Science Fund of the Republic of Serbia through project #7337 ‘Modeling Binary Systems That End in Stellar Mergers and Give Rise to Gravitational Waves’ (MOBY). MA acknowledges support from Universidad de Costa Rica under grant B8267. RB acknowledges funding from the Irish Research Council under the Government of Ireland Postdoctoral Fellowship programme. JM acknowledges support from a Royal Society-Science Foundation Ireland University Research Fellowship (20/RS-URF-R/3712). CBS acknowledges support from a Royal Society Research Fellows Enhancement Award 2021 (22/RS-EA/3810). SL and BV were supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (MSTDIRS) through contract no. 451-03-66/2024-03/200002 made with Astronomical Observatory (Belgrade). PM acknowledges financial support by ANR through the GAMALO project under reference ANR-19-CE31-0014. We thank an anonymous referee for comments and suggestions that greatly improved our paper.
Data availability statement
The data that support the plots/images within this paper and other findings of this study are available from the corresponding author upon reasonable request. The ASKAP data used in this article are available through the CSIRO ASKAP Science Data Archive (CASDA).Footnote k This scientific work uses data obtained from Inyarrimanha Ilgari Bundara/the Murchison Radio-astronomy Observatory.
Appendix A. Naming G278.94+1.35 as Diprotodon
Diprotodon is an extinct genus of Australian marsupial from the Pleistocene period, resembling a giant wombat (see Fig. A1). We adopt this name for G278.94+1.35 to raise awareness of this extinct Australian animal and all of Australia’s prehistorical megafauna, as well as to raise awareness of the current extinction rate of several other species in Australia. As G278.94+1.35 is potentially among the largest SNRs, it is fitting to liken it to this largest of wombats, Diprotodon.
The sole Diprotodon species, D. optatum, was the largest known marsupial, weighing up to 3 500 kg and as long as 3.4 and 2 m tall. It became extinct at the end of the continent-wide extinction of megafauna approximately 46 000 yr ago (Roberts et al. Reference Roberts2001). The first fossils were discovered in Adnyamathanha Country in the Flinders Ranges of South Australia, and more recently, archaeologists have found a bone of a juvenile Diprotodon in a dateable Aboriginal deposit inside a rock shelter in the Flinders Ranges. The shelter was unsuitable for access by a live Diprotodon, and the dating was 46 000–49 000 yr ago (Hamm et al. Reference Hamm2016). It is believed that Aboriginal people co-existed with Diprotodon for up to 20 000 yr. Unfortunately, there is no accepted record in Aboriginal rock art clearly showing a Diprotodon (Bednarik Reference Bednarik2013). Coincidentally (or not), the Adnyamathanha people have a story about a ‘Yamuti’, which was dangerous for children, and if they saw one, they were to climb high on the nearest tree as the Yamuti couldn’t climb (Koolmatrie Reference Koolmatrie2020). Diprotodon, an herbivore, wasn’t a predator; but they also couldn’t climb trees. We now know that Aboriginal stories aren’t just myths but have been shown to be accurate for at least 14 000 yr (Hamacher et al. Reference Hamacher2023), so this story could describe living alongside Diprotodon. Perhaps Aboriginal people and Diprotodon alike witnessed the supernova in the night sky which produced SNR G278.94+1.35.
Figure A1. A Diprotodon. Credit: Anne Musser.
Open access
