INTRODUCTION
Assessing the risk of extinction is important to determine which species are most prone to extinction and may be in need of human intervention. The International Union for Conservation of Nature (IUCN) has defined categories assessing species threat status on the basis of their risk of extinction. Classifications largely rely on quantitative information, but in practice expert opinion plays a strong role. Many different methods have been used to assess extinction risk, including population models (McCarthy et al. Reference McCarthy, Keith, Tietjen, Burgman, Maunder, Master, Brook, Mace, Possingham, Medellin, Andelman, Regan, Regan and Ruckelshaus2004), species-area correlations (Grelle Reference Grelle2005) and genetic analyses (Dunham et al. Reference Dunham, Peacock, Tracy, Nielsen and Vinyard1999). Obtaining the type of data needed to assess extinction risk can be problematic. For example, the assessment of population size and changes in population size can be difficult, particularly when assessing small populations whose individuals are not easily located. Genetic data, which may provide information about the degree of inbreeding and gene flow among populations, is costly, especially if multiple species are to be assessed, and may also be hard to obtain from small populations. However, data on simple ecological or life history characteristics can be obtained using less extensive population monitoring, or from existing knowledge of the natural history of species. In this paper, we assess the potential of such data to provide an alternative and reliable measure of extinction risk.
Among the studies that use ecological characteristics to assess extinction risk, several different types of analyses have been used, including multiple regression (Purvis et al. Reference Purvis, Gittleman, Cowlishaw and Mace2000; Krüger & Radford Reference Krüger and Radford2008), regression tree analysis (Boyer Reference Boyer2008; Davidson et al. Reference Davidson, Hamilton, Boyer, Brown and Ceballos2009; Boyer Reference Boyer2010), logistic regression (Mattila et al. Reference Mattila, Kaitala, Komonen, Kotiaho and Paivinen2006, Reference Mattila, Kotiaho, Kaitala and Komonen2008; Franzen & Johannesson Reference Franzen and Johannesson2007) and risk ranking (Kotiaho et al. Reference Kotiaho, Kaitala, Komonen and Paivinen2005). Several of these studies used multiple tests to assess extinction risk, often initially analysing single ecological or life history characters as predictor variables, followed by one of the single type of statistical tests mentioned above to analyse the complete data set. Bielby et al. (Reference Bielby, Cardillo, Cooper and Purvis2010) compared decision trees and phylogenetic comparative methods. Here we compare three statistical approaches: regression tree analysis, logistic regression and discriminant function analysis. We selected these three statistical methods primarily because they are commonly found in pre-packaged statistical software programs and thus would be easier for conservation managers to access and use than more complicated programs that require writing and editing code. Our aim was to determine if one or a combination of these statistical methods could be used to predict the threat category, threatened or non-threatened, of as yet unclassified species. Such an analysis may determine whether there are unclassified species that merit immediate attention. Reclassification of a formerly non-threatened species to a threatened status is also a possible outcome, and may indicate that a species is in more immediate need of conservation management measures. The specific situation we envision is one in which most species within a particular taxon have been classified as threatened or non-threatened. If it can be shown that this classification is well predicted by one or more of the three statistical approaches using general ecological and life history characters (hereafter, for simplicity, LH characters) then unclassified species of the same taxon that share characteristics with threatened species can be identified to help prioritize further assessments of threat status.
We assess this approach using data on Finnish lepidopterans previously analysed by Komonen et al. (Reference Komonen, Grapputo, Kaitala, Kotiaho and Paivinen2004), Kotiaho et al. (Reference Kotiaho, Kaitala, Komonen and Paivinen2005) and Mattila et al. (Reference Mattila, Kaitala, Komonen, Kotiaho and Paivinen2006, Reference Mattila, Kotiaho, Kaitala and Komonen2008). Komonen et al. (Reference Komonen, Grapputo, Kaitala, Kotiaho and Paivinen2004) used analysis of variance and linear regressions on subsets of LH characters to assess butterfly mobility, but did not relate this to IUCN threat status. Mattila et al. (Reference Mattila, Kaitala, Komonen, Kotiaho and Paivinen2006, Reference Mattila, Kotiaho, Kaitala and Komonen2008) used similar analyses, running logistic regressions of IUCN threat status on single LH characteristics and then using multiple LH characteristics in a multinomial logistic regression to determine the ability to classify species into their correct IUCN threat status. Kotiaho et al. (Reference Kotiaho, Kaitala, Komonen and Paivinen2005) primarily used t-tests and logistic regressions with single LH characteristics to compare differences between threatened and non-threatened species. The four LH characteristics (dispersal ability, larval specificity, adult habitat breadth and length of flight period) that they found to be significantly related to IUCN threat status were used to create an ecological risk ranking of all the species by ranking the species according to each LH characteristic and then summing the four rankings. This summed ranking was used in a logistic regression and compared to the actual IUCN threat status of the species.
In the present analysis, we address the question of whether the LH characteristics of a species may be used directly en masse to predict the probability of unclassified species being threatened or non-threatened, and identify non-threatened species that may need reclassification of their threat status.
METHODS
Regression and classification trees
Roff and Roff (Reference Roff and Roff2003) initially suggested regression tree analysis to determine factors contributing to the risk of extinction. Several studies have since used a regression tree analysis to assess extinction probability (Jones et al. Reference Jones, Fielding and Sullivan2006; Boyer Reference Boyer2008, Reference Boyer2010; Davidson et al. Reference Davidson, Hamilton, Boyer, Brown and Ceballos2009). In our case study the predicted category consisted of two states, ‘threatened’ ( = 1) and ‘non-threatened’ ( = 0), and thus regression and classification trees were identical. In principal, classification trees could be used to identify each different IUCN category. We restricted the analysis to the two states and used the regression tree approach, owing to insufficient data.
Logistic regression
Our aim was to determine the accuracy of models created using logistic regression at predicting the correct assignment of a species as threatened or non-threatened based on LH characteristics. As done with the regression trees, species in the non-threatened category were coded as 0 and those in the threatened category as 1. To use the model as a mechanism for placement of a species into the threatened or non-threatened category, we required a threshold for the fitted value, for example 0.5, above which species were placed into the threated category and below which they were placed into the non-threatened category. Alternatively, we could have selected two thresholds, such as 0.25 and 0.75, and placed species below the lower threshold in the non-threatened category and species above the upper threshold in the threatened category, classifying species lying between the two thresholds as ‘uncertain.’ We explored the consequences of both approaches.
An important point to note in this method of analysis is that, whereas the stopping point for the stepwise regression is defined by a metric such as the Akaike information criterion (AIC), the adequacy of the model in the present context was measured by the assignment to the two categories: because of this, it was possible for the ‘best’ model to contain more or fewer variables than that specified by the ‘best’ stepwise logistic model.
Discriminant function analysis
There are several covariance structures that can be identified when performing a discriminant function analysis: homoscedastic, spherical, proportional, group spherical, equal correlation and heteroscedastic. Principal components can also be specified for analysis in a discriminant function analysis. In the analyses here, to compare statistical tests, we used the covariance structure that correctly assigned the most threatened species based on LH characteristics.
Determining the probability of correct assignment by chance alone
An important consideration is the probability of assigning a species to the correct category, threatened or non-threatened, by chance alone. To determine this we used a simulation model (coding in R given in Appendix 1, see supplementary material at Journals.cambridge.org/ENC). First, we generated a vector, V, of length N, where N was the total number of species in the sample with ones in the first n 1 rows and zeros in the remaining N – n 1 rows, the former being the number of threatened species and the latter the number non-threatened species. These zeros and ones were rearranged at random in the vector. The number of correct assignments in the threatened category, N 1, was given by
N_1 = \sum\limits_{i = 1}^{n_1 } {V_i } ,
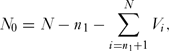N_0 = N - n_1 - \sum\limits_{i = n_1 + 1}^N {V_i } ,
Determining the preferred method
As indicated below, regression tree analysis was not satisfactory for either of the two data sets (butterflies or moths) and, therefore, our further analysis focused upon logistic regression versus discrimination function analysis. We compared the ability of these two methods to correctly classify species into the threatened or non-threatened category with a χ2 analysis. Of particular interest were those species which were incorrectly classified according to one or both methods: we plotted the predicted values from the logistic regression against the predicted values from the discriminant function analysis to see whether the species that were classified differently fell near the 0.5 cutoff. It is safer to classify non-threatened species as threatened than it is to classify threatened species as non-threatened, because in the former case a species will receive attention, but in the latter case a threatened species that needs attention will be overlooked. Therefore, we used the number of correctly classified threatened species in a final comparison of methods to determine which method was to be preferred, at least for the data sets assessed here.
Data sets
The Kotiaho et al. (Reference Kotiaho, Kaitala, Komonen and Paivinen2005) butterfly data set consisted of 94 species and 13 predictor variables: family, genus, species, abundance, distribution, distribution change, resource distribution, extent of range, larval specificity, female size, length of flight period, mobility and habitat breadth (see Komonen et al. Reference Komonen, Grapputo, Kaitala, Kotiaho and Paivinen2004 and Kotiaho et al. Reference Kotiaho, Kaitala, Komonen and Paivinen2005 for variable definitions). Because the primary criterion for listing these species according to IUCN threat status is a function of three ‘distribution’ variables (distribution, distribution change, and extent of range), we included these variables as predictor variables to assess whether any of the other variables were better at predicting IUCN threat status. After initial analysis, these distribution variables were excluded from subsequent analyses to determine whether any more easily accessible variables (such as those obtainable from published natural history descriptions) could be used to predict threat status. One species, Glaucopsyche alexis, was listed using only abundance as the criterion, and so this species was not used in the analyses. Thirteen other species were excluded due to missing data. The analysed data consisted of 18 threatened and 62 non-threatened species. The rest of the variables, excluding resource distribution due to lack of data, were used to predict IUCN threat status as given in the 2000 Finnish Red List (Rassi et al. Reference Rassi, Alanen, Kanerva and Mannerkoski2001). One of the principal aims of the analysis was to investigate the ability of variables that are readily available from published data on the natural history of a species to determine threat status. Therefore, we ran the analyses with and without the variable ‘abundance,’ which might typically be difficult to estimate and, in many cases, unavailable. However, due to the similarity of the results, only the analyses excluding abundance are reported here (Appendix 2 provides a table of the analyses including abundance, see supplementary material at Journals.cambridge.org/ENC).
Two data sets on moths were used, one on noctuids (Mattila et al. Reference Mattila, Kaitala, Komonen, Kotiaho and Paivinen2006) and one on geometrids (Mattila et al. Reference Mattila, Kotiaho, Kaitala and Komonen2008). These two data sets consisted of 284 and 306 species, respectively, and each had the same eight predictor variables: genus, species, male size, length of flight period, larval specificity, resource distribution, overwintering stage, and distribution change. After we ran the analyses with each data set, we combined them into a single data set with the added variable ‘taxonomic family’ to increase the power of the analyses and avoid issues of non-independence by using closely related species. In total, we excluded 40 species from the data sets due to missing data. The analysed data consisted of 68 threatened and 482 non-threatened species. Distribution change was the only distribution variable for these data sets and, after initial analysis, was, as before, excluded to determine which other variables may be important for predicting IUCN threat status. As previously noted, the response variable for all data sets was binomial, threatened or non-threatened. It included all species listed as near threatened or higher according to the IUCN threat status as threatened and the rest as non-threatened.
RESULTS
Among the three distribution variables used in the butterfly data set (distribution, range position, and distribution change), only distribution and range position were highly correlated (r = 0.64; Table 1). Correlations between any of the distribution variables and the other variables was highest for distribution and mobility (r = 0.74) and distribution and length of flight (r = 0.64), although these values were not high enough to cause problems with collinearity since they were < 0.90 (Tabachnick & Fidell Reference Tabachnick and Fidell2007, p. 89–90). None of the correlations among variables for the geometrid or noctuid data sets exceeded an absolute value of 0.26 and thus did not pose problems with collinearity.
Table 1 Correlations among the continuous variables used in the analyses of the butterfly data (sample size = 18 threatened species and 62 non-threatened species). *p < 0.05, **p < 0.01, ***p < 0.001; probabilities not corrected for multiple test.
We first examined the ability of the distribution variables by themselves to classify species status. After this we considered the ability of the other LH characteristics to classify species status.
Regression trees
Distribution variables only
A significant regression tree, with two nodes was obtained (p = 0.0002) using only the distribution variables from the butterfly data set. This split in the regression tree was based on distribution and correctly classified 94% of threatened species and 95% of non-threatened species. When we used the variable distribution change in a regression tree analysis on the geometrid data, the pruned regression tree was significant (p = 0.0006) and had two nodes, but all threatened species were misclassified as non-threatened. The threatened species did not have any defining range of distribution change to use to divide the data. When we used only distribution change in a regression tree analysis on the noctuid data set, the pruned regression tree was significant (p = 0.0002) and had five nodes with a misclassification rate of 11%. Using distribution change in a regression tree analysis on the combined moth data set, we found that the pruned regression tree was significant (p = 0.0002) and had four nodes, but all threatened species were misclassified, again indicating no defined range for the threatened species.
Other LH variables
Using variables from the butterfly data set not explicitly used for determining IUCN threat status (family, mobility, larval specificity, habitat breadth, female size, and flight length), a pruned tree could not be created because only one terminal node was produced during the cross-validation. Thus, in this case, regression tree analysis could not discriminate threatened from non-threatened species.
When all the variables (male size, length of flight period, larval specificity, and overwintering stage) except distribution change were used from the geometrid data set, a non-significant pruned tree with two nodes resulted (p = 0.2826), but no threatened species were correctly classified because both nodes were classified as non-threatened in the regression tree. Thus, breaking the data down into these two nodes based on length of flight period did not allow for enough subdivision of the data to correctly assign IUCN threat status. When all the variables from the noctuid data set or the combined data set (male size, length of flight period, larval specificity, and overwintering stage) except distribution change were used, a pruned tree could not be created because only one terminal node was produced during the cross-validation.
We conclude that for these data sets regression tree analysis did not result in a satisfactory prediction of threat status.
Logistic regression
Distribution variables only
Species with probabilities greater than 0.5 were classified as threatened and those below as non-threatened. A stepwise logistic regression using the distribution variables from the butterfly data set retained the variables distribution and distribution change and was able to correctly classify 94% of threatened species and 95% of non-threatened species. The logistic regression on distribution change in the geometrid data set correctly classified 7% of threatened species and 99% of non-threatened species. Using the noctuid data set or the combined data set, the logistic regression was unable to correctly classify any threatened species.
Other LH variables
We restricted the logistic regression analysis to additive models only (interactions were excluded) because the butterfly data set was limited. Incorporating all the variables except the distribution variables and abundance produced a model that correctly assigned 67% of threatened and 95% of non-threatened species when the fitted value cutoff point was 0.50 (Table 2). This cutoff point (0.5) for the fitted values produced the highest correct assignment for both threatened and non-threatened species. The alternate criterion of 0.25 as the cutoff point for the non-threatened species and anything greater than 0.75 as a cutoff point for the threatened species correctly assigned 39% of the threatened species and 79% of the non-threatened species, with 21 ambiguous species. Moth data produced a similar response to the cutoff values (results not shown), so we opted to use the 0.5 cutoff for all reported classification assignments for the logistic regressions.
Table 2 Classification of threatened and non-threatened species by logistic regression and discriminant function analysis for the butterfly data, when the distribution variables and abundance are excluded from the analysis. Regression tree analysis was excluded because a pruned tree could not be created. When multiple analyses were performed, such as when different structures were used for discriminant analysis, only the analysis with the best result is given. ‡Probability of correctly predicting by chance alone at least as many as observed by a given method.
The stepwise logistic regression on the geometrid data set using all variables except distribution change included interactions due to a larger sample size and retained all variables and their interaction terms except the four-way interaction. This regression correctly assigned 47% of the threatened species (and was able to correctly classify all but one of the non-threatened species (F 47,263 = 2.84, p < 0.001; AIC = 168.11; Table 3). The stepwise logistic regression using all the variables from the noctuid data set except distribution change retained all the variables and their interaction terms, did poorly at correctly assigning threatened species, but well at assigning non-threatened species (21% and 96% respectively; F 61,244 < 0.001, p = 1; AIC = 2887.41; Table 3). The stepwise logistic regression on all variables from the combined data set except distribution change retained all the variables and their four-way interaction terms except the interaction involving family, male size, larval specificity and overwintering stage, correctly assigned one-third of threatened species (29%), and was able to correctly assign almost all the non-threatened species (96%; F 112,477 < 0.001, p = 1; AIC = 4687.5; Table 3).
Table 3 Classification of threatened and non-threatened species by regression tree analysis, logistic regression and discriminant function analysis for the moth data when distribution change was excluded from the analysis. Data for the regression tree analysis was excluded for the noctuid and combined data sets because a pruned tree could not be created.
Discriminant function analysis
Distribution variables only
Discriminant function analysis produced results that were not quite as good as the logistic regression at classifying threatened and non-threatened species (88% and 89%, respectively) using only the distribution variables from the butterfly data set. For the geometrid, noctuid and combined data sets 90%, 100% and 96% of threatened species, respectively, were correctly classified, and 52%, 46% and 53% of non-threatened species were correctly classified using just distribution change.
Other LH variables
The discriminant function analysis on the butterfly data set including all variables except the distribution variables and abundance was significant (Table 2), correctly classifying 56% of threatened species and 90% of non-threatened species. Weighting was highest for family and habitat breadth when classifying threatened species.
The discriminant function analysis for the geometrid data set including all the variables except distribution change performed best using the principal components model, and correctly classified 27% of the threatened species and 95% of the non-threatened species (Table 3). The best discriminant analysis including all the variables from the noctuid data set except distribution change used the equal correlation model and correctly assigned 88% of non-threatened species and 32% of threatened species. The best discriminant analysis on the combined data set including all variables except distribution change used the equal correlation model also, and assigned 94% of non-threatened species, but only 19% of threatened species.
Which method is best?
Logistic regression and discriminant function analysis were able to correctly classify a significant number of threatened and non-threatened species for most analyses. Using the butterfly data set, the logistic regression and the discriminant function analysis did not differ in the number of correctly classified threatened and non-threatened species (χ2 = 0.078, df = 1, p = 0.7804). However, using the combined moth data, the logistic regression and the discriminant function analysis did differ significantly in the number of correctly classified threatened and non-threatened species (χ2 = 6.416, df = 1, p = 0.0113).
Logistic regression and discriminant function analysis agreed on the classification (Table 4), rightly or wrongly, of all but two of the threatened butterfly species, with the logistic regression classifying the species ‘correctly’ according to the published IUCN red list. Interestingly, the incorrectly classified butterfly species did not cluster about the intersection of the 0.5 cutoff (vertical and horizontal lines in Fig. 1) demarking the transition from threatened to non-threatened species for each analysis (the moth data could not be plotted this way because the fitted values for the logistic regression were all 0s and 1s). The two species that were correctly classified by the logistic regression, but not the discriminant function analysis, were not notable outliers. In one case, the species lies close to the ‘decision’ boundary for the discriminant function analysis, while in the other case, the species lies close to the ‘decision’ boundary for the logistic regression. For such species the discrepancy in the analyses invites closer inspection. While the logistic regression correctly classified more species than the discriminant function analysis, the difference overall is relatively minor, and we recommend that both methods be used, with additional attention being paid to those species classified differently.
Table 4 Comparison of classifications by logistic regression and discriminant function analysis for threatened butterfly and moth species.
Figure 1 Plot of the logistic regression (LR) fitted values versus the discriminant function analysis (DFA) predicted values for the butterfly data, indicating the two methods have approximately a 1:1 relationship in their prediction of threat status.
DISCUSSION
All of the analyses on the butterfly data and most of the analyses on the moth data sets were able to correctly assign a significant number of threatened and non-threatened species. Regression tree analysis was not very helpful in classifying species in the two data sets, although previous analyses have suggested it may be a promising tool (Roff & Roff Reference Roff and Roff2003; Jones et al. Reference Jones, Fielding and Sullivan2006; Boyer Reference Boyer2008, Reference Boyer2010; Davidson et al. Reference Davidson, Hamilton, Boyer, Brown and Ceballos2009). Importantly, the approach here did not fail because it incorrectly classified species. For the present data sets, it failed because no trees could be produced. Thus, we recommend that this approach still be tried for other data sets.
There was a decrease in the percentage of correctly classified species when a stepwise logistic regression was used on the butterfly data set and on several moth regressions. As noted above, this is not unexpected, as the criterion for the best fitting model is not the same as the criterion for the stopping point in the stepwise regression. Thus, for logistic regression analysis, a second step, namely a comparison of the models predicting correct assignment is called for, which can be done using simulation (Appendix 1, see supplementary material at Journals.cambridge.org/ENC). Since we were primarily focused on the category the species fell within, and not necessarily how good individual variables were at classifying the species, a case could be made for leaving all the variables in the model, because including variables will not increase the misclassification rate. Comparing the full model and the stepwise model may then be a useful way to identify the ecological characteristics that have the strongest correlation with IUCN threat status, and which variables increase the number of correctly assigned species, even if the difference is not significant.
The overall correct classification rate can be highly misleading. For example, suppose that 90% of species were classified as non-threatened and the statistical analysis classified all species as non-threatened, then the overall correct classification rate would be 90%, which appears to be very good but is actually of little use. This issue was particularly evident in the moth data sets, and illustrates the importance of analysing the ability of the statistical analysis to classify species into each category, as done here. When methods of comparison such as these are used, classification to both categories should always be reported.
Overall, the logistic regression gave the best results based on the number of correctly predicted threatened species, followed by the discriminant function analysis. All variables can be used in these analyses, so deciding among variables is not an issue. Given the ease with which the analyses can be performed, we suggest that multiple analyses be undertaken to identify species that may not be consistently classified as threatened.
Suggested reassessments based on the current analysis
The butterfly species Boloria frigga, B. freija, and B. thore, were classified as threatened by logistic regression and discriminant function analysis, although the IUCN does not list them as threatened. These species may be at an increased risk of extinction. Kotiaho et al. (Reference Kotiaho, Kaitala, Komonen and Paivinen2005) assigned these species ecological risk rankings of 4, 11, and 15, respectively, and our results support a reassessment of their IUCN threat status. Discriminant function analysis classified Pyrgus centaureae as threatened; Kotiaho et al. (Reference Kotiaho, Kaitala, Komonen and Paivinen2005) assigned an ecological risk ranking of 8 to P. centaureae, and thus its threat status may also merit reassessment, although the first three species would be a priority.
For the moth data sets, five non-threatened species were classified as threatened by both logistic regression and discriminant function analysis. All the misclassified moth species fall in the family Noctuidae. Cucullia gnaphalii, Dryobotodes eremita and Orthosia populeti were classified as threatened when the noctuid data set was used. D. eremita, Abrostola triplasia and A. tripartita were classified as threatened when the combined data set was used. We suggest that the threat status of all these species merits re-evaluation; an IUCN threat listing would attract appropriate conservation management, thus enhancing these species’ chance for recovery.
We have shown that a variety of statistical analyses can produce useful assessments of threat status and that readily-available data on ecological and LH characteristics may be used to identify species that merit reassessment of their threat status. Extending the analyses beyond the geographical area of interest should be undertaken cautiously, as important variables may change in different locations and at different scales (Nylin & Bergstrom Reference Nylin and Bergstrom2009). In particular, if abundance is to be used as a variable, understanding its relationship to the species being assessed is essential to determine whether a positive or negative relationship to distribution can be generalized (see the following articles for a debate on positive and negative density-distribution relationships: Paivinen et al. Reference Paivinen, Grapputo, Kaitala, Komonen, Kotiaho, Saarinen and Wahlberg2005; Blackburn et al. Reference Blackburn, Cassey and Gaston2006; Blackburn & Gaston Reference Blackburn and Gaston2009; Komonen et al. Reference Komonen, Paivinen and Kotiaho2009, Reference Komonen, Paivinen and Kotiaho2011; Kotiaho et al. Reference Kotiaho, Komonen and Paivinen2009; Selonen & Helos Reference Selonen and Helos2010). These caveats notwithstanding, the present results suggest that ‘off-the-shelf’ statistical methods such as logistic regression and discriminant function analysis can be extremely valuable in determining the IUCN threat status of a species in areas where there is only limited abundance data.
CONCLUSIONS
Standard statistical analyses may be applied to ecological and life history characteristic data to produce an assessment of threat status where there is limited abundance data. Applying these methods to Finnish butterfly and moth species datasets produced results that were highly consistent with present IUCN threat listings, and identified a few additional candidates that probably deserve increased attention and monitoring. Identifying species that merit reassessment is crucial to allocating conservation management efforts appropriately.
