Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-05-06T02:23:19.738Z Has data issue: false hasContentIssue false
  • English
  • Français

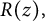Lambert series of logarithm, the derivative of Deninger’s function $R(z),$ and a mean value theorem for 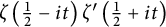$\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$

Part of: Multiplicative number theory Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  11 October 2023

Soumyarup Banerjee ,
Atul Dixit Open the ORCID record for Atul Dixit [Opens in a new window]  and
Shivajee Gupta
Soumyarup Banerjee
Affiliation:
Department of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India Current address: Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur 721302, West Bengal, India e-mail: [email protected]
Atul Dixit*
Affiliation:
Department of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India
Shivajee Gupta
Affiliation:
Department of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India e-mail: [email protected] Current address: Department of Mathematics and Statistics, Indian Institute of Science Education and Research Kolkata, Mohanpur, Nadia 741246 West Bengal, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An explicit transformation for the series 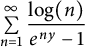$\sum \limits _{n=1}^{\infty }\displaystyle \frac {\log (n)}{e^{ny}-1}$, or equivalently, 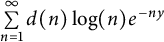$\sum \limits _{n=1}^{\infty }d(n)\log (n)e^{-ny}$ for Re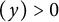$(y)>0$, which takes y to 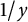$1/y$, is obtained for the first time. This series transforms into a series containing the derivative of 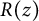$R(z)$, a function studied by Christopher Deninger while obtaining an analog of the famous Chowla–Selberg formula for real quadratic fields. In the course of obtaining the transformation, new important properties of 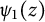$\psi _1(z)$ (the derivative of 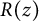$R(z)$) are needed as is a new representation for the second derivative of the two-variable Mittag-Leffler function 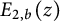$E_{2, b}(z)$ evaluated at 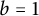$b=1$, all of which may seem quite unexpected at first glance. Our transformation readily gives the complete asymptotic expansion of 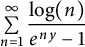$\sum \limits _{n=1}^{\infty }\displaystyle \frac {\log (n)}{e^{ny}-1}$ as 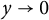$y\to 0$ which was also not known before. An application of the latter is that it gives the asymptotic expansion of 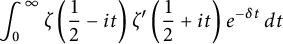$ \displaystyle \int _{0}^{\infty }\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )e^{-\delta t}\, dt$ as 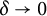$\delta \to 0$.

Keywords

Lambert seriesDeninger’s functionmean value theoremsasymptotic expansions

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$ 11N37: Asymptotic results on arithmetic functions
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 5 , October 2024 , pp. 1695 - 1730
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Dedicated to Christopher Deninger on account of his 65th birthday

Part of this work was done when the first author was a National Postdoctoral Fellow (NPDF) at IIT Gandhinagar funded by the grant PDF/2021/001224, and later, when he was an INSPIRE faculty at IISER Kolkata supported by the DST grant DST/INSPIRE/04/2021/002753. The second author’s research is funded by the Swarnajayanti Fellowship grant SB/SJF/2021-22/08. The third author is supported by CSIR SPM Fellowship under the grant number SPM-06/1031(0281)/2018-EMR-I. All of the authors sincerely thank the respective funding agencies for their support.

References

Apelblat, A., Differentiation of the Mittag-Leffler functions with respect to parameters in the Laplace transform approach . Mathematics 8(2020), 657.CrossRefGoogle Scholar
Apostol, T., Introduction to analytic number theory, Springer Science+Business Media, New York, 1976.Google Scholar
Atkinson, F. V., The mean value of the zeta-function on the critical line . Q. J. Math. (Oxford) 10(1939), 122–128.CrossRefGoogle Scholar
Banerjee, S. and Kumar, R., Explicit identities on zeta values over imaginary quadratic field. Preprint, 2021. arXiv: 2105.04141Google Scholar
Berndt, B. C., On the Hurwitz zeta function . Rocky Mountain J. Math. 2(1972), 151–157.CrossRefGoogle Scholar
Berndt, B. C., On Eisenstein series with characters and the values of Dirichlet $L$ -functions . Acta Arith. 28(1975), 299–320.CrossRefGoogle Scholar
Berndt, B. C., Modular transformations and generalizations of several formulae of Ramanujan . Rocky Mountain J. Math. 7(1977), 147–189.CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s notebooks, Part I, Springer, New York, 1985.CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s notebooks, Part II, Springer, New York, 1989.CrossRefGoogle Scholar
Berndt, B. C. and Straub, A., Ramanujan’s formula for $\zeta (2n+1])$ . In: Montgomery, H., Nikeghbali, A., and Rassias, M. (eds.), Exploring the Riemann zeta function, Springer, Cham, 2017, pp. 13–34.CrossRefGoogle Scholar
Blagouchine, I. V., A theorem for the closed-form evaluation of the first generalized Stieltjes constant at rational arguments and some related summations . J. Number Theory 148(2015), 537–592.CrossRefGoogle Scholar
Bradley, D. M., Series acceleration formulas for Dirichlet series with periodic coefficients . Ramanujan J. 6(2002), 331–346.CrossRefGoogle Scholar
Brychkov, Y. A., Marichev, O. I., and Savischenko, N. V., Handbook of Mellin transforms, Advances in Applied Mathematics, CRC Press, Boca Raton, FL, 2019.Google Scholar
Chatterjee, T. and Khurana, S. S., Shifted Euler constants and a generalization of Euler–Stieltjes constants . J. Number Theory 204(2019), 185–210.CrossRefGoogle Scholar
Coffey, M. W., Series representations for the Stieltjes constants . Rocky Mountain J. Math. 44(2014), 443–477.CrossRefGoogle Scholar
Copson, E. T., Theory of functions of a complex variable, Oxford University Press, Oxford, 1935.Google Scholar
Deninger, C., On the analogue of the formula of Chowla and Selberg for real quadratic fields . J. Reine Angew. Math. 351(1984), 171–191.Google Scholar
Dilcher, K., Generalized Euler constants for arithmetical progressions . Math. Comp. 59(1992), 259–282.CrossRefGoogle Scholar
Dilcher, K., On generalized gamma functions related to the Laurent coefficients of the Riemann zeta function . Aequationes Math. 48(1994), 55–85.CrossRefGoogle Scholar
Dixit, A. and Gupta, R., Koshliakov zeta functions I. Modular relations . Adv. Math. 393(2021), Paper no. 108093.CrossRefGoogle Scholar
Dixit, A., Gupta, R., and Kumar, R., Extended higher Herglotz functions I. Functional equations. Adv. Appl. Math. 153(2024), 102622.CrossRefGoogle Scholar
Dixit, A., Gupta, R., Kumar, R., and Maji, B., Generalized Lambert series, Raabe’s cosine transform and a two-parameter generalization of Ramanujan’s formula for $\zeta (2m+1)$ . Nagoya Math. J. 239(2020), 232–293.CrossRefGoogle Scholar
Dixit, A., Kesarwani, A., and Kumar, R., Explicit transformations of certain Lambert series . Res. Math. Sci. 9(2022), 34.CrossRefGoogle Scholar
Dixit, A. and Maji, B., Generalized Lambert series and arithmetic nature of odd zeta values , Proc. Roy. Soc. Edinburgh Sect. A 150(2020), 741–769.CrossRefGoogle Scholar
Dzhrbashyan, M. M., Integral transforms and representations of functions in the complex domain, Izdat, Nauka, Moscow, 1966, 671 pp.Google Scholar
Erdélyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F. G., Tables of integral transforms. Vol. I. Based, in part, on notes left by Harry Bateman, McGraw-Hill Book Co., Inc., New York, 1954.Google Scholar
Glaisher, J. W. L., On the product ${1}^1.{2}^2.{3}^3\dots {n}^n$ .Mess. Math. (2) VII(1877), 43–47.Google Scholar
Glaisher, J. W. L., On the constant which occurs in the formula for ${1}^1.{2}^2.{3}^3\dots {n}^n$ . Mess. Math. 24(1894), 1–16.Google Scholar
Gonek, S. M., Mean values of the Riemann zeta function and its derivatives . Invent. Math. 75(1984), 123–141.CrossRefGoogle Scholar
Gorenflo, R., Kilbas, A. A., Mainardi, F., and Rogosin, S. V., Mittag-Leffler functions, related topics and applications, Springer Monographs in Mathematics, Springer, Berlin, 2014, 443 pp.CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M., eds., Table of integrals, series, and products, 7th ed., Academic Press, San Diego, CA, 2007.Google Scholar
Gupta, A. and Maji, B., On Ramanujan’s formula for $\zeta (1/2)$ and $\zeta (2m+1)$ . J. Math. Anal. Appl. 507(2022), 125738.CrossRefGoogle Scholar
Hardy, G. H. and Littlewood, J. E., Contributions to the theory of the Riemann zeta-function and the theory of the distribution of primes . Acta Math. 41(1916), 119–196.CrossRefGoogle Scholar
Hardy, G. H. and Littlewood, J. E., On Lindelöf’s hypothesis concerning the Riemann zeta-function . Proc. R. Soc. Lond. (A) 103(1923), 403–412.Google Scholar
Ingham, A. E., Mean-value theorems in the theory of the Riemann zeta-function . Proc. Lond. Math. Soc. 27(1928), 273–300.CrossRefGoogle Scholar
Ishibashi, M., Laurent coefficients of the zeta function of an indefinite quadratic form . Acta Arith. 106(2003), 59–71.CrossRefGoogle Scholar
Ishibashi, M. and Kanemitsu, S., Dirichlet series with periodic coefficients . Res. Math. 35(1999), 70–88.CrossRefGoogle Scholar
Ivić, A., The mean values of the Riemann zeta-function on the critical line, Analytic Number Theory, Approximation Theory, and Special Functions, 3–68, Springer, New York, 2014.Google Scholar
Jahnke, E. and Emde, F., Tables of functions with formulae and curves, 4th ed., Dover Publications, New York, 1945.Google Scholar
Jones, D. S., The theory of electromagnetism, MacMillan, New York, 1964.Google Scholar
Kanemitsu, S., Tanigawa, Y., and Yoshimoto, M., Ramanujan’s formula and modular forms . In: Kanemitsu, S. and Jia, C. (eds.), Number theoretic methods (Iizuka, 2001), Developments in Mathematics, Vol. 8, Kluwer Academic Publishers, Dordrecht, 2002, pp. 159–212.CrossRefGoogle Scholar
Katayama, K., Ramanujan’s formulas for $L$ -functions . J. Math. Soc. Japan 26(1974), 234–240.CrossRefGoogle Scholar
Kinkelin, H., Ueber eine mit der Gammafunction verwandte transcendente und deren anwendung auf die integralrechnung . J. Reine Angew. Math. 57(1860), 122–138.Google Scholar
Komori, Y., Matsumoto, K., and Tsumura, H., Barnes multiple zeta-functions, Ramanujan’s formula, and relevant series involving hyperbolic functions . J. Ramanujan Math. Soc. 28(2013), 49–69.Google Scholar
Languasco, A. and Righi, L., A fast algorithm to compute the Ramanujan–Deninger gamma function and some number-theoretic applications . Math. Comp. 90(2021), 2899–2921.CrossRefGoogle Scholar
Oberhettinger, F., Tables of Mellin transforms, Springer, New York, 1974.CrossRefGoogle Scholar
Olver, F. W. J., Asymptotics and special functions, AKP Classics, reprint of the 1974 original [Academic Press, New York], CRC Press, Boca Raton, FL, 2010.Google Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F., and Clark, C. W., eds., NIST handbook of mathematical functions, Cambridge University Press, Cambridge, 2010.Google Scholar
Paris, R. B. and Kaminski, D., Asymptotics and Mellin-Barnes integrals, Encyclopedia of Mathematics and its Applications, 85, Cambridge University Press, Cambridge, 2001.CrossRefGoogle Scholar
Prudnikov, A. P., Brychkov, Y. A., and Marichev, O. I., Integrals and series. Vol. 1: Elementary functions, Gordon and Breach, New York, 1986.Google Scholar
Prudnikov, A. P., Brychkov, Y. A., and Marichev, O. I., Integrals and series, Vol. 3: More special functions, Gordon and Breach, New York, 1990.Google Scholar
Ramanujan, S., The lost notebook and other unpublished papers, Narosa, New Delhi, 1988.Google Scholar
Ramanujan, S., Notebooks (2 volumes), Tata Institute of Fundamental Research, Bombay, 1957, 2nd ed., 2012.Google Scholar
Riekstins, E., Asymptotic expansions for some type of integrals involving logarithms . Latvian Math. Yearbook 15(1974), 113–130.Google Scholar
Rogers, K., Advanced calculus, Merrill, Columbus, OH, 1976.Google Scholar
Shirasaka, S., On the Laurent coefficients of a class of Dirichlet series . Results Math. 42(2002), 128–138.CrossRefGoogle Scholar
Soundararajan, K., Moments of the Riemann zeta function . Ann. Math. 170(2009), 981–993.CrossRefGoogle Scholar
Temme, N. M., Asymptotic methods for integrals, Series in Analysis, Vol. 6, World Scientific, Singapore, 2015.Google Scholar
Titchmarsh, E. C., The theory of the Riemann zeta function, Clarendon Press, Oxford, 1986.Google Scholar
Turnage-Butterbaugh, C. L., Gaps between zeros of Dedekind zeta-functions of quadratic number fields . J. Math. Anal. Appl. 418(2014), 100–107.CrossRefGoogle Scholar
Voros, A., Spectral functions, special functions and the Selberg zeta function . Commun. Math. Phys. 110(1987), 439–465.CrossRefGoogle Scholar
Widder, D. V., Advanced calculus, Prentice-Hall, Inc., New York, 1947.Google Scholar
Wigert, S., Sur la série de Lambert et son application á la théorie des nombres . Acta Math. 41(1916), 197–218.CrossRefGoogle Scholar
Wiman, A., Uber den fundamental satz in der theorie der funcktionen ${E}_a(x)$ . Acta Math. 29(1905), 191–201.CrossRefGoogle Scholar
Wong, R. and Wyman, M., A generalization of Watson’s lemma . Canad. J. Math. 24(1972), 185–208.CrossRefGoogle Scholar