Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-20T12:47:07.353Z Has data issue: false hasContentIssue false
  • English
  • Français

A better than 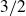$3/2$ exponent for iterated sums and products over 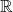$\mathbb R$

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  10 May 2024

OLIVER ROCHE–NEWTON
OLIVER ROCHE–NEWTON*
Affiliation:
Institute for Algebra, Johannes Kepler Universität, Altenberger Straβe 69, Linz 4040, Austria. e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove that the bound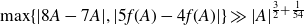

\begin{equation*}\max \{ |8A-7A|,|5f(A)-4f(A)| \} \gg |A|^{\frac{3}{2} + \frac{1}{54}}\end{equation*}
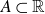holds for all $A \subset \mathbb R$, and for all convex functions f which satisfy an additional technical condition. This technical condition is satisfied by the logarithmic function, and this fact can be used to deduce a sum-product estimate
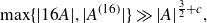\begin{equation*}\max \{ |16A|, |A^{(16)}| \} \gg |A|^{\frac{3}{2} + c},\end{equation*}
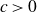for some $c\gt 0$. Previously, no sum-product estimate over 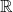$\mathbb R$ with exponent strictly greater than 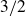$3/2$ was known for any number of variables. Moreover, the technical condition on f seems to be satisfied for most interesting cases, and we give some further applications. In particular, we show that
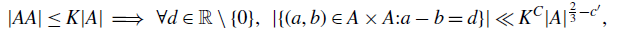\begin{equation*}|AA| \leq K|A| \implies \,\forall d \in \mathbb R \setminus \{0 \}, \,\, |\{(a,b) \in A \times A : a-b=d \}| \ll K^C |A|^{\frac{2}{3}-c^{\prime}},\end{equation*}
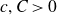where $c,C \gt 0$ are absolute constants.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11A99: None of the above, but in this section
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 177 , Issue 1 , July 2024 , pp. 11 - 22
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bourgain, J. and Chang, M.-C.. On the size of k-fold sum and product sets of integers. J. Amer. Math. Soc. 17 (2004), 473–497.CrossRefGoogle Scholar
Bradshaw, P. J.. Growth in sumsets of higher convex functions. Combinatorica 43(4) (2023), 769–789.CrossRefGoogle Scholar
Elekes, G., Nathanson, M. and Ruzsa, I.. Convexity and sumsets. J Number Theory. 83 (1999), 194–201.CrossRefGoogle Scholar
Erdős, P. and Szemerédi, E.. On sums and products of integers. In Studies in Pure Mathematics (Birkhäuser, Basel, 1983), 213–218.CrossRefGoogle Scholar
Hanson, B., Roche–Newton, O. and Rudnev, M.. Higher convexity and iterated sum sets. Combinatorica 42(1) (2022), 71–85.CrossRefGoogle Scholar
Hanson, B., Roche–Newton, O. and Senger, S.. Convexity, superquadratic growth, and dot products. J. London Math. Soc. 107(5) (2023), 1900–1923.CrossRefGoogle Scholar
Roche–Newton, O. and Zhelezov, D.. Convexity, elementary methods, and distances. To appear in Discrete Comput. Geom. Google Scholar
Rudnev, M. and Stevens, S.. An update on the sum-product problem. Math. Proc. Camb. Phil. Soc. 173(2) (2022), 411–430.CrossRefGoogle Scholar
Ruzsa, I. Z., Shakan, G., Solymosi, J. and Szemerédi, E.. On distinct consecutive differences. Combinatorial and additive number theory IV (Springer Proc. Math. Stat., 347, Springer, Cham, 2021), 425–434.CrossRefGoogle Scholar
Zhelezov, D. and Pálvőlgyi, D.. Query complexity and the polynomial Freiman–Ruzsa conjecture. Adv. Math. 392 (2021), 402–408.CrossRefGoogle Scholar