No CrossRef data available.
Article contents
A SUFFICIENT CONDITION FOR PANCYCLIC GRAPHS
Published online by Cambridge University Press: 20 December 2024
Abstract
A graph G is called an 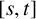 $[s,t]$-graph if any induced subgraph of G of order s has size at least
$[s,t]$-graph if any induced subgraph of G of order s has size at least 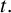 $t.$ We prove that every
$t.$ We prove that every 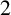 $2$-connected
$2$-connected 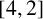 $[4,2]$-graph of order at least
$[4,2]$-graph of order at least 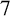 $7$ is pancyclic. This strengthens existing results. There are
$7$ is pancyclic. This strengthens existing results. There are 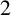 $2$-connected
$2$-connected  $[4,2]$-graphs which do not satisfy the Chvátal–Erdős condition on Hamiltonicity. We also determine the triangle-free graphs among
$[4,2]$-graphs which do not satisfy the Chvátal–Erdős condition on Hamiltonicity. We also determine the triangle-free graphs among 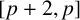 $[p+2,p]$-graphs for a general
$[p+2,p]$-graphs for a general 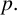 $p.$
$p.$
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by the NSFC grant 12271170 and Science and Technology Commission of Shanghai Municipality grant 22DZ2229014.



