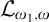1 Introduction
It is well-known that many properties of structures are not expressible in elementary first-order logic, even by a theory rather than a single sentence. Common examples are the property (of graphs) of being connected, the property (of abelian groups) of being torsion, and the property (of linear orders) of being well-founded. To capture such properties, one can pass to extensions of elementary first-order logic. This paper is about a characterization of the common expressive power of two such extensions.
The first extension of elementary first-order logic that we consider allows countably infinite conjunctions and disjunctions; this is, morally, similar to allowing quantifiers over the (standard) natural numbers. One can then express properties such as being torsion by saying “for each group element x, there is an n such that
![]() $nx = 0$
,” or formally,
$nx = 0$
,” or formally,

This infinitary logic is known as
![]() ${\mathcal {L}}_{\omega _1, \omega }$
. One loses compactness, but gains other powerful tools. For example, every countable structure is characterized, up to isomorphism among countable structures, by a sentence of
${\mathcal {L}}_{\omega _1, \omega }$
. One loses compactness, but gains other powerful tools. For example, every countable structure is characterized, up to isomorphism among countable structures, by a sentence of
![]() ${\mathcal {L}}_{\omega _1, \omega }$
[Reference Scott11].
${\mathcal {L}}_{\omega _1, \omega }$
[Reference Scott11].
The second extension of elementary first-order logic allows existential second-order quantifiers. For example, the property of a linear order being non-well-founded can be expressed by the sentence “there is a set with no least element.” We work with existential second-order quantifiers using the framework of pseudo-elementary classes (and so replace existential second-order quantifiers with expansions of the language). More formally, we say that a class
![]() $\mathbb {K}$
of
$\mathbb {K}$
of
![]() $\tau $
-structures is pseudo-elementary (
$\tau $
-structures is pseudo-elementary (
![]() $\operatorname {\mathrm {PC}}_{\Delta }$
) if there is an expanded language
$\operatorname {\mathrm {PC}}_{\Delta }$
) if there is an expanded language
![]() $\tau ^* \supseteq \tau $
and a
$\tau ^* \supseteq \tau $
and a
![]() $\tau ^*$
-theory T such that
$\tau ^*$
-theory T such that
![]() $\mathbb {K}$
consists exactly of the
$\mathbb {K}$
consists exactly of the
![]() $\tau $
-structures admitting an
$\tau $
-structures admitting an
![]() $\tau ^*$
-expansion to a model of T. We will describe both of these extensions of first-order logic in more detail later.
$\tau ^*$
-expansion to a model of T. We will describe both of these extensions of first-order logic in more detail later.
These two extensions of elementary first-order logic have different expressive powers. For example, the class of non-well-founded linear orders is pseudo-elementary but not
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable. Also, the compliment of a pseudo-elementary class is not necessarily pseudo-elementary, but the compliment of an
${\mathcal {L}}_{\omega _1, \omega }$
-definable. Also, the compliment of a pseudo-elementary class is not necessarily pseudo-elementary, but the compliment of an
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable class is again
${\mathcal {L}}_{\omega _1, \omega }$
-definable class is again
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable (by the negation of the original defining sentence). Nevertheless, there are classes that are not elementary first-order axiomatizable, but that are both pseudo-elementary and
${\mathcal {L}}_{\omega _1, \omega }$
-definable (by the negation of the original defining sentence). Nevertheless, there are classes that are not elementary first-order axiomatizable, but that are both pseudo-elementary and
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable. The class of disconnected graphs is such an example; we provide a more detailed discussion of various examples in Section 2.3. The main result of this paper is a complete classification of such properties.
${\mathcal {L}}_{\omega _1, \omega }$
-definable. The class of disconnected graphs is such an example; we provide a more detailed discussion of various examples in Section 2.3. The main result of this paper is a complete classification of such properties.
Theorem 1.1. Let
![]() $\mathbb {K}$
be a class of structures closed under isomorphism. The following are equivalent
$\mathbb {K}$
be a class of structures closed under isomorphism. The following are equivalent
![]() $:$
$:$
1.
 $\mathbb {K}$
is both a pseudo-elementary (
$\mathbb {K}$
is both a pseudo-elementary (
 $\operatorname {\mathrm {PC}}_{\Delta }$
) class and defined by an
$\operatorname {\mathrm {PC}}_{\Delta }$
) class and defined by an
 ${\mathcal {L}}_{\omega _1, \omega }$
-sentence.
${\mathcal {L}}_{\omega _1, \omega }$
-sentence.2.
 $\mathbb {K}$
is defined by a
$\mathbb {K}$
is defined by a
 -sentence.
-sentence.
There is some notation in this theorem that we must explain. The
-sentences in the theorem are the
![]() ${\mathcal {L}}_{\omega _1, \omega }$
sentences which (in normal form) involve infinitary conjunctions, but no infinitary disjunctions (see Definition 2.4). For example, the property of being infinite is definable by the
${\mathcal {L}}_{\omega _1, \omega }$
sentences which (in normal form) involve infinitary conjunctions, but no infinitary disjunctions (see Definition 2.4). For example, the property of being infinite is definable by the
-sentence

The negation, the property of being finite, is
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable by the sentence
${\mathcal {L}}_{\omega _1, \omega }$
-definable by the sentence

but this sentence is not a
-sentence because it involves an infinitary disjunct. Although
-formulas cannot have infinite disjunctions, they can have finite disjunctions.
The proof of (1)
![]() $\Rightarrow $
(2) uses an argument inspired by the proof of Craig Interpolation for
$\Rightarrow $
(2) uses an argument inspired by the proof of Craig Interpolation for
![]() ${\mathcal {L}}_{\omega _1, \omega }$
. This was originally proved by Lopez-Escobar [Reference Lopez-Escobar7] who also gave the following corollary: a class which is both pseudo-elementary and co-pseudo-elementary with respect to
${\mathcal {L}}_{\omega _1, \omega }$
. This was originally proved by Lopez-Escobar [Reference Lopez-Escobar7] who also gave the following corollary: a class which is both pseudo-elementary and co-pseudo-elementary with respect to
![]() ${\mathcal {L}}_{\omega _1, \omega }$
(i.e., both
${\mathcal {L}}_{\omega _1, \omega }$
(i.e., both
![]() $\mathbf {\Sigma }^1_1$
and
$\mathbf {\Sigma }^1_1$
and
![]() $\mathbf {\Pi }^1_1$
) is actually
$\mathbf {\Pi }^1_1$
) is actually
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable.
${\mathcal {L}}_{\omega _1, \omega }$
-definable.
In the direction (2)
![]() $\Rightarrow $
(1), there are several possible proofs. We give the simplest and shortest argument in Section 4. A second proof is to note that any
$\Rightarrow $
(1), there are several possible proofs. We give the simplest and shortest argument in Section 4. A second proof is to note that any
![]() -sentence is equivalent to a closed game formula, and classes defined by such formulas are known to be
-sentence is equivalent to a closed game formula, and classes defined by such formulas are known to be
![]() $\operatorname {\mathrm {PC}}_\Delta $
[Reference Barwise2, Reference Kolaitis6]. We describe this in Section 5. A third proof, for which we do not give the details, proceeds by coding computable formulas in models of weak arithmetic. This is an approach that was taken by Craig and Vaught [Reference Craig and Vaught3] to prove:
$\operatorname {\mathrm {PC}}_\Delta $
[Reference Barwise2, Reference Kolaitis6]. We describe this in Section 5. A third proof, for which we do not give the details, proceeds by coding computable formulas in models of weak arithmetic. This is an approach that was taken by Craig and Vaught [Reference Craig and Vaught3] to prove:
Theorem 1.2 (Craig and Vaught [Reference Craig and Vaught3])
Every computably axiomatizable class in a finite language is a basic pseudo-elementary class (
![]() $\operatorname {\mathrm {PC}}'$
).
$\operatorname {\mathrm {PC}}'$
).
By a basic pseudo-elementary class, we mean the class of reducts of a basic elementary class (one defined by a single sentence) in an expanded language. (See Definition 2.9 for the precise definition of
![]() $\operatorname {\mathrm {PC}}'$
.) The latter two proofs of our main Theorem 1.1 give a strengthening of this result of Craig and Vaught.
$\operatorname {\mathrm {PC}}'$
.) The latter two proofs of our main Theorem 1.1 give a strengthening of this result of Craig and Vaught.
Theorem 1.3. Let
![]() $\mathbb {K}$
be a class of structures in a finite language that is axiomatized by a computable
$\mathbb {K}$
be a class of structures in a finite language that is axiomatized by a computable
![]() -sentence. Then
-sentence. Then
![]() $\mathbb {K}$
is a basic pseudo-elementary class (
$\mathbb {K}$
is a basic pseudo-elementary class (
![]() $\operatorname {\mathrm {PC}}'$
).
$\operatorname {\mathrm {PC}}'$
).
Unfortunately, we do not know how to reverse Theorem 1.3. We conjecture:
Conjecture 1.4. A
![]() $\operatorname {\mathrm {PC}}'$
class which is also
$\operatorname {\mathrm {PC}}'$
class which is also
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-axiomatizable is axiomatizable by a computable
${\mathcal {L}}_{\omega _1, \omega }$
-axiomatizable is axiomatizable by a computable
![]() -sentence.
-sentence.
The argument in Section 4 for (2)
![]() $\Rightarrow $
(1) of Theorem 1.1 goes through for
$\Rightarrow $
(1) of Theorem 1.1 goes through for
![]() -sentences of
-sentences of
![]() ${\mathcal {L}}_{\kappa , \omega }$
for any
${\mathcal {L}}_{\kappa , \omega }$
for any
![]() $\kappa $
. However, we do not know if (1)
$\kappa $
. However, we do not know if (1)
![]() $\Rightarrow $
(2) holds for
$\Rightarrow $
(2) holds for
![]() ${\mathcal {L}}_{\kappa , \omega }$
for
${\mathcal {L}}_{\kappa , \omega }$
for
![]() $\kappa> \omega _1$
.
$\kappa> \omega _1$
.
Question 1.5. For
![]() $\kappa> \omega _1$
, is every
$\kappa> \omega _1$
, is every
![]() $\operatorname {\mathrm {PC}}_\Delta $
class defined by an
$\operatorname {\mathrm {PC}}_\Delta $
class defined by an
![]() ${\mathcal {L}}_{\kappa , \omega }$
sentence actually defined by a
${\mathcal {L}}_{\kappa , \omega }$
sentence actually defined by a
![]() -sentence?
-sentence?
We note that interpolation fails in
![]() ${\mathcal {L}}_{\omega _2,\omega }$
[Reference Malitz9, Theorem 4.2]. Intriguingly, Malitz goes on to give a proof system for
${\mathcal {L}}_{\omega _2,\omega }$
[Reference Malitz9, Theorem 4.2]. Intriguingly, Malitz goes on to give a proof system for
![]() ${\mathcal {L}}_{\kappa , \omega }$
that goes through
${\mathcal {L}}_{\kappa , \omega }$
that goes through
![]() ${\mathcal {L}}_{(2^{<\kappa })^+, \kappa }$
that gives rise to an interpolation theorem [Reference Malitz9, Section 5]. Shelah [Reference Shelah12] uses this to define a logic
${\mathcal {L}}_{(2^{<\kappa })^+, \kappa }$
that gives rise to an interpolation theorem [Reference Malitz9, Section 5]. Shelah [Reference Shelah12] uses this to define a logic
![]() ${\mathcal {L}}^1_\kappa $
that is intermediate between
${\mathcal {L}}^1_\kappa $
that is intermediate between
![]() ${\mathcal {L}}_{\kappa , \omega }$
and
${\mathcal {L}}_{\kappa , \omega }$
and
![]() ${\mathcal {L}}_{\kappa , \kappa }$
that has interpolation and other nice properties (when
${\mathcal {L}}_{\kappa , \kappa }$
that has interpolation and other nice properties (when
![]() $\kappa = \beth _\kappa $
). This suggests the right answer to Question 1.5 goes through
$\kappa = \beth _\kappa $
). This suggests the right answer to Question 1.5 goes through
![]() ${\mathcal {L}}^1_\kappa $
instead of
${\mathcal {L}}^1_\kappa $
instead of
![]() ${\mathcal {L}}_{\kappa , \omega }$
. However, this logic lacks any syntax in the normal sense (formulas are defined by the existence of winning strategies in a delayed Ehrenfeucht–Fraisse game), which causes additional problems, e.g., it is not clear what a
${\mathcal {L}}_{\kappa , \omega }$
. However, this logic lacks any syntax in the normal sense (formulas are defined by the existence of winning strategies in a delayed Ehrenfeucht–Fraisse game), which causes additional problems, e.g., it is not clear what a
![]() -sentence should mean, or what Skolem functions should look like.
-sentence should mean, or what Skolem functions should look like.
2 Notation and definitions
2.1 Infinitary logic
For the most part, we follow Marker’s new book [Reference Marker10]. Elementary first-order logic has a number of properties which, while useful, make it hard to completely characterize structures. For example, the Ryll–Nardzewski theorem says that any countably categorical structure is relatively simple: for each n, there are only finitely many automorphism orbits of n-types. The infinitary logic
![]() ${\mathcal {L}}_{\omega _1, \omega }$
adds more expressive power and hence allows us to characterize every countable structure up to isomorphism among countable structures [Reference Scott11].
${\mathcal {L}}_{\omega _1, \omega }$
adds more expressive power and hence allows us to characterize every countable structure up to isomorphism among countable structures [Reference Scott11].
The infinitary logic
![]() ${\mathcal {L}}_{\omega _1, \omega }$
is defined recursively in the same way as finitary first-order logic, except that for
${\mathcal {L}}_{\omega _1, \omega }$
is defined recursively in the same way as finitary first-order logic, except that for
![]() ${\mathcal {L}}_{\omega _1, \omega }$
we can take countable conjunctions and disjunctions. Throughout the paper, let
${\mathcal {L}}_{\omega _1, \omega }$
we can take countable conjunctions and disjunctions. Throughout the paper, let
![]() $\tau $
be a countable language.
$\tau $
be a countable language.
Definition 2.1. The
![]() ${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formulas are defined inductively as follows:
${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formulas are defined inductively as follows:
1. Every atomic
 $\tau $
-formula is an
$\tau $
-formula is an
 ${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formula.
${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formula.2. If
 $\varphi $
is an
$\varphi $
is an
 ${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formula, then so are
${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formula, then so are
 $\neg \varphi $
,
$\neg \varphi $
,
 $(\exists x) \varphi ,$
and
$(\exists x) \varphi ,$
and
 $(\forall x) \varphi $
.
$(\forall x) \varphi $
.3. If
 $(\varphi _i)_{i \in \omega }$
are
$(\varphi _i)_{i \in \omega }$
are
 ${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formulas with finitely many free variables, then so are
${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-formulas with finitely many free variables, then so are
 and
and
 .
.
In general, we will drop the reference to
![]() $\tau $
when it is clear what we mean.
$\tau $
when it is clear what we mean.
Definition 2.2. An
![]() ${\mathcal {L}}_{\omega _1, \omega }$
formula is in
${\mathcal {L}}_{\omega _1, \omega }$
formula is in
![]() ${\mathcal {L}}_{\omega _1, \omega }$
normal form if the
${\mathcal {L}}_{\omega _1, \omega }$
normal form if the
![]() $\neg $
only occurs applied to atomic formulas.
$\neg $
only occurs applied to atomic formulas.
Every
![]() ${\mathcal {L}}_{\omega _1, \omega }$
can be placed into a normal form. The negation
${\mathcal {L}}_{\omega _1, \omega }$
can be placed into a normal form. The negation
![]() $\neg \varphi $
of a sentence
$\neg \varphi $
of a sentence
![]() $\varphi $
in normal form is not immediately in normal form itself; this gives rise to the formal negation
$\varphi $
in normal form is not immediately in normal form itself; this gives rise to the formal negation
![]() $\mathord {\sim } \varphi $
, which is logically equivalent to
$\mathord {\sim } \varphi $
, which is logically equivalent to
![]() $\neg \varphi $
but is in normal form.
$\neg \varphi $
but is in normal form.
Definition 2.3. For any
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-formula
${\mathcal {L}}_{\omega _1, \omega }$
-formula
![]() $\varphi $
, the formula
$\varphi $
, the formula
![]() $\mathord {\sim } \varphi $
is defined inductively as follows:
$\mathord {\sim } \varphi $
is defined inductively as follows:
1. If
 $\varphi $
is atomic,
$\varphi $
is atomic,
 $\mathord {\sim } \varphi $
is
$\mathord {\sim } \varphi $
is
 $\neg \varphi $
.
$\neg \varphi $
.2.
 $\mathord {\sim } \neg \varphi $
is
$\mathord {\sim } \neg \varphi $
is
 $\varphi $
,
$\varphi $
,
 $\mathord {\sim } (\exists x) \varphi $
is
$\mathord {\sim } (\exists x) \varphi $
is
 $(\forall x) \mathord {\sim } \varphi ,$
and
$(\forall x) \mathord {\sim } \varphi ,$
and
 $\mathord {\sim } (\forall x) \varphi $
is
$\mathord {\sim } (\forall x) \varphi $
is
 $(\exists x) \mathord {\sim } \varphi $
.
$(\exists x) \mathord {\sim } \varphi $
.3.
 is
is
 and
and
 is
is
 .
.
Definition 2.4. An
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-sentence
${\mathcal {L}}_{\omega _1, \omega }$
-sentence
![]() $\varphi $
is a
$\varphi $
is a
![]() -formula if it can be written in normal form without any infinite disjunctions. More concretely, the
-formula if it can be written in normal form without any infinite disjunctions. More concretely, the
![]() -formulas are formed by the following inductive process:
-formulas are formed by the following inductive process:
1. Every finitary quantifier-free sentence is a
 -formula.
-formula.2. If
 $\varphi $
is a
$\varphi $
is a
 -formula, then so are
-formula, then so are
 $(\exists x) \varphi $
and
$(\exists x) \varphi $
and
 $(\forall x) \varphi $
.
$(\forall x) \varphi $
.3. If
 $\varphi $
and
$\varphi $
and
 $\psi $
are
$\psi $
are
 -formulas, then so is
-formulas, then so is
 $\varphi \vee \psi $
.
$\varphi \vee \psi $
.4. If
 $(\varphi _i)_{i \in \omega }$
are
$(\varphi _i)_{i \in \omega }$
are
 -formulas with finitely many free variables, then so is
-formulas with finitely many free variables, then so is
 .
.
Remark 2.5. The third condition allowing one to take the disjunction of finitely many formulas is in some sense unnecessary; any
-formula is equivalent to one in which all of the disjunctions occur on the inside. For example,

is equivalent to

An
![]() ${\mathcal {L}}_{\omega _1, \omega }$
(or
${\mathcal {L}}_{\omega _1, \omega }$
(or
![]() -) formula is computable if, essentially, there is a computable syntactic representation of the formula (see [Reference Ash and Knight1]).
-) formula is computable if, essentially, there is a computable syntactic representation of the formula (see [Reference Ash and Knight1]).
2.2 Pseudo-elementary classes
In this section, we follow the book by Hodges [Reference Hodges4]. Many classes of structures can be described by the existence of some feature that can be added to them; for example, a linear ordering is non-well-founded if it has a subset with no least element, and a group is orderable if there exists an ordering. Such classes of structures may not be elementary, but by thinking of them as pseudoelementary classes we can still apply the tools of model theory to them. The main notion of pseudo-elementary class in infinitary model theory is the following:
Definition 2.6. We say that a class
![]() $\mathbb {K}$
of
$\mathbb {K}$
of
![]() ${\mathcal {L}}$
-structures is a pseudoelementary class (
${\mathcal {L}}$
-structures is a pseudoelementary class (
![]() $\operatorname {\mathrm {PC}}_\Delta $
-class) if there is a language
$\operatorname {\mathrm {PC}}_\Delta $
-class) if there is a language
![]() $\tau ^* \supseteq \tau $
and an elementary first-order
$\tau ^* \supseteq \tau $
and an elementary first-order
![]() $\tau ^*$
theory T such that
$\tau ^*$
theory T such that
Pseudoelementary classes have some nice properties such as being closed under ultraproducts. (On the other hand,
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable classes may not be closed under ultraproducts.)
${\mathcal {L}}_{\omega _1, \omega }$
-definable classes may not be closed under ultraproducts.)
Just as there is a distinction in model theory between elementary classes and basic elementary classes, the former being axiomatized by a theory and the latter by a single sentence, there is a distinction between pseudoelementary classes and basic pseudoelementary classes.
Definition 2.7. We say that a class
![]() $\mathbb {K}$
of
$\mathbb {K}$
of
![]() ${\mathcal {L}}$
-structures is a basic pseudoelementary class (
${\mathcal {L}}$
-structures is a basic pseudoelementary class (
![]() $\operatorname {\mathrm {PC}}$
-class) if there is a language
$\operatorname {\mathrm {PC}}$
-class) if there is a language
![]() $\tau ^* \supseteq \tau $
and an elementary first-order
$\tau ^* \supseteq \tau $
and an elementary first-order
![]() $\tau ^*$
sentence
$\tau ^*$
sentence
![]() $\varphi $
such that
$\varphi $
such that
In finite model theory, it is basic elementary classes that play the more important role, and indeed in finite model theory the term
![]() $\Delta $
-elementary class is often used for what we call elementary classes, while the term elementary class is reserved for what we call basic elementary classes. Similarly, the main notion of pseudoelementary class in finite model theory is that of basic pseudoelementary classes. Basic pseudo-elementary classes seem to have a connection with computability, e.g., Theorems 1.2 and 1.3.
$\Delta $
-elementary class is often used for what we call elementary classes, while the term elementary class is reserved for what we call basic elementary classes. Similarly, the main notion of pseudoelementary class in finite model theory is that of basic pseudoelementary classes. Basic pseudo-elementary classes seem to have a connection with computability, e.g., Theorems 1.2 and 1.3.
Some classes seem like they should be pseudo-elementary but do not immediately fit under the above definitions. For example, consider the class of multiplicative groups of fields, i.e., a group G is in this class if there is a field F such that
![]() $G = F^\times $
. The field F is not going to be a subset of the field G; rather, G will be a subset of F. We can expand our definitions as follows to allow these types of classes, which we call
$G = F^\times $
. The field F is not going to be a subset of the field G; rather, G will be a subset of F. We can expand our definitions as follows to allow these types of classes, which we call
![]() $\operatorname {\mathrm {PC}}'$
and
$\operatorname {\mathrm {PC}}'$
and
![]() $\operatorname {\mathrm {PC}}^{\prime }_\Delta $
. The classes
$\operatorname {\mathrm {PC}}^{\prime }_\Delta $
. The classes
![]() $\operatorname {\mathrm {PC}}'$
and
$\operatorname {\mathrm {PC}}'$
and
![]() $\operatorname {\mathrm {PC}}^{\prime }_\Delta $
differ from
$\operatorname {\mathrm {PC}}^{\prime }_\Delta $
differ from
![]() $\operatorname {\mathrm {PC}}$
and
$\operatorname {\mathrm {PC}}$
and
![]() $\operatorname {\mathrm {PC}}_{\Delta }$
respectively in that in addition to expanding the language, one is allowed to add additional elements.
$\operatorname {\mathrm {PC}}_{\Delta }$
respectively in that in addition to expanding the language, one is allowed to add additional elements.
Definition 2.8. Let
![]() $\tau \subseteq \tau ^*$
be a pair of languages, with a unary predicate
$\tau \subseteq \tau ^*$
be a pair of languages, with a unary predicate
![]() $P \in \tau ^* \setminus \tau $
. Given a
$P \in \tau ^* \setminus \tau $
. Given a
![]() $\tau ^*$
-structure
$\tau ^*$
-structure
![]() ${\mathcal {A}}$
, we denote by
${\mathcal {A}}$
, we denote by
![]() ${\mathcal {A}}_P$
the substructure of
${\mathcal {A}}_P$
the substructure of
![]() ${\mathcal {A}} \mid \tau $
whose domain is
${\mathcal {A}} \mid \tau $
whose domain is
![]() $P^{{\mathcal {A}}}$
(if this is a
$P^{{\mathcal {A}}}$
(if this is a
![]() $\tau $
-structure; otherwise
$\tau $
-structure; otherwise
![]() ${\mathcal {A}}_P$
is not defined).
${\mathcal {A}}_P$
is not defined).
Definition 2.9. We say that a class
![]() $\mathbb {K}$
of
$\mathbb {K}$
of
![]() $\tau $
-structures is a basic pseudoelementary class (
$\tau $
-structures is a basic pseudoelementary class (
![]() $\operatorname {\mathrm {PC}}'$
-class) if there is a language
$\operatorname {\mathrm {PC}}'$
-class) if there is a language
![]() $\tau ^* \supseteq \tau $
, with a unary relation
$\tau ^* \supseteq \tau $
, with a unary relation
![]() $P \in \tau ^* \setminus \tau $
, and a
$P \in \tau ^* \setminus \tau $
, and a
![]() $\tau ^*$
-formula
$\tau ^*$
-formula
![]() $\phi $
, such that
$\phi $
, such that
We say that
![]() $\mathbb {K}$
is a pseudoelementary class (
$\mathbb {K}$
is a pseudoelementary class (
![]() $\operatorname {\mathrm {PC}}^{\prime }_\Delta $
-class) if
$\operatorname {\mathrm {PC}}^{\prime }_\Delta $
-class) if
![]() $\phi $
is a first-order theory.
$\phi $
is a first-order theory.
We will always clarify whether a pseudoelementary class is
![]() $\operatorname {\mathrm {PC}}_\Delta $
or
$\operatorname {\mathrm {PC}}_\Delta $
or
![]() $\operatorname {\mathrm {PC}}_\Delta '$
, and whether a basic pseudoelementary class is
$\operatorname {\mathrm {PC}}_\Delta '$
, and whether a basic pseudoelementary class is
![]() $\operatorname {\mathrm {PC}}$
or
$\operatorname {\mathrm {PC}}$
or
![]() $\operatorname {\mathrm {PC}}'$
.
$\operatorname {\mathrm {PC}}'$
.
Note that in Definition 2.9, if the language is finite (or we are dealing with a
![]() $\operatorname {\mathrm {PC}}^{\prime }_\Delta $
-class), it suffices to ask that
$\operatorname {\mathrm {PC}}^{\prime }_\Delta $
-class), it suffices to ask that
as
![]() $\phi $
can say that
$\phi $
can say that
![]() ${\mathcal {A}}_{P}$
is defined.
${\mathcal {A}}_{P}$
is defined.
We have defined four different types of pseudo-elementary classes. However, it turns out that
![]() $\operatorname {\mathrm {PC}}_\Delta $
and
$\operatorname {\mathrm {PC}}_\Delta $
and
![]() $\operatorname {\mathrm {PC}}_\Delta '$
classes are actually the same; so for example, the class of multiplicative groups of fields, which is easily seen to be
$\operatorname {\mathrm {PC}}_\Delta '$
classes are actually the same; so for example, the class of multiplicative groups of fields, which is easily seen to be
![]() $\operatorname {\mathrm {PC}}_\Delta '$
, is
$\operatorname {\mathrm {PC}}_\Delta '$
, is
![]() $\operatorname {\mathrm {PC}}_\Delta $
.
$\operatorname {\mathrm {PC}}_\Delta $
.
Theorem 2.10 Theorem 5.2.1 of [Reference Hodges4]
Let
![]() $\mathbb {K}$
be a class of structures.
$\mathbb {K}$
be a class of structures.
1.
 $\mathbb {K}$
is a
$\mathbb {K}$
is a
 $\operatorname {\mathrm {PC}}_{\Delta }$
-class if and only if it is a
$\operatorname {\mathrm {PC}}_{\Delta }$
-class if and only if it is a
 $\operatorname {\mathrm {PC}}^{\prime }_{\Delta }$
-class.
$\operatorname {\mathrm {PC}}^{\prime }_{\Delta }$
-class.2. If all the structures in
 $\mathbb {K}$
are infinite, then
$\mathbb {K}$
are infinite, then
 $\mathbb {K}$
is a
$\mathbb {K}$
is a
 $\operatorname {\mathrm {PC}}$
-class if and only if it is a
$\operatorname {\mathrm {PC}}$
-class if and only if it is a
 $\operatorname {\mathrm {PC}}'$
-class.
$\operatorname {\mathrm {PC}}'$
-class.
In Example 2.15 we exhibit a class which is
![]() $\operatorname {\mathrm {PC}}'$
but not
$\operatorname {\mathrm {PC}}'$
but not
![]() $\operatorname {\mathrm {PC}}$
.
$\operatorname {\mathrm {PC}}$
.
The proof of the first point in [Reference Hodges4] is not obvious and quite interesting. For the second, essentially the only reason that
![]() $\operatorname {\mathrm {PC}}$
and
$\operatorname {\mathrm {PC}}$
and
![]() $\operatorname {\mathrm {PC}}'$
are different is that the model might be finite; if a model is infinite, one could just have the elements of the model “wear two hats,” on the one hand being the domain of the expansion of the original model, and on the other hand playing the role of the elements of the new sort P.
$\operatorname {\mathrm {PC}}'$
are different is that the model might be finite; if a model is infinite, one could just have the elements of the model “wear two hats,” on the one hand being the domain of the expansion of the original model, and on the other hand playing the role of the elements of the new sort P.
2.3 Examples
In this section we will give a few examples of classes of various types, separating some of the notions defined in the previous two sections, and including some applications of the theorems of this paper.
The motivating example for this paper was the class of connected graphs. It is easier to think of the compliment, the class of non-connected graphs. This class is both
![]() $\operatorname {\mathrm {PC}}$
and definable by a computable
$\operatorname {\mathrm {PC}}$
and definable by a computable
![]() -sentence. Thus the class of connected graphs is both co-
-sentence. Thus the class of connected graphs is both co-
![]() $\operatorname {\mathrm {PC}}$
and definable by a computable
$\operatorname {\mathrm {PC}}$
and definable by a computable
![]() -sentence (the definition of which should be clear). These classes are not elementary classes.
-sentence (the definition of which should be clear). These classes are not elementary classes.
Example 2.11. Let
![]() $\tau = \{ R \}$
the language of graphs. The class
$\tau = \{ R \}$
the language of graphs. The class
![]() $\mathbb {K}$
of non-connected graphs is a
$\mathbb {K}$
of non-connected graphs is a
![]() $\operatorname {\mathrm {PC}}$
-class. Indeed, an undirected graph
$\operatorname {\mathrm {PC}}$
-class. Indeed, an undirected graph
![]() ${\mathcal {G}} = (G,R)$
is disconnected if and only if there is a binary relation C of connectedness such that:
${\mathcal {G}} = (G,R)$
is disconnected if and only if there is a binary relation C of connectedness such that:
1.
 $(\forall x)(\forall y) \; [R(x,y) \rightarrow C(x,y)]$
,
$(\forall x)(\forall y) \; [R(x,y) \rightarrow C(x,y)]$
,2.
 $(\forall x)(\forall y)(\forall z)\;[ C(x,y) \wedge C(y,z) \rightarrow C(x,z)]$
, and
$(\forall x)(\forall y)(\forall z)\;[ C(x,y) \wedge C(y,z) \rightarrow C(x,z)]$
, and3.
 $\neg (\forall x)(\forall y) \; C(x,y)$
.
$\neg (\forall x)(\forall y) \; C(x,y)$
.
An undirected graph
![]() ${\mathcal {G}}$
is also disconnected if and only if
${\mathcal {G}}$
is also disconnected if and only if

So
![]() $\mathbb {K}$
is also defined by a computable
$\mathbb {K}$
is also defined by a computable
-sentence.
The prototypical example of a
![]() $\operatorname {\mathrm {PC}}$
-class which is not
$\operatorname {\mathrm {PC}}$
-class which is not
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-definable is class of non-well-founded linear orders.
${\mathcal {L}}_{\omega _1, \omega }$
-definable is class of non-well-founded linear orders.
Example 2.12. Let
![]() $\tau = \{ < \}$
the language of linear orders. The class
$\tau = \{ < \}$
the language of linear orders. The class
![]() $\mathbb {K}$
of non-well-founded linear orders is a
$\mathbb {K}$
of non-well-founded linear orders is a
![]() $\operatorname {\mathrm {PC}}$
-class as a linear order
$\operatorname {\mathrm {PC}}$
-class as a linear order
![]() $(S,<)$
is non-well-founded if and only if there is a unary relation U such that
$(S,<)$
is non-well-founded if and only if there is a unary relation U such that
![]() $\mathbb {K}$
is not definable by any
$\mathbb {K}$
is not definable by any
![]() ${\mathcal {L}}_{\omega _1, \omega }$
formula.
${\mathcal {L}}_{\omega _1, \omega }$
formula.
A simple example where one can apply Theorem 1.3 is the class of infinite models.
Example 2.13. Let
![]() $\tau $
be any language and
$\tau $
be any language and
![]() $\phi $
a finitary
$\phi $
a finitary
![]() $\tau $
-sentence. The class
$\tau $
-sentence. The class
![]() $\mathbb {K}$
of infinite models of
$\mathbb {K}$
of infinite models of
![]() $\phi $
is easily seen to be defined by the conjunction of
$\phi $
is easily seen to be defined by the conjunction of
![]() $\phi $
and the computable
$\phi $
and the computable
-sentence

By Theorem 1.3,
![]() $\mathbb {K}$
is a
$\mathbb {K}$
is a
![]() $\operatorname {\mathrm {PC}}'$
-class, and by Theorem 2.10 it is a
$\operatorname {\mathrm {PC}}'$
-class, and by Theorem 2.10 it is a
![]() $\operatorname {\mathrm {PC}}$
-class. Being slightly clever, we can also see that
$\operatorname {\mathrm {PC}}$
-class. Being slightly clever, we can also see that
![]() $\mathbb {K}$
is a
$\mathbb {K}$
is a
![]() $\operatorname {\mathrm {PC}}$
-class by noting that
$\operatorname {\mathrm {PC}}$
-class by noting that
![]() ${\mathcal {A}} \models \phi $
is infinite if and only if there is a linear order
${\mathcal {A}} \models \phi $
is infinite if and only if there is a linear order
![]() $<$
on
$<$
on
![]() ${\mathcal {A}}$
such that
${\mathcal {A}}$
such that
![]() $(\forall x)(\exists y) [ x < y]$
.
$(\forall x)(\exists y) [ x < y]$
.
We have already mentioned the class of orderable groups.
Example 2.14. Orderable groups are a
![]() $\operatorname {\mathrm {PC}}$
-class. By compactness, they are also universally axiomatizable (in elementary first-order logic) by saying that every finite subset can be ordered in a way that is compatible with the group operation.
$\operatorname {\mathrm {PC}}$
-class. By compactness, they are also universally axiomatizable (in elementary first-order logic) by saying that every finite subset can be ordered in a way that is compatible with the group operation.
Example 2.14 is a particular instance of a more general phenomena: if we take a
![]() $\operatorname {\mathrm {PC}}$
-class that such that (a) the expanded vocabulary only adds relations and (b) the added relations are only universally quantified over, then the resulting class is actually elementary (though it may require infinitely many axioms). This is very particular case in which we can answer Conjecture 1.4.
$\operatorname {\mathrm {PC}}$
-class that such that (a) the expanded vocabulary only adds relations and (b) the added relations are only universally quantified over, then the resulting class is actually elementary (though it may require infinitely many axioms). This is very particular case in which we can answer Conjecture 1.4.
As an application of Theorem 1.2, let us give an example of a
![]() $\operatorname {\mathrm {PC}}'$
-class which is not a
$\operatorname {\mathrm {PC}}'$
-class which is not a
![]() $\operatorname {\mathrm {PC}}$
-class.
$\operatorname {\mathrm {PC}}$
-class.
Example 2.15. Define an elementary first-order theory T as follows. The language of T will be the language of graphs. Fix an enumeration of the sentences
![]() $\phi _n$
in finite languages
$\phi _n$
in finite languages
![]() ${\mathcal {L}}_n$
expanding the language of graphs. Note that for every finite graph G, we can decide effectively whether there is an expansion of G to a model of
${\mathcal {L}}_n$
expanding the language of graphs. Note that for every finite graph G, we can decide effectively whether there is an expansion of G to a model of
![]() $\phi _n$
. For each n, let
$\phi _n$
. For each n, let
![]() $C_n$
be cycle of length n. Then, let T be the theory that says that there is no cycle of length n for exactly those n where
$C_n$
be cycle of length n. Then, let T be the theory that says that there is no cycle of length n for exactly those n where
![]() $C_n$
does not have an expansion to a model of
$C_n$
does not have an expansion to a model of
![]() $\phi _n$
.
$\phi _n$
.
Note that T is c.e. and universal. By diagonalization, the models of T are not a
![]() $\operatorname {\mathrm {PC}}$
-class, though by Theorem 1.2 they are a
$\operatorname {\mathrm {PC}}$
-class, though by Theorem 1.2 they are a
![]() $\operatorname {\mathrm {PC}}'$
-class.
$\operatorname {\mathrm {PC}}'$
-class.
As suggested by Theorem 2.10, this example uses finite structures in an integral way.
3 An application of Craig Interpolation
To prove the direction (1) implies (2) of Theorem 1.1, we will adapt a proof of the Craig Interpolation Theorem for
![]() ${\mathcal {L}}_{\omega _1, \omega }$
. We state the standard Craig Interpolation Theorem here for completeness.
${\mathcal {L}}_{\omega _1, \omega }$
. We state the standard Craig Interpolation Theorem here for completeness.
Theorem 3.1 Craig Interpolation Theorem [Reference Lopez-Escobar7]
Suppose
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
are
$\phi _2$
are
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-sentences with
${\mathcal {L}}_{\omega _1, \omega }$
-sentences with
![]() $\phi _1 \models \phi _2$
. There is an
$\phi _1 \models \phi _2$
. There is an
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-sentence
${\mathcal {L}}_{\omega _1, \omega }$
-sentence
![]() $\theta $
such that
$\theta $
such that
![]() $\phi _1 \models \theta $
,
$\phi _1 \models \theta $
,
![]() $\theta \models \phi _2$
, and every relation, function and constant symbol occurring in
$\theta \models \phi _2$
, and every relation, function and constant symbol occurring in
![]() $\theta $
occurs in both
$\theta $
occurs in both
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
.
$\phi _2$
.
The proof we adapt is not the original proof by Lopez-Escobar, but one that appears in the book by Marker [Reference Marker10]. The proof of Craig Interpolation makes use of consistency properties. Consistency properties are the infinitary equivalent of Henkin-style constructions in finitary logic. Consistency properties were first introduced by Makkai [Reference Makkai8]; the exact definition we use seems to be due to Keisler [Reference Keisler5]. See also Definition 4.1 of [Reference Marker10].
Definition 3.2. Let C be a countable collection of new constants. A consistency property
![]() $\Sigma $
is a collection of countable sets
$\Sigma $
is a collection of countable sets
![]() $\sigma $
of
$\sigma $
of
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-sentences with the following properties. For
${\mathcal {L}}_{\omega _1, \omega }$
-sentences with the following properties. For
![]() $\sigma \in \Sigma $
:
$\sigma \in \Sigma $
:
(C1) If
 $\phi \in \sigma $
, then
$\phi \in \sigma $
, then
 $\neg \phi \notin \sigma $
.
$\neg \phi \notin \sigma $
.(C2) If
 $\neg \phi \in \sigma $
, then
$\neg \phi \in \sigma $
, then
 $\sigma \cup \{ \sim \phi \} \in \Sigma $
.
$\sigma \cup \{ \sim \phi \} \in \Sigma $
.(C3) If
 , then for all
, then for all
 $\phi \in X$
,
$\phi \in X$
,
 $\sigma \cup \{\phi \} \in \Sigma $
.
$\sigma \cup \{\phi \} \in \Sigma $
.(C4) If
 , then there is
, then there is
 $\phi \in X$
such that
$\phi \in X$
such that
 $\sigma \cup \{\phi \} \in \Sigma $
.
$\sigma \cup \{\phi \} \in \Sigma $
.(C5) If
 $(\forall v) \phi (v) \in \sigma $
, then for all
$(\forall v) \phi (v) \in \sigma $
, then for all
 $c \in C$
,
$c \in C$
,
 $\sigma \cup \{\phi (c)\} \in \Sigma $
.
$\sigma \cup \{\phi (c)\} \in \Sigma $
.(C6) If
 $(\exists v) \phi (v) \in \sigma $
, then there is
$(\exists v) \phi (v) \in \sigma $
, then there is
 $c \in C$
such that
$c \in C$
such that
 $\sigma \cup \{\phi (c)\} \in \Sigma $
.
$\sigma \cup \{\phi (c)\} \in \Sigma $
.(C7) Let t be a term with no variables and let
 $c,d \in C$
:
$c,d \in C$
:(a) If
 $c = d \in \sigma $
, then
$c = d \in \sigma $
, then
 $\sigma \cup \{d = c\} \in \Sigma $
.
$\sigma \cup \{d = c\} \in \Sigma $
.(b) If
 $c = t \in \sigma $
and
$c = t \in \sigma $
and
 $\phi (t) \in \sigma $
, then
$\phi (t) \in \sigma $
, then
 $\sigma \cup \{\phi (c)\} \in \Sigma $
.
$\sigma \cup \{\phi (c)\} \in \Sigma $
.(c) There is
 $e \in C$
such that
$e \in C$
such that
 $\sigma \cup \{e = t\} \in \Sigma $
.
$\sigma \cup \{e = t\} \in \Sigma $
.
Marker [Reference Marker10] includes another condition, that a consistency property be closed under subsets. However he shows in Exercise 4.1.4 that this is unnecessary. Keisler [Reference Keisler5] states his definition in the same way as ours, and proves that the closure of a consistency property under subsets is against a consistency property.
A consistency property is in some sense a recipe for building a model.
Theorem 3.3 Model Existence Theorem
If
![]() $\Sigma $
is a consistency property and
$\Sigma $
is a consistency property and
![]() $\sigma \in \Sigma $
, there is
$\sigma \in \Sigma $
, there is
![]() ${\mathcal {M}} \models \sigma $
.
${\mathcal {M}} \models \sigma $
.
We are now ready to prove our variant of the Craig Interpolation Theorem. We strengthen the hypotheses to assume that one of the sentences is a
![]() -sentence, and in return, we get that the interpolant is also a
-sentence, and in return, we get that the interpolant is also a
![]() -sentence. The proof follows the same structure as that of the Craig Interpolation Theorem in [Reference Marker10] (Theorem 4.3.1).
-sentence. The proof follows the same structure as that of the Craig Interpolation Theorem in [Reference Marker10] (Theorem 4.3.1).
Theorem 3.4. Suppose
![]() $\phi _1$
is a
$\phi _1$
is a
![]() -sentence and
-sentence and
![]() $\phi _2$
is an
$\phi _2$
is an
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-sentence with
${\mathcal {L}}_{\omega _1, \omega }$
-sentence with
![]() $\phi _1 \models \phi _2$
. There is a
$\phi _1 \models \phi _2$
. There is a
![]() -sentence
-sentence
![]() $\theta $
such that
$\theta $
such that
![]() $\phi _1 \models \theta $
,
$\phi _1 \models \theta $
,
![]() $\theta \models \phi _2$
, and every relation, function and constant symbol occurring in
$\theta \models \phi _2$
, and every relation, function and constant symbol occurring in
![]() $\theta $
occurs in both
$\theta $
occurs in both
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
.
$\phi _2$
.
Proof Let C be a countable collection of new constants. Let
![]() $\tau _i$
be the smallest language containing
$\tau _i$
be the smallest language containing
![]() $\phi _i$
and C, and let
$\phi _i$
and C, and let
![]() $\tau = \tau _1 \cap \tau _2$
.
$\tau = \tau _1 \cap \tau _2$
.
Let
![]() $\Sigma $
be the collection of finite sets of sentences
$\Sigma $
be the collection of finite sets of sentences
![]() $\sigma $
containing only finitely many new constants that can be written as
$\sigma $
containing only finitely many new constants that can be written as
![]() $\sigma = \sigma _1 \cup \sigma _2$
, where
$\sigma = \sigma _1 \cup \sigma _2$
, where
![]() $\sigma _1$
is a finite set of
$\sigma _1$
is a finite set of
![]() -
-
![]() $\tau _1$
-sentences and
$\tau _1$
-sentences and
![]() $\sigma _2$
is a finite set of
$\sigma _2$
is a finite set of
![]() $\tau _2$
-sentences, and such that for all
$\tau _2$
-sentences, and such that for all
![]() $\tau $
-sentences
$\tau $
-sentences
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
, with
$\psi _2$
, with
![]() $\psi _1$
a
$\psi _1$
a
![]() -sentence, if
-sentence, if
![]() $\sigma _1 \models \psi _1$
and
$\sigma _1 \models \psi _1$
and
![]() $\sigma _2 \models \psi _2$
then
$\sigma _2 \models \psi _2$
then
![]() $\psi _1 \wedge \psi _2$
is satisfiable.
$\psi _1 \wedge \psi _2$
is satisfiable.
In the rest of the proof, we make the convention that if
![]() $\sigma \in \Sigma $
and we write
$\sigma \in \Sigma $
and we write
![]() $\sigma = \sigma _1 \cup \sigma _2$
, then
$\sigma = \sigma _1 \cup \sigma _2$
, then
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
are the witnesses that
$\sigma _2$
are the witnesses that
![]() $\sigma \in \Sigma $
, i.e.,
$\sigma \in \Sigma $
, i.e.,
![]() $\sigma _1$
consists of
$\sigma _1$
consists of
![]() -
-
![]() $\tau _1$
-sentences,
$\tau _1$
-sentences,
![]() $\sigma _2$
consists of
$\sigma _2$
consists of
![]() $\tau _2$
-sentences, and they satisfy the satisfiability condition above.
$\tau _2$
-sentences, and they satisfy the satisfiability condition above.
We claim that
![]() $\Sigma $
is a consistency property. The following claim will verify many of the conditions.
$\Sigma $
is a consistency property. The following claim will verify many of the conditions.
Claim. Fix
![]() $\sigma \in \Sigma $
and write
$\sigma \in \Sigma $
and write
![]() $\sigma = \sigma _1 \cup \sigma _2$
. If
$\sigma = \sigma _1 \cup \sigma _2$
. If
![]() $\phi $
is a
$\phi $
is a
![]() $\tau _i$
-sentence (and a
$\tau _i$
-sentence (and a
![]() -sentence if
-sentence if
![]() $i = 1$
) with
$i = 1$
) with
![]() $\sigma _i \models \phi $
, then
$\sigma _i \models \phi $
, then
![]() $\sigma \cup \{\phi \} \in \Sigma $
.
$\sigma \cup \{\phi \} \in \Sigma $
.
Proof We will show the case
![]() $i = 1$
. We can write
$i = 1$
. We can write
![]() $\sigma \cup \{\phi \} = (\sigma _1 \cup \{\phi \}) \cup \sigma _2$
. If
$\sigma \cup \{\phi \} = (\sigma _1 \cup \{\phi \}) \cup \sigma _2$
. If
![]() $\sigma _1 \cup \{\phi \} \models \psi _1$
and
$\sigma _1 \cup \{\phi \} \models \psi _1$
and
![]() $\sigma _2 \models \psi _2$
, with
$\sigma _2 \models \psi _2$
, with
![]() $\psi _1$
a
$\psi _1$
a
![]() -sentence, then since
-sentence, then since
![]() $\sigma _1 \models \phi $
,
$\sigma _1 \models \phi $
,
![]() $\sigma _1 \models \psi _1$
. Hence
$\sigma _1 \models \psi _1$
. Hence
![]() $\psi _1 \wedge \psi _2$
is satisfiable.
$\psi _1 \wedge \psi _2$
is satisfiable.
We now check the conditions of a consistency property.
(C1) Suppose for a contradiction that
 $\phi ,\neg \phi \in \sigma = \sigma _1 \cup \sigma _2$
. If
$\phi ,\neg \phi \in \sigma = \sigma _1 \cup \sigma _2$
. If
 $\phi \in \sigma _i$
while
$\phi \in \sigma _i$
while
 $\neg \phi \in \sigma _j$
for
$\neg \phi \in \sigma _j$
for
 $i\not =j$
, then
$i\not =j$
, then
 $\phi $
is a
$\phi $
is a
 $\tau $
-sentence such that
$\tau $
-sentence such that
 $\sigma _i \models \phi $
and
$\sigma _i \models \phi $
and
 $\sigma _j \models \neg \phi $
, so since
$\sigma _j \models \neg \phi $
, so since
 $\phi \wedge \neg \phi $
is not satisfiable, this witnesses that
$\phi \wedge \neg \phi $
is not satisfiable, this witnesses that
 $\sigma \in \Sigma $
. If both
$\sigma \in \Sigma $
. If both
 $\phi ,\neg \phi \in \sigma _i$
, then
$\phi ,\neg \phi \in \sigma _i$
, then
 $\sigma _i \models \phi \wedge \neg \phi $
. Now since
$\sigma _i \models \phi \wedge \neg \phi $
. Now since
 $\phi \wedge \neg \phi $
is unsatisfiable, letting
$\phi \wedge \neg \phi $
is unsatisfiable, letting
 $\psi _1$
be any unsatisfiable
$\psi _1$
be any unsatisfiable
 $\tau $
-sentence, we also have that
$\tau $
-sentence, we also have that
 $\sigma _i \models \psi _1$
. Letting
$\sigma _i \models \psi _1$
. Letting
 $\psi _2$
be any
$\psi _2$
be any
 $\tau $
-sentence such that
$\tau $
-sentence such that
 $\sigma _j \models \psi _2$
, we see that
$\sigma _j \models \psi _2$
, we see that
 $\psi _1 \wedge \psi _2$
is unsatisfiable and provides a witness to the fact that
$\psi _1 \wedge \psi _2$
is unsatisfiable and provides a witness to the fact that
 $\sigma \in \Sigma $
.
$\sigma \in \Sigma $
.(C2) This follows from the claim.
(C3) This follows from the claim.
(C4) Write
 $\sigma = \sigma _1 \cup \sigma _2$
. We have two cases which are different, depending on whether
$\sigma = \sigma _1 \cup \sigma _2$
. We have two cases which are different, depending on whether
 or
or
 .
.First suppose that
 . Let
. Let
 $\sigma _{2,\phi } = \sigma _2 \cup \{\phi \}$
. We claim that for some
$\sigma _{2,\phi } = \sigma _2 \cup \{\phi \}$
. We claim that for some
 $\phi \in X$
,
$\phi \in X$
,
 $\sigma _{2,\phi } \cup \sigma _1 \in \Sigma $
. If not, then for each
$\sigma _{2,\phi } \cup \sigma _1 \in \Sigma $
. If not, then for each
 $\phi \in X$
there are
$\phi \in X$
there are
 $\tau $
-sentences
$\tau $
-sentences
 $\psi _{2,\phi }$
and
$\psi _{2,\phi }$
and
 $\psi _{1,\phi }$
, with
$\psi _{1,\phi }$
, with
 $\psi _{1,\phi }$
a
$\psi _{1,\phi }$
a
 -sentence, such that
-sentence, such that
 $\sigma _{2,\phi } \models \psi _{2,\phi }$
and
$\sigma _{2,\phi } \models \psi _{2,\phi }$
and
 $\sigma _1 \models \psi _{1,\phi }$
, and such that
$\sigma _1 \models \psi _{1,\phi }$
, and such that
 $\psi _{2,\phi } \wedge \psi _{1,\phi }$
is unsatisfiable. So
$\psi _{2,\phi } \wedge \psi _{1,\phi }$
is unsatisfiable. So
 $\psi _{2,\phi } \models \neg \psi _{1,\phi }$
. Since
$\psi _{2,\phi } \models \neg \psi _{1,\phi }$
. Since 
we have that

On the other hand,

This formula is a
 -sentence as each
-sentence as each
 $\psi _{1,\phi }$
is. Finally,
$\psi _{1,\phi }$
is. Finally, 
which contradicts that
 $\sigma \in \Sigma $
.
$\sigma \in \Sigma $
.Now suppose that
 ; then X is finite. We begin in a similar way as before. Let
; then X is finite. We begin in a similar way as before. Let
 $\sigma _{1,\phi } = \sigma _1 \cup \{\phi \}$
. We claim that for some
$\sigma _{1,\phi } = \sigma _1 \cup \{\phi \}$
. We claim that for some
 $\phi \in X$
,
$\phi \in X$
,
 $\sigma _{1,\phi } \cup \sigma _2 \in \Sigma $
. If not, then for each
$\sigma _{1,\phi } \cup \sigma _2 \in \Sigma $
. If not, then for each
 $\phi \in X$
there are
$\phi \in X$
there are
 $\tau $
-sentences
$\tau $
-sentences
 $\psi _{1,\phi }$
and
$\psi _{1,\phi }$
and
 $\psi _{2,\phi }$
, with
$\psi _{2,\phi }$
, with
 $\psi _{1,\phi }$
a
$\psi _{1,\phi }$
a
 -sentence, such that
-sentence, such that
 $\sigma _{1,\phi } \models \psi _{1,\phi }$
and
$\sigma _{1,\phi } \models \psi _{1,\phi }$
and
 $\sigma _2 \models \psi _{2,\phi }$
, and such that
$\sigma _2 \models \psi _{2,\phi }$
, and such that
 $\psi _{1,\phi } \wedge \psi _{2,\phi }$
is unsatisfiable. So
$\psi _{1,\phi } \wedge \psi _{2,\phi }$
is unsatisfiable. So
 $\psi _{1,\phi } \models \neg \psi _{2,\phi }$
. Since
$\psi _{1,\phi } \models \neg \psi _{2,\phi }$
. Since 
we have that

As X is finite this a
 -sentence. On the other hand,
-sentence. On the other hand, 
and

which contradicts that
 $\sigma \in \Sigma $
.
$\sigma \in \Sigma $
.(C5) This follows from the claim as
 $(\forall x) \phi (x) \models \phi (c)$
for all
$(\forall x) \phi (x) \models \phi (c)$
for all
 $c \in C$
.
$c \in C$
.(C6) If
 $(\exists x) \phi (x) \in \sigma $
, then choose
$(\exists x) \phi (x) \in \sigma $
, then choose
 $c \in C$
which does not appear in
$c \in C$
which does not appear in
 $\sigma $
. Suppose that
$\sigma $
. Suppose that
 $(\exists x) \phi (x) \in \sigma _1$
; the case where
$(\exists x) \phi (x) \in \sigma _1$
; the case where
 $(\exists x)\phi (x) \in \sigma _2$
is similar. We claim that
$(\exists x)\phi (x) \in \sigma _2$
is similar. We claim that
 $\sigma \cup \{\phi (c)\} \in \Sigma $
. Since
$\sigma \cup \{\phi (c)\} \in \Sigma $
. Since
 $(\exists x) \phi (x) \in \sigma _1$
,
$(\exists x) \phi (x) \in \sigma _1$
,
 $\phi (x)$
is a
$\phi (x)$
is a
 -formula, and thus so is
-formula, and thus so is
 $\phi (c)$
.
$\phi (c)$
.Suppose that
 $\sigma _1 \cup \{\phi (c)\} \models \psi _1$
and
$\sigma _1 \cup \{\phi (c)\} \models \psi _1$
and
 $\sigma _2 \models \psi _2$
, where
$\sigma _2 \models \psi _2$
, where
 $\psi _1$
is a
$\psi _1$
is a
 -sentence. Write
-sentence. Write
 $\psi _1 = \theta _1(c)$
and
$\psi _1 = \theta _1(c)$
and
 $\psi _2 = \theta _2(c)$
. We have
$\psi _2 = \theta _2(c)$
. We have
 $\sigma _1 \models \phi (c) \rightarrow \theta _1(c)$
, and so since c does not appear in
$\sigma _1 \models \phi (c) \rightarrow \theta _1(c)$
, and so since c does not appear in
 $\sigma _1$
,
$\sigma _1$
,
 $\sigma _1 \models (\forall x) [\phi (x) \rightarrow \theta _1(x)]$
. Similarly,
$\sigma _1 \models (\forall x) [\phi (x) \rightarrow \theta _1(x)]$
. Similarly,
 $\sigma _2 \models (\forall x) \theta _2(x)$
. Also,
$\sigma _2 \models (\forall x) \theta _2(x)$
. Also,
 $\sigma _1 \models (\exists x) \phi (x)$
and so
$\sigma _1 \models (\exists x) \phi (x)$
and so
 $\sigma _1 \models (\exists x) \theta _1(x)$
. So
$\sigma _1 \models (\exists x) \theta _1(x)$
. So
 $(\exists x)\theta _1(x) \wedge (\forall x) \theta _2(x)$
is satisfiable, say in a model
$(\exists x)\theta _1(x) \wedge (\forall x) \theta _2(x)$
is satisfiable, say in a model
 ${\mathcal {M}}$
. Note that the constant c does not appear in the formula
${\mathcal {M}}$
. Note that the constant c does not appear in the formula
 $(\exists x)\theta _1(x) \wedge (\forall x) \theta _2(x)$
, so we may choose the interpretation of c in
$(\exists x)\theta _1(x) \wedge (\forall x) \theta _2(x)$
, so we may choose the interpretation of c in
 ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
 ${\mathcal {M}} \models \theta _1(c)$
. Then
${\mathcal {M}} \models \theta _1(c)$
. Then
 ${\mathcal {M}} \models \theta _1(c) \wedge \theta _2(c)$
. So
${\mathcal {M}} \models \theta _1(c) \wedge \theta _2(c)$
. So
 $\psi _1 \wedge \psi _2$
is satisfiable, and
$\psi _1 \wedge \psi _2$
is satisfiable, and
 $\sigma \cup \{\phi (c)\} \in \Sigma $
.
$\sigma \cup \{\phi (c)\} \in \Sigma $
.(C7) Let t be a term with no variables and let
 $c,d \in C$
:
$c,d \in C$
:(a) This follows from the claim.
(b) Suppose
 $c=t \in \sigma $
and
$c=t \in \sigma $
and
 $\phi (t) \in \sigma $
. Write
$\phi (t) \in \sigma $
. Write
 $\sigma = \sigma _1 \cup \sigma _2$
. Consider
$\sigma = \sigma _1 \cup \sigma _2$
. Consider
 $\mu = \sigma \cup \{\phi (c)\} = \sigma _1 \cup \sigma _2 \cup \{ \phi (c) \}$
. Suppose
$\mu = \sigma \cup \{\phi (c)\} = \sigma _1 \cup \sigma _2 \cup \{ \phi (c) \}$
. Suppose
 $c=t \in \sigma _i$
and
$c=t \in \sigma _i$
and
 $\phi (t) \in \sigma _j$
. The case
$\phi (t) \in \sigma _j$
. The case
 $i = j$
follows from the claim, so we consider the case
$i = j$
follows from the claim, so we consider the case
 $i \neq j$
. Suppose that
$i \neq j$
. Suppose that
 $\sigma _i \models \psi _i$
and
$\sigma _i \models \psi _i$
and
 $\sigma _j \cup \{\phi (c)\} \models \psi _j$
. Then
$\sigma _j \cup \{\phi (c)\} \models \psi _j$
. Then
 $\sigma _i \models c=t \wedge \psi _i$
and
$\sigma _i \models c=t \wedge \psi _i$
and
 $\sigma _j \models c=t \rightarrow \psi _j$
, so
$\sigma _j \models c=t \rightarrow \psi _j$
, so
 $c=t \wedge \psi _i \wedge (c=t \rightarrow \psi _i)$
is satisfiable. So
$c=t \wedge \psi _i \wedge (c=t \rightarrow \psi _i)$
is satisfiable. So
 $\psi _i \wedge \psi _j$
is satisfiable.
$\psi _i \wedge \psi _j$
is satisfiable.(c) Pick
 $e \in C$
which does not appear in
$e \in C$
which does not appear in
 $\sigma = \sigma _1 \cup \sigma _2$
. Then if
$\sigma = \sigma _1 \cup \sigma _2$
. Then if
 $\sigma _1 \cup \{e = t\} \models \psi _1$
and
$\sigma _1 \cup \{e = t\} \models \psi _1$
and
 $\sigma _2 \cup \{e = t\} \models \psi _2$
, write
$\sigma _2 \cup \{e = t\} \models \psi _2$
, write
 $\psi _1 = \theta _1(e)$
and
$\psi _1 = \theta _1(e)$
and
 $\psi _2 = \theta _2(e)$
. Then since e does not appear in
$\psi _2 = \theta _2(e)$
. Then since e does not appear in
 $\sigma _1$
or
$\sigma _1$
or
 $\sigma _2$
,
$\sigma _2$
,
 $\sigma _1 \models \theta _1(t)$
and
$\sigma _1 \models \theta _1(t)$
and
 $\sigma _2 \models \theta _2(t)$
. Thus
$\sigma _2 \models \theta _2(t)$
. Thus
 $\theta _1(t) \wedge \theta _2(t)$
is satisfiable. Given a model of
$\theta _1(t) \wedge \theta _2(t)$
is satisfiable. Given a model of
 $\theta _1(t) \wedge \theta _2(t)$
, setting the interpretation of c to t, we get a model of
$\theta _1(t) \wedge \theta _2(t)$
, setting the interpretation of c to t, we get a model of
 $\psi _1 \wedge \psi _2$
. So
$\psi _1 \wedge \psi _2$
. So
 $\psi _1 \wedge \psi _2$
is satisfiable.
$\psi _1 \wedge \psi _2$
is satisfiable.
Since
![]() $\phi _1 \models \phi _2$
,
$\phi _1 \models \phi _2$
,
![]() $\{\phi _1,\neg \phi _2\} \notin \Sigma $
as otherwise by the Model Existence Theorem there would be a model of
$\{\phi _1,\neg \phi _2\} \notin \Sigma $
as otherwise by the Model Existence Theorem there would be a model of
![]() $\phi _1 \wedge \neg \phi _2$
. By definition of
$\phi _1 \wedge \neg \phi _2$
. By definition of
![]() $\Sigma $
, there are
$\Sigma $
, there are
![]() $\tau $
-sentences
$\tau $
-sentences
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
, with
$\psi _2$
, with
![]() $\psi _1$
a
$\psi _1$
a
![]() -sentence, such that
-sentence, such that
![]() $\phi _1 \models \psi _1$
,
$\phi _1 \models \psi _1$
,
![]() $\neg \phi _2 \models \psi _2$
, and
$\neg \phi _2 \models \psi _2$
, and
![]() $\psi _1 \wedge \psi _2$
is not satisfiable. So we have that
$\psi _1 \wedge \psi _2$
is not satisfiable. So we have that
![]() $\phi _1 \models \psi _1$
,
$\phi _1 \models \psi _1$
,
![]() $\psi _1 \models \neg \psi _2$
, and
$\psi _1 \models \neg \psi _2$
, and
![]() $\neg \psi _2 \models \phi _2$
. Hence
$\neg \psi _2 \models \phi _2$
. Hence
![]() $\phi _1 \models \psi _1$
and
$\phi _1 \models \psi _1$
and
![]() $\psi _1 \models \phi _2$
.
$\psi _1 \models \phi _2$
.
Thus
![]() $\psi _1$
is the desired interpolant, except that it may contain constants from C. Write
$\psi _1$
is the desired interpolant, except that it may contain constants from C. Write
![]() $\psi _1 = \theta (\bar {c})$
, where
$\psi _1 = \theta (\bar {c})$
, where
![]() $\theta $
is an
$\theta $
is an
![]() $\tau $
-formula with no constants from
$\tau $
-formula with no constants from
![]() $\bar {c}$
. Neither
$\bar {c}$
. Neither
![]() $\phi _1$
nor
$\phi _1$
nor
![]() $\phi _2$
contains constants from C, and so
$\phi _2$
contains constants from C, and so
![]() $\phi _1 \models (\forall \bar {x}) \theta (\bar {x})$
and
$\phi _1 \models (\forall \bar {x}) \theta (\bar {x})$
and
![]() $(\exists \bar {x}) \theta (\bar {x}) \models \phi _2$
. Since
$(\exists \bar {x}) \theta (\bar {x}) \models \phi _2$
. Since
![]() $(\forall \bar {x}) \theta (\bar {x}) \models (\exists \bar {x}) \theta (\bar {x})$
, we can take
$(\forall \bar {x}) \theta (\bar {x}) \models (\exists \bar {x}) \theta (\bar {x})$
, we can take
![]() $(\forall \bar {x}) \theta (\bar {x})$
as the interpolant.⊣
$(\forall \bar {x}) \theta (\bar {x})$
as the interpolant.⊣
We get the following corollary, which is (1) implies (2) of Theorem 1.1. Interestingly, when we apply the interpolation theorem in the proof, one of the languages contains the other (i.e., we have
![]() $\tau _1 \supseteq \tau _2$
so that
$\tau _1 \supseteq \tau _2$
so that
![]() $\tau = \tau _1 \cap \tau _2 = \tau _2$
). If it were not for our added assumptions on the form of the formulas involved, finding an interpolant would be trivial as we could just take the sentence in the smaller language.
$\tau = \tau _1 \cap \tau _2 = \tau _2$
). If it were not for our added assumptions on the form of the formulas involved, finding an interpolant would be trivial as we could just take the sentence in the smaller language.
Corollary 3.5. Let
![]() $\mathbb {K}$
be a class of
$\mathbb {K}$
be a class of
![]() $\tau $
-structures closed under isomorphism. If
$\tau $
-structures closed under isomorphism. If
![]() $\mathbb {K}$
is both a
$\mathbb {K}$
is both a
![]() $\operatorname {\mathrm {PC}}_{\Delta }$
-class and
$\operatorname {\mathrm {PC}}_{\Delta }$
-class and
![]() ${\mathcal {L}}_{\omega _1, \omega }$
-elementary, then it is defined by a
${\mathcal {L}}_{\omega _1, \omega }$
-elementary, then it is defined by a
![]() -sentence.
-sentence.
Proof Let
![]() $\tau ^* \supseteq \tau $
be an expanded language and let X be a set of first-order sentences such that
$\tau ^* \supseteq \tau $
be an expanded language and let X be a set of first-order sentences such that
![]() $\mathbb {K}$
is the class of reducts to
$\mathbb {K}$
is the class of reducts to
![]() $\tau $
of models of
$\tau $
of models of
![]() . Note that
. Note that
![]() $\psi _1$
is a
$\psi _1$
is a
![]() -sentence.
-sentence.
Let
![]() $\psi _2$
be an
$\psi _2$
be an
![]() ${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-sentence defining
${\mathcal {L}}_{\omega _1, \omega }(\tau )$
-sentence defining
![]() $\mathbb {K}$
. We have that
$\mathbb {K}$
. We have that
![]() $\psi _1 \models \psi _2$
, so by the Interpolation Theorem, there is a
$\psi _1 \models \psi _2$
, so by the Interpolation Theorem, there is a
![]() -
-
![]() $\tau $
-sentence
$\tau $
-sentence
![]() $\theta $
such that
$\theta $
such that
![]() $\psi _1 \models \theta $
and
$\psi _1 \models \theta $
and
![]() $\theta \models \psi _2$
.
$\theta \models \psi _2$
.
Every
![]() ${\mathcal {M}} \in \mathbb {K}$
has an expansion which is a model of
${\mathcal {M}} \in \mathbb {K}$
has an expansion which is a model of
![]() $\psi _1$
and hence is itself a model of
$\psi _1$
and hence is itself a model of
![]() $\theta $
; and every model of
$\theta $
; and every model of
![]() $\theta $
is a model of
$\theta $
is a model of
![]() $\psi _2$
, and hence in the class
$\psi _2$
, and hence in the class
![]() $\mathbb {K}$
. So
$\mathbb {K}$
. So
![]() $\theta $
defines
$\theta $
defines
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
4 The Skolem argument
For the direction (2)
![]() $\Rightarrow $
(1) of Theorem 1.1, we must prove the following theorem. The proof works for sentences from
$\Rightarrow $
(1) of Theorem 1.1, we must prove the following theorem. The proof works for sentences from
![]() ${\mathcal {L}}_{\kappa ,\omega }$
for any
${\mathcal {L}}_{\kappa ,\omega }$
for any
![]() $\kappa $
, though the reader should feel free to take
$\kappa $
, though the reader should feel free to take
![]() $\kappa = \omega _1$
. (The logic
$\kappa = \omega _1$
. (The logic
![]() ${\mathcal {L}}_{\kappa ,\omega }$
is defined in the same way as
${\mathcal {L}}_{\kappa ,\omega }$
is defined in the same way as
![]() ${\mathcal {L}}_{\omega _1, \omega }$
except that we allow conjunctions and disjunctions of size
${\mathcal {L}}_{\omega _1, \omega }$
except that we allow conjunctions and disjunctions of size
![]() $< \kappa $
.)
$< \kappa $
.)
Theorem 4.1. Let
![]() $\mathbb {K}$
be a class of structures closed under isomorphism. If
$\mathbb {K}$
be a class of structures closed under isomorphism. If
![]() $\mathbb {K}$
is defined by a
$\mathbb {K}$
is defined by a
![]() -sentence of
-sentence of
![]() ${\mathcal {L}}_{\kappa ,\omega }$
, then it is a pseudo-elementary (PC
${\mathcal {L}}_{\kappa ,\omega }$
, then it is a pseudo-elementary (PC
![]() $_{\Delta }$
) class.
$_{\Delta }$
) class.
We have extended the notion of a
![]() -formula from
-formula from
![]() ${\mathcal {L}}_{\omega _1, \omega }$
to
${\mathcal {L}}_{\omega _1, \omega }$
to
![]() ${\mathcal {L}}_{\kappa , \omega }$
using the same definition (see Definition 2.4).
${\mathcal {L}}_{\kappa , \omega }$
using the same definition (see Definition 2.4).
Remark 4.2. One can extend this theorem to
![]() -theories (sets of
-theories (sets of
![]() -sentences) because every
-sentences) because every
![]() -theory can be turned into a
-theory can be turned into a
![]() -sentence by taking the conjunction, but this might change the logic. For instance, any uncountable first-order theory T is a
-sentence by taking the conjunction, but this might change the logic. For instance, any uncountable first-order theory T is a
![]() -theory in
-theory in
![]() $\mathcal {L}_{\omega _1, \omega }$
, but not a
$\mathcal {L}_{\omega _1, \omega }$
, but not a
![]() -sentence in
-sentence in
![]() $\mathcal {L}_{\omega _1,\omega }$
(this can be proved by noting the lack of countable models). Of course, T is a
$\mathcal {L}_{\omega _1,\omega }$
(this can be proved by noting the lack of countable models). Of course, T is a
![]() -sentence in
-sentence in
![]() $\mathcal {L}_{|T|^+,\omega }$
.
$\mathcal {L}_{|T|^+,\omega }$
.
Morally, the idea of the proof is to Skolemize the language to be left with a universal
![]() -theory in an expanded language, and then the infinitary conjunctions can be dropped. The main construction is the following lemma.
-theory in an expanded language, and then the infinitary conjunctions can be dropped. The main construction is the following lemma.
Lemma 4.3. Let
![]() $\varphi (\bar {x})$
be a
$\varphi (\bar {x})$
be a
![]() -formula in
-formula in
![]() ${\mathcal {L}}_{\kappa , \omega }(\tau )$
. There is an expanded language
${\mathcal {L}}_{\kappa , \omega }(\tau )$
. There is an expanded language
![]() $\tau _\varphi \supset \tau $
and a set
$\tau _\varphi \supset \tau $
and a set
![]() $\Phi (\varphi )$
of first-order
$\Phi (\varphi )$
of first-order
![]() $\tau _\varphi $
-formulas with the same free variables that verifies
$\tau _\varphi $
-formulas with the same free variables that verifies
![]() $\varphi $
in the following sense
$\varphi $
in the following sense
![]() $:$
$:$
1. Given any
 $\tau _{\varphi }$
-structure
$\tau _{\varphi }$
-structure
 ${\mathcal {A}}^+$
and
${\mathcal {A}}^+$
and
 $\bar {a} \in {\mathcal {A}}^+$
,
$\bar {a} \in {\mathcal {A}}^+$
,  $$ \begin{align*} \forall \theta \in \Phi(\varphi), {\mathcal{A}}^+ \models \theta(\bar{a}) \Longrightarrow {\mathcal{A}}^+ \models \varphi(\bar{a}).\end{align*} $$
$$ \begin{align*} \forall \theta \in \Phi(\varphi), {\mathcal{A}}^+ \models \theta(\bar{a}) \Longrightarrow {\mathcal{A}}^+ \models \varphi(\bar{a}).\end{align*} $$
2. Given any
 $\tau $
-structure
$\tau $
-structure
 ${\mathcal {A}}$
, there is an expansion
${\mathcal {A}}$
, there is an expansion
 ${\mathcal {A}}^+_\varphi $
such that for all
${\mathcal {A}}^+_\varphi $
such that for all
 $\bar {a} \in {\mathcal {A}}$
,
$\bar {a} \in {\mathcal {A}}$
,  $$ \begin{align*}{\mathcal{A}} \vDash \varphi(\bar{a}) \iff \forall \theta \in \Phi(\varphi), {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}).\end{align*} $$
$$ \begin{align*}{\mathcal{A}} \vDash \varphi(\bar{a}) \iff \forall \theta \in \Phi(\varphi), {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}).\end{align*} $$
Proof Construction: We work by induction on the formula
![]() $\varphi (\bar {x})$
. Although there is no prenex normal form for formulas of
$\varphi (\bar {x})$
. Although there is no prenex normal form for formulas of
![]() ${\mathcal {L}}_{\kappa ,\omega }$
, formulas are defined inductively. In particular, we follow the definition given for
${\mathcal {L}}_{\kappa ,\omega }$
, formulas are defined inductively. In particular, we follow the definition given for
![]() -formulas from Definition 2.4, using Remark 2.5 to assume that any finite disjunctions occur only as part of finitary, quantifier-free formulas.
-formulas from Definition 2.4, using Remark 2.5 to assume that any finite disjunctions occur only as part of finitary, quantifier-free formulas.
1.
 $\varphi (\bar {x})$
is a finitary, quantifier-free formula.
$\varphi (\bar {x})$
is a finitary, quantifier-free formula.Set
 $\tau _\varphi = \tau $
and
$\tau _\varphi = \tau $
and
 $\Phi (\varphi ) = \{\varphi (\bar {x})\}$
(in fact, this works for any finitary formula).
$\Phi (\varphi ) = \{\varphi (\bar {x})\}$
(in fact, this works for any finitary formula).2.
 $\varphi (\bar {x})$
is
$\varphi (\bar {x})$
is
 $(\exists y) \psi (\bar {x},y)$
.
$(\exists y) \psi (\bar {x},y)$
.Set
 $\tau _\varphi = \tau _\psi \cup \{f_\theta (\bar {x}) \mid \theta \in \Phi (\psi )\}$
where each
$\tau _\varphi = \tau _\psi \cup \{f_\theta (\bar {x}) \mid \theta \in \Phi (\psi )\}$
where each
 $f_\theta $
is a new function symbol, and set
$f_\theta $
is a new function symbol, and set  $$ \begin{align*}\Phi(\varphi) = \left\{\theta\left(\bar{x}, f_\theta(\bar{x})\right) \mid \theta(\bar{x}, y) \in \Phi(\psi)\right\}.\end{align*} $$
$$ \begin{align*}\Phi(\varphi) = \left\{\theta\left(\bar{x}, f_\theta(\bar{x})\right) \mid \theta(\bar{x}, y) \in \Phi(\psi)\right\}.\end{align*} $$
3.
 $\varphi (\bar {x})$
is
$\varphi (\bar {x})$
is
 $(\forall y) \psi (\bar {x}, y)$
.
$(\forall y) \psi (\bar {x}, y)$
.Set
 $\tau _\varphi = \tau _\psi $
and
$\tau _\varphi = \tau _\psi $
and  $$ \begin{align*}\Phi(\varphi) = \left\{(\forall y)\theta\left(\bar{x}, y\right) \mid \theta(\bar{x}, y) \in \Phi(\psi)\right\}\hspace{-1pt}.\end{align*} $$
$$ \begin{align*}\Phi(\varphi) = \left\{(\forall y)\theta\left(\bar{x}, y\right) \mid \theta(\bar{x}, y) \in \Phi(\psi)\right\}\hspace{-1pt}.\end{align*} $$
4.
 $\varphi (\bar {x})$
is
$\varphi (\bar {x})$
is
 .
.Set
 $\tau _\varphi = \cup _{i\in I} \tau _{\psi _i}$
where the union is disjoint over
$\tau _\varphi = \cup _{i\in I} \tau _{\psi _i}$
where the union is disjoint over
 $\tau $
; that is, new functions in
$\tau $
; that is, new functions in
 $\tau _{\psi _i}$
and
$\tau _{\psi _i}$
and
 $\tau _{\psi _j}$
are distinct in
$\tau _{\psi _j}$
are distinct in
 $\tau _\varphi $
. Then set
$\tau _\varphi $
. Then set  $$ \begin{align*}\Phi(\varphi) = \bigcup_{i\in I} \Phi(\psi_i).\end{align*} $$
$$ \begin{align*}\Phi(\varphi) = \bigcup_{i\in I} \Phi(\psi_i).\end{align*} $$
This works: We verify the construction inductively using the same cases. Is is easy to argue inductively that given any
![]() $\tau _{\varphi }$
-structure
$\tau _{\varphi }$
-structure
![]() ${\mathcal {A}}^+$
and
${\mathcal {A}}^+$
and
![]() $\bar {a} \in {\mathcal {A}}^+$
,
$\bar {a} \in {\mathcal {A}}^+$
,
1. Immediate.
2. Suppose that for all
 $\theta \in \Phi (\varphi )$
,
$\theta \in \Phi (\varphi )$
,
 ${\mathcal {A}}^+ \models \theta (\bar {a})$
. Then, for each
${\mathcal {A}}^+ \models \theta (\bar {a})$
. Then, for each
 $\theta (\bar {x},y) \in \Phi (\psi )$
,
$\theta (\bar {x},y) \in \Phi (\psi )$
,
 ${\mathcal {A}}^+ \models \theta (\bar {a},f_\theta (\bar {a}))$
. By the induction hypothesis,
${\mathcal {A}}^+ \models \theta (\bar {a},f_\theta (\bar {a}))$
. By the induction hypothesis,
 ${\mathcal {A}}^+ \models \psi (\bar {a},f_\theta (\bar {a}))$
. So
${\mathcal {A}}^+ \models \psi (\bar {a},f_\theta (\bar {a}))$
. So
 ${\mathcal {A}}^+ \models (\exists y) \psi (\bar {a},y)$
, i.e.,
${\mathcal {A}}^+ \models (\exists y) \psi (\bar {a},y)$
, i.e.,
 ${\mathcal {A}}^+ \models \varphi (\bar {a})$
.
${\mathcal {A}}^+ \models \varphi (\bar {a})$
.3. Suppose that for all
 $\theta \in \Phi (\varphi )$
,
$\theta \in \Phi (\varphi )$
,
 ${\mathcal {A}}^+ \models \theta (\bar {a})$
. Then, for each
${\mathcal {A}}^+ \models \theta (\bar {a})$
. Then, for each
 $\theta (\bar {x},y) \in \Phi (\psi )$
,
$\theta (\bar {x},y) \in \Phi (\psi )$
,
 ${\mathcal {A}}^+ \models (\forall y)\theta (\bar {a},y)$
, and so for each
${\mathcal {A}}^+ \models (\forall y)\theta (\bar {a},y)$
, and so for each
 $b \in {\mathcal {A}}^+$
,
$b \in {\mathcal {A}}^+$
,
 ${\mathcal {A}}^+ \models \theta (\bar {a},b)$
. By the induction hypothesis,
${\mathcal {A}}^+ \models \theta (\bar {a},b)$
. By the induction hypothesis,
 ${\mathcal {A}}^+ \models \psi (\bar {a},b)$
for each
${\mathcal {A}}^+ \models \psi (\bar {a},b)$
for each
 $b \in {\mathcal {A}}^+$
. So
$b \in {\mathcal {A}}^+$
. So
 ${\mathcal {A}}^+ \models (\forall y) \psi (\bar {a}y)$
, i.e.,
${\mathcal {A}}^+ \models (\forall y) \psi (\bar {a}y)$
, i.e.,
 ${\mathcal {A}}^+ \models \varphi (\bar {a})$
.
${\mathcal {A}}^+ \models \varphi (\bar {a})$
.4. Suppose that for all
 $\theta \in \Phi (\varphi )$
,
$\theta \in \Phi (\varphi )$
,
 ${\mathcal {A}}^+ \models \theta (\bar {a})$
. Then, for each
${\mathcal {A}}^+ \models \theta (\bar {a})$
. Then, for each
 $\psi _i$
and each
$\psi _i$
and each
 $\theta (\bar {x}) \in \Phi (\psi _i)$
,
$\theta (\bar {x}) \in \Phi (\psi _i)$
,
 ${\mathcal {A}}^+ \models \theta (\bar {a})$
. By the induction hypothesis,
${\mathcal {A}}^+ \models \theta (\bar {a})$
. By the induction hypothesis,
 ${\mathcal {A}}^+ \models \psi _i(\bar {a})$
for each i, and so
${\mathcal {A}}^+ \models \psi _i(\bar {a})$
for each i, and so
 ${\mathcal {A}}^+ \models \varphi (\bar {a})$
.
${\mathcal {A}}^+ \models \varphi (\bar {a})$
.
Now we will show inductively how to define
![]() ${\mathcal {A}}^+_\varphi $
and verify that
${\mathcal {A}}^+_\varphi $
and verify that
1. Immediate.
2. Fix
 ${\mathcal {A}}$
. By induction, we have an expansion
${\mathcal {A}}$
. By induction, we have an expansion
 ${\mathcal {A}}^+_\psi $
. Expand further to form
${\mathcal {A}}^+_\psi $
. Expand further to form
 ${\mathcal {A}}^+_\varphi $
by picking each
${\mathcal {A}}^+_\varphi $
by picking each
 $f_\theta $
to be a Skolem function for
$f_\theta $
to be a Skolem function for
 $\theta $
; that is, ensure
$\theta $
; that is, ensure  $$ \begin{align*}{\mathcal{A}}^+_\varphi \vDash \forall \bar{x} \left( (\exists y) \theta(\bar{x}, y) \leftrightarrow \theta(\bar{x}, f_\theta(\bar{x}))\right).\end{align*} $$
$$ \begin{align*}{\mathcal{A}}^+_\varphi \vDash \forall \bar{x} \left( (\exists y) \theta(\bar{x}, y) \leftrightarrow \theta(\bar{x}, f_\theta(\bar{x}))\right).\end{align*} $$
Then fix
 $\bar {a} \in {\mathcal {A}}$
.
$\bar {a} \in {\mathcal {A}}$
.  $$ \begin{align*} {\mathcal{A}} \vDash \varphi(\bar{a}) &\iff \exists b \in {\mathcal{A}}, \,\, {\mathcal{A}} \vDash \psi(\bar{a}, b)\\ &\iff \exists b \in {\mathcal{A}}, \, \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\psi \vDash \theta(\bar{a}, b)\\ &\iff \exists b \in {\mathcal{A}}, \, \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}, b)\\ &\iff \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}, f_\theta(\bar{a})). \end{align*} $$
$$ \begin{align*} {\mathcal{A}} \vDash \varphi(\bar{a}) &\iff \exists b \in {\mathcal{A}}, \,\, {\mathcal{A}} \vDash \psi(\bar{a}, b)\\ &\iff \exists b \in {\mathcal{A}}, \, \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\psi \vDash \theta(\bar{a}, b)\\ &\iff \exists b \in {\mathcal{A}}, \, \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}, b)\\ &\iff \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}, f_\theta(\bar{a})). \end{align*} $$
3. Fix
 ${\mathcal {A}}$
and set
${\mathcal {A}}$
and set
 ${\mathcal {A}}^+_\varphi = {\mathcal {A}}^+_\psi $
. Fix
${\mathcal {A}}^+_\varphi = {\mathcal {A}}^+_\psi $
. Fix
 $\bar {a} \in {\mathcal {A}}$
.
$\bar {a} \in {\mathcal {A}}$
.  $$ \begin{align*} {\mathcal{A}} \vDash \varphi(\bar{a}) &\iff \forall b \in {\mathcal{A}}, \,\, {\mathcal{A}} \vDash \psi(\bar{a}, b)\\ &\iff \forall b \in {\mathcal{A}}, \, \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\psi \vDash \theta(\bar{a}, b)\\ &\iff \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\varphi \vDash (\forall y) \theta (\bar{a}, y). \end{align*} $$
$$ \begin{align*} {\mathcal{A}} \vDash \varphi(\bar{a}) &\iff \forall b \in {\mathcal{A}}, \,\, {\mathcal{A}} \vDash \psi(\bar{a}, b)\\ &\iff \forall b \in {\mathcal{A}}, \, \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\psi \vDash \theta(\bar{a}, b)\\ &\iff \forall \theta \in \Phi(\psi), \,\, {\mathcal{A}}^+_\varphi \vDash (\forall y) \theta (\bar{a}, y). \end{align*} $$
4. Fix
 ${\mathcal {A}}$
and set
${\mathcal {A}}$
and set
 ${\mathcal {A}}^+_\varphi $
to be the joint expansion of all of the
${\mathcal {A}}^+_\varphi $
to be the joint expansion of all of the
 ${\mathcal {A}}^+_{\psi _i}$
’s; here we crucially use that the new functions in the different languages are distinct. Fix
${\mathcal {A}}^+_{\psi _i}$
’s; here we crucially use that the new functions in the different languages are distinct. Fix
 $\bar {a} \in {\mathcal {A}}$
.
$\bar {a} \in {\mathcal {A}}$
.  $$ \begin{align*} {\mathcal{A}} \vDash \varphi(\bar{a}) &\iff \forall i \in I, \, {\mathcal{A}} \vDash \psi_i(\bar{a})\\ &\iff \forall i \in I, \, \forall \theta \in \Phi(\psi_i), \,\, {\mathcal{A}}^+_{\psi_i} \vDash \theta(\bar{a})\\ &\iff \forall i \in I, \, \forall \theta \in \Phi(\psi_i), \,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a})\\ &\iff \forall \theta \in \bigcup_{i \in I} \Phi(\psi_i),\,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}). \end{align*} $$
$$ \begin{align*} {\mathcal{A}} \vDash \varphi(\bar{a}) &\iff \forall i \in I, \, {\mathcal{A}} \vDash \psi_i(\bar{a})\\ &\iff \forall i \in I, \, \forall \theta \in \Phi(\psi_i), \,\, {\mathcal{A}}^+_{\psi_i} \vDash \theta(\bar{a})\\ &\iff \forall i \in I, \, \forall \theta \in \Phi(\psi_i), \,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a})\\ &\iff \forall \theta \in \bigcup_{i \in I} \Phi(\psi_i),\,\, {\mathcal{A}}^+_\varphi \vDash \theta(\bar{a}). \end{align*} $$
This completes the proof.
From this lemma, the proof of the theorem is immediate.
Proof of Theorem 4.1
Let
![]() $\varphi $
be a
$\varphi $
be a
![]() -sentence of
-sentence of
![]() ${\mathcal {L}}_{\kappa ,\omega }$
. Apply Lemma 4.3 to
${\mathcal {L}}_{\kappa ,\omega }$
. Apply Lemma 4.3 to
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\varphi $
is a sentence (has no free variables),
$\varphi $
is a sentence (has no free variables),
![]() $\Phi (\varphi )$
is a collection of sentences. Then
$\Phi (\varphi )$
is a collection of sentences. Then
5 Game formulas
In this section, we show how the direction (2)
![]() $\Rightarrow $
(1) of Theorem 1.1 follows from known results on game formulas.
$\Rightarrow $
(1) of Theorem 1.1 follows from known results on game formulas.
Definition 5.1. A closed game formulaFootnote 1 is an expression of the form
where each
![]() $\varphi _n$
is an elementary first-order formula. Such a formula is computable if the sequence
$\varphi _n$
is an elementary first-order formula. Such a formula is computable if the sequence
![]() $\varphi _n$
is computable.
$\varphi _n$
is computable.
Satisfaction for such formulas is defined by a game played between two players, with player I playing the
![]() $\forall $
quantifiers and player II playing the
$\forall $
quantifiers and player II playing the
![]() $\exists $
quantifiers; player II wins, and the formulas is satisfied, if he can make
$\exists $
quantifiers; player II wins, and the formulas is satisfied, if he can make
![]() $\varphi _n(\bar {x},y_1,z_1,\ldots )$
true for every n. Alternatively, satisfaction can be defined by the existence of Skolem functions (which turn out to be the winning strategies for player II).
$\varphi _n(\bar {x},y_1,z_1,\ldots )$
true for every n. Alternatively, satisfaction can be defined by the existence of Skolem functions (which turn out to be the winning strategies for player II).
Note that each
![]() $\varphi _n$
has finitely many free variables. Also, the “closed” adjective refers to use of conjunctions in the formula.
$\varphi _n$
has finitely many free variables. Also, the “closed” adjective refers to use of conjunctions in the formula.
Every (computable)
-formula is equivalent to a (computable) closed game formula by moving all of the quantifiers to the front. In doing this, one must take care to rename bound variables so that each variable is quantified over a single time. This may seem at first to be false by a reader familiar with the fact that one cannot do this and obtain an
![]() ${\mathcal {L}}_{\omega _1, \omega }$
formula, but one can do this and obtain a closed game formula. For example,
${\mathcal {L}}_{\omega _1, \omega }$
formula, but one can do this and obtain a closed game formula. For example,
We can define the game formula inductively; for the inductive step, we have


Essentially we need to merge
![]() $\omega $
-many sequences (or quantifiers) of order type
$\omega $
-many sequences (or quantifiers) of order type
![]() $\omega $
into a single sequence of order type
$\omega $
into a single sequence of order type
![]() $\omega $
, maintaining the order of each of the individual sequences inside the amalgamated sequence.
$\omega $
, maintaining the order of each of the individual sequences inside the amalgamated sequence.
So we can get we get the direction (2)
![]() $\Rightarrow $
(1) of Theorem 1.1 as well as Theorem 1.3 as a corollaries of the following theorem.
$\Rightarrow $
(1) of Theorem 1.1 as well as Theorem 1.3 as a corollaries of the following theorem.
Theorem 5.2 Theorem 2.1.4 of [Reference Kolaitis6], Corollary 6.7 of [Reference Barwise2]
1. Any class of
 $\tau $
-structures defined by a closed game formula is
$\tau $
-structures defined by a closed game formula is
 $\operatorname {\mathrm {PC}}_\Delta $
.
$\operatorname {\mathrm {PC}}_\Delta $
.2. Any class of
 $\tau $
-structures defined by a computable closed game formula is
$\tau $
-structures defined by a computable closed game formula is
 $\operatorname {\mathrm {PC}}'$
.
$\operatorname {\mathrm {PC}}'$
.
The proof given in the previous section is, however, much simpler. Indeed, the proof in Section 4 gives a proof of the first item above because the Skolem functions for closed game formulas are still finitary functions because each stage of the game has only finitely many plays before it (and because each of the formulas
![]() $\varphi _n$
has finitely many free variables). This proof could be further generalized to consider longer games, showing that any class defined by a higher analogue of closed game formulas is
$\varphi _n$
has finitely many free variables). This proof could be further generalized to consider longer games, showing that any class defined by a higher analogue of closed game formulas is
![]() $\operatorname {\mathrm {PC}}$
in some infinitary logic
$\operatorname {\mathrm {PC}}$
in some infinitary logic
![]() ${\mathcal {L}}_{\kappa , \lambda }$
.
${\mathcal {L}}_{\kappa , \lambda }$
.
Acknowledgments
This work grew out of initial discussions with Vakili about the generality of expressing properties not definable in first-order logic in a pseudo-elementary way, and whether such phenomena might be of use for model checking (as the pseudo-elementary definability of graph reachability was used for model checking by Vakili in his thesis [Reference Vakili13] and with the third author in [Reference Vakili and Day14]). We thank one of the referees for pointing us towards some very helpful references.
Funding
The second author is partially supported by Canadian NSERC Discovery Grant. The fourth author was supported by an NSERC Banting Fellowship.