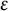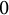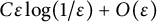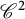Notations
In all the article,
![]() $N \in \mathbb{N}^*$
denotes the dimension of the ambient space
$N \in \mathbb{N}^*$
denotes the dimension of the ambient space
![]() $\mathbb{R}^N$
and
$\mathbb{R}^N$
and
![]() $m \in \mathbb{N}$
is an integer such that
$m \in \mathbb{N}$
is an integer such that
![]() $m\geq 2$
.
$m\geq 2$
.


1 Introduction
We consider an m-uple of probability measures
![]() $\mu _{i}$
compactly supported on sub-manifolds
$\mu _{i}$
compactly supported on sub-manifolds
![]() $X_i\subseteq \mathbb{R}^N$
of dimension
$X_i\subseteq \mathbb{R}^N$
of dimension
![]() $d_i$
and a cost function
$d_i$
and a cost function
![]() $c : X_1 \times \cdots \times X_m \to \mathbb{R}_+$
. The Entropic Multi-Marginal Optimal Transport problem is defined as
$c : X_1 \times \cdots \times X_m \to \mathbb{R}_+$
. The Entropic Multi-Marginal Optimal Transport problem is defined as
where
![]() $\Pi (\mu _1, \ldots , \mu _m)$
denotes the set of all probability measures
$\Pi (\mu _1, \ldots , \mu _m)$
denotes the set of all probability measures
![]() $\gamma $
having
$\gamma $
having
![]() $\mu _i$
as ith marginal, i.e.,
$\mu _i$
as ith marginal, i.e.,
![]() $(e_i)_\sharp \gamma = \mu _i$
, where
$(e_i)_\sharp \gamma = \mu _i$
, where
![]() $e_i : (x_1,\ldots ,x_m) \mapsto x_i$
, for every
$e_i : (x_1,\ldots ,x_m) \mapsto x_i$
, for every
![]() $i \in \{1,\ldots ,m\}$
. The classical multi-marginal optimal transport problem corresponds to the case where
$i \in \{1,\ldots ,m\}$
. The classical multi-marginal optimal transport problem corresponds to the case where
![]() ${\varepsilon =0}$
. In the last decade, these two classes of problems (entropic optimal transport (EOT) and multi-marginal optimal transport (MOT)) have witnessed a growing interest and they are now an active research topic.
${\varepsilon =0}$
. In the last decade, these two classes of problems (entropic optimal transport (EOT) and multi-marginal optimal transport (MOT)) have witnessed a growing interest and they are now an active research topic.
EOT has found applications and proved to be an efficient way to approximate optimal transport (OT) problems, especially from a computational viewpoint. Indeed, when it comes to solving EOT by alternating Kullback–Leibler projections on the two marginal constraints, by the algebraic properties of the entropy, such iterative projections correspond to the celebrated Sinkhorn’s algorithm [Reference SinkhornSin64], applied in this framework in the pioneering works [Reference Benamou, Carlier, Cuturi, Nenna and PeyréBen+15, Reference CuturiCut13]. The simplicity and the good convergence guarantees (see [Reference CarlierCar22, Reference Franklin and LorenzFL89, Reference Ghosal and NutzGN22, Reference Marino and GerolinMG20]) of this method compared to the algorithms used for the OT problems, then determined the success of EOT for applications in machine learning, statistics, image processing, language processing, and other areas (see the monograph [Reference Peyré and CuturiPC19] or the lecture notes [Reference NutzNut] and the references therein).
As concerns MOT, it arises naturally in many different areas of applications, including economics [Reference Carlier and EkelandCE10], financial mathematics [Reference Beiglböck, Henry-Labordere and PenknerBHP13, Reference Dolinsky and SonerDS14a, Reference Dolinsky and SonerDS14b, Reference Ennaji, Mérigot, Nenna and PassEnn+22], statistics [Reference Bigot and KleinBK18, Reference Carlier, Chernozhukov and GalichonCCG16], image processing [Reference Rabin, Peyré, Delon and BernotRab+11], tomography [Reference Abraham, Abraham, Bergounioux and CarlierAbr+17], machine learning [Reference Haasler, Singh, Zhang, Karlsson and ChenHaa+21, Reference Trillos, Jacobs and KimTJK22], fluid dynamics [Reference BrenierBre89], and quantum physics and chemistry, in the framework of density functional theory [Reference Buttazzo, De Pascale and Gori-GiorgiBDG12, Reference Cotar, Friesecke and KlüppelbergCFK13, Reference Friesecke, Gerolin, Gori-Giorgi, Cancès and FrieseckeFGG23]. The structure of solutions to the MOT problem is a notoriously delicate issue, and is still not well understood, despite substantial efforts on the part of many researchers [Reference CarlierCar03, Reference Colombo, De Pascale and Di MarinoCDD15, Reference Carlier and NazaretCN08, Reference Colombo and StraCS16, Reference Gangbo and ŚwięchGŚ98, Reference HeinichHei02, Reference Kim and PassKP14, Reference Kim and PassKP15, Reference Moameni and PassMP17, Reference PassPas11, Reference PassPas12, Reference Pass and Vargas-JiménezPV21a, Reference Pass and Vargas-JiménezPV21b] (see also the surveys [Reference Di Marino, Gerolin and NennaDGN17, Reference PassPas15]). Since
![]() $\mathsf{MOT}_\varepsilon $
can be seen a perturbation of
$\mathsf{MOT}_\varepsilon $
can be seen a perturbation of
![]() $\mathsf{MOT}_0$
, it is natural to study the behavior as
$\mathsf{MOT}_0$
, it is natural to study the behavior as
![]() $\varepsilon $
vanishes. In this paper, we are mainly interested in investigating the rate of convergence of the entropic cost
$\varepsilon $
vanishes. In this paper, we are mainly interested in investigating the rate of convergence of the entropic cost
![]() $\mathsf{MOT}_\varepsilon $
to
$\mathsf{MOT}_\varepsilon $
to
![]() $\mathsf{MOT}_0$
under some mild assumptions on the cost functions and marginals.
$\mathsf{MOT}_0$
under some mild assumptions on the cost functions and marginals.
In particular, we are going to extend the techniques introduced in [Reference Carlier, Pegon and TamaniniCPT23] for two marginals to the multi-marginal case which will also let us generalize the bounds in [Reference Carlier, Pegon and TamaniniCPT23] to the case of degenerate cost functions. For the two marginals and nondegenerate case, we also refer the reader to a very recent (and elegant) paper [Reference Malamut and SylvestreMS23] where the authors push a little further the analysis of the convergence rate by disentangling the roles of
![]() $\int\! \!c{\mathrm {d}}\gamma $
and the relative entropy in the total cost and deriving convergence rate for both these terms. Notice that concerning the convergence rate of the entropic MOT, an upper bound has been already established in [Reference Eckstein and NutzEN23], which depends on the number of marginals and the quantization dimension of the optimal solutions to (MOTε
) with
$\int\! \!c{\mathrm {d}}\gamma $
and the relative entropy in the total cost and deriving convergence rate for both these terms. Notice that concerning the convergence rate of the entropic MOT, an upper bound has been already established in [Reference Eckstein and NutzEN23], which depends on the number of marginals and the quantization dimension of the optimal solutions to (MOTε
) with
![]() $\varepsilon = 0$
. Here we provide an improved, smaller, upper bound, which will depend only on the marginals, but not on the OT plans for the unregularized problem, and we also provide a lower bound depending on a signature condition on the mixed second derivatives of the cost function, that was introduced in [Reference PassPas12]. The main difficulty consists in adapting the estimates of [Reference Carlier, Pegon and TamaniniCPT23] to the local structure of the optimal plans described in [Reference PassPas12].
$\varepsilon = 0$
. Here we provide an improved, smaller, upper bound, which will depend only on the marginals, but not on the OT plans for the unregularized problem, and we also provide a lower bound depending on a signature condition on the mixed second derivatives of the cost function, that was introduced in [Reference PassPas12]. The main difficulty consists in adapting the estimates of [Reference Carlier, Pegon and TamaniniCPT23] to the local structure of the optimal plans described in [Reference PassPas12].
Our main findings can be summarized as follows: we establish two upper bounds, one valid for locally Lipschitz costs and a finer one valid for locally semiconcave costs. The proofs rely, as in [Reference Carlier, Pegon and TamaniniCPT23], on a multi-marginal variant of the block approximation introduced in [Reference Carlier, Duval, Peyré and SchmitzerCar+17]. Notice that in this case the bound will depend only on the dimension of the support of the marginals. Moreover, for locally semiconcave cost functions, by exploiting Alexandrov-type results as in [Reference Carlier, Pegon and TamaniniCPT23], we improve the upper bound by a
![]() $1/2$
factor, obtaining the following inequality for some
$1/2$
factor, obtaining the following inequality for some
![]() $C^*\in \mathbb{R}_{+}$
:
$C^*\in \mathbb{R}_{+}$
:
 $$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \frac 12 \Biggl(\sum_{i=1}^m d_i-\max_{1\leq i\leq m}d_i \Biggr)\varepsilon \log(1/\varepsilon) + C^*\varepsilon.} \end{align} $$
$$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \frac 12 \Biggl(\sum_{i=1}^m d_i-\max_{1\leq i\leq m}d_i \Biggr)\varepsilon \log(1/\varepsilon) + C^*\varepsilon.} \end{align} $$
We stress that this upper bound is smaller than or equal to the one provided in [Reference Eckstein and NutzEN23, Theorem 3.8], which is of the form
![]() $\frac 12 (m-1)D \varepsilon \log (1/\varepsilon ) + O(\varepsilon )$
, where D is a quantization dimension of the support of an OT plan. Thus, D must be greater than or equal to the maximum dimension of the support of the marginals, and of course
$\frac 12 (m-1)D \varepsilon \log (1/\varepsilon ) + O(\varepsilon )$
, where D is a quantization dimension of the support of an OT plan. Thus, D must be greater than or equal to the maximum dimension of the support of the marginals, and of course
![]() $\sum _{i=1}^m d_i - \max _{1\leq i \leq m} d_i \leq (m-1) \max _{1\leq i\leq m} d_i$
. The inequality may be strict, for example, in the two marginals case with unequal dimension, as shown in Section 5.
$\sum _{i=1}^m d_i - \max _{1\leq i \leq m} d_i \leq (m-1) \max _{1\leq i\leq m} d_i$
. The inequality may be strict, for example, in the two marginals case with unequal dimension, as shown in Section 5.
For the lower bound, from the dual formulation of (MOTε ), we have
where
![]() $E(x_1,\ldots ,x_m)=c(x_1,\ldots ,x_m)- \oplus _{i=1}^m\phi _i(x_i)$
is the duality gap and
$E(x_1,\ldots ,x_m)=c(x_1,\ldots ,x_m)- \oplus _{i=1}^m\phi _i(x_i)$
is the duality gap and
![]() $(\phi _1,\ldots ,\phi _m)$
are Kantorovich potentials for the unregularized problem (MOTε
) with
$(\phi _1,\ldots ,\phi _m)$
are Kantorovich potentials for the unregularized problem (MOTε
) with
![]() $\varepsilon = 0$
. By using the singular values decomposition of the bilinear form obtained as an average of mixed second derivatives of the cost and a signature condition introduced in [Reference PassPas11], we are able to prove that E detaches quadratically from the set
$\varepsilon = 0$
. By using the singular values decomposition of the bilinear form obtained as an average of mixed second derivatives of the cost and a signature condition introduced in [Reference PassPas11], we are able to prove that E detaches quadratically from the set
![]() $\{E=0\}$
and this allows us to estimate the previous integral in the desired way as in [Reference Carlier, Pegon and TamaniniCPT23] and improve the results in [Reference Eckstein and NutzEN23] where only an upper bound depending on the quantization dimension of the solution to the unregularized problem is provided. Moreover, this slightly more flexible use of Minty’s trick compared to [Reference Carlier, Pegon and TamaniniCPT23] allows us to obtain a lower bound also for degenerate cost functions in the two marginals setting. Given a
$\{E=0\}$
and this allows us to estimate the previous integral in the desired way as in [Reference Carlier, Pegon and TamaniniCPT23] and improve the results in [Reference Eckstein and NutzEN23] where only an upper bound depending on the quantization dimension of the solution to the unregularized problem is provided. Moreover, this slightly more flexible use of Minty’s trick compared to [Reference Carlier, Pegon and TamaniniCPT23] allows us to obtain a lower bound also for degenerate cost functions in the two marginals setting. Given a
![]() $\kappa $
depending on a signature condition (see (PS(κ))) on the second mixed derivatives of the cost, the lower bound can be summarized as follows:
$\kappa $
depending on a signature condition (see (PS(κ))) on the second mixed derivatives of the cost, the lower bound can be summarized as follows:
 $$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \geq \mathsf{MOT}_0 + \frac \kappa 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon,} \end{align} $$
$$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \geq \mathsf{MOT}_0 + \frac \kappa 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon,} \end{align} $$
for some
![]() $C_*\in \mathbb{R}_+$
.
$C_*\in \mathbb{R}_+$
.
The paper is organized as follows: in Section 2, we recall the MOT problem, some results concerning the structure of the optimal solution, in particular the ones in [Reference PassPas11], and define its entropy regularization. Section 3 is devoted to the upper bounds stated in Theorems 3.1 and 3.5. In Section 4, we establish the lower bound stated in Proposition 4.2. Finally, in Section 5, we provide some examples for which we can get the matching bounds.
2 Preliminaries
Given m probability compactly supported measures
![]() $\mu _i$
on sub-manifolds
$\mu _i$
on sub-manifolds
![]() $X_i$
of dimension
$X_i$
of dimension
![]() $d_i$
in
$d_i$
in
![]() $\mathbb{R}^N$
for
$\mathbb{R}^N$
for
![]() $i\in \{1,\ldots ,m\}$
and a continuous cost function
$i\in \{1,\ldots ,m\}$
and a continuous cost function
![]() $c: X_1 \times X_2 \times \cdots \times X_m \rightarrow \mathbb{R}_+$
, the MOT problem consists in solving the following optimization problem:
$c: X_1 \times X_2 \times \cdots \times X_m \rightarrow \mathbb{R}_+$
, the MOT problem consists in solving the following optimization problem:
where ![]() and
and
![]() $\Pi (\mu _1,\ldots ,\mu _m)$
denotes the set of probability measures on
$\Pi (\mu _1,\ldots ,\mu _m)$
denotes the set of probability measures on
![]() $\boldsymbol X$
whose marginals are the
$\boldsymbol X$
whose marginals are the
![]() $\mu _i$
. The formulation above is also known as the Kantorovich problem, and it amounts to a linear minimization problem over a convex, weakly compact set; it is then not difficult to prove the existence of a solution by the direct method of calculus of variations. Much of the attention in the OT community is rather focused on uniqueness and the structure of the minimizers. In particular, one is mainly interested in determining if the solution is concentrated on the graph of a function
$\mu _i$
. The formulation above is also known as the Kantorovich problem, and it amounts to a linear minimization problem over a convex, weakly compact set; it is then not difficult to prove the existence of a solution by the direct method of calculus of variations. Much of the attention in the OT community is rather focused on uniqueness and the structure of the minimizers. In particular, one is mainly interested in determining if the solution is concentrated on the graph of a function
![]() $(T_2,\ldots ,T_m)$
over the first marginal, where
$(T_2,\ldots ,T_m)$
over the first marginal, where
![]() $(T_i)_\sharp \mu _1=\mu _i$
for
$(T_i)_\sharp \mu _1=\mu _i$
for
![]() $i\in \{1,\ldots ,m\}$
, in which case this function induces a solution à la Monge, that is,
$i\in \{1,\ldots ,m\}$
, in which case this function induces a solution à la Monge, that is,
![]() $\gamma =(\operatorname {\mathrm {Id}},T_2,\ldots ,T_m)_\sharp \mu _1$
.
$\gamma =(\operatorname {\mathrm {Id}},T_2,\ldots ,T_m)_\sharp \mu _1$
.
In the two marginals setting, the theory is fairly well understood and it is well known that under mild conditions on the cost function (e.g., twist condition) and marginals (e.g., being absolutely continuous with respect to Lebesgue), the solution to (MOT) is unique and is concentrated on the graph of a function; we refer the reader to [Reference SantambrogioSan15] to have glimpse of it. The extension to the multi-marginal case is still not well understood, but it has attracted recently a lot of attention due to a diverse variety of applications.
In particular, in his seminal works, Pass [Reference PassPas11, Reference PassPas12] established some conditions, more restrictive than in the two marginals case, to ensure the existence of a solution concentrated on a graph. In this work, we rely on the following (local) result in [Reference PassPas12] giving an upper bound on the dimension of the support of the solution to (MOT). Let P be the set of partitions of
![]() $\{1,\ldots ,m\}$
into two nonempty disjoint subsets:
$\{1,\ldots ,m\}$
into two nonempty disjoint subsets:
![]() ${p=\{p_-,p_+\}\in P}$
if
${p=\{p_-,p_+\}\in P}$
if
![]() $p_-\bigcup p_+=\{1,\ldots ,m\}$
,
$p_-\bigcup p_+=\{1,\ldots ,m\}$
,
![]() $p_-\bigcap p_+=\emptyset $
and
$p_-\bigcap p_+=\emptyset $
and
![]() $p_-,p_+\neq \emptyset $
. Then, for each
$p_-,p_+\neq \emptyset $
. Then, for each
![]() $p\in P$
, we denote by
$p\in P$
, we denote by
![]() $g_p$
the bilinear form on the tangent bundle
$g_p$
the bilinear form on the tangent bundle
![]() $T\boldsymbol X$
$T\boldsymbol X$
for every
![]() $p,q \subseteq \{1,\ldots ,m\}$
, and
$p,q \subseteq \{1,\ldots ,m\}$
, and ![]() , defined for every
, defined for every
![]() $i,j$
on the whole tangent bundle
$i,j$
on the whole tangent bundle
![]() $T \mathbf {X}$
. Define
$T \mathbf {X}$
. Define

to be the convex hull generated by the
![]() $g_p$
, then it is easy to verify that each
$g_p$
, then it is easy to verify that each
![]() $g\in G_c$
is symmetric and therefore its signature, denoted by
$g\in G_c$
is symmetric and therefore its signature, denoted by
![]() $(d^+(g),d^-(g),d^0(g))$
, is well defined. Then, the following result from [Reference PassPas12] gives a control on the dimension of the support of the optimizer(s) in terms of these signatures.
$(d^+(g),d^-(g),d^0(g))$
, is well defined. Then, the following result from [Reference PassPas12] gives a control on the dimension of the support of the optimizer(s) in terms of these signatures.
Theorem 2.1 (Part of [Reference PassPas12, Theorem 2.3])
Let
![]() $\gamma $
a solution to (MOT) and suppose that the signature of some
$\gamma $
a solution to (MOT) and suppose that the signature of some
![]() $g\in G_c$
at a point
$g\in G_c$
at a point
![]() $\boldsymbol x\in \boldsymbol X $
is
$\boldsymbol x\in \boldsymbol X $
is
![]() $(d^+,d^-,d^0)$
, that is, the number of positive, negative, and zero eigenvalues. Then, there exists a neighborhood
$(d^+,d^-,d^0)$
, that is, the number of positive, negative, and zero eigenvalues. Then, there exists a neighborhood
![]() $N_{\boldsymbol x}$
of
$N_{\boldsymbol x}$
of
![]() $\boldsymbol x$
such that
$\boldsymbol x$
such that
![]() $N_{\boldsymbol x}\bigcap \operatorname {\mathrm {spt}}{\gamma }$
is contained in a Lipschitz sub-manifold of
$N_{\boldsymbol x}\bigcap \operatorname {\mathrm {spt}}{\gamma }$
is contained in a Lipschitz sub-manifold of
![]() $\boldsymbol {X}$
with dimension no greater than
$\boldsymbol {X}$
with dimension no greater than
![]() $\sum _{i=1}^m d_i-d^{+}$
.
$\sum _{i=1}^m d_i-d^{+}$
.
Remark 2.2 For the following, it is important to notice that by standard linear algebra arguments, we have for each
![]() $g\in G_c$
that
$g\in G_c$
that
![]() $d^+(g)\leq \sum _{i=1}^m d_i-\max _id_i$
. This implies that the smallest bound on the dimension of
$d^+(g)\leq \sum _{i=1}^m d_i-\max _id_i$
. This implies that the smallest bound on the dimension of
![]() $\operatorname {\mathrm {spt}}{\gamma }$
which Theorem 2.1 can provide is
$\operatorname {\mathrm {spt}}{\gamma }$
which Theorem 2.1 can provide is
![]() $\max _i d_i$
.
$\max _i d_i$
.
Remark 2.3 (Two marginals case)
When
![]() $m=2$
, the only
$m=2$
, the only
![]() $g\in G_c$
coincides precisely with the pseudo-metric introduced by Kim and McCann in [Reference Kim and McCannKM10]. Assuming for simplicity that
$g\in G_c$
coincides precisely with the pseudo-metric introduced by Kim and McCann in [Reference Kim and McCannKM10]. Assuming for simplicity that
![]() $d_1=d_2=d$
, they noted that g has signature
$d_1=d_2=d$
, they noted that g has signature
![]() $(d,d,0)$
whenever c is nondegenerate, so Theorem 2.1 generalizes their result since it applies even when nondegeneracy fails providing new information in the two marginals case: the signature of g is
$(d,d,0)$
whenever c is nondegenerate, so Theorem 2.1 generalizes their result since it applies even when nondegeneracy fails providing new information in the two marginals case: the signature of g is
![]() $(r,r,2d-2r)$
where r is the rank of
$(r,r,2d-2r)$
where r is the rank of
![]() $D^2_{x_1 x_2}c$
. Notice that this will help us to generalize the results established in [Reference Carlier, Pegon and TamaniniCPT23, Reference Eckstein and NutzEN23] to the case of a degenerate cost function.
$D^2_{x_1 x_2}c$
. Notice that this will help us to generalize the results established in [Reference Carlier, Pegon and TamaniniCPT23, Reference Eckstein and NutzEN23] to the case of a degenerate cost function.
It is well known that under some mild assumptions, the Kantorovich problem (MOT) is dual to the following:
 $$ \begin{align} \sup\left\{ \sum_{i=1}^m\int_{X_i}\phi_i(x_i){\mathrm{d}}\mu_i \;|\;\phi_i \in \mathscr{C}_{b}(X_i),\text{ }\sum_{i=1}^m\phi_i(x^i) \leq c(x_1,\ldots,x_m)\right \}. \end{align} $$
$$ \begin{align} \sup\left\{ \sum_{i=1}^m\int_{X_i}\phi_i(x_i){\mathrm{d}}\mu_i \;|\;\phi_i \in \mathscr{C}_{b}(X_i),\text{ }\sum_{i=1}^m\phi_i(x^i) \leq c(x_1,\ldots,x_m)\right \}. \end{align} $$
Besides, it admits solutions
![]() $(\phi _i)_{1\leq i \leq m}$
, called Kantorovich potentials, when c is continuous and all the
$(\phi _i)_{1\leq i \leq m}$
, called Kantorovich potentials, when c is continuous and all the
![]() $X_i$
’s are compact, and these solutions may be assumed c-conjugate, in the sense that for every
$X_i$
’s are compact, and these solutions may be assumed c-conjugate, in the sense that for every
![]() $i \in \{1,\ldots ,m\}$
,
$i \in \{1,\ldots ,m\}$
,
We recall the entropic counterpart of (MOT): given m probability measures
![]() $\mu _i$
on
$\mu _i$
on
![]() $X_i$
as before, and a continuous cost function
$X_i$
as before, and a continuous cost function
![]() $c: \boldsymbol X \rightarrow \mathbb{R}_+$
, the
$c: \boldsymbol X \rightarrow \mathbb{R}_+$
, the
![]() $\mathsf{MOT}_\varepsilon $
problem is
$\mathsf{MOT}_\varepsilon $
problem is
where
![]() ${\mathrm {Ent}}(\cdot |\otimes _{i=1}^m \mu _i)$
is the Boltzmann–Shannon relative entropy (or Kullback–Leibler divergence) w.r.t. the product measure
${\mathrm {Ent}}(\cdot |\otimes _{i=1}^m \mu _i)$
is the Boltzmann–Shannon relative entropy (or Kullback–Leibler divergence) w.r.t. the product measure
![]() $\otimes _{i=1}^m \mu _i$
, defined for general probability measures
$\otimes _{i=1}^m \mu _i$
, defined for general probability measures
![]() $p,q$
as
$p,q$
as
 $$\begin{align*}{\mathrm{Ent}}(p \,|\, q) = \begin{cases} \displaystyle{\int_{\mathbb{R}^d} \rho \log(\rho)\, {\mathrm{d}} q}, & \text{if}\ p = \rho q,\\ +\infty, & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}{\mathrm{Ent}}(p \,|\, q) = \begin{cases} \displaystyle{\int_{\mathbb{R}^d} \rho \log(\rho)\, {\mathrm{d}} q}, & \text{if}\ p = \rho q,\\ +\infty, & \text{otherwise}. \end{cases} \end{align*}$$
The fact that q is a probability measure ensures that
![]() ${\mathrm {Ent}}(p \,|\, q) \geq 0$
. The dual problem of (MOTε
) reads as
${\mathrm {Ent}}(p \,|\, q) \geq 0$
. The dual problem of (MOTε
) reads as
 $$\begin{align} \mathsf{MOT}_\varepsilon = \varepsilon+ \sup\left\{ \sum_{i=1}^m\int_{X_i}\phi_i(x_i){\mathrm{d}}\mu_i -\varepsilon\int_{\boldsymbol X}e^{\frac{\sum_{i=1}^m\phi_i(x_i)-c(\boldsymbol x)}{\varepsilon}}{\mathrm{d}}\otimes_{i=1}^m \mu_i\;|\;\phi_i \in \mathscr{C}_{b}(X_i)\right \}, \end{align}$$
$$\begin{align} \mathsf{MOT}_\varepsilon = \varepsilon+ \sup\left\{ \sum_{i=1}^m\int_{X_i}\phi_i(x_i){\mathrm{d}}\mu_i -\varepsilon\int_{\boldsymbol X}e^{\frac{\sum_{i=1}^m\phi_i(x_i)-c(\boldsymbol x)}{\varepsilon}}{\mathrm{d}}\otimes_{i=1}^m \mu_i\;|\;\phi_i \in \mathscr{C}_{b}(X_i)\right \}, \end{align}$$
which is invariant by
![]() $(\phi _1,\ldots ,\phi _m)\mapsto (\phi _1+\lambda _1,\ldots ,\phi _m+\lambda _m)$
where
$(\phi _1,\ldots ,\phi _m)\mapsto (\phi _1+\lambda _1,\ldots ,\phi _m+\lambda _m)$
where
![]() $(\lambda _1,\ldots ,\lambda _m)\in \mathbb{R}^m$
and
$(\lambda _1,\ldots ,\lambda _m)\in \mathbb{R}^m$
and
![]() $\sum _{i=1}^m\lambda _i=0$
(see [Reference LéonardLéo14, Reference Marino and GerolinMG20, Reference Nutz and WieselNW22] for some recent presentations). It admits an equivalent “log-sum-exp” form:
$\sum _{i=1}^m\lambda _i=0$
(see [Reference LéonardLéo14, Reference Marino and GerolinMG20, Reference Nutz and WieselNW22] for some recent presentations). It admits an equivalent “log-sum-exp” form:
 $$\begin{align} \mathsf{MOT}_\varepsilon = \sup\left\{ \sum_{i=1}^m\int_{X_i}\phi_i(x_i){\mathrm{d}}\mu_i -\varepsilon\log\left(\int_{\boldsymbol X}e^{\frac{\sum_{i=1}^m\phi_i(x_i)-c(\boldsymbol x)}{\varepsilon}}{\mathrm{d}}\otimes_{i=1}^m \mu_i\right)\,|\,\phi_i \in \mathscr{C}_{b}(X_i)\right \}\kern-1pt, \end{align}$$
$$\begin{align} \mathsf{MOT}_\varepsilon = \sup\left\{ \sum_{i=1}^m\int_{X_i}\phi_i(x_i){\mathrm{d}}\mu_i -\varepsilon\log\left(\int_{\boldsymbol X}e^{\frac{\sum_{i=1}^m\phi_i(x_i)-c(\boldsymbol x)}{\varepsilon}}{\mathrm{d}}\otimes_{i=1}^m \mu_i\right)\,|\,\phi_i \in \mathscr{C}_{b}(X_i)\right \}\kern-1pt, \end{align}$$
which is invariant by the same transformations without assuming
![]() $\sum _{i=1}^m\lambda _i=0$
.
$\sum _{i=1}^m\lambda _i=0$
.
From (MOTε
) and (MDε
), we recover, as
![]() $\varepsilon \to 0$
, the unregularized multi-marginal optimal transport (MOT) and its dual (MD) we have introduced above. The link between MOT and its entropic regularization is very strong, and a consequence of the
$\varepsilon \to 0$
, the unregularized multi-marginal optimal transport (MOT) and its dual (MD) we have introduced above. The link between MOT and its entropic regularization is very strong, and a consequence of the
![]() $\Gamma $
-convergence of (MOTε
) toward (MOT) (one can adapt the proof in [Reference Carlier, Duval, Peyré and SchmitzerCar+17] or see [Reference Benamou, Carlier and NennaBCN19, Reference Gerolin, Kausamo and RajalaGKR20] for
$\Gamma $
-convergence of (MOTε
) toward (MOT) (one can adapt the proof in [Reference Carlier, Duval, Peyré and SchmitzerCar+17] or see [Reference Benamou, Carlier and NennaBCN19, Reference Gerolin, Kausamo and RajalaGKR20] for
![]() $\Gamma $
-convergence in some specific cases) is that
$\Gamma $
-convergence in some specific cases) is that
By the direct method in the calculus of variations and strict convexity of the entropy, one can show that (MOTε
) admits a unique solution
![]() $\gamma _\varepsilon $
, called optimal entropic plan. Moreover, there exist m real-valued Borel functions
$\gamma _\varepsilon $
, called optimal entropic plan. Moreover, there exist m real-valued Borel functions
![]() $\phi ^\varepsilon _i$
such that
$\phi ^\varepsilon _i$
such that
 $$ \begin{align} \gamma_\varepsilon = \exp\Bigg(\frac{ \oplus_{i=1}^m \phi^\varepsilon_i - c}{\varepsilon}\Bigg) \otimes_{i=1}^m \mu_i, \end{align} $$
$$ \begin{align} \gamma_\varepsilon = \exp\Bigg(\frac{ \oplus_{i=1}^m \phi^\varepsilon_i - c}{\varepsilon}\Bigg) \otimes_{i=1}^m \mu_i, \end{align} $$
where ![]() , and in particular we have that
, and in particular we have that
 $$ \begin{align} \mathsf{MOT}_\varepsilon = \sum_{i=1}^m \int_{X_i}\phi^\varepsilon_i\,{\mathrm{d}}\mu_i \end{align} $$
$$ \begin{align} \mathsf{MOT}_\varepsilon = \sum_{i=1}^m \int_{X_i}\phi^\varepsilon_i\,{\mathrm{d}}\mu_i \end{align} $$
and these functions have continuous representatives and are uniquely determined up a.e. to additive constants. The reader is referred to the analysis of [Reference Marino and GerolinMG20], to [Reference NennaNen16] for the extension to the multi-marginal setting, and to [Reference Borwein and LewisBL92, Reference Borwein, Lewis and NussbaumBLN94, Reference CsiszarCsi75, Reference Föllmer and GantertFG97, Reference Rüschendorf and ThomsenRT98] for earlier references on the two marginals framework.
The functions
![]() $\phi ^\varepsilon _i$
in (2.3) are called Schrödinger potentials, the terminology being motivated by the fact that they solve the dual problem (MDε
) and are as such the (unique) solutions to the so-called Schrödinger system: for all
$\phi ^\varepsilon _i$
in (2.3) are called Schrödinger potentials, the terminology being motivated by the fact that they solve the dual problem (MDε
) and are as such the (unique) solutions to the so-called Schrödinger system: for all
![]() $i\in \{1,\ldots , m\}$
,
$i\in \{1,\ldots , m\}$
,
where
![]() $\boldsymbol X_{-i} = \prod _{1\leq j\leq m,j\neq i}^m X_j$
. Note that (2.5) is a “softmin” version of the multi-marginal c-conjugacy relation for Kantorovich potentials.
$\boldsymbol X_{-i} = \prod _{1\leq j\leq m,j\neq i}^m X_j$
. Note that (2.5) is a “softmin” version of the multi-marginal c-conjugacy relation for Kantorovich potentials.
3 Upper bounds
We start by establishing an upper bound, which will depend on the dimension of the marginals, for locally Lipschitz cost functions. We will then improve it for locally semiconcave (in particular
![]() $\mathscr {C}^{2}$
) cost functions.
$\mathscr {C}^{2}$
) cost functions.
3.1 Upper bound for locally Lipschitz costs
The natural notion of dimension which arises is the entropy dimension, also called information dimension or Rényi dimension [Reference RényiRén59].
Definition 3.1 (Rényi dimension (following [Reference YoungYou82]))
If
![]() $\mu $
is a probability measure over a metric space X, we set for every
$\mu $
is a probability measure over a metric space X, we set for every
![]() $\delta> 0$
,
$\delta> 0$
,
 $$\begin{align*}H_\delta(\mu) = \inf \left\{ \sum_{n\in\mathbb{N}} \mu(A_n) \log(1/\mu(A_n)) \;|\; \forall n, \operatorname{\mathrm{diam}}(A_n) \leq \delta, \text{ and } X = \bigsqcup_{n\in \mathbb{N}} A_n\right\},\end{align*}$$
$$\begin{align*}H_\delta(\mu) = \inf \left\{ \sum_{n\in\mathbb{N}} \mu(A_n) \log(1/\mu(A_n)) \;|\; \forall n, \operatorname{\mathrm{diam}}(A_n) \leq \delta, \text{ and } X = \bigsqcup_{n\in \mathbb{N}} A_n\right\},\end{align*}$$
where the infimum is taken over countable partitions
![]() $(A_n)_{n\in \mathbb{N}}$
of X by Borel subsets of diameter less than
$(A_n)_{n\in \mathbb{N}}$
of X by Borel subsets of diameter less than
![]() $\delta $
, and we define the lower and upper entropy dimensions of
$\delta $
, and we define the lower and upper entropy dimensions of
![]() $\mu $
, respectively by
$\mu $
, respectively by

Notice that if
![]() $\mu $
is compactly supported on a Lipschitz manifold of dimension d, then
$\mu $
is compactly supported on a Lipschitz manifold of dimension d, then
![]() $N_\delta (\operatorname {\mathrm {spt}}{\mu }) \leq d\log (1/\delta ) + C$
for some constant
$N_\delta (\operatorname {\mathrm {spt}}{\mu }) \leq d\log (1/\delta ) + C$
for some constant
![]() $C> 0$
and
$C> 0$
and
![]() $\delta \in (0,1]$
, where
$\delta \in (0,1]$
, where
![]() $N_\delta (\operatorname {\mathrm {spt}}{\mu })$
is the box-counting number of
$N_\delta (\operatorname {\mathrm {spt}}{\mu })$
is the box-counting number of
![]() $\operatorname {\mathrm {spt}}{\mu }$
, i.e., the minimal number of sets of diameter
$\operatorname {\mathrm {spt}}{\mu }$
, i.e., the minimal number of sets of diameter
![]() $\delta> 0$
which cover
$\delta> 0$
which cover
![]() $\operatorname {\mathrm {spt}}{\mu }$
. In particular, by concavity of
$\operatorname {\mathrm {spt}}{\mu }$
. In particular, by concavity of
![]() $t\mapsto t\log (1/t)$
, we have
$t\mapsto t\log (1/t)$
, we have
We refer to the beginning of [Reference Carlier, Pegon and TamaniniCPT23, Section 3.1] for additional information and references on Rényi dimension.
The following theorem establishes an upper bound for locally Lipschitz costs.
Theorem 3.1 Assume that for
![]() $i \in \{1,\ldots ,m\}$
,
$i \in \{1,\ldots ,m\}$
,
![]() $\mu _i \in \mathscr {P}(X_i)$
is a compactly supported measure on a Lipschitz sub-manifold
$\mu _i \in \mathscr {P}(X_i)$
is a compactly supported measure on a Lipschitz sub-manifold
![]() $X_i$
of dimension
$X_i$
of dimension
![]() $d_i$
and
$d_i$
and
![]() $c\in \mathscr {C}^{0,1}_{\mathrm {loc}}(\boldsymbol X)$
, then
$c\in \mathscr {C}^{0,1}_{\mathrm {loc}}(\boldsymbol X)$
, then
 $$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \Biggl(\sum_{i=1}^m d_i-\max_{j\in\{1,\ldots,m\}}d_j \Biggr)\varepsilon \log(1/\varepsilon) + O(\varepsilon).} \end{align} $$
$$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \Biggl(\sum_{i=1}^m d_i-\max_{j\in\{1,\ldots,m\}}d_j \Biggr)\varepsilon \log(1/\varepsilon) + O(\varepsilon).} \end{align} $$
Proof Given an optimal plan
![]() $\gamma _0$
for
$\gamma _0$
for
![]() $\mathsf{MOT}_0$
, we use the so-called “block approximation” introduced in [Reference Carlier, Duval, Peyré and SchmitzerCar+17]. For every
$\mathsf{MOT}_0$
, we use the so-called “block approximation” introduced in [Reference Carlier, Duval, Peyré and SchmitzerCar+17]. For every
![]() $\delta> 0$
and
$\delta> 0$
and
![]() $i \in \{1,\ldots ,m\}$
, consider a partition
$i \in \{1,\ldots ,m\}$
, consider a partition
![]() $X_i = \bigsqcup _{n\in \mathbb{N}} A^n_{i}$
of Borel sets such thatFootnote
1
$X_i = \bigsqcup _{n\in \mathbb{N}} A^n_{i}$
of Borel sets such thatFootnote
1
![]() $\operatorname {\mathrm {diam}}(A^n_{i}) \leq \delta $
for every
$\operatorname {\mathrm {diam}}(A^n_{i}) \leq \delta $
for every
![]() $n\in \mathbb{N}$
, and set
$n\in \mathbb{N}$
, and set

then for every m-uple
![]() $n = (n_1,\ldots ,n_m)\in \mathbb{N}^m$
,
$n = (n_1,\ldots ,n_m)\in \mathbb{N}^m$
,
and finally,
By definition,
![]() $\gamma _\delta \ll \otimes _{i=1}^m \mu _i$
and we may check that its marginals are the
$\gamma _\delta \ll \otimes _{i=1}^m \mu _i$
and we may check that its marginals are the
![]() $\mu _i$
’s. Besides,
$\mu _i$
’s. Besides,
![]() $\gamma _\delta (\boldsymbol A) = \gamma _0(\boldsymbol A)$
for every
$\gamma _\delta (\boldsymbol A) = \gamma _0(\boldsymbol A)$
for every
![]() $\boldsymbol A = \prod _{i=1}^m A_i^{n_i}$
where
$\boldsymbol A = \prod _{i=1}^m A_i^{n_i}$
where
![]() $n \in \mathbb{N}^m$
, and for
$n \in \mathbb{N}^m$
, and for
![]() $\otimes _{i=1}^m \mu _i$
-almost every
$\otimes _{i=1}^m \mu _i$
-almost every
![]() $\boldsymbol x = (x_1,\ldots ,x_m) \in \prod _{i=1}^m A^{n_i}_i$
,
$\boldsymbol x = (x_1,\ldots ,x_m) \in \prod _{i=1}^m A^{n_i}_i$
,

Let us compute its entropy and assume for simplicity that the measure
![]() $\mu _m$
is the one such that
$\mu _m$
is the one such that
![]() $\overline \dim _R(\mu _m)=\max _{i\in \{1,\ldots ,m\}}\overline \dim (\mu _i)$
:
$\overline \dim _R(\mu _m)=\max _{i\in \{1,\ldots ,m\}}\overline \dim (\mu _i)$
:
 $$ \begin{align*} {\mathrm{Ent}}(\gamma_\delta \,|\, \otimes_{i=1}^m \mu_i) &= \sum_{n\in \mathbb{N}^m} \int_{ \prod_{i=1}^mA^{n_i}_{i}} \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_1(A^{n_1}_{1}) \ldots \mu_m(A^{n_m}_{m})}\right) {\mathrm{d}} \gamma_\delta\\ &= \sum_{n\in \mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_1(A^{n_1}_{1}) \ldots \mu_m(A^{n_m}_{m})}\right)\\ &= \sum_{n\in \mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_m(A^{n_m}_{m})}\right)\\ & \qquad\quad\quad + \sum_{j=1}^{m-1}\sum_{n\in\mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log(1/\mu_j(A^{n_j}_j))\\ &= \sum_{n\in \mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_m(A^{n_m}_{m})}\right)\\ & \qquad\ + \sum_{j=1}^{m-1}\sum_{n_j\in \mathbb{N}} \gamma_0\left(\prod_{i=1}^{j-1}X_i \times A_j^{n_j}\times \prod_{i=j+1}^m X_i\right)\mu_j(A^{n_j}_{j}) \log(1/\mu_j(A^{n_j}_{j}))\\ & \leq \sum_{j=1}^{m-1}\sum_{n_j\in \mathbb{N}}\mu_j(A^{n_j}_{j}) \log(1/\mu_j(A^{n_j}_{j})), \end{align*} $$
$$ \begin{align*} {\mathrm{Ent}}(\gamma_\delta \,|\, \otimes_{i=1}^m \mu_i) &= \sum_{n\in \mathbb{N}^m} \int_{ \prod_{i=1}^mA^{n_i}_{i}} \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_1(A^{n_1}_{1}) \ldots \mu_m(A^{n_m}_{m})}\right) {\mathrm{d}} \gamma_\delta\\ &= \sum_{n\in \mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_1(A^{n_1}_{1}) \ldots \mu_m(A^{n_m}_{m})}\right)\\ &= \sum_{n\in \mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_m(A^{n_m}_{m})}\right)\\ & \qquad\quad\quad + \sum_{j=1}^{m-1}\sum_{n\in\mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log(1/\mu_j(A^{n_j}_j))\\ &= \sum_{n\in \mathbb{N}^m} \gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m}) \log\left(\frac{\gamma_0(A^{n_1}_{1} \times\cdots\times A^{n_m}_{m})}{\mu_m(A^{n_m}_{m})}\right)\\ & \qquad\ + \sum_{j=1}^{m-1}\sum_{n_j\in \mathbb{N}} \gamma_0\left(\prod_{i=1}^{j-1}X_i \times A_j^{n_j}\times \prod_{i=j+1}^m X_i\right)\mu_j(A^{n_j}_{j}) \log(1/\mu_j(A^{n_j}_{j}))\\ & \leq \sum_{j=1}^{m-1}\sum_{n_j\in \mathbb{N}}\mu_j(A^{n_j}_{j}) \log(1/\mu_j(A^{n_j}_{j})), \end{align*} $$
the last inequality coming from the inequality
![]() $\gamma _0(A^{n_1}_{1} \times \cdots \times A^{n_m}_{m}) \leq \mu _m(A^{n_m}_{m})$
. Taking partitions
$\gamma _0(A^{n_1}_{1} \times \cdots \times A^{n_m}_{m}) \leq \mu _m(A^{n_m}_{m})$
. Taking partitions
![]() $(A^n_{j})_{n\in \mathbb{N}}$
of diameter smaller than
$(A^n_{j})_{n\in \mathbb{N}}$
of diameter smaller than
![]() $\delta $
such that
$\delta $
such that
![]() $\sum _{n_j\in \mathbb{N}} \mu _j(A_j^{n_j}) \log (1/\mu _j(A_j^{n_j})) \leq H_\delta (\mu _j) + \frac 1{m-1}$
, we get
$\sum _{n_j\in \mathbb{N}} \mu _j(A_j^{n_j}) \log (1/\mu _j(A_j^{n_j})) \leq H_\delta (\mu _j) + \frac 1{m-1}$
, we get
 $$\begin{align*}{\mathrm{Ent}}(\gamma_\delta \,|\, \otimes_{i=1}^m \mu_i) \leq \sum_{j=1}^{m-1} H_\delta(\mu_j)+1.\end{align*}$$
$$\begin{align*}{\mathrm{Ent}}(\gamma_\delta \,|\, \otimes_{i=1}^m \mu_i) \leq \sum_{j=1}^{m-1} H_\delta(\mu_j)+1.\end{align*}$$
Since the
![]() $\mu _i$
’s have compact support and c is locally Lipschitz, for
$\mu _i$
’s have compact support and c is locally Lipschitz, for
![]() $\delta $
small enough, there exists
$\delta $
small enough, there exists
![]() $L\in (0,+\infty )$
not depending on
$L\in (0,+\infty )$
not depending on
![]() $\delta $
such that
$\delta $
such that
![]() $[c]_{\mathscr {C}^{0,1}(\boldsymbol A)} \leq L$
for every
$[c]_{\mathscr {C}^{0,1}(\boldsymbol A)} \leq L$
for every ![]() . Notice that the
. Notice that the
![]() $\infty $
-Wasserstein distance (see [Reference SantambrogioSan15, Section 3.2]) with respect to the norm
$\infty $
-Wasserstein distance (see [Reference SantambrogioSan15, Section 3.2]) with respect to the norm
![]() $ \left \lVert {\cdot } \right \rVert $
Footnote
2
satisfies
$ \left \lVert {\cdot } \right \rVert $
Footnote
2
satisfies
![]() $W_\infty (\gamma _\delta ,\gamma _0) \leq \delta $
. Indeed,
$W_\infty (\gamma _\delta ,\gamma _0) \leq \delta $
. Indeed,
![]() $\operatorname {\mathrm {diam}} \boldsymbol A \leq \delta $
and
$\operatorname {\mathrm {diam}} \boldsymbol A \leq \delta $
and
![]() $\gamma _0(\boldsymbol A) = \gamma _\delta (\boldsymbol A)$
for every
$\gamma _0(\boldsymbol A) = \gamma _\delta (\boldsymbol A)$
for every
![]() $\boldsymbol A \in \mathcal A$
, so that
$\boldsymbol A \in \mathcal A$
, so that ![]() is a transport plan from
is a transport plan from
![]() $\gamma _\delta $
to
$\gamma _\delta $
to
![]() $\gamma _0$
satisfying
$\gamma _0$
satisfying
![]() $\Gamma -\operatorname *{\mbox {ess sup}}\,(\boldsymbol x,\boldsymbol {x'}) \mapsto \left \lVert {\boldsymbol {x'}-\boldsymbol {x}} \right \rVert \leq \delta $
. Thus, taking
$\Gamma -\operatorname *{\mbox {ess sup}}\,(\boldsymbol x,\boldsymbol {x'}) \mapsto \left \lVert {\boldsymbol {x'}-\boldsymbol {x}} \right \rVert \leq \delta $
. Thus, taking
![]() $\gamma _\delta $
as competitor in (MOTε
), we obtain
$\gamma _\delta $
as competitor in (MOTε
), we obtain

Taking
![]() $\delta = \varepsilon $
and recalling that the
$\delta = \varepsilon $
and recalling that the
![]() $\mu _j$
’s are concentrated on sub-manifolds of dimension
$\mu _j$
’s are concentrated on sub-manifolds of dimension
![]() $d_j$
, which implies that
$d_j$
, which implies that
![]() $H_\delta (\mu _j) \leq d_j \log (1/\delta ) + \frac {C^*-1-L}{m-1}$
for some
$H_\delta (\mu _j) \leq d_j \log (1/\delta ) + \frac {C^*-1-L}{m-1}$
for some
![]() $C^*\geq L+1$
and for every
$C^*\geq L+1$
and for every
![]() $j\in \{1,\ldots ,m\}$
, we get
$j\in \{1,\ldots ,m\}$
, we get
 $$\begin{align*}\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \left(\sum_{j\leq m-1} d_j\right) \varepsilon\log(1/\varepsilon) + C^*\varepsilon.\\[-48pt]\end{align*}$$
$$\begin{align*}\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \left(\sum_{j\leq m-1} d_j\right) \varepsilon\log(1/\varepsilon) + C^*\varepsilon.\\[-48pt]\end{align*}$$
Remark 3.2 If the
![]() $\mu _i$
’s are merely assumed to have compact support (not necessarily supported on a sub-manifold), the above proof actually shows the slightly weaker estimate
$\mu _i$
’s are merely assumed to have compact support (not necessarily supported on a sub-manifold), the above proof actually shows the slightly weaker estimate
 $$ \begin{align} {\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \Biggl(\sum_{i=1}^m \overline\dim_R(\mu_i)-\max_{j\in\{1,\ldots,m\}} \overline\dim_R(\mu_j) \Biggr)\varepsilon \log(1/\varepsilon) + o(\varepsilon\log(1/\varepsilon).} \end{align} $$
$$ \begin{align} {\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \Biggl(\sum_{i=1}^m \overline\dim_R(\mu_i)-\max_{j\in\{1,\ldots,m\}} \overline\dim_R(\mu_j) \Biggr)\varepsilon \log(1/\varepsilon) + o(\varepsilon\log(1/\varepsilon).} \end{align} $$
Indeed, for every i, by definition of ![]() , we have
, we have
![]() $\frac {H_\delta (\mu _i)}{\log (1/\delta )} \leq \sup _{0<\delta ' \leq \delta } \frac {H_{\delta '}(\mu _i)}{\log (1/\delta ')} = d_i + o(1)$
as
$\frac {H_\delta (\mu _i)}{\log (1/\delta )} \leq \sup _{0<\delta ' \leq \delta } \frac {H_{\delta '}(\mu _i)}{\log (1/\delta ')} = d_i + o(1)$
as
![]() $\delta \to 0$
; thus, taking
$\delta \to 0$
; thus, taking
![]() $\delta =\varepsilon $
as above, we have
$\delta =\varepsilon $
as above, we have
![]() $\varepsilon \frac {H_\delta (\mu _i)}{\log (1/\delta )} \log (1/\delta ) \leq (d_i+o(1))\varepsilon \log (1/\varepsilon )$
.
$\varepsilon \frac {H_\delta (\mu _i)}{\log (1/\delta )} \log (1/\delta ) \leq (d_i+o(1))\varepsilon \log (1/\varepsilon )$
.
Besides, notice that by taking
![]() $m=2$
and
$m=2$
and
![]() $d_1=d_2=d$
, one easily retrieves [Reference Carlier, Pegon and TamaniniCPT23, Proposition 3.1].
$d_1=d_2=d$
, one easily retrieves [Reference Carlier, Pegon and TamaniniCPT23, Proposition 3.1].
3.2 Upper bound for locally semiconcave costs
We provide now a finer upper bound under the additional assumptions that the
![]() $X_i$
’s are
$X_i$
’s are
![]() $\mathscr {C}^2$
sub-manifolds of
$\mathscr {C}^2$
sub-manifolds of
![]() $\mathbb{R}^N$
, c is locally semiconcave as in Definition 3.2 (which is the case when
$\mathbb{R}^N$
, c is locally semiconcave as in Definition 3.2 (which is the case when
![]() $c\in \mathscr {C}^2(\boldsymbol X,\mathbb{R}_+)$
), and the
$c\in \mathscr {C}^2(\boldsymbol X,\mathbb{R}_+)$
), and the
![]() $\mu _i$
’s are measures in
$\mu _i$
’s are measures in
![]() $L^\infty ({\mathscr H}^{d_i}_{X_i})$
with compact support in
$L^\infty ({\mathscr H}^{d_i}_{X_i})$
with compact support in
![]() $X_i$
.
$X_i$
.
Definition 3.2 A function
![]() $f : X \to \mathbb{R}$
defined on a
$f : X \to \mathbb{R}$
defined on a
![]() $\mathscr {C}^2$
sub-manifold
$\mathscr {C}^2$
sub-manifold
![]() $X \subseteq \mathbb{R}^N$
of dimension d is locally semiconcave if for every
$X \subseteq \mathbb{R}^N$
of dimension d is locally semiconcave if for every
![]() $x\in X$
there exists a local chart (i.e., a
$x\in X$
there exists a local chart (i.e., a
![]() $\mathscr {C}^2$
diffeomorphism)
$\mathscr {C}^2$
diffeomorphism)
![]() $\psi : U\to \Omega $
where
$\psi : U\to \Omega $
where
![]() $U \subseteq X$
is an open neighborhood of x and
$U \subseteq X$
is an open neighborhood of x and
![]() $\Omega $
is an open convex subset of
$\Omega $
is an open convex subset of
![]() $\mathbb{R}^d$
, such that
$\mathbb{R}^d$
, such that
![]() $f\circ {\boldsymbol \psi }^{-1}$
is
$f\circ {\boldsymbol \psi }^{-1}$
is
![]() $\lambda $
-concave for some
$\lambda $
-concave for some
![]() $\lambda \in \mathbb{R}$
, meaning
$\lambda \in \mathbb{R}$
, meaning
![]() $f\circ {\boldsymbol \psi }^{-1}- \lambda \frac { \left \lvert {\cdot } \right \rvert ^2}2$
is concave on
$f\circ {\boldsymbol \psi }^{-1}- \lambda \frac { \left \lvert {\cdot } \right \rvert ^2}2$
is concave on
![]() $\Omega $
.
$\Omega $
.
Lemma 3.3 (Local semiconcavity and covering)
Let
![]() $c : \boldsymbol X \to \mathbb{R}_+$
be a locally semiconcave cost function and
$c : \boldsymbol X \to \mathbb{R}_+$
be a locally semiconcave cost function and
![]() $(\phi _i)_{1\leq i \leq m} \in \prod _{\leq i\leq m} \mathscr {C}(K_i)$
be a system of c-conjugate functions as in (2.2) defined on compact subsets
$(\phi _i)_{1\leq i \leq m} \in \prod _{\leq i\leq m} \mathscr {C}(K_i)$
be a system of c-conjugate functions as in (2.2) defined on compact subsets
![]() $K_i\subseteq X_i$
. We can find
$K_i\subseteq X_i$
. We can find
![]() $\lambda \in \mathbb{R}, J\in \mathbb{N}^*$
and for every
$\lambda \in \mathbb{R}, J\in \mathbb{N}^*$
and for every
![]() $i\in \{ 1,\ldots , m\}$
a finite open covering
$i\in \{ 1,\ldots , m\}$
a finite open covering
![]() $(U_i^j)_{1\leq j\leq J}$
of
$(U_i^j)_{1\leq j\leq J}$
of
![]() $K_i$
together with bi-Lipschitz local charts
$K_i$
together with bi-Lipschitz local charts
![]() $\psi _i^j : U_i^j \to \Omega _i^j$
satisfying the following properties, having set
$\psi _i^j : U_i^j \to \Omega _i^j$
satisfying the following properties, having set ![]() and
and ![]() for every
for every
![]() $\boldsymbol j = (j_1, \ldots , j_m) \in \{1,\ldots ,J\}^m$
:
$\boldsymbol j = (j_1, \ldots , j_m) \in \{1,\ldots ,J\}^m$
:
-
(1) for every
 $\boldsymbol j \in \{1,\ldots ,J\}^m$
,
$\boldsymbol j \in \{1,\ldots ,J\}^m$
,
 $c \circ ({\boldsymbol \psi }^{\boldsymbol {j}})^{-1}$
is
$c \circ ({\boldsymbol \psi }^{\boldsymbol {j}})^{-1}$
is
 $\lambda $
-concave on
$\lambda $
-concave on
 $\boldsymbol \Omega ^{\boldsymbol j}$
,
$\boldsymbol \Omega ^{\boldsymbol j}$
, -
(2) for every
 $(i,j) \in \{1,\ldots , m\} \times \{1,\ldots , J\}$
,
$(i,j) \in \{1,\ldots , m\} \times \{1,\ldots , J\}$
,
 $\phi _i \circ (\psi _i^j)^{-1}$
is
$\phi _i \circ (\psi _i^j)^{-1}$
is
 $\lambda $
-concave on
$\lambda $
-concave on
 $\Omega _i^j$
.
$\Omega _i^j$
.
In particular, all the
![]() $\phi _i$
’s are locally semiconcave.
$\phi _i$
’s are locally semiconcave.
Proof For every i, by compactness of the
![]() $K_i$
’s, we can find a finite open covering
$K_i$
’s, we can find a finite open covering
![]() $(U_i^j)_{1\leq j\leq J}$
of
$(U_i^j)_{1\leq j\leq J}$
of
![]() $K_i$
and bi-Lipschitz local charts
$K_i$
and bi-Lipschitz local charts
![]() $\psi _i^j : U_i^j \to \Omega _i^j$
such that for every
$\psi _i^j : U_i^j \to \Omega _i^j$
such that for every
![]() $\boldsymbol j = (j_1, \ldots , j_m) \in \{1,\ldots , J\}^m$
,
$\boldsymbol j = (j_1, \ldots , j_m) \in \{1,\ldots , J\}^m$
,
![]() $c \circ ({\boldsymbol \psi }^{\boldsymbol {j}})^{-1} - \lambda ^{\boldsymbol {j}}\frac { \left \lvert {\cdot } \right \rvert ^2}2$
is concave for some
$c \circ ({\boldsymbol \psi }^{\boldsymbol {j}})^{-1} - \lambda ^{\boldsymbol {j}}\frac { \left \lvert {\cdot } \right \rvert ^2}2$
is concave for some
![]() $\lambda ^{\boldsymbol {j}} \in \mathbb{R}$
. We may assume that
$\lambda ^{\boldsymbol {j}} \in \mathbb{R}$
. We may assume that
![]() $\lambda ^{\boldsymbol j} = \lambda $
for every
$\lambda ^{\boldsymbol j} = \lambda $
for every
![]() $\boldsymbol {j}$
, by taking
$\boldsymbol {j}$
, by taking ![]() . Fix
. Fix
![]() $i \in \{1,\ldots ,m\}, j \in \{1,\ldots ,J\}$
, then for every
$i \in \{1,\ldots ,m\}, j \in \{1,\ldots ,J\}$
, then for every
![]() $\boldsymbol k = (k_{\ell })_{\ell \neq i} \in \{1,\ldots ,J\}^{m-1}$
, set
$\boldsymbol k = (k_{\ell })_{\ell \neq i} \in \{1,\ldots ,J\}^{m-1}$
, set
![]() $\boldsymbol {\hat k} = (k_1, \ldots , k_{i-1},j,k_{i+1}, \ldots )$
. Notice that for every
$\boldsymbol {\hat k} = (k_1, \ldots , k_{i-1},j,k_{i+1}, \ldots )$
. Notice that for every
![]() $y\in \Omega _i^j$
,
$y\in \Omega _i^j$
,
 $$ \begin{align*} \quad&\phi_i\circ(\psi_i^j)^{-1}(y)\\ &= \inf_{(x_\ell)_{\ell\neq i} \in \boldsymbol{K}_{-i}} c(x_1,\ldots, x_{i-1},(\psi_i^j)^{-1}(y),x_{i+1}, \ldots) - \sum_{\ell : \ell\neq i} \phi_\ell(x_\ell)\\ &= \min_{\boldsymbol k = (k_\ell)_{\ell\neq i}} \inf_{(y_\ell)_{\ell\neq i}\in \boldsymbol{\Omega^{\hat k}}_{-i}} c\circ ({\boldsymbol \psi}^{\boldsymbol{\hat k}})^{-1}(y_1, \ldots, y_{i-1},y,y_{i+1},\ldots) - \sum_{\ell : \ell\neq i} \phi_\ell\circ (\psi_\ell^{k_\ell})^{-1}(y_\ell), \end{align*} $$
$$ \begin{align*} \quad&\phi_i\circ(\psi_i^j)^{-1}(y)\\ &= \inf_{(x_\ell)_{\ell\neq i} \in \boldsymbol{K}_{-i}} c(x_1,\ldots, x_{i-1},(\psi_i^j)^{-1}(y),x_{i+1}, \ldots) - \sum_{\ell : \ell\neq i} \phi_\ell(x_\ell)\\ &= \min_{\boldsymbol k = (k_\ell)_{\ell\neq i}} \inf_{(y_\ell)_{\ell\neq i}\in \boldsymbol{\Omega^{\hat k}}_{-i}} c\circ ({\boldsymbol \psi}^{\boldsymbol{\hat k}})^{-1}(y_1, \ldots, y_{i-1},y,y_{i+1},\ldots) - \sum_{\ell : \ell\neq i} \phi_\ell\circ (\psi_\ell^{k_\ell})^{-1}(y_\ell), \end{align*} $$
and we see that it is
![]() $\lambda $
-concave as an infimum of
$\lambda $
-concave as an infimum of
![]() $\lambda $
-concave functions.
$\lambda $
-concave functions.
We are going to use an integral variant of Alexandrov’s theorem which is proved in [Reference Carlier, Pegon and TamaniniCPT23].
Lemma 3.4 [Reference Carlier, Pegon and TamaniniCPT23, Lemma 3.6]
Let
![]() $f : \Omega \to \mathbb{R}$
be a
$f : \Omega \to \mathbb{R}$
be a
![]() $\lambda $
-concave function defined on a convex open set
$\lambda $
-concave function defined on a convex open set
![]() $\Omega \subseteq \mathbb{R}^d$
, for some
$\Omega \subseteq \mathbb{R}^d$
, for some
![]() $\lambda \geq 0$
. There exists a constant
$\lambda \geq 0$
. There exists a constant
![]() $C \geq 0$
depending only on d such that
$C \geq 0$
depending only on d such that
 $$ \begin{align} &\int_{\Omega} \sup_{y\in B_r(x)\cap \Omega} \left\lvert {f(y) - (f(x)+ \nabla f(x) \cdot (y-x))} \right\rvert {\mathrm{d}} x \\&\quad\leq C r^2 {\mathscr H}^{d-1}(\partial \Omega) ([f]_{\mathscr{C}^{0,1}(\Omega)} + \lambda\, {\mathrm{diam}}(\Omega)). \nonumber\end{align} $$
$$ \begin{align} &\int_{\Omega} \sup_{y\in B_r(x)\cap \Omega} \left\lvert {f(y) - (f(x)+ \nabla f(x) \cdot (y-x))} \right\rvert {\mathrm{d}} x \\&\quad\leq C r^2 {\mathscr H}^{d-1}(\partial \Omega) ([f]_{\mathscr{C}^{0,1}(\Omega)} + \lambda\, {\mathrm{diam}}(\Omega)). \nonumber\end{align} $$
We may now state the main result of this section.
Theorem 3.5 Let
![]() $c\in \mathscr {C}^{2}(\boldsymbol X)$
and assume that for every
$c\in \mathscr {C}^{2}(\boldsymbol X)$
and assume that for every
![]() $i \in \{1,\ldots , m\}$
,
$i \in \{1,\ldots , m\}$
,
![]() $X_i \subseteq \mathbb{R}^N$
is a
$X_i \subseteq \mathbb{R}^N$
is a
![]() $\mathscr {C}^2$
sub-manifold of dimension
$\mathscr {C}^2$
sub-manifold of dimension
![]() $d_i$
and
$d_i$
and
![]() $\mu _i \in L^\infty ({\mathscr H}^{d_i}_{X_i})$
is a probability measure compactly supported in
$\mu _i \in L^\infty ({\mathscr H}^{d_i}_{X_i})$
is a probability measure compactly supported in
![]() $X_i$
. Then there exist constants
$X_i$
. Then there exist constants
![]() $\varepsilon _0, C^*\geq 0$
such that for
$\varepsilon _0, C^*\geq 0$
such that for
![]() $\varepsilon \in (0,\varepsilon _0]$
,
$\varepsilon \in (0,\varepsilon _0]$
,
 $$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \frac 12 \Biggl(\sum_{i=1}^m d_i-\max_{1\leq i\leq m}d_i \Biggr)\varepsilon \log(1/\varepsilon) + C^*\varepsilon.} \end{align} $$
$$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \leq \mathsf{MOT}_0 + \frac 12 \Biggl(\sum_{i=1}^m d_i-\max_{1\leq i\leq m}d_i \Biggr)\varepsilon \log(1/\varepsilon) + C^*\varepsilon.} \end{align} $$
Proof The measures
![]() $\mu _i$
being compactly supported in
$\mu _i$
being compactly supported in
![]() $X_i$
, take for every
$X_i$
, take for every
![]() $i \in \{1,\ldots ,m\}$
an open subset
$i \in \{1,\ldots ,m\}$
an open subset
![]() $U_i$
of
$U_i$
of
![]() $X_i$
such that
$X_i$
such that
![]() $\operatorname {\mathrm {spt}}{\mu _i} \subseteq U_i \Subset X_i$
and define the compact set
$\operatorname {\mathrm {spt}}{\mu _i} \subseteq U_i \Subset X_i$
and define the compact set ![]() . Take
. Take
![]() $(\phi _i)_{1\leq i \leq m} \in \prod _{1\leq i\leq m} \mathscr {C}(K_i)$
an m-uple of c-conjugate Kantorovich potentials and a transport plan
$(\phi _i)_{1\leq i \leq m} \in \prod _{1\leq i\leq m} \mathscr {C}(K_i)$
an m-uple of c-conjugate Kantorovich potentials and a transport plan
![]() $\gamma _0\in \Pi (\mu _1,\ldots ,\mu _m)$
which are optimal for the unregularized problems (MD) and (MOT), respectively. In particular,
$\gamma _0\in \Pi (\mu _1,\ldots ,\mu _m)$
which are optimal for the unregularized problems (MD) and (MOT), respectively. In particular,

For every
![]() $i \in \{1,\ldots ,m\}$
, we consider the coverings
$i \in \{1,\ldots ,m\}$
, we consider the coverings
![]() $(U_i^j)_{1\leq j\leq J}$
and bi-Lipschitz local charts
$(U_i^j)_{1\leq j\leq J}$
and bi-Lipschitz local charts
![]() $\psi _i^j : U_i^j \to \Omega _i^j$
for
$\psi _i^j : U_i^j \to \Omega _i^j$
for
![]() $j\in \{1,\ldots , J\}$
provided by Lemma 3.3 and we notice by compactness that there exist open subsets
$j\in \{1,\ldots , J\}$
provided by Lemma 3.3 and we notice by compactness that there exist open subsets
![]() $\tilde U_i^j \Subset U_i^j$
such that for a small
$\tilde U_i^j \Subset U_i^j$
such that for a small
![]() $\delta _0> 0$
, the
$\delta _0> 0$
, the
![]() $\delta _0$
-neighborhood of
$\delta _0$
-neighborhood of ![]() is included in
is included in
![]() $\Omega _i^j$
for every j, and
$\Omega _i^j$
for every j, and
![]() $(\tilde U_i^j)_{1\leq j\leq J}$
is still an open covering of
$(\tilde U_i^j)_{1\leq j\leq J}$
is still an open covering of
![]() $K_i$
. For
$K_i$
. For
![]() $\delta \in (0,\delta _0)$
, we consider the block approximation
$\delta \in (0,\delta _0)$
, we consider the block approximation
![]() $\gamma _\delta $
of
$\gamma _\delta $
of
![]() $\gamma _0$
built in the proof of Theorem 3.1, as well as some
$\gamma _0$
built in the proof of Theorem 3.1, as well as some
![]() $\kappa _\delta \in \Pi (\gamma _0,\gamma _\delta )$
such that
$\kappa _\delta \in \Pi (\gamma _0,\gamma _\delta )$
such that
![]() $\sup _{(\boldsymbol {x_0}, \boldsymbol {x})\in \operatorname {\mathrm {spt}}{\kappa _\delta }} \left \lVert {\boldsymbol {x_0}-\boldsymbol {x}} \right \rVert \leq \delta $
. For every
$\sup _{(\boldsymbol {x_0}, \boldsymbol {x})\in \operatorname {\mathrm {spt}}{\kappa _\delta }} \left \lVert {\boldsymbol {x_0}-\boldsymbol {x}} \right \rVert \leq \delta $
. For every
![]() $\boldsymbol j = (j_1,\ldots ,j_m) \in \{1,\ldots ,J\}^m$
, we set
$\boldsymbol j = (j_1,\ldots ,j_m) \in \{1,\ldots ,J\}^m$
, we set ![]() ,
, ![]() , and
, and ![]() , and we write
, and we write
 $$ \begin{align*} \int_{\boldsymbol X} c {\mathrm{d}}\gamma_\delta - \int_{\boldsymbol X} c {\mathrm{d}}\gamma_0 &= \int_{\boldsymbol U} E {\mathrm{d}}\gamma_\delta\\[3pt] &= \int_{\boldsymbol U\times \boldsymbol U} E(\boldsymbol{x}) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x})\\[3pt] &\leq \sum_{\boldsymbol j \in \{1,\ldots,J\}^m} \int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in\tilde U^{\boldsymbol{j}} \times \boldsymbol{U}} E(\boldsymbol{x}) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x})\\[3pt] &\leq \sum_{\boldsymbol j \in \{1,\ldots,J\}^m} \int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in (U^{\boldsymbol{j}})^2} E^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x}). \end{align*} $$
$$ \begin{align*} \int_{\boldsymbol X} c {\mathrm{d}}\gamma_\delta - \int_{\boldsymbol X} c {\mathrm{d}}\gamma_0 &= \int_{\boldsymbol U} E {\mathrm{d}}\gamma_\delta\\[3pt] &= \int_{\boldsymbol U\times \boldsymbol U} E(\boldsymbol{x}) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x})\\[3pt] &\leq \sum_{\boldsymbol j \in \{1,\ldots,J\}^m} \int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in\tilde U^{\boldsymbol{j}} \times \boldsymbol{U}} E(\boldsymbol{x}) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x})\\[3pt] &\leq \sum_{\boldsymbol j \in \{1,\ldots,J\}^m} \int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in (U^{\boldsymbol{j}})^2} E^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x}). \end{align*} $$
Notice that for every
![]() $\boldsymbol j \in \{1,\ldots ,J\}^m$
and
$\boldsymbol j \in \{1,\ldots ,J\}^m$
and
![]() $\gamma _0$
-a.e.
$\gamma _0$
-a.e.
![]() $\boldsymbol {x_0} \in U^{\boldsymbol j}$
,
$\boldsymbol {x_0} \in U^{\boldsymbol j}$
,
![]() $E^{\boldsymbol j}$
is differentiable at
$E^{\boldsymbol j}$
is differentiable at
![]() ${\boldsymbol \psi }^{\boldsymbol j}(\boldsymbol {x_0})$
, or equivalently E is differentiable at
${\boldsymbol \psi }^{\boldsymbol j}(\boldsymbol {x_0})$
, or equivalently E is differentiable at
![]() $\boldsymbol {x_0}$
. Indeed, c is differentiable everywhere, and for every
$\boldsymbol {x_0}$
. Indeed, c is differentiable everywhere, and for every
![]() $i \in \{1,\ldots ,m\}$
and
$i \in \{1,\ldots ,m\}$
and
![]() $j \in \{1,\ldots ,J\}$
,
$j \in \{1,\ldots ,J\}$
,
![]() $\phi _i \circ (\psi _i^j)^{-1}$
is semiconcave thus differentiable
$\phi _i \circ (\psi _i^j)^{-1}$
is semiconcave thus differentiable
![]() ${\mathscr L}^{d_i}$
-a.e.; hence,
${\mathscr L}^{d_i}$
-a.e.; hence,
![]() $\phi _i$
is differentiable
$\phi _i$
is differentiable
![]() $\mu _i$
-a.e. on
$\mu _i$
-a.e. on
![]() $U_i^j$
because
$U_i^j$
because
![]() $\mu _i \ll {\mathscr H}^{d_i}$
and
$\mu _i \ll {\mathscr H}^{d_i}$
and
![]() $\psi _i^j$
is bi-Lipschitz, which in turn implies that
$\psi _i^j$
is bi-Lipschitz, which in turn implies that
![]() $\oplus _{i=1}^m \phi _i$
is differentiable
$\oplus _{i=1}^m \phi _i$
is differentiable
![]() $\gamma _0$
-a.e. on
$\gamma _0$
-a.e. on
![]() $U^{\boldsymbol j}$
because
$U^{\boldsymbol j}$
because
![]() ${\gamma _0 \in \Pi (\mu _1,\ldots , \mu _m)}$
. Moreover, by (3.7), we have
${\gamma _0 \in \Pi (\mu _1,\ldots , \mu _m)}$
. Moreover, by (3.7), we have
![]() $T_{{\boldsymbol \psi }^{\boldsymbol j}(\boldsymbol {x_0})} E^{\boldsymbol j} \equiv 0$
for
$T_{{\boldsymbol \psi }^{\boldsymbol j}(\boldsymbol {x_0})} E^{\boldsymbol j} \equiv 0$
for
![]() $\gamma _0$
-a.e.
$\gamma _0$
-a.e.
![]() $\boldsymbol {x_0} \in U^{\boldsymbol j}$
, where
$\boldsymbol {x_0} \in U^{\boldsymbol j}$
, where
![]() $T_{y_0} f$
designates the first-order Taylor expansion
$T_{y_0} f$
designates the first-order Taylor expansion
![]() $y \mapsto f(y_0) + \nabla f(y_0)\cdot (y-y_0)$
for any function f which is differentiable at
$y \mapsto f(y_0) + \nabla f(y_0)\cdot (y-y_0)$
for any function f which is differentiable at
![]() $y_0$
. We may then compute
$y_0$
. We may then compute
 $$ \begin{align} \begin{aligned} &\qquad \int_{\boldsymbol X} c {\mathrm{d}}\gamma_\delta - \int_{\boldsymbol X} c {\mathrm{d}}\gamma_0\\[3pt] &\leq \sum_{\boldsymbol j \in \{1,\ldots, J\}^m} \int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in (U^{\boldsymbol{j}})^2} \Bigl(E^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x}))-T_{{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} E^{\boldsymbol j}\bigl({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})\bigr)\Bigr) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x})\\[3pt] &= \sum_{\boldsymbol j = (j_1,\ldots, j_m)} \left(\int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in (U^{\boldsymbol{j}})^2} \Bigl(c^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x}))-T_{{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} c^{\boldsymbol j}\bigl({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})\bigr)\Bigr) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x}) \right.\\[3pt] &\quad- \left.\sum_{i=1}^m \int_{(x_0, x) \in (U_i^{j_i})^2} \Bigl(\phi_i^{j_i}(\psi_i^{j_i}(x))-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(\psi_i^{j_i}(x)-\psi_i^{j_i}(x_0)\bigr)\Bigr){\mathrm{d}} (e_i,e_i)_\sharp \kappa_\delta(x_0,x)\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\qquad \int_{\boldsymbol X} c {\mathrm{d}}\gamma_\delta - \int_{\boldsymbol X} c {\mathrm{d}}\gamma_0\\[3pt] &\leq \sum_{\boldsymbol j \in \{1,\ldots, J\}^m} \int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in (U^{\boldsymbol{j}})^2} \Bigl(E^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x}))-T_{{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} E^{\boldsymbol j}\bigl({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})\bigr)\Bigr) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x})\\[3pt] &= \sum_{\boldsymbol j = (j_1,\ldots, j_m)} \left(\int_{(\boldsymbol{x_0}, \boldsymbol{x}) \in (U^{\boldsymbol{j}})^2} \Bigl(c^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x}))-T_{{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} c^{\boldsymbol j}\bigl({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})\bigr)\Bigr) {\mathrm{d}} \kappa_\delta(\boldsymbol{x_0},\boldsymbol{x}) \right.\\[3pt] &\quad- \left.\sum_{i=1}^m \int_{(x_0, x) \in (U_i^{j_i})^2} \Bigl(\phi_i^{j_i}(\psi_i^{j_i}(x))-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(\psi_i^{j_i}(x)-\psi_i^{j_i}(x_0)\bigr)\Bigr){\mathrm{d}} (e_i,e_i)_\sharp \kappa_\delta(x_0,x)\right). \end{aligned} \end{align} $$
Now, since
![]() $c^{\boldsymbol j}$
is
$c^{\boldsymbol j}$
is
![]() $\lambda $
-concave on each
$\lambda $
-concave on each ![]() , whenever
, whenever
![]() $ \left \lVert {\boldsymbol {x_0}-\boldsymbol {x}} \right \rVert \leq \delta $
, we have
$ \left \lVert {\boldsymbol {x_0}-\boldsymbol {x}} \right \rVert \leq \delta $
, we have
 $$ \begin{align} c^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x}))-T_{{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} c^{\boldsymbol j}\bigl({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})\bigr) \leq \lambda \frac{ \left\lvert {{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} \right\rvert ^2}2\leq \frac{m\lambda L^{\boldsymbol j}}2 \delta^2, \end{align} $$
$$ \begin{align} c^{\boldsymbol j}({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x}))-T_{{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} c^{\boldsymbol j}\bigl({\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})\bigr) \leq \lambda \frac{ \left\lvert {{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x})-{\boldsymbol \psi}^{\boldsymbol j}(\boldsymbol{x_0})} \right\rvert ^2}2\leq \frac{m\lambda L^{\boldsymbol j}}2 \delta^2, \end{align} $$
where ![]() . Besides, we may apply Lemma 3.4 to each
. Besides, we may apply Lemma 3.4 to each
![]() $\phi _i^{j_i}$
over
$\phi _i^{j_i}$
over
![]() $\Omega _i^{j_i}$
to get
$\Omega _i^{j_i}$
to get
 $$ \begin{align} \begin{aligned} \qquad& \left\lvert {\int_{(x_0, x) \in (U_i^{j_i})^2} \Bigl(\phi_i^{j_i}(\psi_i^{j_i}(x))-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(\psi_i^{j_i}(x)-\psi_i^{j_i}(x_0)\bigr)\Bigr){\mathrm{d}} (e_i,e_i)_\sharp \kappa_\delta(x_0,x)} \right\rvert \\ \leq& \int_{x_0 \in U_i^{j_i}} \sup_{y \in B_{L^{\boldsymbol j}\delta}({\psi_i^{j_i}(x_0)})\cap \Omega_i^{j_i}} \left\lvert {\phi_i^{j_i}(y)-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(y-\psi_i^{j_i}(x_0)\bigr)} \right\rvert {\mathrm{d}} (e_i,e_i)_\sharp \kappa_\delta(x_0,x)\\ =& \int_{U_i^{j_i}} \sup_{y \in B_{L^{\boldsymbol j}\delta}({\psi_i^{j_i}(x_0)})\cap \Omega_i^{j_i}} \left\lvert {\phi_i^{j_i}(y)-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(y-\psi_i^{j_i}(x_0)\bigr)} \right\rvert {\mathrm{d}} \mu_i(x_0)\\ \leq& \int_{\Omega_i^{j_i}} \sup_{y \in B_{L^{\boldsymbol j}\delta}(y_0)\cap \Omega_i^{j_i}} \left\lvert {\phi_i^{j_i}(y)-T_{y_0} \phi_i^{j_i}\bigl(y-y_0\bigr)} \right\rvert {\mathrm{d}} (\psi_i^{j_i})_\sharp \mu_i(y_0)\\ \leq & \left\lVert {\mu_i} \right\rVert _{L^\infty({\mathscr H}^{d_i})} L^{\boldsymbol j} C (L^{\boldsymbol j} \delta)^2 {\mathscr H}^{d_i-1}(\partial \Omega_i^{j_i}) \left([\phi_i^{j_i}]_{\mathscr{C}^{0,1}(\Omega_i^{j_i})} + \lambda \operatorname{\mathrm{diam}}(\Omega_i^{j_i})\right)\\ \leq& C^{\boldsymbol j} \delta^2, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \qquad& \left\lvert {\int_{(x_0, x) \in (U_i^{j_i})^2} \Bigl(\phi_i^{j_i}(\psi_i^{j_i}(x))-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(\psi_i^{j_i}(x)-\psi_i^{j_i}(x_0)\bigr)\Bigr){\mathrm{d}} (e_i,e_i)_\sharp \kappa_\delta(x_0,x)} \right\rvert \\ \leq& \int_{x_0 \in U_i^{j_i}} \sup_{y \in B_{L^{\boldsymbol j}\delta}({\psi_i^{j_i}(x_0)})\cap \Omega_i^{j_i}} \left\lvert {\phi_i^{j_i}(y)-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(y-\psi_i^{j_i}(x_0)\bigr)} \right\rvert {\mathrm{d}} (e_i,e_i)_\sharp \kappa_\delta(x_0,x)\\ =& \int_{U_i^{j_i}} \sup_{y \in B_{L^{\boldsymbol j}\delta}({\psi_i^{j_i}(x_0)})\cap \Omega_i^{j_i}} \left\lvert {\phi_i^{j_i}(y)-T_{\psi_i^{j_i}(x_0)} \phi_i^{j_i}\bigl(y-\psi_i^{j_i}(x_0)\bigr)} \right\rvert {\mathrm{d}} \mu_i(x_0)\\ \leq& \int_{\Omega_i^{j_i}} \sup_{y \in B_{L^{\boldsymbol j}\delta}(y_0)\cap \Omega_i^{j_i}} \left\lvert {\phi_i^{j_i}(y)-T_{y_0} \phi_i^{j_i}\bigl(y-y_0\bigr)} \right\rvert {\mathrm{d}} (\psi_i^{j_i})_\sharp \mu_i(y_0)\\ \leq & \left\lVert {\mu_i} \right\rVert _{L^\infty({\mathscr H}^{d_i})} L^{\boldsymbol j} C (L^{\boldsymbol j} \delta)^2 {\mathscr H}^{d_i-1}(\partial \Omega_i^{j_i}) \left([\phi_i^{j_i}]_{\mathscr{C}^{0,1}(\Omega_i^{j_i})} + \lambda \operatorname{\mathrm{diam}}(\Omega_i^{j_i})\right)\\ \leq& C^{\boldsymbol j} \delta^2, \end{aligned} \end{align} $$
for some constant
![]() $C^{\boldsymbol j} \in (0,+\infty )$
which does not depend on
$C^{\boldsymbol j} \in (0,+\infty )$
which does not depend on
![]() $\delta $
. Reporting (3.9) and (3.10) in (3.8) yields
$\delta $
. Reporting (3.9) and (3.10) in (3.8) yields

Finally, we proceed as in the end of the proof of Theorem 3.1, taking
![]() $\gamma _\delta $
as competitor in the primal formulation (MOTε
), so as to obtain
$\gamma _\delta $
as competitor in the primal formulation (MOTε
), so as to obtain
 $$ \begin{align*} \mathsf{MOT}_\varepsilon - \mathsf{MOT}_0 &\leq \int_{\boldsymbol X} c {\mathrm{d}}\gamma_\delta - \int_{\boldsymbol X} c {\mathrm{d}}\gamma_0 + \varepsilon \sum_{i\leq m-1} H_\delta(\mu_j) + \varepsilon \\ &\leq C' \delta^2 + \varepsilon \sum_{i\leq m-1} (d_i \log(1/\delta) + C"), \end{align*} $$
$$ \begin{align*} \mathsf{MOT}_\varepsilon - \mathsf{MOT}_0 &\leq \int_{\boldsymbol X} c {\mathrm{d}}\gamma_\delta - \int_{\boldsymbol X} c {\mathrm{d}}\gamma_0 + \varepsilon \sum_{i\leq m-1} H_\delta(\mu_j) + \varepsilon \\ &\leq C' \delta^2 + \varepsilon \sum_{i\leq m-1} (d_i \log(1/\delta) + C"), \end{align*} $$
where
![]() $C" \in (0,+\infty )$
is a constant such that
$C" \in (0,+\infty )$
is a constant such that
![]() $H_\delta (\mu _i) \leq d_i \log (1/\delta ) + C" -1$
. Taking
$H_\delta (\mu _i) \leq d_i \log (1/\delta ) + C" -1$
. Taking
![]() $\delta = \sqrt {\varepsilon }$
for
$\delta = \sqrt {\varepsilon }$
for
![]() $\varepsilon \leq \delta _0^2$
yields
$\varepsilon \leq \delta _0^2$
yields
 $$\begin{align*}\mathsf{MOT}_\varepsilon -\mathsf{MOT}_0 \leq \frac 12 \left(\sum_{i=1}^{m-1} d_i\right)\varepsilon\log(1/\varepsilon) + (C'+(m-1)C")\varepsilon,\end{align*}$$
$$\begin{align*}\mathsf{MOT}_\varepsilon -\mathsf{MOT}_0 \leq \frac 12 \left(\sum_{i=1}^{m-1} d_i\right)\varepsilon\log(1/\varepsilon) + (C'+(m-1)C")\varepsilon,\end{align*}$$
and we obtain the desired estimate recalling that the index
![]() $i=m$
was chosen merely to simplify notations.
$i=m$
was chosen merely to simplify notations.
4 Lower bound for
 $\mathscr {C}^2$
costs with a signature condition
$\mathscr {C}^2$
costs with a signature condition
In this section, we consider a cost
![]() $c \in \mathscr {C}^2(\boldsymbol X,\mathbb{R}_+)$
where
$c \in \mathscr {C}^2(\boldsymbol X,\mathbb{R}_+)$
where
![]() $\boldsymbol X = X_1 \times \cdots \times X_m$
and we will assume that for every
$\boldsymbol X = X_1 \times \cdots \times X_m$
and we will assume that for every
![]() $i\in \{1\ldots ,m\}$
, the measure
$i\in \{1\ldots ,m\}$
, the measure
![]() $\mu _i$
is compactly supported on a
$\mu _i$
is compactly supported on a
![]() $\mathscr {C}^2$
sub-manifold
$\mathscr {C}^2$
sub-manifold
![]() $X_i \subseteq \mathbb{R}^N$
of dimension
$X_i \subseteq \mathbb{R}^N$
of dimension
![]() $d_i$
. We are going to establish a lower bound in the same form as the fine upper bound of Theorem 3.5, the dimensional constant being this time related to the signature of some bilinear forms, following ideas from [Reference PassPas12].
$d_i$
. We are going to establish a lower bound in the same form as the fine upper bound of Theorem 3.5, the dimensional constant being this time related to the signature of some bilinear forms, following ideas from [Reference PassPas12].
Lemma 4.1 Let
![]() $c \in \mathscr {C}^2(\boldsymbol X, \mathbb{R}_+)$
and
$c \in \mathscr {C}^2(\boldsymbol X, \mathbb{R}_+)$
and
![]() $(\phi _1,\ldots , \phi _m) \in \mathscr {C}(K_1)\times \cdots \times \mathscr {C}(K_m)$
be a system of c-conjugate functions on subsets
$(\phi _1,\ldots , \phi _m) \in \mathscr {C}(K_1)\times \cdots \times \mathscr {C}(K_m)$
be a system of c-conjugate functions on subsets
![]() $K_i \subseteq X_i$
for every i. We set
$K_i \subseteq X_i$
for every i. We set ![]() on
on ![]() and we take
and we take
![]() $\boldsymbol {\bar x} \in \boldsymbol K$
as well as some
$\boldsymbol {\bar x} \in \boldsymbol K$
as well as some
![]() $g_{\boldsymbol {\bar x}} \in \{g(\boldsymbol {\bar x}) \;|\; g\in G_c\}$
of signature
$g_{\boldsymbol {\bar x}} \in \{g(\boldsymbol {\bar x}) \;|\; g\in G_c\}$
of signature
![]() $(d^+,d^-,d^0)$
,
$(d^+,d^-,d^0)$
,
![]() $G_c$
being defined in (2.1). Then there exists local coordinates around
$G_c$
being defined in (2.1). Then there exists local coordinates around
![]() $\boldsymbol {\bar x}$
, i.e.,
$\boldsymbol {\bar x}$
, i.e.,
![]() $\mathscr {C}^2$
diffeomorphisms
$\mathscr {C}^2$
diffeomorphisms
U being an open neighborhood of
![]() $\boldsymbol {\bar x}$
, such that if
$\boldsymbol {\bar x}$
, such that if
![]() $\boldsymbol x, \boldsymbol {x'} \in B_r(\boldsymbol {\bar x}) \subseteq U$
,
$\boldsymbol x, \boldsymbol {x'} \in B_r(\boldsymbol {\bar x}) \subseteq U$
,
where
![]() $\eta (r)\geq 0$
tends to
$\eta (r)\geq 0$
tends to
![]() $0$
as
$0$
as
![]() $r\to 0$
.
$r\to 0$
.
Proof Let
![]() $p = \{p_-,p_+\} \in P$
. For
$p = \{p_-,p_+\} \in P$
. For
![]() $y \in \prod _{i\in p_\pm } K_i$
, we set
$y \in \prod _{i\in p_\pm } K_i$
, we set
We identify any
![]() $\boldsymbol x \in \boldsymbol K$
with
$\boldsymbol x \in \boldsymbol K$
with
![]() $(x_{p_-},x_{p_+})$
. Since the
$(x_{p_-},x_{p_+})$
. Since the
![]() $\phi _i$
’s are c-conjugate, for
$\phi _i$
’s are c-conjugate, for
![]() $\boldsymbol x, \boldsymbol {x'} \in \mathbf K$
, it holds
$\boldsymbol x, \boldsymbol {x'} \in \mathbf K$
, it holds
 $$ \begin{align*} E(\boldsymbol{x'}) &= c(x^{\prime}_{p_-}, x^{\prime}_{p_+}) - \phi_{p_-}(x^{\prime}_{p_-}) - \phi_{p_+}(x^{\prime}_{p_+})\\ &\geq c(x_{p_-}',x_{p_+}') - (c(x_{p_-}',x_{p_+})-\phi_{p_+}(x_{p_+}))- (c(x_{p_-},x_{p_+}')-\phi_{p_-}(x_{p_-}))\\ &= c(x_{p_-}',x_{p_+}')-c(x_{p_-}',x_{p_+})-c(x_{p_-},x_{p_+}') + c(x_{p_-},x_{p_+}) - E(\boldsymbol x). \end{align*} $$
$$ \begin{align*} E(\boldsymbol{x'}) &= c(x^{\prime}_{p_-}, x^{\prime}_{p_+}) - \phi_{p_-}(x^{\prime}_{p_-}) - \phi_{p_+}(x^{\prime}_{p_+})\\ &\geq c(x_{p_-}',x_{p_+}') - (c(x_{p_-}',x_{p_+})-\phi_{p_+}(x_{p_+}))- (c(x_{p_-},x_{p_+}')-\phi_{p_-}(x_{p_-}))\\ &= c(x_{p_-}',x_{p_+}')-c(x_{p_-}',x_{p_+})-c(x_{p_-},x_{p_+}') + c(x_{p_-},x_{p_+}) - E(\boldsymbol x). \end{align*} $$
Now we do computations in local charts
![]() $\psi _i : U_i \subseteq X_i \to \psi _i(U_i) \subseteq \mathbb{R}^{d_i}$
which are
$\psi _i : U_i \subseteq X_i \to \psi _i(U_i) \subseteq \mathbb{R}^{d_i}$
which are
![]() $\mathscr {C}^2$
diffeomorphisms such that
$\mathscr {C}^2$
diffeomorphisms such that
![]() $B_R(\bar x_i) \subseteq U_i$
for some
$B_R(\bar x_i) \subseteq U_i$
for some
![]() $R> 0$
and
$R> 0$
and
![]() $\psi _i(U_i)$
are balls centered at
$\psi _i(U_i)$
are balls centered at
![]() $0$
for every
$0$
for every
![]() $i \in \{1,\ldots ,m\}$
. With a slight abuse, we use the same notation for points and functions written in these charts, and use Taylor’s integral formula:Footnote
3
$i \in \{1,\ldots ,m\}$
. With a slight abuse, we use the same notation for points and functions written in these charts, and use Taylor’s integral formula:Footnote
3
where ![]() for
for
![]() $s,t\in [0,1]$
. Since
$s,t\in [0,1]$
. Since
![]() $ \left \lvert {D^2_{p_- p_+} c(\boldsymbol x_{s,t})-D^2_{p_- p_+} c(\boldsymbol {\bar x})} \right \rvert \leq \eta (r)$
where
$ \left \lvert {D^2_{p_- p_+} c(\boldsymbol x_{s,t})-D^2_{p_- p_+} c(\boldsymbol {\bar x})} \right \rvert \leq \eta (r)$
where
![]() $\eta $
is the maximum for
$\eta $
is the maximum for
![]() $p\in P$
of the moduli of continuity of
$p\in P$
of the moduli of continuity of
![]() $D^2_{p^- p^+} c$
at
$D^2_{p^- p^+} c$
at
![]() $\boldsymbol {\bar x}$
. Since
$\boldsymbol {\bar x}$
. Since
![]() $\eta $
is independent from p and tends to
$\eta $
is independent from p and tends to
![]() $0$
as
$0$
as
![]() $r \to 0$
because c is
$r \to 0$
because c is
![]() $\mathscr {C}^2$
, and by definition
$\mathscr {C}^2$
, and by definition
![]() $D^2 c(\boldsymbol {\bar x})(x_{p_-}'-x_{p_-},x_{p_+}'-x_{p_+}) = \frac 12 g_p(\boldsymbol {\bar x})(\boldsymbol {x'}-\boldsymbol {x},\boldsymbol {x'}-\boldsymbol {x})$
, it holds
$D^2 c(\boldsymbol {\bar x})(x_{p_-}'-x_{p_-},x_{p_+}'-x_{p_+}) = \frac 12 g_p(\boldsymbol {\bar x})(\boldsymbol {x'}-\boldsymbol {x},\boldsymbol {x'}-\boldsymbol {x})$
, it holds
Taking
![]() $g_{\boldsymbol {\bar x}} = \sum _{p\in P} t_p g_p(\boldsymbol {\bar x})$
for some
$g_{\boldsymbol {\bar x}} = \sum _{p\in P} t_p g_p(\boldsymbol {\bar x})$
for some
![]() $(t_p)_{p\in P} \in \Delta _P$
and averaging the previous inequality yields
$(t_p)_{p\in P} \in \Delta _P$
and averaging the previous inequality yields
Finally, we can find a linear isomorphism
![]() $Q \in GL(\sum _{i=1}^m d_i, \mathbb{R})$
which diagonalizes
$Q \in GL(\sum _{i=1}^m d_i, \mathbb{R})$
which diagonalizes
![]() $g_{\boldsymbol {\bar x}}$
, such that after setting
$g_{\boldsymbol {\bar x}}$
, such that after setting ![]() and denoting
and denoting
![]() $u = (u^+,u^-,u^0) : \prod _{i=1}^m U_i \to \mathbb{R}^{d^+}\times \mathbb{R}^{d^-} \times \mathbb{R}^{d^0}$
, where
$u = (u^+,u^-,u^0) : \prod _{i=1}^m U_i \to \mathbb{R}^{d^+}\times \mathbb{R}^{d^-} \times \mathbb{R}^{d^0}$
, where
![]() $(d^+,d^-,d^0)$
is the signature of
$(d^+,d^-,d^0)$
is the signature of
![]() $g_{\boldsymbol {\bar x}}$
, it holds
$g_{\boldsymbol {\bar x}}$
, it holds
Reporting this in (4.2), we get the result by replacing
![]() $\eta $
with
$\eta $
with
![]() $ \left \lVert {Q} \right \rVert ^{-1}\eta $
and restricting u to
$ \left \lVert {Q} \right \rVert ^{-1}\eta $
and restricting u to ![]() for some small
for some small
![]() $\rho>0$
.
$\rho>0$
.
We will use the following positive signature condition:
Proposition 4.2 Let
![]() $c\in \mathscr {C}^{2}(\boldsymbol X)$
and assume that for every
$c\in \mathscr {C}^{2}(\boldsymbol X)$
and assume that for every
![]() $i \in \{1,\ldots , m\}$
,
$i \in \{1,\ldots , m\}$
,
![]() $X_i \subseteq \mathbb{R}^N$
is a
$X_i \subseteq \mathbb{R}^N$
is a
![]() $\mathscr {C}^2$
sub-manifold of dimension
$\mathscr {C}^2$
sub-manifold of dimension
![]() $d_i$
and
$d_i$
and
![]() $\mu _i \in L^\infty ({\mathscr H}^{d_i}_{X_i})$
is a probability measure compactly supported in
$\mu _i \in L^\infty ({\mathscr H}^{d_i}_{X_i})$
is a probability measure compactly supported in
![]() $X_i$
. If (PS(κ)) is satisfied, then there exists a constant
$X_i$
. If (PS(κ)) is satisfied, then there exists a constant
![]() $C_*\in [0,\infty )$
such that for every
$C_*\in [0,\infty )$
such that for every
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 $$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \geq \mathsf{MOT}_0 + \frac \kappa 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon.} \end{align} $$
$$ \begin{align} \boxed{\mathsf{MOT}_\varepsilon \geq \mathsf{MOT}_0 + \frac \kappa 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon.} \end{align} $$
Proof The measures
![]() $\mu _i$
being supported on some compact subsets
$\mu _i$
being supported on some compact subsets
![]() $K_i\subseteq X_i$
, consider a family
$K_i\subseteq X_i$
, consider a family
![]() $(\phi _i)_{1\leq i \leq m} \in \prod _{i=1}^m \mathscr {C}(K_i)$
of c-conjugate Kantorovich potentials. Taking
$(\phi _i)_{1\leq i \leq m} \in \prod _{i=1}^m \mathscr {C}(K_i)$
of c-conjugate Kantorovich potentials. Taking
![]() $(\phi _i)_{1\leq i \leq m}$
as competitor in (MDε
), we get the lower bound
$(\phi _i)_{1\leq i \leq m}$
as competitor in (MDε
), we get the lower bound
 $$ \begin{align*} \mathsf{MOT}_\varepsilon &\geq \sum_{i=1}^m \int_{K_i} \phi_i {\mathrm{d}}\mu_i -\varepsilon \log\left(\int_{\boldsymbol K} e^{-\frac{E}\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i\right)\\ &= \mathsf{MOT}_0-\varepsilon \log\left(\int_{\boldsymbol K} e^{-\frac{E}\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i\right), \end{align*} $$
$$ \begin{align*} \mathsf{MOT}_\varepsilon &\geq \sum_{i=1}^m \int_{K_i} \phi_i {\mathrm{d}}\mu_i -\varepsilon \log\left(\int_{\boldsymbol K} e^{-\frac{E}\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i\right)\\ &= \mathsf{MOT}_0-\varepsilon \log\left(\int_{\boldsymbol K} e^{-\frac{E}\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i\right), \end{align*} $$
where ![]() on
on
![]() $\boldsymbol {K} = \prod _{i=1}^m K_i$
as in Lemma 4.1. We are going to show that for some constant
$\boldsymbol {K} = \prod _{i=1}^m K_i$
as in Lemma 4.1. We are going to show that for some constant
![]() $C>0$
and for every
$C>0$
and for every
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
which yields (4.3) with
![]() $C_* = \log (C)$
.
$C_* = \log (C)$
.
For every
![]() $\boldsymbol {\bar x} \in \boldsymbol K$
, we consider a quadratic form
$\boldsymbol {\bar x} \in \boldsymbol K$
, we consider a quadratic form
![]() $g_{\boldsymbol {\bar x}} \in \{g(\boldsymbol {\bar x}) \;|\; g\in G_c\}$
of signature
$g_{\boldsymbol {\bar x}} \in \{g(\boldsymbol {\bar x}) \;|\; g\in G_c\}$
of signature
![]() $(\kappa , d^-, d^0)$
, which is possible thanks to (PS(κ)), and take a local chartFootnote
4
$(\kappa , d^-, d^0)$
, which is possible thanks to (PS(κ)), and take a local chartFootnote
4
as given by Lemma 4.1, such that (4.1) holds with
![]() $\eta (r) \leq 1/2$
for every r such that
$\eta (r) \leq 1/2$
for every r such that
![]() $B_r(\boldsymbol {\bar x}) \subseteq U$
. Notice that
$B_r(\boldsymbol {\bar x}) \subseteq U$
. Notice that
![]() $u_{\boldsymbol {\bar x}}$
is bi-Lipschitz with some constant
$u_{\boldsymbol {\bar x}}$
is bi-Lipschitz with some constant
![]() $L_{\boldsymbol {\bar x}}$
on
$L_{\boldsymbol {\bar x}}$
on ![]() .
.
For every
![]() $i\in \{1,\ldots ,m\}$
, we may write
$i\in \{1,\ldots ,m\}$
, we may write
![]() $\mu _i = f_i {\mathscr H}^{d_i}_{X_i}$
for some density
$\mu _i = f_i {\mathscr H}^{d_i}_{X_i}$
for some density
![]() $f_i : X_i \to \mathbb{R}_+$
. By applying several times the co-area formula [Reference Federer, Eckmann and WaerdenFed96, Theorem 3.2.22] to the projection maps onto
$f_i : X_i \to \mathbb{R}_+$
. By applying several times the co-area formula [Reference Federer, Eckmann and WaerdenFed96, Theorem 3.2.22] to the projection maps onto
![]() $X_i$
, we may justify that
$X_i$
, we may justify that
We set ![]() , and we apply the area formula
, and we apply the area formula
 $$ \begin{align*} \int_{V_{\boldsymbol{\bar x}}} & e^{-E/\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i = \int_{V_{\boldsymbol{\bar x}}} e^{-E/\varepsilon} \otimes_{i=1}^m f_i {\mathrm{d}} {\mathscr H}^d_{\boldsymbol X} \\ &= \int_{B^\kappa_{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} e^{-E_{\boldsymbol{\bar x}}/\varepsilon} \otimes_{i=1}^m f_i J u_{\boldsymbol{\bar x}}^{-1}{\mathrm{d}} {\mathscr H}^\kappa \otimes{\mathscr H}^{d^-} \otimes{\mathscr H}^{d^0}\\ &\leq L_{\boldsymbol{\bar x}} \prod_{i=1}^m \left\lVert {\mu_i} \right\rVert _{L^\infty({\mathscr H}^{d_i}_{X_i})} \int_{B^\kappa_{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} e^{-E_{\boldsymbol{\bar x}}(u^+,u^-,u^0)/\varepsilon} {\mathrm{d}} (u^+, u^-,u^0). \end{align*} $$
$$ \begin{align*} \int_{V_{\boldsymbol{\bar x}}} & e^{-E/\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i = \int_{V_{\boldsymbol{\bar x}}} e^{-E/\varepsilon} \otimes_{i=1}^m f_i {\mathrm{d}} {\mathscr H}^d_{\boldsymbol X} \\ &= \int_{B^\kappa_{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} e^{-E_{\boldsymbol{\bar x}}/\varepsilon} \otimes_{i=1}^m f_i J u_{\boldsymbol{\bar x}}^{-1}{\mathrm{d}} {\mathscr H}^\kappa \otimes{\mathscr H}^{d^-} \otimes{\mathscr H}^{d^0}\\ &\leq L_{\boldsymbol{\bar x}} \prod_{i=1}^m \left\lVert {\mu_i} \right\rVert _{L^\infty({\mathscr H}^{d_i}_{X_i})} \int_{B^\kappa_{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} e^{-E_{\boldsymbol{\bar x}}(u^+,u^-,u^0)/\varepsilon} {\mathrm{d}} (u^+, u^-,u^0). \end{align*} $$
Now, for every
![]() $(u^-,u^0) \in B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)$
, consider a minimizer of
$(u^-,u^0) \in B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)$
, consider a minimizer of
![]() $E_{\boldsymbol {\bar x}}(\cdot ,u^-,u^0)$
over
$E_{\boldsymbol {\bar x}}(\cdot ,u^-,u^0)$
over
![]() $\bar B^\kappa _{R/2}(0)$
denoted by
$\bar B^\kappa _{R/2}(0)$
denoted by
![]() $f^+(u^-,u^0)$
. By (4.1) of Lemma 4.1, for every
$f^+(u^-,u^0)$
. By (4.1) of Lemma 4.1, for every
![]() $(u^+,u^-,u^0)\in B^\kappa _{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)$
,
$(u^+,u^-,u^0)\in B^\kappa _{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)$
,
 $$ \begin{align*} E_{\boldsymbol{\bar x}}(u^+,u^-,u^0) &\geq \frac{1}{2} (E_{\boldsymbol{\bar x}}(f^+(u^-,u^0),u^-,u^0)+ E_{\boldsymbol{\bar x}}(u^+,u^-,u^0))\\ &\geq (1- 1/2) \left\lvert {u^+-f^+(u^-,u^0)} \right\rvert ^2 =\frac{1}{2} \left\lvert {u^+-f^+(u^-,u^0)} \right\rvert ^2. \end{align*} $$
$$ \begin{align*} E_{\boldsymbol{\bar x}}(u^+,u^-,u^0) &\geq \frac{1}{2} (E_{\boldsymbol{\bar x}}(f^+(u^-,u^0),u^-,u^0)+ E_{\boldsymbol{\bar x}}(u^+,u^-,u^0))\\ &\geq (1- 1/2) \left\lvert {u^+-f^+(u^-,u^0)} \right\rvert ^2 =\frac{1}{2} \left\lvert {u^+-f^+(u^-,u^0)} \right\rvert ^2. \end{align*} $$
As a consequence, we obtain
 $$ \begin{align*} &\qquad \int_{B^\kappa_{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} e^{-E_{\boldsymbol{\bar x}}(u^+,u^-,u^0)/\varepsilon} {\mathrm{d}}(u^+,u^-,u^0)\\ &\leq \int_{B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} \int_{B^\kappa_{R/2}(0)} e^{-\frac{ \left\lvert {u^+-f^+(u^-,u^0)} \right\rvert ^2}{2\varepsilon}} {\mathrm{d}} u^+ {\mathrm{d}}(u^-,u^0)\\ &\leq \varepsilon^{\kappa/2} \omega_{d^-}\omega_{d^0} R^{d^- +d^0} \int_{\mathbb{R}^\kappa} e^{- \left\lvert {u} \right\rvert ^2/2} {\mathrm{d}} u = C_{\boldsymbol{\bar x}} \varepsilon^{\kappa/2} \end{align*} $$
$$ \begin{align*} &\qquad \int_{B^\kappa_{R/2}(0) \times B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} e^{-E_{\boldsymbol{\bar x}}(u^+,u^-,u^0)/\varepsilon} {\mathrm{d}}(u^+,u^-,u^0)\\ &\leq \int_{B^{d^-}_{R/2}(0) \times B^{d^0}_{R/2}(0)} \int_{B^\kappa_{R/2}(0)} e^{-\frac{ \left\lvert {u^+-f^+(u^-,u^0)} \right\rvert ^2}{2\varepsilon}} {\mathrm{d}} u^+ {\mathrm{d}}(u^-,u^0)\\ &\leq \varepsilon^{\kappa/2} \omega_{d^-}\omega_{d^0} R^{d^- +d^0} \int_{\mathbb{R}^\kappa} e^{- \left\lvert {u} \right\rvert ^2/2} {\mathrm{d}} u = C_{\boldsymbol{\bar x}} \varepsilon^{\kappa/2} \end{align*} $$
for some constant
![]() $C_{\boldsymbol {\bar x}}> 0$
(which depends on
$C_{\boldsymbol {\bar x}}> 0$
(which depends on
![]() $\boldsymbol {\bar x}$
through R,
$\boldsymbol {\bar x}$
through R,
![]() $d^-$
, and
$d^-$
, and
![]() $d^0$
). The sets
$d^0$
). The sets
![]() $\{V_{\boldsymbol {\bar x}}\}_{\boldsymbol {\bar x}\in \boldsymbol \Sigma }$
form an open covering of the compact set
$\{V_{\boldsymbol {\bar x}}\}_{\boldsymbol {\bar x}\in \boldsymbol \Sigma }$
form an open covering of the compact set ![]() ; hence, we may extract a finite covering
; hence, we may extract a finite covering
![]() $V_{\boldsymbol {\bar x_1}}, \ldots , V_{\boldsymbol {\bar x_L}}$
and for every
$V_{\boldsymbol {\bar x_1}}, \ldots , V_{\boldsymbol {\bar x_L}}$
and for every
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
 $$\begin{align*}\int_{\bigcup_{\ell=1}^L V_{\boldsymbol{\bar x_\ell}}} e^{-E/\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i \leq \varepsilon^{\kappa/2}\Biggl(\sum_{\ell=1}^L L_{\boldsymbol{\bar x_\ell}} C_{\boldsymbol{\bar x_\ell}} \Biggr) \Biggl(\prod_{i=1}^m \left\lVert {\mu_i} \right\rVert _{L^\infty({\mathscr H}^{d_i}_{X_i})}\Biggr) = C_1 \varepsilon^{\kappa/2},\end{align*}$$
$$\begin{align*}\int_{\bigcup_{\ell=1}^L V_{\boldsymbol{\bar x_\ell}}} e^{-E/\varepsilon} {\mathrm{d}} \otimes_{i=1}^m \mu_i \leq \varepsilon^{\kappa/2}\Biggl(\sum_{\ell=1}^L L_{\boldsymbol{\bar x_\ell}} C_{\boldsymbol{\bar x_\ell}} \Biggr) \Biggl(\prod_{i=1}^m \left\lVert {\mu_i} \right\rVert _{L^\infty({\mathscr H}^{d_i}_{X_i})}\Biggr) = C_1 \varepsilon^{\kappa/2},\end{align*}$$
for some constant
![]() $C_1 \in (0,+\infty )$
. Finally, since E is continuous and does not vanish on the compact set
$C_1 \in (0,+\infty )$
. Finally, since E is continuous and does not vanish on the compact set ![]() , it is bounded from below on
, it is bounded from below on
![]() $\boldsymbol {K'}$
by some constant
$\boldsymbol {K'}$
by some constant
![]() $C_2> 0$
. Therefore, for every
$C_2> 0$
. Therefore, for every
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
for some constant
![]() $C> 0$
. This concludes the proof.
$C> 0$
. This concludes the proof.
5 Examples and matching bound
We devote this section to applying the results we have stated above to several cost functions. For simplicity, we can assume that the dimensions of the
![]() $X_i$
are all equal to some common d and the cost function c is
$X_i$
are all equal to some common d and the cost function c is
![]() $\mathscr {C}^2$
. As in [Reference PassPas12], we consider, for the lower bound, the metric
$\mathscr {C}^2$
. As in [Reference PassPas12], we consider, for the lower bound, the metric
![]() $\overline g$
such that
$\overline g$
such that
![]() $t_p=\frac {1}{2^{m-1}-1}$
for all
$t_p=\frac {1}{2^{m-1}-1}$
for all
![]() $p\in P$
, we remind that P is the set of partition of
$p\in P$
, we remind that P is the set of partition of
![]() $\{1,\ldots ,m\}$
into two nonempty disjoint subsets.
$\{1,\ldots ,m\}$
into two nonempty disjoint subsets.
Example 5.1 (Two marginals case)
In previous works [Reference Carlier, Pegon and TamaniniCPT23, Reference Eckstein and NutzEN23] concerning the rate of convergence for the two marginals problem, it was assumed that the cost function must satisfy a nondegeneracy condition, that is,
![]() $D_{x_1x_2}^2c$
must be of full rank. A direct consequence of our analysis is that we can provide a lower bound (the upper bound does not depend on such a condition) for costs for which the nondegeneracy condition fails. Let r be the rank of
$D_{x_1x_2}^2c$
must be of full rank. A direct consequence of our analysis is that we can provide a lower bound (the upper bound does not depend on such a condition) for costs for which the nondegeneracy condition fails. Let r be the rank of
![]() $D_{x_1x_2}^2 c$
at the point where the nondegeneracy condition fails, then the signature of
$D_{x_1x_2}^2 c$
at the point where the nondegeneracy condition fails, then the signature of
![]() $\overline g$
at this point is given by
$\overline g$
at this point is given by
![]() $(r,r,2d-2r)$
meaning that locally the support of the optimal
$(r,r,2d-2r)$
meaning that locally the support of the optimal
![]() $\gamma _0$
is at most (
$\gamma _0$
is at most (
![]() $2d-r$
)-dimensional. Thus, the bounds become
$2d-r$
)-dimensional. Thus, the bounds become
 $$ \begin{align*} \boxed{\frac r 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{OT}_\varepsilon - \mathsf{OT}_0 \leq \frac d 2 \varepsilon\log(1/\varepsilon) + C^*\varepsilon,} \end{align*} $$
$$ \begin{align*} \boxed{\frac r 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{OT}_\varepsilon - \mathsf{OT}_0 \leq \frac d 2 \varepsilon\log(1/\varepsilon) + C^*\varepsilon,} \end{align*} $$
for some constants
![]() $C_*,C^*>0$
. Notice that if
$C_*,C^*>0$
. Notice that if
![]() $D_{x_1,x_2}^2c$
has full rank, then
$D_{x_1,x_2}^2c$
has full rank, then
![]() $r=d$
and we retrieve the matching bound results of [Reference Carlier, Pegon and TamaniniCPT23, Reference Eckstein and NutzEN23].
$r=d$
and we retrieve the matching bound results of [Reference Carlier, Pegon and TamaniniCPT23, Reference Eckstein and NutzEN23].
Example 5.2 (Two marginals case and unequal dimension)
Consider now the two marginals case but unequal dimensional, that is, for example,
![]() $d_1>d_2$
. Then, if
$d_1>d_2$
. Then, if
![]() $D_{x_1,x_2}^2c$
has full rank, that is,
$D_{x_1,x_2}^2c$
has full rank, that is,
![]() $r=d_2$
, we obtain a matching bound depending only on the lower-dimensional marginal
$r=d_2$
, we obtain a matching bound depending only on the lower-dimensional marginal
 $$ \begin{align*} \boxed{\frac{d_{2}} {2} \varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{OT}_\varepsilon - \mathsf{OT}_0 \leq \frac{d_{2}} {2} \varepsilon\log(1/\varepsilon) + C^*\varepsilon,} \end{align*} $$
$$ \begin{align*} \boxed{\frac{d_{2}} {2} \varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{OT}_\varepsilon - \mathsf{OT}_0 \leq \frac{d_{2}} {2} \varepsilon\log(1/\varepsilon) + C^*\varepsilon,} \end{align*} $$
for some constants
![]() $C_*,C^*>0$
. If
$C_*,C^*>0$
. If
![]() $\mu _1$
is absolutely continuous with respect to
$\mu _1$
is absolutely continuous with respect to
![]() ${\mathscr H}^{d_1}$
on some smooth sub-manifold of dimension
${\mathscr H}^{d_1}$
on some smooth sub-manifold of dimension
![]() $d_1$
, then any OT plan would be concentrated on a set of Hausdorff dimension no less than
$d_1$
, then any OT plan would be concentrated on a set of Hausdorff dimension no less than
![]() $d_1$
, and thus the upper bound given in [Reference Eckstein and NutzEN23, Theorem 3.8] would be
$d_1$
, and thus the upper bound given in [Reference Eckstein and NutzEN23, Theorem 3.8] would be
![]() $\frac {d_1}2\varepsilon \log (1/\varepsilon ) + O(\varepsilon )$
, which is strictly worse than our estimate.
$\frac {d_1}2\varepsilon \log (1/\varepsilon ) + O(\varepsilon )$
, which is strictly worse than our estimate.
Example 5.3 (Negative harmonic cost)
Consider the cost
![]() $c(x_1,\ldots ,x_m)=h(\sum _{i=1}^mx_i)$
where h is
$c(x_1,\ldots ,x_m)=h(\sum _{i=1}^mx_i)$
where h is
![]() $\mathscr {C}^2$
and
$\mathscr {C}^2$
and
![]() $D^2h>0$
. Assuming that the marginals have finite second moments, when
$D^2h>0$
. Assuming that the marginals have finite second moments, when
![]() $h(x)=|x|^2$
, this kind of cost is equivalent to the harmonic negative cost that is
$h(x)=|x|^2$
, this kind of cost is equivalent to the harmonic negative cost that is
![]() $c(x_1,\ldots ,x_m)=-\sum _{i<j}|x_i-x_j|^2$
(here
$c(x_1,\ldots ,x_m)=-\sum _{i<j}|x_i-x_j|^2$
(here
![]() $|\cdot |$
denotes the standard euclidean norm) (see [Reference Di Marino, Gerolin and NennaDGN17] for more details). It follows now that the signature of the metric
$|\cdot |$
denotes the standard euclidean norm) (see [Reference Di Marino, Gerolin and NennaDGN17] for more details). It follows now that the signature of the metric
![]() $\overline g$
is
$\overline g$
is
![]() $(d,(m-1)d,0)$
; thus, the bounds between
$(d,(m-1)d,0)$
; thus, the bounds between
![]() $\mathsf{MOT}_\varepsilon $
and
$\mathsf{MOT}_\varepsilon $
and
![]() $\mathsf{MOT}_0$
that we obtain are
$\mathsf{MOT}_0$
that we obtain are
 $$ \begin{align*} \boxed{\frac d 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{MOT}_\varepsilon - \mathsf{MOT}_0 \leq \frac 1 2\Bigl((m-1)d\Bigr) \varepsilon\log(1/\varepsilon) + C^*\varepsilon,} \end{align*} $$
$$ \begin{align*} \boxed{\frac d 2 \varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{MOT}_\varepsilon - \mathsf{MOT}_0 \leq \frac 1 2\Bigl((m-1)d\Bigr) \varepsilon\log(1/\varepsilon) + C^*\varepsilon,} \end{align*} $$
for some constants
![]() $C_*,C^*>0$
. We remark that it is known from [Reference Di Marino, Gerolin and NennaDGN17, Reference PassPas12] that a transport plan
$C_*,C^*>0$
. We remark that it is known from [Reference Di Marino, Gerolin and NennaDGN17, Reference PassPas12] that a transport plan
![]() $\gamma _0$
is optimal if and only if it is supported on the set
$\gamma _0$
is optimal if and only if it is supported on the set
![]() $\{(x_1,\ldots ,x_m)\;|\;\sum _{i=1}^mx_i=l\}$
, where
$\{(x_1,\ldots ,x_m)\;|\;\sum _{i=1}^mx_i=l\}$
, where
![]() $l\in \mathbb{R}^d$
is any constant and there exist solutions whose support has dimension exactly
$l\in \mathbb{R}^d$
is any constant and there exist solutions whose support has dimension exactly
![]() $(m-1)d$
.
$(m-1)d$
.
Example 5.4 (Gangbo–Święch cost and Wasserstein barycenter)
Suppose that
![]() $c(x_1,\ldots ,x_m)=\sum _{i<j}|x_i-x_j|^2$
, known as the Gangbo–Święch cost [Reference Gangbo and ŚwięchGŚ98]. Notice that the cost is equivalent to
$c(x_1,\ldots ,x_m)=\sum _{i<j}|x_i-x_j|^2$
, known as the Gangbo–Święch cost [Reference Gangbo and ŚwięchGŚ98]. Notice that the cost is equivalent to
![]() $c(x_1,\ldots ,x_m)=h(\sum _{i=1}^m x_i)$
where h is
$c(x_1,\ldots ,x_m)=h(\sum _{i=1}^m x_i)$
where h is
![]() $\mathscr {C}^2$
and
$\mathscr {C}^2$
and
![]() $D^2h <0$
, then the signature of
$D^2h <0$
, then the signature of
![]() $\overline g$
is
$\overline g$
is
![]() $((m-1)d,d,0)$
and we have a matching bound
$((m-1)d,d,0)$
and we have a matching bound
 $$ \begin{align*} \boxed{\frac 1 2 \Bigl((m-1)d\Bigr)\varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{MOT}_\varepsilon - \mathsf{MOT}_0 \leq \frac 1 2\Bigl((m-1)d\Bigr) \varepsilon\log(1/\varepsilon) + C^*\varepsilon.} \end{align*} $$
$$ \begin{align*} \boxed{\frac 1 2 \Bigl((m-1)d\Bigr)\varepsilon\log(1/\varepsilon) - C_* \varepsilon \leq \mathsf{MOT}_\varepsilon - \mathsf{MOT}_0 \leq \frac 1 2\Bigl((m-1)d\Bigr) \varepsilon\log(1/\varepsilon) + C^*\varepsilon.} \end{align*} $$
Notice now that considering the
![]() $\mathsf{MOT}_0$
problem with a cost
$\mathsf{MOT}_0$
problem with a cost
![]() $c(x_1,\ldots ,x_m)=\sum _{i}|x_i-T(x_1,\ldots ,x_m)|^2$
, where
$c(x_1,\ldots ,x_m)=\sum _{i}|x_i-T(x_1,\ldots ,x_m)|^2$
, where
![]() $T(x_1,\ldots ,x_m)=\sum _{i=1}^m\lambda _ix_i$
is the Euclidean barycenter, is equivalent to the
$T(x_1,\ldots ,x_m)=\sum _{i=1}^m\lambda _ix_i$
is the Euclidean barycenter, is equivalent to the
![]() $\mathsf{MOT}_0$
with the Gangbo–Święch cost and the matching bound above still holds. Moreover, the multi-marginal problem with this particular cost has been shown [Reference Agueh and CarlierAC11] to be equivalent to the Wasserstein barycenter, that is,
$\mathsf{MOT}_0$
with the Gangbo–Święch cost and the matching bound above still holds. Moreover, the multi-marginal problem with this particular cost has been shown [Reference Agueh and CarlierAC11] to be equivalent to the Wasserstein barycenter, that is,
![]() $T_\sharp \gamma _0=\nu $
is the barycenter of
$T_\sharp \gamma _0=\nu $
is the barycenter of
![]() $\mu _1,\ldots ,\mu _m$
.
$\mu _1,\ldots ,\mu _m$
.