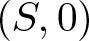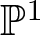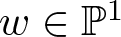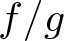1. Introduction
Let
$(S,0)$ be a germ of reduced complex surface and call 
$\mathcal{O}_{S,0}$ its local ring of holomorphic functions. Consider two holomorphic functions f and g in 
$\mathcal{O}_{S,0}$ such that the ideal 
$I= \langle f,g \rangle $ is primary for the maximal ideal 
$ \mathfrak{m} $ of 
$\mathcal{O}_{S,0}$. The pencil 
$\Lambda_{f,g}$ generated by f and g on a representative S of 
$(S,0)$ is the family of curves λw defined on S by the functions 
$\beta f - \alpha g $, where 
$[\alpha : \beta] = w \in \mathbb{P}^1$.
We are interested in characterizing the values 
$w\in \mathbb{P}^1$ for which the curve λw does not have the generic topological behaviour.
This study has been done in the case of pencils of curves on 
$\mathbb{C}^2$ by Lê and Weber in [Reference Lê and C.13]. That work is highly related to the Jacobian conjecture in the complex plane. They express the genericity of the topological type in terms of the minimality of the Milnor number, and they characterize the values for which the Milnor number of λw is not minimal. They start by constructing a resolution of the pencil, which consists of removing the indeterminacy of the meromorphic map 
$f/g$ by a sequence of point blow-ups. Then, they show that the special curves of the pencil are precisely those curves whose strict transform in the resolution contains some special points; they call them ‘special values’ of the pencil.
Still in the case of pencils in the complex plane, Maugendre and Delgado gave in [Reference Delgado and H.5] a characterization of the special values in terms of the discriminant locus of the finite map 
$\pi :=(f,g): (S,0)\rightarrow (\mathbb{C}^2,0)$ associated with the pencil. More precisely, 
$w\in \mathbb{P}^1$ is special if and only if the line of 
$\mathbb{C}^2$ corresponding to w is tangent to the discriminant locus of π. Later on, in [Reference Delgado and Maugendre6], the same authors generalize this characterization to pencils on normal surfaces. They also give a description of the special values from the minimal resolution of the pencil, in the style of [Reference Lê and C.13].
Bondil and Lê studied in [Reference Bondil and D. T.1] families of curves on normal surfaces. Their results apply for pencils and give a description of the special values.
In the present paper, we consider the case of pencils on germs of reduced complex surfaces. In other words, we allow the surface to have non-isolated singularities and to be non Cohen Macaulay. We proceed to explore the impact of these two allowed phenomena on the topology of elements of pencils of curves.
For a pencil 
$\Lambda_{f,g}$ on a reduced complex surface S, we will proceed as in [Reference Bondil and D. T.1], [Reference Snoussi18] and [Reference Snoussi19] and construct the blow-up 
$e_I: S_I \rightarrow S$ of the ideal I generated by f and g. This modification removes the indeterminacy of the quotient map 
$h:=f/g$. Therefore, we obtain a basepoint-free family of curves with a well-defined map to 
$\mathbb{P}^1$. For 
$w\in \mathbb{P}^1$, the curve λw does not have the generic topological behaviour if and only if the family of curves 
$\frac{f\circ e_I}{g\circ e_I}: S_I \rightarrow \mathbb{P}^1$ is not topologically trivial at 
$(0,w)$.
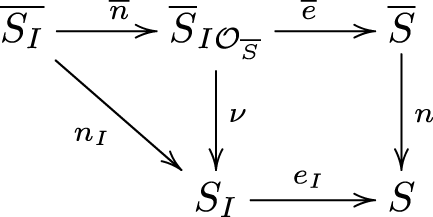
Naturally, the normalization 
$n: (\overline{S}, \overline{0}) \rightarrow (S,0)$ gives rise to pencils 
$\Lambda_{f\circ n, g\circ n}$ on each germ of the multi-germ of normal surface 
$(\overline{S}, \overline{0})$. By blowing-up the ideal 
$I\mathcal{O}_{\overline{S}, \overline{0}}=\langle f\circ n,g\circ n\rangle$, we obtain the following commutative diagram:
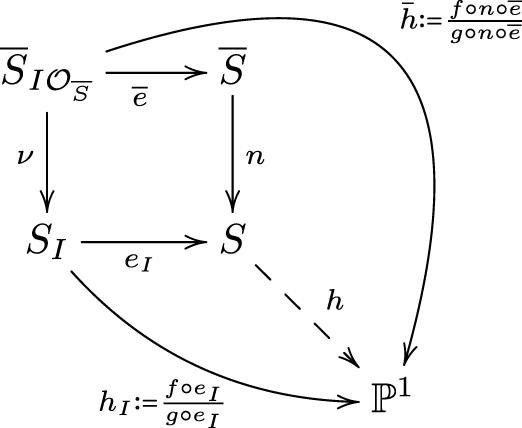
This diagram will allow us to compare the topology of the curves in S with the one in 
$ \overline{S} $ and the family of curves in SI with the one in 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$.
Our main result, stated in Theorem 4.1, says that the topology of an element λw of the pencil on S is different from the generic one if and only if either the corresponding curve in the normalized surface 
$\overline{S}$ does not have the generic topology or the point 
$(0,w)$ of SI belongs to the strict transform of the singular locus of S by eI.
This result gives a complete characterization of curves with non generic topology, for pencils on reduced complex surfaces. Indeed, we know how to characterize non-generic curves of a pencil on a normal surface, and we know that points 
$(0, w)$ of the strict transform of the singular locus of S by eI correspond to limit values of 
$f/g$ at 0 along a component of the singular locus of the surface S.
As a direct consequence of our result, one can notice that for a non-normal surface with an isolated singularity, the topology of the elements of a pencil changes exactly at the same values as for the pulled-back pencil on the normalized surface.
In the process of the proof, it was important to distinguish two types of components of the singular locus 
$(\Sigma, 0)$ of a surface 
$(S,0)$. Namely, let Σ0 be a component of the singular locus of S and consider the restriction of the normalization 
$n_0 := n_{|n^{-1}(\Sigma_0)} :
n^{-1}(\Sigma_0) \rightarrow \Sigma_0$. When n 0 is generically r to 1, we say that Σ0 is an r to 1 component of the singular locus of S. When Σ0 is a one-to-one component of the singular locus, we prove that the surface 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ is not topologically trivial at least at one point lying over the intersection point of the exceptional divisor with the strict transform of Σ0 by eI. Meanwhile, when Σ0 is an r to 1 component with r > 1, we prove the statement directly on SI without checking topological triviality on the surface 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$.
In the first section, we mention generalities on pencils of curves on complex surfaces, such as resolution of pencils and the relation between the pencil and its pull-back to the normalized surface. We also explain how the blow-up of the ideal 
$\langle f,g\rangle$ generated by the generators f and g of the pencil removes the indeterminacy of the quotient map 
$f/g$.
In the second section, in order to simplify the main statement, we define special values of the pencil at the normalization. These are the values w at which the pull-back of the curve λw to the normalized surface has a topology different from the generic one. Then, we define what we call special values of a pencil on a reduced surface. These are the special values at the normalization and the values w corresponding to an intersection point 
$(0,w)$ of the exceptional divisor 
$e_I^{-1}(0)$ with the strict transform of the singular locus of 
$(S,0)$ by eI.
Section three is dedicated to the proof of the main result. It has been cut into several lemmas dealing with different situations. Finally, we give a series of examples in the last section, illustrating situations that arise along the proof.
2. Pencils
Consider a germ of reduced complex surface 
$(S,0)$ with local ring of holomorphic functions 
$\mathcal{O}_{S,0}$ and call 
$\mathfrak{m}$ the maximal ideal of 
$\mathcal{O}_{S,0}$. For the rest of this work, S will denote a sufficiently small representative of 
$ (S,0) $.
Definition 2.1. Consider two holomorphic functions 
$ f,g \in \mathfrak{m} \subset \mathcal{O}_{S,0} $ such that the ideal 
$ \langle f,g \rangle$ is 
$\mathfrak{m}$-primary, i.e., 
$ \sqrt{ \langle f,g \rangle } = \mathfrak{m} $. Define the curve 
$\lambda_{[\alpha : \beta]}\subset S $, 
$[\alpha : \beta] \in \mathbb{P}^1$, to be the zero set on S of the function 
$\alpha f - \beta g \in \mathcal{O}_{S,0}$, with the ring of holomorphic functions 
$\mathcal{O}_{[\alpha:\beta]} =
\mathcal{O}_{S,0}/\langle{\alpha f - \beta g}\rangle$.
The pencil generated by f and g on S is the set:
\begin{equation*} \Lambda_{f,g} = \{ \lambda_w \subset S \, | \, w \in \mathbb{P}^1 \}. \end{equation*} Notice that the condition 
$ \sqrt{ \langle f,g \rangle } = \mathfrak{m} $ implies that, in a sufficiently small representative S of 
$(S,0)$, the only common point of all the elements λw of 
$\Lambda_{f,g}$ is the origin. In particular, the curves defined by f and g do not have any common branch.
We associate with such a pencil a function with an indeterminacy at the origin.
Definition 2.2. Given a pencil 
$ \Lambda_{f,g} $ on S, we define the associated map:
\begin{equation*}\begin{array}{rcl}
h_{f,g} : S \setminus \{ 0 \} & \rightarrow & \mathbb{P}^1 \\
x & \longmapsto & [g(x):f(x)].
\end{array}\end{equation*} For simplicity, and when there is no ambiguity, we will sometimes refer to the map 
$h_{f,g}$ as h.
The elements of the pencil can be compared with fibres of 
$ h_{f,g} $ in the sense that the associated reduced curves are the same:
\begin{align*}
|\lambda_w| = |\overline{ h_{f,g}^{-1} (w) }|;
\end{align*} notice that, depending on the surface 
$(S,0)$, the curve λw may have an embedded component at the origin.
A resolution of the pencil 
$\Lambda_{f,g}$ consists of removing both the indeterminacy of the map 
$h_{f,g}$ and the singularities of the surface 
$ (S,0) $.
Let us recall that a modification 
$ \mu : X \rightarrow S $ of a representative S of 
$ (S,0) $ is a proper map that induces an isomorphism outside a proper closed nowhere dense subspace of S. It is a resolution of singularities of S when X is smooth.
Definition 2.3. A modification 
$ r : S' \rightarrow S $ is a resolution of the pencil 
$ \Lambda_{f,g} $ if r is a resolution of singularities of S and 
$r \circ h $ extends to a well-defined map over Sʹ.
In this situation, if 
$w\neq w' \in \mathbb{P}^1$, then the 
$\overline{r^{-1}(\lambda_w \setminus \{0\})}$ and 
$\overline{r^{-1}(\lambda_{w'} \setminus \{0\})}$ do not intersect. A resolution of the pencil is then a modification that removes the singularities of S and separates the curves λw for all 
$w\in \mathbb{P}^1 $.
Definition 2.4. A resolution 
$ \rho : \hat{S} \rightarrow S $ of 
$ \Lambda_{f,g} $ is minimal if for any other resolution 
$ r : S' \rightarrow S $ of 
$\Lambda_{f,g}$ there exists a holomorphic map 
$ \tau : S' \rightarrow \hat{S} $, such that 
$r = \rho\circ \tau$.
It is well known that any surface singularity admits a minimal resolution which is unique up to isomorphism; see, for example [Reference Laufer12, Theorem 5.9] . Also, in [Reference Lê and C.13, Proposition 2.2], it is proved that any pencil of curves in a small neighbourhood of a point in 
$\mathbb{C}^2$ has a minimal resolution which is also unique up to isomorphism. A combination of these two assertions leads to:
Proposition 2.5. Any pencil 
$\Lambda_{f,g}$ on a surface singularity admits a minimal resolution which is unique up to isomorphism.
Since the map 
$h_{f,g}\circ r$ extends to a well-defined map hr whenever 
$r:S'\rightarrow S$ is a resolution of the pencil 
$\Lambda_{f,g}$, we can distinguish two types of components of the exceptional locus 
$r^{-1}(0)$, the ones where hr is constant and those where it is not.
Definition 2.6. Call 
$E= \bigcup_i E_i$ the decomposition into irreducible components of the exceptional curve 
$r^{-1}(0)$. We say that Ei is a dicritical component if 
$h_r |_{E_i} $ is not constant.
If Ei is a dicritical component of a resolution r of the pencil 
$\Lambda_{f,g}$ then for any point 
$p \in E_i$ there exists a unique 
$w\in \mathbb{P}^1$ such that 
$p \in \overline{r^{-1}(\lambda_w \setminus \{0\})}$. Conversely, if Ei is dicritical, the image of 
$ h_r |_{E_i} $ is 
$ \mathbb{P}^1 $ (since the components Ei are connected). This implies that for any 
$w\in \mathbb{P}^1$ the strict transform of λw by r intersects Ei in at least one point.
Let us now consider a particular modification: the blow-up of the ideal I generated by the functions f and g. Consider the map:
\begin{align*}
\begin{array} {rcl}
l_{f,g} : S \setminus\{0\} & \rightarrow & \mathbb{P}^1\\
x & \mapsto & [g(x) : f(x)].
\end{array}
\end{align*} Define the surface SI to be the closure of the graph of 
$l_{f,g}$ in 
$S\times \mathbb{P}^1 $. Call eI the restriction to SI of the projection onto S. The map 
$e_I : S_I \rightarrow S$ is the blow-up of the ideal I in a representative S of the germ 
$(S,0)$.
This blow-up satisfies the following universal property with respect to the pencil 
$ \Lambda_{f,g} $: a modification µ of the surface S removes the indeterminacy of the map 
$h_{f,g}$ induced by a pencil of curves, if and only if it factors through the blow-up of the ideal 
$\langle f,g \rangle$. It is a direct consequence of the universal property of the blow-up (see [Reference Hartshorne11, Proposition 7.14]).
We have in a more general setting:
Proposition 2.7. Let 
$\mu: Y \rightarrow X$ be a modification map between reduced complex analytic spaces over a neighbourhood of 
$0\in X$. Consider holomorphic functions 
$f_0, \ldots , f_r \in \mathcal{O}_{X,0}$, for which the common zero locus V is a nowhere dense subset of X. Define the map
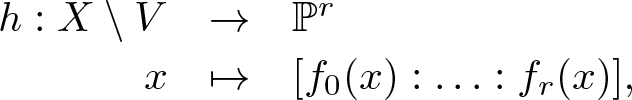\begin{equation*}\begin{array}{rcl}
h: X \setminus V & \rightarrow & \mathbb{P}^r \\
x & \mapsto & [f_0(x) : \ldots : f_r(x)],
\end{array}\end{equation*}whose indeterminacy locus is V.
Then, the composition map 
$ h \circ \mu $ has no indeterminacy on Y if and only if the modification µ factors through the blow-up of the ideal 
$\langle{f_0, \ldots , f_r}\rangle$ in X.
In the case of a pencil of curves 
$\Lambda _{f,g}$ on a representative of a surface singularity 
$(S,0)$, we have then:
Corollary 2.8. Let 
$ e_I : S_I \rightarrow S $ be the blow-up of the ideal 
$ I= \langle f,g \rangle $. The projection from SI to 
$\mathbb{P}^1$ is an extension of 
$h_{f,g} \circ e_I $ on the surface SI.
Remark 2.9. When the germ of surface 
$(S,0)$ is not Cohen–Macaulay, whenever we consider a pencil 
$\Lambda_{f,g}$, the pair (f, g) is not a regular sequence in 
$\mathcal {O}_{S,0}$. Therefore, the surface SI obtained by the blowing-up eI of the ideal generated by f and g need not be given by the equation 
$gt-fs=0$ in 
$S\times \mathbb{P}^1$, where 
$[s:t]$ is a system of homogeneous coordinates in 
$\mathbb{P}^1$.
Indeed, let us call 
$S_1\subset S\times\mathbb{P}^1$ the surface defined by the equation 
$gt-fs=0$. Call π 1 the restriction to S 1 of the projection to 
$\mathbb{P}^1$. One can easily see that for any 
$w\in \mathbb{P}^1$, the fibre 
$\pi_1^{-1}(w)$ is isomorphic to the curve 
$\lambda_w\subset S$. Since 
$(S,0)$ is not Cohen-Macaulay, the curve λw has an embedded component at the origin for any 
$w\in \mathbb{P}^1$. This implies that all the fibres 
$\pi_1^{-1}(w)$ have an embedded component in the point 
$(0, w)\in S_1$. The surface S 1 has then an embedded component along the curve 
$\{0\}\times
\mathbb{P}^1$. By construction of the blow-up eI, the surfaces S 1 and SI coincide outside 
$\{0\}\times \mathbb{P}^1$, and SI is reduced whenever 
$(S,0)$ is, so SI is the reduced surface obtained from S 1.
Corollary 2.8 asserts that the blow-up of the ideal 
$\langle f,g \rangle$ is the easiest way to separate the elements of the pencil 
$\Lambda_{f,g}$ and remove the indeterminacy of the map 
$h_{f,g}$. Theorem 2.10 explains this minimality property and relates it to the minimal resolution of the pencil.
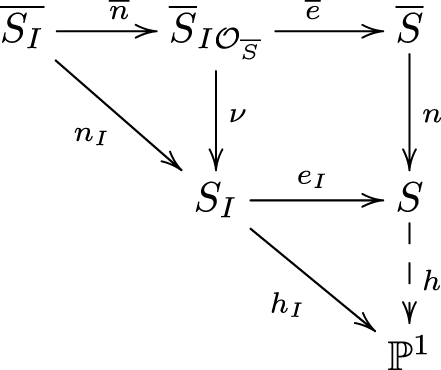
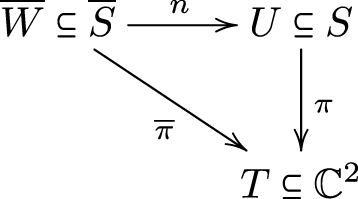
Theorem 2.10. Given a pencil 
$ \Lambda_{f,g} $ on a representative S of a reduced complex surface singularity 
$(S,0)$, we have the following commutative diagram:
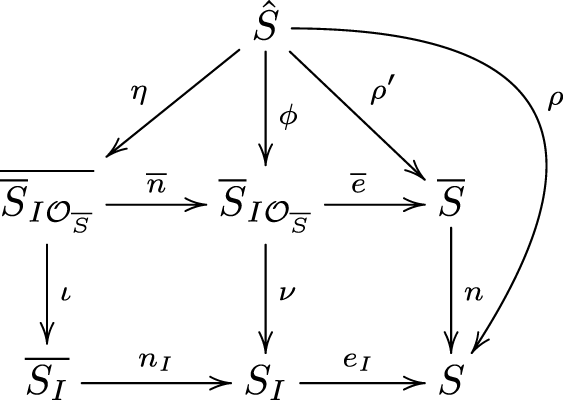
where n is the normalization of S, 
$\rho = n\circ \rho' :
\hat{S} \rightarrow S$ is the minimal resolution of the pencil 
$\Lambda_{f,g}$, eI is the blow-up of the the ideal 
$I= \langle f,
g\rangle$, and 
$\overline{e}$ is the blow-up of the pull-back ideal 
$I\mathcal{O}_{\overline{S}}$. The maps nI and 
$\overline{n}$ are respectively the normalizations of SI and 
$\overline{S}_{I\mathcal{O}_ {\overline{S}}}$.
The map ν is finite, the map ι is an isomorphism, and η is the minimal resolution of the singularities of the normal surface 
$\overline{ \overline{S}_{I \mathcal{O}_S} }$, which is in this case the contraction of all the non-dicritical components of the minimal resolution ρ of the pencil 
$\Lambda_{f,g}$.
Proof. The minimal resolution ρ of the pencil 
$\Lambda_{f,g}$ factors naturally through the normalization 
$n: \overline{S} \rightarrow
S$. We then have 
$\rho = n\circ \rho'$ where 
$\rho' : \hat{S}
\rightarrow \overline{S}$ is the minimal resolution of the pencil 
$\Lambda_{f\circ n, g\circ n}$ defined on 
$\overline {S}$ at each point of 
$n^{-1}(0)$.
By definition of a resolution of 
$\Lambda_{f,g}$, the map 
$h_{f,g}\circ \rho =h_{f\circ n, g\circ n} \circ \rho'$ extends to a well-defined map 
$\hat{h}: \hat{S}\rightarrow \mathbb{P}^1$. Applying Proposition 2.7, there exists a map 
$\phi:\hat{S}\rightarrow \overline
{S}_{I\mathcal{O}_{\overline{S}}}$ such that 
$\rho' = \overline{e}
\circ \phi$.
Since 
$\hat{S}$ is a smooth surface, the map ϕ factors through the normalization 
$\overline{n}$ of 
$\overline
{S}_{I\mathcal{O}_{\overline{S}}}$, so there exists 
$\eta : \hat{S}
\rightarrow \overline{\overline {S}_{I\mathcal{O}_{\overline{S}}}}$ such that 
$\phi = \overline{n}\circ \eta$, and η is the minimal resolution of the singularities of 
$\overline{\overline
{S}_{I\mathcal{O}_{\overline{S}}}}$.
Let us explain the existence and finiteness of the map ν. By Proposition 2.7, the composition map 
$h_{f,g}\circ n \circ \overline{e}$ extends to a well-defined map 
$\overline{h}$ on 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$. Again by Proposition 2.7, there exists a map ν such that 
$e_I \circ \nu = n\circ \overline{e}$. Moreover, the blow-up 
$\overline{e}$ is the blow-up of the pull-back of the ideal I by the normalization n; therefore, the map ν is the pull-back of the normalization n by e. The normalization being finite, ν is also a finite map.
In order to prove that there exists an isomorphism 
$\iota :
\overline{\overline {S}_{I\mathcal{O}_{\overline{S}}}} \rightarrow
\overline{S_I}$, it is enough to notice that 
$\nu\circ \overline{n}$ is a finite modification of SI and that 
$\overline{\overline
{S}_{I\mathcal{O}_{\overline{S}}}}$ is normal; hence, the composition 
$\nu \circ \overline{n}$ coincides with the normalization nI up to the isomorphism ι.
Now let us prove our assertion on η. Consider an irreducible component Ei of the exceptional divisor 
$\rho^{-1}(0)$. If Ei is dicritical for the pencil 
$\Lambda_{f\circ n,g\circ n}$, then the image 
$\eta (E_i)$ cannot be a point; otherwise, two (actually an infinity) different elements of the pencil will have their strict transforms by 
$\overline{e}\circ \overline{n}$ intersecting in a point, which contradicts the fact that 
$h_{f,g}\circ n\circ \overline{e}\circ \overline{n}$ extends to a well-defined map.
If Ei is not dicritical, we are going to prove that its image by η is a point. Indeed, the map 
$\overline{h}: \overline{S}_{I\mathcal{O}_{\overline{S}}} \rightarrow \mathbb{P}^1$ is not constant on any component of the exceptional divisor. Since the normalization 
$\overline{n}$ is finite, the map 
$\overline{h}\circ \overline{n}$ is not constant on any component of the exceptional fibre of 
$\overline{e}\circ \overline{n}$. However, the extended map 
$\hat{h}: \hat{S} \rightarrow \mathbb{P}^1$ is constant over Ei. Therefore, by the commutativity of the above diagram, the map 
$\overline{h} \circ \overline{n}$ is constant on the image 
$\eta(E_i)$ which cannot then be one dimensional. So the non dicritical component Ei contracts to a point by η.
Theorem 2.10 will allow us to compare the pencils 
$\Lambda _{f,g}$ on S and 
$\Lambda_{f\circ n, g\circ n}$ on 
$\overline{S}$ and their respective special values.
Remark 2.11. The pencil 
$\Lambda_{f\circ n,g\circ n}$ has one basepoint for each irreducible component of 
$ (S,0) $ corresponding to a point 
$O_i \in n^{-1}(0)$. Then, the exceptional divisor of the blow-up 
$ \overline{e} : \overline{S}_{I\mathcal{O}_{\overline{S}}}
\rightarrow \overline{S} $ has one connected component 
$\overline{E}_i = \overline{e} ^{-1}(O_i)$ for each basepoint of 
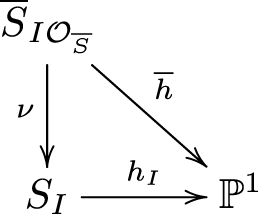
$\Lambda_{f\circ n,g\circ n}$. The restriction 
$ \nu _i: \overline{E}_i =\{O_i\}\times \mathbb{P}^1 \rightarrow S_I $ of ν induces the identity map on 
$ \mathbb{P}^1 $. Indeed, the extension hI of 
$h_{f,g} \circ e_I $ restricted to the exceptional divisor 
$e_I^{-1}(0)$ induces the identity map on 
$\mathbb{P}^1$, and the same is true for the extension 
$\overline{h}$ of 
$ h_{f,g} \circ n
\circ \overline{e} $ restricted to 
$ \overline{E}_i $. This statement is a consequence of the commutativity of the diagram:
3. Special values
Our goal is to understand the generic and particular topological behaviour of the elements of a pencil of curves on a germ of complex surface. We will relate them to the behaviour of the strict transforms of the elements of the pencil, either on the minimal resolution of the pencil or on the blow-up of the ideal generated by the generators of the pencil.
In the case of a pencil 
$\Lambda _{f,g}$ on 
$\mathbb{C}^2$ or on a normal surface, the change of the topology of the curves was measured by the Milnor number at the origin 
$\mu(\lambda_{w},0)$ and related to topological triviality on the blown-up surface 
$S_{\langle f,g \rangle}$. Special values on 
$\mathbb{P}^1$ are defined in terms of the behaviour of the fibres of 
$h_{f,g}$ over these values in the minimal resolution. It is then proved that these are precisely the values where the topology changes. We refer to [Reference Lê and C.13] for 
$\mathbb{C}^2$-case, [Reference Snoussi18] for a particular case on normal surfaces, [Reference Bondil and D. T.1] for linear systems on normal surfaces and [Reference Delgado and Maugendre6] for pencils on normal surfaces.
Following that strategy, we will start by defining special values for a pencil of curves on a germ of a not necessarily normal complex surface 
$(S,0)$.
Definition 3.1. Let 
$ \rho : \hat{S} \rightarrow S $ be the minimal resolution of a pencil 
$ \Lambda_{f,g} $. Take E to be the exceptional divisor of the minimal resolution of the normalized surface 
$\overline {S}$, 
$\rho ' : \hat{S} \rightarrow \overline{S} $. Let 
$ E = \cup E_i $ be the decomposition of E into irreducible components. Consider the extension 
$ \hat{h}$ of 
$h_{f,g} \circ \rho $ to the whole surface 
$\hat{S}$.
We say that 
$ w \in \mathbb{P}^1 $ is a special value for the pencil 
$\Lambda_{f,g}$ in the normalization if one or more of the following are fulfilled:
(1)
$ w= \hat{h} (x) $ with $ x \in E_i \cap E_j $, i ≠ j.(2)
$ w= \hat{h} (E_i) $ with Ei a non-dicritical component.(3)
$ w = \hat{h} (x) $ with x a critical point of $ \hat{h} |_{E_i} $ for a dicritical component Ei.
If w is not special at the normalization, then we say it is a generic value at the normalization.
In other words, a value 
$w\in\mathbb{P}^1$ is special at the normalization for a pencil 
$\Lambda_{f,g}$ on a surface S if and only if it is a special value for the pulled-back pencil 
$\Lambda_{f\circ n, g\circ n}$ on the normal surface 
$\overline{S}$; see [Reference Lê and C.13], [Reference Bondil and D. T.1] and [Reference Delgado and Maugendre6].
Remark 3.2. Since ρ is a resolution of the pencil, there is at least one dicritical component in every connected component of the exceptional divisor by ρ. Therefore, if Ei is a non-dicritical component, it will intersect either a dicritical component or another non-dicritical one. The value 
$\hat{h}(E_i)$ will be equal to 
$\hat{h}(x)$ where x is an intersection point of two irreducible components of the exceptional divisor.
The values in the second point of the definition are included in the ones of the first point. However, we prefer to refer to them separately.
When the surface 
$(S,0)$ has a one-dimensional singular locus Σ, we need to consider the branches of Σ in the definition of special values of a pencil.
Definition 3.3. We say that w is a special value for the pencil 
$\Lambda_{f,g}$ on a representative S of 
$(S,0)$ if:
(1) w is a special value in the normalization,
(2) or
$ w = \hat{h} (x) $ where $ x \in \overline{\rho^{-1}( \Sigma \setminus \{ 0 \} )} \cap E $.
When 
$ w \in \mathbb{P}^1 $ is not special, we say it is generic for the pencil 
$\Lambda_{f,g}$ on S.
Note that in the case of a germ of non-normal surface with an isolated singularity, the special values of a pencil on the surface coincide with the special values at the normalization.
When the surface is not irreducible, its normalization is a disjoint union of normal germs. The special values at the normalization need then to be considered as special values of pencils on each connected component of the normalized surface.
Our main tool for detecting a change in the topology of the elements of a pencil is the topological triviality in a one-parameter flat family of curves. This is to be considered on the surface obtained after the blow-up of the ideal 
$I=\langle{f,g}\rangle$. The reason is that the surface SI obtained by that blow-up is the minimal one where the elements of the pencil can be viewed as fibres of a well-defined map onto 
$\mathbb{P}^1$.
Recall that 
$e_I: S_I \rightarrow S$ is the blow-up of 
$I=\langle{f,g}\rangle$ and call 
$\pi_I : S_I \rightarrow \mathbb{P}^1$ the induced projection onto 
$\mathbb{P}^1$ which coincides with the extension hI of 
$h_{f,g}\circ e_I$ to SI.
Definition 3.4. Let 
$(0,w)\in e_I^{-1}(0)$. We say that the pencil 
$\lambda_{f,g}$ is topologically trivial at w if there exist neighbourhoods 
$(0,w)\in U \subset S_I$ and 
$w\in T \subset \mathbb{P}^1$ such that the induced family of curves 
$\pi_I: U\rightarrow T$ is a topologically trivial family of curves, i.e., there exists a homeomorphism 
$\phi: U \rightarrow \pi_I^{-1}(w) \times T$ which makes the following diagram commutative:
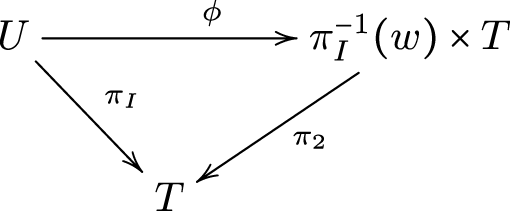
where π 2 is the projection onto the second factor of 
$\pi_I^{-1}(w)\times T$.
In that case, we also say that the surface SI is topologically trivial at 
$(0.w)$.
When the surface 
$(S,0)$ is Cohen-Macaulay, the blow-up of an ideal generated by a regular sequence gives rise to a Cohen-Macaulay surface. However, when 
$(S,0)$ is not Cohen-Macaulay, the blown-up surface SI need not be Cohen-Macaulay at all points of the exceptional fibre, as shown in Example 5.3. Therefore, some of the fibres 
$\pi_I^{-1}(w)$ may have an embedded component at the point 
$(0,w)$. We need then to use equisingularity criteria that consider curves with allowed embedded components. When a curve is possibly with an embedded component and has isolated singularities, we call it a generically reduced curve. We are going to use, along this work, equisingularity criteria on flat families of generically reduced curves as it was done in [Reference Fernández de Bobadilla, Snoussi and Spivakovsky7], [Reference Silva and J.17] and [Reference Greuel9].
4. Main results
In this section, we will state and prove our main result, which establishes the equivalence between generic values and values where the pencil is topologically trivial, for germs of complex surfaces.
Theorem 4.1. A value 
$ w \in \mathbb{P}^1 $ is a special value for a pencil 
$ \Lambda_{f,g} $ on a representative S of a germ of reduced complex surface 
$ (S,0) $, if and only if 
$ \Lambda_{f,g} $ is not topologically trivial at w.
For convenience, we will split the proof into a series of lemmas dealing with different types of special values and types of fibres.
Consider a pencil 
$\Lambda_{f,g}$ on a representative S of a germ of reduced complex surface 
$(S,0) \subset (\mathbb{C}^N,0)$. Call 
$\Sigma = \cup_i \Sigma_i$ the decomposition of the singular locus of S into irreducible components. Consider 
$\rho: \hat{S}\rightarrow S$ the minimal resolution of the pencil 
$\Lambda_{f,g}$ and call 
$\hat{h}$ the extension of 
$h=[g:f]$ to 
$\hat{S}$.
We first consider special values at the normalization:
Lemma 4.2. Suppose 
$ w \in \mathbb{P}^1 $ is a special value in the normalization for 
$ \Lambda_{f,g} $ that is not the image by 
$\hat{h}$ of an 
$ x \in \Sigma^* \cap E \subseteq \hat{S}$, intersection of 
$ \Sigma^* = \overline{\rho^{-1}{( \Sigma \setminus \{ 0 \} )}} $ with 
$ E= \rho^{-1}(0)$ and suppose that the curve λw is generically reduced.
Then, 
$ \Lambda_{f,g} $ is not topologically trivial at w.
Proof. Suppose first that S is irreducible. Then, the inverse image 
$ n^{-1} (0)$ is a single point, the pull-back by the normalization n of the pencil 
$\Lambda_{f,g} $ has only one basepoint and the exceptional fibre of 
$ \overline{e} $ is isomorphic to 
$ \mathbb{P}^1 $. Since the following diagram commutes:
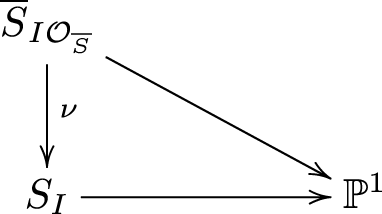
the morphism ν restricted to the exceptional fibre is the identity. If w satisfies the conditions of the lemma, then there exist neighbourhoods 
$ \overline{V} $ and V of 
$ (0,w) $, respectively, in 
$ \overline{S}_{I \mathcal{O}_{\overline{S}}} $ and in SI where ν induces a homeomorphism. By hypothesis, w is a special value at the normalization, so by [Reference Delgado and Maugendre6, Theorem 4] the Milnor number changes at this point. Moreover, the curve 
$ \lambda_w \subset S $ is assumed to be generically reduced, and its strict transform in 
$ \overline{S}_{I \mathcal{O}_{\overline{S}}} $ is therefore reduced. By [Reference Buchweitz and G.-M.3, Theorem 5.2.2], the surface 
$ \overline{S}_{I \mathcal{O}_{\overline{S}}}$ is not topologically trivial at 
$(0,w)$ and neither is SI.
Suppose now that 
$ S =\cup _i S_i$ is a decomposition of S into irreducible components. The normalization 
$ \overline{S} $ of S is a disjoint union
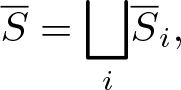\begin{align*}
\overline {S} = {\displaystyle {\bigsqcup _i}} \overline{S}_i,
\end{align*} where each surface 
$\overline{S}_i$ is the normalization of Si.
The pencil 
$\Lambda _{f,g}$ induces a pencil 
$\Lambda^i _{f,g}$ on each component Si. The surface SI obtained by the blow-up of 
$I=\langle{f,g}\rangle$ is a union:
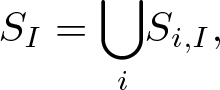\begin{align*}
S_I = {\displaystyle {\bigcup _i}} S_{i,I},
\end{align*} where 
$S_{i,I}$ is the surface obtained by the blow-up of the ideal 
$ I\mathcal{O}_{S_i} $. Note that the exceptional fibre 
$ \{0\} \times \mathbb{P}^1 $ is contained in each component 
$S_{i,I}$.
The morphism 
$\nu : \overline{S}_{I\mathcal{O}_{\overline{S}}}\rightarrow S_I$ induces morphisms:
\begin{align*}
\nu_i : (\overline{S_i})_{I\mathcal{O}_{\overline{S_i}}}\rightarrow S_{i,I}.
\end{align*} When w is as in the hypothesis of the lemma, we have seen in the proof of the irreducible case that there exists an index i 0 such that neither 
$ (\overline{S_{i_0}})_{I\mathcal{O}_{\overline{S_{i_0}}}} $ nor 
$ S_{{i_0},I} $ is topologically trivial at 
$ (0,w) $.
We claim then that SI is not topologically trivial at 
$(0,w)$. Indeed, if SI is topologically trivial at 
$(0,w)$, then there exist neighbourhoods W and U of 
$(0,w)$ in SI and of w in 
$\mathbb{P}^1$, respectively, and a homeomorphism 
$\phi: W\rightarrow \lambda_w \times U$. The homeomorphism ϕ sends every irreducible component of W onto 
$\lambda_{j,w} \times U$, where 
$\lambda_{j,w}$ is a branch of λw. Each of the intersections 
$S_{i,I} \cap W$ is a union of irreducible components of W. Therefore, ϕ induces a homeomorphism between 
$W\cap S_{i,I}$ and 
$\cup_{j \in J_i}\lambda_{j,w}$, proving that each of the surfaces 
$S_{i,I}$ is topologically trivial at 
$(0,w)$. This is a contradiction to the statement in the previous paragraph, and so SI is not topologically trivial at 
$(0,w)$.
In a second step, we propose to deal with points in SI belonging to the strict transform of the singular locus.
For that purpose, we need to distinguish between two different types of branches of the singular locus of the surface S:
Definition 4.3. Consider the normalization 
$n : \overline{S} \rightarrow S$ of S. A branch Σ0 of the singular locus Σ of S is called an r to 1 component of Σ if the normalization is generically r to 1 over Σ0, with 
$r \geq 1$.
We will need to deal separately with the 1 to 1 branches and the r to 1 ones when r > 1.
When Σ0 is an r to 1 component, with r > 1 and 
$ \Sigma_0 \subseteq \lambda_w $, the pull-back 
$ \overline{\lambda_w} $ by the normalization may be reduced and the value w may be generic in the normalization (see Example 5.2). But we still can prove that in this case SI is not topologically trivial at 
$ (0,w) $:
Lemma 4.4. Let Σ0 be an r to 1 component of the singular locus of S, with r > 1. Suppose there exists a 
$ w \in \mathbb{P}^1 $ such that 
$ \Sigma_0 \subseteq \lambda_w $. Then, the surface SI is not topologically trivial at 
$ (0,w) $.
Proof. Let 
$ \Sigma_0^* $ be the strict transform of Σ0 by the blow-up eI. From Theorem 2.10, we have the following diagram:
From the commutativity of the right square we have that a generic point in 
$ \Sigma_0^* $ has exactly r pre-images by ν. Since the normalization map 
$ \overline{n} $ is an isomorphism over 
$ \overline{S}_{I \mathcal{O}_{\overline{S}}} \setminus
\overline{e}^{-1} (n^{-1}(0))$, then by commutativity of the left side of the diagram, a generic point of 
$ \Sigma_0^* $ has exactly r pre-images by nI. In other words, for any 
$ x \in \Sigma_0^* $ sufficiently close to 
$e_I^{-1}(0)\cap \Sigma_0^*$, the surface SI is not irreducible at x.
On the other hand, if SI is topologically trivial at 
$(0,w)$, and since the curve λw is irreducible at its generic points, then there is a sufficiently small neighbourhood V of x in SI which is homeomorphic to a poly-disk of 
$\mathbb{C}^2$ which is everywhere irreducible. So the surface SI cannot be topologically trivial at the point 
$(0,w)$.
When the r to 1 component of the singular locus is not contained in an element of the pencil, we have:
Lemma 4.5. Let Σ0 be an r to 1 branch of the singular locus of S, with r > 1, that is not contained in any element λw of the pencil. Call 
$ (0,w) \in S_I$ the intersection point of the exceptional divisor 
$e_I^{-1}(0)$ with the strict transform 
$\Sigma_0^*$ of Σ0 by eI. Then, the surface SI is not topologically trivial at 
$(0,w)$.
Proof. Recall that the surface 
$(S,0) \subset (\mathbb{C}^N, 0)$ is not assumed to be irreducible. Therefore, the normalized surface 
$\overline{S}$ may be a multi-germ 
$\sqcup _i (\overline{S}_i, O_i)$, and the blown-up surface 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ is also a disjoint union of surfaces 
$\overline{S}^{(i)}_{I\mathcal{O}_{\overline{S}}}$ each of them obtained by the blow-up of the ideal 
$ \langle f\circ n, g\circ n \rangle$ in a representative 
$\overline{S}_i$ of the respective germ 
$(\overline{S}_i, O_i)$.
We claim that for each index i, there exists an open neighbourhood Ui of 
$(O_i,w)$ in 
$\overline{S}_i \times \mathbb{P}^1$ such that the fibre 
$(h_I\circ \nu)^{-1}(w) \cap U_i$ is contractible and for any 
$t\in \mathbb{P}^1$, the fibre 
$(h_I\circ \nu)^{-1}(t)\cap U_i$ is connected; see the commutative diagram below for notation:
In fact, for the contractibility of 
$(h_I\circ \nu)^{-1}(w)\cap U_i$ it is enough to choose each Ui small enough. Consider now, for each germ 
$(\overline{S}_i, O_i)$, the projection 
$\overline{\pi}_i := (f\circ n, g\circ n) :
(\overline{S}_i, O_i) \rightarrow (\mathbb{C}^2,0)$. By abuse of notation, we will call 
$\overline{\pi}_i$ the projection induced on a representative Vi of 
$(\overline{S}_i, O_i)$. Since the projection 
$\overline{\pi}_i$ is finite, we can choose the representative Vi small enough so that 
$\overline{\pi}_i^{-1}(0) = \{O_i\}$.
Let us denote by 
$\Lambda^{(i)}$ the pencil induced by 
$\Lambda_{f,g}$ on 
$\overline{S}_i$. Every element of this pencil is the inverse image by 
$\overline{\pi}_i$ of a line through the origin in 
$\mathbb{C}^2$. For 
$t\in \mathbb{P}^1$ call 
$0\in L_t$ the line in 
$\mathbb{C}^2$ with slope t. Since 
$\overline{\pi}_i^{-1}(0) \cap V_i =\{O_i\}$, the curve 
$\lambda^{i}_t := \overline{\pi}_i^{-1}(L_t) \cap V_i$ is connected. If we choose Ui to be an open set contained in 
$V_i \times \mathbb{P}^1$, then the fibre 
$(h_I\circ \nu)^{-1}(t) \cap U_i$, which is isomorphic to its image in Vi, is connected as claimed above.
We will now prove that since Σ0 is an r to 1 component of the singular locus, then for any 
$t\in \mathbb{P}^1$ close enough to w, the fibre 
$h_I^{-1}(t)$ contains a cycle.
Indeed, the curve Σ0 is not contained in any element of the pencil 
$\Lambda_{f,g}$. The function hI is then non-constant on the strict transform 
$\Sigma_0^*$ of Σ0 by eI. We can then choose neighbourhoods U of 0 in 
$\mathbb{C}^N$ and T of w in 
$\mathbb{P}^1$ such that for any 
$t\in T$ we have
\begin{equation*} h_I^{-1}(t)\cap (U\times T) \cap \Sigma_0^* \neq
\emptyset \neq
h_I^{-1}(t)\cap (U\times T) \cap e_I^{-1}(0). \end{equation*} We will furthermore require that 
$S_I \cap (U\times T)$ is contained in the image by ν of each component 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}\cap U_i$ defined above.
Let us fix a 
$t\in T\setminus \{w\}$. We will call 
$\{x\} := h_I^{-1}(t)\cap (U\times T) \cap e_I^{-1}(0)$ and choose 
$y \in h_I^{-1}(t)\cap (U\times T) \cap \Sigma_0^*$. Since Σ0 is an r to 1 component, with 
$r\geq 2$, there exist at least two points, y 1 and y 2 in 
$\nu^{-1}(y)$. These two points may be in the same open set U 0 defined in the first part of this proof or in different open sets U 1 and U 2.
In the first case, call x 0 a point in 
$\nu^{-1}(0) \cap U_0$ and recall that the fibre 
$(h_I\circ \nu)^{-1}(t)\cap U_0$ is connected. There exist then two continuous paths connecting x 0 to y 1 and x 0 to y 2. The image of these two paths is a non-trivial loop in the fibre 
$h_I^{-1}(t) \cap (U\times T)$. Indeed, for any topological space X, identifying two points 
$ a, b $ results in a space that is homotopically equivalent to the original space with a loop attached:
Then, by an appropriate decomposition and using Van Kampen theorem, we see that the original space and the one with the loop are not homeomorphic.
In the second case, choose two points 
$x_1\in \nu^{-1}(x)\cap U_1$ and 
$x_2 \in \nu^{-1}(x) \cap U_2$. Again the fibres 
$(h_I\circ \nu)^{-1}(t) \cap U_i$ are connected for 
$i=1,2$. Choose two paths on the fibre 
$(h_I\circ \nu)^{-1}(t)$, one in U 1 connecting x 1 to y 1 and the other in U 2 connecting x 2 to y 2. The image of these two paths by ν is again a non-trivial loop in 
$h_I^{-1}(t)\cap (U\times T)$.
In both cases, the fibre 
$h_I^{-1}(t) \cap(U\times T)$ is not contractible; meanwhile, the fibre 
$h_I^{-1}(w)\cap (U\times T)$ is contractible. The surface SI is, therefore, not topologically trivial at 
$(0,w)$.
When Σ0 is a one-to-one branch of the singular locus of S, the preceding argument does not hold anymore. But still we are going to prove that such a component produces a special value at the normalization.
Consider for that a finite map 
$\pi: S \rightarrow \mathbb{C}^2$, defined on a sufficiently small representative of 
$(S,0)$. Recall that we denote by 
$n: \overline{S} \rightarrow S$ the normalization of S.
Lemma 4.6. Let Σ0 be a one-to-one component of the singular locus of S. Then, the inverse image 
$n^{-1} (\Sigma_0) $ is contained in the critical locus of 
$ \pi \circ n $.
Proof. Take a point 
$ p \in n^{-1} ( \Sigma_0 )$. If p is a singular point of 
$ \overline{S} $, then by definition it is in the critical locus of 
$ \pi \circ n $. Then, we can assume that p is not singular.
Since Σ0 is a 1 to 1 component, there exist neighbourhoods 
$ U \subseteq S $ of n(p) and 
$\overline{U}\subset \overline{S}$ of p, such that n induces a homeomorphism 
$\overline{U} \rightarrow U$.
Let 
$ \overline{\pi} := \pi \circ n $, and suppose p is not critical for 
$\overline{\pi}$. Then, there exist neighbourhoods 
$\overline{W} \subset
\overline{U} \subset
\overline{S} $ of p and 
$T \subset \mathbb{C}^2 $ of 
$\overline{\pi}(p)$ where 
$ \overline{\pi}$ induces an isomorphism: 
$\overline{W} \rightarrow T$.
The composition map 
$n\circ \overline{\pi}^{-1}$ defined from 
$T\cap \overline{\pi}(\overline{U}) \rightarrow
U\cap n(\overline{W})$ is the inverse map of the restriction of π to 
$U\cap n(\overline{W})$, with the fact that n(p) is singular for S. Therefore, p is critical for 
$\overline{\pi}$.
In [Reference Delgado and Maugendre6, Theorem 3], Delgado and Maugendre established a relation between critical loci of projections to 
$\mathbb{C}^2$ and special values in the case of normal surfaces. More precisely, if S is a representative of a normal surface germ 
$(S,0)$ and 
$\Lambda _{u,v}$ is a pencil on it, then consider the finite map 
$\pi =(u,v)$ and call 
$C(\pi)$ its critical locus. Consider the blow-up 
$e_{u,v}$ of the ideal generated by u and v, then the intersection points of 
$e_{u,v}^{-1}(0)$ with the strict transform of 
$C(\pi)$ by 
$e_{u,v}$ are special values of the pencil.
We are going to use this relation to prove the following lemma:
Lemma 4.7. Let Σ0 be a one-to-one component of the singular locus of S and call 
$ \Sigma_0^* $ its strict transform by eI. Then, the image by hI of the intersection point 
$\{(0,w)\} =\Sigma_0^* \cap e_I^{-1}(0)$ is a special value in the normalization.
When the corresponding curve λw is generically reduced, the surface SI is not topologically trivial at 
$(0,w)$.
Proof. The first statement is a direct consequence of Lemma 4.6 and [Reference Delgado and Maugendre6, Theorem 3] applied to each component of the normalization of S and to the pencil 
$\Lambda_{f\circ n, g\circ n}$.
When the curve λw is generically reduced, its strict transform on 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ is reduced. We have then a flat family of reduced curves with non-constant Milnor number. The surface 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ is then not topologically trivial at 
$(0,w)$.
We can assume that no r to 1 component of the singular locus with r > 1 has its strict transform in 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ passing through 
$(0,w)$; otherwise, by Lemma 4.5, the pencil will be already non topologically trivial at w. There is then a neighbourhood U of 
$(0,w)$ in 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ on which ν induces a homeomorphism to a neighbourhood V of 
$(0,w)$ in SI. This homeomorphism is compatible with the projections to 
$\mathbb{P}^1$. The surface SI is then not topologically trivial at 
$(0,w)$.
We still need to deal with two cases: when λw contains a one-to-one component of the singular locus, and the case when the curve λw is not generically reduced. In both cases, the strict transform of the curve λw by the normalization is not reduced. Indeed we have:
Lemma 4.8. Let Σ0 be a one-to-one component of the singular locus of S and let λw be an element of the pencil such that 
$ \Sigma_0 \subseteq \lambda_w $. Then, the pre-image, 
$ \overline{\lambda_w} $, of λw by the normalization is non reduced.
Proof. Let S be a sufficiently small representative of 
$(S,0)$. Let 
$x\in \Sigma_0$ be a generic point different from 0 and sufficiently close to 0. Since Σ0 is a one-to-one component of Σ, 
$y:= n^{-1}(x)$ is a unique point.
Consider the inclusion of integral domains induced by the normalization, 
$ n^* : \mathcal{O}_{S,x} \rightarrow \mathcal{O}_{\overline{S},y} $. It makes 
$\mathcal{O}_{\overline{S},y} $ into a finite 
$ \mathcal{O}_{S,x} $-module. Call 
$ h_w = \alpha f - \beta g $, where 
$w= [\alpha : \beta]$. Applying [Reference Matsumura14, Theorem 14.8] to the ideal 
$ \langle h_w \rangle $, we obtain:
\begin{align*}
e( \langle n^* (h_w) \rangle , \mathcal{O}_{\overline{S},y}) =
e( \langle h_w \rangle , \mathcal{O}_{S,x} ),
\end{align*} where 
$e(J, R)$ refers to the multiplicity of the ideal J in the local ring R.
The curve λw is the zero set of hw on S. Since Σ0 is a non-reduced component of λw, the multiplicity 
$e( \langle h_w \rangle , \mathcal{O}_{S,x} )$ is at least two. Therefore, the multiplicity 
$e( \langle n^* (h_w) \rangle , \mathcal{O}_{\overline{S},y})$ is also at least 2, which implies that the curve 
$n^{-1}(\Sigma_0)$ is a non-reduced component of the pre-image , 
$\overline{\lambda_w}$, of λw by the normalization n.
In general, when λw is a non generically reduced element, we loose topological triviality. More precisely:
Lemma 4.9. Let 
$ \Lambda_{f,g} $ be a pencil on a representative S of a reduced surface germ 
$(S,0)$. If 
$ \lambda_{w_0} $ is not generically reduced for some 
$ w_0 \in \mathbb{P}^1 $, then 
$ \Lambda_{f,g} $ is not topologically trivial at w 0.
Proof. Let 
$ \lambda_{w_0} $ be a non generically reduced element of the pencil 
$\Lambda_{f,g}$ on S. Call δ 0 a non reduced component of 
$\lambda_{w_0}$. If δ 0 is an r to 1 component of the singular locus of S, then by Lemma 4.4, the blown-up surface SI is not topologically trivial at 
$(0,w_0) $.
We can assume the surface SI to be irreducible at 
$(0,w_0)$. Indeed, suppose that SI is not irreducible at 
$(0,w_0)$. Two cases may occur. In the first case, 
$ \Sigma_i^* $ will be the strict transform by eI of an r to 1 component 
$\Sigma_i$ of the singular locus of S, with r > 1. We will be then in the situation of the Lemma 4.5. The second case is when the components of SI at 
$ (0,w_0 )$ intersect only along the exceptional divisor 
$ e_I^{-1}(0) $. In this case, the surface SI satisfies the hypothesis of Theorem 4.11 of [Reference Giles Flores, Silva and Snoussi8], i.e., SI is topologically trivial at 
$(0,w_0)$ if and only if each of its irreducible components at 
$(0, w_0)$ is. Then, we have reduced the situation to the case when SI is irreducible at 
$(0,w_0)$.
We are now in the situation where the curve 
$\delta_0 \subset \lambda_{w_0}$ is either a one-to-one component of the singular locus of S or is not contained in the singular locus of S. In both cases, the normalization nI of SI is a homeomorphism in a neighbourhood of 
$(0,w_0)$.
Suppose now that SI is topologically trivial in a neighbourhood U of 
$(0,w_0)$, that is we have a homeomorphism 
$ \phi : S_I \cap U \rightarrow (\lambda_{w_0}\cap U) \times V $, with 
$ V \subseteq \mathbb{C}$ an open disc. Since SI is irreducible at 
$(0,w_0)$ so is the curve 
$\lambda_{w_0}$; in other words, we have 
$ \lambda_{w_0} = \delta_0 $. The normalization 
$ n_0 : W\times V \rightarrow (\lambda_{w_0} \cap U)\times V $ is then also a homeomorphism, W being a disc in 
$\mathbb{C}$.
So we have:
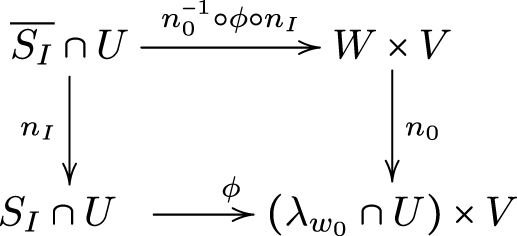
The normalized surface 
$ \overline{S_I}\cap U $ is then homeomorphic to W × V. By a Theorem of Mumford [Reference Mumford15, p. 5], a normal surface is homeomorphic to a non-singular space if and only if it is non-singular.
Consequently, we may assume the surface 
$ \overline{S_I}$ to be non singular in a sufficiently small neighbourhood U of 
$n_I^{-1}(0,w_0)$.
Let us call 
$ \overline{E_0} $ the reduced curve associated to the exceptional divisor in 
$\overline{S_I}$. By hypothesis, 
$ \lambda_{w_0} $ is not generically reduced. If 
$ \lambda_{w_0} $ is a one-to-one component of the singular locus, then by Lemma 4.8, the strict transform of 
$ \lambda_{w_0} $ by nI, 
$ \overline{\lambda_{w_0}} $, is also non-reduced. If 
$ \lambda_{w_0} $ is not part of the singular locus, nI being a normalization is an isomorphism outside the singular locus. This implies again that 
$ \overline{\lambda_{w_0}} $ is non-reduced. Then, the intersection number 
$ i( \overline{\lambda_{w_0}}, \overline{E_0} ) \gt 1 $. Since 
$ \overline{S_I}$ is non-singular at 
$n_I^{-1}(0)$, we can use Theorem 3.14 of [Reference Greuel, Lossen and Shustin10]. Therefore, if t is in a neighbourhood of w 0, the intersection number of 
$ \overline{\lambda_t} $ with 
$ \overline{E_0} $ is greater than 1. Notice that 
$ \overline{\lambda_t} $ is non-singular and the intersection of 
$ \overline{\lambda_t} $ with 
$ \overline{E_0} $ is transversal.
Remember that the projection 
$ h_I : S_I \rightarrow \mathbb{P}^1 $ restricted to E 0 is one to one, where E 0 is the reduced curve associated to the exceptional divisor 
$ e_I^{-1}(0)$. The previous argument implies that t has two pre-images by 
$ h_I \circ n_I $. Then, 
$ ({h_{I}|_{E_0}})^{-1} (t) $ has two preimages by nI. Since nI is a normalization, we have that λt is not irreducible. So it cannot be homeomorphic to 
$ \lambda_{w_0} $, which contradicts the topological triviality of SI at 
$(0,w_0)$.
Now the missing implication:
Lemma 4.10. If w is a generic value, then 
$ \Lambda_{f,g} $ is topologically trivial at w.
Proof. Suppose that w is a generic value. Call 
$x:=(0,w) $ the corresponding point in the blown-up surface SI. By Definition 3.3, w is generic at the normalization and x is not a point of the strict transform by eI of the singular locus Σ of S.
Let us first treat the case when 
$(S,0) $ is irreducible. The surface 
$\overline{S}$ is then connected, and the pencil 
$\Lambda_{f\circ n , g\circ n}$ has a unique indeterminacy point at 
$n^{-1}(0)$. The blow-up 
$\overline{e}: \overline{S}_{I\mathcal{O}_{\overline{S}}} \rightarrow \overline{S}$ produces an irreducible (connected) exceptional divisor 
$\overline{E}$. The map 
$\nu : \overline{S}_{I\mathcal{O}_{\overline{S}}} \rightarrow S_I$ induces a homeomorphism outside the strict transform of the singular locus Σ. The inverse image 
$\nu^{-1}(x)$ is a single point 
$y \in \overline{S}_{I\mathcal{O}_{\overline{S}}}$ satisfying 
$ ( h_I \circ \nu ) (y)= w $.
Each element of the pencil 
$ \Lambda_{f \circ n, g \circ n} $ is isomorphic to the corresponding fibre of 
$ h_I \circ \nu $. Since w is generic in the normalization, [Reference Delgado and Maugendre6, Theorem 4] implies that the Milnor number of the corresponding elements of the pencil 
$ \Lambda_{f \circ n, g \circ n} $ is equal to the minimal value. Then by [Reference Buchweitz and G.-M.3, Theorem 5.2.2], 
$ \overline{S}_{I\mathcal{O}_{\overline{S}}} $ is topologically trivial in a neighbourhood of y.
By the homeomorphism induced by ν, SI is also topologically trivial in a neighbourhood of x.
Now suppose 
$(S,0) $ is reducible. The normalized surface 
$\overline{S}$ is a disjoint union of l components with 
$l\geq 2$ and so is the blown-up surface 
$ \overline{S}_{I \mathcal{O}_{\overline{S}}}$. Call 
$\{y_1, \ldots , y_l\}:=\nu^{-1}(x)$. Since w is generic at the normalization, each connected component of 
$ \overline{S}_{I \mathcal{O}_{\overline{S} }} $ is topologically trivial at yi.
Furthermore, none of the yi’s is a point of the strict transform of the singular locus Σ of S by 
$n \circ \overline{e}$. One can then choose sufficiently small neighbourhoods Wi’s of yi’s, in such a way that the restriction of ν to 
$\displaystyle {\bigcup_i} W_i$ maps each connected component of 
$ (n\circ \overline{e})^{-1}(0) \cap W_i$ homeomorphically onto 
$e_I^{-1}(0) \cap U$, for some neighbourhood U of x in SI. The surface SI is then topologically trivial at x [Reference Giles Flores, Silva and Snoussi8, Proposition 4.11].
Now, putting together all the previous lemmas, we have a proof of Theorem 4.1.
Proof. (of Theorem 4.1) Let 
$w\in \mathbb{P}^1$ be a special value for the pencil 
$\Lambda_{f,g}$. If the curve λw is not generically reduced, then by Lemma 4.9 the surface SI is not topologically trivial at 
$(0,w)$; this situation includes the case when λw contains a component of the singular locus of S.
Assume now that the curve λw is generically reduced. If the point 
$(0,w)\in S_I$ belongs to the strict transform by eI of an r to 1 component of the singular locus of S with r > 1, then by Lemma 4.5, the surface SI is not topologically trivial at 
$(0,w)$. If the point 
$(0,w)$ belongs to the strict transform by eI of a one-to-one component of the singular locus, then by 4.7, the surface SI is not topologically trivial at 
$(0,w)$.
Suppose now w is a special value at the normalization with λw generically reduced and 
$(0,w)\in S_I$ does not belong to the strict transform by eI of any component of the singular locus of S. Then, Lemma 4.2 shows that SI is not topologically trivial at 
$(0,w)$.
So every special value corresponds to a point where the pencil is not topologically trivial.
Conversely, if the pencil is not topologically trivial at w, then Lemma 4.10 shows that w is a special value for the pencil.
One can observe in the proof of Theorem 4.1 that the singular locus of the surface contributes to special values of the pencil in two different ways. The branches of the singular locus that are one-to-one components produce special values at the normalization; meanwhile, the r to 1 components with r > 1 produce special values of the pencil that may not be special at the normalization.
Also, note that when the original surface 
$(S,0)$ is not Cohen-Macaulay, then the surface SI obtained by the blow-up of the ideal 
$I=\langle f,g \rangle$ need not be Cohen-Macaulay in all points of the exceptional fibre. The proof of Theorem 4.1 shows that a point 
$(w,0)\in e_I^{-1}(0)$ where the surface SI is not Cohen-Macaulay does not correspond necessarily to a special value of the pencil, unless it is a special value at the normalization or a point of the strict transform of the singular locus of S.
In particular, when the surface 
$(S,0)$ has an isolated singularity, then for any pencil of curves 
$\Lambda_{f,g}$ on S, the special values are exactly the special values at the normalization.
Remark 4.11. In [Reference Ngô Viêt and Ikeda16], the authors give conditions for a Rees algebra to be Cohen-Macaulay. From their work, one can expect to extract conditions for a pencil 
$\Lambda_{f,g}$ on a non Cohen-Macaulay surface so that the blown-up surface SI is Cohen-Macaulay. But there are cases where the Rees algebra is not Cohen-Macaulay, but the analytic space SI is Cohen-Macaulay.
We are now able to describe special curves of a pencil on a reduced complex surface singularity in terms of their topology on the surface.
Corollary 4.12. Consider a pencil of curves 
$\Lambda_{f,g}$ on a representative of a germ of reduced complex surface singularity 
$(S,0)\subset (\mathbb{C}^N, 0)$. A point 
$w\in \mathbb{P}^1$ is a special value if and only if either the corresponding curve λw is not generically reduced or there exists a neighbourhood U of the origin in 
$\mathbb{C}^N$ such that the curve 
$\lambda_w\cap U$ is contractible and the curves 
$\lambda_t\cap U$ are not, for any 
$t\in \mathbb{P}^1$ sufficiently close to w.
Proof. Consider the surface 
$S_1\subset S\times \mathbb{P}^1$ defined in Remark 2.9 by the equation 
$gt -fs =0$, where (s: t) is a system of homogeneous coordinates in 
$\mathbb{P}^1$ and S is a sufficiently small representative of 
$(S,0)$. Call π 1 the restriction to S 1 of the projection 
$ S \times \mathbb{P}^1 \rightarrow \mathbb{P}^1$. Then, for any 
$t\in \mathbb{P}^1$, the fibre 
$\pi_1^{-1}(t)\subset S\times \{t\}$ is isomorphic to 
$\lambda _t\subset S$. Therefore, in order to compare the topology of the curves λt in a representative S of 
$(S,0)$, it is enough to compare the topology of the fibres 
$\pi_1^{-1}(t)$ in S 1.
On the other hand, the surface SI obtained as the blow-up of the ideal 
$I=\langle f,g\rangle $ is the reduced surface associated to S 1. The reduction map 
$r_I : S_I \rightarrow S_1$ is a homeomorphism that commutes with the respective projections π 1 and hI to 
$\mathbb{P}^1$. The fibres 
$h_I^{-1}(t)\subset S_I$ are then homeomorphic to the corresponding elements 
$\lambda_t \subset S$.
We have a commutative diagram:
Now, let us proceed to prove the equivalence asserted in the Corollary.
If a curve λw is not generically reduced. We have two possibilities: either the curve 
$n^{-1}(\lambda_w)$ is reduced or it is not. In the first case, λw contains a component of the singular locus, so w is a special value. In the second case, the Milnor number of λw at the origin is not minimal, and hence, w is a special value at the normalization and therefore a special value for the pencil.
If now λw is generically reduced, its strict transform in SI is also generically reduced. Suppose there exists a neighbourhood U of 0 in 
$\mathbb{C}^N$ such that 
$\lambda_w\cap U$ is contractible and 
$\lambda_t \cap U$ is not for 
$t\in \mathbb{P}^1$ sufficiently close to w. The fibres 
$h_I^{-1}(t) \cap (U\times \{t\})$ and 
$h_I^{-1}(w) \cap (U \times \{w\})$ cannot be homeomorphic, so that the surface SI is not topologically trivial at 
$(0,w)$, and therefore, by Theorem 4.1, w is a special value.
Conversely, fix a special value 
$w\in \mathbb{P}^1$, and assume λw is generically reduced. Then, in particular, the curve λw does not contain any component of the singular locus Σ of S. We will distinguish two cases:
If 
$(0,w)$ is a point of the strict transform by eI of an r to 1 component of Σ, with r > 1, then we have seen in the proof of Lemma 4.5, that in a fixed neighbourhood 
$U\times T \subset(\mathbb{C}^N \times \mathbb{P}^1)$ of 
$(0,w)$, the fibre 
$h_I^{-1}(w)$ is contractible and 
$h_I^{-1}(t)$ is not for t ≠ w sufficiently close to w. The corresponding curve 
$\lambda_w\cap U$ will be then contractible; meanwhile, 
$\lambda_t \cap U$ will not, for t ≠ w sufficiently close to w.
If 
$(0,w)$ is either a point of the strict transform by eI of a one-to-one component of Σ, or does not belong to the strict transform by eI of Σ, then, by Lemma 4.7 and Definition 3.3, w is a special value at the normalization. Call 
$\overline{\lambda}_w$ the corresponding curve of the pencil on the normalized surface that might be a disjoint union of normal surfaces, and let 
$ \overline{S}= \sqcup \overline{S_i}$ be the decomposition of 
$ \overline{S} $ into irreducible components of 
$ \overline{S}$. By [Reference Delgado and Maugendre6, Theorem 4], there exists a connected component 
$\overline{S}_i$ of 
$\overline{S}$ such that the curve 
$\overline{\lambda}_{w,i}$ of the pencil on 
$\overline{S}_i$ has Milnor number strictly bigger then the minimal one among the curves of the pencil on 
$\overline{S}_i$.
Consider now the surface 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ obtained by the blow-up 
$\overline{e}$ of the ideal 
$I\mathcal{O}_{\overline{S}}= \langle f\circ n, g\circ n\rangle$. It is a disjoint union of surfaces obtained by the blow-up of the corresponding ideals in 
$\overline{S}_j$. The strict transform of 
$\overline{\lambda}_{w,i}$ by 
$\overline{e}$ intersects the exceptional divisor at a point 
$x_i \in \nu^{-1}(0,w)$. By hypothesis on 
$(0,w)$, we can choose a connected neighbourhood Vi of xi in 
$\overline{S}_{I\mathcal{O}_{\overline{S}}}$ such that the restriction 
$\nu |_{V_i} $ is a homeomorphism onto its image, the restriction 
$p_i := (h_I \circ \nu) |_{V_i} : V_i \rightarrow T\subset \mathbb{P}^1$ has all its fibres reduced, where T is a suitable neighbourhood of w in 
$\mathbb{P}^1$ and the fibre 
$p_i^{-1}(w) \subset V_i$ is contractible.
We can then choose a section 
$\sigma : T \rightarrow V_i$, whose image is the exceptional divisor in Vi such that the family of curves 
$p_i : V_i \rightarrow T$ is a family of reduced curves where each fibre 
$p_i^{-1}(t)$ is non-singular outside 
$\sigma(t)$.
Moreover, each fibre of pi is isomorphic to its image in the corresponding 
$\overline{S}_i$. The Milnor number 
$\mu(p_i^{-1}(w), x_i)$ is then strictly bigger than 
$\mu(p_i^{-1}(t), \sigma (t))$ for 
$t\in T$ and t ≠ w.
Using the characterization of topologically trivial families of reduced curves given in [Reference Buchweitz and G.-M.3, Theorem 4.2.4], we conclude that the fibre 
$p_i^{-1}(t)$ is not contractible in Vi. Recall that the morphism ν induces a homeomorphism between Vi and its image Wi in SI compatible with the projections to 
$\mathbb{P}^1$. Therefore, the curve 
$h_I^{-1}(t) \cap W_i$ is not contractible for 
$t\in T$ and t ≠ w; meanwhile, 
$h_I^{-1}(w) \cap W_i$ is contractible. Since these curves are homeomorphic to their respective images in S, there exists a neighbourhood U of 0 in 
$\mathbb{C}^N$ such that 
$\lambda_t \cap U$ is not contractible for t ≠ w and t sufficiently close to w and 
$\lambda_w \cap U$ is contractible.
5. Examples
We give now some examples of pencils on different types of surfaces. Most of the calculations were made using the SINGULAR software [Reference Decker, Greuel, Pfister and Schönemann4].
The first example we give is to illustrate how it is possible to have a special value which is not special at the normalization:
Example 5.1. Consider the polynomial in 
$\mathbb{C}[x, y, z]$:
\begin{align*}
G(x,y,z)= 256x^3-27y^4-128x^2z^2+144xy^2z+16xz^4-4y^2z^3.
\end{align*}Its zero set V(G) is the surface known as the Swallow tail. The normalization of V(G) is given by the parametrization:
\begin{align*}
n : \mathbb{C} ^2 & \rightarrow \mathbb{C}^3 \\
(s,t) & \mapsto \left ( \frac{t^2 (3t^2 +4s)}{16} , \frac{t^3 + 2ts }{2}, s \right ).
\end{align*} The singular locus of this surface has two components. Call Σ1 the one given by the image of 
$ V \left ( s + \frac{3}{2} t^2 \right ) $. It is parametrized by the restriction of n:
\begin{align*}
\sigma_1 : \mathbb{C} & \rightarrow \mathbb{C}^3 \\
(t) & \mapsto \left ( - \frac{3t^4}{16} , - t^3 , - \frac{3}{2} t^2 \right ).
\end{align*}Here, we can see that Σ1 is one-to-one component of the singular locus.
Call Σ2 the second component of the singular locus; it is given by the image of 
$ V \left ( s + \frac{1}{2} t^2 \right ) $ and the parametrization:
\begin{align*}
\sigma_2 : \mathbb{C} & \rightarrow \mathbb{C}^3 \\
(t) & \mapsto \left ( \frac{t^4}{16} , 0 , - \frac{t^2}{2} \right ).
\end{align*}This component is a two-to-one component of the singular locus of the surface.
Consider now the pencil on V(G) generated by the functions 
$f= y-x^2 $ and 
$g = x-z^2 $. The associated rational function with indeterminacy at 0 is defined by 
$ h(x,y,z) = [ y-x^2 : x-z^2 ]$.
By computing limits:
\begin{align*}
\lim_{t \to 0} h \circ \sigma_1 = \lim_{t \to 0} [ -t^3 - \frac{9}{16^2} t^8 : - \frac{3}{16} t^4 - \frac{9}{4} t^4 ]= [1:0]
\end{align*} we obtain that the strict transform of Σ1 passes through the point 
$ (0,1:0) \in S_I \subseteq S \times \mathbb{P}^1 $.
In a similar way:
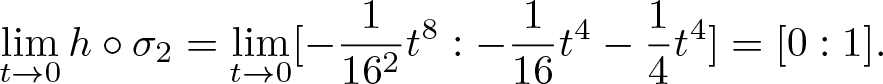\begin{align*}
\lim_{t \to 0} h \circ \sigma_2 = \lim_{t \to 0} [ - \frac{1}{16^2} t^8 : - \frac{1}{16} t^4 - \frac{1}{4} t^4 ]= [0:1].
\end{align*} Then, the strict transform of Σ2 passes through the point 
$ (0,0:1) \in S_I \subseteq S \times \mathbb{P}^1 $.
We obtain the minimal resolution of the pulled back pencil 
$ \Lambda_{f\circ n,g\circ n} $ by blowing-up 3 times. And we get the following diagram:
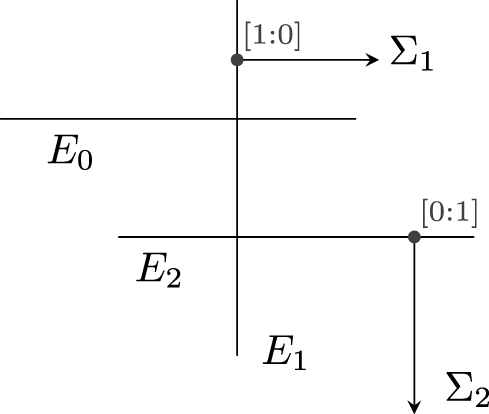
where Ei are the exceptional divisors of the blow-ups.
The component E 0 is dicritical. The restriction to E 0 of 
$ \hat{h} $ is 
$ [s:-t] $, so it has no critical point on E 0.
The component E 1 is non dicritical and 
$ h|_{E_1} \equiv [1,0] $. The last one, E 2, is dicritical. The intersection of Σ2 with E 2 maps to 
$ [0,1] $. And near this intersection, the map 
$\hat{h}$ is defined by 
$h(s,t) =$
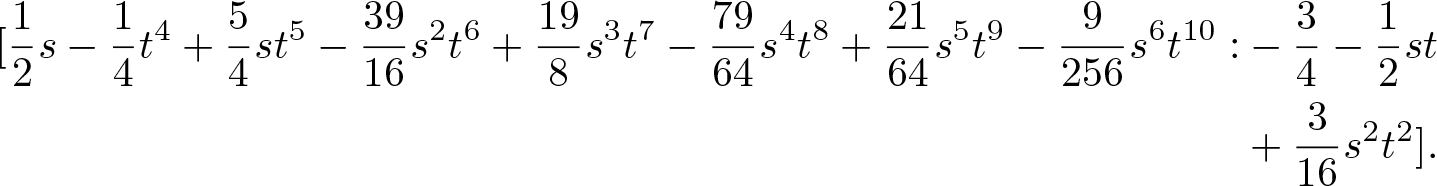\begin{align*}
[ \frac{1}{2}s-\frac{1}{4}t^{4}+\frac{5}{4}st^{5}-\frac{39}{16}s^{2}t^{6}+\frac{19}{8}s^{3}t^{7}-\frac{79}{64}s^{4}t^{8}+\frac{21}{64}s^{5}t^{9}-\frac{9}{256}s^{6}t^{10} : &-\frac{3}{4}-\frac{1}{2}st\\&+\frac{3}{16}s^{2}t^{2}].
\end{align*} Here, the component of the exceptional divisor is defined by t = 0. So we can see that the restriction of 
$\hat{h}$ to this component does not have critical points.
In conclusion, the pencil has two special values: 
$[1:0]$ which is also special at the normalization and 
$ [0,1] $ which is not a special value at the normalization.
Example 5.2. Consider the Whitney umbrella 
$ S = V( x^2 -zy^2 ) $ and the pencil generated by f = z and g = y. Here, the singular locus Σ coincides with the reduced space associated to 
$ \lambda_{[1:0]} = V(y) $. A normalization of S is given by the parametrization:
\begin{align*}
n : \mathbb{C} ^2 & \rightarrow \mathbb{C}^3 \\
(s,t) & \mapsto (st, s, t^2 ).
\end{align*} The pull-back of the pencil by n is generated by s and t 2. The inverse image 
$ n^{-1}(\lambda_{[1:0]}) $ is defined by s = 0; it is a reduced curve. We can then see that the pull-back of a non-reduced curve can be reduced. Since the normalization is 2 to 1 over the singular locus Σ, then by Lemma 4.4, the pencil Λ is not topologically trivial at 
$[1:0]$ which is not a special value at the normalization. The other special value of Λ is 
$[0:1]$ which is special at the normalization.
Example 5.3. Consider the surface defined as the following zero set:
\begin{align*}
S=V( \langle z-x^2, w-y^2 \rangle \cap \langle y+w^2, z+x^2 \rangle) \subseteq \mathbb{C}^4.
\end{align*}It is the union of two smooth surfaces intersecting at one point in a sufficiently small neighbourhood of the origin. It is then a non Cohen-Macaulay surface with an isolated singularity.
Consider the ideal 
$ I = \langle x, y +w\rangle $ generated by two functions that define a pencil on a sufficiently small representative of 
$(S,0)$.
The blow-up of the ideal I in S is a surface in 
$\mathbb{C}^4\times \mathbb{P}^1$ defined in the chart t ≠ 0, where 
$[s,t]$ is a system of homogeneous coordinates in 
$\mathbb{P}^1$, by the intersection of the ideals:
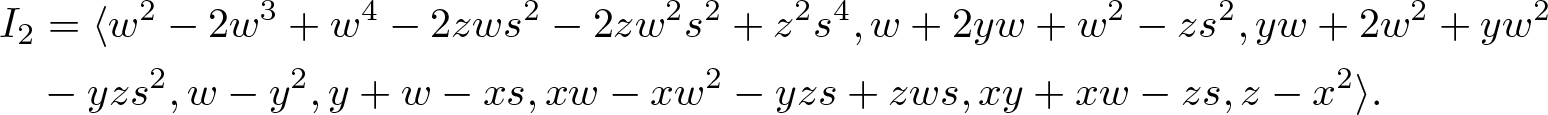\begin{align*}
I_1 = \langle w^2-2w^3+zs^2+w^4, y+w^2, y+w-xs,xw+zs-xw^2, z+x^2 \rangle \, \, {\rm and}
\end{align*}
\begin{align*}
I_2&= \langle w^2-2w^3+w^4-2zws^2-2zw^2s^2+z^2s^4, w+2yw+w^2-zs^2, yw+2w^2+yw^2\\ &-yzs^2, w-y^2, y+w-xs, xw-xw^2-yzs+zws, xy+xw-zs, z-x^2 \rangle.
\end{align*}Intersecting with the hyperplane defined by s = 0, we obtain the curve defined by the ideal:
\begin{align*}
J = \langle
y+w, z2-x4, xw, zw+2x^2y+x^2w-zw^2+x^2w^2, w^2
\rangle .
\end{align*}The primary decomposition of J is:
\begin{align*}
J= \langle w, z-x^2, y \rangle \cap \langle w, z+x^2, y \rangle \cap \langle w^2, z, xw, x^4, y+w \rangle .
\end{align*} The ideal 
$J_3 := \langle w^2, z, xw, x^4, y+w \rangle $ defines an embedded component of the section 
$S_I \cap \{s=0\}$. The surface SI is then non Cohen-Macaulay at the origin of this chart.
The pencil 
$ \Lambda_{x,y+w} $ has no special values. One can check that the surface SI is in fact topologically trivial. In order to do that, in this context, we can compute the Milnor number of the fibres. A generic fibre is a curve with two irreducible smooth non tangent components. Its Milnor number is 1. The fibre defined by s = 0 has an embedded component. Applying the formula of Milnor number of generically reduced curves given in [Reference Brücker and G.-M.2], we obtain that the Milnor number is also 1. Since all the fibres are connected, as seen in the proof of Lemma 4.5, [Reference Greuel9, Theorem 9.3] implies that SI is topologically trivial along 
$\{0\}
\times \mathbb{P}^1$.
Notice that the fibre given by s = 0 in SI has two smooth and tangent irreducible components. Still the family is topologically trivial. The Milnor number stays constant thanks to the embedded component.
Acknowledgements
The authors wish to thank Mark Spivakovsky for his availability and insightful talks, Anne Pichon, Otoniel Nogueira da Silva, Pablo Portilla Cuadrado and Baldur Sigur
$\partial$sson for their time and good ideas. The first Author would like to thank Instituto de Matemáticas UNAN, Unidad Cuernavaca, for financial support and the second author would like to thank the grand PAPIIT117523 by DGAPA-UNAM.
Competing interests
The authors declare not to have any conflict of interests.
