1. INTRODUCTION
With the rapid development of mobile devices and technologies, location-aware applications have become more and more popular. The Global Positioning System (GPS) is known as one of the most effective systems for providing positions for outdoor applications. However, in high-density urban areas and indoor scenes, it is difficult to provide accurate position because of the attenuation and interference of signals. Therefore, indoor positioning technology with high accuracy has become a challenging research problem (Park et al., Reference Park, Charrow, Curtis, Battat, Minkov, Hicks, Teller and Ledlie2010). In recent years, WiFi-based positioning techniques have received considerable attention because of their wide application. A method is proposed using the collection of a dense dataset of WiFi fingerprints and their associated true locations to build a “radio map” (Mahtab Hossain et al., Reference Mahtab Hossain, Jin, Soh and Van2013). Yu and Dutkiewicz (Reference Yu and Dutkiewicz2013) and Mihaylova et al. (Reference Mihaylova, Angelova, Bull and Canagarajah2011) have investigated WiFi multipath distortion and noise to improve localisation accuracy and robustness. Some researchers (Au et al., Reference Au, Feng, Valaee, Reyes, Sorour, Markowitz, Gold, Gordon and Eizenman2013; Jun et al., Reference Jun, Gu, Cheng, Lu, Sun, Zhu and Niu2013; Seitz et al., Reference Seitz, Jahn, Boronat, Vaupel, Meyer and Thielecke2010) have implemented collaborative localisation by combining WiFi and Pedestrian Dead Reckoning. Ferris et al. (Reference Ferris, Fox and Lawrence2007) proposed WiFi-based simultaneous localisation and mapping through related robotics.
Most previous positioning methods employ Received Signal Strength (RSS) as a measurement for position determination. For most off-the-shelf devices, such as WiFi or ZigBee devices, RSS fingerprints are easily available. In these methods, localisation is divided into two phases: training and localisation. The training phase builds a radio map offline, the radio map records RSS received from nearby WiFi Access Points (APs) and the Reference Points’ (RPs) positions where the RSS are collected. In the localisation phase, when users send a location query with the current RSS fingerprint, the localisation algorithm retrieves the radio map to estimate the corresponding location.
The biggest challenge of WiFi-based indoor localisation is timely updating of the radio map as things change. The propagation of wireless signals is easily affected by surrounding environmental changes, such as architectural change, change of interior decoration, and instantaneous interference (Kaemarungsi and Krishnamurthy, Reference Kaemarungsi and Krishnamurthy2012). These changes may cause the radio map to become outdated but re-building the radio map is costly and laborious (Chintalapudi et al., Reference Chintalapudi, Padmanabha Iyer and Padmanabhan2010). In this paper, we apply Gaussian Process Regression (GPR) combined with K-Means to update a global radio map using only one part of the Received Signal Strength Indications (RSSI) to reduce the workload and computational complexity of GPR.
GPR is a non-parametric modelling method, and it is suitable for modelling the received signal strength (Rasmussen and Williams, Reference Rasmussen and Williams2005). The advantage of GPR for modelling WiFi fingerprints is that it includes not only the mean estimation of received signal strength, but also the variance. The mean and variance can be used to reflect the characteristics of the received signal strength even though this may disregard some potentially useful information. However, GPR can require extensive computational resources and may not be suitable for real-time localisation. So, we propose an efficient radio map updating algorithm based on K-Means and GPR. Our experiment shows that the proposed algorithm can greatly reduce the computational complexity and system overhead without sacrificing localisation accuracy.
The contributions of this paper are two-fold. Firstly, a Gaussian mean function-based GPR model is applied for WiFi localisation and compared with other models. Secondly, we propose an efficient algorithm of updating the radio map based on K-Means and GPR. We are able to update the radio map online with a lower computational burden and faster than before.
The rest of the paper is organised as follows. In Section 2, related work is discussed. The details of the proposed algorithm are presented in Section 3. The experimental results are presented in Section 4, and Section 5 provides conclusions.
2. RELATED WORK
Recently, many approaches have been proposed to solve the problem of effectively updating the radio map. Traditional methods including triangulation interpolation, linear interpolation and Kriging interpolation were proposed by Chai and Yang (Reference Chai and Yang2007). However, when fingerprints are sparse, these methods have difficulties in forecasting the RSSI and thus result in poor localisation accuracy. Therefore, other methods have been proposed, including free-calibration methods (Wu et al., Reference Wu, Yang, Liu and Xi2013; Kim et al., Reference Kim, Chon and Cha2012), crowdsourcing methods (Yang et al., Reference Yang, Dessai, Verma and Gerla2013; Rai et al., Reference Rai, Chintalapudi, Padmanabhan and Sen2012; Chang and Han, Reference Chang and Han2014; Wu et al., Reference Wu, Yang and Liu2015a; Reference Wu, Yang, Xiao, Yang, Liu and Liu2015b; Hansen et al., Reference Hansen, Wind, Jensen and Thomsen2010), machine learning models (Pan et al., Reference Pan, Kwok, Yang and Pan2007; Ferris et al., Reference Ferris, Hähnel and Fox2006; Bekkali et al., Reference Bekkali, Masuo, Tominaga, Nakamoto and Ban2011; Richter and Toledano-Ayala, Reference Richter and Toledano-Ayala2015), and the combination of previous methods introduced by Atia et al. (Reference Atia, Noureldin and Korenberg2013).
Wu et al. (Reference Wu, Yang, Liu and Xi2013) proposed Wireless Indoor Localisation (WILL) to record RSSI vectors and the relative distance between them from the embedded sensors to build the radio map. The limitation of WILL is that the quality of fingerprint largely relies on the accuracy of a step counter. Another method introduced by Yang et al. (Reference Yang, Dessai, Verma and Gerla2013) can deal with an unstable signal and construct a metropolitan-cell-based radio map efficiently. However, the proposed interpolation technology is not accurate since it only relies on the relative distance.
The second method is the utilisation of crowdsourcing. The radio map is updated with the most recently measured RSS and inertial sensors’ data uploaded by users. However, designing a sustainable incentive mechanism for crowdsourcing remains a challenge. Chang et al. (Reference Chang and Han2014) used various inertial sensors to collect the users’ path data and update the radio map by interpolation. However, it has limitations in labelling the fingerprints which is rooted in incorrect prediction of a user's path, inaccurate step count and heading. Wu et al. (Reference Wu, Yang and Liu2015a) mapped the fingerprint space to the floor plan in a stress-free form, which results in fingerprints labelled with physical locations. It also relies on inertial sensors’ data.
The third method is based on machine learning. Machine learning algorithms are applied in many fields, such as recommender systems, and so on (Wu et al., Reference Wu, Zhao, Zhang, Meng, Zhang, Zhang and Sun2017; Ji et al., Reference Ji, Ma, Liang, Leung and Zhang2017). Pan et al. (Reference Pan, Kwok, Yang and Pan2007) proposed transferring learning to deal with the signal change. This method can learn the correlation between the locations and fingerprints. However, offline training and online localisation have a high computational cost. A Gaussian process was used to predict Global System for Mobile Communications (GSM) and WiFi signal strength at earlier stages, which adds an offset on the basis of a zero-mean function to solve the limitations (Ferris et al., Reference Ferris, Hähnel and Fox2006). This is limited in practical application because the locations of APs are required. Bekkali et al. (Reference Bekkali, Masuo, Tominaga, Nakamoto and Ban2011) applied a Gaussian process to indoor localisation but did not propose the usage of a hyper-parameter optimisation method and a mean function. The GPR model has been used for predicting Wireless Local Area Networks (WLAN) fingerprints based on mean and covariance functions (Richter and Toledano-Ayala, Reference Richter and Toledano-Ayala2015). Experimental results show that a constant mean function has the best performance, but these mean functions are not in line with the RSS, and do not take into account the impact of reference points’ density on RSS modelling.
Atia et al. (Reference Atia, Noureldin and Korenberg2013) applied a Gaussian process to online-calibrated radio maps for indoor localisation. The gradient descent algorithm was used for hyper-parameter optimisation, and a path loss mean model was proposed. However, sparse deployment of APs may degrade the performance and the APs’ locations are needed. Liu et al. (Reference Liu, Meng and Own2016) focused on a GPRP method based on GPR and the Naive Bayes algorithm to reduce the computational complexity of indoor localisation, and it retains the flexibility of the GPR models. However, the environment is limited, and it requires additional hardware. Kumar et al. (Reference Kumar, Hegde and Trigoni2016) applied GPR which considered the variance of input for indoor localisation. It employed principal component analysis to choose the stronger WiFi AP. However, localisation accuracy is achieved at the expense of O(n 3) computational complexity.
Our study is motivated by these former works, but we solve the problem from a different approach and mainly focus on improving the updating efficiency online without sacrificing localisation accuracy. We propose a novel algorithm to update the radio map by K-Means GPR (KMGPR). We first build a GPR predictive model based on a Gaussian Mean GM) function and then an efficient radio map updating algorithm KMGPR based on K-Means and GPR is applied to reduce the computational complexity of GPR.
3. THE ALGORITHM OF RADIO MAP UPDATING BASED ON K-MEANS AND GAUSSIAN PROCESS REGRESSION
3.1. GPR in fingerprint-based localisation
GPR is a non-parametric and probabilistic approach to regression. It is a probability distribution over functions determined by a mean function m(x) and covariance function ![]() $k(x:x^{\prime})$. Fingerprint-based localisation is used to predict the location based on the RSSI, and we can use GPR to predict the current RSSI. Table 1 introduces the terms used in this work.
$k(x:x^{\prime})$. Fingerprint-based localisation is used to predict the location based on the RSSI, and we can use GPR to predict the current RSSI. Table 1 introduces the terms used in this work.
Table 1. Table of GPR parameter symbols in fingerprint-based localisation.

Here, given the training data X and Y, we could predict the posterior distribution of a function at an arbitrary point x *. The posterior distribution of function values is a Gaussian distribution with ![]() $\mu_{x_{\ast}}$ and
$\mu_{x_{\ast}}$ and ![]() $\sigma_{x_{\ast}}^{2}$:
$\sigma_{x_{\ast}}^{2}$:
The covariance matrix between the n reference points is given in Equation (4).
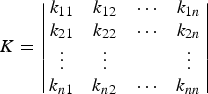 $$K = \left\vert \matrix{k_{11} & k_{12} &\cdots & k_{1n} \cr k_{21} & k_{22} &\cdots & k_{2n} \cr \vdots &\vdots & &\vdots \cr k_{n1} & k_{n2} &\cdots & k_{nn}}\right\vert$$
$$K = \left\vert \matrix{k_{11} & k_{12} &\cdots & k_{1n} \cr k_{21} & k_{22} &\cdots & k_{2n} \cr \vdots &\vdots & &\vdots \cr k_{n1} & k_{n2} &\cdots & k_{nn}}\right\vert$$In fingerprint-based indoor localisation, GPR is used to construct the likelihood model based on WiFi signal strength. The key part is in Equations (2) and (3), which represent the distribution of the RSS prediction.
Fortunately, we can learn and optimise the parameter through maximising the log likelihood function of the observation Y given by
We optimise Equation (5) by conjugating gradient descent and computing the partial derivatives of the log likelihood.
The most complex step of the calculation is the hyper-parameter optimisation in Equation (6). It needs to recalculate the inversion of the covariance matrix K for each new θ, which costs time O(n 3), where n is the number of reference points that collect the WiFi fingerprints. Therefore, the method to reduce the computational complexity requires an effective gradient descent algorithm or other efficient machine learning methods.
3.2. GPR modelling using Gaussian mean function
A Gaussian process is normally a zero-mean prior distribution, and most of the predicted RSS values tend to be zero when lacking training data in a large positioning region. This will result in a higher localisation error. To find a more suitable GPR prior model to predict RSS, a variety of mean functions were evaluated. We used a GPR predictive model based on a Gaussian Mean (GM) function and Equation (2) is displaced by Equations (7) and (8). Moreover, we also compare three other different mean functions: the zero-mean function, the linear mean function and the constant mean function.
When using a GM function to predict RSS, it can effectively capture the RSS feature at a reference point compared with the constant and linear mean functions. This is in line with the characteristics of the signal fluctuations and is conducive to RSS modelling.
3.3. Online radio map updating algorithm
GPR consumes more computational effort when updating the radio map using Equations (3) and (7). So, it is not conducive to indoor real-time localisation. To overcome this problem, we propose an efficient algorithm of radio map updating based on K-Means and Gaussian Process Regression. The KMGPR algorithm can effectively reduce the computational complexity of the GPR predictive model.
This algorithm utilises K-Means clustering on the initial radio map. All the reference points ![]() $\{x_{i}\}_{i = 1}^{n}$ in the target area were divided into several clusters based on the Euclidean distance of locations. In every cluster, we use GPR to predict other fingerprints to update the original radio map. When building the GPR model, we only consider the training data that belongs to the same cluster, so it is very efficient. The KMGPR algorithm can be summarised as the pseudo-code in Table 2.
$\{x_{i}\}_{i = 1}^{n}$ in the target area were divided into several clusters based on the Euclidean distance of locations. In every cluster, we use GPR to predict other fingerprints to update the original radio map. When building the GPR model, we only consider the training data that belongs to the same cluster, so it is very efficient. The KMGPR algorithm can be summarised as the pseudo-code in Table 2.
Table 2. The KMGPR algorithm.

As mentioned above, reducing the GPR computational complexity is an important goal of our work because GPR requires a high computational load. We use clustering to solve the problem. The reference point set of the entire area can be divided into separate sets by K-Means based on the correlation of locations.
When the number of reference points in a cluster is m, the KMGPR algorithm simplifies Equations (2) and (3) by only considering m reference points. Therefore, K * and Y reduce to a m×1 vector, and cov (Y) in Equation (2) to a m×m matrix. So, when updating the radio map online, K clusters can conduct GPR prediction concurrently. Compared to the complexity O(n 3) when considering all n reference points in the region, in the KMGPR, we also use the n reference points and they are divided into K clusters, the complexity is O(m 3) for a cluster and the total complexity is ![]() $K^{\ast}O(m^{3})$ for all K clusters. In general,
$K^{\ast}O(m^{3})$ for all K clusters. In general, ![]() $K^{\ast}O(m^{3}) << O(n^{3})$, because m<n.
$K^{\ast}O(m^{3}) << O(n^{3})$, because m<n.
4. SIMULATION AND EXPERIMENT
We conducted the simulation and experimental study in two scenarios. In the first scenario, we used the experimental data set introduced by Laoudias et al. (Reference Laoudias, Piché and Panayiotou2013), which is a typical office environment with an area of 560 m2 (see Figure 1). In the second scenario, we set up our testbed in a real environment.
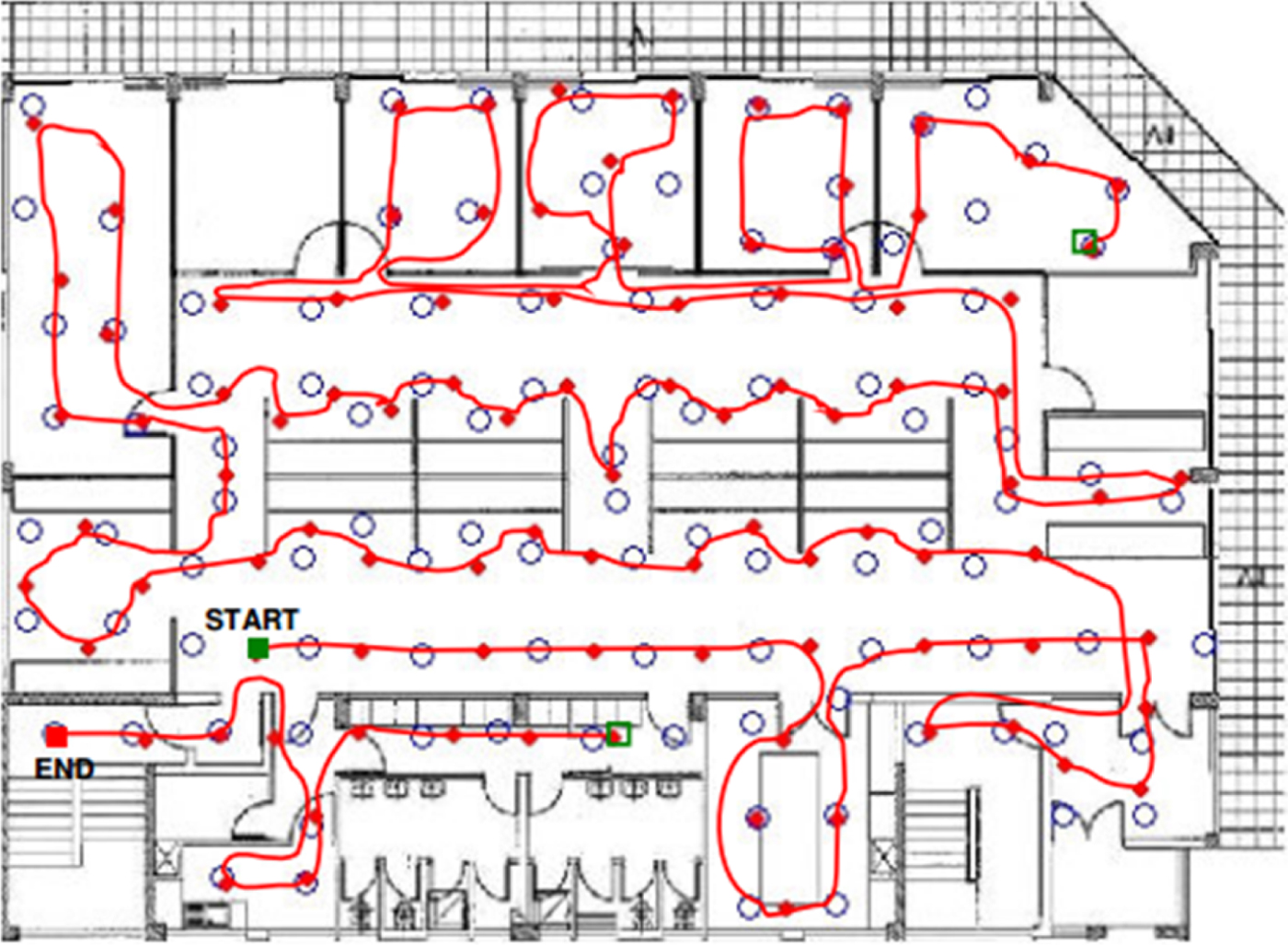
Figure 1. Experimental area introduced by Laoudias et al. (Reference Laoudias, Piché and Panayiotou2013) (Scenario 1).
4.1. Simulations
4.1.1. Simulations setup
There are nine APs in the first scenario. The experimental data set contains RSS from all available APs at 105 distinct reference points and corresponding true locations for comparison. The data set was collected from a Samsung Nexus S containing training and test data. The training data has 2,100 fingerprints for 105 reference points; 20 fingerprints at each reference point. The researcher collected additional test data by walking along a predefined path. The path consists of 96 locations, most of which do not coincide with the reference points. As shown in Figure 1, there are 105 blue circles representing the reference points and the red curve connects 96 red points as the test path.
4.1.2. GPR model evaluation
With a GPR model, we use just a part of the reference point set to update the whole radio map and the final fingerprint density is the same. Different numbers of reference points were randomly selected as training points to update the whole 105 reference points: 20, 40, 60, 80 and 100 and they were not necessarily evenly distributed across the entire indoor area. In order to avoid errors caused by randomness, we conducted 10-fold cross-validation and obtained the mean error as the final result in the RSS estimation and localisation test. To illustrate the quality of GM in updating the RSS radio map, we also compared three other mean functions: (1) the Zero-mean function (Zero), as m(x)=0; (2) the Constant mean function (Const), as m(x)=c and c is a constant; (3) the Linear mean function (Lin), as m(x)=a Tx and a is a linear coefficient vector.
RSS estimation accuracy
In the simulation we used 10-fold cross-validation to determine the quality of the models, and the test error and the Root Mean Squared Error (RMSE) of different models were investigated. Test error is defined as follows:
where F i and ![]() $\overline{F}_{i}$ are estimated RSS values and true RSS values at reference point i respectively. We also computed the RMSE over the remaining reference points which were not training points among the 105 reference points; when the number of reference points is m, the RMSE is as defined in Equation (10).
$\overline{F}_{i}$ are estimated RSS values and true RSS values at reference point i respectively. We also computed the RMSE over the remaining reference points which were not training points among the 105 reference points; when the number of reference points is m, the RMSE is as defined in Equation (10).
 $${RMSE} = \sqrt{\left.\sum\limits_{i = 1}^{m} {Res}_{i}^{2}\right/m}$$
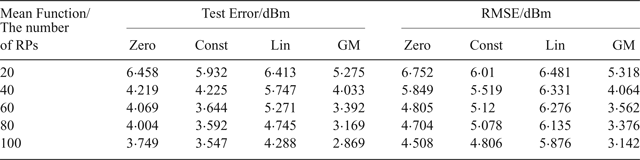
$${RMSE} = \sqrt{\left.\sum\limits_{i = 1}^{m} {Res}_{i}^{2}\right/m}$$Table 3 shows the test error and RMSE of the GPR model for different mean functions. The analysis of the test error and RMSE showed similar experimental results when different numbers of reference points were selected as the training data set. GM consistently outperformed the constant mean function, zero mean function and linear mean function. Compared with other mean functions, the test error and RMSE of GM were 4·41~35·65% and 11·51~46·53% lower, respectively.
Table 3. Test error and RMSE of the GPR model for different mean functions.
Localisation accuracy estimation
In order to further verify the model performance of GPR based on GM, we present the results of the localisation accuracy of the 96 test points using Weighted K-Nearest Neighbour (WKNN). WKNN is a popular algorithm for fingerprint-based indoor localisation, which employs K nearest RPs by Euclidean distance to estimate a user's location. The weight is obtained from the calculated distance and K is the number of RPs whose distance is less than a set threshold. For experimental comparison, the training data of all 105 reference points were used for the construction of the Original radio map (ORI). The Localisation Error is defined as follows:
where (x, y) and ![]() $(\hat{x}, \hat{y})$ are estimated location and true location, respectively. Clearly, the smaller the Localisation Error, the better the algorithm performs.
$(\hat{x}, \hat{y})$ are estimated location and true location, respectively. Clearly, the smaller the Localisation Error, the better the algorithm performs.
Table 4 lists the average localisation accuracy for different GPR models after 10-fold cross-validation. For different training sets of RPs, the most accurate GPR model is the one with the GM function. When compared to other models, the localisation accuracy of GM has improved by an average of 13·76%. When the number of training reference points is 60, the localisation accuracy can be improved by 13·27~19·43%. In Figure 2(a), the CDF of localisation error for different mean functions is shown. The probability of GM's localisation accuracy is a little lower than the ORI, but higher than the other three models.
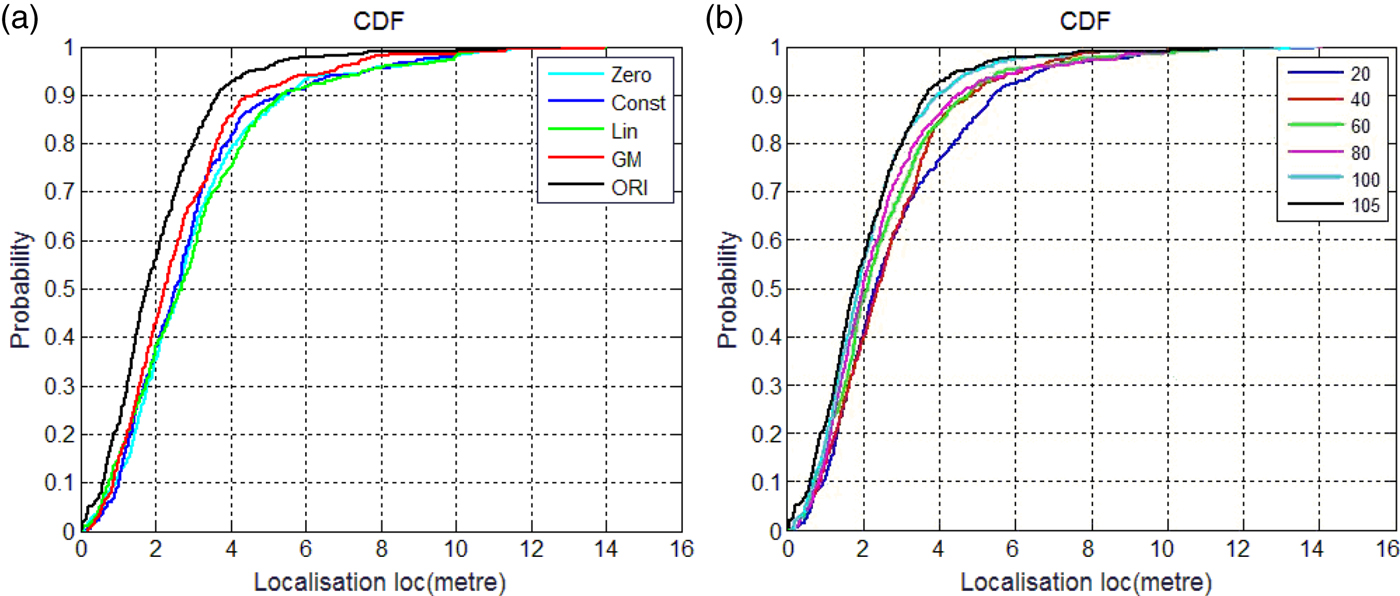
Figure 2. The Cumulative Distribution Function (CDF) of localisation error. (a) different mean functions; (b) different numbers of RPs.
Table 4. Average localisation error for different mean functions.

We also studied the relationship between the number of RPs and the localisation accuracy of different models. Figure 2(b) shows that the model with a larger number of RPs achieves a better performance than with a smaller number of RPs. When the number of RPs is 60, GM has reached 94·6% of the localisation accuracy of the original radio map. This means GM can use only a small amount of resource in updating the radio map.
4.1.3. Evaluation of KMGPR algorithm
To evaluate the performance of the KMGPR algorithm, we also conducted experiments in Scenario 1. In our experiment, we set the number of clusters to 1~ 6 and randomly chose the clusters’ centroid points. The aim was to identify the efficiency of the KMGPR algorithm when compared to GPR.
We used the Gaussian mean function-based GPR prior model to update the radio map. During the experiments, 10-fold cross-validation was performed for GPR and KMGPR. When KMGPR took different clusters with K-Means, the randomly selected RPs were different. In order to keep experimental consistency, GPR applied the same selected RPs as KMGPR. So, the results of GPR were different when KMGPR took different numbers of clusters.
Figure 3(a) depicts the average prediction error of different clusters in Scenario 1. Remarkably, when the number of clusters is 1, the KMGPR algorithm will become the GPR algorithm. The prediction accuracy of the KMGPR algorithm reached about 95% of the prediction accuracy of the GPR model, but the KMGPR algorithm has good performance in computational complexity as shown in Figure 3(b).

Figure 3. RMSE of prediction and running time with varying clusters. (a) RMSE of prediction; (b) Running time.
Figure 3(b) shows the time for updating the radio map with different numbers of clusters in Scenario 1. The results show that the KMGPR algorithm can cut the computation by about 16%~24·1% when compared with GPR.
4.2. Experiments
4.2.1. Experimental setup
To further evaluate our proposed KMGPR algorithm, an experiment was conducted on the third floor of No. 13 office building in Shandong University of Science and Technology (Figure 4). The floor is approximately 70 m by 50 m in size and six APs provide full coverage throughout the building. We developed software for a mobile device (Android 4.4) to collect the RSSI and test data. Fingerprint collections were taken at 65 reference points marked by white dots. For each reference point, we collected 20 RSS samples from each AP and then obtained averages of the results. There was about 2 seconds between consecutive samples. This method can solve the problem of signal fluctuation. We collected other RSS samples at 34 locations marked by red dots as localisation test data. We collected the test data by walking along a predefined path in the corridor, which did not coincide with the reference points. This data can be used to evaluate our algorithm in conjunction with the training data. Figure 5 shows the locations of the real experimental data collection for Scenario 2.
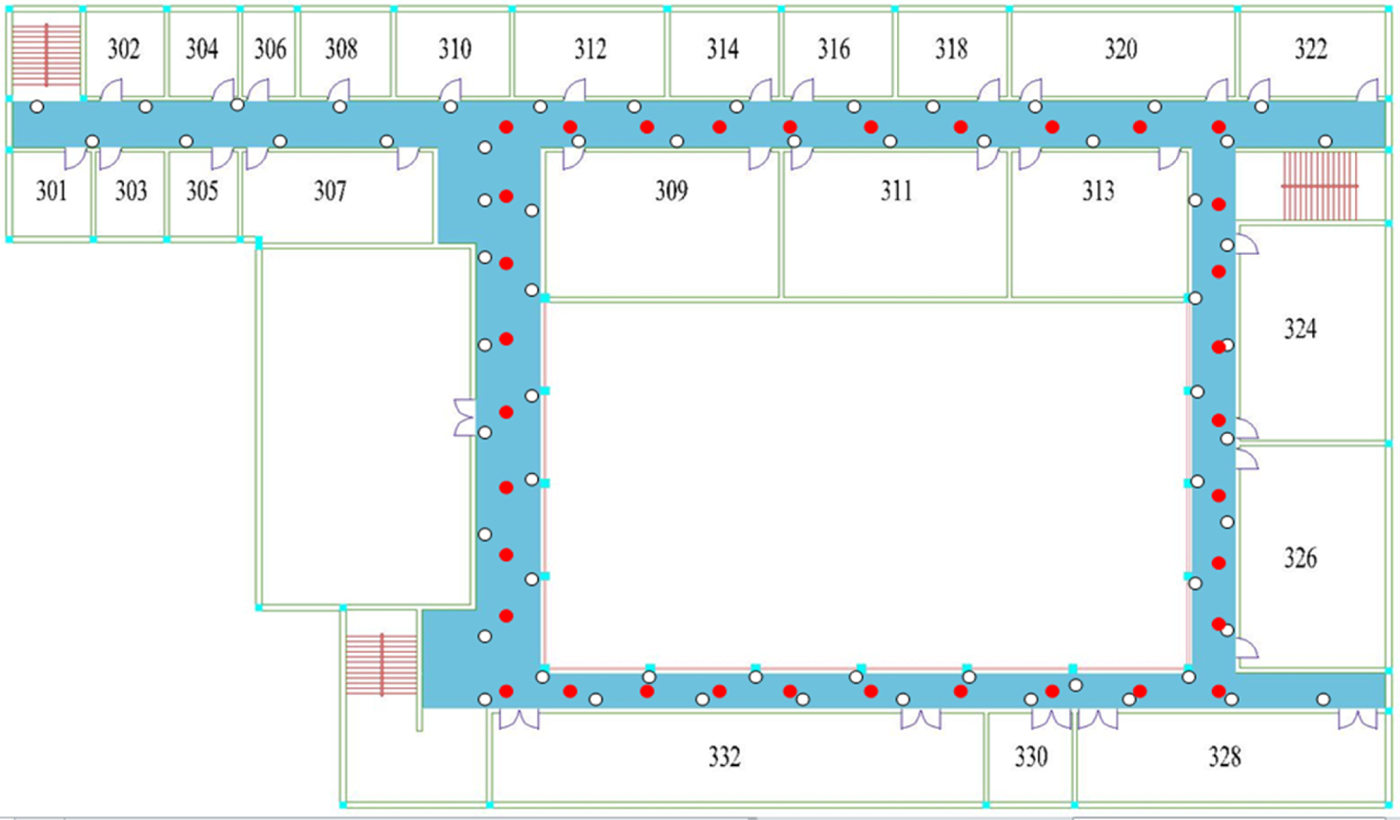
Figure 4. Experimental area (Scenario 2).
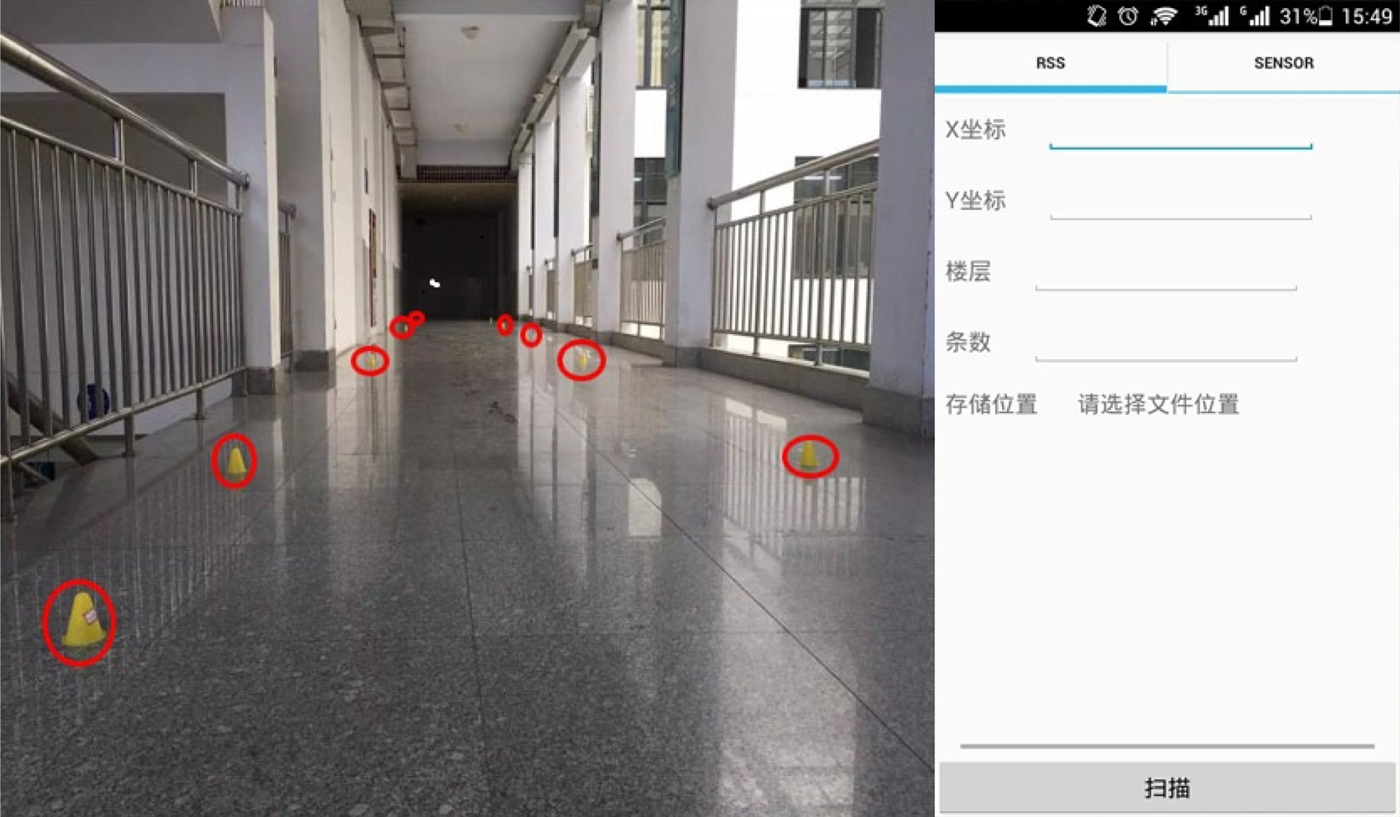
Figure 5. Fingerprint collection in Scenario 2.
4.2.2. GPR model evaluation
In Figure 4, there are 65 reference points in the positioning area. Different numbers of reference points were randomly selected for this experiment: 15, 30, 45 and 60. To illustrate the quality of GM in updating the RSS radio map, we also compared three mean functions: Zero, Const and Lin.
RSS estimation accuracy
In the experiment we used 10-fold cross-validation to determine the quality of the models and the test error and the RMSE of different models were investigated.
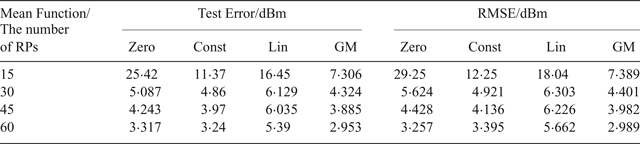
Table 5 shows the test error and RMSE of the GPR model for different mean functions. The analysis of the test error and RMSE showed similar experimental results to Scenario 1. GM can give a better result and consistently outperformed Zero, Const and Lin. Compared with other mean functions, the test error and RMSE of GM were 2·14~71·26% and 8·23~74·74% lower, respectively, in Scenario 2.
Table 5. Test error and RMSE of the GPR model for different mean functions.
Localisation accuracy estimation
In this test, the 34 test points of Scenario 2 were used for localisation to verify the performance of GM. Localisation error is listed in Table 6 using the WKNN algorithm. For different numbers of training data sets, the most accurate GPR model is the GM model. When compared with other models, the localisation accuracy of GM can be improved by an average of 12·50%.
Table 6. Average localisation error for different mean functions.

In Figure 6(a), the CDF of the localisation error for different mean functions is shown. ORI is the original radio map from all the reference points in Scenario 2. The result is consistent with Scenario 1. Figure 6(b) shows the CDF of localisation error for different numbers of RPs. When the number of RPs is 60, GM has almost reached the localisation accuracy of the original radio map.
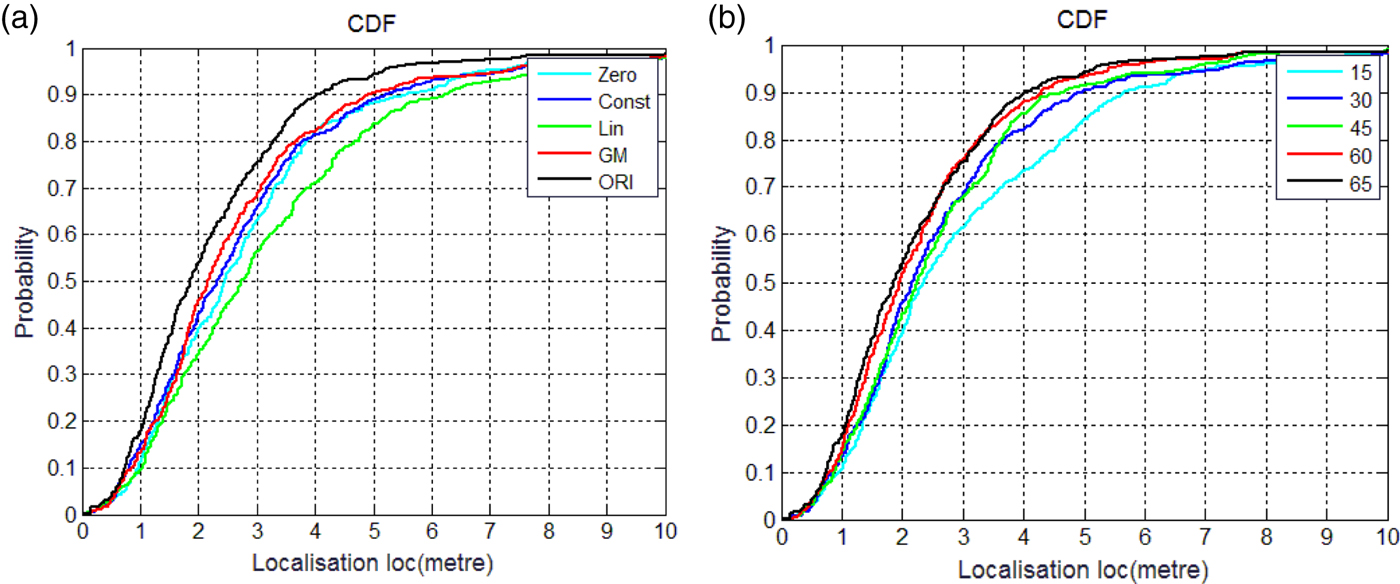
Figure 6. CDF of localisation error. (a) different mean functions; (b) different numbers of RPs.
4.2.3. KMGPR in Scenario 2
Figure 7(a) shows the average prediction error for GPR and KMGPR with different clusters. Compared to the GPR model, the prediction accuracy of the KMGPR algorithm is only slightly reduced.
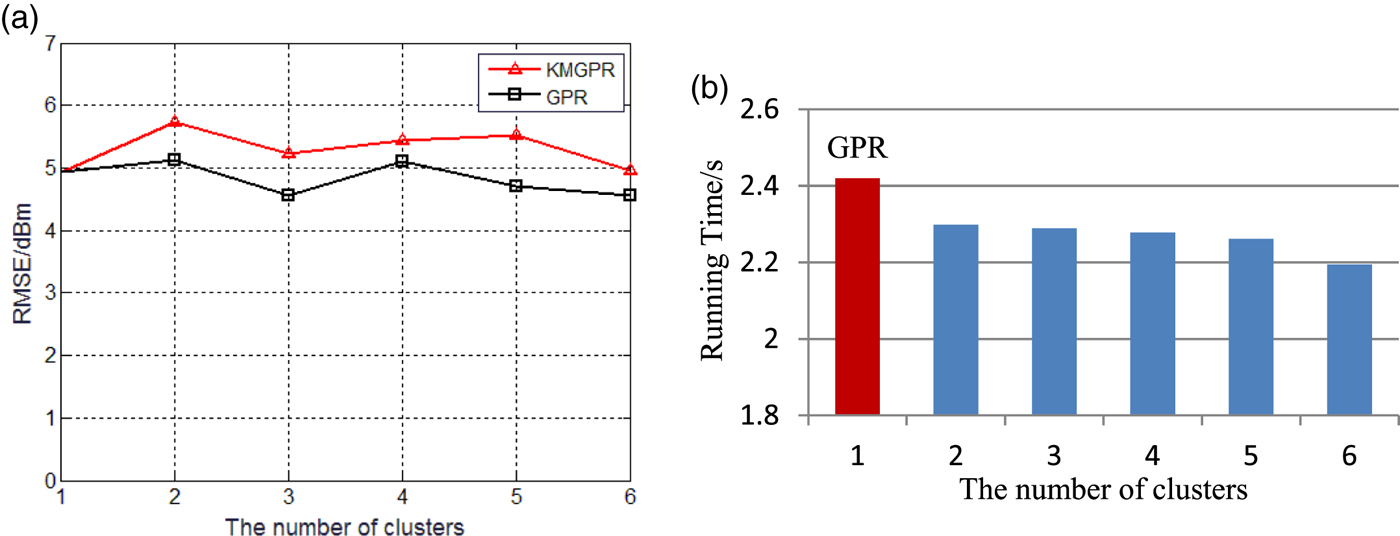
Figure 7. RMSE of prediction and running time with varying clusters. (a) RMSE of prediction; (b) Running time.
Figure 7(b) depicts the running time for updating the radio map with different numbers of clusters in Scenario 2. It shows that the time decreases when the number of clusters increases. The efficiency of our KMGPR algorithm increased by about 5~9·3% compared with GPR.
Figure 8 shows the localisation error versus the number of clusters for GPR and KMGPR in Scenario 2. The localisation errors between GPR and KMGPR are in a small range of fluctuations. As the number of clusters increases, the localisation error decreases first and then increases for KMGPR. This is because with the increase of the number of clusters, some potentially useful information contained in other RPs is lost. In summary, the KMGPR algorithm can have a good localisation performance with less workload compared to GPR.
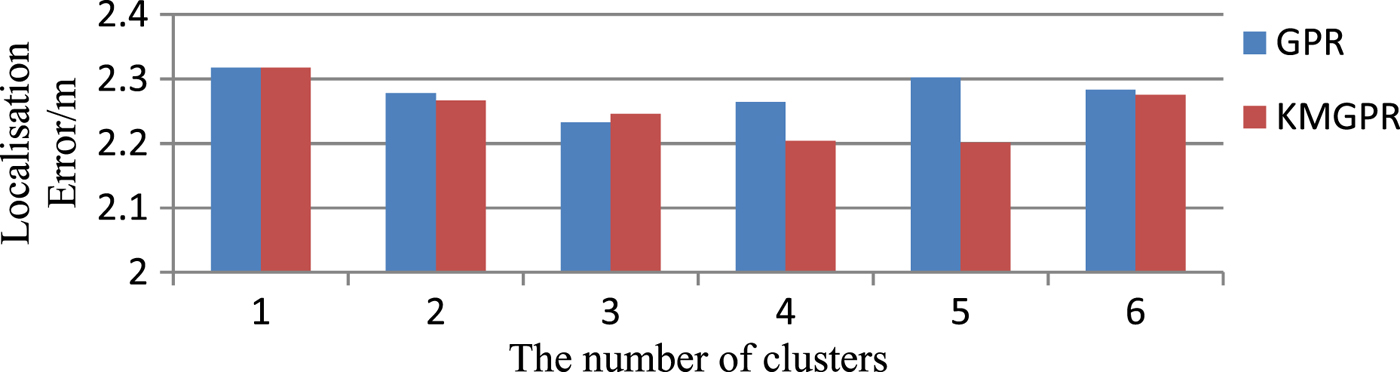
Figure 8. Localisation error comparison between GPR and KMGPR.
Thus, we can see that the KMGPR performs better. The KMGPR algorithm can improve the operating efficiency of online radio map updating and reduce system overhead without sacrificing localisation accuracy.
5. CONCLUSION
In this paper, an efficient algorithm for radio map updating based on K-Means and Gaussian Process Regression is introduced to reduce the workload in updating a fingerprint-based indoor localisation radio map. We first introduce the theory of GPR, parameter optimisation and clustering technology under WLAN-based indoor localisation. Then we build a GPR predictive model based on a Gaussian mean function and update the radio map with online K-Means clustering. Simulations and experiments have been conducted for the proposed KMGPR method and the results show that GPR using Gaussian mean function improves localisation accuracy by about 13·76% compared with other functions and KMGPR can reduce the computational complexity by about 7% and 20%, respectively, in the two scenarios we investigated, with no obvious effects on the localisation accuracy.
ACKNOWLEDGMENTS
This paper is supported by National Key R&D Plan (NO. 2017YFC0804406), Key R&D Plan of Shandong Province (GG201709160017), Project of Industrial Transformation and Upgrading (Made in China 2025 NO.TC170A5SW) and Open Research Fund Program of Beijing Key Laboratory on Integration and Analysis of Large-scale Stream Data (NO.KF201802).
















