1. Introduction
Faults and fractures are abundant discontinuity features in rocks that govern fluid flow in the subsurface (Caine et al. Reference Caine, Evans and Forster1996; Sibson, Reference Sibson1996; Curewitz & Karson, Reference Curewitz and Karson1997; Connolly and Cosgrove Reference Connolly and Cosgrove1999; Sanderson & Zhang, Reference Sanderson and Zhang2004; Kurz et al. Reference Kurz, Imber, Wibberley, Holdsworth and Collettini2008; Zhang et al. Reference Zhang, Schaubs, Zhao, Ord, Hobbs and Barnicoat2008; Bense et al. Reference Bense, Gleeson, Loveless, Bour and Scibek2013; Morley & Nixon, Reference Morley and Nixon2016; La Bruna et al. Reference La Bruna, Bezerra, Souza, Maia, Auler, Araujo, Cazarin, Rodrigues, Vieira and Sousa2021; Pisani et al. Reference Pisani, Antonellini, Bezerra, Carbone, Auler, Audra, La Bruna, Bertotti, Balsamo, Pontes and de Waele2022). These structural features develop at a variety of scales from large-scale regional faults to outcrop scale, fracture and stylolite networks, all of which can either enhance or impede flow in the subsurface (Caine et al. Reference Caine, Evans and Forster1996; Odling et al. Reference Odling, Gillespie, Bourgine, Castaing, Chiles, Christensen, Fillion, Genter, Olsen, Thrane and Trice1999; Bour et al. Reference Bour, Davy, Darcel and Odling2002; Sanderson & Zhang, Reference Sanderson and Zhang2004; Manzocchi et al. Reference Manzocchi, Childs and Walsh2010; Bense et al. Reference Bense, Gleeson, Loveless, Bour and Scibek2013; Bruna et al. Reference Bruna, Lavenu, Matonti and Bertotti2019; Giuffrida et al. Reference Giuffrida, La Bruna, Castelluccio, Panza, Rustichelli, Tondi, Giorgioni and Agosta2019; Araújo et al. Reference Araújo, La Bruna, Rustichelli, Bezerra, Xavier, Audra, Barbosa and Antonino2021). Analysing these networks and characterizing their impact on flow and transport, is paramount for a variety of subsurface applications, e.g. geothermal energy extraction (Lipsey et al. Reference Lipsey, Pluymaekers, Goldberg, van Oversteeg, Ghazaryan, Cloetingh and van Wees2016; Vidal et al. Reference Vidal, Genter and Chopin2017; Smeraglia et al. Reference Smeraglia, Giuffrida, Grimaldi, Pullen, La Bruna, Billi and Agosta2021), hydrocarbon production (Nelson, Reference Nelson2001), mineral exploration (e.g. Cox, Reference Cox, McCaffrey, Lonergan and Wilkinson1999), CO2 sequestration (CSS; e.g. Stork et al. Reference Stork, Verdon and Kendall2015) and hydrogen storage (Saxena et al. Reference Saxena, Nibur and Prakash2018). This is especially important in geothermal reservoirs where host-rock permeability is generally low, e.g. granite geothermal systems (Wibberley & Shimamoto, Reference Wibberley and Shimamoto2002), and fluid flow is controlled at first order by fracture network geometry (Hollinsworth et al. Reference Hollinsworth, Koehn, Dempster and Aanyu2019).
Efficient discretization and simulation techniques are required to obtain reliable prediction of permeability distributions within geothermal reservoirs. We use a field example from an open pit quarry near Kulmbach, Germany, to show how fracture network anisotropy in geothermal reservoirs can be assessed using detailed analysis of outcrop analogues. Specifically, we analyse variation of fracture networks in a cross-section towards the seismic-scale Kulmbach Fault. We present the results of the structural analysis, followed by introducing a mixed-dimensional approach for quick discretization of the network for the numerical analysis of flow in the dense fracture networks. Based on our field data we will demonstrate the importance of linking geological field work to numerical model development. Finally, we propose a new approach to numerical permeability homogenization that is informed by detailed field observations.
1.a. Two-dimensional fracture modelling from surface analogues
Fracture spatial arrangement and variations can be quantified from several data sources at different dimensions such as 1D – scan lines (Priest & Hudson, Reference Priest and Hudson1981), boreholes (e.g. Rajabi et al. Reference Rajabi, Sherkati, Bohloli and Tingay2010) – 2D – drone imagery, pavement analysis (Boersma et al. Reference Boersma, Prabhakaran, Bezerra and Bertotti2019; Smith, Reference Smith2020) – and 3D – seismic analysis (Jaglan et al. Reference Jaglan, Qayyum and Hélène2015), lidar (Pontes et al. Reference Pontes, Bezerra, Bertotti, La Bruna, Audra, De Waele, Auler, Balsamo, De Hoop and Pisani2021), ground-penetrating radar (Grandjean and Gourry, Reference Grandjean and Gourry1996; Elkarmoty et al., Reference Elkarmoty, Tinti, Kasmaeeyazdi, Giannino, Bonduà and Bruno2018) or outcrop mapping (Jones et al. Reference Jones, McCaffrey, Clegg, Wilson, Holliman, Holdsworth, Imber and Waggott2009). Subsurface data allow for larger-scale faults (e.g. seismic surveys) and fractures (e.g. well logs) to be imaged directly from reservoirs which can be implemented into models of the fractured networks at depth (e.g. Boersma et al. Reference Boersma, Bruna, de Hoop, Vinci, Tehrani and Bertotti2021). For geothermal exploration, acquiring reliable subsurface data can be too costly, and, with the resolution limitations of seismic data, small-scale fracture networks are often overlooked (Lei et al. Reference Lei, Latham and Tsang2017). Therefore, surface fractured features can be useful for quantifying fractured networks, in particular the smaller networks, and making predictions at depth (Welch et al. Reference Welch, Souque, Davies and Knipe2015; Gutmanis et al. Reference Gutmanis, i Oró, Díez-Canseco, Chebbihi, Awdal and Cook2018).
Geological analogues are a tool for generating representations of the subsurface from outcrops and reduce uncertainty in developing geological and dynamic models (Pringle et al. Reference Pringle, Howell, Hodgetts, Westerman and Hodgson2006; Howell et al. Reference Howell, Martinius and Good2014). Analogues provide information on the structure of units and fracture systems in place within formations and larger-scale regions where geologists can directly see features in the rocks. Interpreting and utilizing analogues is therefore vital for understanding the fractured networks at depth. For reservoir analogues, scan lines (1D) and fractured pavements (2D) are the most used data techniques and, whilst scan lines can provide statistical information on fracture arrangement, they are not useful for developing further models (Priest and Hudson, Reference Priest and Hudson1976; Dershowitz et al., Reference Dershowitz, Herda, Tillerson and Wawersik1992; Prabhakaran et al. Reference Prabhakaran, Bertotti, Urai and Smeulders2021). Two-dimensional pavement and fracture trace analysis allow for the interpretation and modelling of geometric and topological data (fracture orientation, length, intersections, aperture) from the fracture networks using advanced techniques of data acquisition, e.g. monopod and drone photogrammetry (Bisdom et al. Reference Bisdom, Nick and Bertotti2017; Prabhakaran et al. Reference Prabhakaran, Bruna, Bertotti and Smeulders2019, Smith, Reference Smith2020; Lopes et al. Reference Lopes, Medeiros, La Bruna, de Lima, Bezerra and Schiozer2022).
There are several software solutions that can be used to analyse and capture data within the fractured pavements and 2D outcrops (e.g. Hardebol & Bertotti, Reference Hardebol and Bertotti2013; Healy et al. Reference Healy, Rizzo, Cornwell, Farrell, Watkins, Timms, Gomez-Rivas and Smith2017). These enable the simplification of fracture networks and focus on important parameters such as orientation, connectivity and aperture. Whilst these programs are excellent in producing statistical data on the fracture patterns, they do not provide the functionality to prepare the fracture networks for numerical modelling through the formation of fracture meshes and the clustering of fracture sets.
1.b. Numerical modelling of fractured networks
The analysis and interpretation of fracture networks provides a base from which predictions can be made of the fracture distribution on the surface and within the subsurface. However, to quantify how the fractures affect fluid flow, numerical modelling is required to obtain data that represent the flow response of the fractured network (e.g. permeability tensors; Zhang et al. Reference Zhang, Sanderson, Harkness and Last1996).
Integrating a fractured network into fluid flow simulations can be difficult due to the variability of fracture properties (e.g. length, orientation, aperture), but methods exist to bridge these uncertainties between scales of the fractures and represent the network properties at a multiscale level (Bonnet et al. Reference Bonnet, Bour, Odling, Davy, Main, Cowie and Berkowitz2001; Liu et al. Reference Liu, Li and Jiang2016; Berre et al. Reference Berre, Doster and Keilegavlen2019).
Explicitly representing fracture networks within large-scale simulations poses significant computational challenges. Homogenization of the fractures provides a suitable process to integrate the small-scale networks within these simulations (Berkowitz, Reference Berkowitz1995; Geers et al. Reference Geers, Kouznetsova, Matouš, Yvonnet, Stein, de Borst and Hughes2017; Thovert et al. Reference Thovert, Mourzenko and Adler2017; Berre et al. Reference Berre, Doster and Keilegavlen2019). It is important to accurately homogenize the fractures, as high-density networks (large-scale) effectively act as completely permeable media, and at the small scale fewer fractures will not represent the network (Fourno et al. Reference Fourno, Grenier, Benabderrahmane and Delay2013; Meier et al. Reference Meier, Grühser and Backers2018; Poulet et al. Reference Poulet, Lesueur and Kelka2021).
Fracture networks within reservoirs represent thin features which can be computationally costly to discretize due to the required number of elements in the mesh. Newly developed techniques have allowed for the simulation of fractures as flat features (lower-dimensional elements) such that the fracture aperture is not considered within the mesh but instead is accounted for numerically (e.g. Alboin et al. Reference Alboin, Jaffré, Roberts and Serres2002; Nordbotten et al. Reference Nordbotten, Boon, Fumagalli and Keilegavlen2018; Poulet et al. Reference Poulet, Lesueur and Kelka2021). By considering the fractures as lower-dimensional elements within the mesh, the required number of elements is reduced, resulting in a more efficient simulation (Cacace & Jacquey, Reference Cacace and Jacquey2017; Poulet et al. Reference Poulet, Lesueur and Kelka2021).
An important property in simulating flow through fractured networks is fracture permeability. Faults and fractures can be conceptualized as conduits, barriers or combined conduit–barriers to fluid flow depending on various parameters such as hydraulic or mechanical variations and interactions (Caine et al. Reference Caine, Evans and Forster1996; Poulet et al. Reference Poulet, Lesueur and Kelka2021). Whilst fractures can be exclusively barriers (closed) or conduits (open), many natural fractures present characteristics that are between the end-members, forming conduit–barrier systems with variable permeabilities (Caine et al. Reference Caine, Evans and Forster1996; Korneva et al. Reference Korneva, Tondi, Agosta, Rustichelli, Spina, Bitonte and Di Cuia2014; Bauer et al. Reference Bauer, Schröckenfuchs and Decker2016; Volatili et al. Reference Volatili, Zambrano, Cilona, Huisman, Rustichelli, Giorgioni and Tondi2019; Giuffrida et al. Reference Giuffrida, Agosta, Rustichelli, Panza, La Bruna, Eriksson, Torrieri and Giorgioni2020). For example, strike-slip faults can comprise filled cores surrounded by distributed small-scale damage zones with variable permeabilities (Mitchell & Faulkner, Reference Mitchell and Faulkner2009). Techniques such as discrete fracture network (DFN) or discrete fracture method (DFM) modelling have allowed for efficient simulation of fracture networks; however, variations in permeability are frequently over-simplified (Berre et al. Reference Berre, Doster and Keilegavlen2019). Studies have successfully modelled both end-members of fracture permeability and the integration of fractures within a mesh, separate from the matrix, thus allowing for distinct properties to be applied (e.g. Martin et al. Reference Martin, Jaffré and Roberts2005; Nordbotten et al. Reference Nordbotten, Boon, Fumagalli and Keilegavlen2018). Recent advancements in these methods have enabled the modelling of conduit–barrier systems independently within finite elements (Poulet et al. Reference Poulet, Lesueur and Kelka2021). Applying these approaches to fracture networks and assigning variable permeabilities to the individual fracture generations reduce the uncertainties involved in homogenizing fluid flow through fractured rock.
This contribution primarily focuses on implementing an efficient method for reliable homogenization of fluid flow properties using small-scale fractured outcrop analogues which can be implemented in a large-scale model. The simulations will be analysed based on a regional context assessing how large-scale structures may affect permeability. Improving this type of method is a vital initial step towards developing large-scale models for fractured geothermal systems of low-permeable host rocks (e.g. limestone) where subsurface data may be unavailable or limited and the use of outcrop analogues is essential.
2. Geological setting of the Franconian Basin
2.a. Structural overview of the Franconian Basin
The outcrops analysed in this contribution are located within the Franconian Basin, northern Bavaria (Fig. 1). The Franconian Basin is primarily composed of Late Palaeozoic to Mesozoic sediments with thicknesses up to 3500 m and bounded to the east by the Franconian Lineament and the Bohemian Massif (Schröder, Reference Schröder1987; Peterek et al. Reference Peterek, Rauche, Schröder, Franzke, Bankwitz and Bankwitz1997; Schröder et al. Reference Schröder, Ahrendt, Peterek and Wemmer1997). Subsidence and crustal extension related to the culmination of the Varsican Orogeny formed half-graben and graben structures allowing for deposition to occur from the Late Palaeozoic onwards (Freudenberger & Schwerd, Reference Freudenberger and Schwerd1996; Bauer, Reference Bauer2000; Schäfer et al. Reference Schäfer, Oncken, Kemnitz and Romer2000; Kroner et al. Reference Kroner, Hahn, Romer and Linnemann2007). The Franconian Basin deposition spans from Permian (Rotliegend) to Cretaceous and is formed of sandstones, siltstones, mudstones and limestones (Schröder, Reference Schröder1987; Schäfer et al. Reference Schäfer, Oncken, Kemnitz and Romer2000, Freudenberger et al. Reference Freudenberger, Geyer, Schröder, Lepper and Röhling2013; Kämmlein et al. Reference Kämmlein, Bauer and Stollhofen2017). The outcrops of interest lie within the Malm (Upper Jurassic) limestone unit deposited as an extensive carbonate-dominated platform (Franconian Platform) along the passive Tethyian margin (Meyer & Schmidt-Kaler, Reference Meyer and Schmidt-Kaler1990; Ziegler Reference Ziegler1990; Schintgen & Moeck, Reference Schintgen and Moeck2021).

Fig. 1. Tectonic overview of central Germany and the Franconian Basin showing the main fault lines and basins within the region (modified from Peterek et al. Reference Peterek, Rauche and Schröder1996; Kämmlein et al. Reference Kämmlein, Bauer and Stollhofen2017).
The basin has experienced several major regional events occurring syn- and post- sedimentation along the pre-existing Varsican structures, commencing with a major compressive phase of deformation that occurred during a Late Cretaceous Inversion causing steep-angled reverse and NW–SE-trending strike-slip faults (e.g. Peterek et al. Reference Peterek, Maier, Bankwitz, Franzke, Rauche and Schröder1993, Reference Peterek, Rauche and Schröder1996, Reference Peterek, Rauche, Schröder, Franzke, Bankwitz and Bankwitz1997; Mazur et al. Reference Mazur, Scheck-Wenderoth and Krzywiec2005; Kley & Voigt, Reference Kley and Voigt2008; Navabpour et al. Reference Navabpour, Malz, Kley, Siegburg, Kasch and Ustaszewski2017; Voigt et al. Reference Voigt, Kley and Voigt2021). Compressional structural features related to this phase are primarily found within the main thrust fault zones whilst the strike-slip components are formed in the areas between faults (Peterek et al. Reference Peterek, Rauche and Schröder1996).
Following the inversion, the European Cenozoic Rift System initiated an extensional regime, and normal faults and related structural features formed within the basin (Ziegler, Reference Ziegler1992; Dèzes et al. Reference Dèzes, Schmid and Ziegler2004; Rajchl et al. Reference Rajchl, Uličný, Grygar and Mach2009; Voigt et al. Reference Voigt, Kley and Voigt2021). This rifting system is found across northern Europe and results in the formation of large NE–SW-striking grabens and half-grabens (Eger Graben; see Fig. 1) east of the Franconian Basin (Schröder, Reference Schröder1987; Peterek et al. Reference Peterek, Rauche, Schröder, Franzke, Bankwitz and Bankwitz1997; Schröder et al. Reference Schröder, Ahrendt, Peterek and Wemmer1997; Dèzes et al. Reference Dèzes, Schmid and Ziegler2004).
The final phase of major deformation is the Alpine Orogeny during the Eocene convergence of Africa and Europe (e.g. Scheck-Wenderoth et al. Reference Scheck-Wenderoth, Krzywiec, Zühlke, Maystrenko, Froitzheim and McCann2008; Köhler et al. Reference Köhler, Duschl, Fazlikhani and Köhn2020). This event caused a large strike-slip regime in the region corresponding to a NW–SE compressional NE–SW extensional stress field (Schröder et al. Reference Schröder, Ahrendt, Peterek and Wemmer1997; Wagner et al. Reference Wagner, Coyle, Duyster, Henjes-Kunst, Peterek, Schröder, Stöckhert, Wemmer, Zulauf, Ahrendt, Bischoff, Hejl, Jacobs, Menzel, Nand, van den Haute, Vercoutere and Welzel1997; Zulauf & Duyster, Reference Zulauf and Duyster1997; Köhler et al. Reference Köhler, Duschl, Fazlikhani and Köhn2020). In the Franconian Basin, this phase primarily causes the reactivation of the eastern fault system (Peterek & Schröder, Reference Peterek and Schröder2010).
The deformation caused by these major phases significantly influences the large-scale faults in the region (Köhler et al. Reference Köhler, Duschl, Fazlikhani and Köhn2020). At the site in Kirchleus, the main fault that influences the structural features is the Kulmbach Fault, part of the Franconian Fault System (Heinrichs et al. Reference Heinrichs, Giese, Bankwitz and Bankwitz1994; Peterek et al. Reference Peterek, Rauche and Schröder1996). This fault is located c. 30 m from the quarry (Fig. 2) and records a reverse throw of c. 800 m, positioning the Muschelkalk (Trissaic) beside the Malm units (Behrens et al. Reference Behrens, Jansen and Wurster1967; Franke, Reference Franke, Emmermann and Wohlenberg1989; Fazlikhani et al. Reference Fazlikhani, Bauer and Stollhofen2022).

Fig. 2. Sketch outline of Kirchleus Quarry showing the locations of the studied fractured cliff sections for numerical modelling. Stereonet shows the main fracture orientations observed along the outcrops within the quarry.
2.b. Geothermal potential and exploration of the Franconian Basin
Current geothermal exploration of the Franconian Basin suggests the main heat source may be deep-seated late-Varsican granite intrusions within the Saxothurigan crust underlying the sedimentary cover (Kämmlein et al. Reference Kämmlein, Bauer and Stollhofen2017; de Wall et al. Reference de Wall, Schaarschmidt, Kämmlein, Gabriel, Bestmann and Scharfenberg2019; Drews et al. Reference Drews, Bauer, Fazlikhani, Stollhofen, Kämmlein, Potten, Thuro and de Wall2019). This causes a geothermal gradient of 38 °C km−1 observed in the Obernsees 1 borehole (Stettner & Salger, Reference Stettner and Salger1985; de Wall et al. Reference de Wall, Schaarschmidt, Kämmlein, Gabriel, Bestmann and Scharfenberg2019). Recent studies have primarily focused on characterizing and modelling the deep geothermal potential of the granite systems; however, little research has been undertaken to explore the fractured sedimentary cover and the influence of the fracture networks on geothermal flow (Kämmlein et al. Reference Kämmlein, Bauer and Stollhofen2017; de Wall et al. Reference de Wall, Schaarschmidt, Kämmlein, Gabriel, Bestmann and Scharfenberg2019; Bohnsack et al. Reference Bohnsack, Potten, Pfrang, Wolpert and Zosseder2020). In the Molasse Basin (Fig. 1) to the south, the Malm unit is currently utilized for geothermal energy where structural features (fractures, faults and karst) play a key role in producing high flow rates up to 10−4 m s−1 to the north of the basin (Birner et al. Reference Birner, Fritzer, Jodocy, Savvatis, Schneider and Stober2012; Birner, Reference Birner2013; Przybycin et al. Reference Przybycin, Scheck-Wenderoth and Schneider2017; Bohnsack et al. Reference Bohnsack, Potten, Pfrang, Wolpert and Zosseder2020; Schintgen & Moeck, Reference Schintgen and Moeck2021). It is therefore important that geothermal flow through fractured networks of the Franconian Basin be better understood for future exploration.
3. Structural analysis of outcrop analogue
3.a. Analysis of Kirchleus Quarry
Kirchleus Quarry (4 × 104 km2) is located on the western flank of the Franconian Basin (Fig. 1) within the Malm Formation and in the footwall of the Kulmbach Fault situated 7 km SW of the Franconian Lineament. The quarry complex (Fig. 2) is split into two areas: towards the north, an inactive quarry site contains c. 14 fractured quarry cliff sections (outcrops 1 and 2); towards the south, active quarrying is still operating where the most recently exposed cliff sections are located (outcrop 3). Both sites provide good access, making it possible to measure features within the fractured outcrops and to take detailed images for structural analysis.
These fractures, faults and other structural features can be divided into several stress fields through cross-cutting relationships. The oldest observed structural lineations are observed through normal faults trending NW–SE, with associated striations indicating a NE–SW extension (Fig. 3a).

Fig. 3. Fracture results and interpreted stress fields from Kirchleus Quarry showing the main deformation phases affecting the Malm at the outcrop.
Reverse faults orientated 025/59 and 200/50 (azimuth/dip) are observed within the quarry and as reactivated structural lineations of the previous extensional features. The movement on these faults and associated tectonic stylolites (σ1 ∼ 205°) corresponds to NE–SW compression (Fig. 3b). Strike-slip faults (Fig. 3d) orientated 244/80 and 131/85 are observed to cross-cut these previous structural features and record a NNE compression. Also observed within this set of faults are reverse oblique faults (Fig. 3c) orientated 225/43, recording a similar NE–SW-directed compression. These also appear to cross-cut the structural features observed in Fig. 3b, and these three groups of faults and fractures (Fig. 3b–d) appear the most dominant structural features in the quarry.
A set of dextral strike-slip faults orientated 252/82 and 110/85 (Fig. 3e–f) cross-cut the tectonic stylolites from the previous compressional stress field. Furthermore, tectonic stylolites related to these strike-slip faults are present in a NW–SE compressional direction. These structural features represent the youngest faults that outcrop in the quarry sections.
3.b. Analysis of 2D quarry outcrops
To present the capabilities of the modelling process and the impact of the Kulmbach Fault on the fracture network, three 5 m × 5 m fractured outcrops are imaged at increasing distance from the fault (Fig. 2). The outcrops captured the main fractures within the quarry described in Section 3.a which represent the different deformation phases within the Malm unit. In order to analyse networks present, the images are processed, and fractures are traced using a digital graphics editor (Fig. 4). Geometric analysis of the network is undertaken using FracPaQ which provides results of connectivity and density of the fracture traces (Healy et al. Reference Healy, Rizzo, Cornwell, Farrell, Watkins, Timms, Gomez-Rivas and Smith2017).

Fig. 4. Fractured cliff sections and digitized interpreted fracture traces from Kirchleus Quarry. Sets identified in fracture traces correspond to the sets presented in Table 1.
The fractures vary in orientation, spacing and fill. Five different sets are identified (Table 1; Fig. 4) across the three fractured outcrops identified and measured in the field. Fracture set orientation is averaged for each set by calculating the Fisher distribution mean vector (Fisher et al. Reference Fisher, Lewis and Embleton1993; Cardozo & Allmendinger, Reference Cardozo and Allmendinger2013). Not all sets are observed at every outcrop; however, sets 1–3 are consistent throughout. Bedding is represented within set 1 and is treated as structural lineation. This is due to observed structural movements along the bedding planes acting as faults and fractures and therefore these planes can be considered a structural set. The outcrops are all approximately perpendicular to the main Kulmbach Fault to provide a suitable comparison between sites at increasing distance from the fault.
Table 1. Structural parameters of the measured fracture sets observed and estimated within the fractured outcrops

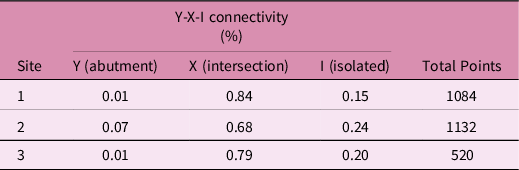
Geometric analysis of the outcrops indicates that whilst average trace length varied between outcrops 3.2 m, 1.86 m, 2.76 m respectively, fracture density (P20) across the 2D traces are similar (5.2 m−2, 5.7 m−2, 4.4 m−2). Connectivity between the nodes of the fracture traces (Table 2) based on Y-X-I analysis (Manzocchi, Reference Manzocchi2002) shows the fractures are well connected with intersections (X) and relatively few are isolated fractures.
Table 2. Y-X-I connectivity of the fractured outcrops
3.c. Integration of geological data into numerical simulations
In order to simulate fluid flow through the fractured outcrops assessed from Kirchleus, several parameters are obtained and estimated from the structural analysis. Based on field observations, the fractures were sorted as open (conduits), closed or filled (barriers) (Fig. 5). As this study focuses primarily on field-based data, the apertures from the field are used for the fluid flow simulations; however, it is known that aperture can vary (increase and decrease) from surface to subsurface due to elevated fluid pressure (e.g. Ghassemi & Kumar, Reference Ghassemi and Kumar2007) or in situ stresses (e.g. Bisdom et al. Reference Bisdom, Bertotti and Nick2016). In order to undertake the fluid flow simulation, a general estimation of aperture and corresponding fracture permeability is required. This is difficult to obtain and for this work we measure aperture for each of the five fracture sets determined from the field through an approximation of fracture widths (Table 1) using image processing software. From these values, permeability along the fracture (longitudinal permeability) is estimated using empirical cubic laws which approximate fracture permeability of each set based on the Hagen–Poiseuille solution of the Navier–Stokes equation (Snow, Reference Snow1969; Witherspoon et al. Reference Witherspoon, Wang, Iwai and Gale1980; Zhang, Reference Zhang and Zhang2019). These values indicate that flow could more likely occur through sets 3 and 4 compared to set 1 which is infilled. The values are used as the initial input for the numerical modelling of the sets to simulate the flow through the network.

Fig. 5. Fracture aperture variation observed at Kirchleus Quarry. (a) Normal fault within the Malm unit observed at site 2 (Fig. 2). (b) Clay infill of the normal fault (Fig. 5a) showing evidence of a fracture barrier to flow. (c) Fractures observed at site 1 showing examples of open and closed sets of fractures which act as conduits and barriers to flow respectively.
In addition to the estimated permeability values, the digitized cliff sections provide the base for a discrete fracture network from which a fractured mesh can be generated for numerical simulations. The fractured mesh is used in combination with the different fracture permeabilities for each set as the initial input for the numerical modelling. This process presents a method that utilizes fractured outcrop analogue structural data in the homogenization and simulation of fractured networks.
4. Fractured numerical modelling
4.a. Numerical homogenization of the permeability tensor
Instead of simply using only empirical laws with the property of the fracture network, a more exact determination of the full permeability tensor can be obtained through a homogenization procedure based on numerical fluid flow simulations through the fracture network. The permeability
![]() $K$
can be expressed in its tensorial form from Darcy’s law:
$K$
can be expressed in its tensorial form from Darcy’s law:
 $$\left( {\matrix{ {{v_x}} \cr {{v_y}} \cr {{v_z}} \cr } } \right) = {1 \over {{\mu _{\rm{f}}}}}\left( {\matrix{ {{K_{xx}}} & {{K_{xy}}} & {{K_{xz}}} \cr {{K_{yx}}} & {{K_{yy}}} & {{K_{yz}}} \cr {{K_{zx}}} & {{K_{zy}}} & {{K_{zz}}} \cr } } \right)\left( {\matrix{ {\nabla {P_x}} \cr {\nabla {P_y}} \cr {\nabla {P_z}} \cr } } \right) $$
$$\left( {\matrix{ {{v_x}} \cr {{v_y}} \cr {{v_z}} \cr } } \right) = {1 \over {{\mu _{\rm{f}}}}}\left( {\matrix{ {{K_{xx}}} & {{K_{xy}}} & {{K_{xz}}} \cr {{K_{yx}}} & {{K_{yy}}} & {{K_{yz}}} \cr {{K_{zx}}} & {{K_{zy}}} & {{K_{zz}}} \cr } } \right)\left( {\matrix{ {\nabla {P_x}} \cr {\nabla {P_y}} \cr {\nabla {P_z}} \cr } } \right) $$
where
![]() ${v_i}$
denotes the flow velocity,
${v_i}$
denotes the flow velocity,
![]() ${\mu _{\rm{f}}}$
the fluid viscosity, and
${\mu _{\rm{f}}}$
the fluid viscosity, and
![]() $\nabla {P_i}$
the pressure gradient.
$\nabla {P_i}$
the pressure gradient.
In order to isolate any specific component of the permeability tensor
![]() ${K_{ij}}$
, Eq. (1) shows that we can constrain the fluid flow to a single direction j such that the resulting pressure gradient vector is equal to
${K_{ij}}$
, Eq. (1) shows that we can constrain the fluid flow to a single direction j such that the resulting pressure gradient vector is equal to
![]() $\nabla {P_j} = {\rm{\Delta }}{P_j}/{L_{j,{\rm{ref}}}}$
, where
$\nabla {P_j} = {\rm{\Delta }}{P_j}/{L_{j,{\rm{ref}}}}$
, where
![]() ${L_{j,{\rm{ref}}}}$
represents the reference length of the model in that direction and
${L_{j,{\rm{ref}}}}$
represents the reference length of the model in that direction and
![]() ${\rm{\Delta }}{P_j}$
is the corresponding pressure differential between the boundaries. In this case, we can extract
${\rm{\Delta }}{P_j}$
is the corresponding pressure differential between the boundaries. In this case, we can extract
![]() ${K_{ij}}$
from Eq. (1), expressed as:
${K_{ij}}$
from Eq. (1), expressed as:
To obtain every component of the permeability tensor, three simulations need to be run, each with a pressure gradient imposed in one different orthogonal direction, from which the longitudinal and transversal fluid velocity can be post-processed. Note that experimental methods cannot calculate the off-diagonal components of the permeability tensor because, as seen from Eq. (4) further below, velocities transversal to the direction of the flow need to be measured, which is very complex to do (Renard et al. Reference Renard, Genty and Stauffer2001). This numerical method is therefore the only way to obtain the full permeability tensor. At the scale of fracture networks, fluid flow is already described by Darcy’s law, with the rock matrix usually having a different permeability than the fractures. The simulations performed for homogenizing the permeability tensor then consist in solving for Darcy’s law through the matrix and the fracture network as explained in the following subsections for a fluid flow in one given orthogonal direction, then post-processing for the value of the fluid velocity.
To homogenize the network, the flow is simulated with the finite element method. Several FEM solvers are available to run numerical simulations of fluid flow through fractured media, including ABAQUS (e.g. Cruz et al. Reference Cruz, Roehl and do Amaral Vargas2019), COMSOL Multiphysics (e.g. Koyama et al. Reference Koyama, Li, Jiang and Jing2009; Lepillier et al. Reference Lepillier, Daniilidis, Gholizadeh, Bruna, Kummerow and Bruhn2019) and MOOSE Framework (e.g. Grimm Lima et al. Reference Grimm Lima, Schädle, Vogler, Saar and Kong2020; Poulet et al. Reference Poulet, Lesueur and Kelka2021), and various methods have been developed through these solvers (Berre et al. Reference Berre, Doster and Keilegavlen2019). We use the open-source finite element simulator REDBACK (Poulet et al. Reference Poulet, Paesold and Veveakis2017) based on the Multi-physics Object Oriented Simulation Environment (MOOSE; Permann et al. Reference Permann, Gaston, Andrš, Carlsen, Kong, Lindsay, Miller, Peterson, Slaughter, Stogner and Martineau2020). The applied REDBACK functionalities have been developed directly for fault-reactivation simulations (e.g. Lesueur et al. Reference Lesueur, Poulet and Veveakis2020; Poulet et al. Reference Poulet, Lesueur and Kelka2021), and MOOSE provides adaptability of the solver for new development and in modifying existing meshes generated initially in GMSH (Geuzaine & Remacle, Reference Geuzaine and Remacle2009).
The simulations require a finite element mesh of the 2D fracture features captured from Kirchleus Quarry as discrete fracture networks (DFN; Fig. 4). The use of the DFN is necessary for the simulations as the individual fractures are required to be treated as infinitely thin geometric features (lower-dimensional elements) whereby their thickness is implemented within the flow equations. By using the fracture networks as lower-dimensional elements within the mesh in which the fractures defined in the DFN are treated as an interface between lower-dimensional elements, the complexities involved can be reduced and the process becomes more efficient compared to continuum-based methods (Cacace & Jacquey Reference Cacace and Jacquey2017; Poulet et al. Reference Poulet, Lesueur and Kelka2021). This process removes the necessity for very small elements within the discretized fracture and reduces the elements within the mesh.
4.c. Outcrop to 2D fractured mesh
A script has been developed to create the 2D fractured mesh from the traced networks (SVG) using GMSH (Geuzaine & Remacle, Reference Geuzaine and Remacle2009) which independently meshes the network of fractures from the matrix. The script identifies the intersection and end nodes of each fracture and converts these into points and lines within GMSH. This provides additional control on the handling of specific nodes, in particular for nearby nodes that should be merged. The geometries are assigned as physical lines within separate groups/sets based on the orientation of the fractures. This tagging process through GMSH allows the fractures to be used in the 2D fluid flow modelling as lower-dimensional elements. This enables the engine to focus the modelling on the fractures independently of the matrix and, when grouping the fractures by orientation, variation of property values can be implemented. To allow the setting of periodic boundary conditions at the numerical stage, extra nodes are also inserted on the bounding box (lines) to ensure that all boundary nodes match on the opposite faces.
4.d. DFN simulation and post-processing
With the mesh generated, finite element simulations can be run to solve for Darcy’s law and the fluid mass balance described in steady state as a diffusion of pressure:
This equation describes the behaviour within the rock matrix. The DFN is treated separately. The fractures are modelled as lower-dimensional interfaces (Poulet et al. Reference Poulet, Lesueur and Kelka2021) allowing simulation of any kind of behaviour for the fracture, from conduit to barrier, and distinguishing longitudinal flow from transversal, allowing for the implementation of more complex conduit–barrier type of behaviour. The system requires as input the aperture (0.1 cm), as well as the longitudinal and the transversal permeability values associated with each fracture. Two simulations are run for each site: (1) fully homogeneous case where all fractures are of equal permeability (transversal = 0.01 mD; longitudinal = 100 mD); (2) non-homogeneous case where longitudinal permeability of each fracture is controlled by orientation (Table 1). This range of permeability values is justified from the measured aperture and previous fault permeability modelling (Cappa & Rutqvist, Reference Cappa and Rutqvist2011).
For the simulation set-up, the pressure gradient is imposed through a high-pressure value as Dirichlet boundary condition at the inlet and a low value at the outlet. On the other sides, periodic boundary conditions of pressure are imposed between parallel faces. Results of the simulations for site 1 of DFN can be seen in Fig. 6.
In order to solve for Eq. (2), the average value of the fluid velocity needs to be computed, where the challenge is to correctly take into account the contribution of the DFN. Specifically, fluid velocity is integrated over the whole domain but the integral over the DFN has to be multiplied by the virtual aperture
![]() $a$
to consider the correct volumetric contribution of the fractures. Similarly, the virtual volume of the fractures needs to be added to the total volume for the averaging. The average of fluid velocity in one direction is eventually post-processed as:
$a$
to consider the correct volumetric contribution of the fractures. Similarly, the virtual volume of the fractures needs to be added to the total volume for the averaging. The average of fluid velocity in one direction is eventually post-processed as:
where
![]() ${V^{\rm{M}}}$
is the total volume of the matrix,
${V^{\rm{M}}}$
is the total volume of the matrix,
![]() ${A^{\rm{F}}}$
the area of the fracture network,
${A^{\rm{F}}}$
the area of the fracture network,
![]() $v_{}^{\rm{M}}$
the fluid velocity in the matrix,
$v_{}^{\rm{M}}$
the fluid velocity in the matrix,
![]() $v_i^{{\rm{F}},{\rm{l}}}$
the fluid velocity longitudinal to the fractures and
$v_i^{{\rm{F}},{\rm{l}}}$
the fluid velocity longitudinal to the fractures and
![]() $\;v_i^{{\rm{F}},{\rm{t}}}$
the fluid velocity transversal to the fractures.
$\;v_i^{{\rm{F}},{\rm{t}}}$
the fluid velocity transversal to the fractures.
4.e. Permeability ellipses
The raw permeability tensors (Table 3) do not allow the properties of the fracture network to be read directly. Instead, most geoscientists prefer to plot ellipses associated with the symmetrical part of the tensor. The ellipses can be plotted using the eigenvalues of the tensor for the radii, and the orientation of the eigenvectors for the rotation of the ellipse. From this plot (Fig. 7), one can visually assess θ, the direction of the principal axis of flow, K max, the maximum value of permeability found on the principal axis, and K min the minimum value.
Table 3. Calculated permeability tensors for both scenarios at each site from the numerical modelling and homogenization


Fig. 7. Permeability ellipses from the homogenization process and tensor calculation. Black permeability ellipse is calculated using a constant permeability for all fractures. Red permeability ellipse is calculated using varying permeabilities based on fracture orientation. Site 1 shows tilting of the ellipse towards the main Kulmbach Fault. Sites 2 and 3 show lessening impact of the fault to the ellipse orientation and magnitude.
The permeability ellipses show that the highest K max for both scenarios is from site 1, closest to the main Kulmbach Fault, whilst the lowest K max is within site 3. The lowest K min is also located at site 1. For both sites 1 and 2 the ellipse from the non-homogeneous case, whereby the fracture permeability is defined by variation in orientation, is larger than the ellipse for the homogeneous case. At site 3, the non-homogeneous case is more spherical and has a lower K max than the corresponding homogeneous case. In general, this points towards the non-homogeneous case showing a higher permeability than the homogeneous case. Site 1 also shows strongly orientated ellipses with θ orientated −29.0° and −42.5° respectively for each scenario, whilst the ellipses for sites 2 and 3 show a more level and spherical shape.
The results of the numerical modelling show the capability of using fault and fracture information from outcrop images to simulate fluid flow through the networks to homogenize and extract permeability tensors which can be used for upscaling to geothermal reservoir scale.
5. Discussion
The results of the structural analysis and numerical simulations show how outcrop analogues can be used to model fluid flow and the effect of varying permeabilities of the fracture sets on fluid transport. Furthermore, this process can act as initial steps towards upscaling and larger-scale numerical simulations of geothermal fluid flow for the Northern Bavarian region, and in particular the use of faults and fractures as flow medium.
5.a. Effect of variable fracture permeability on fluid transport
The permeability tensors and associated ellipses (Fig. 7) presented in the results show that during homogenization varying permeability values of the fractures could have a large impact on the flow magnitude and orientation. For sites 1 and 2, the permeability ellipses for a constant permeability across all fractures (Fig. 7, black ellipses) are smaller than when the permeability is controlled by fracture orientation (Fig. 7, red ellipses). For site 3, it is shown that the ellipses controlled by fracture orientation have a lower K max (0.93D) compared to the tensor with constant fracture permeabilities (K max = 1.07D). To illustrate the effects of varying fracture permeability, we used the tensors from site 1 to simulate transport of a non-reactive tracer through a 5 m × 5 m block (Fig. 8). This allows for transport through a homogenized area using the obtained tensor values to be simulated. The simulation was performed with a constant time increment (1 hour) for 48 hours and with a constant pressure gradient from right (5E5 Pa) to left (1E5 Pa) with a normalized constant tracer concentration of 1 at the source node.

Fig. 8. (a, b) Tracer transport through a 5 m × 5 m block using (a) constant permeability for all fractures and (b) variable permeability controlled by fracture orientation and defined conduit, barrier and conduit–barrier sets. (c) Difference in tracer concentration between the two scenarios. Simulations were performed using the PorousFlow module (Permann et al. Reference Permann, Gaston, Andrš, Carlsen, Kong, Lindsay, Miller, Peterson, Slaughter, Stogner and Martineau2020; Wilkins et al. Reference Wilkins, Green and Ennis-King2021) within MOOSE.
The results of the simulation show that there is a significant difference in tracer concentration (Fig. 8c) between the two simulations such that treating the fractures with varying permeabilities influences the transport orientation compared to fractures with a constant permeability value. Furthermore, given that the differences observed in this simulation over a 5 m × 5 m block are significant, the results over a larger area, for example at reservoir scale (kilometres), would be even more pronounced. Therefore, the data suggest that the homogenization of the fracture network is unlikely to result in a realistic scenario for fluid flow simulations. This highlights the importance of defining the fracture apertures and permeabilities prior to numerical simulations during the homogenization process and understanding the effects of upscaling the fracture networks to larger areas and volumes.
The fracture networks simulated within this contribution are treated as linear lower-dimensional elements with assigned permeability values across the interface. Previous fracture studies have also shown that other fracture properties can influence the fluid flow within the network. Properties such as fracture roughness and tortuosity have been modelled to show the impact on flow from including channelling which reduces the efficiency of the network (Li et al. Reference Li, Liu and Jiang2016; Liu et al. Reference Liu, Li and Jiang2016; Lee & Babadagli, Reference Lee and Babadagli2021). Whilst this property is an important feature in fracture flow simulations, as the networks in this study treat the fractures as lower-dimensional elements within the mesh, the effects of other fracture properties can be accounted for numerically (Cacace & Jacquey Reference Cacace and Jacquey2017; Poulet et al. Reference Poulet, Lesueur and Kelka2021). As this method treats the fracture as a flat interface between lower-dimensional elements, the properties (e.g. aperture and roughness) are accommodated numerically, creating a more efficient simulation.
The numerical methodology presented in this contribution shows a process that can effectively homogenize fracture networks and reduce uncertainties occurring during the upscaling process that can have significant impacts on fluid transport. In terms of geothermal energy, understanding where the tracer is transported to is vital for development planning to create an efficient geothermal system and avoid contamination of the surrounding area.
5.b. Influence of regional events and seismic structures
5.b.1. Regional stress fields from outcrop analysis
The structural features observed in the quarry outcrops (Fig. 3) present several different deformation phases that have affected the units present. The first phase recorded in the Malm unit of the Franconian Basin is the NE–SW extensional phase (Fig. 3a) which causes normal faulting observed in Kirchleus Quarry. This phase occurred at the earliest Late Jurassic, post-Malm sedimentation and into the Early Cretaceous (S Köhler et al., unpub. data. Similar structures have been observed in surrounding basins (e.g. Thuringian Basin) and can be related to the continued subsidence in the Central European Basin System throughout the Mesozoic (Scheck-Wenderoth et al. Reference Scheck-Wenderoth, Krzywiec, Zühlke, Maystrenko, Froitzheim and McCann2008; Stollhofen et al. Reference Stollhofen, Bachmann, Barnasch, Bayer, Beutler, Franz, Kästner, Legler, Mutterlose, Radies, Littke and Bayer2008; Navabpour et al. Reference Navabpour, Malz, Kley, Siegburg, Kasch and Ustaszewski2017; S Köhler et al., unpub. data).
The second stress regime interpreted in the quarry presents a general compressional phase orientated NE–SW (Fig. 3b–d). The structures observed in the outcrops at Kirchleus are related to the Late Cretaceous Inversion deformation phase which involved the uplift and exhumation of the Mesozoic basins (Mazur et al. Reference Mazur, Scheck-Wenderoth and Krzywiec2005; Kley and Voigt, Reference Kley and Voigt2008; Voigt et al. Reference Voigt, Kley and Voigt2021; S Köhler et al., unpub. data. It is observed in Kirchleus that this is a multiphase event whereby the initial deformation is primarily composed of the reactivated reverse faults (Fig. 3b) and its culmination characterized by strike-slip faults (Fig. 3d). Furthermore, it is observed that an intermediary transitional phase occurs during the inversion event which forms the oblique reverse faults (Fig. 3c) within the quarry, possibly due to local stress variations and disturbances (Kley and Voigt, Reference Kley and Voigt2008; Sippel et al. Reference Sippel, Saintot, Heeremans and Scheck-Wenderoth2010; Navabpour et al. Reference Navabpour, Malz, Kley, Siegburg, Kasch and Ustaszewski2017; S Köhler et al., unpub. data. The reactivation of faults during this phase likely also affected the nearby Kulmbach Fault which influenced the deformation observed in the outcrops, and it is generally observed that inversion deformation causes the largest faults and fractures, controlling the structure of the quarry outcrops observed from satellite view (Fig. 2).
The final stress recorded in Kirchleus Quarry formed the strike-slip faulting (Fig. 3e, f) and tectonic stylolites which overprint the structural lineations formed during the Late Cretaceous Inversion. This NW–SE shortening and thrusting is likely related to the Alpine Orogeny and the regional-scale strike-slip regime affecting Central Europe (Schröder et al. Reference Schröder, Ahrendt, Peterek and Wemmer1997; Zulauf & Duyster, Reference Zulauf and Duyster1997; Peterek & Schröder, Reference Peterek and Schröder2010). These are the youngest natural faults observed within the quarry that are cutting all the other faults.
5.b.2. Influence of the Kulmbach Fault
The importance of faults to fluid flow is well documented through reservoir characterization and development (Caine et al. Reference Caine, Evans and Forster1996; Bense et al. Reference Bense, Gleeson, Loveless, Bour and Scibek2013; Vidal et al. Reference Vidal, Genter and Chopin2017; La Bruna et al. Reference La Bruna, Bezerra, Souza, Maia, Auler, Araujo, Cazarin, Rodrigues, Vieira and Sousa2021; Smeraglia et al. Reference Smeraglia, Giuffrida, Grimaldi, Pullen, La Bruna, Billi and Agosta2021), and whilst faults can be observed using subsurface data analysis (e.g. seismic imaging) the fractures related to the faults commonly are not. Therefore, utilizing alternative data sources, such as outcrop analogues, for further understanding the influence of seismic-scale faults on the fracture network and ultimately the fluid flow is vital. Initial results of the structural analysis show that the fractures are well connected and therefore could provide suitable pathways due to the high concentration of fracture intersections. In combination with the results of the numerical simulations they provide a detailed analysis of the impact of the fault on the fracture permeability.
The Kulmbach Fault is a seismic-scale fault, and the fractured cliff sections analysed were an increasing distance from the fault (Fig. 2). Whilst the results of the permeability tensors and ellipses obtained from homogenization of the fractured outcrops showed the importance of classifying fractures through aperture and permeability magnitude, they also show variation in the ellipses by site. In particular, the influence of the fault on the orientation of the flow patterns is clearly seen. The permeability ellipses for site 1 show a tilted nature (−29.0°) in comparison to the generally horizontal nature of the tensors from site 2 (7.4°) and site 3 (7.5°). The increased dip in the anisotropic permeability is noted as also parallel to the main dip of the Kulmbach Fault. Therefore, the fault directly influences the orientation of the permeability tensors and ellipses and thus fluid flow. Fluid flow orientation is important within the reservoir, particularly when primary permeability is controlled by structural features rather than sedimentological properties as observed within the Malm (Birner et al. Reference Birner, Fritzer, Jodocy, Savvatis, Schneider and Stober2012; Schintgen and Moeck Reference Schintgen and Moeck2021).
However, all the fracture outcrops analysed, and modelled from, have generally the same orientation (NE–SW). Therefore, only the fracture network perpendicular to the fault strike is observed in the results. Whilst this could limit the understanding of the fracture flow parallel to the fault, observing perpendicular fracture networks ensures that the horizontal flow and possible fluid pathways away from the fault are captured.
Furthermore, the magnitude (k max) is also larger at site 1 (1.26D) compared to sites 2 and 3 (1.21D and 0.93D respectively). This implies that the permeability increases towards the fault and thus fluid flow transport could be higher. This increased permeability corresponds to a damage zone near the Kulmbach Fault (Fig. 9). This damage zone is situated on the footwall of the reverse fault and impacts on the fracture networks as seen at site 1. Given that site 1 is located c. 30 m from the fault, the damage zone could be up to 100 m from the fault. This large distance could significantly influence the fluid flow around the faults at depth. From the hanging wall towards the ENE another damage zone is expected; however, width is unknown and there are likely additional effects to the fracture networks from the fold–thrust system (e.g. Watkins et al. Reference Watkins, Healy, Bond and Butler2018).
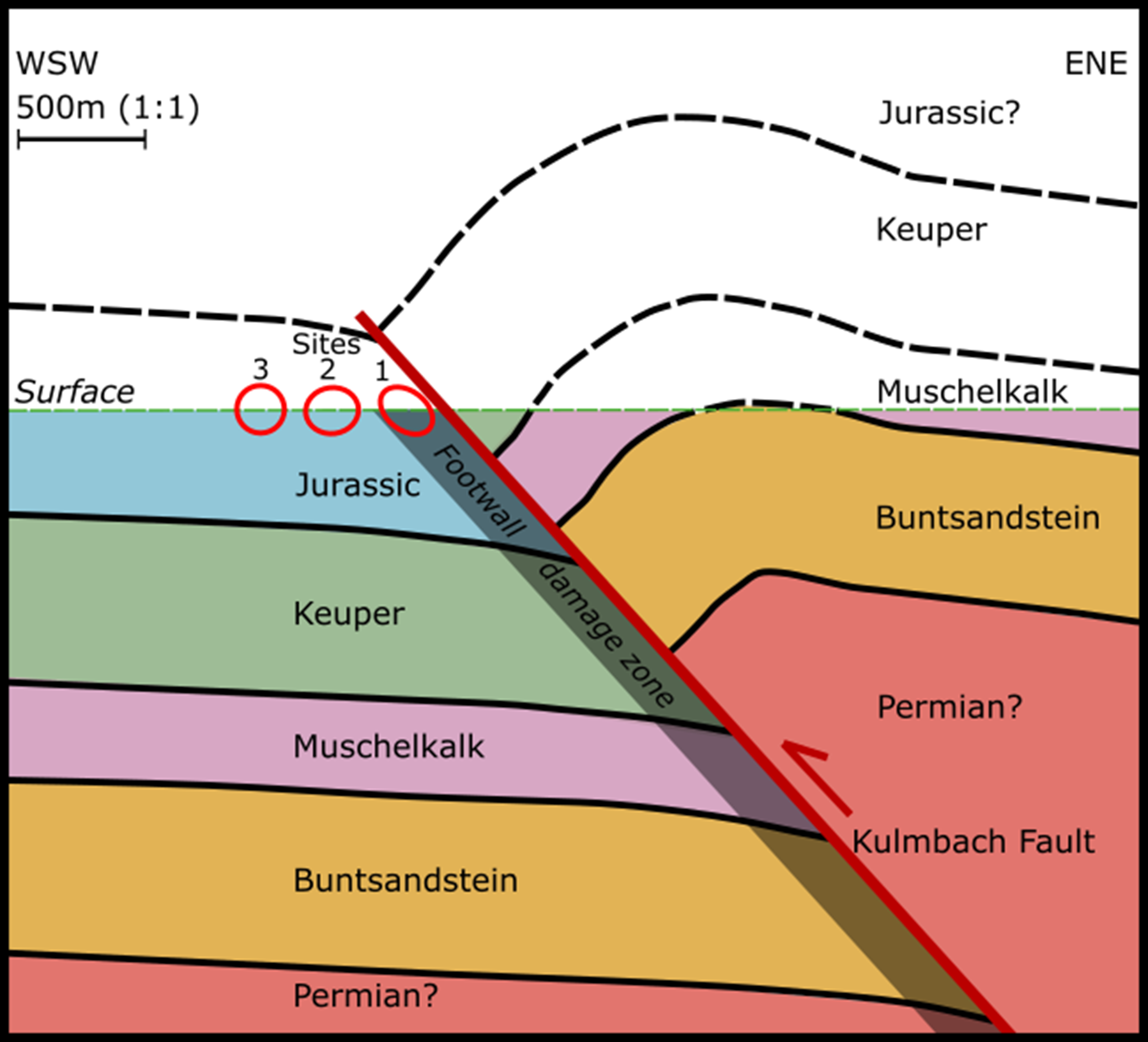
Fig. 9. Conceptual model showing a cross-section through the Kulmbach Fault and how the homogenized permeability of the fracture networks is affected by the fault within the fault damage zone.
Overall, the Kulmbach Fault has a direct influence over fluid transport through the fractured networks. This is important for modelling fractured reservoirs in general, in particular the low-permeability Malm reservoirs, as by further understanding how the faults affect the fracture networks, uncertainties through modelling these faulted systems can be reduced. The outcrop to tensor methodology presented in this paper can be utilized to effectively model, homogenize and upscale these systems, with particular detail on the influence of seismic-scale faults such as the Kulmbach Fault on reservoir flow.
Field-based studies on fracture networks can lead to some uncertainties in the data collection which can be accounted for (e.g. Peacock et al. Reference Peacock, Sanderson, Bastesen, Rotevatn and Storstein2019). Outcrop quality is an important factor to consider when capturing 2D imagery of fracture networks, and it is key that a link to the subsurface is established (Gutmanis et al. Reference Gutmanis, i Oró, Díez-Canseco, Chebbihi, Awdal and Cook2018). Kirchleus Quarry was chosen as a suitable site to assess the fractures within the Malm unit of the Franconian Basin due to its close proximity to the main Kulmbach Fault. The quarry provides excellent access to large cliff sections, some of which have limited weathering effects and therefore good outcrops for analysis. However, this could lead to uncertainties and bias from outcrop quality and choice. For fracture network imaging, unweathered, clean outcrops are most effective for tracing lineations for analysis, and therefore these outcrops are preferred over weathered cliff sections. These sections are therefore discounted from analysis and thus fractures may be missed.
A further consideration when using the fractured analogues is to ensure the captured fractured networks are representative of the modelled network scale. The 5 m × 5 m window size for sampling the fracture networks allows for a large area of the network to be imaged, reducing the sensitivity to bias (Zeeb et al. Reference Zeeb, Gomez-Rivas, Bons and Blum2013). There are several other methods that could be utilized to estimate the representative scale required for the model, such as Monte Carlo simulations (e.g. Rong et al. Reference Rong, Peng, Wang, Liu and Hou2013). However, for the scope of this study we assumed the simulated area is representative of the fracture network observed in outcrop (e.g. Bear, Reference Bear1972; Bear & Bachmat, Reference Bear, Bachmat, Bear and Bachmat1990; Andrianov & Nick, Reference Andrianov and Nick2019) and at outcrop scale (up to tens of metres) the imaged networks are suitable for numerical modelling without over- or undersaturation of fractures (Fourno et al. Reference Fourno, Grenier, Benabderrahmane and Delay2013; Meier et al. Reference Meier, Grühser and Backers2018; Berre et al. Reference Berre, Doster and Keilegavlen2019; Poulet et al. Reference Poulet, Lesueur and Kelka2021). Furthermore, the selection of the outcrops at increasing distance from the main Kulmbach Fault enables a good spread of data to be collected to minimize fractures lost to bias or outcrop quality, thereby limiting the uncertainties that could arise from the data collection and analysis.
5.c. Implications for the Geothermal system and future modelling
Geothermal energy use is increasingly prevalent, and it is a vital necessity to effectively model these systems and reduce uncertainties in reservoir modelling (Witter et al. Reference Witter, Trainor-Guitton and Siler2019). Where data for the exploration and development of geothermal projects are limited, analogues can be a useful tool. In the Franconian Basin, there are limited subsurface data and therefore the modelling of the subsurface is driven by outcrop analysis. Work has primarily focused on the geothermal potential of the deep granite systems within the Fraconian Basin, with limited emphasis on the influence of structural elements (Kämmlein et al. Reference Kämmlein, Bauer and Stollhofen2017). However, it is known that fracture networks within the Malm in southern Germany (Molasse Basin) contribute significantly to flow (Birner et al. Reference Birner, Fritzer, Jodocy, Savvatis, Schneider and Stober2012; Schintgen & Moeck, Reference Schintgen and Moeck2021).
Karstification is also observed at the Kirchleus outcrop affecting the Malm units and can be both advantageous and disadvantageous to production from carbonate reservoirs. Karst within reservoirs can enhance fluid flow in the subsurface depending on the size of the feature, but also can cause serious uncertainties and safety issues regarding drilling and production (e.g. Sloan, Reference Sloan2003). In Kirchleus, several different karst features are observed in and around the fault zones. Wormholes and vugs up to c. 1.5 m wide are recorded within faults, fractures and along stylolites within the limestone. Whilst karstification is outwith the scope of this contribution, it should be noted for future modelling that it is present within the reservoir units and should be considered as a possible subsurface fluid pathway.
The results of the fracture modelling and numerical simulations show that seismic-scale faults are influencing the fracture networks in the vicinity, forming damage zones which could be pathways for geothermal flow at depth. It is also observed that the Malm reservoir in the Franconian Basin hosts good fracture networks formed through several deformation events (Late Cretaceous Inversion and Alpine phases) and that act as the primary conduits for flow. Given that these faults and fractures are linked to deformation phases, it can be predicted that the same networks are located at depth. Therefore, further modelling of the subsurface can use the presence of major faults as a driver for the fracture networks present. The homogenized models presented show the small-scale flow through the Malm units; however, further upscaling (up to km scale) would be required to better model the flow through the reservoir. For this, additional data would be required such as additional larger-scale outcrop sites (e.g. drone imagery) and the use of subsurface data (wells and seismic) to integrate into a reservoir-scale fracture network model.
Currently, new seismic acquisition is underway for northern Bavaria and these additional data could be utilized to directly image the fracture networks at depth to compare with the networks at the surface (Fazlikhani et al. Reference Fazlikhani, Bauer and Stollhofen2022). Similar datasets have already been acquired and analysed in the Molasse Basin, and similar approaches and integration from this basin could be utilized within the Franconian Basin (Budach et al. Reference Budach, Moeck, Lüschen and Wolfgramm2018; Wawerzinek et al. Reference Wawerzinek, Buness, von Hartmann and Tanner2021). Seismic in combination with well and outcrop data can be used to create discrete fracture networks (e.g. Smith, Reference Smith2020; Boersma et al. Reference Boersma, Bruna, de Hoop, Vinci, Tehrani and Bertotti2021). These DFN models can additionally be driven by the outcrops and the understanding of how the faults are tilting the transport direction, as observed at Kirchleus Quarry. The aperture values used for the numerical modelling were determined directly from outcrop; however, future modelling could integrate the numerical flow simulations with aperture modelling based on current stress conditions at depth (Prabhakaran et al. Reference Prabhakaran, Bruna, Bertotti, Mittempergher, Succo, Bistacchi and Storti2018 and references therein). These further fracture acquisition and modelling techniques, in combination with the permeability tensors acquired from outcrop, would enhance understanding of the subsurface structure of the Malm and reduce the uncertainties involved in the geothermal exploration of the Franconian Basin.
6. Conclusions
The Malm units in the Franconian Alps in southern Germany are an important aquifer for geothermal exploration that is dominated by fracture networks which play a vital role in increasing permeability for fluid flow. Structural analysis of the Malm unit within the basin showed that several events have affected the fracture networks present. From the Late Jurassic onwards, an early extensional phase followed by Late Cretaceous Inversion and the Alpine Orogeny have caused movements along major faults (e.g. Kulmbach Fault) which have fractured the limestone formation.
This contribution implements a suitable method for applying 2D outcrop analogue data to the simulation of fluid flow through small-scale fracture networks. The fracture networks have been imaged and digitized to create 2D fracture network models that can be used to analyse and acquire permeability tensors of the Malm units. Analysis of the 2D networks shows that the fractures are well connected through intersections. The networks are meshed and homogenized to acquire the 2D permeability tensors which represent the flow through the rock. The tensors showed that the Kulmbach Fault influences the orientation and magnitude of fluid transport, tilting the flow in the direction of dip. This implies that large-scale (seismic) structures are likely to affect fluid flow in the reservoirs, and, as such, subsurface modelling should account for the effects of these features. There is likely a critical distance at which deformation occurs around the fault. Furthermore, it is shown that variable fracture permeability directly affects the orientation of fluid transport. It is therefore vital for homogenization and upscaling of fracture network flow that conduits, barriers and conduit–barriers are properly quantified. These results of outcrop image to 2D homogenization and permeability tensor acquisition show how using analogues can further improve the understanding of subsurface flow and reduce uncertainty in the modelling of fractured reservoirs.
Acknowledgements
This research was funded by the Bavarian Ministry of Science and Art (StMWK)-funded projects ‘langfristig’ and “regional” of the Geothermal Alliance Bavaria (GAB), which is gratefully acknowledged. Saskia Köhler (FAU) and Jonas Bücker (FAU) are acknowledged for support on the geology of Kirchleus Quarry, and Nico Hoffman (FAU) for work on the Kulmbach Fault. Gary Mullen (University of Glasgow) and Johannes Wiest (FAU) are thanked for assistance in the field. We further acknowledge the support of CSIRO’s Deep Earth Imaging Future science platform and CSIRO INTERCHANGE. Antonino Cilona and an anonymous reviewer are warmly thanked for their constructive remarks.
Conflict of interest
The authors declare that there is no conflict of interest.















