1. INTRODUCTION
Routing algorithms as the main core of navigation systems in Intelligent Transport Systems (ITS), in regard to their user-friendliness, should be able to consider various preferences of their users (Masoomi et al., Reference Masoomi, Sadeghi and Mesgari2011). Route planning is one of the daily decisions of every citizen. The parameters and personal priorities considered by each person when selecting their path can be very diverse, according to their age, occupation, financial status, personal characteristics, etc. Some of the most important parameters/objectives in route planning can be specified so as to minimise the route cost, discomfort, time, and length.
Multimodal transportation networks are public, ordinary networks in urban areas, specifically in metropolises where the citizens may use combinations of different modes of transportation such as private vehicle, taxi, subway, bus, and walking (Abbaspour and Samadzadegan, Reference Abbaspour and Samadzadegan2011). Three major public transport network modes in metropolises are usually metro trains, taxis, and buses. In general, people assume the metro is a fast mode, taxi is a comfortable mode and bus is a low-cost mode. Therefore, using these networks brings real benefits for citizens by saving their time and cost, and also greatly assists sustainable development of metropolises with optimisation of traffic congestion and reduction of air pollution.
Multi-objective routing in a multimodal network means finding a route between two given points by using different modes, while the respective objectives are optimised at the same time. Availability of different modes along with different concerns of people have made route planning a complex and multi-objective problem.
The routing problem is one of the classic problems in network analysis and Geographical Information Sciences (GIS), which has been the subject of much research (Aifadopoulou et al., Reference Aifadopoulou, Ziliaskopoulos and Chrisohoou2007; Berube et al., Reference Bérubé, Potvin and Vaucher2006, Kramer et al., Reference Kramer, Modsching and ten Hagen2006; Chiu and Rizos, Reference Chiu and Rizos2012). Multi-objective methods can incorporate different objectives and preferences of users and are consequently more acceptable. Multi-objective routing in a multimodal network means to search among a large space of routes and find a group of routes that could optimise different objectives simultaneously. These methods normally offer a group of optimal solutions instead of a single optimal solution, called the Pareto front, and the attained solutions are not superior to each other. The efficient performance of meta-heuristic algorithms, such as the Genetic Algorithm (GA), Particle Swarm Optimisation (PSO), and ACO in other complex optimisation problems has led researchers to apply them in various routing problems.
In this study, two different algorithms, i.e., Multi-Colony ACO (MCACO) and Multi-Pheromone ACO (MPACO) algorithms are considered to solve the multi-objective routing problem in the public transportation network of Tehran. The mentioned transportation network consists of four modes (bus, metro, taxi, and walking), which are all large. Three objective functions (i.e. discomfort, expense, and time) are considered as the objectives of the problem due to their significant importance in real conditions. The algorithms are run with various initial parameters and the results of their implementation are compared with each other. They are compared in different ways, including the variation of found routes, convergence trend, repeatability and diversity metrics. In the next section, the existing methods and research in this field are reviewed. In the algorithms section, the main elements and structure of the algorithms are introduced. The data preparation and the implementation results are explained in the implementation section. The main achievements of the study together with conclusions and recommendations are provided in the final section.
2. LITERATURE REVIEW
In general, multi-objective decision-making algorithms are classified into three categories: without weighting, weighting before solving, and weighting after solving. The algorithms with weighting after solving include the methods based on the optimal solution front (Jozefowiez et al., Reference Jozefowiez, Semet and Talbi2008). On the other hand, in the methods without weighting, no preference among different factors is considered by the decision maker. Instead of that, an ideal state is defined and also, a criterion for selecting the options is defined, which is the closeness to the ideal state. In the methods with weighting before solving, the objectives are firstly weighted by the user and then combined to form a single objective (Coello Coello et al., Reference Coello Coello, Lamount and Veldhuizen2007). In contrast to that in the methods with weighting after solving, at first, a collection of optimal solutions is obtained and then by using the preferences stated by the user, the final solution will be selected (Zitzler and Thiele, Reference Zitzler, Thiele, Eiben, Back, Schoenauer and Schwefel1998). The MOACO algorithms are typically considered as types of the methods with weighting after solving.
Deterministic algorithms generally need a great deal of time to solve the routing problem in large networks. For this reason, in recent years, some expeditious techniques have been proposed and utilised to improve the performance (Khezrikhazar, Reference Kheirikhazar2010; Faroqi and Niaraki, Reference Faroqi and Niaraki2015). In general, the outputs of a multi-objective routing problem create a set of optimal routes, which cannot dominate each other. However, deterministic algorithms usually can find one solution in each run, and then they need a number of runs in order to find several solutions. Therefore they are inappropriate for solving multi-objective routing problems. According to the similarity between the nature of the routing problem and optimisation, some research has been accomplished in the recent decade on solving routing problems with the aid of optimisation methods (Mooney and Winstanley, Reference Mooney and Winstanley2006). In addition, Evolutionary Algorithms, PSO algorithms and Artificial Bee Colony (ABC) algorithms have been used for solving various kinds of routing problems (Abbaspour and Samadzadegan, Reference Abbaspour and Samadzadegan2011).
A genetic algorithm as an evolutionary algorithm has been extensively applied for solving routing problems, but has some drawbacks such as its computational complexity, low processing rate, and the non-occurrence problem between its discrete and continuous space of routing problems (Kanoh and Kenta, Reference Kanoh and Kenta2008; Dorigo and Blumb, Reference Dorigo and Blumb2005; Luh and Lin, Reference Luh and Lin2009). In 1992, the ant colony optimisation algorithm was proposed for solving optimisation problems and it resolved numerous drawbacks of the previous algorithms (Dorigo, Reference Dorigo1992; Dorigo and Stutzle, Reference Dorigo and Stutzle2007). In addition, the ACO algorithm has been offered to solve multi-objective routing problems (Chitty and Hernandez, Reference Chitty and Hernandez2004), which is actually a type of weighting of two objectives before solving in a mono-modal network. A solving method for multi-criteria routing problems by the ACO algorithm has been indicated in Doerner et al. (Reference Doerner, Focke and Gutjahr2006), which gives random weights to every neighbour edge of each vertex in the network in order to choose the next route vertex. This method acts randomly and has some downsides in defining the criteria for selecting the next vertex. Additionally, an intelligent routing method based on the multi-pheromone ACO algorithm has been designed in Masoomi et al. (Reference Masoomi, Sadeghi and Mesgari2011), which is typically implemented in a mono-modal network with two objective functions. The results of this research confirmed the efficient performance of the MOACO algorithms in solving the multi-objective problem. Further, a multi-objective evacuation algorithm was designed based on the multi-colony ACO algorithm in Cardoso et al. (Reference Cardoso, Jesus, Guerreiro, Ribeiro, Portillo and Marquez2012) with a relatively very fast run time.
Consequently, the MPACO algorithm is already used for solving multi-objective routing problems in small, simple, and mono-modal transport networks. However, the MCACO algorithm is not used for solving multi-objective routing problems in a transport network.
3. ALGORITHMS
The ACO algorithm is one of the meta-heuristic optimisation methods, which has been designed based on the social behaviour of ants in searching for food. In general, ants leave their colony to search for food, and each ant searches in a different path. In returning to their colony, each ant, based on its success in finding food, leaves some pheromone on the path, which is a smelly material. Actually, pheromone is the trace of ants in seeking for food. In the next search, each ant chooses its path by randomly considering the level of pheromone in each direction. A colony consists of a number of ants, where each one may choose a different route for finding food with the passage of time. The next ants will choose a path with a higher amount of pheromone. Information exchange, information flows, and self-ordering features are the important characteristics of the ACO algorithm, which lead to finding the optimal solutions in the searching population (Dorigo, Reference Dorigo1992). The MOACO algorithm works on the colonies of ants, pheromones, and the number of ants. It operates in two different ways, i.e., multi-pheromone and multi-colony. The main steps of the MOACO algorithm are exhibited in Figure 1 (Lopez-Ibanez, Reference Lopez-Ibanez2004).

Figure 1. The main steps of the MOACO algorithm (Lopez-Ibanez, Reference Lopez-Ibanez2004).
The population of each colony, number of colonies, number of pheromones, and heuristic information are the parameters which are defined in the initialisation step. The population of each colony can be changed according to the complexity of the problem. Heuristic information is set up and changed based on the objective functions of the problem and other information, which are important to take into account in the solving process. In the first run of the algorithm, ants randomly search for the solution due to lack of pheromone in the network. But in the subsequent searches, they can randomly consider pheromones in the network.
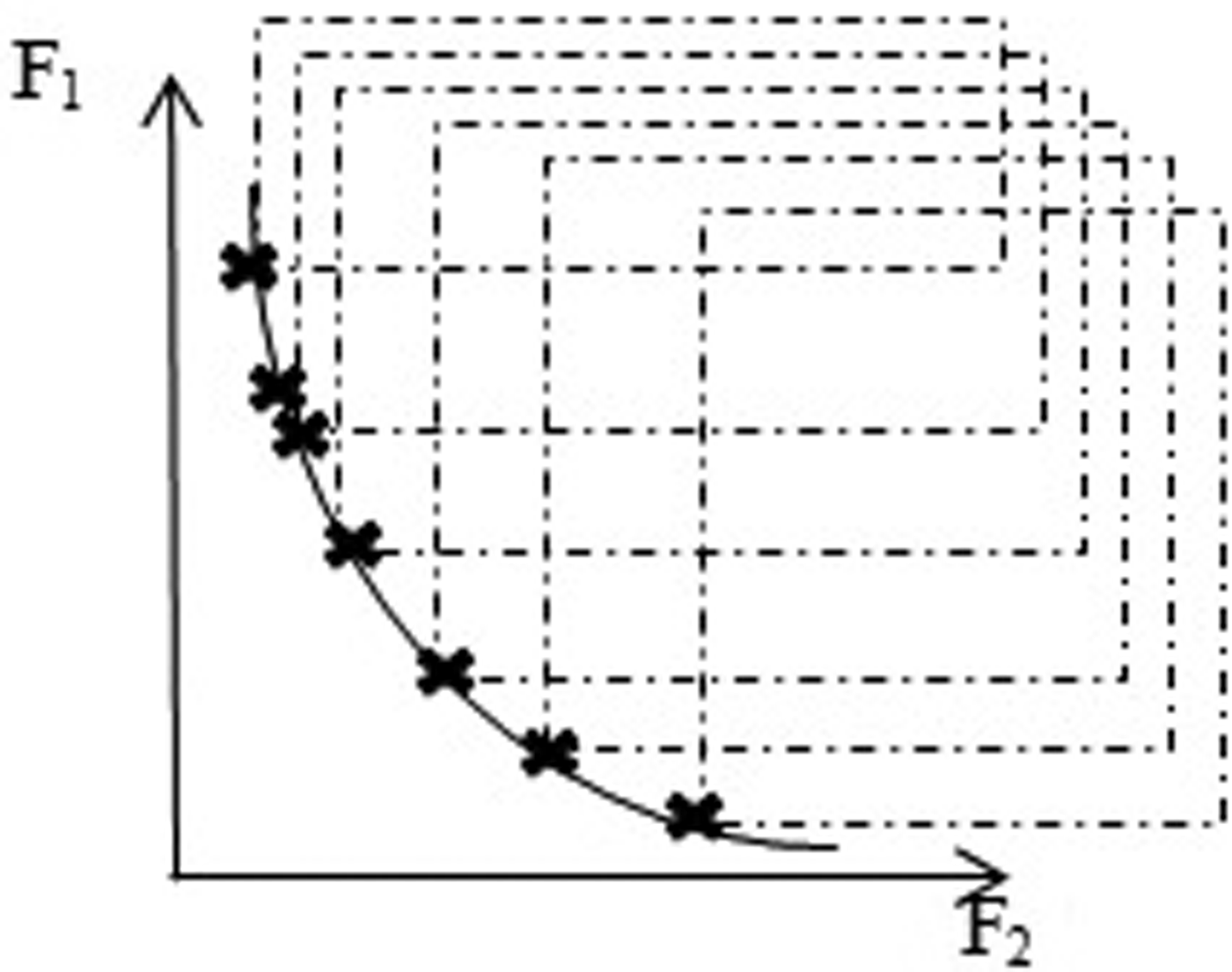
With respect to the multi-objectivity of the problem, a set of non-dominated solutions is determined by the algorithm. The Pareto front concept is used for determining the optimal solutions. According to the definition, solution X1 dominates solution X2 if and only if, firstly, X1 is not worse than X2 in all objectives, and secondly, X1 is better than X2 at least in one objective function (Kalyanmoy and Pratap, Reference Kalyanmoy and Pratap2002). The Pareto front concept is applied for ranking solutions. This last step is the same for both algorithms. In Figure 2, the Pareto front is drawn for a minimisation optimisation problem in the 2-D space of the objective functions, and the confines of the dominated space by each non-dominated solution are determined by rectangles.

Figure 2. The Pareto front.
3.1. The MPACO algorithm
For solving the multi-objective optimisation problem by the MPACO algorithm, it is required to define a different pheromone for each objective function. Therefore, the algorithm consists of a number of pheromone matrices, related to the count of the objective functions. In the MPACO algorithm, all ants are related to one colony and they use different pheromones. Every ant at any point, in order to choose its next point, will calculate the selection probability of all neighbour points based on Equation (1) (Coello Coello et al., Reference Coello Coello, Lamount and Veldhuizen2007)
 $$P_{ij}^k = \displaystyle{{[{\rm \Pi} _{q = 1}^Q \left( {\tau _{Sqj}^q} \right)^{\gamma _q} \left] \ast {[{\rm \Pi} _{q = 1}^Q \left( {\eta _{Sqj}^q} \right)^{\gamma _q}} \right]} \over {{\rm \Sigma} _{l\varepsilon Ni} \left( {\left[ {{\rm \Pi} _{q = 1}^Q \left( {\tau _{Sql}^q} \right)^{\gamma _q}} \right] \ast \left[ {{\rm \Pi} _{q = 1}^Q \left( {\eta _{Sql}^q} \right)^{\gamma _q}} \right]} \right)}}$$
$$P_{ij}^k = \displaystyle{{[{\rm \Pi} _{q = 1}^Q \left( {\tau _{Sqj}^q} \right)^{\gamma _q} \left] \ast {[{\rm \Pi} _{q = 1}^Q \left( {\eta _{Sqj}^q} \right)^{\gamma _q}} \right]} \over {{\rm \Sigma} _{l\varepsilon Ni} \left( {\left[ {{\rm \Pi} _{q = 1}^Q \left( {\tau _{Sql}^q} \right)^{\gamma _q}} \right] \ast \left[ {{\rm \Pi} _{q = 1}^Q \left( {\eta _{Sql}^q} \right)^{\gamma _q}} \right]} \right)}}$$In Equation (1), P ijk is the probability of choosing point j by ant k from point i, q is the number of objective functions, ɳ is related to heuristic information, Y q is the weighting amount for each objective function, and Ni means the neighbour points of point i. In each iteration, Y q is randomly allocated to each ant due to searching different parts of the space of objective functions (Lopez-Ibanez, Reference Lopez-Ibanez2004). Each pheromone matrix is initialised based on one specific objective function and hence the pheromone matrix values will be different from the first run. After calculating P ijk for all Ni points, each ant chooses its next point by using roulette wheel selection. For finding the path, this iteration is repeated until the ant finds the final point. As soon as all ants get their final points, all found solutions based on their objective values will be ranked. In the next step, pheromones will be updated. This stage can be divided into two levels. At first, all the pheromone values are decreased by a pre-specified amount. Second, the pheromones, which are related to the first front solutions, will be increased. In the next iteration of the algorithm, the updated pheromone values will be used. This process will continue until some specific conditions are satisfied by found solutions (Lopez-Ibanez, Reference Lopez-Ibanez2004).
3.2. The MCACO algorithm
Another mode of the MOACO algorithm is the MCACO algorithm, which uses a number of colonies simultaneously. Each colony has its own pheromone matrix and specific ants. The number of colonies is equal to the count of the objective functions. Each colony's ants produce their path based on an objective function, and then, in the ranking step, all found solutions are ranked together and pheromones are updated according to the first front solutions. Therefore the connection between colonies, the objective functions, is established in this step of the MCACO algorithm. The probability of choosing point j from point i by ant k can be observed in Equation (2) (Coello Coello et al., Reference Coello Coello, Lamount and Veldhuizen2007). In fact, the problem is solved separately for each objective function, and then, when the pheromones are updated, all objective functions are considered altogether.
4. IMPLEMENTATION
Based on the graph theory, a network encompasses a set of vertices and edges. A multimodal transportation network comprises different modes, such as automobile, bus, walking, etc. Similarly, a multimodal route can be defined as a route comprising some parts covered by various modes. The network can be presented as a graph, in which more than one edge might exist between two vertices, related to different modes (Joyner et al., Reference Joyner, Van Nguyen and Philips2013). The nature of the ACO algorithms is compatible with the concrete space and hence they are appropriate for solving routing problems.
In this paper, the multi-objective routing is simulated in the public transportation network of Tehran with four possible modes. In addition, three objectives are considered for solving the problem. The MPACO algorithm is initialised with one colony and three pheromone matrices, which are related to the objective functions. On the other hand, the MCACO algorithm is initialised with three colonies and three pheromone matrices, where the colonies and pheromones are related to the objective functions. The initial pheromone value for each edge in the network is assumed equal to the inverse value of the related objective function in the edge. The number of ants and the maximum iteration for the initialised algorithms were taken according to the size of the network. In the MCACO algorithm, ants are divided equally between colonies.
4.1. Data preparation
The data required for the implementation of algorithms include the transportation network map as well as the values of the objective functions assigned to the respective network. The data of the Tehran public transportation network is used for simulating the multimodal network. The public transportation network of Tehran is located in a rectangle (of 25 km by 35 km) and includes three modes (bus, metro, and taxi) and a walking mode to change modes. The walking edges for changing modes and walking between different stations are available just for stations, where the distance between them is less than 1 km. Table 1 shows the characteristics of the simulated network (TCTTS, 2010).
Table 1. Characteristics of the simulated multimodal network (TCTTS, 2010).

Three objective functions (i.e., discomfort, expense, and time) are considered as the objectives of the problem. Discomfort function is calculated based on the applied modes during the trip and the number of changing modes. The expense function is calculated based on the distance as well as the applied modes. Time function is calculated based on the distance, applied modes, and the number of switches between the modes. Moreover, the goal of optimisation in this problem is to minimise the objective functions.
4.2. Results
The Microsoft .NET framework 4 and C# language (on a Vaio laptop with 2·4 GHz Intel® Core i5 with 4·00 GB of RAM) were used as the programming environment for implementation of the offered algorithms. Parameters are initialised based on the results from Coello Coello et al. (Reference Coello Coello, Lamount and Veldhuizen2007) and Chitty and Hernandez (Reference Chitty and Hernandez2004) and according to the size of the simulated network. In order to analyse the results of algorithms, two vertices in the network are assumed as the origin and destination, and algorithms are implemented with different parameters of population and iteration numbers. In Table 2, a summary of the results obtained from nine implementations of the algorithms with different parameter values for the same two vertices can be observed.
Table 2. The results obtained from the implementation of algorithms.

The MCACO algorithm with an average time of 42·4 s for the runs is quicker than the MPACO algorithm with an average time of 65 s. The running time of the algorithms is increased with the increase in the number of iterations and ants. Typically the iteration count has more influence on the running time than the number of ants. In addition, finding more solutions in the first front would reflect a better searching of the problem space and it leads to various available options for users to choose from. The MCACO and MPACO algorithms on average have 4·7 and 3·6 paths in the first front path numbers, respectively. Additionally, the MCACO algorithm has a better performance in finding various solutions and searching the problem space. Moreover, in run eight of the MCACO algorithm, eight non-dominated paths are found, of which the maximum number of solutions is in the first front.
In order to analyse the found non-dominated paths in the real case, each of eight first front path are depicted in Figure 3 on the map of the Tehran city road network. Also, the values of objective functions for each of the non-dominated paths can be observed in Table 3.

Figure 3. Non-dominated found paths on a map of Tehran.
Table 3. Values of objective functions of non-dominated paths.

Figure 3 clearly shows the spatial diversity of optimal paths that are found by the algorithms during different runs. Also, the general trend of the algorithms in searching and constructing the optimal multimodal paths in the public transportation network, consisting of different modes, can be observed. Moreover in Table 3, non-dominating between first front paths based on the values of objective functions and the Pareto front concept is obvious. The Time objective function varies between 31–44 minutes, the Expense objective function varies between 21500–32000 Rial (currency of Iran), and the Discomfort objective function varies between 30–48. The spatial diversity and various values of the objective functions would be useful for different users in order to choose their optimised and favourite path in the public transport network of Tehran.
As was mentioned, the optimisation routing algorithms are used in navigation systems, therefore their performance and usability should be examined analytically (convergence and repeatability tests) and numerically (spacing metric and error ratio). Convergence testing has been used to study the convergence trend of the results, obtained from the algorithm at each run. In the convergence test, variations of the objective function values over time (increase of iterations) are analysed. In Figure 4, the convergence diagrams, with respect to the three objectives, are exhibited for all runs. In each diagram, the variation of the minimum values related to the respective objective function was considered.

Figure 4. The algorithm convergence test.
For comparing the convergence trend of different algorithm runs, the diagrams' gradient and the uniformity of the objective values can be compared. The high gradient of a diagram reflects the algorithm's fast convergence in finding the solutions with minimum objective function values. Added to that, better uniformity of a diagram means a smooth searching of all parts of the related objective function. Therefore the higher gradient and better uniformity in the convergence diagrams means a better convergence performance of the algorithm. It should be noted that the convergence diagram of runs are mostly descending or step toward the lower values of the objective functions. The convergence diagrams of runs related to the MCACO algorithm have a better performance in the expense and time objective functions than the MPACO algorithm. However, in the discomfort objective function, the MPACO's performance is better.
Generally in meta-heuristic algorithms, the initial population is randomly produced. Consequently, the results obtained from different runs, with the same parameters, are dissimilar. Therefore, in order to study the variations in the results and also to evaluate the repeatability of the algorithm it is necessary to run the algorithm with the same parameters several times. Figure 5 displays the repeatability percentage in each run of the algorithms. It should be mentioned that each run of the algorithms is repeated 10 times and the following charts have been drawn based on the results. The MPACO algorithm has a higher repeatability percentage over four runs, while the MCACO algorithm has a better repeatability in run seven. In total, the MPACO algorithm has a better repeatability than the MCACO algorithm. Based on all the tests, 60 ants and 50 iteration numbers are the optimal parameters for both algorithms.

Figure 5. Repeatability Test.
In addition, the numeric tests should be used for quantitative evaluation of the performance of the proposed algorithms. Three goals suggested for multi-objective optimisation algorithms that can be identified and measured (Zitzler et al., Reference Zitzler, Deb and Thiele2000):
(1) The distance of the resulting Non-Dominated Solutions (NDS) to the true Pareto front should be minimised.
(2) A good distribution of the obtained NDS is desirable.
(3) The size of the obtained NDS should be maximised (i.e., a wide range of values should be covered by NDS for each objective).
To quantitatively compare the performance of the algorithms, a convergence metric and a diversity metric are applied. The convergence metrics evaluate how the obtained solutions are far from the true Pareto front. Many metrics for measuring the convergence of a set of approximation NDS towards the Pareto front have been proposed. We select the error ratio (ER) that was proposed by Van Veldhuizen (Reference Van Veldhuizen1999). Let A = {e1, e2, …,en} be an approximation NDS set; ei = 0 if solution i is in the true Pareto front, and ei = 1 otherwise. The metric uses the true Pareto front as a reference set; so we assume that the true Pareto front is the total Pareto-optimal solutions in a combined pool of all approximation NDS obtained from all runs of multi-objective algorithms. In Equation (3) the metric is given, where n is the number of solutions in the approximation NDS. Lower values of the ER are preferable (Samaei et al., Reference Samaei, Bashiri and Tavakkoli2012).
The diversity metrics evaluate the scatter of solutions in the final population on the Pareto front. Like the convergence metrics, many metrics for measuring the diversity of a set of approximation NDS towards the Pareto front have been proposed. We select the Spacing Metric (SM), which was introduced by Schott (Reference Schott1995), to evaluate the applied algorithms. The spacing metric provides a measure of uniformity of the spread of approximation NDS. In Equation (4) the metric is given, where ![]() ${\bar{d}}$ is the mean of all di, n is the size of obtained NDS and fki is the function value of the k-th objective function for solution i. Lower values of the SM are preferable (Zitzler et al., Reference Zitzler, Thiele, Laumanns, Fonseca and Da Fonseca2003; Samaei et al., Reference Samaei, Bashiri and Tavakkoli2012).
${\bar{d}}$ is the mean of all di, n is the size of obtained NDS and fki is the function value of the k-th objective function for solution i. Lower values of the SM are preferable (Zitzler et al., Reference Zitzler, Thiele, Laumanns, Fonseca and Da Fonseca2003; Samaei et al., Reference Samaei, Bashiri and Tavakkoli2012).
 $$SM = \sqrt {\displaystyle{1 \over {n - 1}}\sum\limits_{i = 1}^n {(\bar {d\hskip3.5pt } - d_i )^2}} $
$$SM = \sqrt {\displaystyle{1 \over {n - 1}}\sum\limits_{i = 1}^n {(\bar {d\hskip3.5pt } - d_i )^2}} $where
 $$d_i = _{\,j \in NDS \wedge j \ne i}^{\min} \sum\limits_{k = 1}^k { \vert f_k ^i - f_k ^j} \vert $$
$$d_i = _{\,j \in NDS \wedge j \ne i}^{\min} \sum\limits_{k = 1}^k { \vert f_k ^i - f_k ^j} \vert $$Table 4 shows the result of applying ER and SM metrics for all runs of the algorithms. As was mentioned, the lower value of each metric is preferable. So, the MPACO has better values in the diversity metric. However, the MCACO has better values in the convergence metric.
Table 4. Results of performance metrics.

5. CONCLUSION
Multi-objective routing in a multimodal transport network is a complex problem. This might be due to the presence of different modes, various and even incompatible objectives, numerous possible combinations of edges in creation of the routes etc. In this research, a multi-objective routing problem in a public transportation network has been solved by two different modes of the multi-objective ACO algorithm, and the results obtained from both algorithms are compared and evaluated. The multi-colony and multi-pheromone ACO algorithms are the two modes of the MOACO algorithm.
The real data from the public transportation network of Tehran city was simulated for this problem, using large transportation network data in this study helps to increase complexity and reality of the problem, and it was noted that the simulated network consists of four different modes. In addition, three objective functions were considered for the purpose of optimising the problem. Both algorithms were implemented on the simulated network, and the attained results were examined in different aspects, such as the variation of solutions, run time, convergence trend, repeatability test, convergence and diversity metrics.
By considering the multi-objective routing problem as an optimisation problem and also, by using meta-heuristic for solving this problem, great results were achieved. According to the problem's complexity as well as the large size of the network, the run time of both algorithms is appropriate. Additionally, the variation of found paths in each run of the algorithm is sufficient, because users can make a better decision, when different non-dominated routes are available. Moreover, using the Pareto front concept for determining the front optimal solutions results in better understanding of the solutions status by the user, and highlights the rights for users to choose their optimised favourable route. Evaluating parts are based on examining the user-friendly ability of the proposed algorithms for solving the problem, and comparison between algorithms' usability in order to specify the advantage of each algorithm in real cases.
The convergence test results indicated that both algorithms have a totally uniform trend in searching for better solutions. Furthermore, the repeatability test showed the capability of both algorithms in validation of their results. It was also realized that the MCACO algorithm has a better performance in run time, variation of the found solutions, and the convergence trend for two objective functions. However, the MPACO algorithm has a better performance in repeatability, and also in the convergence in one objective function. Also, the MPACO algorithm has better values in the diversity metric. However, the MCACO algorithm has better values in the convergence metric. Moreover, both algorithms found optimal paths that are shown on the map of Tehran. Regarding the map and the values of the objective functions, these optimal paths have enough spatial diversity and various objective functions to make a proper choice for any citizen of Tehran city, using its public multimodal transport network.
For future studies, both algorithms can be expanded and merged together in order to secure a higher performance. They can be also combined with other algorithms, such as the Evolutionary Algorithm (EA) and PSO. Also, the capability of the algorithms in searching the objective functions' space would be useful in the other usage of optimising the traffic, such as designing optimised public transportation networks, or be used to improve the current multimodal transportation systems. Improving and designing optimisation routing algorithms, with the aim of user-friendly urban navigation systems would change the future of these systems.